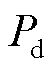 、
、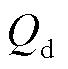 、
、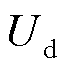 、
、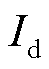 表示;
表示;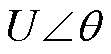 和K分别为逆变侧换流母线电压和逆变侧换流变压器电压比;γ为逆变侧熄弧角;X为逆变侧换相电抗;N为逆变侧换流器串联个数;
和K分别为逆变侧换流母线电压和逆变侧换流变压器电压比;γ为逆变侧熄弧角;X为逆变侧换相电抗;N为逆变侧换流器串联个数;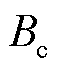 为换流母线上的无功补偿电容。交流电网用戴维南等值电动势E和戴维南等值阻抗Z串联表示,为便于后续分析,假设交流等值线路为纯感性;P和Q分别为从换流母线注入交流电网的有功功率和无功功率;负荷吸收的有功功率和无功功率分别为
为换流母线上的无功补偿电容。交流电网用戴维南等值电动势E和戴维南等值阻抗Z串联表示,为便于后续分析,假设交流等值线路为纯感性;P和Q分别为从换流母线注入交流电网的有功功率和无功功率;负荷吸收的有功功率和无功功率分别为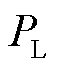 和
和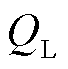 ;则图1中有功功率满足关系
;则图1中有功功率满足关系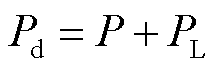 。
。摘要 随着多回直流集中落点受端电网负荷中心,交流电网相对变弱,因此分析负荷对直流多馈入系统电压稳定的影响,对精确度量受端电网电压支撑能力至关重要。该文首先建立了直流、负荷、交流电网的准稳态模型,推导了单馈入系统短路比受负荷影响的定量关系式;其次,基于结构保持和模态摄动理论,将包含负荷的多馈入系统雅克比矩阵近似解耦,分析了负荷对广义短路比的作用机理;最后,给出了基于数据驱动的广义短路比实用计算方法和稳定裕度评估流程。研究表明,考虑负荷影响后,广义短路比实际值改变,而临界值不变。仿真算例验证了所提分析方法的合理性和有效性。
关键词:电压稳定 广义短路比 负荷特性 多馈入系统 模态摄动
我国发电能源与用电负荷在地理分布上具有高度不平衡的特点,能源分布呈现出北富南贫、西多东少的现状[1],而用电负荷则集中于中东部地区,特别是东部沿海地区[2]。远距离大容量高压直流输电工程是实现我国“西电东送”能源战略的主要手段之一[3]。随着负荷不断增长、直流馈入数不断增多,空间尺度上的直流输电走廊资源正被逐步挤占,新建直流落点近区存在负荷中心的情况已难以避免[4-6]。然而目前关于负荷对交直流系统电压稳定性的影响的研究仍不充分。为确保多馈入系统安全稳定运行,准确地量化交直流系统电压稳定裕度,必须计及负荷的影响。
针对上述问题,有学者在单馈入系统中进行了相关研究。其中,一些研究将负荷全部视为等效阻抗,归并到系统阻抗或导纳矩阵中[7]。然而,这种做法未能精确考虑负荷自身特性。文献[8]利用PV曲线分析不同负荷特性对静态电压稳定性的影响,指出考虑负荷影响后静态电压稳定临界点不再与鼻点重合,认为恒阻抗负荷占比越大,静态电压稳定裕度越大。文献[9]利用最大功率曲线法,指出考虑负荷后系统临界短路比有多种可能性,与负荷模型和交流电网参数均有关,负荷类型不同可能会对系统强度产生的影响,但该研究并未从定量角度阐明负荷特性对电压稳定的作用规律。此外,负荷类型与直流换相失败的发生也有着密切关系[10]。
综上所述,目前关于负荷对电压稳定性的影响的研究主要针对直流单馈入系统,倾向于从定性分析的角度总结规律,且部分文献的结论之间相互矛盾。因此,针对多馈入系统,如何从定量的角度解释负荷对直流系统静态电压稳定裕度的具体影响,仍需进一步研究。
近年来,多馈入系统电压稳定问题日益突出。针对多馈入系统电压稳定裕度量化的问题,已有研究提出了多种考虑直流间相互作用的多馈入短路比指标[11-17],大体可以将其分为两类。第一类是等值指标,如文献[11-12]从网络折算的角度提出了多馈入短路比(Multi-Infeed Short Circuit Ratio, MISCR),将其他直流线路功率通过戴维南等值互阻抗与自阻抗之比折算到待研究的直流线路上,从而借鉴单馈入短路比的经验定义多馈入短路比。但该指标在单馈入系统下的临界值与多馈入系统下的临界值往往不相等,且考虑负荷后如何计算戴维南等值阻抗尚不明确。文献[13]利用导纳等值的思路,在电压稳定因子(Voltage Stability Factor, VSF)指标的基础上进一步定义了综合短路比(Integrated Short Circuit Ratio, ISCR)指标,其临界值恒为1。文献[14-15]采用功率等值方法定义了等值有效短路比(Equivalent Effective Short Circuit Ratio, EESCR)等。第二类是模态指标,如文献[16-17]根据电压稳定分岔与系统雅可比矩阵奇异的等价性,建立了交直流系统雅可比矩阵。利用模态解耦的思想,将多馈入系统雅可比矩阵解耦为多个等效单馈入系统雅可比矩阵,定义了广义短路比(generalized Short Circuit Ratio, gSCR)指标。该指标的单馈入系统临界值和多馈入系统临界值相统一。
以上部分指标的计算只需用到交流电网导纳矩阵和设备容量,因此分析方便、使用简单[18]。但这些指标在定义时,多将交流电网等效为由戴维南等值电动势和戴维南等值阻抗构成的理想无穷大系统,忽视了电压稳定分析中系统负荷不能简单地建模为戴维南等值阻抗的事实。因此,在考虑直流落点受端电网负荷中心的情形及负荷模型后,现有短路比指标及其临界值可能会发生变化,这已成为亟待研究的问题。
针对上述问题,本文考虑负荷接入的交直流系统,从定量角度分析了负荷接入对系统静态电压稳定性的影响,并给出了短路比及其临界值的解析表达式。对于多馈入系统,首先,给出了一种复杂系统负荷的等值简化建模方法,避免了“维数灾”问题;其次,基于结构保持模型和模态摄动理论,推导了考虑负荷影响后的直流多馈入系统雅可比矩阵,定义了计及负荷影响的广义短路比及其临界值;最后,提出了一种基于数据驱动的广义短路比实用计算方法,并通过仿真验证了所提方法的有效性。
包含静态负荷的直流单馈入系统等效电路如图1所示。该系统由直流逆变器、交流等值电网和静态负荷三部分组成。在研究交直流系统静态电压稳定时,直流逆变侧通常采用准稳态模型[13]。其中直流系统注入交流系统的有功功率、无功功率、直流逆变侧电压、直流线路电流分别用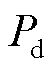 、
、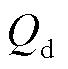 、
、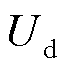 、
、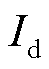 表示;
表示;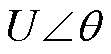 和K分别为逆变侧换流母线电压和逆变侧换流变压器电压比;γ为逆变侧熄弧角;X为逆变侧换相电抗;N为逆变侧换流器串联个数;
和K分别为逆变侧换流母线电压和逆变侧换流变压器电压比;γ为逆变侧熄弧角;X为逆变侧换相电抗;N为逆变侧换流器串联个数;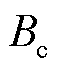 为换流母线上的无功补偿电容。交流电网用戴维南等值电动势E和戴维南等值阻抗Z串联表示,为便于后续分析,假设交流等值线路为纯感性;P和Q分别为从换流母线注入交流电网的有功功率和无功功率;负荷吸收的有功功率和无功功率分别为
为换流母线上的无功补偿电容。交流电网用戴维南等值电动势E和戴维南等值阻抗Z串联表示,为便于后续分析,假设交流等值线路为纯感性;P和Q分别为从换流母线注入交流电网的有功功率和无功功率;负荷吸收的有功功率和无功功率分别为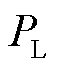 和
和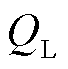 ;则图1中有功功率满足关系
;则图1中有功功率满足关系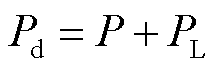 。
。
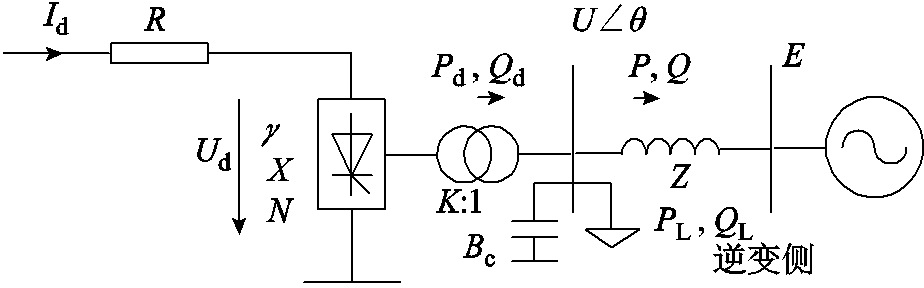
图1 含静态负荷的LCC-HVDC单馈入系统
Fig.1 LCC-HVDC single-infeed system with static load
通常情况下,电力系统中的负荷主要存在于交流电网内部,且数量众多、类型多样。若将负荷视为与直流类似的功率交换“设备”,可以采用网络结构保持的建模思路,建立包含n+m个节点(其中n为直流节点数,m为负荷节点数)的多馈入系统模型。然而,在实际电网中,负荷节点数量庞大,建立这种结构保持模型不利于分析电压稳定的内在规律,并且可能会导致“维数灾”。
因此,为了便于分析负荷对电压稳定性的影响规律,本文采用由特殊到一般的建模分析思路。首先,在单馈入系统中,将交流电网内部的负荷统一折算到换流母线上,并建立了如图1所示的等效电路,这样做的目的在于突出主要矛盾,简化分析流程;然后,后续文中针对多馈入系统将采用更具一般性的系统结构保持模型,并给出相应的等效电路建模方法;最后,通过仿真算例验证了等效电路的有效性。上述分析思路有助于更好地理解负荷对电压稳定性的影响规律,并为复杂的多馈入系统提供了有效的建模方法和分析框架。
潮流雅可比矩阵的奇异点是交直流系统达到静稳极限的常见判据,同时也指示了潮流解存在性的临界状态。本文采用文献[16]的准稳态建模方法,在图1中直流馈入点建立三端口系统雅可比矩阵模型,表示为
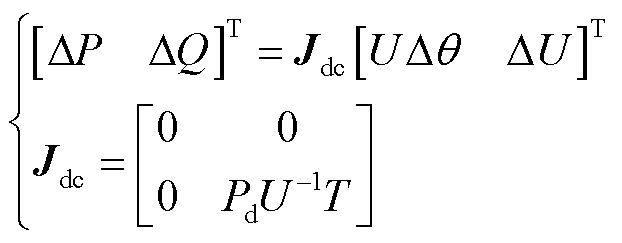 (1)
(1)
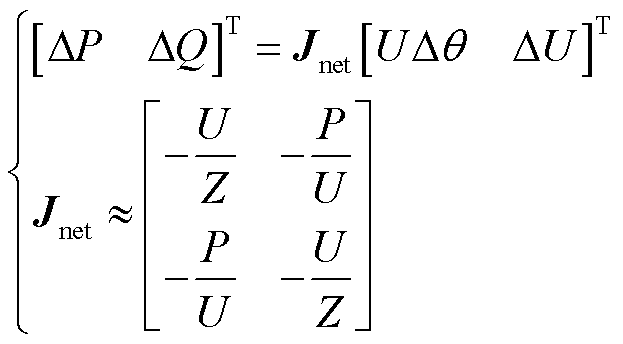 (2)
(2)
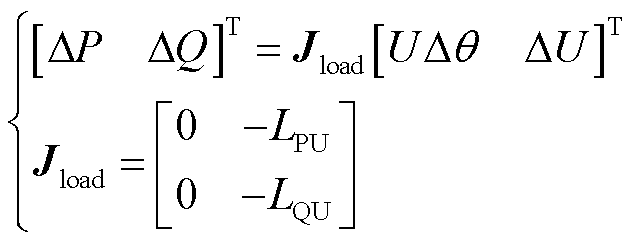 (3)
(3)
式中,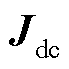 、
、 、
、 分别为直流侧、交流侧和负荷侧雅可比矩阵;T为与直流动态有关的中间变量;
分别为直流侧、交流侧和负荷侧雅可比矩阵;T为与直流动态有关的中间变量;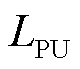 和
和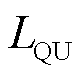 为负荷侧雅可比矩阵中的元素。
为负荷侧雅可比矩阵中的元素。
文献[13]指出,直流系统采用不同控制方式会对交直流系统静态电压稳定产生不同影响。在不同控制方式中,直流采用整流侧定功率/逆变侧定熄弧角(Constant Power Constant Extinction Angle, CP-CEA)控制方式时,系统更容易发生电压失稳,对应最恶劣的情形。故本文分析中假设直流系统采用CP-CEA控制,则式(1)中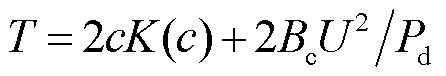 ,其中,中间函数
,其中,中间函数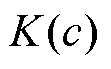 和中间变量
和中间变量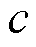 的表达式分别为
的表达式分别为
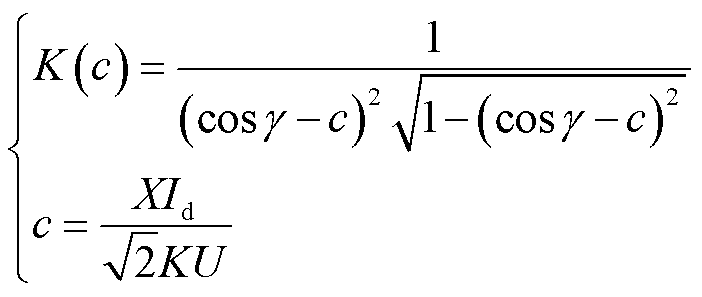 (4)
(4)
设备通过节点从系统中获取的有功和无功功率与该节点的电压及系统频率的关系式即称为该节点负荷的数学模型[19]。不计频率变化时,用多项式表示的负荷静态特性(ZIP)模型为
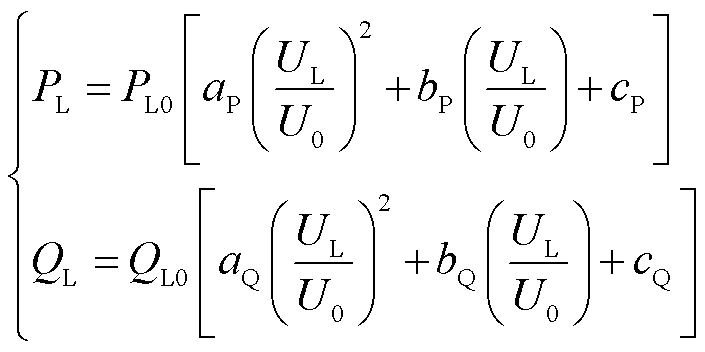 (5)
(5)
式中,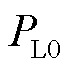 、
、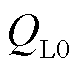 和
和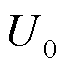 分别为负荷所吸收的有功功率、无功功率和节点电压幅值的初始值;
分别为负荷所吸收的有功功率、无功功率和节点电压幅值的初始值;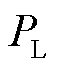 、
、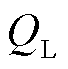 和
和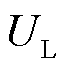 分别为负荷有功功率、无功功率和节点电压幅值的实际值;
分别为负荷有功功率、无功功率和节点电压幅值的实际值;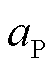 、
、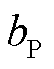 、
、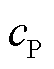 和
和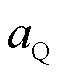 、
、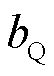 、
、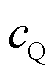 分别为负荷有功功率和无功功率中,恒阻抗负荷、恒电流负荷、恒功率负荷所占的比例,且满足
分别为负荷有功功率和无功功率中,恒阻抗负荷、恒电流负荷、恒功率负荷所占的比例,且满足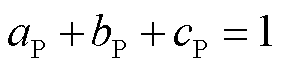 ,
,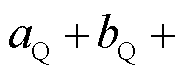
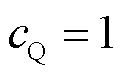 。
。
线性化式(5),则负荷端口雅可比矩阵 (根据功率方向取反号)中元素
(根据功率方向取反号)中元素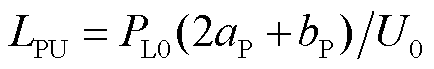 ,
,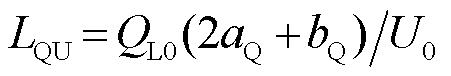 。ZIP负荷模型下,负荷功率和交流母线电压相位无关,而只与电压幅值有关。
。ZIP负荷模型下,负荷功率和交流母线电压相位无关,而只与电压幅值有关。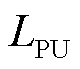 、
、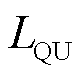 的绝对值大小与负荷类型比例系数直接相关,恒阻抗负荷占比越大,绝对值越大;恒功率负荷占比越大,绝对值越小;恒电流负荷介于两者之间。
的绝对值大小与负荷类型比例系数直接相关,恒阻抗负荷占比越大,绝对值越大;恒功率负荷占比越大,绝对值越小;恒电流负荷介于两者之间。
当交直流系统达到静态电压稳定极限点时,系统雅克比矩阵奇异[17]。图2给出了直流馈入点处三端口雅可比矩阵的关系,结合式(1)~式(3),同时考虑功率流动方向,系统雅克比矩阵表示为
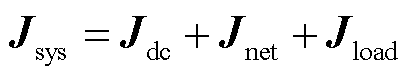 (6)
(6)
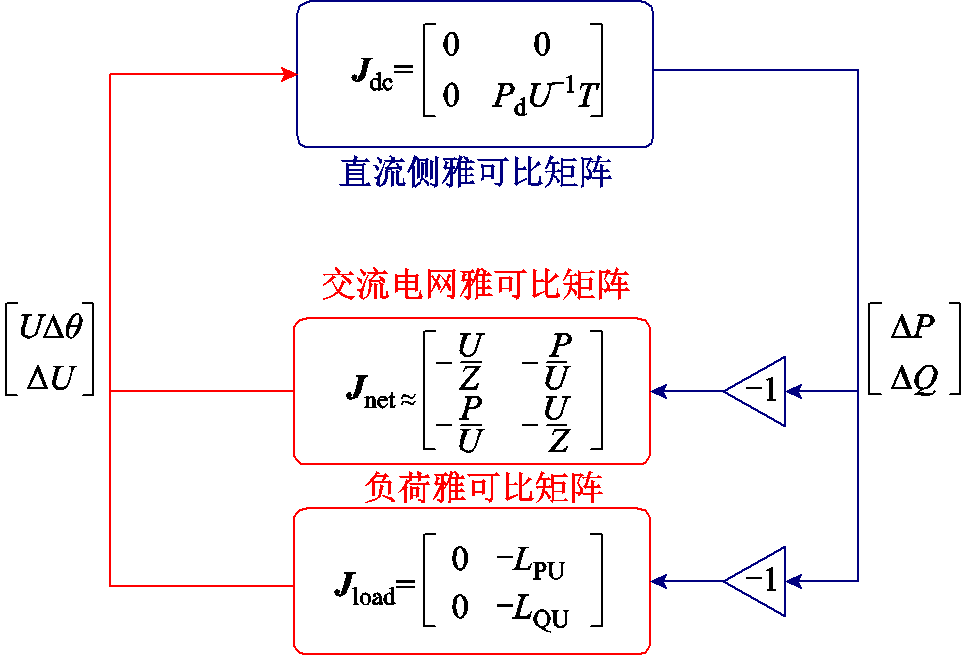
图2 单馈入系统雅可比矩阵关系
Fig.2 Relationship between Jacobi matrices for single-infeed system
令系统雅克比矩阵奇异,即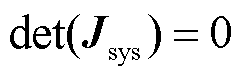 ,利用矩阵Schur变换,可化简得
,利用矩阵Schur变换,可化简得
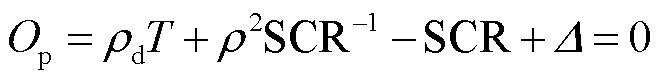 (7)
(7)
其中
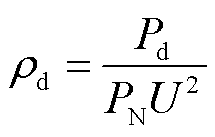
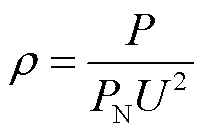
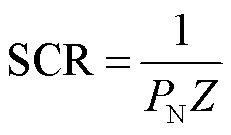
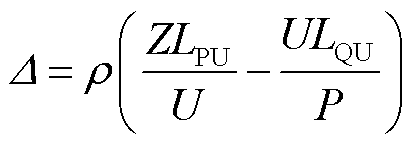
式中,![]() 为交直流系统运行点;SCR为单馈入短路比;
为交直流系统运行点;SCR为单馈入短路比;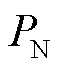 为直流额定有功功率;Δ为系统特征方程中包含负荷特性的项,在本文中将Δ定义为负荷影响因子(Load Effect Factor, LEF)。
为直流额定有功功率;Δ为系统特征方程中包含负荷特性的项,在本文中将Δ定义为负荷影响因子(Load Effect Factor, LEF)。
将式(7)与文献[16]中未考虑负荷的直流系统特征方程进行对比可以发现,式(7)考虑负荷后所带来的影响已被全部折算为负荷影响因子LEF,而式(7)中其余部分基本保持不变。因此,可将式(7)中的负荷影响因子视为对原系统特征方程的修正。具体地,将负荷影响因子LEF折算至交流网络侧,用以修正原直流短路比SCR,则系统雅克比矩阵等价于
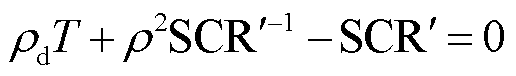 (8)
(8)
式中,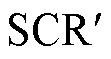 为修正后的实际短路比,满足
为修正后的实际短路比,满足
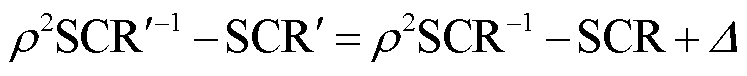 (9)
(9)
式(8)说明实际短路比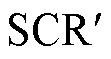 和交直流系统静态电压稳定性直接相关。根据临界短路比的定义,当交直流系统额定运行点与静态电压稳定临界点重合时,满足式(8)的短路比就是临界短路比,因此在额定运行点处求解式(8)能够得到临界短路比的解析表达式为
和交直流系统静态电压稳定性直接相关。根据临界短路比的定义,当交直流系统额定运行点与静态电压稳定临界点重合时,满足式(8)的短路比就是临界短路比,因此在额定运行点处求解式(8)能够得到临界短路比的解析表达式为
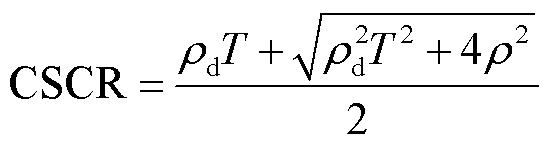 (10)
(10)
综合式(8)~式(10),上述推导过程可以理解为,将负荷折算至交流侧作为交流网络的一部分,而直流侧不受影响。换句话说,接入负荷并不影响短路比的临界值,只影响短路比的实际值。
从临界短路比的解析表达式(10)也可以看出,当运行点确定时,ρ和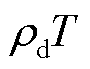 均为定值,因此临界短路比与负荷影响因子LEF无关。但是由式(9)可知,实际
均为定值,因此临界短路比与负荷影响因子LEF无关。但是由式(9)可知,实际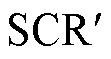 与LEF呈负相关,故通过分析LEF的变化可以获知负荷对实际短路比的影响规律。
与LEF呈负相关,故通过分析LEF的变化可以获知负荷对实际短路比的影响规律。
下面通过分类讨论,具体分析实际短路比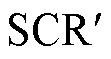 的变化规律。为便于分析,假设有功、无功负荷中ZIP比例系数相同,即
的变化规律。为便于分析,假设有功、无功负荷中ZIP比例系数相同,即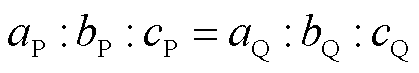 。此时
。此时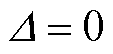 也可等价变换为
也可等价变换为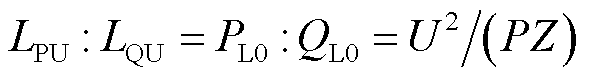 。
。
1)情形1:负荷影响因子LEF为正,即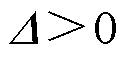 。
。
由上述分析可知,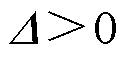 等价于
等价于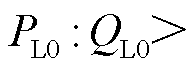
 ,此时实际短路比
,此时实际短路比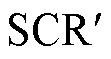 有减小的趋势,并且随着负荷构成中恒阻抗负荷和恒电流负荷占比的增加,Δ的绝对值不断增大,
有减小的趋势,并且随着负荷构成中恒阻抗负荷和恒电流负荷占比的增加,Δ的绝对值不断增大,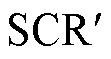 减小,而临界短路比CSCR不变,稳定裕度
减小,而临界短路比CSCR不变,稳定裕度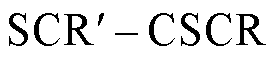 减小,静态电压稳定性削弱。
减小,静态电压稳定性削弱。
2)情形2:负荷影响因子LEF为负,即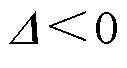 。
。
由上述分析可知,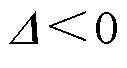 也等价于
也等价于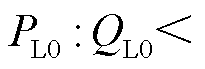
 ,此时实际短路比
,此时实际短路比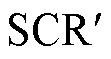 有增大的趋势,并且随着负荷构成中恒阻抗负荷和恒电流负荷占比的增加,Δ的绝对值不断增大,
有增大的趋势,并且随着负荷构成中恒阻抗负荷和恒电流负荷占比的增加,Δ的绝对值不断增大,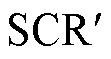 增大,而临界短路比CSCR不变,稳定裕度
增大,而临界短路比CSCR不变,稳定裕度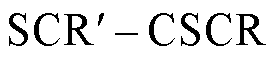 增大,静态电压稳定性增强。
增大,静态电压稳定性增强。
3)情形3:负荷影响因子LEF为0,即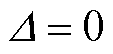 。
。
由上述分析可知,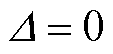 也等价于
也等价于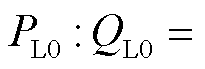
 ,此时无论恒阻抗、恒电流、恒功率负荷占比如何变化,实际短路比
,此时无论恒阻抗、恒电流、恒功率负荷占比如何变化,实际短路比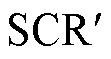 不变。
不变。
不同LEF对短路比及电压稳定的影响见表1,可见负荷接入对实际短路比的影响主要取决于负荷影响因子LEF的正负和大小。在实际应用中,可考虑有功负荷和无功负荷的相对大小,从而快速判断负荷接入后处于哪种情形,如图3所示。
表1 不同LEF对短路比及电压稳定的影响
Tab.1 The impact of different LEF on SCR and voltage stability

ΔPL0:QL0SCRCSCR稳定裕度 >0>U2/(PZ)不变减小不变减小 <0<U2/(PZ)不变增大不变增大 =0=U2/(PZ)不变不变不变不变
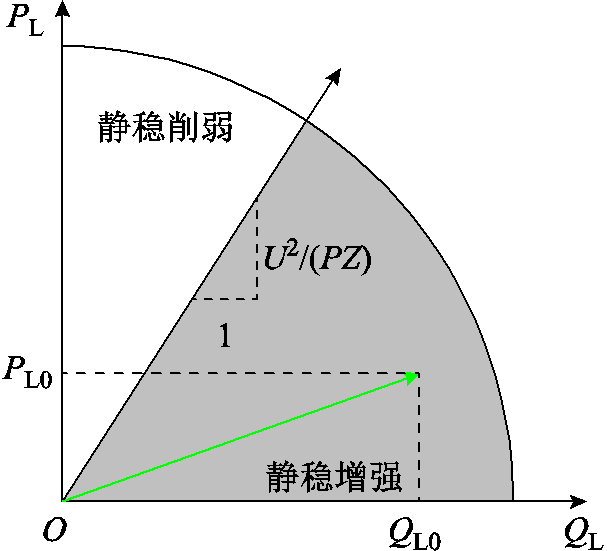
图3 负荷配比对静态电压稳定性的影响
Fig.3 Influence of load ratio on static voltage stability
考虑n条直流馈入的交流系统,该系统中,节点1~n接入直流,节点n+1~n+m接入负荷,红色虚线内部表示无源节点,其余节点为无穷大节点,如图4a所示。因图4中变量具有自明性,故不再赘述。
式(1)构成了第i条直流的端口特性,在此基础上,假设n条直流同构(控制方式相同、以自身容量为基准的主电路参数标幺值相同),可推广得到多馈入直流端口的线性化雅可比矩阵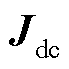 ,表示为
,表示为
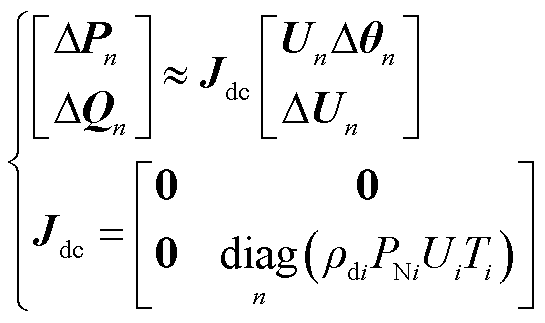 (11)
(11)
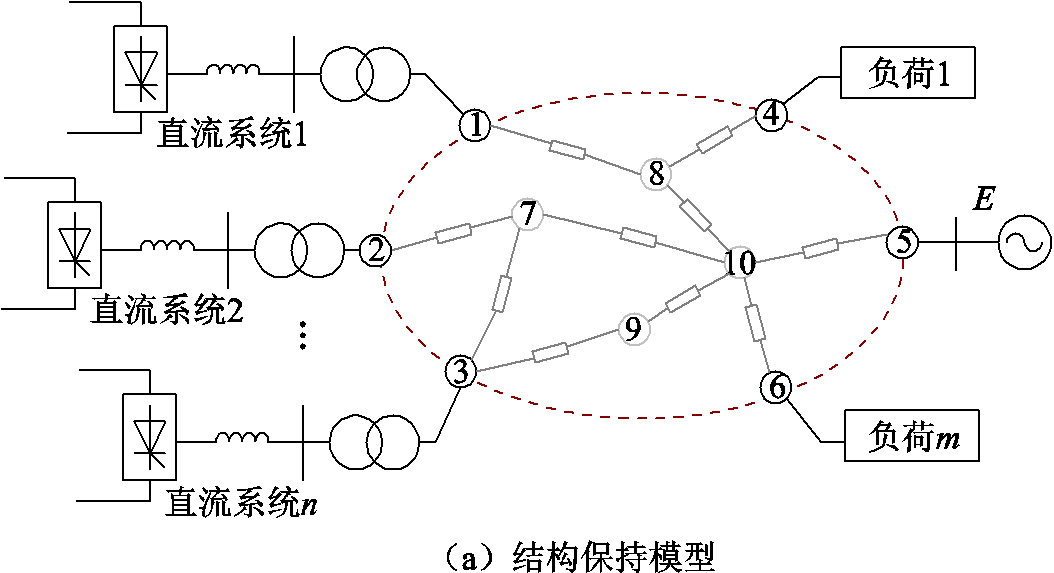
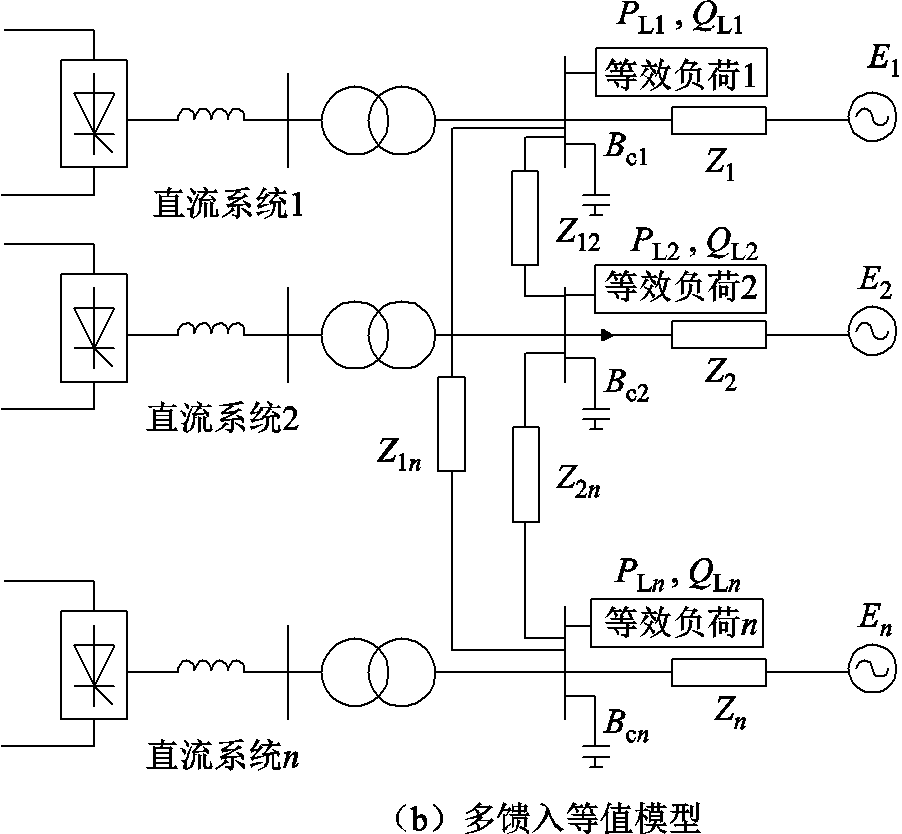
图4 含静态负荷的LCC-HVDC多馈入系统
Fig.4 LCC-HVDC multi-infeed system with static load
其中

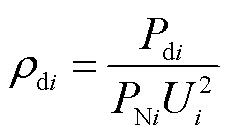
式中,各节点有功功率变化量向量表示为ΔPn=[ΔP1 ΔP2… ΔPn]T;无功功率变化量向量表示为ΔQn= [ΔQ1 ΔQ2… ΔQn]T;电压相位变化量向量表示为UnΔθn= [U1Δθ1 U2Δθ2…UnΔθn]T,电压幅值变化量向量表示为ΔUn=[ΔU1 ΔU2… ΔUn]T;diag(·)代表对角矩阵;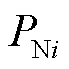 为第i条直流的额定容量;
为第i条直流的额定容量;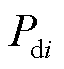 为第i条直流输出有功功率;Ui为第i条直流换流母线电压;ci和K(ci)的含义见式(4)。
为第i条直流输出有功功率;Ui为第i条直流换流母线电压;ci和K(ci)的含义见式(4)。
考虑额定工况下,从直流换流母线及负荷节点向交流电网看去,假设端口节点电压幅值近似为1(pu)(Ui ≈ Uj ≈1(pu)),端口节点之间的相位差较小(cos(θi-θj)≈1),那么交流电网的端口线性化方程可近似表示为
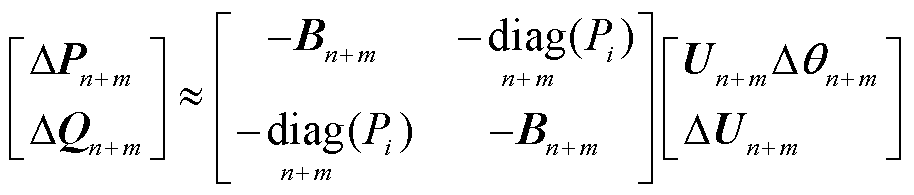 (12)
(12)
式中,![]() 表示以注入交流电网有功功率为对角元素的对角矩阵;导纳矩阵
表示以注入交流电网有功功率为对角元素的对角矩阵;导纳矩阵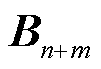 满足主对角元素大于0,且可划分为4个分块矩阵,表示为
满足主对角元素大于0,且可划分为4个分块矩阵,表示为
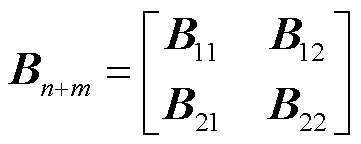 (13)
(13)
基于式(3)推广可得负荷端口线性化方程为
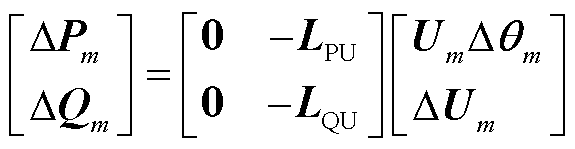 (14)
(14)
其中
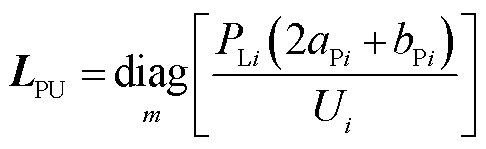
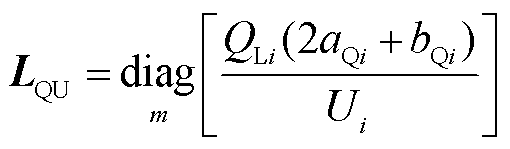
式中,LPU为有功功率对电压幅值的导数构成的对角阵;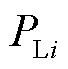 为第i个节点负荷吸收的有功功率;LQU为无功功率对电压幅值的导数构成的对角阵;
为第i个节点负荷吸收的有功功率;LQU为无功功率对电压幅值的导数构成的对角阵;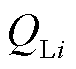 为第i个节点负荷吸收的无功功率。
为第i个节点负荷吸收的无功功率。
结合式(12)和式(14),可推导结构保持下交流电网雅克比矩阵,如附录1所示。在此基础上,仅保留直流端口节点,消去电网内部无源节点后,从换流母线向交流电网看去,交流侧雅克比矩阵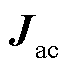 可分解为
可分解为
 (15)
(15)
式中, 为未接入负荷时交流电网雅克比矩阵;
为未接入负荷时交流电网雅克比矩阵; 为等效负荷雅克比矩阵,具体推导过程和参数定义见附录1。等效后多馈入系统可用图4b表示。
为等效负荷雅克比矩阵,具体推导过程和参数定义见附录1。等效后多馈入系统可用图4b表示。
由附录1可知, 可表示为
可表示为
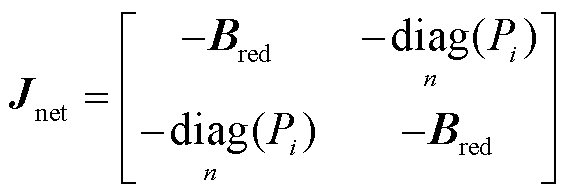 (16)
(16)
其中

式中,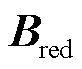 为节点消去后的导纳矩阵。
为节点消去后的导纳矩阵。
等效负荷雅克比矩阵 具有特殊性质,即其前n列元素绝对值远小于后n列元素绝对值,可以认为前n列元素近似为零(后文算例印证了该性质),因此
具有特殊性质,即其前n列元素绝对值远小于后n列元素绝对值,可以认为前n列元素近似为零(后文算例印证了该性质),因此 可近似表示为
可近似表示为
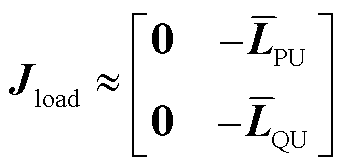 (17)
(17)
式(17)与式(14)不同的是,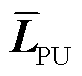 和
和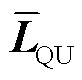 一般不为对角阵,其推导过程见附录1。
一般不为对角阵,其推导过程见附录1。
图5给出了多馈入系统下直流设备、交流电网和等效负荷雅可比矩阵之间的关系。考虑到式(11)和式(15)功率流向相反,大小相等,结合图5可知,二者之和即为多馈入系统雅克比矩阵,即
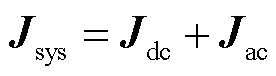 (18)
(18)
引入Schur变换,系统雅克比矩阵奇异等价于
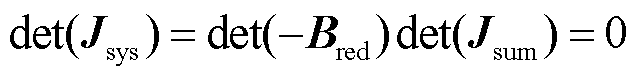 (19)
(19)
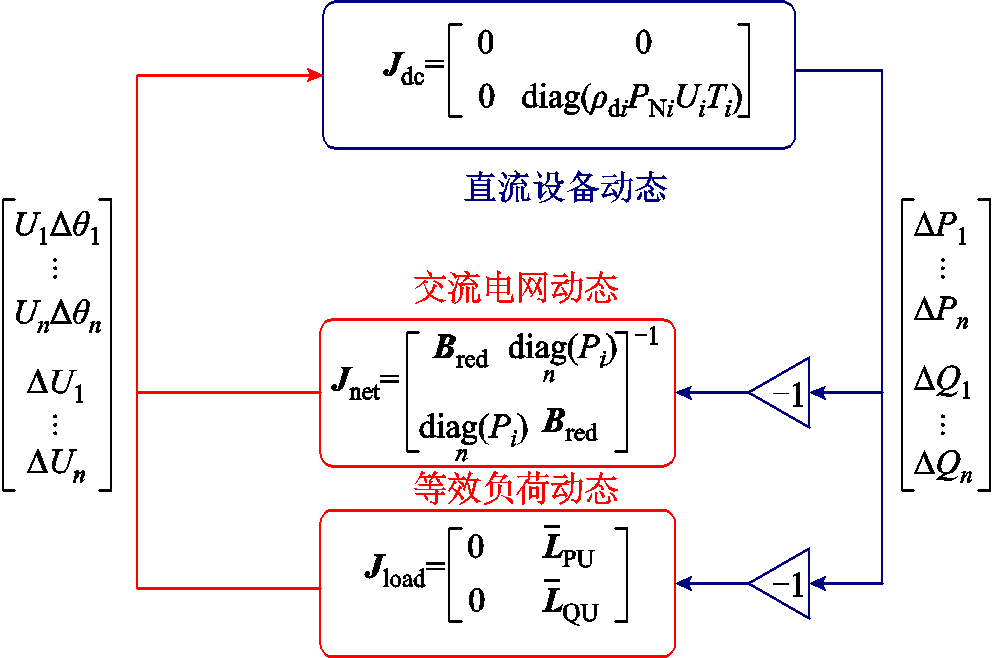
图5 多馈入系统雅可比矩阵关系
Fig.5 Relationship between Jacobi matrices for multi-infeed system
由于矩阵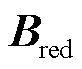 不会奇异,因此系统雅克比矩阵奇异又等价于
不会奇异,因此系统雅克比矩阵奇异又等价于 奇异。因此后文分析系统雅可比矩阵均可用
奇异。因此后文分析系统雅可比矩阵均可用 代替,其表达式为
代替,其表达式为
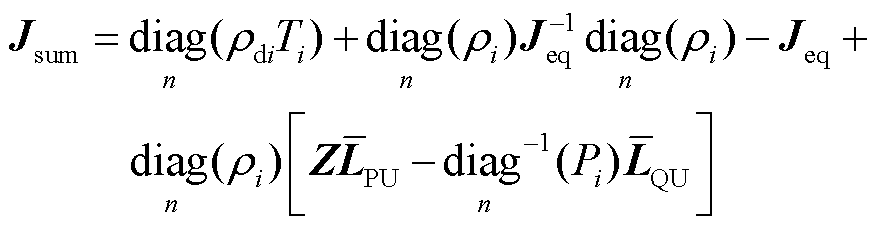 (20)
(20)
其中
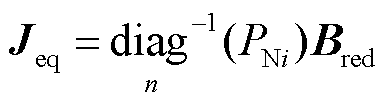
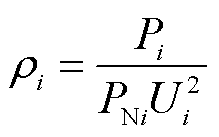
式中,Z为阻抗矩阵,满足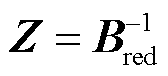 。考虑到n条直流同构,那么对于所有节点i,有
。考虑到n条直流同构,那么对于所有节点i,有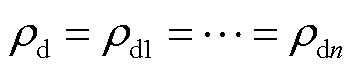 ,
,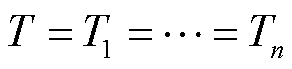 。因此式(20)可化简为
。因此式(20)可化简为
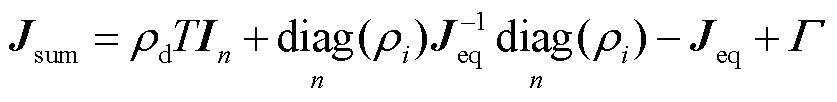 (21)
(21)
其中
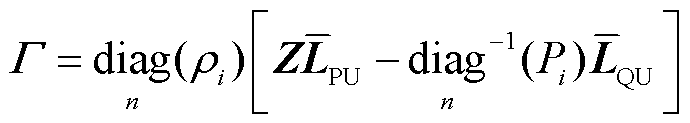
式中,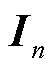 为n阶单位矩阵;Γ为与负荷特性相关的矩阵。由于Γ不为单位阵,式(21)无法类比文献[16]进行直接解耦。为了解决该问题,本文利用模态摄动理论分析静态电压稳定与短路比之间的关系。
为n阶单位矩阵;Γ为与负荷特性相关的矩阵。由于Γ不为单位阵,式(21)无法类比文献[16]进行直接解耦。为了解决该问题,本文利用模态摄动理论分析静态电压稳定与短路比之间的关系。
由Q-V模态分析可知,直流多馈入系统从稳定向不稳定过渡时,系统雅克比矩阵的最小特征值将由正变为零[19]。利用引理1,系统雅克比矩阵最小特征值可通过模态摄动法[20-21]进行分析。
引理1:假设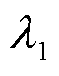 为矩阵
为矩阵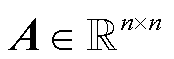 的单特征值,且存在左右特征向量
的单特征值,且存在左右特征向量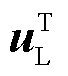 和
和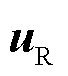 ,令A+E为对矩阵A的一种摄动,那么摄动后的矩阵A+E存在特征值
,令A+E为对矩阵A的一种摄动,那么摄动后的矩阵A+E存在特征值 ,满足
,满足
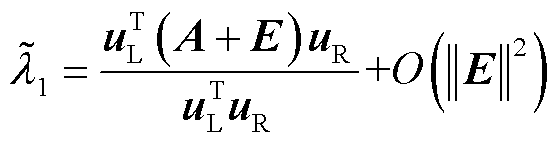 (22)
(22)
式中,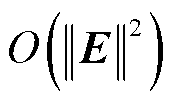 为矩阵E的高阶无穷小量。此外,令
为矩阵E的高阶无穷小量。此外,令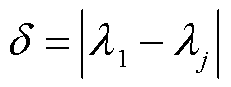 (j=2, 3,…, n)表示特征值
(j=2, 3,…, n)表示特征值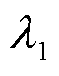 与矩阵A其他特征值
与矩阵A其他特征值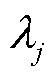 (j=2, 3,…, n)的距离,且
(j=2, 3,…, n)的距离,且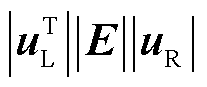 存在上界ε。如果扰动矩阵E较小并满足
存在上界ε。如果扰动矩阵E较小并满足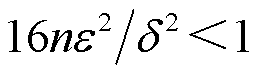 ,那么特征值
,那么特征值 位于以
位于以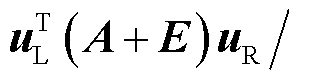
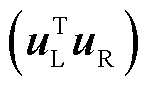 为圆心,
为圆心,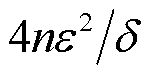 为半径的盖尔圆盘内[20]。
为半径的盖尔圆盘内[20]。
根据引理1,对式(20)进行摄动,可得系统雅克比矩阵 的最小特征值为
的最小特征值为
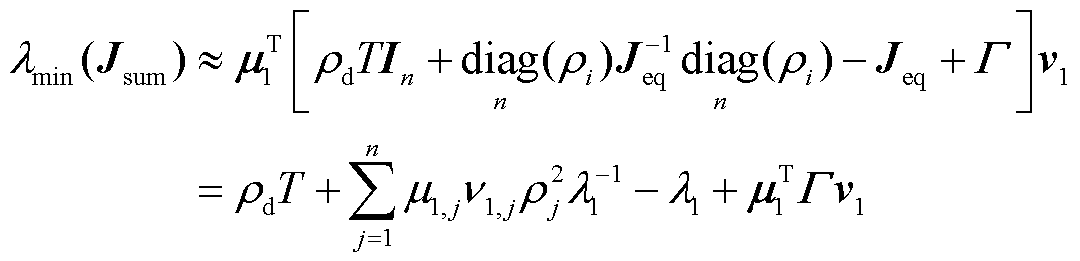 (23)
(23)
式中,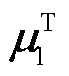 和
和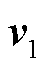 分别为
分别为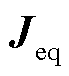 最小特征值
最小特征值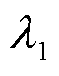 的左右特征向量;
的左右特征向量;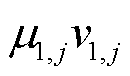 为第j个模态对应的参与因子;
为第j个模态对应的参与因子;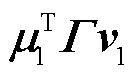 为包含负荷特性的项,类比单馈入系统,将其定义为多馈入负荷影响因子(Multi-infeed Load Effect Factor, MLEF)。与单馈入系统类似,将MLEF折算到交流网络侧,式(23)可表示为
为包含负荷特性的项,类比单馈入系统,将其定义为多馈入负荷影响因子(Multi-infeed Load Effect Factor, MLEF)。与单馈入系统类似,将MLEF折算到交流网络侧,式(23)可表示为
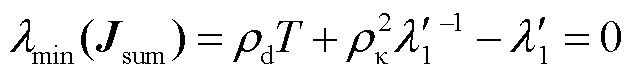 (24)
(24)
其中
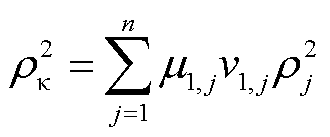
式中,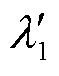 为考虑负荷接入影响的直流多馈入系统主导特征值;
为考虑负荷接入影响的直流多馈入系统主导特征值;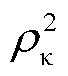 为
为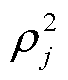 基于参与因子的加权和。
基于参与因子的加权和。
容易发现,式(24)和式(8)具有相似的表现形式,因此定义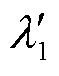 为考虑负荷特性影响的多馈入直流系统的广义短路比gSCR,其临界值CgSCR可通过求解式(24)获得,表达式为
为考虑负荷特性影响的多馈入直流系统的广义短路比gSCR,其临界值CgSCR可通过求解式(24)获得,表达式为
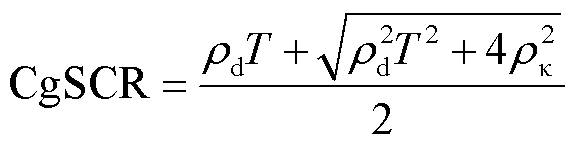 (25)
(25)
和单馈入系统类似,多馈入系统负荷接入后,有功负荷和无功负荷的大小、负荷特性、负荷接入位置以及交流网络参数均会改变MLEF的正负和大小,进而对广义短路比的实际值造成不同的影响。
综上所述,负荷接入后对多馈入系统的影响被多馈入负荷影响因子MLEF量化,而MLEF主要影响广义短路比的实际值,不影响广义短路比的临界值,因此需要计算gSCR和CgSCR的差值,利用该差值量化多馈入系统静态电压稳定裕度。
考虑负荷特性的直流多馈入系统的静态电压稳定裕度可用广义短路比gSCR和临界值CgSCR的差值表征。因此本节给出考虑负荷特性的广义短路比及其临界值计算流程。
由文献[16]可知,未考虑负荷特性时,原广义短路比定义为拓展导纳矩阵的最小特征值,即
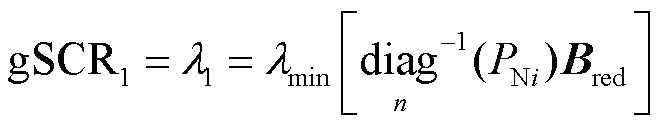 (26)
(26)
上述定义中,计算广义短路比需要获取节点导纳矩阵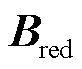 和直流额定功率矩阵
和直流额定功率矩阵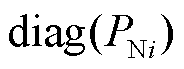 。其中直流额定功率可直接从直流额定参数中获取,导纳矩阵
。其中直流额定功率可直接从直流额定参数中获取,导纳矩阵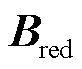 可通过导纳矩阵辨识以及网络矩阵降阶处理计算得到[22]。需要指出的是,式(26)中节点导纳矩阵
可通过导纳矩阵辨识以及网络矩阵降阶处理计算得到[22]。需要指出的是,式(26)中节点导纳矩阵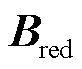 特指交流网络中剔除了所有负荷后,仅由线路阻抗构成的导纳矩阵。
特指交流网络中剔除了所有负荷后,仅由线路阻抗构成的导纳矩阵。
本文在原广义短路比基础上,进一步考虑负荷接入的复杂场景,提出广义短路比的修正形式为
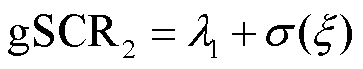 (27)
(27)
其中
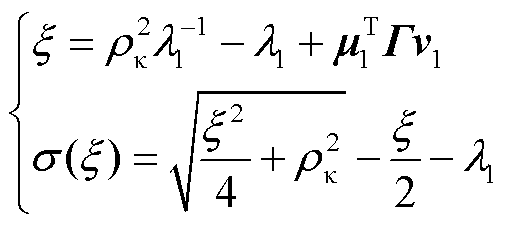
式中,参数ξ可根据式(23)获得。
由式(27)可知,考虑负荷后的广义短路比的修正表达式由ξ和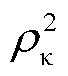 决定,而ξ和
决定,而ξ和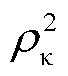 的计算依赖于原广义短路比
的计算依赖于原广义短路比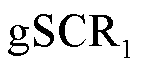 和其对应的左右特征向量
和其对应的左右特征向量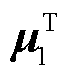 、
、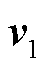 。结合式(26)和式(27)可知,上述计算和分析的前提在于节点导纳矩阵
。结合式(26)和式(27)可知,上述计算和分析的前提在于节点导纳矩阵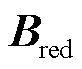 的辨识。
的辨识。
对于存在大量负荷的受端电网,负荷特性势必会对导纳矩阵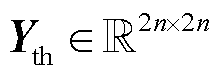 辨识结果产生重要影响。然而,计算原广义短路比
辨识结果产生重要影响。然而,计算原广义短路比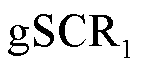 需要的是剔除了所有负荷后,仅由线路阻抗降阶得到的导纳矩阵
需要的是剔除了所有负荷后,仅由线路阻抗降阶得到的导纳矩阵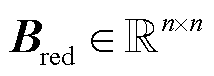 。事实上,由于负荷与线路阻抗按照串并联关系共同构成了
。事实上,由于负荷与线路阻抗按照串并联关系共同构成了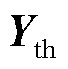 ,在网络拓扑未知的情况下,无法直接由
,在网络拓扑未知的情况下,无法直接由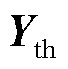 得到
得到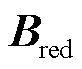 。
。
为了解决上述问题,可考虑将导纳矩阵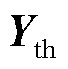 转换为雅克比矩阵
转换为雅克比矩阵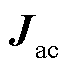 进行分析。附录2推导了这种转换关系,根据导纳矩阵
进行分析。附录2推导了这种转换关系,根据导纳矩阵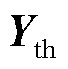 和端口电压、电流数据可间接计算雅克比矩阵
和端口电压、电流数据可间接计算雅克比矩阵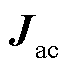 。又由附录1可知,系统内负荷可以近似用折算在换流母线上的等效负荷来代替,因此可按照图4b的等效建模方式,将雅克比矩阵
。又由附录1可知,系统内负荷可以近似用折算在换流母线上的等效负荷来代替,因此可按照图4b的等效建模方式,将雅克比矩阵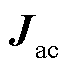 分解为交流电网雅克比矩阵
分解为交流电网雅克比矩阵 与等效负荷雅克比矩阵
与等效负荷雅克比矩阵 之和。根据式(15)和式(17)可知,负荷矩阵
之和。根据式(15)和式(17)可知,负荷矩阵 前n列元素近似为零,故雅克比矩阵
前n列元素近似为零,故雅克比矩阵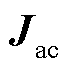 的前n行、前n列元素构成的矩阵即近似为导纳矩阵
的前n行、前n列元素构成的矩阵即近似为导纳矩阵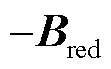 ,据此可计算原广义短路比
,据此可计算原广义短路比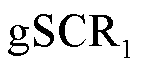 。另一方面,结合
。另一方面,结合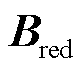 和
和 可计算负荷特性矩阵Γ,代入式(27)即可计算修正后的广义短路比
可计算负荷特性矩阵Γ,代入式(27)即可计算修正后的广义短路比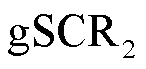 。
。
上述过程可用图6进一步加以说明,同时该图也解释了图1和图4中的等值过程。实际系统中,由于技术受限,电网人员一般只能通过装设在重要节点(如直流换流母线)处的测量装置对交流电网进行等值。因此从直流换流母线向交流电网看去,交流电网及其内部的负荷可以看作一个黑箱系统(图6中①)。基于外特性等值原理,等值后的黑箱系统可用线路阻抗与理想电压源串联的戴维南等值模型表示,如图6中②。等值结果包括黑箱阻抗(导纳)矩阵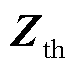 (
(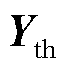 )和理想电压源E。根据黑箱导纳矩阵
)和理想电压源E。根据黑箱导纳矩阵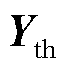 和测得的端口电压、电流数据可间接计算黑箱雅克比矩阵
和测得的端口电压、电流数据可间接计算黑箱雅克比矩阵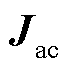 ,该矩阵与附录1中通过结构保持模型化简得到的交流雅克比矩阵等价。因此将黑箱雅克比矩阵分解为
,该矩阵与附录1中通过结构保持模型化简得到的交流雅克比矩阵等价。因此将黑箱雅克比矩阵分解为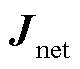 和
和 之和(图6中③),即可用于计算广义短路比。
之和(图6中③),即可用于计算广义短路比。
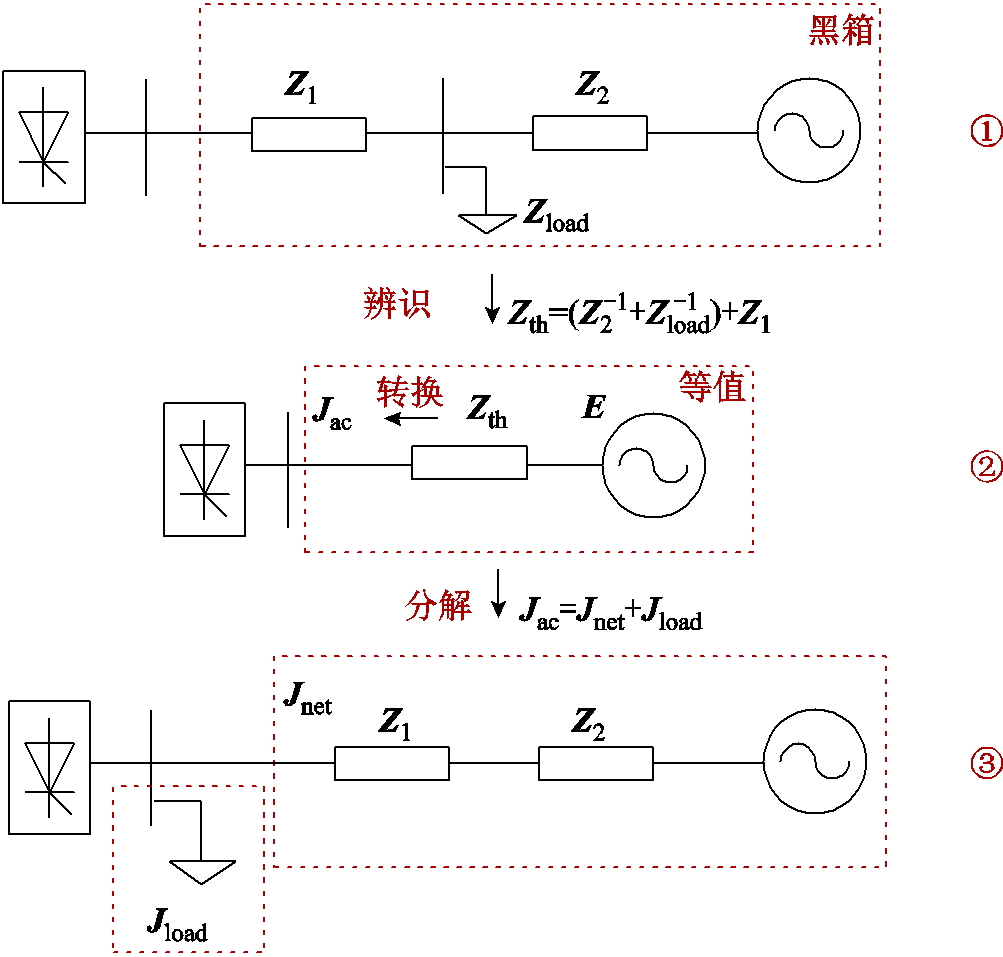
图6 从直流侧看去的交流电网等值模型
Fig.6 AC grid equivalent model seen from DC side
需要说明的是,图6中各个阻抗均表示为2×2的矩阵形式[23],根据电路理论,从直流换流母线看去的黑箱阻抗矩阵理论上可表示为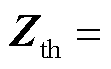
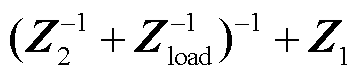 ,其中负荷等值阻抗(导纳)模型见附录3。由附录3可知,当且仅当
,其中负荷等值阻抗(导纳)模型见附录3。由附录3可知,当且仅当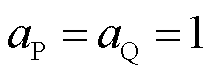 ,即全部负荷均为恒阻抗负荷时,导纳矩阵满足
,即全部负荷均为恒阻抗负荷时,导纳矩阵满足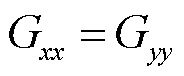 ,
,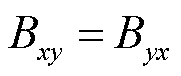 ,本文将这种矩阵定义为反对称矩阵。显然,反对称矩阵中只包含2个未知数,并且易知一般线路阻抗矩阵都为反对称矩阵。然而当负荷不全为恒阻抗负荷时,黑箱的等值导纳矩阵
,本文将这种矩阵定义为反对称矩阵。显然,反对称矩阵中只包含2个未知数,并且易知一般线路阻抗矩阵都为反对称矩阵。然而当负荷不全为恒阻抗负荷时,黑箱的等值导纳矩阵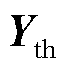 将从反对称矩阵变为不对称矩阵,此时导纳矩阵将包含4个未知数。对于n馈入系统,则需要辨识的导纳矩阵共包含
将从反对称矩阵变为不对称矩阵,此时导纳矩阵将包含4个未知数。对于n馈入系统,则需要辨识的导纳矩阵共包含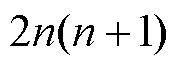 个不重复的未知数。3.2节将介绍一种基于数据驱动的n馈入系统导纳矩阵辨识算法。
个不重复的未知数。3.2节将介绍一种基于数据驱动的n馈入系统导纳矩阵辨识算法。
综上所述,直流多馈入系统gSCR的计算和稳定裕度分析流程可总结如下:
1)采用3.2节算法辨识多馈入系统等值导纳矩阵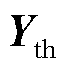 ,根据直流设备信息构建直流容量矩阵
,根据直流设备信息构建直流容量矩阵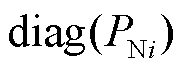 。
。
2)根据附录1计算黑箱雅克比矩阵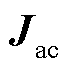 ,并分解得到
,并分解得到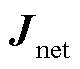 和
和 ,结合直流容量矩阵计算拓展导纳矩阵
,结合直流容量矩阵计算拓展导纳矩阵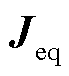 及其最小特征值对应的特征向量
及其最小特征值对应的特征向量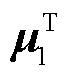 和
和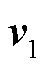 。
。
3)计算直流设备端口特性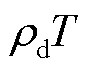 (见式(11)),结合
(见式(11)),结合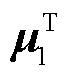 和
和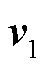 ,对系统雅克比矩阵进行摄动(见式(23))。
,对系统雅克比矩阵进行摄动(见式(23))。
4)计算原广义短路比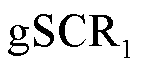 (见式(26))、修正后广义短路比
(见式(26))、修正后广义短路比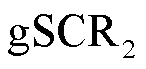 (见式(27)),以及临界广义短路比CgSCR(见式(25))。
(见式(27)),以及临界广义短路比CgSCR(见式(25))。
5)根据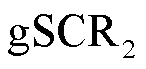 与CgSCR的差值判断多馈入系统的静态电压稳定裕度。
与CgSCR的差值判断多馈入系统的静态电压稳定裕度。
考虑接入n条直流的多馈入系统,在第j个离散时间点,第i条直流换流母线电压相量为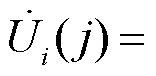
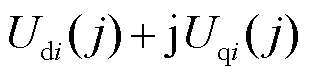 ,通过换流母线注入交流电网的电流相量为
,通过换流母线注入交流电网的电流相量为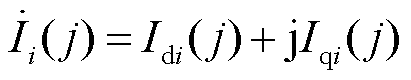 。将j时刻电压、电流与j-1时刻电压、电流作差有
。将j时刻电压、电流与j-1时刻电压、电流作差有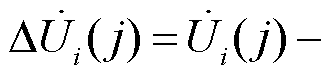
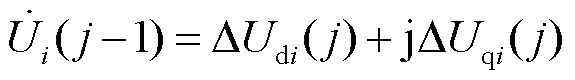 以及
以及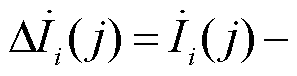
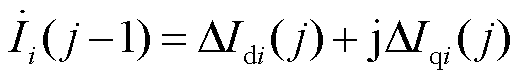 ,并且存在如下关系
,并且存在如下关系
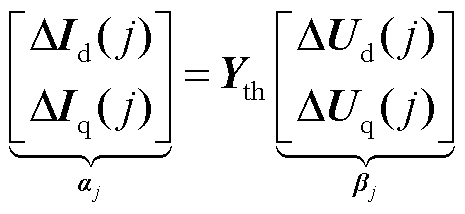 (28)
(28)
式中,电流实部差量向量ΔId(j)=[ΔId1(j) ΔId2(j) …ΔIdn(j)]T;电流虚部差量向量ΔIq(j)=[ΔIq1(j) ΔIq2(j)…ΔIqn(j)]T;电压实部差量向量ΔUd(j)=[ΔUd1(j) ΔUd2(j)…ΔUdn(j)]T;电压虚部差量向量ΔUd(j)=[ΔUq1(j) ΔUq2(j)… ΔUqn(j)]T。
首先考虑式(28)的第l行,有
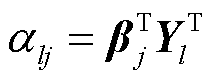 (29)
(29)
式中,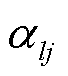 为
为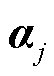 的第l行元素;
的第l行元素;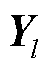 为
为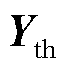 的第l行元素组成的向量。
的第l行元素组成的向量。
估计目标为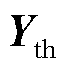 的所有e×e(e=2n)个元素,为此,可将
的所有e×e(e=2n)个元素,为此,可将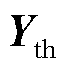 所有元素按照一定的顺序组成向量
所有元素按照一定的顺序组成向量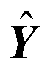 ,表示为
,表示为
将式(30)代入式(29)可得
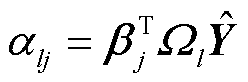 (31)
(31)
式中,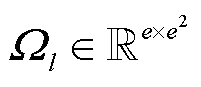 为一种变换矩阵,可将
为一种变换矩阵,可将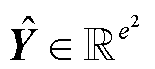 映射为
映射为 。
。
那么将式(31)推广到式(28)的每一行,可得
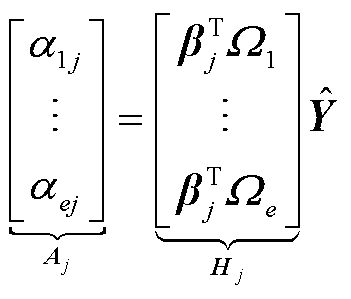 (32)
(32)
对于N个离散时间点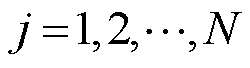 ,联立式(32)可得
,联立式(32)可得
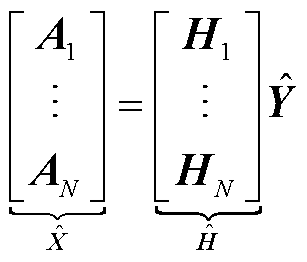 (33)
(33)
式中,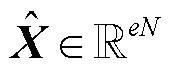 ,
, 。
。
当采样的数据足够多,且对于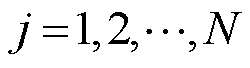 ,
,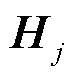 线性不相关时,
线性不相关时,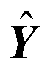 可作为方程的未知数进行求解。例如,式(33)可采用常见的最小二乘逼近算法进行求解,即
可作为方程的未知数进行求解。例如,式(33)可采用常见的最小二乘逼近算法进行求解,即
 (34)
(34)
然而式(34)存在一个明显的缺陷,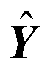 的辨识精度随着采样数据的增多而提高,但当采样值个数不断增加时,每增加一个采样时刻,就需要扩展矩阵
的辨识精度随着采样数据的增多而提高,但当采样值个数不断增加时,每增加一个采样时刻,就需要扩展矩阵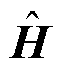 并重新计算
并重新计算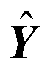 ,因此增加了巨额的计算量。为此,本节提出了一种递推辨识算法[23],无需等到所有采样值都获得之后再去估计导纳矩阵,而是每获得一组采样值之后都能对导纳矩阵的估计值进行递推修正。对导纳矩阵
,因此增加了巨额的计算量。为此,本节提出了一种递推辨识算法[23],无需等到所有采样值都获得之后再去估计导纳矩阵,而是每获得一组采样值之后都能对导纳矩阵的估计值进行递推修正。对导纳矩阵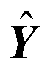 的递推估计算法如下:
的递推估计算法如下:
对于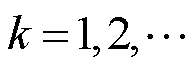 ,有
,有
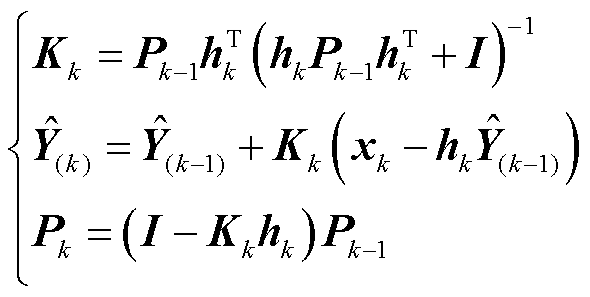 (35)
(35)
式中,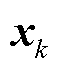 为
为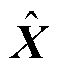 的第k行元素;
的第k行元素;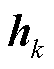 为
为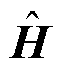 的第k行元素组成的向量;
的第k行元素组成的向量;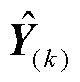 为
为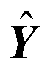 在第k次计算步的估计值;
在第k次计算步的估计值;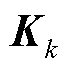 和
和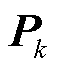 为递推过程中的中间变量。
为递推过程中的中间变量。
综上所述,随着采样数据不断增多,式(35)给出的递推估计算法仅利用第k次计算步的采样数据和第k-1次计算步的估计值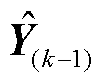 即可计算出
即可计算出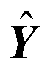 的第k次估计值
的第k次估计值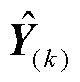 。随着递推算法的不断进行,
。随着递推算法的不断进行,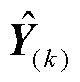 将不断逼近式(34)的结果。即使网络结构发生变化,式(35)也能够通过新的采样值修正原本的估计值,实现对网络参数的跟踪。因此所提算法不需要知道实际网络结构,完全由数据驱动计算,结合图7中广义短路比计算流程,可实现电网强度的估计和电压稳定的判别。
将不断逼近式(34)的结果。即使网络结构发生变化,式(35)也能够通过新的采样值修正原本的估计值,实现对网络参数的跟踪。因此所提算法不需要知道实际网络结构,完全由数据驱动计算,结合图7中广义短路比计算流程,可实现电网强度的估计和电压稳定的判别。
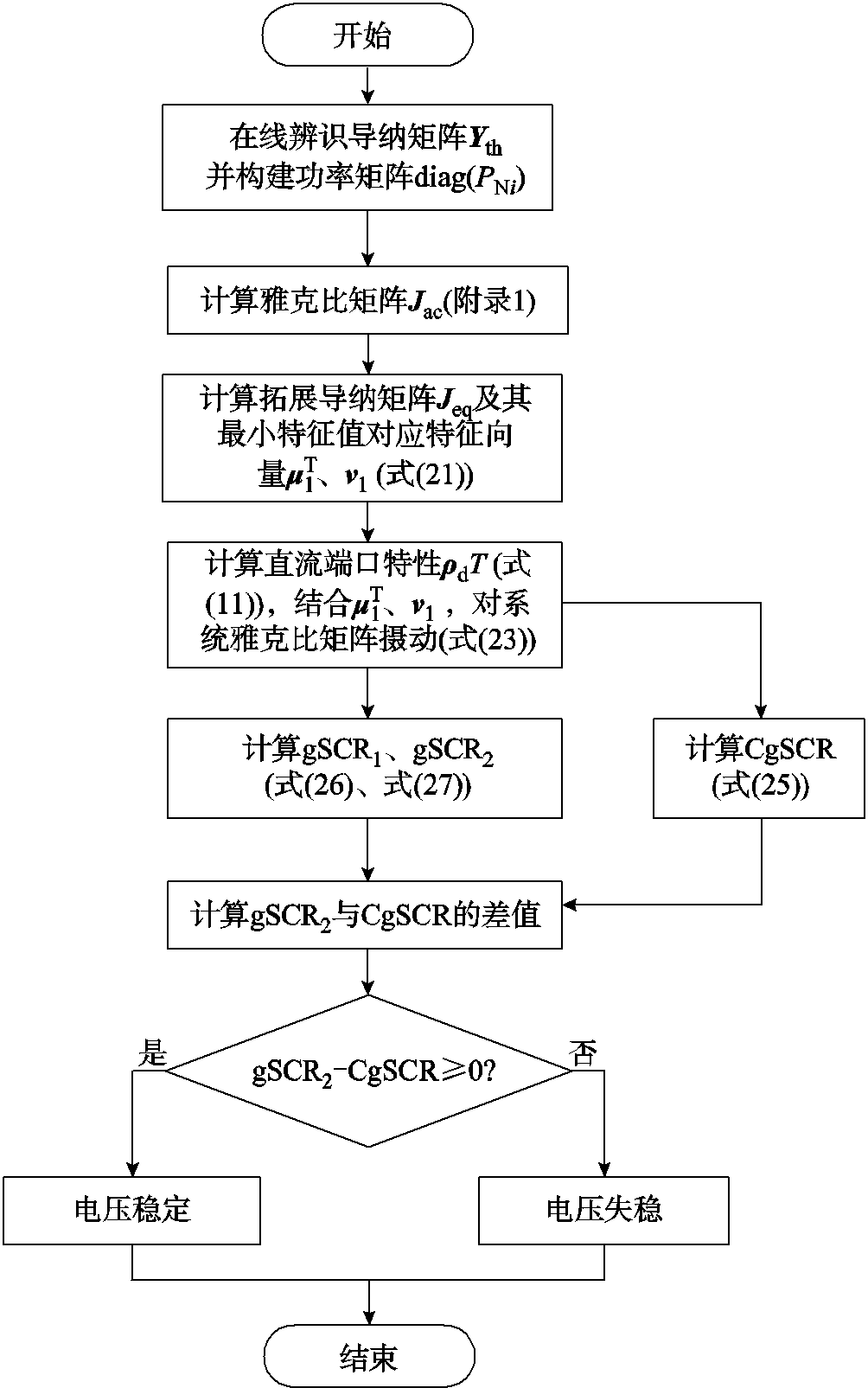
图7 直流多馈入系统gSCR计算和稳定裕度分析流程
Fig.7 Flow chart of gSCR calculation and stability margin analysis in MIDC systems
本节基于PSCAD仿真平台进行仿真计算,直流整流侧控制方式为定功率控制,逆变侧控制方式为定熄弧角控制,系统标幺基准值和直流系统参数见附录4。负荷采用多项式表示的ZIP模型。
首先考察式(7)中不同负荷特性对静态电压稳定的影响。针对图1的单馈入系统,额定工况下交流网络阻抗初始值为L0=0.40(pu),此后通过增加L0直至发生电压崩溃来确定静态电压稳定极限。仿真算例中设置有功、无功负荷ZIP比例系数相同。考虑如下两组算例:算例1接入有功负荷600 MW,无功负荷60 Mvar;算例2接入有功负荷600 MW,无功负荷300 Mvar。由1.2节分析可知U2/(PZ)= 5.814,则算例1中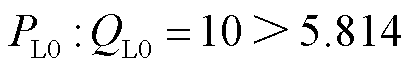 ,满足表1中第一种情形;算例2中
,满足表1中第一种情形;算例2中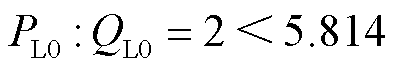 ,满足表1中第二种情形。
,满足表1中第二种情形。
在算例1中,将负荷类型分别设置为恒阻抗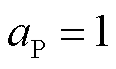 、恒电流
、恒电流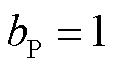 、恒功率
、恒功率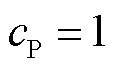 ,建立三组电磁暂态模型。t=3 s时,将L0增加到0.68(pu),三种情况下系统响应过程如图8a所示。由图8a可知,此时仅恒阻抗负荷发生电压崩溃,恒电流和恒功率负荷仍能保持稳定。进一步地,分别在t=5 s、t=7 s时,增加L0至0.70(pu)、0.72(pu),恒电流负荷和恒功率负荷相继发生电压崩溃。说明该情形下,恒阻抗负荷相比于恒功率负荷更易发生静态电压失稳,与表1理论分析一致。
,建立三组电磁暂态模型。t=3 s时,将L0增加到0.68(pu),三种情况下系统响应过程如图8a所示。由图8a可知,此时仅恒阻抗负荷发生电压崩溃,恒电流和恒功率负荷仍能保持稳定。进一步地,分别在t=5 s、t=7 s时,增加L0至0.70(pu)、0.72(pu),恒电流负荷和恒功率负荷相继发生电压崩溃。说明该情形下,恒阻抗负荷相比于恒功率负荷更易发生静态电压失稳,与表1理论分析一致。
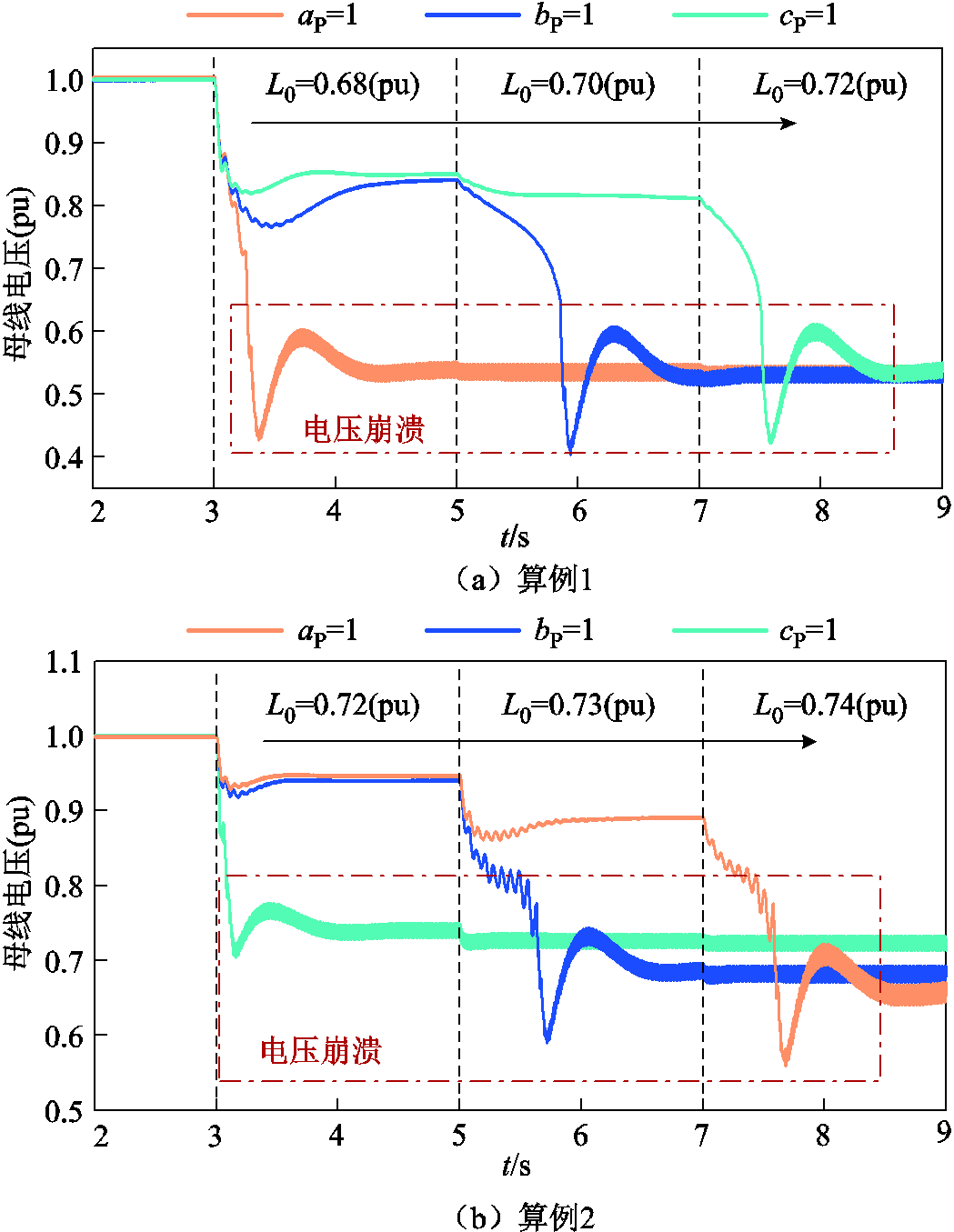
图8 母线电压时域仿真曲线
Fig.8 Time domain simulation curves of bus voltage
在算例2中,将负荷类型分别设置为恒阻抗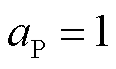 、恒电流
、恒电流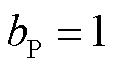 、恒功率
、恒功率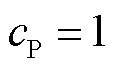 ,建立三组电磁暂态模型。t=3 s时,将L0增加到0.72(pu),三种情况下系统响应过程如图8b所示。由图8b可知,此时仅恒功率负荷发生电压崩溃,恒电流和恒阻抗负荷仍能保持稳定。进一步地,分别在t=5 s、t=7 s时,增加L0至0.73(pu)、0.74(pu),恒电流负荷和恒阻抗负荷相继发生电压崩溃。说明该情形下,恒功率负荷相比于恒阻抗负荷更易发生静态电压失稳,与表1理论分析一致。
,建立三组电磁暂态模型。t=3 s时,将L0增加到0.72(pu),三种情况下系统响应过程如图8b所示。由图8b可知,此时仅恒功率负荷发生电压崩溃,恒电流和恒阻抗负荷仍能保持稳定。进一步地,分别在t=5 s、t=7 s时,增加L0至0.73(pu)、0.74(pu),恒电流负荷和恒阻抗负荷相继发生电压崩溃。说明该情形下,恒功率负荷相比于恒阻抗负荷更易发生静态电压失稳,与表1理论分析一致。
进一步利用附图1所示IEEE 39节点系统算例验证本文所提广义短路比评估计算流程的有效性。基于附表2所给直流参数,将IEEE 39节点系统中节点34、36、37的同步发电机替换为直流,同时保持直流功率与被替换同步机有功功率一致,分别为5.08(pu)、5.60(pu)、5.40(pu)。以直流换流母线为分界线,可将39节点系统划分为直流侧与交流电网侧两部分,其中交流电网侧可通过多端口戴维南等值为图4b所示三馈入系统,故给出等值后三馈入系统的节点导纳矩阵理论值(标幺值)为
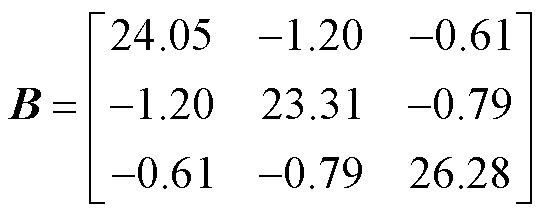 (36)
(36)
值得注意的是,上述给出的导纳矩阵理论值为仅考虑了线路阻抗后进行Kron降阶[23]所得,该过程未计及系统中的负荷。因此可根据式(26)原广义短路比定义直接计算出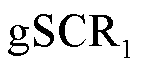 理论值为4.05。
理论值为4.05。
下面利用3.2节算法结合测量数据辨识三馈入系统等值导纳矩阵。首先考虑IEEE 39节点系统中所有负荷均为恒功率负荷(即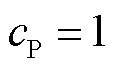 ),通过装设在节点34、36、37节点处的测量装置,对电网电压、功率进行采样。采样数据经处理后代入递推公式(35)得到导纳矩阵
),通过装设在节点34、36、37节点处的测量装置,对电网电压、功率进行采样。采样数据经处理后代入递推公式(35)得到导纳矩阵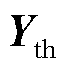 ,由前述分析可知,
,由前述分析可知,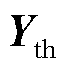 为6×6阶的不对称矩阵,无法直接用于计算短路比。根据图7流程和附录2中的转换关系式,将
为6×6阶的不对称矩阵,无法直接用于计算短路比。根据图7流程和附录2中的转换关系式,将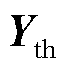 转换为交流系统雅克比矩阵
转换为交流系统雅克比矩阵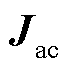 ,其前n行、n列元素(此处n=3)构成的子矩阵即为计算原广义短路比
,其前n行、n列元素(此处n=3)构成的子矩阵即为计算原广义短路比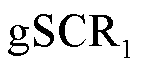 所需的等值导纳矩阵
所需的等值导纳矩阵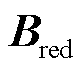 。图9给出了等值导纳矩阵
。图9给出了等值导纳矩阵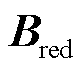 各元素的迭代计算过程。由图9可见,在迭代次数达到30~40次时,导纳矩阵元素迅速收敛至定值。利用最后一次迭代所得导纳矩阵计算原广义短路比
各元素的迭代计算过程。由图9可见,在迭代次数达到30~40次时,导纳矩阵元素迅速收敛至定值。利用最后一次迭代所得导纳矩阵计算原广义短路比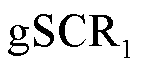 实际值为4.01,与理论值相比误差仅为1%,验证了本文所提基于数据驱动的广义短路比计算方法的有效性。
实际值为4.01,与理论值相比误差仅为1%,验证了本文所提基于数据驱动的广义短路比计算方法的有效性。
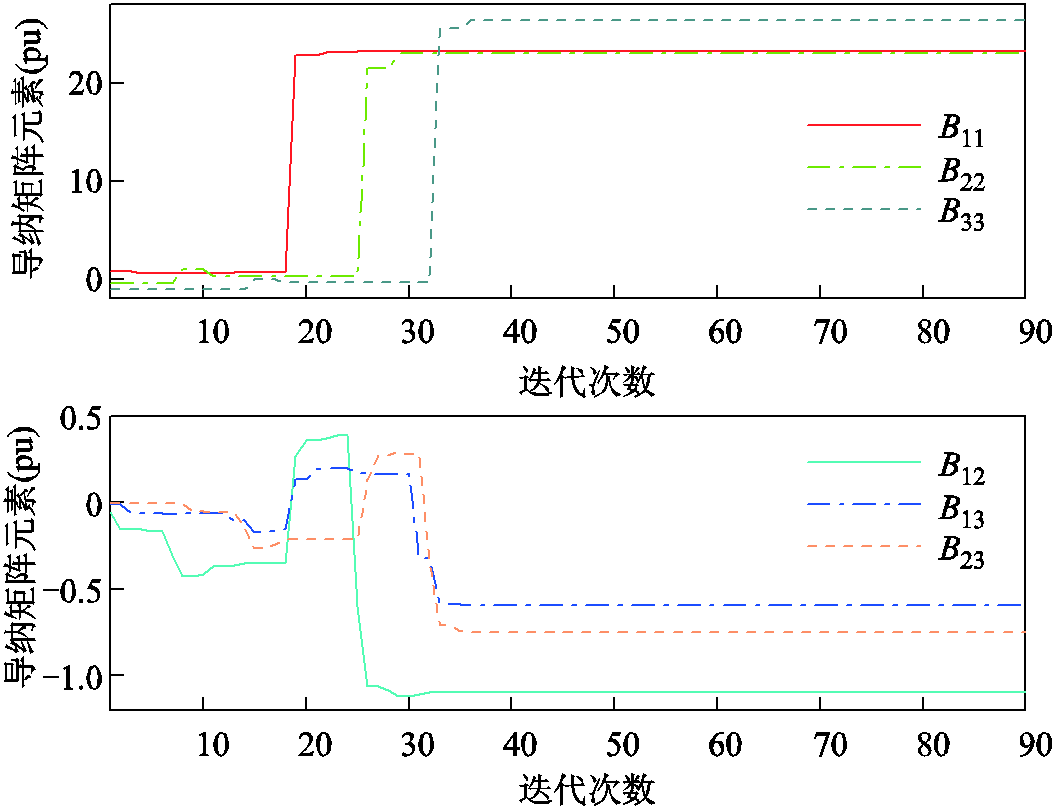
图9 导纳矩阵元素迭代过程
Fig.9 Admittance matrix elements during recursive iterations
在此基础上,考虑负荷类型变化对广义短路比的影响,将IEEE 39节点系统中负荷类型分别修改为恒电流和恒阻抗后,重复上述过程可得到交流电网雅克比矩阵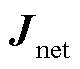 和负荷雅克比矩阵
和负荷雅克比矩阵 。此时计算得到原广义短路比
。此时计算得到原广义短路比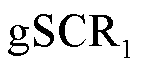 和修正广义短路比
和修正广义短路比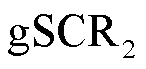 见表2。
见表2。
表2 多馈入系统gSCR1和gSCR2对比
Tab.2 Comparison of gSCR1 and gSCR2 in multi-infeed system

负荷类型MLEF gSCR1gSCR2CgSCR 恒阻抗-0.130.484.024.142.06 恒电流-0.070.484.024.092.06 恒功率00.484.014.012.06
由表2可知,不同负荷类型下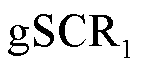 计算结果基本一致,说明原广义短路比
计算结果基本一致,说明原广义短路比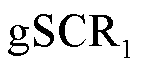 受负荷类型变化影响较小。为了更直观地阐述该结论,图10展示了恒阻抗负荷情形下等值负荷雅克比矩阵
受负荷类型变化影响较小。为了更直观地阐述该结论,图10展示了恒阻抗负荷情形下等值负荷雅克比矩阵 各元素相对大小。由图10可以看出,矩阵
各元素相对大小。由图10可以看出,矩阵 的前3列元素远小于后3列元素,在理论分析时可近似为0,印证了式(17)的近似假设,也验证了图4中等效电路模型的有效性。
的前3列元素远小于后3列元素,在理论分析时可近似为0,印证了式(17)的近似假设,也验证了图4中等效电路模型的有效性。
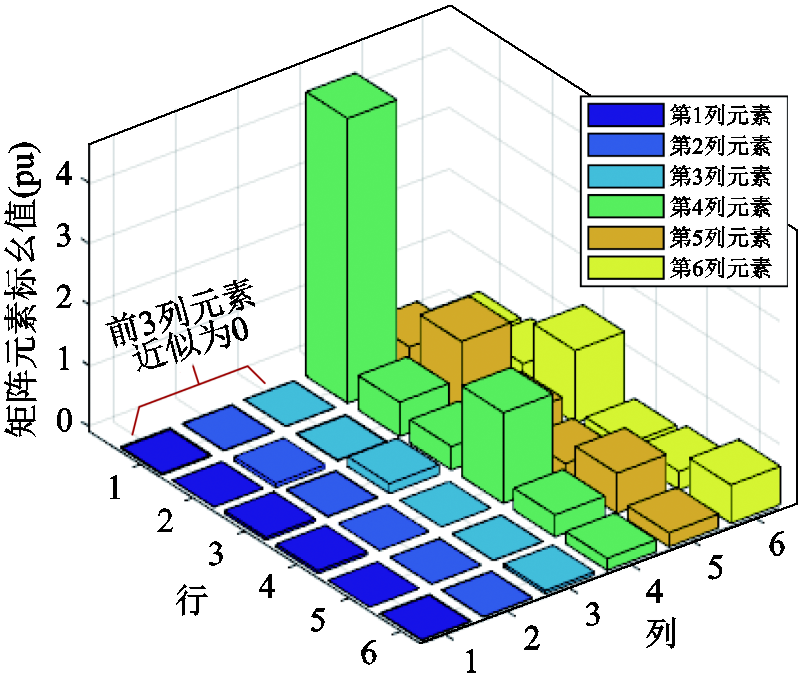
图10 等值负荷雅克比矩阵元素
Fig.10 Jacobi matrix elements of equivalent load
又根据表2可知,恒阻抗和恒电流情形下负荷影响因子MLEF为负(见式(23)及式(24)),说明系统中恒阻抗负荷占比增加,会导致修正广义短路比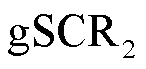 增大(见式(27)),而临界广义短路比CgSCR不变,稳定裕度增大。
增大(见式(27)),而临界广义短路比CgSCR不变,稳定裕度增大。
最后利用辨识得到的雅克比矩阵验证2.4节摄动方法和式(23)所给摄动结果的有效性。根据前文分析,原系统雅克比矩阵最小特征值可由模态摄动后矩阵特征值来近似,因此比较摄动前后的雅克比矩阵最小特征值之间的误差,可以说明模态摄动的近似效果。其中摄动前系统雅克比矩阵最小特征值即为求解式(21)得到的最小特征值,摄动后系统雅克比矩阵特征值可由式(23)得到。表3给出了不同负荷类型下,系统雅克比矩阵最小特征值的实际值和模态近似结果。由表3可知,不同负荷类型下,系统雅克比矩阵最小特征值的实际值与模态近似值之间的误差较小,最大误差不超过3%。因此利用模态摄动理论可近似分析原系统雅克比矩阵的主导模态。
表3 系统雅克比矩阵最小特征值对比
Tab.3 Comparison of minimum eigenvalues of system Jacobi matrix

负荷类型实际值模态近似值相对误差(%) 恒阻抗5.825.880.94 恒电流5.705.791.55 恒功率5.575.692.26
本文研究了负荷接入对直流多馈入系统静态电压稳定性的影响,主要结论如下:
1)本文提出一种面向大电网黑箱的多端口导纳矩阵辨识算法。考虑负荷后,系统导纳矩阵需要由常见的n维扩充为2n维才不会丢失负荷特征信息。所提算法完全由数据驱动计算,无需等到获得所有采样值之后再去估计导纳矩阵,而是每获得一组采样值之后都能对导纳矩阵的估计值进行递推修正。
2)多馈入系统雅可比矩阵经过Schur补之后,负荷主要影响系统雅可比矩阵中与电压相关的列向量。据此提出一种将网络内负荷统一折算至交直流端口处的简化建模方法,避免了大电网稳定分析可能会造成“维数灾”的问题。
3)构造直流、交流电网以及等值负荷的三端口雅克比矩阵,采用矩阵降阶、参数折算的方法,将负荷产生的影响集中归纳,定义了反映负荷影响程度的负荷影响因子指标,利用该指标修正现有广义短路比能够提高广义短路比反映电压稳定的准确性。
4)负荷有功、无功的大小,以及负荷ZIP比例系数均会直接改变负荷影响因子。负荷影响因子的正负决定了静态电压稳定的变化趋势,其绝对值决定了影响的程度。通过计算负荷影响因子能够定量反映负荷对直流静态电压稳定性的影响。
附 录
1. 等效负荷雅克比矩阵推导
对式(12)进行矩阵的初等变换,并将式(14)代表的负荷特性代入其中,则采用结构保持模型[24-25]的交流电网雅克比矩阵可表示为
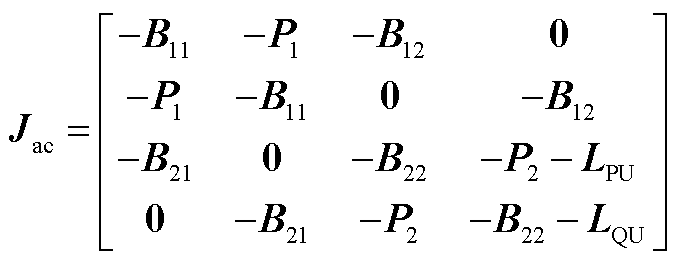 (A1)
(A1)
式中,直流馈入数为n个,负荷节点数为m个;各个分块矩阵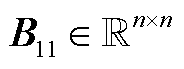 ,
,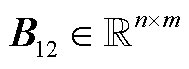 ,
,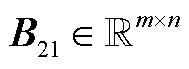 ,
,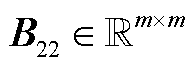 ;P1、P2为矩阵
;P1、P2为矩阵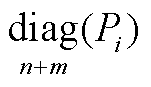 的分块子矩阵,
的分块子矩阵,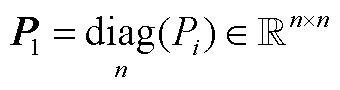 ,
,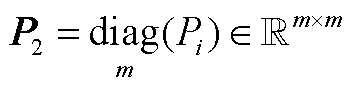 。
。
对式(A1)做Schur补,仅保留直流馈入节点,雅克比矩阵降阶为
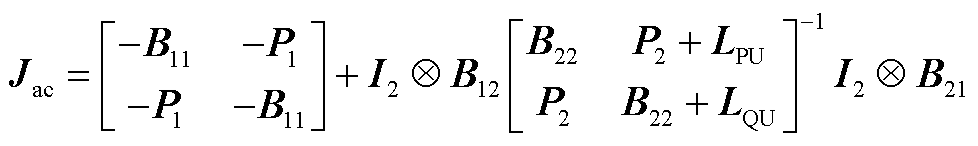 (A2)
(A2)
式中,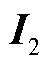 为二阶单位阵;
为二阶单位阵; 表示克罗内克积。
表示克罗内克积。
式(A2)涉及矩阵之和求逆,一般来说,严格的求逆公式非常复杂且不便于计算和分析,因此常用其一阶近似来逼近其逆矩阵。
若矩阵A的谱半径满足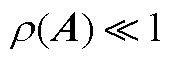 ,则有
,则有
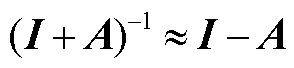 (A3)
(A3)
据此可推得
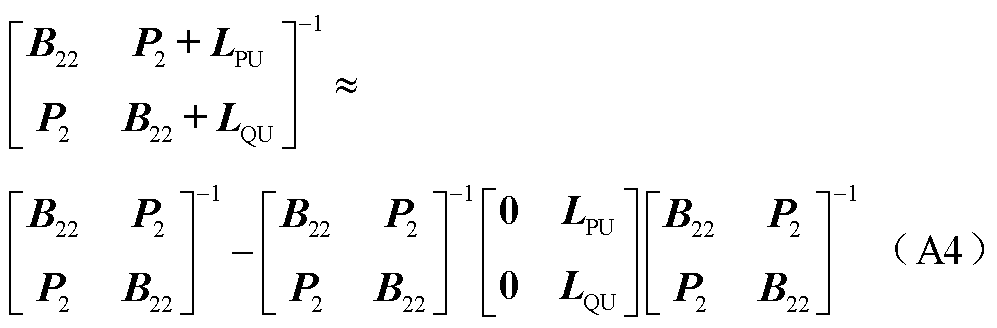
将式(A4)代入式(A2)可得
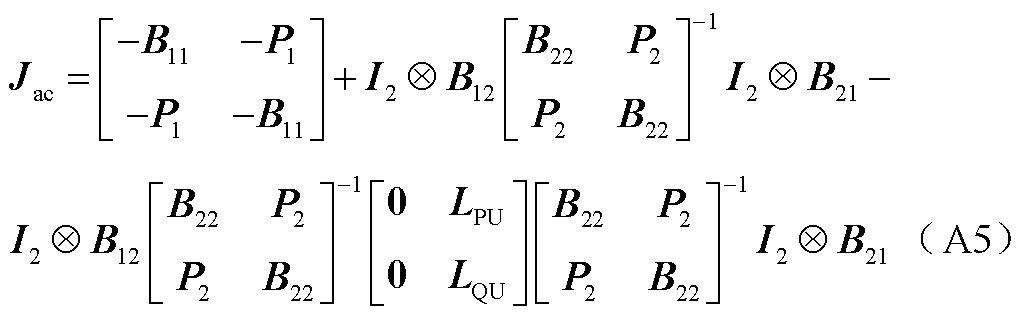
式(A5)等号右侧的前两项即为未接入负荷时的交流电网雅克比矩阵 ,第三项为接入负荷后对
,第三项为接入负荷后对 的修正矩阵,其物理意义为电网中负荷折算在直流馈入点(换流母线)上的等效负荷的雅克比矩阵
的修正矩阵,其物理意义为电网中负荷折算在直流馈入点(换流母线)上的等效负荷的雅克比矩阵 。
。
2. 导纳矩阵与雅克比矩阵转换关系
黑箱系统端口注入功率与端口电压、电流关系为
 (A6)
(A6)
式中,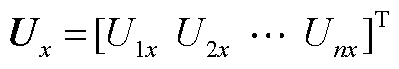 为节点电压的实部分量向量;
为节点电压的实部分量向量;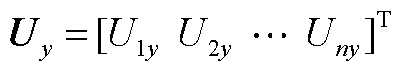 为节点电压的虚部分量向量;
为节点电压的虚部分量向量;![]()
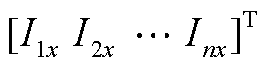 为注入电流的实部分量向量;
为注入电流的实部分量向量;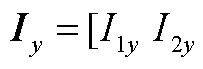
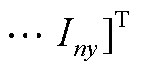 为注入电流的虚部分量向量;
为注入电流的虚部分量向量;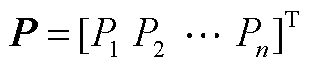 为注入有功功率向量;
为注入有功功率向量;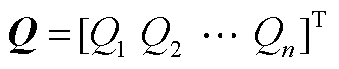 为注入无功功率向量;
为注入无功功率向量; 表示哈达玛积。
表示哈达玛积。
线性化式(A6)可得
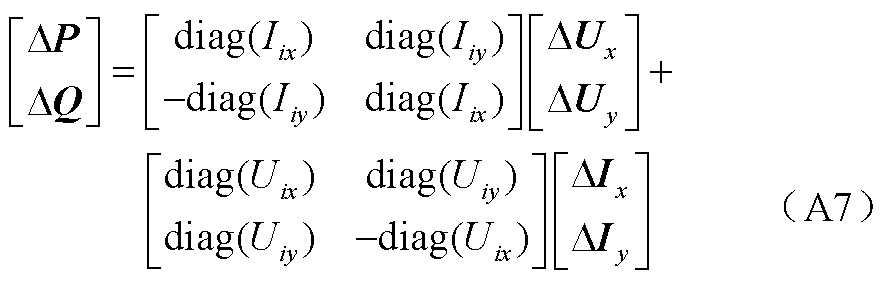
式中,对角矩阵均为n×n维。
黑箱端口导纳矩阵可写为
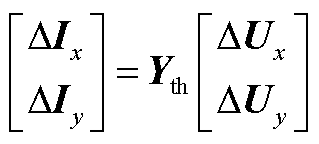 (A8)
(A8)
根据直角坐标与极坐标的转换关系,有
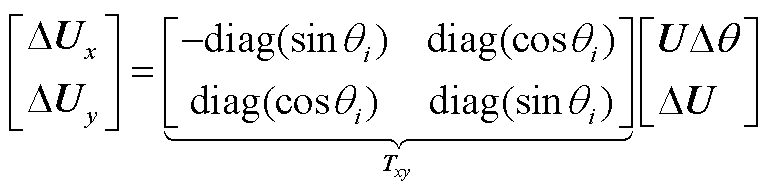 (A9)
(A9)
式中,![]() 为第i个端口电压相位。将式(A8)、式(A9)代入式(A7)可得
为第i个端口电压相位。将式(A8)、式(A9)代入式(A7)可得
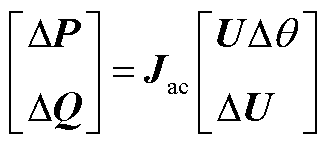 (A10)
(A10)
即导纳矩阵与雅克比矩阵的转换关系为
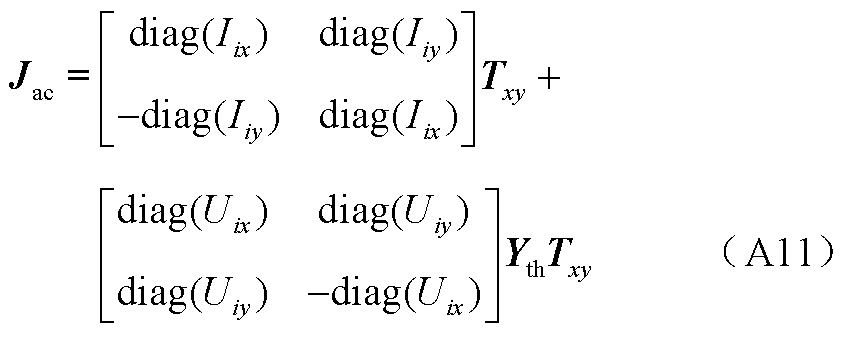
3. 负荷等值导纳模型推导
式(5)给出了负荷ZIP特性方程。负荷节点电压、电流分别为
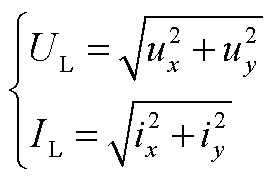 (A12)
(A12)
此外,功率与电压关系满足
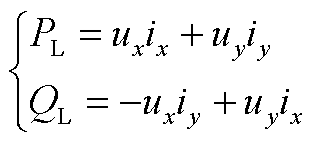 (A13)
(A13)
求解式(A13)可得
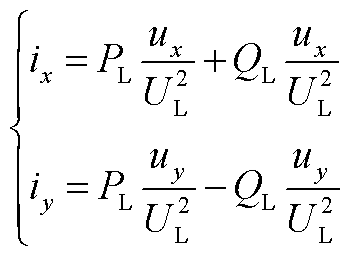 (A14)
(A14)
线性化式(A12)~式(A14),消去中间变量后可得负荷导纳矩阵为
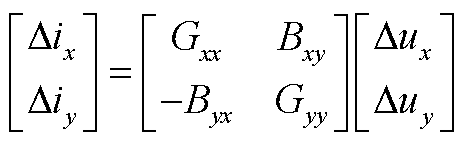 (A15)
(A15)
其中
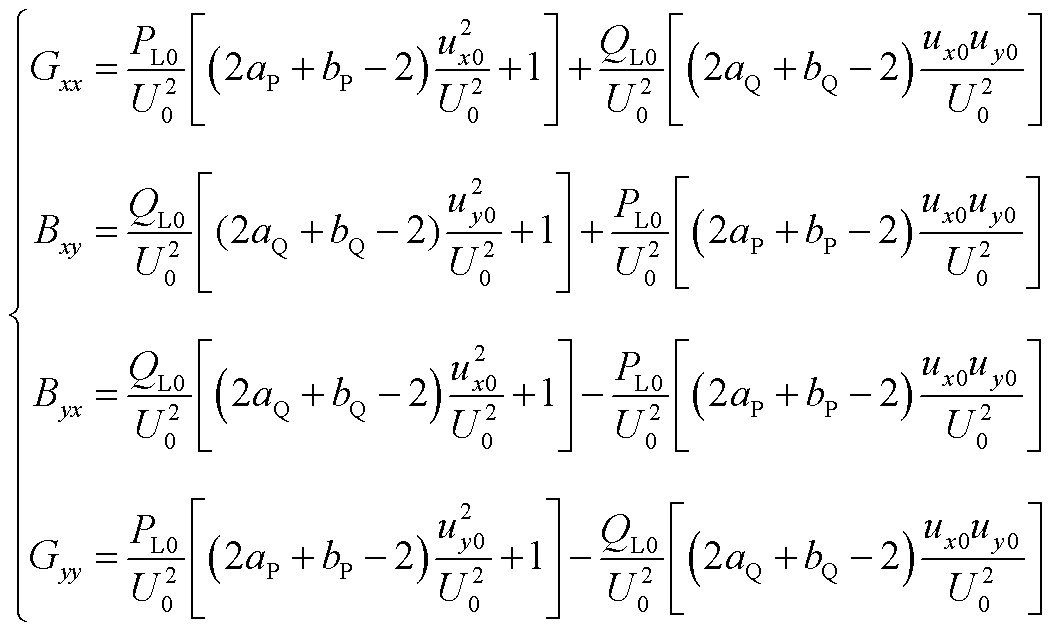 (A16)
(A16)
4. 仿真参数
附表1 系统标幺基准值
App.Tab.1 System per unit values

系统电压/kV功率/MW阻抗/Ω 整流侧交流系统3451 000119.03 逆变侧交流系统2301 00052.90 直流系统5001 000250.00
附表2 直流系统参数
App.Tab.2 DC system parameters

参数数值 补偿电容(pu)0.536 短路电抗(pu)0.18 熄弧角/(°)15 变压器分接头1 定功率控制比例参数1.10 定功率控制积分参数91.58 定熄弧角控制比例参数0.75 定熄弧角控制积分参数18.38
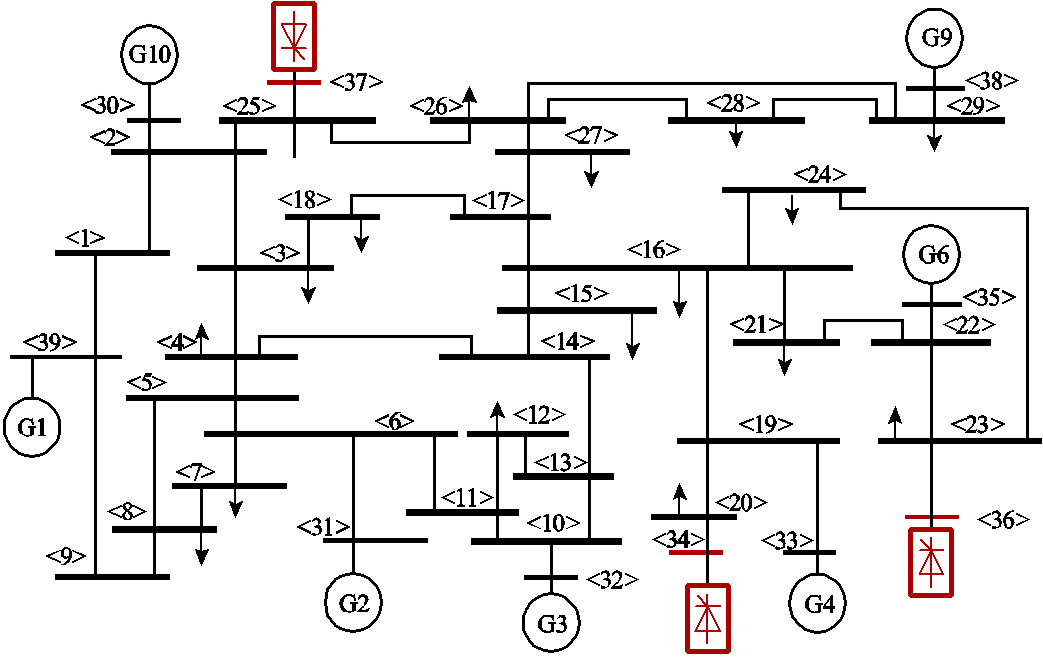
附图1 IEEE 39节点系统
App.Fig.1 IEEE 39-bus system
参考文献
[1] 汪娟娟, 莫泽, 刘岳坤, 等. 基于单边调制映射函数的LCC-HVDC直流侧阻抗精确建模[J]. 电工技术学报, 2024, 39(13): 3928-3942.
Wang Juanjuan, Mo Ze, Liu Yuekun, et al. Accurate modeling of DC side impedance of LCC-HVDC based on single-side modulated mapping function[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3928-3942.
[2] 李少岩, 曹珂, 顾雪平, 等. 多直流馈入受端系统与直流联络线协调恢复的一体化建模与求解[J]. 电工技术学报, 2023, 38(21): 5862-5877.
Li Shaoyan, Cao Ke, Gu Xueping, et al. Integrated modeling and solution for coordinated restoration of multi-infeed receiving-end systems and HVDC Tie lines[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5862-5877.
[3] 郭春义, 吕乃航, 张加卿. 提高LCC-HVDC在弱交流系统下的稳定性和动态性能的控制参数优化方法[J]. 电工技术学报, 2023, 38(7): 1751-1764, 1779.
Guo Chunyi, Lü Naihang, Zhang Jiaqing. Optimization of control parameters to enhance stability and dynamic performance of LCC-HVDC under weak AC condition[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1751-1764, 1779.
[4] CIGRE WG B4.41. Systems with multiple DC infeed[R]. Paris: CIGRE, 2008.
[5] 江岳文, 罗泽宇, 程诺. 基于线性化方法的交直流混合配电系统网架规划[J]. 电工技术学报, 2024, 39(5): 1404-1418.
Jiang Yuewen, Luo Zeyu, Cheng Nuo, et al. Network planning of AC/DC hybrid distribution system based on linearization method[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1404-1418.
[6] 刘杉, 余军, 贺之渊, 等. 基于VSC与LCC混合的多点传输直流输电系统拓扑结构研究与特性分析[J]. 中国电机工程学报, 2018, 38(10): 2980-2988, 3148.
Liu Shan, Yu Jun, He Zhiyuan, et al. Research on the topology and characteristic of multi-terminal HVDC based on VSC and LCC[J]. Proceedings of the CSEE, 2018, 38(10): 2980-2988, 3148.
[7] 汤涌, 易俊, 侯俊贤, 等. 基于时域仿真的戴维南等值参数跟踪计算方法[J]. 中国电机工程学报, 2010, 30(34): 63-68.
Tang Yong, Yi Jun, Hou Junxian, et al. Calculation method for thevenin equivalent parameters based on time domain simulation[J]. Proceedings of the CSEE, 2010, 30(34): 63-68.
[8] 潘学萍, 李乐, 黄华, 等. 综合灵敏度和静态电压稳定裕度的直流受端交流系统电压薄弱区域评估方法[J]. 电力自动化设备, 2019, 39(3): 1-8.
Pan Xueping, Li Le, Huang Hua, et al. Method for evaluating voltage weak area of AC power system at DC receiving end considering sensitivity and static voltage stability margin[J]. Electric Power Automation Equipment, 2019, 39(3): 1-8.
[9] 肖俊, 李兴源. 考虑交流系统负荷模型的直流输电系统特性分析[J]. 电网技术, 2013, 37(9): 2410-2415.
Xiao Jun, Li Xingyuan. Analysis on characteristics of HVDC power transmission system in AC/DC hybrid system considering load model of AC system[J]. Power System Technology, 2013, 37(9): 2410-2415.
[10] 汤奕, 郑晨一. 高压直流输电系统换相失败影响因素研究综述[J]. 中国电机工程学报, 2019, 39(2): 499-513, 647.
Tang Yi, Zheng Chenyi. Review on influencing factors of commutation failure in HVDC systems[J]. Proceedings of the CSEE, 2019, 39(2): 499-513, 647.
[11] 林伟芳, 汤涌, 卜广全. 多馈入交直流系统短路比的定义和应用[J]. 中国电机工程学报, 2008, 28(31): 1-8.
Lin Weifang, Tang Yong, Bu Guangquan. Definition and application of short circuit ratio for multi-infeed AC/DC power systems[J]. Proceedings of the CSEE, 2008, 28(31): 1-8.
[12] 郭小江, 汤涌, 郭强, 等. CIGRE多馈入直流短路比指标影响因素及机理[J]. 电力系统保护与控制, 2012, 40(9): 69-74, 81.
Guo Xiaojiang, Tang Yong, Guo Qiang, et al. Influence factors and theory for CIGRE MISCR index[J]. Power System Protection and Control, 2012, 40(9): 69-74, 81.
[13] 肖浩, 李银红, 段献忠, 等. 计及LCC-HVDC交直流系统静态电压稳定的综合短路比强度指标[J]. 中国电机工程学报, 2017, 37(14): 4008-4017, 4279.
Xiao Hao, Li Yinhong, Duan Xianzhong, et al. Integrated short circuit ratio strength index based on the static voltage stability of the LCC-HVDC systems[J].Proceedings of the CSEE, 2017, 37(14): 4008-4017, 4279.
[14] Lee D H A. Voltage stability assessment using equivalent nodal analysis[J]. IEEE Transactions on Power Systems, 2016, 31(1): 454-463.
[15] Lee D H A, Andersson G. An equivalent single-infeed model of multi-infeed HVDC systems for voltage and power stability analysis[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 303-312.
[16] 辛焕海, 章枫, 于洋, 等. 多馈入直流系统广义短路比: 定义与理论分析[J]. 中国电机工程学报, 2016, 36(3): 633-647.
Xin Huanhai, Zhang Feng, Yu Yang, et al. Generalized short circuit ratio for multi-infeed DC systems: definition and theoretical analysis[J]. Proceedings of the CSEE, 2016, 36(3): 633-647.
[17] Zhang Feng, Xin Huanhai, Wu Di, et al. Assessing strength of multi-infeed LCC-HVDC systems using generalized short-circuit ratio[J]. IEEE Transactions on Power Systems, 2019, 34(1): 467-480.
[18] 辛焕海, 甘德强, 鞠平. 多馈入电力系统广义短路比: 多样化新能源场景[J]. 中国电机工程学报, 2020, 40(17): 5516-5527.
Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5527.
[19] 王锡凡. 现代电力系统分析[M]. 北京: 科学出版社, 2003.
[20] Stewart G W, Sun Jiguang. Matrix Perturbation Theory[M]. Boston: Academic Press, 1990.
[21] Wang Guanzhong, Xin Huanhai, Wu Di, et al. Grid strength assessment for inhomogeneous multi-infeed HVDC systems via generalized short circuit ratio[J]. Journal of Modern Power Systems and Clean Energy, 2023, 11(4): 1370-1374.
[22] Huang Linbin, Xin Huanhai, Li Zhiyi, et al. Identification of generalized short-circuit ratio for on-line stability monitoring of wind farms[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3282-3285.
[23] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[24] 袁辉, 辛焕海, 王冠中, 等. 含SVG的新能源多馈入系统振荡分析和广义短路比计算[J]. 电力系统自动化, 2021, 45(14): 38-46.
Yuan Hui, Xin Huanhai, Wang Guanzhong, et al. Analysis on oscillation of multi-infeed system with renewable energy and static var generator and calculation of its generalized short-circuit ratio[J]. Automation of Electric Power Systems, 2021, 45(14): 38-46.
[25] 王康, 李子恒, 杨超然, 等. 面向大型新能源基地小干扰稳定性提升的调相机选址方法[J]. 电力系统自动化, 2022, 46(4): 66-74.
Wang Kang, Li Ziheng, Yang Chaoran, et al. Siting method of synchronous condenser for small-signal stability improvement of large-scale renewable energy base[J]. Automation of Electric Power Systems, 2022, 46(4): 66-74.
Abstract With the continuous growth of load and the expanding scale of HVDC projects, the spatial resources of HVDCs are gradually being occupied. The situation where new HVDC receiving-end converter stations are established in proximity to load centers has become increasingly unavoidable. Therefore, to ensure the safe and stable operation of the multi-infeed system, the quantification of voltage stability margin in the AC/DC system must take into account the influence of the load. The difference between the generalized short-circuit ratio (gSCR) and the critical generalized short-circuit ratio (CgSCR) is used to quantify the voltage stability margin of the AC/DC system. However, the existing definition of the gSCR has not taken into account the influence of the load, limiting its applicability. When considering the impact of the load in actual systems, the definition and calculation of the gSCR need to be changed. To address this issue, this paper proposes a method for analyzing and calculating the gSCR that considers the impact of the load. The new gSCR is a modification based on the original gSCR, and the modification is determined by various factors such as the size and type of the load.
Firstly, considering a single infeed system, the impact of load on the short-circuit ratio is studied based on the system Jacobi matrix. Analytical expressions for the new short-circuit ratio are derived too. Secondly, for multi-infeed systems, a load equivalent modeling method is proposed which can unify the internal loads of the system onto the HVDC converter bus to avoid the dimension disaster caused by excessive loads. On this basis, the Jacobi matrix for the multi-infeed system is established by clustering the load-related components. Then, based on the modal perturbation method, the multi-infeed system Jacobi matrix is approximately decoupled, and the generalized short-circuit ratio considering the load impact is defined. Moreover, for practical computation of the generalized short-circuit ratio, a data-driven method for calculating the admittance matrix of the multi-infeed system is proposed. Finally, the effectiveness of the proposed methods is validated through a single infeed system and the IEEE 39-bus system simulation cases.
The main contributions of the paper are as follows: (1) The adoption of the load equivalent modeling method overcomes the difficulty of individually modeling and analyzing loads in the system. This makes it possible to quantify the impact of loads in large systems. Since the load equivalent conversion process is independent of load scale, it can avoid the dimension disaster problem in large system analysis. (2) The proposed new gSCR can consider the impact of loads, extending the original gSCR and thereby improving the accuracy of voltage stability analysis. (3) Addressing the challenge of difficult computation of the generalized short-circuit ratio in large systems, a data-driven identification algorithm for the admittance matrix of the multi-infeed system is proposed. The algorithm, combined with the load equivalent modeling method mentioned above, enables the analysis and computation of the gSCR in large systems.
keywords:Voltage stability, generalized short-circuit ratio (gSCR), load characteristics, multi-infeed system, modal perturbation
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.231870
国家电网公司科技项目资助(5108-202218280A-2-437-XG)。
收稿日期 2023-11-08
改稿日期 2024-01-10
王奕鑫 男,1997年生,博士研究生,研究方向为新型电力系统稳定分析与控制。E-mail:11910060@zju.edu.cn
辛焕海 男,1981年生,教授,博士生导师,研究方向为交直流系统稳定分析与控制、新能源并网稳定分析与控制。E-mail:xinhh@zju.edu.cn(通信作者)
(编辑 李 冰)