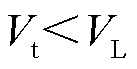；2→1：
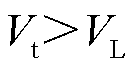且新能源没有穿越后爬坡功能；2→3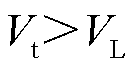：且新能源有穿越后爬坡功能；3→4：经历1个计算步长；4→1：爬坡结束（功率恢复至穿越前的水平）；4→2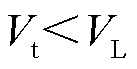：。其中，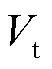
表示新能源的机端电压，
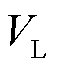表示新能源低电压穿越判断阈值；一般为0.9(pu)。摘要 中国分布式新能源装机容量的不断增加，已成为影响大电网安全稳定的重要因素。目前的分布式新能源等值建模方法尚不成熟，难以用于工程实际中的大电网仿真分析。为此，该文首先介绍了大电网分析中的分布式新能源模型现状，探讨了分布式新能源等值模型的工程要求；然后以大规模工程应用为目标，提出了“含分布式新能源的有源综合负荷模型”的建模思路；最后提出了该模型的结构及参数计算方法，介绍了所提方法在中国S省初步应用的具体案例。应用效果表明，该文提出的有源综合负荷模型能满足高比例分布式新能源的大电网建模、仿真分析需求，具备大规模工程应用潜力。
关键词：大电网 分布式新能源 等值建模 综合负荷模型 安全稳定分析
近年来，分布式新能源在中国呈爆发式增长，因而对大电网安全稳定产生影响，在部分场景下已成为决定大电网稳定性的关键因素。2022年，中国分布式光伏新增并网容量5 111万kW，远超集中式光伏的新增容量[1-2]。在某些高渗透省份，分布式新能源装机可占总新能源装机的50%以上，高峰出力占总负荷功率的近30%。多个省级电网的运行经验表明，目前的大电网分析对分布式新能源考虑不足，极有可能导致分析结论出现重大偏差。澳大利亚、美国等国已发生多起与分布式新能源相关的电网事故[3-5]。
然而，分布式新能源容量小、数量多、电压等级低，在大电网分析中不能一一建模，给稳定分析带来了困难[6-7]。一些研究提出了大量新能源设备的聚合等值建模方法，主要面向集中式新能源场站[8-9]。但分布式新能源一般在35 kV及以下电压等级接入，且与电力系统负荷相互混杂，不能套用集中式新能源的聚合等值方法。
在分布式新能源发展初期，大电网分析常将其出力作为“负的负荷”折算进负荷模型中，与一部分负荷功率相互抵消。但是这一建模方法过于粗放，在高比例分布式新能源渗透地区，可能使大电网分析结论出现严重偏差。部分地区的电力企业使用含分布式新能源的简易配电网模型，代替大电网分析中的负荷模型，以反映分布式新能源的影响。但这类模型的节点数量、元件数量较多，难以应用于省级以上的大型电网。
为解决大电网仿真分析中的分布式新能源建模难题，一些文献借助电力系统的暂态响应数据，使用总体测辨法构建含新能源的配电网等值模型[10]，这种方法有时也被称为“基于量测的方法”，所得到的模型一般被称为广义负荷模型、有源配电网等值模型、微电网等值模型等[11-12]。例如，文献[13]借鉴常规负荷模型的电气结构，借助批量仿真和蒙特卡洛抽样等方法计算模型的电气参数，使其在主网侧体现出的暂态特性尽量接近含分布式新能源的实际配电网；文献[14]基于类似的模型结构，提出基于轨迹灵敏度的等值电气参数计算方法；文献[15]使用传递函数代替实际的电气模型，来表征含分布式新能源的配电网聚合响应特性，并借助无监督学习方法确定传递函数的参数；文献[16]使用长短期记忆神经网络来刻画配电网的响应特性，将神经网络的输出作为等值模型的输出。
虽然目前已有很多基于总体测辨法的建模手段，但鲜有文献报道这些建模手段的工程应用情况。对于大型电力系统，如何获取足够多的配电网响应数据用于辨识（特别是大扰动数据），是制约该方法应用的一个关键瓶颈。另一方面，这类方法较难直观给出实际元件和等值参数间的物理联系，有时还会引发等值参数计算的多解、过拟合等问题，不利于大电网分析和规划。
由于总体测辨法的上述限制，一直以来，中国的工程实践中更多地采用统计综合法来建立负荷及新能源模型[17-22]。该方法借助人工或自动化手段统计负荷及新能源的实际情况，通过分析电力系统的运行机理，计算其等值模型的参数。在这一领域，目前针对负荷的等值建模理论已相对成熟，但对分布式新能源的研究非常少见。其中，文献[17-19]等介绍了常规负荷设备的统计和等值建模方法，但没有考虑分布式新能源对等值模型的影响。文献[22]针对低电压穿越期间定电流控制的新能源设备，推导了穿越期间部分电流控制参数的等值建模方法，但没有涉及使用其他穿越控制策略的新能源设备，也没有讨论穿越后的恢复阶段等其他特性，应用场景较为局限。
总体而言，中国的分布式新能源的装机容量不断提升，对大电网安全稳定产生显著影响，而现有的分布式新能源建模方法不能满足工程计算需求，为电力系统安全带来隐患。
针对上述问题，本文梳理了中国大电网稳定分析中的分布式新能源模型现状，基于综合负荷模型的长期工程应用基础，探讨了等值模型的工程应用要求，提出了“有源综合负荷模型”建模方法，基于中国S省电网介绍了该方法的应用实例。应用效果表明，所提出的模型基本满足大电网稳定分析的工程需求，具备大规模推广应用的潜力。
本节内容将介绍大电网分析中的分布式新能源模型现状，提出等值建模思路，作为本文后续工作的基础。
目前，各类学术文献、标准、政策文件等对“分布式”新能源尚未形成统一定义。本文中的分布式新能源是指：在一般的大电网分析计算中，由于电压等级、容量、并网方式等原因，不作为新能源场站单独建模的新能源设备或集群。
在PSASP等大电网仿真平台中，可将分布式新能源的模型分为三类：①带穿越功能的全功率电压源型换流器（Voltage Source Converter, VSC）并网新能源（A类新能源）；②不带穿越功能的全功率VSC并网新能源（B类新能源）；③双馈风机。
A类分布式新能源是具备穿越功能的全功率VSC并网新能源，一般是按照集中式新能源标准设计制造[23-24]、但以分布式形式接入的光伏和全功率风机。中国尚未发布关于分布式新能源建模的专门标准。实际工程中一般参照相关领域的其他新能源建模标准建立A类分布式新能源的动态模型[25]。
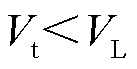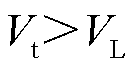A类分布式新能源对负荷模型产生影响的关键在于其切换运行特性。暂态电压波动情况下，其低电压穿越状态转移图如图1所示，图中的状态转移条件简述如下：1→2：；2→1：且新能源没有穿越后爬坡功能；2→3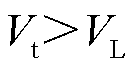：且新能源有穿越后爬坡功能；3→4：经历1个计算步长；4→1：爬坡结束（功率恢复至穿越前的水平）；4→2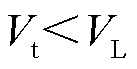：。其中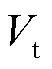，表示新能源的机端电压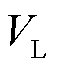，表示新能源低电压穿越判断阈值；一般为0.9(pu)。
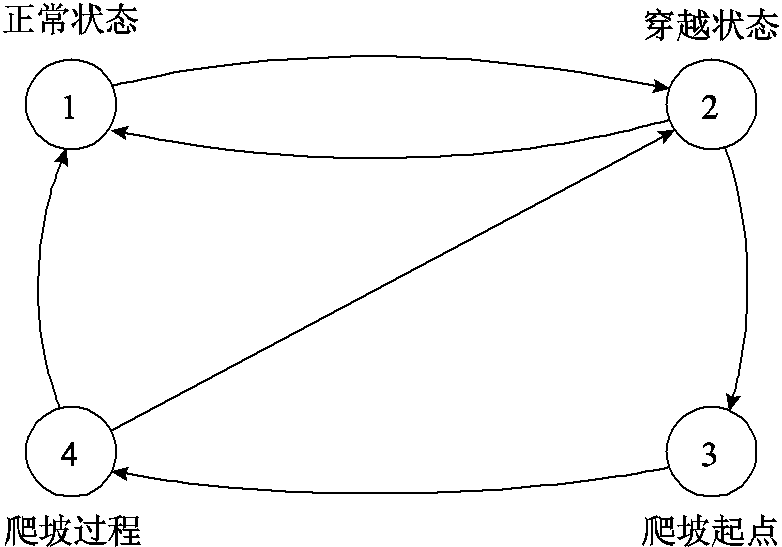
图1 A类分布式新能源的状态转移图
Fig.1 State transition diagram of RES-A
在正常状态下，新能源的暂态特性类似于恒定功率控制，有时也采用定直流电压等控制方式。
在穿越状态下，多数新能源运行在指定电流控制模式，其电流指令为
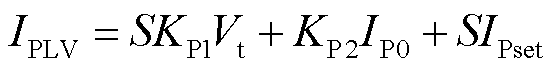（1）
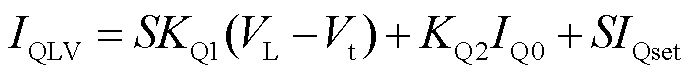（2）
式中，S为新能源的额定容量；IPLV、IQLV分别为新能源低电压穿越期间的有功和无功电流指令；IP0、IQ0分别为新能源进入低电压穿越前的有功、无功电流；其他变量为新能源模型参数。
还有一些新能源在穿越期间运行于指定功率控制模式，其功率指令为
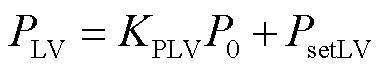（3）
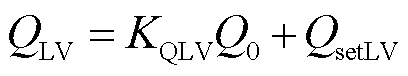（4）
式中，PLV、QLV分别为新能源穿越期间的有功、无功功率指令，P0、Q0分别为新能源穿越前的有功、无功功率；其他变量为新能源的模型参数。
穿越结束后，新能源功率迅速回复到穿越前的水平，或经过爬坡过程回到穿越前水平。新能源的爬坡起点与其穿越前的运行状态有关。在机电暂态仿真时，新能源进入爬坡起点的瞬间可能发生状态跳变。在此之后，新能源将按固定斜率或一阶渐进特性开始爬坡。图2给出了电压扰动下一种典型的A类新能源响应特性。
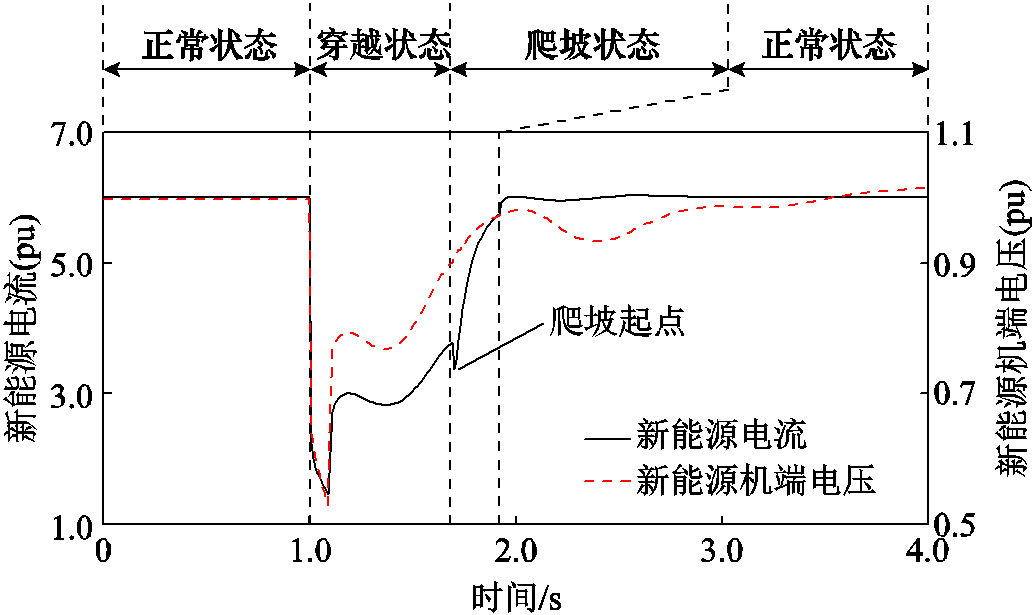
图2 A类新能源的典型暂态特性示意
Fig.2 Typical transient response of RES-A
B类分布式新能源是不具备穿越功能的全功率VSC并网新能源，一般是按照分布式电源标准设计制造的光伏和全功率风机[26-27]。和A类新能源相比，B类新能源在设计制造时未考虑集中式新能源的运行要求，不具备低电压穿越控制措施，但配备有保护设备的“封波（软脱网）”功能。当电压较低时，为了保护换流设备，新能源将停止功率输出，一段时间之后再缓慢恢复至封波前状态。功率恢复过程一般是固定斜率的线性恢复。图3给出了电压扰动下一种典型的B类新能源响应特性。
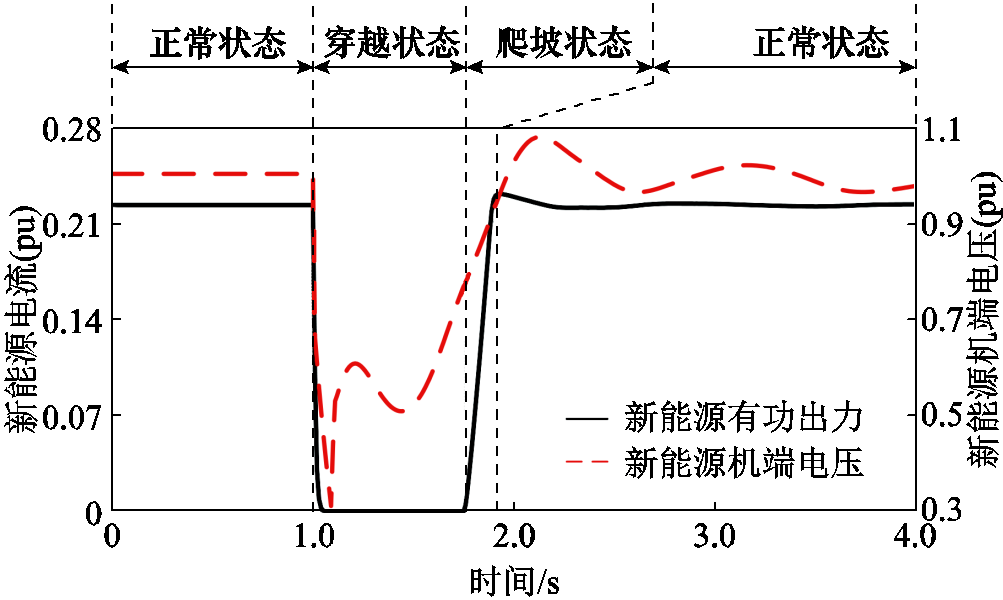
图3 B类新能源的典型暂态特性示意
Fig.3 Typical transient response of RES-B
在大电网工程计算中，双馈风机的切换运行特性与图1中A类新能源基本一致，低电压穿越期间的特性也使用式（1）～式（4）刻画。
双馈风机的并网接口与全VSC设备不同，因而实际上的运行特性也与A类新能源存在差异。这些差异主要体现在式（1）～式（4）中的参数取值，以及风功率转换、转矩控制等环节。
为解决高比例分布式新能源接入导致大电网分析不准的问题，部分电力企业构建了含分布式新能源的简易配电网模型，代替等值负荷模型。一个典型的含新能源的简易配电网模型如图4所示。该模型主要用于电网公司对中国电力系统安全稳定的仿真计算，所以相关分析结论很少公开发表。但在目前的工程实践中，已形成了一套相对完善的数据收资、模型维护、仿真计算流程，对模型的优缺点也有了相对明确的认知。
图4 用于大电网分析的含新能源简易配电网模型
Fig.4 Distribution grid model with DRE for large-scale power system analysis
在建立图4中的新能源模型时，电网公司首先和新能源生产厂家开展合作，对主流新能源机型进行硬件在环仿真测试；然后在此基础上，使用PSASP等大电网仿真软件中的新能源模型，通过填写合理的模型参数，来反映测试得到的实际新能源的外特性；最后，借鉴新能源场站的等值建模方法，将小范围内的分布式新能源集群（例如一个小区的所有屋顶光伏）建模为一个等值分布式新能源设备，接入简易配电网模型。
与实际配电网相比，图4的模型既做了合理的简化、又能满足大电网仿真对准确性的要求。但这类模型的收资、建模、数据维护工作将耗费大量人力，得到的仿真模型节点数量很大。一个省级电网通常包含数百个配电网，其模型包含约10万节点，而PSASP等机电暂态仿真软件所能计算的最大规模系统一般不超过12万节点。因而，这种模型不适用于省级以上规模的大电网仿真分析。
提出更简单的分布式新能源等值模型，可以解决简易配电网模型所面临的一些关键问题，包括但不限于：大电网节点数超出软件计算能力、模型收资维护困难、模型复杂导致稳定机理分析困难等。为此，等值建模工作的具体工作目标可归纳为：提出合理的等值模型，刻画图4中简易配电网模型在主网侧体现出的聚合特性。
目前，不含新能源的配电网特性可以使用综合负荷模型来刻画[18-19]。新能源接入后，一方面引入了新的电气设备，另一方面又会与负荷产生相互作用、使原有的负荷模型不再准确。本文在过去的综合负荷建模的理论基础上，提出有源综合负荷模型构建方法，刻画负荷、新能源、配电网线路等体现出的聚合特性。
本小节基于中国电力企业的大电网分析及建模技术现状，探讨有源综合负荷模型的工程要求，具体包括模型兼容、应用成本、可解释性和等值精度四个方面，见表1。这些要求虽不是对建模方法的强制性约束，但不符合要求的方法在大规模工程应用时需要付出额外代价。
表1 有源综合负荷模型的工程要求
Tab.1 Engineering requirement for equivalent DRE model
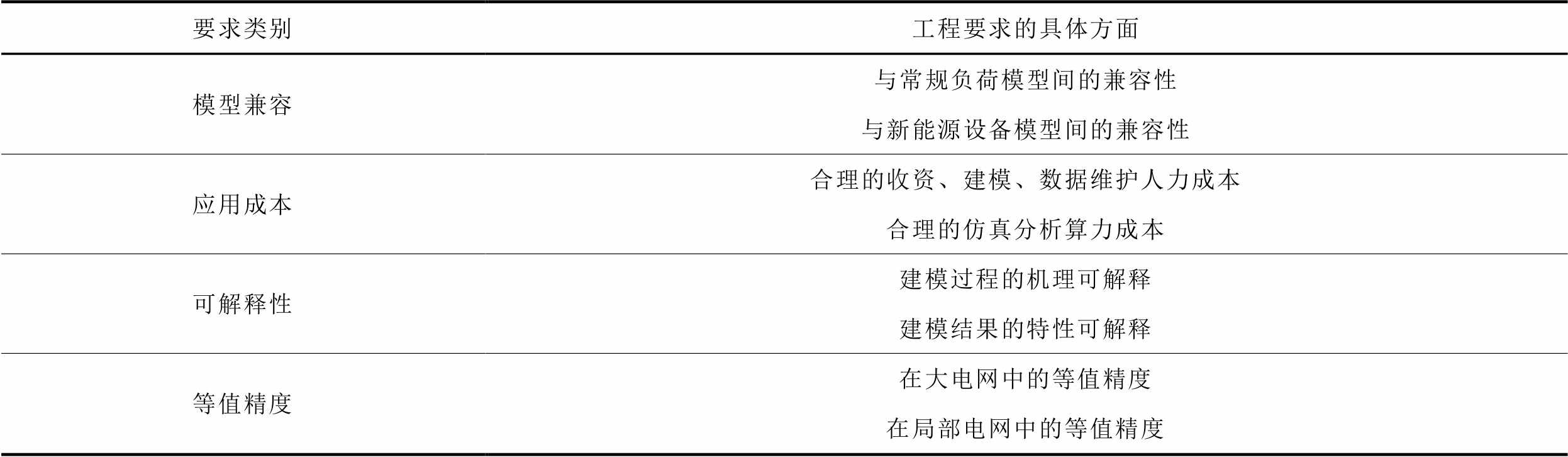
要求类别工程要求的具体方面 模型兼容与常规负荷模型间的兼容性 与新能源设备模型间的兼容性 应用成本合理的收资、建模、数据维护人力成本 合理的仿真分析算力成本 可解释性建模过程的机理可解释 建模结果的特性可解释 等值精度在大电网中的等值精度 在局部电网中的等值精度
在开发建模技术时，需要时刻注意模型的兼容性需求，保证所提模型与已有的大多数建模、仿真、分析技术相互兼容。
2.1.1 与常规负荷模型间的兼容性
分布式新能源在电气结构上与电力负荷混杂接入电网，其运行特性也与电力负荷相互影响。在建立有源综合负荷模型时，需要考虑现有的负荷模型及其应用情况。
中国电力企业广泛使用的负荷模型是经典负荷模型及综合负荷模型（Synthesis Load Model, SLM）[18-19]。以综合负荷模型为例，常用的结构如图5所示，该模型对配电网中的静态负荷、马达负荷、无功补偿等设备已经有了较为合理的考虑[20-21]。在建立有源综合负荷模型时，不宜为了刻画新能源特性而大幅改变现有的负荷模型。当某地区的分布式新能源增加而配电网其他条件不变时，要能平滑地将原有负荷模型过渡为有源综合负荷模型的形式。
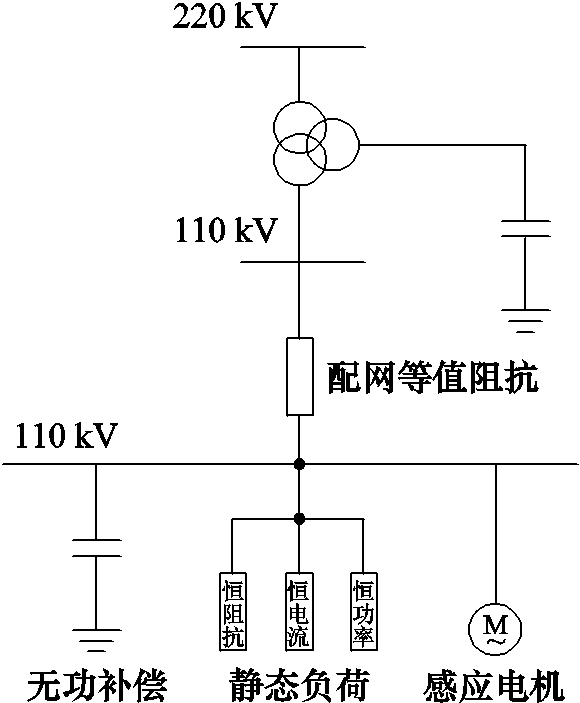
图5 综合负荷模型结构
Fig.5 Structure of synthesis load model
2.1.2 与新能源设备模型间的兼容性
一些文献已经指出，多个新能源设备的聚合特性可能和单个设备特性完全不同。对于新能源设备集群而言，一种理论上可行的等值建模方法是开发出全新的元件级模型，来刻画多个设备的聚合特性。但考虑到物理含义、兼容性、推广性等问题，这类方法在实际工程中较少使用。
在实际工程中，一般使用类似单机倍乘的方式来反映代替多个同类型设备的聚合特性，这一方法在新能源场站建模、负荷建模等工作中有广泛的实践基础，保证了等值模型和实际设备模型间的兼容性。图5中的无功补偿、静态负荷、感应电机等就是基于类似思想来配置的。在对建模精度要求较高的场合，可通过修改倍乘后的模型参数、电气连接方式等，使等值模型的特性更加准确[8-9]。分布式新能源的等值建模也宜采用类似的思路。
任何工程技术都需要考虑成本问题。在高比例分布式新能源接入的未来场景下，其等值模型可能用于成千上万个配电网，需要在应用成本方面符合电力企业的生产要求。
2.2.1 收资建模的人力成本
有源综合负荷模型的收资建模成本主要包括统计调研、模型搭建、数据维护等。对于统计调研，需要通过普查和详查了解某区域内负荷、新能源等设备的情况和参数。对于模型搭建和数据维护，需要在仿真计算软件中搭建等值模型并配置、更新不同运行方式下的模型数据。
所使用的模型宜具备相对较低的收资建模成本，或具备使用自动化手段降低成本的潜力。
2.2.2 仿真分析的算力成本
建立有源综合负荷模型的重要目标之一是降低仿真计算成本。目前使用图4所示的简易配电网模型计算含分布式新能源的大电网特性时，省级电网的仿真节点数量已接近现有仿真软件的极限，相关方法极难推广到更大规模的电网中。所使用的有源综合负荷模型宜具备较低的仿真计算成本，从而满足大电网分析需求。
电力系统是一个人造的物理系统，它的安全运行虽然高度依赖自动化技术，但最为关键的调度决策、建设规划都由人工完成。
所使用的等值模型宜具备高度的可解释性。这里的“可解释”并非理论意义上的可解释，而是面向广大工程技术人员的可解释。可解释的模型更利于实现工程应用，降低推广成本并避免人为失误。
2.3.1 建模过程的机理可解释
模型的构建过程要具备简单明确的物理机理，尽量不使用类似“黑盒”的算法。当新能源机型、容量、同时率、并网位置等发生变化时，在建模过程中如何考虑这些变化、以及这些变化如何对建模结果产生影响，应当有相对明确的结论。
近年来，以人工智能为代表的新型算法展示出了很大的应用潜力，虽然在可解释性方面存在不足，但值得持续关注和研究。
2.3.2 建模结果的特性可解释
模型的构建结果宜具备符合常识的物理特性。一些算法可能导致多解、过拟合等问题，或者得到容性静态负荷、功率为负的电源等罕见结果。这些问题虽然有严格的数学解释，但缺乏工程实际中的物理含义，可能导致工作人员的错误判断或导致大电网分析出现困难，要尽量避免。
目前针对新能源场站的建模方法及精度要求已有国家标准或行业标准[25,28]，但在负荷侧及分布式新能源领域尚无明确规定。本文结合实际工程中的应用经验，进行初步探讨。
2.4.1 大电网的等值精度
使用等值模型代替简易配电网模型进行大电网暂态仿真时，可从临界运行方式和关键暂态特性等方面校验等值精度。
其中，临界运行方式是评价主网层面等值精度的最关键、最易量化的指标，包括电网稳定前提下的最小开机方式、最大负荷水平、最大受电能力等。使用等值模型后，这些临界值不应有大的变化。
关键暂态特性包括故障后的关键联络线功率波动、关键母线电压波动情况等。但是，对于这些特性，目前没有广泛认可的量化评估方法，只能根据经验评估等值效果。
2.4.2 局部电网的等值精度
目前的大多数文献在验证等值精度时，一般关注局部电网的等值效果（一般为1个配电网及附近的主网）。但这并不是实际工程中建模工作的重心。
实际配电网的运行方式非常多样，但大电网分析中一般只考虑典型运行场景下的聚合特性。所使用的建模方法只要能够反映典型配电网在主网侧体现出的暂态响应趋势，一般就能够满足大电网的应用需求（第4节的应用实例）。在此基础上，应当兼顾成本、兼容性、可解释等方面的要求，不宜过度追求局部电网的等值精度。
本文在某高比例新能源渗透省份（S省）的实际大电网分析工作中，初步探索出了一套可实际应用的有源综合负荷模型构建方法。
该方法建立了等值模型各部分结构与简易配电网模型间的直观物理联系，提出等值模型参数的解析计算方法，具备相对明确的低成本工程推广路径，适用于大部分具备放射性网络结构的配电网，并已初步应用于S省电力企业的运行分析工作。
3.1.1 有源综合负荷模型的结构
本文所提出的等值模型结构如图6所示。以现有的综合负荷模型为基础，在同一个等值并网点（是Point of Connection, POC）并联了第1节介绍的三类新能源设备。这一模型结构符合工程应用的兼容性要求。
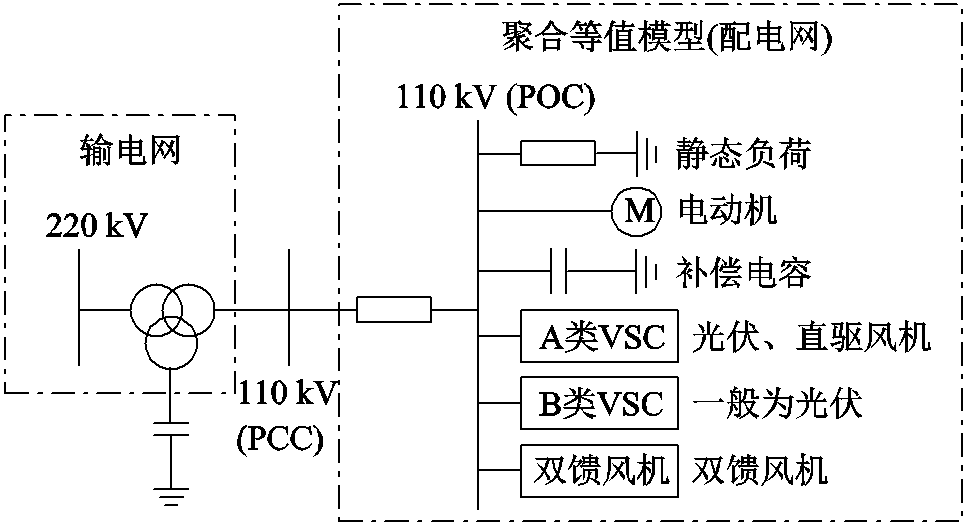
图6 含新能源的有源综合负荷模型结构
Fig.6 Structure of active synthesis load model with renewables
在新增的新能源设备中，A类新能源、双馈风机可以各使用1个等值设备来刻画配电网中所有同类设备的整体影响；B类新能源的运行特性在不同型号间差异较大，需要结合具体工程实际确定等值设备的数量。在S省电网中，使用两个等值设备可以得到较好的建模效果。
3.1.2 模型结构的特点分析
有源综合负荷模型具备与SLM模型不同的暂态特点，在计算和分析时需要加以额外考虑。
1）机端电压特点
实际配电网中，新能源机端电压一般高于负荷母线电压。特别是在电压跌落后的恢复过程中，新能源低电压穿越时发出大量无功功率，对新能源并网点起到电压支撑作用。
在有源综合负荷模型中，新能源与负荷并联在POC。受负荷的影响，等值新能源的机端电压一般低于实际配电网的新能源电压。
以某简易配电网模型及其等值模型为例，这一电压特性的对比如图7所示。机端电压的差别将进一步导致设备暂态响应的差别，需要在计算等值参数时加以额外考虑。第3.2.2节给出了与之相关的一个例子。
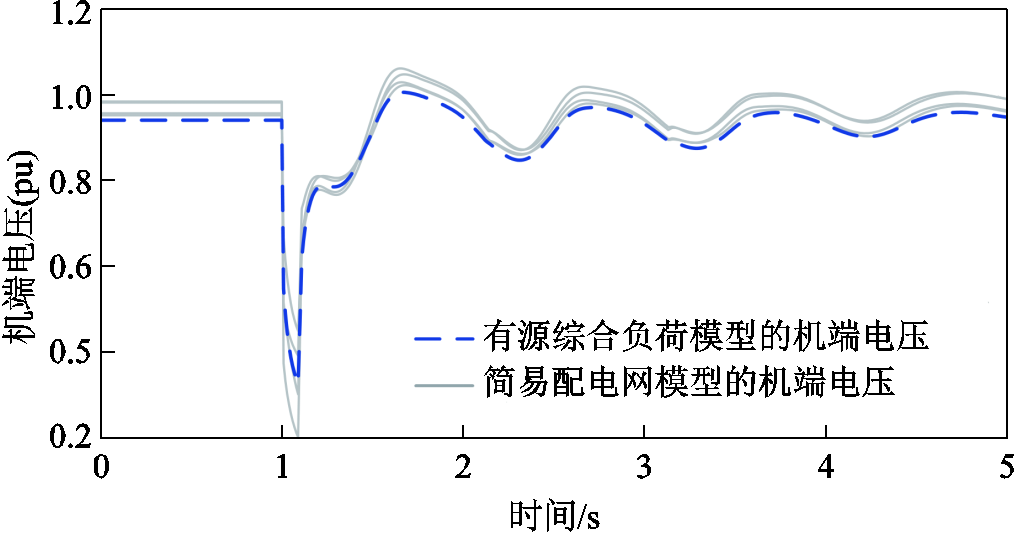
图7 等值前后的新能源机端电压对比
Fig.7 Comparison of renewable terminal voltage of real RESs and the equivalent RES
2）馈线电流特点
在实际配电网中，分布式新能源的输出电流将经过一段相对较长的配电线路，被不同位置的负荷分别消纳（或者反送至主网）。特别是在电压跌落后的恢复过程中，分布式新能源无功输出增加，而负荷消耗的功率减小，分布式新能源电流的流通路径更长。
在有源综合负荷模型中，分布式新能源与负荷连接在同一个节点，大部分功率被负荷就地消纳，没有在线路上的传输过程。这导致模型的暂态网损大幅降低，在主网侧体现为有源综合负荷模型的无功消耗偏小，需要在配置模型参数时加以额外考虑。
3）兼容性特点
在有源综合负荷模型结构中，不含新能源的部分与目前工程计算中的SLM模型完全相同。在优化现有模型或重新建模时，只要获取了新增设备的信息，就可以直接建立新的模型，不需要重新计算原有设备的等值参数。
但另一方面，为实现上述兼容性目标，等值新能源参数不仅需要刻画新能源设备本体的聚合特性，还需要体现出新能源改变配电网电压和电流所引入的新特性（机端电压、馈线电流等）。这给模型参数的计算提出了更高要求。
目前电力企业所使用的PSASP等工程用仿真平台中有近10种新能源模型，每个新能源模型有十余种控制模式和上百个参数。完全推导出一套适用于所有新能源设备的等值计算公式是不现实的。
本文结合机理分析和工程经验，归纳出与大电网暂态特性关系相对密切的参数，见附表1。在此基础上，提出了一般性的、相对通用的建模方法。即使新能源的模型结构或控制策略发生了变化，也可以使用相同的方法、针对新的控制策略加以等值。
所提等值方法的总体思路是叠加原理，即“等值新能源的特性等于所有实际新能源的特性之和”。叠加原理只适用于线性系统，而配电网中的大量非线性特性不能直接相加。为此，将所有的参数分为四个类型，使用不同思路加以修正。
3.2.1 线性独立参数计算
线性独立参数是指在新能源聚合等值过程中可以直接叠加的等值参数。这些参数与其他参数间不存在耦合关系，它们的等值算法为直接相加或加权平均。该方法在经典的负荷建模领域也有应用[18]。
对于含n个A类新能源的配电网，其等值A类新能源的容量为
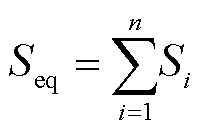（5）
式中，下标eq表示等值参数；Si为第i个新能源的容量。
按照相同的计算思路，式（1）中新能源低电压穿越控制参数KP2的等值算法为
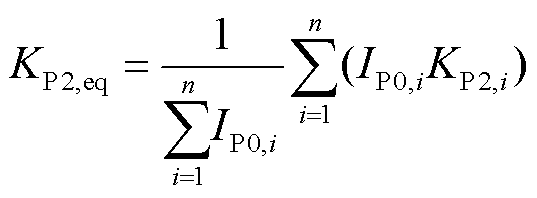（6）
参数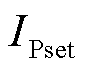
的等值算法为
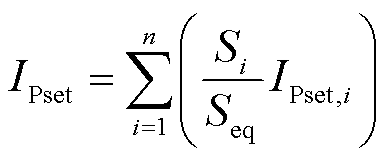（7）
3.2.2 线性耦合参数计算
在新能源输入-输出电气量间建立起线性关系的参数，称为线性耦合参数。例如，式（2）中的KQ1建立起了输入量Vt和输出量IQLV间的线性耦合关系，它是线性耦合参数。
与线性耦合参数相关的电气量一般具备非线性特性，因而不能像线性独立参数一样直接使用叠加定理。此时，可以针对主要非线性特性，使用弱非线性变量替换强非线性变量，然后用叠加定理近似等值。
例如，与线性耦合参数KQ1相关的状态Vt是强非线性变量。暂态过程中，每个新能源机端电压Vt,i都不同。即使配电网中所有新能源的KQ1,i都采用同一个数值，它们的等值KQ1,eq也不是所有参数的加权平均。为此，使用弱非线性变量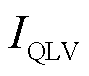
代替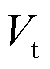
。
针对变量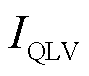，等值的近似要求为
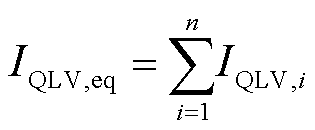（8）
而低电压穿越期间新能源机端电压与电流的关系可近似表示为
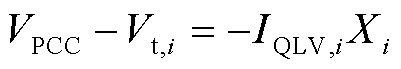（9）
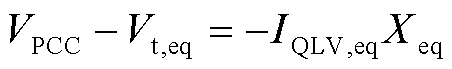（10）
式中，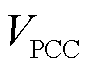
为公共连接点（Point of Common Coupling, PCC）电压；
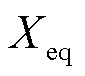为等值新能源机端到PCC间的总电抗；Xi为第i个新能源机端到PCC点间的线路阻抗。
借助式（8）～式（10），可以使用关于新能源电流的函数来表示其机端电压。在此基础上，将式（2）的新能源的电流控制特性代入式（8）～式（10），得到
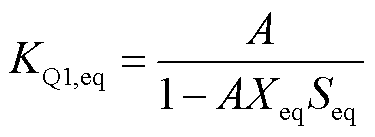（11）
其中
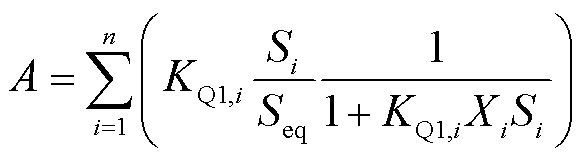（12）
式（11）、式（12）实现了线性耦合参数的等值计算。
3.2.3 非线性耦合参数计算
在新能源输入-输出电气量间建立起非线性关系的参数，称为非线性耦合参数。即使消去了非线性电气量，这些参数所建立的非线性关系也不能直接叠加。
例如，实际的新能源既可能是式（1）、式（2）所描述的指定电流控制模式，也可能是式（3）、式（4）所描述的指定功率控制模式。但在等值模型中，为了降低模型复杂度，一般只使用1个指定电流控制的新能源，代替所有的实际新能源。此时，采用式（3）、式（4）指定功率控制的新能源特性都需要用式（1）、式（2）重新刻画，这使得式（3）中的参数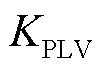
成为非线性耦合参数。
考虑到
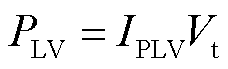（13）
式（3）所表示的特性可转换为类似指定电流控制的形式
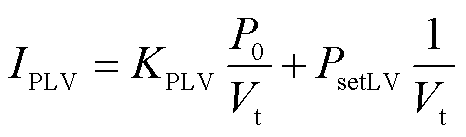（14）
式中，KPLV建立了非线性输入-输出关系（非线性Vt-IPLV关系），不能使用叠加原理来等值。
根据电压稳定分析的原则，当负荷母线的电压在0.8(pu)附近时，是大电网电压稳定的临界状态[29]。考虑到工程应用中对模型“临界运行方式”的要求，当Vt=0.8(pu)时，可以近似刻画大电网在临界状态的运行特性。因而，本文将这一数值代入式（14），使非线性耦合参数KPLV近似转换为线性耦合参数，再借助式（11）、式（12）计算其等值结果。
3.2.4 经验参数计算
当建模工作受工程应用限制，无法使用准确的数学模型时，可以使用经验参数来近似表征某些运行特性。
例如，工程上使用新能源单机模型代替多个新能源的聚合运行特性。当新能源退出低电压穿越、进入功率爬坡状态时，如果多个出力不同的新能源均采用固定斜率的爬坡特性，那么它们的聚合爬坡特性会变为多段斜率不同的折线，如图8所示。此外，还存在爬坡过程中按一阶渐进特性恢复有功功率的新能源（PSASP仿真平台中称为“惯性恢复”）。这一恢复过程的传递函数为
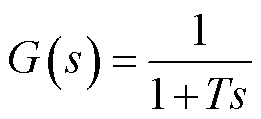（15）
式中，T为时间常数；s为拉普拉斯算子。
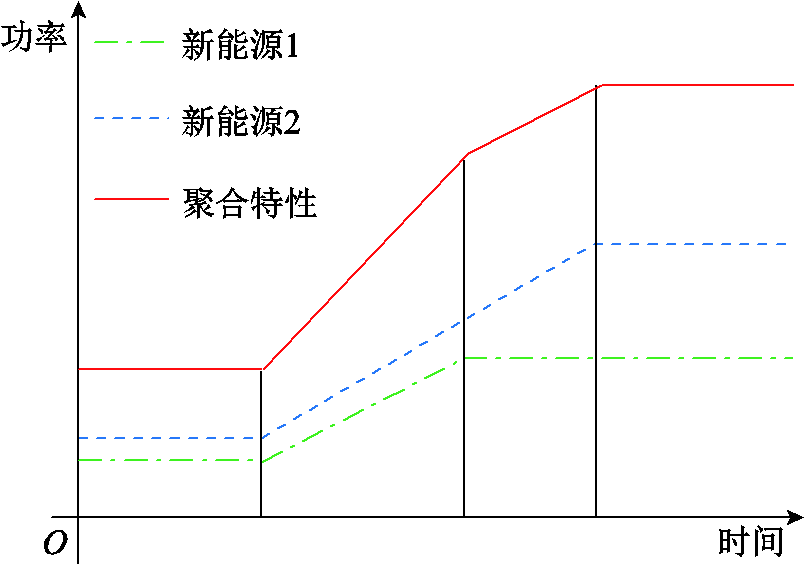
图8 新能源穿越后爬坡特性聚合
Fig.8 Aggregation of renewable post-LVRT ramping
多个这类新能源接入后，总功率的恢复特性需要用高阶的传递函数来刻画。现有工程计算平台的新能源单机模型没有变斜率或高阶渐进恢复模式，不能准确刻画上述特性。在目前的有源综合负荷模型构建工作中，使用折中的计算方法来近似模拟聚合爬坡特性，实验证明可以得到较好效果。例如，对一阶渐进特性T的等值时间常数计算方法为
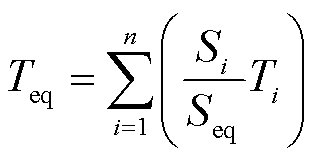（16）
与之相类似，B类新能源的等值一般也采用经验参数。
3.2.5 网络结构补偿
第3.2.1节～3.2.4节在考虑新能源本体特性的基础上，给出了计算等值参数的基本方法。然而在构建综合负荷模型的过程中，配电网的结构发生了变化（由图4变为图6）。此时，新能源与网络、负荷间的相互作用过程也发生了变化（见3.1.2节中的机端电压特点和馈线电流特点）。
为保证模型整体的兼容性，不含新能源部分的负荷模型计算方法与常规SLM模型完全一致。因而，发生变化的源网荷相互作用需要体现在等值新能源参数中。为此对新能源参数做的修正称为网络结构补偿。其中，与机端电压Vt相关的补偿已经体现在式（11）、式（12）等计算过程中，而与馈线电流相关的补偿还没有加以考虑。为此，可通过调整新能源穿越期间的电流控制参数KQ1,eq，减少无功电流值，补偿等值过程导致的网损差异。对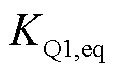
的补偿量B的计算方法为
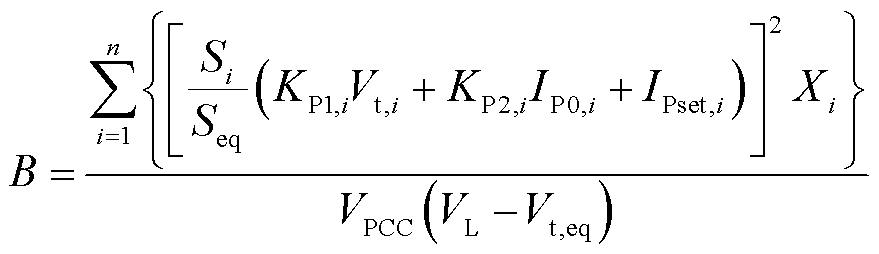（17）
注意到式中的Vt,i、VPCC、Vt,eq都不是常数，会在暂态期间时刻发生变化。本文基于在S省数百个配电网中的仿真经验，给出它们的典型值分别为0.5、0.35、0.45。
将式（17）的网络结构补偿量叠加至式（11）的等值参数的计算过程中，得到等值参数KQ1,eq为
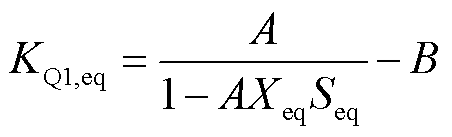（18）
整体而言，在过去SLM建模参数计算流程的基础上，增加本节的新能源参数计算过程，可得到适用于工程应用的大电网仿真有源综合负荷模型。完整的参数计算流程如图9所示。
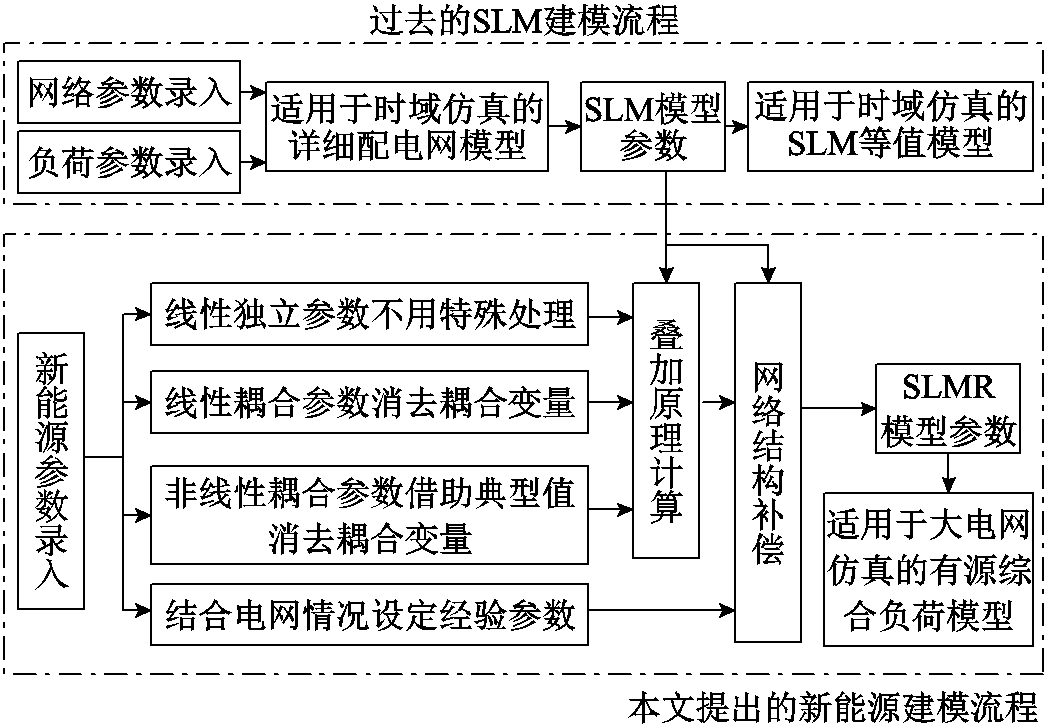
图9 有源综合负荷模型构建流程
Fig.9 Workflow to establish active synthesis load model
第3节所述的建模方法已初步用于某高比例新能源省份（S省）的大电网工程计算。本节将简要介绍其应用过程，展示应用效果，并对未来的工作做出展望。
本节在图10所示的测试系统中模拟高比例分布式新能源接入的局部电网场景，开展仿真测试。图中的绿色母线均为220 kV母线。
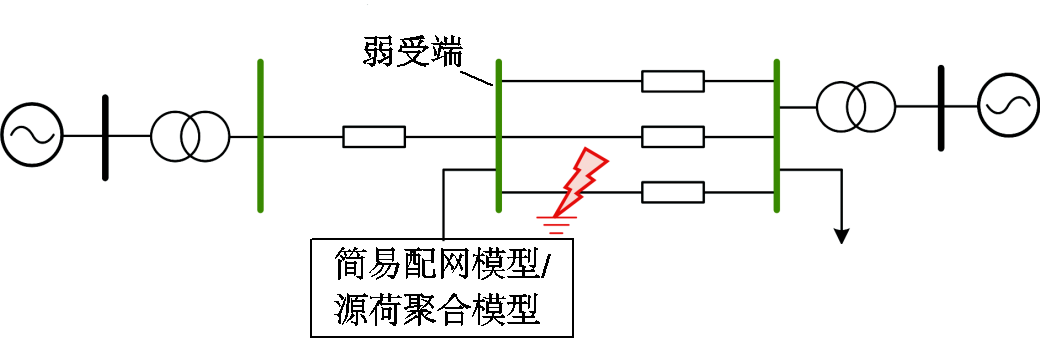
图10 局部电网仿真测试系统
Fig.10 Test system for local power grid
在强电网下，故障消失后电力系统会很快恢复到稳定。电力系统的暂态特性主要受同步电源主导，基本不受分布式新能源影响，不易验证等值方法的有效性。因而，本小节通过增加线路阻抗构造出了弱受端电网场景，在图10中的弱受端母线上接入一个简易配电网模型（图4中的模型）。
所使用的配电网模型是S省的一个实际配电网，其中分布式新能源接入比例较高、暂态特性受分布式新能源的影响较大，可以更好地考验本文所提方法的有效性。配电网中有功总负荷66.02 MW，无功总负荷14.5 Mvar，新能源装机及出力情况见表2。
表2 配电网新能源装机容量及出力
Tab.2 Renewables capacity in the distribution grid
电源类型A类新能源B类新能源双馈风机 装机容量/(MV·A)48.030.099.0 实际出力/MW22.625.246.4
设置一回220 kV输电线路短路接地故障后被切除，计算配电网变压器220 kV侧电压波形及下网总功率，然后将简易配电网模型替换为有源综合负荷模型，在同样故障下计算电压波形及下网总功率。
故障后简易配电网模型与有源综合负荷模型的有功功率特性对比如图11所示（功率下网方向为正），无功功率特性对比如图12所示。220 kV母线电压特性对比如图13所示。所使用的有源综合负荷模型较好地刻画了配电网的暂态特性。
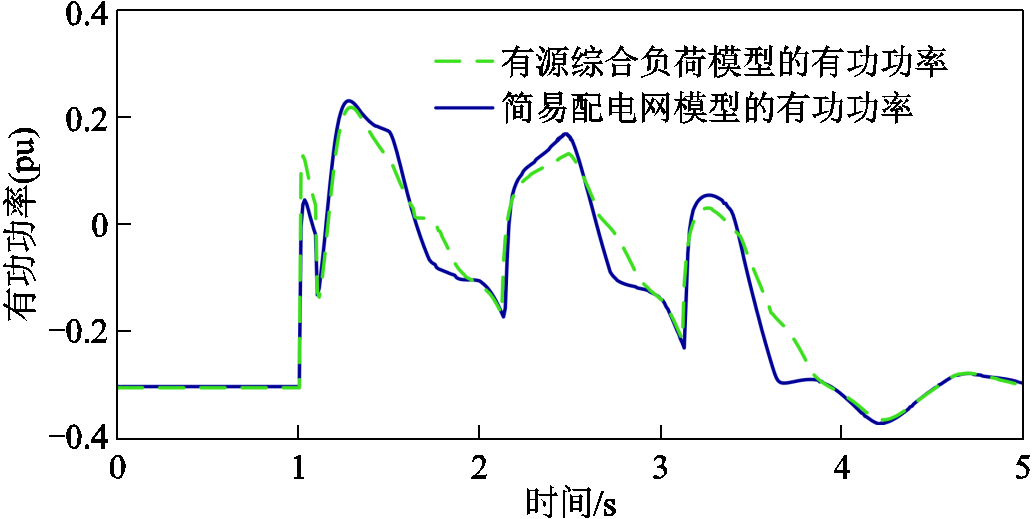
图11 有功功率特性对比
Fig.11 Comparison of active power
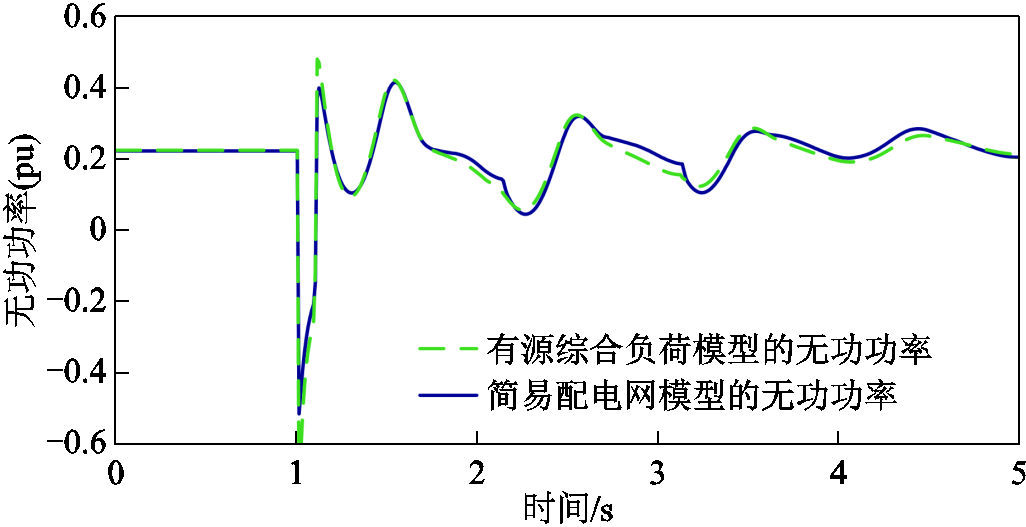
图12 无功功率特性对比
Fig.12 Comparison of reactive power
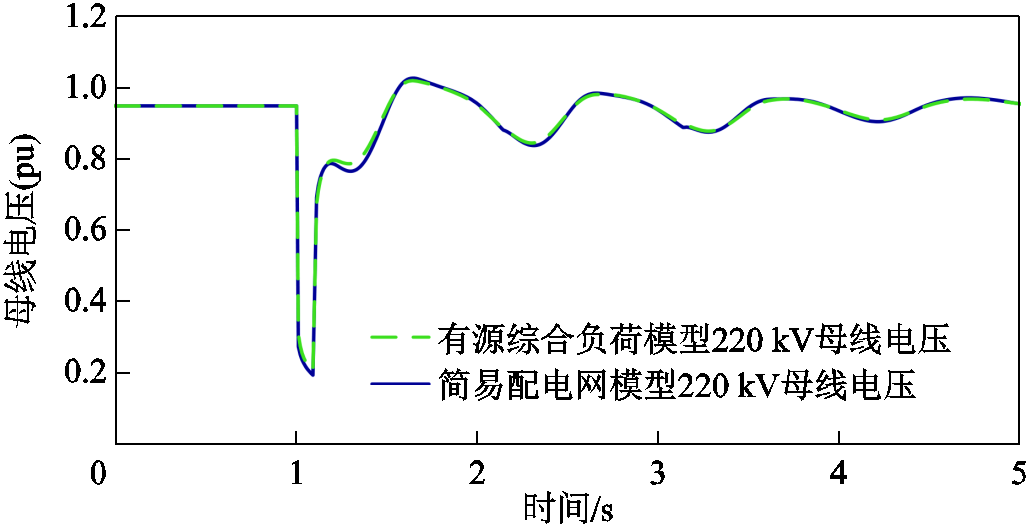
图13 电压特性对比
Fig.13 Comparison of voltage
注意到图11中的有源综合负荷模型仅刻画了配电网有功波动趋势，其响应特性并未与实际特性完全吻合。但这一等值精度已经可以满足工程应用要求，相关分析见4.2节。过度追求局部电网的精度可能导致模型无法满足其他方面的要求。
S省电网的分布式新能源渗透率位居全国前列，常规综合负荷模型不能准确反映其暂态特性。在过去的大电网分析工作中，一直使用含新能源的简易配电网模型。目前的大电网模型节点数已经接近仿真软件能力极限（超过9万节点），且仿真计算耗时长、模型更新的工作量大，亟须使用含分布式新能源的综合负荷模型，克服大电网分析的仿真计算瓶颈。
使用本文提出的有源综合负荷模型代替简易配电网模型后，大电网仿真模型的总节点数缩减到原先的约22%。在系统扩建和运行方式改变时，调整仿真模型的工作量更小。
使用等值模型后，大电网稳定分析的结论变化不大，这表明有源综合负荷模型可以代替实际简易配电网模型，支撑高比例分布式新能源系统的仿真分析。
4.2.1 临界运行方式校验
本文所提的等值建模方法主要用于大型电力系统的机电暂态仿真分析。在这种分析工作中，一般重点关注关键断面的最大输送能力、某区域的最小火电开机量等。在本例中，选择了某年丰水期、大负荷、新能源大发的典型运行场景，调整了四个不同的运行方式。以S省和外部的输电通道为关键断面，通过改变省内的开机数量，计算出符合“N -1”要求的S省最大受电能力，并比较等值模型、详细模型不同运行方式下的计算结论极限受电功率，见表3。仿真结果表明，在大部分的运行方式下，等值模型与详细模型的受电能力计算几乎没有误差（误差小于1个小机组的容量）。仅运行方式3存在1.8%的误差。
表3 不同运行方式下的极限受电功率
Tab.3 Maximum infeed power in different scenarios （单位：MW）
模型方式1方式2方式3方式4 详细模型15 00016 15016 60017 650 等值模型15 00016 15016 30017 650
当受电功率大于表3中的数值时，系统将在“N -1”故障后失稳。因而，表3给出的是临界稳定运行方式。比较临界稳定或失稳时的大电网电压特性如图14～图17所示。从这些波形图中可以直观地判断所提模型的等值效果。结果表明，所提模型在大多数场景下都能较准确地反映大电网暂态特性。
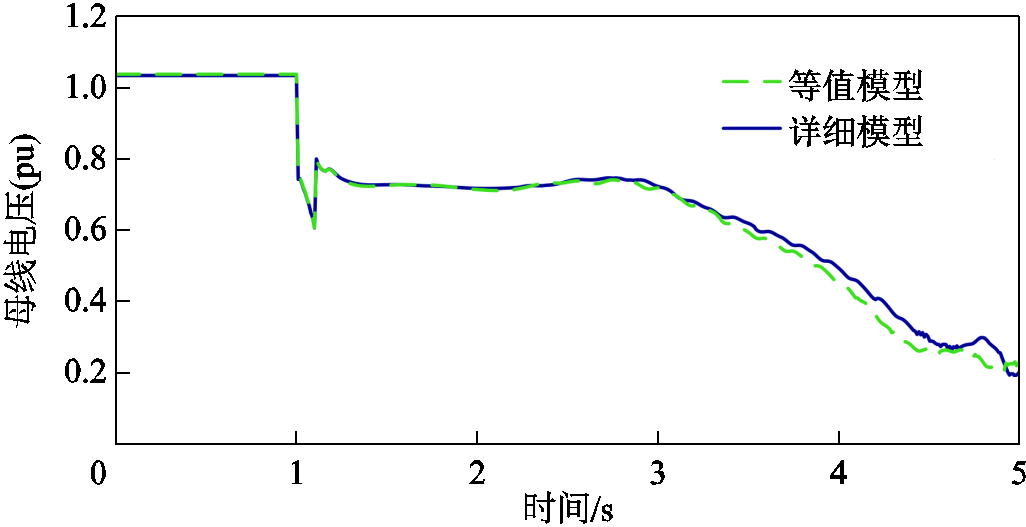
图14 方式1受电15 500 MW时的电压特性
Fig.14 Voltage response in scenario 1 with 15 500 MW power infeed
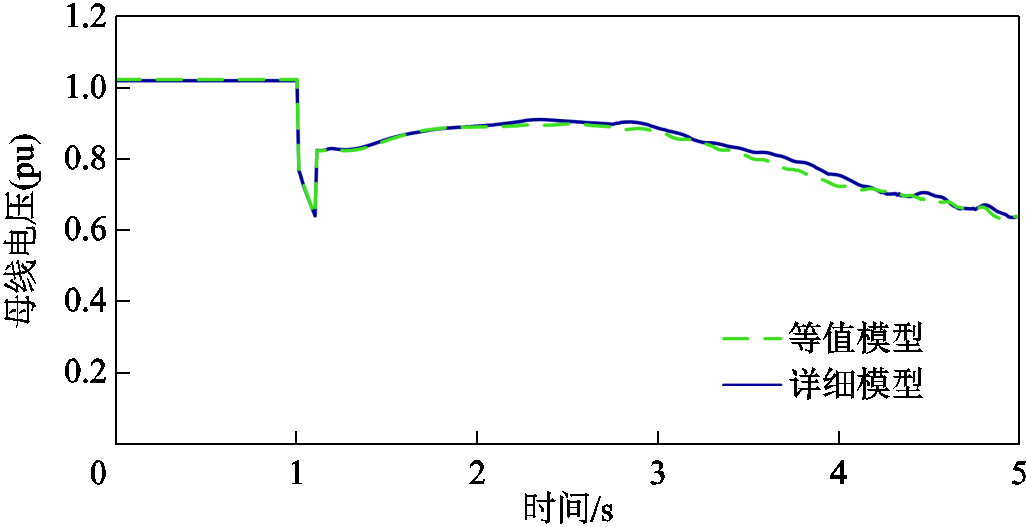
图15 方式2受电16 450 MW时的电压特性
Fig.15 Voltage response in scenario 2 with 16 450 MW power infeed
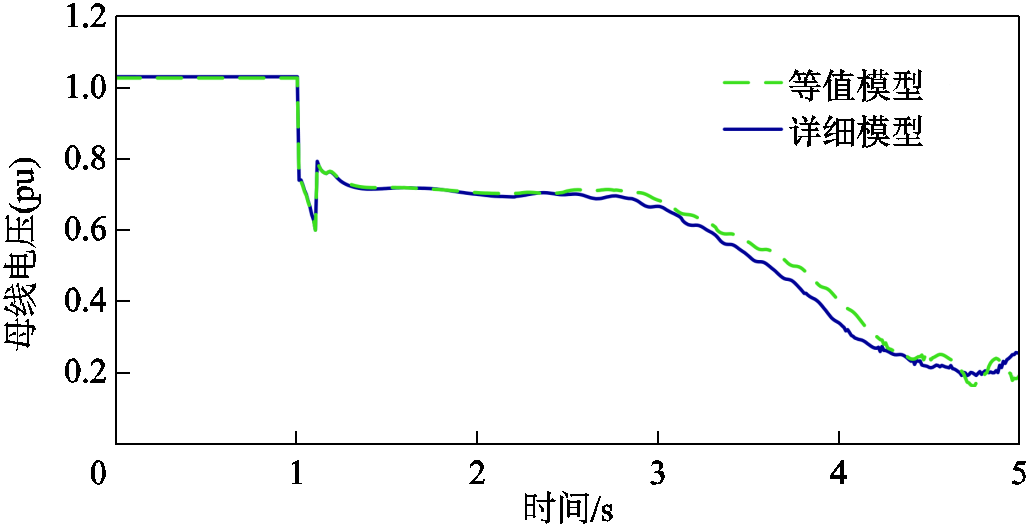
图16 方式3受电16 600 MW时的电压特性
Fig.16 Voltage response in scenario 3 with 16 600 MW power infeed
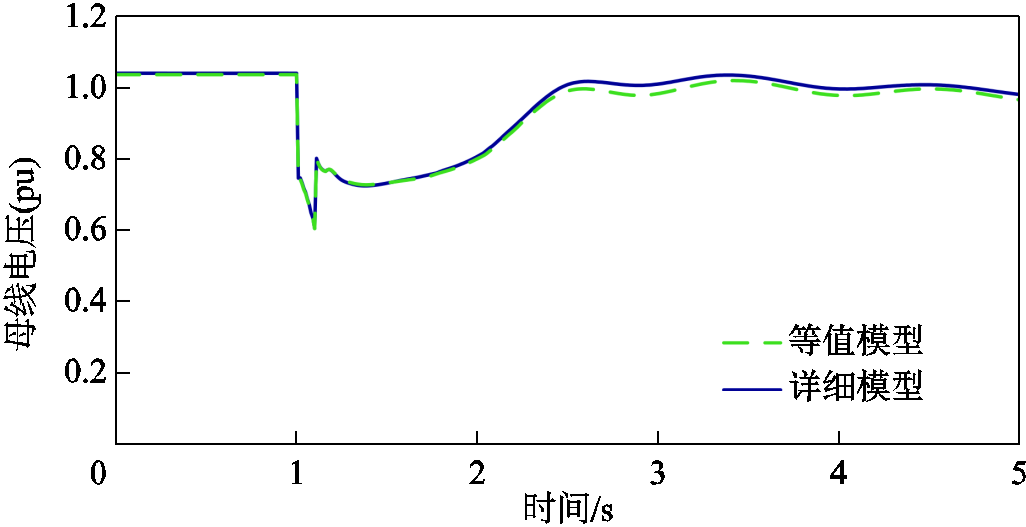
图17 方式4受电17 650 MW时的电压特性
Fig.17 Voltage response in scenario 4 with 17 650 MW power infeed
4.2.2 关键暂态特性校验
在大电网分析中，不仅关注极限受电能力等临界量化指标，也关注电网较弱时的暂态特性。
在某场景下，故障后电网电压恢复较慢，是需要仔细研究的运行方式。对比详细模型和等值模型的母线电压特性及S省与外省间的联络线功率波动特性，如图18～图20所示。出于大电网数据安全考虑，图中没有给出波形的横纵坐标数据，但从波形的形态判断，有源综合负荷模型起到了较好的等值效果。
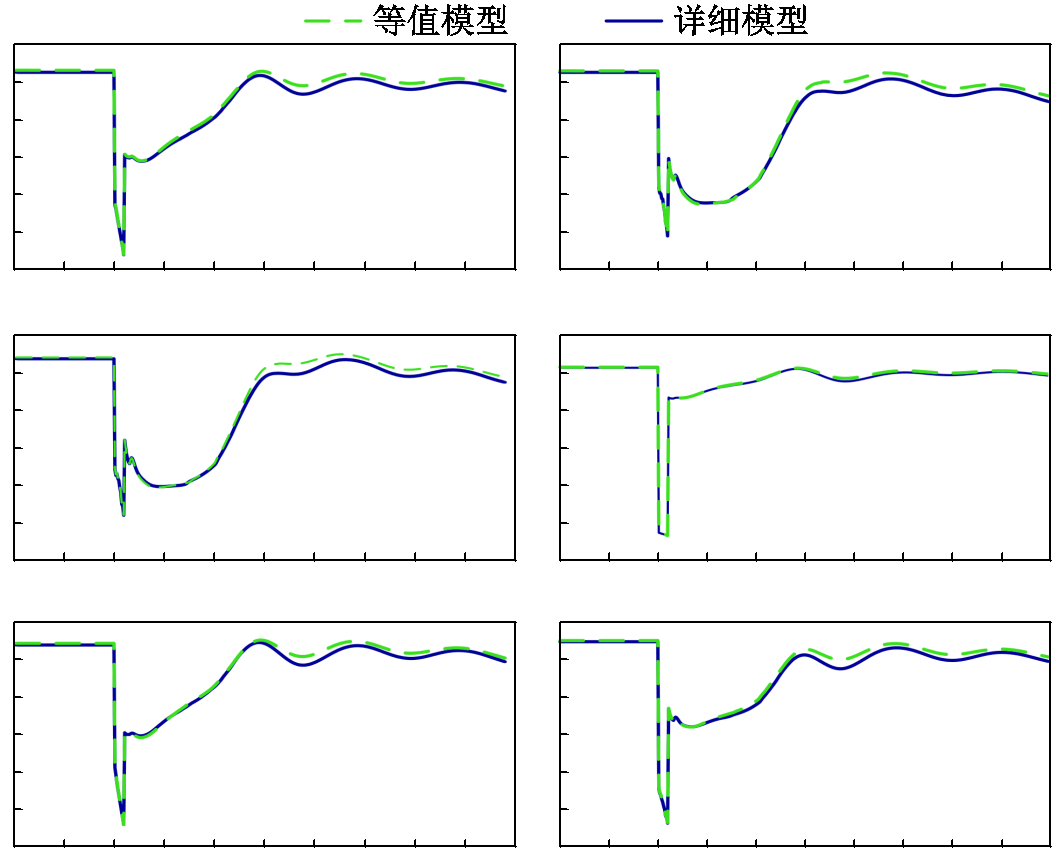
图18 节点电压的对比情况
Fig.18 Comparison of node voltage
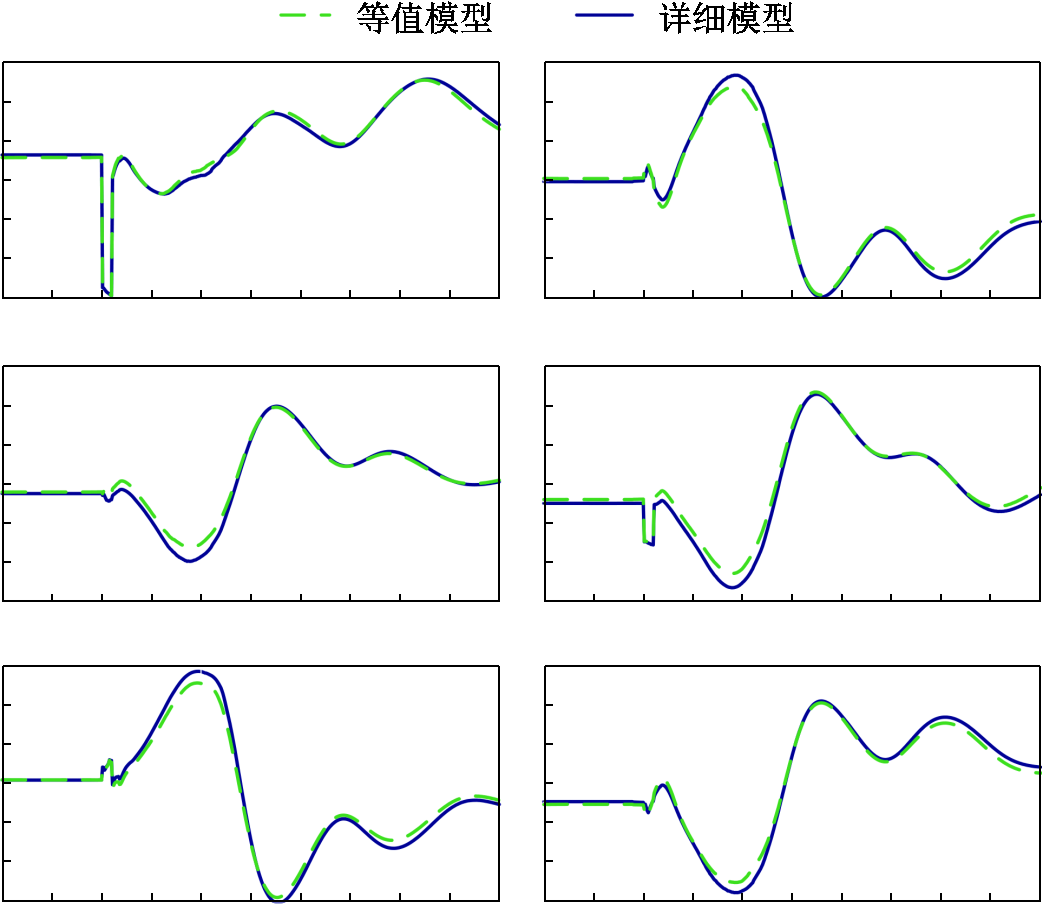
图19 省间联络线有功波动对比情况
Fig.19 Comparison of active power transmission of inter-province lines
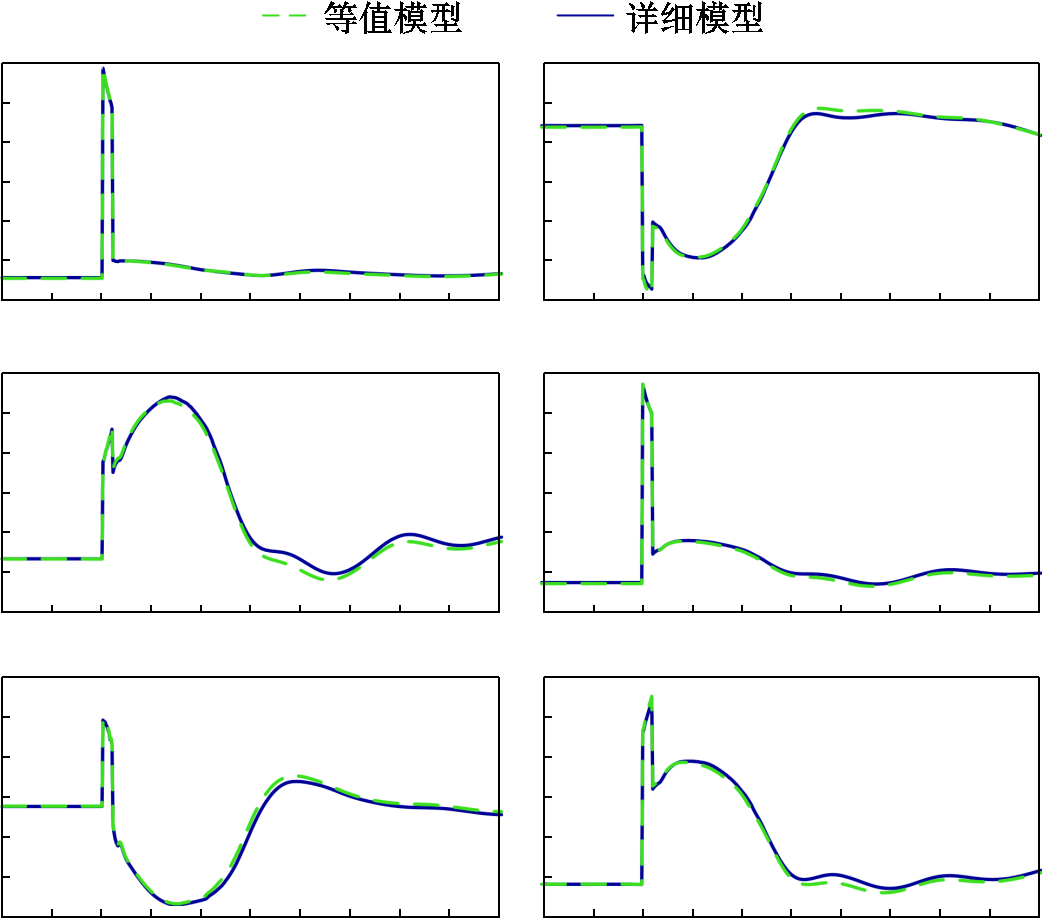
图20 省间联络线无功波动对比情况
Fig.20 Comparison of reactive power transmission of inter-province lines
本文所提的等值建模方法虽然在S省已有了初步应用，但在推广过程中，还应尽量降低其应用成本。为此，在两方面做了初步探索，简要结论如下。
4.3.1 提升自动化水平
S省有数百个220 kV及以下电压等级的高比例分布式新能源配电网，每个配电网的简易模型又含有数十个节点、每个新能源有数十个关键参数。在应用有源综合负荷模型时，如果一一计算配电网的等值模型，将耗费大量人力成本。当电网扩建或运行方式改变时，还需要重新计算等值参数，这在实际工程中是难以接受的。
为此，开发了基于离线数据的参数自动计算软件，并建立该软件和常规负荷参数采集维护系统、大电网机电暂态仿真平台间的数据接口，可以基于现有数据自动生成等值模型。在后续的工作中，计划在线数据与自动计算软件相结合，实现有源综合负荷模型的全自动在线生成。
4.3.2 建立典型参数库
在全国范围的大电网建模中，详细调查每个配电网的新能源特性并建立其等值模型是不现实的。在后续工作中，可以借助小范围应用的数据基础，归纳出不同类型及不同运行方式下的配电网特性，形成几套具有代表性的典型参数，构建有源综合负荷模型参数库。在建立或更新大电网分析模型时，可直接调用参数库中的典型数据，在一定程度上代替成本较高的负荷普查与详查工作。
论文针对含分布式新能源的大电网建模与仿真分析需要，提出了“有源综合负荷模型”建模思路，探讨了实际工程应用对有源综合负荷模型的具体要求，设计了模型结构并提出了参数计算方法，介绍了该建模方法在S省的初步应用情况。具体结论如下：
1）从工程应用角度，有源综合负荷模型宜综合考虑四个方面的要求：模型兼容、应用成本、可解释性和等值精度。其中，等值精度宜从大电网临界运行方式、大电网关键暂态特性等方面衡量。
2）在中国的工程实际中，分布式新能源等值涉及约30个关键机电暂态参数。等值计算时可将这些参数分为四个类型，按不同思路加以处理。这四类参数分别是：线性独立参数、线性耦合参数，非线性耦合参数和经验参数。
3）含分布式新能源的配电网在机端电压、馈线电流等方面具备新的特点，这些特点也体现在了有源综合负荷模型中，在建模时需要额外考虑。
附 录
本文所提到实际工程计算中的分布式新能源参数，是指PSASP计算平台上的分布式新能源模型参数。其中相对重要的部分参数名称列举见附表1。参数的含义见PSASP软件平台说明书《PSASP动态元件库用户手册》。
在不同的电力系统中，受运行方式和主导失稳形态的影响，相关参数的重要性可能会发生变化，这将在后续工作中进一步研究。本文的仿真算例是考虑其中部分参数后，在S省电网的仿真结果。
附表1 分布式新能源模型的关键参数
App.Tab.1 Key parameters of DRE model
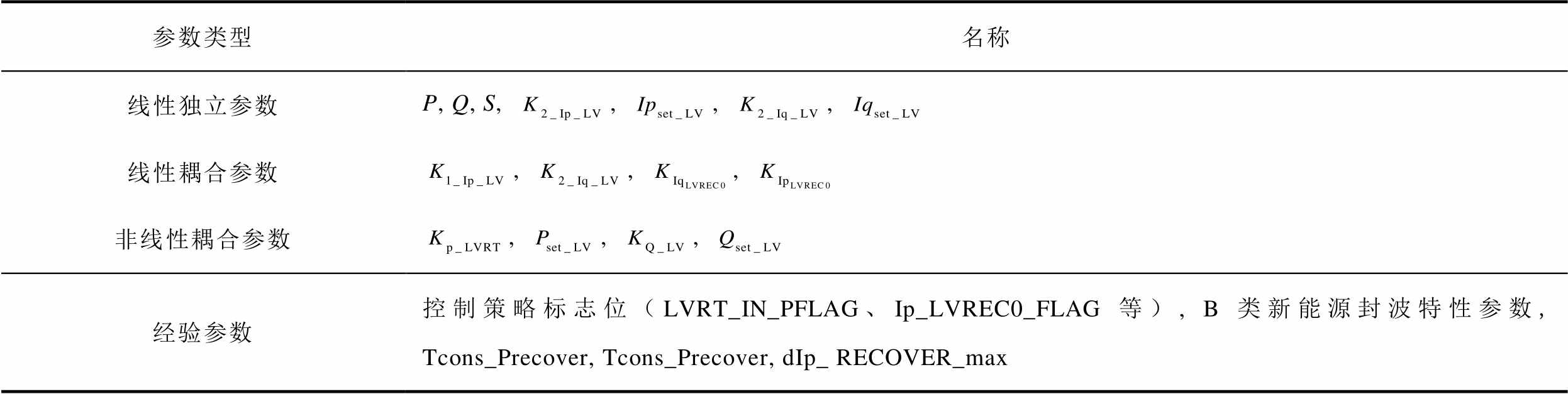
参数类型名称 线性独立参数P, Q, S, , , , 线性耦合参数, , , 非线性耦合参数, , , 经验参数控制策略标志位（LVRT_IN_PFLAG、Ip_LVREC0_FLAG等）, B类新能源封波特性参数, Tcons_Precover, Tcons_Precover, dIp_ RECOVER_max
参考文献
[1] 国家能源局. 2022年光伏发电建设运行情况[EB/ OL]. [2023-02-07]. http://www.nea.gov.cn/2023-02/17/ c_1310698128.htm.
[2] 林雨眠, 熊厚博, 张笑演, 等. 计及新能源机会约束与虚拟储能的电-热系统分布式多目标优化调度[J/OL]. 电工技术学报, 2023: 1-19. https://dgjsxb. ces-transaction.com/CN/abstract/abstract8882.shtml.
Lin Yumian, Xiong Houbo, Zhang Xiaoyan et al. Distributed multi-objective optimal scheduling of integrated electric-heat system considering chance constraint of new energy and virtual storage[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-19. https://dgjsxb.ces-transaction.com/CN/abstract/ abstract8882.shtml.
[3] Joint NERC, Texas RE Staff. Odessa Disturbance Report, Texas Events: May 9, 2021, and June 26, 2021[R]. USA: North American Electric Reliability Corporation, 2021.
[4] Joint NERC, Texas RE Staff. Odessa Disturbance Report, Texas Events: June 4, 2022[R]. USA: North American Electric Reliability Corporation, 2022.
[5] Australian Energy Market Operator. Black System South Australia 28 September 2016[R]. Australia: Australian Energy Market Operator Limited, 2017.
[6] 张天策, 李庚银, 王剑晓, 等. 基于可行域投影理论的新能源电力系统协同运行方法[J]. 电工技术学报, 2024, 39(9): 2784-2796.
Zhang Tiance, Li Gengyin, Wang Jianxiao et al. Coordinated operation method of renewable energy power systems based on feasible region projection theory[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2784-2796.
[7] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[8] 孙华东, 李佳豪, 李文锋, 等. 大规模电力系统仿真用新能源场站模型结构及建模方法研究(二): 机电暂态模型[J]. 中国电机工程学报, 2023, 43(6): 2190-2202.
Sun Huadong, Li Jiahao, Li Wenfeng, et al. Research on model structures and modeling methods of renewable energy station for large-scale power system simulation(Ⅱ): electromechanical transient model[J]. Proceedings of the CSEE, 2023, 43(6): 2190-2202.
[9] Li Jiahao, Sun Huadong, Li Wenfeng, et al. Construction and equivalence of single-machine model of renewable energy for large-scale power system simulation[J/OL]. CSEE Journal of Power and Energy Systems, 2023. doi:10.17775/CSEEJPES.2022. 06490.
[10] 屈星, 李欣然, 宋军英, 等. 考虑配电网调压的综合负荷模型[J]. 电工技术学报, 2018, 33(4): 759-770.
Qu Xing, Li Xinran, Song Junying, et al. Composite load model considering voltage regulation of distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 759-770.
[11] Arif A, Wang Zhaoyu, Wang Jianhui, et al. Load modeling—a review[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5986-5999.
[12] 徐振华, 李欣然, 宋军英, 等. 考虑双馈风电机的配电网广义综合负荷建模[J]. 电工技术学报, 2013, 28(7): 234-242.
Xu Zhenhua, Li Xinran, Song Junying, et al. Load modeling considering doubly-fed induction generator (DFIG) integrated into distribution network[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 234-242.
[13] Chaspierre G, Denis G, Panciatici P, et al. An active distribution network equivalent derived from large-disturbance simulations with uncertainty[J]. IEEE Transactions on Smart Grid, 2020, 11(6): 4749-4759.
[14] 陈忠玉, 徐晋, 汪可友, 等. 计及跟随型和支撑型分布式光伏的广义综合负荷模型及两阶段参数聚合等效方法[J]. 电力自动化设备, 2023, 43(3): 86-93.
Chen Zhongyu, Xu Jin, Wang Keyou, et al. Generalized composite load model and two-stage parameter aggregation and equivalent method considering grid-following and grid-forming distributedphotovoltaic[J]. Electric Power Automation Equipment, 2023, 43(3): 86-93.
[15] Mitrentsis G, Lens H. Data-driven dynamic models of active distribution networks using unsupervised learning techniques on field measurements[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 2952-2965.
[16] Zheng Chao, Wang Shaorong, Liu Yilu, et al. A novel equivalent model of active distribution networks based on LSTM[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(9): 2611-2624.
[17] 王琦, 张文朝, 汤涌, 等. 统计综合法负荷建模中的调查方法及应用[J]. 电网技术, 2010, 34(2): 104-108.
Wang Qi, Zhang Wenchao, Tang Yong, et al. A new load survey method and its application in component based load modeling[J]. Power System Technology, 2010, 34(2): 104-108.
[18] 汤涌. 电力负荷的数学模型与建模技术[M]. 北京: 科学出版社, 2012.
[19] 鞠平, 马大强. 电力系统负荷建模[M]. 2版. 北京: 中国电力出版社, 2008.
[20] 汤涌, 赵兵, 张文朝, 等. 综合负荷模型参数的深化研究及适应性分析[J]. 电网技术, 2010, 34(2): 57-63.
Tang Yong, Zhao Bing, Zhang Wenchao, et al. In-depth study and adaptability analysis on synthesis load models and parameters[J]. Power System Technology, 2010, 34(2): 57-63.
[21] 赵兵, 汤涌, 张文朝, 等. 基于故障拟合法的综合负荷模型验证与校核[J]. 电网技术, 2010, 34(1): 45-50.
Zhao Bing, Tang Yong, Zhang Wenchao, et al. Validation of synthesis load model and its parameter modification based on post-disturbance simulation method[J]. Power System Technology, 2010, 34(1): 45-50.
[22] Lan Tiankai, Sun Huadong, Wang Qi, et al. Synthesis load model with renewable energy sources for transient stability studies[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1647-1663.
[23] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分：陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[24] 国家质量监督检验检疫总局, 中国国家标准化管理委员会.光伏发电站接入电力系统技术规定: GB/T 19964—2012[S]. 北京: 中国标准出版社, 2013.
[25] 国家市场监督管理总局, 国家标准化管理委员会. 风能发电系统通用电气仿真模型: GB/T 36237—2023[S]. 北京: 中国标准出版社, 2013.
[26] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 分布式电源并网技术要求: GB/T 33593—2017[S]. 北京: 中国标准出版社, 2017.
[27] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 分布式电源并网运行控制规范: GB/T 33592—2017[S]. 北京: 中国标准出版社, 2017.
[28] 国家能源局. 风电机组低电压穿越建模及验证方法: NB/T 31053—2014[S]. 北京: 新华出版社, 2015.
[29] 国家市场监督管理总局, 国家标准化管理委员会. 电力系统电压稳定评价导则: GB/T 40615—2021[S]. 北京: 中国标准出版社, 2021.
Abstract Distributed renewable energy (DRE) is experiencing a rapid growth worldwide, and gradually becomes a significant factor that influences stability of bulk power systems. In the year 2022, the increasement of distributed photovoltaic in China has exceeded 51 GW, far exceeding the aggregate photovoltaic increasement. The installed capacity of DRE accounts for over 50% of the total renewable energy sources in several provinces, and peak DRE power output reaches 30% of the overall load power. Bulk power system incidents related to DRE have been reported in countries such as Australia and the United States. It is revealed that current bulk power system analyses inadequately consider the impact of DREs.
However, it is impossible to model every single DRE in bulk power system analysis, as they are with a very large quantity, and integrated in very low voltage level. Although aggregation methods are proposed for renewable energy sources, the methods mainly aim at aggregate renewables. DREs are generally mixed with power loads, and are unsuitable for the methods.
In the early stages of DRE development, they are simply considered as “negative power loads” in bulk power system analysis. This modeling approach is too simplistic for regions with high penetration. To resolve the problem, some power system operators utilize a simplified distribution grid model. However, such model consists too many nodes for bulk power systems, which can comprise hundreds of distribution grids.
To address the modeling challenges of DRE in bulk power system simulation and analysis, measurement-based, data-driven methods are widely utilized. The obtained models are known as generalized load models, microgrid equivalent models, etc., considering both DREs and loads. While the methods are widely seen in literatures, limited engineering application is reported. In large power systems, it is difficult to acquire sufficient transient response data for measurement-based modelling method. Besides, the methods hardly offer physical relations between the equivalent parameters and actual power components. Problems like multiple-solutions and overfitting also exist in the methods. These disadvantages hinder power system analysis.
In view of the above, this paper proposes an active synthesis load model, trying to resolve the DRE modelling problems in China’s practical engineering context. Structure design, parameter calculation, and practical application of the model is described in the paper. The proposed model is tested effective in the application. Conclusions of this paper are briefly drawn as follows:
(1) From the perspective of engineering applications, an equivalent DRE model should consider four aspects: model compatibility, application cost, explainability, and accuracy.
(2) In the practical engineering context in China, the equivalent of DRE involves approximately 30 key electromechanical transient parameters. When calculating equivalents, these parameters can be categorized into four types and treated with different methods. These four types of parameters are: linear independent parameters, linear coupled parameters, nonlinear coupled parameters, and empirical parameters.
(3) Compared to conventional distribution grids, the grids with DRE have important, new features, including but not limited to component terminal voltage and feeder current. Additional attention should be paid to these features when establishing the equivalent model.
Keywords: Large-scale power systems, distributed renewable energy, equivalent modelling, active synthesis load model, security and stability analysis
中图分类号：TM711
DOI: 10.19595/j.cnki.1000-6753.tces.231901
国家自然科学基金项目（52307152）和国家资助博士后研究人员计划（GZB20230688）资助。
收稿日期 2023-11-15
改稿日期 2024-01-10
兰天楷 男，1994年生，高级工程师，研究方向为电力系统电压稳定分析、分布式新能源等值建模。E-mail：lantiankai@epri.sgcc.com.cn
孙华东 男，1975年生，教授级高工，博士生导师，研究方向为电力系统稳定分析与控制。E-mail：sunhd@epri.sgcc.com.cn（通信作者）
（编辑 赫 蕾）