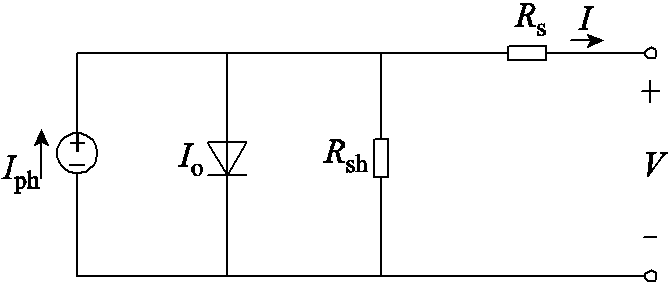
图1 光伏电池模型等效电路
Fig.1 Photovoltaic cell model equivalent circuit
摘要 为了提高光伏电池的参数辨识和输出特性计算的精度,该文提出基于单二极管模型的有效辐照度修正方法。通过研究影响光伏输出特性的环境因素,建立测量辐照度到有效辐照度的修正方程,包含常数修正、角度修正、季节修正和温度修正。首先使用解析方法求解参考条件下的光伏电池单二极管模型物理参数值,根据物理参数与辐照度、温度的转化方程,以I-V曲线的方均根误差(RMSE)为目标函数,拟合得到有效辐照度修正方程中各个参数;然后根据光伏组件实际运行条件,计算有效辐照度数值,将修正后的有效辐照度代入物理参数转化方程,进而得到光伏组件运行物理参数和输出特性;最后通过实测数据对所提出方法进行验证。结果表明,在不同天气条件(晴天、阴天)、不同辐照度区间和温度区间,与未修正结果相比,文中所提方法在I-V、P-V输出特性计算和最大功率估计方面的精度均得到提高。
关键词:单二极管模型 参数辨识 辐照度修正 有效辐照度
随着国家“双碳”目标的提出,我国的能源结构转型正在不断加速[1-4]。近年来,太阳能开发利用已成为全球能源转型的重要领域,光伏发电全面进入规模化发展阶段,呈现出良好的发展前景[5-8]。光伏电池输出特性有多种模型[9-10],其中单二极管模型(Single-Diode Model, SDM)[11-12]是使用最为广泛的光伏电池等效电路模型,它包含光生电流、反向饱和电流、二极管品质因子、串联电阻和并联电阻五个物理参数[13]。光伏电池的输出特性由物理参数决定,并且通过分析这些参数的变化也可以研究光伏电池发生故障的原因,因此光伏电池参数辨识及输出特性建模对研究光伏电池特性及功率预测具有重要意义。
光伏电池参数辨识和输出特性建模分两步完成:首先,在参考条件下求取模型物理参数值,参考条件可以为出厂时的标准测量条件(Standard Testing Condition, STC,1 000 W/m2和25℃)[14],也可为某实测条件[15];其次,根据模型参数对环境条件的依赖性,计算不同运行工况下的模型参数,实现输出特性估计与预测[16]。由于SDM中的物理参数不由制造商提供,也不能通过实验直接测量得到,因此文献中提出了各种不同方法辨识光伏组件中的物理参数。制造商提供的出厂数据通常只包含有限的光伏组件STC下的运行数据,如开路电压、短路电流、最大功率电流和电压,以及开路电压和短路电流下的温度系数(分别为βVoc和αIsc)。STC下的物理参数的求解方法一般有数值方法和解析方法。将STC下的电气数据代入单二极管电流-电压方程,得到了一组关于物理参数的方程组,数值方法采用牛顿拉夫逊法或迭代曲线法求解方程组[17];解析法[18]则求解参考条件下物理参数与出厂信息值之间的解析表达式,往往在保持精度的前提下进行一些近似、简化或假设。对光伏组件具体运行条件下参数辨识和输出特性估计时,需要利用参考条件下的模型参数,根据物理模型参数与环境条件的依赖关系,求解不同工况下的模型参数[19]。在众多环境因素中,辐照度是影响光伏组件物理参数和输出特性的最重要因素,物理参数与辐照度的依赖关系,直接影响光伏组件的参数辨识与输出特性评估精度。
目前工程中使用的辐照度测量传感器往往只记录传感器吸收的多波段辐照度总和,例如,最常用的硅基辐射传感器,具有结构简单、价格便宜的优点,主要响应波长在300~1 200 nm之间,并且在此区间内的光谱响应并不均匀,对红光和近红外光的响应明显高于蓝光和紫外光,这种有限和不均匀的光谱响应导致了宽带辐照度测量的光谱不匹配,使得测量的辐照度与光伏组件的吸收辐照度不一致[20]。针对辐照度传感器的修正研究,主要包括传感器温度补偿、太阳天顶角修正、太阳漫射水平辐照度修正和全球水平辐照度修正[20],目的是减小辐照度传感器入射辐照度与测量值之间的误差。文献[21]研究发现硅基传感器中短路电流随温度升高而升高,根据测量过程中的传感器温度变化,对辐照度测量值予以考虑和校正。然而光伏组件对太阳光的吸收,受到光伏组件地理位置、安装角度、云层对太阳光的吸收与散射等多因素影响,通过物理参数转化方程求解运行条件下光伏组件物理参数过程中,用辐照度直接测量值直接计算物理参数,会影响参数辨识和输出特性估计的精度,在前期研究中并未考虑。
根据影响光伏组件的辐照度测量的因素,本文提出了有效辐照度的概念,对测量辐照度进行修正,得到有效辐照度可以提高光伏电池参数辨识与输出特性建模精度。其中对辐照度的修正包括测量仪器自身误差导致的常数修正、光谱失配导致的角度修正、季节变化导致的最小天顶角修正和温度修正,建立了测量辐照度到有效辐照度的修正方程,通过保证收敛的粒子群算法(Guaranteed Convergence Particle Swarm Optimization, GCPSO)[22]以I-V曲线电流方均根误差(Root Mean Square Error,RMSE)最小为目标函数来对有效辐照度方程中各个参数进行拟合,然后再将有效辐照度代入转化方程当中来求解不同工况下SDM的参数,计算光伏组件的物理参数和输出特性,并在不同天气条件、不同辐照度区间和温度区间,将有效辐照度修正后的I-V、P-V输出特性和最大功率计算结果,与未修正结果进行了对比。
传统的太阳能电池模型等效电路如图1所示,

图1 光伏电池模型等效电路
Fig.1 Photovoltaic cell model equivalent circuit
等效电路的电流与电压关系表达式为
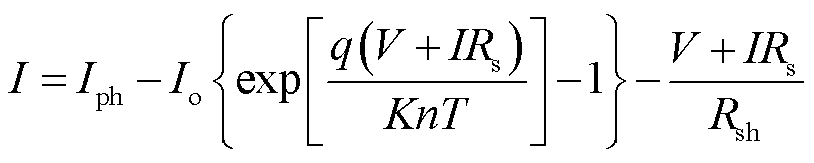 (1)
(1)
式中,V为负载两端电压,V;I为通过负载电流,A;Iph为光生电流,A;Io为二极管反向饱和电流,A;n为二极管品质因子;Rs为电池串联电阻,Ω;Rsh为电池并联电阻,Ω;T为电池的热力学温度,K;K为玻耳兹曼常数,J/K;q为电子电荷,C。
在参数拟合时,方程中的电流I无法通过初等函数处理得到显式的表达式,为此引入Lambert W函数得到解析的I-V方程,经简化后输出电流I的显式表达式为
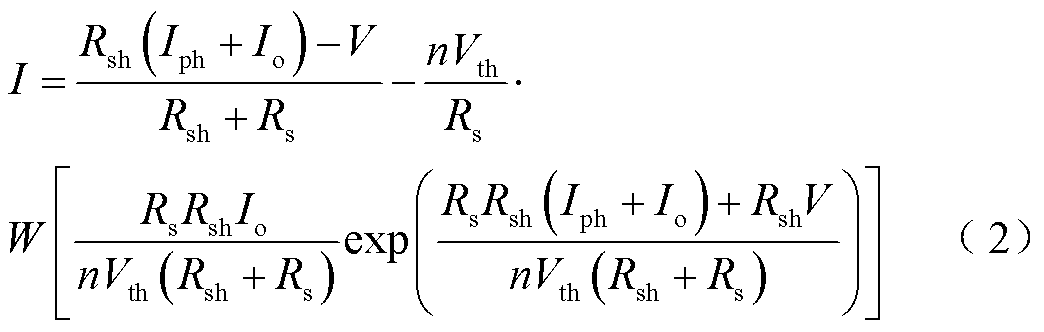
式中,W(·)为Lambert W函数;Vth为二极管热电压,即
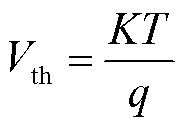 (3)
(3)
本文提出的基于有效辐照度修正的参数辨识方法首先需要求解参考条件下SDM的物理参数值,然后再通过转化方程计算运行条件下的物理参数值,进而拟合辐照度修正方程中的参数,最终得到有效辐照度修正方程,用于光伏组件输出特性计算。
求解STC下光伏电池物理参数的方法有解析法、数值法和寻优法,本文采用解析法进行求解[18,23]。方程式(1)中包含五个物理参数,因此需要STC下五个方程求解参考条件的参数。短路电流点(Isc,ref, 0)、开路电压点(0, Voc,ref)和最大功率点(Imp,ref, Vmp,ref)代入方程式(1)得到三个独立方程为
 (4)
(4)
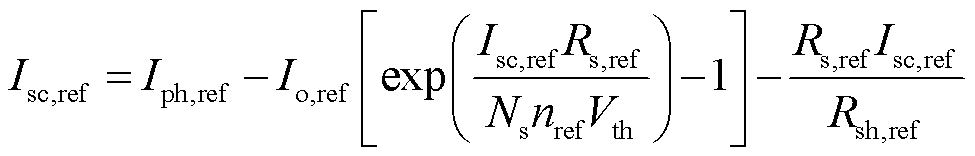 (5)
(5)
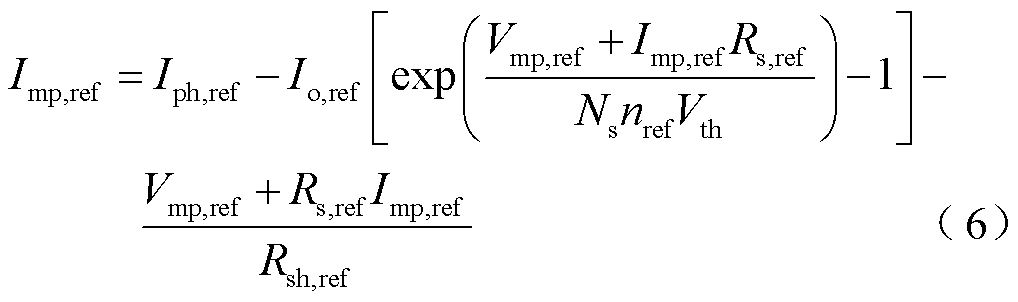
式中,Iph,ref、I0,ref、Rsh,ref、Rs,ref、nref各参数下角标ref代表在标准参考条件STC下的值;Voc,ref为STC下的开路电压参考,V;Isc,ref为STC下的短路电流值,A;Imp,ref为STC下的最大功率点电流参考值,A;Vmp,ref为STC下的最大功率点电压参考值,V;Ns为串联电池数。
最大功率点处导数dP/dV为零为第四个方程。
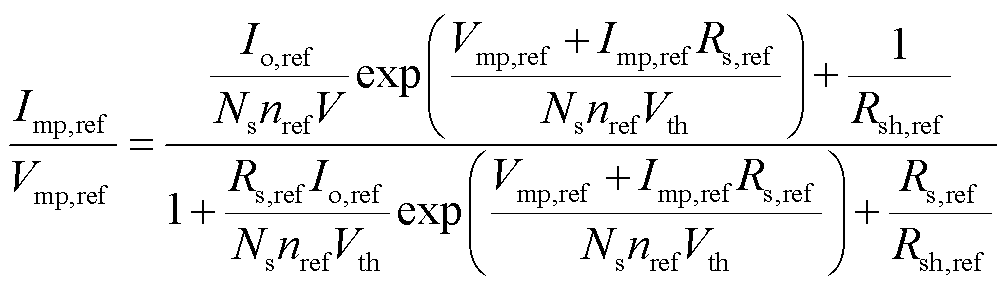 (7)
(7)
在标准环境辐照度下,根据温度增量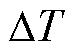 得到最后一个独立方程[23]为
得到最后一个独立方程[23]为
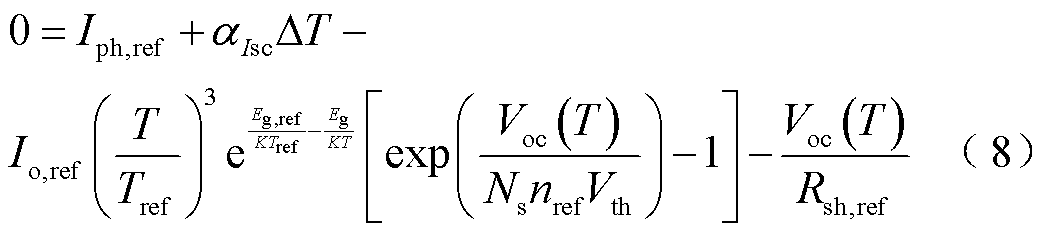
式中,Eg为材料带隙能量,J。
通过式(4)~式(8)解析求解STC下五个物理参数值,方程中所需STC下参数见表1,求解结果见表2。
表1 单晶硅太阳能电池组件规格参数
Tab.1 Specification parameters of xSi12922

参数数据(类型) 光伏组件xSi12922 串联电池数36 地区Cocoa 曲线条数37 997 Isc/A4.983 27 Voc/V21.946 1 Im/A4.486 61 Vm/V17.39
在实际运行条件下,光伏电池单二极管模型中物理参数值根据转化方程得到,转化方程代表了物理参数随环境辐照度G与温度T的依赖关系,具体为
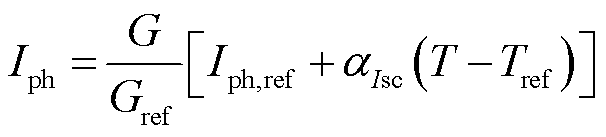 (9)
(9)
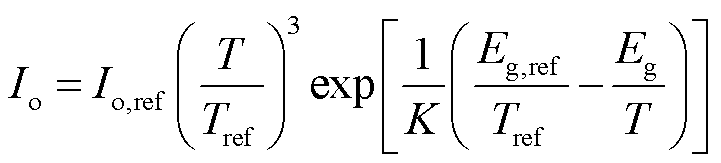 (10)
(10)
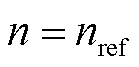 (11)
(11)
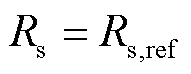 (12)
(12)
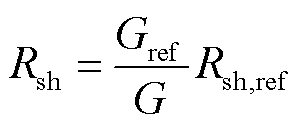 (13)
(13)
将STC下求解的参数值以及待求实际运行条件的辐照度和温度代入式(9)~式(13),可以得到实际运行条件下的五个参数,然后根据方程式(1)得到实际运行条件下的输出特性,如电流电压关系、最大功率等。
表2 STC条件下的单二极管参数辨识结果
Tab.2 SDM parameters identification results under STC

参数数值 Iph/A5.015 7 Io/A5.801 3´10-11 n0.944 6 Rs/Ω0.437 5 Rsh/Ω67.193 8
为提高单二极管运行条件下物理参数求解精度,本文提出了辐照度修正方程为
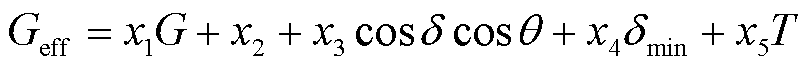 (14)
(14)
式中,Geff为有效辐照度, W/m2;δ为天顶角,(°);θ为方位角,(°);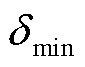 为天顶角最小值,(°)。
为天顶角最小值,(°)。
方程式(14)考虑了常数修正、角度修正、季节修正和温度修正,其中,x2代表常数修正,修正了辐照度测量仪器导致的固有误差;x3cosδcosθ代表太阳角度修正,修正了天顶角δ和方位角θ导致的误差;x4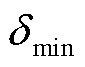 代表天顶角最小值修正,修正了由于季节变化引起的辐照度误差;x5T代表温度修正,修正了温度测量不准确导致的辐照度误差。
代表天顶角最小值修正,修正了由于季节变化引起的辐照度误差;x5T代表温度修正,修正了温度测量不准确导致的辐照度误差。
将修正后的有效辐照度Geff代入转化方程式(9)~式(13),代替测量辐照度G,计算得到实际运行条件下的五个参数,然后根据方程式(1)得到实际运行条件下的输出特性。
在辐照度修正方程式(14)中存在五个未知参数X=[x1 x2 x3 x4 x5],可通过实测条件下光伏组件I-V数据拟合得到。本文采用GCPSO拟合参数,对比传统粒子群算法,该算法解决了粒子群算法过早收敛或停滞的问题,在参数优化问题上展现出了良好性能[24]。算法首先输入拟合所用I-V曲线数据,设置种群数目、空间维度、最大迭代次数和参数搜索区间并初始化程序固有参数,目标函数为
 (15)
(15)
式中,N为所有曲线的总点数;i代表第i个点;Imea为测量电流大小;Ical为通过有效辐照度计算的电流大小。式(15)中电流的计算需用到式(2)中的电流显式表达式。
GCPSO算法通过最小化目标函数拟合参数X,得到最优解,将求解的X代入式(14)得到有效辐照度的修正方程。进而将有效辐照度计算值代入式(9)~式(13)计算光伏组件运行条件下的物理参数与输出特性。参数的拟合过程及光伏组件不同运行条件下输出特性计算流程如图2所示,具体步骤如下:首先初始化GCPSO的各个参数,包括种群数目、空间维度、迭代次数、粒子数目和初始粒子位置;其次进入循环,计算每个种群的最优粒子;然后比较每个种群的RMSE,选取误差最小的粒子位置作为最优解;再次进行粒子位置的调整,比较最优粒子的RMSE,直到满足循环的跳出条件或者达到求解的精度;最后找到全局最优的粒子,作为最优的结果输出。
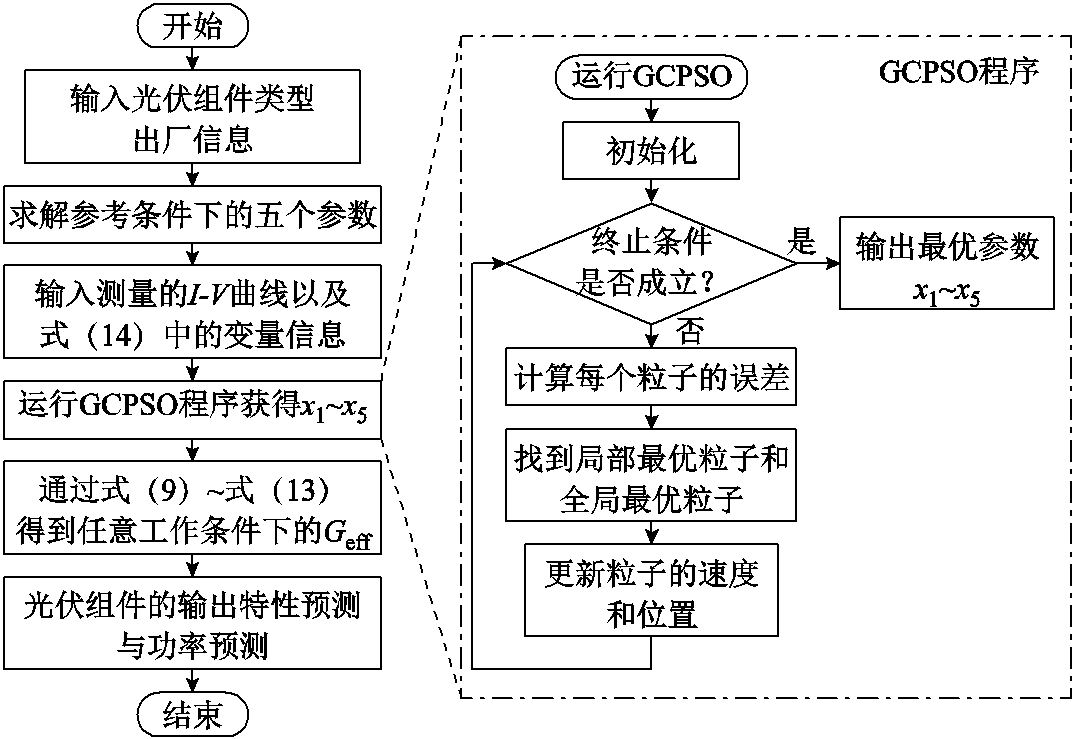
图2 基于有效辐照度修正的参数辨识和输出特性计算流程
Fig.2 Flow chart of parameter identification and output characteristic calculation based on effective irradiance correction
本文采用美国国家可再生能源实验室(NREL)[25]公共数据库中的光伏数据进行结果验证。数据包含实地测量的不同辐照度和温度条件下的光伏电池的I-V实验数据,本文选取具有代表性的单晶硅光伏电池一年的实验数据,实验中每5 min测量一条I-V曲线,共计37 997条,每一条曲线包含大约200个(I, V)数据点。此外,参数拟合使用的计算机为Windows10(64位)操作系统,搭载Intel(R) Core(TM) i5-9400 CPU@2.90 GHz和16 GB内存,同时使用测量辐照度代入物理参数转化方程[18, 23]进行计算并作对比。
式(14)中参数拟合结果见表3。为了验证不同天气情况下的结果,选取晴天(2011年10月20日)和阴天(2011年10月9日)的典型数据进行验证。
表3 参数拟合结果
Tab.3 Parameters fitting results

参数拟合数值 x11.031 9 x2/(W/m2)-9.807 2 x3/(W/m2)-17.853 8 x4/[W/(m2·°)]-13.385 4 x5/[W/m2·K)]0.029 1
典型晴天与阴天的不同方法计算功率与测量功率对比如图3所示,其中包括根据测量辐照度和有效辐照度计算的功率,以及实测功率。由图3可知,在晴天和阴天情况下,由修正后有效辐照度计算的功率与测量功率更接近。表4列出了两种方法计算结果的绝对误差值(Absolute Error, AE),可见不同天气下有效辐照度计算结果均优于测量辐照计算结果。同时图3中显示了测量辐照度与修正的有效辐照度,结果表明,测量辐照度较大时辐照度的修正量较大。

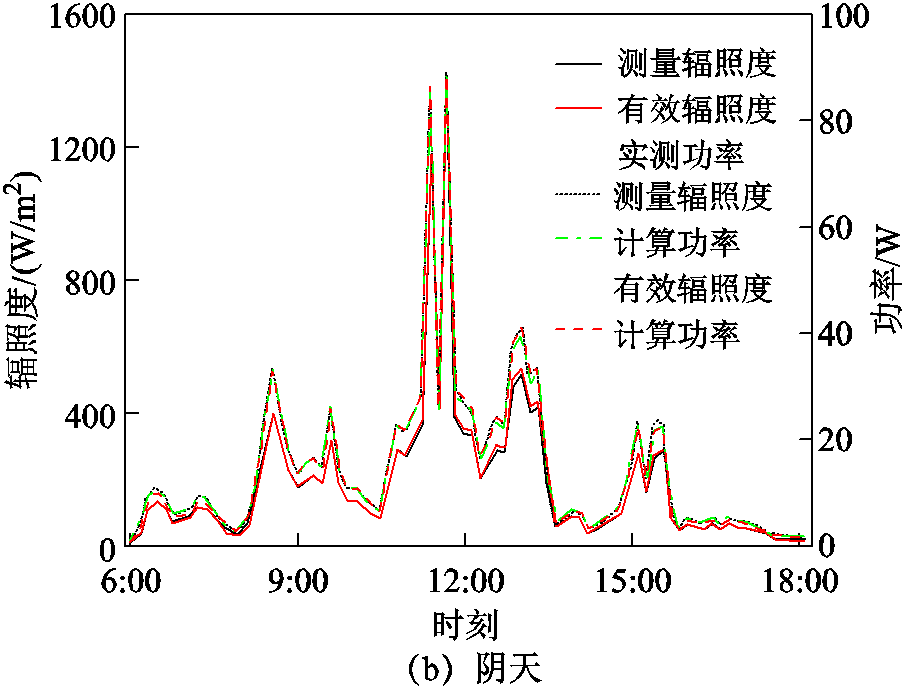
图3 辐照度、功率在晴天和阴天中的变化
Fig.3 Variation of irradiance, power in sunny, cloudy days
表4 测量辐照度、有效辐照度计算功率的绝对误差
Tab.4 AE of measured irradiance and effective irradiance for power calculation

天气类型功率绝对误差AE/W 测量辐照度方法有效辐照度方法 晴天1.764 30.739 8 阴天0.528 00.488 6
图4为晴天和阴天情况下有效辐照度各部分修正值,结果表明常数修正项为负值;在一天内最小天顶角为定值,最小天顶角修正值为负常数;温度修正为正值且与温度正相关,由于温度系数x5的值较小,温度修正项值x5T变化较小;角度修正值随时间变化最明显,由于中午方位角角度变大,角度修正值为正,其余时间为负值;辐照度修正值为有效辐照度与测量辐照度的差值。
为了研究辐照度修正值方程式(14)与环境因素的关系,在不同天顶角、方位角和温度区间下统计了辐照度修正(有效辐照度Geff-测量辐照度Gmea)均值在不同辐照度区间的平均值,如图5所示。由图5可知,在辐照度较低区域,修正值为负值,随着辐照度增大,修正值由负值变为正值并单调增大;随着方位角区间的增大,辐照度修正均值呈现出先增大后减小的趋势;在G<500 W/m2范围内,随着天顶角的增大和温度的减小,辐照度修正均值呈减小的趋势;在G>500 W/m2范围内,辐照度修正均值变化规律不明显。

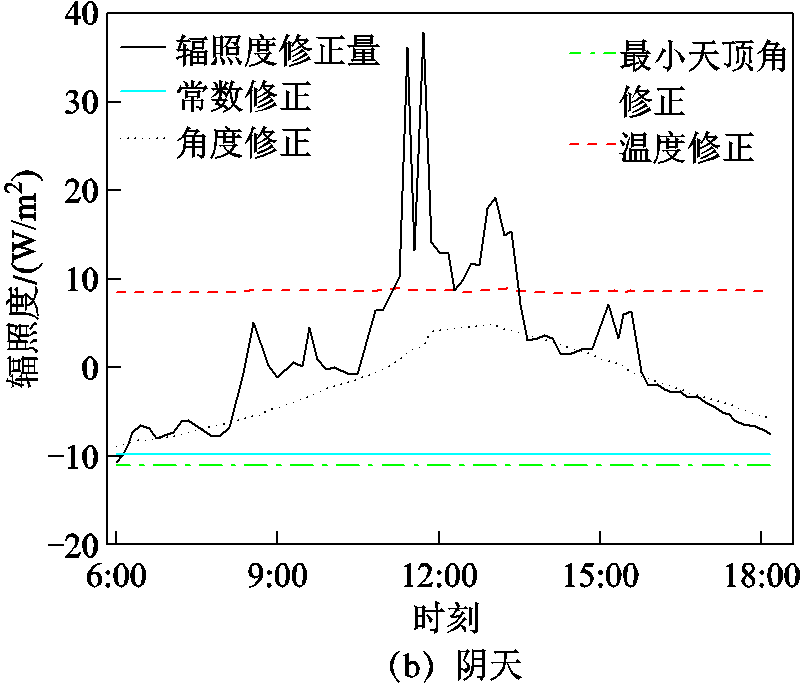
图4 各因素对辐照度修正的影响
Fig.4 Influence of factors on irradiance correction
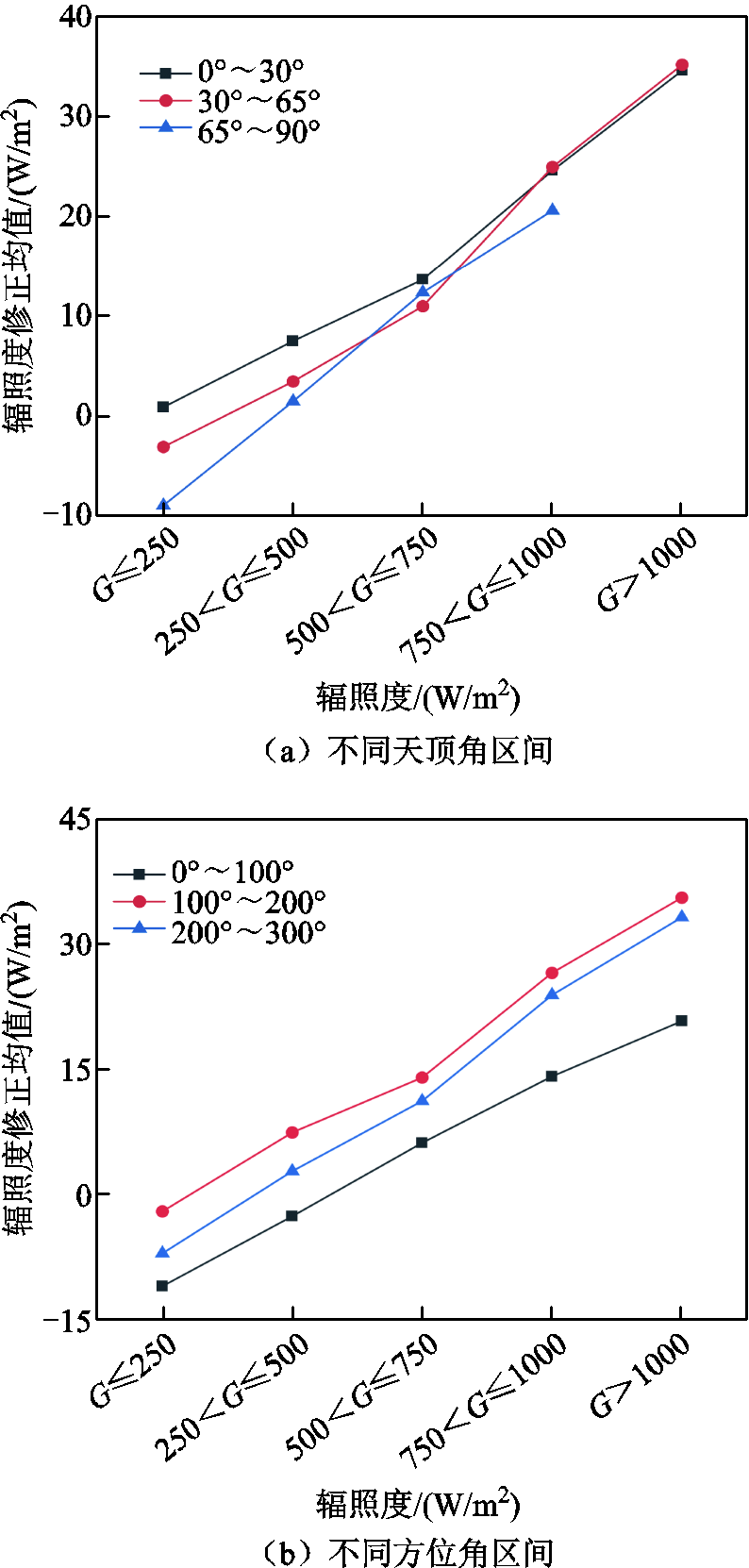
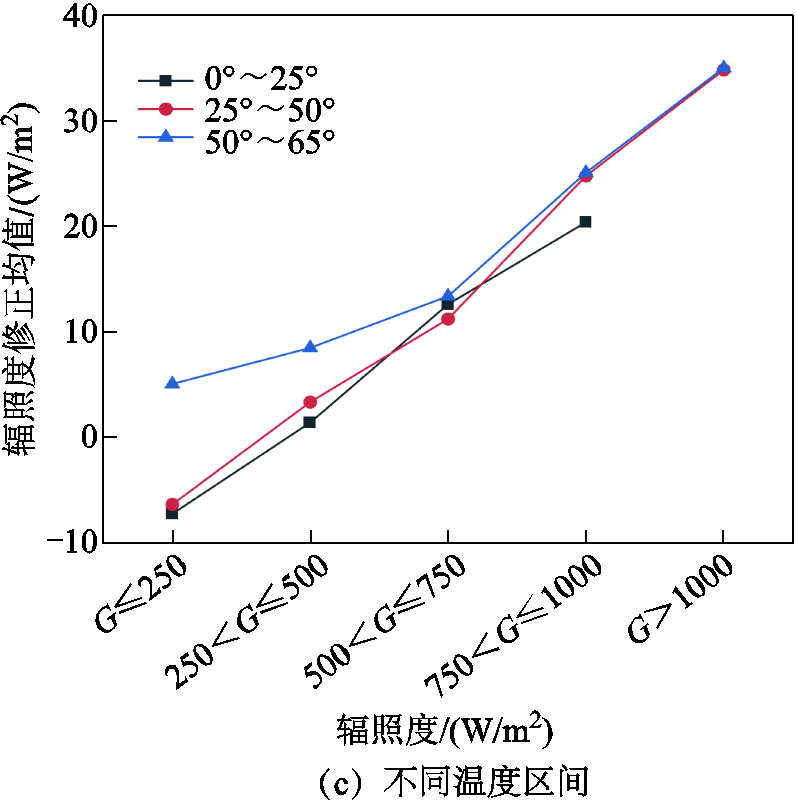
图5 各参数区间的辐照度修正均值
Fig.5 Mean value of irradiance correction for each parameter interval
为了验证辐照度修正结果的准确性,除了将有效辐照度计算的功率与测量辐照度计算的功率进行对比之外,可以根据每个运行条件下的I-V拟合得到辐照度Greal[26]作为真实辐照度,代表光伏组件吸收的光能。将测量辐照度与修正后的有效辐照度与真实辐照度对比,结果如图6所示。图6a为测量辐照度与真实辐照度对比图,图6b为有效辐照度与真实辐照度对比图。由图6和计算R、R2值可知,修正后的辐照度更接近真实辐照度,因此,由有效辐照度计算的功率误差更小,与图3和表4结果一致。
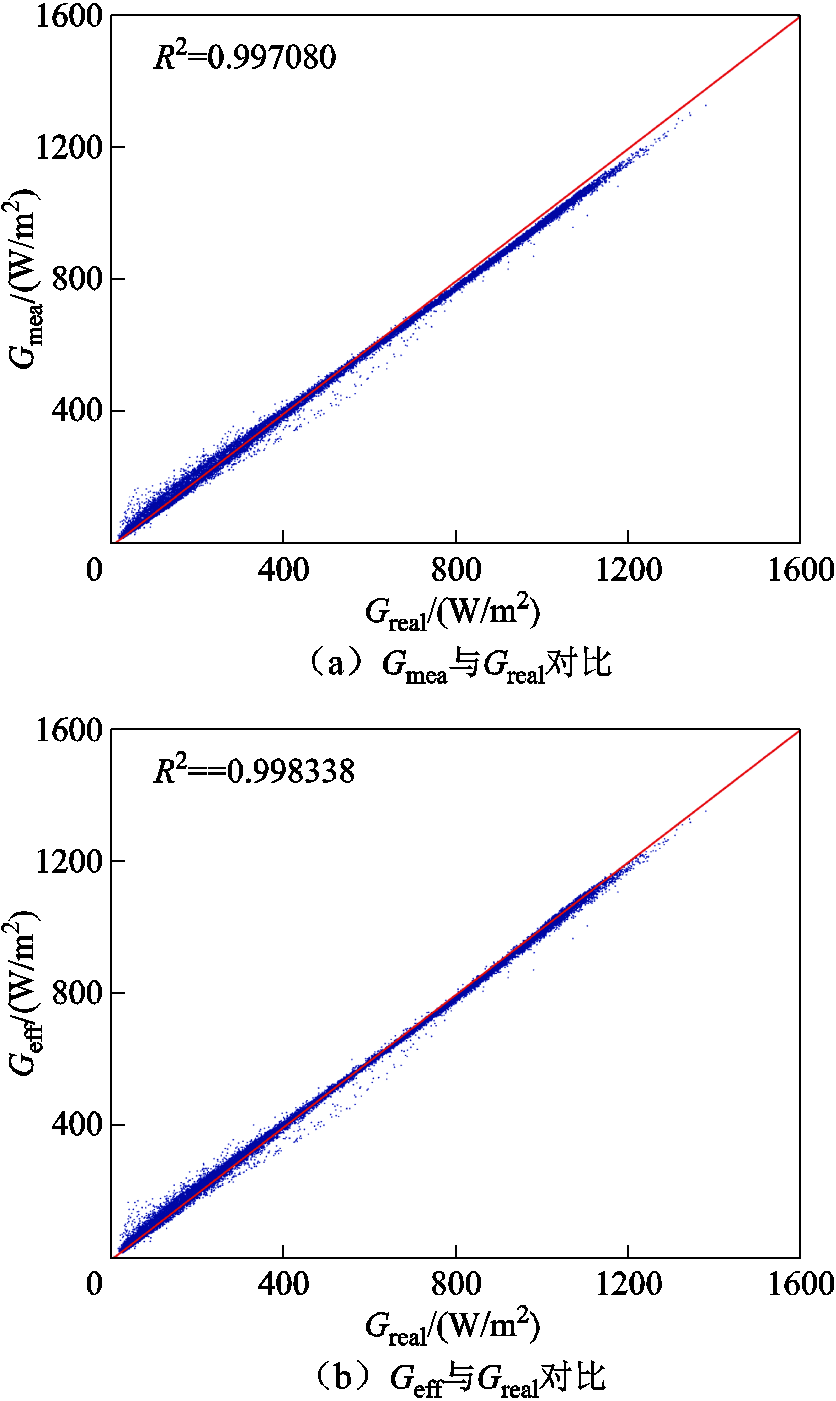
图6 Gmea, Geff分别与Greal的对比
Fig.6 Gmea, Geff compared with Greal respectively
计算全年37 997条I-V曲线的RMSE,并在不同辐照度区间、温度区间和季度区间进行统计,结果如图7所示。结果表明,在所有辐照度、温度和季度区间,由修正后有效辐照度计算的误差RMSE均小于测量辐照度计算结果,验证了本文提出辐照度修正方法的正确性与适用性。同时在辐照度较大区间(大于800 W/m2)精度提高最明显,RMSE减小21.6%;温度较高时精度提升最大,RMSE减小18.6%;所有结果平均RMSE减小9.78%。
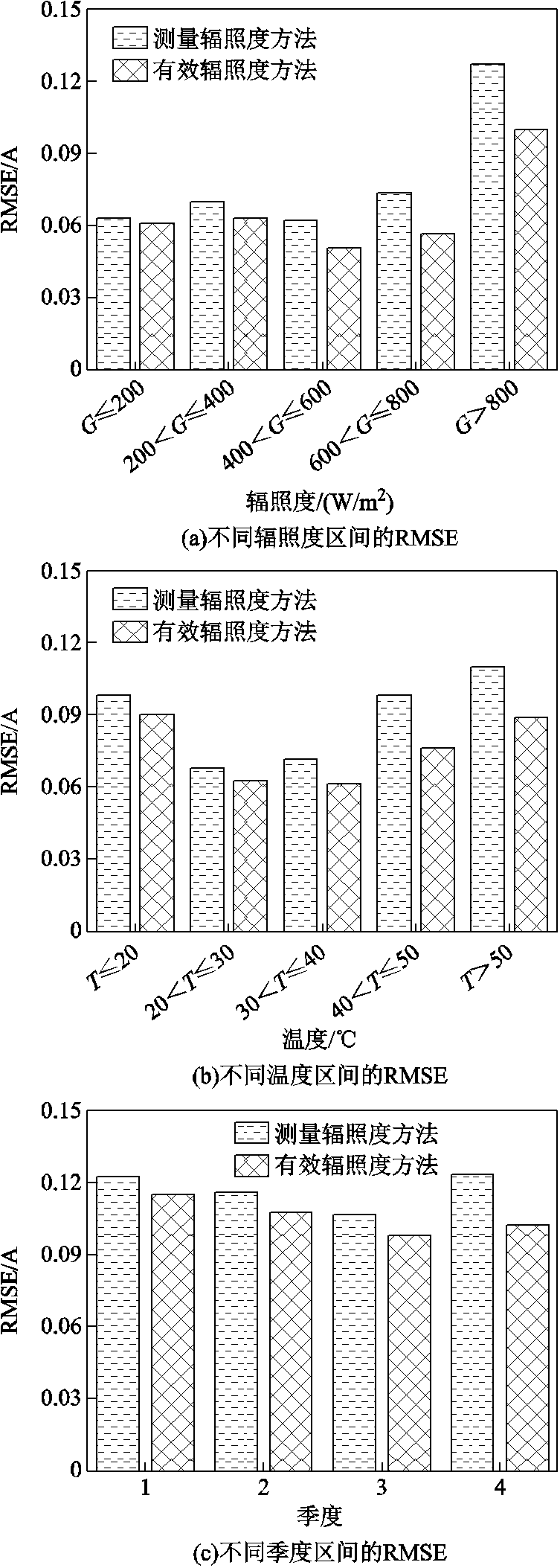
图7 不同辐照度、温度区间和季度区间RMSE对比
Fig.7 Comparison of RMSEbetween different irradiance, temperature and season intervals
图8为在不同运行条件下,由测量辐照度和有效辐照度计算的I-V、P-V曲线,与实测曲线对比,有效辐照度计算结果更接近实测曲线,表明使用有效辐照度在I-V和P-V曲线计算上具有更高精度。表5列出了不同运行条件下I-V和P-V曲线的误差值,结果表明,由有效辐照度计算结果误差均小于测量辐照度计算结果,与图8结果一致。由于光伏组件往往工作在最大功率点处,计算了不同运行条件下由测量辐照度和有效辐照度计算的最大功率,并与实测结果Pm,measured进行对比,如图9所示。结果表明,相比于测量辐照度计算结果Pm,mea,有效辐照度计算结果Pm,eff与实测最大功率Pm,measured符合度更高。
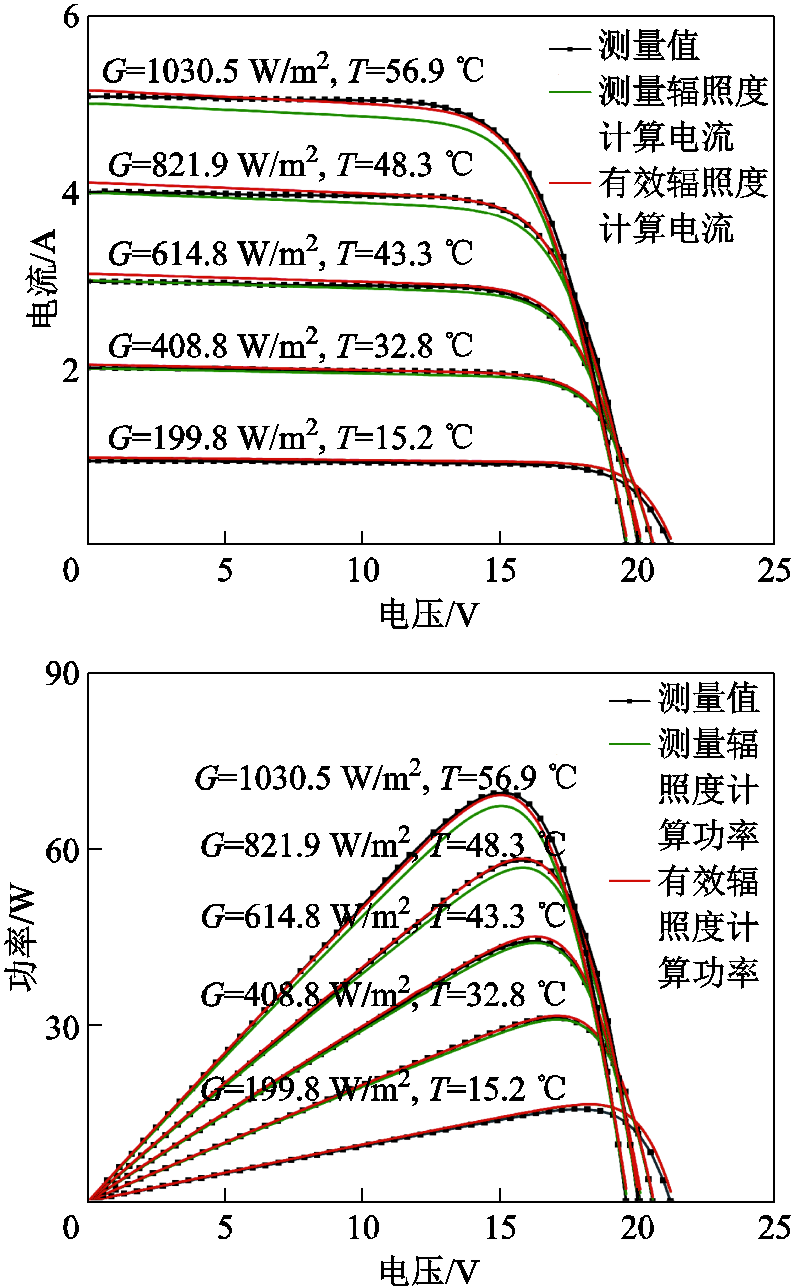
图8 不同方法计算的I-V、P-V曲线
Fig.8 I-V,P-V curves calculated by different methods
表5 不同运行条件下I-V曲线的RMSE
Tab.5 RMSEof I-V curves under different operating conditions
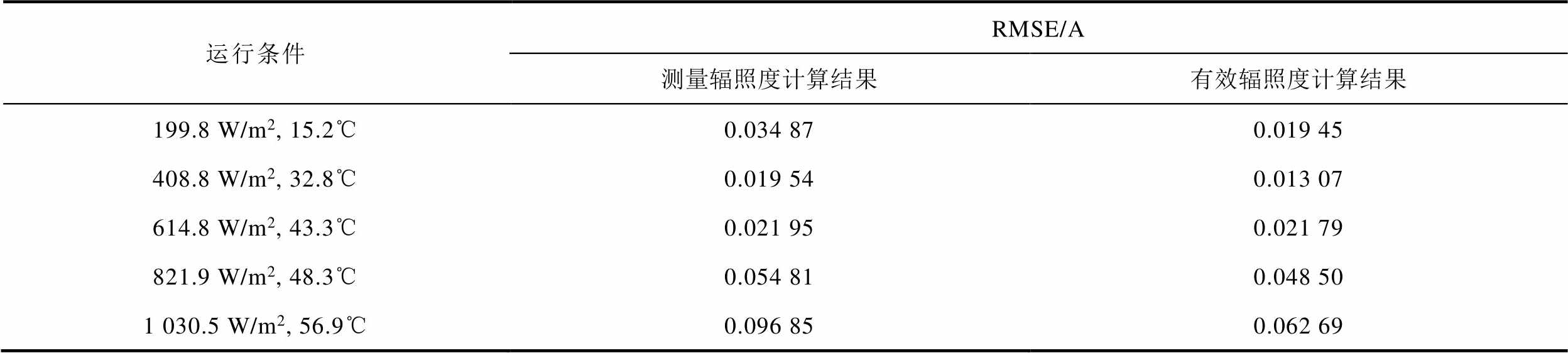
运行条件RMSE/A 测量辐照度计算结果有效辐照度计算结果 199.8 W/m2, 15.2℃0.034 870.019 45 408.8 W/m2, 32.8℃0.019 540.013 07 614.8 W/m2, 43.3℃0.021 950.021 79 821.9 W/m2, 48.3℃0.054 810.048 50 1 030.5 W/m2, 56.9℃0.096 850.062 69
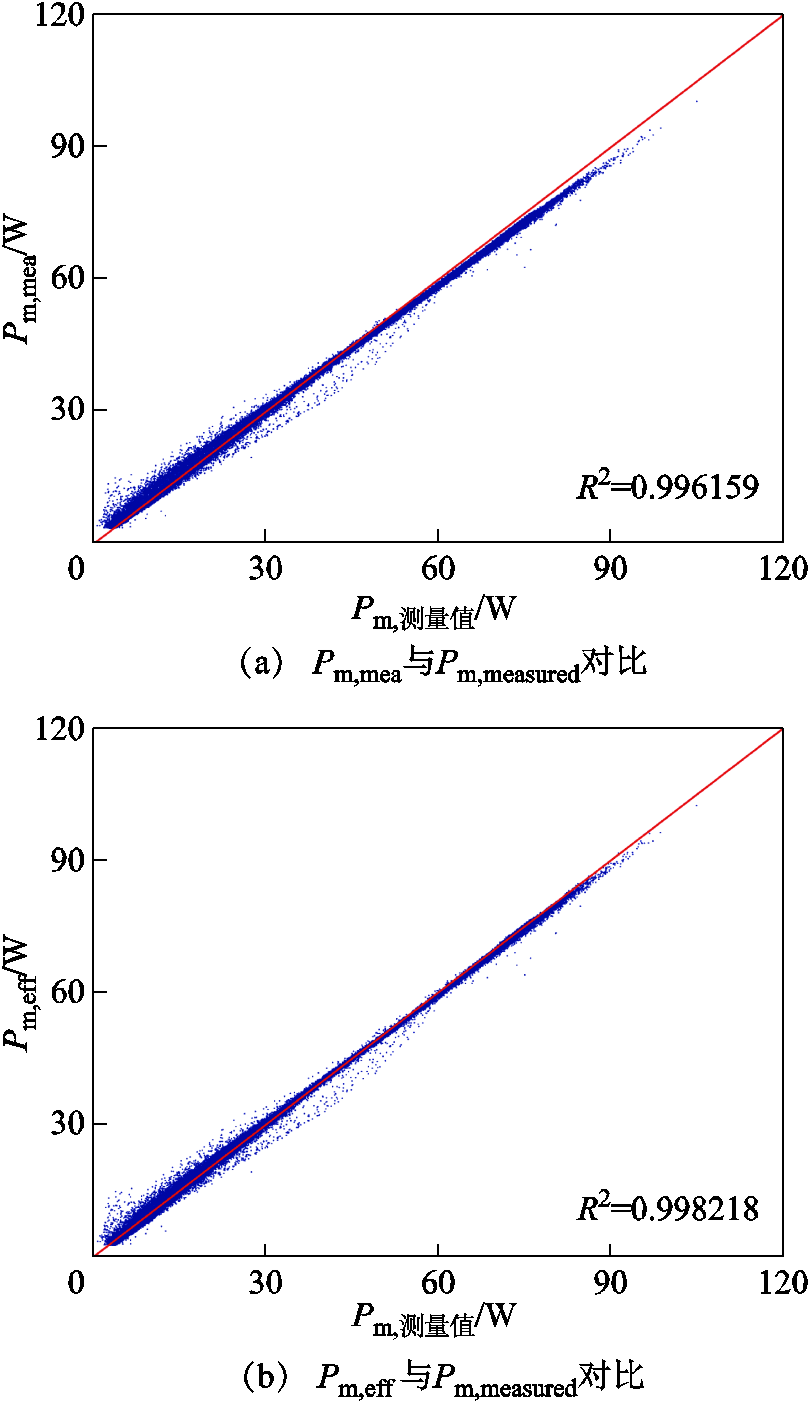
图9 Pm,mea, Pm,eff分别与Pm,measured的比较
Fig.9 Pm,mea, Pm,eff compared with Pm,measured respectively
以上结果说明了有效辐照度在光伏组件输出特性建模与计算方面优于测量辐照度。
本文提出了一种基于有效辐照度的参数辨识和输出特性建模方法,将测量辐照度进行了常数修正、角度修正、季节修正和温度修正,将有效辐照度代入转化方程进行各运行条件下的模型辨识和输出特性计算。通过实测数据对所提出方法进行验证,结果表明,在辐照度较低区域,修正值为负值,随着辐照度增大,修正值由负值变为正值并单调增大。与根据实测I-V数据拟合得到的辐照度对比,有效辐照度更加符合实际情况。在不同天气条件(晴天、阴天)、不同辐照度区间和温度区间,与使用测量辐照度计算结果对比,有效辐照度修正后结果在I-V、P-V输出特性计算和最大功率估计方面的精度均得到提高。本文提出的方法可应用于光伏发电建模、功率预测等方面。在本文工作基础上,建立更准确的辐照度和温度修正方程将是下一步工作的重点。
参考文献
[1] 李桐, 韩学山. 时变追踪并网光伏电站最大输出功率的无功优化方法[J]. 电工技术学报, 2023, 38(11): 2921-2931.
Li Tong, Han Xueshan. Reactive power optimization for time-varying tracking of maximum output power of grid-connected photovoltaic power station[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2921-2931.
[2] 田涵雷, 韩沛松, 唐嵩峰, 等. 计及轻量化设计的多电平光伏逆变器[J]. 电工技术学报, 2023, 38(16): 4301-4311.
Tian Hanlei, Han Peisong, Tang Songfeng, et al. Multi-level photovoltaic inverter considering lightweight design[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4301-4311.
[3] 叶林, 程文丁, 李卓, 等. 光伏集群有功功率分层预测控制策略[J]. 电力系统自动化, 2023, 47(2): 42-52.
Ye Lin, Cheng Wending, Li Zhuo, et al. Hierarchical prediction control strategy of active power for photovoltaic cluster[J]. Automation of Electric Power Systems, 2023, 47(2): 42-52.
[4] 杜磊, 赵涛, 冯之健, 等. 单相短路故障条件下级联模块中压光伏发电系统的有功功率回流抑制[J]. 电工技术学报, 2022, 37(20): 5201-5213.
Du Lei, Zhao Tao, Feng Zhijian, et al. Active power backflow suppression of cascaded module medium-voltage PV power generation system during single-phase short-circuit fault[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5201-5213.
[5] 李勇, 刘珮瑶, 胡斯佳, 等. 基于感应滤波的光伏电站谐波谐振抑制方法[J]. 电工技术学报, 2022, 37(15): 3781-3793.
Li Yong, Liu Peiyao, Hu Sijia, et al. Harmonic resonance damping method of photovoltaic power station based on inductive filtering[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3781-3793.
[6] 王再闯, 陈来军, 李笑竹, 等. 基于合作博弈的产销者社区分布式光伏与共享储能容量优化[J]. 电工技术学报, 2022, 37(23): 5922-5932.
Wang Zaichuang, Chen Laijun, Li Xiaozhu, et al. Capacity optimization of distributed PV and shared energy storage of prosumer community based on cooperative game[J]. Transactions of China Electro-technical Society, 2022, 37(23): 5922-5932.
[7] 程礼临, 臧海祥, 卫志农, 等. 考虑多光谱卫星遥感的区域级超短期光伏功率预测[J]. 中国电机工程学报, 2022, 42(20): 7451-7464.
Cheng Lilin, Zang Haixiang, Wei Zhinong, et al. Ultra-short-term forecasting of regional photovoltaic power generation considering multispectral satellite remote sensing data[J]. Proceedings of the CSEE, 2022, 42(20): 7451-7464.
[8] 任晓琳, 杨奕, 高龙, 等. 基于IBA-KELM模型的TCT光伏阵列故障诊断研究[J]. 电源学报, 2023, 21(5): 67-74.
Ren Xiaolin, Yang Yi, Gao Long, et al. Research on fault diagnosis of tct photovoltaic array based on IBA-KELM Model [J]. Journal of Power Supply, 2023, 21(5): 67-74.
[9] 许杨, 吕雪松, 张科乾, 等. 柔性光伏电池阵列物理参数特性建模[J]. 电气技术, 2023, 24(9): 49-54.
Xu Yang, Lü Xuesong, Zhang Keqian, et al. Modeling of physical parameter characteristics of flexible photovoltaic cell arrays. Electrical Engineering, 2023, 24(9): 49-54.
[10] Younis A, Bakhit A, Onsa M, et al. A comprehensive and critical review of bio-inspired metaheuristic frameworks for extracting parameters of solar cell single and double diode models[J]. Energy Reports, 2022, 8: 7085-7106.
[11] 林泽源, 王宗尧, 张凡, 等. 考虑氢能应用的光伏直流微电网中储能容量配置寻优方法研究[J]. 高压电器, 2024, 60(7): 78-87.
Lin Zeyuan, Wang Zongyao, Zhang Fan, et al. Research on optimization method for energy storage capacity configuration in photovoltaic dc micro grid considering hydrogen energy application[J]. High Voltage Apparatus, 2024, 60(7): 78-87.
[12] 韦明杰, 王聪博, 余越, 等. 适用高比例分布式光伏接入的配电网多级保护优化配置方案[J]. 电力系统自动化, 2023, 47(22): 55-65.
Wei Mingjie, Wang Congbo, Yu Yue, et al. Optimal configuration scheme of multi-staged protection in distribution network for integration of high proportion of distributed photovoltaic[J]. Automation of Electric Power Systems, 2023, 47(22): 55-65.
[13] Hao Peng, Zhang Yunpeng, Lu Hao, et al. A novel method for parameter identification and performance estimation of PV module under varying operating conditions[J]. Energy Conversion and Management, 2021, 247: 114689.
[14] Zhang Yunpeng, Hao Peng, Lu Hao, et al. A novel method for performance estimation of photovoltaic module without setting reference condition[J]. International Journal of Electrical Power & Energy Systems, 2022, 134: 107439.
[15] Zhang Yunpeng, Gao Shuning, Gu Tingkun. Prediction of I-V characteristics for a PV panel by combining single diode model and explicit analytical model[J]. Solar Energy, 2017, 144: 349-355.
[16] Zhang Yunpeng, Hao Peng, Lu Hao, et al. Modelling and estimating performance for PV module under varying operating conditions independent of reference condition[J]. Applied Energy, 2022, 310: 118527.
[17] 简献忠, 翁志远, 王如志. CIJAYA算法在光伏组件参数辨识中的应用[J]. 太阳能学报, 2021, 42(11): 19-26.
Jian Xianzhong, Weng Zhiyuan, Wang Ruzhi. CIJAYA algorithm for parameters identification of photovoltaic module model[J]. Acta Energiae Solaris Sinica, 2021, 42(11): 19-26.
[18] Laudani A, Riganti Fulginei F, Salvini A. High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental I-V curves by using reduced forms[J]. Solar Energy, 2014, 103: 316-326.
[19] Lang Zhe, Zhang Yunpeng. Parameter identification and performance estimation for PV modules based on reduced forms model[J]. Journal of Renewable and Sustainable Energy, 2020, 12(5): 3703.
[20] Mubarak R, Schilke H, Seckmeyer G. Improving the irradiance data measured by silicon-based sensors[J]. Energies, 2021, 14(10): 2766.
[21] Perraki V, Kounavis P. Effect of temperature and radiation on the parameters of photovoltaic modules[J]. Journal of Renewable and Sustainable Energy, 2016, 8(1): 3102.
[22] Nunes H G G, Pombo J A N, Mariano S J P S, et al. A new high performance method for determining the parameters of PV cells and modules based on guaranteed convergence particle swarm optimization[J]. Applied Energy, 2018, 211: 774-791.
[23] Laudani A, Riganti Fulginei F, Salvini A. Identification of the one-diode model for photovoltaic modules from datasheet values[J]. Solar Energy, 2014, 108: 432-446.
[24] He Yubo, Yang Qingzhen, Gao Xiang. Comprehensive optimization design of aerodynamic and electromagnetic scattering characteristics of serpentine nozzle[J]. Chinese Journal of Aeronautics, 2021, 34(3): 118-128.
[25] Marion B, Anderberg A, Deline C, et al. New data set for validating PV module performance models[C]// 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 2014: 1362-1366.
[26] Dang D N, Le Viet T, Takano H, et al. Estimating parameters of photovoltaic modules based on current–voltage characteristics at operating conditions[J]. Energy Reports, 2023, 9: 18-26.
Abstract Parameter identification and output characteristic modelling of photovoltaic (PV) module is a complex task with several significant challenges, including recording and contribution of large amounts of data, data privacy protection anduncertainty of physical parameters of PV modules under varying operating conditions. These poses significant challenges for the efficient implementation of traditional mathematical optimization methods. Recently, many researchers have turned their attention to intelligent optimization algorithm methods, which rely on data-driven principles and exhibit strong adaptability to solve the optimal solution. However, as the prediction accuracy of PV power generation improves, more stringent demands are placed on the accuracy of PV module modeling. The traditional analytical calculation approach alone struggles to meet the heightened requirements for power prediction accuracy, as it involves solving for five parameters under changing operating conditions. To tackle these challenges, this paper introduces a new method for parameter identification and modeling of PV module output characteristics that incorporates effective irradiance correction.
First, the study analyzes environmental factors influencing the output characteristics of photovoltaic modules to establish a correction formula that converts measured irradiance to effective irradiance. This formula accounts for constant, angular, seasonal, and temperature adjustments. Second, the paper employs an analytical method to determine the single-diode model’s physical parameters under standard test conditions, fitting each parameter in the effective irradiance correction formula based on how the physical parameters vary with irradiance and temperature. The fitting process is guided by minimizing the root-mean-square error (RMSE) of the current-voltage (I-V) curve. Then, using the proposed correction method, the actual operating conditions of the PV modules are considered to adjust effective irradiance, which is then used to calculate the modules’ physical parameters and output characteristics. Finally, the method’s efficacy is confirmed using measured data: the corrected results enhance the accuracy of the I-V and power-voltage (P-V) output characteristic computations and maximum power estimation, out performing uncorrected outcomes under varied weather (sunny and cloudy), irradiance levels, and temperature ranges.
The following conclusions can be drawn from the case studies: the results show that the correction value of effective irradiance is negative in low irradiance area, and the correction value changes from negative to positive and increases monotonically with the increase of irradiance. Compared with the irradiance obtained by fitting from the measured I-V data, the effective irradiance is more consistent with fitting irradiance than measured irradiance.In different weather conditions (sunny day, cloudy day), different irradiance, temperature and season intervals, the error RMSE of the proposed effective irradiance method is less than that of the measured irradiance calculation results. And the RMSE of high irradiance (greater than 800 W/m2) and temperature intervals (greater than 50℃) is significantly reduced by 21.6% and 18.6%. The mean RMSE is reduced by 9.78% for all outcomes. Compared with the measured irradiance calculation results, the effective irradiance calculation results is in better agreement with the measured maximum power. The proposed method in this study improves the modelling accuracy of PV modules and the accuracy of PV power prediction. Based on the work in this study, establishing more accurate correction equations for irradiance and temperature is the future work.
keywords:Single diode model, parameter identification, irradiance correction, effective irradiance
中图分类号:TM615
DOI: 10.19595/j.cnki.1000-6753.tces.231694
国家重点研发计划“极高渗透率分布式光伏发电自适应并网与主动同步关键技术(2022YFB2402900)”和国家电网公司总部科技项目(52060023001T)资助。
收稿日期 2023-10-12
改稿日期 2024-02-07
李国荣 男,2000年生,硕士研究生,研究方向为新能源发电预测。E-mail:202214611@mail.sdu.edu.cn
张云鹏 男,1981年生,副教授,硕士生导师,研究方向为电工理论与新技术、新能源发电预测。E-mail:zhangyp@sdu.edu.cn(通信作者)
(编辑 郭丽军)