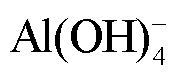 )向阳极电极表面迁移并发生如下沉积反应[14]:
)向阳极电极表面迁移并发生如下沉积反应[14]:摘要 均压电极结垢是导致换流阀冷却系统故障的主要原因之一,传统检修采取的定期拆卸检测方式具有较大的盲目性且易造成系统漏水等故障。现有水质监测或间接检测法不能直接反映垢层沉积情况,而声学检测具有灵敏度高、检测速度快等优点。因此,该文提出了换流阀冷却系统均压电极垢层声学检测方法。首先,根据均压电极结垢特点,提出了适用于均压电极垢层的声学检测装置设计方法;其次,搭建了阀冷系统实验平台,在噪声环境中检验了装置的抗干扰性能,并对比分析无/有垢条件下回波信号的差异性;最后,从回波信号中提取电极垢层厚度的特征指标,建立了其与垢层厚度的数学映射关系,并进一步提出了垢层厚度预测策略。结果表明特征指标减小率与垢层厚度满足Boltzmann数学关系,能够可靠表征电极垢层厚度的变化过程,为均压电极的检修提供依据。
关键词:换流阀冷却系统 均压电极 垢层厚度 声学检测 特征指标
换流阀是特高压直流输电系统的关键设备,直接影响直流输电的稳定性和安全性。然而运行中,由于在大功率晶闸管工作过程中会产生大量热量,目前主要采用基于去离子水的冷却系统对换流阀内部进行散热,以维持可靠的运行温度环境[1]。尽管去离子水电导率很低,但是换流阀阀塔电位差大,冷却系统中会不可避免地产生泄漏电流。为了消散泄漏电流,常采用安装均压电极的方式以平衡电位[2]。然而在长期运行中,铝散热器腐蚀所产生的带电离子在电场作用下游离至电极表面形成垢层,垢层厚度积累至一定程度将导致电极均压能力减弱,进一步加速铝散热器腐蚀[3],形成恶性循环,从而引起水路堵塞、漏水、电抗器和水冷电阻损坏等故障,严重威胁高压直流输电系统的安全运行。
针对阀冷系统均压电极结垢问题,目前主要采用人工逐一筛检拆卸的方式判断和消除结垢的影响。然而电极取出过程极为繁琐,且易导致操作失误,使得垢层脱落至水路中引起堵塞等问题,且在直流换流站中,均压电极的数量众多,各电极结垢情况更是存在差异,使得检修人员工作量庞大且效率低下[4]。而均压电极垢层厚度检测是改变此现状的重要环节,研究均压电极垢层厚度无拆卸检测方法具有重要意义。
为获得均压电极垢层沉积特性,国内外学者开展了相关研究,主要从水质指标、电气参数等角度出发。如文献[5]提出在阀冷系统上安装传感器以监测和控制水质,避免铝散热器快速腐蚀引发严重结垢;文献[6]通过检测水路中的pH值,判断均压电极的结垢趋势;文献[7]提出考虑阀段各支流水路电场分布差异的电压纹波因子和泄漏电流纹波因子,以表征电极结垢后的均压能力并作为电极更换依据,但该思路更多是通过水路中的其他参数间接获得均压电极的结垢程度,检测精度有待提高[8]。声学检测因其灵敏度高、检测速度快、通用性强等优点,近年来已成功应用于如管道[9]、污垢[10]的检测及锂电池荷电状态估计[11],因此,利用声学原理检测均压电极结垢是一种新兴方法,目前正处于起步阶段。文献[12]开展了均压电极垢层厚度的信号处理相关工作,以5 MHz频率下的超声回波信号包络线作为特征参数,识别了0.3 mm及以上均压电极的垢层厚度,但在该频段信号衰减程度大,特征差异性弱;文献[13]研究了均压电极垢层厚度对超声导波回波信号中主模态反射信号和模态转换信号的影响,得出主模态反射信号和转换模态分量随垢层厚度增大而减小的趋势,但在实际检测中电极信号易湮没于管道的频散信号中,难以提取。而且现有工作更多停留于实验室探索阶段,依赖实验仪器设备,便携性能差,是否能应用于换流阀检测仍未知。因此,对均压电极垢层声学检测装置及特征进行分析研究对于换流阀阀冷系统均压电极垢层无拆卸检测具有重要意义。
在现有研究基础上,论文首先提出了换流阀阀冷系统均压电极结垢声学检测方法,设计了均压电极声学检测装置,实现了对声波激励端和接收端的控制,并将回波信号传输至上位PC端,实现了特征提取和分析,该装置具有操作简易、便携性能优异的优点;其次搭建实验平台,对不同厚度的电极垢层进行声学检测,验证了装置对于电极垢层检测的可行性,且在噪声环境中表现出优异的抗干扰性能,并对比分析了无/有垢条件下回波信号的差异性;最后,建立特征指标减小率与垢层厚度的拟合关系,发现采用Boltzmann曲线能够可靠表征特征减小率随电极垢层厚度的变化过程,进而提出一种均压电极垢层厚度预测策略,为均压电极的检修提供指导。
换流阀冷却系统在长期运行中,铝散热器由于去离子树脂粉末的泄漏以及泄漏电流的作用会发生腐蚀,腐蚀离子在电场、湍流场、扩散的共同作用下运动至均压电极表面,进而发生电沉积反应形成垢层。此过程中,负电性致垢离子(主要为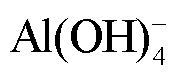 )向阳极电极表面迁移并发生如下沉积反应[14]:
)向阳极电极表面迁移并发生如下沉积反应[14]:
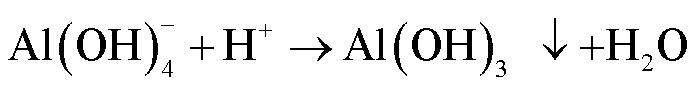 (1)
(1)
正电性致垢离子(如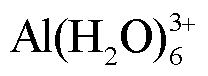 等)向阴极电极表面迁移并发生如下沉积反应:
等)向阴极电极表面迁移并发生如下沉积反应:
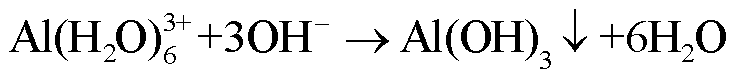 (2)
(2)
反应式中的H+和OH-来源于电解水反应。故垢层主要成分为Al(OH)3,垢层晶型主要为β三羟基铝石,且为多孔隙分布,基于电化学角度,垢层厚度s可表示为Al(OH)3的浓度分布,表达式为[15]
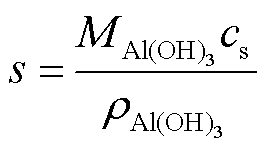 (3)
(3)
式中,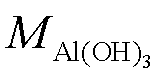 为垢层Al(OH)3的摩尔质量(kg/mol);cs为表面浓度(mol/m2);
为垢层Al(OH)3的摩尔质量(kg/mol);cs为表面浓度(mol/m2);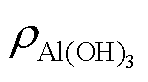 为垢层Al(OH)3的密度(kg/m3)。
为垢层Al(OH)3的密度(kg/m3)。
因此,由式(3)可以看出,垢层厚度的变化反映了Al(OH)3的浓度变化,在微观层面中则表现为密度、孔隙率等介质参数的变化[16],进而导致声阻抗、声速的变化[17]。此外相比吸收衰减和辐射衰减,声波散射衰减在多孔介质的不均匀材料中占主导地位,故同时引起散射衰减系数的变化[18],宏观表现为声学信号,如回波声压等特征量的改变,相关表达式为[11,19]
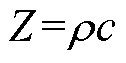 (4)
(4)
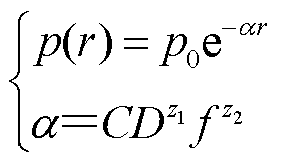 (5)
(5)
式中,Z为介质声阻抗;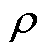 为介质密度(水的密度
为介质密度(水的密度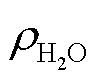 =1 000 kg/m3,铂电极密度
=1 000 kg/m3,铂电极密度 =21 450 kg/m3,垢层密度
=21 450 kg/m3,垢层密度 =3 965 kg/m3);c为声波传播速度(水中声波传播速度
=3 965 kg/m3);c为声波传播速度(水中声波传播速度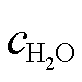 =1 480 m/s,声波在铂电极中的传播速度
=1 480 m/s,声波在铂电极中的传播速度 =3 962 m/s,声波在垢层中的传播速度
=3 962 m/s,声波在垢层中的传播速度 =5 190 m/s);p为回波声压;p0为入射声压;r为声传播距离;α为散射衰减系数;C为与介质性质和声波信号周期数有关的常数;D为晶粒平均直径,金属晶粒直径为nm级,而垢层晶粒直径通常为μm量级[20];f为声波信号中心频率;z1、z2为不同散射机制所对应的常数,本文属于瑞粒散射区(D/λ
=5 190 m/s);p为回波声压;p0为入射声压;r为声传播距离;α为散射衰减系数;C为与介质性质和声波信号周期数有关的常数;D为晶粒平均直径,金属晶粒直径为nm级,而垢层晶粒直径通常为μm量级[20];f为声波信号中心频率;z1、z2为不同散射机制所对应的常数,本文属于瑞粒散射区(D/λ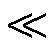 1,其中,λ为声波波长,λ=c/f),此时z1=3,z2=4[18]。
1,其中,λ为声波波长,λ=c/f),此时z1=3,z2=4[18]。
基于上述分析,本文装置采用声波时域反射法对均压电极及其垢层进行声学检测,原理如图1所示。由换能器产生入射声波,在管壁和去离子水的交界面将产生反射回波A和C,在去离子水和均压电极或垢层的交界面将产生反射回波B,在交界面反射系数R满足
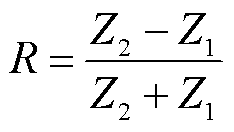 (6)
(6)
式中,Z1为原介质声阻抗;Z2为声波穿透后的介质声阻抗。由式(4)可知:Zse(垢层声阻抗)<Zelectrde(电极声阻抗),此时由式(6)可知在第一重交界面(水-电极/垢层)处Rse<Relectrde,即由于多孔隙垢层的存在,反射回波B主体能量更弱。其余透射声波由于多孔隙垢层的作用,即Dse(垢层晶粒直径)>Delectrode(电极金属晶粒直径),使得αse>αeletrode,从而加剧声波衰减,导致其余界面的反射回波声压p进一步的减小。因此,由于垢层和电极的声学介质参数的不匹配,可通过分析均压电极不同垢层厚度的声反射回波,提取有效的垢层厚度信息,从而反映垢层的状态特征。
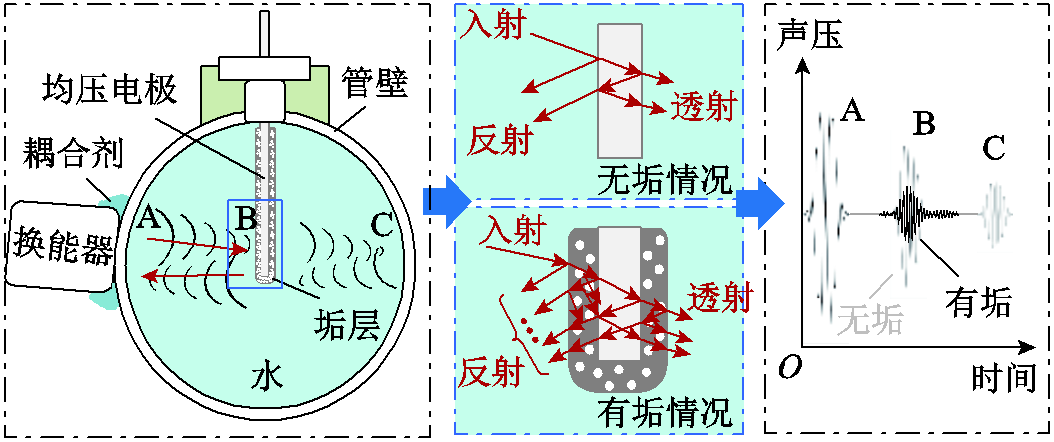
图1 均压电极声学检测原理
Fig.1 Acoustic detection principle of grading electrode
综上所述,声波与电极垢层的交互特性与其厚度密切相关。但在实际工况中,电极的安装位置与检测环境对装置体积提出了严格的要求,且声学检测易受阀冷系统中电磁干扰或其他环境因素的影响,因此,亟须研制出强抗干扰性、强便携性的均压电极垢层检测装置。此外,由于实际垢层沉积具有不均匀性且表面不平整的特点,使得声波与垢层的交互过程变得更为复杂,故而进一步提取分析多角度的、强敏感性的回波特征量,建立垢层厚度和声学指标的强耦合关系对均压电极垢层的无拆卸检测具有重要意义。
均压电极声学检测实验装置结构如图2所示,运用现场可编程门阵列(Field Programmable Gate Array, FPGA)控制声激励端和声接收端,压电换能器在声激励端作用下实现电声能量的变换以及声波能量的聚焦,形成声波与均压电极交互,声接收端采集带有垢层信息的声回波信号,经数据传输导入PC端用于特征分析。依据设计过程,实验装置主要分为三个部分:声激励端、声接收端和FPGA控制。
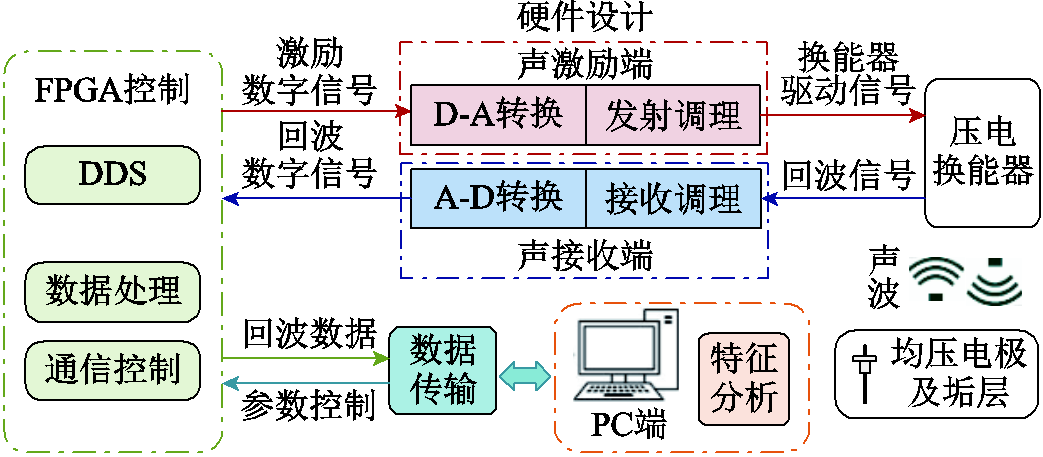
图2 声学检测实验装置结构
Fig.2 Structure of acoustic detection experimental device
声激励端负责将FPGA合成的激励数字信号转换为模拟信号,由发射调理电路对激励信号进行滤波、放大和匹配,以有效驱动压电换能器形成声波。声接收端负责接收换能器的回波信号,由接收调理电路对信号放大和滤波降噪后,通过A-D转换为数字信号,由FPGA接收缓存。FPGA控制过程作为检测装置核心,具体包括用于激励信号生成的直接数字频率合成(Direct Digital Synthesizer, DDS)模块、用于回波数据缓存并累加平均滤波的数据处理模块以及控制数据传输与PC端交互的通信控制模块。
中心频率的选取直接决定超声换能器的选型和检测效果。根据超声检测理论,要保证检测的灵敏度,被检测物尺寸L应至少大于声波波长λ的一半,即应满足
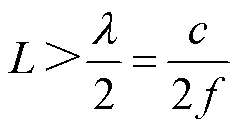 (7)
(7)
对于本文情况,被检测物为结垢电极,电极直径l为2 mm,垢层厚度为t,此时L=l+2t。对式(7)重新整理,可得
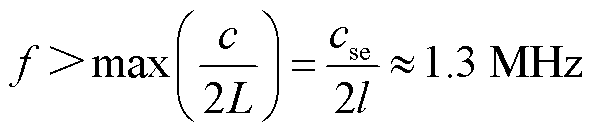 (8)
(8)
另外,选取的f也不宜过大,否则由式(5)可知将会加剧回波信号的衰减,故应留有一定裕度,本文选取激励波形中心频率为1.5 MHz。
本文选取激励信号波形为汉宁窗调制的正弦波脉冲信号,周期数默认为10,在该激励信号下波形具有更好的能量集中性[21]。在实际检测中,可通过PC端对中心频率、周期数进行相应调整。
将激励波形数据预先写入ROM中,通过FPGA内控制模块译码使能对应的DDS模块读取ROM数据,从而输出激励数字信号。选用AD9708数模转换芯片将激励数字信号转换为模拟信号,同时,采用七阶巴特沃斯低通滤波电路去除转换输出信号中的高频噪声。考虑到低通滤波电路输出的电压幅值较低而无法有效驱动压电换能器,故选用AD8065运放器组成前级放大电路,并将低通滤波器输出的差分信号转换为单端信号。后级放大电路选用ADA4870大电流驱动放大器,在保证便携性的前提下,可通过±20 V双电源模式实现最大37 V的输出幅度,且最大驱动电流为1 A,适用于装置所用的双晶压电探头。同时,在末级输出端采用低通L形阻抗匹配电路,将接入压电换能器后的等效负载阻抗匹配至50 Ω,以实现信号的最大功率传输。
本文选用AD9280芯片构成的模数转换电路。接收调理电路包括电路缓冲、放大、带通滤波以及直流偏置,使声回波信号信噪比最优且能作为AD采样的有效输入。缓冲电路使用AD8066双路放大器,其中一路作为电压跟随器,其高输入阻抗以匹配压电换能器的高输出阻抗,另一路则作为可调10倍增益的前级放大电路。带通滤波放大器使用LMH6612芯片组成中心频率1.5 MHz、带宽1 MHz的四阶巴特沃斯有源带通滤波电路,同时利用该电路实现30 dB的电压放大,作为后级放大电路。直流偏置电路选用低噪声放大器TL072,其直流基准源由AD9280内置的可调基准电压提供,将回波信号幅值调制为0~2 V以匹配AD9280采样的输入范围。
FPGA控制设计主要分为DDS输出控制和信号采集发送控制,两路并行工作,提升装置整体效率。FPGA系统时钟信号采用数字锁相环(Phase Locked Loop, PLL)进行锁相优化和分倍频处理。通信接收模块接收PC端指令,对装置参数进行控制与调整。本文选用的FPGA芯片具体型号为EP4CE10F17C8,软件设计的控制流程如图3所示。
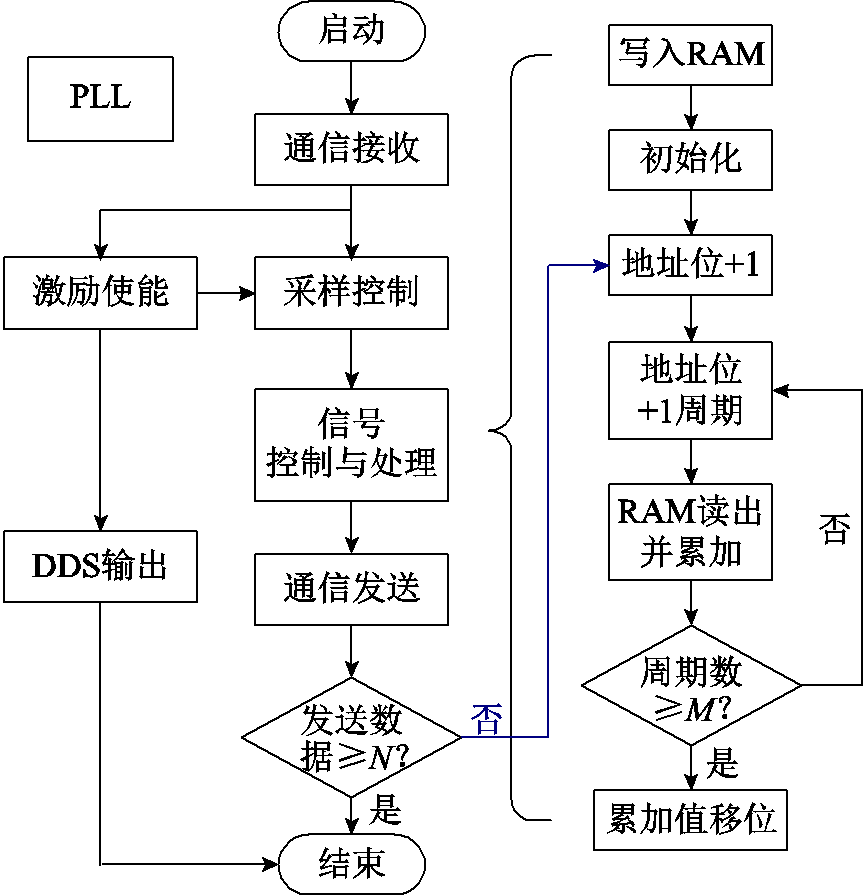
图3 FPGA控制流程
Fig.3 FPGA control flow
激励使能模块接收PC端指令生成预设重复频率的方波脉冲信号,本文预设重复频率为6.67 kHz,在该预设值下能够使得声波在单个重复周期内完成一次完整的管道反射过程。此外,对应的方波脉宽确保DDS模块的输出数据在其脉宽内具有一个完整的波形输出,而周期内其余时刻置零,即实现具有重复频率的激励输出。同时,将激励使能的脉冲上升沿作为单个周期开始时刻的标志信号,且作为采样控制和信号处理的开始时刻。
在DDS模块中,设FPGA系统时钟频率为fs;频率字输入fI,为整数,k为其位宽;设模块输出的频率为fo,满足关系
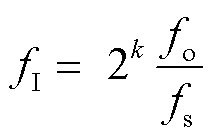 (9)
(9)
对于周期数为n的脉冲信号,频率f为
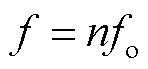 (10)
(10)
因此,调整fI即可设置中心频率f的激励输出。
当装置收到PC端指令且激励使能标志信号有效时,采样控制启动延时,实现对回波信号的时域选取,采集电极回波及周围信号的N个数据点,有效释放FPGA的存储资源,且保证每个重复周期内的采集信号具有一致的时域尺度。信号控制与处理模块将采样得到的共M个时域周期数据缓存至双口RAM中,当RAM写满后,读出每个周期中的相同地址位数据并累加求和,当累加周期数达到预设值M时,移位取其平均值并输出,实现累加平均去噪的功能。最后,通信发送模块将累加平均后的N个数据点经数据传输(USB)发送至PC端,实现与PC端的数据交互。
本文搭建了均压电极垢层厚度声学检测平台搭建如图4所示。其中,水路管道长度为1 m,管道内壁直径为67.8 mm,壁厚为3.6 mm,材质为PVDF,管道内灌满去离子水。均压电极布置在距离管道最左侧0.25 m的中心位置,插入管道的电极针长度为28~30 mm,直径为1.91~1.94 mm。
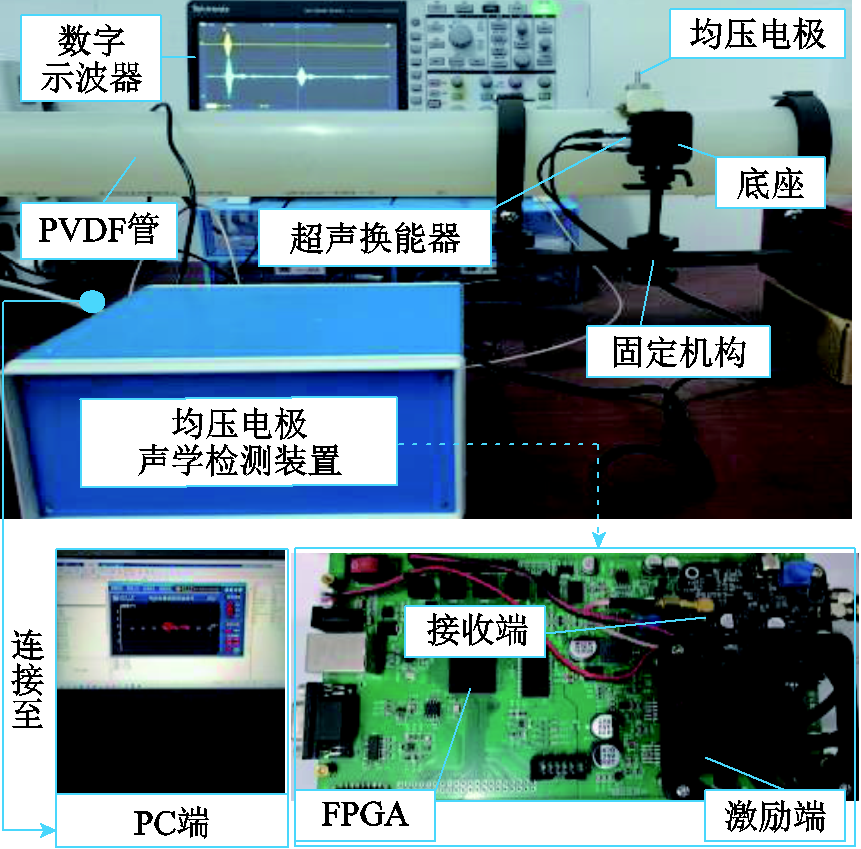
图4 均压电极垢层厚度声学检测平台
Fig.4 Acoustic detection platform for sediment thickness of grading electrode
为最大程度地避免激励端噪声对接收端的影响,实验采用定制的一发一收的双晶压电换能器,其谐振频率为1.5 MHz,晶片尺寸为20 mm。压电换能器安装于固定机构的底座中,通过固定机构可方便地调整和固定换能器的前后、左右、上下位置以及换能器与管壁的贴合角度,提高了检测时探头调整的便利性和一致性。同时,在换能器表面涂抹超声耦合剂(HC-98),保证换能器与管壁的有效贴合和声信号的有效传输。数字示波器用于对装置接收端的前级放大信号进行初步显示,便于确定换能器适宜的贴合位置与角度。本文检测装置参数见表1。
表1 装置参数
Tab.1 Device parameters

参数数值 激励端中心频率f/MHz1.5 重复频率fr/kHz6.67 脉冲波形汉宁窗调制正弦波 脉冲周期数n10 激励峰-峰值Vspp/V36 接收端AD采样率fad/MHz25 累加周期数M8 单周期采样点数N1 024 回波总增益G/dB50
基于实验室已有平台开展电极结垢加速试验,获得了不同垢层厚度的均压电极样品,检测示意图如图5所示。以均压电极的最大结垢厚度作为表征,将样品划分为少垢集、中垢集、多垢集和厚垢集。对少垢集和中垢集各取1组垢厚样本(组Ⅰ和组Ⅱ),多垢集取2组垢厚样本(组Ⅲ和组Ⅳ),厚垢集取3组垢厚样本(组Ⅴ~组Ⅶ)。综上,本次实验共分为7组,记录每组垢层厚度方向上的最大厚度,见表2,同时在对应位置对各组电极进行无垢情况下的检测,作为实验对照。
表2 各组电极垢层最大厚度
Tab.2 Maximum thickness of sediment for each electrode group (单位: mm)

组别最大厚度 组Ⅰ0.10 组Ⅱ0.32
(续)

组别最大厚度 组Ⅲ0.47 组Ⅳ0.58 组Ⅴ0.73 组Ⅵ0.85 组Ⅶ0.98

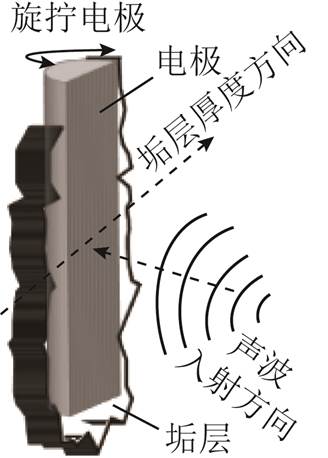
图5 均压电极样品及检测示意图
Fig.5 Sample and detection schematic diagram of grading electrode
图6所示为接入压电换能器后装置产生的激励信号,可见生成的汉宁窗调制正弦脉冲信号稳定且光滑,峰-峰值为35.7 V,无失真现象,符合表1中预期设置,验证了装置激励端的可靠性。
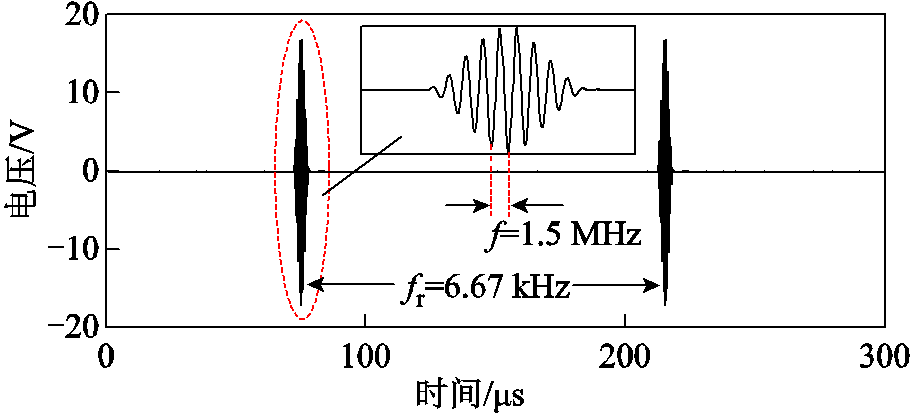
图6 激励信号
Fig.6 Excitation signal
图7所示为对均压电极进行声学检测时装置接收端采集得到的完整周期回波信号(N=3 750)。图中显示的波包可分为四个时域区段:A区为激励原始信号和耦合剂中的反射回波信号;B区为后管壁的二次回波;C区为电极及垢层的回波信号;D区为后管壁一次回波,二次回波由与上周期中的一次回波的时间差确定。与周围时域的其他波包相比,电极及其垢层的回波信号明显,波形清晰,可直观区分,验证了装置接收端的可靠性和本文实验的可行性。
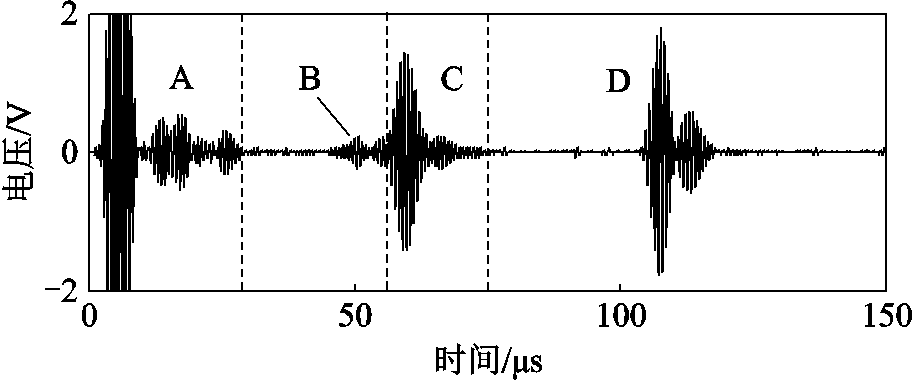
图7 回波信号
Fig.7 Echo signal
在实际换流阀冷却系统工况中,由于存在电磁干扰或其他环境因素,不可避免地会对声检测造成影响。因此,本文通过影响装置各模块间的接线方式及在周围接入其他运行设备,模拟噪声环境,并将降噪前后的B区和C区信号进行对比(N=1 024),如图8所示。
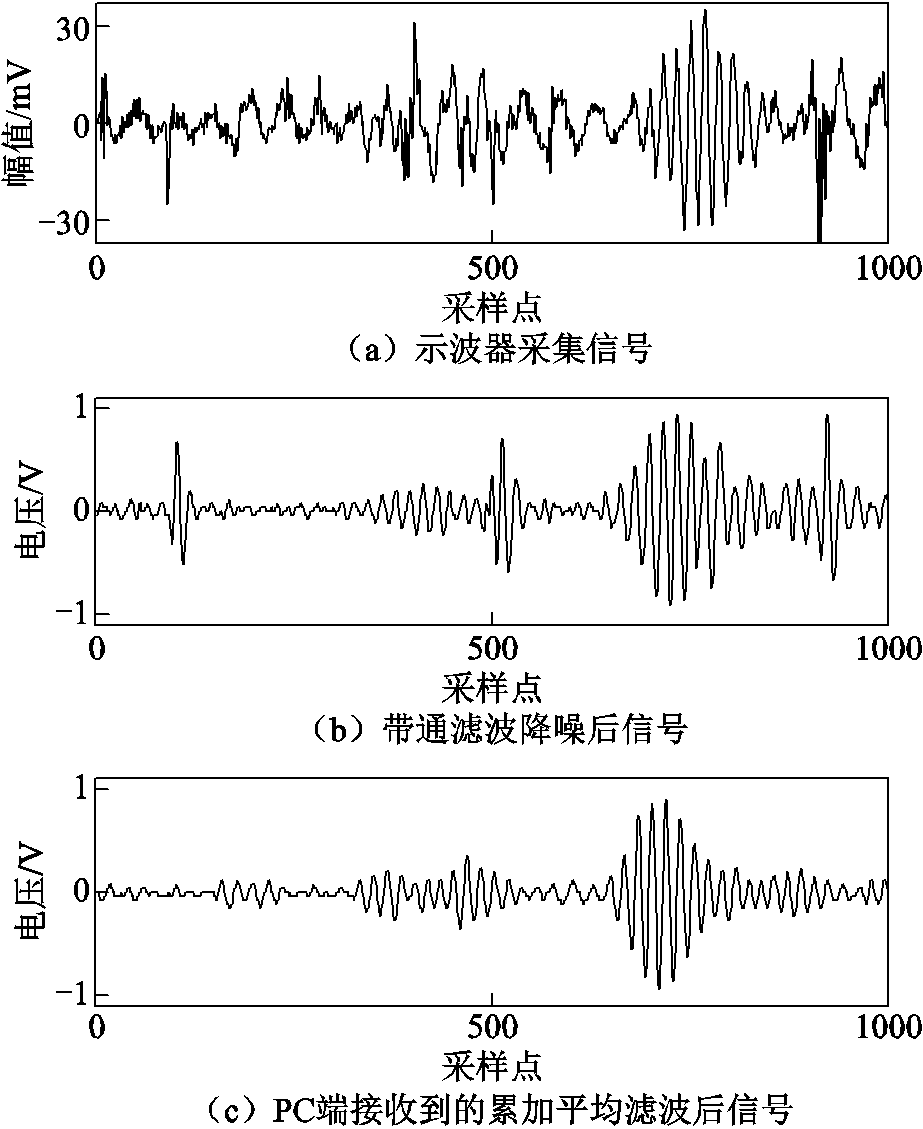
图8 装置降噪前后B区和C区信号
Fig.8 Singnal of B and C domain before and after noise reduction effect of the device
图8a为模拟噪声环境下由示波器直接采集的经接收端前级放大的回波信号,可见回波中存在明显的低频噪声、高频毛刺和随机尖端脉冲,电极回波波包发生严重畸变,而后管壁二次回波由于幅值微弱,已完全湮没在噪声中,难以辨别。经接收端带通滤波电路降噪后的回波信号如图8b所示,可见有效去除了回波中的低频噪声和高频毛刺,且能初步判断后管壁二次回波,较为准确地还原了电极反射波包,但随机尖端脉冲仍旧存在。经由FPGA中8次累加平均滤波后,PC端接收到的信号如图8c所示,随机尖端脉冲已基本滤除,包括后管壁二次回波在内的各波包特征明显,信噪比较高,实现了较强的滤波效果,验证了本文装置在噪声环境中检测的有效性。
图9所示为对表2中各组电极进行声学检测时,PC端接收的声回波信号。值得说明的是,通过调整换能器贴合位置,控制其与管道的贴合切点位于汇流管约中端位置,贴合角度约为5°,此时可有效地增强实验中声波与电极的交互程度,减小甚至消除图7中B区的后管壁二次反射信号,从而在采集范围内得到更为纯净的电极及垢层回波信号。换能器布置方式与对应的回波信号如图9a所示。
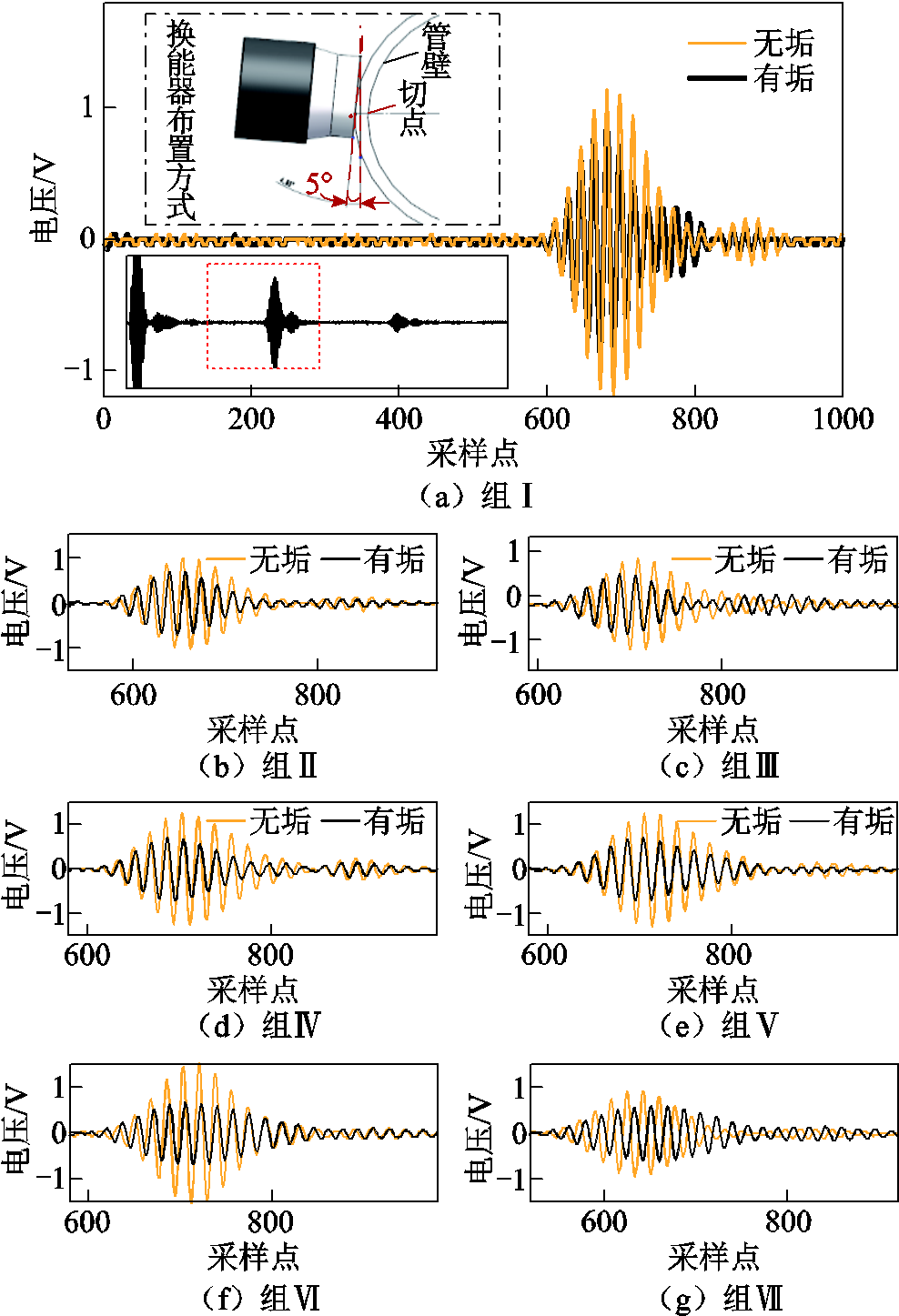
图9 各组电极及垢层的声回波信号
Fig.9 Acoustic echo signals of each electrode and sediment layer
对比图9中各组回波信号可以看出,不同垢层厚度下,无垢与有垢情况下的对应峰值时域差值(横轴)无显著变化趋势,说明回波信号渡越时间(Time Offlight, TOF)难以作为电极垢层检测的特征指标。而各组有垢层情况下的回波信号幅值明显小于无垢情况,验证了垢层相对于电极本身具有更小的声反射系数和更强的声波散射效应,能量衰减程度更大,且信号幅值的减小程度随垢层厚度的增大呈现出先增后减的趋势,这是由于在垢层厚度增大的过程中,声波与垢层的交互面积增大,在声波能量被吸收衰减的同时也伴随着更多的声波能量被反射接收,故当垢层达到一定厚度时,回波信号幅值的减小程度呈减弱趋势。因此,将反映信号能量的幅值指标作为表征垢层厚度的特征指标具有一定的可行性。另外,对各组回波波形进行比较,可以看出,无垢情况下的回波波形与原始激励波形较为接近,振荡周期数较少,分布较为均匀;而在有垢情况下,声波的反射过程复杂,导致各组回波形状发生了不同程度的畸变,主要体现在分布性、波数振荡以及脉冲陡峭程度的变化上。综上分析,本文装置能够有效地反映均压电极垢层厚度的变化情况。
针对装置接收到的回波信号中不同垢层厚度与其无垢层情况下的差异性,本文引入六个时域特征因子指标,具体见表3。其中,A为采样信号;Ai(i=1, 2,…, N)为i点采样信号;Amax为整流最大值;Ā为整流平均值;Arms为方均根值;Ar为方根幅值;σx为标准差。其中,Ā、Arms、Ar及σx的计算公式分别为
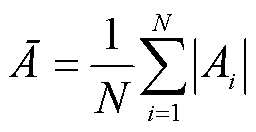 (11)
(11)
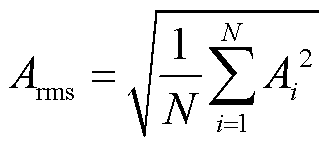 (12)
(12)
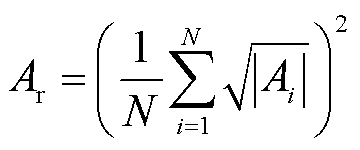 (13)
(13)
表3 特征指标
Tab.3 Characteristic indicators

特征指标公式 波形因子Sf 峰值因子Ip 峭度因子K4 脉冲因子Cf 裕度因子Ce 偏度因子K3
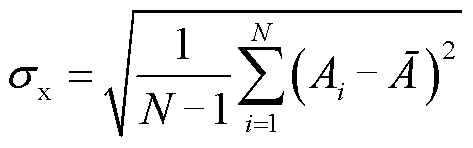 (14)
(14)
Ā、Arms、Ar、σx与峰-峰值Vpp以不同角度皆描述信号的能量情况,具有相似的变化规律;Sf描述声波信号的形状和脉冲特性;Ip描述信号的峰值与平均能量的关系,体现峰值峰谷差异性;Cf和Ce分别描述信号的脉冲特性和幅度分布的尖锐程度;K3和K4分别描述分布的对称性和偏斜情况。基于表3,计算各组无垢情况下的回波信号各特征指标,取重复检测5次下的平均值,见表4。
表4 无垢检测特征值
Tab.4 Characteristic values under sediment-free conditions
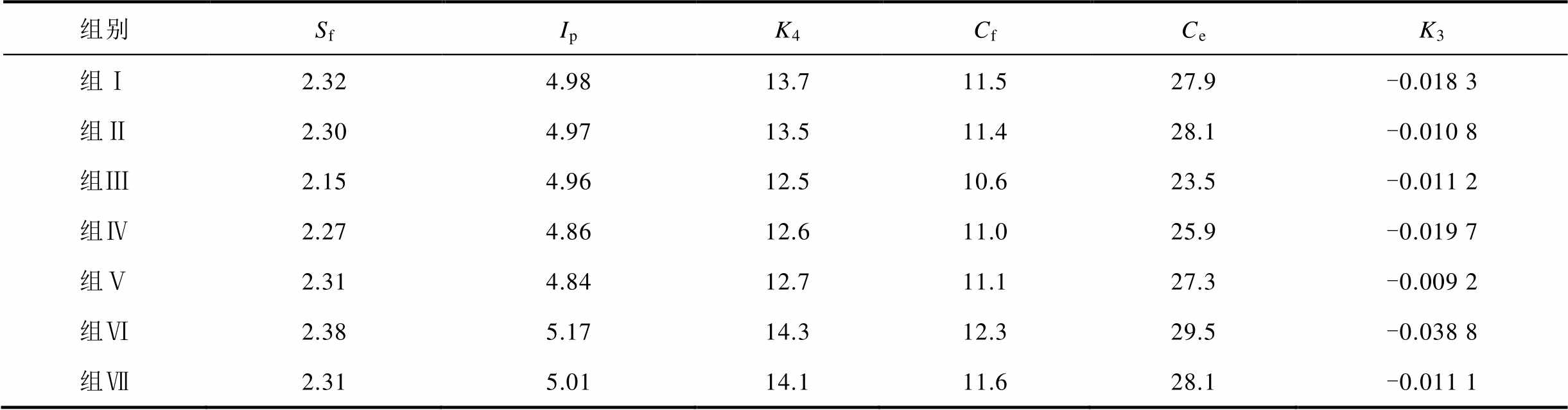
组别SfIpK4CfCeK3 组Ⅰ2.324.9813.711.527.9-0.018 3 组Ⅱ2.304.9713.511.428.1-0.010 8 组Ⅲ2.154.9612.510.623.5-0.011 2 组Ⅳ2.274.8612.611.025.9-0.019 7 组Ⅴ2.314.8412.711.127.3-0.009 2 组Ⅵ2.385.1714.312.329.5-0.038 8 组Ⅶ2.315.0114.111.628.1-0.011 1
为验证各特征指标的稳定性和可靠性,引入变异系数Cv,其可对多组不同量纲的数据集的离散程度进行比较[22]。计算表4中同为无垢情况下的各组电极特征指标的Cv。
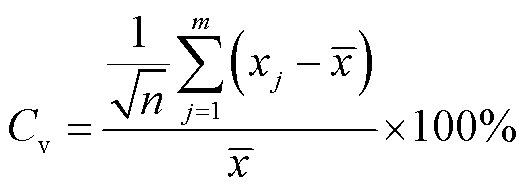 (15)
(15)
式中,m为组数;xj为j组特征值;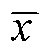 为各组特征值的平均值。同时提取各组回波信号的Vpp进行计算作为对比,结果如图10所示。可见,除偏度因子K3之外,相较于Vpp,其余五个特征指标的变异系数皆小于10%,呈弱变异,反映所用特征指标相比于Vpp具有更好的稳定性和可重复性,能够有效降低不同电极差异对检测结果所带来的影响,验证了本文装置检测结果的可靠性。
为各组特征值的平均值。同时提取各组回波信号的Vpp进行计算作为对比,结果如图10所示。可见,除偏度因子K3之外,相较于Vpp,其余五个特征指标的变异系数皆小于10%,呈弱变异,反映所用特征指标相比于Vpp具有更好的稳定性和可重复性,能够有效降低不同电极差异对检测结果所带来的影响,验证了本文装置检测结果的可靠性。
表5所示为各组有垢情况下重复检测5次的回波特征指标平均值,可以直观地发现,除偏度因子K3外,有垢情况下其余特征指标值皆随着垢层厚度的增大而以不同程度减小。此外,对比表4可得,K3虽波动较大,但在无垢情况下整体小于零;而在有垢情况下整体大于零。以上结果可说明将偏度因子作为有无垢层的定性分析、其余特征指标作为垢层厚度的定量分析的可行性。
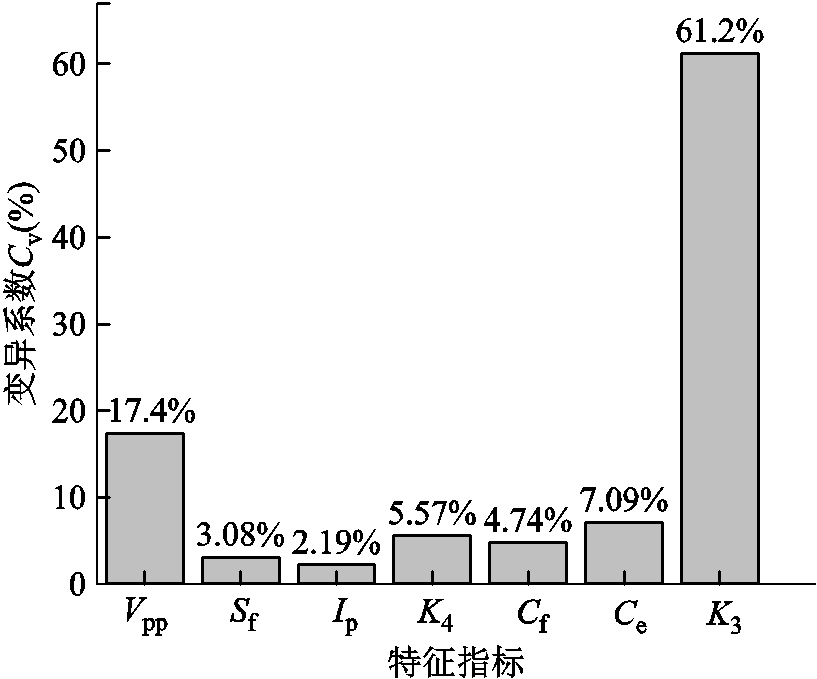
图10 特征指标变异系数
Fig.10 Coefficient of variation of characteristic indexes
表5 有垢检测特征值
Tab.5 Characteristic values under sediment conditions
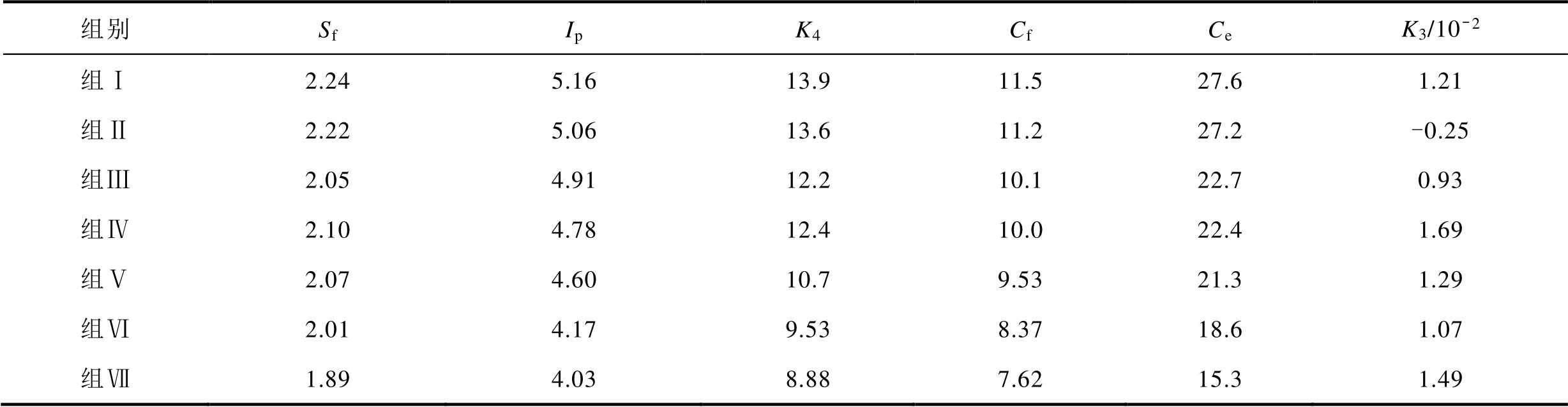
组别SfIpK4CfCeK3/10-2 组Ⅰ2.245.1613.911.527.61.21 组Ⅱ2.225.0613.611.227.2-0.25 组Ⅲ2.054.9112.210.122.70.93 组Ⅳ2.104.7812.410.022.41.69 组Ⅴ2.074.6010.79.5321.31.29 组Ⅵ2.014.179.538.3718.61.07 组Ⅶ1.894.038.887.6215.31.49
图11所示为不同垢层厚度下Sf、Ip、K4、Cf、Ce作为特征指标相较于对应无垢情况下的减小率,以Sf为例,计算公式为
 (16)
(16)
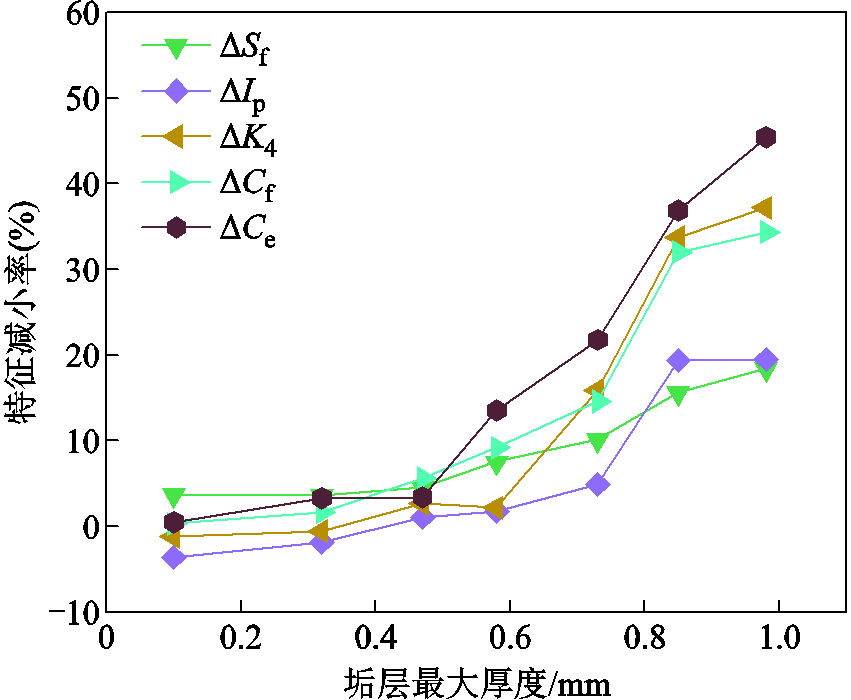
图11 特征指标变化率
Fig.11 Change rate of characteristic indicators
可以发现,特征指标减小率皆随垢层最大厚度呈单调递增性,且在垢层最大厚度小于0.50 mm时,所用特征指标的减小率随厚度的增大而有增大趋势,但较为缓慢;在最大厚度处于0.50~0.85 mm时,减小率迅速增大;而在最大厚度大于0.85 mm后又趋于平缓,即特征指标减小率在整个垢层区间呈“S”形增长。此外,在不同垢层厚度区间各特征指标所反映的灵敏程度存在区别,如当垢层最大厚度小于0.50 mm时,ΔIp和ΔCf的增大趋势较其余指标更为明显;而在垢层最大厚度处于0.50~0.80 mm时,ΔCe和ΔK4则表现出更高的灵敏性;当垢层最大厚度大于0.80 mm时,ΔCe的灵敏性最高,ΔIp的灵敏性最低。综上所述,说明所用声学特征指标能够有效表征均压电极的垢层厚度变化过程,且相较于单一特征指标,采用多个特征指标能够在整个垢层厚度区间提供更加可靠的判断依据,对垢层厚度的定量分析具有实用价值。
Boltzmann函数能够更好地反映数据整体呈“S”形的非线性变化特征[23],建立并运用Boltzmann曲线模型对图11中各特征减小率进行拟合,其函数模型为
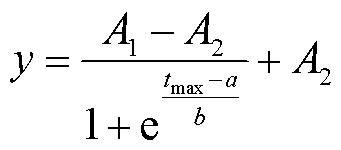 (17)
(17)
式中,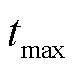 为垢层最大厚度;y为对应
为垢层最大厚度;y为对应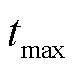 处的特征减小率;A1、A2、a和b为拟合待定系数,其中,A1和A2分别为拟合曲线的最小值和最大值;a为拟合曲线50%,即(A2-A1)/2处对应的垢层最大厚度,此时,y′最大,y″=0,即为拐点(a, (A2-A1)/2);b与拟合曲线拐点处的斜率相关,斜率值为(A2-A1)/(4b)。所得拟合待定系数见表6,可见各特征量的a值为0.76±0.01,稳定性良好,可使用拐点a作为装置垢层厚度阈值评价的有效指标;ΔIp和ΔK4的拐点处斜率表征参数b较小,表明对于拐点处周围的垢层厚度具有更好的特征灵敏性;而ΔCe的A1和A2差值最大,具有更好的整体灵敏性,但分辨精度较低,故可将ΔCe作为垢层厚度的初步评价指标。
处的特征减小率;A1、A2、a和b为拟合待定系数,其中,A1和A2分别为拟合曲线的最小值和最大值;a为拟合曲线50%,即(A2-A1)/2处对应的垢层最大厚度,此时,y′最大,y″=0,即为拐点(a, (A2-A1)/2);b与拟合曲线拐点处的斜率相关,斜率值为(A2-A1)/(4b)。所得拟合待定系数见表6,可见各特征量的a值为0.76±0.01,稳定性良好,可使用拐点a作为装置垢层厚度阈值评价的有效指标;ΔIp和ΔK4的拐点处斜率表征参数b较小,表明对于拐点处周围的垢层厚度具有更好的特征灵敏性;而ΔCe的A1和A2差值最大,具有更好的整体灵敏性,但分辨精度较低,故可将ΔCe作为垢层厚度的初步评价指标。
表6 曲线拟合参数
Tab.6 Curve fitting parameters
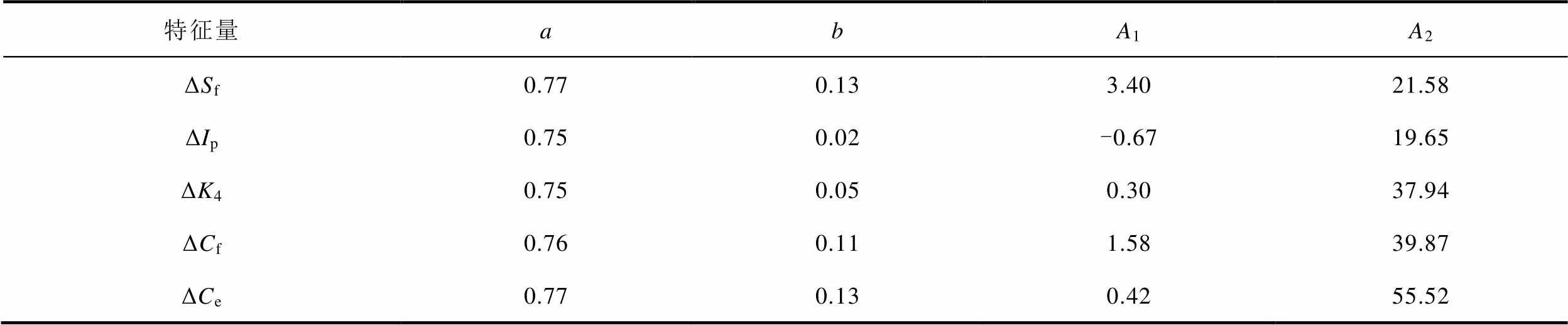
特征量abA1A2 ΔSf0.770.133.4021.58 ΔIp0.750.02-0.6719.65 ΔK40.750.050.3037.94 ΔCf0.760.111.5839.87 ΔCe0.770.130.4255.52
图12为Boltzmann函数拟合结果与实测结果间的对比。可以发现,除ΔIp在t<0.7 mm区间内的拟合效果较差外,其余四个特征量在0~1 mm的垢层厚度区间均有较好的拟合效果,决定系数R2均超过0.96,说明ΔSf、ΔK4、ΔCf和ΔCe与电极垢层厚度存在强相关性,且采用的Boltzmann曲线能够可靠表征电极垢层厚度的变化过程。
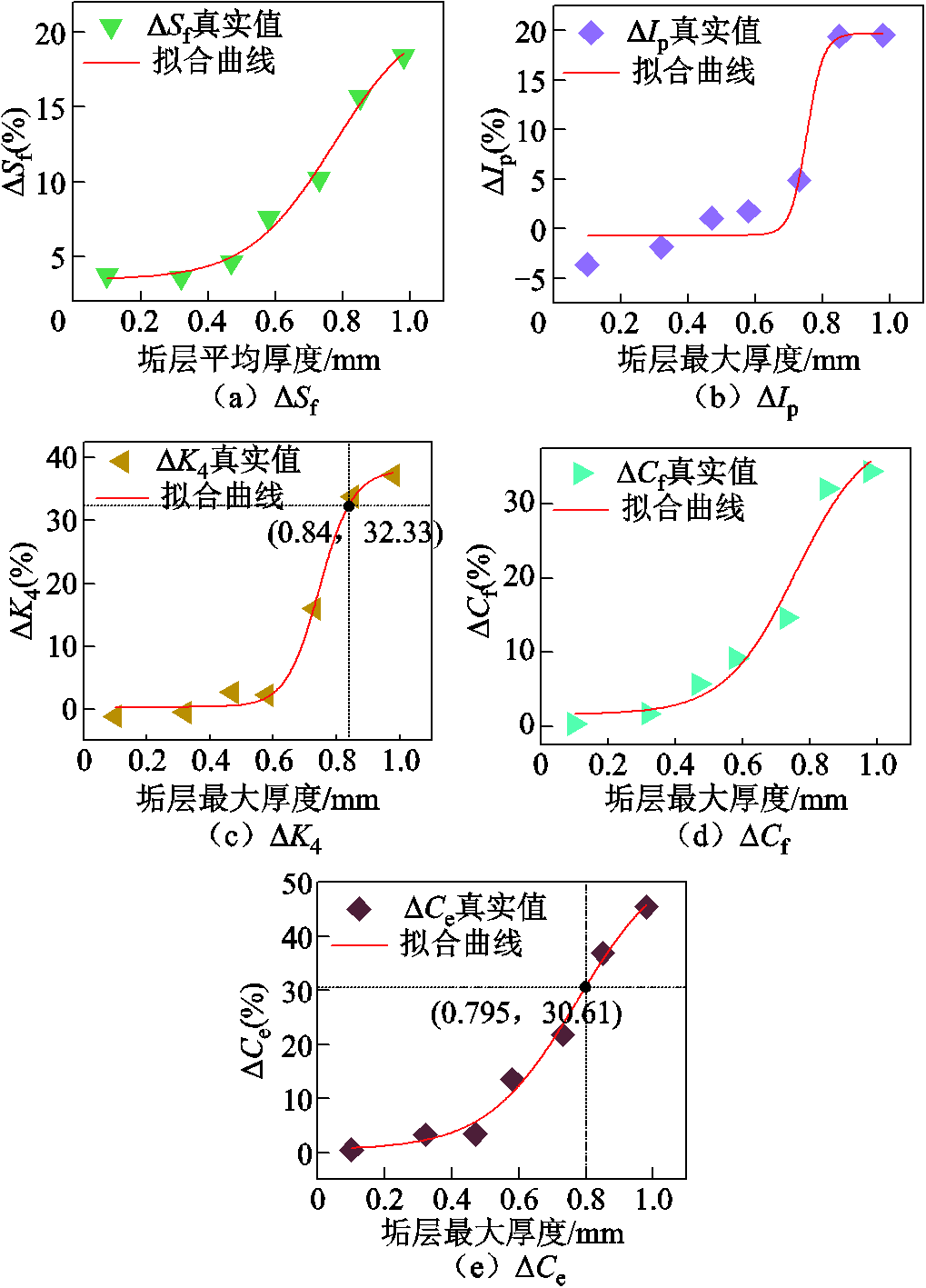
图12 Boltzmann拟合结果
Fig.12 Boltzmann fitting results
基于以上分析,提出一种均压电极垢层厚度预测策略,首先,在对未知结垢程度的均压电极进行检测时,若K3/10-2>-0.5(留有一定裕度),则说明该电极已结垢;其次,将ΔCe值对应式(17)求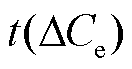 ,将得出三种情况:①若
,将得出三种情况:①若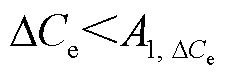 或
或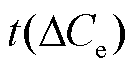 ∈[0, 0.6],则通过ΔCf值对应数学公式(17)求
∈[0, 0.6],则通过ΔCf值对应数学公式(17)求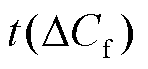 ,若
,若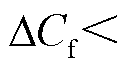
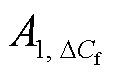 ,则可预测该电极最大结垢厚度t<0.1 mm,反之则所得范围
,则可预测该电极最大结垢厚度t<0.1 mm,反之则所得范围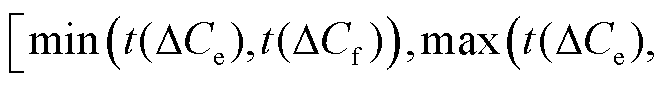
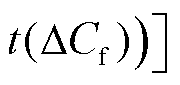 即为最大结垢厚度的最终预测结果;②若
即为最大结垢厚度的最终预测结果;②若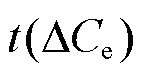 ∈(0.6,0.8],则以ΔK4作为预测指标,预测结果即为
∈(0.6,0.8],则以ΔK4作为预测指标,预测结果即为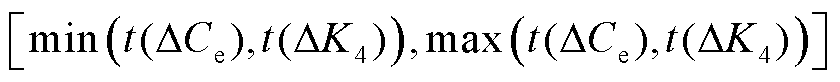 ;③若
;③若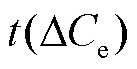 >0.8或
>0.8或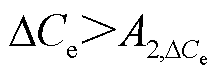 ,过程同理如①。上述具体过程与特征指标的选择依据如图13所示。例如随机对组Ⅵ中的电极进行检测,提取各特征指标,此时K3/10-2=1.58>-0.5,即判定为结垢电极;然后由ΔCe=30.61%,可得出其最大垢层为0.80 mm,处于区间0.6~0.8 mm,故进一步由ΔK4=32.33%得出垢层最大厚度为0.84 mm,故该电极最大结垢厚度的最终预测结果为0.80~0.84 mm,与实验测量结果吻合,从而为均压电极的结垢检修提供指导依据。
,过程同理如①。上述具体过程与特征指标的选择依据如图13所示。例如随机对组Ⅵ中的电极进行检测,提取各特征指标,此时K3/10-2=1.58>-0.5,即判定为结垢电极;然后由ΔCe=30.61%,可得出其最大垢层为0.80 mm,处于区间0.6~0.8 mm,故进一步由ΔK4=32.33%得出垢层最大厚度为0.84 mm,故该电极最大结垢厚度的最终预测结果为0.80~0.84 mm,与实验测量结果吻合,从而为均压电极的结垢检修提供指导依据。
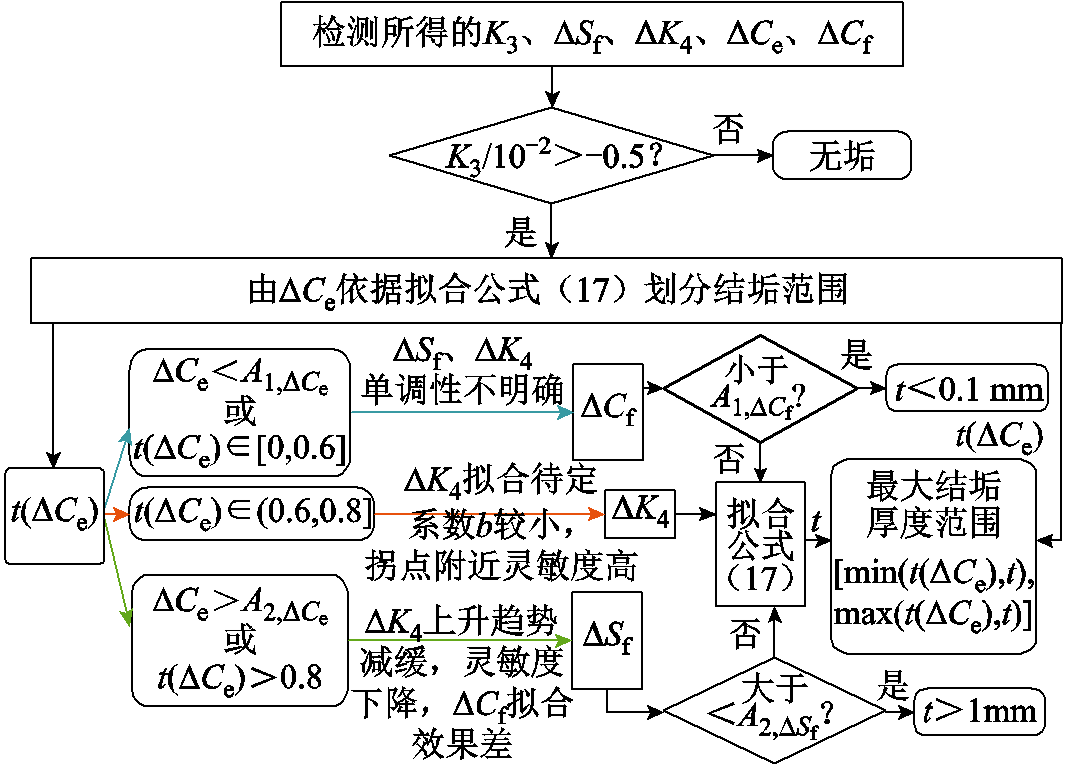
图13 均压电极垢层厚度预测策略
Fig.13 Prediction strategy of sediment of grading electrode
1)本文装置以FPGA为核心,实现声波信号的激励、接收与通信。测试结果表明,装置可有效驱动换能器并接收电极及其垢层的回波信号,且在噪声环境中表现出优异的抗干扰性能,可靠滤除低频噪声、高频毛刺和随机尖端脉冲等噪声信号,得到纯净的电极及垢层回波信号,该装置操作简易、便携性能优异,在阀冷系统实际工况检测中具有良好的应用潜力。
2)以Sf、Ip、K4、Cf、Ce作为特征指标时,对不同电极无垢情况下进行检测时的各指标变异系数均小于10%,具有良好的稳定性和可重复性,且在有垢情况下各指标值随垢层厚度的增大而单调递减;K3在无垢情况下整体为负值,有垢情况下整体为正值。可将K3作为有无垢层的定性分析,其余五个特征指标作为垢层厚度的定量分析。
3)ΔSf、ΔK4、ΔCf和ΔCe与均压电极垢层厚度存在强相关性,其Boltzmann拟合函数能够可靠表征电极垢层厚度的变化过程;基于特征量与垢层厚度的灵敏性关系,提出了均压电极垢层厚度预测策略,能有效预测电极不同结垢阶段中的垢层厚度。
参考文献
[1] Fang Su, Wang Hongtao, Luo Wei, et al. Operational performance of the valve cooling system in Guangzhou converter station[C]//11th IET International Conference on AC and DC Power Transmission, Birmingham, UK, 2015, DOI:10.1049/cp.2015.0092.
[2] 贺婷婷, 高兵, 杨帆, 等. 电-流-传质场作用下的换流阀冷却系统均压电极垢层动态沉积特性研究[J]. 电工技术学报, 2019, 34(14): 2863-2873.
He Tingting, Gao Bing, Yang Fan, et al. The dynamic deposition behavior of grading electrode in converter valve cooling system considering electro-velocity-mass transfer field[J]. Transactions of China Electro-technical Society, 2019, 34(14): 2863-2873.
[3] Wang Xianrong, Liu Xuezhong, Wang Chenxing, et al. Numerical calculation of current through grading electrodes in inner cooling circuit of HV converter valve[C]//2015 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 2015: 411-414.
[4] Gao Bing, He Tingting, Yang Fan, et al. Investigation on deposition behavior of HVDC water cooling system based on electro-mass transfer-velocity coupling model[J]. IEEE Access, 2019, 7: 67960-67971.
[5] 赵文亮, 闫爱军, 付纪华, 等. 高压直流输电换流阀内冷水水质控制指标研究[J]. 陕西电力, 2014, 42(8): 76-81.
Zhao Wenliang, Yan Aijun, Fu Jihua, et al. Study on quality control index of inner cooling water of HVDC converter valve[J]. Shaanxi Electric Power, 2014, 42(8): 76-81.
[6] Qian Yi hua, Zhou Yong yan, Xu Chong wu. Research on the formation and preventive measure of scale in the cooling system of HVDC converter valve[J]. Advanced Materials Research, 2011, 354/355: 1157-1160.
[7] 杨帆, 贺婷婷, 高兵, 等. 基于垢层动态沉积模型的阀冷系统电极均压能力评估方法[J]. 电力自动化设备, 2020, 40(7): 188-197.
Yang Fan, He Tingting, Gao Bing, et al. Evaluation method of voltage-equalizing ability of electrodes in valve cooling system based on sediment dynamic deposition model[J]. Electric Power Automation Equipment, 2020, 40(7): 188-197.
[8] Hynynen K, Jones R M. Image-guided ultrasound phased arrays are a disruptive technology for non-invasive therapy[J]. Physics in Medicine and Biology, 2016, 61(17): R206-R248.
[9] 刘素贞, 张严伟, 张闯, 等. 电磁超声管道周向兰姆波仿真分析及缺陷检测特性研究[J]. 电工技术学报, 2017, 32(22): 144-151.
Liu Suzhen, Zhang Yanwei, Zhang Chuang, et al. Research on simulation analysis of electromagnetic ultrasonic circumferential lamb waves and defect feature detection in pipeline[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 144-151.
[10] Li Xia, Sun Lingfang, Li Jing, et al. Method for acquiring time of flight from high aliasing signal in heat exchange fouling ultrasonic testing[J]. Tran-sactions of the Institute of Measurement and Control, 2021, 43(11): 2438-2449.
[11] 刘素贞, 陈云龙, 张闯, 等. 融合多维超声时频域特征的锂离子电池荷电状态估计[J]. 电工技术学报, 2023, 38(17): 4539-4550, 4563.
Liu Suzhen, Chen Yunlong, Zhang Chuang, et al. State of charge estimation of lithium-ion batteries fused with multi-dimensional ultrasonic time-frequency domain features[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4539-4550, 4563.
[12] 陈伟华, 万晨, 闫孝姮, 等. 基于RWSSA-OMP- DBN的均压电极结垢超声检测[J]. 传感技术学报, 2022, 35(2): 154-161.
Chen Weihua, Wan Chen, Yan Xiaoheng, et al. Ultrasonic detection of scaling of equalizing electrode based on RWSSA-OMP-DBN[J]. Chinese Journal of Sensors and Actuators, 2022, 35(2): 154-161.
[13] 闫孝姮, 光思辰, 胡宇, 等. 换流阀冷却系统均压电极结垢超声导波检测方法研究[J]. 仪器仪表学报, 2021, 42(10): 251-263.
Yan Xiaoheng, Guang Sichen, Hu Yu, et al. Investigation of ultrasonic guided wave mode conversion characteristics in grading electrodes sediments detection of the HVDC converter valve cooling system[J]. Chinese Journal of Scientific Instrument, 2021, 42(10): 251-263.
[14] 卢世才, 李道豫, 王行飞, 等. 高压直流换流阀内水冷系统致垢离子带电特性[J]. 南方电网技术, 2021, 15(8): 64-70.
Lu Shicai, Li Daoyu, Wang Xingfei, et al. Charged property of sediment-forming ions in inner cooling system for HVDC converter valves[J]. Southern Power System Technology, 2021, 15(8): 64-70.
[15] 李通, 刘鹏龙, 李宁瑞, 等. 垢层动态膜阻对换流阀冷却系统内均压电极动态沉积特性影响机理研究[J]. 电工技术学报, 2023, 38(7): 1695-1704.
Li Tong, Liu Penglong, Li Ningrui, et al. Study on the influence of the dynamic film resistance of scale layer on the dynamic deposition characteristics of grading electrodes in inner cooling system of converter calve[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1695-1704.
[16] Majasan J O, Robinson J B, Owen R E, et al. Recent advances in acoustic diagnostics for electrochemical power systems[J]. Journal of Physics: Energy, 2021, 3(3): 032011.
[17] Robinson J B, Pham M, Kok M D R, et al. Examining the cycling behaviour of Li-ion batteries using ultrasonic time-of-flight measurements[J]. Journal of Power Sources, 2019, 444: 227318.
[18] Smith R L. The effect of grain size distribution on the frequency dependence of the ultrasonic attenuation in polycrystalline materials[J]. Ultrasonics, 1982, 20(5): 211-214.
[19] 刘云鹏, 费烨, 陈江波, 等. 特高压GIL故障定位超声衰减特性及试验研究[J]. 电网技术, 2020, 44(8): 3186-3192.
Liu Yunpeng, Fei Ye, Chen Jiangbo, et al. Ultrasonic attenuation characteristics and its experimental research for UHV GIL fault location[J]. Power System Technology, 2020, 44(8): 3186-3192.
[20] 汤庆国, 王丽娟, 梁金生, 等. 水垢晶体的形成及变化规律研究[J]. 人工晶体学报, 2009, 38(3): 602-607.
Tang Qingguo, Wang Lijuan, Liang Jinsheng, et al. Study on the formation process and transformation of fouling crystal[J]. Journal of Synthetic Crystals, 2009, 38(3): 602-607.
[21] Zhang Sida, Guo Chenjun, Cheng Li, et al. Testing method for composite insulators interface based on nonlinear ultrasonic[J]. IEEE Access, 2019, 7: 83111-83119.
[22] 张知先, 陈伟根, 汤思蕊, 等. 基于互补集总经验模态分解和局部异常因子的有载分接开关状态特征提取及异常状态诊断[J]. 电工技术学报, 2019, 34(21): 4508-4518.
Zhang Zhixian, Chen Weigen, Tang Sirui, et al. State feature extraction and anomaly diagnosis of on-load tap-changer based on complementary ensemble empirical mode decomposition and local outlier factor[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4508-4518.
[23] Lu Quan, Zhang Zehao, Zhang Weiping, et al. Point spread function model of grating imaging system based on Boltzmann function edge fitting[J]. Acta Optica Sinica, 2020, 40(14): 1405003.
Abstract Sediment on grading electrodes is one of the main causes of failures in converter valve cooling systems. Traditional maintenance methods mainly involve periodic disassembly and inspection, which are quite blind and can lead to issues such as system leaks from repeated disassembly, severely delaying the maintenance progress of the converter valve system. Most existing research relies on water quality monitoring or other indirect detection methods, which cannot directly reflect the sediment situation. Acoustic detection, however, offers advantages such as high sensitivity, fast detection speed, and strong versatility. Therefore, this paper proposes an acoustic detection method for sediment on grading electrodes in converter valve cooling systems.
Firstly, based on the principles of acoustic detection for grading electrode sediment, an acoustic detection device was designed. This device achieves synchronized control of the sound wave excitation and reception ends, utilizes cumulative averaging for noise reduction in digital signal processing, and transmits the echo signals to a PC for feature extraction and analysis. Secondly, an acoustic detection platform for grading electrode sediment was built. This platform verifies that the designed device can effectively drive the transducer and receive echo signals from the grading electrode and its sediment. It also tests the device's interference resistance in noisy environments, confirming its ability to reliably filter out low-frequency noise, high-frequency spurious signals, and random spikes, thus obtaining clean echo signals. The platform was used to perform acoustic detection on seven groups of grading electrodes with different sediment thicknesses, analyzing the differences in echo signals under sedimented and non-sedimented conditions.
Further, using waveform factors (Sf), peak factors (Ip), kurtosis factors (K4), pulse factors (Cf), peak factors (Ce), and skewness factors (K3) as characteristic indicators for echo signals, it was found that Sf, Ip, K4, Cf and Ce had a coefficient of variation of less than 10% in the non-sedimented condition, indicating good stability. In the presence of sediment, these factors decreased with increasing sediment thickness, while K3 was generally negative without sediment and positive with sediment. Finally, by calculating the variation rates of echo feature values in relation to the non-sedimented conditions, it was found that ΔSf, ΔK4, ΔCf and ΔCe had a strong correlation with the sediment thickness, with the Boltzmann fitting function's determination coefficients (R²) exceeding 0.96, indicating that these measures can reliably characterize changes in electrode sediment thickness. Based on the sensitivity relationship between feature quantities and sediment thickness, a prediction strategy for sediment thickness was proposed, effectively predicting sediment thickness at different stages of sediment.
From the experimental analysis, the following conclusions can be drawn: (1) The designed acoustic detection device for grading electrodes can detect sediment and has advantages of strong portability and interference resistance, showing good application potential in practical valve cooling system inspections. (2) Among the used characteristic indicators, K3 can be used for qualitative analysis of sediment presence, while Sf, Ip, K4, Cf and Ce are suitable for quantitative analysis of sediment thickness. (3) ΔSf, ΔK4, ΔCf and ΔCe show a strong correlation with the sediment thickness, and the Boltzmann fitting function effectively characterizes the thickness change process, providing guidance for the maintenance of grading electrodes.
keywords:Converter valve cooling system, grading electrode, sediment thickness, acoustic detection, characteristic indicators
中图分类号:TM721.1
DOI: 10.19595/j.cnki.1000-6753.tces.231208
国家自然科学基金资助项目(52007013)。
收稿日期 2023-07-05
改稿日期 2024-01-22
高 兵 男,1987年生,副教授,博士生导师,研究方向为多物理场计算和电声换能技术等。E-mail:gbdnbh@hnu.edu.cn
黄 驰 男,2000年生,硕士研究生,研究方向为输变电设备数字孪生技术与无损检测技术。E-mail:951190519@qq.com(通信作者)
(编辑 郭丽军)