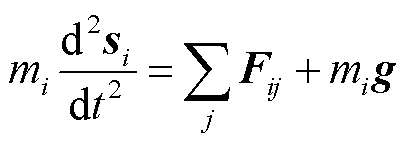 (1)
(1)
摘要 针对目前软磁复合材料(SMC)制造前磁特性预测无法计及颗粒属性和制备参数而导致磁导率和涡流损耗等磁特性评估结果存在偏差的问题,该文提出将离散元(DE)与有限元(FE)相结合的新型SMC材料磁特性预测方法。基于三维DEM研究了颗粒形状、粒径及其分布对SMC样品微观结构的影响,给出DEM模型中最适颗粒参数。为解决所建立的微观尺度SMC材料FE模型求解带来的计算量大的问题,提出一种均质化等效几何模型构建方法。以相对密度为桥梁构建SMC均质化等效FE模型,进而实现对磁导率和涡流损耗的预测评估。最后,利用直流磁化法和环样法分别测量了SMC试样的磁导率和损耗,通过实验与预测结果进行对比分析,验证所提出的磁特性预测方法的可靠性。
关键词:软磁复合材料 颗粒属性 离散元 磁特性
随着全球经济不断深化、科技水平不断提高,现代工业生产逐步由“大而全”向“定制化”“集约化”方向转变。现代电工装备朝向高品质化、差异化方向发展,对电工材料物性参数的独特性需求日益增强[1-3]。
软磁复合材料(Soft Magnetic Composites, SMC)是把铁粉等软磁材料粉末经过表面绝缘处理,再通过粉末冶金工艺制备而成[4],可灵活调整制备工艺参数以满足各类电磁器件,如传感器、电抗器以及电机磁心等应用场景对磁特性的差异化要求[5-7]。与其他磁性材料不同,SMC材料的磁特性既与制备工艺参数,如压制力和退火参数等有关,又与铁磁粉末颗粒属性,如材质、形状、粒径及其分布等有关[8-9]。
关于颗粒属性对SMC材料物性参数的影响,学者们已经开展了相关实验研究[10-12]。研究结果表明,合适的颗粒粒径和形状可以改善软磁复合材料产品的机械强度和磁性能[13-14],且大部分铁磁粉末的尺寸在自然状态下呈正态分布。
目前,SMC材料开发仍然采用以试制-测试-对比-优化为主的方法,通过大量制备试验试错以获得不同参数对材料特性的影响,这不仅增加了试验成本而且需要较长的研发周期。因此,需要一种数值方法模拟SMC的制备过程,预测SMC的磁特性,进而辅助SMC新材料的快速开发。这是提高材料研发效率、降低试验成本的一条可能的解决途径。
传统的磁特性预测方法如三维磁路法[13]、划分单元体法[14]和Ollendorff formula法[15]等能够分析SMC的磁特性,且可以获得颗粒对磁性能影响的规律性认识,但是这些方法无法考虑颗粒形状非均匀性、颗粒间的磁-电接触和孔隙率等因素的影响。 J. Vesa 等[16]利用Voronoi镶嵌法构建了生成SMC微观结构的立方单元模型用于评估SMC的磁特性,虽然能够模拟SMC微观非均匀性,但仍无法考虑粒径分布的影响。
A. Maruo等[17]采用二维离散元(Discrete Element Method, DEM)和有限元(Finite Element Method, FEM)相结合的方法,计算了涡流损耗,分析了SMC内部的磁感应强度分布,发现DEM可以模拟颗粒间的接触,并且讨论了采用该方法得到的二维SMC模型的频率特性,由于SMC材料制成的磁心具有三维磁路结构,因此采用二维DEM模型模拟存在一定的误差。H. Sato等[18]将二维DEM-FEM拓展到了三维,采用球形模拟实际SMC颗粒,比较了磁路法、FEM和DEM-FEM的求解精度,发现DEM-FEM法的计算结果接近实验结果且减少了大量的实验试错成本。此外,DEM-FEM法的优点还在于可以很容易地计及粒径分布和颗粒之间可能的接触影响,但对SMC粉末形状的不规则性和粒径尺寸尚无法考虑。Shi Kaimeng等[19]使用三维DEM-FEM法构建的SMC模型考虑了微观结构中的孔隙和颗粒间隙,模型评估了SMC在不同压制力下的非线性磁性能,计算的等效磁导率与实验结果吻合得较好。该方法虽然与传统模型相比更接近材料真实的非均匀的微观结构,然而复杂的模型意味着更密集的网格,进而带来了沉重的计算负担。
基于此,本文提出了一种基于DEM-FEM的SMC磁导率和涡流损耗评估方法,同时考虑了颗粒属性和制备工艺参数的影响,提高了预制备材料磁特性的预测精度。在DEM建模中,讨论了SMC颗粒模型形状以及粒径分布模型的选择问题。以材料相对密度为桥梁提出了建立SMC均质化等效FE模型的方法,在保证磁特性预测精度的同时降低了有限元求解的负担,并给出了模型参数的参考值。
DEM是一种处理非连续介质问题的数值模拟方法,其理论基础是结合不同本构关系的牛顿第二定律,采用动态松弛法求解方程。该方法能够应用于粉末冶金、颗粒研磨、混合搅拌等多个领域,同时考虑颗粒间相互接触作用的影响,分析离散颗粒间的运动过程。
在DEM中,对颗粒运动进行动态分析,基于牛顿第二定律,第i个颗粒满足的动力学方程为[20]
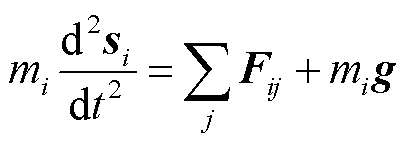 (1)
(1)
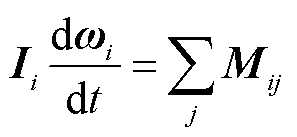 (2)
(2)
式中,si、mi、g、Ii、ωi、Mij、Fij分别为第i个颗粒的位移、质量、重力加速度、转动惯量、角速度,以及第i个和第j个颗粒之间由于接触而产生的相互作用力矩和力。
为研究SMC 材料颗粒属性的影响,在DEM模型中分别设置粒径分布服从正态分布、均匀分布以及等粒径分布,颗粒形状设置为球形(由离散元中单个球形颗粒组成)、长方形(由离散元中两个球形颗粒堆叠组成)和三棱柱(由离散元中三个球形颗粒堆叠组成),粒径尺寸设置为7001P(375 μm)和5001P(150 μm)。
在DEM分析中,初始化10 mm×10 mm×25 mm空间内随机生成4 000个给定属性的颗粒群,引入一个作直线运动的平板来压制颗粒群以模拟SMC的压制过程。粒径分布参数见表1。
表1 粒径分布参数
Tab.1 Parameters of particle size distribution

粒径分布参数范围 正态分布粒径取值1 d(d为颗粒直径) 标准差0.36 d [18] 等粒径分布粒径取值1 d 均匀分布1粒径取值0.5 d~1.5 d 均匀分布2粒径取值0.7 d~1.3 d
经过106个时间步,步长设置为10−5 s,平板以1.5 mm/s匀速运动10 s后停止。当平板和所有的颗粒都停止运动后,分析平板压力数值随时步变化的曲线,提取预设压力值所对应的时间点,导出对应时刻的压制SMC块体模型,模拟SMC制备过程完毕,制备过程如图1所示。
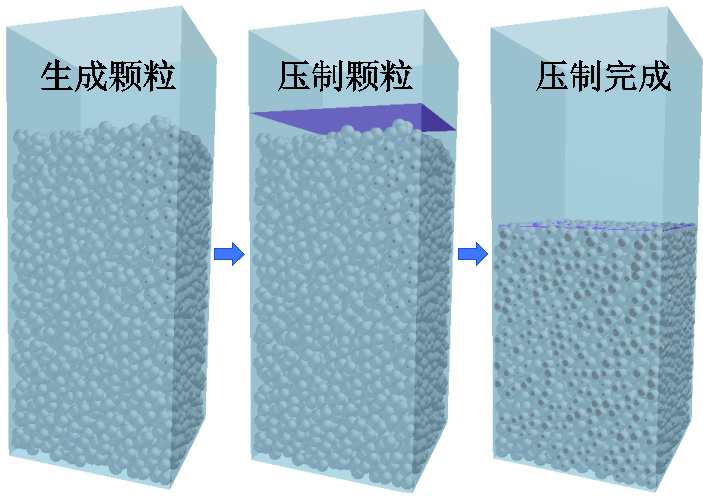
图1 DEM模拟SMC的制备过程
Fig.1 DEM simulation of SMC preparation process
SMC块体中颗粒间的重叠和孔隙能够近似模拟实际SMC材料的微观形态,选取其中两组块体模型进行比较,SMC的DE模型与微观结构如图2所示。可见,设置不同颗粒属性后,压制后的材料模型微观结构不同。为了确定模拟压制过程中的最优颗粒参数组合,以压制后的SMC块体密度作为衡量标准。两种粒径尺寸不同颗粒参数的压制密度统计结果如图3所示。从统计结果可知,当颗粒形状为三棱柱、粒径分布设置为正态分布时,模拟压制的块体质量密度与实际块体的质量密度最接近。因此,将该颗粒参数选为SMC制备模拟的最优参数。
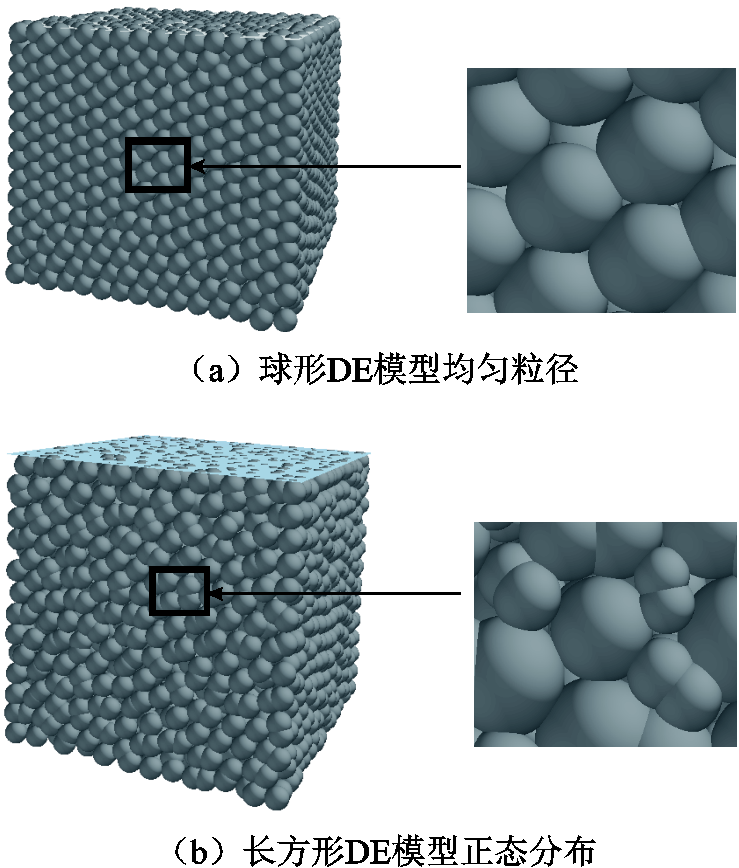
图2 SMC的DE模型与微观结构
Fig.2 DE model and microstructurefor SMC
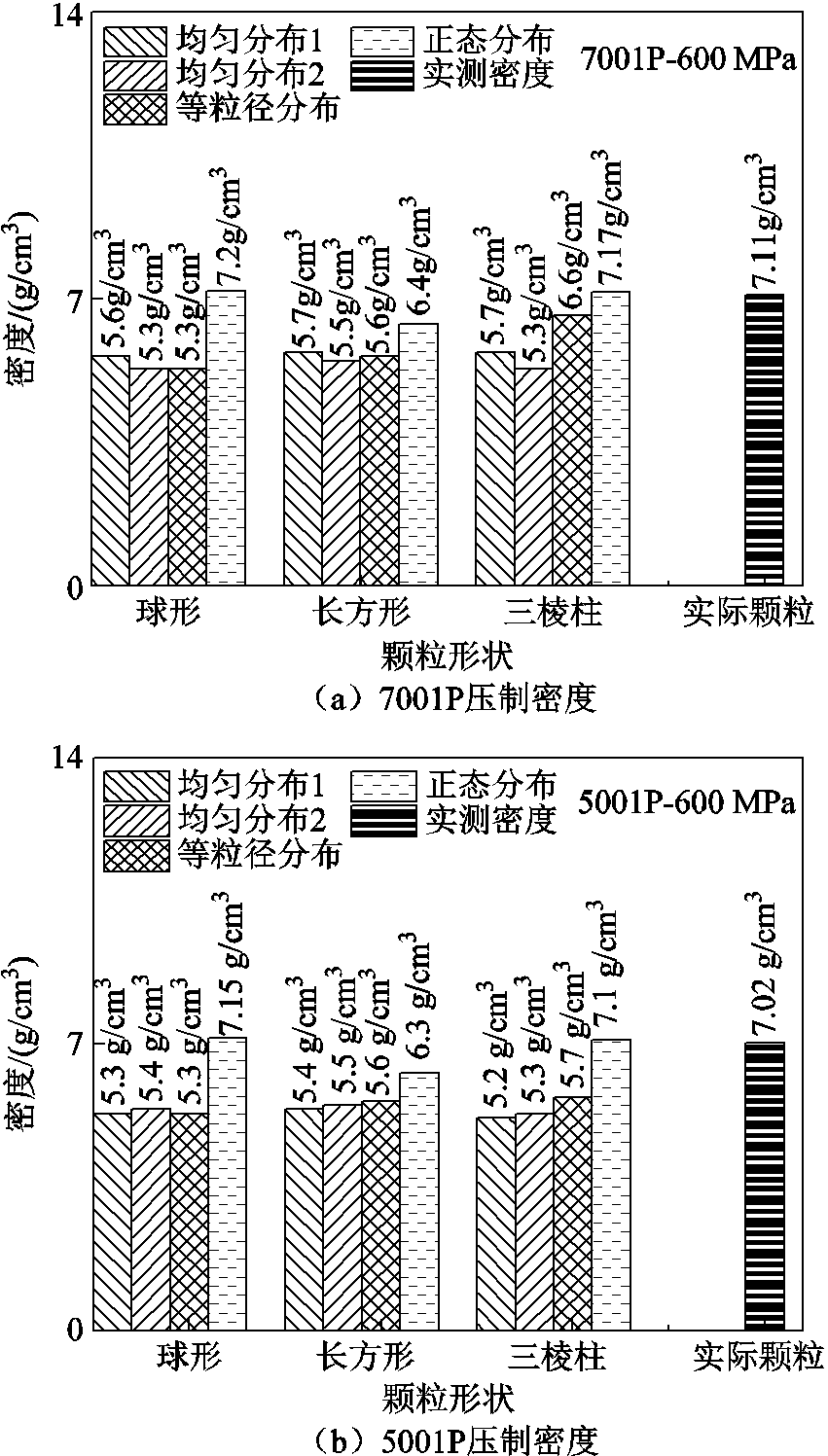
图3 DEM模型压制密度统计结果
Fig.3 Compressing density results for DEM models
SMC材料的磁特性预测采用FEM。首先基于三维DEM的模拟结果建立对应的均质化等效FE几何模型。由于粉末粒径是μm级,若按照实际颗粒形状和尺寸建立FE模型,求解将十分困难,而且颗粒间重叠,因而存在大量交界面,网格数量甚多导致巨大的计算负担,甚至难以完成计算。为解决这一问题,提出一种SMC均质化等效FE模型构建方法,在减少计算成本的同时保证磁特性预测精度。
复合材料的磁特性与其密度密切相关[21],根据1.2节的分析结果,在DEM分析中设定颗粒形状为三棱柱时,模拟计算的材料密度接近实际值。因此,在FE模型中继续采用三棱柱颗粒建立材料均质化等效模型,模型示意图如图4所示。建立边长为 1 mm的立方体作为FE模型的求解域,首先,将M3个小立方体颗粒均匀填充在该求解域内(M为小立方体的单边颗粒数量),然后,沿着小立方体对角线切割形成两个三棱柱形状的颗粒单元,颗粒尺寸计算公式如式(3)~式(6)所示。颗粒间的间隙大小通过相对密度计算,以模拟实际SMC材料微观结构中的孔隙和绝缘层。
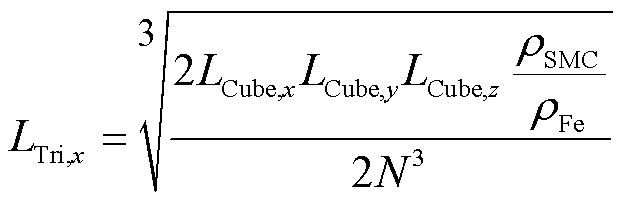 (3)
(3)

图4 均质化等效FE模型的示意图
Fig.4 Schematic of a homogenization FE model
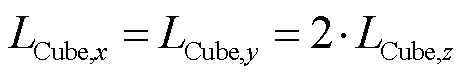 (4)
(4)
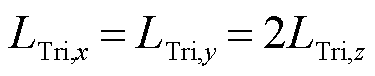 (5)
(5)
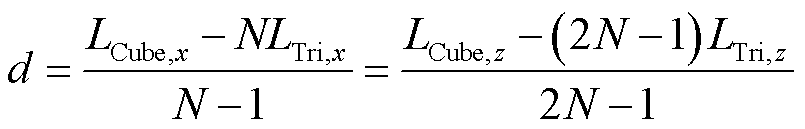 (6)
(6)
式中, 、
、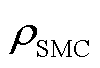 、
、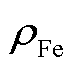 、
、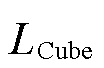 、N、d分别为三棱柱边长、SMC的质量密度、铁的质量密度、立方体边长、三棱柱单边颗粒数量、颗粒间的间隙。
、N、d分别为三棱柱边长、SMC的质量密度、铁的质量密度、立方体边长、三棱柱单边颗粒数量、颗粒间的间隙。
通过以上方法构建的SMC均质化FE等效模型,N=2M,孔隙和绝缘层厚度随模型中包含的颗粒数量N3变化而变化,颗粒数量越多则有限元的计算量越大。综合考虑计算成本,本文N取值范围为6~40。
SMC均质化等效FE模型构建完成后,需要赋予相应的材料属性,模型颗粒赋值铁粉的非线性磁导率,间隙设置为空气,相对磁导率取μr=1。采用静磁场求解器计算均质化等效FE模型的直流磁特性。通过调节边界处磁场强度的大小得到平均磁感应强度Bavg分别为0.5 T、1.0 T和1.5 T。采用时谐场求解计算均质化等效FE模型的涡流损耗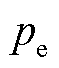 。式(7)~式(9)为Bavg的计算式,式(10)为
。式(7)~式(9)为Bavg的计算式,式(10)为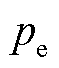 的计算式。
的计算式。
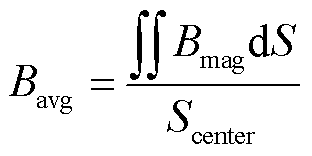 (7)
(7)
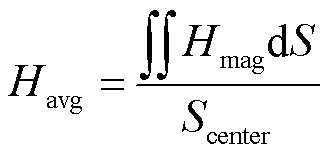 (8)
(8)
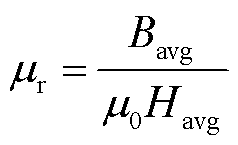 (9)
(9)
 (10)
(10)
式中,Scenter、Bmag、Hmag、μ0、J、V、σ为中心截面的面积、磁感应强度幅值、磁场强度幅值、真空磁导率、电流密度、FE模型的体积、铁的电导率;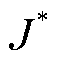 为J的共轭。
为J的共轭。
使用Höganäs公司生产的Somaloy 7001P(375 μm)和Somaloy 5001P(150 μm)绝缘铁粉,通过添加粘结剂、润滑剂并使用液压机按照粉末冶金工艺流程制备了压制力为600 MPa的圆柱形和环形样品,并使用真空管式炉对样品进行退火处理。制备流程和样品如图5所示,制备材料参数见表2。

图5 SMC制备过程与样品
Fig.5 Preparation process and samples for SMC
表2 制备SMC材料参数
Tab.2 Material parameters for the preparation of SMC

项目材质数值 SMC粉末7001P和5001P粒径为375 μm和150 μm 粘结剂Na2SiO3溶胶每100 g粉未加1 mL粘结剂 润滑剂硬脂酸锌每100 g粉未加0.3 g润滑剂
采用环形试样法按照IEC 60404-6标准测量SMC的总损耗,测量装置如图6a所示;采用直流磁化法按照IEC 60404-4标准测量SMC的磁导率,测量装置如图6b所示。分别测量了7001P和5001P两种规格样品,每个数据测量5次取平均值。交流磁特性测量条件见表3。

图6 SMC交、直流磁特性测量装置
Fig.6 AC and DC magnetic properties measurement devices for SMC material
表3 SMC交流磁特性测量
Tab.3 The measurement of SMC AC magnetic properties

测量条件工况参数取值 交流低频一次侧匝数160 二次侧匝数30 磁感应强度0.5~1.5 T, ΔB=0.1 T 频率200~1 000 Hz, Δf =100 Hz 高频一次侧匝数10 二次侧匝数30 磁感应强度0.2 T 频率2~12 kHz, Δf =2 kHz
下面将讨论SMC均质化等效FE模型对磁特性的预测效果。
均质化等效FE模型中的单边颗粒数量N对磁导率和涡流损耗的预测精度影响很大,较大的N值会增加FE计算成本,而N取较小的值会造成颗粒间的间隙变大,对材料微观结构不能准确刻画。因此,需要得到与实际微观结构相符的颗粒间的间隙,通过计算得到了d与N的变化规律,如图7所示。
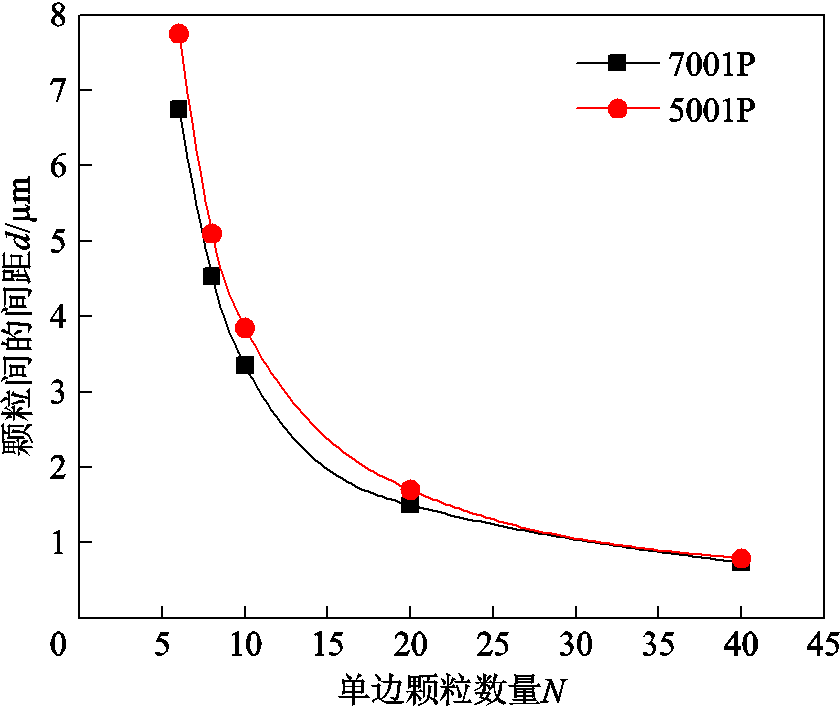
图7 d随N的变化趋势
Fig.7 Variation of d with N
从图7能够看出,颗粒间距离d对单边颗粒数量N的变化非常敏感,通过式(3)~式(6)推导可知d与N之间存在类似反比关系,且N>40后颗粒间间距已无显著变化。
基于1.3节公式计算出7001P和5001P的d分别为0.735 μm和0.79 μm。文献[22]对Somaloy系列的颗粒进行了测量,得到铁粉与绝缘层的体积比为99:1,以球单元计算(方便计算)得到两种粒径尺寸下实际绝缘层厚度分别为0.61 μm和0.252 μm。由于制备过程中添加的粘结剂会填充在颗粒之间的孔隙内,经过高温退火后固化,在宏观尺度上相当于对颗粒进行了二次绝缘层覆盖,所以颗粒间的间隙应大于单个颗粒绝缘层的厚度。此外,5001P相比于7001P的密度较小,孔隙的体积分数较大,所以在绝缘层的基础上5001P实际的颗粒间的间隙增加比例应比7001P大。因此,本文提出的均质化FE模型所计算的微观结构中颗粒间的间隙大小是合理的。
颗粒间的间隙大小对SMC的磁导率有直接影响,SMC磁导率随着颗粒间间隙的降低而增大。在均质化等效FE模型中,随着单边颗粒数量的增加,颗粒间的间距也越小。在磁化过程中,铁粉之间的耦合作用大大加强,因间隙的存在而导致的内部退磁场就会减小,磁导率得以提高。N对相对磁导率μr的影响如图8所示。
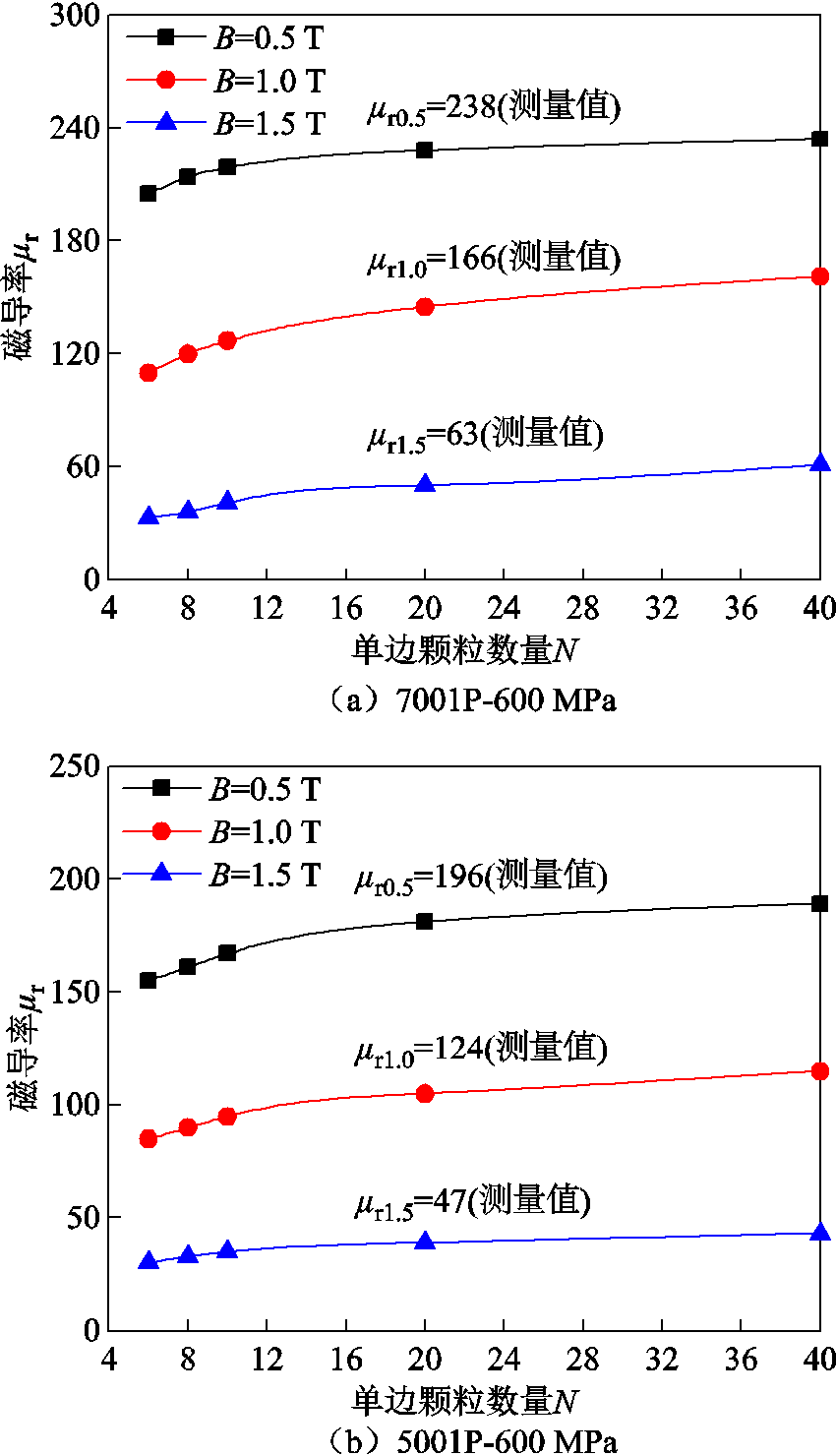
图8 N与μr的关系
Fig.8 Relationship between N and μr
从图8可以看到,对这两种粒径的SMC而言,当N=6时,两种材料在B=1.0 T下与测量值相比误差较大。随着N的增加,颗粒间的间隙越小,均质化等效FE模型预测的磁导率缓慢变大并逐渐接近测量值,这一趋势与Bruggeman模型、Rayleigh模型以及De Loor模型[23]结果的趋势相同。这是因为当FE模型中颗粒数量越多,则越接近实际材料的真实结构,颗粒间的间隙与实际尺寸越趋同。因此N越大,预测结果越准确。但同时,N越大,颗粒间的间隙在FEM中的网格划分就越精细,意味着FEM的计算负担将变大。因此,在实际应用中应在预测精度和计算成本之间做权衡。根据本文的分析,模型N取40时即可兼顾计算精度和计算成本。与文献[19]中SMC微观结构精准构建的方式对比结果见表4,精度上接近,误差都在8%以内,但计算时间上要缩减约50%。
表4 磁导率预测结果的误差
Tab.4 Errors for permeability prediction of SMC
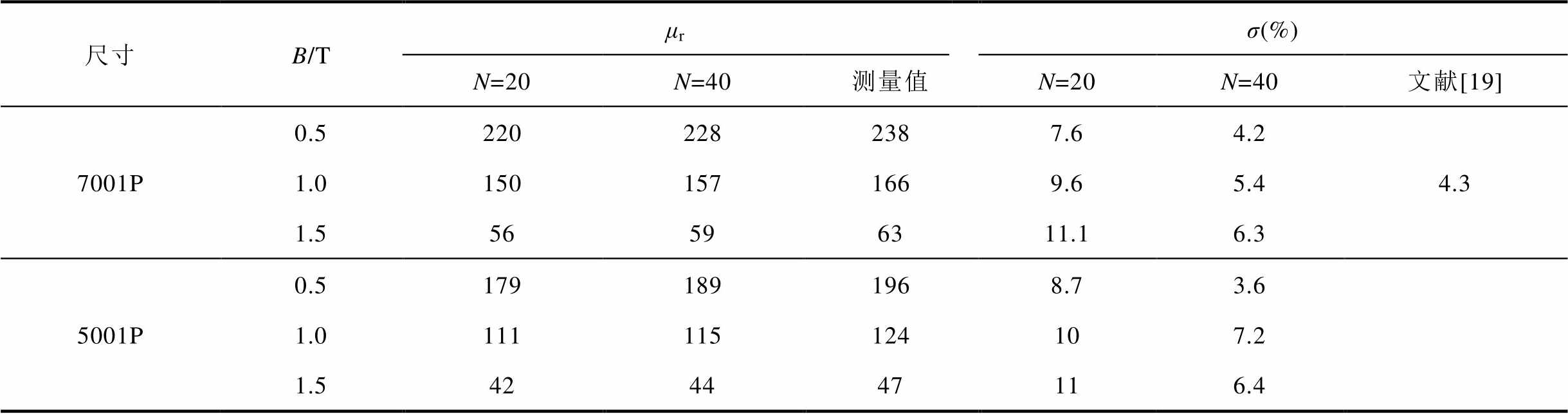
尺寸B/Tμrσ(%) N=20N=40测量值N=20N=40文献[19] 7001P0.52202282387.64.2 1.01501571669.65.44.3 1.556596311.16.3 5001P0.51791891968.73.6 1.0111115124107.2 1.5424447116.4
根据Bertotti的损耗分离理论,总损耗可以分为磁滞损耗、涡流损耗和剩余损耗。一方面,剩余损耗与磁畴的运动有关,产生原理非常复杂,而且在SMC材料中剩余损耗在总损耗中所占比例较小,可以忽略不计[24]。另一方面,SMC应用于高磁感应强度和中高频率的组合工况下,实现了软磁合金和铁氧体难以兼具的特点[25],但随着频率的增加,磁滞损耗占比降低,涡流损耗占比增大,从500 Hz到 1 000 Hz涡流损耗增大接近一倍。因此,本文重点讨论涡流损耗评估方法的准确性。
为了与预测的涡流损耗进行对比验证,首先采用经典的损耗分离方法[26]把涡流损耗从实验的总损耗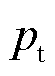 中分离出来。由于磁滞损耗
中分离出来。由于磁滞损耗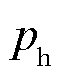 与频率f成正比,涡流损耗
与频率f成正比,涡流损耗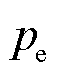 与频率f 2成正比,总损耗可以写成
与频率f 2成正比,总损耗可以写成
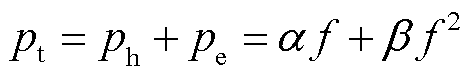 (11)
(11)
将式(11)除以频率f,得到
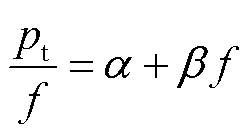 (12)
(12)
式中,α为磁滞损耗系数;β为涡流损耗系数。
从式(12)可以看到,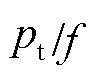 与f呈线性关系。对实测数据进行线性拟合,就可以得到磁滞损耗系数α和涡流损耗系数β,进而实现了涡流损耗的分离。
与f呈线性关系。对实测数据进行线性拟合,就可以得到磁滞损耗系数α和涡流损耗系数β,进而实现了涡流损耗的分离。
以B=1.0 T为例,分析在低频下不同频率f时N对涡流损耗pe的影响,如图9a和图9b所示。对这两种粒径SMC而言,当N值增大时,均质化等效FE模型对SMC低频涡流损耗的预测结果趋于测量值。N=20时,在f =1 000 Hz下7001P的相对误差为20%,5001P的相对误差为16%。当N=40时,这种误差随之降低,相对误差分别降至8.2%和9.4%,低频下涡流损耗预测结果的误差见表5。
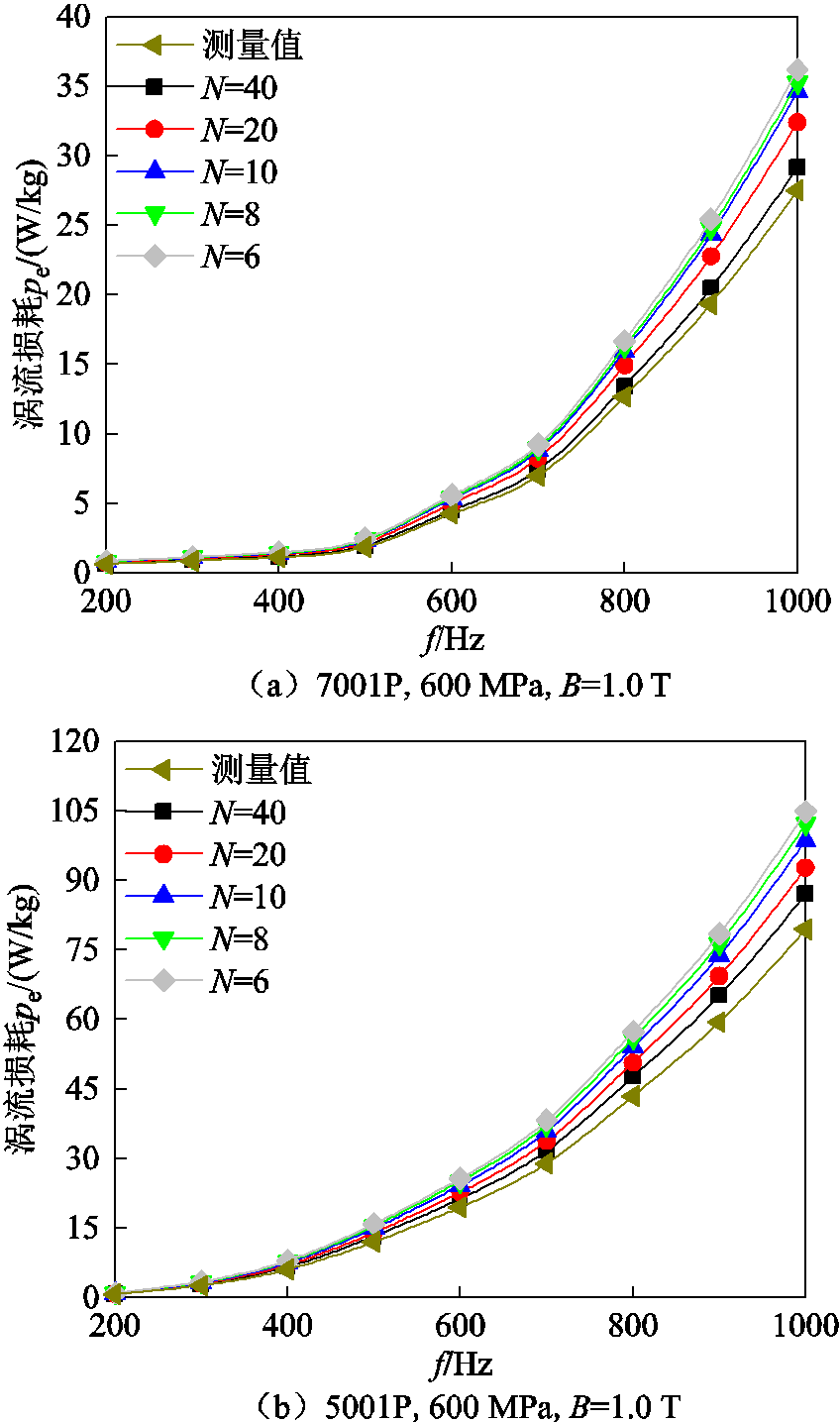
图9 N与pe的关系(低频)
Fig.9 Relationship between N and pe (low frequency)
表5 低频下涡流损耗预测结果的误差
Tab.5 Errors for eddy current loss prediction of SMC at low frequencies

尺寸B/Tf/Hzpe/(W/kg)σ(%) N=20N=40测量值N=20N=40 7001P1.05002.22.01.917.66.4 1 00032.429.227.020.08.2 5001P1.050014.113.712.116.57.4 1 00092.887.580.016.09.4
从上述结果能够看出,随着N的增加,涡流损耗的预测结果更准确。这是因为N越大,铁颗粒总体积分数不变,涡流路径变长,进而造成涡流损耗降低,使预测结果逐渐接近测量值。
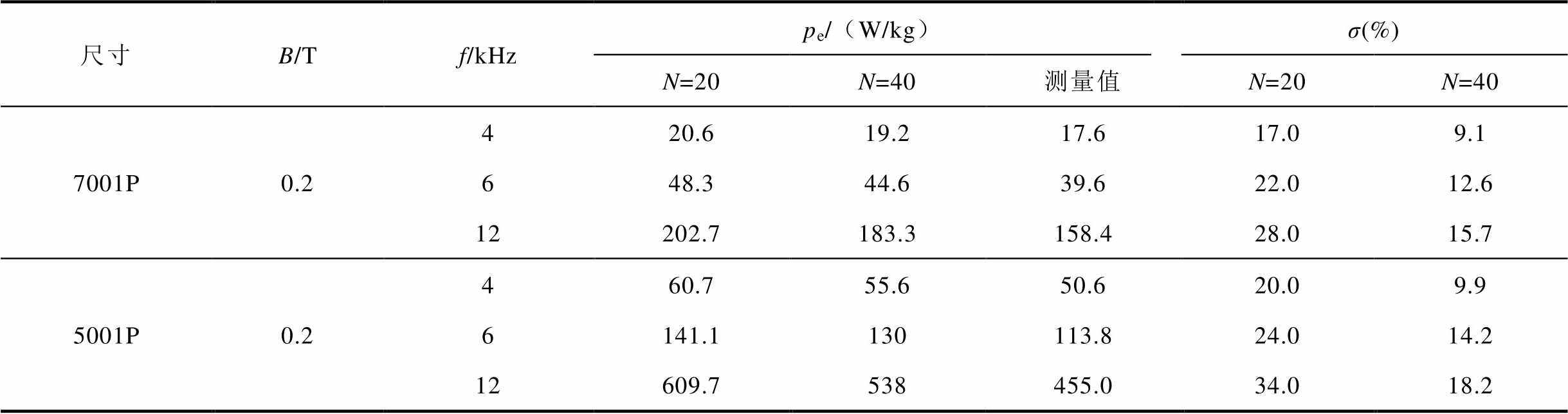
为更详细地分析频率对涡流损耗评估的影响,将磁特性评估的频率范围应用在2~12 kHz。对于一般的电工装备磁性元件,应用在高频时,其工作磁感应强度较低,因此,以B=0.2 T为例,分析在高频时不同频率f对涡流损耗pe的影响,如图10a和图10b所示。对这两种粒径SMC而言,当N值增大时,均质化等效FE模型对SMC高频涡流损耗的预测结果趋向于测量值。N=20时,频率f在4 kHz、6 kHz和12 kHz下,7001P的相对误差分别为17%、22%和28%,5001P的相对误差分别为20%、24%和34%。当N=40时,这种误差随之降低,7001P的相对误差分别降至9.1%、12.6%和15.7%,5001P的相对误差分别降至9.9%、14.2%和18.2%,高频下涡流损耗预测结果的误差见表6所示。
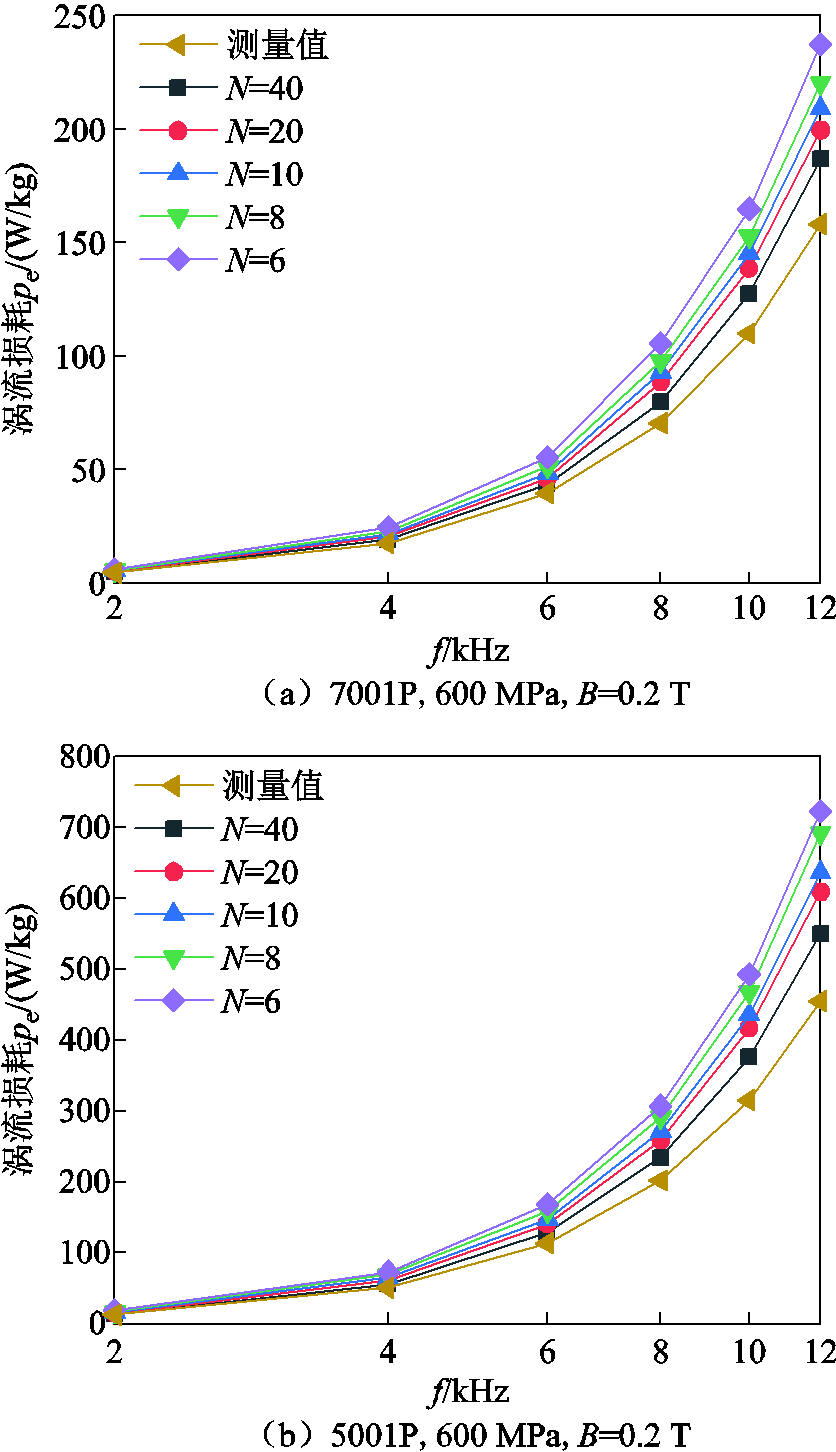
图10 N与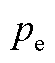 的关系(高频)
的关系(高频)
Fig.10 Relationship between N and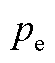 (high frequency)
(high frequency)
从上述结果能够看出,f<6 kHz时均质化FE等效模型对涡流损耗的预测结果是较为准确的;当f>6 kHz时预测误差逐步增大,这可能是该均质化等效FE模型未考虑趋肤效应所导致的计算误差。对于这个问题将在后续的工作中继续研究,进一步拓展该评估方法的应用范围。
表6 高频下涡流损耗预测结果的误差
Tab.6 Errors for eddy current loss prediction of SMC at high frequencies
尺寸B/Tf/kHzpe/(W/kg)σ(%) N=20N=40测量值N=20N=40 7001P0.2420.619.217.617.09.1 648.344.639.622.012.6 12202.7183.3158.428.015.7 5001P0.2460.755.650.620.09.9 6141.1130113.824.014.2 12609.7538455.034.018.2
综上所述,无论是磁导率还是涡流损耗,N的增加均会提高均质化等效FE模型的预测精度,但同时计算时间也会增长。综合考虑当N=40时模型可以在计算量和预测精度之间取得较好的平衡。
本文提出的三维DEM-FEM法解决了SMC磁特性评估中无法考虑制备参数以及颗粒属性影响的问题,构建的SMC均质化FE等效模型解决了在可接受的计算量情况下可靠预测预制备材料磁导率和涡流损耗的问题。DEM-FEM与制备实验的联调机制实现了SMC从制备到磁特性预测的全过程模拟,对辅助SMC新材料开发提供了一条可行的途径。结合制备实验测量与模拟计算结果得出如下结论:
1)在DEM中颗粒采用三棱柱和正态分布时,可以近似模拟SMC的微观结构,模型的压制密度与测量值最接近,颗粒间的间隙与实际结构接近。
2)在磁导率和涡流损耗预测评估中,均质化等效FE模型可以对SMC的交直流磁特性进行有效预测。研究发现:采用三棱柱颗粒模型且取单边颗粒数量N=40时可达到较好的预测效果,兼顾计算精度与FEM计算成本。
本文给出了考虑颗粒属性和制备工艺参数的SMC 材料DEM-FEM联调机制,但对于其他制备参数如退火温度、温压制备和高频下趋肤效应等情况尚未考虑,后续将会进一步进行拓展研究。
参考文献
[1] 郭轩, 肖云昊, 李驰, 等. 综合考虑材料热各向异性与多种传热方式的磁性元件热阻网络精准模型[J]. 电工技术学报, 2024, 39(6): 1806-1817.
Guo Xuan, Xiao Yunhao, Li Chi, et al. An accurate thermal resistance network model for magnetic elements considering thermal anisotropy of materials and various heat transfer ways[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1806-1817.
[2] 李亮, 涂章, 李锐, 等. 大型永磁风力发电机整体充磁系统设计及应用[J]. 电工技术学报, 2023, 38(24): 6596-6608.
Li Liang, Tu Zhang, Li Rui, et al. Design and application of the post assembly magnetization system for large permanent magnet wind generators[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6596-6608.
[3] 徐伟, 李想, 廖凯举, 等. 直线振荡电机拓扑结构及应用综述[J]. 电工技术学报, 2022, 37(21): 5377-5401.
Xu Wei, Li Xiang, Liao Kaiju, et al. Overview of linear oscillatory machines: topology and application [J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5377-5401.
[4] 赵小军, 徐华伟, 刘小娜, 等. 基于PSO-Powell混合算法的软磁复合材料二维矢量磁滞特性模拟[J]. 电工技术学报, 2021, 36(14): 2893-2903.
Zhao Xiaojun, Xu Huawei, Liu Xiaona, et al. Two-dimensional vector hysteresis simulation of soft magnetic composite materials based on the hybrid algorithm of PSO-Powell[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2893-2903.
[5] 杨庆新, 李永建. 先进电工磁性材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-12.
Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1-12.
[6] Silveyra J M, Ferrara E, Huber D L, et al. Soft magnetic materials for a sustainable and electrified world[J]. Science, 2018, 362(6413): eaao0195.
[7] 张文晶, 徐衍亮, 李树才. 新型盘式横向磁通永磁无刷电机的结构原理及设计优化[J]. 电工技术学报, 2021, 36(14): 2979-2988.
Zhang Wenjing, Xu Yanliang, Li Shucai. Structure principle and optimization of a novel disk transverse flux permanent magnet brushless motor[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2979-2988.
[8] Perigo E A, Weidenfeller B, Kollár P, et al. Past, present, and future of soft magnetic composites[J]. Applied Physics Reviews, 2018, 5(3): 031301.
[9] Anhalt M, Weidenfeller B, Mattei J L. Inner demagnetization factor in polymer-bonded soft magnetic composites[J]. Journal of Magnetism and Magnetic Materials, 2008, 320(20): e844-e848.
[10] 李永建, 杨庆新, 安金龙, 等. 软磁复合材料的三维磁特性检测实验研究[J]. 电工技术学报, 2012, 27(9): 160-165.
Li Yongjian, Yang Qingxin, An Jinlong, et al. Three dimensional magnetic properties measurement of soft magnetic composite materials[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 160-165.
[11] 段娜娜, 徐伟杰, 李永建, 等. 基于极限磁滞回线法的软磁复合材料磁特性模拟[J]. 电工技术学报, 2018, 33(20): 4739-4745.
Duan Nana, Xu Weijie, Li Yongjian, et al. Electromagnetic property modeling of the soft magnetic composite material based on the limiting loop method[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4739-4745.
[12] Li Fachang, Li Yi, Liu Xuequan, et al. Influence of iron powder purity and particle size on the magnetic properties of phosphated iron soft magnetic composites[J]. Journal of Functional Materials. 2012, 43(18):2488-2491.
[13] Ito Y, Igarashi H, Suzuki M, et al. Effect of magnetic contact on macroscopic permeability of soft magnetic composite[J]. IEEE Transactions on Magnetics, 2016, 52(3): 9400804.
[14] Gao Yanhui, Fujiki T, Dozono H, et al. Modeling of magnetic characteristics of soft magnetic composite using magnetic field analysis[J]. IEEE Transactions on Magnetics, 2018, 54(3): 7401504.
[15] Ollendorff F. Magnetostatik der massekerne[J]. Archiv Für Elektrotechnik, 1931, 25(6): 436-447.
[16] Vesa J, Rasilo P. Producing 3-D imitations of soft magnetic composite material geometries[J]. IEEE Transactions on Magnetics, 2019, 55(10): 2002510.
[17] Maruo A, Igarashi H. Analysis of magnetic properties of soft magnetic composite using discrete element method[J]. IEEE Transactions on Magnetics, 2019, 55(6): 2002205.
[18] Sato H, Igarashi H. 3-D analysis of soft magnetic composite using discrete element method in frequency domain[J]. IEEE Transactions on Magnetics, 2021, 57(6): 2000504.
[19] Shi Kaimeng, Zhang Dianhai, Ren Ziyan, et al. Evaluation of equivalent permeability of soft magnetic composites considering manufacturing process[J]. IEEE Transactions on Magnetics, 2023, 59(5): 2000204.
[20] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65.
[21] 陈向荣, 黄小凡, 王启隆, 等. 温度和频率对环氧树脂/碳化硅晶须复合材料交流非线性特性的影响[J]. 电工技术学报, 2022, 37(15): 3897-3912.
Chen Xiangrong, Huang Xiaofan, Wang Qilong, et al. Effect of temperature and frequency on AC nonlinear properties of epoxy resin/silicon carbide whisker composites[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3897-3912.
[22] Birčáková Z, Kollár P, Füzer J, et al. Magnetic properties of selected Fe-based soft magnetic composites interpreted in terms of Jiles-Atherton model parameters[J]. Journal of Magnetism and Magnetic Materials, 2020, 502: 166514.
[23] DeLoor G. Dielectric properties of heterogeneous mixtures[D]. Leiden: University ofLeiden, 1956.
[24] Metal Particles, Höganäs (hoganas.com). Electromagnetic Application Particle[EB/OL]. https://www.hoganas. com/zh/particle-technologies/soft-magnetic-composites/products/coated-particles-for-electromagnetic-applications.
[25] Kollár P, Birčáková Z, Füzer J, et al. Power loss separation in Fe-based composite materials[J]. Journal of Magnetism and Magnetic Materials, 2013, 327: 146-150.
[26] 窦润田, 李永建, 张献, 等. 受工艺孔影响的变压器铁心损耗计算与分析[J]. 电工技术学报, 2022, 37(12): 2909-2923.
Dou Runtian, Li Yongjian, Zhang Xian, et al. Calculation and analysis of transformer core loss due to technological hole[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2909-2923.
Abstract The development of modern electric equipment towards high quality and differentiation has led to an increase in the demand for the uniqueness of physical parameters of electric materials. Soft magnetic composites (SMC) is a novel type of soft magnetic material with isotropic magnetic properties that is prepared by the powder metallurgy process. In comparison to metal soft magnetic alloys, it exhibits higher resistivity and three-dimensional molding capabilities. In contrast to ferrite materials, it has a higher saturation magnetic induction strength. Consequently, SMC offer a unique combination of high flux density and low loss for electrical equipment, a characteristic that is challenging to achieve with soft magnetic alloys and ferrites. At present, the prediction of magnetic properties of SMC prior to fabrication does not take into account the particle properties, preparation process parameters, and microstructural parameters, which results in biased evaluation results. In order to address these issues, a novel method for predicting the magnetic properties of SMC materials combining the discrete element method (DEM) and the finite element method (FEM) is proposed. This method is of great significance in facilitating the accelerated development of SMC and in optimizing the design of the global structure of electrotechnical equipment.
A simulation of the preparation of SMC was conducted using DEM. Firstly, the SMC particle properties-including shape, size, and particle size distribution-were analyzed according to scanning electron microscopy. Secondly, the particle properties were simulated using DEM with spherical (single ball), rectangular (two ball stacked fit), and trigonal (three ball stacked fit) shapes. The particle size distributions were homogeneous, isotropic, and normal. Finally, DEM was used to simulate the SMC preparation process, which involved powder filling and pressure pressing.
The magnetic properties of SMC were evaluated using FEM. To address the computational challenges associated with the established FE model of micro-scale SMC, a method to construct a homogenized equivalent FE model for SMC is proposed. This method reduces the computational cost while ensuring the accuracy of the magnetic property prediction. The analysis of DEM revealed that the simulated mass density was in close agreement with the actual value when the particle shape was set to be trigonal. Consequently, trigonal particles were retained for use in the FE model to establish the material homogenization equivalent model. Firstly, a cube is established as the solution domain of the FE model. N3 trigonal particles are uniformly and periodically arranged to fill the solution domain, with N representing the number of particles on one side of the trigonal particles. The volume fraction of the particles in the FE model is calculated by using the relative density. The gap between particles is adjusted by the number of particles on one side N, to simulate the actual microstructure of the SMC. Finally, the relative permeability and eddy current loss of SMC were calculated using FEM.
The following conclusions are drawn from the combination of experimental preparation measurements and computational simulation calculations:
(1) The microstructure of SMC can be approximated when the particles in the DEM use trigonal particles and normal distributions, and the compaction density of the DE model is closest to the measured values.
(2) In the prediction of magnetic properties, the homogenized equivalent FE model is effective in making predictions of relative permeability and eddy current loss. A more accurate prediction can be achieved by using trigonal particles and a number of particles on one side of N=40, taking into account the computational accuracy and the cost of FEM computation.
The DEM-FEM regulation mechanism of SMC was proposed, but the skin effect at high frequency and the process of heat treatment have not yet been considered. Further research will be conducted to address these issues.
keywords:Soft magnetic composites, particle properties, discrete element method, magnetic properties
中图分类号:TM272
DOI: 10.19595/j.cnki.1000-6753.tces.231994
国家自然科学基金(51707125)和辽宁省教育厅科学研究项目(LJKZ0125)资助。
收稿日期 2023-11-29
改稿日期 2024-04-09
赵轩哲 男,1998年生,博士研究生,研究方向为电工材料磁特性测量与模拟。E-mail:zhaoxz@smail.sut.edu.cn
张殿海 男,1984年生,教授,博士生导师,研究方向电工材料磁特性测量与模拟,电工装备多物理场。E-mail:zhangdh@sut.edu.cn(通信作者)
(编辑 郭丽军)