脉冲强磁场磁感应强度测量技术研究进展
魏文琦1,2 张绍哲1,2 谢剑峰1,2 韩小涛1,2
(1. 国家脉冲强磁场科学中心(华中科技大学) 武汉 430074 2. 强电磁技术全国重点实验室(华中科技大学电气与电子工程学院) 武汉 430074)
摘要 脉冲强磁场装置是现代科学研究的重要工具之一,精确地测量脉冲强磁场磁感应强度是发展脉冲强磁场技术、推动相关科学研究的前提和基础。该文介绍了感应线圈法、磁致旋光法、霍尔效应法、磁阻效应法及磁共振法等技术在脉冲强磁场磁感应强度测量中的最新进展,从传感特性、测量系统结构及脉冲强磁场下测量存在的独特问题与解决方案等多个方面进行了总结归纳。此外,该文还介绍了标准探针法及标准磁场法等脉冲强磁场测量标定与校准方法,最后总结并展望了脉冲强磁场磁感应强度测量技术的研究发展。
关键词:脉冲强磁场 磁感应强度测量 磁场标定与校准
0 引言
强磁场装置是现代科学研究的重要工具之一,其在物理学、材料学、化学及生命科学等基础学科中应用广泛,并逐渐拓展到了医疗和工业等领域[1-5]。强磁场装置目前主要包括稳态强磁场装置和脉冲强磁场装置两类。其中脉冲强磁场装置将能量压缩并在短时内释放以产生磁感应强度远高于稳态磁场的脉冲强磁场,是目前进行极端磁场条件下科学研究的重要途径。美国、德国、法国以及日本等国已纷纷建立了脉冲强磁场技术研究与实验中心,目前的脉冲强磁场技术已能产生高达100 T级的非破坏性脉冲磁场[6-7]及高达1 000 T级的破坏性脉冲磁场[8-9]。我国也于2013年在武汉华中科技大学建成脉冲强磁场大科学装置,开展强磁场相关技术与科学研究,目前已成功实现94.8 T的超高脉冲强磁场和64 T的平顶脉冲强磁场[10]。
脉冲强磁场磁感应强度的精确测量是发展脉冲强磁场技术、推动相关科学研究的前提和基础。一方面,精确测量脉冲强磁场能够为脉冲磁体系统提供可靠的磁场性能评估,有利于进一步突破磁感应强度限制壁垒,以及实现高平顶稳定度、高空间均匀度的脉冲磁场;另一方面,场致相变材料的磁场相图绘制及磁共振材料的共振激发等科学研究也需要精确测量脉冲强磁场。然而,相比稳态磁场,脉冲强磁场具有磁感应强度上限高、持续时间短、测量空间小等特点,有效实现脉冲强磁场磁感应强度的精确测量极具挑战。
对于脉冲强磁场磁感应强度测量技术而言,首先,最重要的是满足被测磁场特性,包括磁感应强度的大小与方向、信号带宽以及对测量精确度的要求等。例如,对于非破坏性脉冲磁体产生的磁场,一般要求其测量轴向磁感应强度范围为0~100 T,测量带宽不低于1 kHz,测量精确度为0.1%[2];在平顶调控和磁共振等应用需求领域,更要求磁场测量带宽在100 kHz以上,测量精确度优于0.01%[11-12]。其次,测量环境也对测量技术应用造成了限制。由于脉冲磁体孔径内用于测量的径向空间尺度一般小于10 mm,因此要求磁场传感器体积较小。对于需要同时兼顾磁场测量和物性测量的实验应用而言,磁场传感器的体积要求更为苛刻,且要求能在0.1~400 K温度范围内稳定工作。此外,脉冲强磁场存在固有的电磁脉冲干扰,因此对测量技术的抗电磁干扰能力也提出了要求。最后,磁场测量装置的建造、运行以及维护成本也影响着测量技术的发展。
随着近年来电磁测量技术的进步以及相关强磁场科学研究需求的驱动,脉冲强磁场磁感应强度测量技术在新型传感器研制、测量系统结构改进以及信号处理方法开发等方面有了新发展。为此,本文将详细介绍目前脉冲强磁场下常用的几类磁场测量技术的研究新进展,包括感应线圈法、磁致旋光法、霍尔效应法、磁阻效应法以及磁共振法等。此外,本文也将对常用的脉冲强磁场测量标定校准技术进行总结,并对脉冲强磁场磁感应强度测量技术的发展进行展望。
1 脉冲强磁场磁感应强度测量技术
磁场测量的本质在于观察磁场对电荷和自旋的影响,原子、分子和固态相互作用会改变电荷和自旋的行为及其对外加磁场的反应方式,进而在宏观上表现出不同的状态变量和响应函数[13]。目前用于脉冲强磁场磁感应强度测量的技术方法多种多样,主要包括感应线圈法、磁致旋光法、霍尔效应法、磁阻效应法及磁共振法等。上述每种测量技术都具有独特性并适用于不同的应用需求,表1对其分别进行了总结,并将在下文中进行详细介绍。
表1 脉冲强磁场磁感应强度测量技术分类
Tab.1 Classification of magnetic induction intensity measurement techniques in pulsed high magnetic field

类型测量范围上限/T测量带宽/Hz特点 感应线圈法10+310-3~109最常用,传感器易于设计与制造、高带宽、空心结构不占样品空间体积,但机械稳定性差 磁致旋光法10+3DC~109主要用于破坏性脉冲强磁场测量中,抗电磁干扰,高带宽,磁感应强度测量上限高,性能主要依赖磁光介质的维德尔常数 霍尔效应法10+2DC~106传感器体积小,易于测量磁场空间分布,但电磁兼容性差,且需特殊制备传感器 磁阻效应法10+2DC~105传感器体积小,易于测量磁场空间分布,但电磁兼容性差,温度敏感性高,且需特殊制备传感器 磁共振法10+2DC~104测量精确度高,但连续测量条件下磁感应强度测量范围有限,测量带宽低,实现装置较为复杂
1.1 感应线圈法
感应线圈(induction coil)法又称为拾取线圈(pick-up coil)法、搜索线圈(search coil)法和B-dot探头法等,其一般采用铜线绕制的环形空心线圈作为传感器,并基于法拉第电磁感应定律测量线圈内轴向磁场的平均磁感应强度,即
式中,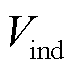 为感应线圈中的感应电压;
为感应线圈中的感应电压;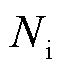 为线圈匝数;
为线圈匝数;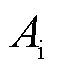 为线圈有效面积。对于有效面积
为线圈有效面积。对于有效面积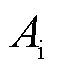 的理论计算可参考文献[14]等,但由于理论误差和绕制误差等导致计算并不精确,因此实际中一般通过已知磁场来标定系数
的理论计算可参考文献[14]等,但由于理论误差和绕制误差等导致计算并不精确,因此实际中一般通过已知磁场来标定系数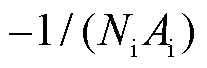 。相比传统导线绕制的感应线圈,基于印制电路板或薄膜技术制造的感应线圈具有更高的精确度、空间分辨率和重复性等优点[14-16]。对于感应电压
。相比传统导线绕制的感应线圈,基于印制电路板或薄膜技术制造的感应线圈具有更高的精确度、空间分辨率和重复性等优点[14-16]。对于感应电压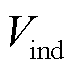 的积分,目前普遍采用模数(A-D)转换并进行数字积分的方法实现。针对固有零点漂移的问题,一般通过减去感应电压噪声信号一段时间内的平均值的方法进行改善。图1所示为典型脉冲强磁场下感应线圈法测量得到的感应电压和磁感应强度波形。
的积分,目前普遍采用模数(A-D)转换并进行数字积分的方法实现。针对固有零点漂移的问题,一般通过减去感应电压噪声信号一段时间内的平均值的方法进行改善。图1所示为典型脉冲强磁场下感应线圈法测量得到的感应电压和磁感应强度波形。
然而,目前脉冲强磁场条件下感应线圈法的应用仍存在以下特有问题[2,17-19]:①当应用于破坏性脉冲强磁场测量时,pick-up线圈产生的感应电压能高达kV量级,且在复杂电磁环境下线圈绝缘击穿电压具有降低的风险,因此测量系统需要较高的绝缘裕度与保护措施;②机械振动、电磁应力或热应力等因素会导致pick-up线圈移动或形变,因此pick-up线圈需被有效固定;③测量回路的频率响应特性会影响其造成测量信号衰减、滞后和振荡。
其中,问题③由于直接影响磁感应强度测量的信号特性以及测量结果的准确性,相关研究得到了学者的广泛关注。图2所示为感应线圈法的测量简化等效电路[14,18,20],其中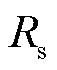 、
、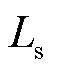 和
和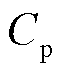 分别为pick-up线圈及引出双绞线和传输同轴电缆的等效串联电阻、等效串联电感以及等效并联电容,
分别为pick-up线圈及引出双绞线和传输同轴电缆的等效串联电阻、等效串联电感以及等效并联电容,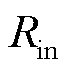 和
和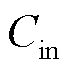 分别为模数转换器(Analog-to-Digital Converter, ADC)的输入电阻和输入电容。可以推导得出感应电压
分别为模数转换器(Analog-to-Digital Converter, ADC)的输入电阻和输入电容。可以推导得出感应电压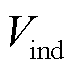 到ADC输入电压
到ADC输入电压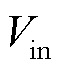 的传递函数为
的传递函数为
其中,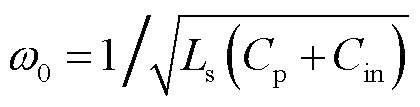 。由式(2)可见该传递函数为二阶,当感应电压
。由式(2)可见该传递函数为二阶,当感应电压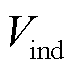 主导频率分量较高时,ADC端输入电压
主导频率分量较高时,ADC端输入电压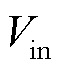 会出现衰减、滞后以及振荡等问题,最终导致相应的测量误差。
会出现衰减、滞后以及振荡等问题,最终导致相应的测量误差。
针对感应线圈高频测量下信号衰减和滞后的问题,文献[18]中通过测量传输系统的频率响应并采用拟合的方式进行信号较正,在一定程度上减小了测量系统误差;针对测量信号振荡的问题,文献[20]中通过测量系统等效电路参数以及采用并联或串联回路电阻的方式改变传输电路的频率响应特性,消除了感应线圈测量电压的振荡。
由于pick-up线圈易于设计与制造,相关测量电路的实现也较为简易,其在测量磁场的同时可以执行其他的科学实验,因此感应线圈法在脉冲强磁场测量中普遍采用。
1.2 磁致旋光法
磁致旋光(magneto-optical rotation)法又称为法拉第旋转(Faraday rotation)法、法拉第效应(Faraday effect)法等,由于具有高达kT量级的磁感应强度测量上限、ms尺度的高响应速度以及突出的抗电磁干扰能力等优点,其在采用单匝线圈以及磁通压缩等技术的超高场破坏性脉冲磁体的磁感应强度测量中应用广泛[2,18,21-26]。
法拉第旋转是一种磁光效应,当线性偏振光穿过置于磁场中的透明介质,且磁场方向和光传播方向平行时,光的偏振面会发生旋转,介质内所测量的平均磁感应强度可计算为
式中,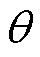 为偏振光旋转角度;
为偏振光旋转角度;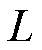 为磁光介质沿磁场方向和光传播方向的长度;
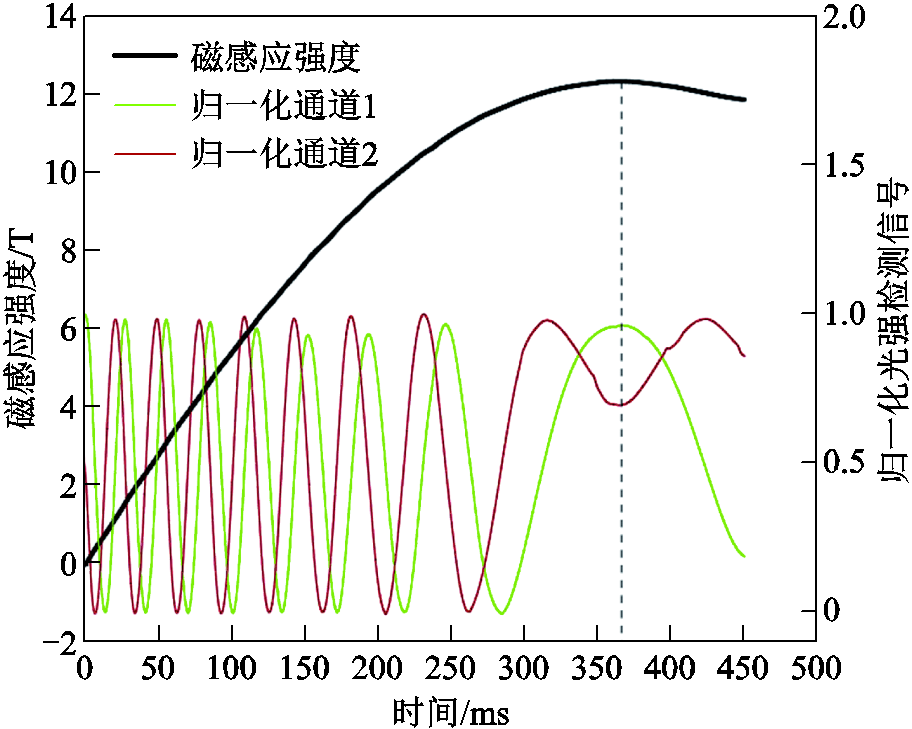
为磁光介质沿磁场方向和光传播方向的长度; 为磁光介质的维尔德(Verdet)常数。基于磁致旋光法的基本测量系统如图3所示,光源(普遍采用激光器)发出特定波长的自然光,其通过起偏器后变为线偏振光并经过磁光介质,在磁体产生的磁场作用下,光的偏振面旋转
为磁光介质的维尔德(Verdet)常数。基于磁致旋光法的基本测量系统如图3所示,光源(普遍采用激光器)发出特定波长的自然光,其通过起偏器后变为线偏振光并经过磁光介质,在磁体产生的磁场作用下,光的偏振面旋转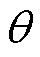 角度并通过检偏器由光电转换器接收,最终由录波仪记录信号波形。为改善光源输出光强波动缺陷,目前普遍采用双正交偏振检测方案:使用沃拉斯顿棱镜(偏振分束器)替代原检偏器产生两个正交线性偏振光束,分别检测两个正交光束的光强
角度并通过检偏器由光电转换器接收,最终由录波仪记录信号波形。为改善光源输出光强波动缺陷,目前普遍采用双正交偏振检测方案:使用沃拉斯顿棱镜(偏振分束器)替代原检偏器产生两个正交线性偏振光束,分别检测两个正交光束的光强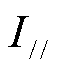 和
和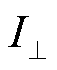 ,可以计算旋转角为
,可以计算旋转角为
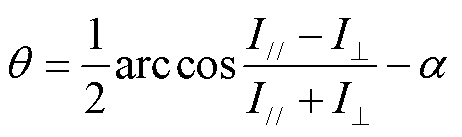 (4)
(4)
式中,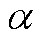 为起偏器和沃拉斯顿棱镜之间的初始夹角。
为起偏器和沃拉斯顿棱镜之间的初始夹角。
由于脉冲磁体的磁场空间不均匀度一般较大,为了精确测量空间中的点磁场,磁光介质长度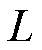 应尽可能小[25-26]。同时为了提高磁感应强度测量的灵敏度,应尽可能使得维尔德常数
应尽可能小[25-26]。同时为了提高磁感应强度测量的灵敏度,应尽可能使得维尔德常数 较大。维尔德常数主要取决于磁光介质的材料性质以及线偏振光的波长[13,21]。典型磁光介质材料如铽镓石榴石(Terbium Gallium Garnet, TGG)具有较高的维尔德常数,其维尔德常数在室温下波长为404 nm时能高达−23.25°/(T·mm)[26]。然而,TGG测量40 T以上的磁场时会出现饱和非线性的现象[27],导致其并不能完全适用于脉冲强磁场的测量。半导体材料如硫化镉(CdS)及磷化镓(GaP)等因其较大的维尔德常数也常用于脉冲强磁场测量中[21],但在较高磁场下也存在非线性行为[23,28]。抗磁性玻璃如石英玻璃(quartz glass)的维尔德常数相对较小,波长404 nm时仅为0.559°/(T·mm)[18],但其具有良好的温度稳定性[29]以及在强磁场下表现出优异的线性特性[24],被广泛应用于磁通压缩等超高脉冲磁场测量中。磁光介质材料的维尔德常数也随着线偏振光波长的变化而变化,其在折射率表现出强色散的吸收线附近变大,但是需避免吸收以保证强度的变化仅由极化导致[13]。此外,通过使线偏振光多次来回穿过磁光介质可以增加测量灵敏度,如文献[24]中在磁光介质端部采用镜面反射的方式使测量灵敏度增加了一倍。
较大。维尔德常数主要取决于磁光介质的材料性质以及线偏振光的波长[13,21]。典型磁光介质材料如铽镓石榴石(Terbium Gallium Garnet, TGG)具有较高的维尔德常数,其维尔德常数在室温下波长为404 nm时能高达−23.25°/(T·mm)[26]。然而,TGG测量40 T以上的磁场时会出现饱和非线性的现象[27],导致其并不能完全适用于脉冲强磁场的测量。半导体材料如硫化镉(CdS)及磷化镓(GaP)等因其较大的维尔德常数也常用于脉冲强磁场测量中[21],但在较高磁场下也存在非线性行为[23,28]。抗磁性玻璃如石英玻璃(quartz glass)的维尔德常数相对较小,波长404 nm时仅为0.559°/(T·mm)[18],但其具有良好的温度稳定性[29]以及在强磁场下表现出优异的线性特性[24],被广泛应用于磁通压缩等超高脉冲磁场测量中。磁光介质材料的维尔德常数也随着线偏振光波长的变化而变化,其在折射率表现出强色散的吸收线附近变大,但是需避免吸收以保证强度的变化仅由极化导致[13]。此外,通过使线偏振光多次来回穿过磁光介质可以增加测量灵敏度,如文献[24]中在磁光介质端部采用镜面反射的方式使测量灵敏度增加了一倍。
在脉冲强磁场测量应用情况下,需特别注意磁体线圈破坏导致的光辐射干扰。通过在光电转换器前放置带通光学滤波器以及进行信号处理可以有效地减小干扰噪声影响[19,24]。此外,为了满足脉冲磁场测量的响应速度,光电转换器需要有较大的带宽,通常采用具有快速上升性能的光电二极管组件或光电倍增器[25]。
在式(4)代表的检测方案中,由于正/余弦函数存在驻点,使得测量灵敏度在驻点附近显著降低,容易导致反演计算得到磁感应强度值畸变;若脉冲磁场波形驻点和光强检测信号驻点恰好重合,则上述方案无法识别后续脉冲磁场的变化趋势[26]。文献[26]中提出了一种双通道正切偏振检测方案,其将通过磁光介质后的偏振光分成两个通道,并分别使用相对角度为45°的检偏器进行检测,两个分量的比例能被转换为正切函数,成功地解决了正/余弦函数驻点导致的脉冲强磁场测量问题。该文献中示例的双通道正切检测信号(绿色实线和红色实线)以及脉冲强磁场磁感应强度测量波形(黑色实线)如图4所示,可见测量的脉冲强磁场磁感应强度波形较为光滑,且当脉冲磁场波形驻点和通道1光强检测信号驻点重合时,通道2光强检测信号能够分辨出脉冲磁场波形的下降趋势,展现了该方案的优势。
1.3 霍尔效应法及磁阻效应法
磁场可以直接通过洛伦兹力或间接通过对磁散射中心作用影响电荷的漂移以改变导体的电响应;结合不同的边界条件和测量配置,产生了部分可用于磁传感器的电荷传输现象,主要包括霍尔效应(Hall effect)以及磁阻效应(magnetoresistance effect)[13]。两者虽然在传感机理上存在明显不同,但在脉冲强磁场测量应用场景下存在诸多类似之处,故本节将两者一起叙述。基于霍尔效应或磁阻效应的传感器最显著的优点在于其体积较小,尺度一般在mm量级,易于在物性实验样品附近测量相关磁场或测量目标磁场的空间分布[30-33]。虽然目前商用的霍尔和磁阻传感器普遍只能用于测量弱磁场或作为磁性开关,但部分实验研究中已制备出特殊用于脉冲强磁场测量的霍尔以及磁阻元件。
当固体导体(一般采用半导体材料)放置在磁场内且通入电流时,导体内的电荷受到洛伦兹力而偏向侧边,继而产生霍尔电压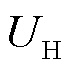 为
为
式中,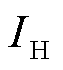 为流经导体的电流;
为流经导体的电流;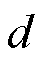 为导体在磁场方向上的厚度;
为导体在磁场方向上的厚度;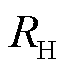 为霍尔系数。霍尔元件在标定后通过测量霍尔电压即可得到磁场大小
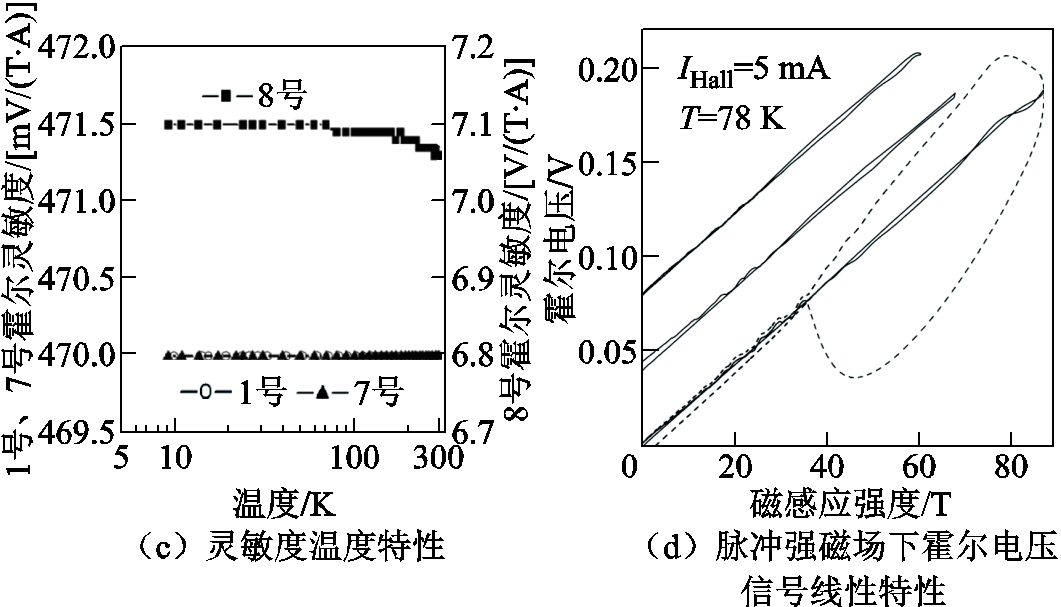
为霍尔系数。霍尔元件在标定后通过测量霍尔电压即可得到磁场大小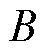 。然而,由于载流子散射机制(取决于温度)、磁阻效应以及传输线闭合回路感应电压干扰等因素的影响,采用霍尔效应法测量脉冲强磁场时并不能保持良好的线性特性[33-35]。目前,仅有O. A. Mironov等[34-35]采用分子束外延方法制备了脉冲强磁场测量用微型霍尔探针,其为Sn掺杂的n-InSb/i-GaAs异质结构,有效传感区域仅为20 mm×20 mm,能在2~300 K温度范围内稳定工作并测量高达87 T的脉冲强磁场,0~52 T磁场范围内线性度优于1%。图5a~图5d分别展现了其结构照片、温度特性以及在脉冲磁场中所测量的霍尔电压信号线性特性。
。然而,由于载流子散射机制(取决于温度)、磁阻效应以及传输线闭合回路感应电压干扰等因素的影响,采用霍尔效应法测量脉冲强磁场时并不能保持良好的线性特性[33-35]。目前,仅有O. A. Mironov等[34-35]采用分子束外延方法制备了脉冲强磁场测量用微型霍尔探针,其为Sn掺杂的n-InSb/i-GaAs异质结构,有效传感区域仅为20 mm×20 mm,能在2~300 K温度范围内稳定工作并测量高达87 T的脉冲强磁场,0~52 T磁场范围内线性度优于1%。图5a~图5d分别展现了其结构照片、温度特性以及在脉冲磁场中所测量的霍尔电压信号线性特性。
在基于磁阻效应的传感器中,其电阻率会随着磁场变化而改变,磁阻通常定义为
式中,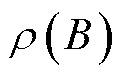 和
和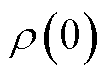 分别为磁感应强度
分别为磁感应强度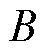 下以及零磁场时的传感器电阻率。大部分商用磁阻传感器具有mT量级较低的饱和磁场上限,限制了其在高场中的应用[32]。N. Žurauskienė教授团队的大量研究[36-46]表明,基于超巨磁阻(Colossal Magneto Resistance, CMR)效应的纳米多晶锰酸镧薄膜材料在外部磁场作用下表现出电阻大幅降低的现象,其在较宽温度和磁场范围内具有较高的测量灵敏度,可作为脉冲强磁场测量的标量传感器。尽管该类传感器具有较大的非线性以及温度敏感性,但在应用范围内标定后通过查表和插值的方式仍可实现精确的磁场测量[36]。目前,基于该类传感器的测量设备能够测量高达91.4 T的脉冲磁场[38],测量带宽能达到100 kHz[36]。图6a~图6c所示分别为一类CMR探头示意图、已成功研制的测量仪照片以及在脉冲强磁场中所测量的磁阻信号特性。目前,该类传感器的研究方向主要包括:①降低传感器中CMR效应的各向异性,减小标量传感误差[36-37];②增加材料磁无序性以及减小晶粒尺寸,提升传感器抗饱和能力以测量更高强度的磁场[37-38];③减小磁阻弛豫(记忆效应)导致的非零剩余磁化,提升传感器测量带宽[39-41];④寻找较优的材料配置,如通过掺杂Co元素、混合石墨烯等方法实现更高的测量灵敏度[42-44];⑤降低传感器老化导致的电阻率变化和磁阻特性变化,提升其时间稳定性[45-46]等。除了锰酸镧薄膜材料外,研究者们还发现在非化学计量的银硫族化物、窄带隙半导体以及石墨烯等材料中引入结构无序性可导致强磁场下的线性磁阻效应[32,47-49],有望进一步开发应用于脉冲强磁场测量中。
下以及零磁场时的传感器电阻率。大部分商用磁阻传感器具有mT量级较低的饱和磁场上限,限制了其在高场中的应用[32]。N. Žurauskienė教授团队的大量研究[36-46]表明,基于超巨磁阻(Colossal Magneto Resistance, CMR)效应的纳米多晶锰酸镧薄膜材料在外部磁场作用下表现出电阻大幅降低的现象,其在较宽温度和磁场范围内具有较高的测量灵敏度,可作为脉冲强磁场测量的标量传感器。尽管该类传感器具有较大的非线性以及温度敏感性,但在应用范围内标定后通过查表和插值的方式仍可实现精确的磁场测量[36]。目前,基于该类传感器的测量设备能够测量高达91.4 T的脉冲磁场[38],测量带宽能达到100 kHz[36]。图6a~图6c所示分别为一类CMR探头示意图、已成功研制的测量仪照片以及在脉冲强磁场中所测量的磁阻信号特性。目前,该类传感器的研究方向主要包括:①降低传感器中CMR效应的各向异性,减小标量传感误差[36-37];②增加材料磁无序性以及减小晶粒尺寸,提升传感器抗饱和能力以测量更高强度的磁场[37-38];③减小磁阻弛豫(记忆效应)导致的非零剩余磁化,提升传感器测量带宽[39-41];④寻找较优的材料配置,如通过掺杂Co元素、混合石墨烯等方法实现更高的测量灵敏度[42-44];⑤降低传感器老化导致的电阻率变化和磁阻特性变化,提升其时间稳定性[45-46]等。除了锰酸镧薄膜材料外,研究者们还发现在非化学计量的银硫族化物、窄带隙半导体以及石墨烯等材料中引入结构无序性可导致强磁场下的线性磁阻效应[32,47-49],有望进一步开发应用于脉冲强磁场测量中。
在基于霍尔传感器或磁阻传感器的测量设备测量脉冲强磁场时,测量回路不可避免地与磁场交链,导致其感应的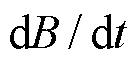 信号耦合到测量信号中(称为环路效应)并造成较大的测量误差[21,33,35,41,43,50]。为减小环路效应影响,目前主要具有以下几类解决方案:①传感器的引出导线采用紧密缠绕的双绞线形式,相邻的回路感应出相反极性的电压并抵消彼此的贡献,需注意由于脉冲磁场一般存在较大的空间梯度,为此需沿导线逐渐改变双绞回路面积[50]。②采用额外的感应线圈测量
信号耦合到测量信号中(称为环路效应)并造成较大的测量误差[21,33,35,41,43,50]。为减小环路效应影响,目前主要具有以下几类解决方案:①传感器的引出导线采用紧密缠绕的双绞线形式,相邻的回路感应出相反极性的电压并抵消彼此的贡献,需注意由于脉冲磁场一般存在较大的空间梯度,为此需沿导线逐渐改变双绞回路面积[50]。②采用额外的感应线圈测量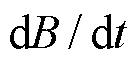 信号并进行补偿消除[21,35,41]。③在两次相同脉冲磁场下通过改变传感器源电流(或源电压)极性进行测量并对信号进行差分运算,
信号并进行补偿消除[21,35,41]。③在两次相同脉冲磁场下通过改变传感器源电流(或源电压)极性进行测量并对信号进行差分运算,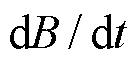 干扰电压由于极性不变因此能被抵消[21]。文献[43]中还提出了一种高频双极性电源供电的方式,使得该类测量能够在单次脉冲磁场中完成。高频双极性电源方案消除环路效应测量波形如图7所示。此外,只改变脉冲磁场极性也能起到类似效果[35]。④将目标测量信号调制至高频段,使其远离
干扰电压由于极性不变因此能被抵消[21]。文献[43]中还提出了一种高频双极性电源供电的方式,使得该类测量能够在单次脉冲磁场中完成。高频双极性电源方案消除环路效应测量波形如图7所示。此外,只改变脉冲磁场极性也能起到类似效果[35]。④将目标测量信号调制至高频段,使其远离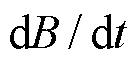 信号频带,高通滤波后进行解调以消除
信号频带,高通滤波后进行解调以消除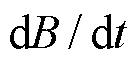 信号干扰[51]。
信号干扰[51]。
1.4 磁共振法
在外部静磁场作用下,物质的磁矩或带电粒子会绕磁场做拉莫尔进动或回旋运动并产生能级差。当对系统施加垂直于静磁场的高频电磁场激励时,若高频电磁场角频率恰好等于拉莫尔进动或回旋运动角频率,则系统将吸收电磁场能量产生能级跃迁,即发生磁共振现象。根据微观机制的不同,磁共振可分为核磁共振(Nuclear Magnetic Resonance, NMR)、电子自旋共振(Electron Spin Resonance, ESR)及回旋共振(Cyclotron Resonance, CR)等。由于共振频率与施加的静磁场磁感应强度呈线性关系,可直接通过测量频率获取磁感应强度,在有利条件下能获得优于0.1×10-6的精度,因此磁共振方法是当今测量和标定磁场最精确的方法[13,52]。磁共振方法被广泛用作分析物质物性的微观探针,其在脉冲强磁场下的测量技术发展也得到了高度重视[2,53-54]。
核自旋不为零的原子核会产生NMR现象,其共振拉莫尔频率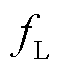 与施加磁感应强度
与施加磁感应强度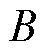 的关系一般表示为
的关系一般表示为
式中,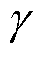 为原子核的旋磁比,一般具有较高的精确值,如国际数据委员会(CODATA)2018推荐的1H核旋磁比为42.577478518(18)MHz/T[55]。需注意的是,原子核的化学环境和温度会影响共振磁场和频率之间的对应关系(例如化学位移)[13,56]。用于脉冲强磁场NMR测量的原子核应具有以下理想特点[2,11]:①为提高NMR信号的检测灵敏度与信噪比,原子核应具有高自然丰度以及高旋磁比;②为提高磁场测量带宽,原子核应具有远低于脉冲磁场时间尺度的纵向弛豫时间T1以快速恢复纵向磁化强度;③在强磁场下和宽温度范围内具有良好的物理稳定性。表2中列出了几种脉冲强磁场NMR测量常用的原子核[11,57-69]。相比其他原子核,1H核具有最高的旋磁比及灵敏度,有利于提高磁场测量的精确度,但缺点是常用样品纯水H2O中其T1过长,在实际脉冲磁场测量中一般通过添加如GdBr3、GdCl3等顺磁盐,来缩短T1至ms量级以下[62-65,69]。2H核作为1H核的同位素,具有类似1H核的电子环境以及较低的旋磁比,适用于NMR谱仪频率性能难以满足的更高磁感应强度的脉冲磁场测量[59,60,65-67,69]。63Cu和93Nb核具有较为适中的NMR特性以及良好的物理稳定性,其单质也常用于脉冲强磁场测量中[11,57,58,61,68]。
为原子核的旋磁比,一般具有较高的精确值,如国际数据委员会(CODATA)2018推荐的1H核旋磁比为42.577478518(18)MHz/T[55]。需注意的是,原子核的化学环境和温度会影响共振磁场和频率之间的对应关系(例如化学位移)[13,56]。用于脉冲强磁场NMR测量的原子核应具有以下理想特点[2,11]:①为提高NMR信号的检测灵敏度与信噪比,原子核应具有高自然丰度以及高旋磁比;②为提高磁场测量带宽,原子核应具有远低于脉冲磁场时间尺度的纵向弛豫时间T1以快速恢复纵向磁化强度;③在强磁场下和宽温度范围内具有良好的物理稳定性。表2中列出了几种脉冲强磁场NMR测量常用的原子核[11,57-69]。相比其他原子核,1H核具有最高的旋磁比及灵敏度,有利于提高磁场测量的精确度,但缺点是常用样品纯水H2O中其T1过长,在实际脉冲磁场测量中一般通过添加如GdBr3、GdCl3等顺磁盐,来缩短T1至ms量级以下[62-65,69]。2H核作为1H核的同位素,具有类似1H核的电子环境以及较低的旋磁比,适用于NMR谱仪频率性能难以满足的更高磁感应强度的脉冲磁场测量[59,60,65-67,69]。63Cu和93Nb核具有较为适中的NMR特性以及良好的物理稳定性,其单质也常用于脉冲强磁场测量中[11,57,58,61,68]。
表2 脉冲强磁场NMR测量常用原子核
Tab.2 Commonly used nuclei for NMR measurement in pulsed high magnetic field

原子核旋磁比/(MHz/T)自然丰度(%)相对灵敏度(%)室温下T1/ms 1H42.577499.99100~3000(H2O) 2H6.535930.0150.000 14~500(D2O) 63Cu11.28569.16.404~4(单质) 93Nb10.40510048.07~1(单质)
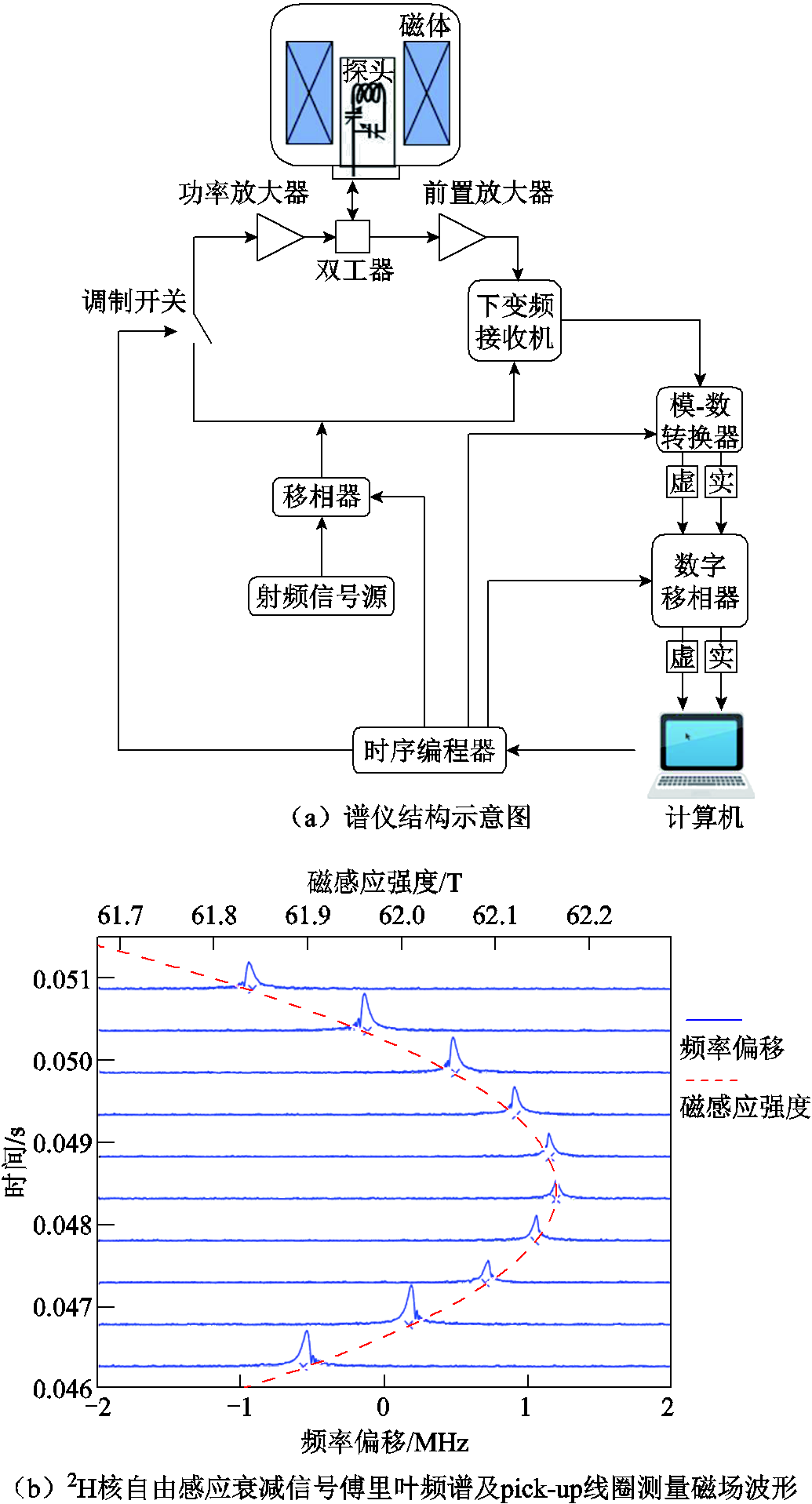
NMR谱仪根据扫描方式的不同,主要分为连续波NMR谱仪和脉冲傅里叶变换NMR谱仪两类。连续波NMR谱仪连续扫描频率或磁场以激发NMR信号,但其因为灵敏度低、扫描时间长以及可测量NMR信息量少等缺点已被脉冲傅里叶变换NMR谱仪取代。然而,近年来,华中科技大学马洪教授团队提出了一种宽带连续波NMR谱仪技术[70-72],可实现非稳态时变磁场的连续测量,具有潜在的脉冲强磁场磁感应强度测量应用价值。脉冲傅里叶变换NMR谱仪以射频脉冲的方式实现宽带频谱激励,图8a中展示了目前常用的脉冲傅里叶变换NMR谱仪结构。对于脉冲强磁场测量应用而言,NMR谱仪需要尽可能满足以下特性[11,53,66]:①谱仪需支持GHz级频率信号的激励和接收以满足高旋磁比核的共振要求;②为了尽可能扩大脉冲磁场磁感应强度跟踪测量范围,射频脉冲激励信号需要有102 W级的功率和μs级的脉宽以扩大激励带宽,接收机对应需要数十兆赫兹以上的实时带宽,探头射频谐振电路的品质因数不应过高;③由于脉冲时变磁场测量时无法实现信号平均以提高信噪比,谱仪电路器件需要较低的噪声系数;④谱仪需要精确的时序控制系统和迅速的瞬态响应以完成脉冲强磁场的跟踪测量;⑤探头的射频谐振电路需要范围较宽且精确的调谐与匹配功能,此外,探头还需实现温度调控与监测以及避免因闭合导电回路产生的涡流给监测带来的影响。图8b展示了脉冲强磁场下测量得到的2H核自由感应衰减信号傅里叶变换频谱随时间的变化曲线(蓝线)以及pick-up线圈测量的磁场曲线(红线)[65],可见通过NMR可以精确测量磁场并标定pick-up线圈。
脉冲磁场的时变性和不均匀性会使得NMR频谱畸变及增宽,最终导致测量精确度下降[11,53]。为此,研究人员一般通过信号处理进行相位校正以改善磁场时变性影响[65,73-74],减小样品体积以改善磁场不均匀性影响[69]。
ESR与NMR类似,其与电子自旋态的磁诱导塞曼分裂有关。ESR在具有不成对电子的顺磁性物质中发生,其共振条件可描述为
式中,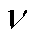 和
和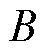 分别为共振频率和共振磁场;
分别为共振频率和共振磁场;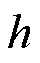 和
和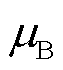 分别为普朗克常量和玻尔磁子常量;
分别为普朗克常量和玻尔磁子常量;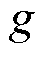 为物质的朗德因子也即g因子。相比NMR,ESR具有数百倍以上的自旋共振频率并拥有更高的灵敏度和响应速度[56]。在脉冲强磁场测量中,一般采用二苯基苦酸基联氨(2,2-diphenyl-1-picrylhydrazyl, DPPH)作为ESR标准样品[21,54,75-77],其具有较窄且单一的共振峰,易于精确测量磁场,g因子为2.003 6,且对温度稳定。此外,Na、Hg、Rb等金属原子蒸气也常被用于脉冲强磁场测量中[78-84]。
为物质的朗德因子也即g因子。相比NMR,ESR具有数百倍以上的自旋共振频率并拥有更高的灵敏度和响应速度[56]。在脉冲强磁场测量中,一般采用二苯基苦酸基联氨(2,2-diphenyl-1-picrylhydrazyl, DPPH)作为ESR标准样品[21,54,75-77],其具有较窄且单一的共振峰,易于精确测量磁场,g因子为2.003 6,且对温度稳定。此外,Na、Hg、Rb等金属原子蒸气也常被用于脉冲强磁场测量中[78-84]。
CR对应于带电粒子中磁诱导分裂的朗道能级之间的共振跃迁,共振频率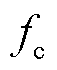 和施加磁场
和施加磁场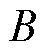 之间的关系为
之间的关系为
式中,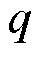 为粒子所带电荷;
为粒子所带电荷;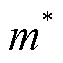 为粒子有效质量。
为粒子有效质量。
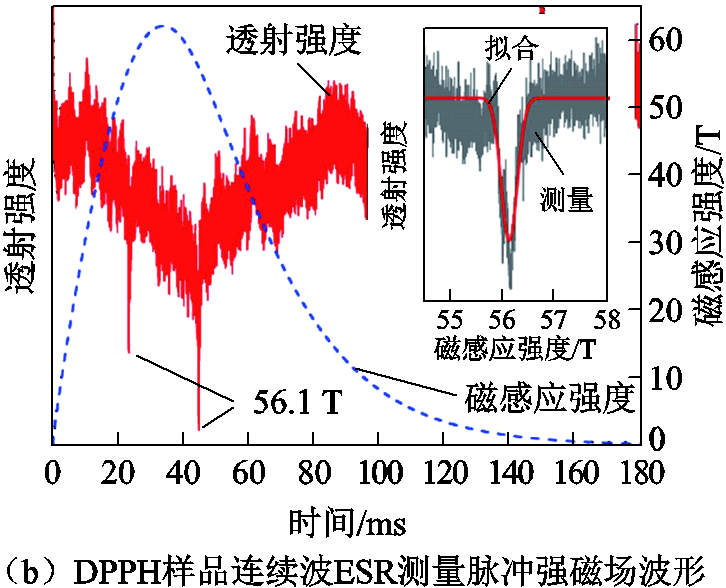
尽管ESR和CR在原理性质上不同,但两者在兆高斯(1 MGs=100 T)磁场范围内的共振频率都对应于THz以及中远红外波段,可以采用基本相同的光谱技术进行测量[21,54,85-86]。图9a所示为连续波ESR/CR装置基本结构示意图,单色连续波源产生的电磁波传输到检测样品后透射到光电探测器或测辐射热计中,当脉冲强磁场经过共振点时样品会吸收电磁波的能量,从而能检测到明显的共振吸收峰以实现磁场测量。图9b展示了脉冲强磁场下测量得到的DPPH样品ESR透射信号随时间的变化曲线(红线)以及pick-up线圈测量的磁场曲线(蓝线)[87],可见在脉冲磁场上升段和下降段出现了明显的共振吸收峰。
为了使得ESR/CR测量具有较高的灵敏度和分辨率,连续波源需要有较高的输出功率和良好的单色性。目前用于脉冲强磁场连续波ESR/CR测量的THz或中远红外波源主要包括返波振荡器、回旋管、自由电子激光器、耿式二极管和倍频器等电子器件波源,以及量子级联激光器和气体激光器等光子器件波源。返波振荡器、耿式二极管及倍频器主要用于1 THz以下激励,功率一般在mW量级以上[21,54,77,87-90]。回旋管在THz宽范围内具有W级以上的高功率、宽频率调谐性和输出高稳定性,具有很好的应用潜力[77,91-92]。自由电子激光器能够灵活提供红外至THz波段的宽调谐频率,但其实现成本过高难以广泛使用[54,86-87,93-94]。气体激光器主要用于覆盖中远红外波段,但其笨重、频率离散以及难以光学对准,逐渐被紧凑和易操作的量子级联激光器所替代[54,86,93-95]。对于探测器而言,需要具有高灵敏度、快速响应和宽频率范围的特性以满足测量,目前主要采用InSb、Ge:Ga、Ge:Cu、HgCdTe等半导体材料器件覆盖THz至中远红外频率波段[21,85,87,90,94,96]。需注意的是,上述探测器一般需要在低温液氦(4.2 K)或液氮(77 K)环境下工作,此外探测器需要远离磁体或使用铜制屏蔽罩来减小脉冲磁场对其测量的干扰[77,94]。
除了利用图9所示的吸收光谱装置外,基于塞曼分裂的光致发光(Photoluminescence, PL)发射光谱技术也常用于脉冲强磁场测量中[78,82,83,97-98]。相比吸收光谱,发射光谱具有更高的检测灵敏度和更容易的光学探测(即可使用反射式单路探测),并且其对样品透明度的要求较低[97]。图10展示了S. George等[78]在脉冲强磁场下的铷蒸气光致发光发射光谱测量装置结构与测量光谱结果,利用该技术实现了58 T下绝对准确度优于2×10-4 T的磁感应强度测量。此外,其研究表明测量的绝对精确度不受实验方法的限制而是受到铷原子激发态的朗德因子g的不确定性的限制,若已知更精确的郎德因子g则测量精确度可进一步提高。
2 磁场测量标定校准技术
在使用感应线圈法、磁阻效应法等方法测量脉冲强磁场磁感应强度时,由于测量方法本身难以反映绝对精确度上的磁感应强度,因此需要进行测量标定校准。根据IEEE Std 1309TM—2013标准[99],目前用于标定校准磁场传感器和探针的通用策略,包括标准探针法、标准磁场法及初级标准传感器法,见表3。
表3 IEEE标准标定校准磁场传感器和探针的通用策略[99]
Tab.3 General strategies for calibrating magnetic field sensors and probes recommended by IEEE standard[99]
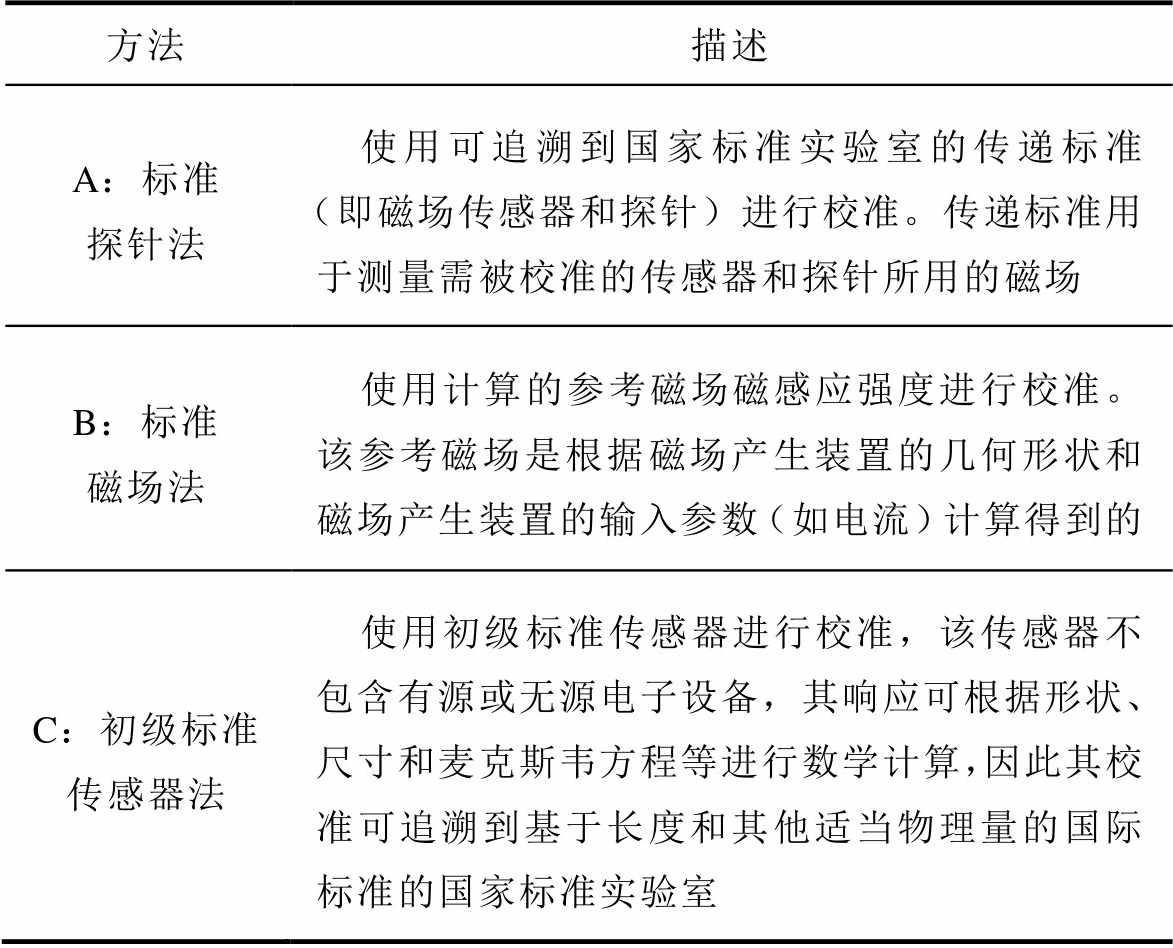
方法描述 A:标准探针法使用可追溯到国家标准实验室的传递标准(即磁场传感器和探针)进行校准。传递标准用于测量需被校准的传感器和探针所用的磁场 B:标准磁场法使用计算的参考磁场磁感应强度进行校准。该参考磁场是根据磁场产生装置的几何形状和磁场产生装置的输入参数(如电流)计算得到的 C:初级标准传感器法使用初级标准传感器进行校准,该传感器不包含有源或无源电子设备,其响应可根据形状、尺寸和麦克斯韦方程等进行数学计算,因此其校准可追溯到基于长度和其他适当物理量的国际标准的国家标准实验室
对于脉冲强磁场的测量标定校准而言,由1.4节中所述,磁共振方法是当今测量和标定磁场最精确的方法,因此磁共振方法可作为实验室的初级标准进行脉冲强磁场测量的标定校准。标准磁场法主要用于感应线圈等磁场测量线性度良好的测量探针标定,且能够校准探针的频率响应特性。标准探针法目前主要包括磁场相变探针标定法以及量子振荡探针标定法等,能够用于实际脉冲强磁场环境下的磁场探针标定校准,相比标准磁场法更为可靠与精确。综上所述,本节将简要介绍标准探针法与标准磁场法两类应用于脉冲强磁场的标定校准技术。
2.1 标准探针法
标准探针法使用可追溯到国家标准实验室的传递标准(即磁场传感器和探针)进行标定校准。为了能够简易且精确地标定校准脉冲强磁场测量,目前主要利用部分样品物质的磁场相变效应以及量子振荡效应等强磁场相关效应的已知测量结果作为标准探针。
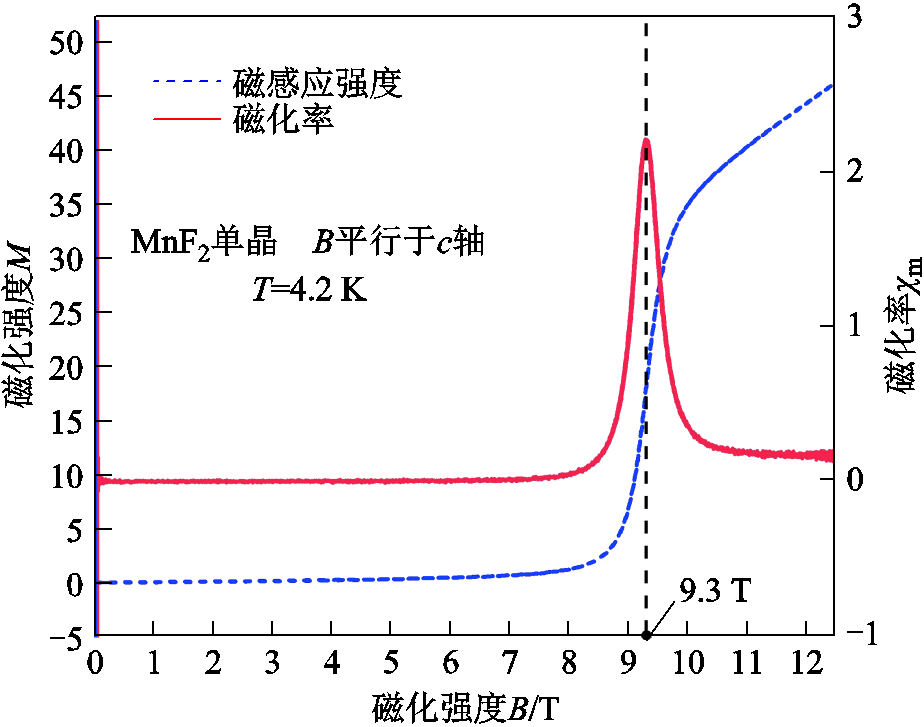
基于磁场相变效应的校准方法中,最常用的校准样品是反铁磁材料MnF2单晶:当磁场平行于样品c轴方向、磁场磁感应强度等于9.3 T以及样品温度等于4.2 K时,反铁磁材料MnF2单晶会发生显著的自旋翻转(spin-flop)转变[100-102],其在宏观上反映为磁化强度的突然跳变,此时具有最大的磁化率,可用于标定校准脉冲强磁场测量。反铁磁材料MnF2单晶的磁化测量曲线如图11所示。
另一常用的标准探针法是基于金属材料纯铜Cu的德哈斯-范阿尔芬(de Haas-van Alphen, dHvA)量子振荡效应校准方法。dHvA效应是指纯金属晶体的磁化强度随外加磁场的增加而发生振荡的量子力学效应,其一般发生在强磁场和低温下,在实际测量中可以观察到材料的磁化强度随磁场磁感应强度的倒数呈周期性振荡。对于单晶铜而言,其在温度1~4.2 K时腹部(belly)〈111〉方向所测量得到的振荡频率约为58.1 kT[103-105]。为了减小涡流效应的影响,脉冲强磁场测量标定校准中一般多采用多晶铜材料,其振荡频率约为59.5 kT[106]。对比实验测得铜的dHvA振荡频率与已知频率即可精确校准脉冲强磁场测量。类似地,除了dHvA效应以外,基于材料的电导率随外加磁场的增加而发生振荡的舒勃尼科夫-德哈斯(Shubnikov-de Haas, SdH)效应也可用于脉冲强磁场标定校准中[21,107]。
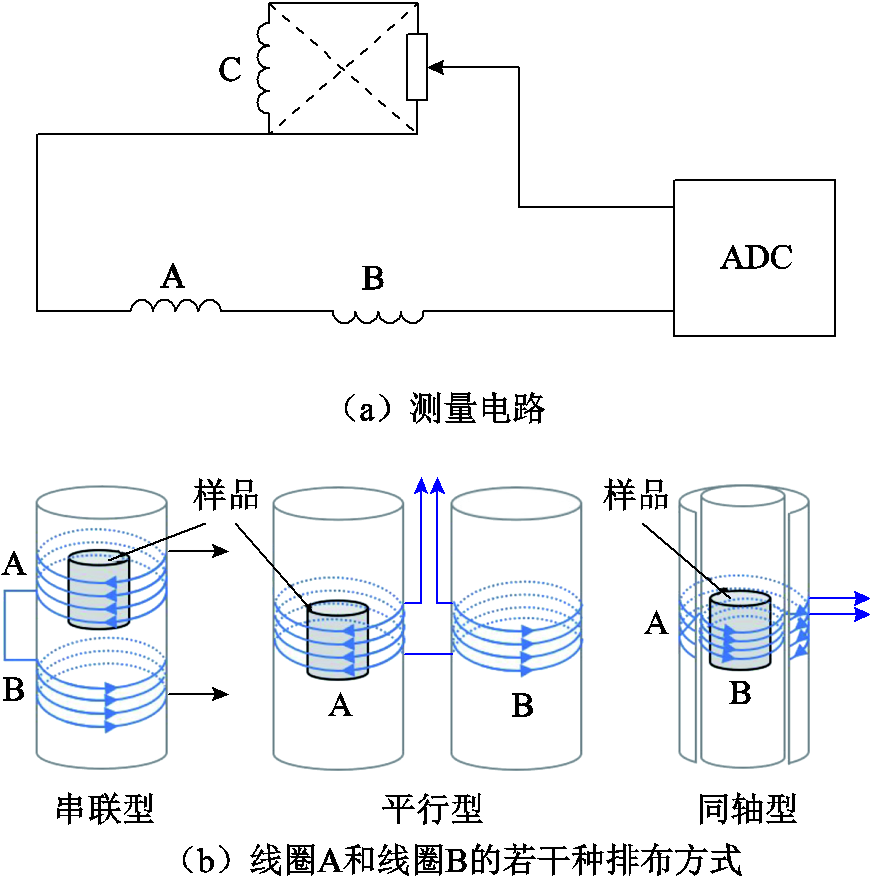
上述两种常用的校准方法需要测量样品物质的磁化强度。在脉冲强磁场磁化强度测量中,一般采用感应线圈法[108-110]:为了消除背景脉冲磁场的干扰,感应线圈应包括一个测量样品磁化的正绕线圈A以及一个不测量样品磁化的串联反绕线圈B,理想情况下两个线圈的磁链设计相等以消除背景脉冲磁场的感应电压。由于线圈A和线圈B在实际绕制过程中存在误差以及磁场的不均匀性分布影响,背景脉冲磁场干扰不可能完全由线圈B消除,为此需引入另一个补偿线圈C通过极性可调的分压电路进一步调节和消除。整体的磁化测量电路以及线圈A和线圈B的若干种排布方式如图12所示。
2.2 标准磁场法
标准磁场法使用计算的参考磁场进行传感器和探针的测量标定校准。用于产生参考磁场的磁体装置须精确确定其几何结构参数和输入参数(如电流)。为了保证传感器和探针所处的磁场较为均匀便于标定校准,IEEE推荐0~10 MHz频率内的标准磁场产生装置为亥姆霍兹线圈[99]。
亥姆霍兹线圈的结构如图13所示,其由两个直径相等、匝数相等的平行圆形线圈串联组成,两者间隔的距离等于线圈的公共半径。亥姆霍兹线圈中心的轴向磁场可计算得到,即
式中,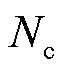 为线圈匝数;
为线圈匝数;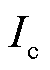 为线圈电流;
为线圈电流;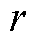 为线圈半径,两个线圈之间的距离
为线圈半径,两个线圈之间的距离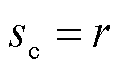 ;
;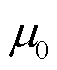 为真空磁导率。磁场计算的相对不确定度可由式(11)进行估计[99,111-112]。
为真空磁导率。磁场计算的相对不确定度可由式(11)进行估计[99,111-112]。
可见线圈的物理空间尺寸、线圈电流供给和测量的精确度、线圈匝数等参数的不确定性会影响磁场计算的准确度。此外,空间磁场的非均匀性、两个线圈之间的错位以及环境磁场噪声等因素也会增加标定校准的不确定度[113]。
虽然亥姆霍兹线圈能够提供较为均匀的用于标定校准的磁场,但其具有较大的装置空间尺寸以及较小的磁场电流比等缺点[114]。为了减小装置尺寸与提高参考磁场磁感应强度,空心或者带磁心的长螺线管[78,114]也可用作标准磁场源。
标准磁场法的独特优势在于能够校准传感器和探针的频率响应特性[115-119]。由于感性磁体负载的阻抗随着频率增加而增加,为了提高高频下的电流驱动能力,可采用串联补偿电容谐振技术措施降低负载阻抗[113,116]。
标准磁场法的缺点在于难以提供强磁场环境,因此不适用于存在高场非线性特性的传感器和探针的标定校准。目前,采用标准磁场法标定校准的相对不确定度普遍在0.1%~1%[78,113-114,120]。
表4中总结了世界上各大脉冲强磁场中心用于最高非破坏性脉冲强磁场磁感应强度记录的感应线圈测量标定校准方法,可见各大实验室都基于初级标准或传递标准进行标定校准以获得更精确可靠的脉冲强磁场磁感应强度测量。
表4 国际上各大脉冲强磁场中心用于最高非破坏性脉冲强磁场磁感应强度记录的感应线圈测量标定校准方法
Tab.4 Induction coil calibration methods for recording the highest non-destructive pulsed high magnetic field at major centers in the world

实验室标定方法不确定度参考文献 NHMFL, 美国铜的dHvA效应未说明[6] WHMFC, 中国NMR、Hall探头协同标定相对0.09 %[121] HLD, 德国ESR、SdH效应以及Hall探头协同标定未说明[122-123] LNCMI, 法国铷蒸气光致发光绝对2×10-4 T[124]
3 总结与展望
本文介绍了目前用于脉冲强磁场磁感应强度测量的主要技术方法及最新研究进展,同时归纳了相关脉冲强磁场测量标定校准技术。针对各具体的脉冲强磁场磁感应强度测量方法,其应用总结如下:
1)感应线圈法由于其简易性仍是技术主流,测量前应进行精确标定与校准,对于频率响应误差的精确补偿方法还有待进一步研究。
2)磁致旋光法具有高测量范围上限、快速响应和优异的抗电磁干扰能力,因此更适合在破坏性脉冲强磁场测量中使用。但仍需寻找或制备维尔德常数较大且不易饱和的磁光材料,以提升测量灵敏度。
3)霍尔效应法和磁阻效应法由于传感器体积较小,易于阵列集成测量脉冲强磁场的空间分布。然而,传感器的稳定性和线性度是影响其应用的关键,提高该方面的性能是未来的研究重点。
4)磁共振方法测量精确度最高,可用作初级标准进行测量标定。但是,由于实现装置较为复杂,其适用于磁共振科学研究场景,有待研发磁感应强度测量专用的、更简易的磁共振装置。
展望未来,脉冲强磁场磁感应强度测量技术需在以下几个方面开展研究:
1)基于强磁场相关场致物理效应,研制高性能脉冲强磁场磁感应强度测量传感器,使其具备高灵敏度、高线性度、高带宽、高稳定度及体积小等特征。
2)实现在线测量与标定校准一体化,提高脉冲强磁场磁感应强度测量的精确性。
3)制定脉冲强磁场磁感应强度测量标准,以确保脉冲强磁场磁感应强度测量的准确性、可重复性与标准化。
随着脉冲强磁场磁感应强度测量技术的不断进步,有望进一步获取精确的脉冲强磁场磁感应强度时空分布并实现磁场调控,推动磁相变、磁共振等脉冲强磁场相关科学研究与应用发展。
参考文献
[1] National Research Council(U.S.). High Magnetic Field Science and Its Application in the United States: Current Status and Future Directions[M]. Washington D. C.: The National Academies Press, 2013.
[2] Battesti R, Beard J, Böser S, et al. High magnetic fields for fundamental physics[J]. Physics Reports, 2018, 765: 1-39.
[3] 韩小涛, 张绍哲, 魏文琦, 等. 平顶脉冲强磁场技术及其应用[J]. 电工技术学报, 2022, 37(19): 5021-5034.
Han Xiaotao, Zhang Shaozhe, Wei Wenqi, et al. Flat-top pulsed high magnetic field technology and its application[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 5021-5034.
[4] 李亮, 涂章, 李锐, 等. 大型永磁风力发电机整体充磁系统设计及应用[J]. 电工技术学报, 2023, 38(24): 6596-6608.
Li Liang, Tu Zhang, Li Rui, et al. Design and application of the post assembly magnetization system for large permanent magnet wind generators[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6596-6608.
[5] 熊奇, 邱爽, 李彦昕, 等. 组合式电磁成形技术研究进展[J]. 电工技术学报,2024, 39(9): 2710-2729.
Xiong Qi, Qiu Shuang, Li Yanxin, et al. Research progress of combined electromagnetic forming technology [J]. Transactions of China Electro-technical Society, 2024, 39(9): 2710-2729.
[6] Sims J R, Rickel D G, Swenson C A, et al. Assembly, commissioning and operation of the NHMFL 100 Tesla multi-pulse magnet system[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 587-591.
[7] Jaime M, Daou R, Crooker S, et al. Magnetostriction and magnetic texture to 100.75 Tesla in frustrated SrCu2(BO3)2[J]. Proc Natl Acad Sci USA, 2012, 109(31): 12404-12407.
[8] Boyko B A, Bykov A I, Dolotenko M I, et al. More than 20 Mg magnetic field generation in the cascade magnetocumulative Mc-1 generator[C]//Megagauss Magnetic Field Generation, Its Application to Science and Ultra-High Pulsed-Power Technology, Tallahassee, Florida, USA, 2004: 61-66.
[9] Nakamura D, Ikeda A, Sawabe H, et al. Record indoor magnetic field of 1200 T generated by electromagnetic flux-compression[J]. The Review of Scientific Instruments, 2018, 89(9): 095106.
[10] Xie Jianfeng, Zhang Shaozhe, Shi Jiangtao, et al. Realisation of the reconfigurable pulsed high magnetic field facility and its scientific application at Wuhan National Pulsed High Magnetic Field Centre[J]. High Voltage, 2023, 8(5): 898-906.
[11] Wei Wenqi, Liu Qinying, Yuan Le, et al. Nuclear magnetic resonance measurements in high flat-top pulsed magnetic field up to 40 T at WHMFC[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 6004309.
[12] 张绍哲, 魏文琦, 樊俊显, 等. 基于双电容器耦合和线性补偿的高稳定度平顶脉冲强磁场调控系统分析与设计[J]. 电工技术学报, 2024, 39(2): 303-312.
Zhang Shaozhe, Wei Wenqi, Fan Junxian, et al. Analysis and design of a high-stability flat-top pulsed magnetic field based on the coupled double capacitor bank circuits and the linear compensation[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 303-312.
[13] Portugall O, Krämer S, Skourski Y. Magnetic fields and measurements[M]//Coey J M D, Parkin S S. Handbook of Magnetism and Magnetic Materials. Cham: Springer, 2021: 1083-1152.
[14] Tumanski S. Induction coil sensors-a review[J]. Measurement Science and Technology, 2007, 18(3): R31-R46.
[15] 韩文杰, 陈庚, 秦斌, 等. 基于PCB方案的多极磁铁谐波测量系统设计与实现[J]. 电工技术学报, 2022, 37(19): 5035-5043.
Han Wenjie, Chen Geng, Qin Bin, et al. Design and implementation of a harmonic coil field measurement system for multipole magnets based on PCB scheme[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 5035-5043.
[16] Lu Y, Mitsuda C, Takaki H, et al. Precise pulsed magnetic field mapping using a compact pick-up probe for a pulsed sextupole magnet[J]. The Review of Scientific Instruments, 2022, 93(12): 123306.
[17] Grossinger R. Pulsed fields: generation, magnetometry and application[J]. Journal of Physics D: Applied Physics, 1982, 15(9): 1545-1608.
[18] Nakamura D, Sawabe H, Matsuda Y H, et al. Precise measurement of a magnetic field generated by the electromagnetic flux compression technique[J]. The Review of Scientific Instruments, 2013, 84(4): 044702.
[19] Gennadiev N N, Demichev V F, Levit P A. Production and measurement of megagauss magnetic fields in single-turn coils[M]//Turchi P J. Megagauss Physics and Technology. Boston, MA: Springer, 1980: 27-36.
[20] Bose S, Kaur M, Barada K K, et al. Understanding the working of a B-dot probe[J]. European Journal of Physics, 2019, 40(1): 015803.
[21] Miura N, Kido G, Herlach F. Measurements in pulsed high magnetic fields[M]//Herlach F, Miura N. High Magnetic Fields: Science and Technology - Volume 1: Magnet Technology and Experimental Techniques. Singapore: World Scientific, 2003: 285-316.
[22] Nakao K, Herlach F, Goto T, et al. A laboratory instrument for generating magnetic fields over 200 T with single turn coils[J]. Journal of Physics E: Scientific Instruments, 1985, 18(12): 1018-1026.
[23] Veeser L R, Rodriguez P J, Marshall B R, et al. Optical magnetic field diagnostics for the MC1 flux compression generator experiments[C]//Digest of Technical Papers. Tenth IEEE International Pulsed Power Conference, Albuquerque, NM, USA, 1995: 1058-1062.
[24] Nakamura D, Ikeda A, Sawabe H, et al. Record indoor magnetic field of 1200 T generated by electromagnetic flux-compression[J]. The Review of Scientific Instruments, 2018, 89(9): 095106.
[25] Dey P, Shukla R, Venkateswarlu D. High magnetic field measurement utilizing Faraday rotation in SF11 glass in simplified diagnostics[J]. Applied Optics, 2017, 56(10): 2873-2877.
[26] Zhang Jue, Zhao Xincai, Chen Guanghua, et al. Dual-channel Faraday rotation measurement for pulsed magnetic field[J]. The Review of Scientific Instruments, 2021, 92(10): 105004.
[27] von Ortenberg M, Puhlmann N, Stolpe I, et al. The Humboldt high magnetic field center at Berlin[J]. Physica B: Condensed Matter, 2001, 294: 568-573.
[28] Druzhinin V V, Tatsenko O M, Bykov A I, et al. Nonlinear Faraday effect in CdS semiconductor in an ultrahigh magnetic field[J]. Physica B: Condensed Matter, 1995, 211(1/2/3/4): 392-395.
[29] Williams P A, Rose A H, Day G W, et al. Temperature dependence of the Verdet constant in several diamagnetic glasses[J]. Applied Optics, 1991, 30(10): 1176-1178.
[30] Balevičius S, Žurauskienė N, Stankevič V, et al. CMR-B-scalar sensor application for high magnetic field measurement in nondestructive pulsed magnets[J]. IEEE Transactions on Magnetics, 2013, 49(11): 5480-5484.
[31] Stankevič T, Medišauskas L, Stankevič V, et al. Pulsed magnetic field measurement system based on colossal magnetoresistance-B-scalar sensors for railgun investigation[J]. The Review of Scientific Instruments, 2014, 85(4): 044704.
[32] Žurauskienė N. Engineering of advanced materials for high magnetic field sensing: a review[J]. Sensors, 2023, 23(6): 2939.
[33] Soika A K, Sologub I O. Measurements of strong pulsed magnetic fields by Hall effect devices[J]. Instruments and Experimental Techniques, 2010, 53(1): 122-123.
[34] Mironov O A, Myronov M, Durov S, et al. Microminiature Hall probes based on n-InSb(Sn)/i-GaAs heterostructure for pulsed magnetic field applications up to 52 T[J]. Physica B: Condensed Matter, 2004, 346: 548-552.
[35] Mironov O A, Zherlitsyn S, Uhlarz M, et al. Microminiature hall probes for applications at pulsed magnetic fields up to 87 Tesla[J]. Journal of Low Temperature Physics, 2010, 159(1): 315-318.
[36] Balevičius S, Žurauskienė N, Stankevič V, et al. Hand-held magnetic field meter based on colossal magnetoresistance-B-scalar sensor[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(6): 2808-2816.
[37] Žurauskienė N, Keršulis S, Medišauskas L, et al. Investigation of magnetoresistance and its anisotropy of thin polycrystalline La0.83Sr0.17MnO3 Films in high pulsed magnetic fields[J]. Acta Physica Polonica A, 2011, 119(2): 186-188.
[38] Balevičius S, Žurauskienė N, Stankevič V, et al. Nanostructured thin manganite films in megagauss magnetic field[J]. Applied Physics Letters, 2012, 101(9): 092407.
[39] Žurauskienė N, Balevičius S, Pavilonis D, et al. Magnetoresistance relaxation in thin La-Sr-Mn-O films exposed to high-pulsed magnetic fields[J]. IEEE Transactions on Plasma Science, 2013, 41(10): 2830-2835.
[40] Žurauskienė N, Pavilonis D, Balevičius S, et al. Fast resistance relaxation in nanostructured La-Ca-Mn-O films in pulsed magnetic fields[J]. IEEE Transactions on Plasma Science, 2015, 43(10): 3445-3450.
[41] Balevičius S, Žurauskienė N, Stankevič V, et al. High-frequency CMR-B-scalar sensor for pulsed magnetic field measurement[J]. IEEE Transactions on Plasma Science, 2013, 41(10): 2885-2889.
[42] Žurauskienė N, Rudokas V, Keršulis S, et al. Magnetoresistance and its relaxation of nanostructuredLa-Sr-Mn-Co-O films: Application for low temperature magnetic sensors[J]. Journal of Magnetism and Magnetic Materials, 2021, 539: 168340.
[43] Stankevič V, Keršulis S, Dilys J, et al. Measurement system for short-pulsed magnetic fields[J]. Sensors, 2023, 23(3): 1435.
[44] Lukose R, Žurauskienė N, Stankevič V, et al. Room temperature Co-doped manganite/graphene sensor operating at high pulsed magnetic fields[J]. Scientific Reports, 2019, 9: 9497.
[45] Stankevič V, Šimkevičius Č, Keršulis S, et al. Improvement in the long-term stability of parameters of encapsulated magnetic field sensors based on LaSrMnO thin films[J]. Sensors and Actuators A: Physical, 2015, 228: 112-117.
[46] Žurauskienė N, Rudokas V, Klimantavičius J, et al. Multistep accelerated aging of magnetic field sensors based on nanostructured La-Sr-Mn-O thin films[J]. IEEE Transactions on Plasma Science, 2017, 45(10): 2787-2793.
[47] Husmann A, Betts J B, Boebinger G S, et al. Megagauss sensors[J]. Nature, 2002, 417(6887): 421-424.
[48] Hu Jingshi, Rosenbaum T F. Classical and quantum routes to linear magnetoresistance[J]. Nature Materials, 2008, 7(9): 697-700.
[49] Kisslinger F, Ott C, Heide C, et al. Linear magnetoresistance in mosaic-like bilayergraphene[J]. Nature Physics, 2015, 11: 650-653.
[50] Žurauskienė N, Balevičius S, Stankevič V, et al. B-scalar sensor using CMR effect in thin polycrystalline manganite films[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 411-416.
[51] Imamura H, Uchida K, Ohmichi E, et al. Magnetotransport measurements of low dimensional conductors under pulsed ultra-high magnetic fields[J]. Journal of Physics: Conference Series, 2006, 51: 303-306.
[52] Bottura L, Henrichsen K N. Field measurements[R]. Geneva, Switzerland: CERN, 2002.
[53] Liu Qinying, Liu Shiyu, Luo Yongkang, et al. Pulsed-field nuclear magnetic resonance: Status and prospects[J]. Matter and Radiation at Extremes, 2021, 6(2): 024201.
[54] Barra A L, Goiran M, Sessoli R, et al. Resonance THz spectroscopy in high magnetic fields[J]. Comptes Rendus Physique, 2013, 14(1): 106-114.
[55] Tiesinga E, Mohr P J, Newell D B, et al. CODATA recommended values of the fundamental physical constants: 2018[J]. Reviews of Modern Physics, 2021, 93(2): 025010.
[56] Ripka P. Magnetic Sensors and Magnetometers[M]. 2nd ed. Norwood: Artech House, 2021.
[57] Haase J, Eckert D, Siegel H, et al. Nuclear magnetic resonance in pulsed high-field magnets[J]. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 2003, 19B(1): 9-13.
[58] Haase J, Eckert D, Siegel H, et al. High-field NMR in pulsed magnets[J]. Solid State Nuclear Magnetic Resonance, 2003, 23(4): 263-265.
[59] Haase J. First 2H NMR at 58 T[J]. Applied Magnetic Resonance, 2004, 27(1/2): 297-302.
[60] Haase J, Eckert D, Siegel H, et al. NMR at the frontier of pulsed high field magnets[J]. Physica B: Condensed Matter, 2004, 346: 514-518.
[61] Haase J, Eckert D, Siegel H, et al. NMR in pulsed high magnetic fields[J]. Journal of Magnetism and Magnetic Materials, 2004, 272: E1623-E1625.
[62] Haase J, Kozlov M, Müller K H, et al. NMR in pulsed high magnetic fields at 1.3 GHz[J]. Journal of Magnetism and Magnetic Materials, 2005, 290: 438-441.
[63] Haase J, Kozlov M B, Webb A G, et al. 2 GHz 1H NMR in pulsed magnets[J]. Solid State Nuclear Magnetic Resonance, 2005, 27(3): 206-208.
[64] Kozlov M B, Haase J, Baumann C, et al. 56T 1H NMR at 2.4 GHz in a pulsed high-field magnet[J]. Solid State Nuclear Magnetic Resonance, 2005, 28(1): 64-67.
[65] Meier B, Greiser S, Haase J, et al. NMR signal averaging in 62T pulsed fields[J]. Journal of Magnetic Resonance, 2011, 210(1): 1-6.
[66] Meier B, Kohlrautz J, Haase J, et al. Nuclear magnetic resonance apparatus for pulsed high magnetic fields[J]. The Review of Scientific Instruments, 2012, 83(8): 083113.
[67] Weickert F, Meier B, Zherlitsyn S, et al. Implementation of specific-heat and NMR experiments in the 1500 ms long-pulse magnet at the Hochfeld-Magnetlabor Dresden[J]. Measurement Science and Technology, 2012, 23(10): 105001.
[68] Abou-Hamad E, Bontemps P, Rikken G L J A. NMR in pulsed magnetic field[J]. Solid State Nuclear Magnetic Resonance, 2011, 40(2): 42-44.
[69] Orlova A, Frings P, Suleiman M, et al. New high homogeneity 55T pulsed magnet for high field NMR[J]. Journal of Magnetic Resonance, 2016, 268: 82-87.
[70] Chen Wenjun, Ma Hong, De Yu. Broadband continuous nuclear magnetic resonance signal in a pulsed magnetic field: numerical solutions of Bloch equations under radio frequency irradiation[J]. Applied Magnetic Resonance, 2016, 47(1): 41-52.
[71] Chen Wenjun, Ma Hong, Yu De, et al. Numerical solution to the Bloch equations: paramagnetic solutions under wideband continuous radio frequency irradiation in a pulsed magnetic field[J]. Chinese Physics C, 2016, 40(8): 088201.
[72] Zeng Xiaohu, Ma Hong, Jin Jiang, et al. Non-steady state NMR effect and application on time-varying magnetic field measurement[J]. Sensors, 2022, 22(24): 9960.
[73] Kohlrautz J, Haase J, Green E L, et al. Field-stepped broadband NMR in pulsed magnets and application to SrCu2(BO3)2 at 54 T[J]. Journal of Magnetic Resonance, 2016, 271: 52-59.
[74] Stork H, Bontemps P, Rikken G L J A. NMR in pulsed high-field magnets and application to high-T C superconductors[J]. Journal of Magnetic Resonance, 2013, 234: 30-34.
[75] Qi Xin, Xiao Houxiu, Han Xiaotao, et al. A broad range frequency measurement method for continuous and pulsed THz waves[J]. The Review of Scientific Instruments, 2020, 91(1): 014710.
[76] Fishman R S, Fernandez-Baca J A, Rõõm T. Spin-wave theory and its applications to neutron scattering and THz spectroscopy[M]. San Rafael, CA, USA: Morgan & Claypool Publishers, 2018.
[77] 王振兴, 欧阳钟文, 肖后秀, 等. 脉冲强磁场电子自旋共振实验测试技术研究进展[J]. 实验技术与管理, 2022, 39(12): 1-9.
Wang Zhenxing, Ouyang Zhongwen, Xiao Houxiu, et al. Research progress on experimental testing technology of electron spin resonance in pulsed high magnetic field[J]. Experimental Technology and Management, 2022, 39(12): 1-9.
[78] George S, Bruyant N, Béard J, et al. Pulsed high magnetic field measurement with a rubidium vapor sensor[J]. The Review of Scientific Instruments, 2017, 88(7): 073102.
[79] Garn W B, Caird R S, Thomson D B, et al. Technique for measuring megagauss magnetic fields using Zeeman effect[J]. Review of Scientific Instruments, 1966, 37(6): 762-767.
[80] King P W, Learner R C M. The application of the Zeeman effect to the precise measurement of pulsed magnetic fields[J]. Proceedings of the Royal Society of London A Mathematical and Physical Sciences, 1971, 323(1554): 431-442.
[81] Hori H, Miki M, Date M. Paschen-back effect of D-lines in sodium under a high magnetic field[J]. Journal of the Physical Society of Japan, 1982, 51(5): 1566.
[82] Jiang Zhiyuan, Wu Jian, Zhang Daoyuan, et al. Measurement of magnetic field distribution produced by high-current pulse using Zeeman splitting of Na emission distributed by laser ablation[J]. The Review of Scientific Instruments, 2021, 92(9): 093502.
[83] Banasek J T, Engelbrecht J T, Pikuz S A, et al. Measuring 20-100 T B-fields using Zeeman splitting of sodium emission lines on a 500 kA pulsed power machine[J]. Review of Scientific Instruments, 2016, 87(11): 11D407.
[84] Gomez M R, Hansen S B, Peterson K J, et al. Magnetic field measurements via visible spectroscopy on the Z machine[J]. Review of Scientific Instruments, 2014, 85(11): 11E609.
[85] Matsuda Y H. THz magneto-spectroscopy in megagauss fields[J]. Journal of the Physical Society of Japan, 2003, 72: 162-171.
[86] Hilton D, Arikawa T, Kono A J. Cyclotron resonance[J]. Characterization of Materials, 2012: 2438.
[87] Zvyagin S A, Ozerov M, Cizmár E, et al. Terahertz-range free-electron laser electron spin resonance spectroscopy: techniques and applications in high magnetic fields[J]. The Review of Scientific Instruments, 2009, 80(7): 073102.
[88] Ohta H, Okubo S, Kawakami K, et al. Submillimeter wave ESR system using the pulsed magnetic field and its applications to one dimensional antiferromagnetic system[J]. Journal of the Physical Society of Japan, 2003, 72: 26-35.
[89] Okubo S, Ohta H, Inagaki Y, et al. High-field ESR systems in Kobe[J]. Physica B: Condensed Matter, 2004, 346: 627-632.
[90] Ohta H, Okubo S, Ohmichi E, et al. Multi-extreme THz ESR: Recent achievements in Kobe[C]//2016 41st International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Copenhagen, Denmark, 2016: 1-2.
[91] Mitsudo S, Higuchi T, Kanazawa K, et al. High field ESR measurements using gyrotron FU series as radiation sources[J]. Journal of the Physical Society of Japan, 2003, 72: 172-176.
[92] Sabchevski S, Glyavin M, Mitsudo S, et al. Novel and emerging applications of the gyrotrons worldwide: current status and prospects[J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2021, 42(7): 715-741.
[93] Drachenko O, Winnerl S, Schneider H, et al. Compact magnetospectrometer for pulsed magnets based on infrared quantum cascade lasers[J]. Review of Scientific Instruments, 2011, 82(3): 033108.
[94] Patane A, Balkan N. Semiconductor Research: Experimental Techniques[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012.
[95] Zhong Kai, Shi Wei, Xu Degang, et al. Optically pumped terahertz sources[J]. Science China Technological Sciences, 2017, 60(12): 1801-1818.
[96] Witters J, Herlach F. ESR in pulsed fields[J]. Bulletin of Magnetic Resonance, 1987, 9: 132-150.
[97] Maes J, Iakoubovskii K, Hayne M, et al. Diamond as a magnetic field calibration probe[J]. Journal of Physics D: Applied Physics, 2004, 37(7): 1102-1106.
[98] Zhong Zhiqiang, Wang Xia, Zhang Junpei, et al. Optical detection of magnetic field with Mn4+: K2SiF6 phosphor from room to liquid helium temperatures[J]. Applied Physics Letters, 2017, 110(21): 212405.
[99] IEEE standard for calibration of electromagnetic field sensors and probes (excluding antennas) from 9 kHz to 40 GHz: IEEE Std 1309TM-2013[S]. New York: IEEE, 2013.
[100] Jacobs I S. Spin-flopping in MnF2 by high magnetic fields[J]. Journal of Applied Physics, 1961, 32(3): S61-S62.
[101] Shapira Y, Foner S. Magnetic phase diagram of MnF2 from ultrasonic and differential magnetization measurements[J]. Physical Review B, 1970, 1(7): 3083-3096.
[102] Felcher G P, Kleb R. Antiferromagnetic domains and the spin-flop transition of MnF2[J]. Europhysics Letters (EPL), 1996, 36(6): 455-460.
[103] O’Sullivan W J, Schirber J E. Accurate de Haas-van Alphen periods for calibration of magnetic fields at lowtemperatures[J]. Cryogenics, 1967, 7(1/2/3/4): 118-119.
[104] Jan J P, Templeton I M. Precision measurements of 〈111〉 de Haas-van alphen frequencies in copper, silver, and gold[J]. Physical Review, 1967, 161(3): 556-558.
[105] Coleridge P T, Templeton I M. High precision de Haas-van Alphen measurements in the noble metals[J]. Journal of Physics F: Metal Physics, 1972, 2(4): 643-656.
[106] Coniglio W A, Williams A F, Yannakopoulos A, et al. High magnetic field calibration using de Haas-van Alphen oscillations in polycrystalline copper[C]// APS March Meeting 2016, Baltimore, USA, 2016: V46.00007.
[107] Hiruma K, Miura N. Magnetoresistance study of Bi and Bi-Sb alloys in high magnetic fields. II. landau levels and semimetal-semiconductor transition[J]. Journal of the Physical Society of Japan, 1983, 52(6): 2118-2127.
[108] Eckert D, Grössinger R, Doerr M, et al. High precision pick-up coils for pulsed field magnetization measurements[J]. Physica B: Condensed Matter, 2001, 294: 705-708.
[109] 刘永杰, 林梓泉, 王俊峰. 脉冲强磁场磁特性科学测量系统及其应用[J]. 物理, 2016, 45(1): 19-25.
Liu Yongjie, Lin Ziquan, Wang Junfeng. A pulsed high magnetic field facility for magnetic property measurements and its applications[J]. Physics, 2016, 45(1): 19-25.
[110] 董超. 脉冲强磁场下Ni3V2O8和GdMnO3单晶的磁热、磁电与磁弹效应研究[D]. 武汉: 华中科技大学, 2021.
Dong Chao. Study on magnetothermal, magnetoelectric and magnetoelastic effects of Ni3V2O8 and GdMnO3 single crystals under pulsed strong magnetic field[D]. Wuhan: Huazhong University of Science and Technology, 2021.
[111] Millanta L M, Agostini A, Lazzerini S. Helmholtz coils: Static and frequency-dependent performance limitations[C]//1993 International Symposium on Electromagnetic Compatibility, Dallas, TX, USA, 1993: 377-378.
[112] Bronaugh E L. Helmholtz coils for calibration of probes and sensors: limits of magnetic field accuracy and uniformity[C]//Proceedings of International Symposium on Electromagnetic Compatibility, Atlanta, GA, USA, 1995: 72-76.
[113] Zhao Pinzhang, Li Lin, Gao Jia, et al. Method of standard field for LF magnetic field meter calibration[J]. Measurement, 2017, 104: 223-232.
[114] Mirzaeva G, Summers T J, Betz R E. A laboratory system to produce a highly accurate and uniform magnetic field for sensor calibration[C]//2012 IEEE International Conference on Industrial Technology, Athens, Greece, 2012: 1020-1025.
[115] Messer S, Blackwell D D, Amatucci W E, et al. Broadband calibration of radio-frequency magnetic induction probes[J]. Review of Scientific Instruments, 2006, 77(11): 115104.
[116] Yang J G, Choi J H, Kim B C, et al. A calibration method of a radio frequency magnetic probe[J]. Review of Scientific Instruments, 1999, 70(9): 3774-3775.
[117] Everson E T, Pribyl P, Constantin C G, et al. Design, construction, and calibration of a three-axis, high-frequency magnetic probe (B-dot probe) as a diagnostic for exploding plasmas[J]. Review of Scientific Instruments, 2009, 80(11): 113505.
[118] Li Fuming, Chen Zhipeng, Zhu Lizhi, et al. Note: a calibration method to determine the lumped-circuit parameters of a magnetic probe[J]. The Review of Scientific Instruments, 2016, 87(6): 066102.
[119] Ratajczak M, Wondrak T. Analysis, design and optimization of compact ultra-high sensitivity coreless induction coil sensors[J]. Measurement Science and Technology, 2020, 31(6): 065902.
[120] de Melo C F, Araújo R L, Ardjomand L M, et al. Calibration of low frequency magnetic field meters using a Helmholtz coil[J]. Measurement, 2009, 42(9): 1330-1334.
[121] Peng T, Jiang F, Sun Q Q, et al. Design and test of a 90-T nondestructive magnet at the Wuhan national high magnetic field center[J]. IEEE Transactions on Applied Superconductivity, 2014, 24(3): 4300604.
[122] Zherlitsyn S, Herrmannsdorfer T, Wustmann B, et al. Design and performance of non-destructive pulsed magnets at the Dresden high magnetic field laboratory[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(3): 672-675.
[123] Zherlitsyn S, Wustmann B, Herrmannsdorfer T, et al. Status of the pulsed-magnet-development program at the Dresden high magnetic field laboratory[J]. IEEE Transactions on Applied Superconductivity, 2012, 22(3): 4300603.
[124] Béard J, Billette J, Ferreira N, et al. Design and tests of the 100-T triple coil at LNCMI[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 4300305.
Progress of Magnetic Induction Intensity Measurement Techniques in the Pulsed High Magnetic Field
Wei Wenqi1,2 Zhang Shaozhe1,2 Xie Jianfeng1,2 Han Xiaotao1,2
(1. Wuhan National High Magnetic Field Center Huazhong University of Science and Technology Wuhan 430074 China 2. State Key Laboratory of Advanced Electromagnetic Technology School of Electrical and Electronic Engineering Huazhong University of Science and Technology Wuhan 430074 China)
Abstract The pulsed high magnetic field is one of the essential tools in modern scientific research. Accurate measurement of the magnetic induction intensity in the pulsed high magnetic field plays a pivotal role in the development of pulsed high magnetic field technology and related scientific studies. However, the pulsed high magnetic field has characteristics such as high field strength, short durations, and limited measurement volumes, which pose significant challenges for achieving accurate measurement of the magnetic induction intensity in the pulsed high magnetic field.
This work introduced recent progress of various magnetic induction intensity measurement techniques in the pulsed high magnetic field, including the induction coil method, magneto-optical rotation method, Hall effect method, magnetoresistance effect method, and magnetic resonance method. Their sensing characteristics, measurement system structures, and unique challenges and solutions in the pulsed high magnetic field were summarized. The induction coil method is one of the most commonly used measurement techniques. In recent years, additional attention has been given to issues such as insulation protection, sensor reinforcement, and frequency response characteristics. The magneto-optical rotation method is widely used in the destructive pulsed magnetic field. However, there is currently a lack of magneto-optical materials that are both less prone to saturation in the high field and have large Verdet constants. Measurement methods based on the Hall effect or magnetoresistance effect have an advantage in that their sensors have a small volume, making it easy to measure the magnetic field near physical experiment samples or the spatial distribution of the target magnetic field. Various solutions have been developed to address the loop effect issues that arise from the coupling between the measurement circuit and the pulsed magnetic field. Magnetic resonance methods are currently the most accurate techniques for measuring and calibrating the magnetic field. Various principles of magnetic resonance phenomena, including nuclear magnetic resonance, electron spin resonance, and cyclotron resonance, are developed and can be employed to measure the pulsed high magnetic field.
Furthermore, we also presented calibration methods for the magnetic induction intensity measurement in the pulsed high magnetic field, such as the standard probe method and standard magnetic field method. The standard probe method currently mainly utilizes known measurement results such as the magnetic field phase transition effect of MnF2 single crystal and the quantum oscillation effect of pure copper metal as the standard probe. The standard magnetic field method is mainly used for calibrating probes with good linearity such as the induction coil, and can evaluate the frequency response characteristics of the probes.
Finally, a summary and outlook of the development of magnetic induction intensity measurement techniques in the pulsed high magnetic field were given.
keywords:Pulsed high magnetic field, magnetic induction intensity measurement, magnetic field calibration
中图分类号:TM93
DOI: 10.19595/j.cnki.1000-6753.tces.232009
国家自然科学基金资助项目(U21A20458, 52107152和51821005)。
收稿日期 2013-12-01
改稿日期 2024-01-16
作者简介
魏文琦 男,1998年生,博士研究生,研究方向为强磁场产生、调控与测量。E-mail:vinkey7wei@hust.edu.cn
韩小涛 男,1974年生,教授,博士生导师,长江学者特聘教授,研究方向为强磁场产生与调控、电磁测量与科学仪器、大功率太赫兹源、电磁成形。E-mail:xthan@mail.hust.edu.cn(通信作者)
(编辑 郭丽军)

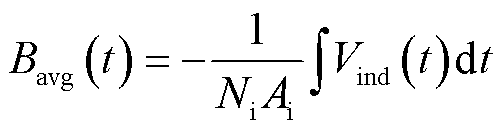 (1)
(1)
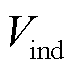 为感应线圈中的感应电压;
为感应线圈中的感应电压;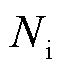 为线圈匝数;
为线圈匝数;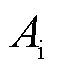 为线圈有效面积。对于有效面积
为线圈有效面积。对于有效面积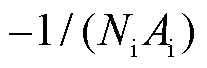 。相比传统导线绕制的感应线圈,基于印制电路板或薄膜技术制造的感应线圈具有更高的精确度、空间分辨率和重复性等优点
。相比传统导线绕制的感应线圈,基于印制电路板或薄膜技术制造的感应线圈具有更高的精确度、空间分辨率和重复性等优点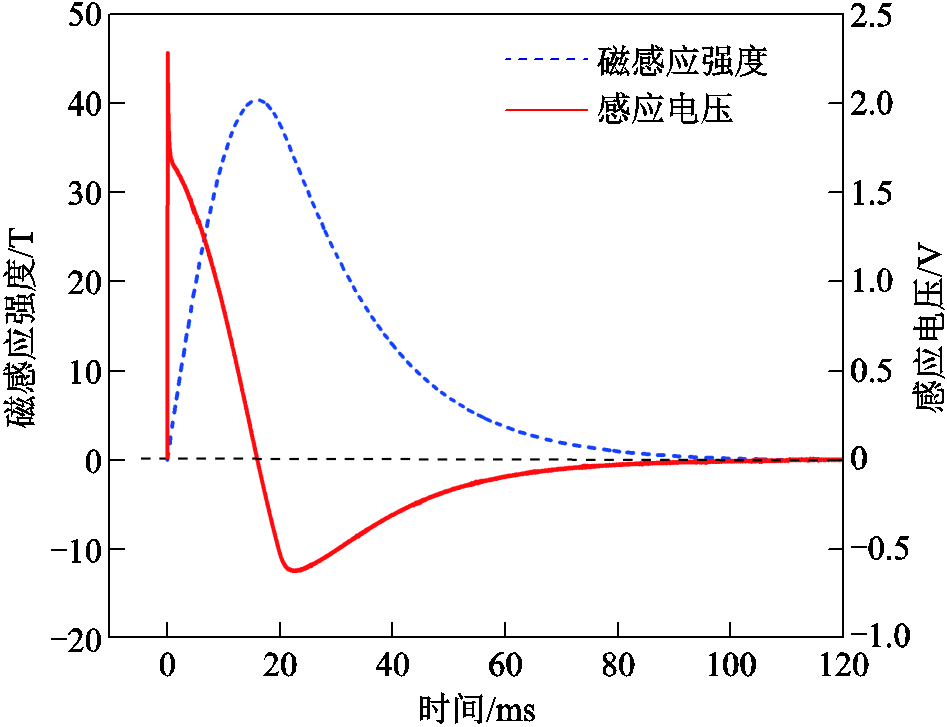
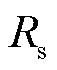 、
、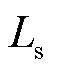 和
和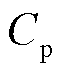 分别为pick-up线圈及引出双绞线和传输同轴电缆的等效串联电阻、等效串联电感以及等效并联电容,
分别为pick-up线圈及引出双绞线和传输同轴电缆的等效串联电阻、等效串联电感以及等效并联电容,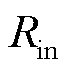 和
和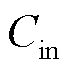 分别为模数转换器(Analog-to-Digital Converter, ADC)的输入电阻和输入电容。可以推导得出感应电压
分别为模数转换器(Analog-to-Digital Converter, ADC)的输入电阻和输入电容。可以推导得出感应电压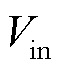 的传递函数为
的传递函数为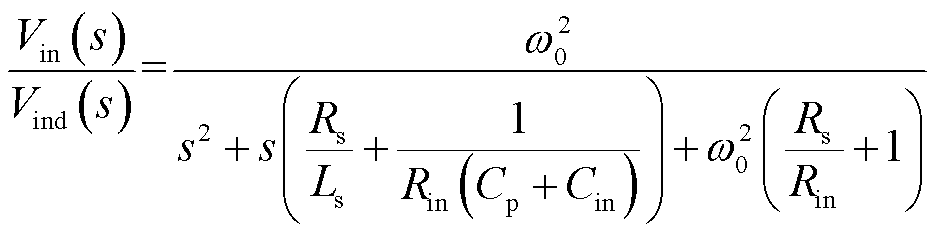 (2)
(2)
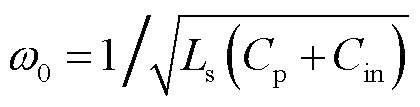 。由式(2)可见该传递函数为二阶,当感应电压
。由式(2)可见该传递函数为二阶,当感应电压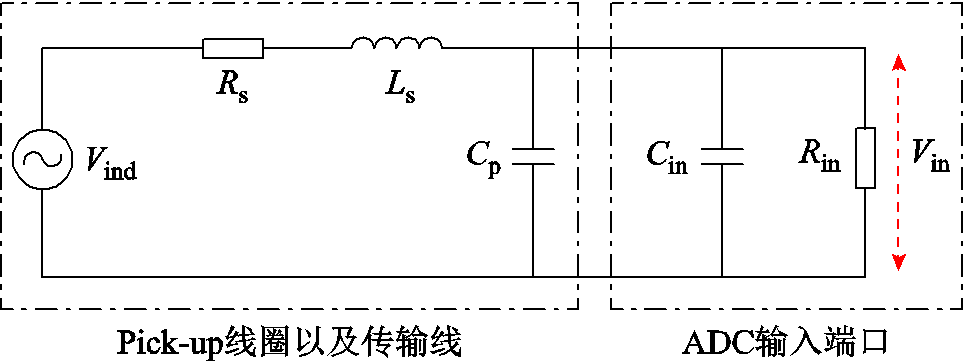
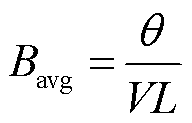 (3)
(3)
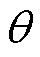 为偏振光旋转角度;
为偏振光旋转角度;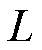 为磁光介质沿磁场方向和光传播方向的长度;
为磁光介质沿磁场方向和光传播方向的长度; 为磁光介质的维尔德(Verdet)常数。基于磁致旋光法的基本测量系统如图3所示,光源(普遍采用激光器)发出特定波长的自然光,其通过起偏器后变为线偏振光并经过磁光介质,在磁体产生的磁场作用下,光的偏振面旋转
为磁光介质的维尔德(Verdet)常数。基于磁致旋光法的基本测量系统如图3所示,光源(普遍采用激光器)发出特定波长的自然光,其通过起偏器后变为线偏振光并经过磁光介质,在磁体产生的磁场作用下,光的偏振面旋转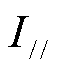 和
和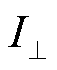 ,可以计算旋转角为
,可以计算旋转角为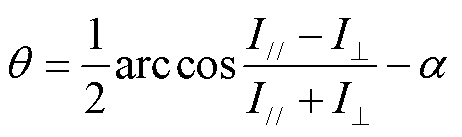 (4)
(4)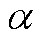 为起偏器和沃拉斯顿棱镜之间的初始夹角。
为起偏器和沃拉斯顿棱镜之间的初始夹角。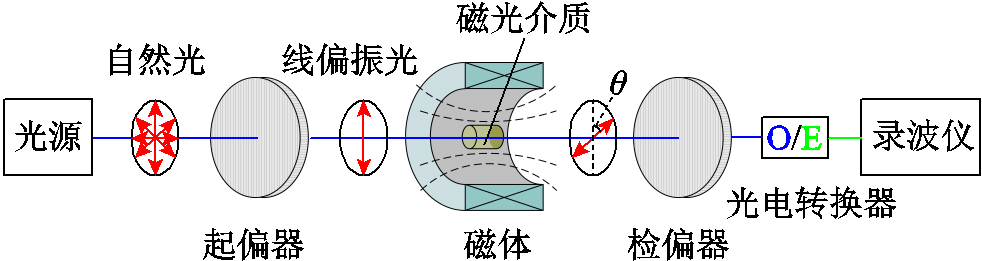
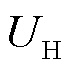 为
为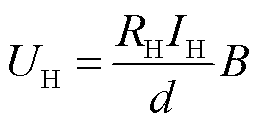 (5)
(5)
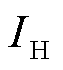 为流经导体的电流;
为流经导体的电流;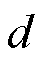 为导体在磁场方向上的厚度;
为导体在磁场方向上的厚度;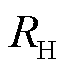 为霍尔系数。霍尔元件在标定后通过测量霍尔电压即可得到磁场大小
为霍尔系数。霍尔元件在标定后通过测量霍尔电压即可得到磁场大小 。然而,由于载流子散射机制(取决于温度)、磁阻效应以及传输线闭合回路感应电压干扰等因素的影响,采用霍尔效应法测量脉冲强磁场时并不能保持良好的线性特性
。然而,由于载流子散射机制(取决于温度)、磁阻效应以及传输线闭合回路感应电压干扰等因素的影响,采用霍尔效应法测量脉冲强磁场时并不能保持良好的线性特性
 (6)
(6)
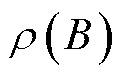 和
和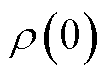 分别为磁感应强度
分别为磁感应强度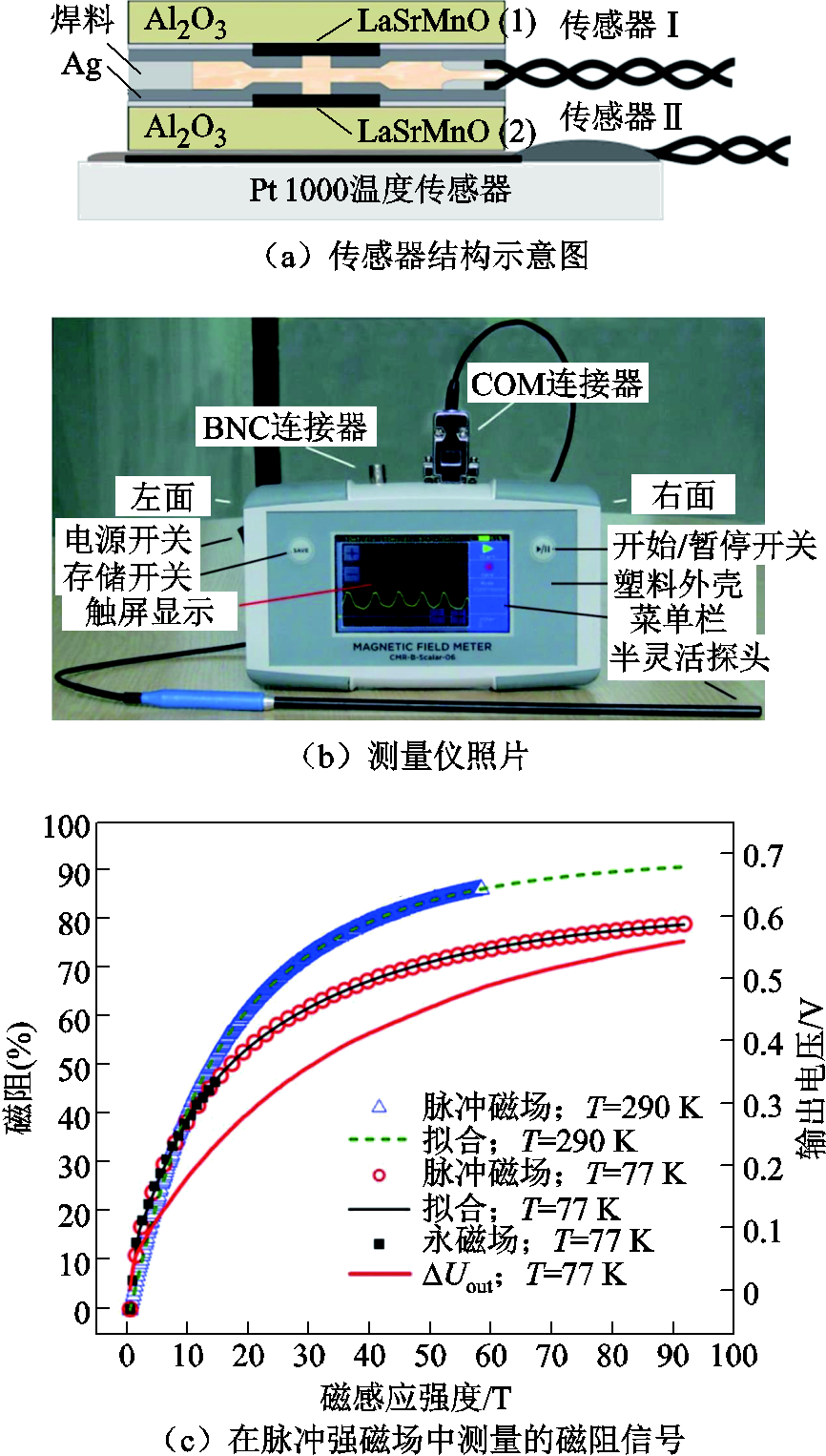
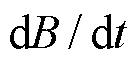 信号耦合到测量信号中(称为环路效应)并造成较大的测量误差
信号耦合到测量信号中(称为环路效应)并造成较大的测量误差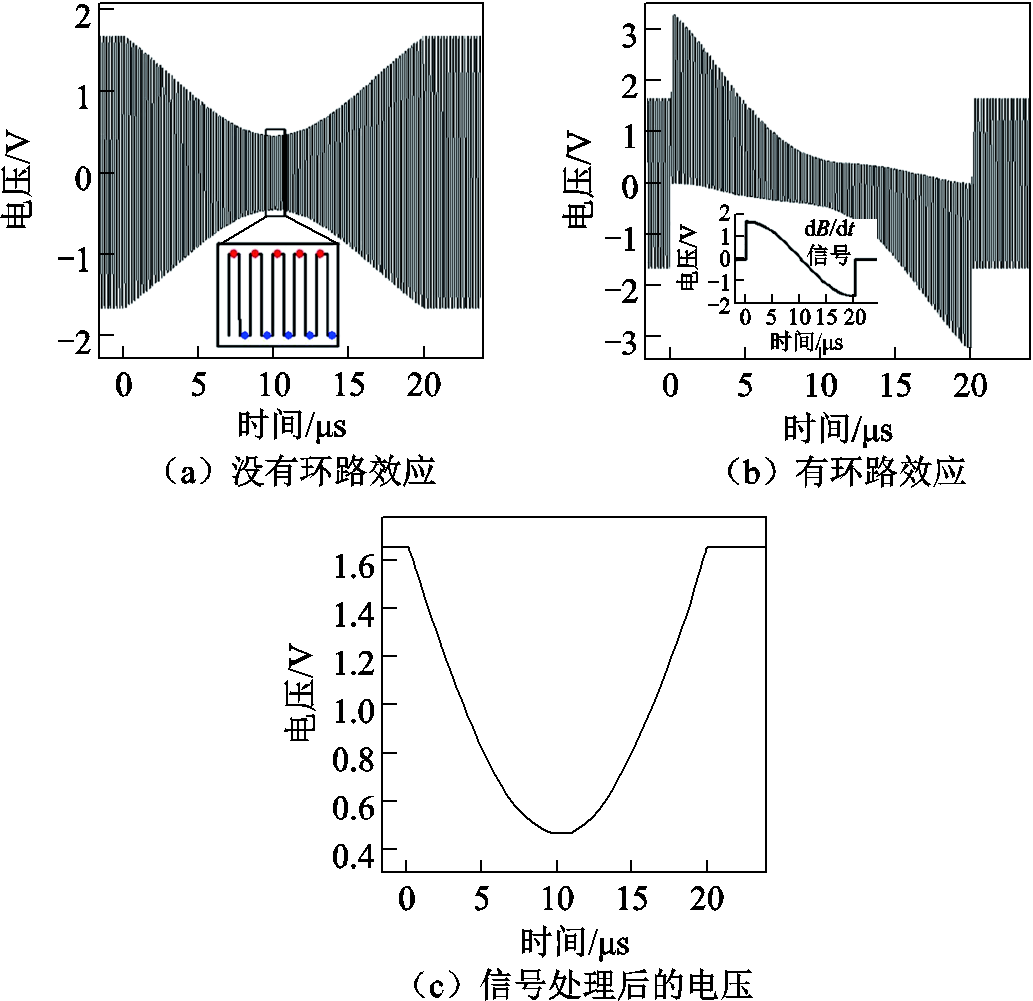
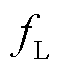 与施加磁感应强度
与施加磁感应强度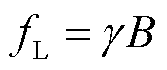 (7)
(7)
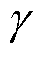 为原子核的旋磁比,一般具有较高的精确值,如国际数据委员会(CODATA)2018推荐的
为原子核的旋磁比,一般具有较高的精确值,如国际数据委员会(CODATA)2018推荐的
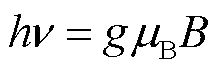 (8)
(8)
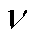 和
和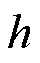 和
和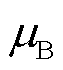 分别为普朗克常量和玻尔磁子常量;
分别为普朗克常量和玻尔磁子常量;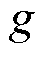 为物质的朗德因子也即g因子。相比NMR,ESR具有数百倍以上的自旋共振频率并拥有更高的灵敏度和响应速度
为物质的朗德因子也即g因子。相比NMR,ESR具有数百倍以上的自旋共振频率并拥有更高的灵敏度和响应速度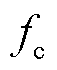 和施加磁场
和施加磁场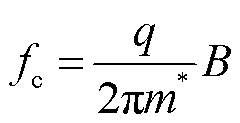 (9)
(9)
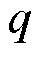 为粒子所带电荷;
为粒子所带电荷;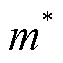 为粒子有效质量。
为粒子有效质量。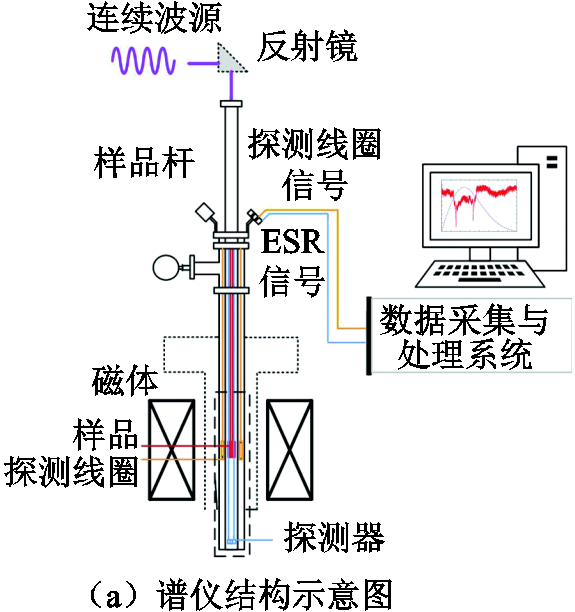


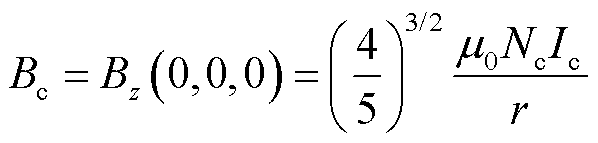 (10)
(10)
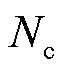 为线圈匝数;
为线圈匝数;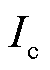 为线圈电流;
为线圈电流;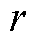 为线圈半径,两个线圈之间的距离
为线圈半径,两个线圈之间的距离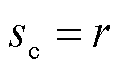 ;
;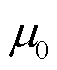 为真空磁导率。磁场计算的相对不确定度可由式(11)进行估计
为真空磁导率。磁场计算的相对不确定度可由式(11)进行估计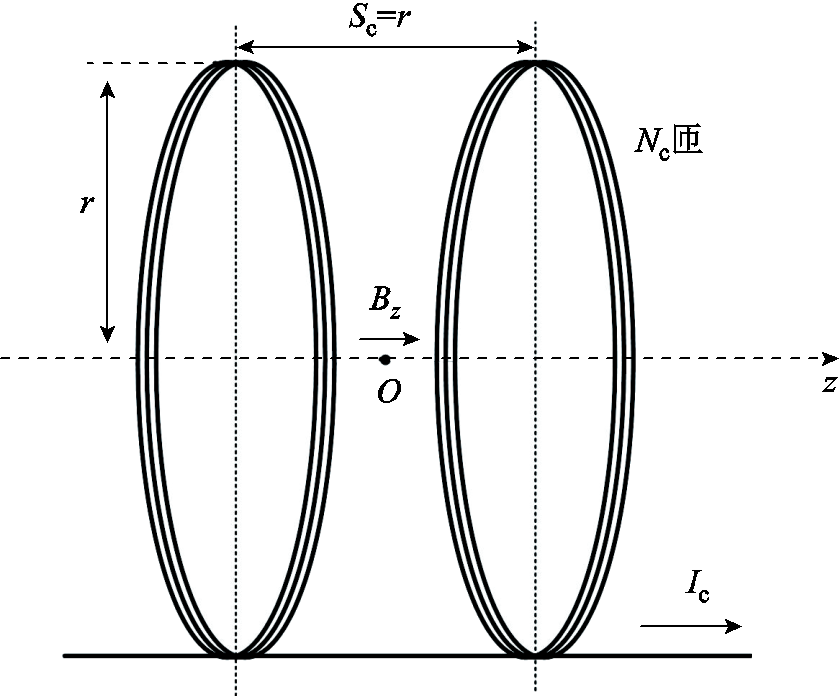
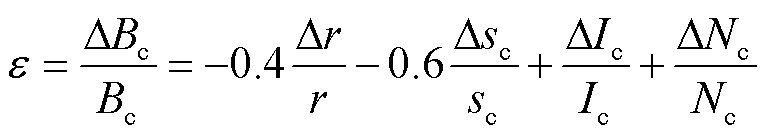 (11)
(11)
