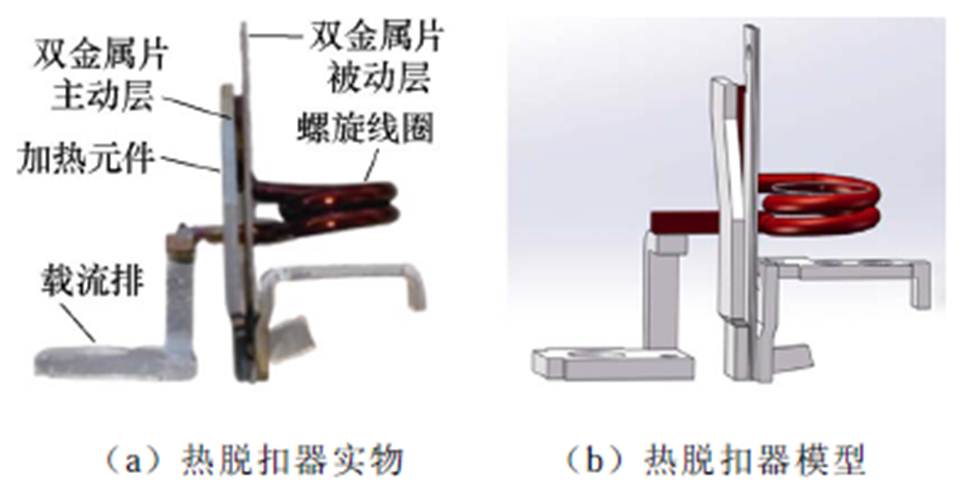
图1 热脱扣器实物和模型
Fig.1 Physical drawing and model diagram of the release devise
摘要 针对低压断路器热脱扣器用双金属片长期服役过程中的性能退化问题，该文首先建立热脱扣器电热结构耦合有限元模型，分析不同电流条件下双金属片表面温度和挠度的分布特性，结合正交试验确定比弯曲为双金属片性能退化关键特征；然后在考虑失效机理不变的前提下设计110、130、150℃三种温度应力下的加速寿命试验，以比弯曲作为特征量，分析双金属片性能与比弯曲的关联关系，对老化前后双金属片主被动层界面处元素分布进行定性分析，揭示了界面间金属原子运动行为，对双金属片比弯曲下降做出微观解释；建立双金属片分子动力学模型，分析主被动层界面原子扩散行为，得到被动层Ni原子与Fe原子向主动层扩散导致双金属片热膨胀系数改变从而影响其宏观动作特性的结论，从微观到宏观阐明双金属片性能退化机理。该文研究有助于揭示低压断路器过载保护系统性能退化规律，为双金属片性能优化提升提供理论基础。
关键词：低压直流断路器 双金属片 有限元仿真 加速寿命试验 分子动力学
直流输配电技术的进步亟需直流关键装备及其技术的跨越式发展，其中低压直流断路器因起到故障跳闸和保护直流系统中其他电力设备的重要作用而得到了越来越多的关注[1-2]。过载工况下低压直流断路器热脱扣器双金属片受热弯曲，推动脱扣机构实现断路器分闸。然而在长期服役过程中，双金属片由于受到电-热-力的影响而产生性能退化，导致动作响应特性改变，不能快速准确地断开电路[3]，严重威胁设备安全，降低直流配电系统运行可靠 性[4]。因此，亟须开展低压直流断路器用双金属片性能退化特性研究，明确其性能退化机理及表征，为低压断路器热过载系统主动运维提供理论参考。
目前，对于低压直流断路器双金属片的研究主要集中在动态响应仿真与脱扣影响因素分析上。周阳等建立双金属片有限元模型，模拟双金属片在电流激励下的发热过程，得到双金属片瞬态温度及形变特性[5]。潘庆元利用仿真模型对双金属片热弯曲特性进行分析，并结合试验建立双金属片参数最优解，降低设计成本[6]。胡建国等建立双金属片式产品动作特性输出模型，利用参数设计方法，实现双金属片动作特性影响因素的定性与定量分析[7]。陈维等采用热电耦合仿真对低压开关电器的温度场进行仿真研究，分析开关电器热稳定性及发热影响因素[8]。因电气设备性能退化时间较长，故通常采用加速退化试验来缩短试验周期。Liu Guojin等以漏电断路器为试验对象，采用应力加速度寿命试验对设备进行寿命预测[9]。李奎等通过建立基于马尔可夫过程的运行状态转移模型，实现了对漏电保护器的实际服役状态准确描述[10]。王国栋等对交联聚乙烯（Cross-Linked Polyethylene, XLPE）进行电压耐久试验，分析XLPE薄片样本失效时间统计特性，对传统基于反幂定律的XLPE电寿命模型进行修正[11]。C. Y. Peng和S. T. Tseng基于非线性退化轨迹模型建立了序进应力加速退化模型，并得到了该模型的首达时失效分布，通过仿真与LED灯试验验证了方法的正确性[12]。利用分子动力学从微观角度对材料属性进行分析能有效对材料失效机理做出解释。代岭均等基于随机各向异性理论，建立了介观尺度下纳米晶合金的三维模型，明确了纳米晶合金高频磁损耗与其微观结构的关系[13]。Li Chang等利用分子动力学技术和嵌入原子法（Embedded Atom Method, EAM）研究了温度对Al-Cu界面扩散键的影响，结果表明Cu原子在扩散键合过程中主要向Al侧扩散，界面区域的厚度与温度有关，温度越高，界面厚度越大[14]。
综上所述，目前鲜有研究空气式低压直流断路器的过载保护系统性能演化规律且大多停留在双金属片温度场仿真方面，本文通过建立热脱扣元件电-热-力耦合有限元模型模拟双金属片受热弯曲的动态响应特性，再经试验验证模型准确性后设计正交方案获得影响双金属片动作特性的关键参数，然后开展加速寿命试验，获得性能退化与特征参数之间的映射关系，最后结合分子动力学揭示性能退化微观机理。
本文选用某公司生产的额定电压Un=500 V、额定电流In=63 A型低压直流断路器为研究对象，其热脱扣器主要由载流排、螺旋线圈、加热元件、双金属片组成，如图1a所示。利用Solidworks软件建立热脱扣器模型，在不影响仿真结果的前提下对模型进行适当简化，将模型导入Ansys workbench中添加材料属性参数并进行网格划分。
图1 热脱扣器实物和模型
Fig.1 Physical drawing and model diagram of the release devise
本文选用的双金属片牌号为5J120110，主被动层厚度相等，均为1 mm，分别由Mn75Ni15Cu10、Ni36Fe64构成，载流排和螺旋线圈为铜，加热元件为康铜。材料属性参数见表1。
由于采用间接加热方式，双金属片热量主要来源于加热元件热传导和空气对流[15-16]，忽略热辐射影响。环境温度设置为20℃，电流从载流排左侧通入，双金属片与加热元件焊接处挠度自由度设置为零。
表1 材料参数
Tab.1 Material parameters
金属材料热膨胀系数/m℃电阻率/(W·m)泊松比弹性模量/(1011 N/m2)导热系数/[W/(m·℃)]密度/(kg/m3)比热容/[J/(kg·℃)] 加热元件1.754.5×10-50.31.17719.68 900386 主动层281.7×10-60.31.176 7227 700514 被动层1.270.78×10-60.31.477227 700514
依据GB 14048.2-2020模拟断路器在1.3In热态条件下响应特性，参照该型号产品反时限特性曲线，设置总模拟时长为5 000 s，前3 600 s接通电流为1.05In，后1 400 s接通电流为1.3In，子步时间设置为2 s。热脱扣元件温度及挠度分布如图2所示。
由图2可知，热脱扣器各元件温度分布由高到低依次为加热元件、螺旋线圈、双金属片和载流排。加热元件温度分布呈现出中间高两端低的趋势，最高温为154.18℃，这是由于加热元件电阻率大，生热多，同时加热元件上下端连接有铜端子和导线，使得加热元件上下端热量更容易传递；双金属片温度分布则呈现出从固定端至自由端依次递减的趋势。双金属片挠度分布由固定端至自由端依次递增，最大挠度3.477 mm出现在双金属片顶端。
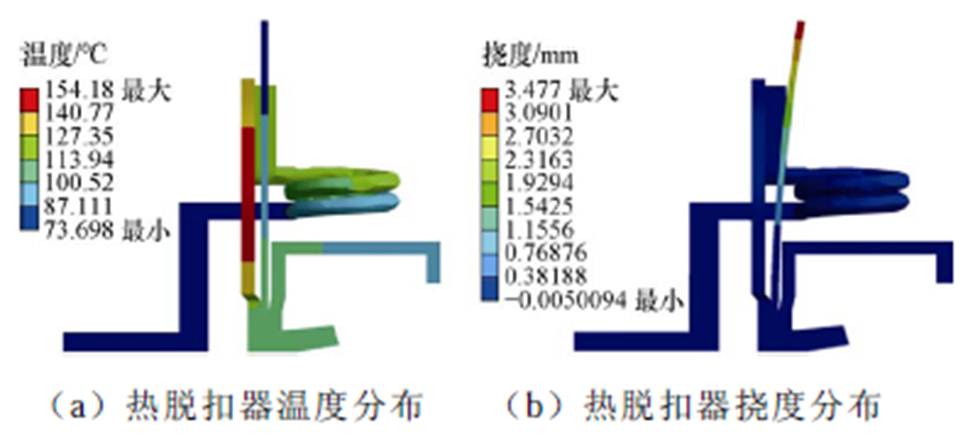
图2 热脱扣器温度和挠度分布
Fig.2 Group diagram of the temperature distribution and group diagram of the deflection distribution of the thermal release device
为验证仿真模型的准确性，开展断路器热脱扣试验，试验条件与仿真条件相同。试验电源采用直流大电流恒流源，利用K型探头的多路温度记录仪和线性可变差动变压器（Linear Variable Differential Transformer, LVDT）高精度位移传感器测量双金属片温度和挠度，采集仿真位置如图3所示。
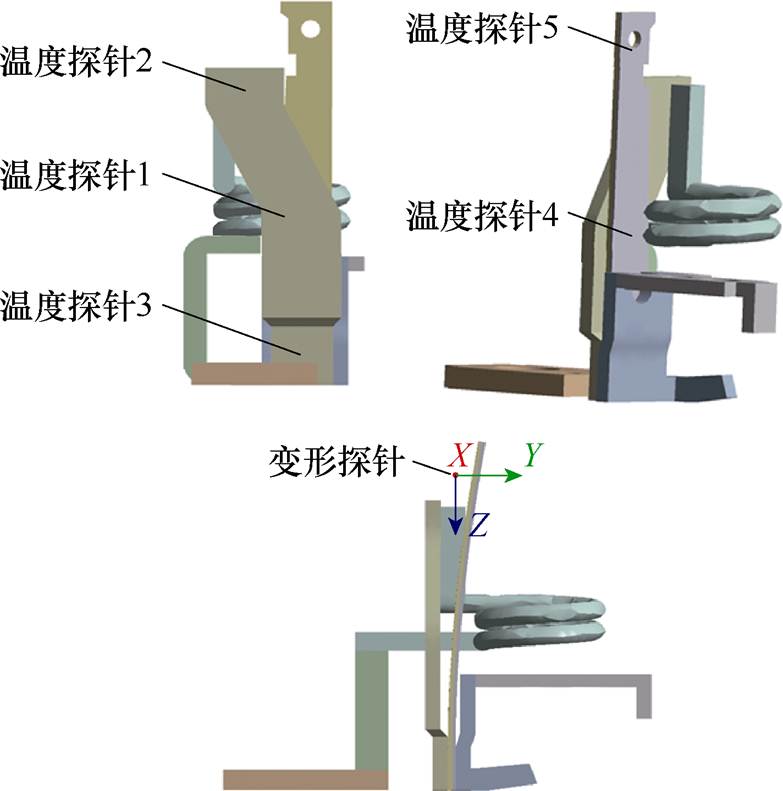
图3 热脱扣器仿真及试验温度、挠度采集位置示意图
Fig.3 Thermal release simulation and experimental temperature and deflection acquisition position schematic
温度与挠度试验和仿真结果对比如图4所示。温度仿真与实测结果随时间的变化趋势一致，经计算仿真与试验各位置点误差均在6.5%以下；挠度仿真与实测变化趋势基本一致，其总体误差均在4%以下。考虑到热脱扣器在现实中电场、温度场分布较为复杂，模型简化了其发热传热过程，加之试验过程中受传感器精度、干扰等影响，难免造成一定误差。误差在可接受范围内，验证了仿真模型的准确性，为下一步利用仿真模型快速、经济地确定性能退化表征关键参数提供理论支撑。
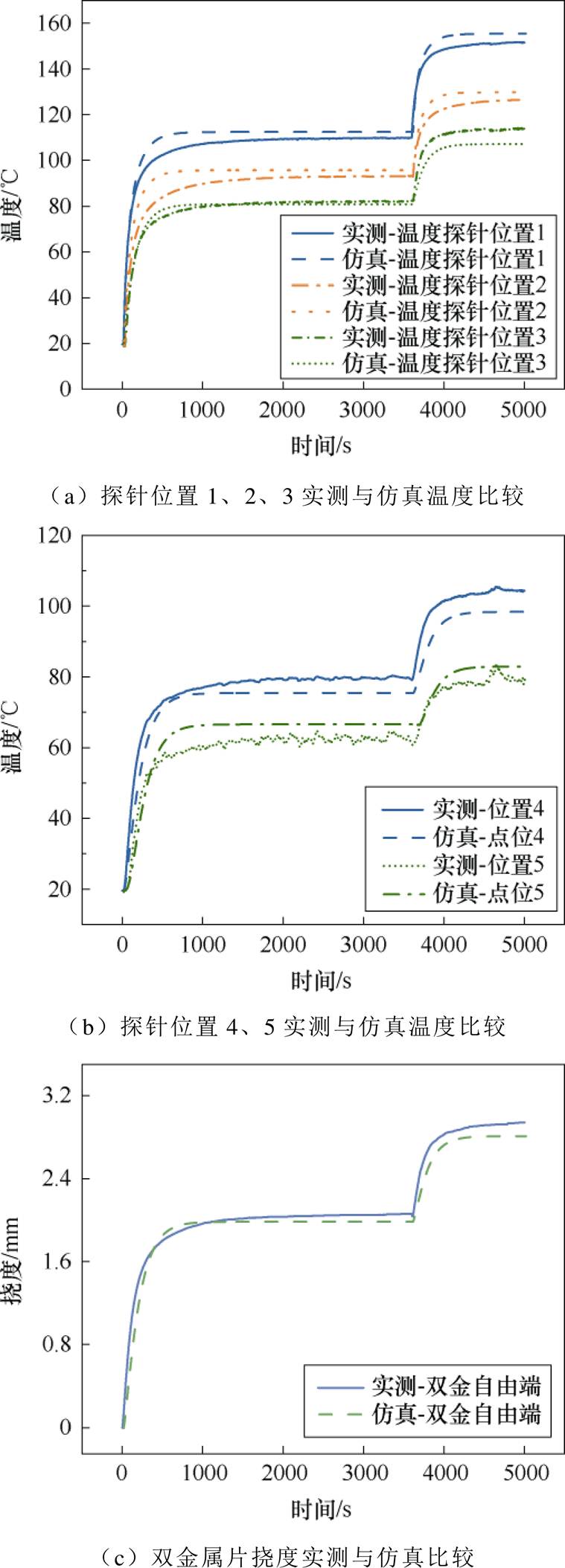
图4 试验温度与挠度和仿真温度与挠度数据对比
Fig.4 Comparison of experimental and simulated temperature and deflection data
低压直流断路器长期服役条件下热脱扣器用双金属片热膨胀系数、弹性模量等属性参数会产生变化，导致脱扣时间发生改变，使得断路器不能及时准确地分断过载回路[17]。为进一步确定影响双金属片性能退化的具体参数，选取主动层热膨胀系数、被动层热膨胀系数、主动层弹性模量、被动层弹性模量四个因素[18]，采用正交设计法安排试验，每个因素选取四个水平来判断该因素对热脱扣元件性能的影响趋势。将四个因素出厂初始值作为第一水平，初始值退化5%、10%和15%分别作为第二、第三、第四水平。
采用正交表L16(45)进行试验，结果见表2。采用极差分析法对正交试验数据进行分析，首先，计算试验参数值在每一水平下的平均值，然后再绘制试验参数平均值与因素水平的关系曲线，由关系曲线可知试验参数值随因素水平变化而变化的趋势。计算求得的影响双金属片自由端挠度的极差R见表3。由表3的极差分析可知，主动层热膨胀系数对双金属片最大位移影响最大。
以因素的退化水平作横坐标，最大位移作纵坐标，根据表3的极差分析，画出水平趋势，如图5所示。从图中可以看出，随着主动层弹性模量和主动层热膨胀系数的不断减小，双金属片最大位移逐渐减小，主动层热膨胀系数对双金属片的最大位移影响最大，主动层热膨胀系数的减小使得双金属片的最大位移呈直线下降趋势，且下降速度较快，主动层弹性模量的影响效果很小。被动层弹性模量数值和被动层热膨胀系数的减小使得最大挠度逐渐增大，但影响效果也同样很小。
表2 正交试验结果
Tab.2 Results of the orthogonal test
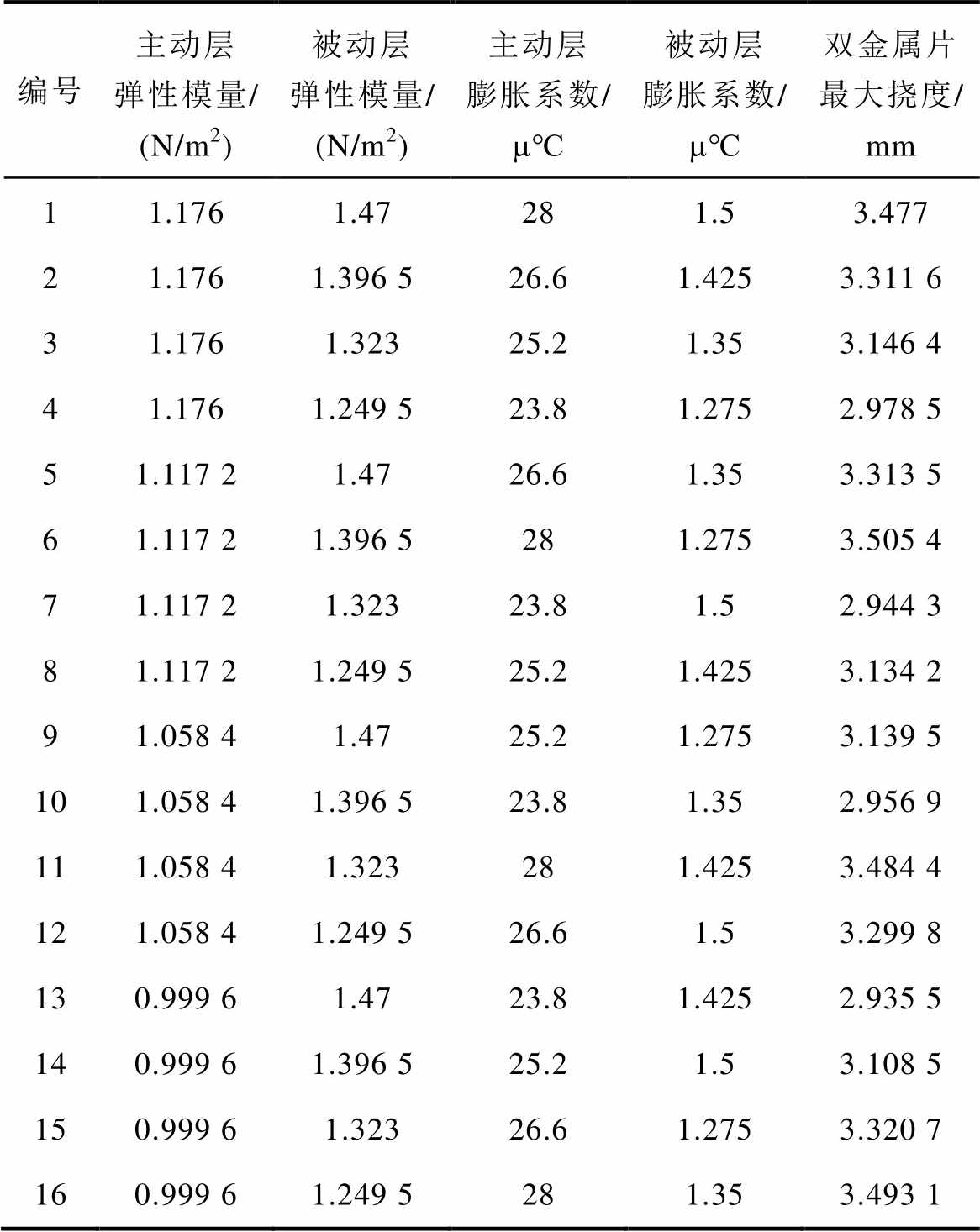
编号主动层弹性模量/(N/m2)被动层弹性模量/(N/m2)主动层膨胀系数/m℃被动层膨胀系数/m℃双金属片最大挠度/mm 11.1761.47281.53.477 21.1761.396 526.61.4253.311 6 31.1761.32325.21.353.146 4 41.1761.249 523.81.2752.978 5 51.117 21.4726.61.353.313 5 61.117 21.396 5281.2753.505 4 71.117 21.32323.81.52.944 3 81.117 21.249 525.21.4253.134 2 91.058 41.4725.21.2753.139 5 101.058 41.396 523.81.352.956 9 111.058 41.323281.4253.484 4 121.058 41.249 526.61.53.299 8 130.999 61.4723.81.4252.935 5 140.999 61.396 525.21.53.108 5 150.999 61.32326.61.2753.320 7 160.999 61.249 5281.353.493 1
表3 影响双金属片最大位移的极差分析
Tab.3 Range analysis affecting the maximum displacement of bimetallic sheet
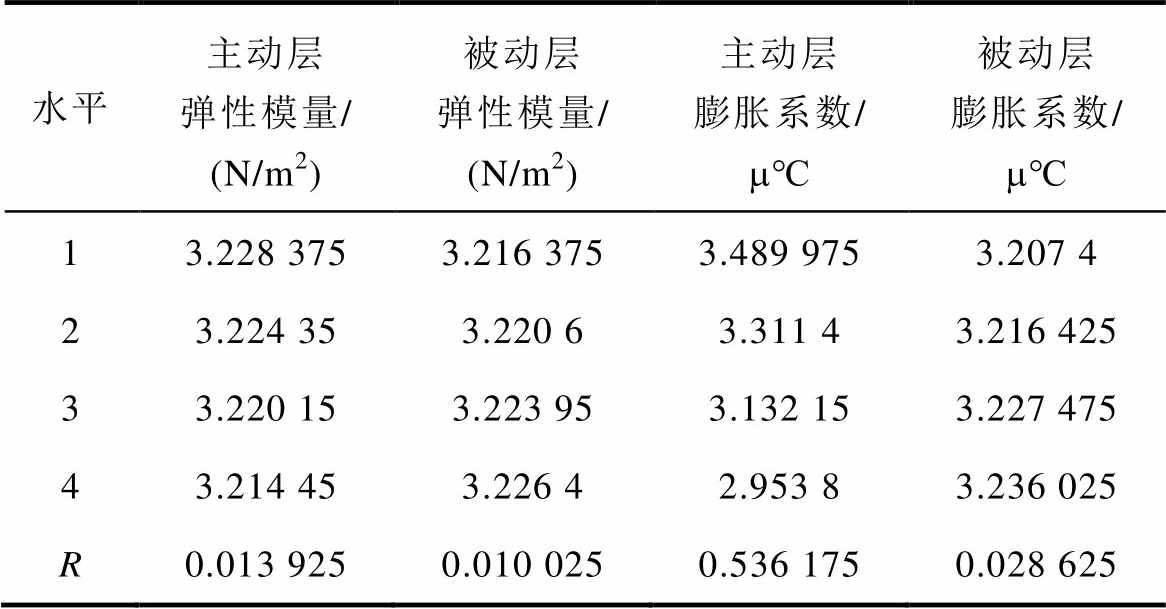
水平主动层弹性模量/(N/m2)被动层弹性模量/(N/m2)主动层膨胀系数/m℃被动层膨胀系数/m℃ 13.228 3753.216 3753.489 9753.207 4 23.224 353.220 63.311 43.216 425 33.220 153.223 953.132 153.227 475 43.214 453.226 42.953 83.236 025 R0.013 9250.010 0250.536 1750.028 625
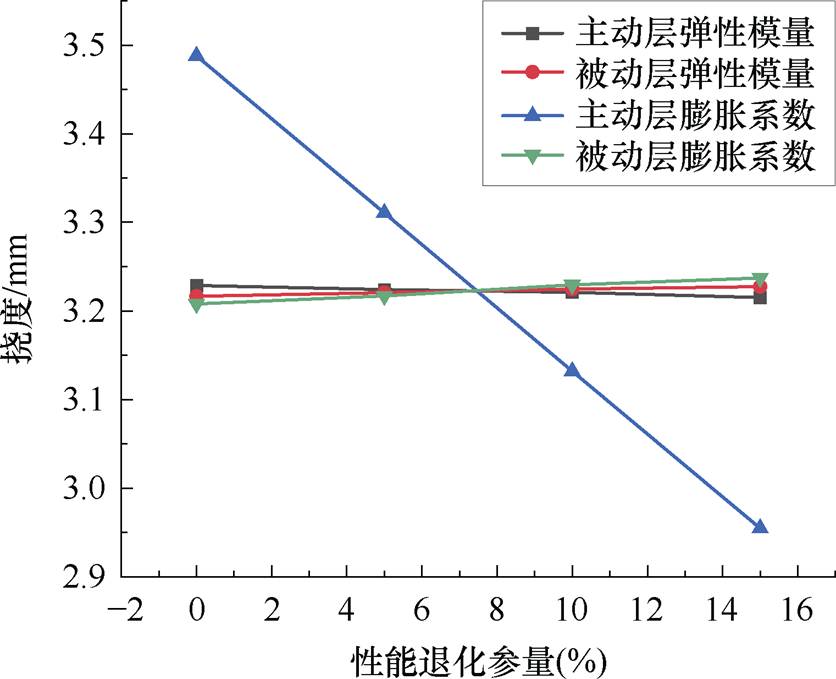
图5 性能影响因素水平趋势
Fig.5 Performance influencing factor horizontal trend
由1.2节可得双金属片性能退化的关键影响因素为主动层热膨胀系数，利用加速寿命试验获得不同性能退化程度的双金属片样品，进一步研究主动层热膨胀系数与性能退化程度的定量关系。由于热膨胀系数检测难度较高，而主动层热膨胀系数与比弯曲K有密切关系[19]，采用中间变量比弯曲K作为性能退化表征量，有
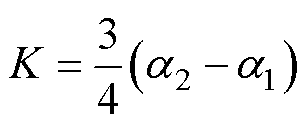（1）
式中，K为比弯曲；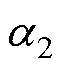
为主动层膨胀系数；
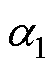为被动层膨胀系数。
根据双金属片实际服役环境，选择只考虑热加速因子的Arrhenius加速退化模型。参考双金属片线性温度范围为20～150℃、服役过程中额定工作温度为70℃、过载保护动作温度为100℃。保证在加速过程中失效机理不变前提下尽可能缩短试验时间，应力水平设置为110、130、150℃。
失效阈值的选定，参考国家标准GB 14048.2—2020可知断路器需满足热态1.3In电流下1 h内脱扣，极限情况下断路器在热态1.3In电流下1 h刚好脱扣。根据式（2）可求出满足脱扣条件的热脱扣元件的最小比弯曲[19]，经推导，最小比弯曲K为
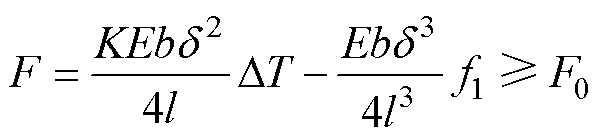（2）
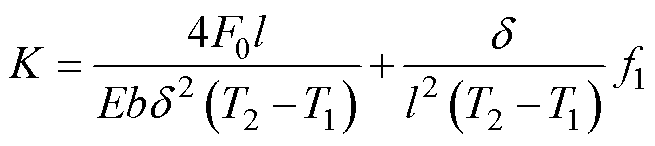（3）
式中，F为双金属片推动联动机构的力；K为双金属片比弯曲；E为双金属片弹性模量，E=1.323× 1011 N/m2；b为双金宽度，b=6.7 mm；d 为双金厚度，d =1 mm；l为双金长度，l=44 mm；DT为试验前后温升；F0为双金属片推动联动机构使断路器脱扣所需的最小力，经试验测量为3.5 N；f1为初始挠度；T2为测量终时温度；T1为初始温度。
考虑到实际样品间初始挠度存在差异性，因此热脱扣元件加速退化试验选取的失效阈值为相对失效阈值。经试验计算得极限情况下最小比弯曲K= 13.4 m℃，将初始比弯曲与最后失效时的比弯曲的差值作为双金属片的相对失效阈值L，即L=Q- 13.4 m℃，其中Q为初始比弯曲，初始比弯曲计算公式为
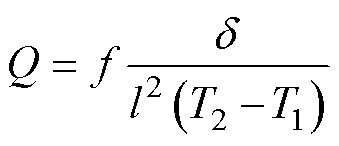（4）
式中，f为初始挠度，可经试验测得。
热脱扣元件加速退化试验过程的流程如图6所示。为了减少内箱壁和样品间的相互干扰，样品放置位置应远离恒温箱内壁，样品间保持间隔。在测量挠度退化数据时，热脱扣元件应先保温至25℃，保持温度1.5 h，再升温至75℃，保持1.5 h，记录温升DT=50℃的挠度值。
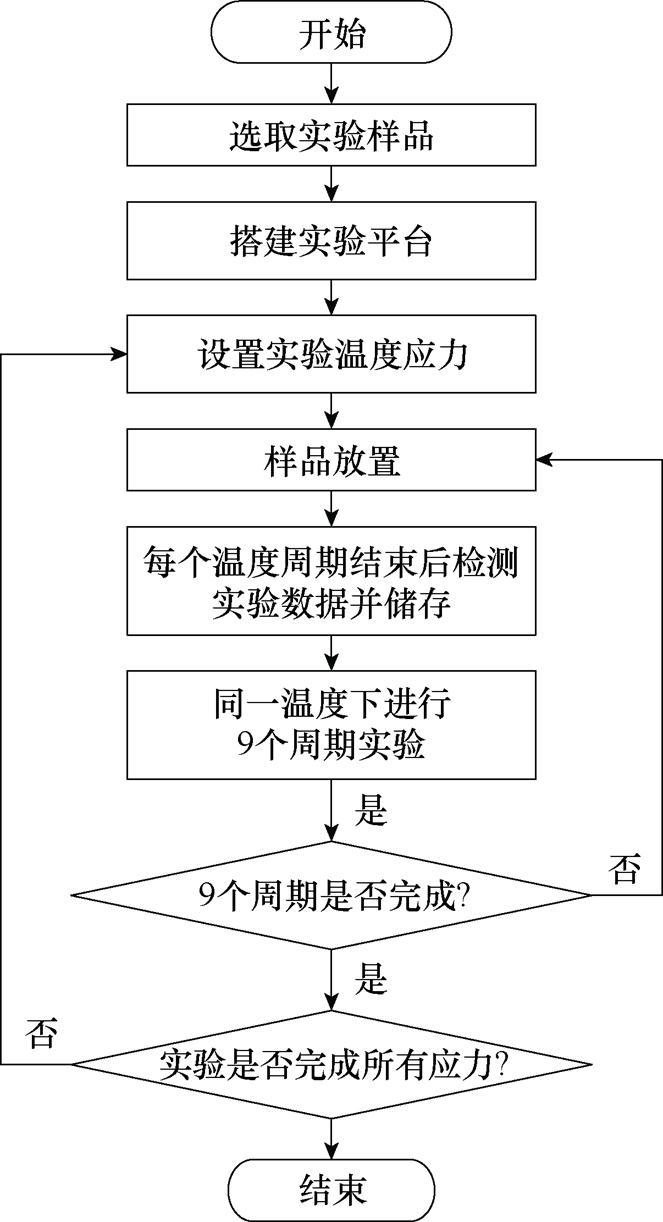
图6 试验流程
Fig.6 Experimental flow chart
图7给出了不同温度应力及不同老化周期条件下15只双金属片样品的比弯曲K，由于受加工工艺影响导致即使同一批样品初始比弯曲K也略有差距，但随着老化时间的增加，各样品比弯曲K都呈下降趋势，表明主动层膨胀系数的变化影响双金属片顶端位移。随着温度应力的升高，下降幅度越大，下降速度越快。定量分析可得，150℃应力下比弯曲K下降约7.01 m℃，130℃温度应力下样品的比弯曲K值总体下降约为3.21 m℃；110℃温度应力样品的比弯曲K值总体下降约为1.03 m℃。
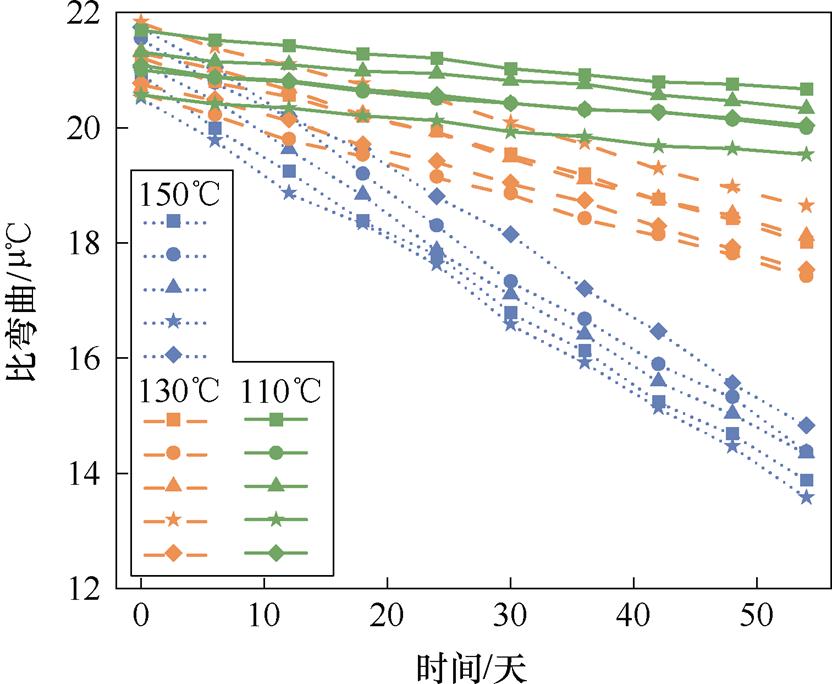
图7 不同温度应力下比弯曲K值的变化
Fig.7 Variation of specific bending K values under different temperature stresses
为进一步研究双金属片性能退化的微观机理，利用具备能谱分析功能的扫描电镜对150℃应力老化前后样品横截面进行元素分析。图8a～图8e给出了老化前双金属片样品横截面能量色散光谱扫描（Energy Dispersive Spectroscopy, EDS）元素分布，绿色部分为含Mn元素较多的主动层，红色部分为含Fe元素较多的被动层。未老化样品主被动层交界面分界较为规则，主被动层厚度基本相等；图8f～图8j给出了经54天加速老化后双金属片样品横截面元素分布情况，与未老化样品不同，老化样品主被动层交界面分界线不规则，且可明显观察到被动层Fe元素扩散进入主动层。分析认为，由于双金属片主被动层Mn75Ni15Cu10/Ni36组成元素浓度不同，原子可顺化学位梯度扩散移动，加之较高温度水平下原子扩散概率增加，使得双金属片交界面发生原子扩散现象，改变了主被动层膨胀系数，造成比弯曲K下降，进而导致双金属片宏观动态响应特性发生变化，验证了正交试验仿真结果的正确性。
图8 退化前后双金属片界面元素分布
Fig.8 Interfacial element distribution of bimetallic sheets before and after degradation
由双金属片老化前后横截面EDS元素分布可知，老化过程中主被动层交界面发生的原子扩散现象是影响宏观性能退化的关键因素，为进一步分析交界面原子扩散行为，本文采用lammps软件构建双金属片分子动力学模型，定量分析双金界面原子扩散现象。
首先创建100a×100a×8a模拟盒子，初始晶格常数a设置为Ni原子晶格常数3.53。将盒子区域填满面心立法晶格（Face Centered Cubic, FCC）结构的Ni原子，然后利用set type/ratio命令按主被动层原子比例替换，得到如图9所示双金属片模型，其上层为主动层，由Mn、Ni、Cu元素组成，下层为被动层，由Ni、Fe元素组成，该体系总共含有73 103个原子。为模拟真实的交界面，在xy轴方向上设置周期性边界条件，z轴方向上设置收缩性边界条件。
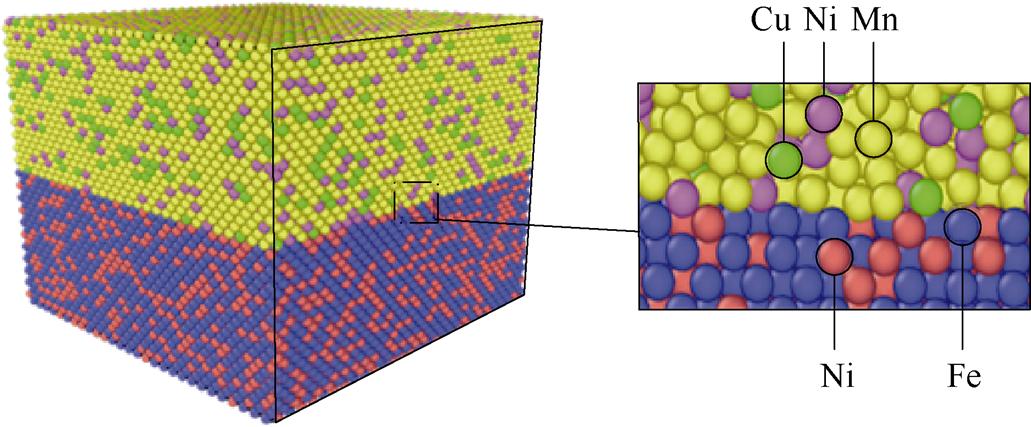
图9 双金属片分子动力学模型
Fig.9 Molecular dynamics model of bimetal
采用混合势函数方式描述各原子间势，主要用到G. Bonny等[20]开发的EAM势函数，W. M. Choi等[21]开发的MEAM势函数，以及D. S. Karls等[22]开发的LJ势函数。其中，Cu-Mn LJ势函数由式（3）、式（4）拟合。
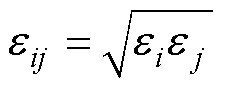（5）
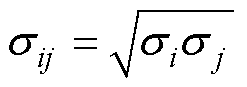（6）
式中，eij为原子i与原子j的LJ势函数e 参数；ei、ej分别为原子i、原子j的LJ势函数e 参数；sij为原子i与原子j之间的LJ势函数s 参数；si、sj分别为原子i、原子j的LJ势函数s 参数。
由于初始模型按理想晶格排列，经随机替换原子后模型存在较大预应力，因此采用共轭梯度法进行能量最小化，释放结构应力。使用Nose-Hoover控温器让模型在相应温度下运行50 000步，使模型得到充分弛豫，时间步长设置为0.001 ps。弛豫结束后，让模型在恒温-体积（constant Number，Volume and Temperature, NVT）系综下控温2 ns[23]。
参照加速试验温度设置模型控温温度为25、110、130和150℃。模拟时长2 ns模型快照如图10所示，常温下界面原子无明显扩散，随着温度升高，扩散的原子逐渐增多，且被动层向主动层扩散原子数量远远大于主动层向被动层扩散的原子数量。
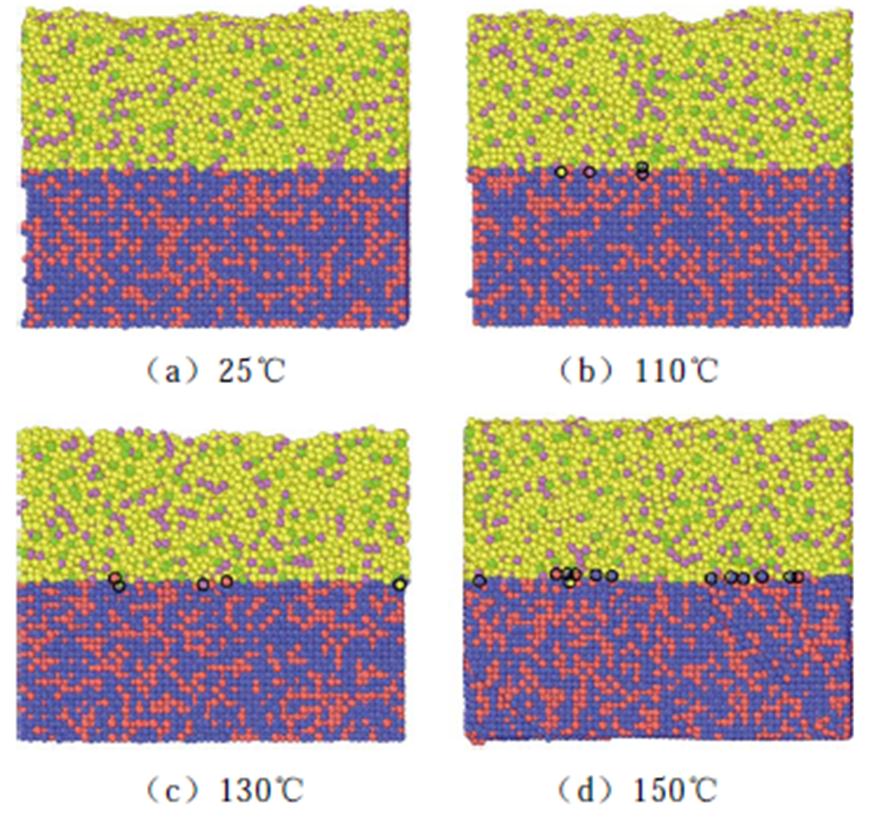
图10 模拟时长2 ns下界面原子扩散情况
Fig.10 Simulate the diffusion of interfacial atoms at 2 ns
利用OVITO后处理软件定量分析每种原子扩散数量，不同温度下主动层与被动层各原子扩散数量随模拟时长变化情况如图11所示。由图11可以看出，被动层原子扩散数量远大于主动层，这是由于被动层原子间相互作用力弱，容易受到温度等外部因素影响打破原子间力平衡而扩散进入主动层，又因为主被动层都含有Ni原子，因此Fe原子化学位梯度大于Ni原子，造成Fe原子扩散数量最多。各原子扩散数量都呈现出随温度升高而增加的趋势。除主动层Cu原子外其余原子扩散数量均随着模拟时间的增长而增加，这是由于Cu原子数量相比其他原子较少，扩散行为受扩散概率影响较小，难以呈现出定向趋势。主动层Mn原子各温度条件下扩散数量随着模拟时长的增加而线性增加，其余原子扩散数量则随着模拟时长增加先快速增加，而后缓慢增加。
为进一步描述各原子的扩散行为，通过方均位移（Mean Square Displacement, MSD）曲线计算不同温度下原子的扩散系数。MSD指的是体系内所有原子在经过t时间后位移变化量的度量，计算公式为
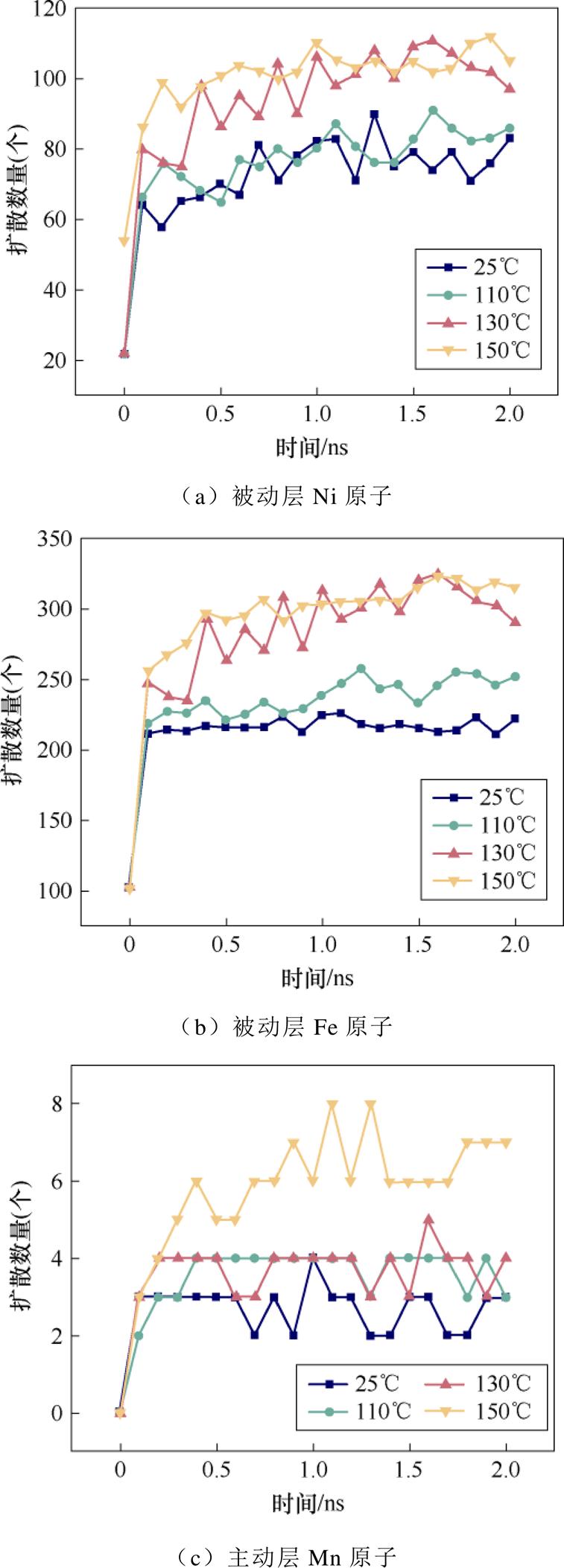
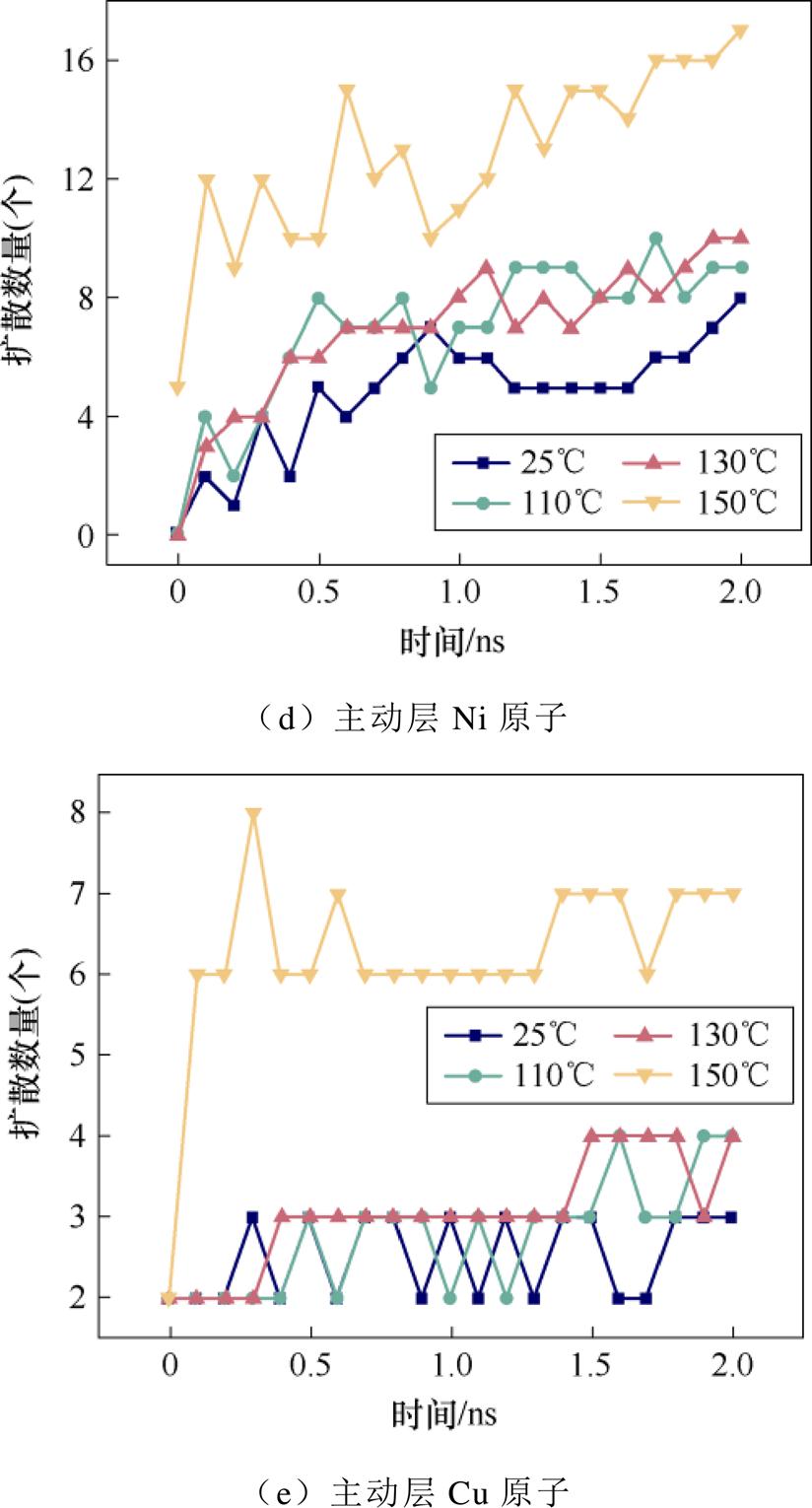
图11 不同温度下主动层与被动层各原子扩散数量随模拟时长变化情况
Fig.11 The variation of atomic diffusion quantities in the active and passive layers with simulation time at different temperatures
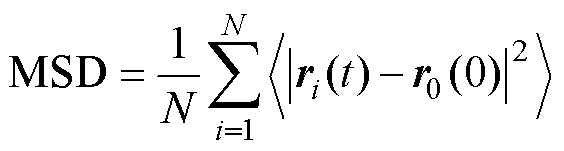（7）
式中，N为体系内原子个数；ri(t)为t时刻原子i的挠度矢量；r0(0)为0时刻原子i挠度矢量。
各原子在不同温度及模拟时长下MSD如图12所示。整体来看，各元素扩散系数都随温度的升高而增加，这是因为温度为原子提供了动能。主动层Mn、Ni、Cu原子表现出了较高的方均位移，被动层Ni、Fe原子则表现出较低的方均位移。在开始阶段（0.5 ns之前）各原子跨越扩散行为较少，只在平衡位置处运动，因此MSD增加缓慢，未表现出线性趋势；在0.5 ns之后，各原子扩散数量和程度增加，MSD呈现线性增长趋势，取此阶段曲线做拟合，计算各元素不同温度下扩散系数，考虑温度对扩散系数的影响，由Arrhenius方程可得扩散系数与扩散活化能和温度的关系为
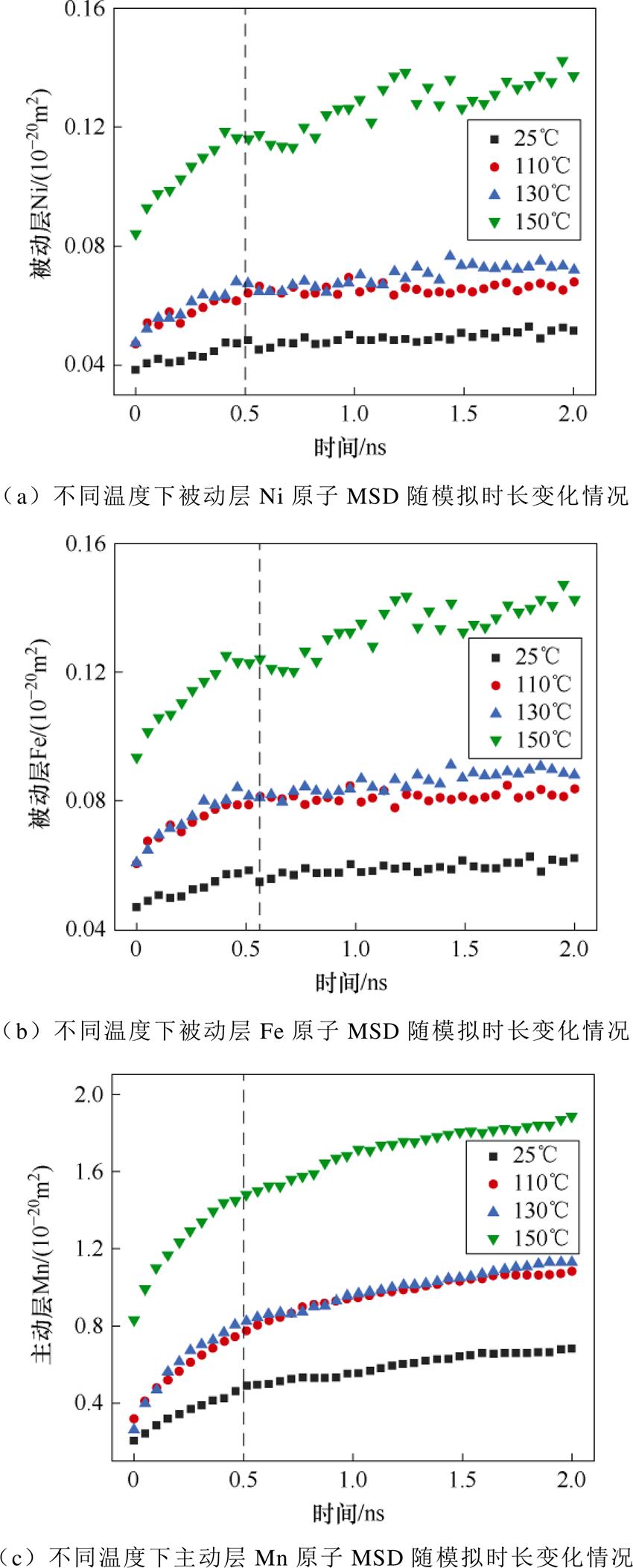
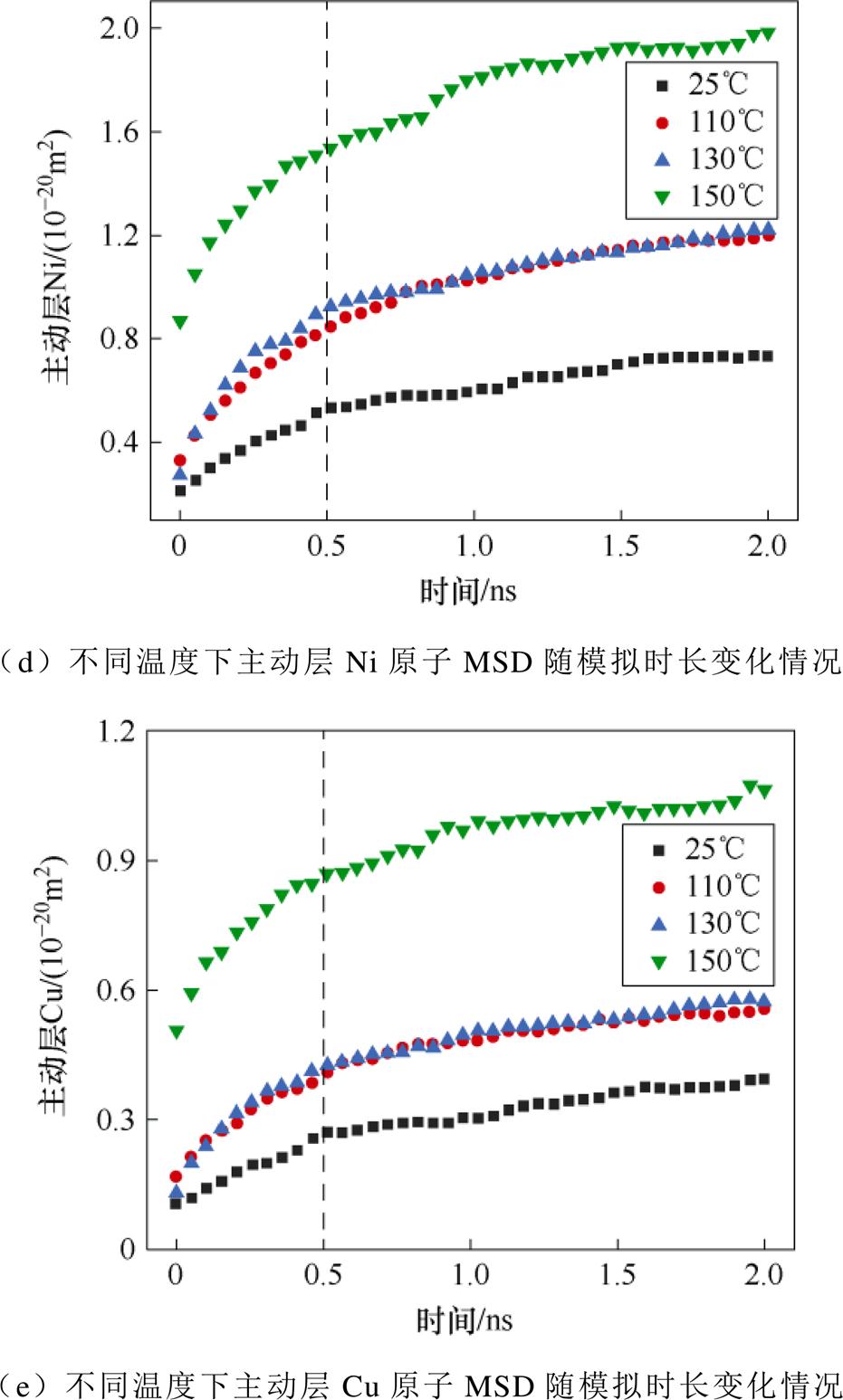
图12 各原子在不同温度及模拟时长下MSD
Fig.12 MSD of each atom at different temperatures and simulation durations
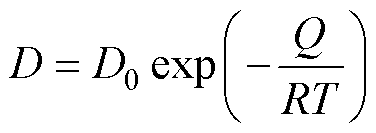（8）
式中，D0为扩散因子；Q为扩散活化能；T为温度；R为气体常数。
各元素在不同温度下的扩散系数如图13所示，298 K下，各原子扩散系数由高到低依次为被动层Ni（均为2.093×10-12 m2/s）、主动层Mn（1.904× 10-12 m2/s）、主动层Cu（1.171×10-12 m2/s）、被动层Fe（0.057×10-12 m2/s）、主动层Ni（0.056×10-12 m2/s）；随着温度的增加，主动层Mn、被动层Ni扩散系数显著增加，而主动层Ni、Cu，被动层Fe增加幅度不大。
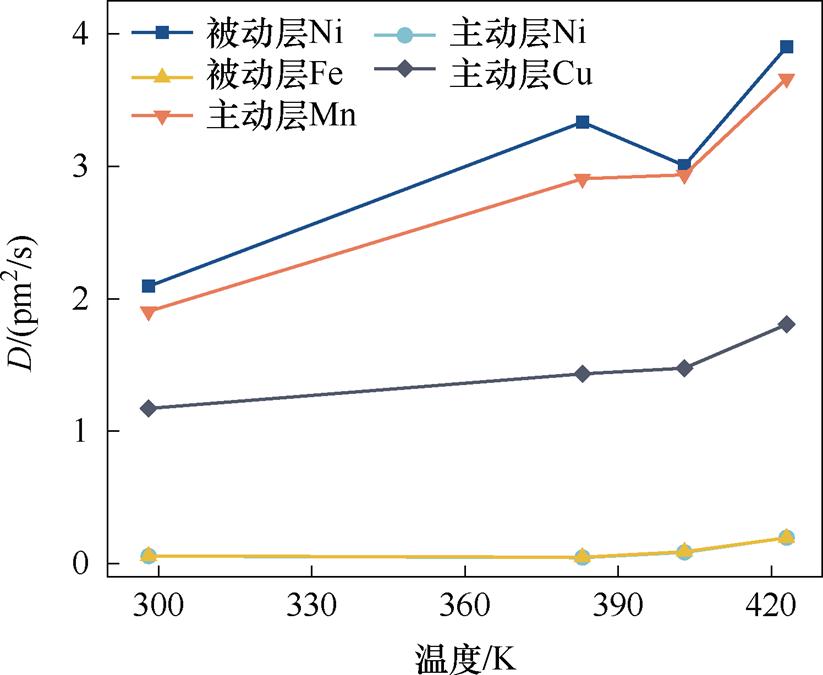
图13 各原子扩散系数与温度的关系
Fig.13 Relationship between atomic diffusion coefficients and temperature
通过拟合数据，可以得到的各金属原子的扩散活化能Q和扩散因子D0，见表4。表中，扩散活化能Q为金属原子扩散时克服周围原子对其束缚的势垒，扩散活化能越低表明原子扩散越容易，扩散因子D0为原子扩散概率。
表4 扩散活化能和扩散因子
Tab.4 Diffusion activation energy and diffusion factor
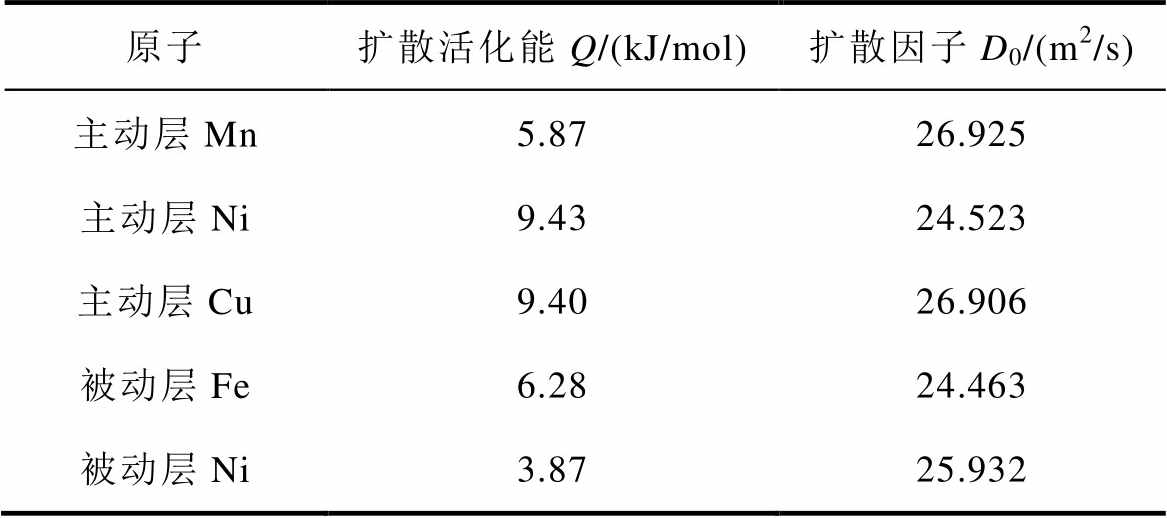
原子扩散活化能Q/(kJ/mol)扩散因子D0/(m2/s) 主动层Mn5.8726.925 主动层Ni9.4324.523 主动层Cu9.4026.906 被动层Fe6.2824.463 被动层Ni3.8725.932
由表4可知，各元素的扩散因子D0差别不大，即各原子扩散概率基本相同，可以不考虑D0对原子扩散的影响。数据表明，被动层Ni原子扩散活化能最低，即被动层Ni原子扩散行为比主动层Ni原子扩散行为更加剧烈，具体表现为扩散数量增多，扩散深度加深，扩散概率增加。而被动层中Fe原子扩散活化能比Ni原子要高，而扩散数量却远大于Ni原子，分析可能是因为主被动层都含有一定数量的Ni原子，其浓度差远小于Fe原子，并且Fe原子数量较多，因此扩散活化能高的Fe原子扩散数量反而比扩散活化能低的Ni原子多。综上所述，被动层的原子扩散活化能较主动层原子扩散活化能低，被动层原子扩散运动较主动层更为剧烈，导致双金热膨胀系数改变，表现为双金属片比弯曲K下降，进而对双金属片的宏观动作特性造成影响。
1）建立了热脱扣元件有限元模型，仿真结果表明，热脱扣元件温度分布最高位置出现在加热元件上，温度分布呈现中间高两端低的特点；双金属片温度分布则从固定端到自由端呈阶梯形递减，双金属片挠度分布与温度分布呈现高度相关，最大挠度位于自由端顶部。通过试验验证了该仿真模型正确性。利用仿真模型进行正交试验，根据正交试验结果，并采用极差法分析可得主动层热膨胀系数对双金属片最大位移影响最大，确定比弯曲K作为反映双金属片性能好坏的特征量。
2）应用Arrhenius模型作为加速寿命模型，试验应力条件范围为100～150℃。试验结果表明，双金属片比弯曲K会随着退化时间的增长而降低，在同一温度应力下产品退化速率相同，应力水平越高比弯曲K退化越明显，150℃应力水平下经54天老化后比弯曲K较未老化时降低了约30%，130℃和 110℃应力水平下分别降低了约10%、4%。
3）元素分析表明老化后双金属片由于主被动层元素浓度不同，主被动层界面间会产生原子扩散现象，金属原子的扩散会导致主被动层界面处元素分布产生改变，进而影响主被动层热膨胀系数，改变比弯曲K数值。采用分子动力学模型进行仿真研究，结果表明，温度的升高及模拟时长的增加会加剧金属原子扩散行为，被动层原子扩散数量远大于主动层原子扩散数量，被动层Fe、Ni原子的大量流失一方面导致该层热膨胀系数改变，另一方面又改变了主动层热膨胀系数，影响比弯曲K，进而造成双金属片宏观性能退化。
参考文献
[1] 贾申利, 史宗谦, 王立军. 真空断路器用于直流开断研究综述[J]. 高压电器, 2017, 53(3): 12-16.
Jia Shenli, Shi Zongqian, Wang Lijun. Review on the research of vacuum circuit breaker for DC breaking[J]. High Voltage Apparatus, 2017, 53(3): 12-16.
[2] 荣命哲, 杨飞, 吴翊, 等. 直流断路器电弧研究的新进展[J]. 电工技术学报, 2014, 29(1): 1-9.
Rong Mingzhe, Yang Fei, Wu Yi, et al. New developments in switching arc research in DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 1-9.
[3] 束洪春, 邵宗学, 旷宇. 基于改进型限流混合式直流断路器的开断时序优化研究[J]. 电工技术学报, 2023, 38(22): 6176-6187.
Shu Hongchun, Shao Zongxue, Kuang Yu. Research of opening timing optimization based on improved current-limiting hybrid DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6176-6187.
[4] 李浩, 裴翔羽, 李泽文, 等. 具备故障电流限制能力的多端口直流断路器[J]. 电工技术学报, 2023, 38(10): 2818-2831.
Li Hao, Pei Xiangyu, Li Zewen, et al. A multi-port DC circuit breaker with fault-current limiting capability[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2818-2831.
[5] 周阳, 王东, 戴铭磊. 小型断路器双金属片瞬时热分布研究[J]. 现代建筑电气, 2022, 13(10): 6-10.
Zhou Yang, Wang Dong, Dai Minglei. Study on instantaneous heat distribution and deformation of bimetallic sheet of miniature circuit breaker[J]. Modern Architecture Electric, 2022, 13(10): 6-10.
[6] 潘庆元. 小型断路器双金属片热弯曲特性的实验仿真[J]. 电器与能效管理技术, 2022(2): 46-52.
Pan Qingyuan. Experimental simulation of bimetallic strip thermal flexivity specialty in miniature circuit breaker[J]. Electrical & Energy Management Tech- nology, 2022(2): 46-52.
[7] 胡建国, 王景凯, 黄和平. 影响双金属片式产品动作特性的因素及其参数设计[J]. 电器与能效管理技术, 2020(6): 30-35.
Hu Jianguo, Wang Jingkai, Huang Heping. Factors affecting performance characteristics of bimetallic strip products and parameter design[J]. Electrical & Energy Management Technology, 2020(6): 30-35.
[8] 陈维, 张国钢, 张鹏飞, 等. 低压开关电器主电路温度场的有限元分析[J]. 低压电器, 2010(20): 1-4.
Chen Wei, Zhang Guogang, Zhang Pengfei, et al. Finite element analysis of temperature field of main circuit in low voltage apparatus[J]. Low Voltage Apparatus, 2010(20): 1-4.
[9] Liu Guojin, Miao Jianhua, Zhao Xingzhou, et al. Life prediction of residual current circuit breaker with overcurrent protection based on BP neural network optimized by genetic algorithm[J]. Journal of Electrical Engineering & Technology, 2022, 17(3): 2003-2014.
[10] 李奎, 郝运佥, 赵成晨, 等. 基于马尔可夫过程的漏电保护器服役状态及其可靠性分析[J]. 电工技术学报, 2023, 38(18): 5061-5076.
Li Kui, Hao Yunqian, Zhao Chengchen, et al. Service states and reliability analysis of residual current device based on Markov process[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5061- 5076.
[11] 王国栋, 周凯, 李原, 等. 基于失效时间统计特性的交联聚乙烯电寿命模型修正[J]. 电工技术学报, 2023, 38(4): 1042-1050.
Wang Guodong, Zhou Kai, Li Yuan, et al. Modification of cross-linked polyethylene electrical life model based on statistical characteristics of failure time[J]. Transactions of China Electro- technical Society, 2023, 38(4): 1042-1050.
[12] Peng C Y, Tseng S T. Progressive-stress accelerated degradation test for highly-reliable products[J]. IEEE Transactions on Reliability, 2010, 59(1): 30-37.
[13] 代岭均, 邹亮, 郭凯航, 等. 纳米晶合金晶粒尺寸与体积分数对高频磁损耗特性影响分析[J]. 电工技术学报, 2023, 38(18): 4853-4863.
Dai Lingjun, Zou Liang, Guo Kaihang, et al. Analysis of grain size and volume fraction of nanocrystalline alloy on high frequency magnetic loss characteri- stics[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4853-4863.
[14] Li Chang, Li Dongxu, Tao Xiaoma, et al. Molecular dynamics simulation of diffusion bonding of Al-Cu interface[J]. Modelling and Simulation in Materials Science and Engineering, 2014, 22(6): 065013.
[15] 崔曼, 胡震, 张腾飞, 等. 基于壳温信息的功率器件可靠性分析[J]. 电工技术学报, 2023, 38(24): 6760-6767.
Cui Man, Hu Zhen, Zhang Tengfei, et al. Reliability analysis of power device based on the case temperatures[J]. Transactions of China Electrotech- nical Society, 2023, 38(24): 6760-6767.
[16] 许文良, 何为龙. 低压电器热过载保护及热双金属片仿真设计[J]. 电器与能效管理技术, 2021(6): 41-46.
Xu Wenliang, He Weilong. Thermal overload protection for low voltage apparatus and simulation of thermal bimetal[J]. Electrical & Energy Management Technology, 2021(6): 41-46.
[17] 胡金利, 卢为民, 姜义非. 小型断路器双金属片温升仿真研究[J]. 电器与能效管理技术, 2020(12): 60-66.
Hu Jinli, Lu Weimin, Jiang Yifei. Simulation study on temperature rise of bimetal in MCB[J]. Electrical & Energy Management Technology, 2020(12): 60-66.
[18] 毛国伟. 塑壳断路器热双金属片动作特性仿真分析[J]. 电子元器件与信息技术, 2022, 6(11): 22-24, 58.
Mao Guowei. Simulation analysis of action characteristics of plastic case circuit breaker hot bimetal[J]. Electronic Components and Information Technology, 2022, 6(11): 22-24, 58.
[19] 于永站, 谭昌柏, 张金泉, 等. 塑壳断路器热脱扣特性的仿真与试验分析[J]. 低压电器, 2012(7): 5-9, 18.
Yu Yongzhan, Tan Changbai, Zhang Jinquan, et al. Simulation and experiment research on thermal tripping capacity of moulded case circuit breaker[J]. Low Voltage Apparatus, 2012(7): 5-9, 18.
[20] Bonny G, Pasianot R C, Castin N, et al. Ternary Fe-Cu-Ni many-body potential to model reactor pressure vessel steels: First validation by simulated thermal annealing[J]. Philosophical Magazine, 2009, 89(34/35/36): 3531-3546.
[21] Choi W M, Jo Y H, Sohn S S, et al. Understanding the physical metallurgy of the CoCrFeMnNi high-entropy alloy: an atomistic simulation study[J]. NPJ Com- putational Materials, 2018, 4: 1.
[22] Karls D S, Bierbaum M, Alemi A A, et al. The OpenKIM processing pipeline: a cloud-based auto- matic material property computation engine[J]. The Journal of Chemical Physics, 2020, 153(6): 064104.
[23] Liu Huaqiang, Deng Wei, Ding Peng, et al. Investigation of the effects of surface wettability and surface roughness on nanoscale boiling process using molecular dynamics simulation[J]. Nuclear Engin- eering and Design, 2021, 382: 111400.
Degradation Characteristics and Mechanism Analysis of Bimetal Sheet of Low Voltage DC Circuit Breaker
Abstract A low-voltage DC circuit breaker plays a role in power distribution, control, and protection in low-voltage DC systems. As the core component of overload protection of low-voltage DC circuit breakers, the reliability of thermal release directly affects the safe and stable operation of the DC system. However, during service, the thermal release is subjected to large temperature stress fluctuations, the degradation mechanism is not clear, and the reliability evaluation is difficult. Therefore, the simulation model of thermal release is established to determine the key parameters of thermal release performance degradation. The degradation mechanism of thermal release is revealed by the accelerated life test, and the degradation mechanism of the bimetal sheet is explained from the perspective of molecular dynamics.
Firstly, a three-dimensional finite element model of thermal release is established to explore the distribution mechanism of temperature, stress, and deflection of the bimetal sheet. An experimental platform is established, and the active layer expansion coefficient is determined as the key parameter of bimetal sheet performance degradation through orthogonal tests. Secondly, the accelerated stress is temperature, and the accelerated life model is the Arrhenius model. The accelerated life test under 110℃, 130℃, and 150℃ is designed, and the specific bending K is used as the degradation parameter. With the increase in temperature stress, the K decreases by 7.01×10-6/℃ at 150℃ and 3.21×10-6/℃ at 130℃. The e overall decrease in the specific bending K at 110℃ is about 1.03×10-6/℃. The distribution of elements at the interface of the bimetal sheet is observed by SEM. Finally, the molecular dynamics model of the bimetal sheet is established. The diffusion behavior of atoms in the passive layer is more intense than in the active layer. The diffusion behavior of atoms at the interface is further explained by analyzing the mean orientation shift, diffusion activation energy, and diffusion factor of different atoms. The results show that the diffusion probability of all atoms was almost the same. Due to the low diffusion activity of the passive layer Ni atom, the diffusion is more intense. The performance degradation mechanism of the overload protection element of low-voltage DC circuit breakers is revealed from a microscopic point of view.
The following conclusions can be drawn. (1) The active layer expansion coefficient is a key parameter affecting the degradation of bimetal sheets, so specific bending K can be used as a characteristic parameter characterizing the degradation of bimetal sheets. (2) The degradation rate of specific bending K is almost the same at the same temperature, and the decrease rate of specific bending K is greater with the increase of temperature. (3) The molecular dynamics analysis shows that the diffusion of atoms at the interface changes active and passive expansion coefficients, and the diffusion of atoms in the passive layer is intense. The degradation mechanism of the bimetal sheet is explained from the microscopic view.
Keywords：Low voltage DC circuit breaker, bimetallic sheet, finite element simulation, accelerated life test, molecular dynamics
中图分类号：TM561
DOI: 10.19595/j.cnki.1000-6753.tces.231721
国家自然科学基金资助项目（51937004）。
收稿日期 2023-10-16
改稿日期 2023-12-07
邢云琪 男，1986年生，教授，研究方向为先进电工材料及装备可靠性提升技术。
E-mail: yqxing@hebut.edu.cn
赵成晨 女，1991年生，讲师，研究方向为开关电器可靠性评估及预测、电器检测技术。
E-mail: zhaocc0827@163.com（通信作者）
（编辑 崔文静）