 (1)
(1)
摘要 模块化多电平变流器(MMC)是柔性直流输电系统的核心装备,其中子模块(SM)金属化薄膜电容器是MMC中的薄弱环节之一,故研究金属化薄膜电容器的状态监测和寿命评估对于提高MMC运行可靠性和制定系统维护计划具有重要意义。目前,现有金属化薄膜电容器的寿命评估方法未考虑电容器老化进程对电容值和等效串联电阻(ESR)的影响,难以准确实现不同服役状态下的电容器剩余寿命评估问题。因此,该文提出考虑当前电容值状态在线监测的金属化薄膜电容器的剩余寿命评估方法。首先,在考虑电容器老化速率与温度耦合关系的基础上建立了电容器ESR和电容值的老化模型。其次,在进行寿命计算时考虑到电容器的老化效应,根据提出的容值在线监测方法得到当前的电容值,推断出电容器已使用年限及电容器目前的ESR值,并代入建立的场路协同仿真电热耦合模型中计算得到电容器温度。最后,根据提出的剩余寿命模型对电容器当前剩余寿命进行预测。该文研究成果将为设备选型、系统设计和MMC系统子模块电容器的可靠性评估提供参考。
关键词:模块化多电平变流器(MMC)系统 金属化薄膜电容器 电热耦合模型 在线监测 寿命评估
为了应对能源危机与化石能源导致的环境气候问题,各国政府越发重视新能源的开发与利用[1]。“十四五”时期,我国可再生能源将进入高质量跃升发展新阶段,为早日实现“碳达峰、碳中和”目标提供主力支撑[2]。由于我国主要的电力消费中心与可再生能源的位置分布具有分散性,因此,具备远距离、大容量输电能力是输电系统的必然要求。大力建设特高压直流输电工程符合我国构建新型电力系统,完成双碳节能减排和解决能源的传输问题的要求[3-4]。基于模块化多电平变流器(Modular Multilevel Converter, MMC)的柔性直流输电凭借其开关频率低、运行效率高等优点已成为目前主要的输电方式之一[5-6]。MMC作为柔性直流输电系统的核心设备,子模块(Submodule, SM)金属化薄膜电容器是失效率最高的部件之一。研究表明,在承受较大负载时子模块电容器核心温度会上升,器件内部产生热应力,在长时间尺度的纹波电压和热应力的作用下电容器发生退化直至失效,最终诱发系统故障。因此,研究金属化薄膜电容器的可靠性对于提高换流器组件的运维计划具有重要意义,影响着电力系统的可靠运行[7]。
目前,针对金属化薄膜电容器的寿命建模和状态评估开展了较多研究,在电容器寿命评估方面:文献[8]对金属化薄膜电容器的高脉冲电流耐受能力进行研究,评估了脉冲模式下不同金属化薄膜电容器的平均寿命。文献[9]利用威布尔分布模型分析了脉冲功率应用场合下金属化薄膜电容器的寿命分布规律,建立了电容器单体元件和整机的寿命预测模型。文献[10]分析了金属化薄膜电容器的退化机理,并根据电容器的加速老化测试结果提出了一种寿命评估模型。文献[11]提出了直流链路电容器寿命模型的经验公式,并认为电容器寿命模型中的温度和电压加速因子分别遵循Arrhenius方程和幂律规则。文献[12]将电极含铝量不同的两种金属化薄膜电容器置于高温高湿的环境下进行加速老化试验,得到了电容值与ESR的老化模型,并对比了二者的平均腐蚀速率。
在电容器状态监测方面:文献[13]基于外加采集电路实现PWM换流器直流侧电容的等效串联电阻(Equivalent Series Resistance, ESR)的监测,该方法需额外添加硬件电路,增加了监测成本。文献[14]将受控的交流电流注入系统电路,并利用数字滤波器提取其在直流输出上感应出的交流纹波电压和电流分量,以便监测ESR值,但该方法额外增加了系统的损耗。文献[15]提出了基于电容器在放电电阻的放电数据监测电容值,但该方法不仅破坏了子模块的原始结构,同时降低了子模块的利用率。文献[16]基于子模块开关器件的死区时间,利用5个工频周期内子模块开关序列计算容值,该方法需实时测量SM的开关状态。文献[17-18]利用电压高频信息建立与ESR映射关系,实现状态的评估,但该方法依赖较高的采样率。
综上所述,现有金属化薄膜电容器的状态监测和剩余寿命评估存在以下不足:①缺乏考虑电容器特性参数与工作温度耦合关系,导致电容器寿命评估不准确;②电容器的容值状态监测方法需要实时获取MMC每个子模块(如厦门柔直工程需采样648通道)的开关信号,存在侵入性、高采样率电路及占控制器计算资源的弊端;③未考虑电容器老化进程对电容值和ESR的影响,难以准确评估不同服役状态下的电容器剩余寿命。因此,本文针对MMC应用场合,首先,提出基于系统已测参数及滑动窗口累积和算法的电容值在线监测方法,结合子模块电容器的电热应力进行分析;其次,考虑电容器容值和ESR的老化与温度间的耦合关系;最后,基于电容器组场路协同仿真模型建立计及电容器状态及其老化效应的寿命模型对电容器的剩余寿命进行评估,为MMC系统和子模块电容器的健康管理与状态维护提供参考。
金属化薄膜电容器失效是电容器内部的自修复特性以及遭受电化学腐蚀的累积结果[19]。与电容器的自愈特性和电化学反应相对应,电压和温度两个物理量是影响电容器寿命的关键因素。因此,分别确定影响子模块电容器寿命的电压和温度加速因子,建立其寿命模型。
电应力和温度对于电容器寿命的影响[20]为
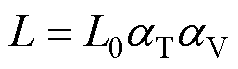 (1)
(1)
式中,L为电容当前使用条件下的寿命;L0为参考条件下的使用寿命;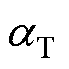 为温度加速因子;
为温度加速因子;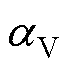 为电压加速因子。
为电压加速因子。
由于金属电极的腐蚀为热激活过程,因此腐蚀速率k的值与温度有关,可用Arrhenius方程表示为
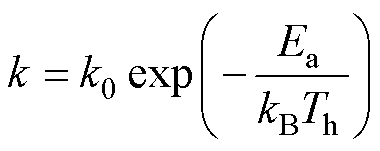 (2)
(2)
式中,k0为常数;kB为玻耳兹曼常数,其数值为8.62× 10-5 eV/K;Ea为化学反应的活化能;Th为电容工作时的实际热点温度。
考虑到温度对腐蚀速率的加速作用,温度加速因子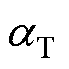 可表示为
可表示为
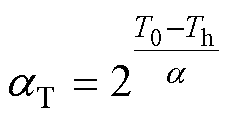 (3)
(3)
式中,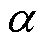 为与温度有关的系数,在薄膜电容器的模型中,其数值约为8~12;T0为参考条件下的额定温度。
为与温度有关的系数,在薄膜电容器的模型中,其数值约为8~12;T0为参考条件下的额定温度。
根据试验数据表明,电压越大,电极腐蚀速率的增长率越快,且每增加一定量的电压幅值,电容器的寿命呈指数下降。因此,引入幂律模型来表征电压对介电材料退化的影响,电压加速因子表示为
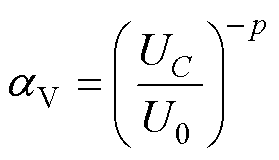 (4)
(4)
式中,UC和U0分别为当前的电容电压和参考条件下的额定电容电压,U0可从数据手册中查询得到;p为经验系数,在薄膜电容器的模型中,其值约为4~12。将温度加速因子和电压加速因子代入式(1)中可得金属化薄膜电容器的寿命评估模型为
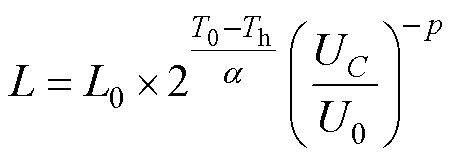 (5)
(5)
对于不同制造商生产的不同规格电容器,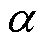 和p的值略有差异。这两个系数可通过加速寿命试验提取[21],即通过拟合得到金属化薄膜电容器在不同恒定应力下的寿命分布如图1所示,p和
和p的值略有差异。这两个系数可通过加速寿命试验提取[21],即通过拟合得到金属化薄膜电容器在不同恒定应力下的寿命分布如图1所示,p和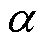 值分别为4.4和10。从图1可知,金属化薄膜电容器在不同电压和不同温度下的寿命分布的数据拟合效果较好。从图1a可知,温度对金属化薄膜电容器的寿命的影响显著,即温度越高电容器寿命越短。同时,从50℃开始,电容器的温度基本上每升高10℃,其寿命则会衰减50%。从图1b可知,当电容器施加在其两端的电压超过工作电压时,其寿命会随着所施加电压的增加而大幅下降,且电压值越高,下降幅度越大。
值分别为4.4和10。从图1可知,金属化薄膜电容器在不同电压和不同温度下的寿命分布的数据拟合效果较好。从图1a可知,温度对金属化薄膜电容器的寿命的影响显著,即温度越高电容器寿命越短。同时,从50℃开始,电容器的温度基本上每升高10℃,其寿命则会衰减50%。从图1b可知,当电容器施加在其两端的电压超过工作电压时,其寿命会随着所施加电压的增加而大幅下降,且电压值越高,下降幅度越大。
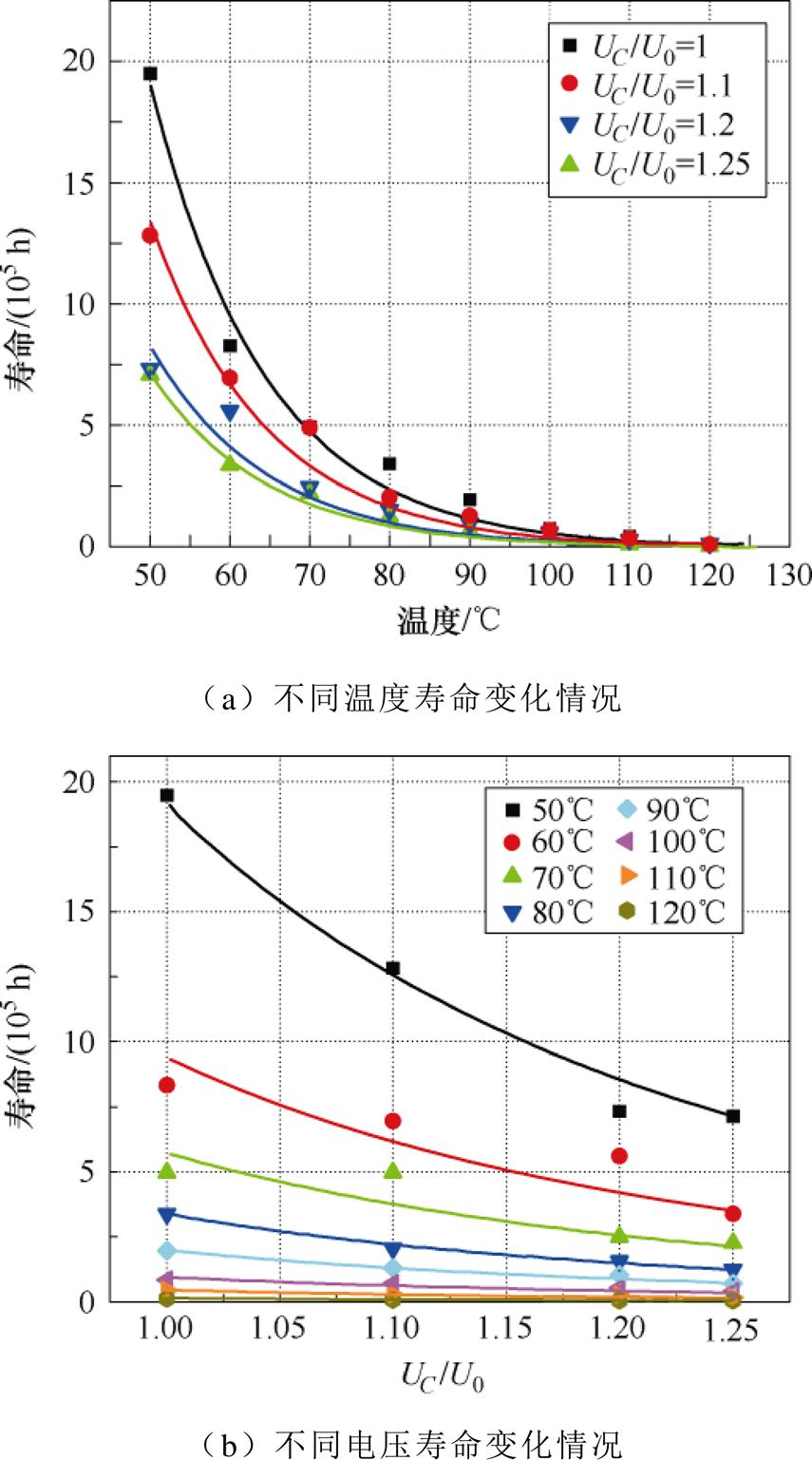
图1 不同恒定应力下金属化薄膜电容器的寿命分布
Fig.1 Lifetime distribution of metallized film capacitor under different constant stress
在使用加速老化试验对寿命模型进行验证时,设电容两端施加的直流电压Udc为额定电压Un的y倍,对于电容器外部温度以及实际电压的增加,加速因子可以使用广义Eyring关系来表示[22],记为Hacc,有
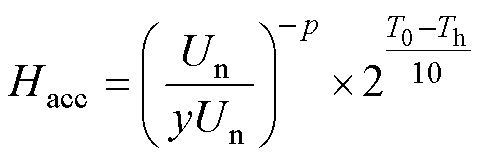 (6)
(6)
在长期服役运行中,电容器发生老化且逐渐加深,表现为电容器ESR上升和电容值下降;损耗增加的同时,热点温度逐渐升高。因此,在相同的工况下,电容器的剩余寿命会随着其老化不断降低。然而,在1.1节解析寿命建模时,未考虑老化的加速影响,导致剩余寿命评估结果存在较大的误差。因此,本节分别建立电容器ESR和电容值的老化 模型。
电容器老化是一个与时间、温度和频率相关的过程。由于操作频率在老化过程中通常保持不变,因此可以在指定的频率下获得老化模型。加速老化试验数据显示,当不考虑金属化薄膜电容器的温度变化时,ESR随时间t呈指数型上升趋势[23],电容值则呈指数型下降趋势[24],有
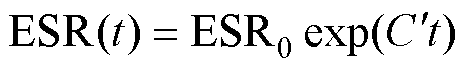 (7)
(7)
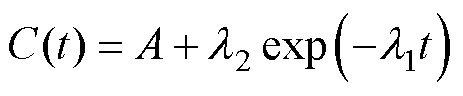 (8)
(8)
式中,ESR(t)和C(t)分别为t时刻金属化薄膜电容器的ESR和电容值;ESR0为初始等效串联电阻;A为与初始电容值C0有关的参数;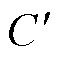 和
和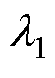 均为与温度相关的老化速率;
均为与温度相关的老化速率;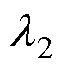 为与温度相关的系数。
为与温度相关的系数。
为了分析ESR0与电容热点温度之间的关系,根据数据手册和不同温度下的实测值对ESR进行拟合。首先,使用Agilent Technologies E4980A LCR测量仪器对电容器的ESR和电容值进行测量,并采用TPS公司的TJR温箱控制电容器环境温度,设置温度测量范围为25~85℃,温度增量为10℃,待温度达到稳定后温箱温度与电容器热点温度保持一致,进行测量并记录数值;对不同温度下的ESR和电容测量值进行线性拟合,结果如图2所示。
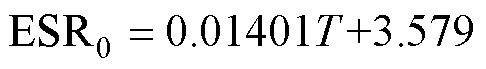 (9)
(9)
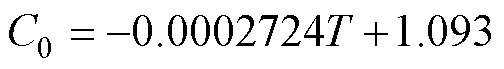 (10)
(10)
获取ESR0和C0与温度T的关系后,对ESR和电容值的老化速率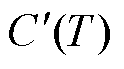 、
、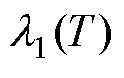 及系数
及系数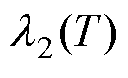 进行分析。考虑ESR的老化速率
进行分析。考虑ESR的老化速率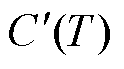 遵循简化后的Arrhenius公式[25],电容值的老化速率
遵循简化后的Arrhenius公式[25],电容值的老化速率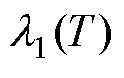 及系数
及系数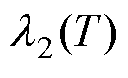 与温度呈指数关系[26],有
与温度呈指数关系[26],有
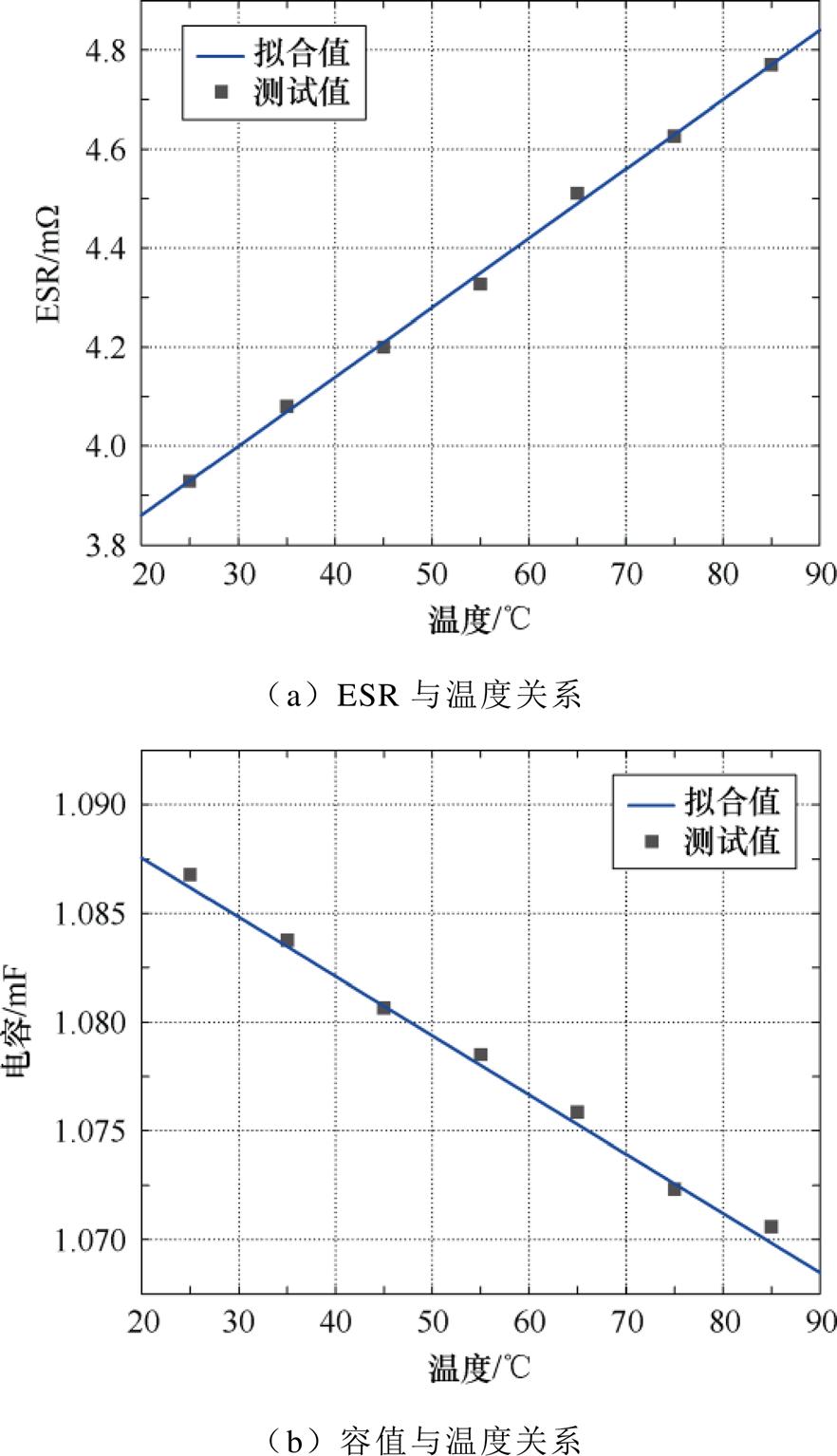
图2 等效串联电阻和电容值随温度变化趋势
Fig.2 ESR and capacitance with temperature
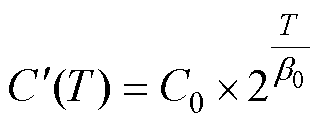 (11)
(11)
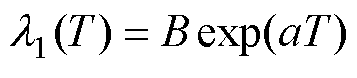 (12)
(12)
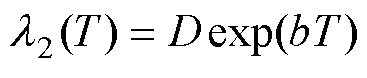 (13)
(13)
式中,C0、B和D为初始值;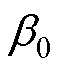 、a、b为与温度相关的系数;T为电容器的运行温度。基于文献[27-28]中不同温度和电压下的加速老化试验数据,对老化速率
、a、b为与温度相关的系数;T为电容器的运行温度。基于文献[27-28]中不同温度和电压下的加速老化试验数据,对老化速率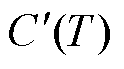 和
和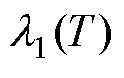 以及相关系数
以及相关系数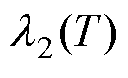 进行数据拟合,结果如图3所示。从图3可知,电容器的老化速率
进行数据拟合,结果如图3所示。从图3可知,电容器的老化速率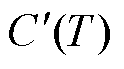 和
和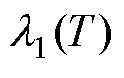 以及相关系数
以及相关系数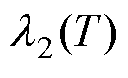 均随着温度的上升而增大。当运行温度不超过50℃时,ESR的老化速率相对较慢,维持在较小的值范围内,处于10-6的数量级,而在50℃之后,ESR的老化速率开始成倍增长。容值的老化速率在运行温度不超过60℃时维持在较低的水平,超过60℃后急剧增大。由此可以看出,ESR和电容值与电容器运行温度之间的相互作用效应较为强烈。等效串联电阻的初始老化速率C0和温度系数
均随着温度的上升而增大。当运行温度不超过50℃时,ESR的老化速率相对较慢,维持在较小的值范围内,处于10-6的数量级,而在50℃之后,ESR的老化速率开始成倍增长。容值的老化速率在运行温度不超过60℃时维持在较低的水平,超过60℃后急剧增大。由此可以看出,ESR和电容值与电容器运行温度之间的相互作用效应较为强烈。等效串联电阻的初始老化速率C0和温度系数 分别为5.024 8×10-7和25.64。电容值的初始老化速率B和D分别为1.501× 10-8和1.107×10-3;温度系数a、b分别为0.061 80、0.035 22。得到
分别为5.024 8×10-7和25.64。电容值的初始老化速率B和D分别为1.501× 10-8和1.107×10-3;温度系数a、b分别为0.061 80、0.035 22。得到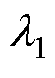 和
和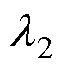 的表达式后,将t =0时电容值的边界条件
的表达式后,将t =0时电容值的边界条件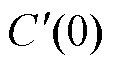 =C0代入式(7),可得A=C0
=C0代入式(7),可得A=C0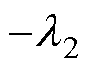 。
。
分别得到初始ESR和容值以及二者的老化速率的表达式后,后文对容值及ESR时变退化模型进行推导。考虑到在老化过程中温度T和时间的变化,则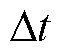 时间内容值和ESR的增量可以表示为
时间内容值和ESR的增量可以表示为
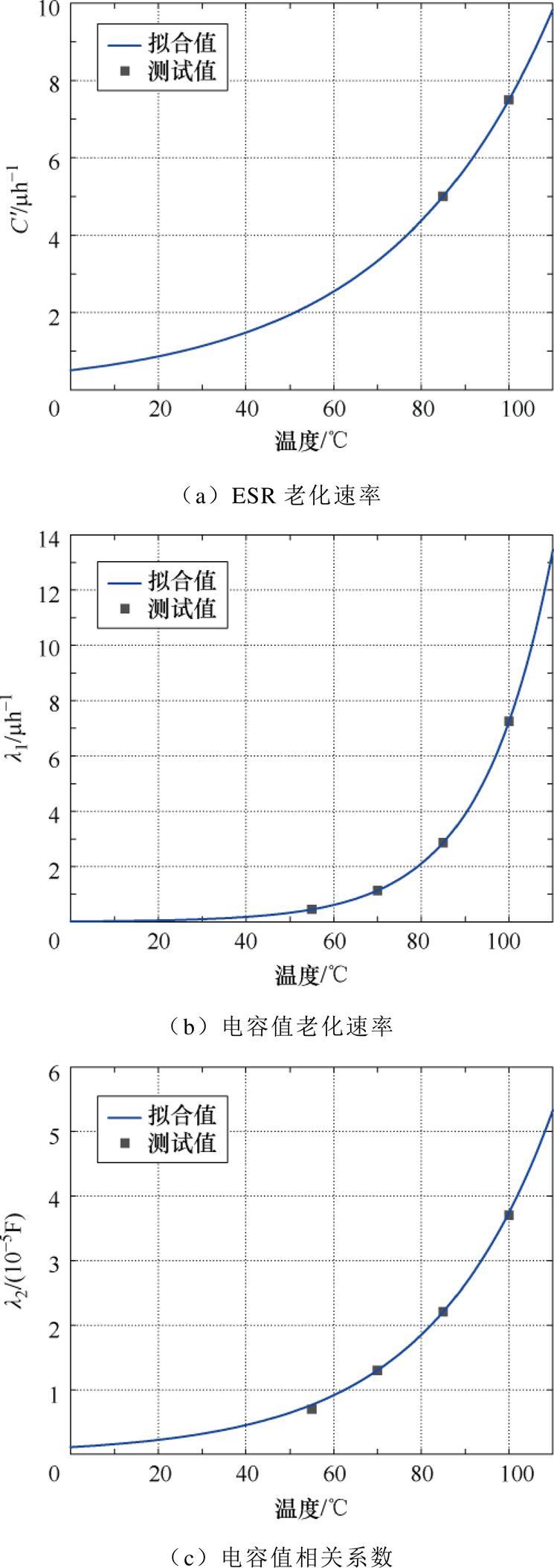
图3 等效串联电阻和电容值的老化速率及相关系数
Fig.3 Degradation rate and correlation coefficient of ESR and C

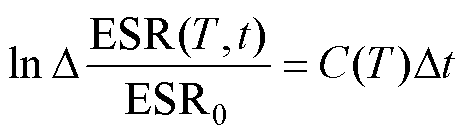 (14)
(14)

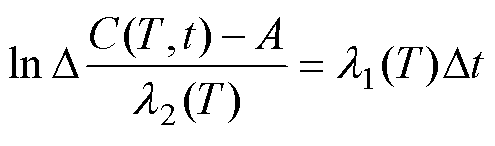 (15)
(15)
因此,从时间0到时间x,累积变化的电容值和ESR可以表示为

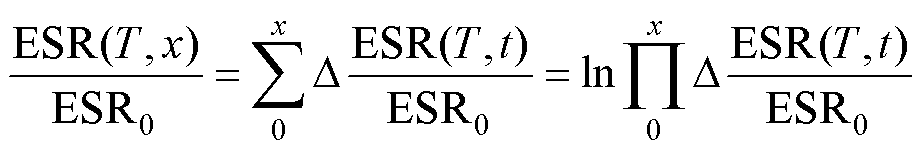 (16)
(16)
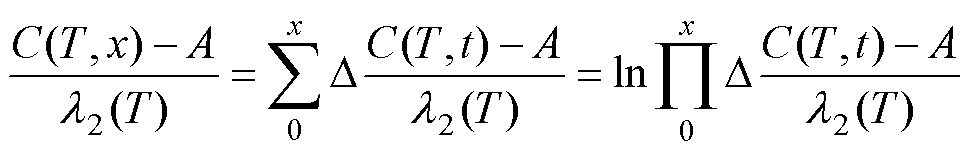 (17)
(17)
将式(16)、式(17)改写成积分的形式,有

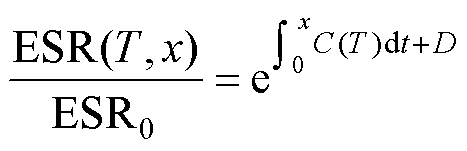 (18)
(18)

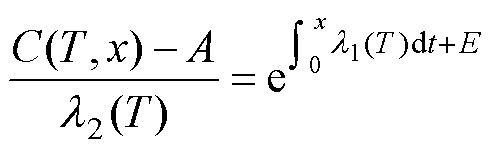 (19)
(19)
式中,D和E为常数。考虑边界条件C(T, 0)=C0,ESR(T, 0)=ESR0,代入式(18)、式(19)可得E=0、D=0,因此C(T, t)和ESR(T, t)从0到时间x的累积可以表示为

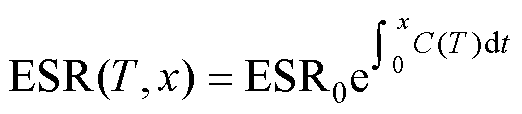 (20)
(20)

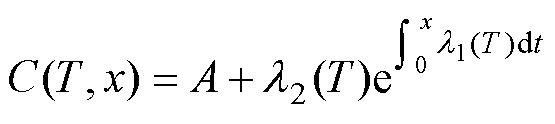 (21)
(21)
本文提出考虑电容器老化效应对参数影响的金属化薄膜电容器剩余寿命预测方法。该方法依赖于电容器的核心温度,而电容器核心温度难以通过工程实施监测。基于此考虑电容器老化和核心温度的耦合关系,提出基于电容器容值的电容器核心温度反演计算方法:①基于提出的滑动窗口累积和算法的电容值在线监测方法,实现电容器容值的在线实时监测;通过电容器容值老化模型计算出电容器服役的时间,基于该时间利用ESR老化模型可计算出当前的ESR值。②基于当前的电容器容值和ESR利用电容器组场路协同仿真模型实现当前电容器核心温度,将计算出的当前电容器老化状态核心温度代入金属化薄膜电容器寿命解析模型可计算出电容器剩余寿命,具体流程如图4所示。首先,根据MMC系统中的桥臂(电感)电流Iarm和电容电压UC对电容器状态进行监测获得当前的电容值Cm,将其代入电容值的老化模型中可以反推出电容器已经服役的年限tuse(如果是新器件则为0),并据tuse计算出电容器当前的ESR。其次,将电容器电流有效值Irms和环境温度Ta代入电热协同仿真模型中计算出电容器的热点温度Th。最后,将Th代入寿命评估模型中并结合电容电压UC对电容器的剩余寿命进行评估。
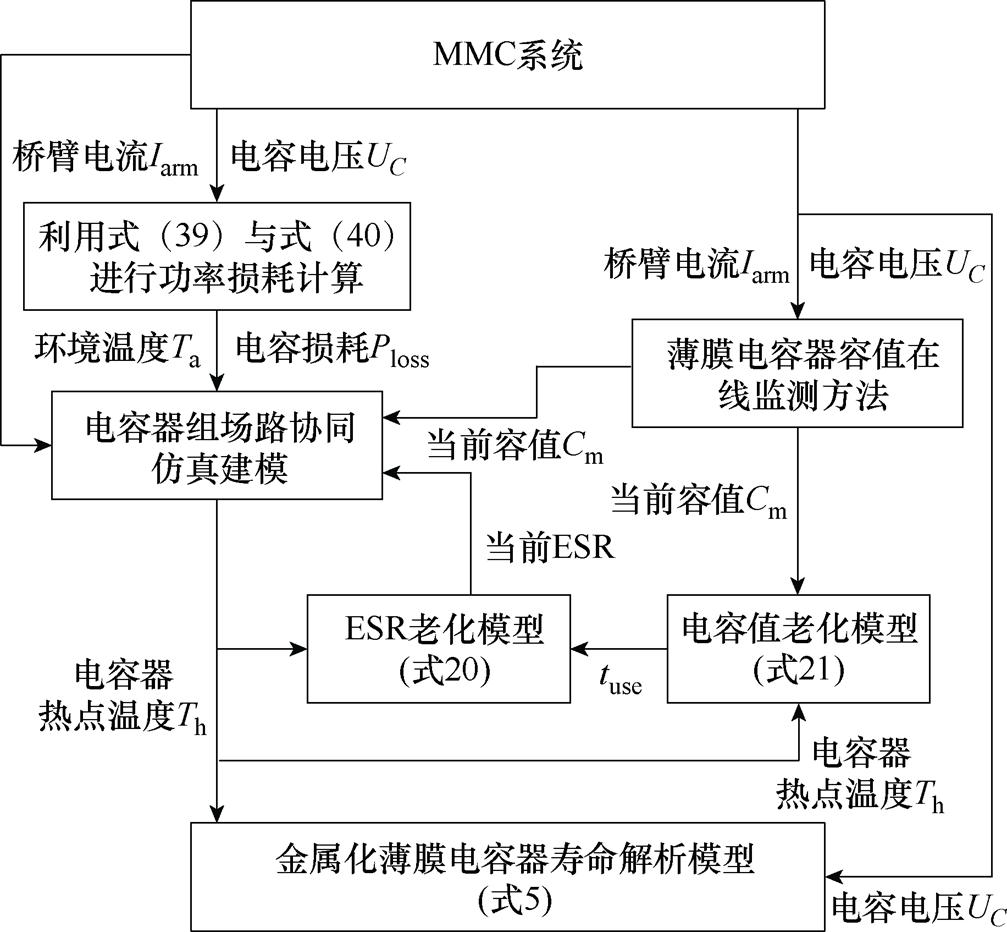
图4 电容器的剩余寿命评估方法
Fig.4 Remaining lifetime estimated process of capacitors
换流器的每个桥臂由一个电抗器和n0个子模块串联而成[29]。每个子模块可以根据触发脉冲来实现子模块的输出电压。MMC系统子模块的电容器电压和开关信号如图5所示。从图5可知,当开关信号为1时,相应的子模块被启用,电容器处于充电或放电状态,从而使得电容电压经历升降变化;相对地,当开关信号为0时,子模块则处于断开状态,电容器与主线路断开,其两端电压维持恒定。
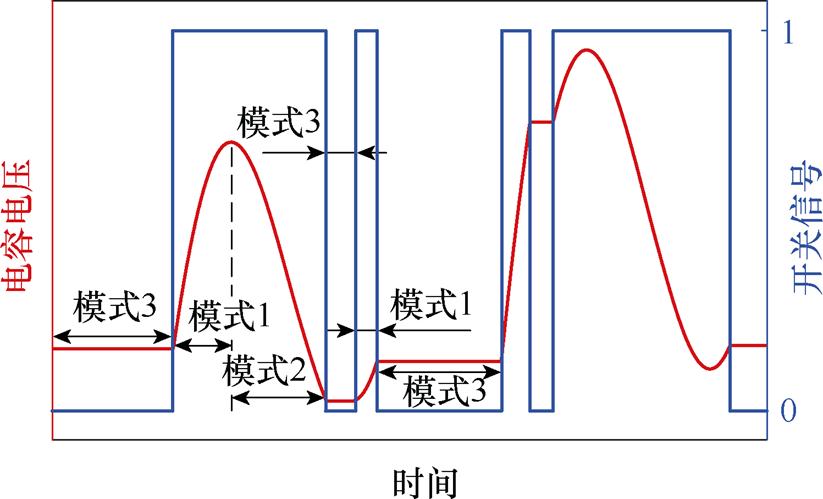
图5 电容器电压和子模块的开关信号
Fig.5 Capacitor voltage and switching signal of SM
子模块的工作模式如图6所示。从图6工作时序可知,定义第i个子模块的开关函数Saui为
 (22)
(22)
如果Saui=1,子模块投入到桥臂中,电容器电流iCaui等于桥臂电流iau,输出电压Usaui=UCaui;相反,如果Saui=0,则子模块从桥臂中被切除,iCaui和Usaui等于0。因此,Usaui和iCaui可以表示为
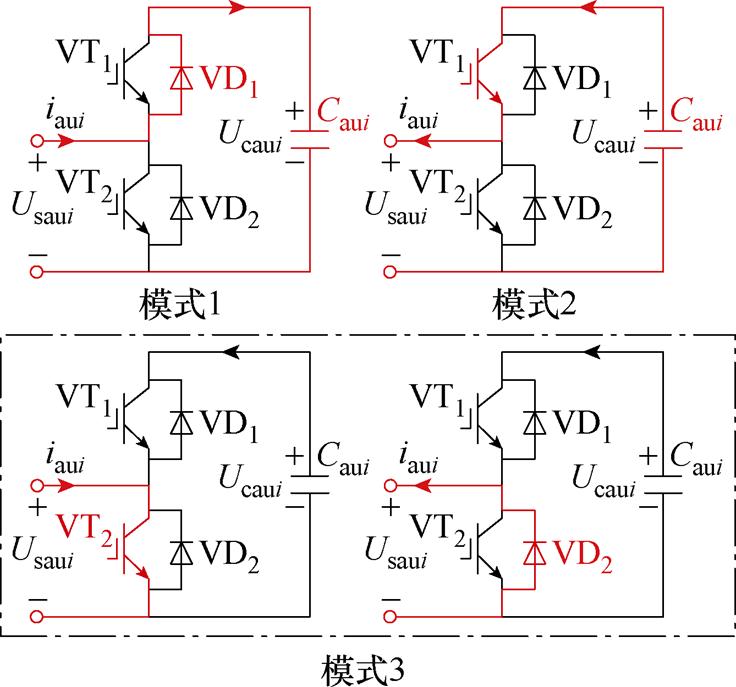
图6 子模块的工作模式
Fig.6 Working mode of SM
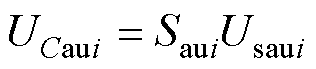 (23)
(23)
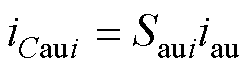 (24)
(24)
根据电容的电压电流关系,在任意时刻t,瞬时电容电压可以表示为
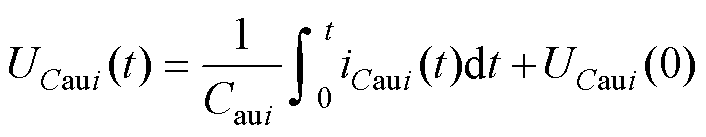 (25)
(25)
式中,iCaui(t)为t时刻的电容电流;UCaui(0)为初始的电容电压。因此,在任意时刻t1和t2的电容电压可以表示为
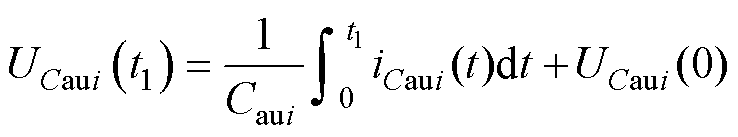 (26)
(26)
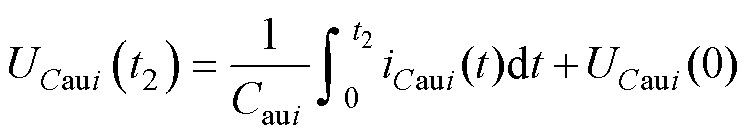 (27)
(27)
式(27)减去式(26),根据定积分定律可得
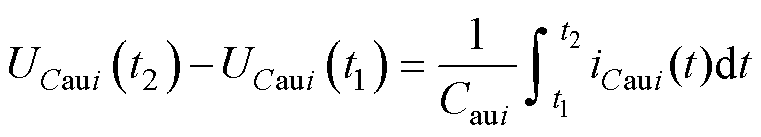 (28)
(28)
将式(27)重新排列,并将式(23)代入可得
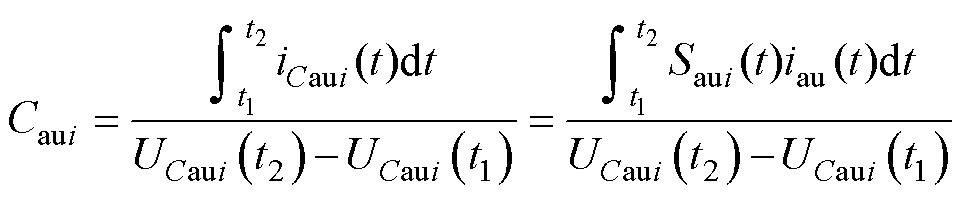 (29)
(29)
子模块的开关序列Saui(t)与实际控制有关,在控制子模块投入的时间段[ton_i, toff_i](i=1, 2, 3,…, N)内,VT1导通,VT2关断,开关序列Saui(t)为1;在控制子模块切除的时间段内,VT1关断,VT2导通,开关序列Saui(t)为0,有
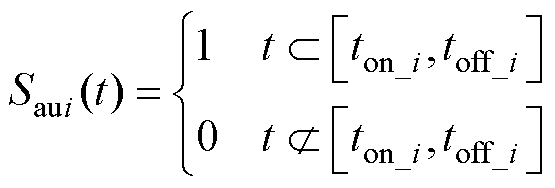 (30)
(30)
将式(30)代入式(29)可得
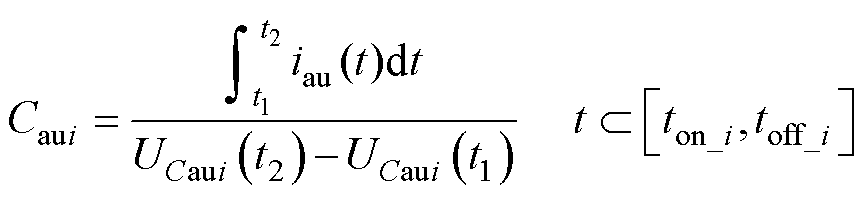 (31)
(31)
式(31)中计算电容值需要电容电压UCaui(t)和桥臂电流iau(t)两个参量,在MMC原系统固有已检测的控制参数。因此,电容器容值的在线监测未增加额外的传感器或采样电路。
在MMC实际运行期间,由于传感器所提取的电压和电流信号是离散信号,因此将式(31)进行离散化得
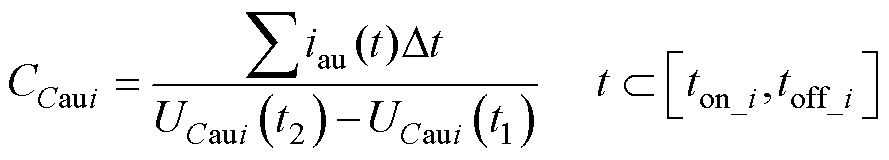 (32)
(32)
式中,[t1, t2]为任意一时间段,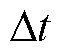 为传感器采样的时间间隔。因此所提出的电容值计算方法的关键是确定开关序列Saui(t)=1时,即控制子模块投入的时间段[ton_i, toff_i](i=1, 2, 3,…, N)。
为传感器采样的时间间隔。因此所提出的电容值计算方法的关键是确定开关序列Saui(t)=1时,即控制子模块投入的时间段[ton_i, toff_i](i=1, 2, 3,…, N)。
根据式(32)可知,确定电容器容值除系统已检测的电压、电流信号外,还需要明确子模块投入或切除的时间段即电容器充电或放电时段。考虑到电容在充电过程中电压增大,而在放电过程中电压减小,电容电压的变化存在正反两种情况,故采用非参数化双边累积和算法。
考察电容电压时间序列U={U(k)}(k=1, 2,…),定义非参数化双边累积和算法中的统计函数为
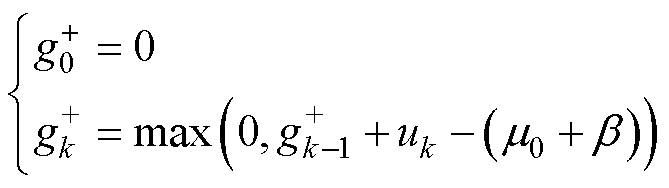 (33)
(33)
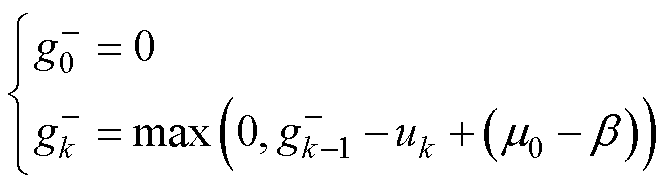 (34)
(34)
式中,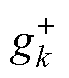 为正向累积和;
为正向累积和;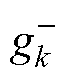 为负向累积和,分别用于检测电容器的充电和放电过程;
为负向累积和,分别用于检测电容器的充电和放电过程;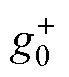 和
和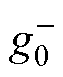 为累积和初始值;uk为采样时间点;
为累积和初始值;uk为采样时间点;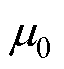 为变点前电压时间序列的平均值;
为变点前电压时间序列的平均值; 为电压时间序列中电压处于稳态时的波动水平。检测过程如图7所示。图中,mk为到时间点k前电容电压的平均值。
为电压时间序列中电压处于稳态时的波动水平。检测过程如图7所示。图中,mk为到时间点k前电容电压的平均值。
(1)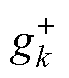 的初始值为零,当电压时间序列处于稳定状态时,累积和
的初始值为零,当电压时间序列处于稳定状态时,累积和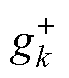 和
和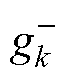 的值均为0。
的值均为0。
(2)若序列表现出正向偏移,导致其平均值增长至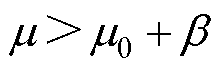 ,此正向偏移将持续积累,从而导致累积和
,此正向偏移将持续积累,从而导致累积和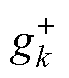 保持增加趋势。反之,若序列出现负向偏移,并使其平均值降低到
保持增加趋势。反之,若序列出现负向偏移,并使其平均值降低到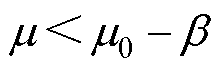 ,则负向偏移将逐步累加,进而导致累积和
,则负向偏移将逐步累加,进而导致累积和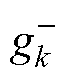 保持增加趋势。
保持增加趋势。
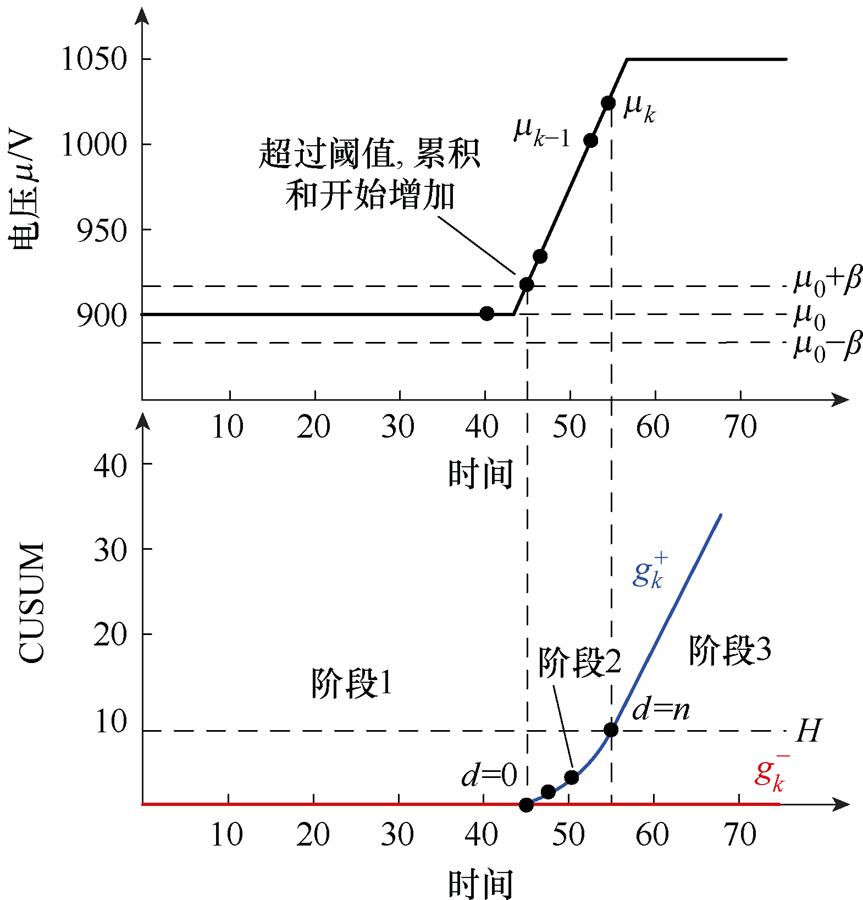
图7 累积和算法检测过程示意图
Fig.7 Schematic diagram of cumulative sum algorithm detection process
(3)当正向累积和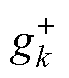 处于0<
处于0<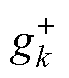 <H这一区间内,表示此时具备发生突变的可能性。然而,至今为止的变化幅度尚未足够明确地标明一个突变的确立。为了进一步诊断序列的持续变化是否会导致突变,引入一个延迟系数d,其初始设定值为0。随后令d=d+1,k=k+1。若
<H这一区间内,表示此时具备发生突变的可能性。然而,至今为止的变化幅度尚未足够明确地标明一个突变的确立。为了进一步诊断序列的持续变化是否会导致突变,引入一个延迟系数d,其初始设定值为0。随后令d=d+1,k=k+1。若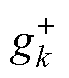 持续上升至
持续上升至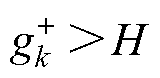 ,则证明了突变点的产生,意味着序列经历了一个明确的突变,此时将突变发生的时刻标记为t=k-d。同理,当序列发生负向突变时也是采用相同的原理进行处理。
,则证明了突变点的产生,意味着序列经历了一个明确的突变,此时将突变发生的时刻标记为t=k-d。同理,当序列发生负向突变时也是采用相同的原理进行处理。
在所考虑的算法中,一个核心假设是电压时间系列的均值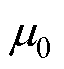 是预先确定的。但在实际的MMC结构中,子模块的电容电压持续波动,导致其均值同样会出现连续的调整。为了应对这种情境,本文引入滑动窗口法来对原算法进行优化。如图8所示,在电容电压序列U={U(k)},(k=1, 2,…)上定义了均值计算窗口(Window Monitor, WM)和检测窗口(Window Detect, WD)两个连续的滑动窗口,这两个窗口长度,即其内部所含电压数据点的数量,分别为m与n。对两个窗口中电容电压平均值Mm和Md进行计算,有
是预先确定的。但在实际的MMC结构中,子模块的电容电压持续波动,导致其均值同样会出现连续的调整。为了应对这种情境,本文引入滑动窗口法来对原算法进行优化。如图8所示,在电容电压序列U={U(k)},(k=1, 2,…)上定义了均值计算窗口(Window Monitor, WM)和检测窗口(Window Detect, WD)两个连续的滑动窗口,这两个窗口长度,即其内部所含电压数据点的数量,分别为m与n。对两个窗口中电容电压平均值Mm和Md进行计算,有
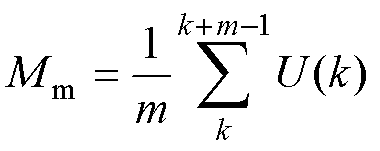 (35)
(35)
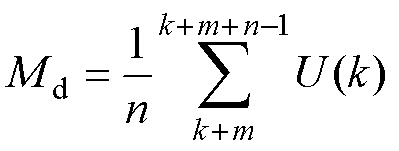 (36)
(36)
改进后的累积和算法的统计函数可以改写为
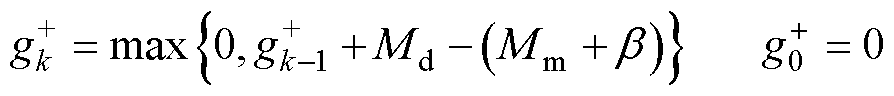 (37)
(37)
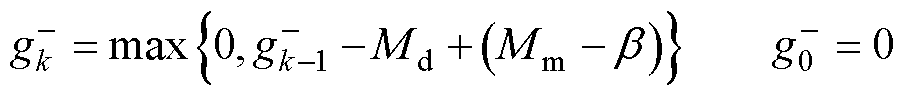 (38)
(38)
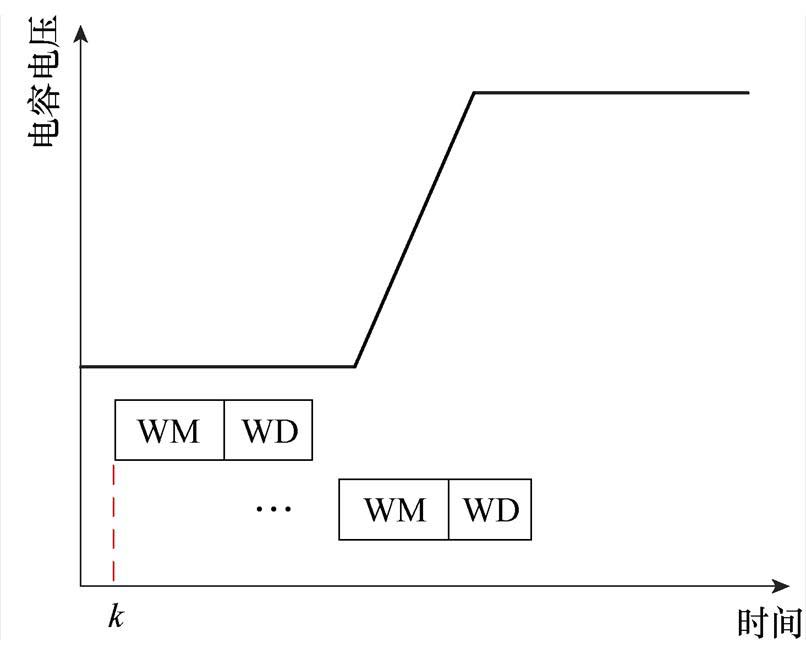
图8 滑动窗口示意图
Fig.8 Schematic diagram of sliding windows
以子模块电容器的充电过程为例进行描述。累积和初始值设置为0,当检测窗平均值Md>Mm+ 时,
时,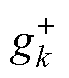 从0开始累积。此时,可以根据实际情况设置累积和阈值H。当0<
从0开始累积。此时,可以根据实际情况设置累积和阈值H。当0<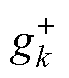 <H时,令d=d+1,k= k+1,然后继续累积。当
<H时,令d=d+1,k= k+1,然后继续累积。当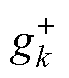 >H时,电容器充电开始的时间可倒推为T_start=k+m+n-d。同时,为了防止因为序列发生振荡而导致的误识别,每递增延迟系数d时,将
>H时,电容器充电开始的时间可倒推为T_start=k+m+n-d。同时,为了防止因为序列发生振荡而导致的误识别,每递增延迟系数d时,将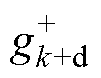 与
与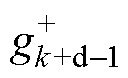 进行比较,如果
进行比较,如果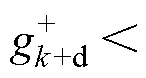
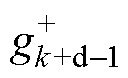 ,则认为此电压变动为单一数据的波动,并且将
,则认为此电压变动为单一数据的波动,并且将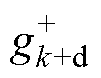 和d都置为0。在检测到电压序列发生突变之后,窗口继续滑动直到累积和不再增加,则将该时刻记录为稳定时刻,表明电容器电压不再增加。类似地,使用相同流程可处理子模块电容器的放电过程。在检测到子模块的控制投入时间段后,即可使用式(31)对电容值进行计算,以实现子模块电容值的状态监测,如图9所示。
和d都置为0。在检测到电压序列发生突变之后,窗口继续滑动直到累积和不再增加,则将该时刻记录为稳定时刻,表明电容器电压不再增加。类似地,使用相同流程可处理子模块电容器的放电过程。在检测到子模块的控制投入时间段后,即可使用式(31)对电容值进行计算,以实现子模块电容值的状态监测,如图9所示。
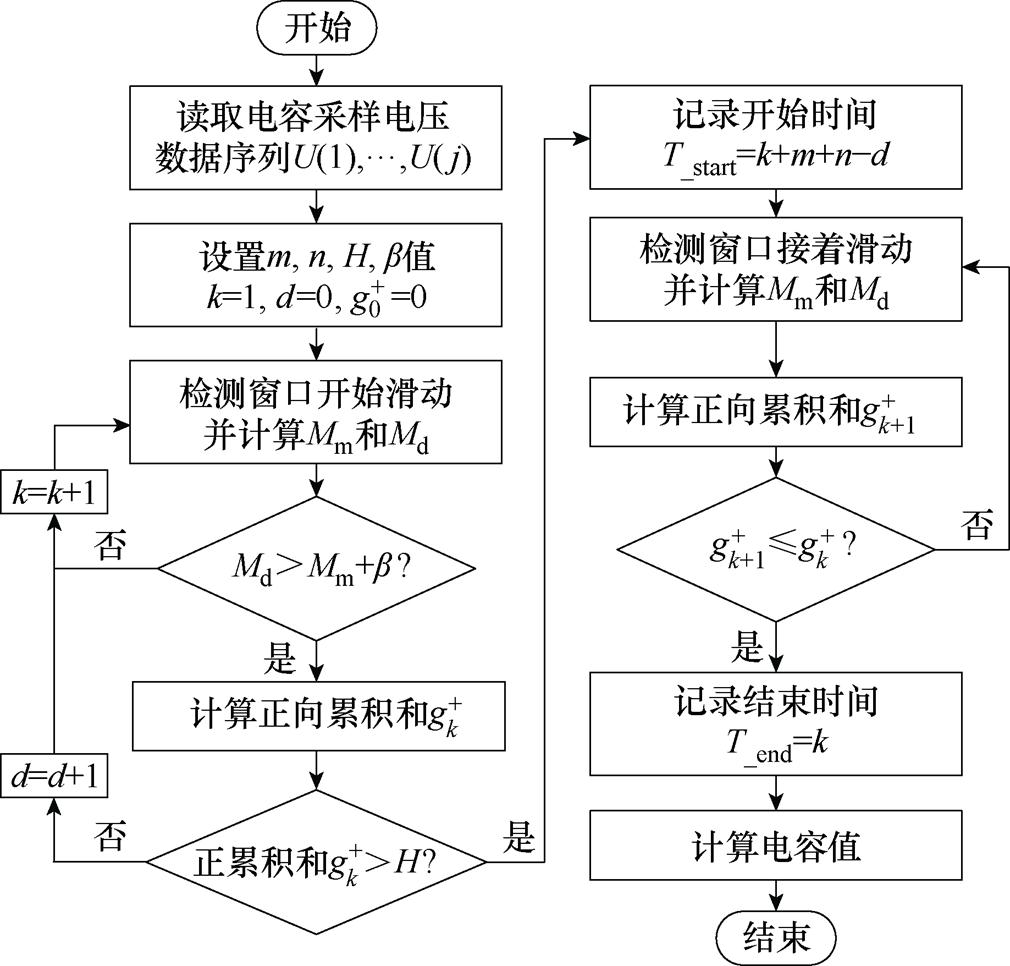
图9 电容值在线监测流程
Fig.9 Capacitance value online monitoring flow chart
为了验证MMC子模块电容器容值监测方法的准确性,搭建了MMC工况等效的试验平台进行试验验证。实际工程中的三相MMC有六个桥臂,每个桥臂至少包含几十个子模块,构建完整的MMC系统成本昂贵。因此,为了降低测试平台的复杂性和成本,采用工况等效的半桥子模块测试电路,其结构如图10所示。
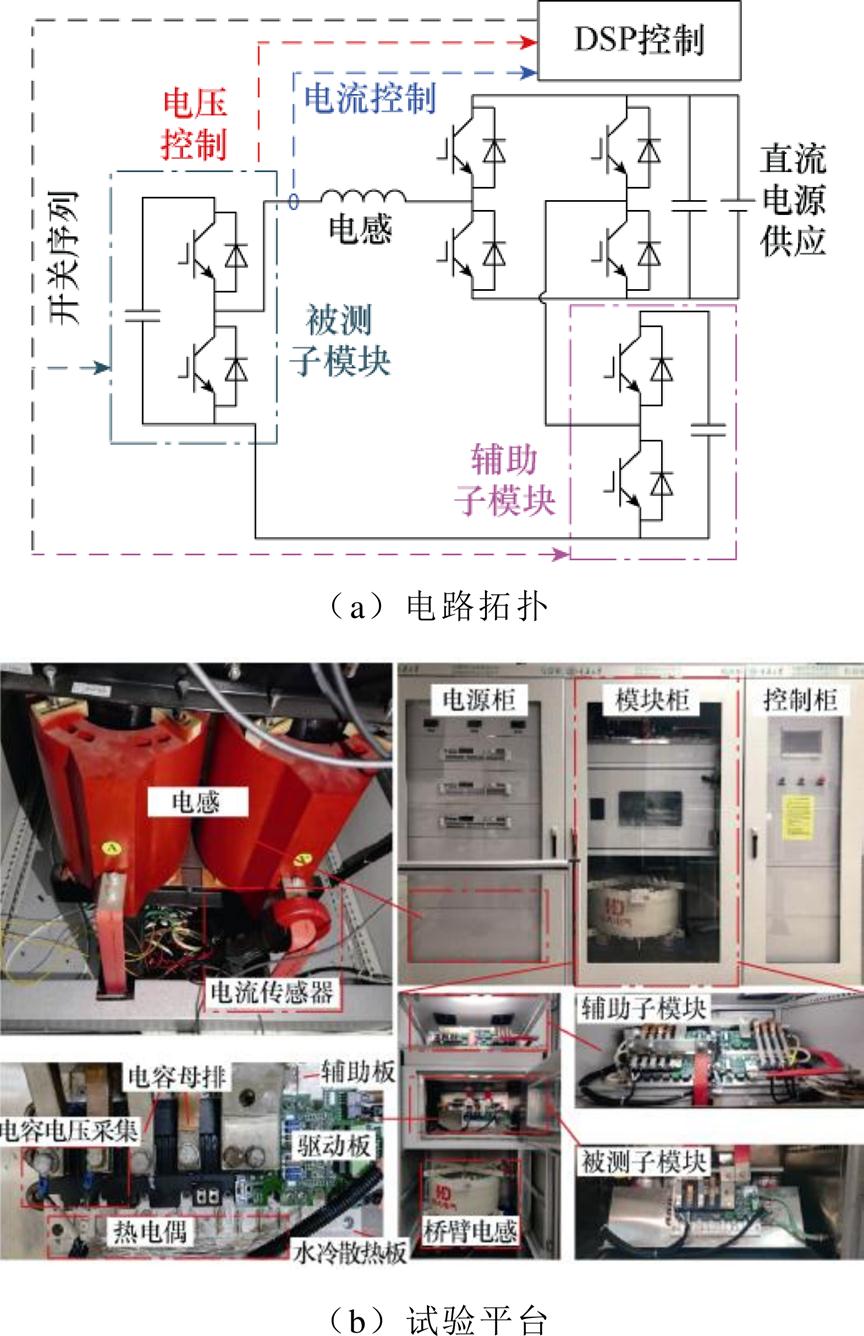
图10 测试平台的结构
Fig.10 Structure of the test platform
该平台可以模拟MMC全系统中桥臂电流、子模块电压和子模块的开关序列,从而使被测子模块的行为特性与在完整MMC系统中保持一致。被测子模块包括一组半桥IGBT模块和电容器组,其中电容器组由10个1 100 V/1 100 mF的金属膜电容器组成,使用LCR测量仪对电容器组电容值进行测量,结果为12.574 8 mF,记为健康电容器组C1。移除1个单体电容器以模拟电容器组老化容值的下降,使用LCR测量仪实际测量的电容值为11.493 mF,记为老化电容器组C2。
提取的子模块电压和电感电流如图11所示,作为基于滑动窗口累积和算法的电容值在线监测模型的输入,计算容值,其结果如图12a和图12c所示。图中,蓝色部分是主要的计算结果,分布在上四分位数和下四分位数之间,红色的点表示计算结果的异常值,主要是由于在采样和量化过程中测量误差造成,提取每秒计算数据的中位数作为真实计算结果,并将结果与LCR测试仪测得的电容值进行比较如图12b和图12d所示。从图中可知,对于不同状态的子模块电容值,计算结果与LCR测量值误差均在0.5%以内,能够用于电容状态的在线监测。
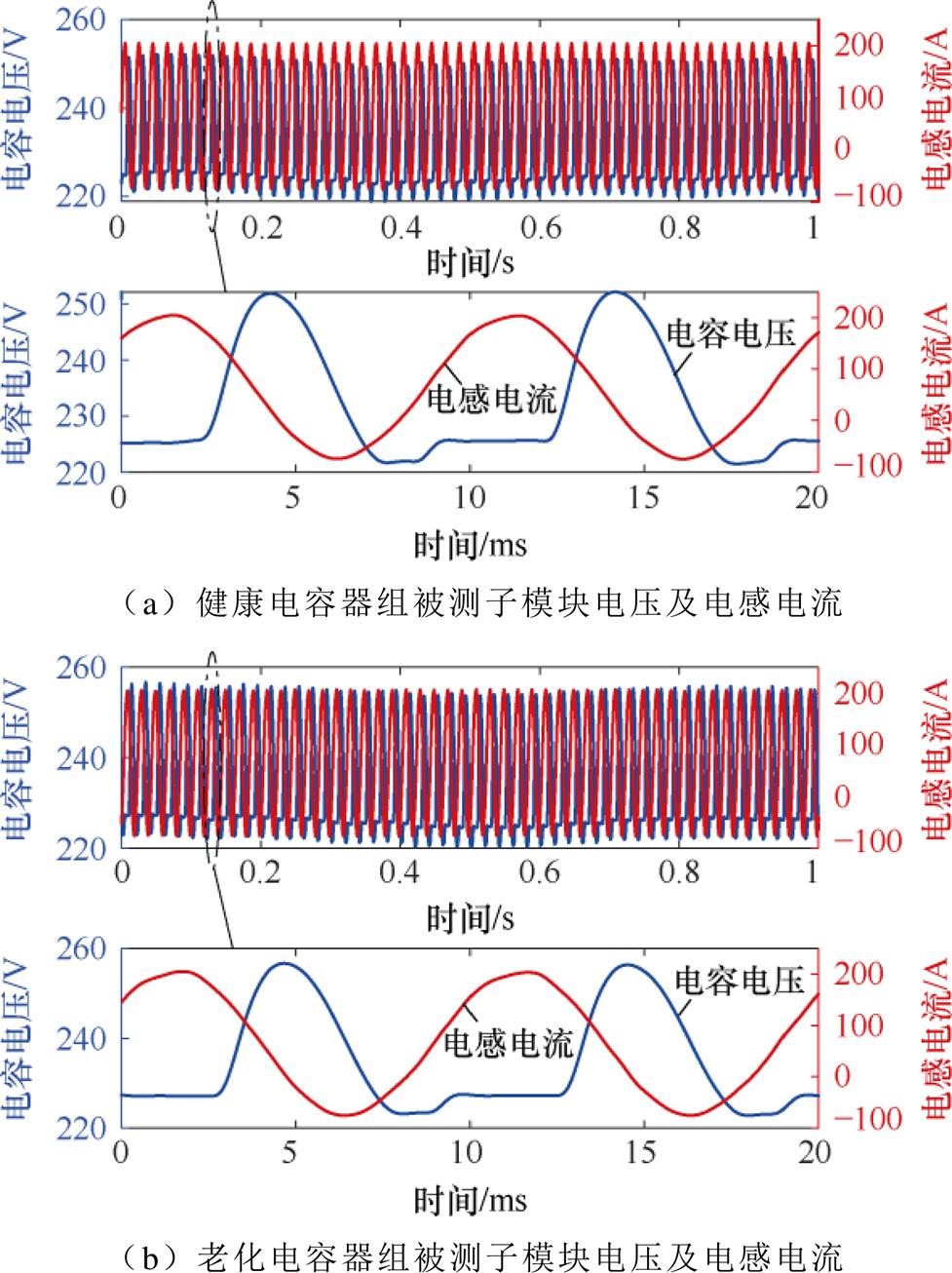
图11 电容电压和电感电流
Fig.11 Capacitor voltage and inductive current


图12 子模块电容器组的容值在线监测结果
Fig.12 Online monitoring results of capacitance of SM capacitor bank
在MMC实际运行过程中,金属化薄膜电容器两端的电压纹波产生功率损耗,致使电容器内部温度升高,是造成电容器失效的关键诱因。因此,为了准确地分析电容器运行时的电热规律及为剩余寿命评估提供输入,建立电-热耦合模型以精确地模拟电容器在实际MMC工况下的电气和温度特性。
电热协同仿真模型的原理如图13所示。电容器特性参数与温度具有耦合关系,故功率损耗与温度是连接Simulink电路仿真与Comsol温度场仿真的重要桥梁,两个模型之间通过相互传递电容器的温度值与损耗值,实现电热协同仿真。由于电路模型和温度场模型分别建立在不同的仿真平台上,因此采用间接耦合的方法进行协同仿真[30]。首先对电路模型进行求解,并将得到的解作为温度场模型的激励,并执行循环的迭代过程。利用Matlab脚本文件进行模型之间的数据传输以及多速率仿真策略的控制。Matlab脚本是通过Comsol提供的Livelink for Matlab接口联合使用Comsol仿真与Matlab编程,通过此双向接口可以实现在Matlab中使用脚本命令调用Comsol仿真模型,对其进行参数设置、创建模型、运行仿真、提取数据等操作。
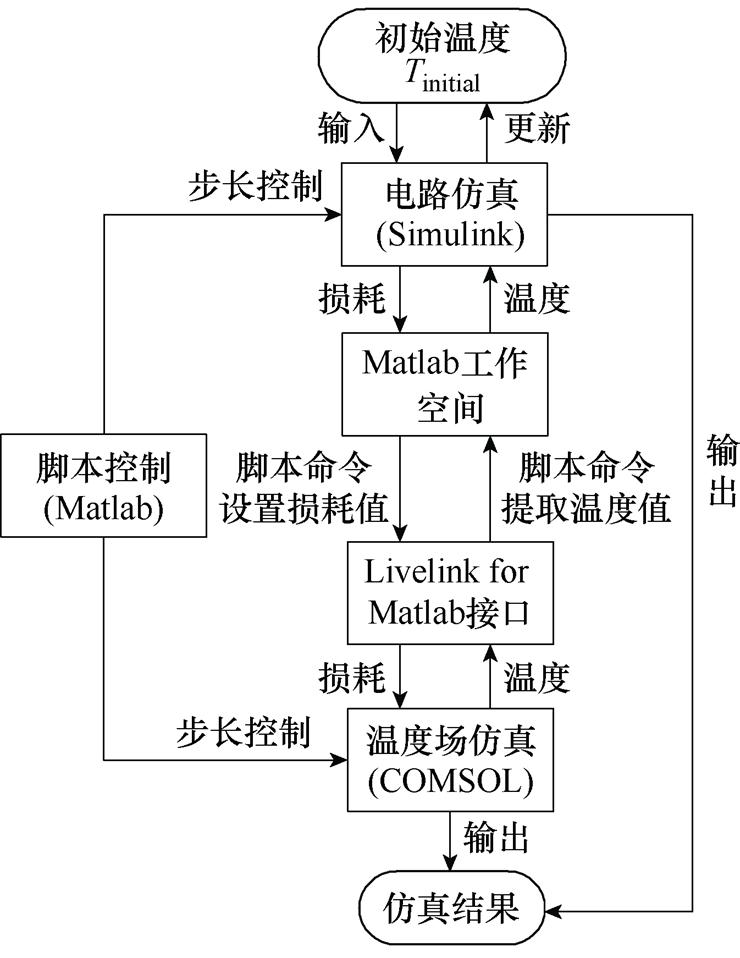
图13 电热协同仿真的原理
Fig.13 Principle of electro-thermal co-simulation
根据上述电热协同仿真的原理,需要在Simulink中对电容器的损耗值进行计算,但考虑到电容器电气参数与温度的依赖关系,需要先对其数学表达式进行拟合。根据电容器的数据手册可知,当温度改变时,电容器的ESR和电容值也会随之发生改变。但是手册上只提供了电容值变化量随温度变化的特性,并没有给出具体容值随温度的变化,因此需要通过试验测试获取电容值。在实际工作环境中要求器件的温度范围是25~85℃,故在此范围内对电容值进行测量。
对于ESR与温度的依赖关系,采用数据手册中给出了ESR随温度和频率变化的非线性曲线[31],温度范围为-40~85℃,涵盖了电容器正常工作的温度范围,且因MMC系统中电容器电流的主频率不高,频率采用1 kHz,建立查找表(Look Up Table, LUT),查表数据如图14所示。
得到容值和ESR与温度的关联关系后,对损耗进行计算,金属化薄膜电容器的损耗主要分为金属电极损耗和介质损耗,可表示[32]为
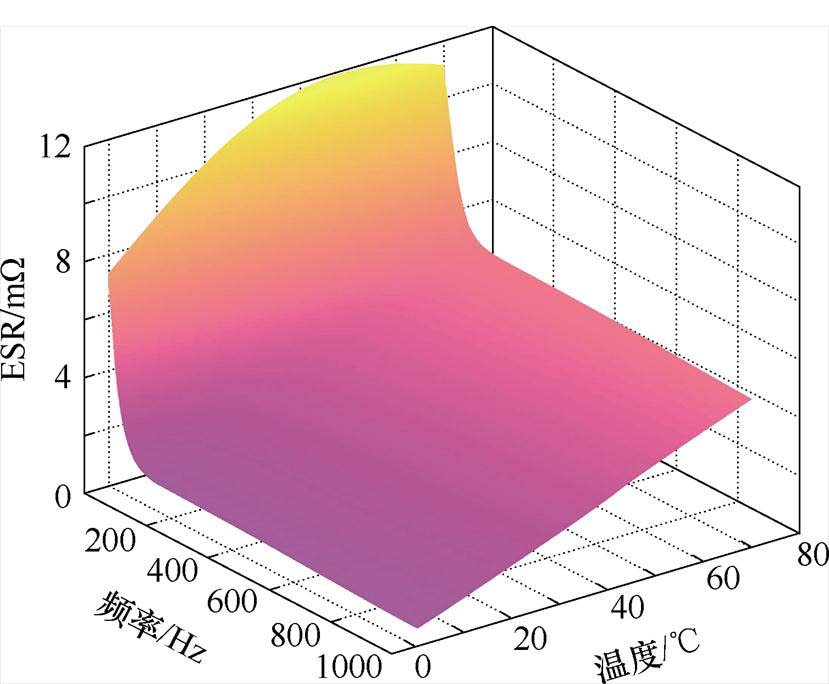
图14 ESR与温度和频率的依赖关系
Fig.14 Trends of ESR with temperature and frequency
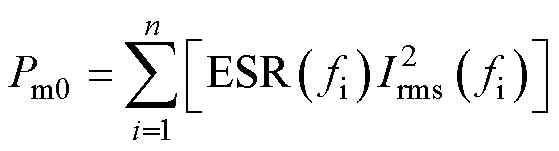 (39)
(39)
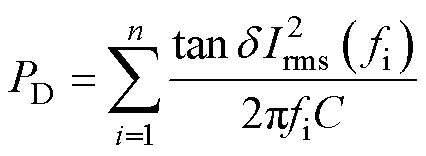 (40)
(40)
式中,Pm0为金属电极损耗;PD为介质损耗;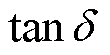 为介质损耗角正切值;C为电容;
为介质损耗角正切值;C为电容;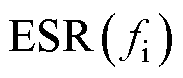 为频率在
为频率在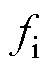 时的ESR;
时的ESR;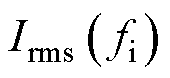 为频率在
为频率在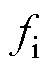 时电容电流的有效值。
时电容电流的有效值。
常见的三相MMC系统主要由交流侧三相电源、交流侧变压器、MMC相单元、直流侧电源组成。其中,每个相单元包含上下两个桥臂,每个桥臂由电抗器和多个子模块构成,每个子模块内含两个IGBT模块和一个电容器。其电路结构如图15所示。
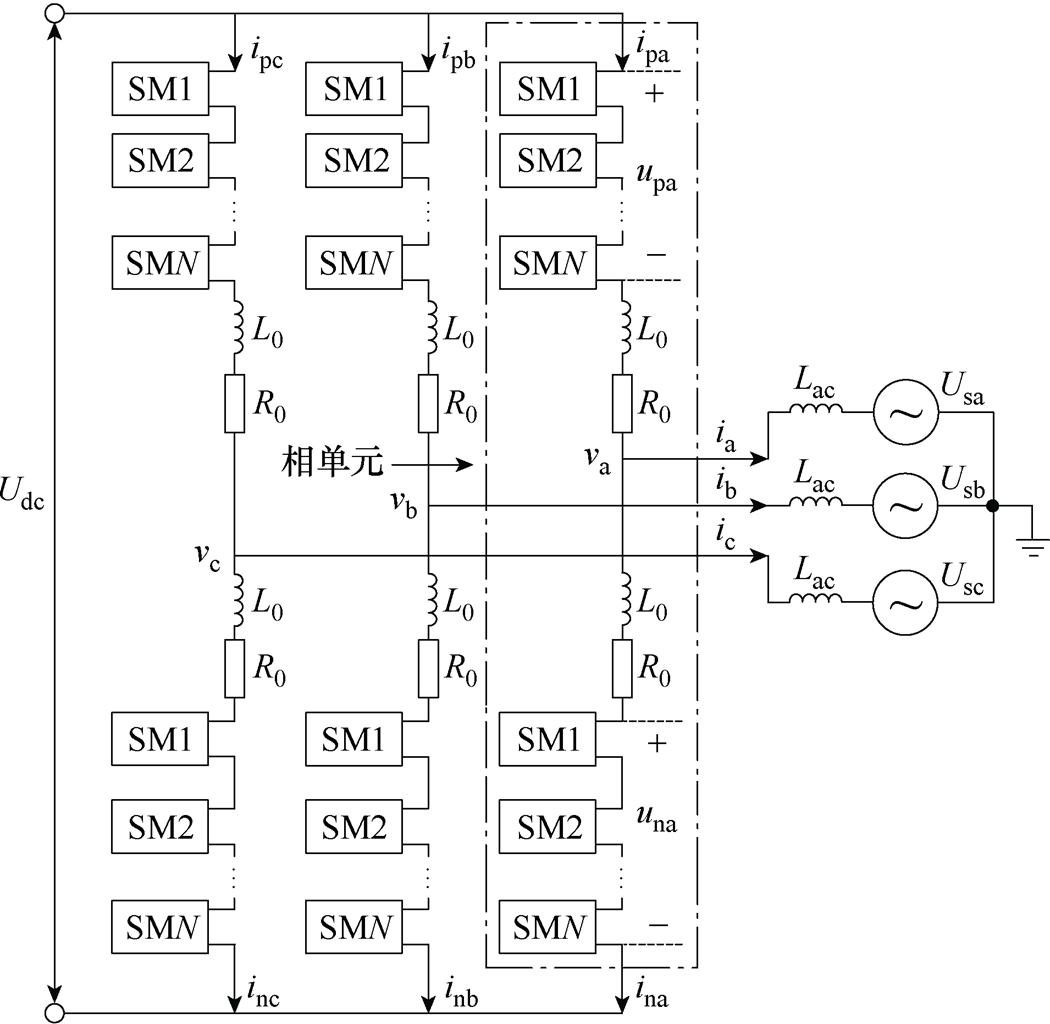
图15 三相MMC系统主电路结构
Fig.15 Three-phase MMC system main circuit structure
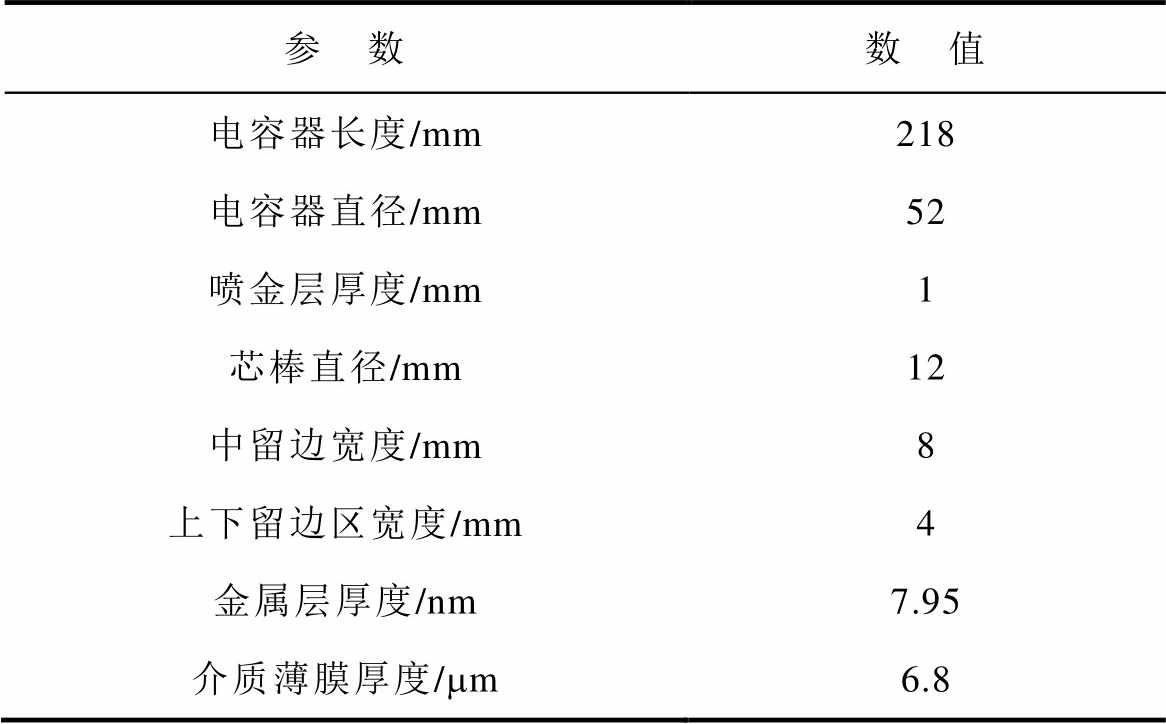
为了分析金属化薄膜电容器的热行为,根据实际电容器的几何尺寸、物理参数和材料特性,通过有限元仿真分别建立电容器组的温度场模型。本文采用型号为B25620B1118K103的金属化薄膜电容器,结合数据手册并测量电容器的实际尺寸,结果见表1。该电容器的结构是中间及两侧留边型,根据其结构特性和物理尺寸在Comsol中建立了单体电容器几何模型,如图16所示。电容器的中心部分为芯棒,两端部分为喷金层,上下留边及中间留边部分为留边区,其余部分则为介质区。在Comsol的几何建模环境中,介质薄膜和金属电极的厚度分别为mm与nm,然而宽度为mm尺度,增加了求解难度。鉴于此,对电容器的介质薄膜和金属电极进行均匀化处理,将其视为均匀材料,并对材料的导热系数、密度等关键参数等效计算。电容器的温度场计算涉及相关材料的密度、导热系数等属性,具体的属性参数见表2。
表1 电容器的尺寸信息
Tab.1 Dimensional information of capacitors
参 数数 值 电容器长度/mm218 电容器直径/mm52 喷金层厚度/mm1 芯棒直径/mm12 中留边宽度/mm8 上下留边区宽度/mm4 金属层厚度/nm7.95 介质薄膜厚度/mm6.8
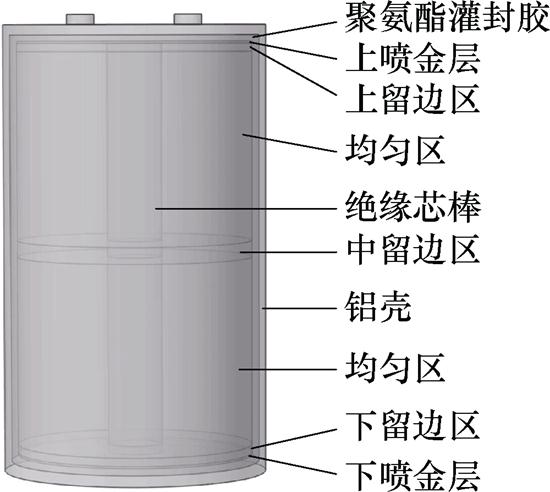
图16 金属化薄膜电容器的几何模型
Fig.16 Geometric model of metallized film capacitors
在实际工程中往往采用多个单体元件并联的方式构成电容器组,以满足电压和电流需求。本文采用10个单体电容器并联,其中单个电容器的额定电压为1 100 V,额定容值为1 100 mF,从而组成了额定电压为1 100 V,额定容值为11 mF的电容器组,元件布置为两列,电极固定在整块铜排上。电容器组整体的长、宽、高分别为592 mm、240 mm和228 mm。电容器内部产生热量后主要通过金属电极、聚丙烯薄膜、绝缘灌封胶传递到铝壳,再通过对流的方式扩散至外部环境,仅极少的热量会从内部直接辐射到环境。在模型中设置热对流系数来等效外壳自然空冷散热,设置为5 W/(m2·K),热边界均设置为绝热等效无热辐射,边界条件如图17a所示。为了提升计算效率,将绝缘树脂、喷金层、铝壳部分进行网格细化,其余部分均采用标准尺寸网格进行划分,如图17b所示。
表2 电容器各材料的属性参数
Tab.2 Property of each material of capacitor
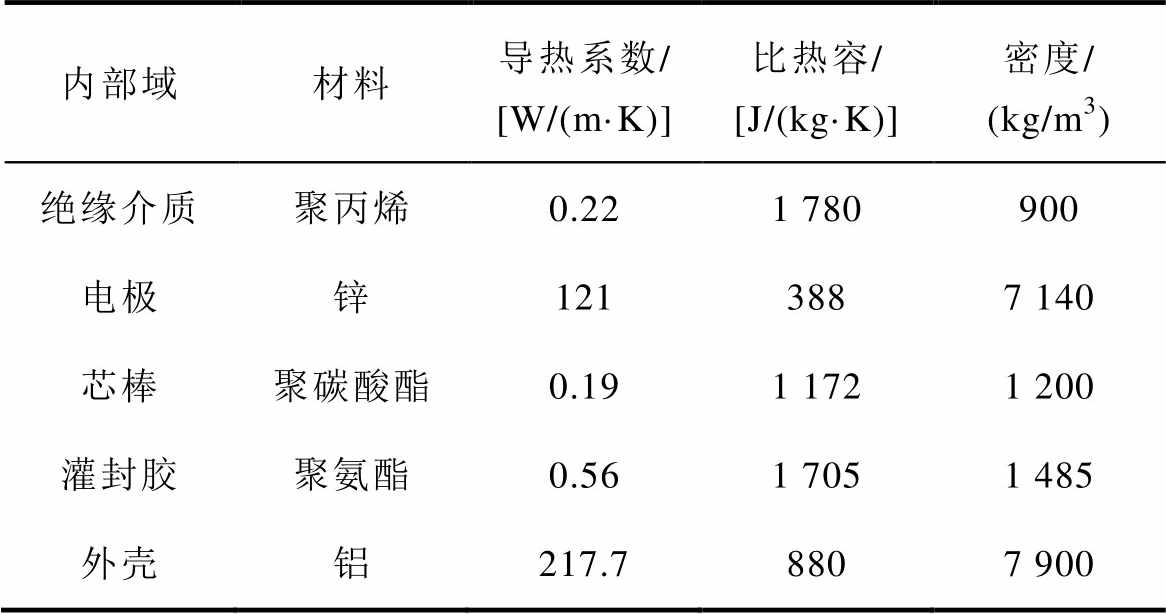
内部域材料导热系数/[W/(m·K)]比热容/[J/(kg·K)]密度/(kg/m3) 绝缘介质聚丙烯0.221 780900 电极锌1213887 140 芯棒聚碳酸酯0.191 1721 200 灌封胶聚氨酯0.561 7051 485 外壳铝217.78807 900

图17 多元件并联电容器组边界条件及网格剖分
Fig.17 Boundary conditions and mesh grid of multi-element shunt capacitor bank
整个电容器组的温度分布如图18所示。从图可知,电容器组外表面的温度明显低于内部的温度,最高温度位于电容的中心。电容器组的最高温升由单个电容的4.9℃变为5.61℃,最低温升为3.66℃,电容器单体间最大温差为1.95℃。
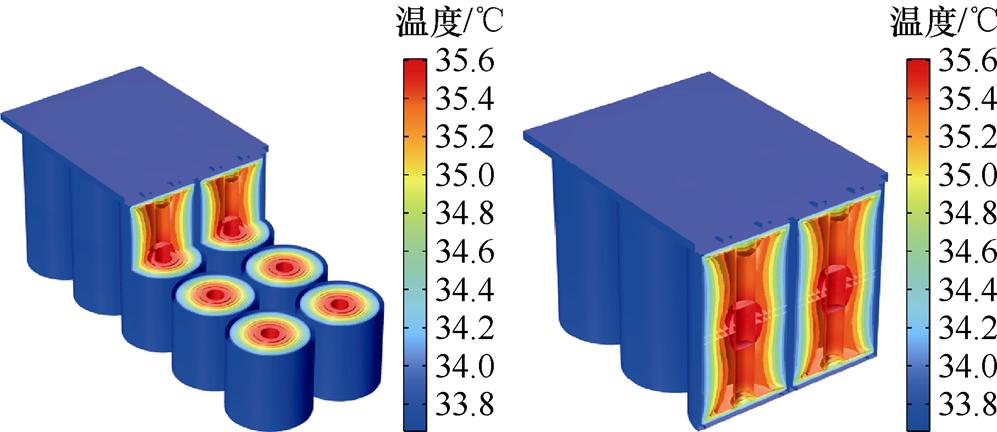
图18 电容器组温度分布
Fig.18 Temperature distribution of capacitors
为了验证电容器组场路协同仿真模型的准确性,将热电偶置于每个单体电容器的中心,用于监测电容器的内部温度。图10所示平台子模块在两个不同运行工况下的电感电流和被测子模块电容电压的波形如图19所示,具体参数见表3。将测试箱的环境温度分别设置为30℃和40℃,对电容器组进行正常工作,采集温度,将测试模型仿真和测量温度进行比较。其中,试验测试中环境温度为30℃时,工况1下电容器内部温度达到稳定时的内部温度为31.6℃,工况2下电容器内部温度达到稳定时的内部温度为32.7℃。将辅助测试平台的数据代入电热协同仿真模型,获得了当前运行条件下被测子模块电容器的热点温度分别为31.9℃和33.2℃。试验测试中环境温度为40℃时,工况1下电容器内部温度达到稳定时的平均温度为41.7℃,工况2下电容器内部温度达到稳定时的平均温度为42.9℃。将辅助测试平台的数据代入电热协同仿真模型,获得了当前运行条件下被测子模块电容器的热点温度分别为42.2℃和43.4℃。电热协同模拟仿真模型的计算结果与实际试验数据的结果基本一致,温升误差小于3%,表明场路协同仿真模型的有效性。
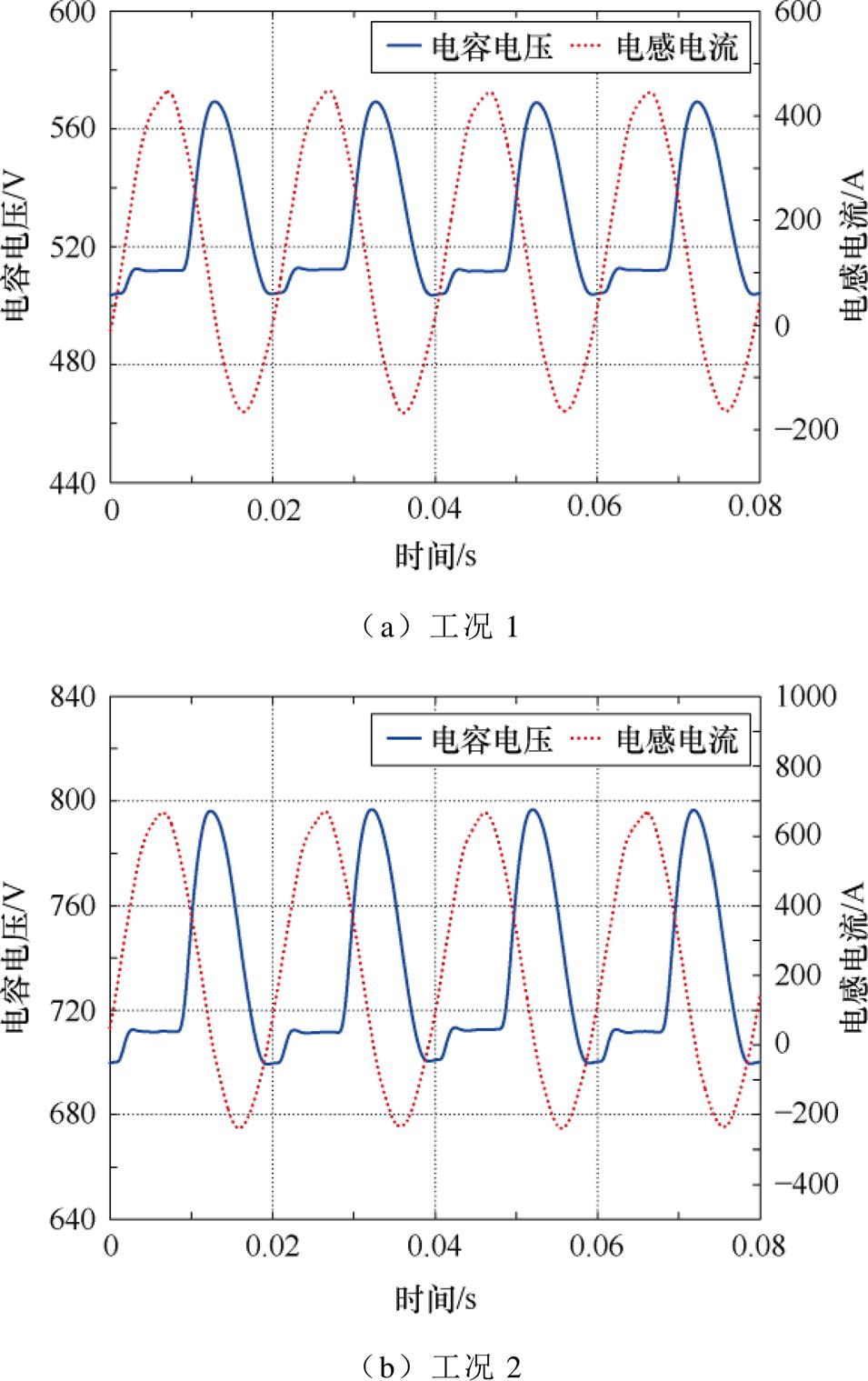
图19 子模块电压及电感电流
Fig.19 Capacitor voltage and inductive current
表3 不同的运行工况
Tab.3 Different working conditions
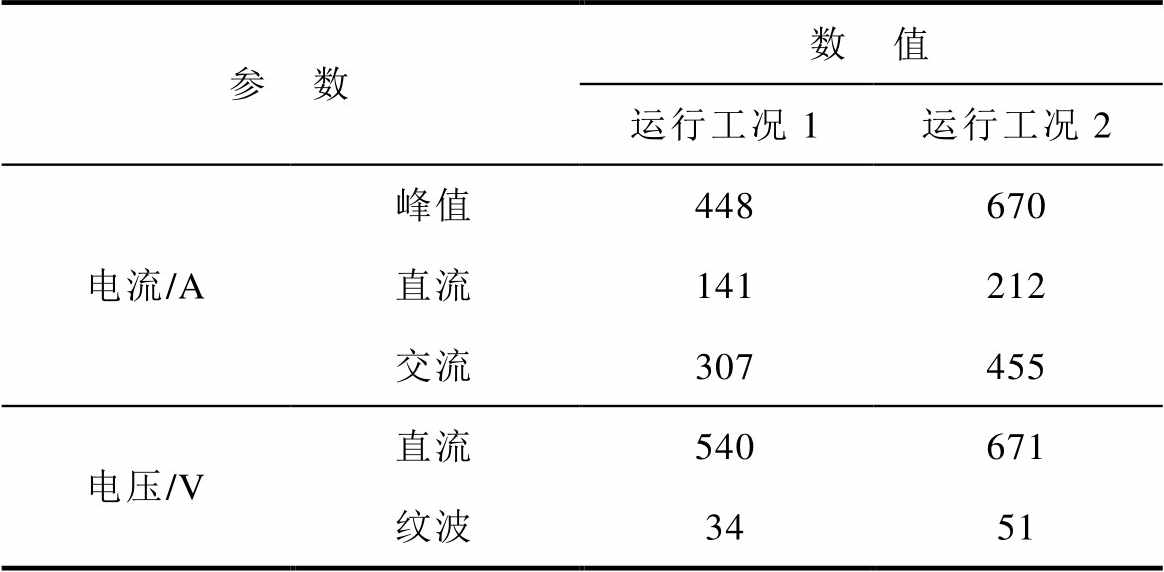
参 数数 值 运行工况1运行工况2 电流/A峰值448670 直流141212 交流307455 电压/V直流540671 纹波3451
为了证明金属化薄膜电容器剩余寿命模型的有效性,先验证其容值及ESR时变退化模型的正确性。将文献[33-34]中加速老化试验数据分别定义为测试1和测试2。在测试1中,在温箱中设置温度为70℃,将电容两端的直流电压Udc增大为额定电压Un的1.2倍。测试2中,加速老化测试系统的温度设置为85℃,电容两端施加的直流电压Udc为额定电压Un。将测试1中进行了2 400 h的测试数据和测试2为期3 500 h的测试数据进行拟合,可得1.1节提到的使用广义Eyring关系所表示的电容器加速因子Hacc1和Hacc2的值分别为37.0和45.25。在测试1和测试2中分别选择了4个时刻记录电容值和ESR值,时刻分布如图20所示,并通过本文提出的金属化薄膜电容器容值及ESR时变退化模型(见式(20)、式(21))计算各个时刻对应的电容值和ESR值,结果见表4。通过比较可知,模型计算结果和试验结果在不同测试工况下非常接近,验证了模型的正确性和有效性。
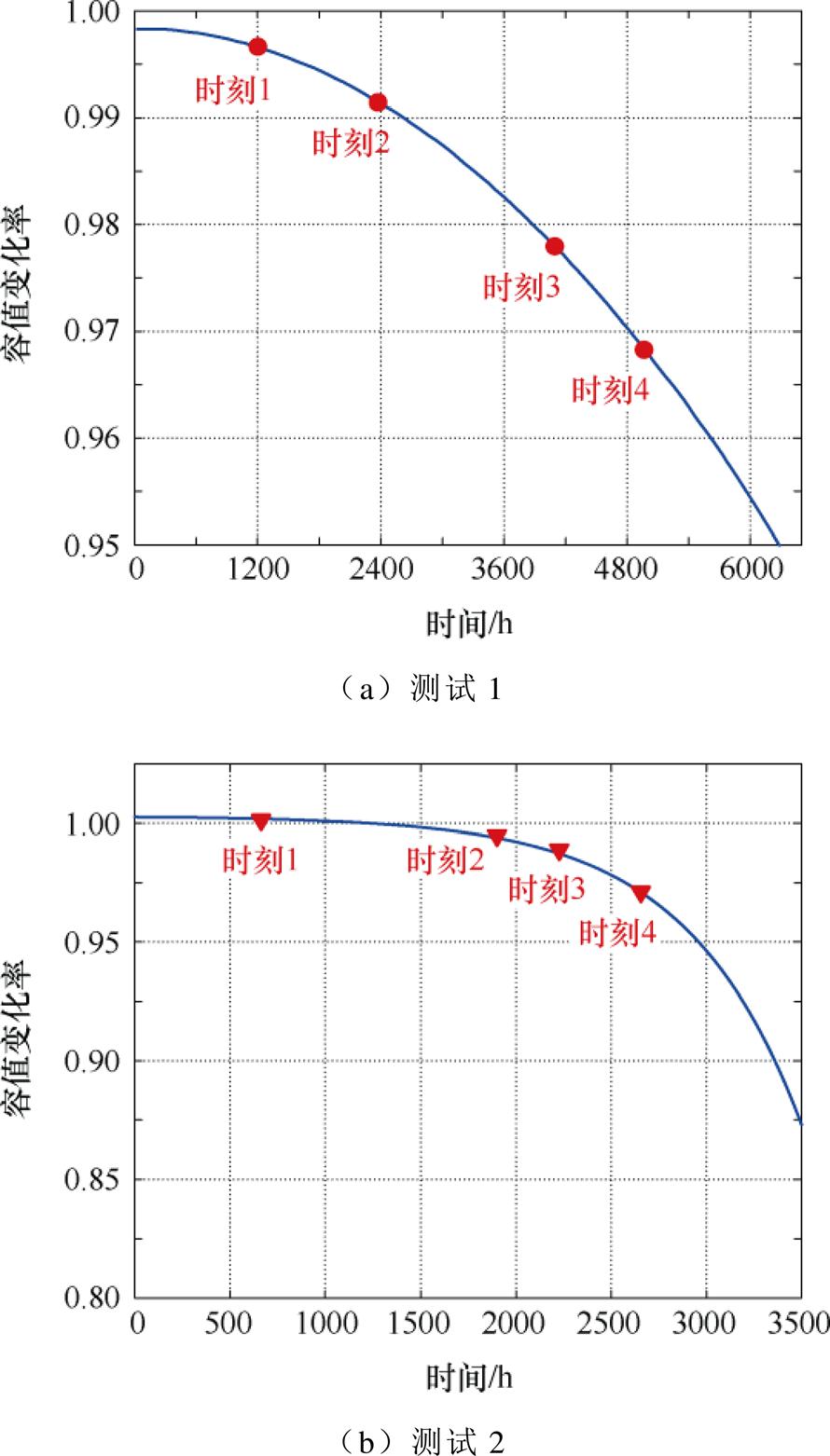
图20 电容值退化测试过程中的运行时刻
Fig.20 Operating time during capacitance degradation testing
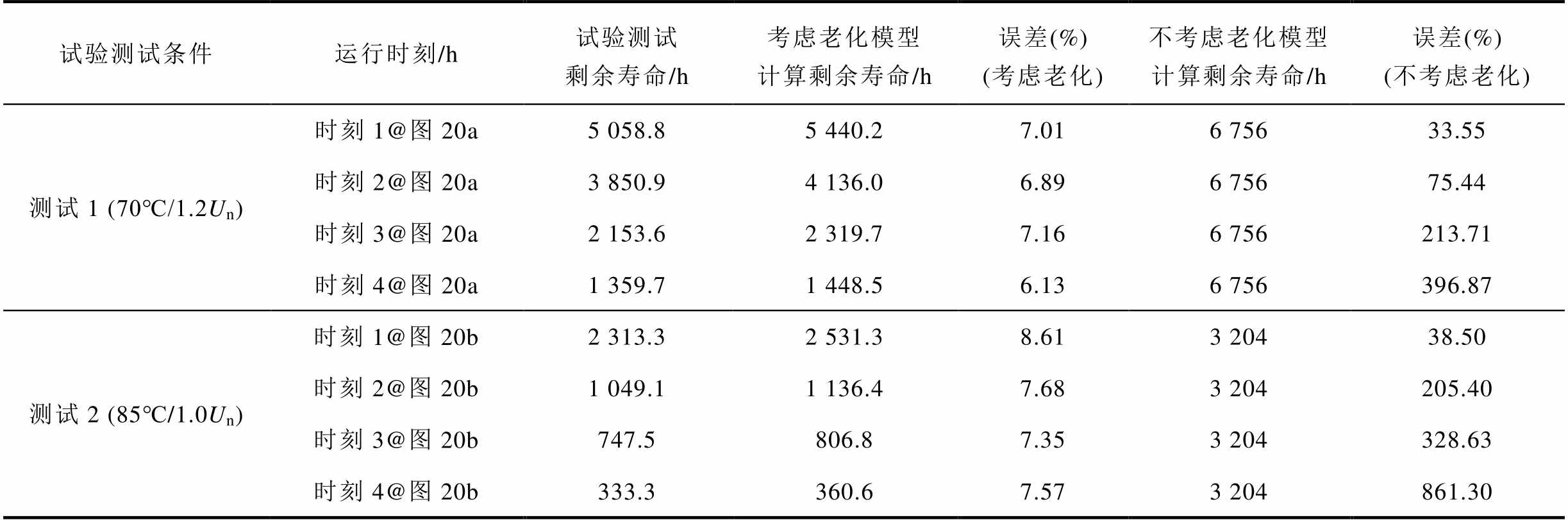
对于金属化薄膜电容器剩余寿命模型的验证,分别采用1.1节和1.2节所提考虑老化和不考虑老化的剩余寿命评估方法对电容器剩余寿命进行计算,在测试1和测试2的老化过程中分别选择了相同的4个时刻计算电容器的剩余寿命,计算结果及误差见表5。从表中可知,计及电容器容值及ESR退化规律的剩余寿命评估方法能够对金属化薄膜电容器的剩余寿命进行评估,误差在10%以下,而不考虑老化的传统寿命评估方法误差很大,因此不宜用于对金属化薄膜电容器的剩余寿命进行评估。这一对比分析验证了该方法的有效性。
表4 金属化薄膜电容器容值及ESR时变退化结果
Tab.4 Metallized film capacitor capacitance and ESR time-varying degradation results
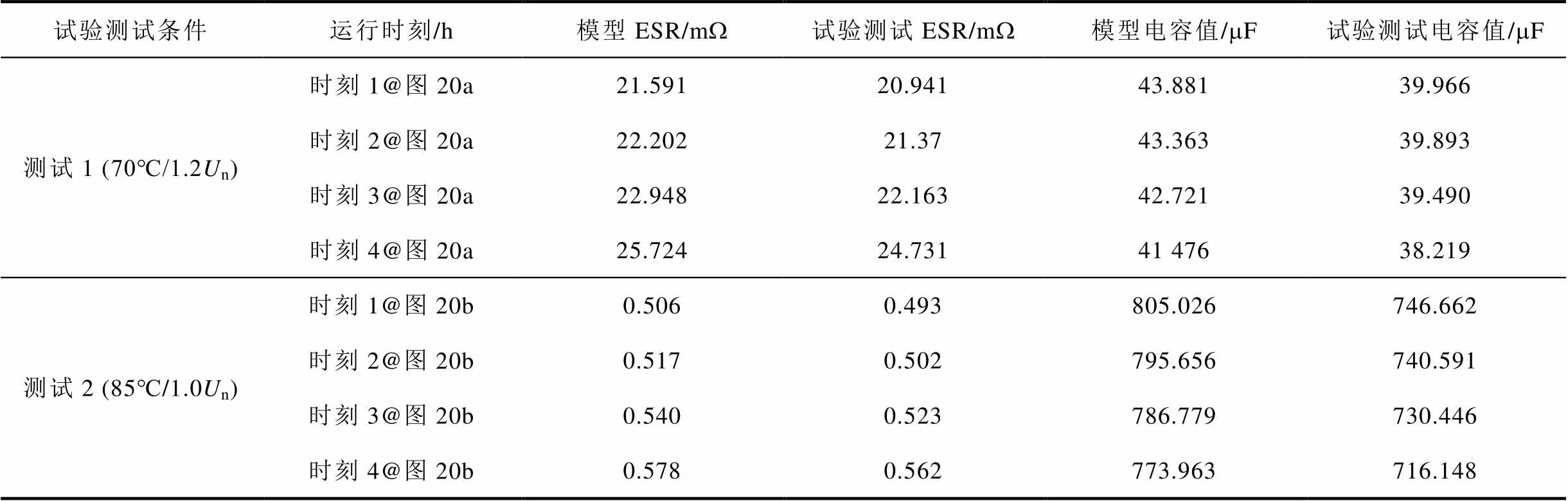
试验测试条件运行时刻/h模型ESR/mW试验测试ESR/mW模型电容值/mF试验测试电容值/mF 测试1 (70℃/1.2Un)时刻1@图20a21.59120.94143.88139.966 时刻2@图20a22.20221.3743.36339.893 时刻3@图20a22.94822.16342.72139.490 时刻4@图20a25.72424.73141 47638.219 测试2 (85℃/1.0Un)时刻1@图20b0.5060.493805.026746.662 时刻2@图20b0.5170.502795.656740.591 时刻3@图20b0.5400.523786.779730.446 时刻4@图20b0.5780.562773.963716.148
表5 金属化薄膜电容器的剩余寿命计算结果及误差
Tab.5 Calculation results and errors of the remaining life of metallized film capacitors
试验测试条件运行时刻/h试验测试剩余寿命/h考虑老化模型计算剩余寿命/h误差(%)(考虑老化)不考虑老化模型计算剩余寿命/h误差(%)(不考虑老化) 测试1 (70℃/1.2Un)时刻1@图20a5 058.85 440.27.016 75633.55 时刻2@图20a3 850.94 136.06.896 75675.44 时刻3@图20a2 153.62 319.77.166 756213.71 时刻4@图20a1 359.71 448.56.136 756396.87 测试2 (85℃/1.0Un)时刻1@图20b2 313.32 531.38.613 20438.50 时刻2@图20b1 049.11 136.47.683 204205.40 时刻3@图20b747.5806.87.353 204328.63 时刻4@图20b333.3360.67.573 204861.30
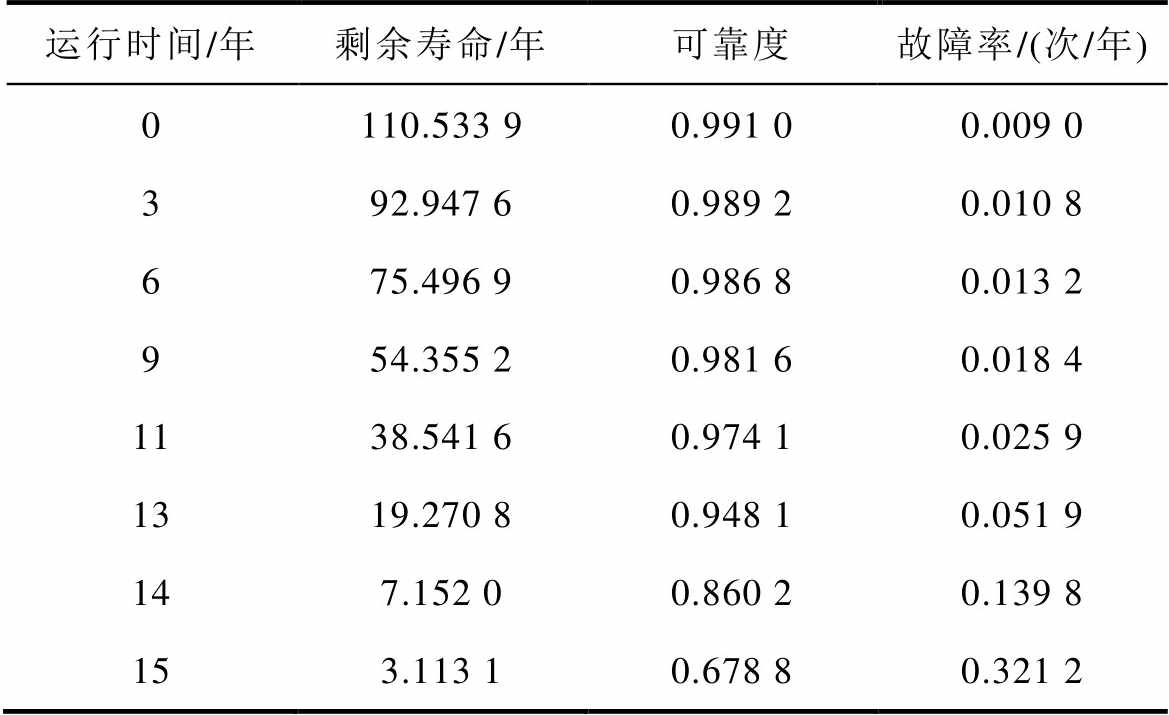
以厦门柔直输电工程逆变工况为例对子模块电容器进行可靠性分析和寿命评估,子模块电容器的平均电容电压为1 600 V,电压波动峰峰值为285 V,电容电流的有效值为680 A,子模块的环境温度为40℃。使用所提方法对不同运行时间的子模块电容器剩余寿命进行评估,结果见表6。电容器的可靠度及故障率与运行时间的关系如图21和图22所示。
表6 金属化薄膜电容器的剩余寿命预测结果
Tab.6 Lifetime estimate result of metallized film capacitor
运行时间/年剩余寿命/年可靠度故障率/(次/年) 0110.533 90.991 00.009 0 392.947 60.989 20.010 8 675.496 90.986 80.013 2 954.355 20.981 60.018 4 1138.541 60.974 10.025 9 1319.270 80.948 10.051 9 147.152 00.860 20.139 8 153.113 10.678 80.321 2
从表4及图21和图22中可知,在MMC系统运行过程中,电容器的老化程度不断加深,其剩余寿命和可靠度均随运行时间的推移而呈指数规律降低,故障率则随着运行时间而增加。在运行初期时,电容器故障率较小,可靠度较高,二者的变化较小,但当服役时间达到约13年时出现了拐点,自此之后电容器的故障率急剧增大,在可靠度保持80%的条件下,电容器的寿命约为14.1年。
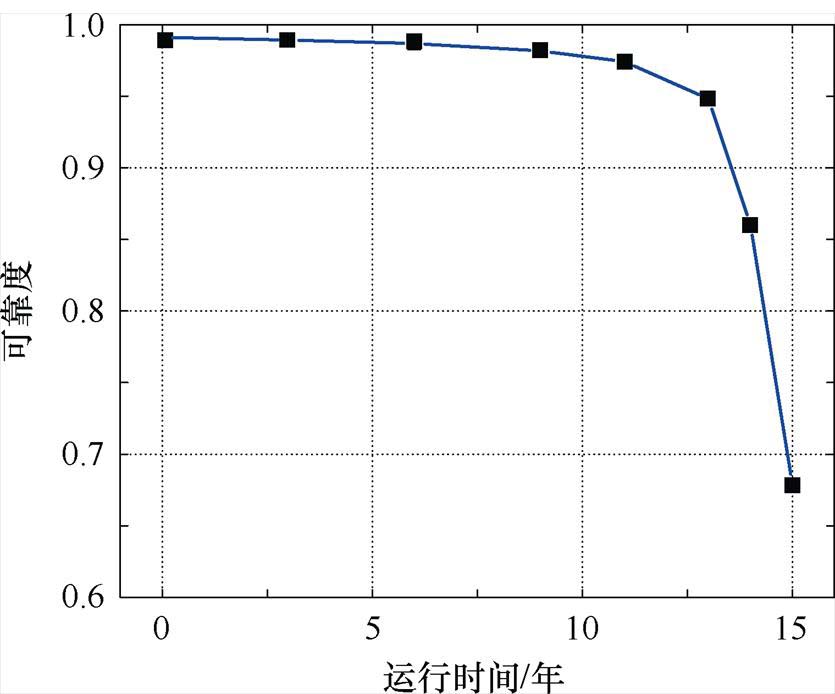
图21 金属化薄膜电容器的可靠度
Fig.21 Reliability curve of metallized film capacitor
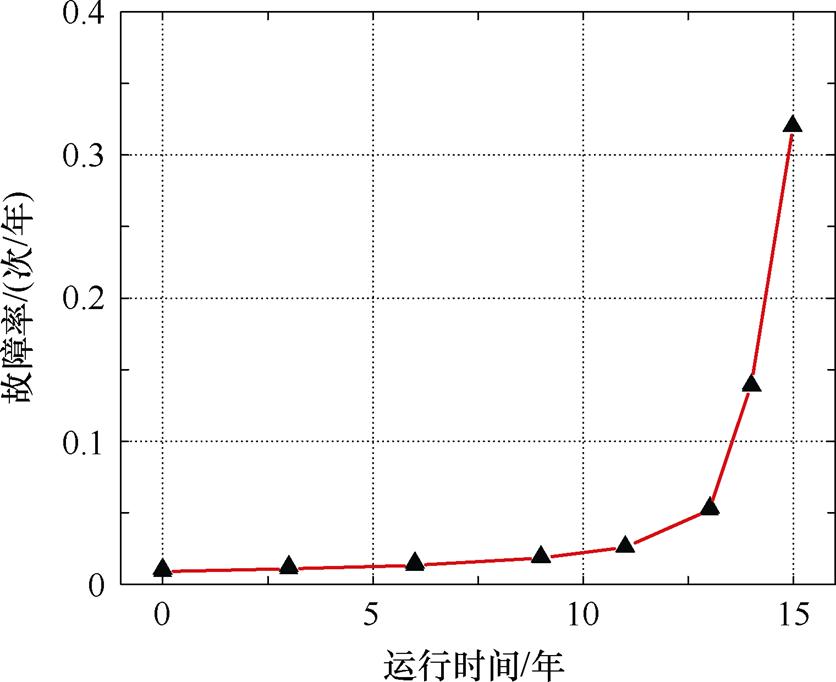
图22 金属化薄膜电容器的故障率
Fig.22 Failure rate curve of metallized film capacitor
此外,为了对比现有方法和本文方法的差异,将计及和不计及电容器老化效应对MMC系统电容器寿命的影响进行评估分析。其中,不计及老化的影响评估寿命为187 500 h(约21.4年),计及老化评估寿命为123 520 h(约14.1年)。根据国家电网的统计数据,实际应用中更换周期为10~15年[35]。因此,不计及电容器老化影响时,其评估结果与实际工程运维统计数据差异较大。采用本文提出的方法对电容器寿命的计算结果约为14.1年,提出的模型评估结果与实际较为一致,为MMC系统电容器的运维提供数据基础。
本文以金属化薄膜电容器为研究对象,分析了导致金属化薄膜电容器失效的主要模式,建立了其解析寿命模型,并提出ESR和电容值的老化模型来描述金属化薄膜电容器的退化过程,表明在长期的服役工况下金属化薄膜电容器的ESR、电容损失随时间呈指数级增加。基于电容器的ESR与电容值的老化速率与温度的相互作用,提出了一种针对金属化薄膜电容器的剩余寿命估算策略。结果表明,所提方法相比于传统的方法结果更准确,更符合工程统计数据结果,为设备选型、系统设计和MMC系统子模块电容器的可靠性评估提供了参考。
参考文献
[1] 潘俊良, 王明渝. 适用于大型海上风电的谐振型飞跨电容式模块化升压变换器[J]. 电工技术学报, 2024, 39(12): 3746-3760.
Pan Junliang, Wang Mingyu. Resonant flying capacitor modular boost converter suitable for large offshore wind power[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3746-3760.
[2] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electro- technical Society, 2022, 37(19): 4808-4822.
[3] 茆美琴, 程德健, 袁敏, 等. 基于暂态能量流的模块化多电平高压直流电网接地优化配置[J]. 电工技术学报, 2022, 37(3): 739-749.
Mao Meiqin, Cheng Dejian, Yuan Min, et al. Optimal allocation of grounding system in high voltage direct current grid with modular multi-level converters based on transient energy flow[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 739-749.
[4] 饶宏, 周月宾, 李巍巍, 等. 柔性直流输电技术的工程应用和发展展望[J]. 电力系统自动化, 2023, 47(1): 1-11.
Rao Hong, Zhou Yuebin, Li Weiwei, et al. Engineering application and development prospect of VSC-HVDC transmission technology[J]. Automation of Electric Power Systems, 2023, 47(1): 1-11.
[5] 雷顺广, 束洪春, 李志民. 基于桥臂功率特征的全-半混合型柔性直流输电线路保护[J]. 电工技术学报, 2023, 38(13): 3563-3575.
Lei Shunguang, Shu Hongchun, Li Zhimin. Full-half bridge hybrid VSC-HVDC transmission line pro- tection method based on power characteristics of bridge arms[J]. Transactions of China Electro- technical Society, 2023, 38(13): 3563-3575.
[6] 罗丹, 陈民铀, 赖伟, 等. 基于Haar小波变换重构开关序列的MMC子模块电容值在线监测方法[J]. 电工技术学报, 2022, 37(20): 5278-5289.
Luo Dan, Chen Minyou, Lai Wei, et al. Online monitoring method for sub-module capacitance in modular multilevel converter based on Haar wavelet transform reconstruction switch sequence[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(20): 5278-5289.
[7] 付华, 陈浩轩, 李秀菊, 等. 含边界元件的MMC- MTDC直流侧单端量故障辨识方法[J]. 电工技术学报, 2021, 36(1): 215-226.
Fu Hua, Chen Haoxuan, Li Xiuju, et al. MMC-MTDC DC side single-ended quantity fault identification method with boundary elements[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 215-226.
[8] Xia Hongjian, Zhang Yi, Chen Minyou, et al. Capacitor condition monitoring for modular multi- level converter based on charging transient voltage analysis[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 3847-3856.
[9] Belko V O, Emelyanov O A, Ivanov I O, et al. Metallized film capacitors degradation under high electrodynamic load[C]//2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St Petersburg and Moscow, Russia, 2017: 1120-1122.
[10] 李化, 李智威, 王国帅, 等. 脉冲功率应用中的金属化膜电容器寿命预测[J]. 强激光与粒子束, 2014, 26(4): 135-140.
Li Hua, Li Zhiwei, Wang Guoshuai, et al. Lifetime prediction of metallized polypropylene film capa- citors in pulsed power applications[J]. High Power Laser and Particle Beams, 2014, 26(4): 135-140.
[11] Zhao Jianyin, Liu Fang. Reliability assessment of the metallized film capacitors from degradation data[J]. Microelectronics Reliability, 2007, 47(2/3): 434-436.
[12] Wang Huai, Blaabjerg F. Reliability of capacitors for DC-link applications in power electronic converters- an overview[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3569-3578.
[13] Li Hua, Lewin P, Fothergill J C. Aging mechanisms of X2 metallized film capacitors in a high temperature and humidity environment[C]//2016 IEEE Inter- national Conference on Dielectrics (ICD), Montpellier, France, 2016: 804-807.
[14] Vogelsberger M A, Wiesinger T, Ertl H. Life-cycle monitoring and voltage-managing unit for DC-link electrolytic capacitors in PWM converters[J]. IEEE Transactions on Power Electronics, 2011, 26(2): 493- 503.
[15] Pu Xingsi, Nguyen T H, Lee D C, et al. Fault diagnosis of DC-link capacitors in three-phase AC/DC PWM converters by online estimation of equivalent series resistance[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 4118-4127.
[16] Wang Hanyu, Wang Huai, Wang Zhongxu, et al. Condition monitoring for submodule capacitors in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10403-10407.
[17] Geng Zhi, Han Minxiao, Zhou Guangyang. Switching signals based condition monitoring for submodule capacitors in modular multilevel converters[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(6): 2017-2021.
[18] 夏宏鉴, 陈民铀, 赖伟, 等. 基于频带能量的模块化多电平换流阀中金属化薄膜电容器失效检测方法[J]. 中国电机工程学报, 2021, 41(22): 7782-7793.
Xia Hongjian, Chen Minyou, Lai Wei, et al. Failure detection method for metalized polypropylene film capacitor in modular multilevel converter based on band energy[J]. Proceedings of the CSEE, 2021, 41(22): 7782-7793.
[19] 盛景, 陈聪, 向鑫, 等. 模块化多电平谐振变换器多自由度调压控制及子模块电容均压方法[J]. 电工技术报, 2022, 37(24): 6216-6229.
Sheng Jing, Chen Cong, Xiang Xin, et al. Multi- degree-of-freedom voltage regulation control of modular multilevel resonant converter and sub- module capacitor voltage balancing method[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6216-6229.
[20] Wang Huai, Diaz Reigosa P, Blaabjerg F. A humidity-dependent lifetime derating factor for DC film capacitors[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 3064-3068.
[21] 邹华碧. 国际金属化薄膜电容器的可靠性发展动态[C]//中国电子元件行业协会电容器分会有机电容器专业委员会技术交流会, 昆明, 中国, 2011: 16-19.
[22] Redondo-Iglesias E, Venet P, Pelissier S. Global model for self-discharge and capacity fade in lithium-ion batteries based on the generalized Eyring relationship[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 104-113.
[23] Lü Chunlin, Liu Jinjun, Zhang Yan, et al. An improved lifetime prediction method for metallized film capacitor considering harmonics and degradation process[J]. Microelectronics Reliability, 2020, 114: 113892.
[24] Makdessi M, Sari A, Venet P. Metallized polymer film capacitors ageing law based on capacitance degradation[J]. Microelectronics Reliability, 2014, 54(9/10): 1823-1827.
[25] Sun Bo, Fan Xuejun, Qian Cheng, et al. PoF- simulation-assisted reliability prediction for elec- trolytic capacitor in LED drivers[J]. IEEE Transa- ctions on Industrial Electronics, 2016, 63(11): 6726-6735.
[26] Soualhi A, Makdessi M, German R, et al. Heath monitoring of capacitors and supercapacitors using the neo-fuzzy neural approach[J]. IEEE Transactions on Industrial Informatics, 2018, 14(1): 24-34.
[27] Makdessi M, Sari A, Venet P, et al. Lifetime estimation of high-temperature high-voltage polymer film capacitor based on capacitance loss[J]. Micro- electronics Reliability, 2015, 55(9/10): 2012-2016.
[28] Makdessi M, Sari A, Venet P. Health monitoring of DC link capacitors[J]. Chemical Engineering, 2013, 33(1): 1105-1110.
[29] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922.
Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of MMC sub-module based on generalized capacitor voltage unbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[30] 贾英杰, 肖飞, 罗毅飞, 等. 基于场路耦合的大功率IGBT多速率电热联合仿真方法[J]. 电工技术学报, 2020, 35(9): 1952-1961.
Jia Yingjie, Xiao Fei, Luo Yifei, et al. Multi-rate electro-thermal simulation method for high power IGBT based on field-circuit coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1952- 1961.
[31] Type polypropylene. (2016). DC link capacitors. [EB/OL]. Available: https://www.cde.com/resources/ catalogs/947D.pdf.
[32] Lü Chunlin, Liu Jinjun, Zhang Yan, et al. A high- resolution analytical thermal modeling method of capacitor bank considering thermal coupling and different cooling modes[J]. IEEE Transactions on Power Electronics, 2023, 38(6): 7674-7684.
[33] Yao Bo, Ge Xinglai, Xie Dong, et al. Electrothermal stress analysis and lifetime evaluation of DC-link capacitor banks in the railway traction drive system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4269-4284.
[34] Wang Huai, Nielsen D A, Blaabjerg F. Degradation testing and failure analysis of DC film capacitors under high humidity conditions[J]. Microelectronics Reliability, 2015, 55(9/10): 2007-2011.
[35] Lü Chunlin, Liu Jinjun, Zhang Yan, et al. Reliability modeling for metallized film capacitors based on time-varying stress mission profile and aging of ESR[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4311-4319.
Remaining Lifetime Assessment Method Based on On-Line Condition Monitoring of Metallized Film Capacitors
Abstract Modular multilevel converter (MMC) is the core equipment in flexible direct current transmission systems, where the sub-module (SM) metalized film capacitors represent one of the weak links within MMCs. Thus, state monitoring and lifetime assessment of metalized film capacitors are of significant importance for enhancing the operational reliability of MMCs and formulating system maintenance plans. Current lifetime assessment methods for metalized film capacitors do not consider the impact of capacitor aging on capacitance value and equivalent series resistance (ESR). It is difficult to accurately assess the remaining lifetime of capacitors under different service conditions. Therefore, this paper proposes a method to assess the remaining lifetime of metalized film capacitors, considering the current capacitance state for online monitoring. The main research contents include the following aspects.
(1) A method based on capacitance value and hotspot temperature is proposed. An analytical lifetime model is established according to the failure mechanism of metalized film capacitors. Subsequently, considering the impact of aging on ESR and capacitance value, a time-varying degradation model for the capacitance and ESR is developed. The nonlinear cumulative damage and degradation process are obtained under actual operational conditions. Based on the coupling relationship between the state of the capacitor, ESR, capacitance value, aging rate, and temperature, the change in failure rate is analyzed at different aging levels.
(2) A non-invasive method for monitoring capacitance value based on sliding window cumulative sum detection is proposed. Firstly, the coupling relationship between changes in capacitor voltage and switching signals is established based on the basic working principle of MMC. Then, the principle of the bilateral cumulative sum algorithm is described, and a sliding window is introduced to process the capacitor voltage, allowing for accurate determination of charging and discharging times within the sliding window. Thus, capacitance values can be calculated online. The effectiveness of the proposed method is validated through simulation and experiment, and the maximum error under different power levels is less than 0.6%. This method uses the existing capacitor voltage and arm current without affecting the original operating state of the MMC system, achieving non-invasive monitoring.
(3) An electrothermal co-simulation model based on field-circuit coupling is proposed to precisely simulate capacitors’ electrical and thermal characteristics under actual MMC conditions. The circuit model of the sub-module capacitor is constructed according to the circuit structure of the MMC system and the equivalent circuit of the capacitor. The temperature field model of the capacitor group is established on a finite element simulation platform of the actual physical structure of the capacitor components. Subsequently, a metalized film capacitor group's electrothermal coupling model is established through the mutual transfer of power loss and temperature parameters in Matlab. Finally, the proposed modeling method is analyzed and validated.
Keywords:Modular multilevel converter (MMC) system, metallized film capacitors, electro-thermal coupling model, online monitoring, lifetime prediction
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.231752
国家自然科学基金项目(U1966213)和中央高校基本科研业务费项目(2022CDJKYJH009)资助。
收稿日期 2023-10-19
改稿日期 2023-12-18
吴云杰 男,2001年生,硕士研究生,研究方向为电力电子器件可靠性。
E-mail: 202311021229T@stu.cqu.edu.cn
赖 伟 男,1986年生,博士,副教授,研究方向为电力电子器件可靠性和状态监测。
E-mail: laiweicqu@126.com(通信作者)