MOSFET输出电容对CLLLC谐振变换器模型的优化
张新闻1 刘文泽1 杨树德2 刘百林1
(1. 北方民族大学电气信息工程学院 银川 750021 2. 扬州大学电气与能源动力工程学院 扬州 225127)
摘要 在CLLLC谐振变换器基波等效建模方法中,未虑及变压器二次电流为零及死区时间内MOSFET输出电容对输出侧H桥桥臂中点电压的影响,当开关频率低于谐振频率(欠谐振)时,变换器输出侧H桥桥臂中点电压模型的准确性有待进一步提高。该文通过解析变换器欠谐振区域模型准确度较低的成因,得到变压器二次电流为零及死区时间内MOSFET输出电容电压方程,对基波等效建模方法进行了更为深入的研究,提出了状态变量(输出侧H桥桥臂中点电压、变压器二次电流)与变换器增益的优化计算方法。该方法计算式中包含开关频率、谐振频率、输出电压和MOSFET输出电容的信息,减小了状态变量稳态值求解误差,使等效输出负载与谐振腔参数更加准确,解决了欠谐振时变换器输出侧H桥桥臂中点电压模型精度相对较低的问题。最后,搭建CLLLC谐振变换器电路仿真模型与实验系统对所提方法进行验证,结果验证了该文理论分析的正确性。
关键词:MOSFET输出电容 CLLLC谐振变换器 基波等效(FHA)模型 时域分析
0 引言
高频隔离双向DC-DC变换器因其可在充电和放电模式之间自由切换[1-2],在电动汽车[3-4]、分布式储能系统[5-6]、不间断供电系统[7]、电力电子变压器[8]等领域中均得到了广泛应用。CLLLC作为高频隔离双向DC-DC变换器的一种典型拓扑,具有高功率、高效率及良好的软开关特性[9-10],已成为变换器研究热点之一。在中小功率应用场景中,普遍选用开关速度快、热稳定性好的MOSFET管作为变换器开关器件[11]。MOSFET输出电容会对变换器性能产生影响,文献[12]讨论了其输出电容对LLC变换器电压增益的影响,文献[13]对其输出电容在CLLLC变换器续流阶段产生的振荡问题进行分析,但都没考虑变压器二次电流为零及死区时间内MOSFET输出电容对变换器输出侧H桥桥臂中点电压模型的影响。本文以此为研究对象,以期提高CLLLC变换器模型的准确性。
基波等效(First Harmonic Approximation, FHA)建模法因其易于理解、准确性较高,常用于研究CLLLC谐振变换器增益特性。具体做法是将CLLLC谐振变换器输入输出侧H桥桥臂中点电压波形作傅里叶变换,取其基波分量,将电路拓扑分析转化为对正弦稳态电路的分析。文献[14]从FHA建模法角度出发,分别对变换器增益特性和阻性边界进行研究。针对非阻性有源负载存在的不足,提出一种基于参数优化的设计方法,得到变换器电压增益曲线,给出了一种新的参数设计方案,但未考虑MOSFET输出电容对FHA建模法的影响,当开关频率低于谐振频率时所建模型精度不高,降低了电压增益曲线的准确性,进而影响变换器参数设计。文献[15]基于FHA建模法,所建变换器增益模型对实际装置特性描述不够准确,直接影响到变换器参数选取以及后续软开关范围的分析。为提高变换器效率,文献[16]从电感比入手,采用FHA建模法推导变换器增益解析式,得到增益曲线不单调、最大增益减小是由于电感比过大造成的结论,但由于所建模型在欠谐振工况下准确度不高,增益曲线单调性的最大电感比与实际值存在较大误差。为提高FHA法建模精度,文献[17]提出扩展谐波近似(Extended Harmonics Approximation, EHA)法,EHA法通过计算各次谐波激励下的电路响应,利用叠加定理得到电路总响应,但计算过程比较复杂,而且EHA模型近似时会带来较大误差。文献[18-19]使用模态分析法(Operation Mode Analysis, OMA),将电路分为P、N、O三种模式,分别对其进行分析,得到各元件的时域解析式,再根据基本模态的具体排列求解,进而推导出增益公式与边界条件。此方法模型准确度较高,但不易找到迭代算法,求解非线性状态方程时计算量大,而且不具备动态分析能力。为简化建模过程中状态变量稳态值的计算,同时提高模型精度,文献[20]对变换器输出侧H桥桥臂中点电压波形进行简化近似,改进了欠谐振时状态量精度低的问题。由于舍弃了变压器二次电流为零及死区时间内MOSFET输出电容对谐振腔输出电压的影响,所得计算式不能准确表示状态量,且开关频率偏离谐振频率越大,模型误差也越大。
通过以上分析可知,传统FHA法未考虑MOSFET输出电容影响,CLLLC变换器处于欠谐振工况时所建模型不能准确描述其实际运行状态,且开关频率较谐振频率越小,模型误差就越大。为此,本文对传统FHA建模法进行优化。在分析模型误差原因的基础上,推导出变压器二次电流为零及死区时间内谐振腔输出电压表达式,将其进行傅里叶变换,提取基波分量,进而得到包含开关频率、谐振频率、输出电压和MOSFET输出电容信息的电压增益与输出等效负载,使变换器电路参数设计更加精准,解决了传统FHA法在变换器欠谐振工况下模型准确性较低的问题。最后,通过仿真和实验对所建模型的准确性进行了验证。
1 CLLLC谐振变换器FHA法模型的优化
CLLLC谐振变换器应用于能量双向流动场景时,必然有一向传输为升压模式,此时变换器工作于欠谐振状态。文中提出一种优化FHA模型,在欠谐振工况时能够为变换器实际参数选择提供更有价值的参考。
1.1 CLLLC谐振变换器基本拓扑
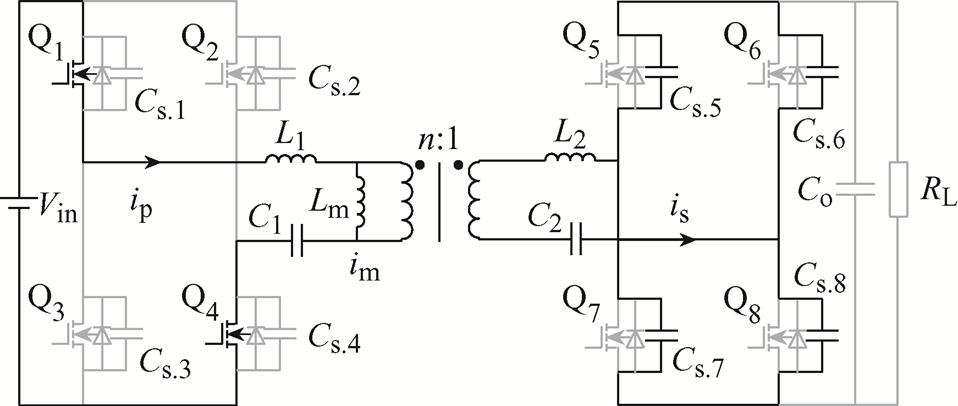
双向CLLLC谐振变换器电路拓扑如图1所示。图中,Q1~Q4构成变换器输入侧H桥,其作用是将直流电源电压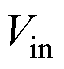 逆变成高频交流电;Q5~Q8构成变换器输出侧H桥,其作用是将谐振腔输出的高频交流电变换成直流输出电压
逆变成高频交流电;Q5~Q8构成变换器输出侧H桥,其作用是将谐振腔输出的高频交流电变换成直流输出电压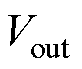 ,再经过滤波电容Co供给负载RL;Cs.1~Cs.8为MOSFET管Q1~Q8的输出电容;变压器一次侧电感L1、电容C1构成一次侧谐振腔,二次侧电感L2、电容C2构成二次侧谐振腔,Lm为变压器励磁电感;A、B、C、D四点分别为变换器输入侧与输出侧H桥桥臂中点。为方便后续分析,设uAB为变压器一次侧谐振腔输入电压,uCD为二次侧谐振腔输出电压,ip为变压器一次侧谐振腔电流,is为变压器二次侧谐振腔电流,n为变压器电压比。
,再经过滤波电容Co供给负载RL;Cs.1~Cs.8为MOSFET管Q1~Q8的输出电容;变压器一次侧电感L1、电容C1构成一次侧谐振腔,二次侧电感L2、电容C2构成二次侧谐振腔,Lm为变压器励磁电感;A、B、C、D四点分别为变换器输入侧与输出侧H桥桥臂中点。为方便后续分析,设uAB为变压器一次侧谐振腔输入电压,uCD为二次侧谐振腔输出电压,ip为变压器一次侧谐振腔电流,is为变压器二次侧谐振腔电流,n为变压器电压比。
1.2 CLLLC基波等效法建模
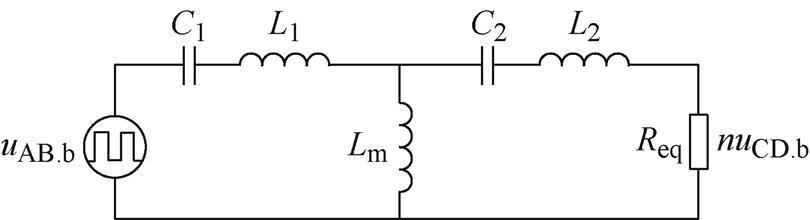
由FHA法得到CLLLC变换器等效电路如图2所示。为简化分析,将变压器二次侧参数折算至一次侧。图中,uAB.b、uCD.b分别为uAB、uCD的基波分量,Req为输出负载RL折算至一次侧的等效负载。
对uAB作傅里叶变换,其基波电压为
式中,ws=2πfs为基波角频率,fs为变换器开关频率。基波有效值为
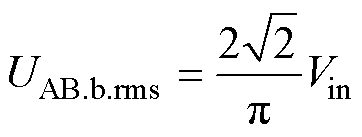 (2)
(2)
同理,输出侧H桥桥臂中点电压基波表示为
其有效值为
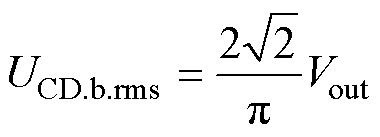 (4)
(4)
定义阻抗Z1、Z2及Z3分别表示为
综合图2与式(2)、式(4)及式(5),可得CLLLC谐振变换器基波简化电路的传递函数为
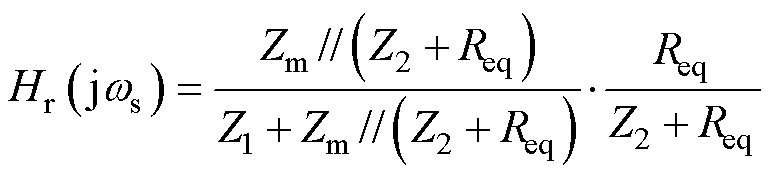 (6)
(6)
电压增益M可表示为
1.3 FHA法误差产生原因分析
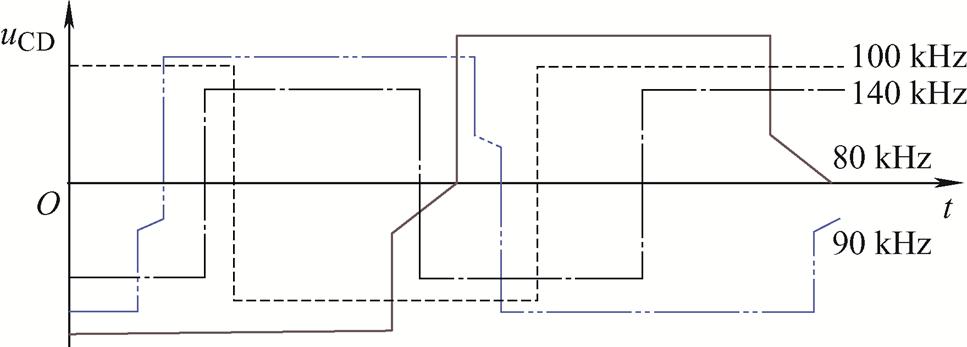
设定CLLLC变换器谐振频率fr=100 kHz,开关频率fs分别为140、100、90和80 kHz时,uCD的时域波形如图3所示。
当CLLLC谐振变换器处于过谐振状态时,由于开关频率大于谐振频率,变压器一次电流ip尚未等于励磁电感电流im时,开关管关闭进入死区时间,此过程中二次电流is只有在换向时刻才会出现等于零的情况。由于is换向时间极短且流过输出电容的电流远远小于下一时刻is,输出电容对uCD的影响可以忽略不计。因此,变换器过谐振时uCD为周期性方波信号。由于uCD波形无简化部分,在此基础上使用FHA建模法准确性很高。
当CLLLC谐振变换器处于准谐振状态时,由于开关频率等于谐振频率,与过谐振状态类似,变压器一次电流ip只在某一个时刻才能与励磁电感电流im相等,即二次电流is在换向时才能为零,因此输出电容对uCD的影响仍可以忽略不计。
当CLLLC谐振变换器处于欠谐振状态时,由于开关频率小于谐振频率,Q1和Q4或者Q2和Q3导通时的某时间段内,变压器一次电流ip等于励磁电感电流im,此时二次电流is为零,变压器二次侧通过输出电容进行续流,对uCD的波形产生影响,使其在此时间段内不再为标准的方波信号,而是具有一定斜率的时变波形。
传统FHA建模法过程中,将时变波形视为方波,并不考虑输出电容对uCD的影响。通过比较开关频率为100、90、80 kHz时uCD的波形可知,开关频率较谐振频率越小,一定斜率的时变波形在方波周期内占比越大,传统FHA建模法的误差也越大。
1.4 FHA法建模的优化
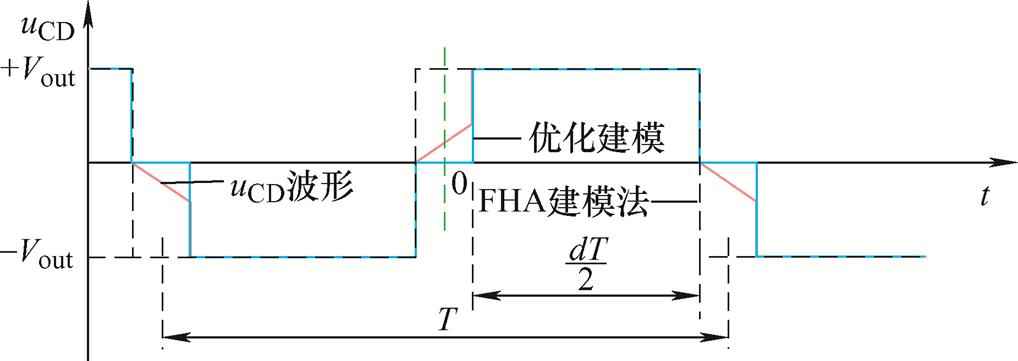
针对1.3节FHA建模法中存在的问题,文献[20]提出了一种简化uCD波形的方法,具体如图4所示,将uCD波形用函数Voutsgn(ip-im)表示。由于省略掉ip-im=0时MOSFET输出电容Cs充放电对uCD的影响,此方法会影响增益M、输出等效负载Req的准确性。
1.4.1 桥臂中点电压uCD的优化
为减小误差,使变换器模型更加准确,不再对uCD进行简化,而是直接求其基波。在Cs.5~Cs.8参与续流的过程中,将其分为运行模态a和运行模态b,模态a为ip-im=0的时段,具体如图5所示。
运行模态a续流阶段,二次侧MOSFET输出电容Cs.5~Cs.8与C2和L2一起形成谐振回路,4个输出电容Cs.5~Cs.8中,Cs.5和Cs.6串联,Cs.7和Cs.8串联,然后相互并联,此时4个输出电容可等效为一个电容Cs.sum,再与C2串联。由于Cs.sum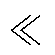 C2,所以Cs.sum与C2串联后约等于Cs.sum。令其串联后两端电压为u2(t),根据图5可以列出运行模态a的暂态方程为
C2,所以Cs.sum与C2串联后约等于Cs.sum。令其串联后两端电压为u2(t),根据图5可以列出运行模态a的暂态方程为
消去式(8)前两个公式中的ip(t)、is(t)和im(t),可得
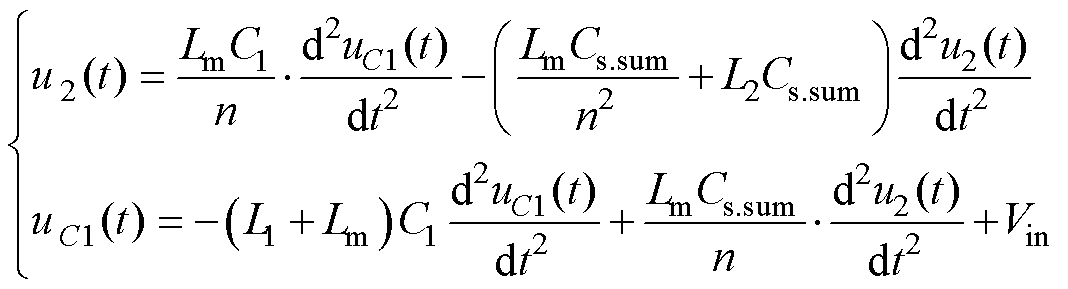 (9)
(9)
解此微分方程,可以得到uC1(t)与u2(t)分别为
式中,Ma1~Ma4为常数,可由初始条件求得
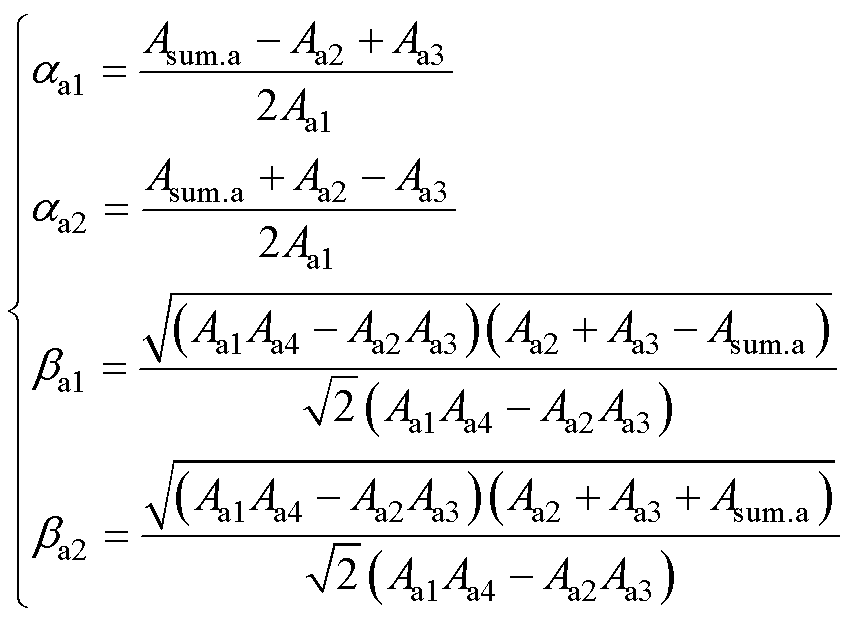
其中
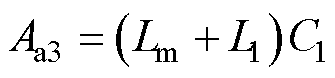
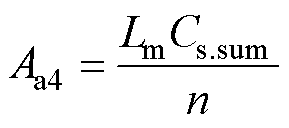
将uC1(t)与u2(t)代入式(8),即可求得is(t),则模态a中MOSFET输出电容的电压变化值为
运行模态b为死区时段,具体如图6所示。
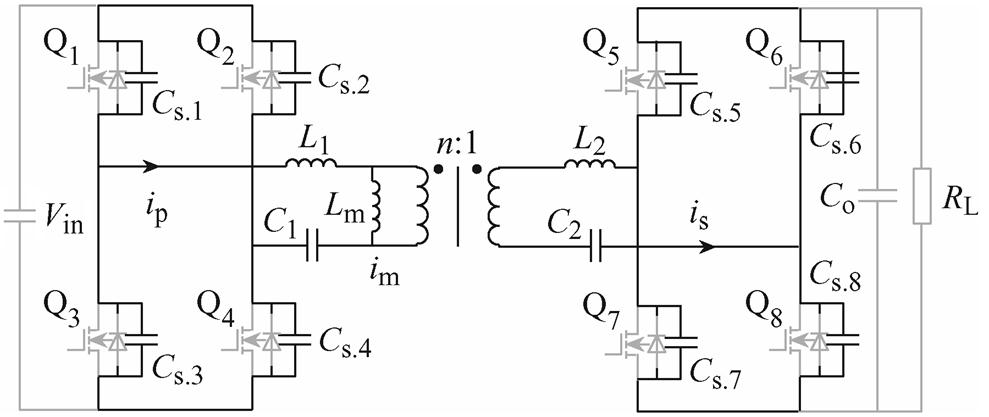
图6 运行模态b
Fig.6 Operation of mode b
根据图6,可以求出运行模态b的暂态方程为
消去式(12)前两个公式中的ip(t)、is(t)和im(t),可得
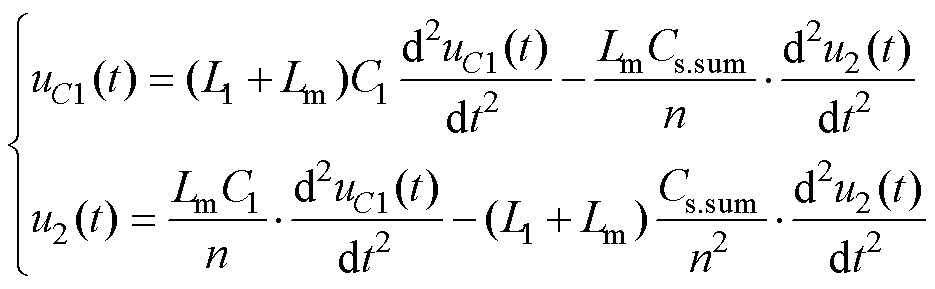 (13)
(13)
同理,解此微分方程,则可以得到uC1(t)、u2(t)分别为
式中,Mb1~Mb4为常数,可由初始条件求得
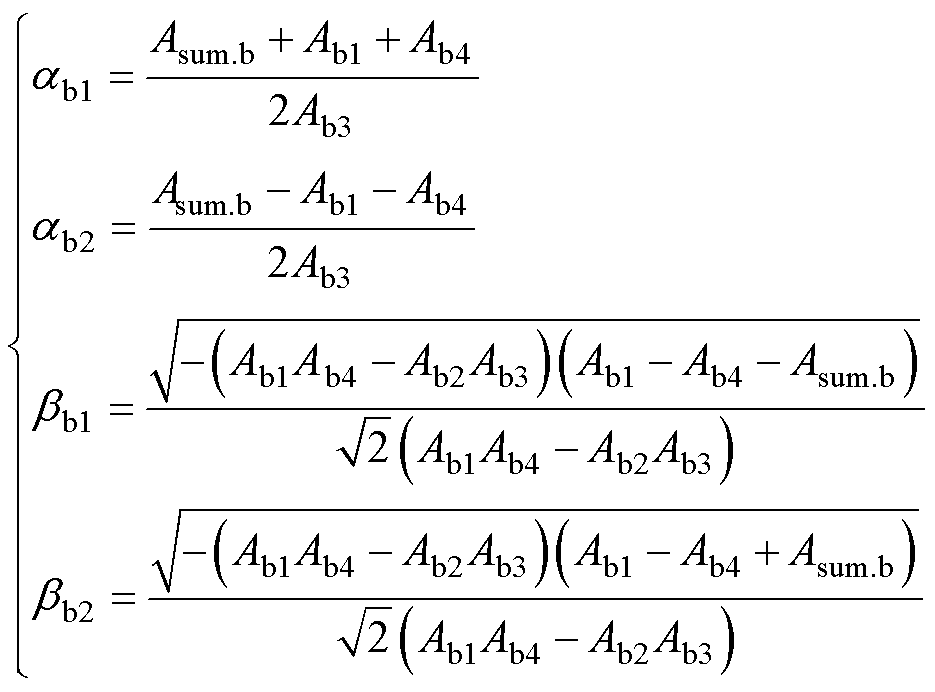
其中
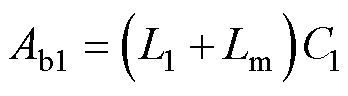
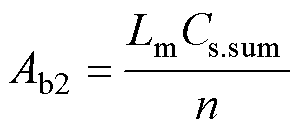
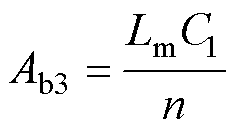
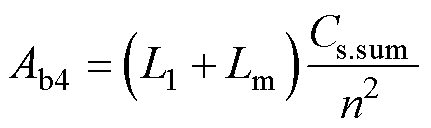
将uC1(t)与u2(t)代入式(12),即可求得is(t),则模态b中MOSFET输出电容电压变化值为
至此,求得a、b两个模态中输出电容总的电压变化值为
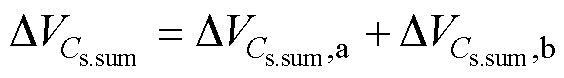 (16)
(16)
简化uCD(t)波形,求得的表达式虽然可以减小工作量,但增加了误差,在开关频率小于谐振频率时误差更加明显。为使模型具有更高的精准度,需要设计更加合理的模型。由于图4中uCD(t)波形以虚线为0刻线、左右各T/2(T为开关周期)作傅里叶变换,其余弦含量最小,有利于后续分析计算,故在[-T/2, T/2]内uCD(t)的分段表达式可写为
式中,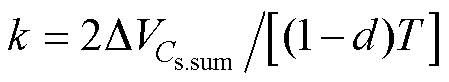 ,d为波形占空比,随开关频率变化而变化。
,d为波形占空比,随开关频率变化而变化。
设uCD(t)优化后为uCD.opti(t),其傅里叶变换后的基波表达式为
其中,l=T/2。令
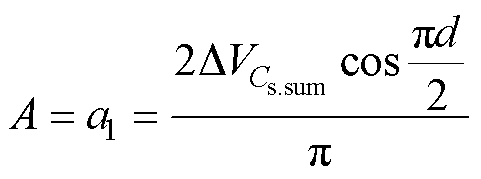
则uCD.opti(t)的基波uCD.b.opti(t)为
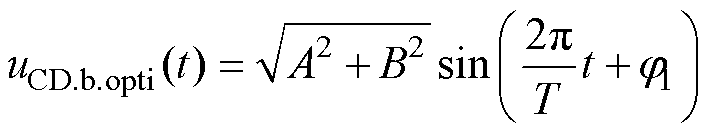 (19)
(19)
式中, 。则uCD.b.opti(t)的有效值uCD.b.opti.rms为
。则uCD.b.opti(t)的有效值uCD.b.opti.rms为
1.4.2 欠谐振时变压器二次电流is的优化
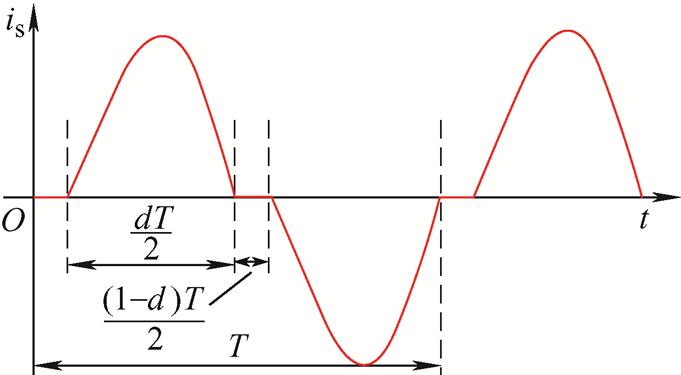
变换器欠谐振状态时,is(t)在dT时间段内近似为正弦函数,在(1-d)T时间段内为零,具体可用图7所示的波形曲线表示。
设变压器二次电流is(t)在dT / 2时间段内为
式中,Is.rms为is(t)的有效值。
负载RL的平均电流Io可由变压器二次电流is(t)经变换器输出侧H桥整流后得到,ip-im=0时及死区时间内is(t)近似为零,考虑到计算平均值应包含is(t)为零的时间段,其平均值应为
式中,Ts=dT。
由式(22)可以求出优化后的变压器二次电流is(t)有效值Is.opti.rms为
1.4.3 优化后的输出等效负载及电压增益M
依据欧姆定律,可知优化后输出等效负载Req.opti的表达式为
式中,d≈fs/fr。
同FHA模型的等效负载相比,优化后的等效负载包含开关频率、谐振频率、输出电压和MOSFET输出电容,能够更好地描述输出等效负载受以上因素的影响,不再呈现Req=8n2RL/p2的线性关系,故式(7)所示的电压增益表达式可改写为
2 基于CLLLC谐振变换器优化FHA模型的参数设计
基于变换器电压增益表达式(25),可更加准确地计算变换器最大最小增益值所需工作频率。为绘制不同情况下增益M的图像,现将电路参数作归一化处理。
设fn为开关频率fs的标幺值,fn=fs/fr,则fr为
设谐振频率的品质因数Q及其他参数分别为
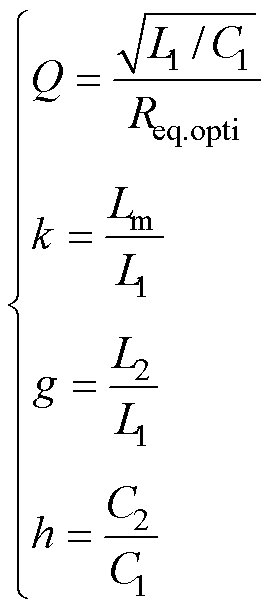 (27)
(27)
进一步将式(25)改写为
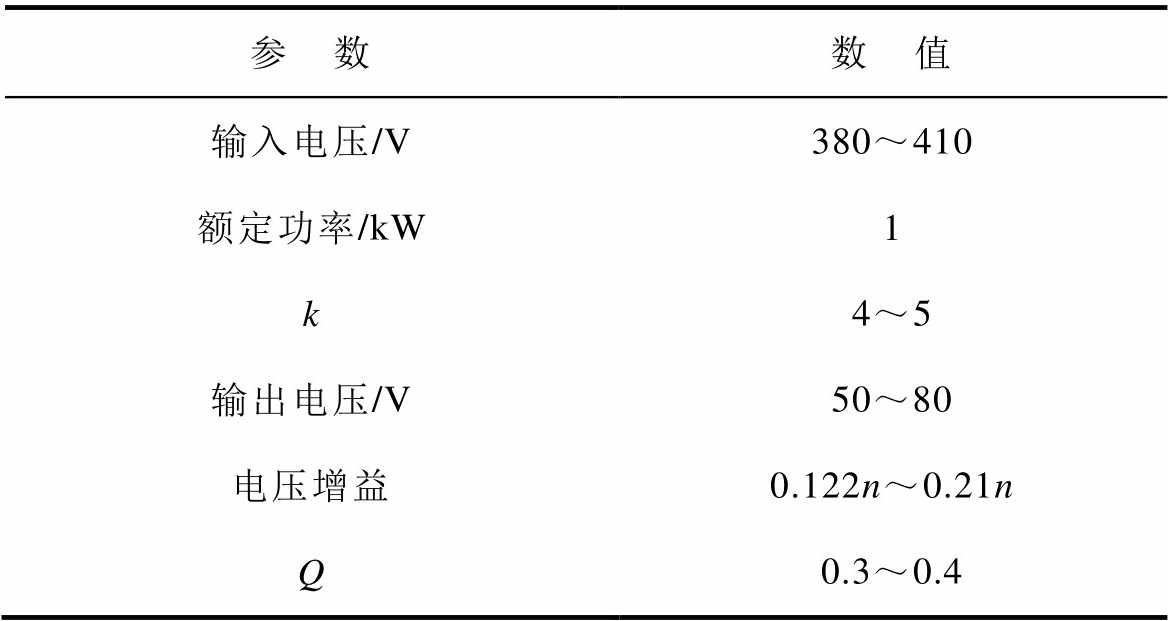
给定变换器主电路性能指标,具体见表1。一般情况下,依据指标设计CLLLC谐振变换器参数时,应基于变换器最大最小增益确定变换器电压比n,此处电压比选取为8。
表1 变换器主电路性能指标
Tab.1 Performance index of converter main circuit
参 数数 值 输入电压/V380~410 额定功率/kW1 k4~5 输出电压/V50~80 电压增益0.122n~0.21n Q0.3~0.4
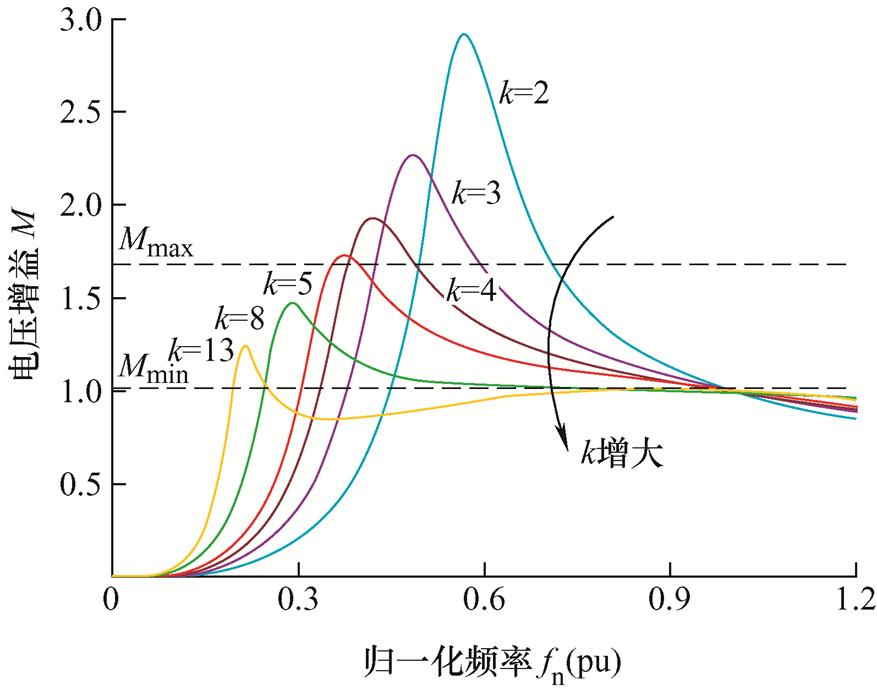
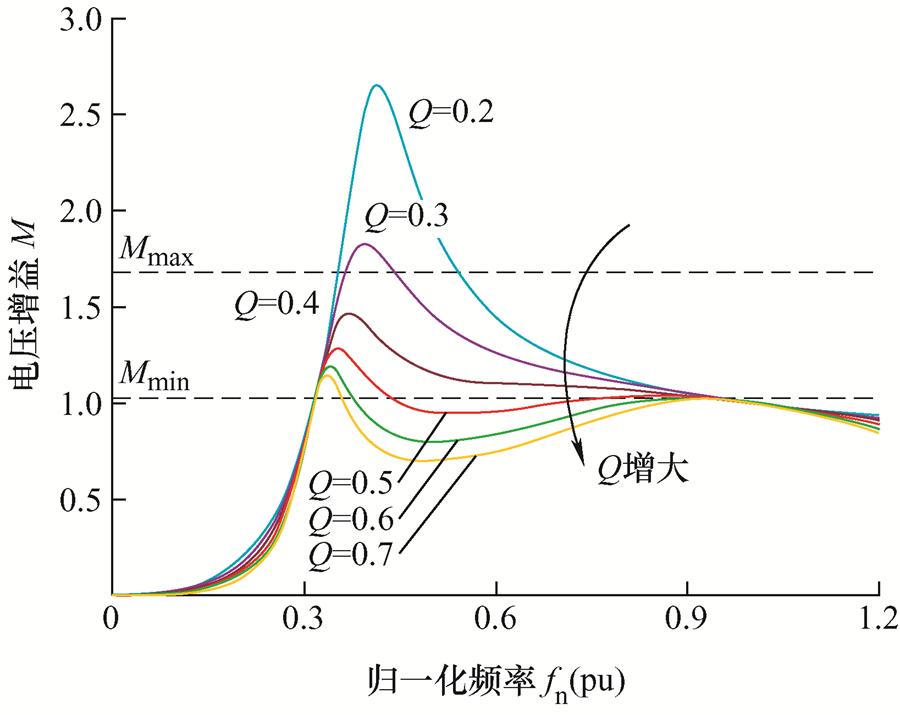
根据式(28)分别绘制Q=0.3时不同k值下的电压增益曲线,以及k=4.5时不同Q值下的电压增益曲线,分别如图8、图9所示。
由电感电流公式可知,励磁电感与电流大小成反比,因此增大励磁电感可以减小环流电流,减小一次侧开关管导通损耗,提高功率变送效率。但另一方面,若励磁电感设计较大,不易保证变换器输入侧H桥开关管在所有电压与负载条件下实现软开关。考虑k、Q参数对电压增益的影响,可通过观察其增益曲线选取合适参数值。选取的参数值既要满足最大和最小增益,又要保持谐振点附近增益的单调性。若k和Q取值过大,不易保证谐振点附近变换器增益的单调性,且增益范围可能不足,使变换器输入侧工作在容性区域,不能确保输入侧H桥开关管软开关的实现。若k和Q取值过小,虽然能保证变换器工作在非容性区域并拥有足够的增益范围,但增益曲线较陡,频率变化相同时,输出电压变化值较大,输出电压不易控制。
综合电压比、励磁电感、k和Q的影响,设计的谐振变换器电路参数见表2。
表2 CLLLC谐振变换器电路参数
Tab.2 Parameters of CLLLC resonant converter
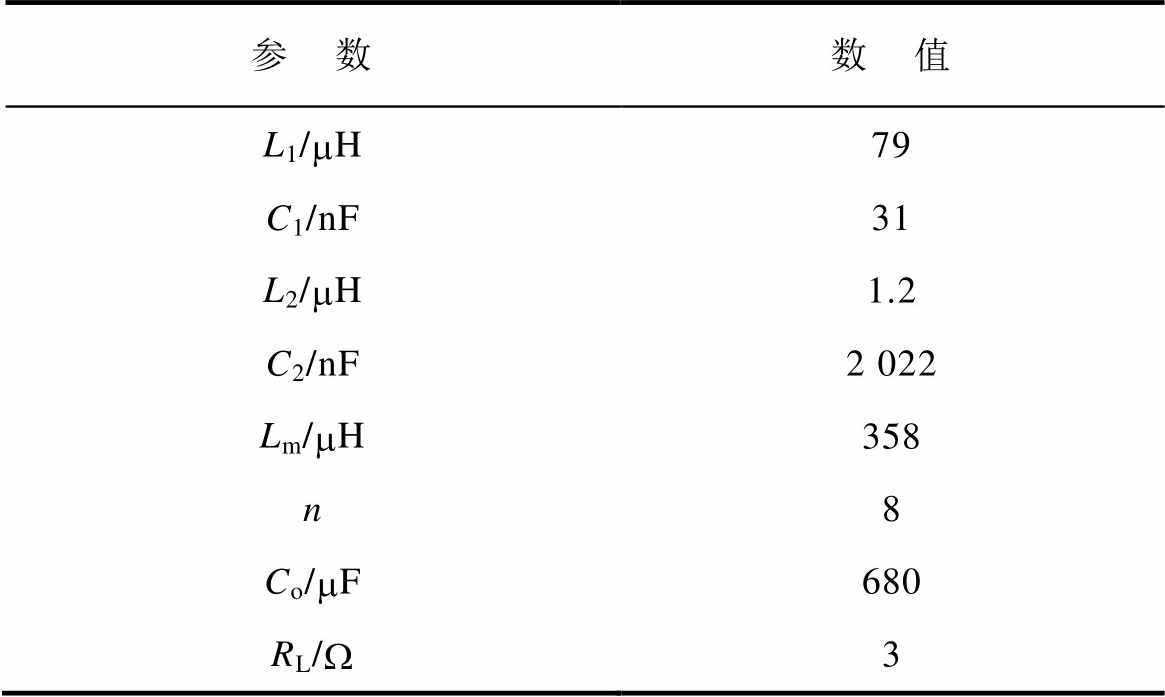
参 数数 值 L1/mH79 C1/nF31 L2/mH1.2 C2/nF2 022 Lm/mH358 n8 Co/mF680 RL/W3
3 仿真与实验
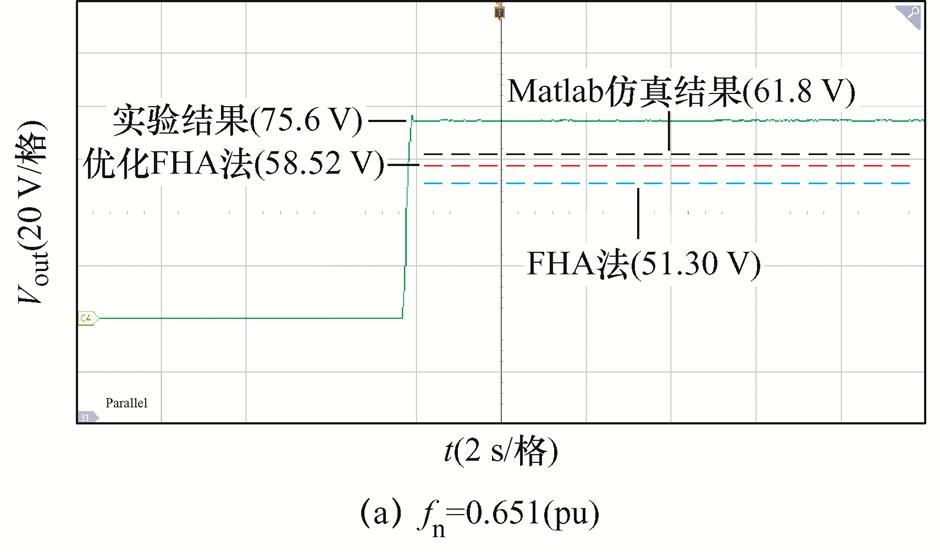
设定归一化频率fn分别为0.651(pu)、0.749(pu)、0.847(pu)与0.952(pu),参照表1主要指标与表2主要参数,利用仿真与实验,对优化FHA法的准确性进行验证。
CLLLC实验样机如图10所示,根据表2参数搭建了一台1 kW实验样机,该系统由CLLLC谐振变换器、直流负载及调试设备组成。
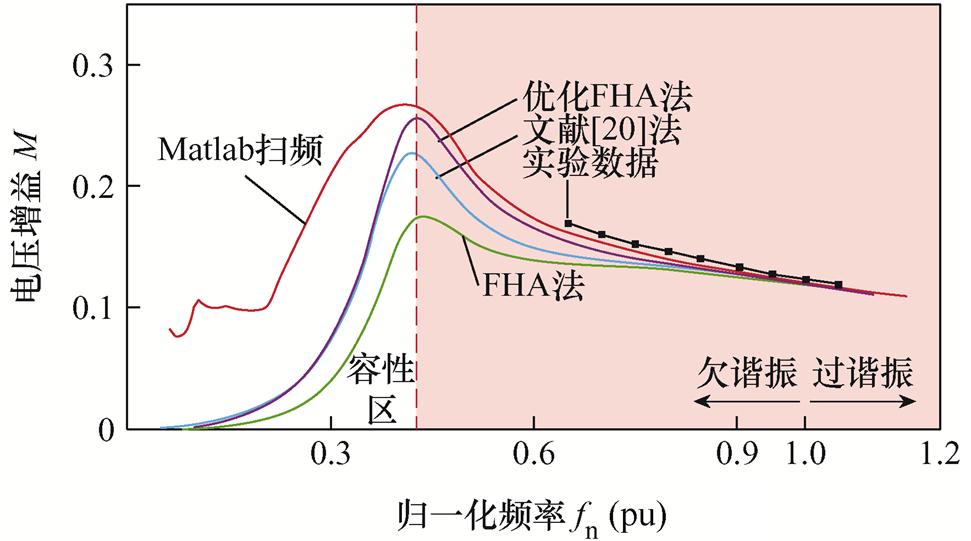
将Matlab扫频、FHA法、文献[20]所述方法、优化FHA法与实验数据绘制在一起进行比较,具体如图11所示。图中,CLLLC谐振变换器工作于容性区域时,谐振腔输入电流ip的相位超前桥臂中点电压uAB的相位,变换器输入侧H桥不能实现零电压软开关(Zero Voltage Switching, ZVS),会增加其导通损耗,为此不对其所处容性区域电压增益进行分析。在其他区域,优化的FHA法比传统的FHA法更接近扫频曲线与实验数据曲线。
优化后的增益曲线与扫频曲线没能完全拟合,两者之间有一定的误差,这主要是因为文中对FHA法进行优化时舍弃了高次谐波分量,并且所求等效输出负载与实际值之间存在差异。此外,欠谐振区域在不同频率下,DVCs.sum的积分时间段也不相同,但图中优化FHA法的曲线以相同积分时间段绘制,这也会产生一点误差。
图12给出了CLLLC谐振变换器FHA法、优化FHA法与Matlab电路仿真、实验在上述fn下的输出电压值。由图可知,变换器工作频率偏离谐振频率值越大,两种FHA方法的计算值与电路仿真模型输出值、实验值相差也越大。相较于传统FHA法,优化FHA法计算值与变换器电路仿真模型输出值、实验值更接近。
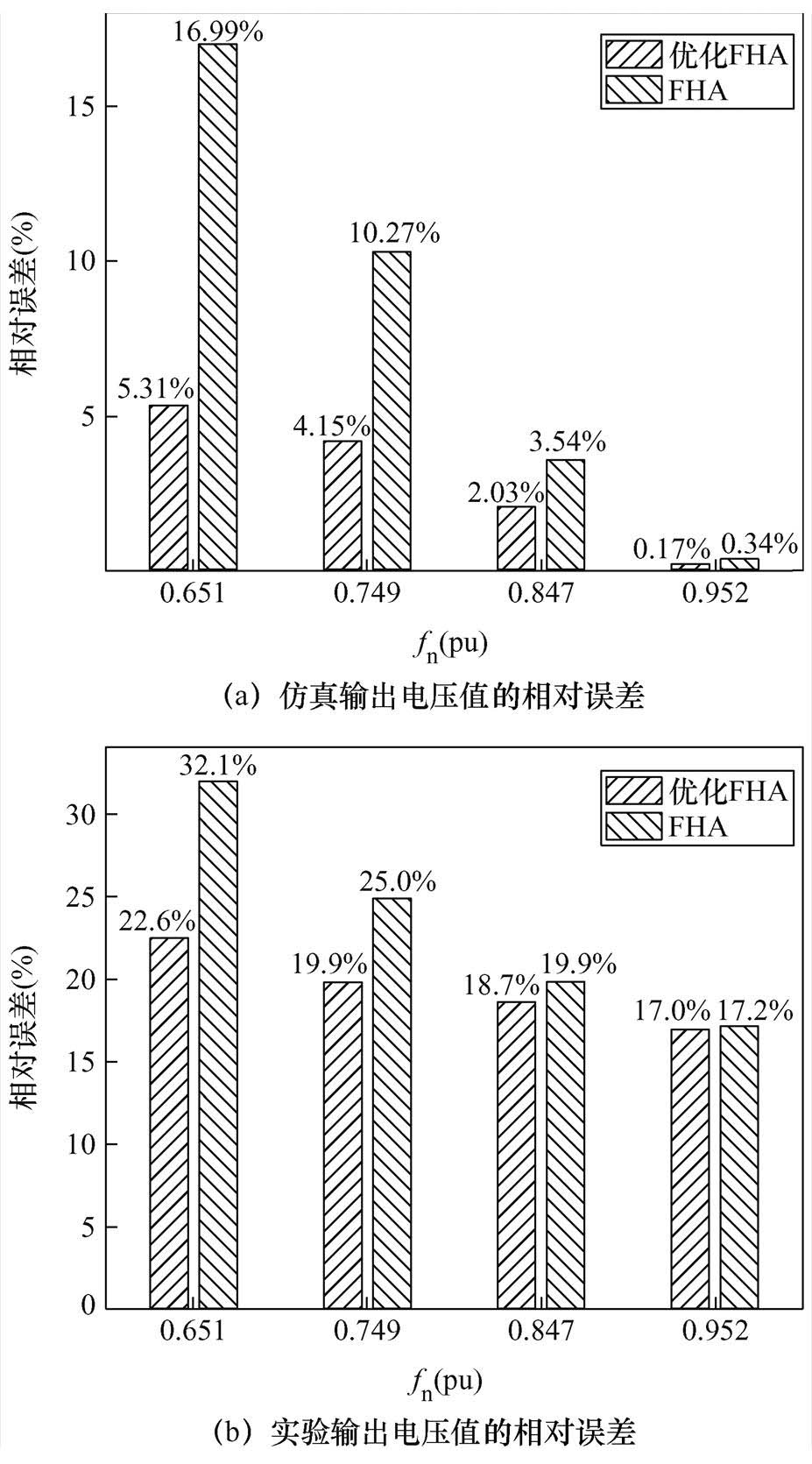
传统FHA法与优化FHA法的相对误差如图13所示。其中,图13a为二者在仿真输出电压值下的相对误差,图13b为二者在实验输出电压值下的相对误差。
图13a中,欠谐振工况下传统FHA法的最大误差是优化FHA法的3.2倍。图13b中,欠谐振工况下传统FHA法最大误差是优化FHA法的1.42倍,且变换器工作频率较谐振频率越小,优化FHA法准确度越高。与图12中的仿真、实验结果规律一致。
综上所述,可见CLLLC谐振变换器优化FHA建模方法的准确性在低频工况下优势更为显著。
4 结论
本文针对CLLLC谐振变换器欠谐振工况下FHA建模法误差较大的问题,提出了变换器输出侧H桥桥臂中点电压、变压器二次电流作为状态变量与变换器增益的优化计算方法。优化后的FHA建模方法减小了状态变量稳态值求解误差,解决了欠谐振时变换器输出侧H桥桥臂中点电压模型精度相对较低的问题。最后,通过Matlab扫频、电路仿真与实验平台分别对理论分析结论进行了验证。结果证实,优化FHA所建模型较传统FHA法欠谐振工况下具有更高的精准度,且变换器工作频率较谐振点频率越小,模型优势越明显,同时也为CLLLC变换器参数设计提供了更准确的理论依据。
参考文献
[1] 朱小全, 刘康, 叶开文, 等. 基于SiC器件的隔离双向混合型LLC谐振变换器[J]. 电工技术学报, 2022, 37(16): 4143-4154.
Zhu Xiaoquan, Liu Kang, Ye Kaiwen, et al. Isolated bidirectional hybrid LLC converter based on SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4143-4154.
[2] Zhao Lie, Pei Yunqing, Wang Laili, et al. Design methodology of bidirectional resonant CLLC charger for wide voltage range based on parameter equivalent and time domain model[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12041-12064.
[3] 周国华, 王淇, 邓伦博. 宽增益高效率CLLLC变换器的变频双移相调制策略[J]. 电工技术学报, 2024, 39(8): 2511-2522.
Zhou Guohua, Wang Qi, Deng Lunbo. Variable- frequency dual-phase-shift modulation strategy for CLLLC converter with wide voltage gain and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2511-2522.
[4] 孙城皓, 孙秋野, 王睿, 等. 基于拓展型双曲正切函数的全桥LLC变换器大信号建模方法[J]. 电工技术学报, 2023, 38(1): 234-245.
Sun Chenghao, Sun Qiuye, Wang Rui, et al. Large- signal modeling method of full-bridge LLC converter based on extended hyperbolic tangent function[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 234-245.
[5] 李福, 邓红雷, 张国驹, 等. 一种中间电容谐振型级联双向DC-DC变换器[J]. 电工技术学报, 2022, 37(20): 5253-5266.
Li Fu, Deng Honglei, Zhang Guoju, et al. A cascaded bidirectional DC-DC converter with intermediate capacitor resonance[J]. Transactions of China Electro- technical Society, 2022, 37(20): 5253-5266.
[6] 廖嘉睿, 杭丽君, 但志敏, 等. 宽范围CLLLC双向同步整流数字控制方法[J]. 电工技术学报, 2022, 37(14): 3632-3642.
Liao Jiarui, Hang Lijun, Dan Zhimin, et al. Digital control method of wide-range CLLLC bidirectional synchronous rectification[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3632-3642.
[7] 王朝强, 曹太强, 郭筱瑛, 等. 三相交错并联双向DC-DC变换器动态休眠控制策略[J]. 电工技术学报, 2020, 35(15): 3214-3223.
Wang Chaoqiang, Cao Taiqiang, Guo Xiaoying, et al. Dynamic dormancy control strategy of three-phase staggered parallel bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3214-3223.
[8] 李俊杰, 吴红飞, 花文敏, 等. CLLC双向谐振变换器电感-变压器矩阵式一体化集成与优化设计[J]. 中国电机工程学报, 2022, 42(10): 3720-3729.
Li Junjie, Wu Hongfei, Hua Wenmin, et al. Matrix inductor-transformer integration and optimization design for CLLC bidirectional resonant converter[J]. Proceedings of the CSEE, 2022, 42(10): 3720-3729.
[9] 李小强, 马永超, 黄金伟, 等. 基于双脉宽调制的交错Boost集成型CLLLC谐振变换器宽增益控制策略[J]. 电工技术学报, 2022, 37(20): 5313-5323.
Li Xiaoqiang, Ma Yongchao, Huang Jinwei, et al. Wide-gain-range control scheme for interleaved boost integrated CLLLC resonant converter based on dual pulse width modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5313-5323.
[10] Zou Shenli, Lu Jiangheng, Mallik A, et al. Bi-directional CLLC converter with synchronous rectification for plug-in electric vehicles[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 998-1005.
[11] Blake C, Bull C. IGBT or MOSFET: choose wisely[J]. International Rectifier, 2015, 19(2): 286-287.
[12] 俞珊, 徐志望, 董纪清. 寄生电容对LLC谐振变换器的影响分析[J]. 电源学报, 2018, 16(2): 124-130.
Yu Shan, Xu Zhiwang, Dong Jiqing. Analysis of impact of stray capacitance on LLC resonant converter[J]. Journal of Power Supply, 2018, 16(2): 124-130.
[13] 陈启超, 纪延超, 王建赜, 等. MOSFET输出电容对CLLLC谐振变换器特性影响分析[J]. 电工技术学报, 2015, 30(17): 26-35.
Chen Qichao, Ji Yanchao, Wang Jianze, et al. Analysis of the influence of MOSFET output capacitance on the bidirectional CLLLC resonant converter[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 26-35.
[14] 赵烈, 裴云庆, 刘鑫浩, 等. 基于基波分析法的车载充电机CLLC谐振变换器参数设计方法[J]. 中国电机工程学报, 2020, 40(15): 4965-4977.
Zhao Lie, Pei Yunqing, Liu Xinhao, et al. Design methodology of CLLC resonant converters for electric vehicle battery chargers[J]. Proceedings of the CSEE, 2020, 40(15): 4965-4977.
[15] 许景慧, 王跃, 李凯. CLLLC谐振型直流变换器参数设计研究[J]. 电气传动, 2021, 51(14): 13-17, 22.
Xu Jinghui, Wang Yue, Li Kai. Research on parameter design of CLLLC resonant DC converter[J]. Electric Drive, 2021, 51(14): 13-17, 22.
[16] 孙欣楠, 陈敏, 李博栋, 等. 基于电感比分析的CLLC谐振变换器效率优化[J]. 中国电机工程学报, 2021, 41(8): 2825-2834.
Sun Xinnan, Chen Min, Li Bodong, et al. Efficiency optimization of CLLC resonant converter based on analysis of the ratio of inductances[J]. Proceedings of the CSEE, 2021, 41(8): 2825-2834.
[17] Sankar A, Mallik A, Khaligh A. Extended harmonics based phase tracking for synchronous rectification in CLLC converters[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6592-6603.
[18] 王菲菲, 张方禹, 戴慧纯, 等. 基于时域分析的CLLC双向谐振变换器优化设计[J]. 电力电子技术, 2019, 53(6): 80-82.
Wang Feifei, Zhang Fangyu, Dai Huichun, et al. Optimal design of CLLC bi-directional resonant converter based on time domain analysis[J]. Power Electronics, 2019, 53(6): 80-82.
[19] 赵子先, 康龙云, 于玮, 等. 基于简化时域模型的CLLC直流变换器参数设计[J]. 电工技术学报, 2022, 37(5): 1262-1274.
Zhao Zixian, Kang Longyun, Yu Wei, et al. Parameter design method of CLLC DC-DC converter based on simplified time domain model[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1262- 1274.
[20] 詹昕明, 何震, 杭丽君, 等. CLLLC谐振电路模型改进方法研究[J]. 中国电机工程学报, 2023, 43(13): 5105-5116.
Zhan Xinming, He Zhen, Hang Lijun, et al. Research on improvement method of CLLLC resonant circuit model[J]. Proceedings of the CSEE, 2023, 43(13): 5105-5116.
Optimization of CLLLC Resonant Converter Modeling by MOSFET Output Capacitance
Zhang Xinwen1 Liu Wenze1 Yang Shude2 Liu Bailin1
(1. School of Electrical and Information Engineering North Minzu University Yinchuan 750021 China 2. College of Electrical Energy and Power Engineering Yangzhou University Yangzhou 225127 China)
Abstract The fundamental harmonic approximation (FHA) modeling method is commonly used to analyze CLLLC resonant converters because of its simple operation and high accuracy. The FHA method uses the fundamental wave component of the input and output voltage of the resonator, so the circuit topology analysis of the CLLLC resonant converter is transformed into the analysis of the sinusoidal steady-state circuit. The voltage gain model of the CLLLC resonant converter established by the FHA modeling method can be used to analyze the characteristics or design the parameters of the CLLLC resonant converter.
However, in the traditional FHA modeling method, the influence of MOSFET output capacitance on the midpoint voltage of the H-bridge arm on the output side is not considered when the secondary current of the transformer is zero and MOSFET is at dead time. When the switching frequency is lower than the resonance frequency (under-resonance condition), the accuracy of the midpoint voltage model of the H-bridge arm needs to be further improved.
The reason that the model accuracy of the traditional FHA modeling method is lower with the decrease of switching frequency is analyzed when the CLLLC resonant converter operates under the under-resonance condition. Two operating states of the CLLLC resonant converter are provided: the current in the secondary winding of the transformer is zero, and the MOSFET is at dead time. The transient equations of the two operating states are established using the time-domain analysis method. The voltage expression of the MOSFET output capacitance is derived by solving the transient equations, and the voltage at the middle point of the H-bridge on the output side of the CLLLC resonant converter is expressed as a complete function. Furthermore, a more precise method for calculating the RMS current on the secondary side of the transformer is given, and a more accurate formula for calculating the output equivalent load is obtained.
The optimized calculation formula of the voltage at the midpoint of the H-bridge arm on the output side of the CLLLC resonant converter and the output equivalent load contains the variables of switching frequency, resonant frequency, output voltage, and MOSFET output capacitance. The obtained voltage gain model can describe the actual gain of the converter more accurately. Therefore, the accuracy of the FHA model can be improved when the CLLLC resonant converter is in under-resonant conditions. Based on the optimized voltage gain model, an accurate parameter design method is presented to provide theoretical support for the parameter design of the CLLLC resonant converter.
Finally, the circuit simulation model and an experimental system of the CLLLC resonant converter are set up with an input voltage of 380 V and power of 1 kW. By comparing the relative errors of output voltage, the accuracy of the proposed optimization method is verified. The results show that: (1) Under simulation conditions, the maximum relative error of the traditional FHA method is 3.2 times the optimized FHA method. (2) Under experimental conditions, the maximum relative error of the traditional FHA method is 1.42 times the optimized FHA method.
Keywords:MOSFET output capacitance, CLLLC resonant converter, fundamental harmonic approximation model, time domain analysis
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231891
宁夏自然科学基金项目(2023AAC03281)和国家自然科学基金项目(52367018)资助。
收稿日期 2023-11-13
改稿日期 2023-11-30
作者简介
张新闻 男,1976年生,博士,教授,研究方向为电能质量与电能变换技术等。
E-mail: cindazm@126.com(通信作者)
刘文泽 男,2000年生,硕士研究生,研究方向为双向直流变换器拓扑及其控制技术等。
E-mail: liu17806267263@163.com
(编辑 陈 诚)
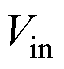 逆变成高频交流电;Q5~Q8构成变换器输出侧H桥,其作用是将谐振腔输出的高频交流电变换成直流输出电压
逆变成高频交流电;Q5~Q8构成变换器输出侧H桥,其作用是将谐振腔输出的高频交流电变换成直流输出电压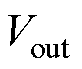 ,再经过滤波电容Co供给负载RL;Cs.1~Cs.8为MOSFET管Q1~Q8的输出电容;变压器一次侧电感L1、电容C1构成一次侧谐振腔,二次侧电感L2、电容C2构成二次侧谐振腔,Lm为变压器励磁电感;A、B、C、D四点分别为变换器输入侧与输出侧H桥桥臂中点。为方便后续分析,设uAB为变压器一次侧谐振腔输入电压,uCD为二次侧谐振腔输出电压,ip为变压器一次侧谐振腔电流,is为变压器二次侧谐振腔电流,n为变压器电压比。
,再经过滤波电容Co供给负载RL;Cs.1~Cs.8为MOSFET管Q1~Q8的输出电容;变压器一次侧电感L1、电容C1构成一次侧谐振腔,二次侧电感L2、电容C2构成二次侧谐振腔,Lm为变压器励磁电感;A、B、C、D四点分别为变换器输入侧与输出侧H桥桥臂中点。为方便后续分析,设uAB为变压器一次侧谐振腔输入电压,uCD为二次侧谐振腔输出电压,ip为变压器一次侧谐振腔电流,is为变压器二次侧谐振腔电流,n为变压器电压比。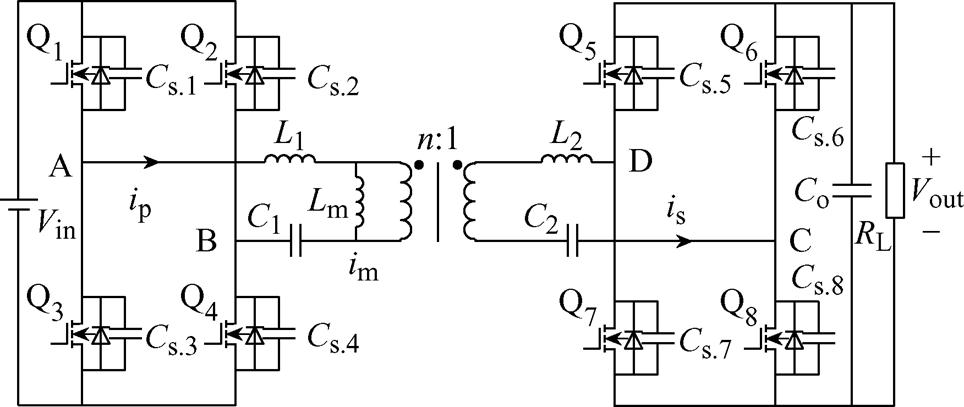
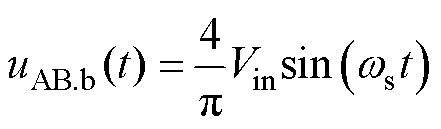 (1)
(1)
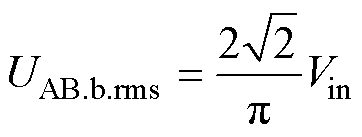 (2)
(2)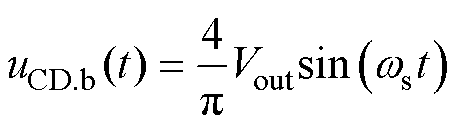 (3)
(3)
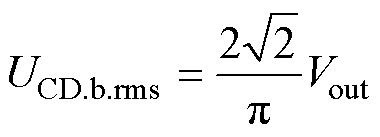 (4)
(4)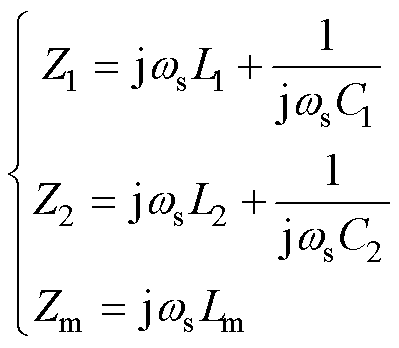 (5)
(5)
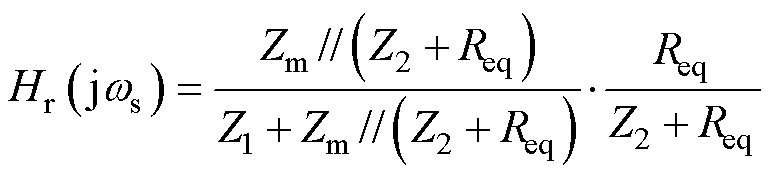 (6)
(6)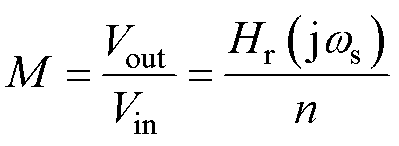 (7)
(7)
 C
C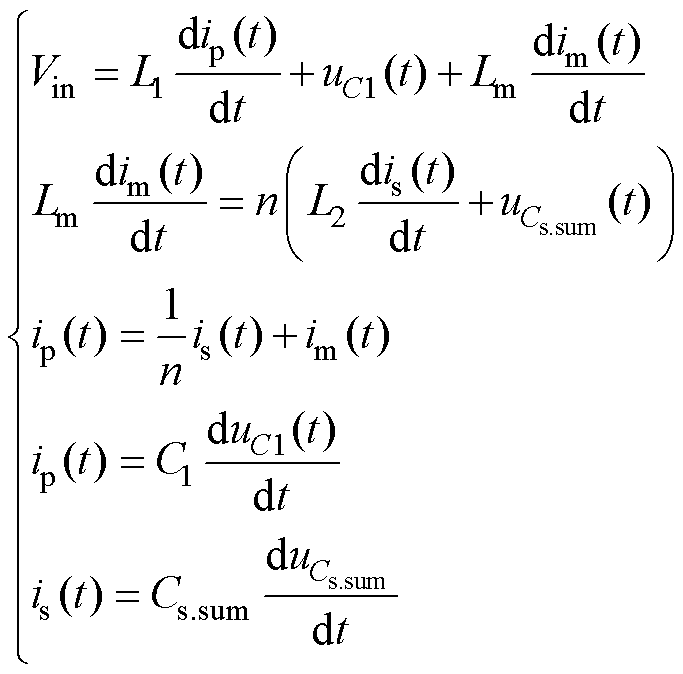 (8)
(8)
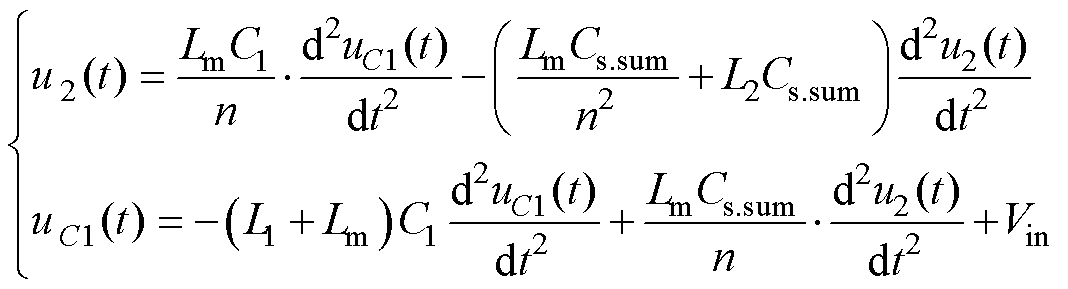 (9)
(9)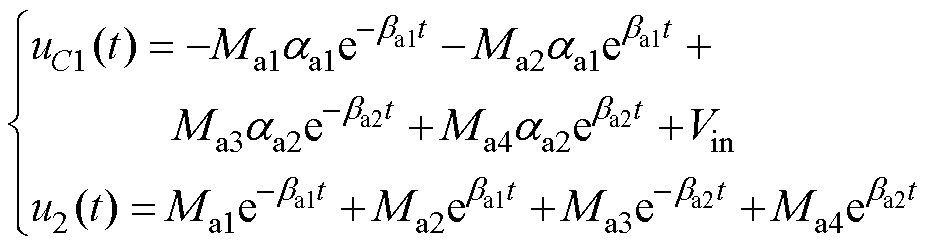 (10)
(10)
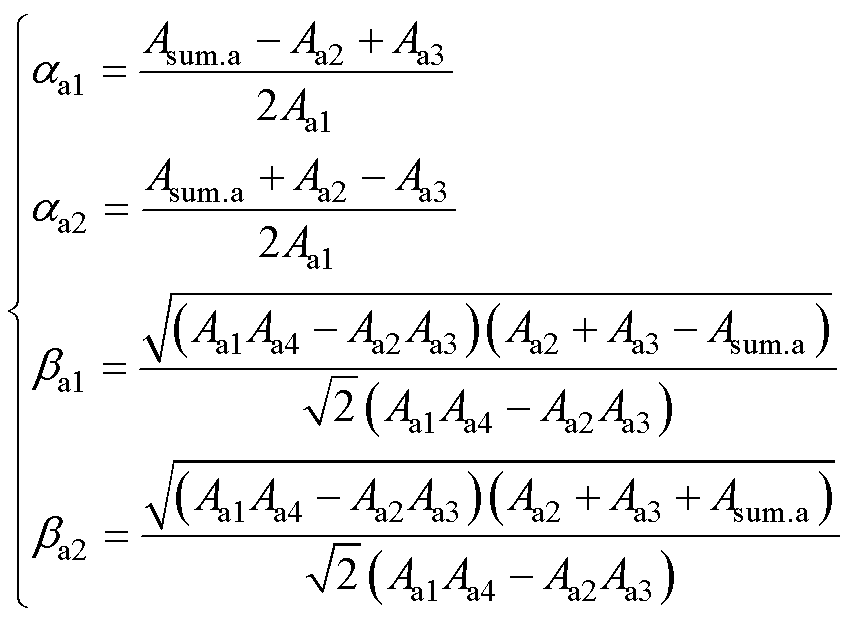
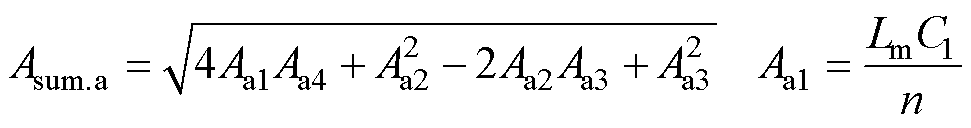
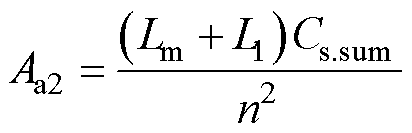
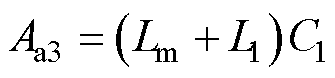
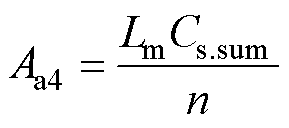
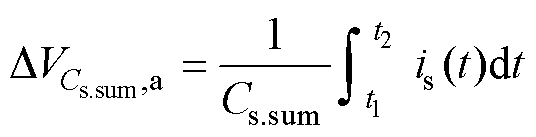 (11)
(11)

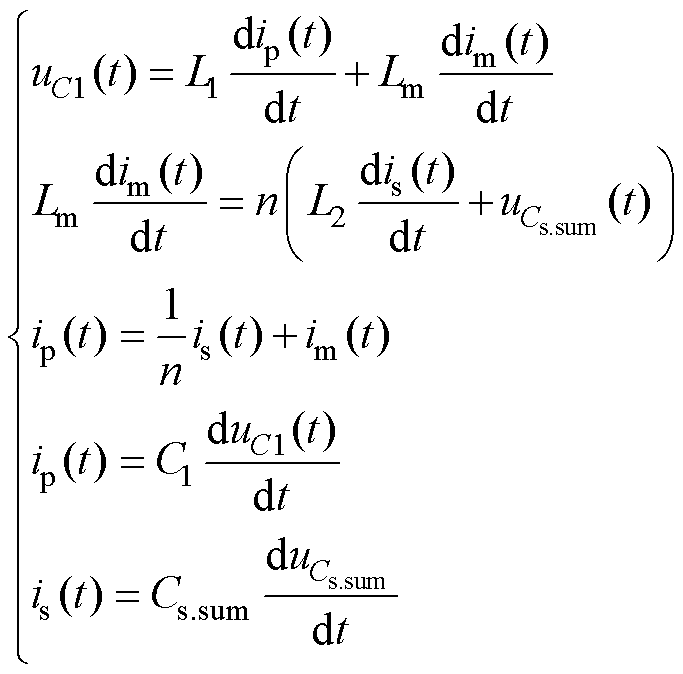 (12)
(12)
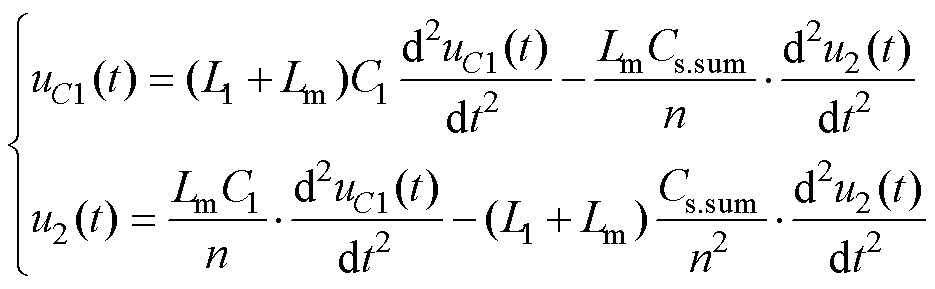 (13)
(13)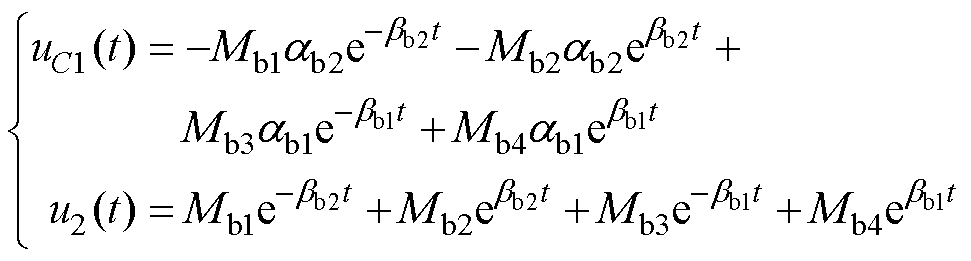 (14)
(14)
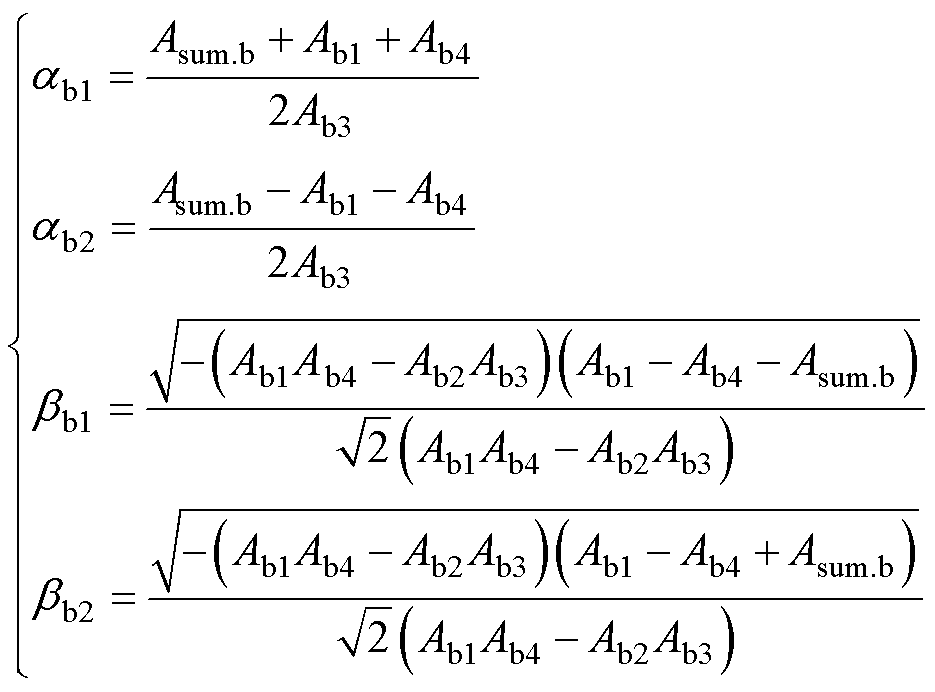
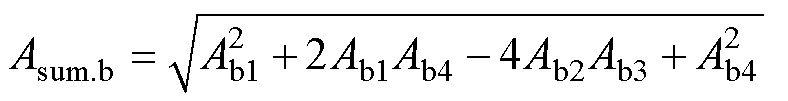
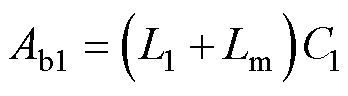
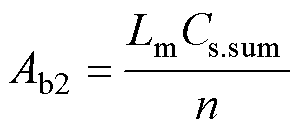
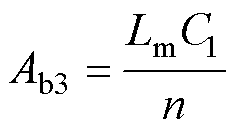
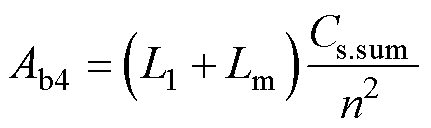
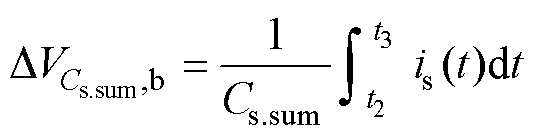 (15)
(15)
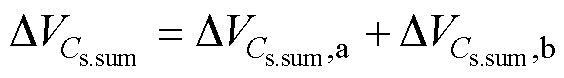 (16)
(16)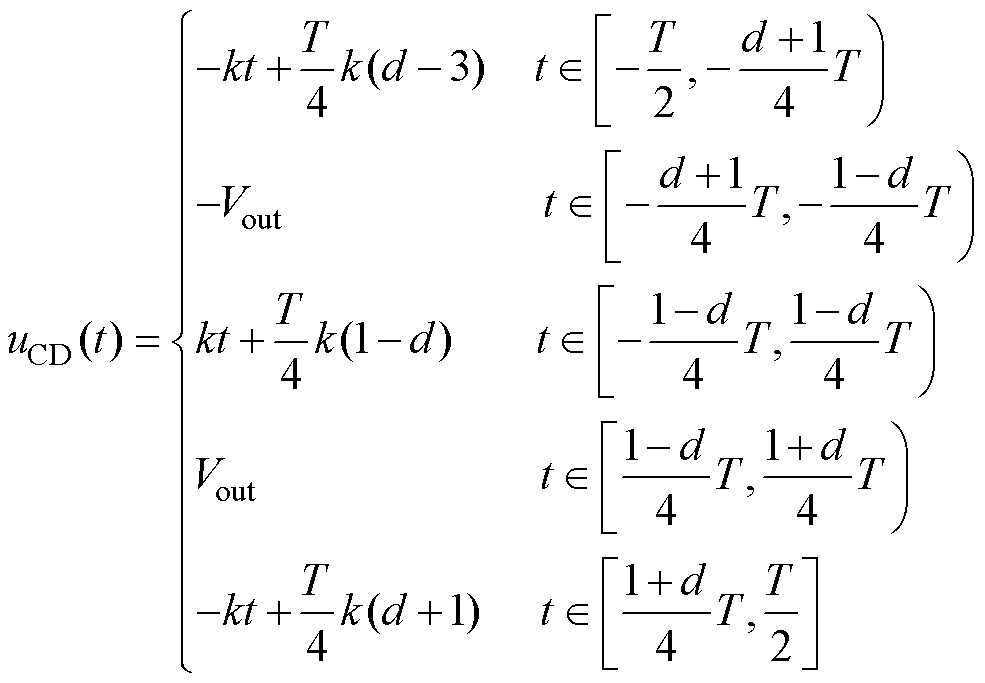 (17)
(17)
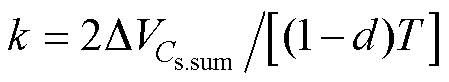 ,d为波形占空比,随开关频率变化而变化。
,d为波形占空比,随开关频率变化而变化。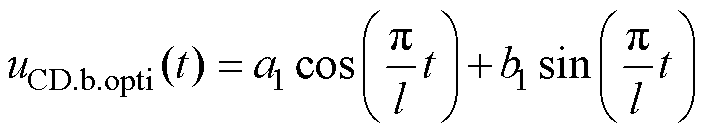 (18)
(18)
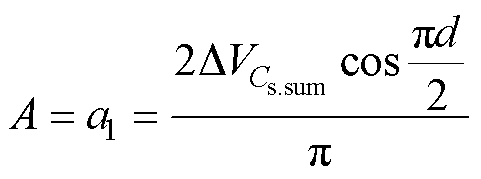
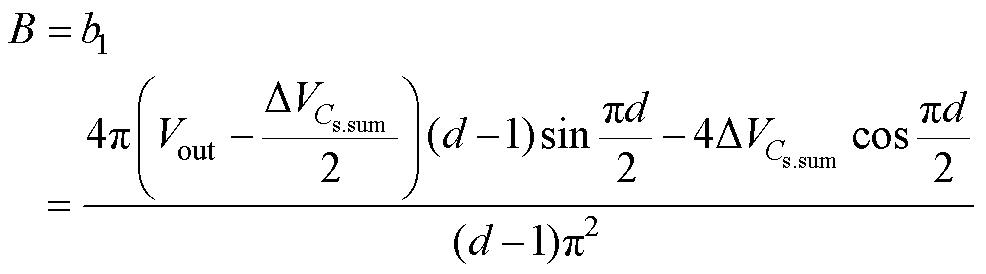
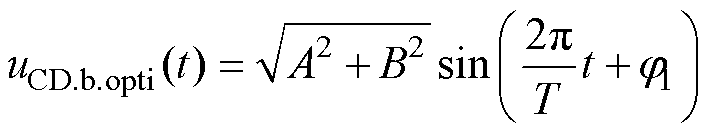 (19)
(19) 。则u
。则u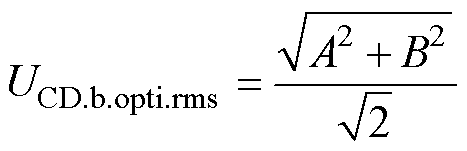 (20)
(20)
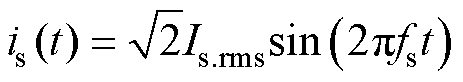 (21)
(21)
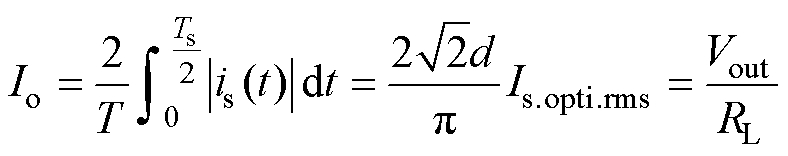 (22)
(22)
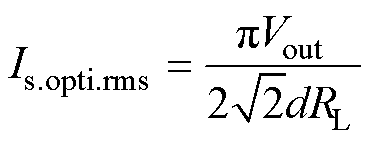 (23)
(23)
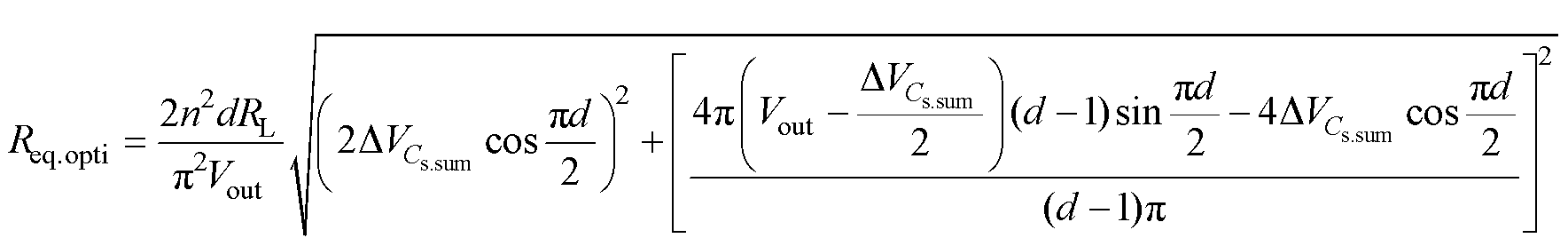 (24)
(24)
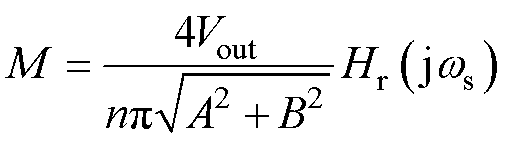 (25)
(25)
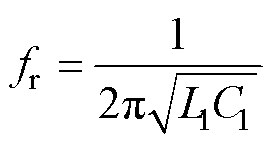 (26)
(26)
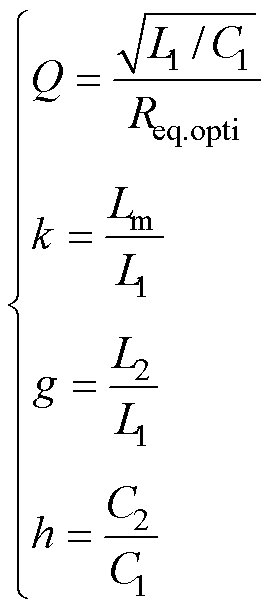 (27)
(27)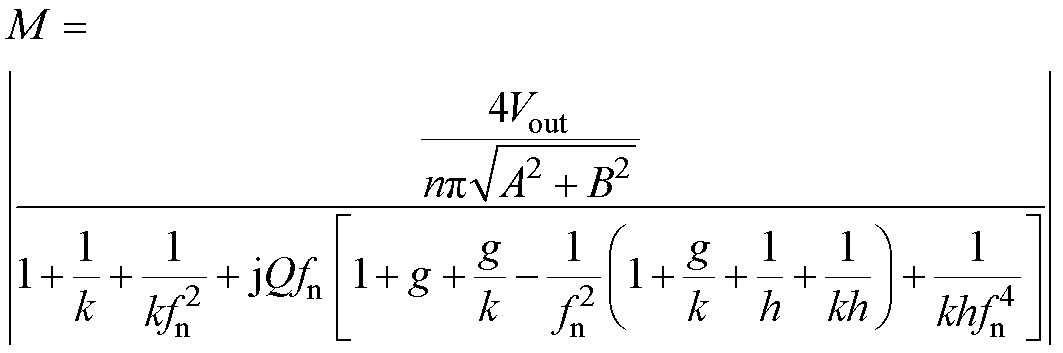 (28)
(28)