图1 GFL并网系统的控制结构
Fig.1 The control structure of the GFL grid-connected system
摘要 直流电压时间尺度与交流电流时间尺度控制耦合可能会导致跟网型变换器阻尼下降,引发相应的同步失稳问题。为此,该文计及多环控制的多时间尺度特性,建立跟网型变换器的小信号同步模型,揭示各时间尺度控制的耦合路径与阻尼分布规律;采用灵敏度分析法,量化控制参数对阻尼特性的影响,筛选出引发系统同步失稳的主导因子;同时,考虑多场景电网工况对控制耦合的影响,从阻尼的角度直观地分析不同工况下系统失稳的机理。针对直流电压时间尺度内部dq耦合及多时间尺度控制耦合对系统阻尼的影响,提出一种基于端电压前馈的阻尼重塑改进控制策略,削弱控制耦合带来的负阻尼效应,增强变换器的同步稳定性。仿真与实验验证了理论分析的正确性和改进控制方案的有效性。
关键词:多时间尺度控制 阻尼特性 同步振荡 灵敏度分析 阻尼重塑
随着新型电力系统建设,以跟网型(Grid Following, GFL)变换器为代表的电力电子装置大规模接入电力系统导致同步振荡频发问题[1-2],严重威胁电力系统安全稳定运行[3-4]。
相较于传统同步电源,GFL变换器一般采用多环级联控制结构,其电源外特性由控制策略主导[5-7]。为简化分析,GFL变换器的稳定性研究大多基于各环路解耦的前提条件[8]。然而,文献[9]指出,实际工况中的复杂控制交互使得环路解耦难度增大,简化模型不再适用于多环控制系统的动力学特性分析,但该文献没有关注多环控制耦合产生的本质。文献[10-12]指出,由于多物理量、多控制目标的约束,多环控制的带宽在时间尺度上存在差异,具有多时间尺度(Multi Timescale, MTS)特征。然而,现有文献在研究多环控制耦合时并没有关注其MTS特性。进一步研究表明,多环控制耦合是由控制频带重叠引起的,其本质为多环控制结构在不同时间尺度下的交互[13-14]。因此,在研究多环控制耦合时,应该关注其MTS特征,重点研究多环控制结构在时间尺度上的差异与联系,从MTS的角度研究多环控制耦合引发系统同步振荡的机理。
根据频带分布不同,MTS控制可以划分为直流电压控制(DC-link Voltage Control, DVC)时间尺度和交流电流控制(Alternating Current Control, ACC)时间尺度[15-16]。其中,DVC时间尺度包含DVC环与端电压控制(Terminal Voltage Control, TVC)环,ACC时间尺度动态主要受电流控制(Current Control, CC)环影响[17]。文献[18-19]计及ACC时间尺度动态,分析ACC与锁相环(Phase Locked Loop, PLL)交互耦合以及参数失配引入负阻尼对系统同步稳定性的影响。文献[20]分析了DVC时间尺度内部dq耦合对变换器同步稳定性的影响,并给出相应解耦控制策略。文献[21-22]考虑DVC环与TVC环的影响,分析得出了DVC时间尺度下影响变换器同步稳定性的关键因素及对应变化规律。然而,上述文献多集中于某一时间尺度展开稳定性研究,忽略了不同时间尺度之间控制耦合的影响。文献[23]指出,PLL不同于其他控制环,具有明显的跨时间尺度特性;进一步研究表明,PLL与DVC、ACC时间尺度存在频带重叠现象,在MTS控制耦合中起到桥梁的作用[24]。“双高”电网下,电网阻抗显著增大,导致PLL作为耦合桥梁的作用进一步增强,使得面向“双高”电网工况的GFL变换器稳定性分析更加复杂。基于MTS解耦简化的稳定性分析模型,可能会导致分析结果存在一定误判。因此,综合考虑MTS交互耦合,建立全局精确控制模型,深入分析MTS耦合影响GFL变换器同步稳定性的内在机理,具有深刻的现实研究意义。
为此,针对现有研究存在的不足,本文计及MTS耦合动态,对GFL变换器展开小信号同步建模及稳定性分析。首先,按照不同时间尺度对GFL变换器的控制环进行划分,建立MTS控制交互模型,揭示各时间尺度控制环的耦合路径。其次,基于灵敏度分析法,量化各环路参数在系统阻尼分布中的参与规律,得出影响系统阻尼分布的主导因子。考虑多场景电网工况对MTS控制耦合的影响,从阻尼的角度直观地分析系统在不同工况下的失稳机理。进一步地,基于理论分析,针对DVC时间尺度内部dq耦合以及MTS耦合对系统阻尼的影响,提出一种基于端电压前馈的阻尼重塑改进控制策略,有效增大系统总阻尼,提升系统的同步稳定性。最后,基于所搭建实验样机,验证了理论分析的正确性和所提改进控制策略的有效性。
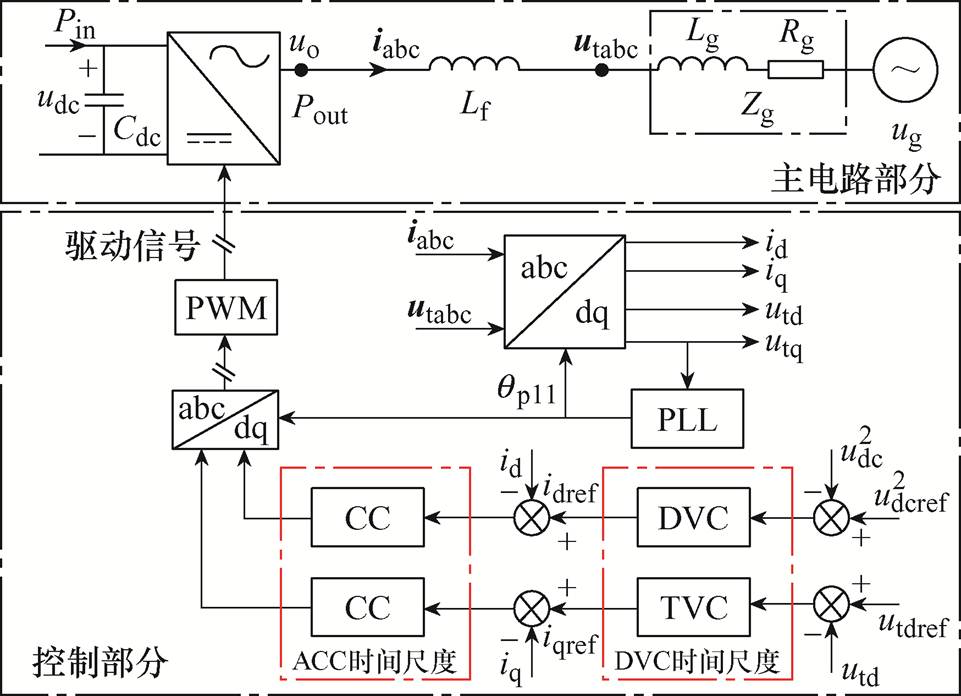
图1为计及MTS控制耦合的GFL并网系统的控制结构。图中,下标d、q和ref分别表示变量d、q分量与参考值,Lf与Zg分别为滤波器电感和并网线路阻抗,ug为电网电压,udc和ut分别为直流母线电压及电网端电压,iabc和uo分别为变流器的输出电流和输出电压。
图1表明,DVC与ACC时间尺度直接串联耦合,ACC时间尺度输出经过线路阻抗影响并网端电压动态,进而影响DVC时间尺度与PLL的输入;同时PLL输出相位qpll通过Park变换参与MTS交互过程,起到耦合桥梁的作用,从而形成了一条完整的“MTS控制闭环耦合路径”,如图2所示。

图1 GFL并网系统的控制结构
Fig.1 The control structure of the GFL grid-connected system
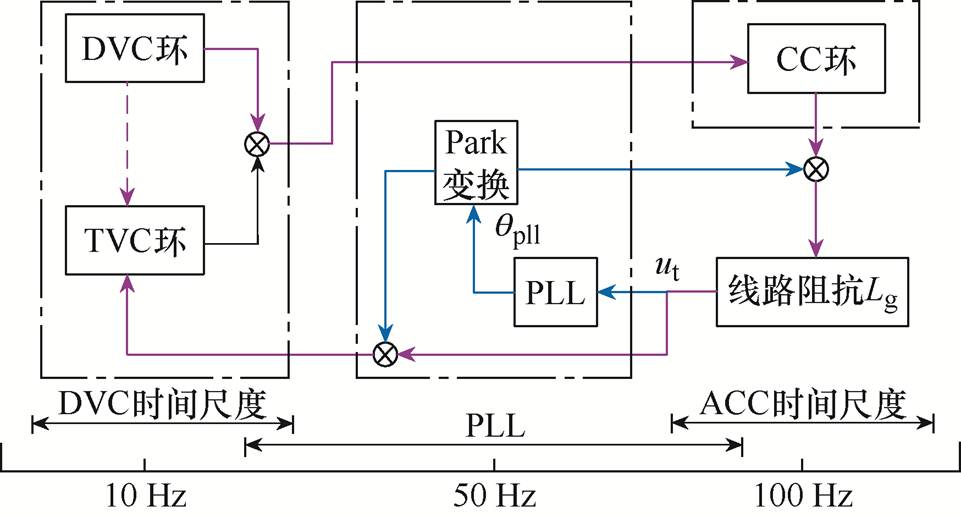
图2 MTS控制频带分布与耦合路径
Fig.2 Bandwidth and coupling paths for MTS control
MTS控制可以分为DVC时间尺度控制、ACC时间尺度控制及PLL控制,下面针对这三个模块分别进行建模。
文献[25]给出了弱电网工况下的PLL小信号模型,如图3所示。图中,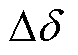 与
与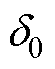 分别为PLL输出功角及其稳态值。
分别为PLL输出功角及其稳态值。
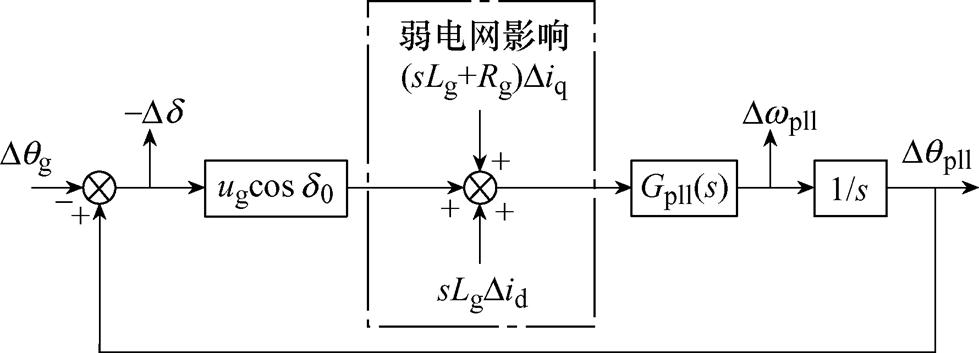
图3 弱电网工况下PLL的小信号模型
Fig.3 Small-signal model of PLL under weak-grid
结合图1与图3可知,PLL动态受到ACC时间尺度输出Did、iq以及弱电网工况的影响。进一步地,考虑ACC时间尺度动态主要受到DVC时间尺度输出与线路阻抗的影响,结合KVL,采用平衡点线性化方法进行处理,推导得出计及ACC时间尺度与PLL耦合的小信号同步模型为
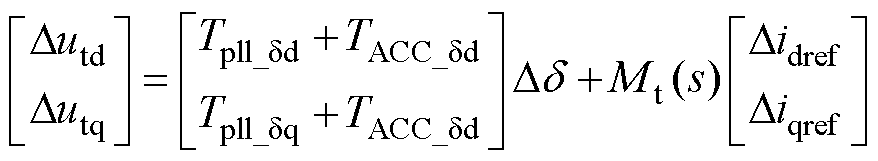 (1)
(1)
式中,Mt(s)与Tpll_dd、Tpll_dq、TACC_dd、TACC_dq的表达式在附录式(A3)、式(A4)中给出。
式(1)中并网电流参考值由DVC时间尺度输出动态主导,下面对DVC时间尺度控制环路进行建模。直流母线有功输入Pin决定DVC环路动态,根据能量守恒定律可得直流侧功率-电压传输关系为
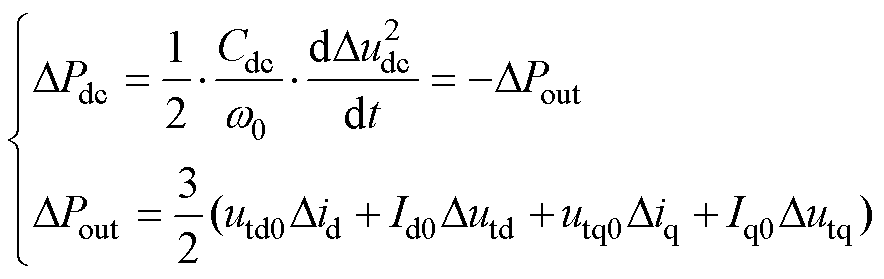 (2)
(2)
并网电流d轴参考值的小信号动态为
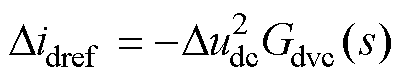 (3)
(3)
式中,Gdvc(s)为DVC环PI控制器,在附录式(A1)中给出。
结合式(2)与式(3),可得idref的小扰动表达式为
 (4)
(4)
TVC环的动态主要由电网端电压ut决定,其中,Gtvc(s)为TVC环PI控制器,表达式见附录式(A1)。
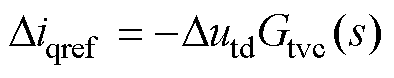 (5)
(5)
结合式(1)、式(4)与式(5),可得DVC时间尺度输出的小信号表达式为
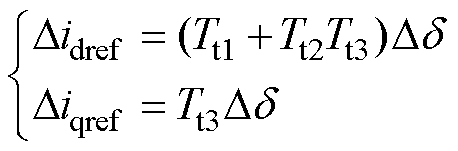 (6)
(6)
式中,Tt1、Tt2与Tt3的表达式在附录式(A5)中给出。
PLL输出相位扰动会给控制坐标系与系统坐标系带来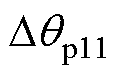 (即
(即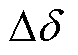 )的相位差[14],结合式(1)、式(6)与图3可得考虑坐标耦合后的小信号模型为
)的相位差[14],结合式(1)、式(6)与图3可得考虑坐标耦合后的小信号模型为
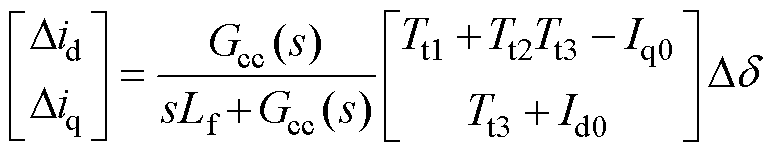 (7)
(7)
根据式(1)、式(6),可获得考虑MTS耦合的端电压输出动态表达式为
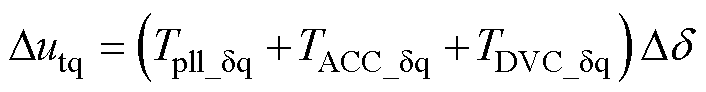 (8)
(8)
式中, 为DVC时间尺度为PLL功角输出引入的动态,其表达式在附录式(A4)中给出。
为DVC时间尺度为PLL功角输出引入的动态,其表达式在附录式(A4)中给出。
根据式(6)~式(8)分析可得计及MTS控制耦合的小信号同步模型,如图4所示。由图4a可知,DVC时间尺度内部通过PLL在dq轴的扰动形成耦合;同时,DVC与ACC以PLL为桥梁形成MTS控制耦合,多个时间尺度控制环节共同参与PLL输出功角动态,进而对系统同步稳定性产生影响。
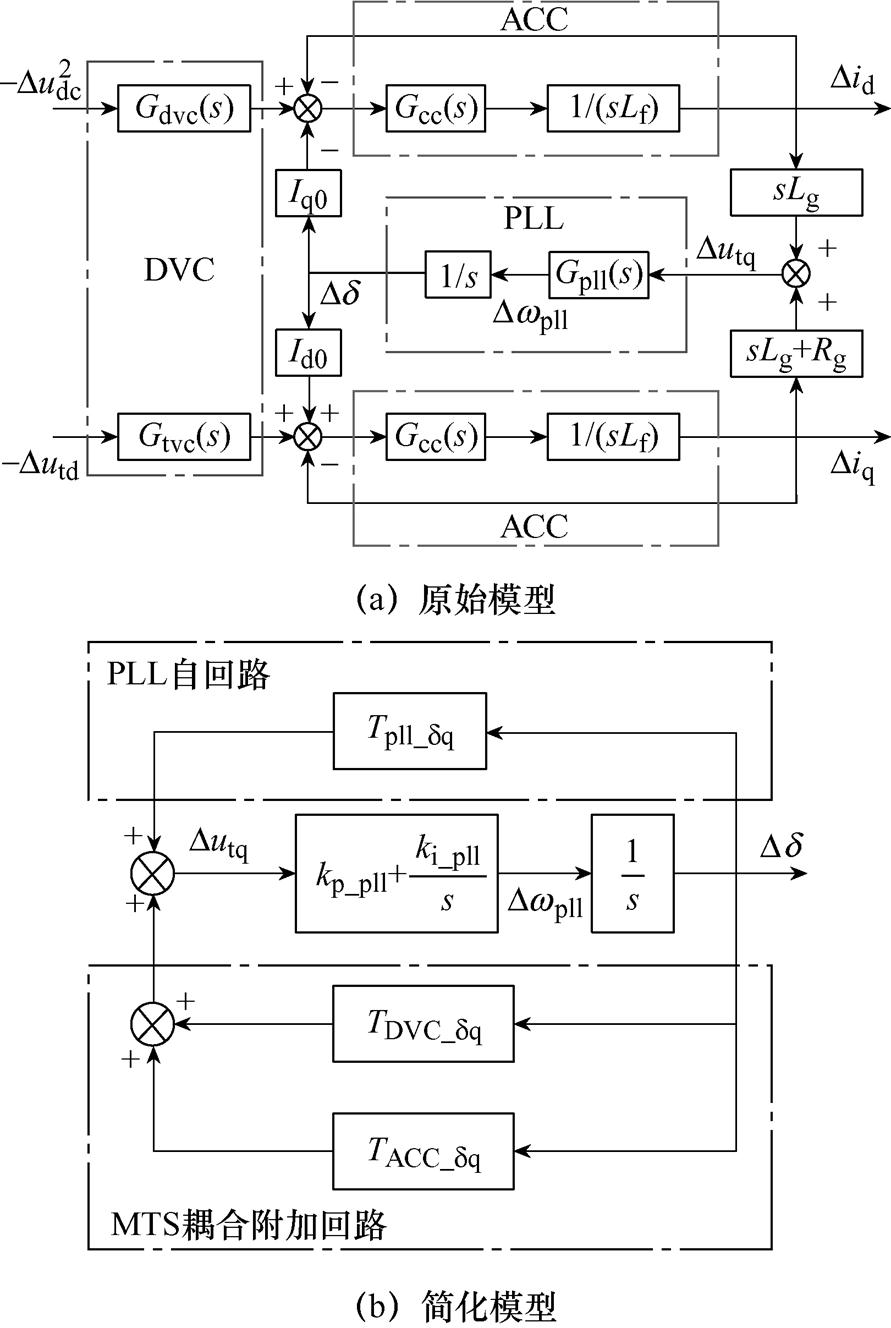
图4 MTS控制系统小信号同步模型
Fig.4 Small-signal synchronization model for MTS systems
综上所述,PLL的功角动态不仅与其自回路有关,与MTS耦合结构同样具有强相关性,而目前针对MTS耦合与系统阻尼分布关系的研究尚待展开。后文将从阻尼分布的角度,量化分析MTS耦合对系统阻尼特性的影响,为系统调参及控制优化提供理论支撑。
并网系统同步振荡常表现为振荡频率处阻尼不足,基于灵敏度分析法[26]对并网系统阻尼特性展开研究,可直观揭示各种工况与控制参数对系统阻尼特性的影响规律,具有明确物理意义。
根据图4中的小信号同步模型,结合PLL自身动态,可推导得出MTS控制系统的特征方程为
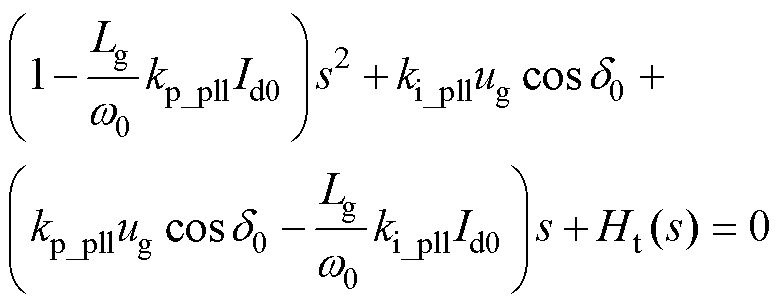 (9)
(9)
式中,Ht(s)为MTS耦合附加回路引入的函数,其表达式为
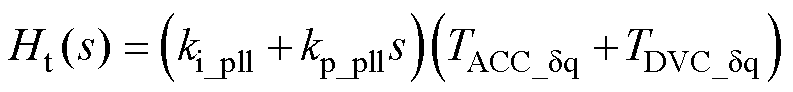 (10)
(10)
PLL主导同步振荡模式 为特征方程式(9)的一组特征根,其中实部
为特征方程式(9)的一组特征根,其中实部 表征
表征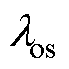 振荡模式的阻尼部分,虚部
振荡模式的阻尼部分,虚部 表征
表征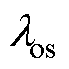 振荡模式的振荡频率部分。
振荡模式的振荡频率部分。
对于弱阻尼振荡模式,可以用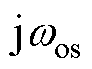 对
对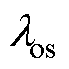 进行近似替换[13],式(10)中环路附加部分可近似为
进行近似替换[13],式(10)中环路附加部分可近似为
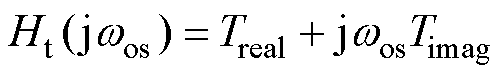 (11)
(11)
式中,Treal与Timag分别反映了MTS控制耦合引入的频率与阻尼动态,即
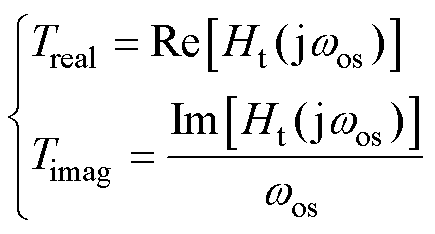 (12)
(12)
结合式(9)与式(11)可以得到,考虑MTS耦合的弱阻尼振荡模式的实部与虚部分别为
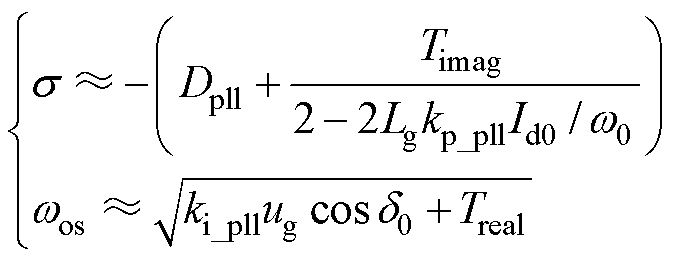 (13)
(13)
式中,Dpll为PLL自回路引入的固有阻尼,表达式为
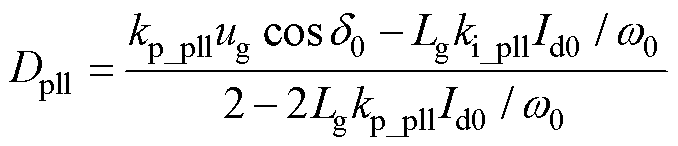 (14)
(14)
由式(14)可知,PLL引入固有阻尼不受MTS耦合的影响,仅与PLL参数以及工作点的选择有关;而根据式(12)可知,MTS引入附加阻尼不仅受到振荡频率的影响,也会受到MTS耦合参与回路参数的影响。
首先,对MTS耦合在系统阻尼稳定性中的作用进行定性分析。观察式(13)与式(14)可知,PLL控制参数一定时,PLL固有阻尼始终保持为正,有利于系统同步稳定,而MTS耦合引入附加阻尼的正负特性与耦合传递函数的频域特性相关,绘制式(10)中各函数的Bode图如图5所示。

图5 MTS耦合支路的Bode图
Fig.5 Bode diagrams of the MTS coupling branches
图5表明,在同步振荡频率范围内,三条曲线相位均处于第三、四象限,根据式(12)可知,DVC时间尺度与ACC时间尺度引入附加阻尼均为负值,两者耦合后引入的附加阻尼将会使系统阻尼特性更加恶化,当MTS耦合引入附加阻尼绝对值超过Dpll时,系统总阻尼为负,就会引发同步振荡失稳问题。
由以上分析可知,MTS控制耦合对系统附加阻尼的影响与各环路参数均有联系,下文将结合灵敏度分析法研究各控制参数在MTS耦合中的参与度。为方便记忆,结合式(13)给出MTS耦合引入附加阻尼Dad与系统总阻尼Dall的表达式为
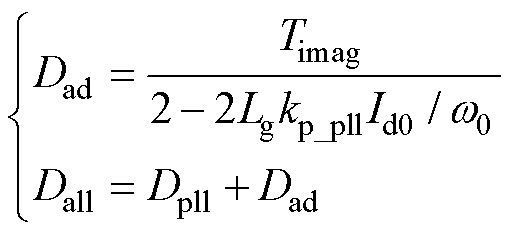 (15)
(15)
定义附加阻尼Dad对参数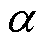 的灵敏度为
的灵敏度为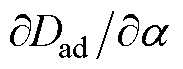 ,该灵敏度为正时表示参数
,该灵敏度为正时表示参数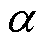 增大会使得Dad增大;为负时则相反,灵敏度绝对值越大,则参数
增大会使得Dad增大;为负时则相反,灵敏度绝对值越大,则参数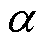 在附加阻尼Dad中的参与度越高。
在附加阻尼Dad中的参与度越高。
为研究控制参数对MTS耦合附加阻尼的影响,选取各环路控制器参数kp_pll、ki_pll、kp_dvc、ki_dvc、kp_tvc、ki_tvc、kp_cc、ki_cc作为研究对象,参考附表1绘制Dad对各参数的灵敏度随频率的变化趋势,如图6所示。
由图6可知,Dad对不同参数的灵敏度存在显著差异,且同一参数的灵敏度也会随频率增加出现较大变化。可以发现,在5~10 Hz振荡频率范围内,Dad对kp_pll与kp_tvc的灵敏度明显大于其他参数,其中参数kp_tvc灵敏度为正值且增大时,Dad也会随之增大,有利于系统同步稳定,而参数kp_pll灵敏度为负值且增大时,Dad有减小趋势,将降低系统同步稳定性。

图6 Dad对控制参数的灵敏度
Fig.6 The sensitivity of Dad to control parameters
为验证以上灵敏度分析结论,以附表1参数为基准,绘制各个参数增大3%对MTS耦合附加阻尼的影响,如图7a所示,图7b为图7a在频率处于6.5 Hz邻域内时的局部细节图。
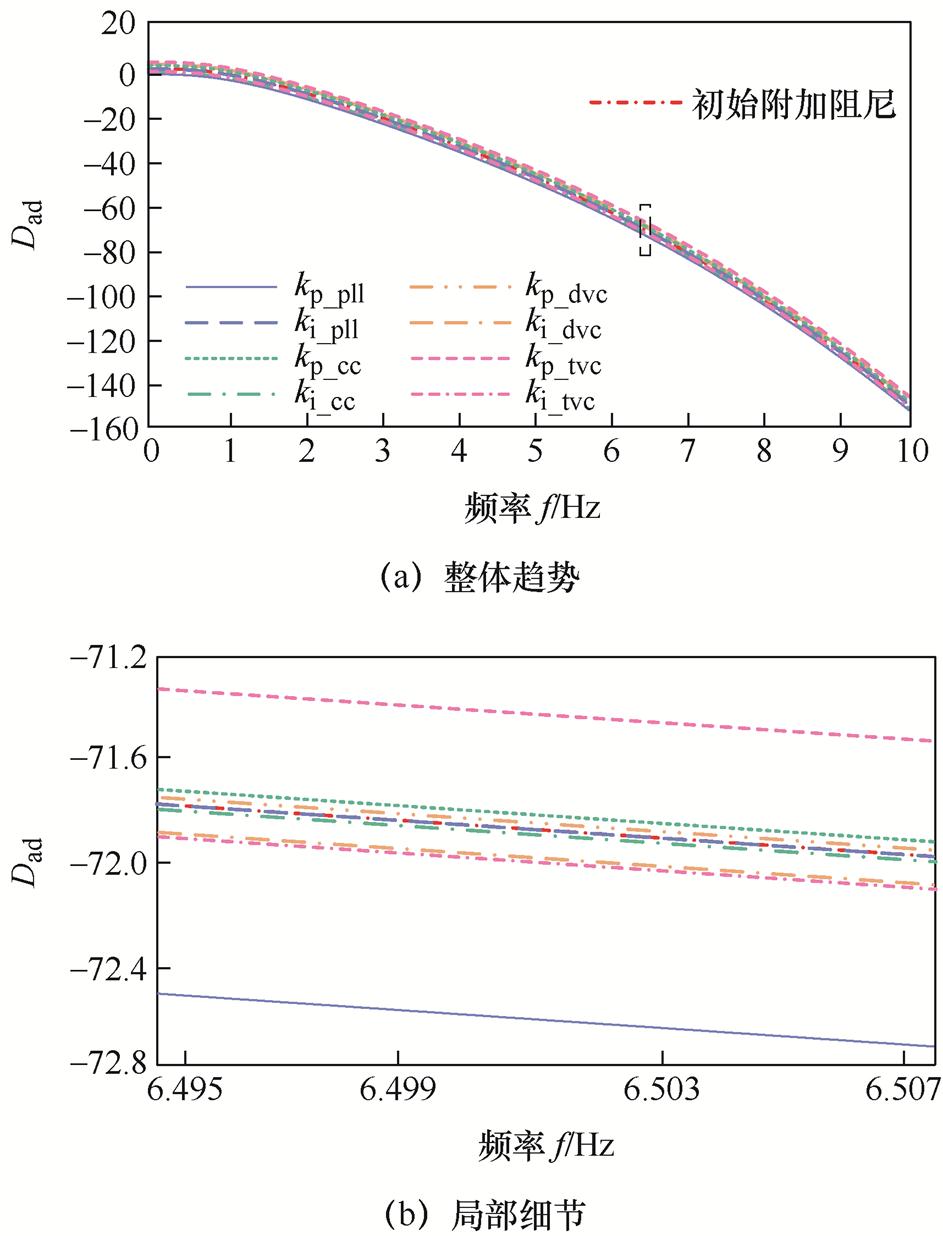
图7 控制参数增大3%时Dad的频率特性
Fig.7 The frequency characteristics of Dad when the control parameters increase by 3%
观察图7可知,当kp_pll增大3%时,Dad较初始值降低,系统负阻尼特性加剧;当kp_tvc增大3%时,Dad较初始值增大,系统负阻尼特性减弱;当ki_dvc与ki_tvc均增大3%时,Dad较初始值也有所降低,负阻尼特性有一定程度加强;其余参数增大3%时,附加阻尼变化不明显。比较图7中各个参数变化对系统阻尼特性的影响,可将参数kp_pll与kp_tvc视为影响MTS耦合系统阻尼特性的主导因子。此结论与图6分析结果一致,验证了灵敏度分析的正确性。
以上灵敏度分析结论可以定性判断控制参数变化时MTS耦合引入附加阻尼的变化趋势,但无法得到系统整体阻尼的大小;同时考虑到MTS耦合附加阻尼的大小受到振荡频率fos的影响,而控制参数变化也会对fos产生扰动,因此结合控制参数与振荡频率变化规律,得到系统在振荡频率点的总阻尼,才能有效判断系统同步稳定性。
选取所提阻尼主导因子为研究对象,定量分析主导参数变化时系统振荡频率fos的大小,并绘制振荡频率变化时系统总阻尼的三维分布图,可从阻尼的角度直观判断系统的同步稳定性。
首先,需要求解控制参数变化时,对应系统振荡频率fos的大小。根据式(13)构造以频率为变量的函数表达式为
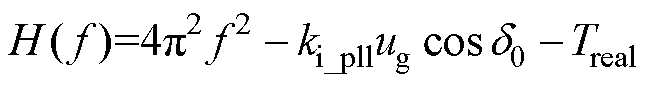 (16)
(16)
观察式(13)与式(16)可知,当H(f)=0时,对应的频率即为系统振荡频率。图8a为根据式(16)绘制的振荡频率fos随kp_pll增大时的变化趋势,其中f11~f14为kp_pll取不同值时对应的振荡频率。可以发现,系统振荡频率分布在5~8 Hz之间,且随着kp_pll增大振荡频率也会逐渐增大。

图8 kp_pll对系统阻尼特性的影响
Fig.8 Effect of kp_pll on the damping characteristics of the system
进一步地,结合图8a与式(15)绘制系统总阻尼随kp_pll增大时的变化图像,如图8b所示,P11~P14为kp_pll取不同值时f11~f14对应的阻尼点。观察图8b可知,在选定参数范围内,随着kp_pll增大,振荡频率增大,对应系统总阻尼降低,负阻尼效应加剧,系统同步稳定性降低,这与在灵敏度分析中关于kp_pll对系统阻尼特性影响的结论一致。
类似地,分别绘制kp_tvc增大时系统振荡频率以及对应阻尼的变化趋势,如图9所示。图9a中,其他参数恒定的情况下,kp_tvc增大时系统振荡频率减小;图9b表明,Dall随着kp_tvc的增大而增大,负阻尼效应减弱,有利于系统稳定。

图9 kp_tvc对系统阻尼特性的影响
Fig.9 Effect of kp_tvc on the damping characteristics of the system
以上定量分析与灵敏度分析结果相互印证,验证了分析结果的正确性与可靠性,为改善系统稳定性的参数调节提供了指导与理论支撑。
上文分析过程未计及不同电网工况对MTS耦合系统阻尼分布的影响,本节对两种不同工况下MTS耦合同步稳定性展开分析。
工况1:电网阻抗变化的影响。观察图3与图4可以发现,MTS耦合产生的负阻尼通过电网阻抗与PLL产生交互,影响系统同步稳定性。电网阻抗Lg越大,MTS耦合引入负阻尼与PLL的交互程度越高,对系统同步稳定性的影响越大。同时式(14)表明,随着Lg的增大,PLL固有阻尼Dpll将会减小,使得GFL系统更容易呈现负阻尼特性,降低系统同步稳定裕度。
图10反映了电网阻抗对MTS耦合阻尼特性的影响,由图10a可以看出,随着Lg的增大,PLL引入固有阻尼Dpll逐渐减小,当Lg接近0.5(pu)时,Dpll由正转变为负,使得系统稳定裕度进一步降低。
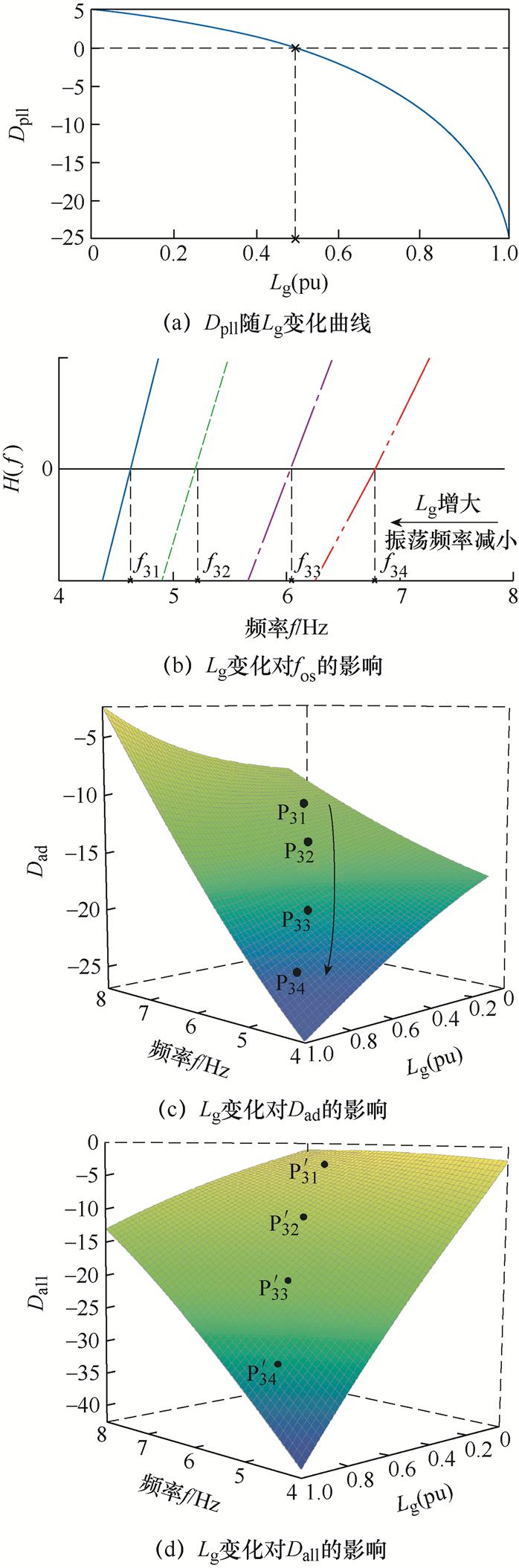
图10 电网阻抗Lg对MTS耦合阻尼特性的影响
Fig.10 Effect of Lg on the damping characteristics of MTS coupling
图10b反映了系统振荡频率随Lg的变化趋势,随着Lg的增大,系统振荡频率减小;图10c、图10d为Lg变化时对应振荡频率下MTS耦合附加阻尼Dad与系统总阻尼Dall的三维图,随着Lg的增大,Dad与Dall均保持减小的趋势,系统负阻尼特性加剧。同时,随着Lg的增大,Dall先大于Dad,后在Lg=0.5(pu)附近开始小于Dad,这与图10a中Lg变化时Dpll分布的分析一致。
工况2:电网电压跌落对系统同步稳定性的影响。图4表明,电网电压跌落会使PLL输入受到干扰,直接影响到MTS耦合系统的同步稳定性。由式(12)、式(14)可知,PLL固有阻尼与MTS耦合引入附加阻尼均有电网电压的参与,因此计及电网电压跌落的影响在研究系统同步稳定性时十分必要。
图11反映了电网电压ug跌落对MTS耦合系统阻尼特性的影响,其中实线和虚线分别表示ug取1.0(pu)和0.9(pu)时总阻尼Dall在不同振荡频率附近的响应特性。当电网电压跌落时,总阻尼Dall随之减小,系统同步稳定性下降。同时,随着电网阻抗增大,电网电压跌落带来的阻尼下降影响加剧,说明电网强度越低,系统同步稳定性受电网跌落的影响越严重。
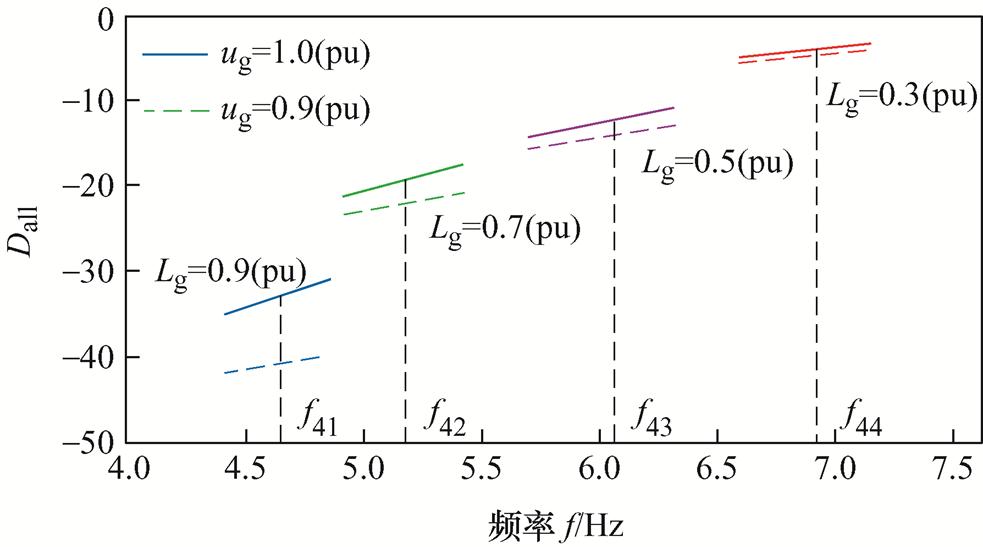
图11 电网电压跌落对MTS耦合阻尼特性的影响
Fig.11 Effect of ug dips on the damping characteristics of MTS coupling
以上关于差异化电网工况下MTS控制耦合影响系统同步稳定性的分析表明,弱电网工况下,系统同步稳定裕度受限,在电网阻抗增大以及电网电压跌落时容易表现为负阻尼特性,降低系统同步稳定性。因此,需要针对MTS控制耦合对系统阻尼特性的影响,寻找合适的改进策略,改善系统阻尼特性,提升系统同步稳定性与抗干扰能力。
为了减小MTS控制耦合对GFL系统阻尼特性的影响,本文提出通过控制环路重塑的方式提升MTS耦合附加回路正阻尼,降低控制参数变化与不同电网工况对系统阻尼特性的影响,增强系统正阻尼特性,提升并网系统同步稳定性与鲁棒性。
由图3可知,DVC时间尺度作为前级单元与ACC时间尺度串联耦合,因此文中对DVC时间尺度控制环路进行改进,可以同时改善双尺度阻尼特性,降低MTS耦合对系统同步稳定性的影响。但同时可以发现,PLL输出功角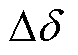 通过并网电流dq轴稳态分量(Id0≠0, Iq0=0)参与MTS耦合过程,使得控制耦合路径更加复杂。量化分析发现,MTS附加阻尼随着Id0增大而减小,负阻尼效应加剧,说明PLL通过Id0参与MTS耦合会降低系统同步稳定性,附图1给出其量化图。因此,在对DVC时间尺度控制进行改进时,需要同时对PLL与MTS耦合的交互进行处理。
通过并网电流dq轴稳态分量(Id0≠0, Iq0=0)参与MTS耦合过程,使得控制耦合路径更加复杂。量化分析发现,MTS附加阻尼随着Id0增大而减小,负阻尼效应加剧,说明PLL通过Id0参与MTS耦合会降低系统同步稳定性,附图1给出其量化图。因此,在对DVC时间尺度控制进行改进时,需要同时对PLL与MTS耦合的交互进行处理。
由图4中小信号模型可知,PLL输出功角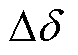 动态反映了MTS耦合引入负阻尼对系统同步稳定的影响,因此本文通过
动态反映了MTS耦合引入负阻尼对系统同步稳定的影响,因此本文通过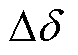 前馈对DVC时间尺度控制环路进行重塑,同时消除PLL参与交互以及MTS控制耦合对系统阻尼特性的影响。考虑到功角
前馈对DVC时间尺度控制环路进行重塑,同时消除PLL参与交互以及MTS控制耦合对系统阻尼特性的影响。考虑到功角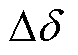 获取难度较大,文中采用q轴端电压前馈的方式进行替代,改进控制框图如图12所示,红色部分为改进控制。
获取难度较大,文中采用q轴端电压前馈的方式进行替代,改进控制框图如图12所示,红色部分为改进控制。
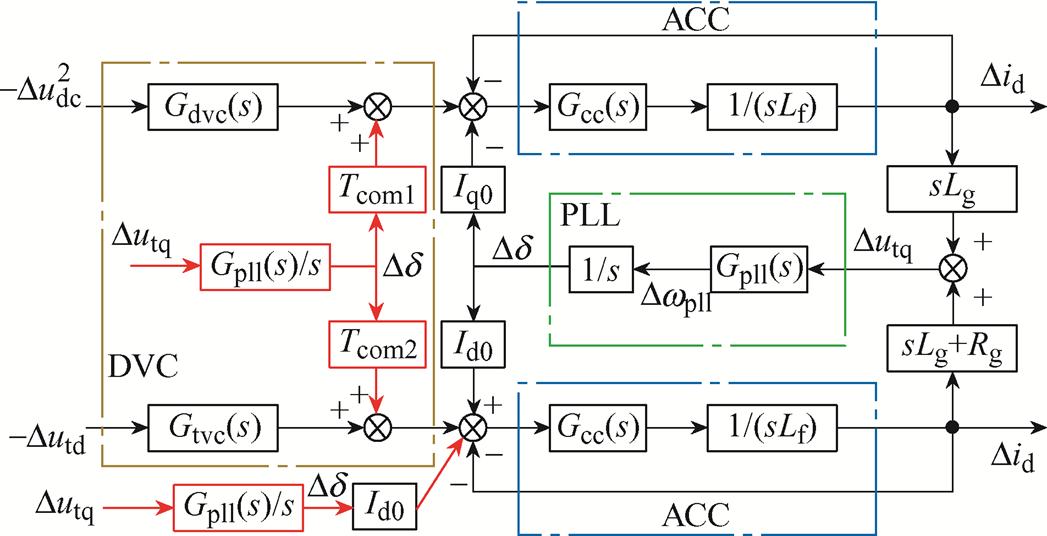
图12 改进后的MTS控制系统小信号同步模型
Fig.12 Improved small-signal synchronization model for MTS control system
根据图12,环路重塑后的并网电流参考值与端电压表达式更新为
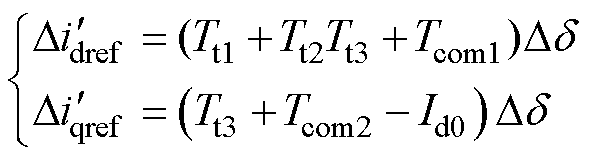 (17)
(17)
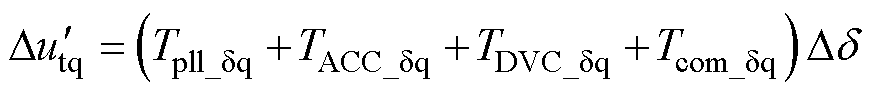 (18)
(18)
式中,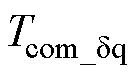 为环路重塑引入的动态,即
为环路重塑引入的动态,即
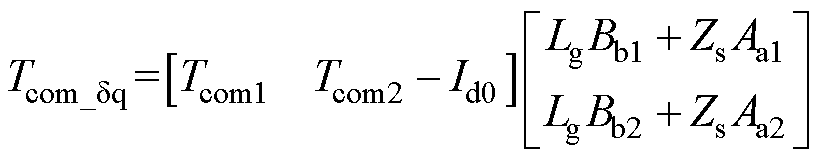 (19)
(19)
式中,Aa1、Aa2、Bb1与Bb2的表达式在附录式(A2)中给出。
参照式(18),可得环路重塑后的MTS小信号同步模型,如图13所示。
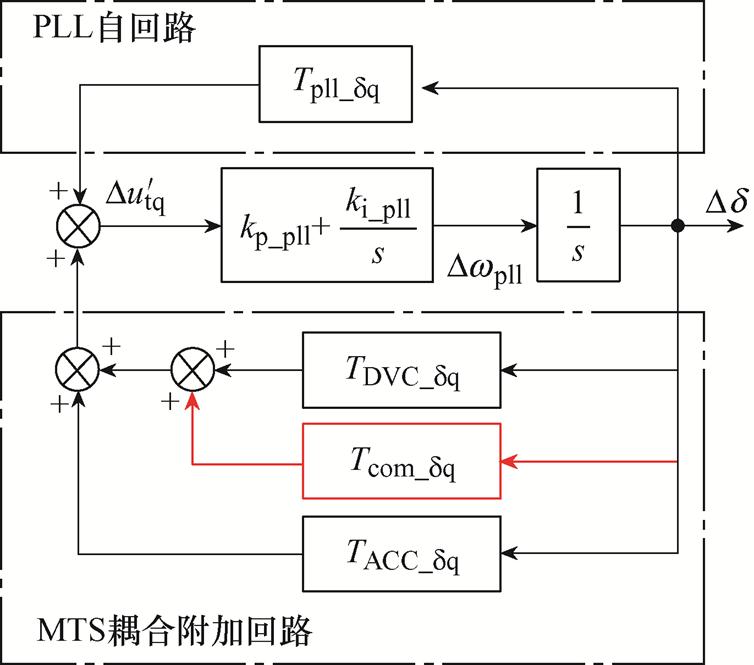
图13 环路重塑后的MTS小信号同步模型
Fig.13 Small-signal synchronization model of MTS after loop reshaping
根据式(11)~式(13)与图5可知,MTS耦合附加回路相位滞后是其引入负阻尼的主要原因,因此将环路重塑环节设计成超前网络,为MTS耦合提供正阻尼,从而改善系统整体阻尼特性,具体设计如下。
为降低参数调节难度,用相同超前控制器设计环路重塑环节,由于文中所提策略只需要控制器超前即可,不需要使用多阶超前环节,选择传递函数为
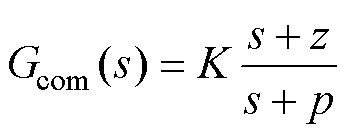 (20)
(20)
式中,K为幅值调节系数;z和p为相位调节参数;Gcom(s)在z<p时提供超前相位,且在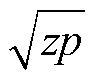 处获取最大相位。
处获取最大相位。
同时,考虑到Gcom(s)会给系统引入高频增益,采用低通滤波器对其进行预处理,设计截止频率为15 Hz,可得重塑环节传递函数为
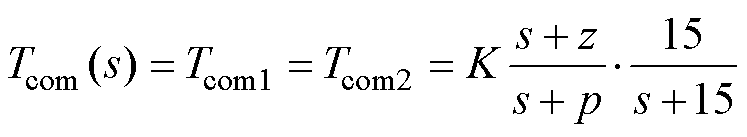 (21)
(21)
以极弱电网工况为例,Lg=0.8(pu)时系统振荡频率fos≈5 Hz,以最大相位利用为准则,Tcom(s)的表达式可简化为
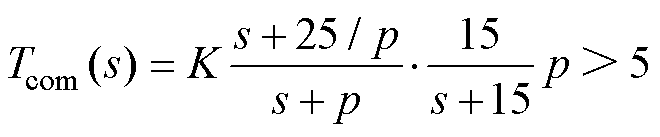 (22)
(22)
结合式(12)、式(13)可知,在添加重塑环节后,系统能够呈现正阻尼特性并保持稳定的条件是:①环路重塑引入附加回路的模态虚部大于原有MTS耦合引入附加回路的模态虚部;②环路重塑引入附加回路的模态实部大于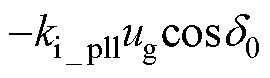 。
。
环路重塑稳定性条件如图14所示。首先计算出极限工况下由MTS耦合引入的模态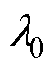 ,然后将Lg≈ 0.8(pu),fos≈5 Hz代入式(11)可得
,然后将Lg≈ 0.8(pu),fos≈5 Hz代入式(11)可得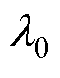 ≈85.96-j642.62,设重塑控制附加回路引入模态为
≈85.96-j642.62,设重塑控制附加回路引入模态为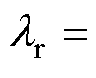
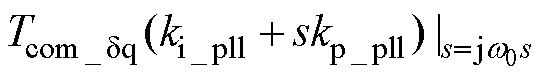 ,则系统同步稳定的条件可转化为:
,则系统同步稳定的条件可转化为: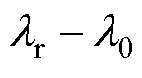 的虚部大于0,实部大于
的虚部大于0,实部大于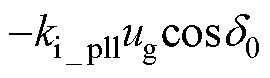 ,即
,即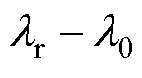 位于图14中区域①与区域②。
位于图14中区域①与区域②。
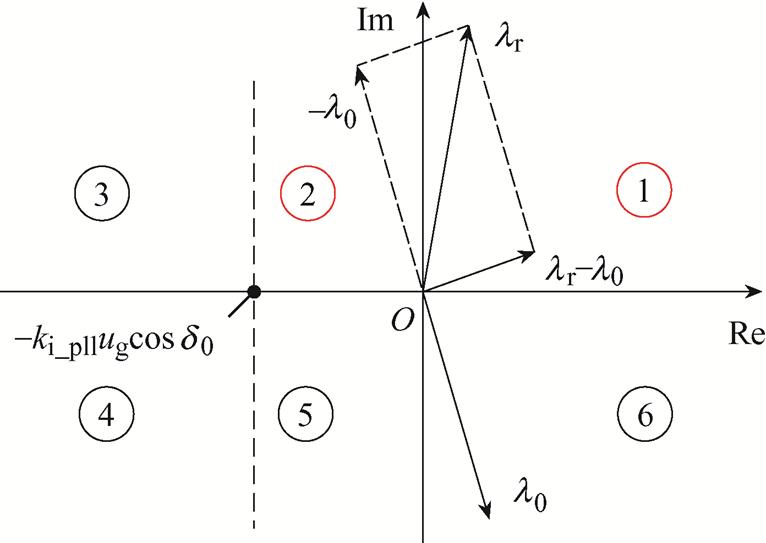
图14 环路重塑稳定性条件
Fig.14 Stability criteria for loop reshaping
绘制 在极弱电网(Lg≈0.8(pu))工况下随参数p和K的变化曲线,如图15所示。
在极弱电网(Lg≈0.8(pu))工况下随参数p和K的变化曲线,如图15所示。
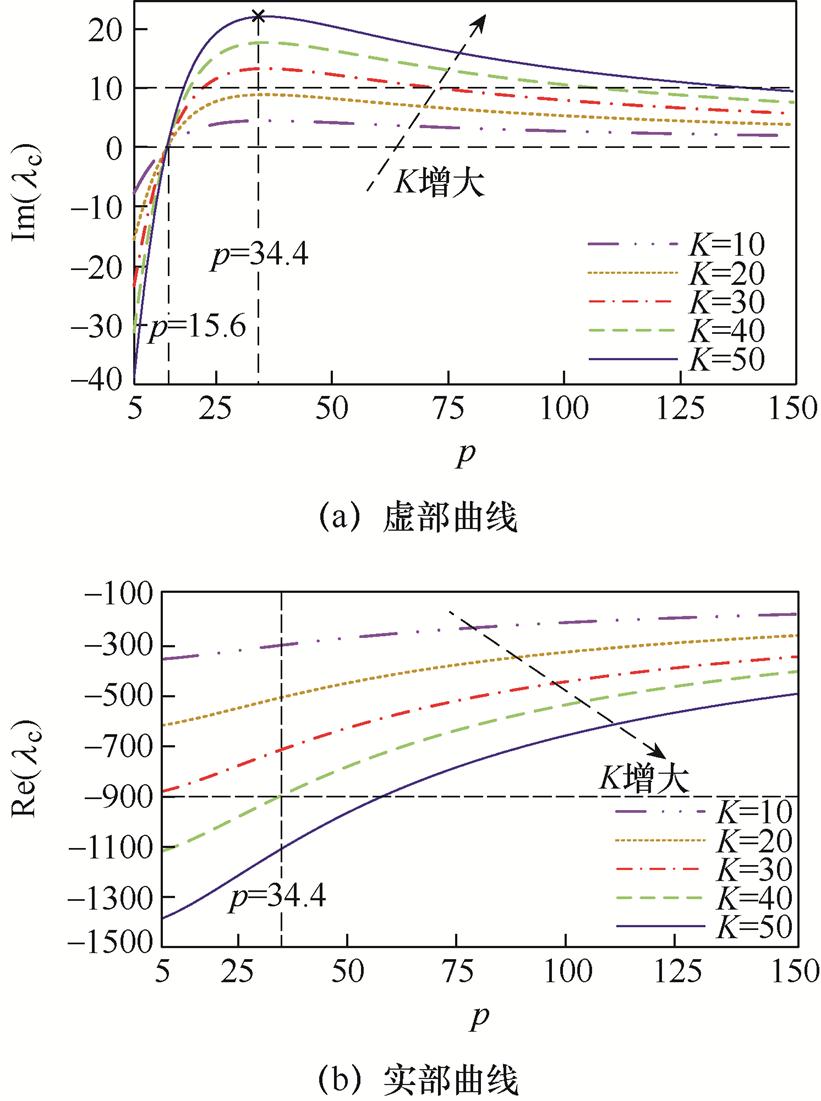
图15 重塑模态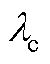 随参数变化曲线
随参数变化曲线
Fig.15 The curves of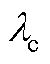 with parameter variation
with parameter variation
如图15a所示,极弱电网工况下,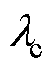 的虚部以p=15.6为正负分界线,根据所提稳定性判据,当p<15.6时,系统不稳定;当p=34.4时,
的虚部以p=15.6为正负分界线,根据所提稳定性判据,当p<15.6时,系统不稳定;当p=34.4时,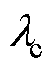 的虚部取最大值,而图15b中显示,随着p的增大,
的虚部取最大值,而图15b中显示,随着p的增大,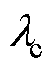 的实部逐渐增大,有利于系统稳定,所以p可在34.4的邻域进行取值。
的实部逐渐增大,有利于系统稳定,所以p可在34.4的邻域进行取值。
进一步对参数K的取值进行判断,首先由阻尼条件进行限制,结合图10a可知,当Lg=0.8(pu)时,Dpll取值约为-10,在极弱电网下,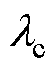 引入的阻尼成分应大于PLL引入的负阻尼。图15a表明,当p=34.4时,随着K的增大,
引入的阻尼成分应大于PLL引入的负阻尼。图15a表明,当p=34.4时,随着K的增大,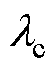 的虚部会逐渐增大,当K>30时可以保证
的虚部会逐渐增大,当K>30时可以保证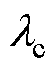 的虚部大于10。其次以频率条件进行限制,由图15b可知,随着K的增大,
的虚部大于10。其次以频率条件进行限制,由图15b可知,随着K的增大,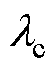 的实部逐渐减小,当K>40时,
的实部逐渐减小,当K>40时,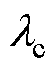 的实部将小于
的实部将小于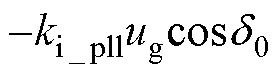 (当Lg=0.8(pu)时,
(当Lg=0.8(pu)时,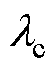 取值约为-900),不满足所提阻尼稳定条件,综合两种限制条件,可得K取值范围为30~40。
取值约为-900),不满足所提阻尼稳定条件,综合两种限制条件,可得K取值范围为30~40。
综上所述,为方便计算,对参数p和K分别取值35和38,则重塑环节Tcom(s)的表达式确定为
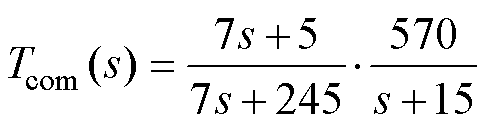 (23)
(23)
根据式(23)绘制环路重塑后Dall随Lg变化的三维曲面图,如图16所示。图16表明,环路重塑后系统总阻尼在极弱电网工况下依然为正,系统同步稳定性大幅提升,验证了所提环路重塑改进控制的有效性。
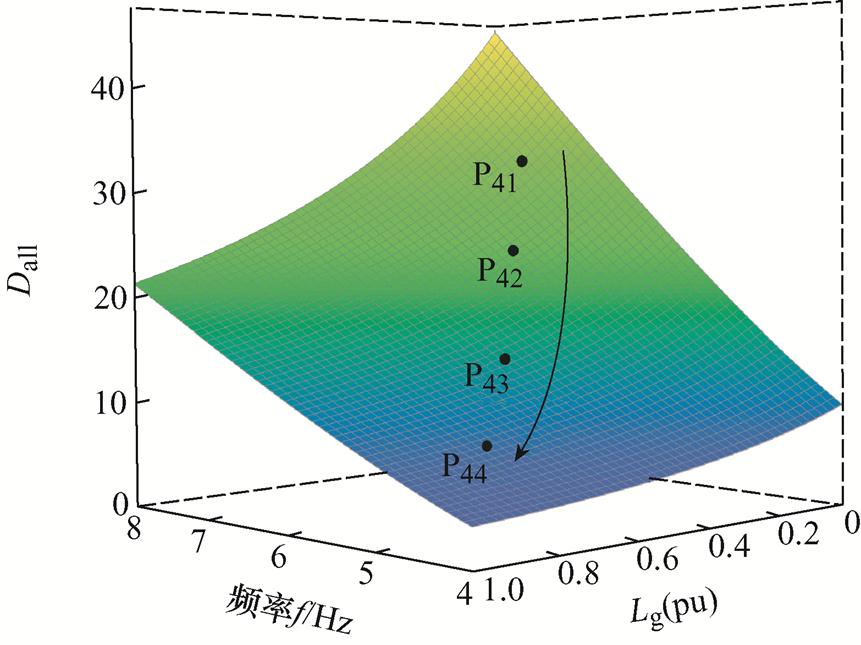
图16 环路重塑后Dall随Lg变化趋势
Fig.16 Trend of Dall with Lg variation after loop reshaping
为验证文中关于MTS耦合并网系统阻尼特性的理论分析与所提阻尼重塑方案的正确性与可行性,基于所搭建仿真模型与实验样机,给出不同工况下的仿真与实验结果,涉及参数详见附表1。
首先,对MTS耦合影响系统同步稳定性的理论分析进行验证。然后分别通过改变Udcref与Idref使得有功功率参考值Pref产生0.1(pu) 的阶跃扰动,绘制Lg = 0.3(pu)时计及MTS耦合与否的阶跃响应如图17所示。
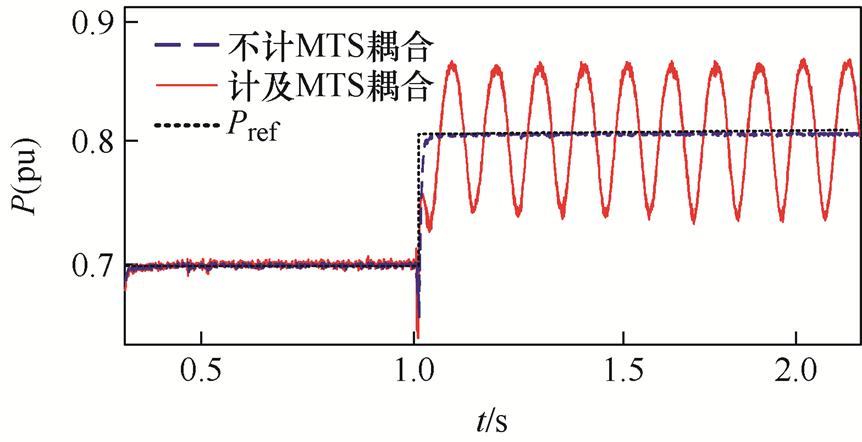
图17 有功功率阶跃响应
Fig.17 The step response of active power
由图17可知,当不考虑MTS耦合时,Lg=0.3(pu)对应的有功功率曲线在参考给定变化后依然能稳定跟踪给定值;当考虑MTS耦合的影响时,对应有功功率曲线出现明显振荡,表明MTS耦合引入的附加回路给系统带来负的附加阻尼,使得系统同步稳定性降低。
进一步验证在不同工况下考虑MTS耦合时的系统同步稳定性。电网阻抗Lg变化工况下有功功率响应曲线如图18所示。由图18可知,Lg从0.1(pu)切换为0.5(pu)时,有功功率P出现明显振荡,且振荡频率fos≈6.15 Hz;当Lg从0.1(pu)切换为极弱电网0.8(pu)时,振荡频率fos减小至约5 Hz,与图10b分析结果一致。
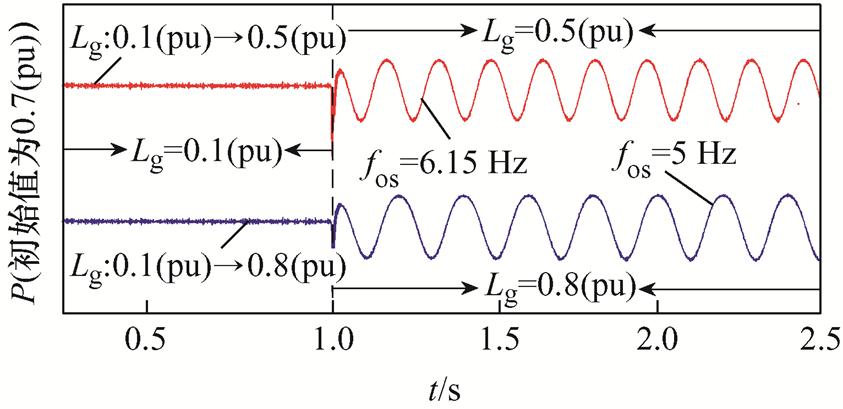
图18 Lg变化工况下有功功率P的响应曲线
Fig.18 Response curves of P when Lg changes
图19为Lg=0.2(pu)时,电网电压跌落故障工况下的有功功率响应。图19表明,Lg=0.2(pu)时,有功功率P能稳定输出,而当电网电压跌落20%时,系统总阻尼下降,P发生振荡失稳,系统同步稳定性失效,符合图11中电网电压跌落对系统阻尼特性影响的分析结果。而投切改进控制后,系统发生电网电压跌落故障时,有功功率P能够稳定输出。
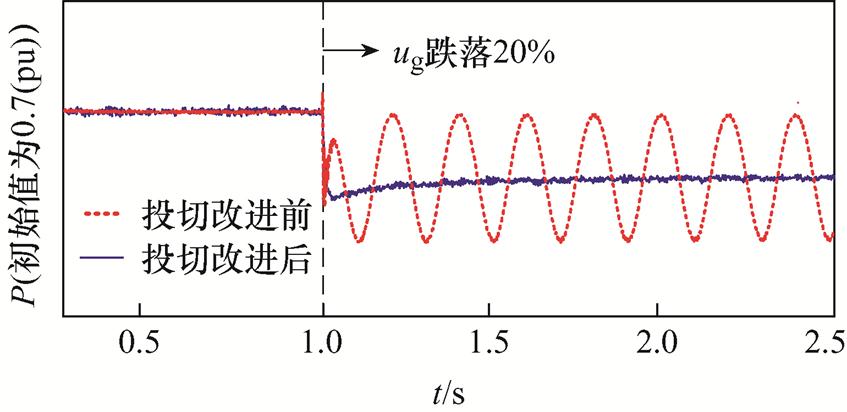
图19 ug跌落时有功功率P的响应曲线
Fig.19 Response curves of P during ug dips
为进一步验证所提策略,结合图1结构与附表1参数搭建额定功率6 kW的RT-Lab硬件在环仿真平台进行实验验证,实验装置如图20所示。其中,采用电网模拟器(Chroma-61815)模拟电网动态,三相全桥逆变器的控制以及采样信号的计算由RT- Lab进行处理。
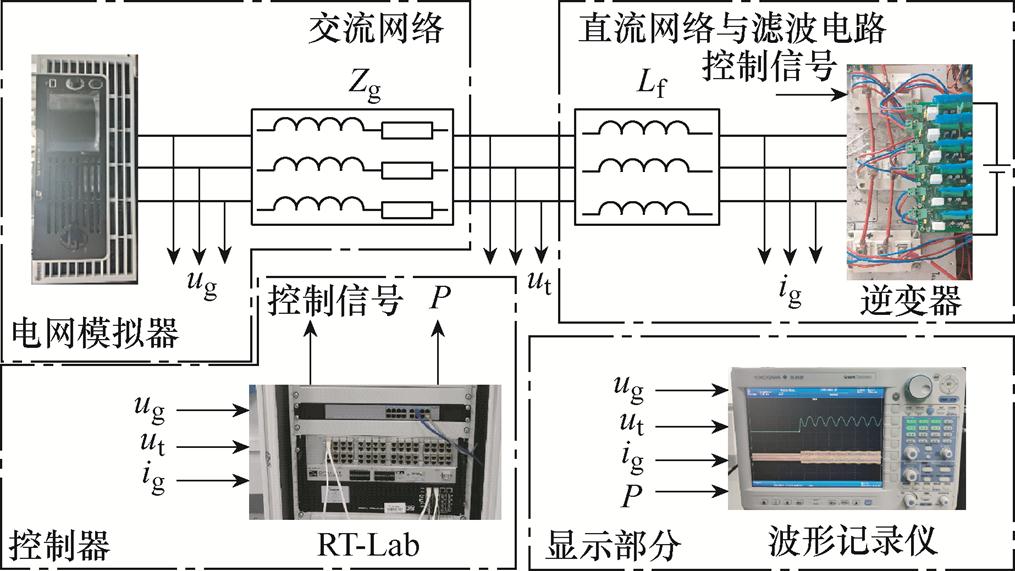
图20 RT-Lab硬件在环实验装置
Fig.20 RT-Lab hardware in the loop experimental setup
首先对MTS控制耦合导致失稳的理论分析进行验证,图21为系统以70%额定功率运行时,改进前后有功功率阶跃的实验波形。图21表明,改进前系统有功出力增加20%时,有功功率P无法稳定跟踪参考值,出现同步振荡现象;而投切改进控制后,当有功出力同样增加20%时,有功功率能够快速稳定地跟踪参考值。

图21 改进前后系统有功功率阶跃实验波形
Fig.21 Step experimental waveforms of P before and after improvement
进一步验证不同工况下所提改进控制策略的有效性。首先验证电网阻抗变化工况下的控制效果,图22为电网阻抗切换时MTS控制耦合对系统稳定性的影响以及改进控制策略的效果。
图22a、图22b表明,当Lg分别从0.1(pu)切换到0.5(pu)和0.8(pu)时,MTS控制耦合引发阻尼下降,系统发生同步振荡,且振荡频率与分析结果一致;图22c显示,极弱电网(Lg=0.8(pu))下,投切改进控制后,有功功率和并网电流逐渐平衡,系统趋于同步稳定。
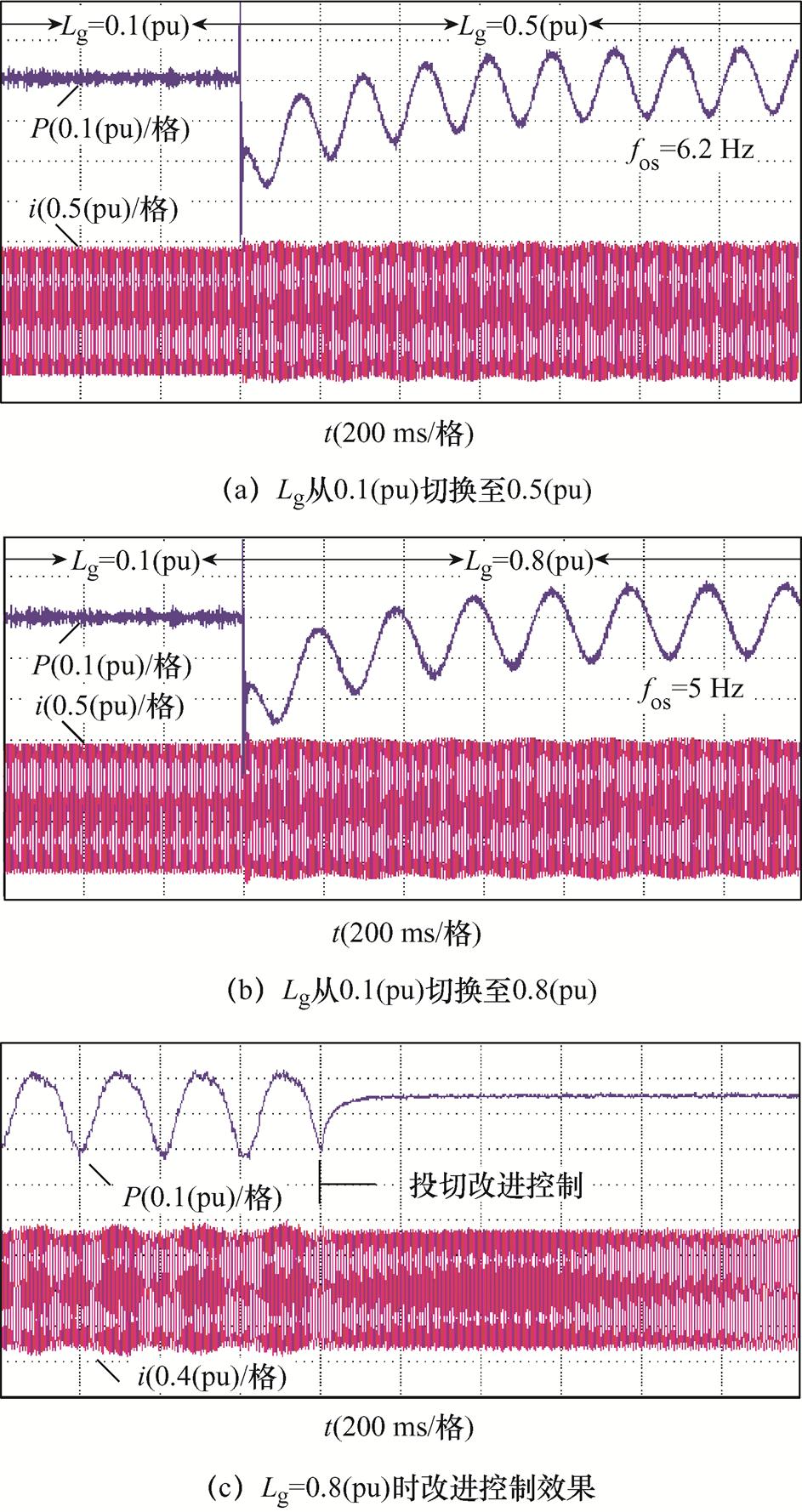
图22 Lg切换时系统同步稳定性
Fig.22 System synchronization stability with switching Lg
电网电压跌落工况下的实验波形如图23所示。图23a表明,投切改进控制前,ug跌落20%时,系统阻尼下降,发生同步振荡现象;图23b表明,投切改进控制后,系统阻尼提升,ug跌落20%时,不再出现振荡现象,使得系统始终保持同步稳定。
为了验证所提改进控制策略的优越性,选用电容电压反馈控制方案进行对比实验,实验结果如附图2所示。可以发现,电容电压反馈控制在Lg=0.5(pu)时可以使系统稳定输出;而当Lg增大到0.8(pu)时,系统同步性能改善程度有限,依然存在振荡现象。同时,采用电容电压反馈控制对本文建立系统进行阻尼重塑时,投切改进控制瞬间的切换过程不够平滑。而在Lg=0.8(pu)时,本文所提方案依然可以有效改善系统阻尼特性,且切换过程平稳快速。
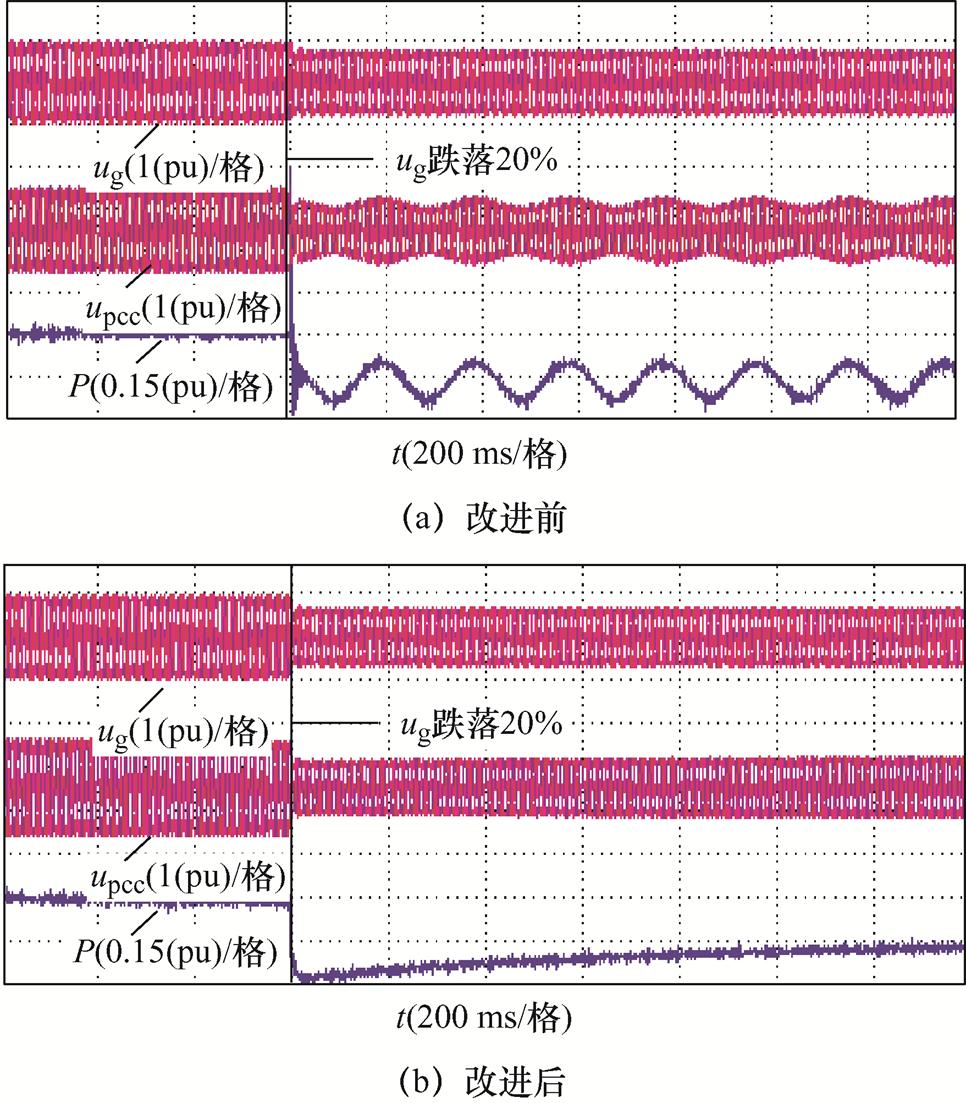
图23 电网电压跌落工况下的实验波形
Fig.23 Experimental waveforms under ug drop conditions
上述仿真与实验结果表明,文中针对MTS控制耦合提出的阻尼重塑改进控制策略有效改善了系统阻尼特性,大幅提升系统在不同工况下的同步稳定性。
本文以跟网型并网系统为研究对象,计及多环控制的MTS特性,建立小信号同步模型,对系统同步稳定性展开研究,得出了以下结论:
1)GFL变换器多环控制耦合的本质是时间尺度上的频带重叠,表现为MTS特性;同时,PLL存在跨时间尺度控制特性,在MTS耦合过程中起到桥梁的作用,从而形成了一条闭合的耦合路径。
2)基于灵敏度分析法量化多控制参数在MTS耦合控制系统阻尼特性中的参与程度,筛选出对系统同步特性影响较大的主导因子kp_pll与kp_tvc。其中,减小kp_pll或增大kp_tvc可以削弱负阻尼效应,提升系统总阻尼,改善系统同步性能。
3)考虑多场景电网工况及DVC时间尺度内部耦合对MTS系统同步稳定性的影响,分别进行量化分析。分析结果表明,电网阻抗增大、电网电压跌落以及DVC内部dq耦合均会导致系统负阻尼效应加剧,可能引起系统同步失稳。
4)提出基于电网端电压前馈的阻尼重塑改进控制方案,在消除DVC时间尺度内部dq耦合影响的同时,可以有效降低多种工况下系统的负阻尼特性,从而增强了MTS耦合控制系统的同步稳定性。
附 录
1. 相关参数
附表1 MTS控制系统主要参数
App.Tab.1 Main parameters of the MTS control system

参 数数 值 电网电压ug/V110(1(pu)) 滤波电感Lf/mH3.6(0.375(pu)) 电网阻抗Lg/mH1(0.1(pu))4.8(0.5(pu))7.6(0.8(pu)) 直流侧电容Cdc/nF4.7mF(4.4(pu)) 直流侧电压参考udcref/V220(2(pu)) 电网端电压参考utdref/V110(1(pu)) kp_pll ki_pll301 250 kp_cc ki_ cc5100 kp_dvc ki_ dvc10190 kp_tvc ki_ tvc0.2595 电网角频率w0/(rad/s)314 阻尼重塑参数p, K35,38
2. 相关表达式
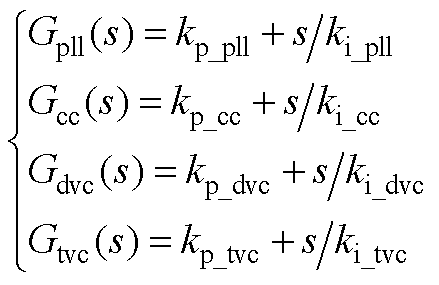 (A1)
(A1)
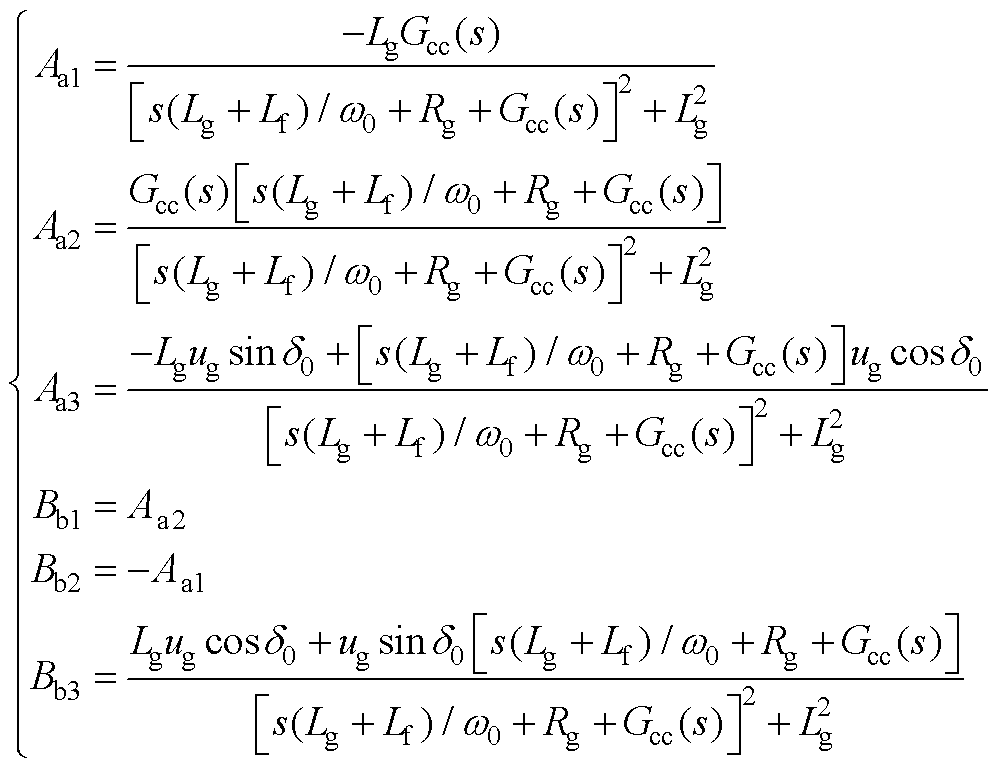 (A2)
(A2)
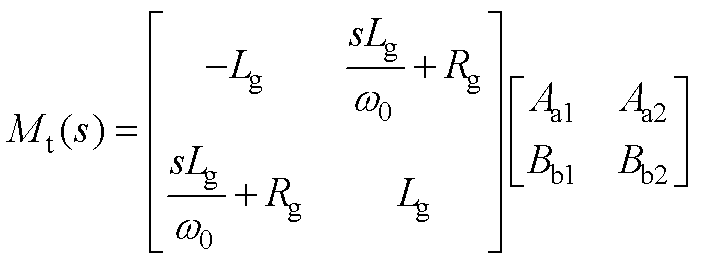 (A3)
(A3)
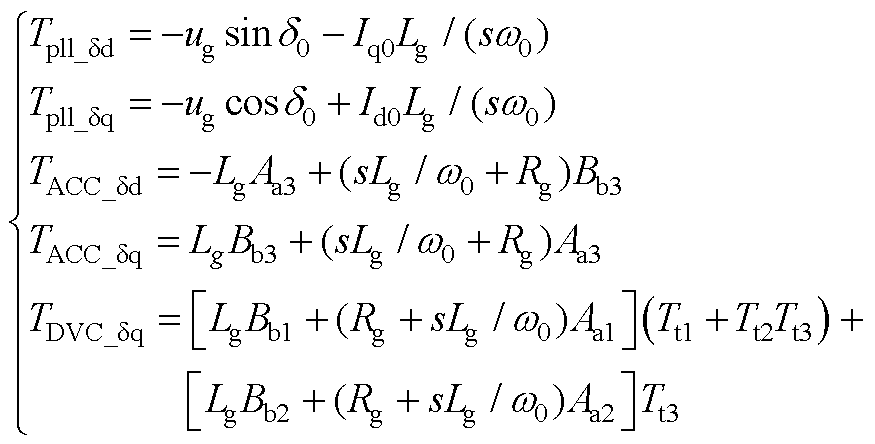 (A4)
(A4)
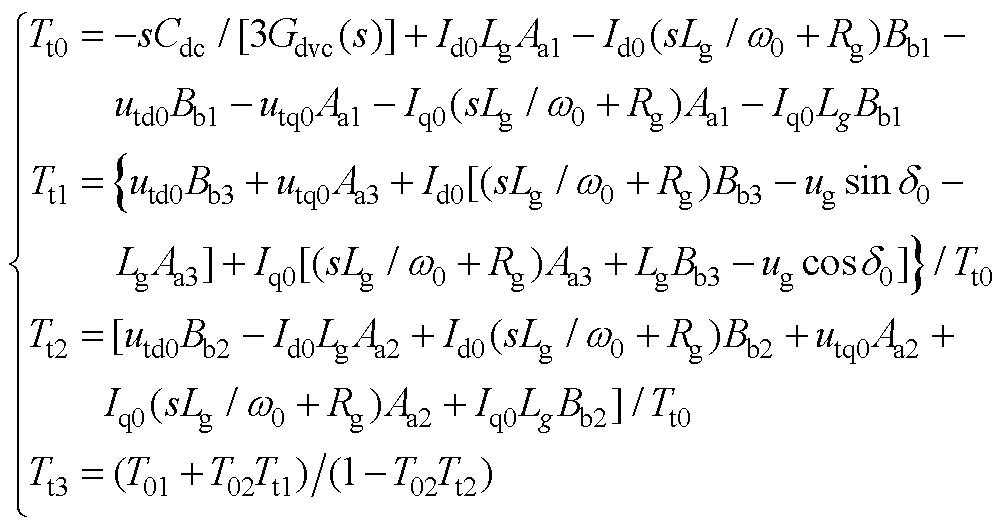 (A5)
(A5)
式中,T00、T01与T02的表达式分别为
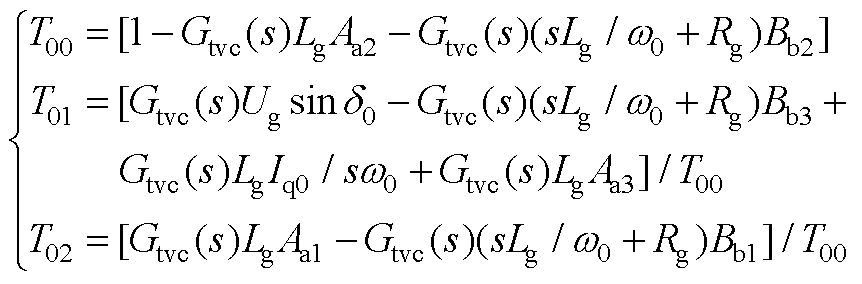 (A6)
(A6)
3. 相关图示
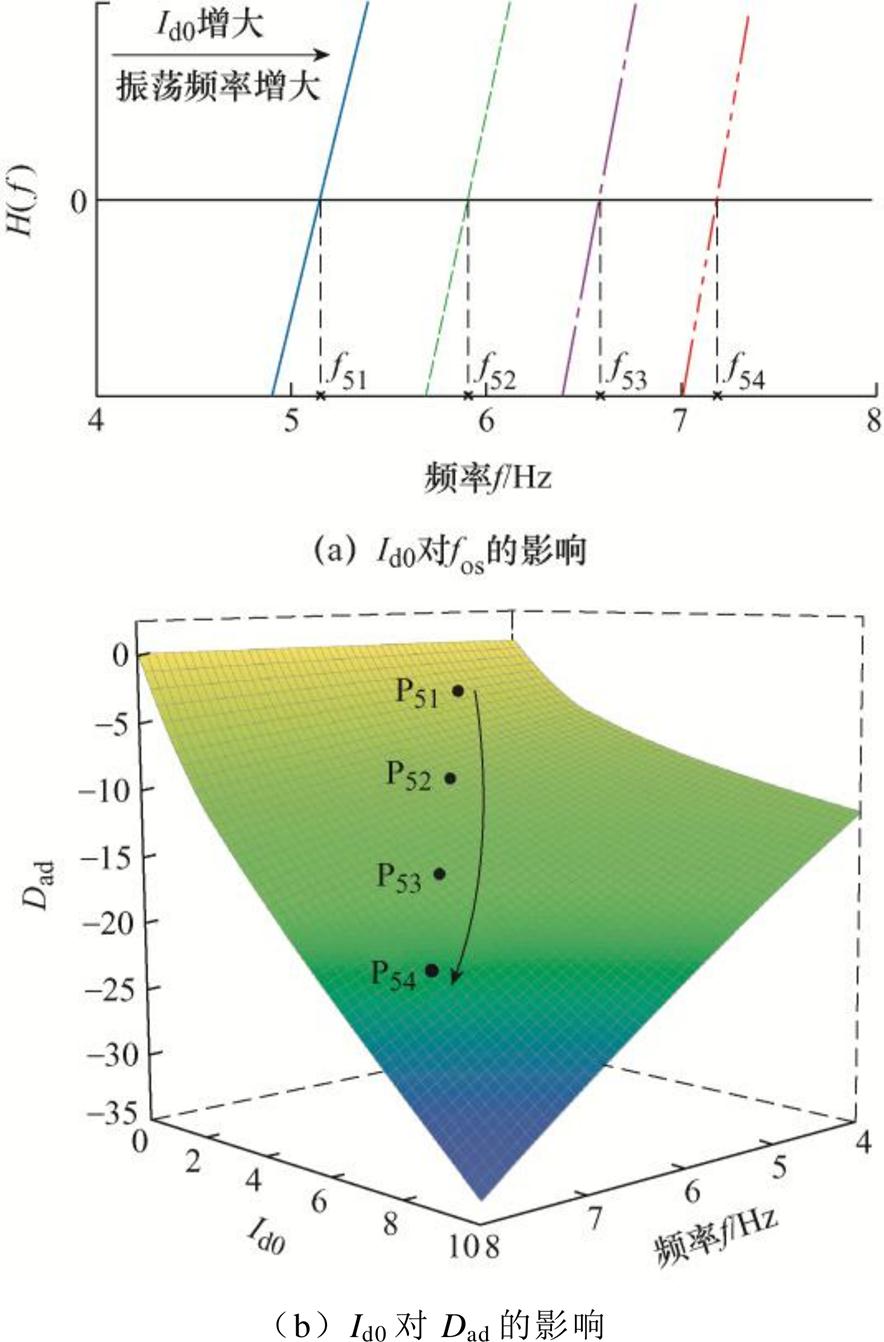
附图1 Id0增大时fos与Dad的变化趋势
App.Fig.1 The trend of fosand Dad when Id0 increases
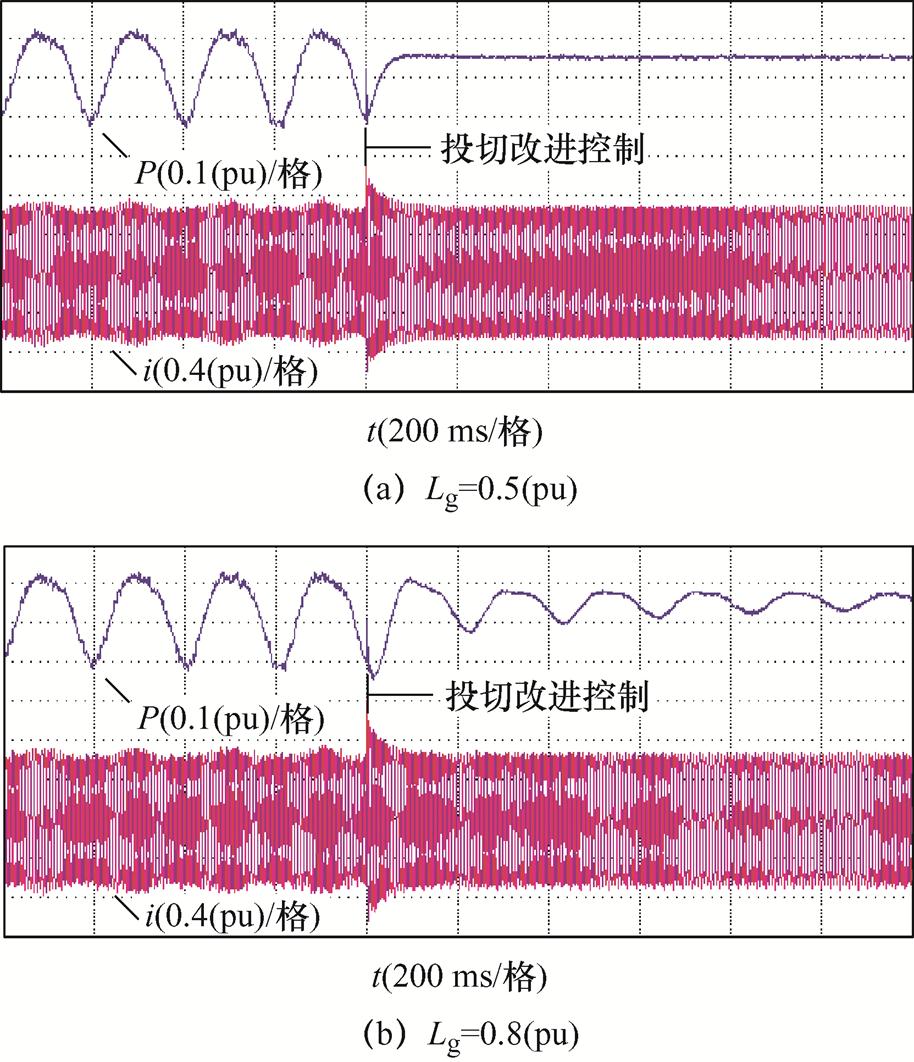
附图2 对比实验波形
App.Fig.2 Waveforms of comparison experiments
参考文献
[1] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low- frequency stability analysis of voltage-sourced doubly- fed wind power grid-connected system under small disturbance[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1312-1324, 1374.
[2] Tian Zhen, Li Xilin, Zha Xiaoming, et al. Transient synchronization stability of an islanded AC microgrid considering interactions between grid-forming and grid-following converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(4): 4463-4476.
[3] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548-5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan.Research on high bandwidth digital control LCL grid-connected inverter and its resonance suppression technology to improve the robustness of grid-connected system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[4] 颜湘武, 常文斐, 崔森, 等. 基于线性自抗扰控制的静止无功补偿器抑制弱交流风电系统次同步振荡策略[J]. 电工技术学报, 2022, 37(11): 2825-2836.
Yan Xiangwu, Chang Wenfei, Cui Sen, et al. Strategy of suppressing sub-synchronous oscillation of weak AC wind power system by static var compensator based on linear active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2825-2836.
[5] Liu C C, Yang Jingxi, Tse C K, et al. Transient syn- chronization stability of grid-following converters considering nonideal current loop[J]. IEEE Transac- tions on Power Electronics, 2023, 38(11): 13757-13769.
[6] Kroposki B, Johnson B, Zhang Yingchen, et al. Achieving a 100% renewable grid: operating electric power systems with extremely high levels of variable renewable energy[J]. IEEE Power and Energy Magazine, 2017, 15(2): 61-73.
[7] 高本锋, 王义, 曾四鸣, 等. 直驱风电场并入弱交流电网的次同步分量通路及阻尼特性分析[J]. 中国电机工程学报, 2022, 42(14): 5089-5103.
Gao Benfeng, Wang Yi, Zeng Siming, et al. Analysis of sub-synchronous component path and damping characteristics of D-PMSG-based wind farm incorporated into weak AC grid[J]. Proceedings of the CSEE, 2022, 42(14): 5089-5103.
[8] 胡宇飞, 田震, 查晓明, 等. 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J]. 电力系统自动化, 2022, 46(24): 121-131.
Hu Yufei, Tian Zhen, Zha Xiaoming, et al. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid- following converters[J]. Automation of Electric Power Systems, 2022, 46(24): 121-131.
[9] 王玉鹏, 严干贵, 穆钢, 等. 交流电流控制尺度下的并网VSC聚合建模研究[J]. 中国电机工程学报, 2022, 42(8): 2900-2910.
Wang Yupeng, Yan Gangui, Mu Gang, et al. Research on aggregation modeling of grid connected VSC under AC current control scale[J]. Proceedings of the CSEE, 2022, 42(8): 2900-2910.
[10] Zhao Zhuoli, Luo Xi, Wu Junhua, et al. Model reduction for grid-forming hybrid renewable energy microgrid clusters based on multi-timescale characterization[J]. IEEE Transactions on Smart Grid, 2024, 15(2): 1227-1242.
[11] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power elec- tronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[12] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758, 3768.
Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid- side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3745-3758, 3768.
[13] Zhang Boshen, Gao Fei, Zhang Yun, et al. An AC-DC coupled droop control strategy for VSC-based DC microgrids[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6568-6584.
[14] 李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一): 宽频带阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2019, 39(22): 6547-6562.
Li Guanghui, Wang Weisheng, Liu Chun, et al. Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part I): analysis of wideband impedance characteristics and oscillation mechanism[J]. Pro- ceedings of the CSEE, 2019, 39(22): 6547-6562.
[15] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid- tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547-5559.
[16] Zheng Wanning, Hu Jiabing, Yuan Xiaoming. Analytic quantification of interactions in MTDC systems based on self-/ en-stabilizing coefficients in DC voltage control timescale[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 2980-2991.
[17] Chang Yuanzhu, Hu Jiabing, Tang W, et al. Fault current analysis of type-3 WTs considering sequential switching of internal control and protection circuits in multi time scales during LVRT[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6894-6903.
[18] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528-3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528-3541.
[19] 胡祺, 付立军, 马凡, 等. 弱电网下基于锁相控制并网变换器小扰动同步稳定分析[J]. 中国电机工程学报, 2021, 41(1): 98-108,401.
Hu Qi, Fu Lijun, Ma Fan, et al. Small signal synchronizing stability analysis of PLL-based VSC connected to weak AC grid[J]. Proceedings of the CSEE, 2021, 41(1): 98-108, 401.
[20] Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. Stability enhancing voltage feed-forward inverter control method to reduce the effects of phase-locked loop and grid impedance[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3000-3009.
[21] Wang Dong, Liang Liang, Shi Lei, et al. Analysis of modal resonance between PLL and DC-link voltage control in weak-grid tied VSCs[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1127-1138.
[22] 黄云辉, 宋泽凡, 唐金锐, 等. 连接弱电网的并网变换器直流电压时间尺度稳定器的设计与分析[J]. 电工技术学报, 2018, 33(增刊1): 185-192.
Huang Yunhui, Song Zefan, Tang Jinrui, et al. Design and analysis of DC voltage time scale stabilizer for grid-connected converter connected to weak current network[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 185-192.
[23] Lin Xianfu, Yu Ruoxue, Yu Jingrong, et al. Constant- coupling-effect-based PLL for synchronization stability enhancement of grid-connected converter under weak grids[J]. IEEE Transactions on Industrial Electronics, 2023, 70(11): 11310-11323.
[24] Qian Qiang, Xie Shaojun, Xu Jinming, et al. Output impedance modeling of single-phase grid-tied inverters with capturing the frequency-coupling effect of PLL[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5479-5495.
[25] Huang Linbin, Xin Huanhai, Li Zhiyi, et al. Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J]. IEEE Transa- ctions on Smart Grid, 2020, 11(1): 501-516.
[26] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
Synchronization Stability Analysis and Enhanced Control of Grid-Following Converters under Multi-Timescale Control
Abstract In the new power systems with increasing penetration of renewable energy and power electronic devices, grid-following (GFL) converters synchronized by a phase-locked loop (PLL) suffer from inadequate damping due to complex control coupling, leading to potential synchronization instability issues. The control loops dominating the dynamic characteristics of the converter can be categorized into DC voltage and AC current timescales, possessing multi-timescale (MTS) features that exhibit strong coupling effects on system damping. However, traditional synchronization stability analysis methods focus on the impact of control on system damping at only one timescale. Thus, the analysis of system synchronous dynamics still needs to be completed. This paper proposes a synchronization stability analysis model, considering the multi-loop control's MTS characteristics. Through sensitivity analysis of system damping, the impact of different operating conditions and control parameters on system synchronization stability is intuitively analyzed.
Firstly, a synchronization stability analysis model that considers multiple timescales for GFL converters is established. The coupling paths and damping distribution patterns of each timescale control are revealed. Secondly, the influence of control parameters on damping characteristics is quantified using sensitivity analysis. The dominant factors causing synchronization instability in the system are identified, and their impact on system damping is visually represented through a three-dimensional graph. Additionally, according to the influence of grid impedance change and grid voltage drop on control coupling, the mechanism of system instability under various conditions is analyzed from a damping perspective. Finally, an improved control strategy based on terminal voltage feedforward for damping reshaping is proposed to mitigate the adverse damping effects of MTS control coupling.
Simulation and experimental results demonstrate that under weak grid conditions, considering the effects of MTS coupling, step changes in active power reference values, an increase in grid impedance, and voltage drops in the grid can lead to sub-synchronous oscillations in the GFL converter system. The proposed improved control can suppress such oscillations, improving system synchronization stability.
The following conclusions can be drawn from theoretical analysis and experiments. (1) The essential nature of the multi-loop control coupling in GFL converters is the frequency band overlap in the timescale, manifesting as MTS characteristics, significantly impacting the synchronization stability of the system. (2) Among the multi-loop control parameters, the dominant factors significantly affecting the system's synchronous characteristics are kp_pll and kp_tvc. Reducing kp_pll or increasing kp_tvc can mitigate adverse damping effects, enhance total system damping, and improve system synchronization performance. (3) Operating conditions, such as an increase in grid impedance, voltage drops in the grid, and internal dq coupling in DC voltage timescales, may exacerbate negative damping effects, potentially causing system synchronization instability. (4) The proposed improved control scheme effectively eliminates the impact of internal dq coupling in DC voltage timescales while significantly reducing adverse damping characteristics, thereby enhancing the synchronization stability of the MTS control system
Keywords:Multi-timescale control, damping characteristics, synchronous oscillation, sensitivity analysis, damping reshaping
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.231732
国家自然科学基金(52207106,52377172)和广西自然科学基金(2021GXNSFAA220132)资助项目。
收稿日期 2023-10-18
改稿日期 2023-12-23
梁军杨 男,1998年生,硕士研究生,研究方向为新能源并网系统的控制与稳定性分析。
E-mail: jamux_liang@163.com
陈延明 男,1966年生,博士生导师,教授,研究方向为新能源发电技术。
E-mail: yanmingchen@126.com(通信作者)
(编辑 陈 诚)