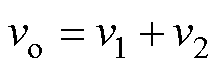（1）
摘要 多电平逆变器具有输出电压谐波含量少、开关器件电压应力低、等效开关频率高等优点，广泛应用于新能源发电场合。悬浮电容H桥级联七电平逆变器，因开关频率低、器件数量少、输出电平数量多得到广泛的关注。为了降低损耗，使H桥逆变单元开关管以低开关频率动作，悬浮电容逆变单元开关管以高开关频率动作，但是会引起过调制和悬浮电容电压失控的问题。为解决过调制问题，该文提出基于调制波分解的混合载波频率调制策略，增加过调制区间的调制过程，分解悬浮电容逆变单元超出载波部分的调制波，使H桥逆变单元开关管以低开关频率运行；同时提出基于工作模式切换的有功功率分解控制，详细分析两种工作模式下的稳压控制原理，根据电容电压的状态改变悬浮电容逆变单元有功功率大小，实现不同工况下悬浮电容电压均衡。最后通过仿真和实验验证了所提调制策略的正确性。
关键词：七电平逆变器 H桥级联 混合载波频率 调制波分解 悬浮电容电压均衡控制
多电平逆变器具有开关应力低、等效开关频率高、输出谐波含量低等优点，在光伏发电、电机驱动、有源电力滤波器等工业、商业领域得到了广泛的应用[1-5]。目前，出现了一些混合七电平拓扑结 构[6-8]，其中，悬浮电容H桥级联七电平逆变器（Seven-Level Flying-Capacitor Cascaded H-Bridge Inverter, 7L-FCCHB）器件数量少、结构简单，选用耐压等级低的器件即可实现较高的开关频率，开关损耗低，减小了滤波器体积，扩大了应用范围[9-11]。
当前，学者们针对7L-FCCHB提出了大量的调制策略，根据开关频率的不同，应用于级联H桥逆变器拓扑的调制策略分为低频调制、高频调制和混合调制[12-13]。其中低频调制主要包括阶梯波合成 法[14]和特定谐波消除法[15]，虽然开关频率低，开关损耗小，但是逆变器输出电平数目较少时，输出电压谐波含量仍然比较高。高频调制策略主要包含载波层叠调制策略[16]和载波移相调制策略[17]，两个桥臂的开关管均以高频动作实现了逆变器七电平输出，谐波含量少，但是开关频率高、开关损耗大。为了降低开关频率同时降低逆变器输出谐波含量，悬浮电容H桥级联多电平逆变器常采用混合调制策略，文献[18]使电压等级高的单元采用低频调制，电压等级低的单元工作于高频调制，但是该方法只适用于悬浮电容电压期望值等于直流源电压值的情况，其余情况会使悬浮电容桥臂出现过调制问题。为解决过调制问题，文献[19]提出了一种新的调制策略，增加额外的采样电路来采样H桥逆变单元输出电压，根据采样结果计算低压单元调制波信号，但是控制复杂。文献[20]提出一种基于调制重组的改进型调制策略，分解问题区间的调制波，调整高、低压单元的调制过程，可有效解决低压单元过调制问题，但是调制范围窄。
控制悬浮电容电压均衡至关重要，但悬浮电容电压的调节同时受调制度和负载功率因数的影响，实现悬浮电容电压均衡较为困难[21]。已经有多种方法实现电容电压均衡，其中一种是通过硬件方式实现，文献[22-23]在悬浮电容前级采用多绕组环形变压器，从单个直流源得到不对称电压源，从而使级联型H桥逆变器输出多电平电压。变压器的引入有助于输入输出电流隔离和提高电压增益，但增大了系统体积。文献[24-25]在逆变器中额外增加了辅助反激变换器，用于将悬浮电容电压调节到独立直流电源电压的1/2，但额外的电路又增加了成本和损耗。
采用控制的方法可以在不增加额外的电路的情况下实现悬浮电容电压均衡，文献[26]利用冗余开关状态实现悬浮电容电压均衡，选择不同电平组合控制电容充放电[26]，虽然利用冗余开关状态可以调节电容电压大小，但是逆变器的输出电流和冗余开关状态的持续时间会影响电容的充放电模式；文献[27]提出了一种基于相移控制电容电压均衡的方法，通过PI控制H桥逆变单元导通角，实现悬浮电容电压均衡，但该控制策略无法负载功率因数为0时保证电容电压均衡。为实现不同工况下的悬浮电容电压均衡，文献[28-29]对不同工况下的电容充放电情况进行分析，根据不同的工作模式切换控制状态，实现对悬浮电容不同的充放电效果，但是该方案是在冗余开关状态控制悬浮电容电压均衡基础上提出的。目前还缺乏一种简单有效的电容电压调节方法，既能兼顾降低开关频率与减小输出电压谐波，又能实现不同工况下悬浮电容电压均衡的控制策略、简化调制策略。
针对悬浮电容H桥级联七电平逆变器，为在降低开关频率的情况下解决过调制问题，同时实现不同工况下悬浮电容电压均衡，本文首先提出了一种基于调制波分解的混合载波频率调制策略，使H桥逆变单元以低开关频率运行；然后，详细分析不同工作模式对电容充放电的影响，提出基于工作模式切换的有功功率分解控制，所提方法输出谐波含量低，降低了H桥逆变单元开关频率，并实现了悬浮电容电压均衡；最后，本文通过仿真和实验验证了所提控制策略的正确性和可行性。
悬浮电容H桥级联七电平逆变器拓扑结构如图1所示，该拓扑由1个H桥逆变电路（称作H桥逆变单元）和1个悬浮电容H桥（称作悬浮电容逆变单元）级联而成。H桥逆变单元使用直流源供电；悬浮电容逆变单元直流侧接悬浮电容，控制悬浮电容电压值VC为直流电压源电压值Vdc的一半；逆变器的输出电压vo可以表示为
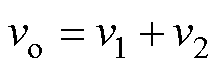（1）
式中，v1为H桥逆变单元输出电压；v2为悬浮电容逆变单元输出电压。逆变器输出等于两个桥臂的调制波之和。
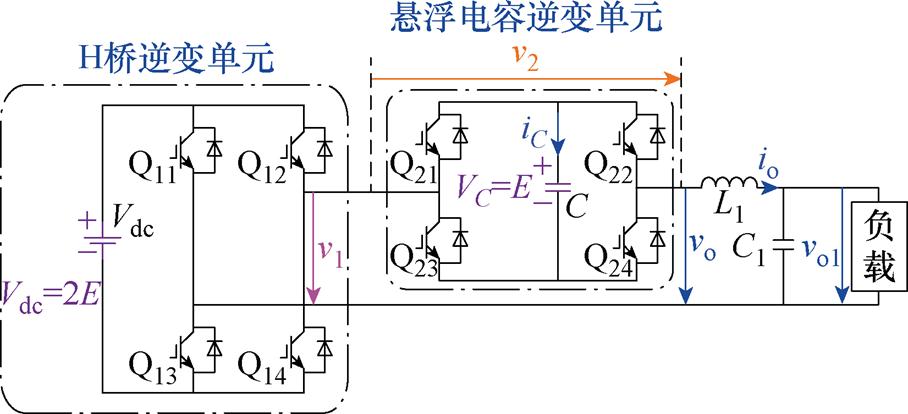
图1 悬浮电容H桥级联七电平逆变器拓扑
Fig.1 Topology of seven-level flying-capacitor cascaded H-bridge inverter
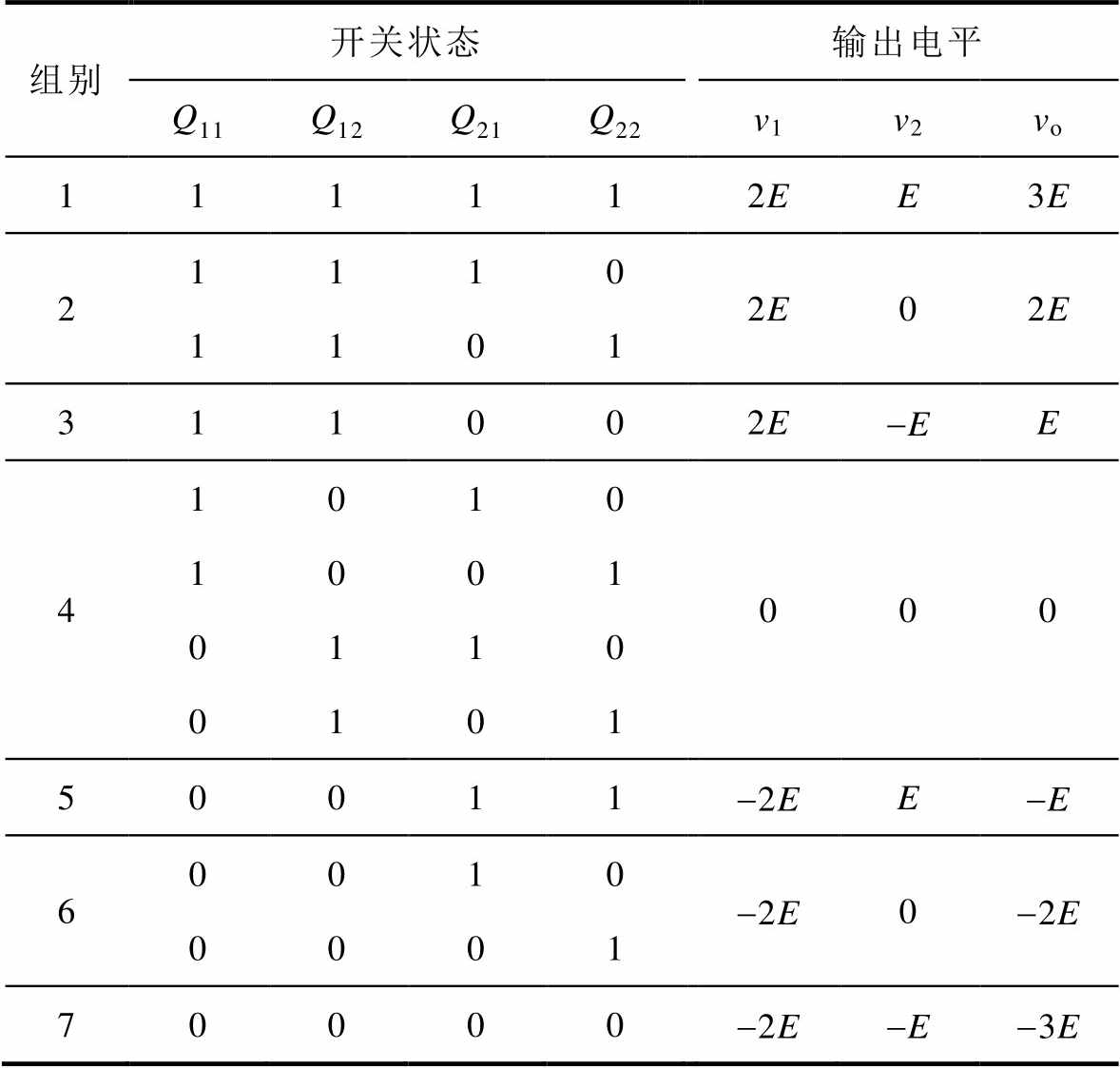
表1给出了逆变器输出七电平的合成方式，并列出了不同输出电平对应的开关状态，“1”表示导通，“0”表示关断。从表1中可以看出，在合成电平数时，H桥逆变单元可以以基频动作，输出基波，悬浮电容逆变单元可以以PWM频率高频动作。
表1 逆变器输出七电平合成方式
Tab.1 Inverter output 7-level synthesis method
组别开关状态输出电平 Q11Q12Q21Q22v1v2vo 111112EE3E 211102E02E 1101 311002E-EE 41010000 1001 0110 0101 50011-2EE-E 60010-2E0-2E 0001 70000-2E-E-3E
图2所示为适用于7 L-FCCHB的混合载波频率调制策略原理[30]，其中H桥逆变单元采用基频调制，悬浮电容逆变单元采用PWM。但是该调制方法受调制度影响，会发生过调制。图2中，vo1为逆变器期望的输出电压，该电压波形为正弦波形，其幅值为Vm，v2r为悬浮电容逆变单元的期望输出电压。
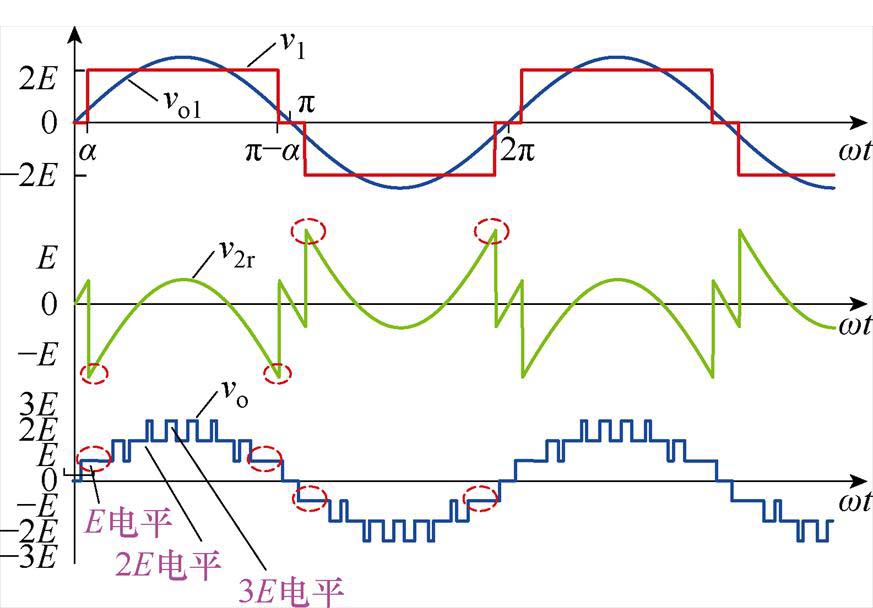
图2 混合载波频率调制策略
Fig.2 Hybrid carrier frequency modulation strategy
为了简化混合调制策略原理分析的描述，做出合理的假设：由于悬浮电容逆变单元采用PWM控制，工作在高频模式，因此假设悬浮电容逆变单元的输出电压等于该调制波波形，即v2(t)=v2r。
由于H桥逆变单元输出电压的频率等于逆变器期望输出电压的频率，且H桥逆变单元输出电压基波幅值为逆变器期望输出的电压幅值。则H桥逆变单元的导通角a 为
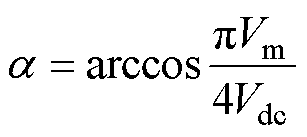（2）
由拓扑工作原理和式（1）可知，逆变器输出电压的剩余部分，即图2中的v2r波形，需要由悬浮电容逆变单元合成，因此悬浮电容逆变单元的期望输出电压可以描述为
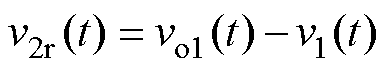（3）
由上述分析可知，H桥逆变单元工作于基频开关状态，H桥逆变单元输出电压的傅里叶级数v1(t)的表达式为
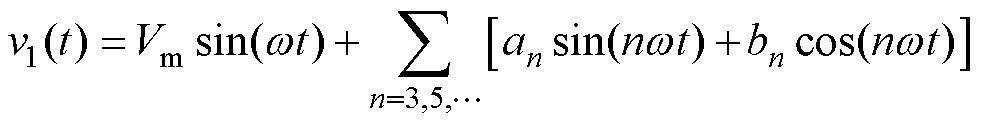
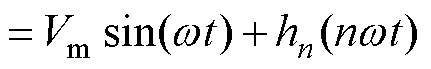（4）
式中，hn(nwt)为此时H桥逆变单元输出的除基波外的所有谐波。将高频率的单极性PWM技术应用于悬浮电容逆变单元，以实现期望输出的电压v2r。因此，悬浮逆变单元输出电压的傅里叶级数v2(t)的表达式为
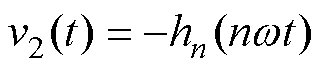（5）
由式（4）和式（5）可知，悬浮逆变单元不产生有功功率，可通过分解H桥逆变单元产生的有功功率实现悬浮电容电压均衡。
观察图2，在H桥逆变单元的开关瞬间，wt=a, p-a, p+a 和2p-a 时，悬浮电容逆变单元输出将达到峰值，将wt代入式（2），可以计算悬浮电容逆变单元在a 处的输出电压幅值va-和va+为
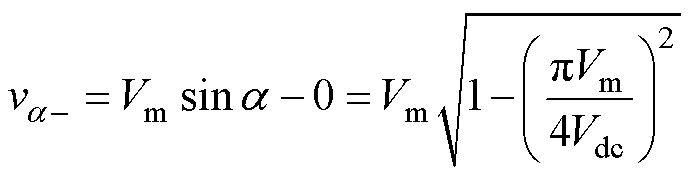（6）
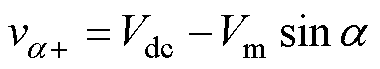（7）
为保证悬浮电容逆变单元不过调制，va-和va+应不超过悬浮电容电压值Vdc。
另外，由调制度m的定义和式（2）可知
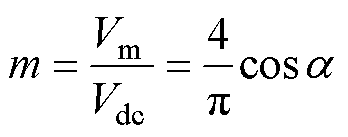（8）
因此，调制度m范围为0＜m≤1.27。
综合式（6）～式（8），得到过调制范围如图3所示。由图3可知，当导通角a 和调制度m变化时，悬浮电容逆变单元的调制波幅值也会随之变化，因此，a 值或者m值变化，都有可能导致悬浮电容逆变单元调制波幅值超过悬浮电容电压值，此时悬浮电容逆变单元会在图2中的E电平处发生过调制，当调制度m在 (0.56, 1.14) 区间时，va-大于电容电压值E；当调制度m在其余区间时，va+大于电容电压值E，因此采用7L-FCCHB逆变器拓扑时，混合调制策略在整个可能的调制度范围内可能会引起悬浮电容逆变单元发生过调制。如果不采取额外的解决方案，过调制的出现会增加逆变器输出电压谐波含量。
图3 过调制范围
Fig.3 Over-modulation range
为从根本上解决过调制问题，本文提出基于调制波分解的混合载波频率调制策略，针对图2中的E电平过调制情况，增加E电平所在区间的调制过程，分解悬浮电容逆变单元超出载波部分的调制波，同时对H桥逆变单元和悬浮电容逆变单元过调制部分的调制波进行调整，使H桥逆变单元输出2E、0电平，悬浮电容单元输出-E、E电平，实现E电平正常输出，具体原理如图4所示。图4a中，UcH、Uch为同频、相位差90°的载波，分别位于[-2E, 2E]和[-E, E]层域，UcH用于H桥逆变单元调制、Uch用于悬浮电容逆变单元调制；vref1、vref2分别为分解后的H桥逆变单元的调制波和悬浮电容逆变单元的调制波；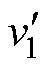
为采用该调制策略下的H桥逆变单元输出电压波形；
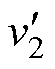为采用该调制策略下的悬浮电容逆变单元输出电压波形，[a1, a2]、[p-a2, p-a1]、[p+a1, p+a2]、[2p-a2, 2p-a1]均为互补区域；图4b中，UcH、Uch为同频同相的载波，其余变量定义与图2一致，其中H桥逆变单元调制波和悬浮电容逆变单元调制波满足
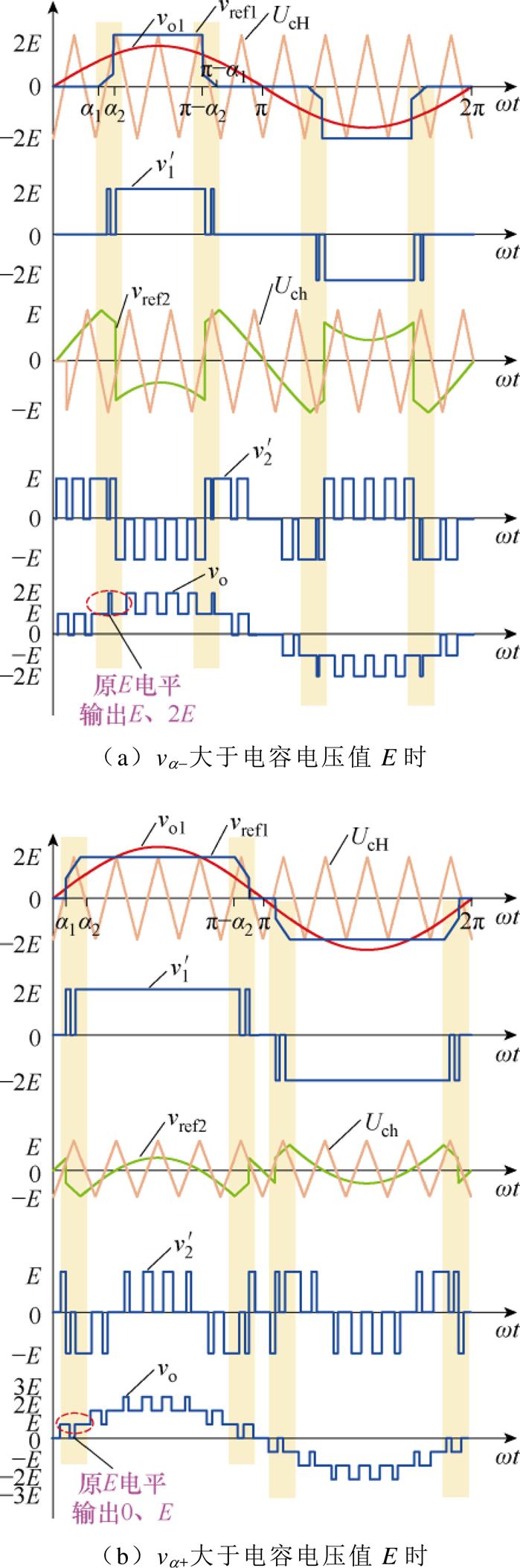
图4 基于调制波分解的混合载波频率调制策略
Fig.4 Hybrid carrier frequency modulation strategy based on modulation wave decomposition
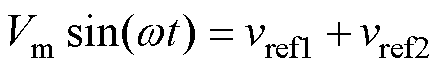（9）
所提策略下，H桥逆变单元在分解后的区间，采用调制波反相的倍频单极性调制方法使H桥逆变单元开关管以高频动作，开关管Q11和Q12采用了幅值相等但相位相差180°的调制波信号，令vref1-为vref1反相后的调制波，在任何一个载波周期内，开关管Q11和Q12的调制波信号与载波均有两个交点：当vref1≥UcH时，驱动开关管Q11导通，反之Q13导通；当vref1-≥UcH时，驱动开关管Q12导通，反之Q14导通。图4中，阴影区域为采用减法分解后的互补区域，H桥逆变单元在该区域做高频变换，输出电压波形为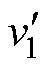，输出基波仍为Vm。
所提策略下，悬浮电容逆变单元在全部区间内采用倍频单极性调制，开关管Q21和Q22采用了幅值相等但相位相差180°的调制波信号vref2和vref2-，调制原理与前述一致。
由前述分析可知，wt在[a1, a2]、[p-a2, p-a1]、[p+a1, p+a2]、[2p-a2, 2p-a1]这些互补区域时，悬浮电容逆变单元会发生过调制，设分解前过调制部分的调制信号H为
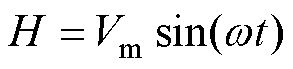（10）
根据上述原理，得到调制策略流程如图5所示，图中列出了1/4周期时修改后的调制波表达式，其余周期的表达式可由波形的对称性得出。
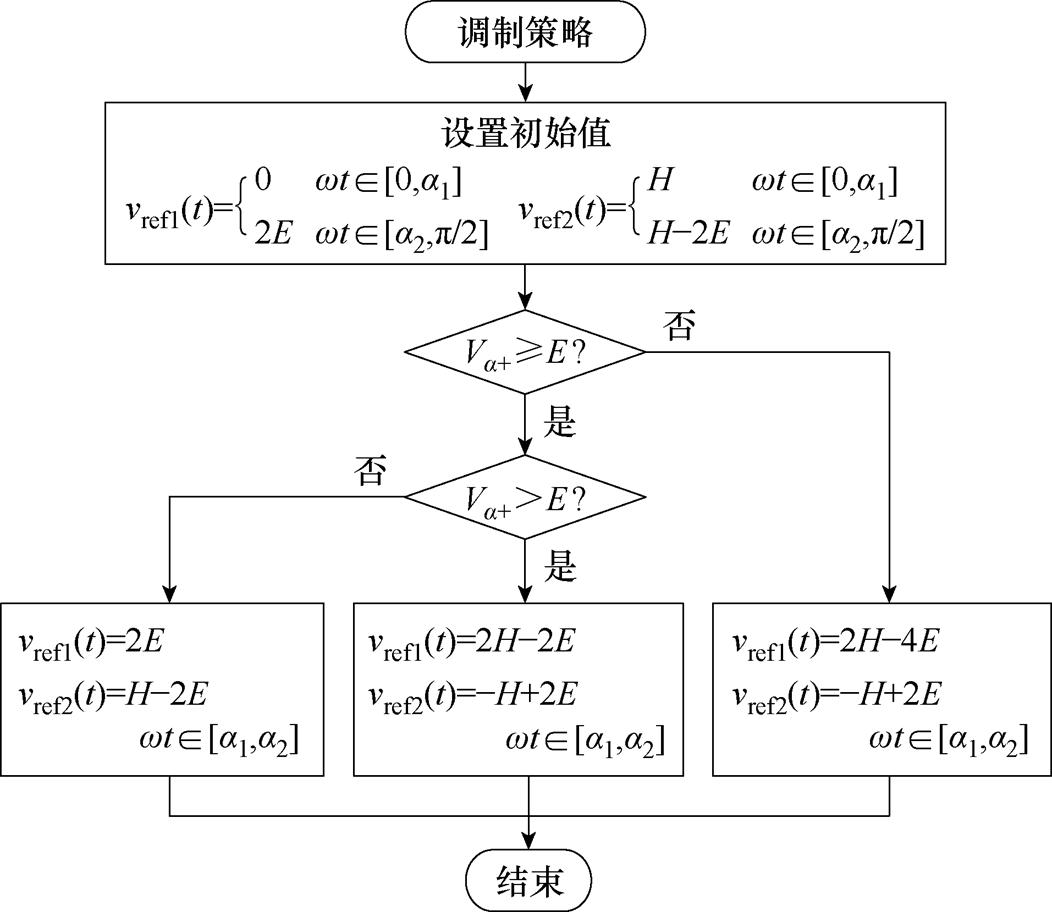
图5 基于调制波分解的混合载波频率调制策略流程
Fig.5 Hybrid carrier frequency modulation strategy based on modulation wave decomposition flow chart
对比图2和图4可知，基于调制波分解的混合载波频率调制策略仅在过调制区间改变H桥逆变单元和悬浮电容逆变单元的输出，使逆变器输出无过调制问题。而在其余区间内，图2和图4中的输出一致。因此，采用基于调制波分解调制策略可以使逆变器的输出符合期望情况。
基于调制波分解的混合载波频率调制策略的本质是增加过调制区间的调制过程，分解过调制区间的调制波，调整调制过程，对互补区域采用高频调制实现E电平，如图4所示。随着阴影部分互补区域[a1, a2]增加，H桥逆变单元开关频率随之增加，因此，分析不同工况下的互补区域大小即可分析H桥逆变单元开关频率。结合式（6）和式（7）可知，va-大于电容电压基准值E时互补区域可由式（11）表示，va+大于电容电压基准值E时互补区域可由式（12）表示。
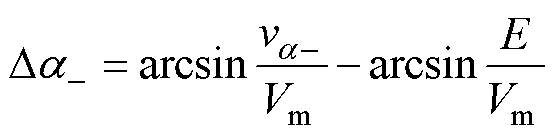（11）
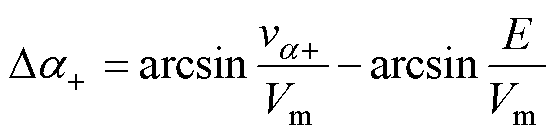（12）
由式（6）～式（8）、式（11）和式（12），可得到不同工况下互补区域随调制度变化的关系曲线如图6所示。
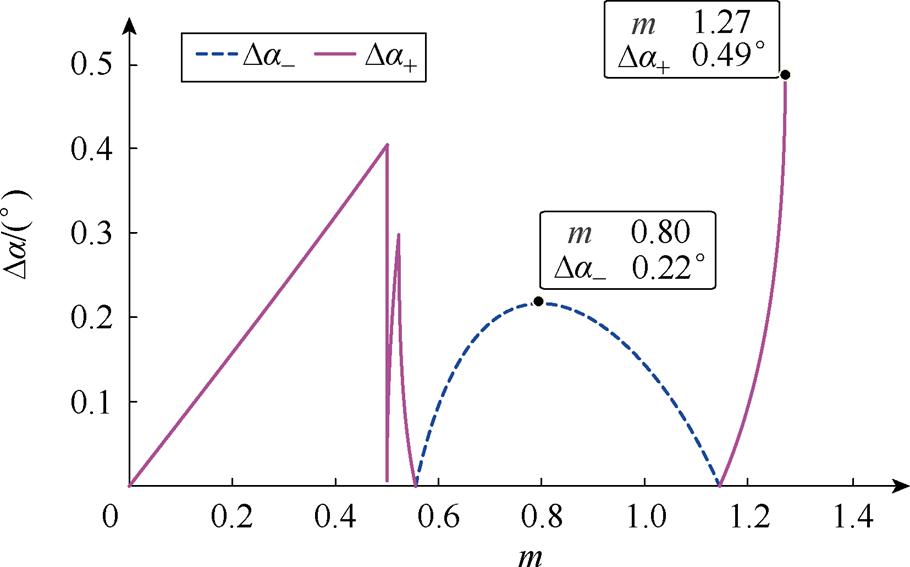
图6 不同工况下互补区域随调制度变化的关系曲线
Fig.6 Relationship curves of complementary regions under different working conditions
理想的情况下H桥逆变单元调制波一直过调制，开关管以工频动作，但是这样会导致有些工况下悬浮电容逆变单元过调制。因此H桥逆变单元应尽量保持过调制，只是在特定区域内未过调制的开关管以高频动作降低开关频率。由图6可看出，调制度m达到最大值1.27时，互补区域值达到最大值，此时逆变器输出为七电平，H桥逆变单元开关频率将达到最大值。由于H桥逆变单元在互补区域做倍频单极性调制，可以得出当Da+=0.49°，载波频率为fs时，H桥逆变单元开关频率为0.32fs，当式（11）和式（12）达到最小值，即Da-=Da+=0时，逆变器输出不发生过调制，此时H桥逆变单元开关频率将达到最小为工频50 Hz，因此H桥逆变单元开关频率范围为[50 Hz, 0.32fs]，远小于载波频率。
为实现电容电压均衡，提出有功功率分解控制策略。基于上述分析，H桥逆变单元输出电压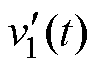
波形的傅里叶级数的表达式为
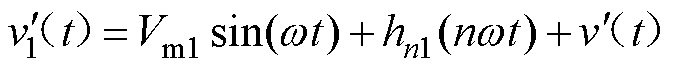（13）
式中，Vm1sin(wt)为H桥逆变单元做工频变换时输出的基波部分，Vm1为基波幅值；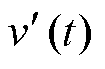
为H桥逆变单元开关管以高频动作时的输出电压；hn1(nwt)为此时H桥逆变单元输出的谐波部分。H桥逆变单元输出基波仍为Vm。
由拓扑工作原理可知，输出电压的剩余部分由悬浮电容逆变单元采用高频PWM策略合成，因此悬浮电容逆变单元期望电压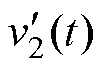
的表达式为
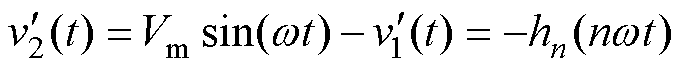（14）
对于一般情况，假设负载功率因数角为q (q∈ [-p, p])，则输出电流可表示为
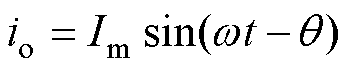（15）
由式（14）可知，在桥臂无损耗情况下，悬浮电容逆变单元平均输出功率P2为谐波在一个周期内发出的平均功率，悬浮电容逆变单元平均输出功率为0，H桥逆变单元平均输出功率等于逆变器输出功率，即
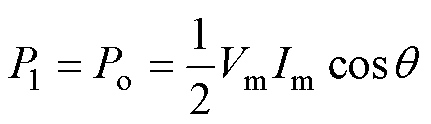（16）
由式（13）～式（15）可知，悬浮电容逆变单元平均输出功率P2可以表示为
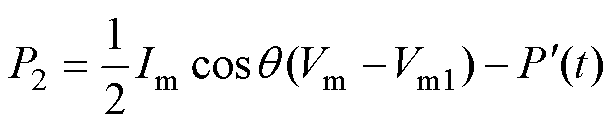（17）
式中，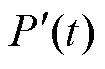
为H桥逆变单元开关管以高频动作时输出的有功功率。
由式（17）可知，通过调节H桥逆变单元互补区域中的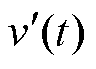
的大小，可间接改变悬浮电容逆变单元平均输出功率P2大小，具体的悬浮电容电压均衡开环控制方案如图7所示。根据逆变器的工作原理，当互补区域发生变化时，H桥逆变单元调制波vref1会随之变化，即H桥逆变单元输出有功功率会变化。由于vo1不变，为保持逆变器输出功率Po不变，悬浮电容逆变单元调制波随之改变，即将根据H桥逆变单元输出功率p1(t)的变化。调整瞬时有功功率p2(t)的大小，当H桥逆变单元中产生的有功功率大于传递给负载的功率时，剩余的功率将被传送到悬浮电容逆变单元，从而给悬浮电容逆变单元上的悬浮电容充电；当H桥逆变单元中产生的有功功率小于传递给负载的功率时，悬浮电容逆变单元输出有功功率，从而使悬浮电容逆变单元上的悬浮电容放电。
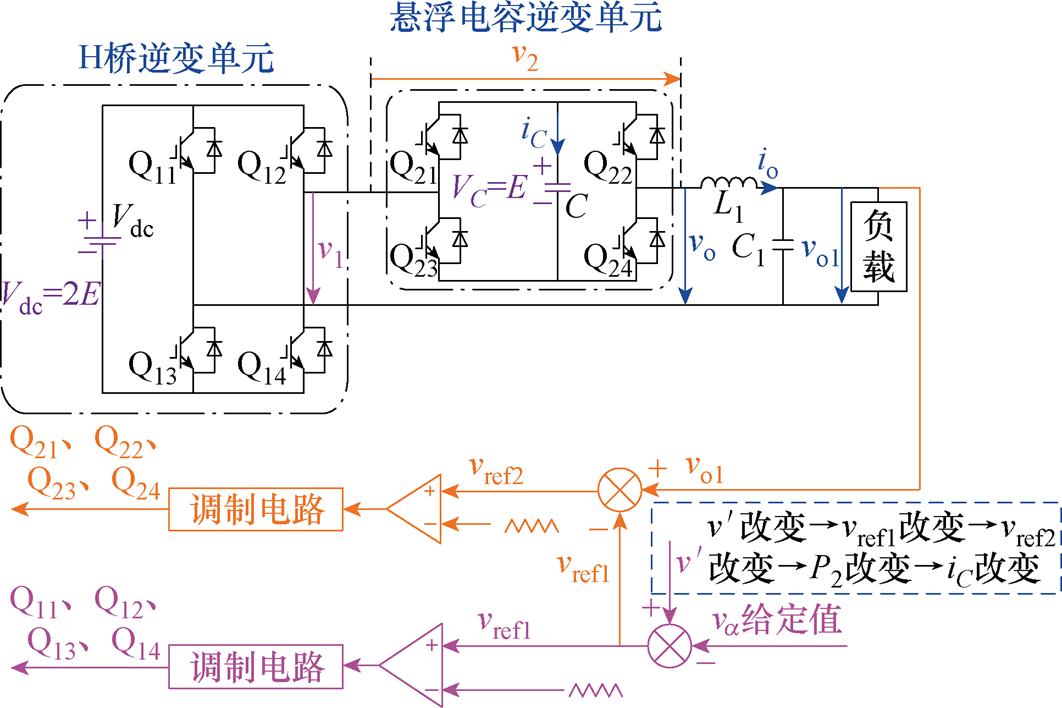
图7 有功功率分解开环控制
Fig.7 Open-loop control diagram for active power decomposition
基于上述原理，可以设计电容电压均衡调节的闭环控制系统，调节H桥逆变单元注入系统中的有功功率实现电容电压均衡。但是电压过零点时，电流方向、大小对悬浮电容电压均衡影响不同，为了实现不同工作模式下悬浮电容电压的均衡，先分析不同工作模式下电容电压充放电情况。
1）工作模式1
该模式下，当逆变器输出电压在正半周过零点时，电流io≤0：当p2(t)＜0时，悬浮电容逆变单元吸收有功功率，iC＞0，控制悬浮电容逆变单元的直流侧悬浮电容将工作于充电状态；当p2(t)＞0时，悬浮电容逆变单元输出有功功率，iC＜0，控制悬浮电容逆变单元的直流侧悬浮电容将工作于放电状态。
当电压vo1在正半周过零点输出电流值io＜0时，互补区域[a1, a2]对悬浮电容电压供电的影响如图8a～图8c所示。当互补区域[a1, a2]不变时，如图8a所示，悬浮电容逆变单元有功功率的平均值为零（p2=0），因此，悬浮电容既不会充电也不会放电；互补区域[a1, a2]减小，输出电流io不变，H桥有功功率增加，悬浮电容逆变单元有功功率P2(t)＜0，在这种情况下，悬浮电容吸收能量，充电，如图8b所示；当互补区域[a1, a2]增加时，悬浮电容逆变单元有功功率P2(t)＞0，因此，悬浮电容放电，如图8c所示。
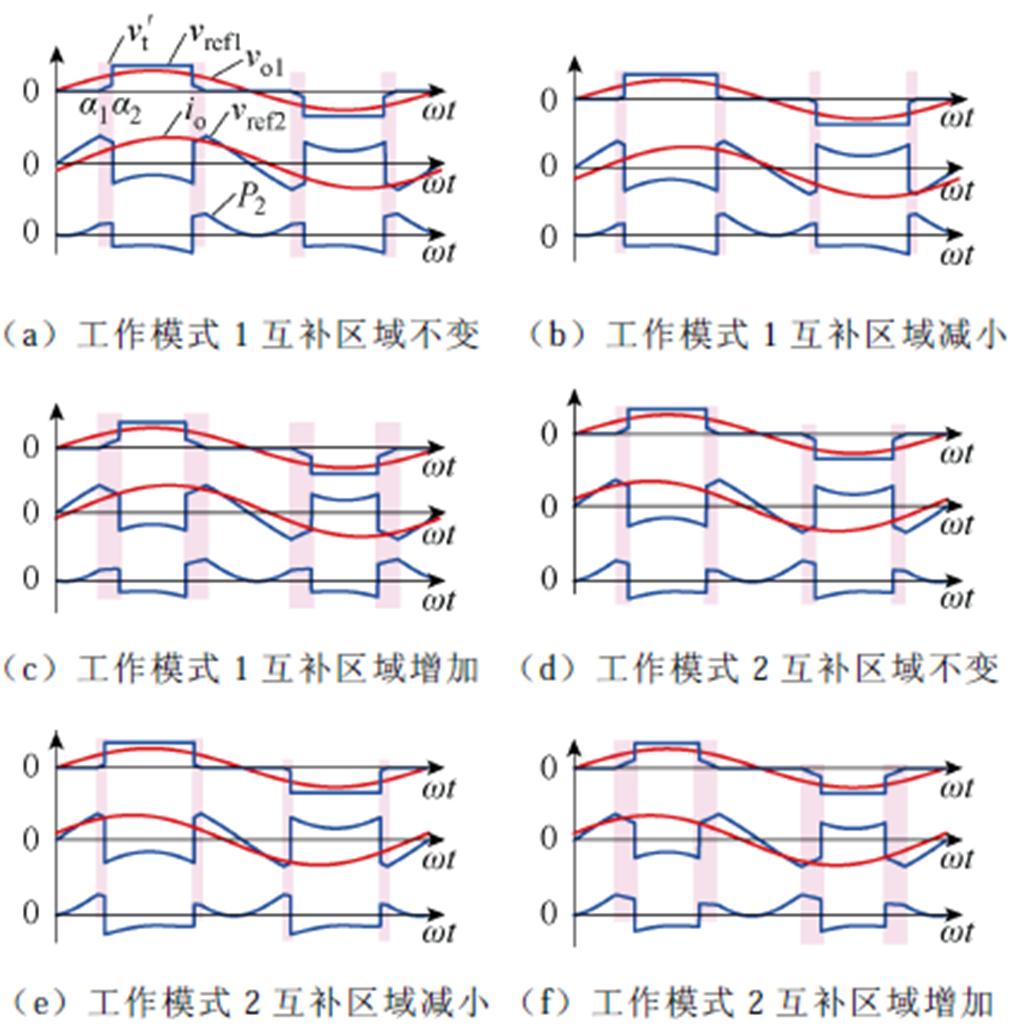
图8 不同工作模式时互补区域影响
Fig.8 Complementary region influence of different modes
2）工作模式2
在这种情况下，当逆变器输出电压在正半周过零点时，电流io＞0：当p2(t)＜0时，悬浮电容逆变单元输出有功功率，iC＜0，控制悬浮电容逆变单元的直流侧悬浮电容将工作于放电状态；当p2(t)＞0时，悬浮电容逆变单元吸收有功功率，iC＞0，控制悬浮电容逆变单元的直流侧悬浮电容将工作于充电状态。
当电压vo1在正半周过零点输出电流io＞0时，互补区域[a1, a2]对悬浮电容电压供电的影响与上述讨论类似，如图8d～图8f所示。当互补区域[a1, a2]不变时，悬浮电容既不会充电也不会放电（图8d）；互补区域[a1, a2]减小，悬浮电容放电（图8e）；当互补区域[a1, a2]增加时，悬浮电容放电（图8f）。
为实现上述效果，设计基于工作模式切换的电容调压系统闭环控制方案如图9所示。先由过零点比较程序检测电压由逆变器输出电压在正半周过零点时，电流值的大小，若电流值io≤0，采用给定电容电压基准值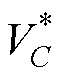
，与实时采样电容电压实际值VC做差得到DVC，经过PI控制器得到所要调节的占空比，从而调节H桥逆变单元的输出电压，调节有功功率大小，如当充电时，DVC增加，H桥逆变单元瞬时有功功率增加，[a1, a2]区域减小，H桥逆变单元开关频率降低，悬浮电容逆变单元输出负的有功功率，控制悬浮电容电压充电；反之，当DVC减小时，控制悬浮电容电压放电；如此能够控制悬浮电容电压实际值趋向于基准值。
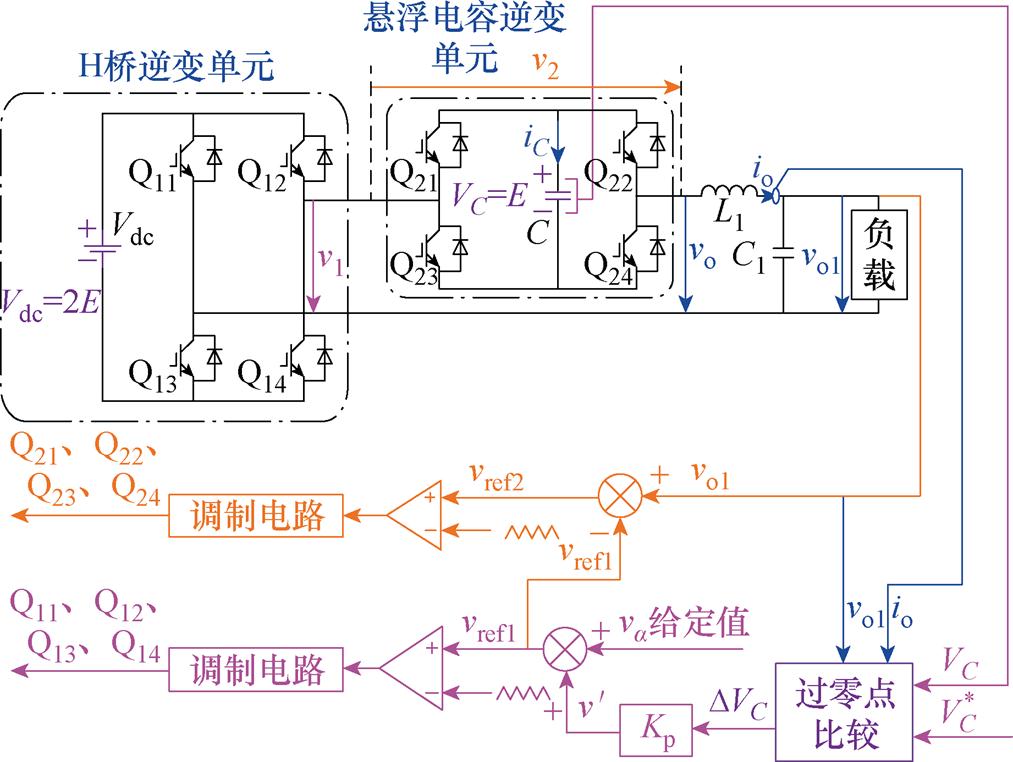
图9 基于工作模式切换的电容调压系统控制策略
Fig.9 Closed-loop control strategy of the capacitor voltage regulation system based on working mode switching
若电流io＞0，设计控制方案与工作模式1相反，如当充电时，DVC减小，H桥逆变单元瞬时有功功率减小，[a1, a2]区域增加，H桥逆变单元开关频率增加，悬浮电容逆变单元输出正的有功功率，控制悬浮电容电压充电；反之，当DVC增加时，控制悬浮电容逆变单元悬浮电容电压放电；如此来实现悬浮电容电压均衡。
综上所述，该方法用当前逆变器输出电压值减去上一次的电压值，将差值与检测得到的逆变器输出电流相乘，所得信号的极性若为非负，则控制逆变器工作于处于工作模式1时的状态，否则工作于处于工作模式2时的状态。
为了验证本文所提调控策略的正确性，基于Matlab/Simulink平台进行仿真研究。仿真参数设置见表2。图10为不同调制度下的逆变器输出电压vo，H桥逆变单元输出电压v1和悬浮电容逆变单元输出电压v2波形，图10a给出了m=0.78时的仿真结果；图10b给出了m=1.22时的仿真结果；图10c给出了m=1.14时的仿真结果。由图10可知，该逆变器在不同调制区间时均不会发生过调制，与理论分析一致。
表2 仿真参数
Tab.2 Simulation parameters
参 数数 值 输入直流电压Vdc/V400 悬浮电容基准电压/V200 悬浮电容值C/mF10 额定功率Pe/W1 000 输出频率fo/Hz50 负载R/W50 L2/mH5 C2/mF10 滤波电感值L1/mH5 滤波电容值C1/mF5 载波频率fs/kHz20 调制比m0＜m≤1.27 输出电压范围vo/V0＜vo≤508 控制器比例参数Kp5
图11给出了采用调制波分解法m=0.78时输出电压的频谱图。由图可知，输出电压谐波主要分布于2倍载波频次，因此实现逆变器的2倍频调制。
图12给出了m=0.78时，不同工作模式下的悬浮电容电压波形和逆变器的输出波形。图12a给出了阻感性负载时的仿真结果（逆变器工作于工作模式1），图12b给出了阻容性负载时的仿真结果（逆变器工作于工作模式2），图12c给出了一个纯阻性负载时的仿真结果（逆变器工作于工作模式1）。由图可知，在不同工作模式下悬浮电容电压均稳定，电容电压纹波小于3%，表明电容调压控制通过改变互补区域大小成功地实现了悬浮电容电压均衡，稳压效果好，输出波形正弦度高，输出电压电流波形质量优良。
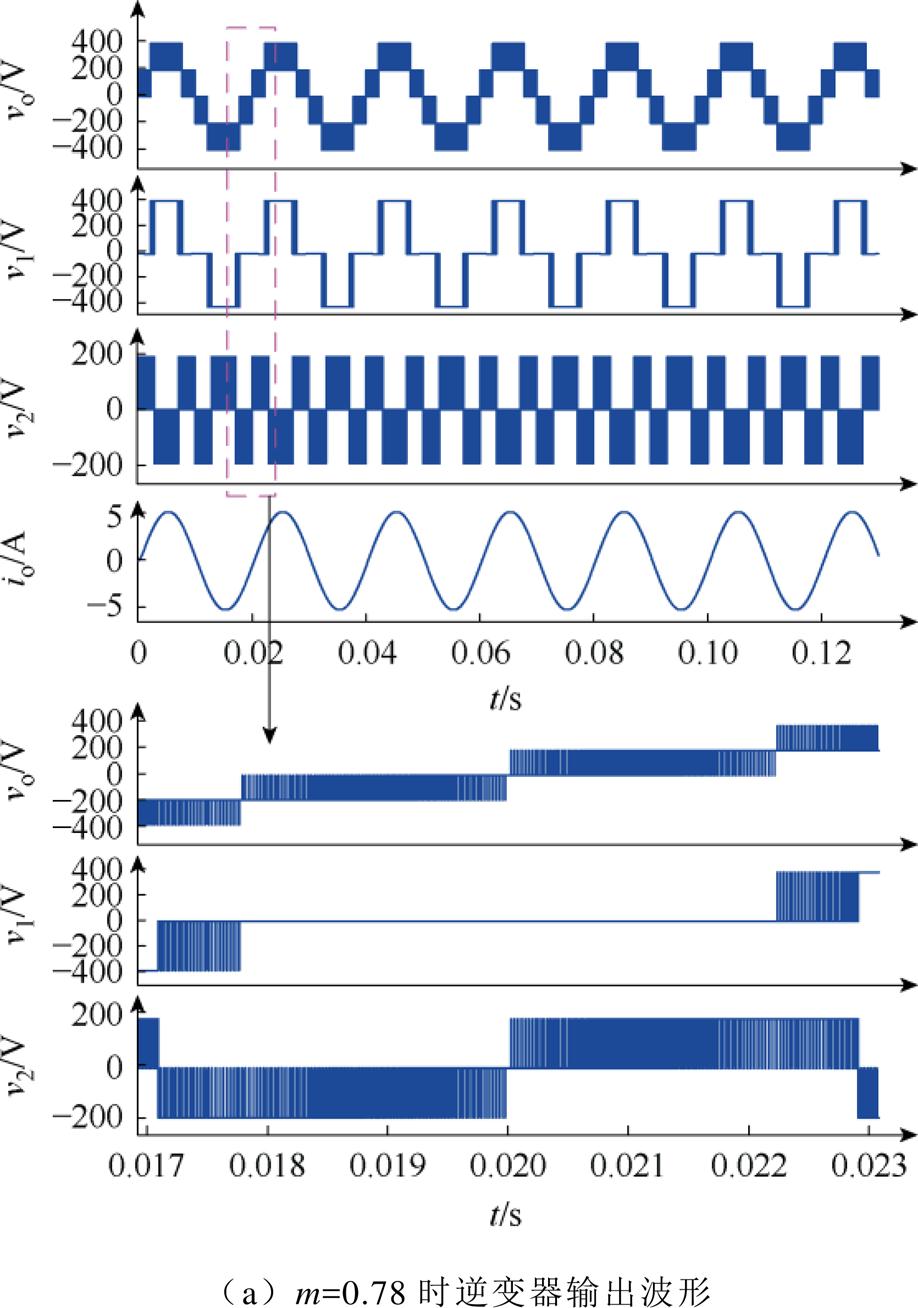
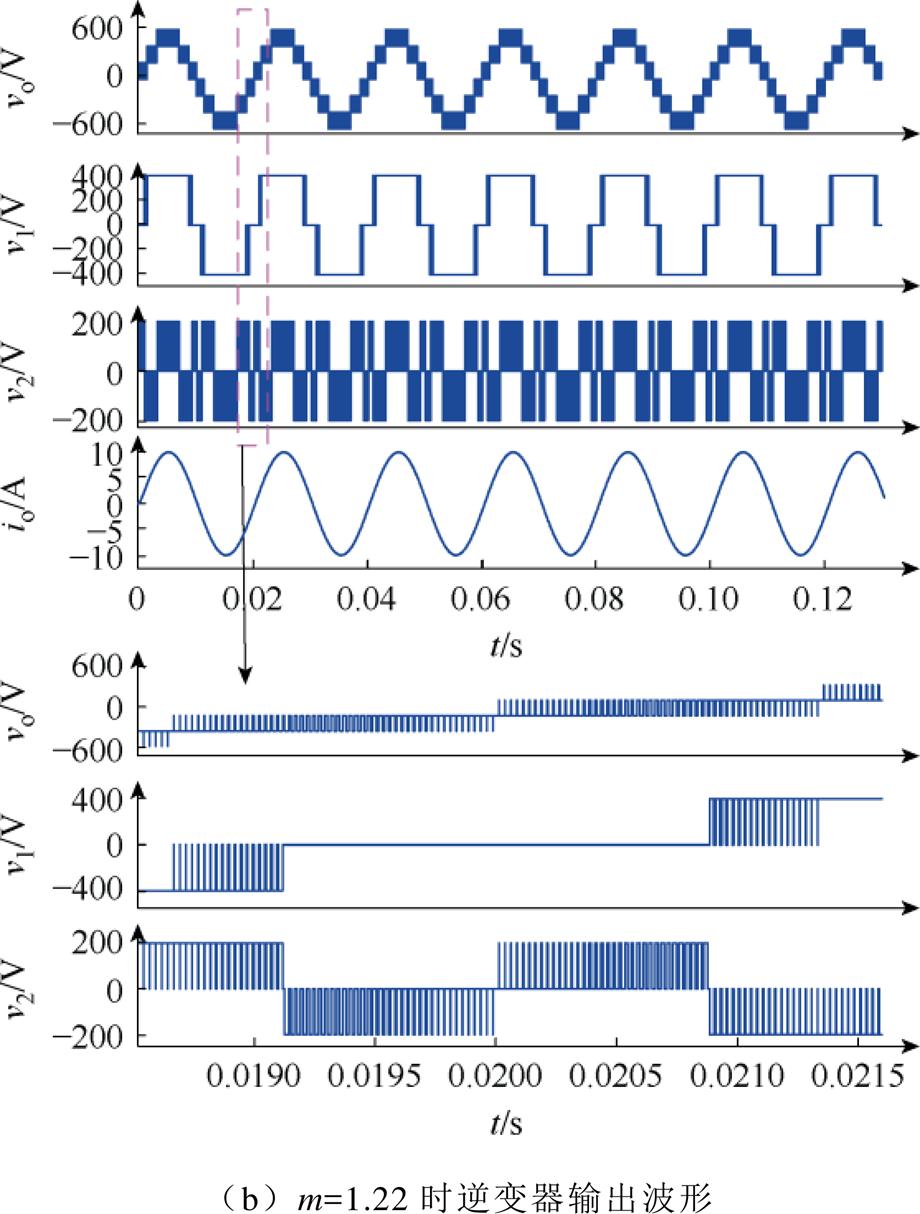
图10 逆变器输出电压输出电流仿真波形
Fig.10 The simulation waveforms for inverter output voltage and output current
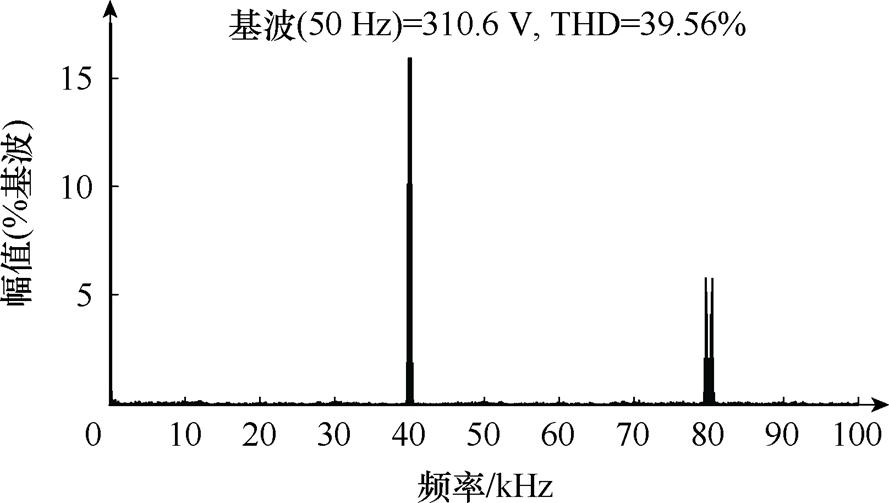
图11 逆变器输出电压频谱图
Fig.11 Inverter output voltage THD diagram
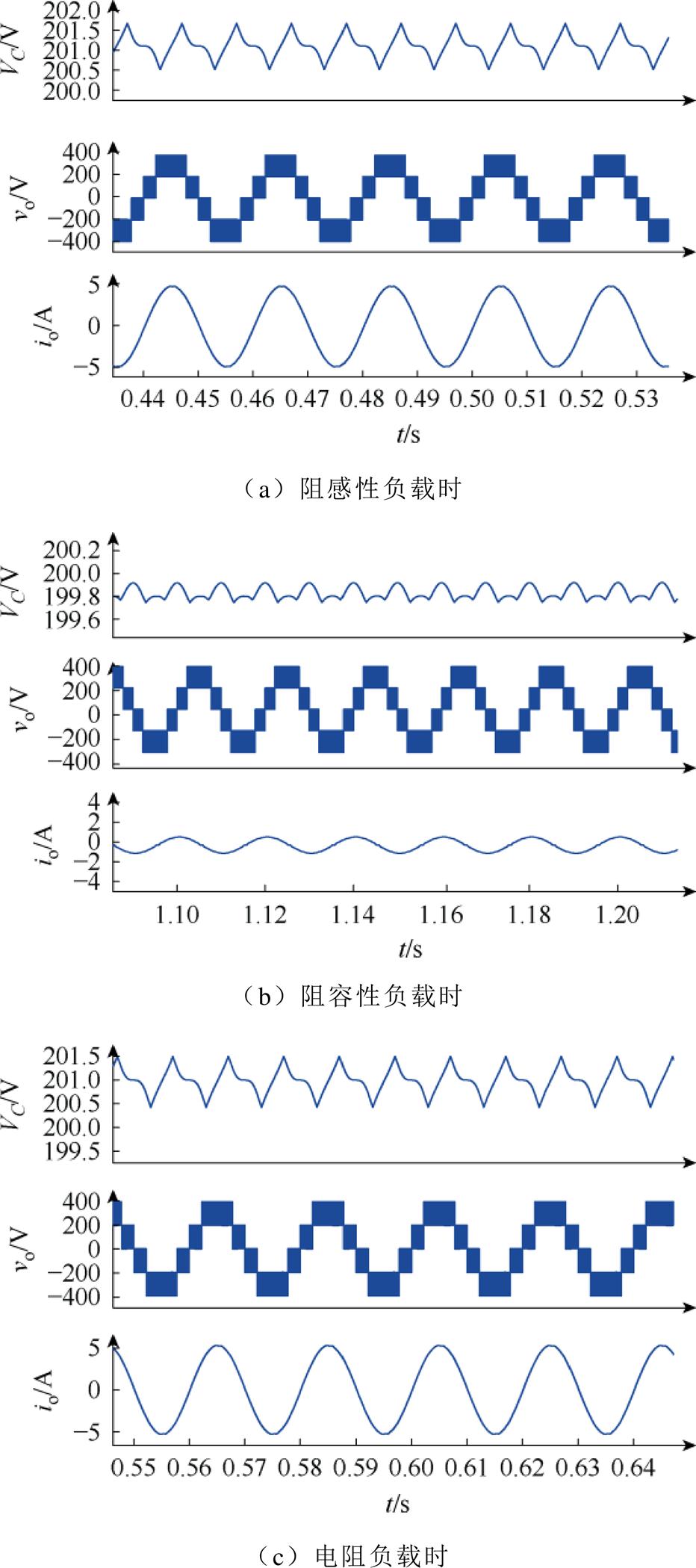
图12 不同工作模式时悬浮电容电压波形及逆变器输出波形
Fig.12 The waveforms for flying capacitor voltage and inverter output in different working modes
为验证悬浮电容电压纹波对输出电压的影响，根据悬浮电容电压表达式
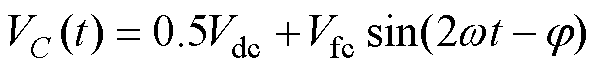（18）
式中，Vfc为悬浮电容电压上纹波分量的幅值。
悬浮电容上的瞬时有功功率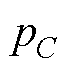
可计算为
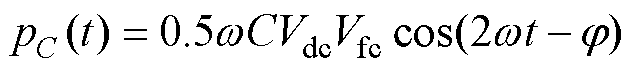（19）
根据交流侧和直流侧之间的功率平衡，可知，当输出功率一定时，即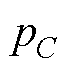一定时，悬浮电容值C越小，Vfc越大，即悬浮电容值会影响电容电压稳定性。
取C=5 mF得到仿真结果如图13所示，图14给出了输出电压频谱图。由仿真结果可以看出，由于控制效果比较好，悬浮电容电压纹波很小，所以对逆变器输出电压THD影响不大，且由于悬浮电容值降低，悬浮电容电压稳定性下降。
为验证所提控制策略的动态特性，图15给出了加入负载突变后的悬浮电容电压仿真波形。0.5 s时输出电阻由50 W 突变至35 W，负载增加，悬浮电容电压纹波增大，电压维持稳定，验证了所设计调节器的合理性。
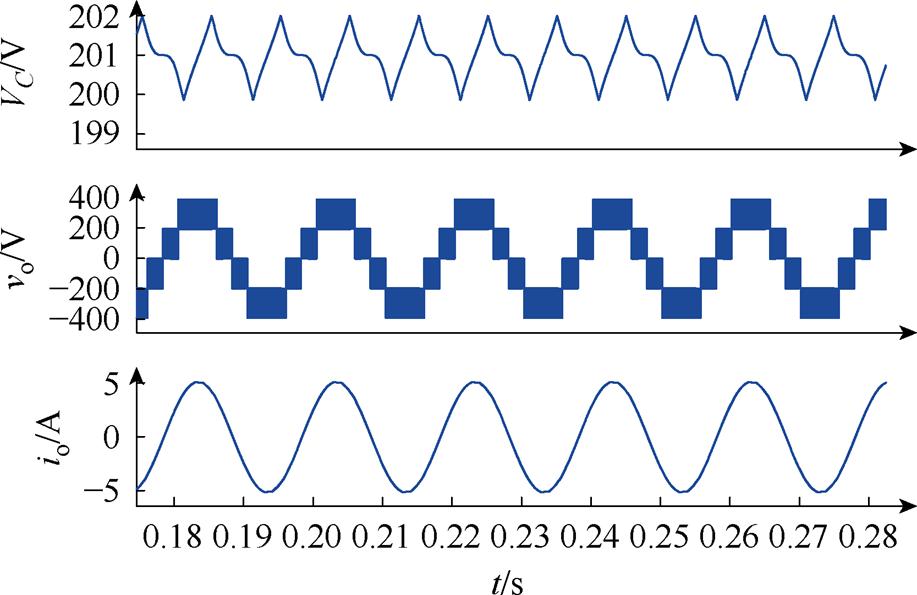
图13 悬浮电容电压波形及逆变器输出波形
Fig.13 The waveforms for flying capacitor voltage and inverter output
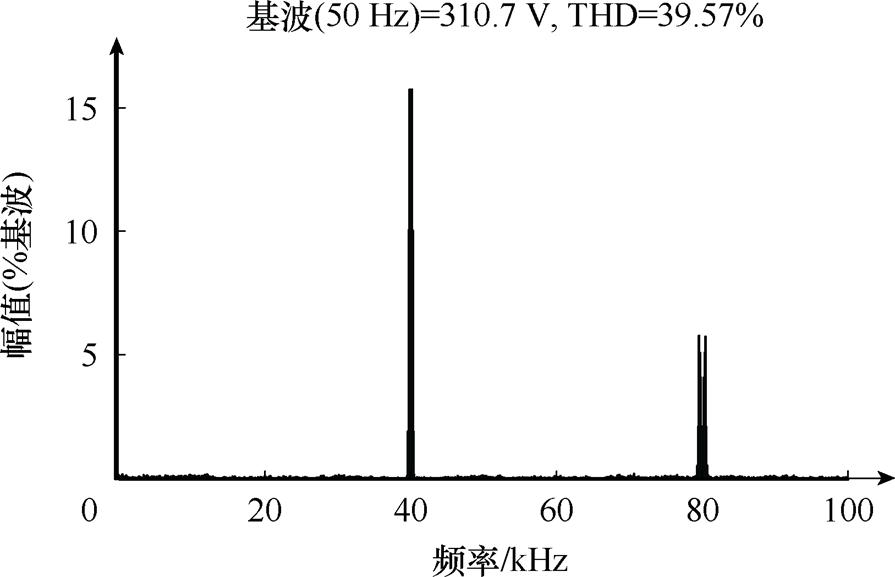
图14 逆变器输出电压频谱图
Fig.14 Inverter output voltage THD diagram
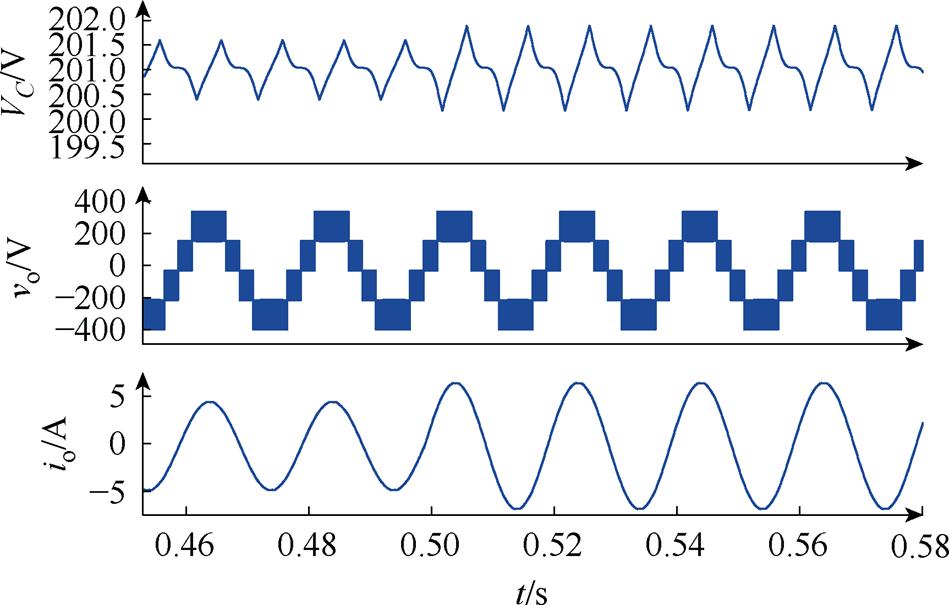
图15 负载突变时仿真波形
Fig.15 Simulation waveforms under sudden load change
将本文与文献[26]所提方法进行仿真对比，输入直流源为200 V，受调制策略限制，调制度M范围为0～1，其余参数与本文一致。
图16所示为基于电容状态切换的改进型载波层叠调制策略下悬浮电容电压VC、逆变器输出电压vo、H1、H2和H3开关输出电压vo1～vo3和逆变器输出电流波形i1，在整个输出周期，无过调制现象。图16a为m=0.52，输出电压为311 V额定工况下的仿真波形。此时H1和H3单元均工作于高频模式。图16b为m=0.75时的仿真波形。图17为m=0.52时的输出电压频谱分析。
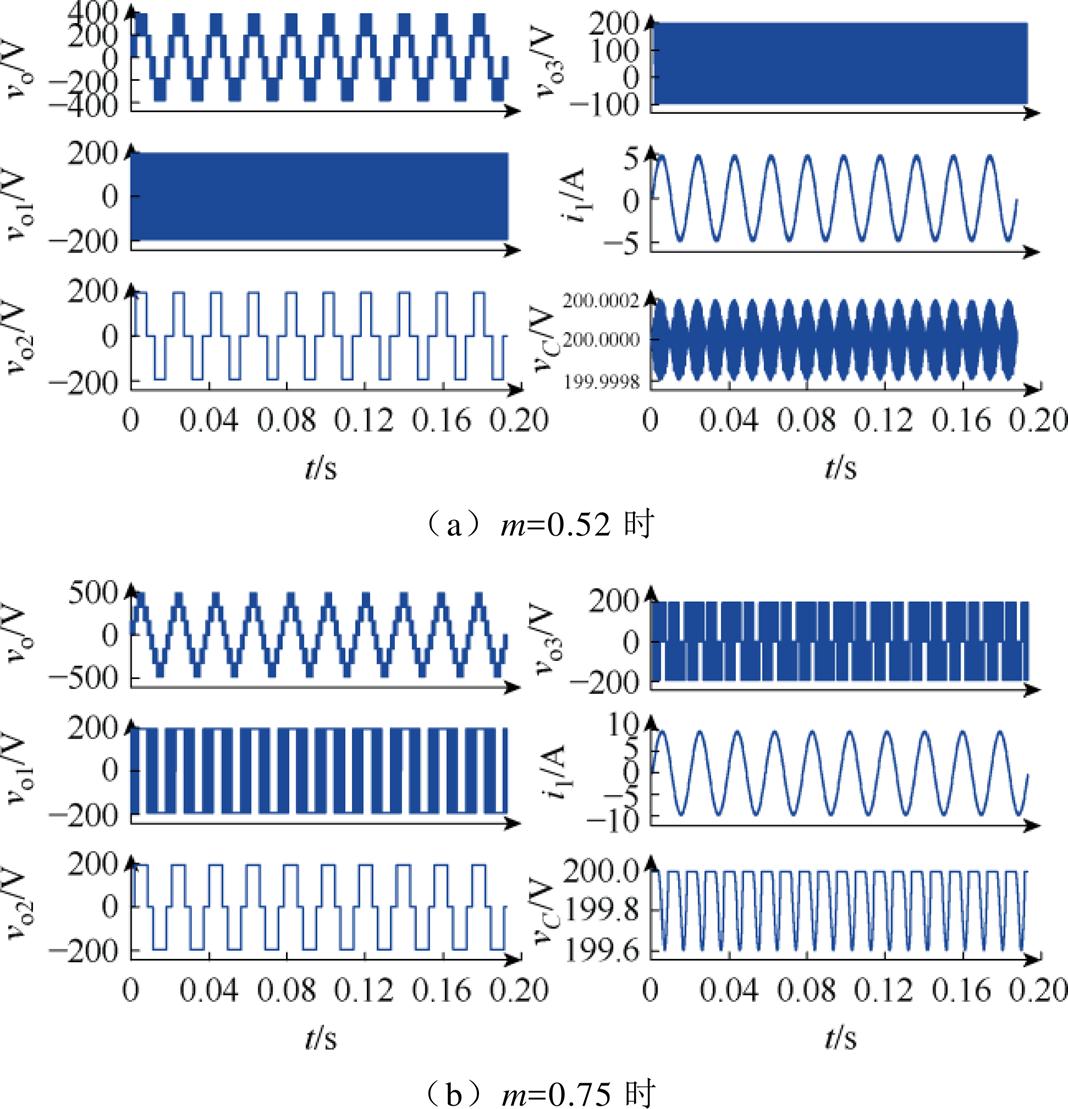
图16 文献[26]调制策略
Fig.16 Document [26] modulation strategy
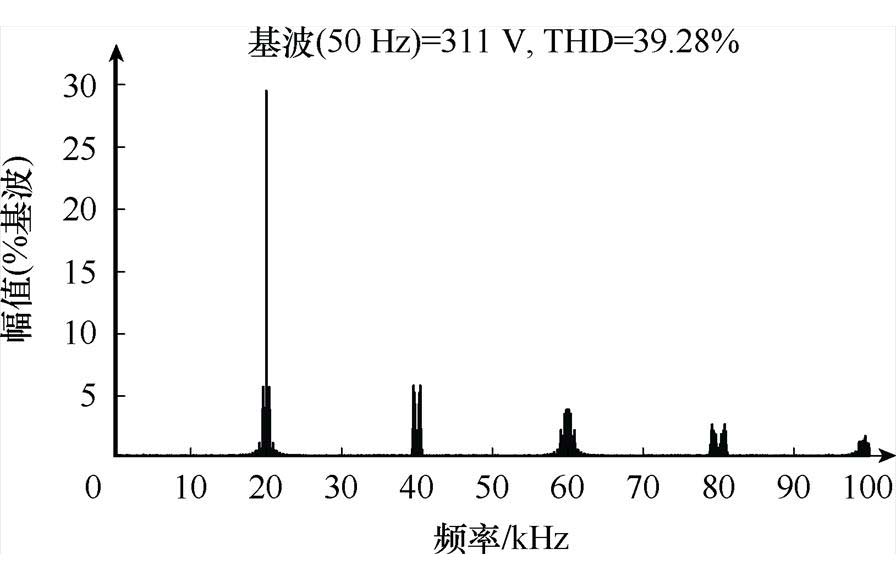
图17 M=0.52时输出电压频谱分析
Fig.17 Inverter output voltage THD diagram when M=0.52
由仿真结果可以看出：
（1）对比文献需要多个隔离直流电源供电，本文采用单直流电源供电，结构简单。
（2）对比文献所提调制策略调制度M最大为1，否则会发生过调制。本文调制度最大为1.27。
（3）对比文献与本文的THD值基本一致，但是谐波分布不同，文献输出电压谐波主要分布于载波频次，因此本文滤波器容量小。
本文搭建了一台如图18所示的七电平逆变器样机，用于原理和功能验证。实验参数见表3。
图18 实验平台
Fig.18 Experimental platform
图19分别为不同调制度下的逆变器输出电压vo，H桥逆变单元输出电压v1和悬浮电容逆变单元输出电压v2波形。图19a给出了m=0.78时的实验结果，此时逆变器输出5电平，与理论一致；图19b给出了m=1.22时的实验结果，此时逆变器输出7电平，与理论一致。由图19可知，该逆变器在不同调制区间时均不会发生过调制；图19c给出了m=1.14时的实验结果。
图20给出了采用调制波分解法m=0.78时输出电压的频谱图，结果表明实现逆变器的2倍频调制，无过调制问题、THD小、波形质量优。
表3 实验参数
Tab.3 Experiment parameters
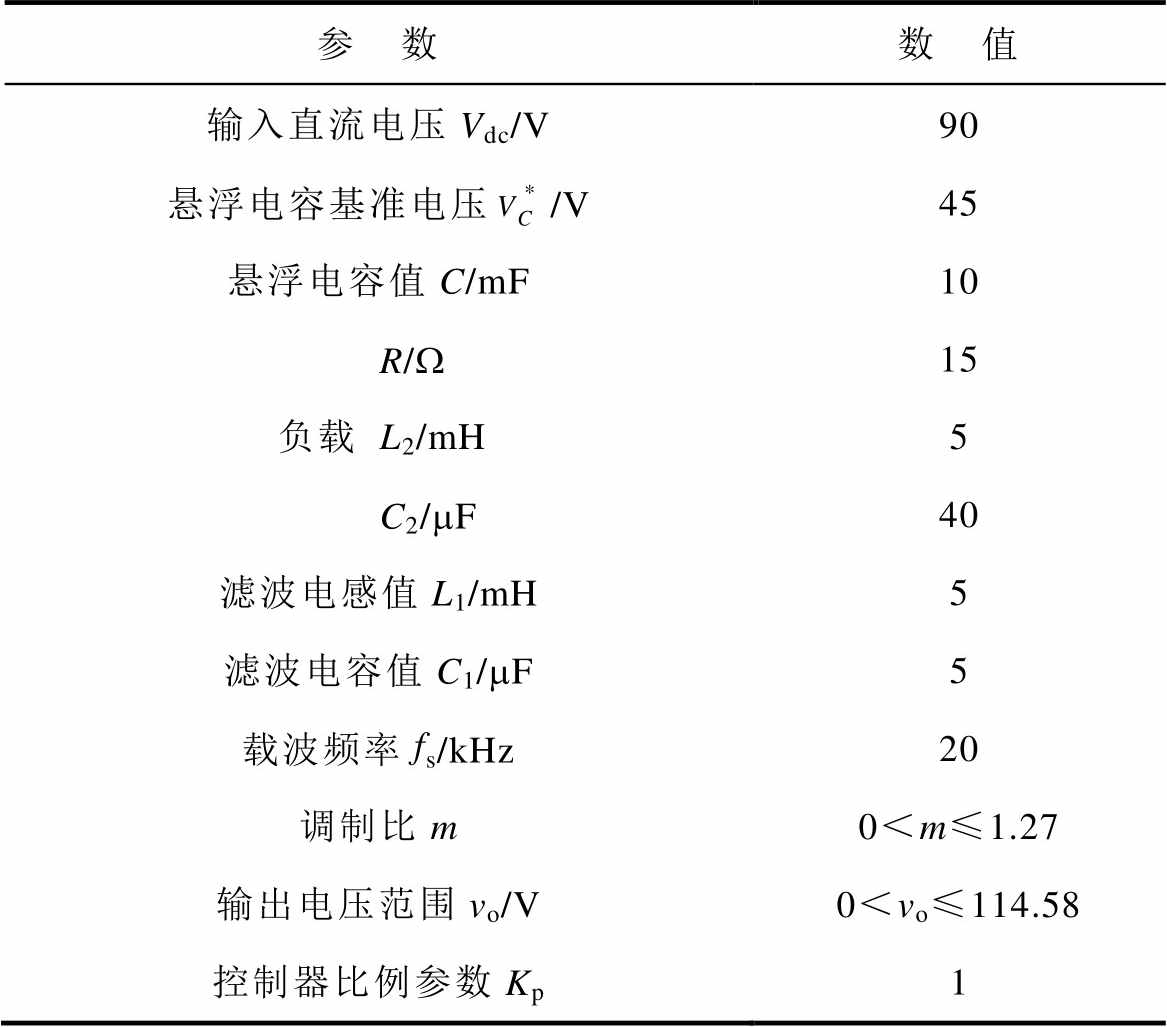
参 数数 值 输入直流电压Vdc/V90 悬浮电容基准电压/V45 悬浮电容值C/mF10 负载R/W15 L2/mH5 C2/mF40 滤波电感值L1/mH5 滤波电容值C1/mF5 载波频率fs/kHz20 调制比m0＜m≤1.27 输出电压范围vo/V0＜vo≤114.58 控制器比例参数Kp1
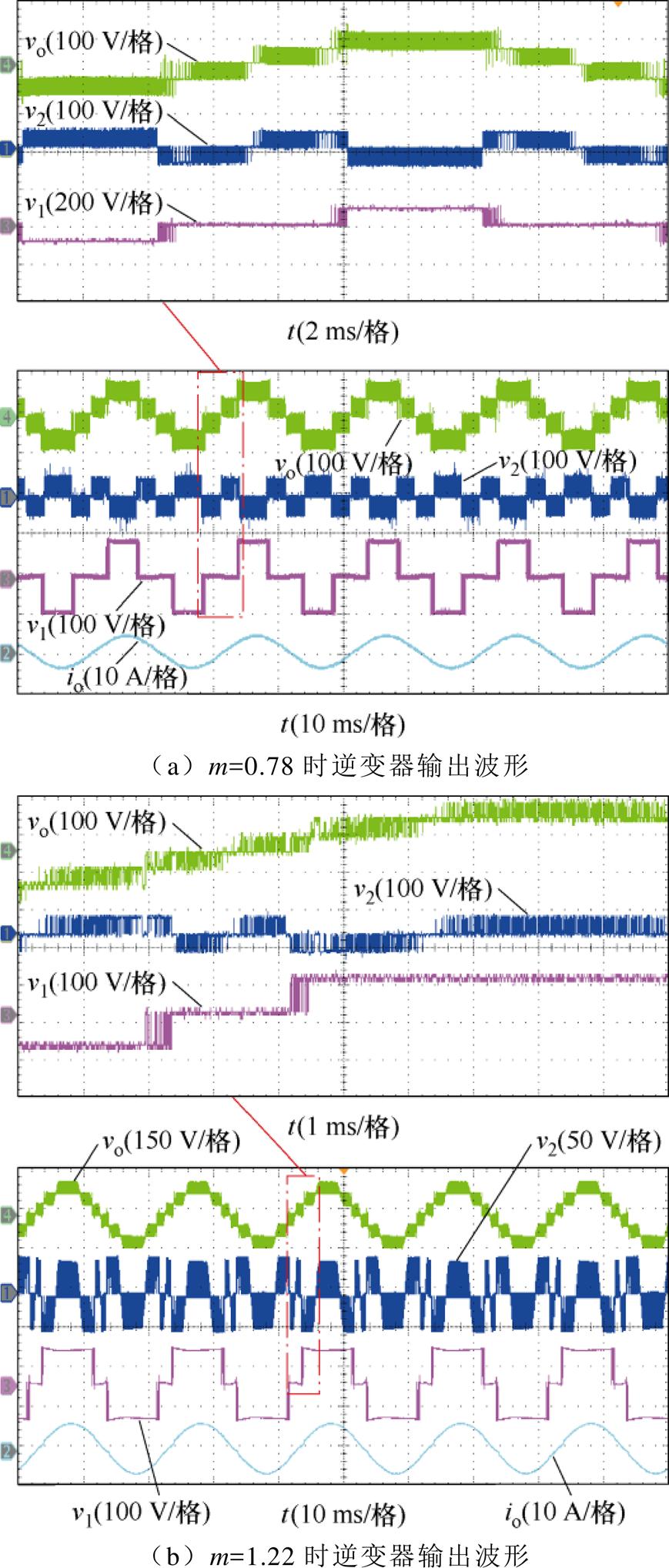
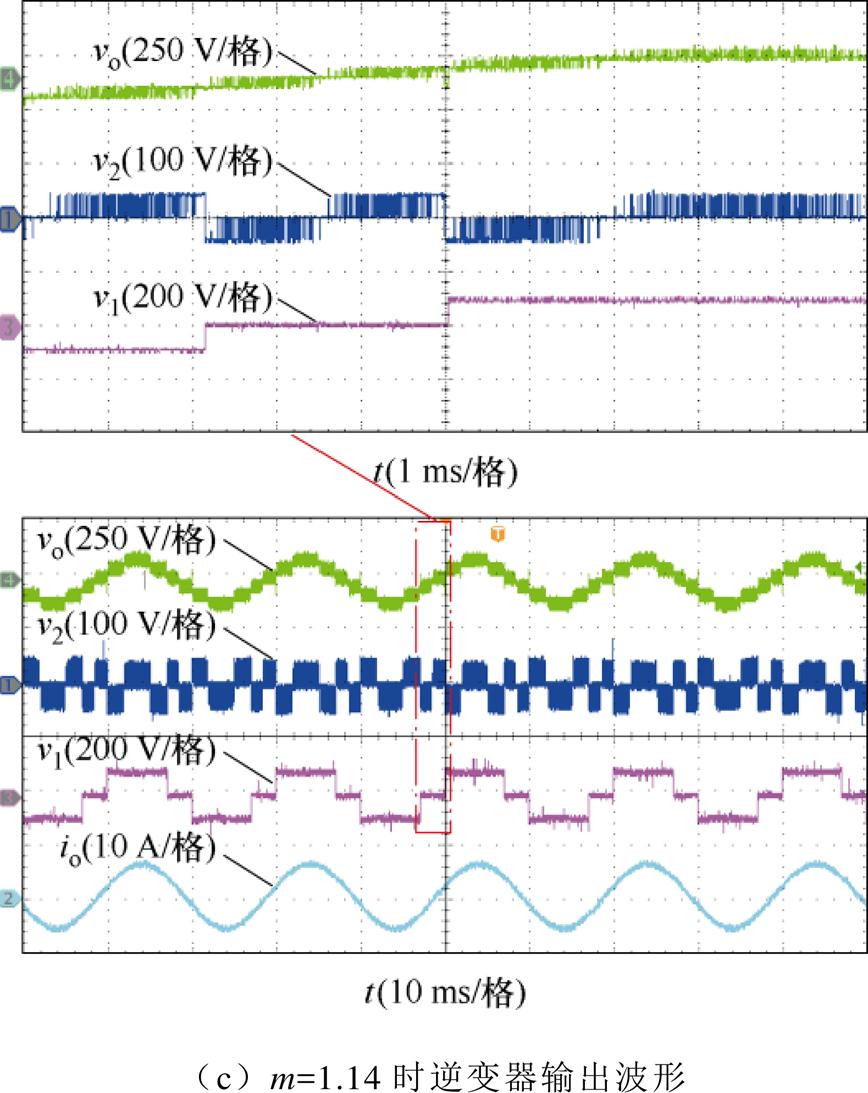
图19 逆变器输出电压和输出电流实验波形
Fig.19 The experiment waveforms for inverter output voltage and output current
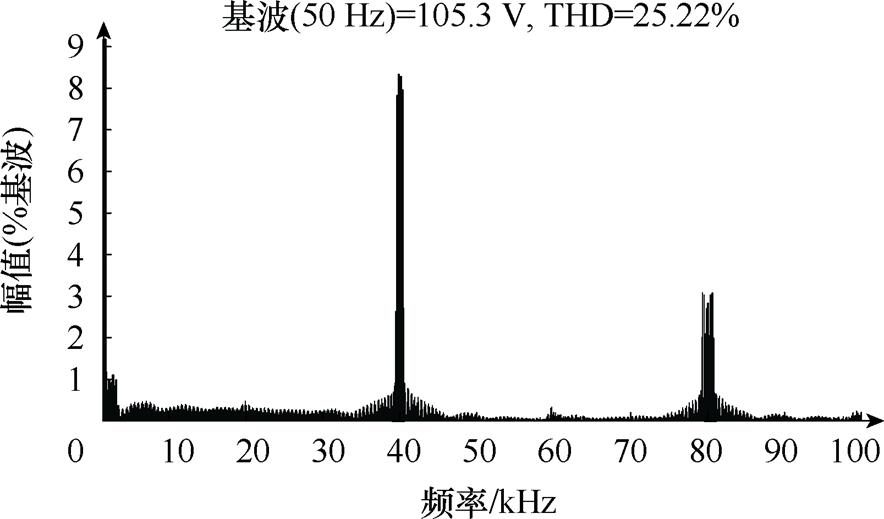
图20 逆变器输出电压频谱图
Fig.20 Inverter output voltage THD diagram
当悬浮电容基准电压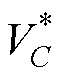=45 V时，图21给出了不同工作模式下的悬浮电容电压波形和逆变器的输出波形。图21a为阻感性负载时的实验结果（逆变器工作于工作模式1），图21b为阻容性负载时的实验结果（逆变器工作于工作模式2），图21c为一个纯阻性负载时的实验结果（逆变器工作于工作模式1）。实验结果均表明逆变器在不同工作模式下，悬浮电容电压均稳定，说明电容调压控制通过改变互补区域大小成功地实现了悬浮电容电压均衡，得到了好的稳压效果，且逆变器输出波形正弦性好。
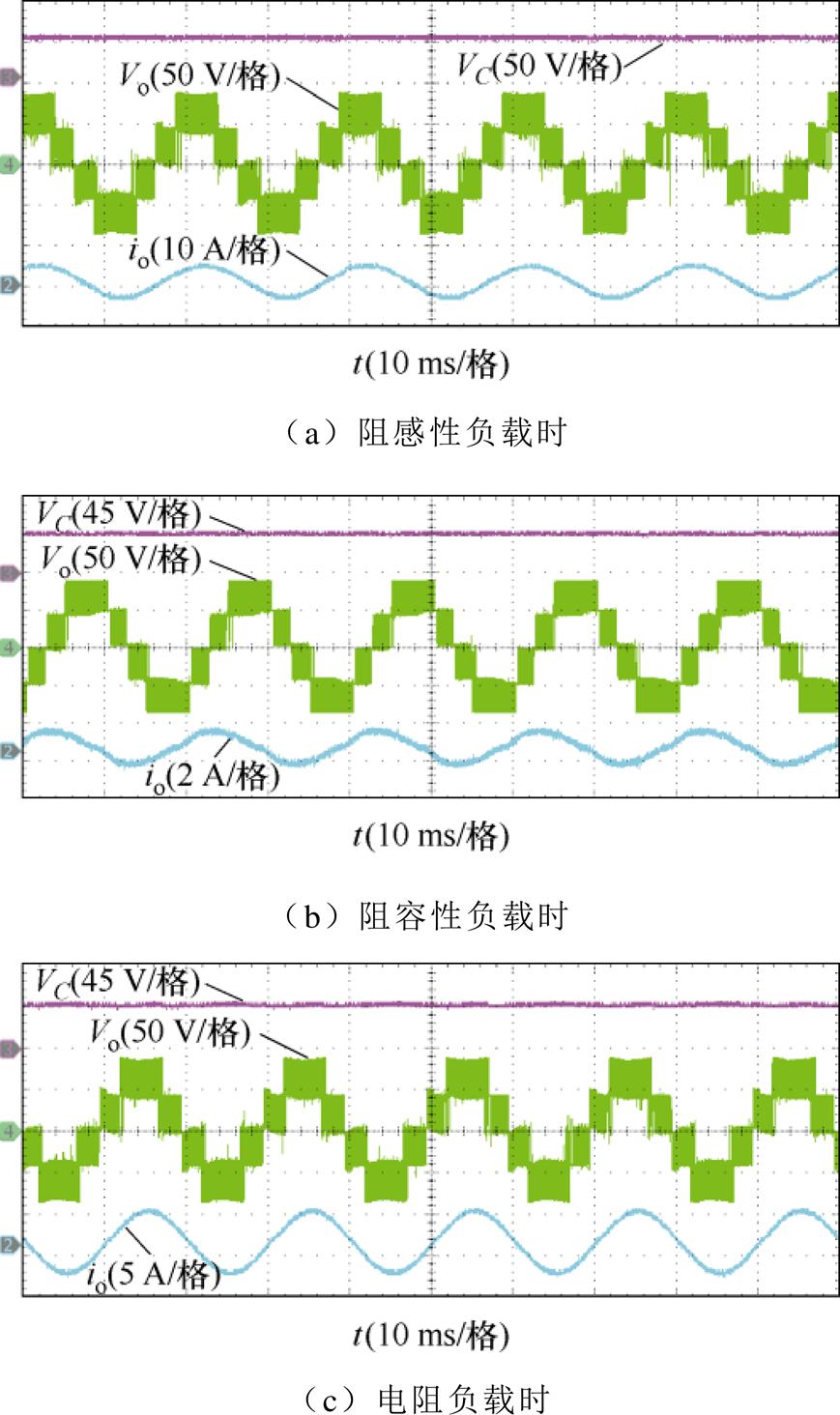
图21 不同工作模式时电容电压波形及逆变器输出波形
Fig.21 The experiment waveforms for capacitor voltage and inverter output in different modes
为验证所提控制策略的动态特性，图22给出了加入负载突变后的悬浮电容电压实验波形。输出电阻由15 W 突变至10 W，负载增加，悬浮电容电压纹波增大，电压维持稳定，验证了所设计调节器的合理性。
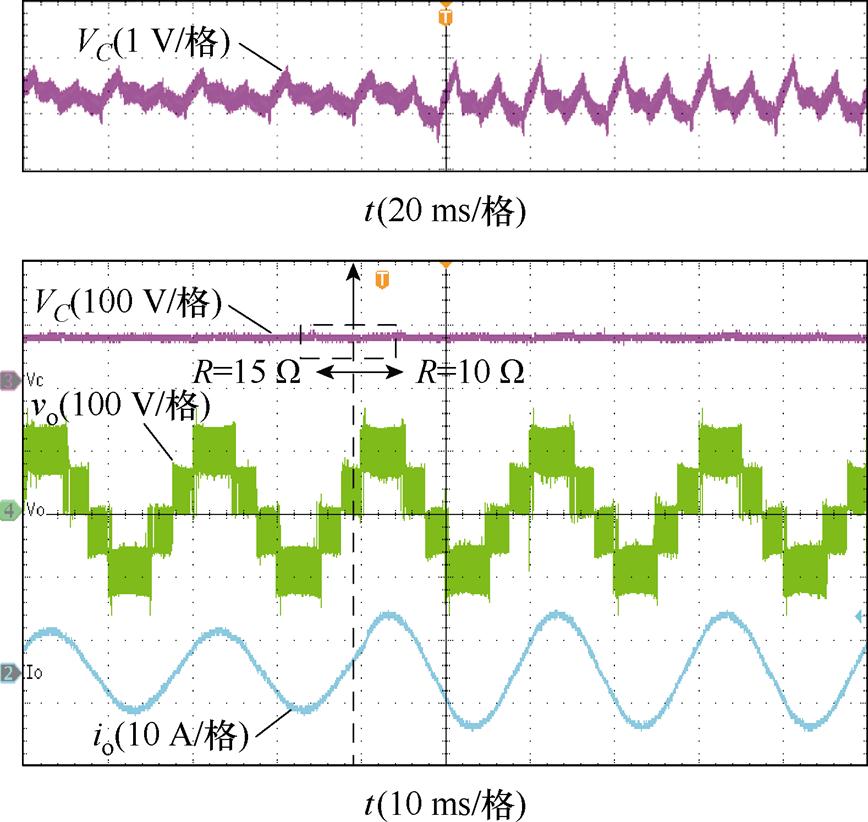
图22 负载突变时实验波形
Fig.22 Experimental waveforms under sudden load
本文针对悬浮电容H桥级联七电平逆变器，为实现H桥逆变单元以低开关频率运行，同时解决悬浮电容H桥单元过调制问题，提出基于调制波分解的混合载波频率调制策略，有效解决了逆变器输出存在的过调制问题同时降低了H桥逆变单元的开关频率。
为实现悬浮电容电压均衡，提出基于工作模式切换的有功功率分解控制，实现了悬浮电容电压在不同工作模式下的稳定控制。
最终，通过分析得到不同工况下H桥逆变单元开关频率与调制度的关系，H桥逆变单元开关频率最大为0.32倍的载波频率，最小为工频50 Hz，该方案采用较少器件实现了逆变器七电平输出，降低H桥逆变单元开关频率，实现逆变器的2倍频调制。
参考文献
[1] Quang-Thang D, Quoc-Trinh V, Thuy-Phuong P, et al. Dynamic power transmission using common RF feeder with dual supply[J]. ZTE Communications, 2022, 20(2): 28-36.
[2] 吴学智, 祁静静, 刘京斗, 等. 采用开关电容/开关电感的多电平逆变器拓扑研究综述[J]. 中国电机工程学报, 2020, 40(1): 222-233, 389.
Wu Xuezhi, Qi Jingjing, Liu Jingdou, et al. Review of multilevel inverter topology research using switched capacitor/switched inductor[J]. Proceedings of the CSEE, 2020, 40(1): 222-233, 389.
[3] 王立乔, 韩胥静, 李占一, 等. 一种新型飞跨电容型Zeta多电平逆变器[J]. 电工技术学报, 2022, 37(1): 254-265.
Wang Liqiao, Han Xujing, Li Zhanyi, et al. A novel flying-capacitor zeta multi-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 254-265.
[4] 王要强, 李娜, 赵朝阳, 等. 一种新型多电平逆变器及其模块化分析[J]. 电工技术学报, 2022, 37(18): 4676-4687.
Wang Yaoqiang, Li Na, Zhao Zhaoyang, et al. A new type of multilevel inverter and its modular analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4676-4687.
[5] 田涵雷, 韩沛松, 唐嵩峰, 等. 计及轻量化设计的多电平光伏逆变器[J]. 电工技术学报, 2023, 38(16): 4301-4311.
Tian Hanlei, Han Peisong, Tang Songfeng, et al. Multi-level photovoltaic inverter considering light- weight design[J]. Transactions of China Electro- technical Society, 2023, 38(16): 4301-4311.
[6] 付博, 曾君, 刘俊峰. 一种基于飞跨电容的升压七电平逆变器[J]. 电力电子技术, 2022, 56(8): 4-7, 49.
Fu Bo, Zeng Jun, Liu Junfeng. A Boost seven-level inverter based on flying capacitor[J]. Power Elec- tronics, 2022, 56(8): 4-7, 49.
[7] Babaie M, Sharifzadeh M, Kanaan H Y, et al. Switching-based optimized sliding-mode control for capacitor self-voltage balancing operation of seven- level PUC inverter[J]. IEEE Transactions on Indu- strial Electronics, 2021, 68(4): 3044-3057.
[8] 张国鑫, 陈仕铠, 叶远茂. 基于开关电容的单输入升压型七电平逆变器[J]. 电源学报, 2024, 22(2): 113-120.
Zhang Guoxin, Chen Shikai, Ye Yuanmao. Single- input step-up seven-level inverter based on switched- capacitor[J]. Journal of Power Supply, 2024, 22(2): 113-120.
[9] Zhu Jihong, Liu Chang, Deng Yan. A capacitor voltage regulation method for Non-redundant cascaded H-bridge converters[C]//2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 2021: 1-6.
[10] Monteiro A P, Jacobina C B, Bahia F A C, et al. Cascaded multilevel rectifiers with reduced number of controlled switches for open-end winding PMSM[C]// 2019 IEEE Energy Conversion Congress and Expo- sition (ECCE), Baltimore, MD, USA, 2019: 3616- 3623.
[11] 邱伟强, 郭谋发, 郑泽胤. 基于单一直流源级联H桥变流器的配电网接地故障柔性消弧方法[J]. 电网技术, 2019, 43(10): 3848-3858.
Qiu Weiqiang, Guo Moufa, Zheng Zeyin. Flexible arc-suppression method based on single-DC-source cascaded H-bridge converter for earth fault in distribution networks[J]. Power System Technology, 2019, 43(10): 3848-3858.
[12] 李金玉, 陈杰, 龚春英, 等. 一种提高级联H桥逆变器功率不平衡运行能力的控制策略[J]. 电工技术学报, 2023, 38(10): 2731-2743.
Li Jinyu, Chen Jie, Gong Chunying, et al. A control strategy to improve working ability of cascaded H-bridge inverter under power imbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(10): 2731-2743.
[13] 叶满园, 喻生铭, 刘文芳, 等. 不对称级联九电平逆变器线性功率均衡控制策略[J]. 电工技术学报, 2024, 39(14): 4495-4507.
Ye Manyuan, Yu Shengming, Liu Wenfang et al. Linear power balance strategy for asymmetric cascaded H-bridge nine-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(14): 4495-4507.
[14] Perez M, Kouro S, Rodriguez J, et al. Modified staircase modulation with low input current distortion for multicell converters[C]//2008 IEEE Power Elec- tronics Specialists Conference, Rhodes, Greece, 2008: 1989-1994.
[15] Manivelan C. A survey on multilevel inverter topo- logies and control schemes with harmonic elimi- nation[C]//2020 International Conference on Elec- trotechnical Complexes and Systems (ICOECS), Ufa, Russia, 2020: 1-7.
[16] 叶伟, 李善寿, 张可, 等. 混合级联H桥逆变器改进功率均衡调制策略[J/OL]. 电源学报, 1-15 [2024- 09-01].
Ye Wei, Li Shanshou, Zhang Ke, et al. Improved power balance modulation strategy for hybrid cascaded H-bridge inverter[J/OL]. Journal of Power Supply, 1-15 [2024-09-01].
[17] 王付胜, 戴之强, 王佳宁, 等. 一种基于级联H桥光伏并网逆变器的变移相角载波移相调制策略[J]. 太阳能学报, 2020, 41(8): 144-150.
Wang Fusheng, Dai Zhiqiang, Wang Jianing, et al. A variable-angle phase-shifted PWM strategy for cascaded H-bridge photovoltaic grid-connected inverter[J]. Acta Energiae Solaris Sinica, 2020, 41(8): 144-150.
[18] Liao Jingsheng, Corzine K, Ferdowsi M. A new control method for single-DC-source cascaded H-bridge multilevel converters using phase-shift modulation[C]//2008 Twenty-Third Annual IEEE Applied Power Electronics Conference and Expo- sition, Austin, TX, 2008: 886-890.
[19] 叶满园, 李宋. 混合级联多电平逆变器的改进混合调制技术[J]. 电机与控制学报, 2015, 19(11): 39-44.
Ye Manyuan, Li Song. Improved hybrid modulation technique for hybrid cascade multi-level inverter[J]. Electric Machines and Control, 2015, 19(11): 39- 44.
[20] 杨真理, 唐红雨. 混合H桥级联逆变器的改进型调制策略[J]. 电气传动, 2021, 51(23): 27-32.
Yang Zhenli, Tang Hongyu. An improved modulation strategy suitable for H-bridge hybrid cascaded inverters[J]. Electric Drive, 2021, 51(23): 27-32.
[21] Monteiro A P, Jacobina C B, Méllo J P R A, et al. Capacitor voltage balancing for single-phase asymmetric cascaded H-bridge inverters[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5129-5141.
[22] Dixon J, Ortuzar M, Carmi R, et al. Static var compensator and active power filter with power injection capability, using 27-level inverters and photovoltaic cells[C]//2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 2006: 1106-1111.
[23] Lee M, Yeh C S, Lai J S. A hybrid binary-cascaded multilevel inverter with simple floating-capacitor- voltage control[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2218-2230.
[24] Sepahvand H, Khazraei M, Corzine K A, et al. Start-up procedure and switching loss reduction for a single-phase flying capacitor active rectifier[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3699-3710.
[25] Manoharan M S, Ahmed A, Kim H W, et al. A single-source photovoltaic power conditioning system using asymmetric cascaded multilevel inverter[C]// 2015 9th International Conference on Power Elec- tronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea (South), 2015: 21-26.
[26] 顾军, 张维国, 卜荣荣, 等. 含电容单元的级联H桥七电平调制策略[J]. 电力自动化设备, 2023, 43(8): 126-132.
Gu Jun, Zhang Weiguo, Bu Rongrong, et al. Seven-level modulation strategy of cascaded H-bridge with capacitor unit[J]. Electric Power Automation Equipment, 2023, 43(8): 126-132.
[27] Sepahvand H, Liao Jingsheng, Ferdowsi M, et al. Capacitor voltage regulation in single-DC-source cascaded H-bridge multilevel converters using phase-shift modulation[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3619-3626.
[28] Ren Lei, Zhang Lei, Wang Li, et al. Capacitor voltage regulation strategy for 7-level single DC source hybrid cascaded inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(5): 5773-5784.
[29] 杨真理, 唐红雨. 单电源型五电平逆变器调控策略的研究[J]. 太阳能学报, 2021, 42(12): 452-458.
Yang Zhenli, Tang Hongyu. Research on regulation strategy of single-supply five-level inverter[J]. Acta Energiae Solaris Sinica, 2021, 42(12): 452-458.
[30] 胡文华, 刘剑锋, 曹仁赢. 混合级联H桥逆变器的改进拓扑及其混合调制方法[J]. 电力系统及其自动化学报, 2020, 32(6): 146-150.
Hu Wenhua, Liu Jianfeng, Cao Renying. Improved topology of hybrid cascaded H-bridge inverter and its hybrid modulation method[J]. Proceedings of the CSU-EPSA, 2020, 32(6): 146-150.
The Hybrid Carrier Frequency Modulation Strategy of Seven-Level Flying-Capacitor Cascaded H-Bridge Inverter
Abstract Multilevel inverters have the advantages of low harmonic content of output voltage, low voltage stress of switching devices, and high equivalent switching frequency, widely used in new energy power generation. Compared to other hybrid seven-level topologies, the seven-level flying-capacitor cascaded H-bridge inverter has attracted attention because of its low switching frequency, small number of devices, and many output levels.
For the seven-level flying-capacitor cascaded H-bridge inverter, the existing modulation strategies, such as low-frequency modulation, have high harmonic content in output voltage. The high-frequency modulation has less harmonic content but a high switching frequency. Hybrid modulation has the problem of over-modulation or narrow modulation range. This paper proposes a hybrid frequency carrier modulation strategy based on modulation wave decomposition. In this strategy, the switching tubes of the H-bridge inverter and the flying capacitor inverter operate at low and high switching frequencies, respectively. However, it causes over- modulation. Thus, the modulation strategy increases the modulation process of the over-modulation interval and decomposes the modulation wave of the flying capacitor inverter beyond the carrier. At the same time, the over-modulating waves of the H-bridge inverter and the flying-capacitor inverter are adjusted. As a result, the switching tube of the H-bridge inverter operates at a low switching frequency.
An active power decomposition control strategy based on working mode switching is proposed to control the voltage equalization of flying capacitors. This method realizes the voltage equalization of the flying capacitor through the control mode without additional hardware circuit. Two working modes of the inverter are obtained according to the influence of current direction and magnitude on voltage equalization of the flying capacitor when the voltage crosses zero. The voltage regulating control principle of the two working modes is obtained by analyzing capacitor charge and discharge. The closed-loop control scheme of the capacitor voltage regulation system based on working mode switching is designed. Capacitor voltage equalization can be realized by adjusting the active power injected into the system by the H-bridge inverter.
Simulation and experimental platforms are established for the seven-level flying-capacitor cascaded H-bridge inverter. The simulation and experimental results indicate that: (1) The proposed method solves the over-modulation problem of inverter output and reduces the switching loss of the H-bridge inverter. The maximum switching frequency of the H-bridge inverter is 0.32 times the carrier frequency, and the minimum power frequency is 50 Hz. (2) The stability control of the flying capacitor voltage under different working modes is realized. (3) The scheme uses fewer devices to realize the seven-level output of the inverter. Under the modulation, the THD value of the output voltage waveform is low, and the inverter has 2 times frequency characteristics.
Keywords：Seven-level inverter, cascaded H-bridge, hybrid carrier frequency, wave decomposition, flying capacitor voltage equalization control
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.231521
收稿日期 2023-09-13
改稿日期 2024-01-14
刘议泽 女，1999年生，硕士研究生，研究方向为电力电子与电力传动。
E-mail: 21121446@bjtu.edu.cn
刘京斗 男，1975年生，高级工程师，硕士生导师，研究方向为大功率变流器、多电平变换器等。
E-mail: jdliu@bjtu.edu.cn（通信作者）
（编辑 郭丽军）