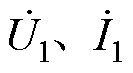分别为换流变网侧输入电压和电流，
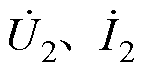分别为换流变网侧输入电压和电流，L1、L2为绕组的漏感，Lm为励磁电感，R1、R2为对应铜耗的等效电阻，Rm为对应铁耗的等效电阻，T为电压比为n1
n2的理想变压器。该模型可有效分析变压器稳态和轻饱和下的低频暂态响应，在低频条件下具有较好的精度。摘要 围绕张北柔直康保站空母线高频谐振问题，重点研究换流变压器在高频段呈现的阻抗特性与建模方法，并应用于模块化多电平换流器（MMC）空母线高频谐振问题的分析。首先介绍换流变压器的高频特性，建立考虑电容效应的换流变压器高频等效模型；其次基于康保站换流变压器实测的频率响应数据，利用改进鲍威尔算法反演计算得到换流变压器的高频等效模型参数，并与实测数据进行对比，校验换流变压器关键参数并确定模型适用范围；再次分析换流变压器等效电容参数对其高频阻抗的影响规律；最后基于换流变压器高频等效模型，仿真复现康保站MMC空母线高频谐振现象，验证了所建换流变压器高频等效模型的准确性以及对研究MMC空母线高频谐振的重要性。
关键词：换流变压器 高频等效模型 反演计算 高频谐振 模块化多电平换流器
近年来，陆上及海上集群风电场通过柔直系统功率外送已成为新能源电力远距离输送技术的一个重要发展方向[1-4]。但是，随着模块化多电平换流器（Modular Multilevel Converters, MMC）高压直流（High-Voltage Direct Current, HVDC）输电技术在工程应用的不断推进，随之而来的高频谐振问题也开始显现[5-9]。在目前国内投运的柔直工程中，高频谐振问题可分为两大类：一类是受端有载运行时，交流系统网架拓扑结构改变导致系统弱化，受端换流站在弱系统条件下发生的高频谐振。例如，鲁西工程广西侧换流站仅通过西百甲线接入交流系统时发生了1 271 Hz左右的高频谐振[6]。另一类是送端换流站启动调试过程中，发生的空载高频谐振。具体而言，空载启动调试第一阶段发生的高频谐振称为MMC空母线高频谐振。例如，如东工程MMC带换流变压器（以下简称“换流变”）启动时，发生了2 000 Hz左右的高频谐振[7]；张北工程康保站带换流变启动时，也发生了3 200 Hz左右的高频谐振[8]。而在空载启动调试第二阶段，出现高频谐振问题多与空载交流线路投入有关。例如，张北工程康保站向诺英线充电时，发生了1 509 Hz左右的高频谐振[9]。
针对柔直系统高频谐振问题，现有研究通过建立MMC-HVDC系统的线性时不变模型，进而利用模态分析法[10-14]或阻抗分析法[15-20]展开研究。文献[15]基于谐波状态空间法建立了MMC谐波阻抗模型，并利用Nyquist判据分析了系统稳定性。文献[17]指出链路延时是引起MMC-HVDC系统高频谐振的主要原因。文献[10]通过Pade近似对延时环节进行等值，建立MMC-HVDC系统的状态空间模型，利用参与因子法探究了引起系统高频谐振的主要因素。文献[18]考虑电流内环、电压前馈和链路延时，建立了MMC高频阻抗简化模型，并用于鲁西工程高频谐振研究，指出弱系统下交流电网出现容性区域，其与带载MMC动态交互将引发系统高频谐振。基于文献[18]建立的MMC模型，文献[9]研究了张北工程康保站向诺英线充电时出现的高频谐振问题，指出诺英线受对地电容影响，其阻抗在高频段出现容性区域，继而与MMC相互影响导致高频谐振，但却忽略了换流变高频特性对谐振的影响。
分析上述文献发现，当前研究主要聚焦在弱系统条件下带载受端换流站高频谐振和空载交流线路投入送端换流站高频谐振两个方面，却鲜有涉及针对送端换流站启动调试过程中出现的MMC空母线高频谐振问题的讨论。而如东工程和张北工程康保站发生MMC空母线高频谐振时，送端换流站处于孤岛运行状态，交流侧仅投入了换流变，未接入其他交流线路[8, 11]，这表明换流变的高频特性与MMC空母线高频谐振具有内在联系。针对MMC空母线高频谐振问题，虽然文献[8, 11]考虑了绕组漏抗和对地电容对换流变高频阻抗的影响，并分析了MMC外环V/f控制与高频谐振的内在关系，但并未对换流变进行精细建模。事实上，由于各绕组的匝间电容以及绕组间的耦合电容在高频情况下对换流变工作特性的影响已较为明显，并且此影响程度会随频率升高而增加[21]，所以如果单纯地将换流变等效为绕组漏抗和对地电容的建模方法，将无法准确刻画其高频特性，继而无法透彻的对MMC空母线高频谐振问题进行分析。
针对以上问题，以康保站带换流变空载启动调试时发生的空母线高频谐振事件为研究背景，构建适用于MMC空母线高频谐振分析的换流变高频等效模型。根据现场换流变频率响应数据反演计算获得模型关键参数，完成换流变模型参数比对校验，并表征出换流变高频阻抗与等效电容间的内在联系。在仿真复现康保站空母线高频谐振的基础上，验证了理论分析和建模的正确性。
在低频情况下，变压器线圈间的磁耦合起主要作用，变压器等效模型的性质主要由电感元件决定。低频条件下对变压器进行分析时，通常采用如图1所示的含理想变压器的电感表征模型。图中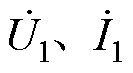，分别为换流变网侧输入电压和电流，分别为换流变网侧输入电压和电流，L1、L2为绕组的漏感，Lm为励磁电感，R1、R2为对应铜耗的等效电阻，Rm为对应铁耗的等效电阻，T为电压比为n1n2的理想变压器。该模型可有效分析变压器稳态和轻饱和下的低频暂态响应，在低频条件下具有较好的精度。
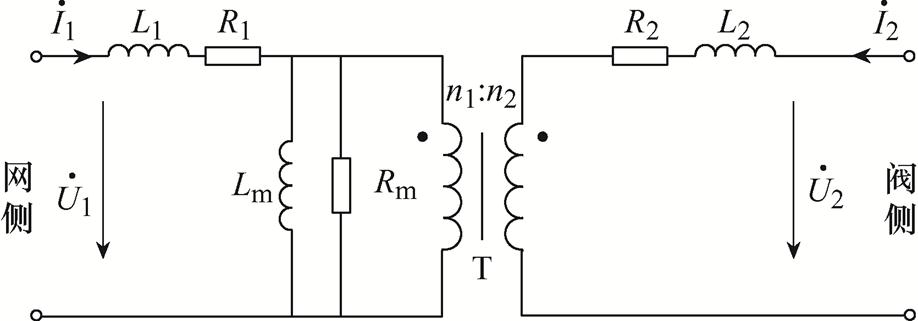
图1 含理想变压器的电感表征模型
Fig.1 Inductor model using an ideal transformer
然而随着频率的提高，特别是当频率超过1 kHz后，变压器的物理特性与低频情况相比有明显不同，变压器的电容效应逐渐显现[22]，此时传统的低频模型已无法正确反映变压器的高频特性，需要充分考虑高频段电容效应的影响。
换流变安装于交流网和MMC阀侧之间，分析时可将三者看作一个整体，并将换流变等效为一个二端口网络，电容效应由5个集中电容参数表示，其高频等效模型如图2所示。图中，C1s和C2s分别为网侧和阀侧绕组的匝间电容，C10和C20分别为网侧和阀侧绕组的对地电容，C12为网侧和阀侧绕组之间的耦合电容。由于该模型结构简单、意义明确，所以在实际工程中得到了广泛应用[23]。考虑到柔直工程中换流变多由三个单相变压器构成，本文研究主要集中在单相变压器高频等效建模上，暂不考虑变压器相间电磁耦合作用。
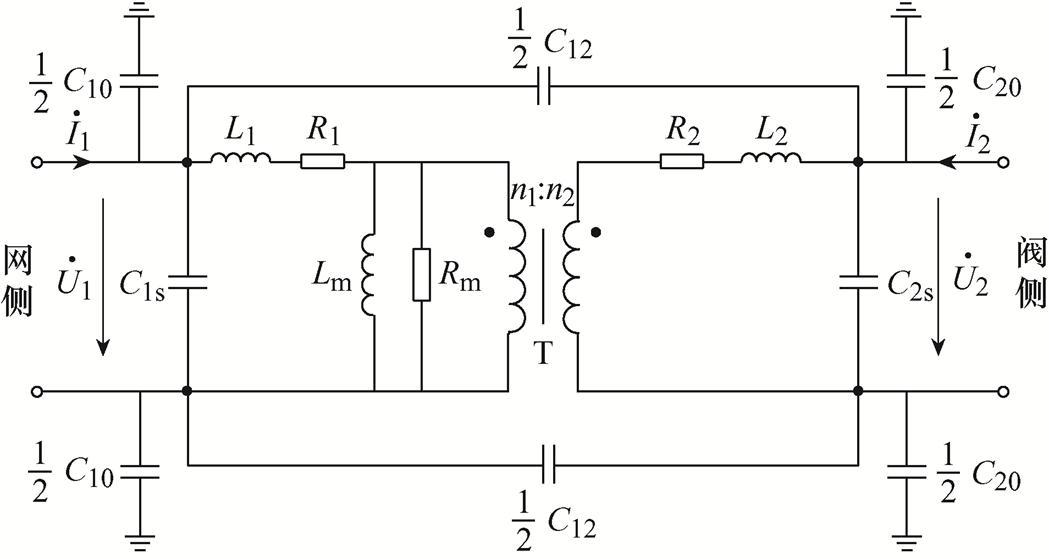
图2 换流变高频等效模型
Fig.2 High-frequency equivalent model of converter transformer
根据研究发现，目前柔直系统发生高频谐振的谐振频率一般低于5 kHz。在该频率范围内，换流变网侧和阀侧绕组的对地电容对其高频特性影响较小，故忽略网侧和阀侧绕组的对地电容，得到换流变高频简化模型如图3所示。
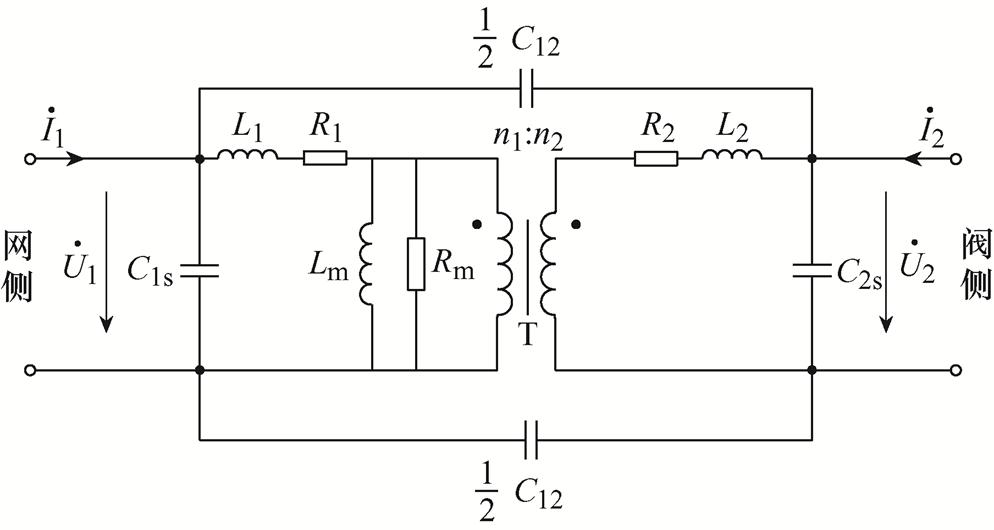
图3 忽略对地支路的换流变高频简化模型
Fig.3 High-frequency simplified model of converter transformer with ignoring the branch to ground
将模型的各支路用阻抗参数表示，各支路的电流正方向规定如图4所示。
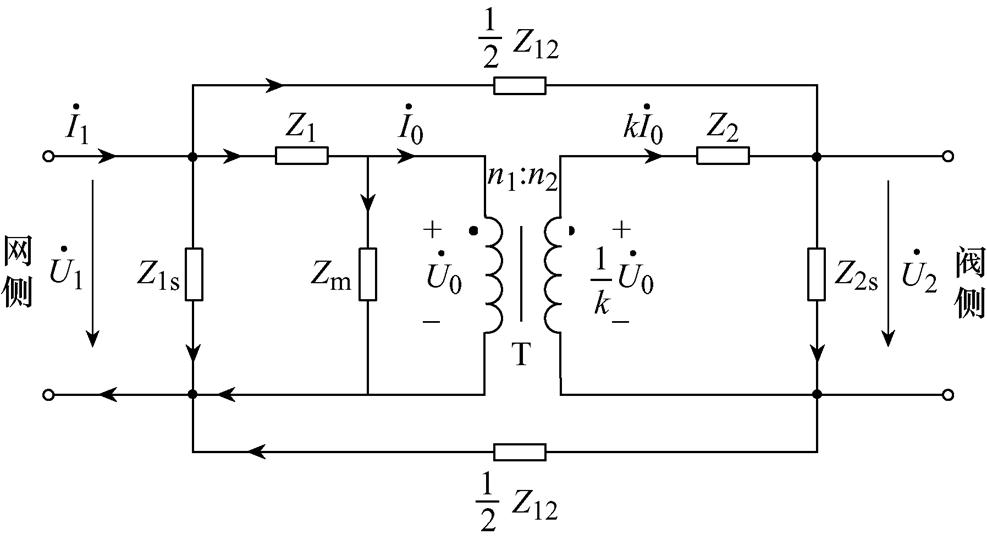
图4 换流变高频阻抗等效模型
Fig.4 High-frequency impedance equivalent model of converter transformer
当换流变阀侧空载运行时，根据基尔霍夫电压电流定律，网侧的输入电压电流关系为
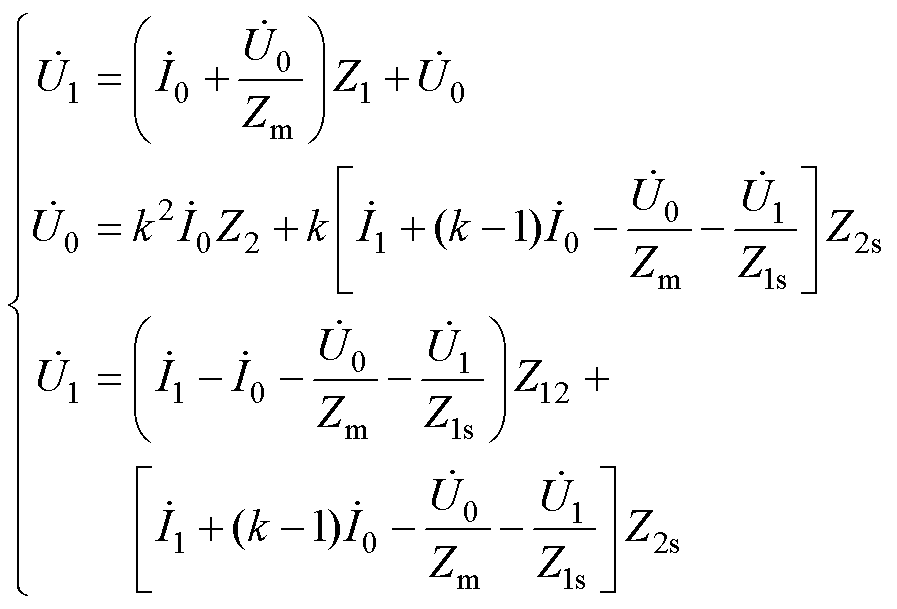（1）
式中，
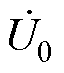和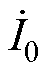
分别为理想变压器网侧电压和电流；k为理想变压器电压比，k=n1n2；Z1和Z2分别为换流变网侧和阀侧绕组漏抗；Zm为换流变励磁支路阻抗；Z1s和Z2s分别为换流变网侧和阀侧绕组匝间电容容抗；Z12为耦合电容容抗。
由式（1）可得换流变阀侧空载运行时网侧端口阻抗为
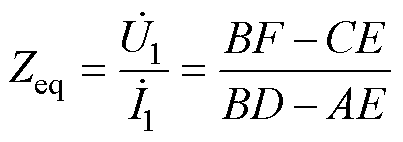（2）
其中
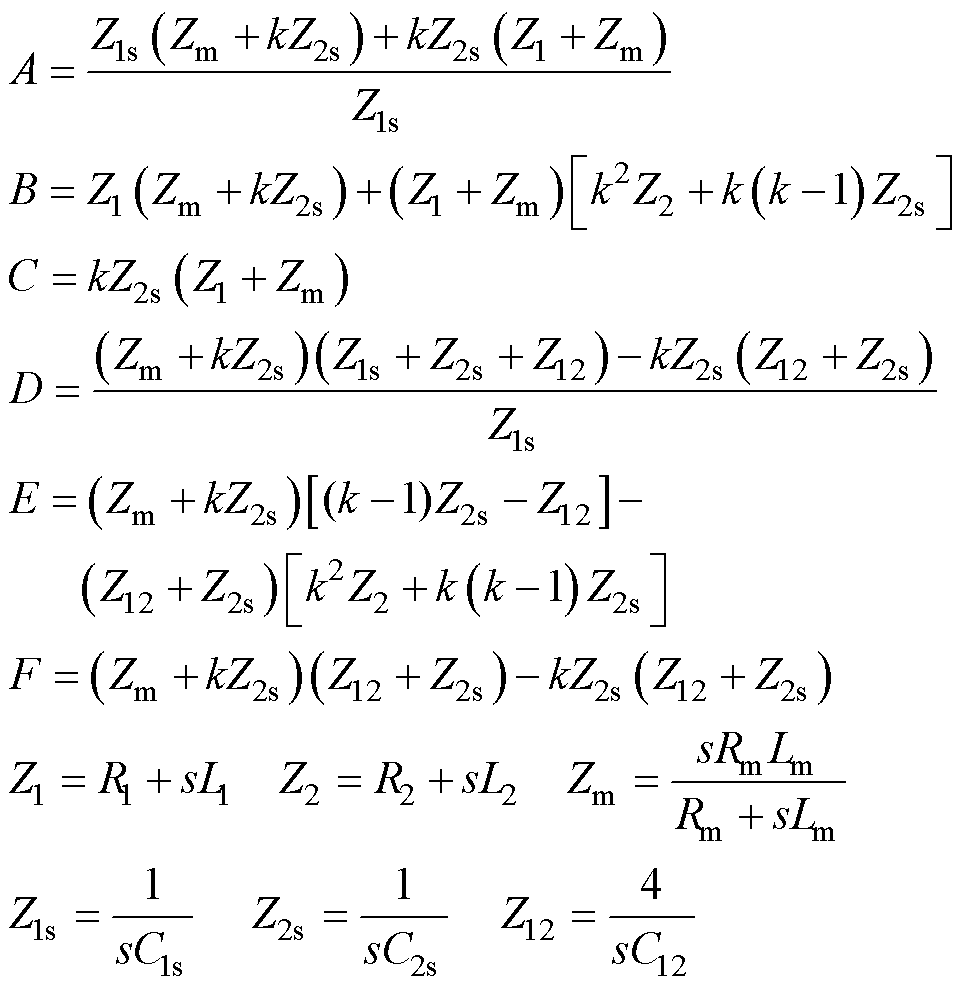
传统变压器的高频等效模型参数是通过电磁场分析计算[24-25]或实验测定[26-27]的方法来获取。电磁场分析计算需要知道变压器的结构、尺寸、媒质参数等详细数据。然而，对于已投运的变压器，上述数据不但较难获得，而且涉及的数值计算也极为复杂。实验测定则依赖操作人员的技术水平，也容易导致获取的参数不准确。针对变压器等效模型参数获取问题，已有学者提出基于变压器的端口特性，借助电路综合理论和数学方法获取模型参数，并已利用遗传算法，通过拟合变压器额定电压电流的方法来获得工频参数[28-29]。对于变压器高频等效模型参数，可以选择频率响应特性作为参数反演依据，利用数学拟合的方法来获取。
变压器作为一个无源线性二端口网络，在较高频率范围内，其内部特性可以通过传递函数H(jω)来描述。变压器内部电感、电容等参数改变，将导致其频率响应特性随之变化。实际工程中变压器的频率响应特性可采用如图5所示的频率响应特性检测回路获得[30]，在变压器网侧绕组的一个端子加频率可变的正弦电压激励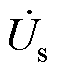
，一个端子连接50 W 的匹配电阻Ro，阀侧绕组的两个端子悬空。通过
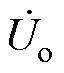测量Ro两端
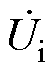的电压，计算不同频率下响应端电压与激励端电压之比，获得描述变压器频率响应特性的传递函数为
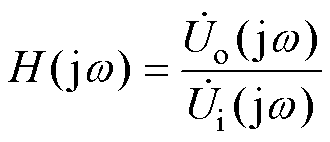（3）
则幅频特性M(jw)和相频特性j(jw)分别表示为
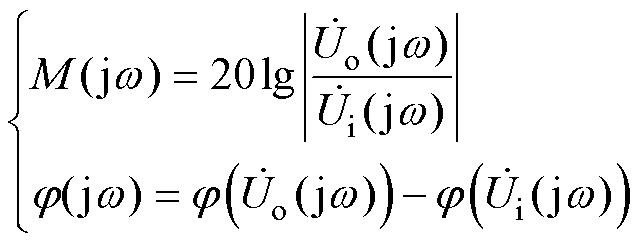（4）
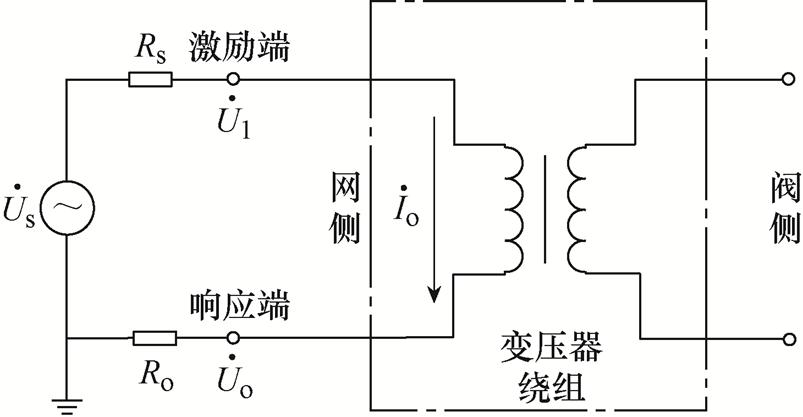
图5 变压器频率响应特性检测回路
Fig.5 Detection circuit for Transformer frequency response characteristics
根据式（4）可知，实际工程中变压器的频率响应特性是用响应端电压与激励端电压之比来描述。因此对1.2节推导的变压器端口阻抗做进一步转化。依据图5所示的检测回路，变压器的端口阻抗可表示为
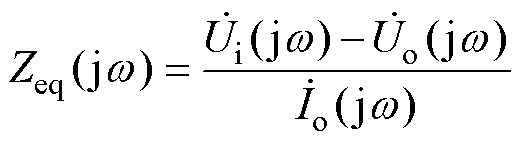（5）
通过变压器绕组的电流表示为
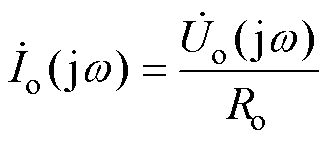（6）
将式（6）代入式（5）可得变压器频率响应特性与其端口阻抗的对应关系为
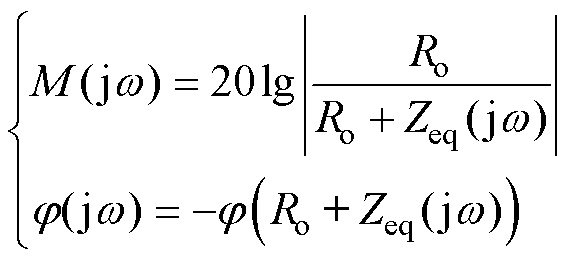（7）
分析式（2）和式（7）可知，变压器的频率响应特性与其高频等效模型的电感、电容等参数存在对应关系。因此利用数学方法，通过拟合变压器实测频率响应特性，即可反演获得高频等效模型参数。
改进鲍威尔算法是利用共轭方向加快收敛速度的性质形成的一种搜索方法，只需计算目标函数即可直接求出用于搜索的共轭方向，加快在极值点附近的收敛速度，具有计算简单、收敛速度快、收敛精度高等优点[31]。因此利用改进鲍威尔算法，结合康保站换流变实测频率响应幅值和相位数据，对1.2节建立的换流变高频简化模型参数进行反演计算。
改进鲍威尔算法目标函数的选取对于算法收敛速度和求解质量具有较大影响，为了使反演计算数据与实测数据更好地拟合，构建两个子目标函数J1和J2[32]。引入J1从频率范围整体考察实测与计算数据的拟合程度；同时，引入J2以增强变压器谐振频率下实测与计算数据的一致性。J1和J2分别表示为
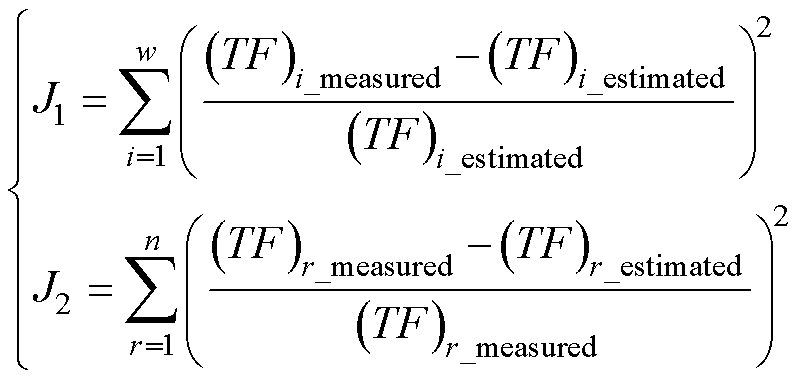（8）
式中，TF为以式（4）形式表征的换流变压器频率响应数据；(TF)i_measured和(TF)i_estimated分别为频率点i处实测和估算的频率响应数据；w为选取频率点的数量；(TF)r_measured和(TF)r_estimated分别为谐振频率点r处实测和估算的频率响应数据；n为谐振频率点的数量；(TF)i_estimated和(TF)r_estimated由式（2）和式（7）计算得到。
算法的总目标函数可表示为
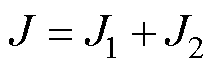（9）
基于改进鲍威尔算法的换流变高频简化模型参数反演计算流程如图6所示。
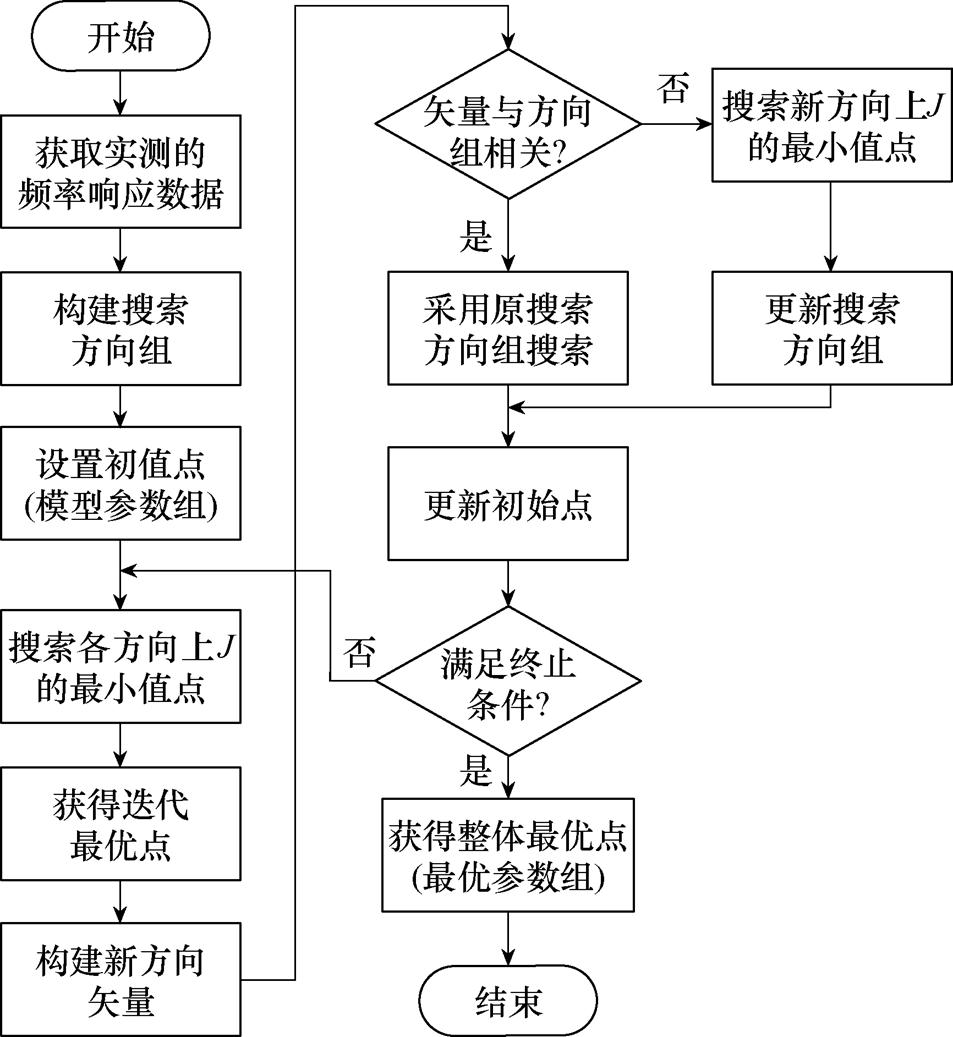
图6 改进鲍威尔算法换流变高频简化反演计算模型参数流程
Fig.6 Flow chart of model parameter inversion calculation based on improved Powell algorithm
利用改进鲍威尔算法反演计算得到的康保站换流变高频简化模型参数，见表1。
表1 康保站换流变高频简化模型参数
Tab.1 High-frequency simplified model parameters of converter transformer of Kangbao converter station
参 数数 值 R1/W0.038 L1/H0.005 C1s/mF2.519 R2/W0.030 L2/H0.005 C2s/mF0.661 9 Rm/W3.267×105 Lm/H1.039×103 C12/mF1.917×10-2
根据表1中所列参数，利用式（2）和式（7）计算出换流变频率响应的幅值和相位，并与实测数据进行对比，结果如图7所示。两者拟合程度可以衡量反演计算所得换流变参数的准确性。
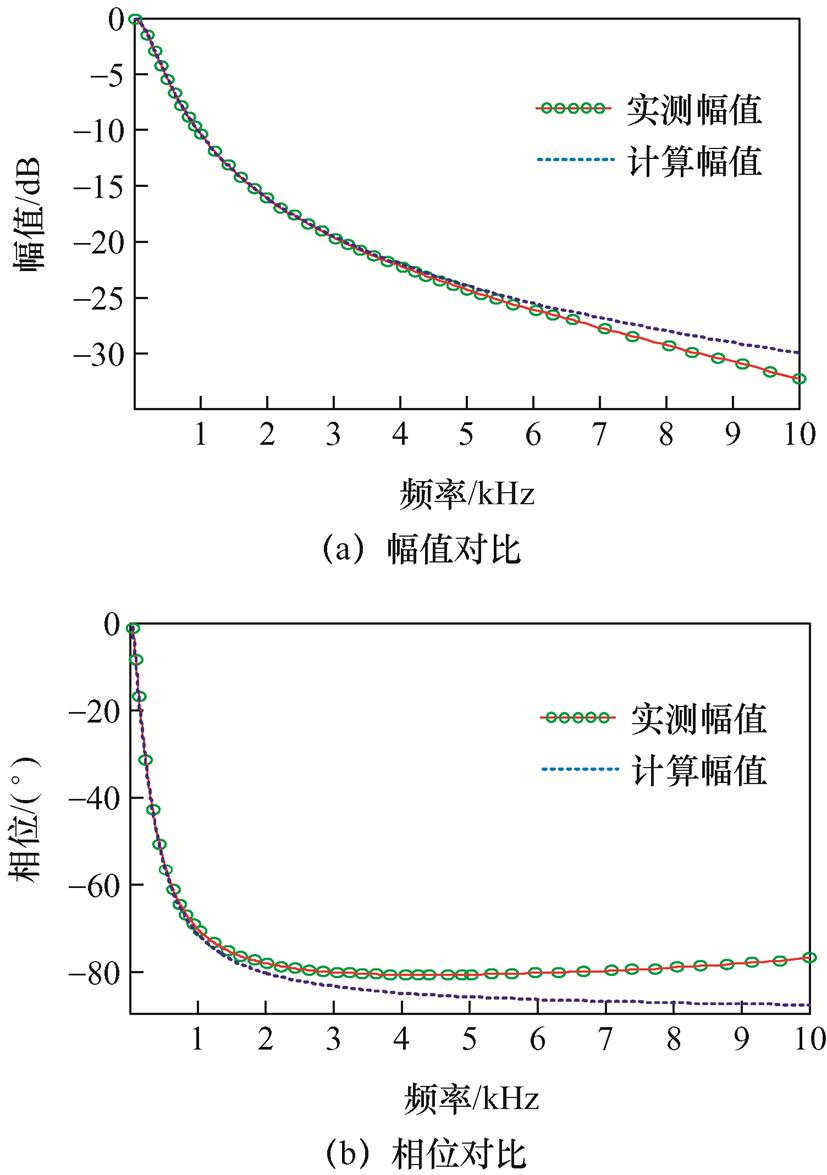
图7 10 kHz内幅值相位对比
Fig.7 Comparison of amplitude and phase below 10 kHz
变压器参数拟合多利用误差率来衡量拟合的效果，并且认为误差率在±5%之内时，拟合的效果较好[28-29,33]，因此取±5%为允许的最大误差率。当误差率超过±5%时，认为实测数据与计算数据的拟合误差较大，建立的换流变高频简化模型的精度不能满足MMC空母线高频谐振分析的要求。
误差率表示为
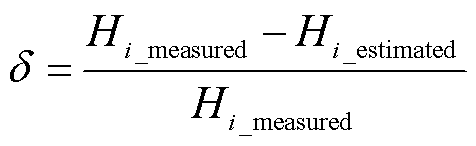（10）
式中，H为以式（3）形式表征的换流变压器频率响应数据；Hi_measured和Hi_estimated分别为频率点i处实测和估算的频率响应数据。10 kHz之内幅值和相位误差率如图8所示。
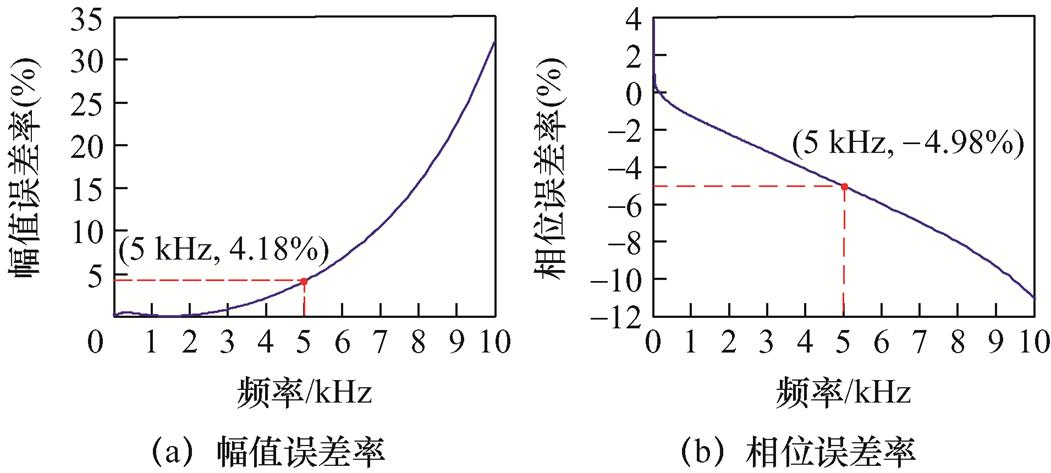
图8 10 kHz内幅值和相位误差率
Fig.8 Error rate of amplitude and phase below 10 kHz
由图8可以看出，随着频率的增加，幅值和相位的误差率都不断上升。5 kHz时，幅值误差率为4.18%，相位误差率为-4.98%，均已接近允许误差上限，因此低于5 kHz时，其计算数据与实测数据拟合程度较高。
所建立换流变高频简化模型在频率低于5 kHz时精度较高，但是随着频率的增加其精度呈下降趋势。这是因为所建模型将换流变绕组看作一个整体，并未考虑绕组的分散特性[34-35]。为保证高频等效模型的准确度，当频率大于5 kHz时，需要将绕组分散化处理，将每段绕组视为一个基本单元进行级联，且级联数与频率呈正相关。考虑到谐振频率低于5 kHz时，绕组分散特性并不明显，因此所建换流变高频简化模型可满足柔直高频谐振分析精度要求。
与工频模型不同，换流变高频等效模型需考虑C1s、C2s、C12对其阻抗的影响。考虑到实际工程中柔直换流站空母线谐振时，换流变阀侧与MMC连接，分析高频谐振时重点涉及阀侧端口的等效阻抗，因此主要讨论三电容不同数值下阀侧端口高频阻抗变化趋势。由于建立的换流变高频简化模型适用范围为5 kHz以内，所以仅研究1～5 kHz范围内，等效电容参数小范围变化时对换流变高频阻抗的影响。
基于表1中提供的C1s、C2s与C12，进一步对其增大和减小5倍，分别绘制不同容值条件下换流变高频阻抗Bode图，如图9所示。
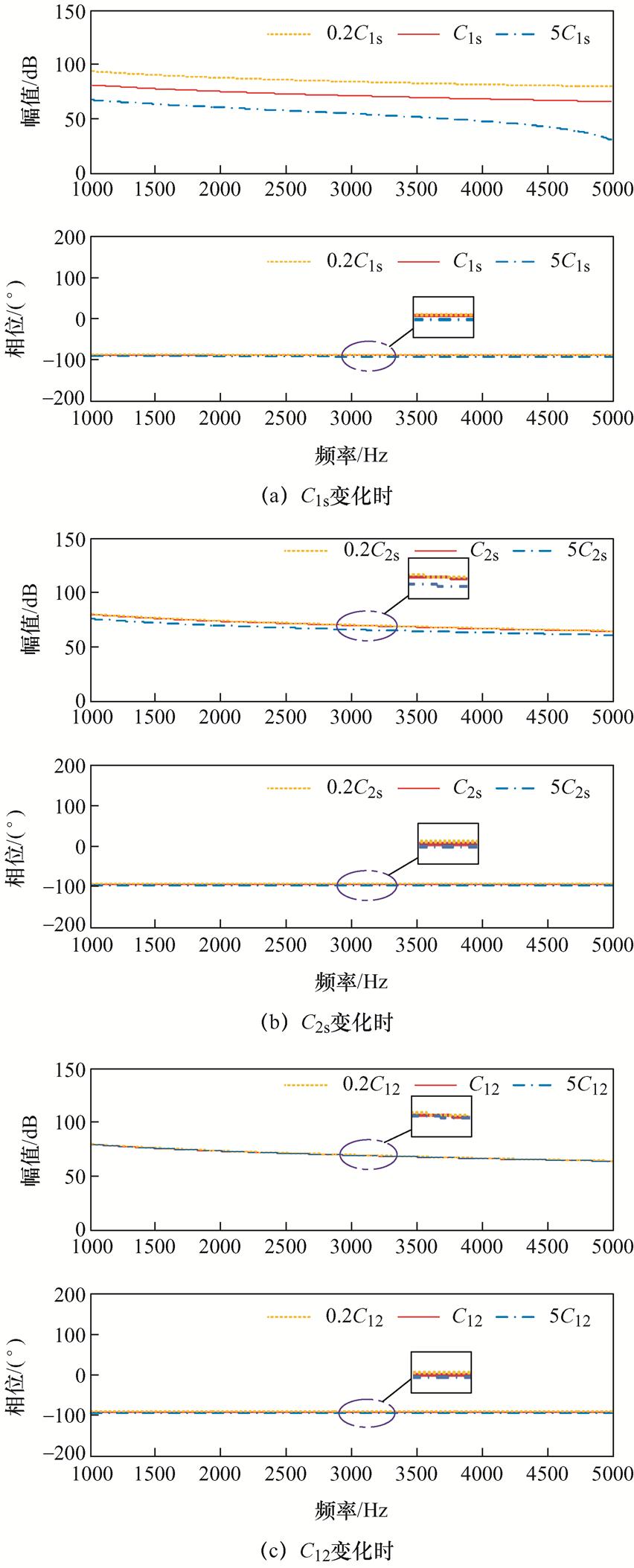
图9 等效电容变化时换流变阻抗Bode图
Fig.9 Converter transformer impedance Bode diagram with changing of equivalent capacitance
由图9a可知，C1s变化对换流变高频阻抗有较大影响。当C1s减小时，换流变高频阻抗幅值上升，当C1s增大时，换流变高频阻抗幅值下降。由图9b可知，换流变高频阻抗对C2s的变化并不敏感。C2s小范围变化时，随着C2s的增大，换流变高频阻抗幅值虽然也有下降趋向，但变化很小。当C2s减小时，换流变高频阻抗幅值上升，但当C2s到达某一临界值后，继续减小容值，对换流变高频阻抗几乎无影响。由图9c可知，C12小范围变化对换流变高频阻抗几乎无影响。
由上述分析可知，C1s对换流变高频阻抗影响最大，C2s对换流变高频阻抗影响较小，C12对换流变高频阻抗几乎无影响。
2020年12月27日，康保站带换流变空载启动调试过程中，交流电压/电流中出现了频率约为3 200 Hz左右的高频谐振，触发极控高频分量保护，继而导致换流阀闭锁，最终系统跳闸，现场故障波形如图10所示。
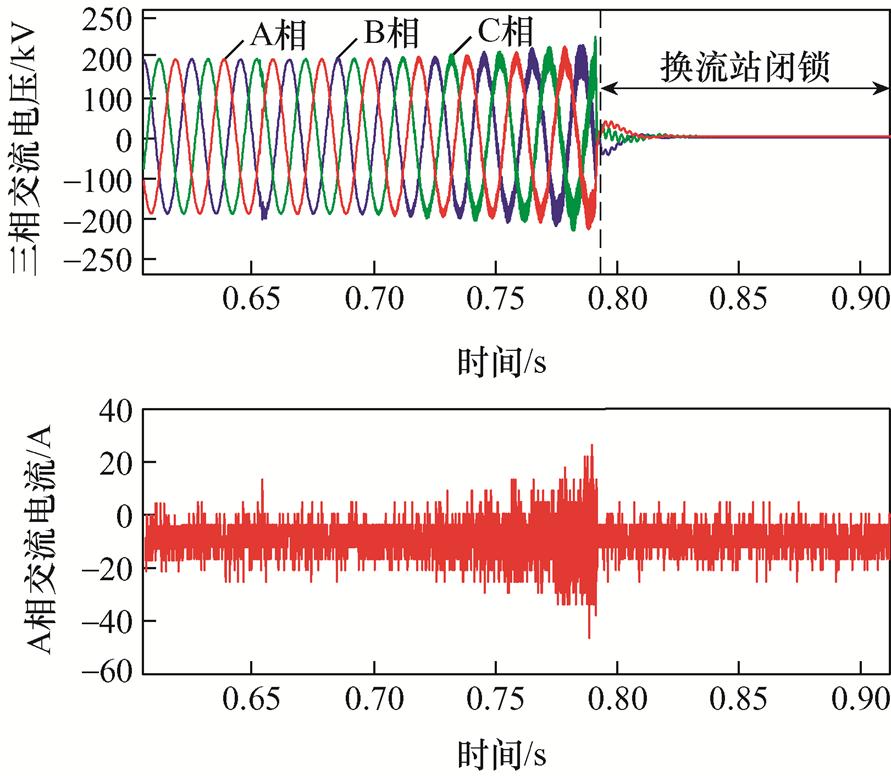
图10 康保站现场高频谐振波形
Fig.10 High-frequency resonance waveforms of Kangbao MMC
发生高频谐振时，诺英线未接入康巴诺尔母线，康保站交流侧仅投入了换流变，初步分析换流变与MMC之间相互作用是诱发高频谐振的主要原因。
为验证换流变高频特性对MMC空母线高频谐振的影响，基于RTLab5600仿真平台搭建四端柔直系统仿真模型如图11所示，其中MMC1参考康保站[7]，参数设置见表2。
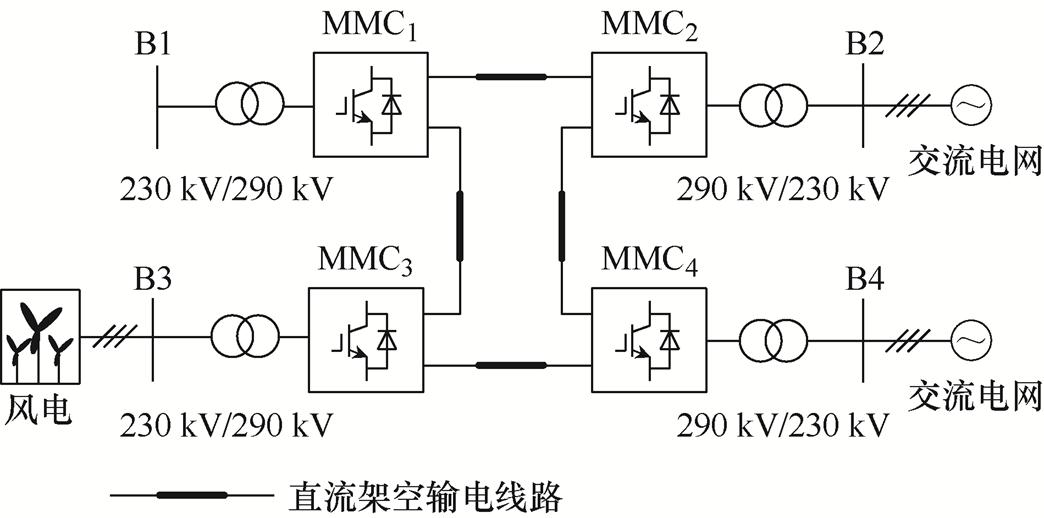
图11 所搭建的四端柔直系统结构
Fig.11 Four terminal MMC-HVDC system structure
表2 MMC1主要参数
Tab.2 MMC1 main parameters
参 数数 值 额定有功功率PN/MW900 换流变压器电压比/kV/kV230/290 额定直流电压UdcN/kV500 桥臂电抗Larm/mH100 桥臂电阻Rarm/W0.3 子模块电容C0/mF8 子模块数量交流电压控制器比例，积分增益交流电流控制器比例，积分增益301,1001,10 链路延时/ms250
图11中，MMC1为送端换流站，交流侧空母线运行，采用V/f控制策略，即外环控制并网点电压dq轴分量，坐标变换角度直接给定，以维持并网点电压幅值和频率恒定。MMC2采用定直流电压控制策略，以维持整个系统直流电压的稳定。MMC3与MMC4采用定功率控制策略。
0～2 s时段内，换流变采用工频模型，2 s后，切换为高频模型，换流变网侧三相交流电压与A相交流电流仿真波形如图12所示。由图12可知，换流变采用工频模型，换流站稳定运行；切换为所建高频模型，换流站与换流变之间交互作用，发生高频谐振。这表明忽略换流变高频特性将无法准确分析柔直换流站空母线高频谐振问题。换流变与MMC之间的交互作用导致高频谐振的理论分析详见附录。
考虑换流变高频特性前后的换流变网侧A相交流电压Up与交流电流Ip的仿真波形及其傅里叶分析结果如图13所示。由图13可知，考虑换流变高频特性后柔直换流站发生高频谐振，主要谐振频率为3 200 Hz，与实际现场谐振频率基本一致，证明换流变高频特性与MMC空母线高频谐振之间具有内在联系。
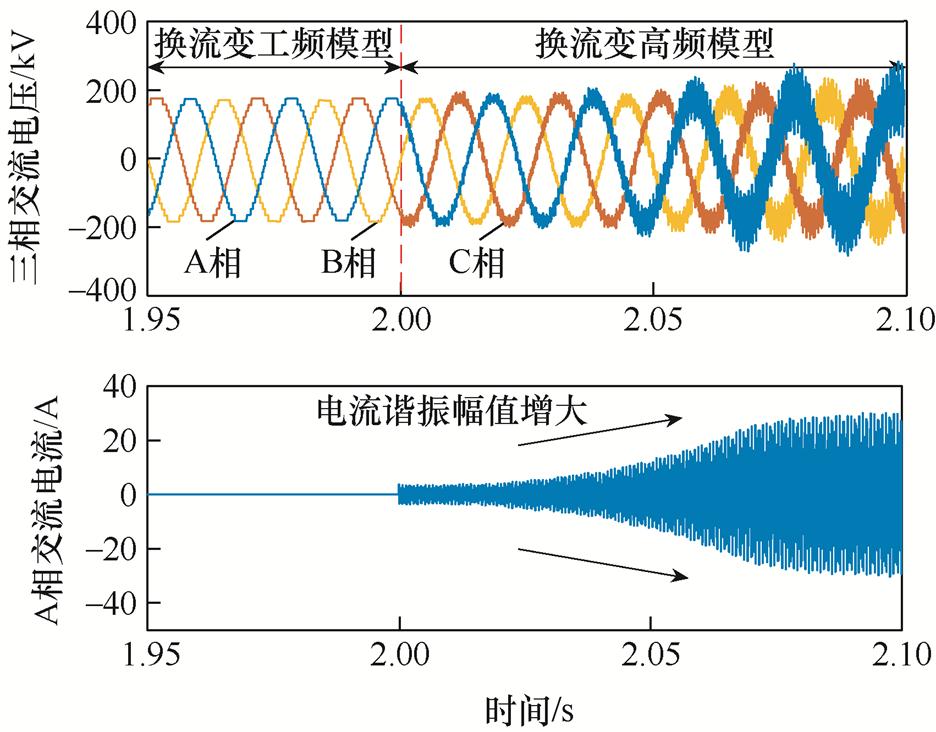
图12 网侧交流电压电流仿真波形
Fig.12 AC voltage and current simulation waveforms of grid side
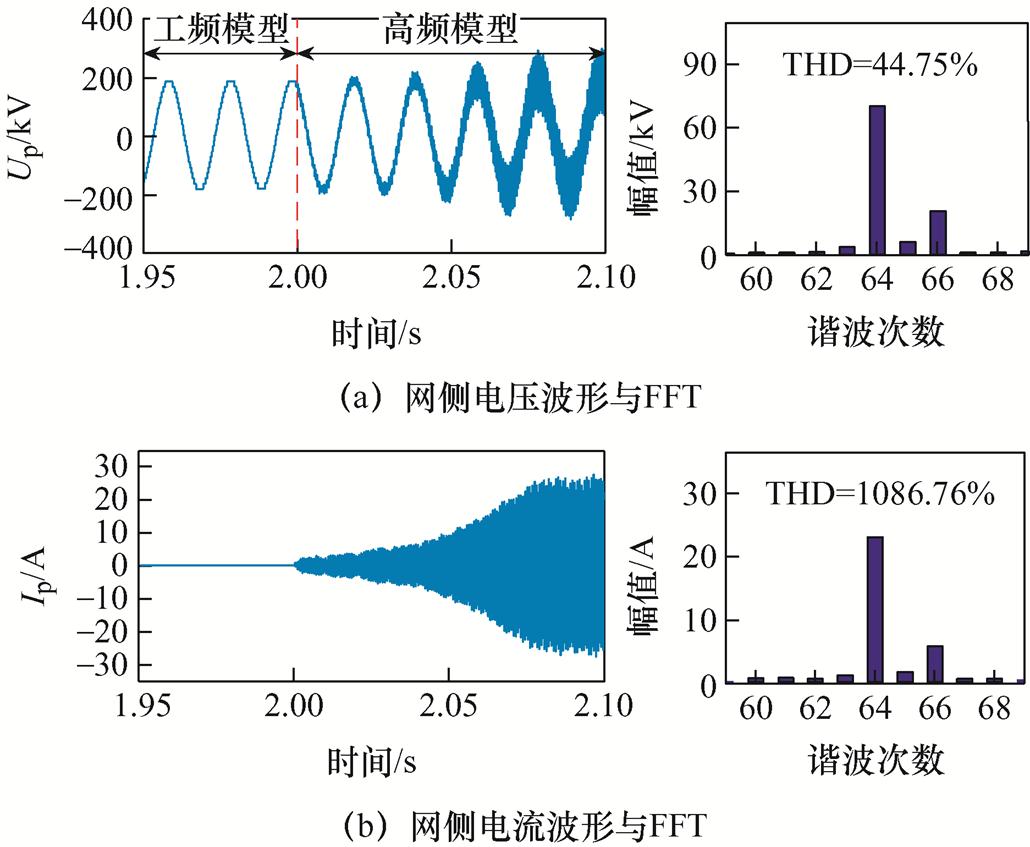
图13 考虑换流变高频特性前后的仿真结果
Fig.13 Simulation results without and with considering high-frequency characteristics of converter transformer
根据第3节可知，针对MMC空母线谐振分析而言，网侧绕组匝间电容C1s对换流变高频阻抗有明显影响。增大C1s对换流站空母线高频谐振的影响效果如图14所示，减小C1s对换流站空母线高频谐振的影响效果如图15所示。
分析图14、图15可知，当C1s增大至12.595 nF时，谐振频率由3 200 Hz减小到2 750 Hz；C1s减小至0.503 8 nF时，谐振频率由3 200 Hz增大到3 500 Hz。所以C1s容值改变能够影响换流站空母线高频谐振频率，当C1s增大时，谐振频率随之降低；C1s减小时，谐振频率随之升高。
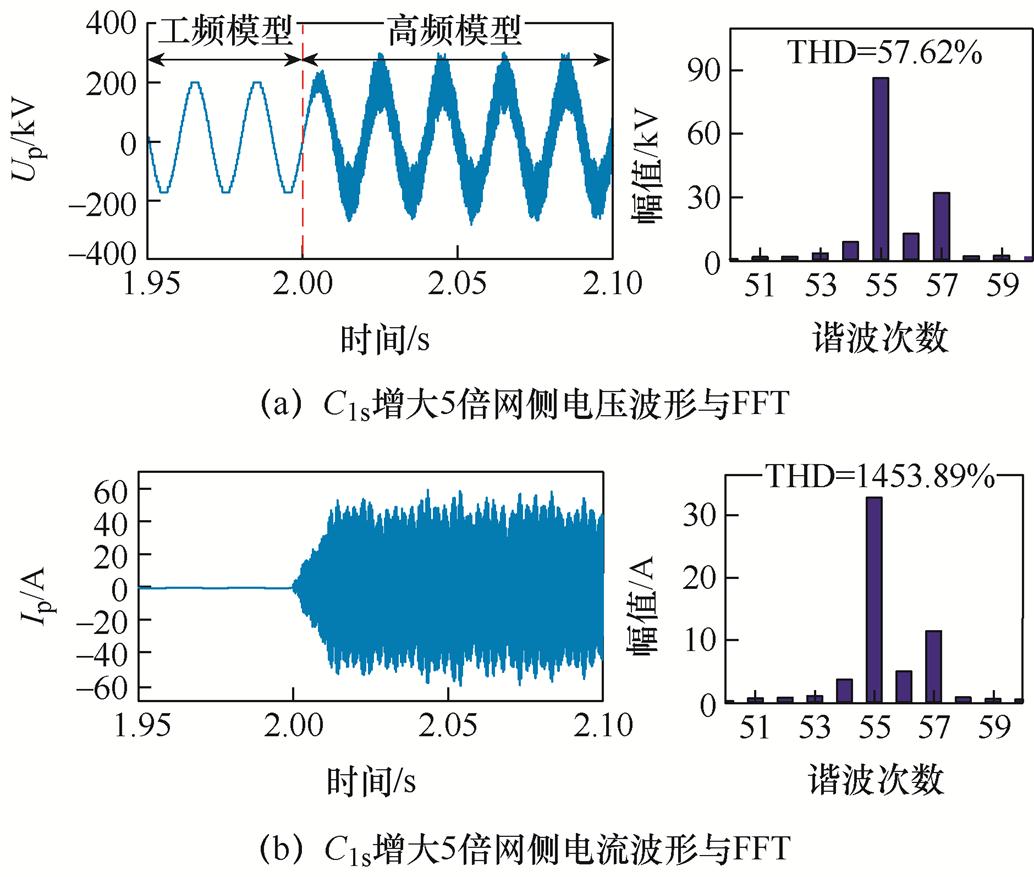
图14 C1s增大时网侧电压电流高频谐振仿真结果
Fig.14 High-frequency resonance simulation results of grid side voltage and current with increasing of C1s
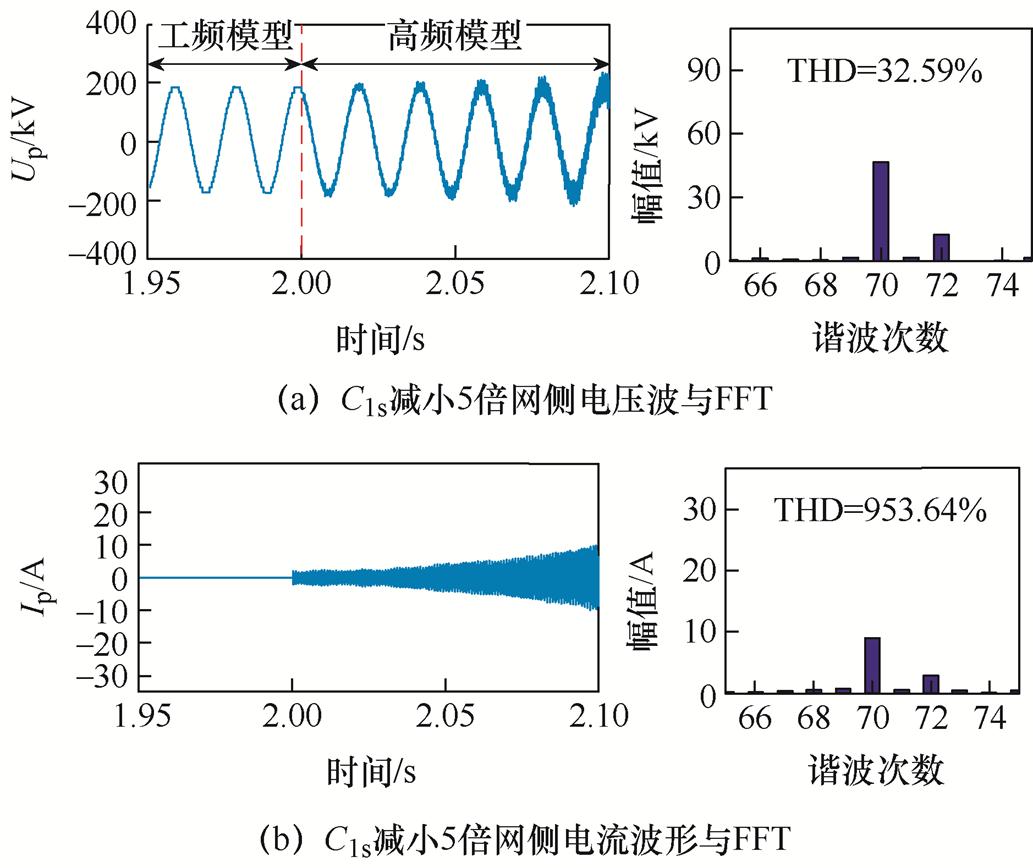
图15 C1s变化时网侧电压电流高频谐振仿真结果
Fig.15 High-frequency resonance simulation results of grid side voltage and current with reducing of C1s
本文重点从换流变高频等效建模和模型参数辨识两方面展开研究，分析了换流变高频特性与MMC空母线高频谐振的内在联系，并通过电磁仿真对理论分析结果进行了验证，得到以下结论：
1）与工频模型不同，高频条件下换流变建模需考虑绕组匝间电容和耦合电容，而本文电容效应会使换流变等效阻抗特征在1～5 kHz频段呈现容性。
2）针对MMC空母线高频谐振分析而言，相较于阀侧绕组匝间电容C2s和耦合电容C12，网侧绕组匝间电容C1s对换流变高频阻抗的影响最大，随着C1s的增大，MMC空母线高频谐振频率将相应减小。
3）在MMC空母线运行工况下，换流变的高频特性是决定换流站发生高频谐振与否的重要因素，忽略换流变高频特性将无法准确分析MMC空母线高频谐振问题。
4）与传统方法相比，在5 kHz以内，所提换流变高频模型参数获取方法能方便地获取换流变高频模型匝间电容、耦合电容、漏感等参数的准确数值。
下一步研究工作计划从拓宽高频谐振分析频带范围入手，考虑换流变绕组的分散特性，建立更精确的换流变高频等效模型，继而获得5 kHz以上高频模型参数。
附 录
考虑桥臂电抗、电流内环、电压前馈、链路延时的MMC高频简化模型结构如附图1所示。图中，L0为MMC的等值电感，L0=Larm/2，Larm为桥臂电感，iref为内环电流参考值，iout为阀侧输出电流，uac为阀侧出口电压，Gi为电流内环的传递函数，Gd为系统的链路延时环节，Gd=e-sT，T为延时。
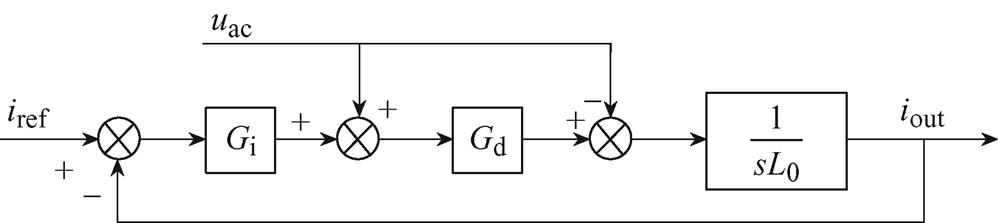
附图1 MMC高频简化模型
App.Fig.1 MMC high frequency simplified model
阀侧输出电流为
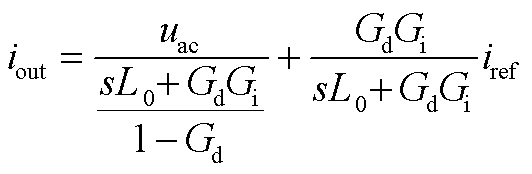（A1）
MMC的高频等效阻抗为
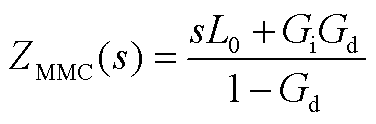（A2）
MMC空母线运行时，系统的稳定性可以根据MMC和换流变的等效阻抗进行判定，系统等效电路如附图2所示。图中，ZT为换流变阀侧端口的等效阻抗，io(s)为换流站的谐波源。
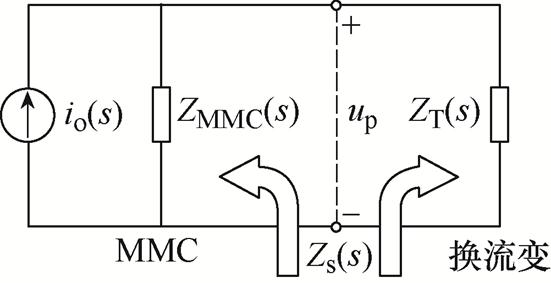
附图2 MMC空母线运行时的等效电路
App.Fig.2 Equivalent circuit of MMC with converter transformer under no-load condition
系统整体等效阻抗为
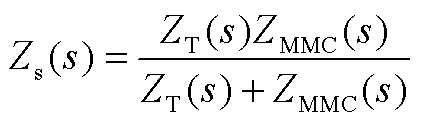（A3）
当系统存在谐振点，并且该点对应的阻尼为负时，在谐振频率处存在高频谐振的风险。换流变阻抗的变化会导致系统整体的谐振频率及负阻尼区域发生变化，进而对系统的高频谐振产生影响。网侧匝间电容C1s是换流变阻抗ZT的重要组成部分，其对系统高频谐振产生影响较大。
C1s容值变化时，系统整体的阻抗变化情况如附图3所示。
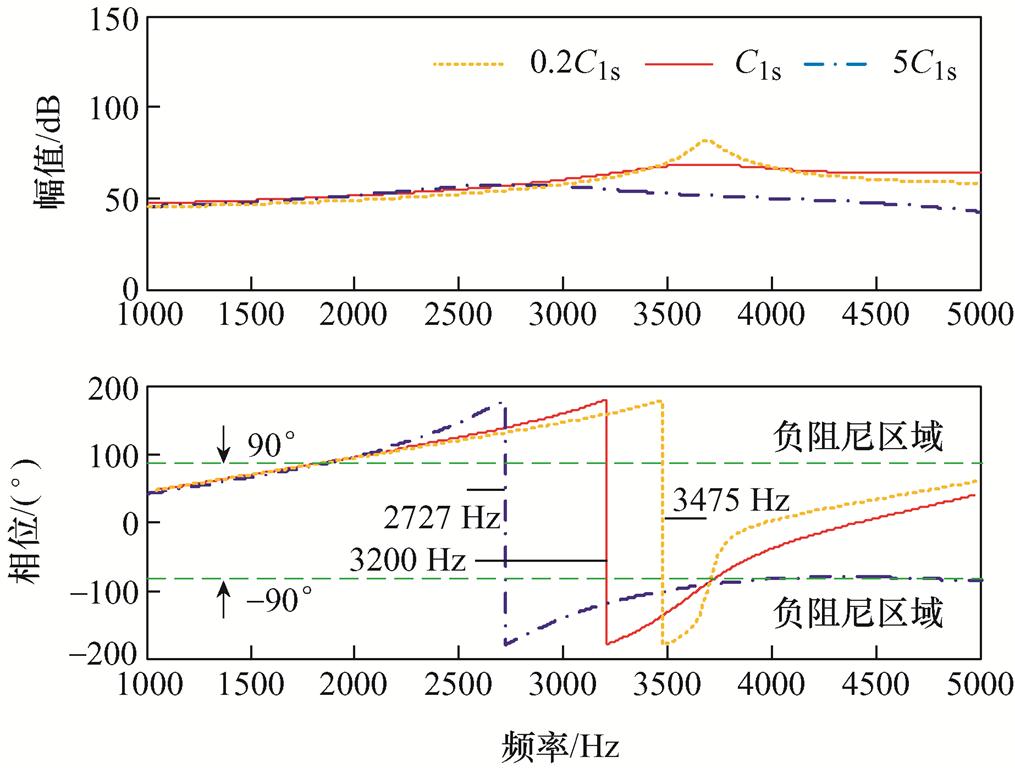
附图3 C1s变化时系统等效阻抗Bode图
App.Fig.3 System equivalent impedance Bode diagram with changing of C1s
C1s容值增大至12.595 nF(5C1s)时，系统谐振频率由3 200 Hz前移至2 727 Hz；C1s容值减小至0.503 8 nF (0.2C1s)时，系统谐振频率由3 200 Hz后移至3 475 Hz，且在谐振频率处系统处于负阻尼区域，存在高频谐振风险。
参考文献
[1] 饶宏, 黄伟煌, 郭知非, 等. 柔性直流输电技术在大电网中的应用与实践[J]. 高电压技术, 2022, 48(9): 3347-3355.
Rao Hong, Huang Weihuang, Guo Zhifei, et al. Practical experience of VSC-HVDC transmission in large grid[J]. High Voltage Engineering, 2022, 48(9): 3347-3355.
[2] 邵冰冰, 赵峥, 肖琪, 等. 多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J]. 电工技术学报, 2023, 38(3): 754-769.
Shao Bingbing, Zhao Zheng, Xiao Qi, et al. Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[3] 汤广福, 贺之渊, 庞辉. 柔性直流输电工程技术研究、应用及发展[J]. 电力系统自动化, 2013, 37(15): 3-14.
Tang Guangfu, He Zhiyuan, Pang Hui. Research, application and development of VSC-HVDC engineering technology[J]. Automation of Electric Power Systems, 2013, 37(15): 3-14.
[4] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[5] Saad H, Fillion Y, Deschanvres S, et al. On resonances and harmonics in HVDC-MMC station connected to AC grid[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1565-1573.
[6] 李岩, 邹常跃, 饶宏, 等. 柔性直流与极端交流系统间的谐波谐振[J]. 中国电机工程学报, 2018, 38(增刊1): 19-23.
Li Yan, Zou Changyue, Rao Hong, et al. Resonance of VSC-HVDC with extreme AC grid[J]. Proceedings of the CSEE, 2018, 38(S1): 19-23.
[7] 赵峥, 李明, 田园园, 等. 江苏如东海上风电柔直工程系统谐振分析与抑制[J]. 电力建设, 2023, 44(6): 144-152.
Zhao Zheng, Li Ming, Tian Yuanyuan, et al. Resonance analysis and suppression in Jiangsu Rudong offshore wind power flexible DC system[J]. Electric Power Construction, 2023, 44(6): 144-152.
[8] 苑宾, 厉璇, 尹聪琦, 等. 孤岛新能源场站接入柔性直流高频振荡机理及抑制策略[J]. 电力系统自动化, 2023, 47(4): 133-141.
Yuan Bin, Li Xuan, Yin Congqi, et al. Mechanism and suppression strategy of high-frequency oscillation caused by integration of islanded renewable energy station into MMC-HVDC system[J]. Automation of Electric Power Systems, 2023, 47(4): 133-141.
[9] 杜镇宇, 阳岳希, 季柯, 等. 张北柔直工程高频谐波振荡机理与抑制方法研究[J]. 电网技术, 2022, 46(8): 3066-3075.
Du Zhenyu, Yang Yuexi, Ji Ke, et al. High frequency harmonic resonance and suppression in Zhangbei Project[J]. Power System Technology, 2022, 46(8): 3066-3075.
[10] 郭春义, 彭意, 徐李清, 等. 考虑延时影响的MMC-HVDC系统高频振荡机理分析[J]. 电力系统自动化, 2020, 44(22): 119-126.
Guo Chunyi, Peng Yi, Xu Liqing, et al. Analysis on high-frequency oscillation mechanism for MMC- HVDC system considering influence of time delay[J]. Automation of Electric Power Systems, 2020, 44(22): 119-126.
[11] 李冠群, 叶华, 宾子君. V/f控制MMC带换流变压器空载充电发生高频振荡的机理分析[J]. 电力系统自动化, 2023, 47(11): 50-59.
Li Guanqun, Ye Hua, Bin Zijun. High-frequency oscillation mechanism analysis of V/f controlled modular multilevel converter charging with converter transformer under no-load condition[J]. Automation of Electric Power Systems, 2023, 47(11): 50-59.
[12] 刘普, 王跃, 雷万钧, 等. 模块化多电平变流器稳态运行特性分析[J]. 电工技术学报, 2015, 30(11): 90-99.
Liu Pu, Wang Yue, Lei Wanjun, et al. Analysis of steady-state operating characteristics for modular multilevel converters[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 90-99.
[13] 李云丰, 贺之渊, 庞辉, 等. 柔性直流输电系统高频稳定性分析及抑制策略(一): 稳定性分析[J]. 中国电机工程学报, 2021, 41(17): 5842-5856.
Li Yunfeng, He Zhiyuan, Pang Hui, et al. High frequency stability analysis and suppression strategy of MMC-HVDC systems (part I): stability analysis[J]. Proceedings of the CSEE, 2021, 41(17): 5842-5856.
[14] 胡畔, 陈红坤, 陈孟忻, 等. 基于动态相量法的改进多端模块化多电平换流器HVDC小干扰稳定模型[J]. 电工技术学报, 2017, 32(24): 193-204.
Hu Pan, Chen Hongkun, Chen Mengxin, et al. Advanced small-signal stability model for multi-terminal modular multilevel converter-HVDC systems based on dynamic phasors[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 193-204.
[15] Lü Jing, Zhang Xin, Cai Xu, et al. Harmonic state-space based small-signal impedance modeling of a modular multilevel converter with consideration of internal harmonic dynamics[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2134-2148.
[16] Zhang Yang, Chen Xin, Sun Jian. Sequence impedance modeling and analysis of MMC in single- star configuration[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 334-346.
[17] 郭琦, 郭海平, 黄立滨. 电网电压前馈对柔性直流输电在弱电网下的稳定性影响[J]. 电力系统自动化, 2018, 42(14): 139-144.
Guo Qi, Guo Haiping, Huang Libin. Effect of grid voltage feedforward on VSC-HVDC stability in weak power grid[J]. Automation of Electric Power Systems, 2018, 42(14): 139-144.
[18] 杜东冶, 郭春义, 贾秀芳, 等. 基于附加带阻滤波器的模块化多电平换流器高频谐振抑制策略[J]. 电工技术学报, 2021, 36(7): 1516-1525.
Du Dongye, Guo Chunyi, Jia Xiufang, et al. Suppression strategy for high frequency resonance of modular multilevel converter based on additional band-stop filter[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1516-1525.
[19] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[20] 王一凡, 赵成勇, 郭春义. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129.
Wang Yifan, Zhao Chengyong, Guo Chunyi. Small signal stability and oscillation suppression method for islanded double fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2116-2129.
[21] Shen Wei, Wang Fei, Boroyevich D, et al. High-density nanocrystalline core transformer for high-power high-frequency resonant converter[J]. IEEE Transactions on Industry Applications, 2008, 44(1): 213-222.
[22] 郝全睿, 徐政, 黄莹, 等. 用于高频干扰计算的HVDC换流变压器模型[J]. 电工技术学报, 2008, 23(8): 47-52.
Hao Quanrui, Xu Zheng, Huang Ying, et al. Models of HVDC converter transformer for calculation of high- frequency interference[J]. Transactions of China Electrotechnical Society, 2008, 23(8): 47-52.
[23] Liu Chen, Qi Lei, Cui Xiang, et al. Experimental extraction of parasitic capacitances for high-frequencytransformers[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4157-4167.
[24] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three-dimensional temperature calculation and optimization design method for high power high- frequency transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[25] Hashemnia N, Abu-Siada A, Islam S. Improved power transformer winding fault detection using FRA diagnostics–part 1: axial displacement simulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1): 556-563.
[26] 张科科, 齐磊, 崔翔, 等. 多绕组中频变压器宽频建模方法[J]. 电网技术, 2019, 43(2): 582-590.
Zhang Keke, Qi Lei, Cui Xiang, et al. Wideband modeling method of multi-winding medium frequency transformer[J]. Power System Technology, 2019, 43(2): 582-590.
[27] 汪涛, 骆仁松, 文继峰, 等. 基于辅助绕组的高频变压器绕组损耗测量方法[J]. 电工技术学报, 2022, 37(10): 2622-2630, 2655.
Wang Tao, Luo Rensong, Wen Jifeng, et al. A measurement method of winding loss for high-frequency transformer based on auxiliary winding[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2622-2630, 2655.
[28] Mossad M I, Azab M, Abu-Siada A. Transformer parameters estimation from nameplate data using evolutionary programming techniques[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2118-2123.
[29] Wu Qiong, Jazebi S, de Leon F. Parameter estimation of three-phase transformer models for low-frequency transient studies from terminal measurements[J]. IEEE Transactions on Magnetics, 2017, 53(7): 1-8.
[30] Abu-Siada A, Hashemnia N, Islam S, et al. Understanding power transformer frequency response analysis signatures[J]. IEEE Electrical Insulation Magazine, 2013, 29(3): 48-56.
[31] 李佳靖, 金荣洪, 耿军平. CDMA系统中一种快速有效的盲波束形成方法[J]. 西安电子科技大学学报(自然科学版), 2007, 34(6): 980-985.
Li Jiajing, Jin Ronghong, Geng Junping. A fast and efficient bind beamforming method for CDMA systems[J]. Journal of Xidian University (Natural Science), 2007, 34(6): 980-985.
[32] Abu-Siada A, Mosaad M I, Kim D, et al. Estimating power transformer high frequency model parameters using frequency response analysis[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1267-1277.
[33] 杨玥坪, 树婷, 吴玖汕, 等. 变压器绕组局部放电量测量误差计算及其修正方法研究[J]. 西安交通大学学报, 2022, 56(10): 122-129.
Yang Yueping, Shu Ting, Wu Jiushan, et al. Error analysis and correction of partial discharge quantity measurement of transformer windings[J]. Journal of Xi’an Jiaotong University, 2022, 56(10): 122-129.
[34] 张旭东, 张重远, 陈涛, 等. 基于多导体传输线模型变压器宽频参数的计算[J]. 变压器, 2014, 51(8): 5-10.
Zhang Xudong, Zhang Zhongyuan, Chen Tao, et al. Calculation of broadband admittance parameters for transformer based on MTL[J]. Transformer, 2014, 51(8): 5-10.
[35] Hashemnia N, Abu-Siada A, Islam S. Detection of power transformer bushing faults and oil degradation using frequency response analysis[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2016, 23(1): 222-229.
Modeling and Parameter Identification of Converter Transformer for High-Frequency Resonance Problem of Flexible DC Converter Station
AbstractIn December 2020, a high-frequency resonance of around 3 200 Hz occurred during the no-load starting process of Kangbao station, triggering high-frequency component protection, which resulted in the converter station blockage and system trip. When the resonance occurred, the converter station charged the converter transformer. However, the bus was not connected to any AC overhead line, which means that the converter transformer participated in the high-frequency resonance of a modular multilevel converter (MMC) with the no-load bus. The modeling method that the converter transformer is equivalent to the leakage reactance can not reflect the high-frequency characteristics of the converter transformer, failing to analyze this high-frequency resonance accurately.
Forthe high-frequency resonance problem in Zhangbei Kangbao MMC with the no-load bus, the research focuses on the physical characteristics of the converter transformer and the modeling method in the high-frequency range. Firstly, the high-frequency equivalent model is established considering the interturn capacitance, the coupling capacitance, and the capacitance to ground. The high-frequency model of the converter transformer is simplified by neglecting the capacitance to ground. Then, based on the measured frequency response data of the Kangbao converter transformer, the improved Powell algorithm is used to calculate the high-frequency equivalent model parameters. The critical parameters are checked, and the application scope of the model is determined. Moreover, the effects of equivalent capacitance parameters on the high-frequency impedance of the converter transformer are analyzed. Finally, based on the high-frequency equivalent model, the high-frequency resonance phenomenon is reproduced in Kangbao MMC with the no-load bus. The simulation results verify the accuracy of the equivalent model.
Different from the power frequency model, interturn and coupling capacitances should be considered in converter transformer modeling at the high-frequency band. The capacitance effect makes the equivalent impedance characteristics of the converter transformer appear capacitive in the frequency band of 1～5 kHz. Compared with the measured frequency response data of the Kangbao converter transformer, the proposed method can easily obtain accurate high-frequency model parameters within 5 kHz, such as the interturn capacitance, the coupling capacitance, and the leakage induction. The simplified high-frequency model of the converter transformer meets the accuracy requirements of the high-frequency resonance analysis of MMC with the no-load bus. The grid side winding's interturn capacitance of the converter transformer has the most obvious influence on its high-frequency impedance, and the high-frequency resonance frequency of MMC with the no-load bus decreases with the increase of its capacity. During the no-load starting process, the high-frequency characteristic of the converter transformer is an essential factor in determining whether the high-frequency resonance risk exists at a converter station. If the high-frequency characteristic of the converter transformer is addressed, the high-frequency resonance problem of MMC with the no-load bus can be accurately analyzed.
Keywords：Converter transformer, high-frequency equivalent model, inversion calculation, high-frequency resonance, modular multilevel converters
中图分类号：TM721.1; TM41
DOI: 10.19595/j.cnki.1000-6753.tces.231665
国网冀北电力有限公司科技资助项目（52018K22001C）。
收稿日期 2023-10-10
改稿日期 2023-12-15
胡应宏 男，1981年生，博士后，正高级工程师，研究方向为新能源并网稳定与控制。
Email: factshu@163.com
陈继开 男，1977年生，教授，博士生导师，研究方向为电能质量分析与控制、柔性直流输电技术等。
Email: chenjikai1977@163.com（通信作者）
（编辑 陈 诚）