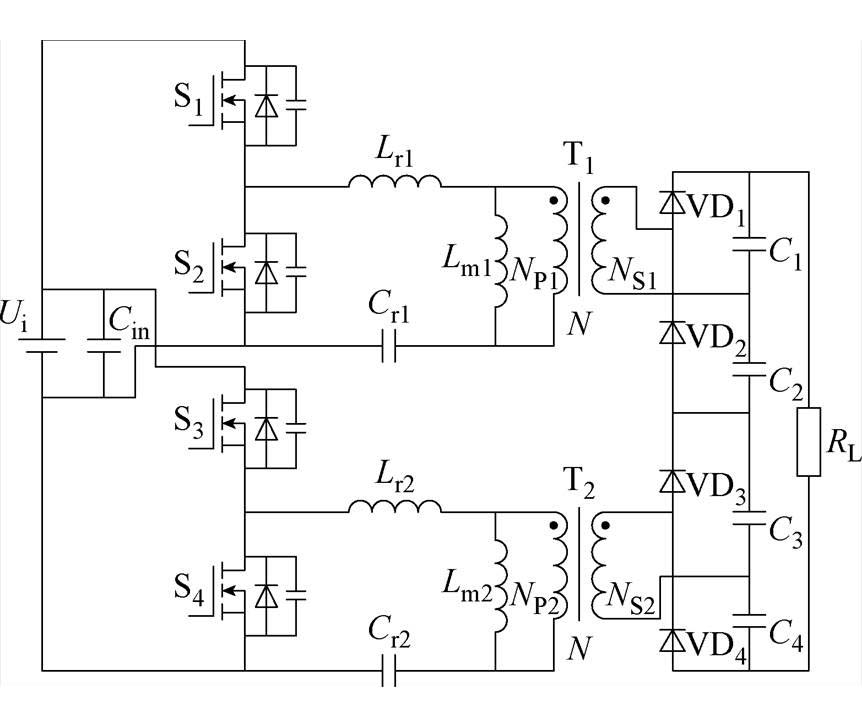
图1 变模态倍压型LLC谐振变换器电路拓扑
Fig.1 Circuit topology of variable mode voltage doubling LLC resonant converter
摘要 传统LLC变换器采用基波分析法,忽略高次谐波的影响,在远离谐振频率点误差较大,宽输出电压场合下变换器精度低。对此,该文深入分析变模态倍压型LLC谐振变换器工作模式,确立PO模式是其最佳工作模式,建立PO模式下状态时域方程,求解状态方程相关系数,得到负载约束、系数约束和角度约束条件,推导谐振电容Cr、电感比系数K和P阶段导通角q 等参数。基于模式边界、谐振电容最值和ZVS多目标约束条件,提出一种多目标参数优化方法,对变换器主电路参数进行优化设计,制作504 W变模态倍压型LLC谐振变换器样机。实验结果表明,基于时域分析的多目标参数优化设计的变换器能够实现全范围内软开关,以满足增益和高效率要求。
关键词:变模态倍压型 PO模式 时域分析 约束条件 多目标参数优化
随着国家“双碳”目标的提出,新能源领域得到快速发展,推动能源消费行业的电气化进程[1-3]。交通电气化发展将“锂”推向了高潮[4]。中小功率领域,“油转电”和“无绳化”趋势加快,同样推动锂电池行业的快速发展。锂电池使用过程中,端电压下降,在深度睡眠状态下电压更低,且充电过程中,随着电池荷电状态的改变,其端电压也会发生改变。为适应待充电锂电池的电压范围,充电器后级DC-DC变换器应具备宽范围电压输出能力[5-6],同时还应确保变换器具有较高的充电效率。LLC谐振变换器可实现电气隔离、软开关且具有高效率、高功率密度的优点,在锂电池充电等领域获得广泛的应用[7]。传统LLC谐振变换器软开关状态下调压能力有限,且存在宽输出电压范围和效率之间的矛盾。
在LLC谐振变换器的设计中,分析方法对参数设计的精度和有效性有很大的影响。基波分析法(Fundamental Harmonic Analysis, FHA)简化了分析难度和计算过程,但开关频率与谐振频率相差较大时增益偏差较大[8],因此为保证锂电池充电的高效率,需对LLC变换器进行精确的时域模型分析。
全桥LLC谐振变换器时域模型在文献[9]中进行了分析,绘制基于时域方程增益曲线,与FHA进行比较,但未给出变换器具体参数设计过程。国内外学者基于时域分析方法分析电路[10-13],给出每个阶段的时域方程,但更多关注开关频率小于谐振频率部分,同时未根据方程相互关系,推导包含电路全部信息的方程组。文献[14]中,进行时域分析时对谐振电流进行简化,导致在远离谐振点处会造成较大偏差。Xu Sen等[15]在FHA频域分析模型的基础上引入时域分析方法,重新定义增益公式中相关部分为谐振因数和负载因数进行分析,但是这种定义没有明确的依据。部分学者对LLC电路的移相控制部分进行了时域分析[16-18],而未对占LLC电路绝大多数的工作状态的变频工作部分进行时域分析。文献[19-21]分别给出了LLC时域模式划分及边界划分,但都未对变换器进行参数优化设计。
针对上述问题,对变模态倍压型LLC变换器工作模态进行分析,确定其最佳工作模式,在此模式下对LLC变换器进行时域分析,推导电路中时域电压电流方程组。根据约束条件对变换器进行多目标优化参数设计,保证变换器在全范围内高效率,通过实验样机验证理论分析的正确性和可靠性。
变模态倍压型LLC谐振变换器电路拓扑如图1所示,前级为交错并联的双谐振腔结构,后级采用倍压整流结构。同等级输出电压时,倍压整流结构可有效降低变压器二次绕组匝数,减小变压器寄生电容高频时LLC谐振变换器增益的影响,高频轻载时有效减小电压“飘升”现象,输出更低的电压,拓宽输出电压范围[22]。通过变模态策略,使变换器可以在半桥模态和双半桥模态运行,变换器电压输出范围为两模式输出电压范围的合集,拓宽了变换器输出电压范围。图1中,Ui为输入电压,Lr1和Lr2为谐振电感,Cr1和Cr2为谐振电容,Lm1和Lm2分别为变压器T1和T2的励磁电感和谐振电感,变压器电压比为N,VD1~VD4为整流管,C1~C4为输出滤波电容,负载用RL表示。

图1 变模态倍压型LLC谐振变换器电路拓扑
Fig.1 Circuit topology of variable mode voltage doubling LLC resonant converter
变换器两个谐振腔的参数完全相同,故只对其中一个谐振腔进行分析,即分析半桥倍压整流型LLC拓扑结构。
以变换器正半周期为例,当开关管S1导通时,谐振槽输入电压为正。由电压条件可知,半桥倍压型LLC谐振变换器工作过程存在三个谐振阶段,其等效电路模型如图2所示。
由图2可知,P阶段:其励磁电感Lm被钳位于NUo/2,励磁电流iLm线性增加。Lr和Cr谐振,谐振电流iLr以正弦形式上升。在此阶段,由于输出电流在一个方向上受到限制,需满足条件iLr>iLm。
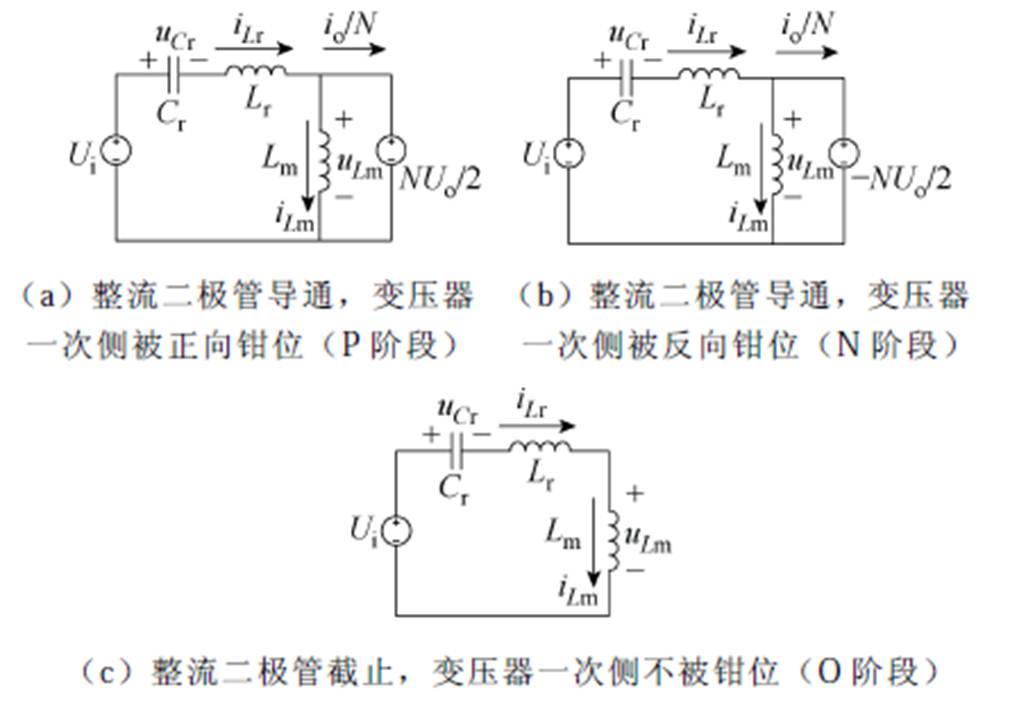
图2 半桥倍压型LLC谐振变换器等效电路
Fig.2 Equivalent circuit diagram of half bridge voltage doubling LLC resonant converter
N阶段:励磁电感Lm被钳位于-NUo/2,因此励磁电流iLm线性减小。Lr和Cr谐振,谐振电流iLr波形以正弦形式下降。同理,在此阶段需要满足条件iLr<iLm。
O阶段:Lr与Lm和Cr一起谐振,整流二极管关断,没有电流流向输出,因此,iLm和iLr相等。
半个开关周期中,根据三个阶段不同顺序组合,用这些组合顺序表示LLC谐振变换器工作模式。一般存在六种主要工作模式:PO、PON、PN、NP、NOP和OPO和三种临界工作模式:P、O和OP。
为确定变换器的最佳工作模式,下面对几种模式进行简单分析。
LLC谐振变换器PO模式工作波形如图3所示。其中,归一化频率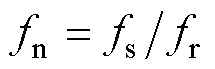 ,
, 为开关频率,
为开关频率,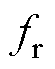 为谐振频率;
为谐振频率;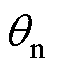 为归一化导通角。P阶段开始,谐振电流iLr和励磁电流iLm具有相同的负初始值。当励磁电感Lm被钳位到NUo/2时,iLm线性增加,而Lr和Cr处于共振阶段时,iLr呈正弦变化。当iLr和iLm在P阶段末相交时,整流二极管关断,此时工作于阶段O。在O阶段,励磁电感电压uLm正弦下降但始终高于-NUo/2,即uLm>-NUo/2,否则半个周期内谐振回路将进入阶段N。
为归一化导通角。P阶段开始,谐振电流iLr和励磁电流iLm具有相同的负初始值。当励磁电感Lm被钳位到NUo/2时,iLm线性增加,而Lr和Cr处于共振阶段时,iLr呈正弦变化。当iLr和iLm在P阶段末相交时,整流二极管关断,此时工作于阶段O。在O阶段,励磁电感电压uLm正弦下降但始终高于-NUo/2,即uLm>-NUo/2,否则半个周期内谐振回路将进入阶段N。

图3 LLC谐振变换器PO模式工作波形
Fig.3 LLC resonant converter PO mode operating waveforms
PO模式开始时,谐振电流iLr为负,表明谐振槽电流滞后谐振槽电压,谐振槽输入阻抗呈感性,在该模式下开关管可实现零电压开通(Zero Voltage Switching, ZVS);结束时,谐振电流iLr等于励磁电流iLm,整流二极管能够实现零电流关断(Zero Current Switching, ZCS)。
PON模式工作波形如图4所示。相较PO模式,存在阶段N,在负载较重或较低的开关频率条件下可能发生该模式。PON模式的前两级与PO模式相同,但以N阶段结束而不是O阶段,故谐振电流iLr和励磁电流iLm以不同的初始值开始。P阶段励磁电感电压uLm被钳位到NUo/2,在O阶段时uLm降低,当下降到-NUo/2时,变压器励磁电感uLm被反向钳位到-NUo/2,谐振变换器开始进入N阶段。N阶段中谐振电流iLr和励磁电流iLm以正弦波形变化且 iLr<iLm。谐振电流iLr和励磁电流iLm再次相交之前,半个周期结束。
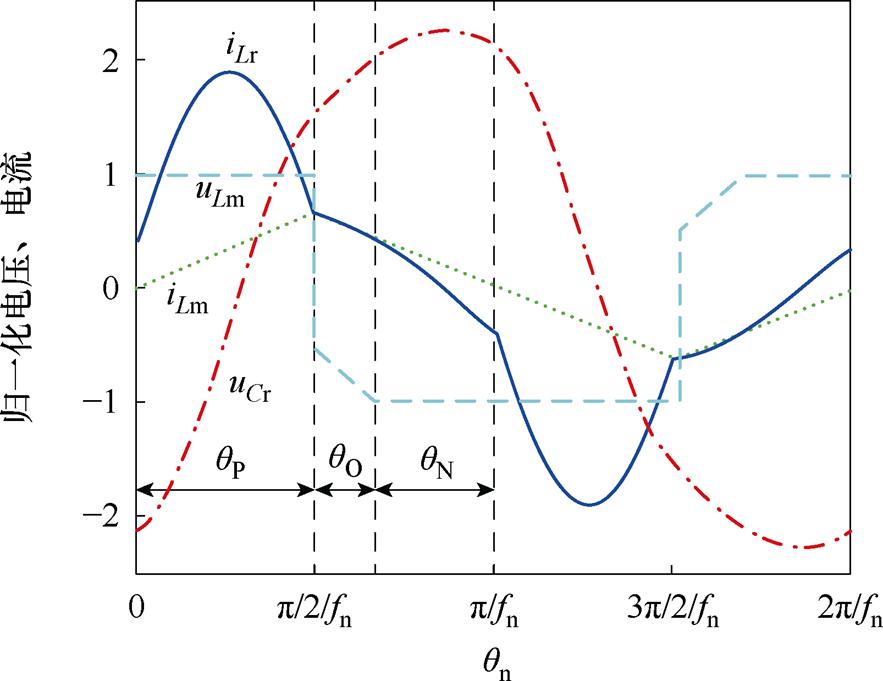
图4 LLC谐振变换器PON模式工作波形
Fig.4 LLC resonant converter PON mode operating waveforms
由于输出电流在开关瞬间不为零,关断时整流二极管存在反向恢复损耗。PON模式开始时谐振电流不一定像PO模式那样始终为负值,因此该模式下开关管可能不满足ZVS。此外,恒定负载条件下的增益-频率关系不再是单调的,此模式下,增益曲线可能会达到峰值并降至1以下,变换器应避免在峰值增益频率点以下运行,因为处于ZCS区域可能导致控制不稳定。
此外,还有PN模式、NP模式、NOP模式、OPO模式等,分析过程同上,工作波形分别如图5所示。

图5 LLC谐振变换器各模式工作波形
Fig.5 Working mode waveforms of LLC resonant converter
为确保变换器的工作效率,应使变换器能够实现开关管的ZVS和整流管的ZCS。PO模式开始时,谐振电流iLr为负,表明谐振槽电流滞后谐振槽电压,谐振槽输入阻抗呈感性,在该条件下开关管可实现ZVS;结束时,谐振电流iLr等于励磁电流iLm,整流二极管能够实现ZCS。PO模式下的直流增益M随着归一化工作频率fn的减小而单调增加,不同负载的增益曲线在谐振频率处相交于一点。该模式下不会出现峰值增益,由负载变化所引起的增益变化较小,可以用较窄的频率变化范围实现增益稳定。此外,PO模式下增益-频率曲线的斜率始终为负,保证了变换器闭环控制的稳定性。因此,PO模式是LLC谐振变换器的首选工作模式。
变模态倍压型LLC谐振变换器拓扑结构为两个半桥并联构成,两个谐振腔参数完全一致,故只研究半桥LLC的PO工作模态。其半桥模态下PO工作模式波形如图6所示。
图6中,定义tf为P阶段初始时刻;tx为P阶段结束时刻;tc为O阶段结束时刻;ts为一个周期结束时刻;q 为P阶段导通角;j 为O阶段导通角。其导通角与阶段时刻关系为
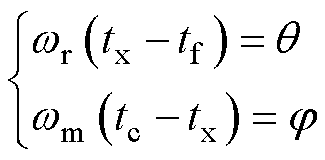 (1)
(1)
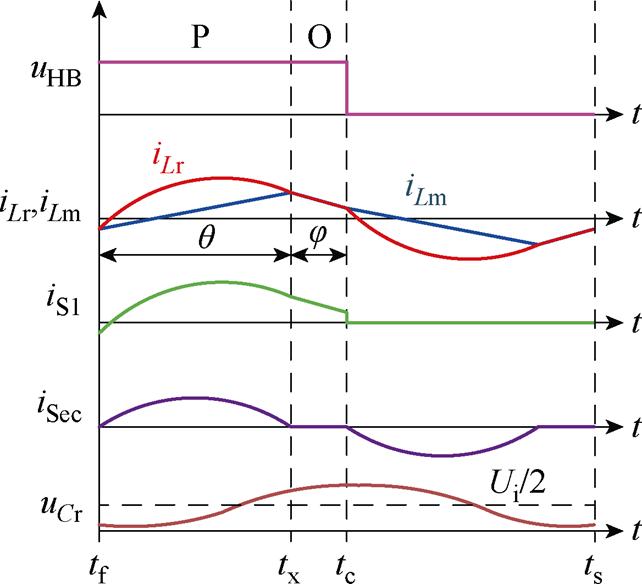
图6 PO工作模式主要波形
Fig.6 Main waveforms of PO working mode
式中,wr为仅有谐振电感和谐振电容参与谐振时的角频率;wm为谐振电感、谐振电容和励磁电感三者共同参与谐振时的角频率。
谐振变换器具有周期对称性,仅对变换器的正半周期进行分析,在正半周内,变换器工作在P阶段和O阶段时的等效电路如图7所示。
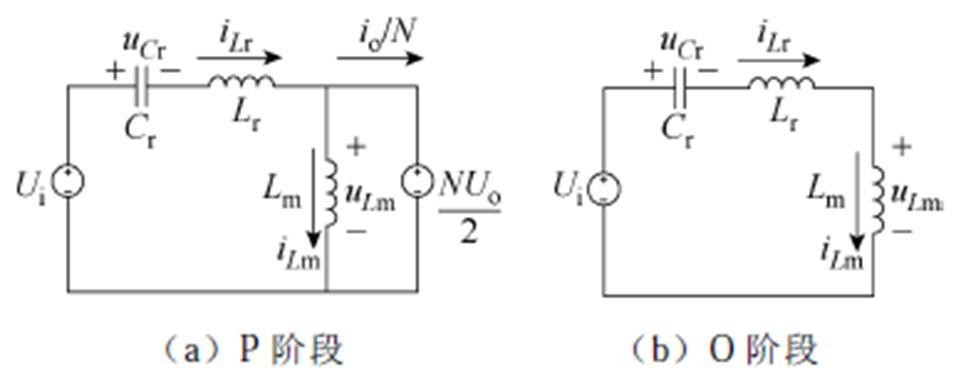
图7 PO模式下P、O阶段等效电路
Fig.7 Equivalent circuit of P and O stages in PO mode
1.2.1 PO模式状态变量时域方程
由P阶段等效电路可知,励磁电流iLm、谐振电流iLr和谐振电容电压uCr三个状态变量满足方程
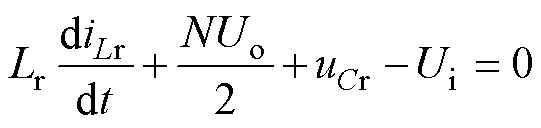 (2)
(2)
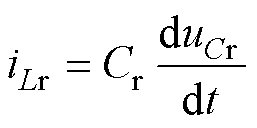 (3)
(3)
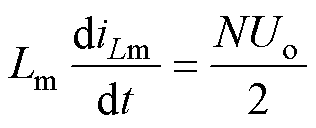 (4)
(4)
由式(2)和式(3)可得
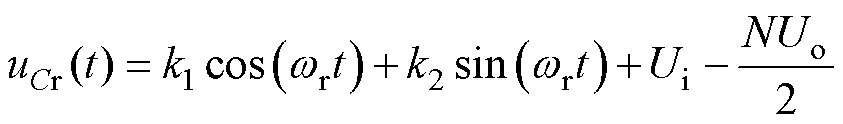 t
t
 [tf, tx
[tf, tx
 (5)
(5)
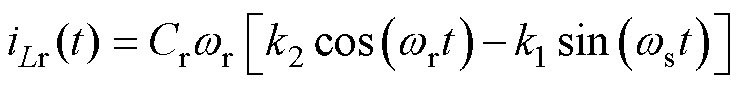 t
t [tf, tx
[tf, tx (6)
(6)
式中,k1、k2为P阶段中与电路初始情况有关的系数。
由图6知,tf时刻定义为P模式的初始时刻,满足wrtf=0。将此条件代入式(4)得
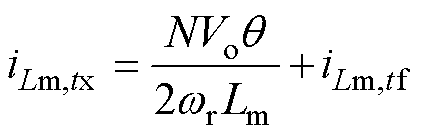 (7)
(7)
式中,iLm,tf为tf时刻励磁电流值;iLm,tx为tx时刻励磁电流值。
由PO模式工作波形可知,在tf时刻和tx时刻满足励磁电流iLm与谐振电流iLr相等,即
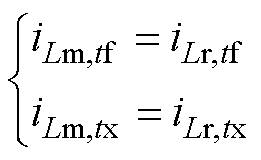 (8)
(8)
由O阶段等效电路得,其谐振变量满足方程可表示为
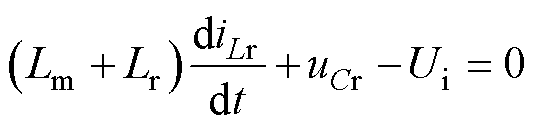 (9)
(9)
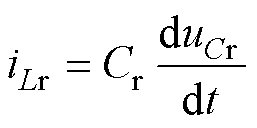 (10)
(10)
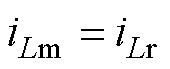 (11)
(11)
由式(9)~式(11)可求解状态变量为
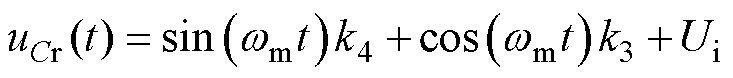 t
t
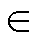 [tx, tc
[tx, tc
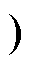 (12)
(12)
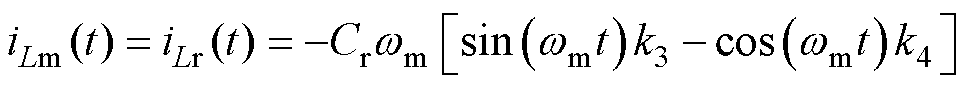
t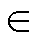 [tx, tc
[tx, tc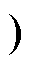 (13)
(13)
式中,k3、k4为O阶段中与电路初始情况有关的系数。
通过式(12)到式(13)就可以求出PO模式下各状态变量的时域方程,但仍存在未知系数k1、k2、k3、k4,因此还需求解系数。
1.2.2 PO模式状态方程系数求解
根据图6和图7,结合电路的初始情况,由PO模式下P阶段初始情况求解对状态方程系数k1、k2。
在正半周期内,电容电压变化量为
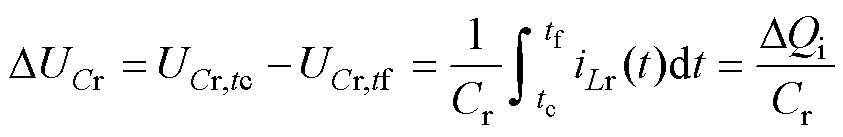 (14)
(14)
式中,DQi为变换器正半周期内谐振网络充电电荷。
而半桥模态下逆变单元为非对称半桥,谐振槽电容存在直流偏置电压,即
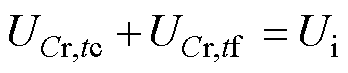 (15)
(15)
结合式(14)、式(15)得
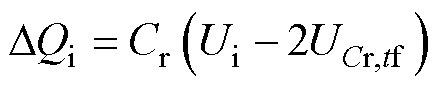 (16)
(16)
忽略电路损耗,在一个开关周期内,输入能量Ei等于输出能量Eo,即
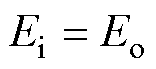 (17)
(17)
对半桥模态而言,变换器输入能量与输出能量可表示为
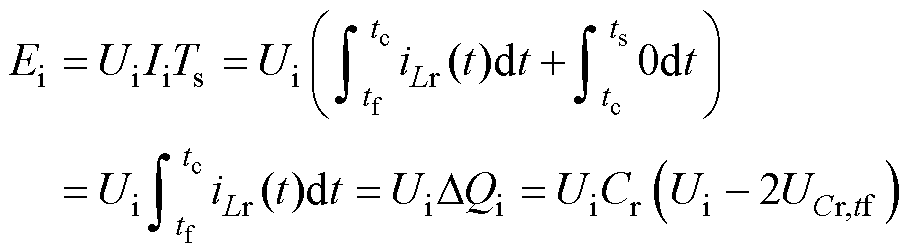 (18)
(18)
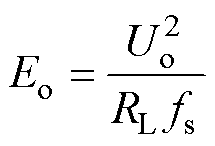 (19)
(19)
结合式(18)、式(19)得到P阶段谐振电容电压的初始值为
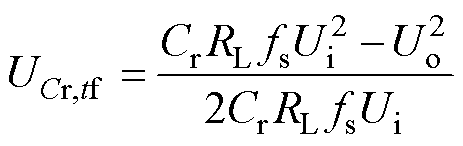 (20)
(20)
P阶段初始时刻wrtf=0,将式(20)代入式(5)得
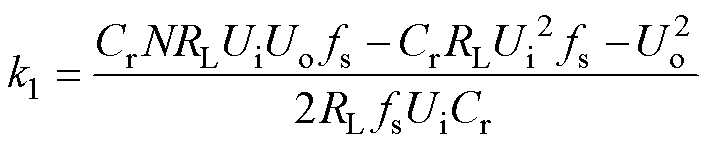 (21)
(21)
P阶段谐振电流iLr在tf时刻满足wrtf=0,代入式(6)得
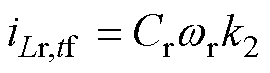 (22)
(22)
由图6和式(8)可得,谐振电流iLr与励磁电流iLm在tf、tx时刻相等,故结合式(7)可得
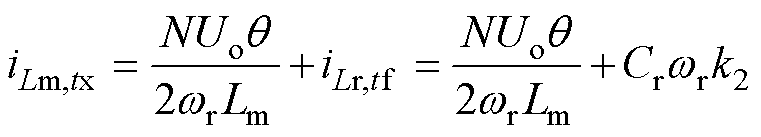 (23)
(23)
分别将wrtf=0和wrtx=q 代入式(6)中,结合式(8)和式(22),得到系数k1与k2之间的关系为
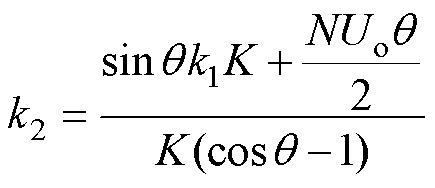 (24)
(24)
式中,K为电感比系数,K=Lm/Lr。
将式(24)中的k1用式(21)替代可得
 (25)
(25)
同理,根据电路在O阶段的初始情况来求解k3、k4,分析过程同P阶段,这里不再赘述。
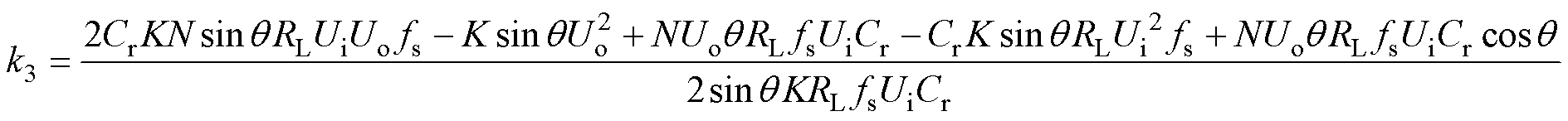 (26)
(26)
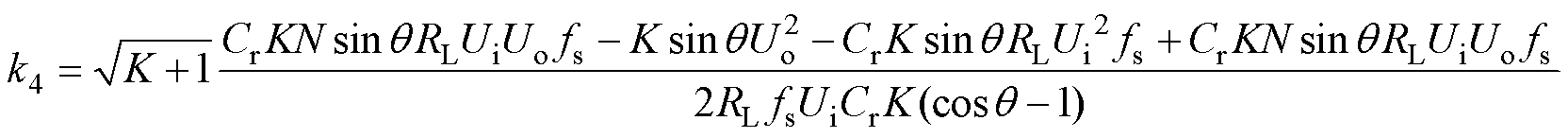 (27)
(27)
通过以上分析得出k1、k2、k3、k4系数解析式,可以看出,在给定谐振变换器输入电压Ui、输出电压Uo、开关频率fs、输出负载RL和变压器电压比N时,PO模式状态方程系数k1、k2、k3、k4只与谐振电容Cr、电感比系数K和P阶段子区间导通角q 三个参数有关。为实现对半桥模态PO工作模式完全时域解析,仍需探究Cr、K和q 之间的关系。
1.2.3 PO模式状态方程约束关系
为实现对半桥模态LLC谐振变换器PO模式的完全时域解析,研究变换器半桥模态下PO模式状态方程中三个参数Cr、K和q 之间的关系,从负载约束条件、系数约束条件和角度约束条件进行探讨。
1)负载约束条件
从图6中可以得到输出电流Io与谐振电流ILr和励磁电流ILm之间的关系为
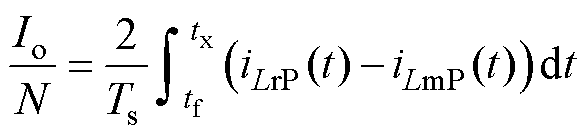 (28)
(28)
式中,输出电流Io=Uo/RL;开关周期Ts=1/fs。
由P阶段子区间下状态变量时域方程可知
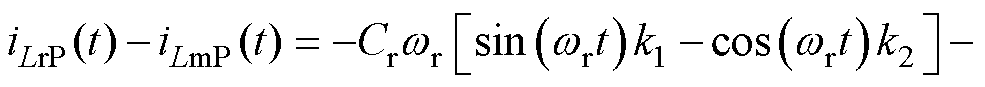
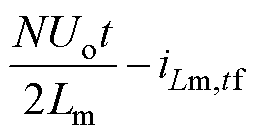 (29)
(29)
联立式(28)和式(29),负载约束关系式可表示为
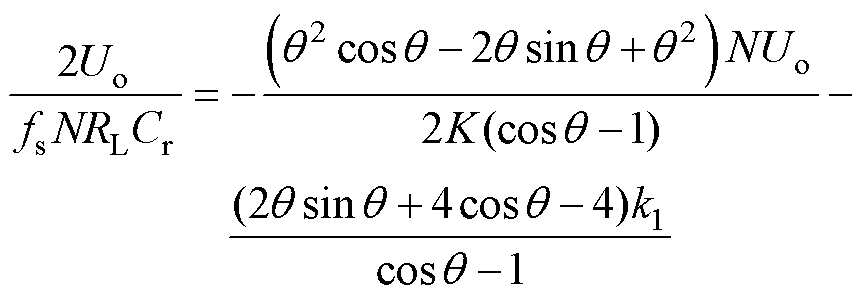 (30)
(30)
由式(21)知,k1是关于Cr的函数,即k1=f(Cr)。
通过负载约束条件可得到Cr、K和q 三者之间的关系,但式(30)为超越方程,需引入数值分析方法进行求解。
2)系数约束条件
LLC谐振变换器PO模式时域分析,O阶段子区间导通角j 的求解对PO模式时域解析也至关重要。因此,下面将从系数约束条件探究j 与系数之间的关系。
由图6可得,因为半桥模态为非对称半桥结构,谐振槽电容存在直流偏置电压,即联立式(15)和P、O阶段时域方程可得
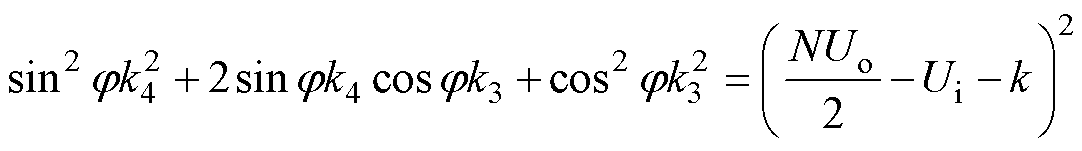 (31)
(31)
同理,谐振电流iLr,在半个周期当中,满足
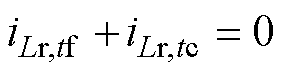 (32)
(32)
将iLr,tf和iLr,tc分别代入式(6)和式(13)可得
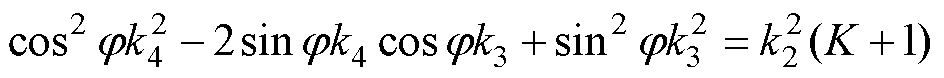 (33)
(33)
将式(31)和式(32)相加可得
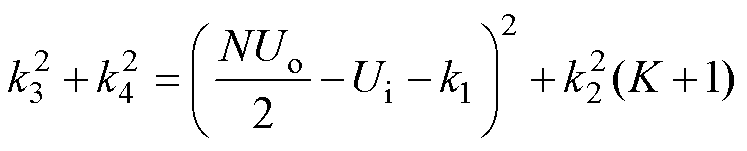 (34)
(34)
联立求解式(15)、式(32)和式(34),得到N阶段子区间导通角j 与状态方程系数之间的关系为
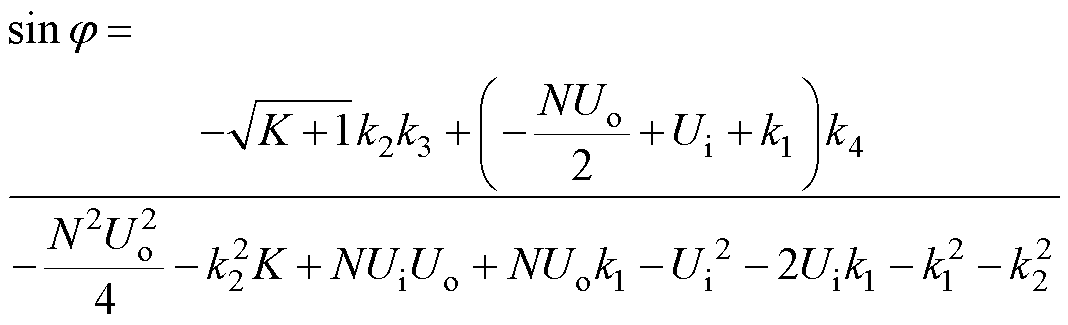 (35)
(35)
3)角度约束条件
通过系数约束条件推导出O阶段子区间导通角j 与状态方程系数之间的函数关系式,但要实现PO模式下的完全时域解析还需探究j 和q 间的关系。
由图6可得q 和j 之间的表达式为
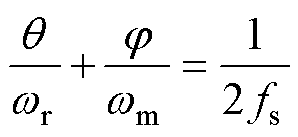 (36)
(36)
将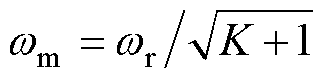 代入式(36)中,得q、j 和wr之间的函数关系为
代入式(36)中,得q、j 和wr之间的函数关系为
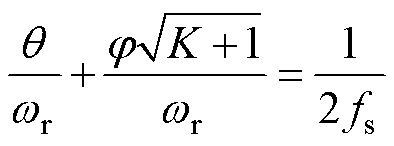 (37)
(37)
式(37)通过角度约束关系探究了j 和q 之间的函数关系。在已知j 和q 时,通过式(37)可求出串联谐振角频率wr。
综上所述,当设计半桥模态LLC谐振变换器在PO模式下工作时,通过给定谐振电容Cr和电感比系数K后,根据相应约束条件和公式求解系数k1~k4及j 和q,从而确定串联谐振角频率wr。通过
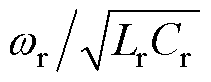 、K=Lm/Lr就可以确定LLC谐振变换器谐振电感Lr和励磁电感Lm的数值。到此,便完成了LLC谐振变换器PO模式下的完全时域解析。
、K=Lm/Lr就可以确定LLC谐振变换器谐振电感Lr和励磁电感Lm的数值。到此,便完成了LLC谐振变换器PO模式下的完全时域解析。
通过对半桥模态LLC谐振变换器PO模式时域分析,还需对参数进行优化设计,确定出一组Cr-K最优解,进一步减小循环无功功率,以实现最苛刻工况下的增益要求和ZVS,得出优化设计理论。
变模态倍压型LLC谐振变换器样机主电路参数见表1。
表1 变换器主要电气参数
Tab.1 Main electrical parameters of transformers

参 数数 值 输入电压Ui/V220 半桥模式输出电压范围Uo1,min~Uo1,max/V20~50 双半桥模式输出电压范围Uo2,min~Uo2,max/V50~84 变换器输出电压范围Uo,min~Uo,max/V20~84 输出功率Po,min~Po,max/W50~504 变压器电压比N8.8 二元谐振频率fr/kHz95
2.2.1 模式边界约束目标
PO模式相临的模式为PON和OPO模式。为保证工作在PO模式,需要探究模式边界约束条件。
1)PO与PON模式边界
由图6知,tc时刻,励磁电感电压ULm,tc恰好等于-NUo/2。因此,为使变换器工作在PO模式而不进入PON模式,半个周期结束前变换器处于O阶段时,ULm,tc终值始终小于-NUo/2,则变换器不会进入N阶段。tc时刻ULm,tc满足不等式
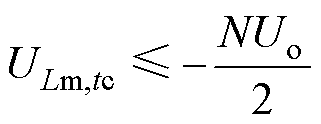 (38)
(38)
由图7中P阶段等效电路可求得tc时刻励磁电感电压ULm,tc,即
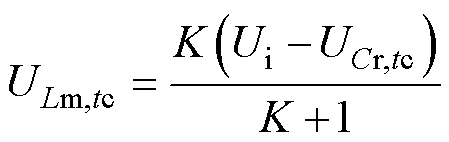 (39)
(39)
将式(15)、式(21)和式(39)代入式(38)中,整理可得不等式关系为
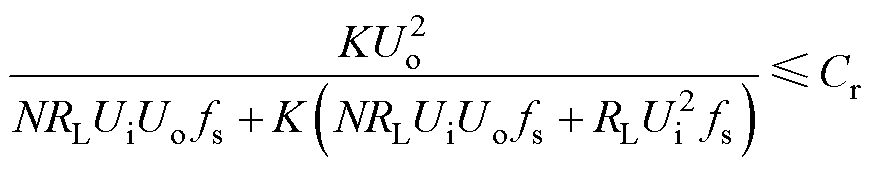 (40)
(40)
根据式(40)和变换器输出电压及输出功率范围,可以画出变换器在不同工况下PO与PON模型边界曲线如图8所示。
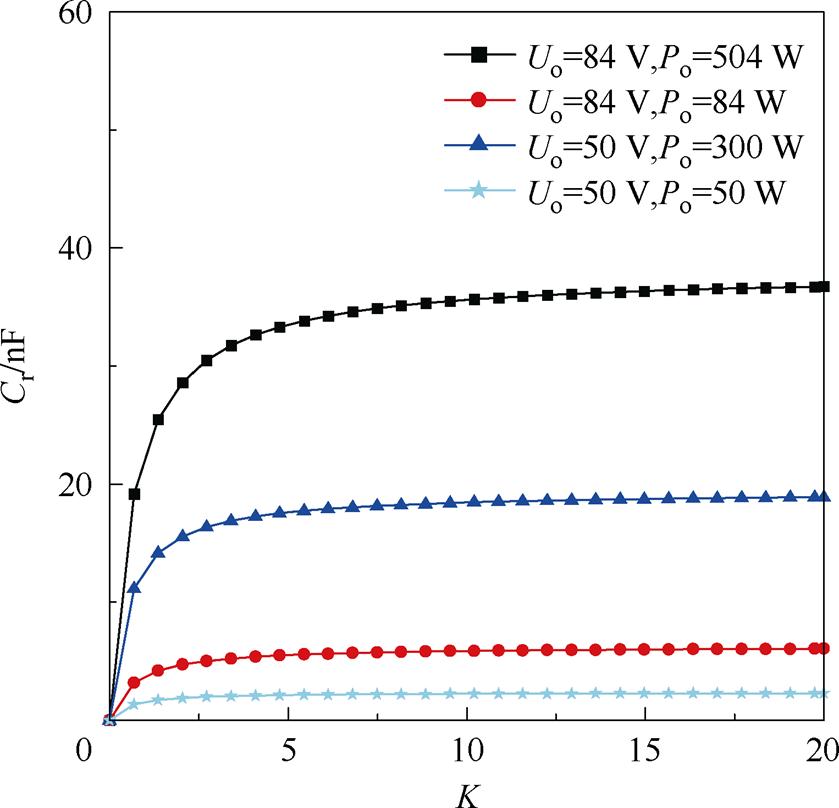
图8 不同工况下PO与PON模式边界
Fig.8 PO and PON mode boundaries under different operating conditions
从图8可以看出,选取四种参数比较PO模式的工作范围,模式边界曲线上方表示变换器工作在PO模式下的Cr、K取值,曲线下方表示变换器工作在PON模式下的Cr、K取值。当输出功率不变,随着输出电压的取值增加,变换器PO模式与PON模式下的边界曲线将向上移动,即Cr、K的取值范围缩小;当输出电压不变,随着输出功率的加重,其边界曲线将向上移动。为保证变换器工作在PO模式下,选取最重载情况下PO和PON模式边界。
2)PO与OPO模式边界
tf时刻,要保证变换器上一个周期结束时刻进入P模式,就要保证励磁电感电压ULm,tf>NUo/2,即PO模式和OPO模式边界关系满足不等式为
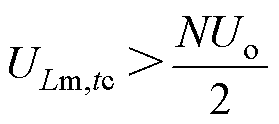 (41)
(41)
图7中P模式下等效电路可得,tf时刻励磁电感电压ULm,tf为
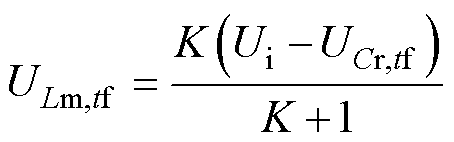 (42)
(42)
同理,将式(42)中的UCr,tf用式(20)表示并代入式(41),得到Cr与K之间的不等式关系为
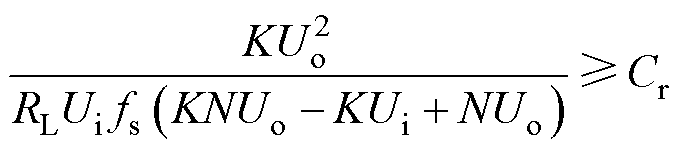 (43)
(43)
在Cr-K平面上画出最重载工况下PO与OPO模式下的模式边界,结合PO与PON最重载情况下边界曲线,得出图9阴影部分所示。
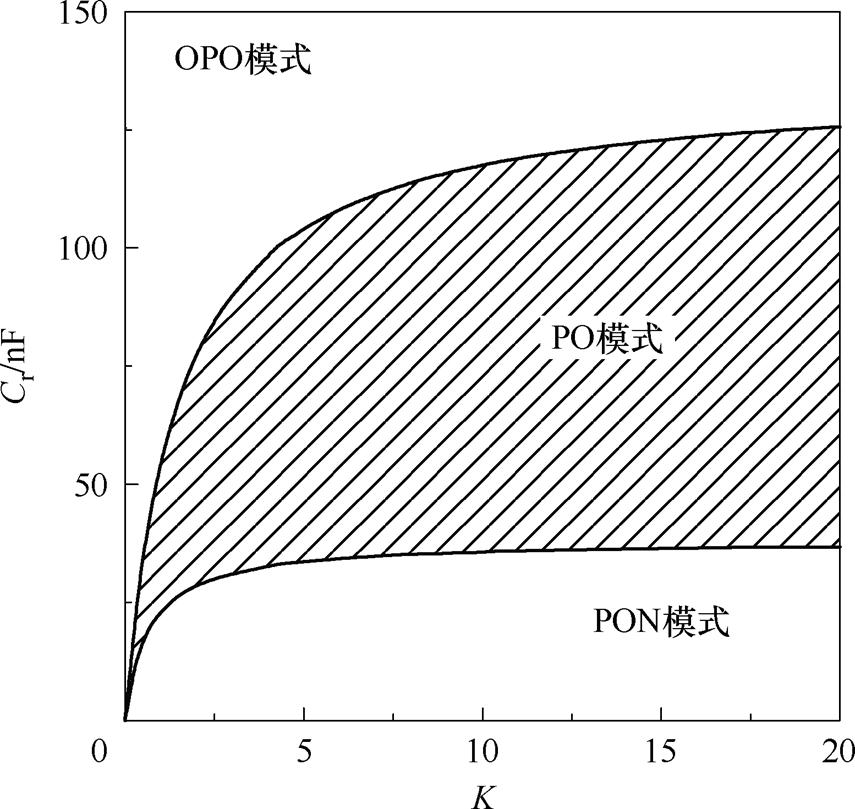
图9 变换器全范围PO模式工作区域
Fig.9 Full range PO mode working area of the converter
重载下,其工作模式的边界在纵轴上从低到高依次为PON模式、PO模式和OPO模式,与LLC谐振变换器模式特点一致。因此,为了实现LLC谐振变换器在全范围内工作在PO模式,需要保证所给定的参数Cr、K取值应在图9中的阴影区域中。
2.2.2 谐振电容最值约束目标
对LLC谐振变换器器件选型和设计时,谐振电容除了电容值外,还需考虑其两端电压应力要求。
由图6可知,谐振电容在P阶段子区间即谐振电流iLr过零时,谐振电容电压uCr取最小值,半桥模态下LLC谐振变换器在一个周期当中,其谐振电容电压最小值uCr,min和最大值uCr,max满足关系式为
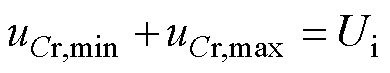 (44)
(44)
在PO工作模式下,其谐振电容电压最小值uCr,min近似等于uCr,tf,故将uCr,tf用式(20)表示并代入式(44)中,则uCr,max与谐振电容Cr的关系式为
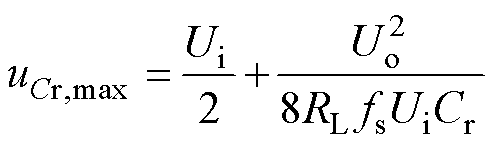 (45)
(45)
在最坏工况下,要保证谐振电容电压最大值uCr,max≤Ui,max,代入式(45)得
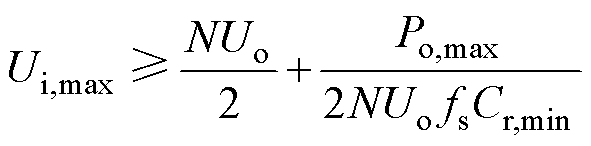 (46)
(46)
将变换器相关参数代入式(46),计算得出谐振电容最小值,将谐振电容不等式曲线加入图9,得到谐振电容参与的最值约束边界条件如图10所示。
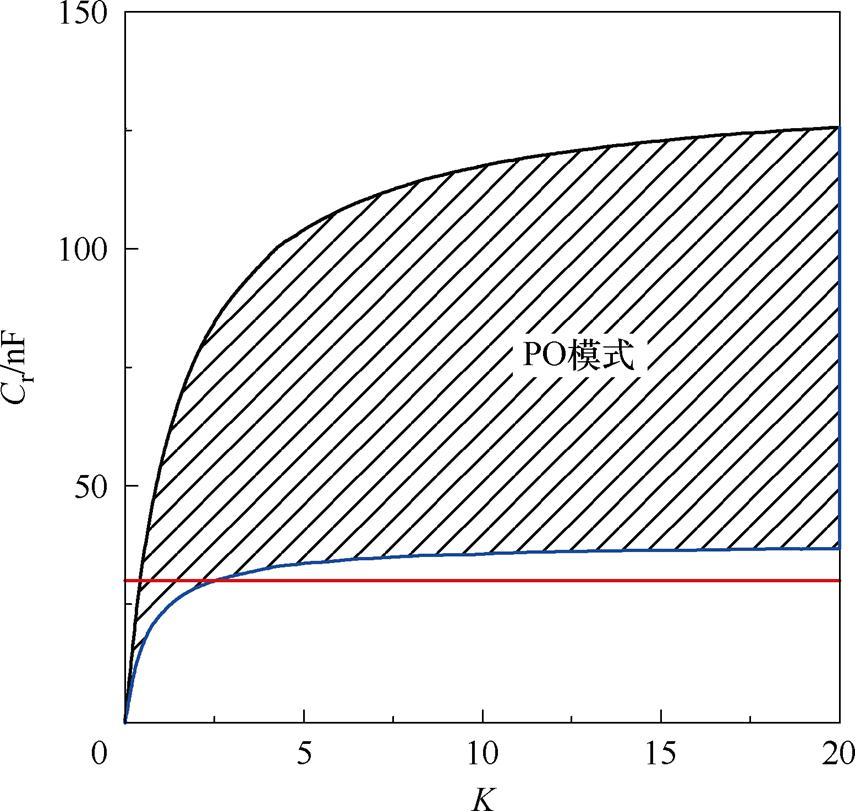
图10 谐振电容最值约束边界条件
Fig.10 Boundary conditions for resonator capacitor maximum constraints
2.2.3 ZVS条件约束目标
为保证开关管实现ZVS,开关管漏源电容存储能量必须在死区时间内完全释放,死区时间较小,谐振电流在该时间内基本保持不变,Coss为开关管输出电容,假设开关管的寄生电容相等。半桥LLC谐振变换器死区内等效电路如图11所示。
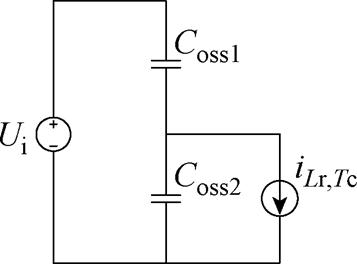
图11 死区内电路等效电路工作状态
Fig.11 Equivalent working state of circuit in dead zone
图11中,死区内变换器满足如下时域方程
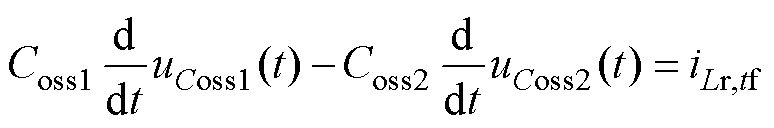 (47)
(47)
式中,Coss1=Coss2=Coss,状态变量所满足的初值条件为uCoss1(0_)=0, uCoss2(0_)=Ui。
由图11利用KVL方程可得
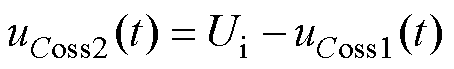 (48)
(48)
将式(47)和式(48)结合可得
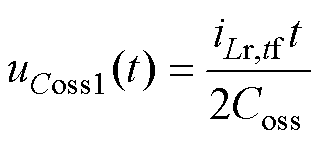 (49)
(49)
由图6中的PO模式波形可知,当t=tdead时,uCoss1=Ui。因此实现ZVS条件需满足
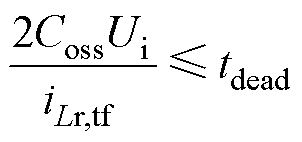 (50)
(50)
式(50)中,死区时间tdead的选择为200 ns。确定死区时间后,结合参数及选型确定Coss。将变换器最重载情况下软开关条件加入图10中,通过前面时域公式推导可知,式(49)中的iLr,tf是关于Cr、K和q 的函数,其中q 与Cr、K是满足式(30)的超越方程,无法直接得出基于ZVS约束的Cr、K函数关系式。因此,借助数值迭代法并结合最小二乘拟合得到ZVS约束边界条件如图12所示。在进行数值迭代求解之前,还需确定P阶段子区间导通角q 的取值范围,以便在迭代计算中确定初值。其ZVS条件约束所拟合函数为图12中的红色曲线。

图12 ZVS约束边界条件
Fig.12 ZVS constraint boundary conditions
通过模式边界、谐振电容最值和ZVS的多目标约束条件,得到多目标参数优化区域如图12阴影部分。从阴影部分选取Cr、K参数,可以保证用较小循环无功实现最苛刻工况下的增益要求和ZVS运行,保证变换器在全范围内高效率。
在保证变换器在阴影区域中设计参数的同时,应进一步减小循环无功功率即减小谐振网络电流有效值,采用迭代递归算法获得多目标优化的最优解,多目标参数设计流程如图13所示。
本文针对所给定的变换器电气参数,通过迭代优化算法,最终选取电感比系数K=4、谐振电容Cr= 46.8 nF一组最优解,代入变换器PO模式时域解析方程式中计算出谐振电感Lr=60 mH、励磁电感Lm= 240 mH。为验证参数优化设计理论的正确性,在该参数下设计样机并进行实验验证。

图13 多目标参数优化设计流程
Fig.13 Multi objective parameter optimization design process
为验证理论分析的正确性,搭建半桥倍压型LLC谐振变换器仿真模型进行仿真验证。
3.1.1 模式边界验证
根据图9分析得到的PO模式工作范围,验证理论分析正确性,选取A、B、C三点进行验证。其中,A点测试谐振电流iLr、励磁电流iLm和变压器一次电流ip波形如图15所示。

图14 最重载下工作模式边界条件
Fig.14 Working mode boundary conditions under maximum load
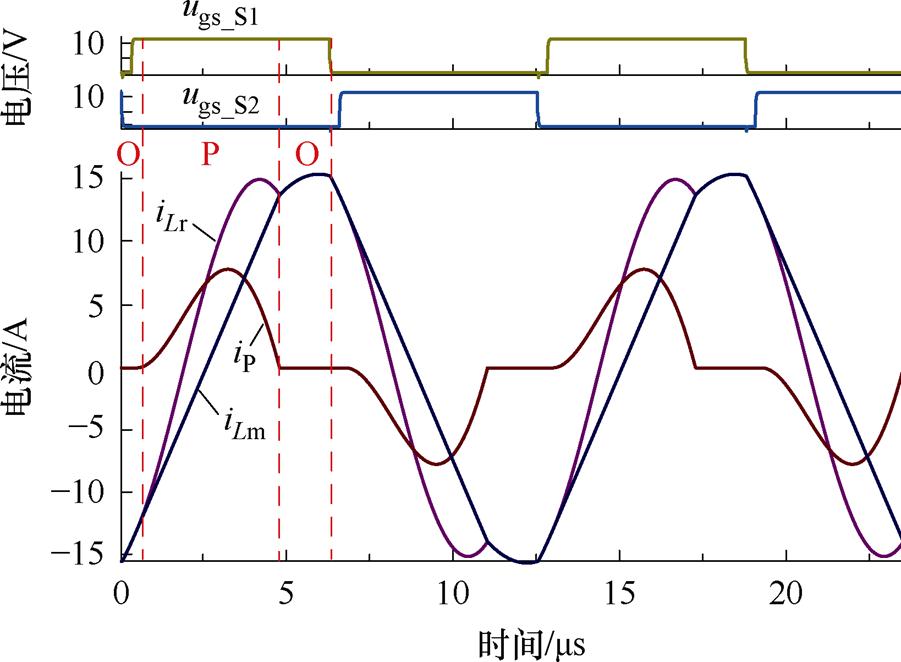
图15 工作点A仿真波形
Fig.15 Simulation waveforms of working point A
同理,取B点和C点参数进行变换器设计时,得到的仿真波形如图16和图17所示。
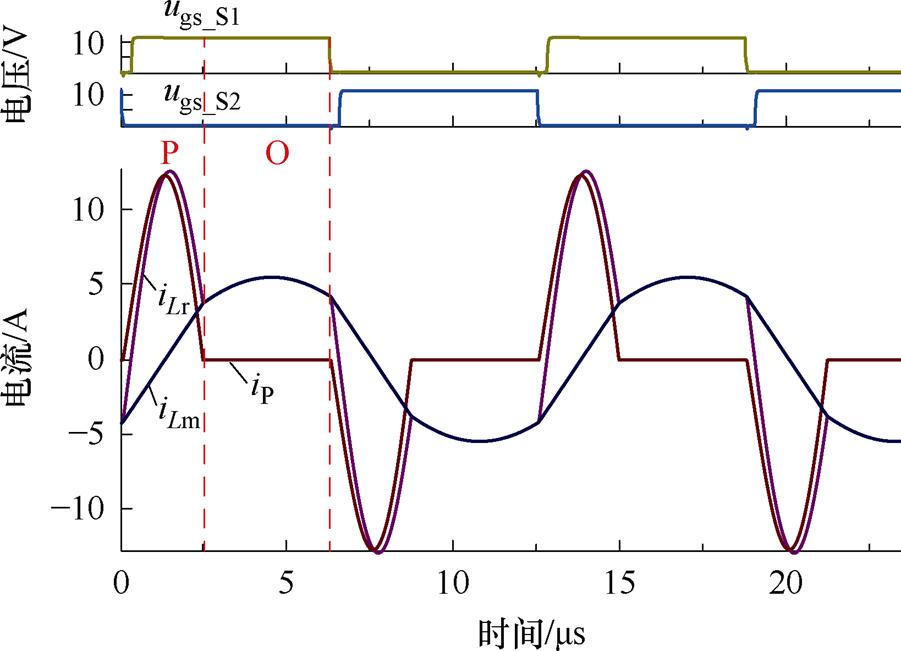
图16 工作点B仿真波形
Fig.16 Simulation waveforms of working point B
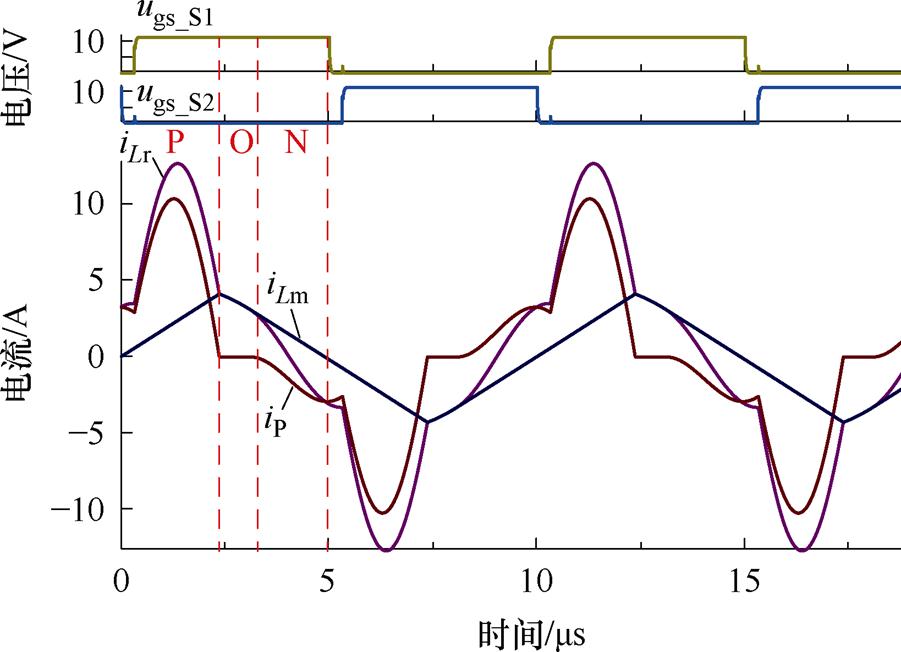
图17 工作点C仿真波形
Fig.17 Simulation waveforms of working point C
仿真波形表明:工作点A情况下变换器为OPO模式;工作点B情况下变换器为PO模式;工作点C情况下变换器为PON模式,与理论分析一致。
3.1.2 谐振电容最值约束目标验证
根据图10谐振电容最值约束边界条件图选取A、B两点,如图18所示,分别对两点进行仿真验证,得到的波形分别如图19和图20所示。
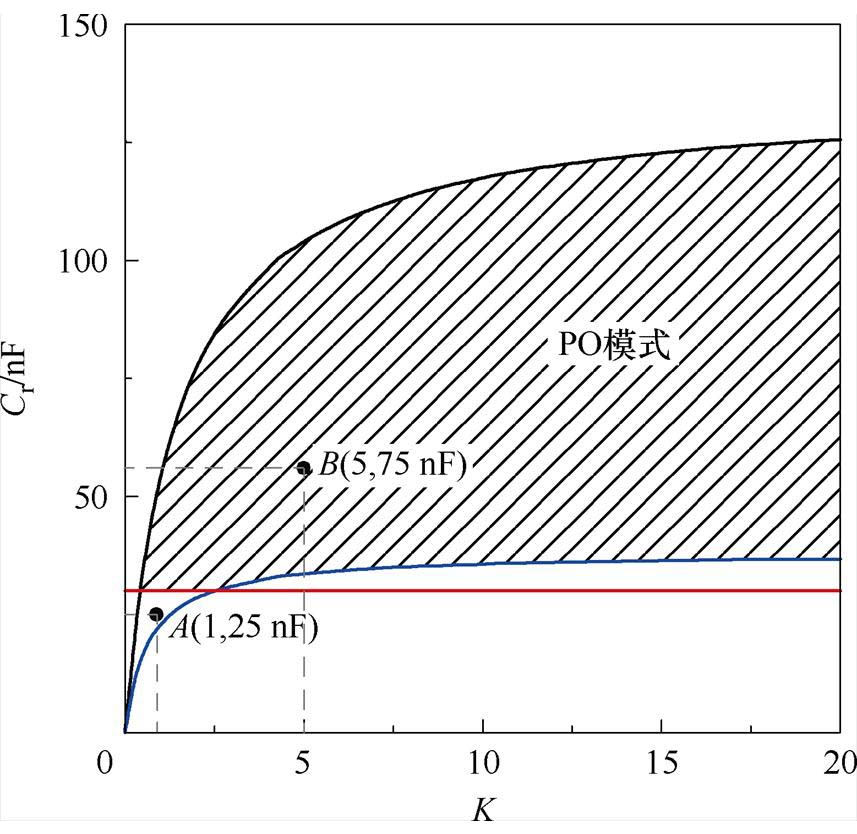
图18 谐振电容最值约束模式边界条件
Fig.18 Boundary conditions for the maximum constrained mode of resonant capacitor

图19 谐振电容最值约束工作点A仿真波形
Fig.19 Simulation waveforms of working point A under the constraint of resonant capacitor
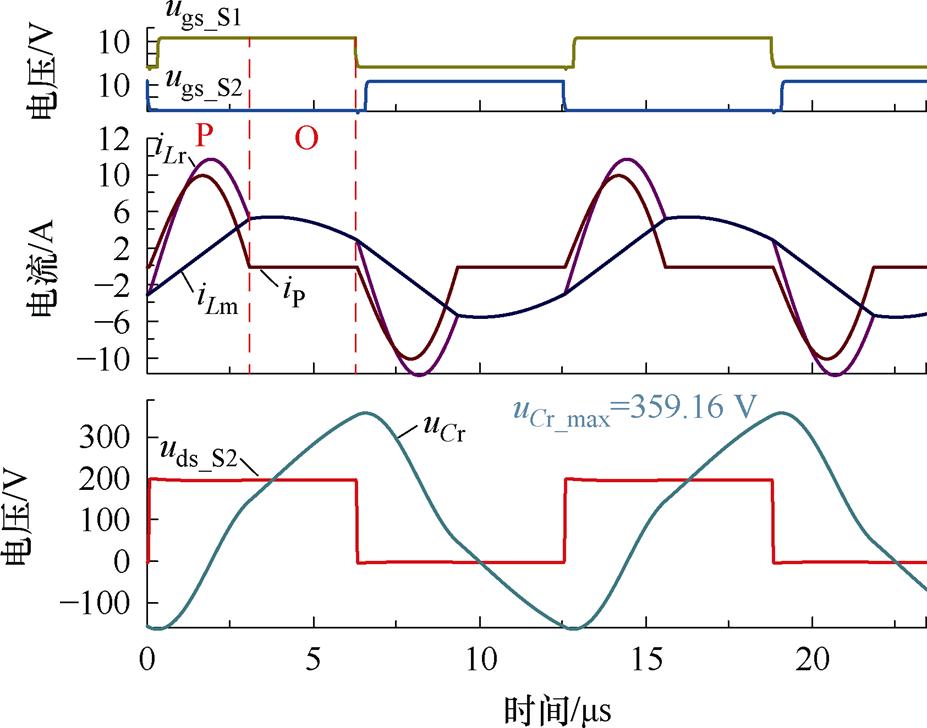
图20 谐振电容约束条件工作点B仿真波形
Fig.20 Simulation waveforms of operating point B under the constraint of resonant capacitor
仿真波形表明:工作点A时变换器工作在PO模式,谐振电容电压最大值大于输入电压最大值,不满足uCr,max≤Uin,max;B情况下变换器为PO模式且满足uCr,max≤Uin,max,仿真验证与理论分析一致。
3.1.4 设计参数验证
将仿真模型代入,并最终选取的谐振腔参数K=4、谐振电容Cr=46.8 nF,谐振电感Lr=60 mH、励磁电感240 mH,得到变换器仿真模型最重载输出时的关键电压电流波形如图21所示。
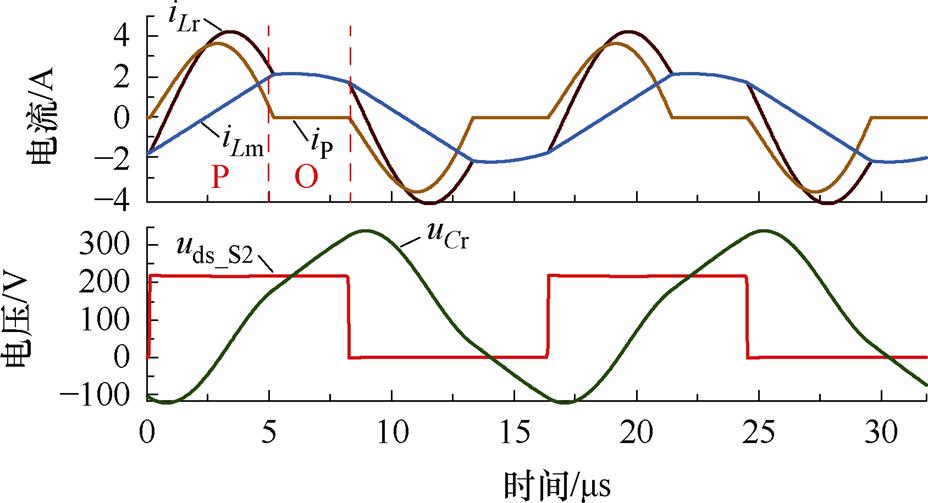
图21 关键电压电流波形
Fig.21 Key voltage and current waveforms
由图20可以看出,变换器在最重载输出时,变换器仍然工作在PO模态,仿真波形验证了理论分析的正确性。同时对其进行ZVS验证,波形如图21所示。
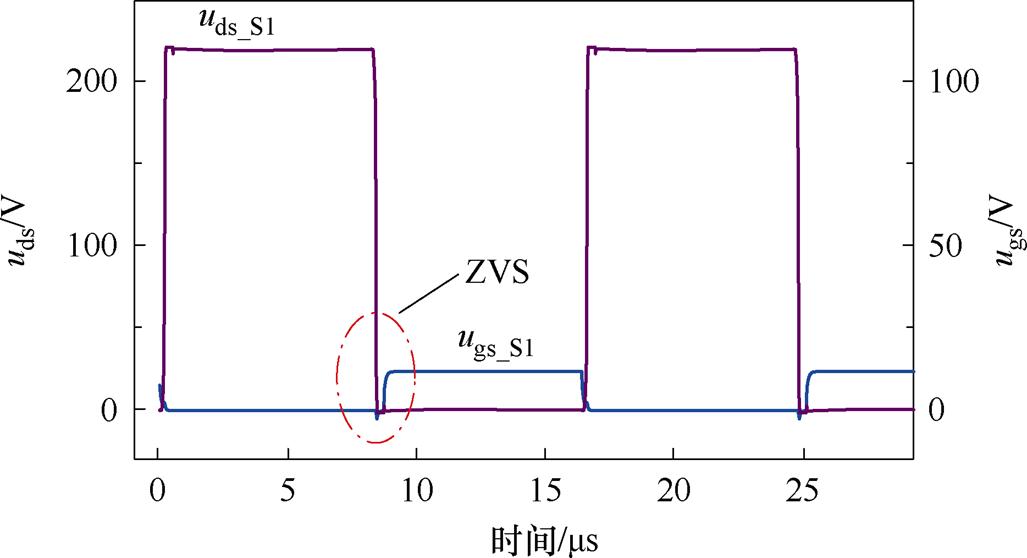
图22 ZVS仿真验证
Fig.22 ZVS simulation verification
由图22可知,当开关管漏源电压uds降为0之后,其栅源电压ugs才到来,开关管实现ZVS开通。
为了验证理论分析的正确性,制作实验样机如图23所示。样机参数见表2。

图23 实验样机
Fig.23 Experimental prototype
表2 变换器主要参数
Tab.2 Main parameters of the converter

参 数数 值 输入电压Ui/V220 输出电压范围Uo,min~Uo,max/V20~84 输出功率Po,min~Po,max/W40~504 变压器电压比N8.8 谐振频率fr/kHz95 电感比K4 谐振电感Lr/mH60 励磁电感Lm/mH240 谐振电容Cr/nF46.8
根据锂电池充电特性,设计三段式充电过程,具体指标见表3。
表3 充电指标
Tab.3 Three stage charging indicators

充电阶段锂电池端电压/V充电电流/A 涓流充电20~50 (深度耗电)2 恒流充电50~84 (正常耗电)6 恒压充电846~0.5
为验证时域分析的LLC谐振变换器多目标优化参数设计理论,对所提出的参数优化设计方法的有效性和准确性进行了实验验证。
1)稳态实验波形
分别对变换器轻载和重载工况时进行测试,得到稳态电压电流波形如图24和图25所示。

图24 Ui=220 V、Io=2 A、Uo=20 V、fs=115 kHz(轻载)条件下得到的稳态电压、电流波形
Fig.24 Steady voltage and current waveforms of Ui=220 V、Io=2 A、Uo=20 V、fs=115 kHz (light load)
由图25a可以看出,变换器最重载工况时工作在PO模式,即变换器最重载工况下,仍能工作在PO模式下,验证了理论分析的正确性。同时由图24b、图25b可以看出变换器开关管S1漏源电压uds_1降为0之后驱动电压ugs_S1才变为高电平,实现了开关管ZVS导通。
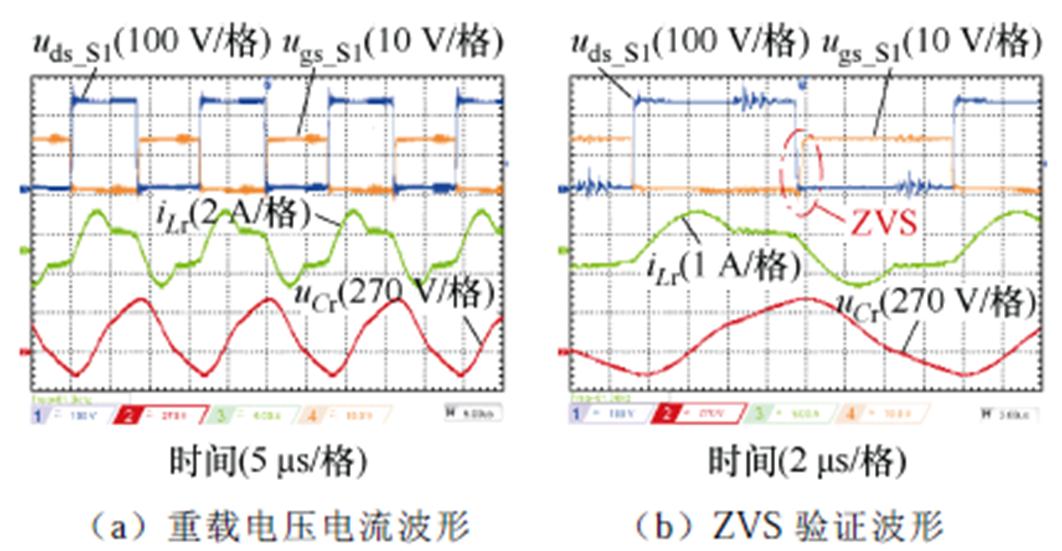
图25 Ui=220 V、Io=6 A、Uo=84 V、fs=62 kHz(重载)条件下得到的稳态电压、电流波形
Fig.25 Steady voltage and current waveforms of Ui=220 V、Io=6 A、Uo=84 V、fs=62 kHz (heavy load)
2)负载突变切换波形
为验证负载扰动对变换器输出的影响,变换器负载电压突变时的电流波形测试结果如图26所示。
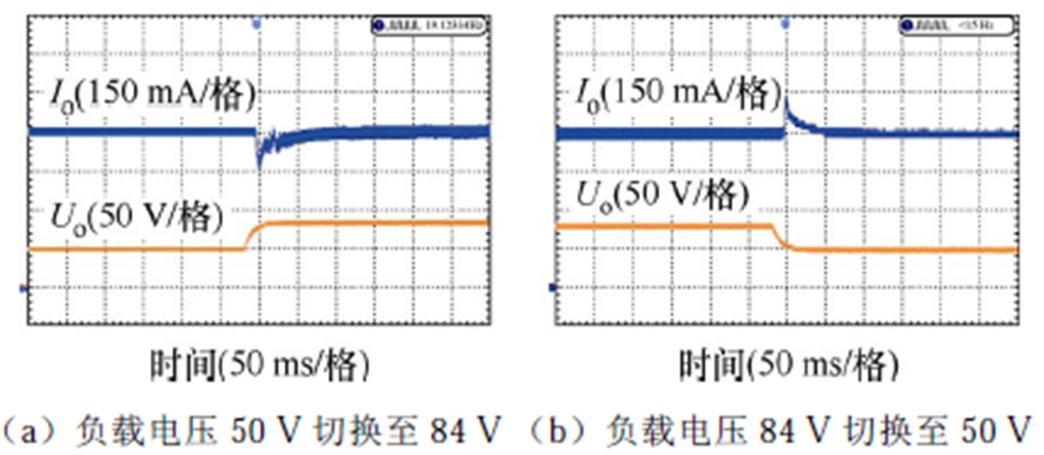
图26 负载电压突变时输出电流波形
Fig.26 Output current waveforms when load voltage suddenly changes
图26可看出,变换器不管是从重载工况下向轻载工况下突变还是轻载向重载工况突变,输出电流最大超调均不超过0.15 A,暂态波形测试结果表明动态特性分析理论的正确性。
3)对比验证
为了验证所提出方法的有效性,在相同的设计指标下,利用FHA和本文提出参数优化设计方法各设计一组参数,并从开关频率变化范围、谐振网络电流等角度进行对比。
传统FHA法设计思路流程如图27所示。两种方法设计的谐振参数对比见表4。
变换器存在两种模态,其中变压器处于半桥模态时,输出电压为20~50 V,双半桥模态时输出电压范围为50~84 V,因此半桥模态时开关频率变化范围大于双半桥模态,故对比两种设计方法在半桥模态时的开关频率范围如图28所示。两种设计方法均以25 V作为额定输出电压,因此谐振频率为95 kHz。由图28可看出,在25~50 V输出电压范围时,本文所提出的设计方法开关频率范围更窄,有利于磁性元件的设计以及变换器的闭环控制。
图27 基于传统基波分析法参数设计流程
Fig.27 Parameter design process based on traditional FHA method
表4 FHA谐振参数及本文方法设计的谐振参数
Tab.4 FHA resonance parameters and the resonance parameters designed by the method in this paper

参 数数 值 FHA本文方法 谐振电感Lr/mH6660 谐振电容Cr/nF42.546.8 励磁电感Lm/mH227.78240
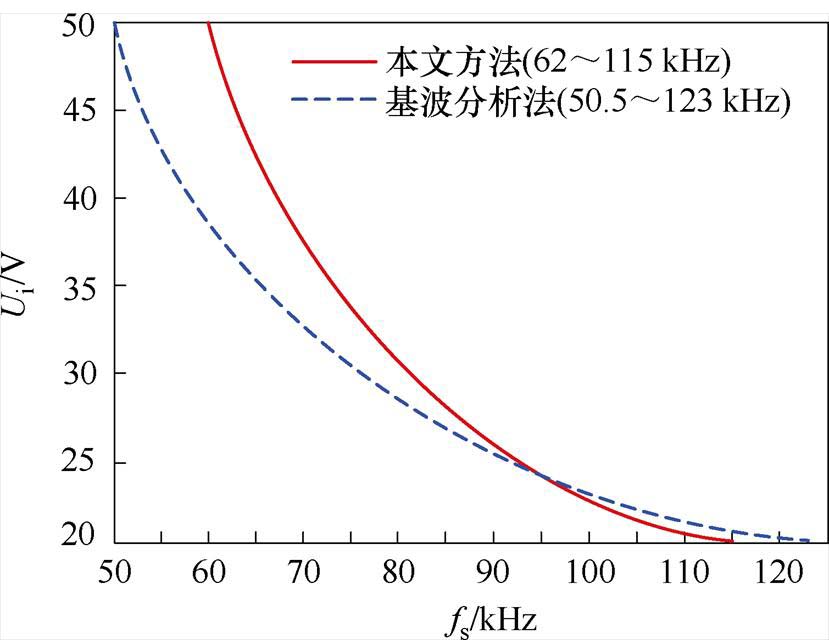
图28 不同输出电压时的开关频率
Fig.28 Switching frequency at different output voltages
为了进一步验证所提方法的优势,本文选取双半桥模态下的谐振电流有效值iLr_rms,开关管关断电流iS1、二次侧二极管电流有效值iVD1_rms三个参数进行比较,结果总结于表5。可以看出,所提方法能够实现电流有效值及开关管关断电流的减小,降低导通损耗,提升变换器效率。
表5 FHA及本文方法关键电流值对比
Tab.5 Comparison of key current values between FHA and the method described in this article
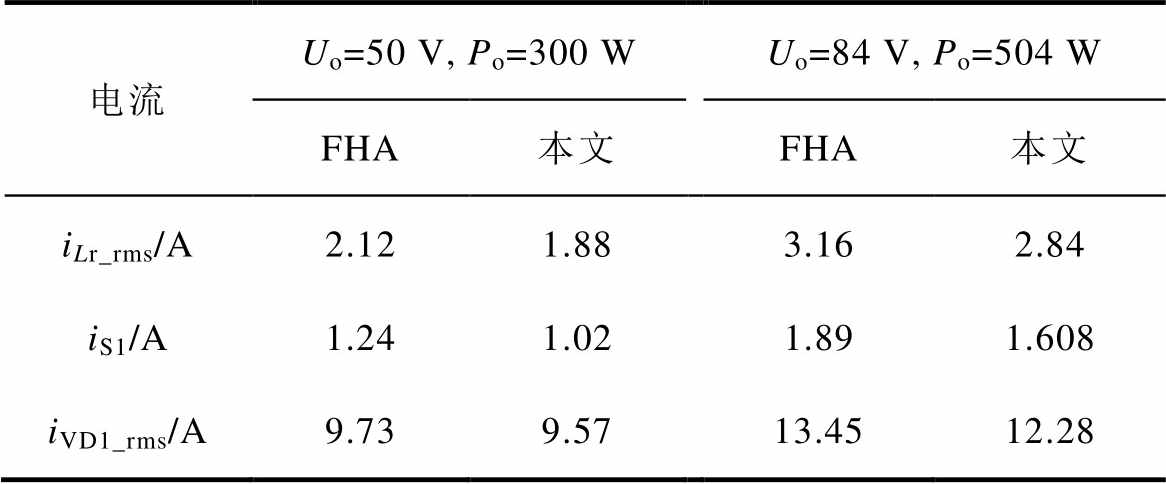
电流Uo=50 V, Po=300 WUo=84 V, Po=504 W FHA本文FHA本文 iLr_rms/A2.121.883.162.84 iS1/A1.241.021.891.608 iVD1_rms/A9.739.5713.4512.28
分别测试两种方法设计的变换器的效率,得到效率对比如图29所示。
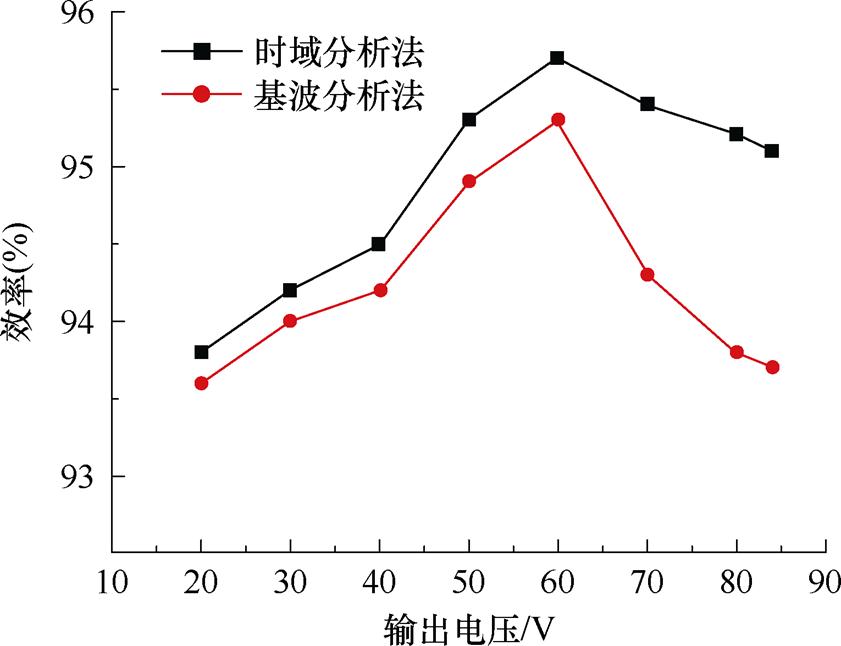
图29 效率对比
Fig.29 Efficiency comparison
由图29可以看出,基于时域分析的多目标优化设计的参数相较于基波分析法设计的参数,在20~84 V宽输出电压范围内,其效率均有所提高,表明本文所提出的参数优化设计方法的正确性。
针对宽范围输出电压应用场合下基波分析法存在误差大、精度低等问题,提出了一种变模态倍压型LLC谐振变换器的多目标参数优化设计方法。得出以下主要结论:
1)为确保开关管的ZVS和整流管的ZCS,同时满足电压增益,对变换器工作模式的运行条件及特点进行分析研究,确立PO模式是LLC谐振变换器最佳工作模式。
2)对LLC谐振变换器PO模式进行时域分析,列写状态变量方程并求解,得到LLC谐振变换器PO模式完全时域解。
3)通过模式边界、谐振电容最值和ZVS的多目标约束条件,得出基于时域分析的多目标参数优化区域,确定一组变换器最优参数,实现变换器增益要求和ZVS运行条件,满足变换器全范围内高效率。
理论和实验验证表明:本文所提出的多目标参数优化设计方法所得的变换器参数具有更高的效率,验证了理论分析和设计方法的正确性。
参考文献
[1] 刘越, 纪国盛, 邹军, 等. 高频LLC谐振变换器的磁集成和一体化PCB绕组优化设计[J]. 电气传动, 2023, 53(2): 24-31.
Liu Yue, Ji Guosheng, Zou Jun, et al. Optimal design of integrated magnetics and PCB winding for high-frequency LLC resonant converter[J]. Electric Drive, 2023, 53(2): 24-31.
[2] 周国华, 邱森林, 张小兵. 宽增益高效率级联式四开关Buck-Boost LLC变换器[J]. 电工技术学报, 2024, 39(4): 1103-1115.
Zhou Guohua, Qiu Senlin, Zhang Xiaobing. Cascaded four-switch Buck-Boost LLC converter with wide gain range and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1103- 1115.
[3] 朱天宇, 纪延超, 王建赜. 一种高效率的宽输出电压范围LLSC谐振变换器及其控制方法[J]. 电工技术学报, 2022, 37(18): 4697-4706.
Zhu Tianyu, Ji Yanchao, Wang Jianze. A high efficiency and wide gain range LLSC resonant converter and its control method[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4697- 4706.
[4] 丁超, 李勇, 姜利, 等. 电动汽车直流充电系统LLC谐振变换器软开关电压边界分析[J]. 电工技术学报, 2022, 37(1): 3-11.
Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant converter for EV DC charging system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 3-11.
[5] 缪哲语, 仝昊, 吕征宇, 等. 一种多模态宽范围箝位桥并联型LLC变换器控制方法[J]. 电源学报, 2022, 20(4): 1-10.
Miao Zheyu, Tong Hao, Lü Zhengyu, et al. Variable-mode control method for wide-range diode clamped bridge paralleled LLC converter[J]. Journal of Power Supply, 2022, 20(4): 1-10.
[6] 张涛. LLC全桥变换器电动汽车充电机设计[J]. 电气技术, 2018, 19(8): 164-167.
Zhang Tao. The design of full bridge EV charger based on LLC[J]. Electrical Engineering, 2018, 19(8): 164-167.
[7] 袁义生, 卢梓意, 刘伟. 一种适合宽范围输出的双向DC-DC变换器[J]. 电机与控制学报, 2024, 28(2): 152-161.
Yuan Yisheng, Lu Ziyi, Liu Wei. Bidirectional DC-DC converter suitable for wide output range[J]. Electric Machines and Control, 2024, 28(2): 152- 161.
[8] Shafiei N, Ordonez M, Craciun M, et al. Burst mode elimination in high-power LLC resonant battery charger for electric vehicles[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1173-1188.
[9] 王志刚, 董长城, 侯凯, 等. 全桥LLC电路时域模型及其分析[J]. 电力系统自动化, 2018, 42(20): 138-143, 164.
Wang Zhigang, Dong Changcheng, Hou Kai, et al. Time domain model of full bridge LLC circuit and its analysis[J]. Automation of Electric Power Systems, 2018, 42(20): 138-143, 164.
[10] 夏潇, 龚春阳, 包俊, 等. 宽增益高效率LLC谐振变换器拓扑[J]. 电力系统保护与控制, 2023, 51(3): 99-107.
Xia Xiao, Gong Chunyang, Bao Jun, et al. LLC resonant converter topology with wide gain and high efficiency[J]. Power System Protection and Control, 2023, 51(3): 99-107.
[11] 刘硕, 苏建徽, 赖纪东, 等. LLC谐振变换器PO模式增益公式与模式边界条件分析[J]. 电力系统自动化, 2020, 44(6): 164-170.
Liu Shuo, Su Jianhui, Lai Jidong, et al. Analysis on gain formula and mode boundary condition for LLC resonant converter in PO mode[J]. Automation of Electric Power Systems, 2020, 44(6): 164-170.
[12] Qian Ting, Qian Chenghui. A combined topology with coupled LLC resonance for wide-range operation[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6593-6600.
[13] Li Mingxiao, Ouyang Ziwei, Andersen M A E. High frequency LLC resonant converter with magnetic shunt integrated planar transformer[C]//2018 IEEE Applied Power Electronics Conference and Expo- sition (APEC), San Antonio, TX, USA, 2018: 2678- 2685.
[14] Jiao Jian, Guo Xizheng, Wang Chenchen, et al. Time-domain analysis and optimal design of LLC-DC transformers (LLC-DCXs) considering discontinuous conduction modes[J]. IEEE Transactions on Trans- portation Electrification, 2023, 9(2): 2308-2323.
[15] Xu Sen, Xie Xiaogao, Chen Chinan, et al. Study on wide dimming range solution for LLC LED driver based on an accurate time-domain analysis con- sidering the parasitical components[J]. IEEE Access, 2022, 10: 120213-120226.
[16] 缪哲语, 仝昊, 姚文熙, 等. 一种柔性多模态宽范围全桥LLC变换器控制方法[J]. 中国电机工程学报, 2022, 42(2): 747-761.
Miao Zheyu, Tong Hao, Yao Wenxi, et al. A flexible variable-mode control method for wide-range full- bridge LLC converter[J]. Proceedings of the CSEE, 2022, 42(2): 747-761.
[17] 张永明, 林嘉伟, 陈俊尧, 等. 计及DCM的电动汽车充电机LLC谐振变换器参数设计与优化[J]. 电力系统保护与控制, 2020, 48(2): 150-156.
Zhang Yongming, Lin Jiawei, Chen Junyao, et al. Parameter design and optimization of LLC resonant converter in electric car charger based on DCM analysis[J]. Power System Protection and Control, 2020, 48(2): 150-156.
[18] 张洪寅, 童朝南, 王泽庭. 基于临界模态的DCM- LCC谐振变换器的归一化分析与设计[J]. 电工技术学报, 2019, 34(1): 103-115.
Zhang Hongyin, Tong Chaonan, Wang Zeting. Normalized analysis and design of DCM-LCC resonant converter based on critical current mode[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 103-115.
[19] 胡海兵, 王万宝, 孙文进, 等. LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56.
Hu Haibing, Wang Wanbao, Sun Wenjin, et al. Optimal efficiency design of LLC resonant con- verters[J]. Proceedings of the CSEE, 2013, 33(18): 48-56.
[20] 赵子先, 康龙云, 于玮, 等. 基于简化时域模型的CLLC直流变换器参数设计[J]. 电工技术学报, 2022, 37(5): 1262-1274.
Zhao Zixian, Kang Longyun, Yu Wei, et al. Parameter design method of CLLC DC-DC converter based on simplified time domain model[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1262- 1274.
[21] Showybul Islam Shakib S M, Mekhilef S. A frequency adaptive phase shift modulation control based LLC series resonant converter for wide input voltage applications[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8360-8370.
[22] 鲁静, 同向前, 尹军, 等. L-LLC谐振型双向DC- DC变换器轻载优化控制策略研究[J]. 电工技术学报, 2022, 37(17): 4458-4465.
Lu Jing, Tong Xiangqian, Yin Jun, et al. The optimal control strategy for L-LLC Bi-directional resonant DC-DC converter under light load[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4458- 4465.
Multi Objective Parameter Optimization of Variable Mode Voltage Doubling LLC Resonant Converter
Abstract LLC resonant converters can achieve electrical isolation and soft switching, exhibit high efficiency and power density advantages, and are widely used in new energy fields such as lithium battery charging. The traditional fundamental analysis method simplifies the analysis difficulty and calculation process. However, significant errors exist when far from the resonant frequency point, and the accuracy is low in wide output voltage scenarios. This paper focuses on the precise time-domain model analysis of a variable mode voltage doubling-type LLC resonant converter with wide output. A multi-objective parameter optimization design method is proposed.
Firstly, the operating modes of LLC resonant converters and the characteristics of each operating mode are analyzed. The PO mode can achieve ZVS of the switching tube and ZCS of the rectifier tube, and the DC gain monotonically increases with the decrease of operating frequency. Accordingly, the PO mode is established as the optimal operating mode. Based on the working waveform of the PO mode and the equivalent circuit of P and O stages, a time-domain equation for the excitation current iLm, resonant current iLr, and resonant capacitor voltage uCr state variables in PO mode is established. The coefficients k1, k2, k3, and k4 in the state equation are solved to obtain the analytical formula for the PO mode state equation system. According to the coefficient analysis formula, it can be seen that k1, k2, k3, and k4 are related to the resonant capacitor Cr, inductance ratio coefficient K, and the conduction angle of the P mode sub-interval q.
Secondly, the parameter design of the main circuit is optimized. A multi-objective parameter optimization method is proposed based on pattern boundary constraints, resonant capacitor maximum constraints, and ZVS constraints. The multi-objective parameter optimization region and the optimal solution are obtained. The gain requirements and ZVS of the switching transistor under the most stringent operating conditions are achieved with a small cyclic reactive power, thereby improving the efficiency of the converter.
Finally, simulation models and experimental prototype platforms are constructed. The correctness of multi-objective parameter optimizationis verified by simulation. Simultaneously, using the traditional fundamental analysis method and the proposed parameter optimization design method, the converter parameters are designed separately, and comparative analysis is conducted from the perspectives of switch frequency variation range and resonant network current. The experimental results show that the proposed multi-objective parameter optimization design method has a narrower operating frequency range and higher operating efficiency than traditional fundamental analysis methods, which can meet the gain requirements and ZVS operating conditions of the converter over the entire load range.
Keywords:Variable mode voltage doubling, PO mode, time-domain analysis, constraint conditions, multi-objective parameter optimization
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231747
收稿日期 2023-10-18
改稿日期 2024-01-17
赵永秀 女,1978年生,博士,副教授,研究方向电力电子与电力传动、本质安全电路放电及防爆理论。
E-mail: yongxiu_zhao@163.com
刘泽伟 男,1995年生,硕士研究生,研究方向为开关变换器。
E-mail: zewei_liu9856@163.com(通信作者)
(编辑 郭丽军)