采用环形变压器的小功率隔离型DC-DC变换器共模电磁干扰噪声建模与抑制
惠 琦 任小永 陈乾宏
(南京航空航天大学自动化学院 南京 211106)
摘要 环形变压器具有隔离电容小、易于实现印制电路板(PCB)和集成电路(IC)等优点,在小功率隔离DC-DC变换器设计中的应用日益广泛。实际产品设计中,针对共模EMI噪声的准确预测和有效抑制是至关重要的,而变压器是隔离变换器共模EMI噪声的主要传播通路。然而,目前鲜有针对环形变压器共模电磁干扰(EMI)特性的相关研究,也缺乏针对性的噪声抑制方法。该文针对多种常见于小功率隔离型DC-DC变换器应用的环形变压器对称绕组结构,推导证明其具有统一的对称共模等效集总电容模型。该模型的参数易于获取,且可直接用于预测共模EMI噪声。分析了常用隔离变换器拓扑采用环形变压器时的共模噪声特性,同时给出噪声预测方法,并经实验验证了模型的正确性和有效性。此外,还提出多种环形变压器的共模EMI噪声抑制方法并加以分析,所提方法已在两台样机上得到验证,共模噪声的抑制效果显著。
关键词:环形变压器 共模电磁干扰(EMI)噪声 隔离变换器
0 引言
环形变压器因具有较低的高度、良好的散热条件、可实现软线连接等优点,广泛应用于高振动等严苛环境,如用作航电设备或星载设备中小功率隔离电源的功率变压器。近年来,环形变压器又因其易于实现超低隔离电容、易于集成至印制电路板(Printed Circuit Board, PCB)与集成电路(Integrated Circuit, IC)等优点,相关应用日益广泛,许多高性能小功率电源设计均采用环形变压器,如低隔离电容的栅极驱动器辅助电源[1]、高压发生器[2]、3D集成功率模块和高频功率IC[3]等。
实际产品设计过程中,对共模噪声实现准确预测和有效抑制至关重要。变压器作为隔离变换器的主要共模噪声传播通路,其共模特性值得研究。然而,当前针对环形变压器的共模等效集总电容模型建模研究相对匮乏,更缺少针对性的抑制手段。已有研究主要针对绕线变压器和平面变压器,根据其物理结构参数可推导得到共模等效集总电容模 型[4-7],由于这些方法得到的模型与变压器具体物理结构有关,而环形变压器与绕线和平面变压器有较大差异,因此无法直接应用相关结论。已有学者基于位移电流守恒原则证明,任何变压器若可忽略漏感,则其最终均可由两电容模型概括表征其共模等效特性[8]。两电容模型作为一种通用的变压器共模噪声集总电路模型已得到广泛应用,其推导过程不依赖变压器的具体物理结构,但也正因忽略了变压器结构信息,该模型中两电容的容值只能依靠实测获取,故较难在变换器早期设计过程中直接用于预测共模噪声。因此,有必要结合常用环形变压器的绕组结构,推导得到其共模等效集总电容模型。
隔离变换器共模噪声抑制的本质是减小一次、二次侧的位移电流,而针对变压器的共模噪声抑制手段,主要分为屏蔽和对消两类方法[4-6]。屏蔽法的主要思想是通过加入屏蔽层,减小甚至阻断一次、二次绕组间的电场耦合,进而减小变压器一次、二次绕组间分布电容的总位移电流。对消法主要是通过增加平衡绕组或外加补偿电容等方式,人为引入与原始位移电流流向相反的位移电流,使得流过一次、二次绕组间分布电容的总位移电流为零。现有针对变压器的共模噪声抑制手段均主要针对特定绕组结构的绕线变压器和平面变压器提出,无法直接应用于环形变压器,因此需要研究环形变压器的共模噪声抑制方法。
本文通过数学推导证明了小功率隔离型DC- DC变换器中常用的环形变压器绕组结构均具有相同的对称共模等效集总电容模型,该模型的唯一参数是变压器结构电容,当获得这一电容值后,便可确定变压器模型并用以预测变换器的原始共模噪声。本文给出变压器模型的验证方法和基于该模型的变换器共模噪声预测流程;进一步地,提出多种适用于环形变压器的共模噪声抑制措施,并分析给出了不同方法的适用条件;最后,在一台6 W模块电源、一台2.4 W隔离驱动辅助电源上分别验证了模型在共模噪声预测方面的有效性和准确性,同时验证了所提共模抑制措施能大幅衰减原始共模噪声,噪声抑制效果可达8 dB以上。
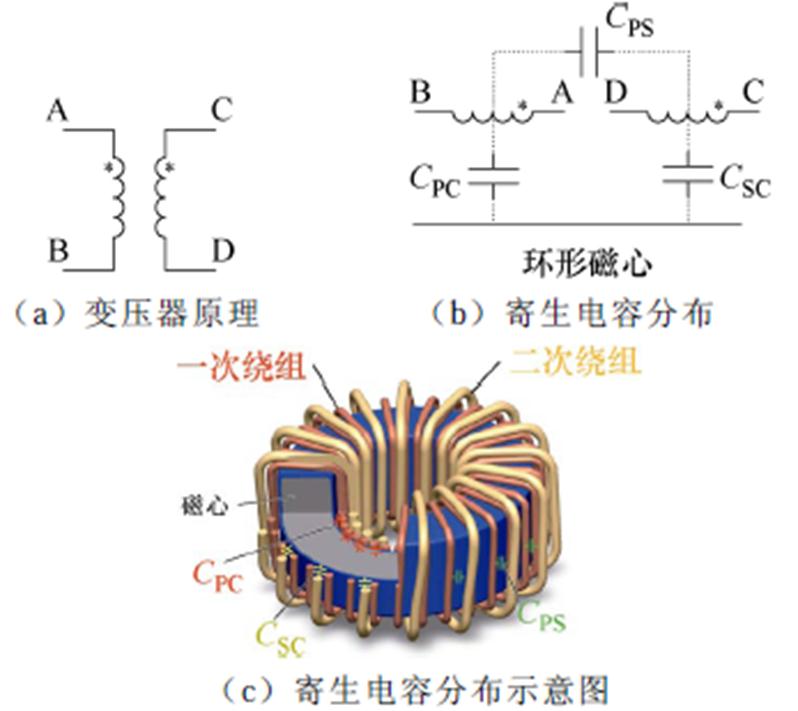
1 环形变压器的共模等效集总电容模型
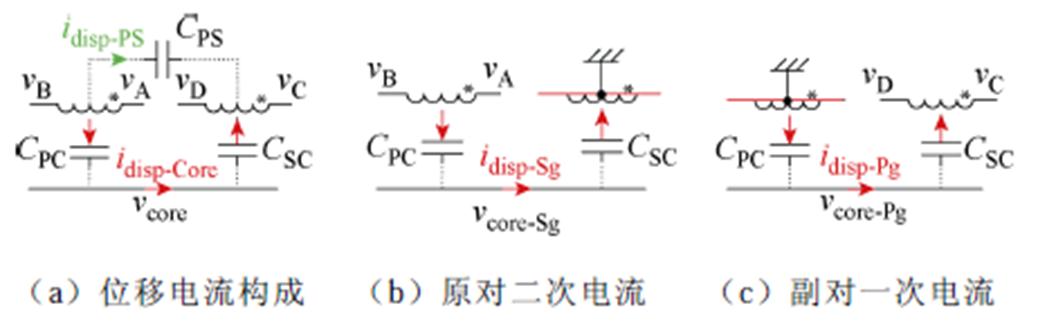
图1a所示的环形变压器,其绕组等效寄生电容可由图1b和图1c所示的三个集总电容表示,分别是假设磁心不存在时一次、二次绕组间的寄生电容CPS、一次绕组对磁心的寄生电容CPC、二次绕组对磁心的寄生电容CSC。定义变压器结构电容C0为一次、二次绕组各自短路时静态测得的总寄生电容,考虑到低频下磁心阻抗相对于电容容抗较小,可将磁环视作导体处理,因此C0可表示为
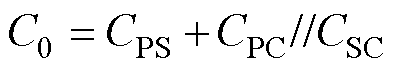
(1)
式中,//表示电容串联。
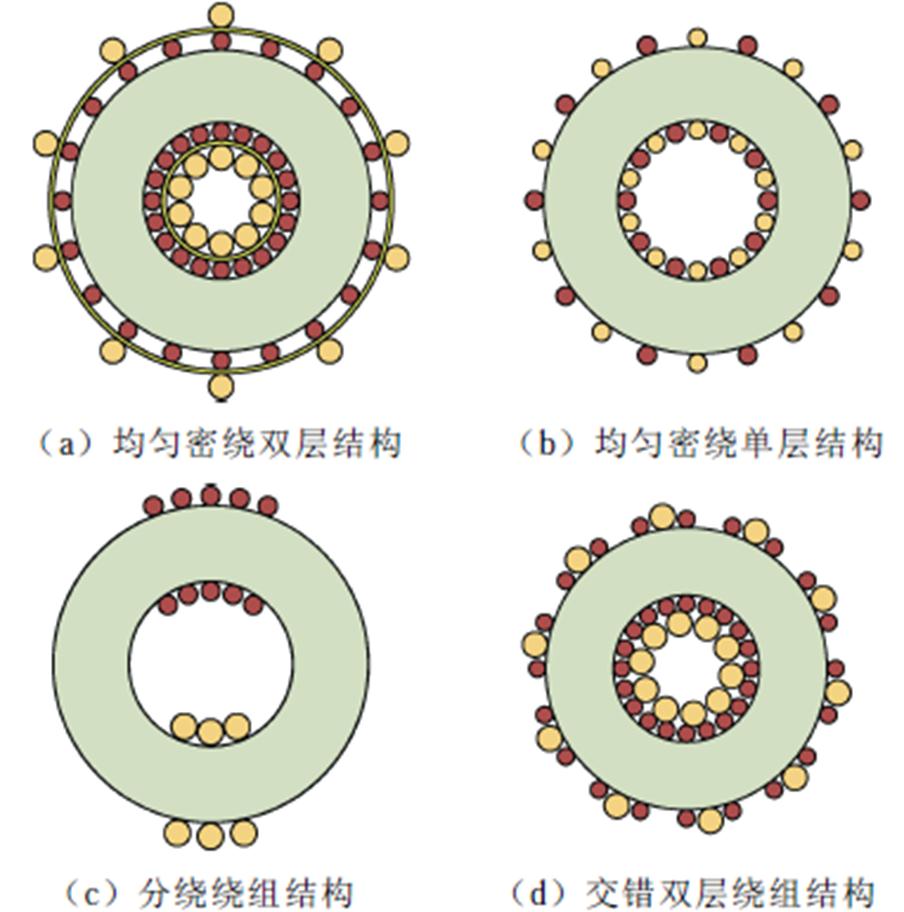
图2是四种常用的环形变压器绕组结构。图2a是均匀密绕双层绕组结构,一次、二次绕组分层绕制,层间用绝缘胶带分隔。采用该绕组结构时,一般一次、二次绕组匝数都很多,内层绕组几乎覆盖了磁环表面,阻断了外层绕组对磁心的电场耦合,因此变压器一次、二次侧的隔离电容主要来源于一次、二次绕组间的电场耦合,即C0=CPS;图2b是均匀密绕单层绕组结构,一次、二次绕组在磁环上均匀交错绕制,显然CPS、CPC、CSC均对结构电容产生贡献,C0由式(1)表示,此结构在小功率电源中常见[3];图2c是分绕结构,由于一次、二次绕组相距很远,CPS忽略不计,结构电容主要由一次、二次绕组对磁心的电容串联构成,即C0=CPC//CPS,该结构容易实现很低的隔离电容,适用于低漏电流应用;图2d的绕法介于图2a与图2b之间,称为交错双层绕组结构。该结构中,磁环内径上一次、二次绕组分成两层绕制,但在外径上一次、二次绕组交错绕制。
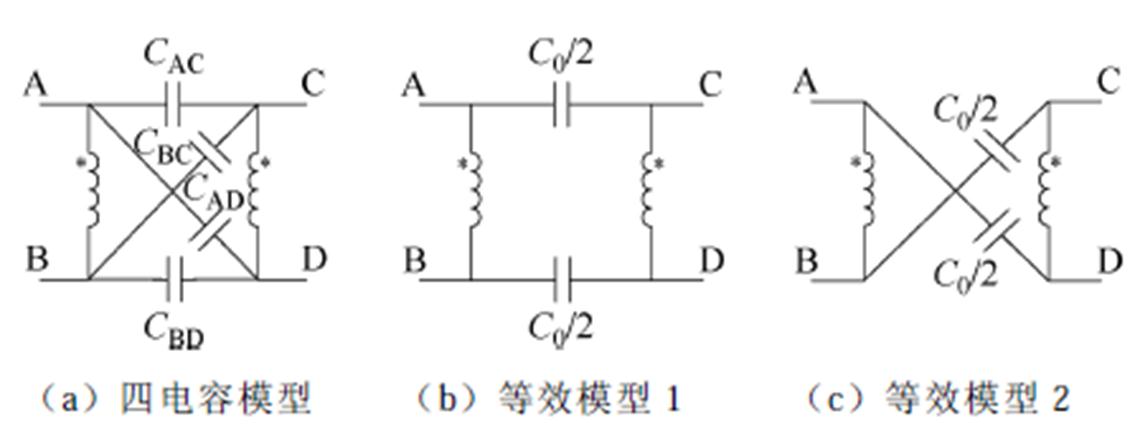
本节将在图3a所示的变压器四电容模型基础上,利用位移电流守恒原则证明以上四种常见的环形变压器绕组结构均具有如图3b或图3c所示的共模等效集总电容模型,上述两种模型是等价的,均能等效表征流经环形变压器的共模位移电流。
1.1 均匀密绕双层/单层绕组结构
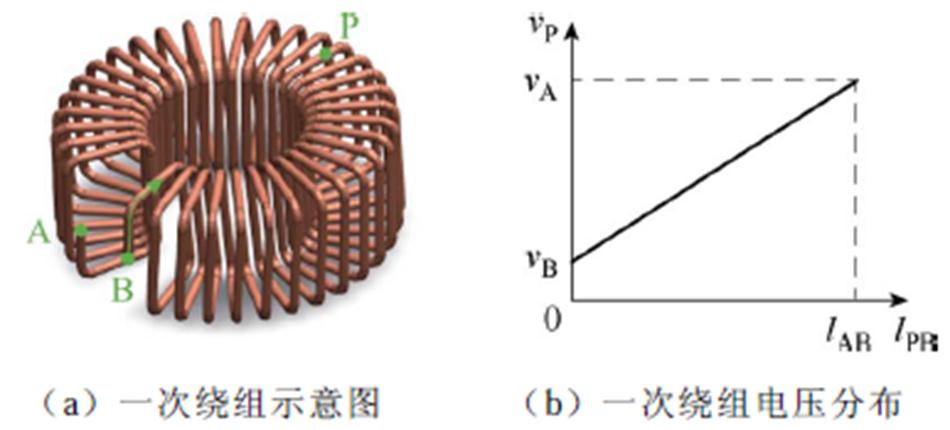
环形变压器一次绕组及其电位分布如图4所示。设一次绕组A、B两端子对参考地的电位为vA和vB,假设一次、二次绕组上电压呈线性分布,则一次绕组上任意一点P的电位可表示为
同理,设二次绕组C、D两端子对参考地的电位为vC和vD,二次绕组任意一点Q的电位为
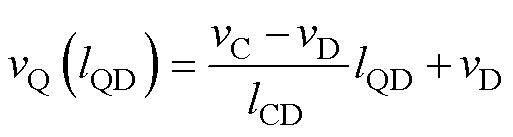 (3)
(3)
对于均匀密绕双层和单层绕组结构,可以假设其结构电容随绕组均匀分布。计算位移电流时,可采用叠加定理[4-5],置二次电位为0,先计算一次电压变化对二次侧产生的位移电流;反之,计算二次侧对一次侧产生的位移电流,并将两者相加,得到位移电流表达式为
将式(2)和式(3)代入式(4)进行计算,可得
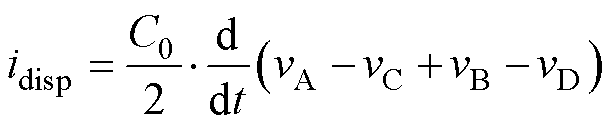 (5)
(5)
对于图3a所示的四电容模型,其位移电流表达式为
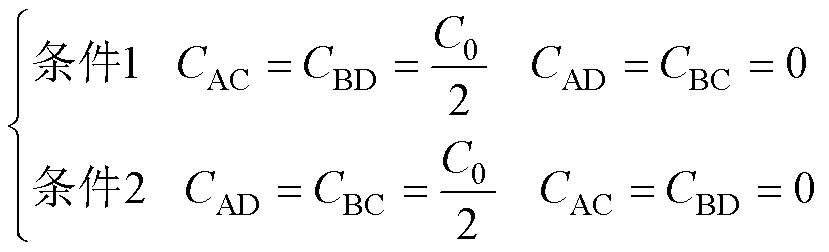 (7)
(7)
对比式(5)和式(6),根据位移电流等效原则,满足式(7)任一条件时,流经变压器的位移电流均与推导所得一致。
由此证明,图3b或图3c均可作为均匀密绕双层或单层绕组结构的共模等效集总电容模型。
1.2 分绕绕组结构
对于分绕绕组结构,虽然漏磁通不能忽略,但一次绕组(或二次绕组)的每一匝所匝链的磁通仍是近似相等的,因此电位线性分布假设即式(2)、式(3)仍成立。如图5a所示,由于CPS可忽略,变压器的总位移电流为流经磁心的位移电流idisp-Core。
如图5b和图5c所示,仍采用叠加定理计算一次、二次电压分别作用时的位移电流idisp-Sg(二次电压置零,一次侧作用)和idisp-Pg(一次电压置零,二次侧作用)。假设CPC随一次绕组长度均匀分布,CSC随二次绕组长度均匀分布。先计算idisp-Sg,二次电压置零、一次电压单独作用时磁环近似为等势体,设磁环电压为vCore-Sg,由KCL可知
化简可得
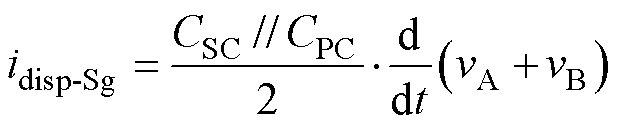 (9)
(9)
同理求得idisp-Pg
将式(9)与式(10)相加,求得总位移电流表达式为
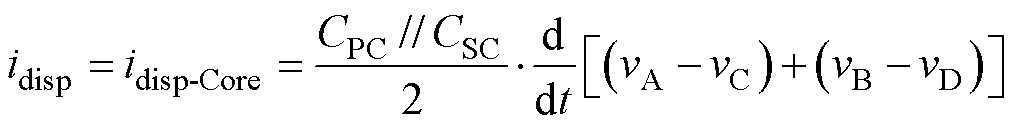 (11)
(11)
考虑到分绕情况下C0=CPC//CSC,证明分绕绕组结构与均匀密绕双层/单层绕组结构具有完全一致的位移电流表达式,因此其也具有图3b或图3c所示的共模等效集总电容模型。
1.3 交错双层绕组结构
交错双层绕组结构中,绕组电位线性分布假设仍成立,但三个分布电容CPS、CPC、CSC对位移电流均有贡献,如图5a所示,仍利用叠加定理分别计算其位移电流并进行加总,即
对于图6a所示的交错双层绕组结构,由于几何对称性,仍可近似认为CPS是随一次、二次绕组均匀线性分布的,因此idisp-PS的表达式为
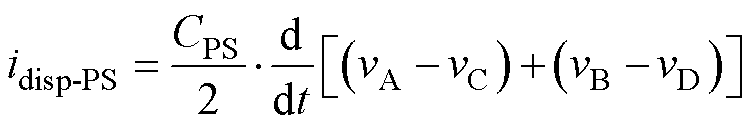 (13)
(13)
idisp-Core的计算参照1.2节,将这一电流分为idisp-Pg和idisp-Sg。对于内层绕组(为方便叙述,后面假设内层绕组为一次绕组),由于其均匀绕制于磁心周围,因此可近似认为其对磁心产生的寄生电容CPC也是随一次绕组均匀线性分布的,因此,很容易得到idisp-Sg的表达式与式(9)一致。
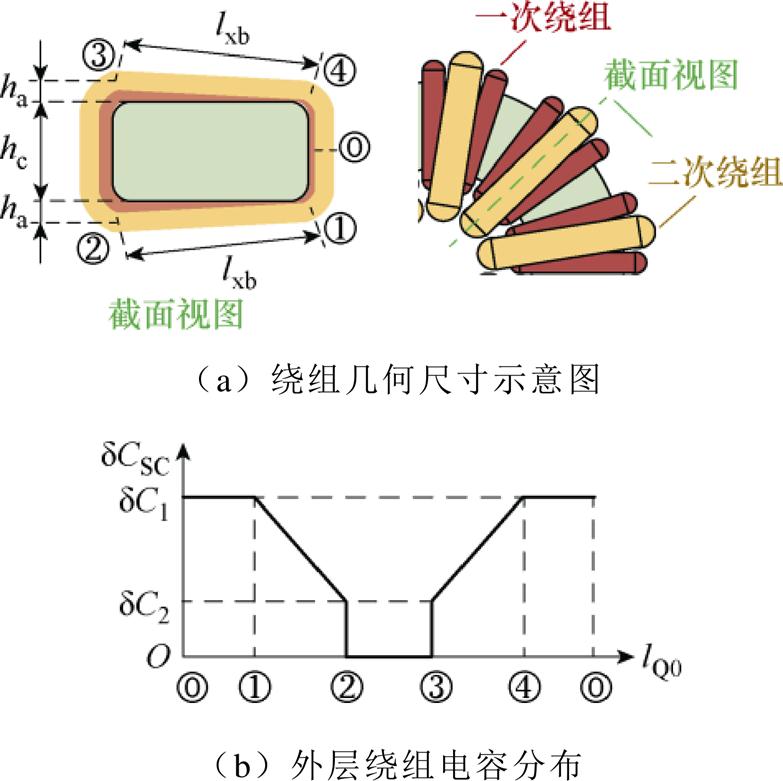
然而,外层绕组(假设为二次绕组)对磁心产生的寄生电容CSC不再随二次绕组均匀线性分布,这是因为外层绕组在磁心内侧被一次绕组阻隔,其对磁心的寄生电容相对很小,而在磁心外侧因其交错绕制在磁心表面,寄生电容相对较大。为处理这一情况,可对二次侧(匝数为Ns)每一匝分别计算其产生的位移电流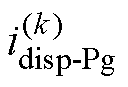 并进行加总,最终得到idisp-Pg为
并进行加总,最终得到idisp-Pg为
先考虑单匝的电容分布情况。可假设二次侧每匝的电容dCSC都相等,即dCSC=CSC/Ns。考虑每匝的几何绕制情况如图6所示,做如下假设,绕组在磁心外侧每单位长度的寄生电容是dC1(长度为磁心厚度hc),而在磁心内侧每单位长度的寄生电容为0(长度为hc+2ha),在磁心内侧向外侧过渡的两边(长度为lxb),其单位长度寄生电容由dC2线性变化为dC1,则单匝二次绕组对磁心的寄生电容满足式(15),且单匝绕组长度lpt满足式(16)。
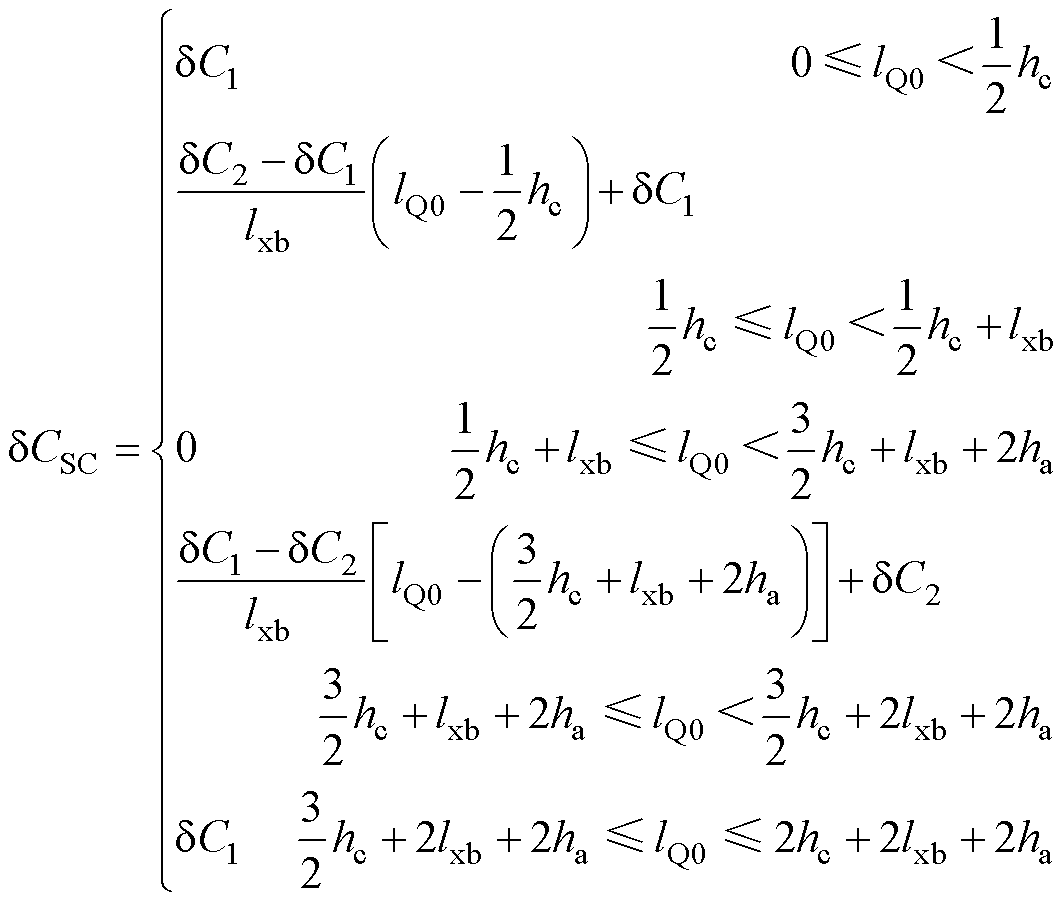 (15)
(15)
且单匝绕组的分布电容应满足
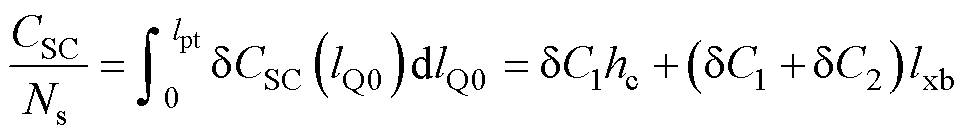 (17)
(17)
再考虑每匝的电位分布情况,以图6所示0位置作为单匝的起点,第k匝Q点的电位可表示为
类似1.2节推导,可得第k匝产生的位移电流为
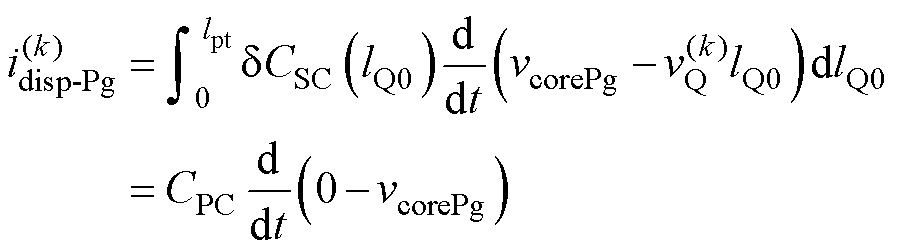 (19)
(19)
根据式(14)~式(19)计算idisp-Pg,可以证明idisp-Pg表达式与式(10)完全一致。
将式(9)、式(10)、式(13)进行相加,最终得到交错双层绕组结构的总位移电流表达式为
考虑到交错叠绕情况下C0=CPS+CPC//CSC,证明该绕组结构也具有图3b和图3c所示的对称共模等效集总电容模型。
2 变压器模型验证与共模噪声预测
2.1 变换器共模等效集总电容模型验证方法
已有许多方法可用于验证共模等效集总电容模型的准确性,如可通过施加正弦激励、测量两电容的分压情况、结合实测结构电容容值计算获得两电容容值[8],基于类似原理,也可以通过仿真[9]或者矢量网络分析仪(Vector Network Analyzer, VNA)测量获得,如图7a和图7b所示。通过测量变压器的共模电流传递函数,亦可间接验证集总电容模型的准确性[4]。然而,这些方法都假定绕组漏感可忽略,这对于部分环形变压器、尤其是采用分绕绕组结构的环形变压器不再适用。因此,本文提出了一种新的两步测量法来实现模型的直接验证。
本文所提方法如图7c所示,首先对端口A-B施加低频正弦激励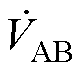 (如150 kHz)并测量端口D-B上的电压
(如150 kHz)并测量端口D-B上的电压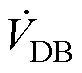 。然后在端口B-A上施加幅值、频率均与此前所加
。然后在端口B-A上施加幅值、频率均与此前所加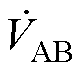 幅值、频率均一致的激励
幅值、频率均一致的激励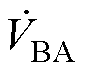 ,并测量在端口C-A上得到的电压
,并测量在端口C-A上得到的电压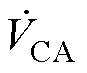 。根据电路理论,这两步测量的电压增益由式(21)给出,其中Lp为一次侧自感,Ls为二次侧自感,M为两绕组的互感,而Cprobe则表示电压探头的寄生电容,即
。根据电路理论,这两步测量的电压增益由式(21)给出,其中Lp为一次侧自感,Ls为二次侧自感,M为两绕组的互感,而Cprobe则表示电压探头的寄生电容,即
其中
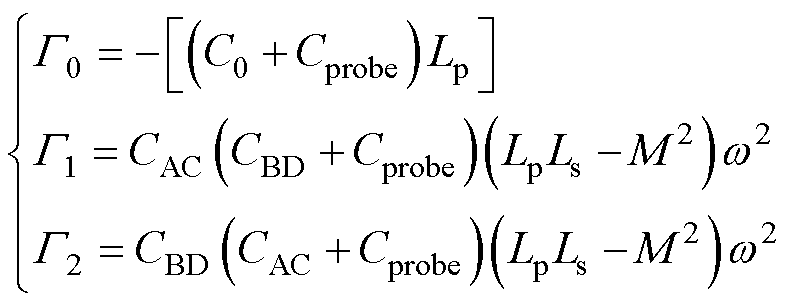 (22)
(22)
考察式(21)右侧分母部分,对于小功率应用中的变压器,Lp、Ls和M一般在数mH到数mH(量级为10-6到10-3),CAC、CBD和Cprobe通常为几pF到几百pF(量级为10-12到10-10),而采用的低频激励信号角频率w 量级为105。此时,G1和G2这两项的数量级远小于G0,因而可以忽略。因此,两次测量的电压增益之比近似为
式(23)给出了CAC、CBD的比例关系,而又有C0=CBD+CAC,因此通过两步测量,可确定环形变压器的共模模型参数。对于第1节分析的四种绕组结构,lC理论上应接近于1,可据此特性进行实验验证。
2.2 采用环形变压器的隔离型DC-DC变换器共模噪声预测方法
环形变压器共模等效集总电容模型中唯一需要确定的参数就是变压器结构电容C0,这一电容的计算方法已有较多研究[10-11],总体上均通过计算电场储能来等效计算结构电容容值,本文所研究不同绕组结构的变压器结构电容均有对应的数值计算方法。然而结构电容数值计算的准确度往往取决于变压器各物理参数的准确性(包括导线绝缘层与磁心绝缘漆层的厚度和介电常数、导线和磁环的具体物理尺寸和几何位置信息等),计算过程相对复杂,因此实际工程中也可采用边界元仿真或者变压器打样实测的方式来更快速地获取结构电容容值。
得到变压器结构电容C0后,变压器模型便可确定,进而可利用等效干扰源方法来预测任意拓扑结构的共模噪声[4, 12-13]。现以图8a所示高侧整流反激变换器为例,说明利用所提模型进行共模噪声预测的方法。根据替代原理,将反激变换器一次侧地、二次侧跳点电压用vp和vs两个电压源替代,并以一次、二次侧地构成一个端口,将整个变换器作戴维南等效,可得其戴维南等效内阻(即共模等效内阻ZCM)由C0 +CPE的阻抗决定,而戴维南等效开路电压voc(等效干扰源ENS)为
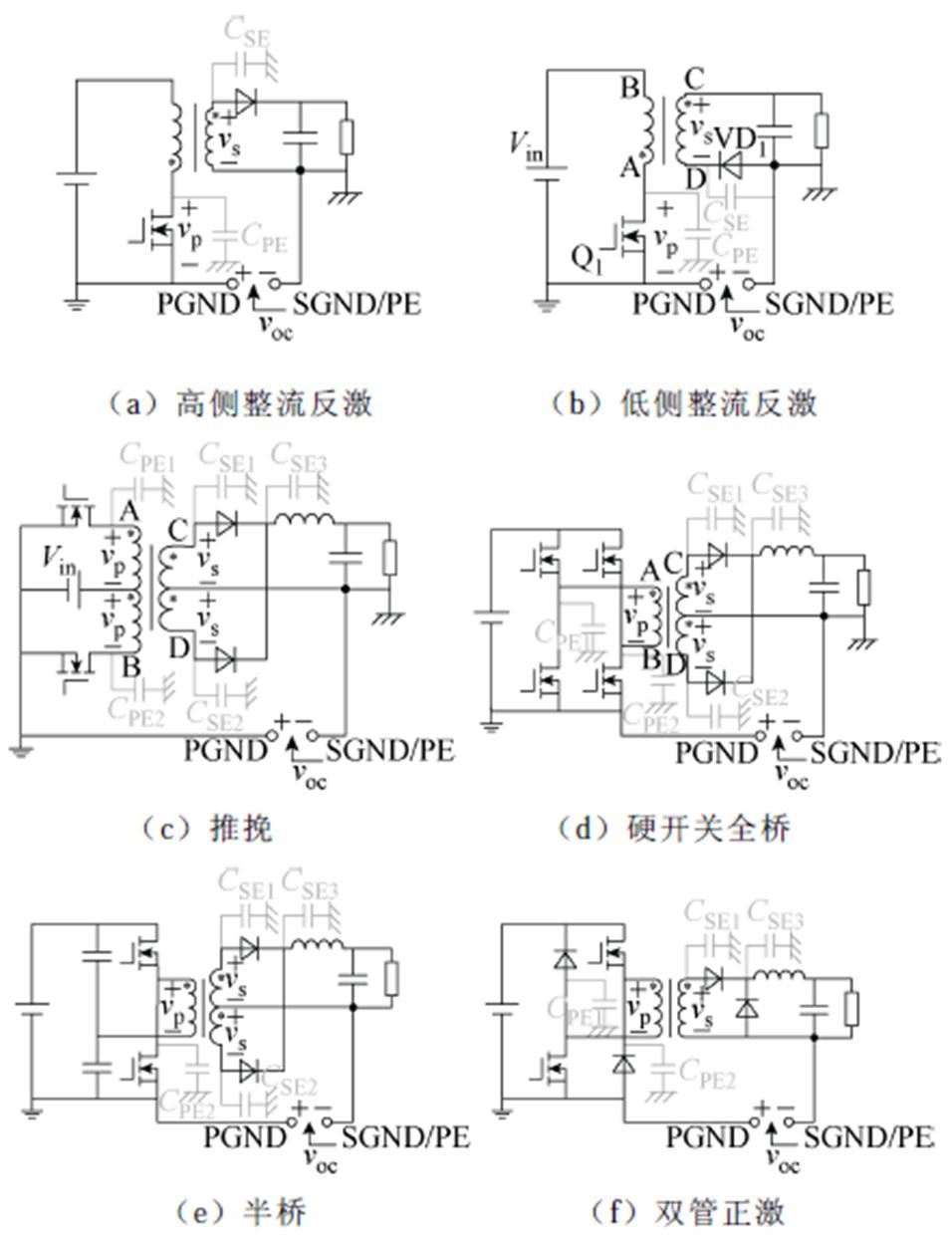
图8 典型的隔离型DC-DC PWM变换器
Fig.8 Typical isolated DC-DC PWM converters
对于没有接地散热器的小功率开关变换器,PCB布局合理情况下一般一次侧跳点对大地的电容CPE非常小,可忽略不计,此时等效开路电压可进一步化简为
进一步地,若变压器漏感较小,一次、二次电压近似满足匝比关系vs=nvp,其中n为匝比,则voc可进一步化简为
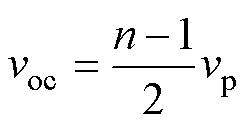 (26)
(26)
任意变换器均可按上述方法进行共模电路等效并得到使用对称环形变压器时的简化等效干扰源。图8所示为部分常用隔离型DC-DC变换器拓扑,当vp、vs、voc的参考方向如图选取、忽略变压器漏感时,其等效干扰源表达式汇总于表1。当忽略CPE和CSE时,其等效共模内阻Zcm均为C0对应的阻抗。
表1 采用环形变压器的典型隔离型DC-DCPWM变换器共模特性与抑制措施可行性
Tab.1 CM characteristics and applicability of CM suppression methods for typical isolated power conveters using toroidal transformer

拓扑结构共模特性共模抑制措施 简化voc零共模噪声条件补偿电容平衡绕组屏蔽绕组 高侧整流反激(n-1)vp/2n=1适用适用适用 低侧整流反激-(n+1)vp/2不具备不适用适用适用 推挽0恒为零——— 半桥 (全波整流)-vp/2不具备适用适用适用 双管正激nvp/2不具备适用适用适用 全桥 (全波整流)0恒为零———
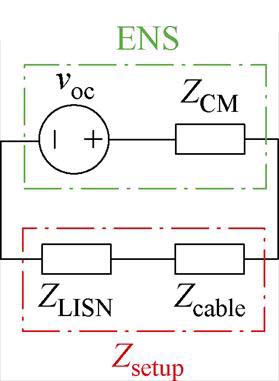
进一步推导共模电流的表达式。变换器等效干扰源与考虑测试环境的共模等效电路如图9所示,等效干扰源作为共模噪声的激励,施加在输入输出线缆和LISN上,因此产生的共模电流为
式中,Zcable为测试线缆、治具等造成的共模等效阻抗;ZLISN为LISN共模等效阻抗;两者可整体视为一个串联阻抗环节Zsetup,共同表征测试环境的作用效果。显然,Zsetup的阻抗特性取决于LISN阻抗、输入输出线缆长度和摆放方式等,不同测试标准、测试场地对这一阻抗会有较大影响,难以精确建模,但一般可通过实测方法获取其宽频阻抗曲线,如可采用矢量网络分析仪(Vector Network Analyzer, VNA)测试其二端口S参数并转换得到其阻抗曲线数据[14]。
进一步通过计算式(27)给出的共模电流在LISN中50 W 电阻上产生的电压,即可得到变换器最终的共模噪声。需要说明的是,上述推导均假设变换器二次侧接大地,若实际二次侧不直接接地,计算流程仍适用,只是此时Zsetup的阻抗在低频段将由二次侧静点(包括二次侧负载等)对大地的寄生电容主导。根据上述流程即可快速计算得到反激变换器的共模噪声电压幅值,一般可在频域进行,其中阻抗特性可由VNA实测获取,而跳点电压的频谱可由时域波形作傅里叶变换得到或通过理论计算得到[15]。
3 环形变压器共模噪声抑制方法
本节介绍采用环形变压器的隔离型开关变换器共模噪声抑制方法。首先讨论采用环形变压器时,变换器自然实现零共模噪声的条件,进而提出三种适用于环形变压器的共模噪声抑制方法,包括补偿电容法、平衡绕组法、屏蔽法(铜箔实现和屏蔽对消线实现)。此外,针对分绕绕组结构,本文提出叠绕平衡方法,实现共模噪声抑制的同时可减小变压器隔离电容。
3.1 自然实现零共模噪声的条件
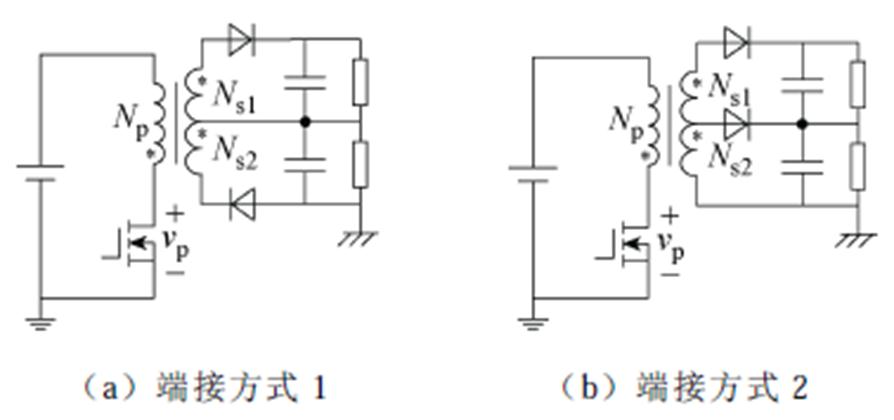
观察表1可以发现,某些拓扑结构在使用环形变压器时,其具有零共模噪声的优异特性,如推挽变换器、全波整流的全桥变换器等。这类拓扑在对共模噪声有严苛要求的场合可优先考虑采用。另一部分变换器虽然共模噪声不恒为零,但在满足特定条件时可实现零共模噪声,然而,其实现零共模噪声的条件往往较为苛刻。以高侧整流的反激变换器为例,小功率应用中若忽略一次、二次侧跳点对大地的寄生电容,由式(26)可知,当且仅当匝比为1时,才能实现自然平衡,这在实际应用中一般很难恰好满足,但有时通过调整变压器的端接方式,可以实现零共模噪声。一个例子是对于需要正负电压输出的反激变换器(如栅极驱动器辅助电源),图10a和图10b实现的输出电压是一致的,当采用本文讨论的环形变压器绕组结构时,若满足Np=Ns1+ Ns2,此时后者能自然实现零共模噪声,而前者则无法实现。工程师可充分利用环形变压器的这一特性,在设计时可根据实际情况综合考虑微调拓扑,有时无需额外措施即可使得变换器具有零共模噪声的特点。
然而,有一些变换器在使用对称环形变压器时理论上无法依靠自身实现自然平衡,如低侧整流的反激变换器,其等效干扰源电压不可能为零。对于这类变换器,可考虑采用后文介绍的其他变压器抑制措施或结合通用电磁干扰(Electromagnetic Inter- ference, EMI)抑制方法[16-17]来进行共模噪声抑制。
3.2 补偿电容法
补偿电容法是最为直接的、基于对消思想实现的共模噪声抑制措施。以低侧整流反激变换器为例,考虑Np>Ns的情况,假设在vs正端和一次侧地之间增加一个补偿电容Cb,则其等效干扰源表达式变为
显然,通过补偿电容实现等效干扰源为零(即实现零共模电流)的条件是
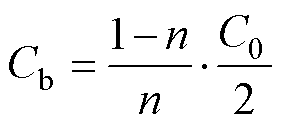 (29)
(29)
补偿电容对低频段共模噪声的抑制是非常有效的,采用环形变压器时,补偿电容的容值也相对容易计算。需要说明两点:①一般而言,一次侧匝数大于二次侧时,一次侧dv/dt相对二次侧更高,因此需要构造反向的位移电流来抵消原有共模电流,故补偿电容需要加在二次侧跳点(图8中vs正端)与一次侧地之间,反之则加在一次侧跳点与二次侧地之间,同样可以基于等效干扰源方法得到实现零共模电流的补偿电容容值;②可以证明,部分拓扑如低侧整流反激变换器无法直接通过补偿电容实现共模抑制,这是因为变压器端接方式使得一次、二次侧跳点产生的共模电流总是向同一侧流动,这种情况只能通过人为构造反向跳变的跳点电压才能实现共模噪声对消(如后文介绍的平衡绕组法)。
补偿电容方法的主要缺点在于:一方面,由于补偿电容是跨接一次、二次侧的电容,实际产品中需要采用安规电容来实现,体积较大、增加成本;另一方面,补偿电容容值往往较小,容差较大,补偿效果一致性难以保证。因此,工程设计中一般仍优先考虑对变压器施加措施来抑制共模噪声。
3.3 平衡绕组法
平衡绕组是绕线变压器中常用的共模抑制措施之一,这一方法可以迁移至环形变压器。平衡绕组本质上仍然是利用对消思想,构造额外的反相位移电流来补偿原有位移电流。以补偿电容无法起效的低侧整流反激变换器为例,图11a为通过平衡绕组实现共模噪声抑制的原理示意图,通过增加平衡绕组(蓝色表示)在一次侧引入一个负向跳变的电压,使能产生由二次侧流向一次侧的位移电流,大小与一次侧流向二次侧的位移电流相等,即可实现共模电流对消。图11b是一种可能的实现方式,其中蓝色绕组为平衡绕组。
通过平衡绕组抑制共模噪声的方法用于绕线变压器时,该绕组往往完全介于一次、二次侧之间且完整填充整个窗口高度,或一般平衡绕组与一次、二次绕组的耦合关系较为简单,因此已有较多方法可比较简单地计算平衡绕组匝数[18]。然而,平衡绕组方法用于环形变压器时,由于其交错分布于一次、二次绕组之间,导致电场耦合关系相对复杂,因此其具体匝数计算依赖变压器具体绕制方法和物理参数,往往需要借助仿真或者多次试错才能取得较好的共模噪声抑制效果。
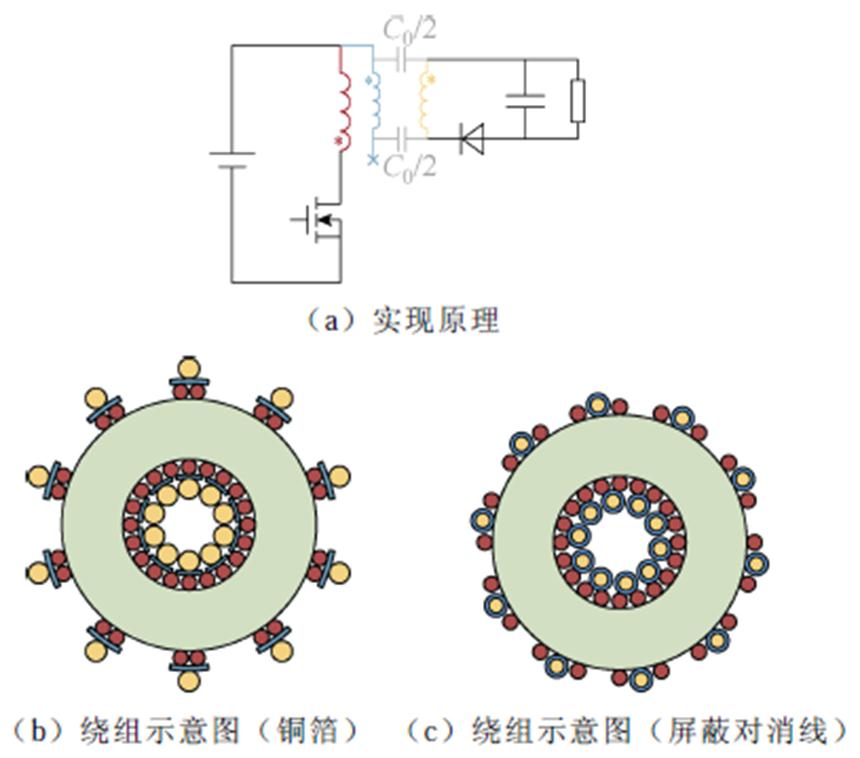
3.4 屏蔽绕组法
一种更简单的方法是采用全屏蔽绕组来进行共模噪声抑制。全屏蔽方法已在平面变压器上得到了广泛应用[19],同样可应用于环形变压器。通过屏蔽绕组实现共模噪声抑制(反激为例)原理如图12所示,以低侧整流反激变换器为例,设Np>Ns,在一次、二次侧之间加上与二次侧匝数相等且电位分布一致的铜箔,构成屏蔽绕组,屏蔽绕组一端接至一次侧地,同名端选取以能使屏蔽绕组电位分布与二次侧一致为准,铜箔宽度合适时可完全阻隔一次、二次主绕组的电场耦合,此时一次、二次侧的电场耦合转换为屏蔽绕组与二次绕组之间的耦合,由于两个绕组电位分布一致,因此总的位移电流为零,因此可以实现很好的共模噪声抑制。该方法下环形变压器的共模等效集总电容模型仍为对称形式,只是结构电容C0变成了屏蔽绕组和二次绕组间的寄生电容,该方法并不严格要求屏蔽绕组每一匝的电位分布均与二次侧完全一一对应,只要求两绕组具有相同的电位分布。
全屏蔽绕组绕制需要采用背胶薄铜带,对于环形变压器来说难以进行机器绕制,且会占据较多绕线空间、增加漏感。一种改良方式是使用屏蔽对消线[4]来实现全屏蔽。屏蔽对消线是类似同轴电缆结构的双层线,本质上是利用外层屏蔽层实现全屏蔽。仍以Np>Ns情况为例,绕组示意图如图12c所示,二次绕组采用屏蔽对消线绕制,外层为屏蔽绕组,一端接一次侧地,且同名端选取以能使屏蔽绕组电位分布与二次侧一致为准,显然这一方法能起到与全屏蔽一样的效果,但相对更容易实现机器绕制。采用屏蔽对消线时,屏蔽绕组与二次绕组是同步绕制的,因此两者电位分布与二次侧也是一一对应的。
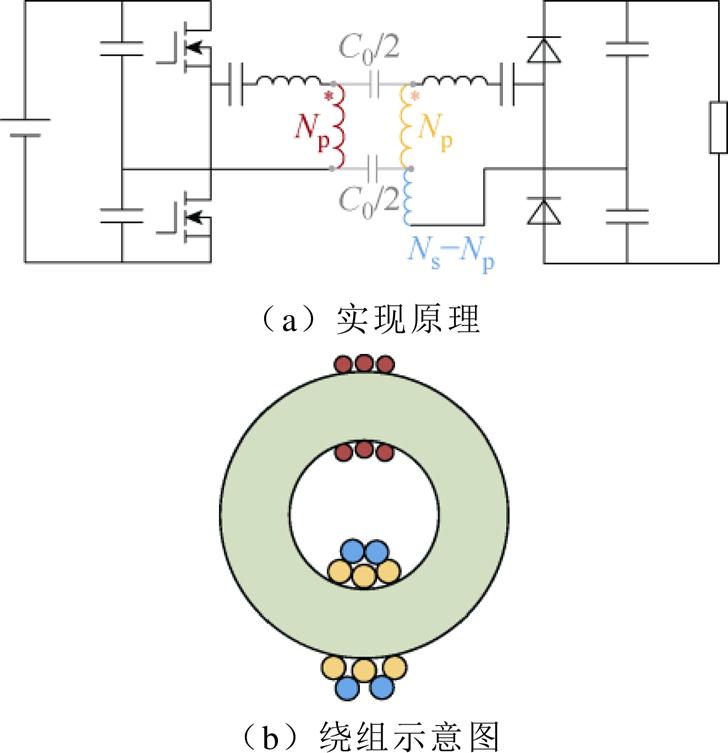
3.5 分绕绕组的叠绕平衡抑制方法
对于分绕绕组结构,自然实现零共模噪声是优选的共模抑制方法,这是因为采用分绕绕组结构的主要目的往往是减小一次、二次侧的结构电容(隔离电容),而上述其他几种抑制措施一般均会增大隔离电容,这与采用分绕绕组绕制环形变压器的初衷相悖。
对于具有可能实现共模噪声抵消的拓扑,本文提出一种改进的分绕绕组结构来帮助实现对消,称为分绕绕组的叠绕平衡抑制方法。由于分绕绕组结构造成的漏感相对较大,一般不适合用于传统PWM变换器,因此本文以倍压整流的半桥串联谐振变换器为例,介绍所提方法的实现原理。该拓扑开环开关频率固定工作时具有很高的转换效率、同时输出电压在一定负载范围内变化很小,结合分绕绕组结构很容易实现很低的隔离电容,因此尤其适合用作隔离栅极驱动器辅助电源。
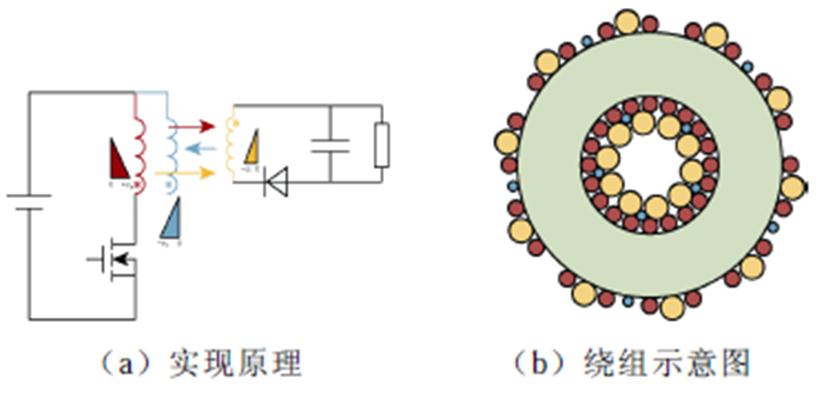
提出的分绕绕组叠绕平衡抑制方法(半桥串联谐振变换器为例)如图13所示,假设Ns>Np,对于二次绕组,先只取与一次绕组dv/dt一致的Np匝绕制一层,剩余Ns-Np匝叠绕在这Ns层上,一次侧Np匝在磁环另一侧单绕一层。此时,因叠绕在外层的二次绕组被内层Np匝绕组阻隔,其对磁心产生的寄生电容可忽略、也不会对位移电流有贡献,因此二次侧只有内层Np匝和一次侧的Np匝耦合,且其dv/dt一致,故位移电流为零,由此实现共模噪声 抑制。
4 实验验证
4.1 变压器模型验证
为验证本文2.1节所提方法的正确性,本文先在一款普通绕线变压器上根据图7a所示的文献[8]所提方法提取模型参数,再利用本文所提方法进行参数提取,比对结果。绕制的变压器磁心采用PQ2016、DMR95材质,匝比为36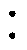 6,三明治绕法,实测其一次侧自感Lp=3.6 mH,二次侧自感Ls= 103.3 mH,互感M=583.3 mH,结构电容C0=30.3 pF。使用信号源(Keysight N5171B)在一次绕组A-B施加5.76 Vpp/150 kHz的正弦激励
6,三明治绕法,实测其一次侧自感Lp=3.6 mH,二次侧自感Ls= 103.3 mH,互感M=583.3 mH,结构电容C0=30.3 pF。使用信号源(Keysight N5171B)在一次绕组A-B施加5.76 Vpp/150 kHz的正弦激励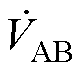 ,在示波器(Tektronix MDO3054)上对应测得D-B之间的响应信号
,在示波器(Tektronix MDO3054)上对应测得D-B之间的响应信号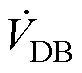 为2.44 Vpp同相正弦信号,测试时采用的无源探头(Tektronix TPP0500B)寄生电容Cprobe实测为3.36 pF,根据文献中的相关折算方法,计算得到模型中两电容CAC和CBD分别是16.93 pF和13.37 pF。进一步地,在一次绕组B-A之间施加同样幅值频率的正弦激励
为2.44 Vpp同相正弦信号,测试时采用的无源探头(Tektronix TPP0500B)寄生电容Cprobe实测为3.36 pF,根据文献中的相关折算方法,计算得到模型中两电容CAC和CBD分别是16.93 pF和13.37 pF。进一步地,在一次绕组B-A之间施加同样幅值频率的正弦激励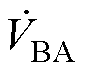 ,实测C-A之间的响应信号
,实测C-A之间的响应信号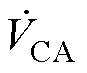 为1.94 Vpp同相正弦信号,根据本文所提方法即式(23),计算得到模型中两电容CAC和CBD分别是16.87 pF和13.42 pF,与已有文献的方法结果一致,由此证明所提方法的正确性。
为1.94 Vpp同相正弦信号,根据本文所提方法即式(23),计算得到模型中两电容CAC和CBD分别是16.87 pF和13.42 pF,与已有文献的方法结果一致,由此证明所提方法的正确性。
进一步地,本文制作了多款变压器,利用2.1节给出的实验方法进行共模等效集总电容模型验证,测试结果见表2,表中汇总的实验结果表明,本文所分析的多种绕组结构确实具有对称两电容等效模型,实验结果与理论分析较为一致。
表2 环形变压器共模等效集总电容模型验证
Tab.2 Verification of CM equivalent lumped capacitance model of different toroidal transformers
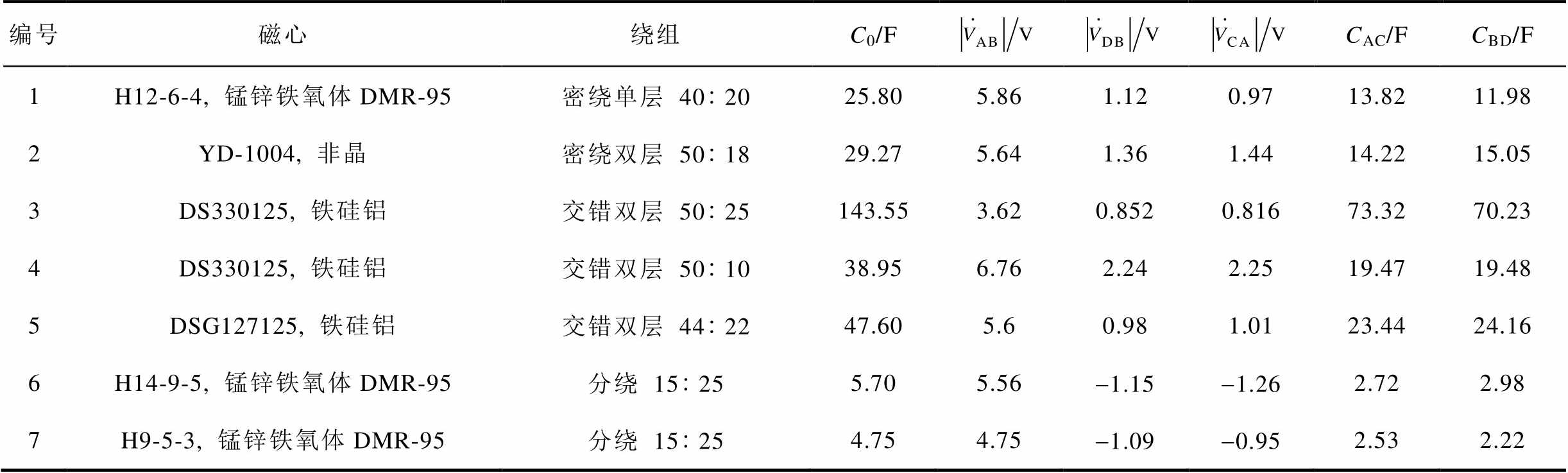
编号磁心绕组C0/FCAC/FCBD/F 1H12-6-4, 锰锌铁氧体DMR-95密绕单层402025.805.861.120.9713.8211.98 2YD-1004, 非晶密绕双层501829.275.641.361.4414.2215.05 3DS330125, 铁硅铝交错双层 5025143.553.620.8520.81673.3270.23 4DS330125, 铁硅铝交错双层501038.956.762.242.2519.4719.48 5DSG127125, 铁硅铝交错双层442247.605.60.981.0123.4424.16 6H14-9-5, 锰锌铁氧体DMR-95分绕15255.705.56-1.15-1.262.722.98 7H9-5-3, 锰锌铁氧体DMR-95分绕15254.754.75-1.09-0.952.532.22
4.2 共模噪声预测
实验样机如图14所示,本文搭建了两台样机用以验证噪声预测和抑制方法。样机1为一台18~36 V输入、5 V/1.2 A输出的高侧整流反激样机(原理见图8a)。样机1使用表2中5号变压器时测得的噪声作为基准比较原始噪声和相关抑制方法。样机2为15 V输入、24 V/0.1 A输出的半桥串联谐振变换器(原理图见图13a)。样机2使用表2中7号变压器时测得的噪声作为原始噪声和相关抑制方法的比较基准。
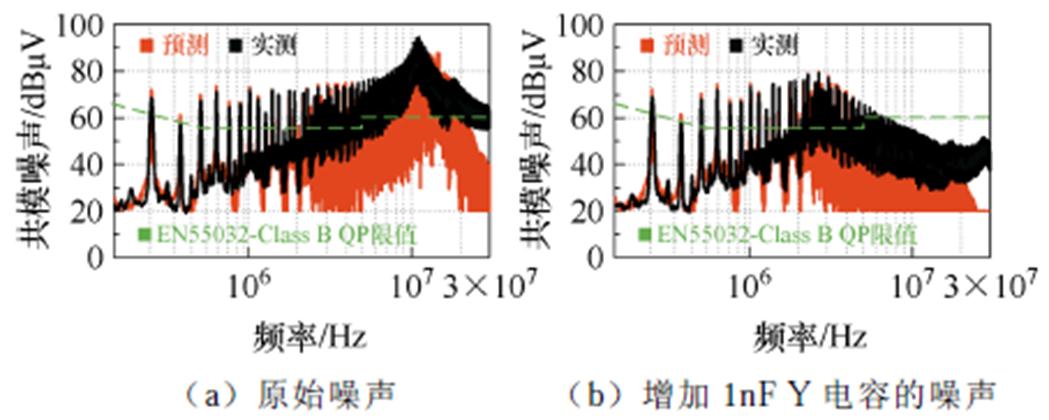
根据2.2节给出的方法,本文先在反激样机上进行了共模噪声预测,以进一步验证所提变压器模型的准确性。EMI测试按EN55032 Class B要求进行,二次侧接地。EMI接收机采用Cybertek EM5080B,LISN和噪声分离器型号为Cybertek EM5040B。按测试要求完成输入输出接线摆放后,不连接待测电源,先采用VNA(Keysight E5063A)实测输入、输出接线之间的S参数,并转换得到测试环境阻抗Zsetup的宽频阻抗特性曲线。在输入24 V、输出5 V/1.2 A条件下,用示波器实测样机1一次侧跳点时域波形vp并作快速傅里叶变换得到vp频谱,由式(26)进一步计算得到等效干扰源voc的频谱。样机1的共模等效内阻Zcm为变压器结构电容C0对应的阻抗。上述过程得到的Zsetup阻抗、voc频谱、Zcm阻抗数据均保留复数表示,即需要保留三者幅值、相位随频率变化的关系,并将其代入式(27)计算得到共模电流的频谱,进一步转换得到LISN上的共模电压,作为共模噪声预测值与实测值进行对比。在同样测试条件下实测共模噪声,实测和预测结果如图15所示,在15 MHz以前,预测值与实测值偏差不超过3 dB,可见所提模型和方法非常准确地预测了样机的共模噪声;观察到原始共模噪声在12 MHz左右出现尖峰,这可以从图9和式(27)得到解释。由于输入输出线以及测试治具的存在,Zsetup在低频段实际呈现出大约3.5 mH的感抗,这一等效电感与变换器共模等效内阻C0(47.6 pF)产生串联谐振,因此在谐振频率(12.3 MHz)附近共模电流幅值增大,出现噪声尖峰。若单纯增加Y电容(增大共模等效内阻的总电容值)或单纯增加共模电感(增加了线路总的低频等效电感值),均只会使谐振峰向较低频率移动,但其对共模噪声的削弱作用是有限的:图15b是单纯增加1nF Y电容时的共模噪声实测值与预测值对比,预测与实测一致,且如前分析,共模噪声尖峰向低频段移动,加入Y电容后谐振尖峰处的噪声相对原始噪声甚至有所提高。
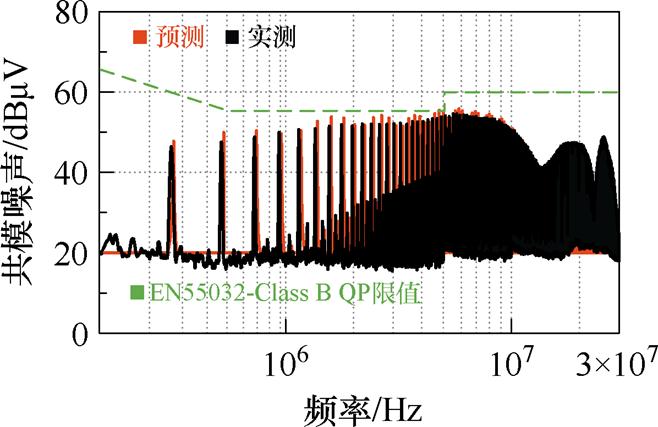
图16是在图14串联谐振变换器样机上进行的共模噪声预测结果,具体实验方法与样机1共模噪声预测实验类似,不再赘述。变换器工作在谐振频率点,一次、二次侧漏感与串联电容谐振。预测共模噪声时,将谐振腔视作短路处理。共模噪声的预测结果仍与实测保持一致,由此再次证明本文所提变压器等效模型在共模噪声预测方面的有效性。
4.3 噪声抑制方法验证
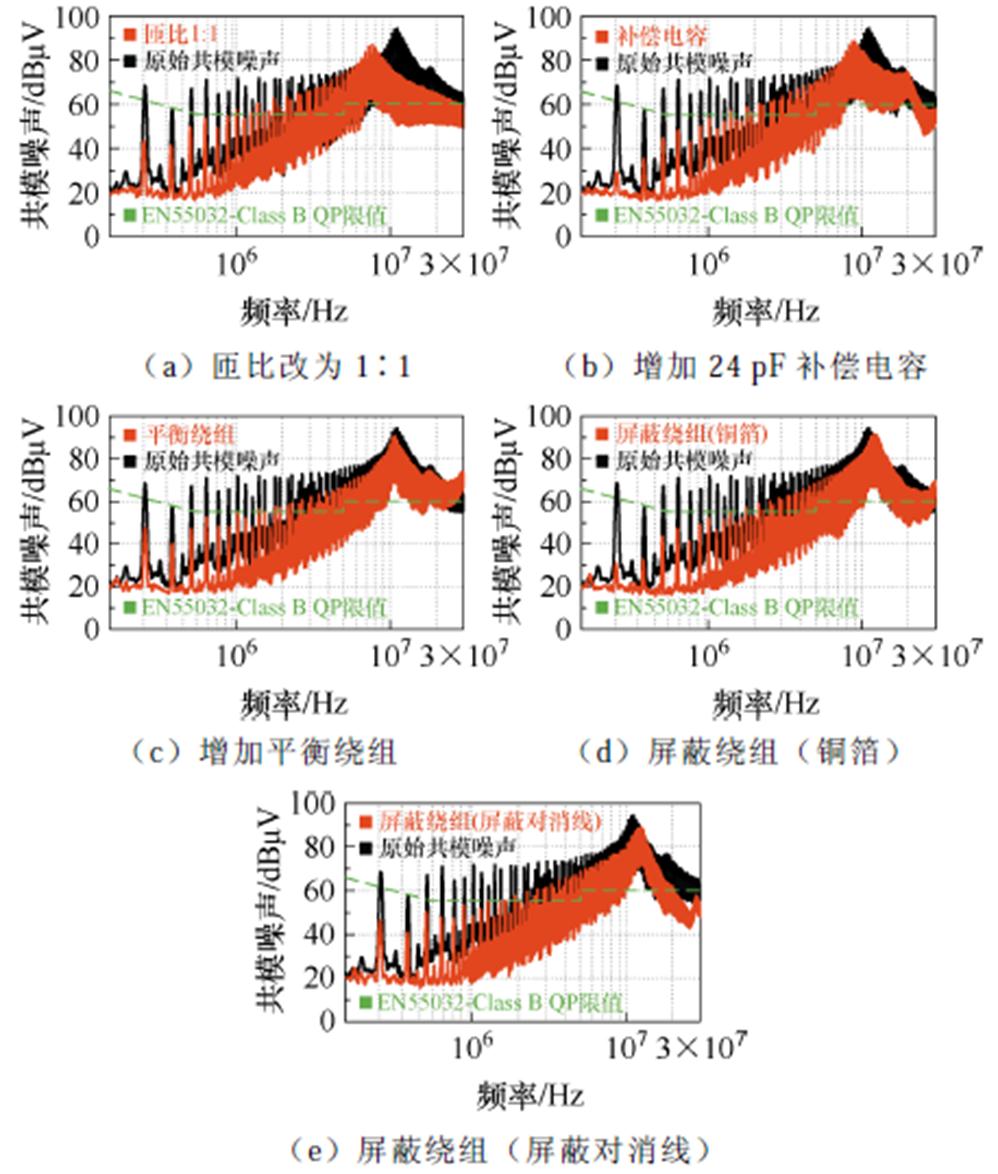
本文先在反激样机上验证了所提多种环形变压器噪声抑制方法,图17为实验结果。其中,图17a为人为改变匝比,将反激变换器匝比改为1 1、采用交错绕制方式时的共模噪声,此条件下自然实现零共模噪声;图17b为人为增加24 pF补偿电容的抑制效果,容值根据式(29)确定;图17c为增加平衡绕组的抑制结果;图17d和图17e分别为铜箔实现全屏蔽和屏蔽对消线实现全屏蔽的效果。可见,所提方法在反激样机上均取得非常良好的共模噪声抑制效果,这些方法在中、低频段的抑制能力达到20 dB以上,而高频段的抑制效果削弱,这主要有两方面的原因:①高频段的共模噪声尖峰如前所述是由于线缆电感和变压器结构电容谐振造成的,无法单纯通过抵消的方式来实现抑制;②因漏感等寄生参数影响,变压器一次、二次电压实际上并不完全满足匝比关系,高频段的噪声可能存在相位差异,因此无法通过抵消的方式实现有效补偿。此外,样机1变压器采用抑制措施后,不增加任何滤波措施的前提下,原始噪声在中低频段得到显著抑制,但高频段仍超过限值的要求,可通过增加高频共模滤波器和Y电容等方法进一步抑制共模噪声,以满足限值要求。
1、采用交错绕制方式时的共模噪声,此条件下自然实现零共模噪声;图17b为人为增加24 pF补偿电容的抑制效果,容值根据式(29)确定;图17c为增加平衡绕组的抑制结果;图17d和图17e分别为铜箔实现全屏蔽和屏蔽对消线实现全屏蔽的效果。可见,所提方法在反激样机上均取得非常良好的共模噪声抑制效果,这些方法在中、低频段的抑制能力达到20 dB以上,而高频段的抑制效果削弱,这主要有两方面的原因:①高频段的共模噪声尖峰如前所述是由于线缆电感和变压器结构电容谐振造成的,无法单纯通过抵消的方式来实现抑制;②因漏感等寄生参数影响,变压器一次、二次电压实际上并不完全满足匝比关系,高频段的噪声可能存在相位差异,因此无法通过抵消的方式实现有效补偿。此外,样机1变压器采用抑制措施后,不增加任何滤波措施的前提下,原始噪声在中低频段得到显著抑制,但高频段仍超过限值的要求,可通过增加高频共模滤波器和Y电容等方法进一步抑制共模噪声,以满足限值要求。
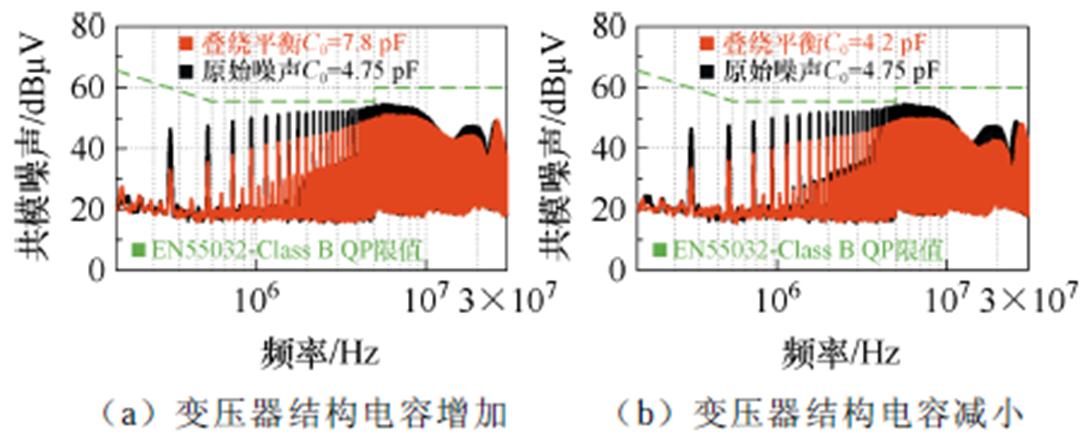
本文所提分绕绕组的叠绕平衡抑制方法在串联谐振变换器上得到验证。由于分绕结构下变压器结构电容很小,仅4.75 pF(见表2中7号变压器),样机原始噪声较低,但5 MHz处裕量不足。验证叠绕平衡方法时,为确保比较的公平性,叠绕时二次侧采用了更粗的导线来绕制,使变压器的结构电容增加至7.8 pF,大于原变压器。此时,所提绕组结构仍然实现了超过8 dB的共模噪声抑制效果如图18a所示。若采用与原变压器一样的线规来绕制叠绕平衡绕组,共模噪声可进一步降低,结果如图18b所示。两组实验在进一步降低了变换器在中低频段共模噪声的同时,有效提高了5 MHz处的噪声裕量。这些结果均证明所提叠绕平衡抑制方法的有效性。
5 结论
本文证明了几种常用绕组结构的环形变压器均具有对称的共模等效集总电容模型,该模型的唯一参数是结构电容容值、易于获取和确定,模型可在变换器设计早期直接用于共模噪声预测。本文给出了常用拓扑使用环形变压器时的共模噪声特性及具体的预测方法,并在两台样机上利用所提模型进行了共模噪声预测,预测结果与实测一致。此外,本文提出并分析了多种适用于环形变压器的共模抑制措施,并提出分绕绕组的叠绕平衡等抑制方法。所提抑制方法已在多台样机上得到实验验证,共模噪声的抑制效果可到8 dB以上。本文研究内容为采用环形变压器的隔离型开关电源共模噪声抑制提供了有益参考。
参考文献
[1] Sun Bingyao, Burgos R, Boroyevich D. Ultralow input-output capacitance PCB-embedded dual-output gate-drive power supply for 650 V GaN-based half- bridges[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1382-1393.
[2] Baktash A, Vahedi A. Calculation of parasitic elements in toroidal core transformers[J]. IEEE Transa- ctions on Plasma Science, 2014, 42(6): 1690-1696.
[3] Li Haiwang, Zhu Kaiyun, Lei Kaibo, et al. Integrated MEMS toroidal transformer with Ni-Zn ferrite core for power supply on chip[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10075-10080.
[4] 谢立宏. 隔离型变换器共模传导干扰的建模与抑制方法研究[D]. 南京: 南京航空航天大学, 2018.
Xie Lihong. Research on modeling and suppression of common mode conducted interference in isolated converter[D]. Nanjing: Nanjing University of Aero- nautics and Astronautics, 2018.
[5] 孔鹏举. 开关电源共模EMI噪声抑制技术的研究[D]. 北京: 清华大学, 2009.
Kong Pengju. Common mode EMI noise reduction techniques in switch mode power supplies[D]. Beijing: Tsinghua University, 2009.
[6] 王议锋, 陈晨, 陈博, 等. 一种基于串联输入并联输出型LLC的噪声抑制磁集成方法[J]. 电工技术学报, 2022, 37(9): 2319-2328.
Wang Yifeng, Chen Chen, Chen Bo, et al. A magnetic integrated method for noise suppression based on input series output parallel LLC[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2319- 2328.
[7] 林苏斌, 陈为, 董纪清, 等. 开关电源变压器传导共模EMI磁电综合模型[J]. 中国电机工程学报, 2017, 37(8): 2436-2445.
Lin Subin, Chen Wei, Dong Jiqing, et al. Magneto- electric composite model of transformer for conducted common-mode EMI in switching-mode power supply[J]. Proceedings of the CSEE, 2017, 37(8): 2436-2445.
[8] Zhang Huan, Wang Shuo, Li Yiming, et al. Two- capacitor transformer winding capacitance models for common-mode EMI noise analysis in isolated DC-DC converters[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(11): 8458-8469.
[9] 徐策, 张方华, 董光冬. 考虑磁场频率特性的变压器共模EMI宽频建模方法[J]. 中国电机工程学报, 2022, 42(13): 4675-4686.
Xu Ce, Zhang Fanghua, Dong Guangdong. Wideband modeling method of transformer common-mode EMI considering frequency characteristics of magnetic field[J]. Proceedings of the CSEE, 2022, 42(13): 4675-4686.
[10] Salomez F, Videt A, Idir N. Modeling and mini- mization of the parasitic capacitances of single-layer toroidal inductors[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12426-12436.
[11] Himanshu, Singh H, Kumar P S, et al. High frequency transformer’s parasitic capacitance minimization for photovoltaic (PV) high-frequency link-based medium voltage (MV) inverter[J]. Electronics, 2018, 7(8): 142.
[12] 王一帆, 刘雪山, 奉榆杰. 浮动式Boost DC-DC变换器共模噪声分析[J/OL]. 电工技术学报, http:// doi.org/10.19595/j.cnki.1000-6753.tces.232092.
Wang Yifan, Liu Xueshan, Feng Yujie. Analysis of common mode noise in floating Boost DC-DC converters[J/OL]. Transactions of China Electro- technical Society, http:// doi.org/10.19595/j.cnki. 1000-6753.tces.232092.
[13] 彭金融, 毛行奎, 崔文玲, 等. 基于插入无源二端口网络的噪声源阻抗提取方法研究[J]. 电工技术学报, 2023, 38(2): 523-532.
Peng Jinrong, Mao Xingkui, Cui Wenling, et al. Research on noise soure impedance extraction method based on inserting passive two-port network[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 523-532.
[14] Yao Juntao, Wang Shuo, Zhao Hui. Measurement techniques of common mode currents, voltages, and impedances in a flyback converter for radiated EMI diagnosis[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(6): 1997-2005.
[15] 吴岳哲, 郑成君, 杜子凯, 等. 推挽变换器共模EMI噪声的预测与抑制[J/OL]. 电源学报, 1-12. 网络首发http://kns.cnki.net/kcms/detail/12.1420.tm. 20230619.1715.012.html.
Wu Yuezhe, Zheng Chengjun, Du Zikai, et al. Common-mode EMI noise prediction and suppression for push-pull converter[J/OL]. Journal of Power Supply, 2024, Early Access Online.
[16] 何杰, 刘钰山, 毕大强, 等. 开关变换器传导干扰抑制策略综述[J]. 电工技术学报, 2022, 37(6): 1455- 1472.
He Jie, Liu Yushan, Bi Daqiang, et al. Review of conducted electromagnetic interference suppression strategies for switching converters[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1455-1472.
[17] 李虹, 张冲默, 丁宇行, 等. 基于混沌脉宽调制的有源EMI滤波器高频抑制效果优化设计方法研究[J]. 中国电机工程学报, 2022, 42(13): 4642-4651.
Li Hong, Zhang Chongmo, Ding Yuhang, et al. Optimization of high frequency noise suppression effect of active EMI filter based on chaotic spread spectrum PWM method[J]. Proceedings of the CSEE, 2022, 42(13): 4642-4651.
[18] Li Yiming, Zhang Huan, Wang Shuo, et al. Investigating switching transformers for common mode EMI reduction to remove common mode EMI filters and Y-capacitors in flyback converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 2287-2301.
[19] Fei Chao, Yang Yuchen, Li Qiang, et al. Shielding technique for planar matrix transformers to suppress common-mode EMI noise and improve efficiency[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1263-1272.
Common-Mode Electromagnetic Interference Noise Modeling and Suppression for Low-Power Isolated Power Converter Using Toroidal Transformer
Hui Qi Ren Xiaoyong Chen Qianhong
(College of Automation Nanjing University of Aeronautics & Astronautics Nanjing 211106 China)
Abstract Featuring low isolation capacitance and ease of integration into PCBs or ICs, toroidal transformers have increasing applications in modern low-power isolated DC/DC converter designs. common-mode (CM) characteristics of toroidal transformers, the main propagation path of CM noises, have yet to beinvestigated. Also, corresponding suppression methods for toroidal transformers are required. A CM equivalent lumped capacitance model of a toroidal transformer is crucial for CM noise modeling and prediction in the early design stage of a power converter. This paper addresses the CM model for toroidal transformers in low-power isolated power converters and proposes several methods to mitigate CM noise.
Four commonly used winding structures (uniformly distributed single/double layer structure, split winding structure, and superimposed double-layer structure) are illustrated as a uniform CM equivalent lumped capacitance model. This model, characterized by its symmetry, relies solely on one parameter—the structure capacitance, which can be easily derived through simple measurement.
Considering leakage inductance, a novel two-step validation approach is introduced to verify the transformer modelutilized in traditional PWM and resonant converters. Moreover, the proposed transformer model can assess CM noise directly in the early stages of transformer design. The concept of equivalent noise sources outlines acomprehensive noise prediction procedure. As a result, an accurate prediction of CM noise for any isolated power converter using toroidal transformers is facilitated.
Additionally, suppression methods for toroidal transformer implementation are discussed. The conditions of converters with toroidal transformers naturally achieving zero CM noise areanalyzed, highlighting several topologies. CM suppression methods are proposed to reduce the CM noise current, including optimal turns ratio or improved terminal configuration, compensation capacitor, balancing winding, and shielding winding (using shielding copper or shielding-cancellation wire). A winding structure suitable for split winding structure application is proposed to eliminate CM noise cancellation and reduce isolation capacitance.
The proposed transformer model is verified on different toroidal transformers. Two prototypes are constructed: a conventional PWM converter (flyback with high-side rectification) and a resonant converter (series-resonant converter). The noise prediction results are consistent with the measurement. All discussed noise mitigation methods are experimentally verified on the prototypes, achieving significant CM noise suppression effects of over 8 dB mitigation in the low-to-mid frequency range, suggesting a possible CM filter size reduction.
Keywords:Toroidal transformer, common-mode electromagnetic interference (EMI) noise, isolated power converter
中图分类号:TM433
DOI: 10.19595/j.cnki.1000-6753.tces.231709
国家自然科学基金资助项目(52177181)。
收稿日期 2023-10-13
改稿日期 2024-01-19
作者简介
惠 琦 男,1993年生,博士研究生,研究方向开关变换器EMI建模与预测、宽禁带器件高频应用。
E-mail: hq@nuaa.edu.cn
任小永 男,1979年生,教授,博士生导师,研究方向为高频/超高频功率电子变换技术、宽禁带器件应用技术、储能与控制、无线充电技术以及高功率密度集成。
E-mail: renxy@nuaa.edu.cn(通信作者)
(编辑 郭丽军)
 (1)
(1)
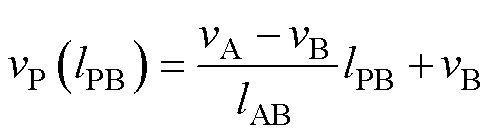 (2)
(2)
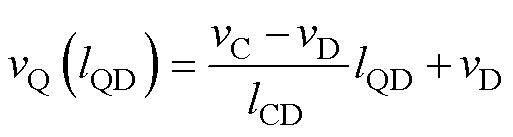 (3)
(3)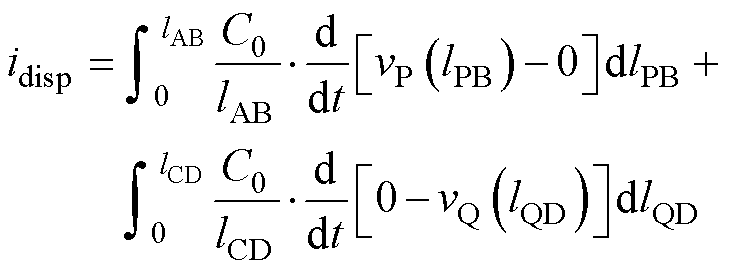 (4)
(4)
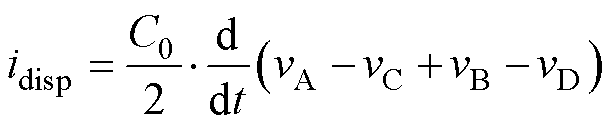 (5)
(5)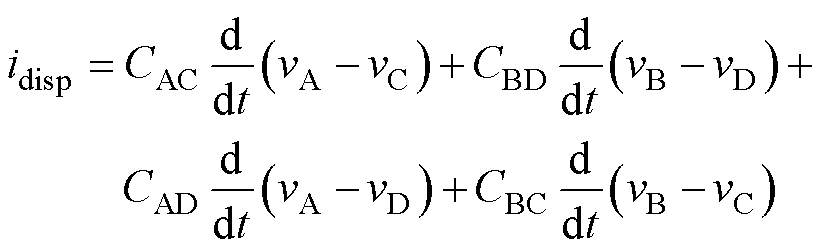 (6)
(6)
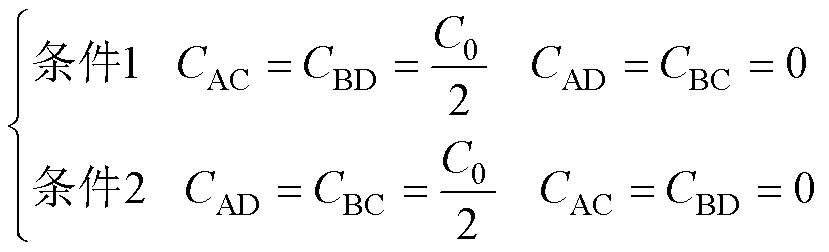 (7)
(7)
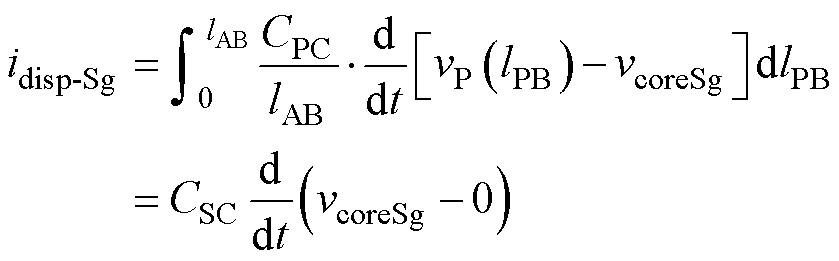 (8)
(8)
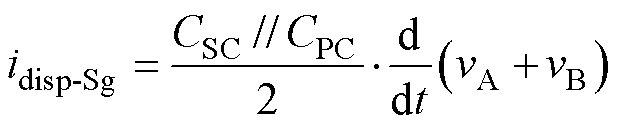 (9)
(9)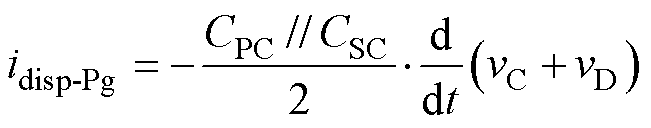 (10)
(10)
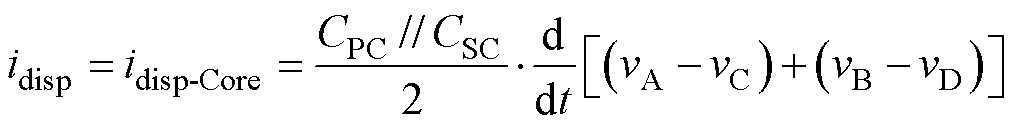 (11)
(11)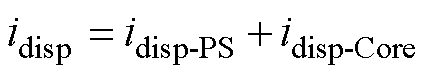 (12)
(12)
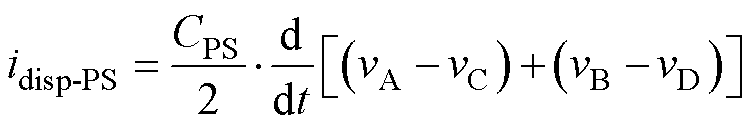 (13)
(13)
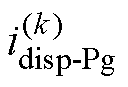 并进行加总,最终得到idisp-Pg为
并进行加总,最终得到idisp-Pg为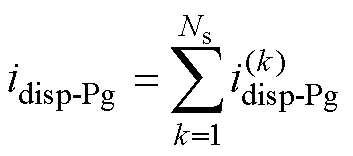 (14)
(14)
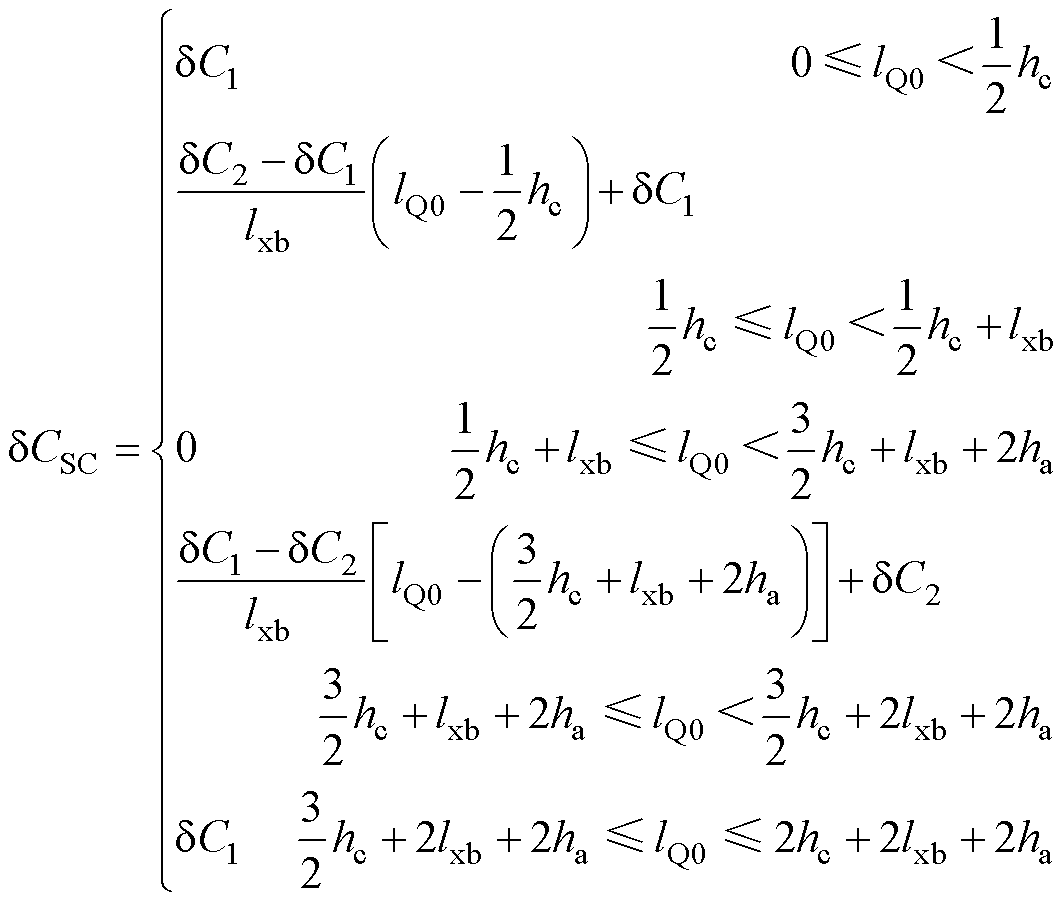 (15)
(15)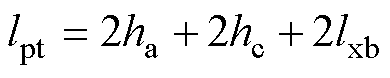 (16)
(16)
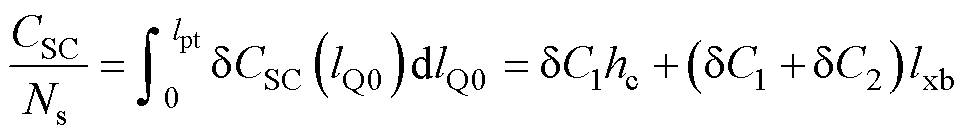 (17)
(17)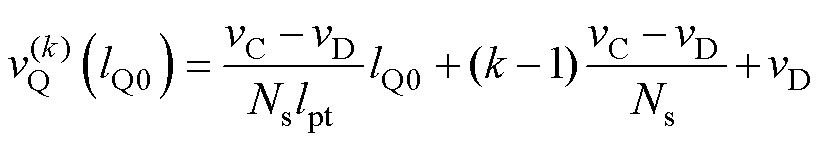 (18)
(18)
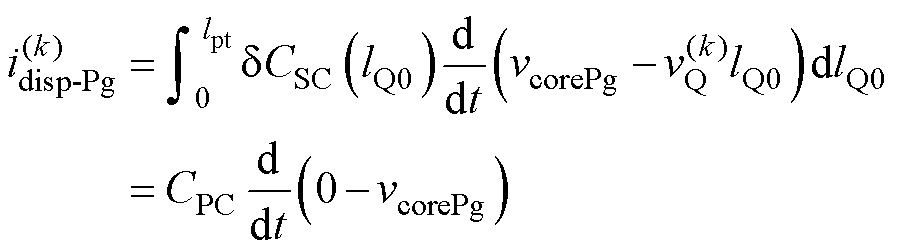 (19)
(19)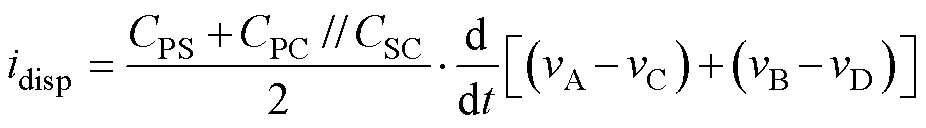 (20)
(20)
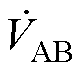 (如150 kHz)并测量端口D-B上的电压
(如150 kHz)并测量端口D-B上的电压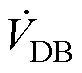 。然后在端口B-A上施加幅值、频率均与此前所加
。然后在端口B-A上施加幅值、频率均与此前所加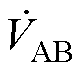 幅值、频率均一致的激励
幅值、频率均一致的激励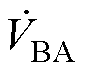 ,并测量在端口C-A上得到的电压
,并测量在端口C-A上得到的电压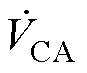 。根据电路理论,这两步测量的电压增益由式(21)给出,其中Lp为一次侧自感,Ls为二次侧自感,M为两绕组的互感,而Cprobe则表示电压探头的寄生电容,即
。根据电路理论,这两步测量的电压增益由式(21)给出,其中Lp为一次侧自感,Ls为二次侧自感,M为两绕组的互感,而Cprobe则表示电压探头的寄生电容,即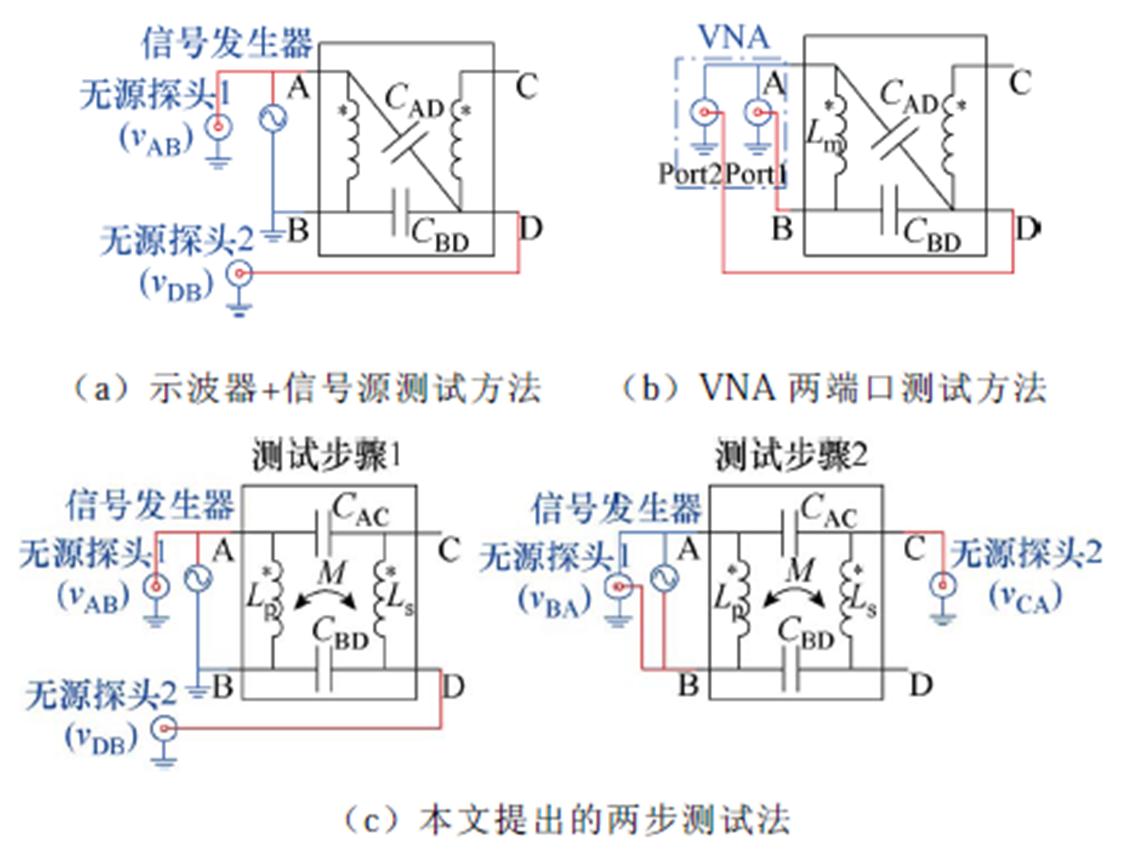
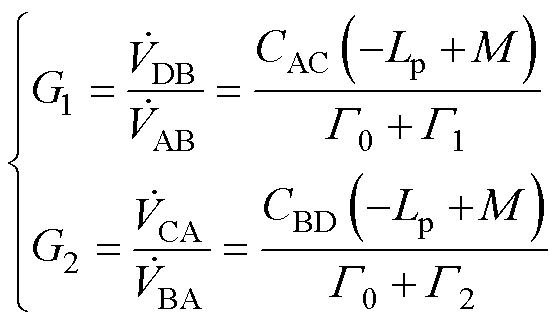 (21)
(21)
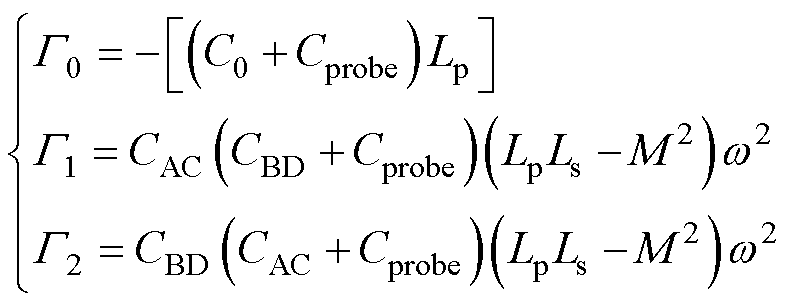 (22)
(22)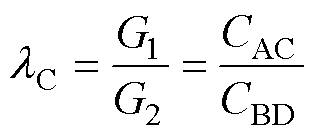 (23)
(23)
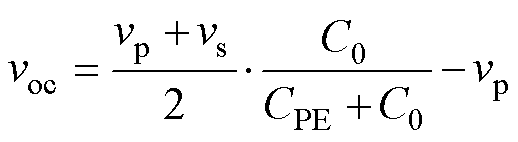 (24)
(24)

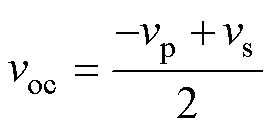 (25)
(25)
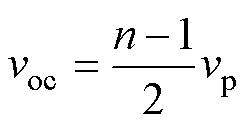 (26)
(26)
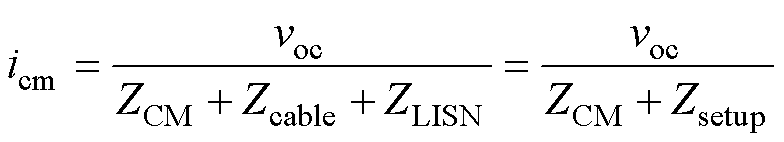 (27)
(27)
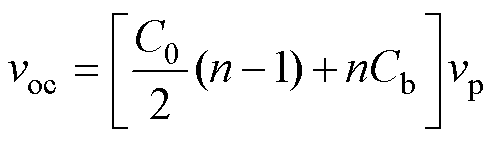 (28)
(28)
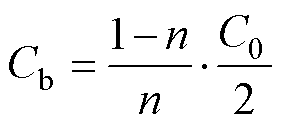 (29)
(29)
 6,三明治绕法,实测其一次侧自感L
6,三明治绕法,实测其一次侧自感L