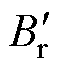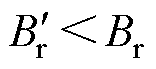（
），从而表现出一定程度的退磁故障，此时永磁体的退磁率DEMrate为摘要 针对电驱动系统用高功率密度永磁驱动电机存在的不可逆退磁问题，以一款8极48槽的双V型永磁同步电机为例对退磁故障的动态识别方法进行了研究。在考虑电机闭合磁路对永磁体退磁故障影响的基础上，通过分析高退磁率电机模型退磁前后的空载和负载参数变化，采用Pearson相关性分析的方法提取了表征退磁故障的特征参量，给出了一种退磁故障的动态识别方法，并分析了转速和电流对特征参量的影响，完成了对退磁故障动态识别方法的修正。通过仿真和实验测试的方法对退磁故障动态识别方法的准确性进行了验证，结果表明，仿真结果的误差为0.68%，实验测试的预测结果最大误差为1.765%，误差均在可接受范围内。
关键词：驱动电机 双V型永磁同步电机 退磁故障 Pearson相关性
在新能源汽车行业，永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因具有高效率、高功率密度[1-2]、低噪声、低转矩脉动等优势，已成为了高性能驱动电机的主流方案之一。随着电动汽车逐渐朝着零部件高度集成化、电压等级高压化、电驱系统多电机化[3-5]的方向发展，永磁同步电机转子永磁体在高温、大电流工况下的退磁问题日益凸 显[6-8]，一旦永磁体发生退磁故障，将会直接导致电机输出转矩质量下降，进而致使电枢电流和电机温度升高，使退磁故障进一步扩散，最终影响整个电驱系统的精准控制和可靠运行。
针对永磁同步电机退磁问题，部分学者从转子结构设计的角度对永磁同步电机进行防退磁设计，分析了磁极拓扑结构[9]、永磁体形状[10]、磁障层 数[11-13]、隔磁桥结构[14]等因素对转子抗退磁性能的影响，为强抗退磁转子结构的设计提供了思路，但该方法仅能开环式防止永磁同步电机退磁故障的发生，无法避免退磁故障的进一步扩散，因此还需要对退磁故障进行在线监测。文献[15-17]采用在电机定子槽内安装探测线圈的侵入式检测方案，通过对探测线圈中的测量信号进行处理，提取退磁故障的特征参量，从而实现对转子永磁体退磁故障的实时检测，众多研究表明，侵入式检测结果的准确度较高，并且该方法可以实现对转子永磁体退磁故障位置的定位，然而由于其需要对电机定子绕组进行特殊设计，因此制造成本较高。文献[18-19]建立了内置式永磁同步电机的等效磁网络模型，对电机的电磁性能以及永磁体的工作点进行计算，在计算速度和精度上均获得了较好的效果，但因磁网络是采用集总参数的原则进行构建，因此该方法难以考虑永磁体的局部退磁故障。文献[20-22]采用小波变换、希尔伯特黄变换等信号处理技术，从电机定子电流信号中提取退磁故障特征参量，实现了永磁体退磁故障的在线诊断。文献[23-26]假设转子永磁体的退磁区域具有几何对称的特点，对永磁同步电机进行了退磁分析，获得了对应的退磁故障诊断方法，但由于所假设的永磁体退磁特点与实际情况有偏差[27]，因此其得到的退磁故障诊断方法的准确性还有待验证。
随着永磁驱动电机不断朝着高功率密度的方向发展，多块永磁体组合成的转子磁极被广泛使用，而空间分布的永磁体因布置位置的不同，其磁极退磁也具有空间特殊性。基于上述存在的问题，本文以一款8极48槽的双V型永磁同步电机为研究对象。为了更好地模拟电机内永磁体的退磁情况，考虑了电机闭合磁路对转子永磁体退磁的影响，首先构建了高退磁率的电机模型，采用Pearson相关性分析的方法，分析了退磁故障对电机空载和负载工况下电机参数的影响，提取退磁故障的特征参量，获得了双V型永磁同步电机退磁故障的动态识别方法。其次为了提高退磁故障动态识别方法的普遍性，分析了电机转速和电枢电流对退磁故障特征参量的影响，对退磁故障动态识别方法进行修正。最后通过仿真和实验对退磁故障动态识别方法的准确性和可行性进行验证。
由于钕铁硼永磁材料具有较高的剩磁Br、矫顽力Hc和磁能积，目前已被广泛应用于高性能的永磁同步电机中。然而，钕铁硼永磁体的磁性能易受电机内工作温度和反向退磁磁场的影响，如图1所示为钕铁硼永磁体的B-H曲线，图中，K为曲线的膝点，一旦永磁体工作在K点以下，永磁体将会沿着新的回复线L进行工作，永磁体的剩磁为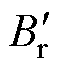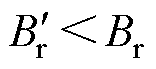（），从而表现出一定程度的退磁故障，此时永磁体的退磁率DEMrate为
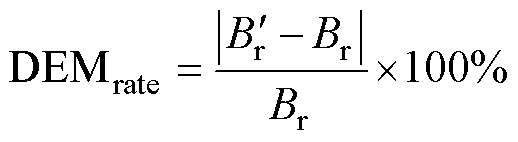（1）
式中，Br和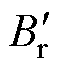分别为永磁体退磁前、后的剩磁值。
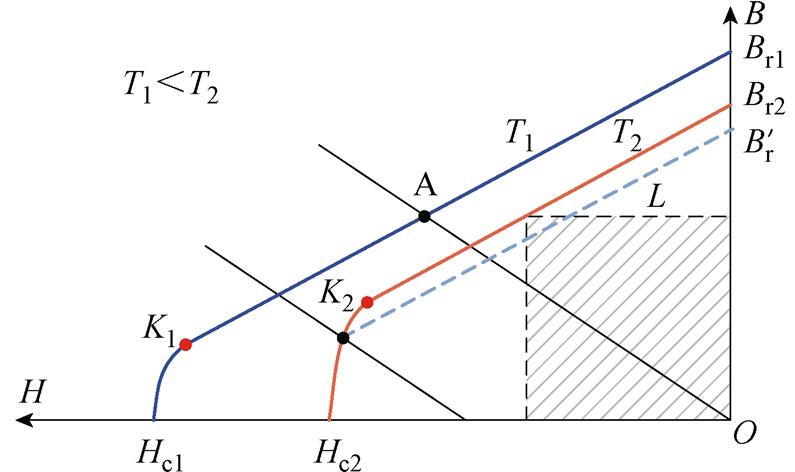
图1 钕铁硼永磁体的B-H曲线
Fig.1 The B-H curves of NdFeB permanent magnet
在电机的实际运行过程中，当永磁体的工作温度（T1＜T2）升高时，其剩磁和矫顽力都将降低，即B-H曲线向原点方向移动，如图1所示，永磁体的实际工作点A更加靠近膝点K2，因此永磁体的退磁风险升高；此外，当电机电枢电流增加导致反向退磁磁场增强时，永磁体的实际工作点A将向K1点移动，同样会增加永磁体发生退磁故障的风险。
永磁同步电机发生退磁故障后，将直接导致永磁体对外提供的磁动势变小，由磁路的欧姆定律式（2）可知，在其他磁路条件不变的情况下，转子永磁体提供的磁通将减小。
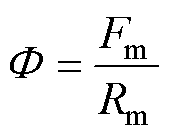（2）
式中，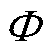
为磁路中的磁通；Rm为磁路的磁阻；Fm为磁路的磁动势。
在空载工况下，根据绕组感应电动势E的产生原理式（3）可知，退磁故障会导致电机在相同转速下的空载反电动势降低。若将空载反电动势的损失率DE作为判断转子退磁故障的参考，可以由式（4）发现，该损失率DE不随空载转速n的变化而变化，而仅与转子永磁体提供的磁通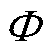有关，因此，常采用空载工况下反电动势的损失率来作为退磁故障的离线检测手段。
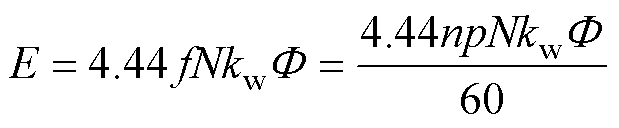（3）
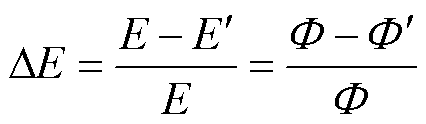（4）
式中，f为频率；N绕组匝数；kw为绕组因数；p为电机转子的极对数；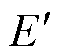
和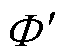
分别为电机退磁后的感应电动势和磁通。
在负载工况下，电机的输出转矩是评估电机负载性能的重要参数，根据永磁同步电机的转矩方程式（5）可知，电机的输出转矩T与永磁磁链yf、电枢电流I、dq轴电感等参数均有关，因此在退磁故障的识别方法研究中，分析退磁故障与各个电机参量之间的关系至关重要。
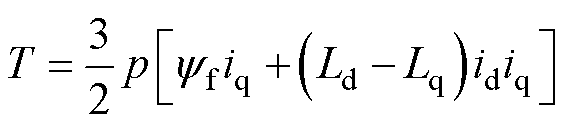（5）
式中，id和iq分别为电枢电流的直轴分量和交轴分量；Ld和Lq分别为直轴电感和交轴电感。
两变量间的关系包括确定性关系和非确定性关系两种，其中，确定性关系是指具有确定的函数关系，而非确定性关系是指宏观上存在相关关系。非确定性相关关系又可分为线性相关和非线性相关，Pearson相关性分析是分析两变量之间线性相关程度的一种方法，具体的计算方法为
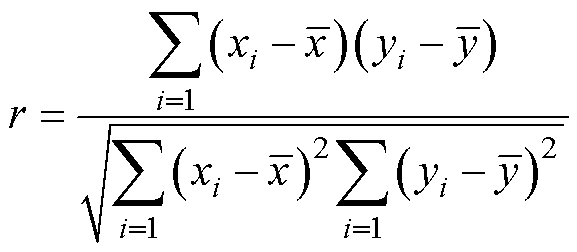（6）
式中，xi和yi分别为待分析的两个变量样本；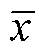
和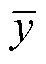
为变量样本的平均值；r为相关系数，取值范围为[-1, 1]，-1表示两变量之间存在显著的负相关关系，+1表示两变量之间存在显著的正相关关系，0表示两变量之间没有线性相关性。
本文以一款8极48槽的双V型组合磁极永磁同步电机为研究对象，结构如图2所示，具体的电磁参数见表1。同时，对模型做如下假设：
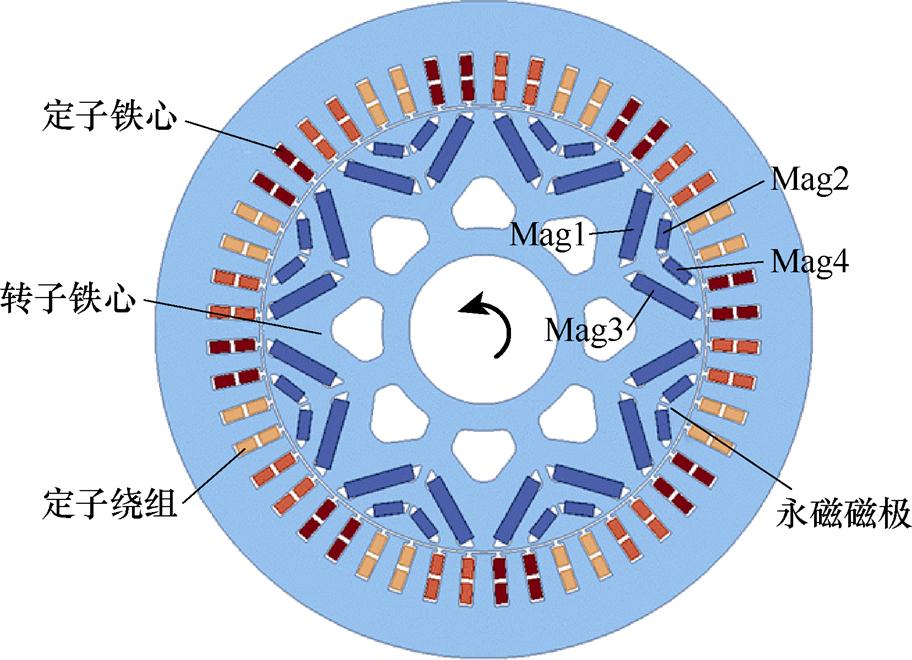
图2 双V型组合磁极永磁同步电机结构
Fig.2 The structure of double V-shaped PMSM
表1 双V型组合磁极永磁同步电机的电磁参数
Tab.1 Electromagnetic parameters of double V-shaped PMSM
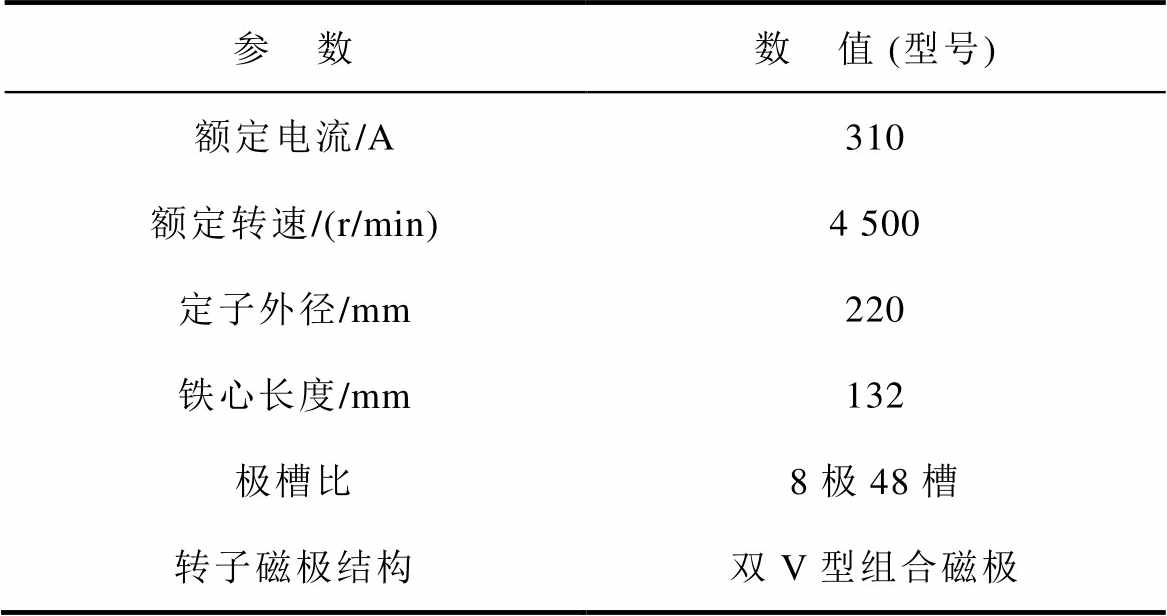
参 数数 值 (型号) 额定电流/A310 额定转速/(r/min)4 500 定子外径/mm220 铁心长度/mm132 极槽比8极48槽 转子磁极结构双V型组合磁极
（1）假设电机的散热性良好，电机轴向的温度具有一致性。
（2）假设电机转子散热充分，且因转子硅钢片的导热系数高，可认为双V型组合磁极各个永磁体的工作温度具有一致性。
（3）由于永磁体的电导率（6.6×105 S/m）和铜导线的电导率（5.7×107 S/m）相差较大，因此，可忽略永磁体的涡流效应。
结合上述的模型假设，为了合理利用计算资源，本文采用1/8电机的二维模型进行计算，图3为1/8电机二维模型对应的网格剖分结果。由于重点关注永磁体的退磁情况，因此，对永磁体区域进行了网格加密，并规定逆时针方向为电机旋转的正方向。图4为永磁体磁性能随温度变化的B-H曲线，本文为了得到较高的退磁率，使用200℃下永磁体的B-H曲线进行分析。
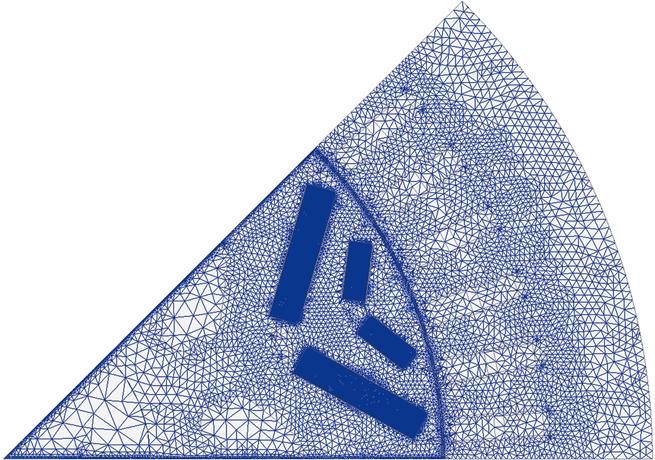
图3 1/8双V型组合磁极永磁同步电机的网格剖分
Fig.3 The meshing of 1/8 2D double V-shaped PMSM
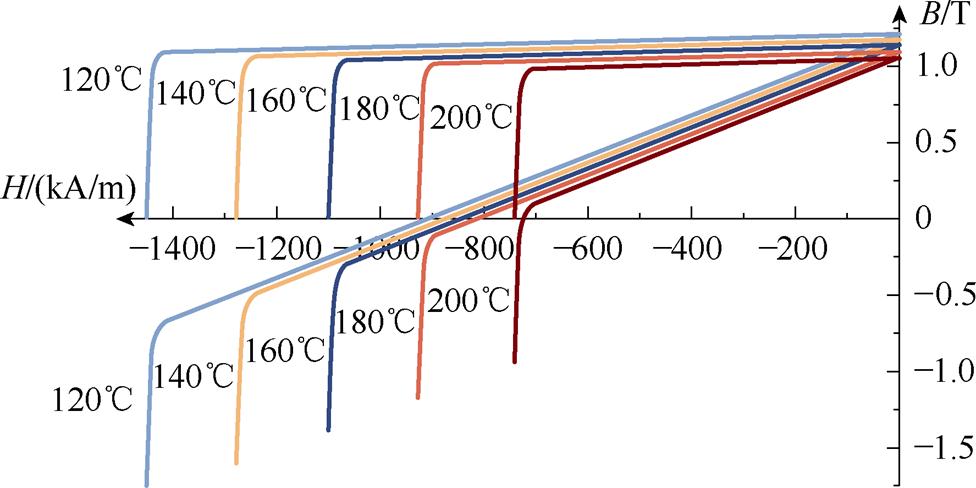
图4 烧结型钕铁硼永磁体的B-H曲线
Fig.4 The B-H curves of sintered NdFeB permanent magnet
为了充分考虑电机内闭合磁路对永磁体退磁的影响，本文通过在电机电枢绕组内施加电流激励，使转子永磁体在电机运行过程中发生退磁故障，最后基于退磁后的电机模型完成对电机空载和负载参数的分析计算。
表2中记录了在内功率因数角分别为70°和90°、电枢电流分别为1 100、1 300、1 500、1 750和2 000 A的工况下，双V型组合磁极各个永磁体的退磁率。图5为两种内功率因数角下，永磁体退磁率随电枢电流的变化。可以看出，当内功率因数角为90°时，双V型组合磁极永磁体的退磁具有明显的对称性，而内功率因数角为70°时，四个永磁体的退磁状态表现出了不对称性，因此通过对两种内功率因数角下电机退磁前后的参数变化进行分析，可以得到更具普适性的退磁故障识别方法。
表2 高退磁率电机模型中各个永磁体的退磁率
Tab.2 The demagnetization rate of PMs in the high demagnetization models
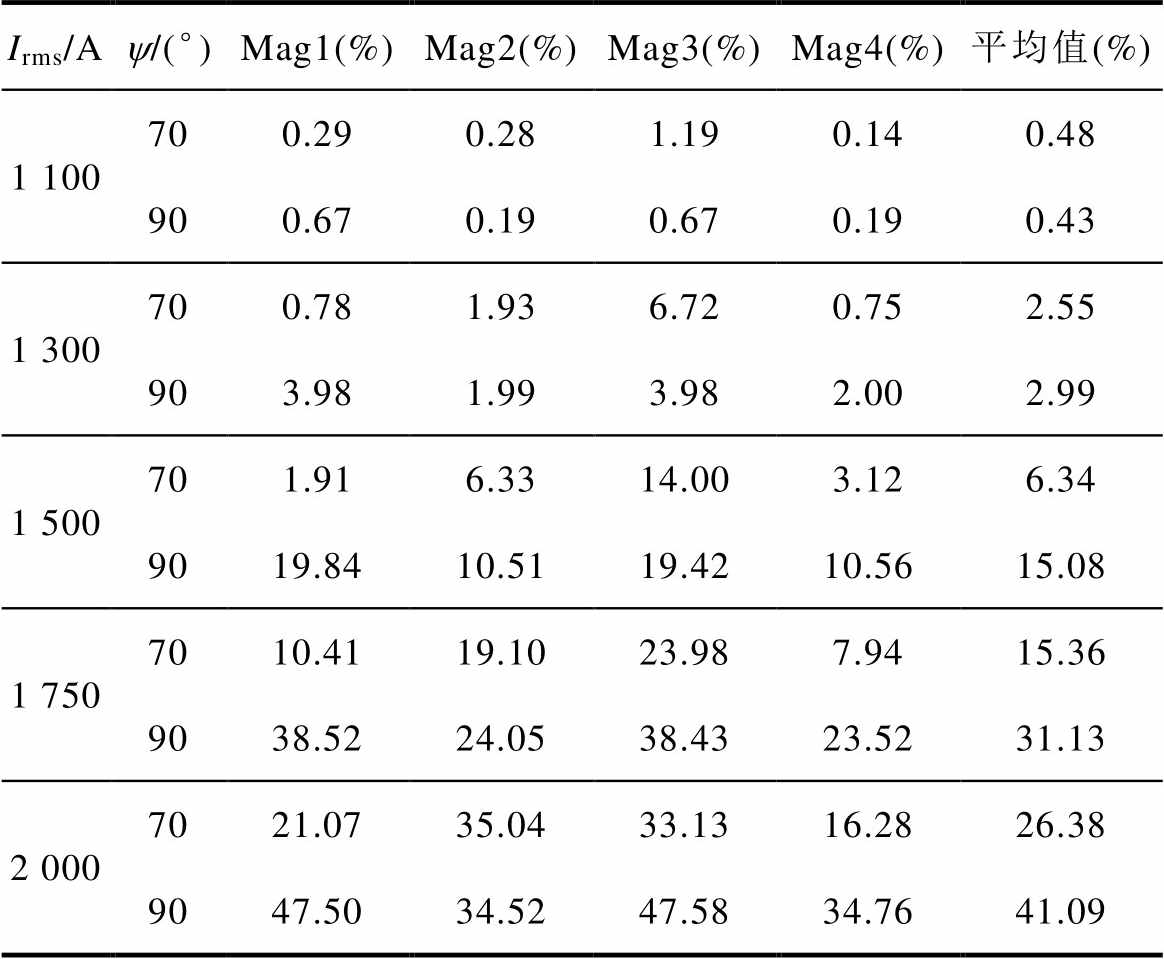
Irms/Ay/(°)Mag1(%)Mag2(%)Mag3(%)Mag4(%)平均值(%) 1 100700.290.281.190.140.48 900.670.190.670.190.43 1 300700.781.936.720.752.55 903.981.993.982.002.99 1 500701.916.3314.003.126.34 9019.8410.5119.4210.5615.08 1 7507010.4119.1023.987.9415.36 9038.5224.0538.4323.5231.13 2 0007021.0735.0433.1316.2826.38 9047.5034.5247.5834.7641.09
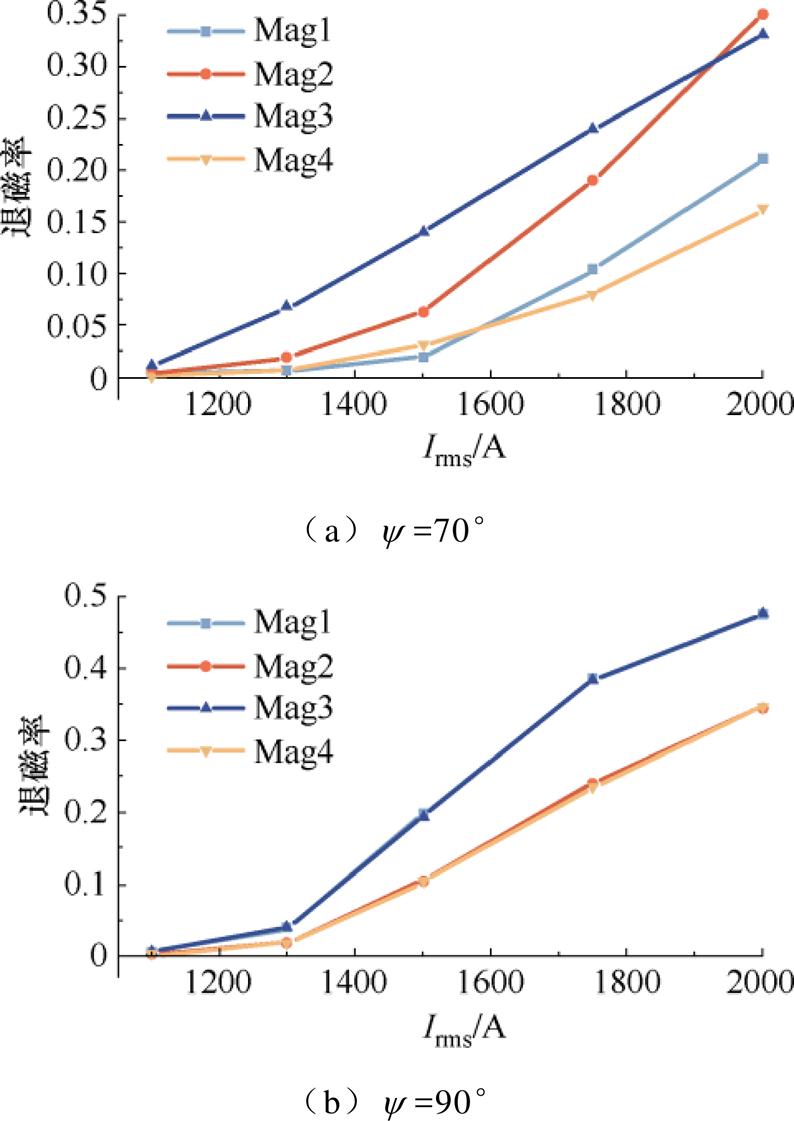
图5 永磁体退磁率随电枢电流的变化
Fig.5 The change of demagnetization rate with armature current
图6为不同工况下永磁体的退磁分布云图，其中红色区域代表永磁体该位置处已发生了退磁，通过对比不同内功率因数角下永磁体退磁区域的分布情况，与上述分析结果相符。为了方便后续对各个高退磁率电机模型进行分析，根据模型所施加电枢电流的不同，将各个电流激励下的高退磁率模型分别记为“M1100、M1300、M1500、M1750、M2000”。
图6 永磁体退磁分布随电枢电流的变化
Fig.6 The demagnetization distribution of PM changes with armature current
3.1.1 空载分析
在电机空载转速为4 500 r/min的工况下，对2.2节中建立的高退磁率电机模型进行空载参数分析，以获得表征退磁故障的空载特征参量。具体参数包括空载反电动势Up0、齿槽转矩T0、齿槽转矩波动T0_ripple、空载气隙磁通密度B0、空载直轴电感Ld0和空载交轴电感Lq0。
图7为空载反电动势随退磁率程度的变化情况。可以明显看出，在不同内功率因数角下，空载反电动势与转子永磁体的退磁率均具有很强的相关性。同时，由式（3）、式（4）的理论分析可知，空载反电动势的损失率与转子永磁体退磁率成绝对的正比关系，因此本文将空载反电动势的损失率作为转子永磁体的标准退磁率，后续将以此为基础进行退磁故障特征参数的进一步分析。
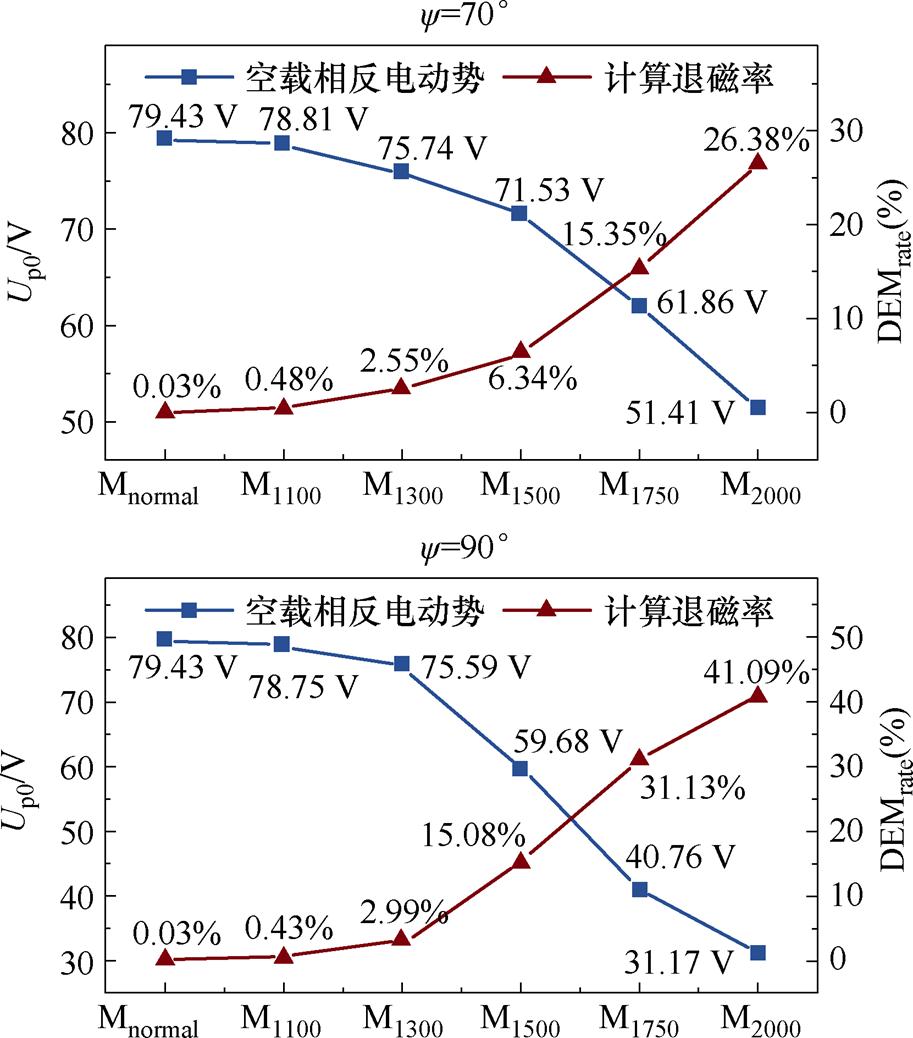
图7 空载相反电动势随退磁率的变化
Fig.7 Change of no-load phase electromotive force with demagnetization rate of PM
表3为2.2节中各个高退磁率模型在转速为4 500 r/min工况下，空载反电动势以及标准退磁率（空载反电动势的损失率）的计算结果。
表3 高退磁率电机模型的标准退磁率
Tab.3 Standard demagnetization rate for high demagnetization motor models
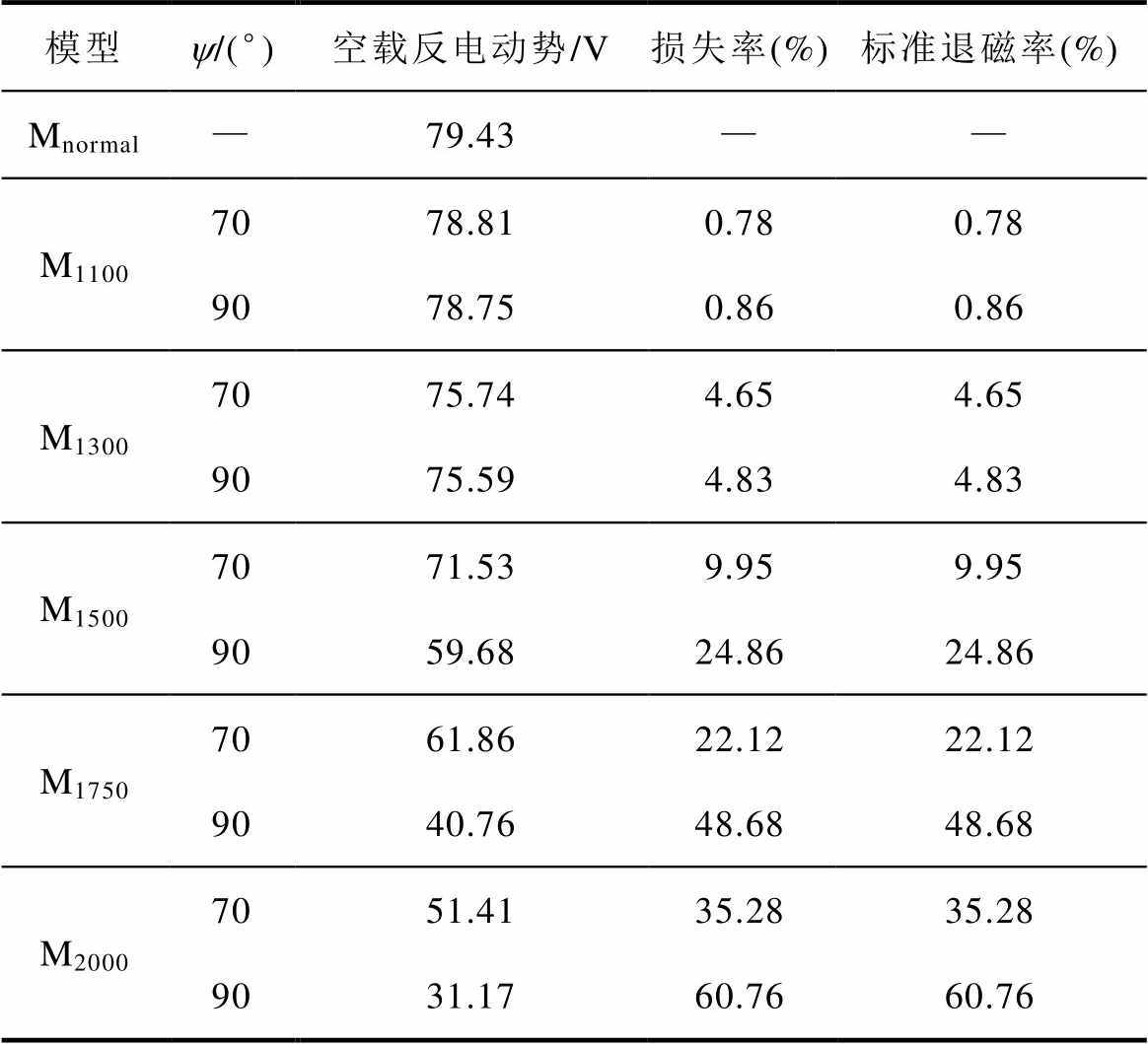
模型y/(°)空载反电动势/V损失率(%)标准退磁率(%) Mnormal—79.43—— M11007078.810.780.78 9078.750.860.86 M13007075.744.654.65 9075.594.834.83 M15007071.539.959.95 9059.6824.8624.86 M17507061.8622.1222.12 9040.7648.6848.68 M20007051.4135.2835.28 9031.1760.7660.76
图8为高退磁率电机模型的齿槽转矩T0、齿槽转矩波动T0_ripple、空载气隙磁通密度Bn0、空载直轴电感Ld0和空载交轴电感Lq0分别与电机退磁率的变化关系。可以看出，当电机发生退磁后，电机空载工况下各个参数的变化均与电机退磁率具有很强的相关性。
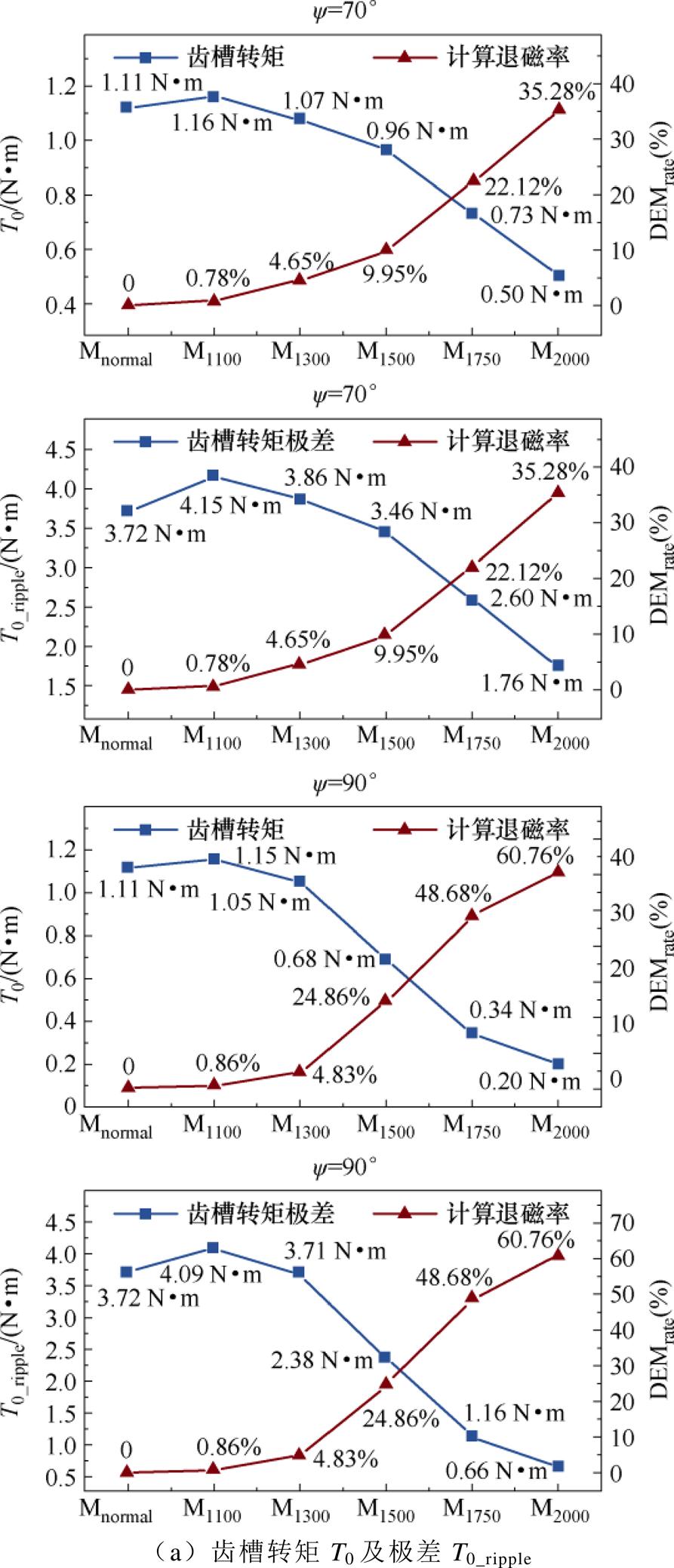
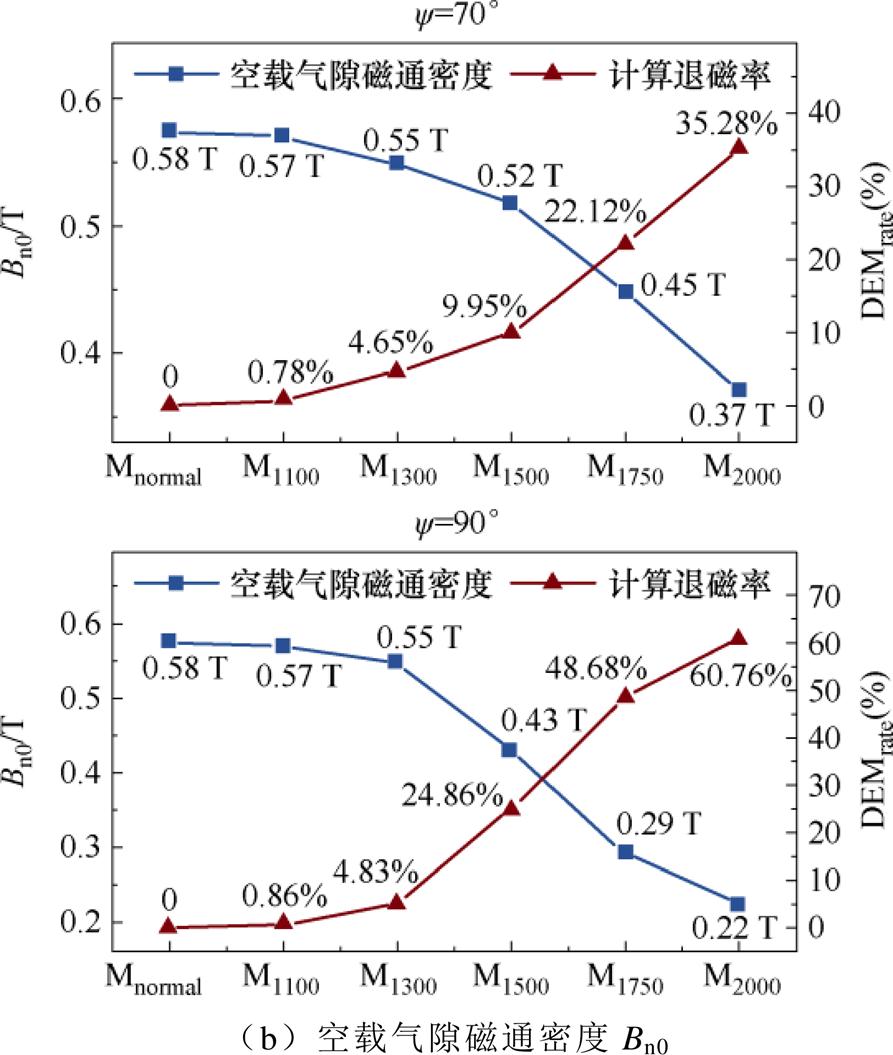
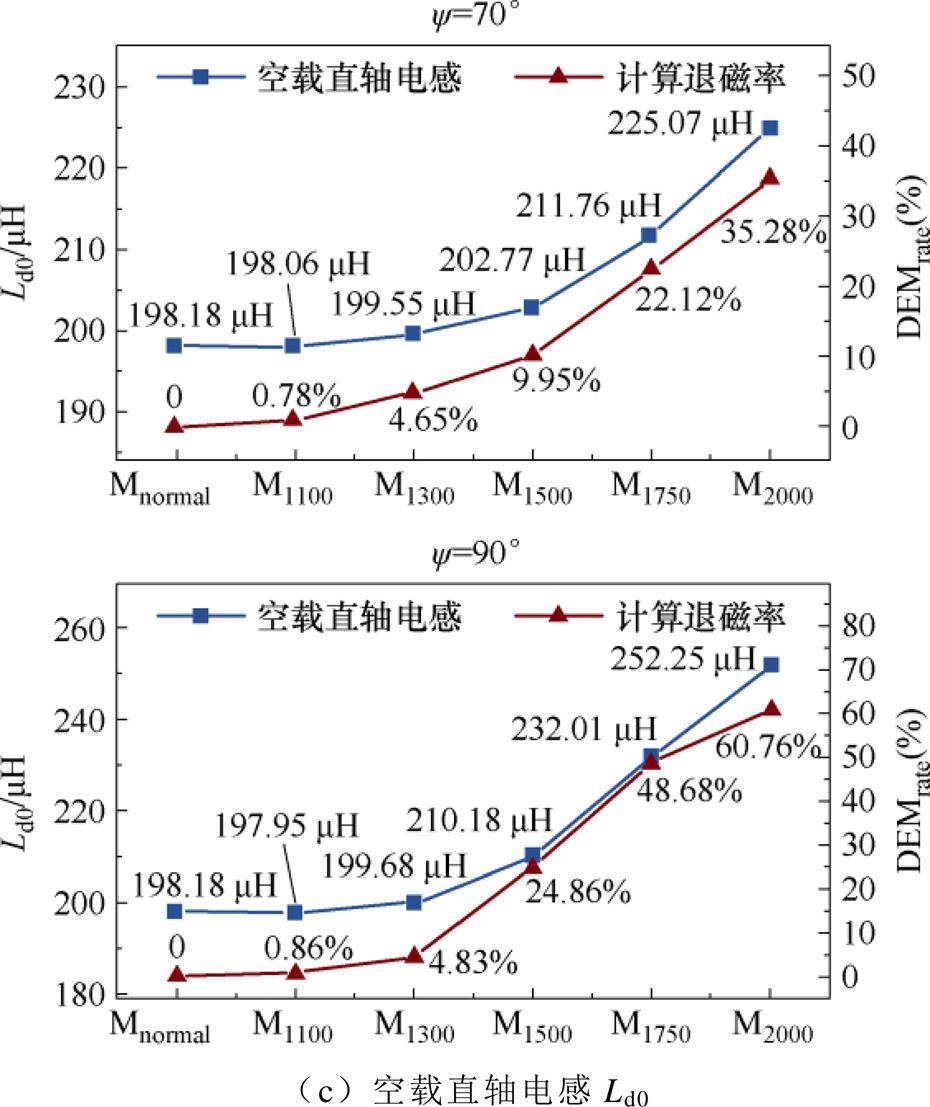
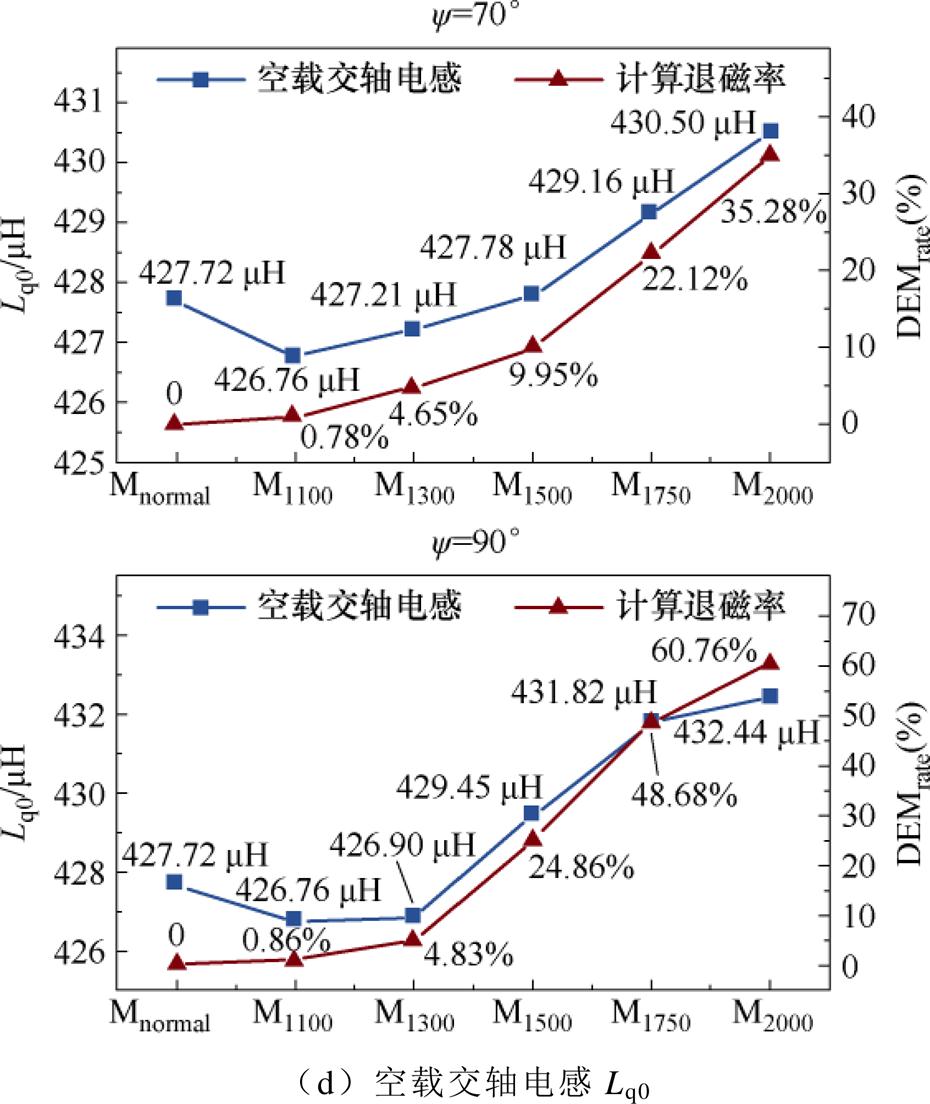
图8 空载参数随退磁率的变化
Fig.8 The change of no-load parameters with demagnetization rate of PM
为了准确描述空载工况下各个参量与电机退磁率的相关性强弱，使用式（6）对空载工况下各个参量与标准退磁率之间的Pearson相关系数进行了计算，并绘制了对应的雷达图，如图9所示。可以直观地看出，空载工况下各个参量与电机标准退磁率之间均具有显著相关性，因此，均可作为电机空载工况下退磁故障的特征参量。
3.1.2 负载分析
为了获得负载工况下表征电机退磁故障的特征参数，本节计算并分析了电机额定工况（Irms=310 A，y =36°，n=4 500 r/min）下的负载参数。
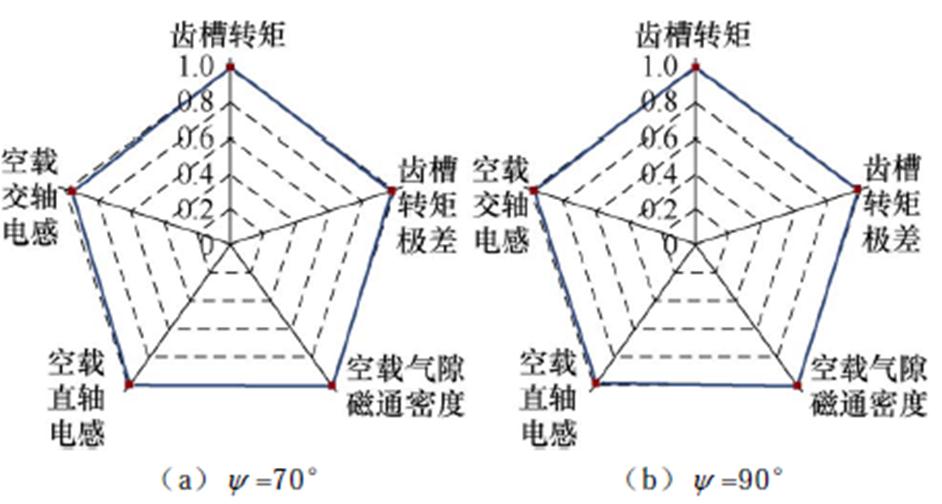
图9 空载参数与退磁率相关系数的雷达图
Fig.9 Radar chart of correlation coefficient between no-load parameters and demagnetization rate
图10为电机的输出转矩T、负载气隙磁通密度Bn、负载相电压Up、负载直轴电感Ld以及负载交轴电感Lq随电机退磁率的变化情况。
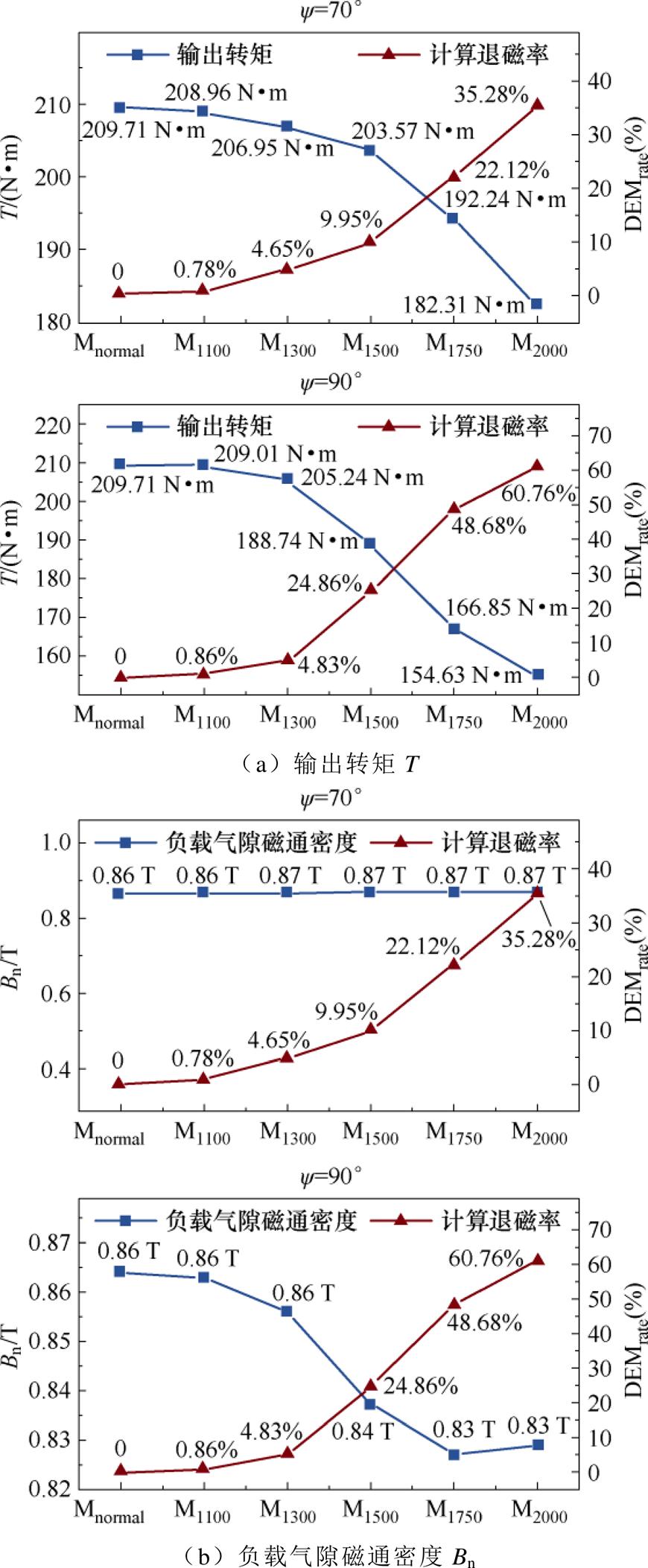
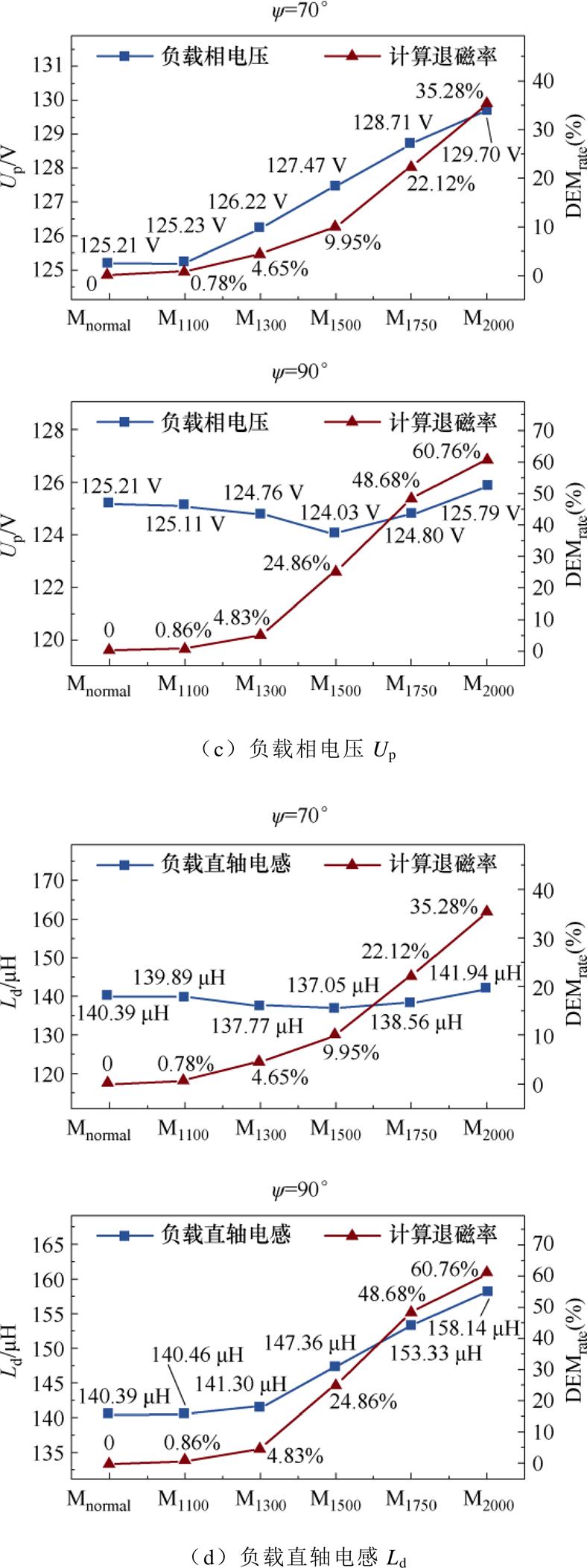
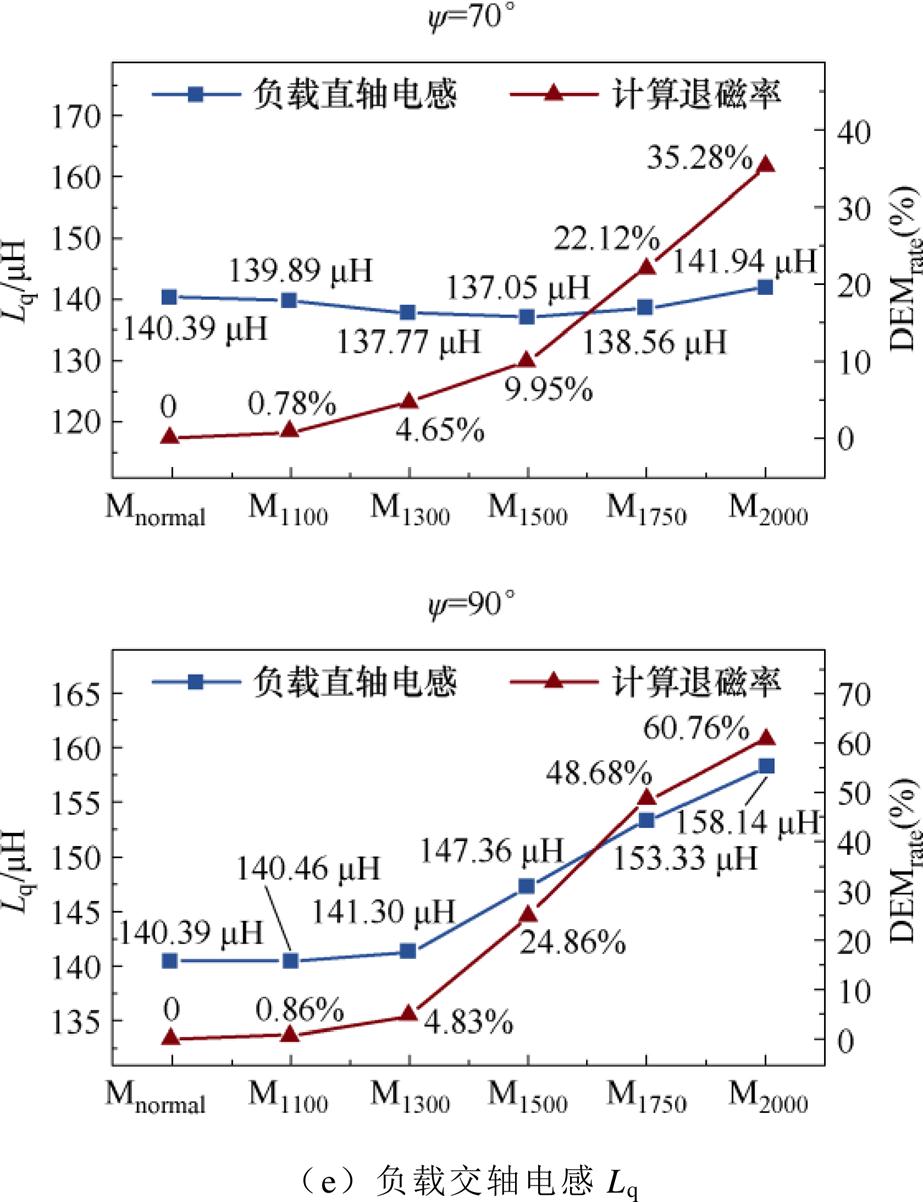
图10 负载参数随退磁率的变化
Fig.10 The change of load parameters with demagnetization rate of PM
从图10中可以看出，除了输出转矩T和负载交轴电感平均值Lq的变化与电机退磁率的相关性较显著外，负载气隙磁通密度Bn、负载相电压的有效值Up和负载直轴电感的平均值Ld与电机退磁率的相关性均不明显，且受内功率因数角的影响较大。
当电机在内功率因数角为70°时发生退磁后，额定工况下电机负载气隙磁通密度Bn和直轴电感Ld的变化与退磁率的相关性较低，而负载电压有效值Up的变化与退磁率的相关性较高。然而，当电机在内功率因数角为90°时发生退磁后，额定工况下电机负载气隙磁通密度Bn和直轴电感Ld的变化与退磁率的相关性较高，而负载电压有效值Up的变化与退磁率的相关性却较低。
为了进一步直观地反映负载工况下各个参量与电机退磁率的相关性，采用式（6）对各个参量与电机退磁率的相关性系数进行计算，并绘制了对应的雷达图，如图11所示。可以看出，当内功率因数角变化时，电机的输出转矩T和交轴电感Lq与电机退磁率的相关性始终较高，即对内功率因数角的敏感度低，而其他参数与电机退磁率的相关性受内功率因数角的影响较大。
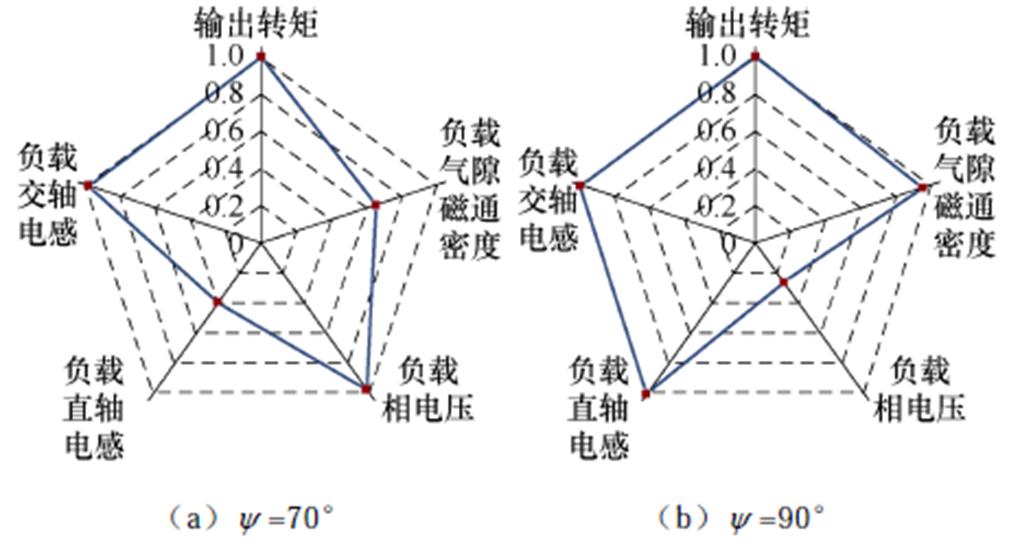
图11 负载参数与退磁率相关系数的雷达图
Fig.11 Radar chart of correlation coefficient between load parameters and demagnetization rate
因此，本文将电机的输出转矩T和负载交轴电感的平均值Lq作为电机负载时退磁故障的两个特征参量，并参与退磁故障动态识别方法的建立。
3.2.1 退磁故障的识别方法
由3.1.2节可知，负载工况下，电机的输出转矩T和交轴电感Lq具有显著相关性，且不受因内功率因数角的不同而导致的永磁体退磁不对称的影响。因此，本节在Pearson相关性分析的基础上，通过数据拟合的方法完成两个特征参量变化率与电机标准退磁率之间的数据映射，如图12所示。图中，R2可以表示曲线拟合的精度，该值越接近1，曲线拟合的精度越高，对应的拟合曲线方程demTN和demLqN分别为
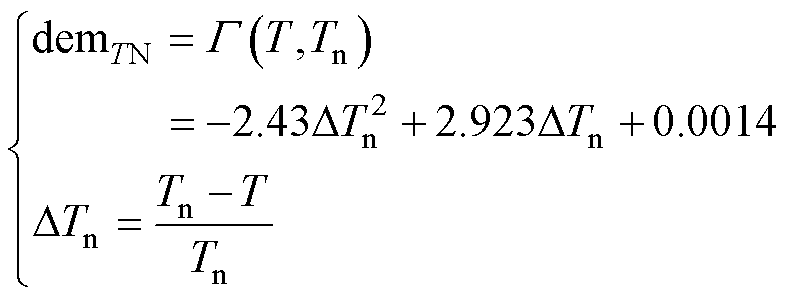（7）
（8）
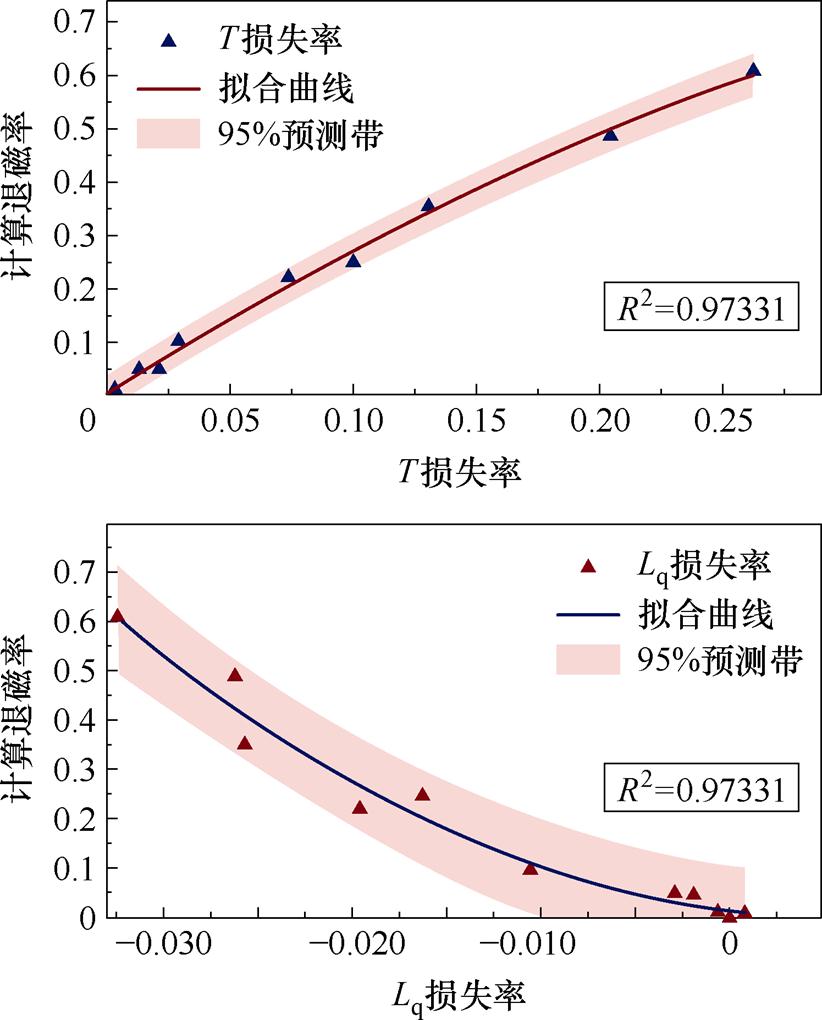
图12 负载特征参量的拟合曲线
Fig.12 Fitting curves of load characteristic parameters
式中，Tn和Lqn分别为电机额定工况未退磁时的输出转矩和交轴电感；T和Lq分别为电机退磁后运行时的输出转矩和交轴电感；DTn和DLqn分别为电机退磁后额定运行时的转矩损失率和交轴电感损失率。
为了实现退磁故障多参量的综合预测，引入特征参量的相关系数r作为各个映射参量值的权重，从而获得额定工况下退磁故障的识别方法，其计算方法为
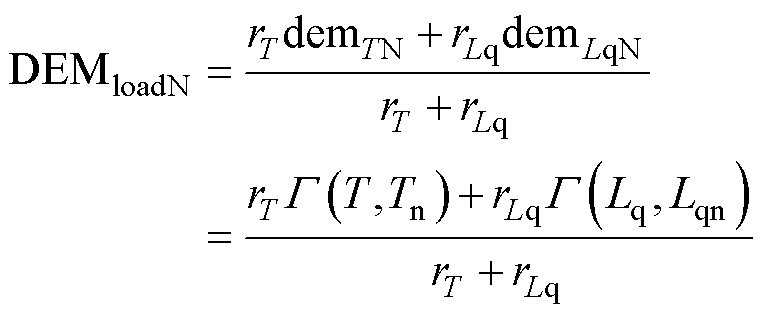（9）
式中，rT和rLq分别为电机额定工况下转矩参量和交轴电感参量与电机退磁故障的相关系数，rT= 0.998 29，rLq=0.989 475。
使用式（9）计算各个高退磁电机模型的退磁率，如图13所示，可以明显看出，预测结果与标准退磁率具有很高的吻合度，且退磁率的最大预测误差仅为2.5%。
图13 额定工况下退磁故障识别方法的精度对比
Fig.13 Accuracy comparison of demagnetization fault prediction method under rated conditions
3.2.2 退磁故障的动态识别方法
在电机的实际运行过程中，转速和电流是时刻变化的，不能完全保持电机在额定工况（Irms=310 A，y =36°，n=4 500 r/min）下运行，3.2.1节中额定工况下的退磁故障识别方法将不再具有普遍性。因此，将退磁故障的识别方法扩展至电机的各个运行工况是非常必要的。
由式（4）可知，空载转速对空载反电动势的损失率没有影响。然而，电枢电流与电机输出转矩和交直电感参数的变化密切相关。因此，本节在额定工况下退磁故障识别方法的基础上，引入电流变量Irms，有
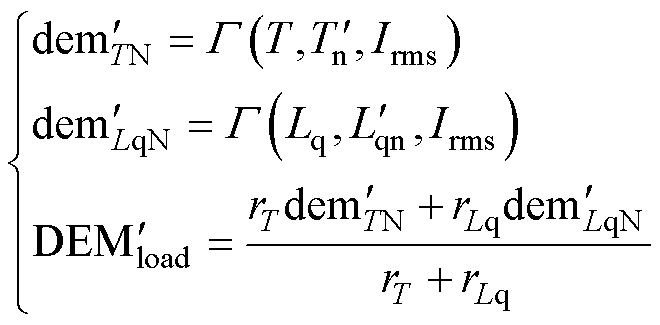（10）
式中，
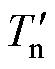和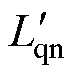
分别为考虑电枢电流后电机额定工况未退磁时的输出转矩和交轴电感。
为了分析电枢电流对输出转矩损失率和交轴电感损失率的影响，在电枢电流分别为110、210、310和410 A的工况下，对高退磁率电机模型的负载参数进行了计算，并据此建立了Irms、T、Lq三个参数分别与额定工况下对应损失率的映射关系，有
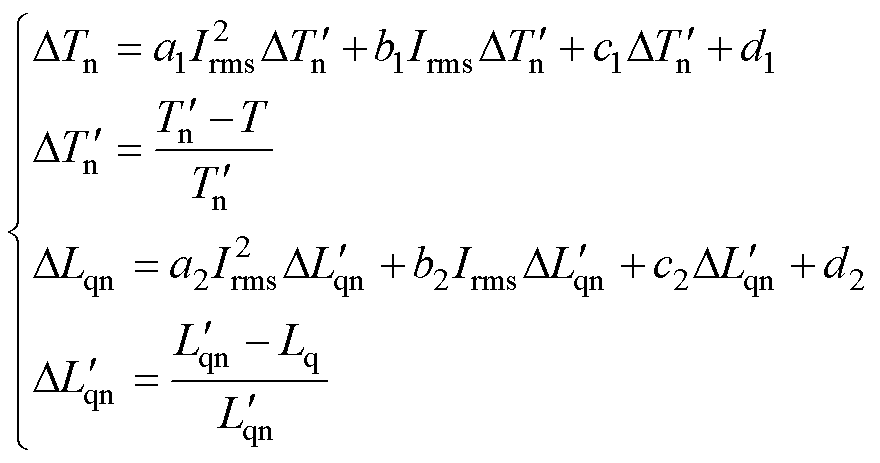（11）
式中，
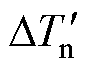和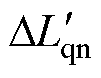
分别为各个电流工况下的转矩损失率和交轴电感损失率；a1、b1、c1、d1、a2、b2、c2、d2分别为映射关系的待定参数。
如图14a为以电枢电流Irms和转矩损失率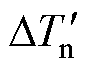为自变量，以额定工况下的转矩损失率
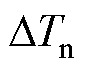为因变量，实现的曲面拟合；图14b为以电枢电流Irms和交轴电感损失率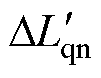为自变量，以额定工况下的交轴电感损失率
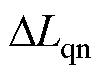为因变量，实现的曲面拟合，两个特征参量曲面拟合的R2值均大于0.9，实现了较高精度的数据拟合，两者具体的映射关系为
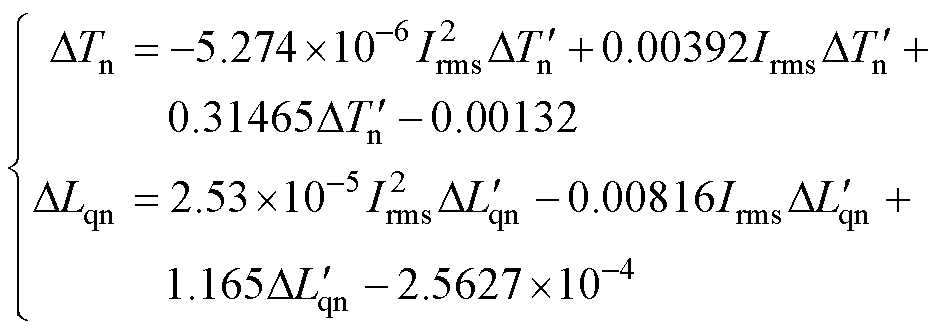（12）
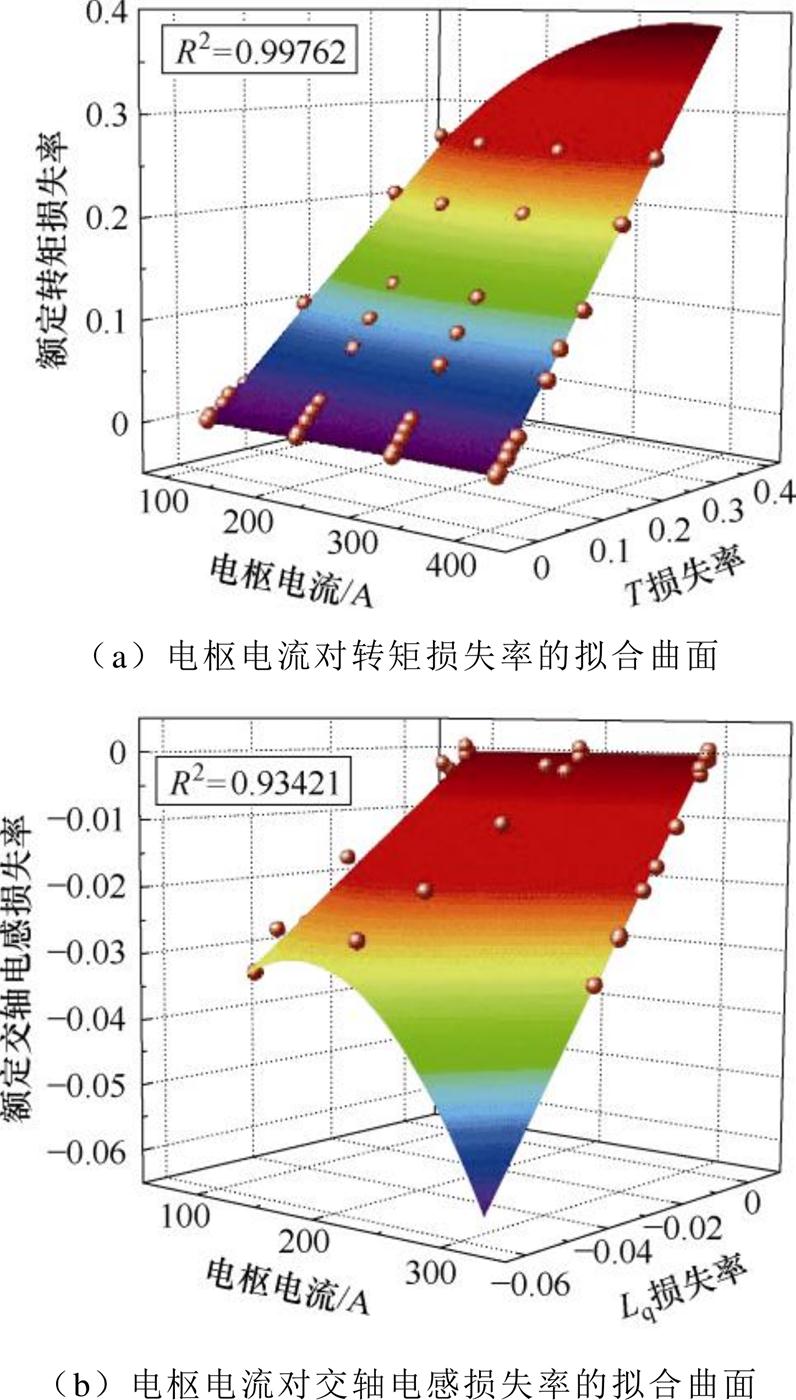
图14 电流对退磁特征参量的影响
Fig.14 The influence of Irms on the characteristic parameters of demagnetization
将式（12）代入式（11）即可得到修正后的退磁故障识别方法，即退磁故障的动态识别方法。为了检验退磁故障动态识别方法的精度，使用高退磁模型在电枢电流为110 A的工况下对其退磁率进行预测计算，得到的结果如图15所示，可以看出，使用退磁故障的动态识别方法可以很好地预测电机退磁故障的程度，最大误差仅为2.94%。
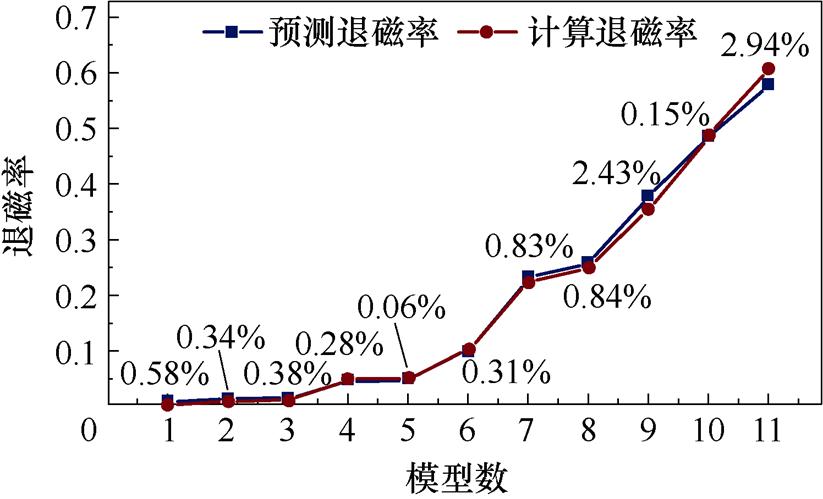
图15 退磁故障动态识别方法的精度对比
Fig.15 Accuracy comparison of the dynamic identification method of demagnetization fault
为了进一步验证所提出的退磁故障动态识别方法的可行性和准确性，本节通过在电枢电流为1 400 A、内功率因数角为70°、转速为4 500 r/min的工况下，重新建立了一个高退磁率电机模型M1400，计算其工作在电枢电流为160 A、内功率因数角为36°、转速为3 000 r/min的工况下，电机的实际输出转矩和交轴电感，并采用退磁故障动态识别方法预测其退磁率。
如图16所示为M1400电机模型在额定转速（n= 4 500 r/min）下，退磁前后的空载反电动势变化曲线，可知空载反电动势损失了7.21%。根据前文对标准退磁率的定义，可以认为M1400电机模型的标准退磁率为7.21%。
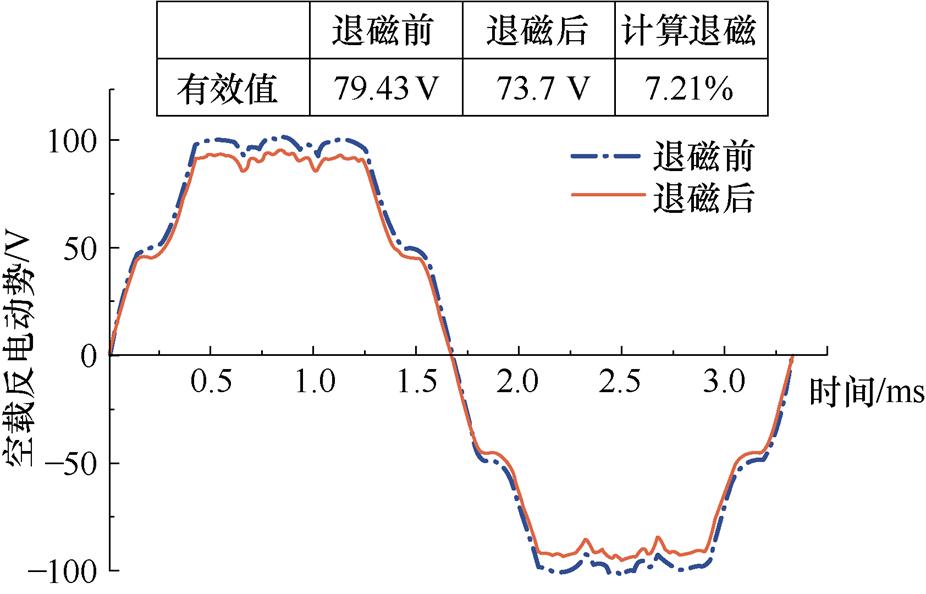
图16 M1400电机模型的空载反电动势波形
Fig.16 The no-load back EMF waveforms of the M1400
图17为M1400电机模型在指定工况（Irms=160 A，y =36°，n=3 000 r/min）下，电机退磁前后的输出转矩和交轴电感波形，其对应的平均值为
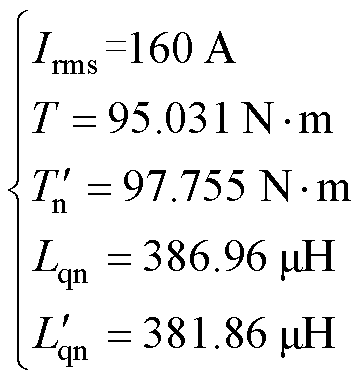（13）
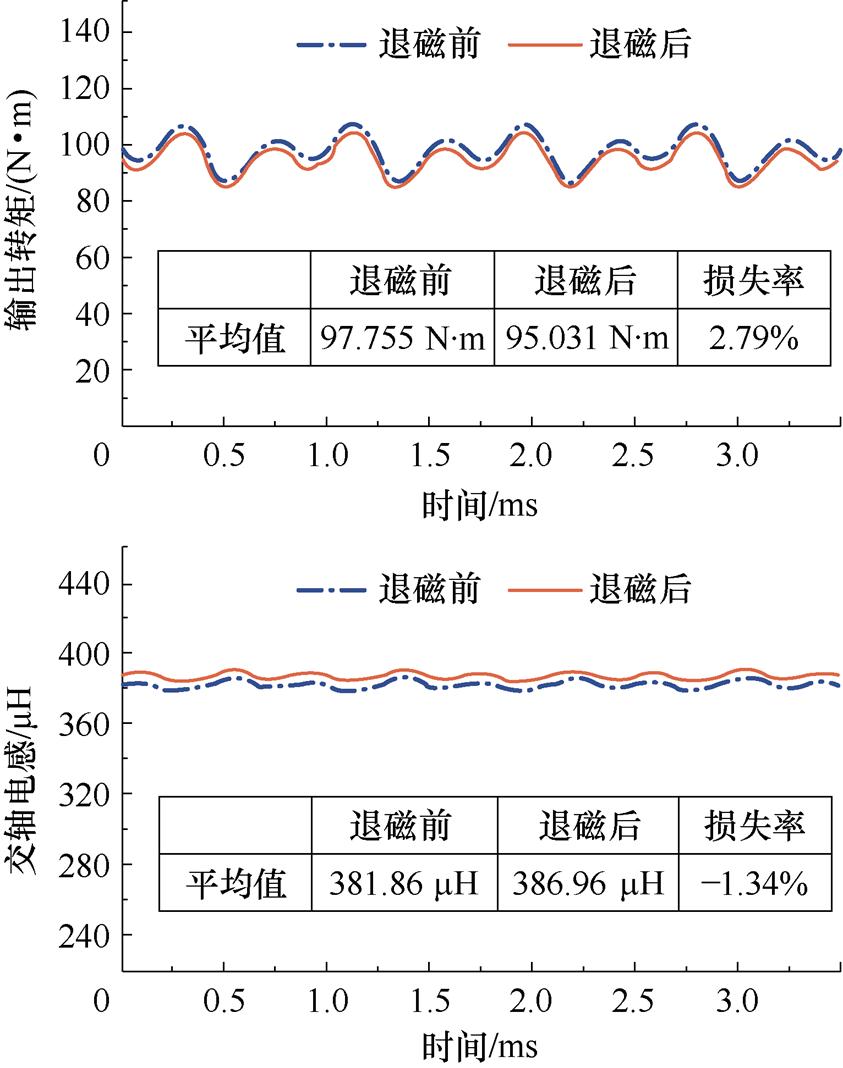
图17 M1400电机模型的负载转矩和交轴电感波形
Fig.17 The load T and Lq waveforms of the M1400
将式（13）中的数据代入退磁故障动态识别方法中，计算结果见表4，可以看出，使用退磁故障动态识别方法得到的预测退磁率与标准退磁率非常接近，误差仅为0.68%，属于可允许的估计误差，进一步验证了本文获得的退磁故障动态识别方法的可行性和准确性。
表4 退磁故障动态识别方法的仿真验证结果
Tab.4 Verification results of the dynamic identification method of demagnetization fault （%）
模型标准退磁率预测退磁率预测误差 M14007.216.530.68
为进一步验证3.2.2节所述退磁故障动态识别方法的有效性和准确性，根据表1的电机性能指标制造了一台测试样机，并对该样机开展了退磁前后电机的空载和负载性能测试及转子退磁实验。
实验测试平台为对拖实验台架，包括测试样机、负载电机、功率分析仪、控制器等设备，如图18所示。
图18 永磁同步电机实验平台
Fig.18 Experimental platform for double V-shaped PMSM
图18中，测试样机与负载电机同轴连接，在空载工况下能够使测试样机以特定转速旋转，在负载工况下可以为测试样机提供负载转矩；功率分析仪可以实时监测和记录被测电机的电枢电流、定子电压、输出转矩、转速等运行参数；控制器通过矢量控制可以使测试样机在目标工况下运行。
为了真实反映电机内转子永磁体的退磁状态，本文开展的电机退磁实验考虑了电机内实际闭合磁路对转子永磁体退磁的影响，因此验证实验具有一定的破坏性。本实验通过采用施加瞬时直轴脉冲电流的方法完成一次电机的退磁实验，并在退磁实验前后，分别开展测试样机的空载性能测试和两组不同工况下的负载性能测试，如图19为退磁故障动态识别方法的验证实验流程。
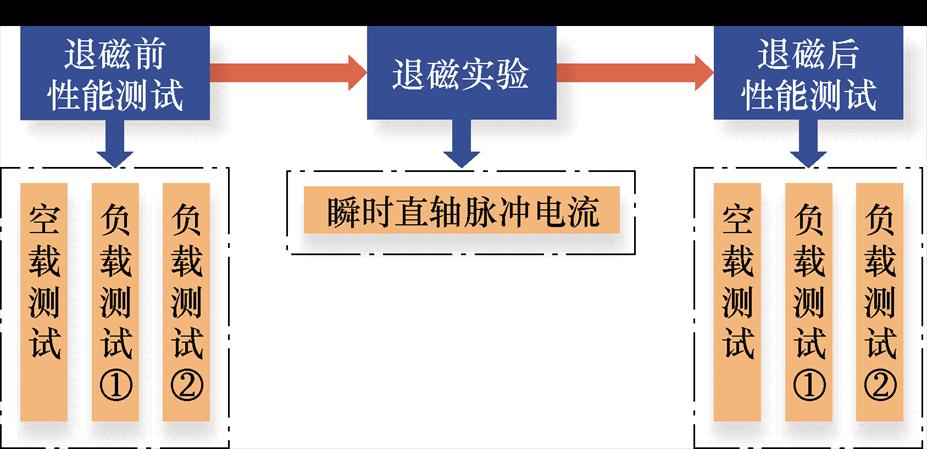
图19 退磁故障动态识别方法的实验验证
Fig.19 Experimental verification of dynamic identification method for demagnetization fault
其中，空载性能测试的实验转速设置为3 000 r/min，负载性能测试的两组代表性工况分别为：①转速为3 010 r/min、定子电流为231 A；②转速为6 509 r/min、定子电流为267 A，退磁前后两组负载工况的电流控制角均保持一致。
5.3.1 空载性能测试结果分析
当空载转速为3 000 r/min时，测试样机在退磁前后的空载反电动势波形如图20所示，且表5记录了各相反电动势的有效值。
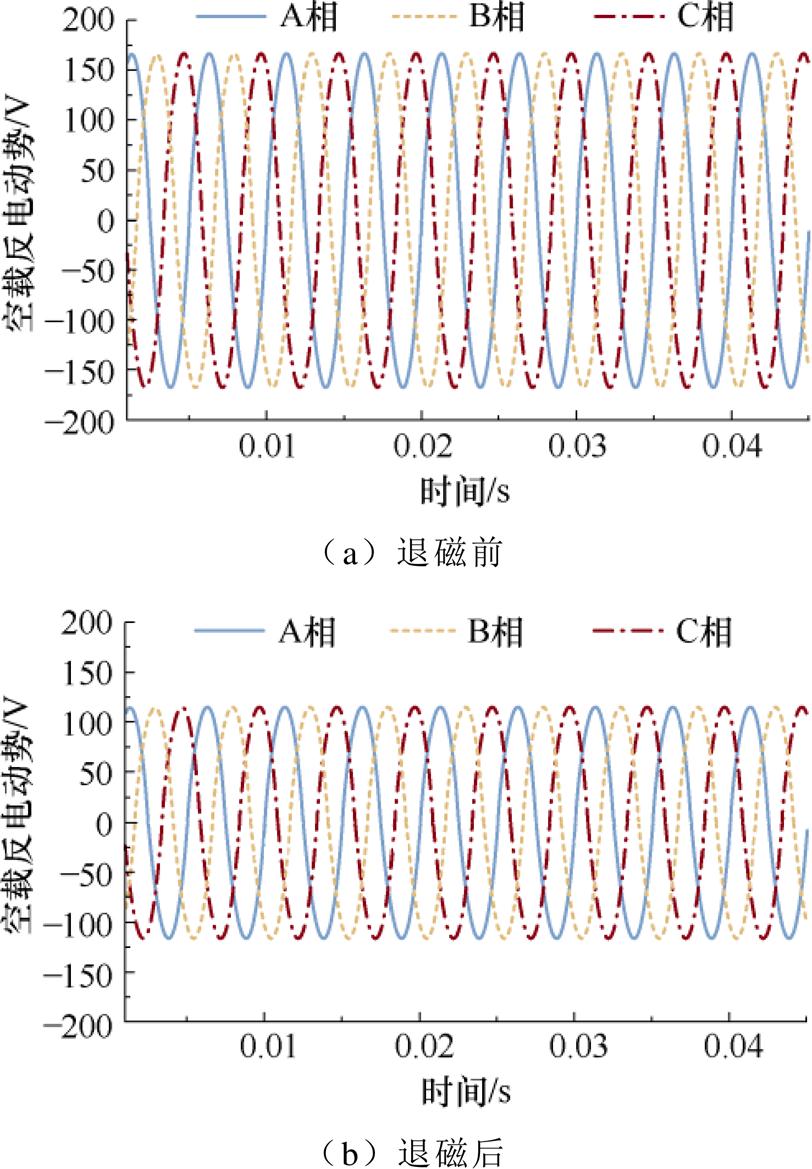
图20 退磁前后测试样机的空载反电动势波形
Fig.20 The no-load back EMF waveforms of the tested prototype before and after demagnetization
经计算，测试样机退磁前后的空载反电动势损失率为31.24%，根据3.1.1节空载工况下的退磁率特征参数分析，可将退磁前后空载反电动势的损失率作为转子永磁体的标准退磁率，即通过本次退磁实验，测试样机产生了31.24%的退磁率。
表5 测试样机的空载性能参数
Tab.5 The no-load performance parameters of the tested prototype
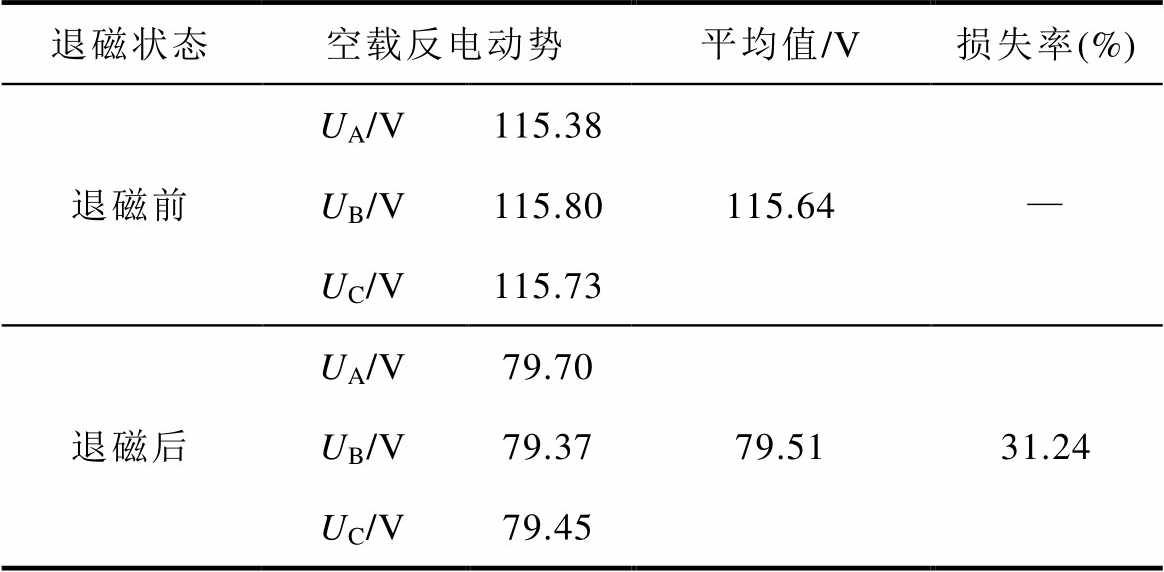
退磁状态空载反电动势平均值/V损失率(%) 退磁前UA/V115.38115.64— UB/V115.80 UC/V115.73 退磁后UA/V79.7079.5131.24 UB/V79.37 UC/V79.45
5.3.2 负载性能测试结果分析
电机负载工况下的稳定运行存在一个建立过程，图21为测试样机在控制参数改变后，电机的温升变化曲线。
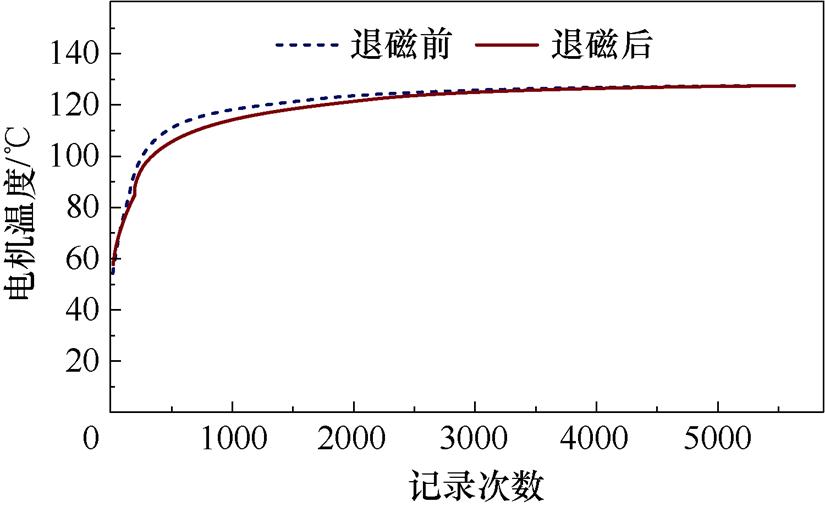
图21 电机性能测试过程中的温升曲线
Fig.21 The temperature curves of the motor during the experiment
为了减小退磁前后电机工作温度对测试结果的影响，本文记录了电机温度稳定后测试数据的平均值，测试样机在两组代表性负载工况下的实测性能参数见表6。其中，交轴电感通过式（14）计算获得。
表6 测试样机的负载性能参数
Tab.6 The load performance parameters of the tested prototype
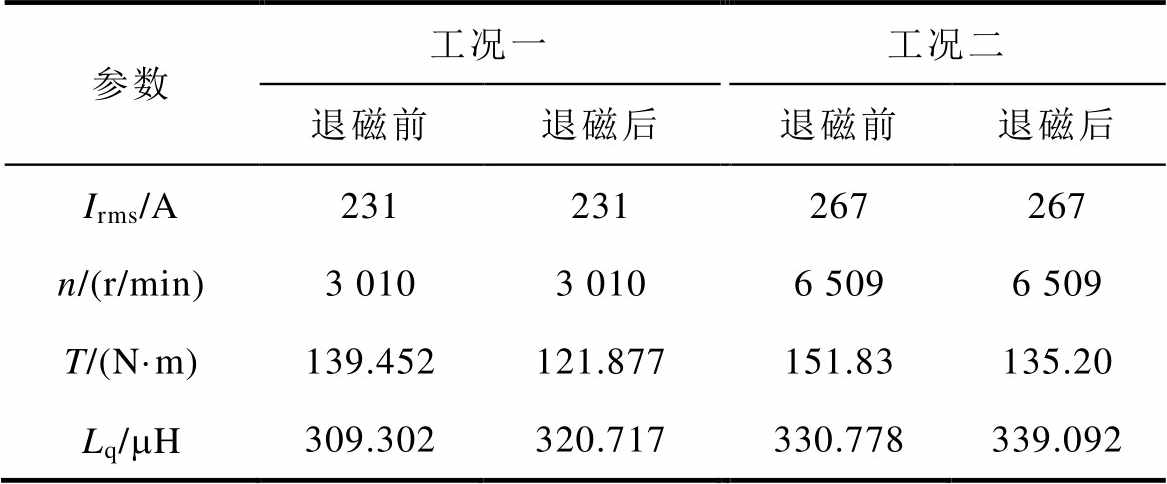
参数工况一工况二 退磁前退磁后退磁前退磁后 Irms/A231231267267 n/(r/min)3 0103 0106 5096 509 T/(N·m)139.452121.877151.83135.20 Lq/mH309.302320.717330.778339.092
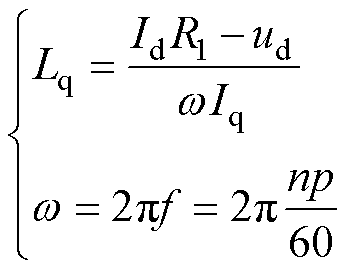（14）
将表6中的实测数据代入退磁故障动态识别方法的计算式（10），获得测试样机的预测退磁率，结果见表7。与标准退磁率相比，两组负载工况下的预测误差分别为1.649%和1.765%，均在可允许的范围内，充分验证了3.2.2节所述的双V型组合磁极永磁同步电机退磁故障动态识别方法的可行性和准确性。
表7 退磁故障动态识别方法的预测误差对比
Tab.7 Prediction error comparison of dynamic identification method for demagnetization fault （%）
标准退磁率预测退磁率预测误差 工况一31.2432.8891.649 工况二31.2429.4951.765
针对双V型永磁同步电机的退磁问题，本文提出了一种基于Pearson相关性分析的退磁故障动态识别方法。获得了以下结论：
1）与采用空气或不导磁介质等效永磁体退磁故障的方法相比，本文考虑了电机闭合磁路对转子永磁体退磁故障的影响，更加接近永磁体实际的退磁状况。
2）基于Pearson相关性分析方法，获得了与退磁故障具有显著相关性的特征参量。在空载工况下的空载反电动势、齿槽转矩、齿槽转矩脉动极差、气隙磁通密度以及交直轴电感均可作为表征退磁故障的特征参量。在负载工况下，电机的输出转矩和负载交轴电感可作为表征退磁故障的特征参量，但还需通过电枢电流对其进行修正，从而得到了任意工况下的退磁故障动态识别方法。
3）退磁故障动态识别方法的仿真验证结果显示，预测退磁率与实际退磁率误差为0.68%。电机的实验测试结果显示，预测退磁率与标准退磁率最大误差也仅为1.765%，两个结果的误差均在可接受的范围内，验证了本文退磁故障动态识别方法的可行性和准确性。
参考文献
[1] 董新伟, 王一飞, 杨磊. 车用高性能永磁同步电机磁极设计综述[J]. 微电机, 2019, 52(11): 97-100.
Dong Xinwei, Wang Yifei, Yang Lei. A survey of magnetic pole design for high performance permanent magnet synchronous motors[J]. Micromotors, 2019, 52(11): 97-100.
[2] 叶宇豪, 彭飞, 黄允凯. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021, 36(14): 2922-2935.
Ye Yuhao, Peng Fei, Huang Yunkai. Overview of multi-motor synchronous motion control tech- nology[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2922-2935.
[3] 王璨, 李国冲, 杨桂林, 等. 基于生物智能环状耦合的嵌入式永磁同步直线电机高精度位置协同控制研究[J]. 电工技术学报, 2021, 36(5): 935-943.
Wang Can, Li Guochong, Yang Guilin, et al. Research on position cooperative control of high-precision embedded permanent magnet synchronous linear motor based on biological intelligence loop coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 935-943.
[4] 李继方, 姚刚, 汤天浩. 共直流母线多电机系统的混杂动态模型及调度[J]. 电工技术学报, 2012, 27(5): 172-179.
Li Jifang, Yao Gang, Tang Tianhao. Hybrid dynamic model and scheduling of multi-motor systems driven by common DC bus[J]. Transactions of China Elec- trotechnical Society, 2012, 27(5): 172-179.
[5] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2016.
[6] 谢颖, 姜佳宁, 蔡蔚, 等. 表贴式高速永磁同步电机失磁故障及磁体选区渗重稀土研究[J]. 电机与控制学报, 2024, 28(2): 44-53.
Xie Ying, Jiang Jianing, Cai Wei, et al. Demagneti- zation failure of surface mount high speed permanent magnet synchronous motor and local infiltration of heavy rare earth[J]. Electric Machines and Control, 2024, 28(2): 44-53.
[7] 谢颖, 孙存峻, 蔡蔚, 等. 电动汽车用永磁同步电机失磁机理与选区渗重稀土研究[J]. 电机与控制学报, 2024, 28(3): 75-83.
Xie Ying, Sun Cunjun, Cai Wei, et al. Demagneti- zation mechanism and local infiltration of heavy rare earth for permanent magnet synchronous motor in electric vehicles[J]. Electric Machines and Control, 2024, 28(3): 75-83.
[8] Zhang Zhouyun, Shi Wei. Review of anti- demagnetization design method for vehicle permanent magnet motor[C]//2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 2014: 1-5.
[9] Kim K C, Lim S B, Koo D H, et al. The shape design of permanent magnet for permanent magnet syn- chronous motor considering partial demagneti- zation[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3485-3487.
[10] Xu Hai, Li Jian, Chen Junhua, et al. Design of a hybrid magnets variable flux memory machine based on hysteresis model[C]//2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 2019: 1889-1894.
[11] Huang Hui, Hu Yusheng, Xiao Yong, et al. Research of parameters and anti-demagnetization of rare- earth-less permanent magnet assisted synchronous reluctance motor[J].IEEE Transactions on Magnetics, 2015, 51(11): 8112504-1-8112504-4.
[12] Liu Wei, Yang Hui, Lin Heyun. A novel dual-layer variable flux memory machine with asymmetric-PM design[C]//2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 2022: 3747-3752.
[13] Yu Fengyuan, Yao Lei, Chen Shangyi, et al. Demag- netization analysis and optimization design of interior permanent magnet synchronous motor[C]//2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 2020: 704-709.
[14] Da Yao, Shi Xiaodong, Krishnamurthy M. A new approach to fault diagnostics for permanent magnet synchronous machines using electromagnetic signature analysis[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 4104-4112.
[15] 杜威, 孙宇光, 田代宗, 等. 基于新型探测线圈的永磁电机转子失磁故障在线监测方法[J]. 电力自动化设备, 2020, 40(6): 218-227.
Du Wei, Sun Yuguang, Tian Daizong, et al. Online monitoring method for rotor demagnetization fault of permanent magnet synchronous machine based on new type of search coil[J]. Electric Power Automation Equipment, 2020, 40(6): 218-227.
[16] 孙宇光, 余锡文, 魏锟, 等. 发电机绕组匝间故障检测的新型探测线圈[J]. 中国电机工程学报, 2014, 34(6): 917-924.
Sun Yuguang, Yu Xiwen, Wei Kun, et al. A new type of search coil for detecting inter-turn faults in synchronous machines[J]. Proceedings of the CSEE, 2014, 34(6): 917-924.
[17] Guo Liyan, Xia Changliang, Wang Zhiqiang, et al. Improving rotor geometry to strengthen anti- demagnetization ability of PM[J]. International Journal of Applied Electromagnetics and Mechanics, 2018, 56(2): 263-274.
[18] Guo Liyan, Xia Changliang, Wang Huimin, et al. Improved equivalent magnetic network modeling for analyzing working points of PMs in interior permanent magnet machine[J]. Journal of Magnetism and Magnetic Materials, 2018, 454: 39-50.
[19] Kao I H, Wang W J, Lai Y H, et al. Analysis of permanent magnet synchronous motor fault diagnosis based on learning[J]. IEEE Transactions on Instru- mentation and Measurement, 2019, 68(2): 310-324.
[20] 李红梅, 陈涛. 电动汽车PMSM退磁故障诊断及故障模式识别[J]. 电工技术学报, 2017, 32(5): 1-8.
Li Hongmei, Chen Tao. Demagnetization fault diagnosis and fault mode recognition of PMSM for EV[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 1-8.
[21] 肖曦, 张猛, 李永东. 永磁同步电机永磁体状况在线监测[J]. 中国电机工程学报, 2007, 27(24): 43-47.
Xiao Xi, Zhang Meng, Li Yongdong. On-line estimation of permanent-magnet flux linkage ripple for PMSM[J]. Proceedings of the CSEE, 2007, 27(24): 43-47.
[22] 卢庆辉, 尹项根, 乔健, 等. 变速抽蓄机组失磁故障分析及保护研究[J]. 电工技术学报, 2024, 39(5): 1390-1403.
Lu Qinghui, Yin Xianggen, Qiao Jian, et al. Study on loss of excitation fault analysis and protection of variable speed pumped storage units[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1390- 1403.
[23] 匡恒. 75kW车用轮毂电机电磁特性及失磁故障研究[D]. 哈尔滨: 哈尔滨理工大学, 2021.
Kuang Heng. Study on Electromagnetic characteristics and loss-of-excitation fault of 75kW vehicle hub motor[D]. Harbin: Harbin University of Science and Technology, 2021.
[24] Huang Song, Lei Jiayin, Zeng Chong, et al. Online rotor fault diagnosis of permanent magnet syn- chronous motors based on stator tooth flux[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[25] 胡土雄, 胡弼, 王伟, 等. 高密度永磁同步电机永磁体失磁特征量分析[J]. 电气工程学报, 2019, 14(2): 121-126.
Hu Tuxiong, Hu Bi, Wang Wei, et al. Analysis of demagnetization characteristics of permanent magnets in high density permanent magnet synchronous motor[J]. Journal of Electrical Engineering, 2019, 14(2): 121-126.
[26] 崔刚, 熊斌, 李振国, 等. 转子温度空间分布差异诱发永磁电机局部失磁特性研究[J]. 中国电机工程学报, 2024, 44(6): 2437-2448.
Cui Gang, Xiong Bin, Li Zhenguo, et al. Research on local demagnetization characteristics of permanent magnet motor induced by spatial distribution difference of rotor temperature[J]. Proceedings of the CSEE, 2024, 44(6): 2437-2448.
[27] 佟文明, 田野, 李晓健, 等. 双层复合护套高速永磁电机转子涡流损耗解析模型[J/OL]. 电工技术学报, https://doi.org/10.19595/j.cnki.1000-6753.tces. 230844.
Tong Wenming, Tian Ye, Li Xiaojian, et al. Analytical modeling for rotor eddy current loss of high-speed surface-mounted permanent magnet motor with double-layer compound retaining sleeve[J/OL]. Transactions of China Electrotechnical Society, https:// doi.org/10.19595/j.cnki.1000-6753.tces.230844.
Dynamic Identification Method of Demagnetization Fault of Double V-Shaped PMSM Based on Pearson Correlation Analysis
Abstract With the gradual development of permanent magnet drive motors in the direction of high speed, high torque, and high power density, the risk of irreversible demagnetization of permanent magnets has increased dramatically. In addition, rotor poles combined with multiple permanent magnets are widely used, and spatial specificity exists in pole demagnetization of space-distributed permanent magnets due to the different arrangement positions. Therefore, real-time detection of special demagnetization faults for permanent magnet drive motors is crucial. Numerous scholars have proposed online diagnostic methods. However, these methods either have the cost increase caused by the stator coil modification, or the assumed demagnetization model of the permanent magnet is far from the actual. Hence, the online diagnostic methods for the demagnetization fault have yet to be verified by experiments. In this paper, taking a permanent magnet motor with an 8-pole 48-slot double V-type as an example, the influence of the closed magnetic circuit of the motor on the demagnetization fault of permanent magnets is considered.
Firstly, Assuming that the motor has good heat dissipation and ignores the axial temperature difference effect on the demagnetization of permanent magnets, the permanent magnet demagnetization caused by the armature reverse magnetic field is analyzed. Meanwhile, this paper establishes a high demagnetization rate motor model under different armature currents, considering the difference between the closed magnetic circuit inside the motor and the magnetic circuit outside the motor. Then, the motor’s no-load and load parameters are analyzed. The Person correlation coefficient method extracts the characteristic parameters of permanent magnet motor demagnetization faults. The dynamic identification method of the demagnetization fault is established, and the armature current is introduced to correct this dynamic identification method. Finally, the simulation error of the dynamic identification method is calculated by establishing a new motor model with a high demagnetization rate, and the experimental error is calculated through two working condition experiments.
The following conclusions can be drawn. (1) Considering the influence of the closed magnetic circuit in the motor on the permanent magnet demagnetization makes the demagnetization model closer to the actual demagnetization condition of the permanent magnet. (2) The no-load parameters of the motor can be used as the characteristic parameters of the no-load demagnetization fault. The loss rate of torque and cross-axis inductance under load conditions is not affected by the current angle, which can be used as the characteristic parameters of the load demagnetization fault. (3) The simulation error of the dynamic identification method is 0.68%, and the experimental error is 1.765%.
Keywords：Drive motor, double V-shaped PMSM, demagnetization fault, Pearson correlation
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231722
国家自然科学基金资助项目（52177064）。
收稿日期 2023-10-16
改稿日期 2023-11-27
黄康杰 男，1997年生，硕士研究生，研究方向为电机与电器。
E-mail: 13593573965@163.com
熊 斌 男，1979年生，研究员，研究方向为电机与电器、冷却技术、电气设备健康状况评估等。
E-mail: xiongbin@mail.iee.ac.cn（通信作者）
（编辑 崔文静）