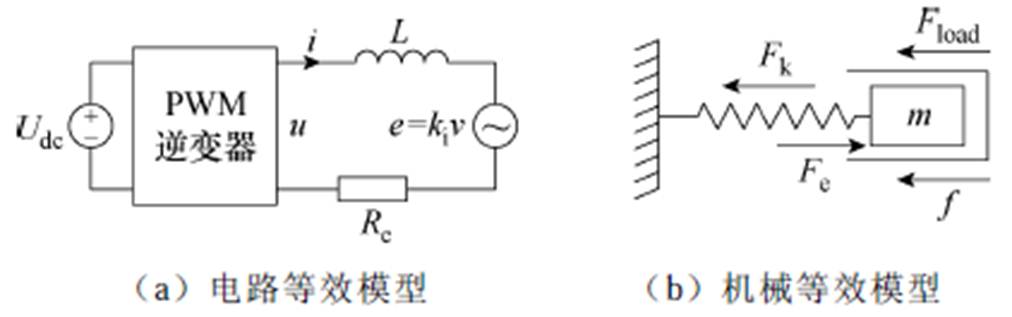
图1 直线振荡电机的系统模型
Fig.1 System model of the linear oscillatory machine
摘要 传统直线振荡电机(LOM)无位置传感器控制方法存在参数敏感性差、行程观测精度低等问题,进而会降低电机运行的可靠性。为减小预设参数不准确及参数非线性变化对行程观测精度的影响,该文提出一种基于在线参数辨识及自适应谐波提取滤波器的改进型直线振荡电机无位置传感器控制策略。首先,采用频域法分析了直线振荡电机行程观测方法的参数敏感性,明确了影响行程观测精度的主要电机参数。然后,根据直线振荡电机数学模型提出了基于高频电压注入法的在线参数辨识方案,并设计了一种基于自适应谐波提取滤波器的高频谐波提取方法。最后,通过大量仿真和实验,验证所提方法的有效性和先进性。
关键词:直线振荡电机 参数辨识 高频电压注入 无位置传感器控制
压缩机是冰箱、空调等制冷设备的核心部件,市场应用前景广阔[1-2]。相比于同功率旋转式压缩机,直线压缩机由直线振荡电机(Linear Oscillatory Machine, LOM)驱动,可将电能直接转化为直线往复运动的机械能,工作效率可提高15%~25%[3-4],具有结构简单、效率高、机械损耗小等优势[5],受到国内外学者的广泛关注。
直线振荡电机有两种常见控制策略:活塞行程控制及谐振频率跟踪控制。首先,直线振荡电机动子行程不受曲轴连杆限位作用,对其实施活塞行程控制能够适应更为广泛的应用需求[6-7]。然而,活塞行程信号的准确性会直接影响行程控制效果,不精确的行程信号可能会导致活塞出现“撞缸”问题,严重危害系统的安全可靠性[8-9]。因此,有必要对该电机实施精确的活塞行程控制。其次,直线振荡电机运行在系统谐振频率时能够获得最大输出效率[10-11],对其实施谐振频率跟踪控制能够实现系统在变负载复杂工况下的高效运行。然而,在弹簧刚度、气体力负载等因素作用下,谐振频率呈现出非线性变化的特点,难以准确建模分析。已有研究多利用直线振荡电机行程-电流特性,即电机运行在系统谐振频率点时活塞行程与电流信号相位互差90°,实现谐振频率跟踪控制[10, 12]。其中,行程-电流相位差计算结果高度依赖活塞行程信号,较小的行程误差即可导致明显的谐振频率计算偏差,严重影响谐振频率跟踪控制的效果[12-14]。
综上所述,准确的活塞行程信号对直线振荡电机安全、高效运行十分重要。考虑到该电机活塞与气缸负载高度一体化,使用位置传感器将面临传感器安装维护困难、系统体积增大、成本增加等问题,因此有必要开展无位置传感器控制策略研究。当前研究中,反电动势积分法是最常用的活塞行程观测方法,可根据电压方程直接计算获得行程信号[10, 15]。然而,该方法严重依赖电机参数,当参数不准时,行程观测结果会受到较大影响。针对该问题,文献[16]提出了一种基于误差符号鲁棒积分的行程观测器,在一定程度上提高了行程观测的参数鲁棒性,但由其观测到的行程信号中含有大量谐波,且未解决电机参数随工况变化等问题。此外,文献[17-18]采用高阶观测器同时获取活塞行程信号及负载参数信息,但由于直线振荡电机系统的强耦合与非线性特点,该方法难以在有限的信息内获取全部参数的变化情况,其参数鲁棒性及参数辨识速度有待提高。
文献[19]提出一种基于最小二乘(Recursive Least Square, RLS)法的直线振荡电机参数估计策略,通过建立LOM的最小二乘估算器,并设置适当的遗忘因子来实现对电阻、电感及推力系数的估算。该算法可以有效得到电机的各项参数,但存在收敛速度较慢、估算结果存在误差等问题,且RLS算法会占用大量的运算量,严重消耗主控芯片算力,不利于工业应用场合。
文献[20]提出了一种基于模型参考自适应的直线压缩机电阻辨识算法。该算法采用自适应律设计定子基于Lyapunov算法的电阻在线辨识,并通过仿真验证了其参数估计的有效性。参数辨识的收敛速度较快,且辨识结果准确性较高,但通过参数敏感性分析可知,电阻参数变化对LOM位置观测的影响较小,对其进行参数辨识对观测精度的提升有限。除此之外,文中未涉及相关内容的实验结果,其在应用场合的有效性还需要进一步验证。
卡尔曼滤波(Kalman Filter, KF)算法可被应用于位置观测及参数辨识的领域。文献[21]设计了一种基于卡尔曼滤波器的LOM电路参数辨识算法。通过构建卡尔曼观测矩阵并使用梯度校正的参数估算法,可以有效地对电阻与电感参数进行修正。该算法的辨识效果优于RLS算法,且收敛速度与稳定性均有所提升,然而卡尔曼滤波算法的复杂度很高,且控制参数整定较为困难,不利于其广泛应用。
综上所述,为提高直线振荡电机活塞行程观测精度,本文提出了一种基于在线参数辨识及自适应谐波提取滤波器的改进型无位置传感器控制策略。其创新性如下:①采用幅频特性曲线对反电动势积分法进行参数敏感性分析,就不同电机参数对活塞行程观测的影响进行定量分析与比较。②设计基于高频注入法的参数辨识策略,通过分析高频激励对电机运行的影响,实现对变化参数的准确跟踪。③设计一种基于自适应谐波提取滤波器的高频谐波提取方法,在基波幅值远大于谐波幅值的应用环境下精确提取谐波信号。通过仿真与实验对比分析,证明了所提方法的先进性与有效性。
直线振荡电机电路与机械等效模型如图1所示[22]。

图1 直线振荡电机的系统模型
Fig.1 System model of the linear oscillatory machine
由图1a可得电机电压方程为
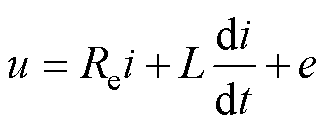 (1)
(1)
式中,u为绕组端电压;i为绕组电流;Re为绕组电阻;L为绕组电感;e为动子运动产生的反电动势。对于直线振荡电机而言,其反电动势与动子运动速度v成正比,比值为电机的电磁推力系数ki,即
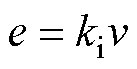 (2)
(2)
由图1b所示的简化机械模型,可得其运动方程为
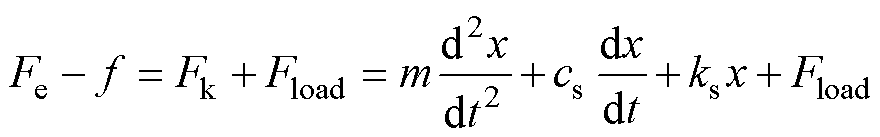 (3)
(3)
式中,m为电机动子与活塞的总质量;x为行程信号;Fk为弹簧作用于动子的力;Fe为电磁推力;f为电机运动所受阻力;Fload为气缸中的气体负载作用于活塞的负载力;ks为弹簧弹性系数;cs为弹簧阻尼系数。
在电机运行过程中,如果压缩机的排出和吸入压力以及活塞行程稳定,那么整个系统可以被视为线性系统[23]。由此,可得线性化气体力方程为
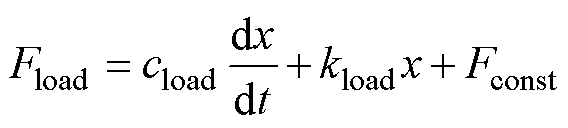 (4)
(4)
式中,kload为负载等效弹性系数;cload为负载等效阻尼系数;Fconst为负载的等效常数力。由电机结构及运行原理可得,电磁推力Fe与电机电流i成正比,比值即为电磁推力系数ki,即
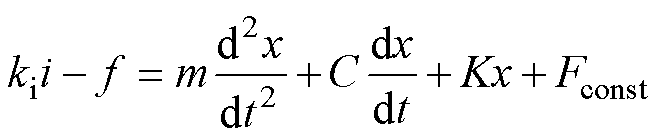 (5)
(5)
其中
C=cs+cload
K=ks+kload
当前针对直线振荡电机无位置传感器控制的研究中,反电动势积分法是最为常用的行程观测方法。其计算表达式为
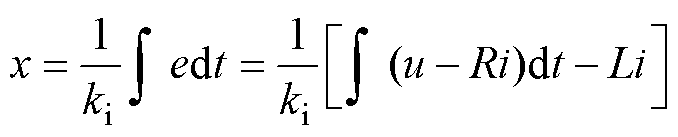 (6)
(6)
式中,R为定子电阻。
反电动势积分法所用的电阻、电感以及推力系数等参数会随着电机运行工况的变化而变化,导致行程计算过程中所用的电机参数与实际参数存在偏差,进而影响行程观测结果。因此,有必要定量分析不同参数偏差对行程观测结果的影响程度,本文将采用相量法对基于反电动势积分的行程观测方法进行参数敏感性分析。
由于直线振荡电机是由一定频率的单相正弦交流电驱动的单相电机,因此可采用相量法分析其稳态特性。将式(1)和式(5)表示成相量形式,有
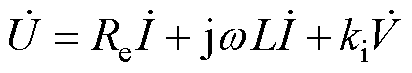 (7)
(7)
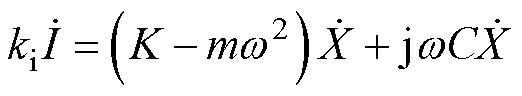 (8)
(8)
设电机实际参数与实际行程分别为R0、L0、ki0、x0,活塞行程计算程序中所设定的参数为R、L、ki、x,观测器观测到的参数为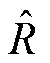 、
、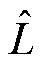 、
、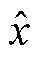 ,可得观测行程与实际行程的表达式为
,可得观测行程与实际行程的表达式为
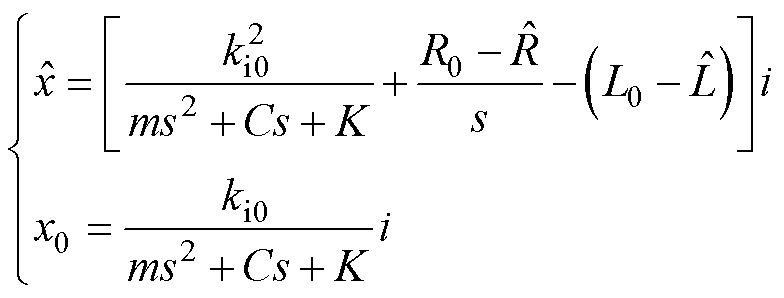 (9)
(9)
由式(9)可得行程观测的比值函数为
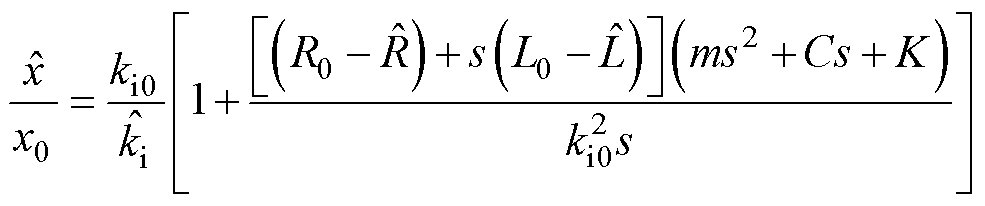 (10)
(10)
由式(10)可知,当观测器中所使用的推力系数ki不准确时,只会导致行程观测结果的幅值产生误差,且该幅值误差大小与推力系数实际值与设置值之比相关。在实际应用中,相较于电机的电感参数,推力系数往往可以测量得到较为精确的结果。且即使在考虑铁心饱和的条件下,推力系数的变化范围一般不超过5%。相较于电路参数偏差,推力系数对行程观测结果的影响较小。
当其他参数准确时,考虑电感参数误差对行程观测结果的影响为
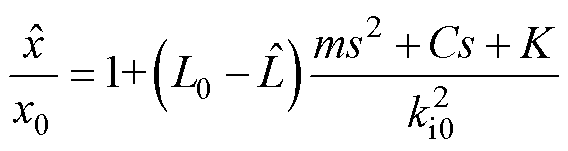 (11)
(11)
同理可得,当其他参数准确时,分析电阻参数误差对观测结果的影响为
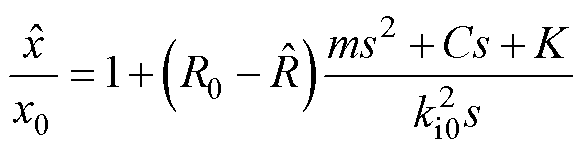 (12)
(12)
由于电感误差来源于测量误差以及电流较大时饱和效应导致的误差,故可认为电感误差不是很大,分析时以电感实际值与设定值有±5%的误差。此外,由于在电机运行过程中常伴有绕组温度变化,这会导致电机电阻参数发生较大变化。在实际应用中,可分别取观测器中电阻设置值R1=0.9R0和R2=1.2R0作为电阻误差进行分析。根据上述内容,可绘制不同电感、电阻参数误差下行程观测偏差的幅频曲线如图2所示。
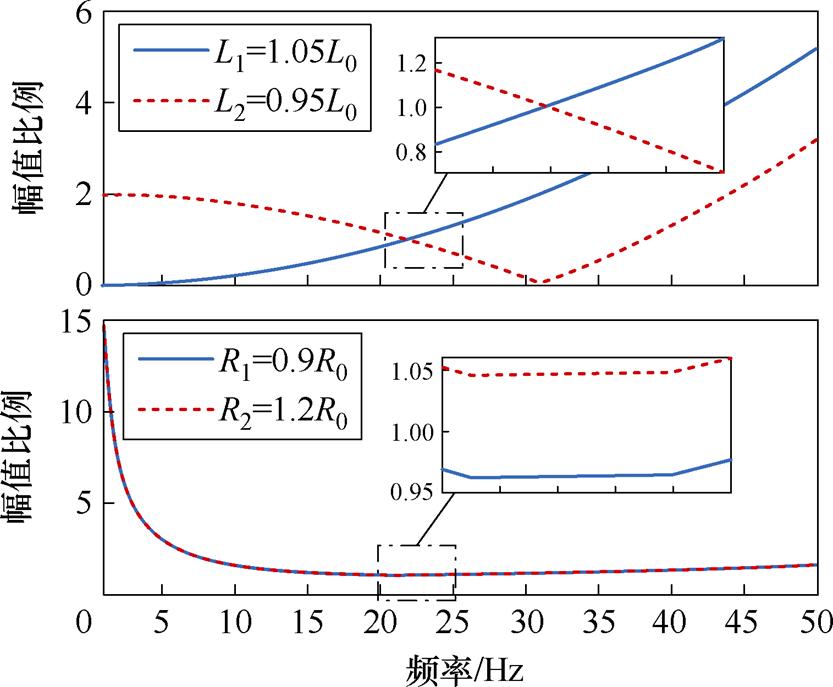
图2 电感、电阻误差下观测行程偏差幅频曲线
Fig.2 Amplitude frequency curves of observed displacement deviation under resistance and inductance errors
本文所分析的直线振荡电机谐振频率为23.5 Hz。由图2可知,在电机运行频率等于电机谐振频率时,行程观测值的偏差最小。由于直线振荡电机主要工作在其谐振频率附近,且负载变化通常不会使其谐振频率发生很大变化,因此针对驱动频率在20~25 Hz的范围内进行分析。在该频率范围内,电感参数误差对行程观测的幅值影响程度远大于电阻参数。电感参数5%的误差即会产生约30%的行程观测幅值误差,而相比之下,电阻参数20%的误差仅会带来5%左右的幅值误差。同时,行程观测的幅值误差不仅会影响正常的振幅与频率控制,还可能导致活塞振幅失控甚至撞缸。因此,相较于电阻参数变化,需要优先解决电感参数的准确性,本文采用电压高频注入法对电感参数进行在线辨识。
高频注入法是永磁同步电机信息计算中的一种常用方法。其主要用途为在低速及零速状态下,获取永磁同步电机的动子位置信息[24-25]。同时,通过对高频注入信号及响应信号的处理,可在电机运行过程中获取电感参数,从而对其进行辨识和修正。本文借鉴传统高频注入法的思想,将其应用于直线振荡电机,实现对电感参数的在线辨识,具体设计原理如下。
高频信号注入可在正弦脉冲宽度调制(Sinusoidal Pulse Width Modulation, SPWM)驱动的基础上,通过逆变器将一个高频的正弦电压信号直接叠加在电机的基波激励上实现。根据式(1)所示的电压方程,假设高频注入电压的角频率为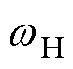 ,幅值为VHm,则注入高频电压信号可表示为
,幅值为VHm,则注入高频电压信号可表示为
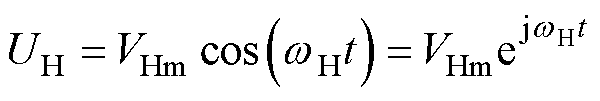 (13)
(13)
高频注入信号的频率一般为0.5~2 kHz,远高于电机基波频率约20~25 Hz。在此高频激励下,电机感抗将远大于其电阻,故高频激励下的电压方程可简化为
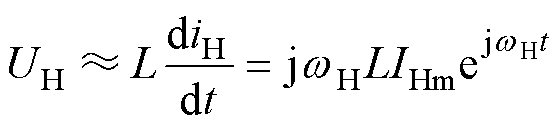 (14)
(14)
式中,IHm为电流高频响应的幅值。此时,可提取高频电流响应信号,然后计算高频电压电流的幅值比,得到电感参数信息。
然而,注入的高频电压/电流信号会对中高速运行状态下的电机产生影响。对于旋转电机,高频信号会产生一个高频脉动的转矩,造成电机抖动并产生较大噪声,影响电机运行性能。与旋转电机不同,直线振荡电机的机械部分为一个受迫振动系统,其运动方程如式(5)所示。分析可知,该受迫振动系统存在固有的机械谐振频率,当系统输入信号的频率远离谐振频率时,受迫振动系统会对激励产生极大的衰减效果。
为便于分析,设式(5)所示的受迫振动系统激励的幅值为AH,角速度为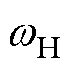 ,可得正弦推力FH满足
,可得正弦推力FH满足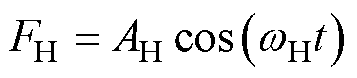 。由此可得最终系统稳定振动的行程表达式为
。由此可得最终系统稳定振动的行程表达式为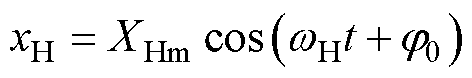 ,其中
,其中
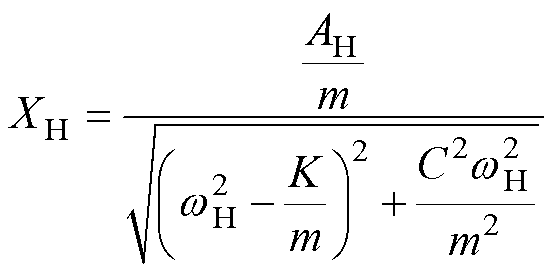 (15)
(15)
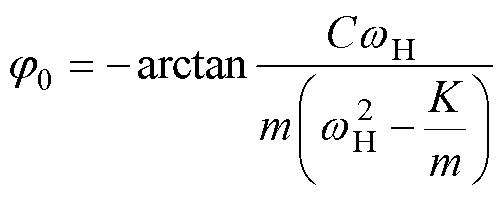 (16)
(16)
由式(15)可知,系统运动响应的幅值与激励的频率有关,且当激励的频率较高时,运动响应的幅值会迅速衰减。当激励的频率超过四倍谐振频率,即90 Hz时,系统运动响应的幅值将小于谐振频率下幅值的1/10,即受迫振动系统会对高频激励信号产生极大的抑制效果。在实验中,对运行中的直线振荡电机注入高频电压信号前后,电机的运行状态及运行噪声不会产生明显变化。因此,可采用高频注入法在线辨识直线振荡电机电感参数。
目前常基于高通滤波器(High-Passed Filter, HPF)和二阶广义积分器(Second-Order Generalized Integrator,SOGI)提取与处理目标信号。然而,HPF会导致滤波信号的幅度衰减和相位偏移[26],而传统的SOGI在基波信号幅值较大的应用条件下效果欠佳。为提取出准确的高频信号,本文设计了一种自适应谐波提取滤波器(Adaptive Harmonic Extraction Filter, AHEF)。AHEF的传递函数可表示为
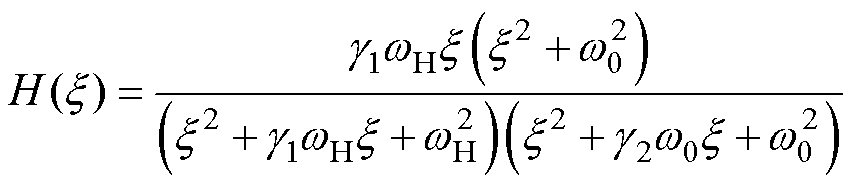 (17)
(17)
式中,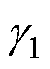 和
和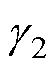 为滤波器设计参数;
为滤波器设计参数;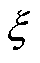 为
为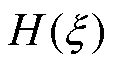 的独立变量;
的独立变量;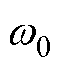 为滤波频率。此外,给出AHEF的原理框图如图3所示。
为滤波频率。此外,给出AHEF的原理框图如图3所示。
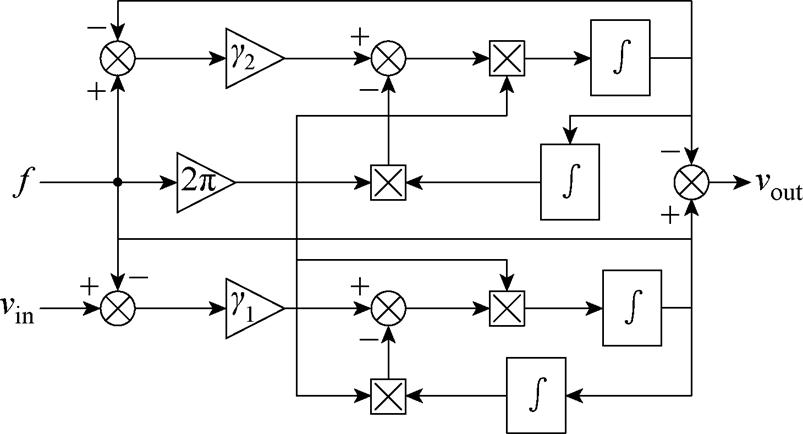
图3 AHEF控制框图
Fig.3 Control block diagram of AHEF
为突出AHEF的谐波提取性能,将其与SOGI进行对比,绘制两种不同滤波器的伯德图如图4所示。由伯德图可知,所设计的AHEF对指定频率的高频谐波的幅值与相位均不会造成影响。并且在带通滤波的同时,对指定频率的基波信号有着额外的衰减效果,能够有效减小基波信号对高频信息提取的影响。在AHEF中,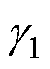 和
和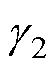 分别用于调整滤波带宽与基波衰减效果。通过合理选择滤波参数,AHEF可准确地提取幅值较小的谐波信息。
分别用于调整滤波带宽与基波衰减效果。通过合理选择滤波参数,AHEF可准确地提取幅值较小的谐波信息。
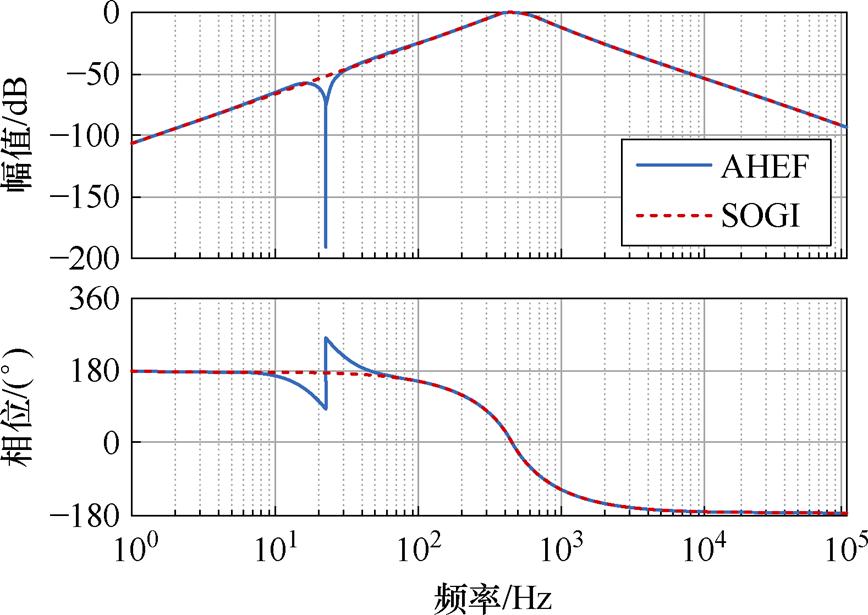
图4 AHEF与SOGI伯德图对比
Fig.4 Comparison of AHEF and SOGI Bode plots
分别采用SOGI和AHEF提取目标信号的谐波信号,结果如图5所示。图中,目标信号为幅值100 dB的23.5 Hz基波与幅值3 dB的500 Hz谐波叠加信号。由图5可知,当基波幅值远大于谐波幅值时,传统SOGI的谐波提取效果不理想。由于没有对基波信号进行特殊的带阻滤波处理,使得滤波器输出的信号受基波信号干扰。而经AHEF处理所得的谐波信号几乎不受基波影响,可以准确获取谐波信号信息。
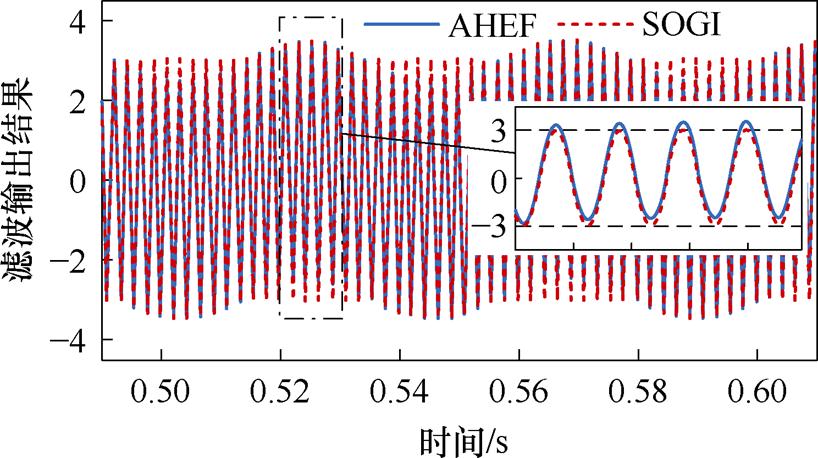
图5 AHEF与SOGI滤波效果对比
Fig.5 Comparison of filtering effects between AHEF and SOGI
在电感参数在线辨识以及活塞振幅获取的过程中,均包含行程幅值计算环节。传统方法常通过检测信号的极大与极小值点来完成对行程幅值的计算与更新。然而,该方法存在占用存储空间较大、易受噪声干扰以及跟踪性能不佳等问题。特别对于高频注入法中所涉及的高频信号的处理,更不宜使用传统幅值检测方法。
针对上述问题,本文设计了一种正交信号发生器(Quadrature Signal Generator, QSG),用于计算行程信号的幅值大小,如图6所示。QSG能够直接计算得到实时幅值信息,避免程序检测与更新过程。与传统算法相比,此方法存储空间占用小、响应速度快、抗扰能力强。
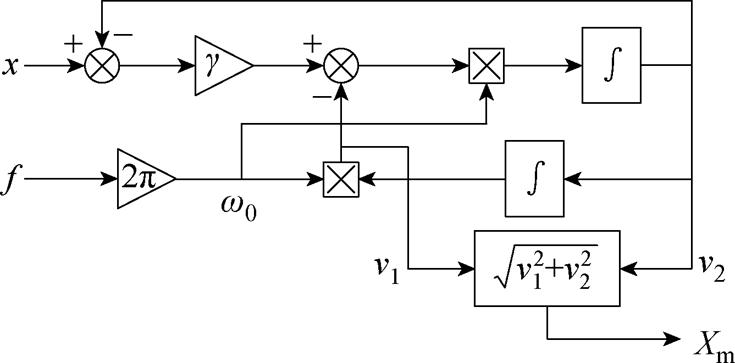
图6 高频信号幅值计算框图
Fig.6 Block diagram of high-frequency signal amplitude calculation
在本节中,仿真模型中使用的电机参数与实验平台的测量值一致,见表1。
表1 直线振荡电机参数
Tab.1 Parameters of linear oscillatory motor

参 数数 值 定子电阻R/W18.4 定子电感L/H0.84 推力系数ki/(N/A)28 弹性系数K/(kN/m)19.75 阻尼系数C/(N·s/m)9 动子质量m/kg1.025 额定功率P/W120 额定推力F/N28
基于在线参数辨识及AHEF的直线振荡电机无传感器控制系统如图7所示。电机使用单相逆变器实现变压变频控制,通过高频谐波注入、谐波提取和幅值检测算法在线辨识电感参数,实时校正行程计算结果。xm为活塞振幅计算结果,与给定振幅比较后经PI得到输出电压Vp。
首先对在线参数辨识环节开展仿真分析。以振幅开环状态起动电机,在t=1 s时切入参数辨识算法。图8为高频谐波注入前后电机的电压、电流与活塞行程仿真结果。由图可知,施加参数辨识算法后,电压信号的波形中存在注入的高频谐波,而电流与行程波形中的谐波相对不明显。由于直线振荡电机的受迫振动系统对高频激励的强衰减效果,仿真结果中可见算法起动前后活塞行程波形几乎没有变化,即高频电压谐波的注入不会影响电机的正常运行,与理论分析结果相符。
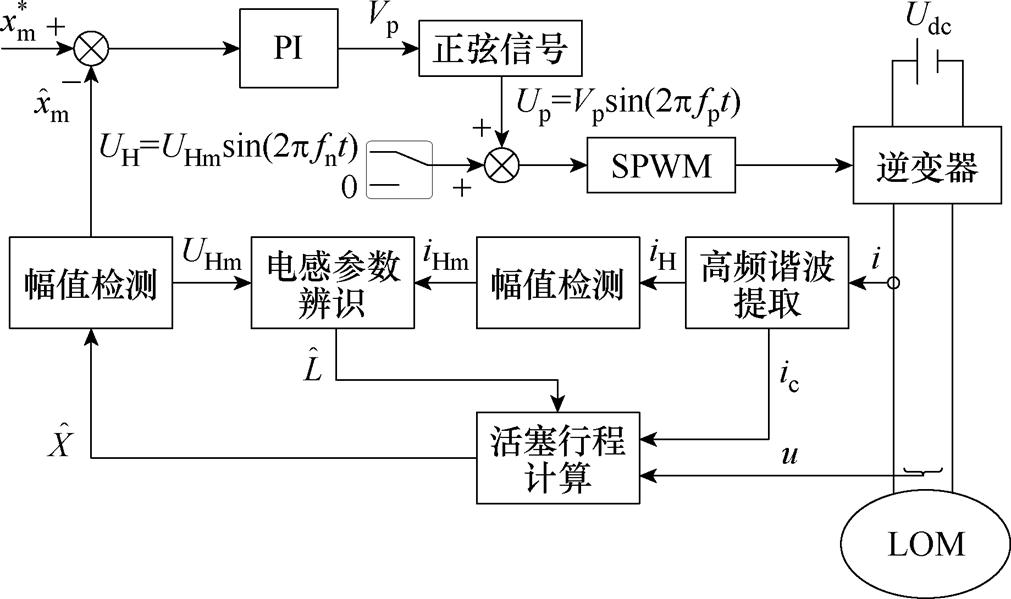
图7 基于在线参数辨识及AHEF的直线振荡电机无位置传感器控制系统
Fig.7 Position sensorless control system for linear oscillatory machine based on online parameter identification and AHEF
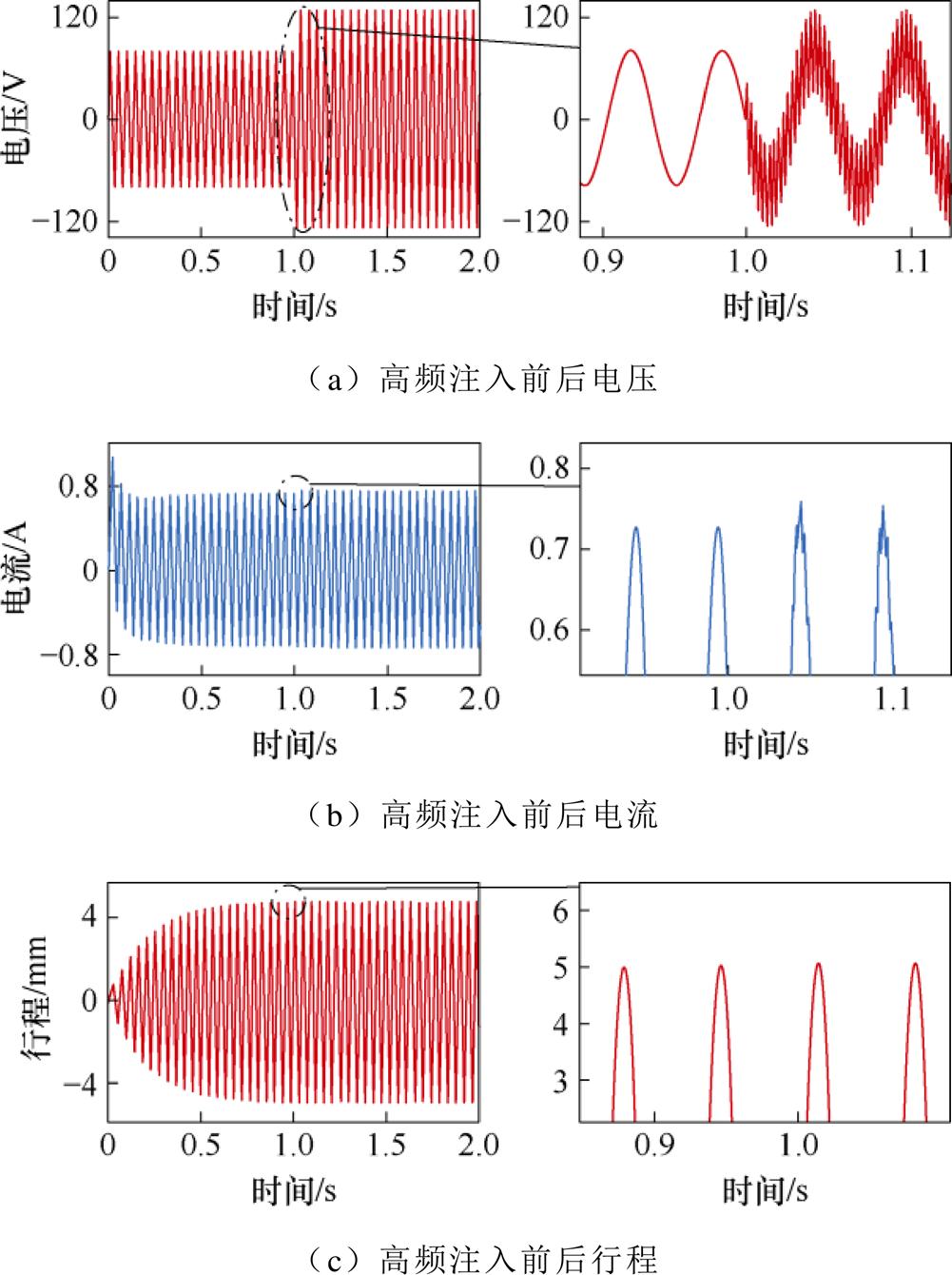
图8 高频注入前后电机波形对比仿真结果
Fig.8 Simulation results of motor waveforms comparison before and after high-frequency injection
然后,针对行程观测中不同电机参数偏差对观测结果的影响进行仿真分析。采用振幅闭环、频率开环模式起动电机,给定活塞振幅为5 mm,频率设定为22 Hz。分别设置电机电感参数5%偏差与电阻参数20%偏差,仿真结果如图9所示。可以看出,当观测器电感参数与实际电感参数存在5%的偏差时,行程观测结果与实际行程存在显著的幅值偏差。而当观测器电阻参数与实际电阻参数存在20%的误差时,行程观测结果相较实际值偏差较小,与理论分析一致。因此,可以认为电感参数是影响行程观测准确性的主要原因。

图9 电机参数偏差下的行程观测仿真结果
Fig.9 Simulation results of position observation under motor parameter deviation
最后,对参数辨识算法的有效性开展仿真分析。电机起动时行程观测器中使用带有偏差的电感参数,设定为0.75 H。在电机运行1 s后起动参数辨识算法,并对行程观测器中的参数进行修正。电机电感参数辨识结果与辨识前后行程观测的仿真结果如图10所示。显然,在起动参数辨识算法后,电感参数迅速从初始给定值0.75 H上升至实际值0.84 H,参数辨识用时约0.2 s,收敛速度较快且稳态下几乎不存在波动。同时,在参数辨识前,由于观测器参数不准确,导致行程观测结果存在一定偏差。在起动参数辨识算法后,随着观测器参数校正的完成,行程观测值与实际行程基本一致,观测精度得到提升。

图10 电感参数辨识与行程观测仿真结果
Fig.10 Simulation results of inductance parameter identification and stroke observation
图11为120 W直线振荡电机实验平台,负载为气缸提供的非线性气体力,三相调压器用于调节母线电压,直线位移传感器(Linear Variable Dis- placement Transducer, LVDT)用于检验行程估算结果,控制系统采用STM32F407芯片,中断周期为5 kHz。

图11 实验平台
Fig.11 Experiment platform
对文中所提基于QSG的活塞振幅计算方法进行实验验证。在电机起动过程中,分别采用传统振幅检测算法与基于QSG的幅值计算方法获取活塞振幅,实验结果如图12所示。
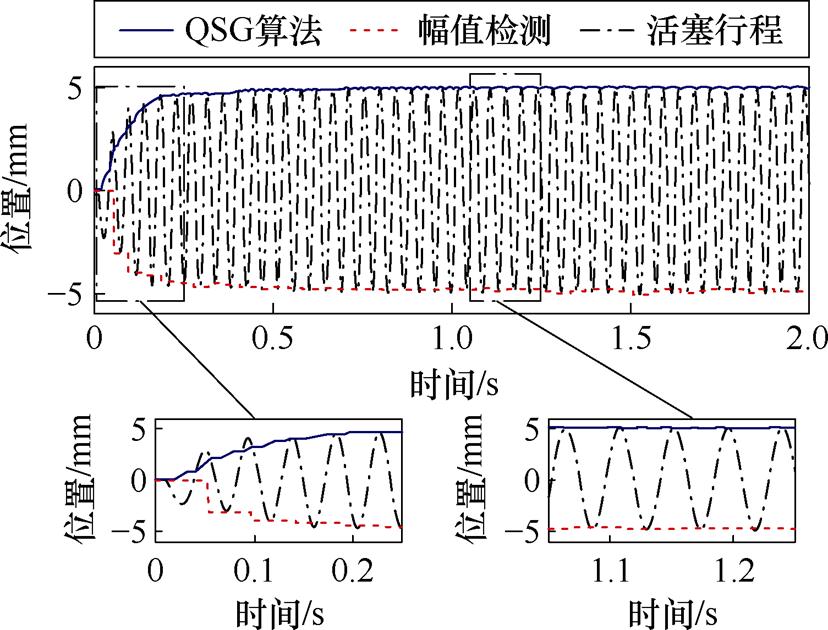
图12 不同幅值计算方法实验结果
Fig.12 Experimental results of different amplitude calculation methods
由图12可知,在电机起动过程中,基于QSG的幅值计算方法所得结果更加平滑稳定,有利于振幅闭环控制,且在稳态运行状态下,其准确度相较传统幅值检测算法更高,减小了活塞振幅的误差。
为验证在不同参数失配情况下参数辨识算法的有效性和鲁棒性,分别设置观测器电感初始参数为0.7 H和1.0 H,以模拟实际运行时电感参数偏小与偏大的情况。在电机运行状态下起动参数辨识算法,电感参数的辨识结果如图13所示,可见无论初始参数偏小或偏大,所设计的参数辨识算法均可有效收敛至真实值。参数辨识的过程用时约0.3 s,收敛速度较快且超调量较小。同时,稳态下参数辨识结果波动较小。实验结果证明了本文所提辨识算法具有较好的动态和稳态性能。
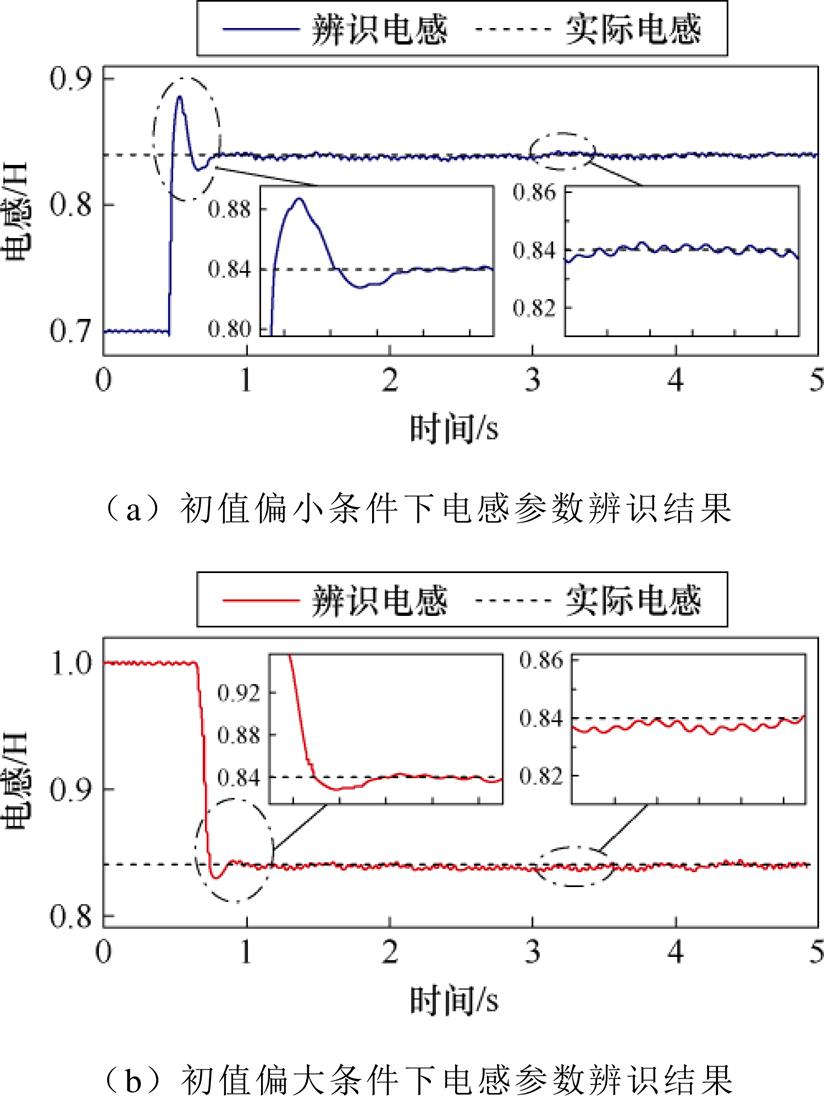
图13 电感参数辨识实验结果
Fig.13 Experimental results of inductance parameter identification
为进一步验证不同驱动频率下参数辨识算法对行程观测精度的影响,分别进行不同频率下的行程观测实验。在观测器中输入有误差的初始电感参数,同时在电机运行过程中起动参数辨识算法并对观测器参数进行校正。驱动频率21、23.5及26 Hz下的实验结果如图14所示。
由图14可知,不同驱动频率下观测器参数误差均会导致观测结果与真实值存在偏差。其中,在谐振频率23.5 Hz时观测误差较小,低于谐振频率时误差主要来自相位偏差,而高于谐振频率时误差主要来自幅值偏差。实验结果与伯德图及理论分析相符。当起动参数辨识算法后,随着观测器参数误差修正,行程观测结果精度得到了显著提升。由实验结果可知,在不同驱动频率下参数辨识算法均可有效提高行程观测的精度,观测结果的幅值和相位误差均得到了改善。相较之下,21 Hz及23.5 Hz驱动下的行程观测精度略优于26 Hz工况,该实验结果与幅频曲线分析结果相符。
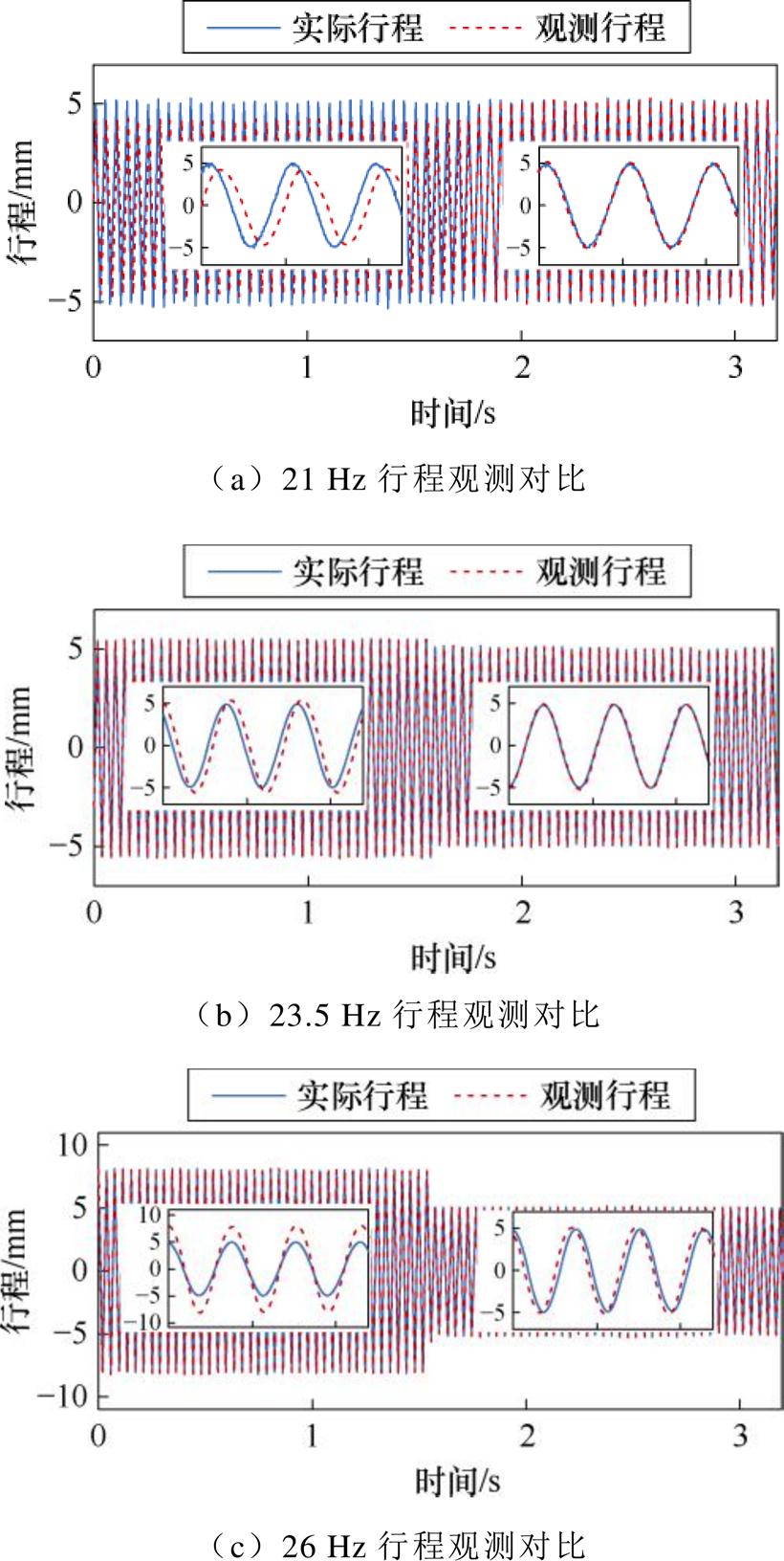
图14 不同驱动频率行程观测实验结果
Fig.14 Observation experimental results at different driving frequency positions
重载时,由于电机电流增大,铁心出现饱和现象,导致电机的电感参数减小。使用20 mm直径活塞气缸作为LOM的负载,采用振幅闭环控制,设定初始振幅为5 mm,在负载工况使用准确的电感参数起动电机,此时气缸内压强为0.06 MPa。随后将给定振幅提升至7 mm,气缸内压强上升至0.1 MPa。待电机运行稳定后,切入参数辨识算法。电感参数辨识结果与行程观测结果如图15所示。
由图15可知,在重载条件下提升行程振幅后,由于饱和现象,电机电感参数发生了变化,导致行程观测结果出现较大偏差。由于活塞振幅闭环中使用观测位置信号进行控制,且观测结果幅值较实际值偏小,故在此状态下活塞振幅略高于给定值7 mm。在切入参数辨识算法后,辨识方法能够有效获取变化后的电感参数。由于铁心饱和现象,电机电感参数的辨识值由0.84 H下降至约0.80 H,尽管难以获取此工况下电感参数的实际值,但通过如图15b所示实验结果中位置观测值准确度的提高,可间接验证本控制算法电感参数辨识结果的准确性。与此同时,由于行程观测误差的降低,活塞振幅与给定值7 mm基本一致,此时电机电流幅值相较切入参数辨识前略有下降。
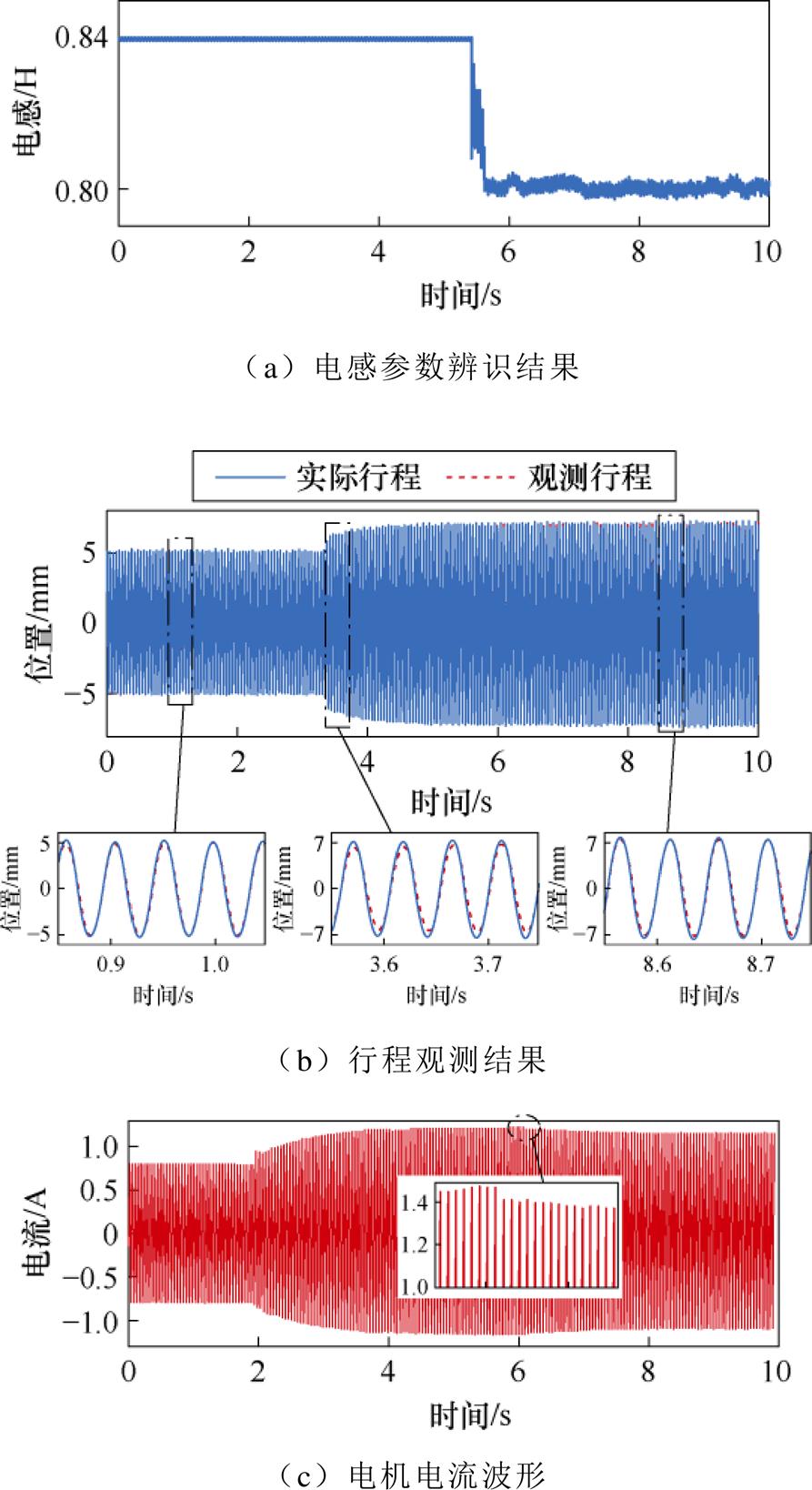
图15 负载变振幅工况实验结果
Fig.15 Experimental results of variable amplitude load conditions
除此之外,为验证参数辨识算法在瞬态工况下的效果,进行参数辨识下的变载实验。对于LOM,无法直接改变气缸中的气体负载性质,因此加减载采用增减活塞振幅的方式进行。采用振幅闭环控制,给定活塞振幅5 mm起动电机,在电机起动过程中即开启参数辨识算法,对位置观测器的参数进行校正。待电机运行至稳态后,将活塞振幅提升至7 mm,此瞬态工况下电感参数辨识结果、位置观测对比结果如图16所示。
由图16可知,负载突增后,电感参数辨识结果经过约1 s收敛至真实值约0.8 H,参数辨识速度较快。在负载突增后的暂态,由于观测器所使用的电感参数存在偏差,在短时间内行程观测结果与实际值有一定误差。当参数辨识完成收敛后,活塞行程观测结果与真实值基本吻合,验证了控制算法在瞬态下的有效性。
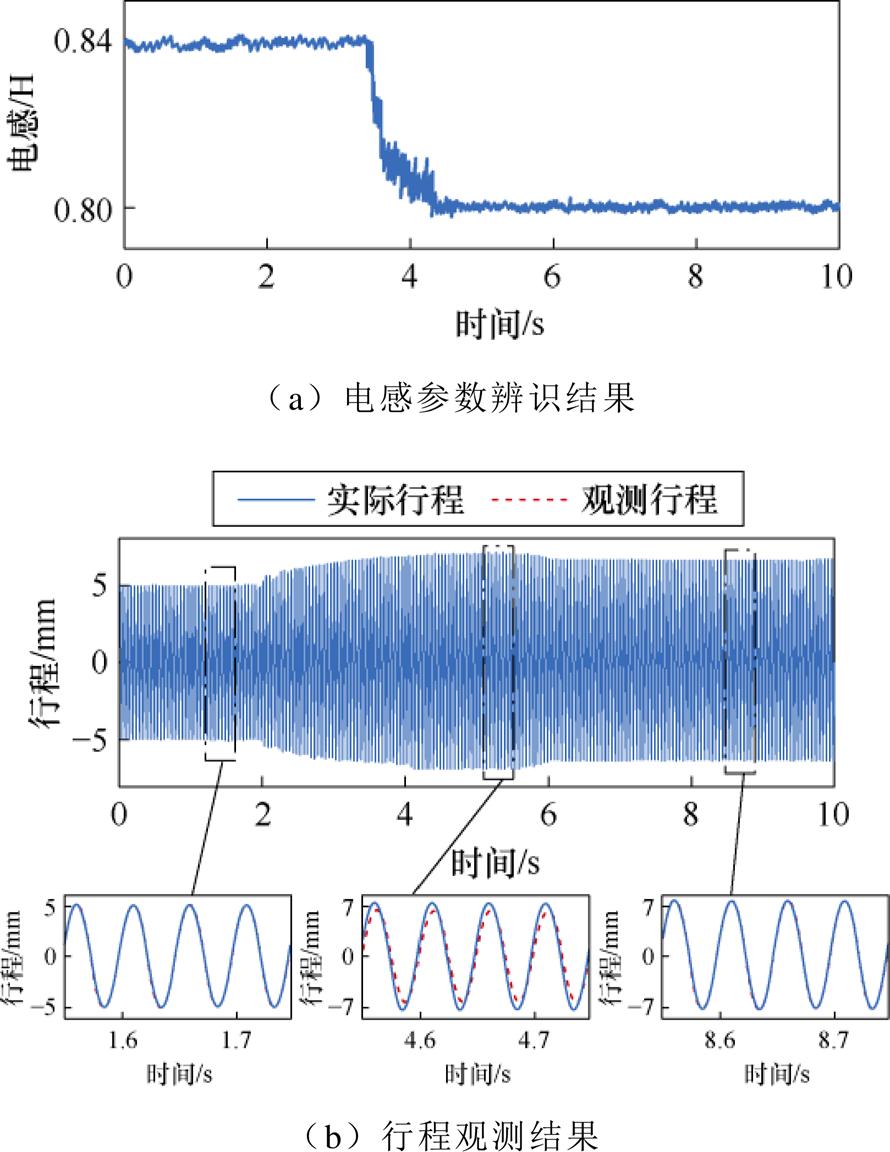
图16 瞬态工况参数辨识实验结果
Fig.16 Experimental results of transient operating condition parameter identification
由上述分析可知,本文提出的控制策略主要适用于绕组电阻变化不大的工作场合,此时铁心饱和导致的电感变化为位置观测误差的主要来源。当绕组电阻因温升变化较大时,该方法观测结果的准确性会受到轻微影响。
为提高直线振荡电机行程观测精度,本文提出一种基于在线参数辨识及AHEF的改进型无位置传感器控制策略。首先,采用频域法对反电动势积分法的参数敏感性进行分析,总结影响观测结果的主要参数。然后,为实现对电机变化参数的精确跟踪,提出一种基于高频电压注入的电机参数在线辨识方法,同时设计了一种基于AHEF的新型谐波信号提取方法,用于精准提取基波信号中所包含的高频谐波分量。最后,仿真和实验结果表明,不同运行工况下,所提方法位置观测幅值误差小于5%,相位误差小于5°,显著提高了行程观测准确度。
参考文献
[1] 徐伟, 李想, 廖凯举, 等. 直线振荡电机拓扑结构及应用综述[J]. 电工技术学报, 2022, 37(21): 5377- 5401.
Xu Wei, Li Xiang, Liao Kaiju, et al. Overview of linear oscillatory machines: topology and appli- cation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5377-5401.
[2] 陈梁远, 李黎川. 压缩机用直线电机及其关键技术发展综述[J]. 中国电机工程学报, 2013, 33(15): 52-68, 15.
Chen Liangyuan, Li Lichuan. Development of the linear motor and its key technologies for reciprocating compressors[J]. Proceedings of the CSEE, 2013, 33(15): 52-68, 15.
[3] Norhisam M, Wong K C, Mariun N, et al. Thrust characteristics of linear oscillatory actuator for liquid pump and its effect to vibration[C]//The fifth inter- national symposium on Linear Drives for Industry Applications, Kobe-Awaji, 2005: 60-63.
[4] Chen Zhiqian, Mutuwo T, Shinji D, Shigeru Okuma, An extended electromotive force model for sensorless control of interior permanent magnet synchronous motors[J]. IEEE Transaction on Industrial Electronics, 50(2): 288-295.
[5] 谢洁飞. 动磁式直线压缩机理论与试验研究[D]. 杭州: 浙江大学, 2005.
Xie Jiefei. Study of theory and testing on a moving magnet linear compressor[D]. Hangzhou: Zhejiang University, 2005.
[6] Liao Kaiju, Xu Wei, Bai Lili, et al. Improved position sensorless piston stroke control method for linear oscillatory machine via an hybrid terminal sliding- mode observer[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14186-14197.
[7] 夏永明. 新型双定子直线振荡电机的研究[D]. 杭州: 浙江大学, 2007.
Xia Yongming. Research on the novel linear oscillatory motor with two separated stators[D]. Hangzhou: Zhejiang University, 2007.
[8] 雷美珍. 新型无内定子动磁式直线振荡执行器的设计及其关键技术研究[D]. 杭州: 浙江理工大学, 2014.
Lei Meizhen. Design and essential technologies research of a novel moving-magnet linear oscillatory actuator with no inner-stators[D]. Hangzhou: Zhejiang Sci-Tech University, 2014.
[9] Suzuki T, Koyama M, Nagata S, et al. Position sensor-less resonant frequency estimation method for linear compressor with assist springs[C]//2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 2020: 1206-1212.
[10] Chun T W, Ahn J R, Lee H H, et al. A novel strategy of efficiency control for a linear compressor system driven by a PWM inverter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 296-301.
[11] Zhang Tao, Yu Haitao. A novel strategy of resonant frequency tracking control for linear compressor[C]// 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-6.
[12] Chun T W, Ahn J R, Tran Q V, et al. Method of estimating the stroke of LPMSM driven by PWM inverter in a linear compressor[C]//APEC 07-Twenty- Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 2007: 403-406.
[13] 廖凯举, 徐伟, 葛健, 等. 基于积分滑模观测器的直线振荡电机谐振频率跟踪控制[J]. 电工技术学报, 2024, 39(14): 4366-4376.
Liao Kaiju, Xu Wei, Ge Jian, et al. Resonant frequency tracking control of linear oscillatory machine based on integral sliding mode observer[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4366-4376.
[14] 余海涛, 张涛. 直线振荡电机谐振频率跟踪控制技术研究[J]. 电机与控制学报, 2019, 23(6): 63-72.
Yu Haitao, Zhang Tao. Strategy of resonant frequency tracking for linear oscillatory actuator[J]. Electric Machines and Control, 2019, 23(6): 63-72.
[15] Xu Wei, Liao Kaiju, Wang Qizhe, et al. A stroke estimation method for linear oscillatory machine using an improved sliding mode observer[J]. IEEE Transactions on Industry Applications, 2022, 58(6): 7286-7296.
[16] Latham J, McIntyre M L, Mohebbi M. Sensorless resonance tracking and stroke control of a linear vapor compressor via nonlinear observers[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3720-3729.
[17] Xu Wei, Wang Qizhe, Li Xiang, et al. A novel resonant frequency tracking control for linear compressor based on MRAS method[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 227-236.
[18] Xu Wei, Wang Qizhe, Liu Yi, et al. Adaptive full-order displacement observer for sensorless resonant frequency tracking control of linear oscillatory machines[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1310-1321.
[19] Zhang Tao, Yu Haitao. Parameter estimation of linear oscillatory actuator with RLS method[C]//20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-6.
[20] Wang Liqiang, Lei Meizhen. Research on observer algorithm of mover displacement for linear oscillatory actuator based on online stator resistance identi- fication[C]//Chinese Control and Decision Confer- ence (CCDC), Shenyang, China, 2018: 6614- 6618.
[21] 李东暘. 直线振荡电机控制系统设计及其无位置控制算法研究[D]. 南京: 东南大学, 2020.
Li Dongyang. Reseach on control system and sensorless control method of linear ocsillatory motor[D]. Nanjing: Southeast University, 2020.
[22] Cadman R V, Cohen R. Electrodynamic oscillating compressors: part 1-design based on linearized loads[J]. Journal of Basic Engineering, 1969, 91(4): 656-663.
[23] 于明湖. 直线压缩机用横向磁通永磁直线振荡电机系统研究[D]. 杭州: 浙江大学, 2011.
Yu Minghu. Research on system of transverse-flux permanent magnet linear oscillatory actuator for linear compressor[D]. Hangzhou: Zhejiang University, 2011.
[24] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Inductance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607-1616.
[25] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[26] 刘亚静, 段超. 全数字自适应滤波器不同离散结构的性能对比分析[J]. 电工技术学报, 2021, 36(20): 4339-4349.
Liu Yajing, Duan Chao. Performance comparison and analysis of all-digital adaptive filter with different discrete methods[J]. Transactions of China Electro- technical Society, 2021, 36(20): 4339-4349.
Improved Sensorless Control of Linear Oscillatory Machine Based on Online Parameter Identification and Adaptive Harmonic Extraction Filter
Abstract Sensorless control is an important control strategy for linear oscillatory machines (LOM). The traditional position observer often has low accuracy and poor anti-interference ability. The deviation of stroke observation affects the closed-loop control of piston stroke and resonance frequency tracking control of LOM. Therefore, this paper provides an improved sensorless control method for LOM based on online parameter identification and adaptive harmonic extraction filters.
Firstly, the amplitude-frequency characteristic is applied to analyze parameter sensitivity for LOM. The impacts of different circuit parameters on stroke observation are analyzed. It is proved that the inductance parameter has a more prominent impact on stroke observation. Therefore, the main object of the parameter identification algorithm is the inductance parameter. Secondly, a parameter identification strategy based on a high-frequency injection method is designed. The influence of high-frequency voltage excitation on LOM is studied by analyzing the forced vibration system, and the feasibility of the algorithm in online parameter identification is demonstrated. Then, a new adaptive harmonic extraction filter is designed to solve the harmonic extraction problem, and the fundamental signal can be effectively decayed. Furthermore, an amplitude calculation method based on an orthogonal generator is designed to accelerate data update speed and improve stability, which can obtain accurate piston amplitude information. Finally, the simulation and experimental results show that this method can accurately identify the motor parameters, thereby improving the accuracy of stroke observation.
The following conclusions can be drawn. (1) The impact of a 5% deviation in inductance parameters on stroke observation is much greater than the 10% deviation in resistance parameters, indicating that the accuracy of the stroke observation algorithm is mainly affected by the inductance parameter. (2) Injecting high-frequency voltage signals during LOM operation has little impact on the movement of the piston. (3) The designed adaptive harmonic extraction filter can extract harmonic signals with smaller amplitudes. The extraction of harmonic signals is more accurate and stable than second-order generalized integrators. (4) Compared with the traditional stroke observation method, the accuracy of the stroke observation after parameter identification and correction is significantly improved.
In conclusion, the proposed stroke observation algorithm solves the traditional algorithm’s high parameter sensitivity problem. It can obtain accurate stroke observation results even in the case of inaccurate parameters and dynamic changes in parameters.
Keywords:Linear oscillatory machine (LOM), parameter identification, high-frequency voltage injection, sensorless control
中图分类号:TM32
DOI: 10.19595/j.cnki.1000-6753.tces.231617
国家自然科学基金面上项目(52277050)、深圳市协同创新计划国际科技合作项目(GJHZ20210705142539007)资助。
收稿日期 2023-10-06
改稿日期 2023-11-14
葛 健 男,1994年生,博士,研究方向为新型直线电机电磁设计与特性分析。
E-mail: gejian1994@hust.edu.cn
徐 伟 男,1980年生,教授,博士生导师,研究方向为直线电机设计及控制。
E-mail: yangsyhfah@163.com(通信作者)
(编辑 崔文静)