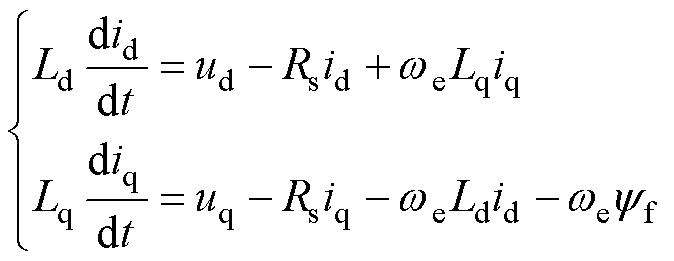 (1)
(1)
摘要 在永磁同步电机(PMSM)有限集模型预测磁链控制策略(FCS-MPFC)中,磁链给定值计算、实际值获取以及未来值预测都要用到电机参数。受工况和温度的影响,电机参数具有变化性,参数偏差将影响实际预测控制性能。为提高控制系统鲁棒性,需要对电机d、q轴电感和永磁磁链进行在线辨识。鉴于此,该文提出了永磁同步电机多参数辨识方案,并基于此设计了FCS-MPFC策略。首先,依据电机稳态方程,设计了广义比例积分观测器(GPIO)对PMSM的q轴电感和永磁磁链进行辨识。其次,利用FCS-MPFC中电机定子电流变化较大的特征,提出了基于电流变化量的d轴电感辨识方法,克服了多参数辨识的欠秩问题。再次,依据FCS-MPFC策略下逆变器电压输出特性,优化设计了电流采样,有效避免了逆变器死区对辨识效果的影响。最后,针对磁链预测过程,设计了基于GPIO的磁链预测模型,进一步提高磁链预测的参数鲁棒性。该文的分析、设计以及性能提升均得到实验验证。
关键词:有限集模型预测磁链控制 广义比例积分观测器 多参数辨识 参数鲁棒性
有限集模型预测控制(Finite Control Set-Model Predictive Control, FCS-MPC)具有概念简单、适用范围广、易于考虑系统非线性约束、无需设计控制器等优点,成为近年来的研究热点之一[1-2]。有限集模型预测磁链控制(FCS-Model Predictive Flux Control, FCS-MPFC)是在有限集模型预测转矩控制(FCS-Model Predictive Torque Control, FCS- MPTC)的基础上发展而来,其将转矩和磁链幅值的控制等效为d、q坐标轴下定子磁链矢量的控制,避免了FCS-MPTC成本函数中的权重系数[3-4]。但FCS-MPFC由于磁链的计算对参数依赖较强,参数偏差将影响实际控制效果[5]。因此,提高FCS-MPC的参数鲁棒性逐渐成为学界研究的热点。就参数鲁棒性而言,主要涉及磁链给定值计算、磁链观测以及磁链预测等环节。
在磁链指令计算方面,目前在FCS-MPFC中可以通过最大转矩电流比(Maximum Torque Per Ampere, MTPA)算法由转矩指令计算定子磁链给定值。在MTPA常见算法中,公式计算法[6]需要电机参数,鲁棒性差;搜索法[7]鲁棒性较强,但会导致电流矢量角在极值处振荡,动态性能不足;注入 法[8]无需模型参数,但会产生转矩脉动和额外损耗;查表法[9]需要繁琐的离线测量。
在磁链观测方面,有电压模型方案和电流模型方案。基于磁链的电压模型进行积分运算获得磁链,具有较强的参数鲁棒性,但存在积分偏置和饱和问题[10],同时也会受到逆变器死区的影响;基于电流模型直接计算获得磁链,需要电机电感和永磁磁链等参数,有着较强的参数依赖性。近年来,基于观测器的磁链观测方案也有研究报道,虽然一定程度上能够降低参数依赖性,但依然会受到逆变器死区的影响,且系统存在稳定性问题。
在磁链预测方面,文献[11]提出无参数模型预测电流控制,基于局部建模原理,采用集总参数对电流进行预测。文献[12]利用时间序列模型反映电机电压、电流等状态变量之间的关系,消除传统参数化建模的影响,提升了鲁棒性。针对模型中的内部扰动量,文献[13-14]分别使用滑模观测器和广义比例积分观测器对其进行补偿。文献[15]提出了一种基于电流差的无模型预测电流控制,但初始阶段无先验信息,实现较为困难。当前预测方案多是建立在当前磁链信息的基础上的,其预测性能依赖当前磁链的观测。
不难发现,上述各个环节均受到参数的影响,若能够对参数进行在线辨识,则可以提升各环节运算精度,从而提升系统的参数鲁棒性。
目前,常用的参数辨识方法有递推最小二乘 法[16]、模型参考自适应法[17]、扩展卡尔曼滤波算 法[18]、粒子群优化算法[19]以及人工智能算法等。但上述方法在进行多参数辨识时都会遇到辨识方程欠秩问题,导致辨识结果不唯一,陷入局部最优解。针对欠秩问题当前解决方案主要有部分辨识和扰动注入方案。前者通过假设部分电机参数恒定不变或者通过分步辨识减少一次辨识参数个数[20],但实际系统中辨识精度不高。后者则通过注入扰动信号构建新的约束方程[21],但扰动信号的注入导致转矩脉动和损耗的增加。因此,寻找一种无需注入信号的多参数辨识方案成为亟待解决的问题。
此外,逆变器死区时间使得通过开关状态计算得到的定子电压值与实际值出现偏差,影响状态量的计算和观测。目前,最常用的解决方案是依据电流的流向对电压补偿[22]。然而,电流过零附近的极性容易出现误判,影响了实际效果。近年来,也有将电压偏差作为扰动项进而通过设计扰动观测器对其进行估算的研究报道[23-24],但观测器本身依赖于电机参数,不适用于参数辨识。此外,针对死区对电流的影响,也有学者直接对电流谐波设计闭环控制[25-26]或者通过自适应补偿器生成死区电压补偿值[27]的研究报道,但这类方法不适用于FCS-MPFC,且多个控制回路相互耦合,设计较为困难。因此,在FCS-MPFC中,参数鲁棒性与死区效应两者相互制约,很难同时解决。
鉴于此,本文提出一种适用于FCS-MPFC的多参数在线辨识方案。所提方案利用广义比例积分观测器(Generalized Proportional Integral Observer, GPIO)构建q轴电感和转子磁链辨识方程,并通过电流差分方程对d轴电感进行辨识以解决欠秩问题。此外,针对FCS-MPFC的电压矢量输出特性通过优化电流采样,避免了逆变器死区对参数辨识的影响,进而同时解决了FCS-MPFC中参数鲁棒性和死区补偿的问题,提升了磁链预测控制的准确性和鲁棒性。最后,本文通过实验验证了所提方案的有效性。
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)在同步旋转坐标系下的数学模型为
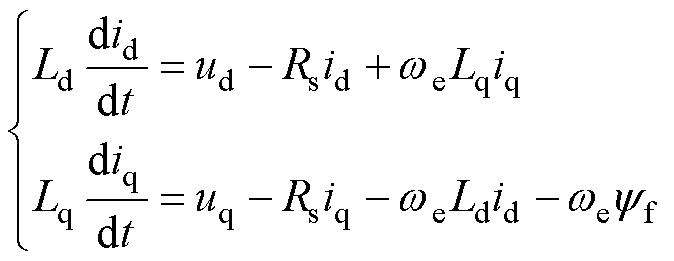 (1)
(1)
式中,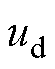 、
、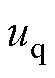 分别为d、q轴定子电压分量;
分别为d、q轴定子电压分量;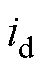 、
、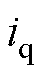 分别为d、q轴定子电流分量;
分别为d、q轴定子电流分量;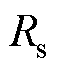 为定子电阻;
为定子电阻;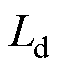 、
、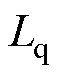 分别为d、q轴的定子电感实际值;
分别为d、q轴的定子电感实际值;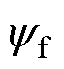 为永磁磁链实际值;
为永磁磁链实际值;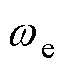 为电角速度。
为电角速度。
定子磁链方程为
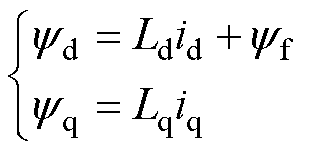 (2)
(2)
式中,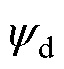 、
、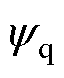 分别为d、q轴定子磁链分量。
分别为d、q轴定子磁链分量。
电磁转矩方程为
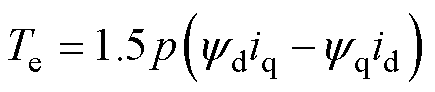 (3)
(3)
式中,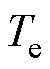 为电磁转矩;
为电磁转矩;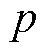 为电机极对数。
为电机极对数。
FCS-MPFC策略的基本思路是通过对电压矢量集中的每个矢量作用下的磁链响应进行预测和评估,从而选出最优电压矢量作为逆变器下一拍的输出量。当使用三相两电平逆变器时,基本电压矢量集由6个非零矢量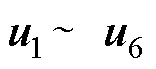 和2个零矢量
和2个零矢量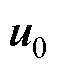 、
、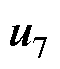 组成。结构上FCS-MPFC包括磁链给定值计算、磁链预测和电压矢量择优三部分。
组成。结构上FCS-MPFC包括磁链给定值计算、磁链预测和电压矢量择优三部分。
依据MTPA原理,磁链给定与电磁转矩指令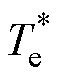 的关系可表示为
的关系可表示为
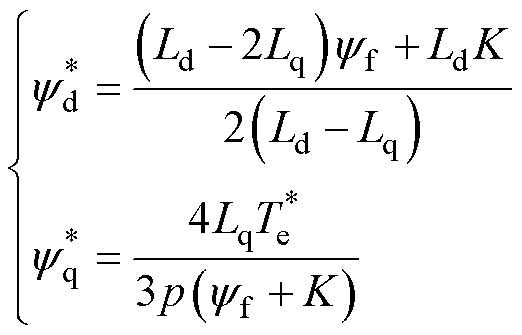 (4)
(4)
其中
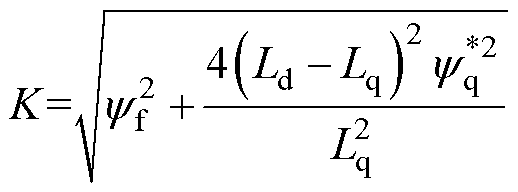
式中,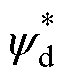 、
、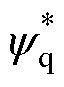 分别为d、q轴定子磁链给定值。
分别为d、q轴定子磁链给定值。
磁链预测值则可根据式(1)、式(2)通过欧拉离散化得到,即
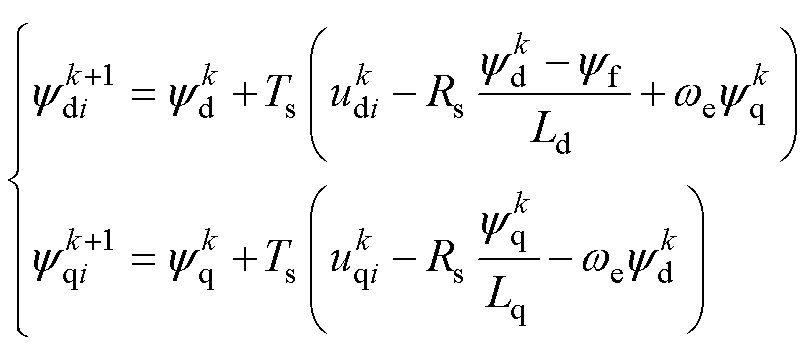 (5)
(5)
式中,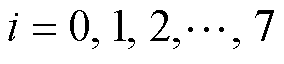 ;
;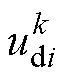 、
、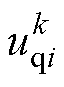 分别为
分别为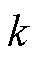 时刻电压矢量
时刻电压矢量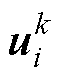 的d、q轴分量;
的d、q轴分量;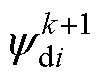 、
、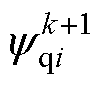 分别为在电压矢量
分别为在电压矢量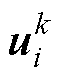 作用下的
作用下的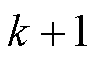 时刻d、q轴磁链预测值;
时刻d、q轴磁链预测值;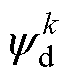 、
、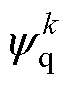 为
为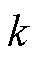 时刻磁链观测值,由式(2)得到;
时刻磁链观测值,由式(2)得到;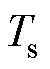 为采样周期。
为采样周期。
电压矢量的择优则通过构建代价函数进行评价,其表达式为
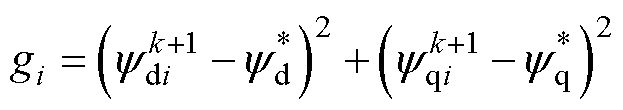 (6)
(6)
将式(5)中的预测磁链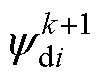 、
、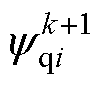 代入式(6),使得
代入式(6),使得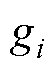 取最小值的电压矢量即为最优矢量,在该矢量作用下一个周期后磁链观测值与给定值之间的误差最小。另外,通常要考虑在数字控制器中存在的一拍延时,即在
取最小值的电压矢量即为最优矢量,在该矢量作用下一个周期后磁链观测值与给定值之间的误差最小。另外,通常要考虑在数字控制器中存在的一拍延时,即在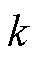 时刻求解得到的最优电压矢量
时刻求解得到的最优电压矢量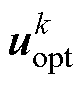 在
在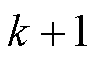 时刻才能施加于逆变器,可通过两步预测对延时进行补偿。
时刻才能施加于逆变器,可通过两步预测对延时进行补偿。
无论是磁链给定值计算还是预测值的估算都要用到电机参数,但电机实际运行时参数会随着工况和温度的变化而变化,参数偏差势必造成控制误差,当偏差较大时更有可能导致控制系统失稳。
本节就参数偏差对控制造成的影响进行分析。所述分析均是在本文所用实验电机参数的基础上进行,其中d轴电感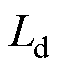 =6.55 mH、q轴电感
=6.55 mH、q轴电感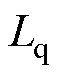 =10.65 mH、永磁磁链
=10.65 mH、永磁磁链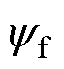 =0.231 Wb以及定子电阻
=0.231 Wb以及定子电阻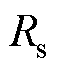 =0.937
=0.937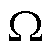 。另外,其他条件为:电机为4对极、逆变器直流侧电压为360 V、给定转矩为额定转矩9.6 N·m以及转速为额定转速1 500 r/min。
。另外,其他条件为:电机为4对极、逆变器直流侧电压为360 V、给定转矩为额定转矩9.6 N·m以及转速为额定转速1 500 r/min。
定子电阻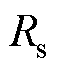 的变化与电机工作温度线性相关,在实际应用中可通过在定子绕组中预埋热敏电阻估算温度进而对电阻值进行实时修正。而且,电阻的影响主要体现在定子电阻压降上,在转速较高时该影响可忽略。因此,在本文后续分析中认为电阻值
的变化与电机工作温度线性相关,在实际应用中可通过在定子绕组中预埋热敏电阻估算温度进而对电阻值进行实时修正。而且,电阻的影响主要体现在定子电阻压降上,在转速较高时该影响可忽略。因此,在本文后续分析中认为电阻值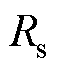 固定。d、q轴定子电感受磁路饱和影响,会随着电流的变化而发生变化。永磁磁链会随温度的升高出现退磁现象,幅值降低,且这一关系具有较强的非线性特征,难以通过温度检测进行校正。当电机参数存在偏差时,定义标称参数与实际参数之间的关系为
固定。d、q轴定子电感受磁路饱和影响,会随着电流的变化而发生变化。永磁磁链会随温度的升高出现退磁现象,幅值降低,且这一关系具有较强的非线性特征,难以通过温度检测进行校正。当电机参数存在偏差时,定义标称参数与实际参数之间的关系为
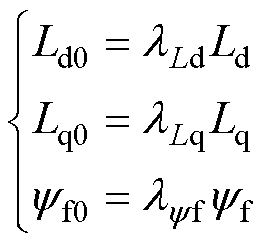 (7)
(7)
式中,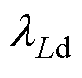 、
、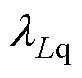 和
和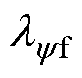 分别为相应参数标称值和实际值之间的偏差系数;
分别为相应参数标称值和实际值之间的偏差系数;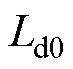 、
、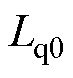 和
和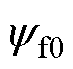 为对应的标 称值。
为对应的标 称值。
考虑到参数偏差,磁链给定计算式(4)将重新表述为
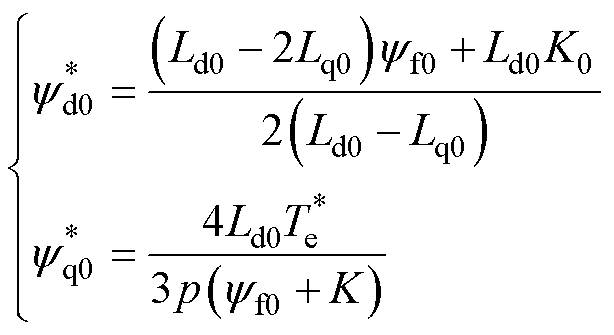 (8)
(8)
其中
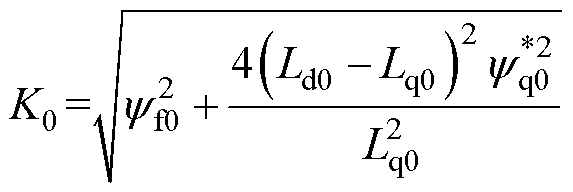
式中,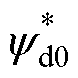 、
、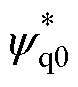 分别为电机参数存在偏差时的d、q轴定子磁链给定值。
分别为电机参数存在偏差时的d、q轴定子磁链给定值。
定义磁链给定值计算误差为
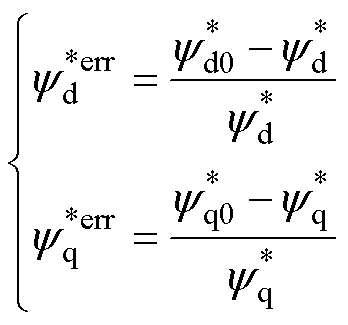 (9)
(9)
将式(4)和式(8)代入式(9)中,可得不同参数偏差下磁链指令的计算误差,如图1所示。对于d轴磁链给定值计算误差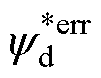 而言,
而言,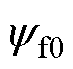 偏差量的影响最大,
偏差量的影响最大,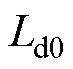 和
和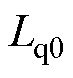 偏差量的影响相对较小。
偏差量的影响相对较小。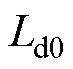 和
和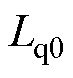 偏差为50%时磁链给定值计算误差
偏差为50%时磁链给定值计算误差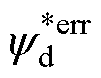 不超过0.4%和0.8%。然而,偏差
不超过0.4%和0.8%。然而,偏差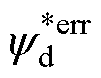 几乎与
几乎与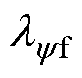 成正比,当
成正比,当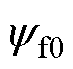 的偏差达到50%时
的偏差达到50%时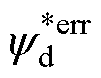 也高达50%,给定值
也高达50%,给定值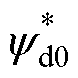 出现严重偏离。q轴磁链给定值计算误差
出现严重偏离。q轴磁链给定值计算误差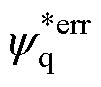 主要受
主要受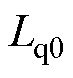 和
和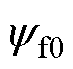 的影响,
的影响,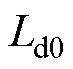 的影响较小。
的影响较小。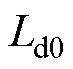 偏差为50%时误差
偏差为50%时误差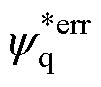 不超过0.9%,而
不超过0.9%,而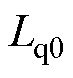 偏差50%时
偏差50%时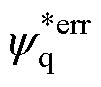 为50%,
为50%,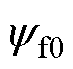 偏差50%时
偏差50%时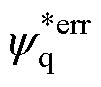 高达88%。
高达88%。
预测模型方程中同样涉及参数,若仍用标称参数,则磁链预测可表示为
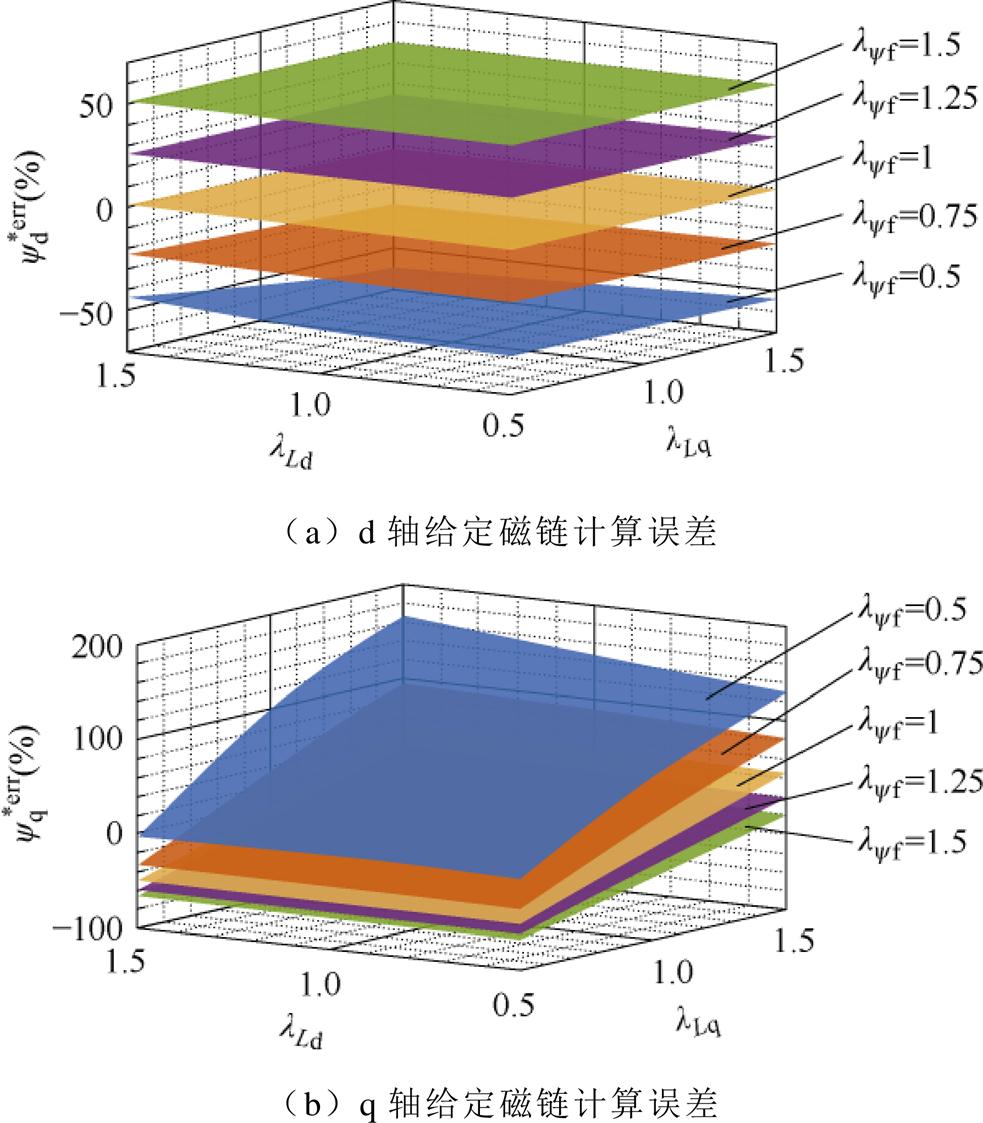
图1 参数偏差时MTPA给定磁链计算误差
Fig.1 Calculation error of the flux linkage reference by MTPA under parameter deviations.
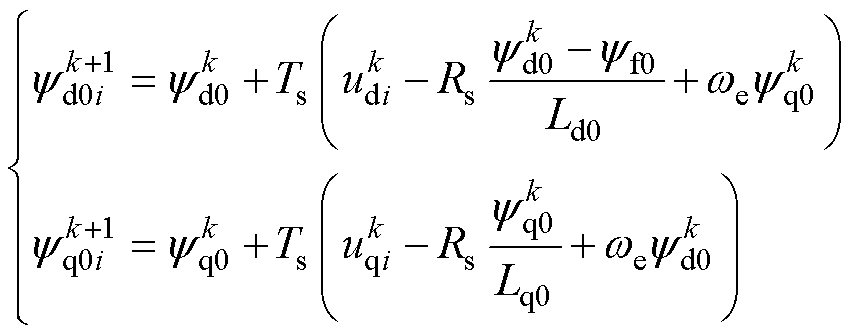 (10)
(10)
其中
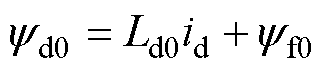
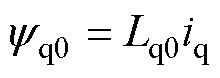
式中,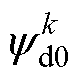 、
、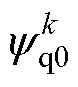 分别为参数存在偏差时当前控制周期的d、q轴磁链观测值;
分别为参数存在偏差时当前控制周期的d、q轴磁链观测值;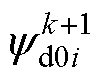 、
、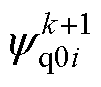 分别为参数存在偏差时在电压矢量
分别为参数存在偏差时在电压矢量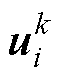 作用下的
作用下的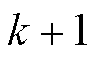 时刻d、q轴磁链预测值。
时刻d、q轴磁链预测值。
由式(5)和式(10)可得预测误差为
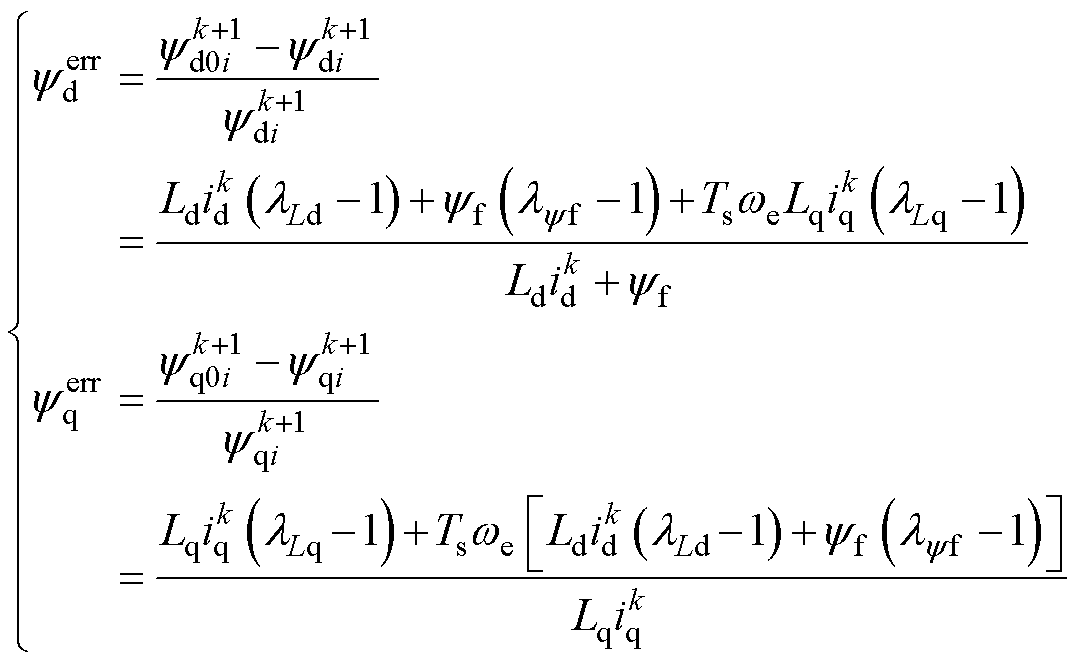 (11)
(11)
由式(11)可得预测误差与参数偏差关系如图2所示。从图中可知,与参数对指令值的影响类似,d轴磁链预测误差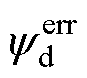 主要受
主要受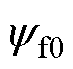 偏差的影响,当
偏差的影响,当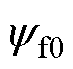 偏差为50%时其误差最大可达50%,而
偏差为50%时其误差最大可达50%,而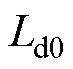 和
和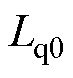 偏差对磁链预测值的影响较小,可忽略不计。q轴磁链预测误差
偏差对磁链预测值的影响较小,可忽略不计。q轴磁链预测误差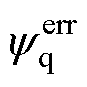 主要受
主要受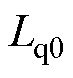 偏差的影响,当
偏差的影响,当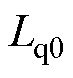 偏差为50%时造成的预测误差最大可达50%,
偏差为50%时造成的预测误差最大可达50%,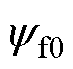 偏差影响次之,其偏差为50%时预测误差为5%,
偏差影响次之,其偏差为50%时预测误差为5%,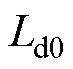 偏差的影响可忽略不计。
偏差的影响可忽略不计。
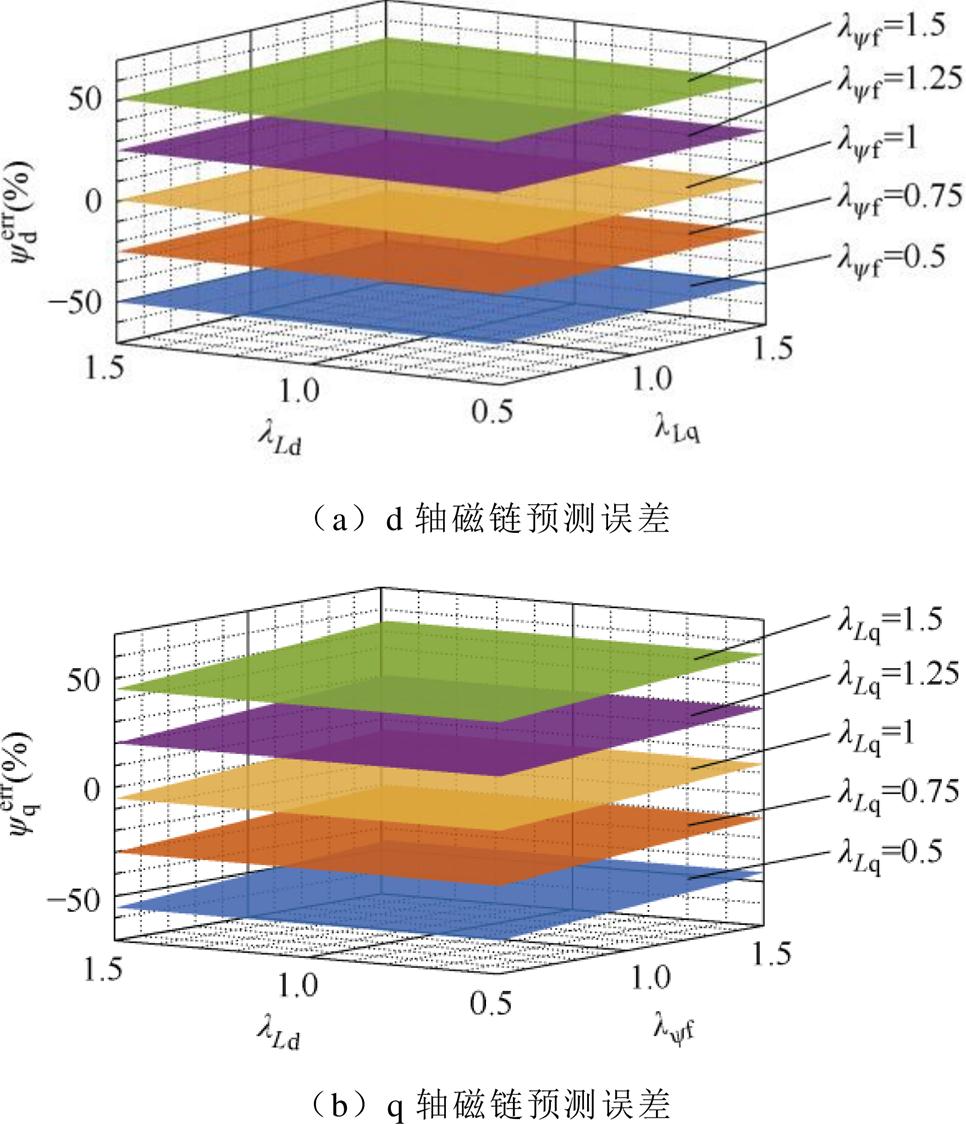
图2 参数偏差时传统预测模型的磁链预测误差
Fig.2 Prediction errors of the flux linkage based on the traditional prediction model under parameters deviations
综上所述,参数的偏差会对d、q轴的定子磁链给定值和预测值造成误差,影响控制性能,其中q轴电感和永磁磁链的影响较大,d轴电感的影响很小可忽略,并且随着参数偏差的增大,控制误差会随之增加,较大的误差甚至会导致系统失稳。因此,为改善系统控制性能,提高系统鲁棒性,需要对电机参数进行在线辨识。
本节通过构建GPIO对由逆变器死区、控制器延迟、采样误差以及电机参数偏差等引起的系统扰动进行观测,并根据扰动观测值对电机参数进行提取,从而实现对参数的辨识。同时,为解决在多参数辨识中存在的欠秩问题,本文根据FCS-MPFC中电机定子电流的特征,利用d轴电流差分方程对d轴的定子电感进行独立辨识。其结构框图如图3所示,图中,PMSM-GPIO为依据电机微分方程建立的广义比例积分观测器,对参数偏差引起的扰动值进行估算,然后通过辨识方程对电机参数进行提取。本节将对各模块的设计过程进行讨论。
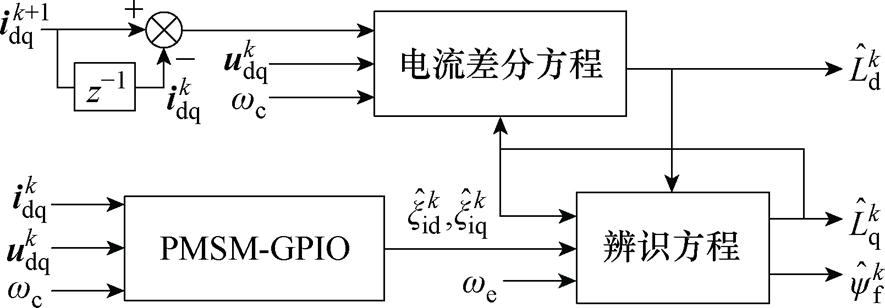
图3 多参数辨识结构框图
Fig.3 Diagram of the multi-parameter identification
采用标称参数可将电机微分方程重新表述为
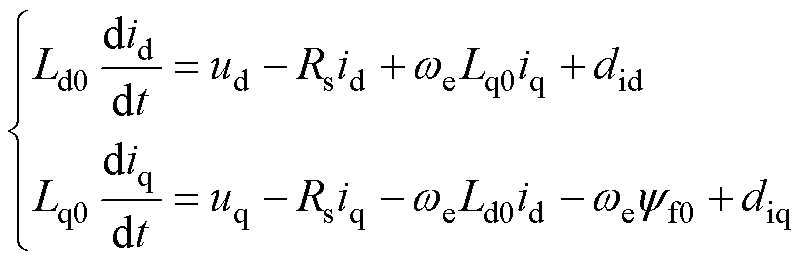 (12)
(12)
式中,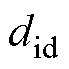 、
、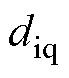 为由参数偏差引起的集总扰动。
为由参数偏差引起的集总扰动。
根据GPIO理论[28],对式(12)设计GPIO如式(13)所示。为便于描述,将其记为PMSM-GPIO。
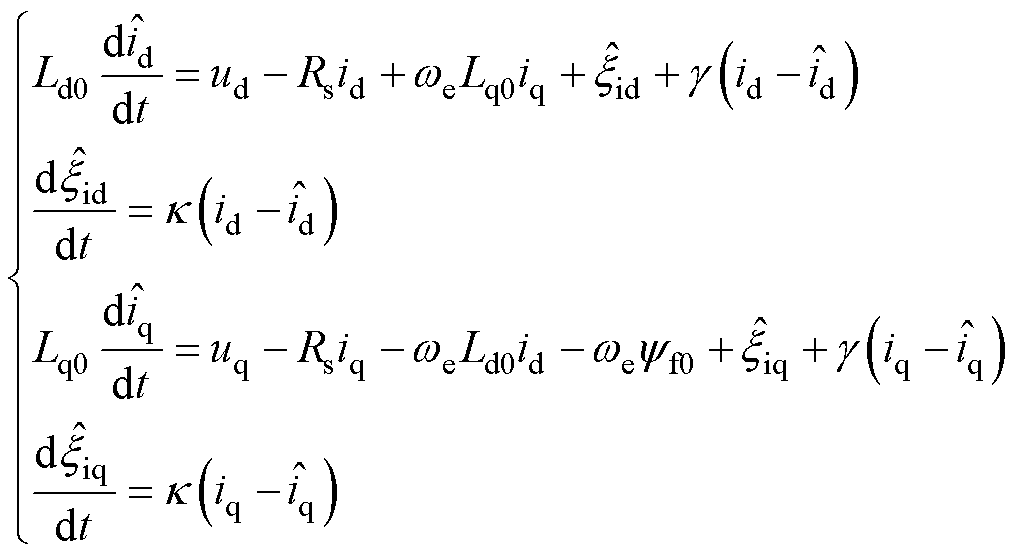 (13)
(13)
式中,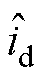 、
、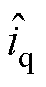 分别为d、q轴的定子电流的观测值;
分别为d、q轴的定子电流的观测值;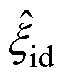 、
、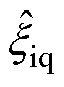 分别为集总扰动
分别为集总扰动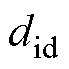 、
、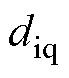 的观测值;g 和k 为观测器参数。
的观测值;g 和k 为观测器参数。
对观测器的收敛性进行验证。由式(12)和式(13)可得PMSM-GPIO观测误差,为了便于分析直接给出其拉氏表达式为
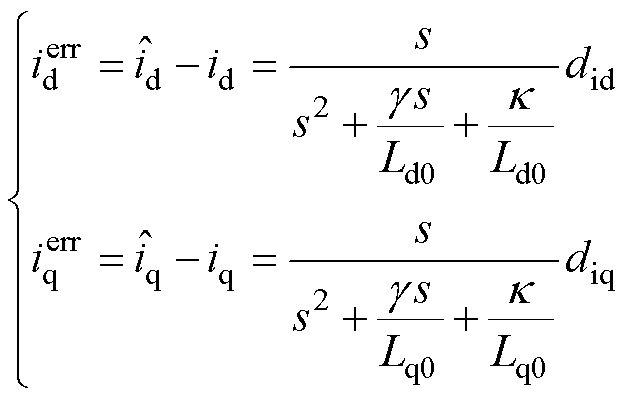 (14)
(14)
令
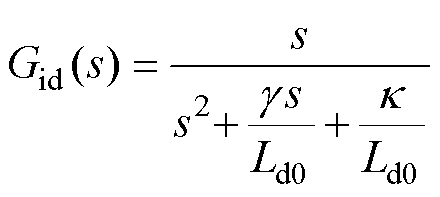
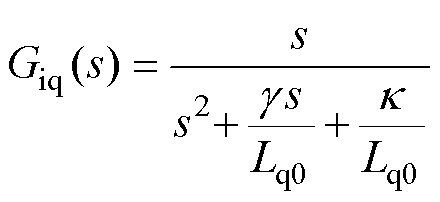
显然,通过观测器参数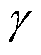 和
和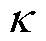 的合理选取,能够使
的合理选取,能够使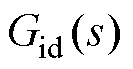 和
和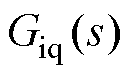 的极点均位于坐标系负半平面,从而在
的极点均位于坐标系负半平面,从而在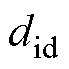 和
和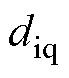 为有限值的情况下,使电流观测误差
为有限值的情况下,使电流观测误差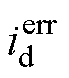 和
和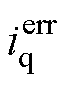 最终收敛于0,电流观测值
最终收敛于0,电流观测值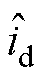 和
和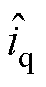 可准确跟踪其实际值
可准确跟踪其实际值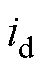 和
和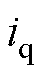 。此时,
。此时,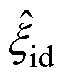 、
、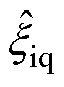 即为集总扰动
即为集总扰动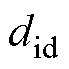 、
、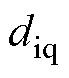 的估计值。
的估计值。
要在数字信号处理器(Digital Signal Processing, DSP)中使用PMSM-GPIO,还需对式(13)进行离散化。为减小离散化误差对参数辨识的影响,这里使用文献[29]中提出的方案4(考虑在一个采样周期内d、q轴的定子电流线性变化)进行离散化,后续对其他方程进行离散化均采用此方案。所得到的离散化PMSM-GPIO为
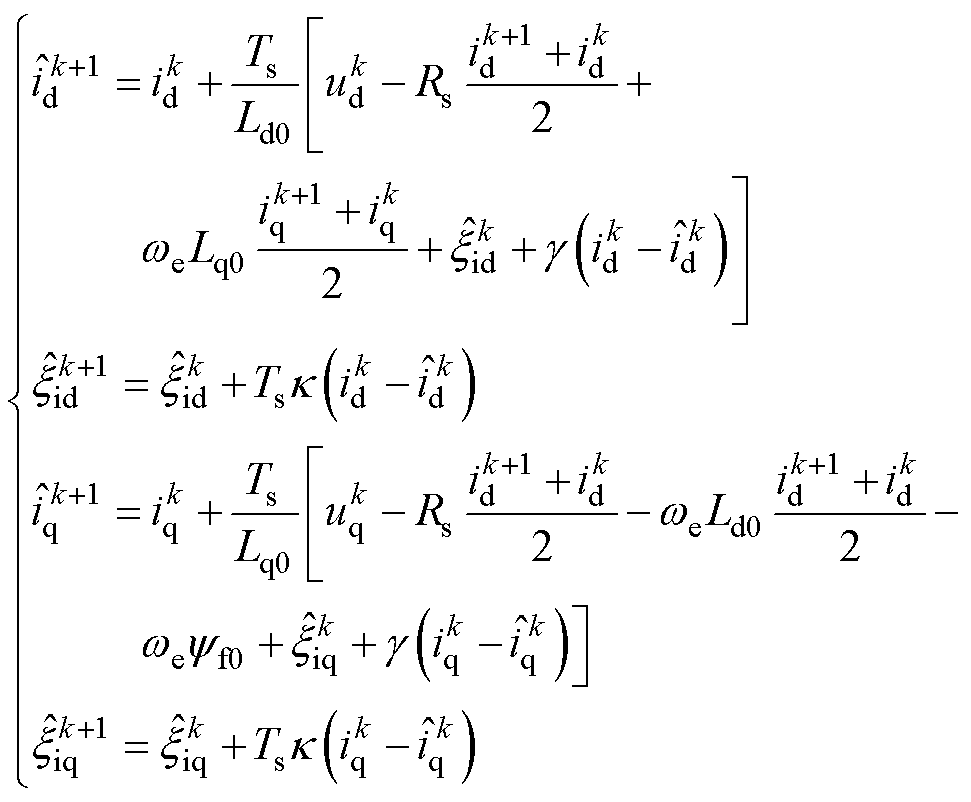 (15)
(15)
首先通过PMSM-GPIO对q轴电感和永磁磁链的辨识方程进行推导。由式(1)和式(13)作差可得
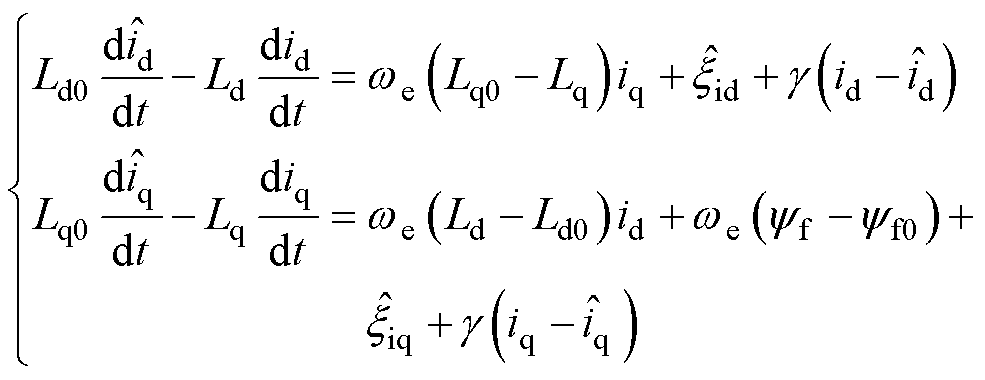 (16)
(16)
稳态时,根据3.1节分析可知,观测器稳定时有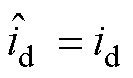 ,
,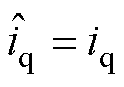 ,
,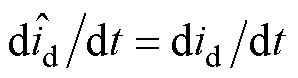 和
和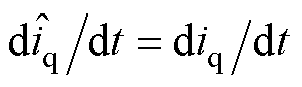 ,因此整理式(16)可得
,因此整理式(16)可得
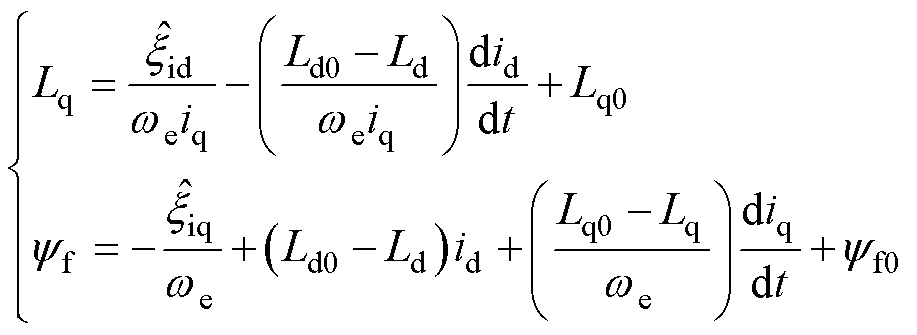 (17)
(17)
由于扰动量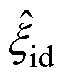 和
和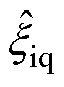 已由式(13)扰动观测器获得,因此可通过式(17)对电机q轴电感和永磁磁链值进行估算。FCS-MPFC离散化的开关控制使得
已由式(13)扰动观测器获得,因此可通过式(17)对电机q轴电感和永磁磁链值进行估算。FCS-MPFC离散化的开关控制使得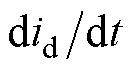 和
和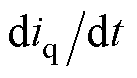 即使在稳态时也并不恒等于零,因此上述两项无法消除。为减小误差,本文选择保留上述两项,但这会分别引入参数实际值
即使在稳态时也并不恒等于零,因此上述两项无法消除。为减小误差,本文选择保留上述两项,但这会分别引入参数实际值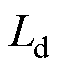 和
和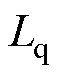 。同时式(17)中
。同时式(17)中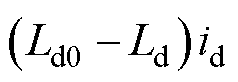 项也包含了
项也包含了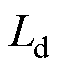 。因此,考虑用辨识值
。因此,考虑用辨识值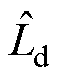 和
和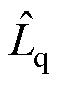 替代
替代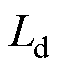 和
和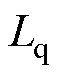 ,即
,即
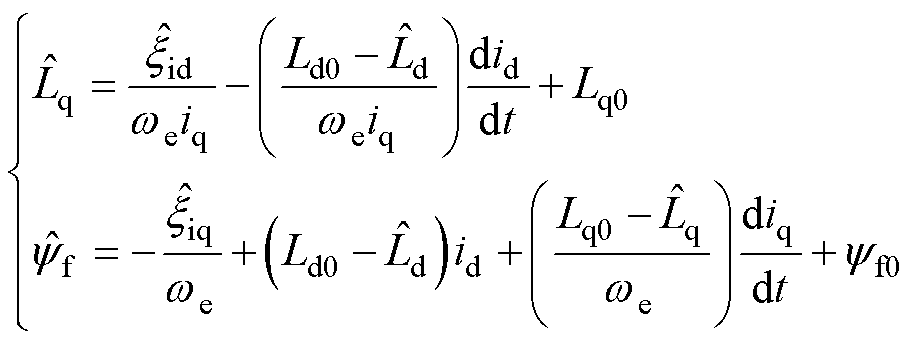 (18)
(18)
式中,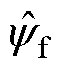 为永磁磁链辨识值。
为永磁磁链辨识值。
但在式(18)中d轴电感辨识值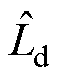 的引入会造成参数辨识中的欠秩问题,为了解决该问题,本文将依据电流变化量另行设计d轴电感的辨识方案,如图3所示。关于
的引入会造成参数辨识中的欠秩问题,为了解决该问题,本文将依据电流变化量另行设计d轴电感的辨识方案,如图3所示。关于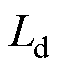 的辨识将在3.3节进行阐述。
的辨识将在3.3节进行阐述。
由式(18)计算得到的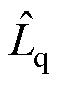 和
和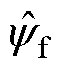 中存在大量的高次谐波噪声。因此,在实际应用时,需要通过低通滤波器对其进行滤波处理。通过对滤波器进行离散化,可得到q轴电感辨识值和永磁磁链辨识值的迭代方程为
中存在大量的高次谐波噪声。因此,在实际应用时,需要通过低通滤波器对其进行滤波处理。通过对滤波器进行离散化,可得到q轴电感辨识值和永磁磁链辨识值的迭代方程为
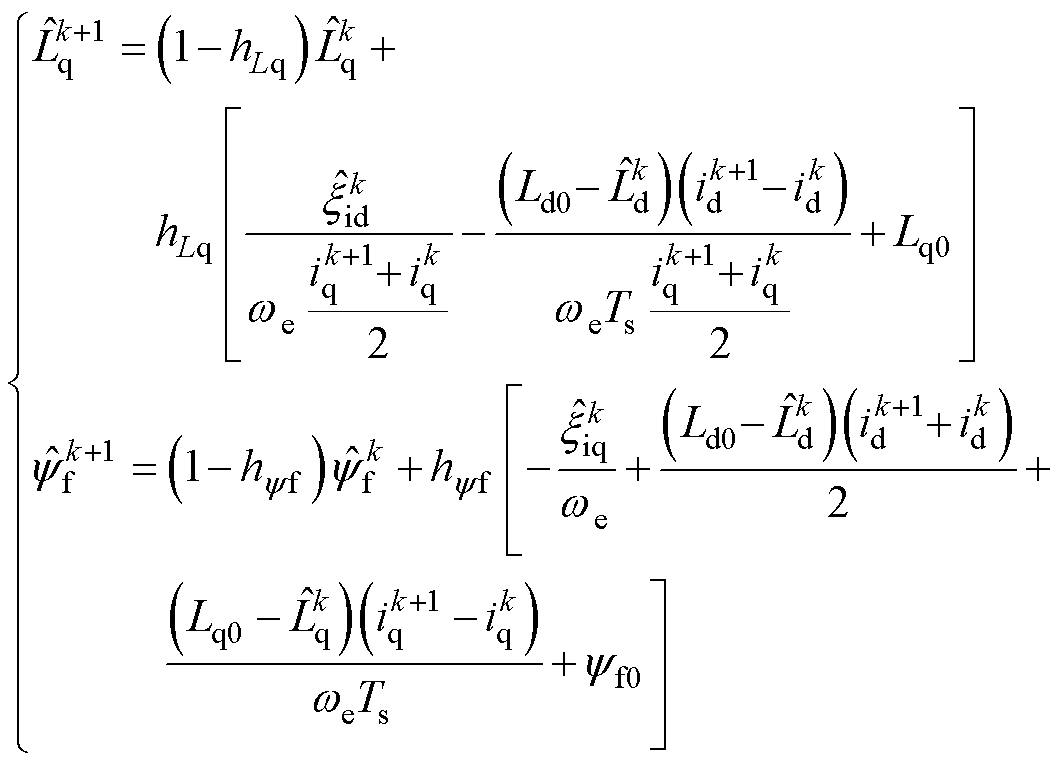 (19)
(19)
式中,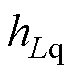 和
和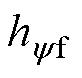 为滤波系数,调节其大小可以控制低通滤波器的截止频率。
为滤波系数,调节其大小可以控制低通滤波器的截止频率。
当转速或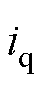 =0时式(19)中
=0时式(19)中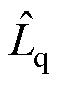 和
和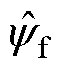 迭代方程分母存在为零的情况,迭代方程缺少激励。考虑到当电流较小时,电感饱和程度较小,标称值和实际值相差较小。因此,只有当
迭代方程分母存在为零的情况,迭代方程缺少激励。考虑到当电流较小时,电感饱和程度较小,标称值和实际值相差较小。因此,只有当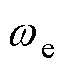 和
和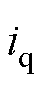 大于一定值时,才使用式(19)对
大于一定值时,才使用式(19)对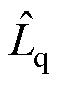 和
和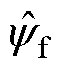 进行辨识。因此,对式(19)设置边界条件为
进行辨识。因此,对式(19)设置边界条件为
 (20)
(20)
式中,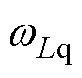 和
和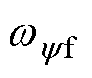 为对应低通滤波器的带宽;
为对应低通滤波器的带宽;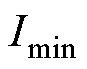 和
和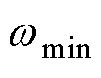 为边界值,其大小通过分析实验中参数辨识的结果进行选取,具体数值实验环节会进行说明。
为边界值,其大小通过分析实验中参数辨识的结果进行选取,具体数值实验环节会进行说明。
虽然在第1节的分析中d轴电感对给定值计算和预测值计算带来的影响较小,但在运用式(19)对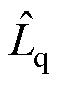 和
和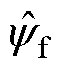 进行辨识时需要用到
进行辨识时需要用到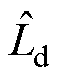 。为了进一步提高精度,这里也对d轴电感进行辨识。通过式(19)本文分别使用了电机的d、q轴稳态电流方程对
。为了进一步提高精度,这里也对d轴电感进行辨识。通过式(19)本文分别使用了电机的d、q轴稳态电流方程对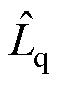 和
和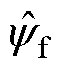 进行辨识,方程组出现欠秩问题使得无法依据稳态方程同时实现对
进行辨识,方程组出现欠秩问题使得无法依据稳态方程同时实现对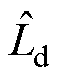 的辨识。为此,本文提出了一种利用定子电流变化量对d轴电感进行辨识的方案。
的辨识。为此,本文提出了一种利用定子电流变化量对d轴电感进行辨识的方案。
对式(1)中d轴方程进行离散化,并将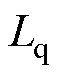 替换为其估计值
替换为其估计值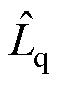 ,可得d轴定子电流差分方程为
,可得d轴定子电流差分方程为
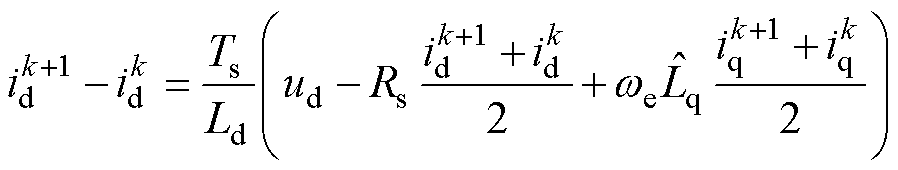 (21)
(21)
不难发现,在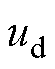 、
、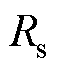 和
和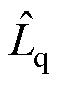 已知的情况下,通过式(21)可对d轴电感值进行估算,即
已知的情况下,通过式(21)可对d轴电感值进行估算,即
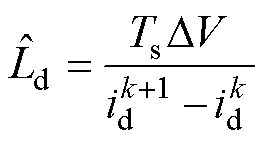 (22)
(22)
其中
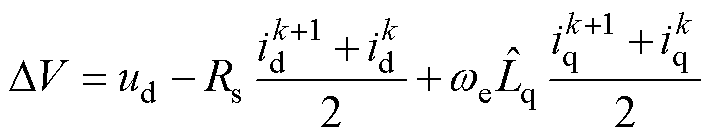
FCS-MPFC在一个控制周期内逆变器只输出一个电压矢量,电压矢量作用时间较长,对应电流变化较大,这为式(22)的可行性提供了条件。同样地,为了滤除谐波噪声的影响,需要对式(22)的估算结果进行滤波。因此,在离散域中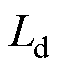 辨识迭代方程为
辨识迭代方程为
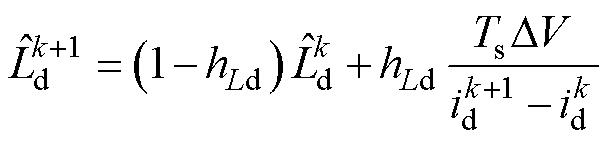 (23)
(23)
式中,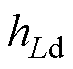 为滤波系数。
为滤波系数。
考虑到电流采样精度的问题,当电流差分值较小时,采样带来的噪声会使得辨识得到的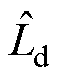 出现较大的波动。因此设置边界条件,只有当电流差分值大于边界条件时才使用式(23)对
出现较大的波动。因此设置边界条件,只有当电流差分值大于边界条件时才使用式(23)对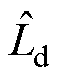 进行迭代运算。由式(21)不难发现,采样周期内电流变化量与
进行迭代运算。由式(21)不难发现,采样周期内电流变化量与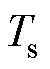 成正比,与d轴电感成反比。定子电阻压降很小,可忽略不计。记
成正比,与d轴电感成反比。定子电阻压降很小,可忽略不计。记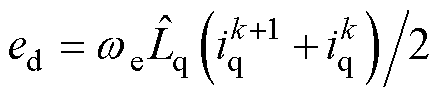 ,通过仿真分析
,通过仿真分析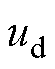 和
和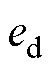 对电流差分值的影响,如图4所示。由图4可以看出,不同控制周期电流变化量主要受
对电流差分值的影响,如图4所示。由图4可以看出,不同控制周期电流变化量主要受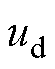 影响,而旋转电动势
影响,而旋转电动势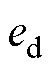 仅会引起恒定的直流偏置,且
仅会引起恒定的直流偏置,且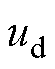 变化范围为
变化范围为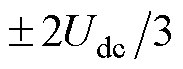 ,其中,
,其中,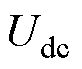 为逆变器直流侧电压幅值,因此可将电流差分值的边界值设为
为逆变器直流侧电压幅值,因此可将电流差分值的边界值设为
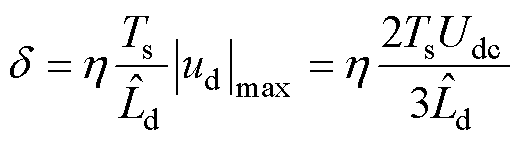 (24)
(24)
式中,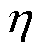 为比例系数,
为比例系数,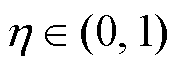 ,通过合理设置
,通过合理设置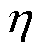 可以调节
可以调节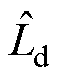 辨识的稳态性能和收敛速度。
辨识的稳态性能和收敛速度。
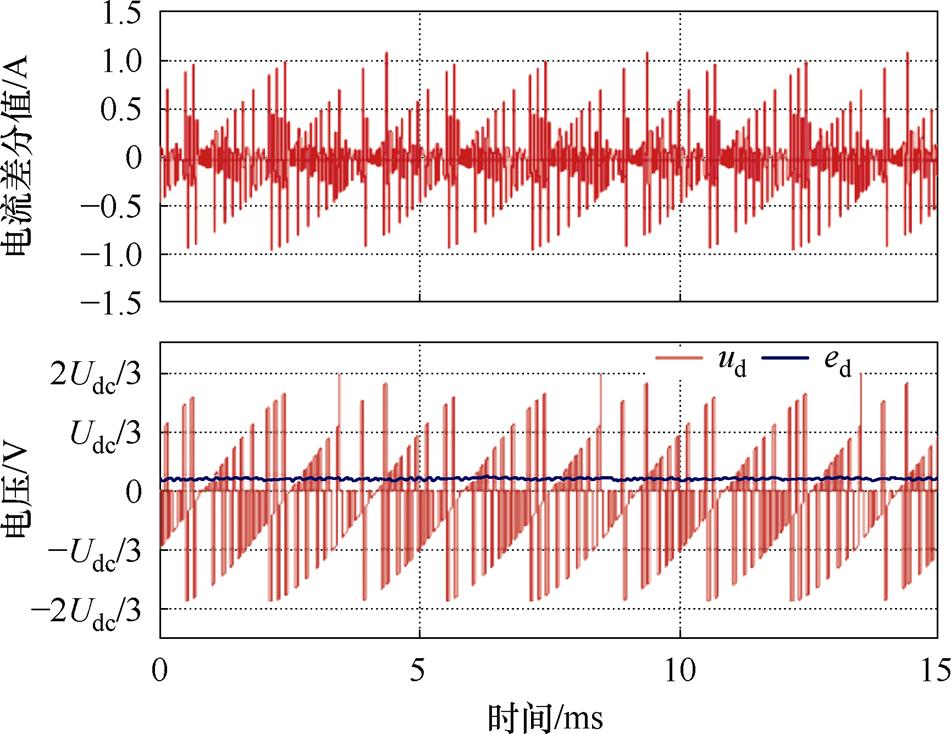
图4 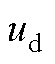 和
和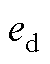 对d轴电流差分值的影响
对d轴电流差分值的影响
Fig.4 Effects of 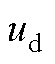 and
and 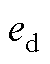 on the d-axis current difference
on the d-axis current difference
综上所述,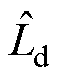 辨识的边界条件为
辨识的边界条件为
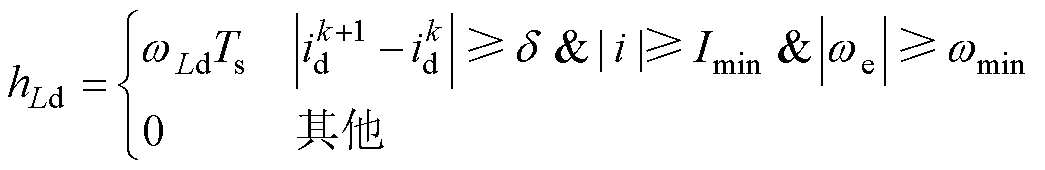 (25)
(25)
式中,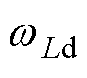 为低通滤波器的带宽。
为低通滤波器的带宽。
基于任何方法辨识参数,一个重要原则是除辨识参数以外的模型应尽可能精确。在d、q轴电感和永磁磁链辨识过程中均要用到定子电压值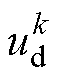 和
和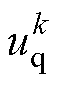 ,而定子电压值的估计通常根据逆变器桥臂的开关状态计算得到,逆变器死区的存在会影响定子电压的估计,使得
,而定子电压值的估计通常根据逆变器桥臂的开关状态计算得到,逆变器死区的存在会影响定子电压的估计,使得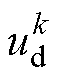 和
和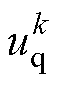 偏离真实值,影响辨识精度。
偏离真实值,影响辨识精度。
由第3节可知,参数的辨识需要对应电压矢量的电流增量。FCS-MPFC在一个控制周期内逆变器只输出一个电压矢量,但死区的存在使得给定的逆变器各桥臂开关状态与实际的开关状态在控制周期开始阶段存在不同。因此,本文采取在一个控制周期内进行两次采样,在得到相应电流增量的同时,又可以通过优化设置两次采样时刻来避免死区的影响。电流采样时刻设置如图5所示,其中以单个桥臂从关断到导通的过程为例进行说明,控制器中死区的处理方式为在PWM的上升沿进行延时。
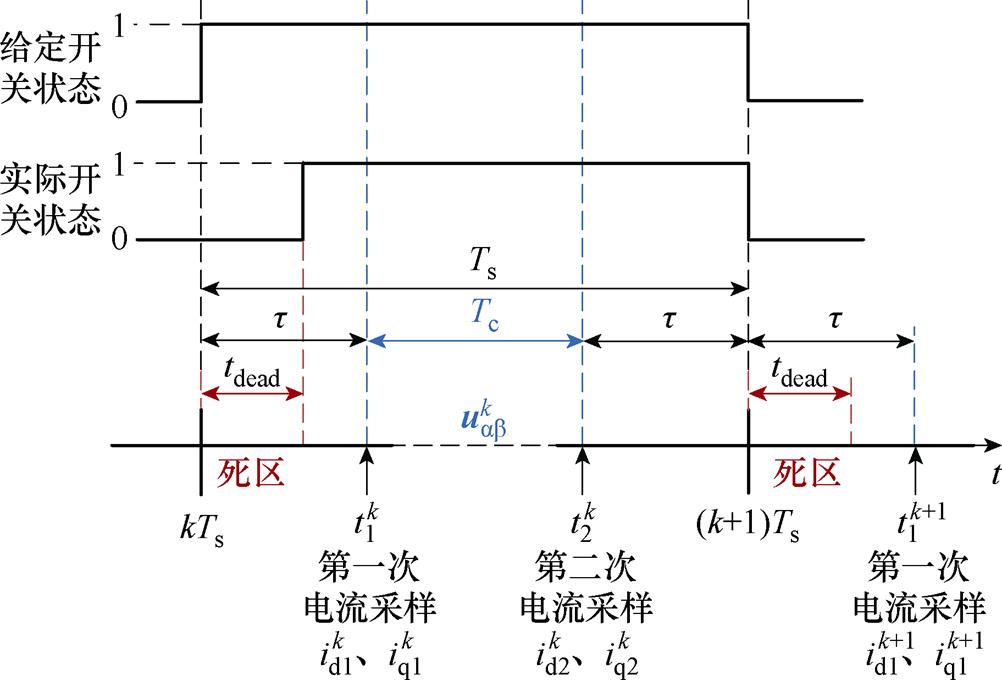
图5 电流双采样死区消除方案
Fig.5 The scheme of current double sampling for dead-time elimination
逆变器死区时间为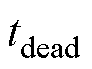 ,但实际死区的大小并不是恒定不变的,会受到桥臂电流的影响而发生变化。因此,设定第一次采样在当前控制周期经过时间裕量
,但实际死区的大小并不是恒定不变的,会受到桥臂电流的影响而发生变化。因此,设定第一次采样在当前控制周期经过时间裕量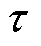 之后的
之后的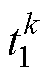 时刻,以避开死区时间,采样获得的电流值记为
时刻,以避开死区时间,采样获得的电流值记为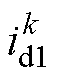 、
、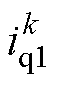 。应尽量增加两次采样时间间隔,以获得尽可能大的电流增量,从而提升辨识精度。在
。应尽量增加两次采样时间间隔,以获得尽可能大的电流增量,从而提升辨识精度。在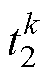 时刻进行第二次采样,采样获得值记为
时刻进行第二次采样,采样获得值记为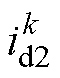 、
、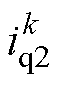 ,两次采样的间隔时间
,两次采样的间隔时间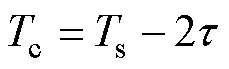 。如图5所示,两次采样间隔内逆变器各桥臂的实际开关状态与给定的开关状态完全相同,进而可以完全避免死区对辨识精度的影响。此时用
。如图5所示,两次采样间隔内逆变器各桥臂的实际开关状态与给定的开关状态完全相同,进而可以完全避免死区对辨识精度的影响。此时用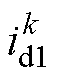 、
、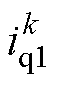 和
和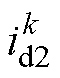 、
、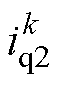 分别代替第3节所有方程中的
分别代替第3节所有方程中的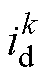 、
、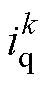 和
和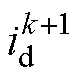 、
、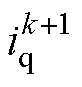 即可,相邻两次采样间隔时间相应地由
即可,相邻两次采样间隔时间相应地由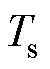 调整为
调整为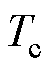 。
。
综上所述,多参数辨识流程如图6所示,图中,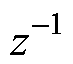 表示延迟一个控制周期。
表示延迟一个控制周期。
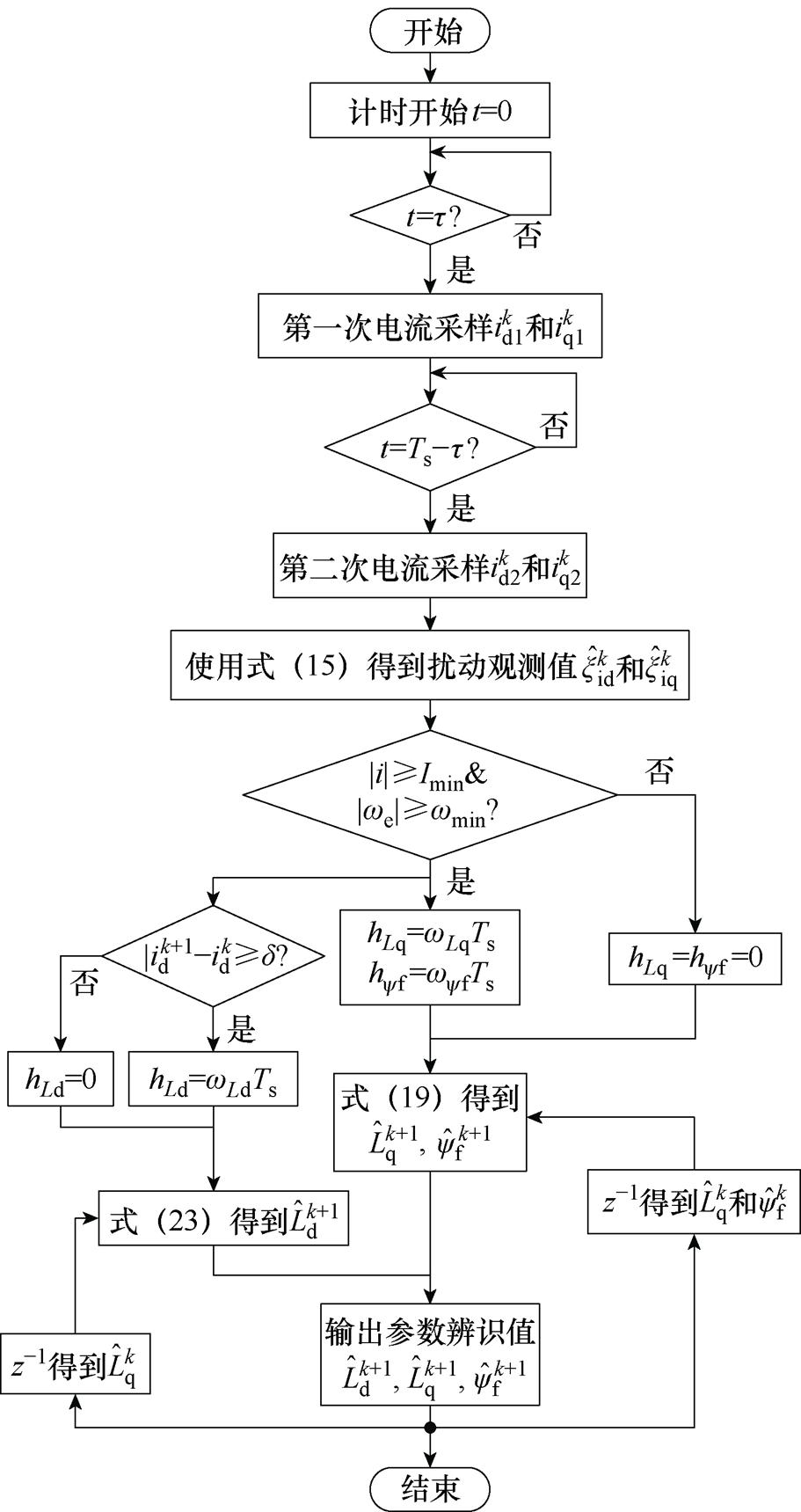
图6 多参数辨识流程
Fig.6 Flow chart of multi-parameter identification
此外,为了进一步提高模型中电压的精度,考虑到定子电压在两相静止坐标系下存在的零阶保持特性,对于同步旋转坐标系下的定子电压在离散化时应该取一个控制周期内的等效电压作用[29]。利用文献[30]中的补偿方法可得
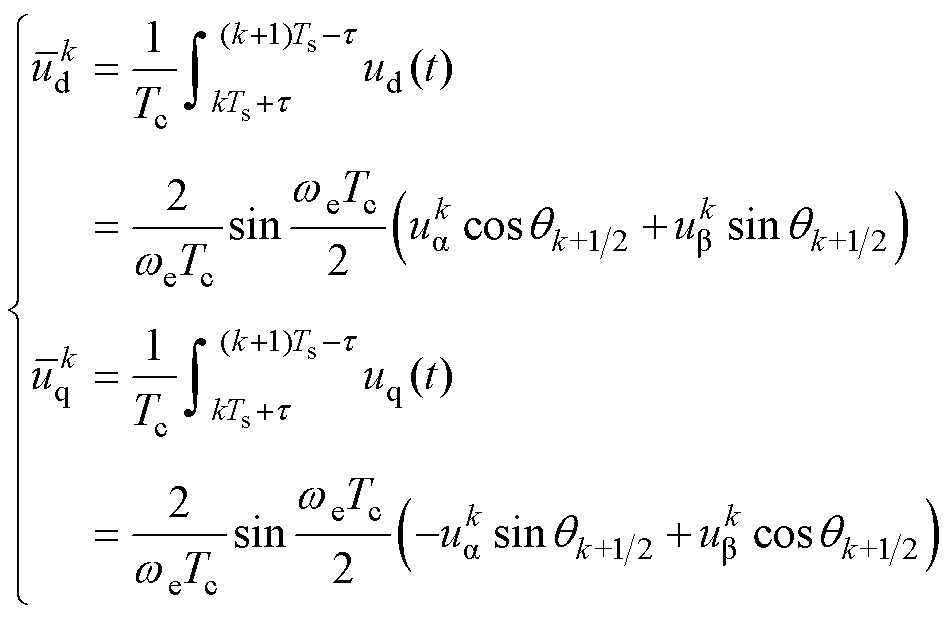 (26)
(26)
其中
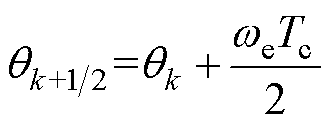
式中,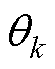 为第一次电流采样时刻电机的电角度;
为第一次电流采样时刻电机的电角度;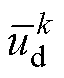 、
、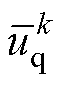 分别为当前控制周期补偿后的d、q轴定子电压分量;
分别为当前控制周期补偿后的d、q轴定子电压分量;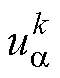 、
、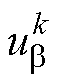 分别为当前控制周期
分别为当前控制周期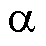 、
、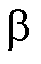 轴的定子电压分量。
轴的定子电压分量。
电压误差不仅仅会影响参数辨识的精度,也会对FCS-MPFC的磁链预测精度造成影响,由式(10)可知,电压误差引起磁链预测误差,且两者之间呈线性关系。但磁链预测需要对一个完整的周期进行计算,因此上述死区影响处理方案不适用于磁链预测。这里同样在预测模型中引入GPIO,继而对预测方程中存在的误差进行集中补偿。实际上通过误差补偿,参数偏差对预测模型的影响也将得到补偿,因此在预测模型中无需使用参数的在线估计值,可简化控制流程。综上所述,基于GPIO的磁链预测模型为
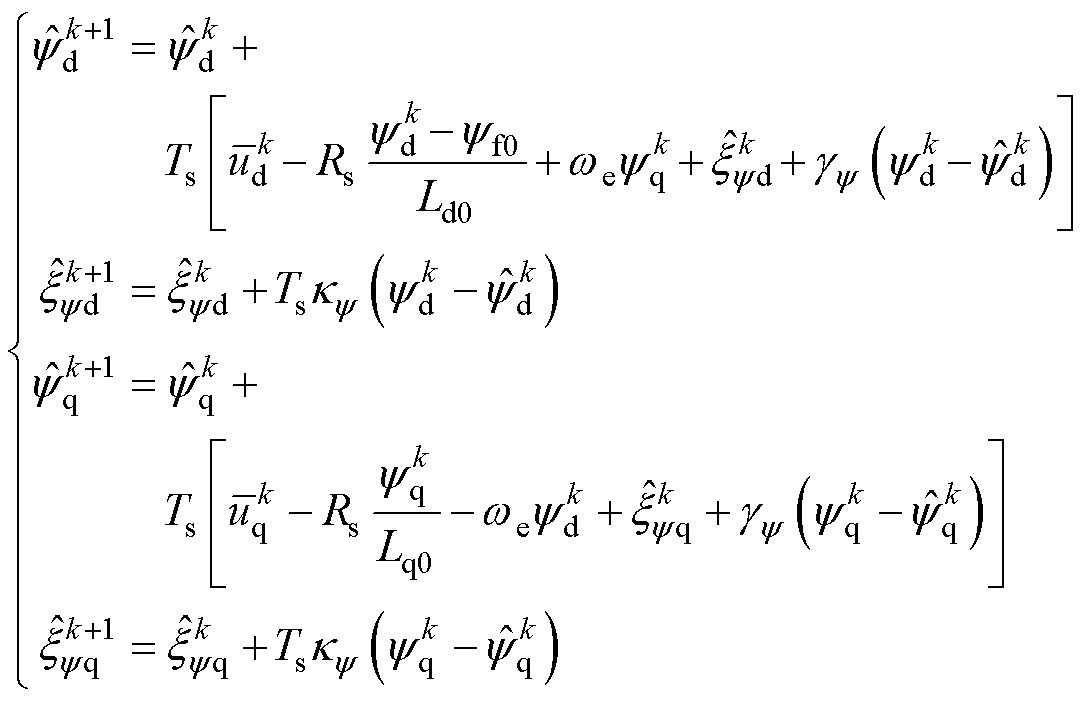 (27)
(27)
其中
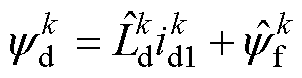
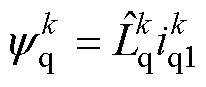
式中,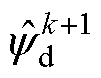 、
、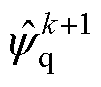 分别为使用改进预测模型时
分别为使用改进预测模型时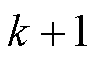 时刻的d、q轴磁链预测值;
时刻的d、q轴磁链预测值;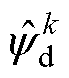 、
、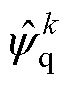 分别为使用改进预测模型时
分别为使用改进预测模型时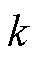 时刻的d、q轴磁链预测值;
时刻的d、q轴磁链预测值;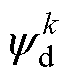 、
、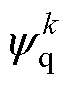 分别为
分别为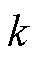 时刻d、q轴磁链观测值;
时刻d、q轴磁链观测值;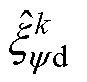 、
、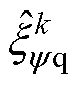 分别为
分别为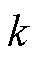 时刻d、q轴磁链预测偏差观测值;
时刻d、q轴磁链预测偏差观测值;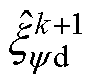 、
、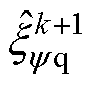 分别为
分别为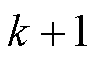 时刻d、q轴磁链预测偏差观测值;
时刻d、q轴磁链预测偏差观测值;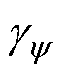 、
、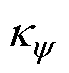 为改进预测模型中的观测器参数。
为改进预测模型中的观测器参数。
考虑到数字控制器中存在的一拍延时,使用两步预测进行补偿,第二步的预测模型为
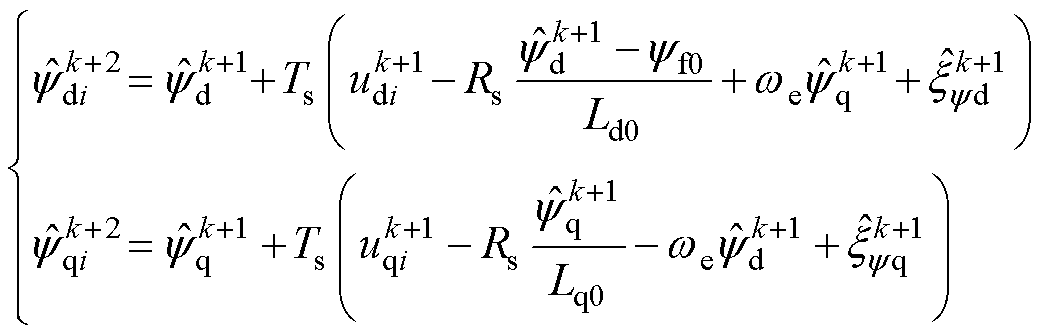 (28)
(28)
式中,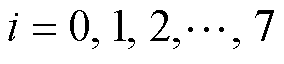 ;
;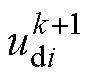 、
、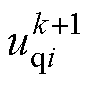 分别为
分别为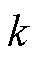 +1时刻电压矢量
+1时刻电压矢量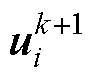 的d、q轴分量;
的d、q轴分量;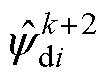 、
、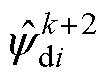 分别为使用改进预测模型在电压矢量
分别为使用改进预测模型在电压矢量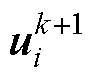 作用下的k+2时刻d、q轴磁链预测值。
作用下的k+2时刻d、q轴磁链预测值。
相应的价值函数为
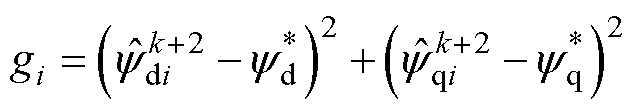 (29)
(29)
FCS-MPFC整体控制框图如图7所示。
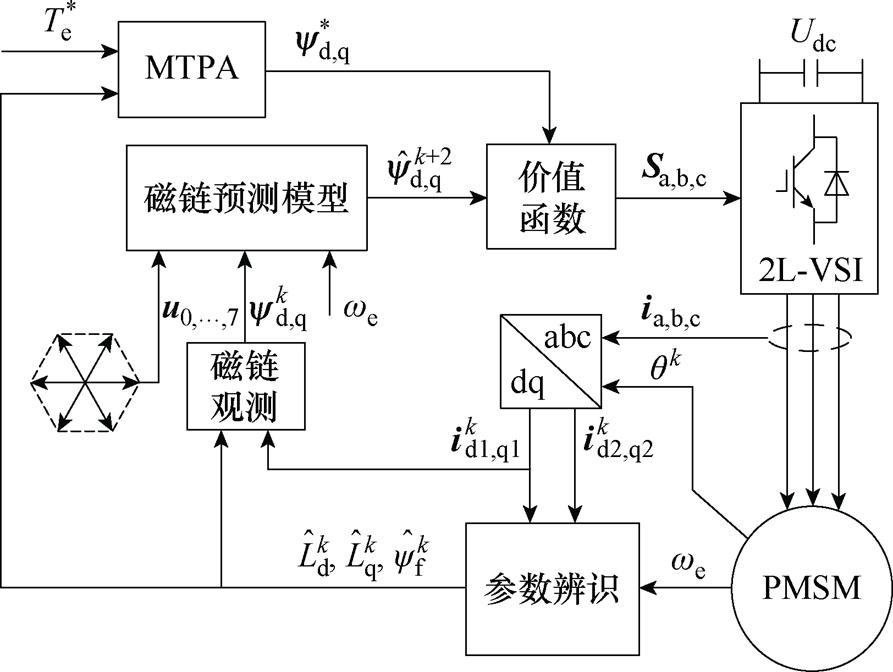
图7 基于多参数辨识的FCS-MPFC控制框图
Fig.7 Control block diagram of FCS-MPFC based on multi-parameter identification
为验证所提FCS-MPFC控制策略的有效性,搭建了PMSM实验平台,如图8所示。测试用永磁同步电机参数见表1。陪试电机由台达伺服驱动器控制,工作在速度控制模式,用于对机组转速进行闭环控制。测试电机由电机控制器控制,控制器采用TI出品的DSP,型号为TMS320F28379D。逆变器主电路功率模块采用三菱PM75CLA120,开关频率设定为20 kHz。在DSP中控制周期设置为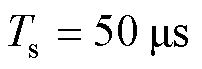 ,死区时间设置为
,死区时间设置为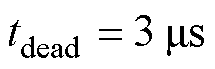 ,电流双采样时间裕量设置为
,电流双采样时间裕量设置为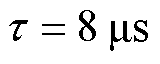 。
。

图8 实验平台
Fig.8 Experimental platform
表1 电机参数
Tab.1 Motor parameters

参 数数 值 极对数p4 定子电阻/W0.937 额定电压/V220 额定电流/A6.2 额定功率/kW1.5 额定转矩/(N·m)9.6 额定转速/(r/min)1 500
实验中电感辨识值、永磁磁链辨识值、dq轴电流以及转速的测量数据均由DSP采集和计算得到,并通过SPI转USB通信模块传输到计算机后使用上位机进行接收和保存。电磁转矩通过转矩传感器进行测量,并使用配套的上位机进行数据的保存,转矩传感器具体型号为大洋传感器出品的DYN-200。电机定子三相电流通过示波器进行观测及数据的保存。本文实验中的波形均是由上述采集到的数据导入Matlab中绘制得到。
由于无法对电机的电感和永磁磁链进行人为修改,因此在实验中人为地将控制器中的标称参数初始化成一定的偏差值,然后验证参数辨识是否可以准确跟踪到实际值,实验波形如图9所示。依据第2节分析,设置控制器中的d、q轴电感和永磁磁链标称值在初始阶段同时存在-30%偏差,对应图9a;同时存在+30%的偏差,对应图9b。在运行中电机给定转速1 000 r/min,初始电磁转矩0 N·m,2 s时电磁转矩阶跃为5 N·m。同时使用第1节中的传统FCS- MPFC作为对比,将其对应的实验结果示于图10中。
在图9a和图9b中,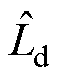 初始值分别为4.585 mH和8.515 mH,
初始值分别为4.585 mH和8.515 mH,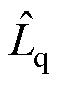 分别为7.455 mH和13.845 mH,
分别为7.455 mH和13.845 mH,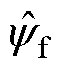 分别为0.161 Wb和0.299 Wb。在第3节中设置了辨识的边界条件,其中电流幅值和电角速度的绝对值要大于0,根据实验情况,设置电流幅值边界条件为
分别为0.161 Wb和0.299 Wb。在第3节中设置了辨识的边界条件,其中电流幅值和电角速度的绝对值要大于0,根据实验情况,设置电流幅值边界条件为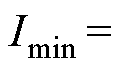 0.36 A,对应电磁转矩为0.5 N·m,设置电角速度边界条件为
0.36 A,对应电磁转矩为0.5 N·m,设置电角速度边界条件为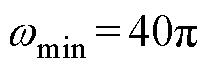 rad/s,设置电流差分边界条件系数
rad/s,设置电流差分边界条件系数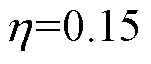 。实验中转速恒定为1 000 r/min对应电角速度为
。实验中转速恒定为1 000 r/min对应电角速度为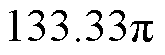 rad/s,满足电角速度的边界条件。因此,在2 s时电磁转矩阶跃5 N·m,此时电流满足边界条件,开始进行参数辨识。两种情况下的5~10 s的辨识结果稳态平均值为:
rad/s,满足电角速度的边界条件。因此,在2 s时电磁转矩阶跃5 N·m,此时电流满足边界条件,开始进行参数辨识。两种情况下的5~10 s的辨识结果稳态平均值为: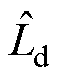 分别为6.557 mH和6.565 mH;
分别为6.557 mH和6.565 mH;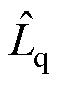 分别为10.648 mH和10.662 mH;
分别为10.648 mH和10.662 mH;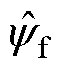 分别为0.231 2 Wb和0.230 5 Wb。两种情况下辨识结果偏差为:
分别为0.231 2 Wb和0.230 5 Wb。两种情况下辨识结果偏差为: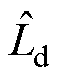 为0.12%、
为0.12%、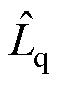 为0.13%以及
为0.13%以及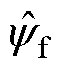 为0.30%。参数偏差较小,验证了参数辨识的准确性。
为0.30%。参数偏差较小,验证了参数辨识的准确性。
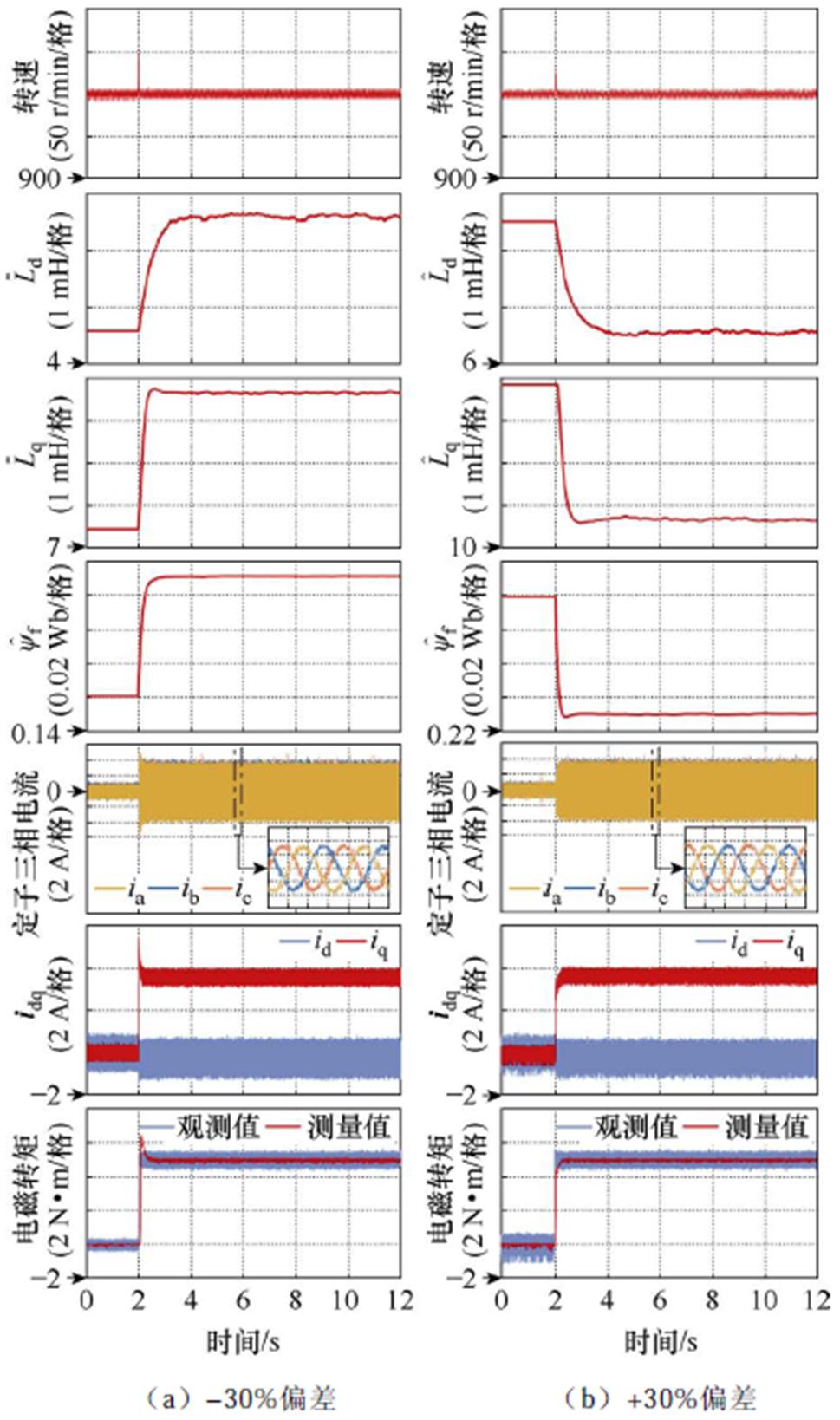
图9 多参数辨识可行性验证
Fig.9 Feasibility verification of multi-parameter identification
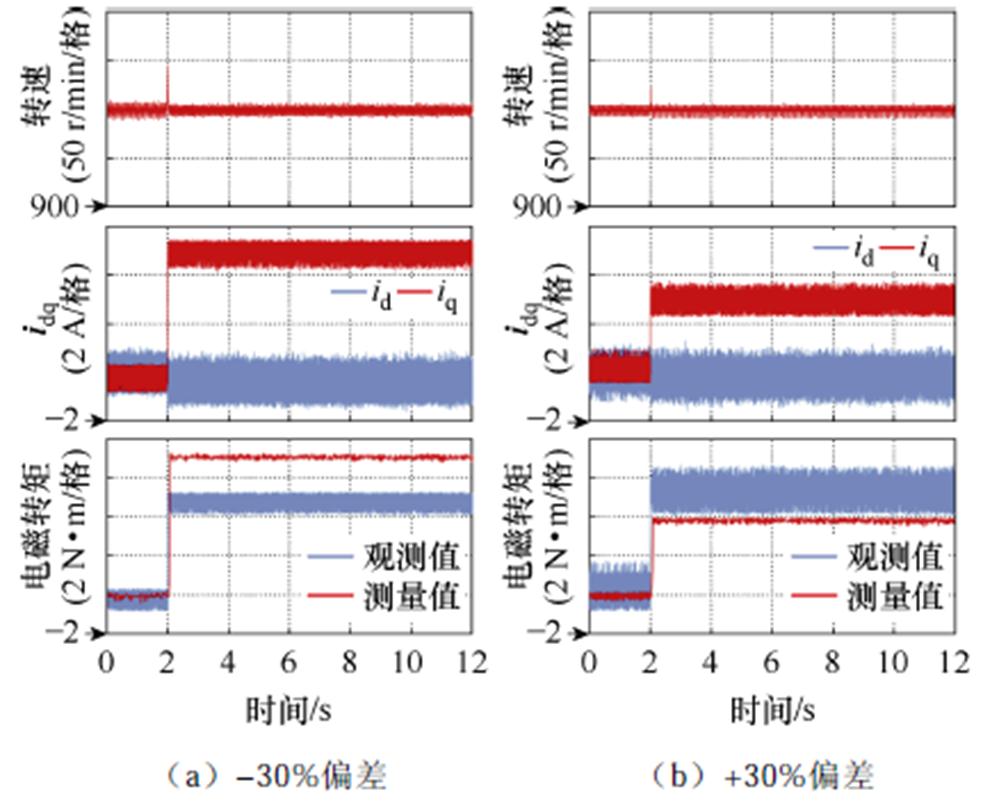
图10 参数偏差时实验结果
Fig.10 Experimental results under parameter deviations
动态性能方面,在标称参数初始值存在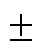 30%偏差的情况下,
30%偏差的情况下,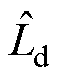 估算过程的上升时间分别为1.10 s和1.20 s,
估算过程的上升时间分别为1.10 s和1.20 s,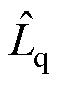 分别为0.40 s和0.58 s、
分别为0.40 s和0.58 s、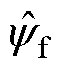 为0.27 s和0.25 s。可见,
为0.27 s和0.25 s。可见,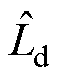 辨识响应速度相对较慢,这是由于在实际采样中存在较多的噪声,为获得较好的稳态性能,降低了低通滤波器的截止频率,提高了电流差分值的边界条件,影响了响应速度。但是,一方面通过第2节的分析可知,d轴电感对控制系统稳态性能的影响较小;另一方面在电机实际正常运行时电机的电感值并不会发生阶跃变化,本方案中参数辨识的响应速度是可以满足实际需求的。
辨识响应速度相对较慢,这是由于在实际采样中存在较多的噪声,为获得较好的稳态性能,降低了低通滤波器的截止频率,提高了电流差分值的边界条件,影响了响应速度。但是,一方面通过第2节的分析可知,d轴电感对控制系统稳态性能的影响较小;另一方面在电机实际正常运行时电机的电感值并不会发生阶跃变化,本方案中参数辨识的响应速度是可以满足实际需求的。
由于无法得知运行中电机参数的真实值,因此也可以从电流和电磁转矩的控制准确性对参数辨识的准确性进行间接的验证。由图9不难看出,在电磁转矩给定值发生阶跃的瞬间由于参数存在偏差,电流和电磁转矩均存在偏差,随着参数辨识过程的逐渐收敛,电流和电磁转矩逐渐跟踪到给定值,两种情况下的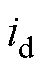 稳态平均值分别为-0.227 A和-0.217 A;
稳态平均值分别为-0.227 A和-0.217 A;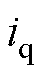 分别为-3.663 A和3.676 A;电磁转矩观测值分别为5.058 N·m和5.056 N·m;电磁转矩测量值分别为5.019 N·m和5.012 N·m。两种情况下电流和电磁转矩控制效果保持一致,均能准确地跟踪给定值。而图10中,初始参数存在-30%偏差时测量电磁转矩的稳态平均值为7.140 N·m,参数的偏差使得电机实际电磁转矩明显偏离给定电磁转矩,且电磁转矩的观测值为4.804 N·m,也明显偏离电磁转矩的测量值;初始参数存在+30%偏差时,测量电磁转矩的稳态平均值为3.874 N·m,参数的偏大使得电机实际电磁转矩偏小,电磁转矩观测值为5.455 N·m,同样与测量值之间存在较大偏差。
分别为-3.663 A和3.676 A;电磁转矩观测值分别为5.058 N·m和5.056 N·m;电磁转矩测量值分别为5.019 N·m和5.012 N·m。两种情况下电流和电磁转矩控制效果保持一致,均能准确地跟踪给定值。而图10中,初始参数存在-30%偏差时测量电磁转矩的稳态平均值为7.140 N·m,参数的偏差使得电机实际电磁转矩明显偏离给定电磁转矩,且电磁转矩的观测值为4.804 N·m,也明显偏离电磁转矩的测量值;初始参数存在+30%偏差时,测量电磁转矩的稳态平均值为3.874 N·m,参数的偏大使得电机实际电磁转矩偏小,电磁转矩观测值为5.455 N·m,同样与测量值之间存在较大偏差。
为进一步验证参数辨识的有效性,分别在不同工况下对电机参数进行辨识,如图11所示。首先转速设置为恒定1 000 r/min,控制电磁转矩递增,依次为3、5、7和9 N·m,实验波形如图11所示。可以看到,随着电磁转矩的增大,电流逐渐增大,d、q轴电感因磁饱和而逐渐减小,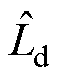 的稳态值依次为6.673、6.560、6.501和6.446 mH,
的稳态值依次为6.673、6.560、6.501和6.446 mH,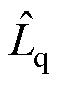 的稳态值依次为10.872、10.637、10.452和10.334 mH。
的稳态值依次为10.872、10.637、10.452和10.334 mH。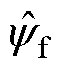 在电磁转矩为3 N·m和5 N·m时因电机功率较小发热不大,未出现明显变化,其值分别为0.230 76 Wb和0.231 03 Wb,两者完全在误差允许范围内。当电磁转矩进一步增大时,
在电磁转矩为3 N·m和5 N·m时因电机功率较小发热不大,未出现明显变化,其值分别为0.230 76 Wb和0.231 03 Wb,两者完全在误差允许范围内。当电磁转矩进一步增大时,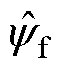 总体上呈下降趋势,这是由于功率增大使电机温度上升进而导致
总体上呈下降趋势,这是由于功率增大使电机温度上升进而导致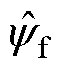 降低,在电磁转矩为7 N·m和9 N·m时的稳态值分别为0.230 48 Wb和0.229 56 Wb。
降低,在电磁转矩为7 N·m和9 N·m时的稳态值分别为0.230 48 Wb和0.229 56 Wb。
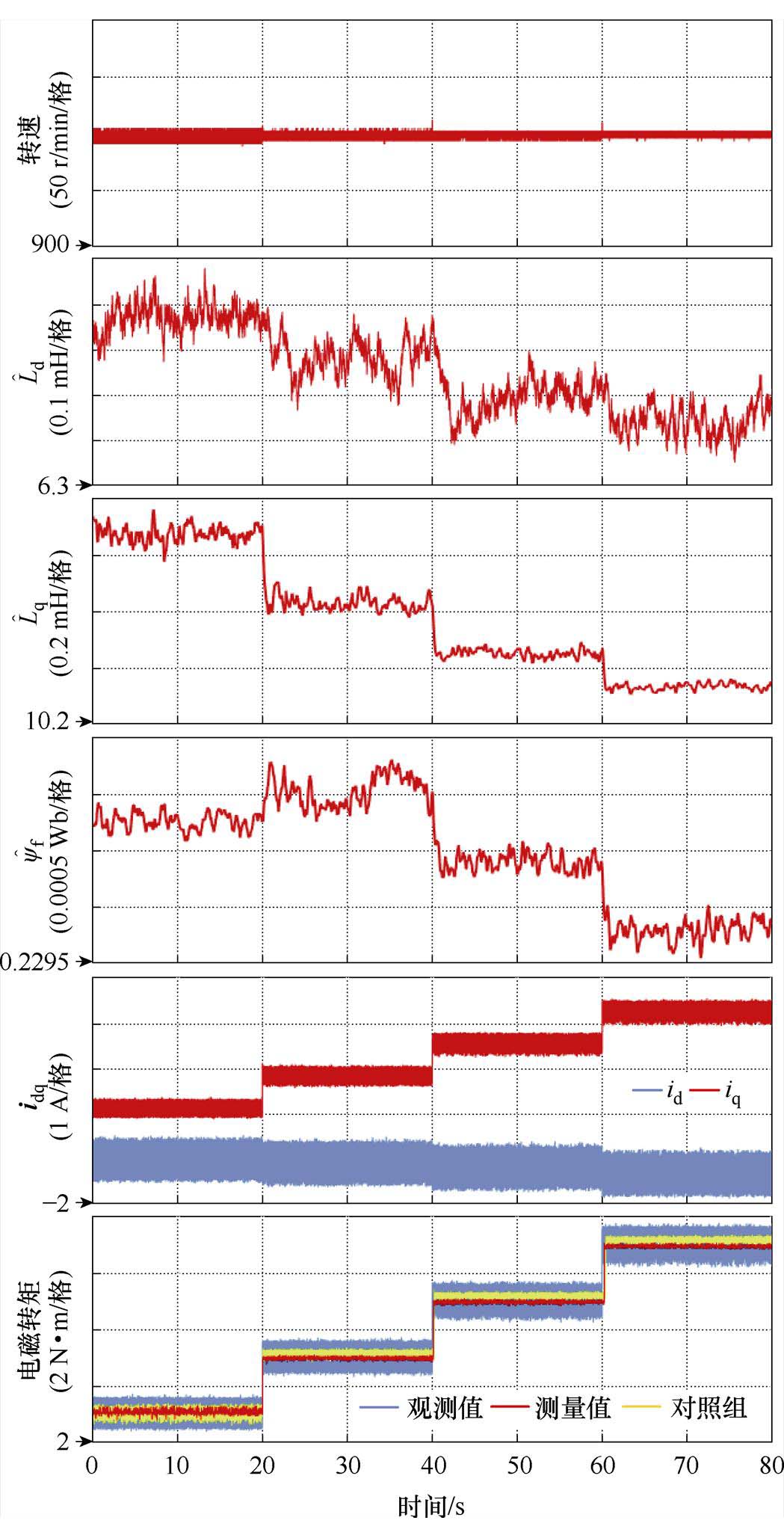
图11 电磁转矩递增实验
Fig.11 Experimental results under electromagnetic torque step increasing
另外设置对照组并测量电磁转矩进行对比,对照组采用标称参数即不同工况下参数保持恒定。为便于对比,对照组中标称参数采用转速1 000 r/min以及电磁转矩3 N·m下的电机参数,具体的标称参数: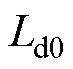 =6.673 mH、
=6.673 mH、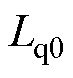 =10.872 mH和
=10.872 mH和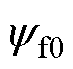 = 0.230 76 Wb。本文所提方案在不同工况下的电磁转矩测量值分别为3.025、5.011、7.005和8.984 N·m,最大误差不超过0.9%,均可以准确地跟踪到给定值。对照组电磁转矩测量值分别为3.012、5.106、7.143和9.192 N·m。可以看到,在3 N·m时因参数相同两种方案控制效果相差很小,但随着给定电磁转矩的上升,对照组的电磁转矩控制逐渐出现误差,最大误差为2.13%。相比之下,本文所提方案控制效果更好。
= 0.230 76 Wb。本文所提方案在不同工况下的电磁转矩测量值分别为3.025、5.011、7.005和8.984 N·m,最大误差不超过0.9%,均可以准确地跟踪到给定值。对照组电磁转矩测量值分别为3.012、5.106、7.143和9.192 N·m。可以看到,在3 N·m时因参数相同两种方案控制效果相差很小,但随着给定电磁转矩的上升,对照组的电磁转矩控制逐渐出现误差,最大误差为2.13%。相比之下,本文所提方案控制效果更好。
考虑转速对辨识结果的影响,分别设置加减速实验,实验波形如图12所示。加减速实验中设置初始转速为1 000 r/min,10 s时控制转速降低到500 r/min或升高到1 500 r/min。同样设置对照组并测量电磁转矩,对照组采用转速1 000 r/min以及电磁转矩5 N·m下的电机参数作为标称参数,具体的标称参数: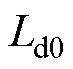 =6.560 mH、
=6.560 mH、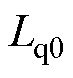 =10.637 mH以及
=10.637 mH以及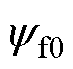 = 0.231 Wb,且控制过程中参数保持恒定。
= 0.231 Wb,且控制过程中参数保持恒定。
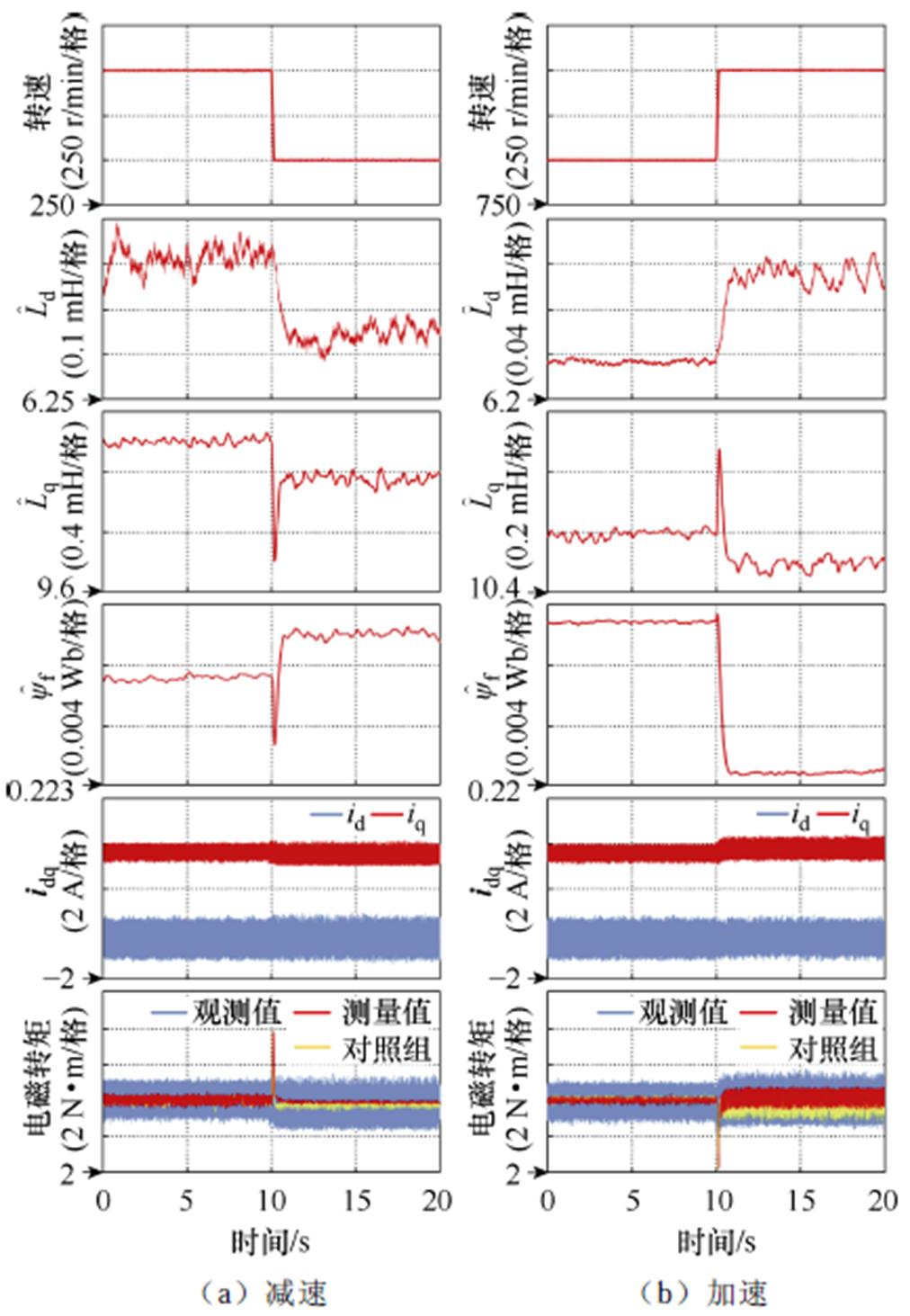
图12 加减速实验
Fig.12 Experimental results under acceleration and deceleration
在所提的控制方案下,可以观察到d、q轴电感辨识结果随转速的不同会发生变化。随着转速上升电机功率增大,电机永磁体温度上升,出现退磁现象,因此,图12中,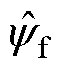 随着转速的上升逐渐减小。电流值随着转速增大会相应增加,电磁转矩则基本保持一致,在500、1 000和1 500 r/min下的稳态值分别为4.969、5.018和5.047 N·m,电磁转矩误差最大不超过1%。对照组电磁转矩测量值分别为4.880、5.024和4.784 N·m。在1 000 r/min工况下,对照组与所提方案使用参数相同,使得对照组的电磁转矩控制误差很小。500 r/min和1 500 r/min下电磁转矩控制误差分别为2.40%和4.32%。相比之下本文所提方案控制效果更好。
随着转速的上升逐渐减小。电流值随着转速增大会相应增加,电磁转矩则基本保持一致,在500、1 000和1 500 r/min下的稳态值分别为4.969、5.018和5.047 N·m,电磁转矩误差最大不超过1%。对照组电磁转矩测量值分别为4.880、5.024和4.784 N·m。在1 000 r/min工况下,对照组与所提方案使用参数相同,使得对照组的电磁转矩控制误差很小。500 r/min和1 500 r/min下电磁转矩控制误差分别为2.40%和4.32%。相比之下本文所提方案控制效果更好。
本文针对传统FCS-MPFC存在参数鲁棒性差的问题,提出了一种基于GPIO的多参数辨识方案,并依据FCS-MPFC的定子电流特性使用电流增量对d轴电感进行辨识以解决欠秩问题。同时根据FCS- MPFC的逆变器电压输出特性,提出一种通过采样时刻优化设置避免死区影响的方法。通过一系列的实验可以得出,本文所提方案可以有效地辨识出不同工况下的d、q轴电感和永磁磁链,消除逆变器死区对参数辨识和预测控制的影响。相比于传统FCS- MPFC,本文所提方案可以消除由参数偏差引起的电磁转矩控制误差。
参考文献
[1] Rodriguez J, Kazmierkowski M P, Espinoza J R, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016.
[2] Lee J H. Model predictive control: review of the three decades of development[J]. International Journal of Control, Automation and Systems, 2011, 9(3): 415- 424.
[3] 张永昌, 杨海涛. 感应电机模型预测磁链控制[J]. 中国电机工程学报, 2015, 35(3): 719-726.
Zhang Yongchang, Yang Haitao. Model predictive flux control for induction motor drives[J]. Pro- ceedings of the CSEE, 2015, 35(3): 719-726.
[4] 牛峰, 韩振铎, 黄晓艳, 等. 永磁同步电机模型预测磁链控制[J]. 电机与控制学报, 2019, 23(3): 34-41.
Niu Feng, Han Zhenduo, Huang Xiaoyan, et al. Model predictive flux control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2019, 23(3): 34-41.
[5] Yan Liming, Wang Fengxiang. Observer-predictor- based predictive torque control of induction machine for robustness improvement[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9477-9486.
[6] Wang Huimin, Li Chongyuan, Zhang Guozheng, et al. Maximum torque per ampere (MTPA) control of IPMSM systems based on controller parameters self-modification[J]. IEEE Transactions on Vehicular Technology, 2020, 69(3): 2613-2620.
[7] Xia Jinhui, Guo Yuanbo, Li Ze, et al. Step-signal- injection-based robust MTPA operation strategy for interior permanent magnet synchronous machines[J]. IEEE Transactions on Energy Conversion, 2019, 34(4): 2052-2061.
[8] Liu Guohai, Wang Jian, Zhao Wenxiang, et al. A novel MTPA control strategy for IPMSM drives by space vector signal injection[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9243-9252.
[9] Feng Guodong, Lai Chunyan, Han Yu, et al. Fast maximum torque per ampere (MTPA) angle detection for interior PMSMs using online polynomial curve fitting[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2045-2056.
[10] 葛扬, 宋卫章, 杨洋. 基于扩张式主从自适应陷波滤波器与动态频率跟踪的永磁同步电机无传感器控制[J]. 电工技术学报, 2023, 38(14): 3824-3835.
Ge Yang, Song Weizhang, Yang Yang. PMSM sensorless control based on extended master-slave adaptive notch filter and dynamic frequency tracking[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3824-3835.
[11] 陈卓易, 邱建琪, 金孟加. 永磁同步电机有限集无参数模型预测控制[J]. 电机与控制学报, 2019, 23(1): 19-26.
Chen Zhuoyi, Qiu Jianqi, Jin Mengjia. Finite control set nonparametric model predictive control for permanent magnet synchronous machines[J]. Electric Machines and Control, 2019, 23(1): 19-26.
[12] 魏尧, 柯栋梁, 黄东晓, 等. 基于超局部化时间序列的永磁同步电机无模型预测电流滑模控制策略[J]. 电工技术学报, 2024, 39(4): 1022-1032.
Wei Yao, Ke Dongliang, Huang Dongxiao, et al. Model-free predictive sliding mode control using ultra-localized time-series for permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1022-1032.
[13] 姚欢, 史婷娜, 王志强, 等. 级联H桥逆变器驱动永磁同步电机的鲁棒预测电流控制策略[J]. 中国电机工程学报, 2022, 42(14): 5266-5278.
Yao Huan, Shi Tingna, Wang Zhiqiang, et al. Robust predictive current control for PMSM fed by CHB inverter[J]. Proceedings of the CSEE, 2022, 42(14): 5266-5278.
[14] 杨帆, 赵希梅, 金鸿雁, 等. 基于GPI观测器的永磁同步电机鲁棒谐振预测电流控制[J]. 电工技术学报, 2024, 39(10): 2995-3006.
Yang Fan, Zhao Ximei, Jin Hongyan, et al. Robust resonant predictive current control based on GPI observer for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2995-3006.
[15] Wang Xing, Zhang Yongchang, Yang Haitao, et al. A model-free predictive current control of induction motor based on current difference[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 2020: 1038-1042.
[16] Li Ze, Feng Guodong, Lai Chunyan, et al. Current injection-based multi-parameter estimation for dual three-phase IPMSM considering VSI nonlinearity[J]. IEEE Transactions on Transportation Electrification, 2019, 5(2): 405-415.
[17] 姚绪梁, 黄乘齐, 王景芳, 等. 具有参数辨识功能的永磁同步电机双矢量模型预测电流控制[J]. 中国电机工程学报, 2023, 43(23): 9319-9330.
Yao Xuliang, Huang Shengqi, Wang Jingfang, et al. A two-vector-based model predictive current control with online parameter identification for PMSM drives[J]. Proceedings of the CSEE, 2023, 43(23): 9319-9330.
[18] Li Xinyue, Kennel R. General formulation of Kalman-filter-based online parameter identification methods for VSI-fed PMSM[J]. IEEE Transactions on Industrial Electronics, 2021, 68(4): 2856-2864.
[19] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet synchronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[20] 吴春, 赵宇纬, 孙明轩. 采用测量电压的永磁同步电机多参数在线辨识[J]. 中国电机工程学报, 2020, 40(13): 4329-4340.
Wu Chun, Zhao Yuwei, Sun Mingxuan. Multi- parameter online identification for permanent magnet synchronous machines using voltage measurements[J]. Proceedings of the CSEE, 2020, 40(13): 4329- 4340.
[21] 马铱林, 袁浩, 尹威, 等. 考虑等效电磁损耗电阻偏移的永磁同步电机直流信号注入在线参数辨识方法[J]. 电工技术学报, 2023, 38(22): 6015-6026.
Ma Yilin, Yuan Hao, Yin Wei, et al. DC-signal- injection-based online parameters identification for permanent magnet synchronous machine considering variation of equivalent electromagnetic loss resistance[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6015-6026.
[22] 陈国真, 黄旭东, 蒋炯炜. 基于死区效应时间补偿的永磁同步电机矢量控制[J]. 微特电机, 2022, 50(4): 52-56.
Chen Guozhen, Huang Xudong, Jiang Jiongwei. Permanent magnet synchronous motor vector control based on dead-time effects time compensation method[J]. Small & Special Electrical Machines, 2022, 50(4): 52-56.
[23] Herran M A, Fischer J R, Gonzalez S A, et al. Adaptive dead-time compensation for grid-connected PWM inverters of single-stage PV systems[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2816-2825.
[24] Yu Kailiang, Wang Zheng. Improved deadbeat predictive current control of dual three-phase variable-flux PMSM drives with composite dis- turbance observer[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8310-8321.
[25] 刘小俊. 基于自适应陷波器的永磁牵引电机死区补偿方法研究[J]. 电机与控制应用, 2019, 46(8): 24-30.
Liu Xiaojun. Method of dead time compensation for permanent magnet traction motor based on adaptive Notch filter[J]. Electric Machines & Control Appli- cation, 2019, 46(8): 24-30.
[26] Qiu Tengfei, Wen Xuhui, Zhao Feng. Adaptive- linear-neuron-based dead-time effects compensation scheme for PMSM drives[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2530-2538.
[27] Joksimovic M G, Levi E, Vukosavic S N. Near- complete suppression of harmonic currents in SPMSMs caused by back EMF and dead time[J]. IEEE Transactions on Industrial Electronics, 2023, 70(5): 4472-4484.
[28] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance- observer-based control and related methods-an overview[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(2): 1083-1095.
[29] 杨淑英, 王奇帅, 东野亚兰, 等. 永磁同步电机离散化建模与分析[J]. 电气传动, 2021, 51(5): 15-24.
Yang Shuying, Wang Qishuai, Dongye Yalan, et al. Discrete-time modeling and analysis of permanent magnet synchronous motor[J]. Electric Drive, 2021, 51(5): 15-24.
[30] Bae B H, Sul S K. A compensation method for time delay of full-digital synchronous frame current regulator of PWM AC drives[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 802-810.
Multi-Parameter Identification Based Flux Predictive Control for Permanent Magnet Synchronous Motor
Abstract In finite control set-model predictive flux control (FCS-MPFC) for permanent magnet synchronous machine (PMSM), the parameters are required for flux linkage reference calculation, actual flux estimation, and flux prediction in the following one or two sampling periods. Due to the influence of operation states and temperature, machine parameters are ready to deviate. Therefore, identifying their values online is crucial to the performance of the actual predictive control system, including the d- and q-axis inductances and the permanent magnet flux. This paper proposes a multi-parameter identification scheme for PMSM. Consequently, with the identified parameters, the flux is treated, and an FCS-MPFC scheme is implemented.
Firstly, this paper designs a generalized proportional integral observer (GPIO) to observe the disturbance caused by parameter deviations. The motor parameter deviations in the disturbance can be extracted based on the mathematical model of the motor. Then, the q-axis inductance and permanent magnet flux can be accurately identified by compensating the nominal parameters. Next, a d-axis inductance identification method is proposed based on the stator current variation characteristics under the FCS-MPFC strategy, which constructs an identification equation for the d-axis inductance using the d-axis current difference equation. It improves identification accuracy by setting appropriate boundary conditions for the differential current values, overcoming the rank deficiency problem in multi-parameter identification. In addition, boundary conditions are set for current and speed to ensure the identification effectiveness. The low-pass filters eliminate high harmonic noises in the identified motor parameters. Furthermore, the identification process is improved by leveraging the characteristics of inverter voltage output under the FCS-MPFC strategy. Specifically, two current samples are taken within a control cycle. By appropriately setting the sampling moments, the dead zone voltage is eliminated from the identification equation. Finally, for the flux prediction process, a flux prediction model based on GPIO is designed to enhance the robustness of flux prediction parameters.
A test platform for PMSM is constructed. Multi-parameter identification, electromagnetic torque increment experiment, and motor acceleration-deceleration experiment are conducted separately. The experimental results demonstrate that the proposed approach can address the rank deficiency issue in multi-parameter identification and eliminate the influence of the inverter dead zone on parameter identification and predictive control. The d-axis inductance, q-axis inductance, and permanent magnet flux under different operating conditions can be identified accurately. Compared to the traditional predictive flux control using nominal parameters, this method eliminates the impact of parameter deviations on torque control. It enables accurate torque control even in the presence of parameter deviations. Furthermore, it outperforms the traditional approach regarding torque control performance under various operating conditions.
Keywords:Finite control set-model predictive flux control, generalized proportional integral observer, multi-parameter identification, parameter robustness
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231680
国家自然科学基金资助项目(51877062)。
收稿日期 2023-10-12
改稿日期 2023-12-29
王祥松 男,1999年生,硕士,研究方向为永磁同步电机驱动控制。
E-mail: 1484997190@qq.com
杨淑英 男,1980年生,教授,博士生导师,研究方向为风力发电系统、电驱动系统。
E-mail: yangsyhfah@163.com(通信作者)
(编辑 崔文静)