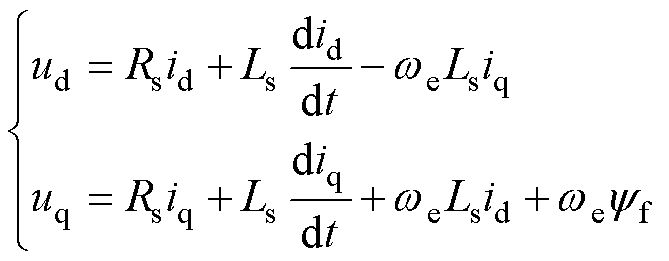 (1)
(1)
摘要 在传统直接转矩控制(DTC)中,参考磁链往往是一个固定值,这将导致五相永磁同步电机(PMSM)在正常及容错情况下运行时效率不高。为解决该问题,该文提出一种基于虚拟方波注入的DTC(VSWI-DTC)策略。首先,建立五相PMSM在正常和开路故障情况下的数学模型,在同步旋转坐标系中推导出恒定转矩下电流幅值与定子磁链幅值的关系。其次,设计最优定子磁链探测器。通过向定子磁链幅值中注入虚拟方波信号,根据电流幅值的变化情况补偿定子磁链幅值,在线探寻最优定子磁链幅值。最后,与无差拍DTC相结合,实现电机高效率DTC运行。实验结果表明,所提策略不但能保持DTC良好的动态性能,抑制开路故障引起的转矩脉动,而且提高了电机在正常和开路故障情况下的效率。
关键词:直接转矩控制 五相永磁同步电机 单相开路故障 最优定子磁链 虚拟方波注入
永磁同步电机(Permanent-Magnet Synchronous Motor, PMSM)具有效率高、转矩密度大等优点,在船舶运输、新能源汽车、航空航天等领域有着广泛的应用[1-3]。相对于三相PMSM,五相PMSM具有母线电压利用率高、转矩脉动小、控制自由度多、容错能力强等优点,在高可靠性场合受到关注[4-6]。
近年来,磁场定向控制(Field-Oriented Control, FOC)[7-10]由于良好的稳态性能在五相PMSM驱动系统中备受欢迎。FOC通过坐标变换,实现了磁链和转矩控制的解耦。相较于FOC,直接转矩控制(Direct Torque Control, DTC)具有优越的转矩动态性能、简单的结构、良好的参数鲁棒性。然而,DTC策略通常采用两个滞环比较器以及开关表分别控制转矩和定子磁链[11-12],导致转矩和定子磁链存在较大的脉动。因此,基于无差拍的DTC(Deadbeat- Based DTC, DB-DTC)策略受到了青睐[13-16]。
在DTC策略中,定子磁链幅值通常取恒定值,这会导致定子电流中包含无功分量,增加电机铜耗。为解决该问题,文献[17]根据当前工况,通过查表法来选择最优定子磁链。然而,这种方法需要提前进行大量的测试且不具备可移植性。文献[18]推导了在定子磁链定向坐标系m-t下t轴电流与定子磁链的数学关系,通过多次迭代获得最优定子磁链,并考虑了磁饱和效应。文献[19]用m轴电流来计算最优定子磁链,无需q轴电感,提高了鲁棒性。文献[20]利用转矩计算最优定子磁链,并提出了d和q轴电感的估算方法,降低了参数变化对最优定子磁链估算的影响,但增加了计算的复杂性。
为降低计算负担并根据运行工况对定子磁链进行实时调整,文献[21-22]采用虚拟信号注入(Virtual Signal Injection, VSI)策略,可有效避免实际信号注入带来的转矩脉动和功率损耗[23-24]。文献[21]将高频虚拟正弦信号注入(Virtual Sinusoidal Signal Injection, VSSI)定子磁链,通过定子电流幅值的变化改变定子磁链。该策略不需q轴电感,具有较好的鲁棒性。文献[22]通过注入虚拟正弦信号以及简单的乘法运算构建了定子磁链探测器,计算简单且无需电机参数,提高了系统的鲁棒性。然而,注入虚拟正弦信号不可避免地需使用多个滤波器,这将导致一定程度的延迟,影响系统的动态性能。文献[25-26]采用虚拟方波信号代替虚拟正弦信号获取最佳电流角,不但实现了最大转矩电流比控制,而且提高了电机的动态性能。这是因为基于虚拟方波信号注入的方法无需使用滤波器。
为提高五相PMSM在正常和容错情况下运行的效率并保持与正常情况下相似的动态性能,本文提出了一种基于虚拟方波注入的直接转矩控制(Virtual-Square-Wave-Injection-based DTC, VSWI- DTC)策略。首先,推导了同步旋转dq坐标系下电流幅值与定子磁链幅值之间的关系,通过向定子磁链中注入虚拟方波信号,根据电流幅值的变化,在线准确、快速地检测出最优定子磁链幅值。其次,基于无差拍控制思想计算出参考电压,进而实现DTC的高效率运行。
图1为20槽22极的外转子五相PMSM。该电机采用分数槽单层集中绕组和容错齿,实现了相间磁和热的物理隔离,有效降低了故障相对非故障相的影响。相间耦合和互感很小,磁阻效应极弱,自感相对转子位置变化很小,可视为常数[27]。此外,由于反电动势谐波很小,假设反电动势仅含基波成分。因此,该五相PMSM在dq坐标系中可表示为
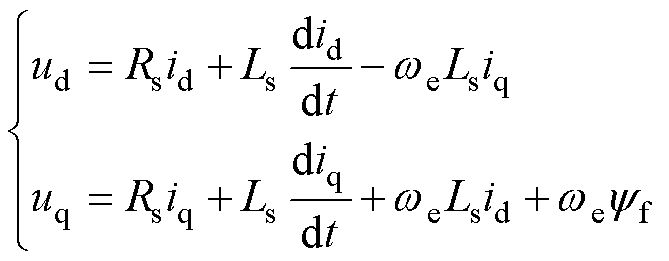 (1)
(1)
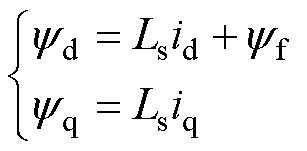 (2)
(2)
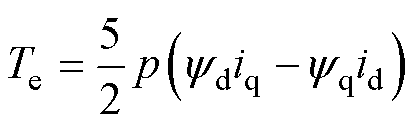 (3)
(3)
式中,Rs为电阻;yf为永磁磁链;we为电角速度;Ls为定子电感;ud、uq、id、iq、yd、yq分别为d、q坐标系中的定子电压、电流、磁链;p为极对数。
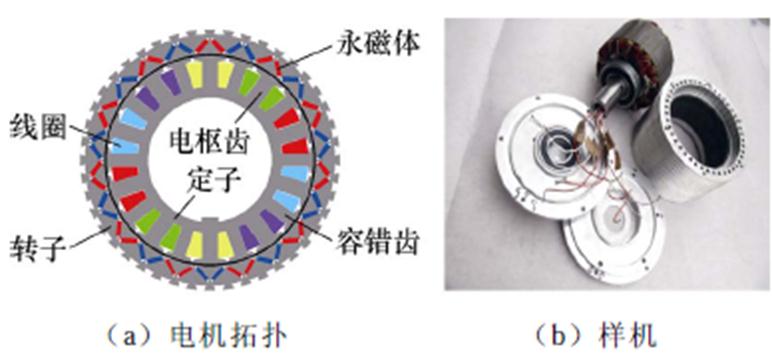
图1 五相PMSM拓扑
Fig.1 Topology of five-phase PMSM
假设A相发生开路故障,基于故障前后磁动势相等、非故障相电流之和为零、非故障相电流关于故障相镜像对称以及铜耗最小原则得到非故障相的容错电流[28]为
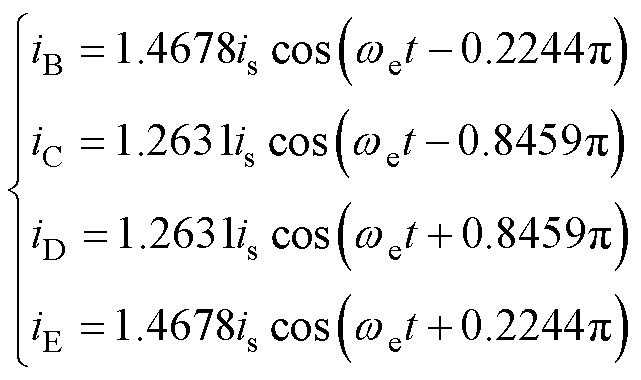 (4)
(4)
式中,iB、iC、iD、iE为非故障相电流;is为电流幅值。在此基础上,得到式(5)所示降阶Clarke变换矩阵[29]。采用该变换矩阵和Park变换矩阵式(6)将自然坐标系上的数学模型变换到dq坐标系上,得到容错后的定子电压、磁链、转矩如式(1)~式(3)所示。可见,容错情况下的定子电压、磁链和转矩与正常情况下一致。
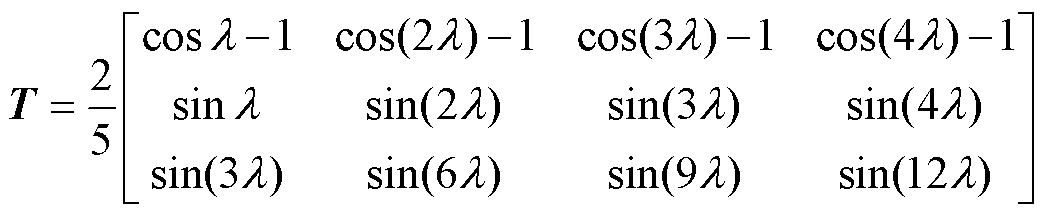 (5)
(5)
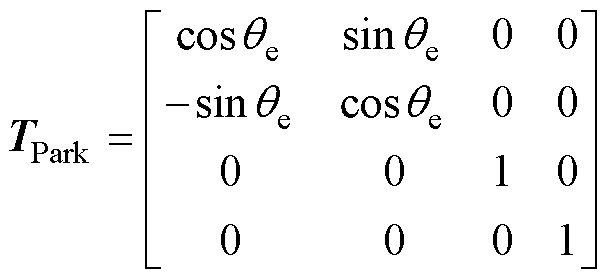 (6)
(6)
式中,l=0.4p;qe为转子电角度。
电流幅值is与定子磁链幅值ys可表示为
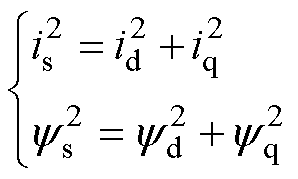 (7)
(7)
由式(2)、式(3)和式(7)得到在转矩恒定时电流幅值与定子磁链幅值之间的关系,如图2所示。可见,当定子磁链幅值小于最优定子磁链幅值时,电流幅值随定子磁链幅值的增大而减小;当定子磁链幅值大于最优定子磁链幅值时,电流幅值随定子磁链幅值的增大而增大。因此,存在最优定子磁链幅值使电流幅值最小。当定子磁链幅值在最优定子磁链幅值附近波动时,电流幅值几乎没有明显变化。
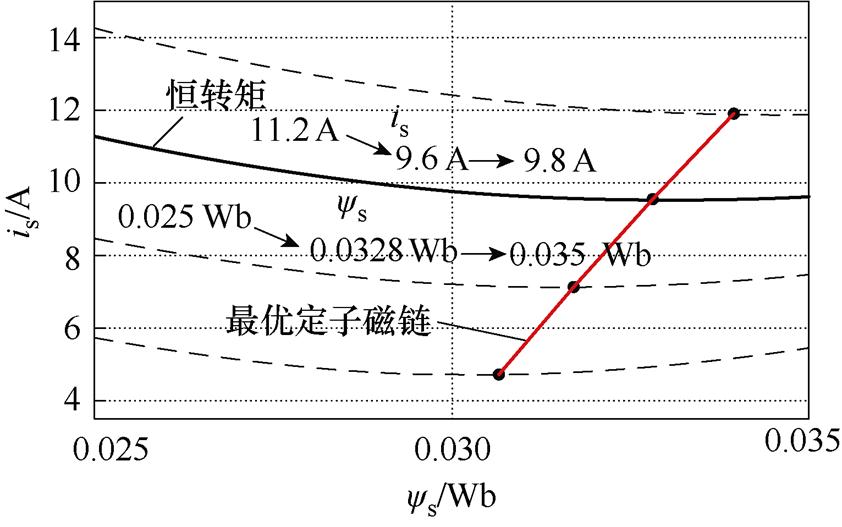
图2 定子磁链幅值与电流幅值在恒转矩下的关系
Fig.2 Current amplitude locus with stator flux linkage amplitude under constant torque
向定子磁链注入的双极性方波信号的占空比为50%,其可表示为
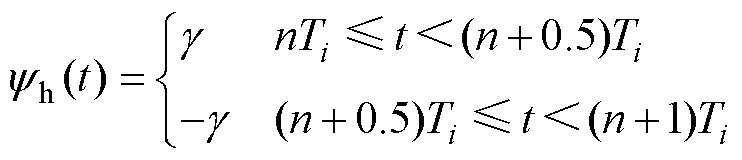 (8)
(8)
式中,g 为虚拟方波信号幅值;Ti为虚拟方波信号周期,设置为采样周期Ts的10倍,即Ti=10Ts;n为第n个虚拟方波信号。
当正极性方波信号注入到定子磁链中,含正极性高频方波信号的定子磁链幅值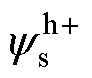 可表示为
可表示为
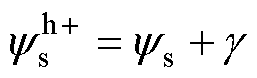 (9)
(9)
根据式(9),注入正极性高频方波信号后,dq坐标系中的定子磁链可表示为
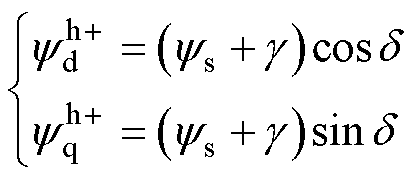 (10)
(10)
式中,d 为定子磁链矢量与d轴的夹角。
将式(10)代入式(2),得到正极性方波注入后dq坐标系中的电流 、
、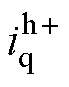 分别为
分别为
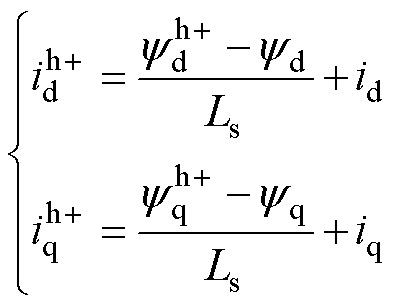 (11)
(11)
根据式(7)和式(11),得到正极性方波注入后的电流幅值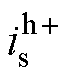 为
为
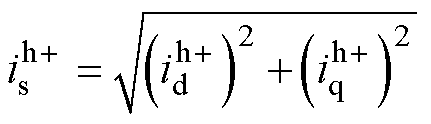 (12)
(12)
同理,当高频负极性方波信号注入定子磁链时,dq坐标系中的定子磁链、电流与电流幅值可分别表示为
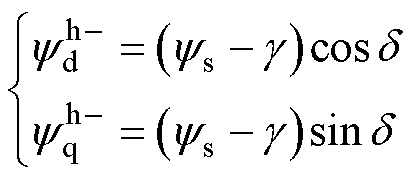 (13)
(13)
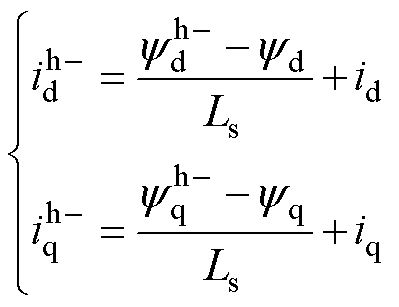 (14)
(14)
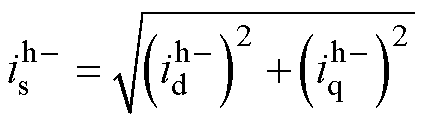 (15)
(15)
由于注入的信号是虚拟高频方波信号,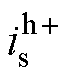 围绕零点进行泰勒级数展开,可得
围绕零点进行泰勒级数展开,可得
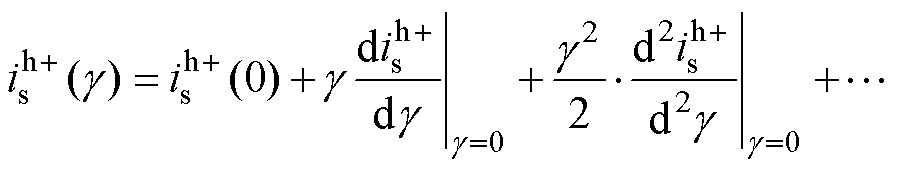
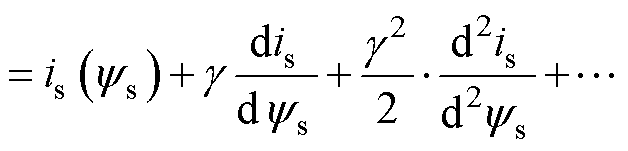 (16)
(16)
由于注入的方波信号幅值非常小;另外,与其他高阶分量相比,式(16)中的一阶项在电流幅值
变化中占主导地位。因此,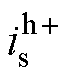 可进一步表示为
可进一步表示为
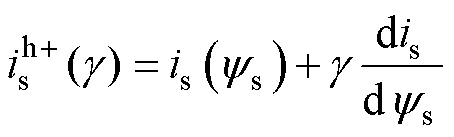 (17)
(17)
同理,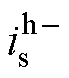 围绕零点进行泰勒级数展开,可得到
围绕零点进行泰勒级数展开,可得到
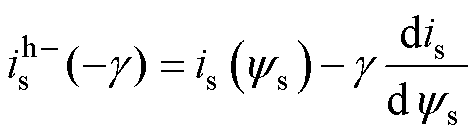 (18)
(18)
由式(17)与式(18)可得误差信号为
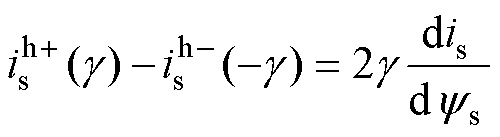 (19)
(19)
根据式(19)可知,若控制dis/dys=0,就能得到电流幅值的最小值,对应的定子磁链幅值即为最优定子磁链幅值。设计的最优磁链探测器如图3所示。将虚拟方波信号注入后得到的电流幅值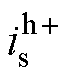 和
和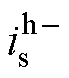 作差得到误差信号h;对h 积分得到定子磁链幅值的补偿值∆ys。可知,当h 被控制为0时,就能获得最优定子磁链幅值。可见,该最优磁链探测器中没有滤波器。
作差得到误差信号h;对h 积分得到定子磁链幅值的补偿值∆ys。可知,当h 被控制为0时,就能获得最优定子磁链幅值。可见,该最优磁链探测器中没有滤波器。
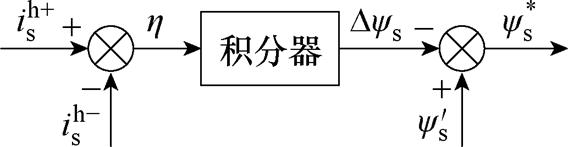
图3 最优定子磁链探测器
Fig.3 Detector of optimal flux linkage
在传统DB-DTC策略中,dq坐标系中的参考电压计算非常复杂[15],为了降低计算负担,本文通过基于磁链微分的DB-DTC策略[13]来简化计算。
根据式(2)与式(7),对dq坐标系中的定子磁链进行微分,并将式(1)代入,可得
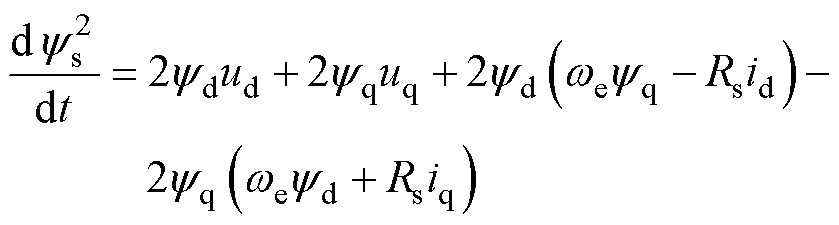 (20)
(20)
对转矩进行微分,并将式(1)代入,可得
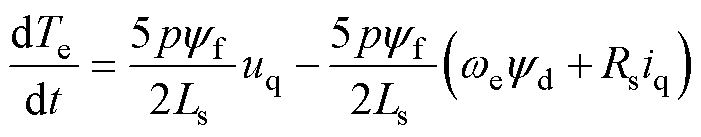 (21)
(21)
离散化式(20)和式(21),可得
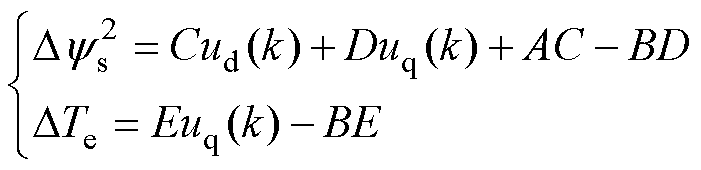 (22)
(22)
其中
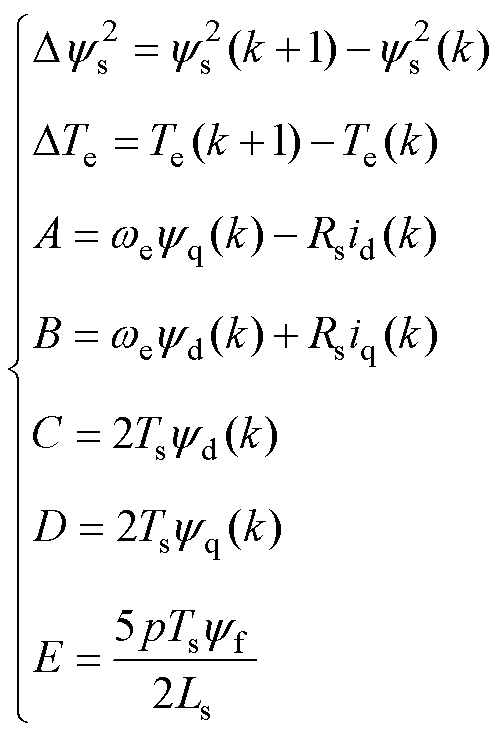 (23)
(23)
式中,k为第k个采样时刻;ys(k+1)与Te(k+1)分别由参考定子磁链幅值和转矩赋值得到。
求解式(22),得到参考电压为
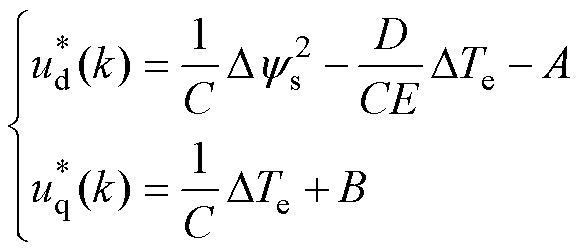 (24)
(24)
式中,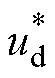 、
、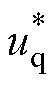 为参考电压在d、q轴的分量。
为参考电压在d、q轴的分量。
将基于虚拟方波信号注入的DTC和基于载波的脉宽调制(Carrier-based Pulse Width Modulation, CPWM)技术相结合,再结合式(24),得到本文所提出的开路故障情况下的VSWI-DTC策略,如图4所示。
为验证本文提出的用于五相PMSM开路故障情况下的VSWI-DTC策略的可行性,搭建如图5所示的基于五相PMSM的实验平台。电机参数见表1。采用文献[21]中的基于虚拟正弦波注入方法的探测器获取最优定子磁链幅值,并将其与DB-DTC策略相结合作为参考对象;同时,将基于MTPA的矢量控制策略[30]作为参考对象。选择TI的数字信号处理(Digital Signal Processing, DSP)(TMS320F2812)作为控制器的核心芯片;使用两块智能功率模块(Intelligent Power Module, IPM)(PM100CVA120)作为功率驱动模块;PMSM所需负载由永磁直流电机连接电阻箱提供;转矩信号通过转矩传感器获取。参考转矩为6 N·m,参考定子磁链初始值为0.04 Wb,采样频率为10 kHz,虚拟正弦波信号和虚拟方波信号的注入频率均为1 kHz。
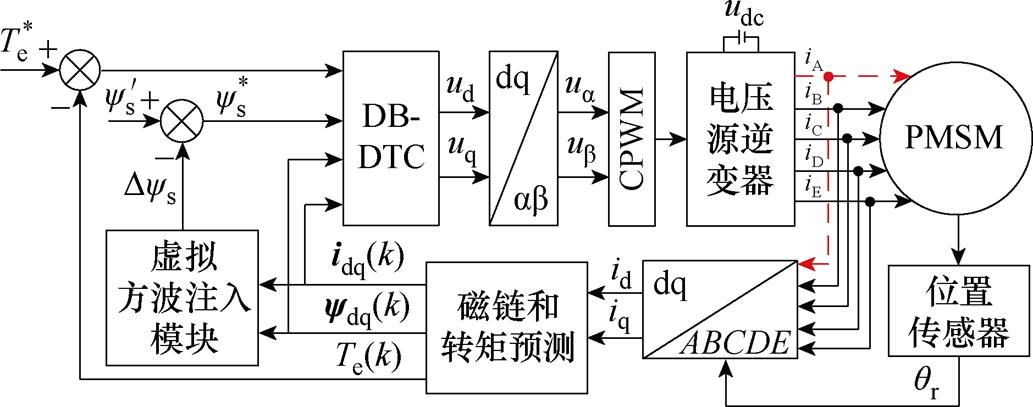
图4 所提出的VSWI-DTC框图
Fig.4 Control diagram of proposed VSWI-DTC

图5 五相PMSM实验平台
Fig.5 Experimental platform of five-phase PMSM
表1 五相PMSM参数
Tab.1 Parameters of five-phase PMSM
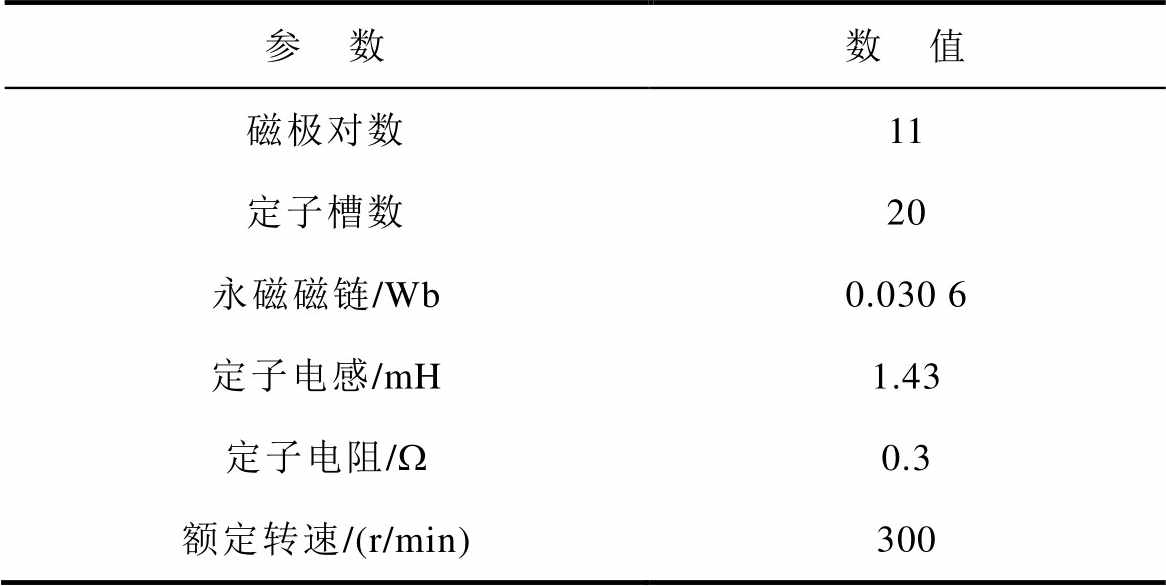
参 数数 值 磁极对数11 定子槽数20 永磁磁链/Wb0.030 6 定子电感/mH1.43 定子电阻/W0.3 额定转速/(r/min)300
所提策略控制五相PMSM以6 N·m负载和额定转速300 r/min在正常情况下稳态运行。图6为五相PMSM在正常情况下稳态运行时,从采用基于恒定定子磁链幅值的DTC (DTC based on Constant Flux Linkage Amplitude, CFLA-DTC)切换到基于虚拟信号注入的DTC(DTC based on VSI, VSI-DTC)过程的转矩、定子磁链幅值和A相电流iA的波形。可见,当策略从CFLA-DTC切换到VSSI-DTC和VSWI-DTC后,电流幅值从9.1 A下降到7.2 A,定子磁链幅值也从0.04 Wb下降到0.032 3 Wb,定子磁链幅值快速并准确地跟踪参考定子磁链的变化。VSSI-DTC需1.384 s才能获得最优定子磁链幅值,而所提出的VSWI-DTC仅需0.082 s。因此,VSWI- DTC能更快地找到最优定子磁链幅值。此外,VSSI- DTC和VSWI-DTC的转矩脉动与CFLA-DTC的转矩脉动基本相同,三种DTC策略的转矩脉动均为3.5%。由于使用的是DB-DTC策略,而非传统的滞环控制策略,故转矩脉动很小。因此,所提VSWI-DTC不会引起额外的转矩波动,在正常情况下具有良好的稳态性能。
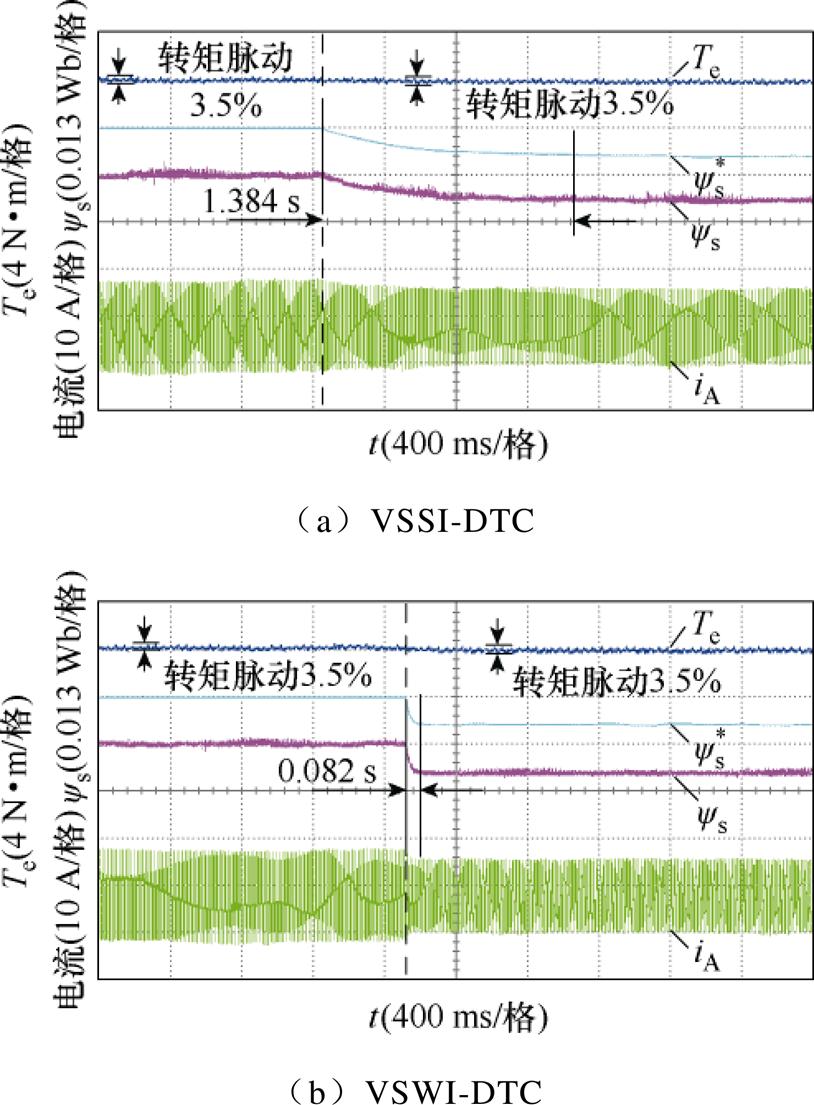
图6 从CFLA-DTC切换到VSI-DTC在正常情况下的转矩、定子磁链幅值和电流波形
Fig.6 Responses of torque, stator flux linkage amplitude and current from CFLA-DTC to VSI-DTC under healthy condition
图7为五相PMSM正常运行过程中发生A相开路故障且容错策略立即启动情况下的转矩、定子磁链幅值和电流波形。可见,容错情况下的平均转矩和转矩波动与正常情况下的基本相同,三种DTC策略的转矩脉动为3.5%。在容错运行时,CFLA- DTC的B相电流幅值为13.3 A,而VSWI-DTC的电流幅值仅为10.6 A,与VSSI-DTC基本相同。在正常及容错情况下,CFLA-DTC的定子电流总谐波畸变率(Total Harmonics Distortion, THD)分别为4.94%和3.37%,而VSSI-DTC和VSWI-DTC在正常和容错情况下的定子电流THD分别为5.67%和3.86%。因此,故障前后相电流波形都具有较好的正弦度,同时由于容错后电流幅值增大致使其THD较小。相比CFLA-DTC在正常和容错情况下的相电流幅值和THD,VSSI-DTC和VSWI-DTC的相电流幅值在相同工况下均较小,因此它们的THD有所增加。当发生A相开路故障后,基于MTPA的矢量控制策略的B相电流幅值由7.2 A变为10.6 A,其B相电流THD在正常及容错情况下分别为5.56%和3.79%,均与VSWI-DTC策略相似,并且两种策略的转矩脉动也基本相同。因此,VSWI-DTC策略在正常及容错情况下的稳态性能和基于MTPA的矢量控制策略相似,能够有效降低电流幅值,实现最小铜耗。此外,基于MTPA矢量控制中定子磁链幅值为0.032 3 Wb,与VSWI-DTC策略得到的最优定子磁链一致。可见,0.032 3 Wb为此工况下的最优定子磁链幅值。因此,所提策略在正常和开路故障情况下具有优良的稳态性能和最小铜耗。

图7 从正常到容错运行的转矩、定子磁链幅值和相电流波形
Fig.7 Waveforms of torque, stator flux linkage amplitude and phase currents from healthy to fault-tolerant condition
图8为PMSM在正常及容错情况下稳态运行时从CFLA-DTC切换到VSWI-DTC过程中的转矩、参考定子磁链幅值和dq轴磁链波形。可见,无论在正常还是在容错情况下,当切换到VSWI-DTC后,d轴磁链从0.038 6 Wb快速下降为0.030 6 Wb左右,而q轴磁链维持在0.010 3 Wb左右。同时,dq轴磁链能快速跟随参考定子磁链幅值的变化。此时d轴磁链与永磁磁链相等,PMSM输出转矩刚好是隐极式PMSM的最大转矩,进一步验证了本文所提策略的有效性。
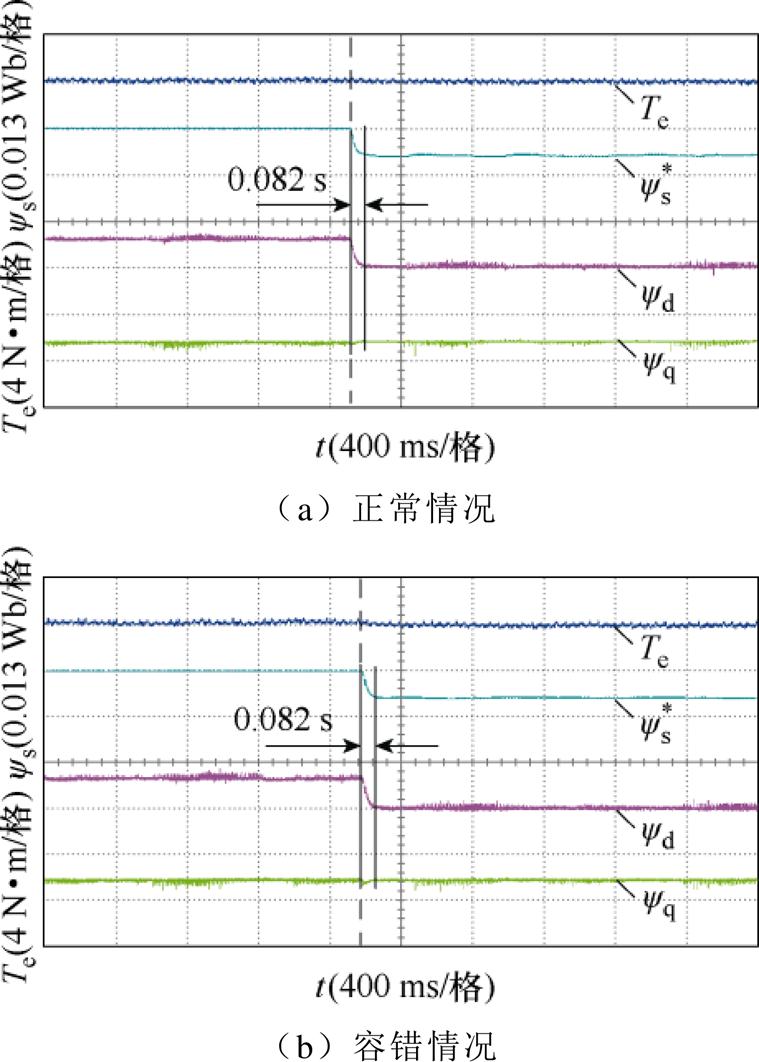
图8 从CFLA-DTC切换到VSWI-DTC的转矩和磁链波形
Fig.8 Responses of torque and flux linkages from CFLA-DTC to VSWI-DTC
图9为电流幅值、h 和定子磁链在正常及容错情况下的关系。当定子磁链幅值从0.04 Wb下降到0.024 Wb再重新上升为0.04 Wb时,定子电流幅值的最小值对应h=0时刻,此时得到的定子磁链幅值即为最优定子磁链幅值。VSWI-DTC在虚线处启动,电流幅值在正常及容错情况下分别阶跃为7.2 A和10.6 A;h和定子磁链幅值快速阶跃为0和0.032 3 Wb,并且此刻电流幅值等于最小值。因此,VSWI-DTC在正常及容错情况下可准确、快速地跟踪最优定子磁链。
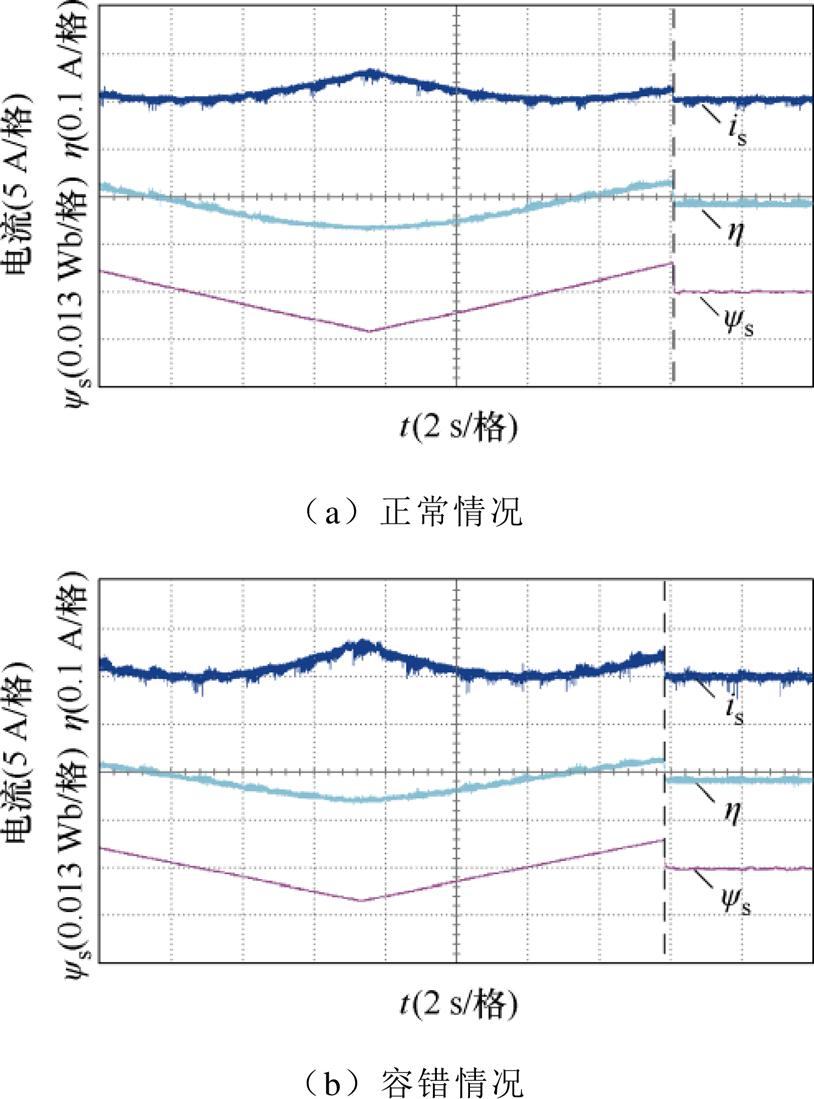
图9 电流幅值、h 与定子磁链幅值的关系
Fig.9 Relationship among current amplitude, h and stator flux linkage amplitude
图10和图11分别为两种策略控制下五相PMSM在正常情况下给定转矩突变时的转矩、定子磁链幅值和电流波形。当给定转矩阶跃变化时,转矩需要大约300 ms才能跟踪其参考。这是由于转矩传感器的响应滞后,致使所测量到的转矩信号存在一定的延迟,但测量转矩与稳态运行时的给定转矩值仍然相等。当给定转矩发生突变时,VSSI-DTC策略需超过1 s才能获得最优定子磁链,而VSWI- DTC策略获得最优定子磁链的时间不到0.1 s。在给定转矩为6 N·m时,最优定子磁链幅值约为0.032 3 Wb;在给定转矩为4 N·m时,最优定子磁链幅值约为0.031 4 Wb。当给定转矩阶跃时,定子磁链能够准确、快速地跟踪其参考值。图12和图13分别为两种策略控制下五相PMSM在容错情况下给定转矩突变时的转矩、定子磁链和电流波形。运行条件与正常情况下相同。与VSSI-DTC策略相比,VSWI- DTC策略可更快地获得最优定子磁链,定子磁链幅值能快速准确地跟踪其最优值。此外,当转矩给定值相同时,最优定子磁链幅值在正常和容错情况下基本一致。因此,无论是正常还是容错情况,VSWI- DTC策略都具有更好的动态性能,能在工况变化时更快地找到最优定子磁链幅值。
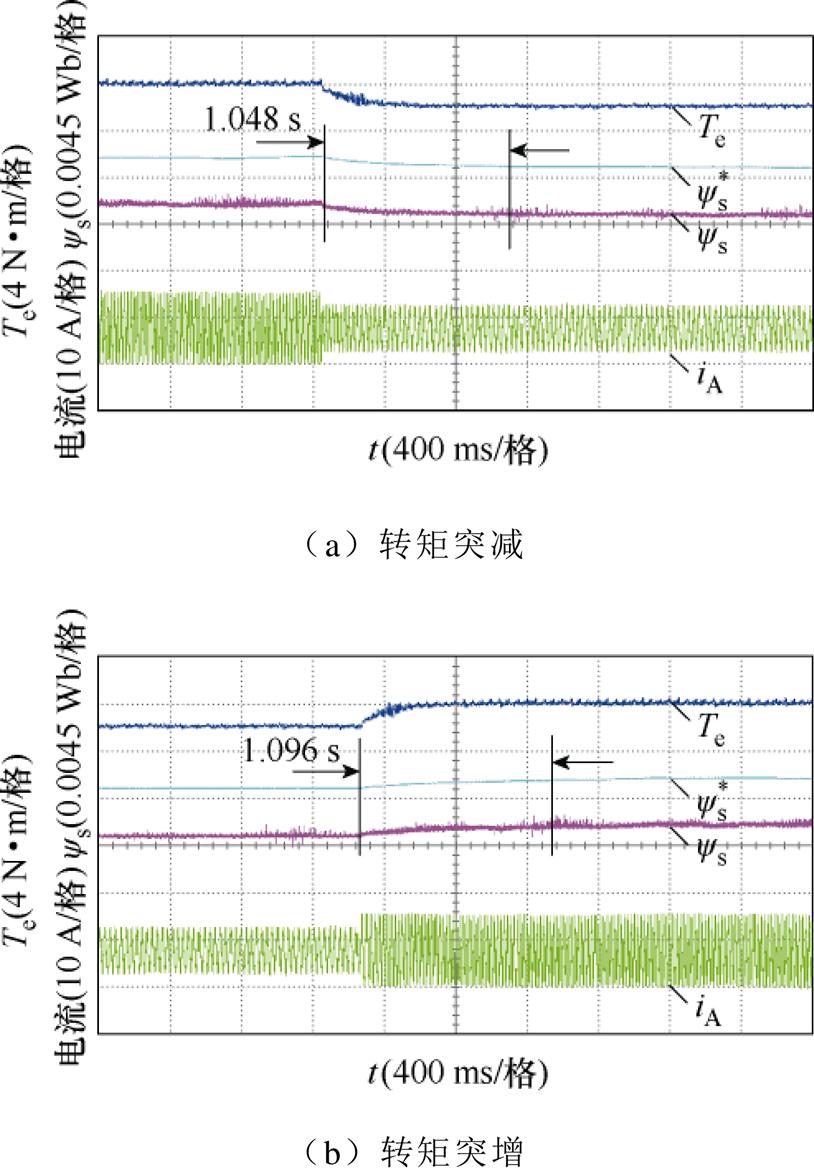
图10 VSSI-DTC在正常情况下给定转矩阶跃时的转矩、定子磁链和电流响应
Fig.10 Responses of torque, stator flux linkage amplitude and current to step changes in torque reference with VSSI-DTC under healthy condition
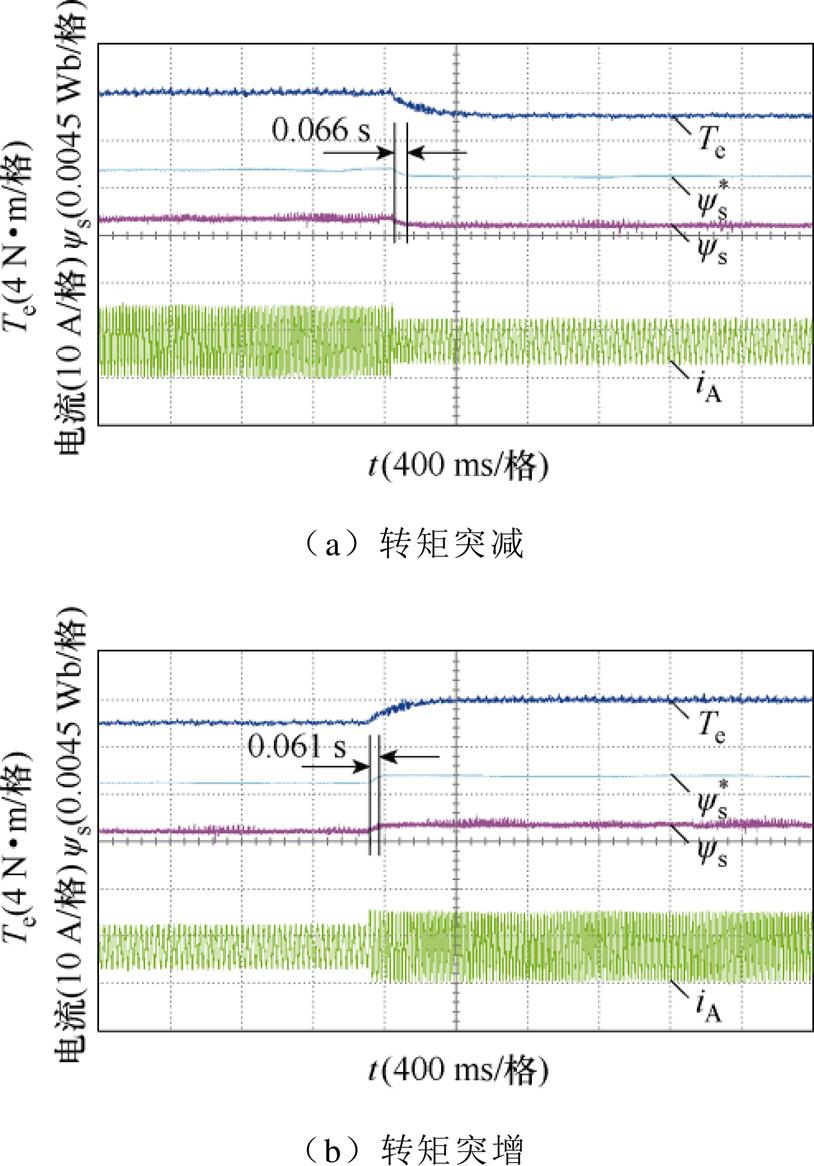
图11 VSWI-DTC在正常情况下给定转矩阶跃时的转矩、定子磁链和电流响应
Fig.11 Responses of torque, stator flux linkage amplitude and current to step changes in torque reference with VSWI-DTC under healthy condition
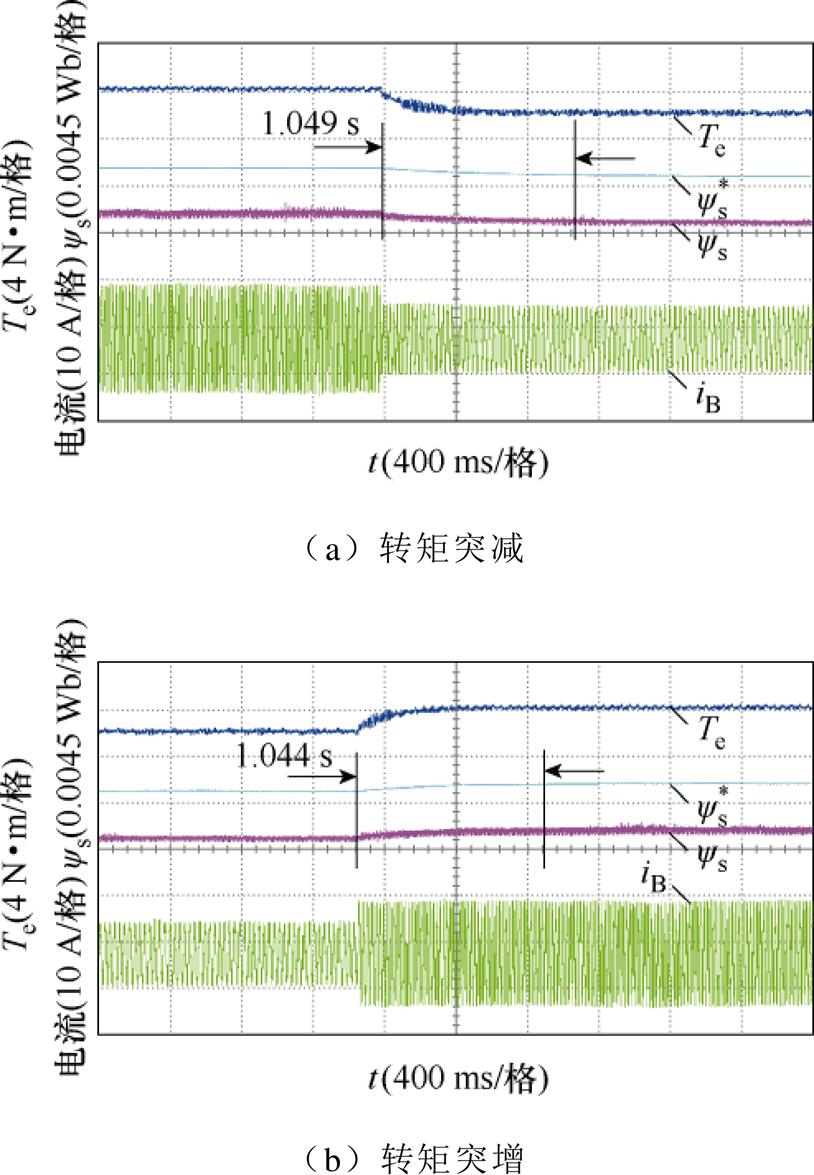
图12 VSSI-DTC在容错情况下给定转矩阶跃时的转矩、定子磁链和电流响应
Fig.12 Responses of torque, stator flux linkage amplitude and currents to step changes in torque reference with VSSI-DTC under fault-tolerant condition
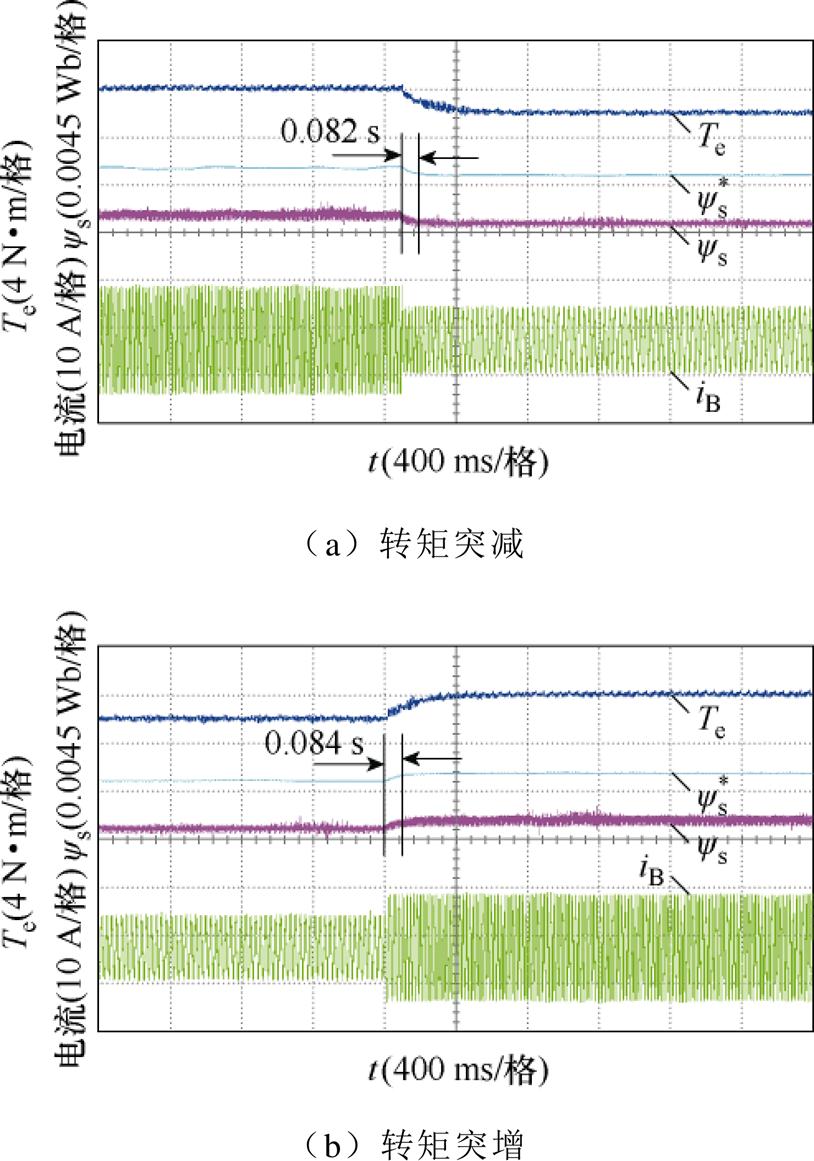
图13 VSWI-DTC在容错情况下给定转矩阶跃时的转矩、定子磁链和电流响应
Fig.13 Responses of torque, stator flux linkage amplitude and currents to step changes in torque reference with VSWI-DTC under fault-tolerant condition
图14和图15分别为正常及容错运行时三种DTC与基于MTPA的矢量控制的效率分布。考虑到实验台架的限制,四种策略的输出转矩范围为1~6 N·m,转速范围为100~300 r/min。无论在正常还是在容错情况下,在相同负载和转速下,VSSI-DTC、VSWI-DTC与基于MTPA的矢量控制的效率均高于CFLA-DTC。此外,VSSI-DTC、VSWI-DTC和基于MTPA的矢量控制的效率基本相同。需要注意的是,所提出的VSWI-DTC容错策略是基于铜耗最小原则;在容错情况下的铜耗相比正常情况下增加了50%;在300 r/min和6 N·m工况下(电机功率很小),所增加的铜耗占输出功率的10.3%。因此,尽管在正常情况下的效率较高,但是在容错情况下的效率有了明显的降低。然而,相比CFLA-DTC,在相同工况下,所提出的VSWI-DTC能够在正常及容错运行时提供更高的效率,且效率与基于MTPA的矢量控制基本相同。
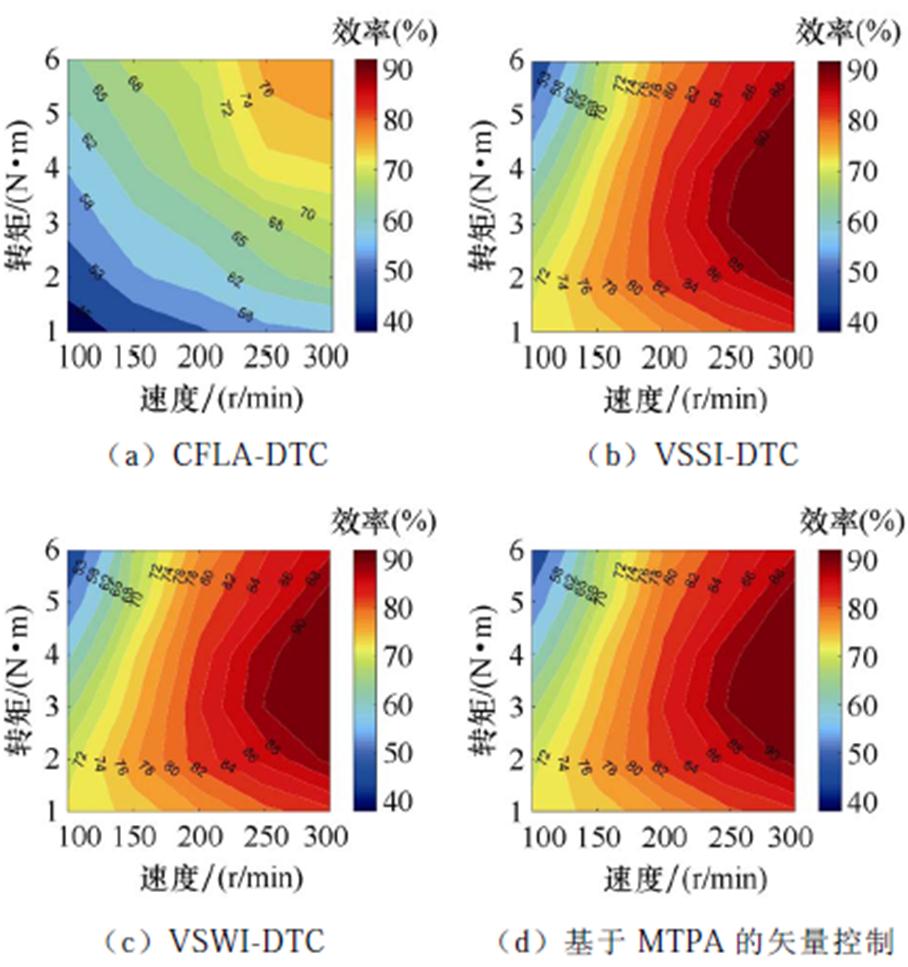
图14 正常情况下效率分布
Fig.14 Efficiency maps under healthy condition
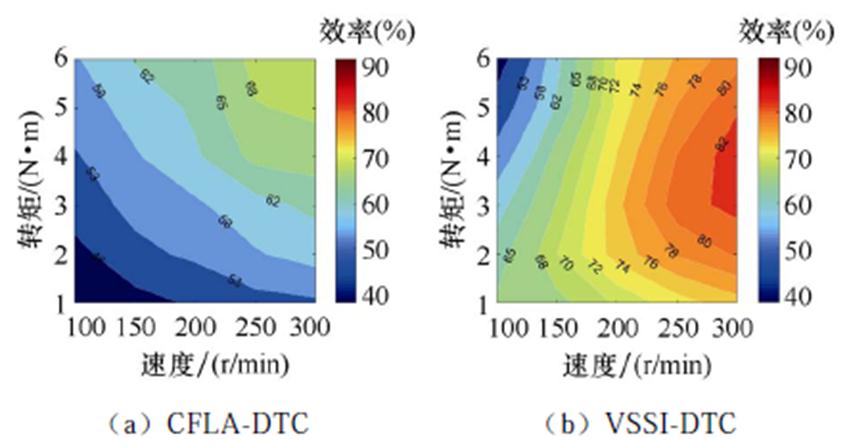
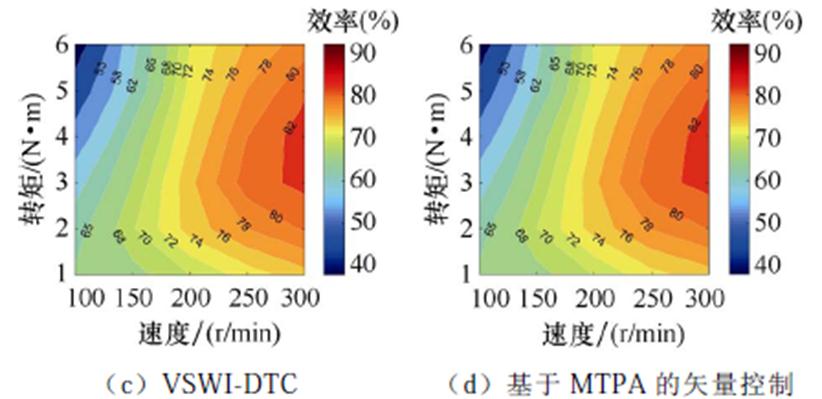
图15 容错情况下效率分布
Fig.15 Efficiency maps under fault-tolerant condition
为提高DTC策略控制的五相PMSM在正常及容错情况下的运行效率,并保证其具有优良的稳态和动态性能,本文提出了一种基于虚拟方波注入的DTC策略。该策略具有如下优点:
1)无论是在正常还是开路故障情况下,都无需使用滤波器,且能在线快速探寻到最优定子磁链幅值,具有优良的稳态和动态性能,提升电机效率的效果与VSSI-DTC策略基本相同,但探测最优定子磁链的速度快于VSSI-DTC。
2)能够抑制开路故障引起的转矩脉动,在开路故障情况下具有和正常情况下相似的动态性能。
3)注入的信号为虚拟信号,不会引起额外的转矩脉动和损耗。
参考文献
[1] 周奇勋, 刘帆, 吴紫辉, 等. 永磁同步电机转矩与定子磁链模型预测控制预测误差补偿方法[J]. 电工技术学报, 2022, 37(22): 5728-5739.
Zhou Qixun, Liu Fan, Wu Zihui, et al. Model predictive torque and stator flux control method for PMSMs with prediction error compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5728-5739.
[2] Chen Shouchuan, Hao Xinhong, Gao Congzhe, et al. An effective nontransient active short-circuit method for PMSM in electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3571-3580.
[3] 孙丹, 赵琛, 柯伟煌, 等. 基于重构电压矢量的共直流母线型开绕组永磁同步电机改进直接转矩控制[J]. 电工技术学报, 2022, 37(7): 1644-1653.
Sun Dan, Zhao Chen, Ke Weihuang, et al. Reconstructed voltage vector based improved direct torque control strategy for open-winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1644-1653.
[4] 陈前, 夏雨航, 赵文祥, 等. 采用无差拍电流跟踪的五相梯形反电动势永磁电机开路容错控制[J]. 电工技术学报, 2022, 37(2): 368-379.
Chen Qian, Xia Yuhang, Zhao Wenxiang, et al. Open-circuit fault-tolerant control for five-phase permanent magnet motors with trapezoidal back-EMF by deadbeat current tracking[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 368- 379.
[5] 周华伟, 叶晨, 陈铖, 等. 基于转子磁链观测器的五相容错PMSM开路故障下的无位置传感器控制[J]. 电工技术学报, 2023, 38(2): 422-434.
Zhou Huawei, Ye Chen, Chen Cheng, et al. Rotor-flux observer based sensorless control of five-phase fault- tolerant PMSM with open-circuit fault[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(2): 422-434.
[6] Saeed M S R, Song Wensheng, Yu Bin, et al. Low-complexity deadbeat model predictive current control with duty ratio for five-phase PMSM drives[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12085-12099.
[7] 周长攀, 刘海峰, 景国秀, 等. 非正弦反电势五相永磁同步电机容错矢量控制[J]. 电气工程学报, 2021, 16(4): 108-119.
Zhou Changpan, Liu Haifeng, Jing Guoxiu, et al. Fault-tolerant vector control of five-phase permanent magnet synchronous motor of non-sinusoidal back EMF[J]. Journal of Electrical Engineering, 2021, 16(4): 108-119.
[8] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[9] Chen Zhiwei, Shi Tingna, Lin Zhichen, et al. Analysis and control of current harmonic in IPMSM field- oriented control system[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9571-9585.
[10] Attaianese C, D’Arpino M, Di Monaco M, et al. Model-based detection and estimation of DC offset of phase current sensors for field oriented PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 6316-6325.
[11] 宋战锋, 毛丰羽, 崔严谨, 等. 基于多级滞环控制器的表贴式双三相永磁同步电机低电流谐波直接转矩控制策略[J]. 中国电机工程学报, 2023, 43(11): 4410-4422.
Song Zhanfeng, Mao Fengyu, Cui Yanjin, et al. Low current harmonic direct torque control strategy for surface-mounted dual-three-phase permanent magnet synchronous machine based on multi-level hysteresis controller[J]. Proceedings of the CSEE, 2023, 43(11): 4410-4422.
[12] Petkar S G, Thippiripati V K. A novel duty-controlled DTC of a surface PMSM drive with reduced torque and flux ripples[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3373-3383.
[13] Wang Wusen, Liu Chunhua, Zhao Hang, et al. Improved deadbeat-direct torque and flux control for PMSM with less computation and enhanced robust- ness[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2254-2263.
[14] 刘国海, 孙汶超, 周华伟, 等. 五相永磁同步电机改进型无差拍直接转矩和磁链控制[J]. 电工技术学报, 2023, 38(24): 6658-6667.
Liu Guohai, Sun Wenchao, Zhou Huawei, et al. An improved deadbeat direct torque and flux control strategy of five-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6658-6667.
[15] Lee J S, Choi C H, Seok J K, et al. Deadbeat-direct torque and flux control of interior permanent magnet synchronous machines with discrete time stator current and stator flux linkage observer[J]. IEEE Transactions on Industry Applications, 2011, 47(4): 1749-1758.
[16] 陈浩, 和阳, 赵文祥, 等. 基于占空比调制的五相容错永磁游标电机直接转矩控制[J]. 电工技术学报, 2020, 35(5): 1055-1064.
Chen Hao, He Yang, Zhao Wenxiang, et al. Direct torque control of five-phase fault-tolerant permanent magnet vernier motor based on duty cycle modu- lation[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1055-1064.
[17] 阎彦, 赵梦圆, 陈志伟, 等. 辅助坐标系下永磁同步电机低载波比无差拍预测转矩控制[J]. 中国电机工程学报, 2023, 43(2): 761-770.
Yan Yan, Zhao Mengyuan, Chen Zhiwei, et al. Low frequency ratio deadbeat predictive torque control of permanent magnet synchronous motor in auxiliary coordinate system[J]. Proceedings of the CSEE, 2023, 43(2): 761-770.
[18] Inoue T, Inoue Y, Morimoto S, et al. Maximum torque per ampere control of a direct torque-controlled PMSM in a stator flux linkage synchronous frame[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2360-2367.
[19] Shinohara A, Inoue Y, Morimoto S, et al. Maximum torque per ampere control in stator flux linkage synchronous frame for DTC-based PMSM drives without using q-axis inductance[J]. IEEE Transa- ctions on Industry Applications, 2017, 53(4): 3663- 3671.
[20] Shinohara A, Inoue Y, Morimoto S, et al. Direct calculation method of reference flux linkage for maximum torque per ampere control in DTC-based IPMSM drives[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2114-2122.
[21] Liu Guohai, Yang Yuqi, Chen Qian. Virtual signal injected MTPA control for DTC five-phase IPMSM drives[J]. Journal of Power Electronics, 2019, 19(4): 956-967.
[22] 刘国海, 黄旭, 周华伟. 基于定子磁链最优的五相永磁电机直接转矩控制[J]. 中国电机工程学报, 2018, 38(20): 6119-6126.
Liu Guohai, Huang Xu, Zhou Huawei. Stator-flux optimization based DTC for five-phase permanent magnet motor drives[J]. Proceedings of the CSEE, 2018, 38(20): 6119-6126.
[23] Chen Qian, Gu Licheng, Lin Zhipeng, et al. Extension of space-vector-signal-injection-based MTPA control into SVPWM fault-tolerant operation for five-phase IPMSM[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(9): 7321-7333.
[24] Yoo J, Kim H S, Sul S K. MTPA tracking control of sensorless IPMSM based on square-wave voltage signal injection[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12525-12537.
[25] Wang Jun, Huang Xiaoyan, Yu Dong, et al. An accurate virtual signal injection control of MTPA for an IPMSM with fast dynamic response[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7916-7926.
[26] Zhou Xinxiu, Zhou Yongping, Wang Huijun, et al. An improved MTPA control based on amplitude- adjustable square wave injection[J]. IEEE Transa- ctions on Energy Conversion, 2020, 35(2): 956-965.
[27] Chen Qian, Liu Guohai, Zhao Wenxiang, et al. Design and comparison of two fault-tolerant interior- permanent-magnet motors[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6615-6623.
[28] 刘国海, 高猛虎, 周华伟, 等. 五相永磁同步电机磁链改进型容错直接转矩控制[J]. 中国电机工程学报, 2019, 39(2): 359-365, 633.
Liu Guohai, Gao Menghu, Zhou Huawei, et al. Flux-modification-based fault-tolerant DTC for five- phase PMSM[J]. Proceedings of the CSEE, 2019, 39(2): 359-365, 633.
[29] Zhou Huawei, Xu Jinhui, Chen Cheng, et al. Disturbance-observer-based direct torque control of five-phase permanent magnet motor under open- circuit and short-circuit faults[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11907-11917.
[30] Chen Qian, Zhao Wenxiang, Liu Guohai, et al. Extension of virtual-signal-injection-based MTPA control for five-phase IPMSM into fault-tolerant operation[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 944-955.
Abstract The five-phase permanent magnet synchronous motor (PMSM) has received attention in electric vehicles and marine transportation due to its more control degrees of freedom, fast response, and high torque density. The most popular control strategies are field-oriented control (FOC) and direct torque control (DTC) strategies. Compared with FOC, a switching table and two hysteresis controllers are applied in DTC to control torque and stator flux linkage. Thus, DTC has the advantages of simple structure, high torque dynamic performance, and fast dynamic response. It also has disadvantages, such as large torque and flux linkage fluctuations. Deadbeat-based DTC (DB-DTC) can solve this problem by discretizing the mathematical model to obtain the voltage vector, which can reduce the fluctuations of torque and stator flux linkage within one sampling period. However, the amplitude of reference flux linkage is usually constant in traditional DTC strategy, resulting in inefficient operation of five-phase PMSM under both healthy and open-circuit fault conditions. This paper proposes a novel DTC based on virtual square wave injection (VSWI-DTC) strategy, which can detect the optimal stator flux linkage amplitude online under healthy and open-circuit fault conditions, achieve the minimum copper loss, improve the operational efficiency, and maintain good dynamic performance.
Firstly, the model of five-phase PMSM is derived in the rotor-flux reference frame under healthy and open-circuit fault conditions, and the relationship between stator current and stator flux linkage under constant torque is deduced. Secondly, the optimal stator flux linkage detector is designed. The virtual square wave signal is injected into the stator flux linkage amplitude, which is compensated according to current amplitude variations under constant torque. Thus, online detection of the optimal stator flux linkage amplitude can be realized. Finally, combined with DB-DTC, the torque and stator flux linkage fluctuations can be reduced.
The experimental results demonstrate that VSWI-DTC has good steady-state and dynamic performance. The proposed strategy requires about 0.1 s to detect the optimal stator flux linkage amplitude, while the DTC based on virtual sinusoidal signal injection (VSSI-DTC) takes about 1 s. Most importantly, the optimal stator flux linkage amplitudes obtained by the two strategies are almost the same. In addition, the optimal stator flux linkage amplitude is almost the same under healthy and open-circuit fault conditions, while the torque reference remains invariable. When the torque reference steps, the amplitude of stator flux linkage can accurately and quickly track its reference. Therefore, the following conclusions can be drawn. (1) The proposed VSWI-DTC strategy can quickly detect the optimal stator flux linkage amplitude online without filters under healthy and open-circuit fault conditions. (2) The proposed VSWI-DTC strategy has similar dynamic performance under healthy and open-circuit fault conditions. Additionally, the torque fluctuations caused by open-circuit faults can be restrained. (3) No additional torque fluctuation and loss exist because the square wave signal injected into the stator flux linkage is virtual.
Keywords:Direct torque control (DTC), five-phase permanent magnet synchronous motor (PMSM), open-circuit fault, optimal stator flux linkage, virtual square wave injection
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231718
国家自然科学基金资助项目(52277052)。
收稿日期 2023-10-16
改稿日期 2023-12-22
周华伟 男,1980年生,教授,博士生导师,研究方向为电动汽车和电磁悬架用特种永磁电机驱动控制、容错控制等。
E-mail: zhouhuawei@ujs.edu.cn(通信作者)
周振伍 男,1999年生,硕士研究生,研究方向为永磁电机驱动控制。
E-mail: 1109466173@qq.com
(编辑 崔文静)