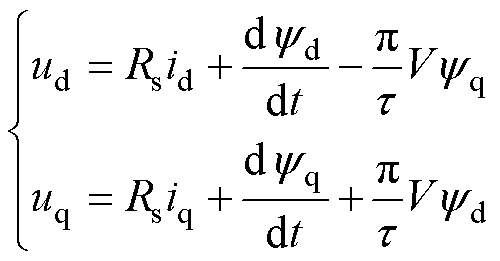 (1)
(1)
摘要 该文研究了一种基于智能在线扩展卡尔曼滤波的永磁同步直线电机高精度循环神经网络多维观测器。首先,为了提高观测器精度,建立了两相旋转坐标系下带有互感和时延扰动的直线电机数学模型;其次,基于此模型设计了循环神经网络多维观测器,并实现了磁链和速度的高精度在线观测;然后,针对系统参数时变的问题,提出了一种智能在线扩展卡尔曼滤波多参数辨识算法,提高了参数辨识的精准度;最后,搭建基于MT1050的半实物永磁同步直线电机控制平台,实验结果验证了所提观测器的准确性和高效性。
关键词:永磁同步直线电机 循环神经网络多维观测器 参数辨识 收敛性分析
近年来,随着计算机技术、控制理论和材料技术的发展,高端数控机床对其性能要求越来越高。以永磁同步直线电机(Permanent Magnet Linear Synchronous Motor, PMLSM)为代表的工作系统,因其响应快、定位准确、可靠性高等特点,已广泛应用于航空航天、半导体和高速自动化加工设备 中[1-3]。PMLSM在运行过程中参数会受工况及环境影响而发生变化[4-5],进而影响到PMLSM的控制性能,甚至会使机器发生严重故障。神经网络观测器能在一定程度上提高系统的鲁棒性和动态性能,被广泛应用于电机速度和参数辨识[6-8]。
电机状态观测技术可以不借助机械传感器而实现对速度和位置的估计,实现电机的无位置传感器控制,成为近年来的研究热点。目前,电机观测器主要有自适应全阶状态观测器[9-10]、滑模观测器[11]及近些年新出现的神经网络观测器[12]。在实际应用中,全阶状态观测器起始角度的不准确会导致估算转子位置产生误差累计及噪声。若起始角度偏差过大则可能会导致起动失败[13]。滑模观测器中固有的高频抖振导致估算出的反电动势需要进行滤波处理,因此就必须对转子位置进行相位补偿[14]。近些年,人工神经网络理论崭露头角,一经提出便得到了广泛的关注。该理论综合了数学、脑科学、神经学、生物学以及计算机学等多种学科的内容、方法和技术思路,可以很好地应对含有未知参数、模型不确定的复杂非线性映射问题,因此被广泛运用在各种算法中,其中较为热门的研究是基于神经网络的电机观测器设计。文献[15]在采用变分理论实现最小绝对值偏差法的基础上,研究了一种基于递归神经网络的辨识方法,该方法能准确地辨识永磁同步电机的定子电阻、交直轴电枢电感及转子磁链等参数,具有很快的收敛速度,但并未进行实验验证。文献[16]提出了一种基于递归小波卡尔曼神经网络的电机伺服驱动智能自适应动态表面控制系统,根据循环神经网络结构设计了一个非线性扰动观测器来估计控制中存在的非线性集总参数不确定性。实验结果表明,该算法在抑制外部负载扰动和参数不确定的鲁棒性方面具有优越性,然而将永磁体磁链假设为已知值,永磁体磁链的误差会对辨识精度产生影响。
在高精尖领域的电机控制系统中,如果计算采用的电阻或电感值与实际值不匹配将会导致位置和速度辨识误差增加,甚至出现观测器不稳定的现 象[17]。因此,有必要对电机电阻和电感进行在线辨识。卡尔曼滤波算法是工业中常用的优化算法之一,由于其优越的数学特性,很多文献已经将它用于神经网络的训练中[18]。文献[19]使用迭代扩展卡尔曼滤波器,在传递近似建议分布的均值和协方差的过程中,充分利用观测值信息,更好地描述了神经网络权值的后验概率分布。实验结果表明,迭代扩展卡尔曼滤波器作为建议分布的粒子滤波算法训练性能明显优于其他训练算法。文献[20]设计了一种递归神经网络结构,可以从混沌信号的单通道输出时间序列中识别非线性系统,使用扩展卡尔曼滤波算法估计神经网络的权重,并使用期望最大化算法来获得卡尔曼滤波的初始状态和协方差。结果表明,扩展卡尔曼滤波算法训练的人工神经网络建模误差值很小,但是辨识精度还是会受到电感误差的影响。
目前,大多数基于神经网络观测器建立的模型复杂度较高,未考虑到电机控制系统中互感和时延等环节带来的影响,导致自适应能力不强,同时对系统中训练硬件要求高。大多数参数辨识算法受逆变器死区等非线性因素的影响,电机参数辨识精度不高。为了解决上述问题,本文在建立带有互感和时延的数学模型基础上设计了基于智能在线扩展卡尔曼的循环神经网络(Recurrent Neural Networks- Intelligent Online Extended Kalman Filtering, RNN- IOEKF)多维观测器,实现了磁链和速度多变量的精确观测。针对系统参数时变问题,提出了一种智能在线扩展卡尔曼滤波(IOEKF)多参数在线辨识算法,提高了辨识精准度。通过实验分析对比RNN- IOEKF观测器、RNN观测器和全阶状态观测器的观测效果,证明了本文所设计观测器的有效性。
假设PMLSM的永磁体是均匀磁化的,忽略端部效应等非理想因素,在旋转dq坐标系下PMLSM的电压方程[21]为
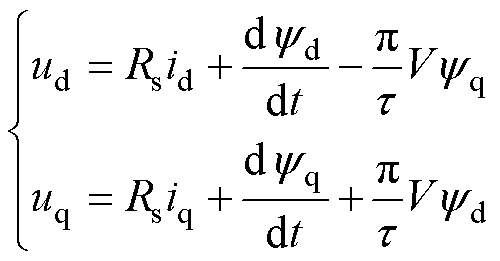 (1)
(1)
磁链方程为
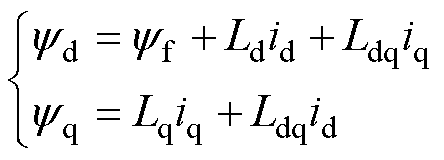 (2)
(2)
电磁推力方程为
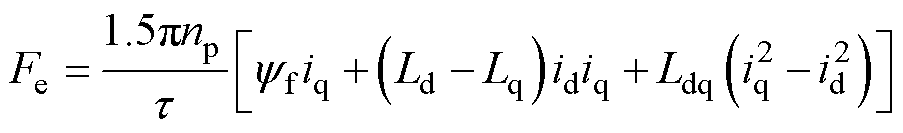
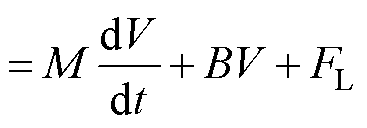 (3)
(3)
式中,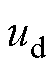 、
、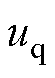 分别为d、q轴电压;
分别为d、q轴电压;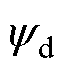 、
、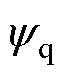 分别为d、q轴磁链;
分别为d、q轴磁链;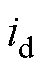 、
、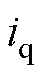 分别为d、q轴电流;
分别为d、q轴电流;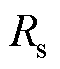 为动子绕组电阻;
为动子绕组电阻;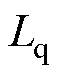 、
、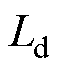 、
、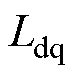 分别为交、直轴电感和互感;
分别为交、直轴电感和互感;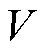 为电机的动子速度;
为电机的动子速度;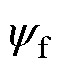 为永磁体磁链;
为永磁体磁链;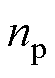 为电机极对数;
为电机极对数;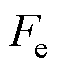 为电磁推力;
为电磁推力;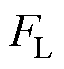 为扰动阻力;
为扰动阻力; 为电机极距;M为动子质量;B为摩擦系数。
为电机极距;M为动子质量;B为摩擦系数。
将式(2)代入式(1),结合式(3)并将其离散化,可得电机的状态方程为
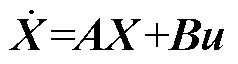 (4)
(4)
其中

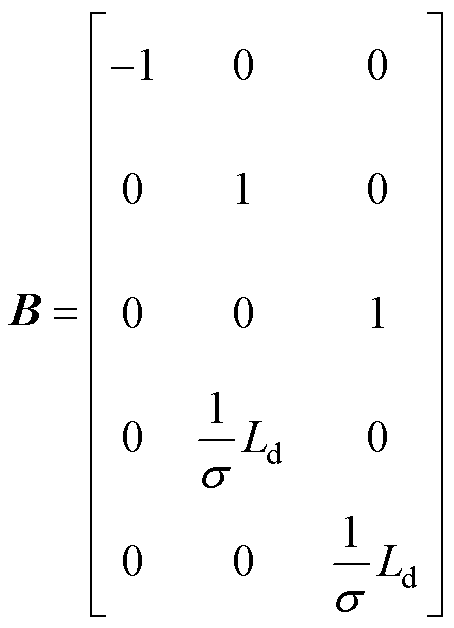
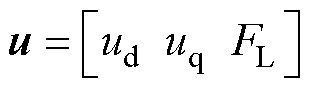
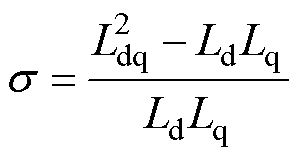
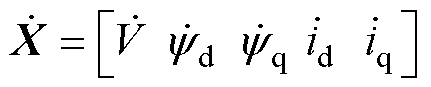
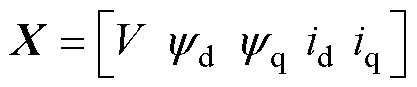
考虑外界扰动干扰等因素时,矩阵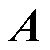 和矩阵
和矩阵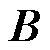 分别发生变化
分别发生变化 和
和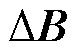 ,那么整个系统的扰动可以表示为
,那么整个系统的扰动可以表示为
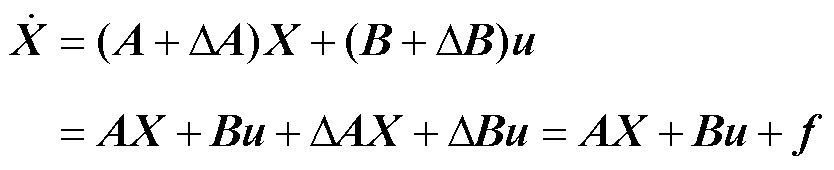 (5)
(5)
式中,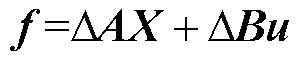 ,包含外界工况、环境变化、端部效应等各种扰动引起的电机模型变化。
,包含外界工况、环境变化、端部效应等各种扰动引起的电机模型变化。
本文在传统电机矢量控制基础上提出了基于RNN-IOEKF的电机状态观测器。电机控制系统框图如图1所示,将电机循环神经网络多维观测器以及IOEKF参数辨识算法加入电机的矢量控制系统中。逆变器输出电压同时输入电机和观测器中,观测器将观测变量及误差输入IOEKF。IOEKF在每个控制周期在线更新系统参数并输入观测器,实现对电机状态的精确观测。

图1 电机控制系统框图
Fig.1 Block diagram of the motor control system
RNN观测器原理框图如图2所示。
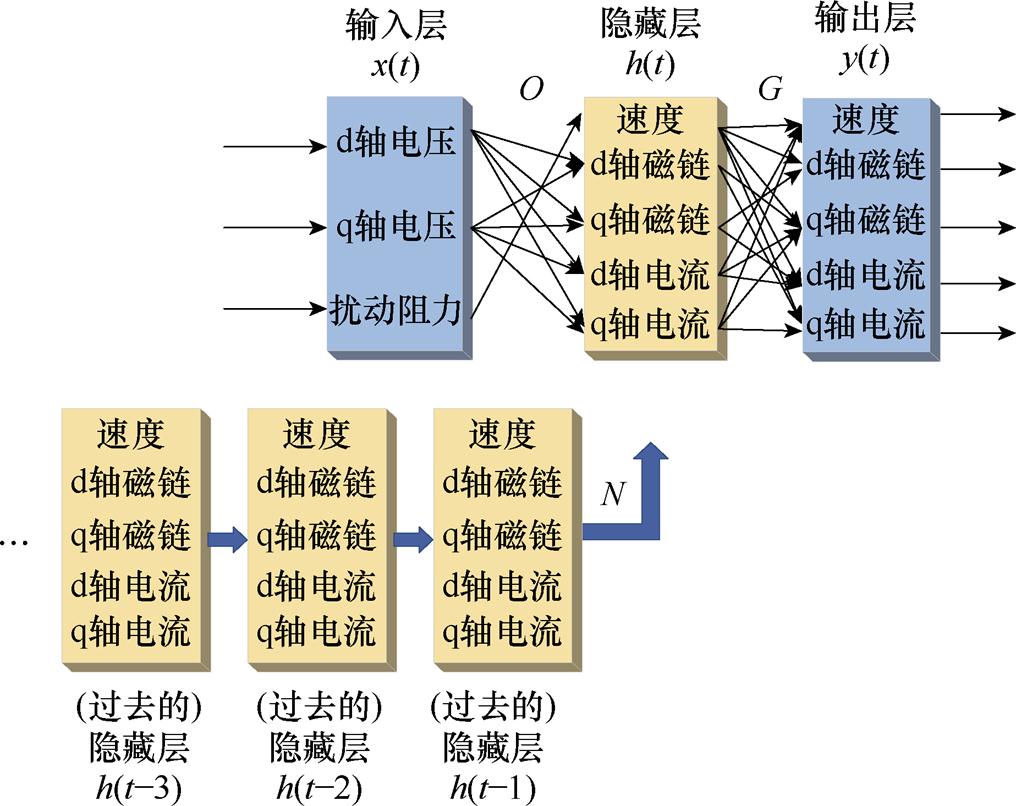
图2 RNN观测器原理框图
Fig.2 Block diagram of RNN observer
相较于传统神经网络和卷积神经网络等其他神经网络结构,循环神经网络的设计引入了连续的时序样本数据,可以充分使用历史数据,共享时序数据,将同一隐藏层的神经元按照顺序相连,实现闭环优化。针对三相永磁同步直线电机的结构和特性,构建了电机的RNN-IOEKF观测器,可以智能高效且准确地观测磁链和速度。
输入层包含3个源节点,负责将输入信号传递至隐藏层,隐藏层包含5个非线性节点,并且将上一时刻隐藏层的输出结果加入该时刻的隐含层中。
输入向量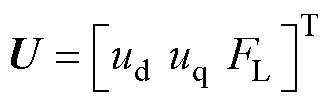 ,输入层的公式为
,输入层的公式为
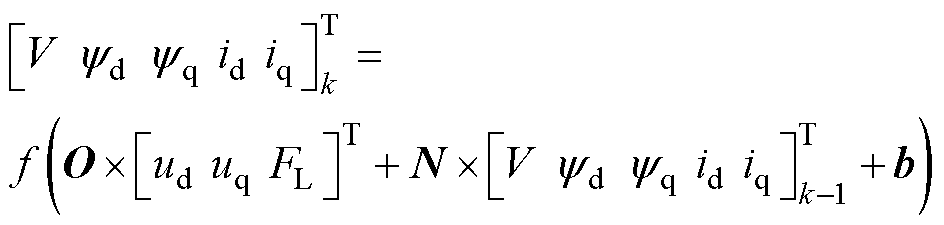 (6)
(6)
式中,N为上一时刻到该时刻隐藏层权重系数矩阵;O为输入层到隐藏层的权重系数矩阵;b为偏置。
输出层包含5个线性节点,对隐藏层输出进行线性组合,可得
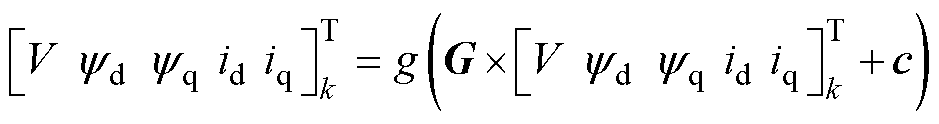 (7)
(7)
式中,G为隐藏层到输出层的权重系数矩阵;c为偏置。
根据第1节介绍的三相永磁同步直线电机的dq轴数学模型,将电机的状态变量设为自变量,有
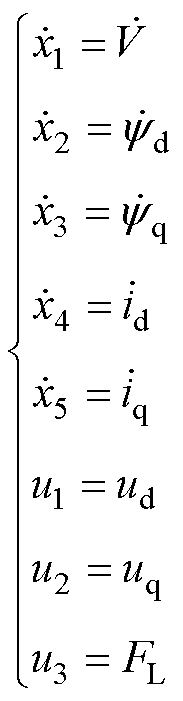 (8)
(8)
可得电机的RNN-IOEKF观测器的结构为
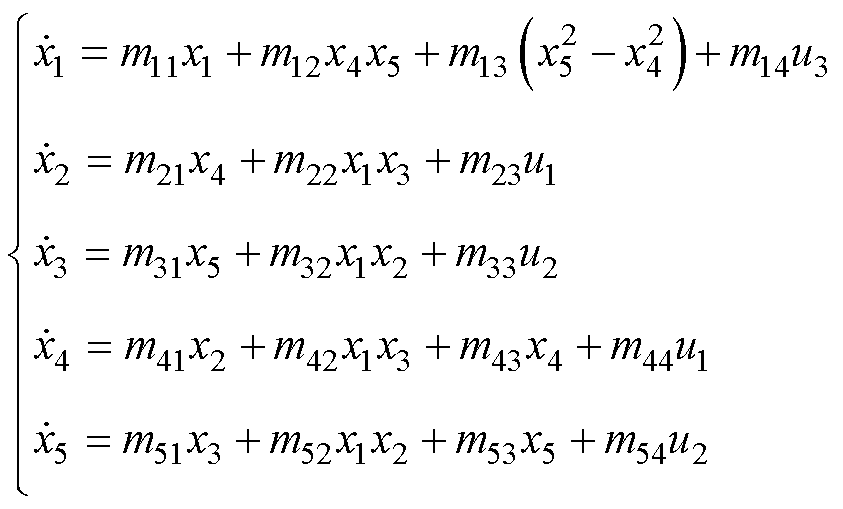 (9)
(9)
式中,m参数表示的是电机参数的组合,也是网络的权重系数。权重系数通过扩展卡尔曼滤波算法进行更新,且更新时间很短,对电机控制性能的影响几乎可以忽略不计。
循环神经网络根据给定参数与观测参数的偏差值,利用学习算法动态调整网络的权值以及相关参数,最终使得误差值最小,实现动态跟踪。IOEKF算法可以减少所需的神经元数,提高学习收敛性,提供在线和离线两种实现方式,计算效率更高。由IOEKF算法[15]可得
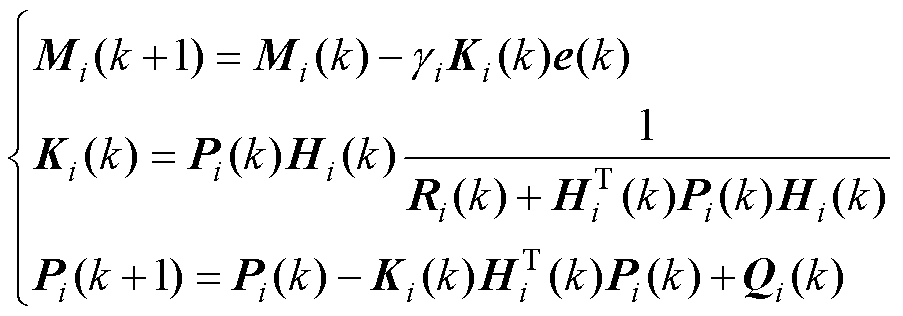 (10)
(10)
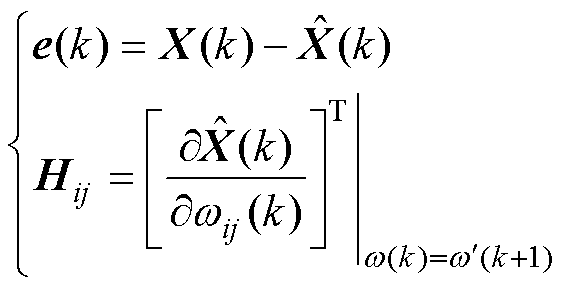 (11)
(11)
式中,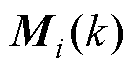 为需要训练的权重系数组;i为变量序号,
为需要训练的权重系数组;i为变量序号,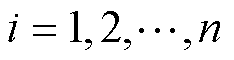 ;
;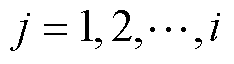 ;
;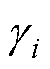 为第i个权重向量的卡尔曼滤波器学习率;
为第i个权重向量的卡尔曼滤波器学习率;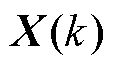 作为系统输出;
作为系统输出;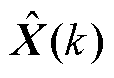 作为系统输出的估计;
作为系统输出的估计;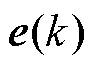 为系统输出误差;
为系统输出误差;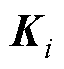 为卡尔曼增益矩阵;
为卡尔曼增益矩阵;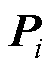 为预测误差的协方差矩阵;
为预测误差的协方差矩阵;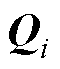 为估计噪声的协方差矩阵;H为一个矩阵,其中每个元素为神经网络输出
为估计噪声的协方差矩阵;H为一个矩阵,其中每个元素为神经网络输出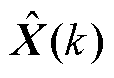 关于神经网络每一个权重
关于神经网络每一个权重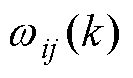 的导数。
的导数。
神经网络观测器与IOEKF算法原理框图如图3所示。以观测电流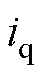 为例实现电阻R和电感
为例实现电阻R和电感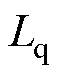 的辨识。RNN多维观测器的输出是观测值
的辨识。RNN多维观测器的输出是观测值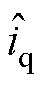 ,与由采样后经过坐标变换的电流
,与由采样后经过坐标变换的电流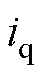 相减,误差输入IOEKF多参数在线辨识算法中,输出的电阻R和电感
相减,误差输入IOEKF多参数在线辨识算法中,输出的电阻R和电感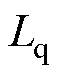 又反馈到观测器中,由式(4)可知,
又反馈到观测器中,由式(4)可知,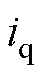 的表达式为
的表达式为
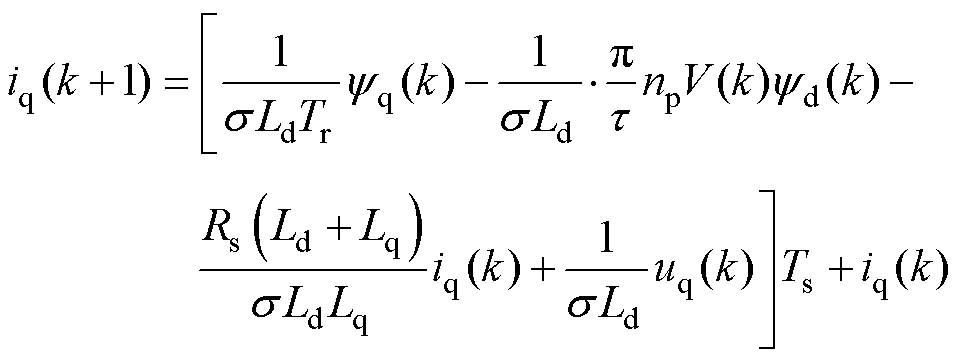 (12)
(12)
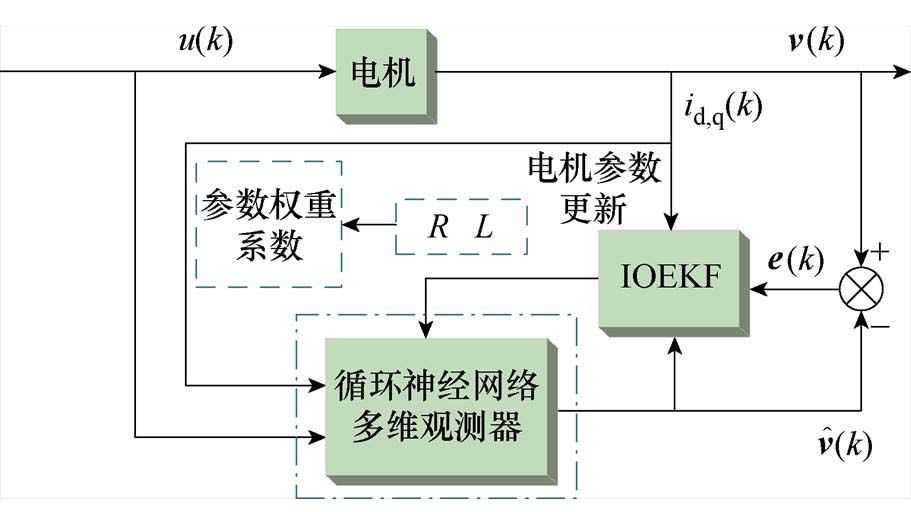
图3 神经网络观测器与IOEKF算法原理框图
Fig.3 Principle block diagram of RNN observer and IOEKF algorithm
由式(12)可知,当待辨识电阻或电感变化时,则将该电阻或电感作为自变量,此时有
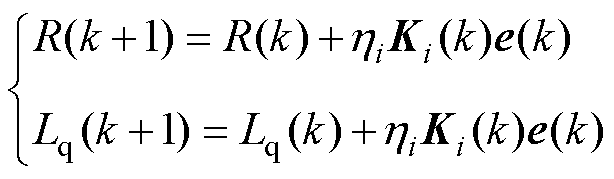 (13)
(13)
式中,hi为学习率。
经过计算可得辨识电阻的矩阵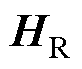 为
为
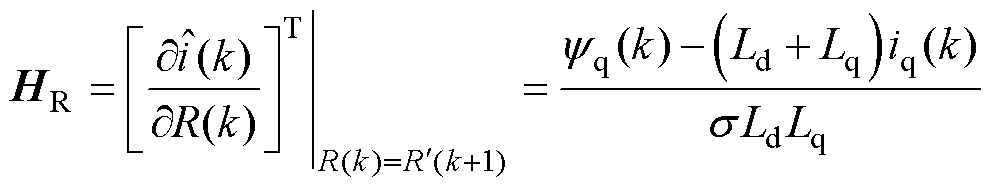 (14)
(14)
辨识电感的矩阵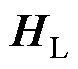 为
为
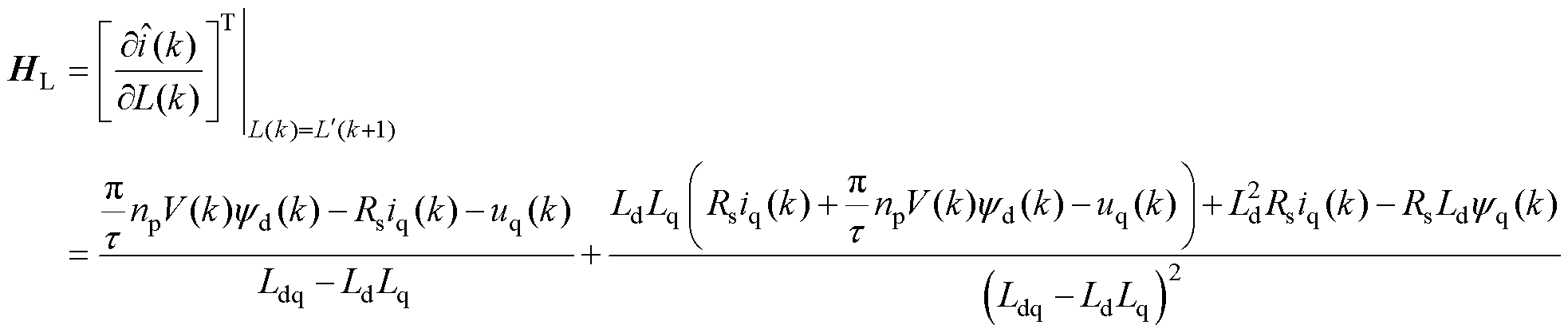 (15)
(15)
针对不同的待辨识参数,可以得到不同的辨识矩阵,避免了对所有的参数进行矩阵求逆,保证了辨识系统的稳定性和快速性。
选取李雅普诺夫方程为
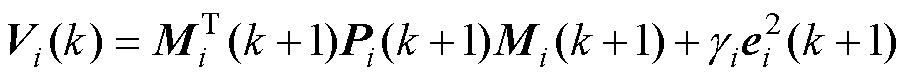 (16)
(16)
式中,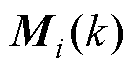 为网络权重系数矩阵。则
为网络权重系数矩阵。则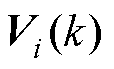 增量为
增量为
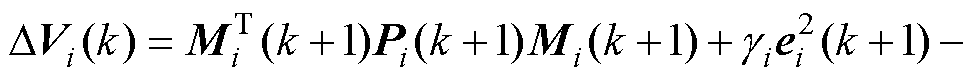
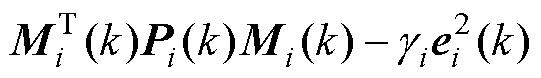 (17)
(17)
由IOEKF式(10)可知
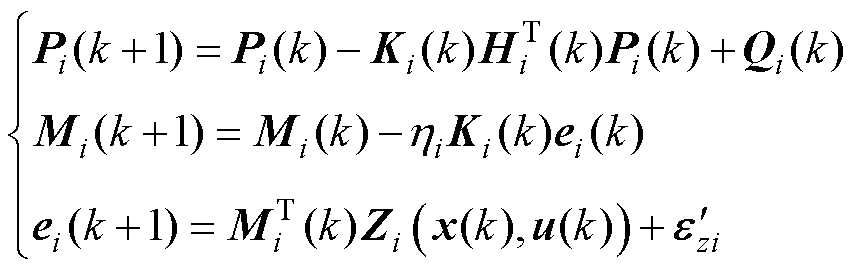 (18)
(18)
式中,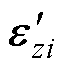 为一个有界的近似误差;
为一个有界的近似误差;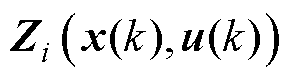 为一个关于输入向量和状态向量的高阶函数。
为一个关于输入向量和状态向量的高阶函数。
将式(18)代入式(17)可得
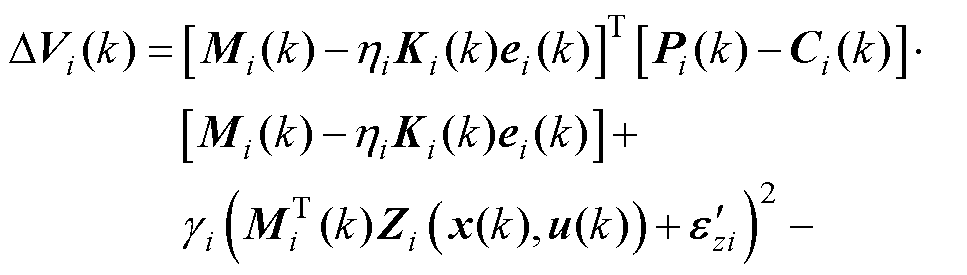
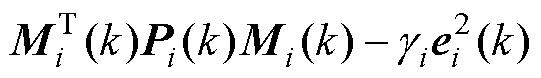 (19)
(19)
其中
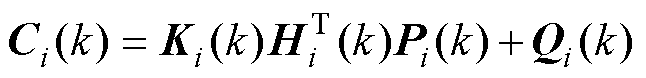
根据Cauchy-Schwarz不等式可得
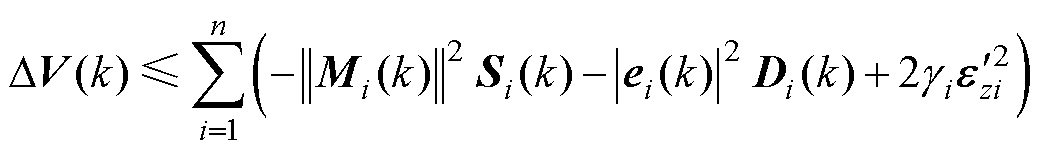 (20)
(20)
式中,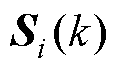 和
和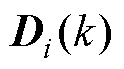 为变量。
为变量。
要使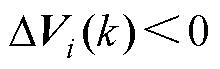 ,则需要满足以下两式之一。
,则需要满足以下两式之一。
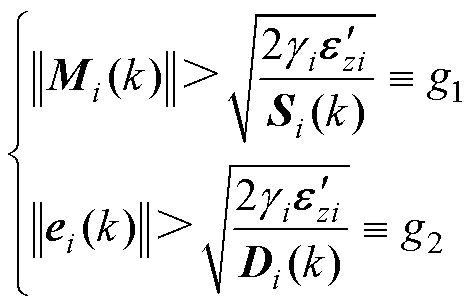 (21)
(21)
当学习率满足不等式(21)时可以确保观测器的误差是收敛的。这意味着本文的观测误差和辨识误差始终是有界的,且网络的权重系数同样也是有界的,那么观测变量和辨识变量最终都会达到稳定状态。具体推导公式见附录。
为了验证本文所提算法,搭建了三相永磁同步直线电机实验平台。本文采用高性能实时数字仿真机MT 1050建立了快速控制原型实验平台,以验证所提出的控制算法。实验平台如图4所示,主要包括四部分:上位机、MT 1050控制器、硬件调理电路和三相永磁同步直线电机。

图4 实验平台
Fig.4 Experimental platform
本文的控制对象为双边动初级无铁心三相永磁同步直线电机。电机主要参数见表1。
为了分析RNN-IOEKF观测器的性能,设计了稳定工况,即给定电机的负载为10 N,速度为1 m/s。将RNN-IOEKF观测器与全阶状态观测器和未用IOEKF的RNN观测器进行对比。
表1 电机主要参数
Tab.1 Main parameters of the motor
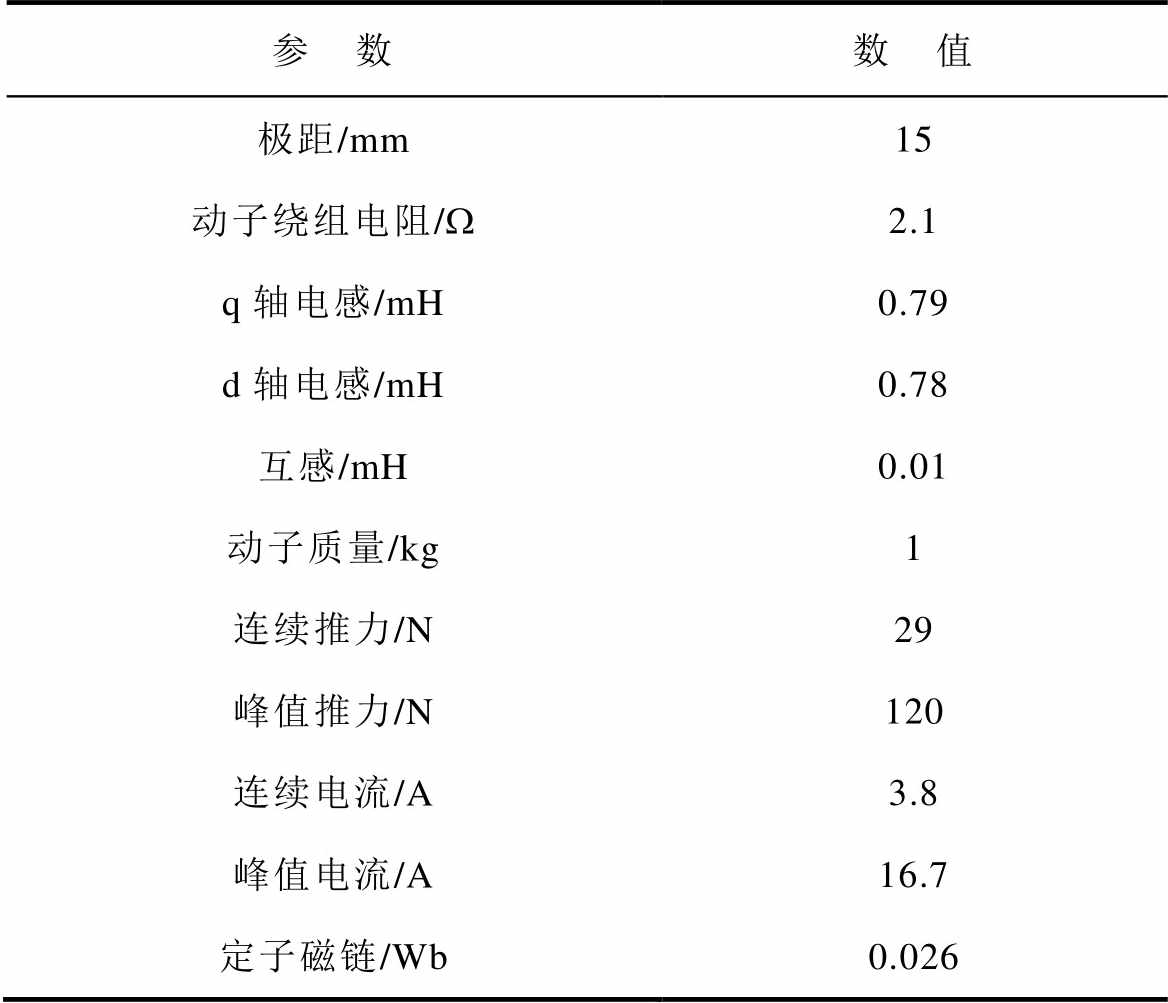
参 数数 值 极距/mm15 动子绕组电阻/W2.1 q轴电感/mH0.79 d轴电感/mH0.78 互感/mH0.01 动子质量/kg1 连续推力/N29 峰值推力/N120 连续电流/A3.8 峰值电流/A16.7 定子磁链/Wb0.026
将电机动子速度设为1 m/s,对比三种观测器的观测效果,如图5所示。速度观测性能(稳态工况)对比见表2。由表2可知,RNN-IOEKF观测器观测速度的效果相较于RNN观测器和全阶状态观测器的效果更好,调节时间更短。在观测速度时,RNN- IOEKF多维观测器的方均根误差为0.106 3 m/s,RNN观测器的方均根误差为0.114 8m/s,而全阶状态观测器的方均根误差为0.110 6m/s。RNN-IOEKF多维观测器调节时间为0.31 s,RNN观测器的调节时间为0.35 s,全阶状态观测器的调节时间为0.48 s。综合各项指标,RNN-IOEKF多维观测器提高了速度观测的精度。
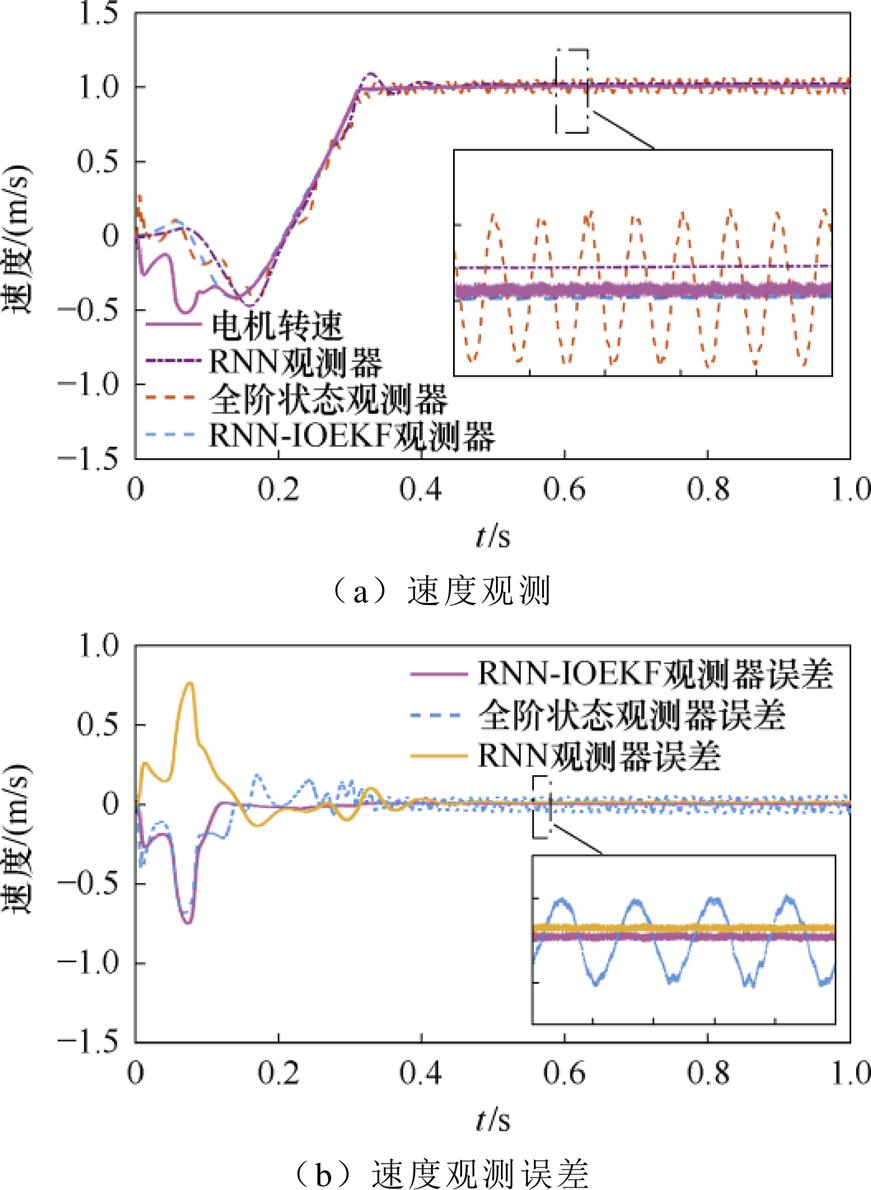
图5 速度观测及误差(稳态工况)
Fig.5 Speed observation and error under steady state conditions
表2 速度观测性能(稳态工况)对比
Tab.2 Comparison of speed observation under steady state conditions
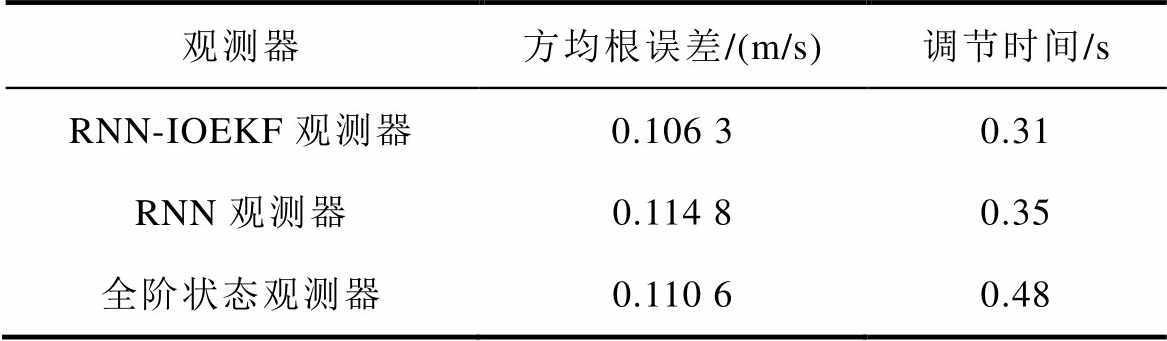
观测器方均根误差/(m/s)调节时间/s RNN-IOEKF观测器0.106 30.31 RNN观测器0.114 80.35 全阶状态观测器0.110 60.48
通过在直线电机运行方向上加装滑轮组,利用悬挂重物的重力作为水平运动电机的突加突卸负载。为了研究观测器在动态工况下的性能,起始时刻,给定电机速度为1 m/s,给定电机的负载为10 N,在0.75 s时将电机速度降低到0.5 m/s,负载降低到0 N。
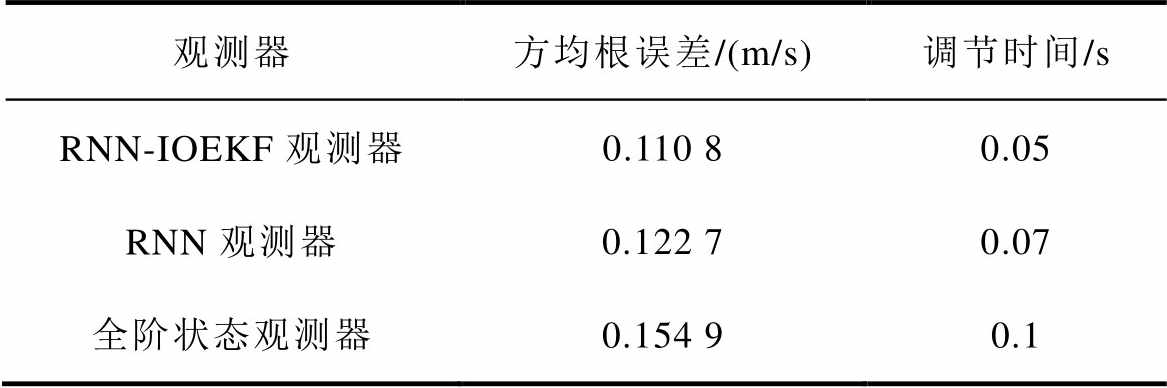
将电机动子初速度设为1 m/s,0.75 s时设为0.5 m/s,对比三种观测器观测效果,如图6所示。速度观测性能(动态工况)对比见表3。由表3可知,RNN-IOEKF观测器观测磁链的效果相较于RNN观测器和全阶状态观测器的效果更好,调节时间更短。在观测速度时,RNN-IOEKF多维观测器的方均根误差为0.110 8m/s,RNN观测器的方均根误差为0.122 7m/s,而全阶状态观测器的方均根误差为0.154 9m/s。RNN-IOEKF多维观测器调节时间为0.05 s,RNN观测器的调节时间为0.07 s,全阶状态观测器的调节时间为0.1 s。综合各项指标,RNN- IOEKF多维观测器观测速度可以快速且无超调地跟随工况变化,动态响应好,鲁棒性强。
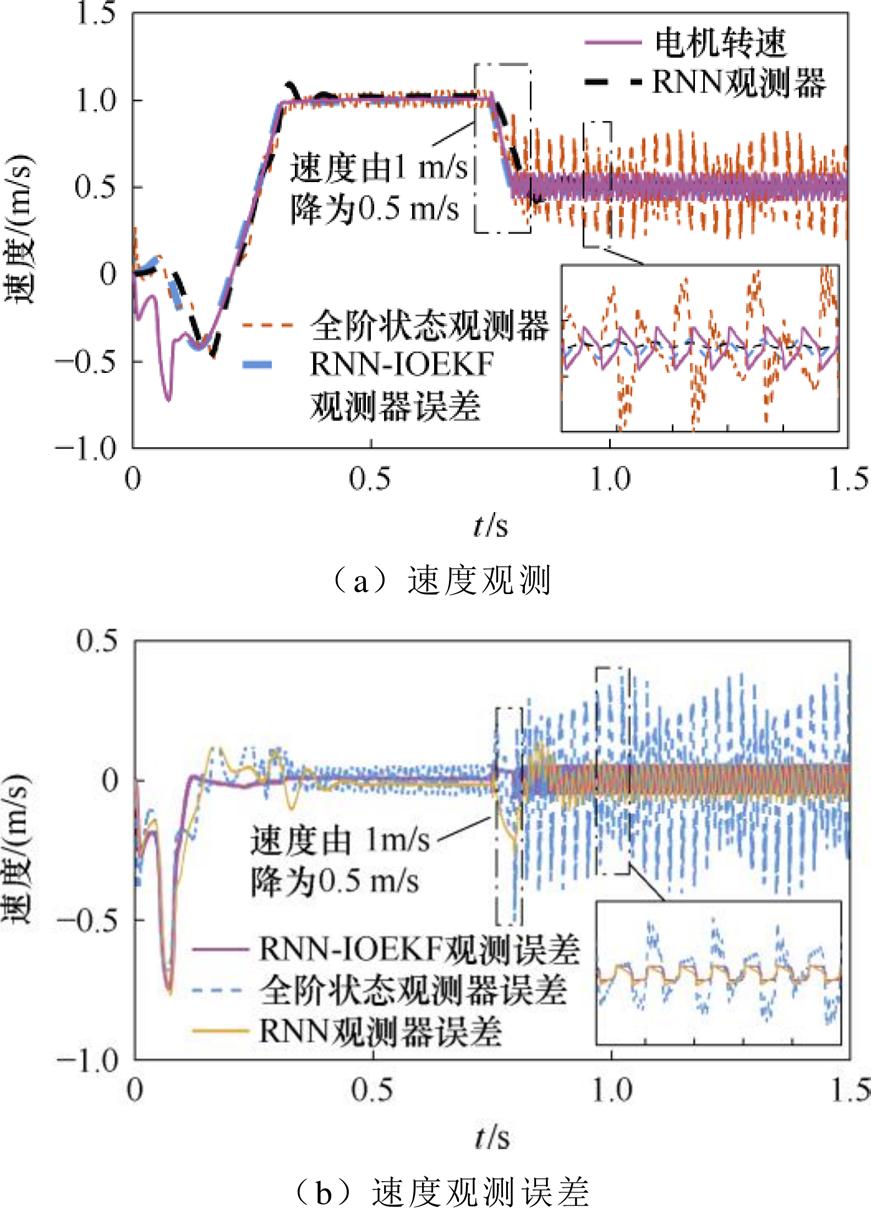
图6 速度观测及误差(动态工况)
Fig.6 Speed observation and error under dynamic state conditions
表3 速度观测性能(动态工况)对比
Tab.3 Comparison of speed observation under dynamic state conditions
观测器方均根误差/(m/s)调节时间/s RNN-IOEKF观测器0.110 80.05 RNN观测器0.122 70.07 全阶状态观测器0.154 90.1
为了分析RNN-IOEKF多维观测的性能,在稳态工况下观测速度的同时观测磁链,给定电机的负载为10 N,速度为1 m/s。将RNN-IOEKF观测器与全阶状态观测器和未用IOEKF的RNN观测器进行对比。为了更好地分析磁链观测效果,将磁链转换到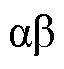 坐标系中。
坐标系中。
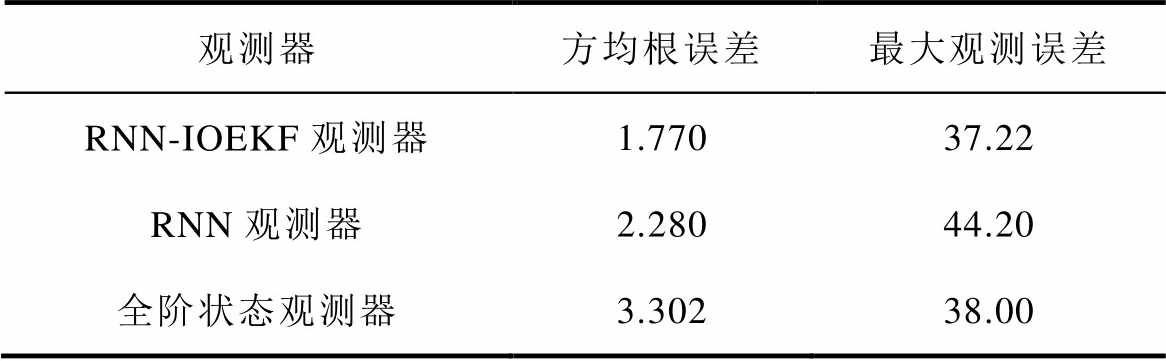
磁链观测及误差(稳态工况)如图7所示。磁链观测性能(稳态工况)对比见表4。由表4可知,RNN-IOEKF观测器观测磁链的效果相较于RNN观测器和全阶状态观测器的效果更好,观测误差更小。RNN-IOEKF多维观测器的方均根误差为1.770 Wb,RNN观测器的方均根误差为2.280 Wb,全阶状态观测器的方均根误差为3.302 Wb。RNN-IOEKF多维观测器的最大观测误差为37.22 Wb,RNN观测器的最大观测误差为44.20 Wb,而全阶状态观测器的最大观测误差为38.00 Wb。由此可见,RNN-IOEKF多维观测器有效提高了磁链观测性能,增强了磁链观测的稳定性。
为了研究观测器在动态工况下的性能,起始时刻,给定电机速度为1 m/s,给定电机的负载为10 N,在0.75 s时将电机速度降低到0.5 m/s,负载降低到0 N。
磁链观测及误差(动态工况)如图8所示。磁链观测性能(动态工况)对比见表5。由表5可知,在动态工况下,RNN-IOEKF观测器观测磁链的效果相较于RNN观测器和全阶状态观测器的效果更好,观测误差更小。RNN-IOEKF多维观测器、RNN观测器和全阶状态观测器的方均根误差分别为1.834、6.021、3.969 Wb。最大观测误差分别为38.95、51.96、41.88 Wb。由此可见,RNN-IOEKF多维观测器的抗干扰能力更强,观测精度更高。
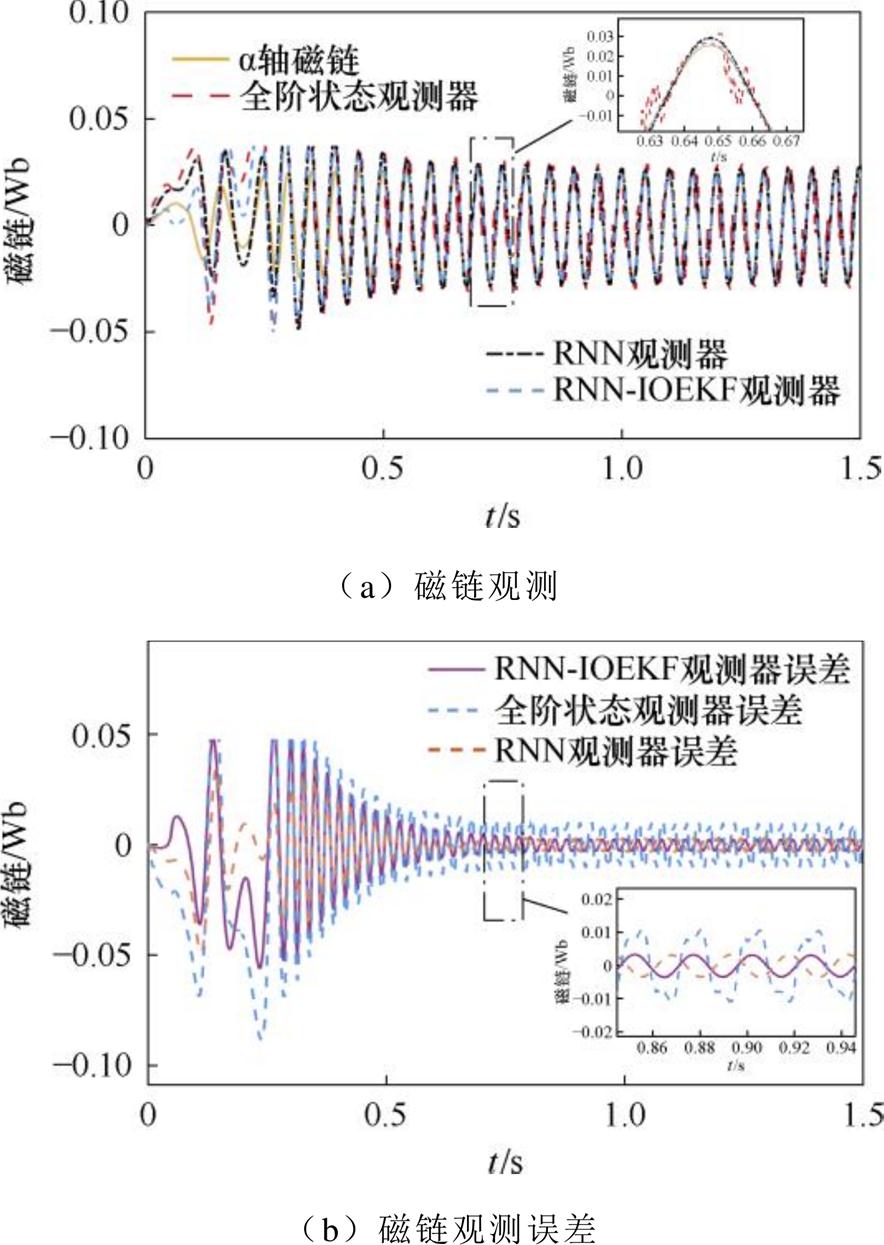
图7 磁链观测及误差(稳态工况)
Fig.7 Flux linkage observation and error
表4 磁链观测性能(稳态工况)对比
Tab.4 Comparison of flux linkage observation under steady state conditions (单位: Wb)
观测器方均根误差最大观测误差 RNN-IOEKF观测器1.77037.22 RNN观测器2.28044.20 全阶状态观测器3.30238.00
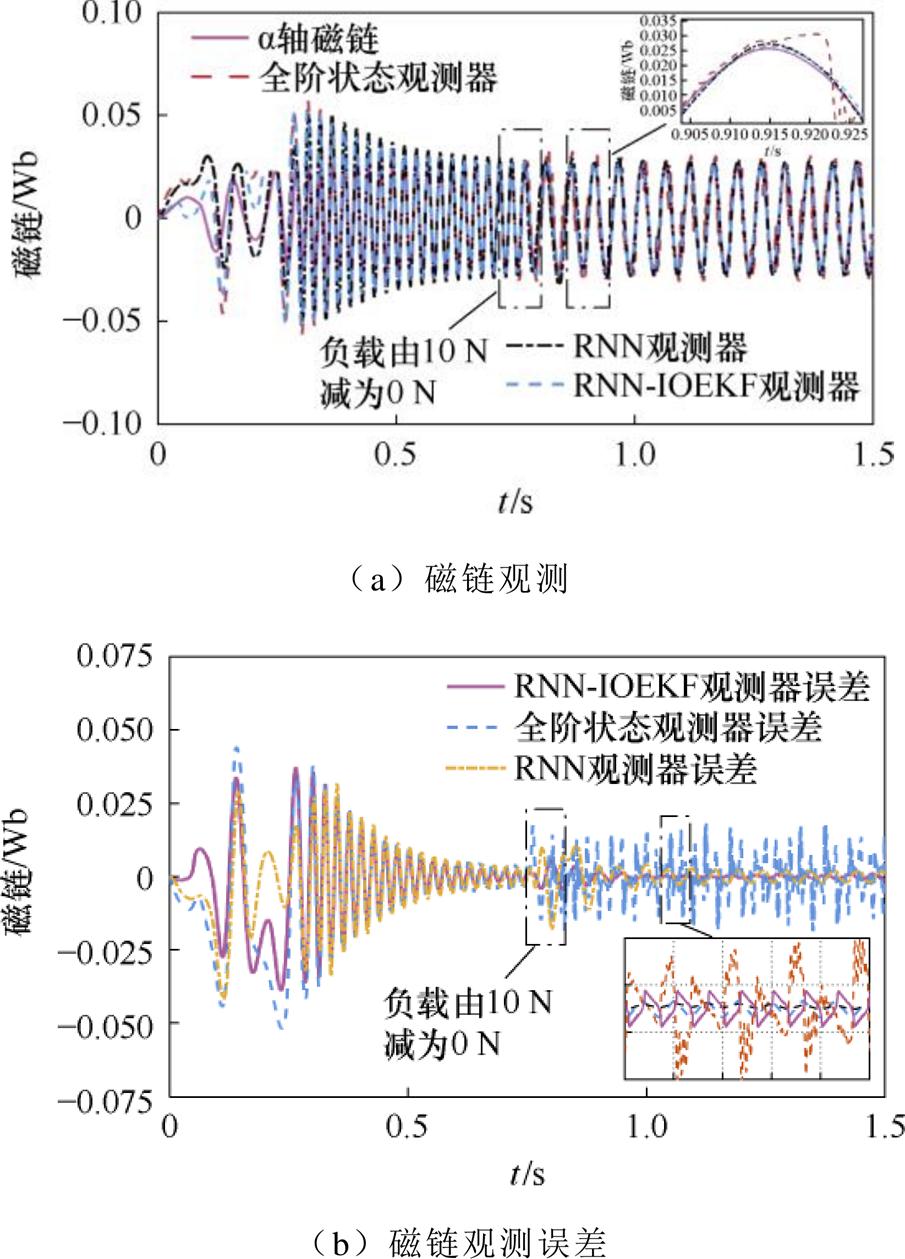
图8 磁链观测及误差(动态工况)
Fig.8 Flux linkage observation and error under dynamic state conditions
表5 磁链观测性能(动态工况)对比
Tab.5 Comparison of flux linkage observation under dynamic state conditions (单位: Wb)
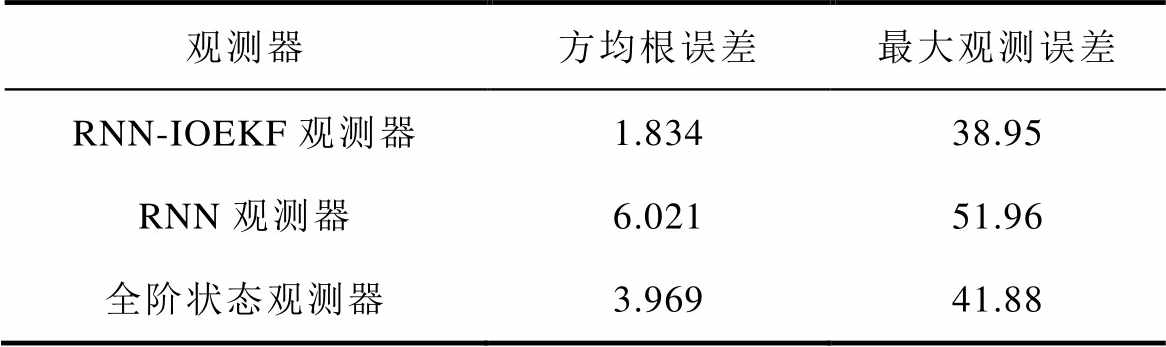
观测器方均根误差最大观测误差 RNN-IOEKF观测器1.83438.95 RNN观测器6.02151.96 全阶状态观测器3.96941.88
根据式(14)和式(15)可以得到参数辨识结果,为排除电阻和电感初始值的设定对参数辨识的影响,将电阻和电感的初始值设为不同的值,即大于真实值和小于真实值。分别在稳定负载工况和动态工况两种情况下,将最小二乘法作为对照,验证所提参数辨识算法的有效性。
本文所使用的电机参数中动子电阻为2.1 W,为了使算法更有说服力,将电阻的初始值分别设为3 W 和0.5 W,电机进行双闭环控制且处于空载工况,对动子电阻进行辨识,如图9所示。
电阻辨识性能对比见表6。由表6可知,电阻从不同初始值开始进行参数辨识时,IOEKF多参数辨识算法在0.004 s时已经稳定,而最小二乘法在0.04 s时趋于稳定。当电阻初始值为0.5 W 时,IOEKF多参数辨识算法的超调为3.00%,而最小二乘法的超调为19.05%;当电阻初始值为3 W 时,IOEKF多参数辨识算法的超调为3.00%,而最小二乘法的超调为66.67%。因此,IOEKF多参数辨识算法的超调更小,调节时间更短,精度更高。
不同初始值的电感辨识(带稳定负载)如图10所示。由图10可知,在电感辨识算法中,最小二乘法的超调明显比IOEKF算法的超调大。电感辨识性能对比见表7。由表7可知,电感从不同初始值开始进行参数辨识时,IOEKF多参数辨识算法在0.08 s时就已经稳定,而最小二乘法在0.1 s时趋于稳定。由图10可知,无论电感初始值为0.000 1 H还是0.001 H,最小二乘法的超调均是IOEKF多参数辨识算法的10倍左右。因此,在辨识电感时,IOEKF多参数辨识算法的动态响应速度更快,可以达到高效的应用需求。
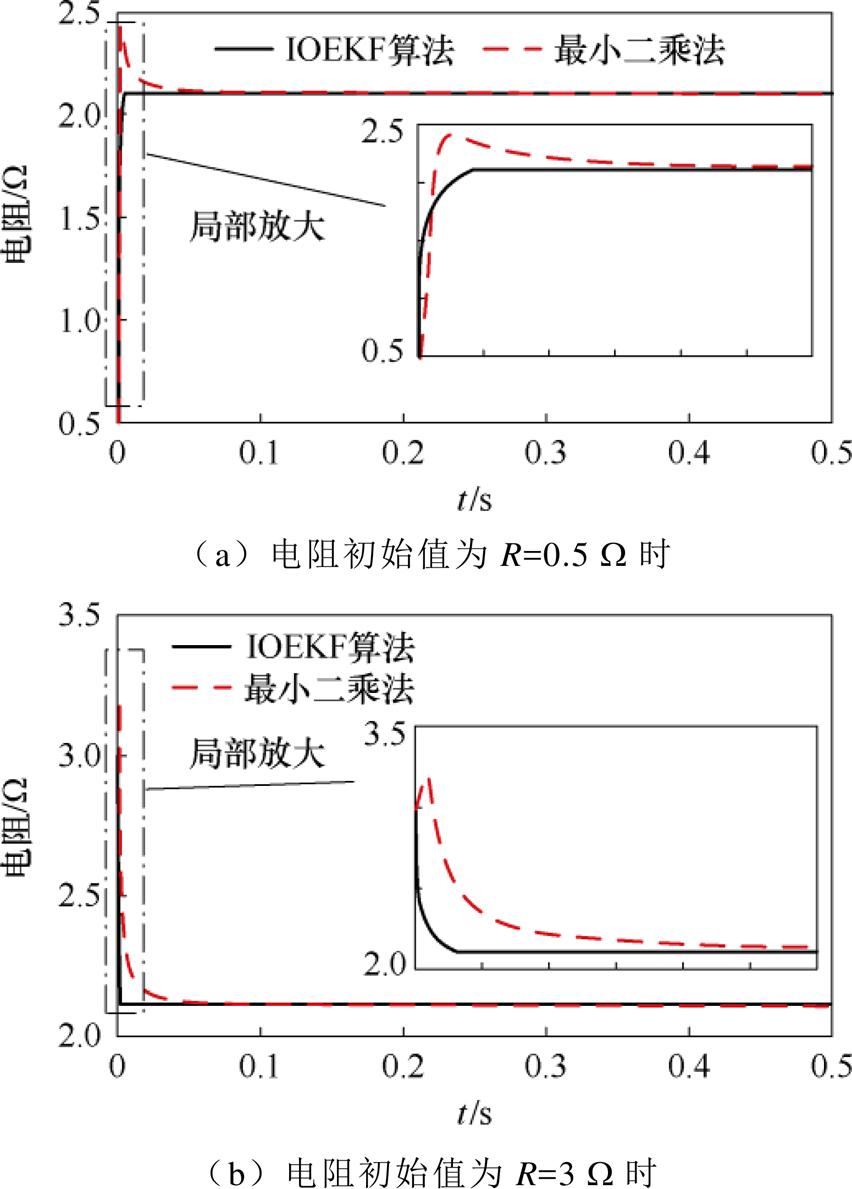
图9 不同初始值的电阻辨识
Fig.9 Resistance identification with different initial values
表6 电阻辨识性能对比
Tab.6 Comparison of resistance identification
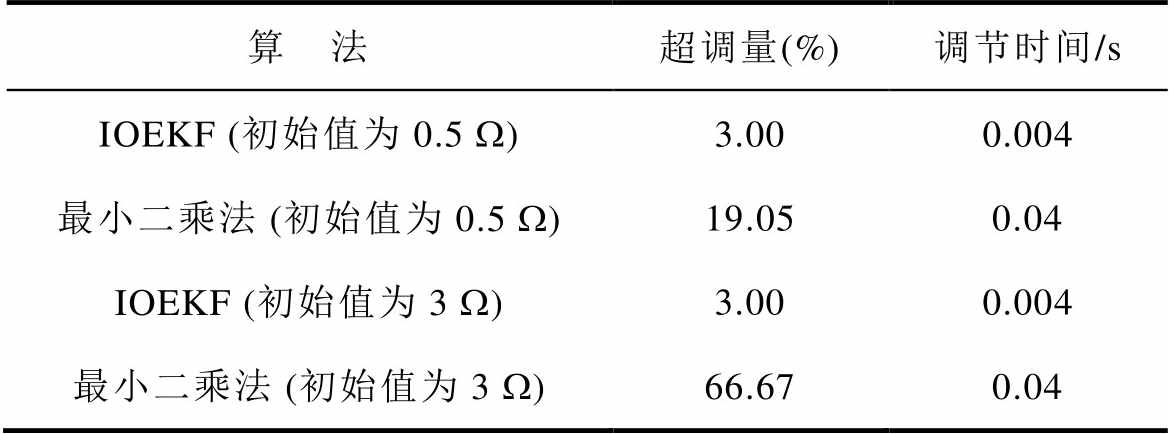
算 法超调量(%)调节时间/s IOEKF (初始值为0.5 W)3.000.004 最小二乘法 (初始值为0.5 W)19.050.04 IOEKF (初始值为3 W)3.000.004 最小二乘法 (初始值为3 W)66.670.04
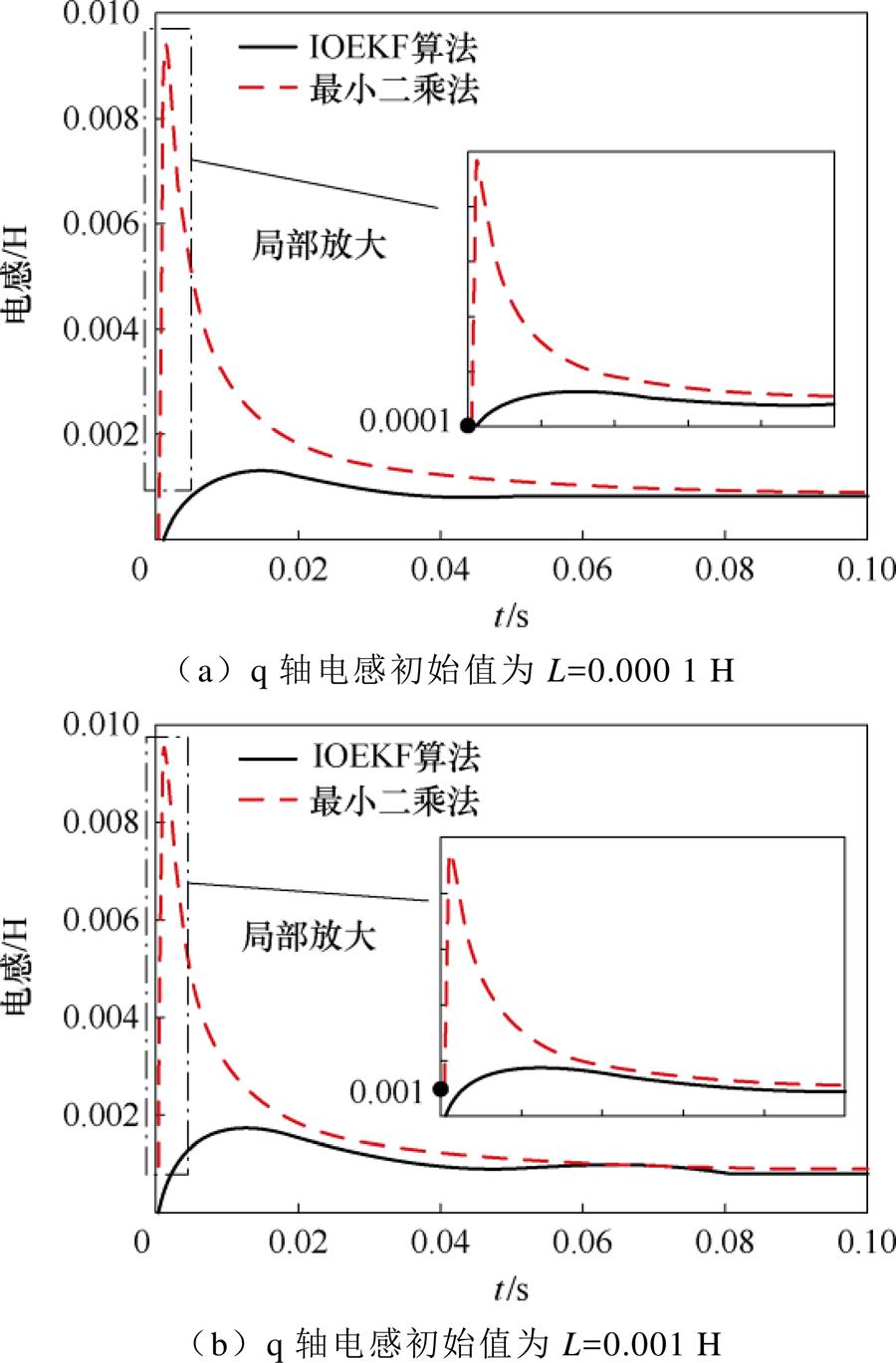
图10 不同初始值的电感辨识(带稳定负载)
Fig.10 Inductor identification with different initial values (with stable load)
表7 电感辨识性能对比(带稳定负载)
Tab.7 Comparison of inductance identification (with stable load)
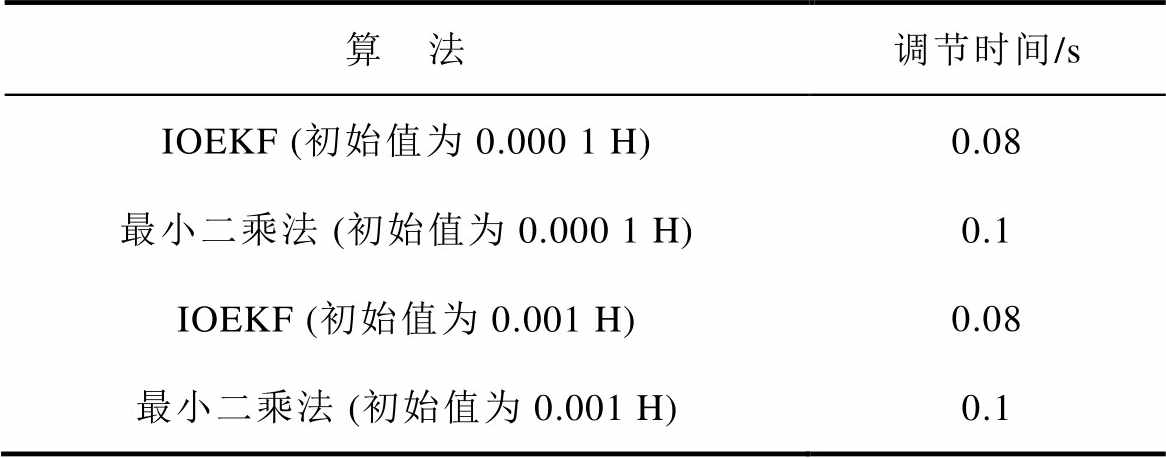
算 法调节时间/s IOEKF (初始值为0.000 1 H)0.08 最小二乘法 (初始值为0.000 1 H)0.1 IOEKF (初始值为0.001 H)0.08 最小二乘法 (初始值为0.001 H)0.1
为了验证辨识算法在扰动状态下的性能,在实验中进行负载的突变,在实验中设置速度为0.3 m/s不变,负载起始时刻为0 N,0.7 s时加入负载为10 N,1.7 s时卸去负载到0 N。由于实验时间较短,电阻辨识结果与空载结果类似,因此主要辨识q轴电感。实验结果波形如图11所示。
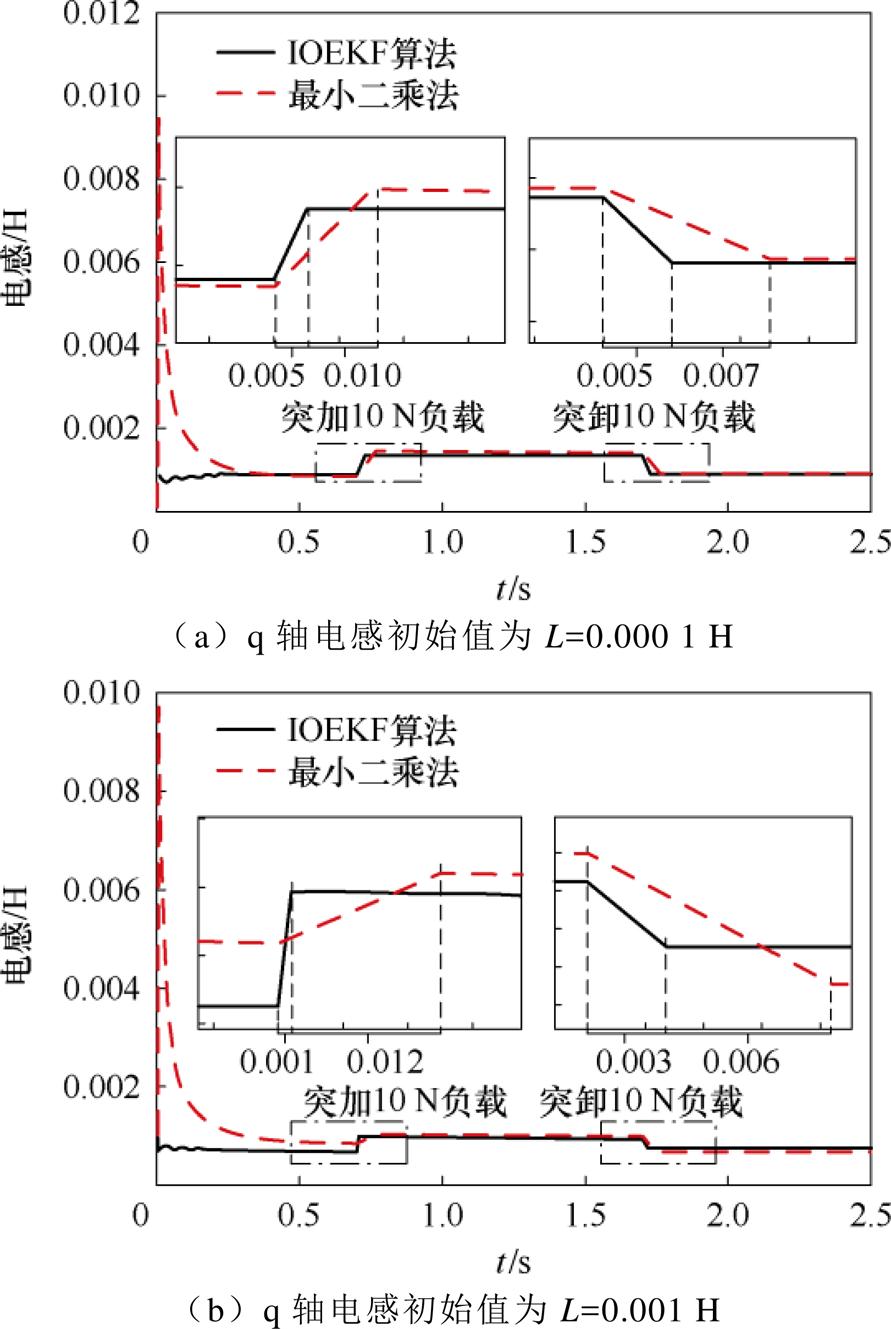
图11 不同初始值的电感辨识(突加突卸负载)
Fig.11 Inductor identification with different initial values (sudden loading and unloading)
电感辨识性能对比见表8。由表8可知,传统的最小二乘法收敛速度慢,且误差大,扰动性能较差,而IOEKF算法的收敛速度是传统方法的2~4倍,抗干扰能力强且具有良好的精度。
表8 电感辨识性能对比(突加突卸负载)
Tab.8 Comparison of inductance identification(sudden loading and unloading)
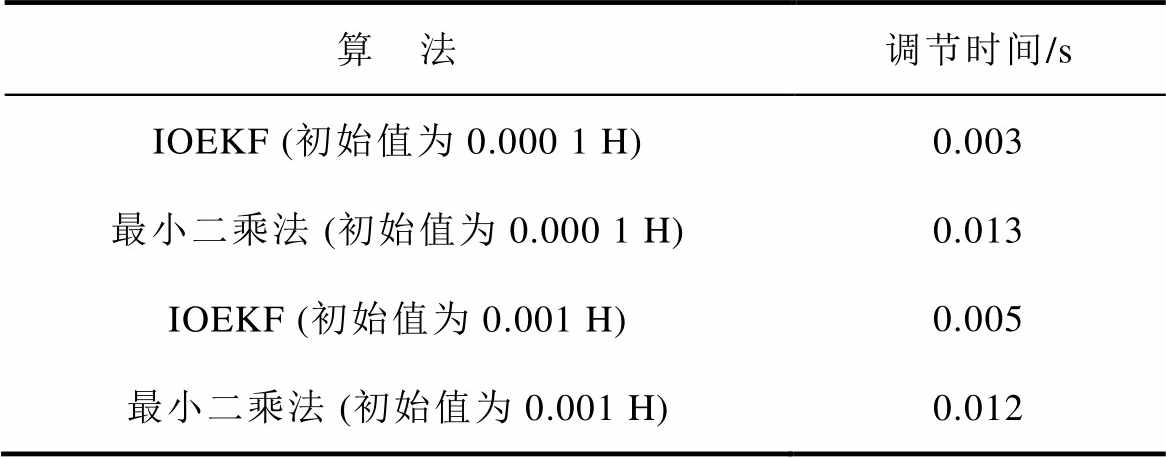
算 法调节时间/s IOEKF (初始值为0.000 1 H)0.003 最小二乘法 (初始值为0.000 1 H)0.013 IOEKF (初始值为0.001 H)0.005 最小二乘法 (初始值为0.001 H)0.012
综上所述,不论是稳态还是动态工况,在不同初始值的情况下,IOEKF多参数辨识算法都不仅可以更快地实现参数辨识,而且超调更小,准确性更高,实验结果证明了算法的有效性。
本文主要对三相永磁同步直线电机的循环神经网络多维观测器及参数辨识算法展开研究。首先基于三相永磁同步直线电机的数学模型和循环神经网络的结构,设计了RNN多维观测器,用于同时观测磁链和速度。针对观测器严重依赖电机参数的问题,采用了IOEKF多参数辨识算法,建立了电阻和电感参数在线辨识模型,实现电机参数的在线更新。采用最小二乘法作为对照,分别在稳定负载和突加突卸负载的工况下进行实验,通过实验结果对比分析验证了IOEKF多参数辨识算法的可行性与高效性。同时,将RNN-IOEKF观测器、传统RNN观测器和全阶状态观测器三者进行对比分析,实验结果证明了RNN-IOEKF多维观测器的有效性。
附 录
1. 本文在给电机建模时,考虑到外界扰动等因素,矩阵A和矩阵B发生变化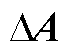 和
和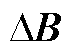 ,那么整个系统的扰动可以表示为
,那么整个系统的扰动可以表示为
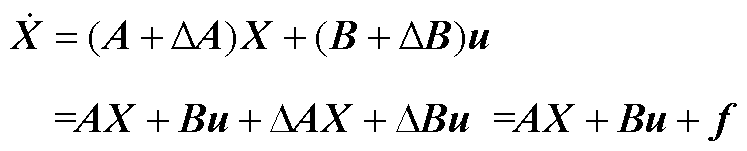 (A1)
(A1)
式中,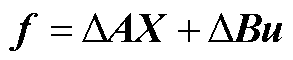 ,包含外界工况、环境变化、端部效应等各种扰动引起的电机模型变化。具体解释如下:
,包含外界工况、环境变化、端部效应等各种扰动引起的电机模型变化。具体解释如下:
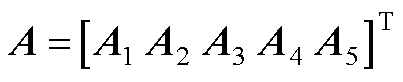 ,
,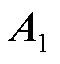 ~
~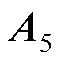 分别为1×5的矩阵,当电阻
分别为1×5的矩阵,当电阻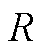 发生变化
发生变化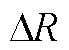 、电感不变时,系数矩阵发生变化为
、电感不变时,系数矩阵发生变化为
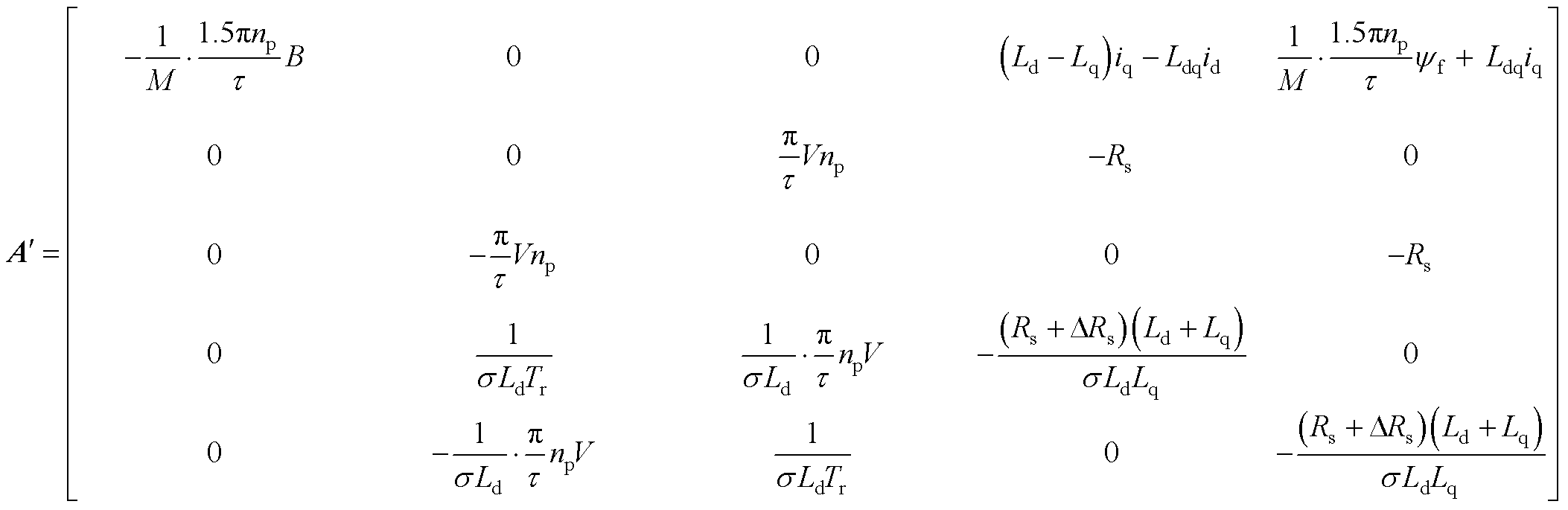
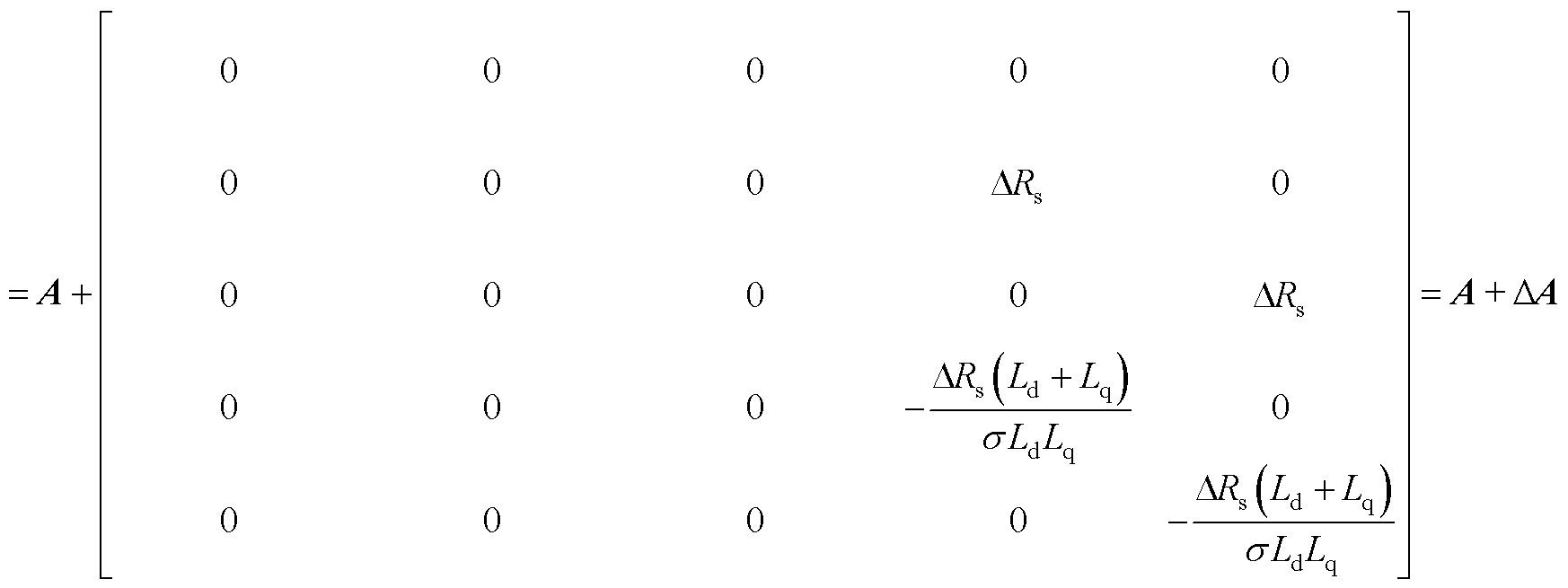 (A2)
(A2)
由式(A2)可知,当电机运行工况及环境发生变化导致电阻发生变化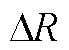 时,系数矩阵A会变化到
时,系数矩阵A会变化到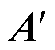 ,且
,且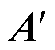 可以分解成
可以分解成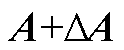 。
。
假设电阻不变,电感L变化相对较小时,通常在工程应用中,可以将电感的变化过程看作是线性过程,此时系数矩阵A和B都会发生相应的改变,有
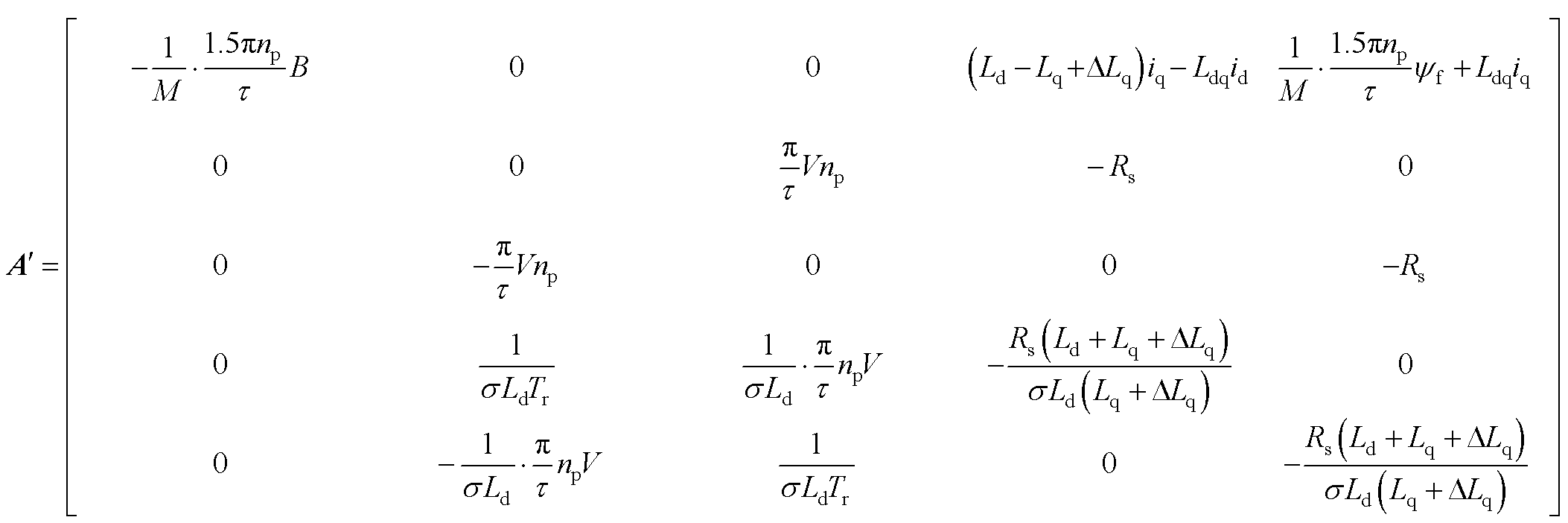
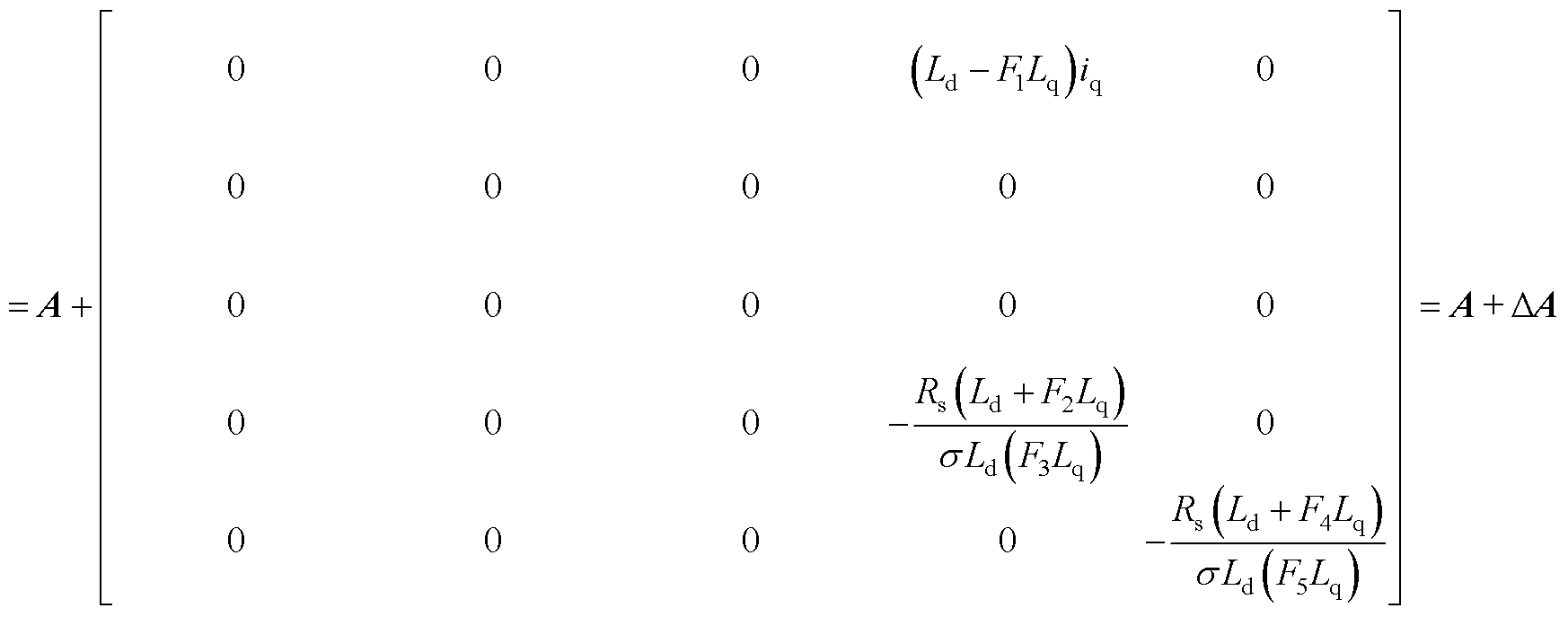 (A3)
(A3)
式中,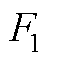 ~
~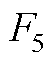 为线性变化比例系数。
为线性变化比例系数。
同样地,系数矩阵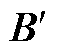 也可以分解为
也可以分解为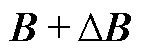 。
。
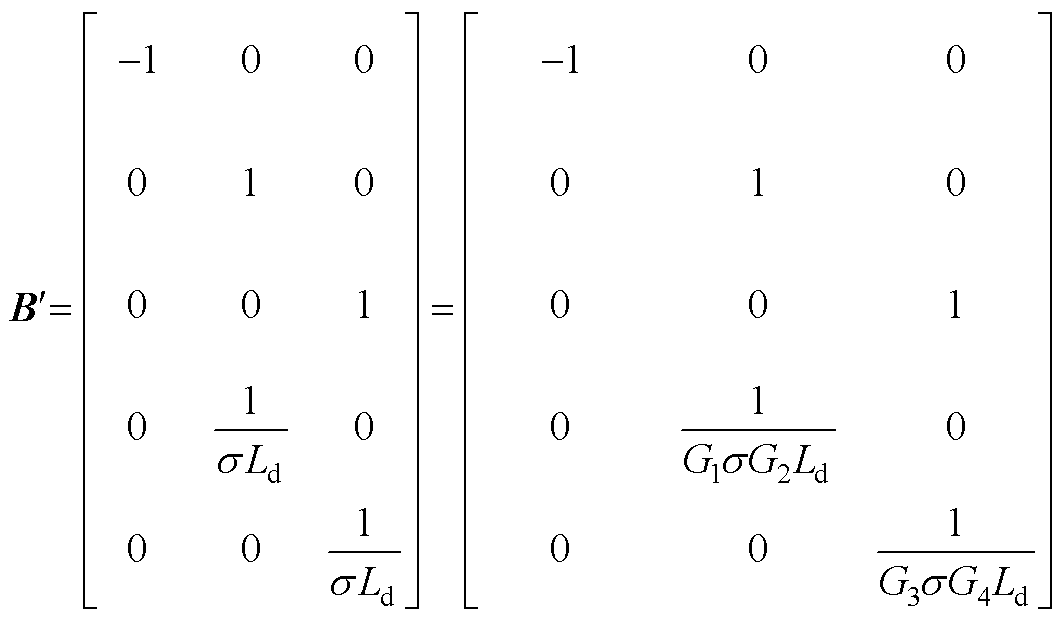
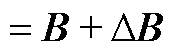 (A4)
(A4)
式中,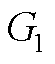 ~
~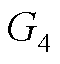 为线性变化比例系数。
为线性变化比例系数。
可以得到,基于电机方程构建RNN-IOEKF观测器时,电机模型可以化简为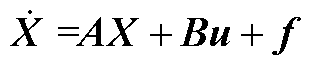 ,用
,用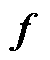 来表示当电机运行工况、环境变化以及端部效应等引起的三相电感、磁链不对称、产生的推力波动等扰动引起的电机模型变化。
来表示当电机运行工况、环境变化以及端部效应等引起的三相电感、磁链不对称、产生的推力波动等扰动引起的电机模型变化。
2. 将式(19)展开为
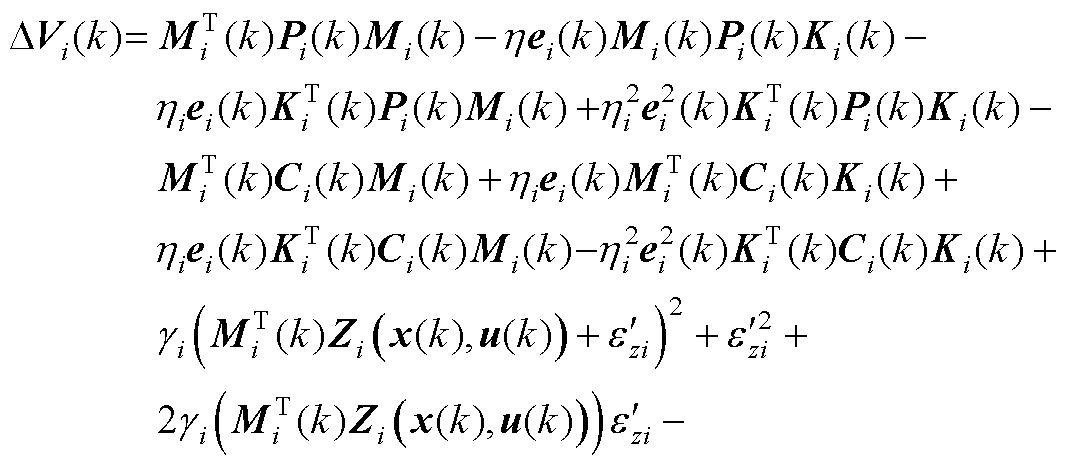
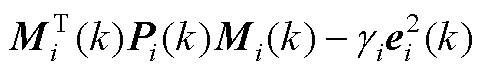 (A5)
(A5)
有Cauchy-Schwarz不等式为
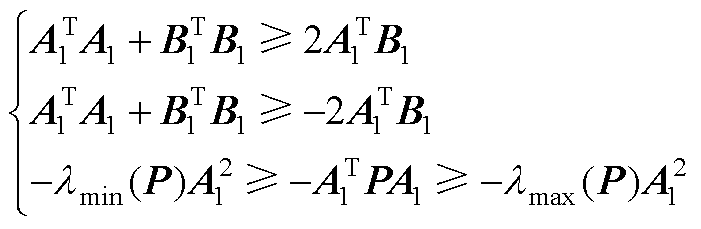 (A6)
(A6)
其中
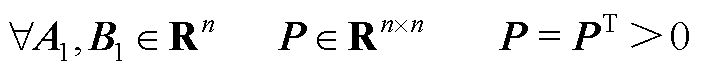
此时根据不等式(A6),将式(A5)化简为
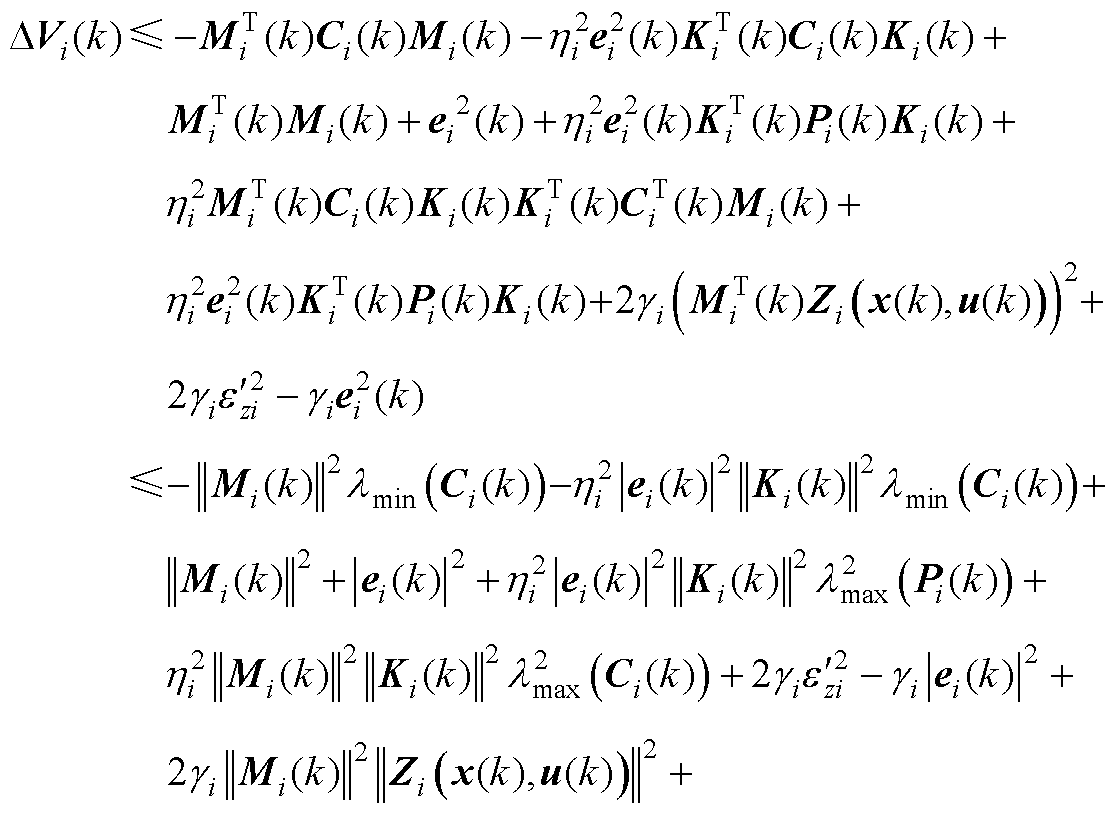
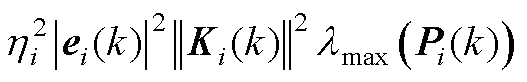 (A7)
(A7)
定义两个变量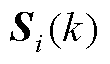 和
和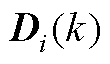 ,有
,有
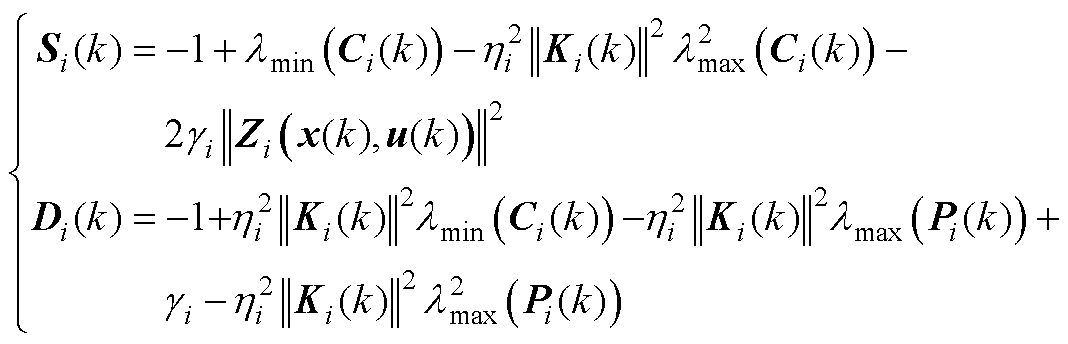 (A8)
(A8)
将式(A8)代入式(A7)可得
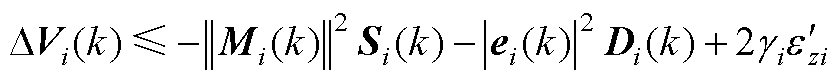 (A9)
(A9)
要使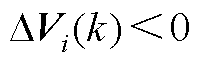 ,则需要满足以下两式之一。
,则需要满足以下两式之一。
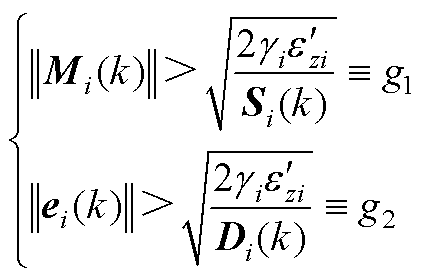 (A10)
(A10)
式中,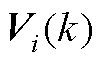 和
和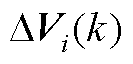 为网络中的某一项变量组成的李亚普诺夫函数,要证明整个神经网络的收敛性,则令
为网络中的某一项变量组成的李亚普诺夫函数,要证明整个神经网络的收敛性,则令
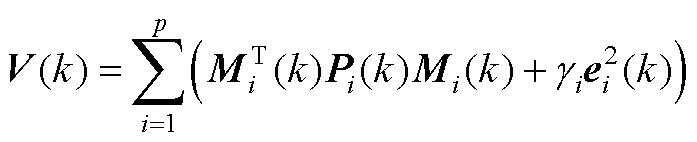 (A11)
(A11)
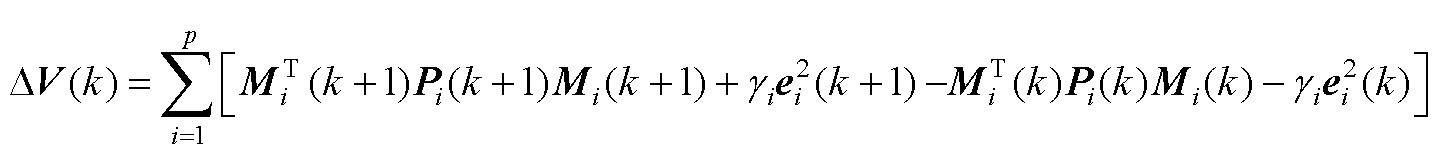 (A12)
(A12)
经过同样的方法化简证明可得
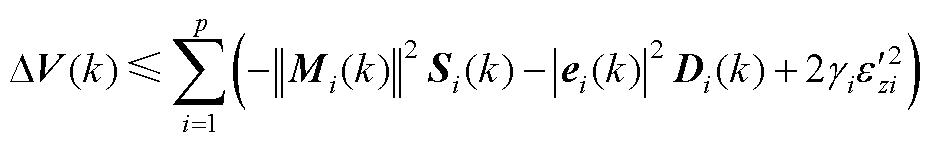 (A13)
(A13)
当学习率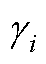 满足不等式(A10)时可以确保观测器的误差是收敛的。这意味着本文的观测误差和辨识误差始终是有界的,且网络的权重系数同样也是有界的,那么观测变量和辨识变量最终都会达到稳定状态。
满足不等式(A10)时可以确保观测器的误差是收敛的。这意味着本文的观测误差和辨识误差始终是有界的,且网络的权重系数同样也是有界的,那么观测变量和辨识变量最终都会达到稳定状态。
参考文献
[1] 周世炯, 李耀华, 史黎明, 等. 分段式双三相永磁直线同步电机的无模型电流预测控制[J]. 电工技术学报, 2024, 39(4): 996-1009, 1021.
Zhou Shijiong, Li Yaohua, Shi Liming, et al. Model- free predictive current control of segmented dual three-phase permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 996-1009, 1021.
[2] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[3] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[4] 郭科宇, 李耀华, 史黎明. 分段供电双三相永磁同步直线电机电流解耦与扰动抑制[J]. 电工技术学报, 2022, 37(24): 6332-6344.
Guo Keyu, Li Yaohua, Shi Liming. Current decoupling and force disturbance suppression of dual three-phase permanent magnet linear synchronous motors with section power supply[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6332- 6344.
[5] 鲍明堃, 周扬忠. 基于复合神经网络重构对象的永磁同步直线电机变参数型位移速度并行控制[J]. 电工技术学报, 2024, 39(8): 2470-2484.
Bao Mingkun, Zhou Yangzhong. Parallel dis- placement velocity control of permanent magnet synchronous linear motor with variable parameters based on composite neural network reconstruction object[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2470-2484.
[6] Nguyen N D, Nam N N, Yoon C, et al. Speed sensorless model predictive torque control of induction motors using a modified adaptive full-order observer[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(6): 6162-6172.
[7] 杨阳, 赵吉文, 宋俊材, 等. 基于深度神经网络模型的无铁心永磁同步直线电机结构优化研究[J]. 中国电机工程学报, 2019, 39(20): 6085-6094, 6189.
Yang Yang, Zhao Jiwen, Song Juncai, et al. Structural optimization of air-core permanent magnet syn- chronous linear motors based on deep neural network models[J]. Proceedings of the CSEE, 2019, 39(20): 6085-6094, 6189.
[8] Bai Chenyao. AGA-GRU: an optimized GRU neural network model based on adaptive genetic algorithm[J]. Journal of Physics: Conference Series, 2020, 1651(1): 012146.
[9] Volpato Filho C J, Vieira R P. Adaptive full-order observer analysis and design for sensorless interior permanent magnet synchronous motors drives[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 6527-6536.
[10] Auger F, Hilairet M, Guerrero J M, et al. Industrial applications of the Kalman filter: a review[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5458-5471.
[11] Geng Yiwen, Lai Zou, Li Yonggang, et al. Sensorless fault-tolerant control strategy of six-phase induction machine based on harmonic suppression and sliding mode observer[J]. IEEE Access, 2019, 7: 110086- 110102.
[12] Fu Zhijun, Xie Wenfang, Na Jing. Robust adaptive nonlinear observer design via multi-time scales neural network[J]. Neurocomputing, 2016, 190: 217-225.
[13] Yu Xiangqian, Zhang Chi, Su Tao. Speed sensorless of induction motor with adaptive full order state observer[J]. Journal of Physics: Conference Series, 2020, 1550(4): 042058.
[14] Sun Xiaodong, Wu Jiangling, Lei Gang, et al. Torque ripple reduction of SRM drive using improved direct torque control with sliding mode controller and observer[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(10): 9334-9345.
[15] 荆禄宗, 吴钦木. 基于递归神经网络的永磁同步电机参数辨识研究[J]. 电气传动, 2020, 50(3): 87-91, 101.
Jing Luzong, Wu Qinmu. Research on identification of PMSM based on recurrent neural network[J]. Electric Drive, 2020, 50(3): 87-91, 101.
[16] El-Sousy F F M, Abuhasel K A. Intelligent adaptive dynamic surface control system with recurrent wavelet Elman neural networks for DSP-based induction motor servo drives[C]//2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 2017: 1-16.
[17] 苏有成, 陈志辉. 基于电感扰动的三相横向磁通永磁电机参数辨识与估算位置偏差修正[J]. 电工技术学报, 2023, 38(12): 3165-3175.
Su Youcheng, Chen Zhihui. Parameter identification and estimation of three-phase transverse flux per- manent magnet motor based on inductive disturbance, correction of position deviation[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3165- 3175.
[18] Zheng Tianyu, Yao Yu, He Fenghua, et al. An RNN- based learnable extended Kalman filter design and application[C]//2019 18th European Control Con- ference (ECC), Naples, Italy, 2019: 3304-3309.
[19] 王法胜, 郭权. 基于扩展卡尔曼粒子滤波算法的神经网络训练[J]. 计算机工程与科学, 2010, 32(5): 48-50.
Wang Fasheng, Guo Quan. Neural network training based on the extended Kalman particle filter[J]. Computer Engineering & Science, 2010, 32(5): 48-50.
[20] Archana R, Unnikrishnan A, Gopikakumari R. An improved EKF based neural network training algorithm for the identification of chaotic systems driven by time series[C]//2012 International Con- ference on Power, Signals, Controls and Computation, Thrissur, India, 2012: 1-6.
[21] 张明远, 史黎明, 徐飞, 等. 单变流器驱动多分段并联长初级双边直线感应电动机模型与控制策略[J]. 中国电机工程学报, 2022, 42(22): 8343-8352.
Zhang Mingyuan, Shi Liming, Xu Fei, et al. Modeling and control strategy of long primary double-sided linear induction motor segmented in parallel fed by a single inverter[J]. Proceedings of the CSEE, 2022, 42(22): 8343-8352.
Multidimensional Observer of Permanent Magnet Synchronous Linear Motor Recurrent Neural Network Based on Parameter Identification
Abstract In recent years, with the development of computer technology, control theory, and material technology, the performance requirements for computer numerical control (CNC) machine tools have become increasingly high. The permanent magnet linear synchronous motor (PMLSM) has been widely used in aerospace, semiconductor, and high-speed automated processing equipment due to its fast response, accurate positioning, and high reliability. During the operation of PMSLM, the parameters change correspondingly with operation conditions and environment, which affects the high-performance control of PMSLM and even causes serious machine failures. Neural network observers are studied for speed and motor parameter identification to improve the robustness and dynamic performance of the system. This paper studies a high-precision recurrent neural network (RNN) for multi-dimensional observation of PMSLM based on intelligent online extended Kalman filtering (IOEKF).
Since PMSLM is a complex nonlinear time-varying system with multiple variables and strong coupling, it is necessary to simplify the actual system for analysis when establishing the mathematical model. Starting from the basic structure and equivalent circuit of the motor, a three-phase PMSLM model with mutual inductance is derived in a synchronous rotating coordinate system. A closed-loop control system for the three-phase PMLSM is established.
Secondly, based on the principle and structure of RNN, a multi-dimensional observer for three-phase PMSLM is established. The weight coefficient update of the neural network online is solved using the EKF algorithm. A semi-physical PMSLM control platform based on MT 1050 is built. Simulation and experimental results show that the proposed multi-dimensional observer has higher accuracy than the full-order state observer and the observer without EKF algorithm update under steady-state and dynamic conditions. The Lyapunov stability criterion provides theoretical validation for the observer's stability. The stability of the observer is theoretically ensured by constructing an appropriate Lyapunov function and demonstrating the negativity of its derivative.
Based on the variations of resistance and inductance, the corresponding identification models are established, and the EKF multi-parameter online identification method is proposed. The least squares method is used as a comparison. The results show that the EKF multi-parameter identification algorithm for motor parameter identification has better dynamic and steady-state performance.
The proposed observation method for PMLSM enhances the overall performance and reliability of CNC machine tools. The RNN-based multi-dimensional observer, supported by IOEKF, reduces the training time of the control algorithm, achieving real-time and high-precision performance in the control of linear motors.
Keywords:Permanent magnet linear synchronous motor, recurrent neural network multidimensional observer, parameter identification, convergence analysis
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231621
国家自然科学基金(52077219, 52307051)和电磁能技术全国重点实验室资助课题(614221720220201)资助项目。
收稿日期 2023-10-06
改稿日期 2024-03-11
宋 琳 女,1998年生,博士研究生,研究方向为人工智能技术在电力电子中的应用。
E-mail: 3203502540@qq.com
李华玉 男,1989年生,助理研究员,研究方向为电机高性能驱动。
E-mail: lihuayu23@nue.edu.cn(通信作者)
(编辑 崔文静)