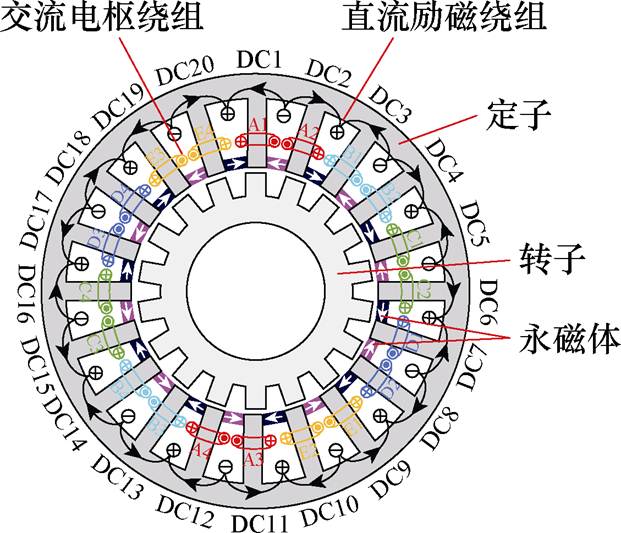
图1 20/18极混合励磁电机结构
Fig.1 Structure of 20/18 pole hybrid excitation machine
摘要 五相定子槽口永磁型混合励磁双凸极电机定子槽内绕组与永磁体的耦合对优化设计提出了更高的要求,为进一步提升此类电机的功率密度和过载能力,该文提出一种五相20/18极的拓扑结构,对电机的空载特性和功率特性进行分析,确定初始优化参数和目标后进行六参数四目标的分层分期优化。首先,在电机直流饱和前提下,通过槽满率和绕组电流密度的限制提出基本的约束条件并合理分配好定子槽面积;其次,结合正交试验设计法和综合灵敏度分析对电机的本体结构参数进行分层优化,通过有限元分析建立高敏感层参数的数据库并建立数学模型,在此基础上运用改进的非支配排序遗传算法对模型实现分期优化设计,引入佳点集并在算法迭代前期基于线性排名加快收敛速度,在迭代后期施加均值约束避免畸形解,与其他智能算法对比验证了改进算法的优越性;最后,根据优化结构制造实验样机进行实验,验证了所提优化算法的可行性与有效性。
关键词:定子槽口永磁 混合励磁 槽面积 多目标优化 分层分期
定子励磁电机由于具有高可靠性、易冷却、宽调速范围和无刷结构等优势在电机领域备受关注。永磁双凸极电机[1-2]和电励磁双凸极电机[3-4]是两种典型的定子励磁电机,然而单一的励磁源使得电机应用受到限制。“混合励磁”技术[5-6]同时引入永磁磁钢和直流励磁线圈作为励磁源,有效地缓解了直流偏置饱和效应,获得了很好的输出性能。
电机的本体优化是一个多目标、非线性、强耦合问题[7-8],槽口永磁型混合励磁电机由于定子槽内绕组与永磁体的耦合对优化设计提出了更高的要求,难点在于精确且快速地建立多个优化目标和多个本体结构之间的数学模型。为克服解析建模法[9]精度低、有限元分析法[10]效率低、试验设计法不具备全局最优性的问题,结合智能算法[11]的多目标优化[12]成为了重要的技术手段之一。
文献[13]提出一种四相16/18极容错磁阻发电机,通过遗传算法得到优化结果并分析了优化后电机的电磁特性。文献[14]提出一种系统的多目标优化方法,根据所有参数对目标的影响划分为三个子空间并依次对子空间进行优化,在不同子空间内结合灵敏度分析、近似模型和遗传算法来减少计算量从而快速收敛。文献[15]针对六个优化目标提出一种结合中心复合表面设计和响应曲面设计的分层响应面法,实现了电机的多目标分层优化。文献[16]在参数敏感性分析和分层优化策略的基础上利用响应面代理模型构建了优化目标和优化变量之间的回归方程,并采用改进布谷鸟算法对代理模型进行多目标寻优。文献[17]基于中心复合设计和响应面模型的敏感度分析实现结构参数的降维,并采用多目标遗传算法获得了最优解集,在此基础上通过多目标加权权衡设计选择最优解方案。文献[18]引入了一种回归机器学习算法,通过映射电机本体结构因素与输出性能之间的非线性复杂关系对电机建立数学模型,并采用灰狼优化算法搜索最优性能的结构。上述研究虽然对电机进行了优化,但优化目标普遍不多,优化过程的本质还是把多目标的优化转变成单目标的函数优化问题,在四目标优化问题中很容易产生畸形解,优化结果缺乏全面性。
本文提出了一种20/18极结构的五相定子槽口永磁型混合励磁双凸极发电机(Stator Slotted Permanent Hybrid-excited Double Salient Machine, SSPHDSM),根据此类电机定子槽面积有限的特点,以发电机工作在直流饱和状态为前提,以槽满率和绕组电流密度为约束条件,合理分配槽面积后对发电机进行六参数四目标的多目标分层分期优化。首先,结合正交试验设计法和综合灵敏度对电机的优化结构参数进行分层,运用单参扫描法确定低敏感度参数的值,将有限元分析方法与径向基函数(Radial Basis Function, RBF)神经网络相结合,通过有限元仿真出高敏感度参数的数据库,再对数据进行RBF建模。其次,运用改进的非支配排序遗传算法Ⅱ(Non-dominated Sorting Genetic Algorithm Ⅱ, NSGA-Ⅱ)对模型进行优化,引入佳点集生成优秀的初始种群后,在迭代过程前期使用基于线性排名的父代选择方式快速收敛到优选解,在优化后期依据样本库的平均值对合并种群施加均值约束从而避免畸形解,得到电机的Pareto解集之后根据优化的多目标加权函数获得最优设计方案,并进一步与改进前算法和其他优化算法进行对比,验证了改进算法的优越性,在此基础上搭建了优化前后的有限元模型,分析了发电机的电磁特性。最后,制造一台3 kW的样机并进行了实验验证。
为了提高电机发电运行时的容错能力和降低输出电压脉动,本文基于五相结构对电机进行设计并根据电机相数和体积大小,选取定子极数为20。不同于传统电机集中励磁结构导致有限的极槽配合,电机的分布励磁设计给出了更多拓扑结构的选择。为了保证电机五相磁路和周围气隙磁通密度的对称性,转子极数需为偶数且一般都接近于定子极数来达到高的绕组因数。相比20/22极结构而言,20/18极结构的转子极宽和极长更加合理且质量更小,在有限元分析中拥有更佳的性能。
本文提出20/18极结构的SSPHDSM,电机结构如图1所示,定子侧每极分槽,槽口放置切向充磁的永磁体且相邻永磁体充磁方向相反,定子槽内还存在交流电枢绕组线圈和直流励磁绕组线圈。

图1 20/18极混合励磁电机结构
Fig.1 Structure of 20/18 pole hybrid excitation machine
电枢绕组结构如图2所示,在每个定子极上都均匀放置电枢绕组,四个定子极上串联而成的电枢绕组组成了电机的一个相绕组。励磁绕组结构如图3所示,DC1~DC20这二十个直流绕组被交替串联起来形成一个单一的绕组。为了避免了不同相绕组之间的直接接触,提高容错能力,所有绕组都采用非重叠集中式绕组结构。
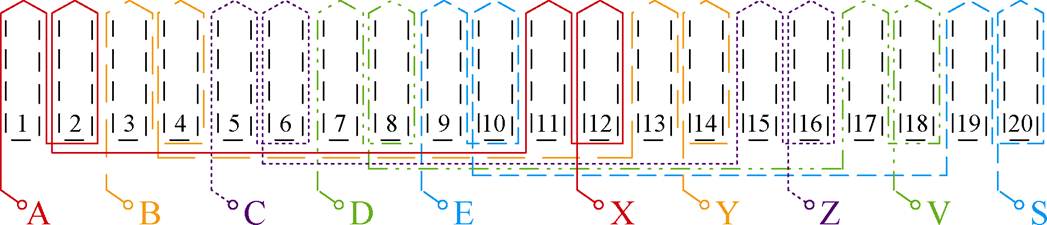
图2 电枢绕组结构
Fig.2 Armature winding structure
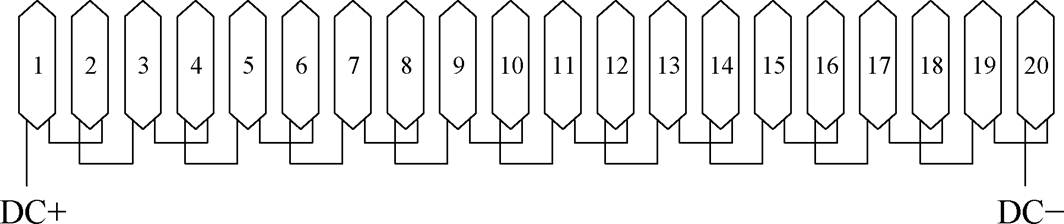
图3 励磁绕组结构
Fig.3 Excitation winding structure
电机的关键几何参数和槽面积分布如图4所示,图中,tr、hr、ts和hs分别为转子极宽、转子极长、定子极宽和定子极长,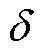 为定转子之间的气隙长度,hpm为永磁体的厚度。每个定子槽内的两个电枢线圈和两个励磁线圈都分别占有相同的匝数和槽面积,电枢线圈所占槽面积用SA表示,两个励磁线圈合并在一起所占槽面积用SDC表示。
为定转子之间的气隙长度,hpm为永磁体的厚度。每个定子槽内的两个电枢线圈和两个励磁线圈都分别占有相同的匝数和槽面积,电枢线圈所占槽面积用SA表示,两个励磁线圈合并在一起所占槽面积用SDC表示。
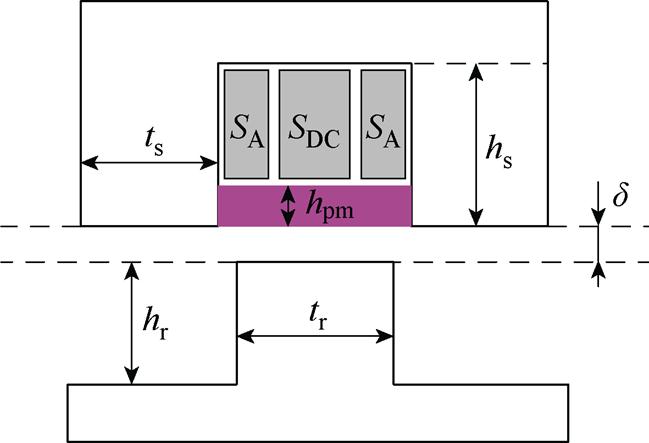
图4 关键几何参数和槽面积分布
Fig.4 Key geometric parameters and groove area distribution
根据不同绕组分布情况,可以得到如图5所示的电枢线圈矢量图和反电动势(基波)相量。从图5b和图5c中可以看出,五相电机每个相位的线圈由同相或36°相移的线圈组成,不能像三相电机那样利用线圈相差180°互补的原理来消除每一相反电动势的偶次谐波,每相电枢绕组的磁链都是单极性的,在一定程度上减小输出功率且影响过载能力。
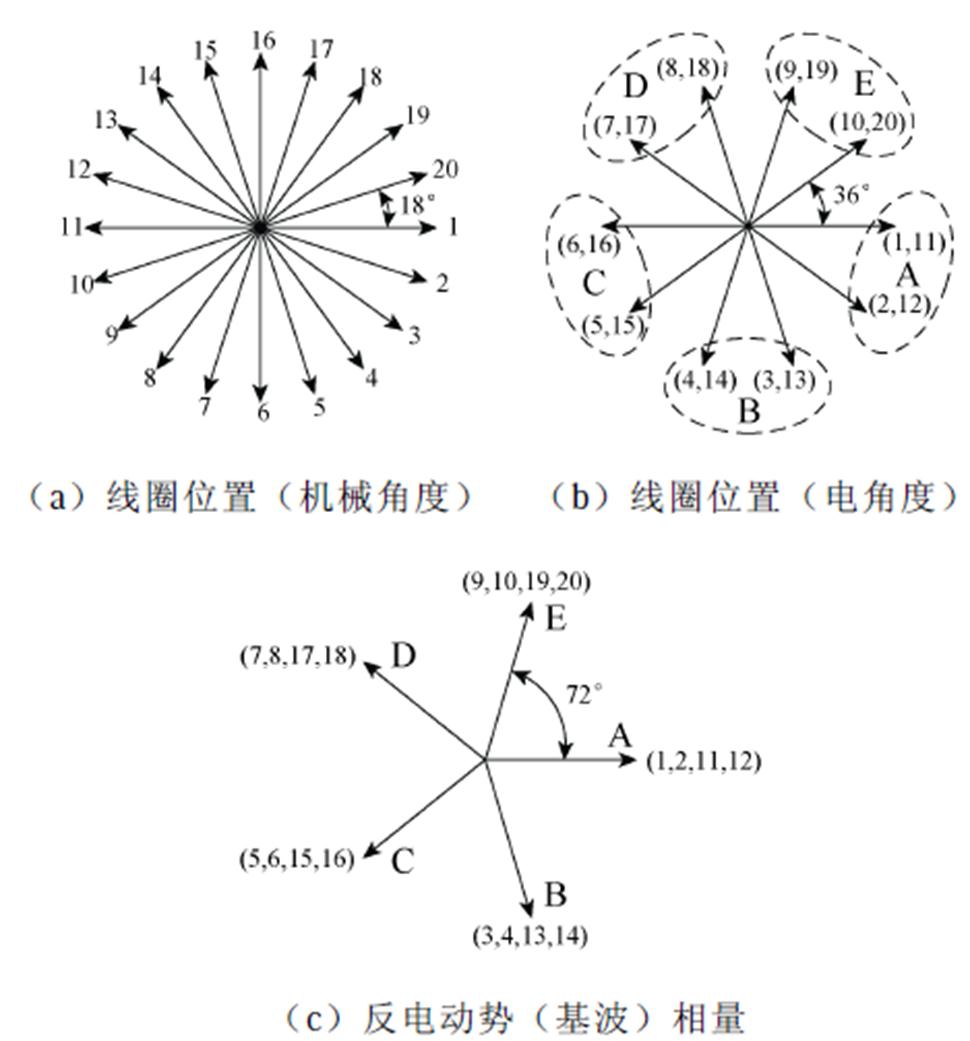
图5 电枢线圈矢量图和反电动势(基波)相量
Fig.5 Armature coil vector diagram and back electromotive force (fundamental) phasor
假设磁路是线性的,励磁源磁路的简化模型如图6所示。图6a和图6b分别为只有永磁体和直流励磁作用时的磁路情况,可以看出,永磁磁通FDC恒定不变,直流励磁通电被激发产生单极性变化的直流励磁磁通FPM穿过气隙连接定子和转子,在定子铁心处产生明显的直流偏置饱和效应;图6c和图6d分别为永磁体和直流励磁同时工作且在定子铁心处磁路同向和异向时的磁路情况,可以看出,同向时定子铁心处极易饱和,会引起较大的损耗且限制了输出性能的上限,异向时两者磁通相互抵消,很大程度上缓解了定子处的直流偏置饱和,有效提高了发电机输出性能的上限。这两种情况下FPM在两个励磁源磁场磁拉力的作用下连接定子和转子,当FPM与FDC在定子侧异向时,两者在转子侧方向一致,可以增大电枢线圈中的感应电动势,进一步提高了发电机的输出性能。值得注意的是,由于永磁体切向充磁且相邻永磁体极性相反,所以每一个定子极上的励磁源磁路都保持一致。
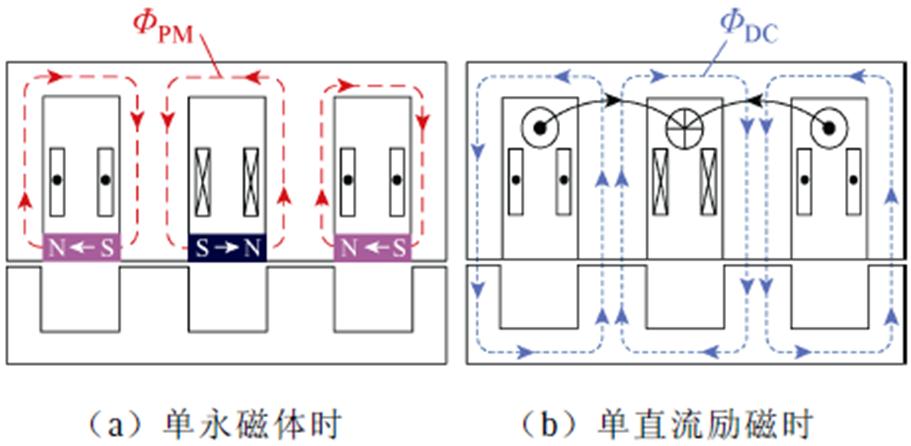
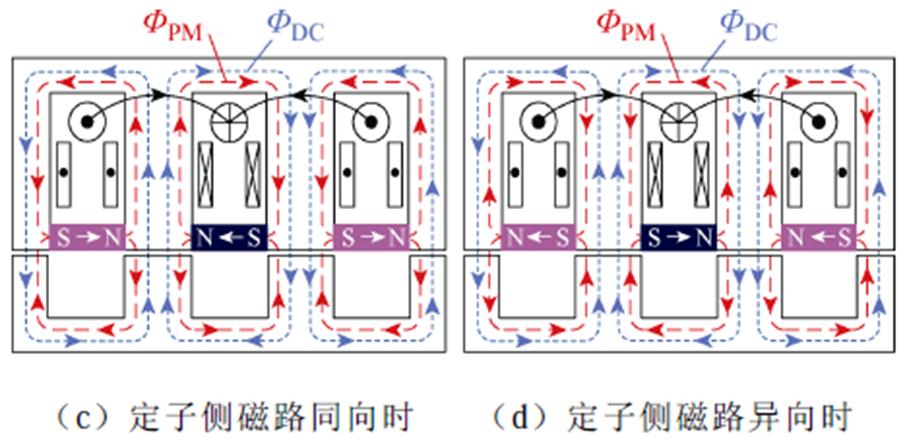
图6 简化模型中的励磁源磁路分析
Fig.6 Analysis of excitation source magnetic circuit in simplified model
基于直流励磁绕组的磁动势和气隙磁导模型,电枢线圈磁链可以分解为各次磁链谐波与直流磁链ydc和永磁磁链ypm之和,ydc和ypm分别可以表示为
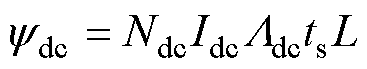 (1)
(1)
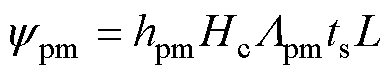 (2)
(2)
式中,Ndc和Idc分别为直流绕组的匝数和电流;Ldc为直流励磁磁链所经磁路的磁导平均值;L为电机轴长;Hc为永磁体的矫顽力;Lpm为永磁体磁链所经磁路的磁导平均值。为了提高定子铁心的利用率,减少定子侧的铁耗,需要尽可能让ydc与ypm相等,从而相互抵消,达到理想的缓解直流饱和的效果。故先保持Ndc=80匝和其他条件相同,得到如图7所示不同Idc对电机功率特性和空载特性的影响。可以看出,空载状态下,空载电压在Idc=12 A时达到最大值,之后随着Idc的增大逐渐减小,电机进入饱和状态。在功率特性曲线中,最大功率点随着Idc的增加而增加,且最大功率点对应的输出电流也在逐步增加,这是因为Idc增加之后导致电机相电感及电抗随之减小,故输出电流也随之增加。Idc达到14 A之后,电机进入饱和状态,最大功率点对应的输出电流保持不变,Idc达到16 A之后,电机进入深度饱和状态,最大功率点开始下降,此时直流励磁源对电机输出起负面作用,定子铁耗急剧上升。综合空载和负载特性曲线,为了最优化缓解直流饱和的效果,也为后续hpm的优化留下调整的空间,将Idc设定为14 A。此外,根据不同电枢绕组匝数N下的功率特性曲线,选择N=40匝,综上所述,电机的初步基本参数见表1,此外,本电机的额定转速为1 000 r/min,本文所有仿真数据和实验样机数据都是在此转速下得出。
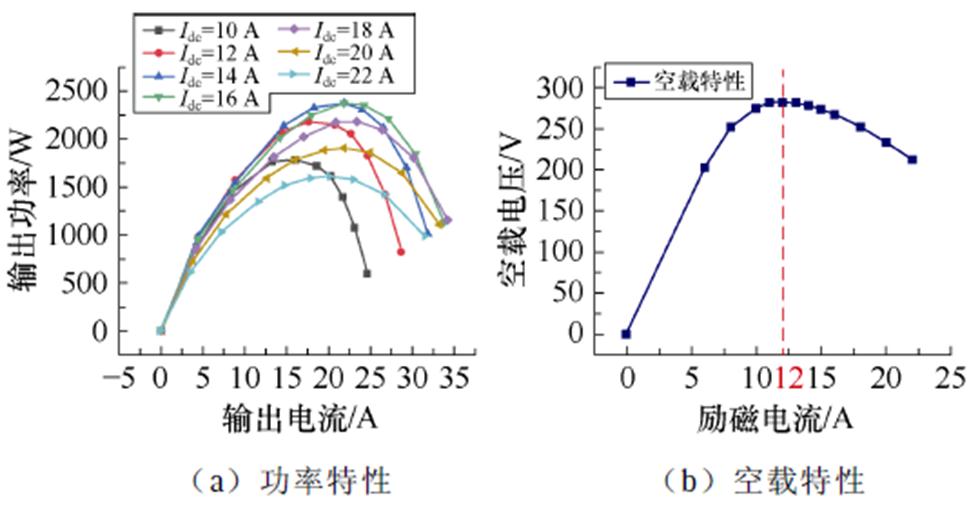
图7 不同励磁下电机的特性
Fig.7 Characteristics of machine under different excitation
表1 电机的初步基本参数
Tab.1 Preliminary basic parameters of the machine

参 数数 值 (型号) 轴长/mm100 定子外径/mm240 定子内径/mm149 气隙宽度/mm0.5 转子外径/mm148 转子内径/mm100 定子极长/mm36.5 转子极长/mm12.5 定子极宽/mm8 转子极宽/mm8.4 永磁体材料NdFeB35 永磁体高度/mm4 输出功率/W3 327.2 电枢铜损/W244.5 输出电压脉动0.137 输出转矩脉动0.305
由于SSPHDSM的两个励磁源和电枢绕组都在定子侧,导致定子槽结构复杂,槽面积紧张,所以对定子槽面积进行合理分配是此类电机优化的前提。每个定子槽约束条件为
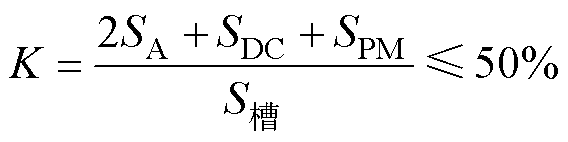 (3)
(3)
式中,K为定子槽满率;SPM为每块永磁体所占的槽面积; 为整个槽的面积。考虑到二维理论计算的局限性以及实际绕组绕制中工艺的限制,约束K不超过0.5。
为整个槽的面积。考虑到二维理论计算的局限性以及实际绕组绕制中工艺的限制,约束K不超过0.5。
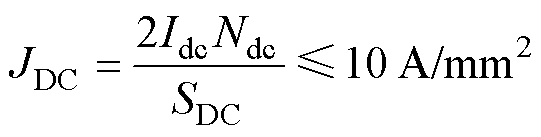 (4)
(4)
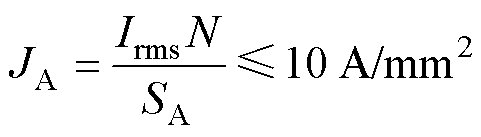 (5)
(5)
式中,JDC为励磁线圈的电流密度;JA为电枢线圈中的电流密度;Irms为相绕组电流的有效值。为了防止电机运行过程中线圈过载导致烧毁,约束电流密度不超过10 A/mm2。
为了最大化发电机的性能,本文取K=0.5,JDC= JA=10 A/mm2。结合1.3节Idc和Ndc的值以及式(4),得到每个定子槽内分配给直流励磁的槽面积为224 mm2。在优化过程中,根据不同的电机本体参数可以得到不同的SA,从而影响电枢绕组的电阻,每相电枢绕组的电阻R表示为
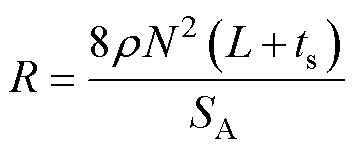 (6)
(6)
式中,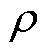 为电枢线圈的电阻率,考虑到电机工作时温度上升,本文取
为电枢线圈的电阻率,考虑到电机工作时温度上升,本文取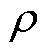 =0.02 W·m。
=0.02 W·m。
为提升电机的综合性能,除了最大化输出功率P之外,还以降低电枢铜损Pa和降低输出电压脉动Uri与输出转矩脉动Tri为目标,并提出相应的约束条件,优化模型方程为
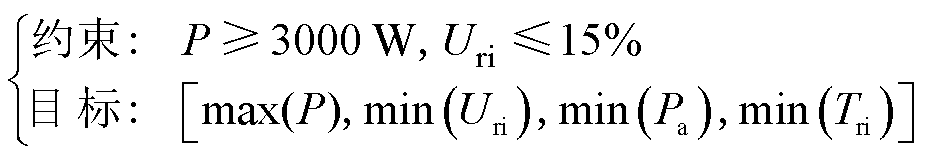 (7)
(7)
其中
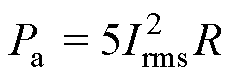 (8)
(8)
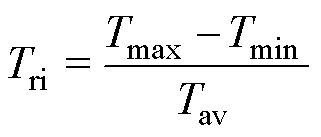 (9)
(9)
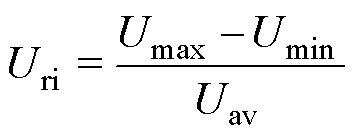 (10)
(10)
式中,Tmax、Tmin和Tav分别为输出转矩的最大值、最小值和平均值;Umax、Umin、Uav分别为输出电压的最大值、最小值和平均值。为了量化Pareto解中的最优解,提出多目标加权的目标函数F(xi)min,其表达式为
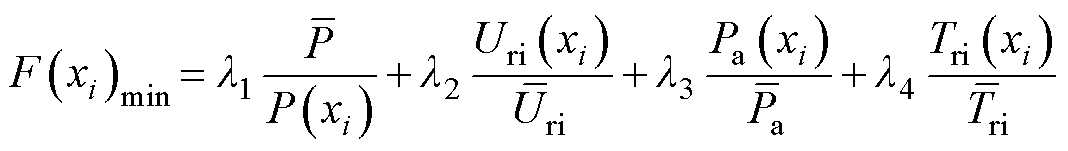 (11)
(11)
式中,xi为参数变量;P(xi)、Uri(xi)、Pa(xi)和Tri(xi)分别为输出功率、电压脉动、电枢铜损和转矩脉动的优化值;l1、l2、l3和l4为权重系数,表示各目标在优化过程中的重要性,和为1,分别取为0.35、0.35、0.15和0.15。此外,为了避免初始尺寸对目标函数的影响,体现目标函数的实际优化能力,本文提出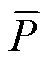 、
、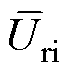 、
、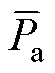 和
和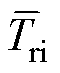 ,分别为输出功率、电压脉动、电枢铜损和转矩脉动的样本平均值,大小由样本库中所有同一目标数据平均后得出。由定义可知,当F(xi)min>1时,电机整体优化呈负向作用;F(xi)min<1时,电机整体优化呈正向作用,且其值越小,电机的优化效果越好。
,分别为输出功率、电压脉动、电枢铜损和转矩脉动的样本平均值,大小由样本库中所有同一目标数据平均后得出。由定义可知,当F(xi)min>1时,电机整体优化呈负向作用;F(xi)min<1时,电机整体优化呈正向作用,且其值越小,电机的优化效果越好。
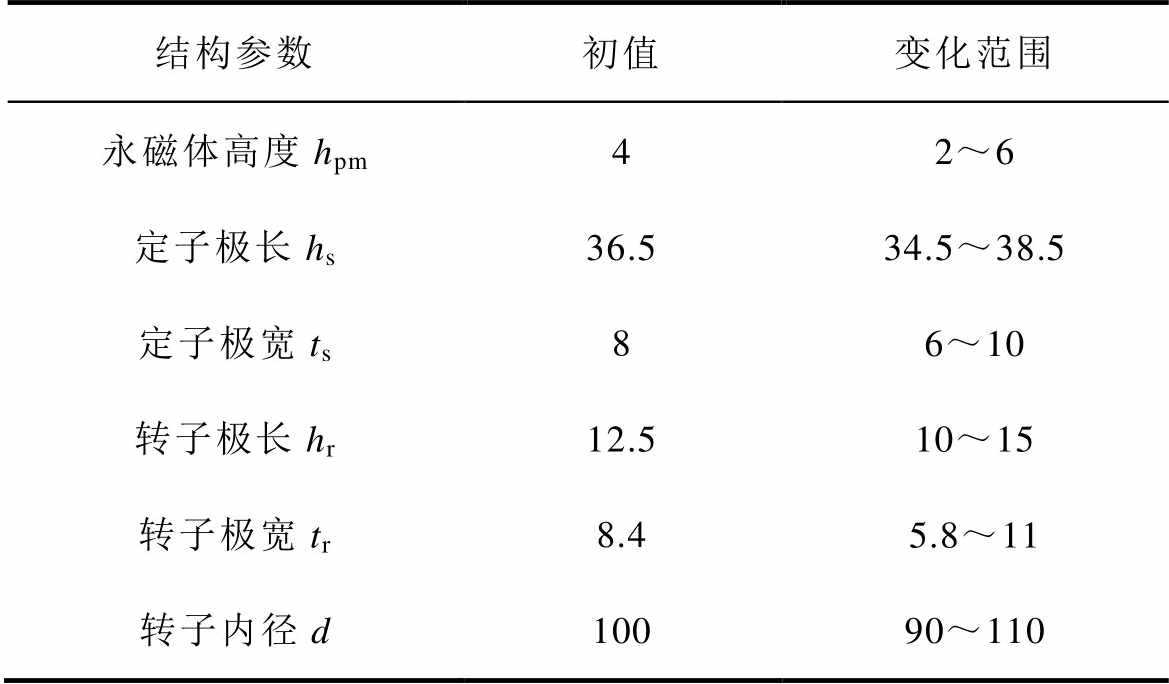
根据上述理论推导和工程经验,在保证电机定子外径、轴向长度和转速不变的前提下,对电机本体结构参数进行优化,相关优化参数的初值和变化范围见表2。需要注意的是,当定子极长和转子极长变化时,定子轭部和转子轭部也随之变化。
表2 电机优化参数的初值和变化范围
Tab.2 Initial values and ranges of machine optimization parameters (单位: mm)
结构参数初值变化范围 永磁体高度hpm42~6 定子极长hs36.534.5~38.5 定子极宽ts86~10 转子极长hr12.510~15 转子极宽tr8.45.8~11 转子内径d10090~110
在建立数学模型之前,对每个参数取五个水平分量,并通过有限元仿真出样本库,进而对数据进行建模和优化。若直接对表2中6个参数进行同时优化,则需要56=15 625次仿真,计算量极大且耗时过长;若逐次对单个参数进行优化,则会忽略各参数之间的相互耦合,难以保证优化结果的可靠性。本文采用多目标分层次的优化思路,引入灵敏度指数和综合灵敏度函数的概念,对优化参数进行分层后逐个优化。
为了表现单个结构参数对单个优化目标的影响,采用Pearson相关系数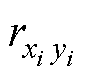 来表现两者之间的线性关系,表示为
来表现两者之间的线性关系,表示为
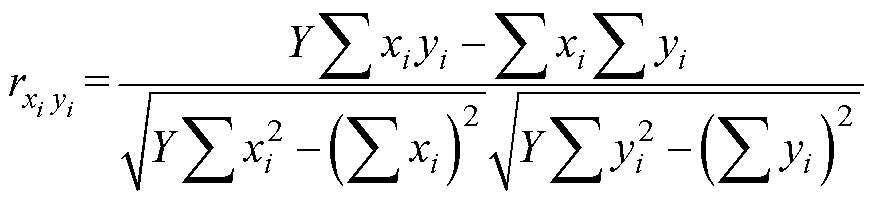 (12)
(12)
式中,yi为单个优化目标对应结构参数变化的第i个值;Y为样本容量,即单个设计参数变量。为了摆脱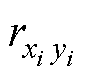 对其他固定尺寸的依赖,通过正交试验设计法引入六因素五水平分量的正交表L25(56),求任一相关系数时,选取其他25组有代表性的固定尺寸,用这些相关系数的均值来表示第m个结构参数Xm对第n个优化目标的灵敏度指数Hn(Xm),表示为
对其他固定尺寸的依赖,通过正交试验设计法引入六因素五水平分量的正交表L25(56),求任一相关系数时,选取其他25组有代表性的固定尺寸,用这些相关系数的均值来表示第m个结构参数Xm对第n个优化目标的灵敏度指数Hn(Xm),表示为
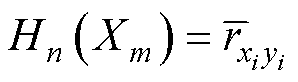 (13)
(13)
为了评价单个结构参数对所有优化目标的综合影响,引入增加权重系数后综合灵敏度G(Xm)的概念,表示为
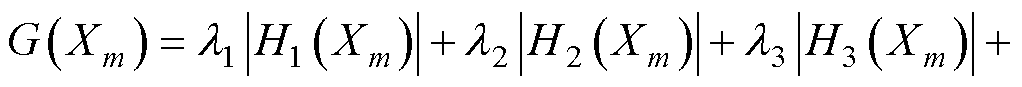
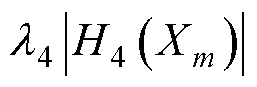 (14)
(14)
式中,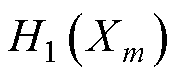 、
、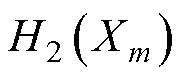 、
、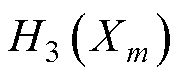 和
和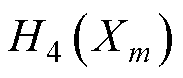 分别为结构参数对输出功率、电压脉动、电枢铜损和转矩脉动的灵敏度指数。
分别为结构参数对输出功率、电压脉动、电枢铜损和转矩脉动的灵敏度指数。
灵敏度分析结果如图8所示,转子侧的结构参数对电机性能的影响普遍较小,转子极宽与定子极宽之间相互耦合程度很高,需要一起分析。根据式(14)得到综合灵敏度的分析结果见附表1,以G(Xm)=0.1为分界将设计参数分为两个层次:①hr和dn为低敏感层次,采用单参扫描法直接优化; ②hpm、hs、ts和tr为高敏感层次,仿真出数据样本库后建立数学模型再用改进的NSGA-Ⅱ进行优化。
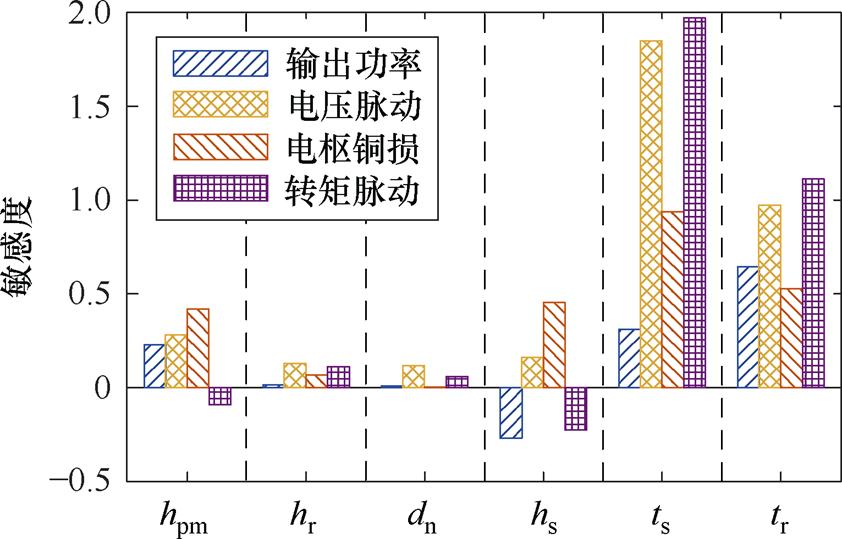
图8 灵敏度分析结果
Fig.8 Sensitivity analysis results
为了满足后续优化迭代中数据库可以实时性变化,对仿真出的数据样本库结果建立径向基函数(Radial Basis Function, RBF)数学模型。首先,根据附表2结构设计参数水平表中给出的四因素五水平分量得到54=625种正交组合方式,通过有限元软件仿真出各种参数组合下设计目标的样本库见附表3,并根据样本库得到式(11)中的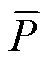 、
、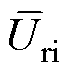 、
、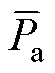 和
和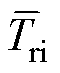 分别为3 032.5 W、0.132、198.2 W和0.337。其次,将样本库中的625组数据按照4
分别为3 032.5 W、0.132、198.2 W和0.337。其次,将样本库中的625组数据按照4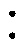 1的比例分为500组训练样本和125组检测样本,并对样本数据进行归一化处理,确定输入层、隐藏层和输出层的神经元个数,在隐层中选取Gaussian函数为激活函数对训练组神经元进行训练。
1的比例分为500组训练样本和125组检测样本,并对样本数据进行归一化处理,确定输入层、隐藏层和输出层的神经元个数,在隐层中选取Gaussian函数为激活函数对训练组神经元进行训练。
最后,为了提高函数拟合的精确性和平滑性,针对P、Pa、Uri和Tri四个目标网络依次选取扩展速度为0.3、0.3、0.2和0.22。通过检测样本对RBF模型的精度进行验证,针对P、Pa、Uri和Tri四个目标网络的决定系数R2值分别为0.999 6、0.999 6、0.999 7和0.999 7,都超过了0.99,认为RBF模型准确。RBF模型对P、Pa、Uri和Tri四个目标检测样本的回归拟合如图9所示,可见RBF模型预测值与真实值保持一致,可以进行下一步算法优化。
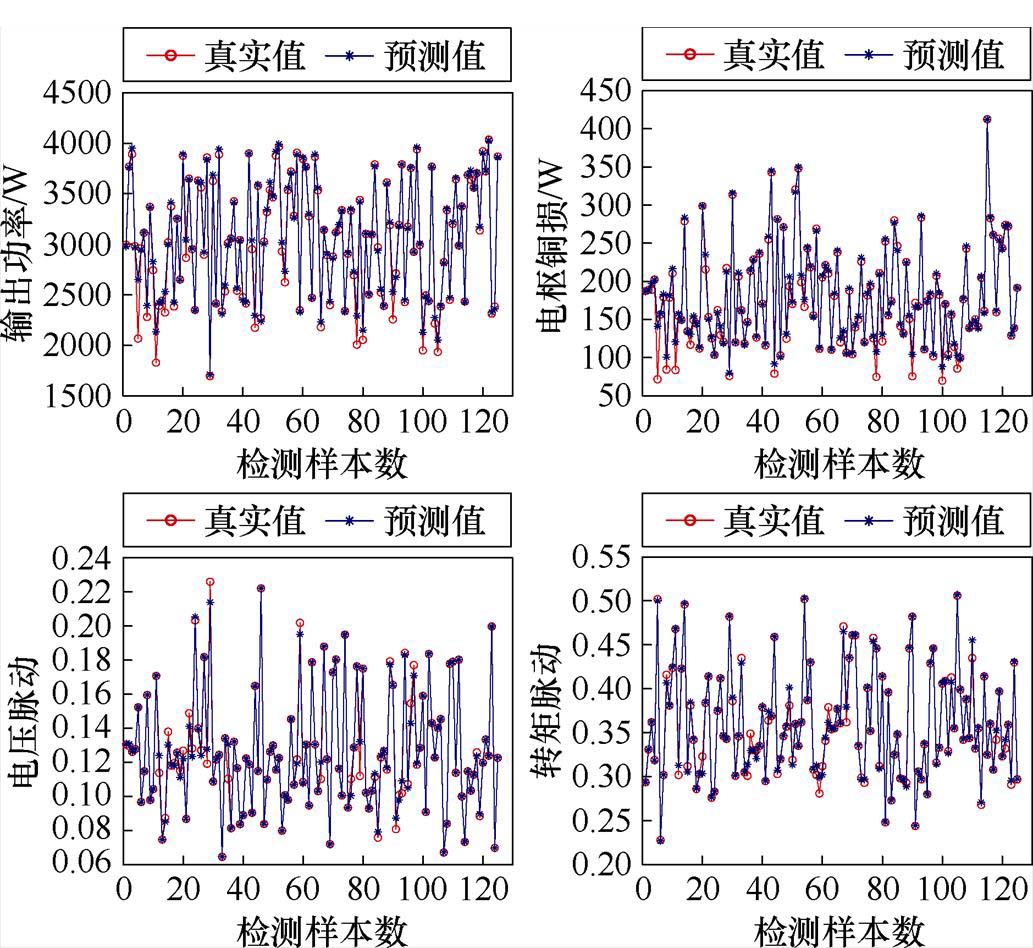
图9 模型的回归拟合
Fig.9 Regression fitting diagram of the model
2.5.1 低敏感度参数优化
对于低敏感度层的参数hr和d,根据制造工艺精度,采用缩小步长、逐个单参扫描的方法进行优化,二者的变化范围分别为10~15 mm和90~110 mm,结合式(11)的多目标加权的目标函数,有限元仿真出目标函数随hr和dn的变化情况如图10a和图10b所示,可以看出,当hr和dn分别为13 mm和102 mm时目标函数达到最小,可以用这两个固定的参数代入后续高敏感层的优化中。
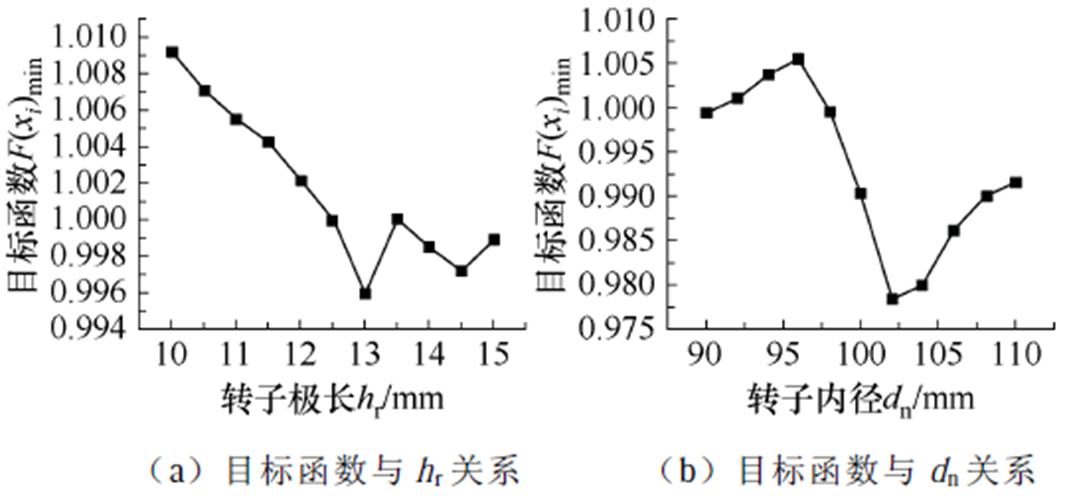
图10 单参扫描法优化
Fig.10 Optimization of single parameter scanning method
2.5.2 高敏感度参数分期优化
对于高敏感层的参数hpm、hs、ts和tr,考虑到各个结构参数之间复杂的耦合关系,难以逐一优化,故采用改进的NSGA-Ⅱ对其建立的整个RBF模型进行优化。
区别于传统优化问题将多目标优化转变成单目标函数优化只能得到一个最优解,NSGA-Ⅱ可以得到具有多样性的一组Pareto解,再根据设计要求从所有Pareto解中选取符合条件的最优解,拥有更多的选择。为了达到更好的优化效果,本文根据电机具体情况对NSGA-Ⅱ进行以下改进:①在初始化种群阶段引入佳点集生成优秀的初始种群,避免了传统随机生成法在空间上的分布不均匀,最大程度预防后续迭代中受到初始种群影响陷入局部最优解,全面考虑了所有电机结构参数的可能性,使最终优化的结果具有更高的可靠性;②在父代选择阶段,区别于传统的二元锦标法选择方式,基于线性排名来选择父代,保证了在进化过程中的搜索能力,并且能够加快前期的收敛速度,缩短了电机整个优化流程的时间;③在算法迭代过程中进行分期优化,在算法前期扩大搜索能力,在算法后期对合并种群实施目标均值约束,剔除种群中的畸形解,使最优解设计出的电机结构具有更均衡的输出性能,同时加大对父代选择的压力来保证算法更好地逼近最 优解。
算法的主体实现流程如图11所示。首先在e维空间下取Z个佳点集表示为
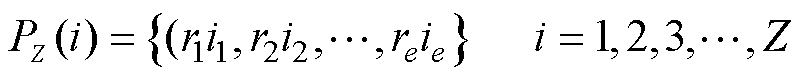 (15)
(15)
式中,Z为种群数量;e为种群的空间维度,本文设计参数变量为四个,故e=4;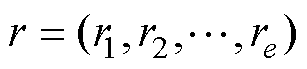 表示一个佳点,其中的rj可表示为
表示一个佳点,其中的rj可表示为
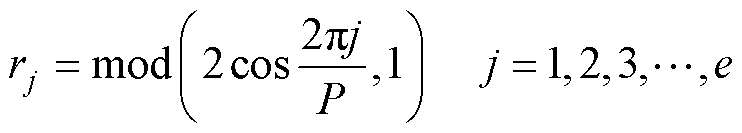 (16)
(16)
式中,P为满足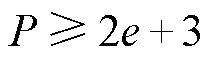 的最小素数,本文取P=11。将rj映射到搜索空间,可表示为
的最小素数,本文取P=11。将rj映射到搜索空间,可表示为
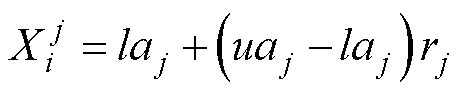 (17)
(17)
式中,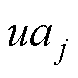 和
和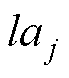 分别为第j维的上、下限。
分别为第j维的上、下限。
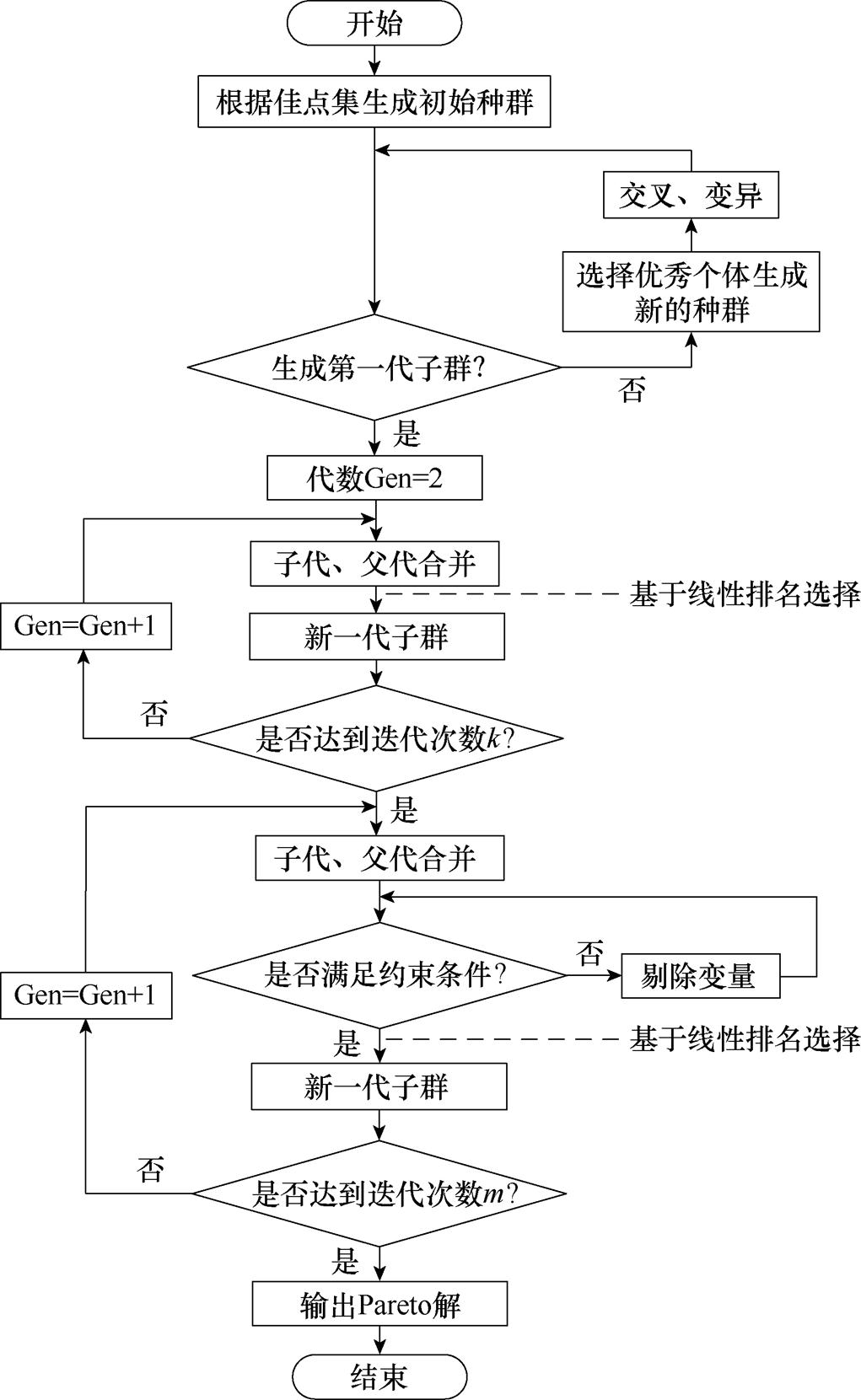
图11 算法流程
Fig.11 Algorithm flow chart
首先,根据佳点集生成的规模为Z的初始父代种群Pt经过选择、交叉和变异后产生第一代子群Qt且合并在一起形成大小为2Z的种群Rt;其次,在优化前期对合并种群Rt采用基于线性目标函数排名的选择方式生成新的父代Pt+1,使算法能够快速收敛,生成新一代子群Qt+1后与父代合并再重复以上操作;最后,在迭代k次后进入优化后期,对合并种群Rt+i实施目标均值约束,剔除种群中的畸形解后重复上述操作,直到迭代L次后结束程序。约束模型可表示为
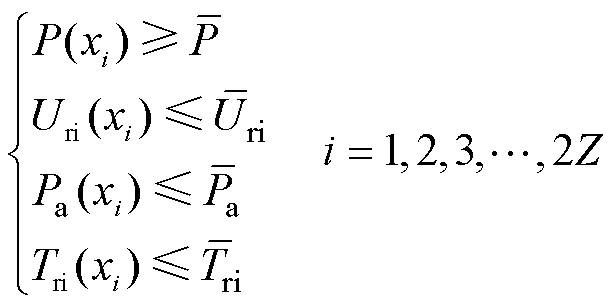 (18)
(18)
只有当对应的P、Uri、Pa和Tri这四个优化目标的值都优于样本库中的均值时,才认为这一组变量没有发生畸变。值得注意的是,此时在算法前期经过k次迭代后的种群已经足够优秀,可以保证经过约束后的种群数目大于Z,能够顺利生成下一代子群。
其中,父代选择阶段的流程如图12所示,在对合并种群排序时,先按照适应值从小到大排序,再对拥挤距离进行升序排序,然后根据线性函数来决定每组变量被选中的概率,按照排序先后,分派给排名i个体的选择概率pi可以表示为
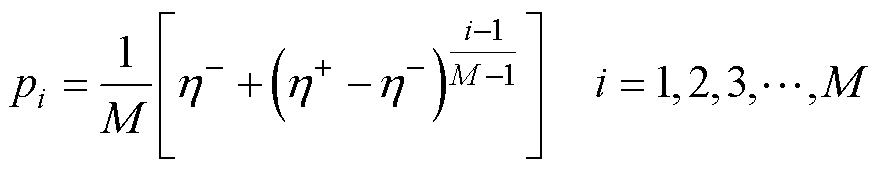 (19)
(19)
式中,M为种群数量,在优化前期大小为2Z,在优化后期由每次剔除畸变个体后的种群数量决定;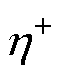 和
和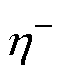 为指定的常数,和为2,且
为指定的常数,和为2,且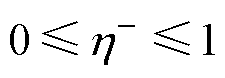 ,当两者越接近时,种群的选择压力越小。为了在迭代过程中逐步加大父代的选择压力,定义
,当两者越接近时,种群的选择压力越小。为了在迭代过程中逐步加大父代的选择压力,定义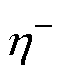 的值为
的值为
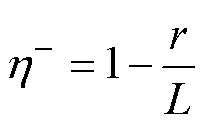 (20)
(20)
式中,r为当前代数。
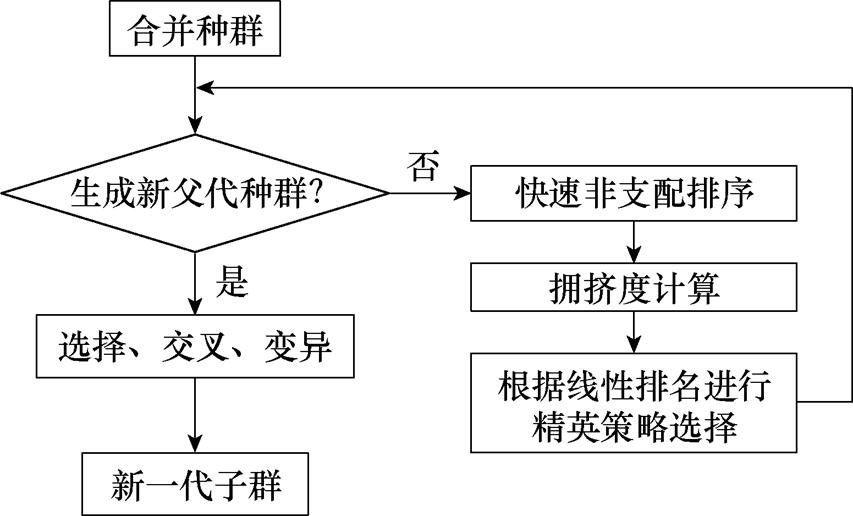
图12 基于线性排名选择父代
Fig.12 Selecting parents based on linear ranking
在保证优化准确的前提下设置前期迭代次数k=300,总迭代次数L=500,种群大小Z=100,交叉比例为0.7,变异比例为0.4,变异率为0.02,此时迭代结果趋于稳定,电机结构参数0.1 mm数量级无变化,满足了设计要求。得到算法改进前后优化结果的对比如图13所示,图中,y1~y4分别为输出功率P、电枢铜损Pa、输出电压脉动Uri和输出转矩脉动Tri。可以看出,算法改进后的Pareto解集更集中且更加逼近Pareto前沿,可以生成更优秀的个体。
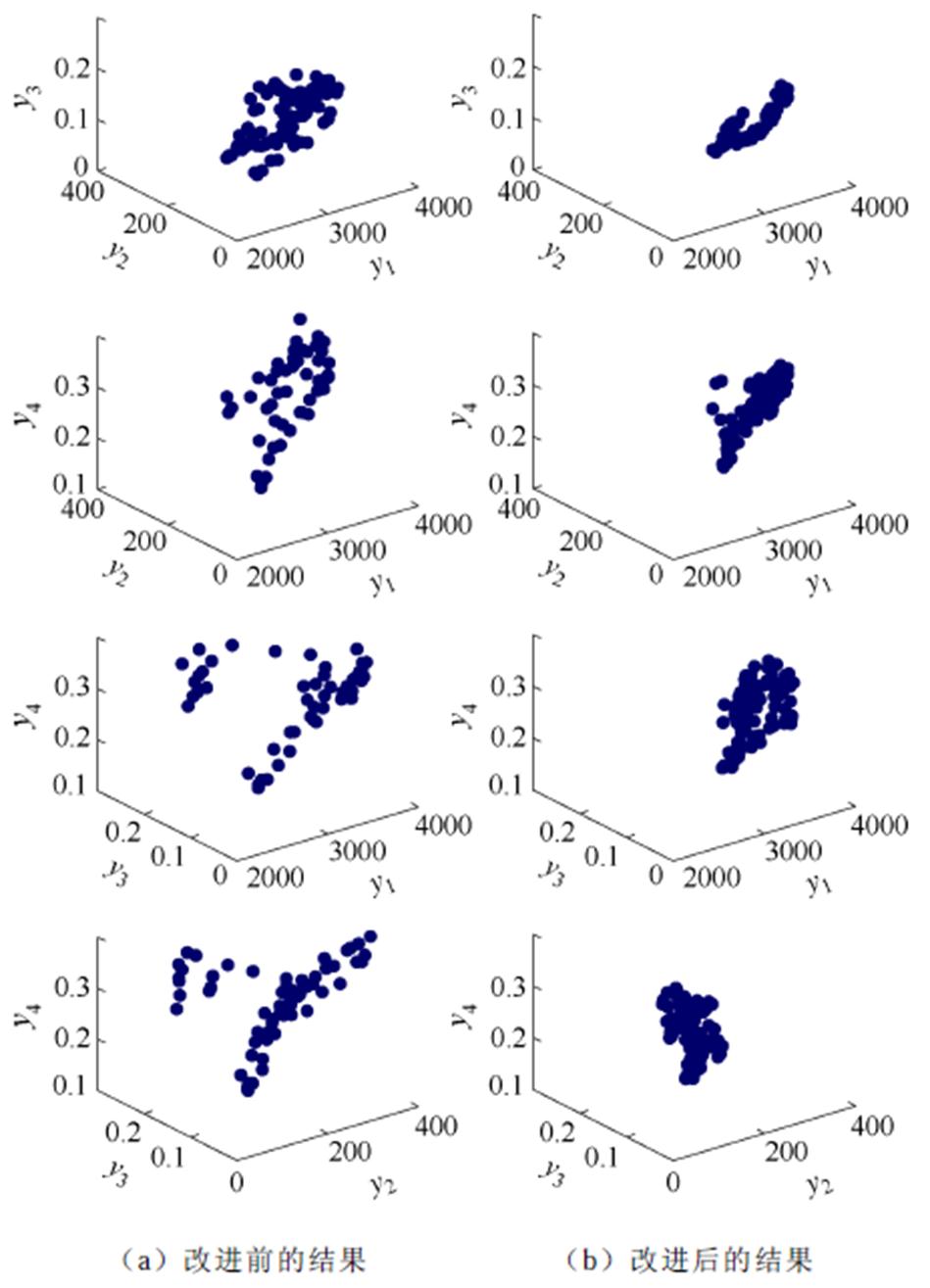
图13 算法改进前后优化结果对比
Fig.13 Comparison of optimization results before and after algorithm improvement
为了进一步验证本文所改进的NSGA-Ⅱ的优越性,将其与NSGA、NSGA-Ⅱ和灰狼优化算法进行对比分析,得到迭代误差与迭代次数的关系如图14所示,可以看出,改进的NSGA-Ⅱ拥有更优秀的初始种群、更快的收敛速度以及更小的误差。值得注意的是,当改进算法进入后期对种群进行均值约束时,由于较多新的种群出现会导致迭代误差短时间内有所增加,但其能够快速收敛到比优化前期精度更高的程度。为了直观比较优化前后期的迭代精度,此改进算法的误差曲线是在k=300的情况下绘制的,实际上k值可以设定为更小的值,在优化前期还未迭代稳定时就能进行均值约束,此时可以有效减少总迭代次数。
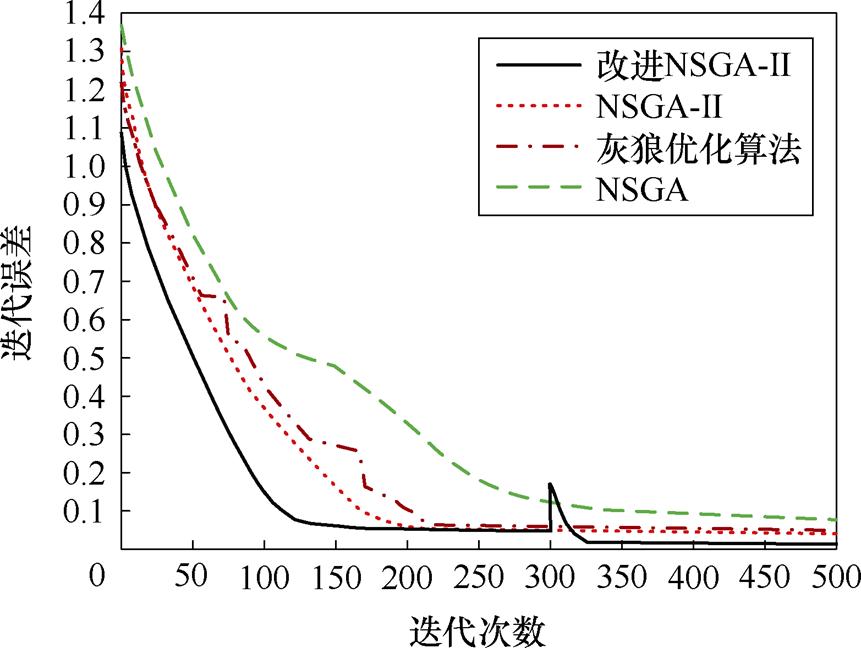
图14 改进NSGA-Ⅱ与其他算法对比
Fig.14 Comparison of improved NSGA-Ⅱwith other algorithms
2.6.1 优化结果
根据优化结果中的Pareto前沿生成最优解候选集,再结合式(11)得到优化目标的最优结果,优化前后电机的结构参数和目标结果对比分别见附表4和表3,由表3可以看出,经过算法优化的目标结果普遍比初始尺寸和样本库均值要好,只有算法改进前的输出转矩脉动性能发生了畸变,高于平均值。虽然算法改进前的电枢铜损很小,但考虑到电机多目标的均衡性,不考虑此方案。算法改进后的各目标结果性能优异,相对样本库的均值,输出功率提高了19.8%,电枢铜损降低了6.7%,电压脉动降低了24.5%,转矩脉动降低了21.5%。通过有限元分析发现,改进算法优化的结果与仿真结果十分接近,这进一步验证了数学模型的准确性。此时,根据有限元分析计算出电枢线圈中的电流密度为5.61 A/mm2,满足式(5)的要求,且电机输出功率和输出电压脉动的值满足式(7)优化模型方程中的约束条件,故优化结果达到了设计要求。
表3 优化目标结果对比
Tab.3 Comparison of optimization target results
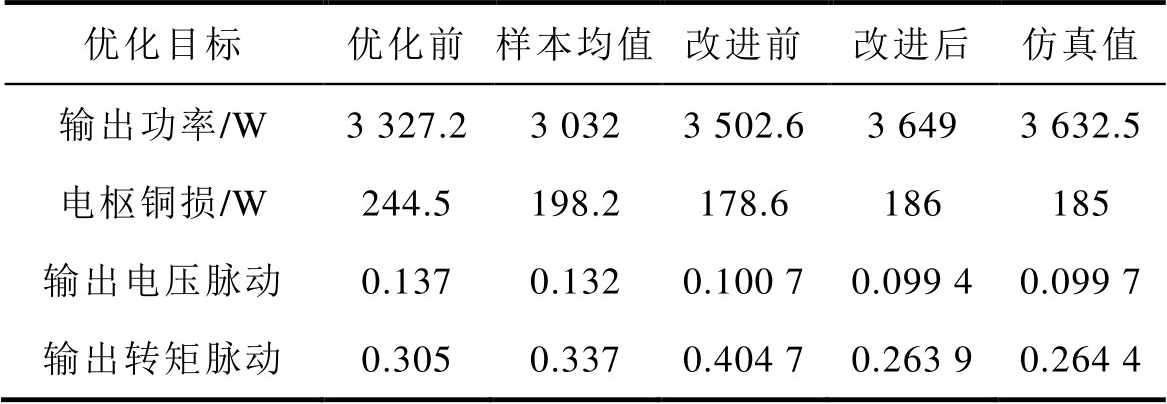
优化目标优化前样本均值改进前改进后仿真值 输出功率/W3 327.23 0323 502.63 6493 632.5 电枢铜损/W244.5198.2178.6186185 输出电压脉动0.1370.1320.100 70.099 40.099 7 输出转矩脉动0.3050.3370.404 70.263 90.264 4
2.6.2 空载特性
以算法改进后的电机结构为优化结果,与优化前的基础结构进行电磁特性的对比分析。图15为Idc不变的情况下同一周期内优化前后空载磁链的对比,其中交流电枢磁链以A相为例。可以看出,优化后的直流磁链降低,相交流磁链峰值减小且整体变化率增大,这表明电机优化后更好地缓解了直流偏置饱和效应,从而具备更强的输出性能。
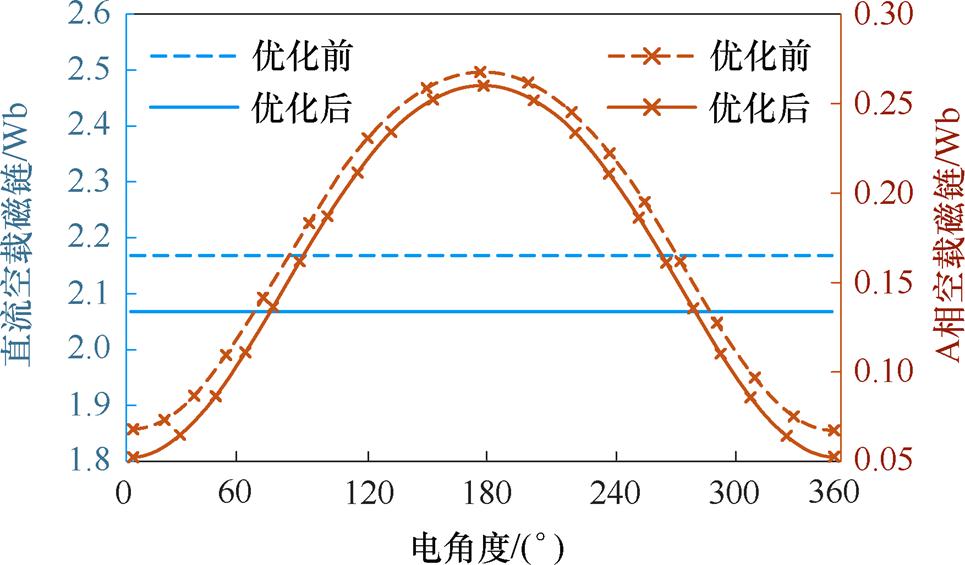
图15 优化前后空载磁链对比
Fig.15 Comparison of no-load magnetic flux before and after optimization
以A相为例,其他条件不变时,不同Idc下的空载反电动势和空载磁链对比如图16所示。当Idc= 0 A时,电机没有直流励磁的存在,几乎不工作;当Idc=7 A时,电机处于直流励磁欠饱和状态,此时空载磁链较小,空载反电动势峰值较小且在峰值时为一段平直状态,总体呈畸形状态;当Idc=14 A时,电机处于直流励磁饱和状态,此时空载磁链较大,空载反电动势较大且波形呈正弦波状态;当Idc= 21 A时,电机处于直流励磁过饱和状态,此时空载磁链相对于饱和状态稍有增加,但空载反电动势峰值较小且呈畸形状态。
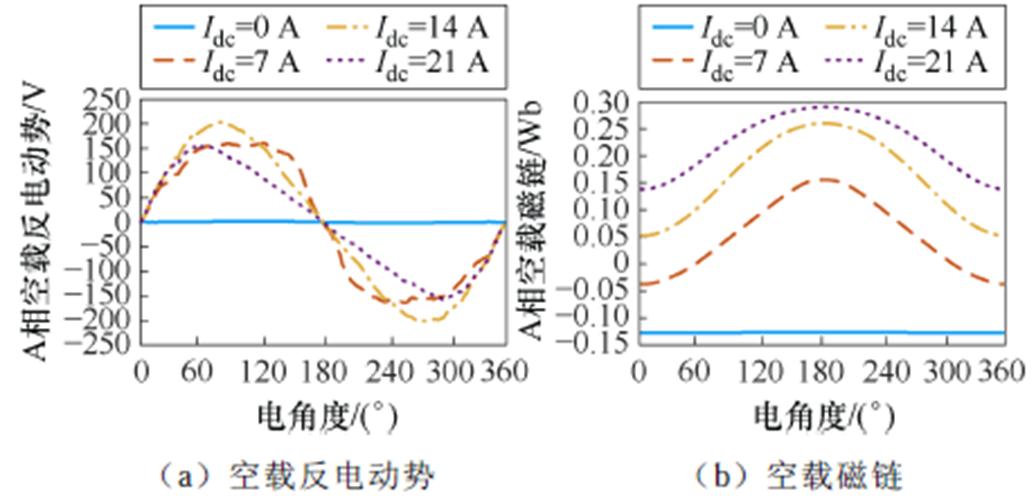
图16 不同励磁下空载反电动势和空载磁链对比
Fig.16 Comparison of no-load back electromotive force and no-load magnetic flux under different excitation
2.6.3 负载特性对比
负载电阻为10 W 且其他条件都不变时,最大功率点优化前后负载特性一个周期内的对比如图17所示。
图17a为输出功率的前后对比,在一个周期内输出功率呈十次有规律的波动,且优化后的输出功率显著提高,均值提高了9.2%;图17b为相绕组电流的前后对比,虽然两者相差不大,但根据式(6)可以得出优化前电机的相电阻为0.688 W,优化后为0.505 W,根据式(8)可以计算出优化后的电枢铜损降低了24.3%;图17c为输出电压的前后对比,在一个周期内输出电压呈十次有规律的波动,且优化后的输出电压数值提高,波动变小,根据式(10),优化后的输出电压脉动降低了27.2%;图17d为输出转矩的前后对比,在一个周期内输出转矩呈十次有规律的波动,且优化后的输出转矩数值提高,波动变小,根据式(9),优化后的输出转矩脉动降低了13.3%。这表明优化后电机的带载能力显著提高,损耗和各类脉动得到了有效抑制,进一步验证了优化的正确性。
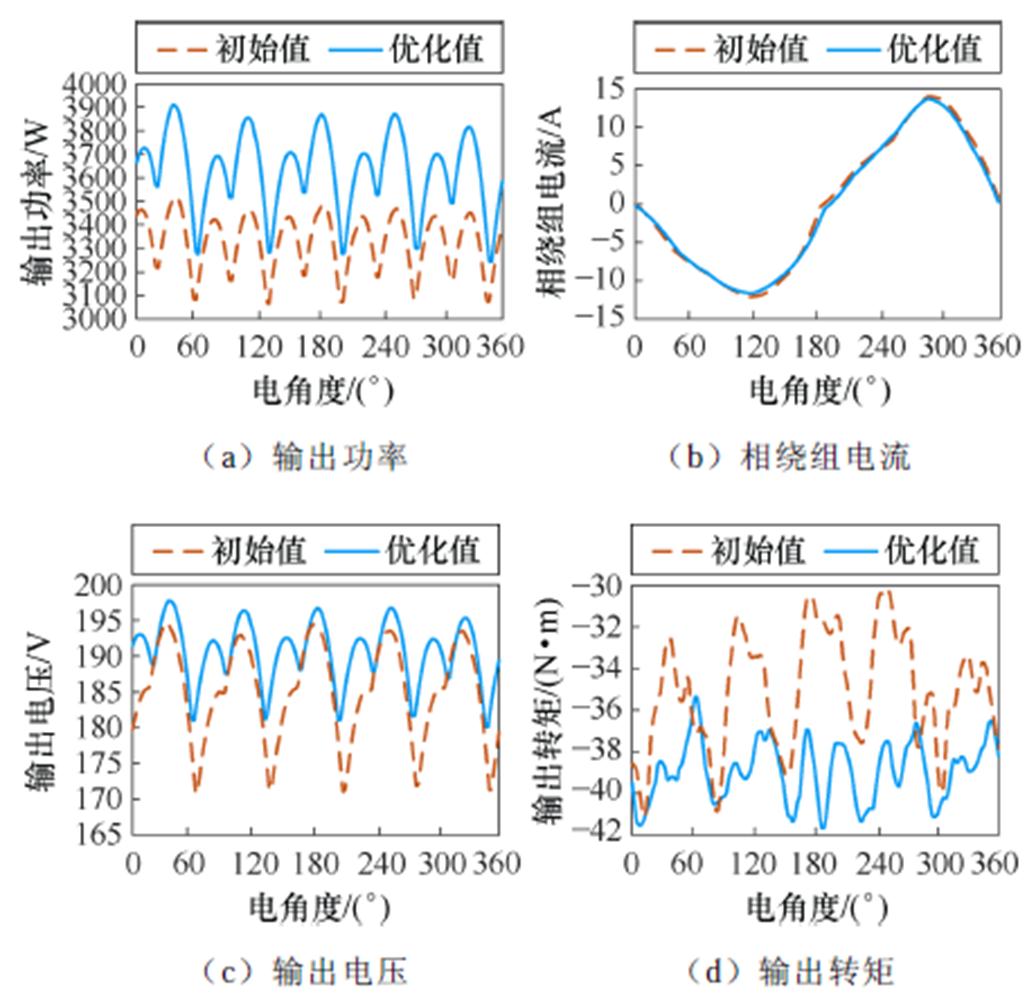
图17 优化前后负载特性对比
Fig.17 Comparison of load characteristics before and after optimization
为了验证理论研究的正确性,根据优化结果制造出一台五相20/18极结构的实验样机并搭建实验平台如图18所示。实验平台包括发电机本体、直流输入装置、转速输入装置和转速控制器、五相全桥整流装置、功率负载和可调电子负载以及示波器、普通探头、电流探头、高倍差分探头等测量装置。
样机实测中,当直流励磁反接时,电机定子侧迅速发热且输出性能极差,当直流励磁正连时,电机可以长时间运转且定子侧几乎不发热,这从实践角度验证了设计中永磁体缓解直流励磁饱和的有效性。
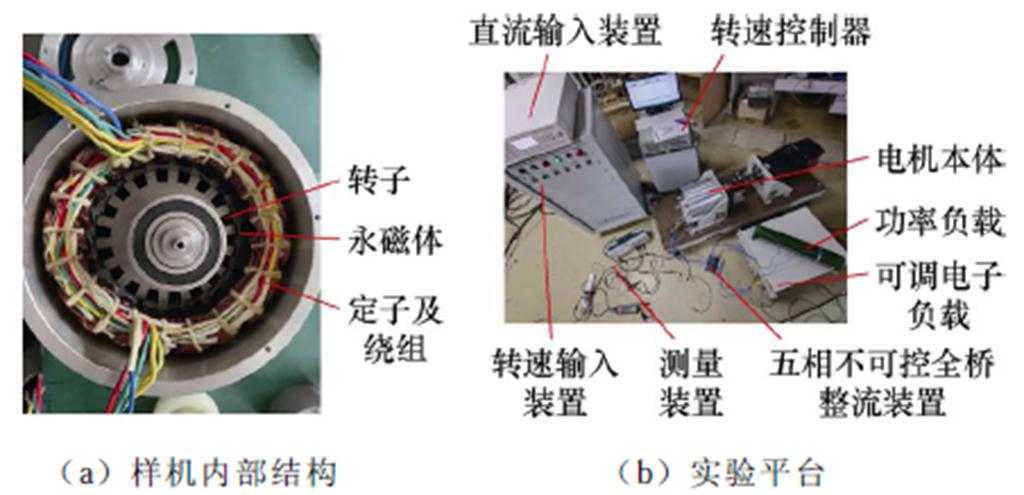
图18 实验样机和实验平台
Fig.18 Experimental prototype and platform
其他条件不变时,测得不同Idc下的空载反电动势对比如图19所示,由于示波器接口有限,仅取五相中A、B、C三相为例。图中,A、B、C三相相差电角度相同,且波形与图16中的仿真波形一致。
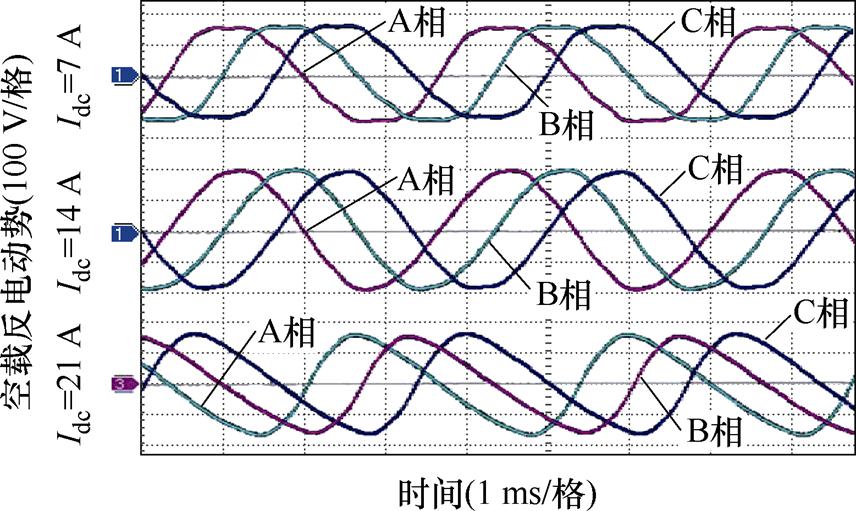
图19 不同Idc下空载反电动势对比
Fig.19 Comparison of no-load back electromotive force under different Idc
当Idc=7 A时,A相空载反电动势峰值实测值为160 V左右,仿真值为160.8 V,相差约0.5%;当Idc= 14 A时,A相空载反电动势峰值实测值为200 V左右,仿真值为203.7 V,相差约1.85%;当Idc=21 A时,A相空载反电动势峰值实测值为155 V左右,仿真值为156.6 V,相差约1.03%。由此可见,实验样机测得的数据与仿真数据相差很小,误差在2%之内,这从实践角度验证了本电机设计的合理性。
其他条件不变时,测得负载电阻为10 W 时电机的相反电动势如图20a所示,对比的仿真波形如图20b所示。可以看出,两者波形基本一致,实验波形幅值为115 V左右,仿真幅值为123 V。
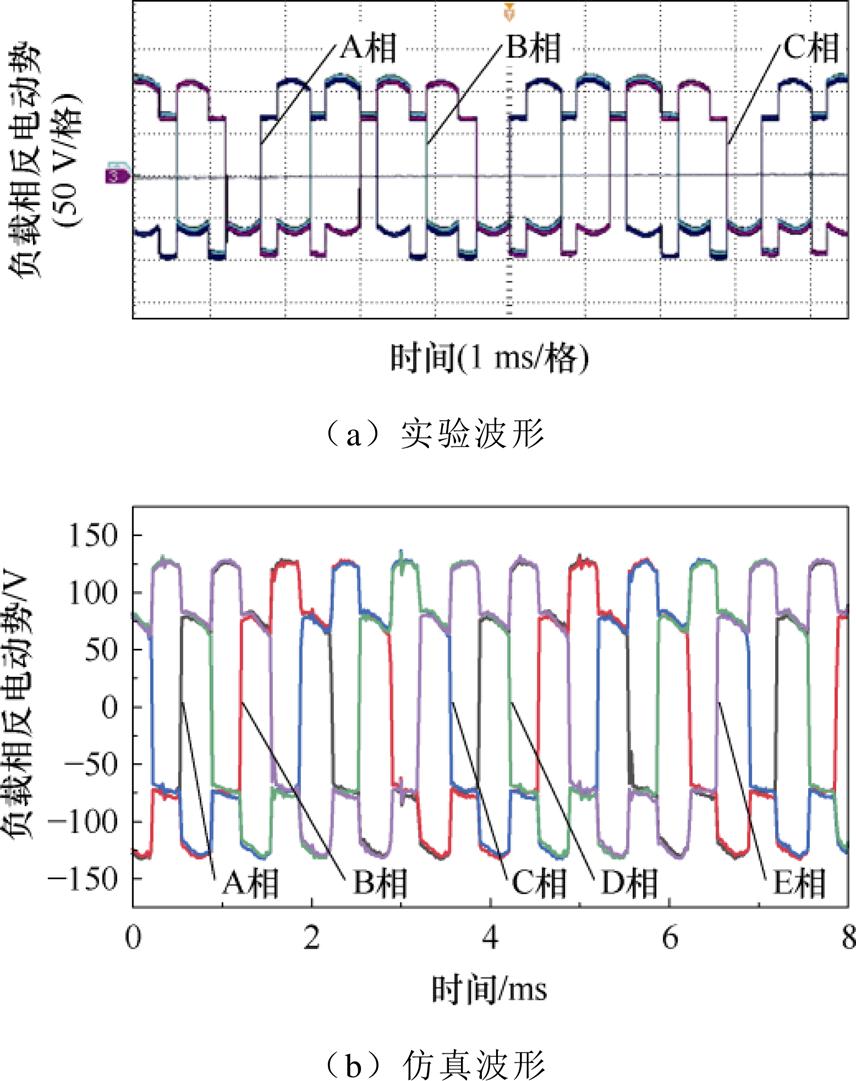
图20 负载运行时的相反电动势
Fig.20 Phase electromotive force with load
此外,电机空载及负载时输出的整流电压实测波形如图21所示,空载电压的均值为345 V左右,仿真值为364 V,相差约5.51%,负载输出电压的均值为175 V左右,仿真值为183 V,相差约4.57%,负载输出电压的脉动为11.43%左右,仿真值为9.97%,根据输出电压得到输出功率为3 062.5 W,与仿真值保持了良好的一致性,表明本发电机具备优越的输出性能。
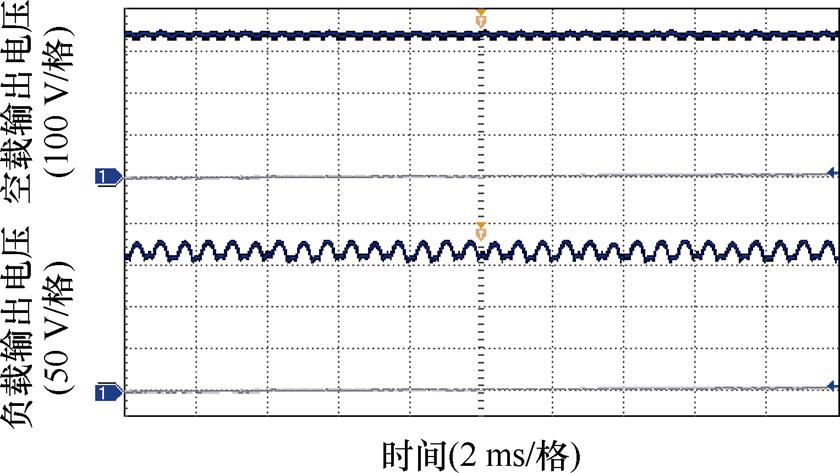
图21 空载及负载运行时的输出电压
Fig.21 Output voltage at no load and load
图22a和图22b分别为负载运行时的相绕组电流实测和仿真波形,对比可以看出,实测值的波形和幅值基本与仿真值保持一致,这表明本文电机不仅拥有理想的输出能力,而且在设计过程中考虑到的对电流密度的约束得到了有效验证,充分证明了电机设计和多目标优化的正确性。
通过上述样机实验和仿真分析的对比,本文设计的电机基本达到了理想效果,其中负载时实测值相比于仿真值有所减少,这是电机制作工艺的限制以及绕组绕制过程中重叠引起的电枢绕组阻值偏大带来了更多损耗造成的,这些损耗导致的误差在允许范围之内。
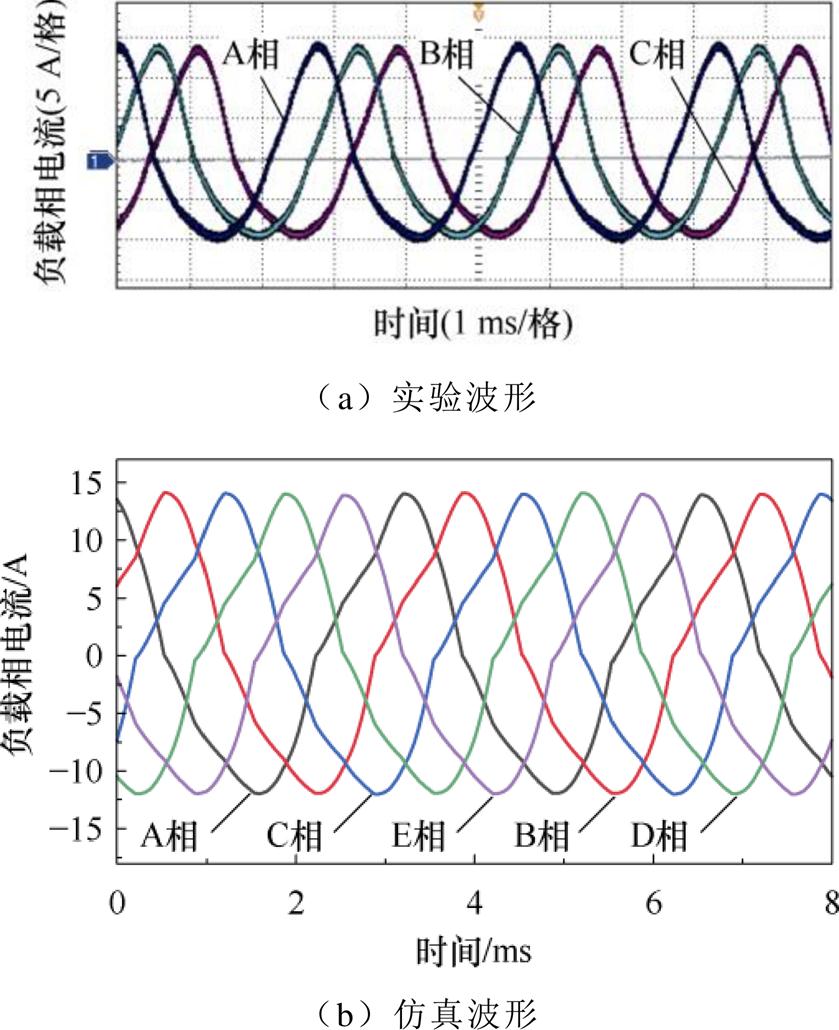
图22 负载运行时的相电流
Fig.22 Phase current with load
本文提出了一种五相20/18极结构的SSPHDSM和一个改进的NSGA-Ⅱ,在对电机定子槽面积合理分配的基础上进行了多目标分层分期优化,实现了电机发电运行的最佳输出性能,并通过有限元仿真和样机实验验证了理论的有效性,具体的研究成果如下:
1)提出了五相20/18极结构的槽口永磁型混合励磁双凸极电机,根据此类电机定子槽面积有限的特点,以定子槽面积的分配为切入点,兼顾了工业制造中的实际问题,提出了基于该电机结构的多目标优化方法。
2)结合正交试验设计法和综合灵敏度分析对电机的本体结构参数进行分层优化,根据灵敏度进行分层优化在近年来的研究中也有所提及,但大多只是简单运用一个灵敏度计算公式,难以摆脱耦合的固定尺寸的影响,本文结合了正交试验设计法,既保证了准确度又提高了设计效率。
3)面对四个优化目标给优化流程带来的更高要求,采用仿真数据库建模和智能算法对模型优化的思路,大大减少了有限元的仿真量,并运用了改进的NSGA-Ⅱ对电机的数学模型进行了分期优化,更适合多目标的优化场合,在优化后期剔除了畸形解,使根据迭代出来的最优解设计出的电机结构具有更均衡的输出性能。
4)通过优化,电机输出功率提高了9.2%,电枢铜损降低了24.3%,输出电压脉动降低了27.2%,输出转矩脉动降低了13.3%,样机的实测数据也基本保持一致,这表明本电机的设计和优化是正确有效的。
附 录
附表1 综合灵敏度分析结果
App.Tab.1 Comprehensive sensitivity analysis results

参数H1H2H3H4G敏感层次 hpm0.229 60.281 40.418 7-0.091 00.255 3高 hs-0.270 10.161 80.453 0-0.226 50.253 1高 ts0.312 11.849 20.938 61.970 71.192 8高 hr0.015 80.127 70.068 60.112 60.077 0低 tr0.643 60.973 00.526 81.112 10.811 6高 dn0.010 50.117 10.002 30.058 70.053 8低
附表2 结构设计参数水平
App.Tab.2 Structural design parameter level (单位: mm)

参数水平1水平2水平3水平4水平5 hpm23456 hs34.535.536.537.538.5 ts678910 tr5.87.18.49.711
附表3 样本库
App.Tab.3 Sample library
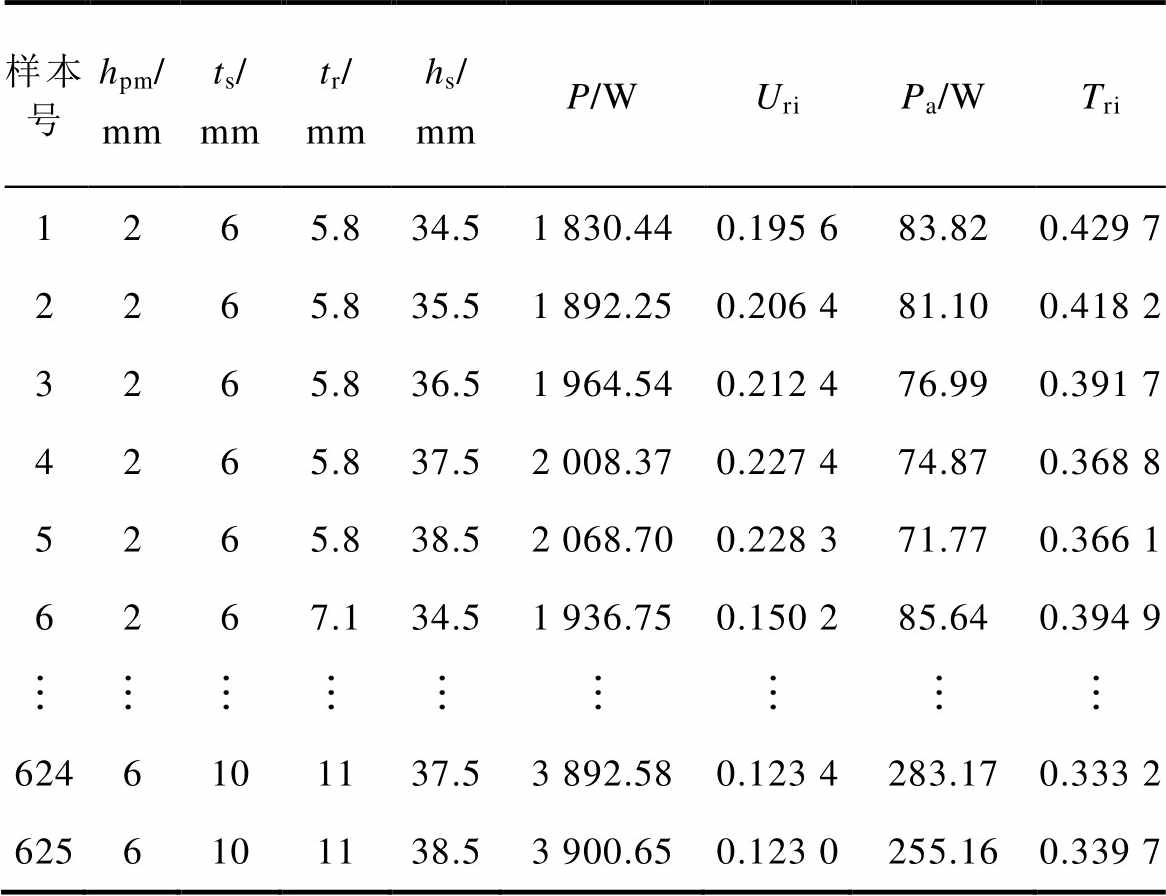
样本号hpm/mmts/mmtr/mmhs/mmP/WUriPa/WTri 1265.834.51 830.440.195 683.820.429 7 2265.835.51 892.250.206 481.100.418 2 3265.836.51 964.540.212 476.990.391 7 4265.837.52 008.370.227 474.870.368 8 5265.838.52 068.700.228 371.770.366 1 6267.134.51 936.750.150 285.640.394 9 6246101137.53 892.580.123 4283.170.333 2 6256101138.53 900.650.123 0255.160.339 7
附表4 电机结构参数对比
App.Tab.4 Comparison of machine structural parameters (单位: mm)

结构参数优化前算法改进前算法改进后 hpm42.73.3 hs36.538.438.1 ts89.29.3 hr12.51313 tr8.47.410.6 dn100102102
参考文献
[1] 程明, 张淦, 花为. 定子永磁型无刷电机系统及其关键技术综述[J]. 中国电机工程学报, 2014, 34(29): 5204-5220.
Cheng Ming, Zhang Gan, Hua Wei. Overview of stator permanent magnet brushless machine systems and their key technologies[J]. Proceedings of the CSEE, 2014, 34(29): 5204-5220.
[2] Neethu S, Nikam S P, Pal S, et al. Performance comparison between PCB-stator and laminated- core-stator-based designs of axial flux permanent magnet motors for high-speed low-power appli- cations[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(7): 5269-5277.
[3] 陈旭, 张卓然, 于立, 等. 基于改进型准比例谐振控制的电励磁双凸极电机电流谐波抑制方法[J]. 电工技术学报, 2023, 38(14): 3836-3848, 3861.
Chen Xu, Zhang Zhuoran, Yu Li, et al. Current harmonic suppression method of doubly salient electro-magnetic machine based on improved quasi proportional resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3836- 3848, 3861.
[4] 赵耀, 沈翀, 李东东, 等. 极端条件下基于特征层面信号融合的电励磁双凸极电机匝间短路故障诊断[J]. 电工技术学报, 2023, 38(10): 2661-2674.
Zhao Yao, Shen Chong, Li Dongdong, et al. Inter-turn short circuit diagnosis of wound-field doubly salient machine based on multi-signal fusion on feature level under extreme conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2661-2674.
[5] 张卓然, 王东, 花为. 混合励磁电机结构原理、设计与运行控制技术综述及展望[J]. 中国电机工程学报, 2020, 40(24): 7834-7850, 8221.
Zhang Zhuoran, Wang Dong, Hua Wei. Overview of configuration, design and control technology of hybrid excitation machines[J]. Proceedings of the CSEE, 2020, 40(24): 7834-7850, 8221.
[6] 马昕晨, 陈志辉. 高压直流轴向混合励磁双凸极发电机的结构及特性分析[J]. 电气工程学报, 2022, 17(2): 65-72.
Ma Xinchen, Chen Zhihui. Topology and characteri- stic analysis of HVDC axial hybrid excitation doubly salient machine[J]. Journal of Electrical Engineering, 2022, 17(2): 65-72.
[7] 周嗣理, 李国丽, 王群京, 等. 基于改进粒子群优化算法的永磁球形电机驱动策略研究[J]. 电工技术学报, 2023, 38(1): 166-176, 189.
Zhou Sili, Li Guoli, Wang Qunjing, et al. Improved particle swarm optimization algorithm based driving strategy research for permanent magnet spherical motor[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 166-176, 189.
[8] 张玉峰, 高文韬, 史乔宁, 等. 基于改进迭代田口法的双余度永磁同步电机优化设计[J]. 电工技术学报, 2023, 38(10): 2637-2647, 2685.
Zhang Yufeng, Gao Wentao, Shi Qiaoning, et al. Optimization design of dual-redundancy permanent magnet synchronous motor based on improved iterations taguchi method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2637-2647, 2685.
[9] 支凡, 张鸣, 朱煜, 等. 无铁心永磁同步直线电机推力谐波分析与消除[J]. 中国电机工程学报, 2017, 37(7): 2101-2110.
Zhi Fan, Zhang Ming, Zhu Yu, et al. Analysis and elimination of harmonics in force of ironless permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2017, 37(7): 2101-2110.
[10] 李思泽, 徐炜, 金振, 等. 一种基于有限元法与改进无网格法耦合的双定子电机振动噪声分析方法[J]. 电工技术学报, 2023, 38(19): 5112-5127.
Li Size, Xu Wei, Jin Zhen, et al. A novel vibration-noise calculation method by coupling finite element analysis and optimized meshless method for dual-stator electric machine[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5112-5127.
[11] 李东东, 蒋海涛, 赵耀, 等. 极端条件下基于改进深度森林的行星齿轮箱故障诊断方法[J]. 电力系统保护与控制, 2023, 51(11): 39-50.
Li Dongdong, Jiang Haitao, Zhao Yao, et al. Fault diagnosis technology of a planetary gearbox based on an improved deep forest algorithm under extreme conditions[J]. Power System Protection and Control, 2023, 51(11): 39-50.
[12] 赵耀, 陆传扬, 李东东, 等. 基于改进距离权重双电枢绕组电励磁变磁阻电机多目标优化研究[J]. 电机与控制学报, 2023, 27(11): 90-103.
Zhao Yao, Lu Chuanyang, Li Dongdong, et al. Multi- objective optimization of double armature winding wound field variable reluctance machine based on improved distance weighted[J]. Electric Machines and Control, 2023, 27(11): 90-103.
[13] 赵耀, 滕登晖, 李东东, 等. 四相容错型缓解直流偏置饱和的混合励磁磁阻发电机电磁特性研究[J]. 中国电机工程学报, 2022, 42(18): 6880-6893.
Zhao Yao, Teng Denghui, Li Dongdong, et al. Research on the electromagnetic characteristics of four-phase fault-tolerant Relieving-DC-saturation hybrid excited reluctance generator[J]. Proceedings of the CSEE, 2022, 42(18): 6880-6893.
[14] Diao Kaikai, Sun Xiaodong, Lei Gang, et al. Multiobjective system level optimization method for switched reluctance motor drive systems using finite-element model[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10055-10064.
[15] 曹永娟, 冯亮亮, 毛瑞, 等. 轴向磁场永磁记忆电机多目标分层优化设计[J]. 中国电机工程学报, 2021, 41(6): 1983-1992.
Cao Yongjuan, Feng Liangliang, Mao Rui, et al. Multi-objective stratified optimization design of axial-flux permanent magnet memory motor[J]. Proceedings of the CSEE, 2021, 41(6): 1983-1992.
[16] 王晨, 黄健, 江明, 等. 聚磁式永磁轮毂电机多目标优化设计[J]. 中国电机工程学报, 2024, 44(3): 1173-1184.
Wang Chen, Huang Jian, Jiang Ming, et al. Multi- objective optimization and design of flux- concentrating permanent magnet In-wheel motor[J]. Proceedings of the CSEE, 2024, 44(3): 1173-1184.
[17] 郑诗玥, 朱孝勇, 徐磊, 等. 永磁助磁式同步磁阻电机高转矩质量比设计与性能分析[J]. 中国电机工程学报, 2022, 42(19): 7236-7248.
Zheng Shiyue, Zhu Xiaoyong, Xu Lei, et al. Design and performance analysis of PM-assisted synchronous reluctance motor considering high torque-quality ratio[J]. Proceedings of the CSEE, 2022, 42(19): 7236-7248.
[18] Song Juncai, Dong Fei, Zhao Jiwen, et al. An efficient multiobjective design optimization method for a PMSLM based on an extreme learning machine[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1001-1011.
Abstract The coupling between the winding and the permanent magnet in the stator slot of the five-phase stator slotted permanent magnet hybrid excitation doubly salient machine puts forward high requirements for optimization design. The multi-objective optimization process produces deformed solutions easily, and the optimization results are not comprehensive. Therefore, a five-phase 20/18 pole topology is proposed. According to the limited stator slot area of the machine structure, the no-load and power characteristics are analyzed after the slot area is rationally allocated under the DC saturation state. The slot filling rate and winding current density are taken as constraint conditions to determine the initial optimization parameters and objectives. Multi-objective layered and phased optimization with six parameters and four objectives is carried out.
Combined with the orthogonal experimental design method and comprehensive sensitivity analysis, the structure parameters of the machine body are layered, and the low-sensitivity parameters are determined by the single-parameter scanning method. A parameter database of the high-sensitivity layer is established by finite element analysis, and radial basis function neural network modeling is conducted. Secondly, the improved non-dominated sorting genetic algorithm II is used to optimize the model by phases. The best data set is introduced to generate an excellent initial population. In the early phase, the parent selection method based on linear ranking accelerates the convergence speed. In the later phase, the mean value constraint is applied to the merged populations according to the average value of the database to avoid deformed solutions. The optimal design scheme is obtained according to the optimized multi-objective weighting function. Finally, the experiments verify the feasibility and effectiveness of the proposed optimization method.
Using the proposed optimization method, the electromagnetic performance of the optimized machine is superior. The output power of the machine is 3649W, increased by 9.2%; the armature copper loss is 186 W, decreased by 24.3%; the output voltage pulsation is 0.0994, decreased by 24.3%; the output torque pulsation is 0.2639, decreased by 13.3%.
The following conclusions can be drawn. (1) The optimization problem with six parameters and four objectives is reduced to two parameters/four objectives and four parameters/four objectives to layer the structure parameters of the machine body. The influence of fixed dimensions is eliminated, and the overall optimization workload is reduced. (2) The proposed simulation database modeling and intelligent algorithm only need 625 times of finite element simulation, while the traditional finite element optimization method requires 3652,813 times to achieve the same accuracy. In contrast, the proposed method reduces the number of finite element simulations and accelerates the machine optimization speed. (3) The improved algorithm optimizes the mathematical model of the machine by phases and removes deformed solutions in the later phase of optimization. The machine structure can balance output performance, which is suitable for the multi-objective optimization of the machine.
Keywords:Stator slotted permanent magnet, hybrid excitation, slot area, multi-objective optimization, layered and phase
中图分类号:TM352
DOI: 10.19595/j.cnki.1000-6753.tces.231796
国家自然科学基金(52377111)、上海市青年科技启明星计划(21QC1400200)和上海市自然科学基金(21ZR1425400)资助 项目。
收稿日期 2023-10-30
改稿日期 2023-12-28
赵 耀 男,1986年生,博士,副教授,硕士生导师,研究方向为电机设计与控制。
E-mail: zhaoyao@shiep.edu.cn
李东东 男,1976年生,博士,教授,博士生导师,研究方向为电力系统建模分析与运行控制和风力发电系统。
E-mail: shiepldd@163.com(通信作者)
(编辑 崔文静)