表1 电机结构参数
Tab.1 Motor structure parameters
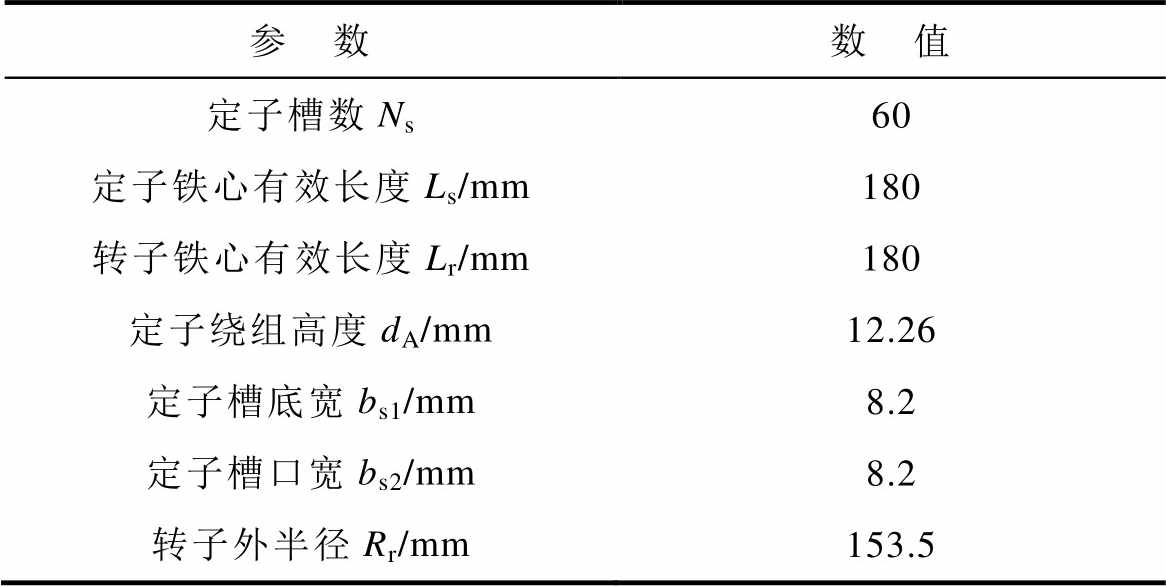
参 数数 值 定子槽数Ns60 定子铁心有效长度Ls/mm180 转子铁心有效长度Lr/mm180 定子绕组高度dA/mm12.26 定子槽底宽bs1/mm8.2 定子槽口宽bs2/mm8.2 转子外半径Rr/mm153.5
摘要 在变频电机驱动系统中，变频器输出的高频共模电压会在电机内部感应出轴电压和轴电流，继而引发轴承电腐蚀，危害系统运行的安全性和可靠性。建立精确的轴电流高频模型对于预测轴承电腐蚀风险、制定维护计划和设计抑制方案具有重要意义。该文对现有的轴电流高频模型的误差来源和范围进行了分析，指出了现有方法在阻抗特性中频部分与实测曲线存在不匹配的问题。为了克服这一缺陷，提出了一种改进的轴电流高频模型，以及相应的参数提取方法。该方法考虑了电机在不同频率下的谐振机理和等效电路，利用特征频率点阻抗值求解参数，以确保模型充分还原各频段的阻抗特性。针对一台190 kW异步电机，分别采用改进模型和现有模型进行对比。结果表明，改进模型更接近电机实际端口阻抗特性，验证了所提方法的准确性。
关键词：交流电机 轴电流 高频模型 阻抗特性
脉冲宽度调制（Pulse Width Modulation, PWM）变频器被广泛应用于电机驱动系统中，其输出端固有的高频共模电压，在电机内部杂散电容的耦合下，于轴承内、外圈之间感应出轴电压。当轴电压超出润滑脂膜电气强度时，会以火花放电的形式产生短时放电电流，即轴电流[1]。轴承作为电机运行的关键部件，电腐蚀问题会直接影响电机驱动系统的安全运行[2-3]。建立轴电流高频模型可以对轴电流进行精确仿真和预测。在实际应用中，有助于识别轴电流的关键参数和影响因素[4-5]，评估潜在的电腐蚀风险，进而制定预测性维护计划。此外，在精确模型的基础上可以对比不同抑制措施的效果，指导轴电流抑制方案的设计[6-7]。总体而言，精确建模对于提高电机驱动系统的可靠性，降低维护成本具有重要意义。
不同类型的轴电流，其建模和分析方法也不相同。目前，部分学者针对磁路不对称引起的低频轴电流进行了分析[8-9]，但是更多研究集中于变频器共模电压引起的高频轴电流[10]。Chen Shaotang等[11-12]将电机定子绕组与机壳、定子绕组与转轴、转轴与机壳间的电气联系等效为三个电容元件，认为这些电容元件为共模电流提供通路，提出了轴电流集中参数模型。文献[13-15]利用解析法和有限元法计算了电机内部杂散电容参数，并使用LCR表提取电机端口电容，验证模型的准确性。然而，集中参数模型在宽频范围的适用性存在一定的局限，特别是对于大容量电机，内部电气耦合关系复杂，需要建立轴电流高频模型表征其频域阻抗特性。文献[16]以大功率永磁同步电机为研究对象，利用向量拟合法对实测端口阻抗的网络函数进行数据拟合，根据网络函数与电路元件的对应关系建立高频阻抗模型，使其在100 kHz以上的高频段具有较高的精度。文 献[17]对一台三级式电机进行建模，将阻抗模型视为一个多端口的“黑匣子”，利用二端口理论中的Z参数求解等效模型，模拟电机测试端口的实际情况。上述方法为了使模型与实际端口阻抗测试结果相匹配，需要设计高阶传递函数进行拟合，阶次越高，模型精度越高。但是随着迭代次数增多，计算难度也随之增加。此外，由于模型缺乏实际物理意义，无法有效指导抑制方案的设计。
由于具有参数提取简便、模型精度高、物理含义清晰等优点，根据电机实测阻抗曲线建立轴电流高频模型的方法引起了广泛关注。针对异步电机的分析主要包括三种模型：①集中参数模型[11]，由电机的电阻、电感与内部多导体间寄生电容的集中元件组成，具有电路拓扑简单、物理意义明确等优点。但是集中参数模型在高频段存在阻抗特性曲线与实际测量结果不匹配的问题[18]。例如，集中参数模型的共模阻抗特性曲线仅有一个串联谐振点，而实际电机的共模阻抗在整个频率区间内会出现两次甚至多次串联谐振。②O. Magdun等将绕组与机壳、绕组与转子间寄生电容分为高频和低频支路，模拟了共模端口阻抗特性的两次串联谐振，但是模型在谐振点处的精确度不佳[19]。赵秦聪等在上述模型基础上，增加了匝间电容和电阻支路，提高了模型在中高频段的准确性[20]。③考虑高频下定子绕组的分布参数效应，王禹等提出一种分布参数的轴电流模型，将电机绕组沿轴向长度等分为两段，考虑了两段绕组与机壳、绕组与转子间的杂散参数[21]。但是，由于在参数提取过程中，对于首末端杂散电容的简化等效处理，使得电机在中频段阻抗特性与实测结果存在较大误差。
综上所述，现有的交流电机轴电流高频模型分别在不同的频段范围内存在一定的误差。针对这一问题，本文首先对三种基于阻抗测试的轴电流建模方法的误差来源和范围进行了分析；其次在分布参数模型的基础上进行改进，提出了一种具有更高精度的高频轴电流模型；然后分析了电机在不同频率下的谐振机理和等效电路，利用特征频率点处的阻抗值求解参数，以确保模型充分还原各频段的阻抗特性；最后针对一台190 kW异步电机，采用现有模型、改进模型与实测结果进行对比，分析不同模型的误差，验证改进模型的精确性。
目前，国内外学者多利用电机端口阻抗测试曲线计算模型参数，建立比较准确的轴电流高频模型。为了求解模型参数以及后续模型验证，首先要进行静止状态下的电机端口阻抗测试。
本文的测试样机为一台190 kW异步电机，为了使转子与机壳电气绝缘，使用表面喷涂Al2O3陶瓷的绝缘轴承。电机结构参数见表1。阻抗测试设备为WK6500B型阻抗分析仪，在100 Hz～10 MHz频率范围内测量电机定子绕组、转子、机壳以及差模端口的阻抗特性曲线。试验测量设备如图1所示。电机端口阻抗测试接线原理如图2所示。
表1 电机结构参数
Tab.1 Motor structure parameters
参 数数 值 定子槽数Ns60 定子铁心有效长度Ls/mm180 转子铁心有效长度Lr/mm180 定子绕组高度dA/mm12.26 定子槽底宽bs1/mm8.2 定子槽口宽bs2/mm8.2 转子外半径Rr/mm153.5
图1 电机阻抗测试
Fig.1 Port impedance measurement of motor
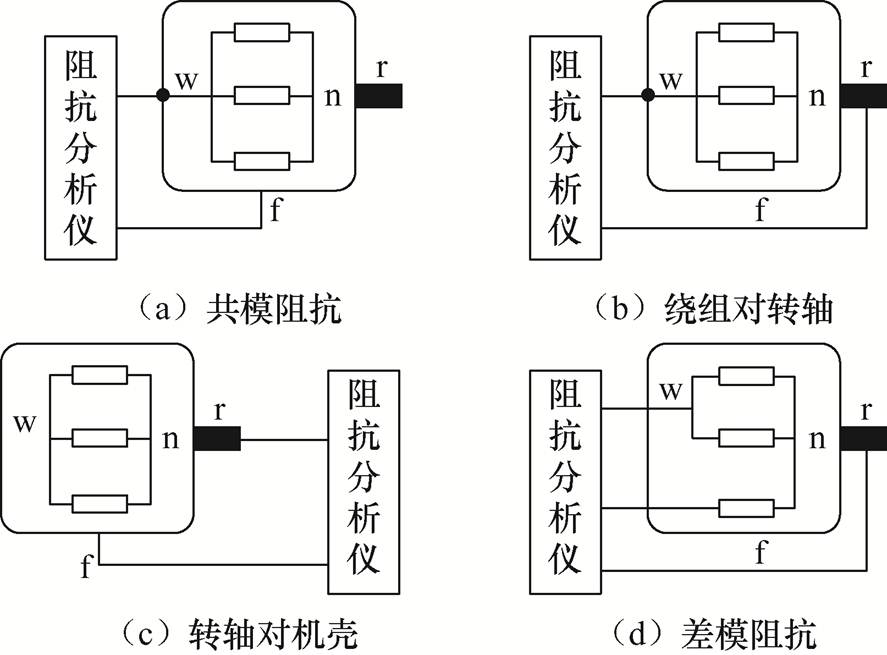
图2 电机端口阻抗测试原理
Fig.2 Principle of motor port impedance measurement
图2中，w为三相定子绕组短接点，r为转轴测试点，f为电机机壳测试点，n为三相定子绕组中性点。将定子绕组短接点w与机壳f作为测试点，可以得到定子绕组-机壳端口的阻抗特性曲线，如图2a所示；选取w和r为测试点，可以测试定子绕组-转轴端口的阻抗特性曲线，如图2b所示；选取r和f为测试点，测试转轴-机壳端口的阻抗特性曲线，如图2c所示。差模阻抗测试是将定子绕组两相短接，然后测量短接点与第三相绕组之间的阻抗，如图2d所示。
针对集中参数模型端口阻抗特性在高频段误差较大的问题，O. Magdun从实际电机结构出发，提出了将杂散电容分别考虑高、低频的轴电流高频模 型[19]，如图3所示。
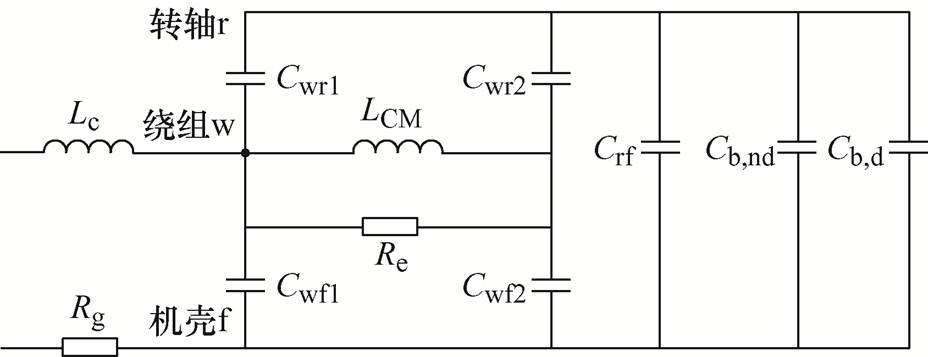
图3 高-低频支路模型
Fig.3 High-low frequency branch model
图3中，Lc为电机进线电感，Rg为接地电阻，Re为涡流电阻，LCM为共模电感，Crf为转子和机壳间电容，Cwf1和Cwf2分别为高频、低频时电机定子绕组与机壳间的杂散电容，Cwr1和Cwr2分别为高频、低频时电机定子绕组与转轴间的杂散电容，Cb,d、Cb,nd分别为驱动端与非驱动端轴承等效电容。
针对本文试验所用的190 kW异步电机，采用文献[19]的建模方法，提取模型参数。仿真共模阻抗特性与实测结果对比如图4所示。
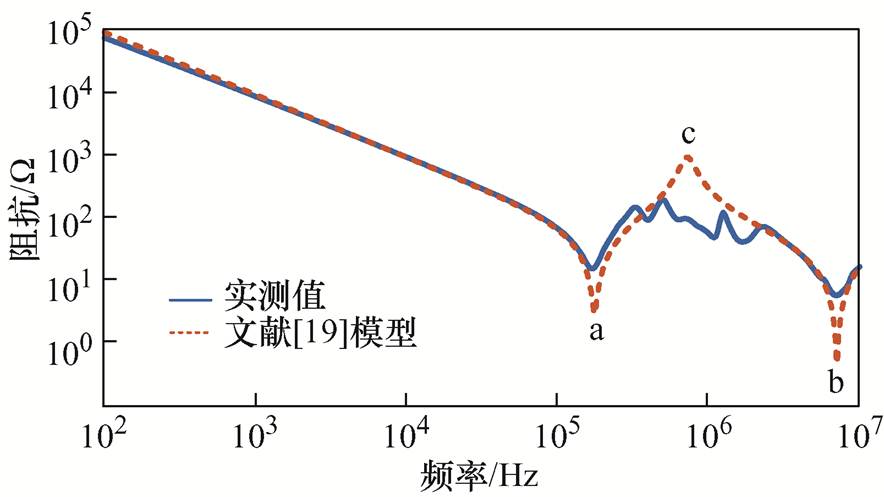
图4 共模阻抗仿真与实测对比[19]
Fig.4 Comparison between simulation and measurement of common mode impedance[19]
由图4可以看出，仿真的阻抗曲线有两个串联谐振点a、b和一个并联谐振点c，总体上阻抗特性变化趋势与实测结果一致。但是，谐振点处阻抗误差较大，两个串联谐振点阻抗小于实测值，原因是该模型中未考虑绕组-机壳支路的谐振电阻；而并联谐振点阻抗高于实测值，原因是未考虑绕组匝间电容和电阻的影响。
针对以上的不足，赵秦聪等[20]对模型进行改进，增加定子绕组匝间电容Cww和匝间电阻Rww，使并联谐振点阻抗幅值接近实测值；在定子绕组-机壳端口杂散电容支路串联高频、低频时电机定子绕组与机壳间的谐振电阻Rwf1和Rwf2，提高低频、高频串联谐振时的阻抗幅值，如图5所示。图5中，Ciso,d、Ciso,nd分别为驱动端与非驱动端绝缘涂层电容。
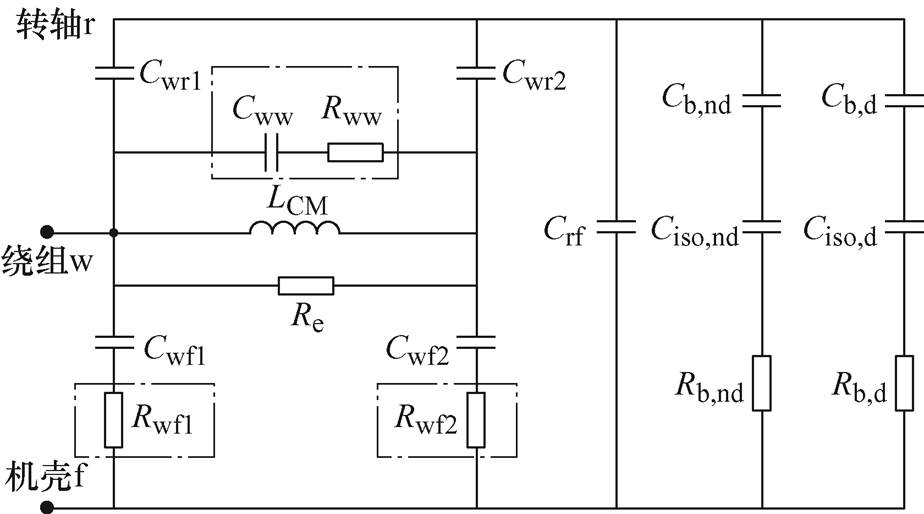
图5 改进的高-低频支路模型
Fig.5 Improved high-low frequency branch model
按照文献[20]中的模型进行共模阻抗仿真验证，与实测曲线对比，如图6所示。
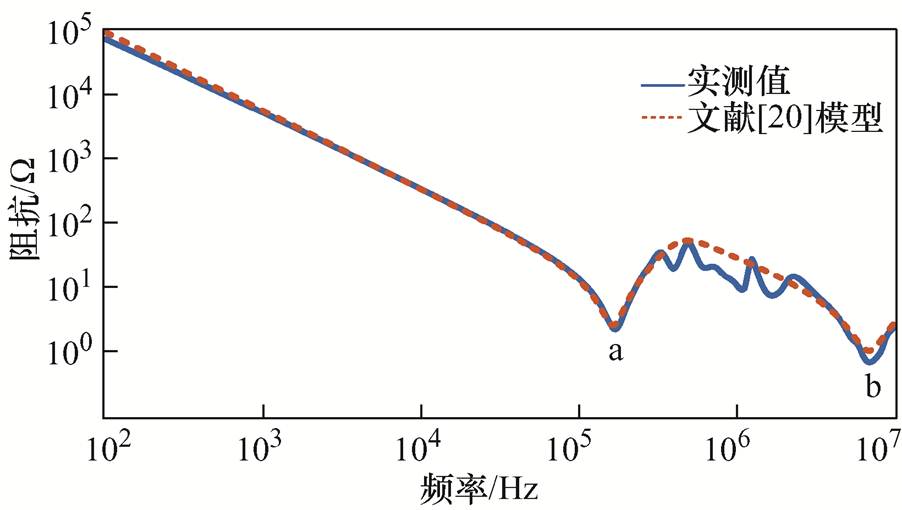
图6 共模阻抗仿真与实测对比[20]
Fig.6 Comparison between simulation and measurement of common mode impedance[20]
由图6可看出，文献[20]中的模型改进了高-低频模型中串联谐振点和并联谐振点处阻抗值偏离过大的问题，提升了精度。但是实测曲线在两个串联谐振点a、b之间中频段的谐振点较多，仿真模型完全忽略了中频段出现的谐振。
王禹等考虑定子绕组的分布参数特性，建立了分布参数的轴电流电路模型[21]，如图7所示。
图7中，Cww为绕组寄生电容，Rs为绕组电阻，Lws为绕组电感，Rc为谐振电阻。绕组沿轴向分为两段，将绕组对定子铁心电容分为Cwft、Cwfa、Cwfn三个部分，Cwft、Cwfn为绕组两端对定子的电容，Cwfa为绕组中间段的电容；同理，绕组到转子电容分为Cwrt、Cwra、Cwrn三个部分。绕组参数由定子绕组单相测试求得，杂散电容参数由端口阻抗测试求解。参数提取过程如下：
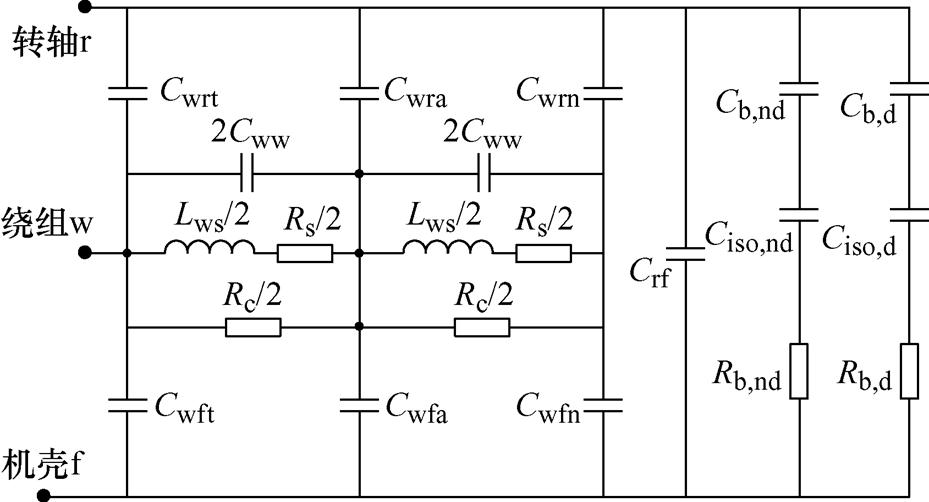
图7 分布参数模型
Fig.7 Distributed parameters model
（1）绕组参数提取。对电机进行单相绕组测试。低频段忽略电容的作用，Lws为相位最接近90°的点对应的电感。以Lws为基础，Rs由低频段任意一点求得，Cww由并联谐振求得，Rc为并联谐振时对应阻抗。
（2）杂散电容提取。以定子绕组-机壳端口为例，低频段相位最接近-90°的点对应的阻抗为总杂散电容Cwf的容抗；当超过1 MHz时认为仅Cwft作用，选择1 MHz以上相位最接近-90°的点，其对应阻抗为Cwft的容抗；令Cwrt=Cwrn，Cwf=Cwft+Cwfa+Cwfn。按照相同的方法计算全部的杂散电容参数。
采用文献[21]中的参数计算方法，190 kW电机仿真结果与实测结果对比如图8所示。
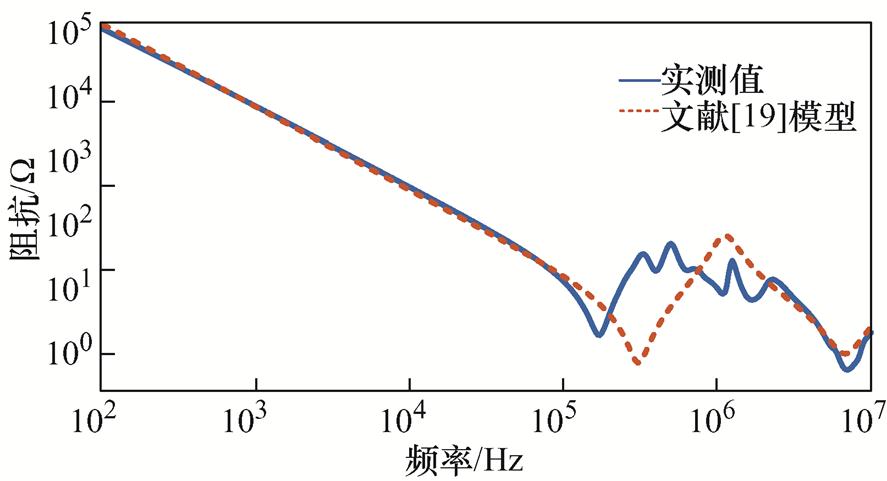
图8 共模阻抗仿真与实测对比[21]
Fig.8 Comparison between simulation and measurement of common mode impedance[21]
由图8可以看出，该模型的端口仿真曲线与实测值差距很大，主要原因如下：
（1）计算分布参数时把绕组的电感、电阻、电容平均分为两部分，导致低频串联谐振点偏移以及低频段阻抗整体小于实测值。应考虑低频、中频谐振特征，合理分配参数在两部分中所占的比例。
（2）该模型利用高频串联谐振点求出Cwft后，令Cwrt=Cwrn，而后期计算结果表明Cwrn＜Cwra，导致低频、中频段Cwrn的影响效果小，只出现2次串联谐振和1次并联谐振。如果能够根据中频和低频串联谐振点确定Cwrn和Cwra的值，会使谐振情况更接近实测值。
（3）计算该模型时忽略了谐振点电阻，导致仿真曲线与实测曲线的串联谐振点幅值差距过大。应根据实测的串联谐振的阻抗幅值，确定Cwft、Cwfa、Cwfn支路上的谐振电阻。
综上所述，文献[21]的模型具有一定的参考意义，但是将绕组简单平均分为两段，导致模型仿真结果与实测值不匹配。为了解决上述问题，本文结合文献[20-21]各自的优点，提出一种改进的轴电流高频模型，并给出相应参数计算方法，使仿真模型的端口特性在中频段更接近实测阻抗曲线。
本文提出的改进轴电流高频模型如图9所示。
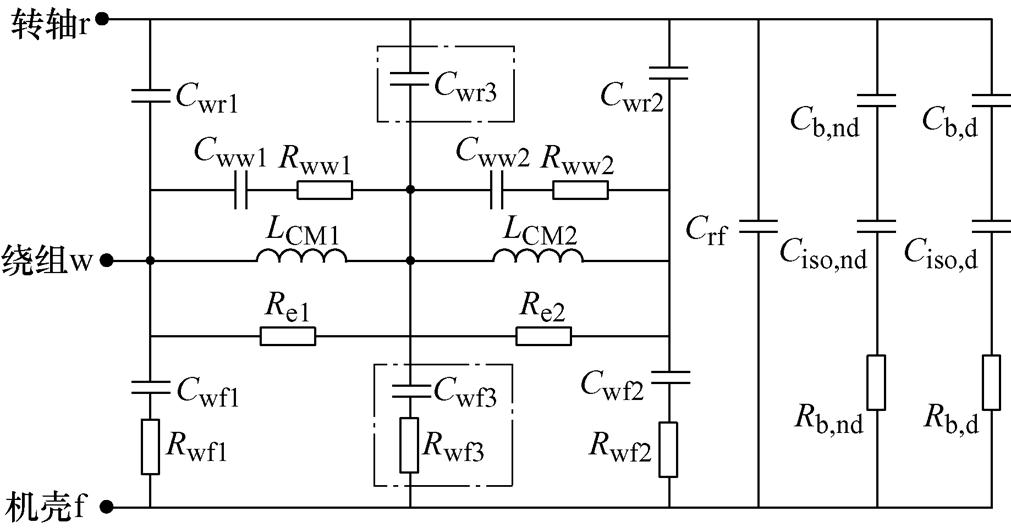
图9 改进后的轴电流高频模型
Fig.9 Improved high-frequency model of bearing currents
与高-低频支路模型相比，改进模型考虑了绕组端口的高频、中频和低频阻抗，增加了中频支路（如点画线框所示）。与分布参数模型相比，改进模型总体结构相近，但是参数含义和确定方法不同。分布参数模型把电机绕组一分为二，定子绕组与机壳间电容分为两个相同的端部电容Cwft、Cwfn和中间段电容Cwfa；而改进模型中绕组与机壳的三个电容分别与阻抗特性的高频、中频和低频时的阻抗值相关，需要利用谐振原理和端口拓扑结构求得轴电流高频模型的电路参数。此外，改进模型中还增加了高、中、低频谐振点电阻Rwf1、Rwf2、Rwf3，以更好地匹配阻抗谐振点的阻抗。改进模型中的涡流电阻Re1、Re2，共模电感LCM1、LCM2，绕组寄生电容Cww1、Cww2也不是简单的平均分配，需要根据阻抗测试中谐振点频率和阻抗关系来确定。
以190 kW异步电机为例，说明利用改进模型的参数提取方法。
3.2.1 差模端口
差模阻抗测试结果如图10所示。利用差模阻抗曲线，可以提取总的涡流电阻Re。
由于共模电感和绕组匝间寄生电容并联谐振，差模阻抗曲线中出现一个并联谐振点。谐振点处，差模阻抗有最大值，等效电路如图11所示。
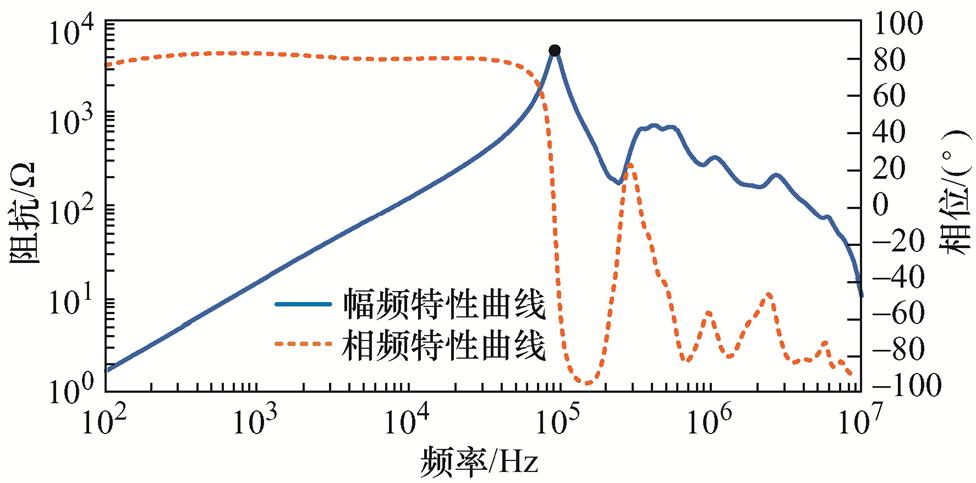
图10 差模阻抗曲线
Fig.10 Differential-mode impedance curve
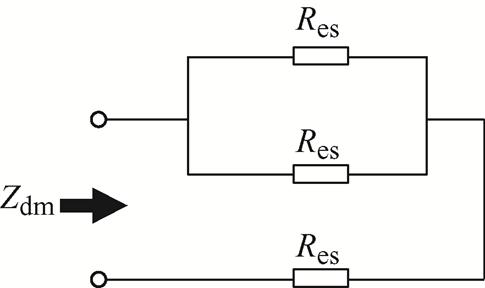
图11 差模端口谐振等效电路
Fig.11 Differential mode port resonant equivalent circuit
图11中，Res为单相涡流电阻，Zdm为差模阻抗在谐振点处的阻抗值。根据等效电路可得
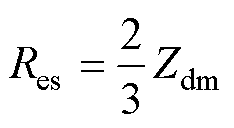（1）
总涡流电阻Re视为三个单相涡流电阻的并联。即Re=1/3Res。差模测试得到并联谐振点的阻抗Zdm=4 698 W，将其代入式（1）可得涡流电阻Re= 1 044 W。总涡流电阻Re是图9中两段涡流电阻Re1和Re2的和。
3.2.2 定子绕组-机壳端口
定子绕组-机壳端口的阻抗幅频特性与相频特性如图12所示。
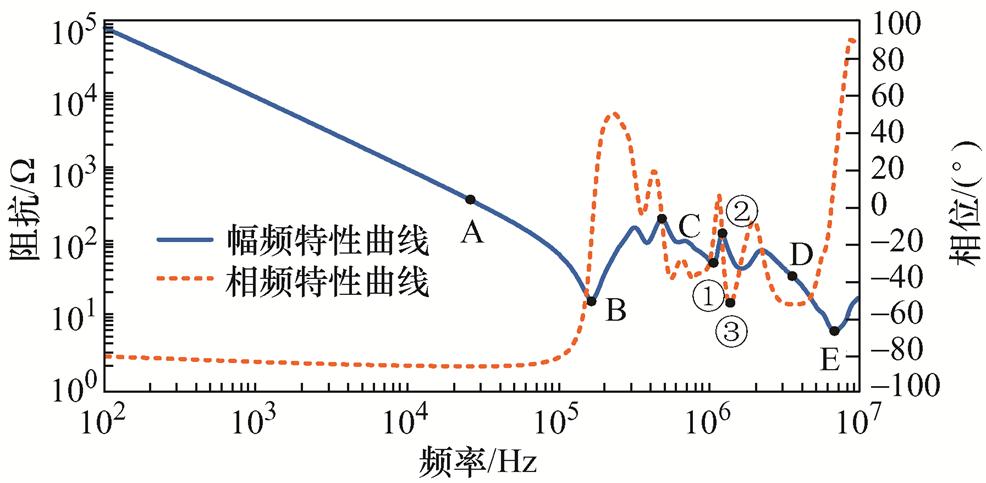
图12 定子绕组-机壳端口阻抗特性曲线
Fig.12 Impedance characteristic curves of stator winding to frame port
在图12标记了8个特征点，B、E分别为低频段和高频段串联谐振点，C为低频并联谐振点，A、D分别为低频段与高频段相位接近-90°的点，此外，①点为中频串联谐振点，②点为中频并联谐振点，③点为中频段相位最接近-90°的点。上述标记点的频率、阻抗和相位，见表2。
表2 定子绕组-机壳端口阻抗特征点信息
Tab.2 Impedance characteristic points of stator windings and frame port
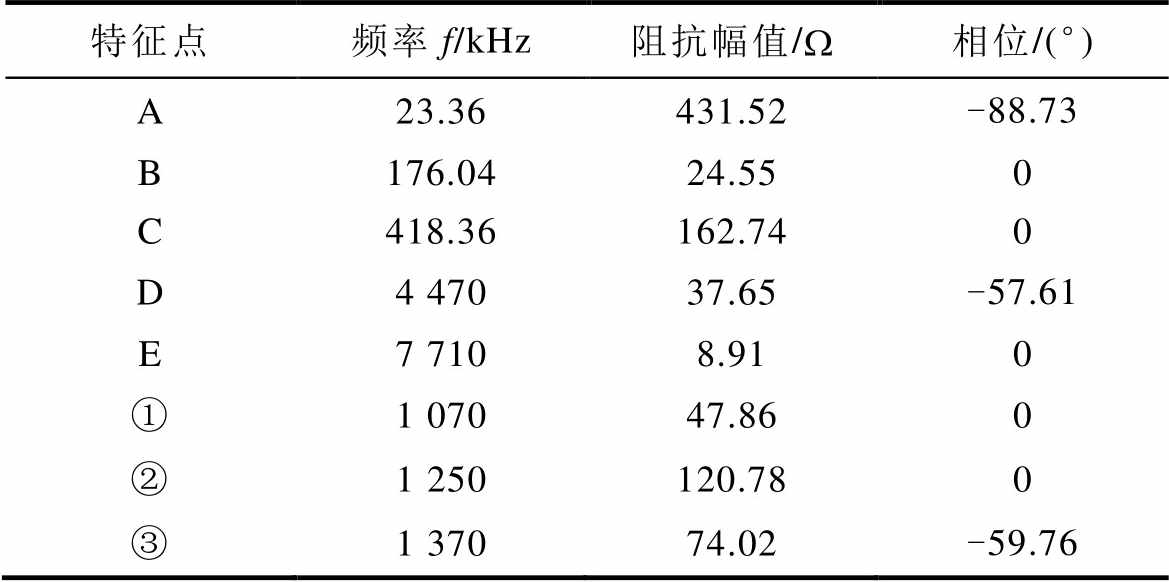
特征点频率f/kHz阻抗幅值/W相位/(°) A23.36431.52-88.73 B176.0424.550 C418.36162.740 D4 47037.65-57.61 E7 7108.910 ①1 07047.860 ②1 250120.780 ③1 37074.02-59.76
（1）A点为低频段相位最接近-90°的点，此时端口阻抗接近纯容性，可以根据A点确定定子绕组到机壳的低频等效电容Cwf_low为
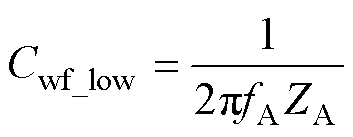（2）
将表2中特征点A的频率fA和阻抗值ZA代入式（2），可得到低频下绕组与机壳间寄生电容Cwf_low=15.79 nF。
（2）B点为低频段串联谐振点，总共模电感LCM与低频电容Cwf_low在该点发生串联谐振，即
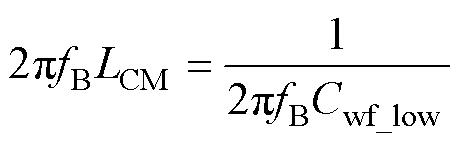（3）
将表2中特征点B的频率fB和阻抗值ZB代入式（3），可得共模电感LCM=51.75 mH。
（3）C点为阻抗极大值点，该点发生并联谐振，此时的总感抗和容抗相抵消，C点端口阻抗的极小值为总谐振电阻Rww，即ZC=Rww。并联电容应为总匝间电容Cww，与感抗ZCM=1/LCM相抵消，即
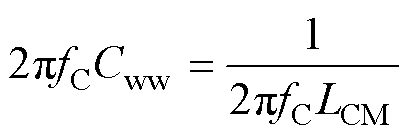（4）
根据表2中C点频率fC和LCM代入式（4），可得到Cww=2.79 nF，而Rww=ZC=162.74 W。
（4）D点为高频段阻抗相位接近-90°的点，与E点配合求解高频电容。E点为高频串联谐振点，在频率fE下，绕组与机壳间电容的高频分量Cwf_high与外部引线电感LE发生谐振。由D、E两点可得
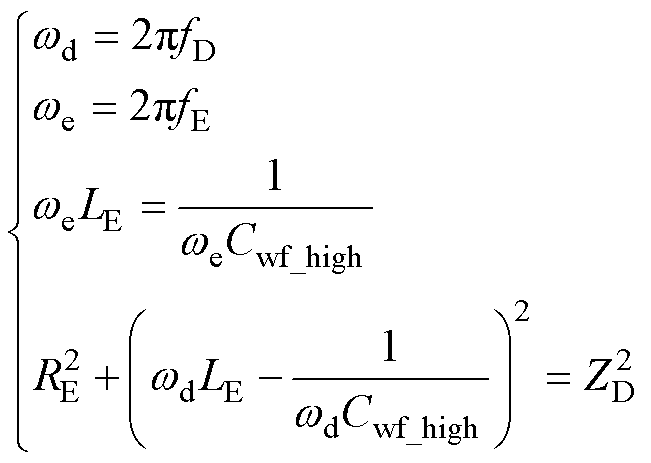（5）
式中，fD、ZD对应D点的频率和阻抗；fE、ZE对应E点的频率和阻抗；wd、we为D、E点对应的角频率；LE为外部引线电感；RE为频率fE下共模回路的串联谐振电阻。
将表2中D、E点的数据代入式（5），求得LE= 0.66 mH，Cwf_high=1.014 nF。
（5）绕组与机壳间谐振电阻。对于改进的轴电流高频模型，低频串联谐振时，定子绕组-机壳端口的求解模型可近似表示为如图13所示。
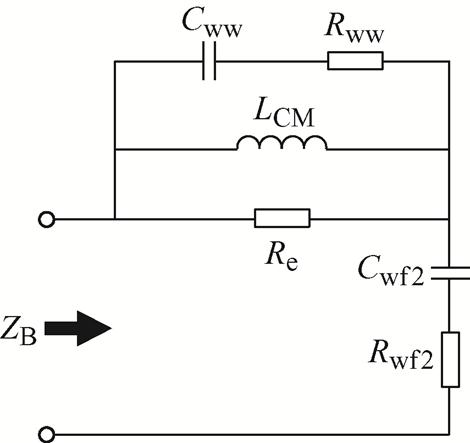
图13 定子绕组-机壳端口低频等效电路
Fig.13 Low-frequency equivalent circuit of stator winding to frame port
在B点发生串联谐振时，端口阻抗幅值为纯电阻，端口阻抗为Rwf2与并联部分等效电阻之和，即
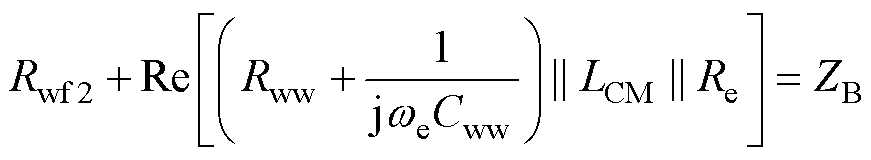（6）
根据表2得到ZB，将差模阻抗测试得到的涡流电阻Re、总谐振电阻Rww和总匝间电容Cww代入 式（6），求得高频支路电阻Rwf2=15.42 W。
在高频段，随频率增加，LCM的感抗上升可以近似为开路，可仅考虑图9中的Rwf1和Cwf1，结合表2中E点阻抗幅值和式（5）中高频谐振点D、E的求解方式，可得
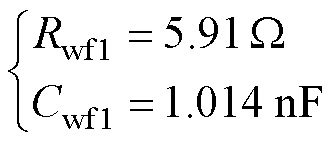（7）
（6）中频谐振计算模型如图14所示。①点为中频段串联谐振点，②点为中频段并联谐振点，③点为中频段最接近-90°的点。
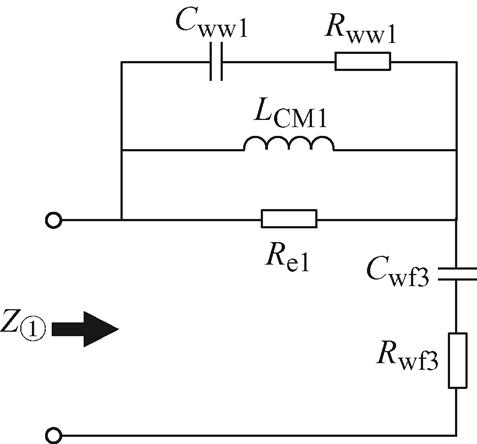
图14 定子绕组-机壳端口中频等效电路
Fig.14 Intermediate frequency equivalent circuit of stator winding to frame port
根据③点的阻抗可确定中频等效电容Cwf_mid；Cwf_mid与中频共模电感LCM1在①点对应的频率发生串联谐振；匝间电容Cww1与LCM1在②点对应的频率发生并联谐振；②点阻抗即为中频谐振电阻Rww1。上述关系如方程组式（8）所示。
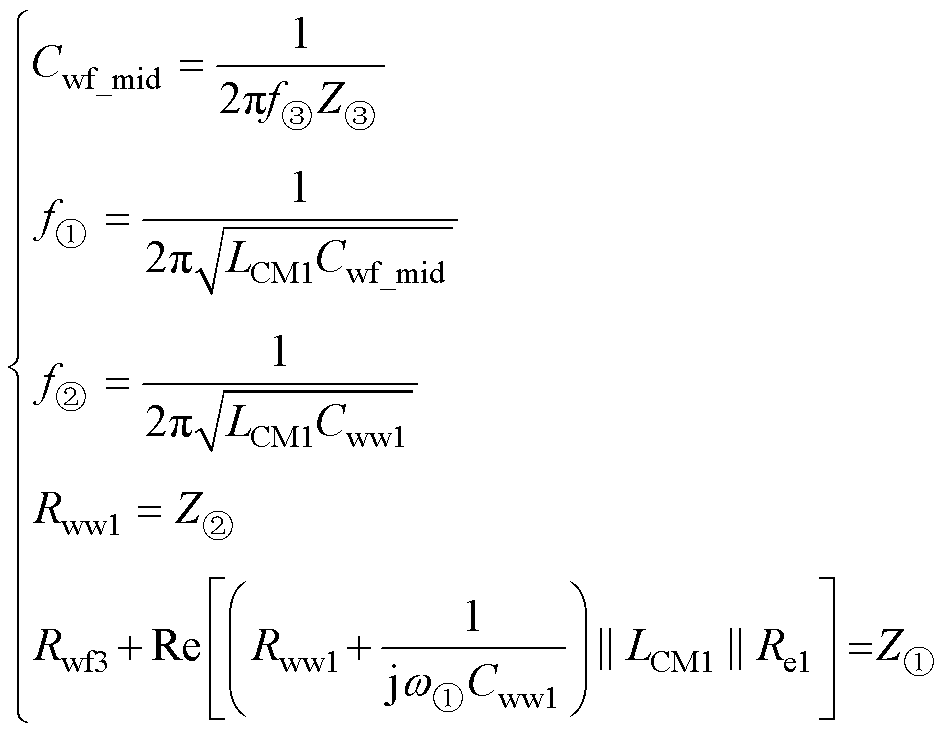（8）
式中，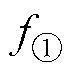
、
、
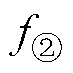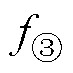分别为特征点①、②、③的频率；
、
、
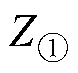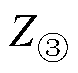为特征点①、②、③的阻抗；Cwf_mid为中频等效电容；LCM1为中频共模电感；Cww1为中频段匝间电容；Rww1为中频谐振电阻；Re1为中频段对应的涡流电阻；Rwf3为中频绕组-机壳支路的电阻。
将①、②、③点的数据代入式（8），联立求解可得LCM1=13.83 μH，Cww1=1.17 nF，Rww1=120.78 Ω，Rwf3=5.85 Ω，Cwf3 =Cwf_mid=1.57 nF。
绕组共模电感LCM、涡流电阻Re、匝间电容Cww和匝间电阻Rww与图9模型各分支的电感、电阻、电容关系为
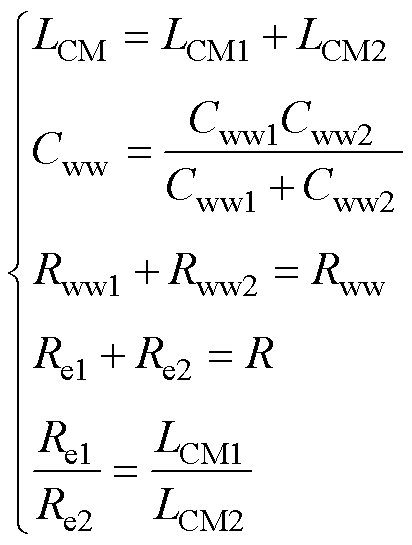（9）
联立求解，可得LCM2=36.42 mH，Cww2=1.62 nF，Rww2=68.12 W，Re1=287.6 W，Re2=756.39 W。
3.2.3 定子绕组-转轴端口
定子绕组-转轴端口阻抗测试结果如图15所示，主要用于计算绕组-转轴端口低频等效电容Cwr_low。
在图15中标记了1个特征点，F点为低频段相频特性最接近-90°的点。F点对应的频率及幅值和相位见表3。
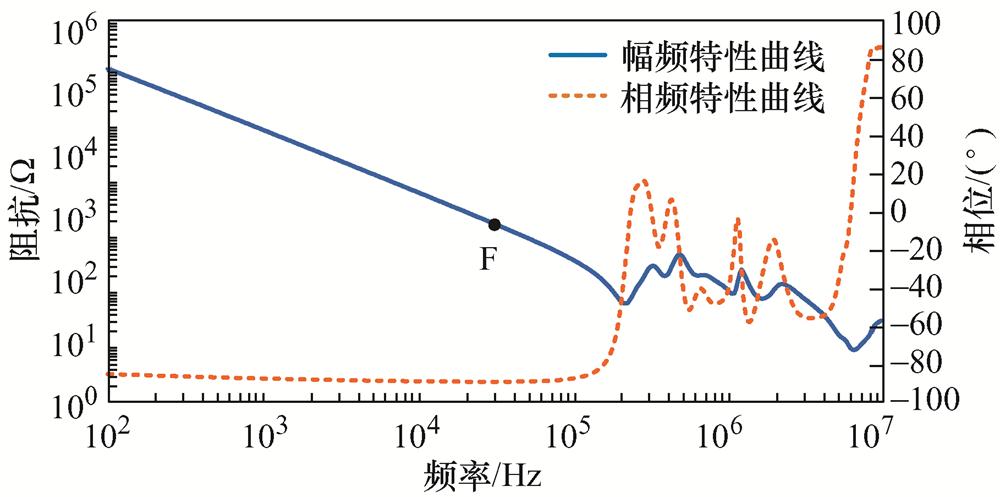
图15 定子绕组-转轴端口阻抗特性曲线
Fig.15 Impedance characteristic curves of stator winding to rotating shaft port
表3 定子绕组-转轴端口阻抗特征点信息
Tab.3 Impedance characteristic points of stator windings and rotating shaft port
特征点频率/kHz幅值/Ω相位/(°) F32.01604.2-87.5
由于F点相位接近-90°，可由该点求得低频下定子绕组-转轴端口电容Cwr_low，即
（10）
式中，fF、ZF分别为特征点F对应的频率和阻抗。
将表3中的数据代入式（10）可得，Cwr_low= 7.714 1 nF。
3.2.4 转轴-机壳端口
转轴-机壳端口的阻抗特性曲线如图16所示。
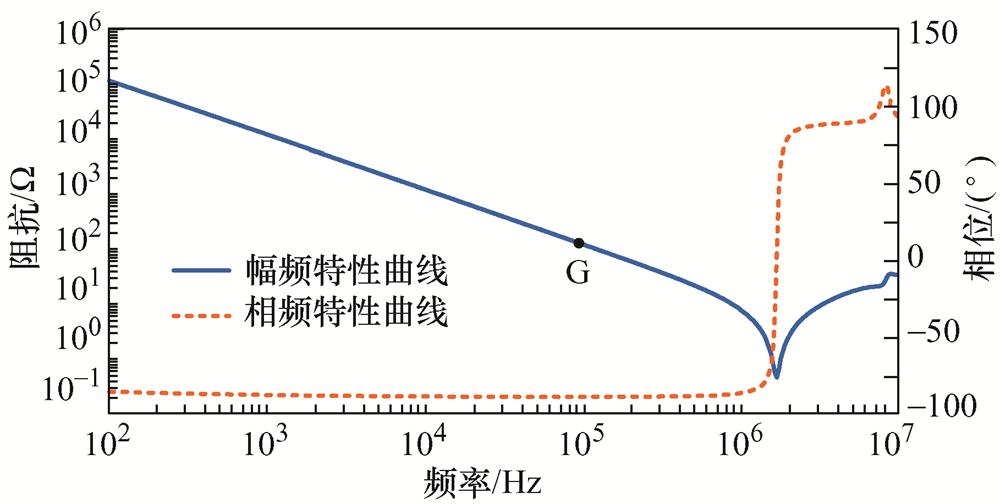
图16 转轴-机壳端口阻抗特性曲线
Fig.16 Impedance characteristic curves of the rotating shaft-frame port
在图16中标记了1个特征点，由幅频特性曲线可得，G点为低频段阻抗相位最接近-90°的点，G点频率及对应的幅值和相位见表4。
表4 转轴-机壳端口阻抗特征点信息
Tab.4 Impedance characteristic points of frame and rotating shaft port
特征点频率/kHz幅值/W相位/(°) G93.31125.7-89.4
由于G点相位接近-90°，可由该点求得低频下转轴-机壳端口电容Crf_low的容抗，即
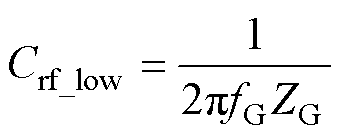（11）
式中，fG、ZG分别为特征点G对应的频率和阻抗。
将表4中的数据代入式（11）可得，Crf_low= 13.496 nF。
3.2.5 绝缘轴承参数
为了使转子与机壳之间不导通，试验电机使用了表面喷涂高绝缘性Al2O3涂层的绝缘轴承，轴承静态时的等效电气参数见表5。
表5 轴承等效电气参数
Tab.5 Equivalent electrical parameters of bearings
类型非驱动端驱动端 轴承电阻/WRb,nd=5.00Rb,d=0.76 涂层电容/nFCiso,nd=5.438Ciso,d=5.740
3.2.6 低频端口电容
经过3.2.1～3.2.5小节的计算，改进模型中仅剩Cwf2、Cwr1、Cwr2、Cwr3和Crf五个参数未知。低频段可忽略共模电感LCM的作用，端口电容与电机内部杂散电容的关系如图17所示。利用阻抗曲线中提取的低频端口电容值，可求取Cwf2、Cwr、Crf。
图17 电机端口电容与杂散电容关系
Fig.17 Relation between port capacitance and stray capacitance of motor
图17中，Cwf_low、Cwr_low、Crf_low为阻抗曲线提取的端口电容，Cwf、Cwr、Crf为低频时电机内部杂散电容。为了便于计算，将Crf与Ciso,nd和Ciso,d的并联表示为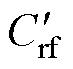
，即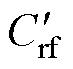=Crf+Ciso,nd+Ciso,d。根据图17，推导得出低频端口电容和电机内部杂散电容的关系，有
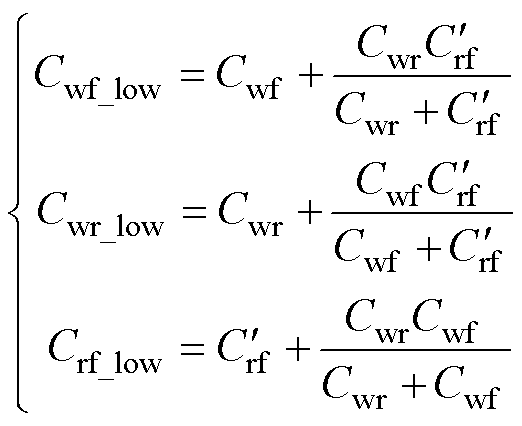（12）
代入端口电容提取结果，求解式（12），可得
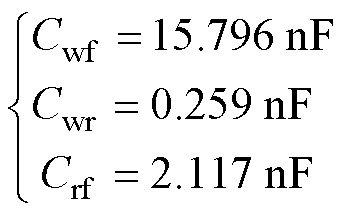（13）
低频时，共模电感的感抗小，可忽略共模电感的影响，Cwf1、Cwf2与Cwf3之和为Cwf，有
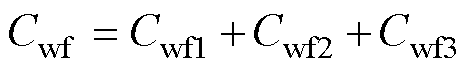（14）
由式（7）和式（8）已经得到Cwf1和Cwf3，代入式（14），可得Cwf2=13.21 nF。Cwr1、Cwr2与Cwr3之和为低频时总电容Cwr，其高-中-低频电容比例可根据Cwf1、Cwf2与Cwf3之间的比例求得，有
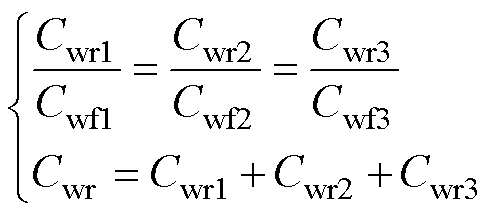（15）
由式（15）可得Cwr1=0.017 nF、Cwr2=0.22 nF、Cwr3=0.026 nF。
综上所述，得到190 kW异步电机的改进轴电流高频模型参数见表6。
表6 改进的高频模型参数
Tab.6 Model parameters of high frequency bearing currents
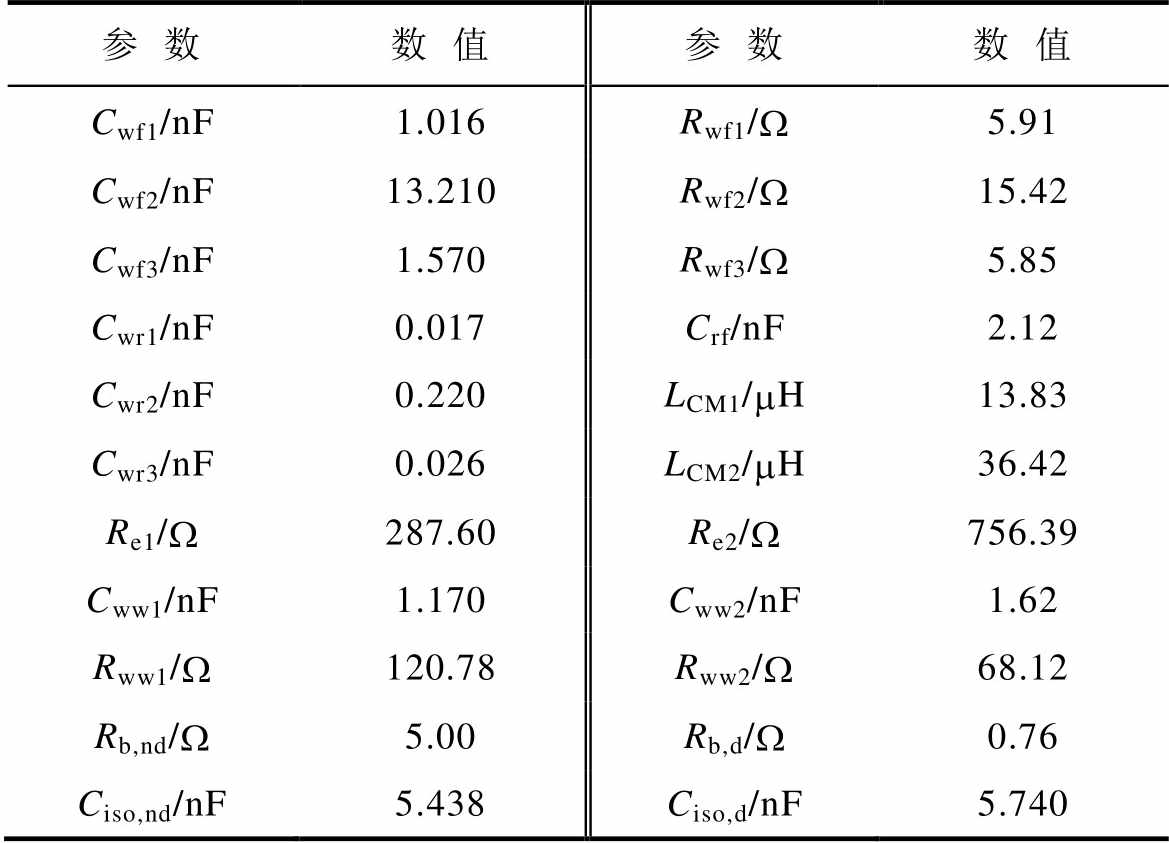
参数数值参数数值 Cwf1/nF1.016Rwf1/W5.91 Cwf2/nF13.210Rwf2/W15.42 Cwf3/nF1.570Rwf3/W5.85 Cwr1/nF0.017Crf/nF2.12 Cwr2/nF0.220LCM1/mH13.83 Cwr3/nF0.026LCM2/mH36.42 Re1/W287.60Re2/W756.39 Cww1/nF1.170Cww2/nF1.62 Rww1/W120.78Rww2/W68.12 Rb,nd/W5.00Rb,d/W0.76 Ciso,nd/nF5.438Ciso,d/nF5.740
为了验证本文建立的高频轴电流模型以及参数提取方法的准确性，在Matlab/Simulink中搭建了高频模型的等效电路仿真。在各端口分别连接阻抗测量模块，获取仿真模型端口阻抗的幅频特性和相频特性，如图18所示。
将文献[20]模型、文献[21]模型和本文所提出的改进模型的仿真结果与实测电机阻抗特性曲线进行对比。以定子绕组-机壳端口为例，如图19所示。图19a为阻抗幅频特性曲线对比，图19b为相频特性曲线对比。
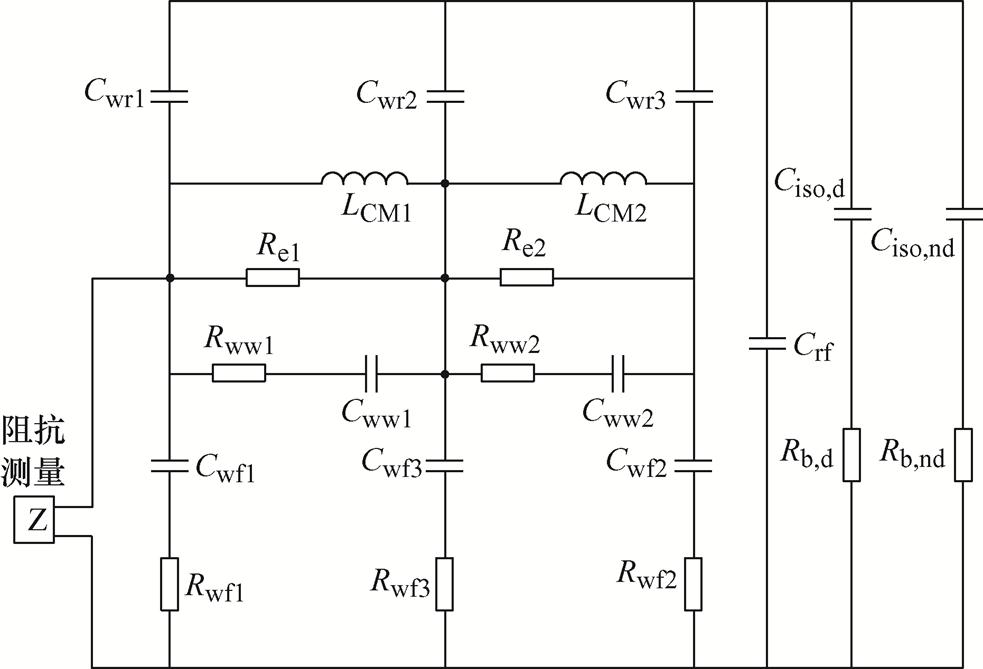
图18 高频仿真模型的等效电路
Fig.18 Equivalent circuit simulation of high frequency bearing currents model
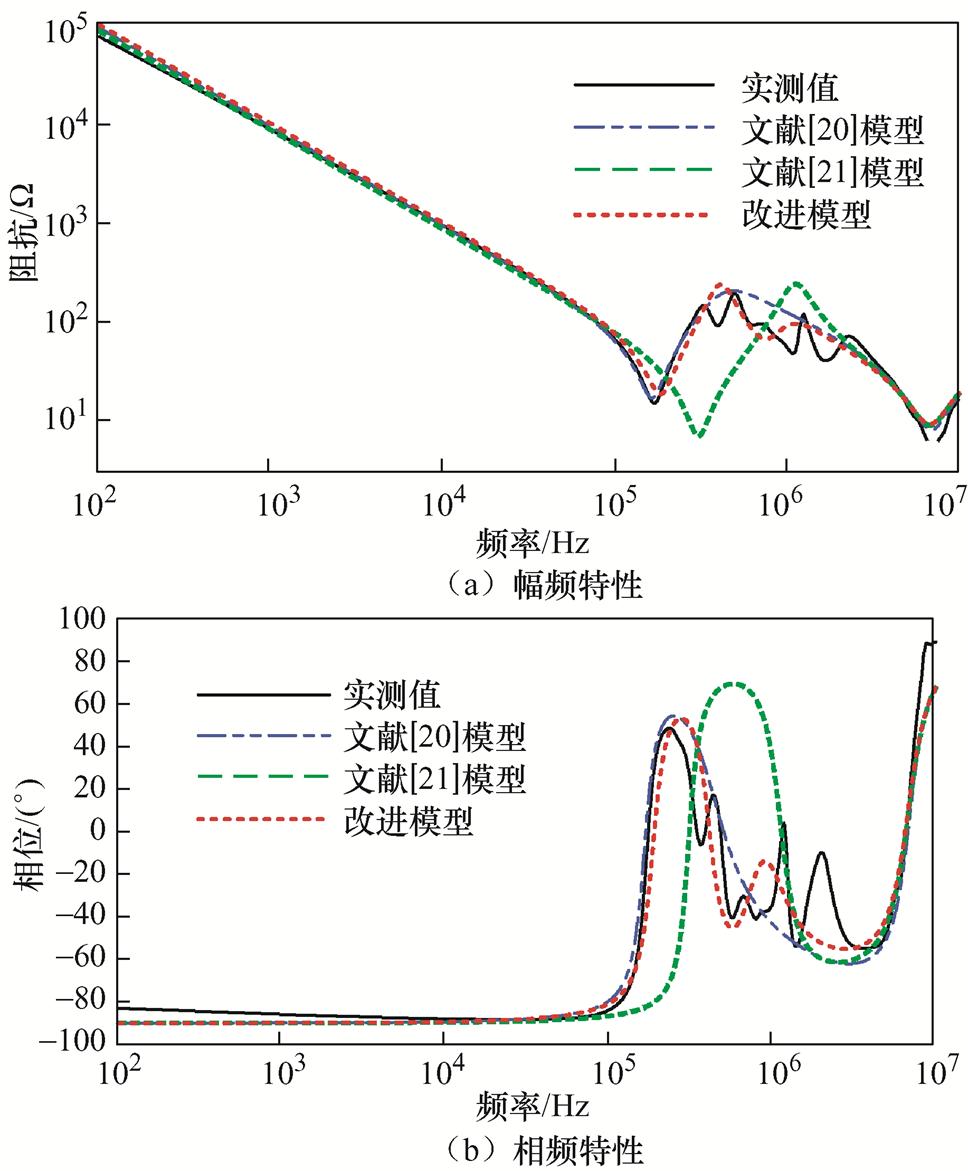
图19 定子绕组-机壳端口仿真与实测阻抗特性对比
Fig.19 Comparison of simulation and measured impedance characteristics of stator windings and the frame port
可以看出，定子绕组-机壳端口阻抗幅频特性，相较于文献[20]模型的阻抗特性曲线，改进后的模型增加了1次串联谐振和1次并联谐振，使幅频和相频特性更接近实测值。相较于文献[21]模型，本文提出的改进模型，无论是幅频特性还是相频特性，都具有更好的吻合度。
为了量化分析各种模型的精确度，本文以阻抗幅频特性曲线的仿真值与实测值在关键频率点处的方均根误差作为评价指标，定义如式（16）所示。鉴于100 kHz以下，各种模型均具有较高的精确度，选取高频段100 kHz～10 MHz范围内实测曲线的10个极值点进行计算。
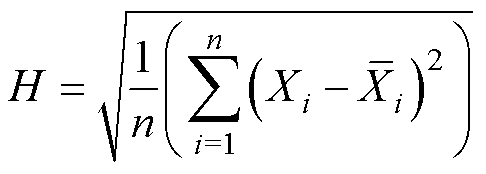（16）
式中，Xi为模型仿真的特征点阻抗值；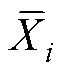
为实测的特征点阻抗值；n为特征点个数，n=10。
记录特征频率点处实测阻抗幅值、文献[20]、文献[21]模型以及改进模型仿真的端口阻抗幅值，并计算各种模型方均根误差H，见表7。
表7 特征频率点处的阻抗仿真值及实测值
Tab.7 Simulated and measured impedance amplitudes at key frequency points
频率f/kHz实测曲线阻抗/W改进模型阻抗/W文献[20]模型阻抗/W文献[21]模型阻抗/W 173.7815.1317.923.3125.53 322.11144.54125.89128.838.54 391.9190.78177.82229.0827.81 478.63186.21173.78206.7476.8 608.7895.8390.16186.2188.67 703.2795.5469.18165.96185.67 1 07047.8695.5116.9596.42 1 62041.1570.881.2851.3 2 34070.7950.1154.9566.74 6 1805.759.318.138.63 误差H—35.21 62.95 67.23
由表7可知，改进模型、文献[20]模型和文献[21]模型三种方法的方均根误差分别为35.21、62.95、67.23，本文提出的改进模型误差仅为文献[20]误差的55.9%，为文献[21]误差的52.4%。改进模型相比其他两种模型的误差更小，具有更高的准确性。
本文针对变频电机高频轴电流建模问题进行研究，分析了现有分布参数模型中频段误差较大的问题，提出了一种具有更高精度的高频轴电流模型和参数提取方法，并得出以下结论：
1）该方法利用阻抗分析仪提取电机端口阻抗的幅频和相频曲线，分别采用阻抗曲线的低频、中频和高频特征谐振点求解参数，解决了传统高频轴电流模型在中频段误差较大的问题。
2）搭建了改进电机高频轴电流模型的仿真电路，对比了改进后模型与其他模型的端口阻抗曲线，结果表明，新方法的误差远小于其他仿真模型，本文模型具有更高的精确性。
3）本文提出的电机高频轴电流精确建模方法可以推广应用于其他类型电机的高频轴电流问题的分析中。在提高设备可靠性、降低维护成本以及预防电腐蚀方面有一定的工程价值。
参考文献
[1] 白保东, 刘威峰, 王禹, 等. PWM驱动感应电机轴电压轴承电流[J]. 电工技术学报, 2013, 28(增刊2): 434-440.
Bai Baodong, Liu Weifeng, Wang Yu, et al. PWM driving induction motor shaft voltage bearing current[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 434-440.
[2] Busse D, Erdman J, Kerkman R J, et al. System electrical parameters and their effects on bearing currents[J]. IEEE Transactions on Industry Applications, 1997, 33(2): 577-584.
[3] Busse D, Erdman J, Kerkman R J, et al. Bearing currents and their relationship to PWM drives[J]. IEEE Transa- ctions on Power Electronics, 1997, 12(2): 243-252.
[4] 陈立珂, 刘瑞芳, 李知浩, 等. 电缆参数对变频驱动电机轴电压和轴电流的影响[J/OL]. 电工技术学报, 1-13[2023-12-06]. DOI: 10.19595/j.cnki.1000-6753. tces.231160.
Chen Like, Liu Ruifang, Li Zhihao, et al. The influence of cable parameters on the bearing voltage and bearing current of the variable frequency drive motor[J/OL]. Transactions of China Electrotechnical Society, 1-13[2023-12-06]. DOI: 10.19595/j.cnki.1000- 6753. tces.231160.
[5] 贾磊, 刘瑞芳, 李知浩, 等. 永磁同步风力发电机高频共模电流谐波分布及幅值影响因素研究[J]. 电工技术学报, 2023, 38(增刊1): 101-113.
Jia Lei, Liu Ruifang, Li Zhihao, et al. Study on the influence factors of harmonic distribution and amplitude of common-mode current of permanent magnet syn- chronous wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 101-113.
[6] 李知浩, 刘瑞芳, 张亮亮, 等. 绝缘轴承对变频电机高频轴电流的抑制机理与效果[J]. 电工技术学报, 2024, 39(4): 1046-1058.
Li Zhihao, Liu Ruifang, Zhang Liangliang, et al. The suppression mechanism and effects of insulated bearings on high frequency bearing current[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1046-1058.
[7] 孙全增, 张志锋. 双三相永磁同步电机低共模电压模型预测电流控制[J]. 电工技术学报, 2023, 38(14): 3708-3722.
Sun Quanzeng, Zhang Zhifeng. Low common-mode voltage model predictive current control for dual three-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3708-3722.
[8] 赵方伟, 王秀和, 赵文良, 等. 内置式永磁同步电机动态偏心故障下的轴电压解析分析和削弱[J]. 电工技术学报, 2022, 37(4): 837-848.
Zhao Fangwei, Wang Xiuhe, Zhao Wenliang, et al. Analysis and reduction of shaft voltage in interior permanent magnet synchronous motors under dynamic eccentricity fault[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 837-848.
[9] 李剑立, 武玉才, 卢伟甫. 水轮发电机机电故障的轴电压特征分析及诊断[J]. 电机与控制学报, 2023, 27(9): 10-18.
Li Jianli, Wu Yucai, Lu Weifu. Shaft voltage characteristics analysis and diagnosis of hydro- generator electromechanical faults[J]. Electric Machines and Control, 2023, 27(9): 10-18.
[10] 白保东, 王禹, 陈志雪, 等. 基于电磁屏蔽法变频电机轴承电流抑制研究[J]. 电工技术学报, 2016, 31(7): 33-39.
Bai Baodong, Wang Yu, Chen Zhixue, et al. Inhibition of bearing currents in frequency variable motor based on electromagnetic shielding[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 33-39.
[11] Chen Shaotang, Lipo T A, Fitzgerald D. Modeling of bearing currents in PWM inverter drives[C]// IEEE Industry Applications Conference, Orlando, FL, USA, 1995, 388-393.
[12] Chen Shaotang, Lipo T A, Fitzgerald D. Source of induction motor bearing currents caused by PWM inverters[J]. IEEE Transactions on Energy Conversion, 1996, 11(1): 25-32.
[13] Mohammed O A, Ganu S, Abed N, et al. High frequency PM synchronous motor model determined by FE analysis[J]. IEEE Transactions on Magnetics, 2006, 42(4): 1291-1294.
[14] 贾磊, 刘瑞芳, 王芹芹. 变频驱动感应电机轴电流问题中端部杂散电容的解析计算[J]. 电机与控制学报, 2022, 26(8): 30-39.
Jia Lei, Liu Ruifang, Wang Qinqin. Analytical calculation of stray capacitance of motor end in bearing current problem of induction motor driven by frequency convertor[J]. Electric Machines and Control, 2022, 26(8): 30-39.
[15] Maki K, Funato H, Shao Liang. Motor modeling for EMC simulation by 3-D electromagnetic field analysis[C]//2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 2009: 103-108.
[16] 汪泉弟, 张飞, 彭河蒙, 等. 基于向量拟合法的永磁同步电机EMI高频模型[J]. 电工技术学报, 2015, 30(6): 77-84.
Wang Quandi, Zhang Fei, Peng Hemeng, et al. Permanent magnet synchronous AC motor EMI model based on vector-fitting[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 77-84.
[17] 赵丹, 申科, 刘卫国, 等. 基于二端口理论的航空三级式起动/发电机宽频阻抗模型研究[J]. 中国电机工程学报, 2021, 41(22): 7841-7850.
Zhao Dan, Shen Ke, Liu Weiguo, et al. Two-port theory based wide frequency impedance modeling method for aircraft three-stage starter/generator[J]. Proceedings of the CSEE, 2021, 41(22): 7841-7850.
[18] Magdun O, Binder A. High-frequency induction machine modeling for common mode current and bearing voltage calculation[J]. IEEE Transactions on Industry Applications, 2014, 50(3): 1780-1790.
[19] Magdun O, Binder A. The high-frequency induction machine parameters and their influence on the common mode stator ground current[C]//2012 XX th International Conference on Electrical Machines, Marseille, France, 2012: 505-511.
[20] 赵秦聪, 杨二乐, 刘瑞芳, 等. 一种变频供电感应电机高频轴电流建模方法[J]. 中国电机工程学报, 2021, 41(23): 8139-8148.
Zhao Qincong, Yang Erle, Liu Ruifang, et al. Modeling of high frequency bearing currents of induction motors powered by frequency converters[J]. Proceedings of the CSEE, 2021, 41(23): 8139-8148.
[21] 王禹, 白保东, 刘威峰, 等. 分布参数共模等效电路关键参数确定及轴承电流计算[J]. 电工技术学报, 2014, 29(增刊1): 124-131.
Wang Yu, Bai Baodong, Liu Weifeng, et al. Deter- mination of key parameters in distribution parameters common mode equivalent circuit and calculation of the bearing currents[J]. Transactions of China Electro- technical Society, 2014, 29(S1): 124-131.
Abstract The regulation technology for PWM variable frequency speed significantly enhances the dynamic performance of the motor drive system. However, it also introduces adverse effects like bearing electric corrosion. The high-frequency common-mode voltage output by the frequency converter induces bearing voltage and bearing currents inside the motor, leading to bearing electric corrosion and reducing the bearings' lifespan. The high-frequency model of motor bearing current can accurately simulate and predict the bearing current. In practical applications, it helps to identify key parameters and influencing factors of the bearing current, evaluate potential bearing electric corrosion risks, develop predictive maintenance plans, and guide the design of suppression schemes.
Due to the advantages of simple calculation, high precision, and clear physical meaning, the establishing method of the high-frequency model of bearing currents based on the impedance curve has garnered wide attention. This paper analyzes the error sources and ranges of three existing high-frequency models, pointing out the poor fitting performance of existing models in the mid-frequency range. A high-frequency bearing currents model with high accuracy is proposed based on the distributed parameter model. Then, the impedance analyzer is used to test a 190 kW motor, and the port impedance characteristic curves are obtained. The resonance mechanism and equivalent circuit of the motor under low frequency, medium frequency, and high frequency are analyzed. The characteristic points at different frequencies are used to solve the parameters to consider the influence of each frequency band. Finally, multiple simulation circuits are constructed to verify the new model’s accuracy.
The root mean square error of the port impedance at the key frequency points is taken as the evaluation index. Compared with the existing methods, the new method reduces the impedance error between the stator winding and the frame by more than 50% in the frequency range 100 kHz～10 MHz, which has higher accuracy. In the wideband range of 100 Hz～10 MHz, the amplitude-frequency and phase-frequency characteristics of the improved model are in good agreement with the measured impedance curves. It is proved that this method has universal applicability in modeling the high-frequency bearing current of AC motors.
In summary, an improved high-frequency model of the distributed-parameter bearing current is presented. The model parameters are calculated according to the characteristic resonance points in each frequency band of the motor impedance characteristic curve. Thus, the problem of large frequency band error is solved, showing high accuracy in the wide frequency range 100 Hz～10 MHz. This method can be applied to analyze the high-frequency bearing current in other types of motors, providing theoretical and technical support for the bearing corrosion risk assessment and bearing current suppression design. It has practical engineering significance for improving equipment reliability, reducing maintenance costs, and preventing bearing electric corrosion.
Keywords：AC motor, bearing current, high frequency model, impedance characteristics
中图分类号：TM315
DOI: 10.19595/j.cnki.1000-6753.tces.231618
北京市自然科学基金（3222055）和2021年高功率高效电驱动总成系统开发及产业化项目（TC210H02Q）资助。
收稿日期 2023-10-06
改稿日期 2023-11-24
刘瑞芳 女，1971年生，教授，博士生导师，研究方向为电机及电力电子系统集成分析。
E-mail: rfliu@bjtu.edu.cn（通信作者）
李知浩 男，1995年生，博士研究生，研究方向为电机及电力电子系统集成分析。
E-mail: lizhihao@bjtu.edu.cn
（编辑 崔文静）