图1 磁特性测试平台
Fig.1 Platform for magnetic characterization testing
摘要 应力作用会影响磁性材料的磁性能，准确快速地模拟磁性材料在不同应力下的磁化特性对设计承受机械应力的装备铁心具有重要意义。该文研究拉应力作用下取向电工钢磁畴结构沿轧制方向的变化规律，将拉应力与畴壁平移运动之间的关系量化处理，由此采用基于畴壁平移运动的J-A模型对材料的磁化特性进行描述，通过提出适用于低磁通密度范围的新型无磁滞磁化公式替代传统J-A理论中的郎之万公式以考虑拉应力对取向电工钢磁化特性的影响；通过将磁畴简化为独立个体，将磁致伸缩效应在高磁通密度范围对取向电工钢磁化特性的影响转换为磁畴之间的摩擦作用，提出适用于高磁通密度范围的改进磁滞模型；应用BP神经网络寻找出最佳比例参数，将两种不同适用范围的磁滞模型构建为完整的磁-力耦合模型。通过对比实验结果与模型计算结果，验证了所提混合磁滞模型的准确性。
关键词：J-A模型 BP神经网络 取向电工钢 拉应力 磁畴运动
电工装备的损耗构成中最复杂的部分由磁性材料磁化过程中的磁化特性造成，而取向电工钢作为应用最广泛的电力变压器铁心材料，其磁特性的精确测量和模拟工作越来越受到重视[1]。实验证明，应力对磁性材料的磁化特性具有显著的影响，为了提高装备的工作性能，研究不同应力工况条件下的磁化特性，对电工装备的优化设计和安全运行至关重要。
考虑应力条件的磁滞模型一般分为唯象模型和物理模型，唯象模型一般精度较高，但缺乏物理意义，Preisach模型作为典型的唯象模型，可准确地描述磁性材料的磁滞特性，但分布函数辨识困难且模型比较复杂[2]。文献[3-5]根据热力学平衡原理推导出力磁耦合磁化模型，该模型并未考虑磁性材料的磁滞现象。文献[6]将基于热力学平衡原理推导的力磁耦合磁化模型与J-A（Jiles-Atherton）模型相结合以考虑磁性材料的磁滞特性，但所能模拟的应力范围较小。部分磁化模型基于磁畴总能量计算，通过寻找磁畴总能量的最小值来模拟磁化过程[7-9]。然而，该类模型的准确性在很大程度上取决于假定的磁畴结构，且该类模型需要计算各种磁畴能量，求解过程复杂。在文献[1]中，基于磁畴结构模型（Assembled Domain Structure Model, ADSM）与磁畴能量最小值的建模思想，通过添加磁弹性能来定量表征应力对磁滞特性的作用。由于其简化了磁畴结构并且未考虑磁弹性能与其他磁畴能量之间的耦合关系，使模型更适用于应力较小的情况。
目前，对于磁-力耦合的磁滞模型研究多数针对无取向电工钢材料等各向同性磁性材料，而对于各向异性极强的取向电工钢材料的相关研究较少[5-6]。这是由于各向异性材料的内部磁畴结构与磁化过程中的磁畴运动相较于各向同性材料更加复杂[10-11]，因此，考虑应力工况影响，建立一种数学表达简单且计算精度较高的磁滞模型具有重要意义。J-A模型具有一定的物理意义且具有参数简洁等优点[12]，因此，本文基于J-A模型，结合神经网络算法建立考虑拉应力作用的混合磁滞模型。
首先，利用二维宽频磁特性测量装置沿轧制方向测量取向电工钢片在不同拉应力下的磁化特性，并通过与不同应力下磁畴结构的变化趋势进行对比，建立取向电工钢在应力影响下的磁化特性和畴壁平移运动之间的联系，通过量化两者之间的关系，提出新的无磁滞磁化公式替代传统J-A理论的无磁滞磁化公式，从而提出一种适用于低磁通密度范围并可以描述拉应力影响下取向电工钢片磁化特性的磁滞模型。将磁性材料的磁致伸缩特性以摩擦作用的形式引入J-A理论中，从而提出一种适用于高磁通密度范围内可以描述取向电工钢磁化特性的模型。由于低磁通密度范围与高磁通密度范围的磁化特性分别采用了不同的模型进行描述，利用反向传播（Back Propagation, BP）神经网络对拉应力影响的取向电工钢的磁化特性进行完整描述。最后，通过模型的计算结果与实验数据的对比，验证所提混合磁滞模型的有效性与准确性。
本文采用图1a所示的二维宽频磁特性测量装置对实验样品沿轧制方向在应力工况下进行磁特性测量实验，其中采用压电纤维复合材料（Macro Fiber Composite, MFC）作为应力加载元件[13]，MFC的输出力与加在其两端的直流电压之间存在着一种明确的线性关系，本文主要研究取向电工钢片轧制方向（Rolling Direction, RD）的磁化特性，因此，将MFC的长度方向沿轧制方向粘贴到样片的上表面，进而在样品的中心区域产生均匀的局部拉应力，同时在样品表面粘贴应变片检验施加的应力大小，被测样品、压电执行器与应变片构成的应力施加-检测结构示意图如图1b所示。为了防止引入弯曲应力从而影响实验数据的准确性，设计了样品固定垫片结构。
图1 磁特性测试平台
Fig.1 Platform for magnetic characterization testing
选取测试样品为取向电工钢GT100，被测样品尺寸为50 mm×50 mm×0.1 mm，拉应力与激励磁场均与取向电工钢轧制方向平行，拉应力的施加范围为0～40 MPa，最高测量磁通密度为1.5 T。
本文采用B线圈法测量磁通密度B(t)，即
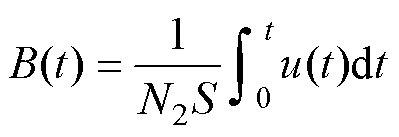（1）
式中，N2为二次绕组线圈；S为样品的截面积；u(t)为B线圈的感应电压。
本文采用隧道磁电阻（Tunnel Magneto- Resistance, TMR）传感器作为磁场强度H的测量元件，理想状态下TMR元件的磁阻R随着外部磁场强度H的变化呈线性关系，本文中所用的TMR传感器型号为TMR2602-P5，图2所示为该传感器输出电压随外加磁场强度H变化的示意曲线。图中LL、UL分别代表保持传感器线性变化的最小磁场强度与最大磁场强度。
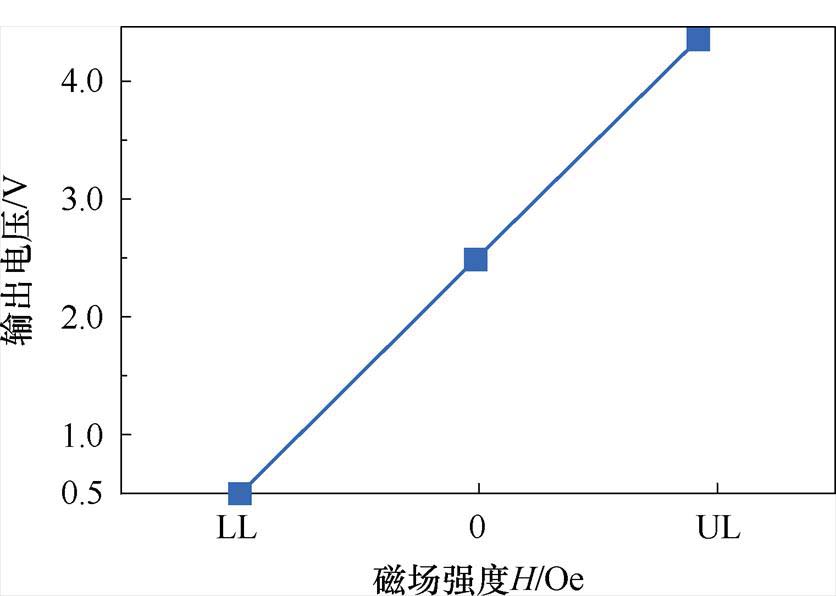
图2 TMR2602-P5输出曲线
Fig.2 TMR2602-P5 output curve
对压电执行器施加电压u从而产生均匀的应力s。样品磁滞回线的测量结果如图3所示，图中Bm为最大磁通密度。
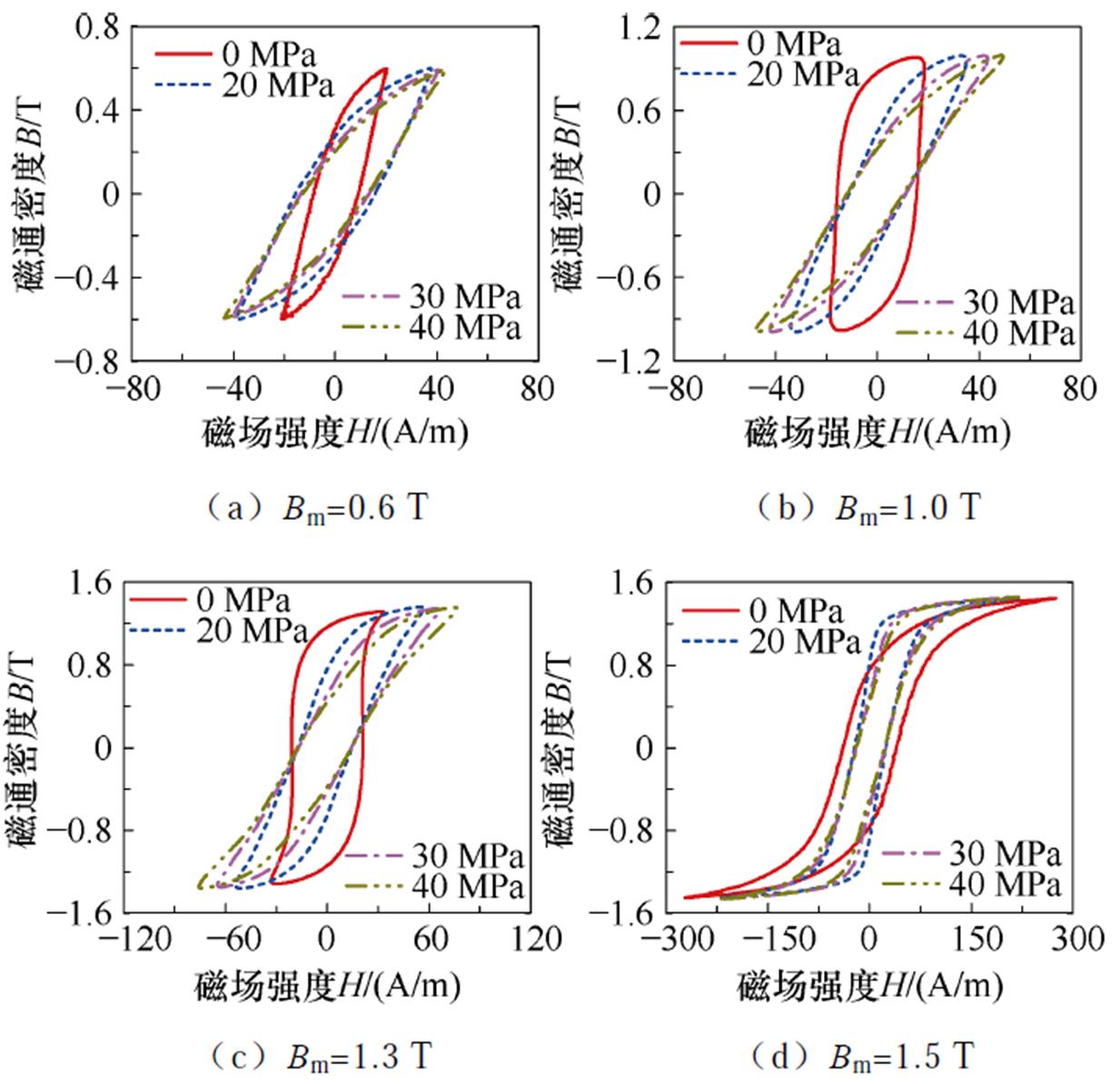
图3 不同磁通密度与不同拉应力下样品磁滞回线
Fig.3 Hysteresis loops of samples with different flux densities and different tensile stresses
根据磁畴运动方式，可以将取向电工钢的磁化进程划分为两个阶段：第一阶段是磁畴壁的平移运动；第二阶段是磁畴磁矩的旋转运动，如图4所示。
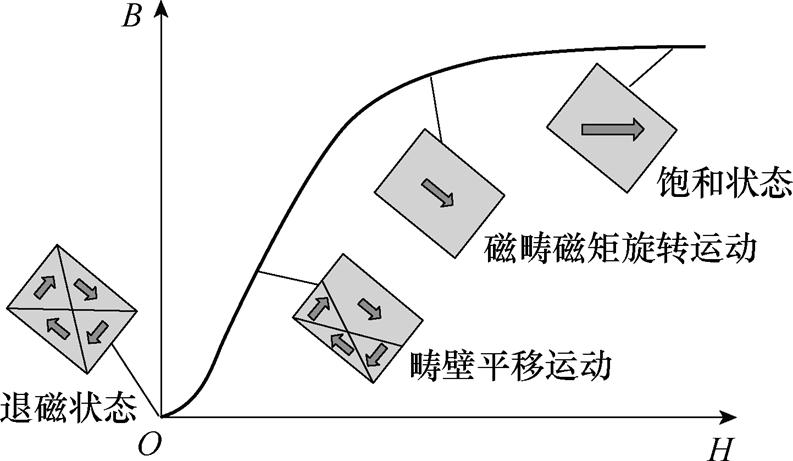
图4 磁性材料磁化过程
Fig.4 Magnetization process of magnetic materials
在磁化进程中材料的每一个磁化状态为该状态下磁畴总能量的极小值，其中磁畴能量包括静磁能、各向异性能、磁弹性能和赛曼能[14]。在赛曼能的作用下，材料内部磁畴开始运动并将状态锁定于磁畴能量总和的极小值；静磁能将整块磁性材料分成若干磁畴；各向异性能使磁畴的磁矩按照易磁化轴方向排列；根据磁弹性能式（2）可知[1, 8]，受磁弹性能的作用，材料内部磁畴的磁化方向转向应力方向，应力的作用改变了材料的初始磁畴结构。
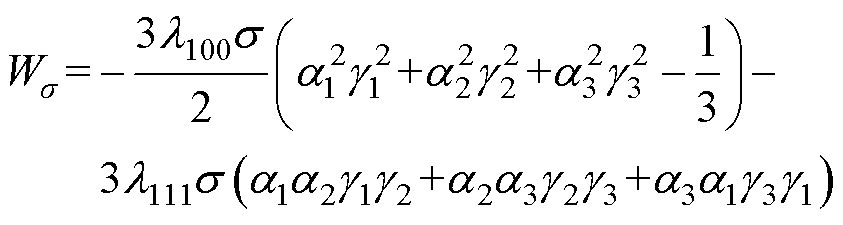（2）
式中，l100、l111分别为沿着[1 0 0]与[1 1 1]晶相方向的饱和磁滞致伸缩常数；（a1, a2, a3）为磁畴与晶粒的三个易磁化轴方向的余弦值；（g1, g2, g3）为应力与晶粒三个易磁化轴方向的余弦值。图5为材料在拉应力加载条件下磁畴结构随磁化过程的变化趋势。
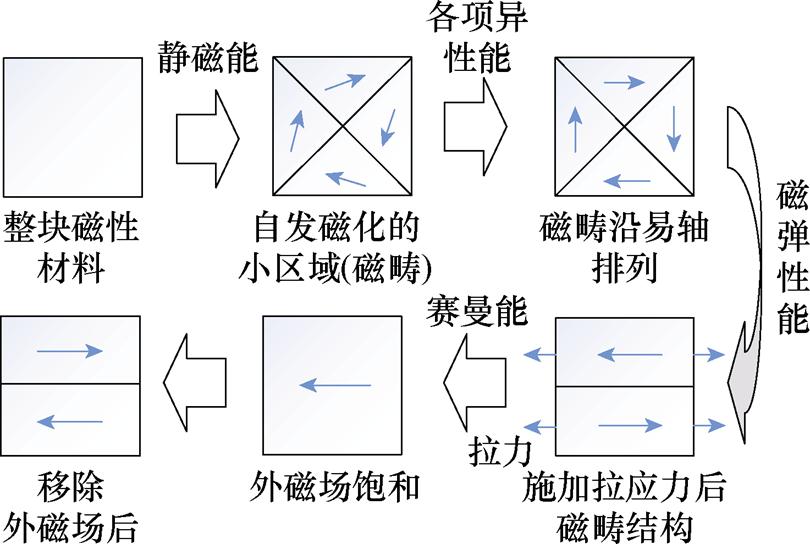
图5 磁畴的变化趋势
Fig.5 Trend of magnetic domains
磁性材料的宏观磁特性是微观特性在应用层面的表现，通过磁光成像技术应力检测系统观测取向电工钢沿RD施加拉应力后磁畴结构在磁化过程中的变化规律[15-18]。由此，本文假设在以畴壁平移运动为主导的过程中，磁性材料的磁化特性为线性变化；在以磁矩旋转运动为主导的过程中，材料的磁化特性为非线性变化，基于此建立了材料磁化特性与磁畴之间的联系。
受沿RD拉应力的影响，磁弹性能促使磁畴的磁化方向转向拉应力方向，即材料内部非RD的磁畴向RD的磁畴转变。随着拉应力的增加，材料内部磁畴结构以沿RD磁畴为主，由此表明，在材料磁化过程的前期（即低磁通密度范围）内磁畴的运动方式以RD磁畴的畴壁平移运动为主。假设材料内部缺陷为均匀分布，在外部磁场均匀增强的过程中，磁畴随磁场的变化可视为恒定，由此可将磁畴随磁场强度的变化率视为常数。此外，非RD磁畴的存在降低了磁性材料内部的退磁场能[19]，由此表明，拉应力使取向电工钢内部退磁场能增加。退磁场能的增加导致了材料激励至相同磁通密度时所需的磁场强度增大，因此，磁畴随磁场的变化率降低，宏观表现为低磁通密度范围内材料磁导率的减小，如图3所示。
图6对比了在不同磁通密度、拉应力作用下取向电工钢磁滞回线的测量值与传统J-A模型的计算值。结果表明，传统J-A模型在模拟无应力低磁通密度时偏差较大；此外，传统J-A模型也无法准确地模拟拉应力影响下取向电工钢的磁特性。传统J-A模型[20-21]为
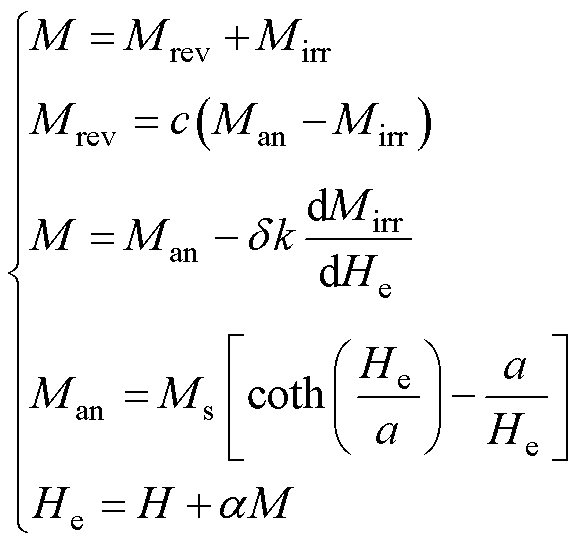（3）
式中，M为磁化强度；Mrev和Mirr分别为可逆磁化强度与不可逆磁化强度；Man和Ms分别为无磁滞磁化强度与饱和磁化强度；He为有效磁场强度；k为磁畴之间的牵制系数；d 为方向系数；c为可逆磁化系数；a 为磁畴耦合平均场系数；a为无磁滞磁化曲线的形状参数。
综上所述，对取向电工钢沿RD施加拉应力导致材料内部非RD磁畴在磁化之前转变为RD磁畴，由此认为拉应力对取向电工钢的影响主要集中于低磁通密度范围的畴壁平移运动，而对磁畴在高磁通密度范围内的磁矩旋转运动影响较小。因此，可以基于拉应力对取向电工钢磁畴结构的影响特点，提出适用于低磁通密度范围的磁-力耦合模型，而对于高磁通密度范围内磁矩旋转运动的描述则需另一种模型。本文将取向电工钢畴壁平移运动结束时的磁场强度作为低磁通密度状态与高磁通密度状态的分界点，称为分界磁场Ht。
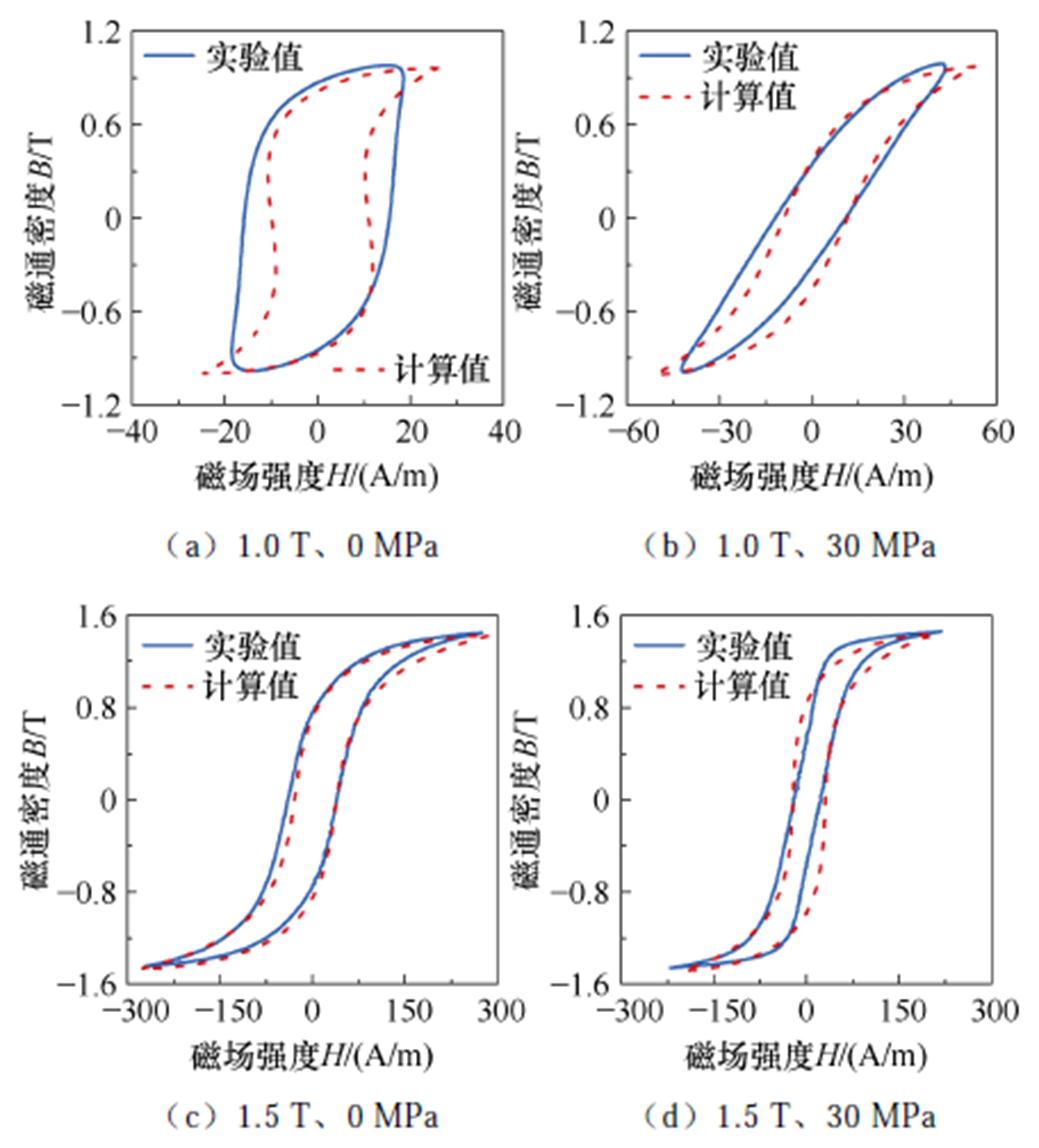
图6 传统J-A模型计算值与实验值
Fig.6 Calculated values of traditional J-A model and experimental values
式（3）中无磁滞磁化公式Man=f(H)基于朗之万经典顺磁理论建立，该理论假定顺磁性物质内部原子磁矩间没有明显的相互作用，无外施磁场激励条件下，由于热运动的作用，原子磁矩无规则混乱取向。当施加磁场激励时，原子磁矩有沿磁场方向的趋势，在磁场和热运动的共同作用下，确定稳 态[20]。然而，取向电工钢本身的磁畴结构导致其具有较强的各向异性，在拉应力影响下的磁畴结构进一步强化了其各向异性。因此，使用朗之万顺磁公式描述拉应力影响下取向电工钢的磁化特性具有理论上的局限性，需要建立能够描述取向电工钢在承受拉应力状态下的磁化过程的数学表征方法。
根据第2节，在低磁通密度范围内，受拉应力影响的取向电工钢磁畴随磁场的变化率可近似为恒定，同时退磁场能的增大导致材料的磁化难度增加。由此提出可以描述材料受拉应力影响的无磁滞磁化强度Man的数学表达式为
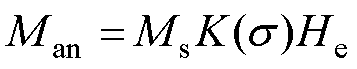（4）
式中，K(s)为关于拉应力的函数，称为磁化效率，其意义为磁滞回线线性区域内材料磁通密度随磁场的变化率，代表取向电工钢在低磁通密度范围内的磁化特性。
在低磁通密度状态下，磁畴的变化效率视为恒定，由于不同应力状态下材料内部畴壁平移运动结束时的状态一致，由此，采用1/Ht表示在拉应力改变取向电工钢内部磁畴结构的条件下，磁性材料到达磁饱和状态的效率，称为磁畴变化效率ntp，代表取向电工钢在低磁通密度范围内的磁畴特性。因此，磁畴的变化效率ntp决定了磁化效率K的大小，磁化效率K可以表示为
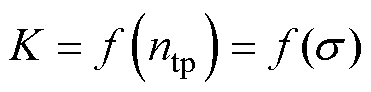（5）
本文将磁滞回线上升沿的膝点作为畴壁平移运动结束的标志，基于磁特性测试平台的测试结果，磁畴变化效率ntp与拉应力s 之间的关系如图7a所示，二者之间视为反比关系，可以表述为
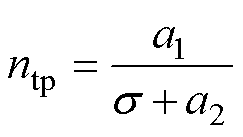（6）
式中，a1、a2为与材料相关的比例系数。
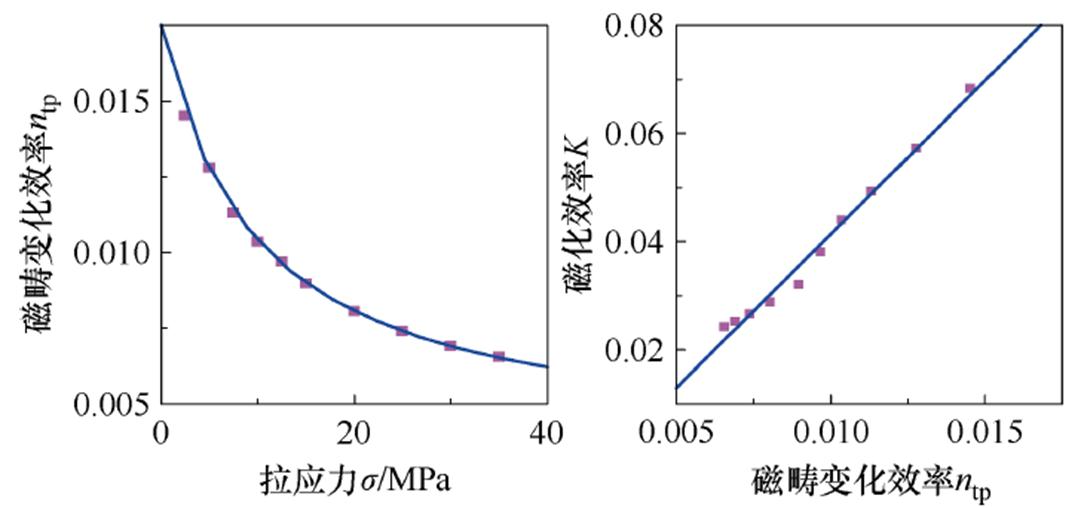
图7 磁畴变化效率ntp与拉应力s、材料磁化效率K之间的关系示意图
Fig.7 Relationship between magnetic domain change efficiency ntp and tensile stress s, material magnetization efficiency K
磁化效率K基于磁滞回线上升沿膝点位置所对应的B、H值进行计算，其值为B/H。基于磁特性测试平台的测试结果，磁化效率K与磁畴变化效率ntp的关系如图7b所示，二者之间视为正比关系，有
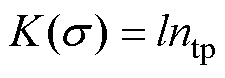（7）
式中，l为比例系数。此时式（4）可以表述为
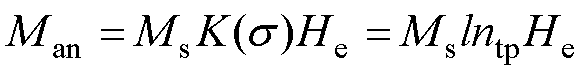（8）
在J-A理论中，磁化强度M、可逆磁化强度Mrev、不可逆磁化强度Mirr、无磁滞磁化强度Man之间的关系见式（3）中第1式和第2式，有
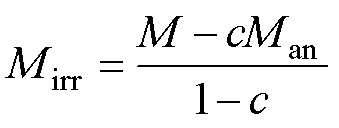（9）
将式（9）代入J-A能量平衡公式可得
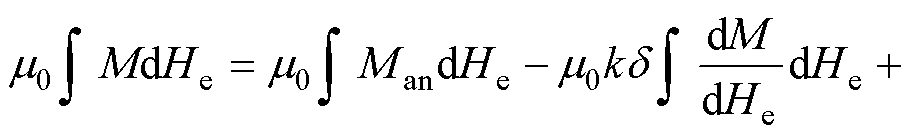
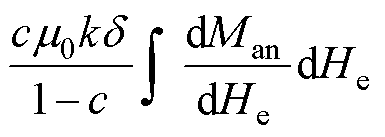（10）
式中，m0为真空磁导率。
将式（10）的等号两边同时进行微分可得
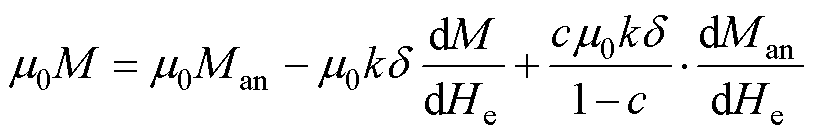（11）
若以磁通密度B为激励，为了表达出激励与磁场强度H之间的关系，将式（11）的等号两边同时乘以dHe/dB得到
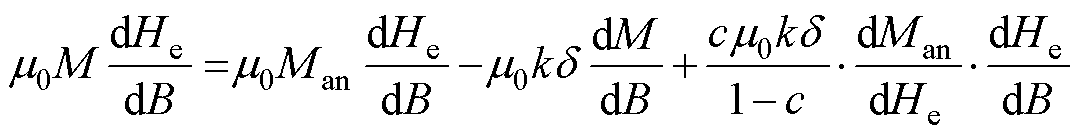（12）
由于dHe/dB为
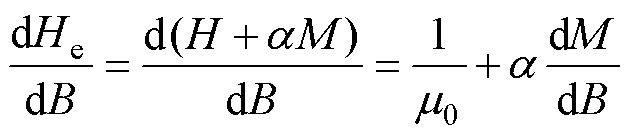（13）
将式（13）代入式（12）中，最终推导出M与B之间的微分关系，有
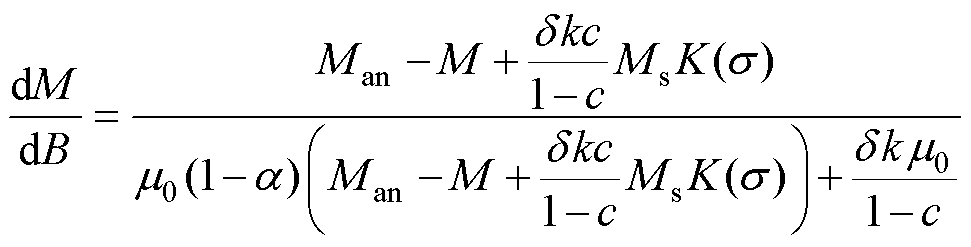（14）
上述所提模型能够模拟受拉应力影响的取向电工钢在低磁通密度范围内的畴壁平移运动。而在高磁通密度范围内需要采用另一种模型对取向电工钢内部磁畴磁矩的旋转运动进行模拟。依据第2节可知，分界磁场Ht为高、低磁通密度范围的分界点，如图8所示为分界磁场Ht与拉应力s 的关系曲线，拉应力与分界磁场可视为正比关系，通过实验数据拟合得到两者之间数学关系为
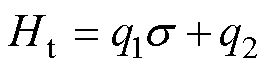（15）
式中，q1、q2为与材料相关的参数。通过式（15）可确定不同拉应力下取向电工钢的分界磁场。
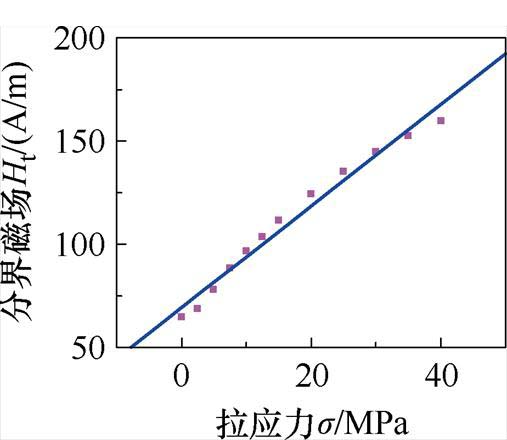
图8 分界磁场与拉应力的关系曲线
Fig.8 Relationship between dividing magnetic field and tensile stress
第2、3节表明，拉应力的作用不会对取向电工钢在高磁通密度范围内的磁化过程造成显著影响，尤其在材料的磁饱和阶段。由于拉应力向材料中输入的磁弹性能仅改变材料内部磁畴的初始结构，不能改变磁畴最终向磁化方向转变的结果。根据图6c、图6d可知，传统J-A模型模拟取向电工钢片高磁通密度范围内的磁化特性具有良好的模拟精度，由此采用传统J-A模型模拟受拉应力影响的取向电工钢片在高磁通密度范围内的磁矩旋转运动。由磁致伸缩模型中的二次畴转模型式（16）可知[22]，磁性材料的磁致伸缩与磁化强度密切相关。因此，当磁通密度较高时，取向电工钢的磁致伸缩效应会对其宏观磁化特性造成一定程度的影响，传统J-A模型未考虑该因素的影响。因此，考虑引入磁性材料的磁致伸缩效应以提高传统J-A模型在高磁通密度范围内的模拟精度。
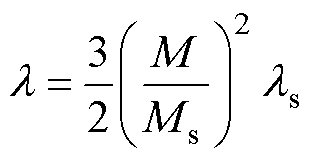（16）
式中，l 为磁致伸缩系数；ls为材料饱和磁致伸缩系数。
磁致伸缩现象的本质是由于材料中微观磁畴受外部磁场的影响而发生变化，引起材料宏观形状的改变。磁畴演变过程中其形态的变化是一个复杂的过程，本文假设每个磁畴为独立的个体，由此材料的磁致伸缩现象可以等效为单一磁畴形态变化的集合，如图9所示，磁畴之间由于各自形态的变化导致发生相对位移，造成摩擦损耗。可将磁致伸缩效应造成的影响等效为磁畴之间相互摩擦力的影响。
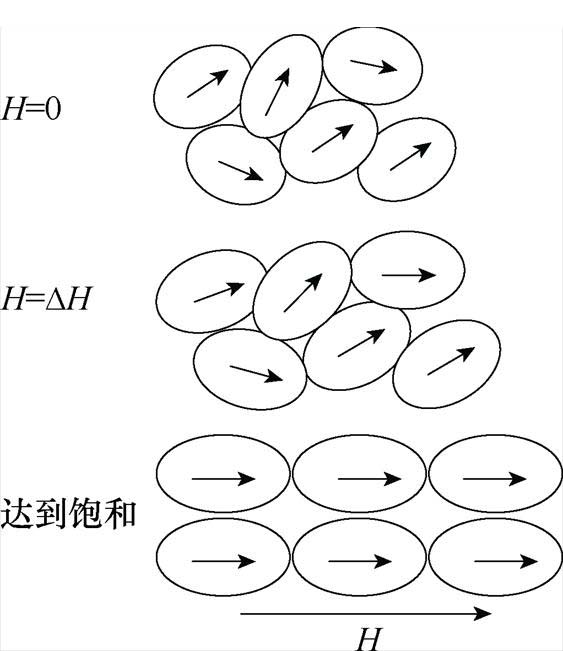
图9 磁致伸缩效应等效示意图
Fig.9 Equivalent diagram of magnetostrictive effect
根据摩擦力做功公式
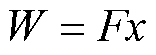（17）
式中，F为等效摩擦力；x为等效相对位移。假设单个磁畴的摩擦做功为w，可以表示为
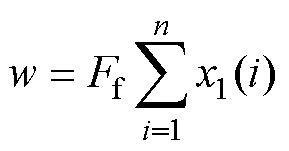（18）
式中，x1为两个磁畴的相对位移量，可以表示为式（19）；Ff为两个磁畴之间的摩擦力，可以表示为式（20）。
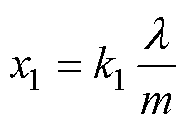（19）
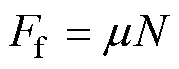（20）
式中，k1为比例系数；m为材料内部的磁畴数量；m 为磁畴之间的摩擦系数；N为每个磁畴所受到的正应力，可以表示为
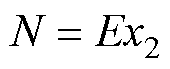（21）
式中，E为材料的杨氏模量；x2为两磁畴之间挤压形变量，可以表示为
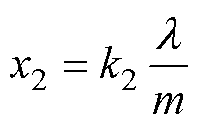（22）
式中，k2为比例系数。由此可以推导出材料整体由于磁致伸缩效应引起的摩擦损耗为
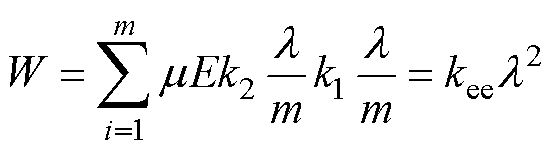（23）
式中，kee为与材料相关的参数，可通过实验数据进行参数识别。而磁致伸缩系数l 可利用式（17）计算，将摩擦做功的能量代入J-A理论的能量公式 中，有
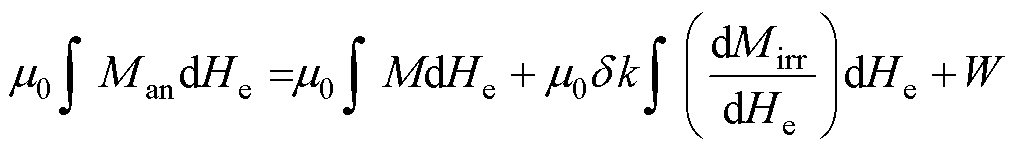（24）
最终推导出M与B的微分关系式为
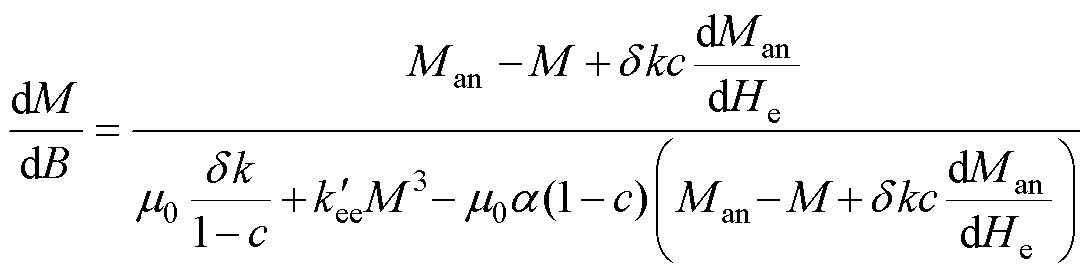（25）
式中，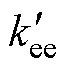
为与材料相关的系数。
第3、4节提出了两种不同模型用以描述拉应力影响下取向电工钢低磁通密度范围内畴壁的平移运动与高磁通密度范围内磁矩的旋转运动。然而，在实际磁化过程中，磁畴的运动方式并不是独立存在的，畴壁的平移运动与磁矩的旋转运动共同作用于材料的整个磁化进程，而第3、4节所提出的两种模型无法单独模拟拉应力影响下取向电工钢的完整磁化过程。由于BP神经网络具有学习和储存大量输入-输出模式映射关系的能力，无需揭示描述映射关系的数学方程[23]，因此，为了能够模拟拉应力加载条件下取向电工钢完整的磁化过程，本文采用BP神经网络作为连接两个模型的桥梁。
利用BP神经网络构建考虑拉应力影响的磁-力耦合模型，其基本结构如图10所示。在低磁通密度范围内，由于材料内部磁畴运动方式以畴壁的平移运动为主，因此，以第3节的模型为主导；在高磁通密度范围内，材料内部磁畴运动方式以磁矩旋转运动为主，以第4节的模型为主导。而在低磁通密度范围与高磁通密度范围的过渡区域，畴壁平移与磁矩旋转两种运动方式共同存在，为了模拟真实材料内部磁畴的运动规律，引入模型比例参数D，表示材料在磁化过程中畴壁平移运动的占比。
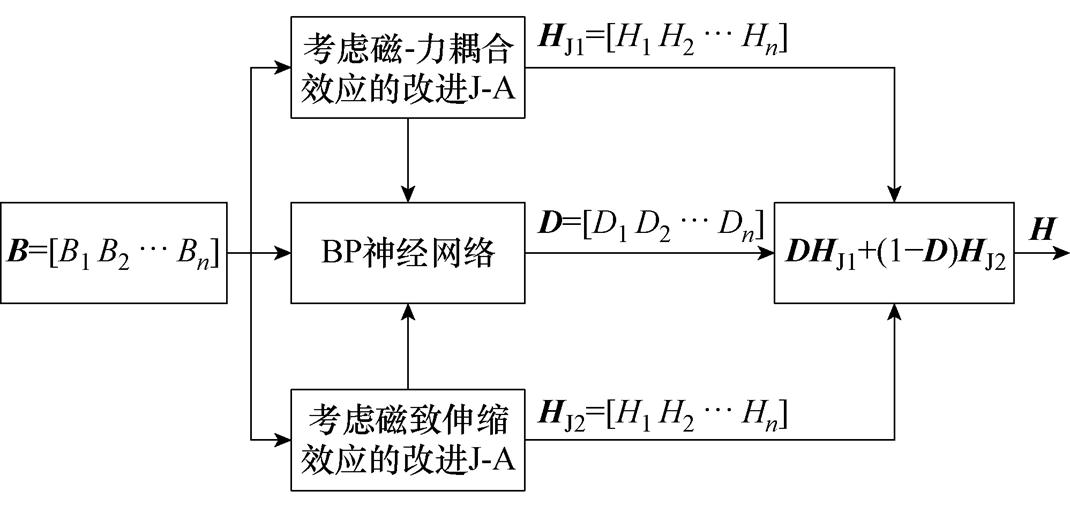
图10 混合磁滞模型基本结构
Fig.10 Basic structure of hybrid hysteresis model
考虑拉应力影响的磁-力耦合模型最终的输出磁场强度为
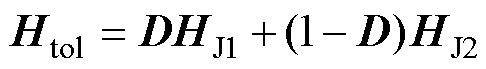（26）
式中，HJ1为考虑畴壁平移运动的模型输出磁场强度；HJ2为考虑磁矩旋转运动的模型输出磁场强度。
由于仅需求解模型比例参数D，本文建立了三层结构的BP神经网络。其中，特征值的设置如下：
（1）材料磁化过程中不同时刻的磁通密度值B。
（2）材料磁化过程中不同时刻下磁通密度值与所对应的磁场强度的乘积Ssr。
（3）材料磁化过程中不同时刻下磁通密度与所对应的磁场强度的比值mst。
图11为BP神经网络的算法流程。
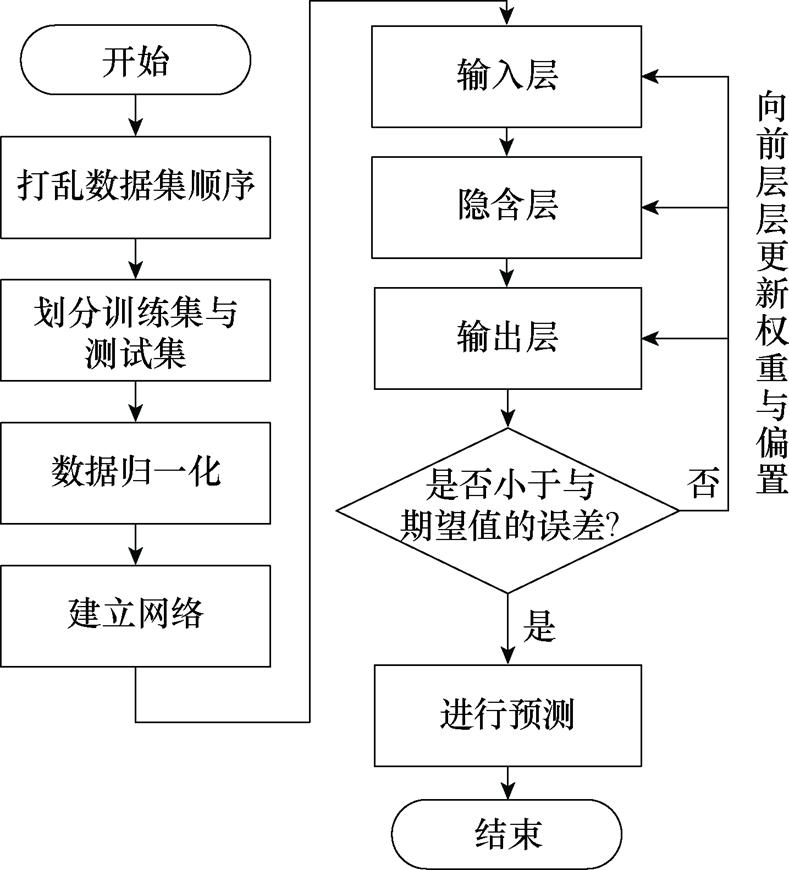
图11 BP神经网络的算法流程
Fig.11 Algorithm flow of BP neural network
本文中BP神经网络的数据样本为不同应力等级下测量得到的磁滞回线，其中80%被随机选择作为BP神经网络的训练集，其余20%的测量结果用作BP神经网络的验证集。为了提高BP神经网络的学习效率，需要对输出数据D进行预处理。用于预处理的运算可以表示为
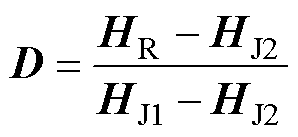（27）
式中，HR为实验测量的磁场强度。
为了验证网络的预测效果，图12a对比了部分BP神经网络预测的比例参数D与经过预处理计算的比例参数D，结果表明，预测值与预处理的比例参数之间的误差被严格控制在5%以内，表明本节所建立的BP神经网络具有良好的预测效果。图12b为BP神经网络在不同拉应力等级下预测得出的比例参数D随磁场强度的变化趋势。观察图12b可以发现比例参数D有以下特征：
（1）在磁通密度较低时D值接近于1，而在磁通密度逐渐升高时D值随之下降，这表明D值的变化规律与磁化过程的划分相符合，即低磁通密度范围内材料磁化特性的模拟以第3节代表畴壁平移运动的模型为主导，而高磁通密度范围内材料磁化特性的模拟以第4节代表磁矩旋转运动的模型为主导。
（2）随着拉应力的增加，参数D接近于1的范围也随之扩大，以上特点与磁化过程中畴壁运动与磁畴旋转的机理可以互相印证。
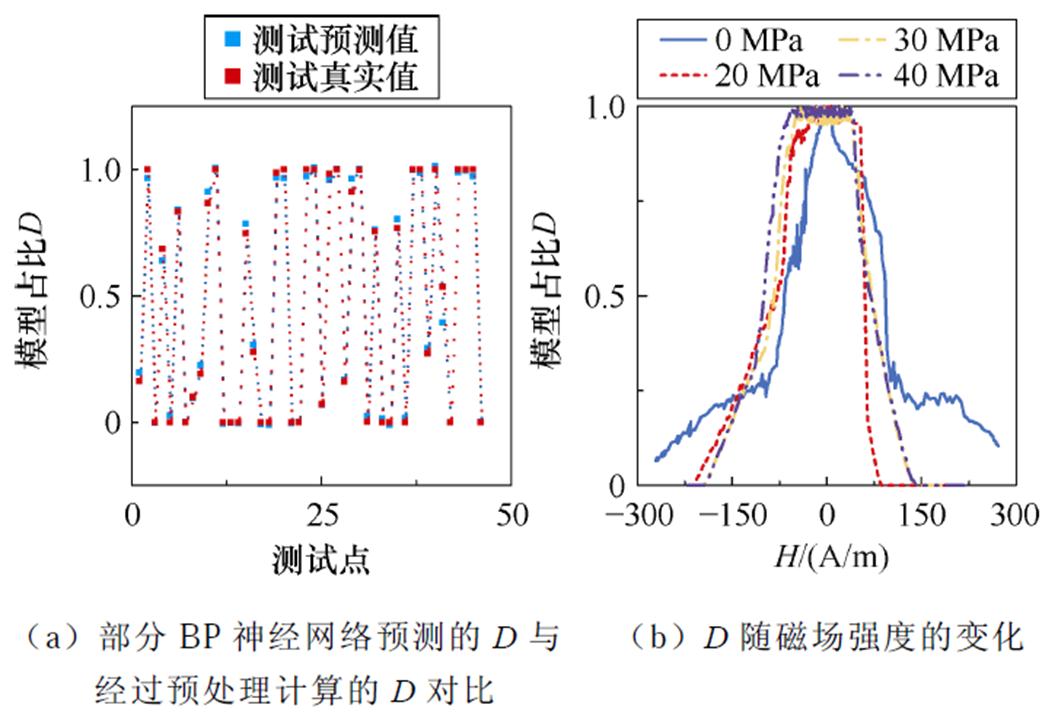
图12 神经网络验证与磁通密度为1.5 T时不同拉应力等级的比例参数
Fig.12 Neural network validation and ratio parameters for different tensile stress levels at 1.5 T
粒子群种群寻优（Particle Swarm Optimization, PSO）算法是一种进化计算技术，源于对鸟群捕食的行为研究，通过种群中个体之间的协作和信息共享来寻找最优解[24]。采用PSO对模型进行参数识别，将目标函数设置为计算磁场强度与实验磁场强度的均方差，有
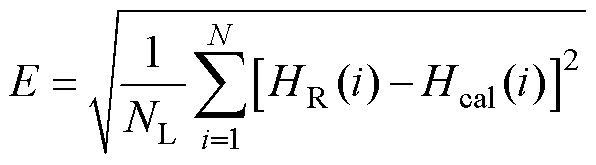（28）
式中，NL为采样点数；Hcal为计算磁场强度。图13为粒子群算法流程。
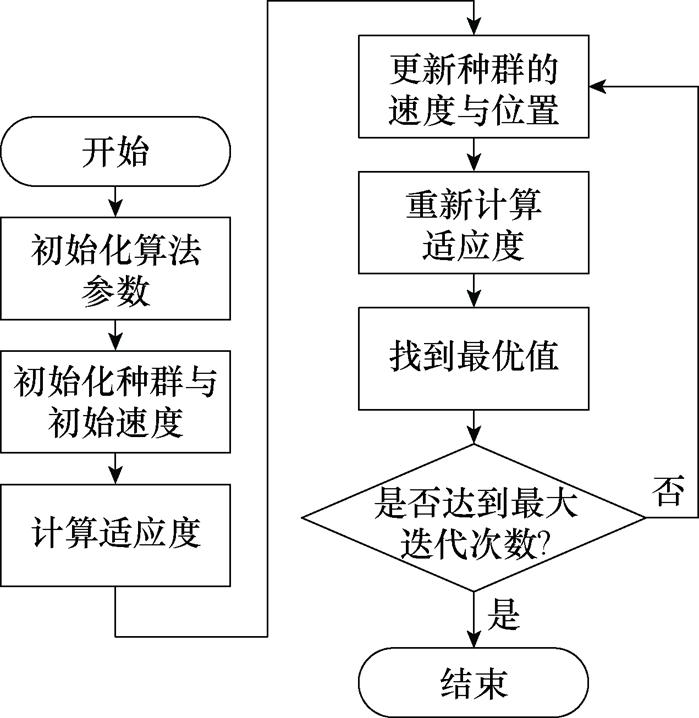
图13 PSO的算法流程
Fig.13 Algorithm flow of PSO
图14为所提磁-力耦合模型计算值与实验测量值的对比。
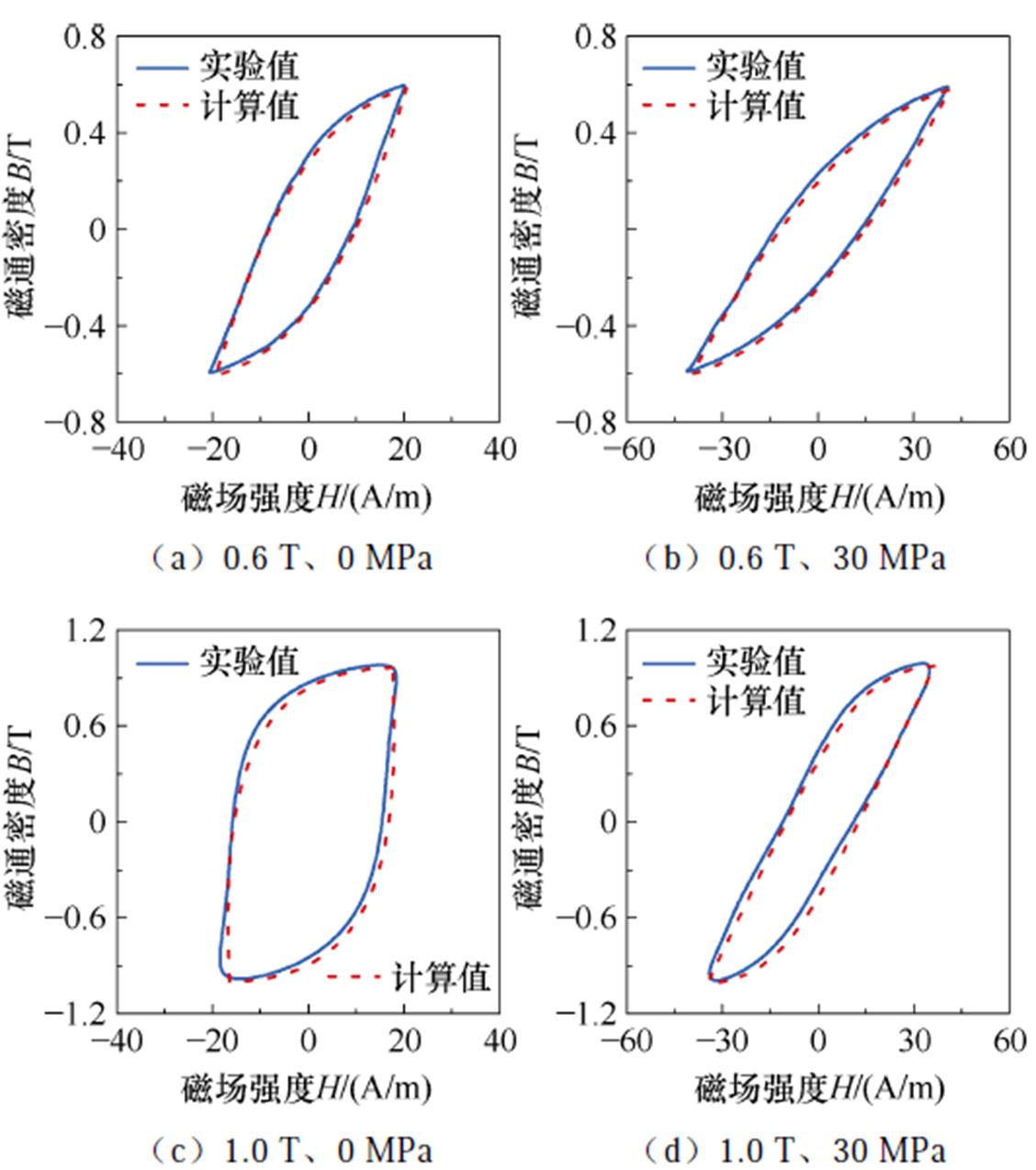
图14 低磁通密度范围内模型计算值与实验值
Fig.14 Calculation values of the model and experimental values at low magnetic flux density
图14证明所提磁-力耦合模型在Bm＜1.0 T时，具有较高的计算精度，该结果表明，磁-力耦合模型能够更好地模拟材料磁化过程中畴壁的平移运动。图15给出了Bm=1.5 T时，磁-力耦合模型计算值与实验测量值的对比。图15证明混合模型能够准确地模拟取向电工钢在拉应力作用下的磁化特性，但该模型在磁滞回线膝点位置的计算精度稍差。
此外，通过对所提混合模型计算结果进行积分求解，得到样品在不同应力条件下的损耗计算值。
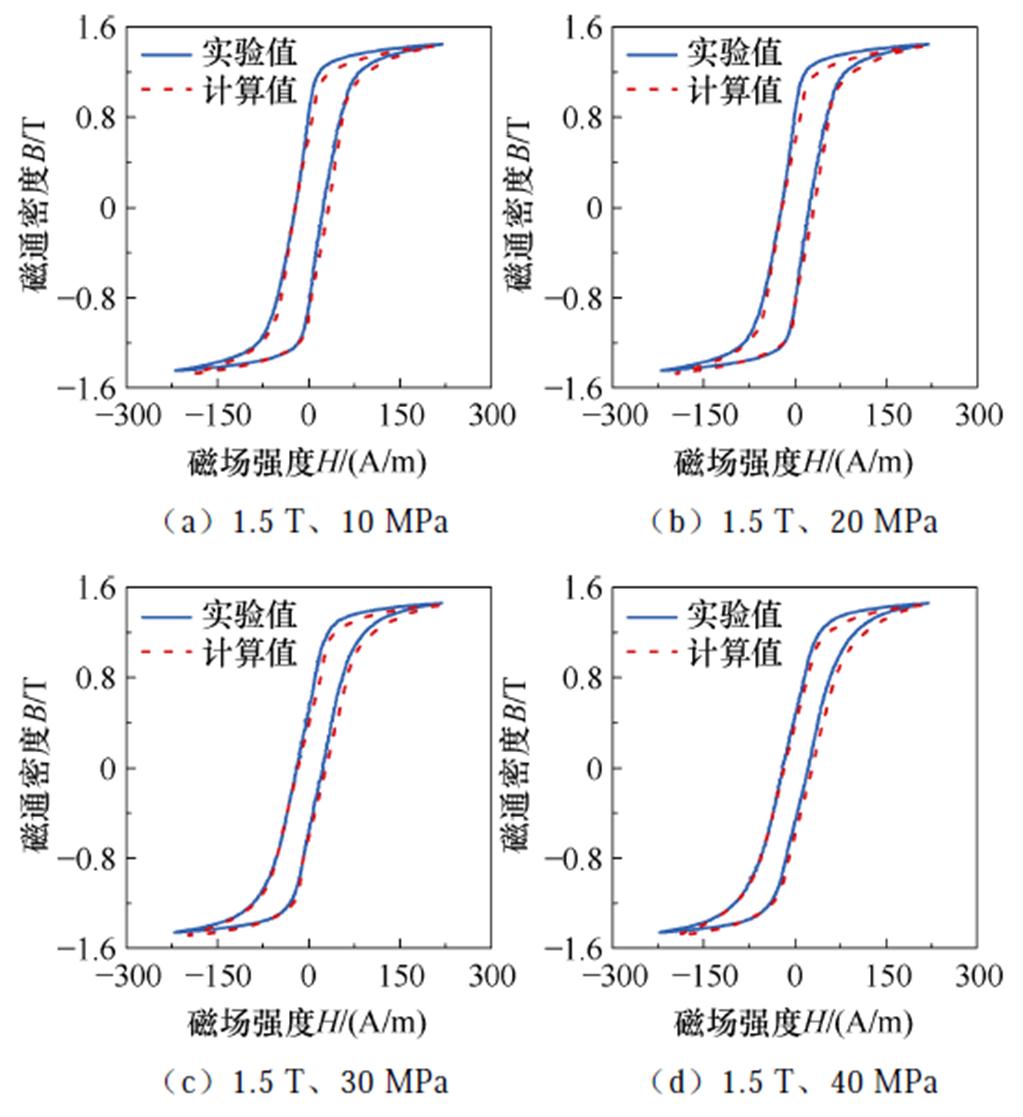
图15 高磁通密度范围内模型计算值与实验值
Fig.15 Calculation values of the model and experimental values at high magnetic flux density
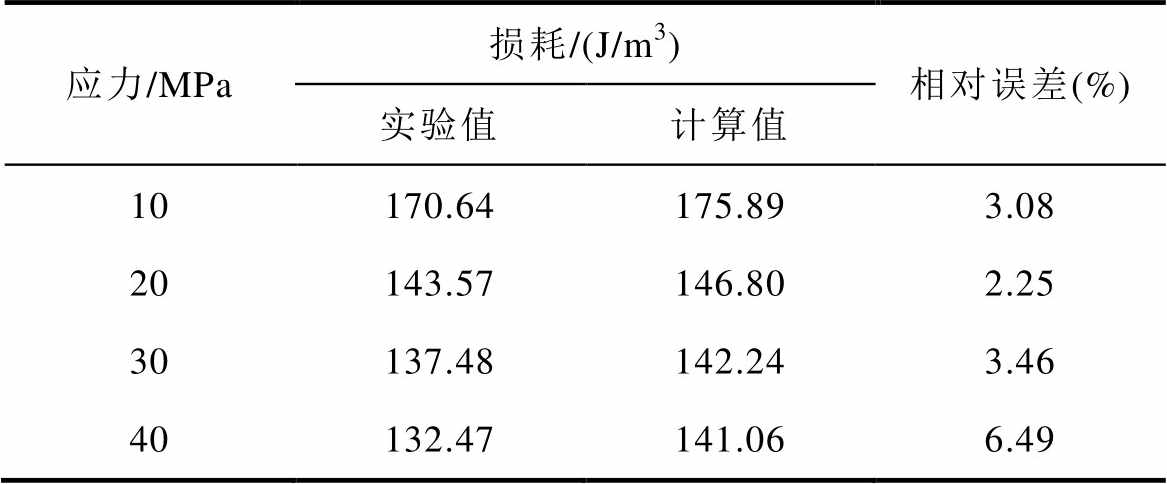
表1对比了样品实验测量的损耗值与所提模型的计算值，混合模型的损耗计算结果与实验测量结果接近，误差最大不超过6.49%。由此验证了所提出的磁-力耦合模型的计算误差在允许范围以内。
表1 考虑拉应力影响下总损耗计算值与实验值对比
Tab.1 Comparison of calculated and experimental values of total loss considering the effect of tensile stress
应力/MPa损耗/(J/m3)相对误差(%) 实验值计算值 10170.64175.893.08 20143.57146.802.25 30137.48142.243.46 40132.47141.066.49
通过分析施加拉应力条件下取向电工钢的磁畴结构变化，并与材料的宏观磁特性建立联系，对拉应力状态下的磁畴变化规律进行定性描述与定量计算，考虑了传统J-A模型中适用于各向同性材料的无磁滞磁化公式的局限性，提出适用于取向电工钢的新型无磁滞磁化公式，能够描述低磁通密度范围内的畴壁平移运动；将材料的磁致伸缩效应等效为磁畴之间的摩擦作用从而向传统J-A模型中引入了磁致伸缩效应的影响，能够描述高磁通密度范围内的磁矩旋转运动。应用BP神经网络有效预测了不同激磁水平下两种模型的混合比例，建立了考虑拉应力影响的磁滞模型，通过与实验测量值对比，验证了所提混合模型的准确性与有效性。
参考文献
[1] 李梦星, 张艳丽, 姜伟, 等. 机械应力下电工钢片磁滞与磁致伸缩回环滞后特性模拟[J]. 电工技术学报, 2022, 37(11): 2698-2706.
Li Mengxing, Zhang Yanli, Jiang Wei, et al. Simulation of hysteresis and magnetostrictive loop hysteretic characteristics of electrical steel sheets under mechanical stress[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2698-2706.
[2] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 2606.
Chen Long, Yi Qiongyang, Ben Tong, et al. Appli- cation and performance comparison of global optimi- zation algorithms in the parameter identification problems of the Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 2606.
[3] 周浩淼. 铁磁材料非线性磁弹性耦合理论及其在超磁致伸缩智能材料中的应用[D]. 兰州: 兰州大学, 2007.
Zhou Haomiao. Nonlinear coupled magneto-elastic theory in ferromagnetic materials and the appli- cation in giant magnetostrictive smart materials[D]. Lanzhou: Lanzhou University, 2007.
[4] 张黎, 王国政, 董攀婷, 等. 基于磁致伸缩本征特性的晶粒取向性变压器铁心振动模型[J]. 中国电机工程学报, 2016, 36(14): 3990-4001.
Zhang Li, Wang Guozheng, Dong Panting, et al. Study on the vibration of grain-oriented transformer core based on the magnetostrictive intrinsic characteristics[J]. Proceedings of the CSEE, 2016, 36(14): 3990-4001.
[5] Perevertov O. Influence of the applied elastic tensile and compressive stress on the hysteresis curves of Fe-3%Si non-oriented steel[J]. Journal of Magnetism and Magnetic Materials, 2017, 428: 223-228.
[6] 贲彤, 陈芳媛, 陈龙, 等. 考虑力-磁耦合效应的无取向电工钢片磁致伸缩模型的改进[J]. 中国电机工程学报, 2021, 41(15): 5361-5370.
Ben Tong, Chen Fangyuan, Chen Long, et al. An improved magnetostrictive model of Non-oriented electrical steel sheet considering force-magnetic coupling effect[J]. Proceedings of the CSEE, 2021, 41(15): 5361-5370.
[7] Daniel L, Hubert O, Buiron N, et al. Reversible magneto-elastic behavior: a multiscale approach[J]. Journal of the Mechanics and Physics of Solids, 2008, 56(3): 1018-1042.
[8] Daniel L, Rekik M, Hubert O. A multiscale model for magneto-elastic behaviour including hysteresis effects[J]. Archive of Applied Mechanics, 2014, 84(9): 1307-1323.
[9] Ito S, Mifune T, Matsuo T, et al. Macroscopic magnetization modeling of silicon steel sheets using an assembly of six-domain particles[J]. Journal of Applied Physics, 2015, 117(17): 17D126.
[10] Liu Jia, Tian Guiyun, Gao Bin, et al. Domain wall characterization inside grain and around grain boundary under tensile stress[J]. Journal of Mag- netism and Magnetic Materials, 2019, 471: 39-48.
[11] Perevertov O, Schäfer R. Influence of applied tensile stress on the hysteresis curve and magnetic domain structure of grain-oriented Fe-3%Si steel[J]. Journal of Physics D: Applied Physics, 2014, 47(18): 185001.
[12] 李岱岩, 张艳丽, 荆盈, 等. 基于J-A模型的电工钢片磁致伸缩特性模拟与实验[J]. 电工技术学报, 2022, 37(20): 5081-5091.
Li Daiyan, Zhang Yanli, Jing Ying, et al. Modeling of magnetostrictive characteristics in an electrical steel sheet based on the J-A model and its experimental verification[J]. Transactions of China Electrotech- nical Society, 2022, 37(20): 5081-5091.
[13] Wilkie W K, Bryant R G, High J W, et al. Low-cost piezocomposite actuator for structural control appli- cations[J]. Proceedings of Spie the International Society for Optical Engineering, 2000, 3991: 323- 334.
[14] Hubert A, Schäfer R. Magnetic domains: the analysis of magnetic microstructures[M]. Berlin: Springer Science & Business Media, 2008.
[15] Qiu Fasheng, Ren Wenwei, Tian Guiyun, et al. Characterization of applied tensile stress using domain wall dynamic behavior of grain-oriented elec- trical steel[J]. Journal of Magnetism and Magnetic Materials, 2017, 432: 250-259.
[16] Perevertov O, Thielsch J, Schäfer R. Effect of applied tensile stress on the hysteresis curve and magnetic domain structure of grain-oriented transverse Fe- 3%Si steel[J]. Journal of Magnetism and Magnetic Materials, 2015, 385: 358-367.
[17] 吴鑫. 介观尺度下电工钢片磁化过程磁畴结构动态特性研究[D]. 沈阳: 沈阳工业大学, 2022.
Wu Xin. Study on dynamic characteristics of mag- netic domains structure during magnetization process of electrical steel sheet at mesoscopic scale[D]. Shenyang: Shenyang University of Technology, 2022.
[18] 邱发生. 基于磁畴动态行为特征的应力表征研究[D]. 成都: 电子科技大学, 2019.
Qiu Fasheng. Research on magnetic domain wall dynamic behaviors for stress characterization[D]. Chengdu: University of Electronic Science and Technology of China, 2019.
[19] 宛德福, 马兴隆. 磁性物理学[M]. 成都: 电子科技大学社, 1994.
[20] 李贞, 李庆民, 李长云, 等. J-A磁化建模理论的质疑与修正方法研究[J]. 中国电机工程学报, 2011, 31(3): 124-131.
Li Zhen, Li Qingmin, Li Changyun, et al. Queries on the J-A modeling theory of the magnetization process in ferromagnets and proposed correction method[J]. Proceedings of the CSEE, 2011, 31(3): 124-131.
[21] 莫仕勋, 杨皓, 蒋坤坪, 等. 基于改进秃鹰搜索算法的变压器J-A模型参数辨识[J]. 电工电能新技术, 2022, 41(4): 67-74.
Mo Shixun, Yang Hao, Jiang Kunping, et al. Parameter identification of transformer J-A model based on improved BES algorithm[J]. Advanced Technology of Electrical Engineering and Energy, 2022, 41(4): 67-74.
[22] 李晶晶. 基于J-A磁滞模型硅钢片磁致伸缩模型的研究[D]. 天津: 天津工业大学, 2020.
Li Jingjing. Study on magnetostrictive model of silicon steel sheet based on J-A hysteresis model[D]. Tianjin: Tianjin Polytechnic University, 2020.
[23] 闻枫, 荆凡胜, 李强, 等. 基于改进BP神经网络的无线电能传输系统接收线圈参数优化[J]. 电工技术学报, 2021, 36(增刊2): 412-422.
Wen Feng, Jing Fansheng, Li Qiang, et al. Optimization on receiver parameters of wireless power transfer system based on improved BP neural network[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 412-422.
[24] 李永建, 利雅婷, 林志伟, 等. 基于改进Bouc-Wen模型的谐波激励条件下电工钢片磁滞特性模拟与验证[J]. 电工技术学报, 2022, 37(17): 4259-4268.
Li Yongjian, Li Yating, Lin Zhiwei, et al. An improved Bouc-Wen based hysteresis model under harmonic magnetization[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4259-4268.
Abstract The magnetization characteristics cause the most complex part of the loss composition in electrical equipment during the magnetization process of magnetic materials. Grain-oriented electrical steel, the widely used core material for power transformers, has its magnetic properties affected by stress, thereby impacting the performance of power transformers. Therefore, accurately and quickly simulating the hysteresis characteristics of magnetic materials under different stresses is significant for designing equipment cores that withstand mechanical stress.
Firstly, a magnetic property measurement device is used to measure the magnetization characteristics of grain-oriented electrical steel sheets under different tensile stresses along the rolling direction. The relationship between the magnetization characteristics of grain-oriented electrical steel and different movement modes of magnetic domains is established by comparing with the changes in the domain structure of grain-oriented electrical steel under different stress levels. It is assumed that the magnetization characteristics of magnetic materials are linear when domain wall motion is dominant and non-linear when magnetization rotation is dominant. Tensile stress mainly affects the domain wall motion of grain-oriented electrical steel in the low magnetic flux density range. Additionally, assume that the change efficiency of the magnetic domain in the low magnetic flux density range is constant under constant stress. The magnetic domain change efficiency ntp is expressed as 1/Ht (Ht is the magnetic field strength at the end of the domain wall translational motion), and the relationship between ntp and tensile stress is quantified into a specific mathematical expression. A new anhysteretic magnetization formula based on the relationship between ntp and stress is proposed to replace the traditional J-A model’s formula based on Langevin theory. Thus, a mathematical model is proposed as Model 1 for the low magnetic flux density range to describe the domain wall motion of grain-oriented electrical steel sheets under tensile stress. Assuming that each magnetic domain within the material is an independent entity, the magnetostrictive phenomenon of the material can be equivalent to the aggregation of the changes in the form of a single magnetic domain. During the magnetization process, changes in the shapes of magnetic domains lead to relative displacement, resulting in frictional losses. Therefore, the magnetostrictive characteristics of magnetic materials are introduced into the J-A theory in the form of friction, and a mathematical model is proposed as Model 2 for the high magnetic flux density range that can describe the magnetization rotation movement of grain-oriented electrical steel. In the actual magnetization process, the domain wall motion and the magnetization rotation movement affect the entire magnetization process. Thus, the hybrid ratio of the two models under different magnetization levels is effectively predicted using a BP neural network, and a hybrid hysteresis model considering the influence of tensile stress is proposed.
The calculation accuracy of the hybrid model is much higher than that of the traditional J-A model and is slightly worse at the knee point of the hysteresis loop. The calculated loss of the hybrid model is close to the measured results, with a maximum error not exceeding 6.49%.
The following conclusions can be drawn. (1) The hybrid hysteresis model can accurately describe the domain wall motion of oriented electrical steel in the low magnetic flux density range. (2) It can also accurately describe the magnetic moment rotation movement of oriented electrical steel in the high magnetic flux density range. The calculation error of the proposed magneto-mechanical coupling model is within the allowable range, which verifies the accuracy and effectiveness of the hybrid model.
Keywords：J-A model, BP neural network, oriented electrical steel, tensile stress, magnetic domain motion
中图分类号：TM275
DOI: 10.19595/j.cnki.1000-6753.tces.231491
国家自然科学基金项目（52130710, 52277008）和河北省教育厅在读研究生创新能力培养项目（CXZZSS2024014）资助。
收稿日期 2023-09-09
改稿日期 2023-12-29
李永建 男，1978年生，教授，博士生导师，研究方向为工程电磁场与磁技术、三维磁特性测量与建模。
E-mail: liyongjian@hebut.edu.cn（通信作者）
李宗明 男，1998年生，硕士研究生，研究方向为工程电磁场与磁技术。
E-mail: mkyhuo@163.com
（编辑 崔文静）