。充电完成之后，表面电荷注入材料内部，并在材料体中形成电场[25]。在电荷注入过程中，表面电位的衰减率不同[26]。100 μm XLPE在90℃下正负电晕的等温表面电位衰减曲线如图1所示。摘要 交联聚乙烯绝缘层厚度设计是高压直流电缆研发的关键任务之一。然而，实验室中难以获得厚绝缘样品的直流击穿性能参数，绝缘层厚度设计缺少直接的数据支撑，因此研究交联聚乙烯绝缘直流击穿的厚度效应具有重要意义。该文获得了不同厚度交联聚乙烯绝缘样品在90℃下的直流击穿特性，揭示了交联聚乙烯绝缘威布尔特征击穿场强和形状参数随样品厚度的增加而减小的厚度效应。采用电荷输运和分子链位移调制模型计算了交联聚乙烯的直流击穿过程，结果表明击穿威布尔形状参数受陷阱能级、陷阱密度、载流子迁移率随机变量标准差的影响。在厚试样中，三种电荷陷阱参数的高斯分布更宽、标准差大，导致击穿场强分散性增大，其中电荷陷阱能级随机变量标准差的影响最显著。因此，交联聚乙烯绝缘电荷陷阱参数分布是决定其高温直流击穿厚度效应的关键。该研究可为高压电缆绝缘设计提供理论指导和实验依据。
关键词：交联聚乙烯 厚度效应 威布尔分布 电荷输运
由于我国电力能源分布不均，对于电力系统的规划有着更高的要求，而采用高压直流（High Voltage Direct Current, HVDC）输电方式，能够远距离输送电力至现有电网中，具有容量大、损耗小等特点。高压直流电缆输电作为高压直流输电的关键部分，在远距离输电、区域电网互联和风电并网等方面发挥着至关重要的作用[1-3]。交联聚乙烯（Cross-Linked Polyethylene, XLPE）因其优异的导热性能和介电性能被广泛地用作高压电缆的绝缘材料[4]。其长期工作温度一般为70℃，短时间能够承受130℃的高温[5-6]，具有较高的耐热性能和较强的载流性能。
提高直流电缆的载流量，需要迫切提升XLPE绝缘电缆的长期工作温度[7]。如何将XLPE直流电缆长期工作温度从70℃提升至90℃，是现今研究的热点之一。交联聚乙烯绝缘层厚度设计是高压直流电缆研发制造的关键任务之一[8-9]，直流击穿场强随着厚度的增加和温度的升高而减小[10-12]，且电缆在长期运行过程中会受电-热耦合影响，导致电缆的绝缘性能下降[13-15]。然而，实验室中难以获得厚绝缘样品的直流击穿性能参数，绝缘层厚度设计缺少直接的数据支撑。因此，研究高温直流电压下交联聚乙烯绝缘的厚度效应具有重要意义。
研究学者对击穿场强的厚度效应已有一定程度的研究，最早可以追溯到20世纪中后期。一般认为，绝缘介质击穿场强随厚度的增加而下降的原因是厚绝缘介质的宏观缺陷相对更多。1968年，W. S. Nicol[16]获得了15～600 nm范围内等离子体氧化铝薄膜击穿场强随厚度的增加而减小的特征，但尚不明确所发现的厚度依赖关系是否适用于更大的厚度以及其他的电介质薄膜。1992年，T. Mizutani等[17]研究了10 nm～10 μm的聚对二甲苯薄膜的空间电荷效应与薄膜厚度、温度和击穿场强之间的关系，认为聚对二甲苯击穿场强不依赖温度变化、随着厚度增大而减小的关系符合雪崩击穿机理，且认为空间电荷对击穿场强有较大影响。之后，Y. Yamano和H. Endoh[18]在5～25 μm的聚乙烯薄膜中掺杂了不同浓度的偶氮化合物，以获得试样厚度以及不同浓度偶氮化合物掺杂对于试样击穿强度的影响。实验结果表明，试样的击穿场强与厚度呈负相关，但没有关于击穿分散性的报道。2005年，H. Zhou等[19]认为击穿场强与薄膜厚度逆幂关系的指数因子有关，薄膜厚度阈值与温度有关，温度加速了电子的捕获过程。2018年，钱恺羽等[12]研究了不同温度下XLPE击穿场强的厚度效应，认为逆幂关系指数因子随着温度变化，且厚度效应同时受空间电荷、自由体积击穿和热击穿等机制的影响。
本课题组提出电荷输运与分子链位移相结合的模型（Charge Transport and Molecular Displacement modulated model, CTMD）以仿真低密度聚乙烯（Low Density Polyethylene, LDPE）的击穿场强与样品厚度、温度的关系[20-21]，后续开展了实验和CTMD仿真模拟的研究，对比实验结果与仿真结果表明，同时考虑电荷输运与分子链位移过程的模型能有效解释LDPE与厚度、温度相关的击穿机理[21]。电介质绝缘材料中载流子输运与能量积累过程最终导致电介质的击穿，而介质击穿的威布尔分布与电荷输运参数密切相关。本课题组通过CTMD模型，模拟了聚丙烯（Polypropylene, PP）/Al2O3纳米复合材料的击穿强度，认为威布尔分布受陷阱能级的影响较强，受试图逃逸频率和载流子迁移率的影响较弱，受注入势垒和陷阱捕获概率的影响最弱[22]。前期仿真研究表明[23]，常温下XLPE击穿场强大小随厚度的增加呈逆幂关系，击穿威布尔概率分布受陷阱能级随机变量影响较大。
综上所述，对于固体电介质击穿场强的厚度效应以及击穿威布尔概率分布虽有持续的关注与研究，但主要是分析宏观缺陷与厚度效应之间的关系，而本文关注厚度效应和电荷输运参数之间的影响，揭示了绝缘厚度效应对试样威布尔特征击穿场强和击穿概率分布的定量关系。通过实验得到160、300、400、550、650 μm五种厚度的试样在90℃下的击穿场强结果，仿真研究了不同电荷输运随机变量标准差对威布尔分布形状参数的影响，分析了厚度效应对试样击穿场强的影响，为高电压等级电缆设计以及绝缘厚度减薄提供了理论指导和实验依据。
采用北欧化工（Borealis）生产的超纯净交联聚乙烯绝缘料，其熔体流动速率为2 g/(10 min)，密度为0.922 g/cm3。首先将交联聚乙烯绝缘料颗粒放入模具内，在平板硫化机170℃下预压20 min，然后施加10 MPa压力热压30 min，最后保持相同压力冷却至室温，制备出不同厚度的交联聚乙烯绝缘样品。样品采用无水乙醇清洗，并在60℃真空烘箱中干燥脱气处理24 h。
高温直流击穿实验采用直径为25 mm的球-球电极系统，对160、300、400、550、650 μm五种厚度的XLPE试样进行90℃下的高温直流击穿实验。实验电压以1 kV/s的速率升高，直至薄膜试样被击穿。对每种厚度的试样至少进行20次高温直流击穿实验，记录所得击穿电压数值，用测厚仪对每个击穿点进行厚度测量，精度控制在±10 μm，计算得到击穿场强结果。
通过等温表面电位衰减（Isothermal Surface Potential Decay, ISPD）实验可以得到绝缘材料的载流子迁移率以及深陷阱能级和深陷阱密度参数。ISPD方法是通过电晕充电在绝缘介质的表面沉积电荷，电荷在等温条件下脱陷导致电位衰减[24]，从而得到载流子迁移率以及深陷阱能级和深陷阱密度。
本文采用100 μm厚的XLPE试样进行ISPD实验测试。施加充电电压13 kV，针-栅电极产生电晕对试样表面充电10 min。充电完成后，将Trek表面电位计探头快速移动至试样表面，表面电位开始衰减，并用计算机记录衰减过程的数据。实验在环境温度(90±1)℃、相对湿度(22±1)%的条件下进行。
由于薄膜绝缘介质试样表面电位与表面电荷近似呈线性关系，因此可以采用ISPD实验来研究绝缘材料的表面载流子迁移特性。以正极性电晕为例，在对样品施加正极性电压的过程中，在XLPE表面积累了正电荷，产生表面电位。充电完成之后，表面电荷注入材料内部，并在材料体中形成电场[25]。在电荷注入过程中，表面电位的衰减率不同[26]。100 μm XLPE在90℃下正负电晕的等温表面电位衰减曲线如图1所示。
通过双指数函数拟合，可以得到tdφs/dt和时间t之间的函数关系，如图1b所示。图中峰值时间为载流子到达接地电极的渡越时间tT。浅陷阱控制的载流子迁移率表示为[26-27]
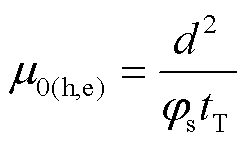（1）
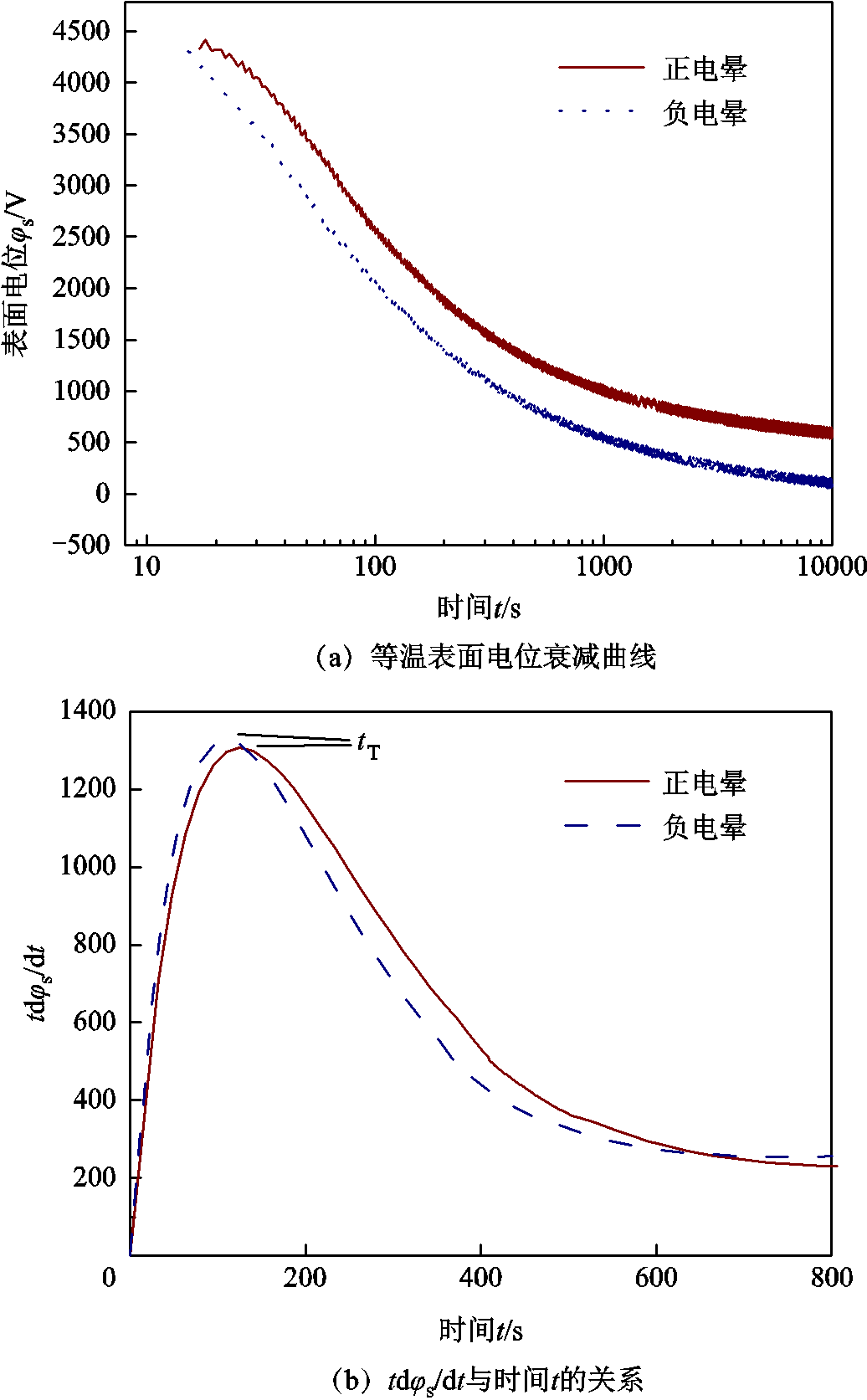
图1 XLPE在90℃下的等温表面电位衰减曲线和tdφs/dt与时间t的关系
Fig.1 ISPD curves of XLPE at 90℃ and the relationship between tdφs/dt and t
式中，下标h和e分别表示空穴和电子；μ0(h,e)为浅陷阱控制的载流子迁移率，m2/(V·s)；d为绝缘试样厚度，m；φs为表面电位，V。通过计算可以得到空穴和电子的迁移率分别为μ0(h)=6.15×10-15 m2/(V·s)和μ0(e)=6.63×10-15 m2/(V·s)。
XLPE的电荷输运、消散过程与陷阱特性以及电荷的捕获/脱陷过程密切相关，因此可以通过ISPD方法来研究聚合物的陷阱特性。陷阱连续分布函数Nt(u)[28]可以表示为
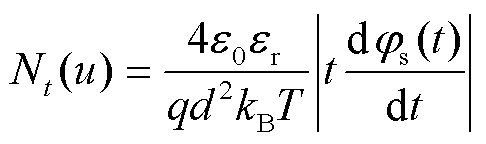（2）
式中，u为陷阱能级，eV；ε0为真空介电常数；εr为绝缘介质的相对介电常数；q为空穴电荷量，C；kB为玻耳兹曼常数，
=1.380 649×10-23 J/K；T为温度，K。
陷阱能级u可以表示为[28]
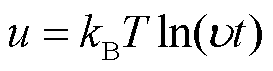（3）
式中，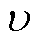
为陷阱电荷的逃逸频率因子。
通过对测量得到的XLPE等温表面电位衰减曲线进行双指数函数拟合可以得到t时刻试样表面电位函数φs(t)表达式为[28]
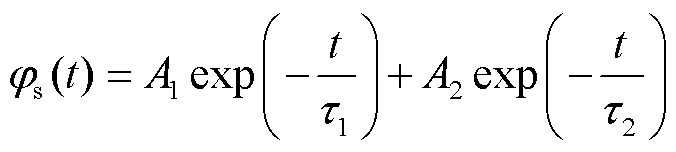（4）
式中，A1、A2、τ1、τ2均为拟合参数。
通过式（2）和式（3）对双指数函数φs(t)中的两个部分分别进行计算，即可得到总陷阱的分布特征，如图2所示。从图2中可以看出，空穴的深陷阱能级和电子的深陷阱能级都在1.16 eV左右，电子的深陷阱密度为3.85×1020 eV-1·m-3，空穴的深陷阱密度为3.39×1020 eV-1·m-3。
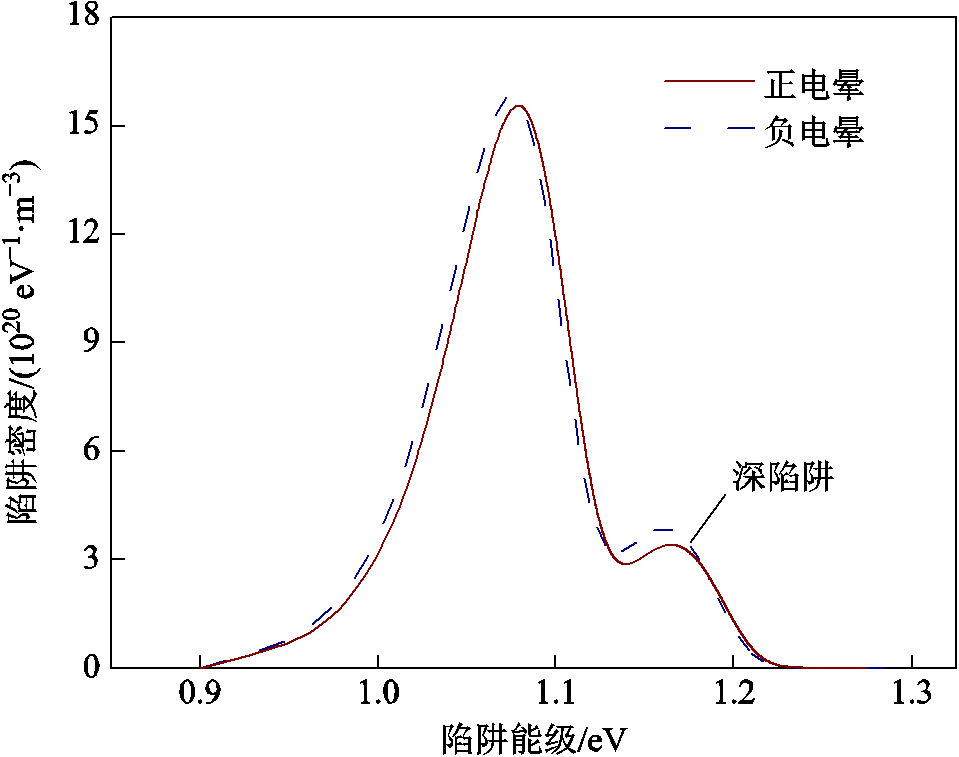
图2 ISPD曲线拟合得到的陷阱能级分布
Fig.2 Trap energy level distribution obtained by ISPD curve fitting
绝缘击穿场强具有一定的随机性和分散性，需要用到统计学理论来分析。威布尔（Weibull）分布是目前运用较为广泛的寿命诊断和可靠性分析的方法之一，一般使用双参数威布尔分布来分析击穿数据，其表达式为[29]
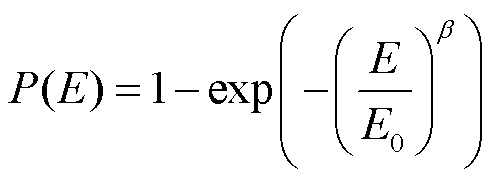（5）
式中，E0为对应于63.2%击穿概率的特征击穿场强，反映电介质材料的击穿性能，kV/mm；β为威布尔分布的形状参数，表示实验数据的分散性，β越小，数据分散性越大。
不同厚度XLPE试样在90℃下的直流击穿场强威布尔分布特性实验结果如图3a所示。从图中可以看出，威布尔分布曲线随着XLPE厚度的增加逐渐左移，并且斜率随着厚度的增加而略微减小，即XLPE直流击穿场强随着厚度的增加逐渐降低。
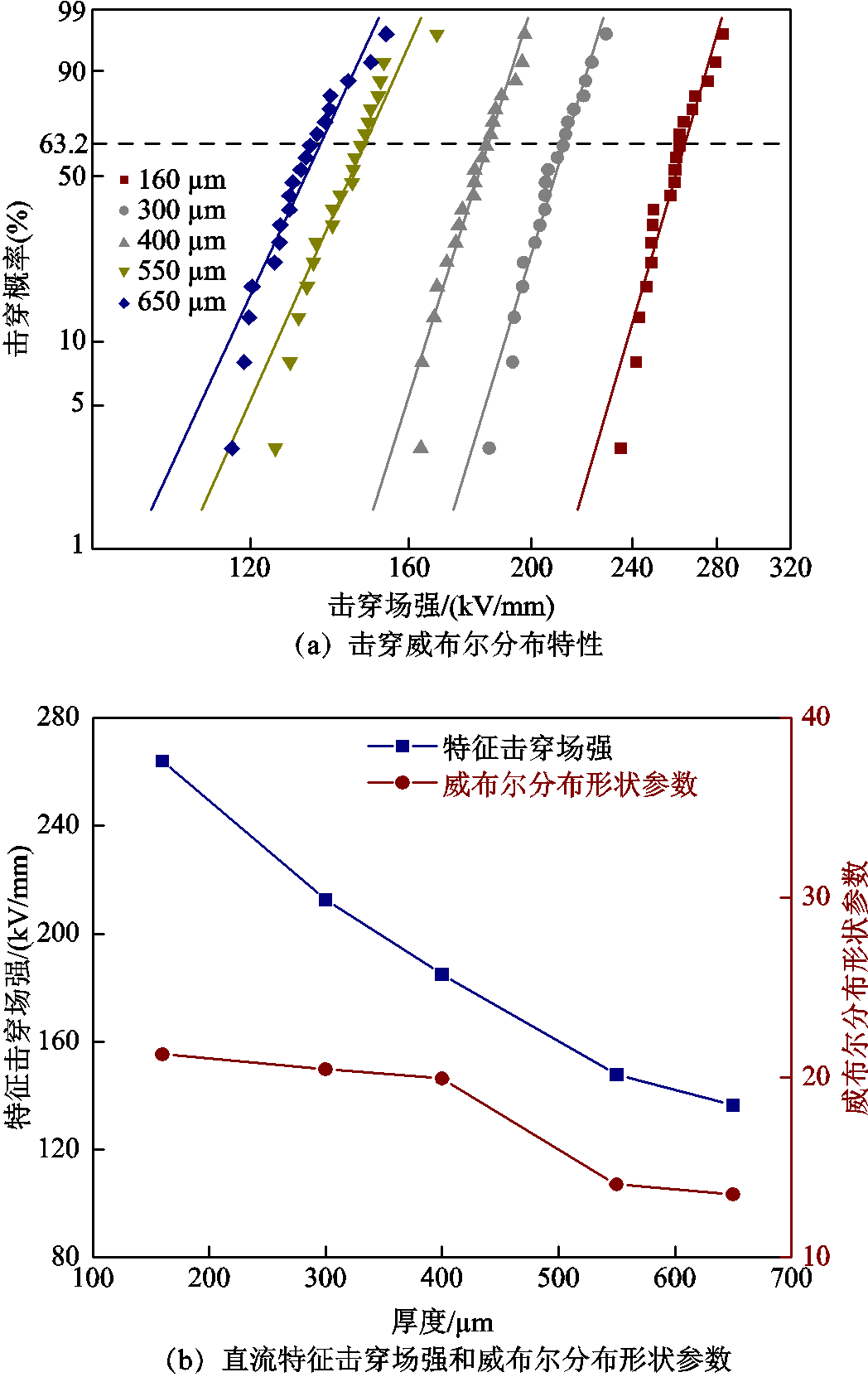
图3 90℃下不同厚度XLPE试样的直流击穿实验结果
Fig.3 DC breakdown test results of XLPE with different thicknesses at 90℃
160～650 μm厚度绝缘试样的直流威布尔特征击穿场强和威布尔分布形状参数见表1。图3b为90℃下交联聚乙烯直流特征击穿强度和威布尔分布形状参数实验结果随试样厚度的变化关系。160、300、400、550、650 μm厚度的XLPE试样的威布尔分布形状参数分别为21.3、20.5、19.9、14.1、13.5，可见威布尔分布形状参数随着厚度的增加而减小，击穿场强数据的分散性随着厚度的增加而增大。
表1 不同厚度绝缘试样的直流威布尔特征击穿场强
Tab.1 DC Weibull characteristic breakdown field strengths of insulation specimens of different thicknesses
厚度/μm特征击穿场强/(kV/mm)形状参数 160264.121.3 300212.620.5 400185.019.9 550147.714.1 650136.413.5
较厚的电介质内部陷阱参数分布更宽，加之电介质内部分子链定向运动会产生积聚效应，使内部导电路径发展得更为容易，从而导致更低的击穿强度。同时，厚电介质中更宽的陷阱分布使其击穿场强威布尔分布的随机性更强，分散性更大，这将在第4节中进行进一步论证。
本文将通过实验测试得到的XLPE绝缘介质陷阱参数以及载流子迁移率作为仿真模型输入参数，建立电荷输运和分子链位移调制模型（CTMD）以研究高温下交联聚乙烯绝缘介质的直流电击穿强度随试样厚度的变化规律。
3.1.1 CTMD模型
在电荷输运中考虑四种载流子，即自由和捕获电子以及自由和捕获空穴。根据聚合物的能带结构理论，物理缺陷会形成靠近导带及价带的浅陷阱，化学缺陷会形成靠近费米能级的深陷阱[30]。深陷阱由于其作用时间长，库仑力作用强，对电荷输运以及分子链位移作用影响更大。深陷阱捕获载流子，捕获电子的分子链向阳极移动，捕获空穴的分子链向阴极移动，在绝缘介质的界面处形成空间电荷，空间电荷的不断积聚使得电场强度发生畸变。同时，因受库仑力作用，分子链的位移使得自由体积扩张，电荷能量剧增。当电荷能量增加到可以跃过陷阱势垒时，绝缘材料发生击穿。因此，电介质材料的击穿与电荷输运以及载流子的位移过程密切相关。电荷输运和分子链位移调制模型示意图如图4所示，包含了电荷注入、电荷迁移、电荷捕获/脱陷、电荷复合和分子链位移等过程[20-21]。
在厚度为d的绝缘介质两端对绝缘介质施加斜坡电压，升压过程可以表示为电场对空间位置的积分。
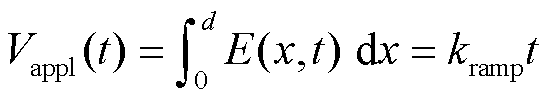（6）
式中，Vappl为施加电压，V；E为电场强度，V/m；x为空间位置，m；kramp为升压速率，V/s。
根据肖特基热发射注入原理，载流子电荷密度可以表示为式（7）[20-21]，该过程中电荷需要克服金属电极和绝缘电介质之间的界面势垒。
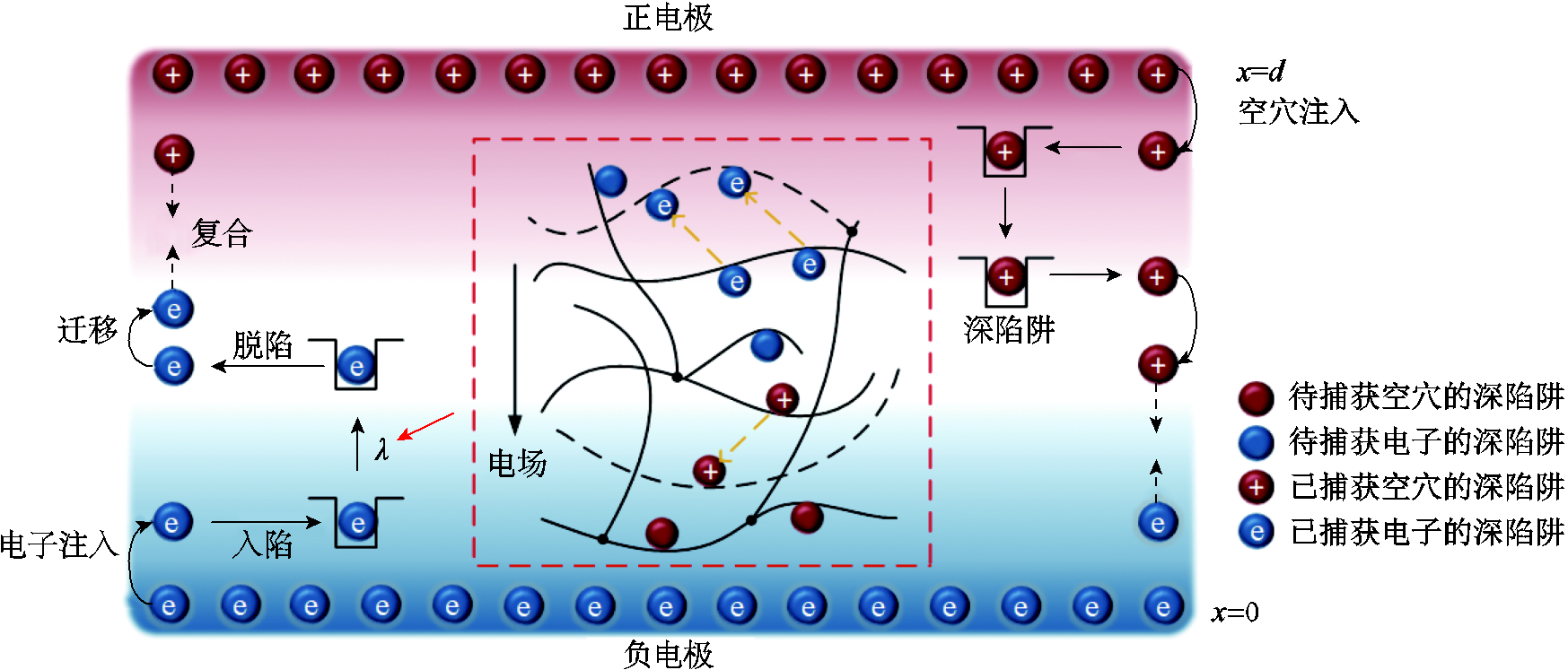
图4 电荷输运和分子链位移调制模型示意图[20-21]
Fig.4 Schematic diagram of charge transport and molecular displacement modulated electrical breakdown model[20-21]
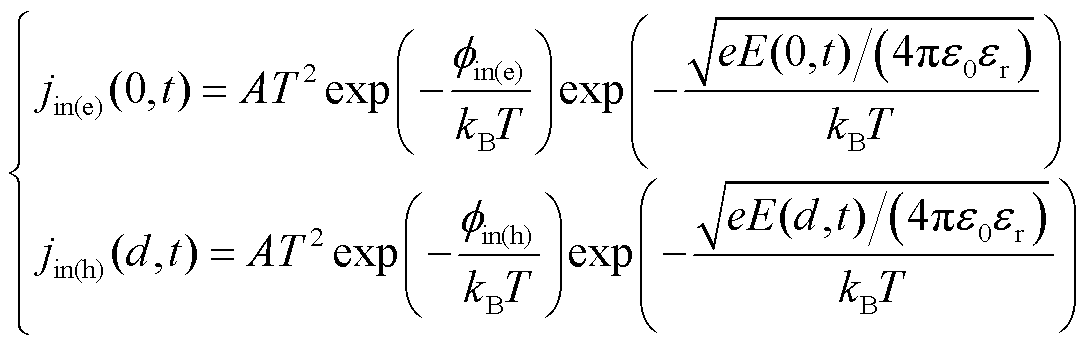（7）
式中，
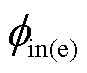和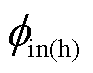
分别为电子和空穴的有效注入势垒，eV；A为Richardson常数；e为元电荷量，C。
注入到介质中的载流子受电场作用，在绝缘材料内部分别向阴极和阳极迁移，其过程服从电荷连续性方程、电流传导方程以及泊松方程。在绝缘介质中的任一位置，电荷密度大小随时间的变化与流入、流出的电流密度之差大小相等。电荷连续性方程为[31-32]
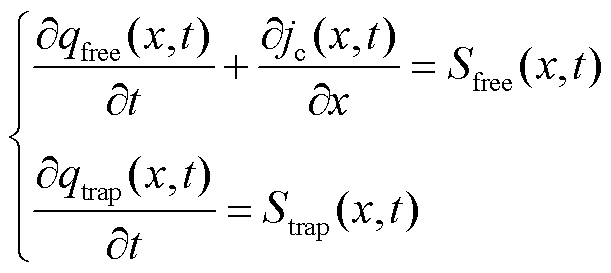（8）
式中，qfree和qtrap分别为自由电荷和捕获电荷的密度，C/m3；jc为传导电流密度，A/m2；Sfree和Strap分别为自由电荷和陷阱电荷的反应项。
电荷输运过程形成的电流密度遵循电流传导方程，表示为
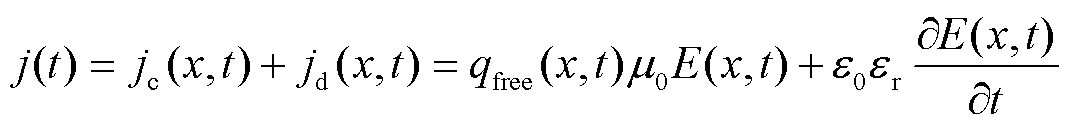（9）
式中，j为总电流密度，A/m2；jd为位移电流密度，A/m2。
空间电荷与电位j的关系满足泊松方程，表示为
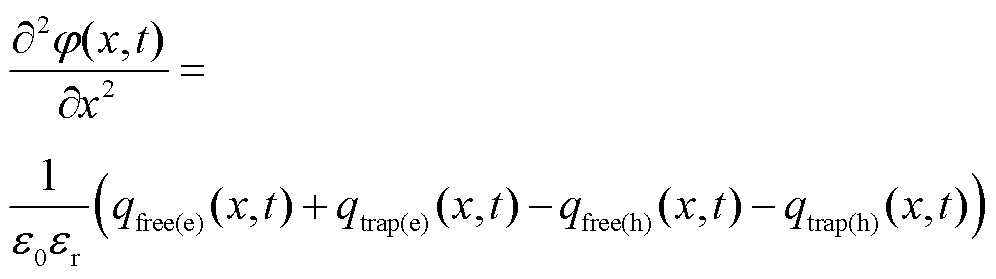（10）
电荷输运过程中，载流子会受深陷阱影响被捕获，在介质界面处形成空间电荷。本文只考虑单一陷阱对于电荷的捕获作用。而被捕获的载流子受热激发影响，会从深陷阱中脱陷。同时，当电子和空穴在绝缘介质中相遇时会发生电荷复合。式（8）中Sfree(x,t)和Strap(x,t)的扩展式如式（11）所示[20,32]，其描述了电荷的捕获-脱陷-复合的过程。
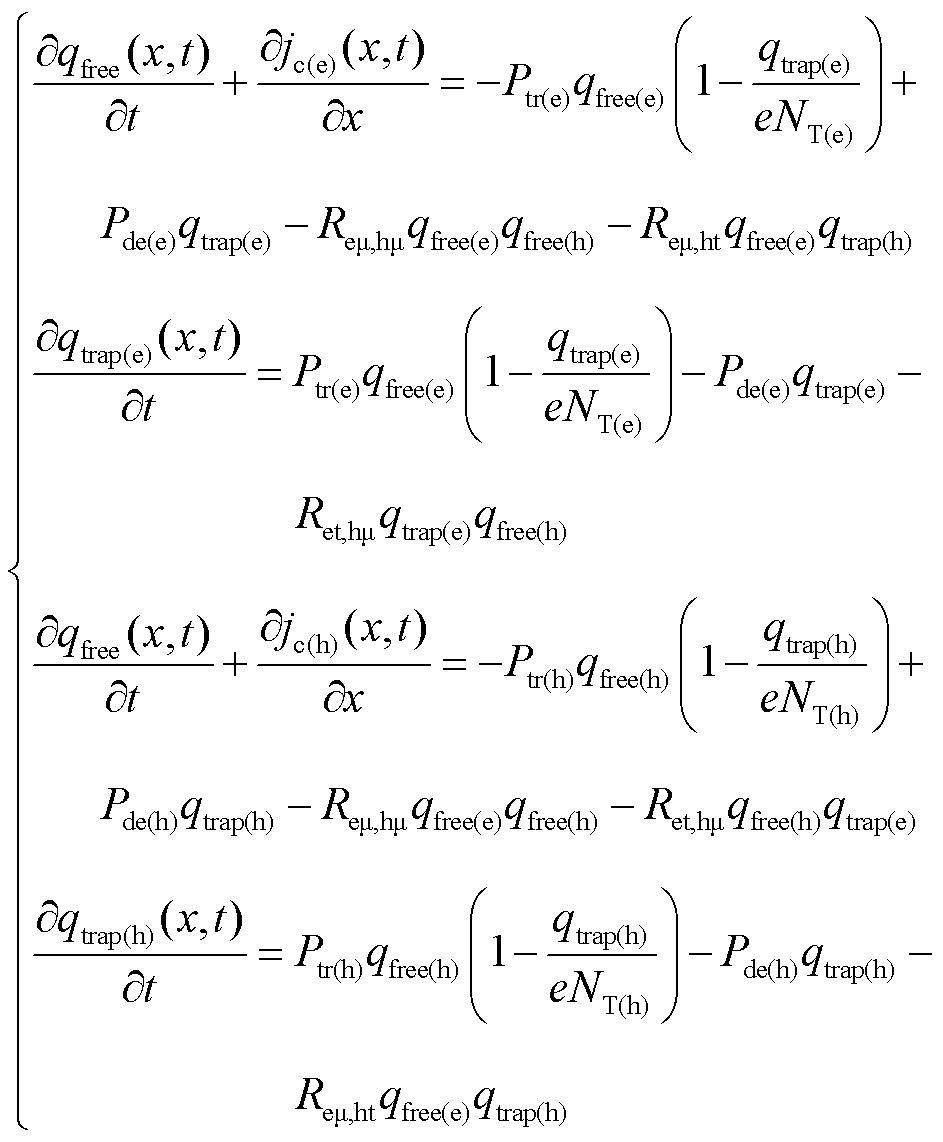（11）
式中，下标μ和t分别表示可移动（自由）和被捕获。
式（11）中，由于强库仑力作用，电荷在迁移过程中可能被深陷阱捕获，捕获概率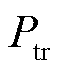
可表示为[33]
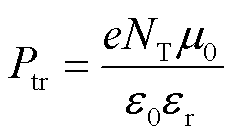（12）
式中，NT为深陷阱捕获密度，m-3。
热激发过程使得深陷阱释放电荷，电荷脱陷概率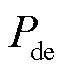
为[20-21]
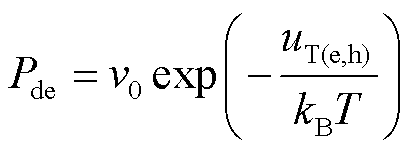（13）
式中，uT为深陷阱能级，eV；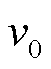
为试图逃逸频率。
自由电子与自由空穴的复合系数Reμ,hμ、自由电子与捕获空穴的复合系数Reμ,ht、捕获电子与自由空穴的复合系数Ret,hμ（单位均为m3/(C∙s)）分别表示[34-36]为
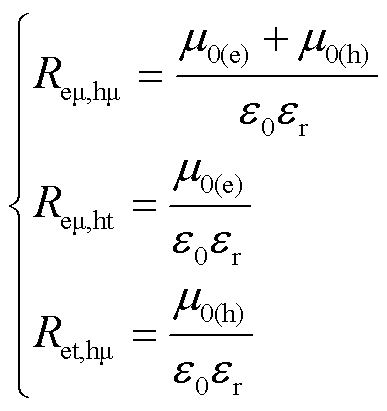（14）
如图4所示，载流子被深陷阱捕获后，与其相连的分子链受库仑力影响迁移，从而引起自由体积的扩张。捕获电子、带负电荷的分子链向阳极运动；捕获空穴、带正电荷的分子链向阴极运动。深陷阱分子链的运动特征可表示为
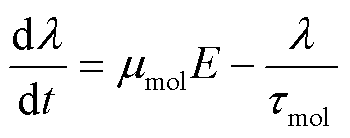（15）
式中，λ为分子链的位移，m；μmol为分子链的迁移率，m2/(V∙s)；τmol为分子链的弛豫时间，s。
3.1.2 输入参数与方程求解
仿真计算中采用的试样厚度范围与高温直流击穿实验中的试样厚度范围相同，温度设置为90℃，外加斜坡电压的升压速率为1 kV/s。电子和空穴的深陷阱密度、深陷阱能级和载流子迁移率采用2.1节ISPD实验得到的结果。CTMD仿真模型中XLPE的输入参数见表2。
电荷输运仿真计算采用高阶精度龙格库塔间断伽辽金法，泊松方程采用有限边界元法求解[23,30]。
表2 CTMD仿真模型中XLPE的输入参数
Tab.2 Input parameters of XLPE in CTMD model
参数数值 温度T/K363 相对介电常数εr2.35 空穴和电子的注入势垒/eV1.15 空穴的深陷阱密度NT(h)/(eV-1·m-3)3.39×1020 电子的深陷阱密度NT(e)/(eV-1·m-3)3.85×1020 空穴和电子的深陷阱能级uT/eV1.16 空穴的载流子迁移率μ0(h)/[m2/(V∙s)]6.15×10-15 电子的载流子迁移率μ0(e)/[m2/(V∙s)]6.63×10-15
电介质绝缘材料中载流子输运与能量积累过程最终导致电介质的击穿，而此过程与电荷输运参数密切相关。因此，在CTMD模型中引入三种电荷输运随机变量：陷阱能级、陷阱密度和载流子迁移率。通过调控输运随机变量的标准差来仿真电荷输运、分子链位移以及自由体积扩张的过程，进而调控载流子能量的积累和消逝过程[37]。
采用400 μm的XLPE试样进行仿真实验，当三种电荷输运随机变量标准差不同时，计算得到的击穿场强威布尔分布如图5所示，其中σ为高斯分布的标准差。图5a中，当陷阱能级的σ分别为0.000 1、0.000 5、0.001、0.003、0.008 eV时，威布尔分布的形状参数分别为494.9、143.6、75.1、34.2、10.0。图5b中，当陷阱密度的σ分别为0.001、0.01、0.1、0.2、0.3eV-1·m-3时，威布尔分布形状参数分别为4 451.6、467.9、39.2、26.8、13.0。图5c中，当载流子迁移率的σ分别为0.001、0.01、0.1、0.215、0.3 m2/(V∙s)时，威布尔分布形状参数分别为3 268.6、333.9、37.0、17.6、14.4。结果表明，基于CTMD模型，当陷阱能级、陷阱密度和载流子迁移率为符合高斯分布的随机变量时，得到的击穿场强是服从威布尔分布的。随着随机变量标准差的增大，击穿场强数据的形状参数减小，分散性增大。
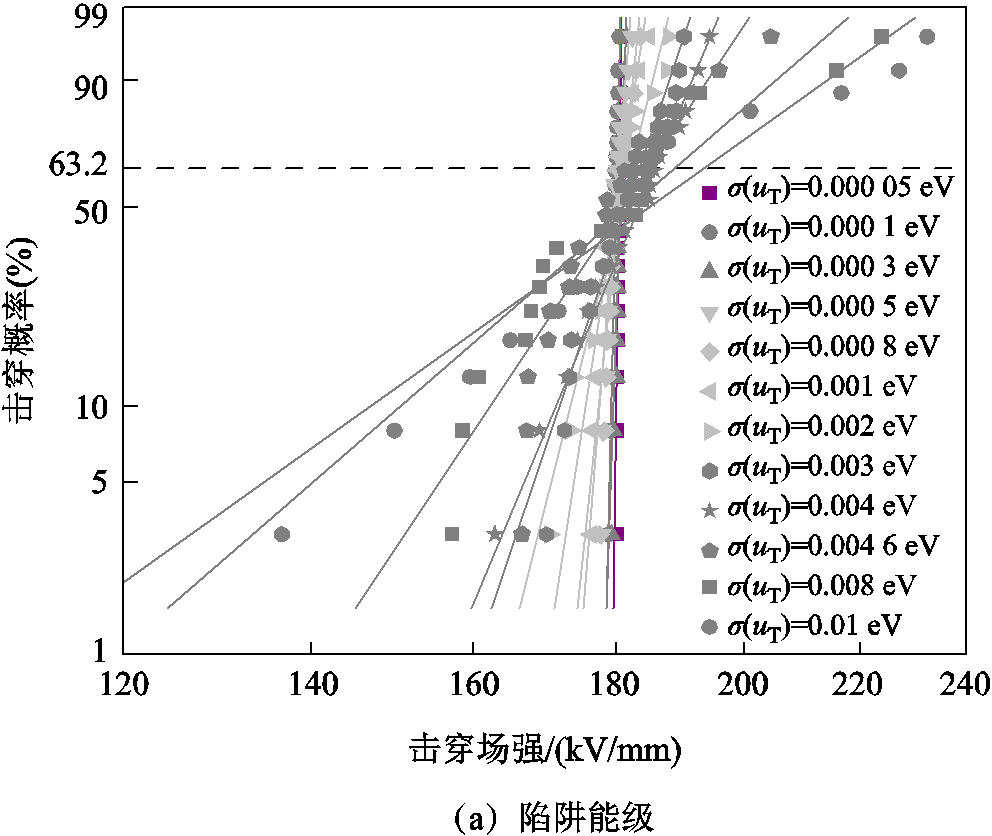
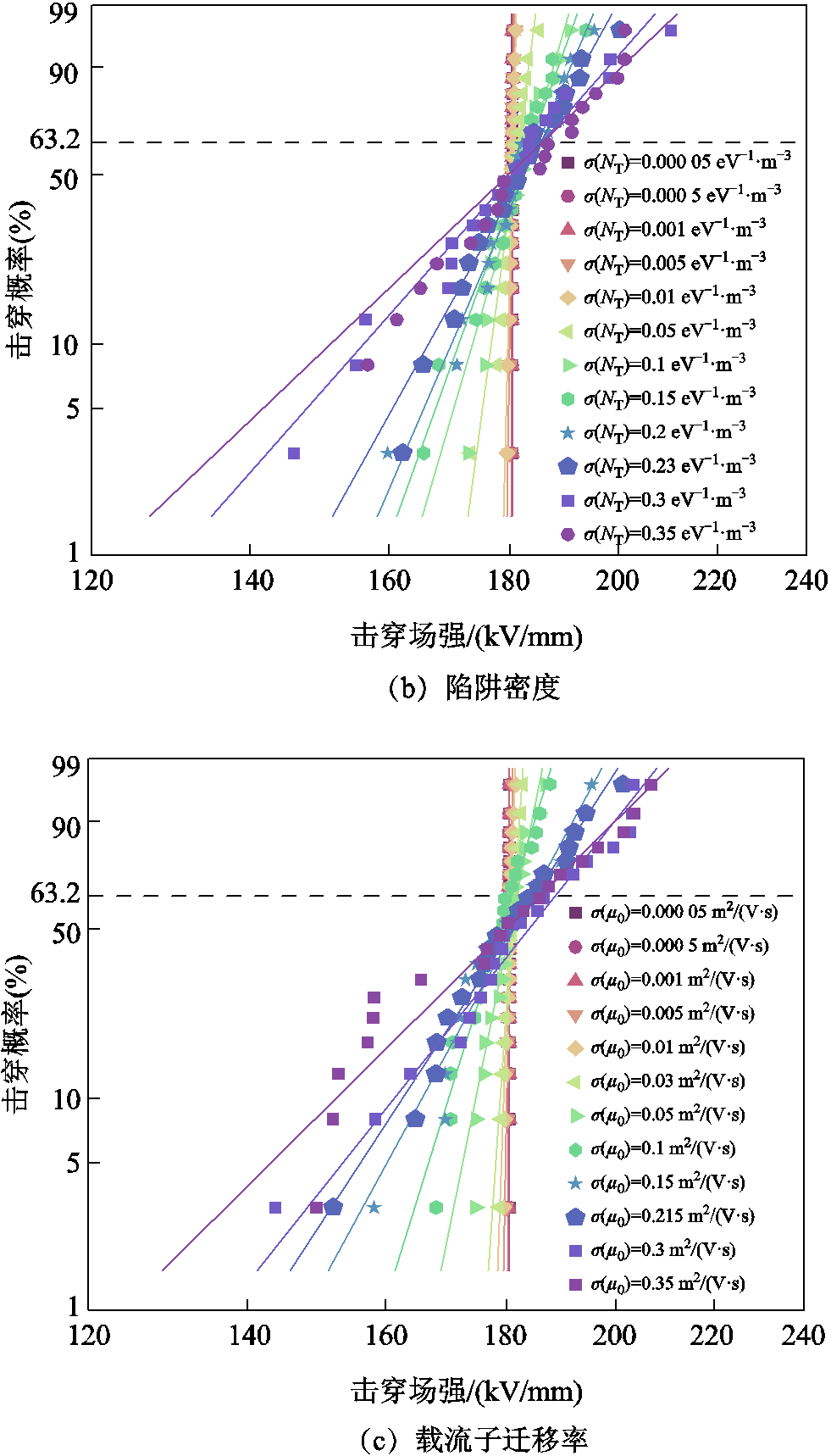
图5 电荷输运随机变量标准差不同时的击穿威布尔分布
Fig.5 Breakdown Weibull distribution with different standard deviations
从图5中可以看出，XLPE击穿概率的威布尔分布特性可以通过调节输运随机变量的标准差进行调控。据此建立了这三种电荷输运随机变量的威布尔分布形状参数和特征击穿场强与随机变量标准差σ的关系，如图6所示。
形状参数变化曲线呈现下降趋势，随着随机变量标准差的增加，威布尔分布形状参数急剧减小，如图6a所示。这是由于电荷输运随机变量的增大使得载流子输运和能量积累过程的波动幅度增大，绝缘材料击穿场强的分散性也随之增加。可以看出，威布尔分布形状参数随着随机变量标准差的增大而减小，并趋于实验值附近。对比陷阱能级、陷阱密度和载流子迁移率这三种随机变量形状参数的变化曲线可以发现，与陷阱密度和载流子迁移率随机变量相比，陷阱能级的形状参数最小，陷阱密度和载流子迁移率的形状参数下降趋势类似。当威布尔形状参数值与实验结果值相同时，陷阱能级、载流子迁移率与陷阱密度对应的标准差依次增加。说明基于CTMD模型，威布尔分布形状参数受陷阱能级影响最大，受陷阱密度和载流子迁移率影响较小。
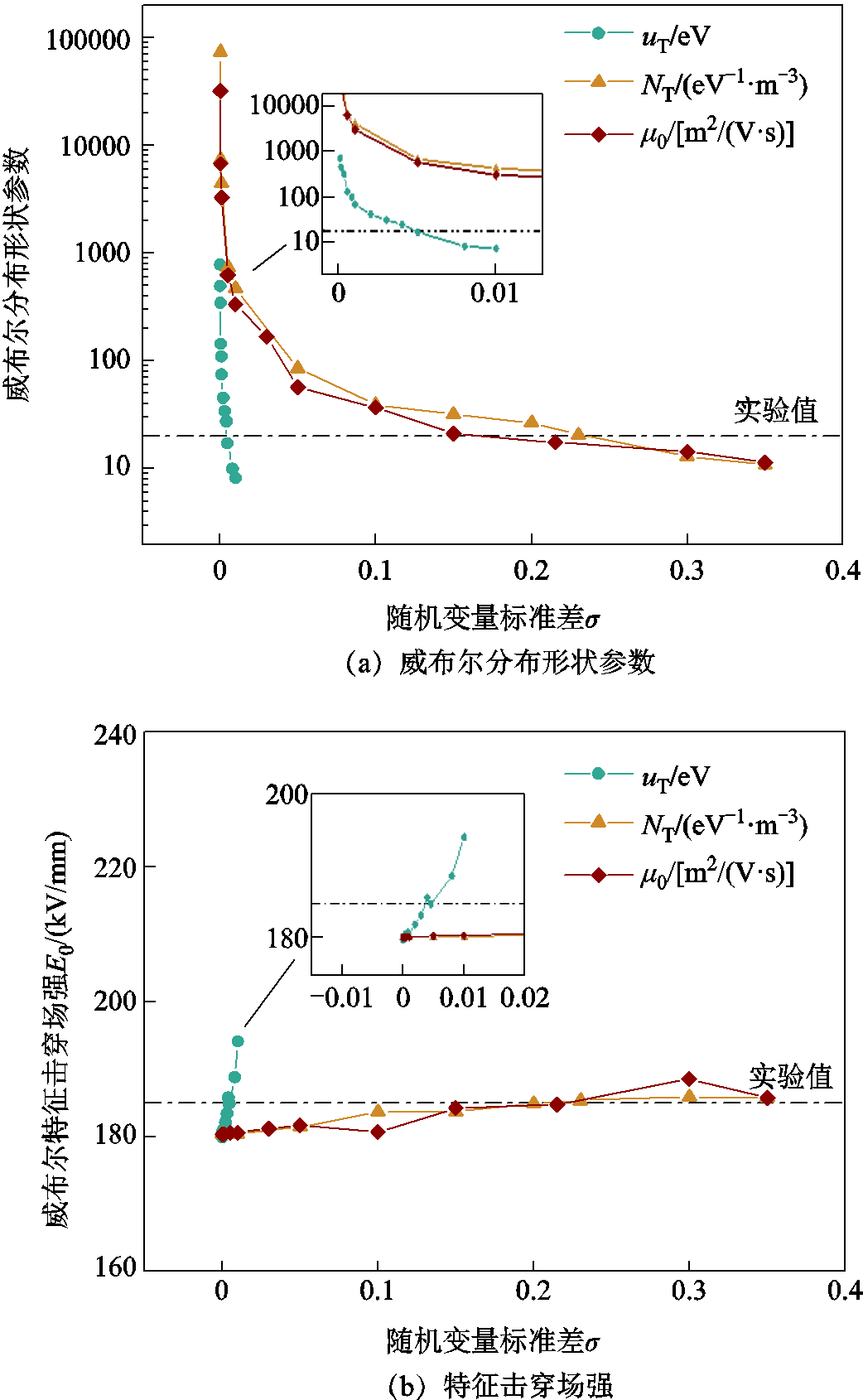
图6 威布尔分布形状参数和特征击穿场强与电荷输运随机变量标准差的关系
Fig.6 Standard deviation plot of shape parameters of the Weibull distribution and characteristic breakdown field strength and charge transport random variables
建立威布尔特征击穿场强和随机变量标准差的关系如图6b所示，随机变量的分布范围可以表明电荷输运参数对于威布尔分布的影响程度，分布范围越小，影响作用越强。对比图6b中曲线发现，威布尔特征击穿场强随陷阱能级增大而变化的程度最明显。因此，可以证明陷阱能级是影响威布尔分布的主要参数。图6b中特征击穿场强最大值为194.1 kV/mm，最小值为180.0 kV/mm，稳定在实验值185.0 kV/mm附近。因此，CTMD模型可以很好地模拟仿真XLPE的高温直流电击穿过程，得到较为准确的特征击穿场强。
在之前的研究过程中，已对室温下的直流击穿模型进行了仿真研究[23]。室温下试样中电导形成的焦耳热比较小，温升不明显；而高温下电导率较大，导致试样中的焦耳热大幅增加，温升比较明显。 160 μm试样在30℃和90℃下的直流击穿过程如图7所示。从图7中可以看到，随着斜坡电压的逐步升高，试样温度也逐渐升高。此外，高温下的分子链运动速率更快，载流子积累能量，自由体积扩张迅速，载流子迁移速度快，引起局部电流升高和局部温度的上升。自由移动的载流子则会与聚合物晶格发生激烈碰撞，产生电离，试样迅速被击穿，因此高温下的击穿强度会远低于室温下的击穿强度。与之前的常温模型相比较，高温模型中分子链迁移率的前置系数有所增强。
图7 160 μm试样在不同温度下的直流击穿过程
Fig.7 DC breakdown process of 160 μm sample at different temperatures
调节CTMD模型中的陷阱能级、陷阱密度和载流子迁移率三种电荷输运随机变量的标准差，对不同厚度的XLPE进行仿真拟合，得到的结果与实验结果进行对比，如图8所示。调节随机变量的标准差大小，使不同厚度下的XLPE威布尔分布仿真结果的特征击穿场强和形状参数接近于实验结果。
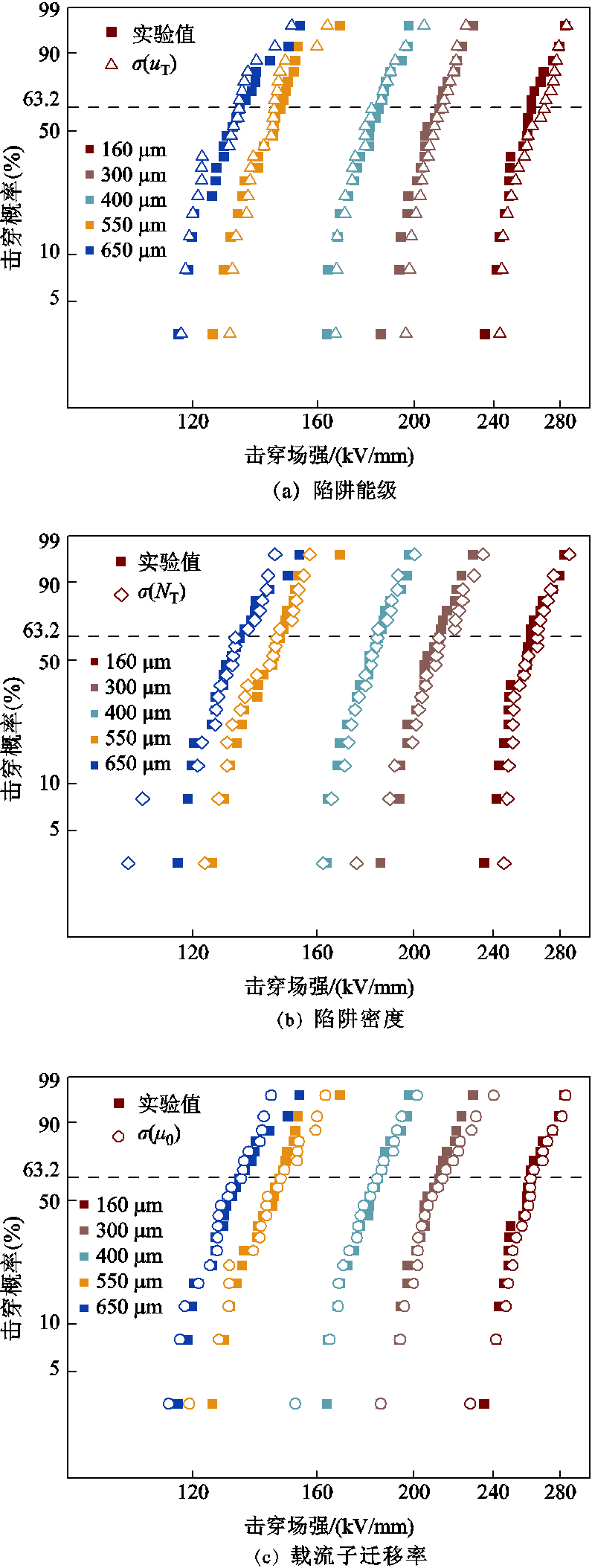
图8 威布尔分布仿真结果与实验结果对比
Fig.8 Comparison of simulation and experimental results for the Weibull distribution
图9为绘制的不同厚度下XLPE的随机变量标准差曲线。通过调节陷阱能级参数，得到160、300、400、550、650 μm厚度的XLPE试样的对应标准差分别为0.004 2、0.004 4、0.004 6、0.004 7、0.004 8 eV；通过调节陷阱密度参数，得到五种厚度XLPE试样对应的标准差值分别为0.22、0.225、0.23、0.235、0.245 eV-1·m-3；通过调节载流子迁移率标准差参数，得到五种厚度XLPE试样对应的标准差值分别为0.18、0.195、0.215、0.245、0.265 m2/(V∙s)。随着XLPE试样厚度的增加，随机变量的标准差逐渐增大，其中陷阱能级的标准差变化的程度最小，标准差值介于0.004～0.005 eV之间，载流子迁移率与陷阱密度的标准差变化趋势类似。仿真结果表明，影响XLPE击穿概率分散性的原因之一是电介质绝缘厚度影响了电荷输运参数的标准差大小。
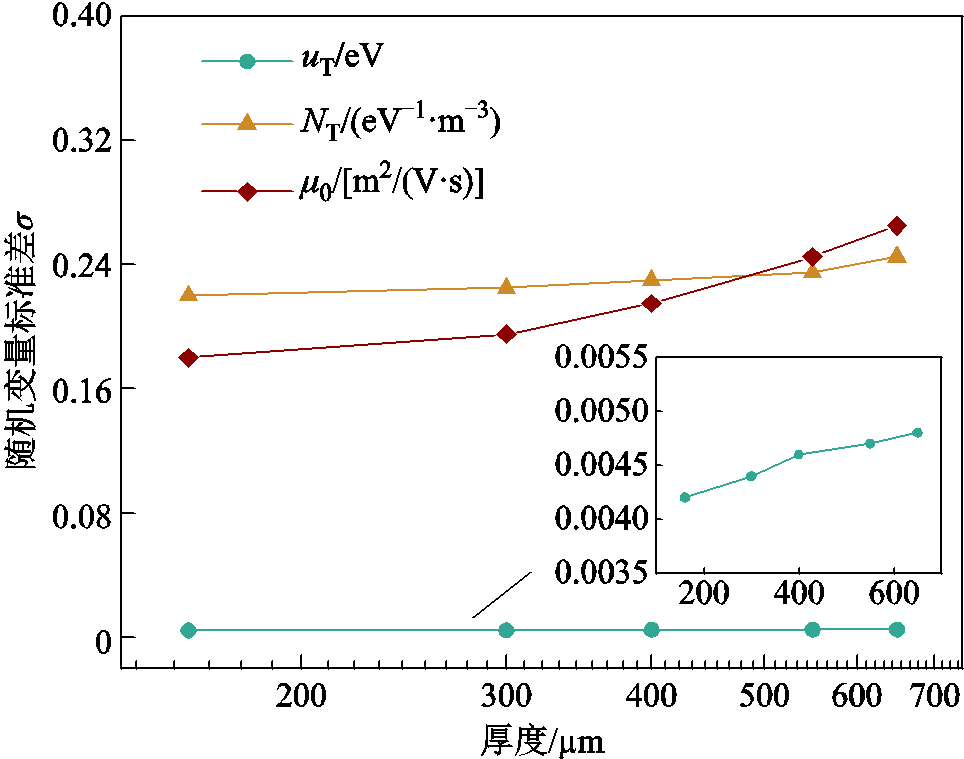
图9 不同厚度下XLPE的随机变量标准差曲线
Fig.9 Random variable standard deviation curves for XLPE in different thicknesses
不同厚度下特征击穿场强仿真结果与实验结果对比如图10所示。通过调节陷阱能级标准差，可以获得160、300、400、550、650 μm厚度的XLPE试样的特征击穿场强分别为268.5、224.5、184.9、146.4、134.1 kV/mm；调节陷阱密度标准差，五种厚度XLPE试样的特征击穿场强分别为266.4、216.0、185.4、147.7、134.9 kV/mm；调节载流子迁移率标准差，五种厚度XLPE试样仿真的特征击穿场强分别为265.9、216.8、184.8、148.6、133.9 kV/mm。XLPE的击穿实验结果在双对数坐标下与试样厚度呈线性关系，即逆幂形式E=kd-n，其中实验值的n=0.45，调节陷阱能级、陷阱密度、载流子迁移率标准差得到n的仿真结果分别为0.47、0.46、0.46。仿真结果与实验结果接近，说明考虑电荷输运和载流子位移的CTMD模型可以较好地模拟厚度对绝缘电介质直流击穿的影响。
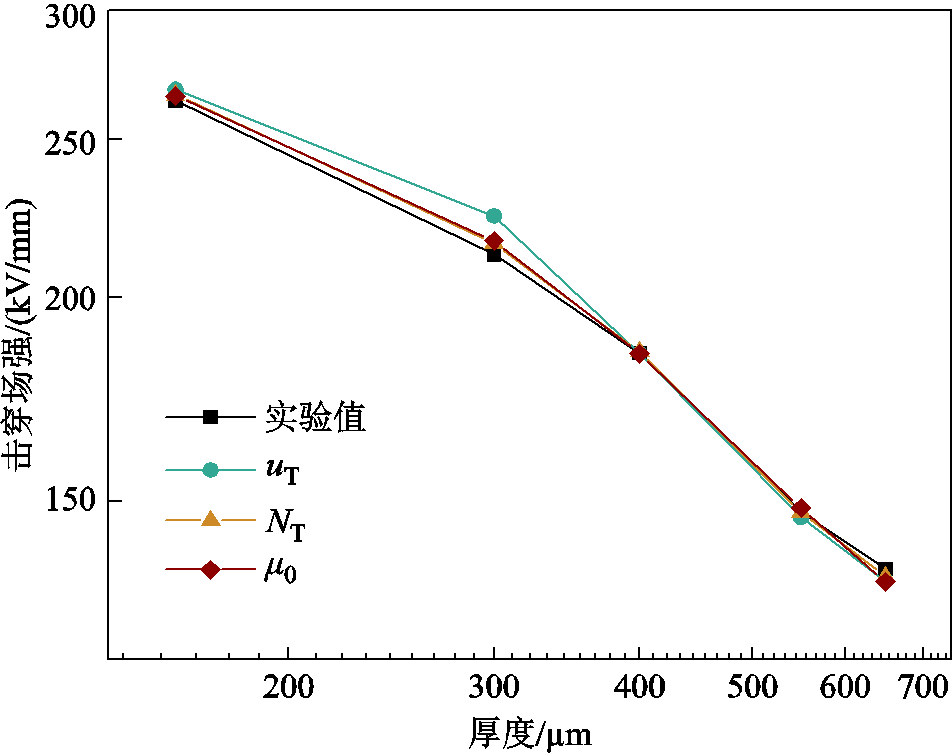
图10 特征击穿场强仿真结果与实验结果对比
Fig.10 Comparison of simulation and experimental results for the characteristic breakdown field strength
对于较薄的绝缘介质，导电击穿路径由较少的陷阱组成，陷阱分布窄；而对于较厚的绝缘介质，击穿路径由大量的陷阱组成，更多的陷阱意味着其有更宽的分布，因此直流击穿场强的威布尔分布随机性更强，击穿概率更加分散。实验结果表明，在不同厚度下的XLPE击穿概率分布仿真结果与实验结果相吻合，且在CTMD模型中陷阱能级输运参数是影响威布尔分布形状参数的主要因素，该模型能有效地模拟不同厚度下交联聚乙烯的击穿机理。绝缘电介质厚度效应不仅会导致其特征击穿场强的减小，也会使其击穿概率分散性增大，因此，在高电压等级电缆的绝缘设计过程中，需要同时考虑使特征击穿场强降低和击穿场强分散性增大的厚度效应。
本文为探究交联聚乙烯电缆绝缘的厚度效应，研究了高温直流电压下交联聚乙烯绝缘特征击穿场强和威布尔分布形状参数随试样厚度的变化规律，针对160、300、400、550、650 μm五种厚度的XLPE试样在90℃下进行了直流击穿实验，并提出用CTMD模型进行仿真分析。通过实验与仿真对比分析，可以得出以下结论：
1）交联聚乙烯绝缘的高温直流击穿场强的分散性与其厚度相关。厚交联聚乙烯绝缘陷阱参数有更宽的高斯分布，使直流击穿场强分散性更为明显。因此，在进行高电压等级电缆绝缘设计时，既需要考虑厚度效应导致的特征击穿场强的降低，还需要考虑其导致的击穿场强分散性的增大。
2）采用CTMD模型引入随机变化的电荷输运变量进行仿真得到，随着电荷输运随机变量标准差的增大，XLPE击穿概率威布尔分布形状参数减小，击穿场强数据的分散性增大。对比陷阱密度、电荷注入势垒和载流子迁移率三种电荷输运随机变量，威布尔特征击穿场强分散性随陷阱能级标准差的增大而变化的程度最明显。
3）交联聚乙烯绝缘的高温直流击穿场强随着厚度的增大而减小，呈逆幂函数关系，且电荷输运参数标准差的变化不影响其特征击穿场强大小。绝缘电介质内部分子链定向运动，更厚的交联聚乙烯绝缘介质中其陷阱含有更宽的分布，更易产生积聚效应而发生击穿现象。
参考文献
[1] 周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612.
Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612.
[2] 尚恺, 李加才, 王诗航, 等. 高压电缆交联聚乙烯绝缘料黏度参数对挤出特性影响的仿真研究[J]. 电工技术学报, 2024, 39(3): 810-819.
Shang Kai, Li Jiacai, Wang Shihang, et al. Simulation study on the extrusion performances based on the viscosity parameters of cross-linked polyethylene insulating materials for high-voltage cables[J]. Transactions of China Electrotechnical Society,2024, 39(3): 810-819.
[3] 魏艳慧, 郑元浩, 龙海泳, 等. 绝缘层厚度对高压直流电缆电场和温度场分布的影响[J]. 电工技术学报, 2022, 37(15): 3932-3940.
Wei Yanhui, Zheng Yuanhao, Long Haiyong, et al. Influence of insulation layer thickness on electric field and temperature field of HVDC cable[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3932-3940.
[4] 石逸雯, 陈向荣, 孟繁博, 等. 电压稳定剂及其含量对高压直流用500kV XLPE电缆材料绝缘性能的影响[J]. 电工技术学报, 2022, 37(22): 5851-5861.
Shi Yiwen, Chen Xiangrong, Meng Fanbo, et al. The effect of voltage stabilizer and its content on the insulation properties of 500kV HVDC cable insulation materials[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5851-5861.
[5] Ouyang Yingwei, Pourrahimi A M, Lund A, et al. High-temperature creep resistant ternary blends based on polyethylene and polypropylene for thermoplastic power cable insulation[J]. Journal of Polymer Science, 2021, 59(11): 1084-1094.
[6] Lü Hongkun, Lu Tianhao, Xiong Lingqi, et al. Assessment of thermally aged XLPE insulation material under extreme operating temperatures[J]. Polymer Testing, 2020, 88: 106569.
[7] 陈向荣, 洪泽林, 朱光宇, 等. 高温下电压稳定剂对交联聚乙烯电树枝化及局部放电特性的影响[J]. 电工技术学报, 2023, 38(3): 577-586.
Chen Xiangrong, Hong Zelin, Zhu Guangyu, et al. Effect of voltage stabilizer on electrical treeing and partial discharge characteristics of crosslinked polyethylene at high temperature[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 577-586.
[8] 王泽瑞, 赵学童, 赵远涛, 等. 66 kV交联聚乙烯海底电缆绝缘厚度设计[J]. 高电压技术, 2023, 49(6): 2634-2643.
Wang Zerui, Zhao Xuetong, Zhao Yuantao, et al. Insulation thickness design of 66 kV XLPE submarine cable[J]. High Voltage Engineering, 2023, 49(6): 2634-2643.
[9] 李栋, 王宇, 朱智恩, 等. ±400kV高压直流电缆绝缘厚度设计与验证[J]. 绝缘材料, 2021, 54(6): 91-95.
Li Dong, Wang Yu, Zhu Zhien, et al. Thickness design and verification for ±400kV HVDC cable insulation[J]. Insulating Materials, 2021, 54(6): 91-95.
[10] Min Daomin, Li Shengtao, Ohki Y. Analysis on the thickness and temperature dependent DC breakdown of low density polyethylene[C]//2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, Australia, 2015: 368-371.
[11] Akram S, Bhutta M S, Zhou Kai, et al. DC breakdown of XLPE modulated by space charge and temperature dependent carrier mobility[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(5): 1514-1522.
[12] 钱恺羽, 苏鹏飞, 吴建东, 等. 不同温度下高压直流电缆绝缘击穿场强的厚度效应[J]. 中国电机工程学报, 2018, 38(24): 7121-7130.
Qian Kaiyu, Su Pengfei, Wu Jiandong, et al. The effect of thickness on breakdown strength in high voltage direct current cable insulation at different temperatures [J]. Proceedings of the CSEE, 2018, 38(24): 7121-7130.
[13] 王兆琛, 段玉兵, 魏艳慧, 等. 高压电缆绝缘热老化特性及破坏机理研究[J]. 高压电器, 2023, 59(11): 56-64.
Wang Zhaochen, Duan Yubing, Wei Yanhui, et al. Research on insulation thermal aging characteristic and destruction mechanism of high voltage cable[J]. High Voltage Apparatus, 2023, 59(11): 56-64.
[14] 张伟, 胡修翠, 高超, 等. 长期服役XLPE电缆绝缘的空间电荷与热性能[J]. 高电压技术, 2022, 48(9): 3533-3541.
Zhang Wei, Hu Xiucui, Gao Chao, et al. Space charge and thermal characteristics of long-service crosslinked polyethylene cable insulation[J]. High Voltage Engineering, 2022, 48(9): 3533-3541.
[15] 王威望, 汪朝辉, 卜文, 等. 高压海底电缆电-热耦合仿真分析和电压极性反转的影响研究[J]. 广东电力, 2019, 32(12): 43-50.
Wang Weiwang, Wang Zhaohui, Bu Wen, et al. Simulation analysis on thermoelectric coupling characteristics of HV submarine cables and study of effect of voltage polarity reversal[J]. Guangdong Electric Power, 2019, 32(12): 43-50.
[16] Nicol W S. Thickness variation of breakdown field strength in plasma oxidized aluminum films[J]. Proceedings of the IEEE, 1968, 56(1): 109-110.
[17] Mizutani T, Mori T, Matsuoka T. Space charge and breakdown of poly-p-xylylene thin film[J]. Proceedings of the 4th International Conference on Conduction and Breakdown in Solid Dielectrics, ICSD 1992, 1992: 488-491.
[18] Yamano Y, Endoh H. Increase in breakdown strength of PE film by additives of azocompounds[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1998, 5(2): 270-275.
[19] Zhou H, Shi F G, Zhao B, et al. Temperature accelerated dielectric breakdown of PECVD low-k carbon doped silicon dioxide dielectric thin films[J]. Applied Physics A, 2005, 81(4): 767-771.
[20] Min Daomin, Li Shengtao, Ohki Y. Numerical simulation on molecular displacement and DC breakdown of LDPE[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(1): 507-516.
[21] Min Daomin, Li Yuwei, Yan Chenyu, et al. Thickness-dependent DC electrical breakdown of polyimide modulated by charge transport and molecular displacement[J]. Polymers, 2018, 10(9): 1012.
[22] Cai Shurao, Gao Ziwei, Ji Minzun, et al. Simulation on weibull-distribution of PP nanocomposites modulated by carrier transport and molecular displacement[C]//22nd International Symposium on High Voltage Engineering (ISH 2021), Xi’an, China, 2021: 1887-1891.
[23] 朱敏慧, 闵道敏, 高梓巍, 等. 直流电缆用交联聚乙烯绝缘的击穿概率及其尺度效应仿真[J]. 电工技术学报, 2024, 39(4): 1172-1184.
Zhu Minhui, Min Daomin, Gao Ziwei, et al. Breakdown probability and size effect simulation of XLPE insulation for DC power cables[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1172-1184.
[24] Ma Zhipeng, Yang Lijun, Bhutta M S, et al. Effect of thickness on the space charge behavior and DC breakdown strength of cross-linked polyethylene insulation[J]. IEEE Access, 2020, 8: 85552-85566.
[25] Zhou Fusheng, Li Jianying, Yan Zhimin, et al. Investigation of charge trapping and detrapping dynamics in LDPE, HDPE and XLPE[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(6): 3742-3751.
[26] Sonnonstine T J, Perlman M M. Surface-potential decay in insulators with field-dependent mobility and injection efficiency[J]. Journal of Applied Physics, 1975, 46(9): 3975-3981.
[27] Bhutta M S, Yang Lijun, Ma Zhipeng, et al. Simulation of thickness controlled DC breakdown of XLPE regulated by space charge & molecular chain movement[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(4): 1143-1151.
[28] 李忠磊, 韩晨磊, 赵伟铭, 等. 基于等温表面电位衰减法的氧化石墨烯/低密度聚乙烯纳米复合材料陷阱分布特性[J]. 高电压技术, 2017, 43(11): 3583-3590.
Li Zhonglei, Han Chenlei, Zhao Weiming, et al. Characteristics of trap level distribution in graphene oxide/low density polyethylene nanocomposites based on the isothermal surface potential decay method[J]. High Voltage Engineering, 2017, 43(11): 3583-3590.
[29] Cheng Hongyi, Zhao Jiankang, Zheng Peng, et al. Simulation calculation and analysis of insulation thermal breakdown of XLPE cable under DC voltage[C]//The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online, 2021: 2026-2032.
[30] 谢东日. 聚丙烯纳米复合界面调控及其与击穿特性关联的研究[D]. 西安交通大学, 2020.
Xie Dongri. Investigation into interface tailoring of polypropylene nanocomposite and its relationship with breakdown properties[D]. Xi’an Jiaotong University, 2020.
[31] Teyssedre G, Laurent C. Charge transport modeling in insulating polymers: from molecular to macroscopic scale[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(5): 857-875.
[32] Li Shengtao, Min Daomin, Wang Weiwang, et al. Modelling of dielectric breakdown through charge dynamics for polymer nanocomposites[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(6): 3476-3485.
[33] Kuik M, Koster L J, Wetzelaer G A, et al. Trap-assisted recombination in disordered organic semiconductors[J]. Physical Review Letters, 2011, 107(25): 256805.
[34] van der Holst J J M, van Oost F W A, Coehoorn R, et al. Electron-hole recombination in disordered organic semiconductors: validity of the Langevin formula[J]. Physical Review B, 2009, 80(23): 235202.
[35] Kuik M, Koster L J A, Dijkstra A G, et al. Non-radiative recombination losses in polymer light-emitting diodes[J]. Organic Electronics, 2012, 13(6): 969-974.
[36] Shockley W, Read W T. Statistics of the recombinations of holes and electrons[J]. Physical Review, 1952, 87(5): 835-842.
[37] 蔡姝娆, 高梓巍, 纪民尊, 等. 聚丙烯载流子输运与能量积累调制直流击穿威布尔分布特性仿真研究[J]. 电气工程学报, 2021, 16(2): 50-59.
Cai Shurao, Gao Ziwei, Ji Minzun, et al. Simulation of carrier transport and energy accumulation modulated DC breakdown Weibull distribution in polypropylene[J]. Journal of Electrical Engineering, 2021, 16(2): 50-59.
Abstract The design of XLPE insulation thickness is one of the key tasks in the development and manufacturing of HVDC cables. However, it is difficult to obtain the DC breakdown performance parameters of thick insulation samples in the laboratory, and the design of insulation thickness lacks direct data support. Meanwhile, although there are continuous attention and researches on the thickness effect of breakdown field strength and the breakdown Weibull probability distribution of solid dielectric, there are few studies on the DC breakdown field thickness effect based on XLPE at high temperatures, and there are few reports on the dispersion of the DC breakdown field strength. Therefore, it is of great significance to study the effect of thickness on DC breakdown of XLPE insulation. In this paper, the high temperature DC breakdown experiment of XLPE insulation samples with different thicknesses was carried out, and charge transport and molecular displacement modulated model (CTMD) was used to simulate and analyze the breakdown process. Besides, the characteristic breakdown field strength and Weibull distribution shape parameters of XLPE insulation under high temperature DC voltage are studied with sample thickness.
In dielectric insulation, the deep trap captures carriers, forming space charges at the interface of the insulating medium, and the continuous aggregation of space charges make the electric field strength distorted. At the same time, by the Coulomb force, the displacement of the molecular chains make the expansion of the free volume, the charge energy increases dramatically. When the charge energy increases to the point where it can leap over the trap barrier, the insulating material breaks down. DC breakdown experiments were carried out on 160, 300, 400, 550 and 650 μm XLPE specimens at 90℃. The characteristic DC Weibull breakdown field strengths were 264.1, 212.6, 185.0, 147.7, 136.4 kV/mm and the shape parameters of the Weibull distribution were 21.3, 20.5, 19.9, 14.1 and 13.5.
The process of carrier transport and energy accumulation in dielectric insulating materials ultimately leads to the breakdown of the dielectric, and this process is closely related to the charge transport parameters. Therefore, three charge transport random variables, which are trap energy level, trap density and carrier mobility, are introduced into the CTMD model. By adjusting the trap charge transport random variables, the standard deviations of trap energy level, trap density and carrier mobility corresponding to XLPE are obtained.
The following conclusions are obtained from the experiment and simulations: (1) Thick XLPE insulation has a wider Gaussian distribution trap, making the DC breakdown field strength dispersion more obvious. Therefore, the thickness effects of reduced characteristic breakdown strength and increased breakdown strength dispersion need to be considered simultaneously in the design of high-voltage-rated cable insulation. (2) CTMD simulations yield that the shape parameter of the Weibull distribution decreases with increasing standard deviation of the charge transport random variable, and the dispersion of the breakdown field strength data increases. The dispersion of the characteristic Weibull breakdown field strength varies most significantly with increasing standard deviation of the trap energy level. (3) The high-temperature DC breakdown field strength of XLPE insulation decreases with increasing thickness in an inverse power function relationship, and variations in the standard deviation of the charge transport parameter do not affect the characteristic breakdown field strength.
keywords：XLPE, thickness effect, Weibull distribution, charge transport
中图分类号：TM215; TM85
DOI: 10.19595/j.cnki.1000-6753.tces.231759
国家自然科学基金（52077162, 51777162）和中央高校基本科研业务费专项资金（xzy012019022）资助项目。
收稿日期 2023-10-22
改稿日期 2023-12-08
朱敏慧 女，1999年生，硕士研究生，研究方向为交联聚乙烯的介电、击穿性能，交联聚乙烯的多物理仿真特性。E-mail：zzzminhui@stu.xjtu.edu.cn
闵道敏 男，1985年生，副教授，博士生导师，研究方向为先进绝缘材料与技术，高储能密度复合电介质，多物理场高效计算，局部放电、击穿、沿面闪络建模仿真与性能提升方法。E-mail：forrestmin@foxmail.com（通信作者）
（编辑 李 冰）