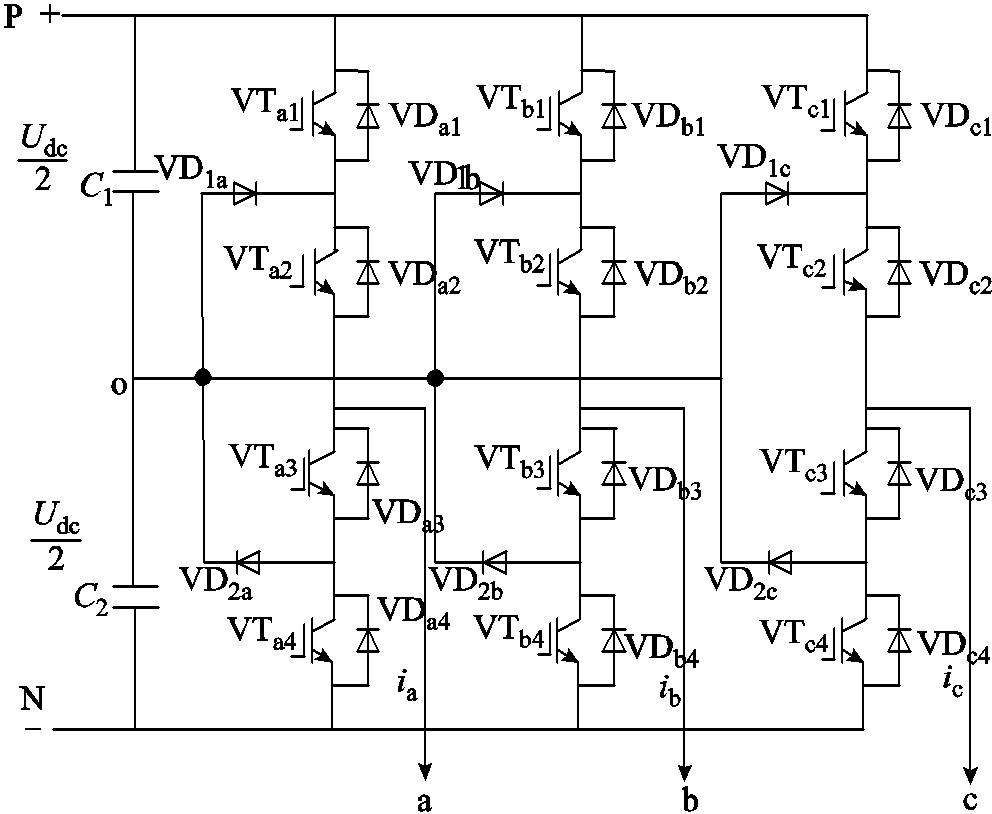
图1 NPC型三电平逆变器的主电路拓扑结构
Fig.1 The main circuit topology of NPC three-level inverter
摘要 在基于解析模型的故障诊断系统中,为了显化残差信号所包含故障信息的能力,提出一种面向残差评价的中点钳位型三电平三相逆变器快速开路故障诊断方法。首先,构建诊断观测器获取三相电流观测值并通过观测矩阵计算电流残差;其次,通过引入基于范数的标准评价函数,计算残差性能指标与阈值,将残差转换为可用的特征信号并与阈值相比较实现高效实时的故障检测;再次,推导不同功率开关器件开路故障状态下的电流残差特性,并依据此特性实现精准的故障隔离;最后,在仿真平台及半实物实验平台上验证了该文所提算法的有效性与可行性。仿真与实验平台结果表明,相较于传统基于信号与知识的诊断方法,残差性能评价的引入使得诊断速度提高80%以上。针对NPC型三电平三相逆变器常见的四种开路故障情况,均可实现快速且精准的故障检测及定位。
关键词:中点钳位(NPC)型三电平三相逆变器 开路故障诊断 残差评价 阈值 诊断观测器
电机是风机、泵、压缩机、机床、传输带等各种设备的驱动装置,广泛应用于冶金、石化、化工、煤炭、建材、公用设施等多个行业和领域,是用电量最大的耗电设备。因此,保障电机及其驱动系统的安全性、稳定性,提升电机系统性能已成为当今工业界与学术界的研究热点。
电机驱动系统主要由电源、电机驱动器、电机、传感器以及控制器组成。然而逆变器内部的核心单元功率开关器件,例如,IGBT(insulate gate bipolar transistor)管和MOSFET(metal oxide semiconductor field effect transistor)管,不仅在高开关频率下持续工作,而且需承受电与热的过应力,易出现故障。相关研究结果表明,电机驱动系统各部件的年故障率中,电力电子器件年故障率占总电气故障率的47.2%[1];变速驱动系统中约38%的故障是由半导体功率器件故障导致的[2]。在逆变器的各元器件中,电容元件、功率开关器件及印制电路板(Printed Circuit Board, PCB)是导致逆变器故障发生的主要来源[3]。其中,由功率开关器件所导致的逆变器故障占比21%,位居第二[4]。因此,功率器件被认为是电机驱动系统中最脆弱的部件。导致功率开关器件故障失效的原因主要来源于热应力、湿度及高电流密度应力三方面。在高开关频率的工作条件下,由器件温度所导致的热应力是功率开关器件故障失效的首要原因[5]。逆变器功率器件的故障类型包含开路故障与短路故障[6]。功率开关器件短路故障主要由驱动器电路故障、辅助电源故障、过电压/雪崩应力或温度过冲引起的固有故障。短路故障通过串联快速熔断器产生保护动作进而迅速转换为开路故障。现有的大多数IGBT短路检测和保护方法都是基于硬件电路的保护策略,并且已集成为标准功能模块[7]。功率开关器件开路故障主要是由于其所承高电场应力和高温应力、键合线的抬起以及栅极控制电路中的故障引起的[8]。然而开路故障会导致输出波形谐波增大和电机转矩脉动增大等问题,进而出现二次故障,给系统带来不良影响[9]。因此,逆变器开路故障诊断方法研究在降低经济损失、提高驱动系统稳定性等方面具有重要意义[10]。
目前,国内外针对逆变器开路故障诊断开展了相关研究。故障诊断方法可划分为基于解析模型的故障诊断方法[11-13]、基于信号处理的故障诊断方法[14-16]和基于知识的故障诊断方法[17-19]。其中基于解析模型的诊断方法依赖被控对象的精确数学模型,一旦数学模型参数不准确,容易出现误诊断问题。在传统基于解析模型的故障诊断方案中,以下的两个问题长时间被视为一种挑战:
(1)在故障检测环节中对于阈值的设定。以往基于解析模型的方案中,故障检测阈值大多根据前期人工经验设定,在系统处于复杂工况和受到噪声与扰动时,基于人工经验法的阈值难以实时检测故障,易出现故障误报与故障虚警现象。
(2)如何有效地提取残差信号中的故障信息[20]。基于解析模型故障诊断方案的核心可以抽象为从残差信号中过滤与提取有效的故障信息。然而在传统方案中,残差是通过观测器生成的观测信号与实际信号相减获得。残差信号通常被参数变化造成的扰动和不确定性所破坏。因此,如何解决上述两个问题,成为优化基于解析模型故障诊断技术中待解决的问题。
同时,在基于解析模型的故障诊断方法中,尽管故障诊断系统是由残差生成器、带有自适应阈值的残差评价器以及决策器组成的,但是残差评价和阈值计算的相关研究成果却很少。残差评价最初是为了确立一个残差信号的物理特性以实现有效的故障诊断[20]。在残差评价中有两个主要的方法:一个是在统计学方法中已经成熟的统计检验;另一个是基于范数的残差评价。其中基于范数的残差评价不仅具有较少的在线计算量,而且还可以用较完善的鲁棒控制原理进行系统自适应阈值的计算[20]。A. Emami-naeini等在基于模型的故障诊断技术上最先提出了基于范数的残差评价理念。在他们的先驱性工作中,A. Emami-naeini等提出了使用方均根(Root-Mean-Square, RMS)范数进行残差评价,并且基于残差评价函数推导出一个自适应阈值[21]。这个方法已经被用来诊断含干扰和模型不确定因素的动态系统中的故障。受此思想的启发,国内外许多研究者开始采用这个理念来处理H∞方法中的残差评估问题。其中,L2范数是作为残差估计函数来使用的。针对故障诊断与分离系统的综合设计,X. D. Steven等于2000年首次在基于范数的残差评估技术基础上提出了面向故障误报率与故障检测率的故障诊断系统集成设计[22]。目前,基于残差性能评价的故障诊断技术在国内外所开展的研究中,较多用于网络通信系统这一被控对象。
综上所述,针对残差性能评价,现有的两种方案均成功地将残差信号中的故障信息进行显化,通过残差性能这一中间“桥梁”,将残差信号、故障信息两个原本存在较少映射关系的变量联系起来。然而,对于在逆变器功率开关器件的开路故障诊断领域,国内外至今鲜有较为成熟的研究成果,是基于解析模型的开路故障诊断方法在电机驱动系统故障诊断框架下暂未被涉及的领域。
本文提出一种基于残差性能评价的逆变器开路故障诊断方法。首先,依据混杂系统建模理论构建逆变器与电机的混合逻辑动态统一模型,以系统输出的三相线电流为监测量,建立诊断观测器对线电流进行实时估计,并根据观测器的数学机理计算三相电流残差;然后,引入基于范数的评价函数计算残差性能指标与自适应阈值,通过残差特征信号与阈值比较,实现故障检测;最后,结合PSIM软件仿真平台与PTS-1000电力电子实验平台进行实验,验证本文所提残差性能评价诊断方法的快速性与准确性。相较于传统方案,通过残差性能评价设定的故障报警阈值是根据标准评价函数计算所得,相比于人工先验阈值更加具有客观性,并且考虑了外部干扰与不确定性所带来的影响。同时,残差性能评价方案通过生成残差信号的特征,显化并提取故障信息,实现残差信号对噪声扰动具有鲁棒性,但对故障信号具备敏感性。
中点钳位(Neutral Point Clamped, NPC)型三电平三相逆变器最早由日本长冈科技大学学者A. Nabae提出,是一种应用最为广泛的多电平拓扑结构。图1为NPC型三电平三相逆变器拓扑结构。图1中包含两个串联的直流电容C1和C2,C1和C2是两个电容值相等且具有分压和缓冲能量作用的直流侧输入电容,两电容间的点称为中点o。NPC型三电平逆变桥由对称的a、b、c三相桥臂组成,其中每一相桥臂包括4个功率开关器件VTx1~VTx4(x = a,b,c),4个续流二极管VDx1~VDx4以及2个钳位二极管VD1x、VD2x。P、N分别为直流侧电源正、负端,Udc为直流母线电压,ia、ib、ic为逆变器三相输出电流。

图1 NPC型三电平逆变器的主电路拓扑结构
Fig.1 The main circuit topology of NPC three-level inverter
由图1可知,电机状态方程为
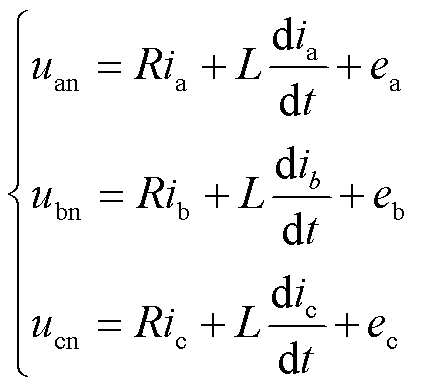 (1)
(1)
式中,uan、ubn、ucn为三相绕组电压;ea、eb、ec为三相反电动势;R为定子绕组;L为定子电感。
根据图1电路星形联结和基尔霍夫电压定律可知
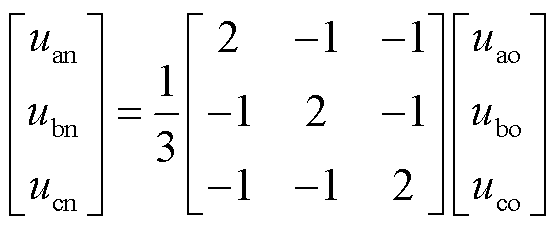 (2)
(2)
在建模时,每一相桥臂由4个功率开关器件VTx1~VTx4的开关信号由符号sx1~sx4表示,sxi=1(i=1,2,3,4)表示开关管VTxi处于导通状态,sxi=0表示开关管VTxi处于断开状态。此外,令da、db、dc为电机三相绕组的电流流向,dk=1(k=a,b,c)表示电流流入绕组,dk=0表示电流流出绕组。
根据逆变器正常工作时电流的流向路径得到三相对地电压的运行状态,表达式为
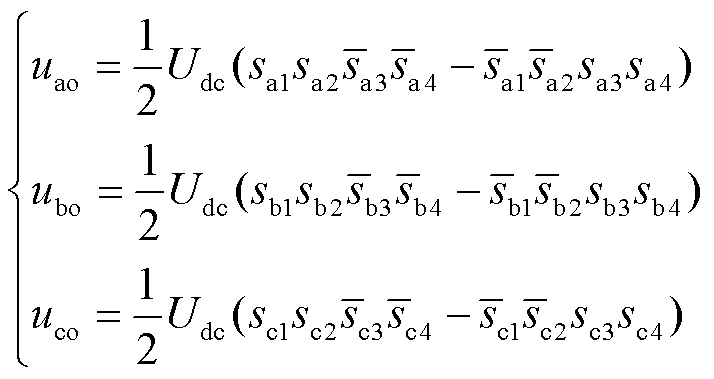 (3)
(3)
联立式(2)、式(3)可得
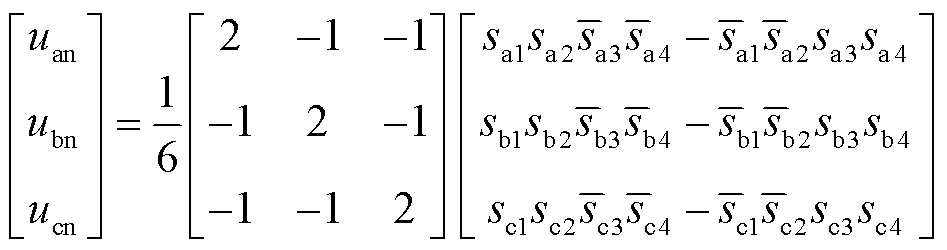 (4)
(4)
联立式(1)、式(4)可得基于混合逻辑动态模型的电机驱动系统状态空间模型为
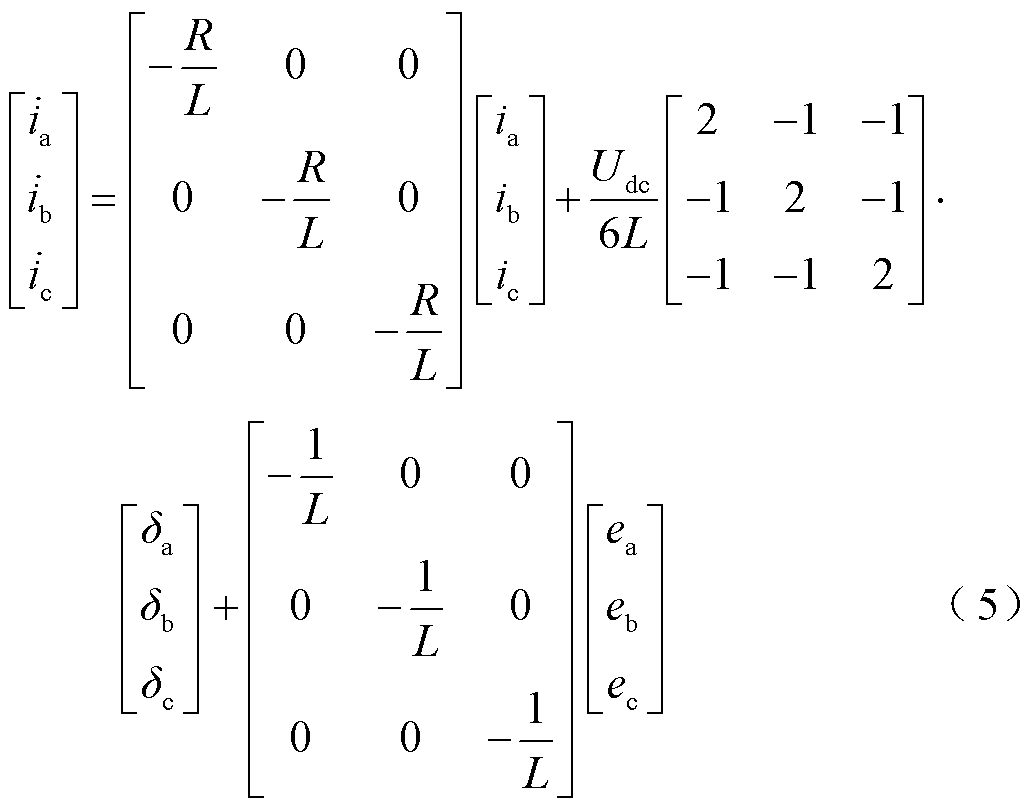
令i=[ia ib ic]T,δ=[δa δb δc]T,e=[ea eb ec]T,式(5)可改写为
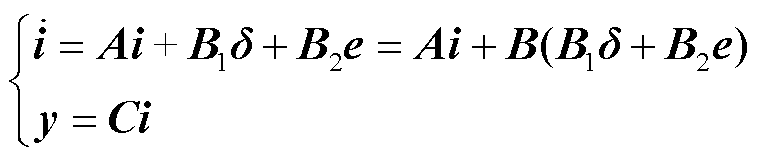 (6)
(6)
式中,A=diag(-R/L -R/L -R/L);![]() ;B1=
;B1=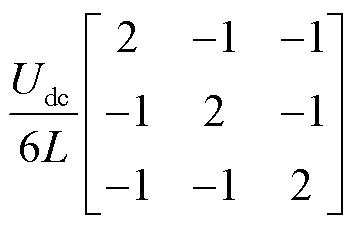 ;B2=diag(-1/L -1/L -1/L)。
;B2=diag(-1/L -1/L -1/L)。
本文提出的故障诊断策略如图2所示。首先,采用空间矢量脉冲调制技术产生控制12个功率开关管的脉宽调制(Pulse Width Modulation, PWM)开关信号,从而逆变生成三相电流输出至电机;然后,在基于混合逻辑动态法的电机系统状态空间模型基础上,构建诊断观测器对被控系统进行等价,作为逆变器正常情况下的估计电流输出,当逆变器发生故障时,实际电流值与观测器所估计的正常电流值相减形成三相电流残差;最后,在获得电流残差信号后,通过评价函数生成残差信号相关特征与自适应阈值实现故障诊断。
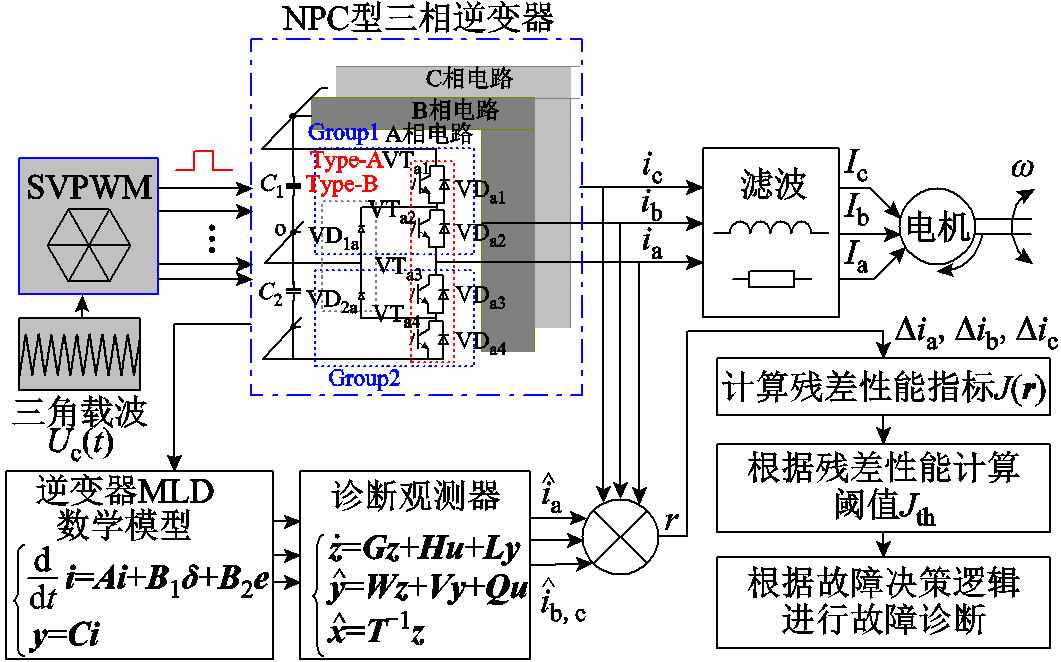
图2 面向残差评价的NPC逆变器开路故障诊断框图
Fig.2 Open circuit fault diagnosis block diagram of NPC inverter for residual evaluation
考虑n维连续时间线性时不变被观测系统为
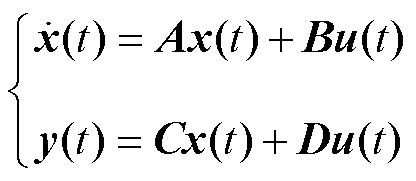 (7)
(7)
式中,x(t)为状态向量;y(t)为输出向量;u(t)为控制向量;矩阵A,B,C,D均为常系数矩阵[23]。
诊断观测器(Diagnostic Observer, DO)的核心部分为Luenberger型输出观测器,即
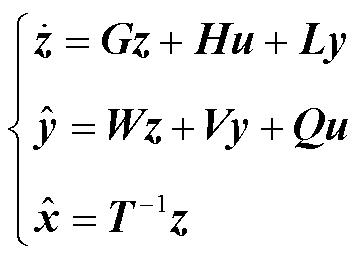 (8)
(8)
式中,对角矩阵G、H、L、Q、V、W和矩阵T需满足Luenberger条件,即
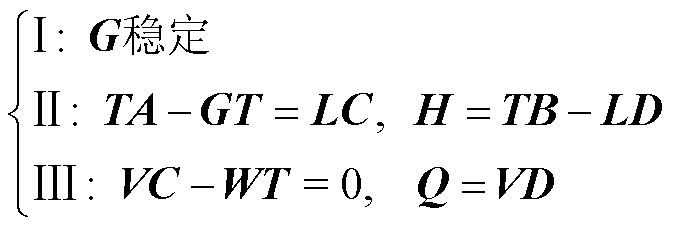 (9)
(9)
为了找出用于解决式(9)中Luenberger方程的矩阵G、L、T、V、W,本文将介绍一种数值求解方法。
首先,对矩阵A、C进行分解,得到
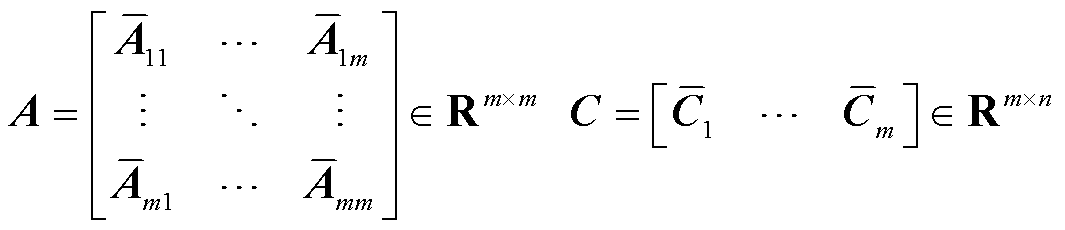 (10)
(10)
其中
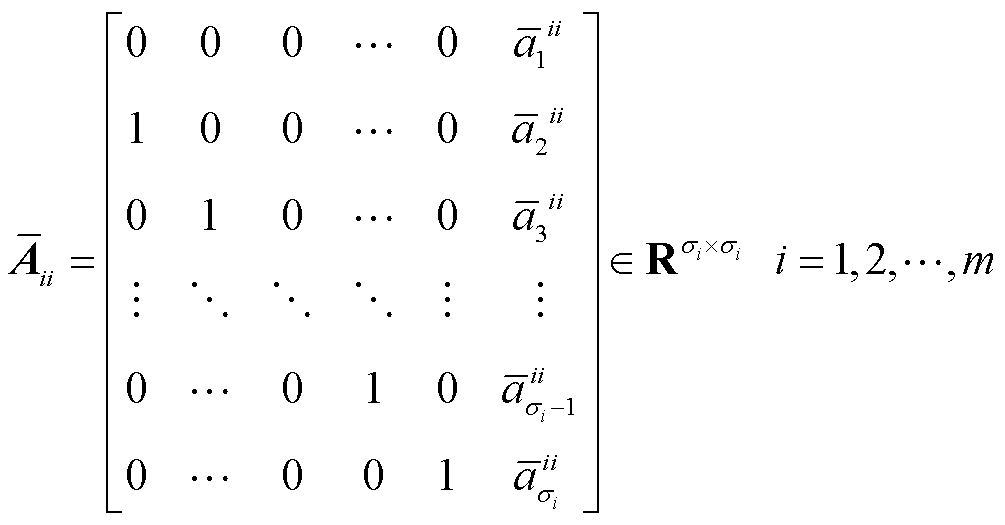 (11)
(11)
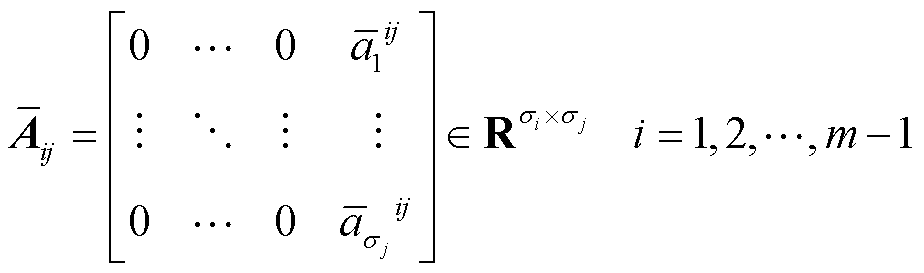 (12)
(12)
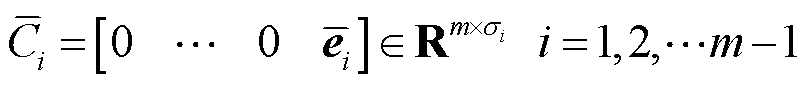 (13)
(13)
式中,σ1,…,σm为可观性指标,并且满足
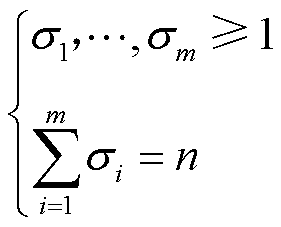 (14)
(14)
令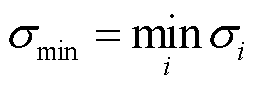 和
和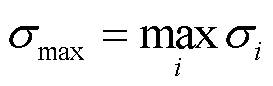 分别表示最小与最大可观测性指标。
分别表示最小与最大可观测性指标。
其次,对于式(8)中,矩阵G、W表示为
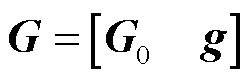 (15)
(15)
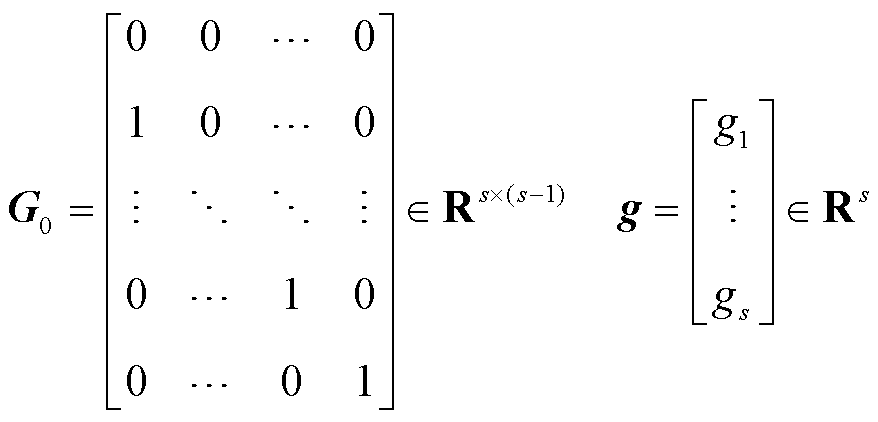 (16)
(16)
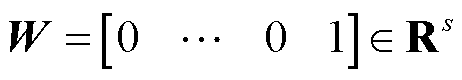 (17)
(17)
式中,s为被观测系统阶数。
定理1:当且仅当被观测系统阶数s与最小可观测性指标满足式(18)时,式(9)中条件Ⅱ、Ⅲ是可解的。
定理2:若满足式(18),则矩阵L、T、V、W定义为
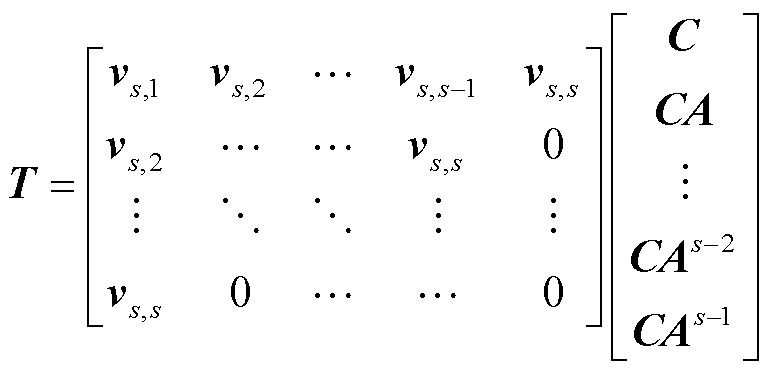 (19)
(19)
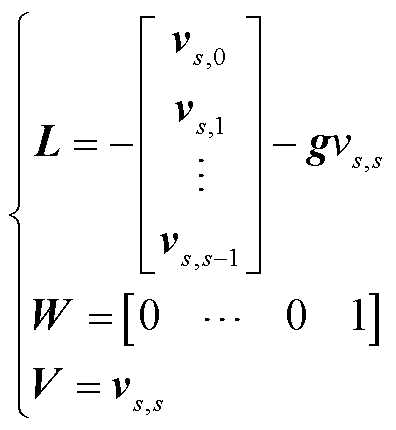 (20)
(20)
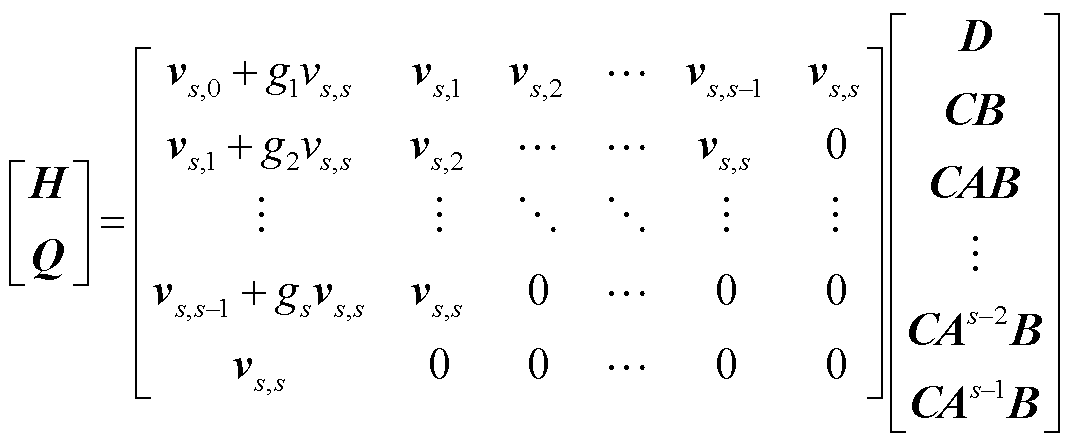 (21)
(21)
式(19)~式(21)中,vs,1,…,vs,s为式(22)的解。
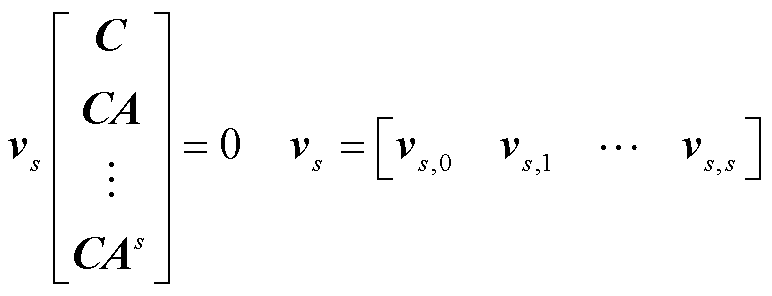 (22)
(22)
式中,对于向量g,即所有的g1, g2,…, gs,需要保证矩阵G的稳定性。也就是矩阵G的全部特征值λi, i=1,2,…,n均具有负实部,同时也需满足矩阵A和G不具有公共特征值这一条件[24]。
最终,根据以上定理,可得出诊断观测器DO的设计算法步骤:
1)确定系统阶数s与最小可观测性指标σmin。
针对三电平三相NPC型逆变器系统,阶数s=1,输入状态变量与输出状态变量均为3,即m=n=3。根据式(14),该系统的可观测性能指标为σ1、σ2、σ3,并满足
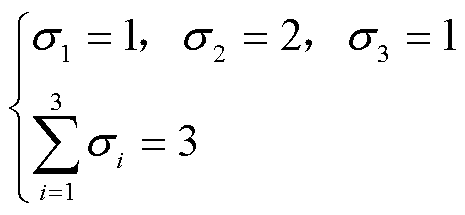 (23)
(23)
2)求解式(22)得向量vs为
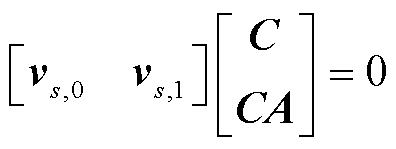 (24)
(24)
令vs,0=[a b c],vs,1=[a1 b1 c1],可得
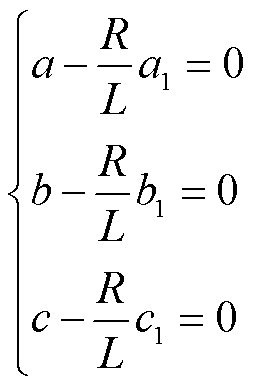 (25)
(25)
解得vs,0、vs,1为
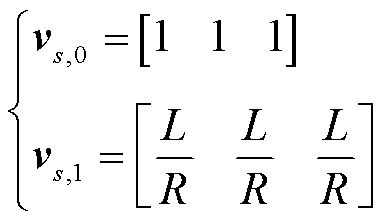 (26)
(26)
3)定义期望极点,计算向量g使矩阵G稳定。
首先,矩阵A和G不具有公共特征值[24],即极点设置需满足
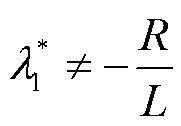 (27)
(27)
令希望极点λ1*=-1000R/L,则向量g、矩阵G表示为
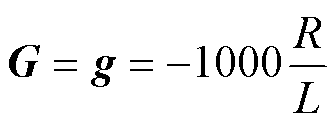 (28)
(28)
4)根据式(17),式(19)~式(21),计算矩阵T、H、L、V、W。
5)根据式(8),将重构状态变量z还原为实际系统状态观测量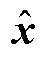 。
。
6)计算残差r。
根据式(9),基于诊断观测器DO的残差计算公式为
式(29)的计算证明过程如下。
证明:原Luenberger型输出观测器表达式为
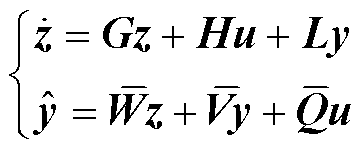 (30)
(30)
对于连续时间线性时不变状态空间方程式(7),将Luenberger条件Ⅱ代入,则有
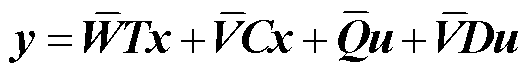 (31)
(31)
设e=Tx-z为状态向量,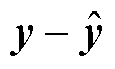 为输出。联立式(30)和式(31)可得
为输出。联立式(30)和式(31)可得
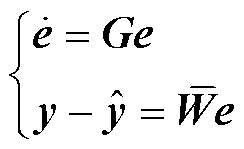 (32)
(32)
根据式(32),可定义龙伯格型输出观测器的残差为
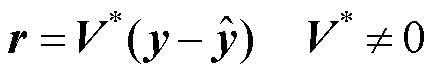 (33)
(33)
联立式(32)、式(33)可得
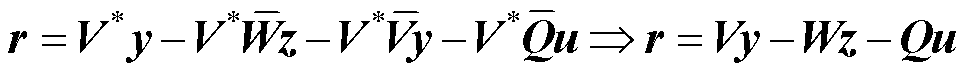 (34)
(34)
其中
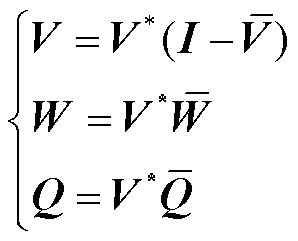 (35)
(35)
联立式(35)与式(9)中Luenberger条件Ⅱ可得
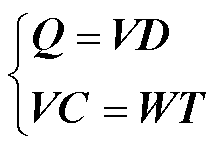 (36)
(36)
式(36)与式(9)中条件Ⅱ一致且吻合,证毕。
在故障诊断与分离技术领域内,范数的一个直接应用就是对残差进行评价,生成残差的特征。在实际工程应用中,将会在线计算范数意义下的残差特征信号,然后生成基于特征的自适应阈值进行比较,从而成功实现故障诊断。本文基于范数,通过生成三相电流残差的特征信号及对应的阈值实现故障诊断。
1)定义残差评价函数J(r)。
首先介绍L2范数的基本概念,定义如下。
对于信号u和v有
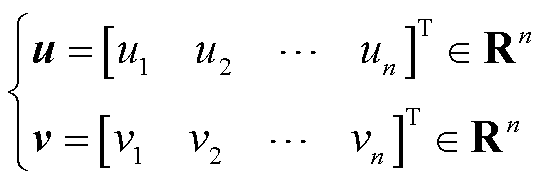 (37)
(37)
向量u(k)、信号u(t)的L2范数定义为
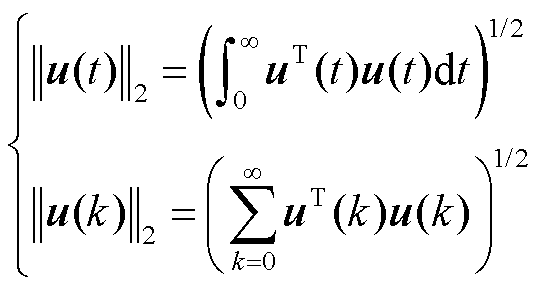 (38)
(38)
对于残差信号r(k),引入残差评价函数J(r),有
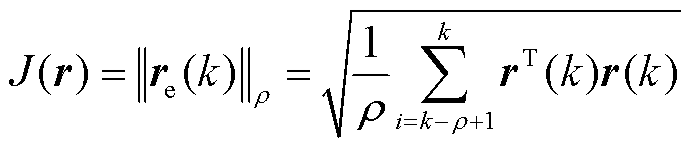 (39)
(39)
式中,ρ为时间窗口;r(k)为残差信号。对于三相电流残差信号Δia、Δib、Δic,式(39)可改写为
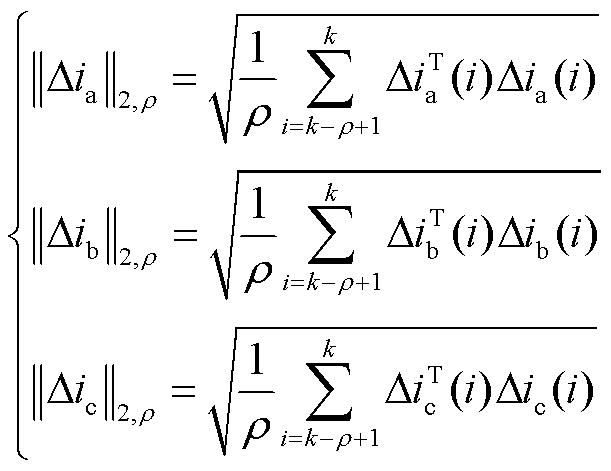 (40)
(40)
2)根据残差评价函数J(r)计算阈值Jth。
根据残差评价函数J(r),阈值为
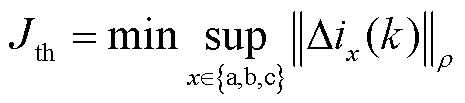 (41)
(41)
3)定义故障决策逻辑。
基于L2范数的故障诊断决策逻辑定义为
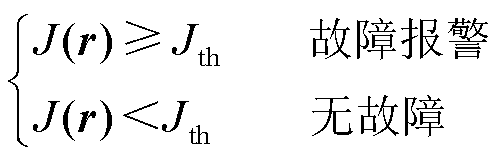 (42)
(42)
结合三相电流残差信号Δia、Δib、Δic,可将具体的故障决策逻辑,即式(42)改写为
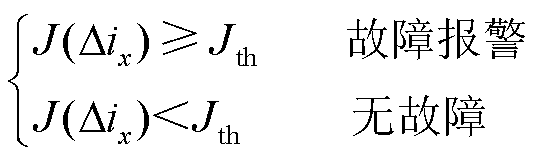 (43)
(43)
以L2范数评价函数相关理论为起点,同样可以推导出基于L1及L∞范数的残差性能评价函数J(r)与阈值Jth,如下所示。
对于L1范数,残差性能评价函数J(r)为
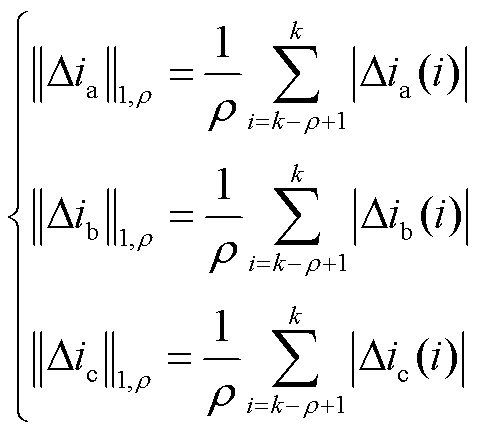 (44)
(44)
对于L1范数,对应阈值Jth设定为
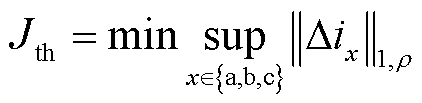 (45)
(45)
同理,对于L∞范数,残差性能评价函数J(r)为
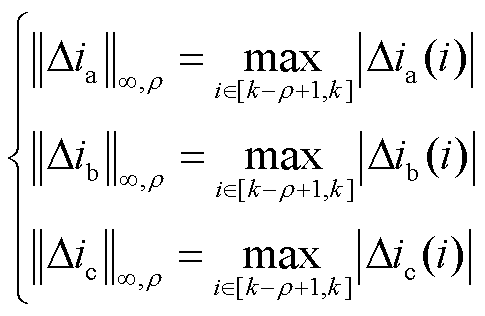 (46)
(46)
对于L∞范数,对应阈值Jth设定为
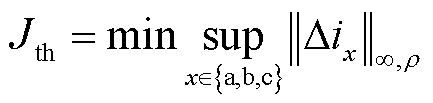 (47)
(47)
对于故障决策逻辑,与L2范数一致,即式(42)、式(43)所示。根据上述理论,基于范数的残差性能评价故障诊断流程如图3所示。
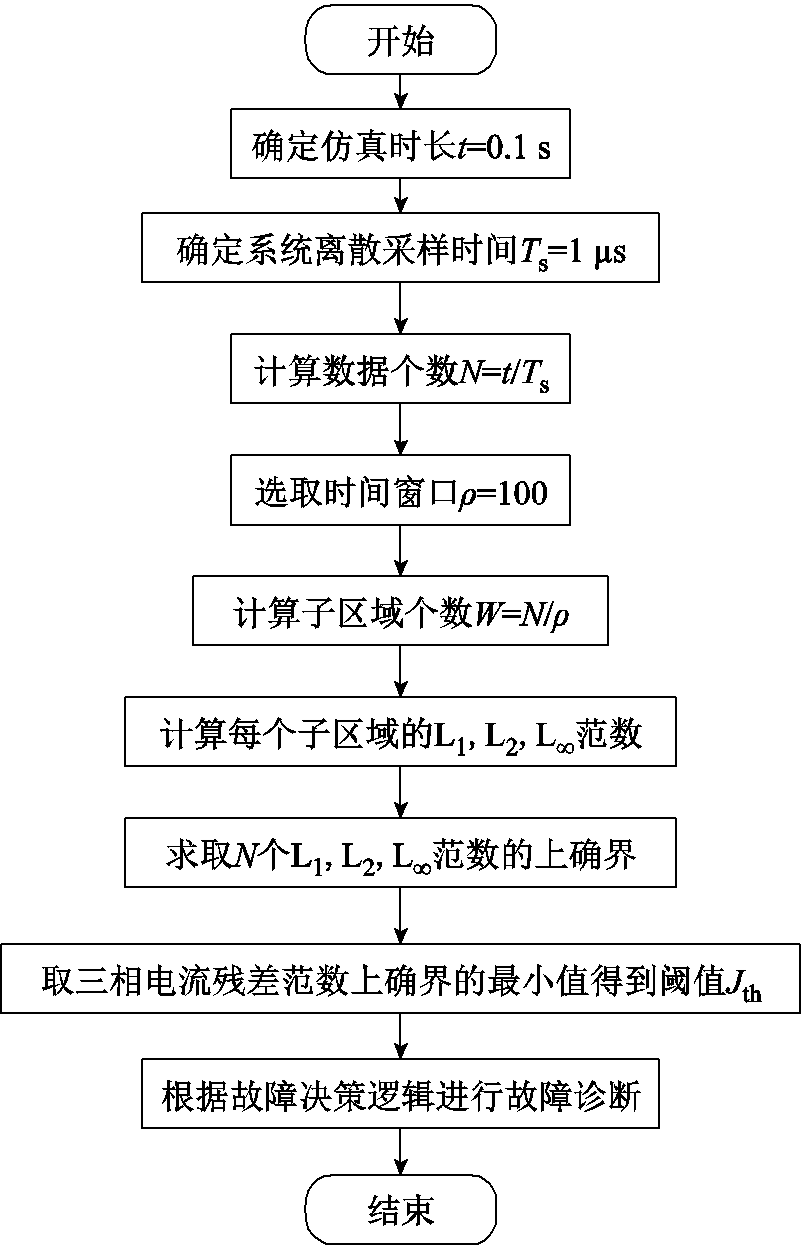
图3 基于范数的残差性能评价故障诊断流程
Fig.3 Fault diagnosis flow chart of norm-based residual performance evaluation
在成功实现故障诊断之后,需要对NPC型三电平逆变器具体的开路故障类型进行精确定位,实现故障隔离。在第4节,针对NPC型三电平逆变器的四种功率开关器件故障类型,通过残差评价方案均实现了故障检测。接下来针对四种具体的开路故障类型,首先得到故障状态下的三相开关信号,记为δ′,代入逆变器状态空间表达式,即式(6)中,得到故障电流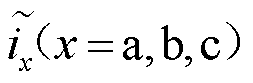 表达式;其次,将健康状态下的三相电流与故障三相电流表达式相减,得到对应故障状态下三相电流残差的数学表达式;最后,根据此获得三相电流残差信号的代数特征,实现故障定位及隔离[25-28]。
表达式;其次,将健康状态下的三相电流与故障三相电流表达式相减,得到对应故障状态下三相电流残差的数学表达式;最后,根据此获得三相电流残差信号的代数特征,实现故障定位及隔离[25-28]。
1)逆变器单管故障情况——以VTb2为例
当NPC型逆变器b相功率开关器件VTb2发生开路故障时,VTb2功率管的开关信号sb2=0,则VTb2故障时的三相开关信号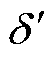 为
为
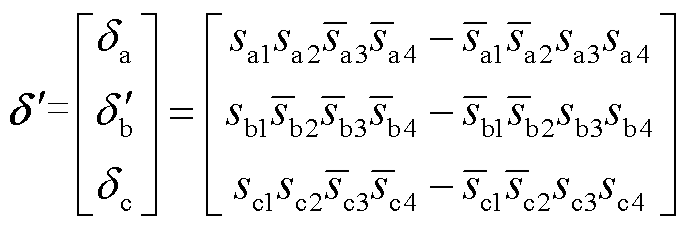 (48)
(48)
将式(48)代入逆变器状态空间表达式,即式(6)中,可得当VTb2开路故障状态下逆变器状态空间表达式为
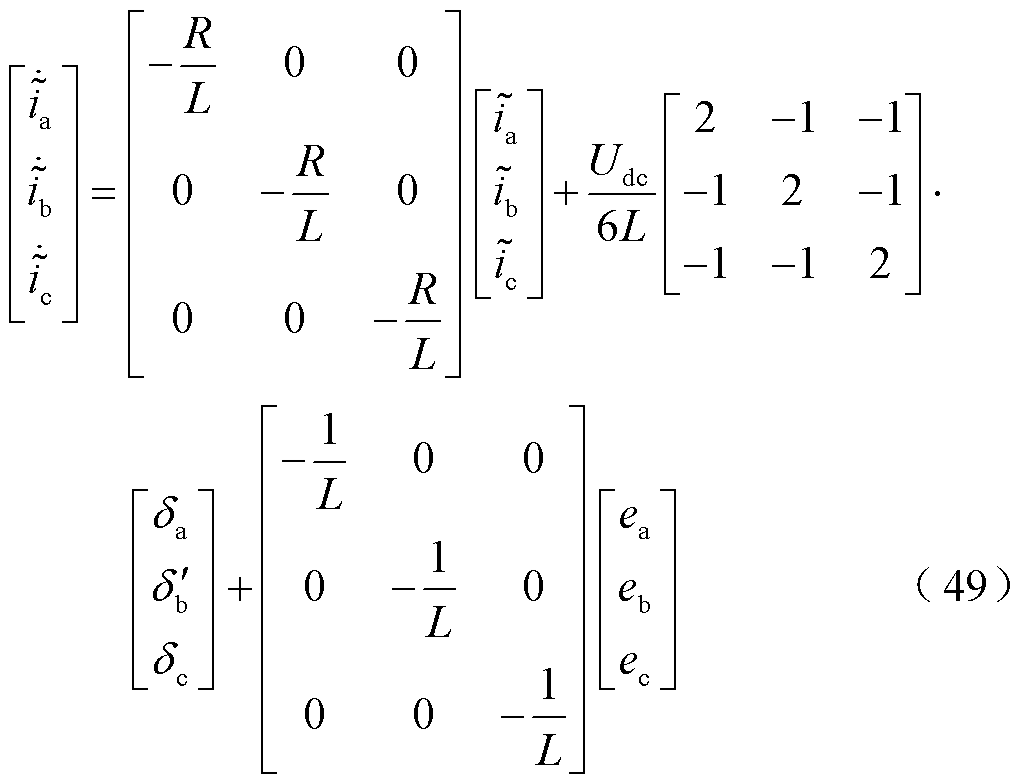
将式(49)与逆变器健康状态下状态空间表达式相减,可得VTb2开路故障状态下三相电流残差数学表达式为
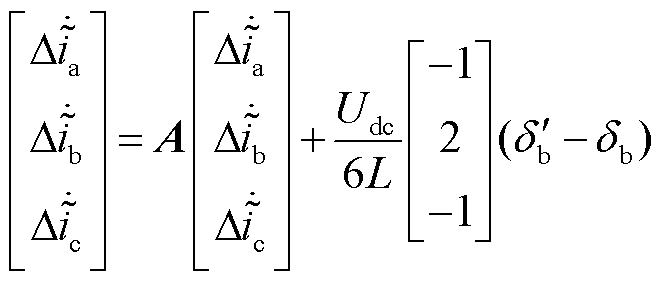 (50)
(50)
式中,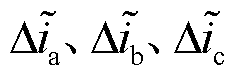 为三相电流残差信号。
为三相电流残差信号。
令Δδb=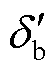 -δb=
-δb=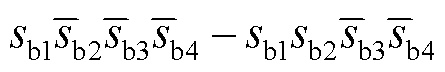 ,并且假设三相电流残差信号初始值均为0,求解式(50)可得
,并且假设三相电流残差信号初始值均为0,求解式(50)可得
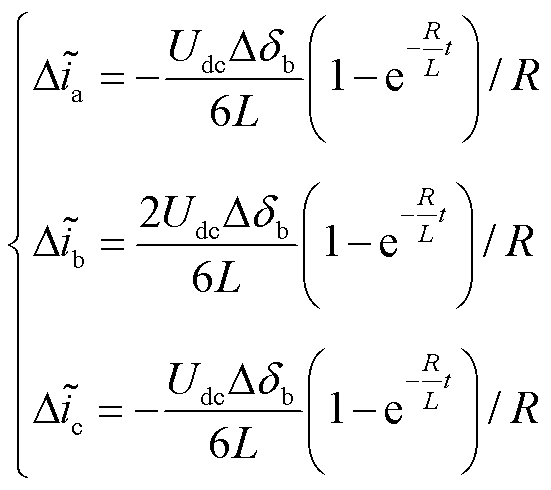 (51)
(51)
式中,R与L分别为三相绕组与滤波电感。
根据式(51),当VTb2发生开路故障时,b相电流残差小于等于0,然而a、c两相电流残差信号均大于等于0。进一步地,根据式(51),b相电流残差信号在数值上是另外两相电流残差的两倍,满足
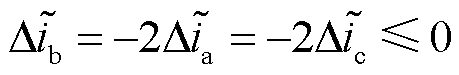 (52)
(52)
2)逆变器同相管故障情况——以VTc2VTc4为例
针对同相双管开路故障类型,此处以c相的VTc2VTc4开路故障为例。当NPC型逆变器c相功率开关器件VTc2VTc4发生开路故障时,VTc2与VTc4功率管的开关信号sc2=sc4=0,则VTc2VTc4故障时的三相开关信号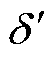 为
为
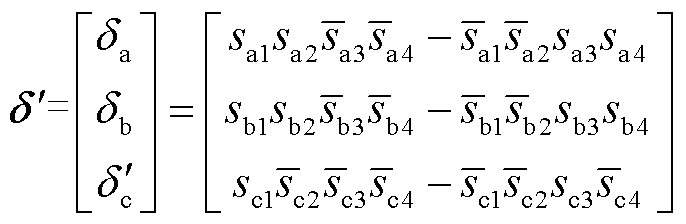 (53)
(53)
与VTb2发生开路故障的分析机理相同,将式(53)代入逆变器状态空间表达式,得当VTc2VTc4开路故障状态下逆变器状态空间表达式,并与健康状态下逆变器系统的状态空间表达式相减,得VTc2VTc4开路故障状态下三相电流残差数学表达式为
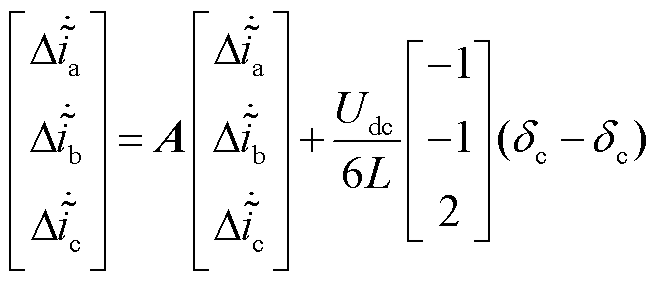 (54)
(54)
令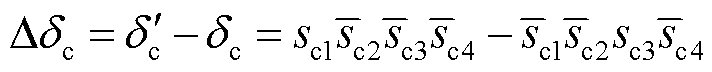 ,并且假设三相电流残差信号初始值均为0,求解式(54)可得
,并且假设三相电流残差信号初始值均为0,求解式(54)可得
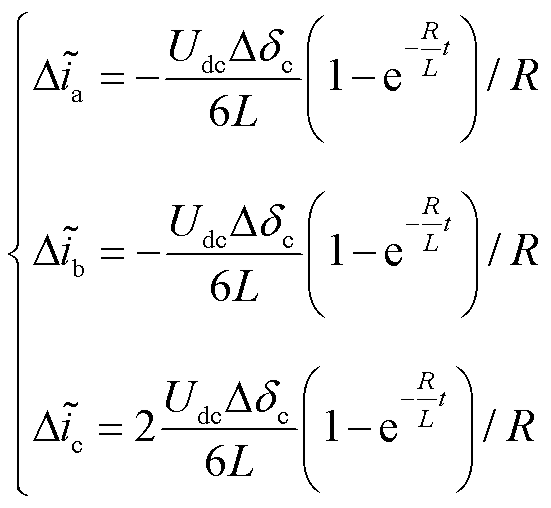 (55)
(55)
根据式(55),当VTc2VTc4发生开路故障时,c相电流残差信号在数值上是另外两相电流残差的两倍,满足
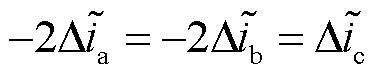 (56)
(56)
然而,与单管故障情况下的电流残差不同的是,VTc2VTc4故障状态下三相电流残差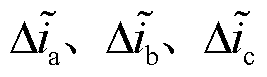 可正可负,电流残差信号不具备单一极性。
可正可负,电流残差信号不具备单一极性。
3)逆变器异相同臂双管故障情况——以VTb2 VTc2为例
针对异相同臂的双管开路故障类型,此处以b、c两相的VTb2VTc2开路故障为例。当VTb2VTc2同时发生开路故障时,VTb2与VTc2功率管的开关信号sb2=sc2=0,则VTb2VTc2故障时的三相开关信号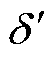 为
为
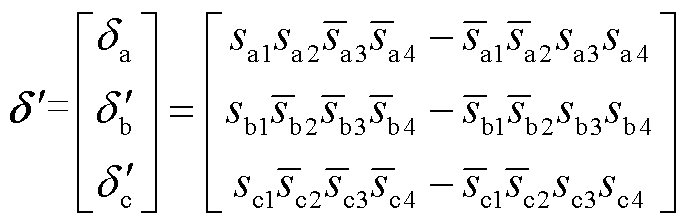 (57)
(57)
将VTb2VTc2开路故障状态下逆变器状态空间表达式与健康状态下的状态空间表达式相减,得VTb2VTc2开路故障状态下三相电流残差数学表达式为
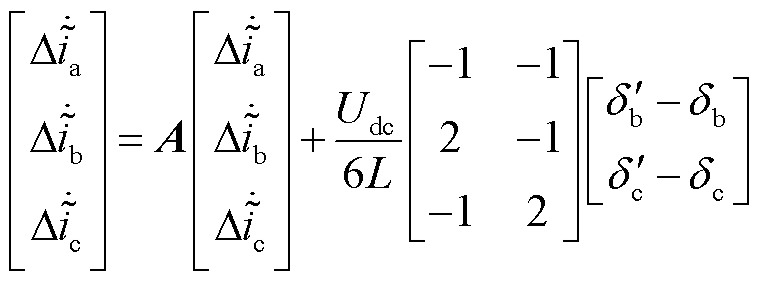 (58)
(58)
令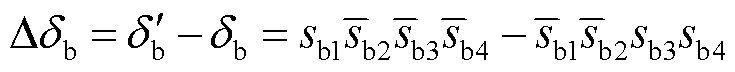 ,
,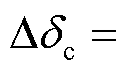
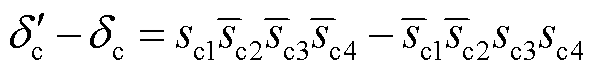 ,并且假设三相电流残差信号初始值均为0,求解式(51)可得
,并且假设三相电流残差信号初始值均为0,求解式(51)可得
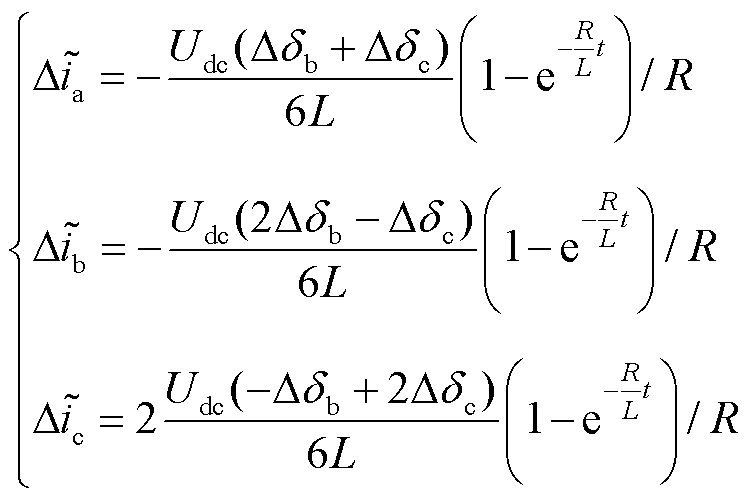 (59)
(59)
根据式(59),当VTb2VTc2发生开路故障时,b、c相电流残差信号在数值上满足
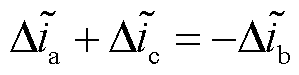 (60)
(60)
4)逆变器异相异臂双管故障情况——以VTa1VTc3为例
针对异相异臂的双管开路故障类型,此处以a、c两相的VTa1VTc3开路故障为例。当VTa1VTc3同时发生开路故障时,VTa1与VTc3功率管的开关信号sa1=sc3=0,则VTa1VTc3故障时的三相开关信号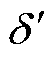 为
为
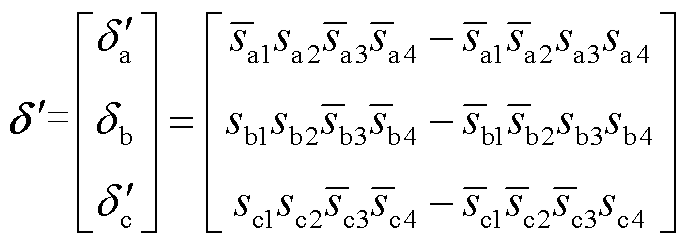 (61)
(61)
同理,将VTa1VTc3开路故障状态下逆变器状态空间表达式与健康状态下的状态空间表达式相减,得VTa1VTc3开路故障状态下三相电流残差数学表达式为
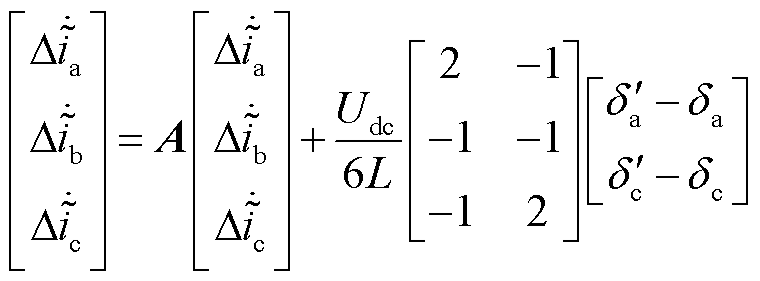 (62)
(62)
令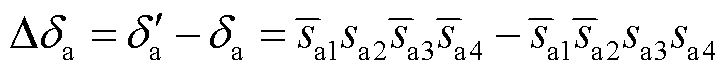 ,
,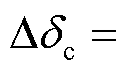
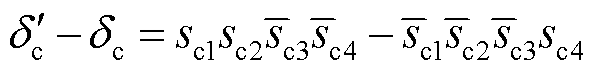 ,并且假设三相电流残差信号初始值均为0,求解式(62)可得
,并且假设三相电流残差信号初始值均为0,求解式(62)可得
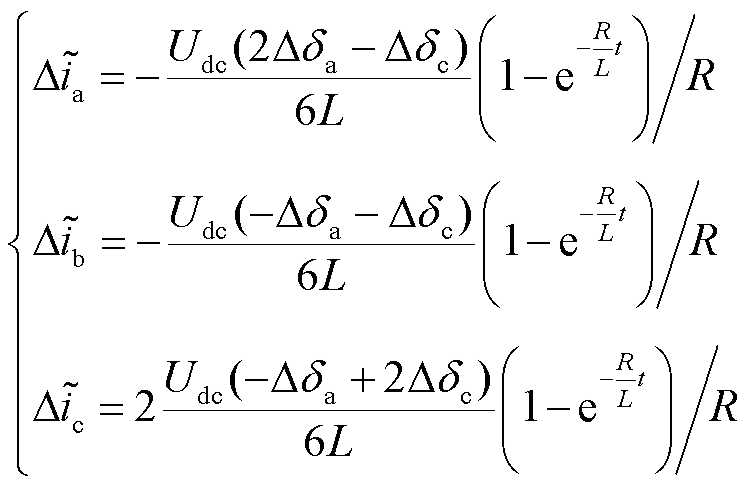 (63)
(63)
根据式(63),当VTa1VTc3发生开路故障时,a、c相电流残差信号在数值上满足
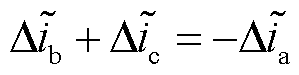 (64)
(64)
在上述对NPC型三相逆变器不同故障类型的电流残差机理分析后,表1对b相单个功率开关器件开路故障下的电流残差特性进行归纳总结。
表1 b相单管故障时三相电流残差信息
Tab.1 Current residual considering single-tube fault in b phase

分类故障管状态各相的电流残差之间的关系 无故障无 单管故障VTb1 VTb2 VTb3 VTb4
同时,表2以c相为例,归纳总结两个功率开关器件同时开路故障下的电流残差特性。
表2中需注意的是,同相双管故障状态下仅凭三相电流残差数值特征无法实现故障隔离与识别,需结合电流残差极性与故障相电流极性联合判断。
对异相两个功率开关器件同时开路故障下的电流残差特性一并进行归纳总结,但由于篇幅限制,仅选择部分故障状态纳入表3。
表2 c相同相双管故障时三相电流残差信息
Tab.2 Current residual considering double-tube fault in c phase

分类故障管状态各相的电流残差之间的关系 无故障无 同相双管故障VTc1VTc2 VTc1VTc3 VTc1VTc4 VTc2VTc3 VTc2VTc4 VTc3VTc4
表3 异相双管故障时三相电流残差信息
Tab.3 Current residual considering different-phase-tube fault

分类故障管状态各相的电流残差之间的关系 无故障无 异相同臂VTb2VTc2 VTa1VTb1 异相异臂VTa1VTc3 VTa2VTc4
综上所述,当NPC型逆变器正常工作时,三相电流残差应满足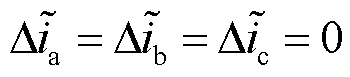 。当NPC型逆变器的功率开关器件发生开路故障时,首先根据第4节提出的基于范数的残差评价方案对逆变器进行故障检测,判断是否出现故障。在故障诊断后,依照表1~表3归纳总结的三相电流残差特性,实现故障隔离与定位。
。当NPC型逆变器的功率开关器件发生开路故障时,首先根据第4节提出的基于范数的残差评价方案对逆变器进行故障检测,判断是否出现故障。在故障诊断后,依照表1~表3归纳总结的三相电流残差特性,实现故障隔离与定位。
在Matlab/Simulink中搭建NPC型三电平逆变器电机驱动系统仿真模型,仿真参数见表4。
表4 仿真参数
Tab.4 Simulation parameters

参数数值 仿真时长t/s0.1 功率管故障时间t-break/s0.05 离散系统采样时间/s10-6 直流母线电压Udc/V380 正弦调制波Us(t)频率fs/Hz50 三角载波Uc(t)频率fc/Hz104 三相负载绕组Ri/Ω0.435 三相滤波电感Li/mH4 评价窗口ρ100
6.1.1 正常工作情况
图4为NPC型逆变器正常工作情况下输出三相电流仿真波形。
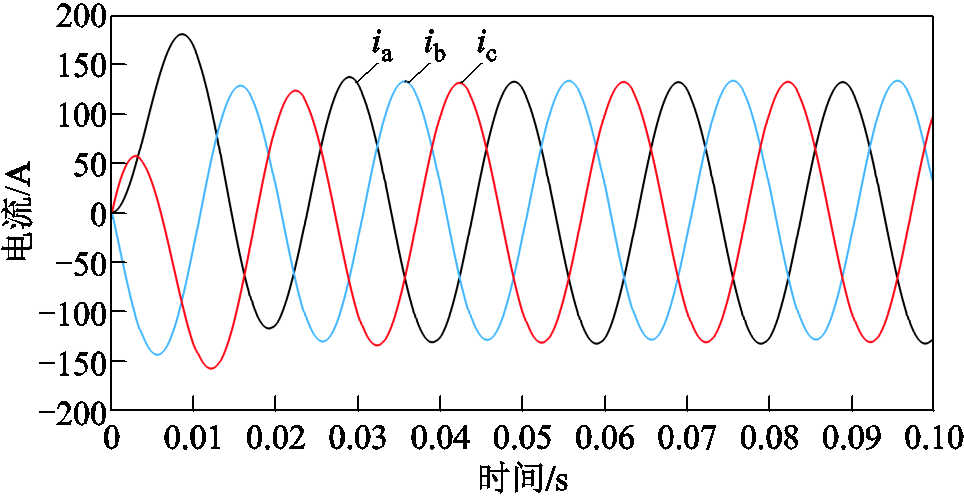
图4 正常情况下NPC型逆变器电流仿真波形
Fig.4 Normal NPC inverter current waveforms
从图4中可以得出,正常情况下输出的三相电流波形均为正弦波,周期均为0.02 s,每相间相差2π/3。
6.1.2 单管开路故障情况
以b相为例,VTb2发生开路故障时逆变器输出电流波形如图5所示。

图5 VTb2开路故障时逆变器的电流波形
Fig.5 Inverter current waveforms under VTb2 open circuit fault
当VTb2功率开关管处于开路故障状态时,逆变器b相失去P状态与O状态,仅N状态正常,因此逆变输出电流负半周期正常。
6.1.3 同相双管开路故障
以b相为例,VTb2VTb3发生开路故障时逆变器输出电流波形如图6所示。

图6 VTb2VTb3开路故障时逆变器的电流波形
Fig.6 Inverter current waveforms under VTb2VTb3 open circuit fault
当VTb2VTb3功率开关管同时处于开路故障状态时,逆变器b相P状态、N状态与O状态均失去,因此逆变器b相输出电流趋近于0。
6.1.4 异相双管开路故障
在异相双管开路故障中,可细分为异相同侧与异相异侧双管故障。针对异相同侧双管故障情况,选取VTa1VTb2为例,仿真结果如图7所示。对于异相异侧双管故障情况,选取VTb1VTc4为例,仿真结果如图8所示。

图7 VTa1VTb2开路故障时逆变器的电流波形
Fig.7 Inverter current waveform under VTa1VTb2 open circuit fault

图8 VTb1VTc4开路故障时逆变器的电流波形
Fig.8 Inverter current waveforms under VTb1VTc4 open circuit fault
图7中,功率开关管VTa1开路故障,说明a相失去P状态,仅有O和N状态,故黑色曲线代表的a相电流输出电流负半周期正常。并且由于续流二极管的存在,有且仅有小部分正电流存在。功率开关管VTb2开路故障,b相同时失去P和O状态,仅有N状态,因此蓝色曲线代表的b相电流输出仅有负半周期电流[29-31]。
同理,在图8中,功率开关管VTb1开路故障,说明b相失去P状态,仅有O和N状态,故蓝色曲线代表的b相电流输出电流负半周期正常。并且由于续流二极管的存在,有且仅有小部分正电流存在。功率开关管VTc4开路故障,说明c相仅失去N状态,P、O状态均存在,因此红色曲线代表的c相电流输出电流正半周期正常,并且由于续流二极管的存在,有且仅有小部分负电流存在。
NPC三电平逆变器正常工作情况下,诊断观测器DO观测所得b相电流仿真结果如图9所示。
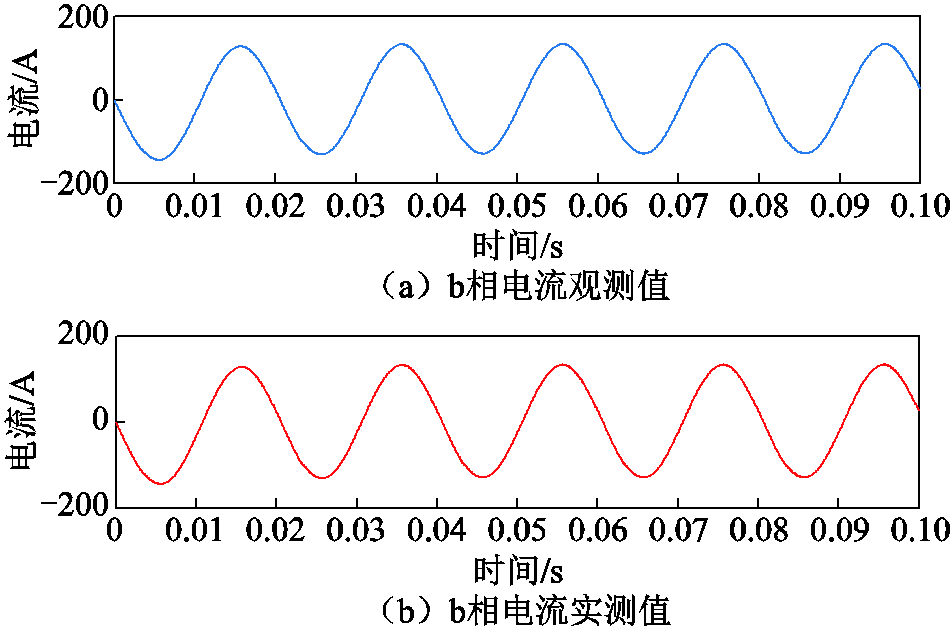
图9 b相电流观测值与实测值对比
Fig.9 Comparison of observed and actual current in b phase
从图9中可明显看出,诊断观测器DO观测所得三相电流值在全仿真时间段内,同样可以很好地跟踪逆变器输出的三相电流。
针对诊断观测器DO的估计精度,以0~0.1 s为例,绘制在该仿真时段内三相线电流估计值与实际系统实测值之间的误差输出如图10所示。
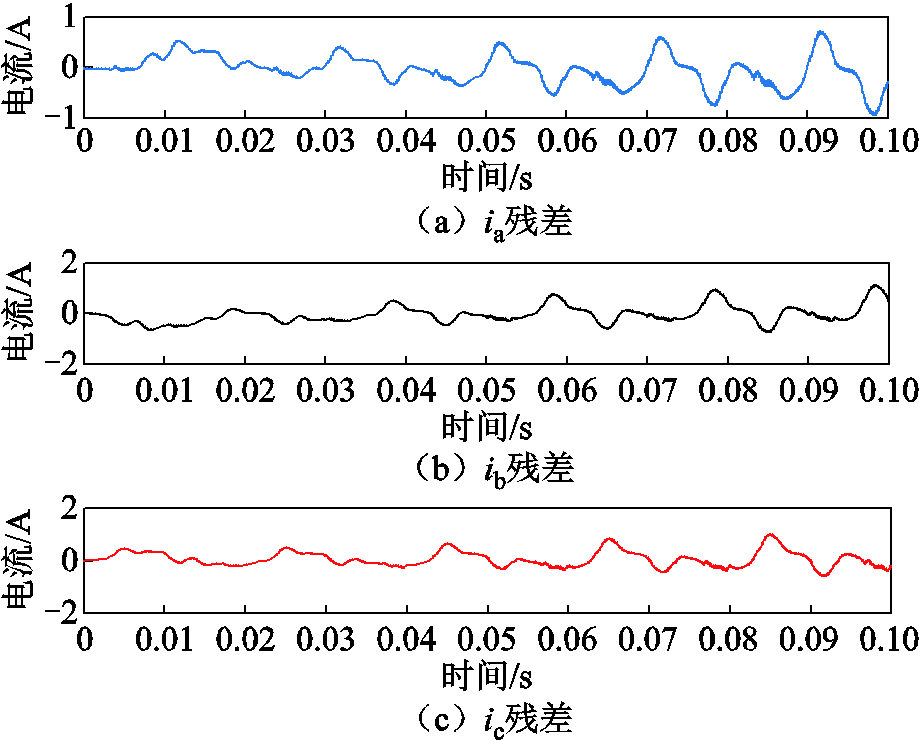
图10 逆变器健康状态下诊断观测器DO误差输出
Fig.10 Error output of DO under inverter health condition
在图10中,基于诊断观测器DO观测所得三相电流值与实测值相比,在仿真时间0~0.1 s内误差较小且平稳分布。
针对NPC型逆变器单管故障情况,以VTb1故障为例,绘制诊断观测器DO所得电流观测值与实测值进行比对,并绘制三相电流残差信号,仿真结果如图11、图12所示。
从图11中可以看出,当逆变器VTb1管发生开故障时,b相实测电流在故障发生后正半周消失。同时,诊断观测器DO观测所得b相电流跟随实测电流值,发生畸变。这是由于诊断观测器状态变量表达式中存在输出项y,致使观测值跟随实测值。

图11 VTb1故障状态下三相电流观测值与实测值对比
Fig.11 Comparison of three-phase observed current and actual value in VTb1 fault state
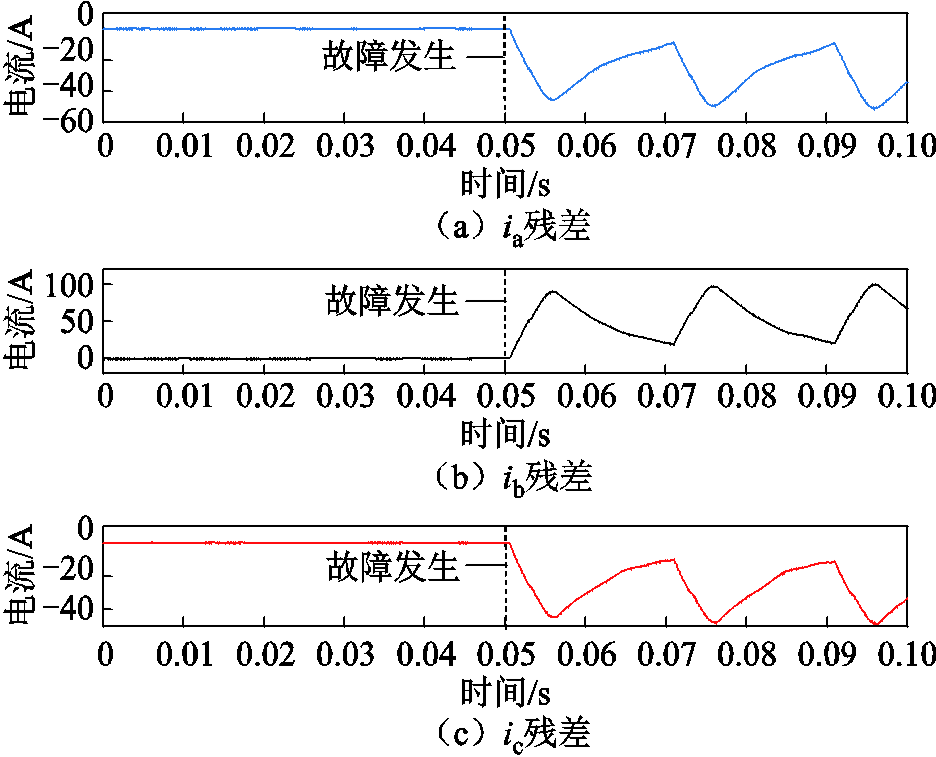
图12 VTb1故障状态下三相电流残差
Fig.12 Three-phase current residuals in VTb1fault state
在图12中,三相电流残差在故障发生后出现跃变。在此需强调,基于诊断观测器DO的残差信号采用式(29)直接计算获得。
6.3.1 逆变器单管故障情况——以VTb2为例
针对NPC型逆变器单管开路故障情况,以VTb2为例,基于范数的残差评价故障诊断仿真如图13所示。
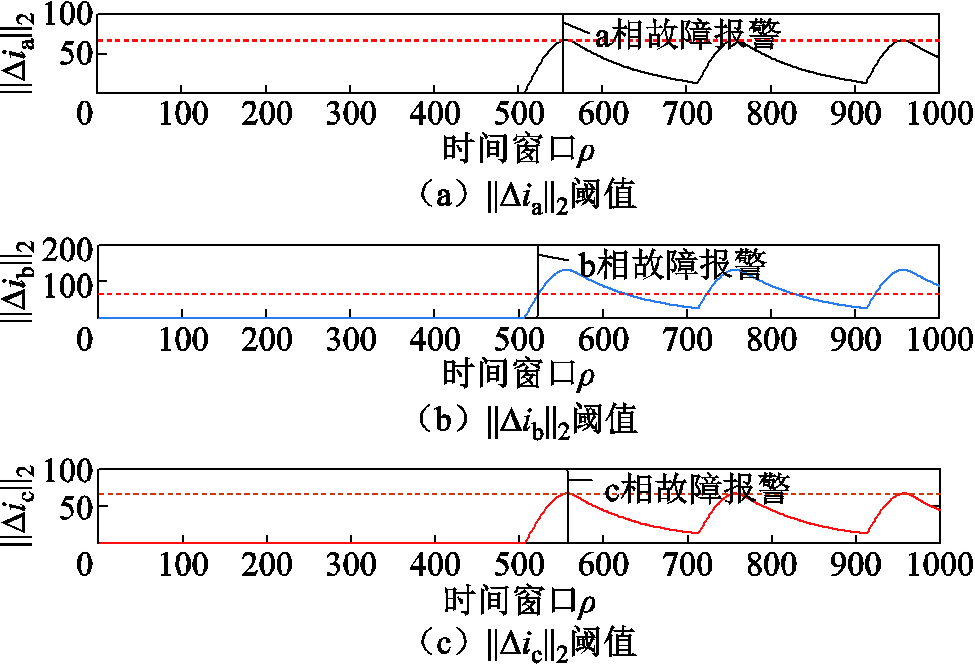

图13 VTb2故障下残差评价指标与阈值及故障标志位信号
Fig.13 Residual evaluation indicators and threshold and fault flag signal under VTb2 fault
在图13中,红色虚线代表阈值Jth,蓝色实线为三相电流残差信号的L2范数,也是评价指标J(r)。三个子图中黑色竖线所代表的是评价指标J(r)首次超越阈值Jth的时刻。根据故障决策逻辑,即式(54),三相残差信号的评价函数J(r)中哪一相最先超越阈值,此时故障报警。从图13中可知,b相残差评价指标J(Δib)最先超越阈值,此时立即故障报警,时间为t-flag=0.052 3 s。故障发生时间为0.05 s,因此故障诊断系统的反应决策时间为2.3 ms。
6.3.2 逆变器同相双管故障情况——以VTc2VTc4为例
针对逆变器同相双管开路故障情况,以VTc2VTc4为例,基于范数的残差评价故障诊断仿真如图14所示。
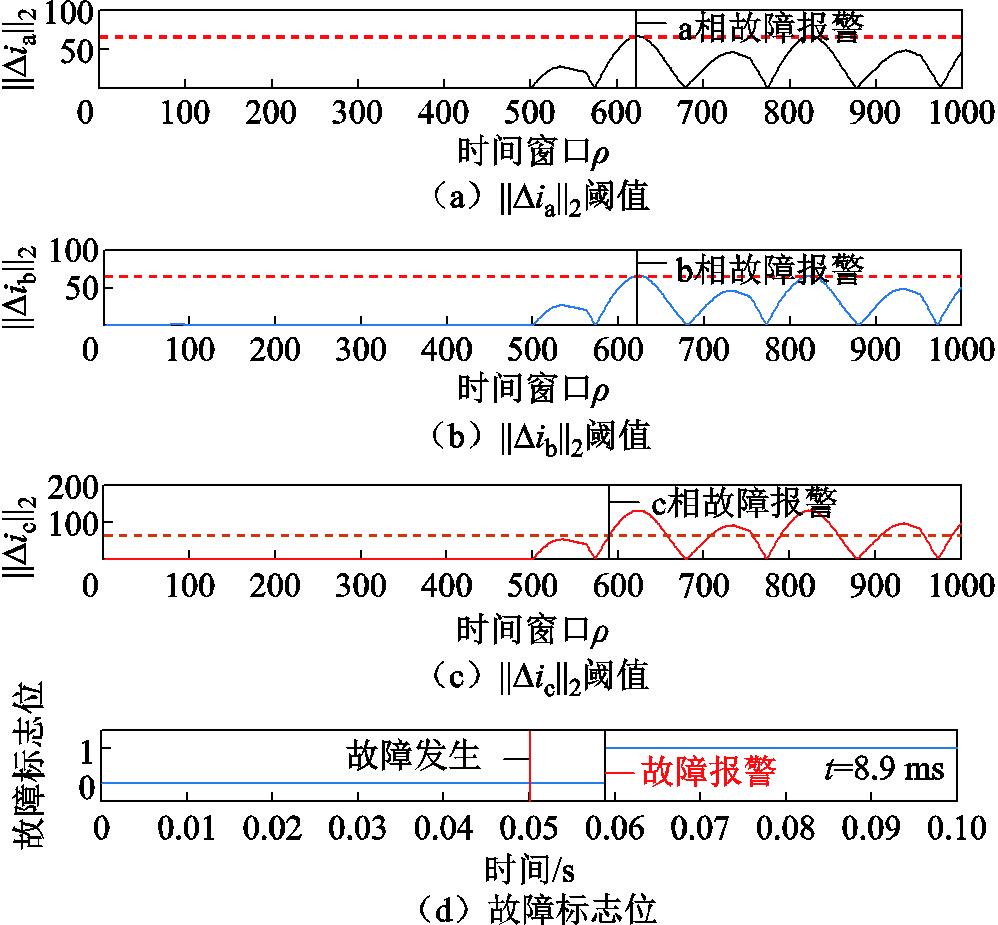
图14 VTc2VTc4故障下残差评价函数与阈值及故障标志位信号
Fig.14 Residual evaluation indicators and threshold and fault flag signal under VTc2VTc4 fault
根据图14,c相残差评价指标J(Δic)最先超越阈值Jth,此时立即故障报警,时间为t-flag=0.058 9 s。故障发生时间为0.05 s,因此故障诊断系统的反应决策时间为8.9 ms。
6.3.3 逆变器异相同臂双管故障——以VTb2VTc2为例
针对逆变器异相同臂双管开路故障情况,以VTb2VTc2为例,基于范数的残差评价故障诊断仿真如图15所示。
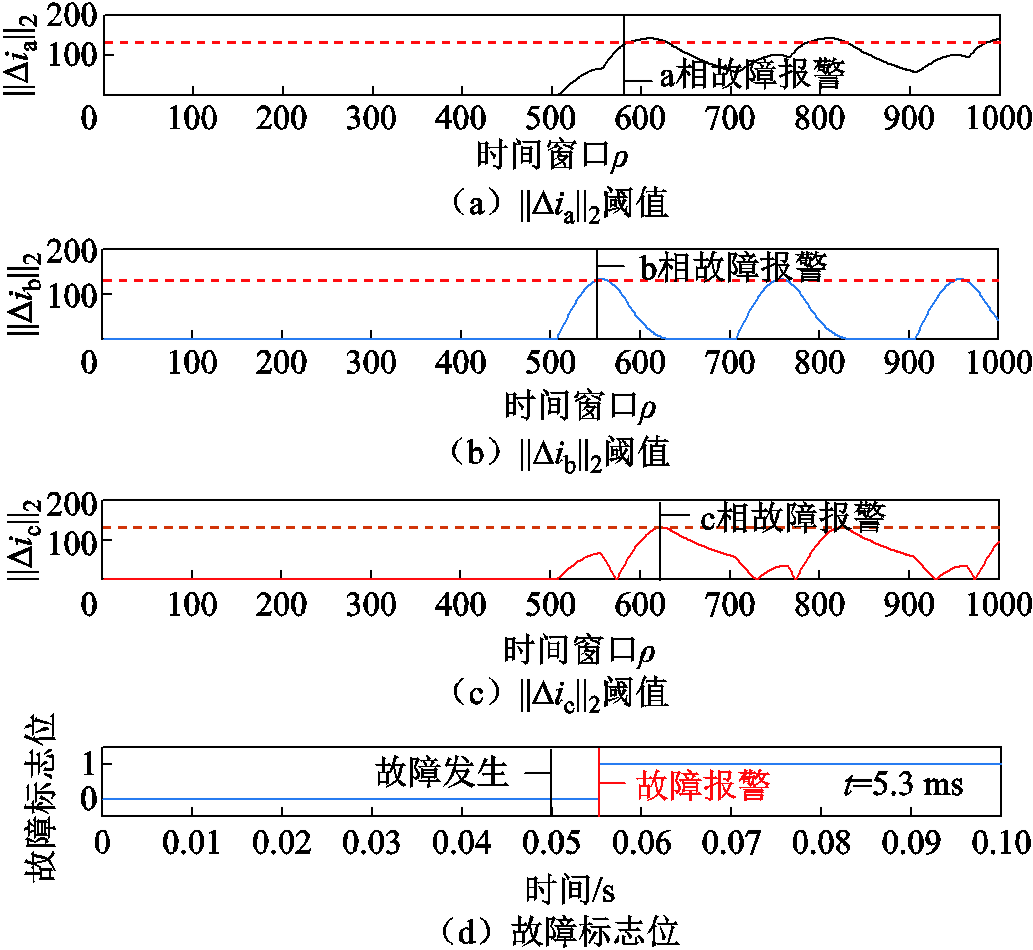
图15 VTb2VTc2故障下残差评价函数与阈值及故障标志位信号
Fig.15 Residual evaluation indicators and threshold and fault flag signal under VTb2VTc2 fault
在图15中,b相残差评价指标J(Δib)最先超越阈值Jth,此时立即故障报警,时间为t-flag=0.055 3 s。故障发生时间为0.05 s,因此故障诊断系统的反应决策时间为5.3 ms。
6.3.4 逆变器异相异臂双管故障——以VTa1VTc3为例
针对逆变器异相同臂双管开路故障情况,以VTa1VTc3为例,基于范数的残差评价故障诊断仿真如图16所示。
从图16中可知,c相残差评价指标J(Δic)最先超越阈值Jth,此时刻立即故障报警,时间为t-flag=0.051 2 s。故障发生时间为0.05 s,因此故障诊断系统的反应决策时间为1.2 ms。
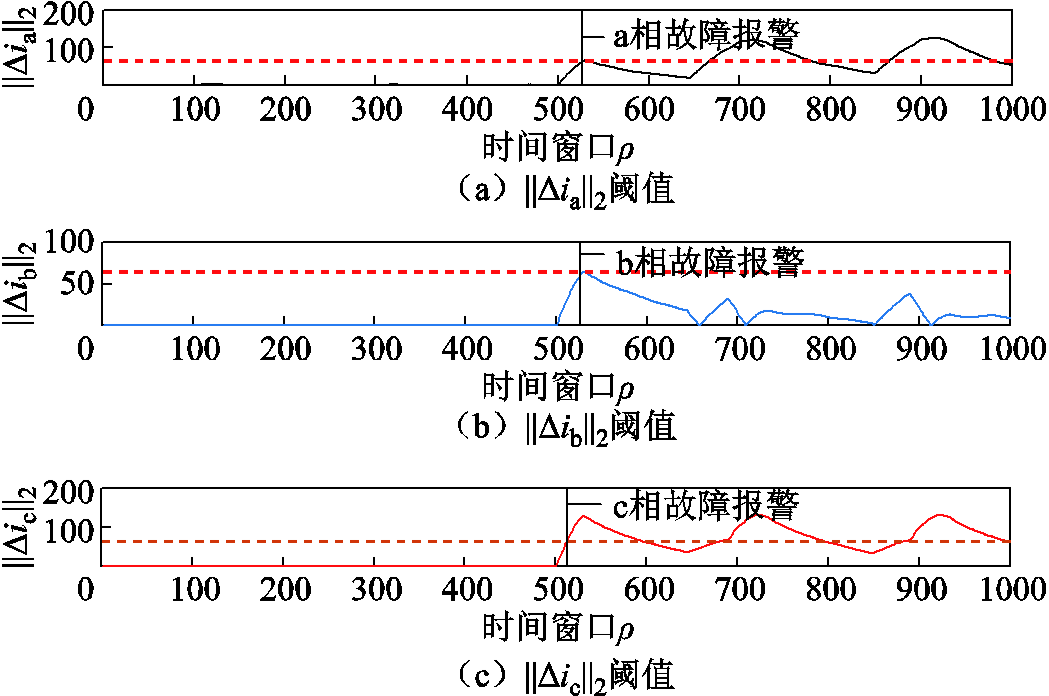
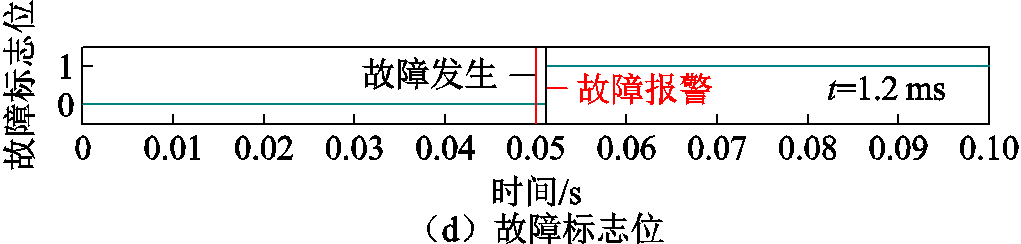
图16 VTa1VTc3故障下残差评价函数与阈值及故障标志位信号
Fig.16 Residual evaluation indicators and threshold and fault flag signal under VTa1VTc3 fault
同理,L1范数与L∞范数的残差评价函数J(r)与阈值Jth根据上述计算公式均可计算并绘制图像,得到故障诊断时间及故障报警flag标志位。下面将比较在逆变器发生相同类型的故障时,基于L1范数、L2范数与L∞范数的残差性能评价诊断算法的反应决策时间。
以逆变器单管VTb1故障情况为例,图17为基于L1范数、L2范数与L∞范数的残差性能评价诊断算法的反应决策时间比对结果。
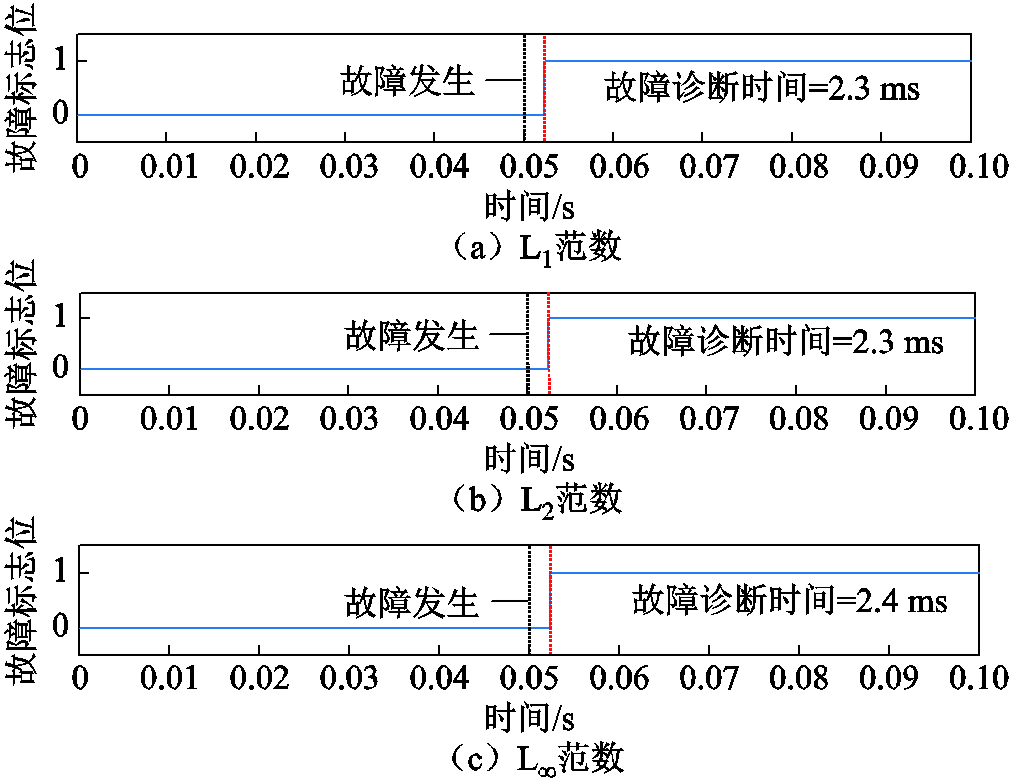
图17 L1范数、L2范数、L∞范数的反应决策时间对比
Fig.17 Comparison of fault decision time of L1 norm, L2 norm and L∞ norm
从图17可以看出,基于L1范数与L2范数的诊断算法诊断时间相同,L∞范数相较于前两者诊断时间略长。然而,以上三者诊断时间均达到4 ms以内,小于三相电流基波周期的1/5。Lu Bin等在2009年总结归纳了IGBT开路故障诊断方法[25]。在汇总的表格中,基于信号处理的故障诊断算法诊断时间大于20 ms,基于知识的故障诊断算法诊断时间为5个基波周期[25]。综上所述,本文提出的故障诊断算法,通过残差性能评价的引入使得故障诊断速度提高80%以上。
6.3.5 逆变器复杂工况下残差性能评价仿真结果
由于在实际工况中,逆变器系统中存在过程扰动与随机噪声,加大了逆变器功率器件开路故障检测与隔离方案的难度[32-34]。下面,以b相功率开关器件VTb2开路故障为例,将实际工况下残差性能评价仿真结果与理想情况下残差评价结果进行对比,如图18所示。同时,根据文献[28]与多次仿真,设定干扰v(t)=1+0.5sin(pt),噪声e(t)为均值为0,方差为1的高斯白噪声。
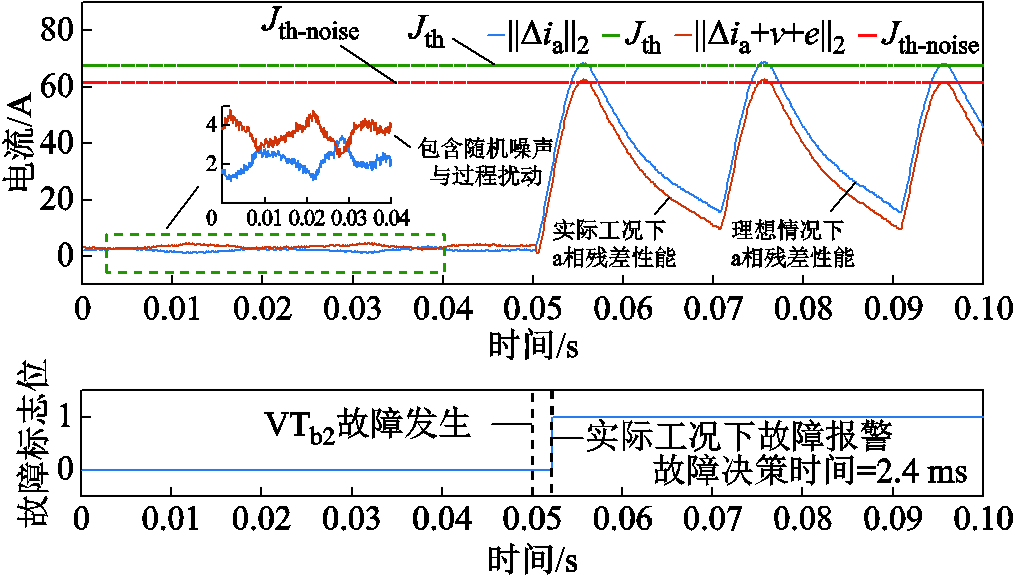
图18 实际工况下残差性能评价结果与理想情况间对比
Fig.18 Comparison of residual performance evaluation results under actual working condition and ideal condition
在图18中,实际工况下的a相残差性能评价信号略小于理想状态下的残差性能评价信号。相对应地,实际工况下的阈值Jth-noise也略小于理想状态下计算所得阈值Jth。根据图18,结合图13可得,理想工况下VTb2开路故障故障决策时间为2.3 ms,在实际工况中,故障决策时间为2.4 ms,两者相差0.1 ms。
同时,由于v(t)+e(t)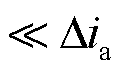 ,结合式(39)可得,实际工况下的残差性能评价信号对干扰v(t)与噪声e(t)具有较强的鲁棒性。因此,在实际工况中,基于残差性能评价的诊断方案依然可以保证快速且精准的故障检测与隔离。
,结合式(39)可得,实际工况下的残差性能评价信号对干扰v(t)与噪声e(t)具有较强的鲁棒性。因此,在实际工况中,基于残差性能评价的诊断方案依然可以保证快速且精准的故障检测与隔离。
6.4.1 逆变器单管故障电流残差仿真结果
图19为NPC型逆变器VTb2功率开关器件开路故障时,三相电流残差仿真结果。
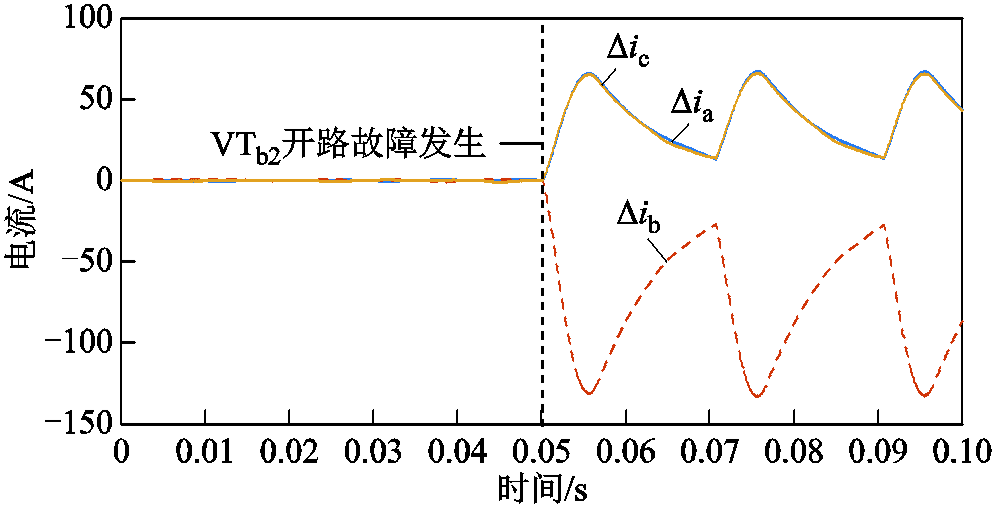
图19 VTb2单管故障情况下三相电流残差仿真结果
Fig.19 Three phase current residual simulation under VTb2 fault
根据图19可知,在故障发生后,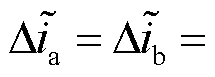
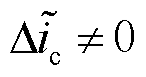 ,且
,且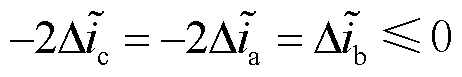 ,满足式(52)的机理分析结果。因此验证了表1所得单管故障状态下三相电流残差特征的准确性,可根据表3进行故障定位,得到VTb2单管开路故障。
,满足式(52)的机理分析结果。因此验证了表1所得单管故障状态下三相电流残差特征的准确性,可根据表3进行故障定位,得到VTb2单管开路故障。
6.4.2 逆变器同相双管故障电流残差仿真结果
图20为NPC型逆变器VTc2VTc4功率开关器件开路故障时,三相电流残差仿真结果。
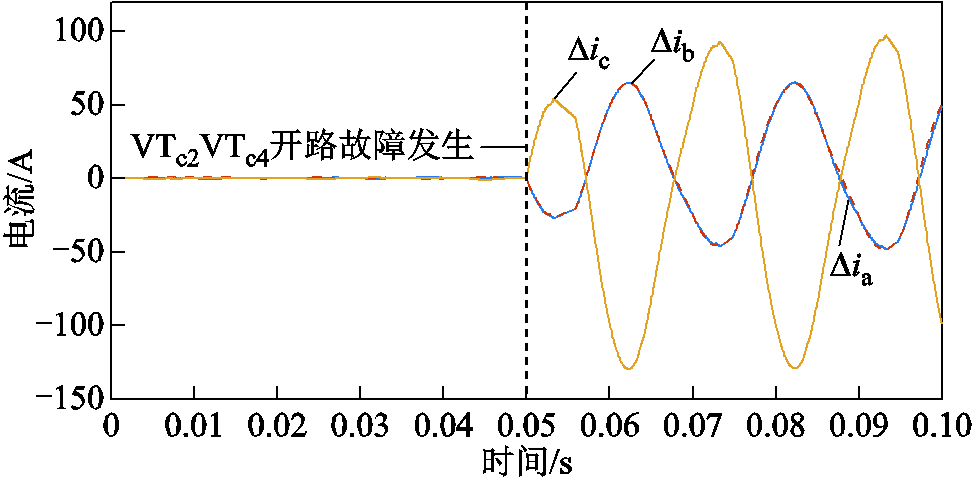
图20 VTc2VTc4双管故障情况下三相电流残差仿真结果
Fig.20 Three phase current residual simulation under VTc2VTc4 fault
根据图20可得,在故障发生后,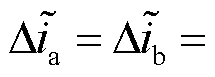
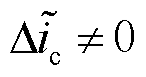 ,且满足
,且满足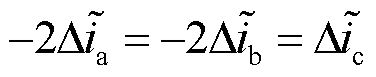 ,满足式(56)的机理分析结果。因此验证了表2所得同相双管故障状态下三相电流残差特征的准确性,可根据表2进行故障定位,得到VTc2VTc4同相双管开路故障。
,满足式(56)的机理分析结果。因此验证了表2所得同相双管故障状态下三相电流残差特征的准确性,可根据表2进行故障定位,得到VTc2VTc4同相双管开路故障。
6.4.3 逆变器异相同臂双管故障电流残差仿真结果
图21为NPC型逆变器VTb2VTc2功率开关器件开路故障时,三相电流残差仿真结果。
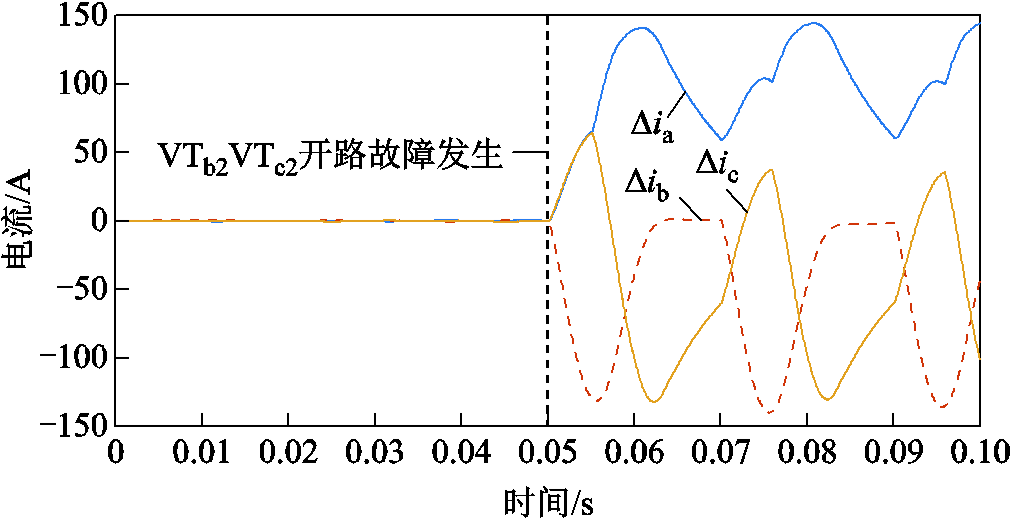
图21 VTb2VTc2双管故障情况下三相电流残差仿真结果
Fig.21 Three phase current residual simulation under VTb2VTc2 fault
根据图21可得,在故障发生后,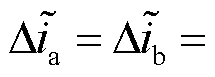
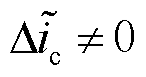 ,且满足
,且满足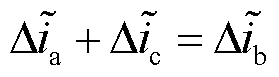 ,满足式(60)的机理分析结果。因此验证了表3所得异相同臂双管故障状态下三相电流残差特征的准确性,根据表3进行故障定位,得VTb2VTc2同相双管开路故障。
,满足式(60)的机理分析结果。因此验证了表3所得异相同臂双管故障状态下三相电流残差特征的准确性,根据表3进行故障定位,得VTb2VTc2同相双管开路故障。
6.4.4 逆变器异相异臂双管故障电流残差仿真结果
图22为NPC型逆变器VTa1、VTc3功率开关器件开路故障时,三相电流残差仿真结果。
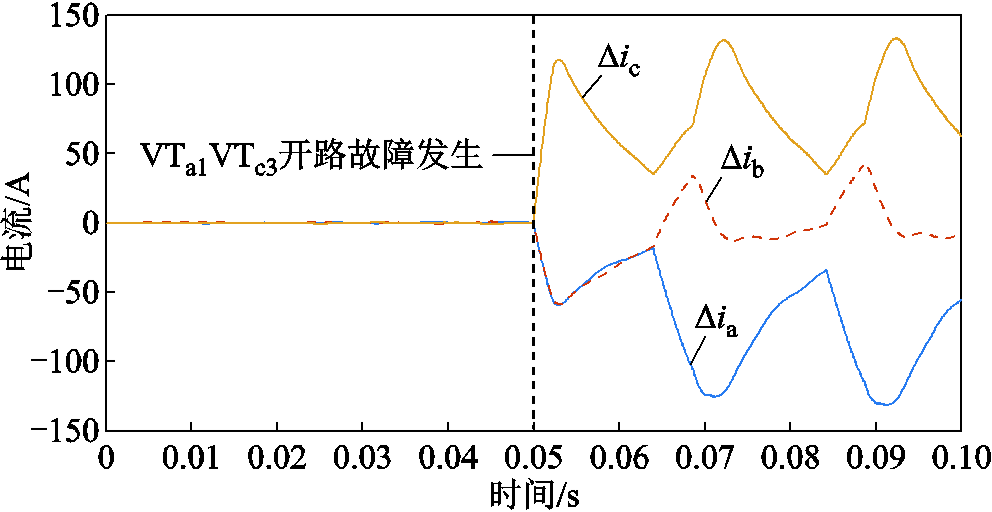
图22 VTa1VTc3双管故障情况下三相电流残差仿真结果
Fig.22 Three phase current residual simulation under VTa1VTc3 fault
根据图22可得,在故障发生后,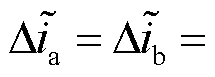
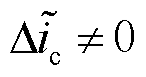 ,且满足
,且满足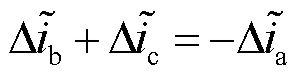 ,满足式(64)的机理分析结果。因此验证了表3所得异相异臂双管故障状态下三相电流残差特征的准确性,根据表3进行故障定位,得到VTa1、VTc3同相双管开路故障。
,满足式(64)的机理分析结果。因此验证了表3所得异相异臂双管故障状态下三相电流残差特征的准确性,根据表3进行故障定位,得到VTa1、VTc3同相双管开路故障。
图23为逆变器开路故障诊断系统实验平台实物图,包括直流电压源、NPC型三电平逆变器、驱动模块和电机等。NPC型三电平逆变器模块作为电机驱动电路。控制电路在主控芯片TMS320F28335基础上搭建。当需要模拟故障时,上位机PSIM软件平台发送模拟故障的控制信号,获取故障波形。实验平台及电机相关参数见表5。

图23 NPC型逆变器实验平台
Fig.23 NPC inverter test platform
表5 实验平台参数
Tab.5 Test platform parameters

参数数值 直流侧电压udc/V100 额定电压U/V36 额定输出功率P/W200 额定电流I/A7.5 额定转速nN/(r/min)3 000 额定转矩Tn/(N·m)0.637 转动惯量J/(kg·m2)1.89×10-5 极对数p8
图23中的实验平台上电后,不提供故障模拟信号,使其工作于正常状态,采集到的三相电流波形如图24所示。从图24中可以看出,电流波形均为稳定的50 Hz正弦波,任意两相信号之间相位相差120°,与图4仿真结果一致。

图24 正常工作时NPC型逆变器的电流波形
Fig.24 Current waveforms of NPC inverter under normal operation
在进行故障实验时,通过移除驱动信号模拟开路故障的发生。图25、图26分别为VTb2单管、VTb2VTb3同相双管发生开路故障时的逆变器输出三相电流实验波形,与图5、图6仿真波形基本一致。同理,图27为异相双管VTa1VTb2发生开路故障时三相电流波形,与Simulink仿真波形结果,即图7相吻合。
本文以NPC型三电平逆变器为研究对象,采用基于解析模型的故障诊断方法,提出了一套较为完备的故障诊断系统,用于解决逆变器功率开关器件开路故障这一工程实际问题。本文从残差评价角度出发,通过基于范数的标准评价函数计算残差性能指标与阈值,通过两者间对比实现故障检测。在后续的故障隔离中,根据逆变器功率开关器件的不同开路故障类型,求解三相电流残差表达式,得到三相电流残差间的数值特性从而实现精准故障隔离与定位。在残差生成环节中,构建诊断观测器观测三相电流,并且根据观测矩阵直接计算电流残差信号。这不仅实现了对被控系统状态变量的解析重构,同时规避了由于硬件电路和传感器加入而降低故障诊断率的问题。仿真结果表明,采用残差评价的故障检测方法缩短了诊断时间,使得故障诊断速度提高80%以上。在此基础上,今后研究中可加入容错方案,以确保逆变器在尽可能短的时间内检测出故障且仍可以正常运行。

图25 VTb2开路故障时NPC型逆变器实验电流波形
Fig.25 Current waveform of NPC inverter under VTb2 open circuit fault

图26 VTb2VTb3开路故障时NPC型逆变器实验电流波形
Fig.26 Current waveforms of NPC inverter under VTb2VTb3 open circuit fault

图27 VTa1VTb2开路故障时NPC型逆变器实验电流波形
Fig.27 Current waveforms of NPC inverter under VTa1VTb2 open circuit fault
参考文献
[1] 魏书荣, 黄苏融, 符杨, 等. 永磁同步电机及其驱动系统故障处理与容错机制研究综述[J]. 电力自动化设备, 2016, 36(10): 100-107.
Wei Shurong, Huang Surong, Fu Yang, et al. Overview on fault disposal and fault-tolerance mechanism of PMSM and its driving system[J]. Electric Power Automation Equipment, 2016, 36(10): 100-107.
[2] Yang Shaoyong, Bryant A, Mawby P, et al. An industry-based survey of reliability in power electronic converters[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1441-1451.
[3] Tian Xinlei, Guo Hong, Xu Jinquan, et al. Online inverter open-circuit fault diagnosis for fault tolerant permanent magnet synchronous motor system under multi-fault condition[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[4] Zhang Zeliang, Luo Guangzhao, Zhang Zhengbin, et al. A hybrid diagnosis method for inverter open-circuit faults in PMSM drives[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 180-189.
[5] Wang Borong, Li Zhan, Bai Zhihong, et al. Real-time diagnosis of multiple transistor open-circuit faults in a T-type inverter based on finite-state machine model[J]. CPSS Transactions on Power Electronics and Applications, 2020, 5(1): 74-85.
[6] Rahimpour S, Tarzamni H, Kurdkandi N V, et al. An overview of lifetime management of power electronic converters[J]. IEEE Access, 2022, 10: 109688-109711.
[7] Riccio J, Kumar R R, Cirrincione G, et al. Fault diagnosis using shallow neural networks for voltage source inverters in SynRM drives[C]//2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2022: 1-6.
[8] Freire N M A, Estima J O, Marques Cardoso A J. Open-circuit fault diagnosis in PMSG drives for wind turbine applications[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3957-3967.
[9] Ku H K, Jung J H, Park J W, et al. Fault-tolerant control strategy for open-circuit fault of two-parallel-connected three-phase AC–DC two-level PWM converter[J]. Journal of Power Electronics, 2020, 20(3): 731-742.
[10] Fan Jisheng, Yuan Wei. Review of parametric fault prediction methods for power electronic circuits[J]. Engineering Research Express, 2021, 3(4): 042002.
[11] 余运俊, 裴石磊, 谢玉麟. NPC三电平逆变器混杂建模及开路故障诊断[J]. 电测与仪表, 2020, 57(11): 16-23.
Yu Yunjun, Pei Shilei, Xie Yulin. Hybrid modeling and open-circuit fault diagnosis of NPC three-level inverter[J]. Electrical Measurement & Instrumentation, 2020, 57(11): 16-23.
[12] 史丽萍, 李衡, 马也, 等. 一种T型三电平拓扑APF故障诊断方法[J]. 电机与控制学报, 2022, 26(2): 94-101.
Shi Liping, Li Heng, Ma Ye, et al. Fault diagnosis method of T-type three-level topologyAPF[J]. Electric Machines and Control, 2022, 26(2): 94-101.
[13] 夏志凌, 胡凯波, 刘心悦, 等. 基于变模态分解的异步电机转子断条故障诊断[J]. 电工技术学报, 2023, 38(8): 2048-2059.
Xia Zhiling, Hu Kaibo, Liu Xinyue, et al. Fault diagnosis of rotor broken bar in induction motor based on variable mode decomposition[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2048-2059.
[14] Wu Feng, Zhao Jin. A real-time multiple open-circuit fault diagnosis method in voltage-source-inverter fed vector controlled drives[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1425-1437.
[15] Laadjal K, Sahraoui M, Cardoso A J M. On-line fault diagnosis of DC-link electrolytic capacitors in boost converters using the STFT technique[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6303-6312.
[16] 周晨阳, 沈艳霞. 基于小波分析的二重三相电压型逆变器开路故障诊断[J]. 电机与控制学报, 2020, 24(9): 65-75, 94.
Zhou Chenyang, Shen Yanxia. Open circuit fault diagnosis of dual three-phase voltage source inverter based on wavelet analysis[J]. Electric Machines and Control, 2020, 24(9): 65-75, 94.
[17] Henao H, Capolino G A, Fernandez-Cabanas M, et al. Trends in fault diagnosis for electrical machines: a review of diagnostic techniques[J]. IEEE Industrial Electronics Magazine, 2014, 8(2): 31-42.
[18] Ypma A, Tax D M J, Duin R P W. Robust machine fault detection with independent component analysis and support vector data description[C]//Neural Networks for Signal Processing IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop (Cat. No.98TH8468), Madison, WI, USA, 2002: 67-76.
[19] Martins J F, Pires V F, Pires A J. PCA-based on-line diagnosis of induction motor stator fault feed by PWM inverter[C]//2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 2006: 2401-2405.
[20] Ding S X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms and Tools[M]. London: Springer London, 2013.
[21] Emami-Naeini A, Akhter M M, Rock S M. Effect of model uncertainty on failure detection: the threshold selector[J]. IEEE Transactions on Automatic Control, 1988, 33(12): 1106-1115.
[22] Ding S X, Frank P M, Ding E L, et al. Fault detection system design based on a new trade-off strategy[C]//Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 2002: 4144-4149.
[23] Barhoumi L, Bemri H, Soudani D. Discretization of uncertain linears systems with time delay via Euler’s and Tustin’s approximations[C]//2016 4th International Conference on Control Engineering & Information Technology (CEIT), Hammamet, Tunisia, 2016: 1-6.
[24] 郑大钟. 线性系统理论[M]. 2版. 北京: 清华大学出版社, 2002.
[25] Lu Bin, Sharma S K. A literature review of IGBT fault diagnostic and protection methods for power inverters[J]. IEEE Transactions on Industry Applications, 2009, 45(5): 1770-1777.
[26] 许水清, 黄文展, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开路故障诊断[J]. 电工技术学报, 2023, 38(4): 1010-1022.
Xu Shuiqing, Huang Wenzhan, He Yigang, et al. Open-circuit fault diagnosis method of neutral point clamped three-level grid-connected inverter based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1010-1022.
[27] 陈勇, 刘志龙, 陈章勇. 基于电流矢量特征分析的逆变器开路故障快速诊断与定位方法[J]. 电工技术学报, 2018, 33(4): 883-891.
Chen Yong, Liu Zhilong, Chen Zhangyong. Fast diagnosis and location method for open-circuit fault in inverter based on current vector character analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 883-891.
[28] 陈超波, 王霞霞, 高嵩, 等. 基于区间滑模观测器的逆变器开路故障诊断方法[J]. 中国电机工程学报, 2020, 40(14): 4569-4579, 4736.
Chen Chaobo, Wang Xiaxia, Gao Song, et al. A diagnosis method for open-circuit faults in inverters based on interval sliding mode observer[J]. Proceedings of the CSEE, 2020, 40(14): 4569-4579, 4736.
[29] 杜厚贤, 刘昊, 雷龙武, 等. 基于振动信号多特征值的电力变压器故障检测研究[J]. 电工技术学报, 2023, 38(1): 83-94.
Du Houxian, Liu Hao, Lei Longwu, et al. Power transformer fault detection based on multi-eigenvalues of vibration signal[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 83-94.
[30] 褚旭, 鲍泽宏, 许立强, 等. 基于时序卷积残差网络的主动配电系统线路短路故障诊断方案[J]. 电工技术学报, 2023, 38(8): 2178-2190.
Chu Xu, Bao Zehong, Xu Liqiang, et al. Fault line diagnosis scheme of active distribution system based on time-sequence convolution residual network[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2178-2190.
[31] 杨贺雅, 邢纹硕, 向鑫, 等. 基于多元高斯分布异常检测模型的MMC子模块开路故障诊断方法[J]. 电工技术学报, 2023, 38(10): 2744-2756.
Yang Heya, Xing Wenshuo, Xiang Xin, et al. A sub-module open-circuit fault detection and location strategy for modular multilevel converters based on multivariate Gaussian distribution[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2744-2756.
[32] 刘帼巾, 刘达明, 缪建华, 等. 基于变分模态分解和改进灰狼算法优化深度置信网络的自动转换开关故障识别[J]. 电工技术学报, 2024, 39(4): 1221-1233.
Liu Guojin, Liu Daming, Miao Jianhua, et al. Fault identification of automatic transfer switching equipment based on VMD-WPE and IGWO optimized DBN[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1221-1233.
[33] 龙寰, 杨婷, 徐劭辉, 等. 基于数据驱动的风电机组状态监测与故障诊断技术综述[J]. 电力系统自动化, 2023, 47(23): 55-69.
Long Huan, Yang Ting, Xu Shaohui, et al. Review of data-driven condition monitoring and fault diagnosis technologies for wind turbines[J]. Automation of Electric Power Systems, 2023, 47(23): 55-69.
[34] 陈宁铤, 黄文焘, 杨欢红, 等. 多端环型海底观测网供电系统故障主动定位方法[J]. 电力系统自动化, 2023, 47(19): 147-155.
Chen Ningting, Huang Wentao, Yang Huanhong, et al. Active fault location method for power supply system of multi-terminal undersea observation ring networks[J]. Automation of Electric Power Systems, 2023, 47(19): 147-155.
Abstract During the contemporary scenario of "Industry 4.0 era", motors and theirs drive systems are widely used in metallurgy, petrochemical, chemical and other industrial fields. They are the largest power consumption machinery. Therefore, to guarantee the safety and stability of motors and theirs drive systems and improve the performance of them, it has become a research hotspot in the present industry and academia. However, the power switching devices in the motor drive system, such as the insulated gate bipolar transistor, work continuously at high switching frequency. They have to withstand the electrical and thermal overstress. It is prone to open circuit failure. It causes the output waveform harmonics increase, the motor torque ripple increase and brings bad effects on the system. Hence, it is urgent to solve the problem of open circuit fault of inverter power switching devices.
In the fault diagnosis system based on analytical model,the system is composed of residual generator, residual evaluation with threshold and fault decision part.In this process, the difference information obtained by comparing the actual variable with the reconstructed variable is called the residual. Residual signals can reveal fault information and reflect fault signals.However, the technique of filtering and extracting effective fault information from residual signals has been regarded as a challenge. Furthermore, there are few research results on residual evaluation and threshold calculation. In order to manifest the ability of fault information contained in residual signals, a fast open circuit fault diagnosis method for NPC three-level three-phase inverter is proposed via residual performance evaluation.
Firstly, aiming at the hybrid characteristics of the inverter, the health state mathematical model of the inverter based on hybrid logic dynamic method was established. Meanwhile, the diagnostic observer was constructed to obtain the three-phase current observations and calculate current residuals.Three phase current residuals were calculated by observation matrixes. Next, by introducing the standard evaluation function based on norm, the residual performance indicators and threshold were calculated. Current residuals were converted into usable characteristic signals and compared with the threshold to achieve efficient and accurate fault detection. At the same time, by means of analyzing the residual current numerical characteristics of different power switching devices under the open fault condition, the fault isolation table of the NPC inverter was derived. The accurate fault isolation is achieved according to the fault isolation table.
Ultimately, the proposed algorithm was verified on the simulation and semi-physical experiment platform. The simulation and semi-experimental platform results show that compared with the traditional signal and knowledge-based diagnosis method, the introduction of residual performance evaluation can improve the diagnosis speed by more than 80%. In the fault isolation simulation, three phase residual signals are generated for four different open circuit fault types of the inverter power switching device. The numerical characteristics are consistent with the fault isolation conditions derived in Tab.1~Tab.3. It verifies the effectiveness and accuracy of fault isolation.Furthermore, the fault diagnosis scheme proposed in this paper is simulated and discussed under the complex working condition, that is, under the condition of process disturbance and random noise. The simulation results indicate that the residual performance evaluation has good robustness under noise and disturbance. In summary, in this paper, the fast and accurate fault detection and isolation can be realized for the four common open circuit fault conditions of NPC three-level three-phase inverters.
Keywords:NPC type three-level three-phase inverter,open circuit fault diagnosis, residual performance evaluation, threshold, diagnostic observer
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.231519
国家重点研发计划(2022YFE0123400)和陕西高校青年创新团队项目(自主无人系统智能化测试与协同控制创新团队)资助。
收稿日期 2023-09-13
改稿日期 2024-02-16
陈超波 男,1978年生,博士,教授,研究方向为电机故障诊断与容错控制。E-mail:chenchaobo@xatu.edu.cn
高 嵩 男,1966年生,教授,博士生导师,研究方向为自动化控制系统和并网逆变。E-mail:gaos@xatu.edu.cn(通信作者)
(编辑 赫 蕾)