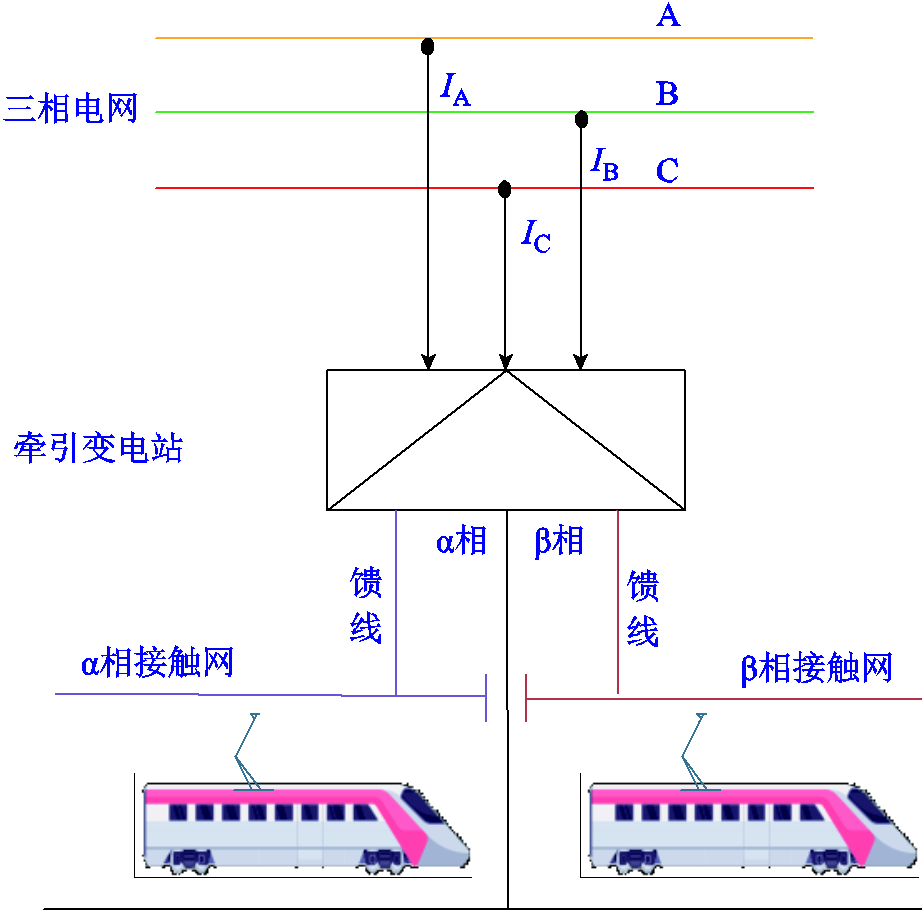
图1 牵引供电系统结构
Fig.1 Structure of traction power supply system
摘要 针对电气化铁路牵引负荷难以预测的问题,构建了一种由集合经验模态分解(EEMD)、改进型卷积块注意力模块(CBAM)和双向长短期神经网络(BiLSTM)组合成的EEMD-CBAM-BILSTM预测方法,有效地降低了牵引负荷超短期预测误差与计算成本。首先,通过EEMD将牵引负荷数据分解为多个稳定、有规律的时序模态函数,突出负荷数据的时序特征;其次,将分解后的各分量整体通入由卷积神经网络(CNN)和改进型CBAM组成的特征提取模块提取全局时序特征;最后,利用贝叶斯优化(BO)搜寻BiLSTM最优参数,并将全局特征通入优化后的神经网络进行超短期时序预测。仿真算例表明,该文所提预测框架在各预测步长下均能很好地把握牵引负荷变化趋势,显著提升了牵引负荷预测的精度。
关键词:牵引负荷预测 集合经验模态分解 双向长短期神经网络 贝叶斯优化 卷积块注意力模块卷积神经网络
我国拥有世界上最大规模的轨道交通网络[1],总里程超15万km,电气化率超过70%[2],铁路耗能是最大的单体负荷类别。随着我国电气化铁路网络的迅猛发展,以高铁动车为代表的铁路运输已经成为我国运输系统的重要组成部分。
随着“网-源-储-车”协同供能技术的发展[3-5],系统内部的能量管理与协同控制部分亟须源荷两侧精确的秒级超短期预测提供技术支撑[6-7]。为了保障电网的安全稳定运行和日前与实时的经济调度,铁路部门需向国家电网公司上报各牵引变电站购电量的预测值。若实际购电量超出预测误差阈值,国家电网公司将在日内增加电费结算价格[8],造成轨道交通系统整体运营成本增加。同时,精准地牵引负荷超短期预测也可以为轨道交通电能质量分析、牵引变电站的优化调度、牵引变电站选址定容等研究[9-11]提供数据源侧的支持。因此,亟须开展电气化铁路牵引负荷(下文简称为“牵引负荷”)精确预测课题研究。
目前已有的针对牵引负荷预测的研究主要分为两类:一类是基于牵引计算和供电计算的仿真;另一类是基于实测的负荷数据和列车运行图。其中,基于牵引计算和供电计算方面的技术已经非常成熟[12-14]。由于其数学上的本质是根据列车运动方程和受力情况进行计算,需要详尽准确的列车与轨道参数,故只能预测运行情况稳定的客运线路,对新站和重载铁路等行车随机的路段预测准确度会大大降低,且整体计算规模十分庞大,无法满足能量管理系统的预测需求。随着电气化铁路系统信息化程度的提高,数据采集与监视控制系统(Supervisory Control And Data Acquisition, SCADA)的落地,使得通过实测数据建模进行负荷预测变为可能。文献[8]基于滑动窗法从实测数据中提取典型运行过程的负荷曲线并建立相应的负荷库,建立典型运行过程的动态负荷模型,并结合行车运行图的信息进行牵引变电站的负荷预测。但现有的这些研究还保留在较大的时间尺度进行预测,并未有效地利用规模化的数据,且基于运行图的方法无法应用在重载铁路等无固定运行图的情况。文献[15]通过稀疏高斯过程拟合负荷历史特征和时间信息与牵引负荷之间的关系,从而实现牵引负荷超短期秒级点预测与概率预测,但该研究模型无法深入捕捉时间序列的隐含特征。总体上,牵引负荷预测的相关研究工作方兴未艾。同时,数据驱动的崛起也可为牵引负荷预测的发展提供了有力支撑。然而,基于数据驱动的牵引负荷预测研究尚处于起步阶段,并无充足的示范性研究作为技术支持。对此,可在较为成熟的电力负荷预测领域中进行合理借鉴,有效迁移。
在电力系统负荷预测领域,已取得了较多的研究成果。目前,主流的电力系统负荷预测方法主要分为传统统计学方法、机器学习方法和组合预测方法三类。①基于传统统计学的方法,包括多元线性回归法[16]、时间序列法[17-18]等。该类方法应用于平稳性、周期性和趋势性较强的时间序列数据时,拥有良好的表现,但面对随机性强、波动性较大的时序数据时,其结果往往较差。②基于机器学习的方法,包括神经网络法[19-20]、支持向量机[21]等。与传统算法相比,虽然机器学习算法拥有鲁棒性强、适应性强和自动化程度高等优点,但也存在超参数确定难、易出现欠拟合、过拟合情况的问题。而且,此类方法对非线性时序数据之间的隐藏特征提取较为困难。③“分解-预测”型的组合预测方法[22-24]:由于统计学方法和机器学习的不足,研究者们提出“分解-预测”型的预测方法。首先将负荷进行分解,突出时序特征,然后建立神经网络模型对各个分量依次训练、预测并将最终的分量预测结果叠加,虽然在一定程度上能突出时序特征,但多个神经网络的训练大大增加了预测过程的计算量,且在多个网络预测结果的加和过程中,误差也可能出现叠加,导致预测精度下降。考虑到牵引负荷波动大、突变性和动态特性强等特性与“网-源-储-车”协同供能体系下能量管理系统的超短期负荷预测需求,这些方法无法直接应用于牵引负荷预测中。
鉴于此,本文针对牵引负荷的时序特征,提出一种基于经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)、改进型卷积块注意力模块(Convolutional Block Attention Module, CBAM)、双向长短期神经网络(Bidirectional Long Short-Term Memory Neural Network, BiLSTM)等技术的牵引负荷超短期预测框架,主要贡献如下:
1)在方法层面,本文创新性地将深度学习方法应用于牵引负荷预测领域,相较于已有预测方法来说,在数据端仅需要历史负荷数据作为输入,无需车辆运行图、车辆信息、铁路信息等其他输入,适用于重载铁路等特殊预测场景。
2)在技术层面,将集合经验模态分解、改进型卷积块注意力模块、双向长短期神经网络、贝叶斯优化(Bayesian Optimization, BO)等技术有机结合起来,突出各技术优势,有效地解决了现有研究无法深入地捕捉负荷的实时动态特性的缺陷,从模型端提升牵引负荷预测精度。
3)在架构层面,提出新型预测架构,相较于传统“分解-预测”型预测架构,大幅降低了计算成本,更好地适应超短期牵引负荷预测任务,从而满足“网-源-储-车”能量管理系统高时间分辨率的预测数据需求。
牵引负荷作为一类电力系统的特殊负荷,与传统电网负荷相比,具有较大的区别。牵引变电所通常采用Vv、YNd11、Scott等两相牵引变压器将电网三相电转换为两相27.5 kV供电[25],如图1所示,牵引供电所引出的两条供电线之间存在电分相,α相供电线与β相供电线上机车牵引负荷相互独立。因此,可直接对单条桥臂进行预测。

图1 牵引供电系统结构
Fig.1 Structure of traction power supply system
由于电力机车在行进间存在不同运行状态的频繁切换,同时受人为操作、气象条件、路面情况等随机因素的影响,牵引负荷具备较强的突变性及波动性[26]。图2~图4显示了朝脑沟、关碾房、万水泉牵引变电所的单日有功功率变化情况。从图2~图4可知,三个牵引变电所的两条供电桥臂的有功功率的变化范围基本相同,均处于0~14 MW的范围内,变化情况相似,在曲线的峰值点呈现出“阶跃信号”的特性,该处相邻功率点所连成的曲线的斜率接近1或-1,这种波动源于该变电所供电区域内运行电力机车的数量变化[27],而这种剧烈波动所发生的时刻,具有强烈的随机性。
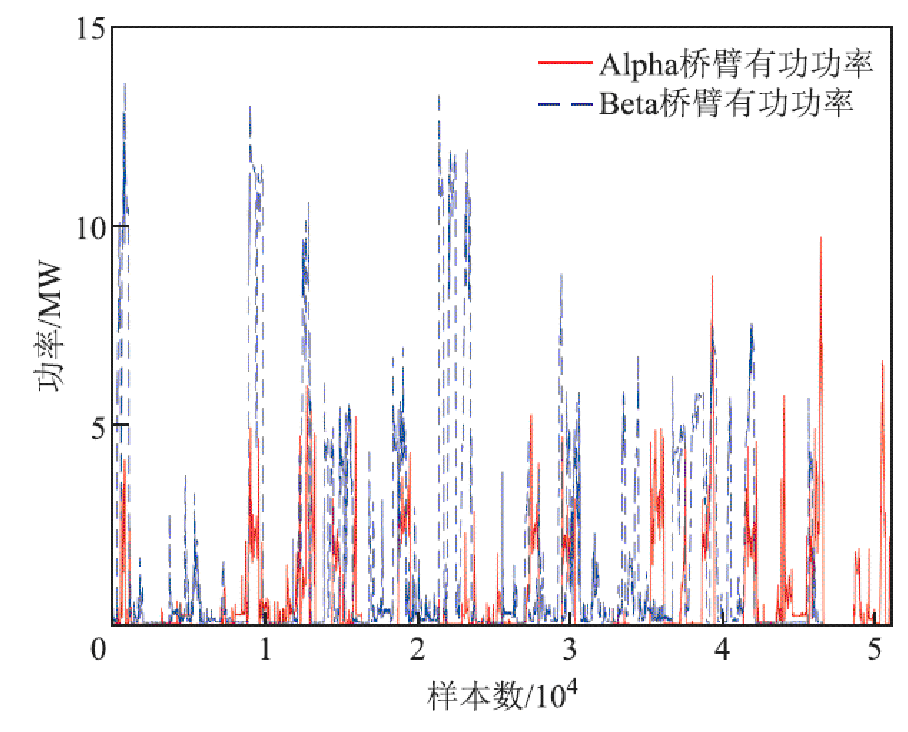
图2 朝脑沟牵引变电站负荷
Fig.2 Load of Chaonaogou traction substation
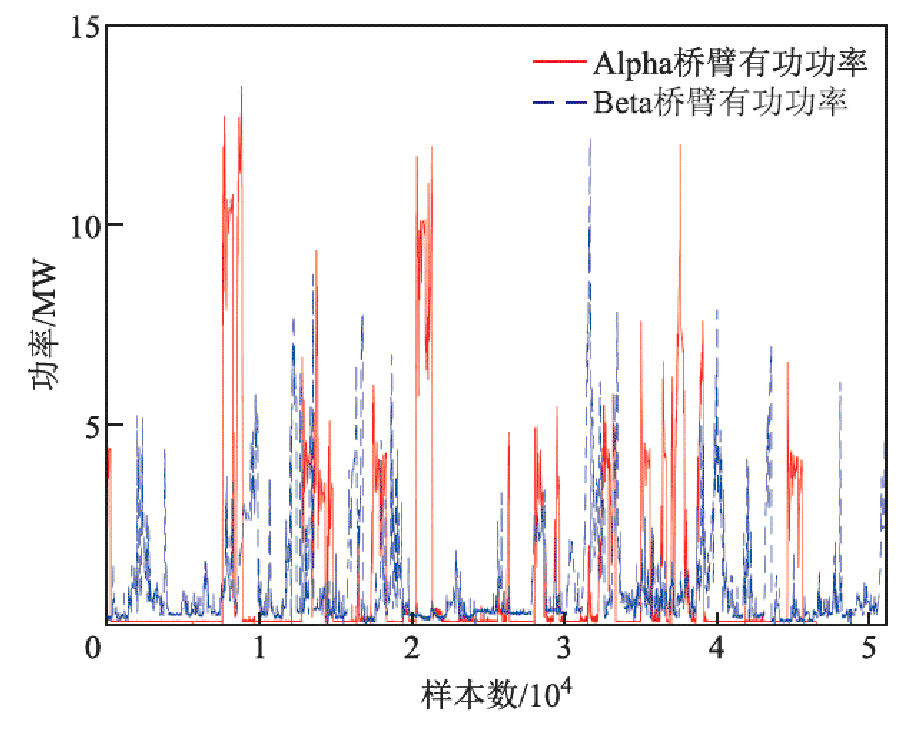
图3 关碾房牵引变电站负荷
Fig.3 Load of Guannianfang traction substation
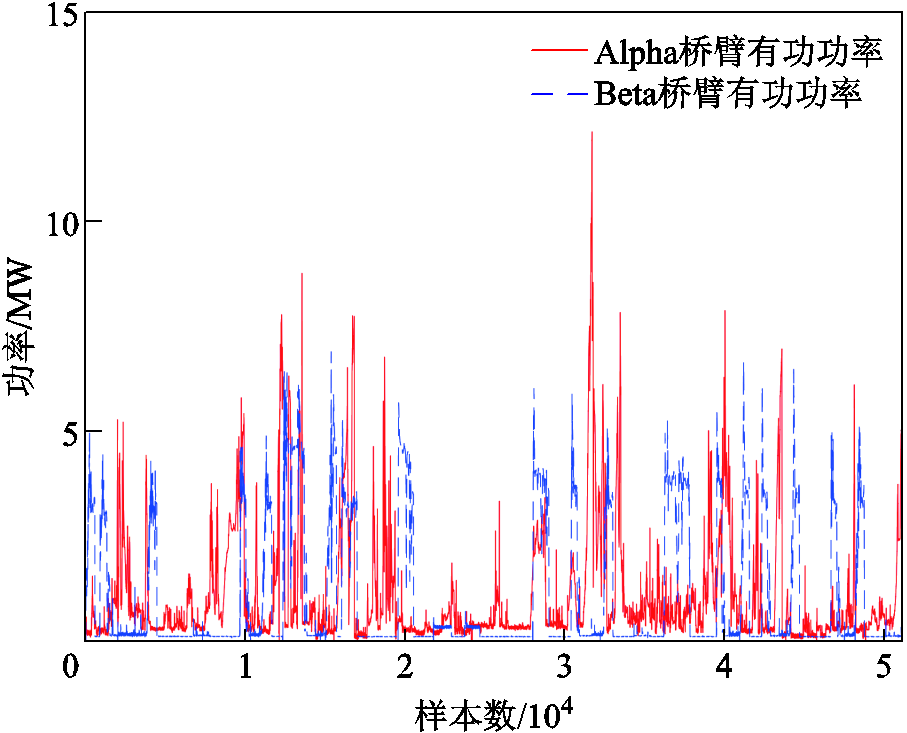
图4 万水泉牵引变电站负荷
Fig.4 Load of Wanshuiquan traction substation
为了对比牵引负荷与电力负荷的差别,在上述基础上,本文从数据侧的视角出发,选取江苏某地区电力负荷实测数据,运用统计学的相关知识对牵引负荷与电力负荷数据进行研究分析,通过指标量化的方式研究两者之间的差别。首先观察两负荷的突变性,即动态变化情况。在相同时间跨度下,为了描述这种动态变化,参照离散点集的梯度计算方法,定义一阶差分变化率为
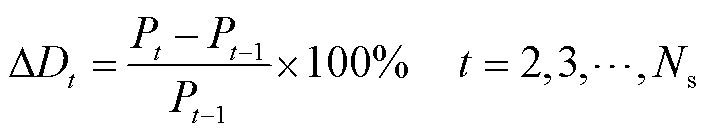 (1)
(1)
式中,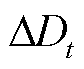 为第t个负荷点处的一阶差分变化率;
为第t个负荷点处的一阶差分变化率;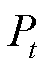 为第t时刻的负荷数值;
为第t时刻的负荷数值;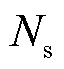 为负荷序列包含的功率点数量。通过计算一阶差分变化率,可获取相邻功率点间的变化率,快速查看序列的突变情况。电力负荷和牵引负荷的一阶差分变化率分别如图5、图6所示。由图可知,两种负荷功率变化率各具有一条密集数据带,但牵引负荷所对应的图像包含较多离群数据点,表明列车牵引负荷序列更易出现数值突变情况。相比之下,电力负荷更加稳定,功率将保持相对固定的变化率增长或减小。
为负荷序列包含的功率点数量。通过计算一阶差分变化率,可获取相邻功率点间的变化率,快速查看序列的突变情况。电力负荷和牵引负荷的一阶差分变化率分别如图5、图6所示。由图可知,两种负荷功率变化率各具有一条密集数据带,但牵引负荷所对应的图像包含较多离群数据点,表明列车牵引负荷序列更易出现数值突变情况。相比之下,电力负荷更加稳定,功率将保持相对固定的变化率增长或减小。
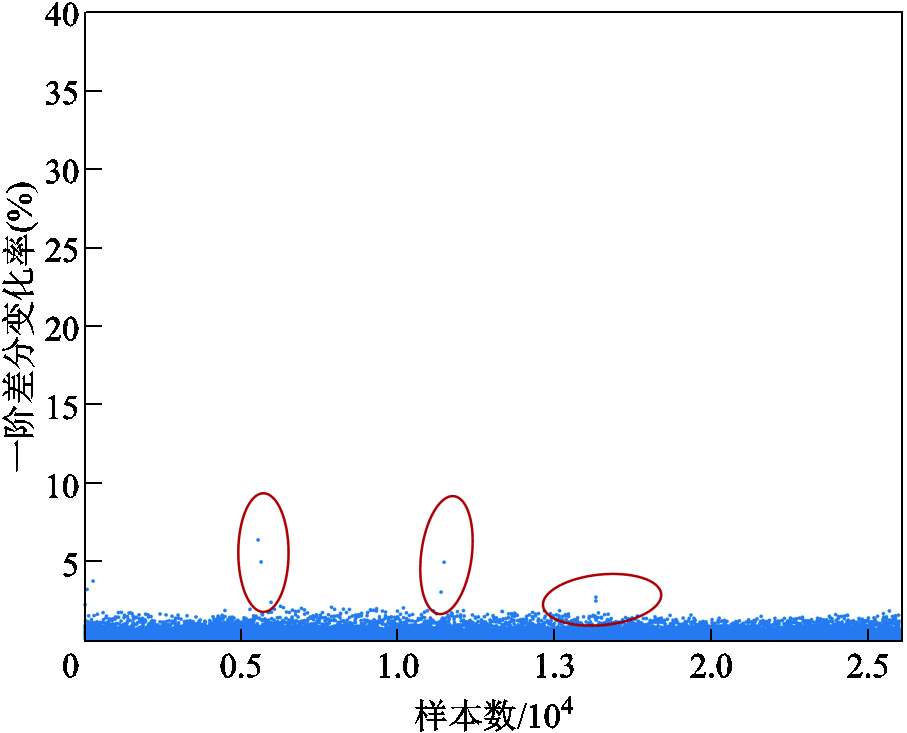
图5 电力负荷一阶差分变化率
Fig.5 First order differential change rate of power load

图6 牵引负荷一阶差分变化率
Fig.6 First order differential change rate of traction load
为了进一步分析与描述两种负荷在增、减区间的波动性,本文提出了一种自适应区间的方差(Adaptive Interval Variance, AIV),通过分析更小范围内的序列特征,关注局部的剧烈波动,进而描述总体的波动性。指标对两组负荷数据进行对比分析。计算分析过程如图7所示。
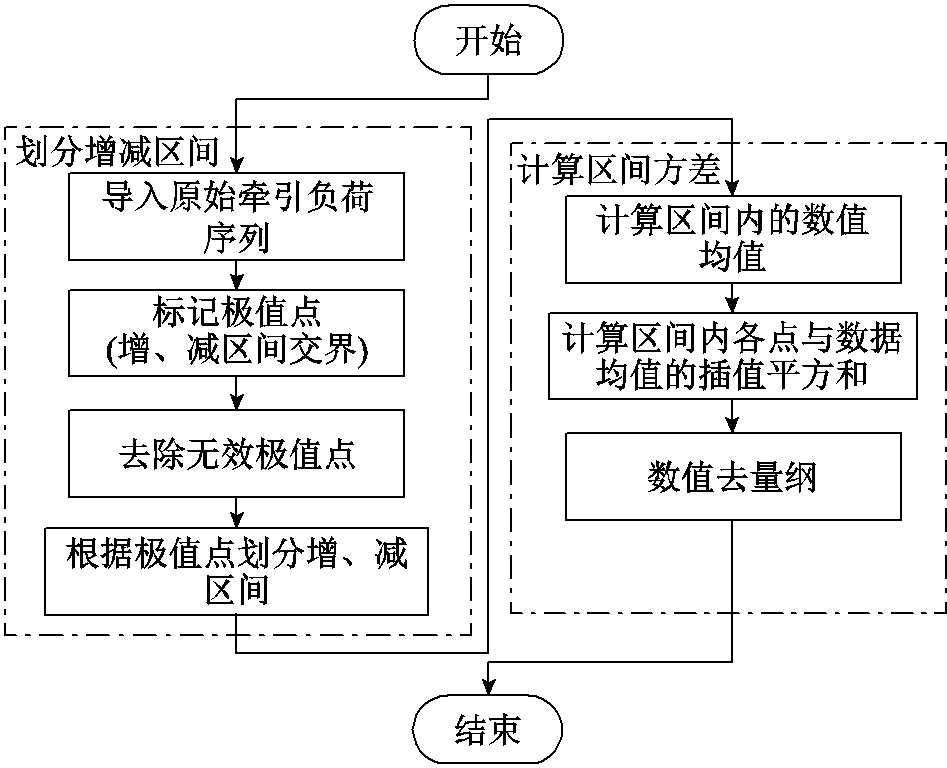
图7 AIV的计算过程
Fig.7 Calculation flow chart of AIV
针对电力负荷序列及牵引负荷序列的AIV计算结果对比见表1。由表1可见,相较于电力负荷,牵引负荷所包含的增(减)区间增加15.47%,且具有更高的AIV,表明牵引负荷的趋势变化更加频繁,且在同一趋势下变化幅度更大。
表1 电力负荷与牵引负荷AIV计算结果对比
Tab.1 Comparison of AIV calculation results between electric load and traction load

类型区间数AIV 电力负荷3 1730.022 9 牵引负荷3 6640.393 9
由1.1节和1.2节对牵引负荷的特性分析可知,与传统电力负荷相比,牵引负荷是具有单相独立性、突变性和波动性,其反映在时间序列数据上后,使得原始牵引负荷序列为一列具有复杂、深度隐含特征的数据,需面向牵引负荷时序特征,针对性地设计预测模型。
牵引负荷相较于传统电力负荷具有较强的突变性与波动性,同时,此类负荷在时序上存在着一定的隐含规律,如何“突显”其规律成为需要聚焦的问题。EEMD是一种常用于信号分解和模态分析的方法,是对EMD的改进和扩展,可将复杂的信号数据分解为若干个较平稳信号,从而突出数据内部隐含的时序特征,利用多维度的序列共同描述牵引负荷的时序变化过程。其基本思想是通过将随机噪声引入原始信号中,进行多次的EMD分解,并对分解结果进行平均化来获得稳定和可靠的模态成分。
EEMD拥有自适应分解、无需设置基函数、优秀的去噪性能等优点,特别是对长序列和非平稳性特征的信号具有较好的适应能力。经EEMD处理后的牵引负荷原始信号会被分解为处于不同频段的IMF,这些IMF可从不同层面反映原始信号的负荷波动性及随机性。相较于原始波动性、突变性较强的时间序列数据,IMF的波形更加平稳,具备一定的规律。因此EEMD的使用可在一定程度上降低信号的杂糅,剥离出信号的深层特征,从而降低神经网络的预测难度。
相较于传统电力负荷,牵引负荷序列的突变性及波动性更强,而s级的高分辨率时序数据代表着在较短时间内,时序便可包含大量的功率点,其数据特征隐含于长序列中。虽然EEMD分解后的时序特征更加明显,但同时增加了后续预测的数据量,如何整体提取经EEMD分解之后的各特征序列的隐含特征成为关注的重点。对此,本文结合卷积神经网络(Convolutional Neural Network, CNN)和CBAM[28]技术提出一种增强的特征提取模块,通过融入通道注意力及空间注意力两种机制,提升预测架构面向横向数据(维度)的特征提取能力。该模块包含两个核心结构,用于连接CNN的改进型CBAM结构及两层CNN,分别完成特征放大及特征提取的任务。改进型CBAM赋予了一种可以同时考虑空间及通道的复合注意力机制,经过CBAM处理的数据将带有明显的特征,但这只是一个标记的过程,仍需利用CNN进行特征提取。二者的结合就是一个突显特征进而提取的流程,是对各自功能的有效利用和延续。本文的特征提取模块的结构如图8所示。
2.2.1 改进型CBAM
CBAM通过自适应地对特征图进行注意力加权,使网络能够更关注重要的特征,并抑制无关的信息。这有助于提高网络的表征能力,使其能够更好地捕捉数据中的关键特征。同时CBAM可作为不同层间的数据通道,灵活地嵌入不同的CNN架构中。CBAM模块包含两个子模块:通道注意力模块和空间注意力模块。这两个子模块分别对特征图的通道维度和空间维度进行注意力加权。
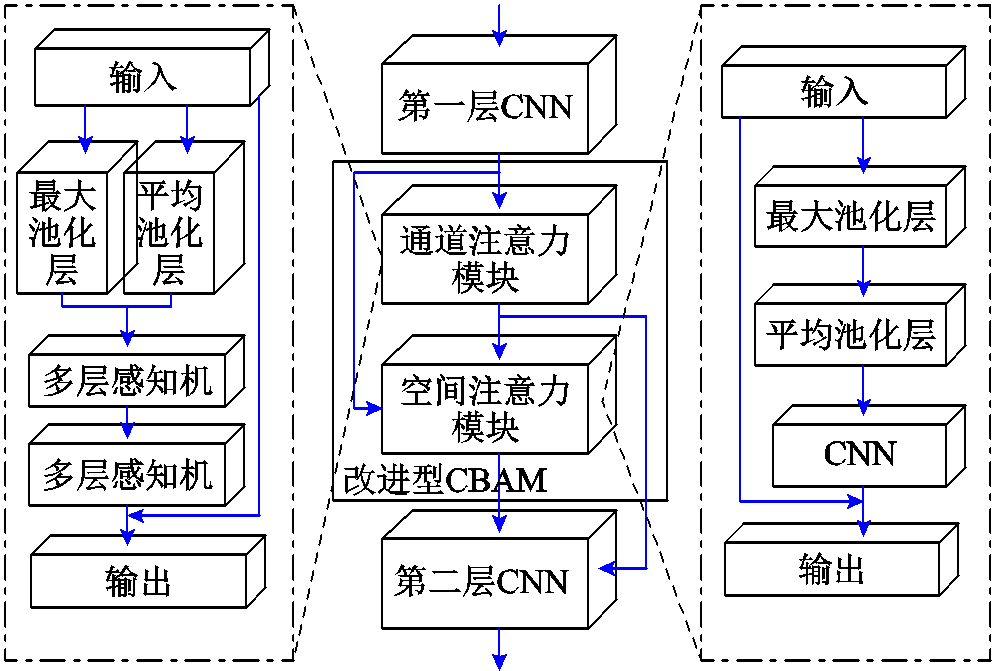
图8 包含改进型CBAM的全局特征提取模块结构
Fig.8 Global feature extraction module structure including improved CBAM
传统的CBAM以Sigmoid为激活函数,由于其分布两极化明显,常应用于二分类问题,但在处理复杂特征时可能会丢失特征信息。所以本文在提取模块的搭建中,选择Elu作为线性单元。Elu会将数值映射在非负范围内,从而避免了“神经元死亡”的问题。
通道注意力模块通过全局平均池化将特征图在空间维度上进行压缩,然后经过两个全连接层,其中使用了激活函数(如Elu)和Sigmoid函数。这个过程旨在学习每个通道的重要性权重,然后将权重应用于原始特征图上,使得网络能够自适应地调整通道之间的重要性。通道注意力模块的计算过程为
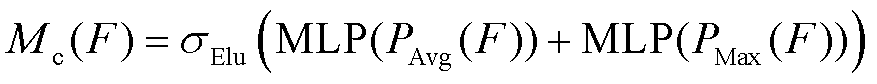 (2)
(2)
式中, 为激活函数,
为激活函数,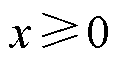 时,
时,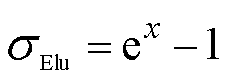 ,
,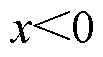 时,
时,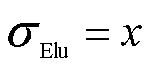 ;
;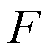 为输入通道注意力模块的原始数据;
为输入通道注意力模块的原始数据;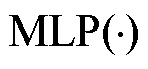 表示多层感知机;
表示多层感知机;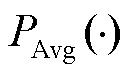 表示全局平均池化;
表示全局平均池化;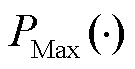 表示全局最大池化。
表示全局最大池化。
空间注意力模块则通过对特征图在通道维度上进行压缩和扩展,使用了两个卷积层和激活函数(如ReLU),生成了一个二维的注意力图。注意力图表示不同位置上的像素对于最终特征表示的重要性权重。这样,网络可以自适应地关注不同空间位置的信息。空间注意力模块的计算过程为
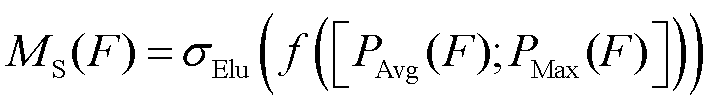 (3)
(3)
式中,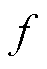 为卷积。整个CBAM模块将通道注意力和空间注意力相结合,通过对特征图进行通道维度和空间维度的注意力加权,使得网络能够更加关注重要的特征并抑制无关的信息。这有助于提高网络的表示能力、感知能力和鲁棒性,进而提升任务性能。
为卷积。整个CBAM模块将通道注意力和空间注意力相结合,通过对特征图进行通道维度和空间维度的注意力加权,使得网络能够更加关注重要的特征并抑制无关的信息。这有助于提高网络的表示能力、感知能力和鲁棒性,进而提升任务性能。
2.2.2 CNN
CNN包含两个主体结构:卷积层和池化层。卷积层是加权求和的过程。通过卷积运算,原始数据的局部低维特征被映射到高维特征。考虑到经EEMD处理后的牵引负荷序列更易被整理为二维特征图的形式,本文选择二维CNN为体征提取工具。经过卷积层提取特征之后,进行池化操作。经过池化操作后的数据对应原始数据会拥有更大的感受野,通过降低图的空间维度,减少计算量,同时提取并强化特征。本文利用的是最大池化(Max Pooling)。
本文所提出的全局特征提取结构包含两层CNN结构。由于牵引负荷序列的高分辨率,短时内便包含大量数据,并且EEMD处理后会出现数据量的倍增,导致数据环境复杂,使得CBAM的特征识别与标记受阻。所以,第一层CNN将用来进行特征的初步提取,降低CBAM的工作量,提升CBAM的特征处理性能;第二层将对由CABM标记后的简化特征进行处理。
秒级分辨率的牵引负荷序列包含了大量样本,为了适应实际工程应用需求,所拟合的特征应为一个长序列。传统的预测网络无法很好地适用于该长度序列,为此,本文借助BiLSTM对经由特征提取结构处理后的数据进行拟合,通过前向以及后向的同时推演捕捉序列中的关键时序特征。
BiLSTM是一种循环神经网络(Recurrent Neural Network, RNN)的变体,它能够在处理序列数据时考虑前后信息,可以有效地处理长序列,并且能够捕捉到序列中的关键特征。其基本结构是由两个LSTM组成的,一个按时间步从前到后处理序列(前向LSTM),另一个按时间步从后到前处理序列(后向LSTM)。这样,每个时间步的输入将同时考虑过去和未来的上下文信息。BiLSTM神经网络预测示意图如图9所示。
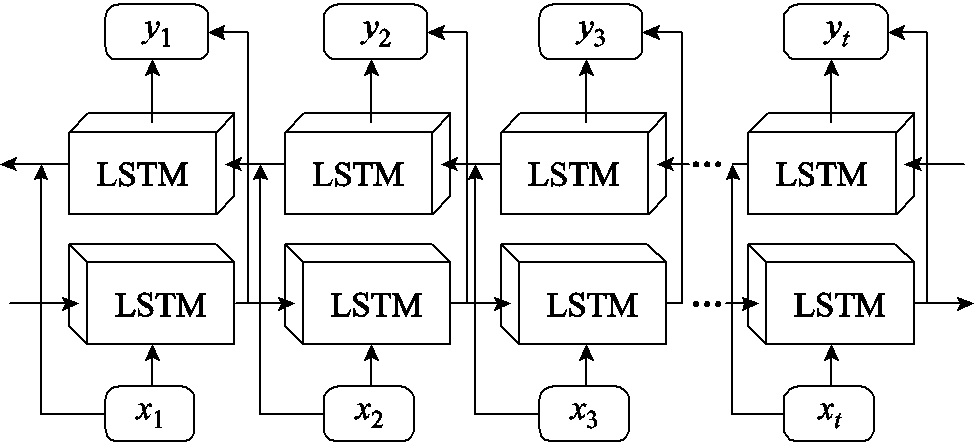
图9 BiLSTM神经网络预测示意图
Fig.9 Schematic diagram of BiLSTM neural network prediction
在神经网络训练过程中,其超参数的选择往往采用人工经验法取得,导致容易出现欠拟合和过拟合的情况。本文采用贝叶斯优化的方法求解神经网络模型的超参数,其优化过程如图10所示。
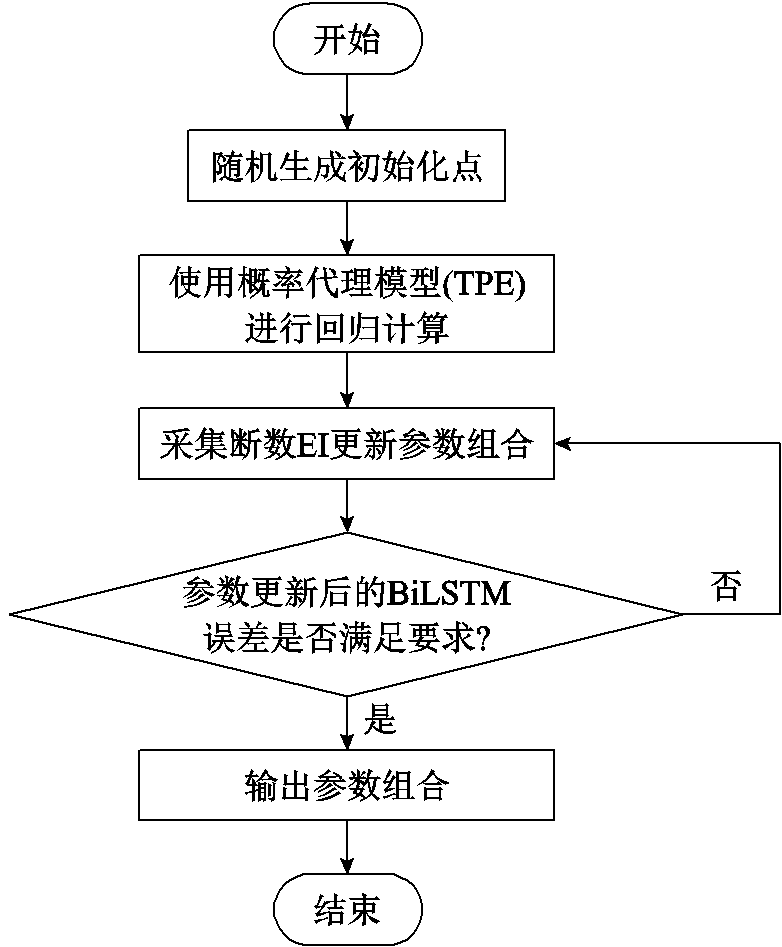
图10 贝叶斯优化过程
Fig.10 Bayesian optimization process
由图10知,贝叶斯优化包含四个核心步骤:
1)建立概率代理模型。在开始优化之前,需要定义一个概率模型来代表目标函数的分布。概率代理模型包括高斯过程(Gaussian Process)、随机森林和树状结构Parzen估算器(Tree-structured Parzen Estimator, TPE)。
2)通过采集函数补充模型的描述。根据当前的先验模型,通过一定的策略选择下一个样本点进行评估,该策略被称为采集函数。常用的采集函数有期望改进(Expected Improvement, EI)、置信区间(Confidence Bound)等。
3)评估目标函数。选择的样本点被送入目标函数进行评估,获取其函数值。
4)更新后验模型。将新的样本点和其对应的函数值加入已有的数据集中,使用贝叶斯推断方法更新后验模型。
迭代优化:重复步骤2)~步骤4),直到达到预定的迭代次数或满足迭代停止准则。
由于贝叶斯的序贯式进程,后序优化建立在前序优化的计算结果上,在缩短计算时长的同时,保证了模型的高精度。
本文选择TPE及EI对框架中的BiLSTM的部分参数进行优化,具体见表2。文献[29]已对相关技术进行充分描述,在此不再赘述。
表2 优化参数汇总
Tab.2 Summary of optimization parameters

变量搜索范围 学习率 Learning Rate[10-4,0.1] 批次数 Batch Size[1,1,32] 隐含层Hidden Size[1,1,64]
本文构建的牵引负荷预测框架流程如图11所示。
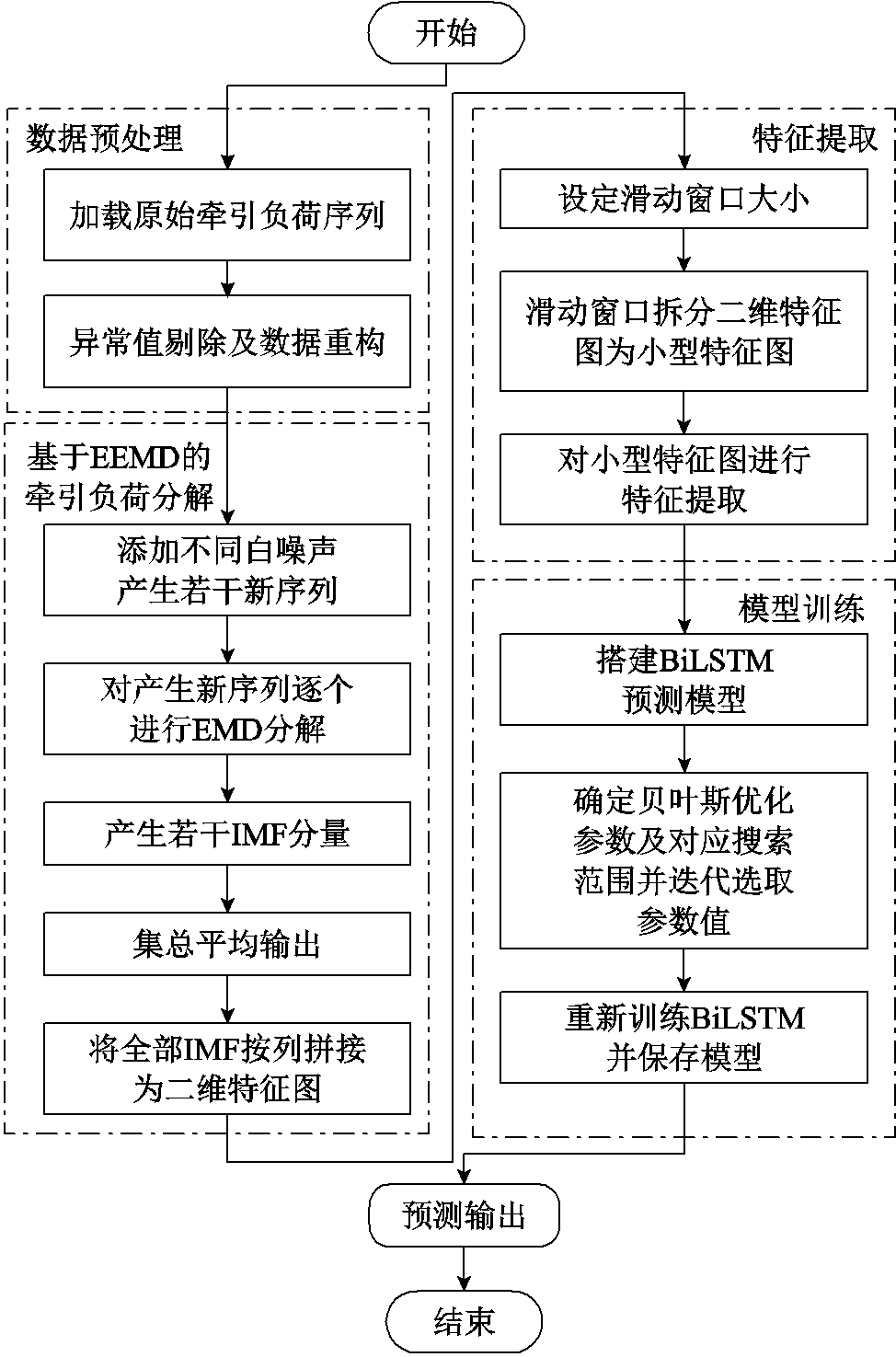
图11 本文牵引负荷预测框架流程
Fig.11 Flow chart of traction load prediction framework in this paper
具体流程为:
1)数据预处理。识别原始牵引负荷序列(长度为m)中的异常数据,主要包括极少量数值为负以及局部突变过于强烈的负荷点。之后,利用三次样条插值生成异常数据的替代值,完成数据重构。
2)基于EEMD的牵引负荷序列分解。通过在重构后的牵引序列上分别添加n个白噪声,产生n个新序列,分别进行EMD分解,对分解结果进行平均化输出,最终获得n个简单、稳定的负荷子序列,分别命名为IMF1, ,IMFn,并按照编号顺序按列拼接为大小为m×n的二维特征图。
,IMFn,并按照编号顺序按列拼接为大小为m×n的二维特征图。
3)特征提取。设定滑动窗口的大小(时间步长×特征数);然后利用滑动窗口将由步骤2)获得的二维特征图拆分为若干小型特征图,并滚动输入至第一层CNN、改进型CBAM以及第二层CNN,分别完成初步的整体特征提取、自适应加权的特征强化和深度的特征提取;最后,获得特征更加突出的特征图,并输入后续结构进行模型训练。
4)模型训练。搭建BiLSTM预测模型,确定贝叶斯优化的目标,并设定各目标的搜索范围;其次通过建立概率代理模型TPE,根据采集函数EI添加可补充描述代理模型的样本点,以调整、更新参数值;然后对更新参数后的BiLSTM进行误差评估,若满足迭代条件,则输出当前的参数组合,若不满足,则继续更新参数值;最后将输出预测误差最小的参数组合,将该组合代入BiLSTM,重新训练模型,并以可直接调用的格式保存该模型。
图12展示了本文架构与其他“分解-预测”框架的对比。如图12所示,在经过EEMD处理将牵引负荷序列分解为若干IMF后,传统“分解-预测”框架注重各个特征的短期时序特征,并分别对不同特征进行预测,这一过程中需要训练等同于特征数的BiLSTM,最后叠加输出预测结果,这会导致整体模型运算量过大、最后预测结果叠加过程会造成误差叠加、不同IMF之间的隐含特征无法识别等问题,进而使得预测准确度降低、计算时间过长;而本文架构将重组后的数据集直接拼接转换为二维特征图,之后经过滑动窗口处理拆分为小型特征图,利用CNN和改进型CBAM,对短期内的全局特征进行识别、标记和提取,之后通过一个BiLSTM模型完成预测。相较于其他框架,本文框架更注重对数据整体特征的提取,认为不同IMF分量反映不同层级的数据特征,且均会关联到实际的牵引负荷,由于单个滑动窗口包含多种信息,更有利于挖掘深层关联性,实现精准的预测。同时,全程仅需训练一个预测模型,在一定程度上节约了计算成本,简化了计算过程,也可避免叠加输出时对预测误差的累积。
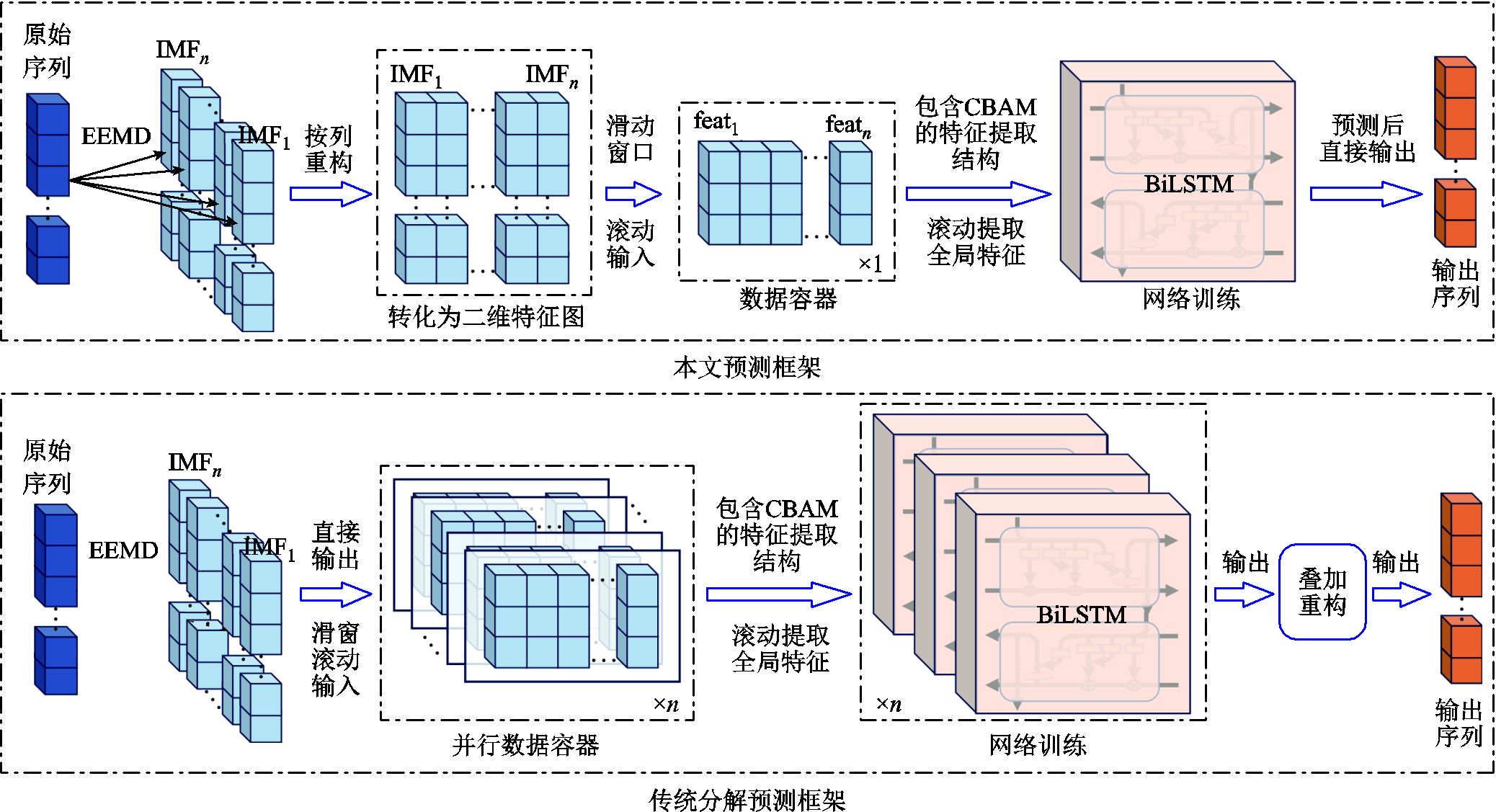
图12 本文预测框架与传统“分解-预测”框架结构对比
Fig.12 Comparison between the prediction framework of this article and the traditional "decomposition prediction" framework structure
本文仿真通过Pytorch框架的Python语言实现,主机系统为Windows11,仿真主机硬件参数为:CPU为Intel Core i7-13700H 2.40 GHz,内存RAM为16 GB,GPU为Nvidia GeFore RTX 4060,并利用CUDA架构实现GPU加速运算。本文预测架构及其参数设置见表3。
表3 本文预测框架结构与参数设置
Tab.3 Prediction framework structure and parameter settings in this article
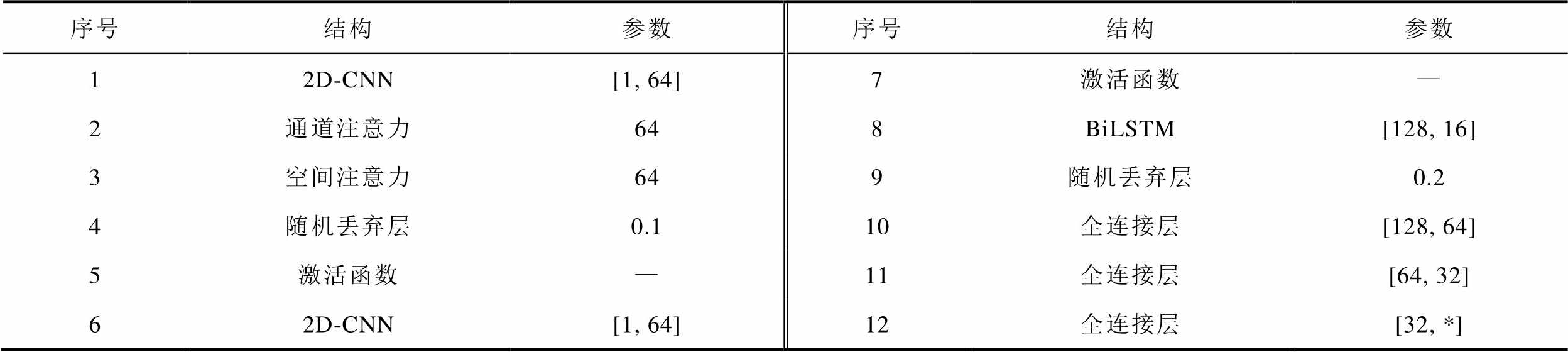
序号结构参数序号结构参数 12D-CNN[1, 64]7激活函数— 2通道注意力648BiLSTM[128, 16] 3空间注意力649随机丢弃层0.2 4随机丢弃层0.110全连接层[128, 64] 5激活函数—11全连接层[64, 32] 62D-CNN[1, 64]12全连接层[32, *]
注:*表示输出的预测负荷点数量;各结构按照序号顺序连接。
本算例参考功率预测和新能源预测国标,采用方均根误差(Root Mean Square Error, RMSE)、平均误差(Mean Absolute Error, MAE)和拟合优度(Goodness of Fit, R2)作为仿真的综合评估损失函数。各指标的计算过程为
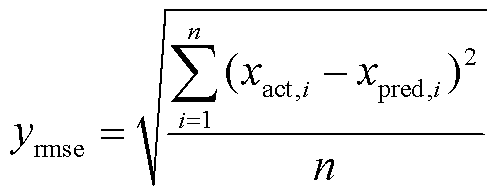 (4)
(4)
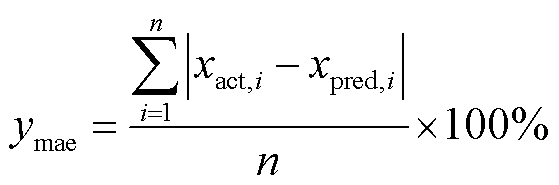 (5)
(5)
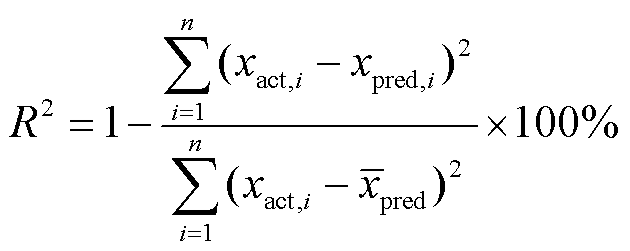 (6)
(6)
式中,n为预测样本数;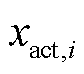 和
和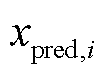 分别为i时刻的实际值和预测值;
分别为i时刻的实际值和预测值;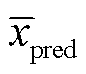 为预测样本均值。
为预测样本均值。
为了验证本文预测框架的准确性,项目组在内蒙某高铁牵引变电站进行了实地采集,数据时间分辨率为1 s,不间断采集16 h数据(共77 400条),以保证数据来源的真实性与可靠性。
整体数据集划分为训练集、验证集和测试集。训练集用来训练预测模型的各种参数,验证集用来验证模型是否建立合适,而测试集用来进行实际的预测。取其中1~61 720条数据作为训练集,61 721~7 304条数据作为验证集,74 305~77 400条数据作为测试集。本文利用滑动窗口输入数据,并定义单次滑动窗口输入数据的条数为时间步长,单次滑动窗口输出的预测结果数为预测步长。考虑到牵引负荷序列的分辨率仅为1 s,按照其实际分辨率进行预测输出对运算速度提出极高的要求,且不具备实际工程应用需求。所以,在仿真中,按照不同时间步长以及预测步长分为不同的预测形式,包括:①10-2(时间步长-预测步长);②10-4;③20-4;④20-8;⑤40-8;⑥40-16。
本文主要对所提出架构的批次大小、学习率和隐含层数量进行优化。使用贝叶斯优化前后的EEMD-CNN-CBAM-BiLSTM(ECCBL)的预测结果对比见表4(以10-2的模式进行预测)。由表4可知,优化后的MAE、RMSE分别降低了76.8%、76.0%;R2提高了5.29%,表明优化的介入提升了模型的数据拟合能力从而降低了预测误差,证明通过贝叶斯优化可使本文模型获得的较好参数值。虽然人工调节参数也可近似达到该预测水平,但过程繁琐,且依赖经验。而贝叶斯优化的调参过程,可设置的效率更高,具有更高的解释性和可靠性。
表4 贝叶斯优化结果对比
Tab.4 Comparison of Bayesian optimization results

ECCBL优化目标模型性能 学习率批次数隐含层ymaeyrmseR2(%) 优化后0.007 314570.044 40.067 399.68 优化前0.00110640.191 30.280 494.19
本次仿真首先将原始牵引负荷序列进行EEMD分解,共得到15个IMF,连同原始序列构成数据集的16个分量,如图13所示。可知,相比于原始序列,所得IMF的波形突变和波动明显减少,未出现模态混叠的情况。通过EEMD,原始复杂信号被极大简化。目前主流的模态分解方式包括EEMD以及VMD。为了验证模态分解对预测效果提升的有效性、EEMD相较于VMD的优势以及3.2节中新构建的分解预测框架的有效性,本文构建VMD-CNN-CBAM-BiLSTM(VCCBL)架构与本文的ECCBL以及CNN-CBAM-BiLSTM(CCBL)进行对比,不同预测模式的结果汇总见表5,并选取200个数据点进行可视化描述,结果如图14所示。其中,ECCBL*表示使用传统分解-预测框架的ECCBL。由表5可知,随着输出的增加,全部预测的精度都有不同程度的降低。然而,总体上,ECCBL的性能明显高于其他对比模型。

图13 EEMD分解结果
Fig.13 EEMD decomposition results
表5 模态分解对比及预测框架对比数据
Tab.5 Modal decomposition comparison and prediction framework comparison data

预测模式误差水平10-210-420-420-840-840-16 ECCBLymae0.044 40.049 00.083 10.092 40.094 50.137 4 yrmse0.067 30.088 30.129 60.170 80.163 50.200 8 R2(%)99.6899.4398.7497.7197.8696.87
(续)

预测模式误差水平10-210-420-420-840-840-16 ECCBL*ymae0.209 6 0.213 1 0.207 4 0.185 7 0.191 4 0.204 1 yrmse0.305 5 0.326 9 0.310 5 0.350 5 0.342 1 0.379 5 R2(%)95.7395.1995.6894.3894.6592.42 VCCBLymae0.206 30.161 30.188 90.2160.232 30.283 5 yrmse0.252 10.253 70.279 20.370 30.430 10.477 1 R2(%)96.0295.5795.4492.1090.0989.13 CCBLymae0.191 4 0.230 3 0.228 3 0.312 8 0.322 5 0.359 3 yrmse0.298 2 0.348 9 0.344 6 0.474 7 0.486 1 0.586 4 R2(%)95.9494.4494.7689.7089.5484.29

图14 模态分解对比及预测框架对比
Fig.14 Modal decomposition comparison and prediction framework comparison
对比ECCBL及CCBL可知,从10-2增加至40-16,ECCBL的R2仅下降2.81%;相同情况下,CCBL的R2下降了11.65%。由图14可知,CCBL的预测输出存在明显偏移波动,且这种波动趋势并不符合实际值的变化趋势。这是由于CCBL的预测模型前端无序列分解结构,使得CCBL无法解析数据深层隐含的变化规律。因此可知,模态分解对信息的深度分解,可降低预测模型对信息变化的理解难度,显著提升预测精度。
对比ECCBL和精度仅次之的VCCBL可知,从10-2增加至40-16,ECCBL的R2仅下降2.81%;相同情况下,VCCBL的R2下降了6.89%。ECCBL的性能优于VCCBL可在图14中得到交叉验证。在20-4及40-8两种模式下,ECCBL对于实际值序列(黑色序列)的跟随效果更好,更接近实际数值。二者的唯一差别为序列分解方法。VMD在针对长序列分解时,信号分解不完全,更易出现模态混叠。将复杂序列输入CCBL,其内部神经元不能充分拟合隐含的深层数据关系,使得CCBL的性能出现较大损失。上述分析表明,经EEMD处理后的数据更适于牵引负荷的预测。
对比ECCBL和ECCBL*可知,从10-2增加至40-16,ECCBL的R2仅下降2.81百分点;相同情况下,ECCBL*的R2下降了3.31百分点。ECCBL的性能优于ECCBL*。这表明,传统预测框架在分解-预测-叠加的过程中会不断积累误差,使得最终的预测偏移较大。而使用新构建预测框架的ECCBL在CBAM的加持下,搜索模态数据包含的全域信息,可深度解析模态信息中的关键因素,提升预测过程中对信息的利用效率。
将本文所提出的ECCBL预测框架与CNN-BiLSTM(CBL)、CNN-LSTM-Attention(CLA)、BiLSTM及RNN进行对比实验,数据集的划分情况一致。本文所涉及的全部预测模型或框架(包含单一以及复合模型)的预测数据见表6,可见,不同场景下,本文框架的R2均保持在95%以上,MAE以及RMSE处于最小水平。即使CBL及CLA在多预测输出时,如20-8以及40-16时,也会出现明显的性能衰减,二者的R2跌至90%左右。在与其他模型比较时发现,本文框架在40-16下的性能提升最为明显,MAE分别缩小了31.2%、39.1%、47.5%、45.8%;RMSE分别缩小了40.0%、42.6%、53.6%、47.5%;R2分别提高了5.2%、5.9%、10.65%、7.7%。
表6 整体预测数据
Tab.6 Overall forecast data

预测模型误差水平10-210-420-420-840-840-16 ECCBLymae0.044 40.049 00.083 10.092 40.094 50.137 4 yrmse0.067 30.088 30.129 60.170 80.163 50.200 8 R2(%)99.6899.4398.7497.7197.8696.87 CBLymae0.104 30.169 00.135 70.174 70.138 00.198 2 yrmse0.176 20.243 30.224 30.272 60.347 10.334 8 R2(%)97.7195.6496.3994.5891.1091.65 CLAymae0.106 90.116 70.108 40.175 30.145 70.225 1 yrmse0.138 10.168 30.180 60.222 40.235 50.349 7 R2(%)98.5797.9197.5796.3395.8890.99 RNNymae0.134 60.122 00.136 20.165 70.174 30.261 4 yrmse0.226 80.258 40.262 50.321 70.318 10.433 2 R2(%)96.1895.1094.9092.2992.5386.22 BiLSTMymae0.155 80.157 30.181 00.201 40.188 60.253 1 yrmse0.204 60.236 30.300 90.322 10.354 70.383 2 R2(%)96.8895.8793.2392.2690.6689.20
为了进一步对比各模型预测的性能细节差异,图15和图16从单一模型和复合模型两个角度详细展示了本文框架与其他模型的结果(200个负荷点)对比。由图15、图16可知,复合模型的预测性能要优于单一模型。在不同预测模式下,复合模型输出的误差更小,对实际序列的还原度更高。在复合预测模型中,本文框架输出的预测曲线在大部分情况下的要更接近实际值曲线;整体上的趋势变化与真实值序列一致。图15、图16还展示了该段负荷序列中既存在上升趋势又存在下降趋势的一小段序列。随着预测输出的增加,BiLSTM和RNN的输出曲线已逐渐不具备牵引负荷的波动性特点,对实际曲线的还原程度大大降低;CLA、CBL的表现尚属良好,但对于第70个负荷点附近出现的“下降后迅速上升”波形的预测效果不及本文框架,相似情况还出现在第50个负荷点附近。综上所述,相对于传统方法,本文框架的预测精度更高,对突变、波动序列的预测效果有着明显的提升,且优势在多预测输出的情况下体现得更加充分。
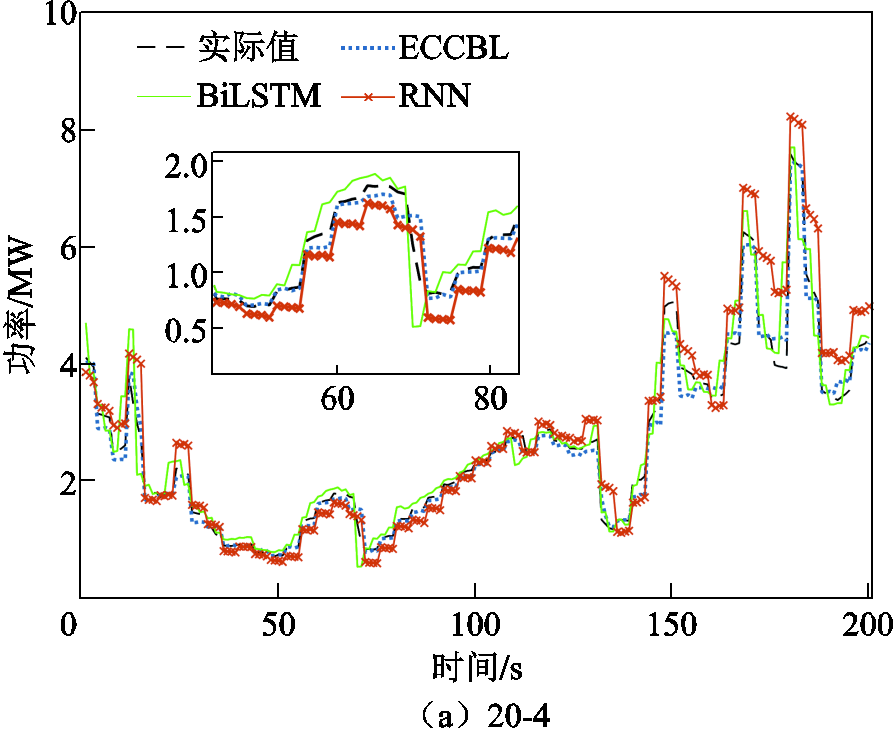
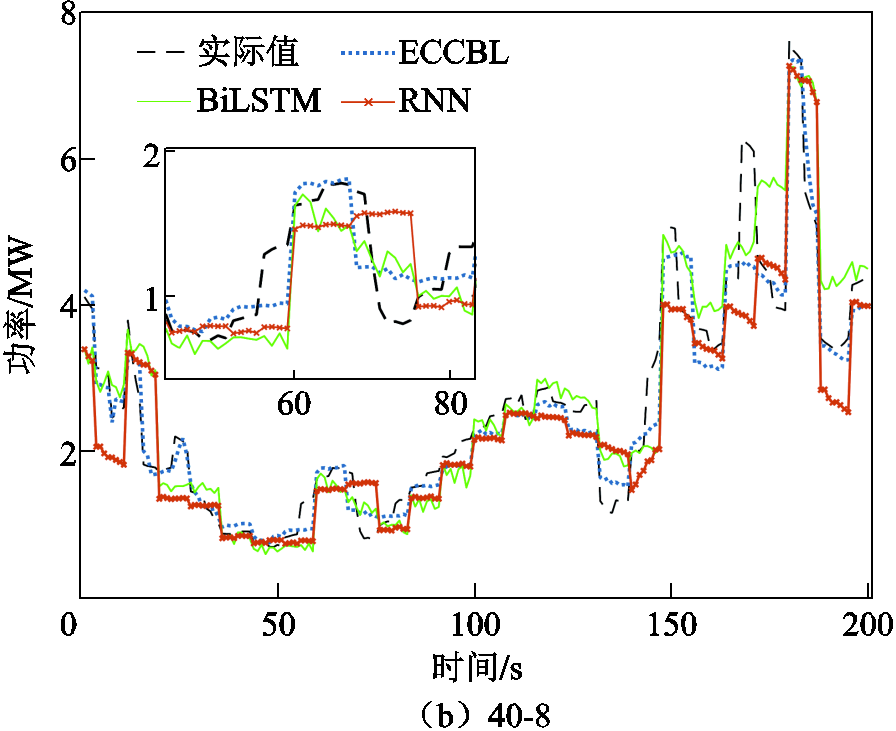
图15 ECCBL与单一模型结果对比
Fig.15 Comparison of ECCBL and single model results
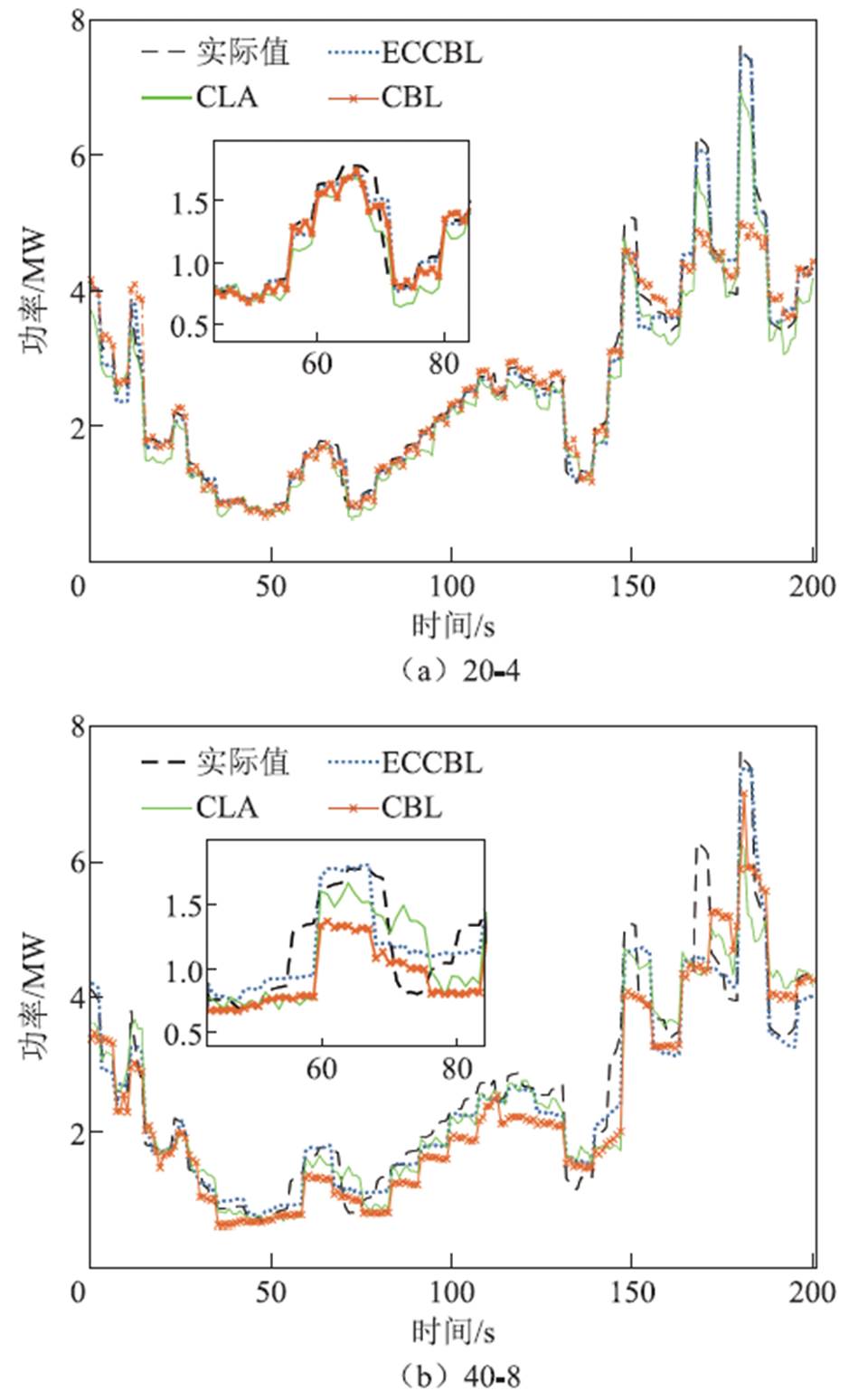
图16 ECCBL与复合模型结果对比
Fig.16 Comparison of ECCBL and composite model results
面向“网-源-储-车”协同供能体系下能量管理系统的超短期负荷预测需求,针对牵引负荷时序特征,本文提出一种基于EEMD-CBAM-BILSTM的牵引负荷超短期预测框架。通过EEMD分解将牵引负荷数据分解为不同频率的平稳分量,然后将各分量拼接成整体特征矩阵,利用由CNN与改进型CBAM组成的全局特征提取模块提取各分量之间的时序特征矩阵,并利用BiLSTM对该矩阵进行精准的时序预测,主要得出了以下的结论:
1)相对于其他分解算法,在面对波动较大、不平稳的牵引负荷长序列时,EEMD拥有较好的效果,不易出现模态混叠的情况,更好地突出时序隐含的深层数据关系与时序特征。
2)提出一种包含改进型CBAM的特征提取模块和全局特征提取结构,能显著减少由于“分解-预测”型方法带来的计算量。提高牵引负荷数据的隐含时序特征的表征能力,更好地捕捉数据中的关键特征,提升后续神经网络预测精度。
3)经过贝叶斯优化超参数后的BiLSTM模型在处理长特征序列时,性能较为稳定,相较于其他的神经网络,能更好地捕捉前后时间方向上的信息,充分考虑以当前点为基准点的过去和未来的时序信息,同时避免了传统RNN训练时,容易出现梯度消失和爆炸的问题。
4)本文框架集合了EEMD、CBAM、CNN、BO和BiLSTM技术的优势和特点,在实测数据下的仿真实验结果表明:该预测框架在各预测步长下均能显著地提升电气化铁路牵引负荷超短期预测精度,具有良好的工程应用价值。
参考文献
[1] 熊嘉阳, 沈志云. 中国高速铁路的崛起和今后的发展[J]. 交通运输工程学报, 2021, 21(5): 6-29.
Xiong Jiayang, Shen Zhiyun. Rise and future development of Chinese high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2021, 21(5): 6-29.
[2] 唐圣德, 胡海涛, 肖冬华, 等. 基于阻抗测量信息的电气化铁路“多车共网”系统稳定性分析[J]. 电工技术学报, 2024, 39(19): 6039-6053.
Tang Shengde, Hu Haitao, Xiao Donghua, et al. Stability analysis of electrified railway "multi-vehicle common network" system based on impedance measurement information[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6039-6053.
[3] 胡海涛, 郑政, 何正友, 等. 交通能源互联网体系架构及关键技术[J]. 中国电机工程学报, 2018, 38(1): 12-24, 339.
Hu Haitao, Zheng Zheng, He Zhengyou, et al. The framework and key technologies of traffic energy Internet[J]. Proceedings of the CSEE, 2018, 38(1): 12-24, 339.
[4] 高仕斌, 罗嘉明, 陈维荣, 等. 轨道交通“网-源-储-车”协同供能技术体系[J]. 西南交通大学学报, 2024, 59(5): 959-979, 989.
Gao Shibin, Luo Jiaming, Chen Weirong, et al. Rail transit ‘network-source-storage-vehicle’ collaborative energy supply technology system[J]. Journal of Southwest Jiaotong University, 2024, 59(5): 959-979, 989.
[5] 罗嘉明, 高仕斌, 韦晓广, 等. 基于模糊Petri网的“网-源-储-车”动态阈值能量管理策略研究[J]. 工程科学与技术, 2023, 55(1): 48-58.
Luo Jiaming, Gao Shibin, Wei Xiaoguang, et al. Research on “grid–source–storage–vehicle” dynamic threshold energy management based on fuzzy Petri nets[J]. Advanced Engineering Sciences, 2023, 55(1): 48-58.
[6] Liu Yuanli, Chen Minwu, Cheng Zhe, et al. Robust energy management of high-speed railway co-phase traction substation with uncertain PV generation and traction load[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(6): 5079-5091.
[7] 李俊豪, 涂春鸣, 王鑫, 等. 基于“规则+优化”的电气化铁路站点实时能量管控策略[J]. 电工技术学报, 2024, 39(11): 3339-3352.
Li Junhao, Tu Chunming, Wang Xin, et al. Real-time energy management strategy for electrified railroad stations based on “rules + optimization”[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3339-3352.
[8] 魏波, 胡海涛, 王科, 等. 基于实测数据和行车运行图的高铁牵引变电站负荷预测方法[J]. 电工技术学报, 2020, 35(1): 179-188.
Wei Bo, Hu Haitao, Wang Ke, et al. Research on traction load forecasting method for high-speed railway traction substation based on measured data and train timetable[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 179-188.
[9] Langerudy A T, Mariscotti A, Abolhassani M A. Power quality conditioning in railway electrification: a comparative study[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 6653-6662.
[10] Wang Xiaoyu, Han Ying, Li Luoyi, et al. CVaR quantitative uncertainty-based optimal dispatch for flexible traction power supply system[J]. IEEE Transactions on Transportation Electrification, 2024, 10(1): 1900-1910.
[11] Chen Minwu, Cheng Zhe, Liu Yuanli, et al. Multitime-scale optimal dispatch of railway FTPSS based on model predictive control[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 808-820.
[12] 薛艳冰, 马大炜, 王烈. 列车牵引能耗计算方法[J]. 中国铁道科学, 2007, 28(3): 84-87.
Xue Yanbing, Ma Dawei, Wang Lie. Calculation method of energy consumption in train traction[J]. China Railway Science, 2007, 28(3): 84-87.
[13] 王琪. 川藏铁路再生制动能量利用方案研究[D]. 北京: 北京交通大学, 2021.
Wang Qi. Study on energy utilization scheme of regenerative braking in sichuan-tibet railway[D]. Beijing: Beijing Jiaotong University, 2021.
[14] 王科, 胡海涛, 魏文婧, 等. 基于列车运行图的高速铁路动态牵引负荷建模方法[J]. 中国铁道科学, 2017, 38(1): 102-110.
Wang Ke, Hu Haitao, Wei Wenjing, et al. Modelling method for dynamic traction load of high speed railway based on train working diagram[J]. China Railway Science, 2017, 38(1): 102-110.
[15] 刘福, 廖启术. 电气化铁路牵引负荷预测研究[J]. 机车电传动, 2023(2): 142-150.
Liu Fu, Liao Qishu. Research on traction load forecasting of electrified railway[J]. Electric Drive for Locomotives, 2023(2): 142-150.
[16] Hong Tao, Gui Min, Baran M E, et al. Modeling and forecasting hourly electric load by multiple linear regression with interactions[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-8.
[17] Lee Chengming, Ko C N. Short-term load forecasting using lifting scheme and ARIMA models[J]. Expert Systems with Applications, 2011, 38(5): 5902-5911.
[18] 刘达. 基于误差校正的中长期负荷预测模型[J]. 电网技术, 2012, 36(8): 243-247.
Liu Da. A model for medium-and long-term power load forecasting based on error correction[J]. Power System Technology, 2012, 36(8): 243-247.
[19] 赵洋, 王瀚墨, 康丽, 等. 基于时间卷积网络的短期电力负荷预测[J]. 电工技术学报, 2022, 37(5): 1242-1251.
Zhao Yang, Wang Hanmo, Kang Li, et al. Temporal convolution network-based short-term electrical load forecasting[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1242-1251.
[20] 王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-58.
Wang Zengping, Zhao Bing, Ji Weijia, et al. Short-term load forecasting method based on GRU-NN model[J]. Automation of Electric Power Systems, 2019, 43(5): 53-58.
[21] 李元诚, 方廷健, 于尔铿. 短期负荷预测的支持向量机方法研究[J]. 中国电机工程学报, 2003, 23(6): 55-59.
Li Yuancheng, Fang Tingjian, Yu Erkeng. Study of support vector machines for short-term load forecasting [J]. Proceedings of the CSEE, 2003, 23(6): 55-59.
[22] 孔祥玉, 李闯, 郑锋, 等. 基于经验模态分解与特征相关分析的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 46-52.
Kong Xiangyu, Li Chuang, Zheng Feng, et al. Short-term load forecasting method based on empirical mode decomposition and feature correlation analysis[J]. Automation of Electric Power Systems, 2019, 43(5): 46-52.
[23] 张淑清, 李君, 姜安琦, 等. 基于FPA-VMD和BiLSTM神经网络的新型两阶段短期电力负荷预测[J]. 电网技术, 2022, 46(8): 3269-3279.
Zhang Shuqing, Li Jun, Jiang Anqi, et al. A novel two-stage model based on FPA-VMD and BiLSTM neural network for short-term power load forecasting[J]. Power System Technology, 2022, 46(8): 3269-3279.
[24] 邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测[J]. 电网技术, 2020, 44(2): 593-602.
Deng Daiyu, Li Jian, Zhang Zhenyuan, et al. Short-term electric load forecasting based on EEMD-GRU-MLR[J]. Power System Technology, 2020, 44(2): 593-602.
[25] 陈映月. 基于数据挖掘的牵引负荷统计方法及应用研究[D]. 成都: 西南交通大学, 2019.
Chen Yingyue. Research on traction load statistics method and application based on data mining[D]. Chengdu: Southwest Jiaotong University, 2019.
[26] 高锋阳, 宋志翔, 高建宁, 等. 计及光伏和储能接入的牵引供电系统能量管理策略[J]. 电工技术学报, 2024, 39(3): 745-757.
Gao Fengyang, Song Zhixiang, Gao Jianning, et al. Energy management strategies for traction power systems with PV and energy storage access[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 745-757.
[27] 张浩, 熊浩清, 陈谦, 等. 电铁牵引负荷的构成分析及其功率模型[J]. 电力系统及其自动化学报, 2015, 27(6): 37-42.
Zhang Hao, Xiong Haoqing, Chen Qian, et al. Component analysis and power model of traction load[J]. Proceedings of the CSU-EPSA, 2015, 27(6): 37-42.
[28] Woo S, Park J, Lee J Y, et al. CBAM: convolutional block attention module[C]//European conference on computer vision, Cham, 2018: 3-19.
[29] Bergstra J, Bardenet R, Bengio Y, et al. Algorithms for hyper-parameter optimization[J]. Advances in neural information processing systems, 2011, 24: 2546-2554.
Abstract China has the world's largest rail transit network, with a total mileage of more than 150,000 kilometers, the electrification rate of more than 70 percent, and railway energy consumption is the largest single load category. With the rapid development of China's electrified railway network, the railway transportation represented by high-speed rail has become an important part of China's transportation system. With the development of "net-source-storage-vehicle" collaborative energy supply technology, the internal energy management and collaborative control of the system need the technical support of accurate second-level ultra-short-term prediction on both sides of the source and load. At the same time, accurate ultra-short-term prediction of traction load can also provide data source support for research on power quality analysis of rail transit, optimal scheduling of traction substation, location and capacity determination of traction substation, etc.
This paper constructs an ultra-short-term forecast framework for traction load based on EEMD-CBAM-BiLSTM, aiming at the problem of difficulty in predicting rail transit traction load due to strong mutability and volatility. Firstly, based on the analysis of the time series characteristics of rail transit traction load, the data of rail transit traction load is decomposed into several stable and regular time series mode functions by ensemble empirical mode decomposition (EEMD) to highlight the time series characteristics of load data. Secondly, the decomposed components are integrated into the feature extraction module composed of convolutional neural network (CNN) and improved convolutional block attention module (CBAM) to extract the global timing features. After that, Bayesian optimization (BO) is used to search the optimal parameters of BiLSTM neural network to make the network structure reach the best state.In this paper, the traction load data in a single day (with a resolution of 1 s) is selected to build a prediction model, and the model is compared with the mainstream single prediction model and composite model by starting from three output modes: predicting the load in the next 4 seconds, the load in the next 8 seconds, and the load in the next 16 seconds.
The calculation results show that compared to other models, the framework in this paper reduces MAE by 31.2%, 39.1%, 47.5%, and 45.8% in the 40-16 prediction mode, respectively; RMSE decreased by 40.0%, 42.6%, 53.6%, and 47.5% respectively; R2 increased by 5.2%, 5.9%, 10.65%, and 7.7% respectively. Therefore, the following conclusion can be drawn: EEMD has good performance in avoiding modal aliasing and better highlighting the deep data relationships and temporal features hidden in time series. The improved CBAM feature extraction module and global feature extraction structure can significantly reduce the computational workload caused by the "decomposition prediction" method, improve the representation ability of hidden temporal features in traction load data, better capture key features in the data, and improve the accuracy of subsequent neural network predictions. After Bayesian optimization of hyperparameters, the BiLSTM model can better capture information in the front and back temporal directions when processing long feature sequences, fully considering the past and future temporal information based on the current point as the reference point. This article framework combines the advantages and characteristics of EEMD, CBAM, CNN, BO, and BiLSTM technologies, and can significantly improve the accuracy of ultra short term prediction of electrified railway traction loads at various prediction steps, which has good engineering application value.
keywords:Traction load forecasting, ensemble empirical mode decomposition (EEMD), bidirectional long short-term memory neural network (BiLSTM), Bayesian optimization (BO), convolutional block attention module (CBAM), convolutional neural network (CNN)
中图分类号:TM922.3
DOI: 10.19595/j.cnki.1000-6753.tces.231515
国家重点研发计划项目(2021YFB2601504)和国家自然科学基金项目(52377097)资助。
收稿日期 2023-09-13
改稿日期 2024-05-31
钟吴君 男,1994年生,博士研究生,研究方向为负荷与新能源预测。E-mail:395236969@qq.com(通信作者)
李培强 男,1975年生,博士,博士生导师,研究方向为智能电网及其分布式发电研究。E-mail:lpqcs@hnu.edu.cn
(编辑 赫 蕾)