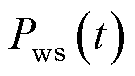 无法超过最大输出功率预测值
无法超过最大输出功率预测值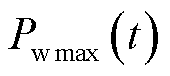 与基准值
与基准值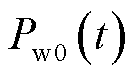 之差,即
之差,即摘要 与传统水火电机组相比,参与调频辅助服务市场的风电资源具备灵活性强和调节速率快等优势。然而,风电资源存在不确定性的缺点,影响可调容量与调频性能,干扰调频市场出清与调度,引发调频安全风险。基于此,该文通过分析风电不确定性对不同调频市场运行阶段的影响,结合特定市场运行阶段的目标,提出考虑安全风险与调频性能的多时间尺度出清与调度策略。首先,在日前和日内时段,分别使用条件风险价值方法量化风电可调容量不确定性风险;其次,根据考虑风电资源参与的调频风险与调节成本,构建调频市场出清模型;最后,量化分析风电不确定性对调频精度指标的影响,提出考虑综合调频性能指标最优的调度策略。仿真算例分析表明,所提出清策略下的日前累计风险成本相较于传统策略降低35%;所提调度策略可以最大限度地保证调频综合调频性能好的资源优先参与调度。
关键词:电力系统频率控制 调频性能 多时间尺度能量管理 风电不确定性
为实现“双碳”目标,电力行业正积极发展新能源。新能源与常规电源共同参与调频市场,形成多元调频资源协调运作方式,发挥互补与灵活性优势,提升调频性能并降低市场运行成本。然而,制约新能源参与调频市场的首要因素是不确定性。以风电资源为例,其出力的随机与波动性可能导致市场违约风险,损害调频市场运行安全。因此,亟须明确风电不确定性对调频市场运行的影响机制,构建考虑不确定性安全风险的市场出清与调度方法。
目前,国内外学者主要从投标和市场出清两个维度对多元资源参与调频辅助服务市场展开研究。调频资源往往采用优化投标策略,使其参与调频市场的收益最大化[1]。在调节资源方面,针对电动汽车[2-3]、储能[4]、虚拟电厂[5]和新能源[6]等资源参与调频辅助服务市场投标策略展开广泛研究。
多元调频资源接入为实现提升市场效率和竞争力的调频市场出清与调度提供了重要手段。文献[7]提出了一种考虑频率控制的实时市场出清机制,可以有效降低调频容量需求。除了考虑单一调频辅助模式,在电能量和调频联合调度中,可以同时考虑一次与二次调频备用约束以提升系统频率响应能力[8]。近年来,伴随电池储能技术的不断发展,学术界针对电池储能如何参与调频市场的优化运行决策展开研究[9]。储能可以快速抑制新能源波动与不确定性;然而,储能调节成本较高,可能在一定程度上影响调频经济性。不同于水火电、储能等调频资源,主动参与调频的新能源会带来不确定性风险,影响调频市场安全出清。
目前针对不确定性风电资源参与调频市场的出清调度已有一定研究。在考虑风电功率预测误差不确定性的情况下,文献[10]构建了电网调频极限的形成方法,提出了利用储能辅助风电跟踪日前调度计划并参与调频的策略。文献[11]提出了基于鲁棒优化的调频市场出清策略。文献[12]提出了风电参与能量-调频联合市场的调度策略。为提高风电可调度性,文献[13]构建了考虑风电调频风险损失的出清模型。文献[14-16]考虑了含碳交易机制的风电调度策略。文献[17]分析了风电灵活性调节需求,并且提出了基于主从博弈的灵活性供需均衡分析方法。然而,鲜见研究人员能结合市场不同运行阶段特定要求量化分析风电确定性影响,并给出考虑风电不确定性的多时间尺度出清调度策略。
多时间尺度优化调度近年来在电力系统领域得到广泛关注。文献[18]提出了并网型多微电网系统多时间尺度“报量不报价”交易机制,激励各子微电网积极参与协作运行。文献[19]综合考虑了储能与需求响应资源的多时间尺度特性,提出了日前主辅市场的主动配电网经济调度模型。文献[20]提出了虚拟电厂的日前计划-滚动计划-实时计划全时域调度框架。此外,研究人员对综合能源系统的多时间尺度调度问题也展开了研究[21-22]。在考虑风电的多时间尺度能量管理方面,文献[23]根据不同时间尺度下风电消纳调度需求,提出了利用海水淡化、电制热等灵活性负荷消纳富余风电的多时间尺度优化调度策略。文献[24]提出了一种考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度方法。尽管多时间尺度分析方法在日前或日内等能量市场有一定应用;然而,针对调频市场在风电不确定性情况下的多时间尺度出清调度鲜有研究。
不确定性会影响新能源参与市场的可靠性。以本文研究的风电为例,在日前与日内调频市场中,风电随机波动将导致出清容量偏差(中标容量与实际提供的容量不匹配),提升出清风险并降低市场参与可靠性;在实时调度层面,风电随机波动会影响调频与调度性能。考虑到风电在多时间尺度下随机波动的差异性,需要结合不同时间尺度的风电功率预测信息对风电进行逐层出清与调度。
本文基于“多层优化+逐层细化”思想,提出了多时间尺度下考虑调频市场安全风险与调频性能的出清与调度策略。在日前和日内时段,结合各时段的调频需求和资源申报信息,提出了考虑调频风险成本的预出清和正式出清策略;在调度阶段,基于模型预测控制(Model Predictive Control, MPC)理念,根据上一轮优化调度后的资源执行结果更新调频性能指标,并反馈给下一轮滚动优化调度,实现以综合调频性能最优为目标的实时调度。通过考虑风险成本的多时间尺度出清与基于调频性能最优的调度策略,降低了调频市场风险,提升了优质机组的市场参与度,最后通过仿真算例证明了所提策略的有效性。
在国内当前高比例新能源接入新型电力系统发展背景下,传统水火电资源的调频空间被不断压缩。为确保电网保有充足的调频能力,风电等新型资源越发需要参与调频任务。尤其是新疆等风力资源丰富、风电装机容量高的西部地区,风电越发需要参与调频。根据《新疆电力辅助服务市场运营规则》,风电可以作为市场主体参与调频。相比传统资源,风电具有调节灵活性高和速率快等优点。然而,风电资源同样存在不确定性的缺点,会影响其参与调频市场的可靠性,给市场与系统安全与稳定运行带来风险。以调频市场日前出清阶段为例,风电资源在t时段申报的可调容量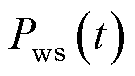 无法超过最大输出功率预测值
无法超过最大输出功率预测值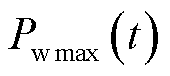 与基准值
与基准值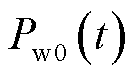 之差,即
之差,即
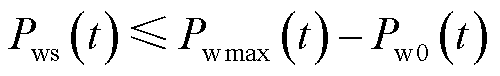 (1)
(1)
式中,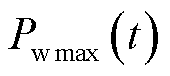 的不确定性将导致可调容量
的不确定性将导致可调容量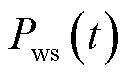 的不确定性。通过市场出清得到中标容量
的不确定性。通过市场出清得到中标容量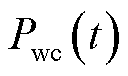 可能高于可调容量
可能高于可调容量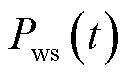 ,引发调频市场安全风险。除了可调容量,风电不确定性还会影响调频性能指标(本文主要考虑调节精度指标
,引发调频市场安全风险。除了可调容量,风电不确定性还会影响调频性能指标(本文主要考虑调节精度指标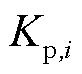 )。
)。
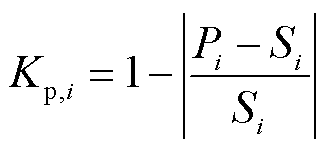 (2)
(2)
式中,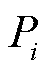 为风电资源i的实际响应量;
为风电资源i的实际响应量;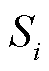 为风电资源i接收的调频指令。对特定调节过程而言,风电资源i接收到的调频指令
为风电资源i接收的调频指令。对特定调节过程而言,风电资源i接收到的调频指令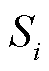 是给定的;而实际响应量
是给定的;而实际响应量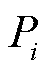 受到风电不确定影响呈现波动性,导致调频精度
受到风电不确定影响呈现波动性,导致调频精度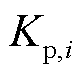 也存在不确定性。
也存在不确定性。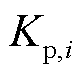 的不确定性会影响以综合调频性能指标最优为目标的调度表现。综上所述,通过影响可调容量与调节精度,风电不确定性将干扰调频市场运行。
的不确定性会影响以综合调频性能指标最优为目标的调度表现。综上所述,通过影响可调容量与调节精度,风电不确定性将干扰调频市场运行。
为应对风电不确定性给调频市场运行带来的挑战,本文提出了一种改进型出清与调度基本框架,其核心是在市场不同运行阶段量化评估风电不确定性影响,根据量化评估结果构建市场出清与调度模型,继而得到出清与调度方案。所提出的改进型调频市场出清与调度基本框架如图1所示。

图1 考虑风电不确定性的调频市场出清与调度基本框架
Fig.1 The basic framework of frequency regulation market clearing and dispatch considering wind power uncertainty
图1所示的基本框架主要包括:①日前市场出清;②日内市场出清;③实时市场出清;④实时调度。在日前、日内和实时市场出清阶段,主要利用条件风险价值量化评估风电资源可调容量不确定性与风险成本,然后给出考虑调频运行与风险综合成本的出清策略。在多时间尺度出清框架下,上一层出清结果为下一层出清提供了发电计划曲线边界条件,例如:日前预出清结果为日内预出清提供了发电计划曲线边界条件,保证了资源参与其他市场的安全可靠性。在实时调度阶段,主要利用最新调度结果与预测信息修正风电资源调频性能指标,并根据模型预测控制理念,给出考虑综合调频性能指标最优的滚动优化调度方案。
为了构建考虑风电资源不确定性风险的出清与调度模型,本节首先设计两种风险指标,以刻画可调容量与调节精度指标不确定性影响,然后利用风险指标量化评估风电资源不确定性给出清与调度带来的风险成本。
由1.1节可知,风电预测不确定性会导致申报市场的可调容量不准。尤其是当实际可调容量低于中标容量的情况下,导致风电资源发生违约行为。本文将中标容量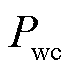 与实际可调容量
与实际可调容量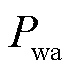 的差值占中标容量的比率定义为中标容量违约率
的差值占中标容量的比率定义为中标容量违约率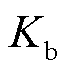 ,即
,即
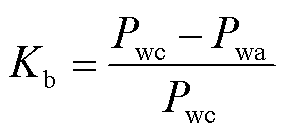 (3)
(3)
由式(3)可知,实际可调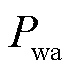 与中标容量
与中标容量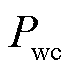 差值越大,中标容量违约率
差值越大,中标容量违约率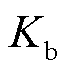 越大,市场出清安全风险越高。调频资源的中标容量违约率可由其历史表现平均值近似表示为
越大,市场出清安全风险越高。调频资源的中标容量违约率可由其历史表现平均值近似表示为
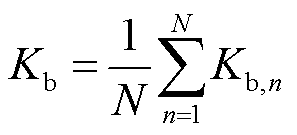 (4)
(4)
式中,N为历史观测次数;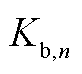 为第n次观测中调频资源测得的中标容量违约率。
为第n次观测中调频资源测得的中标容量违约率。
不确定性风险量化评估方法主要包括蒙特卡洛模拟法、价值风险(Value-at-Risk, VaR)法和条件价值风险(Conditional Value-at-Risk, CVaR)法。蒙特卡洛法通过大规模场景模拟与指标计算实现风险评估,该方法计算量大。VaR无需场景模拟,直接通过损失概率模型获得置信水平下可能的最大损失。不同于VaR,CVaR可以定量描述超过置信度的调频市场出清风险成本,提供了更加详细的风险描述,更能反映潜在风险。出清风险成本的计算步骤包括:①根据风电资源违约率构建风险函数;②结合违约率概率密度函数构建风险函数不低于特定边界值的概率分布函数;③利用概率分布函数建立风险价值VaR以描述给定置信水平下预期的最大损失;④基于VaR构建条件风险价值CVaR作为出清风险成本。
置信度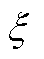 下的条件风险价值
下的条件风险价值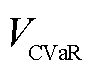 为
为
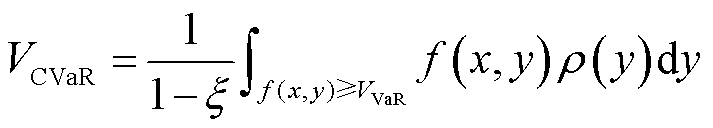 (5)
(5)
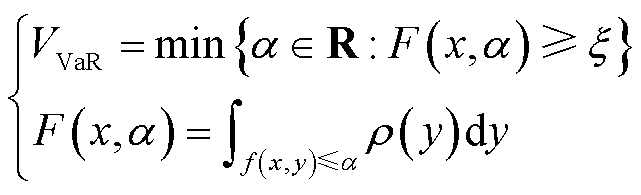 (6)
(6)
式中,x为决策变量;y为随机变量;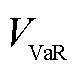 为风险价值;
为风险价值;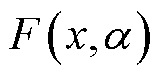 为风险函数
为风险函数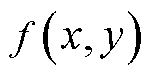 不大于边界值
不大于边界值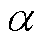 的分布函数;
的分布函数;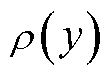 为随机变量y的概率密度函数。根据式(5)和式(6),本文将风电中标容量违约给调频市场造成损失的风险函数
为随机变量y的概率密度函数。根据式(5)和式(6),本文将风电中标容量违约给调频市场造成损失的风险函数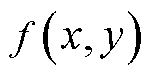 定义为
定义为
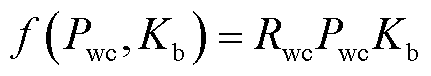 (7)
(7)
式中,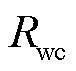 为风电资源的调频容量报价。利用条件风险价值量化风电可调容量不确定性带来的风险,有
为风电资源的调频容量报价。利用条件风险价值量化风电可调容量不确定性带来的风险,有
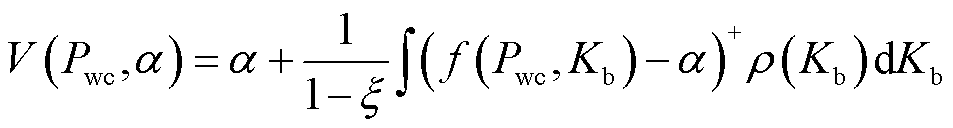 (8)
(8)
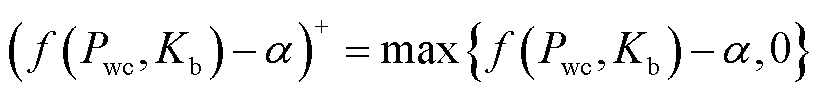 (9)
(9)
式中,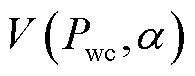 为风电资源参与出清的风险成本。对风险成本进行离散化变换得
为风电资源参与出清的风险成本。对风险成本进行离散化变换得
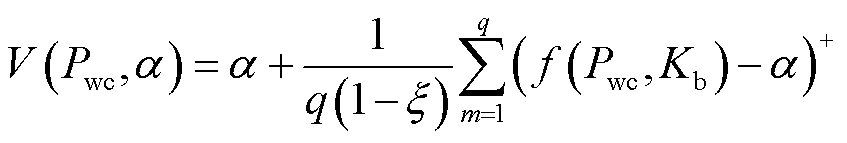 (10)
(10)
式中,q为采样数量。
考虑风电不确定性的调频辅助服务市场出清调度架构如图2所示。在调频辅助服务市场出清调度中,日前预出清根据出清结果为次日调频资源预留出调频容量,封存调频资源申报的容量、报价作为次日出清的依据。日内出清根据每次滚动更新后的调频备用容量需求、机组状态,以及风电短期预测调整的申报容量进行。预出清结果预留调频容量,正式出清中标容量作为资源参与调频调度的边界条件。滚动调度基于模型预测控制方法,引入反馈,调度调频性能最优资源实现系统功率平衡。
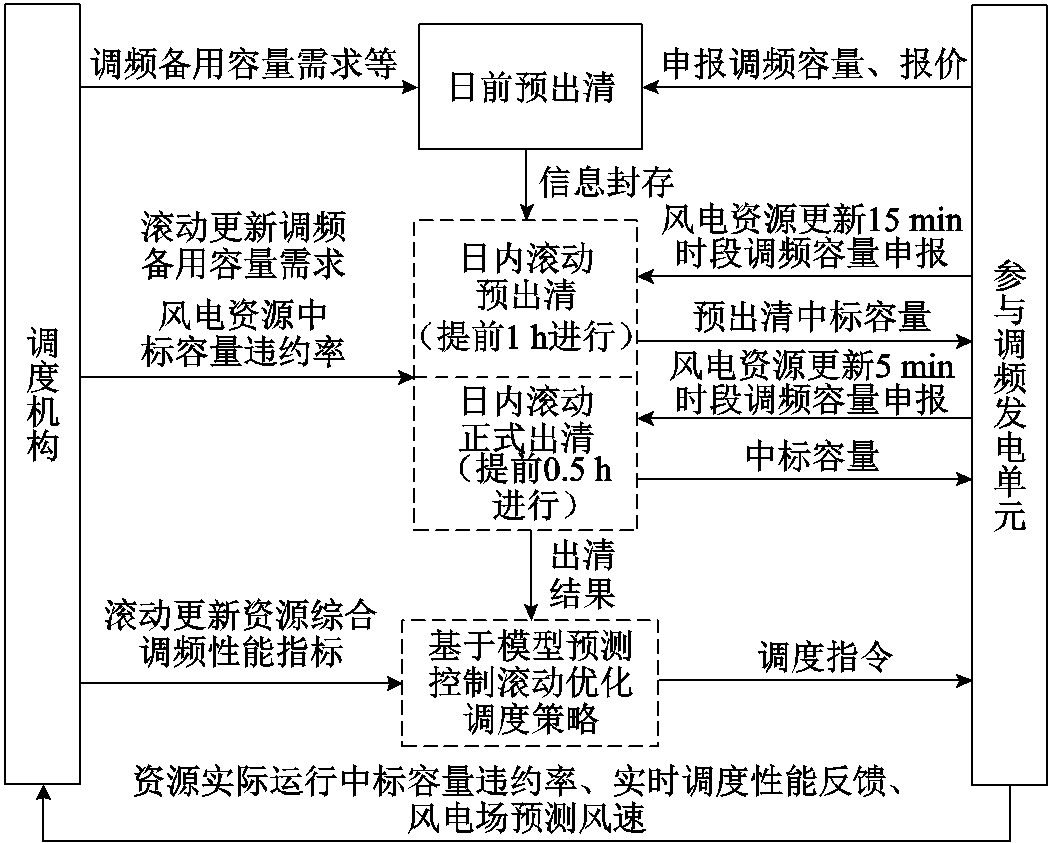
图2 考虑风电不确定性的多时间尺度出清调度架构
Fig.2 Diagram of multi-time-scale frequency regulation market clearing and scheduling strategy considering wind power uncertainty
本文提出的多时间尺度滚动出清调度框架包括日前预出清、日内预出清和日内正式出清。日前预出清以次日每1 h为时间尺度,其中标容量形成次日发电计划曲线边界条件,为调频资源预留调频容量。日内预出清计划以15 min为时间尺度,短期预测更新预出清时段调频容量供需信息,包括:调频备用容量需求和风电资源申报容量。根据日内预出清得到的中标容量,修正日内预出清时段调频资源发电计划曲线边界条件。正式出清以5 min为时间尺度,通过超短期预测修正出清时段调频容量供需信息,最终中标容量确定正式出清时段发电计划曲线边界条件。在多时间尺度滚动出清框架下,通过多阶段发电计划曲线边界条件修正,增强了市场交易调度中心的可调节与灵活性;同时,不断缩短预测时间跨度提升供需预测信息精确度,降低风电资源可调容量不确定性给出清带来的风险。
3.1.1 考虑风电不确定性风险的日前预出清
在竞价日的日前预出清中,调度机构收集市场准入调频资源的调频里程报价、调频容量等信息,根据预测的次日调频备用容量需求以调频成本和风险成本最低为目标进行预出清,即
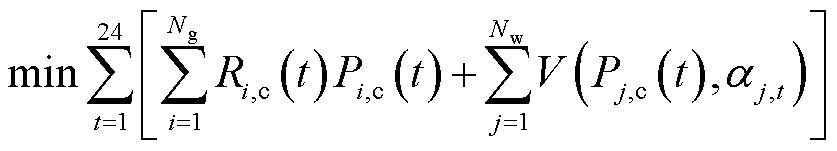 (11)
(11)
式中,t为时间尺度(1 h)编号;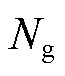 和
和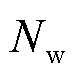 分别为所有调频资源个数和风电资源个数;
分别为所有调频资源个数和风电资源个数;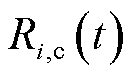 为资源i在时刻t的容量报价;
为资源i在时刻t的容量报价;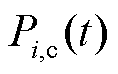 为资源i在时刻t的中标容量;
为资源i在时刻t的中标容量;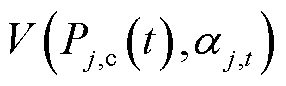 为风电资源j在时刻t的风险成本。
为风电资源j在时刻t的风险成本。
调频需求约束为
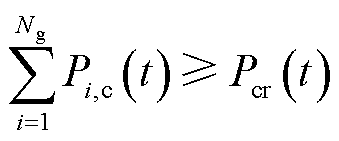 (12)
(12)
式中,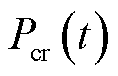 为系统在日前预出清t时段的调频备用容量需求。
为系统在日前预出清t时段的调频备用容量需求。
资源i日前预出清t时段的中标容量不能超过其申报容量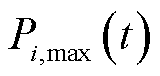 ,即
,即
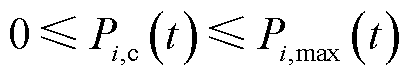 (13)
(13)
3.1.2 考虑风电不确定性风险的日内滚动预出清
在运行日当天,日内滚动预出清提前1 h进行,预出清时间尺度为15 min,滚动周期为1 h。每次滚动,市场交易调度中心和风电资源通过短期预测分别更新预出清时段系统调频备用容量需求和申报容量,并根据风电资源在正式出清时可调容量与中标容量偏差,更新其中标容量违约率。以调频成本与风险成本最低为目标、更新后的供需平衡和申报容量限制为约束,市场交易调度中心构建并求解预出清模型,使用第一时段预出清决策值为资源预留调频容量,有
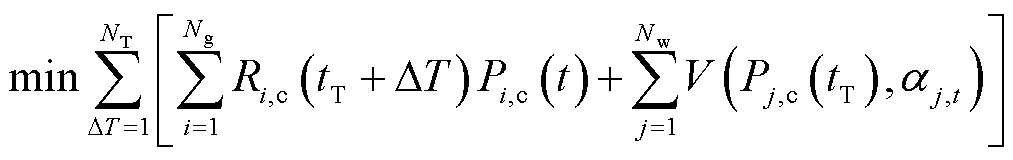 (14)
(14)
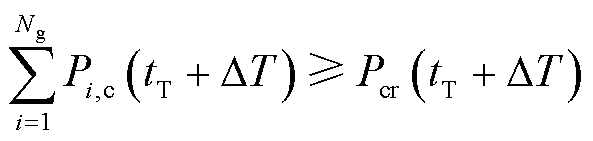 (15)
(15)
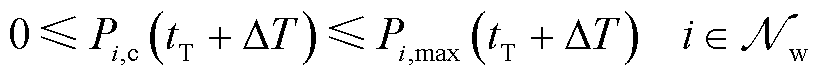 (16)
(16)
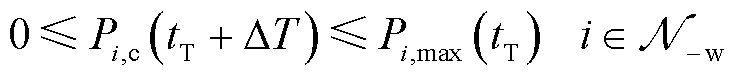 (17)
(17)
式中,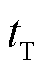 为时间尺度(15 min)编号;
为时间尺度(15 min)编号;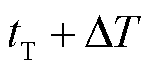 为以编号
为以编号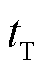 为起始值增加
为起始值增加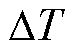 后的编号;
后的编号;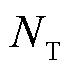 为滚动优化预测周期数,NT=4(60 min/15 min);
为滚动优化预测周期数,NT=4(60 min/15 min);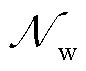 为风电资源集合;
为风电资源集合;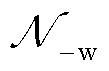 为非风电资源集合。日内滚动预出清模型与日前模型结构相同。主要区别在于,日内预出清
为非风电资源集合。日内滚动预出清模型与日前模型结构相同。主要区别在于,日内预出清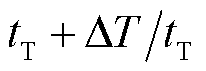 时段调频需求
时段调频需求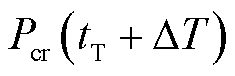 和风电资源申报容量
和风电资源申报容量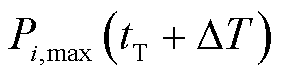 发生变化。式(17)考虑传统资源可调容量相对稳定,因此其申报容量同日前出清阶段。
发生变化。式(17)考虑传统资源可调容量相对稳定,因此其申报容量同日前出清阶段。
3.1.3 考虑风电不确定性风险的日内滚动正式出清
本文规定日内滚动正式出清提前运行0.5 h进行,时间尺度为5 min,滚动周期为15 min。与日内滚动预出清类似,调度交易中心更新出清时段系统调频备用容量需求、风电中标容量违约率;风电更新申报调频容量,然后通过计算滚动出清模型得到出清策略。滚动周期第一时段的决策作为资源正式出清的中标容量,有

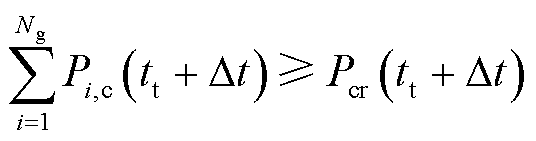 (19)
(19)
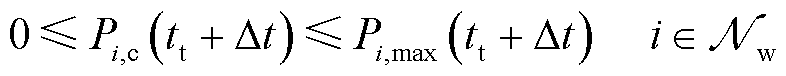 (20)
(20)
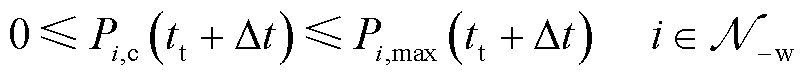 (21)
(21)
式中,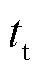 为时间尺度(5 min)编号;
为时间尺度(5 min)编号;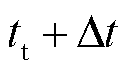 为以编号t为起始值增加
为以编号t为起始值增加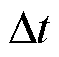 后的编号;
后的编号;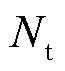 为滚动优化预测周期数,Nt=3(15 min/5 min)。日内滚动出清模型与日内滚动预出清模型结构相同。根据超短时预测信息,日内正式出清时段
为滚动优化预测周期数,Nt=3(15 min/5 min)。日内滚动出清模型与日内滚动预出清模型结构相同。根据超短时预测信息,日内正式出清时段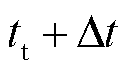 调频需求
调频需求 和风电资源申报容量
和风电资源申报容量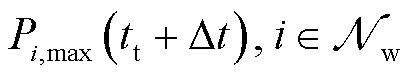 发生变化。同样地,式(21)考虑传统资源在正式出清
发生变化。同样地,式(21)考虑传统资源在正式出清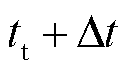 时段的申报容量保持不变。
时段的申报容量保持不变。
在正式出清后的实时调度中,中标资源按照特定调频指令实时调整出力参与调频。风电出力波动性导致实际出力与调频指令存在偏差,影响频率质量和系统安全。本文为降低调节偏差的安全风险,采用基于模型预测控制的滚动优化调度策略。实时滚动优化调度为自动发电控制(Automatic Generation Control, AGC)提供了调频资源选择与备用容量基础。一方面,实时滚动优化调度决定每个调节时段选用哪些资源执行AGC指令;另一方面,实时滚动优化调度决定每个调节时段参与AGC资源的调频备用容量。模型预测控制主要由预测模型、反馈校正和滚动优化三部分组成。调度机构根据调频资源当前有功出力,发布调度指令并预测机组未来出力。滚动优化中,通过反馈将资源当前出力以及根据执行上一调度的调频性能更新后的综合调频性能指标作为初始条件,以综合调频性能指标最优为目标,发布未来的调度指令。基于MPC的滚动优化调度通过引入反馈,根据资源参与调度情况实时更新调频性能指标。本文构建计及改进型调节精度指标的调度方法,以1 min为时段,5 min为滚动周期的模型预测控制滚动优化调度,对资源参与调频进行调度决策。目标函数为
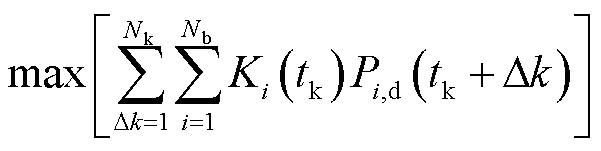 (22)
(22)
式中,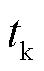 为时间尺度(1 min)编号;
为时间尺度(1 min)编号;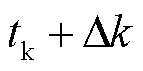 为以编号
为以编号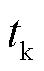 为起始值增加
为起始值增加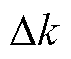 后的编号;
后的编号;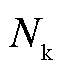 为滚动优化预测周期数,Nk=5(5 min/1 min);
为滚动优化预测周期数,Nk=5(5 min/1 min);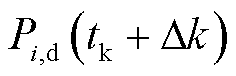 为决策变量,表示资源
为决策变量,表示资源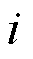 在调度时刻
在调度时刻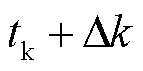 的调度出力;
的调度出力;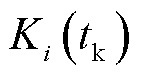 为
为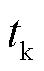 滚动周期资源i的综合调频性能指标;滚动优化调度每推进一步,
滚动周期资源i的综合调频性能指标;滚动优化调度每推进一步,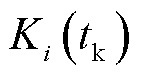 更新一次,即
更新一次,即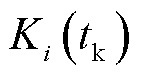 的更新周期为1 min;
的更新周期为1 min;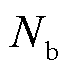 为中标调频资源的个数。本文综合调频性能指标,参考广东调频市场交易实施细则规定的确定方式,通过调节速率、响应时间、调节精度三方面评估机组调频性能,计算方法为
为中标调频资源的个数。本文综合调频性能指标,参考广东调频市场交易实施细则规定的确定方式,通过调节速率、响应时间、调节精度三方面评估机组调频性能,计算方法为
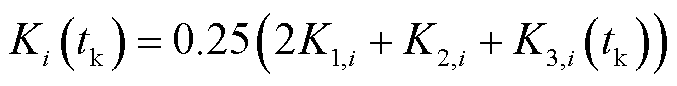 (23)
(23)
式中,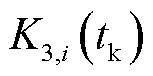 为tk时段的调节精度指标;
为tk时段的调节精度指标;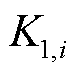 、
、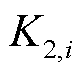 分别为调节速率指标与响应时间指标,通常由通过最近历史N次调节过程的平均和求出,即
分别为调节速率指标与响应时间指标,通常由通过最近历史N次调节过程的平均和求出,即
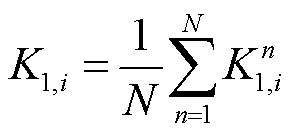 (24)
(24)
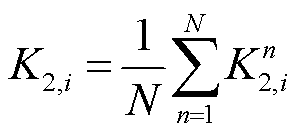 (25)
(25)
式中,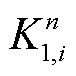 和
和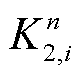 分别为第n次测得资源i的调节速率与响应时间指标值,有
分别为第n次测得资源i的调节速率与响应时间指标值,有
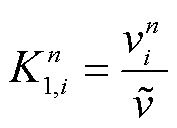 (26)
(26)
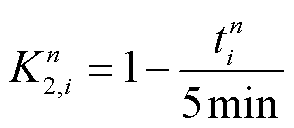 (27)
(27)
式中,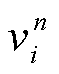 为资源i第n次调度实测速率;
为资源i第n次调度实测速率;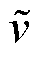 为调频资源分布区内AGC发电平均标准调节速率;
为调频资源分布区内AGC发电平均标准调节速率;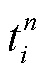 为资源i第n次调度响应时间。由于速率和响应时间主要由资源内部的控制结构和参数决定,时变性不大,因此设为常数。
为资源i第n次调度响应时间。由于速率和响应时间主要由资源内部的控制结构和参数决定,时变性不大,因此设为常数。
不同于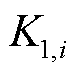 和
和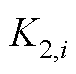 ,调节精度指标
,调节精度指标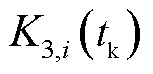 受不确定性偏差
受不确定性偏差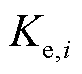 影响存在时变特性。本文使用上一轮滚动优化后的实测调节精度指标
影响存在时变特性。本文使用上一轮滚动优化后的实测调节精度指标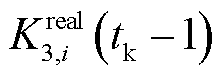 评估
评估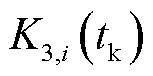 。
。
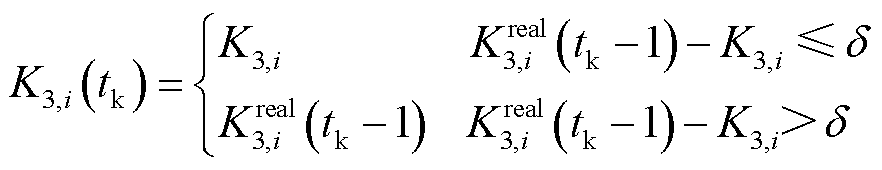 (28)
(28)
式中,K3,i为基准调节精度指标,通过历史调节精度指标求均值获得;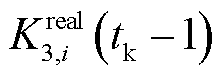 为
为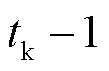 时段调节精度指标的实测值;
时段调节精度指标的实测值;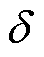 为调节精度指标偏差阈值。
为调节精度指标偏差阈值。
滚动优化调度的约束条件包括调频资源调度出力之和满足总调度指令,即
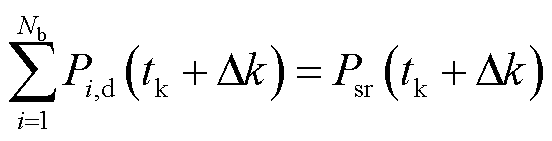 (29)
(29)
式中,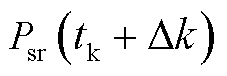 为调度时刻
为调度时刻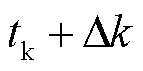 系统调频需要的功率。同时,调频资源调度出力指令不超过其中标容量,即
系统调频需要的功率。同时,调频资源调度出力指令不超过其中标容量,即
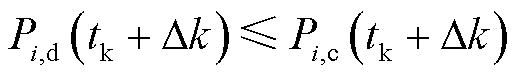 (30)
(30)
为了避免过大的调度出力波动,设置波动幅度限制为
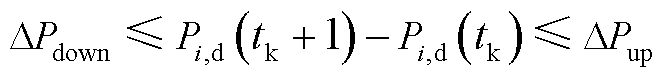 (31)
(31)
式中,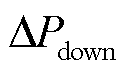 和
和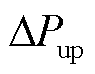 为允许的调度出力改变阈值。由于每轮滚动优化调度仅执行控制时域(第一个 1 min),因此调度出力改变要求仅针对
为允许的调度出力改变阈值。由于每轮滚动优化调度仅执行控制时域(第一个 1 min),因此调度出力改变要求仅针对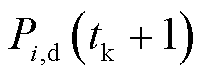 。
。
每一轮滚动优化调度接收的反馈信息包括资源调度出力实测值与综合调频性能指标实测值,有
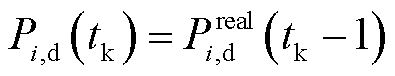 (32)
(32)
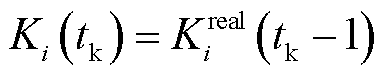 (33)
(33)
式中,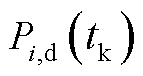 为滚动周期
为滚动周期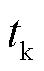 对应的资源i的初始调度出力;
对应的资源i的初始调度出力;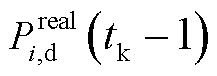 为
为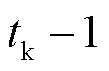 滚动周期执行第1时段决策后资源i的实际调度出力;
滚动周期执行第1时段决策后资源i的实际调度出力;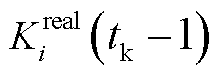 为
为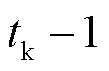 滚动周期执行第1时段决策后资源i的实际综合调频性能指标。
滚动周期执行第1时段决策后资源i的实际综合调频性能指标。
整个基于MPC的滚动优化调度时序关系如图3所示。每个滚动调度窗口时长(滚动周期或预测周期)为5 min,滚动调度窗口推进步长为1 min。每轮滚动优化调度的时间步长为1 min,即每个滚动调度窗口包含5个步长。例如:t0滚动周期为t0~t0+5(共5个时段,每个时段步长为1 min)的红色虚线方框;t0+1滚动周期为t0+1~t0+6(共5个时段,每个时段步长为1 min)的黄色虚线方框。每一轮滚动每个步长对应的可调容量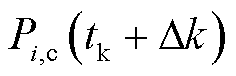 来自正式出清后对应时段的中标容量。
来自正式出清后对应时段的中标容量。
每轮滚动调度按照式(22)~式(33)求出滚动(预测)周期内的5个1 min调度出力。由于基于MPC的滚动优化调度控制周期为1 min;因此,机组仅执行第1时段(第1个1 min)决策得到的调度出力。当前滚动调度窗口向后一滚动调度窗口推进时,通过观测机组前一轮优化后的执行效果反馈校正调频性能指标Ki(t)。例如,t0滚动周期按照式(22)~式(33)求出滚动(预测)周期内的5个1 min调度出力,仅执行第1时段(第1个1 min)决策获得的调度出力Pi,d(t0+1)。紧接着,调度推进到t0+1滚动周期,根据t0滚动周期的执行效果反馈校正得到Ki(t0+1),求解并执行第1时段(第1个1 min)决策获得的调度出力Pi,d(t0+2),依此类推,得到每轮调度的优化调度出力和执行结果。
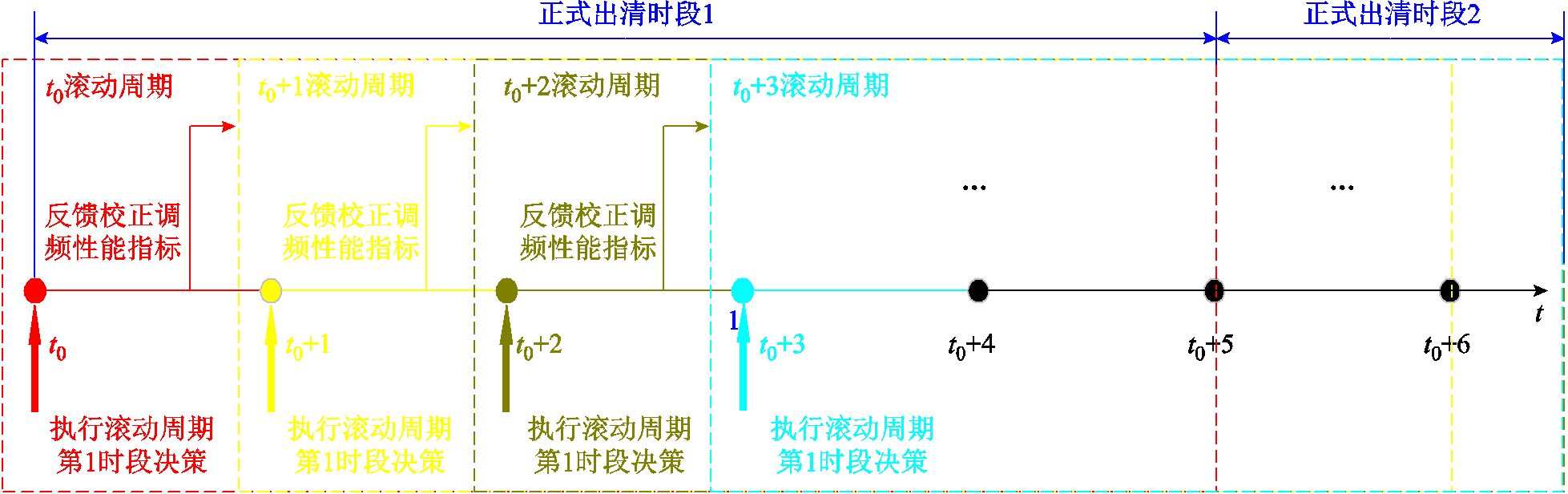
图3 基于模型预测控制滚动优化调度时序图
Fig.3 Diagram of rolling optimization scheduling sequence based on MPC
算例仿真在Matlab R2023a编译环境下,采用Yalmip优化工具建模。本文所提模型为凸优化模型,直接调用Gurobi(版本10.0.2)求解。计算机配置为Intel(R) Core(TM) i7-9750H CPU@2.60 GHz,内存RAM为8 GB。
为了简便分析,本文模拟3座风电场和1座火电厂参与调频市场竞标。其中,调频参数(申报价格、申报容量、调频性能指标)不同的3座风电场作为主导资源,最后1座火电厂类似于潮流计算中的平衡节点机组,作为后备资源弥补因调频需求突增或风电停运导致的功率缺失。根据ISO New England(ISO-NE)调频市场数据确立调频市场申报价格、调频需求和资源申报容量。3座风电场与1座火电厂在日前(日内)市场的申报价格分别为10、7、7、20 $/MW。表1和表2分别给出日前市场调频需求和风电场申报容量。日内市场预出清阶段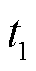 时刻的调频需求
时刻的调频需求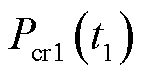 基于日前市场对应时刻t的调频需求
基于日前市场对应时刻t的调频需求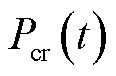 进行修正
进行修正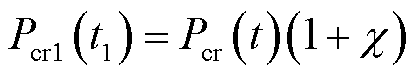 ,
,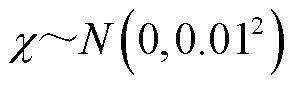 ;采取相同的修正方法得到日内市场预出清阶段
;采取相同的修正方法得到日内市场预出清阶段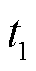 时刻风电场的申报容量
时刻风电场的申报容量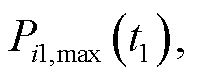
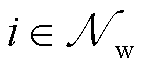 ;正式出清阶段
;正式出清阶段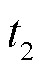 时刻调频需求
时刻调频需求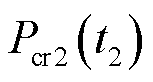 基于预出清阶段对应时刻
基于预出清阶段对应时刻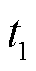 的调频需求
的调频需求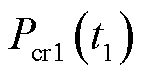 进行修正
进行修正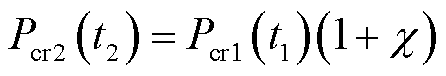 ,
,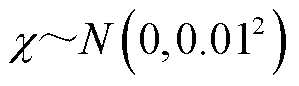 ;采取相同的修正方法得到日内市场正式出清阶段
;采取相同的修正方法得到日内市场正式出清阶段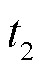 时刻风电场的申报容量
时刻风电场的申报容量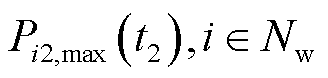 。3座风电场容量中标违约率
。3座风电场容量中标违约率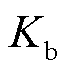 分别满足:N(0.05,0.012),N(0.2,0.022)和N(0.5,0.052)。在调度阶段,3座风电场与1座火电厂的调频节速率指标
分别满足:N(0.05,0.012),N(0.2,0.022)和N(0.5,0.052)。在调度阶段,3座风电场与1座火电厂的调频节速率指标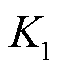 分别为1.29、1.07、0.97和0.6;响应时间指标
分别为1.29、1.07、0.97和0.6;响应时间指标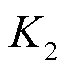 分别为0.99、0.98、0.99和0.8。考虑到风电出力的不确定性,假设3座风电场和1座火电厂的初始调节精度指标
分别为0.99、0.98、0.99和0.8。考虑到风电出力的不确定性,假设3座风电场和1座火电厂的初始调节精度指标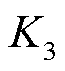 分别为0.8、0.7、0.7和0.6。基于MPC的滚动优化调度控制时域与预测时域分别为1 min和5 min。
分别为0.8、0.7、0.7和0.6。基于MPC的滚动优化调度控制时域与预测时域分别为1 min和5 min。
表1 日前调频市场容量需求数据
Tab.1 Day-ahead frequency regulation capacity requirement
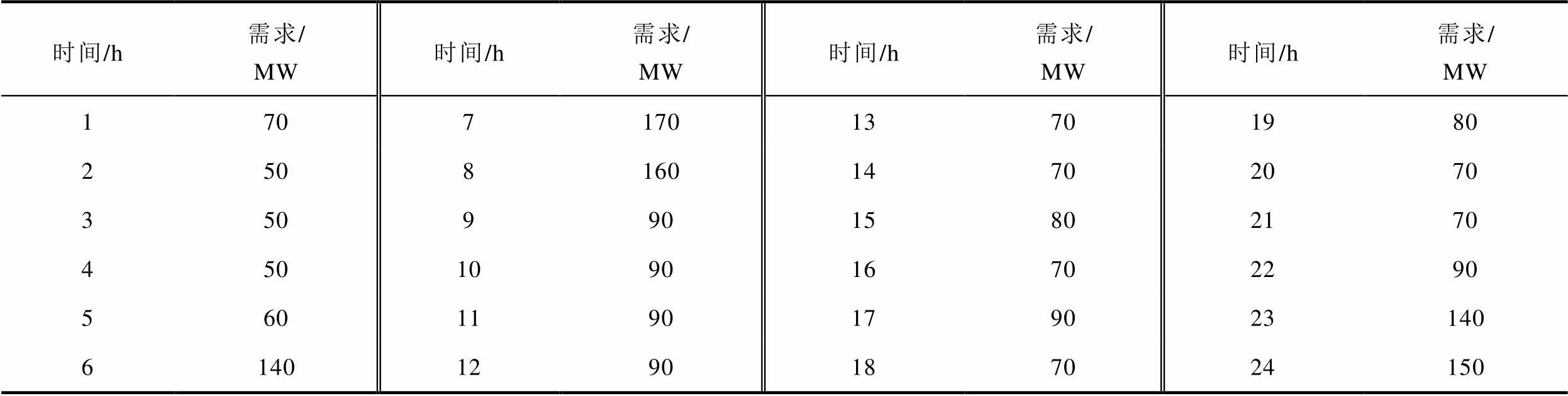
时间/h需求/MW时间/h需求/MW时间/h需求/MW时间/h需求/MW 170717013701980 250816014702070 35099015802170 450109016702290 5601190179023140 61401290187024150
表2 日前调频市场机组申报容量数据
Tab.2 Day-ahead frequency regulation market regulation capacity offer
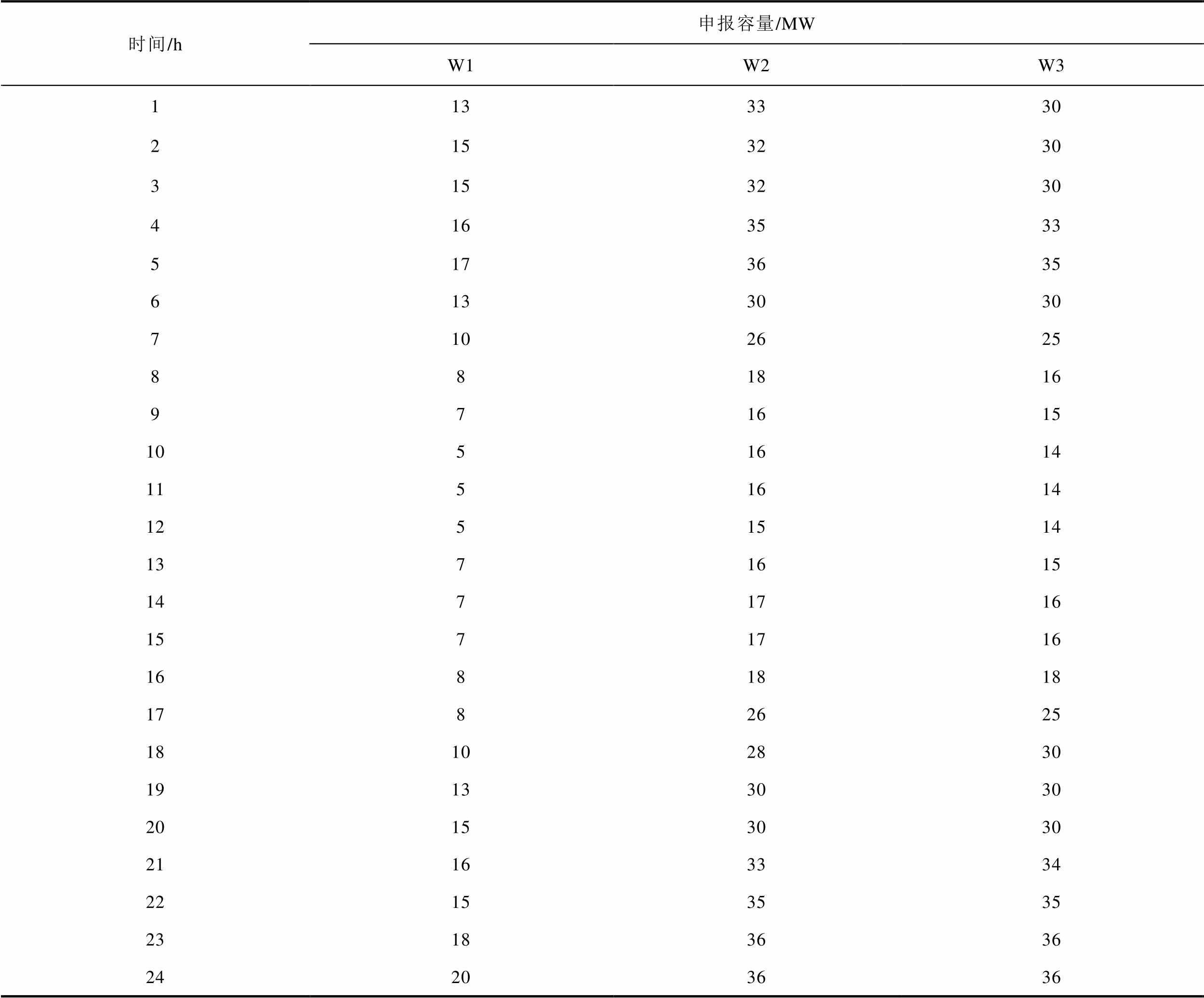
时间/h申报容量/MW W1W2W3 1133330 2153230 3153230 4163533 5173635 6133030 7102625 881816 971615 1051614 1151614 1251514 1371615 1471716 1571716 1681818 1782625 18102830 19133030 20153030 21163334 22153535 23183636 24203636
根据4.1节日前调频市场数据,计算得到出清结果如图4和图5所示。图4给出了4个资源(W1、W2和W3代表3座风电场,T1代表火电厂)参与日前调频市场后的剩余容量(申报容量-出清容量)。图5给出了出清后风电场的CVaR风险值(火电厂的CVaR恒为0 $)。接下来对两组日前时段出清结果进行分析。

图4 风电与火电在日前调频市场的申报与出清容量差
Fig.4 The difference of offered and cleared regulation capacity of wind and thermal power plants in the day-ahead frequency regulation market
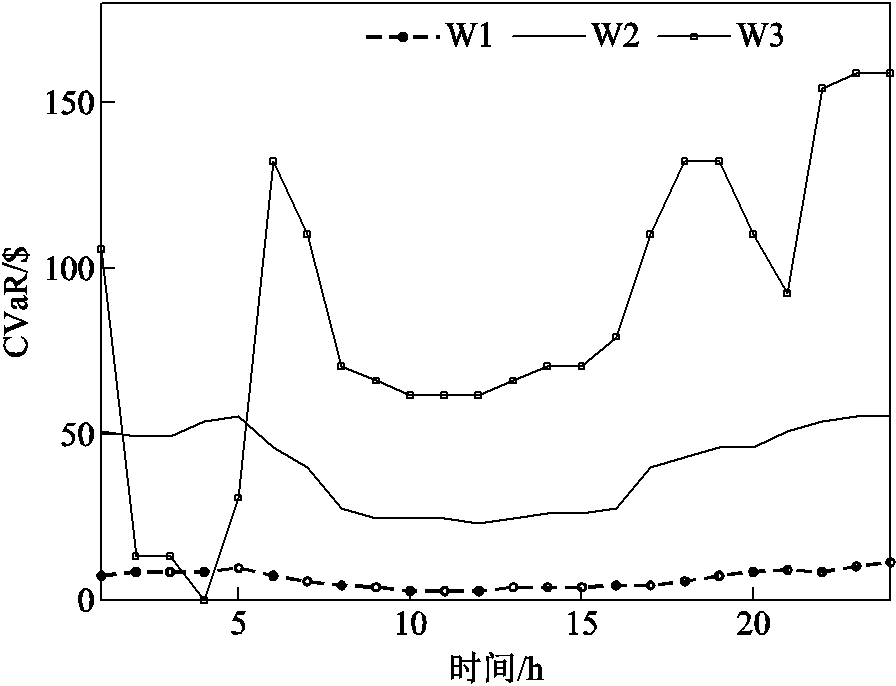
图5 风电在日前调频市场的条件风险价值
Fig.5 CVaR value of wind power plants in the day-ahead frequency regulation market
4.2.1 时段1出清结果分析
时段1为1~5 h与20~21 h。由图4可知,火电厂的剩余容量在该时段维持在申报容量100 MW。两个时段风电的总申报容量大于调频需求,市场可以选择风电或火电提供调频服务。相较于风电,尽管火电的风险价值始终维持在最低水平(CVaR=0 $),其过高的报价(20 $/MW)造成调频与总成本过大,因此火电厂未能出清。在风电场选择方面,尽管1号风电场的申报价格略高于2号与3号风电场(10 $/ MW>8 $/MW),但是超低违约率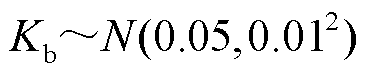 导致风险值远低于2号与3号风电场。因此,1号风电场优先出清。同时,尽管2号、3号风电场的申报价格相同,但是2号风电场的违约率
导致风险值远低于2号与3号风电场。因此,1号风电场优先出清。同时,尽管2号、3号风电场的申报价格相同,但是2号风电场的违约率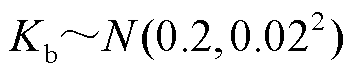 小于3号
小于3号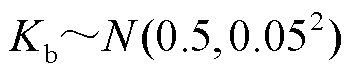 ;因此,2号风电场次优先出清。综上分析,出清优先级从高到低依次为:1号风电场—2号风电场—3号风电场—火电厂。图5中2~5 h时段3号风电场的CVaR值低于2号风电场(4 h的CVaR值甚至为0),主要因为CVaR值同时受到违约率
;因此,2号风电场次优先出清。综上分析,出清优先级从高到低依次为:1号风电场—2号风电场—3号风电场—火电厂。图5中2~5 h时段3号风电场的CVaR值低于2号风电场(4 h的CVaR值甚至为0),主要因为CVaR值同时受到违约率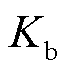 与出清量
与出清量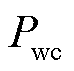 的影响。由于2~5 h时段3号风电场出清量很低:3 MW(2 h)、3 MW(3 h)、0 MW(4 h)和7 MW(5 h),因此风险值低于出清量更大的2号风电场。在4 h时刻,3号风电场由于没出清,CVaR值直接变为0 $。
的影响。由于2~5 h时段3号风电场出清量很低:3 MW(2 h)、3 MW(3 h)、0 MW(4 h)和7 MW(5 h),因此风险值低于出清量更大的2号风电场。在4 h时刻,3号风电场由于没出清,CVaR值直接变为0 $。
4.2.2 时段2出清结果分析
时段2为6~19 h与22~24 h。由图4可知,火电厂的剩余容量在该时段不再是100 MW。调频需求在该时段超过风电的总申报量,导致市场必须向火电厂购买部分调频容量满足调频需求。相应地,3座风电场在该时段全部完成出清;3座风电场的风险值呈现递增现象,与违约率递增现象相符。
根据图5计算得到日前调频市场所有资源在24 h内的累计条件风险价值为3 200 $,相较于不考虑风险(仅考虑调频资源使用成本(4 925 $))下的累计条件风险价值降低了35%。采用鲁棒优化方法和机会约束规划方法与本文使用的条件风险价值方法进行对比,结果见表3。可以看出,条件风险价值方法不仅可以通过CVaR量化评估不确定性风险(见图5),而且调频成本低于基于鲁棒优化与机会约束规划的出清。
表3 日前调频市场调频成本
Tab.3 Frequency regulation cost in day-ahead frequency regulation market

条件风险价值法鲁棒优化法机会约束规划法 调频成本/$28 30030 70029 500
4.3.1 日内预出清阶段结果分析
根据4.1节日内调频市场数据,计算得到风电与火电在日内调频市场的申报与预出清容量差如图6所示,风电在日内调频市场预出清阶段的条件风险价值如图7所示。图6给出了四个资源日内预出清后的剩余容量(申报容量-出清容量)。图7给出了预出清后风电场的CVaR风险值(火电厂的CVaR恒为0 $)。
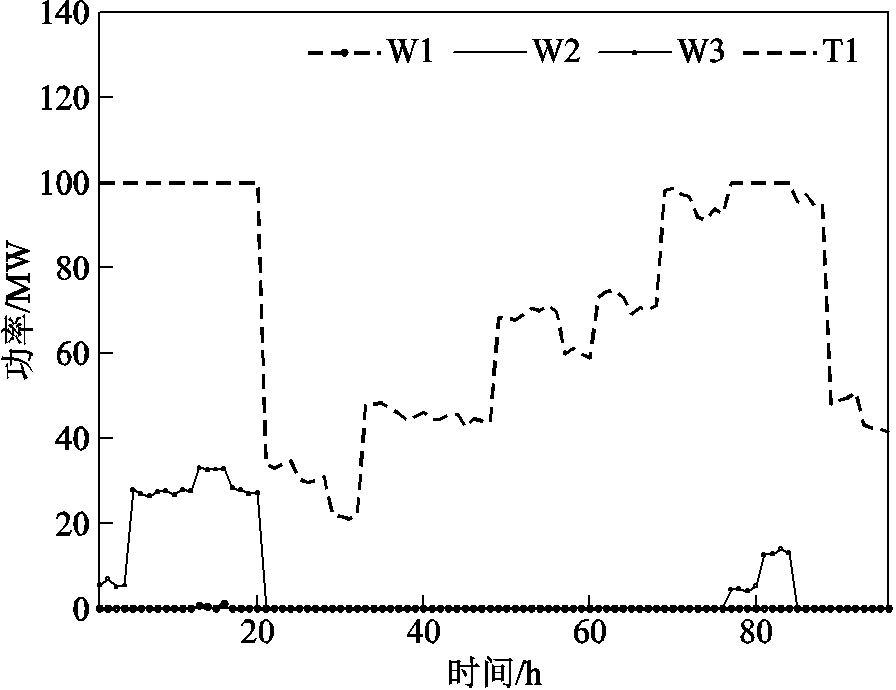
图6 风电与火电在日内调频市场的申报与预出清容量差
Fig.6 The difference of offered and cleared regulation capacity of wind and thermal power plants in the intraday frequency regulation market (pre-clearing)
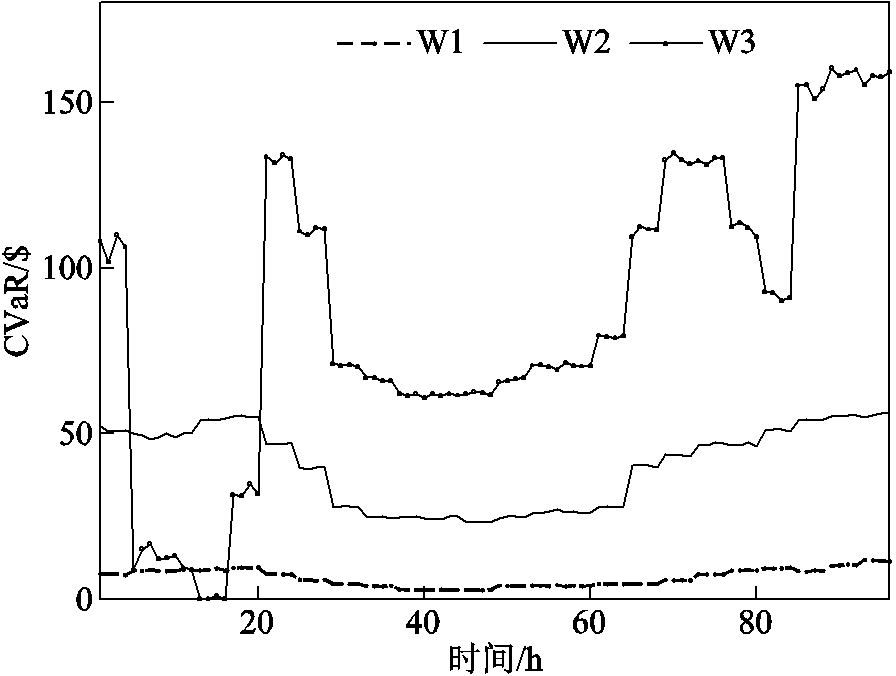
图7 风电在日内调频市场预出清阶段的条件风险价值
Fig.7 CVaR value of wind power plants in the intraday frequency regulation market pre-clearing phase
由于预出清是在短时间尺度(15 min)对长时间尺度(1 h)日前出清的微调,图6与图4、图7与图5的曲线走势基本相同。进一步,表4比较了1 h、12 h和20 h对应的日前与日内预出清结果。由表4可知,日内预出清阶段1 h、12 h和20 h对应的四个15 min时段出清容量与1 h、12 h和20 h的出清容量基本相同。表明在日内与日前(需求和申报容量)预测值相差不大的情况下(预测更新量小),资源预出清与日前出清容量基本相同。
4.3.2 日内正式出清阶段结果分析
根据4.3.1节日内调频市场数据和预出清结果,计算得到正式出清结果如图8和图9所示。图8给出了四个资源日内正式出清后的剩余容量(申报容量-出清容量)。图9给出了正式出清后风电场的CVaR风险值(火电厂的CVaR恒为0 $)。
表4 日前与日内预出清阶段不同时刻出清容量
Tab.4 Day-ahead and intra-day frequency regulation market regulation cleared capacity at different time
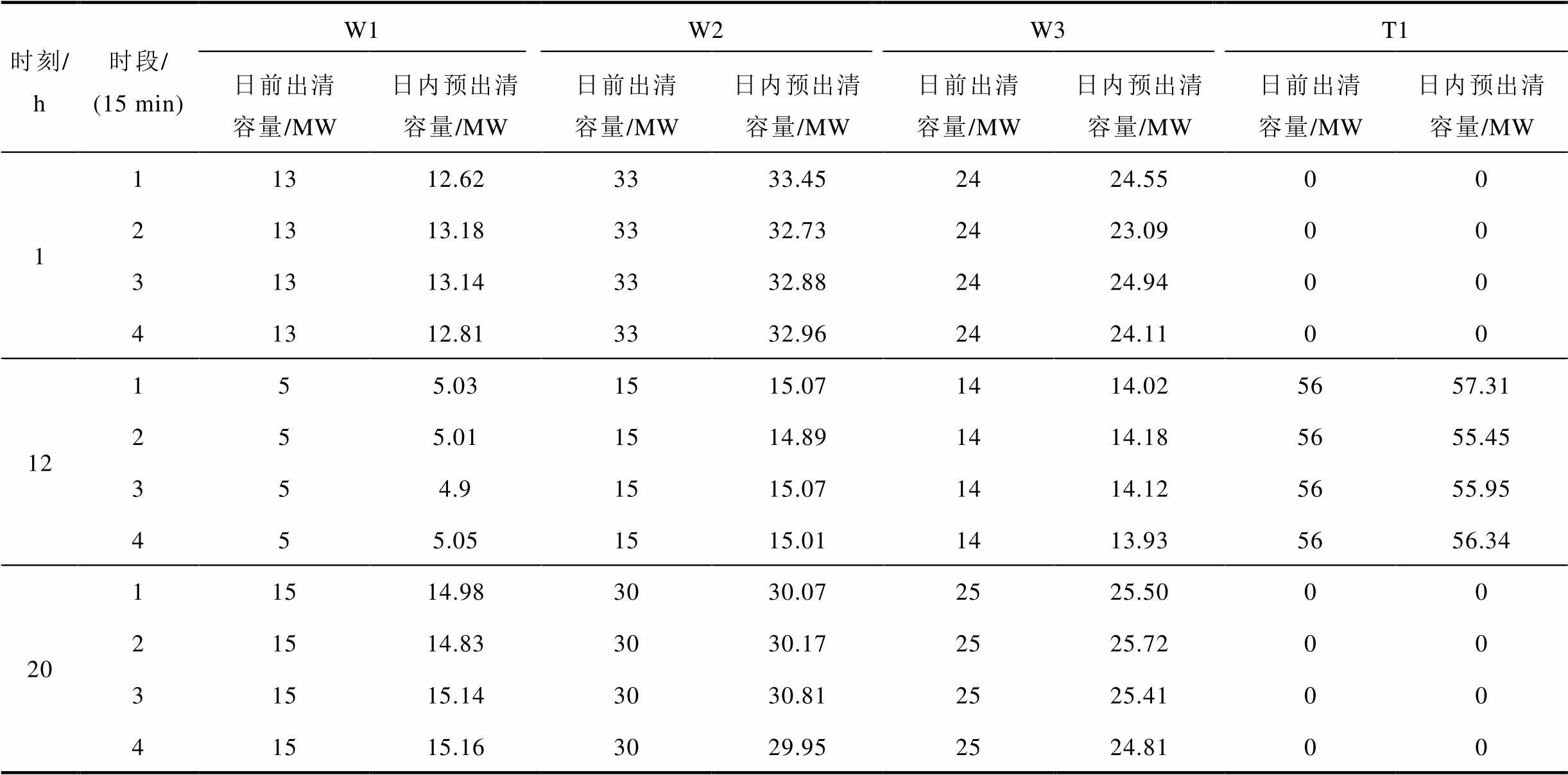
时刻/h时段/(15 min)W1W2W3T1 日前出清容量/MW日内预出清容量/MW日前出清容量/MW日内预出清容量/MW日前出清容量/MW日内预出清容量/MW日前出清容量/MW日内预出清容量/MW 111312.623333.452424.5500 21313.183332.732423.0900 31313.143332.882424.9400 41312.813332.962424.1100 12155.031515.071414.025657.31 255.011514.891414.185655.45 354.91515.071414.125655.95 455.051515.011413.935656.34 2011514.983030.072525.5000 21514.833030.172525.7200 31515.143030.812525.4100 41515.163029.952524.8100
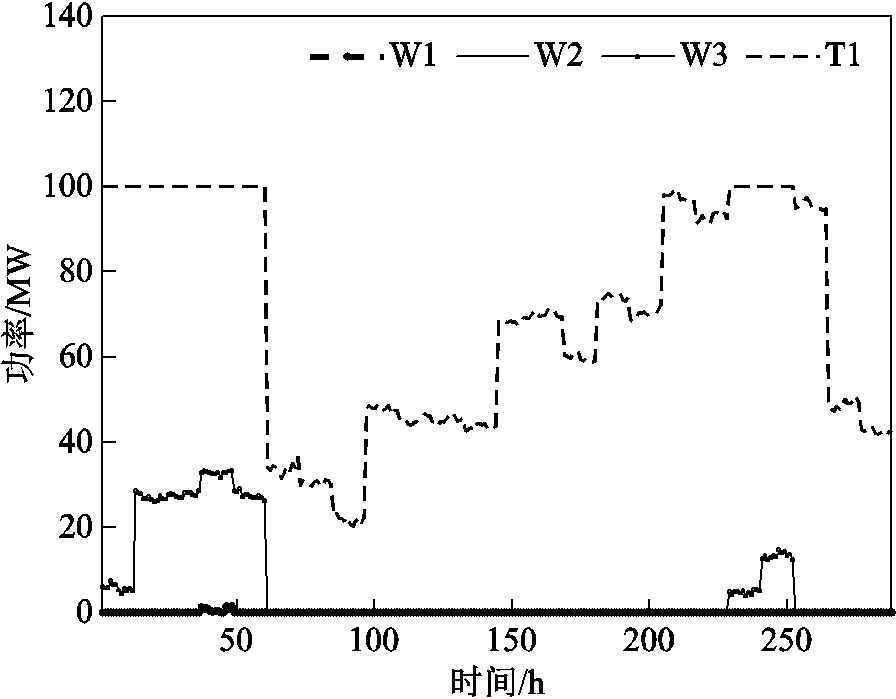
图8 风电与火电在日内调频市场的申报与正式出清容量差
Fig.8 The difference of offered and cleared regulation capacity of wind and thermal power plants in the intraday frequency regulation market
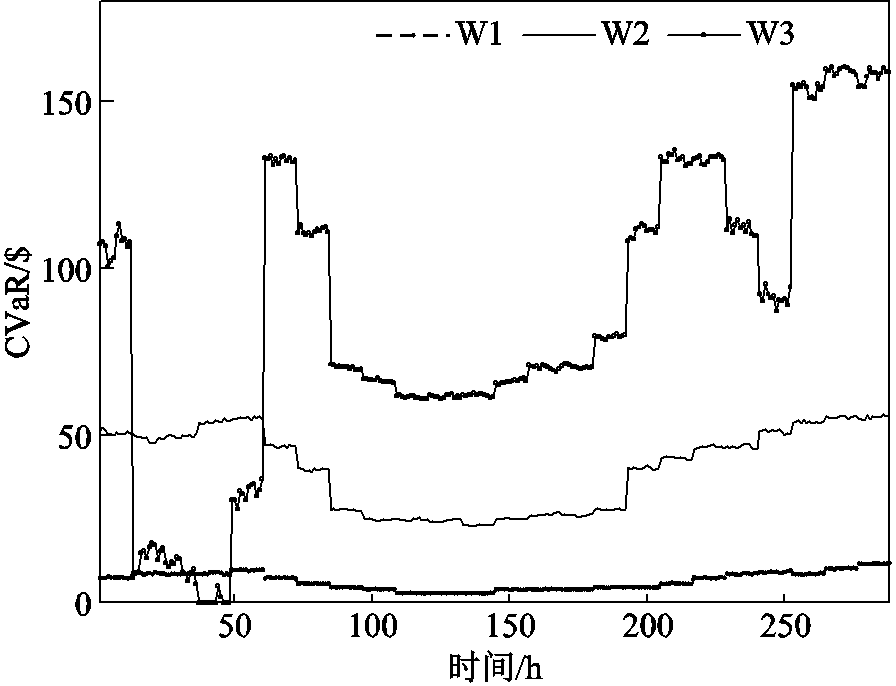
图9 风电在日内调频市场正式出清阶段的条件风险价值
Fig.9 CVaR value of wind power plants in the intraday frequency regulation market clearing phase
由于正式出清是在短时间尺度(5 min)对长时间尺度(15 min)预出清的微调,图8与图6、图9与图7的曲线走势基本相同。进一步地,表5比较了第1、45和77个15 min对应的日内预出清与正式结果。其中,第1个15 min对应表4中1 h的第1个15 min;第45个15 min对应表4中12 h的第1个15 min;第77个15 min对应表4中20 h的第1个15 min。由表5可知,日内正式出清阶段第1、45和77个15 min对应的3个5 min时段出清容量与日内第1、45和77个15 min的预出清容量基本相同;表明在日内预出清与正式出清阶段(需求和申报容量)预测值相差不大的情况下(预测更新量小),资源正式出清与预出清容量基本相同。
利用4.1节调度参数与4.3.2节正式出清结果对四个资源的调频调度进行仿真验证。具体地,表6给出了第1、133和229个5 min的滚动优化调度结果。其中,第1个5 min对应表5中第1个15 min的第1个5 min;第133个5 min对应表5中第45个15 min的第1个5 min;第229个5 min对应表5中第77个15 min的第1个5 min。假设每个资源在第1、3、4和5轮滚动优化后的实测调节精度指标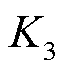 与初始值之差均保持在允许误差之内。1号风电资源在第2轮滚动后的实测误差超过允许误差。本文采用PJM调频市场规则,出清阶段不区分上下调频容量。在调度阶段根据调频信号确定上下调频阶段。表6中第1和133个5 min对应的5个滚动周期为上调频阶段,第229个5 min对应的5个滚动周期为下调频阶段。
与初始值之差均保持在允许误差之内。1号风电资源在第2轮滚动后的实测误差超过允许误差。本文采用PJM调频市场规则,出清阶段不区分上下调频容量。在调度阶段根据调频信号确定上下调频阶段。表6中第1和133个5 min对应的5个滚动周期为上调频阶段,第229个5 min对应的5个滚动周期为下调频阶段。
表5 日内预出清与正式出清阶段不同时刻出清容量
Tab.5 Intra-day frequency regulation market regulation pre-cleared and cleared capacity at different time
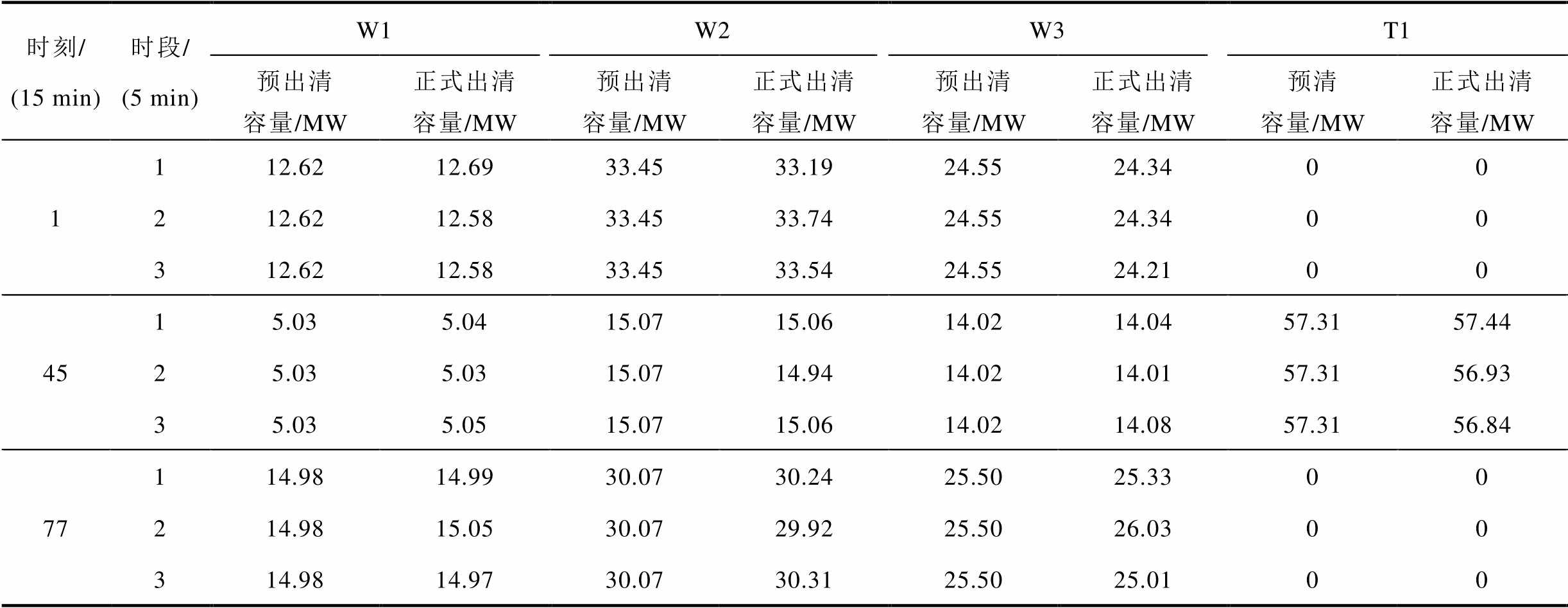
时刻/(15 min)时段/(5 min)W1W2W3T1 预出清容量/MW正式出清容量/MW预出清容量/MW正式出清容量/MW预出清容量/MW正式出清容量/MW预清容量/MW正式出清容量/MW 1112.6212.6933.4533.1924.5524.3400 212.6212.5833.4533.7424.5524.3400 312.6212.5833.4533.5424.5524.2100 4515.035.0415.0715.0614.0214.0457.3157.44 25.035.0315.0714.9414.0214.0157.3156.93 35.035.0515.0715.0614.0214.0857.3156.84 77114.9814.9930.0730.2425.5025.3300 214.9815.0530.0729.9225.5026.0300 314.9814.9730.0730.3125.5025.0100
表6 不同时刻滚动优化调度的指令分配结果
Tab.6 Dispatch order allocation at different rolling optimization cycle
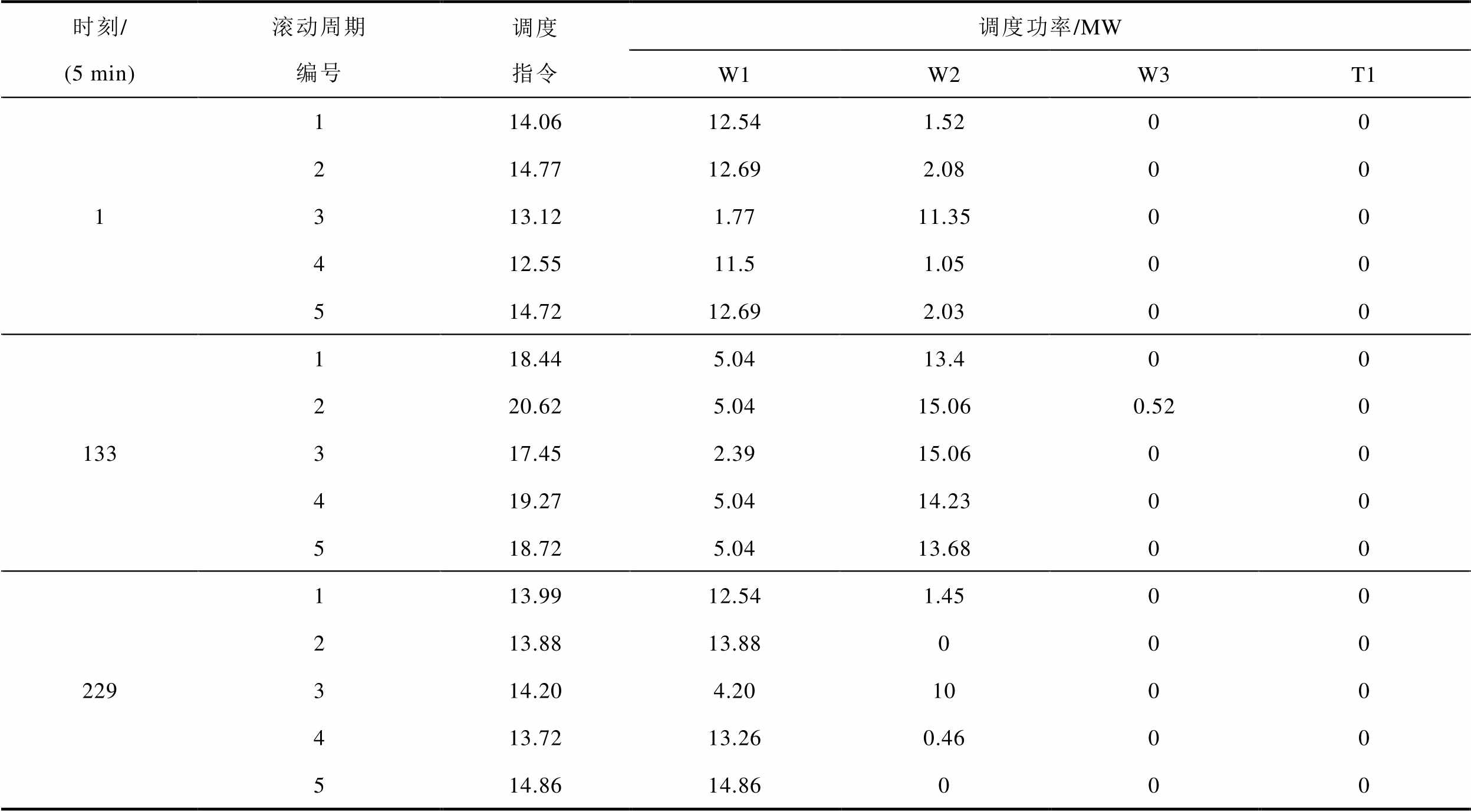
时刻/(5 min)滚动周期编号调度指令调度功率/MW W1W2W3T1 1114.0612.541.5200 214.7712.692.0800 313.121.7711.3500 412.5511.51.0500 514.7212.692.0300 133118.445.0413.400 220.625.0415.060.520 317.452.3915.0600 419.275.0414.2300 518.725.0413.6800 229113.9912.541.4500 213.8813.88000 314.204.201000 413.7213.260.4600 514.8614.86000
在第1个5 min的第1轮滚动优化过程中,利用4.1节中根据调节误差与式(28)计算得到调节精度指标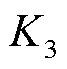 ,结合调节速率
,结合调节速率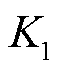 和响应时间指标
和响应时间指标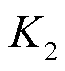 ,得到四个资源的综合性能指标值为1.09、0.96、0.91和0.65。因此,根据以综合性能最优为目标的优化调度模型,在不超过正式出清容量的情况下,资源调度的优先级从高到底依次为1号风电场—2号风电场—3号风电场—火电厂。由于1号风电场(因风速陡降)在第2轮滚动优化后实测调节精度指标
,得到四个资源的综合性能指标值为1.09、0.96、0.91和0.65。因此,根据以综合性能最优为目标的优化调度模型,在不超过正式出清容量的情况下,资源调度的优先级从高到底依次为1号风电场—2号风电场—3号风电场—火电厂。由于1号风电场(因风速陡降)在第2轮滚动优化后实测调节精度指标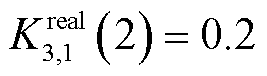 ,因此1号风电场更新
,因此1号风电场更新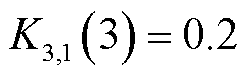 。在第1个5 min的第3轮滚动优化对应的综合性能指标更新为0.94、0.96、0.91和0.65。资源调度的优先级从高到底依次为2号风电场-1号风电场-3号风电场-火电厂。因此,1号风电场调度出力由第2轮的12.69 MW降低至1.77 MW;2号风电场调度出力由第2轮的2.08 MW增至11.35 MW。由于第2轮滚动优化后1号风电场的实测功率
。在第1个5 min的第3轮滚动优化对应的综合性能指标更新为0.94、0.96、0.91和0.65。资源调度的优先级从高到底依次为2号风电场-1号风电场-3号风电场-火电厂。因此,1号风电场调度出力由第2轮的12.69 MW降低至1.77 MW;2号风电场调度出力由第2轮的2.08 MW增至11.35 MW。由于第2轮滚动优化后1号风电场的实测功率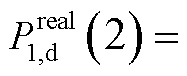
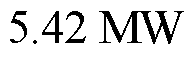 ,调度功率变化量为
,调度功率变化量为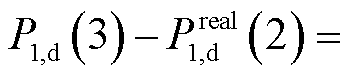
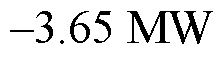 ,并未超过阈值10 MW。1号风电场在第3轮滚动优化后恢复指令执行效果,优先级重新变成1号风电场—2号风电场—3号风电场—火电厂。因此,1号风电场调度出力由第3轮的1.77 MW增至11.5 MW;2号风电场调度出力由第3轮的11.35 MW降至1.05 MW。类似地,在第133个5 min的第1~2轮滚动优化过程中,资源调度的优先级从高到底依次为1号风电场—2号风电场—3号风电场—火电厂。在第2轮滚动优化中,由于总指令超过了1号与2号风电场的正式出清容量(5.04 MW,15.06 MW),剩余的0.52 MW由3号风电场承担。由于1号风电场(因风速陡降)在第2轮滚动优化后执行指令效果差导致实测调节指标
,并未超过阈值10 MW。1号风电场在第3轮滚动优化后恢复指令执行效果,优先级重新变成1号风电场—2号风电场—3号风电场—火电厂。因此,1号风电场调度出力由第3轮的1.77 MW增至11.5 MW;2号风电场调度出力由第3轮的11.35 MW降至1.05 MW。类似地,在第133个5 min的第1~2轮滚动优化过程中,资源调度的优先级从高到底依次为1号风电场—2号风电场—3号风电场—火电厂。在第2轮滚动优化中,由于总指令超过了1号与2号风电场的正式出清容量(5.04 MW,15.06 MW),剩余的0.52 MW由3号风电场承担。由于1号风电场(因风速陡降)在第2轮滚动优化后执行指令效果差导致实测调节指标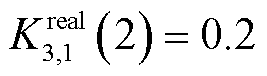 ,调度指令分配优先级从高到低变为2号风电场—1号风电场—3号风电场—火电厂。因此,1号风电场调度出力由第2轮的5.04 MW降至2.39 MW。伴随第3轮执行效果的恢复,1号风电场恢复至5.04 MW。同样地,1号风电场在第229个5 min的第2轮滚动优化过程后执行效果差,优先级降低,因此在第3轮的调度出力降至4.20 MW。由于在第3轮后执行效果恢复,1号风电场在第4轮的调度出力伴随优先级重新提升增至13.26 MW。
,调度指令分配优先级从高到低变为2号风电场—1号风电场—3号风电场—火电厂。因此,1号风电场调度出力由第2轮的5.04 MW降至2.39 MW。伴随第3轮执行效果的恢复,1号风电场恢复至5.04 MW。同样地,1号风电场在第229个5 min的第2轮滚动优化过程后执行效果差,优先级降低,因此在第3轮的调度出力降至4.20 MW。由于在第3轮后执行效果恢复,1号风电场在第4轮的调度出力伴随优先级重新提升增至13.26 MW。
风储联合系统可以有效平抑风电波动,降低不确定性风险。以日前预出清为例比较不同配套储能占比情况下的出清结果。设风储联合系统i中配套储能比例为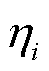 ,风储联合系统中标容量为
,风储联合系统中标容量为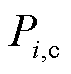 。设中标容量按照装机比例进行分配:储能承担
。设中标容量按照装机比例进行分配:储能承担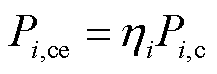 ;风电承担
;风电承担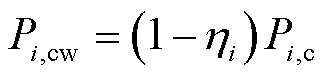 。对于风储联合系统,式(3)中的违约率由风电引起(储能调频性能好)。因此,设中标容量为
。对于风储联合系统,式(3)中的违约率由风电引起(储能调频性能好)。因此,设中标容量为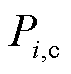 的风电违约率为
的风电违约率为 ,则中标容量为
,则中标容量为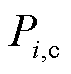 的风储联合系统所对应的违约率
的风储联合系统所对应的违约率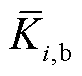 为
为
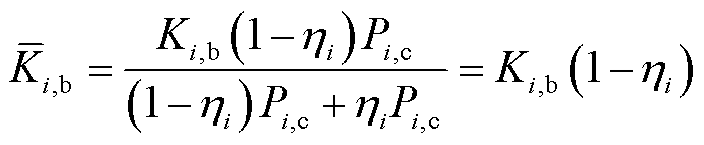 (34)
(34)
式中,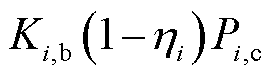 为风电承担部分
为风电承担部分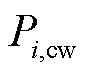 对应的违约量(中标容量乘以违约率),储能承担部分
对应的违约量(中标容量乘以违约率),储能承担部分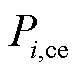 不产生违约量。结合风电违约率
不产生违约量。结合风电违约率 ,通过式(34)计算风储联合系统不同配套储能比例
,通过式(34)计算风储联合系统不同配套储能比例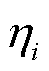 下的
下的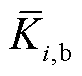 。除了将3座风电场换成3座风储联合电站,其余参数均沿用4.1节,不同
。除了将3座风电场换成3座风储联合电站,其余参数均沿用4.1节,不同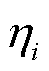 下的系统总成本与风险成本见表7。由表7可知,
下的系统总成本与风险成本见表7。由表7可知,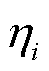 增加导致违约水平与成本(包括风险成本)降低。由于本文假设储能低配比情况下风电和风储系统的报价相同;随着储能配比增加,风储系统的报价会高于风电场;储能调频成本增加量可能超过风险成本减少量,导致总成本增加。在后续研究中,会结合特定的报价策略研究最佳储能配比。
增加导致违约水平与成本(包括风险成本)降低。由于本文假设储能低配比情况下风电和风储系统的报价相同;随着储能配比增加,风储系统的报价会高于风电场;储能调频成本增加量可能超过风险成本减少量,导致总成本增加。在后续研究中,会结合特定的报价策略研究最佳储能配比。
表7 不同储能配比下的日前市场预出清成本
Tab.7 Pre-clearing cost of day-ahead frequency regulation market under different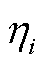

储能配比总成本/$风险成本/$ 0.0528 1443 031 0.127 9852 872 0.1527 8252 712 0.227 6662 553 0.2527 5062 393
为了应对风电等不确定性新型资源参与调频市场的调频安全与性能问题,迫切需要在多时间尺度开展考虑风电不确定性的出清与调度方法的研究。为此,本文分别从日前预出清、日内预出清、日内正式出清和实时调度四个层面,给出了考虑不确定性的出清与调度策略。通过理论与仿真算例分析可知,报价低但违约率高的风电资源可能因风险成本无法优先出清,可以通过降低风电资源违约水平(例如用风储联合系统替代风电)提升风电出清优先级并降低不确定性风险成本。此外,所提基于MPC的滚动优化调度可以结合反馈校正的调频性能指标实时修正中标资源调度出力,使得综合调频性能最优。
本文主要以风电为对象,后续研究需考虑光伏、电动汽车和可调负荷等不确定性资源,以及风储、光储等联合储能系统的调频市场出清策略。增加储能虽然提升储能成本,却可有效地抑制新能源不确定与波动性,降低不确定性资源风险成本。如何从博弈或多目标优化等角度平衡储能成本与不确定性资源风险成本,是未来的重点研究方向之一。
参考文献
[1] Sadeghi-Mobarakeh A, Mohsenian-Rad H. Optimal bidding in performance-based regulation markets: an MPEC analysis with system dynamics[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1282-1292.
[2] 徐湘楚, 米增强, 詹泽伟, 等. 考虑多重不确定性的电动汽车聚合商参与能量-调频市场的鲁棒优化模型[J]. 电工技术学报, 2023, 38(3): 793-805.
Xu Xiangchu, Mi Zengqiang, Zhan Zewei, et al. A robust optimization model for electric vehicle aggregator participation in energy and frequency regulation markets considering multiple uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 793-805.
[3] 张谦, 邓小松, 岳焕展, 等. 计及电池寿命损耗的电动汽车参与能量-调频市场协同优化策略[J]. 电工技术学报, 2022, 37(1): 72-81.
Zhang Qian, Deng Xiaosong, Yue Huanzhan, et al. Coordinated optimization strategy of electric vehicle cluster participating in energy and frequency regulation markets considering battery lifetime degradation[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 72-81.
[4] 叶晨, 王蓓蓓, 薛必克, 等. 考虑超售的共享分布式光储混合运营模式协同策略研究[J]. 电工技术学报, 2022, 37(7): 1836-1846.
Ye Chen, Wang Beibei, Xue Bike, et al. Study on the coordination strategy of sharing distributed photovoltaic energy storage hybrid operation mode considering overselling[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1836-1846.
[5] 关舒丰, 王旭, 蒋传文, 等. 基于可控负荷响应性能差异的虚拟电厂分类聚合方法及辅助服务市场投标策略研究[J]. 电网技术, 2022, 46(3): 933-944.
Guan Shufeng, Wang Xu, Jiang Chuanwen, et al. Classification and aggregation of controllable loads based on different responses and optimal bidding strategy of VPP in ancillary market[J]. Power System Technology, 2022, 46(3): 933-944.
[6] 王浩浩, 陈嘉俊, 朱涛, 等. 计及储能寿命与调频性能的风储联合投标模型及算法[J]. 电网技术, 2021, 45(1): 208-217.
Wang Haohao, Chen Jiajun, Zhu Tao, et al. Joint bidding model and algorithm of wind-storage system considering energy storage life and frequency regulation performance[J]. Power System Technology, 2021, 45(1): 208-217.
[7] Shiltz D J, Cvetković M, Annaswamy A M. An integrated dynamic market mechanism for real-time markets and frequency regulation[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 875-885.
[8] 王霞, 应黎明, 卢少平. 考虑动态频率约束的一次调频和二次调频联合优化模型[J]. 电网技术, 2020, 44(8): 2858-2867.
Wang Xia, Ying Liming, Lu Shaoping. Joint optimization model for primary and secondary frequency regulation considering dynamic frequency constraint[J]. Power System Technology, 2020, 44(8): 2858-2867.
[9] 肖云鹏, 张兰, 张轩, 等. 包含独立储能的现货电能量与调频辅助服务市场出清协调机制[J]. 中国电机工程学报, 2020, 40(增刊1): 167-180.
Xiao Yunpeng, Zhang Lan, Zhang Xuan, et al. Coordination mechanism of spot electric energy with independent energy storage and market clearing of FM auxiliary service[J]. Proceedings of the CSEE, 2020, 40(S1): 167-180.
[10] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804.
Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions ofChina Electrotechnical Society, 2021, 36(9): 1791-1804.
[11] 郭钰锋, 潘梦琪. 基于风功率三参数幂律模型预测日前调频需求的调频辅助服务市场研究[J]. 中国电机工程学报, 2021, 41(20): 6941-6949.
Guo Yufeng, Pan Mengqi. Research on frequency modulation ancillary service market based on three parameter power law model of wind power to predict the day-ahead frequency modulation demand[J]. Proceedings of the CSEE, 2021, 41(20): 6941-6949.
[12] 崔达, 史沛然, 陈启鑫, 等. 风电参与能量-调频联合市场的优化策略[J]. 电力系统自动化, 2016, 40(13): 5-12.
Cui Da, Shi Peiran, Chen Qixin, et al. Optimal strategy for wind power bidding in energy and frequency regulation markets[J]. Automation of Electric Power Systems, 2016, 40(13): 5-12.
[13] 杨家琪, 喻洁, 田宏杰, 等. 考虑新能源性能风险的调频辅助服务市场出清与调度策略[J]. 电力系统自动化, 2020, 44(8): 66-73.
Yang Jiaqi, Yu Jie, Tian Hongjie, et al. Clearing and scheduling strategy of frequency regulation ancillary service market considering performance risk of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(8): 66-73.
[14] 韩丽, 王冲, 于晓娇, 等. 考虑风电爬坡灵活调节的碳捕集电厂低碳经济调度[J]. 电工技术学报, 2024, 39(7): 2033-2045.
Han Li, Wang Chong, Yu Xiaojiao, et al. Low-carbon and economic dispatch considering the carbon capture power plants with flexible adjustment of wind power ramp[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2033-2045.
[15] 吴含欣, 董树锋, 张祥龙, 等. 考虑碳交易机制的含风电电力系统日前优化调度[J]. 电网技术, 2024, 48(1): 70-80.
Wu Hanxin, Dong Shufeng, Zhang Xianglong, et al. Optimal dispatching of power system with wind power considering carbon trading mechanism[J]. Power System Technology, 2024, 48(1): 70-80.
[16] 王彦红, 刘浩, 李洪伟. 碳交易机制下旁路补偿供热消纳风电的电热经济调度[J]. 南方电网技术, 2024, 18(4): 50-58.
Wang Yanhong, Liu Hao, Li Hongwei. Economic dispatch of electric and thermal energy with wind power integration and bypass heat compensation under carbon trading mechanisms[J]. Southern Power System Technology, 2024, 18(4): 50-58.
[17] 潘郑楠, 邓长虹, 徐慧慧, 等. 考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度[J]. 电工技术学报, 2023, 38(增刊1): 56-69.
Pan Zhengnan, Deng Changhong, Xu Huihui, et al. Game optimization scheduling of high proportion wind power and multiple flexible resources considering flexibility compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 56-69.
[18] 黄弦超, 封钰, 丁肇豪. 多微网多时间尺度交易机制设计和交易策略优化[J]. 电力系统自动化, 2020, 44(24): 77-88.
Huang Xianchao, Feng Yu, Ding Zhaohao. Design of multi-time scale trading mechanism and trading strategy optimization for multiple microgrids[J]. Automation of Electric Power Systems, 2020, 44(24): 77-88.
[19] 唐杰, 吕林, 叶勇, 等. 多时间尺度下主动配电网源-储-荷协调经济调度[J]. 电力系统保护与控制, 2021, 49(20): 53-64.
Tang Jie, Lü Lin, Ye Yong, et al. Source-storage-load coordinated economic dispatch of an active distribution network under multiple time scales[J]. Power System Protection and Control, 2021, 49(20): 53-64.
[20] 李翔宇, 赵冬梅. 基于模糊-概率策略实时反馈的虚拟电厂多时间尺度优化调度[J]. 电工技术学报, 2021, 36(7): 1446-1455.
Li Xiangyu, Zhao Dongmei. Research on multi-time scale optimal scheduling of virtual power plant based on real-time feedback of fuzzy-probability strategy[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1446-1455.
[21] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. Multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1419-1435.
[22] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7): 1864-1881.
Chen Minghao, Sun Yi, Xie Zhiyuan. The multi-time-scale management optimization method for park integrated energy system based on the Bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[23] 楚帅, 葛维春, 滕云, 等. 海水淡化与电制热负荷联合消纳风电的多时间尺度调度策略[J]. 电力系统自动化, 2023, 47(8): 120-131.
Chu Shuai, Ge Weichun, Teng Yun, et al. Multi-time-scale scheduling strategy for combined accommodation of wind power by seawater desalination and electric heating loads[J]. Automation of Electric Power Systems, 2023, 47(8): 120-131.
[24] 胡俊杰, 赖信辉, 郭伟, 等. 考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度[J]. 电力系统自动化, 2022, 46(16): 52-60.
Hu Junjie, Lai Xinhui, Guo Wei, et al. Multi-time-scale scheduling for regional power grid considering flexibility of electric vehicle and wind power accommodation[J]. Automation of Electric Power Systems, 2022, 46(16): 52-60.
Abstract To meet the requirements of the modern power system construction, the National Energy Administration introduces guidance and management requirements for new resources such as renewable energy and energy storage systems. In western regions with abundant wind energy resources, such as Xinjiang Province, wind farms meeting certain installed capacity requirements can participate in the frequency regulation ancillary services market. The dispatching agency optimizes clearing based on frequency demands. Wind farms provide frequency services and obtain settlement fees according to the clearing results.
Unlike conventional units, declared capacity of wind farms is subject to uncertainty. In this situation, despite the desire of wind farms to occupy market share and increase revenue by utilizing the full capacity quota, the uncertainty in declared capacity may lead to actual capacity being lower than the reported value, posing a risk to the frequency regulation market. Therefore, this paper proposes a multi-time scale clearing and scheduling method for the frequency regulation market considering wind power uncertainty.
Firstly, the impact of wind power uncertainty on the frequency regulation market clearing and scheduling process is analyzed through the analysis of the bid capacity default rate. By designing a risk cost based on conditional value-at-risk, the paper quantitatively evaluates the impact of wind power uncertainty on the frequency regulation market clearing. Secondly, by analyzing the frequency demand characteristics at different timescales, a multi-timescale clearing model and strategy considering frequency risk cost are proposed, providing generation plan boundary conditions for the next level of clearing and ensuring market safety and reliability. Finally, the paper quantitatively analyzes the impact of wind power uncertainty on frequency accuracy indicators and proposes a scheduling strategy considering the optimal comprehensive frequency performance indicators. The proposed scheduling strategy adopts a rolling mode, where the dispatching agency updates frequency performance indicators based on the previous round of scheduling performance, improving the participation and quality of high-quality regulation units in frequency regulation.
Simulation analysis is conducted using a 3-wind-farm-and-1-thermal power system to reproduce the market clearing and scheduling process. The simulation results indicate that despite offering low prices of wind farms, if their default rate is too high, they may not clear priority due to risk costs. Thermal power units have the lowest default rate and lowest frequency regulation risk cost. To increase the clearing capacity of uncertain wind power, wind storage systems can be used to reduce the bid default rate. Through simulated rolling scheduling processes, it is observed that the performance of units in one round of scheduling affects their frequency performance indicators in the next round, thereby altering their regulation quantity.
Through simulation analysis, the following conclusions can be drawn: (1)Wind farms with low quotes but high default rates may not be cleared due to the associated risk costs. To enhance the priority of wind power clearing and reduce uncertainty risk costs, it is possible to lower the default levels of wind power resources (e.g., by using a wind and storage joint system to replace standalone wind power). (2)The rolling optimization scheduling based on model predictive control (MPC) can dynamically adjust the dispatched output of bid resources in real-time using feedback-corrected frequency performance indicators, achieving optimal comprehensive frequency regulation performance. Future research should consider uncertainties from other resources like photovoltaics and controllable loads, as well as develop clearing strategies for their participation in the frequency regulation market. Additionally, approaches considering game theory or multi-objective optimization could be explored to optimize the trade-off between storage costs and uncertainty resource risk costs, thereby enhancing the economic efficiency and security of frequency regulation.
keywords:Power system frequency control, frequency regulation performance, multi-time-scale energy management, wind power uncertainty
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.231477
国家自然科学基金(52207142)、江苏省自然科学基金(BK20210512)和上海市启明星培育扬帆专项(22YF1414800)资助。
收稿日期 2023-09-07
改稿日期 2024-06-05
陈春宇 男,1991年生,副教授,硕士生导师,研究方向为新能源电力系统运行与控制。E-mail:chunyuchen@cumt.edu.cn
王剑晓 男,1992年生,助理教授,博士生导师,研究方向为电力市场、能源环境政策和数据挖掘技术。E-mail:wang-jx@pku.edu.cn(通信作者)
(编辑 赫 蕾)