
图1 分时电价的制定与EV灵活调度框架
Fig.1 Time-of-use price formulation and EV flexible scheduling framework
摘要 针对新能源随机性较大而出现一些极端情况时,现有分时电价下弃风、弃光与火电机组调节能力不足而导致切负荷成本较大的问题仍较为突出的现象,提出了一种考虑风光消纳与电动汽车灵活性的调度策略。首先,制定综合考虑风电、光伏、火电机组调节能力与基础负荷的分时电价,新增凹谷与尖峰电价时段,并引入价格弹性系数定量描述电动汽车对新增时段的响应;其次,基于电价信息建立电动汽车充放电模型,确定电动汽车充放电调度的电量信息;再次,统筹考虑电网、电动汽车聚合商以及电动汽车用户的三方利益,构建以负荷波动最小,弃风、弃光与用户充电成本最小和最大化聚合商收益为目标的电动汽车充放电优化调度模型;最后,通过算例验证所提模型的可行性与有效性。
关键词:电动汽车 切负荷 分时电价 调度策略
电动汽车(Electric Vehicle, EV)作为一种低碳绿色环保的交通工具,在其大规模入网无序充电时将会加重电网负担,造成“峰上加峰”的现象[1-2]。风能和太阳能等可再生能源凭借其环保、高效的优点,在新能源发电领域得到广泛应用。但由于自身存在随机性和波动性较大的问题,在大规模入网后也会对电网的可靠性与稳定性造成影响[3-4]。因此,为降低负荷波动,减少弃风、弃光与电力供应不足时的切负荷现象,制定包含新能源与EV的优化调度策略是目前研究的热点。
现有研究常将EV作为一种具有灵活调节能力的负荷资源,使其在电力系统调峰和新能源消纳方面得到了广泛应用[5-10]。文献[5]建立了考虑EV与跟踪光伏出力的凸优化模型,通过车联网(Vehicle-to-Grid, V2G)技术实现平抑光伏波动的目的。文献[6-7]提出了通过V2G技术考虑EV储能特性与可再生能源协同调度的策略,实现了平抑负荷波动并消纳可再生能源的目标。文献[8]建立了包含风电、火电及EV的双层调度模型,降低了火电机组成本并增加了风光消纳量。文献[9]提出一种通过调度EV充电减少可再生能源浪费的方法,结果表明该方法能够有效地降低弃光现象。文献[10]提出了考虑V2G的EV调度策略,增加了电网负荷的调峰和填谷效果,提高了系统的经济效益。上述文献通过优化EV充放电行为达到实现负荷调峰与消纳新能源的目标,但未考虑分时电价,忽略了其在EV调度中对用户的引导作用和经济效益。
为促进新能源消纳、降低负荷峰谷差,许多文献采用分时电价策略引导用户的充放电行为[11-16],调动EV用户参与电网调度的积极性。文献[11]基于分时电价建立了包含风电与EV的多时间尺度调度模型,降低了电网机组的运行成本与用户的用电成本。文献[12]提出分时电价动态优化方法,优化EV的有序充放电,在减小负荷峰谷差的同时降低用户的用电成本。文献[13]建立基于价格弹性系数矩阵的实时电价模型,通过调控EV充放电行为实现了减少负荷峰谷差和弃风、弃光的目标。文献[14]提出一种基于EV参与调峰定价策略的区域电网两阶段优化调度方案,通过两阶段优化,缓解了区域电网的调峰压力,降低了用户用电成本,提高了风电光伏的消纳水平。文献[16]制定了考虑动态电价的优化调度策略,建立多目标优化调度模型,引导电动汽车用户在负荷高峰时放电,在负荷较低时充电,增加了风电消纳、降低了用户的充电成本。但文献[11-15]未综合考虑电网、EV聚合商及EV用户三者的利益。文献[16]根据预测的负荷与风电出力,制定了动态分时电价,结果表明在风电正反调峰的情况下能够降低用户的用电成本,同时在反调峰时还可以平抑负荷波动,增加风电消纳。但文献[16]制定的电价策略未考虑火电机组的调节能力,在新能源不确定性较大的情况下,负荷需求降至低谷时,风电、光伏消纳受阻导致弃风、弃光成本较大;忽略了负荷需求超出火电机组的能力范围时,为应对电力供应不足而产生的切负荷成本较大的现象。因此,为进一步降低弃风、弃光以及切负荷成本,需要充分考虑火电机组调节能力,在风光不确定性较大的情况下,制定能够更加调动用户充放电积极性的凹谷与尖峰电价。
综上所述,本文提出了考虑风光消纳与电动汽车灵活性的调度策略。该策略通过综合考虑风光功率、基础负荷以及火电机组调节能力,制定并新增了凹谷与尖峰电价时段;基于电价信息在电价峰谷时段调度EV充放电,实现多目标函数的优化。最后通过算例仿真验证了本文方法的有效性。
本文的调度策略主要有电网、EV聚合商及EV用户三个主体参与。分时电价的制定与EV灵活调度框架如图1所示。电网根据日前预测的负荷信息,制定风电、光伏和基础的等效负荷,并基于等效负荷制定尖峰、峰、平、谷与凹谷电价及其时段,随后将电价信息传达给EV聚合商;EV聚合商从EV用户处获取所需信息,同时根据市场情况调整电价,通过移动程序发布电价与充电站位置等信息,并根据电网需求将EV放电的电能出售给电网;EV得知电价信息之后提供充电需求、初始位置等信息,根据自身情况前往充电点进行充放电操作。最后在本文的电价引导下,EV参与充放电调度后能够显著降低电网负荷波动,实现新能源消纳和减少切负荷的目标。

图1 分时电价的制定与EV灵活调度框架
Fig.1 Time-of-use price formulation and EV flexible scheduling framework
随着风电和光伏大规模入网,固定的分时电价无法有效调控用户的用电行为,导致电网供需不平衡的问题日益突出。因此,为准确减少负荷波动与消纳风电、光伏,需要制定合适的分时电价方案。
根据历史数据预测日前风光功率和基础负荷的数据并计算出等效负荷及其平均值与峰谷差,将等效负荷的平均值和峰谷差作为划分时段的依据。分时电价制定策略示意图如图2所示。当某个时段的等效负荷低于其均值减去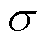 倍峰谷差时,制定该电价为谷电价;当某个时段的等效负荷高于其均值加上
倍峰谷差时,制定该电价为谷电价;当某个时段的等效负荷高于其均值加上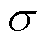 倍峰谷差时,制定该电价为峰电价;其他时段则为平电价。
倍峰谷差时,制定该电价为峰电价;其他时段则为平电价。
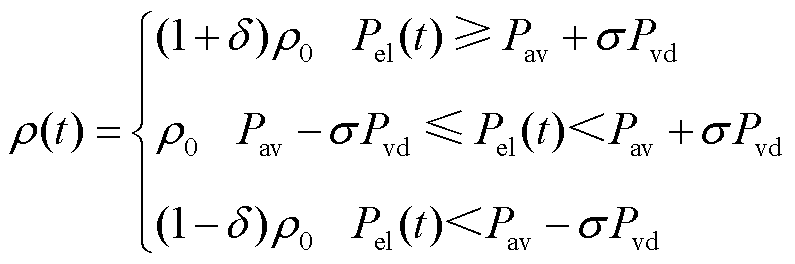 (1)
(1)
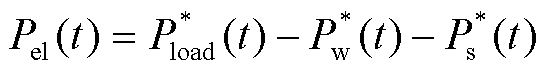 (2)
(2)
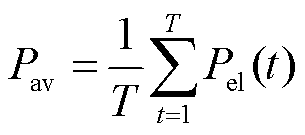 (3)
(3)
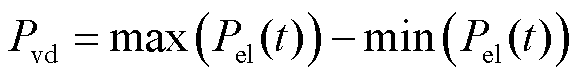 (4)
(4)
式中,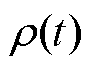 为动态分时电价;
为动态分时电价;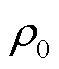 为平时段电价;
为平时段电价;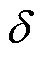 为电价波动范围;
为电价波动范围;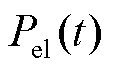 为某一风电、光伏和基础负荷的等效负荷;
为某一风电、光伏和基础负荷的等效负荷;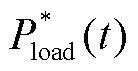 为日前预测的基础负荷;
为日前预测的基础负荷;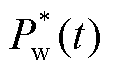 为日前预测的风电出力;
为日前预测的风电出力;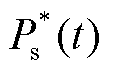 为日前预测的光伏发电出力;
为日前预测的光伏发电出力; 为调度周期;
为调度周期;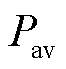 为等效负荷的平均值;
为等效负荷的平均值;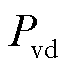 为等效负荷的峰谷差。
为等效负荷的峰谷差。
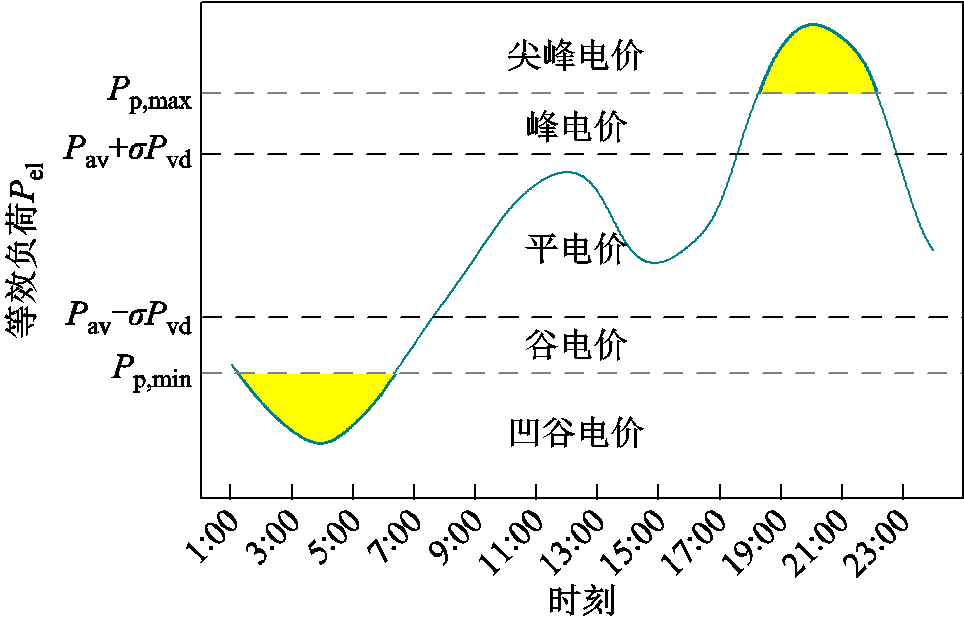
图2 分时电价制定策略示意图
Fig.2 Formulation strategy diagram of time-of-use price
考虑到风电、光伏的波动性,当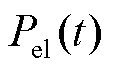 小于火电机组最小出力时,会增加弃风、弃光现象,造成资源浪费;当
小于火电机组最小出力时,会增加弃风、弃光现象,造成资源浪费;当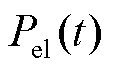 大于火电机组的最大出力或当
大于火电机组的最大出力或当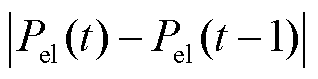 超出火电机组的爬坡能力时,会出现电力供应不足现象,为保证电力系统的稳定性,电网侧会进行切负荷操作。因此,为进一步减少弃风、弃光与切负荷现象,降低惩罚成本,本文以上述研究为基础,将考虑火电机组的调节能力加入电价策略制定中,通过凹谷与尖峰电价提高EV用户的积极性,吸引更多EV参与电网的充放电调度。制定策略同样如图2阴影部分所示,当某个时段的等效负荷低于火电机组的最小出力时,制定该时段电价为凹谷电价;当某个时段的等效负荷高于火电机组的最大出力或等效负荷的变化超出火电机组爬坡能力时,制定该时段电价为尖峰电价。
超出火电机组的爬坡能力时,会出现电力供应不足现象,为保证电力系统的稳定性,电网侧会进行切负荷操作。因此,为进一步减少弃风、弃光与切负荷现象,降低惩罚成本,本文以上述研究为基础,将考虑火电机组的调节能力加入电价策略制定中,通过凹谷与尖峰电价提高EV用户的积极性,吸引更多EV参与电网的充放电调度。制定策略同样如图2阴影部分所示,当某个时段的等效负荷低于火电机组的最小出力时,制定该时段电价为凹谷电价;当某个时段的等效负荷高于火电机组的最大出力或等效负荷的变化超出火电机组爬坡能力时,制定该时段电价为尖峰电价。
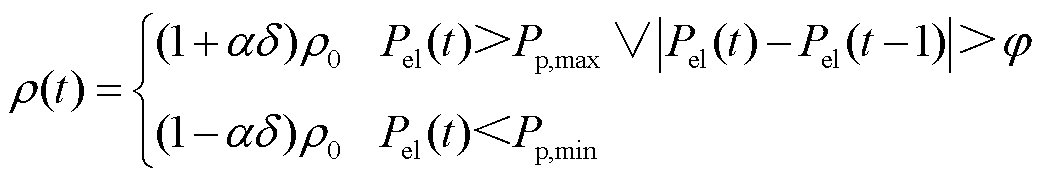 (5)
(5)
式中,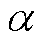 为波动系数;
为波动系数;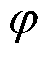 为火电机组的爬坡率;
为火电机组的爬坡率;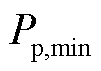 与
与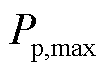 分别为火电机组最小出力和最大出力。
分别为火电机组最小出力和最大出力。
凹谷电价和尖峰电价的设定根据电网负荷和可再生能源出力波动情况进行调整。通过考虑火电机组调节能力,制定价格更高或更低的电价能够吸引更多用户参与充放电调度,能够减少弃风、弃光与切负荷现象,降低能源浪费、提高电力系统的稳定性,实现电网供需的平衡。
基于上述电价制定策略,本文利用需求价格弹性系数来描述电价变化与EV用户用电量之间的关系,即描述本文方法下凹谷与尖峰电价能够吸引更多EV用户参与充放电调度的行为。根据经济学原理,电力负荷的价格弹性系数[17-18]是指电价的变动所引起用户用电量的变化。在实际生活中,用户的用电量不仅与当前时刻的电价相关,还受到相邻时刻电价的影响。因此为更准确地描述用户用电行为对价格的反应,需要引入自弹性系数和交叉弹性系数,它们分别表示当前时段电价变化造成的当前时段用电量的变化与其他时段电价变化造成的当前时段用电量的变化,具体公式为
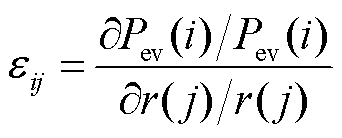 (6)
(6)
式中,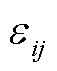 为弹性系数;
为弹性系数; 和
和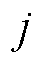 为时刻,当
为时刻,当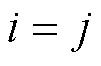 时,
时,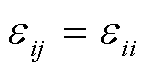 为自弹性系数,当
为自弹性系数,当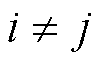 时,
时,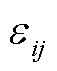 为交叉弹性系数;
为交叉弹性系数;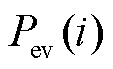 和
和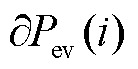 分别为第
分别为第 时刻电价变化前的EV用户用电量与电价变化后的EV用户用电变化量;
时刻电价变化前的EV用户用电量与电价变化后的EV用户用电变化量;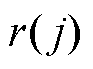 和
和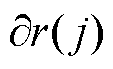 分别为
分别为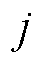 时刻EV聚合商发布的EV充放电电价变化前的电价与电价变化后的电价变化量。通常情况下,用户用电量与本时间段内的价格成反比,与其他时间段的价格成正比。
时刻EV聚合商发布的EV充放电电价变化前的电价与电价变化后的电价变化量。通常情况下,用户用电量与本时间段内的价格成反比,与其他时间段的价格成正比。
定义EV充放电模型用车辆类型、电池荷电状态(State of Charge, SOC)及容量和充放电功率等描述。鉴于灵活性较强的电动私家车在私人交通领域的广泛应用,以及本文的调度策略是引导EV前往充电点参与充放电调度,因此参与充放电调度的EV类型为电动私家车,而不考虑其他类型如电动公交车、电动出租车等。同时EV的充放电功率设为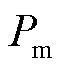 。
。
EV日行驶里程的概率密度函数满足正态分布,有
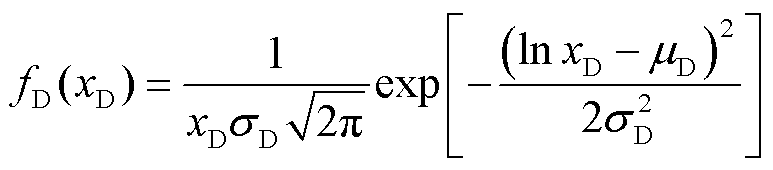 (7)
(7)
式中,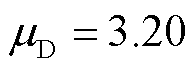 ;
;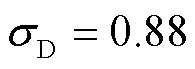 ;
; 为日行驶里程。
为日行驶里程。
EV到达充电点时的初始电量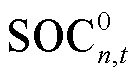 为
为
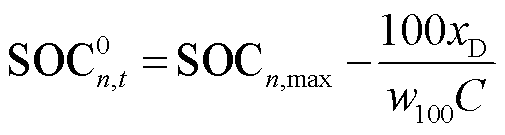 (8)
(8)
式中,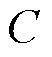 为电池容量;
为电池容量;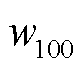 为百公里能耗;
为百公里能耗;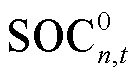 为第
为第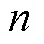 辆EV在
辆EV在 时刻到达充电点的初始电量;
时刻到达充电点的初始电量;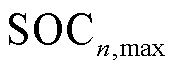 为第
为第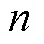 辆EV所能充到的
辆EV所能充到的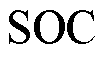 的最大值。
的最大值。
为降低EV无序充电对电网负荷的影响、提高电网的稳定性以及促进风电、光伏的有效利用,综合考虑电网、EV用户和EV聚合商的利益,构建多个目标函数。
1)负荷方差与弃风、弃光和切负荷成本
为了减少负荷峰谷差、降低负荷波动,以风光并网后的负荷方差最小作为目标;为提高可再生能源的利用率,增加电网的稳定性,以弃风弃光量与切负荷成本最小为目标,有
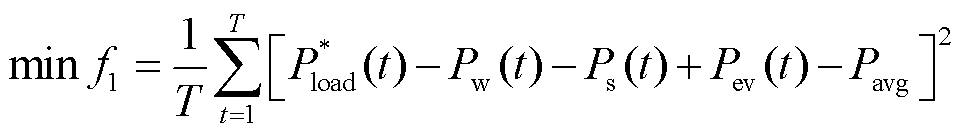 (9)
(9)
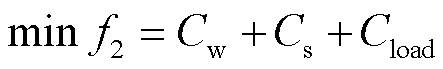 (10)
(10)
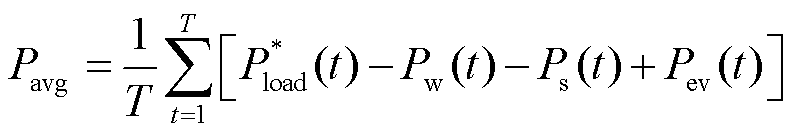 (11)
(11)
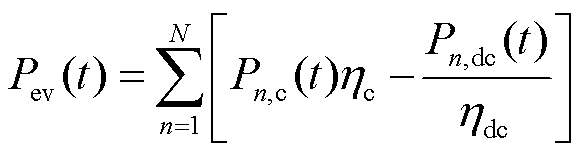 (12)
(12)
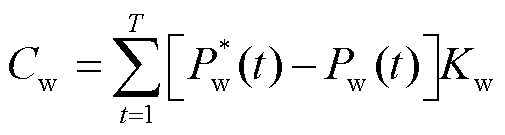 (13)
(13)
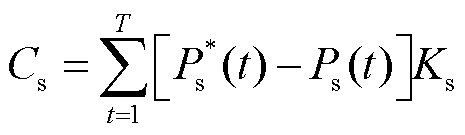 (14)
(14)
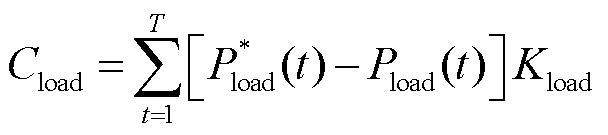 (15)
(15)
式中,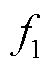 为负荷方差的目标函数;
为负荷方差的目标函数;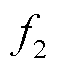 为弃风、弃光与切负荷总成本的目标函数;
为弃风、弃光与切负荷总成本的目标函数;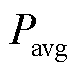 为调度周期内的平均负荷;
为调度周期内的平均负荷;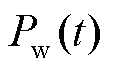 为风电在
为风电在 时段的实际出力;
时段的实际出力;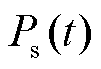 为光伏在
为光伏在 时段的实际出力;
时段的实际出力; 为调度中的负荷出力;
为调度中的负荷出力;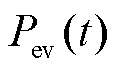 为
为 时段所有EV的总充放电功率;
时段所有EV的总充放电功率;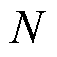 为参与调度的EV的数量;
为参与调度的EV的数量;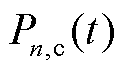 为第
为第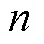 辆EV在
辆EV在 时段的充电功率;
时段的充电功率;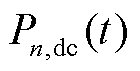 为第
为第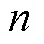 辆EV在
辆EV在 时段的放电功率;
时段的放电功率;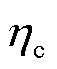 与
与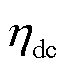 分别为电动汽车的充电效率与放电效率;
分别为电动汽车的充电效率与放电效率;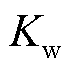 、
、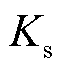 、
、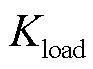 分别为弃风、弃光、切负荷惩罚成本系数;
分别为弃风、弃光、切负荷惩罚成本系数;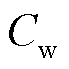 为弃风调度周期内的弃风成本;
为弃风调度周期内的弃风成本; 为弃风调度周期内的弃光成本;
为弃风调度周期内的弃光成本;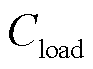 为弃风调度周期内的切负荷成本。
为弃风调度周期内的切负荷成本。
2)EV用户用电成本
为满足用户希望以较低成本满足用电需求的要求,提高用户满意度,以用户用电成本最低为目标,有
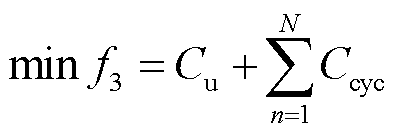 (16)
(16)
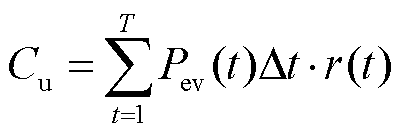 (17)
(17)
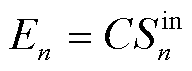 (18)
(18)
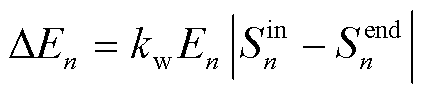 (19)
(19)
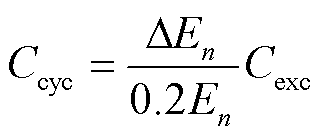 (20)
(20)
式中, 为用户用电成本的目标函数;
为用户用电成本的目标函数;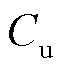 为参与调度的EV的充放电成本;
为参与调度的EV的充放电成本;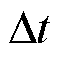 为时段长度;
为时段长度; 为充电站发布的EV充放电电价;
为充电站发布的EV充放电电价;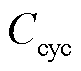 为单辆EV的电池损耗成本;
为单辆EV的电池损耗成本;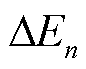 为第
为第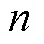 辆EV电池一次放电过程造成的容量损失;
辆EV电池一次放电过程造成的容量损失;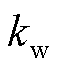 为计算系数;
为计算系数;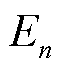 为第
为第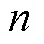 辆EV调度前电池的初始容量;
辆EV调度前电池的初始容量;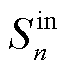 为第
为第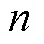 辆EV放电前的
辆EV放电前的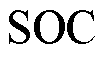 ;
;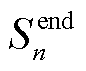 为第
为第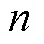 辆EV放电后的
辆EV放电后的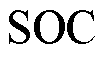 ;
;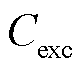 为单辆EV电池的更换成本。
为单辆EV电池的更换成本。
本文通过考虑火电机组的调节能力制定了凹谷与尖峰时段。用户在凹谷时段充电时成本会低于谷时段;用户在尖峰时段放电时收益会高于峰时段。通过需求价格弹性系数可得此时用户的成本为
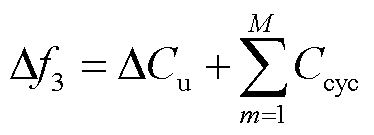 (21)
(21)
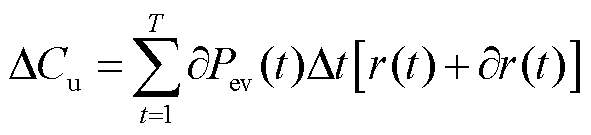 (22)
(22)
式中,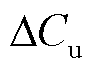 为凹谷与尖峰时段EV用户的充放电成本;
为凹谷与尖峰时段EV用户的充放电成本;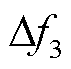 为需求价格弹性下凹谷与尖峰时段EV用户的用电成本;
为需求价格弹性下凹谷与尖峰时段EV用户的用电成本;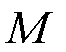 为尖峰时段参与放电调度的EV的数量。
为尖峰时段参与放电调度的EV的数量。
3)EV聚合商收益
为了激励EV聚合商更有效地运营电动汽车充电服务,以EV聚合商收益最高为目标,有
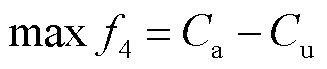 (23)
(23)
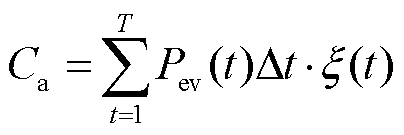
 (24)
(24)
式中,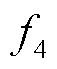 为EV聚合商收益的目标函数;
为EV聚合商收益的目标函数;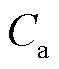 为EV聚合商对于EV参与充放电调度的总收入;
为EV聚合商对于EV参与充放电调度的总收入;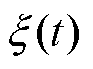 为EV聚合商的购售电价,其数值与
为EV聚合商的购售电价,其数值与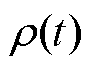 相等。
相等。
由于目标函数负荷方差与弃风弃光和切负荷成本、用户用电成本以及聚合商收益的量纲和数量级不同,且聚合商收益以利润最大为目标,因此本文选择通过使用权重系数加权的方法对多个目标函数进行归一化处理,引入负荷方差成本系数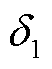 ,并令
,并令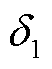 是一个非常小的数,以避免数量级过大造成的多目标数据求解不准确,将求解的多目标问题转换为单目标问题。
是一个非常小的数,以避免数量级过大造成的多目标数据求解不准确,将求解的多目标问题转换为单目标问题。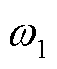 、
、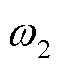 、
、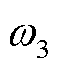 、
、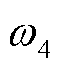 四个权重系数在保证
四个权重系数在保证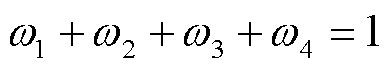 的情况下,对于不同利益主体的应用场景,可取不同权重系数。例如当负荷波动比较大,弃风弃光或切负荷现象较严重时,需要适当地提高负荷曲线方差
的情况下,对于不同利益主体的应用场景,可取不同权重系数。例如当负荷波动比较大,弃风弃光或切负荷现象较严重时,需要适当地提高负荷曲线方差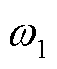 与
与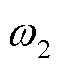 的权重系数,以确保系统的稳定运行。本文在确定权重系数时,考虑到各利益主体之间的协调和平衡,故令四个权重系数的取值均为0.25。
的权重系数,以确保系统的稳定运行。本文在确定权重系数时,考虑到各利益主体之间的协调和平衡,故令四个权重系数的取值均为0.25。
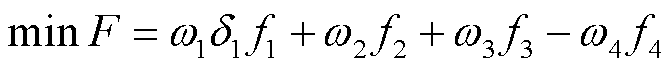 (25)
(25)
式中,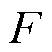 为归一化成统一量纲单位为元的目标函数;
为归一化成统一量纲单位为元的目标函数;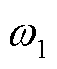 、
、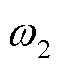 、
、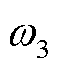 、
、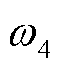 分别为目标函数
分别为目标函数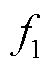 、
、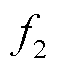 、
、 、
、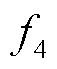 对应的权重系数。
对应的权重系数。
1)系统功率平衡约束
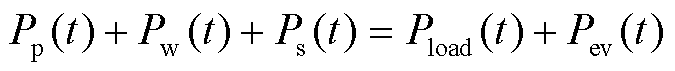 (26)
(26)
式中,Pp(t)为火电机组在t时段的实际出力。
2)火电机组运行约束
本文主要考虑火电机组的出力约束和爬坡约束,即
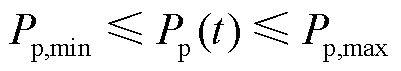 (27)
(27)
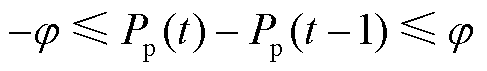 (28)
(28)
3)风电出力、光伏出力与负荷出力约束
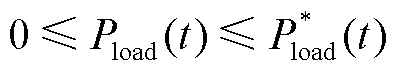 (29)
(29)
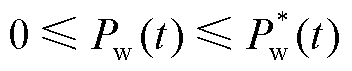 (30)
(30)
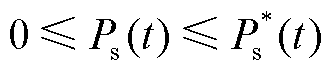 (31)
(31)
4)EV充放电约束
本文假设EV恒功率充放电,同时在EV到达充电点之后令EV仅在谷时段充电,在峰时段放电,在平时段既不充电也不放电;同时为保证电动汽车能够正常行驶,即任意时刻电动汽车的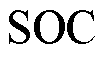 不能超过电池
不能超过电池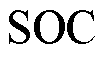 的上、下限,有
的上、下限,有
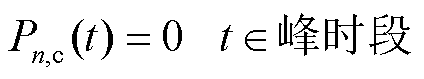 (32)
(32)
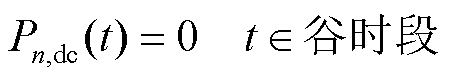 (33)
(33)
 (34)
(34)
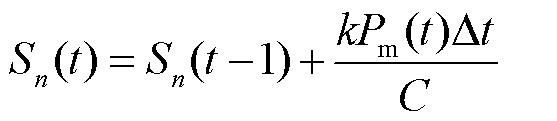 (35)
(35)
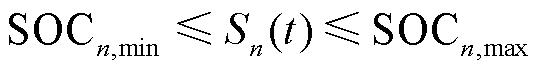 (36)
(36)
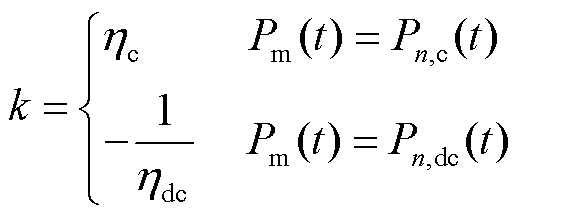 (37)
(37)
式中,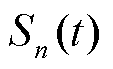 为第
为第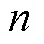 辆EV在
辆EV在 时刻的
时刻的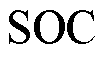 ;
;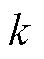 为充放电功率系数;
为充放电功率系数;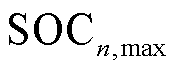 、
、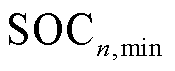 分别为第
分别为第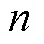 辆EV的
辆EV的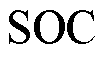 上、下限;
上、下限;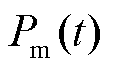 为EV充放电功率。根据式(7)、式(8)日行驶里程模拟EV到达充电点时的初始电量,保证了EV到充电点时的
为EV充放电功率。根据式(7)、式(8)日行驶里程模拟EV到达充电点时的初始电量,保证了EV到充电点时的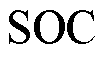 不会低于下限
不会低于下限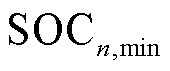 。
。
为充分体现本文方法的优越性,参考文献[7]选取某区域电力系统进行分析。其中包括最小出力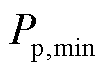 与最大出力
与最大出力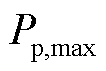 分别为12 MW与40 MW、爬坡率
分别为12 MW与40 MW、爬坡率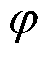 为20 MW/h的火电机组[19],1个20 MW容量的风电场,1个5 MW容量的光伏电站。本文的调度周期T=24 h,调度单位时段时长为1 h,电价波动范围为0.4,波动系数为0.9,平时段电价为0.6元/(kW·h),
为20 MW/h的火电机组[19],1个20 MW容量的风电场,1个5 MW容量的光伏电站。本文的调度周期T=24 h,调度单位时段时长为1 h,电价波动范围为0.4,波动系数为0.9,平时段电价为0.6元/(kW·h),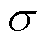 =0.2,
=0.2,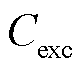 =78 000元;
=78 000元;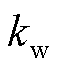 =0.000 15[20];弃风、弃光惩罚成本系数均为0.6元/(kW·h)。切负荷惩罚成本系数为4元/(kW·h);为实现多方利益的平衡,令
=0.000 15[20];弃风、弃光惩罚成本系数均为0.6元/(kW·h)。切负荷惩罚成本系数为4元/(kW·h);为实现多方利益的平衡,令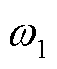 、
、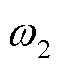 、
、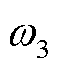 、
、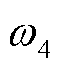 取值均为0.25。基础负荷数据来自文献[16],风电、光伏发电数据来源于Elia比利时电力运营商公开的2023年5月5日的运行数据,具体数据如图3所示;EV的参数见表1。考虑到弹性系数一般通过历史数据分析、市场调研等方式获得,且多个时段的交叉弹性系数较难获取,因此本文仅考虑并引入文献[21]中的自弹性系数-0.25,同时仅考虑价格变化时用电量的变化,价格不变时用电量视为不变。算例在Matlab R2022a环境下调用YALMIP+CPLEX求解器求解。
取值均为0.25。基础负荷数据来自文献[16],风电、光伏发电数据来源于Elia比利时电力运营商公开的2023年5月5日的运行数据,具体数据如图3所示;EV的参数见表1。考虑到弹性系数一般通过历史数据分析、市场调研等方式获得,且多个时段的交叉弹性系数较难获取,因此本文仅考虑并引入文献[21]中的自弹性系数-0.25,同时仅考虑价格变化时用电量的变化,价格不变时用电量视为不变。算例在Matlab R2022a环境下调用YALMIP+CPLEX求解器求解。
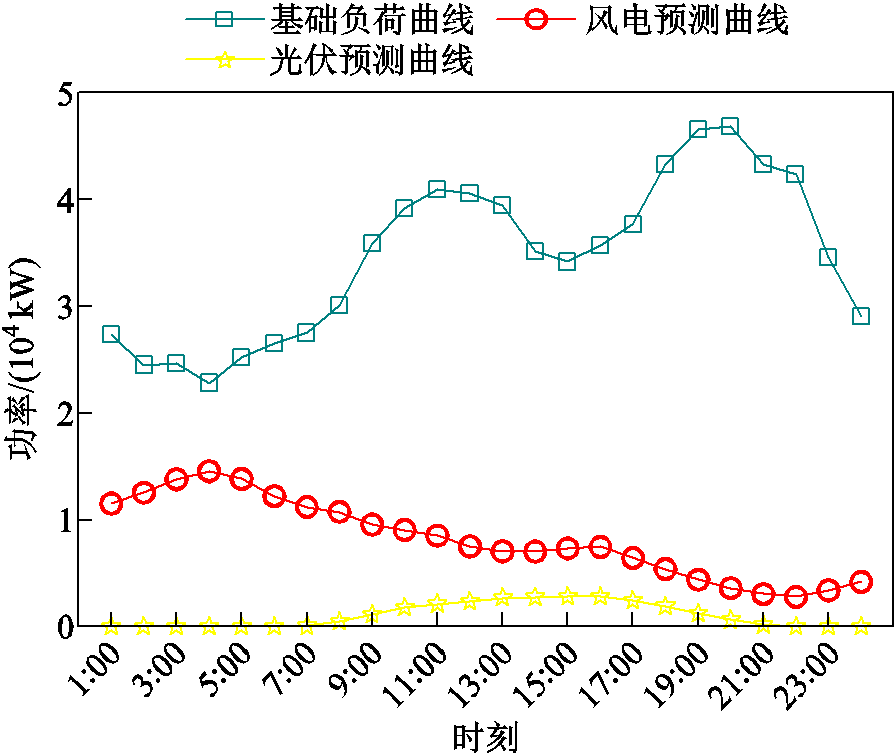
图3 基础负荷、风电和光伏出力预测曲线
Fig.3 Forecast curves of load ,wind power and photovoltaic output
表1 EV的参数
Tab.1 Parameters of EV

参数数值 充放电功率/kW7 充放电效率0.92 电池容量/(kW·h)55 百公里能耗/[kW·h/(100km)]18.18 0.2 0.9
表2展示了根据本文电价策略制定的EV聚合商购售电电价与向用户发布的EV充放电电价具体参数。由文献[22]建立的用户价格响应模型可知,本文EV谷-凹谷与尖峰-峰充放电电价差0.3元/(kW·h)均超出了死区阈值,用户响应处在线性区内,因此EV用户在凹谷与尖峰时段会有相应的响应。
表2 EV聚合商购售电与EV充放电分时电价
Tab.2 EV aggregator purchasing and selling and EV charging and discharging time-of-use price

电价水平电价时段聚合商购售电电价/[元/(kW·h)]EV充放电电价/[元/(kW·h)] 尖峰时段19:00—21:001.141.34 峰时段18:00, 22:000.841.04 平时段8:00—17:00,23:00—24:000.60.8 谷时段1:00, 6:00—7:000.360.56 凹谷时段2:00—5:000.060.26
将本文电价策略与文献[16]电价策略进行对比,对比结果如图4所示。文献[16]根据等效负荷与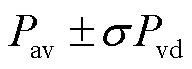 制定了以蓝色箭头线分隔的峰平谷电价与电价时段。但在谷时段2:00—5:00时,等效负荷大小分别为11 967、10 851、8 257与11 407 kW,均低于火电机组最小出力
制定了以蓝色箭头线分隔的峰平谷电价与电价时段。但在谷时段2:00—5:00时,等效负荷大小分别为11 967、10 851、8 257与11 407 kW,均低于火电机组最小出力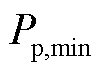 ,此时会有多余的风电未被消纳,产生弃风现象,造成了新能源资源的浪费;在峰时段19:00—21:00时,等效负荷大小分别为40 926、42 647与40 101 kW,均高于火电机组最大出力
,此时会有多余的风电未被消纳,产生弃风现象,造成了新能源资源的浪费;在峰时段19:00—21:00时,等效负荷大小分别为40 926、42 647与40 101 kW,均高于火电机组最大出力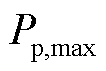 ,此时为减少电力供应不足现象电网侧会进行切负荷操作,增加了切负荷成本。文献[16]的电价制定策略忽略了在风电、光伏波动性较大时火电机组的调节能力。因此,本文通过考虑火电机组的调节能力,将以黄色圆头线分隔的等效负荷出力低于
,此时为减少电力供应不足现象电网侧会进行切负荷操作,增加了切负荷成本。文献[16]的电价制定策略忽略了在风电、光伏波动性较大时火电机组的调节能力。因此,本文通过考虑火电机组的调节能力,将以黄色圆头线分隔的等效负荷出力低于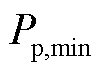 的电价制定为凹谷电价,对应的1:00—3:00时段制定为凹谷时段,通过吸引更多EV用户参与充电调度来增加对风电资源的消纳;同时将等效负荷出力高于
的电价制定为凹谷电价,对应的1:00—3:00时段制定为凹谷时段,通过吸引更多EV用户参与充电调度来增加对风电资源的消纳;同时将等效负荷出力高于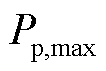 对应的电价制定为尖峰电价,对应的18:00—21:00时段制定为尖峰时段,以通过吸引更多EV用户参与放电调度来减少切负荷现象,从而降低切负荷成本并缓解电网的供电压力。
对应的电价制定为尖峰电价,对应的18:00—21:00时段制定为尖峰时段,以通过吸引更多EV用户参与放电调度来减少切负荷现象,从而降低切负荷成本并缓解电网的供电压力。
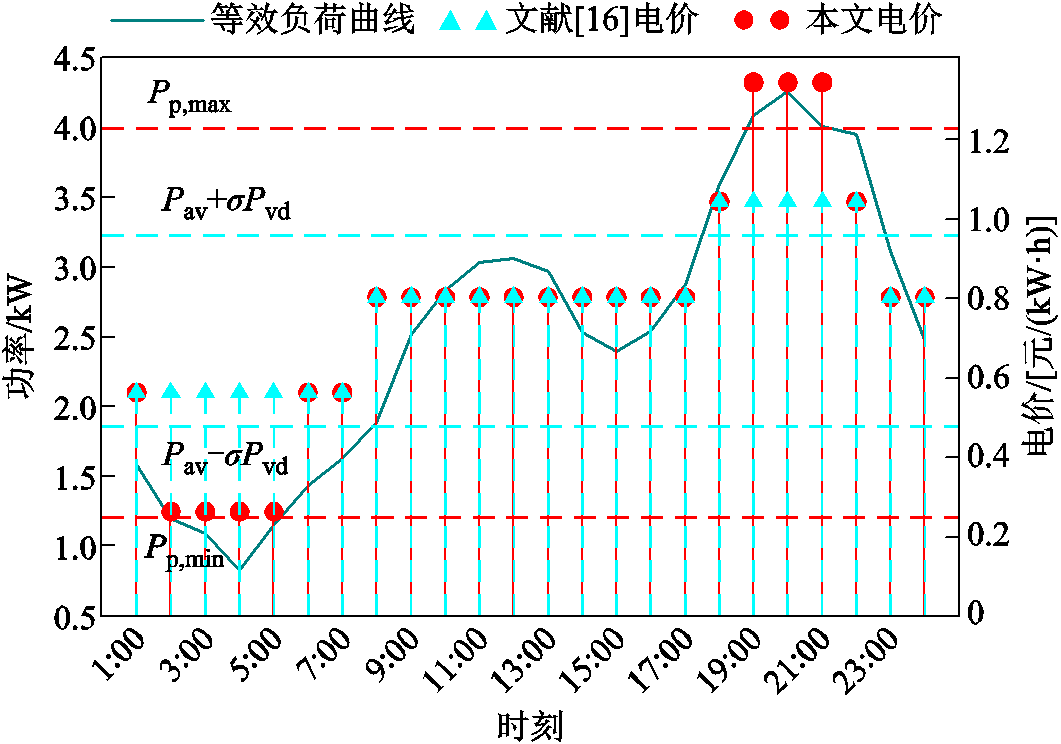
图4 不同电价策略下电价时段划分与大小对比
Fig.4 The time division and size comparison of time-of-use price under different price strategies
对比文献[16]电价下50辆EV参与调度时,本文凹谷与尖峰电价通过价格弹性系数计算吸引来的EV数量,结果如图5所示。相较于文献[16]的峰谷电价时段,本文制定的凹谷电价能够在2:00—5:00时段吸引更多EV用户充电;尖峰电价能够在19:00—21:00时段吸引更多EV用户放电。本文电价策略更利于提高用户参与调度的积极性,在电网产生负荷需求时提供更多的需求响应。
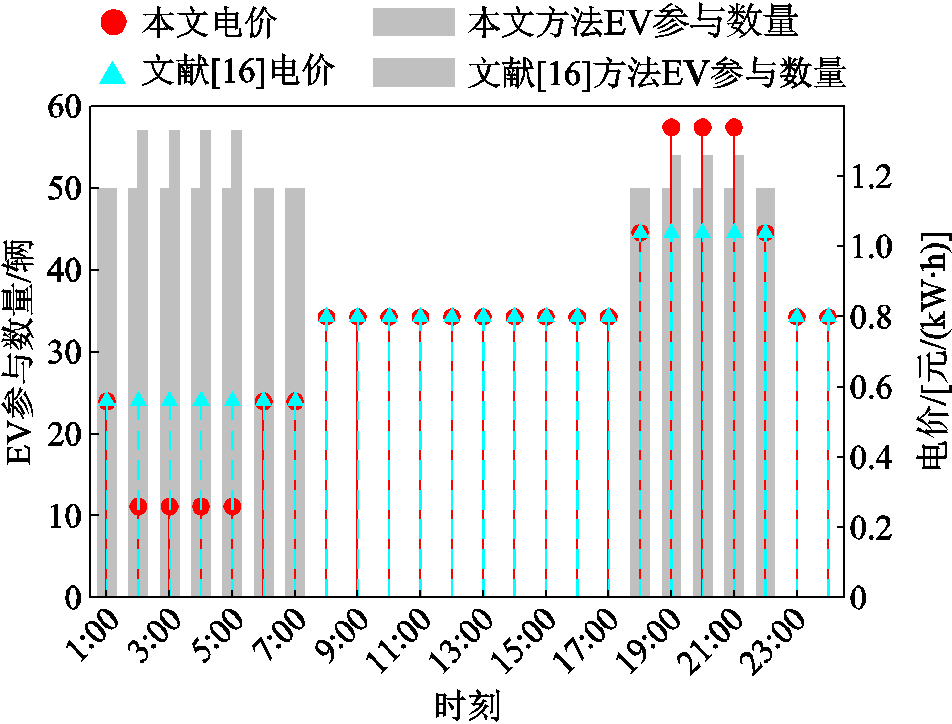
图5 不同电价策略下EV参与数量的对比
Fig.5 Comparison of the number of EV participation under different price strategies
表3展示了文献[16]电价下不同数量EV参与调度后弃风、弃光与切负荷成本,以及通过需求价格弹性系数得出的本文凹谷、峰谷与尖峰电价下参与调度的EV数量和相应数量EV参与调度后弃风、弃光与切负荷成本。
表3 不同电价策略下EV充放电的弃风、弃光与切负荷成本
Tab.3 The cost of wind curtailment, photovoltaic curtailment and load shedding of EV charging and discharging under different price strategies
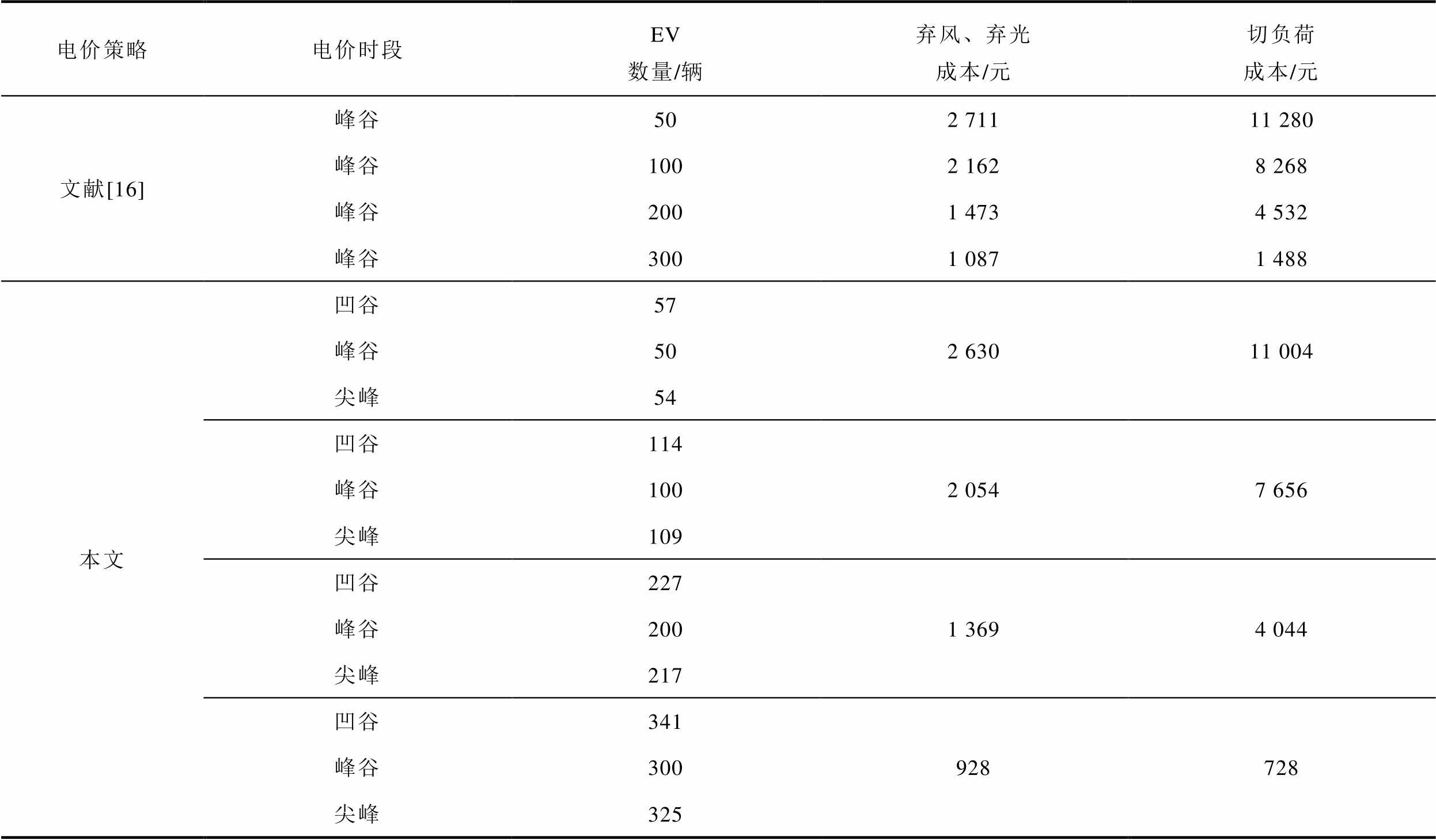
电价策略电价时段EV数量/辆弃风、弃光成本/元切负荷成本/元 文献[16]峰谷502 71111 280 峰谷1002 1628 268 峰谷2001 4734 532 峰谷3001 0871 488 本文凹谷572 63011 004 峰谷50 尖峰54 凹谷1142 0547 656 峰谷100 尖峰109 凹谷2271 3694 044 峰谷200 尖峰217 凹谷341928728 峰谷300 尖峰325
由表3可知,随着峰谷时段参与调度的EV数量的增加,凹谷和尖峰电价时段EV参与的数量也随之增加。以200辆与300辆EV参与峰谷调度为例,相较于文献[16]电价,200辆EV参与时,本文凹谷电价能够多吸引27辆EV用户参与充电调度,尖峰电价能够多吸引17辆EV用户参与放电调度,弃风弃光成本减少了7%,切负荷成本减少了11%;300辆EV参与时,凹谷电价能够多吸引41辆EV用户参与充电调度,尖峰电价能够多吸引25辆EV用户参与放电调度,弃风弃光成本减少了15%,切负荷成本减少了51%。由此可见,本文电价策略通过制定凹谷与尖峰电价调动更多EV用户参与充放电调度,能够进一步降低弃风、弃光与切负荷成本,并随着参与调度的EV数量的增多,优化效果越明显。在EV保有量大的地区,借助凹谷与尖峰电价机制,可以更好地调动EV用户的积极性,减少电网弃风弃光与切负荷现象,实现电力系统的可持续发展。
为了更直观地看到本文电价的优化效果,根据表3,对比文献[16]电价下200、300辆EV和通过需求价格弹性系数得出的本文电价下EV参与电网调度的充放电量、弃风弃光量、切负荷量以及负荷曲线,结果如图6所示:当200辆与300辆EV参与时,在4:00与20:00会发生弃风与切负荷现象。与文献[16]相比,在4:00风电消纳不足时,本文凹谷电价能够吸引更多EV参与充电调度,进而减少弃风现象;在20:00火电机组供电能力不足时,本文尖峰电价能够吸引更多EV参与放电调度,进而减少切负荷现象,降低切负荷成本。本文通过凹谷电价吸引更多EV用户在2:00—5:00充电;通过尖峰电价吸引更多EV用户在19:00—21:00放电,能够进一步减轻电网的压力,对负荷曲线的“削峰填谷”效果更加明显。同时,随着参与调度的EV数量的增加,本文凹谷与尖峰电价吸引参与调度的EV数量也随之增加,对弃风、弃光与切负荷的减少效果更加显著,“削峰填谷”的优化效果也更为出色。
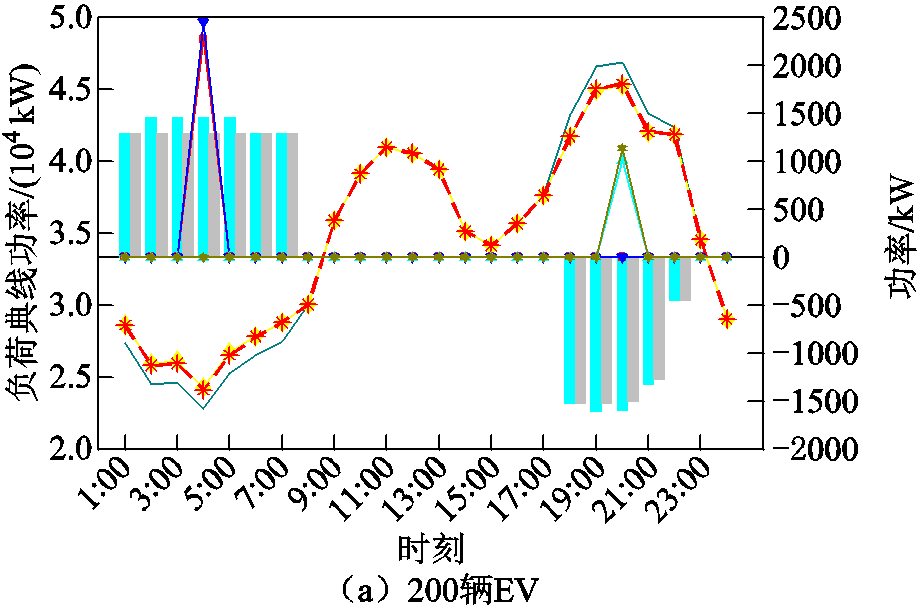
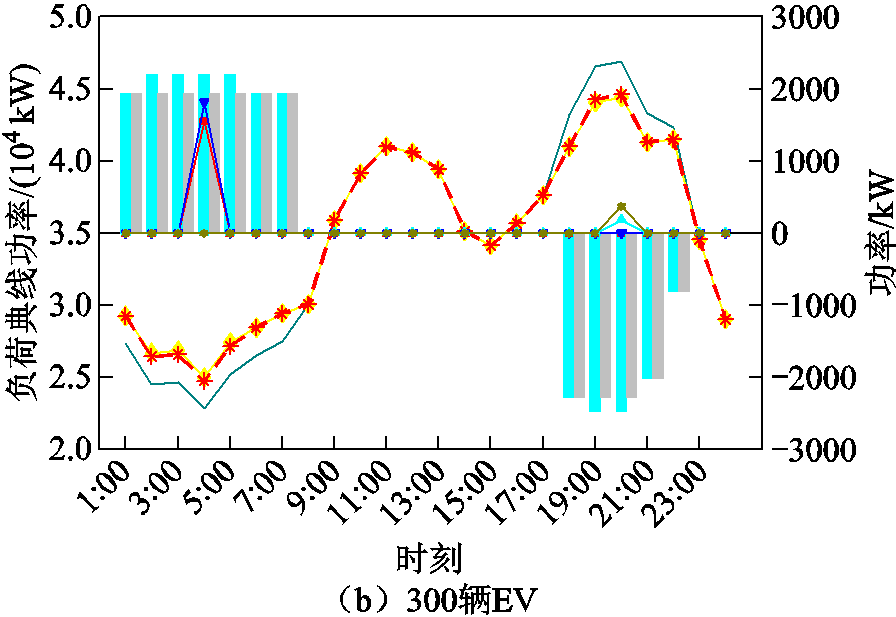

图6 不同电价策略下EV参与电网调度的充放电量、弃风弃光量、切负荷量以及负荷曲线
Fig.6 The charging and discharging amounts, wind and photovoltaic curtailment amounts, load shedding amounts and load curve of EV participating in power grid scheduling under different price strategies
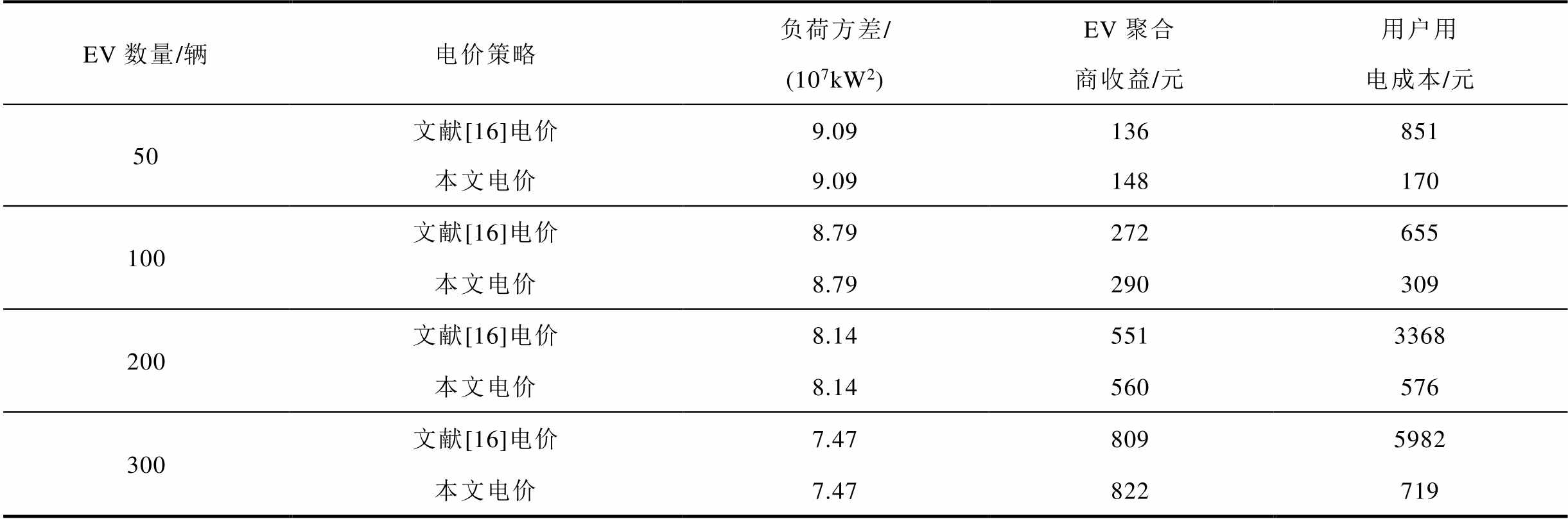
为进一步探讨本文电价策略对电网、EV聚合商以及EV用户之间的影响,对比在两种电价策略下均有相同数量,即不考虑需求价格弹性的EV参与后的负荷方差、聚合商收益与用户用电成本,对比结果见表4。
表4 不同电价策略不同EV数量参与下多目标优化效果
Tab.4 Multi-objective optimization effect under differentprice strategies and different number of EVs
EV数量/辆电价策略负荷方差/(107kW2)EV聚合商收益/元用户用电成本/元 50文献[16]电价9.09136851 本文电价9.09148170 100文献[16]电价8.79272655 本文电价8.79290309 200文献[16]电价8.145513368 本文电价8.14560576 300文献[16]电价7.478095982 本文电价7.47822719
由表4可知,在两种电价策略下,随着参与调度的EV数量的增加,多目标的优化效果越明显。以200辆EV参与调度为例,与文献[16]相比,由于参与调度的EV数量相同,所以本文方法在负荷方差上的优化效果一致,EV聚合商的收益增加了9元,用户用电成本降低了83%。因此,本文方法在增加EV聚合商的收益的同时大幅度降低了用户的用电成本,能够有效提高用户参与调度的积极性。
为充分利用可再生能源,引导EV有序充放电并解决风电光伏不确定性较大时弃风、弃光以及切负荷成本较大的问题,本文提出一种关于风光消纳与电动汽车灵活性的调度策略方法。通过算例分析,得出以下结论:
1)本文制定的分时电价模型与调度策略能够在风电、光伏功率较大,负荷需求较小时,利用凹谷电价吸引更多EV用户参与充电调度,消纳多余的风电与光伏;在风电、光伏功率较小,火电机组供电能力不足时利用尖峰电价吸引更多EV用户参与放电调度,减少切负荷成本。
2)随着EV参与调度的数量的增加,负荷方差越小,负荷曲线更为平滑,弃风、弃光与切负荷成本更小;EV聚合商收益更高;EV用户用电成本更低,平衡了电网、EV聚合商与EV用户三者之间的利益,具有良好的应用前景。
本文的调度策略充分利用EV的移动性和储能特性,综合考虑电网、用户成本与EV聚合商的利益,实现了多目标的优化,在一定程度上解决了风电、光伏不确定性较大时弃风、弃光与切负荷成本较大的问题,具有一定的实际意义。下一步研究方向为EV参与多时间尺度调度,充分利用EV的移动储能性解决电力系统与用户之间的供需问题。
参考文献
[1] 王海鑫, 袁佳慧, 陈哲, 等. 智慧城市车-站-网一体化运行关键技术研究综述及展望[J]. 电工技术学报, 2022, 37(1): 112-132.
Wang Haixin, Yuan Jiahui, Chen Zhe, et al. Review and prospect of key techniques for vehicle-station-network integrated operation in smart city[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 112-132.
[2] 毛玲, 张钟浩, 赵晋斌, 等. 车-桩-网交融技术研究现状及展望[J]. 电工技术学报, 2022, 37(24): 6357-6371.
Mao Ling, Zhang Zhonghao, Zhao Jinbin, et al. Research status and prospects of fusion technology of vehicle-charging pile-power grid[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6357-6371.
[3] 何晨可, 朱继忠, 刘云, 等. 计及碳减排的电动汽车充换储一体站与主动配电网协调规划[J]. 电工技术学报, 2022, 37(1): 92-111.
He Chenke, Zhu Jizhong, Liu Yun, et al. Coordinated planning of electric vehicle charging-swapping-storage integrated station and active distribution network considering carbon reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 92-111.
[4] 房宇轩, 胡俊杰, 马文帅. 计及用户意愿的电动汽车聚合商主从博弈优化调度策略[J]. 电工技术学报, 2024, 39(16): 5091-5103.
Fang Yuxuan, Hu Junjie, Ma Wenshuai. Optimal dispatch strategy for electric vehicle aggregators based on stackelberg game theory considering user intention [J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5091-5103.
[5] 胡俊杰, 周华嫣然, 李阳. 集群电动汽车平抑光伏波动实时调度策略[J]. 电网技术, 2019, 43(7): 2552-2560.
Hu Junjie, Zhou Huayanran, Li Yang. Real-time dispatching strategy for aggregated electric vehicles to smooth power fluctuation of photovoltaics[J]. Power System Technology, 2019, 43(7): 2552-2560.
[6] 陈中, 刘艺, 陈轩, 等. 考虑移动储能特性的电动汽车充放电调度策略[J]. 电力系统自动化, 2020, 44(2): 77-85.
Chen Zhong, Liu Yi, Chen Xuan, et al. Charging and discharging dispatching strategy for electric vehicles considering characteristics of mobile energy storage[J]. Automation of Electric Power Systems, 2020, 44(2): 77-85.
[7] 胡俊杰, 赖信辉, 郭伟, 等. 考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度[J]. 电力系统自动化, 2022, 46(16): 52-60.
Hu Junjie, Lai Xinhui, Guo Wei, et al. Multi-time-scale scheduling for regional power grid considering flexibility of electric vehicle and wind power accommodation[J]. Automation of Electric Power Systems, 2022, 46(16): 52-60.
[8] 葛晓琳, 郝广东, 夏澍, 等. 考虑规模化电动汽车与风电接入的随机解耦协同调度[J]. 电力系统自动化, 2020, 44(4): 54-62.
Ge Xiaolin, Hao Guangdong, Xia Shu, et al. Stochastic decoupling collaborative dispatch considering integration of large-scale electric vehicles and wind power[J]. Automation of Electric Power Systems, 2020, 44(4): 54-62.
[9] Bayani R, Manshadi S D, Liu Guangyi, et al. Autonomous charging of electric vehicle fleets to enhance renewable generation dispatchability[J]. CSEE Journal of Power and Energy Systems, 2022, 8(3): 669-681.
[10] Yin Wanjun, Jia Leilei, Ji Jianbo. Energy optimal scheduling strategy considering V2G characteristics of electric vehicle[J]. Energy, 2024, 294: 130967.
[11] 史文龙, 秦文萍, 王丽彬, 等. 计及电动汽车需求和分时电价差异的区域电网LSTM调度策略[J]. 中国电机工程学报, 2022, 42(10): 3573-3587.
Shi Wenlong, Qin Wenping, Wang Libin, et al. Regional power grid LSTM dispatch strategy considering the difference between electric vehicle demand and time-of-use electricity price[J]. Proceedings of the CSEE, 2022, 42(10): 3573-3587.
[12] 张良, 孙成龙, 蔡国伟, 等. 基于PSO算法的电动汽车有序充放电两阶段优化策略[J]. 中国电机工程学报, 2022, 42(5): 1837-1852.
Zhang Liang, Sun Chenglong, Cai Guowei, et al. Two-stage optimization strategy for coordinated charging and discharging of EVs based on PSO algorithm[J]. Proceedings of the CSEE, 2022, 42(5): 1837-1852.
[13] 石文超, 吕林, 高红均, 等. 考虑需求响应和电动汽车参与的主动配电网经济调度[J]. 电力系统自动化, 2020, 44(11): 41-51.
Shi Wenchao, Lü Lin, Gao Hongjun, et al. Economic dispatch of active distribution network with participation of demand response and electric vehicle[J]. Automation of Electric Power Systems, 2020, 44(11): 41-51.
[14] 杨镜司, 秦文萍, 史文龙, 等. 基于电动汽车参与调峰定价策略的区域电网两阶段优化调度[J]. 电工技术学报, 2022, 37(1): 58-71.
Yang Jingsi, Qin Wenping, Shi Wenlong, et al. Two-stage optimal dispatching of regional power grid based on electric vehicles' participation in peak-shaving pricing strategy[J]. Transactions of China Electro-technical Society, 2022, 37(1): 58-71.
[15] Yin Wanjun, Wen Tao, Zhang Chao. Cooperative optimal scheduling strategy of electric vehicles based on dynamic electricity price mechanism[J]. Energy, 2023, 263: 125627.
[16] 朱磊, 黄河, 高松, 等. 计及风电消纳的电动汽车负荷优化配置研究[J]. 中国电机工程学报, 2021, 41(增刊1): 194-203.
Zhu Lei, Huang He, Gao Song, et al. Research on optimal load allocation of electric vehicle considering wind power consumption[J]. Proceedings of the CSEE, 2021, 41(S1): 194-203.
[17] 秦祯芳, 岳顺民, 余贻鑫, 等. 零售端电力市场中的电量电价弹性矩阵[J]. 电力系统自动化, 2004, 28(5): 16-19, 24.
Qin Zhenfang, Yue Shunmin, Yu Yixin, et al. Price elasticity matrix of demand in current retail power market[J]. Automation of Electric Power Systems, 2004, 28(5): 16-19, 24.
[18] 王守相, 王瀚樟, 赵倩宇, 等. 面向配电网光伏接纳能力提升的分时电价优化方法[J]. 电力系统自动化, 2023, 47(10): 38-46.
Wang Shouxiang, Wang Hanzhang, Zhao Qianyu, et al. Optimization method of time-of-use electricity price for improving photovoltaic hosting capacity of distribution network[J]. Automation of Electric Power Systems, 2023, 47(10): 38-46.
[19] 崔杨, 修志坚, 薄利明, 等. 考虑火–储深度调峰容量二次分配的含风电电力系统分层优化调度[J]. 电网技术, 2022, 46(7): 2520-2531.
Cui Yang, Xiu Zhijian, Bo Liming, et al. Hierarchical optimal scheduling of power systems with wind generation considering secondary allocation of thermal-storage deep peaking capacity[J]. Power System Technology, 2022, 46(7): 2520-2531.
[20] Hou Hui, Wang Yifan, Chen Yue, et al. Long-time scale vehicle-to-grid scheduling strategy considering psychological effect based on Weber-Fechner law[J]. International Journal of Electrical Power & Energy Systems, 2022, 136: 107709.
[21] 宋艺航, 谭忠富, 李欢欢, 等. 促进风电消纳的发电侧、储能及需求侧联合优化模型[J]. 电网技术, 2014, 38(3): 610-615.
Song Yihang, Tan Zhongfu, Li Huanhuan, et al. An optimization model combining generation side and energy storage system with demand side to promote accommodation of wind power[J]. Power System Technology, 2014, 38(3): 610-615.
[22] 常方宇, 黄梅, 张维戈. 分时充电价格下电动汽车有序充电引导策略[J]. 电网技术, 2016, 40(9): 2609-2615.
Chang Fangyu, Huang Mei, Zhang Weige. Research on coordinated charging of electric vehicles based on TOU charging price[J]. Power System Technology, 2016, 40(9): 2609-2615.
Abstract As a clean means of transport, electric vehicles (EVs) can improve the peak-to-valley difference of grid load and promote renewable energy consumption while facilitating users' travelling, and the scale of their application is constantly expanding. However, the disorderly charging of large-scale EVs will increase the burden on the power grid, which will have a counterproductive effect in load regulation or renewable energy consumption. The orderly charging and discharging of EVs can be effectively guided by time-of-use (TOU) price. At present, with stochastic large and some extreme situations of the renewable energy, the wind curtailment, photovoltaic curtailment and thermal power unit regulation capacity under the existing TOU price under are insufficient to lead to the larger cost of load-shedding, which remains a more prominent phenomenon. Therefore, proposing a scheduling strategy considering wind and photovoltaic power consumption and the flexibility of EVs.
Firstly, based on the wind power and photovoltaic output values and load information of each time period predicted in the day-ahead, the equivalent load of wind power, photovoltaic and base load and their average values are derived, and the peak-valley difference of the equivalent load in this time period is calculated. Based on the average value of the equivalent load and the peak-valley difference, the peak-valley price is formulated; when the equivalent load is lower than the minimum output of the thermal power unit, it will increase the phenomenon of wind and photovoltaic curtailment, resulting in a waste of resources, which will be formulated as the sunken valley price; when the equivalent load is larger than the maximum output of the thermal power unit, or the neighbouring difference in the equivalent load exceeds the ramping capacity of the thermal power unit, it will be insufficient to supply electricity, and it will be formulated as the sharp peak price. At the same time, the price elasticity coefficient is introduced to quantitatively describe the response of EVs to the sunken valley and sharp peak price.
Secondly, an EV charging and discharging model is established based on the TOU price information to determine the electricity information for EV charging and discharging scheduling. Then, an optimal EV charging and discharging scheduling model is constructed with the goal of minimizing load fluctuation and wind and photovoltaic curtailment costs, minimizing the cost of electricity for users and maximizing the revenue for the aggregator, taking into account the interests of the power grid, the EV aggregator and the EV users.
Finally, conducting an analysis of a specific power system, compared to the TOU price strategy in the peak-to-valley period, the TOU price strategy in this paper can attract more EVs to participate in the charging scheduling. The phenomenon of wind and photovoltaic curtailment can be reduced through the sunken valley TOU price in the period of renewable energy surplus. In the period of insufficient regulation capacity of thermal power unit, more EVs are attracted to participate in discharge scheduling through sharp peak TOU price to provide load resource for the power grid and reduce load shedding. Meanwhile, the price strategy can improve the revenue of aggregators and reduce the electricity cost of users while reducing the load fluctuation of power grid.
Keywords: Electric vehicle, load shedding, time-of-use electricity price, scheduling strategy
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.231603
国家自然科学基金项目(62076243)和徐州市科技项目(KC22343)资助。
收稿日期 2023-10-06
改稿日期 2024-04-10
韩 丽 女,1977年生,教授,博士生导师,研究方向为可再生能源发电技术以及电网优化调度等。E-mail:dannyli717@163.com(通信作者)
陈 硕 男,2000年生,硕士研究生,研究方向为电网优化调度。E-mail:2661206313@qq.com
(编辑 赫 蕾)