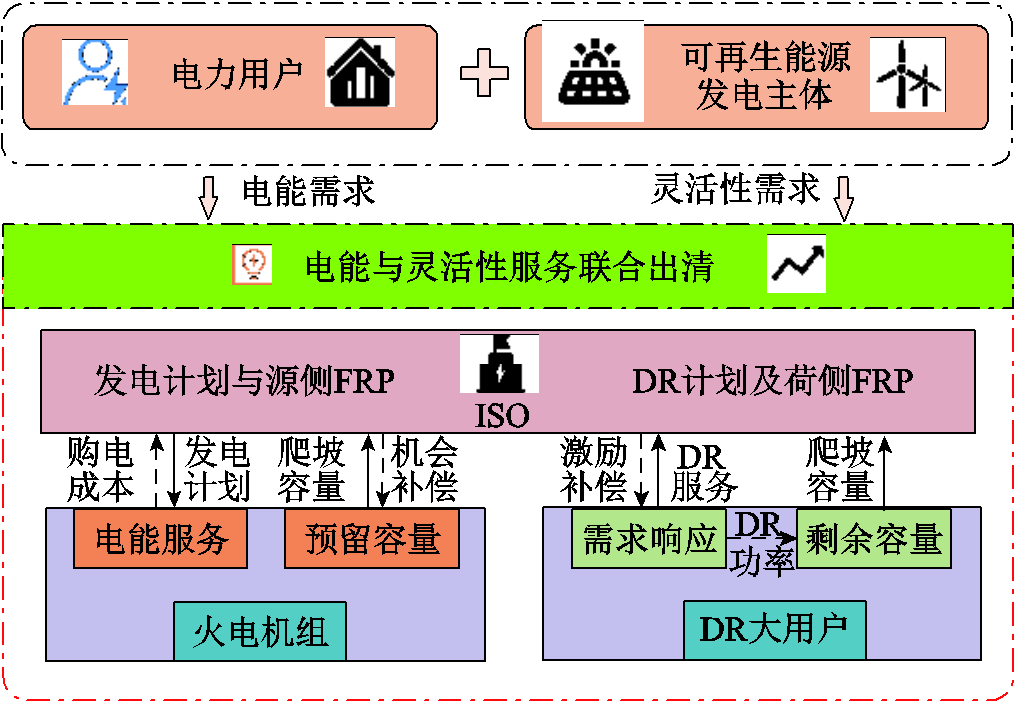
图1 考虑需求响应的电能与FRP服务联合运营模式
Fig.1 Energy and flexibility service co-operation mode considering demand response
摘要 针对大规模可再生能源接入电力系统所导致的灵活爬坡产品(FRP)需求激增问题,提出一种大用户激励型需求响应(DR)策略,为独立系统运营商(ISO)获取需求侧灵活性资源提供有效途径。采用用户需求管理行为模型(CDMBM),估计能够反映DR行为差异化的用户响应成本函数;构建ISO与多个大用户之间的激励型DR主从博弈模型,以ISO为决策主体的电能与FRP联合出清优化模型作为上层模型,以大用户参与联合市场DR决策的优化模型作为下层模型,通过将主从博弈问题转换为带均衡约束的数学优化问题,求解博弈均衡解进而得到具有差异化的用户DR单位补偿费用。通过算例分析,验证了所提策略的有效性。
关键词:需求响应 灵活爬坡产品市场 主从博弈 均衡约束 单位激励补偿费用
随着可再生能源发电比例的不断攀升,其发电功率波动性和不确定性使电力系统运行调控面临严峻挑战,系统净负荷(负荷与可再生能源出力之差)曲线变得更为陡峭[1-2],仅靠发电侧灵活性资源跟随净负荷变化已不能满足系统运行需求。面向大用户实施需求响应(Demand Response, DR)已成为提升系统灵活性的重要途径。DR分为激励型与价格型两类[3],相较于价格型DR,激励型DR在系统中实施更加灵活,且对用户更具吸引力[4]。如何设计合理的激励补偿措施,以引导大用户提供DR服务参与灵活性市场,对提升系统灵活性具有重要意义[5]。
已有学者对激励补偿机制及相关DR优化策略开展了较多的研究。在电能市场中,大用户利用其负荷转移特性,为系统提供削减型DR或消纳型DR服务。文献[6]提出基于主从博弈的灵活性供需均衡模型,风电运营商为上层领导者,DR用户、火电机组及储能为跟随者,建立考虑高比例风电与多元灵活性资源博弈的灵活调节激励机制。文献[7]提出综合考虑用户响应能力与电网激励成本的评估指标,为电网激励机制及用户响应方案提供参考。文献[8]基于马尔可夫决策过程,综合考虑微网激励成本与用户状态,通过供需双方反复信息交互,获得多时段的最优激励补偿费用。文献[9]在现货市场中求解售电商与多个DR用户之间的主从博弈模型,以合理的单位激励补偿费用规避售电商因现货市场价格波动带来的风险。以上研究在市场环境下提出了合理的激励补偿机制与DR策略,但未考虑DR用户的响应意愿差异与响应成本之间的关系。
灵活爬坡产品(Flexible Ramping Products, FRP)包括上行灵活爬坡产品(Flexible Ramp-Up products, FRU)和下行灵活爬坡产品(Flexible Ramp-Down products, FRD)两类。与发电侧灵活性资源类似,DR用户可通过预留响应容量为系统提供FRP服务[10],需要从市场均衡理论出发,合理设计FRP的获取机制[11],依据用户响应意愿的不同给予其相应的补偿费用或定价策略,并满足激励相容的市场设计准则[12-13]。文献[14]针对价格型DR,提出日内和实时两阶段鲁棒优化模型,FRP在第一阶段的出清结果制约第二阶段不确定场景下的灵活调节能力。文献[15-16]设计了DR用户参与FRP市场的机制,引导DR用户同时参与电能市场和FRP市场交易,对提供FRP服务的DR用户采用相同的单位补偿费用,但未考虑用户差异化补偿。文献[17]利用日前出清的备用服务在实时阶段提供FRP,为了避免出现备用服务与FRP服务“双重付费”的现象,对从备用中获取的FRP将不进行补偿。如果机组提供的FRP容量在实时运行中被系统调用,可能会出现FRP与电能的费用重叠[10]。因此,在电能与FRP联合出清市场中,如何在净负荷大幅波动的场景下,对响应意愿差异化的DR用户提供合理的单位激励补偿费用,避免灵活性市场中的“双重付费”现象,保证DR用户按响应意愿参与DR服务并提供有效的FRP,成为提升电力系统灵活性与经济性的关键。
本文提出一种适应电能与FRP联合出清的用户DR优化策略。采用用户需求管理行为模型(Customer Demand Management Behavior Model, CDMBM)[18],估计用户响应成本函数,以响应意愿参数作为用户DR行为的差异化指标;构建独立系统运营商(Independent System Operator, ISO)与多个大用户之间的激励型DR主从博弈模型,上层模型为以ISO为决策主体的电能与FRP联合出清优化模型,下层模型为大用户参与联合市场DR决策的优化模型;通过将下层模型的KKT条件作为上层模型的约束条件,将主从博弈问题转换为带有线性均衡约束的数学优化问题进行求解,以主从博弈均衡刻画ISO与DR用户之间的博弈行为,获取考虑用户差异化的DR单位补偿费用。
2016年美国加州辅助服务市场设计FRP以应对两个时段之间的净负荷不确定性变化,缓解电力系统爬/滑坡能力不足的问题[19-21],其FRP交易仅在实时市场中[22],而在美国中部电力市场中的FRP交易包含日前和实时两个时间尺度[19]。为了突出FRP这一新型交易品种对市场的影响,本文不考虑调频与备用辅助服务等传统辅助服务。参考美国中部日前发电侧电能与FRP市场联合出清市场,并引入DR大用户成员通过激励型DR为系统提供FRP服务,联合运营模式如图1所示。
本文分析的电能与FRP联合出清市场为日前市场,每15 min为一个交易时段[23],ISO根据净负荷预测曲线的波动性与不确定性计算每个时段的FRU和FRD灵活性需求。火电机组以报量不报价的形式参与FRP市场,由ISO以机会成本进行补偿,其机会成本来源于预留灵活爬坡容量而产生的电能收益损失。ISO根据火电机组的日前电能报价信息、风电预测曲线以及用户侧申报的日负荷曲线,获得未考虑FRP的常规经济调度结果并作为参考[24],以发电收益损失作为机会成本在FRP市场中补偿火电机组。DR用户则以接受激励补偿费用的方式参与系统功率调节,利用DR用户的剩余调节能力提供FRP。ISO通过调整DR单位激励补偿费用的方式改变大用户DR功率,进而改变其提供的灵活爬坡容量。在此市场机制下,本文研究合理确定大用户单位激励补偿费用的DR优化策略,以提升系统灵活性。

图1 考虑需求响应的电能与FRP服务联合运营模式
Fig.1 Energy and flexibility service co-operation mode considering demand response
一方面,ISO需要分析系统灵活性需求,通过统筹系统内各类灵活性资源以满足系统所需的灵活性;另一方面,ISO需要预估大用户的响应能力及响应成本,通过确定与各大用户之间的单位激励补偿费用,激励用户提供DR功率,满足电能需求,利用DR大用户的剩余的爬坡能力提供FRP。本文所提的大用户DR优化策略的基本框架示意图如图2所示。
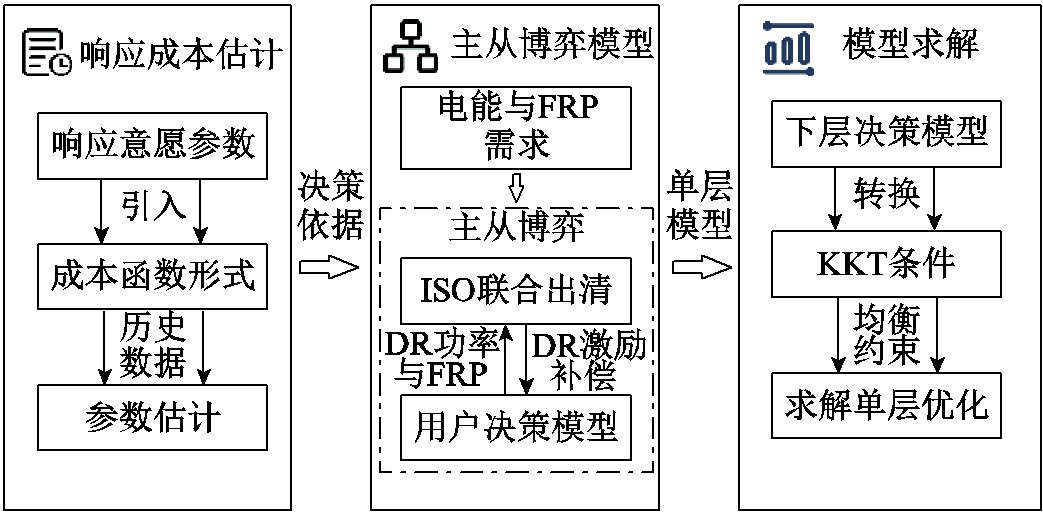
图2 DR优化策略基本框架示意图
Fig.2 Basic framework diagram of DR optimization strategy
ISO希望以更低的成本在不确定性场景下降低失负荷及可再生能源削减的概率,即以更低的激励补偿费用代价换取DR大用户的响应功率,并根据预估的响应能力,利用剩余的爬坡容量提供FRP。对于大用户而言,其响应成本随着响应量的增加而增大,若ISO不能提供令大用户满意的激励措施,则用户将降低其提供的DR功率。ISO在满足灵活性需求的基础上,以激励补偿费用最小为目标,大用户以提供DR服务的收益最大为目的,双方彼此制约。为此,建立ISO-DR大用户主从博弈模型,上层决策者为ISO,下层决策者为各大用户,在电能与FRP联合出清市场中主从博弈的结构示意图如图3所示。

图3 主从博弈结构示意图
Fig.3 Master-slave game structure diagram
主从博弈下的单位激励补偿费用结果满足大用户响应意愿,因此,无需对其FRP进行补偿,仅通过调整与大用户之间的激励补偿费用即可获得对应的灵活爬坡容量。ISO根据系统负荷及灵活性需求确定各时段火电机组的出力水平、大用户的单位补偿费用及灵活爬坡容量,将单位补偿费用传递至下层模型;各DR大用户以效益最大化为目标进行决策,将响应功率及FRP反馈至上层模型;通过求解主从博弈的均衡解集,在ISO与DR大用户之间生成适应电能与FRP联合出清的大用户DR优化策略。
各大用户的响应能力以及响应意愿存在差异,设置响应意愿参数并采用CDMBM估计大用户的响应成本,为大用户提供削减型DR与消纳型DR的决策行为精准建模提供依据。
通过大用户用电调节量与边际收益之间的关系,分析响应成本产生的原因。其中,边际收益曲线的线性表达形式在较为精准地表现用户意愿的同时,可降低用户成本信息维度,其对应的响应成本函数为二次形式,相较于指数形式,在制定激励补偿措施时用户参与的响应程度较高[18]。因此,采用大用户的边际收益线性函数,分别建立削减型DR及消纳型DR的响应成本函数。
大用户参与DR的用户剩余损失如图4所示。图中不参与DR的利润为S1与S2之和,即用户总剩余价值;当大用户以削减形式参与DR时,用户剩余损失为S2,此部分为削减型DR的响应成本;当大用户以增加用电形式参与DR时,会造成大用户亏损S3,此为消纳型DR的响应成本。

图4 剩余损失示意图
Fig.4 Remaining loss diagram
用电量削减场景下的用户剩余损失表示由于参与DR而未达到生产目标导致的损失,大用户的生产计划受到影响以致不能满足生产数量的要求而导致亏损;在用电量增加的场景下,大用户的生产偏离经济工作范围,单位用电量所创造的价值降低,进而降低大用户的经济收益水平,其响应成本表示参与消纳型DR导致生产经济性降低而造成的用户亏损。
考虑到各用户参与DR的意愿与能力不同,因此在响应成本函数预估过程中引入表征用户参与削减型DR的响应意愿参数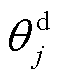 和参与消纳型DR的响应意愿参数
和参与消纳型DR的响应意愿参数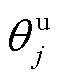 。由于大用户削减型DR与消纳型DR的响应成本估计过程类似,首先进行削减型DR的成本函数估计。在大用户边际效益函数线性形式的基础上,引入用户响应意愿参数后,其削减型DR的响应成本函数Cdd表示为[18]
。由于大用户削减型DR与消纳型DR的响应成本估计过程类似,首先进行削减型DR的成本函数估计。在大用户边际效益函数线性形式的基础上,引入用户响应意愿参数后,其削减型DR的响应成本函数Cdd表示为[18]
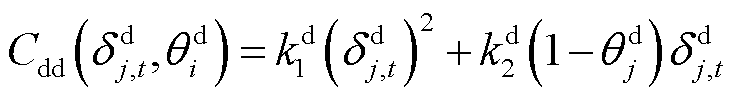 (1)
(1)
式中,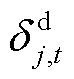 为t时段DR大用户j的用电削减功率;
为t时段DR大用户j的用电削减功率;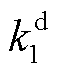 与
与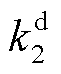 分别为与削减功率相关的二次项系数和一次项系数;
分别为与削减功率相关的二次项系数和一次项系数;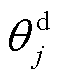 为DR大用户j参与削减型DR的响应意愿,
为DR大用户j参与削减型DR的响应意愿,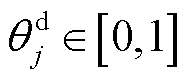 ,
,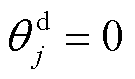 表示用户参与意愿最低,
表示用户参与意愿最低,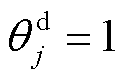 表示用户参与意愿最高。
表示用户参与意愿最高。
大用户参与DR的收益来源于ISO提供的激励补偿费用,效益函数Bdd表示为
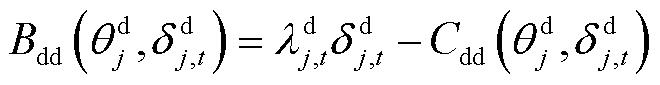 (2)
(2)
式中,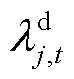 为t时段大用户j削减型DR的单位激励补偿费用。
为t时段大用户j削减型DR的单位激励补偿费用。
大用户以自身效益最大为目标参与DR,根据极值条件可得
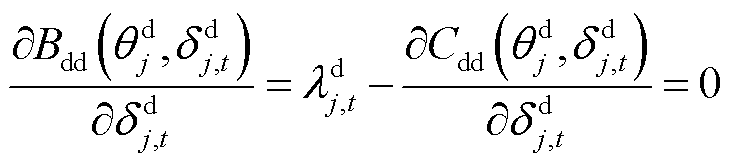 (3)
(3)
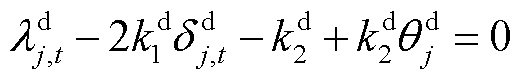 (4)
(4)
同理,消纳型DR的响应成本函数与用于响应成本函数估计的等式关系为
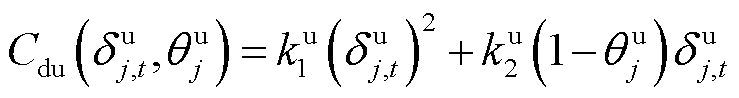 (5)
(5)
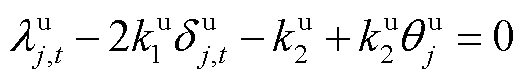 (6)
(6)
式中,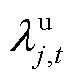 和
和 分别为t时段大用户j消纳型DR的单位激励补偿费用和用电增加功率;
分别为t时段大用户j消纳型DR的单位激励补偿费用和用电增加功率;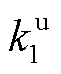 与
与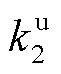 分别为与增加功率相关的二次项系数和一次项系数;
分别为与增加功率相关的二次项系数和一次项系数;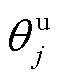 为大用户j参与消纳型DR的响应意愿。
为大用户j参与消纳型DR的响应意愿。
在现有单一的激励补偿机制下获得DR大用户响应历史数据,按照响应意愿高低对所有大用户进行排序。根据n个大用户参与DR的历史数据,求解待定系数方程中n-2项响应意愿参数、一次及二次项系数。
ISO需承担可再生能源并网消纳的责任,因此在竞争性的市场环境下,ISO希望以电能与FRP成本最小为目标消纳可再生能源。在电能与FRP联合出清市场中,ISO以火电机组购电成本、大用户激励补偿费用和火电机组FRP补偿成本最小为目标,具体表示为
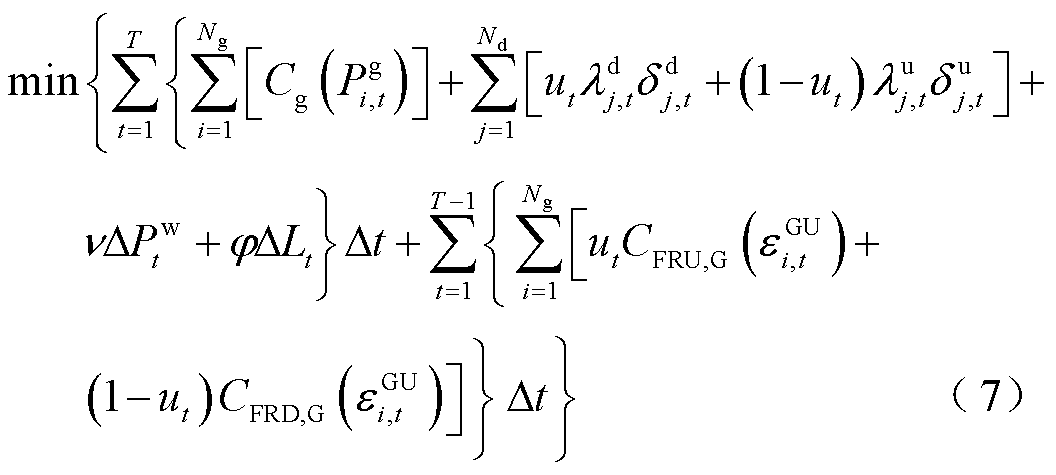
其中,各项成本函数具体表示为
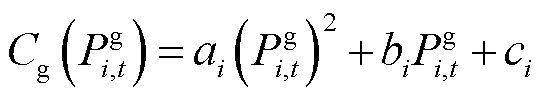 (8)
(8)
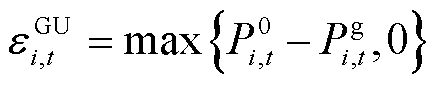 (9)
(9)
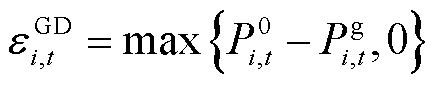 (10)
(10)
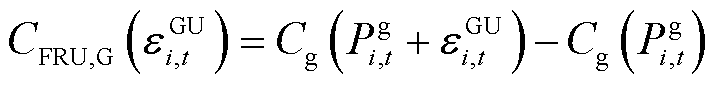 (11)
(11)
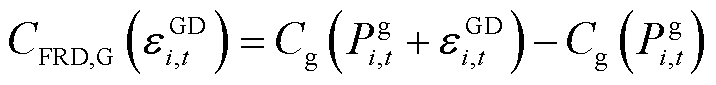 (12)
(12)
式中,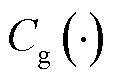 、
、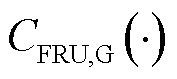 和
和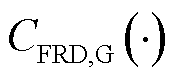 分别为火电机组发电、提供FRU和FRD的补偿成本函数;
分别为火电机组发电、提供FRU和FRD的补偿成本函数;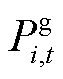 为t时段火电机组i发电功率;
为t时段火电机组i发电功率;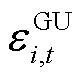 和
和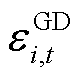 分别为t时段火电机组i提供FRU和FRD的补偿量;
分别为t时段火电机组i提供FRU和FRD的补偿量; 为t时段火电机组i未考虑FRP出清的发电功率;
为t时段火电机组i未考虑FRP出清的发电功率;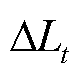 和
和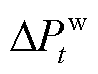 分别为t时段系统失负荷量与可再生能源削减量;
分别为t时段系统失负荷量与可再生能源削减量;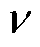 和
和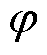 分别为单位可再生能源削减损失惩罚和失负荷损失惩罚;
分别为单位可再生能源削减损失惩罚和失负荷损失惩罚;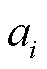 、
、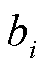 和
和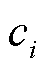 为购买火电机组发电功率成本函数系数;T为调度时段数;
为购买火电机组发电功率成本函数系数;T为调度时段数;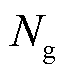 和
和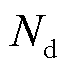 分别为火电机组数量和大用户数量;
分别为火电机组数量和大用户数量;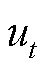 为ISO表征DR服务类型的0-1标识量,当系统出现正的净负荷波动时,大用户提供削减型DR服务,此时
为ISO表征DR服务类型的0-1标识量,当系统出现正的净负荷波动时,大用户提供削减型DR服务,此时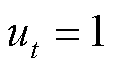 ,若系统出现负的净负荷波动,大用户提供消纳型DR服务,此时
,若系统出现负的净负荷波动,大用户提供消纳型DR服务,此时 。
。
火电机组通过预留向上爬坡容量提供FRU,其补偿成本按因降低发电功率而造成电能收益损失的机会成本进行补偿;出力水平较低的火电机组因提供FRD而增加发电功率并获得更高的电能收益,为满足固定的电能需求,出力水平较高的机组需减少发电功率,因此需按机会成本对降低出力的机组进行补偿,而提供FRD的机组由于增加电能收益将不受到补偿。
由于机组存在固有调节能力,若灵活性需求小于整个系统的固有调节能力,则含FRP的经济调度与常规经济调度结果相同,不产生机会成本[24]。因此,对于未影响电能出清结果并提供FRP的机组将不受到补偿,若产生机会成本,其补偿量为降低出力而额外预留的灵活爬坡容量。另外,若对FRU和FRD进行双重补偿,会导致补偿费用超出机会成本。虽然火电机组在当前时刻可同时预留FRU和FRD,但在下一时段发生确定性的偏差后,仅两者之一发挥灵活性的作用,因此每个时段仅对FRU与FRD中需求较大者进行补偿[25]。
为了计算火电机组提供FRP而产生的机会成本,以常规经济调度模型中火电机组发电计划 为参考[24],计算火电机组在FRP市场中因降低出力而造成的电能收益损失,补偿相应的火电机组。
为参考[24],计算火电机组在FRP市场中因降低出力而造成的电能收益损失,补偿相应的火电机组。
为避免式(7)中失负荷及可再生能源削减的高额惩罚,需满足FRP在各时段的需求。预留灵活爬坡容量是为了应对下一时段的净负荷的波动性与不确定性,FRP需求包括净负荷预测功率的波动性及不确定性两部分,具体分析过程如附图1所示。其FRU和FRD需求分别为
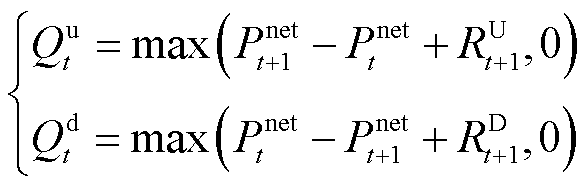 (13)
(13)
式中,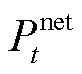 为t时段净负荷预测功率;
为t时段净负荷预测功率;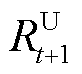 和
和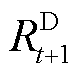 分别为t+1时段为预测不确定性预留的向上安全裕度和向下安全裕度,具体计算见附录。
分别为t+1时段为预测不确定性预留的向上安全裕度和向下安全裕度,具体计算见附录。
约束条件为
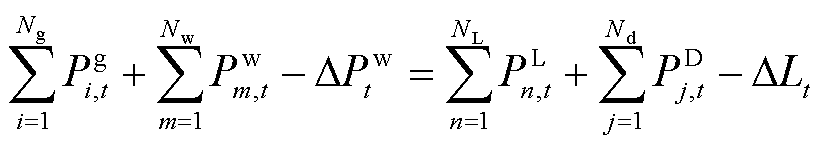 (14)
(14)
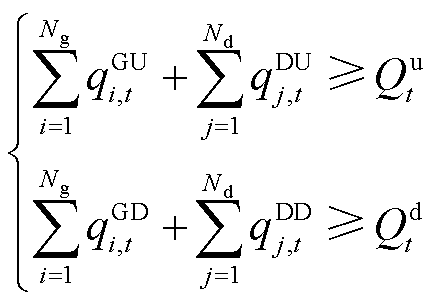 (15)
(15)
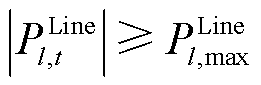 (16)
(16)
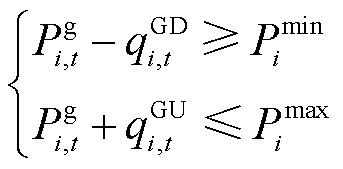 (17)
(17)
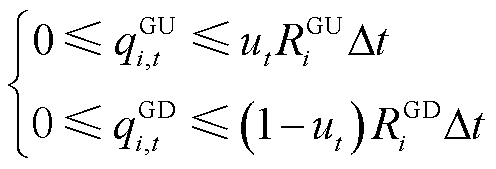 (18)
(18)
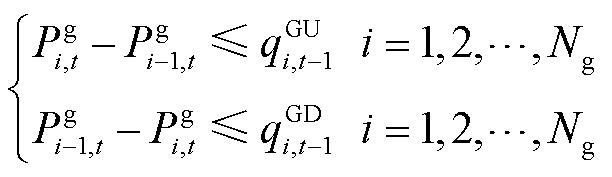 (19)
(19)
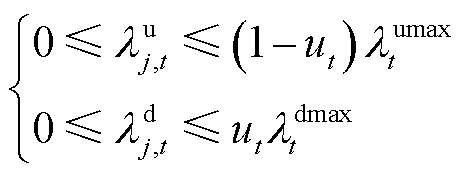 (20)
(20)
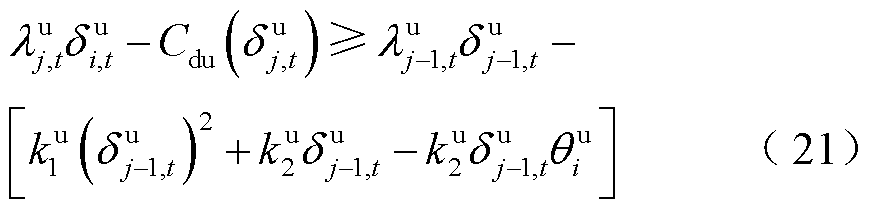
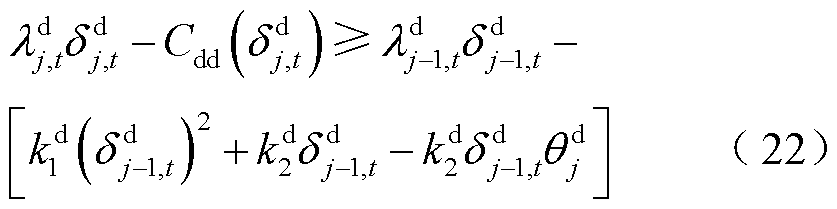
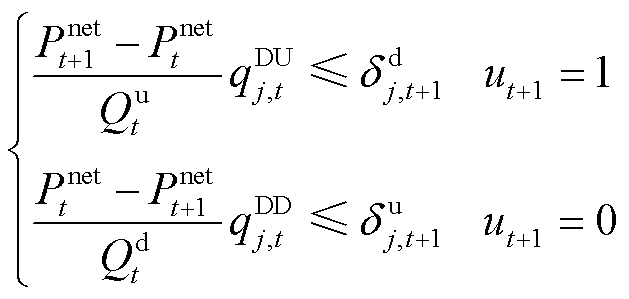 (23)
(23)
式中,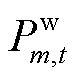 、
、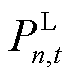 和
和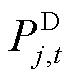 分别为t时段可再生能源出力、负荷用电功率和DR大用户用电功率;
分别为t时段可再生能源出力、负荷用电功率和DR大用户用电功率;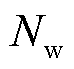 、
、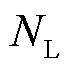 分别为可再生能源场站数量、常规负荷数量;
分别为可再生能源场站数量、常规负荷数量;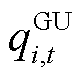 、
、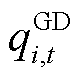 分别为t时段火电机组i的向上、向下灵活爬坡容量;
分别为t时段火电机组i的向上、向下灵活爬坡容量;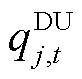 、
、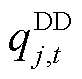 分别为t时段大用户j为提供FRU和FRD而预留的爬坡容量;
分别为t时段大用户j为提供FRU和FRD而预留的爬坡容量;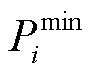 、
、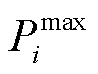 分别为火电机组最小、最大出力;
分别为火电机组最小、最大出力;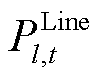 、
、 分别为第l条线路的有功功率、最大传输容量;
分别为第l条线路的有功功率、最大传输容量;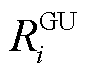 、
、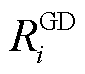 分别为火电机组爬坡、滑坡速率;
分别为火电机组爬坡、滑坡速率;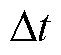 为调度时间;
为调度时间;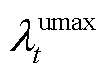 、
、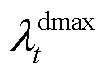 分别为t时段消纳型DR、削减型DR的单位激励补偿费用最大值。
分别为t时段消纳型DR、削减型DR的单位激励补偿费用最大值。
大用户用电功率与DR功率之间的关系表示为
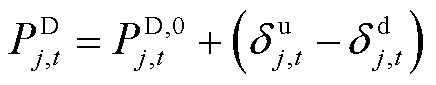 (24)
(24)
式中,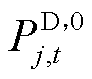 为大用户j未参与DR时的用电功率。
为大用户j未参与DR时的用电功率。
约束式(14)为功率平衡约束;约束式(15)表示各时段灵活性需求约束;约束式(16)表示线路传输能力上限约束;约束式(17)表示火电机组出力约束;约束(18)表示火电机组的灵活爬坡容量限制在爬坡能力范围之内;约束式(19)表示火电机组出力变化受前一时段预留的灵活爬坡容量限制;约束式(20)为单位激励补偿费用约束。
约束式(21)与式(22)为激励相容约束,按响应意愿参数由低到高进行排序,在相同响应意愿参数下,DR大用户j的收益高于DR大用户j-1,即保证提供DR服务积极性高的用户获益更高。系统为应对t+1时段净负荷的波动性与不确定性而预留灵活爬坡容量,大用户在t时段预留爬坡容量,t+1时段通过DR服务为系统提供灵活爬坡能力。考虑到大用户预留的爬坡容量受t+1时段响应能力限制,如约束式(23)所示,大用户t+1时段所提供的DR功率需大于t时段应对净负荷波动而预留的那部分爬坡容量。因此,ISO可利用DR的激励机制为系统预留FRP。
ISO根据净负荷波动方向,确定各时段的DR类型,进而确定削减型DR或消纳型DR的调节功率,其剩余灵活爬坡容量可为系统提供FRP。大用户以提供DR服务收益最大为目标与ISO进行博弈。大用户决策模型的目标函数具体表示为
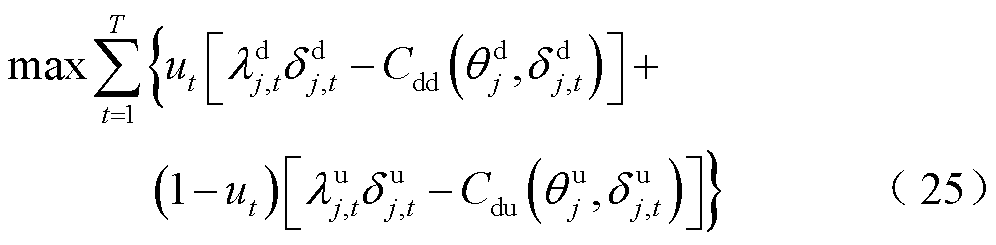
下层模型根据对应时段ISO所需灵活性的方向,选择相应的目标函数进行决策优化。上述目标函数中第一项为削减型DR收益,若当前时段系统需要大用户增加用电功率,此部分收益为零;第二项为消纳型DR收益,若当前时段系统需要大用户削减用电功率,此部分收益为零。
约束条件为
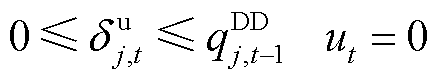 (26)
(26)
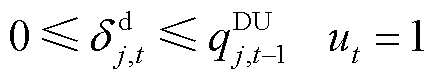 (27)
(27)
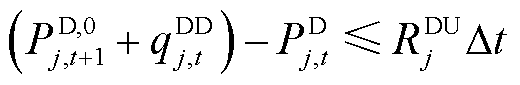 (28)
(28)
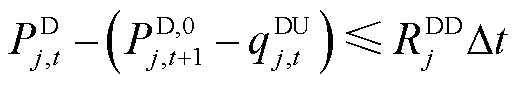 (29)
(29)
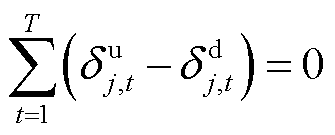 (30)
(30)
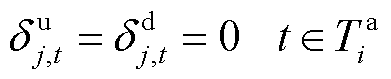 (31)
(31)
式中,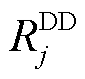 和
和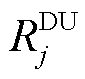 分别为大用户j的爬坡和滑坡速率;
分别为大用户j的爬坡和滑坡速率;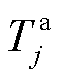 为大用户j不参与DR的时间集合。
为大用户j不参与DR的时间集合。
上述公式中,约束式(26)和式(27)表示大用户提供削减型或消纳型DR受限于前一时段预留的灵活爬坡容量;约束式(28)和式(29)表示大用户预留的爬坡容量受爬坡能力约束;约束式(30)表示大用户参与DR不能影响其一天的用电总量,即不影响正常的生产用电需求;约束式(31)表示大用户在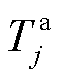 时间段内不参与需求响应。另外,大用户预留的爬坡容量在下一时段的调节范围之内。
时间段内不参与需求响应。另外,大用户预留的爬坡容量在下一时段的调节范围之内。
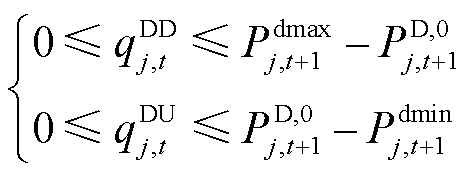 (32)
(32)
式中,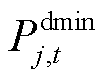 、
、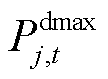 分别为t时段大用户j用电功率的下限、上限,即考虑大用户在每个时段DR上限的不同。
分别为t时段大用户j用电功率的下限、上限,即考虑大用户在每个时段DR上限的不同。
ISO问题式(7)~式(23)和大用户问题式(25)~式(32)构成了主从博弈模型。该博弈最早由H.Von Stackelberg提出[26],主从博弈双层优化模型直接求解复杂,可将下层优化决策模型利用 KKT(Karush-Kuhn-Tucker)条件转换为均衡约束,将约束式代入上层优化模型中联立求解,进而将基于主从博弈的双层优化问题转换为带有均衡约束的单层优化问题。
双层优化模型的求解具有一定的复杂度,且解的最优性无法证明,将双层模型转变为单层问题可降低模型的求解难度。下层大用户进行DR决策时,单位激励补偿费用与FRP需求是上层ISO问题优化后既定的结果,若将优化问题式(25)~式(32)用KKT条件代替,即可消去此下层优化问题,重新生成关于电能与FRP及其单位激励补偿费用的单层优化问题,则大用户优化决策问题的KKT条件为
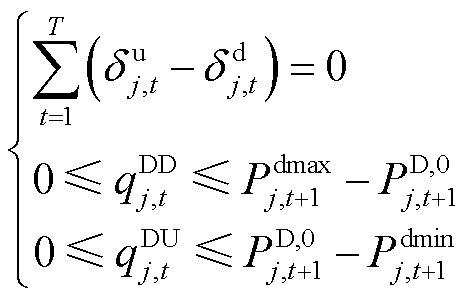 (33)
(33)
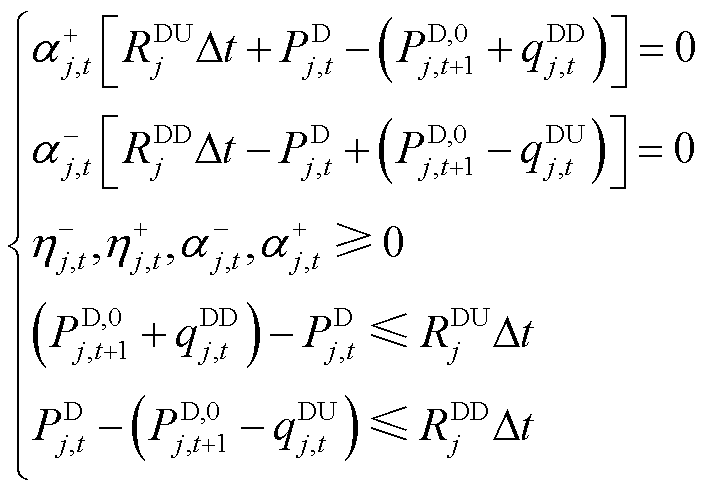 (34)
(34)
当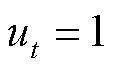 时,有
时,有
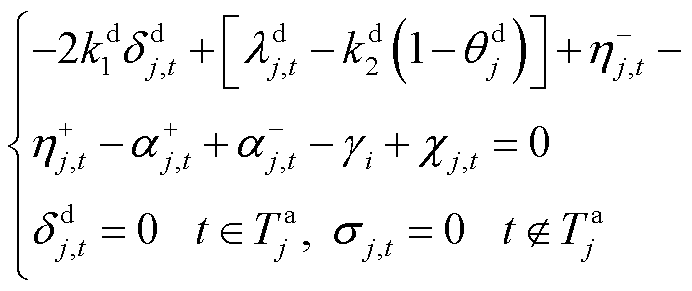 (35)
(35)
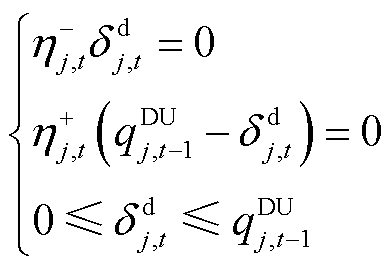 (36)
(36)
当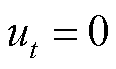 时,有
时,有
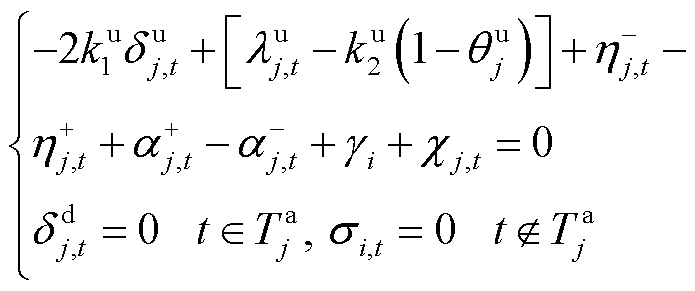 (37)
(37)
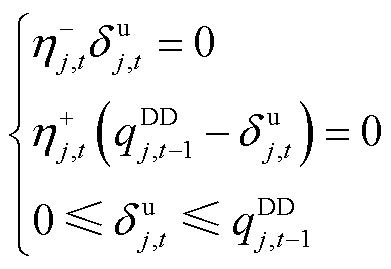 (38)
(38)
式中,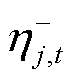 、
、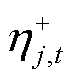 分别为约束式(26)、式(27)对应的对偶变量;
分别为约束式(26)、式(27)对应的对偶变量;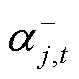 、
、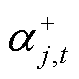 分别为约束式(28)、式(29)对应的对偶变量;
分别为约束式(28)、式(29)对应的对偶变量;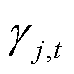 和
和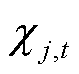 分别为等式约束式(30)、式(31)对应的对偶变量;
分别为等式约束式(30)、式(31)对应的对偶变量;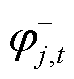 和
和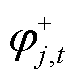 为约束式(32)对应的对偶变量。
为约束式(32)对应的对偶变量。
采用文献[27]的方法,通过引入0-1变量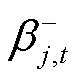 、
、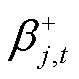 、
、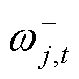 、
、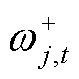 将约束式(34)、式(36)和式(38)转换为线性约束式,即
将约束式(34)、式(36)和式(38)转换为线性约束式,即
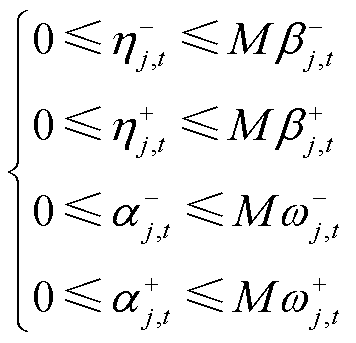 (39)
(39)
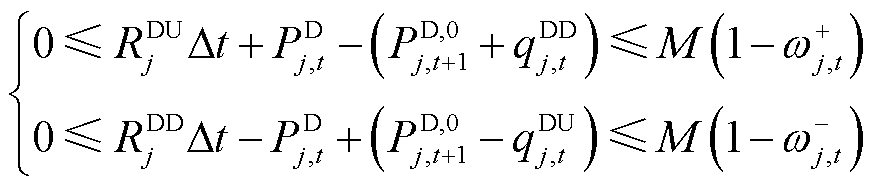 (40)
(40)
当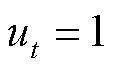 时,有
时,有
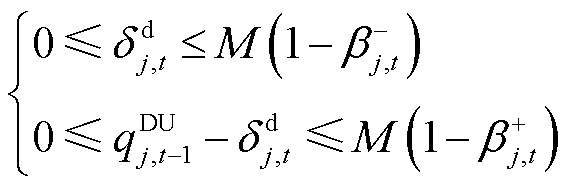 (41)
(41)
当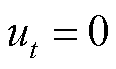 时,有
时,有
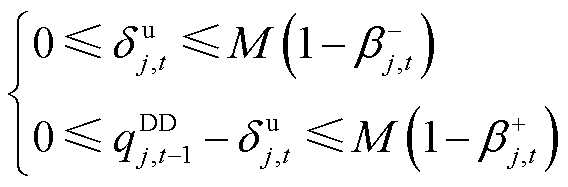 (42)
(42)
综上所述,面向系统灵活性提升的主从博弈模型可转换为带有均衡线性约束的单层优化问题:
目标函数:式(7)
s.t. 式(14)~式(24)、式(33)、式(35)、式(37)、式(39)~式(42)。
此带有线性均衡约束的单层优化模型最优解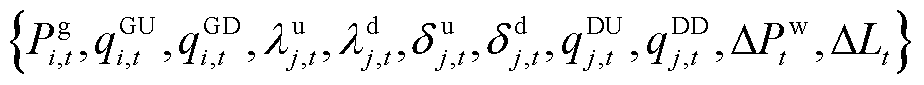 构成ISO与大用户主从博弈的Stackelberg均衡解集。在Matlab环境下调用Gurobi求解器对带有线性均衡约束的单层优化模型进行求解。
构成ISO与大用户主从博弈的Stackelberg均衡解集。在Matlab环境下调用Gurobi求解器对带有线性均衡约束的单层优化模型进行求解。
本文算例在PJM-5系统结构的基础上引入可再生能源及DR大用户进行验证,PJM-5系统如图5所示。网络线路参数来源于文献[28],各火电机组的容量、购电成本函数及爬坡滑坡能力见附表1[29]。风电厂位于节点C,系统日负荷预测曲线、日风电预测出力曲线及净负荷曲线如图6所示,失负荷损失和可再生能源削减损失分别设置为2 500元/(MW·h)和420元/(MW·h)[30]。
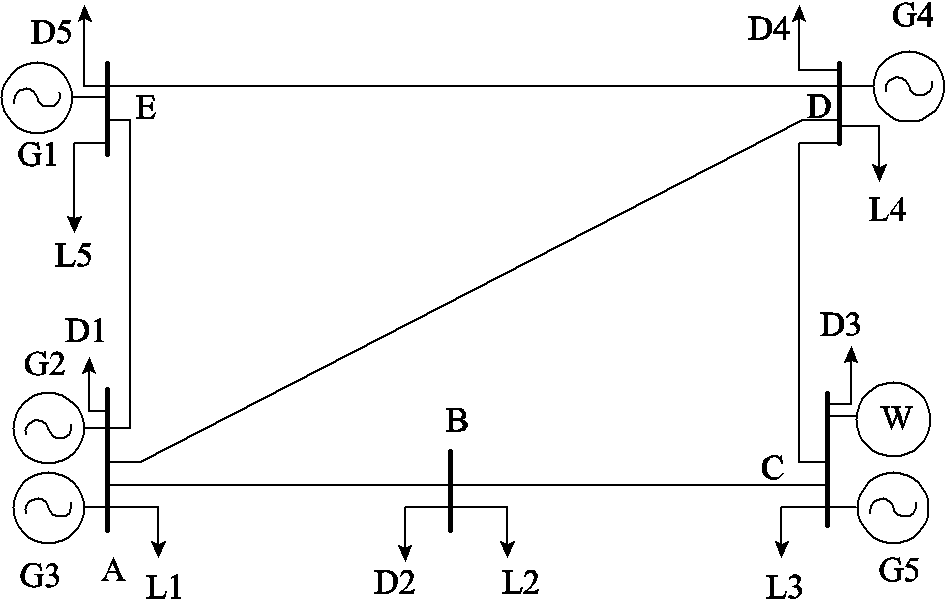
图5 PJM-5系统
Fig.5 PJM-5 system
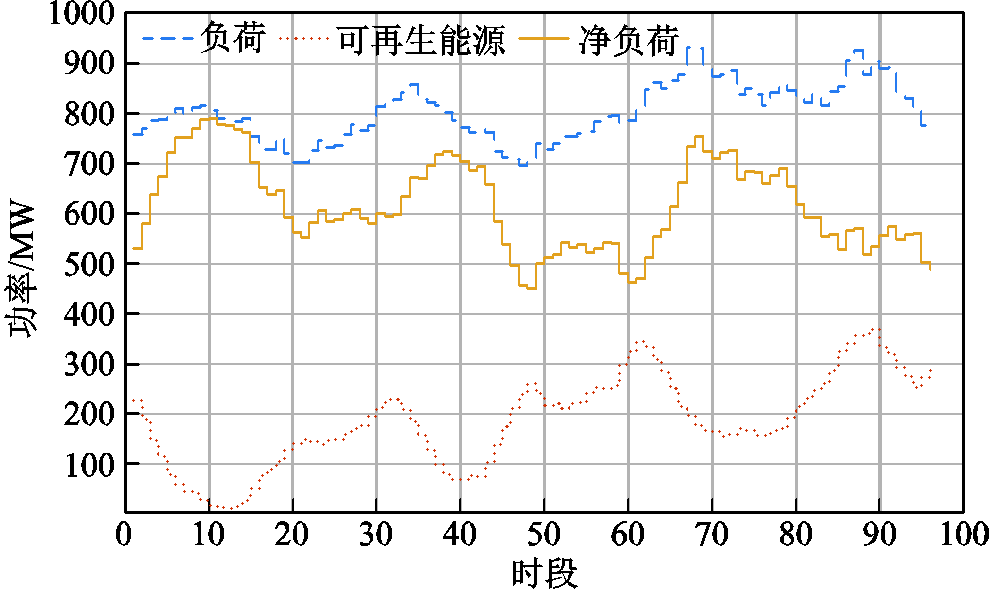
图6 净负荷功率曲线
Fig.6 Net load power curve
大用户参与DR前的负荷曲线如附图2所示,其调节范围均为参与DR前负荷曲线的±15%,大用户的爬/滑坡速率等其他DR参数见附表2。削减型和消纳型DR的单位激励补偿单位费用上限均为1 500元/(MW·h)。
现有激励机制分别以200、800和850元/ (MW·h)三个分段的单位补偿费用激励用户提供削减型或消纳型DR服务,并生成用户DR历史数据。在单位补偿费用为200元/(MW·h)时,可获得L3~L5的DR历史数据,L1与L2未参与DR服务;当单位补偿费用提升至800元/(MW·h)时,可获得L2的DR响应历史数据,L3~L5均以最大响应能力提供DR服务,而L1未参与DR服务;当单位补偿费用为850元/(MW·h)时,可获得L1的DR历史数据。在此激励措施下,所有大用户的DR具体历史数据见附表3。
将大用户按响应意愿从低到高排序,根据DR响应历史数据并采用CDMBM估计响应成本,大用户的响应意愿参数计算结果见表1,其中一次项系数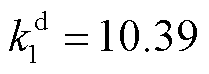 ,
,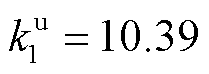 ,二次项系数
,二次项系数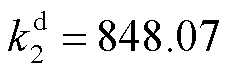 ,
,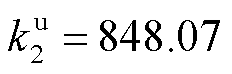 。
。
表1 大用户意愿参数
Tab.1 Large-scale user intention parameters

大用户编号 L100 L20.1110.111 L30.7890.789 L40.8260.826 L511
根据图6净负荷曲线可知,净负荷向上波动主要集中在时段1~10、30~38、61~68,净负荷向下波动主要集中在时段11~21、39~48、69~96,在可再生能源波动的影响下净负荷曲线呈现“三峰三谷”的形状。在本文提出的DR策略下,不同的DR大用户在各时段的单位激励补偿费用如图7所示。
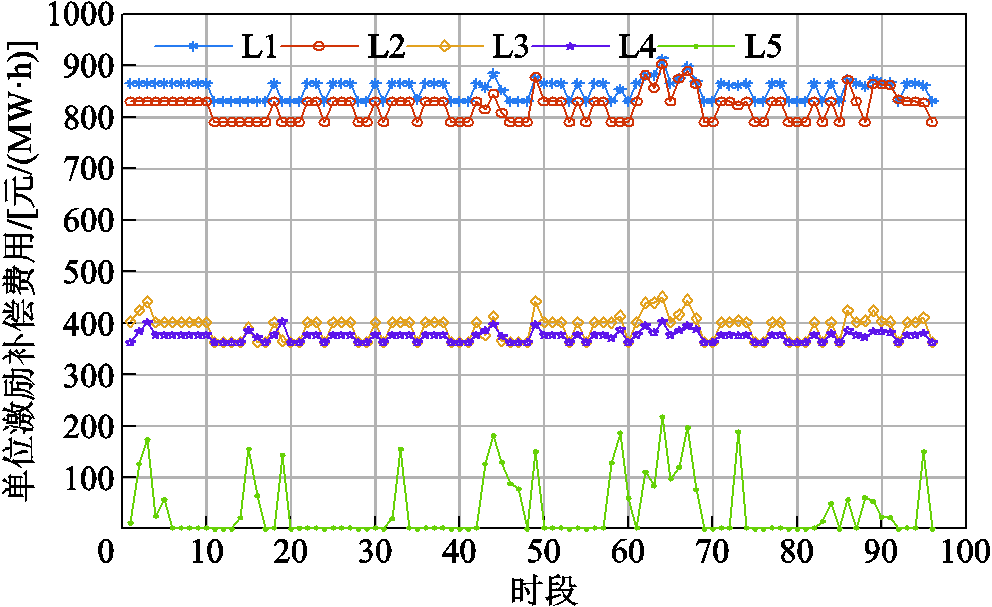
图7 单位激励补偿费用
Fig.7 Unit incentive compensation cost
由图7可以看出,通过本文提出的DR优化策略引导,大用户在各时段的单位激励补偿费用随着净负荷波动幅度的增加而提高,ISO按照单位激励补偿费用由低到高确定不同大用户的DR功率。
从DR类型来看,净负荷向上波动时段的单位激励补偿费用高于向下波动时段。从单位激励补偿费用的解析表达上可知,电量平衡约束对应的对偶变量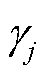 在向上和向下波动时段的数值正负存在差异,而导致净负荷波动方向对单位激励补偿费用产生影响。因此,若大用户在不参与DR服务时,其单位激励补偿费用在净负荷向上和向下波动时段的平均值为大用户响应的平均边际成本。对ISO而言,在净负荷向下波动时段更希望减少发电机的出力并降低购电成本,而非额外支付激励补偿费用引导大用户增加用电量;对大用户而言,希望以较低的激励补偿在净负荷向下波动时段恢复周期总用电量。
在向上和向下波动时段的数值正负存在差异,而导致净负荷波动方向对单位激励补偿费用产生影响。因此,若大用户在不参与DR服务时,其单位激励补偿费用在净负荷向上和向下波动时段的平均值为大用户响应的平均边际成本。对ISO而言,在净负荷向下波动时段更希望减少发电机的出力并降低购电成本,而非额外支付激励补偿费用引导大用户增加用电量;对大用户而言,希望以较低的激励补偿在净负荷向下波动时段恢复周期总用电量。
若净负荷波动相对较缓,火电机组可以在每个时段预留足够的灵活爬坡容量,且电能市场下负荷在各火电机组上进行经济分配,电能出清价格较低,因此在本文提出的激励补偿措施下,ISO以较低的单位激励补偿费用保证系统功率实时平衡和灵活性的充足,如时段4~14、21~31等,仅依靠响应意愿最高且响应成本最小的大用户L5即可满足系统所需的DR服务,此时激励相容机制不起约束作用,以边际成本补偿大用户L5。
为了进一步说明其他时段单位激励补偿费用较高的原因,图8展示了大用户在各时段DR功率的分配情况,图9展示了火电机组与大用户在各时段提供向上或向下爬坡容量分布(向上或向下爬坡容量由净负荷波动方向确定)。
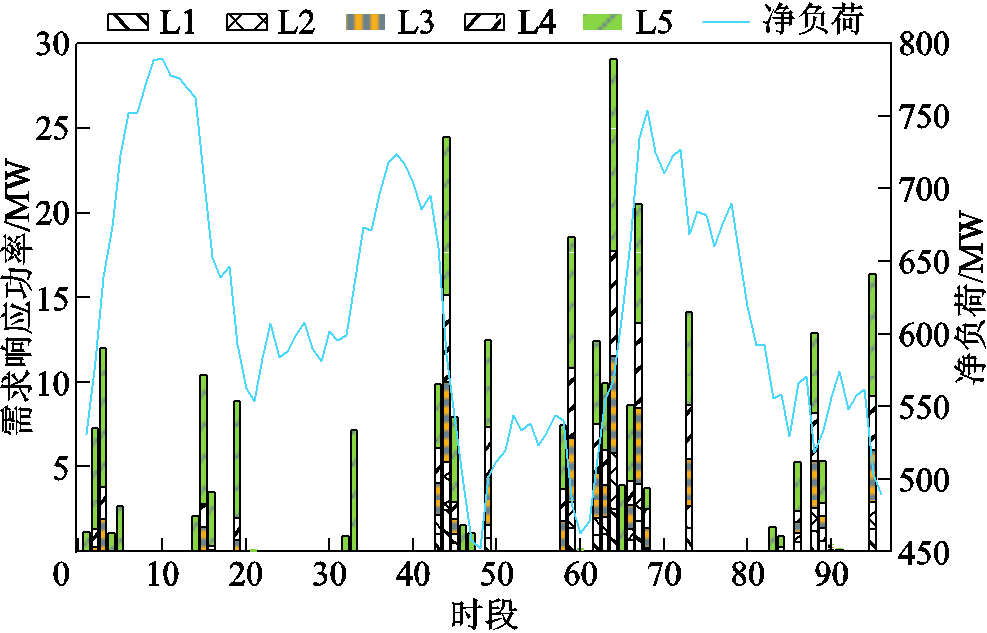
图8 需求响应功率
Fig.8 Demand response power
在时段15、19、43~45、58~59,大用户提供消纳型DR服务的单位激励补偿费用较高,这是由于此时刻净负荷急剧下降,火电机组本身的爬/滑坡能力不足,为了降低可再生能源的削减,通过提供较高的激励补偿提高消纳型DR成本较低的大用户用电功率;尤其在时段44下,净负荷出现剧烈的向下波动,在时段43所有大用户提供较多的灵活爬坡容量应对净负荷的波动性与不确定性。时段62~68净负荷剧烈向上波动,大用户通过在前一时段预留爬坡容量以保证下一时刻提供充足的DR服务。
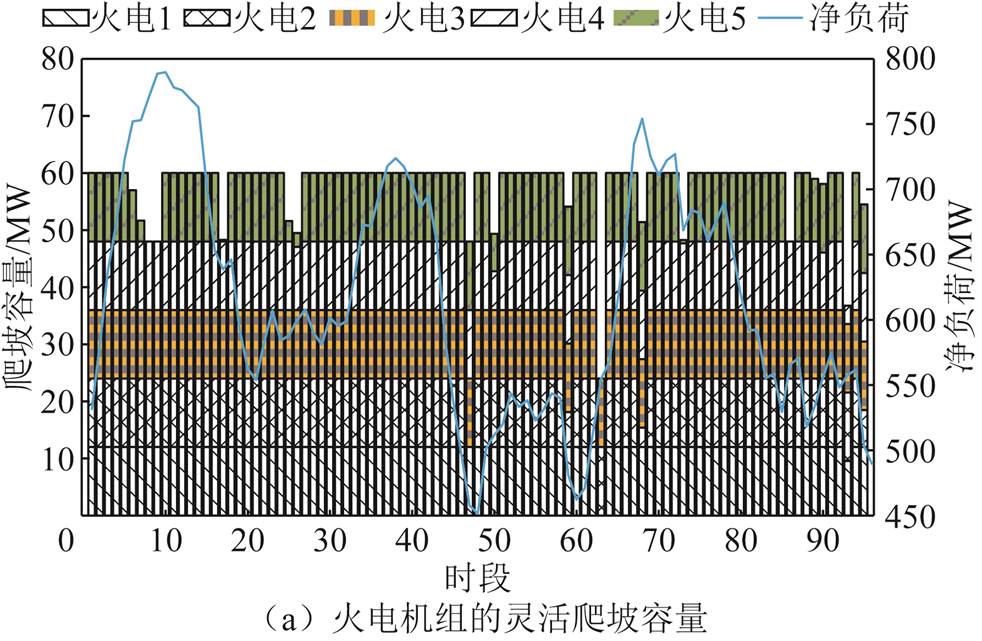
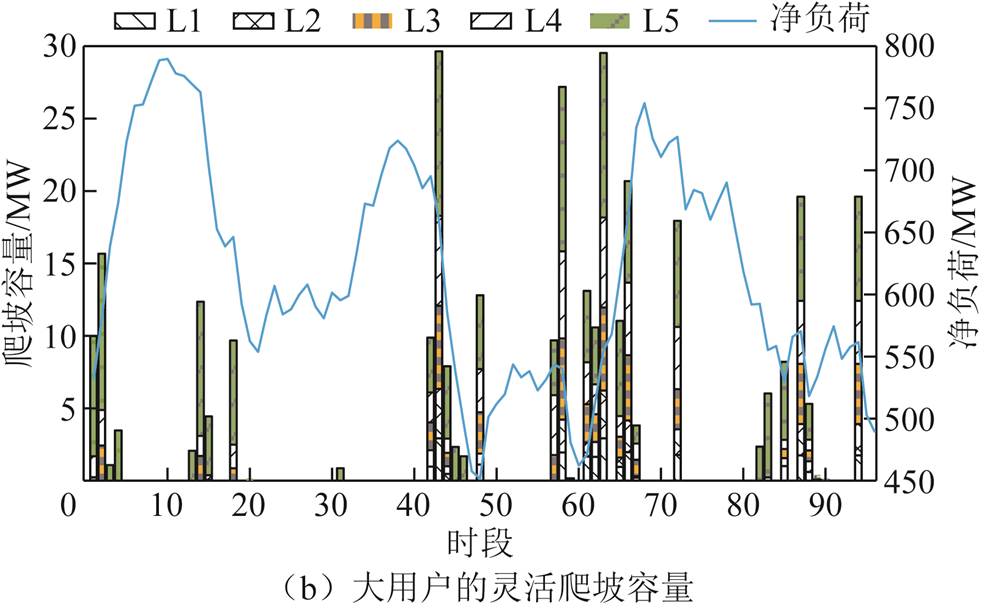
图9 灵活爬坡产品出清结果
Fig.9 Flexible ramping products clearing results
在峰荷时段6~14、36~40,净负荷波动较缓且火电机组在前一时段预留了足够的爬坡容量,ISO无需增加单位激励补偿费用和大用户的DR服务。L5作为响应成本较低的大用户,ISO未以降低此时段电能成本为目的来增加此用户的DR服务。这是因为大用户提供DR服务需满足周期用电量约束,虽然大用户L5提供电能服务较火电机组更低,但其提供削减型DR与消纳型DR总量在周期内维持相等,而在净负荷向下波动时段降低发电成本比额外支付用户激励补偿更经济,消纳型DR在系统滑坡能力不足时才能发挥其经济性。因此,在一定周期内的削减型DR总量受其消纳型DR经济性的影响,ISO希望用户提供的DR服务在净负荷波动较大时段满足FRP需求或能够避免负荷损失与可再生能源削减。
若大用户的爬/滑坡速率能使其用电功率在调节范围内快速变化,则大用户在各时段之间的调节能力将不受影响,无需在前一时刻预留FRP;但若大用户的爬/滑坡速率存在限制,前一时刻的大用户DR功率将影响下一时刻大用户的DR能力。因此,为了在爬/滑坡能力限制下满足下一时段的灵活性需求,应通过改变单位激励补偿费用的方式以预留FRP,提高应对净负荷波动的能力。例如时段63、64为净负荷连续向上波动时段,在时段63通过增加单位补偿费用以提高大用户L5提供的削减型DR功率,使其在时段64获得足够的爬坡能力,在用电功率下限提供了11.349 MW的削减型DR;若前一段未激励L5提供消纳型DR,则时段64仅能提供7.19 MW的削减型DR。在净负荷连续下降时段43、44,同样通过增加前一时段的激励补偿,为下一时段预留了足够的滑坡容量。而时段88净负荷向下波动,时段89净负荷向上波动,通过减少时段88的单位激励补偿费用以降低其提供的消纳型DR功率,为时段89提供了2.47 MW的爬坡容量。另外,系统在每个时段应对净负荷波动后的剩余爬坡容量平均值为37.65 MW,可有效应对实时阶段的不确定。
在本文提出的DR策略下,各DR用户以差异化的单位激励补偿费用进行补偿,大用户通过预留FRP,缓解了净负荷剧烈波动时段出现的爬/滑坡能力不足的问题,通过满足由净负荷波动引起的灵活性需求,为实时阶段的不确定性预留了较多的灵活调节能力。
为验证本文提出的DR优化策略在灵活性与经济性上的优势,与文献[9]提及的统一单位激励补偿费用策略进行对比。对比策略:不考虑FRP机制且各时段所有大用户的单位激励补偿费用无差异,建立基于主从博弈的DR优化策略。在对比策略中,上层以火电机组、削减型/消纳型DR服务、失负荷及可再生能源削减惩罚最小为目标,下层以大用户效益最大为目标,所有大用户设置相同的单位激励补偿费用,用户的响应能力和响应成本与本文策略一致。两种策略下各项成本对比情况见表2。
表2 两种策略下各成本对比
Tab.2 Cost comparison under two strategies (单位:元)
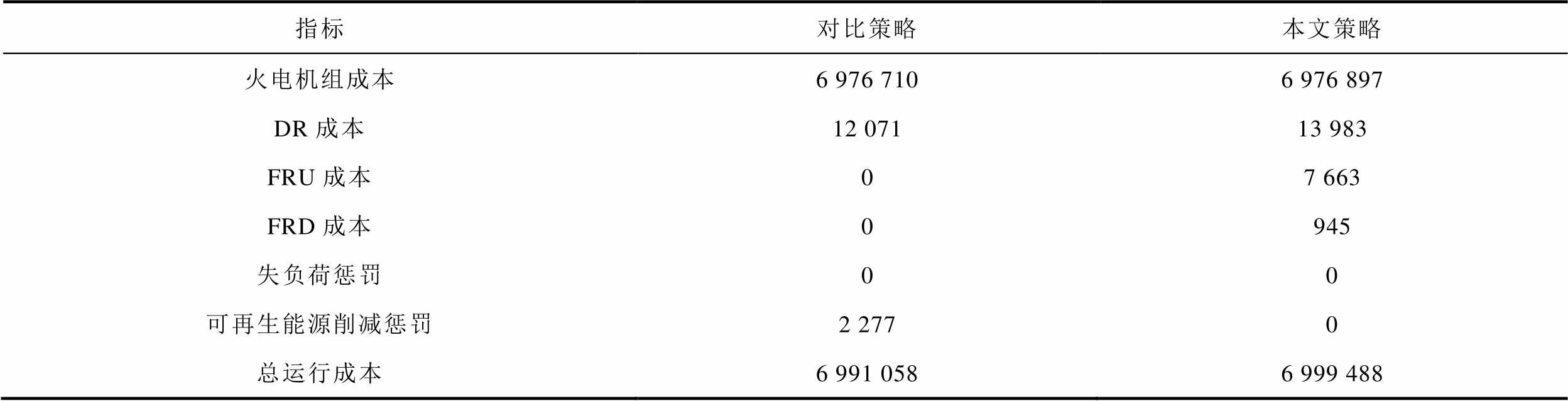
指标对比策略本文策略 火电机组成本6 976 710 6 976 897 DR成本12 07113 983 FRU成本07 663 FRD成本0945 失负荷惩罚00 可再生能源削减惩罚2 2770 总运行成本6 991 058 6 999 488
本文策略的总运行成本略高,原因在于火电购电成本略高,且需支付额外的FRP补偿。本文策略火电运行成本略高的原因在于其提供灵活爬坡容量而使火电机组偏离经济运行点。本文策略的DR成本虽较对比策略高出15.84%,但提供的DR功率总量却高出26.28%,本文策略的DR单位成本为198.63元/(MW·h),而对比策略的DR单位成本为216.52元/(MW·h),在本文提出的DR策略下,不仅能提高DR的经济性,而且能够提高用户参与DR的积极性。对比策略中由于出现可再生能源削减惩罚,导致总的电能成本较高。
本文策略虽额外支付了FRP补偿费用,但在每个时段预留了足够的FRP,不存在可再生能源削减,且应对实时阶段不确定性的各时段爬坡容量平均值高出24.71%。对比策略中由于未预留FRP,在净负荷向上剧烈波动时段,如时段67等,向上爬坡能力不足,难以应对实时阶段的不确定性,易出现失负荷现象;在净负荷向下剧烈波动的44等时段,日前计划中已出现可再生能源削减,在实时阶段可能加剧可再生能源削减的现象。在本文策略下,通过单位激励补偿费用的引导,为火电机组分担提供灵活爬坡容量的压力,使火电机组的FRP成本仅占总成本的0.31%,并为实时阶段的不确定性提供爬/滑坡能力,提升系统日前阶段与实时阶段的灵活性。
为了进一步说明本文策略在提供DR服务时其经济性上的优越性,分析两种策略在单位激励补偿费用上的区别,图10展示了对比策略下净负荷剧烈波动时段40~70的单位激励补偿费用结果及每个时段下的DR功率。
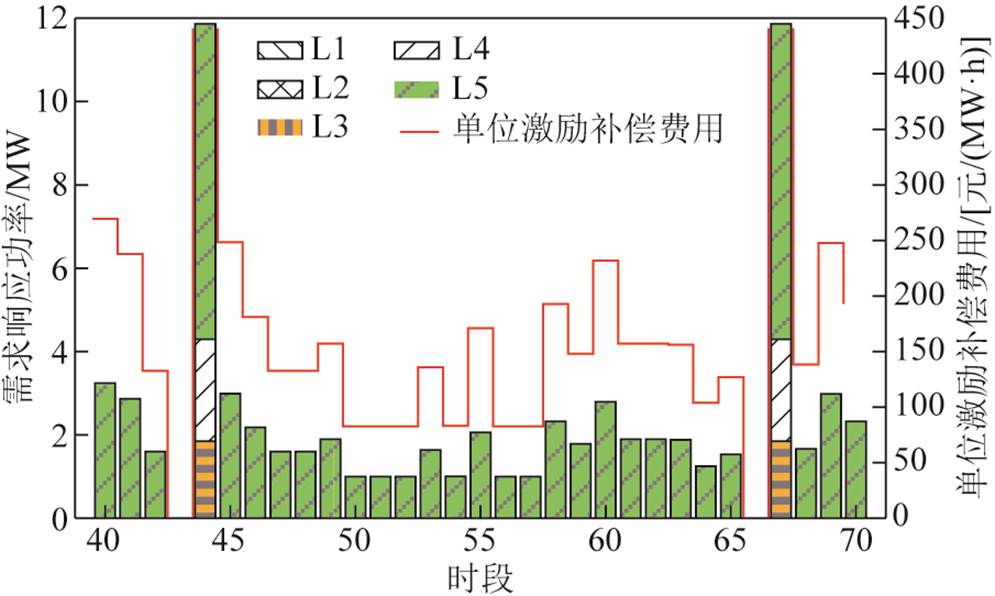
图10 对比策略的单位激励补偿费用及DR功率结果
Fig.10 The unit incentive compensation cost and the DR power results for contrast strategy
从图10可以看出,对比策略的单位激励补偿费用结果也随着净负荷波动量的增加而提高,但在系统出现较大波动时,如时段44与时段67,由于大用户L3的响应成本较高,为了保证大用户提供DR服务时不产生亏损,单位激励补偿费用急剧上升,相比相邻时段提高了近2倍,所有大用户的单位激励补偿以最高的响应成本进行决策,而单位激励补偿费用的大幅波动影响响应成本低的用户在其他时段的DR意愿,并且此统一的单位激励补偿措施为了保证系统的经济性难以发挥L1与L2的DR能力。
本文考虑不同大用户的响应意愿,通过建立激励相容机制,避免了对响应成本较低的用户激励补偿过高的现象,有利于市场的稳定运行,刻画了DR意愿较高的用户所表现的低成本特性,对DR大用户进行有针对性地补偿。
总体来说,在本文提出的DR优化策略下,通过估计响应意愿和响应成本及考虑FRP机制,降低了失负荷和可再生能源削减量,以较少的FRP代价提升了系统的灵活性,且对不同响应意愿用户进行差异化补偿,生成契合ISO与DR大用户双方利益的单位激励补偿费用策略。
在本节中,采用改进的IEEE 118节点系统,原系统包含54个火电机组,在此基础上增加17个风电场和5个DR大用户,其位置分布信息见附表4,系统净负荷曲线变化趋势与PJM-5算例类似。可再生能源发电量约占总发电量的10%,所有DR大用户的负荷总和占系统总负荷的5.5%,其响应成本参数与PJM-5算例一致,调节范围增加到参与DR前负荷曲线的±30%,爬滑坡能力提升了2倍。42~69时段为净负荷剧烈变化时段,图11和图12给出了此时段区间的单位激励补偿费用与DR功率以及预留的灵活爬坡容量。
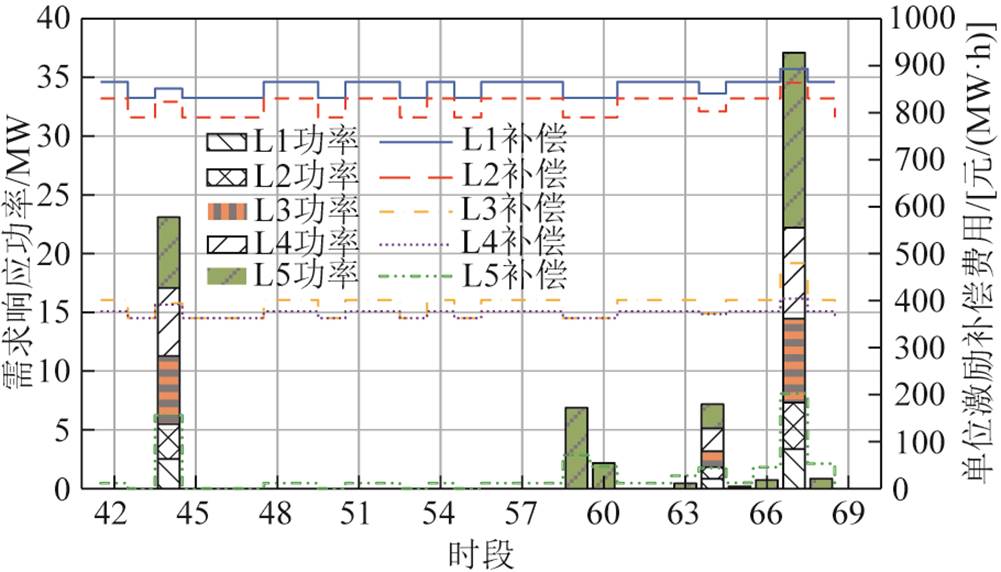
图11 单位激励补偿费用及DR功率结果
Fig.11 The unit incentive compensation cost and the DR power results
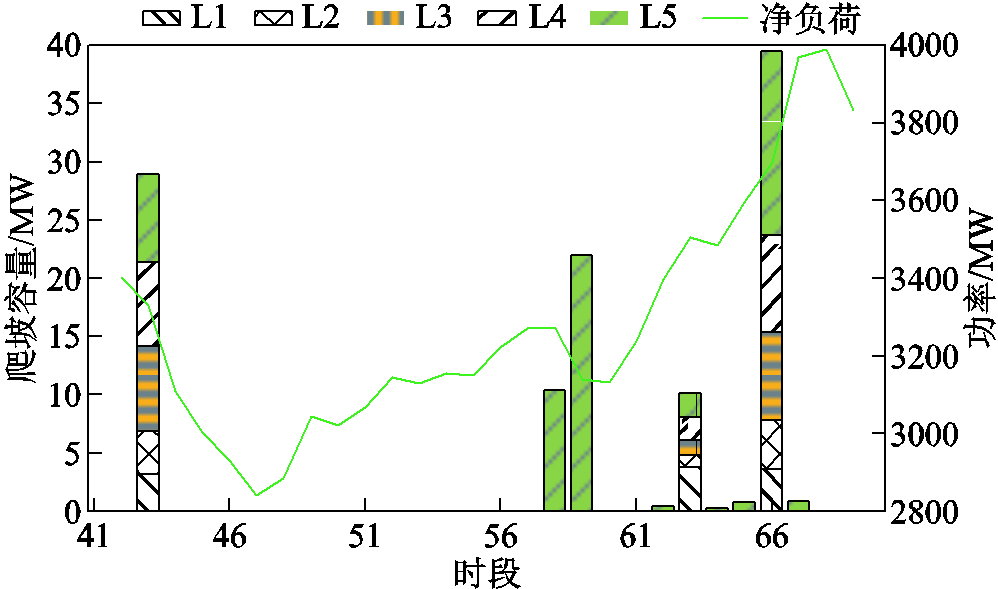
图12 大用户各时段预留灵活爬坡容量
Fig.12 Flexible ramping capacity reserved for large-scale users at different time periods
本算例与PJM-5具有相似的结果,在所提策略下,按照大用户的响应意愿差异化地补偿其DR服务。在净负荷剧烈波动时段44和67等,ISO通过调整单位激励补偿费用为火电机组分担提供FRP的压力,提升下一时段系统的爬坡能力,引导大用户提供系统所需的电能服务,不仅能够适应净负荷的剧烈变化,而且提升了系统的灵活性。
本文通过同时考虑ISO与各DR大用户主体利益,为系统提供电能与FRP服务,在所提的主从博弈DR优化策略下,ISO以差异化的单位激励补偿费用对不同响应意愿的DR大用户给予补偿,得到以下结论:
1)通过引入DR大用户的响应意愿参数,分别对削减型DR和消纳型DR的响应成本进行估计,建立激励相容机制以协调DR大用户的响应意愿差异。在电能与FRP联合出清市场中,其单位激励补偿费用结果契合ISO与DR大用户双方意愿,充分发挥低成本且响应意愿更高的大用户调节能力,在电能服务上具有较好的经济性。本策略通过调整单位激励补偿费用改变大用户预留的灵活爬坡容量,提升系统应对净负荷波动性与不确定性的爬/滑坡能力。
2)在本文提出的DR优化策略下,大用户在FRP市场中预留灵活爬坡容量,为火电机组分担提供灵活爬坡容量的压力,以仅占总运行成本0.31%的FRP代价降低电能惩罚并提升实时阶段应对不确定性的能力。对不同响应意愿用户进行有差异的合理补偿,此单位激励补偿费用能适应不同的净负荷波动水平,有效地缓解在灵活爬坡能力不足时激励费用过高的现象,避免DR大用户的单位激励补偿费用大幅波动。
本文所构建的主从博弈模型通过FRP机制考虑相邻时段的耦合关系以提高系统的灵活性,但仅针对日前市场的博弈过程进行研究,未考虑多时段的动态博弈过程。未来可进一步研究动态博弈模型,以模拟ISO和大用户的动态决策行为。
附 录
1. 预测误差不确定性
为了抵御净负荷的波动性与不确定性而预留灵活调节能力,FRP需求包括预测净负荷波动量和预测误差变动量两部分,FRU和FRD需求示意图如附图1所示。
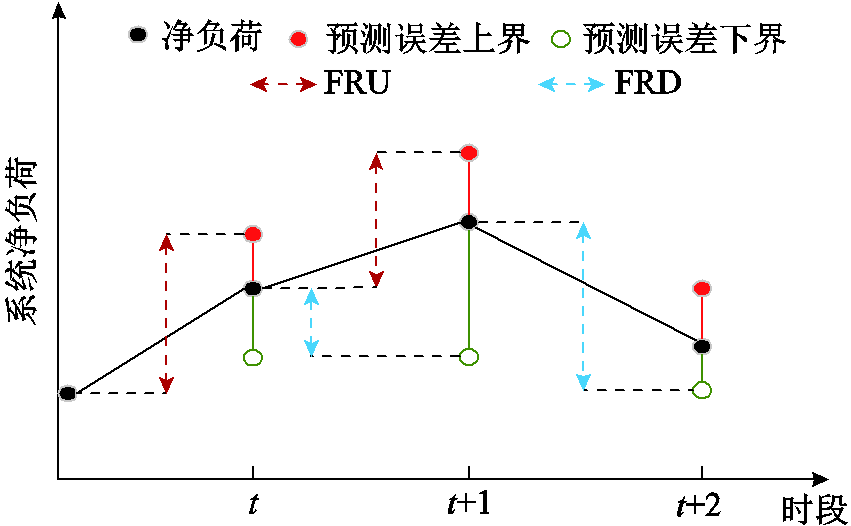
附图1 FRU与FRD需求示意图
App.Fig.1 FRU and FRD requirements diagram
预测误差变动量包括两部分,可再生能源的预测误差与负荷预测误差。已知预测误差服从正态分布,负荷预测误差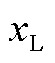 服从均值为
服从均值为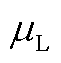 且标准差为
且标准差为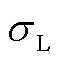 的正态分布,可再生能源预测误差
的正态分布,可再生能源预测误差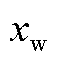 服从均值为
服从均值为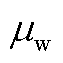 且标准差为
且标准差为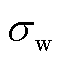 的正态分布,即
的正态分布,即
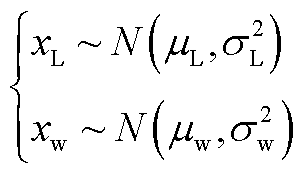 (A1)
(A1)
由于随机变量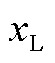 和
和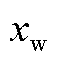 相互独立,其净负荷预测误差
相互独立,其净负荷预测误差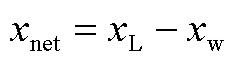 服从均值为
服从均值为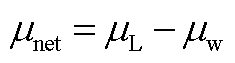 ,方差为
,方差为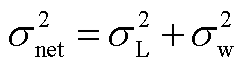 的正态分布,即
的正态分布,即
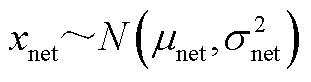 (A2)
(A2)
式中,负荷和可再生能源预测误差均值一般为0,而标准差与负荷功率或可再生能源出力存在比例关系,即
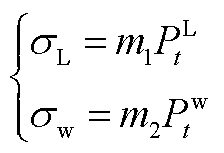 (A3)
(A3)
式中, 和
和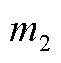 分别为负荷和可再生能源标准差比例系数,一般由历史数据计算获得,本文
分别为负荷和可再生能源标准差比例系数,一般由历史数据计算获得,本文 和
和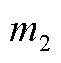 分别取为0.01和0.05。
分别取为0.01和0.05。
净负荷预测不确定性导致的FRU和FRD需求分别为
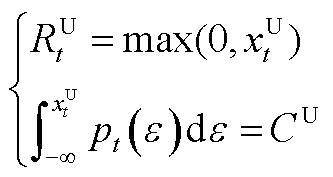 (A4)
(A4)
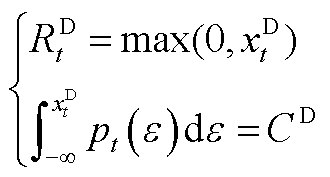 (A5)
(A5)
式中,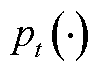 为t时段的净负荷预测误差的概率分布函数;
为t时段的净负荷预测误差的概率分布函数;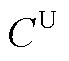 和
和 分别为置信区间的上界和下界;
分别为置信区间的上界和下界;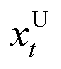 和
和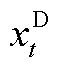 分别为对应置信水平下的t时段净负荷预测误差上界和下界。
分别为对应置信水平下的t时段净负荷预测误差上界和下界。
本文置信区间取为90%,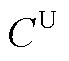 和
和 分别为95%和5%。
分别为95%和5%。
2. 系统参数
附表1 火电机组参数
App.Tab.1 Generator parameters
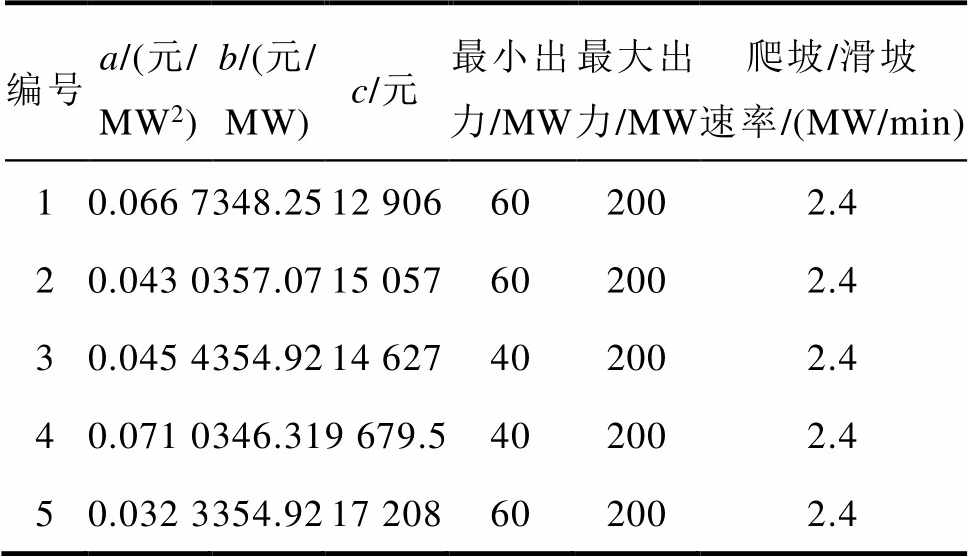
编号a/(元/MW2)b/(元/MW)c/元最小出力/MW最大出力/MW爬坡/滑坡速率/(MW/min) 10.066 7348.2512 906602002.4 20.043 0357.0715 057602002.4 30.045 4354.9214 627402002.4 40.071 0346.319 679.5402002.4 50.032 3354.9217 208602002.4
附表2 大用户爬坡速率
App.Tab.2 Ramping rate of large-scale users
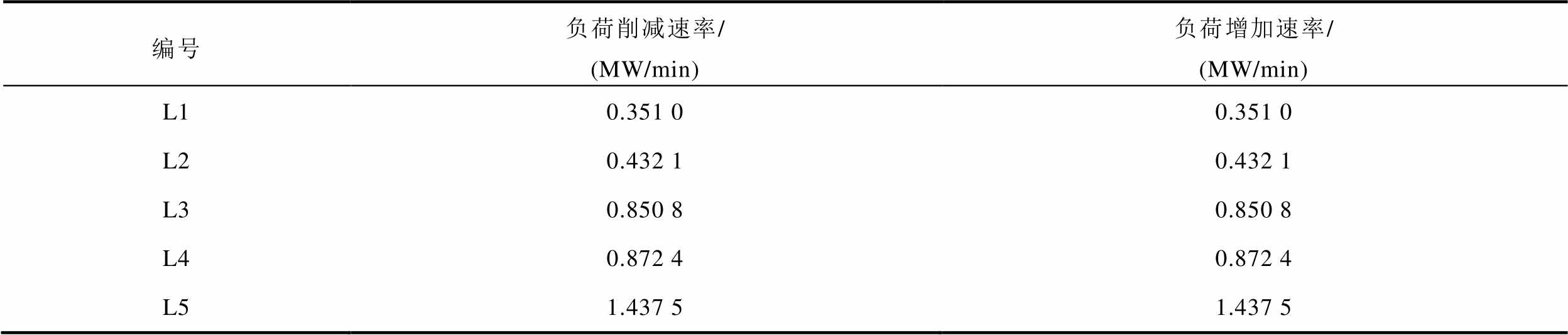
编号负荷削减速率/(MW/min)负荷增加速率/(MW/min) L10.351 00.351 0 L20.432 10.432 1 L30.850 80.850 8 L40.872 40.872 4 L51.437 51.437 5
附表3 大用户需求响应历史数据
App.Tab.3 Large-scale users DR historical data
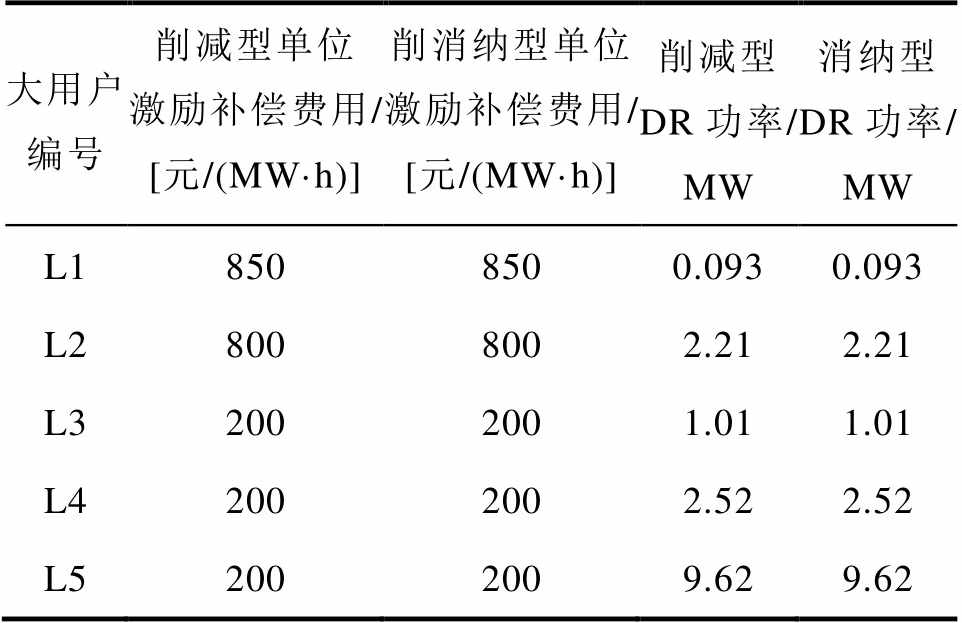
大用户编号削减型单位激励补偿费用/[元/(MW·h)]削消纳型单位激励补偿费用/[元/(MW·h)]削减型DR功率/MW消纳型DR功率/MW L18508500.0930.093 L28008002.212.21 L32002001.011.01 L42002002.522.52 L52002009.629.62
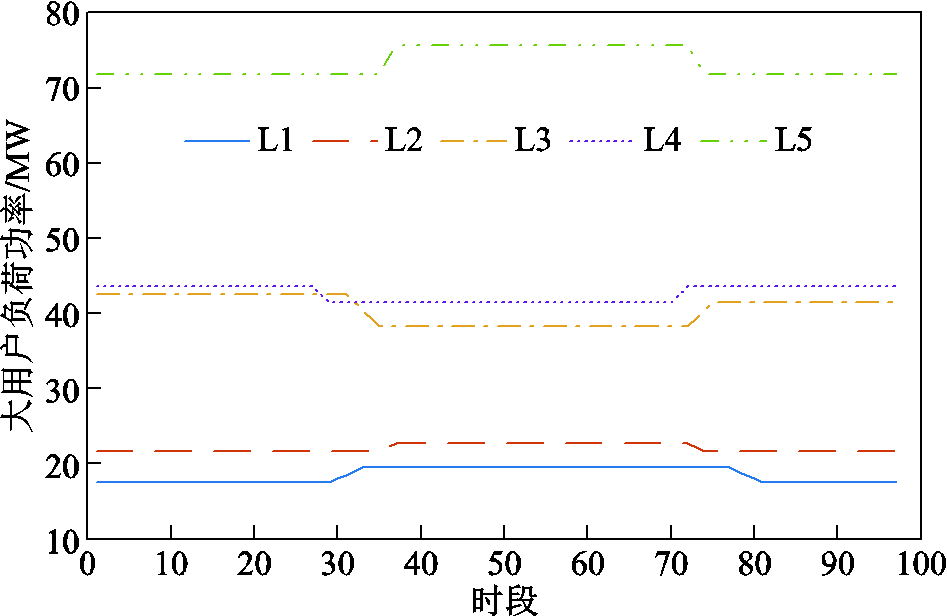
附图2 大用户负荷功率曲线
App.Fig.2 Large-scale users load power curves
附表4 IEEE 188系统的风电与大用户位置分布
App.Tab.4 The location distribution of wind power and large-scale users in IEEE 188 system

类型节点位置 风电2,9,16,18,19,21,35,43,49,54,56,59,62,69,76,83,107 DR大用户17,51,82,110,116
参考文献
[1] 韩丽, 王冲, 于晓娇, 等. 考虑风电爬坡灵活调节的碳捕集电厂低碳经济调度[J]. 电工技术学报, 2024, 39(7): 2033-2045.
Han Li, Wang Chong, Yu Xiaojiao, et al. Low-carbon and economic dispatch considering the carbon capture power plants with flexible adjustment of wind power ramp[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2033-2045.
[2] 杨雪, 王明强, 胡召永, 等. 精细考虑时刻间净负荷波动不确定性的机组组合[J]. 高电压技术, 2023, 49(11): 4839-4848.
Yang Xue, Wang Mingqiang, Hu Zhaoyong, et al. Unit commitment considering fluctuation uncertainty of net load between adjacent periods[J]. High Voltage Engineering, 2023, 49(11): 4839-4848.
[3] Shen Bo, Ghatikar G, Lei Zeng, et al. The role of regulatory reforms, market changes, and technology development to make demand response a viable resource in meeting energy challenges[J]. Applied Energy, 2014, 130: 814-823.
[4] Asadinejad A, Tomsovic K. Optimal use of incentive and price based demand response to reduce costs and price volatility[J]. Electric Power Systems Research, 2017, 144: 215-223.
[5] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[6] 潘郑楠, 邓长虹, 徐慧慧, 等. 考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度[J]. 电工技术学报, 2023, 38(增刊1): 56-69.
Pan Zhengnan, Deng Changhong, Xu Huihui, et al. Game optimization scheduling of high proportion wind power and multiple flexible resources considering flexibility compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 56-69.
[7] 郑若楠, 李志浩, 唐雅洁, 等. 考虑居民用户参与度不确定性的激励型需求响应模型与评估[J]. 电力系统自动化, 2022, 46(8): 154-162.
Zheng Ruonan, Li Zhihao, Tang Yajie, et al. Incentive demand response model and evaluation considering uncertainty of residential customer participation degree[J]. Automation of Electric Power Systems, 2022, 46(8): 154-162.
[8] 张全明, 崔晓昱, 张笑弟, 等. 计及用户不确定性的多时段耦合需求响应激励优化策略[J]. 中国电机工程学报, 2022, 42(24): 8844-8853.
Zhang Quanming, Cui Xiaoyu, Zhang Xiaodi, et al. Incentive optimization strategy of multi period coupling demand response considering user uncertainty[J]. Proceedings of the CSEE, 2022, 42(24): 8844-8853.
[9] 郭昆健, 高赐威, 林国营, 等. 现货市场环境下售电商激励型需求响应优化策略[J]. 电力系统自动化, 2020, 44(15): 28-35.
Guo Kunjian, Gao Ciwei, Lin Guoying, et al. Optimization strategy of incentive based demand response for electricity retailer in spot market environment[J]. Automation of Electric Power Systems, 2020, 44(15): 28-35.
[10] 郭鸿业, 陈启鑫, 夏清, 等. 电力市场中的灵活调节服务: 基本概念、均衡模型与研究方向[J]. 中国电机工程学报, 2017, 37(11): 3057-3066.
Guo Hongye, Chen Qixin, Xia Qing, et al. Flexible ramping product in electricity markets: basic concept, equilibrium model and research prospect[J]. Proceedings of the CSEE, 2017, 37(11): 3057-3066.
[11] 胡嘉骅. 电力系统灵活性提升方法及灵活调节产品获取机制[D]. 杭州: 浙江大学, 2018.
Hu Jiahua. Power system flexibility improvement method and flexible adjustment product acquisition mechanism[D]. Hangzhou: Zhejiang University, 2018.
[12] 武昭原, 周明, 王剑晓, 等. 双碳目标下提升电力系统灵活性的市场机制综述[J]. 中国电机工程学报, 2022, 42(21): 7746-7763.
Wu Zhaoyuan, Zhou Ming, Wang Jianxiao, et al. Review on market mechanism to enhance the flexibility of power system under the dual-carbon target[J]. Proceedings of the CSEE, 2022, 42(21): 7746-7763.
[13] Wu Chenye, Hug G, Kar S. A functional approach to assessing flexible ramping products' impact on electricity market[C]//2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 2015: 1-5.
[14] Zhao Yuzhou. Real-time dispatch of flexible ramping products for energy storage and demand response[C]// 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia), Chengdu, China, 2019: 1936-1941.
[15] Hu Jiahua, Wen Fushuan, Wang Ke, et al. Simultaneous provision of flexible ramping product and demand relief by interruptible loads considering economic incentives[J]. Energies, 2017, 11(1): 46.
[16] Makhdoomi H, Moshtagh J. Optimal scheduling of electrical storage system and flexible loads to participate in energy and flexible ramping product markets[J]. Journal of Operation and Automation in Power Engineering, 2023, 11(3): 203-212.
[17] Khoshjahan M, Dehghanian P, Moeini-Aghtaie M, et al. Harnessing ramp capability of spinning reserve services for enhanced power grid flexibility[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7103-7112.
[18] Fahrioglu M, Alvarado F L. Using utility information to calibrate customer demand management behavior models[C]//2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 2002: 317-322.
[19] Wang Qin, Hodge B M. Enhancing power system operational flexibility with flexible ramping products: a review[J]. IEEE Transactions on Industrial Informatics, 2017, 13(4): 1652-1664.
[20] Sreekumar S, Yamujala S, Sharma K C, et al. Flexible Ramp Products: a solution to enhance power system flexibility[J]. Renewable and Sustainable Energy Reviews, 2022, 162: 112429.
[21] Villar J, Bessa R, Matos M. Flexibility products and markets: Literature review[J]. Electric Power Systems Research, 2018, 154: 329-340.
[22] Xu Lin, Tretheway D. Flexible ramping products[R]. CAISO Proposal, 2012.
[23] 刘英琪. 高比例风电参与的电力市场灵活运营策略研究[D]. 广州: 华南理工大学, 2020.
Liu Yingqi. Research on flexible operation strategy of power market with high proportion of wind power participation[D].Guangzhou: South China University of Technology, 2020.
[24] 钟佳宇, 陈皓勇, 陈武涛, 等. 含灵活性资源交易的电力市场实时出清[J]. 电网技术, 2021, 45(3): 1032-1040.
Zhong Jiayu, Chen Haoyong, Chen Wutao, et al. Real-time clearing of electricity markets with flexible resource transactions[J]. Power System Technology, 2021, 45(3): 1032-1040.
[25] 王玲玲, 刘恋, 张锞, 等. 电力系统灵活调节服务与市场机制研究综述[J]. 电网技术, 2022, 46(2): 442-452.
Wang Lingling, Liu Lian, Zhang Ke, et al. A review of power system flexible ramping product and market mechanism[J]. Power System Technology, 2022, 46(2): 442-452.
[26] Von Stackelberg H. Marketform and gleichgewicht [M]. Vienna: Springer, 1934.
[27] Fortuny-Amat J, McCarl B. A representation and economic interpretation of a two-level programming problem[J]. Journal of the Operational Research Society, 1981, 32(9): 783-792.
[28] Li Fangxing, Bo Rui. Small test systems for power system economic studies[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-4.
[29] Kazarlis S A, Bakirtzis A G, Petridis V. A genetic algorithm solution to the unit commitment problem[J]. IEEE Transactions on Power Systems, 1996, 11(1): 83-92.
[30] Park H, Baldick R. Transmission planning under uncertainties of wind and load: sequential approximation approach[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2395-2402.
Abstract With the increasing scale of renewable energy such as wind and solar energy into the power system, its generation power volatility and uncertainty make the system net load curve steeper. Independent system operators (ISO) needs to introduce more flexible resources to cope with the surge in flexibility ramping products (FRP) demand. Implementing demand response (DR) for large-scale users has become an important way to improve system flexibility. How to design reasonable incentive compensation measures to guide large-scale users to provide DR services and participate in the FRP market is of great significance to improve the flexibility of the system. Existing studies have proposed reasonable incentive compensation mechanisms and DR strategies under the market environment, but have not considered the relationship between the difference of large-scale users' response willingness and response cost. Therefore, this paper proposed a DR optimization strategy that adapts to the joint clearing of electric energy and FRP, and realized differentiated compensation according to the response willingness of large-scale users.
First, the customer demand management behavior model (CDMBM) was used to estimate the response cost function of users by using the historical DR participation data of large- scale users. Characterizing the differences in user response costs by introducing a response willingness parameter in the cost function. The higher the willingness of large-scale users to respond, the lower the cost of response. CDMBM provided a basis for the accurate modeling of large-scale users' decision behaviors of reduction-type DR and absorption-type DR.
Secondly, an incentive DR master-slave game model was constructed between ISO and multiple large-scale users. The upper level model was the optimization model of joint clearing of electric energy and FRP with ISO as the decision-making body, and the lower level model was the optimization model of DR decision-making with large-scale users participating in the joint market.ISO aimed to minimize incentive compensation costs with the goal of meeting the flexibility requirements, while large-scale users aimed to maximize the benefits of providing DR services. Both parties are interdependent.
Finally, by taking the KKT condition of the lower model as the constraint condition of the upper model, the master-slave game problem was transformed into a mathematical optimization problem with linear equilibrium constraint for solving. The game behavior between ISO and large-scale users was described by the master-slave game equilibrium. The DR unit incentive compensation cost considering user differentiation was obtained according to the equilibrium result of the game between both parties.
The results show that differentiated compensation is carried out according to the response willingness of large-scale users. Large-scale users are effectively encouraged to participate in the joint clearing market of electric energy and FRP market. The unit incentive compensation cost not only meets the needs of large-scale users and ISO, but also effectively alleviates the sharp increase in incentive compensation costs when there is a lack of flexible ramping capability.Large-scale users reserve flexible ramping capacity in the FRP market to provide flexible climbing capacity, which reduce the pressure of thermal power units. The cost of FRP accounts for only 0.31% of the total system cost. The proposed DR optimization strategy enhances the system's flexibility while considering economic efficiency.
keywords:Demand response, flexible ramping products (FRP) market, master-slave game, equilibrium constraints, unit incentive compensation cost
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.240822
国家重点研发计划(2018YFB1503101)和国家自然科学基金(51307019)资助项目。
收稿日期 2024-05-21
改稿日期 2024-08-06
黄大为 男,1976年生,副教授,硕士生导师,研究方向为综合能源系统运行与规划、电力系统运行与控制等。E-mail:hdw76@163.com
于 娜 女,1977年生,副教授,硕士生导师,研究方向为电力市场需求侧研究等。E-mail:yuna0616@163.com(通信作者)
(编辑 赫 蕾)