Tab.1 Framework for multi-level energy storage collaborative optimization operation

调度层级场站级调度系统级调度 调度目的最大化利用风能资源最小化电力系统运行成本 储能类型风电场内自备电池储能大型电站级抽水蓄能 储能效用平抑风电出力波动、提高风电PFR能力风电消纳、削峰填谷、PFR 两层调度间的关系场站级调度为系统级调度提供风电场的运行边界
摘要 高比例风电的接入使得电力系统调峰及消纳负担加重。为缓解上述压力,火电机组的开机规模通常会缩减,弱化了其在系统运行期间的频率电压支撑能力,致使系统静态电压及小扰动频率失稳风险增加。对此,该文考虑多元储能的协同互补作用,计及频率电压稳定性约束,提出一种多层级储能协同优化运行策略。首先,搭建风电场站级-电力系统级储能协同优化运行框架,据此提出场站级及系统级调度模型构建方法,并将线性化频率电压稳定性约束嵌入系统级调度模型;然后,采用主子问题分解迭代方法求解混合整数二阶锥系统级调度模型,避免直接求解导致的收敛缓慢或内存溢出问题;最后,开展算例分析,结果表明,所提策略能够有效地平抑风电出力波动、提高风电场调频支撑能力,同时可有效兼顾系统运行的经济性与频率电压的稳定性要求。
关键词:静态电压稳定 小扰动频率稳定 多层级储能 主子问题分解迭代 优化调度
能源生产和消费活动是最主要的二氧化碳排放源,大力推动能源领域碳减排,尤其是促进以风电为代表的新能源和清洁能源发展,是实现“碳达峰、碳中和”目标、加快构建现代能源体系的重要举措。近年来,我国风电行业有力应对各类风险挑战,实现了由小到大到强、由跟跑到并跑到领跑的跨越式发展。截至2023年6月底,我国风电累计装机容量达3.89亿kW,已成为推进“双碳”目标的中坚力量。
然而,风电的大规模接入同样为电力系统带来了前所未有的挑战。一方面,风电的反调峰特性与出力波动性,加重了系统的调峰与消纳负担;另一方面,高比例风电挤占传统同步机发电空间,弱化了系统电压支撑、惯性响应、一次调频(Primary Frequency Regulation, PFR)能力,使得系统静态电压稳定(Steady-State Voltage Stability, SSVS)及小扰动频率稳定(Small-Disturbance Frequency Stability, SDFS)的失稳风险增加。为解决上述问题,可从资源与策略两个角度入手。资源层面,在风电场站侧及电力系统侧设置合适的功率型及能量型储能,可缓解系统调控压力;策略层面,在常规日前调度策略中计及SSVS及SDFS约束,可保证系统运行方案远离临界稳定及失稳状态,并留有足额的稳定裕度。双管齐下,可有效地保障系统的安全稳定经济运行。
现阶段,已有学者在计及SSVS及SDFS约束的调度策略领域开展研究。将SSVS约束引入调度模型中,首先应构建表征SSVS裕度的指标,最为常用的是区域负荷有功功率裕度[1]及雅可比矩阵最小奇异值[2]。前者含义为:区域负荷按给定方式增长,得到的系统最大载荷量相对于当前载荷量的增长比例;后者含义为:系统当前潮流雅可比矩阵奇异分解后获得的最小奇异值。在调度领域,负荷裕度[3-5]与奇异值[6-8]均有应用:文献[4]在最优潮流模型中引入负荷裕度约束以保证SSVS,并通过再调度的方式避免了系统载荷量最大时各发电机功角失稳;文献[6]构造了基于雅可比矩阵非奇异的电-气耦合系统SSVS约束,并通过McCormick包络实现约束的凸松弛。然而,上述两种SSVS指标各有局限性。前者需要计算给定调度方案下各时段的最大载荷量,即在min问题中嵌套数量等于调度时段数的max问题,调度模型整体求解难度大。后者的局限性体现为两点:①标准给定的安全负荷裕度下限为8%[1],而最小奇异值目前缺乏权威的参考边界;②调度寻优过程中,当机组达到运行边界时,所在节点类型将改变,雅可比矩阵结构随之改变,导致最小特征值跳变,难以客观地评价电压稳定程度。在计及SSVS约束的调度问题中,需避免或改善上述局限性。
在SDFS方面,文献[9]将频率稳定判据定义为:系统受扰后频率能迅速恢复至额定值附近,既不发生振荡或崩溃,也不长期悬浮于某一过高或过低的数值。在维持SDFS过程中,惯性响应与PFR起主导作用。因此,现有研究主要通过限制在预设扰动、惯性响应、PFR等因素作用下系统的初始频率变化率、最大频差、稳态频差来保障SDFS[10-14]。文献[11]推导了计及火电与新能源调节特性的频率最低点解析式,并将其置入机组组合模型中;文献[12]构造了电-气耦合系统的频率变化率、最低点以及准稳态频率约束,将频率最低点约束替换为其线性充分条件,以实现频率约束体系的混合整数线性化。然而,该方法仍存在一定的局限性:①忽略机组调频死区及功率限幅等非线性控制环节,致使调度求解的频率指标与实际情况存在出入;②仅考核单一扰动方向的频率指标(多为功率突增方向),忽略了机组PFR上调与下调能力的差异性。与SSVS相同,在调度模型计及SDFS约束后,需要处理上述问题。
为缓解系统调峰及消纳压力,提高系统抵御SSVS及SDFS失稳风险的能力,改善现有研究的局限性,本文提出一种计及频率电压稳定性约束的电力系统多层级储能协同优化运行策略。首先,阐述多层级储能协同运行原理,构造含有风电场站级、电力系统级双层调度的优化运行框架;其次,分别构建场站级调度与系统级调度模型,后者计及SSVS与SDFS约束;然后,针对系统级调度模型为大规模混合整数二阶锥规划模型(Mixed-Integer Second- Order Cone Programming, MISOCP)而难以直接求解的问题,提出一种主子问题分解迭代(Master & Sub Problem Decomposition Iteration, MSDI)算法;最后,基于改进IEEE 39节点系统进行算例分析。
多层级储能协同优化运行框架见表1,由风电场站级调度、电力系统级调度两层构成。
电力系统对风电场有出力波动性及PFR的考核要求。对于无自备储能的风电场,若风电出力波动性过大或通过超速、变桨减载等方式提供PFR功能,将导致弃风。通过设置具有快速响应能力的功率型储能可缓解上述问题,本文选取电池储能。场站级调度的任务为:合理地调控风机与电池储能,使得风电场在满足考核要求的同时,最大化场站出力。
表1 多层级储能协同优化运行框架
Tab.1 Framework for multi-level energy storage collaborative optimization operation

调度层级场站级调度系统级调度 调度目的最大化利用风能资源最小化电力系统运行成本 储能类型风电场内自备电池储能大型电站级抽水蓄能 储能效用平抑风电出力波动、提高风电PFR能力风电消纳、削峰填谷、PFR 两层调度间的关系场站级调度为系统级调度提供风电场的运行边界
在高比例风电接入条件下,电力系统的安全稳定运行受到严峻挑战,一方面SSVS、SDFS失稳风险增大,另一方面风电消纳、削峰填谷的需求更为迫切。通过设置具有大规模能量转移及PFR功能的能量型储能可有效地应对上述风险及需求,本文选取抽水蓄能。系统级调度的任务为:合理地调控风电场、抽水蓄能、常规机组等资源,使得系统在满足SSVS及SDFS要求的同时,实现整体运行经济性最优。
风电场站级调度的目标是在上报出力最大化的基础上,尽量由电池储能预留PFR调节空间以满足系统对风电场的PFR考核要求,风机作为补充。具体表示为
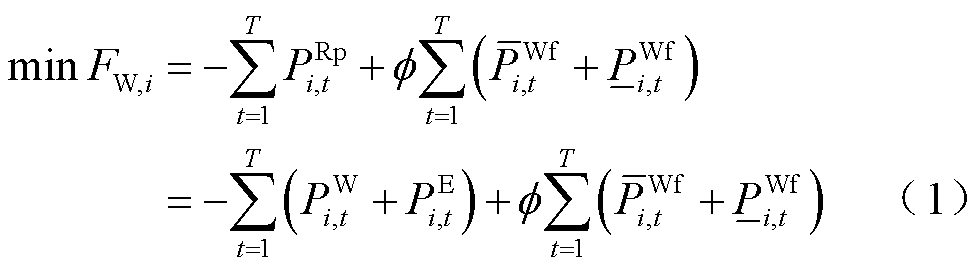
式中,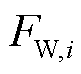 为风电场i的场站级调度目标;T为调度总时段数,本文设置调度步长为15 min,则T=96;
为风电场i的场站级调度目标;T为调度总时段数,本文设置调度步长为15 min,则T=96;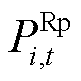 为t时段风电场i向系统上报的计划出力;
为t时段风电场i向系统上报的计划出力;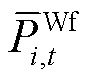 、
、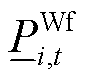 分别为场站内风机的PFR上调、下调空间;
分别为场站内风机的PFR上调、下调空间;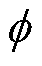 为风机PFR预留空间的惩罚系数;
为风机PFR预留空间的惩罚系数;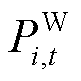 、
、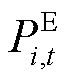 分别为风机、电池储能的场站级调度功率。本文以下角标t代表时段编号,i代表风电场编号,下同。
分别为风机、电池储能的场站级调度功率。本文以下角标t代表时段编号,i代表风电场编号,下同。
约束条件包括风机出力约束、电池储能功率及能量约束、风电场上报出力平滑性约束、风电场PFR预留空间约束,前两项详见文献[14],后两项表示为
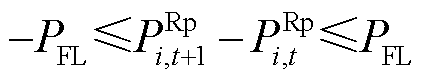 (2)
(2)
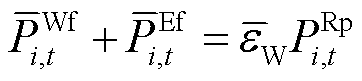 (3)
(3)
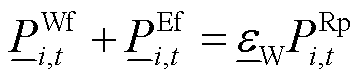 (4)
(4)
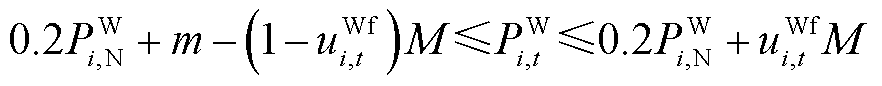 (5)
(5)
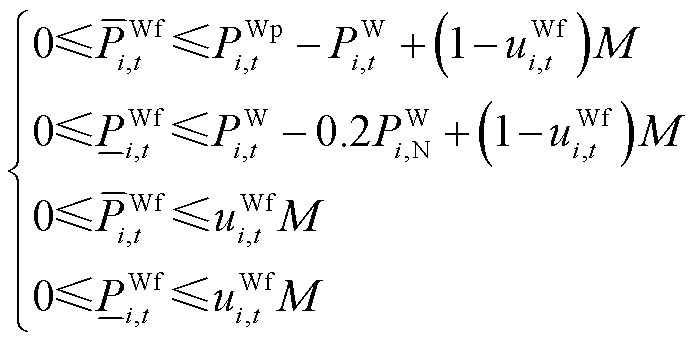 (6)
(6)
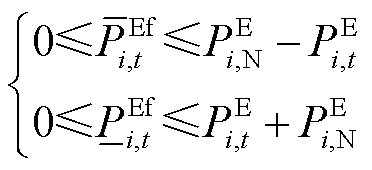 (7)
(7)
式中,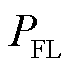 为相邻时段风电场上报出力的变化限值;
为相邻时段风电场上报出力的变化限值;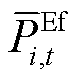 、
、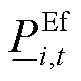 分别为场站内电池储能的PFR上调、下调空间;
分别为场站内电池储能的PFR上调、下调空间;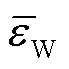 、
、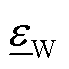 为系统对风电场的PFR限幅要求,本文均取10%[15-16];
为系统对风电场的PFR限幅要求,本文均取10%[15-16];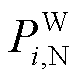 为场站内风机容量;
为场站内风机容量;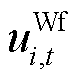 为场站内风机PFR使能状态,当风机场站级调度功率大于20%容量时,可提供PFR功能,
为场站内风机PFR使能状态,当风机场站级调度功率大于20%容量时,可提供PFR功能,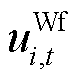 为1,否则为0[15];
为1,否则为0[15];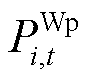 为风机预测功率;
为风机预测功率;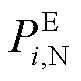 为电池储能额定功率;M、m分别为足够大和足够小的正数。
为电池储能额定功率;M、m分别为足够大和足够小的正数。
系统级调度以经济性最优为目标,表示为
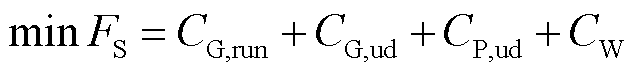 (8)
(8)
式中,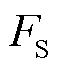 为系统级调度目标;
为系统级调度目标;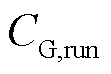 、
、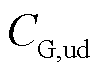 分别为火电机组运行及起停成本;
分别为火电机组运行及起停成本;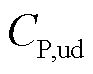 为抽水蓄能机组起停成本;
为抽水蓄能机组起停成本;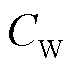 为弃风惩罚成本。各项成本具体表示为
为弃风惩罚成本。各项成本具体表示为
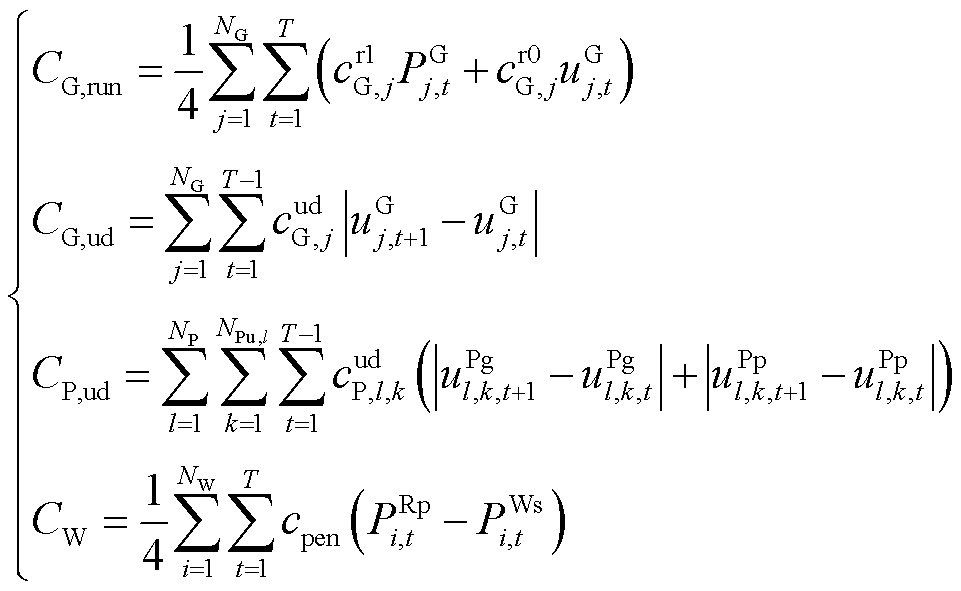 (9)
(9)
式中,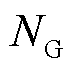 、
、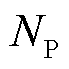 、
、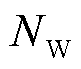 分别为系统内火电机组、抽水蓄能电站、风电场的数量;
分别为系统内火电机组、抽水蓄能电站、风电场的数量;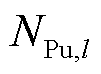 为抽水蓄能电站l内的机组数量;
为抽水蓄能电站l内的机组数量;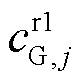 、
、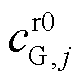 及
及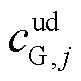 分别为火电机组j运行及起停成本系数;
分别为火电机组j运行及起停成本系数;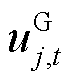 、
、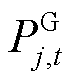 分别为火电机组j运行状态及出力,运行时
分别为火电机组j运行状态及出力,运行时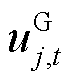 为1,停机为0;
为1,停机为0;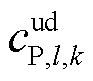 为抽水蓄能机组起停成本系数;
为抽水蓄能机组起停成本系数;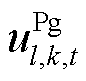 、
、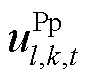 分别为抽水蓄能机组的发电及抽水状态,发电时
分别为抽水蓄能机组的发电及抽水状态,发电时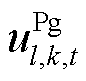 为1,而
为1,而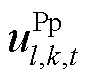 为0,抽水时相反,停机时均为0,二者不同时为1;
为0,抽水时相反,停机时均为0,二者不同时为1;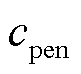 为弃风惩罚成本系数;
为弃风惩罚成本系数;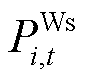 为风电场系统级调度出力。本文以下角标j代表火电机组编号,l代表抽水蓄能电站编号,k代表抽水蓄能电站内机组编号,下同。
为风电场系统级调度出力。本文以下角标j代表火电机组编号,l代表抽水蓄能电站编号,k代表抽水蓄能电站内机组编号,下同。
常规约束是指除SSVS、SDFS约束之外的系统级约束,包括火电机组运行约束[17-18](有功及无功出力约束、起停时间约束、爬坡率约束),风电场运行约束(有功[18]及无功出力约束),抽水蓄能运行约束(状态约束[18]、功率约束、上水库水量约束[18]、起停机次数约束),系统运行约束(节点电压约束[17]、线路功率约束[17]、节点功率平衡约束[17]、备用约束[14]、支路功率形式的改进直流潮流约束[19])。其中,注有参考文献的不再赘述,其他约束描述如下。
1)风电场无功出力约束
假设风电场内变流器、无功补偿装置等无功电源整体面向系统的功率因数在超前0.95至滞后0.95范围内动态可调[15],则无功出力约束为
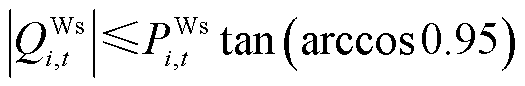 (10)
(10)
式中,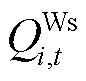 为风电场无功出力。
为风电场无功出力。
2)抽水蓄能功率约束
本文讨论的是封闭式抽水蓄能电站,不考虑上游水源对上水库补充水量的情况,以及下水库释放水量至下游水电站进行发电的情况,其机组均为全功率型变速抽水蓄能机组。此类机组通过全功率变流器并网,在水轮机工况与水泵工况下均能提供可调有功及无功功率,在静止工况下变流器还可充当静止同步补偿器[20]。假设抽水蓄能机组额定发电功率与额定抽水功率相同,变流器容量略高于发电电动机容量,以使抽水蓄能机组在额定功率下,功率因数在超前0.95至滞后0.95范围内动态可调,则机组四象限运行示意图如图1所示。
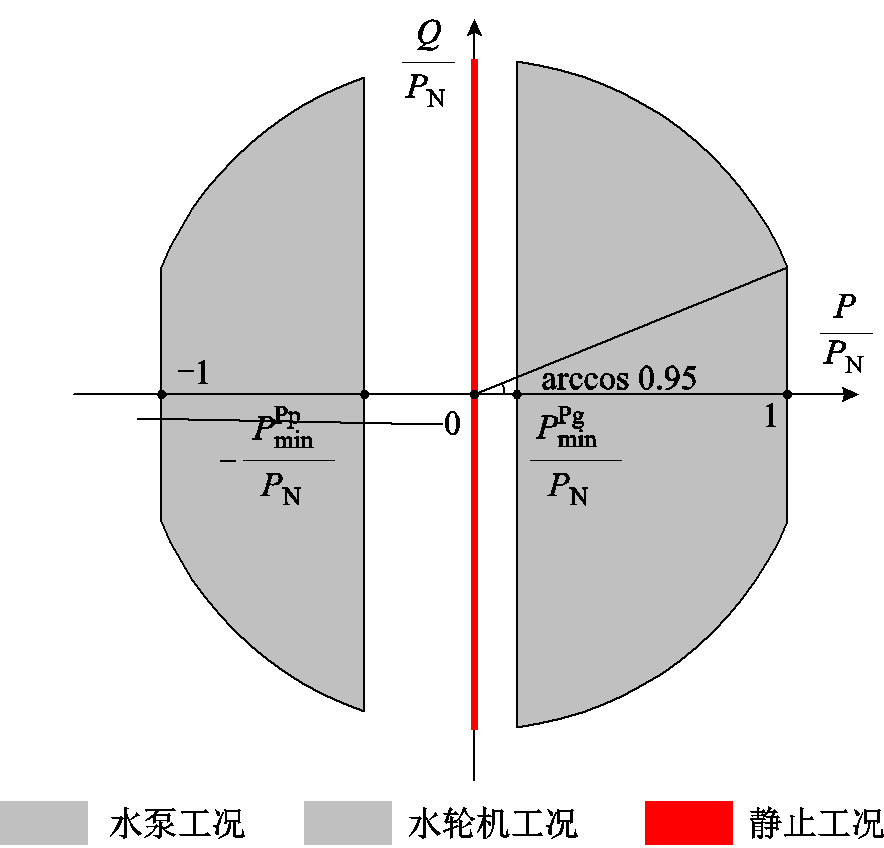
图1 抽水蓄能机组四象限运行示意图
Fig.1 Four quadrant operation diagram of pumped storage
根据图1,可得抽水蓄能机组功率约束为
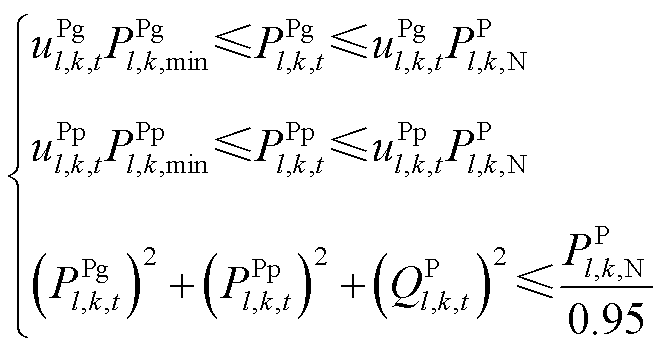 (11)
(11)
式中,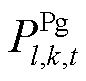 、
、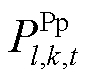 分别为机组发电及抽水功率;
分别为机组发电及抽水功率;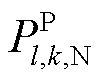 、
、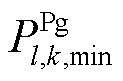 及
及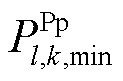 分别为机组额定功率、最小发电及抽水功率;
分别为机组额定功率、最小发电及抽水功率;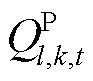 为机组无功功率。
为机组无功功率。
3)抽水蓄能起停机次数约束
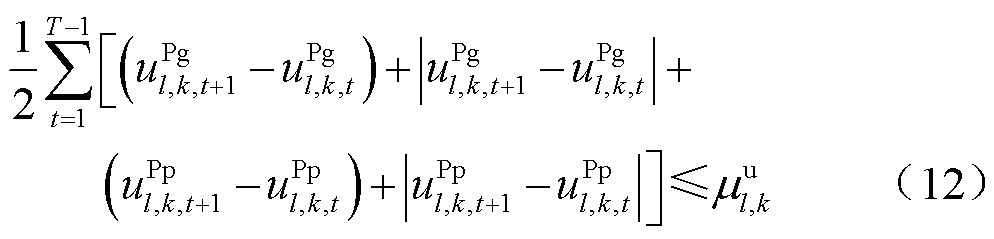
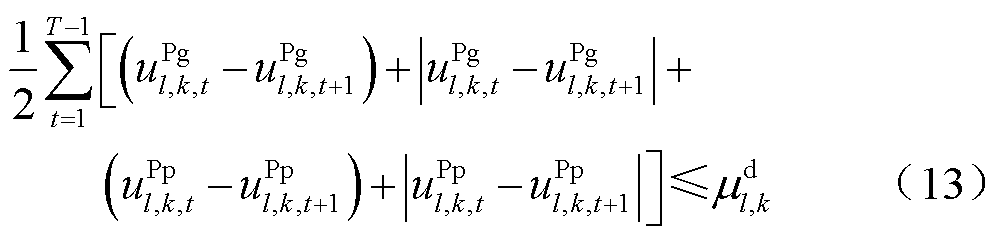
式中,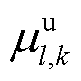 、
、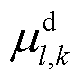 分别为机组起、停机次数上限。
分别为机组起、停机次数上限。
本文以区域负荷有功功率裕度作为评价系统SSVS的指标。假设负荷增长方式为各节点负荷比例及功率因数不变,增加系统有功负荷总量。系统对裕度的要求是大于8%[1],则SSVS约束为
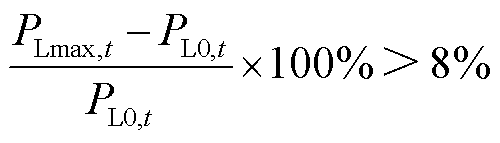 (14)
(14)
式中,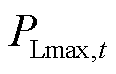 、
、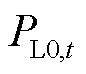 分别为t时段系统最大载荷量及实际负荷。
分别为t时段系统最大载荷量及实际负荷。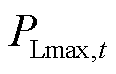 是通过求解以系统负荷最大为目标、潮流及功率平衡约束为边界的优化问题得到的。若将式(14)嵌入系统级调度模型,将显著提升求解复杂度,因此本文不直接使用式(14),而是采用校核方式实现系统SSVS。
是通过求解以系统负荷最大为目标、潮流及功率平衡约束为边界的优化问题得到的。若将式(14)嵌入系统级调度模型,将显著提升求解复杂度,因此本文不直接使用式(14),而是采用校核方式实现系统SSVS。
图2展示了采用连续潮流法绘制的系统典型P-V曲线[1,21]。随着负荷增长,系统电压不断逼近当前运行方式下的鞍结分岔(Saddle-Node Bifurcation, SNB)点或极限诱导分岔(Limit Induced Bifurcation, LIB)点,达到分岔点后继续增加负荷,则会导致电压崩溃,潮流无解。因此,若系统潮流在1.08倍实际负荷的条件下有解,则说明该负荷点未达到SNB点或LIB点,负荷裕度至少为8%。从而,系统最大载荷量求解问题可转换为1.08倍实际负荷条件下的潮流可解校核问题。后者包括火电机组*及风电场出力约束,抽水蓄能状态、功率、上水库水量*约束,节点电压约束*,线路功率约束,潮流约束*,节点功率平衡约束*等,本文重点介绍注有*角标的约束,其他约束可从常规约束或*角标约束类比。
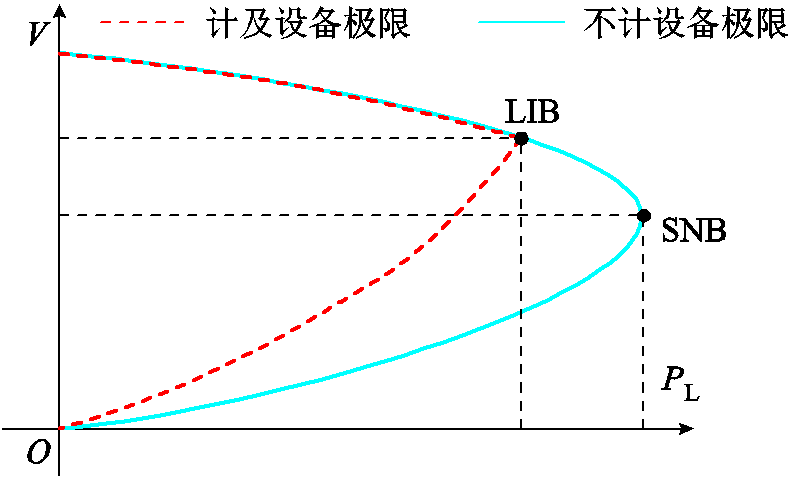
图2 P-V曲线
Fig.2 P-V curves
1)火电机组出力约束
SSVS校核中,火电机组运行状态继承常规约束的取值,出力可自由调节,表示为
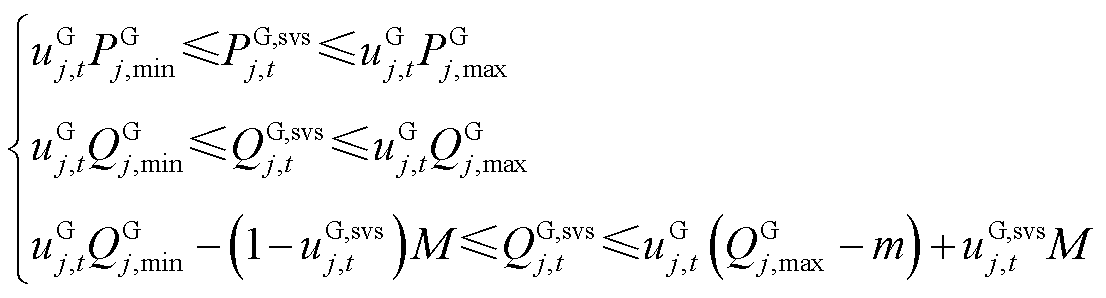 (15)
(15)
式中,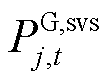 、
、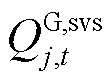 分别为SSVS校核中的火电有功及无功出力;
分别为SSVS校核中的火电有功及无功出力;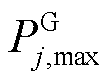 及
及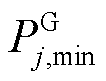 、
、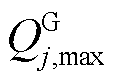 及
及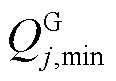 分别为火电有功、无功出力边界;
分别为火电有功、无功出力边界;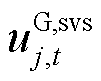 为SSVS校核中的火电无功指示状态,达到上限时为1,否则为0。
为SSVS校核中的火电无功指示状态,达到上限时为1,否则为0。
2)抽水蓄能上水库水量约束
SSVS校核中,抽水蓄能电站上水库水量继承常规约束的取值,机组状态及功率均可自由调节,但功率受限于上水库当前剩余水量,表示为
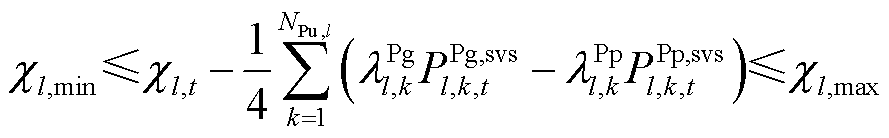 (16)
(16)
式中,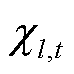 、
、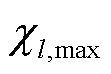 、
、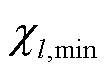 分别为抽水蓄能电站上水库水量及其边界;
分别为抽水蓄能电站上水库水量及其边界;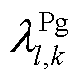 、
、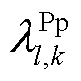 分别为水轮机、水泵工况下的抽水蓄能机组水电转换系数;
分别为水轮机、水泵工况下的抽水蓄能机组水电转换系数;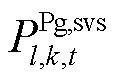 、
、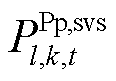 分别为SSVS校核中的抽水蓄能机组发电、抽水功率。
分别为SSVS校核中的抽水蓄能机组发电、抽水功率。
3)节点电压约束
常规约束中,节点电压标幺值被限制在[0.95(pu), 1.05(pu)]内。SSVS校核中,负荷增长将导致静态电压下降。本文根据节点所接设备类型设置电压下限:①火电节点,机组运行且无功未达到上限时,电压下限取0.95(pu),无功达到上限或机组停运时取0.8(pu)[21-22];②风电场或抽水蓄能电站节点,为避免电压超出低穿边界导致设备脱网,电压下限取0.9(pu)[15,23];③纯负荷节点或连接节点,电压下限取0.8(pu)[24]。
4)潮流约束
常规约束中,节点电压幅值维持在1(pu)附近,线路两端相位差近似为0,可采用支路功率形式的改进直流潮流。SSVS校核中,节点电压明显偏离额定值,直流潮流假设条件不成立。因此,本文采用基于二阶锥松弛的交流潮流,详见文献[25]。
5)节点功率平衡约束
常规约束中,节点电压幅值维持在1(pu)附近,无需考虑负荷的静态电压特性。SSVS校核中,节点电压明显偏离额定值,负荷应采用ZIP模型[26]。由于ZIP模型中恒定电流部分是节点电压的一次项,而交流潮流中电压变量以二次项形式出现[25],因此本文在电压[0.8(pu), 1.05(pu)]范围内采用最小二乘法消除恒定电流部分,将负荷静态电压特性从a2V2+ a1V+a0(a2+a1+a0=1)形式简化为b2V2+b0(b2+b0=1)。
本文主要通过约束预想功率扰动场景下系统的初始频率变化率、最大频差、稳态频差来保障SDFS。预想扰动场景包括由负荷及风电随机性导致的功率突增和突减场景,两类场景具有相似性和对称性,因此重点介绍功率突增场景的SDFS约束。
构造SDFS约束首先应构建系统小扰动动态频率响应模型。参考文献[14],构建模型如图3所示。图中,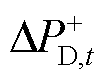 为功率突增扰动阶跃函数;
为功率突增扰动阶跃函数;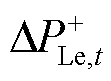 、
、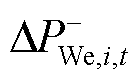 分别为负荷增及风电减方向的预测误差;
分别为负荷增及风电减方向的预测误差;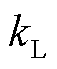 为负荷频率响应系数;
为负荷频率响应系数;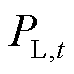 为负荷预测值;
为负荷预测值;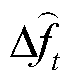 为系统频差,上标
为系统频差,上标 代表标幺值,下同。
代表标幺值,下同。
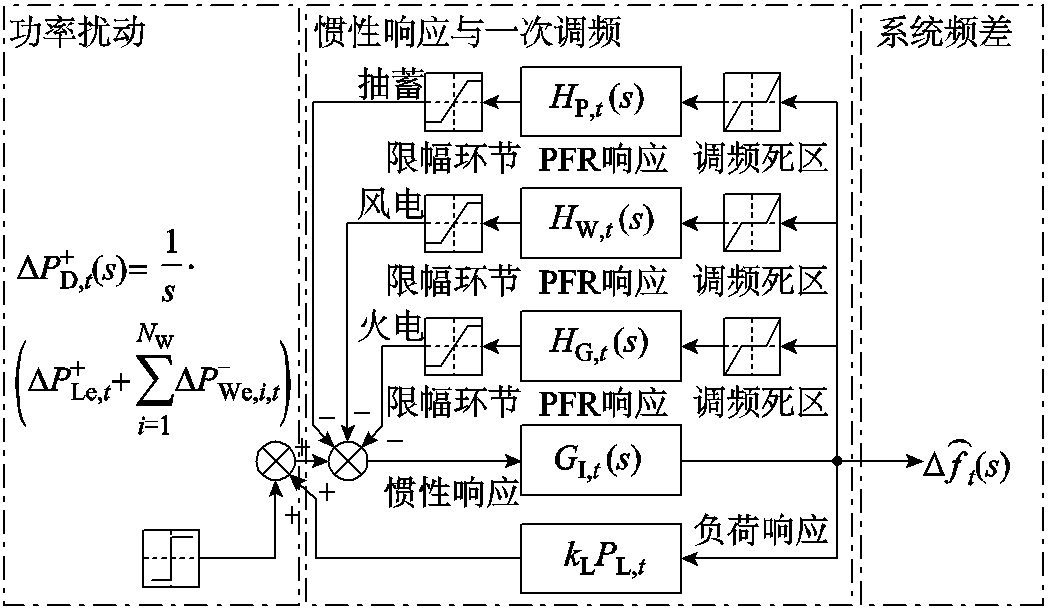
图3 系统动态频率响应模型(t时段)
Fig.3 Dynamic frequency response model of power system (time interval t)
图3中PFR及惯性响应环节分别表示为
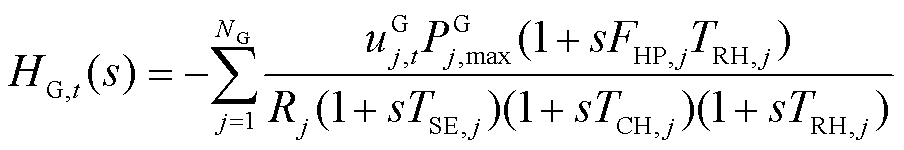 (17)
(17)
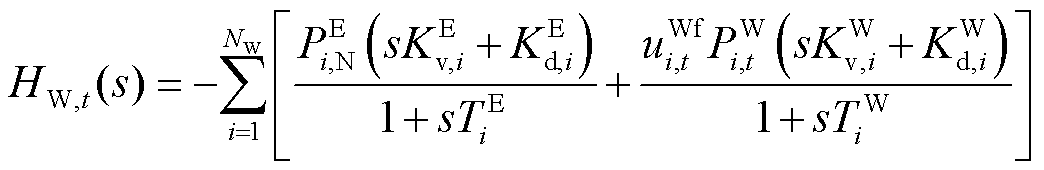 (18)
(18)
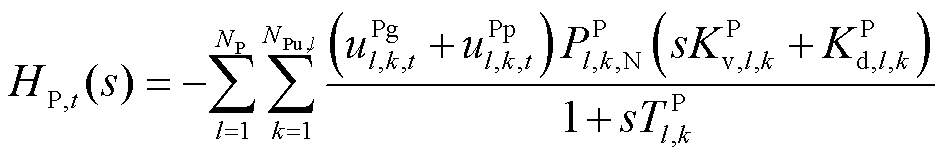 (19)
(19)
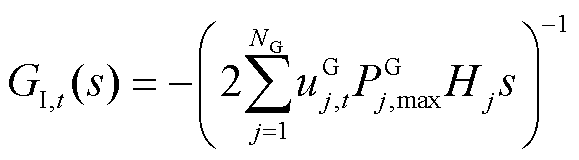 (20)
(20)
式中,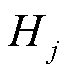 、
、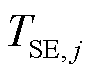 、
、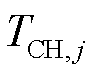 、
、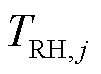 分别为火电机组惯性、伺服、高压缸前汽室容积、再热器容积时间常数;
分别为火电机组惯性、伺服、高压缸前汽室容积、再热器容积时间常数;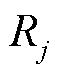 、
、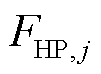 分别为火电机组调差系数及高压缸输出功率占比;
分别为火电机组调差系数及高压缸输出功率占比;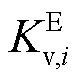 、
、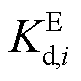 、
、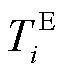 分别为风电场内电池储能的虚拟惯量系数、频率下垂系数、变流器时间常数;
分别为风电场内电池储能的虚拟惯量系数、频率下垂系数、变流器时间常数;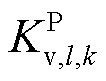 、
、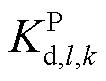 、
、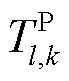 及
及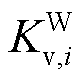 、
、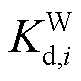 、
、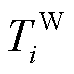 与上述参数含义相同,分别对应于抽水蓄能机组及风电场内风机。
与上述参数含义相同,分别对应于抽水蓄能机组及风电场内风机。
由于调频死区与限幅环节的存在,无法直接通过Laplace反变换得出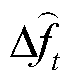 的时域解析式,需要对两环节进行省略。即便如此,省略后获得的最大频差仍为非线性[14],直接嵌入系统级调度会显著提升求解复杂度。对此,本文基于简化调频死区、松弛功率限幅的思路,给出一种新的SDFS约束构造方法。其中初始频率变化率、最大频差约束通过差分方程实现,稳态频差约束通过终值定理实现,具体如下。
的时域解析式,需要对两环节进行省略。即便如此,省略后获得的最大频差仍为非线性[14],直接嵌入系统级调度会显著提升求解复杂度。对此,本文基于简化调频死区、松弛功率限幅的思路,给出一种新的SDFS约束构造方法。其中初始频率变化率、最大频差约束通过差分方程实现,稳态频差约束通过终值定理实现,具体如下。
1)初始频率变化率、最大频差约束
系统受扰后通常在10 s内达到最大频差,时间尺度较小,适合采用差分方程构造线性化约束。
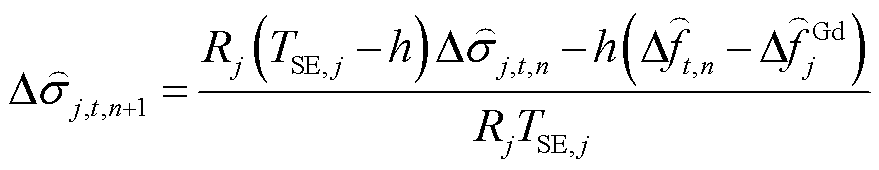 (21)
(21)
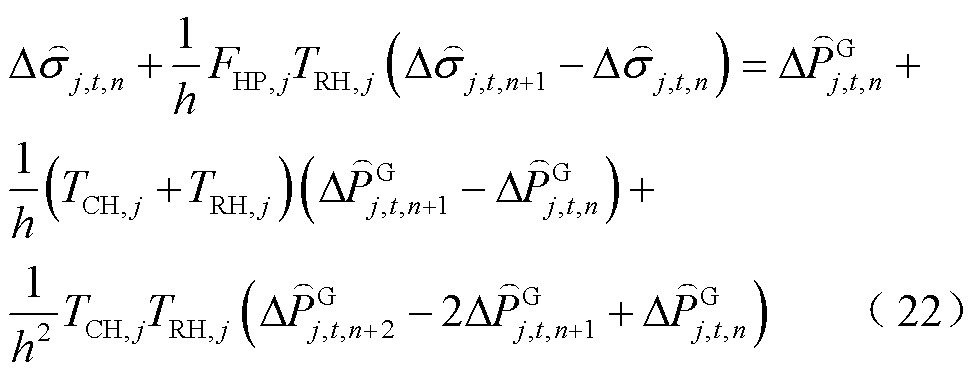
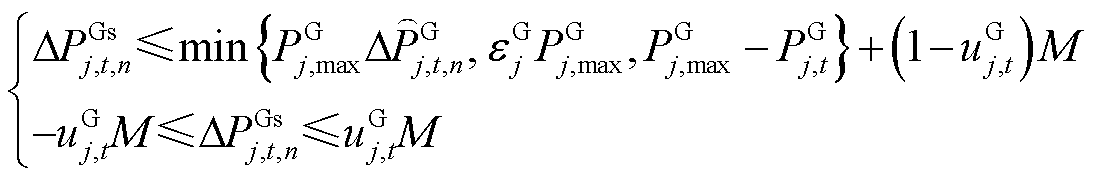 (23)
(23)
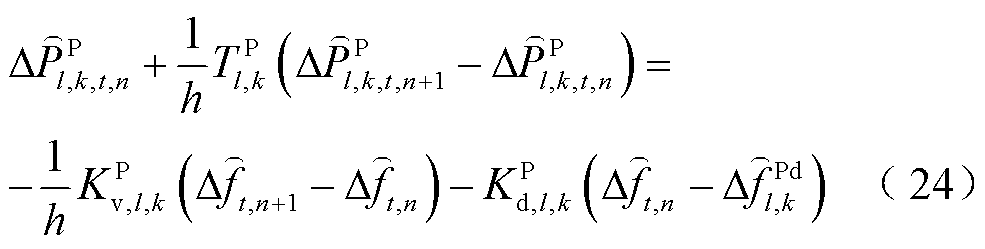
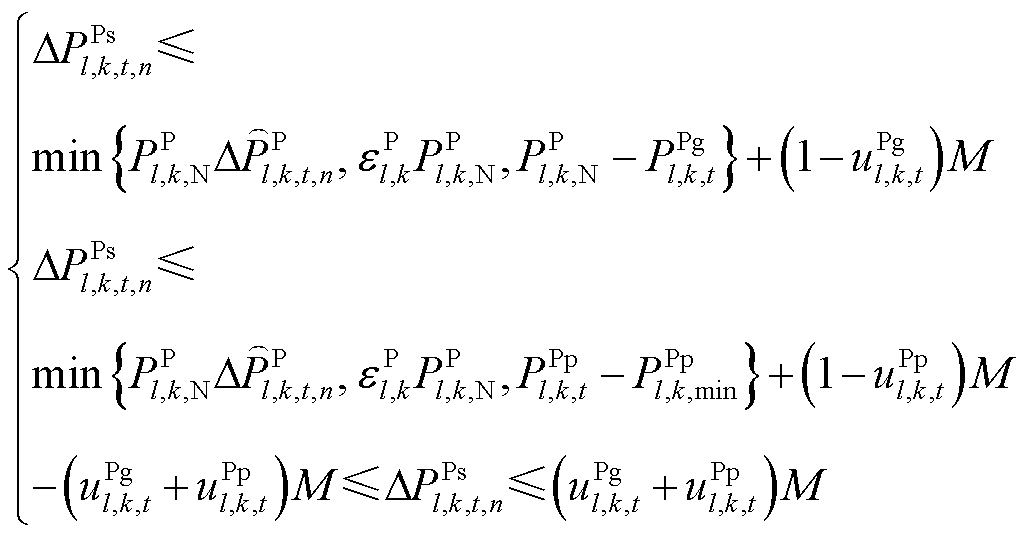 (25)
(25)
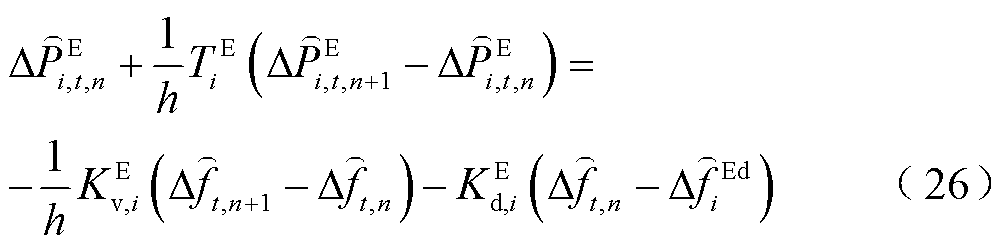
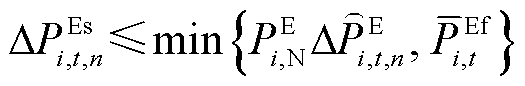 (27)
(27)
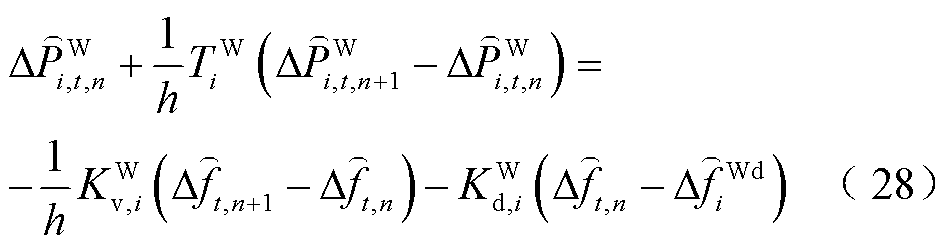
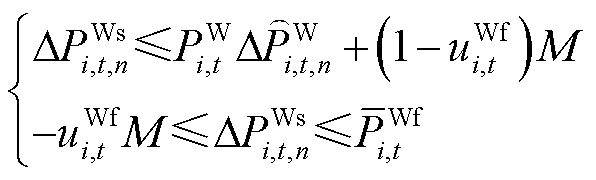 (29)
(29)
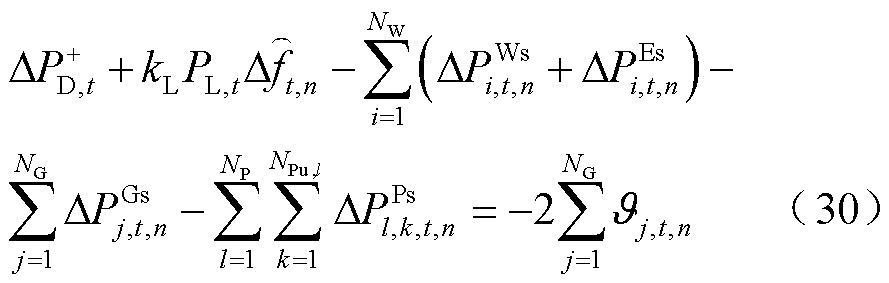
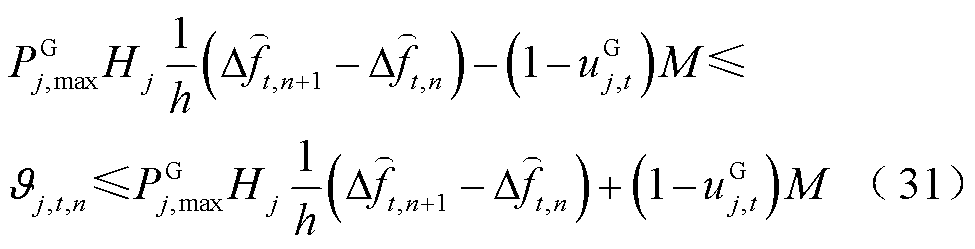
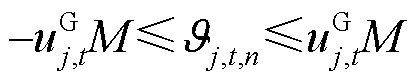 (32)
(32)
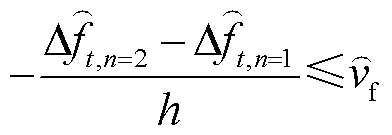 (33)
(33)
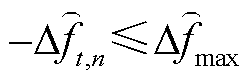 (34)
(34)
式中,h为差分步长;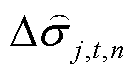 为火电机组高压调节汽阀阀组等效开度变化量,其中n为差分时步编号,下同;
为火电机组高压调节汽阀阀组等效开度变化量,其中n为差分时步编号,下同;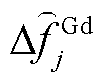 、
、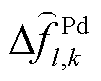 、
、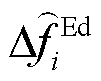 及
及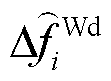 分别为火电机组、抽水蓄能机组、风电场内电池储能及风机的调频死区下界;
分别为火电机组、抽水蓄能机组、风电场内电池储能及风机的调频死区下界;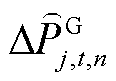 、
、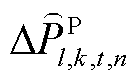 、
、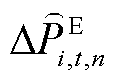 及
及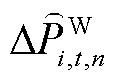 分别为未经限幅作用的火电机组、抽水蓄能机组、风电场内电池储能及风机的PFR调节功率;
分别为未经限幅作用的火电机组、抽水蓄能机组、风电场内电池储能及风机的PFR调节功率;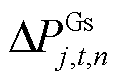 、
、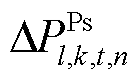 、
、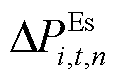 及
及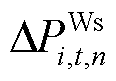 分别为经过限幅作用的火电机组、抽水蓄能机组、风电场内电池储能及风机的PFR调节功率松弛变量;
分别为经过限幅作用的火电机组、抽水蓄能机组、风电场内电池储能及风机的PFR调节功率松弛变量;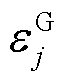 、
、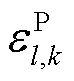 分别为火电及抽水蓄能机组的功率限幅比例;
分别为火电及抽水蓄能机组的功率限幅比例;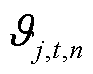 为火电惯量辅助变量,以避免机组状态与频差相乘;
为火电惯量辅助变量,以避免机组状态与频差相乘;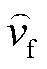 、
、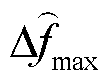 分别为初始频率变化率、最大频差限值。
分别为初始频率变化率、最大频差限值。
式(21)~式(32)与图3的对应关系为:式(21)~式(23)为火电机组PFR环节;式(24)、式(25)为抽水蓄能机组PFR环节;式(26)~式(29)为风电场PFR环节;式(30)~式(32)为负荷及惯性响应环节。
式(21)中,调频死区被线性化为频差超出死区的部分,即从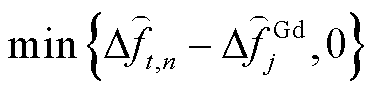 线性化为
线性化为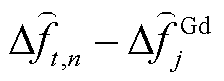 ,这在扰动量较大以至于频差必然超过各机组调频死区的条件下引起的误差很小,具体分析详见附录3。
,这在扰动量较大以至于频差必然超过各机组调频死区的条件下引起的误差很小,具体分析详见附录3。
式(23)中,功率限幅的原始形式为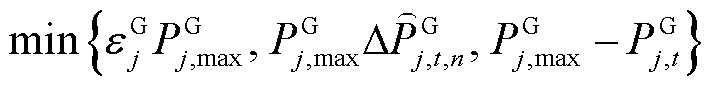 ,此处采用松弛变量
,此处采用松弛变量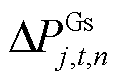 消除非线性。在突增场景下,各机组将提供上调功率,如果系统在不高于限幅边界的
消除非线性。在突增场景下,各机组将提供上调功率,如果系统在不高于限幅边界的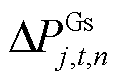 处满足式(33)、式(34)约束,那么实际限幅环节输出的上调功率也必定满足。此外,
处满足式(33)、式(34)约束,那么实际限幅环节输出的上调功率也必定满足。此外,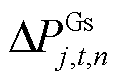 的引入,一方面将使得按式(33)、式(34)计算所得的初始频率变化率及最大频差绝对值略大于或等于实际绝对值;另一方面将使得差分时序递推关系出现断裂,导致
的引入,一方面将使得按式(33)、式(34)计算所得的初始频率变化率及最大频差绝对值略大于或等于实际绝对值;另一方面将使得差分时序递推关系出现断裂,导致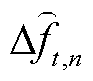 的差分时序曲线出现锯齿。对此,本文将频差惩罚项引入目标函数,即
的差分时序曲线出现锯齿。对此,本文将频差惩罚项引入目标函数,即
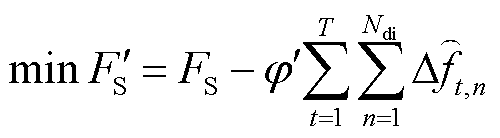 (35)
(35)
式中,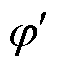 为差分频差惩罚系数;
为差分频差惩罚系数;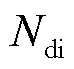 为差分总时步数。如此处理后,理论上将使得
为差分总时步数。如此处理后,理论上将使得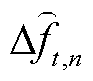 的绝对值在系统可用PFR调节资源下达到最小,促使
的绝对值在系统可用PFR调节资源下达到最小,促使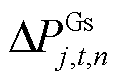 等于限幅边界,进而消除按式(33)、式(34)计算所得的初始频率变化率及最大频差绝对值与实际绝对值之间的误差。应当指出,引入频差惩罚项不应动摇经济性目标的首要地位。
等于限幅边界,进而消除按式(33)、式(34)计算所得的初始频率变化率及最大频差绝对值与实际绝对值之间的误差。应当指出,引入频差惩罚项不应动摇经济性目标的首要地位。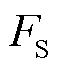 的数量级通常为106,若按
的数量级通常为106,若按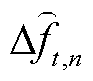 =-0.01、
=-0.01、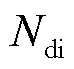 =1 001(差分总时长及步长分别为10 s、0.01 s)计算,则
=1 001(差分总时长及步长分别为10 s、0.01 s)计算,则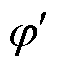 推荐取值为10-3。
推荐取值为10-3。
死区与限幅分析虽然是基于火电机组开展的,但对于抽水蓄能机组、风电场内风机及电池储能均成立。
2)稳态频差约束
系统受扰后再次达到稳态的用时通常超过30 s,时间尺度较大,如果采用差分方程构造稳态频差约束,则会大幅加重系统级调度模型的求解负担。对此,本文利用终值定理构造线性化稳态频差约束。
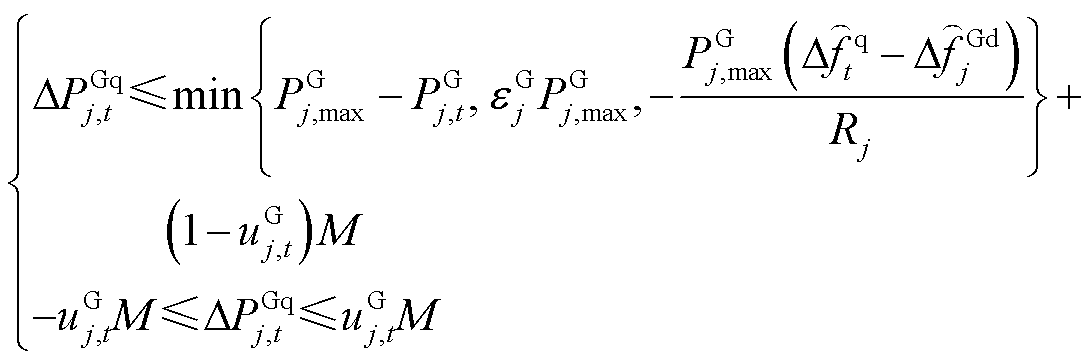 (36)
(36)
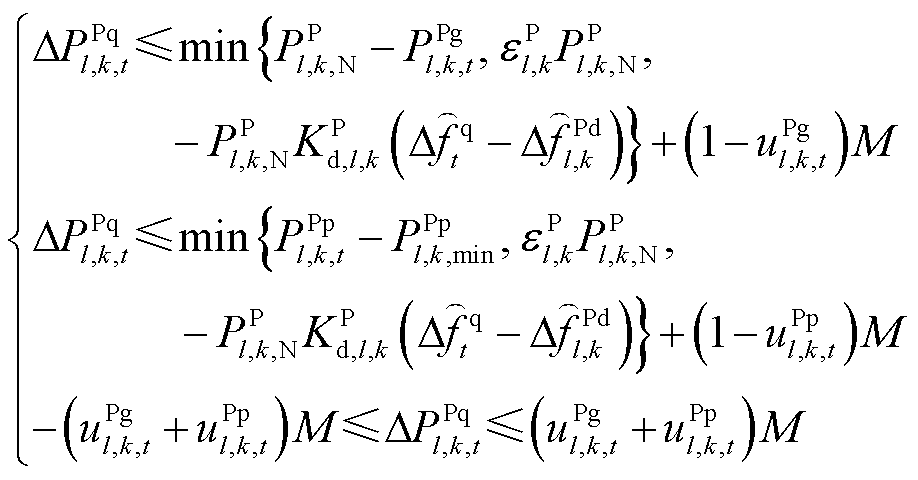 (37)
(37)
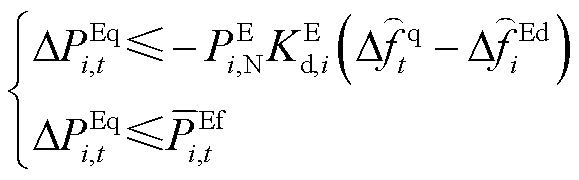 (38)
(38)
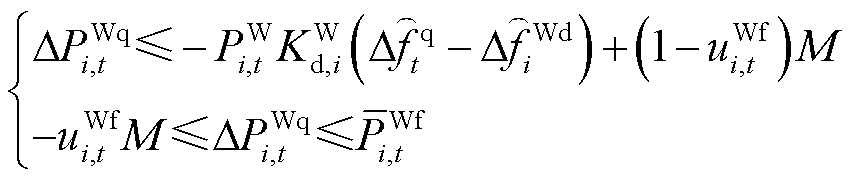 (39)
(39)
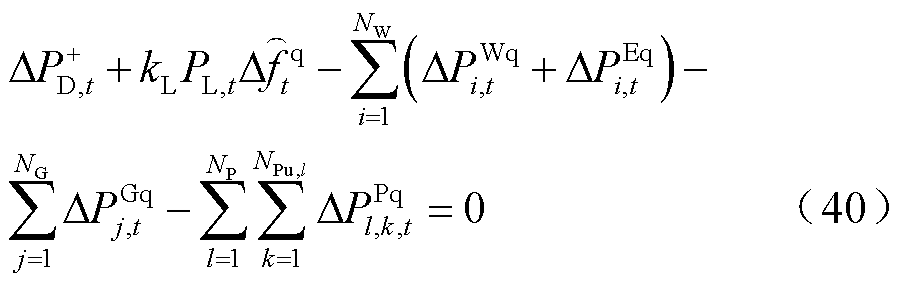
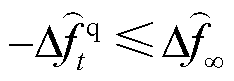 (41)
(41)
式中,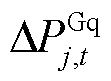 、
、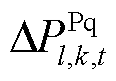 、
、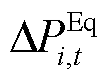 及
及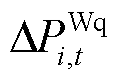 分别为火电机组、抽水蓄能机组、风电场内电池储能及风机的稳态PFR调节功率松弛变量;
分别为火电机组、抽水蓄能机组、风电场内电池储能及风机的稳态PFR调节功率松弛变量;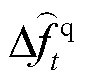 、
、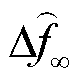 分别为稳态频差及其限值。式(36)~式(39)中,首行约束右侧均为终值定理计算结果;式(40)为系统达到稳态频差的条件,即图3的惯性响应环节输入为0。
分别为稳态频差及其限值。式(36)~式(39)中,首行约束右侧均为终值定理计算结果;式(40)为系统达到稳态频差的条件,即图3的惯性响应环节输入为0。
由于使用了松弛变量,仍需要引入频差惩罚项,即
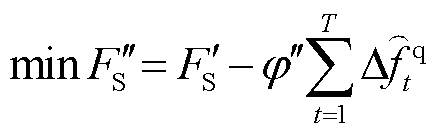 (42)
(42)
式中,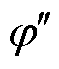 为稳态频差惩罚系数。为保证经济性优先,若按
为稳态频差惩罚系数。为保证经济性优先,若按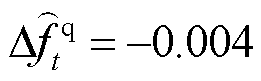 计算,则
计算,则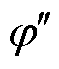 推荐取值为1。
推荐取值为1。
由于大量布尔变量及SSVS校核中交流潮流的存在,系统级调度模型为大规模MISOCP模型,难以一次性完成求解。本文将原调度问题拆分为四部分:只包含常规约束及稳态频差约束的系统级调度主问题(MP)、SSVS约束校核子问题(SP1)、功率突增及突减场景的差分频差约束校核子问题(SP2及SP3),MP与SP1~SP3交互迭代实现模型求解。由于SP1~SP3均为非凸问题,无法直接套用benders分解[27]、列与约束生成(Column-and-Constraint Generation, C&CG)[28-29]等经典算法。借鉴上述算法思想,提出一种适用于所建模型的MSDI算法,其数学模型详见附录1,下面重点介绍算法原理及求解流程。
在任意一次迭代中,MP首先求解,得到各调控资源的运行计划。之后,将求解结果传递至SP1~SP3,校核给定运行计划下的SSVS约束、初始频率变化率及最大频差约束的越限情况。由于SP1~SP3具有时间解耦性,即各时段的校核互不干涉,故SP1~SP3可多时段并行计算。若某时段SP1校核为越限,则向MP增补该时段的SP1修正约束,调整MP可行域边界,引导MP向满足SSVS约束的方向求解,SP2、SP3同理。待所有时段的SP1~SP3均完成校核并向MP增补修正约束后,则开始新一次迭代。若所有时段的SP1~SP3校核结果均未越限,则停止迭代,输出本次迭代中MP的求解结果。MSDI算法流程如图4所示。
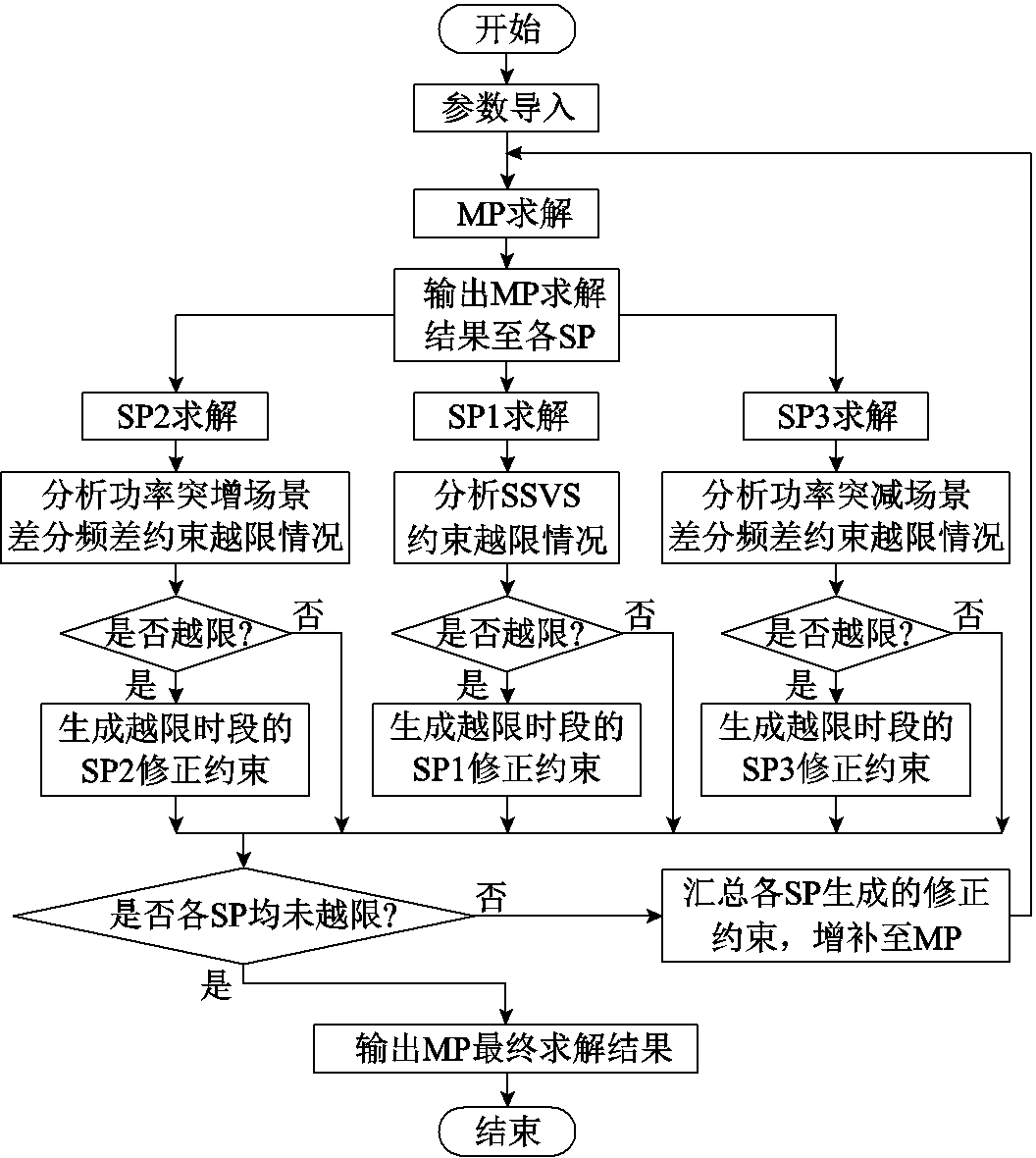
图4 MSDI算法流程
Fig.4 MSDI algorithm flow chart
本文基于改进IEEE 39节点系统开展算例分析,系统内有8个火电机组、2个风电场、1个抽水蓄能电站(包含2个抽水蓄能机组)。系统拓扑、负荷及风电预测结果、设备及系统参数见附录2,附图2中负荷及风电的增、减方向预测误差大小相同。
对2个风电场W1、W2开展场站级调度,结果如图5~图7所示。
由图5可知,为满足出力波动性及PFR考核要求,电池储能动作频繁。受限于储能容量上限以及能量转换效率,风电场上报出力有所损失,W1、W2损失率分别为0.84%、0.59%,在可接受范围内。
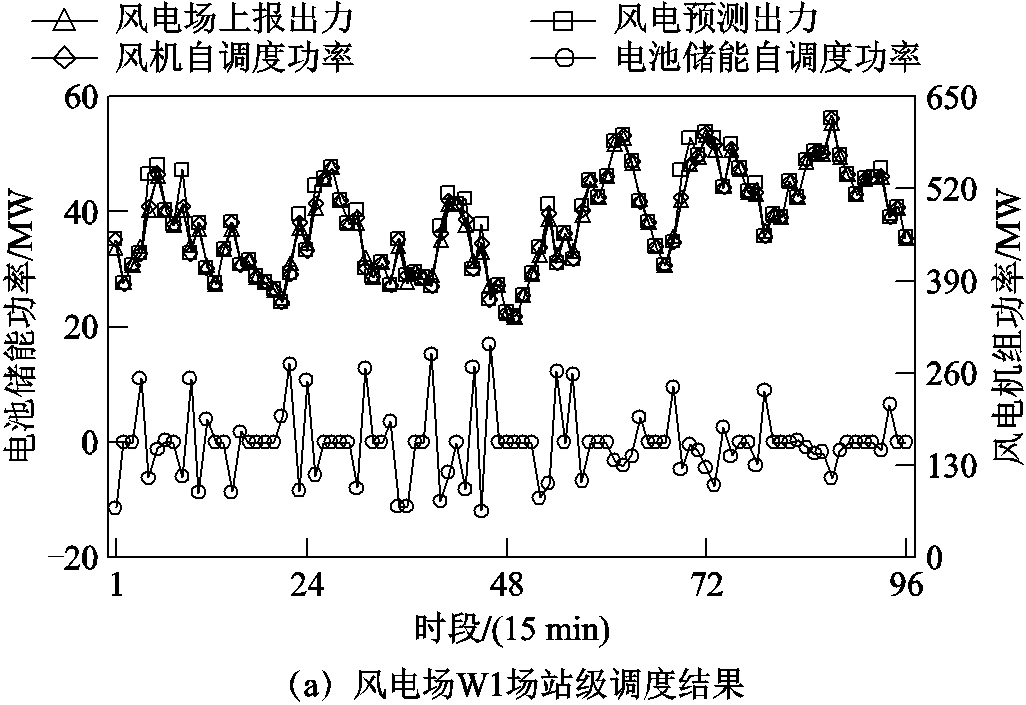
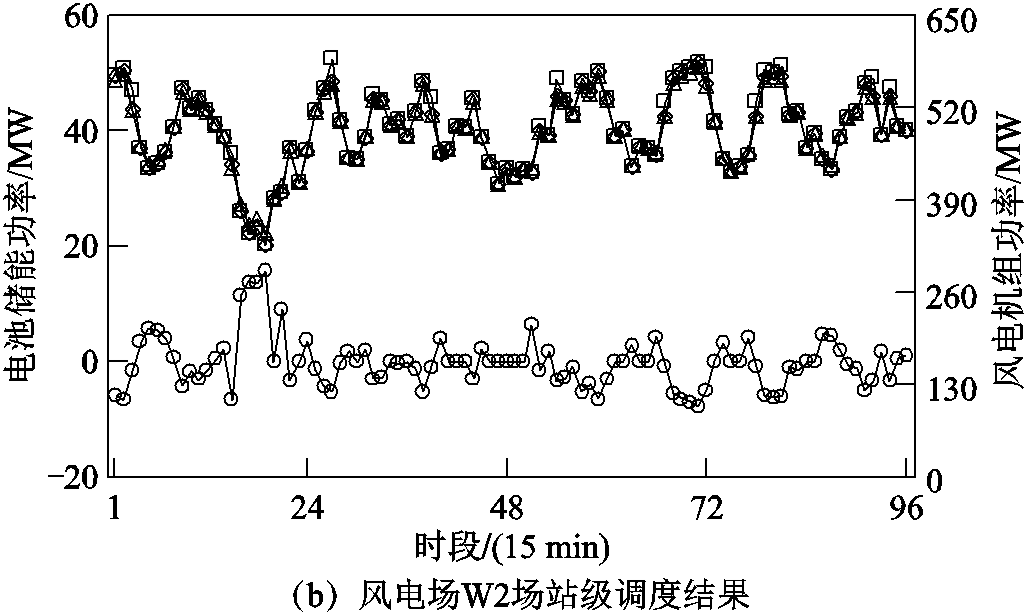
图5 风电场站级调度出力
Fig.5 Station level dispatch output of wind farms
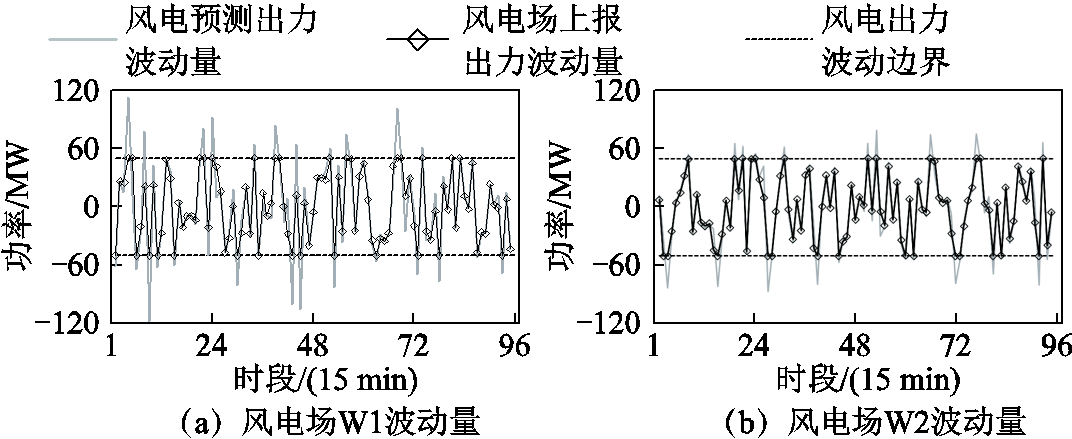
图6 风电场站级调度出力波动量
Fig.6 Station level dispatch output fluctuation of wind farms
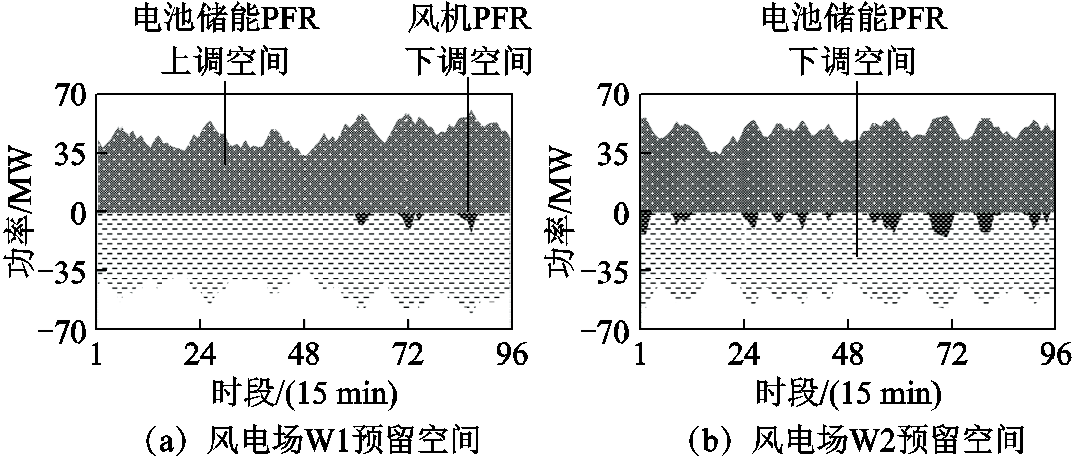
图7 风电场PFR预留空间
Fig.7 Reserved power space for wind farms PFR
由图6可知,电池储能可有效吸收或填补风电预测出力的上波动冗余能量或下波动缺额能量,从而将风电场上报出力波动限制在考核要求范围内。
由图7可知,通过吸纳风机过剩能量,电池储能获得PFR上调能力,从而实现过剩能量在时间尺度上的分散转移,避免风机预留PFR上调空间造成弃风。在PFR下调方向,当且仅当电池储能预留空间不足以达到系统考核要求时,风机补充下调备用,从而尽可能避免风机PFR减出力造成弃风。
为验证所提系统级调度策略的有效性,设计算例EP1,包含四组场景:场景A考虑SSVS、SDFS约束;场景B、C分别仅考虑SSVS约束、SDFS约束;场景D两类约束都不考虑。调度结果如表2及图8~图12所示。
表2 各场景成本
Tab.2 Cost of each scenes

场景编号火电机组运行成本/$火电机组起停成本/$抽水蓄能起停成本/$弃风惩罚成本/$总成本/$ A738 496.674 9002 4000745 796.67 B717 099.814 9001 2000723 199.81 C737 663.443 1002 4000743 163.44 D716 347.733 1001 2000720 647.73
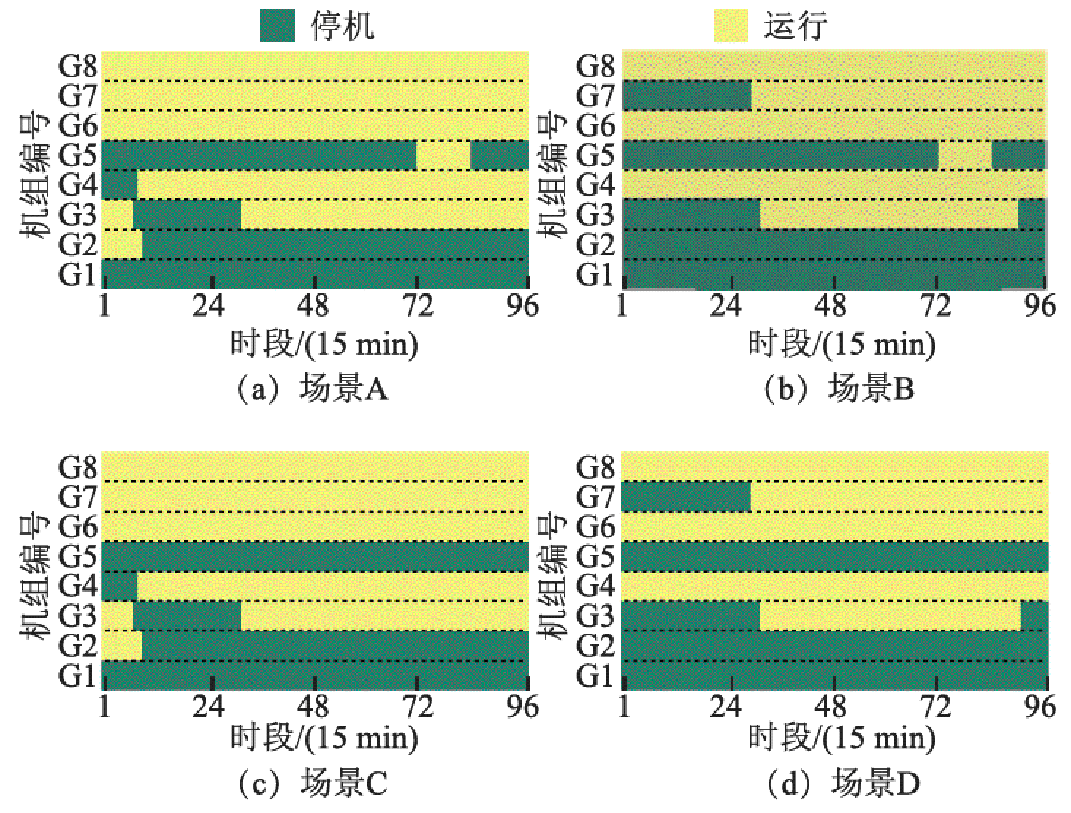
图8 火电机组起停状态
Fig.8 Startup and shutdown status of thermal power units
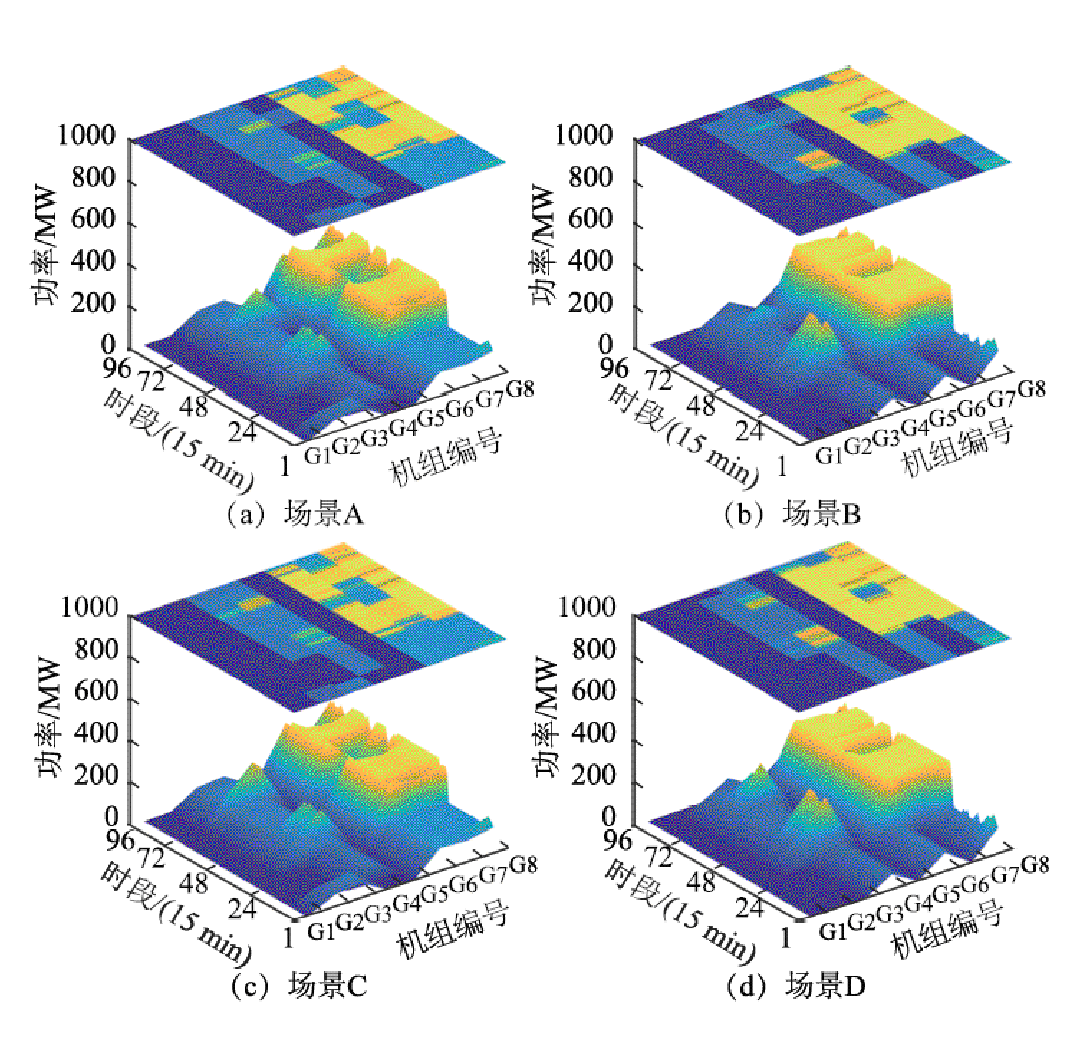
图9 火电机组出力计划
Fig.9 Output plan of thermal power units
由表2可知,场景A~C相对于D的成本提升比例分别为3.49%、0.35%、3.12%。场景D为经济性调度,考虑SSVS、SDFS约束后,系统的经济运行域受到稳定边界的限制,主要体现在:①为提升系统最大载荷量及PFR能力,增开了经济性较差的中小容量火电机组;②火电增开挤占了风电出力空间,为保证风电全额消纳,抽水蓄能工作强度提升,但其能量转换效率仅为75.05%,抽水蓄能的频繁使用导致经济性损失增大;③火电需预留PFR上调空间,导致部分经济性较好的大容量机组无法满发。
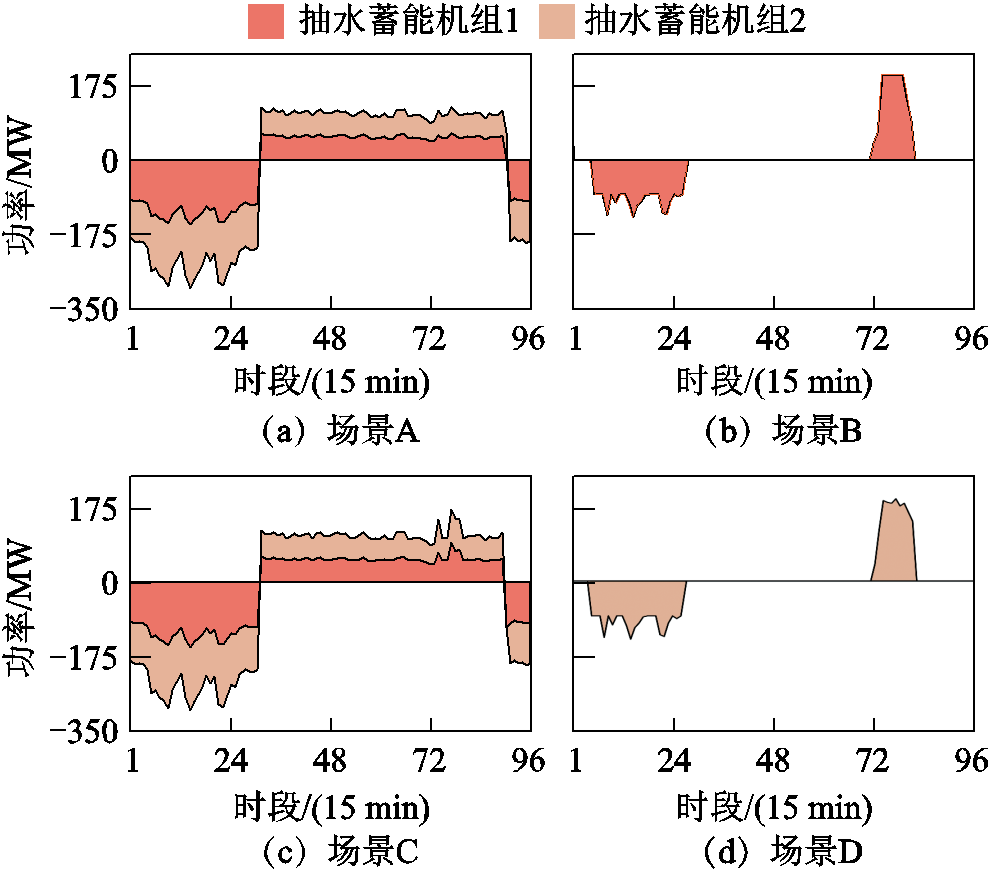
图10 抽水蓄能机组出力计划
Fig.10 Output plan of pumped-storage units
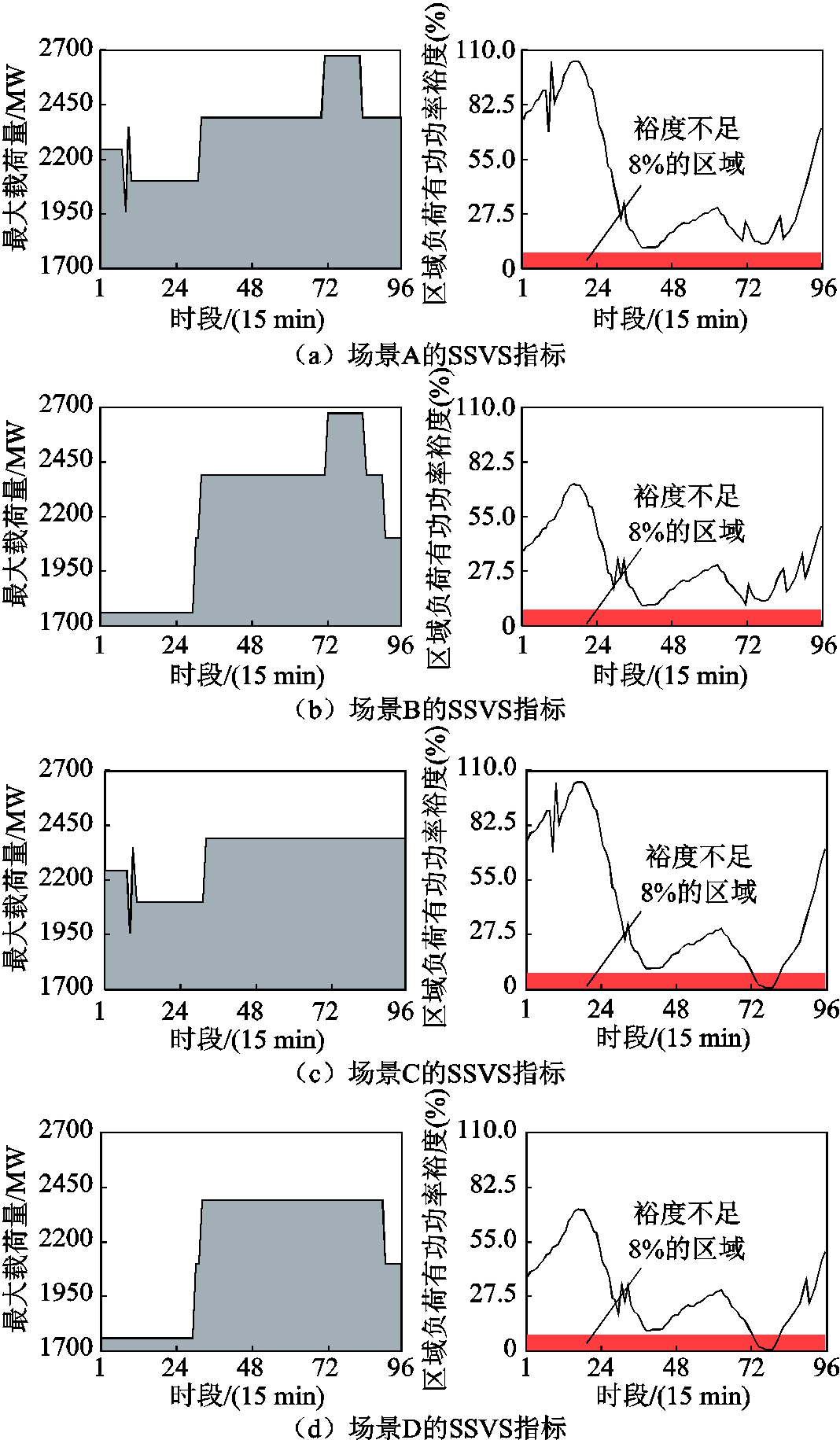
图11 SSVS指标
Fig.11 SSVS indexes
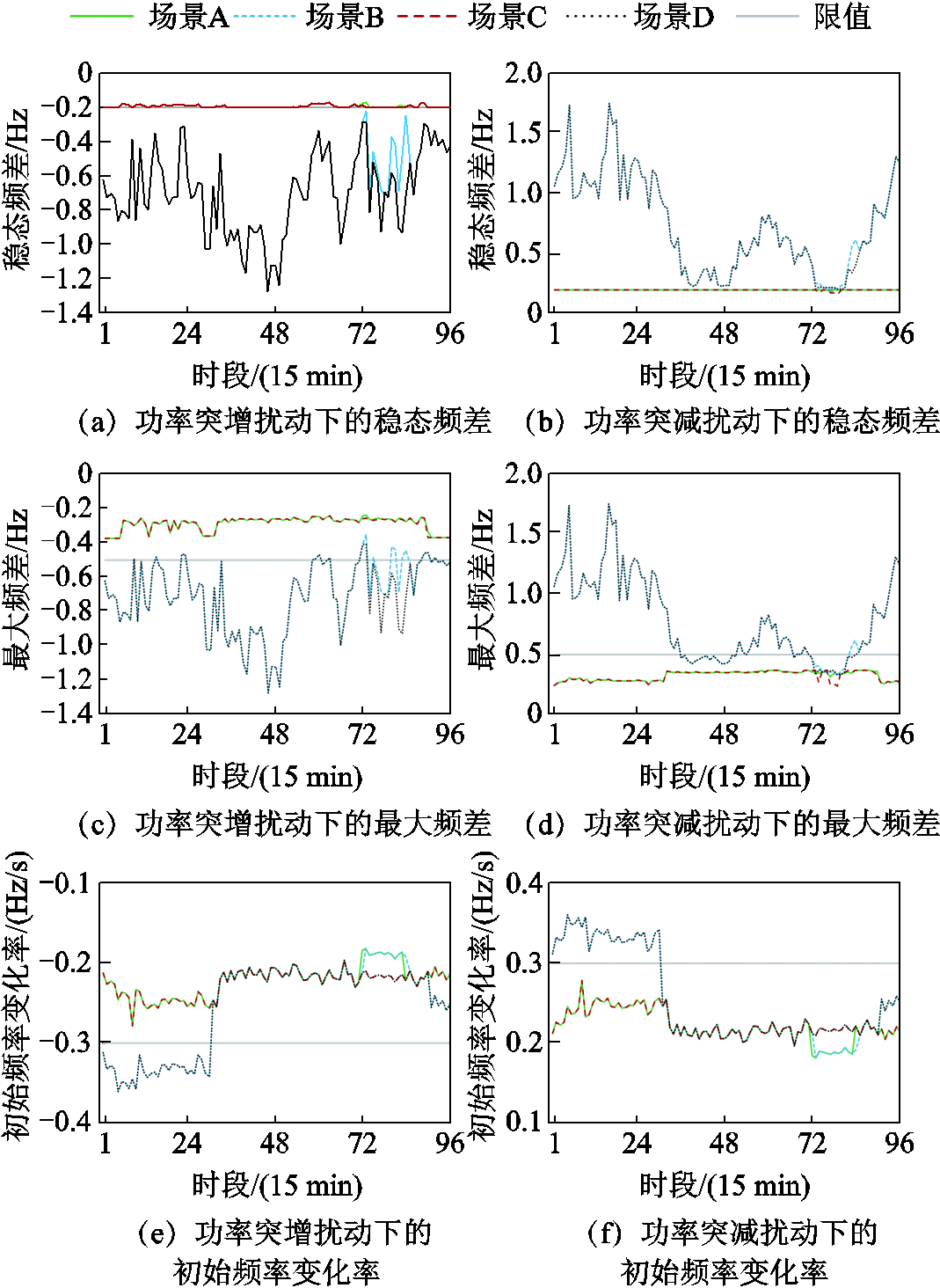
图12 SDFS指标
Fig.12 SDFS indexes
由图8可知,相对于场景D,场景B在72~83时段增开了火电机组G5,以满足SSVS约束;场景C在1~10时段增开了火电机组G2,在1~8时段增开了火电机组G3,在1~30时段增开了火电机组G7,以满足SDFS约束。而场景A统筹兼顾SSVS与SDFS约束,其火电起停计划相当于B、C的并集。
由图9可知,计及SDFS约束后,为接纳增开火电机组的最小技术出力以及预留PFR上调空间,同一时段下场景A、C的大容量火电机组出力低于D。对于场景B,其大容量火电机组的出力不受PFR所牵制,在经济性目标引导下遵循应发尽发原则,仅有负荷尖峰时段(72~83时段)增开机组G5,与G4分享出力空间,以保证系统预留足额的静态电压储备。
由图10可知,场景B、D中抽水蓄能机组仅执行基本的削峰填谷任务以稀释风电的反调峰特性,在风电顺调峰时段抽水蓄能机组不动作,避免能量转换损失。场景A、C在SDFS约束作用下,一方面,火电机组整体出力增大,导致风电出力空间被压缩,为保证风电的充分消纳,抽水蓄能机组全时段能量转换规模显著提升;另一方面,系统对抽水蓄能机组有PFR需求,使其始终保持投运并预留足够的PFR调节空间。
由图11可知,计及SSVS约束后,场景A、B在负荷尖峰时段(72~83时段)的系统最大载荷量显著提升,两种场景在全时段的区域负荷有功功率裕度均大于8%;相反,场景C、D在负荷尖峰时段的裕度不足8%,其中77时段最低,仅为0.59%。
由图12可知,计及SDFS约束后,场景A、C在预想功率突增或突减扰动下的稳态频差、最大频差、初始频率变化率均维持在限值以内;相反,场景B、D难以抵御由相同扰动引发的频率越限风险。此外,在不计SDFS约束情况下,基于经济性原则,中小容量火电机组倾向于以最小技术出力运行,大容量火电机组倾向于以系统净负荷值运行,火电整体PFR下调空间低于上调空间;计及SDFS约束后,火电机组增开,为避免功率突减扰动下频率指标越限,部分中小容量机组出力提升,以拓宽PFR下调空间,但从整体上仍低于上调空间。基于图12数据计算,场景A~D的全时段两类扰动稳态频差总和分别为0.62、6.07、0.45、3.37 Hz,最大频差总和分别为3.53、7.34、3.15、5.24 Hz,均为正值,说明系统PFR下调能力相对更弱。对于初始频率变化率,在相同扰动下,其仅与机组惯量或虚拟惯量有关,不受限于PFR调节空间及下垂系数,因此场景A~D的初始频率变化率总和均为0,即两类扰动下的初始频率变化率大小相同而符号相反。
针对高比例风电电力系统调峰、消纳压力大,静态电压、小扰动频率失稳风险高的问题,本文提出一种计及频率电压稳定性约束的电力系统多层级储能协同优化运行策略,所得结论如下:
1)所提出的SSVS约束构造方法,将对区域负荷有功功率裕度的限制,转换为裕度边界条件下的系统潮流有解校核问题,避免在系统级调度min问题中求解大规模潮流可解临界载荷量max问题,提高了计及SSVS约束的系统级调度模型求解效率。
2)所提出的SDFS约束构造方法,计及了各机组的调频死区与功率限幅环节,利用差分方程计算初始频率变化率、最大频差,利用终值定理计算稳态频差,实现了SDFS约束的线性化,进而通过Simulink仿真验证了所提指标计算方法的准确性。
3)所提出的计及频率电压稳定性约束的电力系统多层级储能协同优化运行策略,既能充分发挥风电场自备电池储能的快速调节作用,有效平抑风电场出力波动并提高其PFR支撑能力,又能充分发挥电站级抽水蓄能的PFR及规模化能量转移作用,实现系统运行经济性与频率电压稳定性的统筹兼顾。
附 录
1. 求解算法数学模型
1)MP模型
MP模型的优化目标为
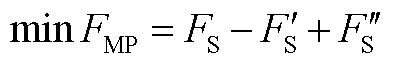 (A1)
(A1)
约束条件包括所有常规约束、功率突增及突减场景的稳态频差约束、SP1~SP3反馈的修正约束。最后一项用于当SP1~SP3校核越限后,修正MP的可行域,使其向满足SSVS及差分频差约束的方向求解。由3.3节可知,提高系统最大载荷能力的措施为增开火电机组及提高抽水蓄能电站上水库水量。由3.4节可知,提高系统频率响应能力的措施为增开火电、抽水蓄能机组及增大两类机组的PFR调节空间。因此,可通过调整相关变量修正MP的可行域。
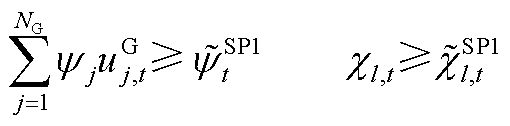 (A2)
(A2)
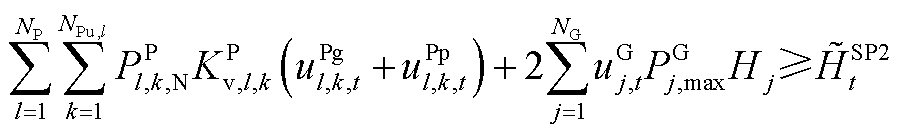 (A3)
(A3)
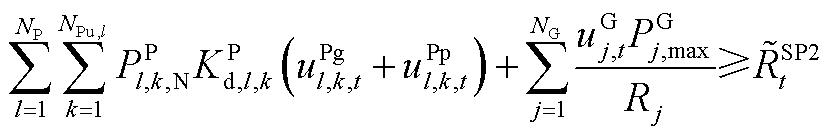 (A4)
(A4)
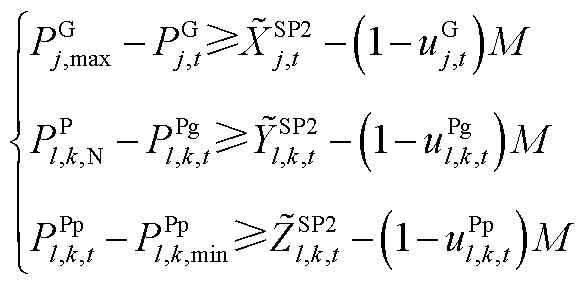 (A5)
(A5)
式中,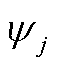 为系统最大载荷量对火电机组运行状态的灵敏度;
为系统最大载荷量对火电机组运行状态的灵敏度;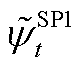 、
、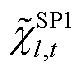 、
、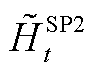 、
、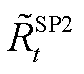 、
、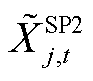 、
、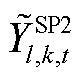 、
、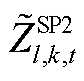 分别为SP1、SP2反馈的修正约束边界,此处为上次迭代的求解结果,均为常数。由于SP2、SP3具有相似性和对称性,因此本文对SP3不再赘述。
分别为SP1、SP2反馈的修正约束边界,此处为上次迭代的求解结果,均为常数。由于SP2、SP3具有相似性和对称性,因此本文对SP3不再赘述。
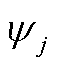 的计算流程如下:
的计算流程如下:
(1)假设风电场可用功率为场内风机装机容量,抽水蓄能电站上水库水量为最大水量,所有火电机组均投运,令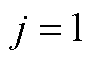 ,计算该条件下的系统最大载荷量
,计算该条件下的系统最大载荷量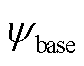 。
。
(2)退出第j台火电机组,其他机组投运,计算该条件下的系统最大载荷量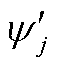 ,则
,则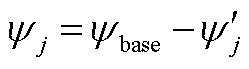 。
。
(3)令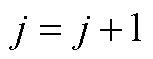 ,若
,若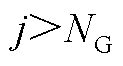 则完成,否则返回(2)。
则完成,否则返回(2)。
2)SP1模型
SP1模型具有时间解耦性,即各时段的SSVS校核互不干涉。t时段SP1模型的优化目标为
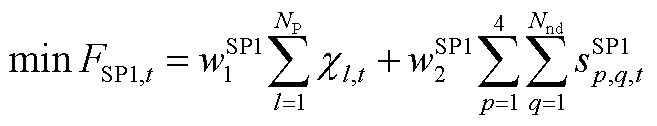 (A6)
(A6)
式中,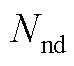 为系统节点数量;
为系统节点数量;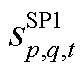 为节点功率平衡约束松弛变量;p为松弛变量类型索引,取1时
为节点功率平衡约束松弛变量;p为松弛变量类型索引,取1时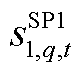 为节点有功功率平衡约束的正松弛变量,取其他值时同样代表有功或无功、正或负的松弛变量,详见式(A7);q为节点编号,下同;
为节点有功功率平衡约束的正松弛变量,取其他值时同样代表有功或无功、正或负的松弛变量,详见式(A7);q为节点编号,下同;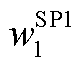 、
、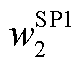 为SP1优化目标权重,应满足松弛变量的优先级高于抽水蓄能电站上水库水量的优先级。
为SP1优化目标权重,应满足松弛变量的优先级高于抽水蓄能电站上水库水量的优先级。
约束条件包括松弛变量约束及3.3节所有约束。其中,火电机组运行状态为本次迭代中MP的求解结果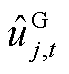 。节点功率平衡及松弛变量约束为
。节点功率平衡及松弛变量约束为
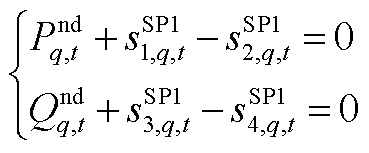 (A7)
(A7)
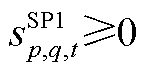 (A8)
(A8)
式中,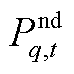 、
、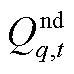 分别为节点有功、无功功率之和。
分别为节点有功、无功功率之和。
SP1反馈的MP修正约束边界需分情况更新:
(1)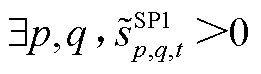 ,其中,
,其中,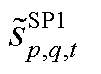 为本次迭代SP1求解的松弛变量结果。该情况说明,在给定
为本次迭代SP1求解的松弛变量结果。该情况说明,在给定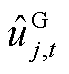 条件下,即使抽水蓄能电站上水库水量最大,节点功率仍不平衡,故需增开火电机组,即
条件下,即使抽水蓄能电站上水库水量最大,节点功率仍不平衡,故需增开火电机组,即
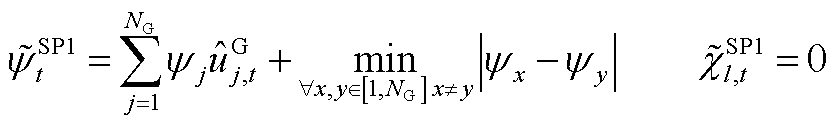 (A9)
(A9)
式中,x、y为任意两个不同的发电设备的编号。
(2)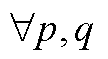 ,
,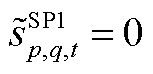 ;
;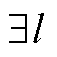 ,
,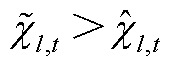 ,其中,
,其中,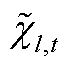 、
、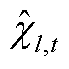 分别为本次迭代SP1及MP求解的抽水蓄能电站上水库水量结果。该情况说明,在给定
分别为本次迭代SP1及MP求解的抽水蓄能电站上水库水量结果。该情况说明,在给定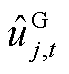 条件下,系统有能力在1.08倍实际负荷处达到功率平衡,但需要提高抽水蓄能电站上水库水量,即
条件下,系统有能力在1.08倍实际负荷处达到功率平衡,但需要提高抽水蓄能电站上水库水量,即
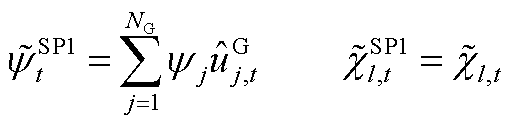 (A10)
(A10)
(3)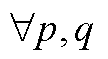 ,
,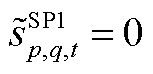 ;
;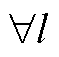 ,
,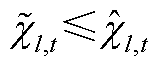 。该情况说明,在给定
。该情况说明,在给定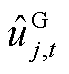 条件下,系统有能力在1.08倍实际负荷处达到功率平衡,且无需提高抽水蓄能电站上水库水量,无需更新修正约束边界。
条件下,系统有能力在1.08倍实际负荷处达到功率平衡,且无需提高抽水蓄能电站上水库水量,无需更新修正约束边界。
由于时间解耦性,各时段SP1模型可并行求解。
3)SP2与SP3模型
SP2、SP3模型具有时间解耦性,即各时段的差分频差约束校核互不干涉。由于SP2、SP3具有相似性、对称性,故仅介绍SP2,其t时段优化目标为
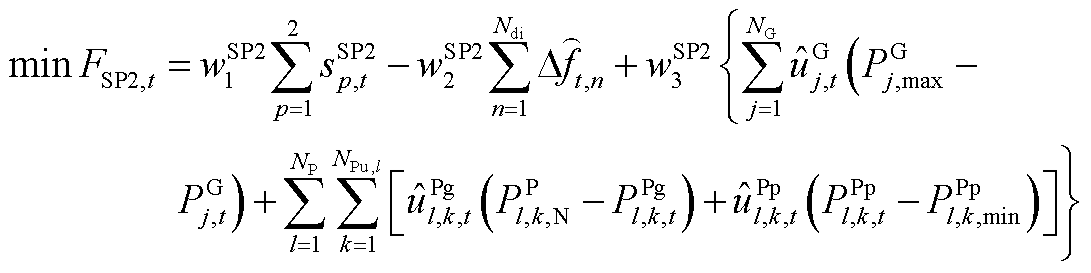 (A11)
(A11)
式中,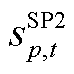 为初始频率变化率及最大频差约束松弛变量;
为初始频率变化率及最大频差约束松弛变量;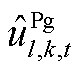 、
、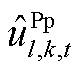 分别为本次迭代中MP求解的抽水蓄能机组发电及抽水状态结果;
分别为本次迭代中MP求解的抽水蓄能机组发电及抽水状态结果;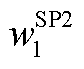 、
、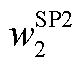 、
、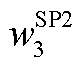 为优化目标权重,应合理取值,使得各目标优先级降序依次为松弛变量、PFR调节空间、差分频差。
为优化目标权重,应合理取值,使得各目标优先级降序依次为松弛变量、PFR调节空间、差分频差。
约束条件包括松弛变量约束、PFR调节空间约束及3.4节中所有差分形式的约束。初始频率变化率、最大频差、PFR调节空间、松弛变量约束分别为
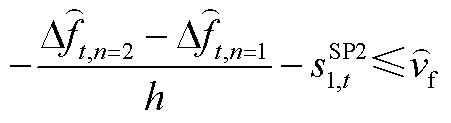 (A12)
(A12)
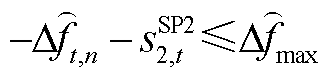 (A13)
(A13)
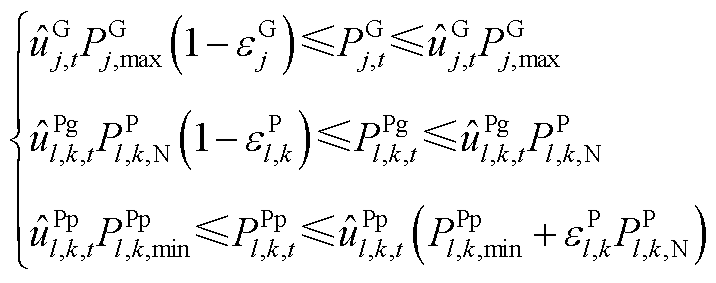 (A14)
(A14)
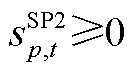 (A15)
(A15)
SP2反馈的MP修正约束边界也需分情况更新:
(1)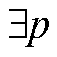 ,
,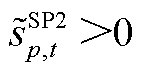 ,其中,
,其中,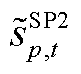 为本次迭代SP2求解的松弛变量结果。该情况说明,在给定
为本次迭代SP2求解的松弛变量结果。该情况说明,在给定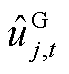 、
、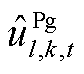 、
、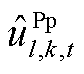 条件下,即使各机组预留PFR调节空间最大,初始频率变化率或最大频差仍越限,因此需要增开火电或抽水蓄能机组,表示为
条件下,即使各机组预留PFR调节空间最大,初始频率变化率或最大频差仍越限,因此需要增开火电或抽水蓄能机组,表示为
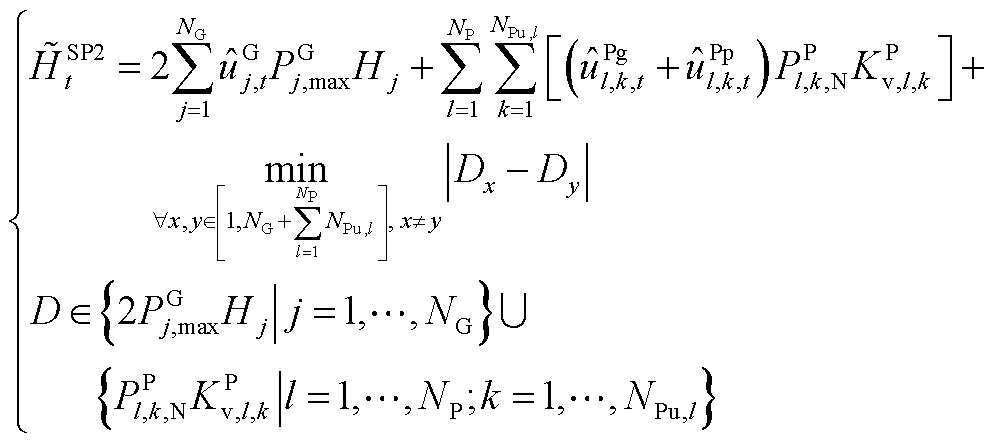 (A16)
(A16)
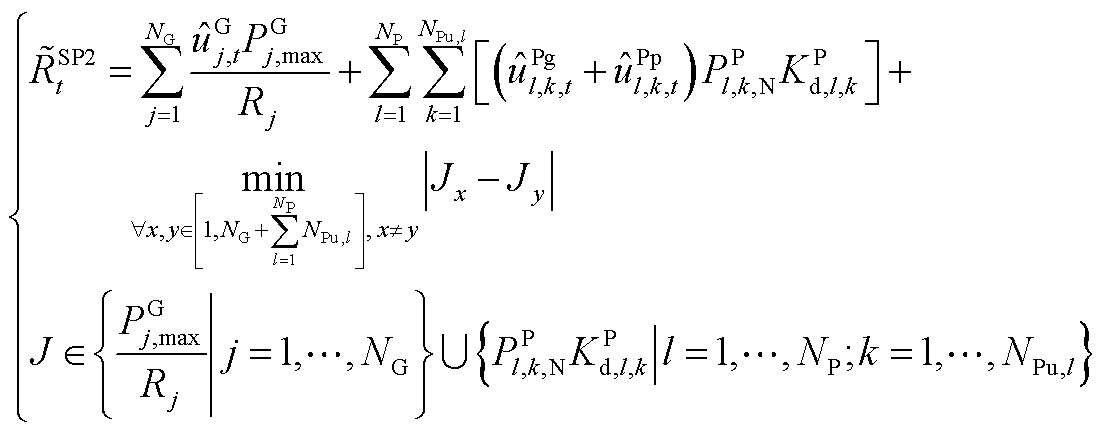 (A17)
(A17)
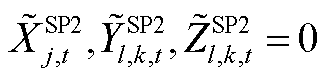 (A18)
(A18)
(2)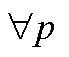 ,
,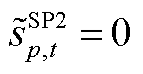 ;
;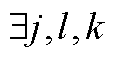 ,
,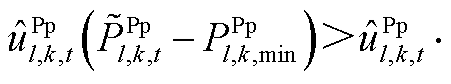
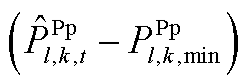 或
或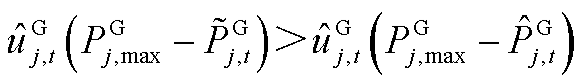 或
或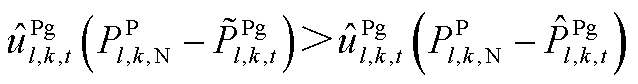 ,其中,
,其中,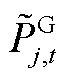 、
、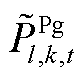 、
、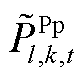 及
及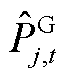 、
、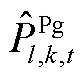 、
、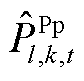 分别为本次迭代SP2及MP求解的火电、抽水蓄能发电、抽水蓄能抽水功率结果。该情况说明,在给定
分别为本次迭代SP2及MP求解的火电、抽水蓄能发电、抽水蓄能抽水功率结果。该情况说明,在给定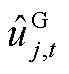 、
、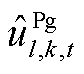 、
、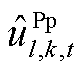 条件下,系统有能力保证初始频率变化率及最大频差不越限,但需要增大PFR调节空间,表示为
条件下,系统有能力保证初始频率变化率及最大频差不越限,但需要增大PFR调节空间,表示为
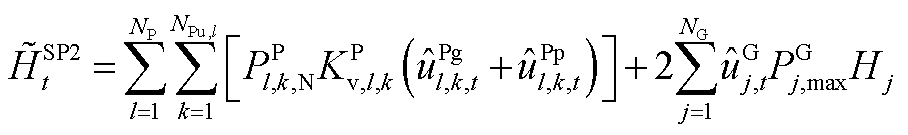 (A19)
(A19)
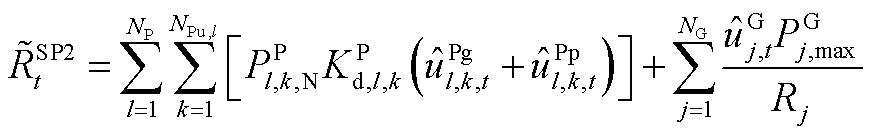 (A20)
(A20)
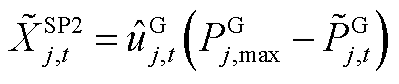 (A21)
(A21)
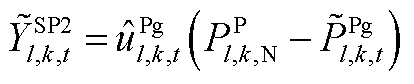 (A22)
(A22)
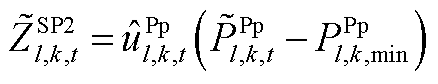 (A23)
(A23)
(3)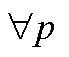 ,
,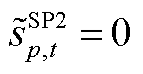 ;
;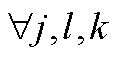 ,
,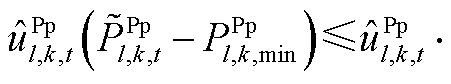
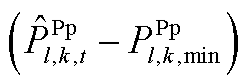 且
且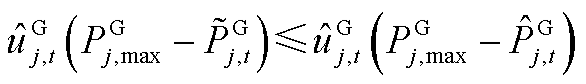 且
且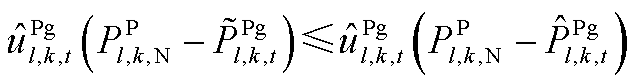 。该情况说明,在给定
。该情况说明,在给定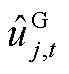 、
、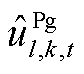 、
、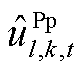 条件下,系统有能力保证初始频率变化率及最大频差不越限,且无需增大PFR调节空间,无需更新修正约束边界。
条件下,系统有能力保证初始频率变化率及最大频差不越限,且无需增大PFR调节空间,无需更新修正约束边界。
由于时间解耦性,各时段SP2模型可并行求解。
2. 算例参数设置
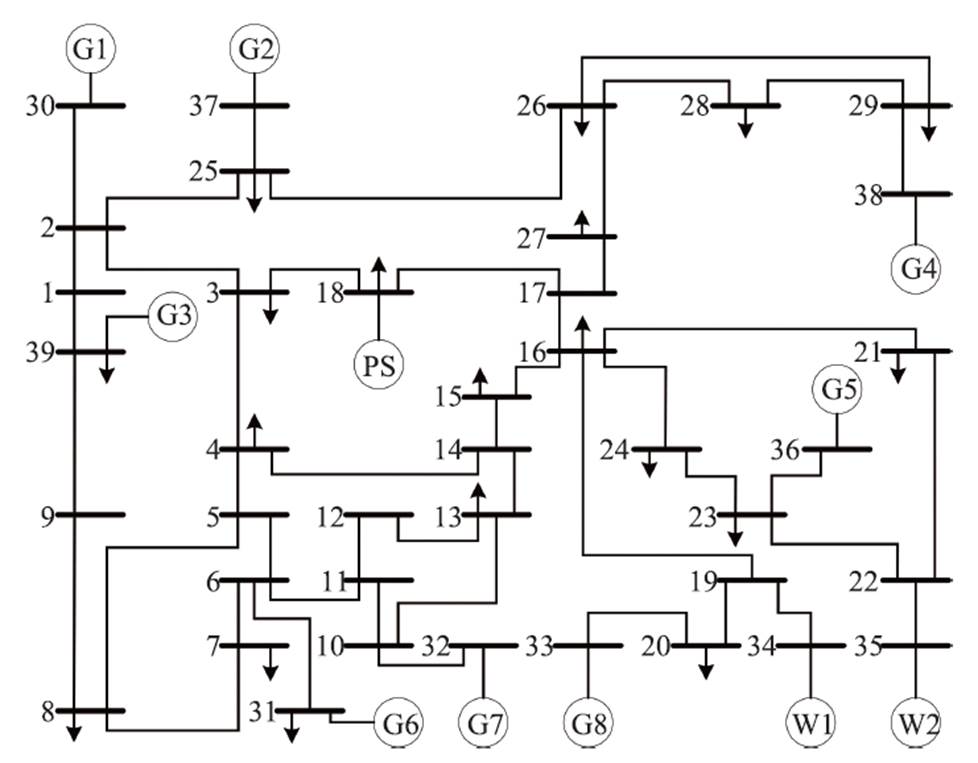
附图1 系统拓扑
App.Fig.1 System topology
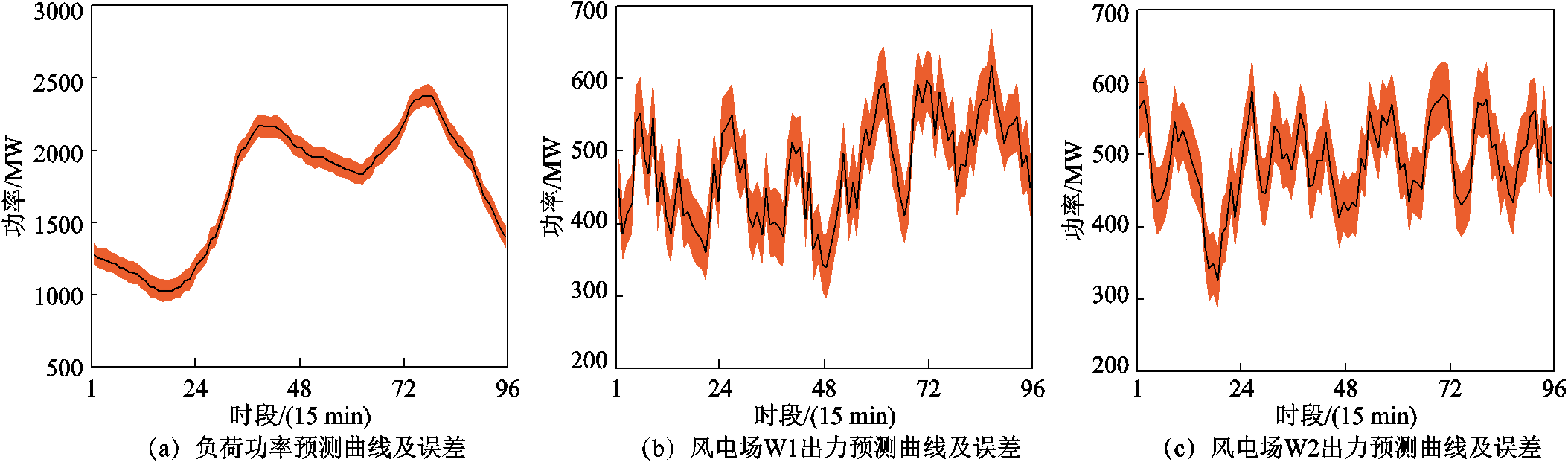
附图2 负荷及风电预测结果
App.Fig.2 Forecast results of load and wind farms
附表1 火电机组参数
App.Tab.1 Parameters of thermal power units

参数G1G2G3G4G5G6G7G8 额定有功出力/MW200200250250250300300300 有功出力下限/MW6060757575909090 额定无功出力/Mvar123.95123.95154.94154.94154.94185.92185.92185.92 无功出力下限/Mvar00000000 单次起停成本/$6007008008009001 4001 5001 500 最小起停机时间/h22333444 爬坡率/(MW/min)4.54.95.45.967.588.8 购电成本系数1/[$/(MW·h)]54.8255.6443.6843.0844.5137.1237.3635.96 购电成本系数2/($/h)105.18104.25116.02117.41115.44122.62122.27123.57 调差系数0.0420.0420.0430.0430.0430.0440.0440.044 伺服机构时间常数/s0.250.30.290.260.310.290.330.32 高压缸输出功率占比0.3010.2690.2870.2730.2960.3070.2550.282 高压缸前汽室容积时间常数/s0.2550.2510.2790.2870.2720.3090.3210.317 再热器容积时间常数/s10.1239.94211.24511.78711.00812.10412.09412.119 惯性时间常数/s14.211.510.613.61112.312.914.7 调频死区边界绝对值(pu)0.000 660.000 660.000 660.000 660.000 660.000 660.000 660.000 66 功率限幅比例绝对值0.10.10.10.10.10.10.10.1 载荷灵敏度/MW238255294517360363358276
附表2 抽水蓄能机组参数
App.Tab.2 Parameters of pumped-storage units

参数数值 抽水蓄能机组数量2 抽水蓄能机组额定功率/MW200 抽水蓄能机组发电功率下限/MW40 抽水蓄能机组抽水功率下限/MW80 上水库水量上限/m34 442 467 上水库水量下限/m31 075 118 上水库初始水量/m32 221 234 抽水蓄能机组单次起停成本/$300
(续)

参数数值 抽水蓄能机组单日开机次数上限2 抽水蓄能机组单日停机次数上限2 发电工况水电转换系数/[m3/(MW·h)]998 抽水工况水电转换系数/[m3/(MW·h)]749 变流器时间常数/s0.15 虚拟惯量控制增益系数7 频率下垂控制增益系数50 调频死区边界绝对值(pu)0.001 功率限幅比例绝对值0.2
附表3 风电场参数
App.Tab.3 Parameters of wind farms
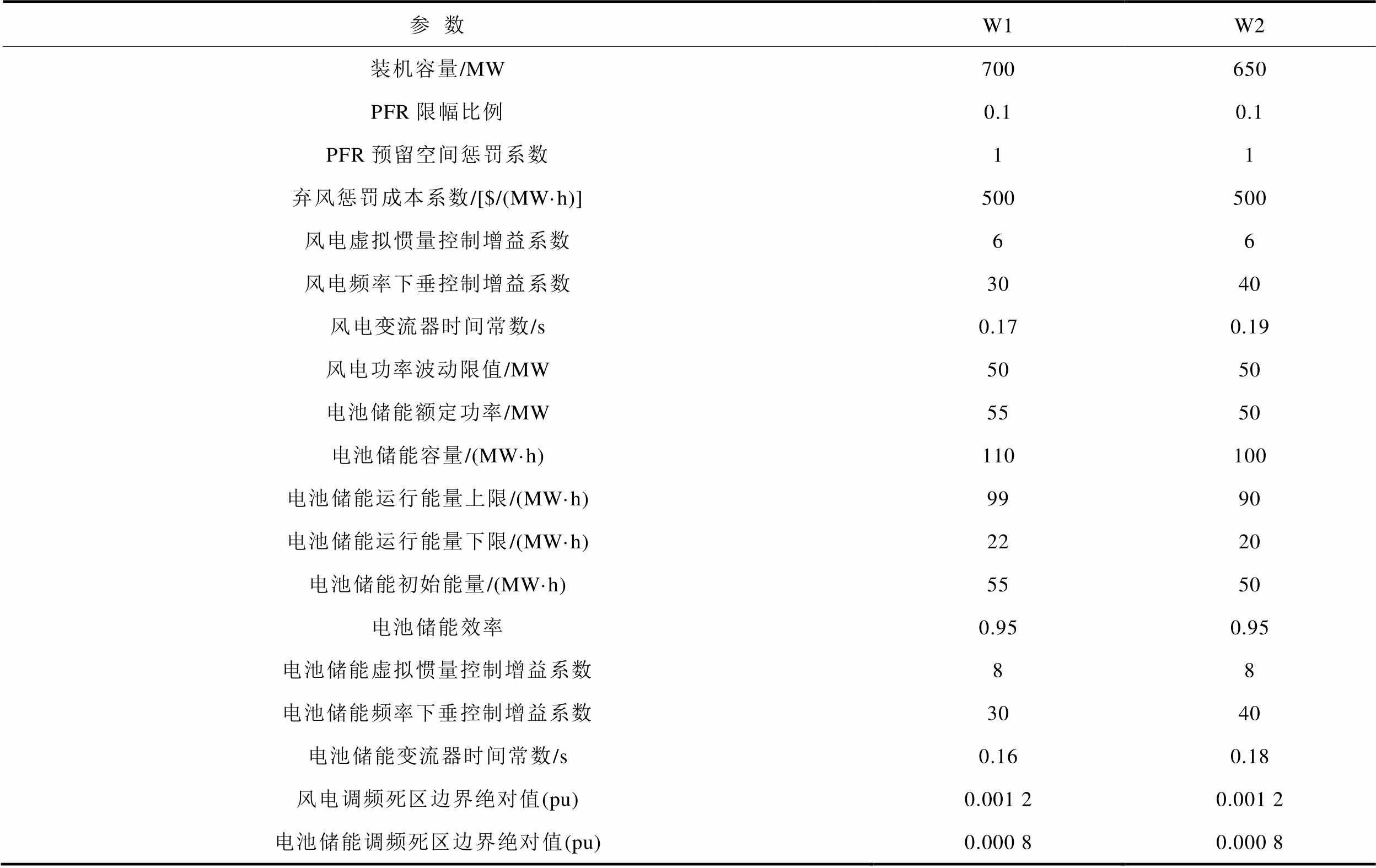
参数W1W2 装机容量/MW700650 PFR限幅比例0.10.1 PFR预留空间惩罚系数11 弃风惩罚成本系数/[$/(MW·h)]500500 风电虚拟惯量控制增益系数66 风电频率下垂控制增益系数3040 风电变流器时间常数/s0.170.19 风电功率波动限值/MW5050 电池储能额定功率/MW5550 电池储能容量/(MW·h)110100 电池储能运行能量上限/(MW·h)9990 电池储能运行能量下限/(MW·h)2220 电池储能初始能量/(MW·h)5550 电池储能效率0.950.95 电池储能虚拟惯量控制增益系数88 电池储能频率下垂控制增益系数3040 电池储能变流器时间常数/s0.160.18 风电调频死区边界绝对值(pu)0.001 20.001 2 电池储能调频死区边界绝对值(pu)0.000 80.000 8
附表4 线路参数
App.Tab.4 Parameters of transmission lines
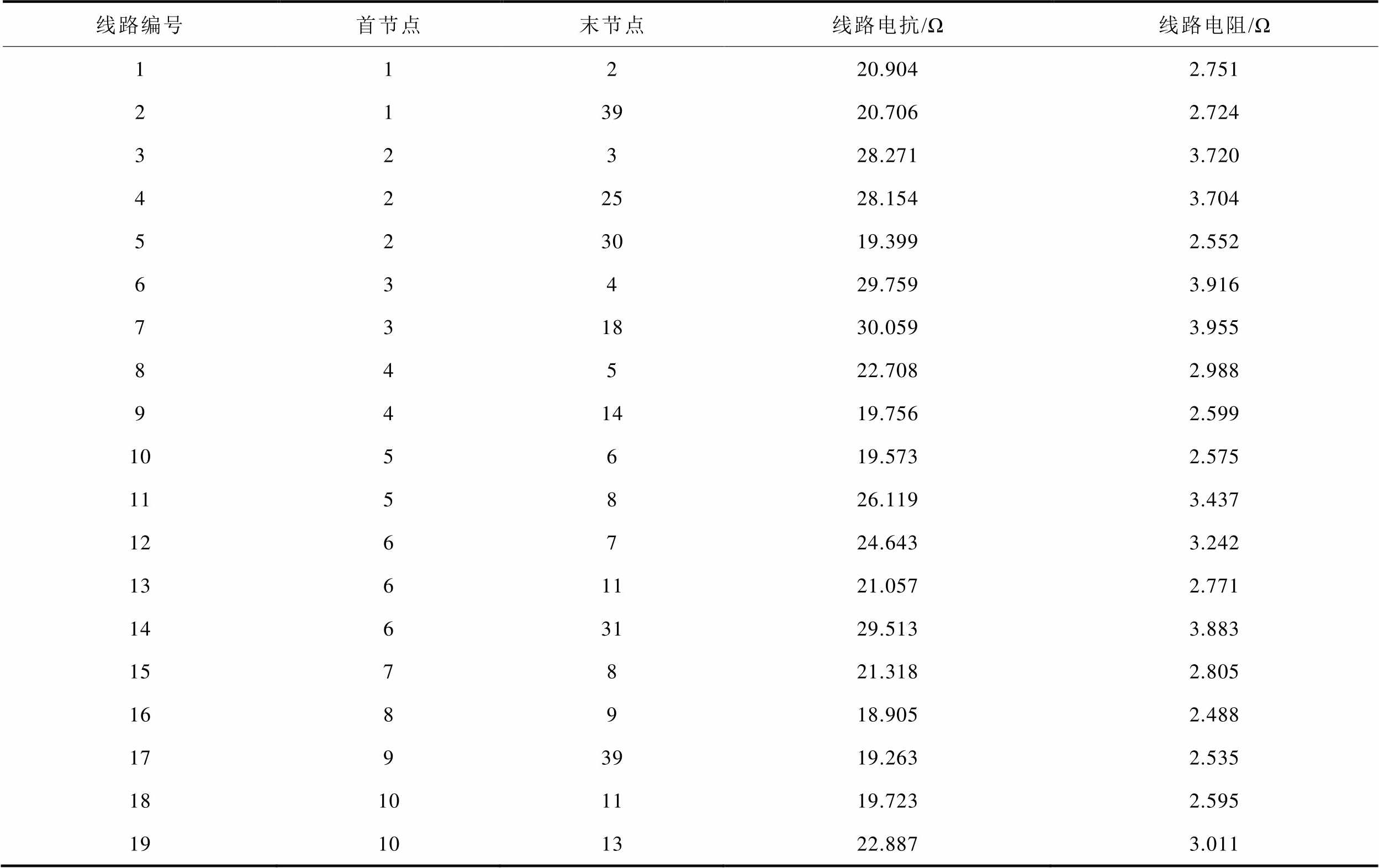
线路编号首节点末节点线路电抗/Ω线路电阻/Ω 11220.9042.751 213920.7062.724 32328.2713.720 422528.1543.704 523019.3992.552 63429.7593.916 731830.0593.955 84522.7082.988 941419.7562.599 105619.5732.575 115826.1193.437 126724.6433.242 1361121.0572.771 1463129.5133.883 157821.3182.805 168918.9052.488 1793919.2632.535 18101119.7232.595 19101322.8873.011
(续)
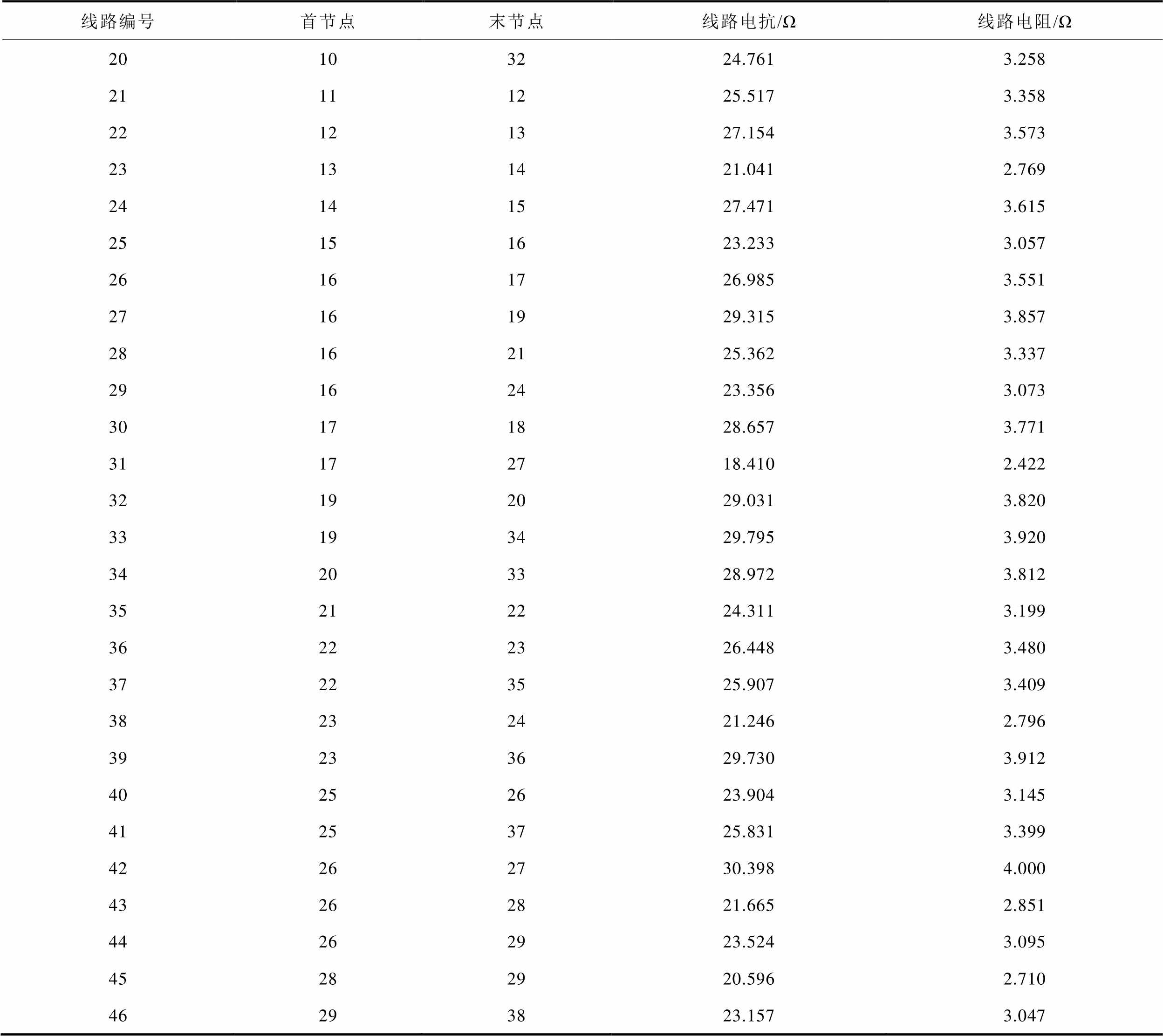
线路编号首节点末节点线路电抗/Ω线路电阻/Ω 20103224.7613.258 21111225.5173.358 22121327.1543.573 23131421.0412.769 24141527.4713.615 25151623.2333.057 26161726.9853.551 27161929.3153.857 28162125.3623.337 29162423.3563.073 30171828.6573.771 31172718.4102.422 32192029.0313.820 33193429.7953.920 34203328.9723.812 35212224.3113.199 36222326.4483.480 37223525.9073.409 38232421.2462.796 39233629.7303.912 40252623.9043.145 41253725.8313.399 42262730.3984.000 43262821.6652.851 44262923.5243.095 45282920.5962.710 46293823.1573.047
附表5 节点负荷参数
App.Tab.5 Load parameters of nodes
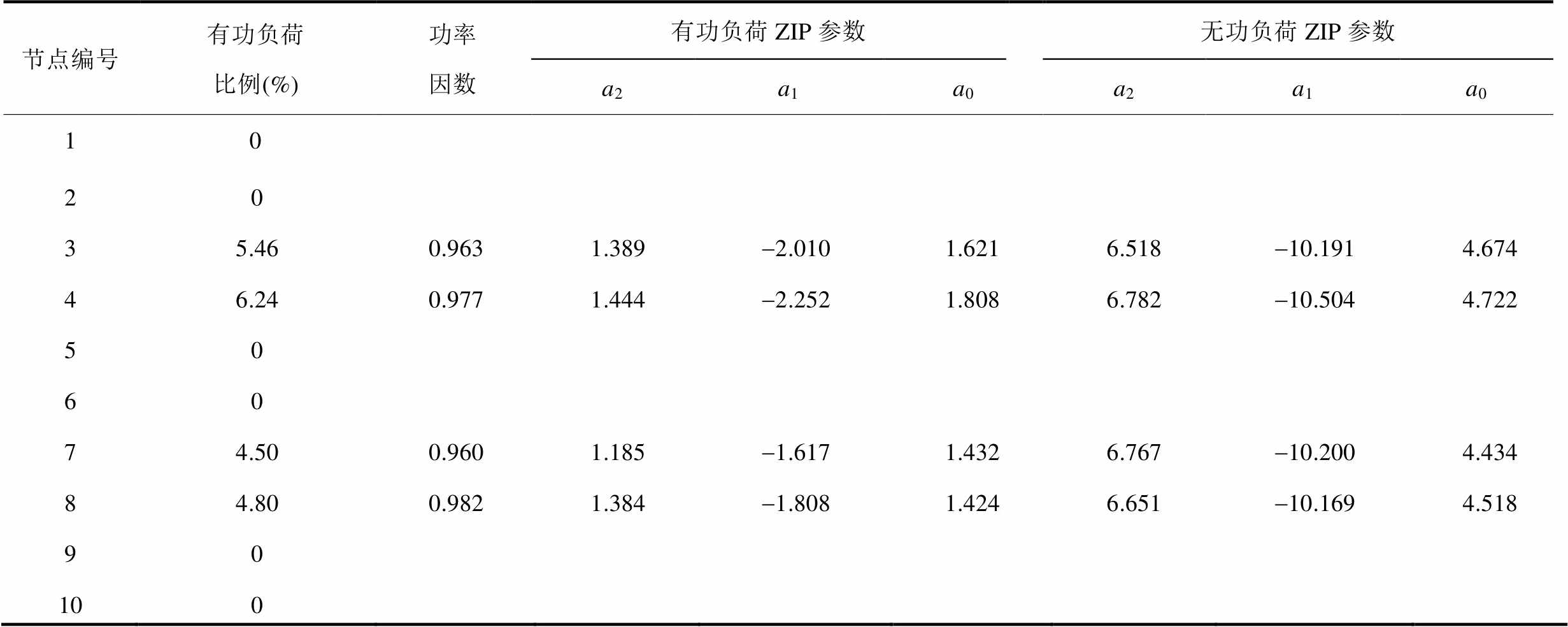
节点编号有功负荷比例(%)功率因数有功负荷ZIP参数无功负荷ZIP参数 a2a1a0a2a1a0 10 20 35.460.9631.389-2.0101.6216.518-10.1914.674 46.240.9771.444-2.2521.8086.782-10.5044.722 50 60 74.500.9601.185-1.6171.4326.767-10.2004.434 84.800.9821.384-1.8081.4246.651-10.1694.518 90 100
(续)
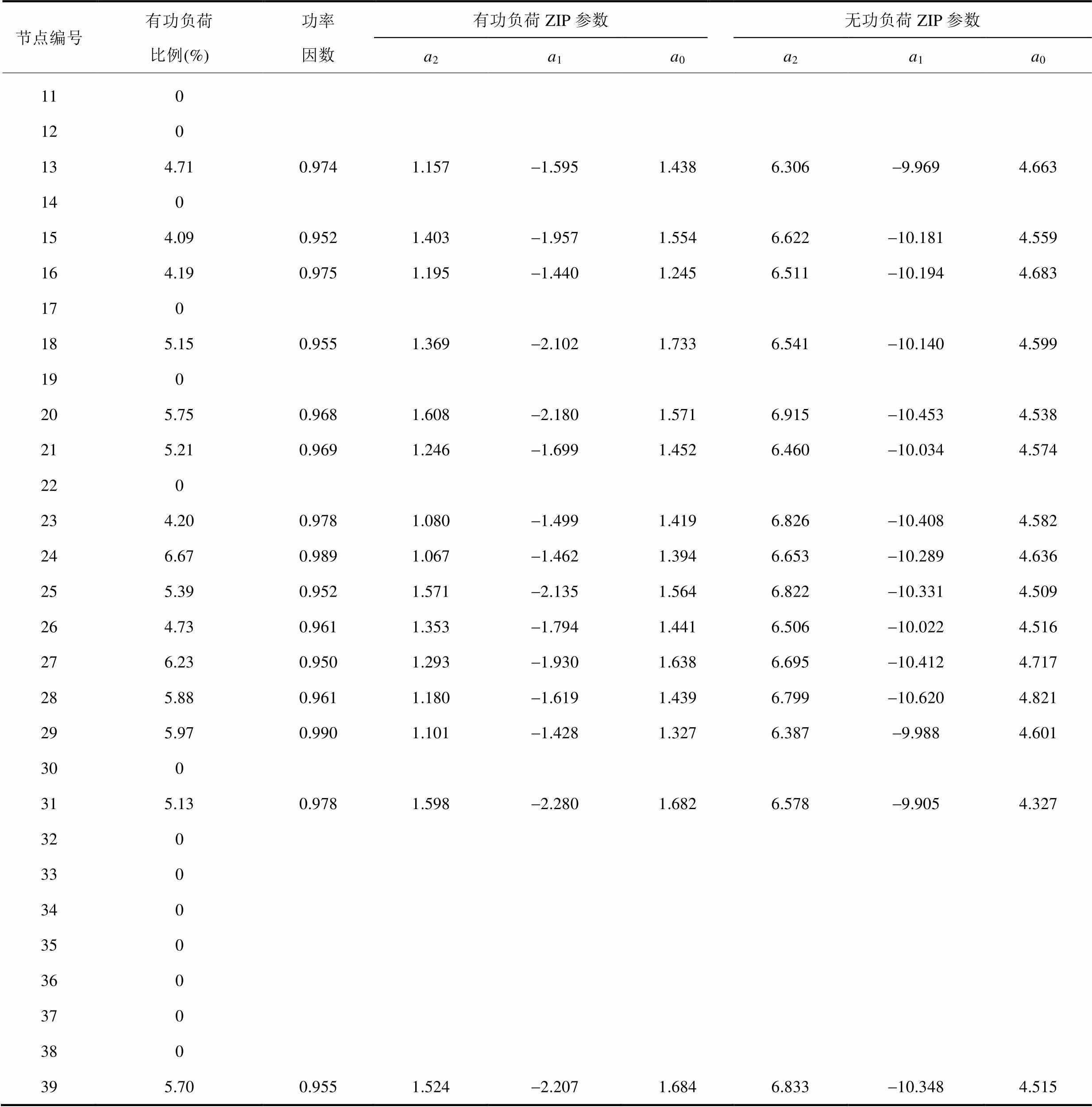
节点编号有功负荷比例(%)功率因数有功负荷ZIP参数无功负荷ZIP参数 a2a1a0a2a1a0 110 120 134.710.9741.157-1.5951.4386.306-9.9694.663 140 154.090.9521.403-1.9571.5546.622-10.1814.559 164.190.9751.195-1.4401.2456.511-10.1944.683 170 185.150.9551.369-2.1021.7336.541-10.1404.599 190 205.750.9681.608-2.1801.5716.915-10.4534.538 215.210.9691.246-1.6991.4526.460-10.0344.574 220 234.200.9781.080-1.4991.4196.826-10.4084.582 246.670.9891.067-1.4621.3946.653-10.2894.636 255.390.9521.571-2.1351.5646.822-10.3314.509 264.730.9611.353-1.7941.4416.506-10.0224.516 276.230.9501.293-1.9301.6386.695-10.4124.717 285.880.9611.180-1.6191.4396.799-10.6204.821 295.970.9901.101-1.4281.3276.387-9.9884.601 300 315.130.9781.598-2.2801.6826.578-9.9054.327 320 330 340 350 360 370 380 395.700.9551.524-2.2071.6846.833-10.3484.515
附表6 其他系统参数
App.Tab.6 Other system parameters

参数数值 差分计算步长/s0.01 差分计算总时长/s10 初始频率变化率限值/(Hz/s)0.3 稳态频差限值/Hz0.2 最大频差限值/Hz0.5 线路容量上限/(MV·A)700 电压等级/kV220 负荷频率响应系数1
(续)

参数数值 功率基准值/(MV·A)100 额定频率/Hz50 差分频差惩罚系数0.001 各差分变量及火电机组PFR功率变化率初值0 稳态频差惩罚系数1 SP1优化目标惩罚系数10.000 000 1 SP1优化目标惩罚系数210 000 000 SP2、SP3优化目标惩罚系数1100 000 SP2、SP3优化目标惩罚系数21 SP2、SP3优化目标惩罚系数30.000 5 足够大的正数M10 000 000 足够小的正数m0.000 000 1
3. 调频死区简化及频差惩罚项对求解SDFS指标的影响
为分析3.4节中调频死区简化及频差惩罚项对求解SDFS指标的影响,设计算例EP2,包含8组场景:场景a~d基于EP1场景A中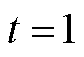 的调度结果分析功率突增扰动下的系统频率及各机组PFR功率变化量波形,场景a、b采用Simulink仿真,二者分别考虑未简化及已简化的调频死区,场景c、d求解SP2模型,场景c考虑差分频差惩罚项而场景d不考虑;场景e~h基于EP1场景A全天的调度结果分析功率突增扰动下的各时段稳态频差,场景e、f条件与场景a、b相同,场景g、h求解MP模型,场景g考虑稳态频差惩罚项而场景h不考虑。仿真及求解结果如附图3所示。
的调度结果分析功率突增扰动下的系统频率及各机组PFR功率变化量波形,场景a、b采用Simulink仿真,二者分别考虑未简化及已简化的调频死区,场景c、d求解SP2模型,场景c考虑差分频差惩罚项而场景d不考虑;场景e~h基于EP1场景A全天的调度结果分析功率突增扰动下的各时段稳态频差,场景e、f条件与场景a、b相同,场景g、h求解MP模型,场景g考虑稳态频差惩罚项而场景h不考虑。仿真及求解结果如附图3所示。
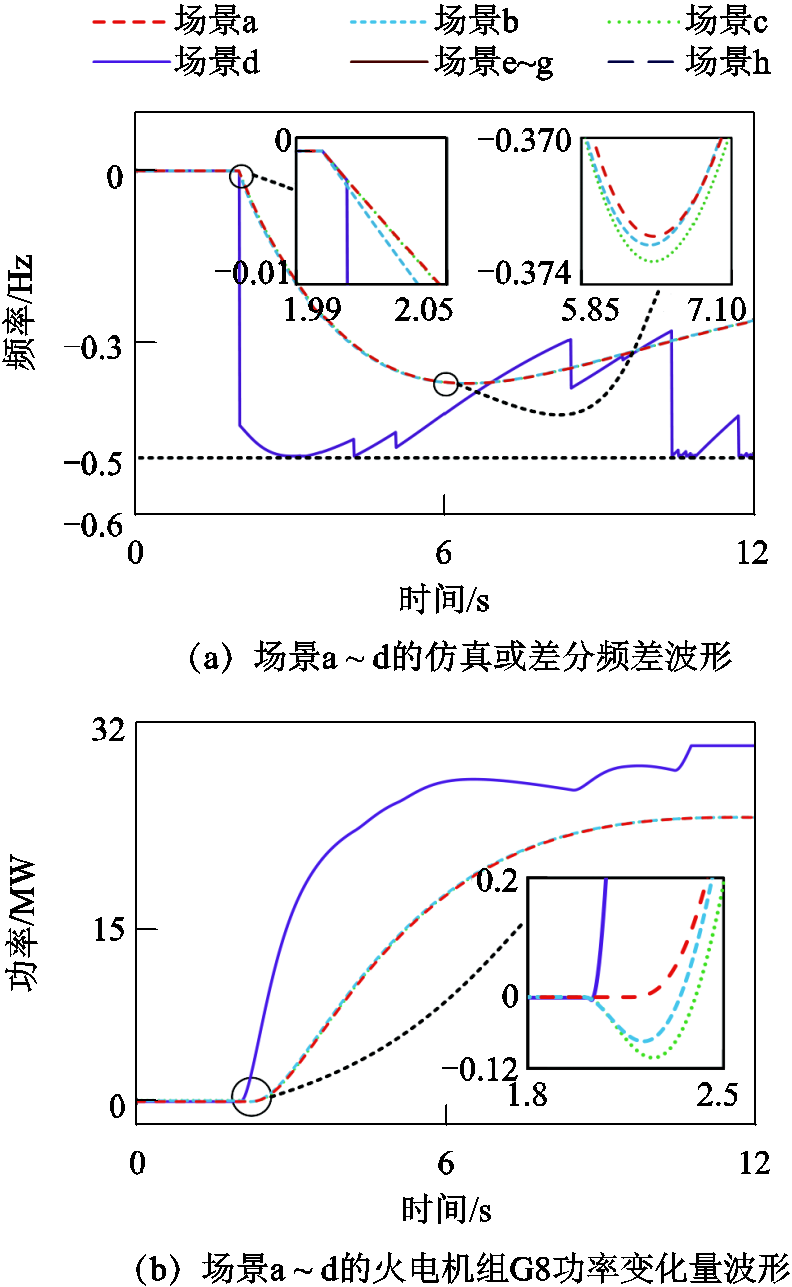
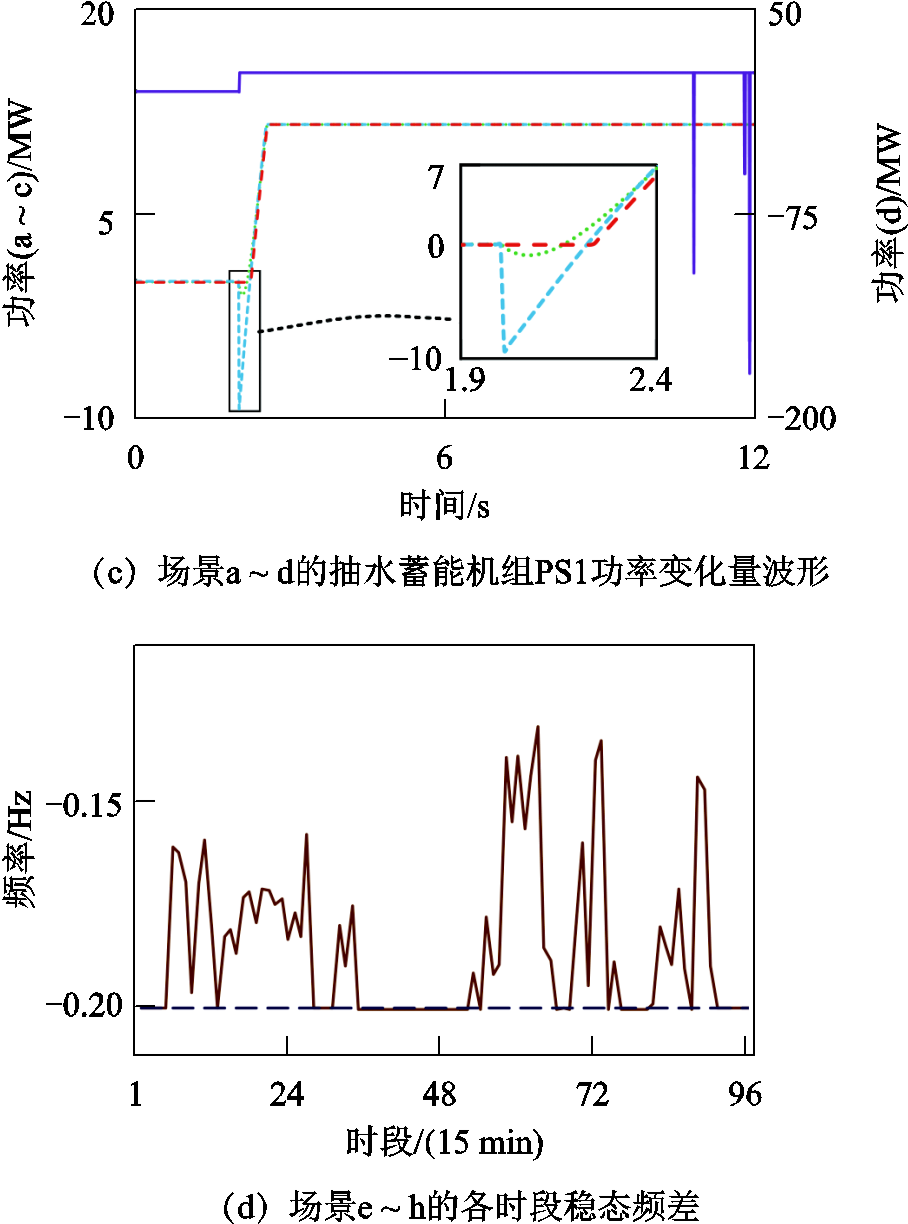
附图3 场景a~h的仿真及求解结果
App.Fig.3 Simulation and solution results of scene a to h
附图3中,扰动发生时刻为2 s,此时频差仍为0。对比场景a~c火电机组G8功率变化量,由于场景b、c采用简化死区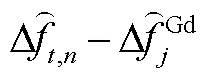 ,故此时场景b、c中G8调速系统输入频差为
,故此时场景b、c中G8调速系统输入频差为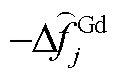 。由附表1可知,输入频差为0.033 Hz,这将在PFR初期引起功率反调量,对于其他机组也类似。反观场景a,由于采用标准死区
。由附表1可知,输入频差为0.033 Hz,这将在PFR初期引起功率反调量,对于其他机组也类似。反观场景a,由于采用标准死区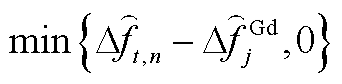 ,2 s时G8调速系统输入频差为0,其功率变化量也为0。功率反调量的出现,将导致场景b、c初始频率变化率及最大频差绝对值偏大。相较于场景a,场景b、c初始频率变化率各提升23.41%、0.02%,最大频差各提升0.06%、0.18%,说明场景c(本文调度方法)求解所得的SDFS稳定域具有微小的保守性。
,2 s时G8调速系统输入频差为0,其功率变化量也为0。功率反调量的出现,将导致场景b、c初始频率变化率及最大频差绝对值偏大。相较于场景a,场景b、c初始频率变化率各提升23.41%、0.02%,最大频差各提升0.06%、0.18%,说明场景c(本文调度方法)求解所得的SDFS稳定域具有微小的保守性。
对比场景c、d,不计差分频差惩罚项时,虽然d的初始频率变化率及最大频差未越限,但各差分变量仅满足式(21)~式(32)的代数关系,其时序递推关系混乱,存在未来取值决定当前取值的现象,致使频差波形出现毛刺,机组功率变化量出现跳变。
对比场景e~g,根据终值定理,无论调频死区是否简化,各机组达到稳态时,其功率变化量均响应于稳态频差剔除调频死区的部分,从而场景e~g各时段的稳态频差均相同。只不过由于功率反调量的存在,场景f、g达到稳态的时间会略晚于场景e。对比场景g、h,不计稳态频差惩罚项时,式(36)~式(39)中各PFR调节功率松弛变量均可在调频限幅之下自由取值,只需保证稳态频差不越限即可,因此场景h解得的全时段稳态频差均为-0.2 Hz,并非真实稳态频差。
参考文献
[1] 国家市场监督管理总局, 国家标准化管理委员会. 电力系统电压稳定评价导则: GB/T 40615—2021[S]. 北京: 中国标准出版社, 2021.
[2] 冯治鸿, 刘取, 倪以信, 等. 多机电力系统电压静态稳定性分析——奇异值分解法[J]. 中国电机工程学报, 1992, 12(3): 10-19.
Feng Zhihong, Liu Qu, Ni Yixin, et al. Analysis of steady-state voltage stability in multimachine power systems by singular value decomposition method[J]. Proceedings of the CSEE, 1992, 12(3): 10-19.
[3] Omi S, Shirai Y. Benders-decomposition-based voltage-stability-constrained unit-commitment taking reactive power limit into account[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2023, 18(3): 375-385.
[4] Hamidreza Adeli S, Rabiee A, Taghipour Boroujeni S. Optimal re-dispatch of generating units ensuring small signal stability[J]. IET Generation, Transmission & Distribution, 2020, 14(18): 3692-3701.
[5] Zhang Ningyu, Wu Shengjun, An Haiyun, et al. Security-constraint unit commitment for AC/DC transmission systems with voltage stability constraint[J]. Journal of Electrical Engineering & Technology, 2020, 15(6): 2459-2469.
[6] Wang Chong, Ju Ping, Wu Feng, et al. Long-term voltage stability-constrained coordinated scheduling for gas and power grids with uncertain wind power[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 363-377.
[7] Song Tianhao, Han Xiaoqing, Zhang Baifu. Multi-time-scale optimal scheduling in active distribution network with voltage stability constraints[J]. Energies, 2021, 14(21): 7107.
[8] Chu Zhongda, Teng Fei. Voltage stability constrained unit commitment in power systems with high penetration of inverter-based generators[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1572-1582.
[9] 国家市场监督管理总局, 国家标准化管理委员会. 电力系统安全稳定导则: GB 38755—2019[S]. 北京: 中国标准出版社, 2019.
[10] Li Kun, Ai Xiaomeng, Fang Jiakun, et al. Frequency security constrained robust unit commitment for sufficient deployment of diversified frequency support resources[J]. IEEE Transactions on Industry Applications, 2024, 60(1): 1725-1737.
[11] Zhang Ziyang, Du Ershun, Teng Fei, et al. Modeling frequency dynamics in unit commitment with a high share of renewable energy[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4383-4395.
[12] Yang Lun, Xu Yinliang, Zhou Jianguo, et al. Distributionally robust frequency constrained scheduling for an integrated electricity-gas system[J]. IEEE Transactions on Smart Grid, 2022, 13(4): 2730-2743.
[13] 李少岩, 曹珂, 顾雪平, 等. 多直流馈入受端系统与直流联络线协调恢复的一体化建模与求解[J]. 电工技术学报, 2023, 38(21): 5862-5877.
Li Shaoyan, Cao Ke, Gu Xueping, et al. Integrated modeling and solution for coordinated restoration of multi-infeed receiving-end systems and HVDC Tie lines[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5862-5877.
[14] 王廷涛, 苗世洪, 姚福星, 等. 计及动态频率响应约束的高比例风电电力系统日前-日内联合调度策略[J]. 中国电机工程学报, 2024, 44(7): 2590-2604.
Wang Tingtao, Miao Shihong, Yao Fuxing, et al. Day-ahead and intra-day joint dispatch strategy of high proportion wind power system considering dynamic frequency response constraints[J]. Proceedings of the CSEE, 2024, 44(7): 2590-2604.
[15] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分:陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[16] 国家市场监督管理总局, 国家标准化管理委员会. 并网电源一次调频技术规定及试验导则: GB/T 40595—2021[S]. 北京: 中国标准出版社, 2021.
[17] 谭晶, 何川, 陈保瑞, 等. 考虑水光蓄互补和直流外送的电力系统分布鲁棒优化调度方法[J]. 中国电机工程学报, 2024, 44(15): 5947-5959.
Tan Jing, He Chuan, Chen Baorui, et al. Distributionally robust optimal scheduling method of power system considering hydropower-photovoltaic-pumped storage complementarity and DC transmission [J]. Proceedings of the CSEE, 2024, 44(15): 5947-5959.
[18] 王廷涛, 苗世洪, 张松岩, 等. 基于状态评估的多类型储能系统检修优化策略[J]. 电力自动化设备, 2021, 41(10): 234-243.
Wang Tingtao, Miao Shihong, Zhang Songyan, et al. Maintenance optimization strategy of multi-type energy storage systems based on state evaluation[J]. Electric Power Automation Equipment, 2021, 41(10): 234-243.
[19] 蔡杰, 王廷涛, 徐小琴, 等. 考虑输配协同的电网机组组合与技改计划联合优化模型[J]. 电力自动化设备, 2023, 43(1): 174-183.
Cai Jie, Wang Tingtao, Xu Xiaoqin, et al. Joint optimization model of power grid unit commitment and technical transformation plan considering transmission and distribution coordination[J]. Electric Power Automation Equipment, 2023, 43(1): 174-183.
[20] 李晓鹏, 李岩, 刘舒然, 等. 基于可变速抽水蓄能技术提升区域电网新能源消纳水平的研究[J]. 智慧电力, 2021, 49(10): 52-58, 112.
Li Xiaopeng, Li Yan, Liu Shuran, et al. Research on promotion of renewable energy integration into regional power grid by variable speed pumped storage technology[J]. Smart Power, 2021, 49(10): 52-58, 112.
[21] 姜涛, 张明宇, 崔晓丹, 等. 电力系统静态电压稳定域边界快速搜索的优化模型[J]. 电工技术学报, 2018, 33(17): 4167-4179.
Jiang Tao, Zhang Mingyu, Cui Xiaodan, et al. A novel optimization model to explore static voltage stability region boundary in bulk power systems[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4167-4179.
[22] Grigsby L L. Power System Stability and Control[M]. 3rd ed. Boca Raton: CRC Press, 2012.
[23] 国家市场监督管理总局, 国家标准化管理委员会. 风力发电机组全功率变流器第1部分:技术条件: GB/T25387.1—2021[S]. 北京: 中国标准出版社, 2021.
[24] 陈刚, 刘万彬, 杨悦荣, 等. 考虑新能源不确定波动的交直流混联电网静态电压稳定裕度区间计算[J]. 电网技术, 2023, 47(3): 1127-1137.
Chen Gang, Liu Wanbin, Yang Yuerong, et al. Calculation of static voltage stability margin interval for AC/DC hybrid power system considering the uncertainty of renewable energy[J]. Power System Technology, 2023, 47(3): 1127-1137.
[25] 李超, 苗世洪, 盛万兴, 等. 考虑动态网络重构的主动配电网优化运行策略[J]. 电工技术学报, 2019, 34(18): 3909-3919.
Li Chao, Miao Shihong, Sheng Wanxing, et al. Optimization operation strategy of active distribution network considering dynamic network reconfiguration[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3909-3919.
[26] 国家市场监督管理总局, 国家标准化管理委员会. 电力系统安全稳定计算规范: GB/T 40581—2021 [S]. 北京: 中国标准出版社, 2022.
[27] 朱浩昊, 朱继忠, 李盛林, 等. 基于Benders分解和纳什议价的分布式热电联合优化调度[J]. 电工技术学报, 2023, 38(21): 5808-5820.
Zhu Haohao, Zhu Jizhong, Li Shenglin, et al. Distributed combined heat and power optimal scheduling based on Benders decomposition and Nash bargaining[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5808-5820.
[28] 吴晗, 欧阳森, 梁炜焜. 计及储能循环寿命的柔性配电网优化运行及效益均衡策略[J]. 电力系统自动化, 2023, 47(17): 99-109.
Wu Han, Ouyang Sen, Liang Weikun. Optimal operation and benefit balance strategy for flexible distribution network considering cycle life of energy storage[J]. Automation of Electric Power Systems, 2023, 47(17): 99-109.
[29] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477.
Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
Abstract The large-scale integration of wind power brings unprecedented challenges to the power system. On the one hand, the wind power characteristics of fluctuation and anti-peak regulation increase the burden of peak regulation and wind power consumption on the system. On the other hand, a high proportion of wind power occupies the output space of traditional synchronous generators, weakening the system's voltage support, inertial response, and primary frequency regulation (PFR) capabilities, increasing the risk of instability in the system's steady-state voltage stability (SSVS) and small-disturbance frequency stability (SDFS).
To solve the above problems, we can start from two perspectives: resources and strategies. At the resource level, setting up appropriate power-type and energy-type energy storage systems on the wind farm side and power system side respectively can alleviate the pressure of system regulation. At the strategy level, SSVS and SDFS constraints are taken into account in the conventional day-ahead dispatch strategy, which can ensure that the system operation scheme is far away from critical stability and instability and has sufficient stability margin. A dual approach can effectively ensure the safe and stable economic operation of the system. Based on the above ideas, a multi-level energy storage collaborative optimization operation strategy for power systems considering frequency and voltage stability constraints is proposed. Firstly, a energy storage collaborative optimization operation framework for wind farm level and power system level is designed. Based on this, the wind farm level and power system level dispatching models are constructed, incorporating linearized frequency and voltage stability constraints into the latter. Secondly, The master & sub problem decomposition iteration method is used to solve the power system level dispatching model with mixed integer second-order cone characteristics, avoiding slow convergence or memory overflow problems caused by direct solving. Finally, the case studies were conducted to verify the effectiveness of the proposed method.
The following conclusions can be drawn from the case studies analysis: (1) The proposed SSVS constraints construction method transforms the limitation on the active power margin of regional loads into the system flow solvable verification problem under margin boundary conditions, avoiding solving the max-problem of the large-scale system flow solvable critical load in the min-problem of the system level dispatch, and improving the efficiency of solving the system level dispatch model. (2) The proposed SDFS constraints construction method takes into account the frequency regulation dead zone and power limiting of each unit. The initial frequency change rate and maximum frequency difference are calculated using difference equations, and the steady-state frequency difference is calculated using the final value theorem. The linearization of SDFS constraints is achieved, and the accuracy of the proposed frequency indexes calculation method is verified through Simulink simulation. (3) The proposed multi-level energy storage collaborative optimization operation strategy for power systems considering frequency and voltage stability constraints can not only fully leverage the rapid adjustment effect of the wind farm self-owned battery energy storage, effectively suppress the wind farm output fluctuations and improve the wind farm PFR support capacity, but also fully leverage the PFR and large-scale energy transfer effect of the pumped storage, achieving a comprehensive balance between system operation economy as well as frequency and voltage stability.
keywords:Steady-state voltage stability, small-disturbance frequency stability, multi-level energy storage, master & sub problem decomposition iteration, optimal dispatch
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.231727
国家电网有限公司总部管理科技项目资助(5419-202199551A-0-5-ZN)。
收稿日期 2023-10-17
改稿日期 2023-12-05
王廷涛 男,1997年生,博士研究生,研究方向为压缩空气储能系统、电力系统优化调度等。E-mail:vvtt@hust.edu.cn
苗世洪 男,1963年生,教授,博士生导师,博士,研究方向为电力系统保护与控制、压缩空气储能系统等。E-mail:shmiao@hust.edu.cn(通信作者)
(编辑 李 冰)