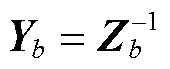（1）
摘要 大规模新能源接入和外地送电的增加，使得受端电网本地传统发电机无功支撑大大减少，面临暂态电压稳定问题，需要快速筛选出严重故障，以备系统预防控制和安控策略制定。该文提出了基于节点阻抗矩阵的故障点对电网暂态电压影响度指标，可用于快速筛选引发电网暂态电压失稳的关键故障点。首先，介绍了节点阻抗矩阵及其支路追加法；其次，提出反映节点故障对电网暂态电压影响程度的指标，可用于快速筛选高风险关键故障点；再次，结合升阶矩阵给出线路故障点的影响度指标；最后，改进IEEE 39节点系统及某省级电网仿真结果表明，所提指标可以快速筛选出对电网暂态电压影响显著的关键故障点。
关键词：暂态电压 关键故障点 节点阻抗矩阵 支路追加法
新能源大规模接入的受端电网由于本地传统发电机减少，存在无功支撑不足问题，使得电压稳定问题尤为突出。故障将直接改变电网拓扑结构，以及原电网的静态电压稳定域，进一步削弱电源对电压的支撑能力，极易造成故障并引起暂态电压失稳，甚至引发电网大停电事故。例如英国“8·9”大停电，给人民生活及社会稳定造成了严重的影响[1-3]。特别地，受端电网本地新能源出力不确定，使得上述风险增加。为预防暂态电压失稳问题，需要快速定位高风险故障。
现有暂态电压稳定性分析方法主要基于时域仿真。文献[4]通过计算不同工况下系统等效电容确定暂态电压稳定性；文献[5]通过改进连续潮流法确定系统的电压稳定域，分析得出对电压稳定性贡献较大的节点；文献[6-7]提出了暂态过程中的电压可接受性概念；文献[8]基于电压可接受性提出加权多二元表判据指标以衡量暂态电压稳定性。然而，这些分析方法大多存在计算量大、时空复杂度高的问题，在需要实时调控平衡的实际电网中应用时，时效性不足，难以及时定位和跟踪关键故障[9]。
另一方面，现有的定位电网关键元件的相关研究大多基于复杂网络的小世界特性[10-13]和无标度特性[14]。文献[14]将度概念与Thevenin等值定理结合，构建电气耦合连接度指标评价节点关键性，并验证了小电网的无标度性；文献[15-17]基于网络方程提出电气介数并用于关键线路识别；文献[18]则引入最小生成树算法，并在大电网中进行模拟寻优，求取关键区域网络。可以看出，这些方法都从拓扑角度出发确定电网的关键节点、支路或小网络[19-24]。这些结合图论概念的方法计算速度较快，但同时大多由于：①采用无向无权图[25]；②认为功率仅沿最短路径传输[26]；③不考虑暂态过程[27-28]等原因，并未充分考虑电力系统的物理特性，如电网各节点间的电压支撑关系，因此缺乏相关物理意义，难以准确反映电力系统的本质特征，从而难以精确辨识实际大电网的关键元件。
特别地，文献[29]借鉴了网络分析技术的概念及其分析方法，提出稳定影响度指标用于分析电网所具有的电气特性。但是，其未考虑电源侧尤其是新能源接入及负荷侧动态特性对阻抗矩阵及网络方程的影响，对各个节点的分析也未能拓展至全网。
鉴于此，本文基于电网加权拓扑和暂态参数，结合节点阻抗矩阵，分析节点对电网暂态电压稳定性影响程度，以快速筛选高风险故障。本文主要工作及贡献如下：
1）提出了一种反映节点故障对其他节点暂态电压影响程度的指标，可用于高风险关键故障点快速筛选。
2）对于线路故障点，构造了升阶矩阵计算其影响度指标，综合节点故障影响因子，形成了全网高暂态电压失稳风险关键故障点筛选方法。
3）将上述筛选方法应用于改进IEEE 39节点系统与实际受端大系统，将影响度指标与故障下电网平均最低电压及临界切除时间（Critical Clearing Time, CCT）对比，验证了筛选方法的有效性。
本文提出的暂态电压影响度指标，能够较为准确地反映新能源接入的受端电网中节点及线路发生故障对全网的暂态电压影响程度。此外，其集成的快速筛选方法在对可能引起电网暂态电压失稳的高风险关键故障点筛选时具有快速、有效的优势，后续可为系统的预防控制和安控策略制定提供参考，为相关高风险区域重点巡检工作提供备选方案，具有一定的工程实用性。
本节主要阐明了网络阻抗对节点电压的支撑机理，并在此基础上简要介绍了节点阻抗矩阵及其支路追加时的修正方法。
对于含N个节点（其中G个节点为发电机节点，其他L=N-G个节点为负荷节点）、b条支路的电力系统，可获得其支路阻抗矩阵为Zb，不计互感情况下，为b×b的对角阵。也可得其支路导纳矩阵为Yb，包含电网每条支路的导纳参数，其关系为
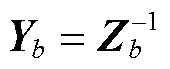（1）
根据高等电力网络分析[30]，结合支路特性和网络拓扑约束，考虑变压/流器等移相器作用，可得
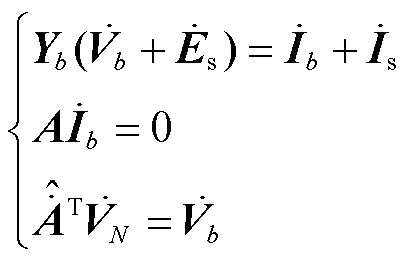（2）
式中，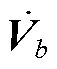
为支路电压；
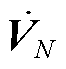为节点电压；
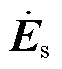为电源内电动势；
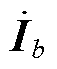为支路电流；
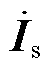为电源内电流；A为节-支关联矩阵，储存电网拓扑连接关系；上标ˆ表示取共轭分量。
消去支路分量，可推得
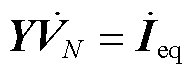（3）
式中，Y为电力网络的节点导纳矩阵，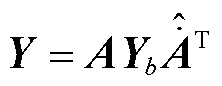
。
此外，等效注入电流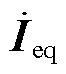
为
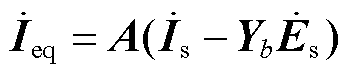（4）
最终，可得到节点阻抗矩阵为
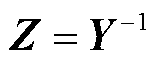（5）
用Z表示的电网电压方程为
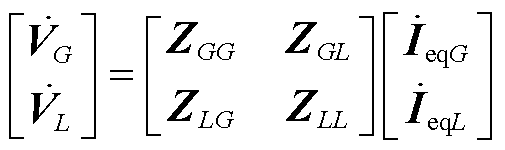（6）
式中，
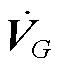与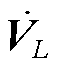
分别为G和L节点的电压；ZGG、ZGL、ZLG和ZLL分别为节点阻抗矩阵中G节点和G节点、G节点和L节点、L节点和G节点、L节点和L节点对应的行和列组成的分块矩阵；
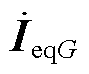和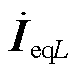
分别为G和L节点的等效注入电流。
式（6）阐明了各节点电压是由电源节点的注入电流经由网络阻抗所支撑。因此，从节点阻抗矩阵中可以提取节点的关键性信息，从而筛选出电网关键节点，即对电网电压稳定性影响程度较大的高风险故障节点。
注1：发电机节点处的节点注入电流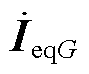并不是发电机端电流，而是发电机基本支路经过Norton等值得到的等效注入电流。
当支路发生变化时，可使用支路追加法[30]直接对原阻抗矩阵进行修正，从而获得新运行状态下的节点阻抗矩阵。以在k节点增加一条对地支路为例，支路追加法如图1所示，可得
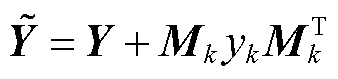（7）
式中，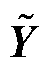
为原节点导纳矩阵Y经支路追加产生的新节点导纳矩阵；yk为追加支路的导纳值；Mk为所追加支路对应的关联矢量，为N×1矢量，其通常的结构形式为Mk=[0 … 0 1(k) 0 … 0]T。
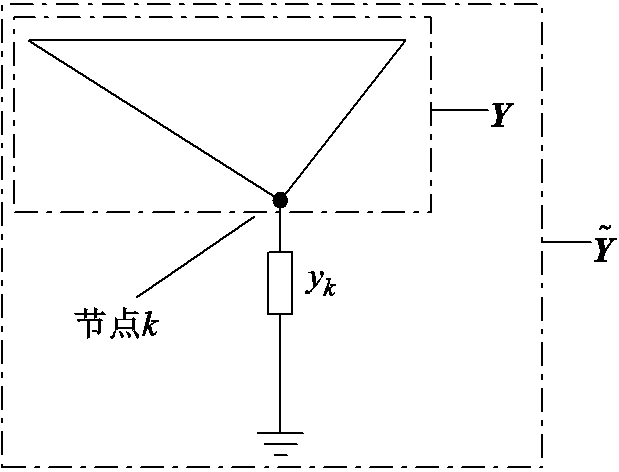
图1 支路追加法（以增加一条对地支路为例）
Fig.1 Branch addition method (take the example of adding a branch to the ground)
基于Sherman-Morrison-Woodburg定理（亦称矩阵求逆引理）[31]，可得
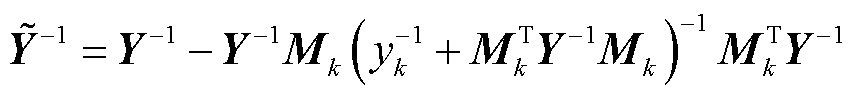（8）
将节点导纳矩阵与节点阻抗矩阵之间的互逆关系代入式（8）可得
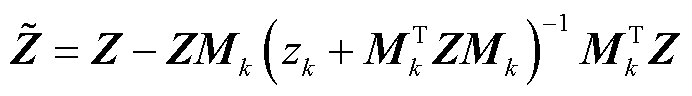（9）
式中，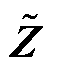
为修正后的节点阻抗矩阵；zk为所追加支路的阻抗值。
式（9）描述了当在节点阻抗矩阵为Z的网络中增添阻抗值为zk的对地支路时新的节点阻抗矩阵的计算方法，同时也包含了追加支路所产生的阻抗矩阵的修正量。
由式（6）可知，当电网中出现故障时，各节点电压的变化主要是节点间电气联系和等效注入电流的变化造成的。其中节点间电气联系的改变表现为节点阻抗矩阵Z的变化；同时，由式（4）可知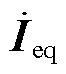，主要与发电机参数有关。受端电网中，本地发电机较少，发电机的支撑效应相较于传统电网大大削弱。在快速筛选需求下，考虑各节点等效注入电流变化不大，各节点电压变化可近似主要由节点阻抗变化造成，即
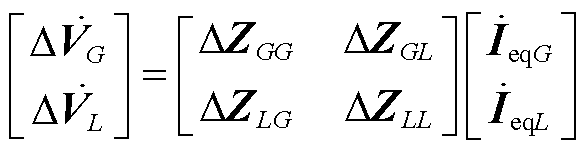（10）
式中，ΔZ为故障发生导致的节点阻抗矩阵各部分的变化量；ΔZGG、ΔZGL、ΔZLG和ΔZLL分别为ZGG、ZGL、ZLG和ZLL的变化量矩阵。
由式（10）可知，故障导致的网络结构变化影响了电源对于各节点电压的支撑能力，使得各节点电压降低，而节点在网络中的位置越关键，其故障对电网电压的影响就越严重。通过节点故障时阻抗矩阵的变化可以反映该故障对于暂态电压的影响程度，进而评价该节点在电网中的关键性。
当网络节点k处发生任意横向故障（包括对称及非对称故障）时，可等价为在节点k添加一条阻抗为zk的对地支路，根据支路追加法，式（9）可得
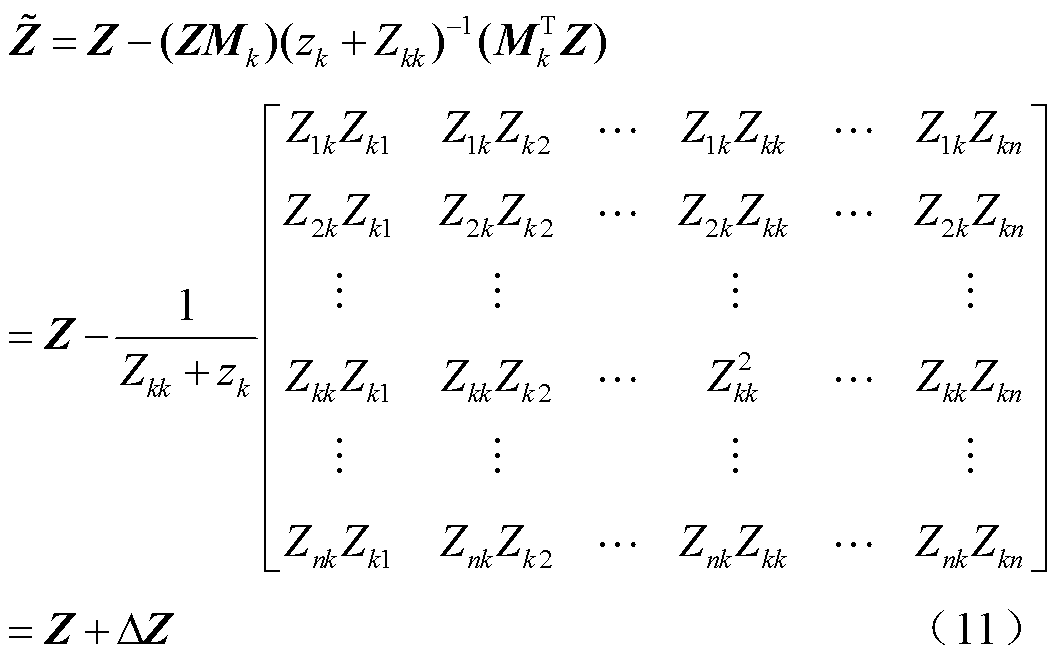
式中，Zij为原节点阻抗矩阵中的元素。
2.1.1 对称故障的影响因子矩阵
特别地，对称故障下，三相电流平衡，系统三相解耦，可取一相进行分析。其中，当发生三相短路直接接地故障时，zk=0，式（11）变为
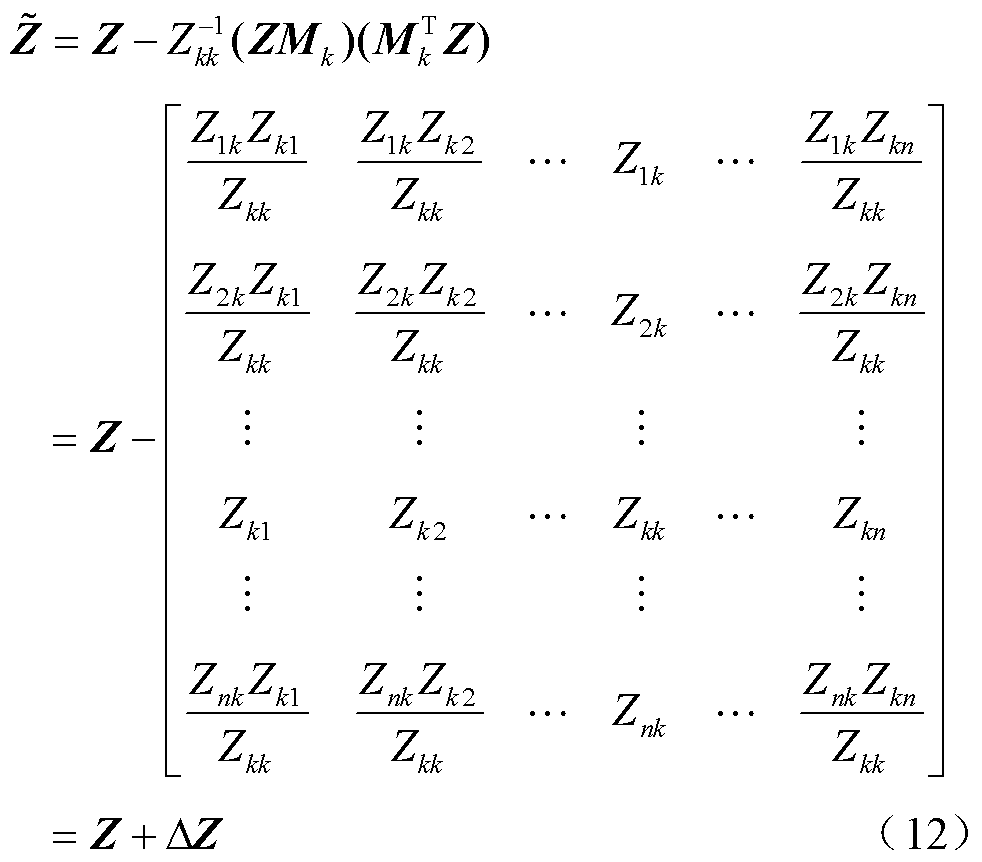
即原节点阻抗矩阵中的任意元素Zij均会产生一个ΔZij=-(ZikZkj)/Zkk的变化量。
当i=j=k时，其对应的修正后的节点阻抗方程中的元素Zij=0，对应其物理意义即故障节点k电压将下降为0，并失去对其他节点的电压支撑能力，其他节点也将产生不同程度的电压下降。因此以ΔZij表示故障导致的节点阻抗矩阵元素的变化，可以定义故障影响因子矩阵Fk，其各元素(i, j)满足
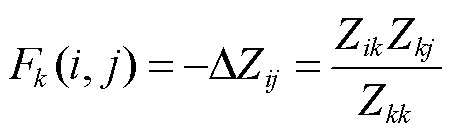（13）
式中，Fk(i, j)为网络节点k处发生三相金属性短路故障导致的节点阻抗矩阵各元素的减小量。
2.1.2 非对称故障的影响因子矩阵
不失一般性，k处发生非对称故障时，三相分量耦合，需对zk进行序分量分解以解耦，其在不同非对称故障下取值不同，具体取值可参考附录。
根据不同故障下的序分量修正式（11），有
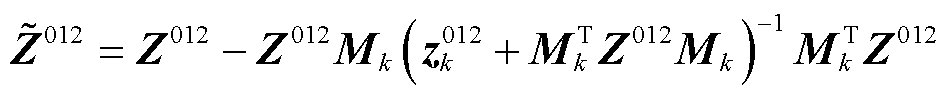（14）
相似地，其故障影响因子矩阵为
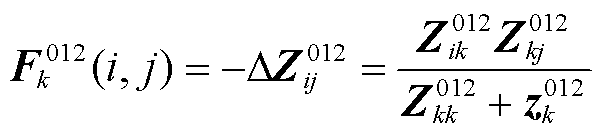（15）
需要说明的是，以上所有带“012”上标的物理量均为计及序分量的3×3矩阵形式，计算时，三序解耦，需分别计算，最后统一至三相分量。
事实上，一般故障情况下该接地阻抗三序分量均较小，可近似认为zk=0，即三相金属性短路故障。后文主要对最严重的三相短路直接接地故障进行分析。
下面给出基于故障影响因子矩阵的节点故障对于电网电压影响程度的评价方法。
当节点k处发生横向故障时，各节点电压变化近似为
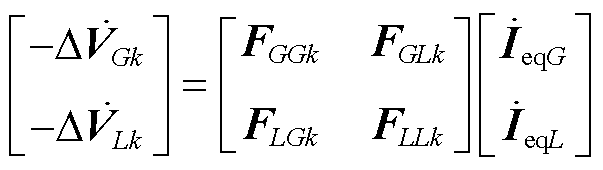（16）
式中，FGGk、FGLk、FLGk、FLLk为故障影响因子矩阵Fk中相对应的子矩阵，分别反映了G节点和L节点对自身内部以及之间的阻抗变化关联关系。
在故障的暂态过程中，负荷节点L的等效注入电流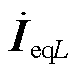=0，G节点处的等效注入电流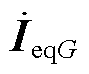会对网络节点电压产生影响。
2.2.1 对称故障的暂态电压影响度指标
当k（k=1, 2,…, N）处发生三相短路故障，网络中任意节点i（i=1, 2,…, N）的电压减小量可表示为
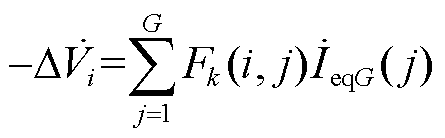（17）
式（17）也反映了任意节点电压跌落量与故障影响因子矩阵之间的关系。
进一步地，为评估单个节点故障对区域网络电压的整体影响，可构建反映故障对电网各节点暂态电压平均影响程度的指标FAC，其各元素满足
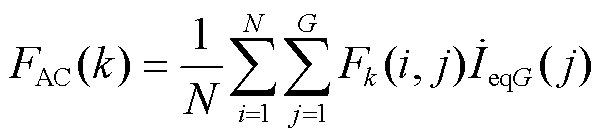（18）
由式（18）可知，FAC(k)为节点k三相故障时电网各节点电压的综合减小量，表征了该故障对于整个电网的暂态电压影响程度，也可以反映该节点发生故障造成电力系统暂态电压失稳的风险性大小。
2.2.2 非对称故障的暂态电压影响度指标
类似地，非对称故障下，根据序分量法，可得
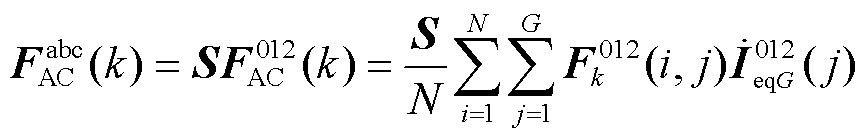（19）
式中，S为序分量变换矩阵。
然而，由于发电机只提供正序分量，可以正序分量表示k点的影响度，则其表达式与式（18）相同，不同点在于，其各序阻抗分量之间耦合。
综上所述，FAC(k)为节点k的暂态电压影响度指标（下文简称影响度指标或FAC），该指标值越大则表明相应节点故障导致电网发生电压失稳的风险越高。可以通过计算各节点的FAC指标值并排序来定位网络中的关键母线节点。
注2：考虑到暂态过程中，传统机组的暂态电动势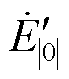
和直轴暂态电抗
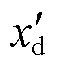可近似为恒定，故其节点注入电流的Norton等值计算式为
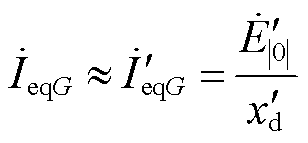（20）
注3：对于新能源机组，可采取等效阻抗模的方法，以近似其等效暂态电抗，进而计算等效注入电流，即
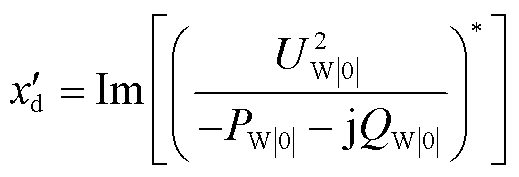（21）
式中，UW|0|为新能源并网点故障时刻的电压幅值；PW|0|和QW|0|分别为故障时刻由并网点向电网输送的有功和无功功率；*为共轭。
实际电网中，母线处通常具备较为完善的保护措施，因而故障概率较小，而线路故障的发生概率在电力系统中相对较高，因此线路上发生故障的情况往往不可忽略。分析输电线路上的影响度指标，有助于对线路采取针对性的后备保护。
本文将线路中间的某一故障点当作一个等效节点。相应地，节点阻抗矩阵的阶数应当升高一阶。因此，首先需要得到阶数升高后的节点阻抗矩阵，然后再根据第2节的方法评估故障点的影响程度。
然而，将某线路的一处故障点当作节点会改变原线路阻抗值及原电网的拓扑关系，最终会改变原电网的节点阻抗矩阵。为分析此情况，得到升阶后的节点阻抗矩阵，本节基于1.2节的支路追加修正方法，将线路上增加故障点的过程分为三步。
假设增加故障点前电网的节点阻抗矩阵为Z(0)。取某线路分析，其两端母线分别为节点i和节点j，如图2所示。
图2 原始线路
Fig.2 Original line
1）增加树支ip：此时线路拓扑关系如图3所示。
图3 增加树支ip后线路
Fig.3 Line after addition of tree branch ip
相应地，电网的节点阻抗矩阵变为
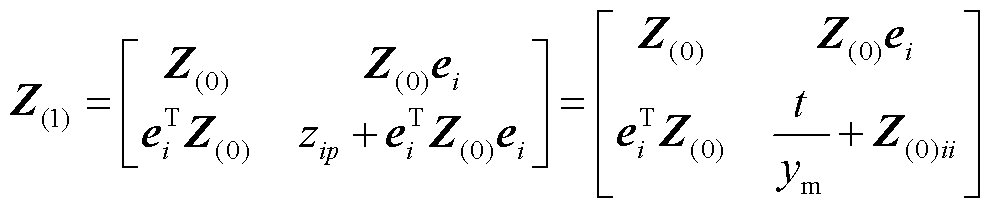（22）
式中，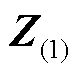
为增加树支后的系统节点阻抗矩阵；t为所取线路中故障点距i点距离占输电线路ij总长的比例，t
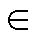[0,1]；
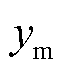为线路ij的导纳；ei为列向量，只有元素i为1，其余元素为0，即ei=[0 …1(i)…0]T。
2）消去原支路ij：此时线路拓扑关系如图4所示。
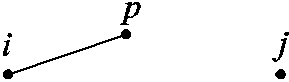
图4 消去原支路ij后线路
Fig.4 Line after elimination of original branch ij
相应地，电网的节点阻抗矩阵变为
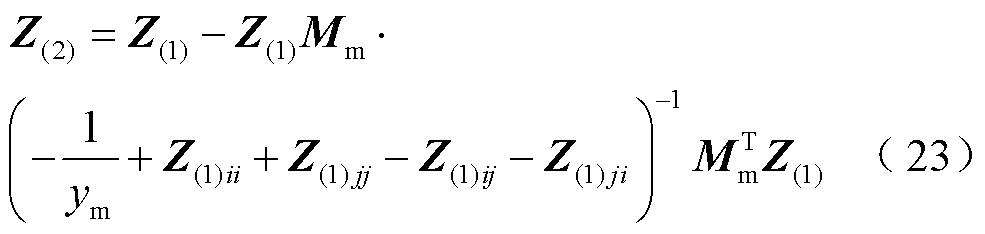
式中，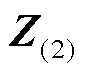
为消去原支路后的系统节点阻抗矩阵；Mm为线路ij对应位置的节-支关联矩阵中的关联矢量，元素i为1，元素j为-1，其余元素为0，即Mm=[0 …1(i)…-1(j)…0]T。
3）增加连支jp：此时线路拓扑关系如图5所示。
图5 增加连支jp后线路
Fig.5 Line after addition of consecutive branch jp
相应地，电网的节点阻抗矩阵变为
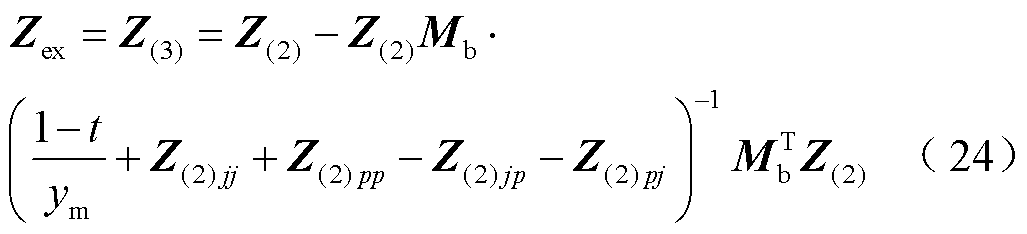
式中，Mb为新增连支jp对应的关联矢量，其中元素j为1，元素p为-1，其余元素为0，即Mb=[0 …1(j)…-1(p)…0]T。
电网的原始节点阻抗矩阵Z(0)经过以上三个步骤的变换，完成升阶，变为新节点阻抗矩阵Zex，Zex包含了电网所有母线节点和线路上一个故障点的节点阻抗信息。
对于得出的节点阻抗矩阵Zex，可以在故障点p根据式（13）计算故障影响因子矩阵Fp，再根据式（18）求取p点故障对整个电网暂态电压的影响度指标，即FAC(p)。
通过不断改变所取线路中故障点距线路母线节点i距离占输电线路ij总长的比例t，使之从0到1变化，可以得到线路全长各处的FAC。在此基础上，不断迭代线路ij序号，可以实现对电网任意物理位置的FAC的计算。
基于节点阻抗的电网高暂态电压失稳风险关键故障点快速筛选方法的基本思路如下：
1）读取当前运行工况下计及边界点潮流约束的整体/区域电网拓扑信息和相关线路参数，以识别节点-线路的拓扑匹配关系，通过自适应化简和Ward等值形成原始节点阻抗矩阵Z(0)。
2）在每次求解故障点的FAC前，判断所选定的节点k是否为母线节点，若为母线节点则可直接对其求Fk以提高计算速度；若为线路中故障点，则需要按照第3节的方法对原始阻抗矩阵Z(0)进行升阶，形成Zex后再对其所选定的故障点计算故障影响因子矩阵Fk。
3）根据机组数据求得等效注入电流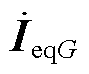后将其与Fk相乘并加权平均得到节点影响度指标FAC。
4）遍历节点，按指标大小导出节点及其指标，所得指标较大的节点即为所求关键节点。具体流程如图6所示。
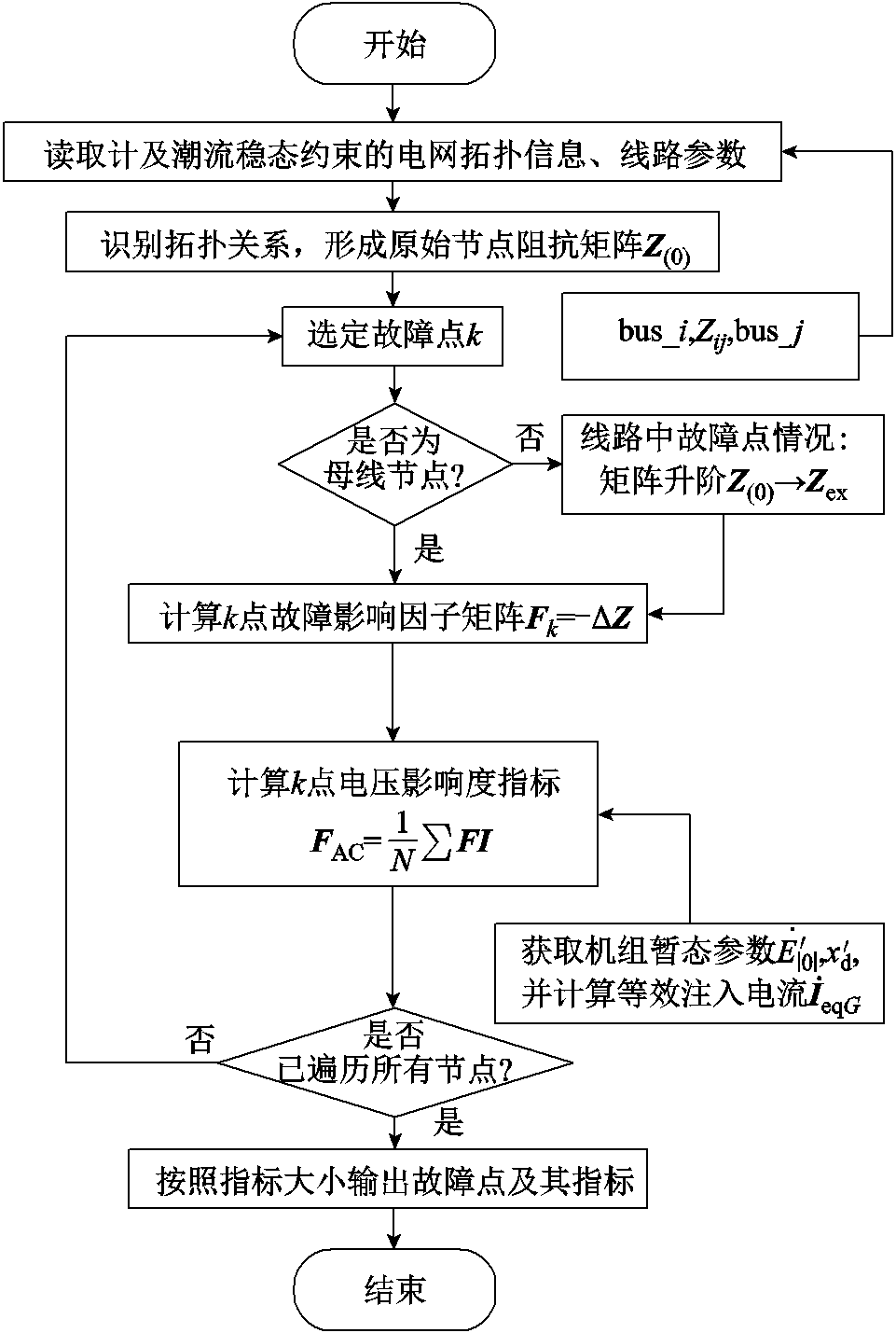
图6 电网高暂态电压失稳风险关键故障快速筛选流程
Fig.6 Fast screening process for high-risk critical fault points causing transient voltage instability in grids
本节将上述的筛选方法分别应用于改进IEEE 39节点系统和实际受端大电网，结合暂态仿真结果，证明所提指标及筛选方法的有效性。
将IEEE 10机39节点模型的32～36节点的火电机组改为典型参数的双馈风电机组，以模拟分布式新能源大量接入的受端电网，如图7所示。暂态仿真采用PSD-BPA软件，基于电网数据生成正序节点定阻抗矩阵进行分析。
5.1.1 母线节点
对于以上改进模型，计算各母线节点对应的节点三相短路故障下对全网暂态电压的影响度指标值FAC，结果见表1。
由表1可知，改进IEEE 39节点系统中高暂态电压失稳风险故障关键节点为节点16。
进一步，暂态仿真方面，在各母线节点处设置10周波后切除的三相故障，记录故障周波内的电网平均最低电压UAVL并获取每个节点的临界切除时间（CCT）。FAC排序前十位和后三位的节点FAC及其暂态仿真结果见表2。
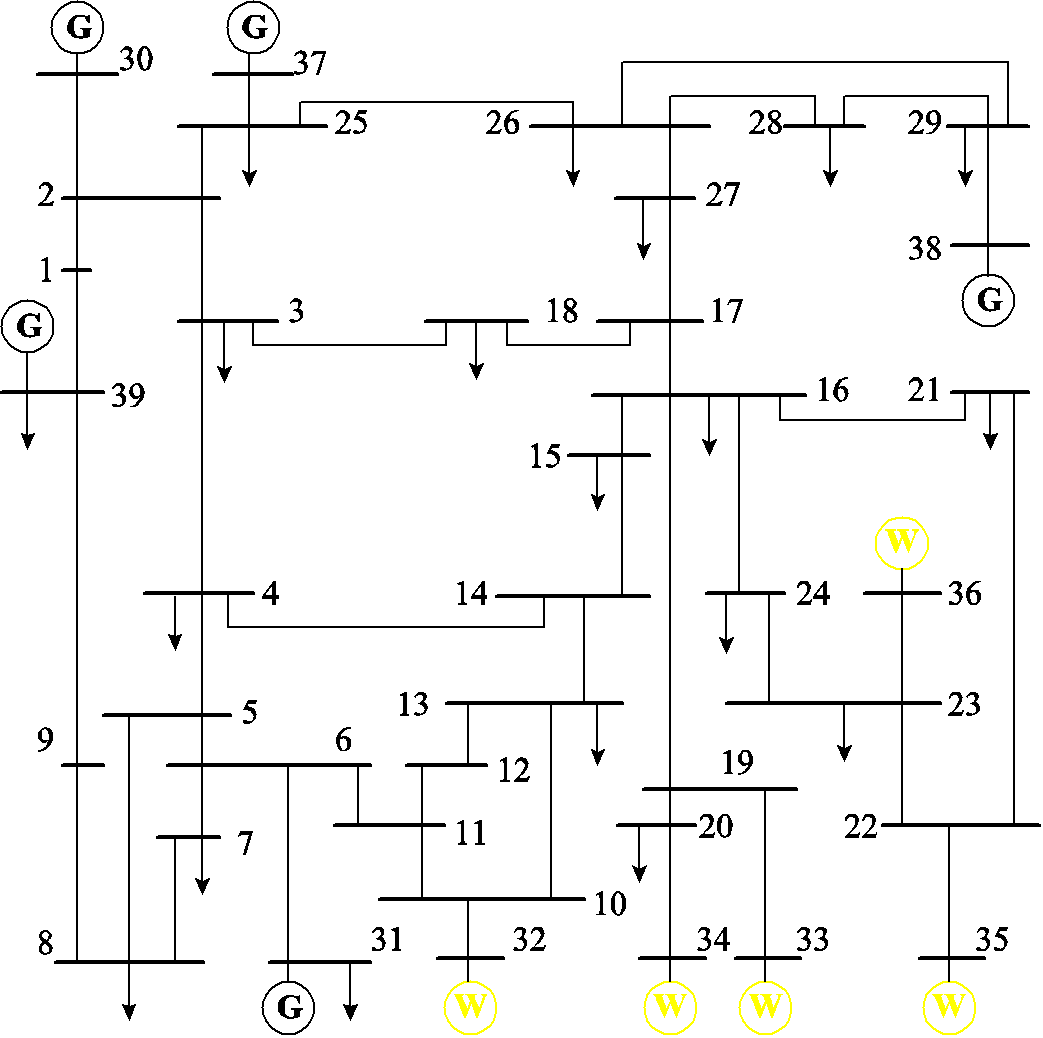
图7 改进IEEE 10机39节点测试系统
Fig.7 Improved IEEE 10-generator 39-bus test system
表1 改进IEEE 39节点系统母线节点FAC计算结果
Tab.1 FAC calculations for buses of the system
母线节点FAC母线节点FAC 300.121 6110.251 6 310.111 2120.122 2 320.143 1130.249 7 330.171 7140.270 1 340.123 7150.263 8 350.131 1160.350 0 360.110 9170.298 8 370.095 1180.253 7 380.093 8190.232 9 390.130 6200.161 1 10.084 1210.217 5 20.229 6220.201 4 30.262 5230.189 9 40.261 2240.264 0 50.256 0250.189 9 60.263 5260.182 5 70.208 2270.198 7 80.210 7280.104 1 90.100 9290.113 5 100.254 1——
表2 改进IEEE 39节点系统部分典型节点的FAC、UAVL、与CCT
Tab.2 FAC, UAVL & CCT of typical buses of the system
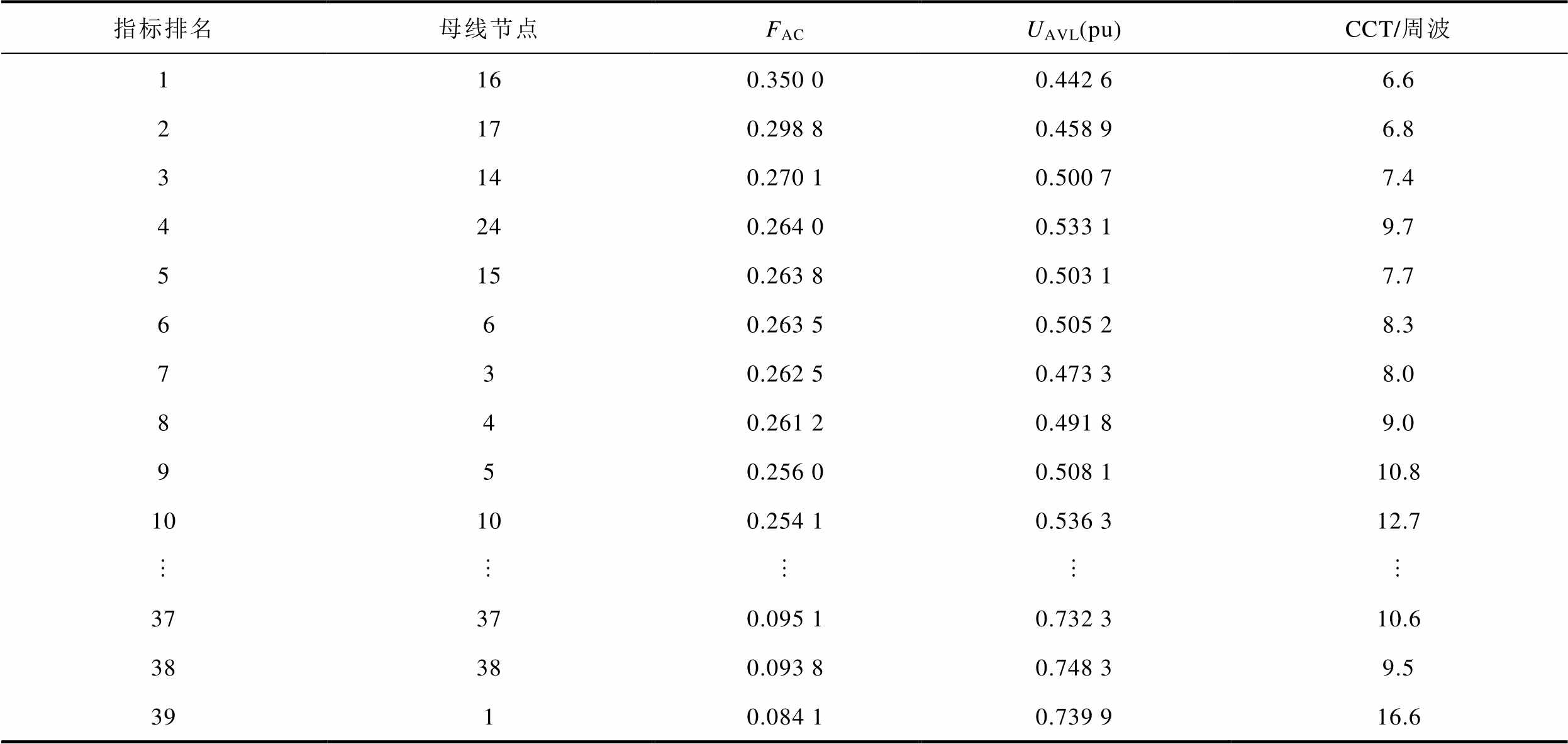
指标排名母线节点FACUAVL(pu)CCT/周波1160.350 00.442 66.62170.298 80.458 96.83140.270 10.500 77.44240.264 00.533 19.75150.263 80.503 17.7660.263 50.505 28.3730.262 50.473 38.0840.261 20.491 89.0950.256 00.508 110.810100.254 10.536 312.737370.095 10.732 310.638380.093 80.748 39.53910.084 10.739 916.6
表2表明，在各母线节点的FAC及UAVL与CCT的对应关系上，总体而言，FAC越大，UAVL越低，CCT越短，说明该母线故障对于整体电网暂态电压稳定性影响越大。相对而言，影响度指标与UAVL一致性较高；与CCT一致性一般，这主要是因为暂态功角稳定性受一部分传统发电机惯量的影响。
5.1.2 线路中故障点
考虑线路影响中式（22）的t=0.1，以与节点21相连的两条线路为例，可得线路不同点的FAC如图8所示。
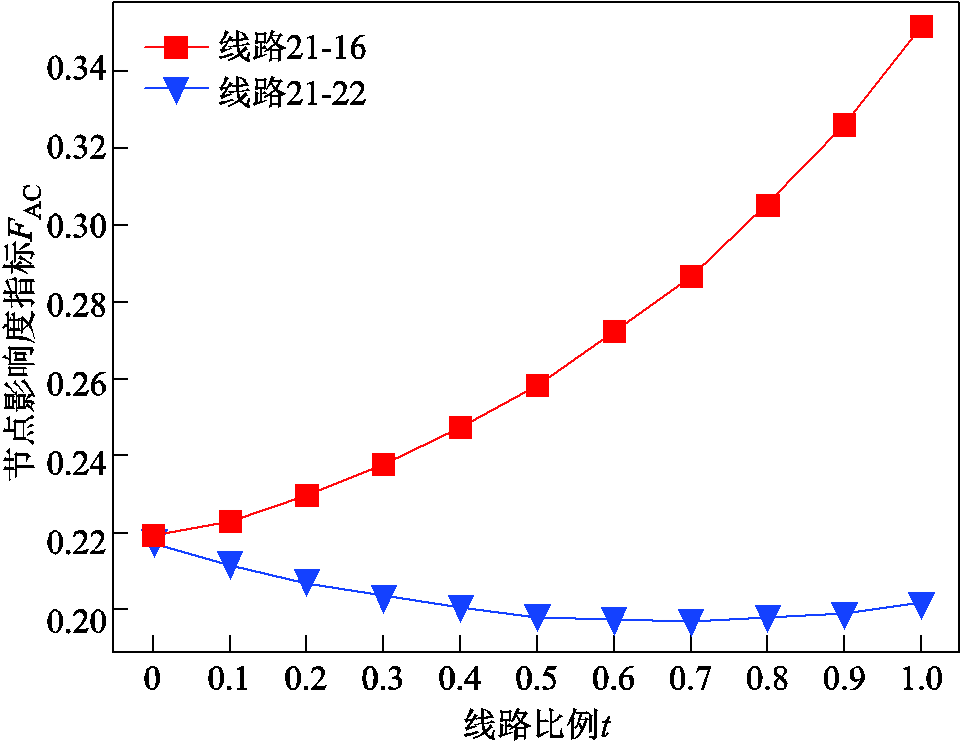
图8 典型线路的FAC
Fig.8 FAC of typical lines
图8表明，线路21-16的FAC呈现“单调增”的特点，在线路末端即节点16处取得最大值，在线路始端即节点21处取得最小值；线路21-22的FAC呈现“先减后增”的特点，在线路始端即21节点处取得最大值，在线路中取得最小值。对这两条线路而言，FAC的最大值出现在首末两节点的较大值处。
保持t变化步长为0.1以覆盖单条线路，遍历改进IEEE 39节点系统所有线路，同时计算所有节点的FAC，可得改进IEEE 10机39节点电网的FAC分布的色彩渲染图如图9所示。图9表明对于此系统，暂态电压稳定性影响较大的关键节点和线路都集中于节点16附近区域，该区域的FAC明显偏高。
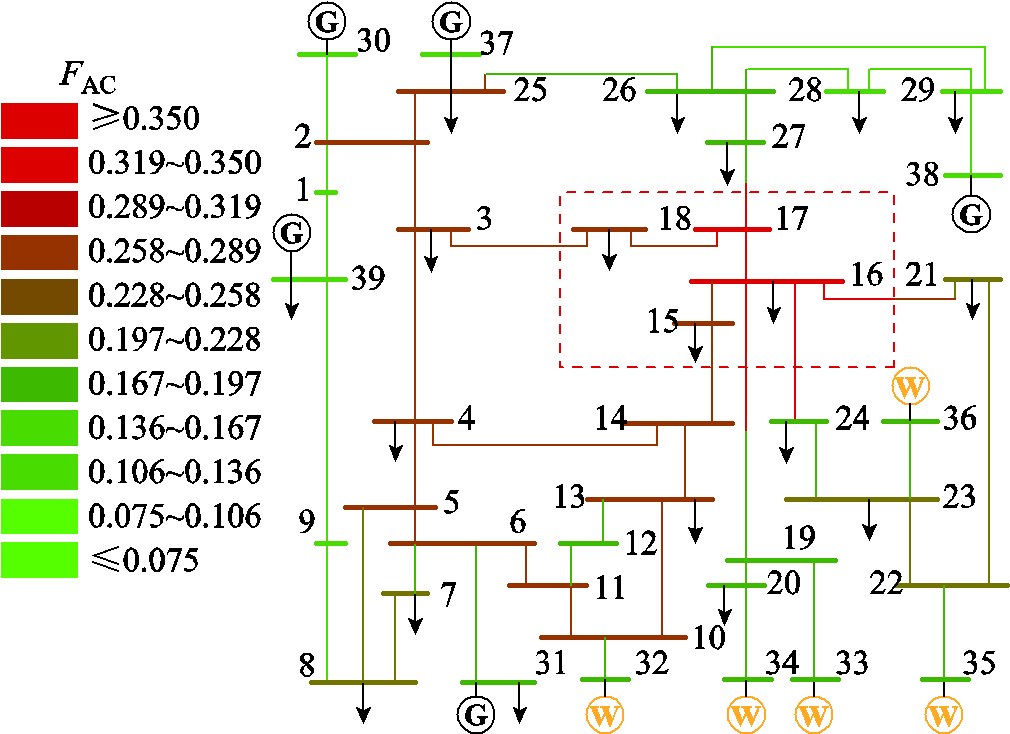
图9 改进IEEE 10机39节点电网FAC分布渲染
Fig.9 Color rendering of the FAC distribution for the improved system
5.1.3 负荷特性对FAC的影响
将算例中节点16的恒阻抗负荷分别修改为等容量标准静态负荷与重载异步电机动态负荷，设原和新负荷特性模型的等效阻抗为ZL0与ZL1，具体取值可参考附录，则其对节点导纳矩阵的贡献为
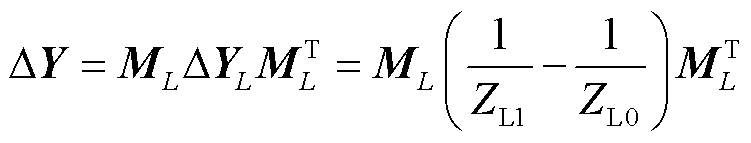（25）
式中，ML为列向量，取值为ML=[0 …1(L)…0]T。
根据矩阵求逆引理，可得阻抗修正矩阵为
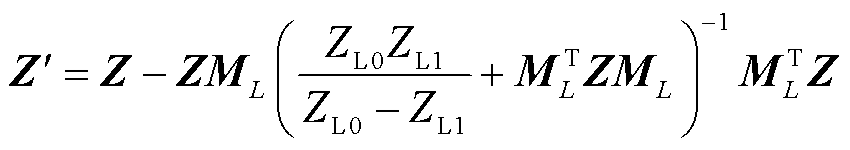（26）
式中，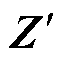
为考虑新负荷特性的阻抗矩阵。
根据
，重新对FAC(16)进行计算，并对其UAVL和CCT进行仿真，与恒阻抗负荷对比，结果见表3。
表3 不同负荷特性下节点16的FAC、UAVL与CCT
Tab.3 FAC, UAVL & CCT of bus16 with different load characteristics
节点16FACUAVL(pu)CCT/周波 恒阻抗0.350 00.442 66.6 静态负荷0.360 10.433 36.4 动态负荷0.412 70.377 25.7
表3表明，相同容量下，恒阻抗负荷的FAC依次小于标准静态负荷和动态负荷，即动态负荷会放大节点对全网的暂态电压影响程度，指标计算值和仿真结果仍能够较好地吻合。此外，全网节点的FAC均有所上升，但节点16及其相邻节点的FAC升高较为明显，最高点仍为节点16。
5.1.4 故障类型对FAC的影响
在算例中的节点16处，除已计算的三相短路外，分别设置以ZF=j0.01、Zg=0的a相单相接地短路f(1)、bc两相接地短路f(1,1)及bc相间短路f(2)，利用非对称故障的影响度指标算法对FAC(16)进行计算，并对其UAVL和CCT进行仿真，结果见表4。
表4 不同故障类型下节点16的FAC、UAVL与CCT
Tab.4 FAC, UAVL & CCT of bus16 with different fault types
节点16FACUAVL(pu)CCT/周波 f(3)0.350 00.442 66.6 f(1)0.332 60.816 29.3 f(1,1)0.339 70.805 910.5 f(2)0.344 80.769 410.1
表4表明，在相同条件下，非对称故障对暂态电压的影响程度小于三相故障，且非对称故障的FAC趋同，这与仿真结果较好地吻合。但FAC虽能够筛选出影响程度较大的故障类型，却不能很灵敏地反映不同非对称故障间对全网暂态电压影响的差异。此外，不同故障下全网FAC最大的点仍为节点16，且指标排名结果基本不变。
5.1.5 计算性能分析
本文方法从筛选指标算法本身出发，无需迭代，因此没有收敛性问题。将本文算法的筛选结果与标准算例的节点平均计算时间同文献[8]基于暂态仿真的方法与文献[5]的稳定域算法进行对比，结果见表5。
表5 不同方法筛选结果与计算时间
Tab.5 Screening results and calculation time of methods
计算方法本文方法文献[8]文献[5] 筛选结果节点16节点16节点16 节点平均计算时间/ms1.974121.62414.747
除此以外，文献[14]基于电气耦合连接度指标、文献[32]基于风险熵权与文献[33]基于图谱理论所得的筛选结果都与本文结果一致，均为节点16。
以上表明，本文筛选算法具有占用内存少、计算速度快的优势，且能准确地筛选出关键故障点。
采用某省级电网的实际算例，该电网新能源渗透率超过25%，含多回直流，为典型高比例受电的受端电网。其中，TZ—OH片区尤为特殊，其网架为该地区计算得出的一个骨干网架[34]，如图10所示。
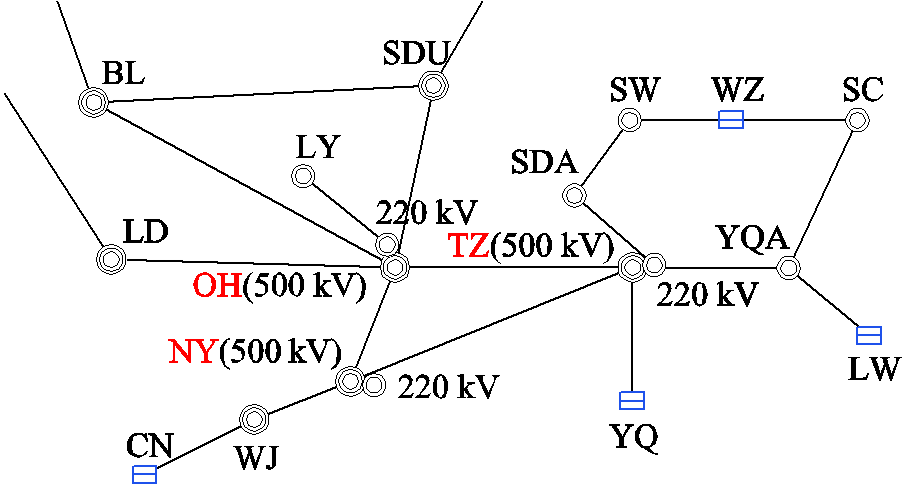
图10 某省级电网区域结构示意图
Fig.10 Schematic of the regional structure of a provincial power grid
该区域电网同外界的功率交换均会经过OH变电站，且从拓扑角度而言，区域内部少数节点的度明显高于其他节点，当关键元件发生故障时，将导致区域电网的电压发生明显下降，甚至电压失稳。
为验证节点快速筛选指标的有效性，在仿真中同时设置对应母线三相短路，并得出相应故障的FAC、UAVL与CCT暂态仿真结果见表6。
表6 区域关键母线的FAC、UAVL与CCT
Tab.6 FAC, UAVL & CCT of regional critical buses
母线节点FACUAVL(pu)CCT/周波 TZ 500 kV0.325 80.109 66.2 OH 500 kV0.303 90.127 05.7 NY 500 kV0.294 30.184 86.8 YQA0.267 30.377 78.0 SC0.259 50.403 010.0 WJ0.252 00.328 08.7 WZ0.246 00.451 69.0 SDA0.234 00.439 812.8 LW0.230 00.458 515.5 CN0.229 70.409 19.4 YQ0.226 10.447 111.5 SW0.219 90.482 612.6
表6表明，总体而言，FAC越大，对应的电网平均暂态电压越低，临界切除时间越短，表明该母线故障对于区域电网的电压稳定性影响越大。指标计算结果与暂态仿真的相符性证明了所提影响度指标的有效性。
此外，指标结果与仿真结果表明，对于TZ—OH片区各母线节点而言，TZ、OH及NY三处500 kV母线对于区域电网电压稳定性的影响程度较大，对这些母线故障需要重点防范。
本文针对新能源接入的受端电网中某些关键节点故障将会严重影响暂态电压稳定的问题，提出将各节点发生故障时阻抗矩阵的变化情况作为节点对暂态电压影响程度的评价依据，免去了导纳阵的求逆工作，具体工作如下：
1）提出了反映母线节点故障对电网的暂态电压的影响程度的指标。
2）通过构造升阶矩阵的方法，计算得出了线路故障点对电网的暂态电压影响度指标。
3）结合以上指标，提出了高风险关键故障点的快速筛选方法。
改进IEEE 39与实际受端大电网仿真表明：
1）本文方法下，输电线路故障点对电网暂态电压影响度随线路延伸呈现下凸特征，线路指标最高值取决于两侧母线较高者。
2）节点影响度指标和全网平均电压一致性较好，和临界切除时间一致性一般。
3）本文方法计算速度快，能够准确筛选出高风险节点，但不能精确刻画电压下降的过程。
本文方法为近似方法，且在求解等值网络方程时只考虑阻抗变化，其他因素有待后续进一步考虑。
附 录
1. 不同负荷特性及其等值阻抗
1）恒阻抗特性负荷模型，其等值阻抗为
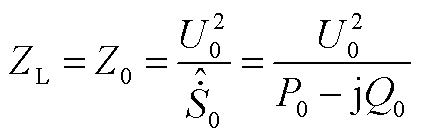（A1）
2）静态负荷特性模型，其等值阻抗为
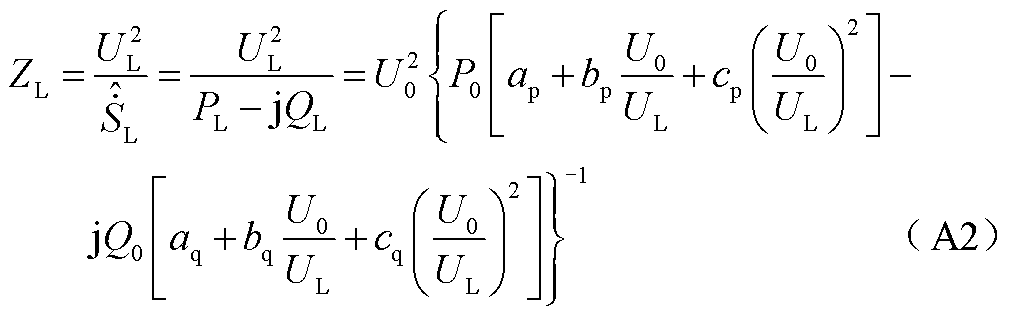
3）动态负荷特性模型，其等值阻抗为
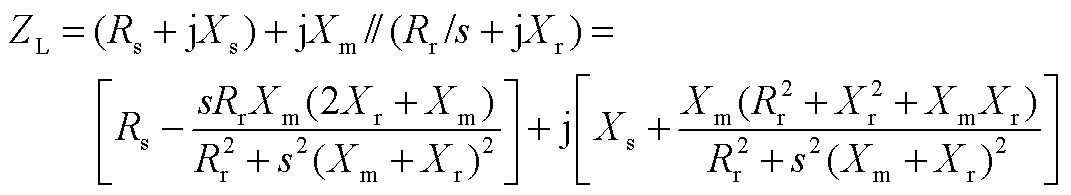（A3）
式中，含“0”下标的均为额定值；含“L”下标的均为运行值；ap、bp和cp分别为恒阻抗、恒电流和恒功率模型在有功功率中的占比；aq、bq和cq分别为恒阻抗，恒电流和恒功率模型在无功功率中的占比；s为转子的转差率，为提高计算速度，取初始转差率s0；Rr和Xr分别为定子绕组的电阻和漏抗；Rs和Xs分别为定子绕组的电阻和漏抗；Xm为励磁电抗。以上物理量均为以感应电动机自身容量为基准的标幺值。
2. 双馈风机和动态负荷参数
附表1 双馈风机控制和运行参数
App.Tab.1 The control and operation parameters of DFIG
参数数值(pu) RSC控制器功率外环比例/积分系数kp1, ki11, 3.75 RSC控制器电流内环比例/积分系数kp2, ki20.135, 20 GSC控制器直流电压比例/积分系数kp3, ki38, 400 GSC控制器电流内环比例/积分系数kp4, ki40.83, 5 定子电阻Rs0.011 4 转子电阻Rr0.010 4 定子电抗L1s0.075 2 转子电抗L1r0.146 9 激磁电抗Lm3.927
附表2 动态负荷参数
App.Tab.2 The parameters of dynamic loads
参数数值 惯性时间常数TJ/s2.037 2 初始转差率s0(pu)0.008 4 定子电阻Rs(pu)0.037 1 转子电阻Rr(pu)0.019 2 定子电抗Xs(pu)0.202 5 转子电抗Xr(pu)0.110 0 激磁电抗Xm(pu)2.965
3. 接地支路序参数
设广义横向故障电路如附图1所示。其中，ZF为故障电路等效三相并联阻抗，Zg为故障电路等效串联阻抗，可得不同非对称故障电路的等效接地支路序参数为
1）三相短路故障：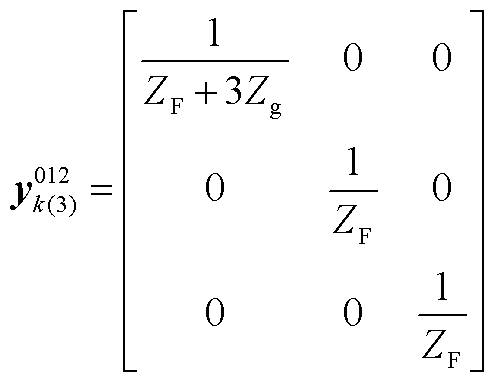
2）a相单相接地故障：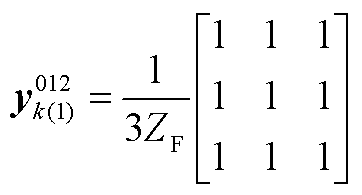
3）bc两相接地故障：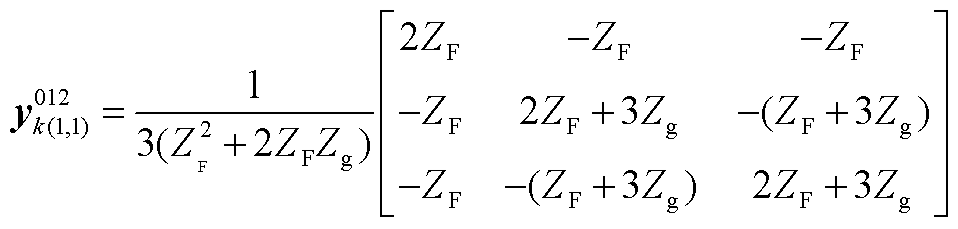
4）bc两相相间故障：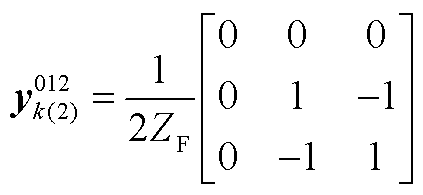
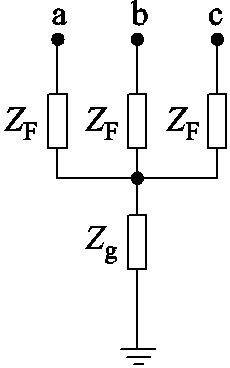
附图1 广义横向故障电路
App.Fig.1 Generalized lateral faults circuits
参考文献
[1] 项胜, 何怡刚, 吴可汗. 基于分形理论的国内大停电分析[J]. 电工技术学报, 2013, 28(增刊2): 367-371.
Xiang Sheng, He Yigang, Wu Kehan. Blackout analysis of domestic power based on fractal theory[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 367-371.
[2] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192.
Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[3] 胡秦然, 丁昊晖, 陈心宜, 等. 美国加州2020年轮流停电事故分析及其对中国电网的启示[J]. 电力系统自动化, 2020, 44(24): 11-18.
Hu Qinran, Ding Haohui, Chen Xinyi, et al. Analysis on rotating power outage in California, USA in 2020 and its enlightenment to power grid of China[J]. Automation of Electric Power Systems, 2020, 44(24): 11-18.
[4] 唐欣, 蔡明君, 唐惟楚, 等. 辐射型直流配电网母线电压跌落峰值的定量计算方法[J]. 电工技术学报, 2022, 37(12): 3108-3116.
Tang Xin, Cai Mingjun, Tang Weichu, et al. Quantitative calculation method of bus voltage sag peak value in radial DC distribution network[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3108-3116.
[5] 姜涛, 李雪, 李国庆, 等. 含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J]. 电工技术学报, 2022, 37(7): 1746-1759.
Jiang Tao, Li Xue, Li Guoqing, et al. A predictor-corrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1746-1759.
[6] 全国电网运行与控制标准化技术委员会. 电力系统安全稳定计算技术规范: DL/T 1234—2013[S]. 北京: 中国电力出版社, 2013.
[7] 中国南方电网电力调度通信中心. 南方电网安全稳定计算分析导则: Q/CSG 11004—2009[S]. 广州: 中国南方电网公司, 2009.
[8] 薛安成, 周健, 刘瑞煌, 等. 采用多二元表判据的实用暂态电压稳定裕度指标研究[J]. 中国电机工程学报, 2018, 38(14): 4117-4125, 4317.
Xue Ancheng, Zhou Jian, Liu Ruihuang, et al. A new practical transient voltage stability margin index based on multiple-two-element notation criterion[J]. Proceedings of the CSEE, 2018, 38(14): 4117-4125, 4317.
[9] 王东旭, 乐健, 刘开培, 等. 基于虚拟节点的复杂电网电压跌落随机评估方法[J]. 电工技术学报, 2011, 26(8): 190-197.
Wang Dongxu, Le Jian, Liu Kaipei, et al. Stochastic assessment method of voltage dip in complex power grid based on virtual bus[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 190-197.
[10] Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440-442.
[11] 孟仲伟, 鲁宗相, 宋靖雁. 中美电网的小世界拓扑模型比较分析[J]. 电力系统自动化, 2004, 28(15): 21-24, 29.
Meng Zhongwei, Lu Zongxiang, Song Jingyan. Comparison analysis of the small-world topological model of Chinese and American power grids[J]. Automation of Electric Power Systems, 2004, 28(15): 21-24, 29.
[12] Crucitti P, Latora V, Marchiori M. A topological analysis of the Italian electric power grid[J]. Physica A: Statistical Mechanics and Its Applications, 2004, 338(1/2): 92-97.
[13] Mishkovski I, Biey M, Kocarev L. Vulnerability of complex networks[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(1): 341-349.
[14] 谭玉东, 李欣然, 蔡晔, 等. 基于电气距离的复杂电网关键节点识别[J]. 中国电机工程学报, 2014, 34(1): 146-152.
Tan Yudong, Li Xinran, Cai Ye, et al. Critical node identification for complex power grid based on electrical distance[J]. Proceedings of the CSEE, 2014, 34(1): 146-152.
[15] Motter A E, Lai Yingcheng. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102.
[16] Kinney R, Crucitti P, Albert R, et al. Modeling cascading failures in the North American power grid[J]. The European Physical Journal B - Condensed Matter and Complex Systems, 2005, 46(1): 101-107.
[17] 王涛, 李渝, 顾雪平, 等. 电网关键线路序元搜索方法[J]. 电工技术学报, 2016, 31(2): 153-162.
Wang Tao, Li Yu, Gu Xueping, et al. Study of grid’s key line sequence search method[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 153-162.
[18] 单政博. 电网重要节点、脆弱线路及骨干网架识别研究[D]. 杭州: 浙江大学, 2017.
Shan Zhengbo. Research on identifications of important node, vulnerable transmission line and backbone grid[D]. Hangzhou: Zhejiang University, 2014.
[19] Carreras B A, Newman D E, Dobson I, et al. Evidence for self-organized criticality in a time series of electric power system blackouts[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(9): 1733-1740.
[20] Crucitti P, Latora V, Marchiori M. Model for cascading failures in complex networks[J]. Physical Review E, 2004, 69(4): 045104.
[21] Rosas-Casals M, Valverde S, Solé R V. Topological vulnerability of the European power grid under errors and attacks[J]. International Journal of Bifurcation and Chaos, 2007, 17(7): 2465-2475.
[22] 顾雪平, 刘彤, 李少岩, 等. 用于未来态预测的电网运行断面时空相似性挖掘[J]. 电工技术学报, 2022, 37(23): 6145-6156.
Gu Xueping, Liu Tong, Li Shaoyan, et al. Temporal and spatial similarity mining of power grid running section for future state prediction[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6145-6156.
[23] 李雪, 姜涛, 李国庆, 等. 基于相关增益的电压稳定关键注入区域识别[J]. 电工技术学报, 2018, 33(4): 739-749.
Li Xue, Jiang Tao, Li Guoqing, et al. Voltage stability critical injection area determination via cross-relative gain[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 739-749.
[24] 王涛, 李渝, 顾雪平, 等. 考虑地理分区边界优化的电网关键输电断面辨识[J]. 电工技术学报, 2014, 29(4): 220-228, 245.
Wang Tao, Li Yu, Gu Xueping, et al. Identification of the key transmission sections considering optimization of geographical partition boundary for power grids[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 220-228, 245.
[25] 徐林, 王秀丽, 王锡凡. 电气介数及其在电力系统关键线路识别中的应用[J]. 中国电机工程学报, 2010, 30(1): 33-39.
Xu Lin, Wang Xiuli, Wang Xifan. Electric betweenness and its application in vulnerable line identification in power system[J]. Proceedings of the CSEE, 2010, 30(1): 33-39.
[26] 李昌超, 康忠健, 于洪国, 等. 基于PageRank改进算法的电力系统关键节点识别[J]. 电工技术学报, 2019, 34(9): 1952-1959.
Li Changchao, Kang Zhongjian, Yu Hongguo, et al. Identification method of key nodes in power system based on improved PageRank algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1952-1959.
[27] 谭玉东. 复杂电力系统脆弱性评估方法研究[D]. 长沙: 湖南大学, 2013.
Tan Yudong. Research on complex power system vulnerability assessment methods[D]. Changsha: Hunan University, 2013.
[28] 向洁, 蔡静谊, 刘小林, 等. 基于改进奇异值分解法的电力系统弱节点研究[J]. 电气技术, 2012(8): 55-58.
Xiang Jie, Cai Jingyi, Liu Xiaolin, et al. Research on weak node of power system based on modified singular value decomposition[J]. Electrical Engineering, 2012(8): 55-58.
[29] 胡臻, 李欣然, 刘光晔, 等. 基于稳定影响度指标的电压稳定脆弱点分析[J]. 电工技术学报, 2017, 32(7): 150-157.
Hu Zhen, Li Xinran, Liu Guangye, et al. Analysis of voltage fragility area based on the stability influence index[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 150-157.
[30] 张伯明, 陈寿孙, 严正. 高等电力网络分析[M]. 2版. 北京: 清华大学出版社, 2007: 89-117.
[31] Sherman J, Morrison W J. Adjustment of an inverse matrix corresponding to a change in one element of a given matrix[J]. The Annals of Mathematical Statistics, 1950, 21(1): 124-127.
[32] 丁明, 过羿, 张晶晶, 等. 基于效用风险熵权模糊综合评判的复杂电网节点脆弱性评估[J]. 电工技术学报, 2015, 30(3): 214-223.
Ding Ming, Guo Yi, Zhang Jingjing, et al. Node vulnerability assessment for complex power grids based on effect risk entropy-weighted fuzzy comprehensive evaluation[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 214-223.
[33] 栗然, 靳保源, 张凡, 等. 基于图谱理论的电力系统关键节点识别方法[J]. 电力系统保护与控制, 2018, 46(11): 14-22.
Li Ran, Jin Baoyuan, Zhang Fan, et al. Research on identification of key nodes in power system based on spectral graph theory[J]. Power System Protection and Control, 2018, 46(11): 14-22.
[34] 杨文辉, 毕天姝, 黄少锋, 等. 基于电网生存性评估的关键线路识别方法[J]. 中国电机工程学报, 2011, 31(7): 29-35.
Yang Wenhui, Bi Tianshu, Huang Shaofeng, et al. An approach for critical lines identification based on the survivability of power grid[J]. Proceedings of the CSEE, 2011, 31(7): 29-35.
Abstract The receiving-end power grid interconnected with large-scale new energy lack reactive power support from local conventional generators, so that transient voltage stability problems are particularly prominent, easy to cause grid blackout. However, existing transient voltage stability analysis methods are mainly based on time-domain simulations, and most of these methods have large computational volume and high complexity, which are not fast enough to locate the critical fault point in time in the actual power grids. On the other hand, most of the existing studies related to locating critical fault points of power grids utilize graph-theoretic concepts to construct indexes. Although these methods are faster in computation, most of them lack relevant physical meanings, making it difficult to accurately identify the critical fault point of the actual large power grid.
In view of this, this paper analyzes the degree of influence of points on the transient voltage stability of the grid based on the weighted topology and transient parameters of the grid, combined with the impedance matrix, in order to quickly screen high-risk fault points. Specifically, firstly, an index reflecting the degree of influence of node faults on the transient voltages of power grid (degree index, also the point influence factor,FAC) is proposed, which can be used for fast screening of high-risk critical fault points; secondly, for the line fault points, an ascending matrix is constructed to calculate their FAC, and the point influence factor array forms a screening method for the whole grid of high-risk critical fault points with high transient voltage instability risk; lastly, the above screening method is applied to the improved IEEE 39 bus test system and the actual receiving-end grid.
In the improved IEEE 39-bus system, firstly, the FAC of the bus nodes are calculated, and it is concluded that bus 16 has the highest FAC of 0.350 0, and the indexes are compared with the average minimum voltage (UAVL) of the grid under fault and critical clearing time (CCT) to prove its validity; secondly, the FAC of the equivalent buses on the line are calculated, and it is found that the FAC in the line is not the highest, and the color rendering of the system shows the area around the bus 16 has a higher level of risk; furthermore, the effects of load characteristics and fault types on FAC are also considered; finally, the computational efficiency of the screening methods is analyzed and compared. In the actual large receiving-end grid, the FAC of the buses are calculated, and it can be seen that the FAC of the TZ, OH and NY are higher, which are 0.325 8, 0.303 9 and 0.294 3, respectively, and the simulation results also proved that these nodes play a key role in the transient voltage stability of the whole grid.
The main work and conclusions of this paper are as follows: (1) this paper attributes the change of voltage during transient process to the change of impedance based on the supporting role of impedance on voltage, and accordingly proposes the FAC. (2) This paper puts forward a way of thinking to construct the ascending matrix in order to calculate the FAC of the line fault point and summarize it as a fast screening method for the critical fault point. (3) Simulation results show that the proposed FAC index can effectively reflect the degree of influence of fault point on the transient voltage, and the screening method using the FAC can quickly screen the high-risk faults and visualize the results, which has a certain degree of engineering practicability, and can provide a theoretical basis for the subsequent development of security & control strategies.
keywords：Transient voltage, critical fault points, impedance matrix, branch addition method
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.231728
国家自然科学基金资助项目（51477050）。
收稿日期 2023-10-17
改稿日期 2023-12-08
杨金洲 男，2001年生，硕士研究生，研究方向为新型电力系统动暂态稳定性分析。E-mail：1563185817@qq.com
薛安成 男，1979年生，教授，博士生导师，研究方向为模型和数据驱动的新型电力系统稳定性分析及安全防御、二次设备评估等。E-mail：acxue@ncepu.edu.cn（通信作者）
（编辑 赫 蕾）