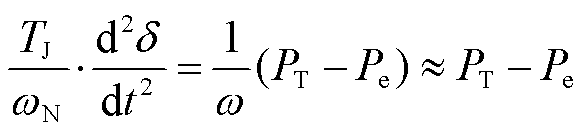（1）
摘要 直流换相失败引起的功率瞬降易增加送端交流系统的功角失稳风险，但当前研究尚缺少应对多直流换相失败的暂态功角稳定实时控制方法。针对这一问题，该文首先分析了换相失败功率冲击下送端系统发电机相对动能和转速的变化规律，指出送端系统的相对动能变化可仅由等值发电机的相对转速表征，不依赖于直流系统功率跌落和恢复的曲线态势；然后根据直流功率恢复至稳态时等值发电机的相对转速计算转子运动剩余加速面积，进而得到维持送端系统暂态功角稳定性所需的减速面积及相应的切机量；最后根据切机量计算结果制定了实时切机控制策略，并基于简单系统和实际电网进行了仿真分析和验证。仿真结果表明，所提方法能够较准确地计算维持送端系统暂态功角稳定性所需的切机量，有效减小换相失败后送端系统的暂态功角失稳风险。
关键词：高压直流 换相失败 功角失稳 切机策略
基于电网换相换流器的高压直流输电为解决我国能源与负荷的逆向分布问题提供了广泛、有效的技术支撑[1-2]。但受端交流系统发生故障时，直流系统易发生换相失败从而导致功率传输瞬降等问题，影响交直流混联系统的安全稳定运行[3]。
随着直流输送功率的提升及电网互联规模的扩大，换相失败对系统稳定性的影响程度和范围逐渐扩大[4-5]。换相失败引起的功率瞬降冲击会导致送端交流系统产生大量的功率盈余，当盈余功率转移到区域间的互联线路时，可能会破坏薄弱交流断面稳定，增大送端系统暂态功角失稳风险[6-7]。
交流系统暂态功角稳定是一个相对传统、研究较为成熟的课题，目前国内外工程界广泛采用的是基于预想故障集和控制策略表的“离线决策、在线匹配”的应对方法[8]。但随着电力系统规模和复杂度的提升，依赖离线仿真和故障枚举的传统方法，难以覆盖电力系统多变的运行方式，离线制定的控制策略难以完全匹配实时的运行状况，甚至可能导致控制策略失效[9]。
广域测量系统的发展为复杂电力系统电气量的实时感知和获取提供了技术保障，也为暂态稳定问题的在线实时决策和控制奠定了基础。文献[10]在传统等面积法则的基础上提出了扩展等面积理论，将发电机群分为加速机组和滞后机组，并根据系统等效惯量中心解释复杂电力系统的功角稳定问题。相关研究在此基础上根据系统加速能量实时计算维持系统暂态稳定性所需的切机方案，但该类方法依赖于发电机同调机群的准确识别和划分[11-12]。为减小对同调分群的依赖，文献[13]提出了基于动态安全域的紧急控制策略；文献[14]利用修正势能边界曲面出口处势能的变化情况估算维持暂态稳定所需的切机量；文献[15]基于发电机转子在全时域空间内的积分特性，根据临界切机量下系统加速能量所满足的特性方程制定实时的发电机切机方案；文献[16]根据离线仿真轨迹与实测功角轨迹之间的差异计算暂态能量偏差，据此评估控制策略的有效性并附加相应的控制；文献[17]提出了考虑主导不稳定平衡点变化的切机策略，从而提升切机的响应速度和控制精度。
基于上述暂态稳定相关研究，少数文献针对换相失败后送端系统暂态功角稳定问题进行了研究。文献[18-19]分析了换相失败导致送端互联系统暂态功角失稳的机理，并指出可通过延长重合闸时间、增开火电机组和适当切机等方式减小功角失稳风险，但未涉及相关措施的定量计算；文献[20]根据换相失败累积时间制定了切机方案的离线策略表；文献[21]则提出利用直流系统短时功率过载能力补偿换相失败期间送端机组转子运动的加速面积。由此可见，当前研究主要集中在定性分析、离线决策及直流控制等方面，缺少切机方案的量化方法及实时控制策略。
针对上述问题，本文提出换相失败后提升送端系统暂态功角稳定性的实时控制方法。在分析换相失败后送端机组相对动能和转速变化规律的基础上，计算换相失败功率冲击引起的转子运动相对动能及剩余加速面积，依据维持暂态稳定性所需的减速面积实施切机策略，从而有效提升换相失败功率冲击下送端系统的功角稳定性。
对于单机无穷大系统，当以标幺值表示时发电机转子运动方程为
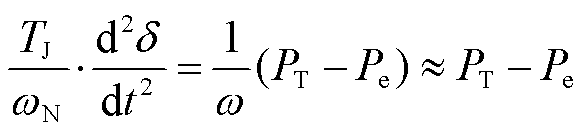（1）
式中，TJ为惯性时间常数；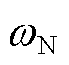
为同步转速；
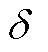为发电机功角；w为发电机转速；PT和Pe分别为机械功率和电磁功率。
故对于图1所示的交直流混联系统，假设由G1向G2送电，则送端交流系统等值发电机的转子运动方程为
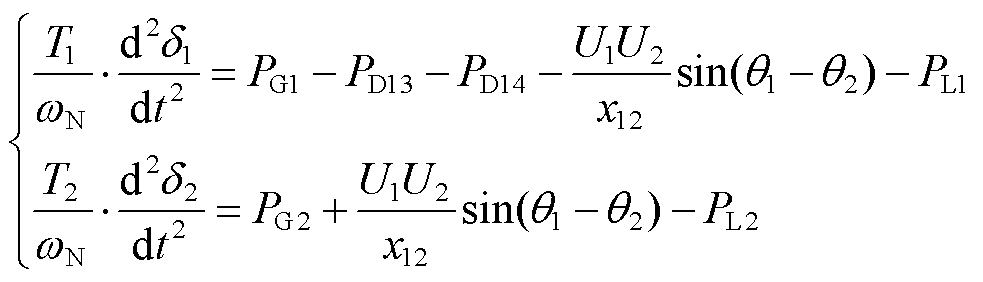（2）
式中，T1和T2分别为等值发电机G1和G2的惯性时间常数；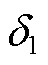
和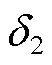
分别为等值发电机G1和G2的功角；PG1和PG2分别为等值机械功率；PD13和PD14分别为直流系统D1和D2的输送功率；U1和U2分别为两侧等值母线电压幅值；
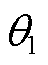和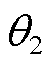
分别为两侧等值母线电压相角；PL1和PL2为等值负荷；x12为联络线电抗。
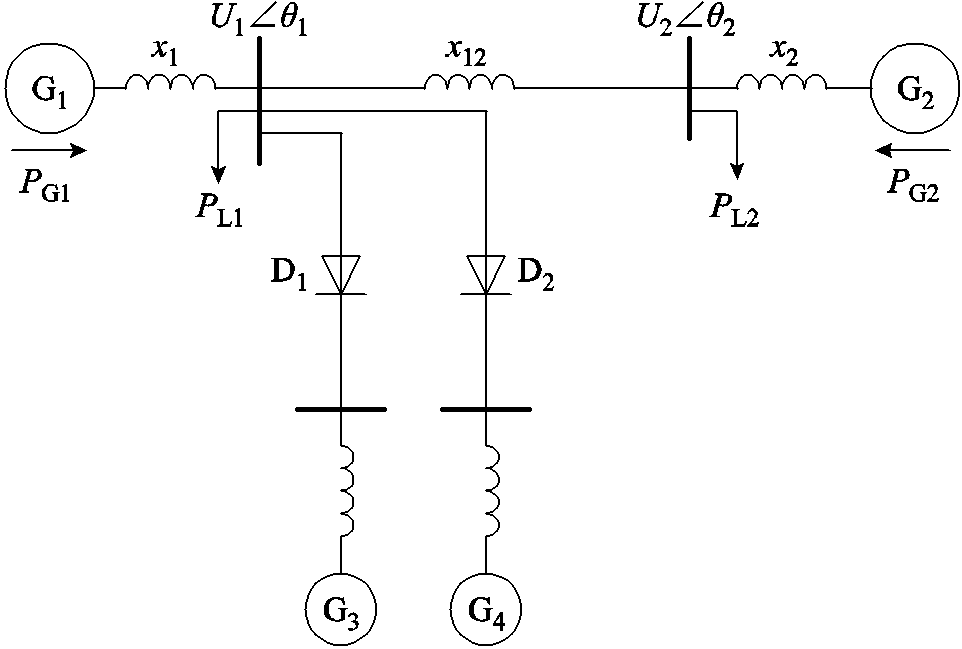
图1 交直流混联系统简化模型
Fig.1 Simplified model of the AC/DC hybrid system
图1中，G1和G2表示送端两区域等值发电机，G3和G4表示受端系统等值发电机，x1和x2为等值电抗。
将式（2）化简为
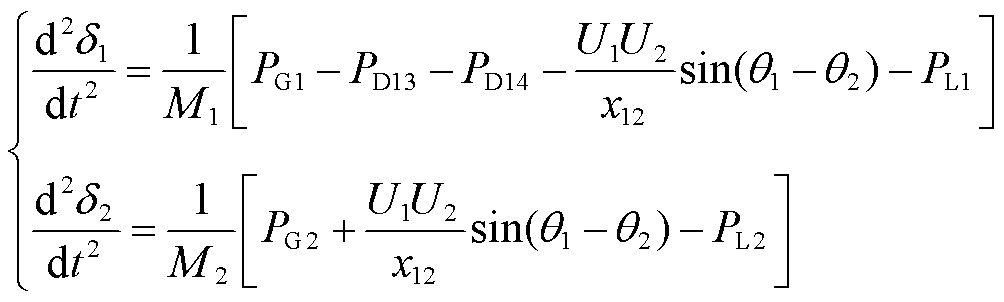（3）
式中，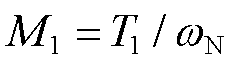
；
。
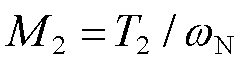将式（3）中两式相减并整理化简后可得
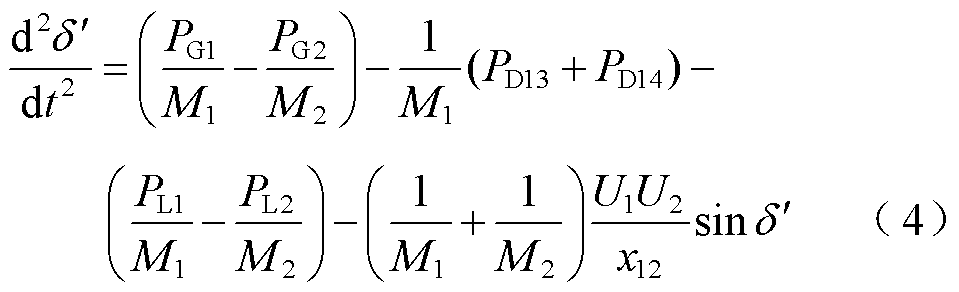
式中，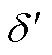
为等值发电机功角差。
式（4）为送端交流系统的等值发电机转子运动方程，其中等值机械功率和电磁功率为
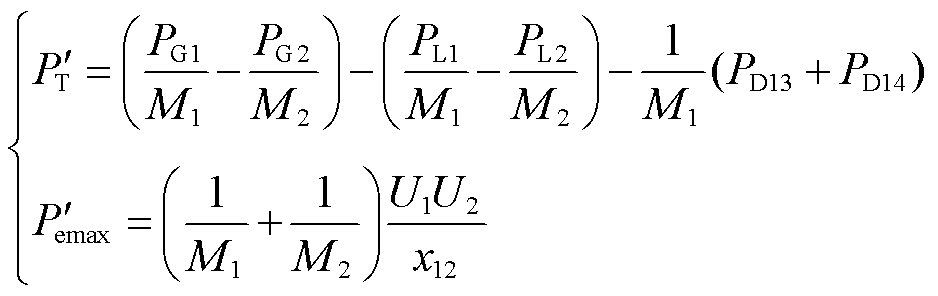（5）
式中，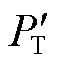
为等值机械功率；
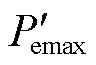为等值电磁功率最大值。
由式（5）可知，若换相失败引起直流输送功率大幅下降时，则等效于送端系统等值机械功率上升。
换相失败后等值发电机功率特性曲线如图2所示。文献[18-19]基于上述推导过程并结合图2阐明了等值机械功率增大是导致送端系统暂态功角失稳的原因。本文简要说明如下：正常工况下系统运行工作点为a，当直流系统发生换相失败，其输送的功率会出现瞬降，等效于等值机械功率上升，此时系统运作工作点由a点变化至b点，等值功角差由于发电机转子惯性而继续保持在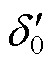
。当等值机械功率大于等值电磁功率时，若直流功率持续保持在最低值，则系统运行工作点将随着等值功角差增大而由b点运行至c点。随着直流输送功率的恢复，等值机械功率小于电磁功率，发电机转子开始减速但仍然大于同步转速，等值功角差将继续增大。若等值功角差增大至
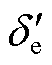时，等值发电机转速仍然未恢复至同步转速，则系统运行工作点将越过e点，此时等值机械功率再次大于电磁功率，进而造成系统功角失稳。
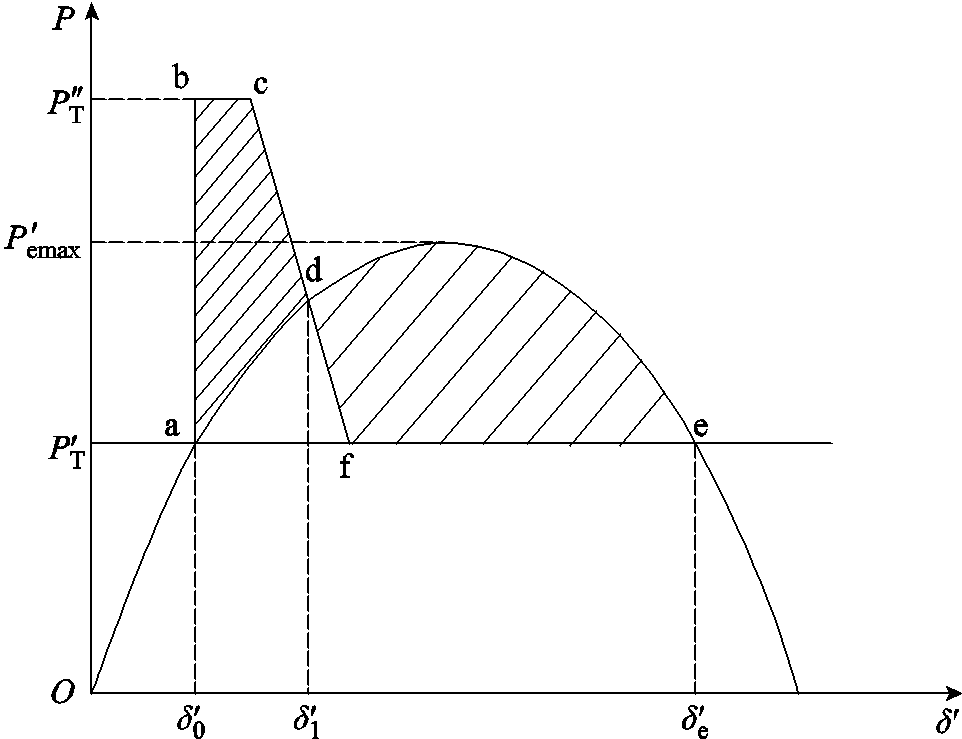
图2 换相失败后等值发电机功率特性曲线
Fig.2 Equivalent generator power characteristic curve after commutation failure
尽管当前研究已说明了换相失败导致送端系统功角失稳的原因，但未能对发电机转子的相对动能进行量化，故根据其结论仅能得到针对控制措施的定性原则。且在分析时假设直流功率的变化是瞬时下降后持续一段时间再瞬时恢复的阶跃过程，忽略了直流功率恢复过程及多次换相失败问题。
当以状态方程的形式进行表征时，图1所示交直流混联系统的送端等值发电机转子运动方程为
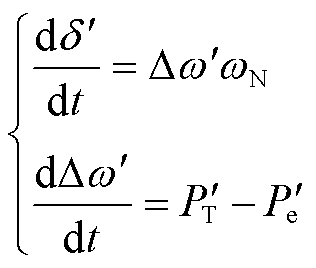（6）
式中，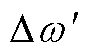
为等值发电机的相对转速；
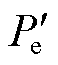为等值电磁功率。
图2中的加速面积Sabcd为
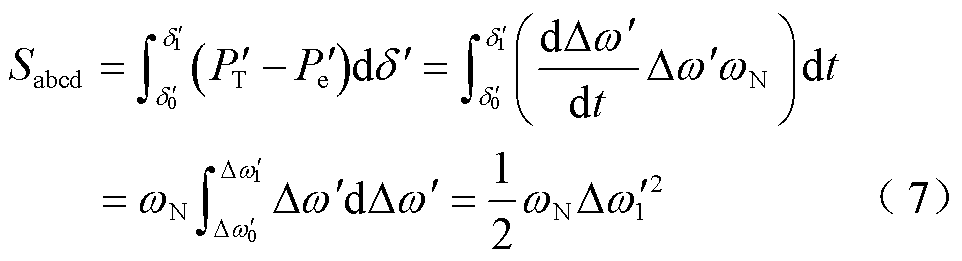
式中，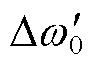
和
分别为在等值功角差为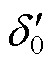和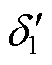
时的相对转速。
由式（7）可以看出，加速面积所产生的加速动能大小与加速面积结束时刻的相对转速大小有关。
若直流系统发生后续换相失败而引起多次功率冲击，如图3所示，等值机械功率恢复到初始值之前再次因直流的功率瞬降而增加并形成加速面积，同理可推导换相失败连续功率冲击下的相对动能变化。
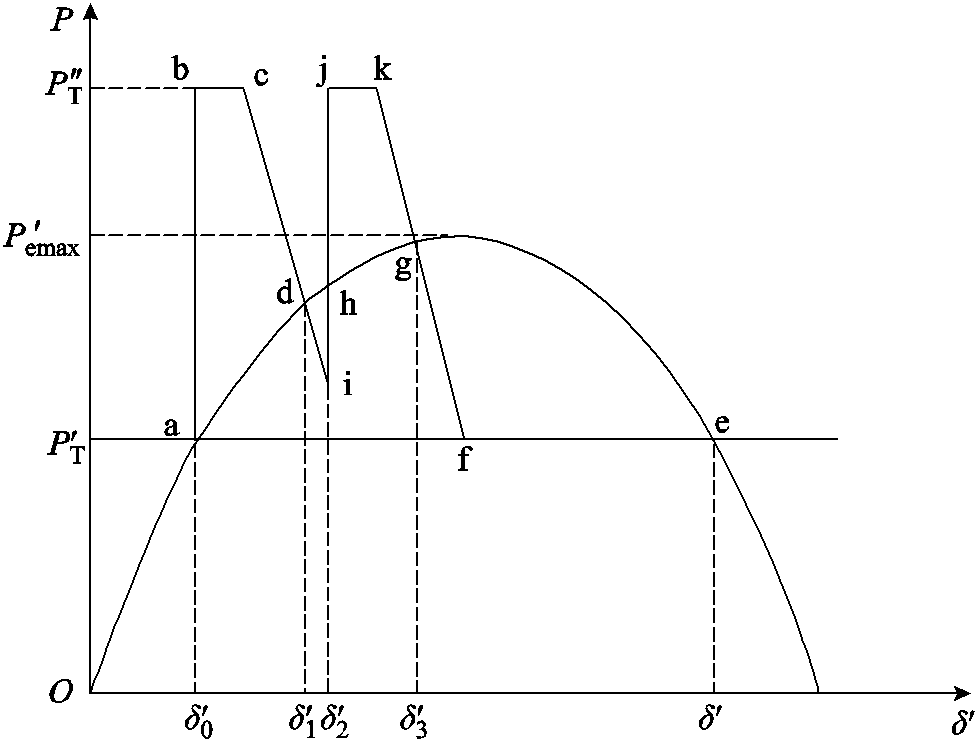
图3 连续功率冲击下等值发电机功率特性曲线
Fig.3 Equivalent generator power characteristic curve after continuous commutation failure
由图3可知，此时总的加速面积为Sabcd与Shjkg，其间有一小段由于直流功率逐渐恢复而形成的减速面积Sdih。故此时总的加速面积可表示为
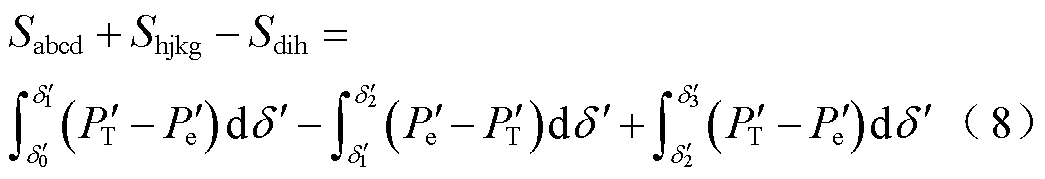
式中，Sabcd、Shjkg、Sdih分别为点abcd、hjkg、dih围成的面积。
同理对式（8）进行计算和化简后可得
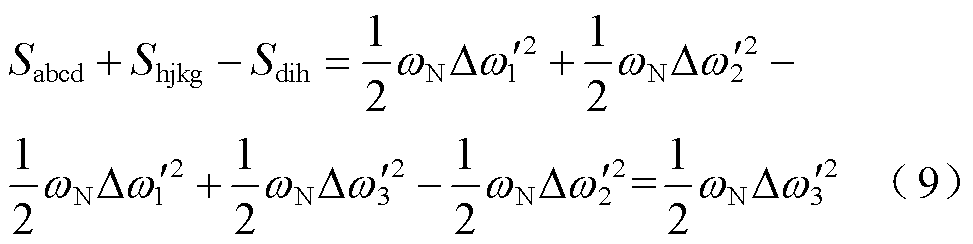
式中，、
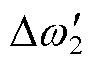和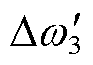
分别为图3中等值功角差为
、
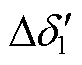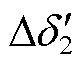和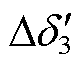
时的等值功角差。
结合式（7）和式（9）可以看出，加速面积作用下等值发电机转子最终增加的动能可仅由加速面积结束时刻的相对转速表征。若能够实时读取等值发电机相对转速，则送端交流系统的相对动能变化与直流系统功率跌落和恢复的曲线态势无关，也与换相失败的持续时间和功率冲击次数无关。
根据电力系统暂态功角稳定的等面积法则可知，增大系统最大可能的减速面积是提升暂态功角稳定性、减小功角失稳风险的有效措施。因此若能通过切机方式弥补换相失败产生的加速面积，则应能较好地维持送端系统的暂态功角稳定性。切机控制措施示意图如图4所示。
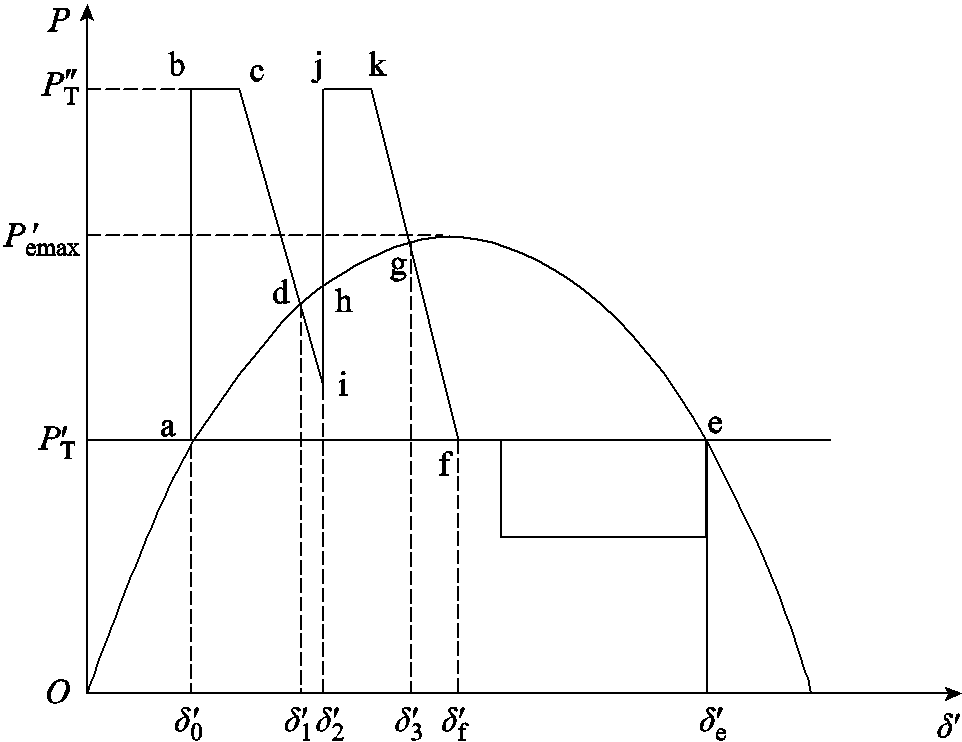
图4 切机控制措施示意图
Fig.4 Diagram of the generator tripping strategy
本文以直流功率恢复到稳态值的时间为界线计算所需补偿的减速面积：一方面，这样可以避免求取等值机械功率曲线与等值电磁功率曲线的交点（图4中的g点和h点），从而减小了实时计算的复杂度；另一方面，直流功率完全恢复到稳态值之前实际上已产生一小段时间的减速面积（图4中Sdhi），在这部分减速面积之后，根据f点的相对转速进行计算能够在一定程度上减小实际所需的切机控制量。
设直流功率恢复到稳态值时f点所对应的等值功角差为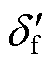
，由2.1节可知在换相失败及其恢复期间的加速面积和减速面积作用下，此时等值发电机转子最终所获得动能为
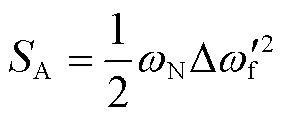（10）
式中，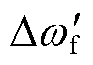
为在等值功角差为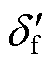时的相对转速。
而系统所能提供的最大可能减速面积为
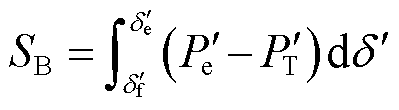（11）
式中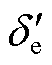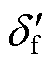，、分别为e点、f点对应的等值功角差。
忽略电磁功率特性曲线的变化，并考虑切机策略以矩形的形式增加减速面积，则切机控制措施的示意图如图4所示。根据式（10）和式（11），为维持系统暂态功角稳定性所需补偿的面积为
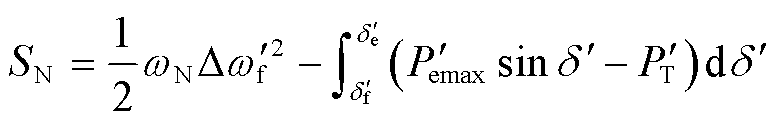（12）
因此，根据图4所示矩形面积，可由式（13）计算所需的切机量。
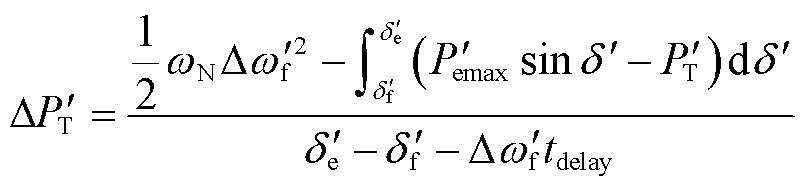（13）
式中，tdelay为切机控制的时间延迟。
考虑到数据计算、控制决策及控制实施的延迟，切机策略难以在直流功率恢复到稳态值时立即同步实施，故在计算切机方案时应当考虑时间延迟。在文献[11]中，对于其提出的传统交流电网切机控制措施，时间延迟主要是控制动作实施和数据传输，并假设控制动作时间为50 ms，控制决策计算时间为10 ms，数据传输时间为40 ms。本文面向交直流混联电网，虽然送、受端系统的空间距离较远，但由于同一个直流系统在送、受端换流站间具备高速通信功能，故进一步附加了100 ms的信息交互延时，将控制策略的时间延时设定为200 ms。
事实上，随着直流功率恢复等值发电机转子运动进入减速面积，相对转速是逐渐减小的，仍然以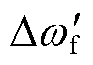计算时间延时期间的面积可能会导致式（13）中分母偏小，但相对保守的切机计算结果也符合电力系统稳定控制的原则和要求。
式（13）的计算结果对应于图4中的等值机械功率所需的改变量，故应进一步转换为发电机的实际切机量，如式（14）所示，然后根据各台发电机出力的实际情况分配切机台数。
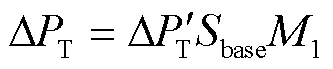（14）
式中，Sbase为基准容量。
此外，在实际计算过程中为得到等值功率特性及转子运动方程，需要先对送端系统的发电机、负荷及惯性时间常数进行等值，即
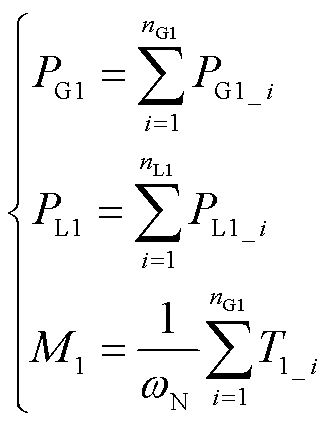（15）
式中，PG1_i和T1_i分别为等值机群G1中各台发电机的机械功率和惯性时间常数；nG1和nL1分别为发电机和负荷节点的数量；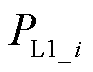
为该区域内的各负荷节点功率。同理可对等值机群G2及其区域内的负荷节点进行相关等值参数计算。
综上所述，所提实时切机控制策略的流程如图5所示。
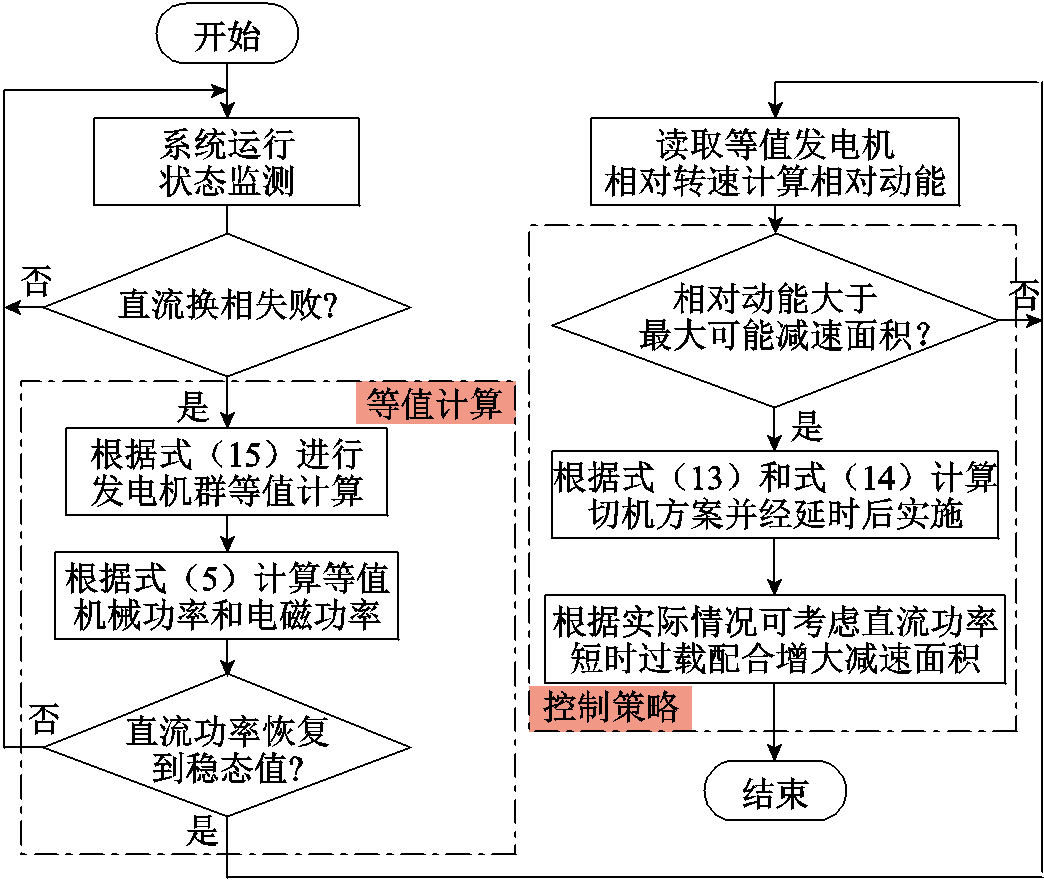
图5 实时切机方案的计算与控制流程
Fig.5 Calculation and control flow chart of the real-time generator tripping strategy
1）监测系统运行状态，若直流系统逆变侧发生换相失败，则启动计算及控制策略。根据式（15）对发电机群进行等值计算，由式（5）得到等值发电机机械功率和电磁功率，联立可得等值发电机功率特性曲线。
2）监测直流系统输送功率是否恢复到稳态值，若是，则读取此时的等值发电机相对转速，并根据式（10）计算换相失败后增大的相对动能；同时根据式（12）计算最大可能的减速面积。若最大可能的减速面积小于换相失败功率冲击增大的相对动能，则启动切机控制策略。
3）根据式（13）和式（14）计算所需的切机量，经200 ms延时后实施切机策略。此外，直流系统具有短时过载能力，能够在较长时间尺度内维持1.05(pu)～1.10(pu)过载运行[21]。直流过载运行相当于减小了等值机械功率，可根据实际情况及需要配合实施。本文考虑在直流系统功率恢复至稳态值后，将直流系统输送功率参考值提升至稳态值的1.1倍。由于切机策略在200 ms延时后才能实施到位，故令直流系统过载运行持续200 ms后将直流功率参考值恢复至原态。
本节基于中国电力科学研究院开发的PSD-BPA仿真平台和程序，搭建简单电力系统对所提控制方法进行仿真分析。发电机均采用考虑励磁作用的经典次暂态模型。
首先搭建了如图6所示的简单仿真系统，送端两区域简化为单机-无穷大系统，直流输送功率 1 500 MW，稳态运行时送端区域联络线传输功率300 MW，联络线两端交流电压分别为1.052(pu)和1.0(pu)，联络线电抗为0.2(pu)，发电机惯性时间常数为36 s。
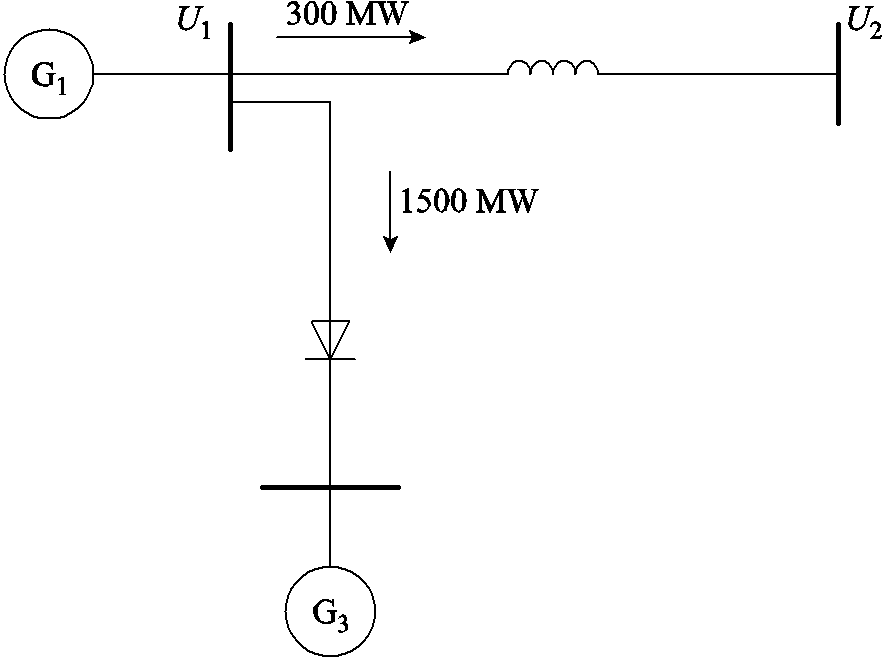
图6 简单仿真系统
Fig.6 The simple simulation system
根据相关初始参数可得到送端系统转子运动方程为
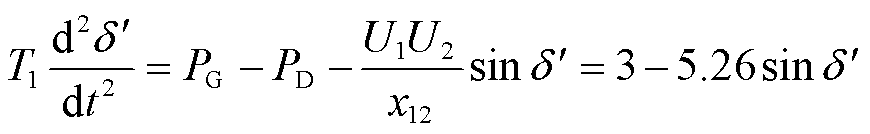（16）
式中，PG为等值机械功率；PD为直流系统输送功率。
可解得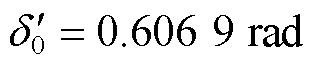
，
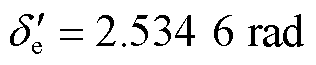。设置受端系统母线在0.2 s时发生三相短路，0.36 s故障清除。直流系统发生换相失败，其输送功率在约0.5 s恢复，此时转速差为0.009 02(pu)，可求解得切机量为372.15 MW，故在0.7 s时切机375 MW。需要指出的是，实际当中切机策略一般是整台切除，该仿真系统中送端区域仅有一台发电机，故按照计算结果减小机械功率。
相关电气量的响应曲线如图7所示。由图7a所示的直流功率曲线可知，直流系统在故障后发生换相失败并在约0.5 s内恢复。但图7b中发电机转速并未在减速面积作用下减速到0并穿过横轴，而是呈现持续上升的趋势，这意味着换相失败功率冲击将引起送端系统暂态功角失稳。从图7c中功角曲线亦可看出发电机与无穷大系统的功角差超过了180°。而在直流系统输送功率恢复至稳态值后采取相应的切机策略，能够有效地抑制发电机转速和功角的持续增大，从而维持送端系统的暂态功角稳定，如图7d所示。
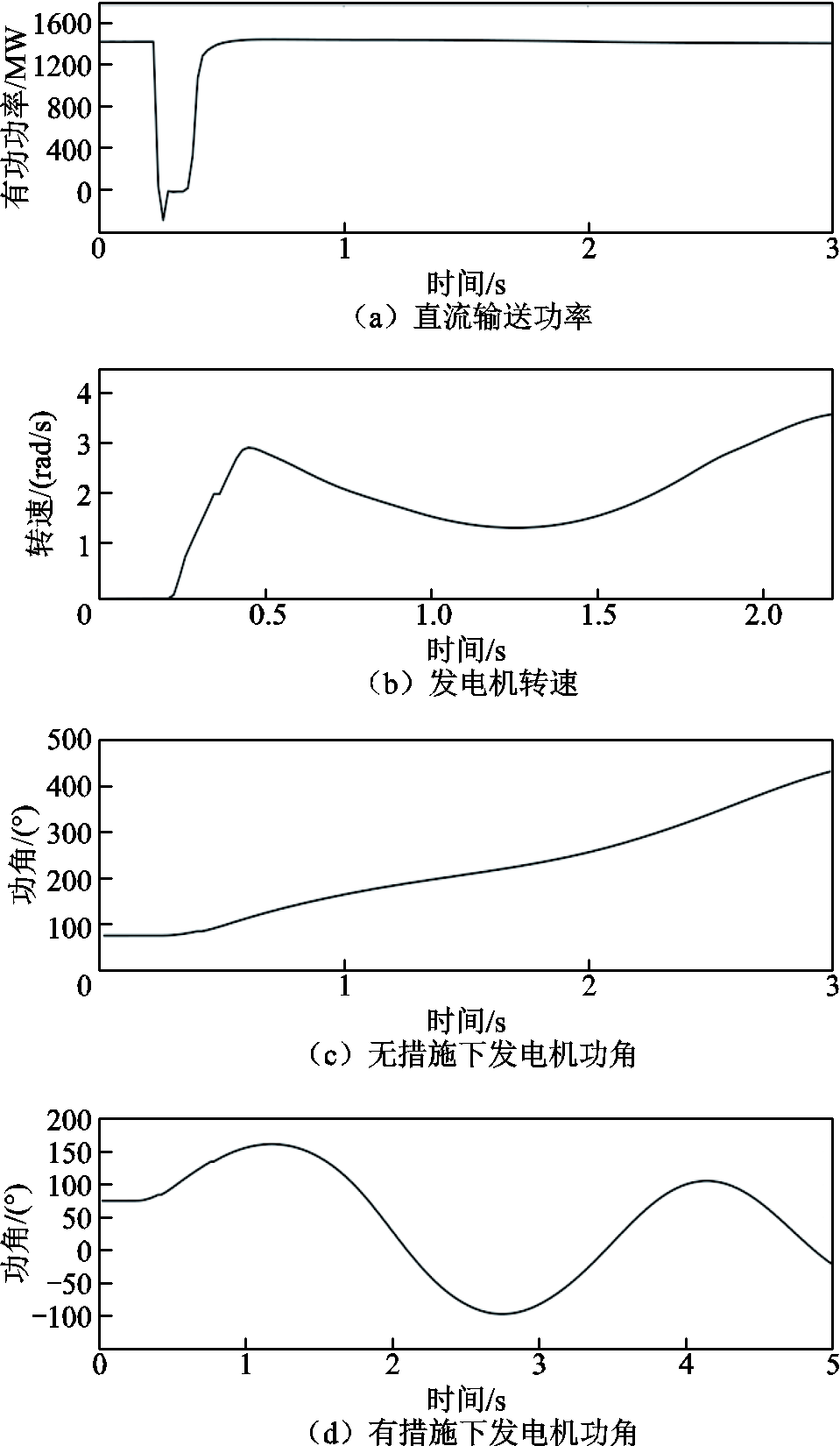
图7 相关电气量响应曲线
Fig.7 Response curves of relevant electrical variables
进一步基于10机39节点系统搭建交直流混联系统如图8所示，交流系统相关参数详见参考文献[22]。稳态运行时直流输送功率1 200 MW，送端系统区域间联络线传输功率200 MW，联络线两端母线交流电压分别为1.011 6(pu)和1.035 1(pu)，联络线电抗为0.251 6(pu)，10台发电机的等值惯性时间常数为318.7 s。根据相关初始参数可得送端系统转子运动方程为
（17）
可解得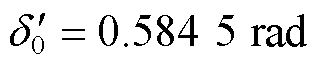
，
。
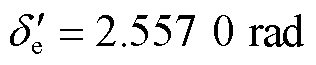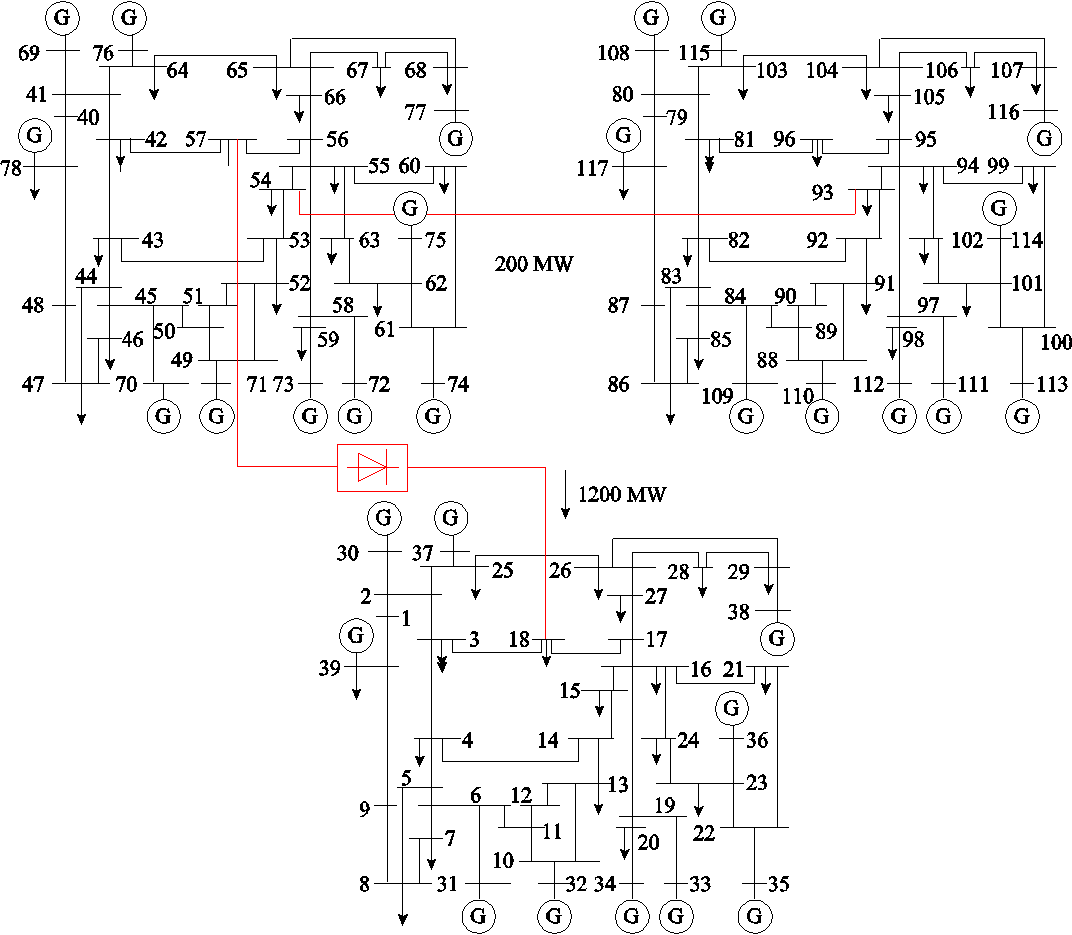
图8 基于39节点系统的交直流混联系统
Fig.8 The AC/DC hybrid power system based on the 39-nodes system
设置直流功率分别在0.20 s、0.62 s发生持续0.4 s的功率瞬降，直流功率在1.0 s恢复，相关电气量的响应曲线如图9所示。由图9所示的发电机功角曲线可以看出，送端两区域发电机呈现典型的两机群状态，系统1中发电机在换相失败功率冲击下功角迅速增大，两机群等值功角差超过180°而导致两机群功角失稳。直流功率恢复至稳态值时，等值功角差为56.539 4°，等值转速差为0.359 2 rad/s，代入解得切机量为250.24 MW，并在1.2 s切除70～77号机各30 MW。采取切机措施后加速机群等值功角增大趋势有所缓解，两机群等值功角差被限制在180°以内，如图9c和图9d所示。控制策略计算和实施过程如图10所示。
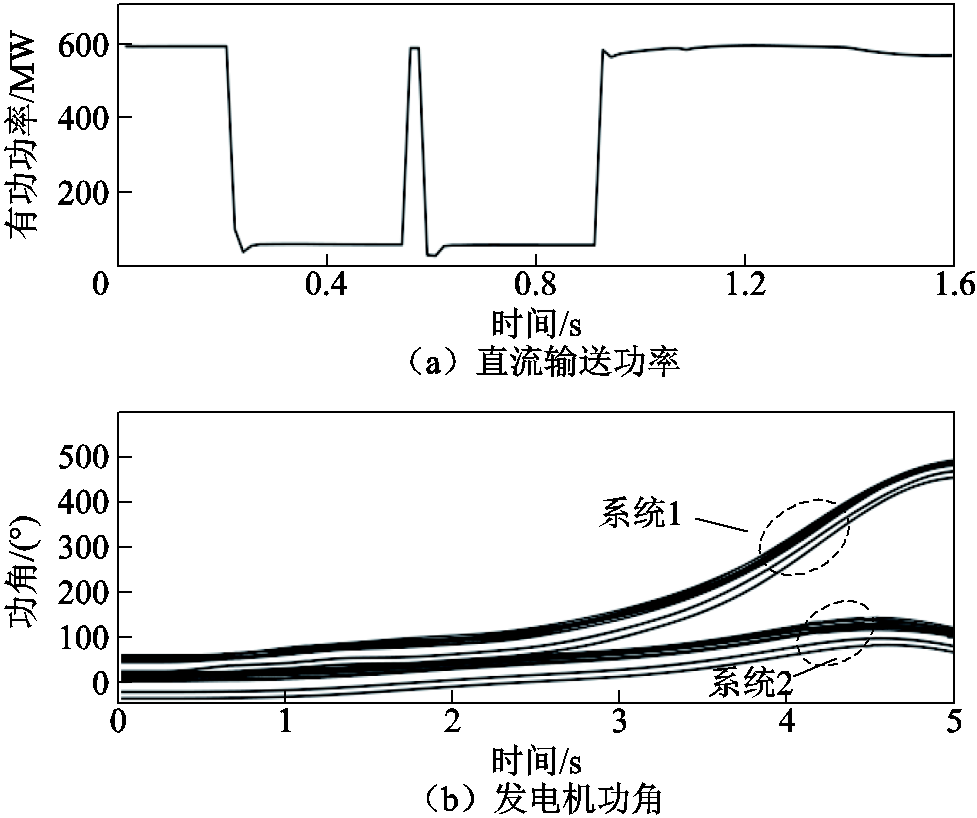
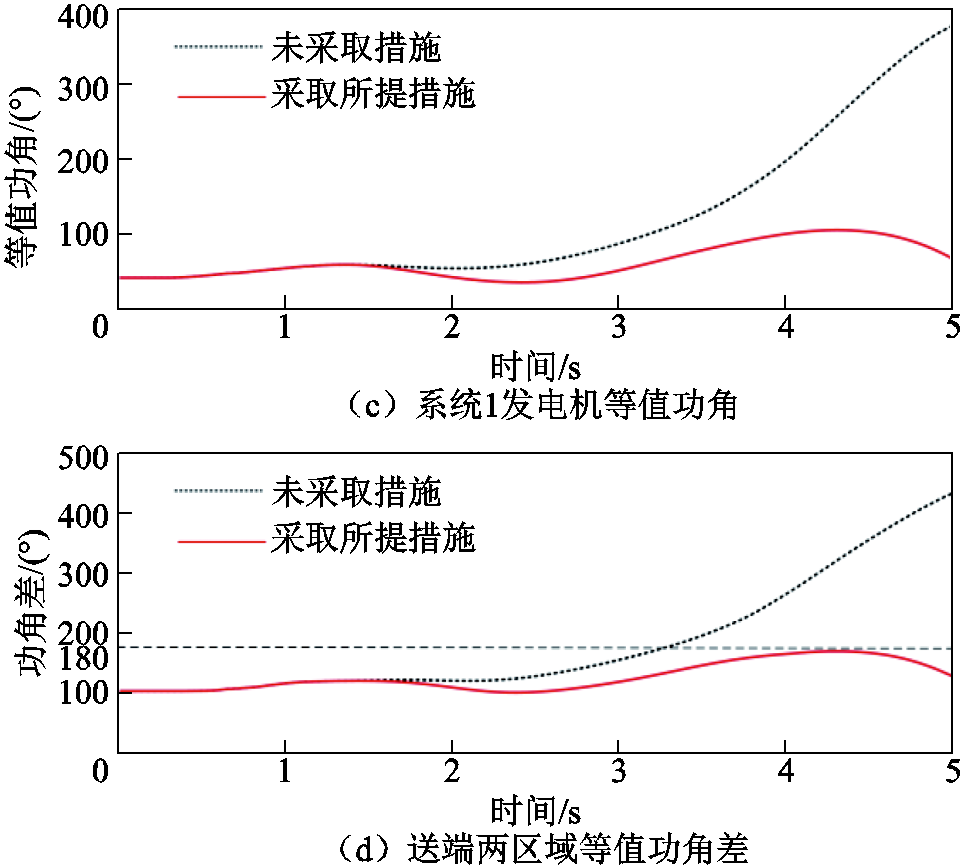
图9 交直流混联系统相关电气量的响应曲线
Fig.9 Response curves of related electrical variables of the AC/DC hybrid power system
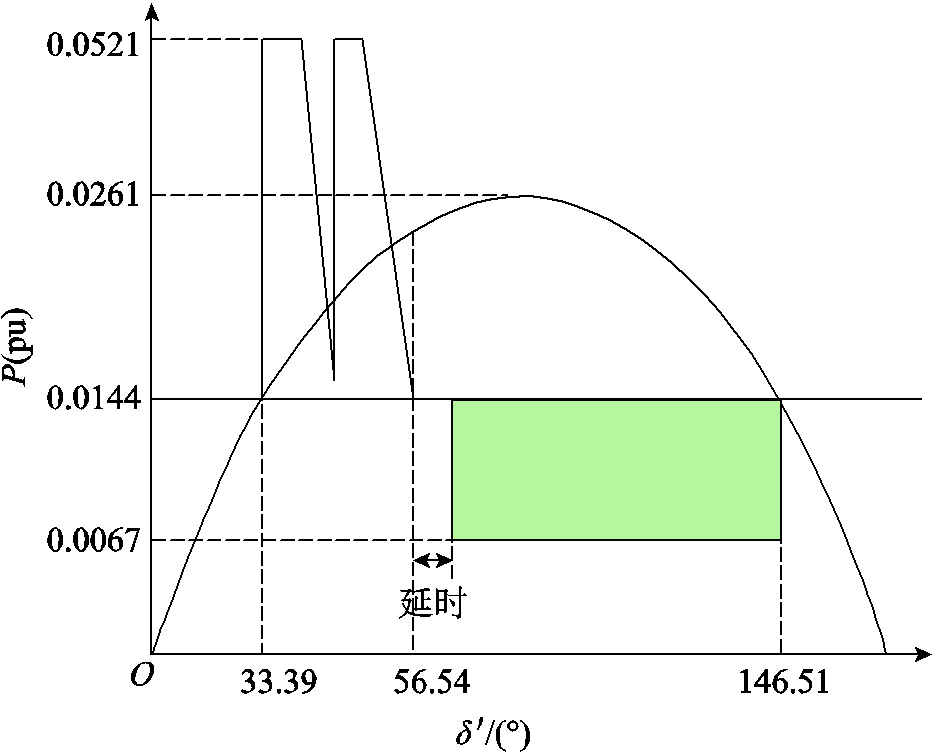
图10 控制策略计算和实施示意图
Fig.10 Schematic diagram of control strategy calculation and implementation
设置受端系统bus18-bus17在0.2 s三相短路，0.3 s故障清除，直流系统发生1次功率冲击，相关电气量响应曲线如图11所示。由图11a所示的直流功率曲线可知，直流功率在约1.0 s恢复到稳态值，此时两机群等值转速差和等值功角差分别为0.292 7 rad/s和61.785 8°，如图11b和图11c所示。由于此时换相失败功率冲击引起的加速面积小于系统可能提供的最大减速面积，可不必采取切机措施，但若为提升系统的暂态功角稳定性，可根据加速面积大小确定切机方案。以加速面积大小代入式（13）解得所需切机量为175.32 MW，并在1.2 s切除70～75号机各30 MW。相应的等值功角仿真曲线如图11d所示，可见发电机群的功角加速趋势能够得到进一步缓解。
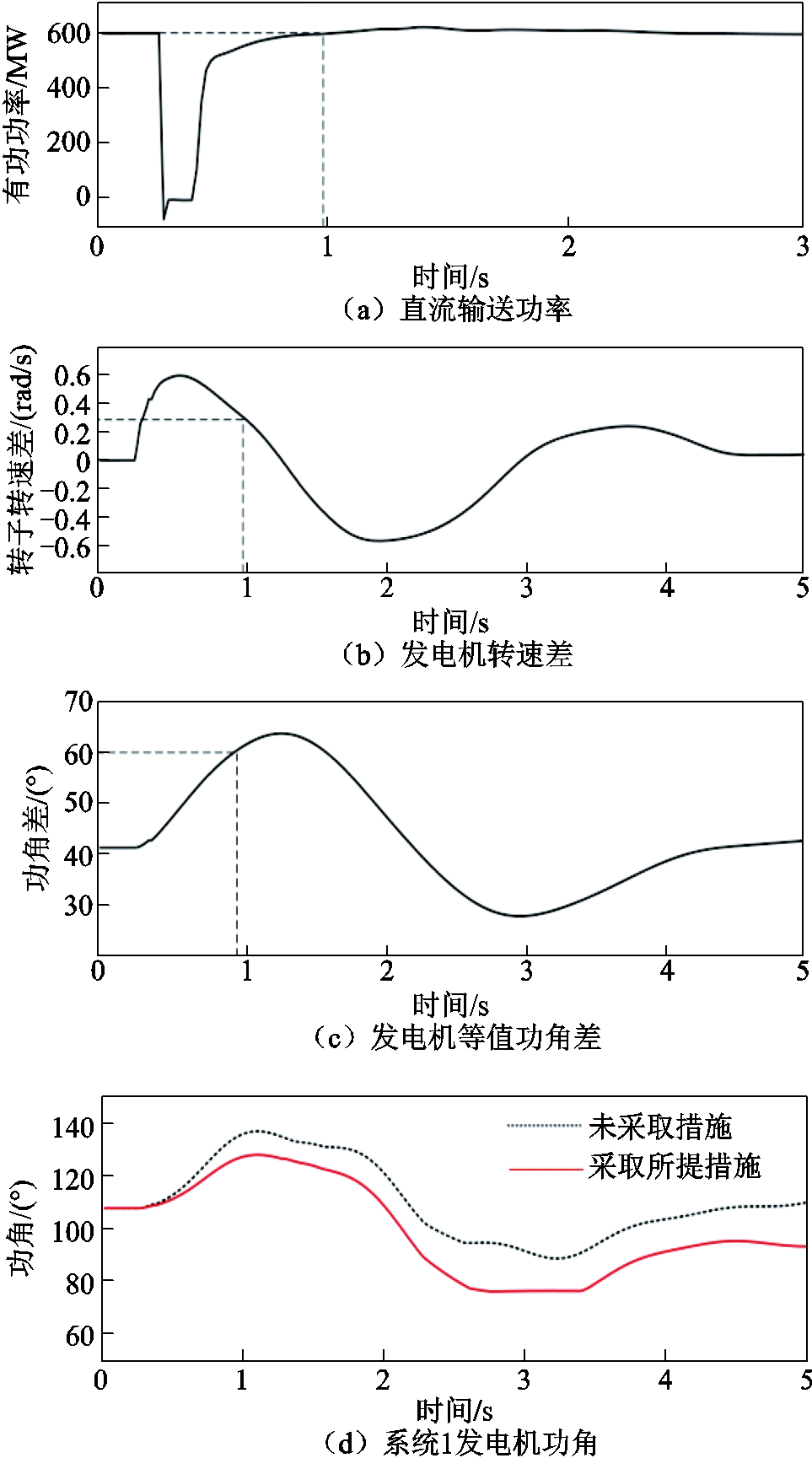
图11 暂态功角稳定性较好时相关电气量的响应曲线
Fig.11 Response curves of relevant electrical variables under better transient angle stability
此外，当系统暂态功角稳定性较高时，根据加速面积大小确定切机方案不会产生负面的影响。根据图12所示的不同控制措施下系统频率情况可知，采取适当的切机措施不会影响系统的频率稳定性。
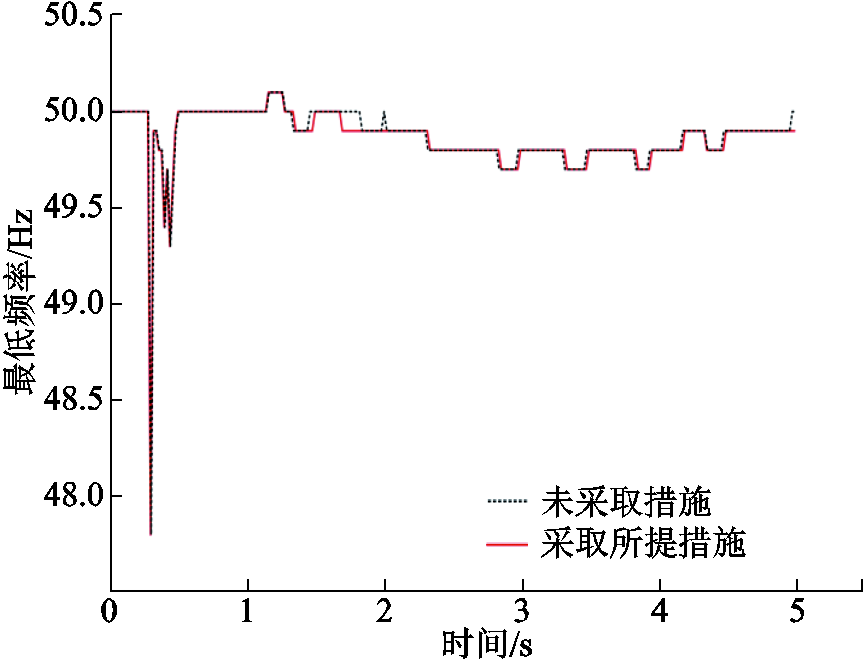
图12 系统最低频率情况对比
Fig.12 Contrast curves of the lowest system frequency
本节基于我国华北—华中（西南）—华东交直流混联电网某年某方式进行仿真分析。实际交直流混联电网如图13所示，其中华中电网向华东电网馈入直流系统7回，包括起于四川境内的复奉直流、锦苏直流和宾金直流，以及起于湖北境内的葛南直流、林枫直流、宜华直流和龙政直流。
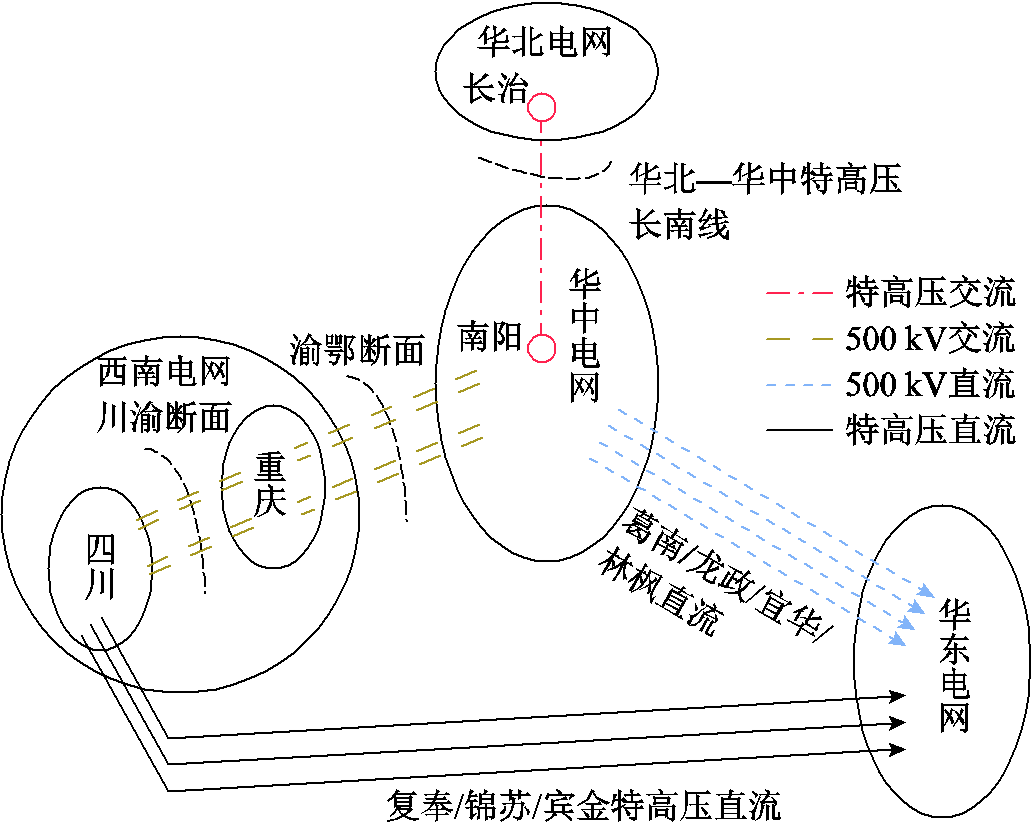
图13 实际交直流混联电网
Fig.13 The actual AC/DC hybrid power system
在渝鄂断面改为柔性直流背靠背联系之前，川渝断面、渝鄂断面分别通过交流双回线路联系，华北-华中区域通过长治—南阳单回特高压交流线路（长南线）联系。当华东电网发生交流故障导致多回直流换相失败，功率冲击下华中送端的盈余功率将从川渝断面和渝鄂断面涌出，进而威胁长南线功率传输极限及华北-华中的暂态功角稳定性。由此可见，3.1节中基于10机39节点系统搭建的简单电力系统具有一定的现实意义。
设置华东电网内部交流故障引起复奉直流和锦苏直流换相失败，并产生连续的功率冲击，两回直流传输功率曲线如图14a和图14b所示。在换相失败功率冲击作用下，华中电网内部发电机组功角迅速摆开和增大，图14c中华中和华北电网发电机组功角差最终超过180°而呈现两群暂态功角失稳，对特高压长南线的功率传输造成巨大冲击，如图14d所示。
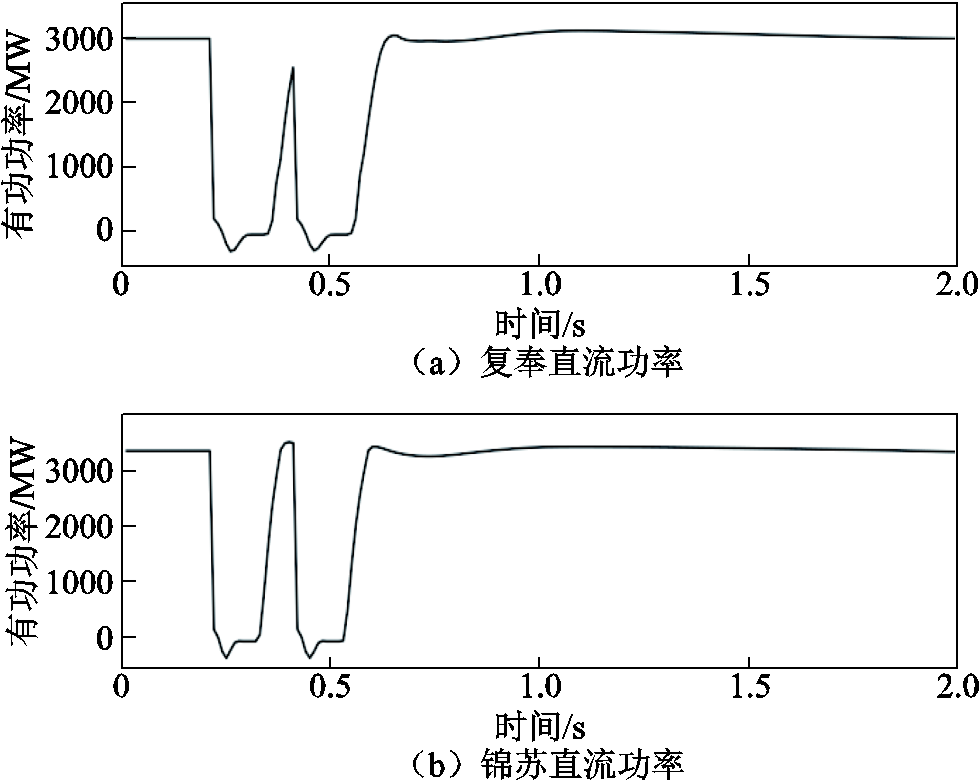
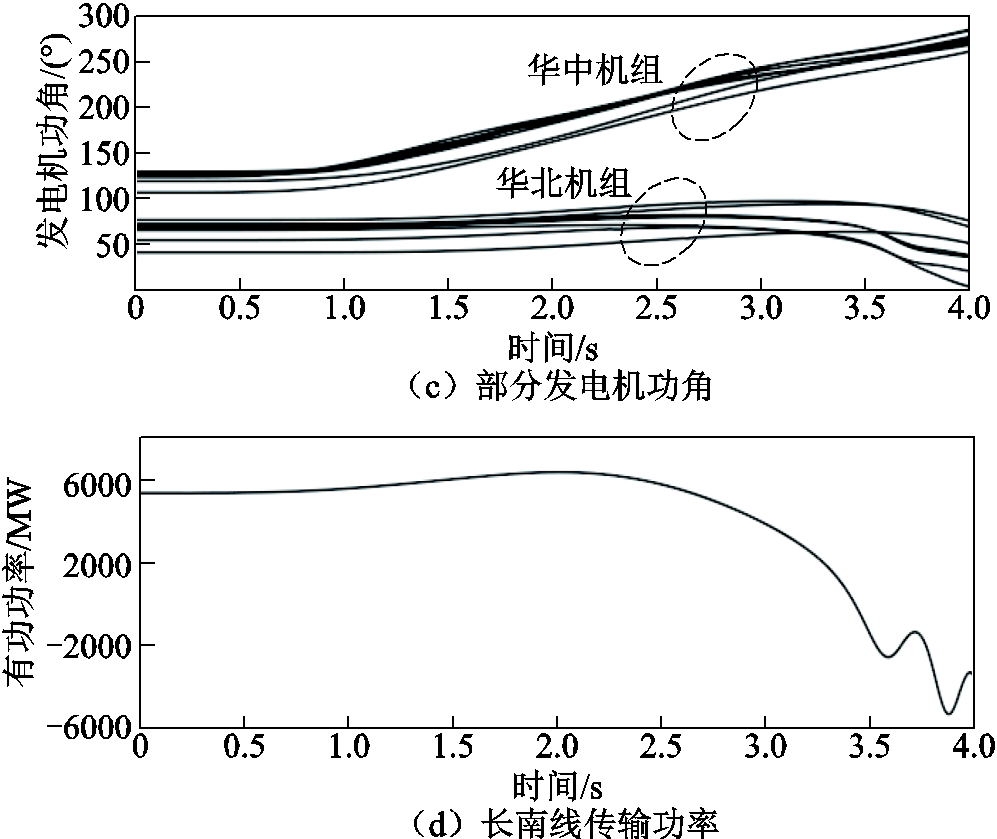
图14 未采取措施时的电气量仿真曲线
Fig.14 Simulation curves of electrical variables without control strategy
采用所提方法计算直流功率恢复到稳态值后所需补偿的加速面积及相应的切机量。由于实际电网中切机通常是按照整台发电机进行切除，故确定在约0.80 s切除四川电网内换流站近区水电机组600 MW，相关电气量的仿真曲线如图15所示。由图15a中的发电机功角曲线可以看出，华中机组和华北机组的相对功角虽然摆开，但并未达到功角失稳的程度，功角差维持在180°以内。长南线传输功率在盈余功率的冲击下迅速增大至6 500 MW，但在切机后未突破稳定极限，如图15b所示。图15c和图15d分别显示了不同控制策略下长南线相关电气量的状态，切机后南阳站母线电压能够保持稳定状态并维持在较高水平，两侧母线电压相位差持续增大的趋势得到有效抑制，相位差保持在180°以内。
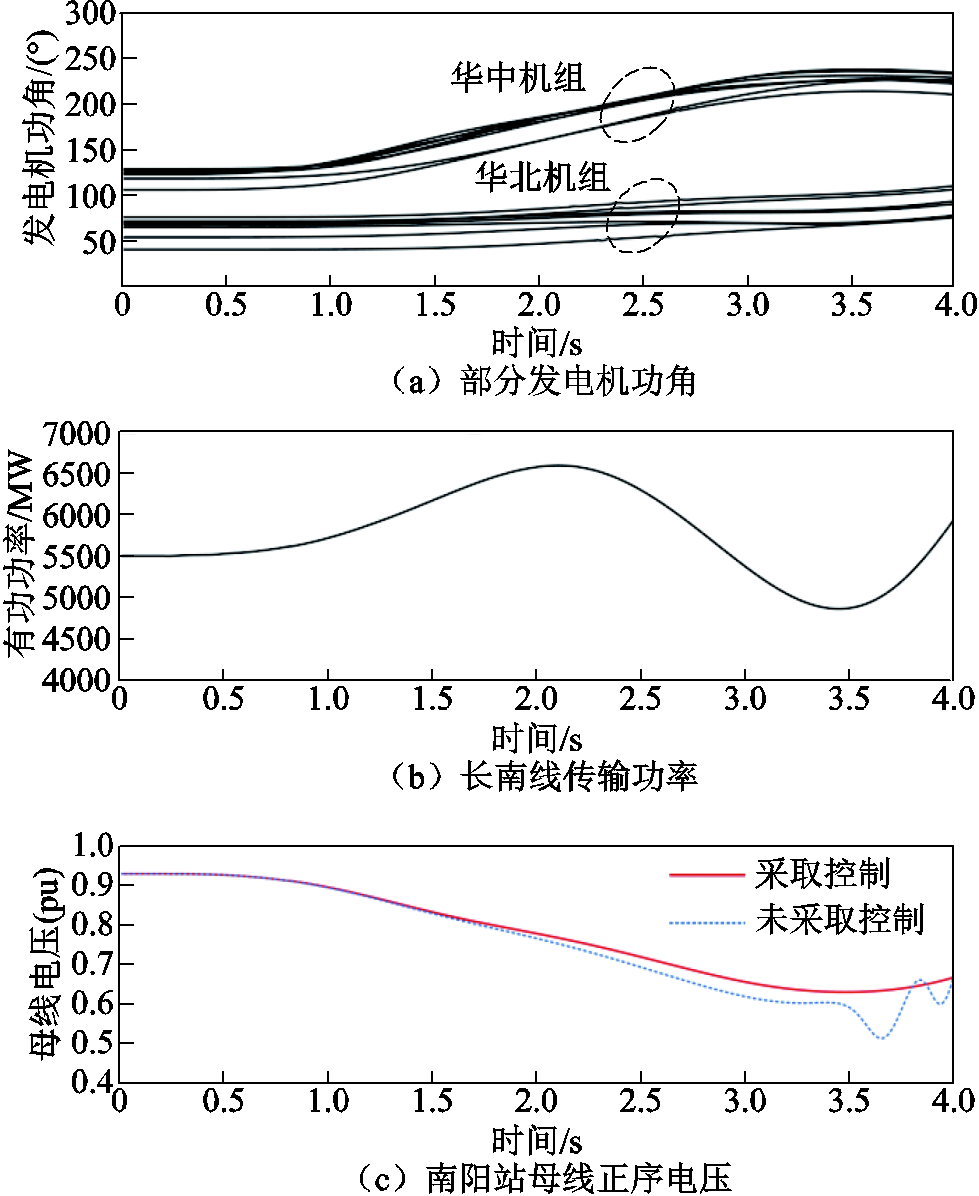
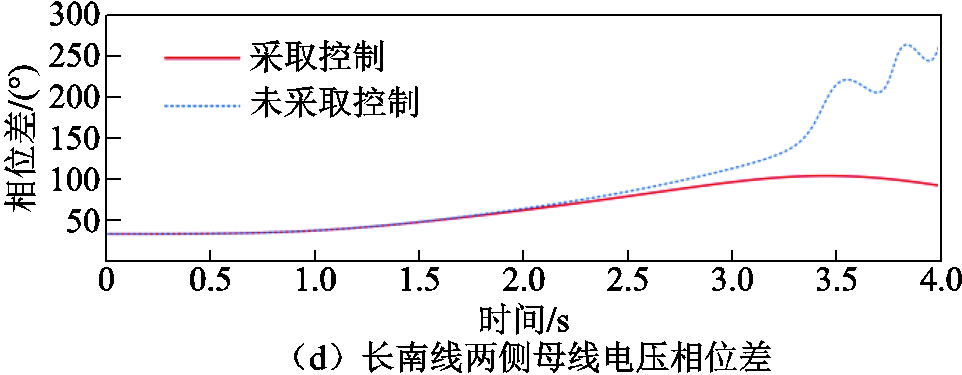
图15 采取措施时的电气量仿真曲线
Fig.15 Simulation curves of electrical variables under the control strategy
本文进一步考虑在直流系统功率恢复至稳态值后，将直流系统输送功率参考值提升至稳态值的1.1倍。设置与上例相同的交流故障，则在复奉直流和锦苏直流功率恢复后分别将各自功率参考值提升320 MW和360 MW，持续时间200 ms，同时本文所提控制方法在经过200 ms延时后实施切机控制策略。考虑到直流输送功率短时过载能够增大减速面积，与仅依靠切机控制相比少切除一台发电机。由图16所示的仿真曲线可以看出，尽管少切除了一台发电机，但配合实施直流输送功率调节后仍可有效维持系统暂态功角稳定性。
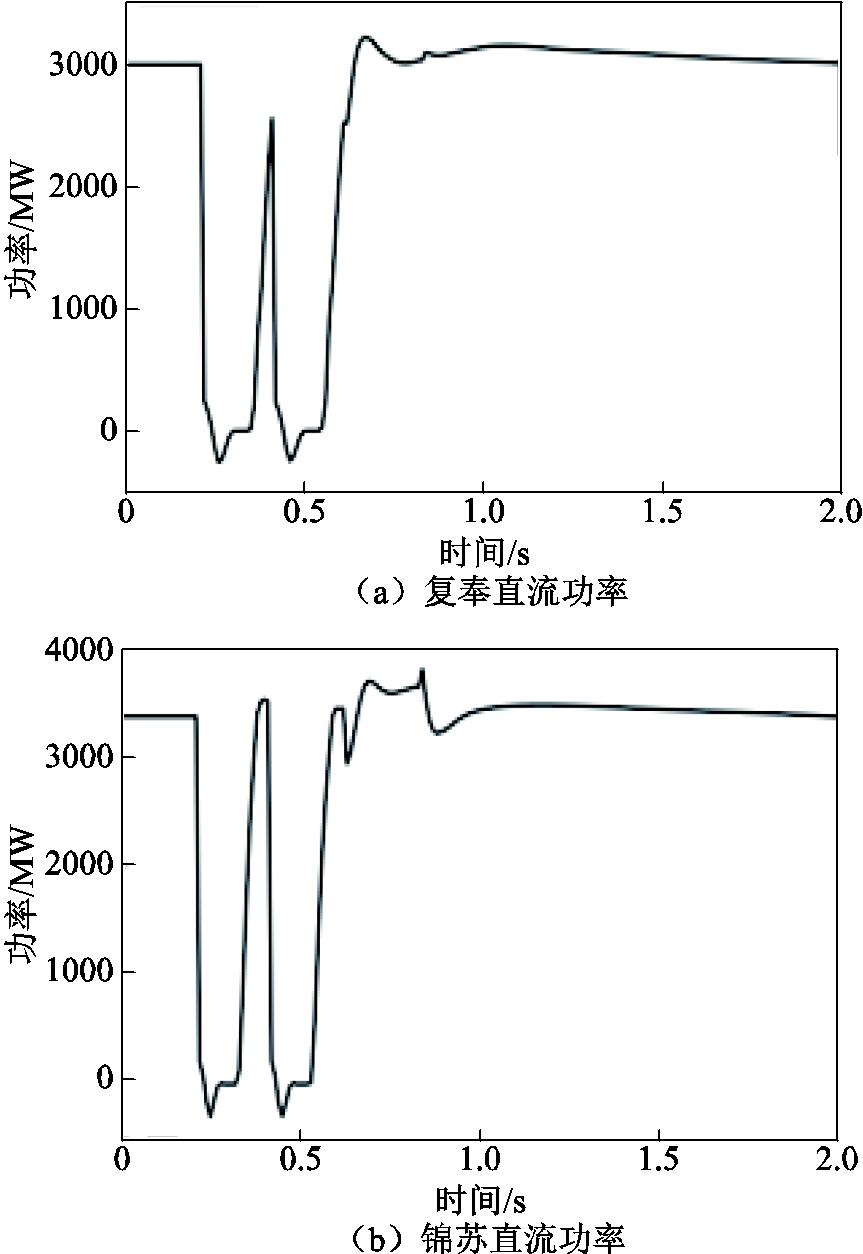
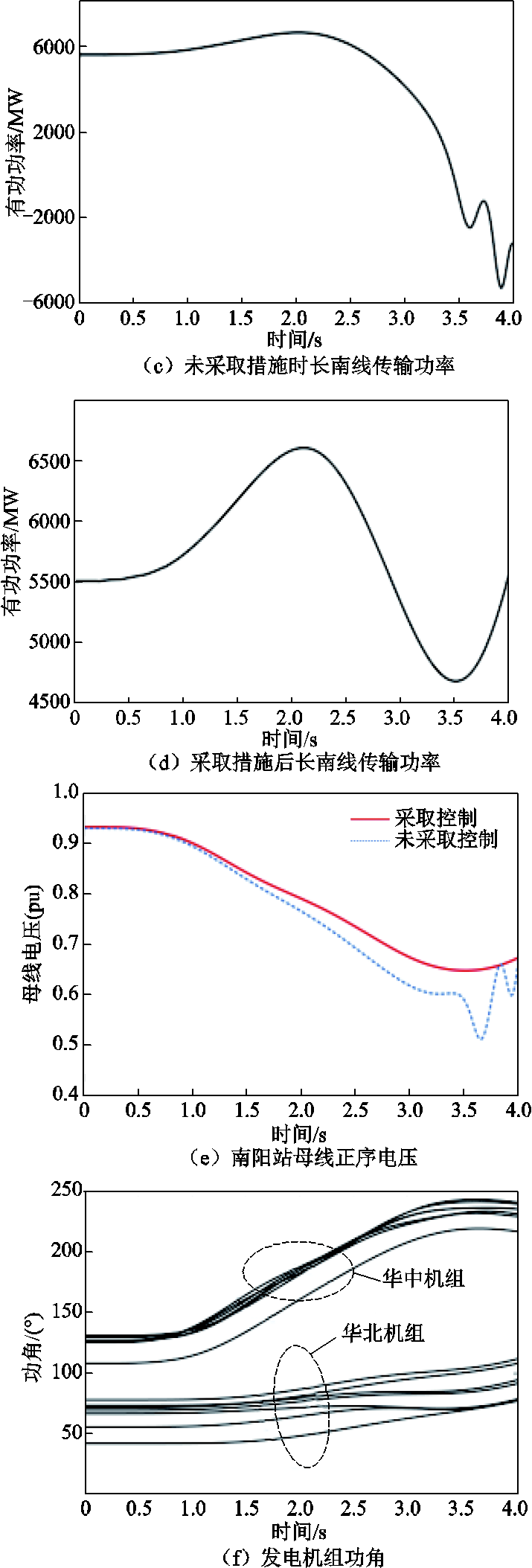
图16 采取直流功率控制措施时的电气量仿真曲线
Fig.16 Simulation curves of electrical variables under the DC power control strategy
本文提出了换相失败后维持送端交流系统暂态功角稳定的切机量计算方法及控制策略，根据理论和仿真分析得到以下结论：
1）换相失败引起的直流功率瞬降对送端交流系统的影响相当于等值机械功率上升，加速面积作用下送端交流系统等值发电机转子最终增加的动能，可仅由加速面积结束时刻的相对转速表征。
2）基于所提方法，在直流功率恢复至稳态值时依据等值发电机的相对转速计算转子运动剩余加速面积，进而可得出维持送端系统暂态功角稳定性所需的减速面积及相应的切机量。
3）将所提切机控制方法与直流系统功率短时过载进行有效配合，能够在一定程度上减小维持功角稳定所需的切机量。
如何综合考虑不同机组类型、不同分布区域确定机组之间的切机量分配方案，从而制定更符合实际电网情况的切机策略，是下一步研究工作的重点。
参考文献
[1] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[2] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205.
[3] Rahimi E, Gole A M, Davies J B, et al. Commutation failure analysis in multi-infeed HVDC systems[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 378-384.
[4] 汪娟娟, 郑睿娜, 傅闯, 等. 基于逆变站动态无功控制的后续换相失败抑制方法[J]. 电工技术学报, 2023, 38(17): 4672-4682.
Wang Juanjuan, Zheng Ruina, Fu Chuang, et al. A method based on constant reactive power control of inverter to suppress the subsequent commutation failure in HVDC system[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4672-4682.
[5] 郑晨一, 汤奕. 考虑多直流无功交互影响的换相失败预防协调控制方法[J]. 电力系统自动化, 2023, 47(4): 102-110.
Zheng Chenyi, Tang Yi. Coordinated control method for commutation failure prevention considering reactive power interaction among multiple HVDC systems[J]. Automation of Electric Power Systems, 2023, 47(4): 102-110.
[6] 汤奕, 郑晨一. 高压直流输电系统换相失败影响因素研究综述[J]. 中国电机工程学报, 2019, 39(2): 499-513, 647.
Tang Yi, Zheng Chenyi. Review on influencing factors of commutation failure in HVDC systems[J]. Proceedings of the CSEE, 2019, 39(2): 499-513, 647.
[7] 张炎, 丁明, 韩平平, 等. 直流闭锁后风电送端系统暂态稳定及控制策略研究[J]. 电工技术学报, 2020, 35(17): 3714-3726.
Zhang Yan, Ding Ming, Han Pingping, et al. Study on the transient stability and control schemes of the sending-end system involving wind power after UHVDC block[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3714-3726.
[8] 汤奕, 崔晗, 党杰. 基于继承思想的时变性电力系统暂态稳定预测[J]. 中国电机工程学报, 2021, 41(15): 5107-5119.
Tang Yi, Cui Han, Dang Jie. Transient stability prediction of time-varying power systems based on inheritance[J]. Proceedings of the CSEE, 2021, 41(15): 5107-5119.
[9] 王科, 游大海, 尹项根, 等. 基于支路势能脊的电力系统暂态稳定分析和临界割集识别[J]. 电工技术学报, 2013, 28(11): 262-269.
Wang Ke, You Dahai, Yin Xianggen, et al. Power system transient stability analysis and critical cutset detection based on branch ridge[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 262-269.
[10] 顾卓远, 汤涌, 张健, 等. 基于相对动能的电力系统暂态稳定实时紧急控制方案[J]. 中国电机工程学报, 2014, 34(7): 1095-1102.
Gu Zhuoyuan, Tang Yong, Zhang Jian, et al. Real-time power system transient stability emergency control scheme based on the relative kinetic energy[J]. Proceedings of the CSEE, 2014, 34(7): 1095-1102.
[11] 王佳丽, 刘涤尘, 廖清芬, 等. 基于暂态能量的电力系统切机控制措施[J]. 电力系统保护与控制, 2016, 44(10): 1-9.
Wang Jiali, Liu Dichen, Liao Qingfen, et al. Generator tripping strategy based on transient energy of power system[J]. Power System Protection and Control, 2016, 44(10): 1-9.
[12] 卢锦玲, 郭鲁豫. 基于改进深度残差收缩网络的电力系统暂态稳定评估[J]. 电工技术学报, 2021, 36(11): 2233-2244.
Lu Jinling, Guo Luyu. Power system transient stability assessment based on improved deep residual shrinkage network[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2233-2244.
[13] 余贻鑫, 刘辉, 曾沅. 基于实用动态安全域的紧急控制策略[J]. 电力系统自动化, 2004, 28(6): 6-10.
Yu Yixin, Liu Hui, Zeng Yuan. A novel emergency control strategy based on practical dynamic security regions[J]. Automation of Electric Power Systems, 2004, 28(6): 6-10.
[14] 任伟, 房大中, 陈家荣, 等. 大电网暂态稳定紧急控制下切机量快速估计算法[J]. 电网技术, 2008, 32(19): 10-15, 55.
Ren Wei, Fang Dazhong, Chen Jiarong, et al. A fast algorithm to estimate generation capacity tripped by emergency control for transient stability of large power system[J]. Power System Technology, 2008, 32(19): 10-15, 55.
[15] 吴为, 汤涌, 孙华东. 基于系统加速能量的切机控制措施量化研究[J]. 中国电机工程学报, 2014, 34(34): 6134-6140.
Wu Wei, Tang Yong, Sun Huadong. Quantitative research of generation capacity tripped based on acceleration energy of power system[J]. Proceedings of the CSEE, 2014, 34(34): 6134-6140.
[16] 陈长胜, 马世英, 郑超, 等. 基于暂态偏差能量的紧急控制效果超前评估方法[J]. 中国电机工程学报, 2018, 38(17): 5118-5125, 5308.
Chen Changsheng, Ma Shiying, Zheng Chao, et al. The advance evaluation of emergency control based on transient deviation energy[J]. Proceedings of the CSEE, 2018, 38(17): 5118-5125, 5308.
[17] 朱劭璇, 王彤, 王增平, 等. 考虑主导不稳定平衡点变化的电力系统暂态稳定切机控制策略[J]. 电力系统保护与控制, 2021, 49(5): 20-28.
Zhu Shaoxuan, Wang Tong, Wang Zengping, et al. Generator tripping strategy in transient stability control of a power system considering the change of the controlling unstable equilibrium point[J]. Power System Protection and Control, 2021, 49(5): 20-28.
[18] 屠竞哲, 张健, 王建明, 等. 大规模直流异步互联系统受端故障引发送端稳定破坏的机理分析[J]. 中国电机工程学报, 2015, 35(21): 5492-5499.
Tu Jingzhe, Zhang Jian, Wang Jianming, et al. Mechanism analysis on the sending-side instability caused by the receiving-side contingencies of large-scale HVDC asynchronous interconnected power systems[J]. Proceedings of the CSEE, 2015, 35(21): 5492-5499.
[19] 贾俊川, 张健, 仲悟之, 等. 应对多回并列直流换相失败的送端系统安全稳定控制措施研究[J]. 中国电机工程学报, 2017, 37(21): 6320-6327.
Jia Junchuan, Zhang Jian, Zhong Wuzhi, et al. Research on the security and stability control measures of the sending side system coping with multiple parallel-operation HVDCs simultaneous commutation failure[J]. Proceedings of the CSEE, 2017, 37(21): 6320-6327.
[20] 苏寅生, 陈董秀, 鲍颜红, 等. 应对直流连续换相失败的紧急控制策略[J]. 电力系统保护与控制, 2017, 45(4): 126-131.
Su Yinsheng, Chen Dongxiu, Bao Yanhong, et al. An emergency control strategy coping with continuous commutation failure in DC system[J]. Power System Protection and Control, 2017, 45(4): 126-131.
[21] 王少辉, 唐飞, 刘涤尘, 等. 应对多直流同时换相失败的直流功率能量补偿调制方法[J]. 电网技术, 2018, 42(9): 2876-2884.
Wang Shaohui, Tang Fei, Liu Dichen, et al. DC power energy compensation modulation method coping with simultaneous multiple HVDC commutation failures[J]. Power System Technology, 2018, 42(9): 2876-2884.
[22] Ramon G L F. Prediction and control of transient instability using wide area phasor measurement[D]. Winnipeg, Canada: University of Manitoba, 2011.
Abstract The active power impact caused by commutation failure (CF) at the inverters of line-commutated-converter-based high voltage direct current (LCC-HVDC) can easily increase the risk of power angle instability in the sending-end ac system. However, the real-time control methods to maintain the transient power angle stability after suffering CF are still insufficient in the existing literatures, since the current researches mainly focus on the qualitative analysis, offline decision and dc control strategy, lacking the quantitative methods and real-time control strategies generator tripping.
To solve the issue, the principle of generator rotor acceleration and power angle instability caused by the power impact of CF is firstly analyzed. When a dc system suffers CF, the transmitted active power would experience a sudden drop, equivalent to an increase of the equivalent mechanical power in the sending-end system. If dc system suffers continuous CFs, causing multiple power impacts, the equivalent mechanical power would increase again and form an acceleration area due to the power drop before returning to its initial value. Similarly, the relative kinetic energy under continuous power impacts of CFs can be derived. The analysis results indicate the relative kinetic energy change of the sending-end system can be characterized only by the relative speed of the equivalent generator. If the relative speed of the equivalent generator can be obtained in real time, the relative kinetic energy change of the sending-end ac system is independent of the curve trend of the dc power drop and recovery, as well as the duration of CF.
Then the remaining acceleration area of the rotor movement is calculated based on the relative speed of the equivalent generator when DC power is restored to steady state, and the deceleration area and cutting amount required to maintain the transient power angle stability of the system can thus be obtained. Based on the theory researches, a real-time generator tripping control strategy is developed, the specific steps are as follows:
(1) IfCF occurs at the inverter of dc system, start the calculation and control strategy, calculate the equivalent mechanical power and electromagnetic power of the generators.
(2) Monitor whether the transmission power of dc system has recovered to the steady-state value. If so, record the equivalent relative speed of generators at this time and calculate the increased relative kinetic energy after CF. At the same time, calculate the maximum possible deceleration area, if the value of which is less than the relative kinetic energy of increased by power impact, implement the generator tripping control strategy.
(3) Calculate the required tripping amount of the generators, and implement the strategy after 200 ms time delay. Since dc overload operation is equivalent to reducing equivalent mechanical power, increase the reference value of the transmitted power of the dc system to the 1.1 times of steady state value during the time delay.
Simulations are implemented based on the simple system and actual power grid, which shows that the proposed method can accurately calculate the required cutting amount to maintain the transient power angle stability and effectively reduce the risk of power angle instability after commutation failure. Owing to the generator tripping strategy, voltages of the critical nodes can be maintained at a relatively higher level and the trend of continuous increase of the phase angle difference is effectively suppressed, with the phase angle difference maintained within 180°.
Keywords: High voltage direct current (HVDC), commutation failure (CF), power angle instability, generator tripping strategy
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.231792
国家重点研发计划资助项目（2021YFB2400900）。
收稿日期 2023-10-30
改稿日期 2023-12-21
朱益华 男，1988年生，硕士，研究方向为电力系统稳定分析、高压直流输电等。E-mail：zhuyih@csg.cn
郑晨一 男，1994年生，博士研究生，研究方向为电力系统稳定分析、高压直流输电等。E-mail：zhengchenyi@seu.edu.cn（通信作者）
（编辑 赫 蕾）