 、
、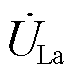 为HPFC两端电压。以a相为例,
为HPFC两端电压。以a相为例,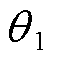 、
、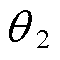 为移相角,
为移相角,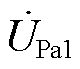 、
、 、
、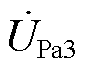 分别为ET与CHBC输出电压。给定的潮流对应HPFC的两端电压相位差为
分别为ET与CHBC输出电压。给定的潮流对应HPFC的两端电压相位差为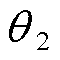 ,此时PST通过挡位调节产生的相位差为
,此时PST通过挡位调节产生的相位差为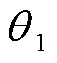 ,线路潮流接近给定的潮流指令。CHBC通过控制输出与
,线路潮流接近给定的潮流指令。CHBC通过控制输出与 同相的电压
同相的电压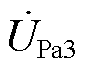 ,PST与CHBC协同控制,使得相位差增加到
,PST与CHBC协同控制,使得相位差增加到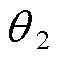 ,线路功率达到目标指令。
,线路功率达到目标指令。摘要 随着新能源并网的占比不断提高,新能源输送通道受到电网结构及线路热稳定极限的限制。为此,提出一种混合型潮流控制器(HPFC)用于灵活、精准调控潮流,平衡潮流分布,提高断面输送能力。HPFC由无源移相器(PST)部分与有源级联H桥换流器(CHBC)部分组合而成,结合了PST调节潮流容量大与CHBC灵敏性高的优点,实现了对潮流的快速精准调节。首先,利用PST阻抗特性分析了潮流与PST挡位之间的非线性耦合关系,并提出一种基于sinh函数的变步长高效求解的迭代算法;其次,对PST有载调压过程进行仿真建模与暂态分析,推导出切换过程中PST输出电压解析式,为实现暂态应力协同控制(TSCC)提供理论基础;再次,针对有源CHBC与无源PST调节区域及速度之间的差异问题,提出一种潮流柔性协同控制策略,实现了暂态应力协同控制,减小了HPFC调控过程中对电网的潮流冲击及换流阀承受的应力集中;最后,基于PSCAD/EMTDC的仿真结果验证了理论分析的正确性及协调控制策略的有效性。
关键词:混合潮流控制器 移相变压器 级联H桥换流器 等值阻抗 协同控制
随着新能源的快速发展,新能源接入电网所占比例越来越大,而由于电网潮流分配不均和线路热稳定极限的限制,导致电网中出现输电断面瓶颈和线路输电能力闲置并存的情况。因此,采用安全、可靠、经济的新型柔性交流输电(Flexible Alternative Current Transmission System, FACTS)装备,改善现有电网潮流调控能力和提升电网对新能源的承载能力[1]是传统交流电网向柔性电网升级的重要方向。
统一潮流控制器(Unified Power Flow Controller, UPFC)[2-4],可独立调节节点电压幅值、相位及线路阻抗,兼具线路潮流独立控制、无功动态补偿及系统振荡平抑[5]等功能,是功能最强大的FACTS装置。但其需要较多的电力电子器件,控制较为复杂,价格昂贵,占地面积大,难以广泛应用。文献[6-7]提出了一种基于Sen变压器与小容量UPFC结合的混合式统一潮流控制器,降低了电力电子装置的容量,节省了制造成本,但Sen变压器在机械式挡位切换过程中产生的电流暂态应力会对UPFC产生影响[8]。传统移相器(Phase Shifter Transformers, PST)[9-10]通过改变电压相位和幅值从而改变潮流的分布,但由于PST挡位为固定值,只能离散地改变潮流大小,无法实现对潮流的平滑、连续、精确调节;文献[11-12]通过多端口网络理论,对PST进行等值阻抗建模,推导出PST电压比与阻抗之间的函数关系式,但对于PST电压比与潮流的函数关系式没有进一步讨论分析。级联H桥换流器(Cascaded H-Bridge Converter, CHBC)[13-14]在电力电子装置中是较为重要的拓扑结构,相对于模块化多电平换流器(Modular Multilevel Converter, MMC)[15-16]结构与控制算法较为简单,且耐受过电压、过电流能力更强。
本文提出了一种基于PST与CHBC组合而成的混合式潮流控制器(Hybrid Power Flow Controller, HPFC),结合了PST调节容量大和小容量CHBC灵敏性高的优点,实现了对潮流的精准快速控制,安全性和可靠性指标更佳,且相对于UPFC占地面积少、工程造价较低、运行维护方便,具有显著的经济优势。针对无源PST部分,详细分析了PST电压比与潮流之间的影响机理,推导出两者之间的函数关系式。但由于电网潮流特性与PST内部的电磁耦合关系复杂,因此函数关系式呈现复杂的非线性,需要采用迭代方法进行求解,计算量很大,仿真速度缓慢。基于此,本文提出了基于sinh函数的变步长迭代算法,高效解算出目标潮流对应的电压比,从而获得PST需要调节的挡位。针对有源CHBC部分采用了直流电压分层控制策略和载波移相脉宽调制策略(Carrier Phase-Shift Pulse Width Modulation, CPS-PWM),实现了内部直流电压的稳定。针对PST与CHBC的协同控制部分,在PST有载分接开关(On-Load Tap-Changer, OLTC)切换期间,利用CHBC的快速调节特性抑制功率、电流等电气量的快速变化,减小对电网的冲击及CHBC承受的电流应力,实现暂态应力协同控制(Transient Stress Co-Control, TSCC);PST调挡完成后,剩余的功率差由CHBC进行补偿,完成对功率的精准调节。
HPFC结构主要由PST与CHBC串联组成,本文采用的PST结构为双心对称型移相变压器[17](Two-core Symmetrical Phase Shifting Transformer, TSPST),主要由串联变压器(Series Transformer, ST)和励磁变压器(Excitation Transformer, ET)组成。TSPST具有改变电压相位[18]的功能,相对于其他结构的变压器,调节方式简单,稳定性更好。CHBC通过串联在PST的ET低压侧与PST结合,实现对潮流的精准控制,且通过这种连接方式,能够有效保护CHBC,提高CHBC耐受过电压、过电流的能力。CHBC在工作时通过开关的通断将直流侧的电压转换成与网侧同频率的交流电压,可将其等效为一个交流电压源,其幅值和相位都可以控制[19]。HPFC结构及工作原理如图1所示。
如图1a所示,无源的PST与有源的CHBC串联,利用PST改变线路电压相位的功能,通过改变励磁变压器低压侧电压,从而大幅度调节线路潮流[20]。但由于PST挡位是离散的,PST调节的潮流为固定值,无法满足线路潮流指令灵活多变的情况。基于此,本文通过利用CHBC灵活可控的优点来补偿PST调节潮流因挡位离散产生的死区。其基本原理如图1b所示,图中 、
、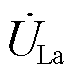 为HPFC两端电压。以a相为例,
为HPFC两端电压。以a相为例,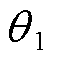 、
、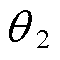 为移相角,
为移相角,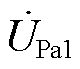 、
、 、
、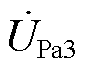 分别为ET与CHBC输出电压。给定的潮流对应HPFC的两端电压相位差为
分别为ET与CHBC输出电压。给定的潮流对应HPFC的两端电压相位差为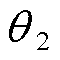 ,此时PST通过挡位调节产生的相位差为
,此时PST通过挡位调节产生的相位差为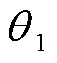 ,线路潮流接近给定的潮流指令。CHBC通过控制输出与
,线路潮流接近给定的潮流指令。CHBC通过控制输出与 同相的电压
同相的电压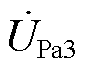 ,PST与CHBC协同控制,使得相位差增加到
,PST与CHBC协同控制,使得相位差增加到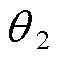 ,线路功率达到目标指令。
,线路功率达到目标指令。
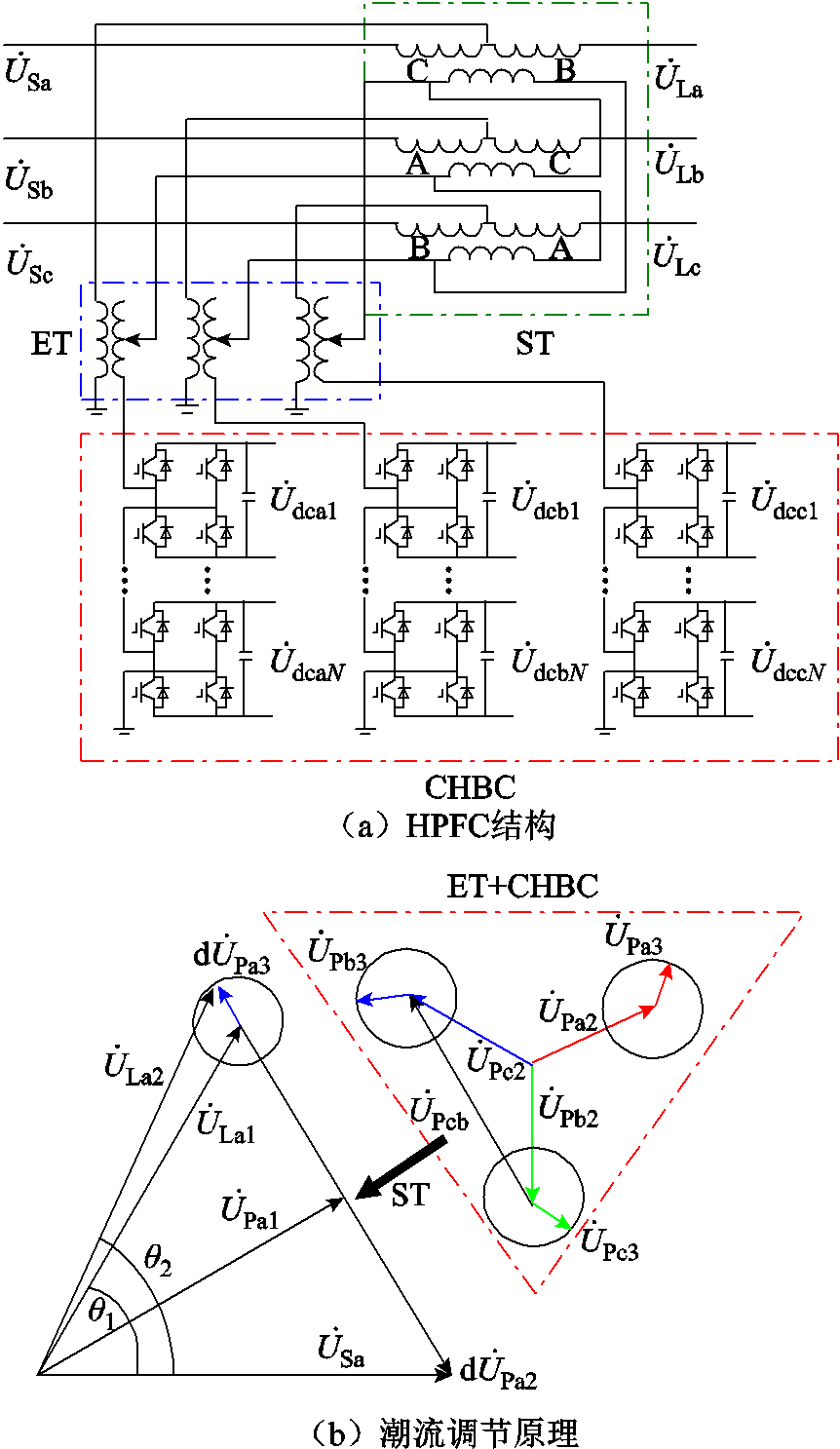
图1 HPFC结构及工作原理
Fig.1 HPFC structure and working principle
HPFC调控潮流首先是PST通过有载调压逐级调节挡位接近目标功率,其次由CHBC补偿剩下的功率差值。但由于系统潮流特性和PST内部的电磁耦合特性较为复杂,无法确定合适的挡位值,因此需要研究PST的阻抗特性,推导出线路潮流与PST挡位之间的函数关系式,求解出目标潮流对应的挡位值,从而更加准确地调节潮流。
由于PST内部电磁耦合关系复杂,需要通过建立PST等效模型,利用多端口网络理论推导出PST等值阻抗关系式。
PST的拓扑结构及等效电路如图2所示。
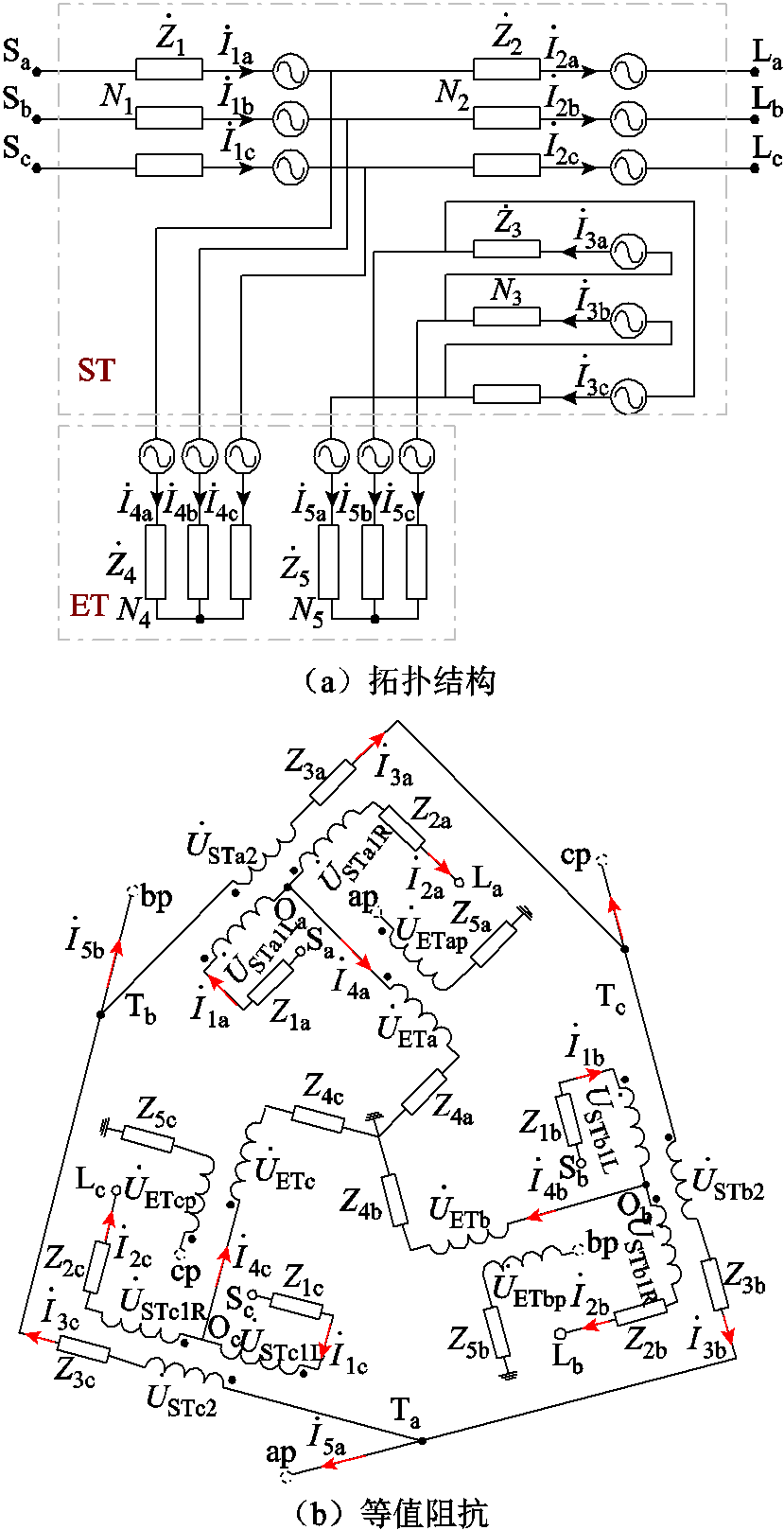
图2 双心对称移相变压器
Fig.2 Twin-core symmetrical phase-shifter transformer
图2中,ET为励磁变压器,ST为串联变压器,Sh、Lh分别为电源侧和负荷侧;Z1h、Z2h、Z3h分别为串联变压器一次侧、二次侧、三次侧等效阻抗,Z4h、Z5h分别为励磁变压器一次侧、二次侧等效阻抗,USTh1L、USTh1R、USTh2分别为串联变压器一次侧、二次侧、三次侧感应电动势,UETh、UEThp分别为励磁变压器一次侧、二次侧感应电动势,I1h、I2h、I3h分别为串联变压器一次、二次、三次电流,I4h、I5h分别为励磁变压器一次、二次电流,h=a,b,c三相。ke=N5/N4为励磁变压器二次侧与一次侧绕组匝数比值;ks=N3/N1=N3/N2为串联变压器匝数比。
根据PST的功能与特性,将PST看作由理想电源与内阻抗串联组成,等效模型如图3所示。
附录中式(A1)~式(A8)详细推导了PST移相角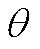 与ke之间的关系及PST的等值阻抗Zeq与ke的关系,有
与ke之间的关系及PST的等值阻抗Zeq与ke的关系,有
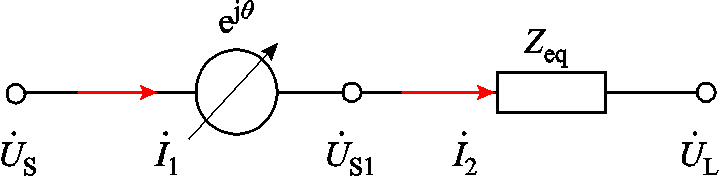
图3 等效模型
Fig.3 Equivalent model
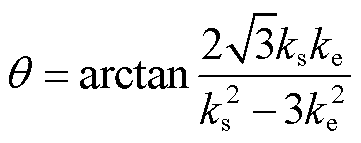 (1)
(1)
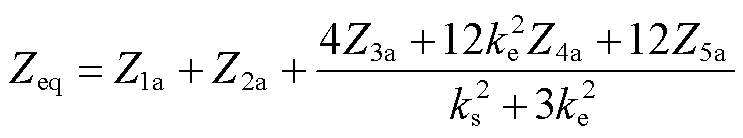 (2)
(2)
根据式(2)可知,PST的等值阻抗主要与变压器的电压比及漏抗等参数有关,为详细分析PST的阻抗特性,本文采用控制变量法,通过改变其中一个变量进行理论计算与仿真,并将数据绘制成三维视图。不同ST短路阻抗等值曲面如图4所示。

图4 不同ST短路阻抗等值曲面
Fig.4 Isometric surfaces with different ST short-circuit impedances
图4中z轴为阻抗值,x轴为ET挡位,y轴为ST挡位,Uk%为变压器中短路电压百分比。分析图4可知,随着ST短路阻抗的增大,等值曲面整体向上平移。
附图1为不同ET短路阻抗下的等值阻抗曲面,随着短路阻抗的增大,曲面的陡度增大,说明ET短路阻抗主要影响等值曲面的陡度。
综合图4和附图1可以看到,随着ET/ST挡位增大,等值阻抗呈现非线性增长,且正、负挡位呈现的阻抗曲面具有对称性。
当PST投入工程应用之后,其中的ST电压比ks及变压器漏抗是确定的,通过式(2)可得PST等值阻抗只与ET的电压比ke有关。对图4进行y轴切面分割,转换为只含ke变量的二维视图,可以得到PST阻抗与ke呈现复杂的非线性关系。以典型的双机互联系统为例,搭建PST潮流调控模型,如图5所示。
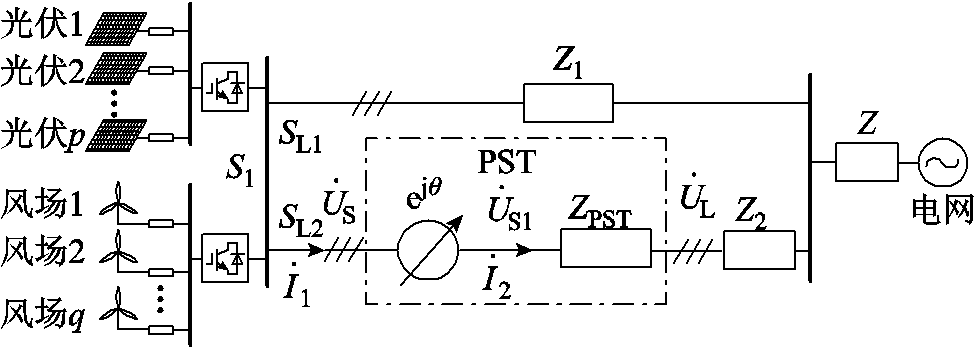
图5 PST潮流调控模型
Fig.5 PST power flow regulation model
由图5可知,线路潮流分布不平衡时,PST通过改变线路电压相位从而平衡线路潮流。根据潮流计算公式可得,PST所在线路的潮流SL2与PST电压比ke之间的函数关系式为
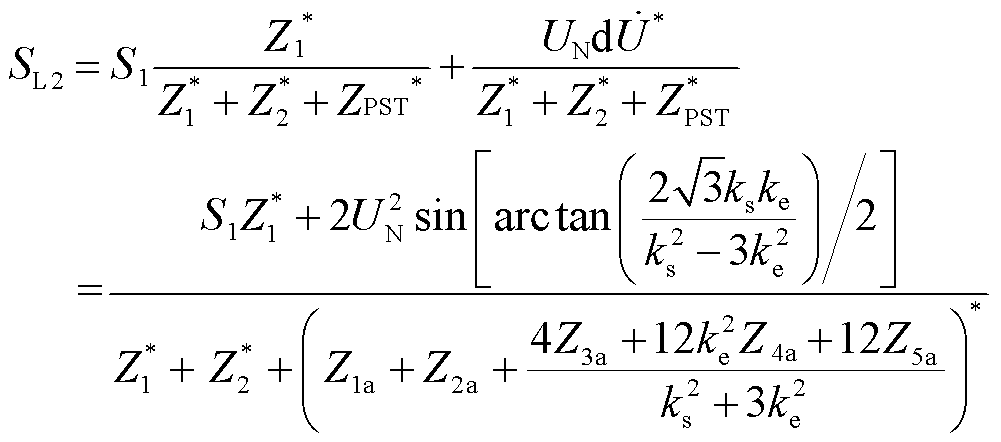 (3)
(3)
式中,*为共轭;Z1、Z2为线路阻抗;ZPST为PST等值阻抗;dU为HPFC在线路中呈现的电压差;SL1、SL2为线路功率;S1为总功率;UN为额定电压。
通过式(3)可以求解出目标功率对应的PST电压比。但由于PST内部复杂的电磁耦合关系和目标功率的不确定性,功率与电压比之间呈现的是复杂的非线性关系。为保证求解方程的快速性和收敛性,本文提出了一种基于sinh函数的变步长迭代方法,利用sinh函数接近目标值的良好收敛性对迭代步长进行实时调整,提高求解效率与准确率。PST电压比求解过程如图6所示。
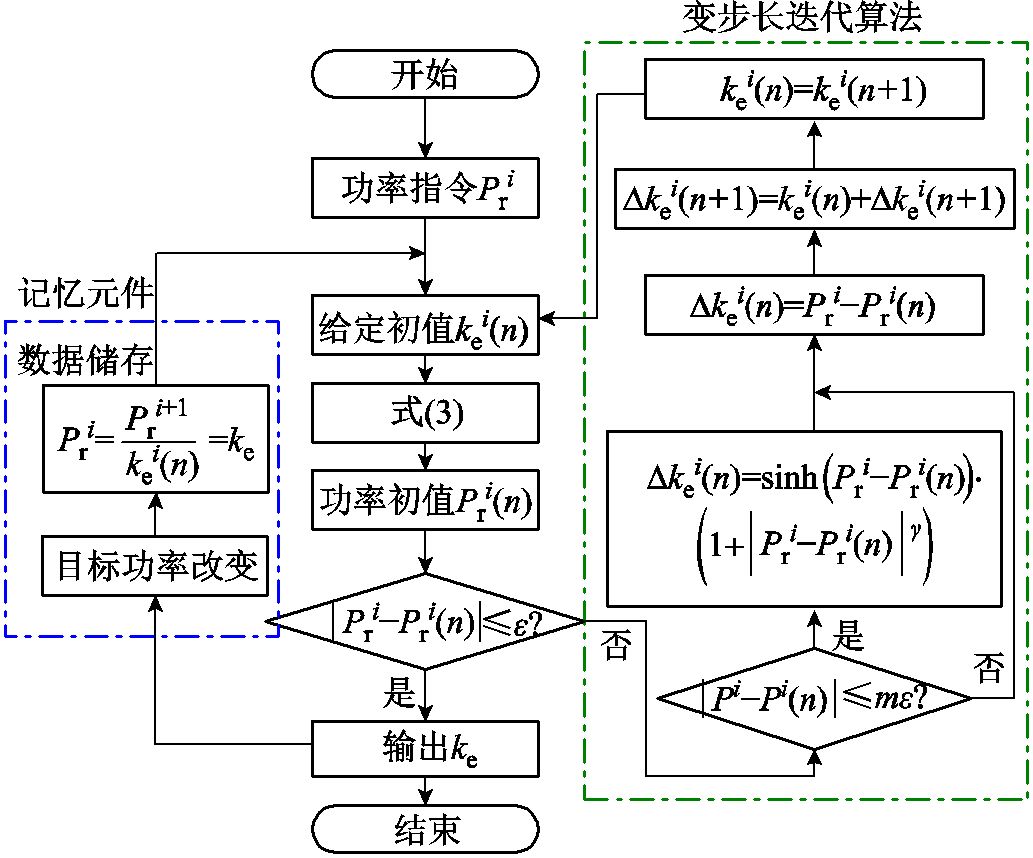
图6 PST电压比求解过程
Fig.6 PST transformation ratio solution process
图6中,i为目标功率Pr改变的次数,n为求解一次电压比ke的迭代次数,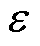 为允许的误差,
为允许的误差,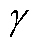 为收敛因子。以目标功率Pr与迭代功率
为收敛因子。以目标功率Pr与迭代功率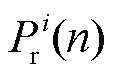 之间的差值作为迭代步长的参考值,大大减小了迭代次数,提高了计算效率。当功率误差减小到设定值
之间的差值作为迭代步长的参考值,大大减小了迭代次数,提高了计算效率。当功率误差减小到设定值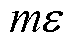 值时,为保证迭代的收敛精确性,本文引入了sinh函数对步长进行实时调整,实现了函数在迭代求解过程中的快速性与准确性,既节省了运算时间,又加快了收敛。
值时,为保证迭代的收敛精确性,本文引入了sinh函数对步长进行实时调整,实现了函数在迭代求解过程中的快速性与准确性,既节省了运算时间,又加快了收敛。
考虑到目标功率指令多变的情况,每次功率的变化意味着需要重新求解一次ke,运算效率大大降低。本文设计一个记忆元件,对上个时间段的功率与电压比进行储存,作为下个时间段的迭代初值,缩短了运算时间。两种给定不同的目标功率Pr迭代算法的电压比求解过程如图7所示。
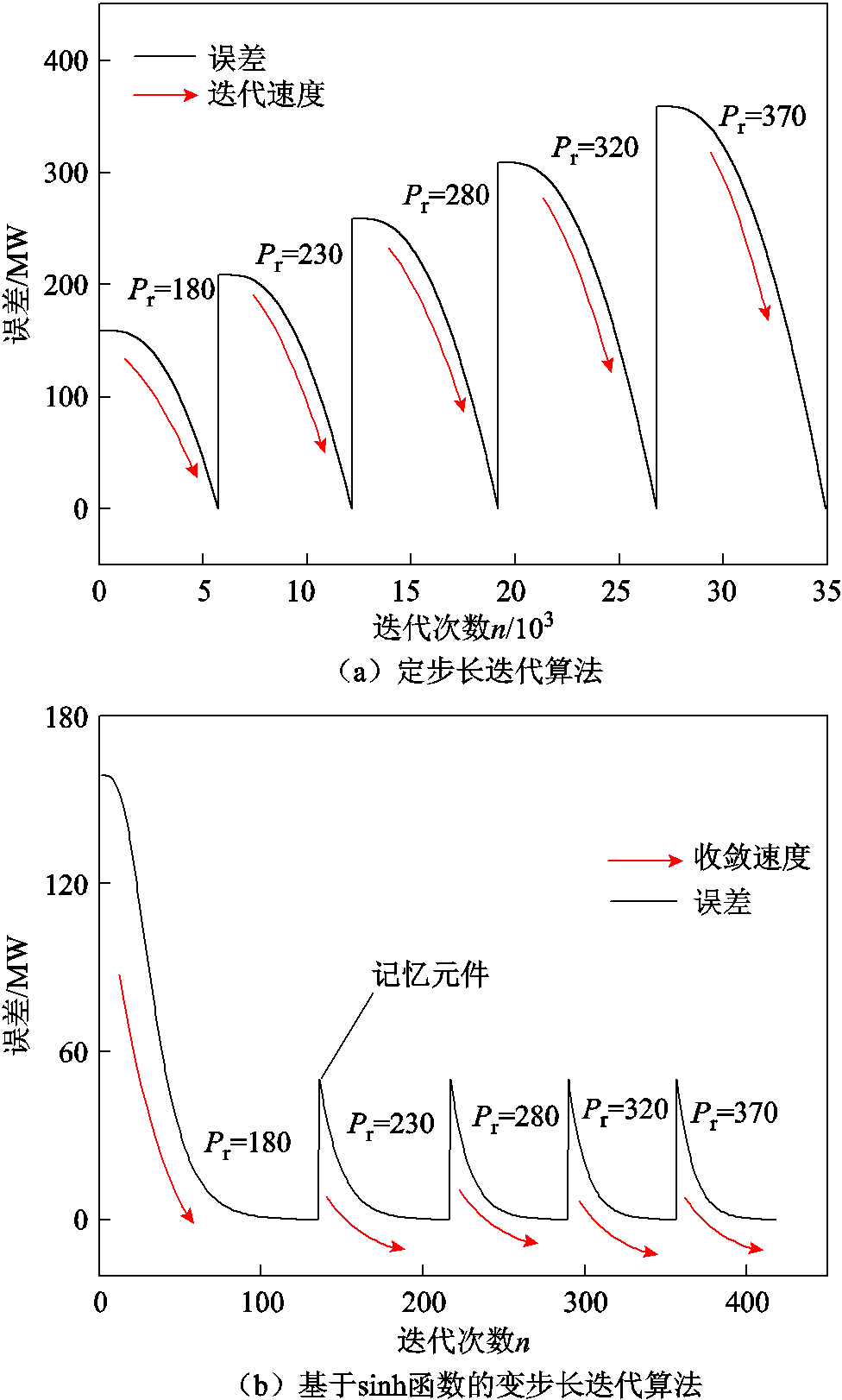
图7 不同算法求解对比
Fig.7 Comparison of different algorithms
图7a为普通定步长迭代算法1,每次Pr改变,都需要重新进行迭代求解,求解5次总共需要迭代约35 000次,且随着迭代次数增加,迭代速度越快,收敛性较差;图7b为基于sinh函数的变步长迭代算法2求解过程,每次迭代完成以后,对迭代结果进行记忆,用于下次求解,5次求解只需要迭代大约430次,且收敛速度先快后慢,因此具有较高的准确性和效率。
在PSCAD中分别利用两种迭代算法的仿真效率见表1。
表1 不同算法仿真效率
Tab.1 Simulation efficiency of different algorithms

参数数值 算法1算法2 仿真时间/s9 9 仿真步长/ms1010 实际时间/min127.645 54.601 3
由表1中数据可知,基于sinh函数的变步长迭代算法提高了仿真效率。
根据线路潮流与PST电压比之间的函数关系式可以求解出目标潮流Pr对应的ke。由于PST的挡位M为离散值,即PST可调电压比KM为固定值,因此只能选择离ke较近的KM对应的挡位作为目标挡位T。
PST通过有载调压[21-22]过程调整挡位至目标值,通过每个挡位之间的触头开关动作来进行挡位的调节[23-24],换挡开关结构及动作逻辑如图8所示。
图8a为PST有载分接开关结构,MC为主抽头,TC为过渡触头,R为过渡电阻[25]。当PST接收到调挡指令以后,各触头开始协同动作,如图8b所示,以1挡调到2挡为例:①首先MC1接通,0 ms TC1接通;②10 ms断开MC1,20 ms接通TC2;③40 ms断开TC1,50 ms接通MC2;④60 ms断开TC2。经过60 ms[26]即可完成一次挡位的切换。具体切换流程如附图2所示,仿真结果如图9所示。
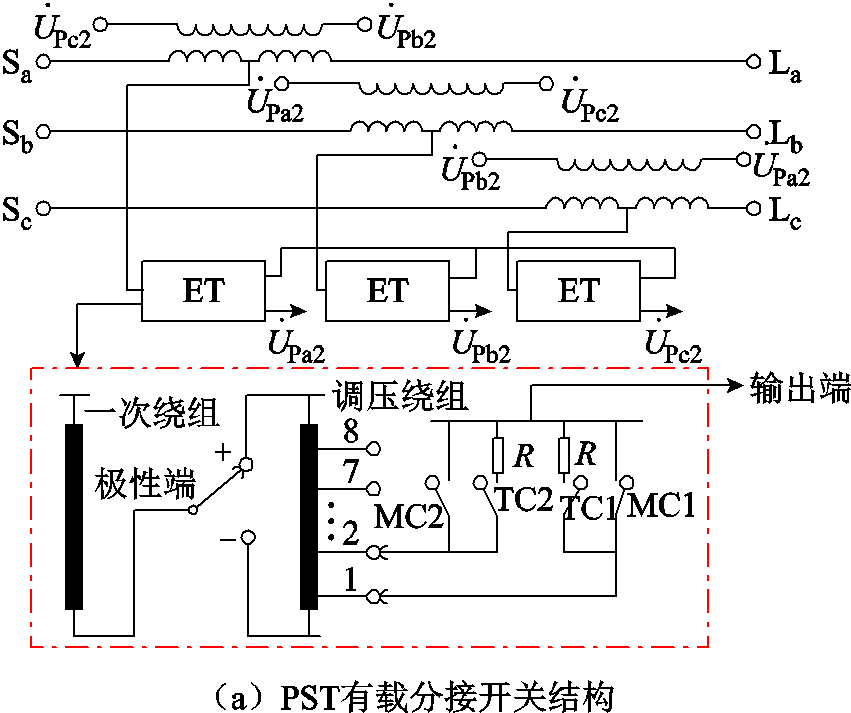
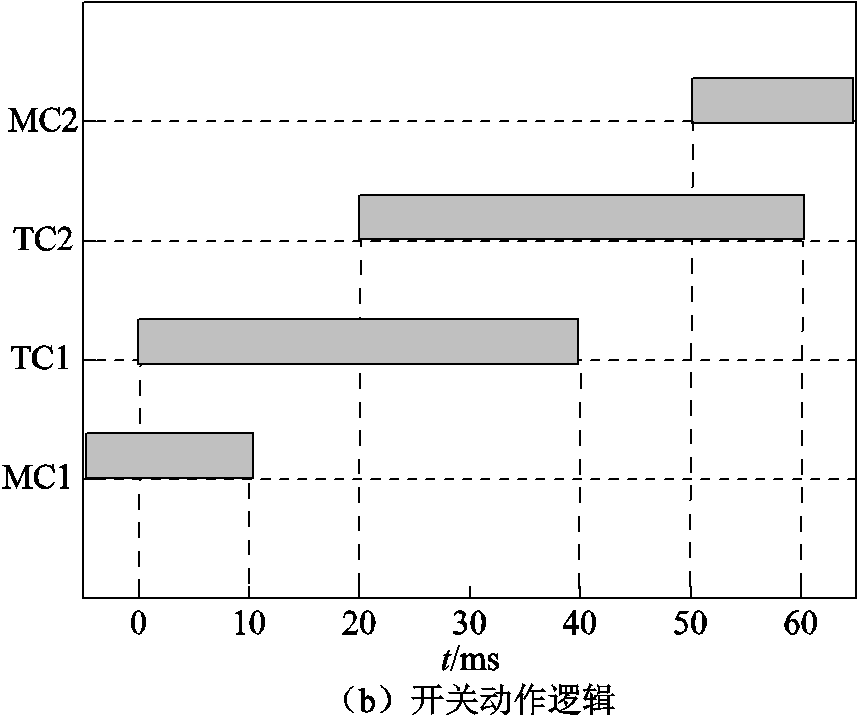
图8 有载调压过程分析
Fig.8 Analysis of on-load pressure regulation process
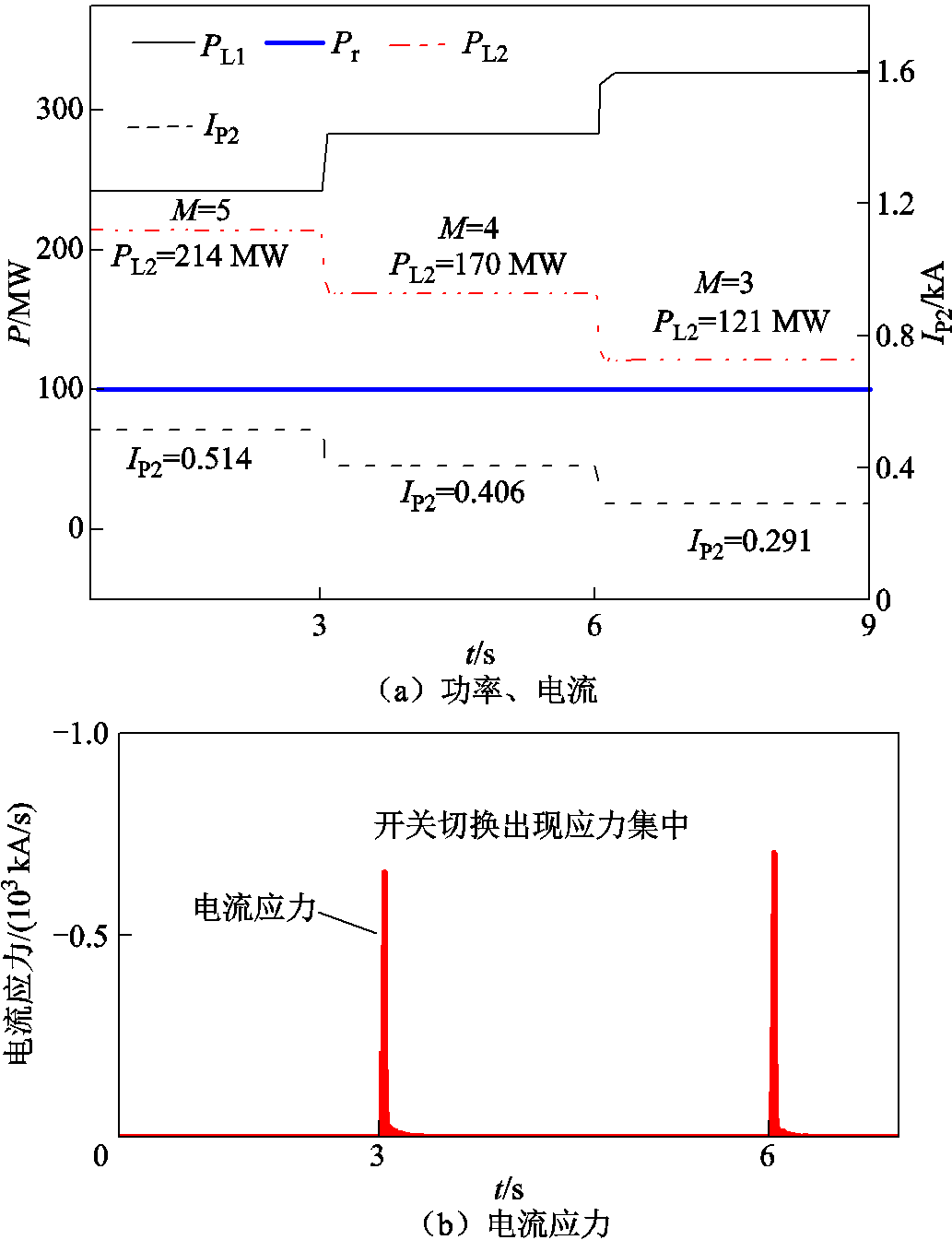
图9 PST调控潮流过程
Fig.9 PST flow control process
给定目标功率Pr为100 MW,通过图6所示方法进行迭代,计算出PST对应的电压比为0.030 5,选择较为接近的目标挡位T为3挡,PST初始挡位为5挡。PST在进行有载调压过程中,实际功率PL2、阀级电流IP2如图9a所示,在PST的潮流调控下,线路功率接近目标功率,但由于PST的挡位离散,存在一定的功率差值。根据HPFC调控潮流机理,剩余的功率差将由CHBC进行补充。同时在有载调压过程中,由于挡位切换速度较快,功率变化率较大,影响了电网的稳定性。图9b为CHBC在PST进行调挡时承受的电流应力,在换挡瞬间,产生了电流应力集中,可能对换流阀造成影响。考虑到电力电子设备的安全性,本文设计利用CHBC的快速灵敏性,抑制PST在换挡过程中电压及电流的变化率,实现功率的平滑调节。
通过上述有载调压分接开关动作逻辑,本文将一次挡位切换过程分为7个步骤,并获取等效电路如图10所示。
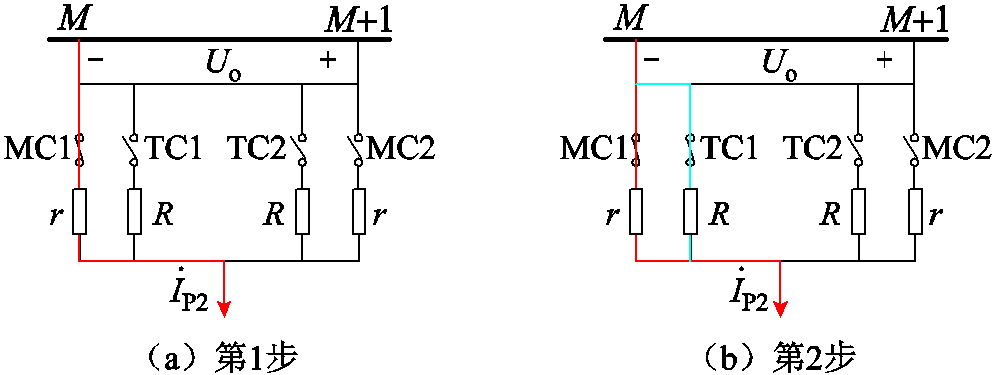
图10 等效电路
Fig.10 Equivalent circuit
图10为切换过程中1、2两步等效电路。图中r为导线电阻,Uo为每挡的电压差值。ET输出电压为
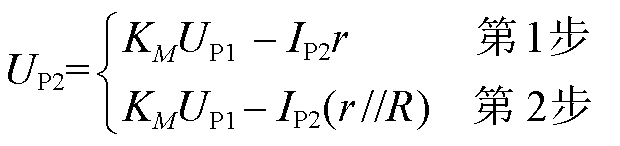 (4)
(4)
式中,UP1为ET一次电压有效值;KM为当前挡位对应电压比。全部步骤等效电路及输出电压如附图3及式(A9)~式(A15)所示。挡位切换过程中ET输出电压如图11所示。
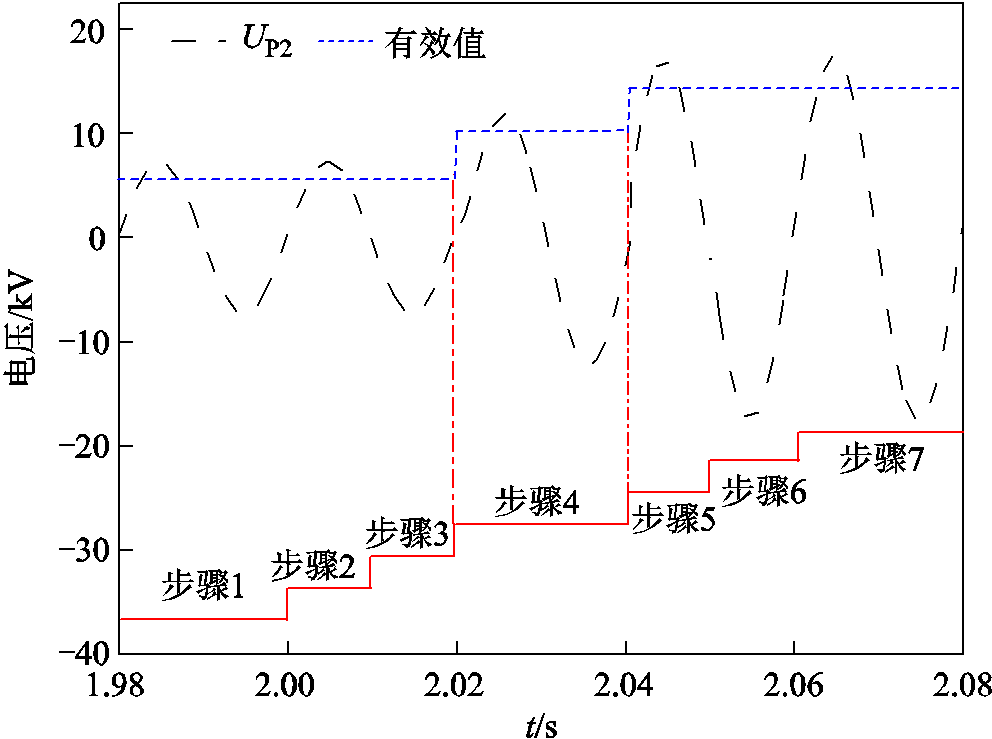
图11 挡位切换ET输出电压
Fig.11 Switching the ET output voltage in gear
由图11可知,引起输出电压的变化主要由步骤1、4、7产生。为简化分析与控制过程,在理论计算过程中将PST换挡过程简化为三个过程:步骤1为换挡前,MC1接通;步骤4为过渡阶段,过渡触头TC1、TC2接通;步骤7为换挡完成,MC2接通。由于导线电阻r较小,为简化分析将其忽略。三个过程的变压器输出电压UP2为
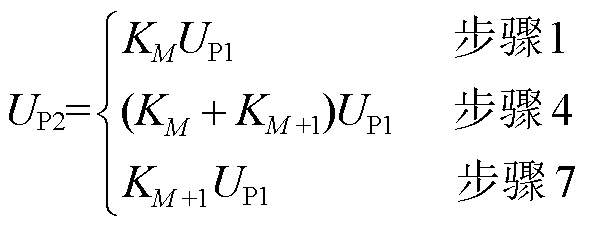 (5)
(5)
式中,KM+1为下一挡位对应的电压比。将简化过程进行理论计算并与实际仿真结果对比,有载调压波形如图12所示。
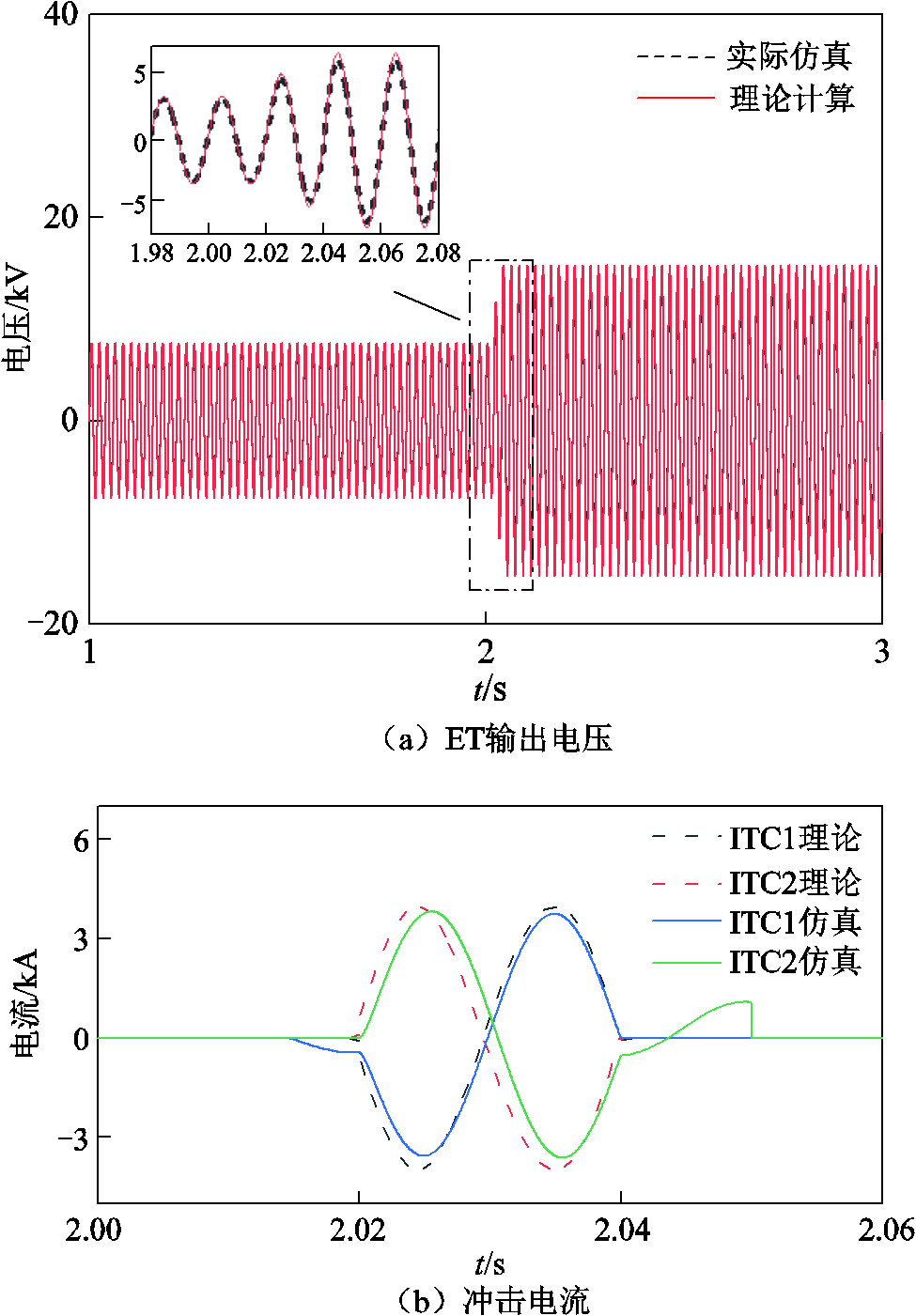
图12 有载调压波形
Fig.12 On-load regulation waveforms
图12a为换挡过程中ET输出电压的理论值与实际值对比,发现简化过程与实际结果较为吻合。图12b为冲击电流的实际值与理论值,结果证明冲击电流主要产生于步骤4中。
通过上述暂态分析,可以通过计算近似得到有载调压暂态过程中ET输出电压及电流幅值,为后续CHBC进行柔性调节控制提供了理论基础。
CHBC串联在ET低压侧,通过控制输出电压与PST进行协同配合,对潮流进行柔性、精准调节。针对PST换挡迅速导致功率变化较快的问题,本文通过利用CHBC的快速灵敏性,在PST换挡过程中进行控制使线路功率平滑变化。实现目标如图13所示。
由图13所得,未加CHBC控制的情况下,原始功率在t1~t2换挡期间迅速上升,变化率较大。因此CHBC协同控制主要分为两步:
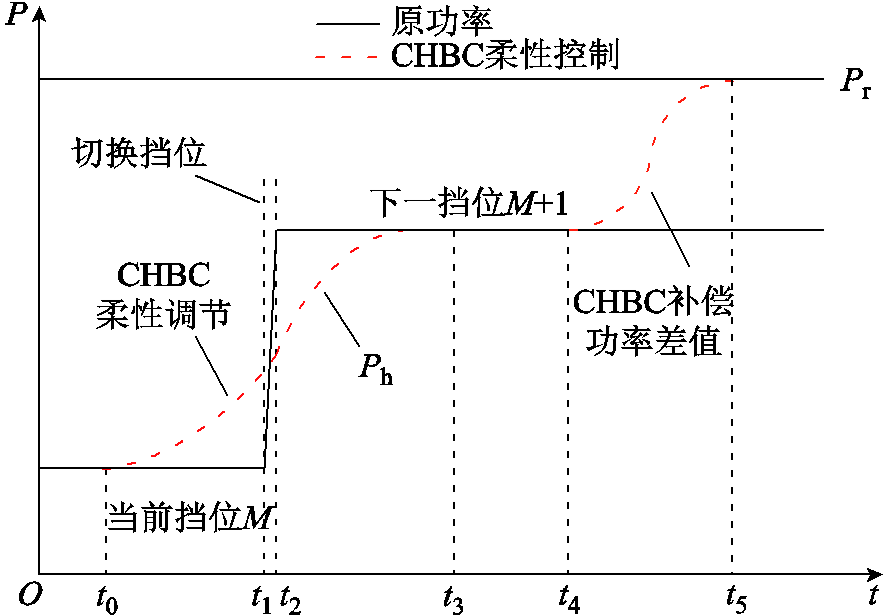
图13 CHBC柔性调节
Fig.13 CHBC flexible adjustment
1)在PST切换挡位期间,利用CHBC的快速调节特性,使功率平滑变化:在CHBC的柔性控制下,在t0时刻,先由CHBC控制功率沿着给定功率Ph上升,为保证功率平滑上升,设定Ph为平滑效果较好的指数函数;到达PST换挡瞬间t1时,利用CHBC的快速响应,抑制HPFC因PST换挡导致的电压跳跃;当换挡结束以后,t2时刻再由CHBC控制功率上升至PST该挡位下对应的功率;t3换挡过程结束,此时实际功率接近目标值Pr,PST停止动作。
2)PST停止动作后,剩余的功率差再由CHBC进行单独调节:t4时刻CHBC改变输出指令,平滑调节功率至Pr。
根据HPFC的工作原理可知,通过CHBC输出与PST励磁电压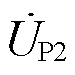 同相或者反相的电压
同相或者反相的电压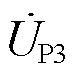 与
与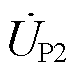 进行叠加,即可覆盖PST潮流调控死区。已知当前ET电压比为KM,目标功率对应的电压比为ke,则剩余的电压差值即CHBC输出电压值,为ET理想输出电压keUP1与实际输出电压KMUP1之间的差值。CHBC不同时刻的输出电压为
进行叠加,即可覆盖PST潮流调控死区。已知当前ET电压比为KM,目标功率对应的电压比为ke,则剩余的电压差值即CHBC输出电压值,为ET理想输出电压keUP1与实际输出电压KMUP1之间的差值。CHBC不同时刻的输出电压为
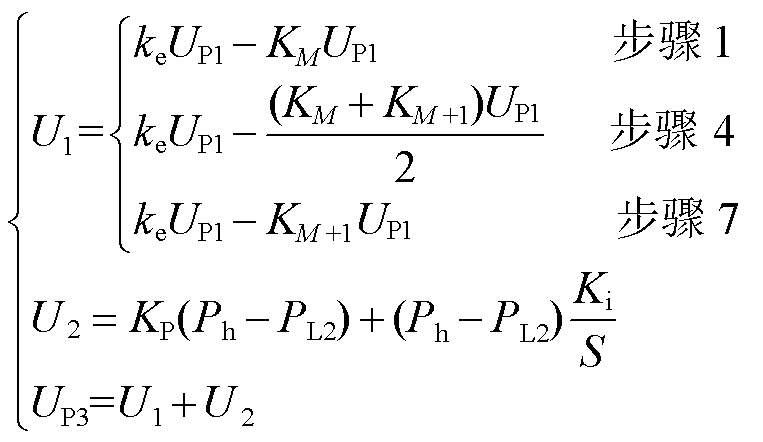 (6)
(6)
式中,U1为CHBC近似输出电压;U2为补偿电压,直接由功率差值进行PI控制;KP、Ki为比例积分系数,用来实时补偿U1的计算误差。经过计算的前馈解耦控制,PI承担的调节量较小,调节速度较快。
CHBC内部的电压控制策略采用直流电压分层控制[27-28],分别对整体侧直流平均电压Udcv、每相换流链的直流平均电压Udchv、每个单元电容的直流电压Udchx进行控制,x为每相单元电容的个数。三层控制策略为
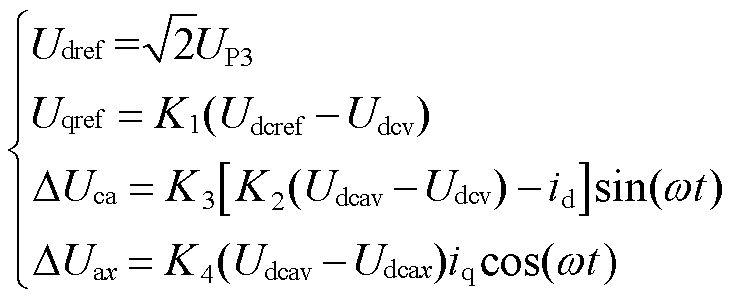 (7)
(7)
式中,Udref、Uqref分别为dq轴的参考电压;id、iq分别为ET二次电流![]() 经过分解后dq轴上的电流;Udcref为CHBC整体侧直流参考电压;
经过分解后dq轴上的电流;Udcref为CHBC整体侧直流参考电压;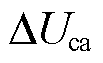 为a相直流电压补偿量;Udcav为a相直流平均电压;
为a相直流电压补偿量;Udcav为a相直流平均电压;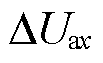 为单元电容电压补充量;K1、K2、K3、K4为比例系数。
为单元电容电压补充量;K1、K2、K3、K4为比例系数。
将上述潮流协同指令与各级直流电压指令进行叠加生成调制波,利用CPS-SPWM技术[29-30]输出对应的绝缘栅双极晶体管(Insulated-Gate Bipolar Transistors, IGBT)的开关信号ShN1~ShN4。
结合内部直流电压控制策略,CHBC的整体控制策略如图14所示。
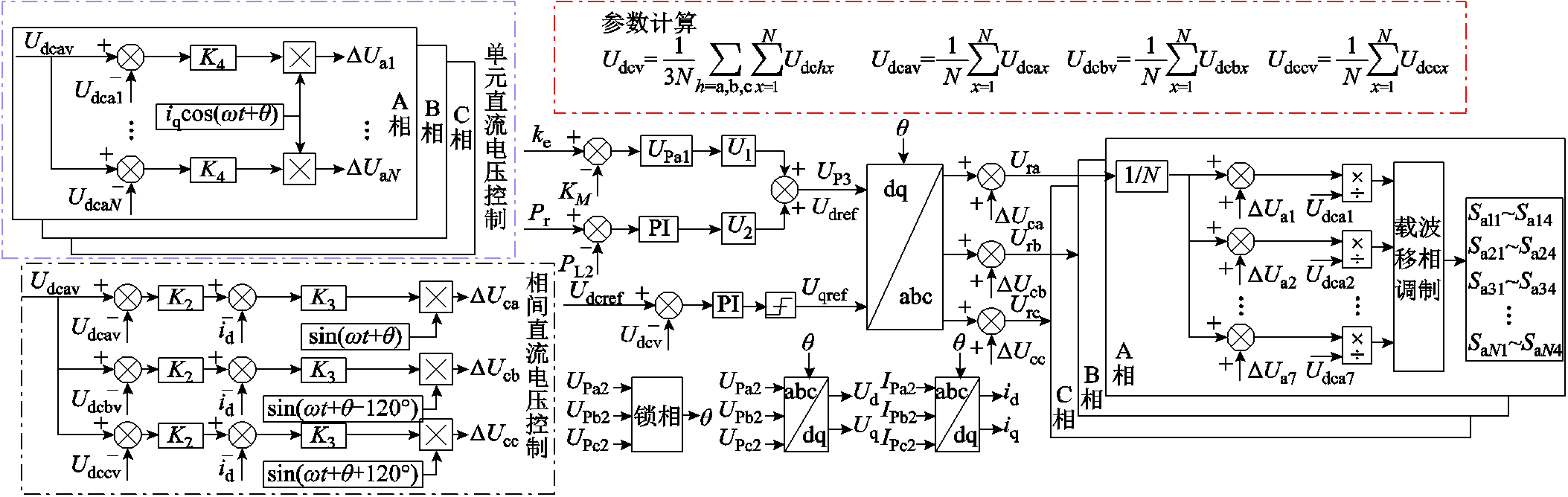
图14 CHBC控制策略
Fig.14 CHBC control strategy
在PSCAD/EMTDC中搭建图5所示新能源并网系统,并在一条线路中搭建HPFC模型。HPFC参数见表2。
表2 HPFC参数
Tab.2 HPFC parameters

装置参数数值 HPFC额定容量/(MV·A)370 ST额定电压/kV220 短路电压百分比(%)8 电压比ks3.225 8 ET额定电压/kV220 挡位M-8~8 移相角度/(°)-10~10 CHBC整体直流侧电压/kV11.2 单相直流侧电压/kV11.2 单元电容直流电压/kV1.6 级联子模块个数7
将数据代入式(2)中求出每挡对应的理论阻抗Zeq1与实际阻抗Zeq2,整理数据绘制PST等值阻抗如图15所示。
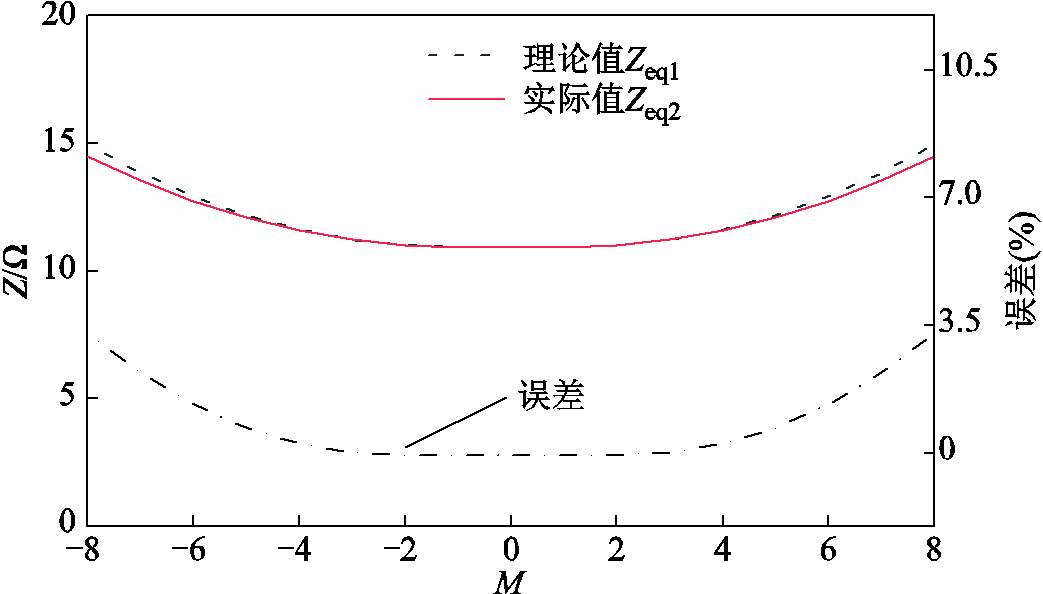
图15 PST等值阻抗
Fig.15 PST equivalent impedance
由图15可以得到,PST实际阻抗与理论阻抗是基本重合的,最高挡位时误差为3.5 %,说明等值阻抗的推导公式是可行的,可为推导出目标功率Pr与PST电压比ke之间的关系式提供理论基础。
CHBC在直流电压分层控制下的直流电压波形如图16所示。由图16可得,直流电压稳定在参考值附近,当CHBC参与调控潮流时,直流电压纹波率小于10%,说明直流电压控制效果较好。
在仿真模型中给定HPFC调节的潮流Pr为 100 MW,具体CHBC柔性协同控制波形如图17所示。
由图17a的功率波形可得,PST当前挡位为5挡,对应的潮流为209.39 MW,当HPFC接收到潮流指令Pr=100 MW后,通过式(3)求解PST的目标挡位T=3,通过有载调压分接触头的动作进行调挡。以5挡换到4挡为例,2 s时刻开始准备调挡,此时CHBC先进行功率的调节,使线路潮流PL2沿着Ph先缓慢下降,3~3.06 s换挡,4 s时刻,经过CHBC与PST协同控制使得PL2到达4挡对应的功率157.7 MW。7 s换挡结束,此时实际潮流PL2与目标潮流还有差值,8 s时刻CHBC再进行控制,使得功率到达目标潮流;图17b为CHBC输出电压指令,在CHBC的辅助调节下,功率呈现平滑变化,减小了对电网的冲击;图17c为调节过程中CHBC换流阀承受的电流暂态应力协同控制,相对于无CHBC辅助调节,应力值下降71.2%,有效地保护了电力电子装置。调节过程中PST输出电压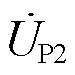 与CHBC输出电压
与CHBC输出电压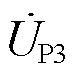 及CHBC阀侧电流
及CHBC阀侧电流![]() 的波形如图18所示。
的波形如图18所示。
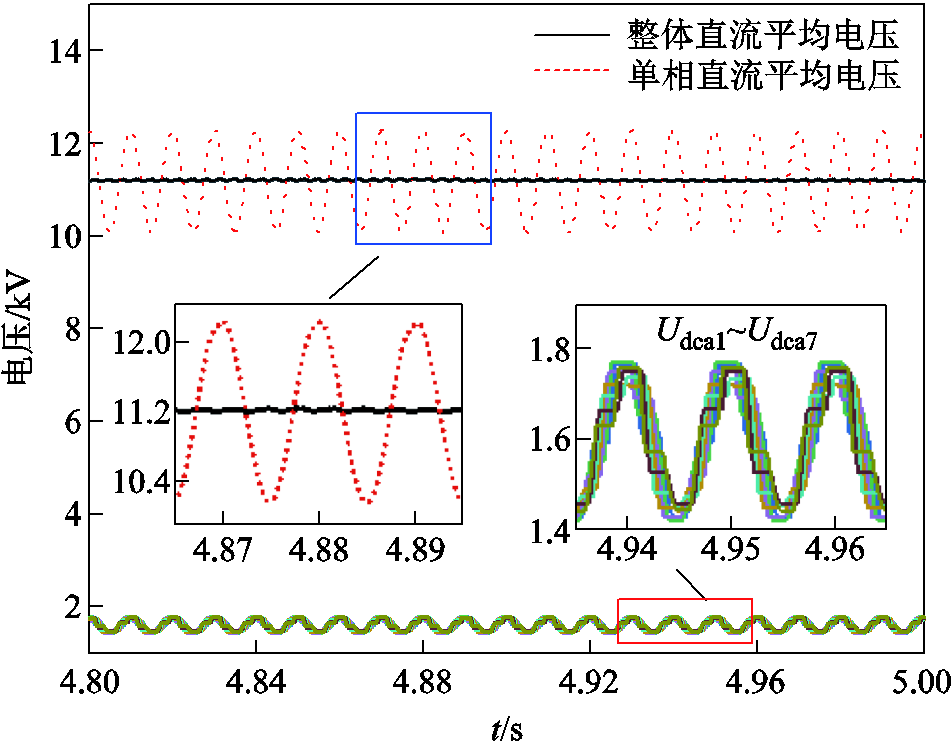
图16 CHBC直流电压波形
Fig.16 CHBC DC voltage waveforms

图17 CHBC柔性协同控制波形
Fig.17 CHBC flexible collaborative control waveforms
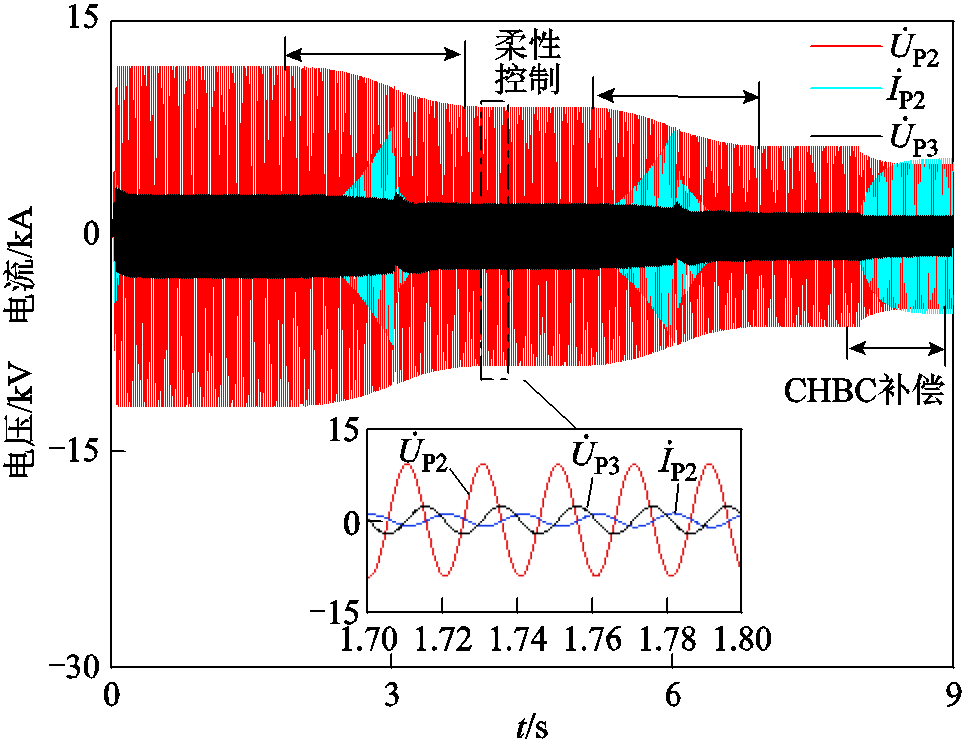
图18 电压电流波形
Fig.18 Voltage and current waveforms
如图18所示,在CHBC的辅助调节下,PST输出电压电流波形呈现平滑变化,且CHBC输出电压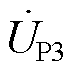 与PST输出电压
与PST输出电压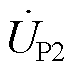 为反相,与电流
为反相,与电流![]() 呈90°,说明CHBC与系统主要进行的是无功交换。
呈90°,说明CHBC与系统主要进行的是无功交换。
本文针对电网潮流分布不平衡问题,提出了一种由无源PST与有源CHBC组合而成的混合潮流控制器,利用PST调节容量大和CHBC快速、精准的优点实现了对潮流的快速精准控制。
1)对于无源PST调控潮流机理,利用移相器等值阻抗表达式,并结合典型的双机互联系统求解出PST挡位与潮流之间的函数关系式,利用关系式可以求解出目标功率对应的挡位;针对函数关系式的复杂非线性求解问题,提出了一种基于sinh函数的变步长迭代求解方法,提升了求解效率和仿真速度。
2)对于PST有载调压过程,设计分接抽头动作逻辑,进行挡位切换电流暂态应力过程分析,对OLTC切换过程进行理论简化,推导出PST输出电压解析式,并通过PSCAD进行仿真,验证理论结果的正确性,为CHBC暂态应力协同控制提供理论基础。
3)对于无源与有源配合问题,本文提出两种阶段的协同控制策略。对于PST在进行有载调压过程中功率阶梯变化对电网的冲击问题,利用CHBC的快速调节特性,使功率平滑变化,同时降低CHBC承受的电流应力,实现暂态应力协同控制;PST完成调挡后,由CHBC补偿剩余的功率差值,达到精准控制潮流的目的。
附 录
1. 等值阻抗推导过程
利用KCL定理对图2b中节点Oa和节点Ta分析可得
 (A1)
(A1)
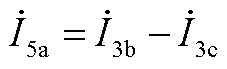 (A2)
(A2)
基于三相电流相序关系变换式(A2)可得
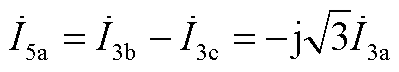 (A3)
(A3)
基于图2b中所示电流参考方向,对于ST和ET忽略励磁电流时磁势平衡方程为
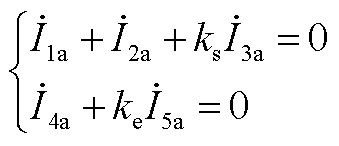 (A4)
(A4)
联立式(A1)~式(A4)得到各绕组电流之间的关系为
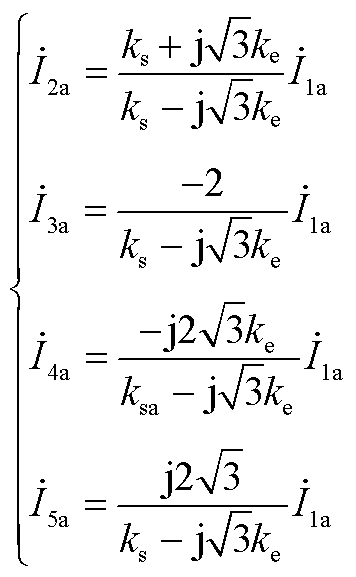 (A5)
(A5)
由式(A5)可得移相角与电压比之间的关系为
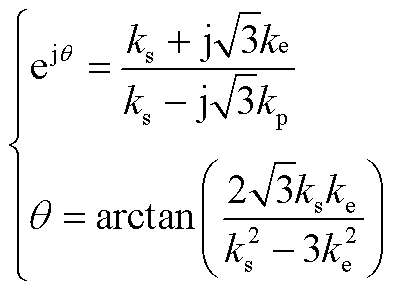 (A6)
(A6)
利用KVL定理与电流关系通过消去内部感应电动势可得PST两端电压关系式为
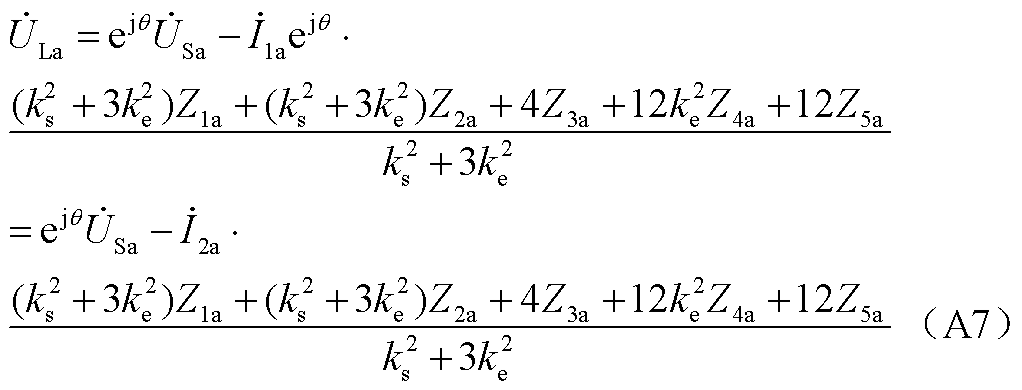
等值阻抗关系式为
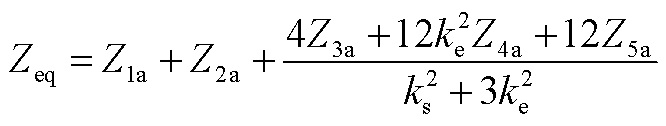 (A8)
(A8)
附图1为PST的等值阻抗,将ET、ST分别设置成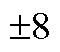 个挡位,并计算出对应挡位的阻抗值Zeq,绘制成三维曲面。
个挡位,并计算出对应挡位的阻抗值Zeq,绘制成三维曲面。

附图1 不同ET短路阻抗等值曲面
App.Fig.1 Isometric surfaces of different ET short-circuit impedances
2. OLTC切换过程分析
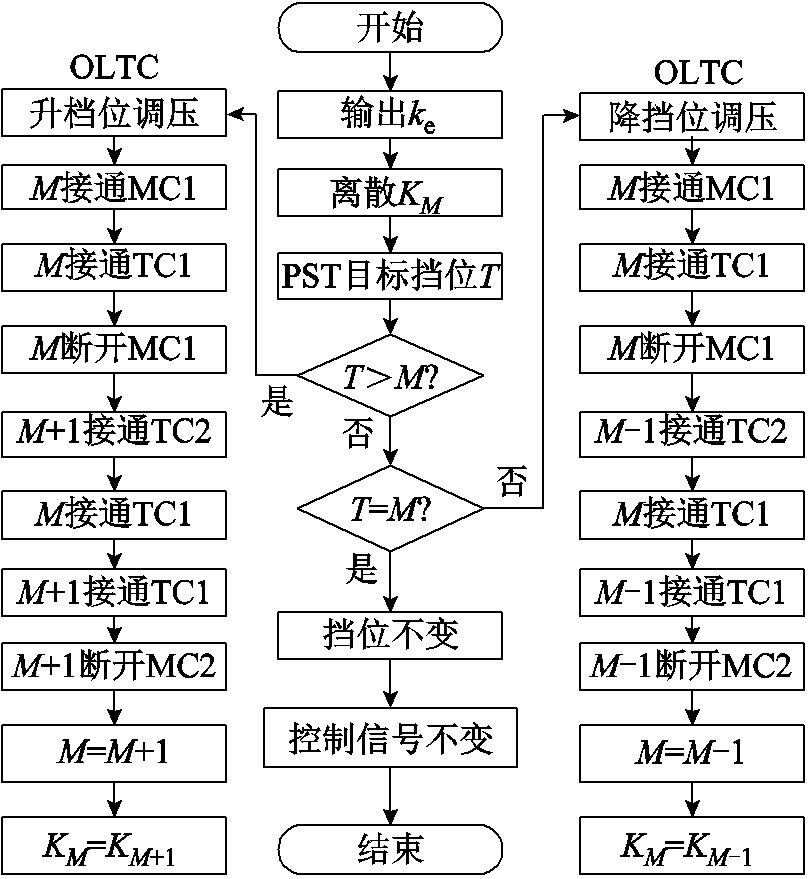
附图2 OLTC动作过程
App.Fig.2 OLTC action process
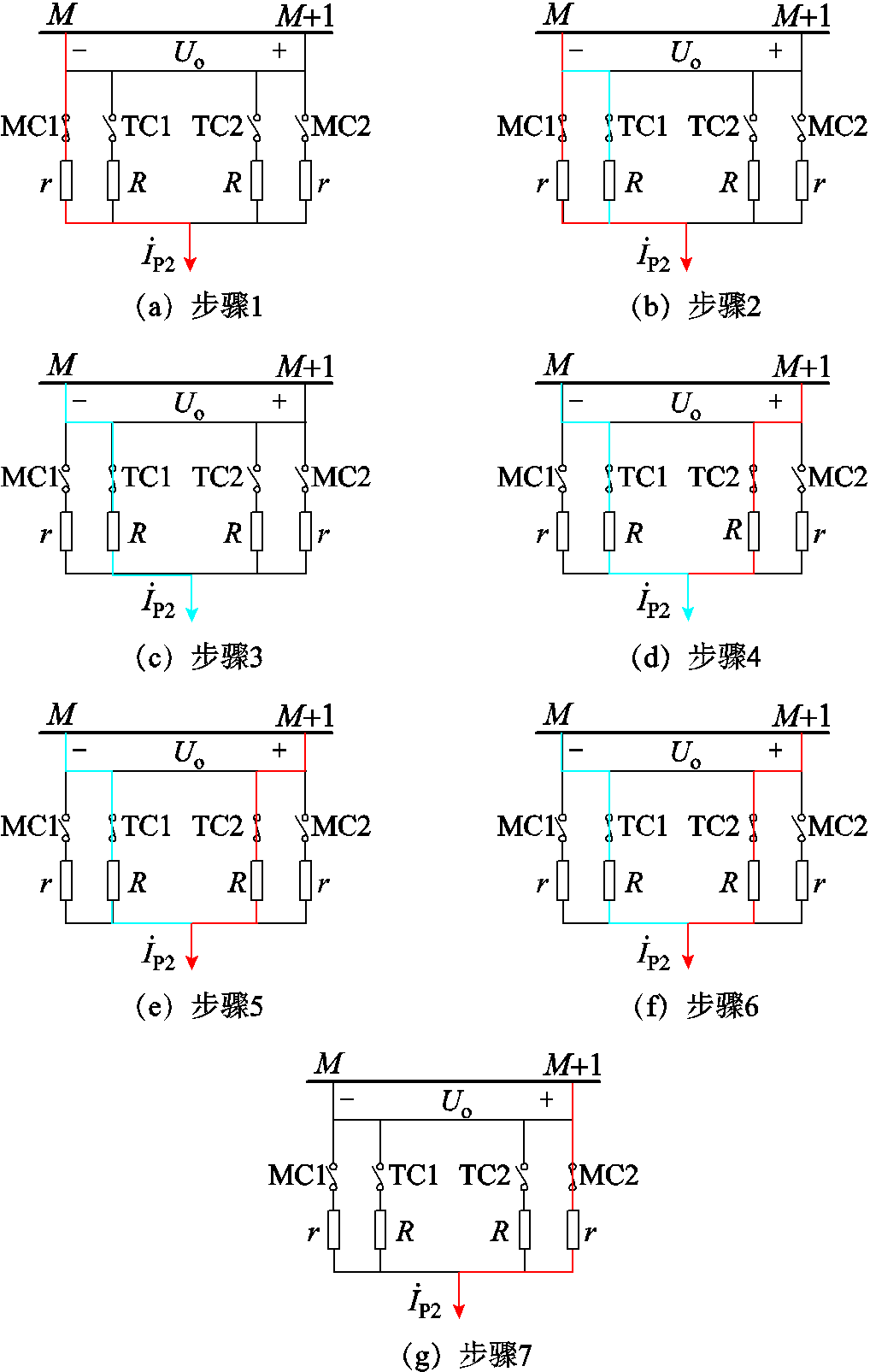
附图3 挡位切换过程分析
App.Fig.3 Analysis of gear switching process
根据各个触头动作顺序可分为7个步骤:
1)主触头MC1接通。
输出电压 及电流
及电流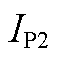 大小为
大小为
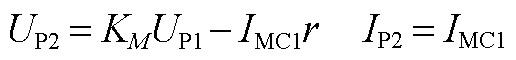 (A9)
(A9)
式中, 为流过主触头MCl的电流。
为流过主触头MCl的电流。
2)辅助触头TC1接通。
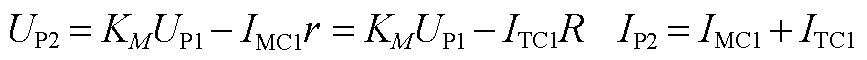 (A10)
(A10)
式中,![]() 为流过过渡触头TCl的电流。
为流过过渡触头TCl的电流。
3)主触头MC1断开。
4)辅助触头TC2接通。
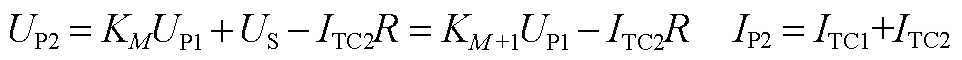 (A12)
(A12)
式中,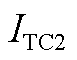 为流过过渡触头TC2的电流。
为流过过渡触头TC2的电流。
5)辅助触头TC1断开。
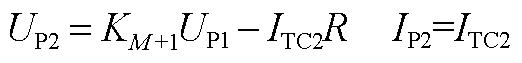 (A13)
(A13)
6)主触头MC2接通。
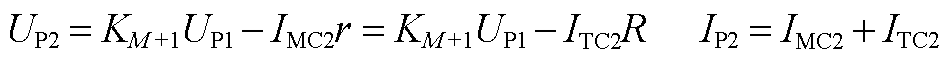 (A14)
(A14)
式中, 为流过主触头MC2的电流。
为流过主触头MC2的电流。
7)辅助触头TC2断开。
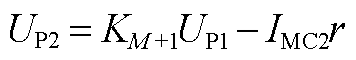 (A15)
(A15)
参考文献
[1] 刘俊磊, 刘新苗, 卢洵, 等. 高比例新能源系统供需平衡分析方法和对策[J]. 高电压技术, 2023, 49(7): 2711-2724.
Liu Junlei, Liu Xinmiao, Lu Xun, et al. Analysis methods and countermeasures of supply and demand balance of high proportion of new energy system[J]. High Voltage Engineering, 2023, 49(7): 2711-2724.
[2] Wu Xi, Wang Rui, Wang Yifei, et al. A novel UPFC model and its convexification for security-constrained economic dispatch[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4202-4213.
[3] 罗玉春, 王毅, 闪鑫, 等. 调控系统中统一潮流控制器稳态建模的实现[J]. 电力系统保护与控制, 2022, 50(1): 148-157.
Luo Yuchun, Wang Yi, Shan Xin, et al. Realization of steady state modeling of unified power flow controller in a control system[J]. Power System Protection and Control, 2022, 50(1): 148-157.
[4] 吴烈鑫, 余梦泽, 李作红, 等. 电磁式统一潮流控制器及其在环网潮流调节中的应用[J]. 高电压技术, 2018, 44(10): 3241-3249.
Wu Liexin, Yu Mengze, Li Zuohong, et al. Electromagnetic unified power flow controller and its application in the power flow control of loop network power grid[J]. High Voltage Engineering, 2018, 44(10): 3241-3249.
[5] 蒋平, 陈琼, 吴熙, 等. 利用重复控制跟踪的统一潮流控制器抑制系统强迫振荡方法[J]. 电力系统自动化, 2018, 42(18): 64-69, 168.
Jiang Ping, Chen Qiong, Wu Xi, et al. Suppressing method of power system forced oscillation by unified power flow controller based on repetitive control tracking[J]. Automation of Electric Power Systems, 2018, 42(18): 64-69, 168.
[6] 余梦泽, 李俭, 刘雷, 等. 电磁混合式统一潮流控制器的拓扑结构与控制策略优化[J]. 电工技术学报, 2015, 30(增刊2): 169-175.
Yu Mengze, Li Jian, Liu Lei, et al. Topology structure and control strategy optimization of electromagnetic hybrid unified power flow controller[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 169-175.
[7] 韩旭东, 牛胜锁, 孟令钊. 基于PST和UPFC的混合潮流控制器协同控制策略研究[J]. 电气技术与经济, 2023(4): 43-48.
Han Xudong, Niu Shengsuo, Meng Lingzhao. Research on cooperative control strategy of hybrid power flow controller based on PST and UPFC[J]. Electrical Technology and Economy, 2023(4): 43-48.
[8] 陈凯龙. 混合式统一潮流控制器建模及其控制策略研究[D]. 北京: 华北电力大学, 2021.
Chen Kailong. Research on modeling and control strategy of hybrid unified power flow controller[D]. Beijing: North China Electric Power University, 2022.
[9] 沈涛. 移相变压器在电力系统中的应用研究[D]. 北京: 华北电力大学, 2018.
Shen Tao. Research on the application of phase shifter transformer in power system[D]. Beijing: North China Electric Power University, 2019.
[10] Verma D, Agarwal P K, Jain P. Congestion management in transmission system using PST[C]// 2021 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 2021: 1-5.
[11] 杨永前, 崔勇, 杨增辉, 等. 双芯对称离散型可控移相器的数学建模[J]. 陕西电力, 2014, 42(11): 61-67.
Yang Yongqian, Cui Yong, Yang Zenghui, et al. Modeling of two-core symmetrical discrete thyristor controlled phase shifting transformer[J]. Shaanxi Electric Power, 2014, 42(11): 61-67.
[12] 申旭辉, 印永华, 卜广全, 等. 双输出移相器的建模研究[J]. 电网技术, 2012, 36(5): 215-218.
Shen Xuhui, Yin Yonghua, Bu Guangquan, et al. Research on modeling of dual output phase-shifting transformers[J]. Power System Technology, 2012, 36(5): 215-218.
[13] 李金玉, 陈杰, 龚春英, 等. 一种提高级联H桥逆变器功率不平衡运行能力的控制策略[J]. 电工技术学报, 2023, 38(10): 2731-2743.
Li Jinyu, Chen Jie, Gong Chunying, et al. A control strategy to improve working ability of cascaded H-bridge inverter under power imbalance[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2731-2743.
[14] 王要强, 李娜, 赵朝阳, 等. 一种新型多电平逆变器及其模块化分析[J]. 电工技术学报, 2022, 37(18): 4676-4687.
Wang Yaoqiang, Li Na, Zhao Chaoyang, et al. A novel multilevel inverter and its modularization analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4676-4687.
[15] 潘子迅, 杨晓峰, 赵锐, 等. 不平衡电网下模块化多电平换流器的直流环流均衡策略[J]. 电工技术学报, 2024, 39(2): 541-553.
Pan Zixun, Yang Xiaofeng, Zhao Rui, et al. DC circulating equalization strategy of modular multilevel converter under unbalanced power grid[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 541-553.
[16] 张建坡, 赵成勇. 模块化多电平换流器环流及抑制策略研究[J]. 电工技术学报, 2013, 28(10): 328-336.
Zhang Jianpo, Zhao Chengyong. Research on circulation current and suppressing strategy of modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 328-336.
[17] 杨用春, 唐健雄, 牛超群, 等. 基于移相变压器的灵活合环控制装置及控制策略研究[J]. 华北电力大学学报(自然科学版), 2022, 49(1): 48-57.
Yang Yongchun, Tang Jianxiong, Niu Chaoqun, et al. Research on flexible loop-closing control device and control strategy based on phase shifting transformer[J]. Journal of North China Electric Power University (Natural Science Edition), 2022, 49(1): 48-57.
[18] 郭家鹏, 郝正航, 陈卓, 等. 对称双芯移相变压器阻抗计算及仿真建模研究[J]. 高压电器, 2022, 58(4): 80-86.
Guo Jiapeng, Hao Zhenghang, Chen Zhuo, et al. Research on impedance calculation and simulation modeling of symmetrical dual-core phase-shifting transformer[J]. High Voltage Electrical Apparatus, 2022, 58(4): 80-86.
[19] 徐榕. H桥级联STATCOM非线性控制策略及系统实现技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
Xu Rong. Research on H-bridge cascade STATCOM nonlinear control strategy and system implementation technology[D]. Harbin: Harbin Institute of Technology, 2016.
[20] 董靓媛, 李晓军, 戎士洋, 等. 双芯对称型移相变压器应用场景分析[J]. 河北电力技术, 2022, 41(5): 20-24.
Dong Jingyuan, Li Xiaojun, Rong Shiyang, et al. Application scenario analysis of dual-core symmetrical phase-shifting transformers[J]. Hebei Electric Power, 2022, 41(5): 20-24.
[21] 高飞, 刘欣, 王利桐, 等. 对称双芯移相变压器有载分接开关最大级电压计算方法研究[J]. 中国电机工程学报, 2017, 37(7): 2110-2120.
Gao Fei, Liu Xin, Wang Litong, et al. Study on the maximum step voltage calculation method of on-load tap changer in symmetrical two-core phase shifting transformer[J]. Proceedings of the CSEE, 2017, 37(7): 2110-2120.
[22] 司马文霞, 王大森, 杨鸣, 等. 适配变压器全挡位切换暂态分析的有载分接开关电路模型构建[J].高电压技术, 2024, 50(2): 472-488.
Sima Wenxia, Wang Dasen, Yang Ming, et al. Model construction of on-load tap-changer circuit for transient analysis of full-gear switching of transformer[J]. High Voltage Technology, 2024, 50(2): 472-488.
[23] 司马文霞, 刘蕙, 厉璇, 等. 换流变压器真空有载分接开关切换过程电气应力解析方法[J]. 中国电机工程学报, 2022, 42(18): 6908-6919.
Sima Wenxia, Liu Hui, Li Xuan, et al. Analysis method of electrical stresses during switching process of vacuum on-load tap-changer in converter transformers[J]. Proceedings of the CSEE, 2022, 42(18): 6908-6919.
[24] 雷园园, 赵林杰, 彭在兴, 等. 换流变压器有载分接开关切换过程仿真及选型技术[J]. 南方电网技术, 2018, 12(7): 14-19.
Lei Yuanyuan, Zhao Linjie, Peng Zaixing, et al. Switching process simulation and type-selection technology of on-load tap changer of converter transformer[J]. Southern Power System Technology, 2018, 12(7): 14-19.
[25] 王金丽, 马钊, 潘旭, 等. 配电变压器有载调压技术[J]. 中国电力, 2018, 51(5): 75-79, 100.
Wang Jinli, Ma Zhao, Pan Xu, et al. On-load tap-changing technology of distribution transformer[J]. Electric Power, 2018, 51(5): 75-79, 100.
[26] 张伟, 张志杰, 宋欣原, 等. 一种新型有载调压转换开关的研制[J]. 变压器, 2010, 47(9): 34-36, 54.
Zhang Wei, Zhang Zhijie, Song Xinyuan, et al. Development of new on-load tap-changer[J]. Transformer, 2010, 47(9): 34-36, 54.
[27] 高伟娟. 级联式H桥多电平STATCOM的控制策略研究[D]. 哈尔滨: 哈尔滨理工大学, 2019.
GaoWeijuan. Research on control strategy of cascaded H-bridge multilevel STATCOM[D]. Harbin: Harbin University of Science and Technology, 2019.
[28] 徐高祥. 级联H桥变换器直流电压二倍频波动抑制策略研究[D]. 徐州: 中国矿业大学, 2022.
Xu Gaoxiang. Research on suppression strategy of DC voltage doubled frequency fluctuation of cascaded H-bridge converter[D]. Xuzhou: China University of Mining and Technology, 2022.
[29] 孙大伟, 刘振兴. 基于CPS-SPWM策略控制的级联H桥逆变器研究[J]. 东北电力技术, 2022, 43(12): 9-14.
Sun Dawei, Liu Zhenxing. Research on cascaded H-bridge inverter based on CPS-SPWM strategy control[J]. Northeast Electric Power Technology, 2022, 43(12): 9-14.
[30] 许胜, 赵剑锋. 基于不对称规则采样法的级联H桥型变流器CPS-SPWM输出电压谐波特性分析[J]. 电工技术学报, 2011, 26(6): 121-128.
Xu Sheng, Zhao Jianfeng. Analysis of the harmonic characteristics of the CPS-SPWM output voltage of cascaded H-bridge converters based on irregular sampling[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 121-128.
Abstract With the rapid development and large-scale application of new energy power generation technology, the rapid development of renewable energy (such as wind energy, solar energy) and large-scale grid connection, the capacity of new energy power generation has grown rapidly, but the capacity of new energy transmission to the power grid is limited by the structural characteristics of the power grid itself and the thermal stability limit of the transmission line, which hinders the transmission capacity. In order to solve this problem, this paper proposes a hybrid power flow controller (HPFC) for flexible and accurate regulation of power flow, balancing the power flow distribution of power grid lines, and improving the cross-section transportation capacity. HPFC is a combination of the more common passive phase-shifting transformer (PST) and the active cascaded H-bridge converter (CHBC) power electronics, which connects the CHBC in series on the low-voltage side of the excitation transformer part of the PST, combining the advantages of large power flow capacity of PST regulation and high sensitivity of CHBC, so as to achieve accurate, fast and large-capacity regulation of power flow. In order to improve the efficiency of the solution, an iterative algorithm based on Sinh is proposed to solve the problem with variable step size, which greatly saves the simulation time. Secondly, the process of on-load voltage regulation of PST is analyzed in detail, the simulation model is established, the analytical formula of the output voltage in the process of PST switching is derived, and the theoretical results are compared with the simulation results, which verifies the accuracy of the theory and provides a theoretical basis for the subsequent transient stress cooperative control (TSCC). Thirdly, aiming at the difference between the regulation area and speed of active CHBC and passive PST, a flexible collaborative control strategy for power flow was proposed, which realized the cooperative control of transient stress, reduced the power flow impact on the power grid and the stress concentration of the converter valve in the process of HPFC regulation, realized the smooth regulation of power flow, ensured the stability of the power grid, and effectively protected the device to improve the ability of HPFC to withstand overvoltage and overcurrent. Finally, the simulation model of HPFC power flow control is built in PSCAD/EMTDC simulation software, and the simulation results verify the ability of PST and CHBC to change the power flow and the effectiveness of the flexible collaborative control strategy of power flow, which can ensure the safety and reliability of the device while regulating the power flow.
keywords:Hybrid power flow controller, phase shift transformer, cascade H-bridge converter, equivalent impedance, collaborative control
中图分类号:TM571
DOI: 10.19595/j.cnki.1000-6753.tces.231653
国家电网公司总部科技项目资助(5500-202213121A-1-1-ZN)。
收稿日期 2023-10-08
改稿日期 2023-11-20
杨用春 男,1982年生,博士,讲师,研究方向为柔性交流输电技术、交直流电力变换及电能质量分析与控制。E-mail:yongchunyang@126.com.
杜翔宇 男,2000年生,硕士研究生,研究方向为混合潮流控制器。E-mail:xiangyudu218@163.com(通信作者)
(编辑 赫 蕾)