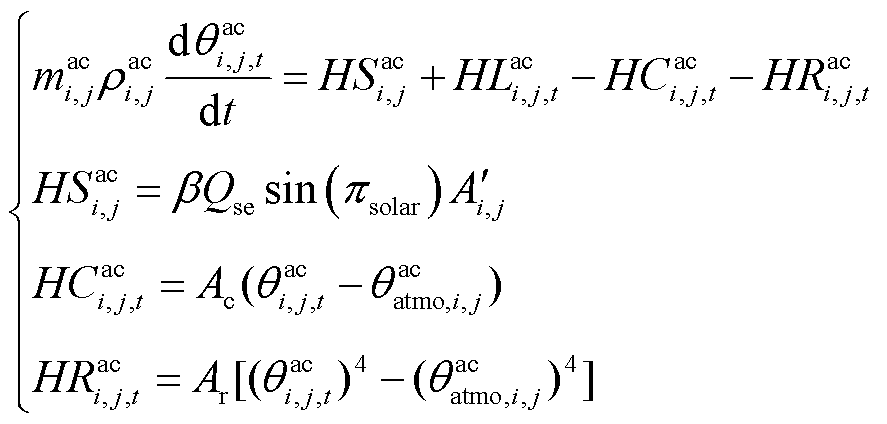 (1)
(1)
摘要 为了充分发挥交直流线路耐热特性、提高系统在不确定运行环境下应对故障的调控能力,以含柔性直流输电技术(VSC-HVDC)的交直流系统为研究对象,提出一种考虑线路动态电热特性的分布鲁棒潮流优化策略。首先,根据热传导理论分别建立交流架空线路、直流电缆线路的动态电热模型,而后在校正控制中引入交、直流输电线路短期最高允许温度(SAOT)约束及校正期间最大热积累量来代替长期允许温度(LAOT)作为在校正期间的暂时安全约束,以达到充分利用线路的短期过载/耐热特性的目的;其次,将故障后的校正过程划分成两个子校正过程,通过最大化储能及VSC-HVDC的快速校正能力,弥补常规调控装置难以快速响应指令的缺陷,进一步,在基于Kullback-Leibler(KL)散度所构建的风荷概率分布模糊集上,通过在考虑风荷最恶劣概率分布的情况下进行潮流优化,改善了传统鲁棒优化方法过于保守的问题;再次,在列和约束生成(C&CG)算法和Multi-cut Benders分解算法的基础上,提出一种融合物理知识的双循环分解算法,不仅能避免对非过载线路热平衡方程的线性化,同时还能避免多场景多故障协同求解;最后,在基于改进的IEEE 39测试系统中对所提模型及算法的有效性进行了验证。
关键词:柔性直流输电(VSC-HVDC) 分布鲁棒 线路短时耐热特性 动态电热模型 潮流优化
现阶段安全校正方法大多考虑的是切负荷及调整机组输出功率等常规控制手段[1]。然而,由于常规机组爬坡约束及响应间隙的限制,使得机组难以快速响应校正指令,这会加重故障后果,且易造成故障扩散[2-3]。故依据传统安全校正优化模型所获的校正指令会丧失一定的安全性。为了解决上述问题,文献[4-5]指出系统所处运行状态应当能够保证事故发生后的安全性,即便是在常规校正手段动作之前。但由于事先就保证了事故发生后系统的安全性,而故障并非一定会发生,所以会降低系统运行经济性。而在含柔性直流输电技术(Voltage Source Converter High Voltage Direct Current, VSC-HVDC)的交直流混合系统中,由于核心器件通常为全控型器件,不仅能避免换相失败,还能实现有功与无功的独立控制;故当电网发生故障时,决策者能够利用VSC-HVDC向故障区域提供紧急功率支撑,从而改善系统整体运行状态[6-7]。文献[3, 8]提出运用VSC-HVDC来消除N-1故障后电网过载问题。与此同时,储能同样是一种灵活性资源,尤其是以电化学为代表的储能装置,可通过所配置的电力电子接口实现与电网间的双向互动,为此亦能在故障发生后为电网提供快速调节能力和频率支撑能力[9-11]。文献[11]针对交直流混合微电网,提出考虑储能校正能力的安全约束最优潮流;文献[12]协同利用VSC-HVDC与储能装置来维持事故发生后系统的安全性。虽然上述文献发挥了VSC-HVDC及储能装置的校正能力,但并未将机组爬坡约束及响应间隙的限制纳入其中,使得所获结果丧失了一定的安全性。
与此同时,文献[13]指出不确定运行环境会加重故障带来的负面影响。因此,还需将不确定量所带来的负面影响纳入考虑范畴。当前,对于不确定量的处理,主要包含随机优化[14]、鲁棒优化[15]及分布鲁棒优化[16]等方法。前者依赖不确定参数的精准概率分布信息,所获分布信息越真实,所得结果越准确,但在实际中很难获取不确定参数的真实概率分布。由于中间者仅关注最差运行场景,忽略了不确定参数的分布信息,且最差运行场景并不一定会发生,因此中间者具有较大的保守性。而后者结合随机优化和鲁棒优化的优点,通过构建概率分布模糊集优化得到最坏的概率分布,故该方法能够在不依赖不确定量的精确分布的前提下具备鲁棒性[17]。文献[18]利用混合Copula函数及Kullback-Leibler(KL)散度建立风电概率分布模糊集,并在所构建的概率分布模糊集上提出交直流低碳分布鲁棒优化模型。文献[19]提出考虑分布式电源无功支撑和开关重构的无功优化分布鲁棒模型,通过综合范数来构建风光出力概率分布的不确定性。文献[20]提出基于Wasserstain距离的电-耦合系统分布鲁棒优化模型,同时结合机会约束限制含不确定变量的不等式约束成立的概率。
此外,对于线路潮流的限制通常采用静态传输容量;而静态传输容量通常都是在给定的环境下指定的,因此具有一定的保守性[21]。为了充分考虑线路所处的运行环境,文献[22]提出考虑线路动态容量的安全约束机组组合模型,通过线路动态容量机制挖掘线路传输能力。根据线路热平衡方程,线路温度变化滞后于线路传输功率变化。由于在故障前线路温度不会超过其长期允许最高温度,同时温度的变化是非瞬变过程,故在故障发生后的短期内线路传输功率可以等于或者超过其静态传输容量,这使得其传输能力得到短暂的提升[22]。基于此,文献[23-24]提出一种考虑输电元件电热耦合效应的安全约束最优潮流模型,该模型能够保证故障后的校正控制时间在设定值之内,同时能够避免校正控制期间线路出现过温的情况。但上述文献大多数考虑的是线路长时间运行允许最高温度的限制。
进一步,文献[25]指出,对于因过载而出现故障的线路,其发生故障的根本原因是承受了过高的温度或者处于非正常温度的时间过长。同时,文献[26-27]提出,线路可以在长期允许最高温度和短期允许最高温度之间运行一段时间,而这并不会影响线路的机械强度与寿命。因此,文献[27-28]提出利用线路短期最高允许温度及最大热积累量来限制线路在校正期间的传输功率,最大限度地挖掘线路传输能力。虽然上述文献考虑了线路的耐热特性,但大多数仅考虑了交流线路的动态传输容量与耐热特性,而在交直流系统中,直流线路的动态传输容量与耐热特性亦可得到利用。
针对上述问题,本文面向含VSC-HVDC的交直流系统,提出一种考虑线路动态电热特性的分布鲁棒潮流优化策略。首先,根据热传导理论分别建立交流架空线路、直流电缆线路的动态电热模型,在校正控制中引入交、直流输电线路短期最高允许温度约束及校正期间最大热积累量来代替长期允许温度作为在校正期间的暂时安全约束,以达到充分利用交、直流输电线路的短期过载/耐热特性的目的;其次,将故障后的校正过程划分成两个子校正过程,实现传统常规慢速校正手段与快速校正手段(VSC-HVDC及储能装置)之间的协同利用,提高系统处理故障的能力,在KL散度的基础上构建了风荷概率分布模糊集,通过在最恶劣概率分布的情况下进行潮流优化的方式,改善传统鲁棒优化方法过于保守的问题;再次,考虑到只有线路潮流超过其静态热容量时,线路运行温度才有可能超过其长期运行最高温度的物理特性,同时考虑到离散场景间互不影响、各N-1故障间相互独立的模型特点,在列和约束生成(Column-and-Constraint Generation, C&CG)算法和Multi-cut Benders分解算法的基础上,提出一种融合物理知识的双循环分解算法。结果表明,所提算法不仅能够完全避免对非过载线路热平衡方程线性化而引入大量冗余约束和变量,同时还能避免多场景多故障协同求解造成优化问题规模过大的缺陷。
在交直流混合系统中,陆上交流电网输电线路通常是由裸导线采用架空方式装设,而海上直流电网通常是由电缆采用海底埋设方式进行装设[29]。因此,采用架空方式的交流线路动态电热模型不适用于采用海底埋设的直流线路,故有必要分开构建两者的动态电热模型。
根据文献[21],交流架空线路的动态电热模型可表示为
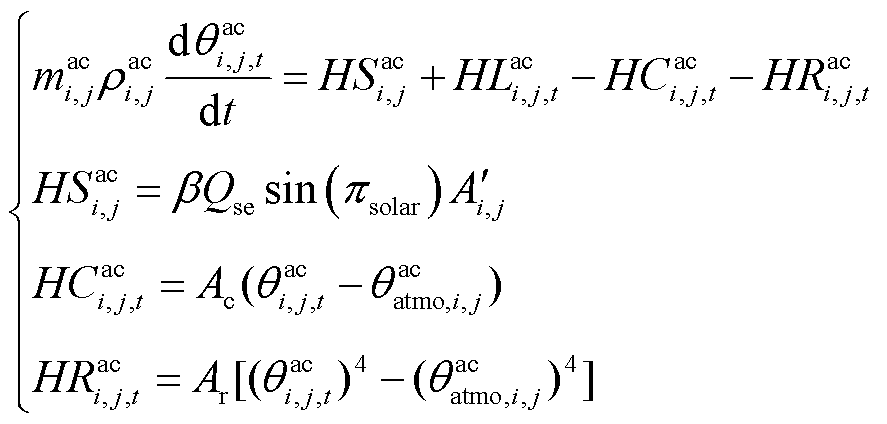 (1)
(1)
式中,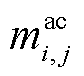 和
和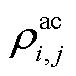 分别为交流线路ij的质量和比热容;
分别为交流线路ij的质量和比热容;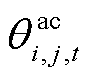 为交流线路ij在时刻t的导体温度;
为交流线路ij在时刻t的导体温度;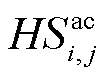 为交流线路ij由于太阳辐射所吸收的热量;
为交流线路ij由于太阳辐射所吸收的热量;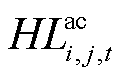 为交流线路ij在时刻t因自身电热效应所产生的热量;
为交流线路ij在时刻t因自身电热效应所产生的热量;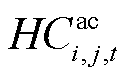 为交流线路ij在时刻t因空气对流所释放的热量;
为交流线路ij在时刻t因空气对流所释放的热量;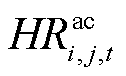 为交流线路ij在时刻t由于表面辐射所释放的热量;
为交流线路ij在时刻t由于表面辐射所释放的热量;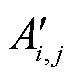 为交流线路ij的单位长度投影面积;
为交流线路ij的单位长度投影面积;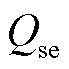 、
、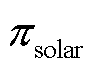 、
、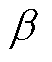 分别为太阳辐射率、辐射角及吸收效率;
分别为太阳辐射率、辐射角及吸收效率;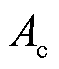 为空气表面传热系数;
为空气表面传热系数;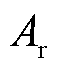 为表面辐射换热系数;
为表面辐射换热系数;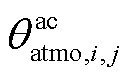 为线路所处的环境温度。
为线路所处的环境温度。
根据文献[30],直流电缆线路的动态电热模型可表示为
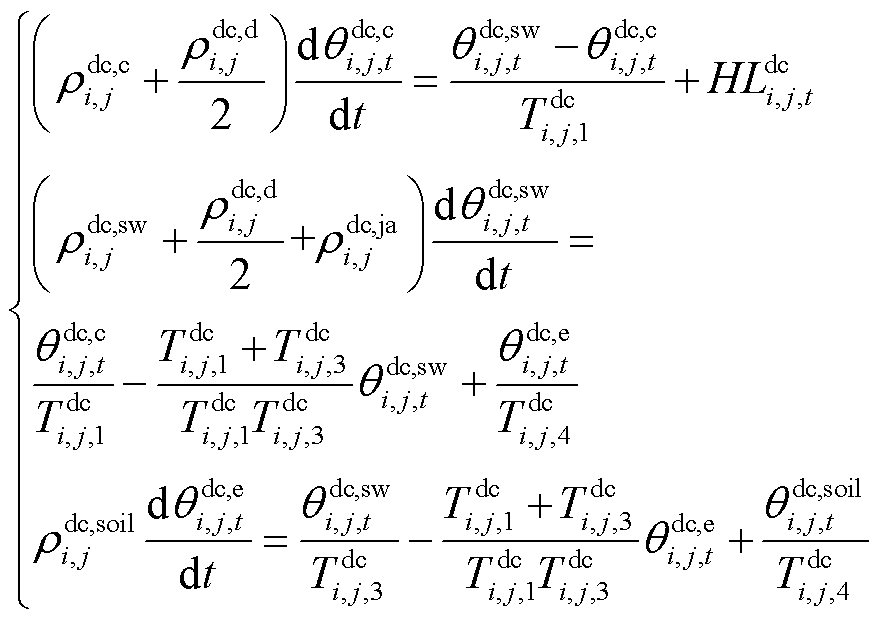 (2)
(2)
式中,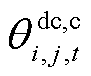 、
、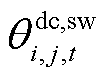 、
、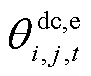 及
及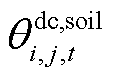 分别为直流线路ij在时刻t的导体温度、金属套温度、外护套温度及周围土壤温度;
分别为直流线路ij在时刻t的导体温度、金属套温度、外护套温度及周围土壤温度;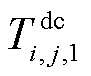 、
、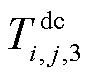 及
及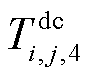 分别为直流线路ij的绝缘介质热阻、外护套热阻及土壤热阻;
分别为直流线路ij的绝缘介质热阻、外护套热阻及土壤热阻;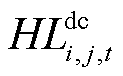 为直流线路ij在t时刻因自身电热效应所产生的热量;
为直流线路ij在t时刻因自身电热效应所产生的热量;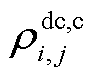 、
、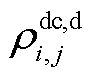 、
、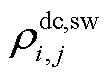 、
、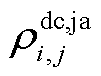 及
及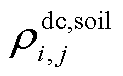 分别为直流线路ij的导体热容、绝缘介质热容、金属护套热容、外护套热容及土壤热容。
分别为直流线路ij的导体热容、绝缘介质热容、金属护套热容、外护套热容及土壤热容。
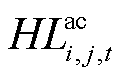 和
和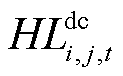 可表示为
可表示为
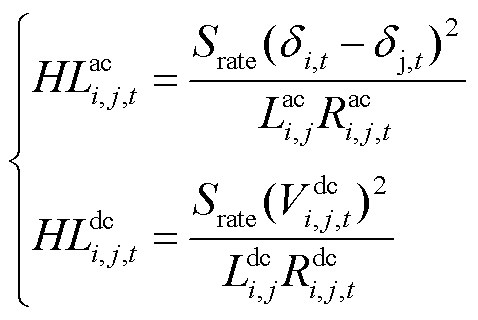 (3)
(3)
式中,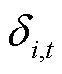 为交流节点i在时刻t的电压相角;
为交流节点i在时刻t的电压相角;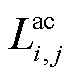 为交流线路ij的线路长度;
为交流线路ij的线路长度;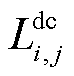 为直流线路ij的线路长度;
为直流线路ij的线路长度; 为功率基准值;
为功率基准值;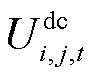 为直流线路ij在时刻t两端的电压差;
为直流线路ij在时刻t两端的电压差;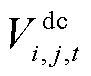 为在时刻t直流节点i和j之间的电压;
为在时刻t直流节点i和j之间的电压;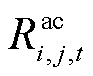 为交流线路ij在温度
为交流线路ij在温度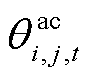 时的电阻,
时的电阻,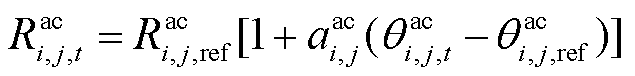 ,
,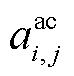 为电阻温度系数,
为电阻温度系数,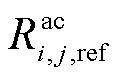 为交流线路ij在额定运行温度
为交流线路ij在额定运行温度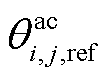 时的阻值。根据文献[22]可知,由于决策者更加倾向于发挥线路的电热特性,所以可将交流线路ij阻值固定成
时的阻值。根据文献[22]可知,由于决策者更加倾向于发挥线路的电热特性,所以可将交流线路ij阻值固定成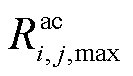 (恒等于线路温度处于长期运行最高温度
(恒等于线路温度处于长期运行最高温度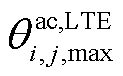 时的阻值)。同样,可将直流线路ij阻值固定成
时的阻值)。同样,可将直流线路ij阻值固定成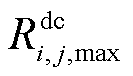 。此外,由于电抗基本上不受运行温度的影响,故在交流线路ij阻值固定成
。此外,由于电抗基本上不受运行温度的影响,故在交流线路ij阻值固定成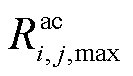 后,其电导和电抗分别为
后,其电导和电抗分别为
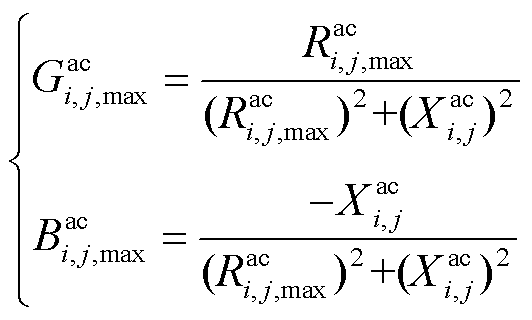 (4)
(4)
式中,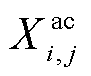 为交流子系统线路ij的电抗。
为交流子系统线路ij的电抗。
图1所示为典型含VSC-HVDC的交直流系统的结构示意图,主要由海上风电场、多端柔性直流系统、风电场侧VSC换流站(Wind farm-side VSC, WVSC)、电网侧VSC换流站(Grid-side VSC, GVSC)、交流系统及发电机组构成;同时,VSC换流站主要包括变压器、滤波器、电抗器及电压源型变流器[31]。
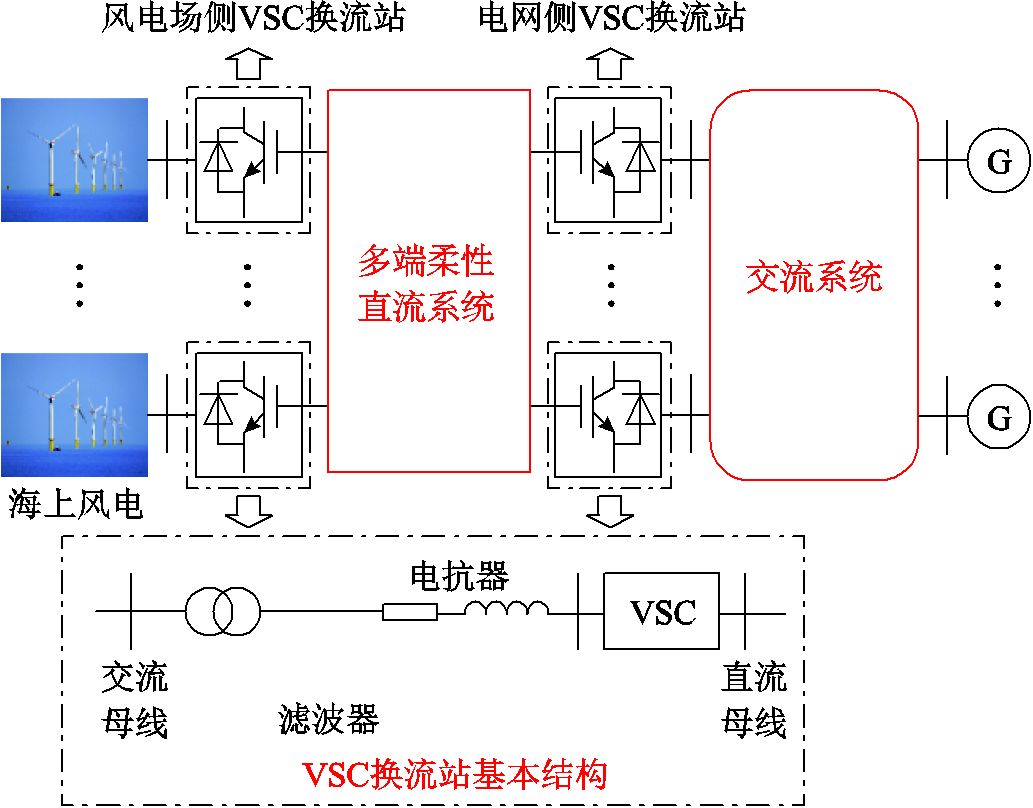
图1 基于VSC-HVDC的交直流系统结构示意图
Fig.1 Configuration of a hybrid AC/VSC-HVDC grids
图2为所提考虑线路动态电热特性的三层分布鲁棒潮流优化模型的整体框架图。最上层模型:在给定的风荷预测值的前提下,确定系统最优运行状态;同时,确保在故障发生后系统不仅能利用可控装置维持系统功率平衡,且能避免非故障元件再次故障。中间层模型:在给定的风荷不确定概率分布模糊集中,通过最大化校正成本,寻找风荷最恶劣场景概率分布。最下层模型:根据所确定的最优运行状态与最恶劣风荷概率分布,最小化安全校正成本。
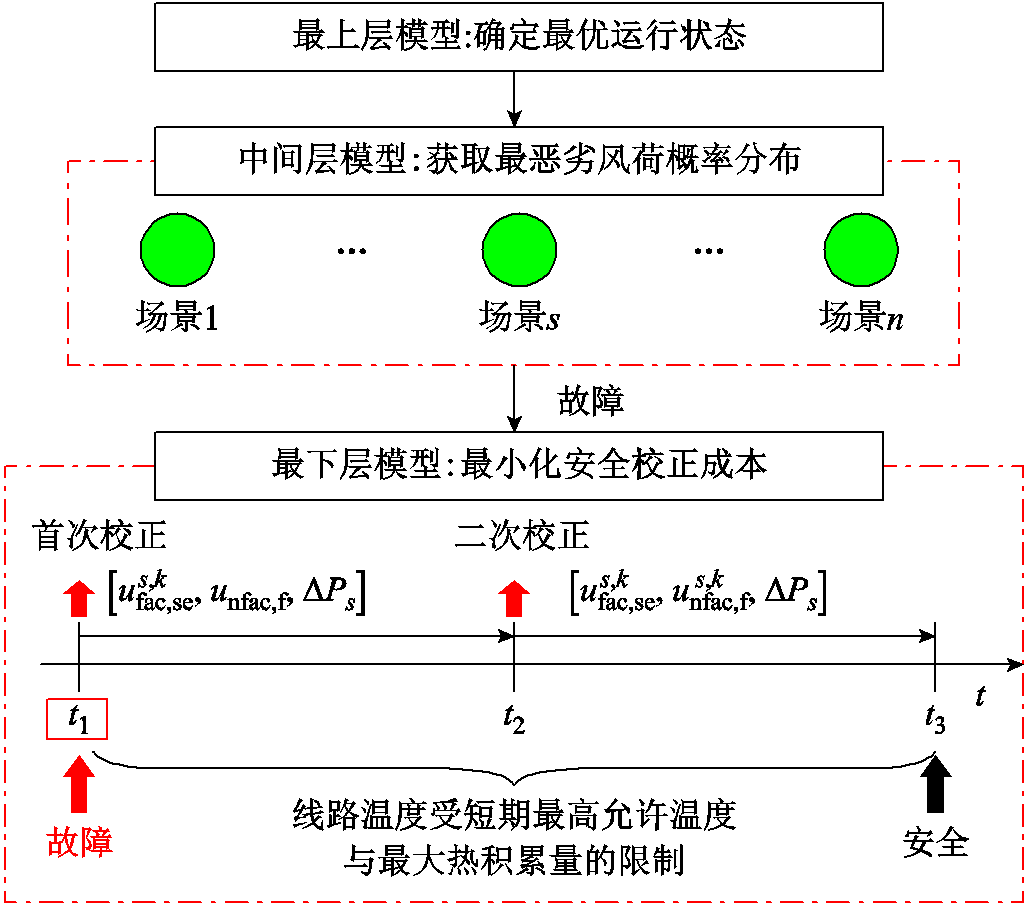
图2 所提分布鲁棒安全潮流优化策略的框架
Fig.2 Framework of the proposed distributionally robust security power flow optimization strategy
考虑到常规传统机组(如火电机组)具有较大的惯性,存在响应时间间隔(Dt=t2-t1),难以快速响应系统的调度指令,故可先利用系统中的快速调控装置(GVSC和储能)进行快速校正,避免其他非故障元件再次故障。故在文献[2]的基础上,将故障后的安全校正环节划分为首次校正与二次校正过程。
1)在首次校正过程(t1≤t<t2)中,通过利用快速调控装置确保系统暂时运行安全,避免非故障元件再次故障。故在此期间,常规传统机组维持故障前电压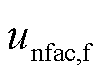 保持不变,而具有快速校正能力的GVSC和储能将转变成
保持不变,而具有快速校正能力的GVSC和储能将转变成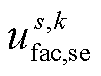 。同时,还需消除系统中的不平衡功率,维持系统功率平衡。
。同时,还需消除系统中的不平衡功率,维持系统功率平衡。
2)在二次校正过程(t2≤t<t3)中,常规调控装置可与快速响应装置GVSC进行综合调整,将系统重新调整至长期运行安全稳定点。故在此期间,常规传统机组将由维持故障前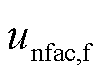 转变为
转变为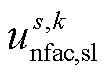 ,而系统中的快速调控装置GVSC将由首次校正后的
,而系统中的快速调控装置GVSC将由首次校正后的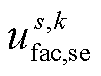 转变成
转变成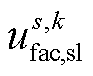 ;同时,仍需维持系统功率平衡。需要注意的是,本文中的二次校正过程不考虑储能装置,故储能装置的输出功率会逐渐下降到0[2]。
;同时,仍需维持系统功率平衡。需要注意的是,本文中的二次校正过程不考虑储能装置,故储能装置的输出功率会逐渐下降到0[2]。
需要说明的是:①包含“k”符号的变量说明此变量考虑了元件k的N-1故障;②包含“s”符号的变量说明此变量属于场景s;③包含“f”符号的变量说明此变量属于最上层子模型;④包含“se”或“sl”符号的变量说明此变量属于最下层子模型中故障发生后的首次校正或二次校正过程。
所提分布鲁棒潮流优化模型的目标函数为
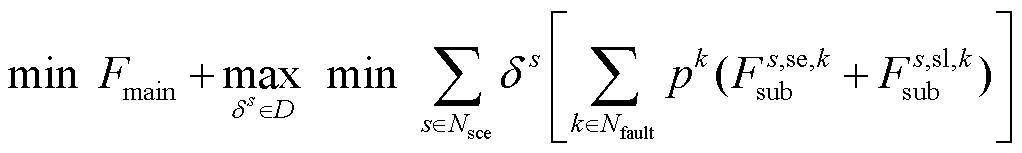 (5)
(5)
式中,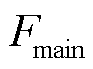 为机组成本;
为机组成本;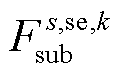 与
与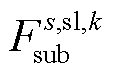 分别为系统在场景s中元件k故障后的短期或长期校正成本;
分别为系统在场景s中元件k故障后的短期或长期校正成本;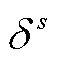 为场景s概率;
为场景s概率;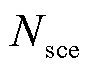 为场景集合;
为场景集合;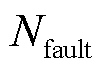 为故障集;
为故障集;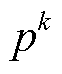 为元件k的强迫停运概率;D为概率分布模糊集。
为元件k的强迫停运概率;D为概率分布模糊集。
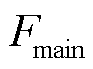 、
、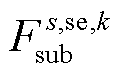 及
及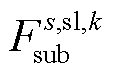 分别为
分别为
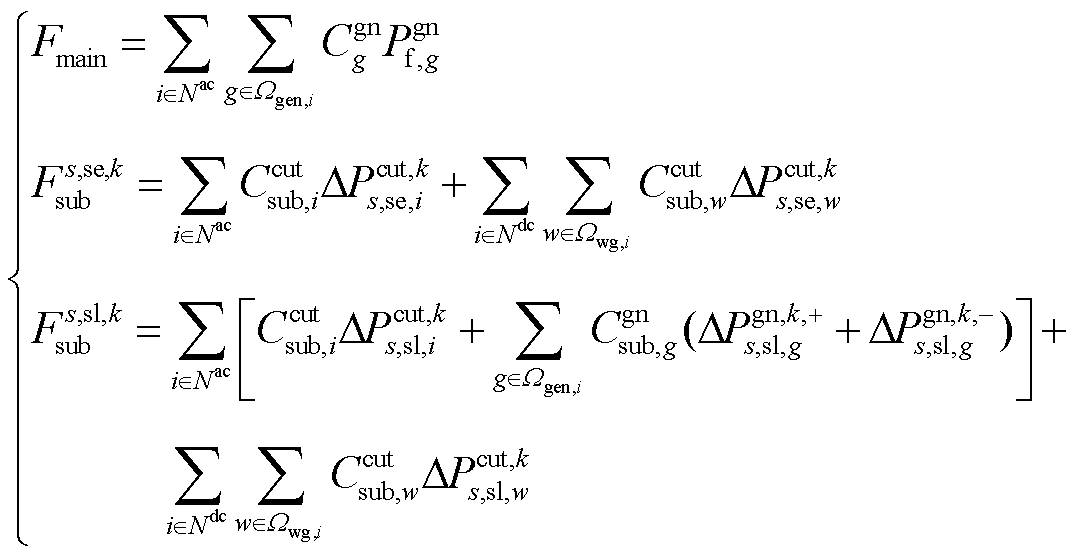 (6)
(6)
式中,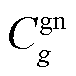 、
、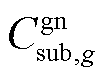 分别为机组g单位燃料成本、单位调用成本;
分别为机组g单位燃料成本、单位调用成本;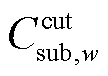 、
、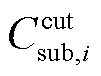 分别为风电场w单位弃风成本、节点i单位切负荷成本;
分别为风电场w单位弃风成本、节点i单位切负荷成本;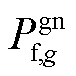 为机组g的有功功率;
为机组g的有功功率;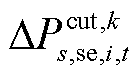 、
、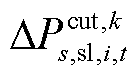 分别为节点i在场景s中元件k故障后的短期或长期校正阶段过程中的切负荷量;
分别为节点i在场景s中元件k故障后的短期或长期校正阶段过程中的切负荷量;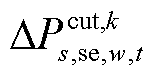 与
与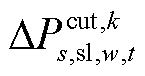 分别为风电场w在场景s中元件k故障后短期或长期校正阶段过程中的弃风量;
分别为风电场w在场景s中元件k故障后短期或长期校正阶段过程中的弃风量;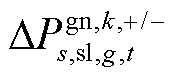 为机组g在场景s中元件k故障后长期校正过程中的上/下调功率;
为机组g在场景s中元件k故障后长期校正过程中的上/下调功率;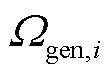 为与交流节点i连接的机组集合;
为与交流节点i连接的机组集合;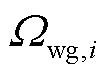 为与直流节点i连接的风电场集合;
为与直流节点i连接的风电场集合;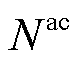 、
、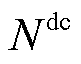 分别为交流子系统/直流子系统的节点集合。
分别为交流子系统/直流子系统的节点集合。
2.2.1 上层约束条件(最优运行状态)
上层min模型主要是确定事故发生前系统的最优运行状态,相关约束如下。
1)功率平衡约束
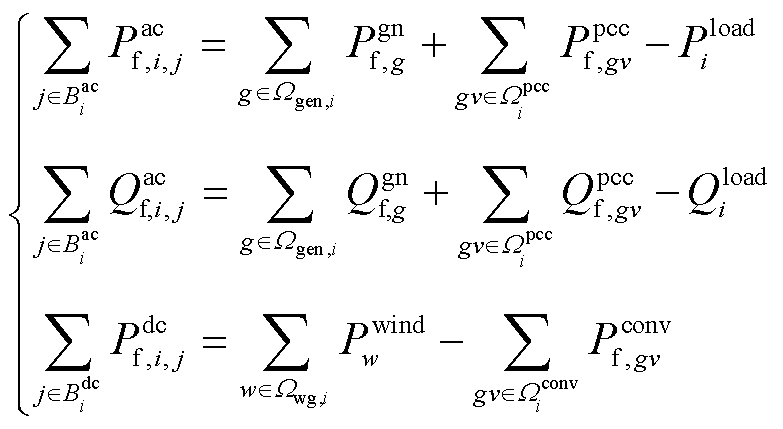 (7)
(7)
式中,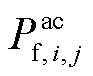 和
和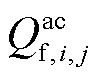 分别为交流线路ij传输的有功功率、无功功率;
分别为交流线路ij传输的有功功率、无功功率;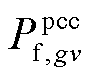 和
和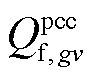 分别为第gv个VSC注入交流系统的有功功率、无功功率;
分别为第gv个VSC注入交流系统的有功功率、无功功率;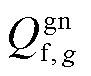 为机组g的无功功率;
为机组g的无功功率;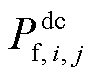 为直流线路ij传输的有功功率;
为直流线路ij传输的有功功率;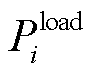 和
和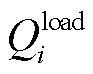 分别为节点i的有功功率、无功功率;
分别为节点i的有功功率、无功功率;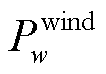 为风电场w注入到直流子系统的有功功率;
为风电场w注入到直流子系统的有功功率;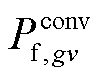 为第gv个VSC从直流系统吸收的有功功率;
为第gv个VSC从直流系统吸收的有功功率;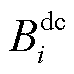 为与直流节点i连接的直流线路集合;
为与直流节点i连接的直流线路集合;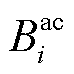 为与交流节点i连接的交流线路集合。
为与交流节点i连接的交流线路集合。
2)线路潮流方程[32-33]与长期运行约束[21]
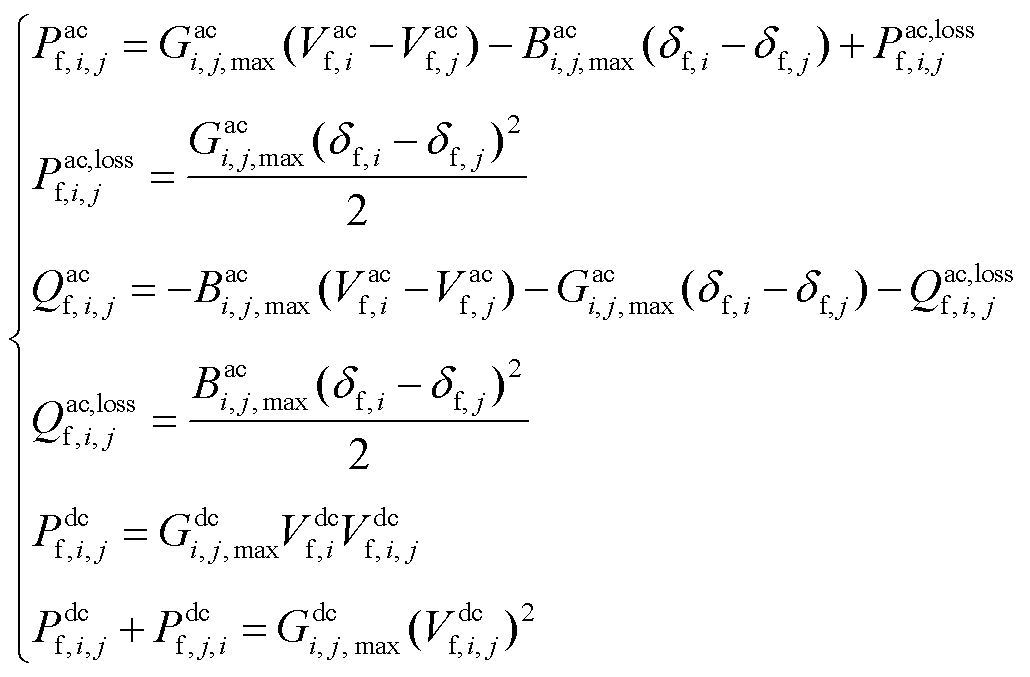 (8)
(8)
式中,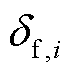 为交流节点i电压相角;
为交流节点i电压相角;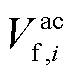 、
、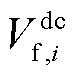 分别为在交流系统、直流系统中节点i的电压值。
分别为在交流系统、直流系统中节点i的电压值。
除了上述方程之外,线路动态电热模型式(1)~式(4)及式(9)也包含在内。在正常运行过程中,线路近似处于热平衡状态,故动态电热模型中温度对时间的导数可视为0,即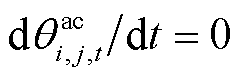 、
、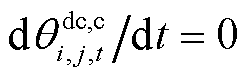 、
、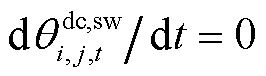 、
、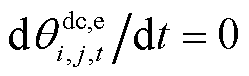 。同时,在正常运行过程中,线路导体温度不应超过其长期允许最高温度,故线路导体温度还需满足
。同时,在正常运行过程中,线路导体温度不应超过其长期允许最高温度,故线路导体温度还需满足
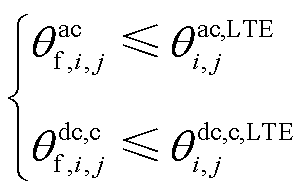 (9)
(9)
式中,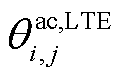 和
和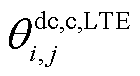 分别为交流线路ij和直流线路ij的长期允许最高温度。
分别为交流线路ij和直流线路ij的长期允许最高温度。
3)VSC传输功率约束和下垂控制方程[3,32]
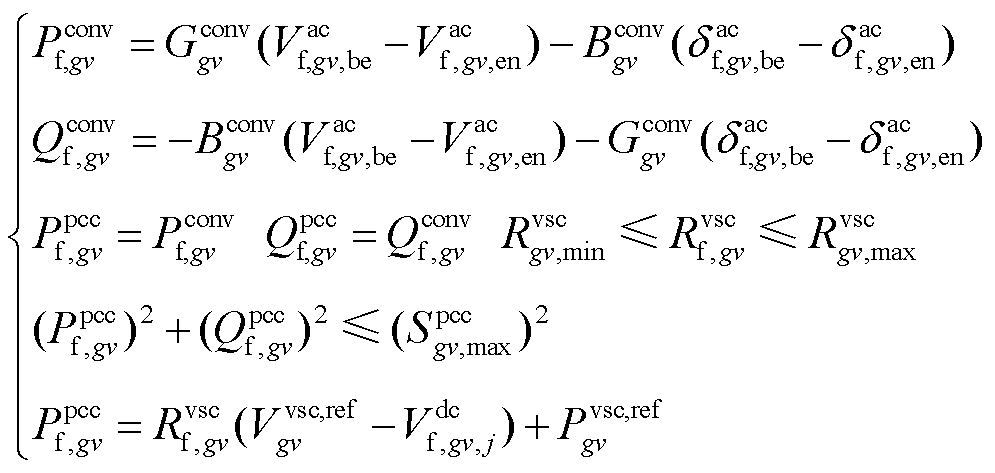 (10)
(10)
式中,换流站的电抗器和变压器已被等效为一条线路,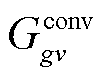 和
和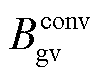 分别为第gv个VSC中等效线路的电导和电纳;
分别为第gv个VSC中等效线路的电导和电纳;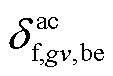 和
和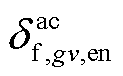 分别为第gv个VSC中等效线路的首端、末端电压相角;
分别为第gv个VSC中等效线路的首端、末端电压相角;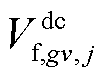 为与第gv个VSC相连的直流节点j的电压值;
为与第gv个VSC相连的直流节点j的电压值;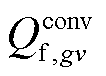 为第gv个VSC从直流系统吸收的无功功率;、
为第gv个VSC从直流系统吸收的无功功率;、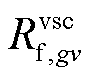 、
、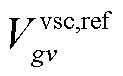 、
、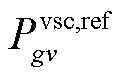 、
、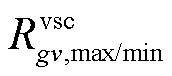 及
及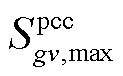 分别为第gv个VSC的下垂控制系数、参考电压、参考功率、下垂控制系数上/下限及最大视在功率。上述约束忽略了VSC功率损耗[34-35]。
分别为第gv个VSC的下垂控制系数、参考电压、参考功率、下垂控制系数上/下限及最大视在功率。上述约束忽略了VSC功率损耗[34-35]。
4)火电机组运行约束
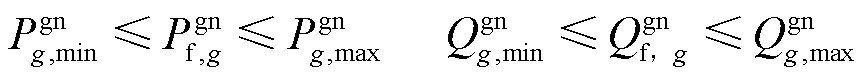 (11)
(11)
式中,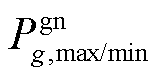 与
与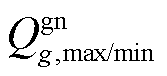 分别为机组g有功功率上/下限与无功功率上/下限。
分别为机组g有功功率上/下限与无功功率上/下限。
5)交直流系统电压约束
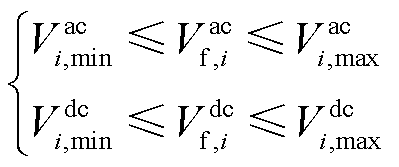 (12)
(12)
式中,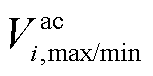 为交流节点i的电压上/下限;
为交流节点i的电压上/下限;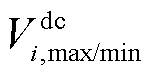 为直流节点i的电压上/下限。
为直流节点i的电压上/下限。
2.2.2 中间层约束条件(概率分布模糊集)
中间层max模型主要是在所构建的概率分布模糊集中寻找不确定量的最差概率分布。相对基于多离散场景、Wasserstain距离的概率密度型分布模糊集或者是基于确定距、不确定距的距信息型分布模糊集而言,基于KL散度所构建的概率密度型分布模糊集的可解性更高。因此,本文采用KL散度构建风荷不确定量的概率分布模糊集,可表述[17]为
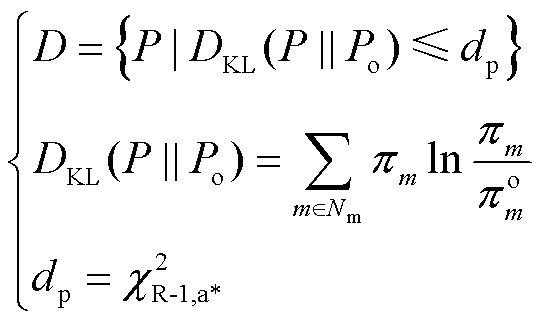 (13)
(13)
式中,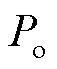 为参考分布;
为参考分布;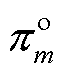 和
和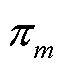 分别为第m个区间样本在参考分布
分别为第m个区间样本在参考分布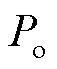 中或实际分布P中的离散概率;
中或实际分布P中的离散概率;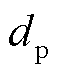 为距离容差,范围为[0,¥],反映决策者对参考分布的信赖程度;Nm为区间样本集合;
为距离容差,范围为[0,¥],反映决策者对参考分布的信赖程度;Nm为区间样本集合;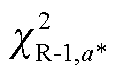 为卡布分布
为卡布分布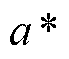 上分位数,保证实际分布以不小于
上分位数,保证实际分布以不小于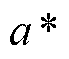 的概率被包含在模糊集D中。
的概率被包含在模糊集D中。
2.2.3 下层约束条件(多阶段安全校正)
下层min模型主要是在第一阶段所确定的最优状态下,当事故发生后,通过调整快速性和非快速性的调控装置维持系统正常运行。
在事故k发生后,先利用快速调控装置(GVSC和储能)进行快速校正,避免在常规校正动作前,系统中其他非故障元件再次故障。事故k发生后首次校正过程中的相关约束如下。
1)交直流系统功率平衡方程
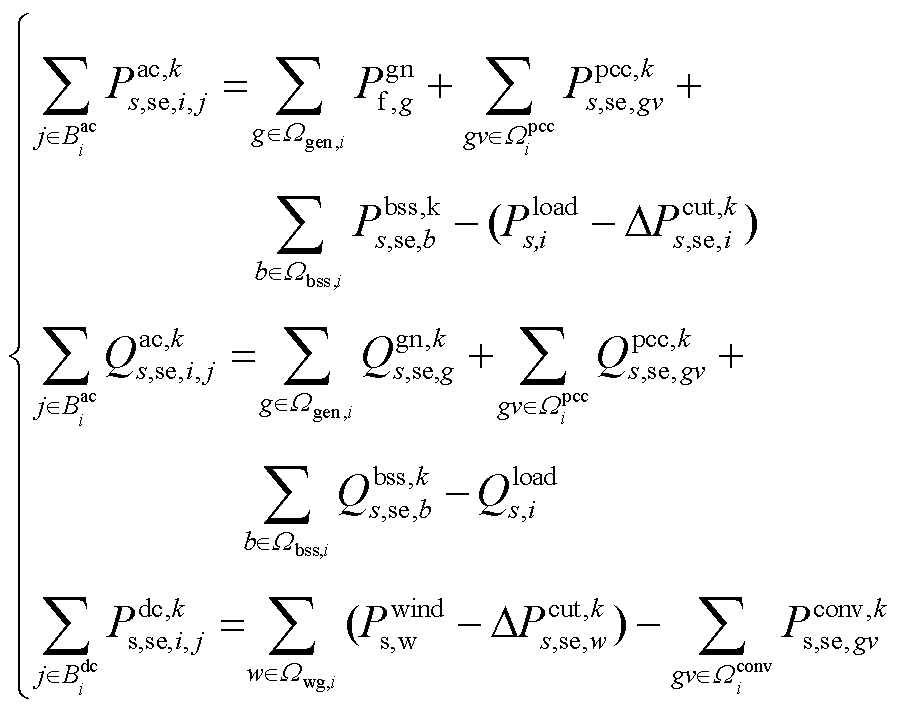 (14)
(14)
式中,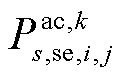 和
和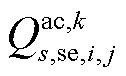 分别为交流线路ij在场景s中首次校正动作后传输的有功/无功功率;
分别为交流线路ij在场景s中首次校正动作后传输的有功/无功功率;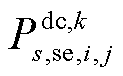 为在场景s中首次校正动作后直流子系统线路ij传输的有功功率;
为在场景s中首次校正动作后直流子系统线路ij传输的有功功率;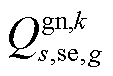 为机组g在场景s中首次校正动作后的输出无功功率;
为机组g在场景s中首次校正动作后的输出无功功率;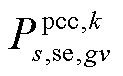 和
和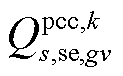 分别为在场景s中首次校正动作后第gv个VSC注入交流子系统的有功/无功功率;
分别为在场景s中首次校正动作后第gv个VSC注入交流子系统的有功/无功功率;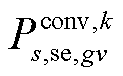 为在场景s中首次校正动作后第gv个VSC从直流子系统吸收的有功功率;
为在场景s中首次校正动作后第gv个VSC从直流子系统吸收的有功功率;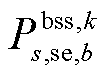 和
和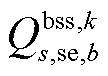 分别为在场景s中首次校正动作后储能装置b的注入交流子系统的有功、无功功率;
分别为在场景s中首次校正动作后储能装置b的注入交流子系统的有功、无功功率;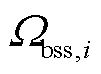 为交流子系统中与节点i相连的储能集合;
为交流子系统中与节点i相连的储能集合;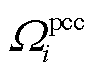 为与交流节点i连接的GVSC集合;
为与交流节点i连接的GVSC集合;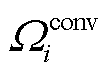 为与直流节点i连接的WVSC集合。
为与直流节点i连接的WVSC集合。
2)火电机组无功调整约束
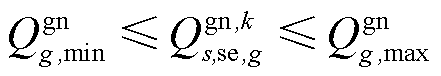 (15)
(15)
3)储能装置运行约束[13]
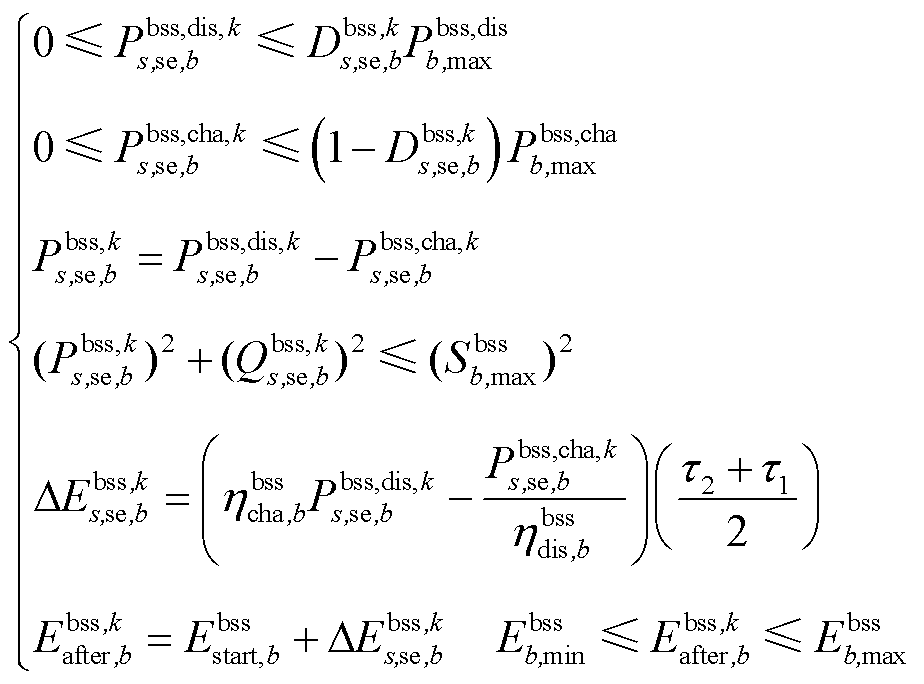 (16)
(16)
式中,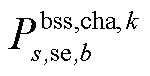 、
、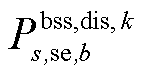 分别为储能装置b在场景s中首次校正中的充、放电功率;
分别为储能装置b在场景s中首次校正中的充、放电功率;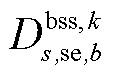 为充放电状态,0表示放电,1表示充电;
为充放电状态,0表示放电,1表示充电;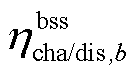 、
、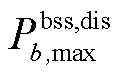 、
、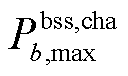 、
、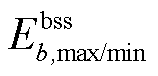 、
、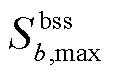 分别为储能装置b的充/放电效率、充/放电功率上限、能量水平上/下限、视在功率上限;
分别为储能装置b的充/放电效率、充/放电功率上限、能量水平上/下限、视在功率上限;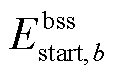 为储能装置b在故障发生前的起始能量水平。需注意的是,
为储能装置b在故障发生前的起始能量水平。需注意的是,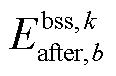 为储能装置b在场景s中故障校正(包括首次、二次校正)完成后的能量水平;此外,有关校正过程中的储能能量平衡方程的更多细节,可查阅文献[2]。
为储能装置b在场景s中故障校正(包括首次、二次校正)完成后的能量水平;此外,有关校正过程中的储能能量平衡方程的更多细节,可查阅文献[2]。
4)弃风约束和切负荷约束
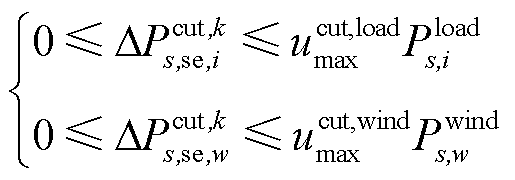 (17)
(17)
式中,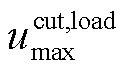 、
、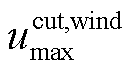 分别为最大切负荷、弃风比例。
分别为最大切负荷、弃风比例。
除上述约束式(14)~式(17)之外,首次校正过程中的相关约束还包括线路潮流方程、交直流系统电压约束及VSC传输功率约束与下垂控制方程,这些约束已在第一阶段中阐述,不再赘述。
常规调控装置经过响应时间后开始进入调整阶段,可以与快速响应装置进行综合调整。事故k发生后二次校正过程中的相关约束如下。
1)交直流系统功率平衡方程
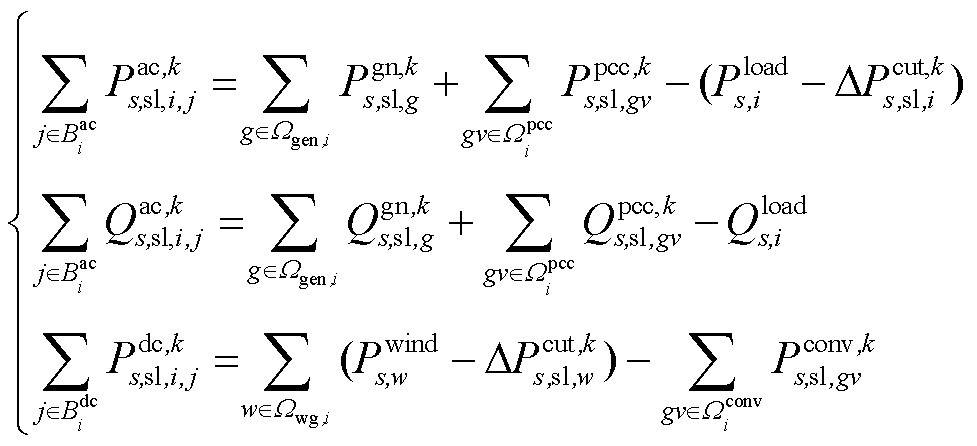 (18)
(18)
式中,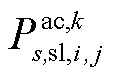 和
和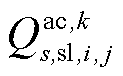 分别为交流线路ij在场景s中二次校正动作完成后传输的有功、无功功率;
分别为交流线路ij在场景s中二次校正动作完成后传输的有功、无功功率;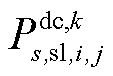 为在场景s中二次校正动作完成后直流子系统线路ij传输的有功功率;
为在场景s中二次校正动作完成后直流子系统线路ij传输的有功功率;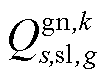 为机组g在场景s中二次校正动作完成后的无功输出功率;
为机组g在场景s中二次校正动作完成后的无功输出功率;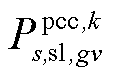 和
和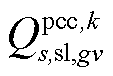 分别为在场景s中二次校正动作完成后第gv个VSC注入交流子系统的有功、无功功率;
分别为在场景s中二次校正动作完成后第gv个VSC注入交流子系统的有功、无功功率;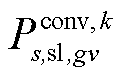 为在场景s中二次校正动作完成后第gv个VSC向直流子系统吸收的有功功率;
为在场景s中二次校正动作完成后第gv个VSC向直流子系统吸收的有功功率;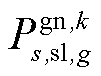 为机组g在场景s中完成爬坡过程后的最终有功输出功率。
为机组g在场景s中完成爬坡过程后的最终有功输出功率。
2)火电机组有功与无功调整约束
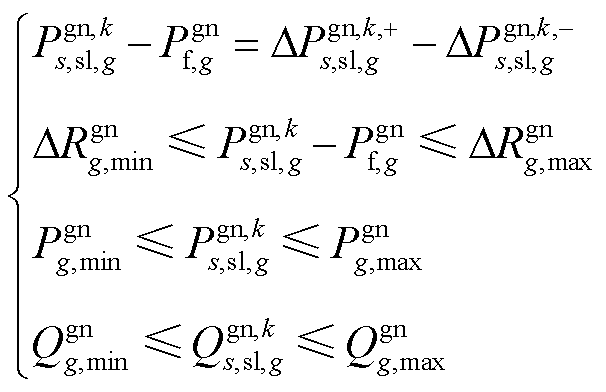 (19)
(19)
式中,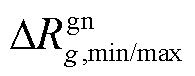 为机组g有功调整量的上/下限。
为机组g有功调整量的上/下限。
除上述约束式(18)、式(19)外,二次校正的相关约束还包括线路潮流方程、交直流系统电压约束、VSC传输功率约束与下垂控制方程,弃风与切负荷约束,而这些约束在前文中已阐述,故在此不再赘述。
进一步,为了挖掘交、直流线路的功率传输能力,通过引入线路的短期最高允许温度及校正期间最大热积累量约束来代替长期允许温度作为线路在校正期间的暂时安全约束,表示为
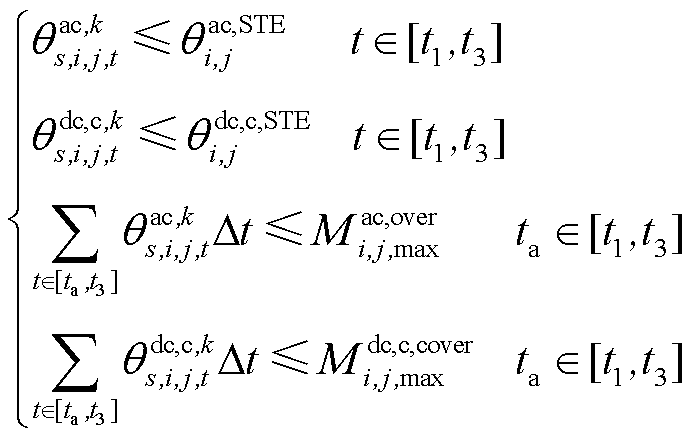 (20)
(20)
式中,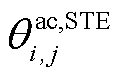 和
和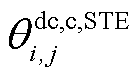 分别为交流线路ij和直流线路ij的短期最高温度;
分别为交流线路ij和直流线路ij的短期最高温度;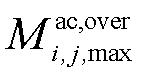 和
和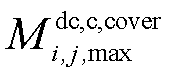 分别为交流线路ij和直流线路ij的最大热积累量;
分别为交流线路ij和直流线路ij的最大热积累量;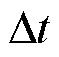 为时间步长。
为时间步长。
再者,还需确保校正完成后,线路的运行温度重新处于长期允许最高温度之内,故线路传输功率应当不超过其静态传输容量。所述约束为
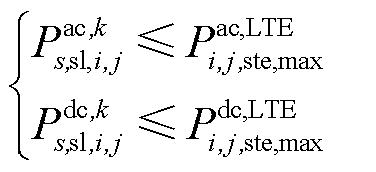 (21)
(21)
此外,根据文献[2, 31]可知,VSC和储能通常可以在几秒甚至几百毫秒内完成响应;而对于常规机组而言,由于爬坡约束的限制,其不能在短时间内完成响应。因此,在首次校正后,交流线路ij的有功损耗直接从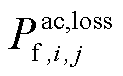 过渡到
过渡到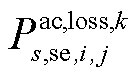 ,直流线路ij的有功损耗直接从
,直流线路ij的有功损耗直接从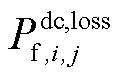 过渡到
过渡到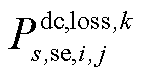 ;而在二次校正后,常规传统机组进入机组爬坡过程,交流线路ij的有功损耗需经过“爬坡过程”最终才能从
;而在二次校正后,常规传统机组进入机组爬坡过程,交流线路ij的有功损耗需经过“爬坡过程”最终才能从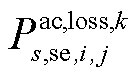 变化到
变化到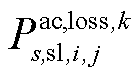 ,同样直流线路ij的有功损耗亦是如此。为了降低模型的复杂度,同时考虑有功损耗的变化过程,本文假定有功损耗的变化过程是一个线性增加或者线性递减的过程,故在常规传统机组进入机组爬坡过程中,单位长度的交、直流线路在
,同样直流线路ij的有功损耗亦是如此。为了降低模型的复杂度,同时考虑有功损耗的变化过程,本文假定有功损耗的变化过程是一个线性增加或者线性递减的过程,故在常规传统机组进入机组爬坡过程中,单位长度的交、直流线路在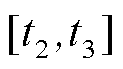 所产生的热量可表示为
所产生的热量可表示为
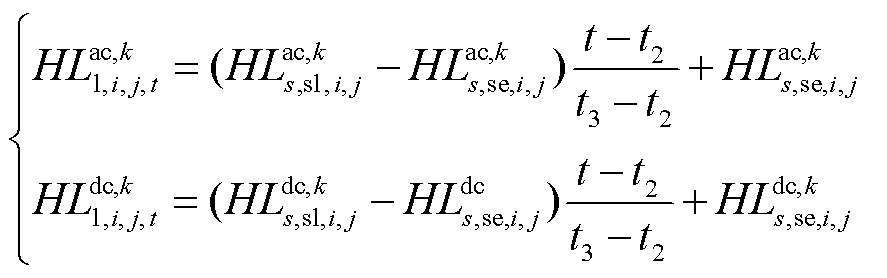 (22)
(22)
针对min-max-min三层模型,最常用的求解方法为C&CG算法[36-37]。但本文下层min模型是一个大规模多场景多阶段的校正问题,使得C&CG算法主问题的规模会随着迭代次数的递增而呈现极大的增长,严重影响模型的求解效率。而Multi-cut Benders分解算法对于包含多场景多阶段且各场景间、各阶段间均互不影响的单层模型是最为适合的[38]。考虑到只有传输功率超过其静态传输容量的线路在校正期间的最高温度才有可能超过其长期运行最高温度,故在校正过程中仅需考虑传输功率超过其静态传输容量的线路的暂时安全约束,而对其他非过载线路传输功率的限制依然沿用其静态传输容量,以避免对非过载线路热平衡方程的线性化,达到降低模型规模与提高求解速度的目的。为此,本文在C&CG算法与Multi-cut Benders分解算法的基础上,提出融合所述物理特性的双循环分解算法。
在运用融合所述物理特性的双循环分解算法之前,还需要利用相关的数学处理方法(包括梯形隐式积分法[22]、分段线性法[22]、McCormick松弛法[39]、六边形松弛法[40-41])对模型中的非线性项和非线性约束进行线性处理,将原问题近似转换成混合整数线性规划模型,该过程详见附录。为了清晰地说明求解过程,将线性化后的模型写成紧凑式,有
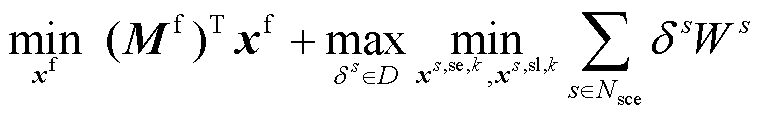 (23)
(23)
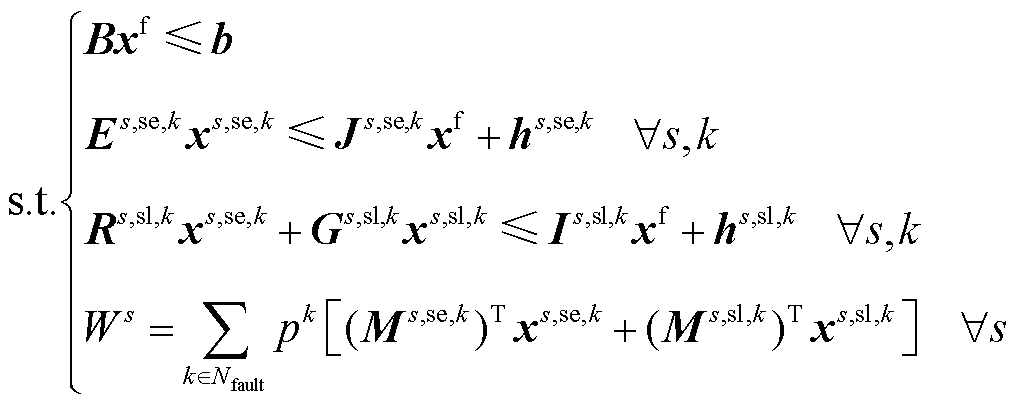 (24)
(24)
该紧凑式中的变量/参数相关说明见附录。
1)外循环主问题
每当中间层max模型寻找到一组更恶劣的概率分布,就需返回一组新的约束到外循环主问题中,故第i次外循环中的外循环主问题可表示为
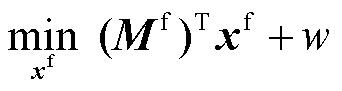 (25)
(25)
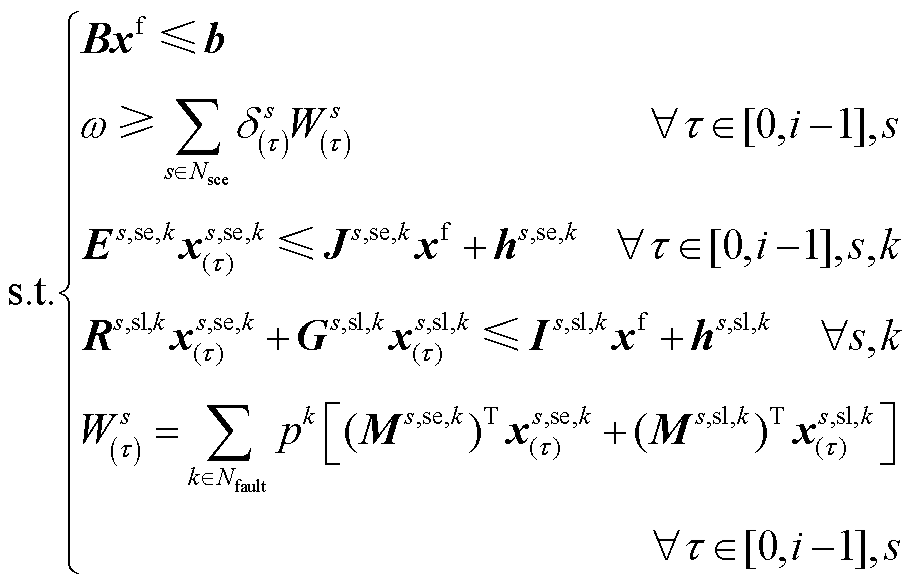 (26)
(26)
式中,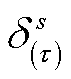 为第t 次所获得的更坏场景概率分布;
为第t 次所获得的更坏场景概率分布;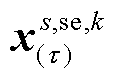 与
与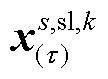 为新增优化变量;w为第二阶段目标值。
为新增优化变量;w为第二阶段目标值。
2)外循环子问题
外循环子问题由中间层max模型构成,在外循环主问题解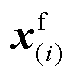 的前提下,通过求解中间层max模型,寻找更场景概率分布,其模型可表示为
的前提下,通过求解中间层max模型,寻找更场景概率分布,其模型可表示为
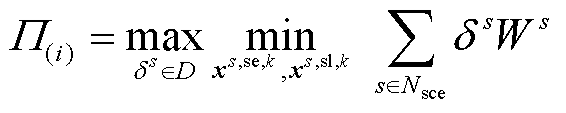 (27)
(27)
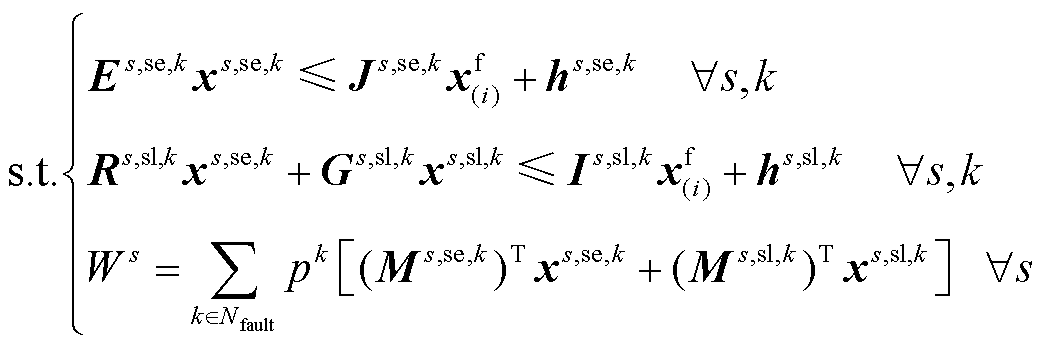 (28)
(28)
由于函数式(27)中包含双线性变量且约束中有整数变量,故该问题难以通过KKT条件转换成单层问题;考虑到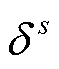 在下层模型中为常数,并不会影响min模型的可行域,故可解耦成以下两个独立步骤。
在下层模型中为常数,并不会影响min模型的可行域,故可解耦成以下两个独立步骤。
(1)并行求解Ns´Nk个混合整数线性模型
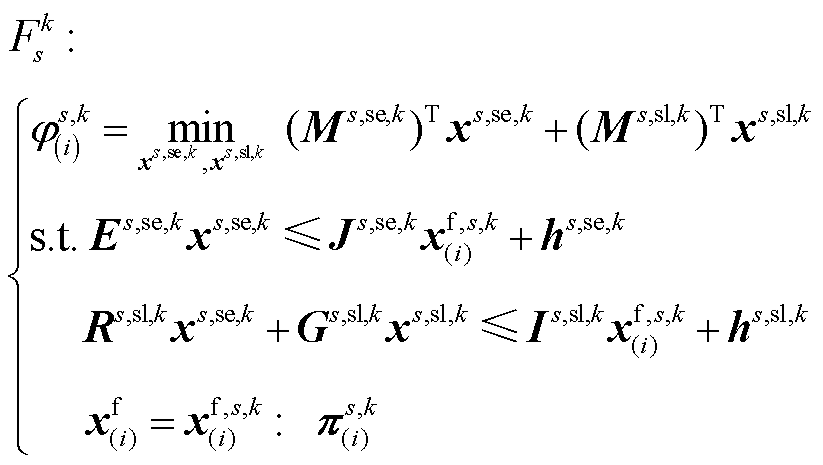 (29)
(29)
考虑到只有线路潮流超过其静态传输容量时,线路运行温度才有可能超过其长期运行最高温度,故在子问题中可只考虑传输功率大于静态传输容量的线路暂时安全约束,而对其他非过载线路的传输功率的限制依然沿用静态传输容量。为此,需在上述模型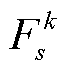 的基础上,重新构建该问题的辅助模型
的基础上,重新构建该问题的辅助模型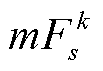 ,用以辨识故障后传输功率大于静态传输容量的线路。为了使得所辨识的线路集能完全包含所有传输功率大于静态传输容量的线路,故将模型
,用以辨识故障后传输功率大于静态传输容量的线路。为了使得所辨识的线路集能完全包含所有传输功率大于静态传输容量的线路,故将模型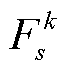 中所有调控手段去掉,最终形成模型
中所有调控手段去掉,最终形成模型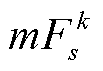 ,用以模拟最坏故障情形;而后再根据最坏情形,辨识需补充暂时安全约束的线路。
,用以模拟最坏故障情形;而后再根据最坏情形,辨识需补充暂时安全约束的线路。
在模型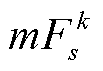 中,对所有线路的潮流采用静态传输容量进行限制,同时为了防止子问题的辅助模型出现无解的情况,引入非负辅助变量对原有静态传输容量进行松弛,松弛后的静态传输容量如式(30)所示。而后,将所添加的非负松弛变量之和构建成辅助模型的目标函数如式(31)所示。
中,对所有线路的潮流采用静态传输容量进行限制,同时为了防止子问题的辅助模型出现无解的情况,引入非负辅助变量对原有静态传输容量进行松弛,松弛后的静态传输容量如式(30)所示。而后,将所添加的非负松弛变量之和构建成辅助模型的目标函数如式(31)所示。
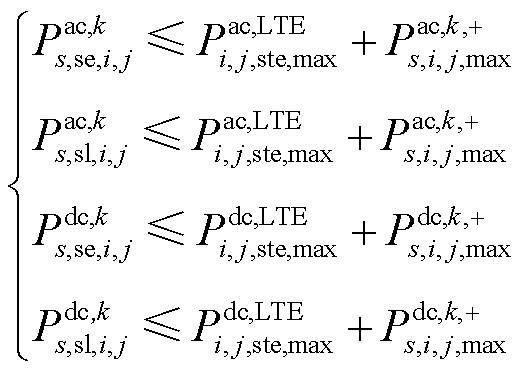 (30)
(30)
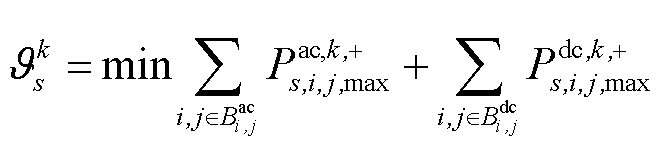 (31)
(31)
式中,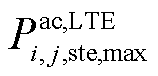 、
、 分别为交流、直流线路ij最大静态传输容量极限;
分别为交流、直流线路ij最大静态传输容量极限;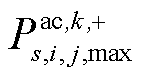 、
、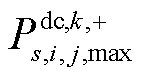 分别为交流、直流线路ij静态传输容量非负松弛变量。
分别为交流、直流线路ij静态传输容量非负松弛变量。
当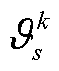 >0时,说明存在故障后传输功率大于静态传输容量的线路;反之,则不存在。当
>0时,说明存在故障后传输功率大于静态传输容量的线路;反之,则不存在。当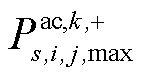 >0时,说明在场景s中元件k故障后交流线路ij潮流超过其静态传输容量;当
>0时,说明在场景s中元件k故障后交流线路ij潮流超过其静态传输容量;当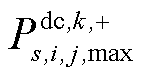 >0时,说明在场景s中元件k故障后直流线路ij潮流超过其静态传输容量。在辨识完过载线路后,再将这些线路的动态电热模型补充至原模型
>0时,说明在场景s中元件k故障后直流线路ij潮流超过其静态传输容量。在辨识完过载线路后,再将这些线路的动态电热模型补充至原模型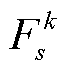 中,而模型
中,而模型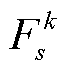 中其他线路的潮流限制沿用静态传输容量。
中其他线路的潮流限制沿用静态传输容量。
(2)将所获得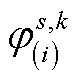 代入中间层max模型中,可得如下模型(标记为OS-max);而后通过求解模型OS-max,即可得到一组最坏场景概率分布
代入中间层max模型中,可得如下模型(标记为OS-max);而后通过求解模型OS-max,即可得到一组最坏场景概率分布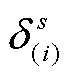 。
。
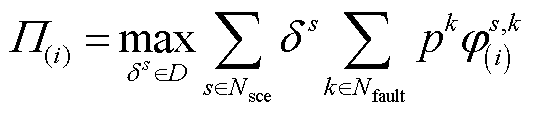 (32)
(32)
本文运用Multi-cut Benders分解算法求解外循环主问题,通过返回多割约束的方式降低外循环主问题规模。Multi-cut Benders分解算法同样需将外循环主问题分解成主问题与子问题,因此Multi-cut Benders分解算法将构成内循环分解算法。
1)内循环主问题
根据第i次迭代过程中外循环主问题,可分解得到第j次内循环主问题,其表达式为
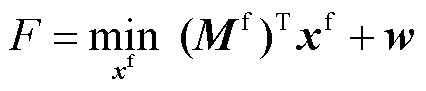 (33)
(33)
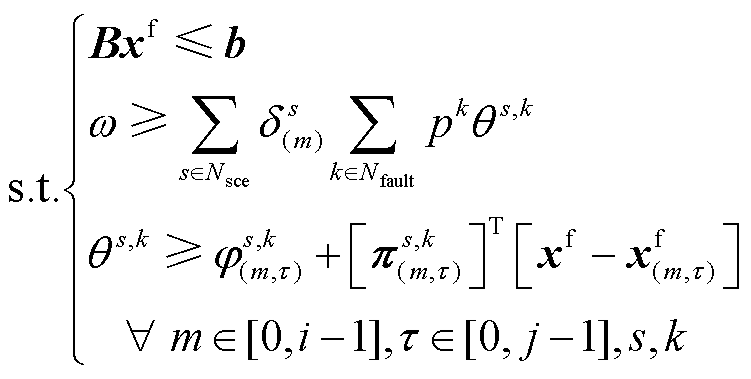 (34)
(34)
式中,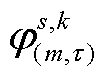 与
与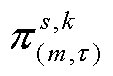 分别为第m次外循环中第t 次求解内循环子问题时所获的目标函数值与变量传递约束的拉格朗日乘子;
分别为第m次外循环中第t 次求解内循环子问题时所获的目标函数值与变量传递约束的拉格朗日乘子;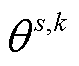 为中间辅助变量。
为中间辅助变量。
2)内循环子问题
根据第i次迭代过程中外循环主问题,可分解得到第j次内循环子问题,其表达式为
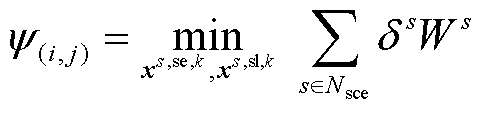 (35)
(35)
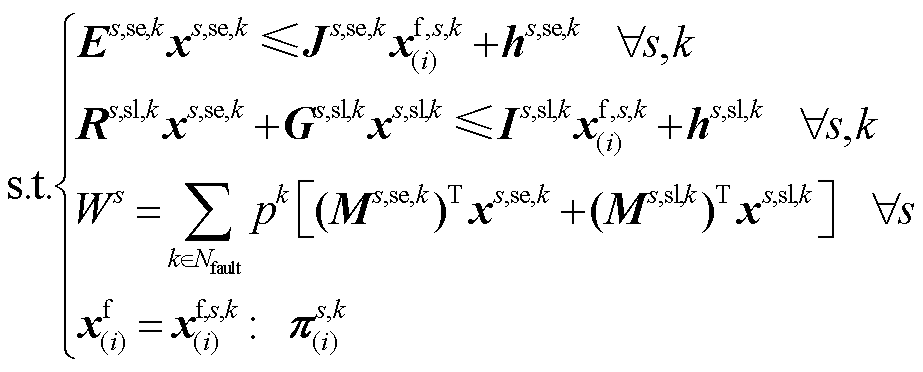 (36)
(36)
值得注意的是,在内循环子问题中,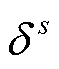 为常数。同样内循环子问题可分成两个独立步骤。步骤(1)与求解外循环子问题的步骤(1)相同,故不再赘述。此外,考虑到在本文中,内循环子问题包含整数变量,对偶变量
为常数。同样内循环子问题可分成两个独立步骤。步骤(1)与求解外循环子问题的步骤(1)相同,故不再赘述。此外,考虑到在本文中,内循环子问题包含整数变量,对偶变量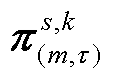 不能直接获得,但可先求解该混合整数线性模型,然后将该所求得的整数解固定代入原问题中,得到原子问题的线性模型,最后,在通过求解所得线性模型后,便可获得该对偶变量[2]。
不能直接获得,但可先求解该混合整数线性模型,然后将该所求得的整数解固定代入原问题中,得到原子问题的线性模型,最后,在通过求解所得线性模型后,便可获得该对偶变量[2]。
在步骤(1)后,得到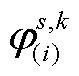 与
与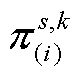 ;而后,通过式(37)即可直接得到内循环子问题目标函数。
;而后,通过式(37)即可直接得到内循环子问题目标函数。
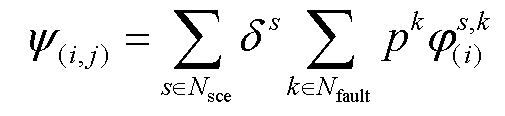 (37)
(37)
图3所示为融合物理知识的双循环分解算法计算流程。
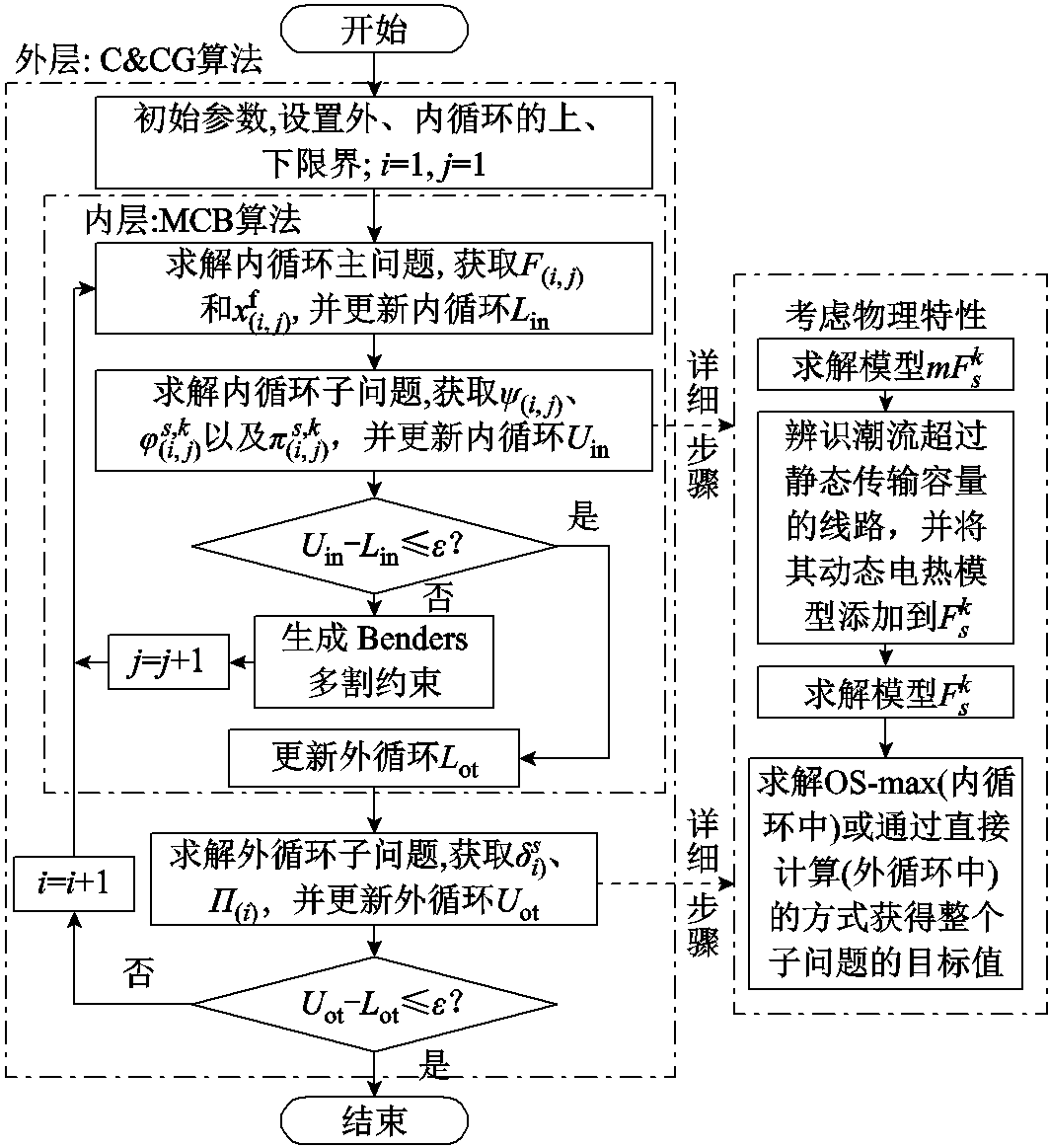
图3 所提算法的流程
Fig.3 Flow chart of the proposed method
该算法的计算步骤如下所示:
(1)初始参数及内外循环迭代次数i=1与j=1;设置外循环上、下限Uot=+¥ ,Lot=-¥ ,及内循环上、下限Uin=+¥ ,Lin=-¥ ;获取各场景初始概率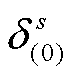 。
。
(2)求解第j次内循环主问题,得目标值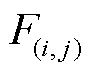 及
及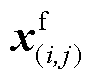 ,更新Lin=
,更新Lin=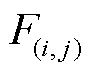 ;将
;将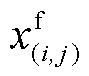 传递给内循环子问题,并转入步骤(3)。
传递给内循环子问题,并转入步骤(3)。
(3)求解内循环子问题中的模型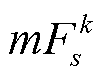 ,得目标值
,得目标值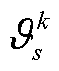 及松弛变量
及松弛变量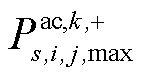 与
与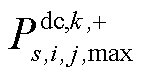 ;根据松弛变量
;根据松弛变量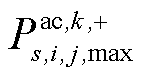 与
与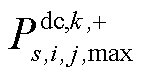 确定元件k故障后出现传输功率超过静态传输容量的线路,并将它们的动态电热模型添加到模型
确定元件k故障后出现传输功率超过静态传输容量的线路,并将它们的动态电热模型添加到模型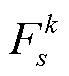 之中;而后求解模型
之中;而后求解模型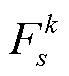 ,可得
,可得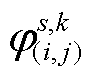 与
与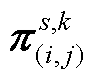 ;紧接着,求解OS-max模型得
;紧接着,求解OS-max模型得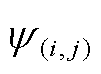 ,并更新Uin=min[Uin,
,并更新Uin=min[Uin,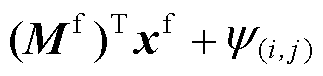 ],再转入步骤(4)。
],再转入步骤(4)。
(4)如果Uin-Lin≤e成立(e为收敛阈值,可取为极小的正数),则步骤(2)中所得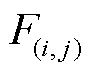 及
及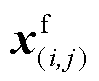 即为第i次外循环主问题的目标值和最优决策值,更新Lot=
即为第i次外循环主问题的目标值和最优决策值,更新Lot=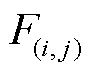 ,进入步骤(5);否则,生成Benders多割约束,更新j=j+1,并返回步骤(2),继续寻找当前第i次外循环主问题的目标值和最优决策值。
,进入步骤(5);否则,生成Benders多割约束,更新j=j+1,并返回步骤(2),继续寻找当前第i次外循环主问题的目标值和最优决策值。
(5)在步骤(2)所获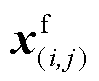 的基础上,求解第i次外循环子问题,即可得到新的
的基础上,求解第i次外循环子问题,即可得到新的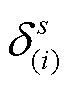 及外循环子问题目标
及外循环子问题目标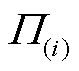 ,并更新Uot=min[Uot,
,并更新Uot=min[Uot,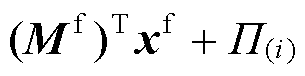 ],同时转到步骤(6)。求解外循环子问题和求解内循环子问题的步骤相似,故不再赘述。
],同时转到步骤(6)。求解外循环子问题和求解内循环子问题的步骤相似,故不再赘述。
(6)如果Uot-Lot≤e成立,则问题收敛,停止迭代;否则,i=i+1,同时重置内循环上、下限,并返回步骤(2)。
本节以改进IEEE 39测试系统为算例进行分析,验证所提模型与算法的有效性。改进IEEE 39测试系统中的交流子系统为IEEE 39标准测试系统,相关参数及拓扑结构可见文献[42]。图4所示为该测试系统的直流部分。此外,VSC的相关参数可见文献[3]。交流系统节点11及15中配置储能装置,所配置的储能装置的容量为60 MW·h,充放电效率分别为0.94及0.90,最小/最大荷电状态分别为所配置储能装置容量的10%及90%,输出的最大视在功率为30 MV·A。常规调控装置(火电机组)的响应间隙假设为5 min。校正周期设定为15 min。梯形隐式积分法中的时间步长设置为1 min。初始容差系数设定为0.01。线路长期允许最高温度和短期允许最高温度分别假设为70℃和80℃;最大热积累量设定为100℃∙min。本文通过历史数据获得5 000个随机场景,而后利用K-Means聚类算法[32]筛选出4个离散典型场景,并获得各个离散场景的初始概率值;各场景的负荷水平及风电出力可见附录。算例运行在CPU为Intel Core(TM) i5-7400U、内存为8 GB的便携式计算机中,并利用GAMS商业求解软件进行求解。需要注意的是BL(i,j)表示该线路联结了节点i和节点j,节点i的编号始终小于节点j的编号;与此同时,线路排序由两级规则决定,其中节点i的优先级高于节点j。交流线路BL(4,5)与BL(12,13)及直流线路BL(42,43)为预想故障线路。
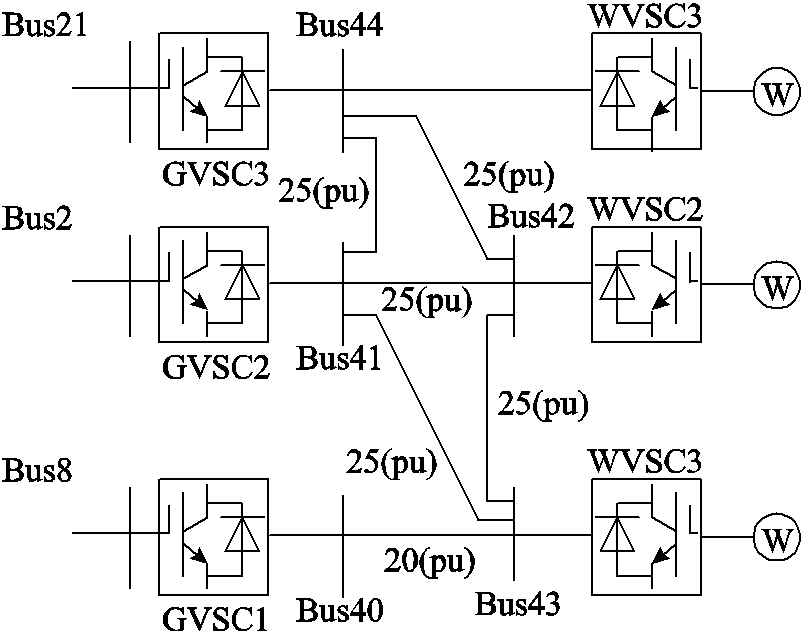
图4 改进IEEE 39测试系统中的直流子系统
Fig.4 DC grid in the modified IEEE 39-bus system
为了验证所提方法的有效性,本文在测试系统中设定六个案例进行对比分析,对比案例的环境设定见表1。
表1 对比案例的环境设定
Tab.1 Environment configurations of all cases
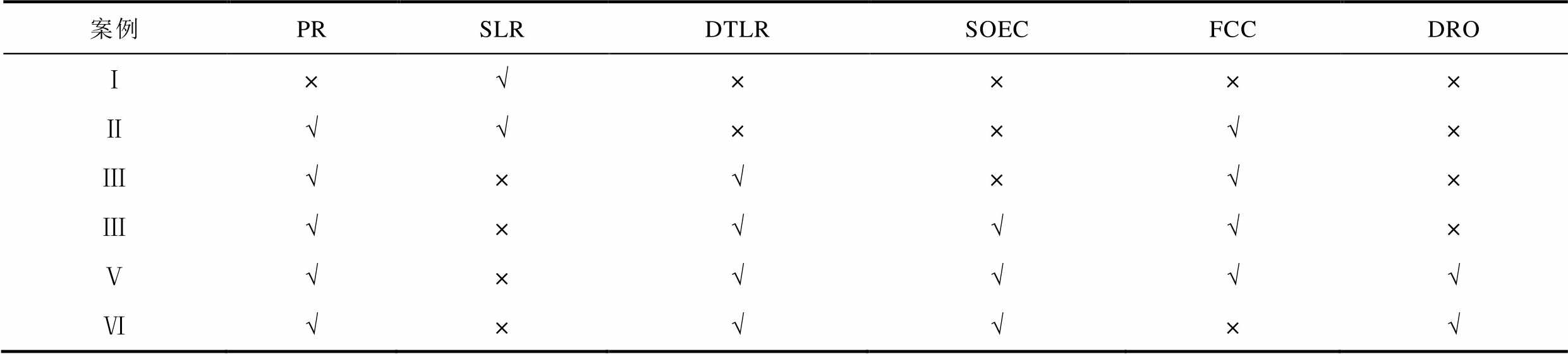
案例PRSLRDTLRSOECFCCDRO Ⅰ×√×××× Ⅱ√√××√× Ⅲ√×√×√× Ⅲ√×√√√× Ⅴ√×√√√√ Ⅵ√×√√×√
注:“×”和“√”分别代表考虑和未考虑;PR表示N-1事故;SLR表示静态传输容量;DTLR表示动态传输容量;SOEC表示暂时安全约束;FCC表示快速校正控制;DRO表示分布鲁棒。
图5为测试系统中交流线路BL(4,5)与BL(12,13)及直流线路BL(42,43)发生故障后上述案例下各非故障线路在校正环节中的最高温度。从图5中可以看出,只有非故障线路编号23的交流线路BL(13,14)在校正期间中出现温度大于长期允许温度(Long-term Allowable Operation Temperature, LAOT)的情况,而其他非故障线路在校正期间的最高温度均低于其LAOT。这说明只有非故障交流线路BL(13,14)运行处于非长期安全状态。非故障交流线路BL(13,14)在各案例中的最高温度依次为78.41、69.70、70.00、80.00、77.73及80.00℃。可以明显看出,案例Ⅱ中交流线路BL(13,14)的最高温度未达到70.00℃,这是因为该案例采用的是静态传输容量机制,所以在校正期间,线路传输量不能超过静态传输容量,而线路升温到长期运行最高温度的时间相对采取动态电热模型的案例Ⅲ而言较长,以致线路原本传输能力也并未得到完全发挥。此外,案例Ⅰ、Ⅳ、Ⅴ及Ⅵ的最高温度均超过70.00℃,说明在这些案例中线路BL(13,14)的耐热特性在校正期间得到利用。
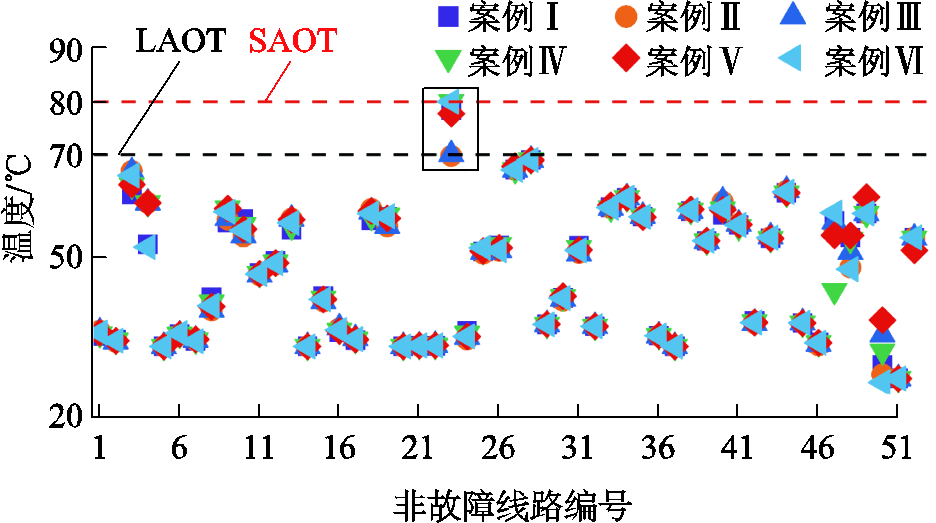
图5 非故障线路在校正期间的最高温度
Fig.5 Highest temperature of all no-fault lines during the correction period
改进测试系统中上述六个案例下的计算结果见表2。从表2中可以看出,虽然案例Ⅰ的所得最优指令的经济性最高,但是由于并未考虑故障情况,致使故障阶段维持系统正常运行所需的校正成本及紧急切荷量将明显高于其他案例。进一步,在采用动态电热模型的案例Ⅲ~Ⅵ中线路最大传输功率为1.031、1.204、1.170及1.209(pu),均超过其静态传输容量1.000(pu)。这说明考虑线路动态电热特性能够在一定程度上提高线路的传输能力。此外,在动态电热模型的基础上,再考虑线路暂时安全状态,能够进一步激发线路的传输潜力,故相比案例Ⅲ,考虑线路暂时安全状态的案例Ⅳ、Ⅴ及Ⅵ具有更大的线路传输功率。与此同时,由于案例Ⅴ是在最恶劣概率分布下进行的鲁棒决策,故案例Ⅴ的经济性低于案例Ⅳ,但依据案例Ⅴ所获结果的鲁棒性更高。再者,通过对比案例Ⅴ与Ⅵ可知,案例Ⅴ的总成本、运行成本及校正成本均低于案例Ⅵ。这是因为案例Ⅴ考虑了GVSC和储能的快速校正能力,而在故障校正期间运用GVSC和储能的快速校正能力,不仅能够降低整体校正成本,同时还能降低对故障后系统安全程度的考虑,最终达到提高系统经济性的目的。
表2 各案例的计算结果
Tab.2 Optimal results of all cases
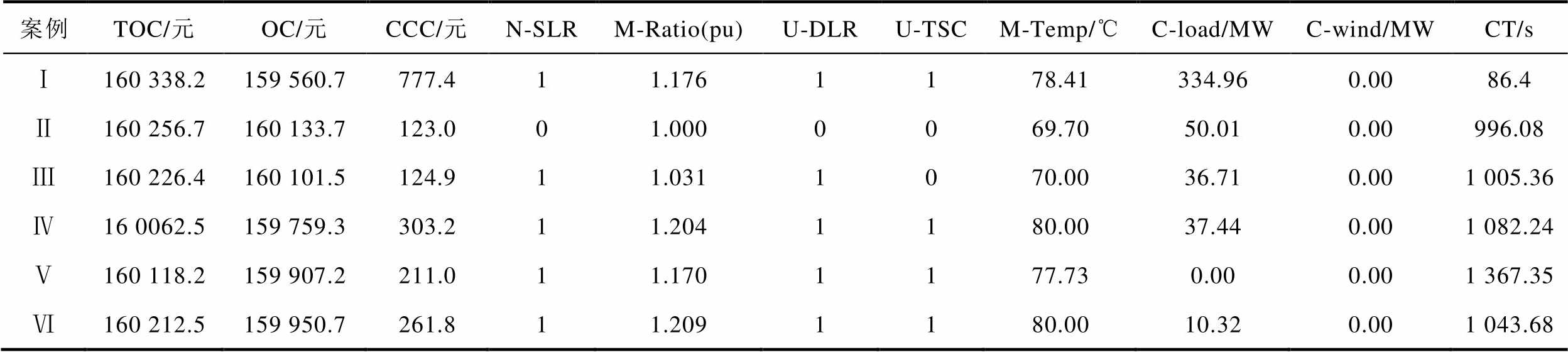
案例TOC/元OC/元CCC/元N-SLRM-Ratio(pu)U-DLRU-TSCM-Temp/℃C-load/MWC-wind/MWCT/s Ⅰ160 338.2159 560.7777.411.1761178.41334.960.0086.4 Ⅱ160 256.7160 133.7123.001.0000069.7050.010.00996.08 Ⅲ160 226.4160 101.5124.911.0311070.0036.710.001 005.36 Ⅳ16 0062.5159 759.3303.211.2041180.0037.440.001 082.24 Ⅴ160 118.2159 907.2211.011.1701177.730.000.001 367.35 Ⅵ160 212.5159 950.7261.811.2091180.0010.320.001 043.68
注:OC、CCC与TOC分别为运行成本、校正成本与总成本;N-SLR为不满足静态传输容量的线路数量;M-Ratio为线路最大负载率;U-TSC为线路暂态安全约束得到利用的线路数量;U-DLR为线路动态电热特性得到利用的线路数量;M-Temp为全系统线路最高温度;C-load与C-wind为所有场景切荷量与弃风量;CT为时间。
图6为在案例Ⅴ中不同场景下所有预想N-1故障发生后交流线路BL(13,14)处于校正期间的最高温度。图7为在案例Ⅴ中不同预想N-1故障发生后所有场景下交流线路BL(13,14)处于校正期间的最高温度。从图6中可以看出,交流线路BL(13,14)在各场景中的最高温度均处于短期最高允许温度(Short-term Allowable Operation Temperature, SAOT)与LAOT之间,其中场景Ⅳ的温度最高达到77.73℃,这说明线路BL(13,14)的耐热能力在各随机场景中均得到了利用,而在场景Ⅳ中发挥得最为充分。此外,从图7中可以看出,交流线路BL(4,5)与BL(12,13)及直流线路BL(42,43)发生N-1故障后,线路BL(13,14)的温升分别为15.96、0.17及0.45℃,这说明交流线路BL(4,5)故障后会加重交流线路BL(13,14)潮流传输负重,进而导致该线路出现较大温升。进一步,结合图6和图7可知,交流线路BL(13,14)的耐热能力在场景Ⅳ中交流线路BL(4,5)发生N-1故障时发挥得最为充分。
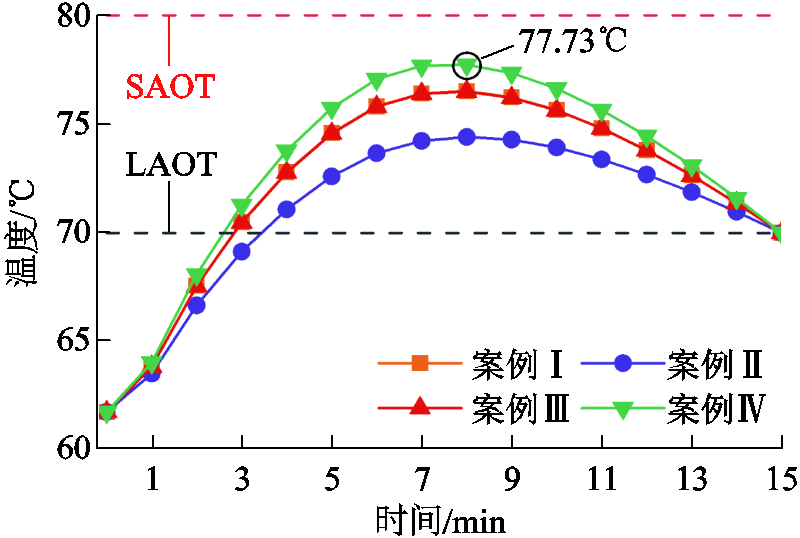
图6 在案例Ⅴ中不同场景下所有预想N-1故障发生后线路BL(13,14)处于校正期间的最高温度
Fig.6 Highest temperature of BL(13,14)in different scenes during the correction period of all N-1 failures at Case Ⅴ
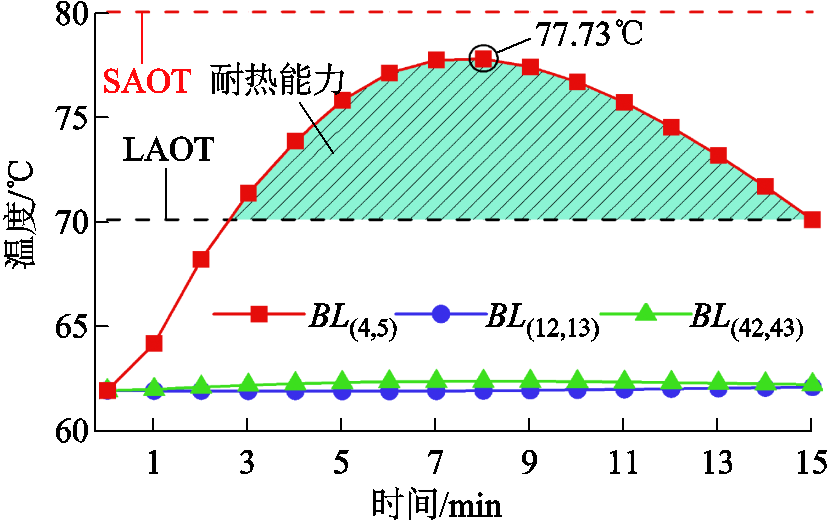
图7 在案例Ⅴ中不同预想N-1故障发生后所有场景下BL(13,14)处于校正期间的最高温度
Fig.7 Highest temperature of BL(13,14) in different N-1 failures during the correction period of all scenes at Case Ⅴ
表3和表4为在案例Ⅴ中场景Ⅳ下交流线路BL(4,5)故障后快速校正装置与常规装置的校正动作。除此之外,有关案例Ⅴ的其他优化结果可见附录。如果交流线路BL(4,5)发生故障,节点11的储能需要释放15×(5+10/2)/60=2.50 MW·h的能量,而安装在节点15上的储能装置需吸收5.00 MW·h的能量;此外通过VSC-1与VSC-2注入交流系统的有功功率分别减少21.66 MW、5.33 MW,通过VSC-3注入交流系统的有功功率增加26.97 MW。在二次校正环节中,节点30与节点38上的机组分别需上调56.86 MW、86.51 MW,节点9及节点12上的机组则均需要上调20 MW的有功功率。
表3 案例Ⅴ中场景Ⅳ下线路BL(4,5)故障后快速校正动作
Tab.3 Corrective action provided by fast control resources in Scene-Ⅳ at CaseⅤafter BL(4,5) failure

阶段类型GVSC-1GVSC-2GVSC-3储能-11储能-15 首次校正有功/MW-5.62+64.05+79.15-15.00+30.00 无功/Mvar+43.52+27.63+1.48+25.980.00 二次校正有功/MW-5.77+64.02+79.18—— 无功/Mvar+43.75+27.67+1.42——
注:“+”和“-”分别表示注入交流系统的有功出力与无功出力;“—”表示不参加校正控制。
表4 案例Ⅴ场景Ⅳ下线路BL(4,5)故障后非快速校正动作
Tab.4 Corrective action provided by non-fast control resources in Scene Ⅳ at CaseⅤafter BL(4,5) failure
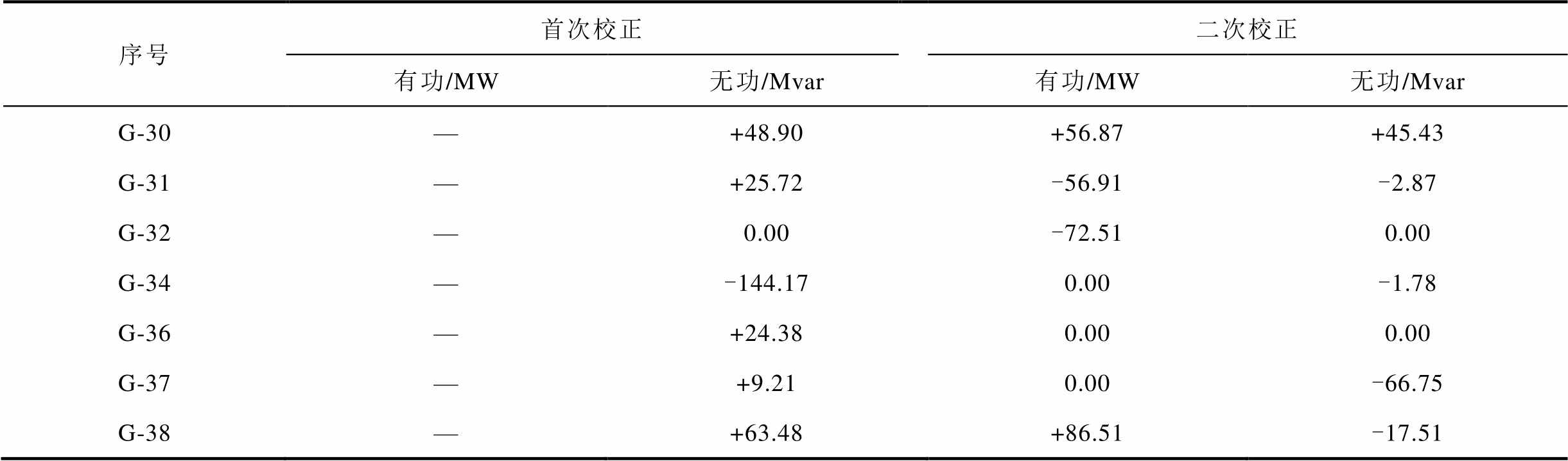
序号首次校正二次校正 有功/MW无功/Mvar有功/MW无功/Mvar G-30—+48.90+56.87+45.43 G-31—+25.72-56.91-2.87 G-32—0.00-72.510.00 G-34—-144.170.00-1.78 G-36—+24.380.000.00 G-37—+9.210.00-66.75 G-38—+63.48+86.51-17.51
注:“+”和“-”分别代表增加和减少;“—”表示不参加校正控制。
图8为决策者设定不同容差系数时各场景的场景概率,图9为不同容差系数下的累计概率变化量及总成本。容差系数可用来表示决策者对所获不确定量的概率分布的信赖程度。该系数取值越小,信赖度越大;反之则信赖度越小。从图8中可以看出,随着容差系数不断增大,所有场景的概率均发生变化,其中场景Ⅱ与Ⅳ的概率变化最大。场景Ⅰ与Ⅳ处于上升通道,最大上升幅度为场景Ⅳ,从24.42%上升到33.27%,上升幅度为8.85百分点;场景Ⅱ与Ⅲ处于下降通道,最大下降幅度为场景Ⅲ,从25.16%下降到16.37%,下降幅度为8.79百分点。这说明通过降低场景Ⅱ与Ⅲ的概率而抬升场景Ⅰ与Ⅳ的概率,能够获得更差概率分布。从图9中同样可以看出,随着容差系数不断增大,累计概率变量及总成本均呈上升的趋势,这是由搜索范围扩大所致;而正是因为搜索范围的扩大,使得决策者在决策过程中能够考虑更为恶劣的概率分布。虽然考虑更为恶劣的概率分布会降低决策指令的经济性,但所获决策指令应对不确定性的能力得到增强。
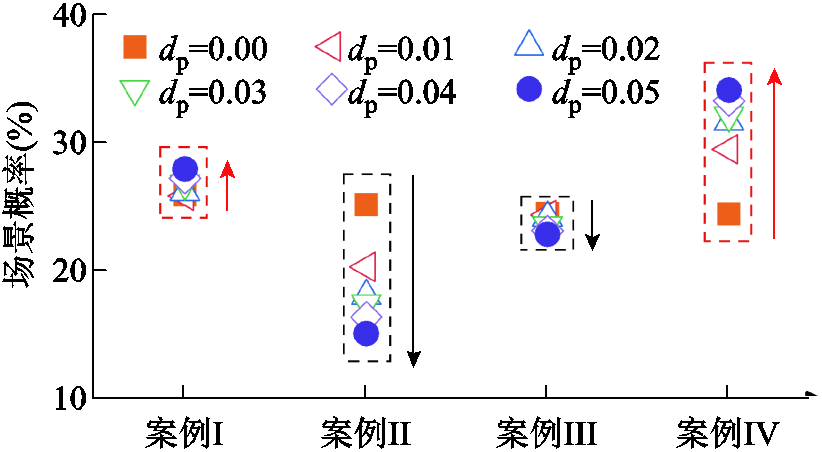
图8 不同容差系数下的场景概率
Fig.8 Probability of these discrete scenes in different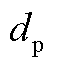
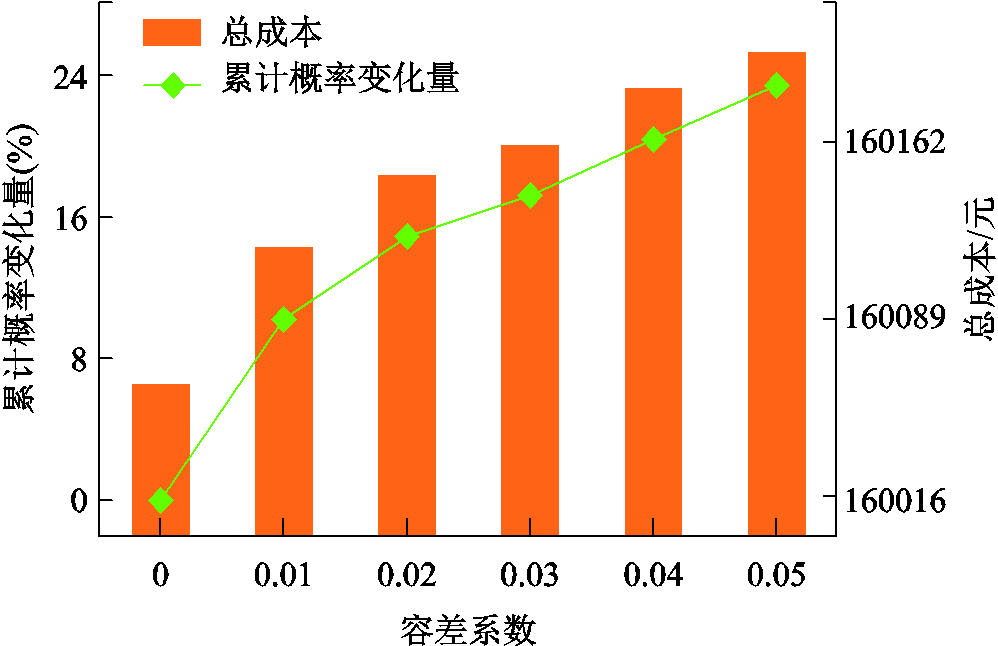
图9 不同容差系数下的累计概率变化量及总成本
Fig.9 Cumulative probability changes and cost in different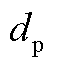
此外,M. Nick等[22]提出通过松弛非过载线路的动态电热模型来削减线性非过载线路的动态电热模型的影响,但是该方法在计算过程中会引入大量无效约束和整数变量,尤其是在采用分段线性化及梯形隐式积分法处理线路的热平衡约束的过程中。而考虑到只有传输功率超过其静态传输容量的线路在校正期间的最高温度才有可能超过其长期运行最高温度的物理特性,本文在C&CG算法与Multi-cut Benders分解算法的基础上,提出融合所述物理特性的双循环分解算法。表5为所提方法和其他方法的计算结果(计算时间上限为6 h)。从表5中可以看出,由于下层min模型的限制,传统C&CG算法已不能在设定的计算时间内完成求解;而所提方法与C&CG+MCB及C&CG+MCB+松弛电热模型三种方法均能完成求解。三种方法之间的总成本的平均误差不超过0.1%,而所提方法与其他两种方法相比计算时间分别下降了89.0%、72.3%。故可说明所提方法能够在保证准确度的前提下,提高整体模型求解效率。
表5 所提求解方法与其他求解方法的计算结果
Tab.5 Comparation of proposed method and other methods

求解算法总成本/元计算时间/s C&CG—— C&CG+MCB160 109.412 402.88 C&CG+MCB+松弛电热模型160 123.84 937.12 C&CG+MCB+物理特性160 118.21 367.35
为了充分发挥交直流线路的耐热特性、提高系统在不确定运行环境下应对N-1故障的能力、弥补常规调控手段在故障校正期间难以快速响应调度指令的缺陷,本文提出考虑线路动态电热特性的交直流系统分布鲁棒潮流优化策略。通过分析不同优化方案,得到以下结论:
1)通过构建交流架空线路、直流电缆线路的动态电热模型,同时在校正控制中引入线路的短期最高允许温度及校正期间线路的热积累量约束来代替长期允许温度作为线路在校正期间的暂时安全约束,使得交流线路和直流线路的功率传输能力在校正期间均能够得以最大限度的利用。
2)在常规调控装置动作前,通过充分利用具有更快的校正速度和响应速度的VSC及储能装置,能够避免其他非故障元件再次故障。同时,在基于KL散度的概率分布模糊集上进行分布鲁棒潮流优化,可改善传统鲁棒优化方法过于保守的问题。
3)所提融合物理知识的双循环求解方法,不仅能够完全避免对非过载线路热平衡方程线性化而引入大量冗余约束和变量,同时还能避免多场景多故障协同求解造成优化问题规模过大的缺陷。
附 录
1. 线性过程
1)利用梯形隐式积分法[22]对交、直流线路热平衡方程进行线性近似。
以交流线路热平衡方程为例进行说明。当采用梯形隐式积分法对其线性化时,可得
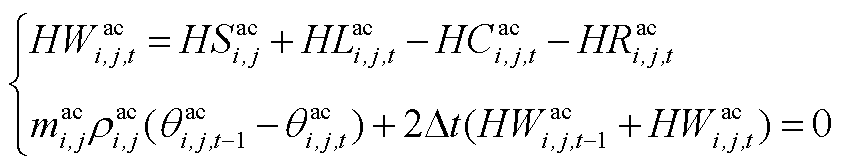 (A1)
(A1)
式中,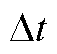 为梯形隐式积分法中的步长。
为梯形隐式积分法中的步长。
2)利用分段线性法[22]对非线性凸项(交流线路动态电热模型中的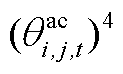 、潮流方程中的
、潮流方程中的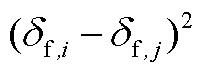 与
与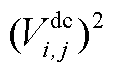 )进行线性处理。
)进行线性处理。
以交流线路的电热模型中的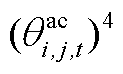 为例进行说明。当采用分段线性法对交流线路电热模型中的
为例进行说明。当采用分段线性法对交流线路电热模型中的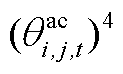 进行线性化时,可首先用
进行线性化时,可首先用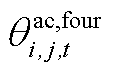 替代
替代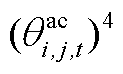 ,再设置如下相关的约束。
,再设置如下相关的约束。
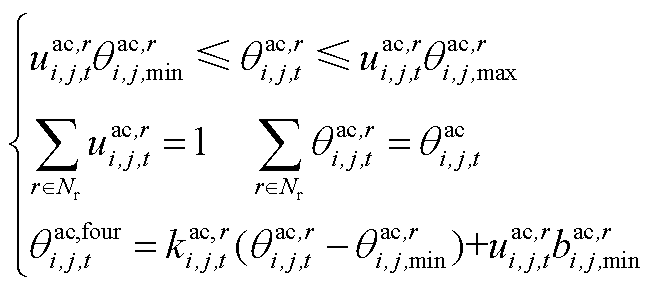 (A2)
(A2)
式中,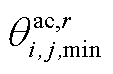 、
、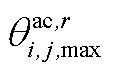 分别为第r段的起始点、终止点;
分别为第r段的起始点、终止点;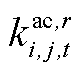 、
、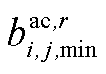 为第r段拟合直线的表达式的方程参数;
为第r段拟合直线的表达式的方程参数;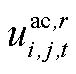 为二进制辅助变量,用于判断
为二进制辅助变量,用于判断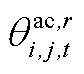 所处分段的位置;
所处分段的位置;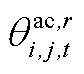 为第r段的分段值。
为第r段的分段值。
3)利用McCormick松弛法[39]对模型中的双线性项(直流线路潮流方程中的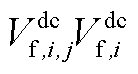 、VSC下垂控制中的
、VSC下垂控制中的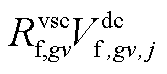 )进行线性处理。
)进行线性处理。
以直流线路潮流方程中的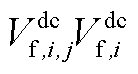 为例进行说明。当采用McCormick松弛法对直流线路潮流方程中的
为例进行说明。当采用McCormick松弛法对直流线路潮流方程中的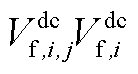 进行线性化时,可首先用
进行线性化时,可首先用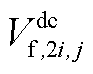 替代
替代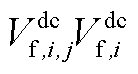 ,再设置如下相关的约束。
,再设置如下相关的约束。
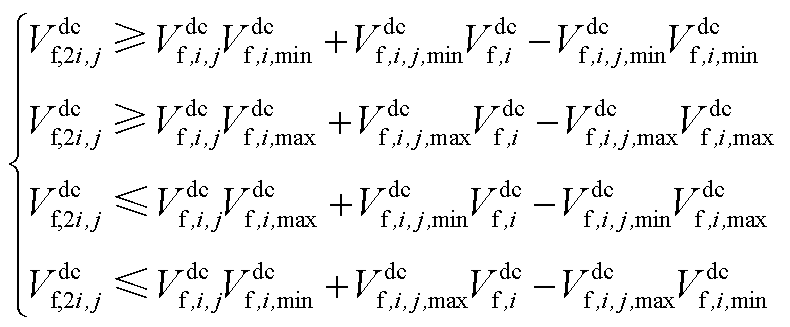 (A3)
(A3)
4)利用六边形松弛法[40-41]对VSC视在功率约束、储能系统视在功率约束进行线性近似。
以VSC视在功率约束为例进行说明。当采用六边形松弛法对其线性化时,可得
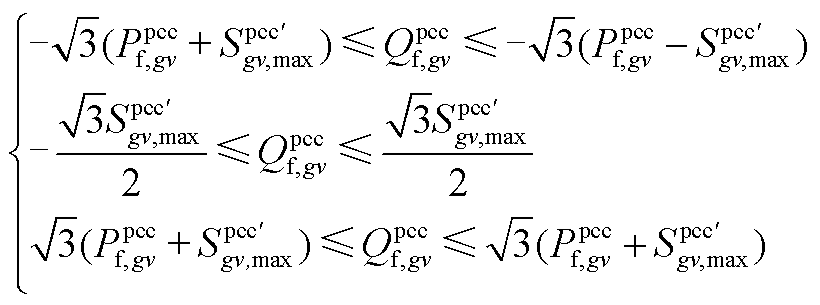 (A4)
(A4)
式中,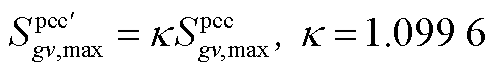 。
。
2. 本文所提分布鲁棒模型的紧凑形式
为了更清晰地说明求解过程,本文将线性化后的分布鲁棒模型改写为
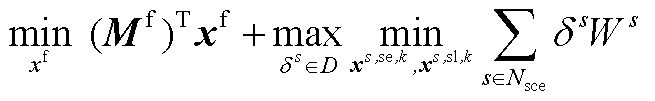 (A5)
(A5)
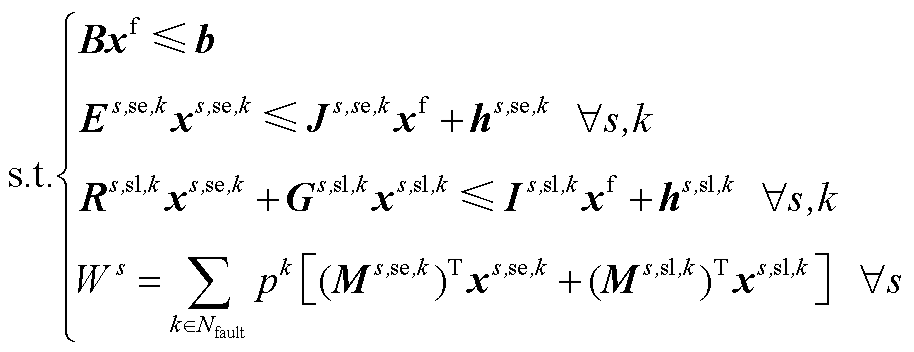 (A6)
(A6)
式中,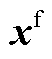 为上层min模型中的控制变量,包含
为上层min模型中的控制变量,包含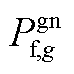 、
、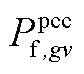 、
、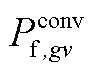 、
、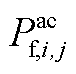 、
、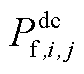 、
、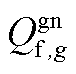 、
、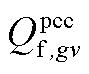 、
、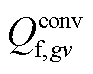 、
、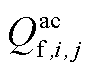 、
、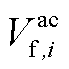 、
、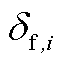 、
、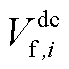 、
、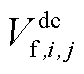 、
、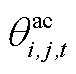 、
、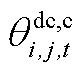 、
、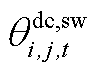 、
、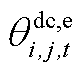 、
、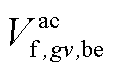 、
、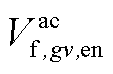 、
、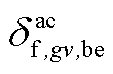 、
、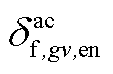 、
、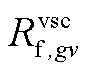 、
、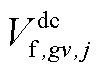 ;D和
;D和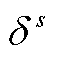 分别为中间max模型中的模糊集与场景s概率;
分别为中间max模型中的模糊集与场景s概率;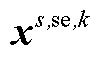 为下层min模型中场景s下元件k故障后短期运行子阶段的控制变量,包含
为下层min模型中场景s下元件k故障后短期运行子阶段的控制变量,包含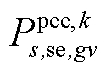 、
、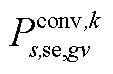 、
、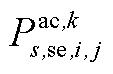 、
、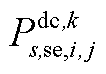 、
、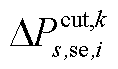 、
、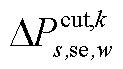 、
、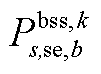 、
、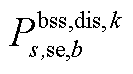 、
、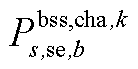 、
、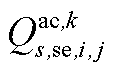 、
、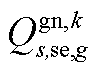 、
、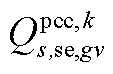 、
、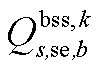 、
、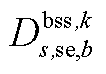 、
、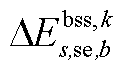 、
、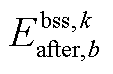 、
、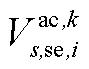 、
、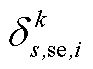 、
、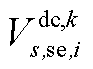 、
、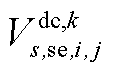 、
、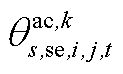 、
、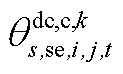 、
、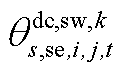 、
、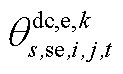 、
、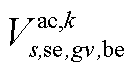 、
、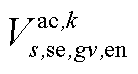 、
、 、
、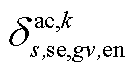 、
、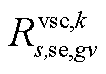 、
、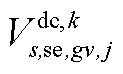 ;
;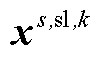 为下层min模型中场景s下元件k故障后长期运行子阶段的控制变量,包含
为下层min模型中场景s下元件k故障后长期运行子阶段的控制变量,包含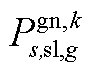 、
、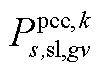 、
、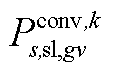 、
、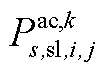 、
、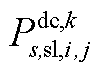 、
、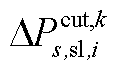 、
、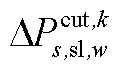 、
、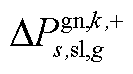 、
、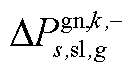 、
、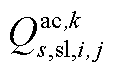 、
、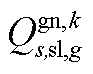 、
、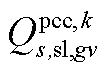 、
、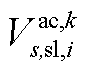 、
、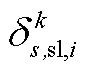 、
、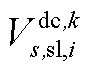 、
、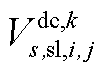 、
、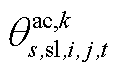 、
、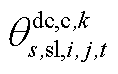 、
、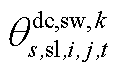 、
、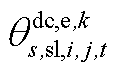 、
、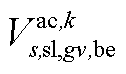 、
、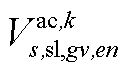 、
、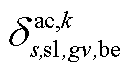 、
、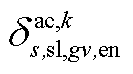 、
、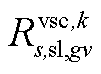 、
、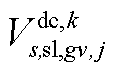 。此外,需要注意的是
。此外,需要注意的是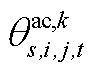 由
由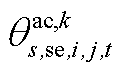 和
和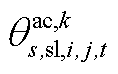 构成,
构成,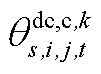 由
由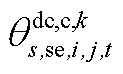 和
和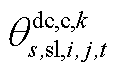 构成,
构成,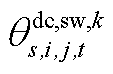 由
由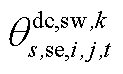 和
和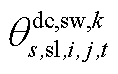 构成,
构成,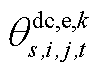 由
由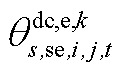 和
和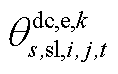 构成,
构成,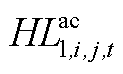 由
由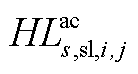 和
和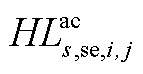 构成,
构成,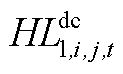 由
由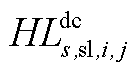 和
和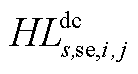 构成。
构成。
式(A5)为整个分布鲁棒模型的目标函数,由式(5)构成。式(A6)第一项为上层约束条件,由约束式(7)~式(12)所构成,同时还包含导数项为0的稳态线路动态电热模型,即约束式(1)~式(4)中所有导数项均等于0。式(A6)第二项主要是事故k发生后首次校正过程中的相关约束,除约束式(14)~式(17)之外,还包括线路潮流方程、交直流系统电压约束及VSC传输功率约束与下垂控制方程,该部分约束与约束式(8)、式(12)及式(10)类似。式(A6)第三项主要是事故k发生后二次校正过程中的相关约束,除约束式(18)、式(19)、式(21)、式(22)之外,还包括线路潮流方程、交直流系统电压约束、VSC传输功率约束与下垂控制方程,弃风与切负荷约束,该部分约束与约束式(8)、式(12)、式(10)及式(17)类似。由于在第二阶段中引入线路的短期最高允许温度及校正期间最大热积累量约束来代替长期允许温度作为线路在校正期间的暂时安全约束,因此暂态线路动态电热模型将被同时包含在式(A6)第二项与第三项中,即导数项不等于0的约束式(1)~式(4)被包含在式(A6)第二项与第三项中;与此同时,该两项中的线路运行温度均由约束式(20)进行限制。进一步,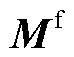 、
、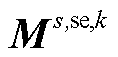 、
、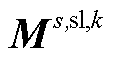 、B、
、B、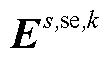 、
、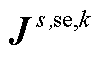 、
、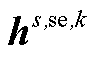 、
、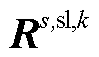 、
、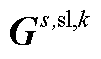 、
、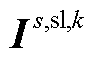 与
与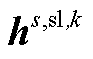 为目标函数或约束条件中的常数矩阵。此外,需要注意的是,
为目标函数或约束条件中的常数矩阵。此外,需要注意的是,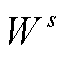 为所引入的中间量。
为所引入的中间量。
3. 算例相关参数和最终优化结果
附表1 负荷水平预测值、风力出力预测值及各聚类场景下的负荷水平、风力出力与初始场景概率
App.Tab.1 Initial scenario probability, scenario value of load and wind power in every clustering scene, predicted value of load and wind power
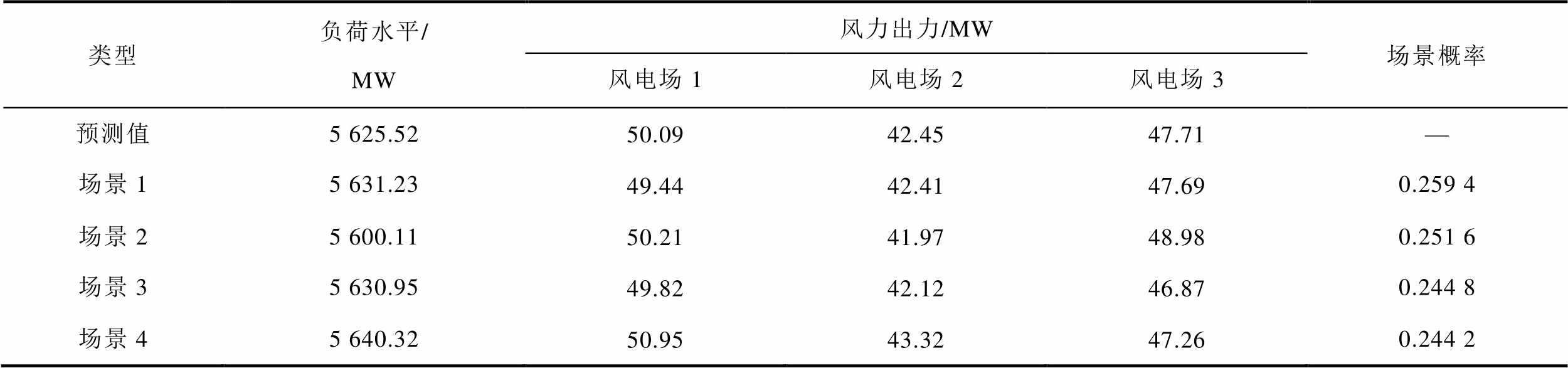
类型负荷水平/MW风力出力/MW场景概率 风电场1风电场2风电场3 预测值5 625.5250.0942.4547.71— 场景15 631.2349.4442.4147.690.259 4 场景25 600.1150.2141.9748.980.251 6 场景35 630.9549.8242.1246.870.244 8 场景45 640.3250.9543.3247.260.244 2
附表2 常规火电机组在故障前的有功出力与无功出力
App.Tab.2 Active/reactive power output of TG before a contingency

序号有功/MW无功/Mvar序号有功/MW无功/Mvar G-30335.51299.47G-35687.00300.00 G-31385.24153.93G-36580.00215.61 G-32725.00300.00G-37564.00197.37 G-33652.00250.00G-380.0030.49 G-34508.00167.00G-391 100.00300.00
附表3 在故障前通过GVSC注入交流系统的有功出力与无功出力
App.Tab.3 Active/reactive power injected to AC grid from GVSC before a contingency

序号有功/MW无功/Mvar GVSC-116.0441.20 GVSC-269.3818.38 GVSC-352.1730.29
附表4 在首次校正过程中通过GVSC或储能装置注入交流系统的有功出力与无功出力
App.Tab.4 Active/reactive power injected to AC grid from GVSC or BSS in the primary corrective stage
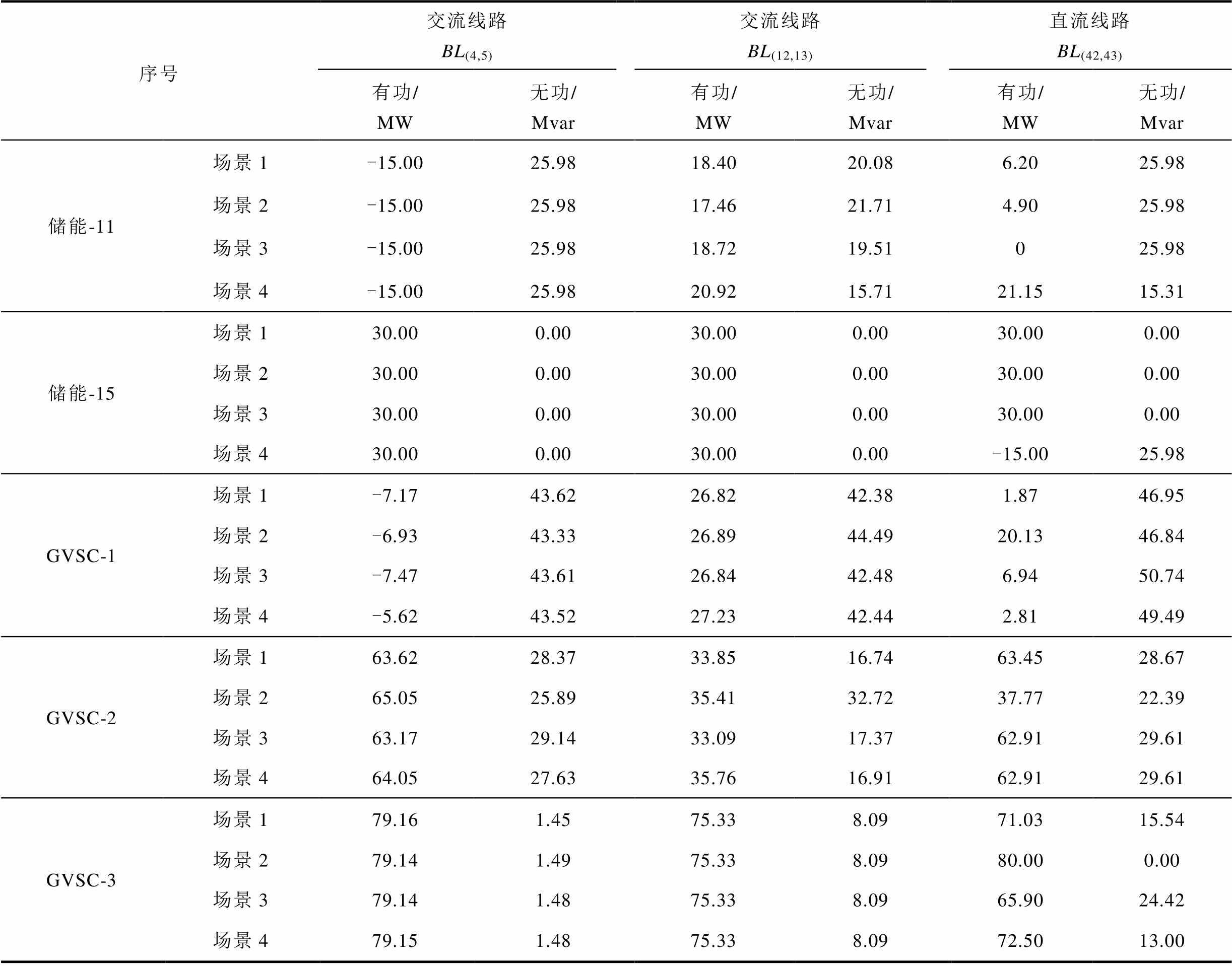
序号交流线路BL(4,5)交流线路BL(12,13)直流线路BL(42,43) 有功/MW无功/Mvar有功/MW无功/Mvar有功/MW无功/Mvar 储能-11场景1-15.0025.9818.4020.086.2025.98 场景2-15.0025.9817.4621.714.9025.98 场景3-15.0025.9818.7219.51025.98 场景4-15.0025.9820.9215.7121.1515.31 储能-15场景130.000.0030.000.0030.000.00 场景230.000.0030.000.0030.000.00 场景330.000.0030.000.0030.000.00 场景430.000.0030.000.00-15.0025.98 GVSC-1场景1-7.17 43.62 26.82 42.38 1.87 46.95 场景2-6.93 43.33 26.89 44.49 20.13 46.84 场景3-7.47 43.61 26.84 42.48 6.94 50.74 场景4-5.62 43.52 27.23 42.44 2.81 49.49 GVSC-2场景163.62 28.37 33.85 16.74 63.45 28.67 场景265.05 25.89 35.41 32.72 37.77 22.39 场景363.17 29.14 33.09 17.37 62.91 29.61 场景464.05 27.63 35.76 16.91 62.91 29.61 GVSC-3场景179.16 1.45 75.33 8.09 71.03 15.54 场景279.14 1.49 75.33 8.09 80.00 0.00 场景379.14 1.48 75.33 8.09 65.90 24.42 场景479.15 1.48 75.33 8.09 72.50 13.00
附表5 常规火电机组在首次校正过程中的无功调整量
App.Tab.5 Reactive power adjustment injected to AC grid from TG in the primary corrective stage (单位:Mvar)
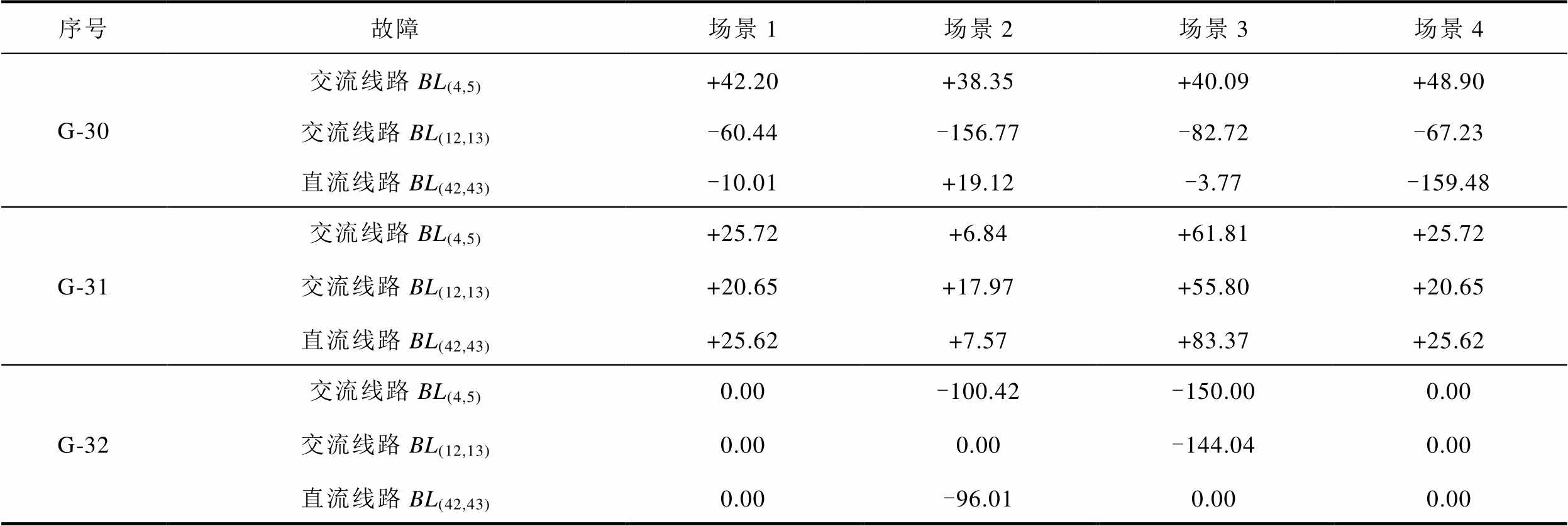
序号故障场景1场景2场景3场景4 G-30交流线路BL(4,5)+42.20 +38.35 +40.09 +48.90 交流线路BL(12,13)-60.44 -156.77 -82.72 -67.23 直流线路BL(42,43)-10.01 +19.12 -3.77 -159.48 G-31交流线路BL(4,5)+25.72 +6.84 +61.81 +25.72 交流线路BL(12,13)+20.65 +17.97 +55.80 +20.65 直流线路BL(42,43)+25.62 +7.57 +83.37 +25.62 G-32交流线路BL(4,5)0.00 -100.42 -150.00 0.00 交流线路BL(12,13)0.00 0.00 -144.04 0.00 直流线路BL(42,43)0.00 -96.01 0.00 0.00
(续)
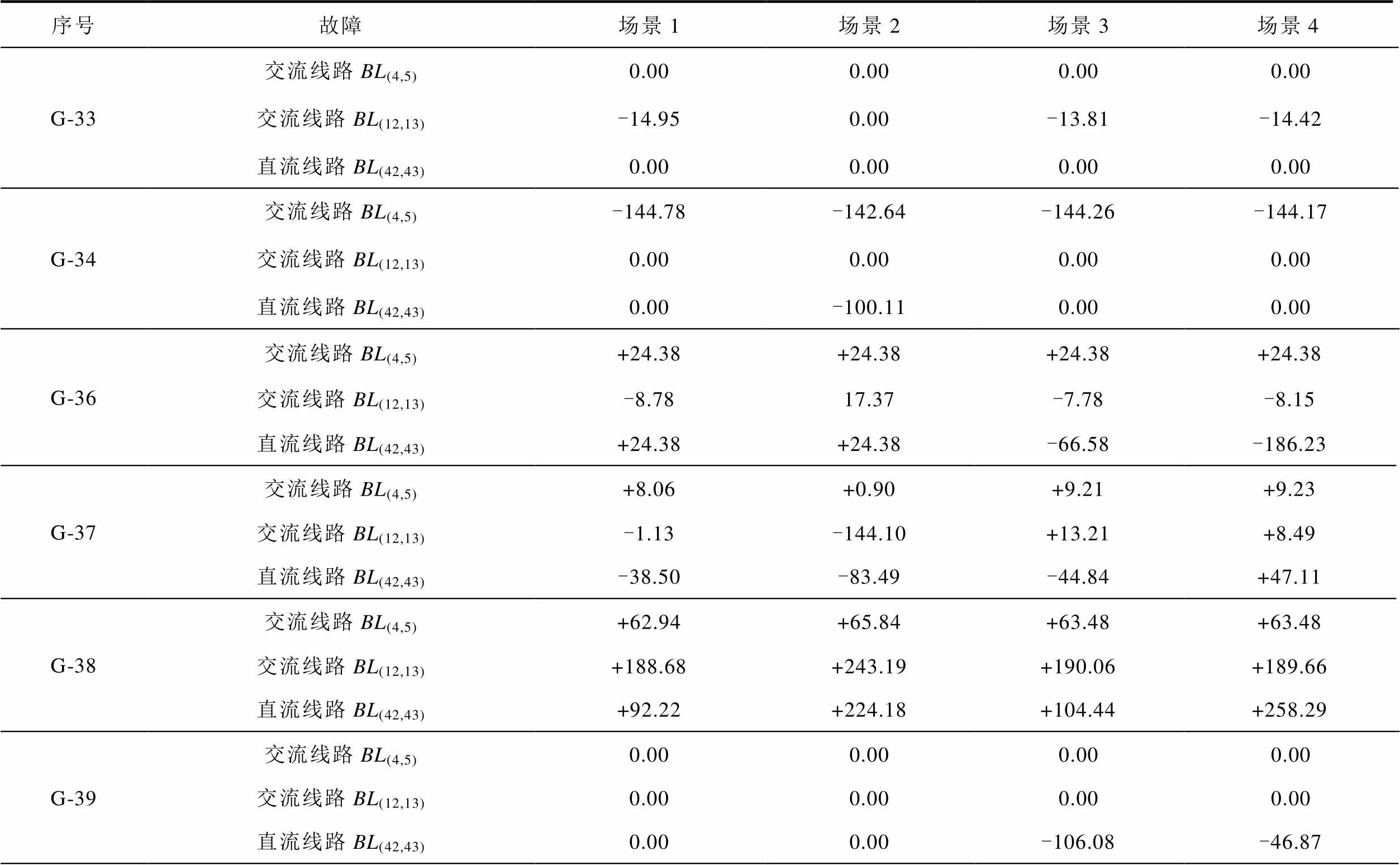
序号故障场景1场景2场景3场景4 G-33交流线路BL(4,5)0.000.000.000.00 交流线路BL(12,13)-14.95 0.00 -13.81 -14.42 直流线路BL(42,43)0.000.000.000.00 G-34交流线路BL(4,5)-144.78 -142.64 -144.26 -144.17 交流线路BL(12,13)0.000.000.000.00 直流线路BL(42,43)0.00-100.11 0.000.00 G-36交流线路BL(4,5)+24.38 +24.38 +24.38 +24.38 交流线路BL(12,13)-8.78 17.37 -7.78 -8.15 直流线路BL(42,43)+24.38 +24.38 -66.58 -186.23 G-37交流线路BL(4,5)+8.06 +0.90 +9.21 +9.23 交流线路BL(12,13)-1.13 -144.10 +13.21 +8.49 直流线路BL(42,43)-38.50 -83.49 -44.84 +47.11 G-38交流线路BL(4,5)+62.94 +65.84 +63.48 +63.48 交流线路BL(12,13)+188.68 +243.19 +190.06 +189.66 直流线路BL(42,43)+92.22 +224.18 +104.44 +258.29 G-39交流线路BL(4,5)0.000.000.000.00 交流线路BL(12,13)0.000.000.000.00 直流线路BL(42,43)0.000.00-106.08 -46.87
注:“+”和“-”分别代表增加和减少。
附表6 在二次校正过程中通过GVSC注入交流系统的有功出力与无功出力
App.Tab.6 Active/reactive power injected to AC grid from GVSC in the Secondary corrective stage
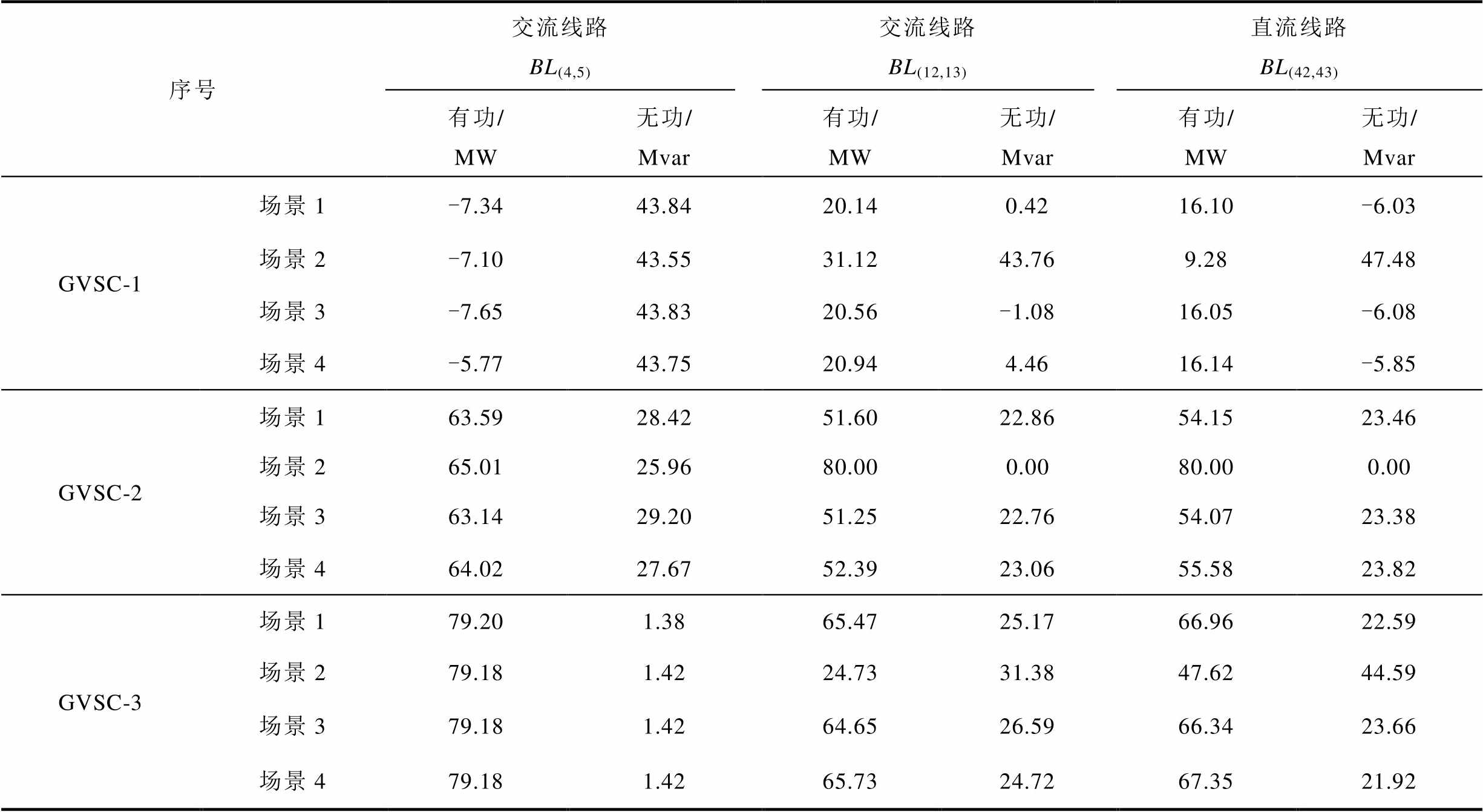
序号交流线路BL(4,5)交流线路BL(12,13)直流线路BL(42,43) 有功/MW无功/Mvar有功/MW无功/Mvar有功/MW无功/Mvar GVSC-1场景1-7.34 43.84 20.14 0.42 16.10 -6.03 场景2-7.10 43.55 31.12 43.76 9.28 47.48 场景3-7.65 43.83 20.56 -1.08 16.05 -6.08 场景4-5.77 43.75 20.94 4.46 16.14 -5.85 GVSC-2场景163.59 28.42 51.60 22.86 54.15 23.46 场景265.01 25.96 80.00 0.0080.00 0.00 场景363.14 29.20 51.25 22.76 54.07 23.38 场景464.02 27.67 52.39 23.06 55.58 23.82 GVSC-3场景179.20 1.38 65.47 25.17 66.96 22.59 场景279.18 1.42 24.73 31.38 47.62 44.59 场景379.18 1.42 64.65 26.59 66.34 23.66 场景479.18 1.42 65.73 24.72 67.35 21.92
附表7 常规火电机组在二次校正过程中的有功调整量
App.Tab.7 Active power adjustment injected to AC grid from TG in the seconday corrective stage (单位:MW)
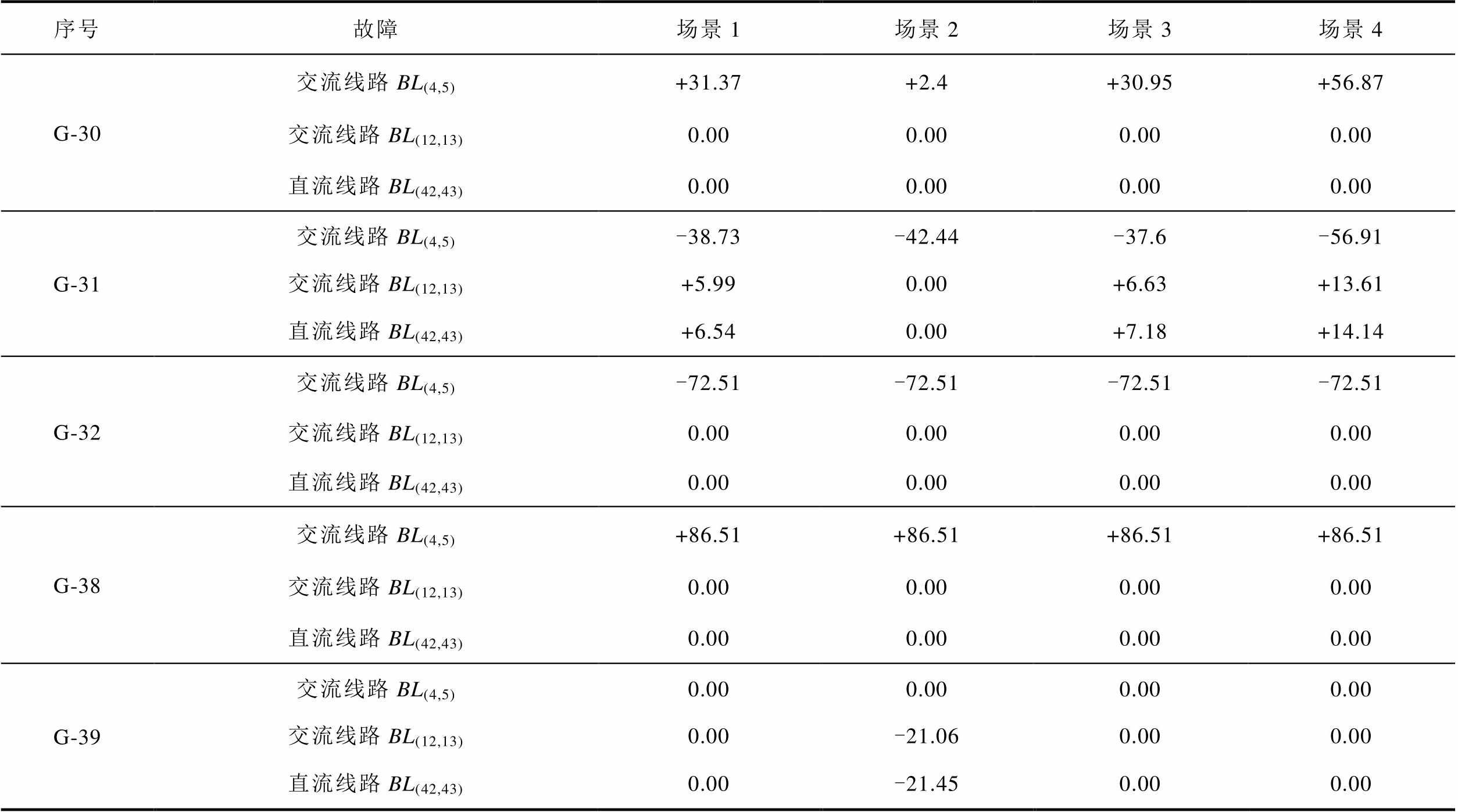
序号故障场景1场景2场景3场景4 G-30交流线路BL(4,5)+31.37+2.4+30.95+56.87 交流线路BL(12,13)0.000.000.000.00 直流线路BL(42,43)0.000.000.000.00 G-31交流线路BL(4,5)-38.73-42.44-37.6-56.91 交流线路BL(12,13)+5.990.00+6.63+13.61 直流线路BL(42,43)+6.540.00+7.18+14.14 G-32交流线路BL(4,5)-72.51-72.51-72.51-72.51 交流线路BL(12,13)0.000.000.000.00 直流线路BL(42,43)0.000.000.000.00 G-38交流线路BL(4,5)+86.51+86.51+86.51+86.51 交流线路BL(12,13)0.000.000.000.00 直流线路BL(42,43)0.000.000.000.00 G-39交流线路BL(4,5)0.000.000.000.00 交流线路BL(12,13)0.00-21.060.000.00 直流线路BL(42,43)0.00-21.450.000.00
注:“+”和“-”分别代表增加和减少。
附表8 常规火电机组在二次校正过程中的无功调整量
App.Tab.8 Reactive power adjustment injected to AC grid from TG in the seconday corrective stage (单位:Mvar)
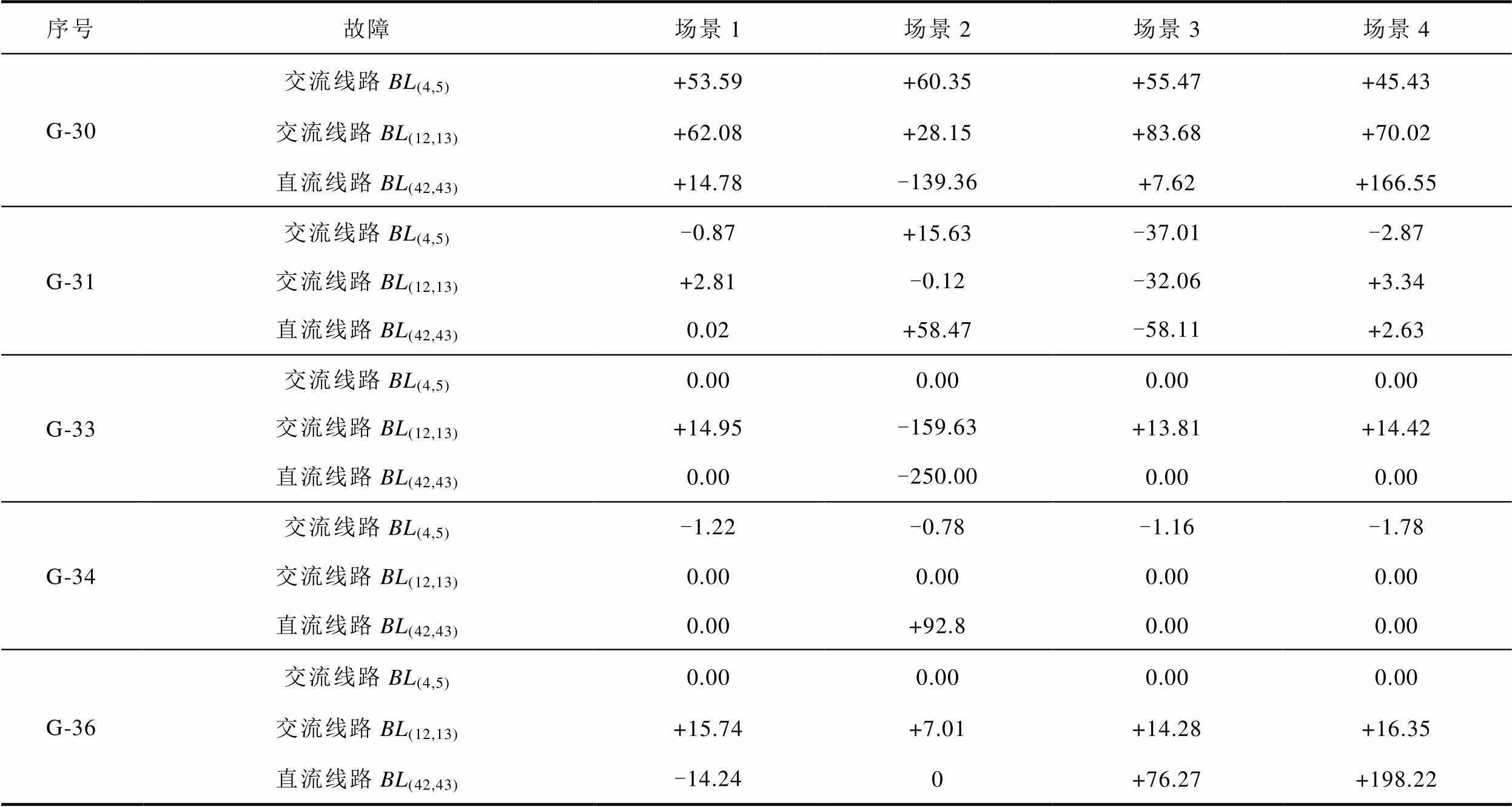
序号故障场景1场景2场景3场景4 G-30交流线路BL(4,5)+53.59+60.35+55.47+45.43 交流线路BL(12,13)+62.08+28.15+83.68+70.02 直流线路BL(42,43)+14.78-139.36+7.62+166.55 G-31交流线路BL(4,5)-0.87+15.63-37.01-2.87 交流线路BL(12,13)+2.81-0.12-32.06+3.34 直流线路BL(42,43)0.02+58.47-58.11+2.63 G-33交流线路BL(4,5)0.000.000.000.00 交流线路BL(12,13)+14.95-159.63+13.81+14.42 直流线路BL(42,43)0.00-250.000.000.00 G-34交流线路BL(4,5)-1.22-0.78-1.16-1.78 交流线路BL(12,13)0.000.000.000.00 直流线路BL(42,43)0.00+92.80.000.00 G-36交流线路BL(4,5)0.000.000.000.00 交流线路BL(12,13)+15.74+7.01+14.28+16.35 直流线路BL(42,43)-14.240+76.27+198.22
(续)
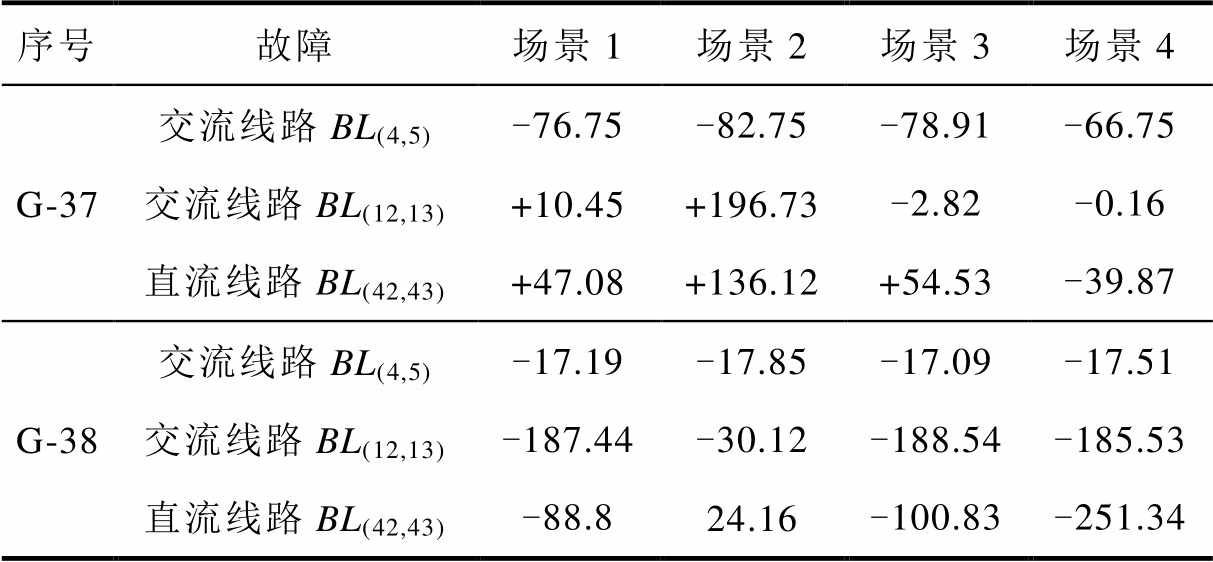
序号故障场景1场景2场景3场景4 G-37交流线路BL(4,5)-76.75-82.75-78.91-66.75 交流线路BL(12,13)+10.45+196.73-2.82-0.16 直流线路BL(42,43)+47.08+136.12+54.53-39.87 G-38交流线路BL(4,5)-17.19-17.85-17.09-17.51 交流线路BL(12,13)-187.44-30.12-188.54-185.53 直流线路BL(42,43)-88.824.16-100.83-251.34
注:“+”和“-”分别代表增加和减少。
参考文献
[1] 林涛, 毕如玉, 陈汝斯, 等. 基于二阶锥规划的计及多种快速控制手段的综合安全校正策略[J]. 电工技术学报, 2020, 35(1): 167-178.
Lin Tao, Bi Ruyu, Chen Rusi, et al. Comprehensive security correction strategy based on second-order cone programming considering multiple fast control measures[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 167-178.
[2] Wen Yunfeng, Guo Chuangxin, Kirschen D S, et al. Enhanced security-constrained OPF with distributed battery energy storage[J]. IEEE Transactions on Power Systems, 2015, 30(1): 98-108.
[3] Cao Jun, Du W, Wang H F. An improved corrective security constrained OPF for meshed AC/DC grids with multi-terminal VSC-HVDC[J]. IEEE Transactions on Power Systems, 2016, 31(1): 485-495.
[4] Xu Yan, Dong Zhao yang, Zhang Rui, et al. Solving preventive-corrective SCOPF by a hybrid computational strategy[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1345-1355.
[5] Meng Ke, Zhang Wang, Li Yujun, et al. Hierarchical SCOPF considering wind energy integration through multiterminal VSC-HVDC grids[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4211-4221.
[6] 饶宏, 周月宾, 李巍巍, 等. 柔性直流输电技术的工程应用和发展展望[J]. 电力系统自动化, 2023, 47(1): 1-11.
Rao Hong, Zhou Yuebin, Li Weiwei, et al. Engineering application and development prospect of VSC-HVDC transmission technology[J]. Automation of Electric Power Systems, 2023, 47(1): 1-11.
[7] 李湘旗, 周洋, 章德, 等. VSC-HVDC线路接入点选址及容量优化配置方法[J]. 电力自动化设备, 2020, 40(12): 113-120, 126.
Li Xiangqi, Zhou Yang, Zhang De, et al. Method of access point selection and capacity optimal configuration for VSC-HVDC line[J]. Electric Power Automation Equipment, 2020, 40(12): 113-120, 126.
[8] Sennewald T, Linke F, Westermann D. Preventive and curative actions by meshed bipolar HVDC-overlay-systems[J]. IEEE Transactions on Power Delivery, 2020, 35(6): 2928-2936.
[9] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804.
Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.
[10] 张智, 周明, 武昭原, 等. 考虑动态频率支撑的储能选址定容规划方法[J]. 中国电机工程学报, 2023, 43(7): 2708-2721.
Zhang Zhi, Zhou Ming, Wu Zhaoyuan, et al. Energy storage location and capacity planning method considering dynamic frequency support[J]. Proceedings of the CSEE, 2023, 43(7): 2708-2721.
[11] Gong Kai, Wang Xu, Jiang Chuanwen, et al. Security-constrained optimal sizing and siting of BESS in hybrid AC/DC microgrid considering post-contingency corrective rescheduling[J]. IEEE Transactions on Sustainable Energy, 2021, 12(4): 2110-2122.
[12] Zhou Yang, Rehtanz C, Luo Pei, et al. Joint corrective optimization based on VSC-HVDC and distributed energy storage for power system security enhancement[J]. International Journal of Electrical Power & Energy Systems, 2022, 135: 107573.
[13] Wu Lei. Robust SCUC considering continuous/discrete uncertainties and quick-start units: a two-stage robust optimization with mixed-integer recourse[C]//2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 2016: 1.
[14] Lai T L. Stochastic approximation: invited paper[J]. The Annals of Statistics, 2003, 31(2): 391-406.
[15] Ben-Tal A, El Ghaoui L, Nemirovskiĭ A S. Robust Optimization[M]. Princeton: Princeton University Press, 2009.
[16] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[17] 贺帅佳, 阮贺彬, 高红均, 等. 分布鲁棒优化方法在电力系统中的理论分析与应用综述[J]. 电力系统自动化, 2020, 44(14): 179-191.
He Shuaijia, Ruan Hebin, Gao Hongjun, et al. Overview on theory analysis and application of distributionally robust optimization method in power system[J]. Automation of Electric Power Systems, 2020, 44(14): 179-191.
[18] 席俊烨, 童晓阳, 李智, 等. 考虑风电不确定性的交直流配电网低碳分布鲁棒优化调度[J]. 电力自动化设备, 2023, 43(11): 59-66.
Xi Junye, Tong Xiaoyang, Li Zhi, et al. Low-carbon distributionally robust optimal scheduling for AC/DC distribution network considering wind power uncertainty[J]. Electric Power Automation Equipment, 2023, 43(11): 59-66.
[19] 郑义, 白晓清, 苏向阳. 考虑风电不确定性的φ-散度下基于条件风险价值的鲁棒动态经济调度[J]. 电力自动化设备, 2021, 41(2): 63-70.
Zheng Yi, Bai Xiaoqing, Su Xiangyang. Robust dynamic economic dispatch considering uncertainty of wind power based on conditional value-at-risk under φ-divergence[J]. Electric Power Automation Equipment, 2021, 41(2): 63-70.
[20] 曾捷, 童晓阳, 范嘉乐. 计及需求响应不确定性的电-气耦合配网系统动态分布鲁棒优化[J]. 电网技术, 2022, 46(5): 1877-1888.
Zeng Jie, Tong Xiaoyang, Fan Jiale. Dynamic distributionally robust optimization of integrated electric-gas distribution system considering demand response uncertainty[J]. Power System Technology, 2022, 46(5): 1877-1888.
[21] 王孟夏, 韩学山, 韦志清, 等. 电网运行环境下基于电热耦合潮流的架空线路应力预估[J]. 电工技术学报, 2019, 34(5): 1078-1087.
Wang Mengxia, Han Xueshan, Wei Zhiqing, et al. Tension prediction of overhead transmission line based on electrothermal coupling power flow in operating power systems[J]. Transactions of China Electro-technical Society, 2019, 34(5): 1078-1087.
[22] Nick M, Alizadeh-Mousavi O, Cherkaoui R, et al. Security constrained unit commitment with dynamic thermal line rating[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2014-2025.
[23] 王孟夏, 韩学山, 黄金鑫, 等. 计及输电元件热惯性效应的安全约束最优潮流[J]. 中国电机工程学报, 2016, 36(5): 1181-1189.
Wang Mengxia, Han Xueshan, Huang Jinxin, et al. Security constrained optimal power flow considering thermal inertia effect of transmission component[J]. Proceedings of the CSEE, 2016, 36(5): 1181-1189.
[24] 王孟夏, 韩学山. 基于电热协调的电网安全校正控制方法[J]. 电力系统自动化, 2011, 35(12): 32-36.
Wang Mengxia, Han Xueshan. Realization of security corrective control considering electro-thermal coordination[J]. Automation of Electric Power Systems, 2011, 35(12): 32-36.
[25] Hu Jian, Wang Jian, Xiong Xiaofu, et al. A post-contingency power flow control strategy for AC/DC hybrid power grid considering the dynamic electrothermal effects of transmission lines[J]. IEEE Access, 2019, 7: 65288-65302.
[26] 戴沅, 程养春, 钟万里, 等. 高压架空输电线路动态增容技术[M]. 北京: 中国电力出版社, 2013.
[27] 胡剑, 王建, 熊小伏, 等. 计及线路动态电热特性的交直流混联电网过载控制策略[J]. 电力系统保护与控制, 2020, 48(7): 66-75.
Hu Jian, Wang Jian, Xiong Xiaofu, et al. An overload control strategy for AC/DC hybrid power grid considering dynamic electro-thermal characteristics of transmission lines[J]. Power System Protection and Control, 2020, 48(7): 66-75.
[28] Nick M, Mousavi O A, Cherkaoui R, et al. Integration of transmission lines dynamic thermal rating into real-time optimal dispatching of power systems[C]// 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 2015: 1-6.
[29] 王孟夏, 周生远, 杨明, 等. 计及海底电缆热特性的可接纳海上风电装机容量评估方法[J]. 电力系统自动化, 2021, 45(6): 195-202.
Wang Mengxia, Zhou Shengyuan, Yang Ming, et al. Assessment method for acceptable installed capacity of offshore wind farms considering thermal characteristics of submarine cables[J]. Automation of Electric Power Systems, 2021, 45(6): 195-202.
[30] Zhang Ruiqi, Sun Hua, Dong Xiaoming. The comparison of thermal characteristics of AC cable and DC cable[J]. Journal of Physics: Conference Series, 2019, 1187(2): 022051.
[31] Wen Yunfeng, Zhan Junpeng, Chung C Y, et al. Frequency stability enhancement of integrated AC/VSC-MTDC systems with massive infeed of offshore wind generation[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5135-5146.
[32] Yang Zhifang, Zhong Haiwang, Xia Qing, et al. Solving OPF using linear approximations: fundamental analysis and numerical demonstration[J]. IET Generation, Transmission & Distribution, 2017, 11(17): 4115-4125.
[33] Wiget R, Andersson G. DC optimal power flow including HVDC grids[C]//2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 2013: 1-6.
[34] Beerten J, Cole S, Belmans R. A sequential AC/DC power flow algorithm for networks containing Multi-terminal VSC HVDC systems[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-7.
[35] 曾子龙, 李勇, 李培强, 等. 综合多阶段安全校正与风险管控的储能分布鲁棒优化配置[J]. 高电压技术, 2023, 49(10): 4150-4162.
Zeng Zilong, Li Yong, Li Peiqiang, et al. Distributional Robust configuration of energy storage considering risk management and multi-stage security correction[J]. High Voltage Engineering, 2023, 49(10): 4150-4162.
[36] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477.
Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[37] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. Multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1419-1435.
[38] You Fengqi, Grossmann I E. Multicut Benders decomposition algorithm for process supply chain planning under uncertainty[J]. Annals of Operations Research, 2013, 210(1): 191-211.
[39] Tan Yi, Li Yong, Cao Yijia, et al. Integrated optimization of network topology and DG outputs for MVDC distribution systems[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1121-1123.
[40] Ahmadi H, Martı´ J R. Linear current flow equations with application to distribution systems reconfiguration[J]. IEEE Transactions on Power Systems, 2015, 30(4): 2073-2080.
[41] Gholami A, Shekari T, Grijalva S. Proactive management of microgrids for resiliency enhancement: an adaptive robust approach[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 470-480.
[42] Zimmerman R D, Murillo-Sánchez C E, Thomas R J. Matpower: steady-state operations, planning, and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19.
Abstract Due to the limits of the ramp constraints and response buffer time, the traditional corrective control provided by the thermal generator cannot finish in a short time, which may aggravate the damage caused by the contingency. Meanwhile, the predict error of power output in the off-shore wind farm at the hybrid AC/VSC-HVDC grids could reduce the accuracy of the corrective control even amplify the fault coverage, especially in the response buffer time of traditional corrective resource. In addition, for the limits of power flow in AC/DC lines, the static maximum line rating (SMLR) is normally used. But the SMLR not only ignores the actual environmental condition but also has difficulty in exerting the short-term overheat characteristic that could temporarily boosts the transmission capacity. To address these issues, this paper proposes a distributionally robust power flow optimization strategy considering dynamic electro-thermal properties of lines for hybrid AC/DC grids with VSC-HVDC. By considering the dynamic electro-thermal properties of lines and the joint utilization of VSC-HVDC and battery storage system (BSS), the proposed distributionally robust strategy could improve the quickly handing ability for N-1 contingency.
Firstly, the dynamic electro-thermal models of AC overhead line and DC cable line are respectively established, according to the theory of heat conduction. Then, the short-term maximum allowable temperature and the maximum thermal accumulation are introduced into the correction control to replace the long-term allowable temperature as the temporary security constraint for lines during correction period, so as to make full use of the short-term overload capacity of lines. Secondly, in order to make-up the slow respond speed of traditional control resources, the corrective control after a contingency is divided into the primary and secondary corrective action, which realize the joint utilization of traditional control resources and convert fast control provided by VSC-HVDC and BSS. Furthermore, based on the Kullback-Leibler divergence, the fuzzy set of the probability distribution of wind power and load demand is built. And then, by searching the worst probability in the built fuzzy set, the conservative of power flow optimization is improved when comparing with the traditional robust optimization. In addition, based on the column-and-constraint generation (C&CG) algorithm and Multi-cut Benders decomposition algorithm, a double-cycle decomposition algorithm including the physical characteristic is developed, which avoids the unnecessary linearization for the heat balance equation of lines and the multi-scenario and multi-fault simultaneous solving process.
The numerical results show that the coordinated optimization of BSS and VSC is better for reducing the load shedding for keeping the security of the system after a contingency. Meanwhile, when the short-term maximum allowable temperature and the maximum thermal accumulation are regarded as the temporary security constraint for AC/DC transmission lines, the operation cost and the load shedding could be further reduced.In addition, the utilization of distributionally robust strategy increases the operation cost of the scheduling instruction due to the consideration of the worst probability for random factors, the robustness of scheduling instruction is similarly increased. Furthermore, compared with other algorithms, a double-cycle decomposition algorithm including the physical characteristic has several times faster computational speed while ensures the average error below 0.1%.
The following conclusions can be drawn from the study: (1) Compared with the limits of SMLR for AC/DC lines, the proposed temporary security constraint considering the short-term maximum allowable temperature and the maximum thermal accumulation can make full use of the short-term overload capacity. (2) The distributionally robust security power flow optimization strategy included the convert fast control provided by VSC and BSS could improve the robustness of the scheduling instruction considering the N-1 contingency. (3) This proposed double-cycle decomposition algorithm including the physical characteristic has high solving efficiency under the premise of the high precision.
Keywords: Voltage source converter high voltage direct current (VSC-HVDC), distributionally robust, short-term over-heat capacity, dynamic electro-thermal properties, power flow optimization
中图分类号:TM614; TM711
DOI: 10.19595/j.cnki.1000-6753.tces.231606
国家重点研发计划政府间国际科技创新合作重点项目(2022YFE0129300)、国家自然科学基金联合基金重点支持项目(U22B200134)和国家电网公司科技项目(5216A223000J)资助。
收稿日期 2023-10-06
改稿日期 2024-03-19
曾子龙 男,1993年生,博士研究生,研究方向为交直流系统规划与运行。E-mail:zengzilong@hnu.edu.cn
李 勇 男,1982年生,教授,博士生导师,研究方向为能源/电力系统优化运行与控制、电能变换系统与装备方面等。E-mail:yongli@hnu.edu.cn(通信作者)
(编辑 赫 蕾)