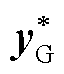 (即机组有功功率预测值)近似如下最优潮流问题式(1)和式(2)的最优解
(即机组有功功率预测值)近似如下最优潮流问题式(1)和式(2)的最优解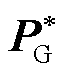 。
。摘要 为应对新型电力系统以最优潮流为核心的精细化资源配置与运行分析需求,基于深度神经网络的最优潮流计算方法受到广泛关注。然而深度神经网络具有“黑箱特性”,现有方法普遍仅基于有限训练、测试集进行深度神经网络的训练与评估,难以从理论上量化计算误差,导致可信度缺乏理论保障。为此,该文提出基于可信深度神经网络的最优潮流计算方法。首先,以理论定量评估深度神经网络映射误差为核心,提出基于min-max双层规划问题的深度神经网络可信训练模型,实现深度神经网络的可信度量化训练;然后,基于KKT最优性条件与激活函数解析表征技术,将所提可信训练模型解析构建为以混合整数规划模型为基础的双层规划问题,并提出基于Danskin定理的精确求解策略;最后,提出基于凸松弛技术与模式识别思想的快速近似求解策略以减轻整数变量计算负担。仿真算例表明:所提方法可将基于有限测试集的深度神经网络映射评估精度提升28.73%,可更为精准地量化深度神经网络可信度;相较于基于有限训练集的现有深度神经网络训练方法,该方法可将计算误差减少87.49%,实现更为可信的深度神经网络训练。
关键词:新能源 最优潮流 深度神经网络 可信训练
绿色发展指引中国可持续发展,对于全球气候治理,亦具有重要意义[1-2]。由于我国近90%的温室气体排放源自能源体系[3-4],构建蕴含高比例清洁能源的低碳电力系统是实现“碳达峰、碳中和”目标的核心支撑[5-6]。我国目前已设立2030年全国风电、太阳能装机容量达到12亿kW以上的发展目标[7]。为应对风/光等新能源带来的强间歇性、随机性和波动性,在精细时间颗粒度实现以最优潮流为核心的电力系统资源优化配置与运行分析对于电力系统的安全、经济运行至关重要[8-9],例如,分钟级/秒级时间颗粒度的海量场景最优潮流计算,以制定新型电力系统调度方案[10];IEEE PES可靠性评估工作组建议引入运行可靠性评估技术,而运行可靠性评估需在较短时间内求解海量新能源场景的最优潮流计算问题[11]。
可见,实现上述目标的主要挑战在于最优潮流的快速计算。求解最优潮流问题以往多采用简化梯度法[12]、牛顿法[13]、内点法[14]等迭代型算法,往往难以满足精细时间颗粒度的海量最优潮流问题计算需求[15]。不同于传统迭代型算法,深度神经网络凭借其“端到端”(end-to-end)的特性,为精细时间颗粒度的最优潮流快速计算提供了新契机[16]:基于深度神经网络的最优潮流计算方法,可实现由新能源功率至最优潮流计算结果的快速映射。已有专家学者实现基于深度神经网络的最优潮流计算速度数量级提升,例如,文献[17]将深度学习引入基于蒙特卡洛法的最优潮流海量场景计算,将计算时间大幅缩减。
此外,现有研究还从特征构造、训练策略、数据特性挖掘增强等方面,研究了基于深度神经网络的最优潮流计算精度提升方法。
在特征构造方面,文献[18]在映射输出中用机组有功功率量表示相角量,从而有效地降低映射维数,缩减深度神经网络模型的大小和所需的训练数据量,并采用均匀采样来避免通用深度神经网络方法中常见的过拟合问题;文献[19]为解决深度学习中因特征维数过高而导致的数值湮没问题,提出基于深度神经网络的最优潮流关键决策变量的优先辨识策略,并以此为导向基于关联性分析和聚类分析挖掘最优潮流输入与输出特征的关联性匹配度,通过构建样本数据的分块特征库来降低学习难度;文献[20]针对输出空间维数过高可能导致计算误差过大、可伸缩性差的问题,提出基于主成分分析法的输出空间维数压缩策略,即深度神经网络先在低维子空间学习最优潮流映射关系,随后再将低维空间映射关系还原至原始输出空间。
在训练策略方面,文献[21]基于最优潮流计算结果对负荷水平的偏导数信息,设计基于负荷水平灵敏度感知的深度神经网络训练策略;为提高深度神经网络的约束满足能力,文献[22]提出基于投影感知策略的深度神经网络训练策略,即将隐含层向量投影至最优潮流可行区域,并将投影向量与最优潮流计算间的反向传播误差嵌入损失函数;文献[23]基于拉格朗日对偶思想,将深度神经网络最优潮流学习任务转换为考虑最优潮流约束的经验风险最小化问题,以提高深度神经网络学习性能;不同于上述利用深度神经网络直接映射最优潮流计算结果,文献[24]首先仅基于深度神经网络预测最优潮流电压结果,而后通过求解线性方程获得剩余最优潮流计算结果。
在数据特性挖掘增强方面,主流思想为:以最优潮流历史数据及噪声数据为训练样本,基于生成对抗网络(Generative Adversarial Network, GAN),通过优化整定GAN生成器及判别器参数,从训练样本参数分布特征角度深度挖掘由新能源功率至最优潮流计算结果的映射关系。例如,文献[25]通过可行性过滤层与最优性过滤层构建生成器,并经由判别器评估训练样本标签概率分布与基于生成器的最优潮流计算结果概率分布间的偏差;文献[26]采用自编码器构建生成器生成最优潮流计算结果,并结合判别器筛选基于生成器的最优潮流计算结果,使得GAN生成结果概率分布趋向于最优潮流最优解概率分布。应当注意的是,部分电力系统研究亦基于GAN增添训练集样本多样性以实现数据特性的挖掘增强,如文献[27]的暂态稳定性分析、文献[28]的输电线路异物检测、文献[29]的设备故障诊断。上述研究也为基于数据特性挖掘增强的深度神经网络最优潮流计算精度提升方法提供了新的思路。
尽管上述研究已展示深度神经网络具备最优潮流高效计算的应用潜力,但是基于深度神经网络的最优潮流计算在实际应用中仍存在困难[30]。其重要原因在于调度运行人员对于深度神经网络“黑箱特性”的担忧,即现有方法普遍难以解释深度神经网络训练参数与最优潮流计算结果映射误差的理论关系。目前,现有方法普遍依赖有限训练集(即部分新能源场景)指导深度神经网络训练,进而基于有限测试集评估训练参数可能导致的映射误差。随着风/光等新能源装机容量迅速攀升,训练集与测试集可能难以完备地反映未来新能源运行场景,使得深度神经网络在部分新能源场景中具有显著映射误差[31]。因此,即使是在训练集/测试集上表现良好的深度神经网络,其后续应用效果可能仍旧不佳,使得现有基于深度神经网络的最优潮流计算方法存在可信度担忧,阻碍其实际应用。
为此,本文提出基于可信深度神经网络的最优潮流计算方法,以期通过基于深度神经网络映射误差的理论评估实现基于深度神经网络的最优潮流计算结果可信度量化,并实现以提升可信度为目标的深度神经网络参数更新,最终达成基于可信深度神经网络的最优潮流计算。本文主要工作包括:
1)提出基于min-max双层规划问题的深度神经网络可信训练模型(第1节)。首先,在内层规划问题构建基于优化理论的深度神经网络映射误差理论评估方法,以此量化深度神经网络映射结果可信度。进而,利用该可信度评估结果指导外层规划问题,更新深度神经网络参数。
2)提出深度神经网络可信训练模型的求解方法(第2节)。首先,基于KKT最优性条件与激活函数解析表征技术,将所提可信训练模型解析构建为以混合整数规划模型为基础的双层规划问题。其次,基于Danskin定理,构建基于梯度下降思想的精确求解策略。最后,为减轻整数变量计算负担,提出基于凸松弛技术与模式识别思想的快速近似求解策略。
本节首先简述基于深度神经网络的最优潮流计算思想。在此基础之上,研究基于min-max双层规划问题的深度神经网络可信训练模型。
考虑到目前工业界广泛采用直流最优潮流模型[32],本文特别关注:给定输入向量PR(即新能源有功功率标幺值),由深度神经网络G输出向量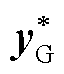 (即机组有功功率预测值)近似如下最优潮流问题式(1)和式(2)的最优解
(即机组有功功率预测值)近似如下最优潮流问题式(1)和式(2)的最优解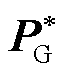 。
。
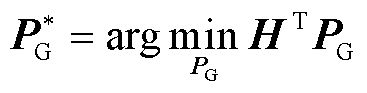 (1)
(1)
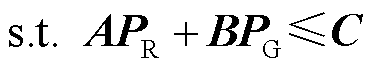 (2)
(2)
式中,PR为新能源有功功率标幺值向量,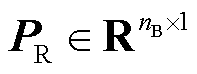 ,nB为新能源场站数量;PG为机组有功功率标幺值向量,
,nB为新能源场站数量;PG为机组有功功率标幺值向量,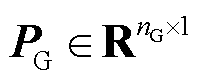 ,nG为机组数量;A和B为最优潮流约束的常数矩阵;C为最优潮流约束的常数向量;H为发电成本系数向量[33]。约束式(2)的具体形式见附录。负荷功率也可包含于PR。
,nG为机组数量;A和B为最优潮流约束的常数矩阵;C为最优潮流约束的常数向量;H为发电成本系数向量[33]。约束式(2)的具体形式见附录。负荷功率也可包含于PR。
基于深度神经网络的最优潮流计算框架如图1所示。由图1可知:①深度神经网络G具有K个全连接隐含层;②第k层具有nk个神经元(k=1, 2,…, K),其第i个神经元输出向量为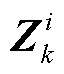 (i=1, 2,…, nk);③第k层输出向量为
(i=1, 2,…, nk);③第k层输出向量为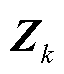 =[
=[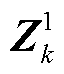 ;
; 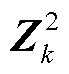 ;…;
;…; 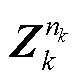 ](“;”代表列向量的拼接)。基于上述定义,图1所示深度神经网络G 可写为
](“;”代表列向量的拼接)。基于上述定义,图1所示深度神经网络G 可写为
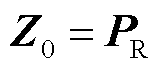 (3)
(3)
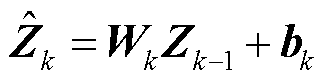 (4)
(4)
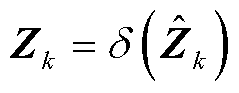 (5)
(5)
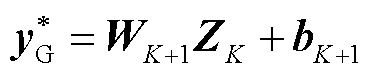 (6)
(6)
式中,Wk为深度神经网络第k层权重矩阵,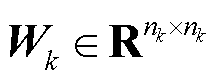 ;bk为深度神经网络第k层偏置向量,
;bk为深度神经网络第k层偏置向量,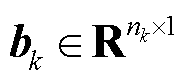 ;
;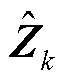 为第k层输入特征向量;
为第k层输入特征向量;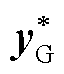 为深度神经网络输出特征向量,
为深度神经网络输出特征向量,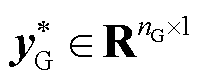 ;δ(·)为激活函数,本文选取ReLU激活函数[34],即
;δ(·)为激活函数,本文选取ReLU激活函数[34],即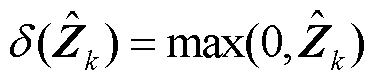 。
。
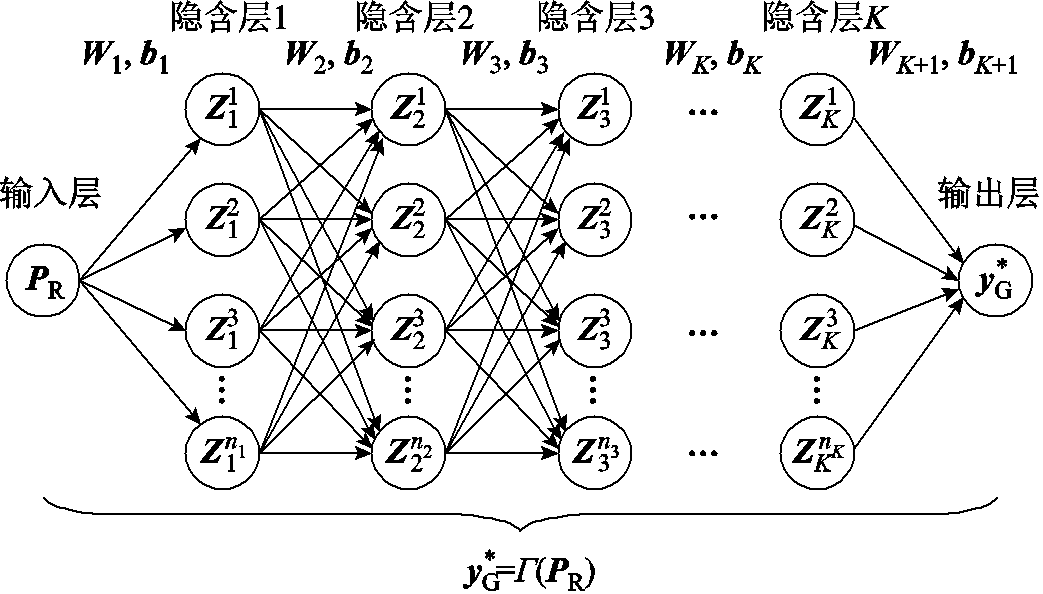
图1 基于深度神经网络的最优潮流计算框架
Fig.1 Framework of optimal power flow by deep neural networks
由式(3)~式(6)可知:①深度神经网络的输入特征向量为新能源有功功率向量PR(其维数为节点数量nB),输出特征向量为直流最优潮流机组有功功率预测值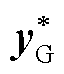 (其维数为机组数量nG);②当完成离线训练W=[W1W2…WK+1]和偏置向量b= [b1; b2; …; bK+1]后,深度神经网络可直接由给定的新能源功率PR输出
(其维数为机组数量nG);②当完成离线训练W=[W1W2…WK+1]和偏置向量b= [b1; b2; …; bK+1]后,深度神经网络可直接由给定的新能源功率PR输出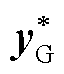 ,作为直流最优潮流模型式(1)和式(2)最优解
,作为直流最优潮流模型式(1)和式(2)最优解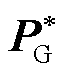 的预测值,而无需再通过传统优化算法求解最优潮流模型,从而实现海量最优潮流优化问题的在线高效计算。
的预测值,而无需再通过传统优化算法求解最优潮流模型,从而实现海量最优潮流优化问题的在线高效计算。
现有研究通过调整深度神经网络参数(W, b),以在训练集上最小化深度神经网络输出向量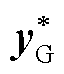 与真实计算结果
与真实计算结果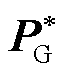 的偏差。进而,基于测试集数值验证深度神经网络的最优潮流计算结果映射误差。然而,由于训练集与测试集可能难以完备地反映未来新能源运行场景,使得相应深度神经网络可能在后续应用中仍旧存在显著的映射误差,导致基于深度神经网络的最优潮流计算方法存在可信度担忧。为此,本文在1.2节提出深度神经网络可信训练模型。
的偏差。进而,基于测试集数值验证深度神经网络的最优潮流计算结果映射误差。然而,由于训练集与测试集可能难以完备地反映未来新能源运行场景,使得相应深度神经网络可能在后续应用中仍旧存在显著的映射误差,导致基于深度神经网络的最优潮流计算方法存在可信度担忧。为此,本文在1.2节提出深度神经网络可信训练模型。
构建深度神经网络可信训练模型的核心在于:如何精准地评估深度神经网络参数对最优潮流计算结果映射误差的影响,并引导深度神经网络进行训练。为此,本文构建min-max双层规划问题,表示为
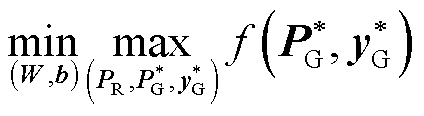 (7)
(7)
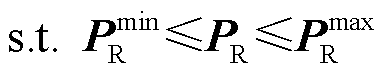 (8)
(8)
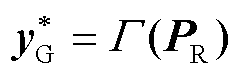 (9)
(9)
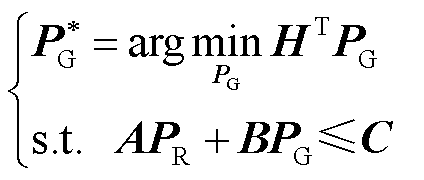 (10)
(10)
式中,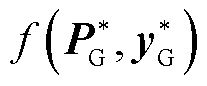 为深度神经网络映射误差评估函数,如方均根类型误差评估函数为
为深度神经网络映射误差评估函数,如方均根类型误差评估函数为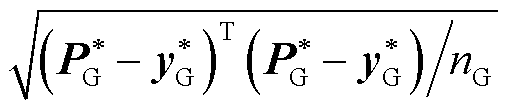 ;
;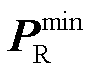 和
和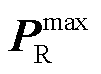 分别为新能源可消纳区间下界与上界,可由文献[35]计算获得。
分别为新能源可消纳区间下界与上界,可由文献[35]计算获得。
所提深度神经网络可信训练模型式(7)~式(10)解释如下:
1)内层最大化问题期望通过在式(8)所示的所有新能源场景中找到新能源功率PR,使得式(9)中经由深度神经网络G 的最优潮流计算结果预测值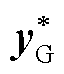 与式(10)中最优潮流真实计算结果
与式(10)中最优潮流真实计算结果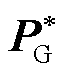 的映射误差评估函数值
的映射误差评估函数值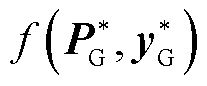 最劣。
最劣。
2)外层最小化问题期望通过调整深度神经网络参数(W, b),使得内层优化问题的最劣误差评估函数值趋于最小。
3)基本思想是基于构建的min-max双层规划模型,内层max优化问题通过优化手段定位到使深度神经网络映射误差最大的输入特征,从而可在避免对所有新能源场景进行最优潮流真实值的计算情况下,找到映射误差最劣时的新能源功率场景PR;进而,外层min优化问题通过更新深度神经网络参数(W, b)使得最劣误差评估结果趋于最小。
因此,通过求解可信训练模型式(7)~式(10),可达成下述两大目标:
1)通过内层优化问题,本文所提方法可为指定深度神经网络提供映射误差的理论评估,而非基于测试集的数值化验证。具体而言,基于深度神经网络映射误差上界,量化深度神经网络可信度,为调度运行人员提供指导。
2)通过外层最小化问题,本文所提方法可引导训练参数(W, b)改善深度神经网络映射误差,提升深度神经网络可信度,实现基于可信深度神经网络的最优潮流计算。
然而,所提深度神经网络可信训练模型式(7)~式(10)难以通过现有商业求解器直接求解。这是由于:①约束式(9)和式(10)为非解析模型,内层最大化问题难以由现有商业求解器直接求解;②所提模型式(7)~式(10)为min-max双层规划问题,现有求解器难以直接求解。
为此,本文将在第2节研究深度神经网络可信训练模型的求解方法。
本节首先基于KKT最优性条件与激活函数解析表征技术,将所提可信训练模型式(7)~式(10)解析构建为以混合整数规划模型为基础的双层规划问题;其次,提出基于Danskin定理的精确求解策略;最后,为减轻整数变量计算负担,提出基于凸松弛技术与模式识别思想的快速近似求解策略。
由前述可知:所提可信训练模型式(7)~式(10)的解析化依赖于解析表征约束式(9)和式(10)。本节详述如下。
2.1.1 约束式(9)的解析化构建
约束式(9)的解析化构建在于实现ReLU激活函数的激活区域解析化选择。为实现上述目的,本文将约束式(9)解析构建为
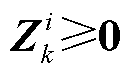 (11)
(11)
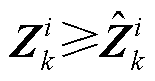 (12)
(12)
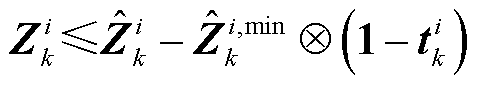 (13)
(13)
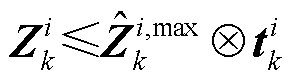 (14)
(14)
式中,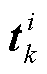 为第k层第i个神经元所对应的二进制变量,表征第k层第i个神经元的ReLU函数是否处于激活状态(
为第k层第i个神经元所对应的二进制变量,表征第k层第i个神经元的ReLU函数是否处于激活状态(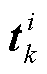 =0表征ReLU函数处于未激活状态;反之,表征ReLU函数处于激活状态);
=0表征ReLU函数处于未激活状态;反之,表征ReLU函数处于激活状态); 为Hadamard乘法算符;
为Hadamard乘法算符;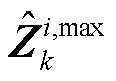 和
和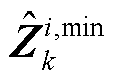 分别为第k层的第i个神经元输入向量
分别为第k层的第i个神经元输入向量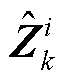 的上界与下界,可由附录式(A6)和式(A7)获得。
的上界与下界,可由附录式(A6)和式(A7)获得。
约束式(11)~式(14)与原始ReLU激活函数的等价性可通过图2解释。
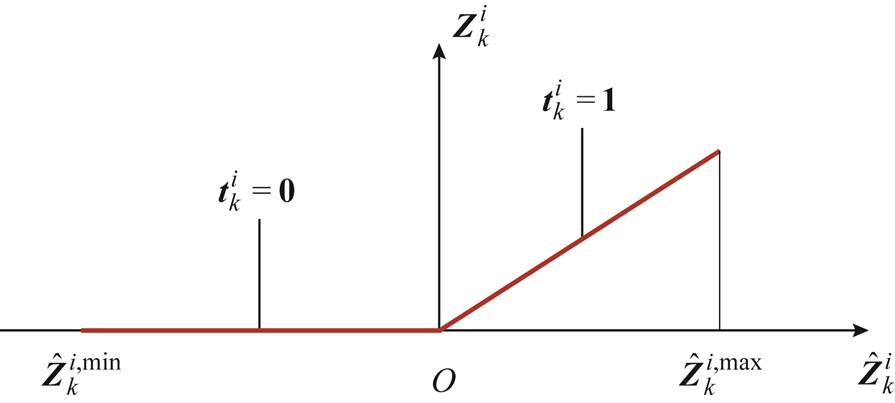
图2 基于二进制变量的ReLU激活函数解析构建
Fig.2 Explicit construction of the ReLU activation function based on binary variables
1)当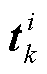 =1时,式(13)和式(14)分别变为
=1时,式(13)和式(14)分别变为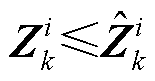 和
和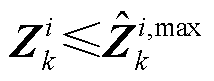 。进而,根据式(11)和式(12)可知
。进而,根据式(11)和式(12)可知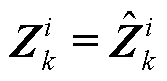 ,即ReLU函数处于激活状态(图2右侧红线部分)。
,即ReLU函数处于激活状态(图2右侧红线部分)。
2)当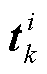 =0时,式(13)和式(14)分别变为
=0时,式(13)和式(14)分别变为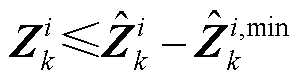 和
和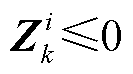 。进而,根据式(11)和式(12)可知此时
。进而,根据式(11)和式(12)可知此时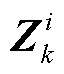 =0,即ReLU函数处于未激活状态(图2左侧红线部分)。
=0,即ReLU函数处于未激活状态(图2左侧红线部分)。
2.1.2 约束式(10)的解析化构建
约束式(10)的解析化核心在于构建优化问题式(1)和式(2)的最优解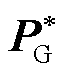 与给定输入向量PR间的约束关系。本文通过下述最优性条件,实现上述目的。
与给定输入向量PR间的约束关系。本文通过下述最优性条件,实现上述目的。
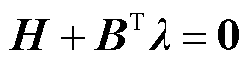 (15)
(15)
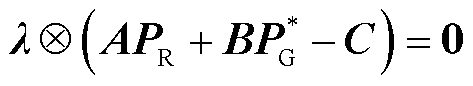 (16)
(16)
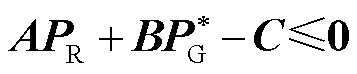 (17)
(17)
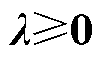 (18)
(18)
式中,λ为约束式(2)的对偶乘子向量。
依据最优化理论[36],优化问题式(1)和式(2)的最优解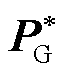 需满足驻点条件式(15)、互补松弛约束式(16)、原可行性条件式(17)以及对偶可行性条件式(18)。为此,可将约束式(10)等价替换为约束式(15)~式(18)。基于大M法[37],非线性约束式(16)可进一步等价表征为
需满足驻点条件式(15)、互补松弛约束式(16)、原可行性条件式(17)以及对偶可行性条件式(18)。为此,可将约束式(10)等价替换为约束式(15)~式(18)。基于大M法[37],非线性约束式(16)可进一步等价表征为
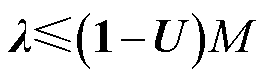 (19)
(19)
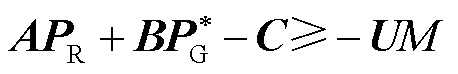 (20)
(20)
式中,U为二进制整数变量向量;M为充分大的正数。
由2.1节可知,所提可信训练模型式(7)~式(10)等价为
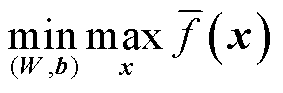 (21)
(21)
s.t. 式(3)、式(6)、式(11)~式(15)
式(17)~式(20) (22)
其中
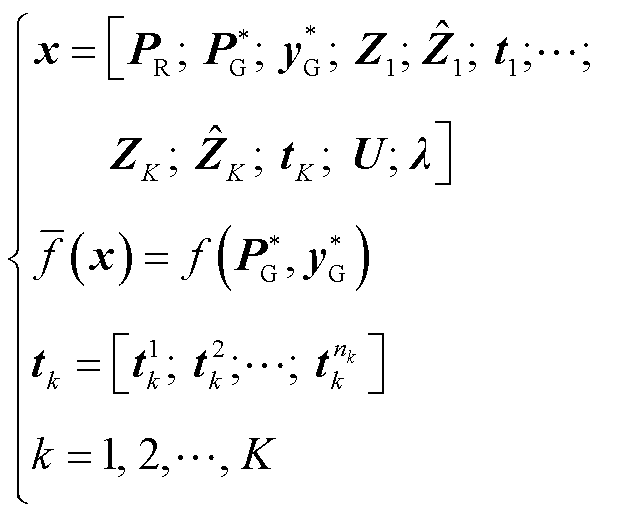
然而,现有商用求解器难以直接求解上述双层规划问题式(21)和式(22)。为此,本文提出梯度下降求解策略,即外层最小化问题中基于梯度下降更新后的(W, b),可使内层最大化问题目标函数值下降。
依据梯度下降原理,双层规划问题式(21)和式(22)的外层问题优化变量W和b的第s+1轮更新公式分别为
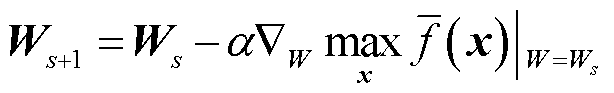 (23)
(23)
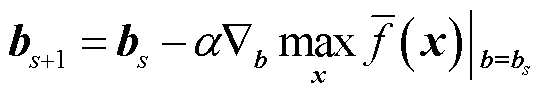 (24)
(24)
式中,α为学习率; 为梯度算子;(Ws, bs)为(W, b)的第s轮计算结果。
为梯度算子;(Ws, bs)为(W, b)的第s轮计算结果。
由式(23)和式(24)可知,(W, b)的更新难点在于计算其梯度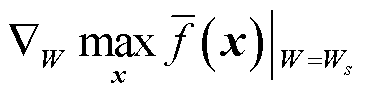 与
与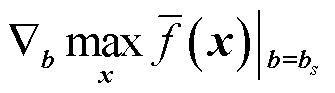 ,为此,本文引入Danskin定理[38]计算上述梯度。
,为此,本文引入Danskin定理[38]计算上述梯度。
Danskin定理 若有:实数空间连续变量y和z,以及具有可变优化变量z的连续函数g(y, z),则函数h(y)=maxg(y, z)在y方向上的导数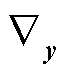 h(y)为
h(y)为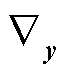 g(y, z*),其中z*为maxg(y, z)的最优解。
g(y, z*),其中z*为maxg(y, z)的最优解。
在Danskin定理中,令(y, z)=(W, x)及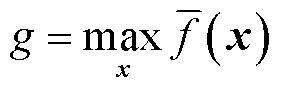 ,则式(23)中的梯度
,则式(23)中的梯度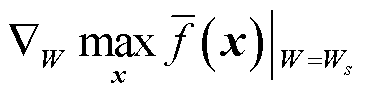 可写为
可写为
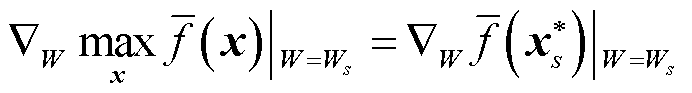 (25)
(25)
式中,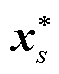 为式(21)和式(22)的内层优化问题在(W, b)=(Ws, bs)时的最优解。
为式(21)和式(22)的内层优化问题在(W, b)=(Ws, bs)时的最优解。
同理,式(24)中的梯度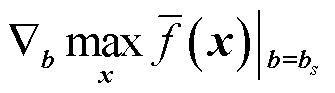 为
为
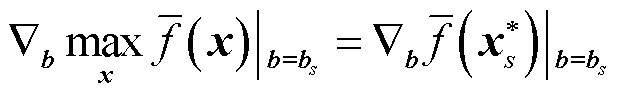 (26)
(26)
因此,本文可通过式(23)和式(24)迭代更新深度神经网络参数以降低深度神经网络理论映射误差函数值,提升深度神经网络可信度。上述深度神经网络可信训练方法求解策略流程如图3所示。
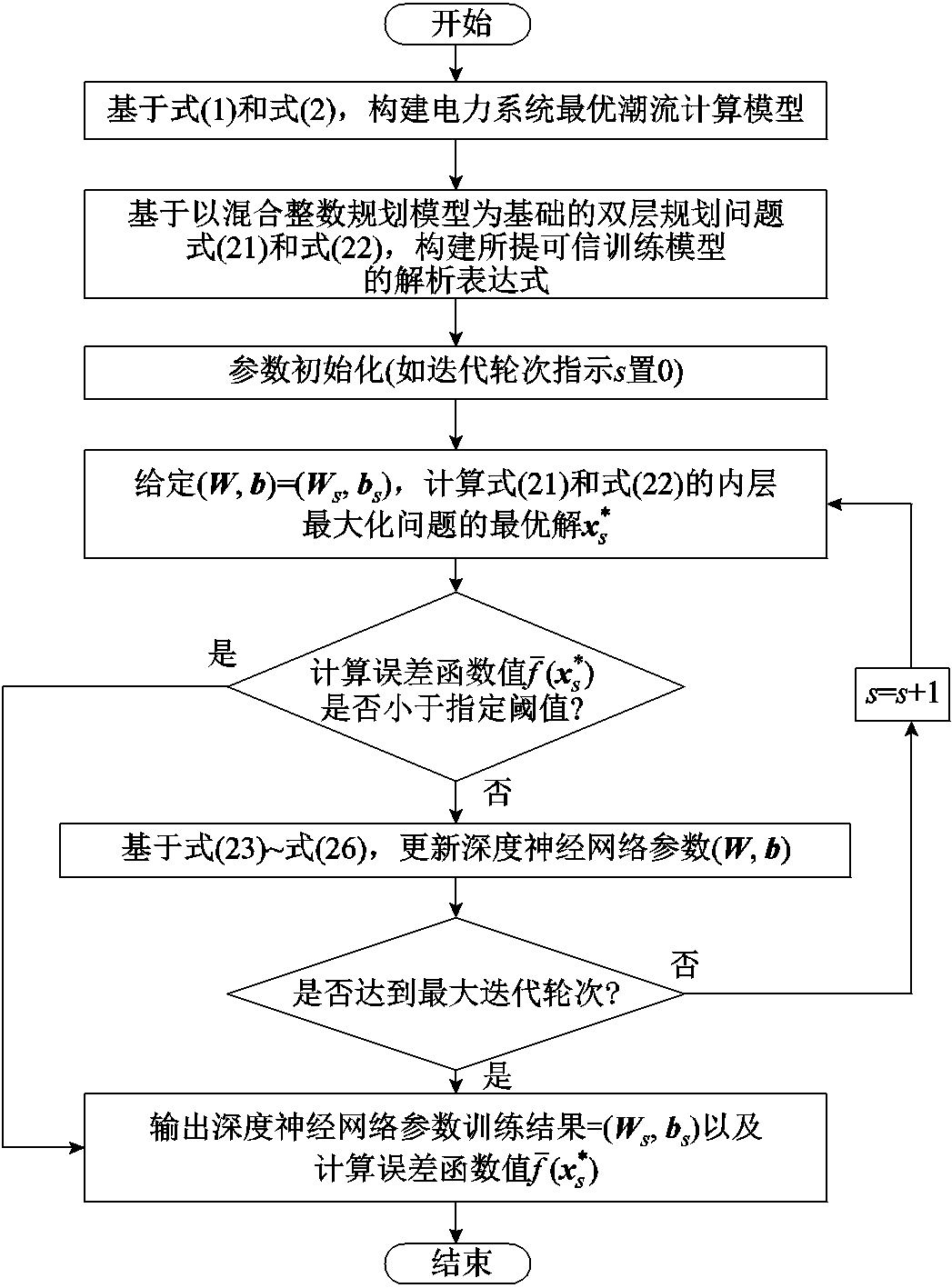
图3 基于Danskin定理的求解策略流程
Fig.3 Flow chart of the strategy using Danskin’s theorem
2.2节求解策略的计算负担主要在于所提可信训练模型式(21)和式(22)内层优化问题的整数变量t。为此,本文进一步研究减轻整数变量t所带来计算负担的深度神经网络可信训练模型快速近似求解策略。应当注意的是,本节快速近似求解策略与2.2节精确求解策略的区别在于可信训练模型式(21)和式(22)内层优化问题的求解方式。特别地,2.2节的精确求解策略需在内层优化问题中考虑整数变量t的精确求解;本节所提快速近似求解策略希望实现无需整数变量t的内层优化问题快速近似求解。
由2.1节可知,整数变量t的引入是为实现约束式(11)~式(14)中的ReLU函数激活区域选择。为避免整数变量t,本节首先基于凸松弛思想,将约束式(11)~式(14)松弛为
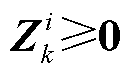 (27)
(27)
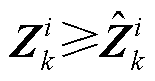 (28)
(28)
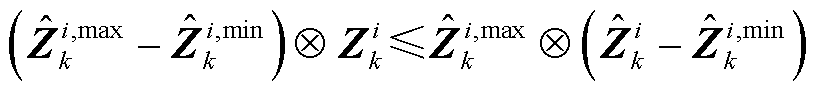 (29)
(29)
松弛后约束式(27)~式(29)与松弛前约束式(11)~式(14)的关系如图4所示。
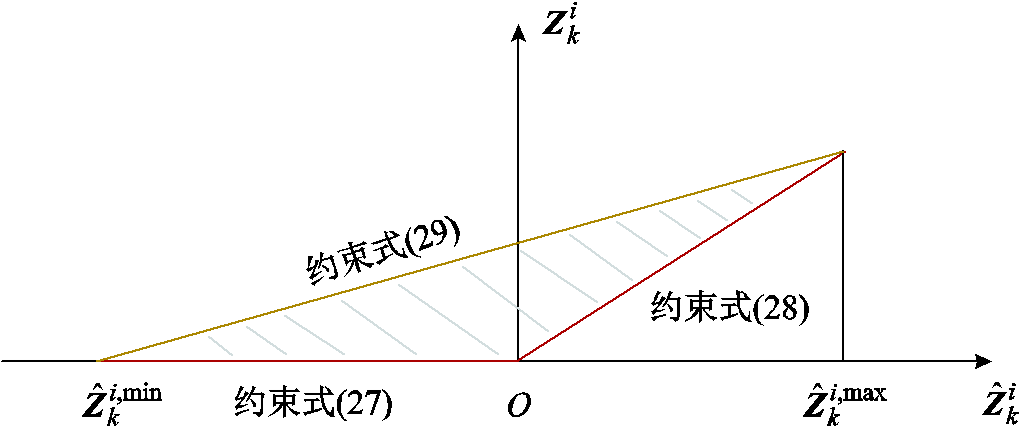
图4 基于凸松弛技术的ReLU激活函数重构
Fig.4 Reformation of ReLU activation functions based on convex relaxation
由图4可知,若将所提可信训练模型式(21)和式(22)中的约束式(11)~式(14)替换为约束式(27)~式(29),所提可信训练模型式(21)和式(22)的内层优化问题可行域将由红线部分扩大为灰色阴影区域。为避免由于内层优化问题可行域扩大而显著高估深度神经网络的最优潮流计算结果映射误差,本文在上述快速近似求解策略中进一步融合模式识别思想。本文模式识别思想的核心在于:提前辨识当内层优化问题最优时,深度神经网络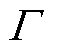 中各神经元的激活模式。为实现上述模式识别,本文基于两轮快速近似迭代求解结果,将两轮迭代中一直处于未激活状态的神经元在下一轮次迭代中设为未激活状态,如图5所示。上述模式识别思想可解释如下:深度神经网络的训练本质是学习优化问题式(1)和式(2)中由输入向量PR至其最优解
中各神经元的激活模式。为实现上述模式识别,本文基于两轮快速近似迭代求解结果,将两轮迭代中一直处于未激活状态的神经元在下一轮次迭代中设为未激活状态,如图5所示。上述模式识别思想可解释如下:深度神经网络的训练本质是学习优化问题式(1)和式(2)中由输入向量PR至其最优解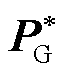 的映射关系。同时,为实现深度神经网络精细化训练,深度神经网络参数迭代式(23)和式(24)中的学习率不应取得太大[39],即意味着邻近两轮迭代内层优化问题最优解
的映射关系。同时,为实现深度神经网络精细化训练,深度神经网络参数迭代式(23)和式(24)中的学习率不应取得太大[39],即意味着邻近两轮迭代内层优化问题最优解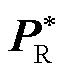 处于某一邻域内。由多参数规划理论[40]可知,优化问题式(1)和式(2)中的输入向量PR至其最优解
处于某一邻域内。由多参数规划理论[40]可知,优化问题式(1)和式(2)中的输入向量PR至其最优解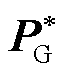 的映射关系为分段映射函数关系,且当PR在一定邻域范围内变化时,分段映射函数关系不变。因此,由于深度神经网络的训练本质为模拟分段映射关系,且前后两轮内层优化问题最优解处于邻域范围,可认为邻近迭代轮次中的神经元激活状态应处于类似模式,即未激活神经元位置相似。
的映射关系为分段映射函数关系,且当PR在一定邻域范围内变化时,分段映射函数关系不变。因此,由于深度神经网络的训练本质为模拟分段映射关系,且前后两轮内层优化问题最优解处于邻域范围,可认为邻近迭代轮次中的神经元激活状态应处于类似模式,即未激活神经元位置相似。
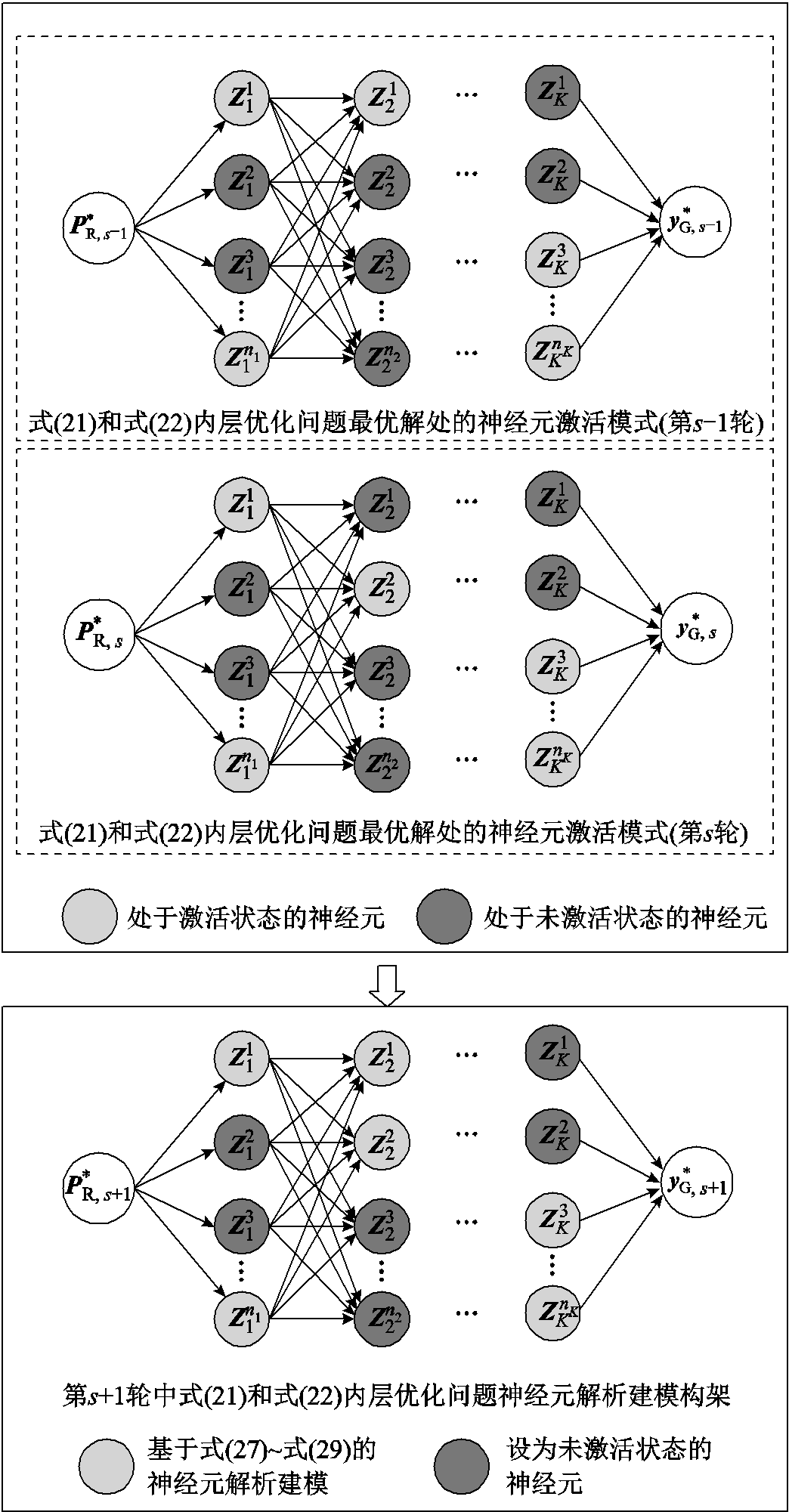
图5 模式识别基本思想
Fig.5 Basic idea of pattern recognition
本文以2机4节点与54机IEEE 118节点测试系统,验证所提基于可信深度神经网络的最优潮流计算方法。本文仿真环境为AMD Ryzen 5 3600X 6-Core Processor 3.80 GHz、16 GB RAM,并采用Pytorch开源包[41]、Pyomo开源包[42]及其Gurobi求解器[43]实现所提方法。本文在4节点测试系统的节点1、3上连接新能源场站,节点1、4连接发电机组;在IEEE 118节点测试系统中的99个节点均连接新能源场站,54个节点连接发电机组。测试系统具体参数设置(包括新能源场站容量、发电机组成本系数、线路参数等)见文献[44]。
首先,3.1节通过4节点系统验证所提可信训练模型及其基于Danskin定理的精确迭代求解策略的有效性,并对所提方法与传统最优潮流方法的计算效率进行对比。然后,3.2节通过IEEE 118节点系统验证所提基于凸松弛技术与模式识别思想的快速近似求解策略的有效性。
本节基于4节点测试系统验证2.1节所提可信训练模型及2.2节精确求解策略的有效性。特别地,本节对比下述两类深度神经网络训练方法。
M1:基于训练集的传统深度神经网络训练方法。本文以文献[18]为该类典型方法进行对比。
M2:基于2.1节可信训练模型及2.2节精确求解策略的可信深度神经网络训练方法。特别地,所提可信训练模型式(21)和式(22)的映射误差函数选为机组功率累计映射方均根误差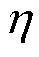 ,表示为
,表示为
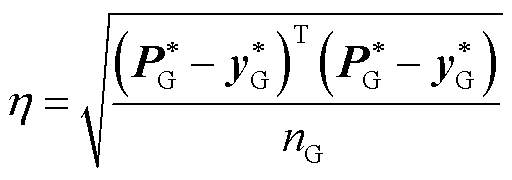 (30)
(30)
在M1与M2方法中,深度神经网络均包含2个全连接隐含层,每层包含20个神经元,学习率均设置为1×10-4。其中M1的迭代次数、批次样本数分别设置为200、5,M2的最大迭代次数设置为200。
本文首先基于有限测试集和可信训练模型内层优化问题式(21)和式(22),在图6中对比了M1和M2方法所训练的深度神经网络在这两种评估方法下的机组功率累计映射方均根误差最大值,并在图7和图8中对比了两种评估方法下的机组功率最大映射偏差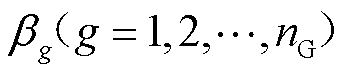 ,表达式为
,表达式为
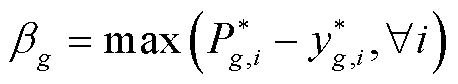 (31)
(31)
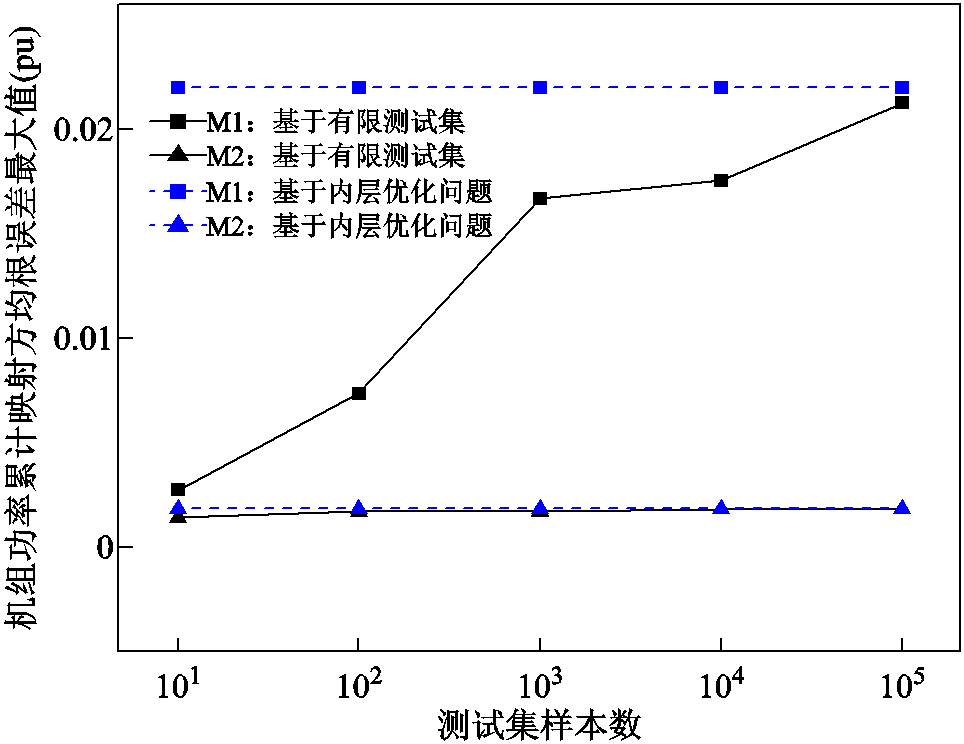
图6 机组功率累计映射方均根误差最大值
Fig.6 Maximum root mean squared cumulative errors of generation levels
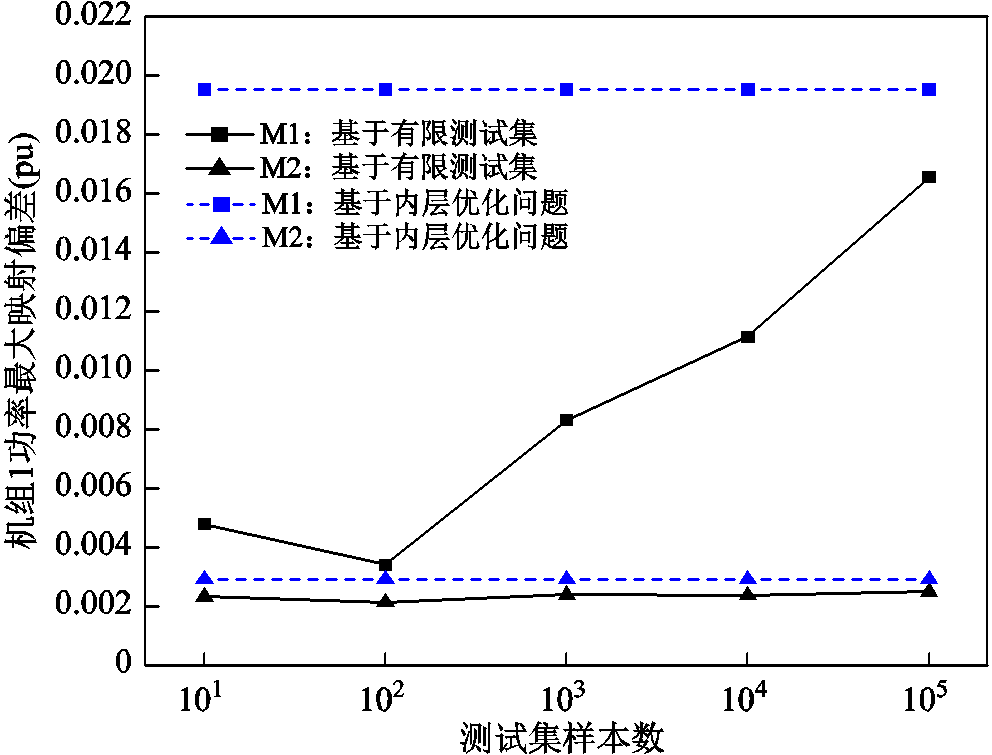
图7 机组1功率最大映射偏差
Fig.7 Maximum mapping errors of Unit 1
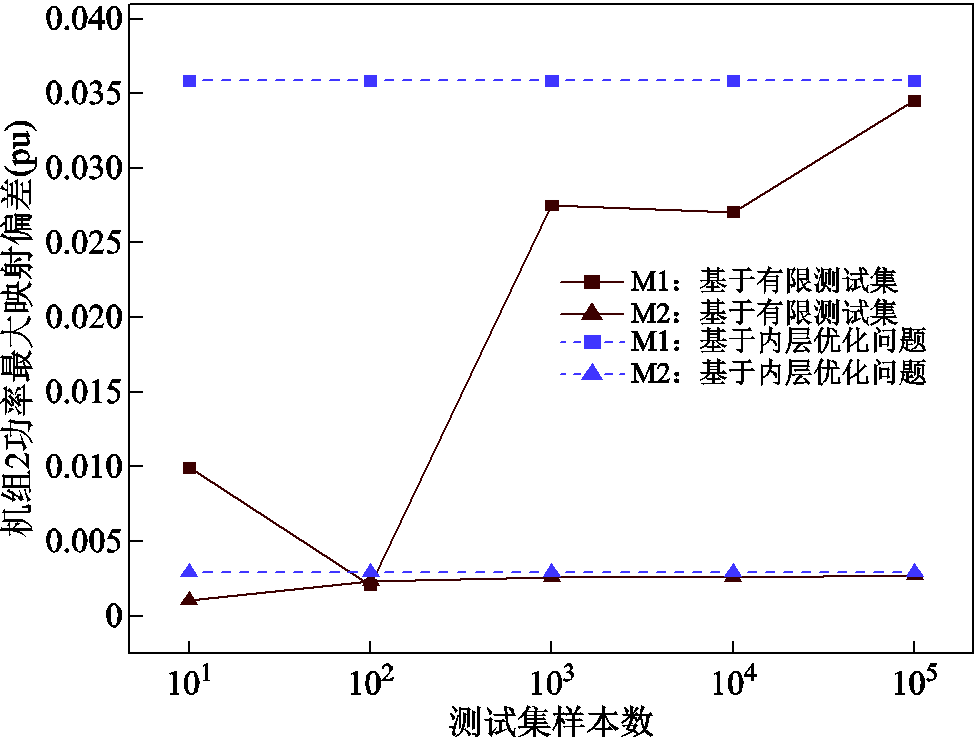
图8 机组2功率最大映射偏差
Fig.8 Maximum mapping errors of Unit 2
式中,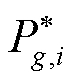 为第g个机组在第i个测试数据的最优潮流真实计算结果;
为第g个机组在第i个测试数据的最优潮流真实计算结果;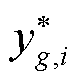 为第g个机组在第i组测试数据中基于深度神经网络的最优潮流计算结果预测值。
为第g个机组在第i组测试数据中基于深度神经网络的最优潮流计算结果预测值。
其次在4节点测试系统中,本文还基于可信训练模型内层优化问题式(21)和式(22),在图6~图8中对比了深度神经网络在M1和M2这两种不同训练方法下的映射误差最大值。
由图6~图8可知:
1)为验证现有基于有限测试集评估的局限性,本文在M1及M2两种训练方法下,对比了基于所提可信训练模型内层优化问题式(21)和式(22)评估得到的映射误差最大值与基于有限测试集的映射误差最大值。结果表明,前者映射误差最大值均大于后者,例如,在图6中,M1方法基于内层优化问题的映射误差为0.022 0(pu),而M1方法基于有限测试集的映射误差即使在测试集样本数达到1×105时,也仅为0.021 2(pu);M2方法基于内层优化问题的映射误差为0.001 9(pu),而M2方法基于有限测试集的映射误差即使在测试集样本数达到1×105时,也仅为0.001 8(pu)。上述结果的出现是由于:有限测试集本质是式(21)和式(22)内层优化问题可行域的部分可行点,即基于有限测试集的映射误差评估是通过有限可行点表征式(21)和式(22)内层优化问题目标函数最值;而本文所提方法通过直接求解式(21)和式(22)内层优化问题实现映射误差的精准评估。换言之,有限测试集仅通过部分新能源场景实现映射误差的有限估计,而所提方法可认为是在完备新能源场景下实现映射误差评估的精准评估。基于上述原因,从图6~图8中还可观察到,当测试集数量逐渐上升时,两者间的误差评估结果可能趋近。
2)为验证所提M2训练方法相较于M1训练方法的优势,本文基于可信训练模型内层优化问题式(21)和式(22),分别评估了M1和M2两种训练方法下深度神经网络的最大映射误差。结果表明,M1方法下深度神经网络的最大映射误差远大于M2方法下最大映射误差,如在图7中,M1方法映射误差为0.019 5(pu),而M2方法映射误差为0.002 9(pu);在图8中,M1方法映射误差为0.035 8(pu),而M2方法映射误差为0.002 9(pu)。上述结果产生的原因在于:M1方法仅基于有限训练集进行深度神经网络参数训练,难以完备考虑所有新能源场景以更新深度神经网络参数;而本文所提M2方法通过评估深度神经网络在所有新能源场景下的可信度,将可信评估结果引入深度神经网络参数更新中,最终实现映射误差评估结果的改善。应当注意的是,上述结果是在M1方法数据量和M2方法迭代轮次相当的情况下对比获得的。因此,相较于M1方法,所提M2方法可为深度神经网络参数的训练提供更为有效的引导信息,指导深度神经网络参数有效降低映射误差。
本文还基于4节点测试系统,验证所提计算方法相较于传统最优潮流方法的计算效率优势。特别地,所提方法利用深度神经网络的“端到端”特性,实现由新能源功率至最优潮流计算结果的快速映射,为非迭代型算法;而传统最优潮流方法普遍为迭代型算法(如Gurobi求解器中配置的单纯型算法)。以求解1×104组不同新能源场景下的最优潮流问题式(1)和式(2)为例,本文所提方法在4节点测试系统中,可将计算时间由1 286.3 s缩减至6.1 s,显著体现所提方法的计算效率优势。
本节基于IEEE 118节点测试系统验证2.3节快速近似求解策略的有效性。特别地,本文对比如下三类训练方法的深度神经网络映射误差。
S1:基于训练集的传统深度神经网络训练方法。本文以文献[18]为该类典型方法进行对比。
S2:2.3节仅考虑凸松弛技术的快速近似求解策略的可信深度神经网络训练方法。
S3:2.3节同时考虑凸松弛技术与模式识别思想的快速近似求解策略的可信深度神经网络训练方法。
特别地,三种训练方法中深度神经网络均包含4个全连接隐含层,每层采用50个神经元,学习率均设置为5×10-5。其中S1的迭代次数、批次样本数分别设置为200、20,S2、S3的最大迭代次数设置为100。
在给定深度神经网络参数后,上述三类方法仍可采用式(21)和式(22)内层优化问题进行映射误差评估。但如2.3节所述,当神经元较多时,式(21)和式(22)内层优化问题与神经元个数相关的整数变量增加,使得内层优化问题可能不易求解。为此,本文将2.3节凸松弛技术与模式识别思想应用到内层优化问题中,实现无需引入与神经元个数相关的整数变量的映射误差高效评估。
为验证所提方法的有效性,本文首先在图9中对比S1~S3方法所训练的深度神经网络的机组功率最大映射误差。由图9可知,S1方法下机组功率最大映射误差基本均远大于S2和S3方法;S2方法的映射误差总体而言又大于S3方法。特别地,所提S3方法的机组功率最大映射误差平均值为0.062 8(pu),低于S1和S2方法的0.502 6(pu)和0.120 5(pu),其中S3方法相较于S1方法计算误差降低了87.49%。这是由于S1方法仅考虑有限新能源场景训练深度神经网络参数,而S2和S3方法将深度神经网络在所有新能源场景下的可信评估结果引入到参数更新中,以实现对最大映射误差的改善。同时,由于S3方法在快速近似求解策略中进一步考虑模式识别思想,可缓解凸松弛技术所导致的映射误差高估,在可信评估结果改善上更具引导性,从而使得S3方法又优于S2方法。
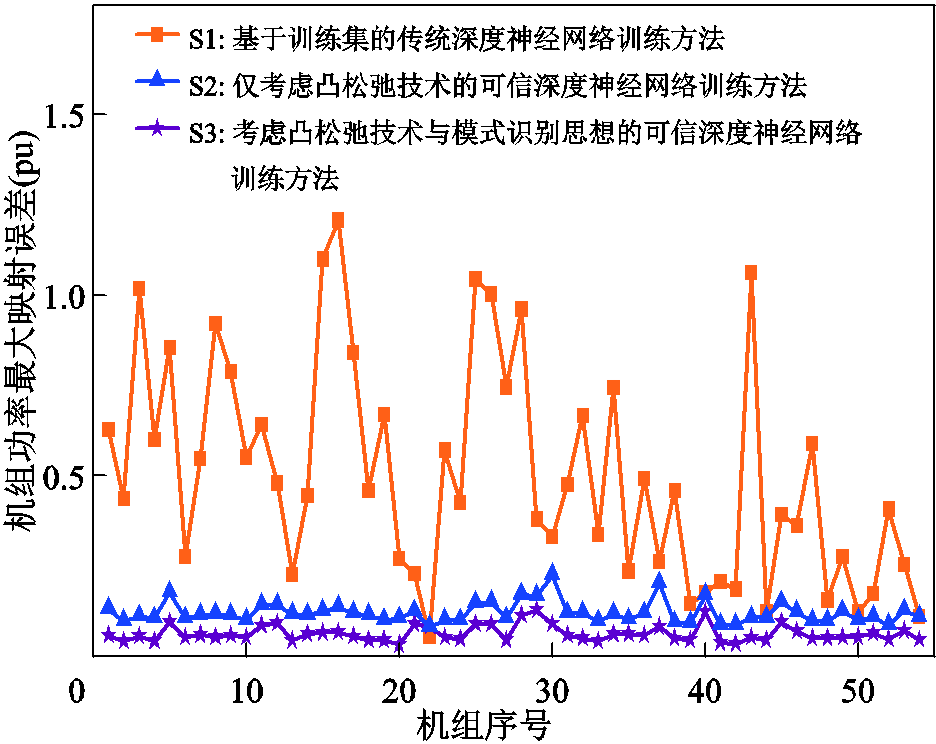
图9 机组功率最大映射误差
Fig.9 Maximum mapping errors of units
特别地,本文还基于1×104个测试样本统计了机组功率最大映射误差评估结果。仿真结果发现:基于测试集样本的映射误差评估结果仍旧小于式(21)和式(22)内层优化问题的评估结果。例如:机组35的基于测试集样本的映射误差评估结果为0.043 9(pu),而基于内层优化问题的评估结果为0.061 6(pu),映射评估结果精度提升了28.7%。这是由于基于有限测试集的评估方法只能考虑部分新能源场景来实现映射误差的有限估计,而基于式(21)和式(22)内层优化问题的评估方法可认为是在完备新能源场景下实现映射误差的更为精准的评估。
另外,本文还在IEEE 118节点测试系统中对比了采用不同求解策略的内层优化问题计算时间,结果见表1。其中,精确求解策略即为本文2.2节所述不采用凸松弛技术与模式识别思想的求解策略;快速近似求解策略指代本文2.3节所述采用凸松弛技术与模式识别思想的求解策略。
表1 内层优化问题不同求解策略求解效率对比
Tab.1 Relationship between forecast performance and forecast horizon

求解策略求解耗时/min 精确求解策略>1 440 快速近似求解策略①25
①求解50次内层优化问题求解的平均时间。
由表1可知,若采用精确求解策略,内层优化问题难以在一天之内(即1 440 min)完成计算,使得所提基于Danskin定理迭代框架的可信训练模型求解具有较重的计算负担。上述计算负担主要来源于精确求解策略需对深度神经网络的每一个神经元上的ReLU激活函数均引入一组二进制变量以表征其激活状态(见图2)。快速近似求解策略由于采用凸松弛技术与模式识别思想,避免了上述表征ReLU激活状态的大量二进制变量,从而使得内层优化问题的平均求解时间仅为25 min,大幅缓解了整数变量所带来的计算负担。
本文也在IEEE 118节点测试系统中,以求解1×104组不同新能源场景下的最优潮流问题式(1)和式(2)为例,阐述所提方法相较于传统最优潮流方法的计算优势。仿真结果发现,在IEEE 118节点测试系统中,可将计算时间由1 611.8 s大幅缩减至7.6 s。
随着风/光等新能源大规模并网,需在精细时间颗粒度上实现以最优潮流为核心的电力系统资源配置与运行分析。虽然深度神经网络具备最优潮流高效计算的应用潜力,但是目前由于其“黑箱特性”,基于深度神经网络的最优潮流计算方法的可信应用仍有待探究。为此,本文研究了基于可信深度神经网络的最优潮流计算方法。主要结论如下:
1)本文所提基于min-max双层规划问题的深度神经网络可信训练模型,可在给定深度神经网络参数下,基于内层优化问题实现深度神经网络计算性能的理论评估,实现无需有限测试集的最优潮流计算结果可信度精准量化。进而,所提可信训练模型可通过所提基于Danskin定理的梯度下降求解方法实现精确求解。
2)本文所提基于考虑凸松弛技术与模式识别思想的快速近似迭代求解策略,可在减轻精确迭代求解策略中的整数变量计算负担的同时,保持以可信度改善为导向的深度神经网络参数更新。
附 录
1. 约束式(2)具体形式
约束式(2)的具体形式可写作
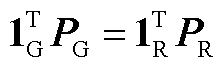 (A1)
(A1)
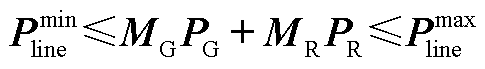 (A2)
(A2)
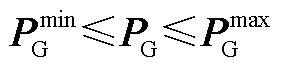 (A3)
(A3)
式中,1G和1R为全1向量;MG和MR分别为机组和新能源的功率转移分布因子矩阵;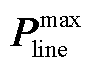 和
和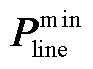 分别为线路传输容量上界与下界;
分别为线路传输容量上界与下界;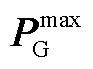 和
和 分别为机组有功功率上界与下界。
分别为机组有功功率上界与下界。
2. 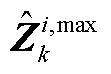 与
与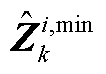 计算方法
计算方法
为便于计算,定义两类算子符号为
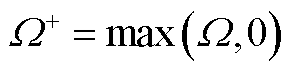 (A4)
(A4)
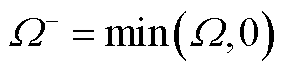 (A5)
(A5)
基于式(A4)和式(A5),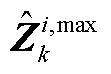 与
与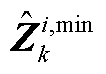 可表示为
可表示为
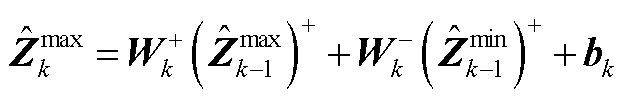 (A6)
(A6)
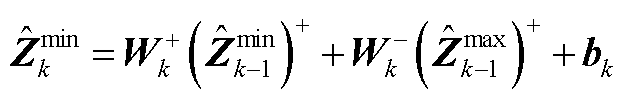 (A7)
(A7)
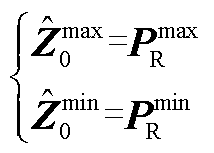 (A8)
(A8)
其中,k=1, 2,…, K。
参考文献
[1] 习近平. 决胜全面建成小康社会夺取新时代中国特色社会主义伟大胜利——在中国共产党第十九次全国代表大会上的报告[EB/OL]. (2017-10-18) [2023-08-03]. https://www.gov.cn/zhuanti/2017-10/ 27/content_5234876.htm.
[2] 秦博宇, 周星月, 丁涛, 等. 全球碳市场发展现状综述及中国碳市场建设展望[J]. 电力系统自动化, 2022, 46(21): 186-199.
Qin Boyu, Zhou Xingyue, Ding Tao, et al. Review on development of global carbon market and prospect of China’s carbon market construction[J]. Automation of Electric Power Systems, 2022, 46(21): 186-199.
[3] International Energy Agency. An energy sector roadmap to carbon neutrality in China[R/OL]. (2021-09-01)[2023-08-03]. https://iea.blob.core.windows. net/assets/9448bd6e-670e-4cfd-953c-32e822a80f77/ AnenergysectorroadmaptocarbonneutralityinChina.pdf.
[4] 李军徽, 邵岩, 朱星旭, 等. 计及碳排放量约束的多区域互联电力系统分布式低碳经济调度[J]. 电工技术学报, 2023, 38(17): 4715-4728.
Li Junhui, Shao Yan, Zhu Xingxu, et al. Carbon emissions constraint distributed low-carbon economic dispatch of power system[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4715-4728.
[5] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207.
Zhang Shenxi, Wang Danyang, Cheng Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207.
[6] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[7] 中华人民共和国中央人民政府. 中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见[EB/OL]. (2021-10-24)[2023-08-03]. https://www.gov.cn/zhengce/2021-10/24/content_ 5644613.htm.
[8] Wu Jianghua, Luh P B, Chen Yonghong, et al. Synergistic integration of machine learning and mathematical optimization for unit commitment[J]. IEEE Transactions on Power Systems, 2023: 1-10.
[9] 韩丽, 王冲, 于晓娇, 等. 考虑风电爬坡灵活调节的碳捕集电厂低碳经济调度[J]. 电工技术学报, 2024, 39(7): 2033-2045.
Han Li, Wang Chong, Yu Xiaojiao, et al. Low-carbon and economic dispatch considering the carbon capture power plants with flexible adjustment of wind power ramp[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2033-2045.
[10] Zhang Yijian, Dall'Anese E, Hong Mingyi. Dynamic ADMM for real-time optimal power flow[C]//2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, 2017: 1085-1089.
[11] Bagen B, Bhavaraju M, Choi J, et al. Composite power system reliability[R]. IEEE Power and Energy Society, 2022.
[12] 张伯明, 陈寿孙. 高等电力网络分析[M]. 北京: 清华大学出版社, 1996.
[13] Sun D, Ashley B, Brewer B, et al. Optimal power flow by Newton approach[J]. IEEE Transactions on Power Apparatus and Systems, 1984, PAS-103(10): 2864-2880.
[14] Jabr R A, Coonick A H, Cory B J. A primal-dual interior point method for optimal power flow dispatching[J]. IEEE Transactions on Power Systems, 2002, 17(3): 654-662.
[15] Huang Shengjun, Dinavahi V. Fast batched solution for real-time optimal power flow with penetration of renewable energy[J]. IEEE Access, 2018, 6: 13898-13910.
[16] Yang Yan, Yu Juan, Yang Zhifang, et al. A trustable data-driven framework for composite system reliability evaluation[J]. IEEE Systems Journal, 2022, 16(4): 6697-6707.
[17] 余娟, 杨燕, 杨知方, 等. 基于深度学习的概率能量流快速计算方法[J]. 中国电机工程学报, 2019, 39(1): 22-30, 317.
Yu Juan, Yang Yan, Yang Zhifang, et al. Fast probabilistic energy flow analysis based on deep learning[J]. Proceedings of the CSEE, 2019, 39(1): 22-30, 317.
[18] Pan Xiang, Zhao Tianyu, Chen Minghua. DeepOPF: deep neural network for DC optimal power flow[C]// 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, Beijing, China, 2019: 1-6.
[19] 武新章, 郭苏杭, 代伟, 等. 基于特征降维与分块的输电网概率最优潮流深度学习方法[J]. 电力自动化设备, 2023, 43(8): 174-180.
Wu Xinzhang, Guo Suhang, Dai Wei, et al. Feature dimension reduction and partitioning based deep learning method for probabilistic optimal power flow of transmission network[J]. Electric Power Automation Equipment, 2023, 43(8): 174-180.
[20] Park S, Chen Wenbo, Mak T W K, et al. Compact optimization learning for AC optimal power flow[J]. IEEE Transactions on Power Systems, 2024, 39(2): 4350-4359.
[21] Singh M, Kekatos V, Giannakis G. Learning to solve the AC-OPF using sensitivity-informed deep neural networks[C]//2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 2022: 1.
[22] Kim M, Kim H. Projection-aware deep neural network for DC optimal power flow without constraint violations[C]//2022 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, Singapore, Singapore, 2022: 116-121.
[23] Fioretto F, Mak T W K, van Hentenryck P. Predicting AC optimal power flows: combining deep learning and Lagrangian dual methods[C]//Proceedings of the AAAI Conference on Artificial Intelligence, New York, USA, 2020: 630-637.
[24] Huang Wanjun, Pan Xiang, Chen Minghua, et al. DeepOPF-V: solving AC-OPF problems efficiently[J]. IEEE Transactions on Power Systems, 2022, 37(1): 800-803.
[25] Li Yuxuan, Zhao Chaoyue, Liu Chenang. Solving non-linear optimization problem in engineering by model-informed generative adversarial network (MI-GAN)[C]//2022 IEEE International Conference on Data Mining Workshops (ICDMW), Orlando, FL, USA, 2022: 198-205.
[26] Wang Junfei, Srikantha P. Fast optimal power flow with guarantees via an unsupervised generative model[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4593-4604.
[27] 杨东升, 吉明佳, 周博文, 等. 基于双生成器生成对抗网络的电力系统暂态稳定评估方法[J]. 电网技术, 2021, 45(8): 2934-2945.
Yang Dongsheng, Ji Mingjia, Zhou Bowen, et al. Transient stability assessment of power system based on DGL-GAN[J]. Power System Technology, 2021, 45(8): 2934-2945.
[28] 杨剑锋, 秦钟, 庞小龙, 等. 基于深度学习网络的输电线路异物入侵监测和识别方法[J]. 电力系统保护与控制, 2021, 49(4): 37-44.
Yang Jianfeng, Qin Zhong, Pang Xiaolong, et al. Foreign body intrusion monitoring and recognition method based on Dense-YOLOv3 deep learning network[J]. Power System Protection and Control, 2021, 49(4): 37-44.
[29] 朱永利, 张翼, 蔡炜豪, 等. 基于辅助分类-边界平衡生成式对抗网络的局部放电数据增强与多源放电识别[J]. 中国电机工程学报, 2021, 41(14): 5044-5053.
Zhu Yongli, Zhang Yi, Cai Weihao, et al. Data augmentation and pattern recognition for multi-sources partial discharge based on boundary equilibrium generative adversarial network with auxiliary classifier[J]. Proceedings of the CSEE, 2021, 41(14): 5044-5053.
[30] Yang Yafei, Wu Lei. Machine learning approaches to the unit commitment problem: current trends, emerging challenges, and new strategies[J]. The Electricity Journal, 2021, 34(1): 106889.
[31] Chen Yize, Tan Yushi, Deka D. Is machine learning in power systems vulnerable?[C]//2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, Aalborg, Denmark, 2018: 1-6.
[32] Lin Wei, Yang Zhifang, Yu Juan, et al. Toward fast calculation of probabilistic optimal power flow[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3286-3288.
[33] 刘承锡, 徐慎凯, 赖秋频. 基于全纯嵌入法的非迭代电力系统最优潮流计算[J]. 电工技术学报, 2023, 38(11): 2870-2882.
Liu Chengxi, Xu Shenkai, Lai Qiupin. Non-iterative optimal power flow calculation based on holomorphic embedding method[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2870-2882.
[34] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90.
[35] Lin Wei, Chen Yue, Li Qifeng, et al. An AC-feasible linear model in distribution networks with energy storage[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1224-1239.
[36] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997.
[37] Lin Wei, Yang Zhifang, Yu Juan, et al. Transmission expansion planning with feasible region of hydrogen production from water electrolysis[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2863-2874.
[38] Danskin J M. The Theory of Max-Min and Its Application to Weapons Allocation Problems[M]. Berlin: Springer, 1967.
[39] (美)伊恩·古德费洛, (加)约书亚·本吉奥, (加)亚伦·库维尔. 深度学习[M]. 赵申剑, 黎彧君, 符天凡, 等, 译. 北京: 人民邮电出版社, 2017.
[40] 张林, 杨高峰, 汪洋, 等. 基于多参数规划理论的互联电网直流联络线功率可行域确定方法[J]. 中国电机工程学报, 2019, 39(19): 5763-5771, 5904.
Zhang Lin, Yang Gaofeng, Wang Yang, et al. Determination of the DC tie-line transfer capacity region of the interconnected power grid: a multi-parametric programming approach[J]. Proceedings of the CSEE, 2019, 39(19): 5763-5771, 5904.
[41] Paszke A, Gross S, Massa F, et al. PyTorch: an imperative style, high-performance deep learning library[C]//Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 8026-8037.
[42] Hart W E, Watson J P, Woodruff D L. Pyomo: modeling and solving mathematical programs in Python[J]. Mathematical Programming Computation, 2011, 3(3): 219-260.
[43] Gwyneth Butera. Getting started with Gurobi optimizer[EB/OL]. (2023-08-03)[2023-08-03]. https: //support.gurobi.com/hc/en-us/articles/14799677517585.
[44] Lin Wei. SystemParameters_NN_OPF[EB/OL]. (2023-05-11)[2023-08-03]. https://figshare.com/articles/dataset/ SystemParameters_NN_OPF/22799744.
Abstract To conduct the optimal power flow (OPF) for resource allocation and system analysis within small time resolutions in renewable power systems, deep neural network-based (DNN-based) optimal power flow calculation methods have gained much attention. Nevertheless, since DNNs possess a black-box nature, the existing methods generally rely on limited training and testing sets for DNNs in the training and evaluation process. This makes difficulties in theoretically quantifying computational errors, and lacks the theoretical support for their trustworthiness. Consequently, this paper proposes an optimal power flow calculation method based on a trustworthy DNN.
First, this paper focuses on the theoretical quantitative evaluation of mapping errors in DNNs and introduces a trustworthy DNN training model based on a bi-level min-max programming problem, enabling a training process with trustworthiness quantifications. Furthermore, based on the KKT conditions and the analytical representation of activation functions, this paper explicitly reformulates the proposed model as a bi-level programming problem by introducing integer variables, followed by developing an exact solution strategy based on Danskin’s theorem. Moreover, this paper proposes a fast approximate solution strategy using convex relaxation and pattern recognition to alleviate the computational burden of integer variables.
Numerical experiments in a 4-bus test system showcase: (1) Compared with existing methods, the proposed trustworthy DNN training model solved by our exact solution strategy can more accurately quantify the trustworthiness of DNNs. The mapping error evaluated based on a limited testing set (in existing methods) is smaller than that based on the proposed trustworthy DNN model (in the proposed method), even if the sample number in the testing set has been set to 1×104. (2) The mapping error of DNNs which are trained based on existing methods can reach up to 0.022 0(pu), while the mapping error of the proposed method is only 0.001 9(pu). Numerical experiments in the IEEE 118-bus system further verify: (1) Compared with existing methods, the average maximum mapping error of generation levels can decrease from 0.502 6(pu) to 0.120 5(pu) once the proposed trustworthy DNN training model and our solved by our fast approximate solution strategy with convex relaxation. (2) When pattern recognition is additionally added in our fast approximate solution strategy, the average maximum mapping error can decrease to 0.062 8(pu). Compared with the exact solution strategy which cannot complete one solution iteration within 1 440 minutes, the computational time of our fast approximate solution strategy with convex relaxation and pattern recognition can decrease to 25 minutes. These observations indicate the synergic combination of the proposed trustworthy DNN training model and the fast approximation solution strategy can contribute to improving the trustworthiness of a DNN with improved computational efficiency.
The following conclusions can be drawn from this paper: (1) The proposed trustworthy DNN training model can theoretically quantify the computational performance of DNNs. This distinguishes us from existing methods, which quantify the computational performance of DNNs using limited testing sets, by paving a promising way for precise quantification of the trustworthiness for DNN-based OPF calculations. Furthermore, the proposed model can be exactly solved using our gradient-descent method based on Danskin’s theorem. (2) Our fast approximate solution strategy, which considers convex relaxation and pattern recognition, can alleviate the computational burden of integer variables involved in our previous exact solution strategy, while still maintaining the direction of updating DNN parameters toward improved trustworthiness.
keywords:Renewable source, optimal power flow calculation, deep neural network, trustworthy training
中图分类号:TM711
DOI: 10.19595/j.cnki.1000-6753.tces.231295
国家重点研发计划资助项目(2021YFE0191000)。
收稿日期 2023-08-10
改稿日期 2023-09-27
冉晴月 男,1999年生,硕士研究生,研究方向为电力系统调度分析。E-mail:r2018199927@163.com
林 伟 男,1994年生,博士后研究员,研究方向为电力系统运筹优化、可信AI技术、新能源电力市场。E-mail:wlin1994@hotmail.com(通信作者)
(编辑 李 冰)