
图1 环形水冷变压器结构及热单元
Fig.1 Structure and thermal unit of toroidal water-cooled transformer
摘要 干式高频变压器结构紧凑且损耗较高,而低导热系数的灌封材料使得热量易在变压器内部累积,从而导致温升成为限制大功率变压器容量与功率密度提升的重要因素。该文以环形水冷变压器为研究对象,建立了考虑中心圆柱热阻的变压器集总参数热路模型,并通过有限元仿真验证了所建模型的准确性。基于所建热路模型,解释了变压器温度降幅随着水流量的提高趋于稳定的现象。为了进一步增强散热效果,该文提出了一种基于高导热绝缘材料氮化铝的新型散热结构。该结构在热源与水冷板之间建立起低热阻通道,增强了变压器与水冷板之间的传热,变压器的容量和功率密度可进一步提高。最后,通过有限元仿真与25 kHz/160 kV·A高频变压器样机实验验证了所提散热结构的有效性。
关键词:大功率高频变压器 环形水冷变压器 等效热路模型 氮化铝材料
大功率高频变压器是解决清洁能源并网、直流负荷供电等需求的关键设备。在高频(>5 kHz)、大功率(>10 kW)应用场合,纳米晶材料具有优异的综合磁性能[1-2]。纳米晶带材一般卷绕为环形或者矩形磁心,由于环形磁心不存在直角拐角,损耗分布更为均匀,且环形变压器漏感低、效率高,因此环形变压器在高频大功率场合下优势明显,应用前景广阔。
变压器高频化的意义在于缩小磁元件体积和提高功率密度,这也导致高频变压器的热负荷密度相对于工频变压器急剧增大[3]。随着变压器容量的增加,变压器温升越发严重,已成为制约高频变压器容量和功率密度提升的主要瓶颈,因此目前亟须针对环形高频变压器开展散热优化研究。干式变压器常用的散热方式分为风冷和水冷,其中风冷式散热多采取增加散热面积的思路。文献[4-5]改进骨架形状,增大绕组与空气接触面积,以此加强变压器散热,但是骨架形状复杂,制作困难。文献[6]提出了强制风冷工况下翅片阵列换热器最佳尺寸的获取方法,但不适用于环形变压器。与风冷相比,水冷具有更强的散热能力[7],在大功率变压器的实际工程中更具应用潜力。
评判变压器散热能力好坏的指标是温升。常用的变压器温升分析方法有经验公式[8]、集总参数热路模型和有限元仿真三种。相比于经验公式的较大误差,集总参数热路模型和有限元仿真虽然需消耗更多计算资源,但提供了更高的准确度。在热路建模方面,文献[9]基于静电场和热场的对比,类比推导了绕组导线之间的热阻,为热阻建模提供了新思路;文献[10]建立了壳式变压器的6节点集总参数热路模型,但其磁心形状为EE型,不适用于环形变压器;文献[11]建立了绕组区域详细的热网络模型,但其侧重点在于列车风冷却的湍流对流传热计算,不适用于水冷变压器;文献[12]建立了干式变压器热网络模型,考虑了干式变压器空气域的流体动力学特征,但计算的节点数较多,增加了热路模型的复杂性;文献[13-14]建立了环形变压器的集总参数热路模型,其中文献[14]还建立了利兹线绕组的热模型,但都未对磁环灌封后所形成的中心圆柱区域的热阻进行建模。在有限元仿真方面,文献[15]建立了高频变压器瞬态电磁场-温度场的耦合仿真模型,这种方式求解精度高,但计算耗时长,且存在不同时间尺度下的耦合仿真收敛困难的问题,仅适用于验证散热设计的有效性。集总参数热路模型本质上与有限元方法相似,但节点数量少了几个数量级[16],从而能在保证计算精度的前提下大幅减小计算量,适合作为变压器设计过程中的温升分析方法[17-18]。然而目前关于环形水冷变压器的热路模型还不成熟,需要进一步开展研究。
固体灌封绝缘可有效地降低绝缘距离,是目前高频变压器的主流绝缘方式[19]。灌封式高频变压器的绝缘主要依靠有机材料(如环氧树脂、聚酰亚胺、ABS塑料等)实现。有机材料的缺点在于导热系数较低(仅有0.2~1 W/(m·K)),容易导致变压器内部热点温度过高。文献[20]以10 kV全环氧固封水冷高频变压器为研究对象,分析了水流量、水管材质和环氧树脂导热系数等因素对变压器温升的影响,发现环氧树脂的导热系数是主要影响因素。环氧树脂的导热系数通常在0.2 W/(m·K)左右,添加氧化硅填料可使其导热系数增加到1.494 W/(m·K)。但受限于环氧树脂材料固有特点,改性环氧树脂的导热系数很难超过5 W/(m·K)[21],与铜的导热系数(399 W/(m·K))相差两个数量级,不利于变压器内部热量的散出,因此需要找到一种导热性能较强的绝缘材料以满足灌封式变压器的散热需求。
针对环形水冷高频变压器的热管理,本文选择集总参数热路模型作为变压器散热设计中的指导方法,根据环形变压器的轴对称结构建立了考虑中心圆柱热阻的二维等效热路模型,并通过有限元仿真对中心圆柱热阻及整个热路模型的准确性进行了验证。针对水流量高于某值后变压器温度基本不再随水流量增大而降低的现象,基于热阻模型分析发现是热源与水冷板之间的热阻较大所致。针对该传热过程中的瓶颈环节,提出了一种基于高导热绝缘材料氮化铝的新型散热结构。该结构在灌封的变压器与水冷板之间建立低热阻通道,可将更多热量传导至水冷板散出,从而降低了变压器温升,使得变压器容量和功率密度可进一步提升。有限元仿真与25 kHz/160 kV·A样机实验均可证明所提散热结构的有效性。
本文集总参数热路模型针对单面水冷环形变压器建立,所研究变压器的结构如图1所示。利兹线绕组和纳米晶磁心各自被绝缘材料包覆后完全被灌封材料密封。绕组结构为低压绕组在内层,高压绕组在外层,灌封完成后在其底部放置水冷板散热。绝缘与灌封材料的导热系数通常较低,这会带来较大的热阻,降低变压器的散热性能,因此准确的热路建模是大功率环形变压器设计中的关键。

图1 环形水冷变压器结构及热单元
Fig.1 Structure and thermal unit of toroidal water-cooled transformer
基于环形变压器的轴对称结构,可将环形变压器沿其圆周均匀分段,将每段视为一个热单元,如图1所示。基于热电类比理论,将热流类比为电流,通过分析热流的流通路径,即可建立变压器集总参数热路模型。由于热容仅影响变压器温度到达稳态的时间而不影响温升的幅值,热路建模时仅需考虑热阻。
每个热单元是完全相同的,因此二维等效热路足以对环形变压器进行精确建模。环形变压器热单元的纵剖面及二维热量传递路径如图2所示。
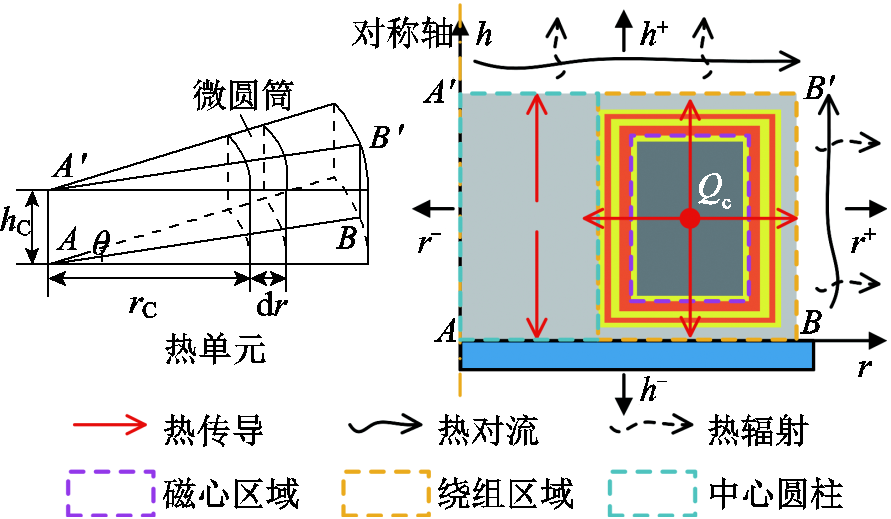
图2 热单元的纵剖面及二维热量传递路径
Fig.2 Cross section and 2D heat transfer path of thermal unit
对于磁心区域,磁心发热沿径向不均匀,但难以对此不均匀度进行量化,故本文采取文献[22]中的建模方式,将磁心发热处理为点热流源并考虑r-、r+、h-、h+四个方向的磁心热阻。对于绕组区域,由于四个方向的绕组层数分布不同,本文分别建立各方向的分层热路。热路建模需要根据几何结构及热源对变压器进行节点化,本文选取的节点为磁心截面中心温度(Tc,对应磁心最高温度)、磁心内表面温度(Tcr-)、磁心外表面温度(Tcr+)、磁心上表面温度(Tch+)以及磁心下表面温度(Tch-)。根据温度节点之间的热流传递路径可得如图3所示的环形变压器二维等效热路模型,其中各热路参数的含义见表1。
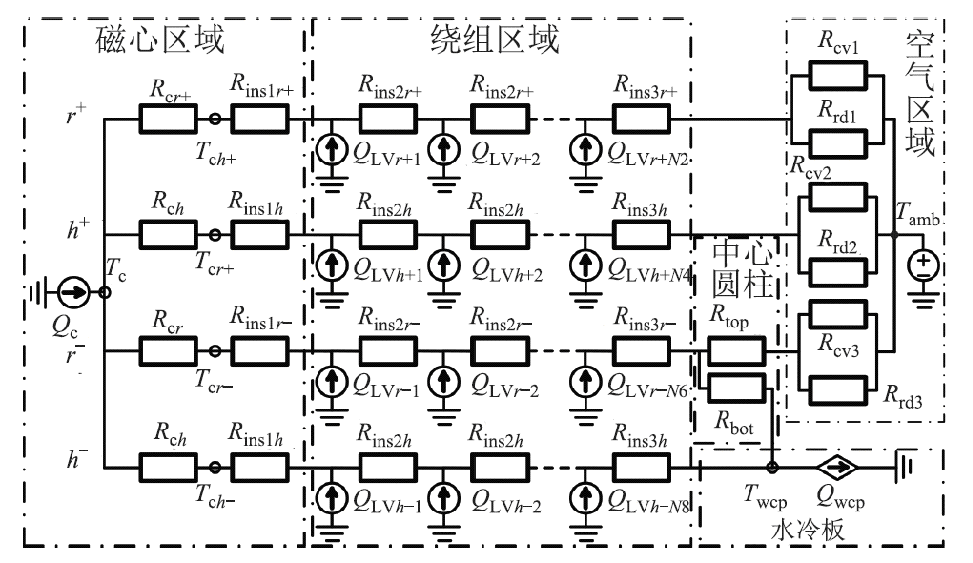
图3 环形变压器的二维等效热路模型
Fig.3 2D equivalent thermal circuit model of toroidal transformer
表1 等效热路模型参数说明
Tab.1 Parameter interpretation of equivalent thermal circuit model

参数类型表达式含义 热阻传导Rcr+, Rcr-磁环截面中心到内/外表面的圆筒热阻 Rch磁环截面中心到上/下表面的平壁热阻 Rins1r+, Rins1r-磁环内/外表面到第一层绕组的圆筒热阻 Rins1h磁环上/下表面到第一层绕组的平壁热阻 Rins2r+,Rins2r-磁环内/外方向不同层绕组间的圆筒热阻 Rins2h磁环上/下方向不同层绕组间的平壁热阻 Rins3r+磁环向外方向最外层绕组绝缘层与环氧树脂层叠加而成的圆筒热阻 Rins3r-磁环向内方向最外层绕组绝缘层的圆筒热阻 Rins3h磁环上/下方向最外层绕组绝缘层与环氧树脂层叠加而成的平壁热阻 Rtop,Rbot中心圆柱侧面到其上/下底面的圆柱热阻 对流与辐射Rcv1,Rrd1变压器侧表面与空气间的对流与辐射热阻 Rcv2, Rrd2磁心区域对应的变压器上表面与空气间的对流与辐射热阻 Rcv3, Rrd3中心圆柱区域对应的变压器上表面与空气间的对流与辐射热阻 热流源发热Qc磁心发热量 QLV磁心四周低压绕组的分层发热量 QHV磁心四周高压绕组的分层发热量 散热Qwcp冷却水带走的热量
传统二维等效热路模型法不考虑中心圆柱区域的热阻,按照热流路径的横截面形状将环形变压器的传导热阻分为平壁热阻以及圆筒热阻,其中平壁热阻Rth1计算式为
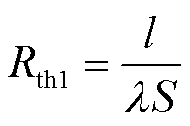 (1)
(1)
式中,S为平壁的横截面积;l为平壁的厚度;λ为材料的导热系数。
圆筒的导热可看作只沿径向变化的一维稳态导热。如图2所示,对于圆心角为θ、与圆柱中轴距离为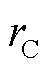 、厚度为dr、高度为
、厚度为dr、高度为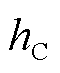 的微圆筒来说,其热阻dR的表达式为
的微圆筒来说,其热阻dR的表达式为
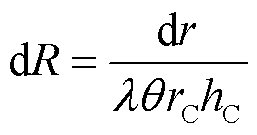 (2)
(2)
设实际圆筒的内外半径分别为r1、r2,则对于实际圆筒来说,其热阻Rth2为
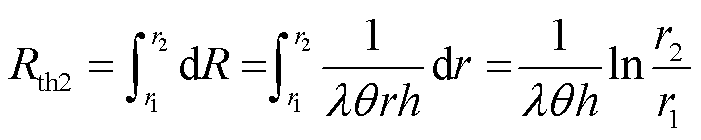 (3)
(3)
工程上常用特征数方程来描述流体的单相对流传热现象,获得不同换热条件下的特征数方程是研究对流传热现象的基础。在研究变压器外表面与空气间的对流传热现象时,格拉晓夫数Gr及普朗特数Pr(均无量纲)是已定特征数,而努塞尔数Nun为待定特征数,因为其中的表面传热系数hn是需要求解的未知量。努塞尔数Nun的定义式为
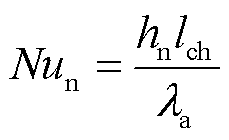 (4)
(4)
式中,hn为待求表面的表面传热系数,W/(m2·K);lch为待求表面的特征长度,m;λa为空气的导热系数,W/(m·K)。求得Nun后即可根据式(4)求得hn。
认为变压器不同外表面是分别等温的,设某一外表面的温度为Tw(K),环境温度为Tamb(K),则该待求表面努塞尔数Nun的计算式为
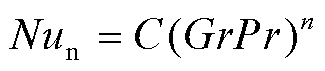 (5)
(5)
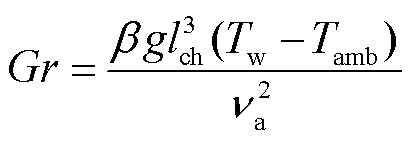 (6)
(6)
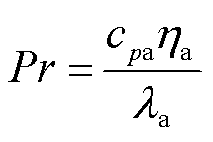 (7)
(7)
式中,β为空气的体胀系数,K-1,β=1/Ta,其中Ta=(Tw+Tamb)/2为空气的定性温度;g为重力加速度,g= 9.8 m/s2; 为空气的运动黏度,m2/s;cpa为空气的比定压热容,J/(kg·K);ηa为空气的动力黏度,Pa·s;C和n为常数,其值可按换热表面的形状及Gr或GrPr的数值范围从表2中选取。可以看到,表2中流态转变判据分别采用了Gr和GrPr,这是因为文献[23]指出,采用Gr作为转变判据时,克服了GrPr作为判据时不同流体转变判据数值各异的缺陷,更能反映自然对流传热的本质,但该文献仅对垂直平壁及垂直圆柱开展了研究,因此水平壁面的判据仍沿用GrPr。
为空气的运动黏度,m2/s;cpa为空气的比定压热容,J/(kg·K);ηa为空气的动力黏度,Pa·s;C和n为常数,其值可按换热表面的形状及Gr或GrPr的数值范围从表2中选取。可以看到,表2中流态转变判据分别采用了Gr和GrPr,这是因为文献[23]指出,采用Gr作为转变判据时,克服了GrPr作为判据时不同流体转变判据数值各异的缺陷,更能反映自然对流传热的本质,但该文献仅对垂直平壁及垂直圆柱开展了研究,因此水平壁面的判据仍沿用GrPr。
表2 式(5)中的常数C和n的取值
Tab.2 The values of constants C and n in Equ.(5)

形状与位置流态数值特征长度适用范围 Cn 垂直平壁及垂直圆柱层流0.590.25壁面高度1.43×104<Gr≤3×109 过渡0.0290.393×109<Gr≤2×1010 湍流0.111/3Gr>2×1010 热面朝上的水平壁面层流0.540.25面积除以周长2×104<GrPr≤8×106 湍流0.151/38×106<GrPr≤8×1011
综上所述,对于一个面积为Aw(m2)的变压器外表面,其自然对流热阻为
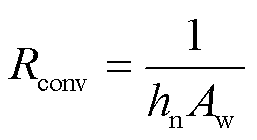 (8)
(8)
变压器某一外表面与空气之间的辐射换热量与该表面面积Aw、表面温度Tw、环境温度Tamb以及表面材料及状态有关,表面材料及状态由发射率ε(无量纲)表征,则对于一个面积为Aw的外表面,其辐射热阻为
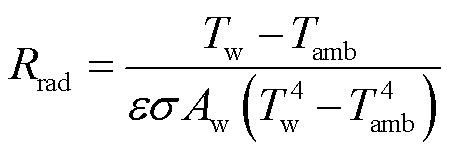 (9)
(9)
式中,σ为斯忒藩-玻耳兹曼常数,数值为5.67×10-8 W/(m2·K4)。
1.3.1 发热热流源
磁心发热已等效为点热流源,无需处理。本节介绍由绕组发热计算绕组分层热流源QLV和QHV的方法。环形磁心内外半径不同导致磁心的内周长和外周长不相等,因此,在绕组均匀绕制在磁环上的情况下,绕组在磁环四个方向的层数不同,四个方向的绕组绝缘层层数也就不同。由于绝缘材料导热系数低,会导致较大的温度梯度,因此热路建模时磁环不同方向绕组的不均匀分布应加以考虑。本文采用文献[13]中的方法,假设单位长度导体的损耗为固定值,根据各方位匝长与完整匝长的比值及各方位绕组层数对绕组的分层热流源大小进行计算,具体过程参见文献[13],此处不再赘述。
1.3.2 散热热流源
本文将水冷板的散热作用建模为受控热流源Qwcp,等效过程如下。磁心与绕组产生的热量经热传导到达水冷板上表面,由于水冷板较薄且材质为铜,水冷板上表面与水冷管内壁之间的热阻可忽略不计,故热路建模时只需考虑水冷管内壁与冷却水之间的管内强迫对流的传热过程。建模时认为水冷管是等温的,设水冷管温度为Twcp,进水口水温为Ti=Tamb,出水口水温为To,水冷管内壁面积为Awcp,强制对流换热系数为hf,则水冷管换热量Qwcp为
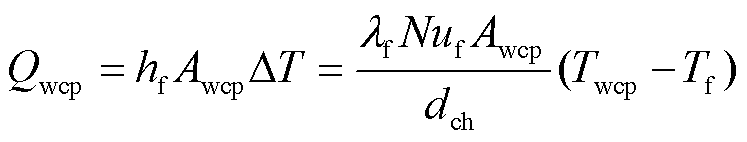 (10)
(10)
式中,λf为水的导热系数,W/(m·K);Tf为水温,本文取为进、出水口的平均水温,即
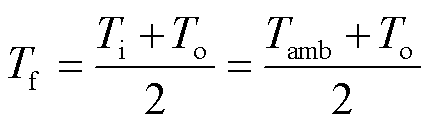 (11)
(11)
水冷管的特征长度为水冷管的当量直径dch(m),dch取决于水冷管横截面积Ac(m2)及水冷管内壁周长P(m)。圆形及非圆形截面水冷管当量直径的计算公式统一为
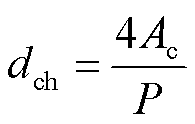 (12)
(12)
为求hf,需计算强制对流换热的努塞尔数Nuf,Gnielinski公式是迄今为止计算准确度最高的等壁温条件下强制对流传热实验关联式,表示为
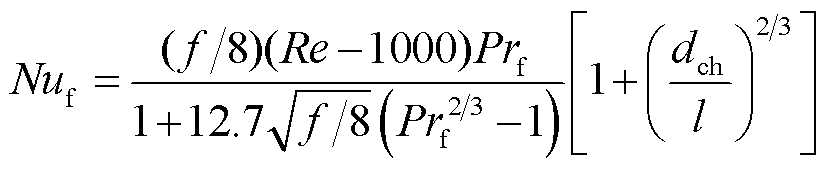 (13)
(13)
式中,Prf为普朗特数,Prf=cpf ηf/λf,其中cpf为水的比定压热容,J/(kg·K),ηf为水的动力黏度,Pa·s;l为水冷管的总长度,m;f为管内湍流流动的Darcy阻力系数,无量纲,按Konakov公式计算,表示为
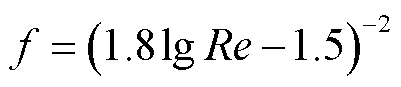 (14)
(14)
式中,Re为雷诺数,无量纲,与水流速度u(m/s)有关,计算式为
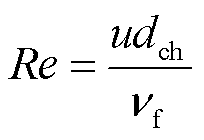 (15)
(15)
式中,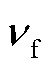 为水的运动粘度,m2/s。在管内强迫对流问题中,换热量Qwcp与壁温Twcp、水温Tf之间存在耦合关系,这与电路中的电压控制电流源类似,因此本文将水冷管与冷却水之间的热路等效为温差控制热流源。上述三者之间的耦合关系为
为水的运动粘度,m2/s。在管内强迫对流问题中,换热量Qwcp与壁温Twcp、水温Tf之间存在耦合关系,这与电路中的电压控制电流源类似,因此本文将水冷管与冷却水之间的热路等效为温差控制热流源。上述三者之间的耦合关系为
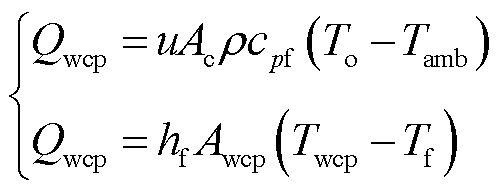 (16)
(16)
式中,ρ为水的密度,kg/m3。式(16)中第一个等式为能量守恒公式,代表冷却水吸收热量导致其温度升高。联立式(11)和式(16)可计算出受控热流源Qwcp的表达式为
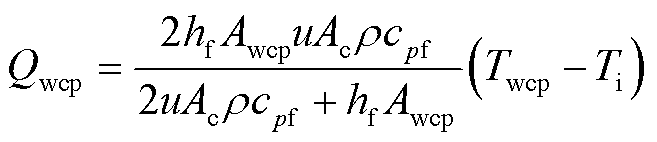 (17)
(17)
环形变压器完全灌封后会形成中心圆柱,但传统二维热路模型缺少对中心圆柱侧面到其上、下底面热阻的建模,本节对此进行补充。对于环形变压器的中心圆柱,热量从其侧面流入,从其上、下底面流出到达变压器上、下表面,因此建模的目的是获得圆柱侧面到其上、下底面的解析热阻Rtop、Rbot。热阻定义为温差与热流之比,为了能够使用此定义式对所求热阻进行验证,求解热阻时应认为圆柱侧面为等温面,其温度记为T1,圆柱的上、下底面也是等温面且温度分别记为T2、T3。
热流路径是获得热阻解析式的关键,因此首先运用有限元方法对圆柱侧面到底面的热流路径进行分析。本节分析上、下底面等温的情况,有限元仿真条件设为T1=50℃,T2=T3=30℃,此时圆柱纵剖面温度仿真结果如图4所示。
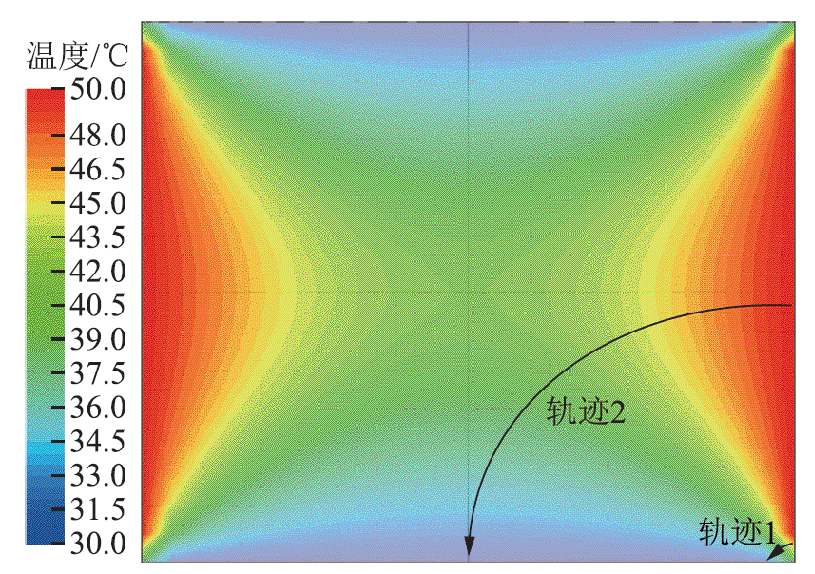
图4 圆柱纵剖面温度仿真结果
Fig.4 Simulation results of temperature in the longitudinal section of the cylinder
热流流经热阻产生温度差,因此热流方向为温度的负梯度方向。由图4可见,热流路径具有上下对称性,因此求解圆柱侧面到圆柱上、下底面的热阻Rcyl与求解圆柱侧面下半部分到圆柱下底面的热阻是等价的。热流路径为曲线,沿曲线求解热阻较为困难,本文对其进行简化:将热流路径分为横向段与纵向段,横向段对应径向热阻,纵向段对应轴向热阻,获得横向段与纵向段的微分热阻后,分别积分再相加获得总热阻。设中心圆柱的半径和高分别为rcyl和hcyl,对于圆柱侧面上纵坐标为h,长度为dh的微分区域而言,横向段的微分热阻dR1与该坐标处对应的热流径向透入深度δr有关。对于圆柱底面上横坐标为r,长度为dr的微分区域而言,纵向段的微分热阻dR2与该坐标处对应的热流轴向透入深度δh有关。dR1、dR2的表达式分别为
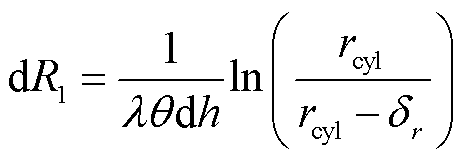 (18)
(18)
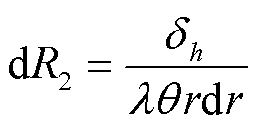 (19)
(19)
式中,由于求的是整个中心圆柱的热阻,所以θ=2π。由图4可知,径向透入深度δr与h的关系和轴向透入深度δh与r的关系均为曲线,本文以二次函数对其进行拟合,结果如图5所示。由于热流可从圆柱侧面沿图4中的轨迹1、2两条路径流动到达圆柱下底面,故同一位置的径向与轴向透入深度难以直接界定,本文取轨迹1、2的平均值对透入深度进行建模,故拟合曲线的顶点为透入方向最大深度的一半,即径向透入深度最大值δrmax=rcyl/2,轴向透入深度最大值δhmax=hcyl/4,最后得到径向与轴向透入深度的表达式为
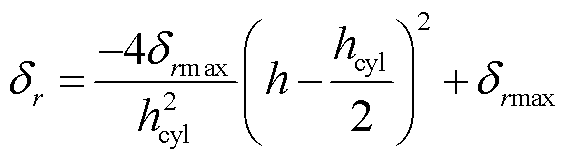 (20)
(20)
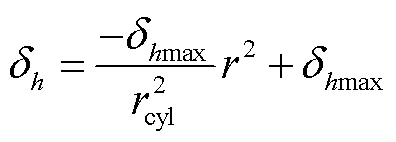 (21)
(21)
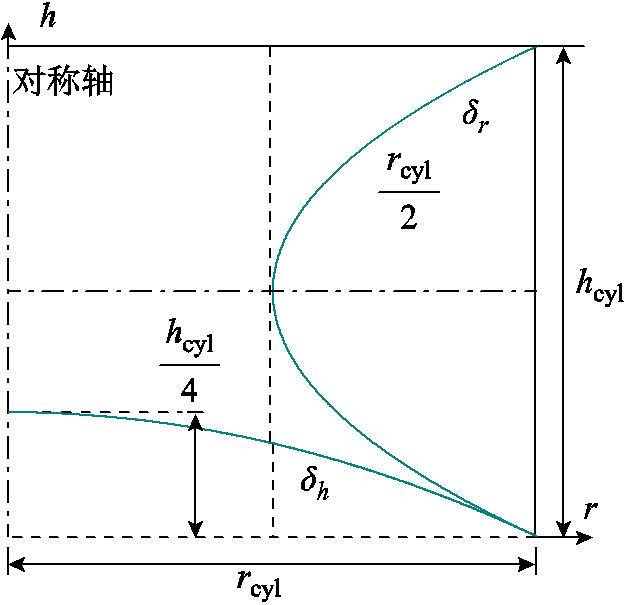
图5 热流透入深度拟合曲线
Fig.5 Fitting curves of heat flow penetration depth
将式(20)和式(21)分别代入式(18)和式(19)即可求得径向与轴向的微分热阻,由于微分热阻在各自方向为并联关系,因此取其倒数可得到微分热导。对微分热导在各自方向进行积分,结果分别取倒数即为径向热阻R1、轴向热阻R2,表示为
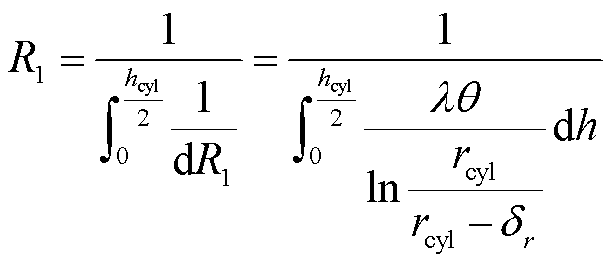 (22)
(22)
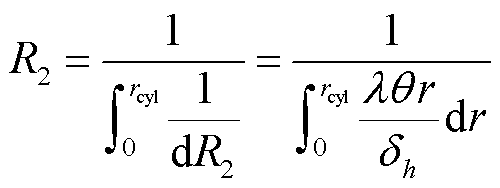 (23)
(23)
圆柱侧面到圆柱上、下底面的热阻Rcyl为径向热阻R1与轴向热阻R2之和,即
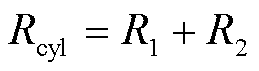 (24)
(24)
由于此时上、下底面等温,从侧面流入的热流从上、下底面均分流出,由热阻定义式可知此时有Rtop=Rbot=2Rcyl。
下面通过有限元仿真验证上述热阻解析模型的准确性。在图4所示有限元仿真模型基础上,通过对温度边界T1上的热流密度进行积分,可以计算得到稳态热流Q(W),圆柱侧面到上、下底面的热阻Rcyl即为(T1–T2)/Q。有限元计算结果与解析计算结果对比如图6所示。
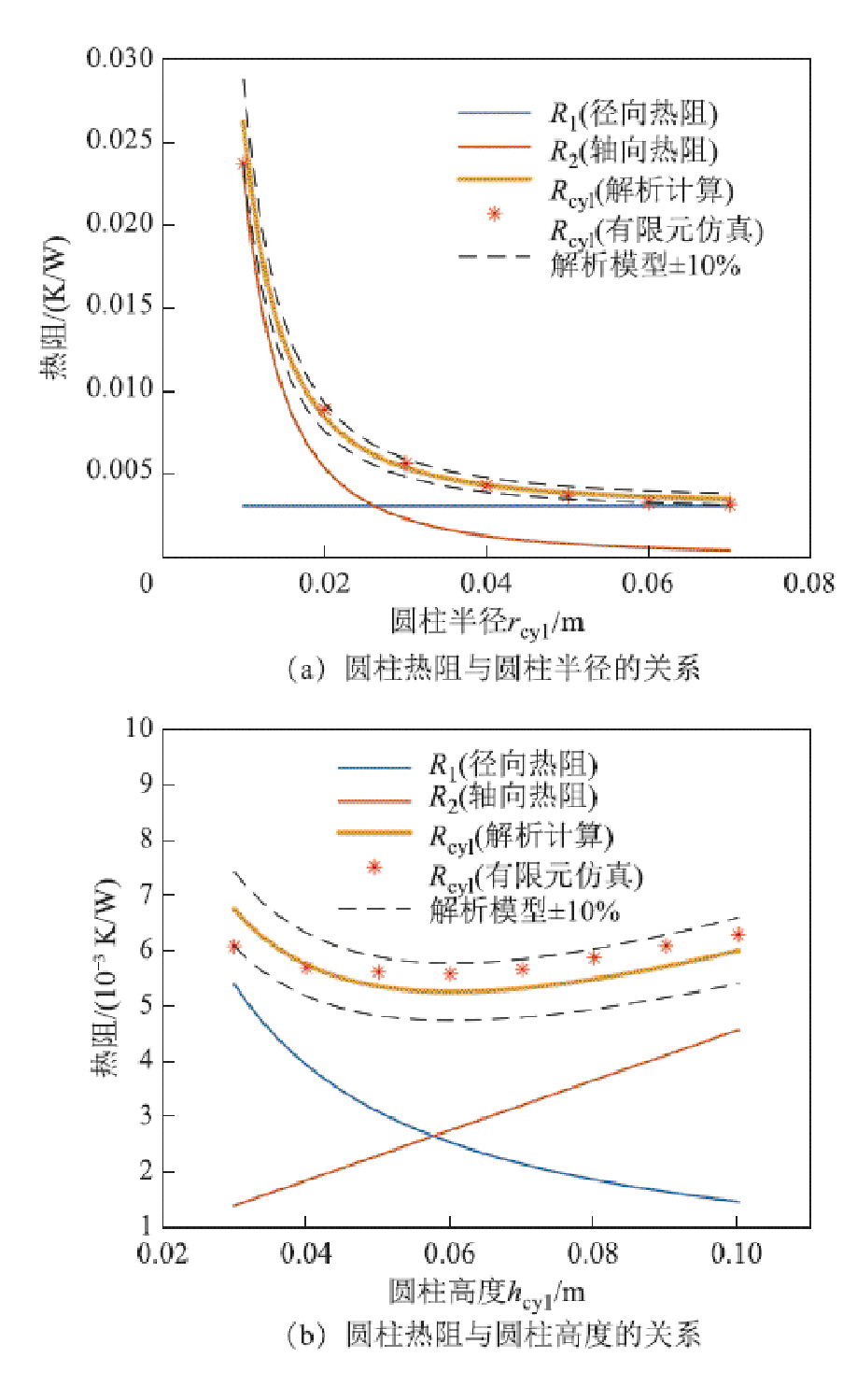
图6 有限元计算结果与解析计算结果的对比
Fig.6 Comparison of finite element calculation results and analytical calculation results
Rcyl的大小由圆柱高度、半径以及圆柱材料的导热系数决定,由于热阻与导热系数呈线性关系,故只需对圆柱高度及半径进行扫描仿真。由图6a可知,径向热阻与rcyl无关,故改变rcyl只会影响轴向热阻,当rcyl增大时,轴向热阻减小而径向热阻不变,因此,总热阻减小,故实际应用时中心圆柱的半径应尽可能大。如图6b所示,改变hcyl对径向和轴向热阻均有影响,当hcyl增大时,轴向热阻增大而径向热阻减小,总热阻变化趋势由式(24)决定。由图6可知,在所取参数范围内,本文所建立的圆柱热阻解析结果与有限元计算结果的误差都在±10%以内,证明了所建圆柱热阻解析模型的准确性。
上述热阻解析模型是在上、下底面等温时求得的,但在实际应用时会出现上、下底面不等温的情况,本节对此情况进行分析。在原有单圆柱有限元仿真的基础上改变边界条件,设置中心圆柱侧面温度T1固定为50℃;圆柱下底面温度T3固定为30℃;圆柱上底面温度T2则是变化的,初始值为30℃,按1℃的步长增加至40℃进行参数扫描仿真。由于第一个扫描点对应上、下底面等温时的情况,因此以该点为基准观察上、下底面不等温对热阻的影响,最终所得结果如图7所示。
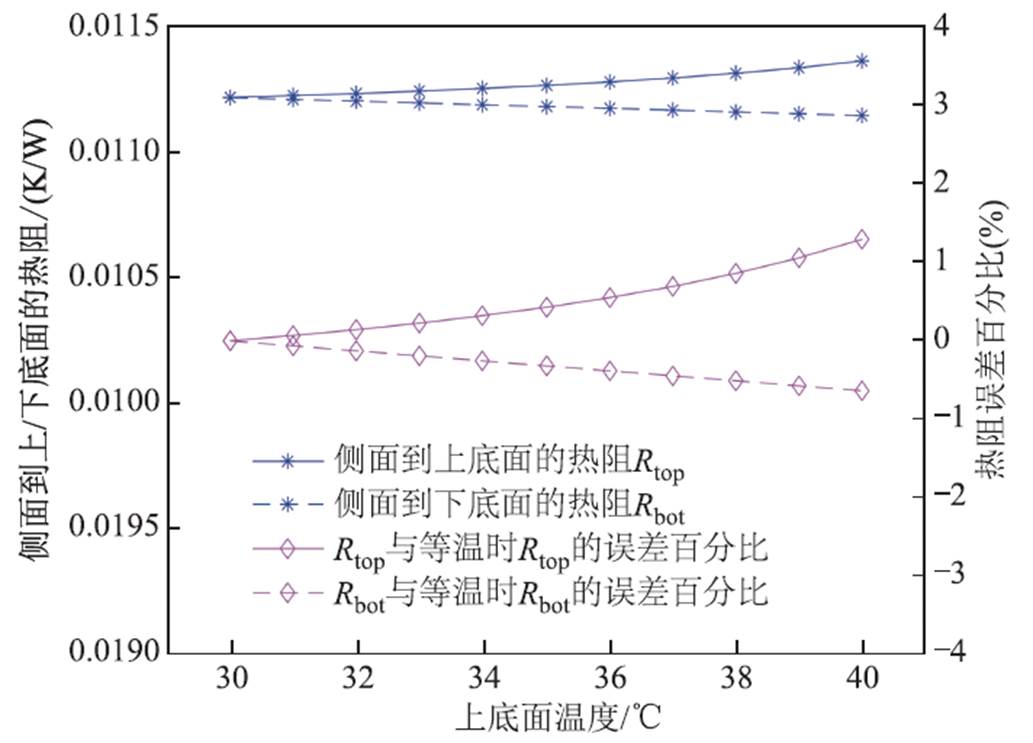
图7 上、下底面不等温对热阻的影响
Fig.7 The influence of temperature difference between upper and lower surfaces on thermal resistance
由图7可知,在上、下底面温差达到10℃时,圆柱侧面与上底面之间的热阻Rtop与上、下底面等温时该热阻的误差绝对值小于2%,圆柱侧面与下底面之间的热阻Rbot与上、下底面等温时该热阻的误差绝对值小于1%,即上、下底面不等温时,Rtop、Rbot与等温时的值相差都很小。因此,无论上、下底面是否等温,热路模型中的Rtop、Rbot都可认为是上、下底面等温时求得的圆柱侧面到圆柱上、下底面的热阻Rcyl的两倍。
为验证本文所建环形变压器二维等效热路模型的准确性,在Ansys中建立了环形变压器有限元仿真模型。设置环境温度为20℃,水流量为1.5 L/min,此条件下变压器温度有限元仿真结果如图8所示。将有限元仿真中的相应参数代入等效热路模型中进行计算,得到有限元仿真结果与热路模型计算结果的对比见表3,变压器各处温度的误差都小于10%,证明了本文所建立热路模型的准确性。

图8 变压器温度有限元仿真结果
Fig.8 Finite element simulation results of transformer temperature
表3 有限元仿真结果与热路模型计算结果的对比
Tab.3 Comparison of finite element simulation results and thermal circuit model calculation results
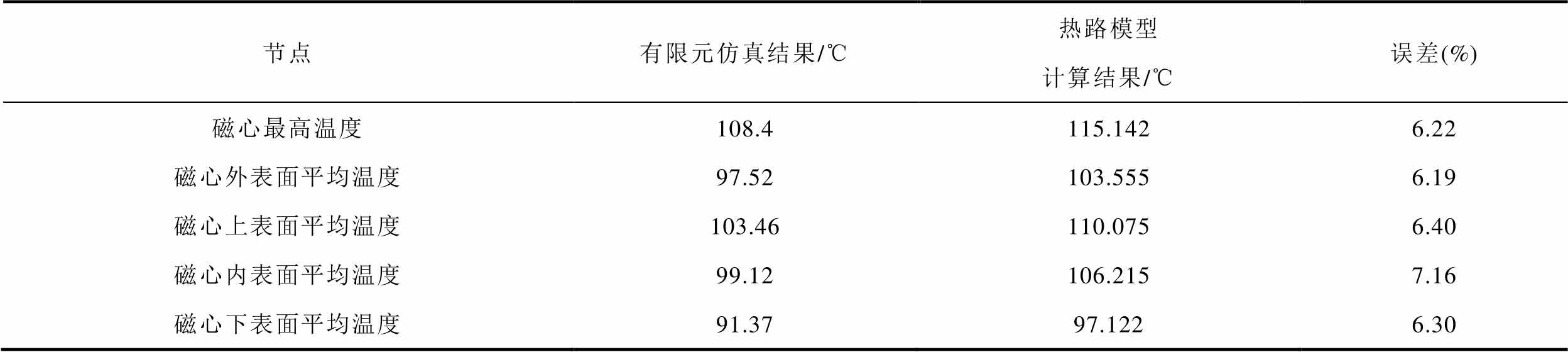
节点有限元仿真结果/℃热路模型计算结果/℃误差(%) 磁心最高温度108.4115.1426.22 磁心外表面平均温度97.52103.5556.19 磁心上表面平均温度103.46110.0756.40 磁心内表面平均温度99.12106.2157.16 磁心下表面平均温度91.3797.1226.30
水流量的大小是水冷系统的关键参数,水冷板水流量越大,冷却水所能带走的热量就越多,但与此同时水冷系统的功耗也越大,因此应对此进行详细分析。采用所建立的热路模型对水流量进行参数扫描,按照0.5 L/min的步长从1 L/min增加到 10 L/min,得到不同水流量下各节点的温度如图9所示。由图9可知,当水流量大于5 L/min后,绕组和铁心温度随着水流量增大的降幅微弱,此时继续增加水流量的经济性较差。
基于所建立的热路模型对此现象进行分析,出现上述现象的原因是热源与水冷板之间的热阻较大,故到达水冷板的热流较小,冷却水流速达到5 L/min后即可将该部分热流近乎完全吸收,因此继续增大水流量并不能有效降低变压器温度,而此时变压器热点温度仍高于110℃,将导致绝缘系统加速老化甚至失效[24],为此需研究新的散热结构。
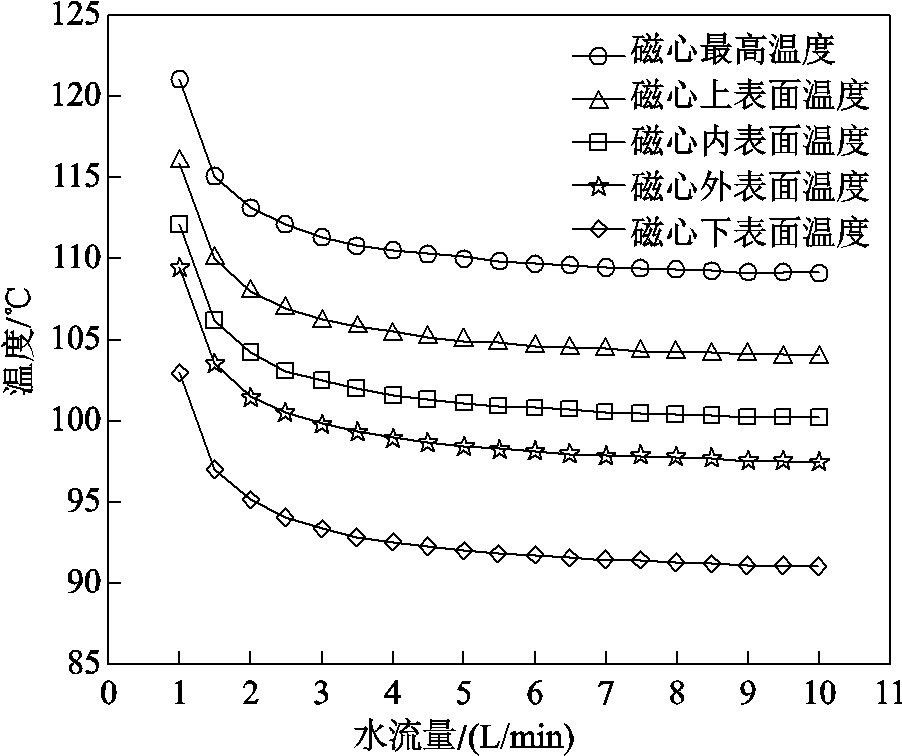
图9 水流量对变压器温度的影响
Fig.9 The influence of water flow rate on transformer temperature
变压器中常用材料的物理特性见表4。磁心与绕组区域所用的绝缘材料导热系数普遍较低,且难以对其进行改进;而中心圆柱区域的材料选择具有较强的灵活性,可通过改进该区域的导热特性减小r-支路热阻,更多的热流便会通过此支路到达水冷板被冷却水带走,与此同时其他支路的热流会减小,因此各节点温度都会降低,变压器散热能力由此增强。
表4 变压器常用材料的物理特性
Tab.4 Physical properties of commonly used materials for transformers
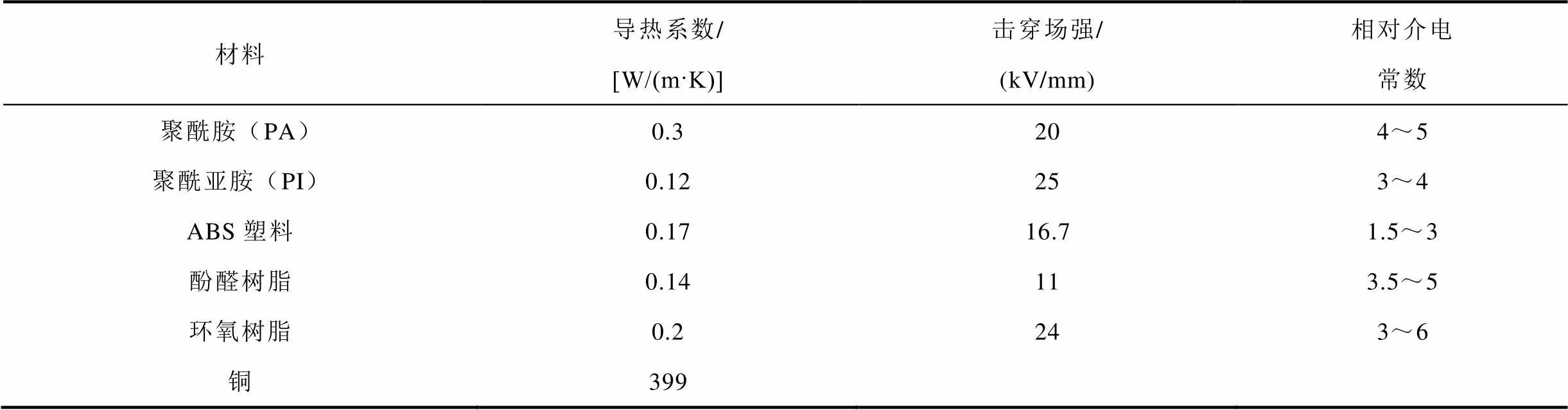
材料导热系数/[W/(m·K)]击穿场强/(kV/mm)相对介电常数 聚酰胺(PA)0.3204~5 聚酰亚胺(PI)0.12253~4 ABS塑料0.1716.71.5~3 酚醛树脂0.14113.5~5 环氧树脂0.2243~6 铜399
变压器对中心圆柱的材料有两大要求:高导热与高绝缘。从大功率半导体模块电路的封装材料中得到启发,一些新型陶瓷材料兼具优良的绝缘能力与散热能力,可以引入大功率变压器中加以应用。可用的绝缘导热陶瓷材料有四种:氧化铝、氧化铍、氮化硼及氮化铝,其中氧化铝和氮化硼导热系数较低,大约在30~40 W/(m·K),氧化铍和氮化铝材料导热系数较高,可达230 W/(m·K)以上,但氧化铍材料有剧毒,因此本文使用氮化铝陶瓷作为中心圆柱的材料。氮化铝的击穿场强比环氧树脂更高,在增强导热的同时也能保证系统整体的绝缘强度,在中压场合实用性较强,是解决大功率高频变压器热管理问题的理想材料。
采用氮化铝陶瓷的环形变压器结构如图10所示,图中白色部分为氮化铝陶瓷。
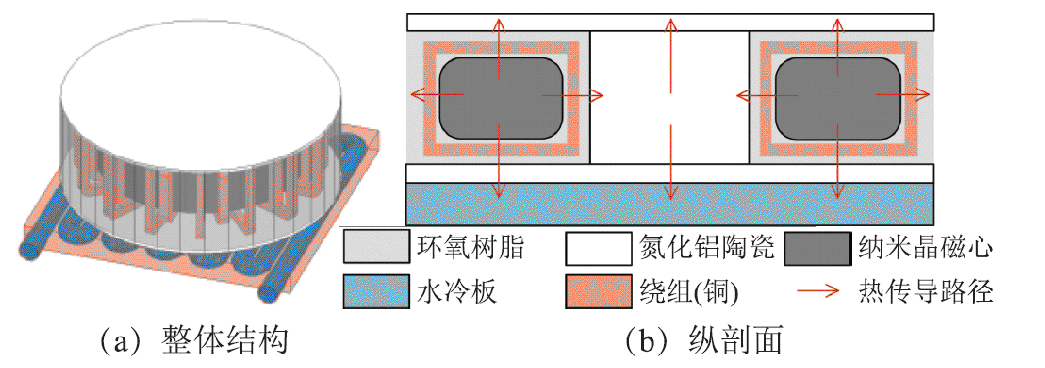
图10 采用氮化铝陶瓷的灌封式环形变压器结构
Fig.10 Potted toroidal transformer structure using aluminum nitride ceramics
所提新型散热结构使用氮化铝陶瓷代替一部分易老化且导热能力差的环氧树脂,由上、下两个平板和一个圆柱组成的工字形陶瓷与灌封后的磁心及绕组紧密接触,该结构可使Rins3h、Rtop、Rbot都有所减小。由于氮化铝陶瓷导热系数很高,工字形结构在灌封的变压器与水冷板之间建立低热阻通道,将更多磁心与绕组产生的热量传导到水冷板上,加强了变压器与水冷板之间的热量交换。此外,由于环形变压器磁心内圆磁损更大且磁心内侧绕组比外侧更密集,变压器r-方向的热密度比r+方向更大,而本文所提散热结构是对r-方向导热的增强,与环形变压器极为适配,可避免热量在变压器内部的累积,有利于高频变压器的安全稳定运行。
将采用氮化铝散热结构的Rins3h、Rtop、Rbot代入热路模型重新对水流量进行参数扫描,所得结果如图11所示。对比图9,图11中各节点温度明显降低,且图11中磁心内表面温度变得低于外表面的温度,说明采用氮化铝后流过r-支路的热流变大,这意味着更多热流可通过r-支路到达水冷板,提高了水冷的利用率,证明了3.2节散热结构有效性理论分析的正确性。与此同时其他支路的热流会减小,各节点温度由此降低。
采用与2.3节中有限元仿真相同的参数对所提新型散热结构进行热仿真验证,结果如图12所示。两种散热结构的变压器温度对比见表5。采用氮化铝后,变压器热点温度降低了35.72℃,改善了变压器的工作环境,延长了变压器绝缘系统的寿命,从而增强了变压器的可靠性。
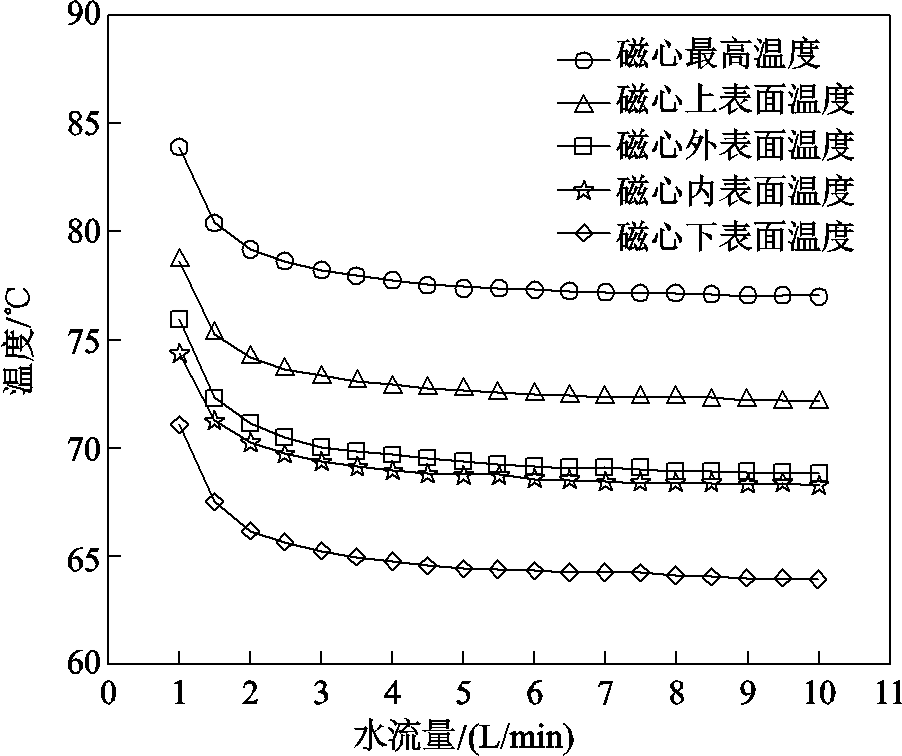
图11 采用氮化铝后水流量对变压器温度的影响
Fig.11 The influence of water flow rate on transformer temperature after adopting aluminum nitride heat dissipation structure

图12 采用氮化铝散热结构的变压器温度仿真结果
Fig.12 Temperature simulation results of transformers using aluminum nitride heat dissipation structure
表5 两种散热结构的变压器各节点温度对比
Tab.5 Comparison of temperature at each node of transformers with two heat dissipation structures

节点无氮化铝仿真结果/℃有氮化铝仿真结果/℃降温(%) 磁心最高温度108.472.6832.95 磁心外表面平均温度97.5263.8534.53 磁心上表面平均温度103.4667.9034.37 磁心内表面平均温度99.1262.6036.84 磁心下表面平均温度91.3758.5835.89
本文采用对比实验验证所提散热结构的有效性。所制作的两台环形高频变压器样机关键参数见表6,一台为全环氧树脂灌封,另一台采取本文所提氮化铝散热结构,二者除了散热结构外其他部分完全相同。待测试变压器实物如图13所示。变压器样机浇注为长方体,这是由于水冷板表面为长方形,这样可以增大变压器与水冷板的接触面积。
表6 高频变压器样机关键参数
Tab.6 Key parameters of the HFT prototype

参数数值 工作频率/kHz25 额定容量/(kV·A)160 一次侧额定电压/kV1.5 二次侧额定电压/kV1.2 一、二次侧耐压/kV8 磁环尺寸(外半径×内半径×高度)/(mm×mm×mm)100×50×84 一次侧匝数15 二次侧匝数12

图13 待测试变压器
Fig.13 Transformers under test
高频变压器温升实验平台如图14所示,直流电压经逆变电路变为双极性方波后作为变压器的输入,由于满容量有功实验难度较大,本文采取满容量无功方式使变压器发热与额定工况相当,即变压器所接负载为电感。

图14 高频变压器温升实验平台
Fig.14 Experiment platform for temperature rise of high frequency transformer
实验过程中,变压器内部温度由变压器制作过程中埋在变压器磁心与低压绕组之间的Pt100温度传感器传出,采用万用表测量其两端电阻值即可获得变压器内部温度。在输入相同、负载相同、环境温度相同、冷却水水流量相同的情况下对两台变压器分别进行满容量无功升温实验。实验过程中每隔5 min记录一次万用表测量到的电阻值,待其读数基本不再随时间变化时即可认为达到稳态并停止记录。最后根据Pt100阻值与温度的对应关系将阻值转换为温度,所得结果如图15所示。
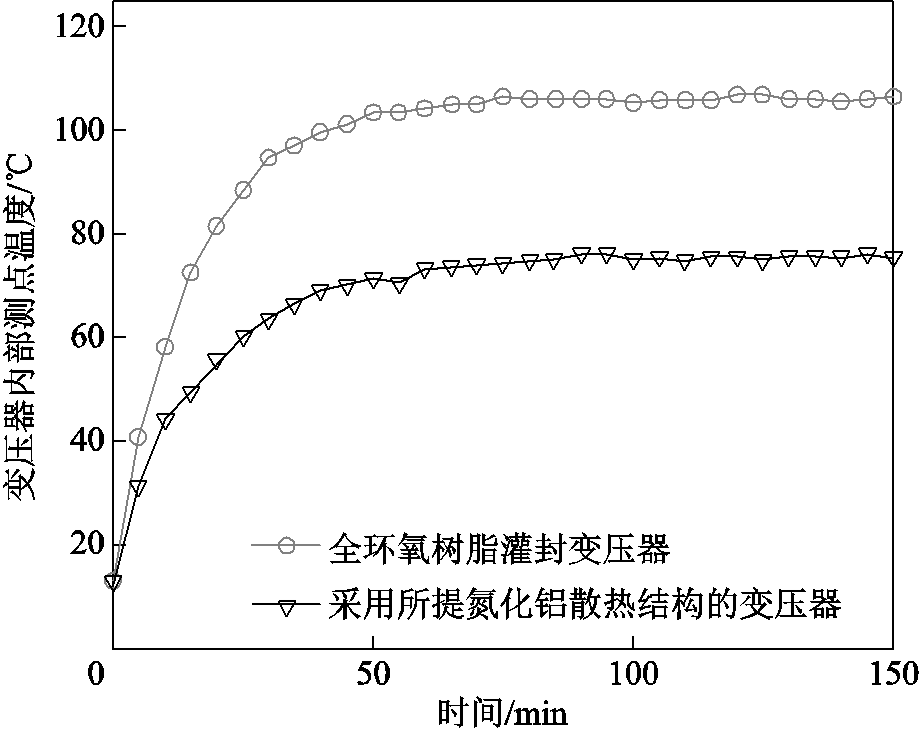
图15 不同散热结构变压器温度曲线
Fig.15 Temperature curves of transformers with different heat dissipation structures
由实验结果可知,采取氮化铝散热结构的变压器的稳态温度比全环氧树脂灌封的变压器降低了30.68℃,证明了本文所提散热结构的有效性。但降温幅度相比于仿真结果有所降低,这是由于实际样机中的绕组与氮化铝之间填充的环氧树脂更厚,产生了更大的热阻。
针对环形水冷高频变压器的热管理问题,本文基于热流路径建立了考虑中心圆柱热阻的二维热路模型,并提出了一种采用氮化铝材料的新型散热结构,主要结论如下:
1)建立了变压器中心圆柱侧面到底面的热阻模型,对现有二维等效热路模型进行补充,并通过有限元仿真对所建立的完整二维等效热路模型的准确性进行了验证。
2)分析所建完整二维热路模型发现,热源与水冷板之间的热阻较大,导致到达水冷板的热量较少,制约了水冷效果。针对此传热薄弱环节,本文提出了一种基于高导热绝缘材料氮化铝的新型散热结构,该结构在灌封的变压器与水冷板之间建立起低热阻通道,可增强变压器与水冷板之间的传热。
3)开展了有限元仿真验证和实验验证,二者均证明了相比于全环氧树脂灌封变压器,采用氮化铝散热结构的变压器温升更低,验证了本文所提散热结构的有效性。
参考文献
[1] 孙凯, 卢世蕾, 易哲嫄, 等. 面向电力电子变压器应用的大容量高频变压器技术综述[J]. 中国电机工程学报, 2021, 41(24): 8531-8545.
Sun Kai, Lu Shilei, Yi Zheyuan, et al. A review of high-power high-frequency transformer technology for power electronic transformer applications[J]. Proceedings of the CSEE, 2021, 41(24): 8531-8545,.
[2] 杨庆新, 李永建. 先进电工磁性材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-29.
Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1-29.
[3] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid-state transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 110-123.
[4] Guo Zhicheng, Yu Ruiyang, Xu Wei, et al. Design and optimization of a 200-kW medium-frequency transformer for medium-voltage SiC PV inverters[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10548-10560.
[5] Guo Zhicheng, Rajendran S, Tangudu J, et al. A novel high insulation 100 kW medium frequency transformer[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 112-117.
[6] Chen Bin, Liang Xu, Wan Nina. Design methodology for inductor-integrated Litz-wired high-power medium-frequency transformer with the nanocrystalline core material for isolated DC-link stage of solid-state transformer[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 11557-11573.
[7] Mudawar I. Assessment of high-heat-flux thermal management schemes[J]. IEEE Transactions on Components and Packaging Technologies, 2001, 24(2): 122-141.
[8] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal-fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
[9] Jaritz M, Hillers A, Biela J. General analytical model for the thermal resistance of windings made of solid or Litz wire[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 668-684.
[10] 陈彬, 李琳, 赵志斌, 等. 电感集成式大容量高频变压器精细化设计方法[J]. 中国电机工程学报, 2018, 38(5): 1356-1368.
Chen Bin, Li Lin, Zhao Zhibin, et al. Design method of inductor-integrated high-power high-frequency transformers[J]. Proceedings of the CSEE, 2018, 38(5): 1356-1368.
[11] 袁帅, 周利军, 勾小凤, 等. 干式车载牵引变压器列车风冷却对流传热计算与绕组区域热网络建模[J]. 中国电机工程学报, 2022, 42(15): 5719-5729.
Yuan Shuai, Zhou Lijun, Gou Xiaofeng, et al. Train induced wind cooling convection heat transfer calculation and winding area thermal network modeling of dry-type on-board traction transformer[J]. Proceedings of the CSEE, 2022, 42(15): 5719-5729.
[12] 唐钊, 刘轩东, 陈铭. 考虑流体动力学的干式变压器热网络模型仿真分析[J]. 电工技术学报, 2022, 37(18): 4777-4787.
Tang Zhao, Liu Xuandong, Chen Ming. Simulation analysis of dry-type transformer thermal network model considering fluid dynamics[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4777-4787.
[13] Purushothaman S, de Leon F. Heat-transfer model for toroidal transformers[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 813-820.
[14] Kyaw P A, Delhommais M, Qiu Jizheng, et al. Thermal modeling of inductor and transformer windings including litz wire[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 867-881.
[15] 刘洁苇, 吕运强, 李琳, 等. 高频变压器磁场和温度场的瞬态特性分析[J]. 高电压技术, 2019, 45(4): 1191-1200.
Liu Jiewei, Lü Yunqiang, Li Lin, et al. Transient simulation analysis of electromagnetic field and temperature field of high-frequency transformer[J]. High Voltage Engineering, 2019, 45(4): 1191-1200.
[16] Scoltock J, Wang Yiren, Calderon-Lopez G, et al. Rapid thermal analysis of nanocrystalline inductors for converter optimization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2276-2284.
[17] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three-dimensional temperature calculation and optimization design method for high power high-frequency transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[18] 孙晨茜, 李琳. 非正弦激励下高频变压器的温度分布计算与分析[J]. 高压电器, 2022, 58(10): 96-105.
Sun Chenxi), Li Lin. Calculation and analysis of temperature distribution of high-frequency transformer under non-sinusoidal excitation[J]. High Voltage Apparatus, 2022, 58(10): 96-105.
[19] 王威望, 刘莹, 何杰峰, 等. 高压大容量电力电子变压器中高频变压器研究现状和发展趋势[J]. 高电压技术, 2020, 46(10): 3362-3373.
Wang Weiwang, Liu Ying, He Jiefeng, et al. Research status and development of high frequency transformer used in high voltage and large capacity power electronic transformer[J]. High Voltage Engineering, 2020, 46(10): 3362-3373.
[20] 靳艳娇, 乔光尧, 邓占锋, 等. 全环氧固封高频变压器散热优化设计研究[J]. 电网技术, 2022, 46(7): 2531-2537.
Jin Yanjiao, Qiao Guangyao, Deng Zhanfeng, et al. Heat dissipation optimization design of epoxy resin sealing high frequency transformer[J]. Power System Technology, 2022, 46(7): 2531-2537.
[21] 曾柏顺, 饶保林, 韦衍乐, 等. 干式变压器用高导热抗开裂环氧浇注料[J]. 绝缘材料, 2013, 46(2): 7-10.
Zeng Baishun, Rao Baolin, Wei Yanle, et al. High thermal conductive and anti-cracking epoxy resin casting material for dry-type transformer[J]. Insulating Materials, 2013, 46(2): 7-10.
[22] Militão L A, Bertoldi B, Furlan A G L, et al. Thermal network models for toroidal and E-core inductors in still air[J]. IEEE Transactions on Power Electronics, 2023, 38(12): 15879-15892.
[23] 刘学来, 宋永军, 金洪文. 热工学理论基础[M]. 2版. 北京: 中国电力出版社, 2008.
[24] 蒋起航, 王威望, 钟禹, 等. 环氧树脂高频松弛的交流电导与双极性方波击穿特性[J]. 电工技术学报, 2024, 39(4): 1159-1171.
Jiang Qihang, Wang Weiwang, Zhong Yu, et al. AC conductivity with high frequency relaxation and breakdown characteristics of epoxy resin under bipolar square wave voltage[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1159-1171.
Abstract Dry-type high-frequency transformers typically have compact structures and significant losses. The use of potting materials with low thermal conductivity can lead to heat accumulation within the large-capacity transformer, resulting in temperature rise becoming a limiting factor in increasing the power density of high-frequency transformers. Due to the significant advantages of toroidal cores and water-cooling heat dissipation method, this paper focuses on the thermal management issue of toroidal water-cooling transformers.
Because of the axisymmetric structure of the toroidal transformer, the thermal circuit of the transformer can be equivalently described using a two-dimensional model. In order to calculate the temperature rise, this paper establishes a lumped parameter two-dimensional equivalent thermal circuit model of the toroidal transformer based on the thermoelectric analogy theory, with the center and the four surfaces of the magnetic core as temperature nodes. Compared with existing models, the proposed model takes into account the thermal resistance of the central cylinder formed after sealing. The modeling of the thermal resistance between the side and bottom surfaces of the central cylinder is based on the analysis of heat flow path. This heat flow path is a curve, but solving the thermal resistance along the curve is difficult. This paper simplifies it by dividing the heat flow path into horizontal and vertical sections. The thermal resistances of these two sections are in series, so the thermal resistance of the cylinder is the sum of them. The accuracy of the simplification method is verified by finite element simulation.
With the established thermal circuit model, the phenomenon that the temperature decrease of the transformer tends to remain constant as the water flow rate increases is explained. The cause of this phenomenon is the relatively high thermal resistance between the heat source and the water-cooling plate, resulting in less heat reaching the water-cooling plate and limited cooling effect. Therefore, it is necessary to find an insulation material with strong thermal conductivity to meet the heat dissipation requirements of potting transformers.
Taking inspiration from the packaging materials of high-power semiconductor module, Aluminum Nitride material with both insulation and heat dissipation capabilities is suggested and applied in high-power transformers. Based on this high thermal conductivity insulation material, this paper proposes a new heat dissipation structure. This structure provides a low thermal resistance channel between the heat source and the water-cooling plate, and allows further increase in capacity and power density of high-frequency transformers. In addition, due to the larger core loss in the inner circle of the toroidal core and the denser winding on the inner side of the core, the thermal density in the inner direction of the transformer is higher than that in the outer direction, and the proposed heat dissipation structure enhances the thermal conductivity in the inner direction, so it is highly suitable for the toroidal transformers.
Finite element simulation and experiments conducted on the 25 kHz/160 kV·A high-frequency transformer prototype prove that the temperature rise of the transformer using aluminum nitride heat dissipation structure is lower than that of the fully epoxy resin potted transformer, verifying the effectiveness of the proposed heat dissipation structure.
keywords:High-power high-frequency transformer, toroidal water-cooling transformer, equivalent thermal circuit model, aluminum nitride material
中图分类号:TM433
DOI: 10.19595/j.cnki.1000-6753.tces.231685
国家自然科学基金资助项目(52177191)。
收稿日期 2023-10-12
改稿日期 2023-12-26
王开国 男,1998年生,硕士研究生,研究方向为大功率高频变压器精细化设计。E-mail:wangkaiguo@whu.edu.cn
宫金武 男,1981年生,副教授,博士生导师,研究方向为高效率高功率密度电力电子变换技术、宽禁带半导体器件应用、电能质量分析与治理。E-mail:gongjinwu@whu.edu.cn(通信作者)
(编辑 李 冰)