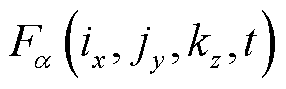 表示t时刻场分量的值,有
表示t时刻场分量的值,有摘要 时程精细积分(PITD)法是一种全波电磁数值方法,具有相当宽松的数值稳定性条件,且数值色散误差几乎不受时间步长的影响,因而近年来在电磁学领域中受到广泛关注。在有源区域的电磁数值模拟中,PITD法需要计算激励源添加引入的非齐次项所产生的矩阵积分,其计算或存在矩阵求逆运算,易不稳定,或难以在大时间步长下保证计算结果的精度,这使得PITD法的推广应用受到一定限制。该文将响应矩阵法引入有源区域的电磁波PITD仿真中,不仅避免了矩阵的求逆运算,并且能够在保证计算结果精度的条件下,增大时间步长的选择范围,提高算法的计算效率。最后,进行了实例计算,并与直接近似积分方法和数值积分方法的结果进行了对比,验证了该文所提方法的实用性和有效性。
关键词:电磁波数值模拟 矩阵积分 矩阵求逆问题 响应矩阵法
时域有限差分(Finite Difference Time Domain, FDTD)法是一种简单直观的全波电磁数值方法,已被广泛应用于电磁学研究的众多领域中[1-4]。在电磁系统的FDTD仿真中一般都包含两个不同的空间尺度,分别是激励源的波长和系统的空间尺寸。随着加工技术的不断改进,各类电磁器件的集成度不断提高,且尺寸逐渐向着亚毫米、纳米级发展[5]。因此,高度集成的芯片元件[6-7]等电小尺寸系统的电磁特性分析受到了人们的广泛关注。在电小尺寸系统的电磁仿真中,激励源的波长往往比系统的空间尺寸大得多。然而,根据Courant Friedrichs Lewy(CFL)稳定性条件[8],FDTD法的时间步长受限于空间网格尺寸却成为制约提高计算效率的一个瓶颈因素。时程精细积分(Precise Integration Time Domain, PITD)法[9-11]突破了CFL稳定性条件的限制,在保证计算精度的前提下,它不仅具有相当宽松的时间步长选取范围,且数值色散误差几乎不受时间步长大小的影响,这使得PITD法在提高计算效率方面具有自然的优势,近年来在计算电磁学领域中受到了广泛关注。目前,PITD法的数值稳定性分析、数值色散特性分析、吸收边界处理等关键技术已经相当成熟,掣肘其广泛应用的存储占用大的问题也得到了比较明显的缓解[12-14],其应用也已推广到运动介质、时变媒质等的电磁波问题分析中[15-20]。
在有源区域的电磁仿真中,PITD法需要计算添加激励源引起的非齐次项积分——矩阵积分项。目前,PITD法中常用的矩阵积分项计算方法有两类。一类是直接近似积分方法[9,16],采用线性函数或三角函数对非齐次项进行近似后直接积分,得到相应的时域递推计算公式。它虽然具有良好的数值计算精度,但存在矩阵的求逆运算。矩阵求逆不仅计算量大,而且容易数值不稳定,有时还会有逆矩阵不存在的情况。为了确保逆矩阵存在,马西奎等[9]给出了去除系数矩阵线性相关关系的公式,其缺点是在实际计算中会遇到其他问题且编程难度大。另一类是数值积分方法[15],例如辛普森积分方法、高斯积分方法等,这类方法虽然不涉及矩阵的求逆运算,但数值计算精度较低,在时间步长较大时尤其明显。如何避免矩阵求逆运算和在大时间步长下保证计算结果的精度,仍然是在PITD法应用中亟待解决的问题。
基于加法定理和增量存储思想,钟万勰等提出了一种用于非齐次动力方程[21]和非线性动力方程[22]中Duhamel积分项计算的响应矩阵法。本文将响应矩阵法引入PITD法的非齐次项计算中,将非齐次项产生的矩阵积分的计算转换为一系列基本形式函数的响应矩阵的计算,成功地避免了矩阵求逆,实现了在大时间步长下的高精度计算。由于避免了矩阵的求逆运算,所以不受矩阵性态的限制,更便于扩展PITD法的应用范围。采用PITD法分析电磁问题时,常用的激励源按随时间变化的形式分为两类:一类是周期性变化的时谐源;另一类是脉冲形式变化的脉冲源,例如,高斯脉冲源、升余弦脉冲源、微分高斯脉冲源、截断三余弦脉冲源、双指数脉冲源和调制高斯脉冲源。通常时谐源、升余弦脉冲源、截断三余弦脉冲源和双指数脉冲源都能写成e指数函数展开形式;而高斯脉冲源、微分高斯脉冲源、调制高斯脉冲源可以采用Taylor展开写成多项式函数展开形式。因此,本文给出了这两种基本形式函数的响应矩阵的计算公式。
PITD法是一种半解析时域数值计算方法,在对Maxwell旋度方程进行离散化处理时,仅对空间偏导数进行差分近似,将旋度方程转换为常微分方程(Ordinary Differential Equation, ODE),再应用常微分方程理论和精细积分(Precise Integration, PI)方法就可以求得各个时刻电磁场的空间分布。
PITD法的空间离散与FDTD法相似,沿着x、y和z三个方向将电场强度和磁场强度离散到Yee元胞的各条棱边与各个表面。在离散的空间域中,采用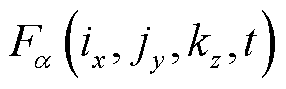 表示t时刻场分量的值,有
表示t时刻场分量的值,有
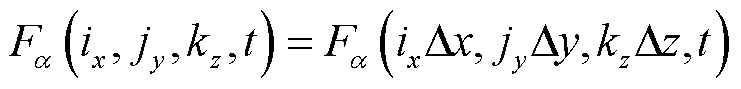 (1)
(1)
式中, =x, y, z;
=x, y, z;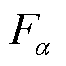 为电场强度
为电场强度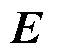 、磁场强度
、磁场强度 或电流密度
或电流密度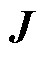 的某一分量;ix、jy和kz分别为场分量在空间中沿着x、y和z方向的序号;
的某一分量;ix、jy和kz分别为场分量在空间中沿着x、y和z方向的序号;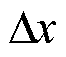 、
、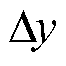 和
和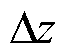 分别为沿着x、y和z方向的空间步长。
分别为沿着x、y和z方向的空间步长。
若在一个有源区域内,媒质参数不随时间变化并各向同性,则Maxwell旋度方程表示为
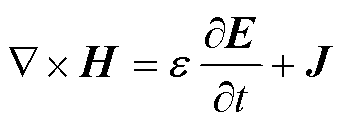 (2)
(2)
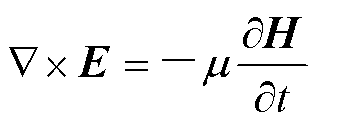 (3)
(3)
式中,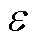 为介电常数;
为介电常数;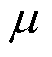 为磁导率。将
为磁导率。将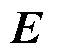 、
、 和
和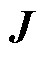 采用式(1)格式进行空间离散后,利用中心差分仅对式(2)、式(3)中的空间偏导数进行近似,可将Maxwell旋度方程在每个空间节点上转换为常微分方程。以
采用式(1)格式进行空间离散后,利用中心差分仅对式(2)、式(3)中的空间偏导数进行近似,可将Maxwell旋度方程在每个空间节点上转换为常微分方程。以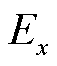 为例,它的空间离散形式为
为例,它的空间离散形式为
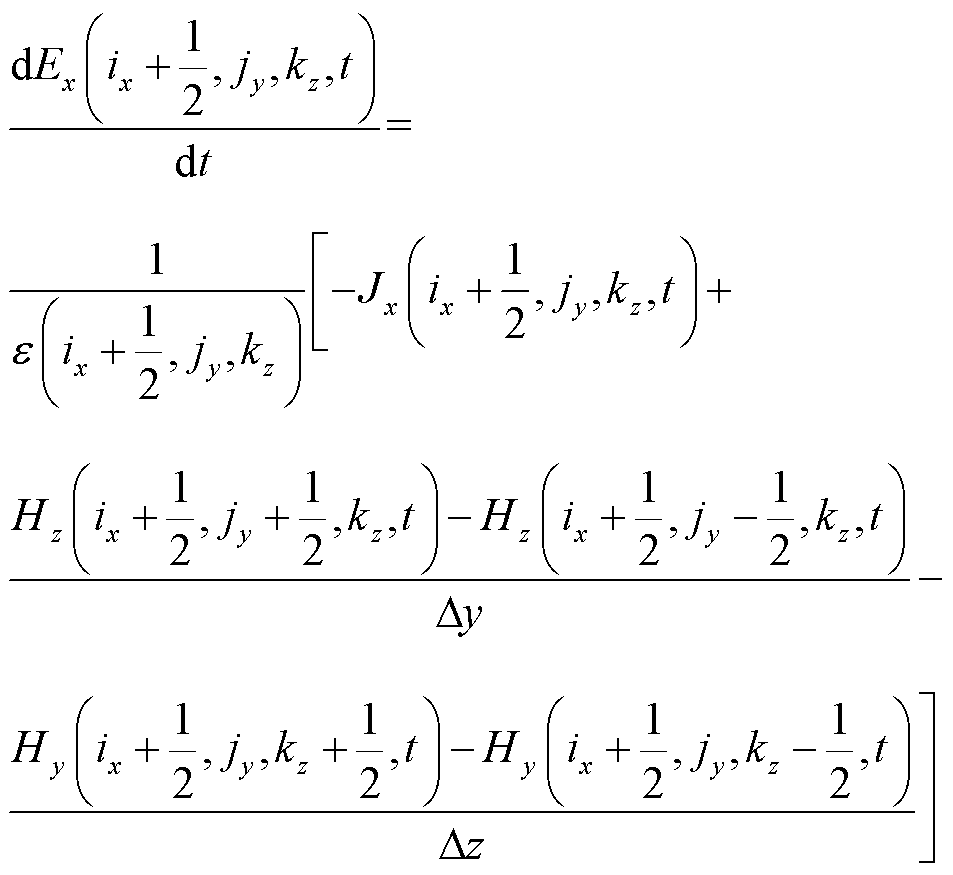 (4)
(4)
其余各个场分量的空间离散形式与式(4)类似,这里不再赘述。显然,在空间中所有节点上各场分量的常微分方程构成了一个常微分方程组,其解表示在各个时刻电磁场的空间分布。
综合空间各节点上的常微分方程,可以写成矩阵形式,有
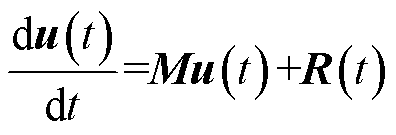 (5)
(5)
式中,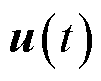 为一个包含全部节点上的电场和磁场分量的列向量;
为一个包含全部节点上的电场和磁场分量的列向量;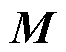 为由离散网格尺寸和媒质参数确定的系数矩阵;
为由离散网格尺寸和媒质参数确定的系数矩阵;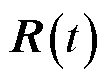 为由于引入激励源和边界条件所产生的非齐次项。应该注意到,
为由于引入激励源和边界条件所产生的非齐次项。应该注意到,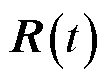 的形式与具体问题有关。
的形式与具体问题有关。
根据ODE理论,式(5)的通解可以表示为
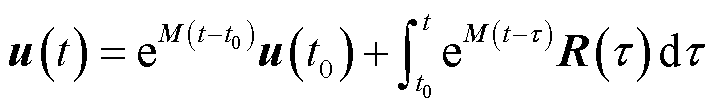 (6)
(6)
式中,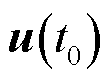 为
为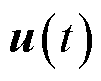 的初始值;t为初始值为t0、终止值为t的时间变量。对时间变量t进行离散化,令时间步长为
的初始值;t为初始值为t0、终止值为t的时间变量。对时间变量t进行离散化,令时间步长为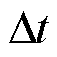 ,则一系列等步长
,则一系列等步长 的时刻为
的时刻为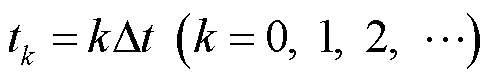 ,记
,记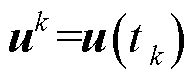 。那么,由式(6)得到逐步递推计算公式为
。那么,由式(6)得到逐步递推计算公式为
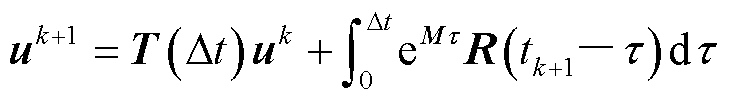 (7)
(7)
式中, 为状态传递矩阵,
为状态传递矩阵,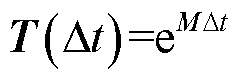 。对于
。对于 的计算可以采用PI方法[9],它能够在计算机字长范围内精确计算矩阵指数。然而,由于
的计算可以采用PI方法[9],它能够在计算机字长范围内精确计算矩阵指数。然而,由于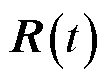 的一般性,所以式(7)右边的矩阵积分项的计算就应根据特定形式选择一种合适的方法。
的一般性,所以式(7)右边的矩阵积分项的计算就应根据特定形式选择一种合适的方法。
对于矩阵积分项的计算,文献[9,16]中分别给出用线性函数和三角函数近似非齐次项的直接近似积分方法。例如,假设在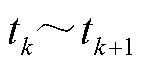 时间段内,
时间段内,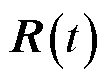 是线性变化的,即
是线性变化的,即
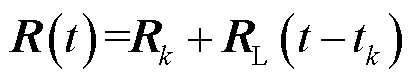 (8)
(8)
式中,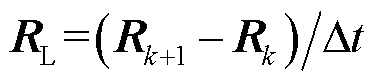 ;
; 、
、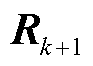 分别为
分别为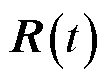 在
在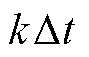 、
、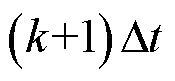 时刻的值。将式(8)代入式(7)中,得到在线性函数近似下PITD法的递推计算公式为
时刻的值。将式(8)代入式(7)中,得到在线性函数近似下PITD法的递推计算公式为
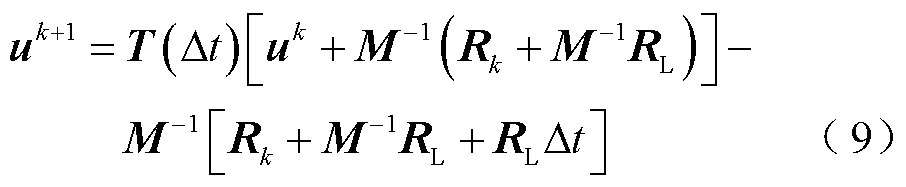
假设在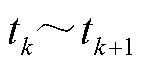 时间段内,
时间段内,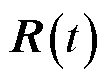 是以三角函数形式变化的,即
是以三角函数形式变化的,即
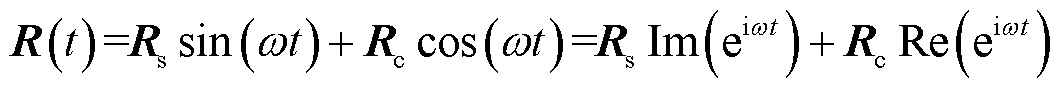 (10)
(10)
式中,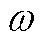 为角频率;
为角频率;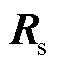 、
、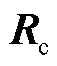 分别为正弦分量、余弦分量的幅值。将式(10)代入式(7)中,得到在三角函数近似下PITD法的递推计算公式为
分别为正弦分量、余弦分量的幅值。将式(10)代入式(7)中,得到在三角函数近似下PITD法的递推计算公式为
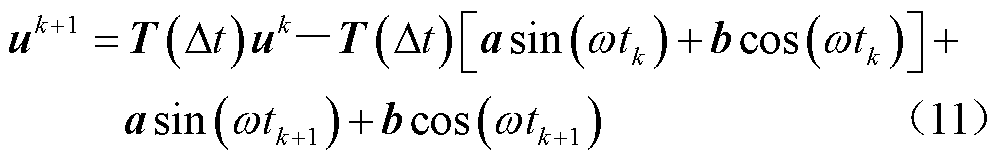
其中
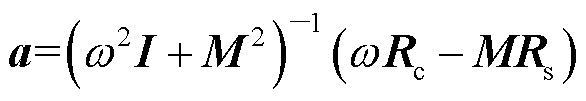
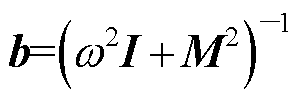
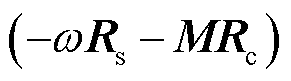
容易知道,直接近似积分方法的误差主要来自于用线性函数或三角函数近似非齐次项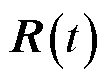 。显然,当
。显然,当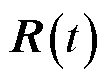 是线性函数或三角函数时,直接近似积分方法能够得到矩阵积分项在计算机上的精确解。然而,直接近似积分方法涉及系数矩阵
是线性函数或三角函数时,直接近似积分方法能够得到矩阵积分项在计算机上的精确解。然而,直接近似积分方法涉及系数矩阵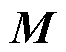 或其相关矩阵
或其相关矩阵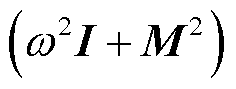 的求逆运算,容易产生数值不稳定,甚至逆矩阵不存在。
的求逆运算,容易产生数值不稳定,甚至逆矩阵不存在。
为了避免矩阵的求逆运算,文献[15]提出采用数值积分方法计算矩阵积分项。目前,常用的数值积分方法有辛普森积分方法和高斯积分方法。采用辛普森积分方法计算矩阵积分项时,PITD法的递推计算公式为
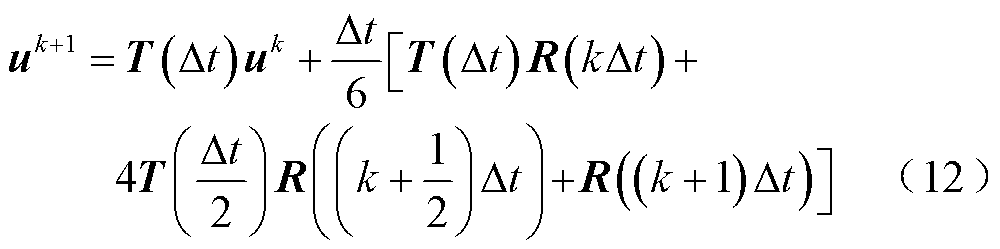
而采用高斯积分方法计算矩阵积分项时,PITD法的递推计算公式为
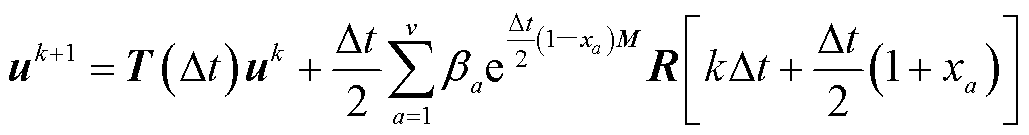 (13)
(13)
式中,v为积分点数量;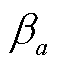 为加权系数;
为加权系数;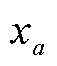 为积分点的坐标。
为积分点的坐标。
数值积分方法已被广泛应用于有源区域电磁场的PITD计算,但计算精度较低,在大时间步长下尤为明显。因此,发展一种避免矩阵求逆运算的大时间步长矩阵积分高精度计算方法,对PITD法用于有源区域电磁场的仿真计算来说是十分有意义的。
用响应矩阵法计算非齐次项引起的矩阵积分,不仅能够避免矩阵求逆运算,并且能在大时间步长下实现高精度计算。响应矩阵法首先将矩阵积分转换为一系列基本形式函数的矩阵积分,然后应用加法定理和增量存储思想构造响应矩阵的计算公式。根据常用的激励源类型,本文给出了e指数函数展开形式和多项式函数展开形式的响应矩阵计算公式。值得指出,在非齐次项就是e指数函数或多项式函数形式的情况下,响应矩阵法可以得到矩阵积分项在计算机上的精确解。
首先,根据具体问题选择一个适合的基本形式函数进行非齐次项的近似。假设在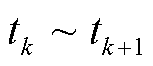 时间段内,
时间段内,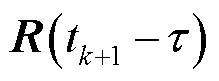 以式(14)形式变化。
以式(14)形式变化。
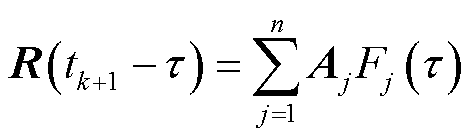 (14)
(14)
式中,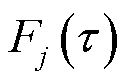 为基本形式函数;n为基本形式函数的数量;
为基本形式函数;n为基本形式函数的数量;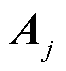 为第j个基本形式函数对应的幅值。将式(14)代入式(7)右边的矩阵积分项中,得到
为第j个基本形式函数对应的幅值。将式(14)代入式(7)右边的矩阵积分项中,得到
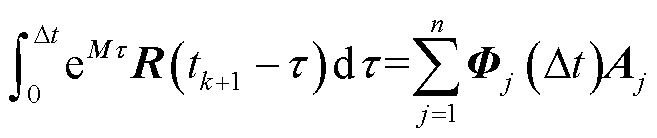 (15)
(15)
其中
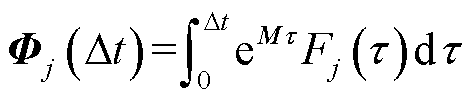 (16)
(16)
因此,矩阵积分项的计算转换为基本形式函数与指数矩阵函数乘积的积分。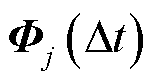 可以被看成外加激励源的响应矩阵,它能够基于加法定理和增量存储思想进行计算。在此过程中,令
可以被看成外加激励源的响应矩阵,它能够基于加法定理和增量存储思想进行计算。在此过程中,令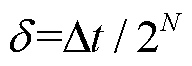 ,其中,
,其中,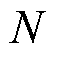 为任意正整数,一般取
为任意正整数,一般取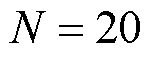 。首先,根据式(16),可推导出
。首先,根据式(16),可推导出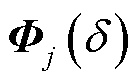 的加法定理,有
的加法定理,有
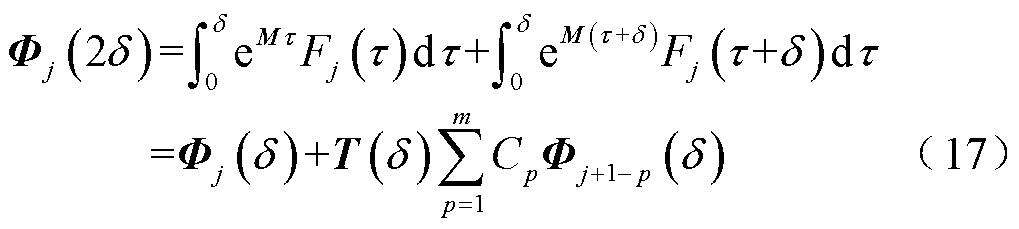
式中,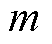 和
和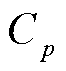 为待定常数,由选择的基本形式函数确定。显然,
为待定常数,由选择的基本形式函数确定。显然,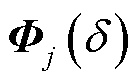 加法定理的实现需要
加法定理的实现需要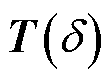 ,其加法定理为
,其加法定理为
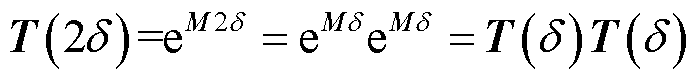 (18)
(18)
有了加法定理后,就可以根据在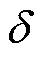 区段内对应的
区段内对应的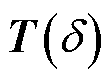 和
和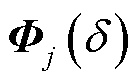 ,通过循环计算的方式,合并得到在
,通过循环计算的方式,合并得到在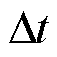 区段内对应的
区段内对应的 及
及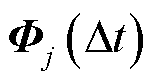 。可采用Taylor级数来展开
。可采用Taylor级数来展开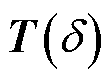 和
和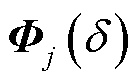 ,即
,即
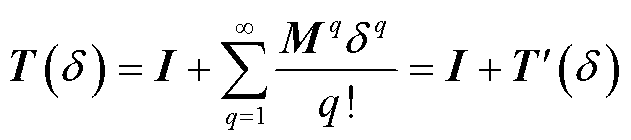 (19)
(19)
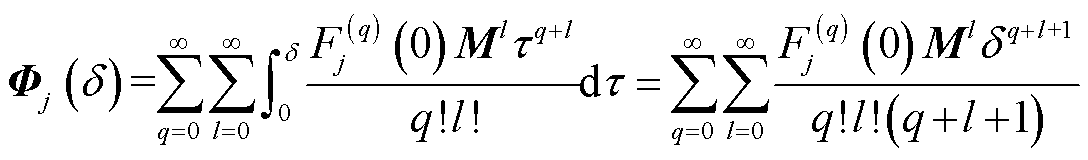 (20)
(20)
式中,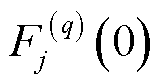 为
为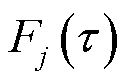 在
在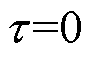 时的q阶导数;
时的q阶导数;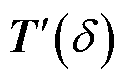 为
为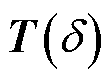 相对于单位矩阵
相对于单位矩阵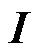 的增量矩阵,
的增量矩阵,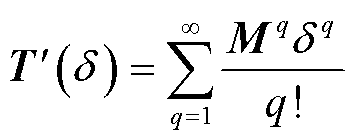 。考虑到
。考虑到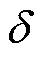 很小,式(19)和式(20)一般截断到
很小,式(19)和式(20)一般截断到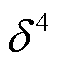 就足够了。应该注意,增量矩阵
就足够了。应该注意,增量矩阵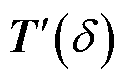 为小量。为避免小量在合并过程中由于计算机的舍入操作严重丧失计算精度,将其单独存储计算得到
为小量。为避免小量在合并过程中由于计算机的舍入操作严重丧失计算精度,将其单独存储计算得到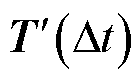 ,最后再与单位矩阵
,最后再与单位矩阵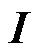 进行加法运算。
进行加法运算。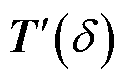 的加法定理为
的加法定理为
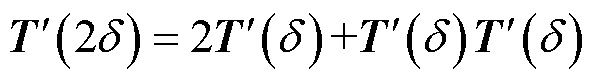 (21)
(21)
此时,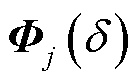 的加法定理式(17)改写为
的加法定理式(17)改写为
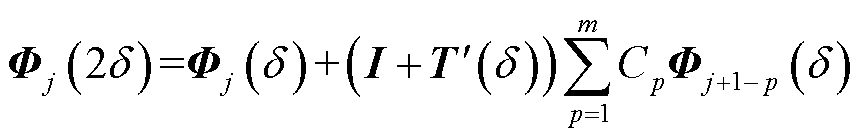 (22)
(22)
下面介绍基于加法定理,合并得到在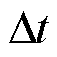 区段内对应的
区段内对应的 和
和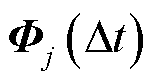 。首先,将
。首先,将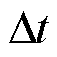 区段均匀划分为
区段均匀划分为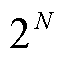 份小区段
份小区段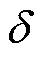 ,并根据式(19)和式(20)计算得到
,并根据式(19)和式(20)计算得到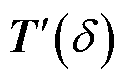 和
和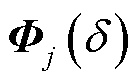 。然后,将
。然后,将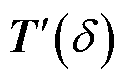 和
和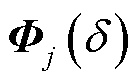 代入算法1中,通过循环计算的方式合并得到在
代入算法1中,通过循环计算的方式合并得到在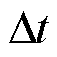 区段内对应的
区段内对应的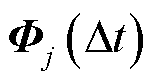 。
。

算法1 响应矩阵的循环合并计算 for i=1:Nfor j=1:n执行的加法定理式(22), 得到;令;end执行的加法定理式(21),得到;令;end执行。
现在,以基本形式函数为e指数函数和多项式函数为例,分别给出PITD法的时域递推计算公式。例如,假设在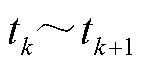 时间段内,
时间段内,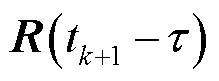 是以e指数函数展开形式变化,即
是以e指数函数展开形式变化,即
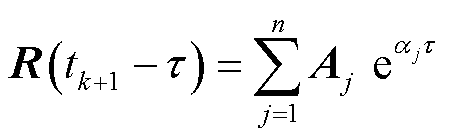 (23)
(23)
式中,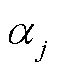 为复数,记
为复数,记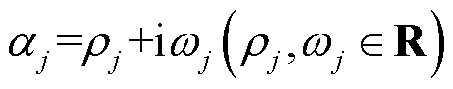 。此时,
。此时,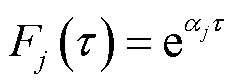 ,将式(23)代入式(17)中确定
,将式(23)代入式(17)中确定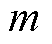 和
和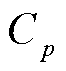 分别为1和
分别为1和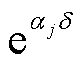 ,就能够通过算法1计算得到在
,就能够通过算法1计算得到在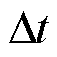 区段内对应的
区段内对应的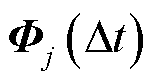 。然后,将
。然后,将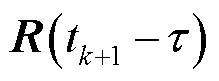 代入式(7)中,可以推导出PITD法的递推计算公式。例如,对于式(10)所示三角函数形式,相应的递推计算公式为
代入式(7)中,可以推导出PITD法的递推计算公式。例如,对于式(10)所示三角函数形式,相应的递推计算公式为
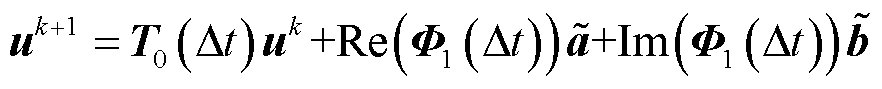 (24)
(24)
式中,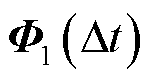 为响应矩阵;
为响应矩阵;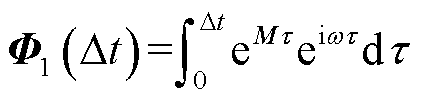 ;
;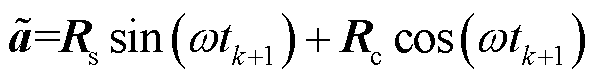 ;
;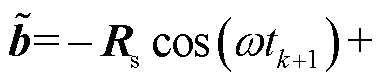
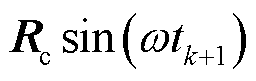 。
。
假设在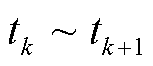 时间段内,
时间段内,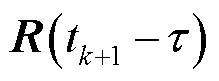 是以多项式函数展开形式变化,即
是以多项式函数展开形式变化,即
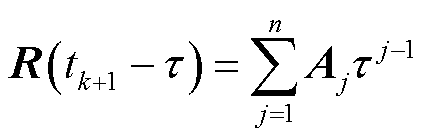 (25)
(25)
此时,式(17)中的m和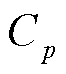 分别为j和
分别为j和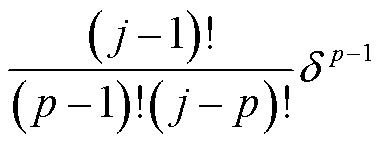 。例如,对于式(8)所示线性函数形式,相应的递推计算公式为
。例如,对于式(8)所示线性函数形式,相应的递推计算公式为
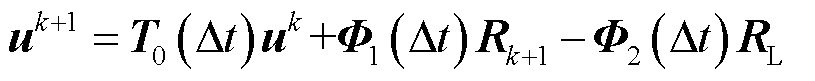 (26)
(26)
式中,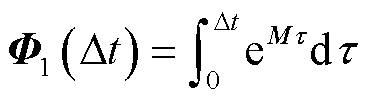 和
和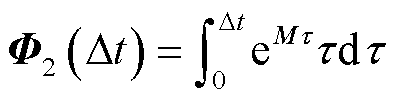 为响应矩阵。
为响应矩阵。
显然,与直接近似积分方法相比,递推计算公式(24)和式(26)不仅避免了矩阵求逆运算且格式更加简洁。
在对电磁系统进行宽带特性分析时,常会用到脉冲激励源。由于高斯脉冲源的最高频率和频宽可以通过参数调节,很容易就能保证在空间中的信号采样精度,因此被广泛应用在宽带特性分析中。然而,由于高斯脉冲源的脉冲持续时间短且变化迅速,若采用低阶多项式近似,则在大时间步长下的计算精度较差;反之,若采用高阶多项式近似,虽然能够在保证精度的前提下选择大时间步长,但响应矩阵的数量随多项式阶数的增加而增加,导致计算机资源消耗大量增加和对算法效率的提升效果有限,甚至有可能降低算法效率。考虑到高斯脉冲源应用的广泛性,本文对其提出了一种新的近似函数,在提高计算精度的同时尽量降低计算机资源消耗。
首先,对升余弦脉冲函数进行时移,确保其脉冲峰值与高斯脉冲函数出现在同一时刻。如图1所示,时移后升余弦脉冲的时域波形及频谱图中主要频率成分的幅值相位与高斯脉冲高度相似,且能够通过e指数函数展开形式求解。
因此,本文采用升余弦函数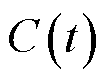 作为高斯脉冲函数
作为高斯脉冲函数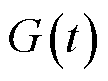 的近似形式。它们的表达式分别为
的近似形式。它们的表达式分别为
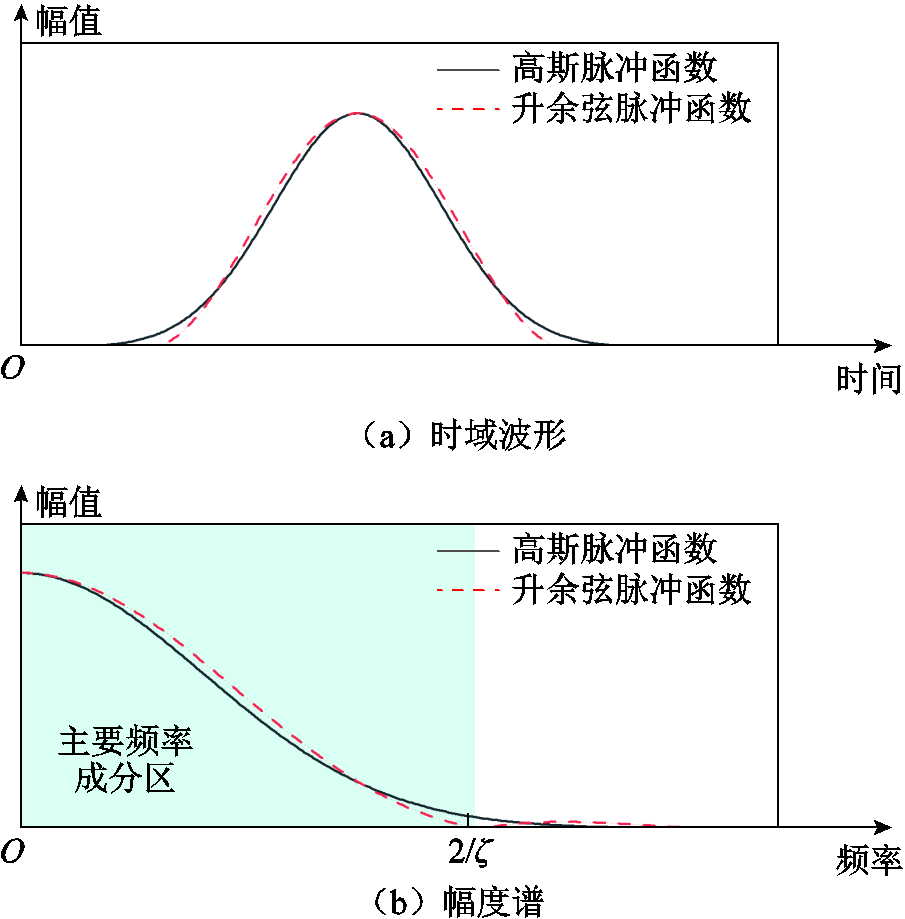
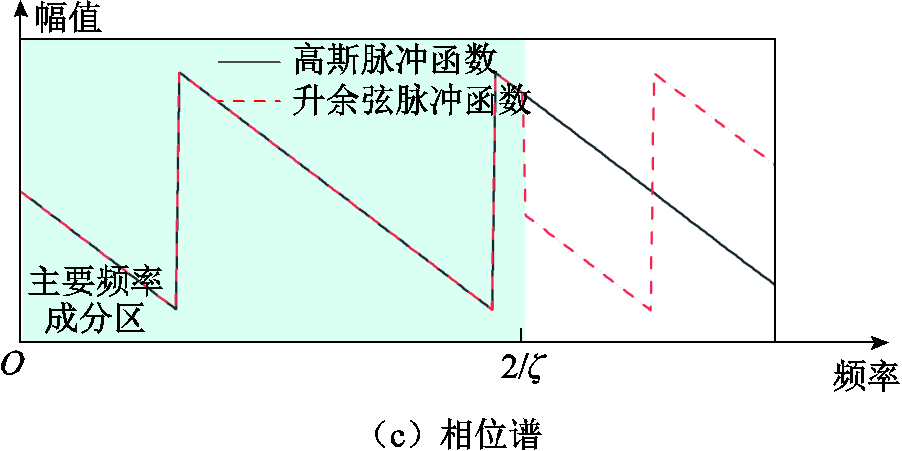
图1 高斯脉冲、时移后升余弦脉冲的时域波形和频谱
Fig.1 Time-domain waveforms and spectra of Gaussian pulses, time-shifted raised cosine pulses
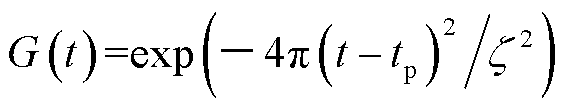 (27)
(27)
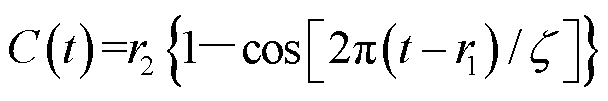 (28)
(28)
式中,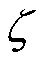 为常数,决定了高斯脉冲的宽度和最高频率;
为常数,决定了高斯脉冲的宽度和最高频率;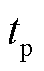 为常数,决定了脉冲峰值出现的时刻,一般令
为常数,决定了脉冲峰值出现的时刻,一般令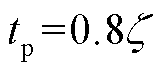 。采用
。采用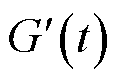 和
和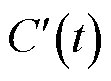 分别表示
分别表示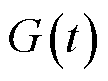 和
和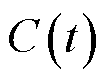 的时间一阶导数。如果在
的时间一阶导数。如果在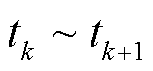 时间段内满足
时间段内满足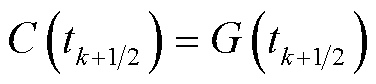 和
和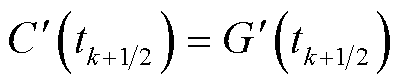 ,即
,即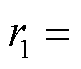
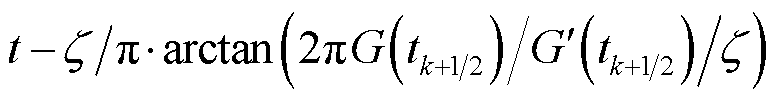 ,
,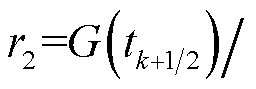
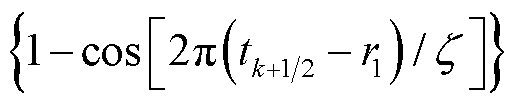 ,则有
,则有
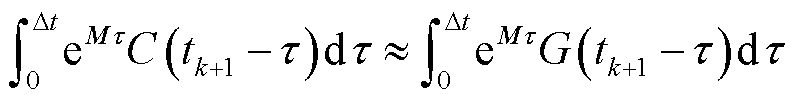 (29)
(29)
若激励源为高斯脉冲源,即
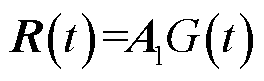 (30)
(30)
式中,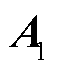 为代表幅值的常数。将式(29)和式(30)代入式(7)中右边的非齐次积分项中,得到
为代表幅值的常数。将式(29)和式(30)代入式(7)中右边的非齐次积分项中,得到
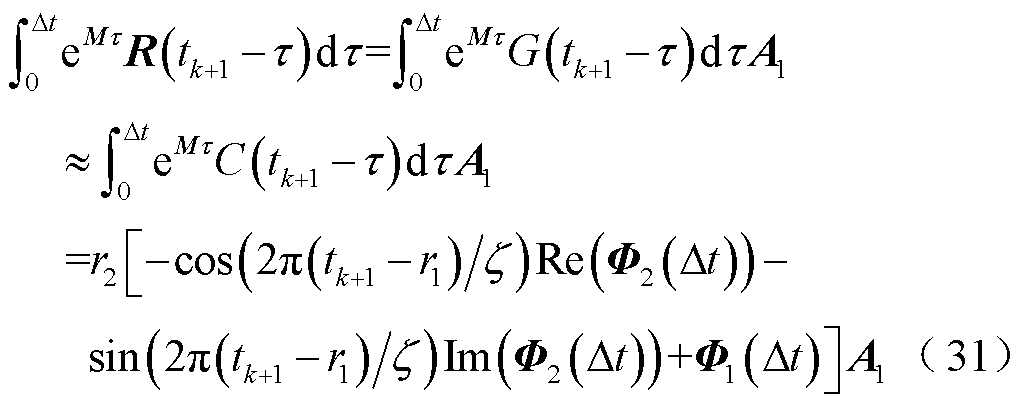
式中, 。因此,在高斯脉冲源激励下,采用升余弦函数近似非齐次项时PITD法的递推计算公式为
。因此,在高斯脉冲源激励下,采用升余弦函数近似非齐次项时PITD法的递推计算公式为
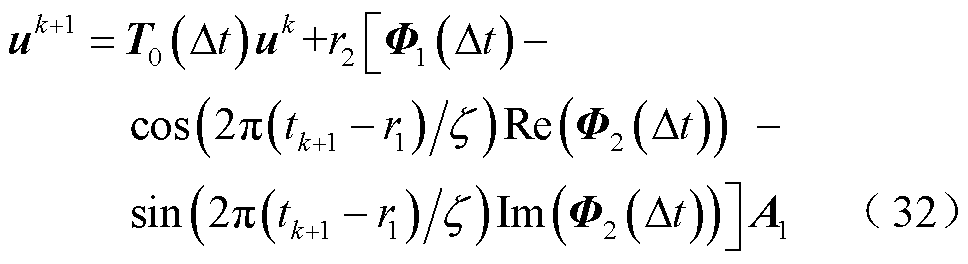
为了验证响应矩阵法的有效性,在这里以实例将它与直接近似积分方法和数值积分方法进行了比较。在处理有源区域电磁仿真问题时,PITD法的误差主要来自空间网格剖分和矩阵积分项的计算。例如,设有一个长10 cm的一维仿真区域,在边界处采用吸收边界条件进行截断,采用的离散网格空间步长为0.1 cm。现在,分别采用响应矩阵法、直接近似积分方法和数值积分方法来仿真正弦平面波在自由空间中的传播。任选一点作为观测点进行场量采集,并以解析解为参考值得到计算误差为
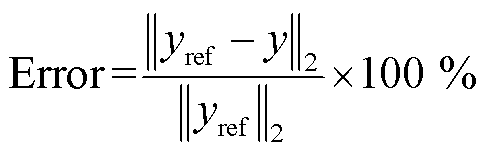 (33)
(33)
式中,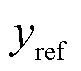 为参考值;
为参考值;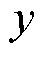 为观测点处采集到的电场计算值。在100 MHz正弦波激励下得到的计算结果如图2所示。在图2中,S为
为观测点处采集到的电场计算值。在100 MHz正弦波激励下得到的计算结果如图2所示。在图2中,S为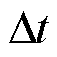 的倍数,
的倍数,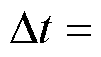 3.335 ps,它等于CFL稳定条件给出的最大时间步长。
3.335 ps,它等于CFL稳定条件给出的最大时间步长。
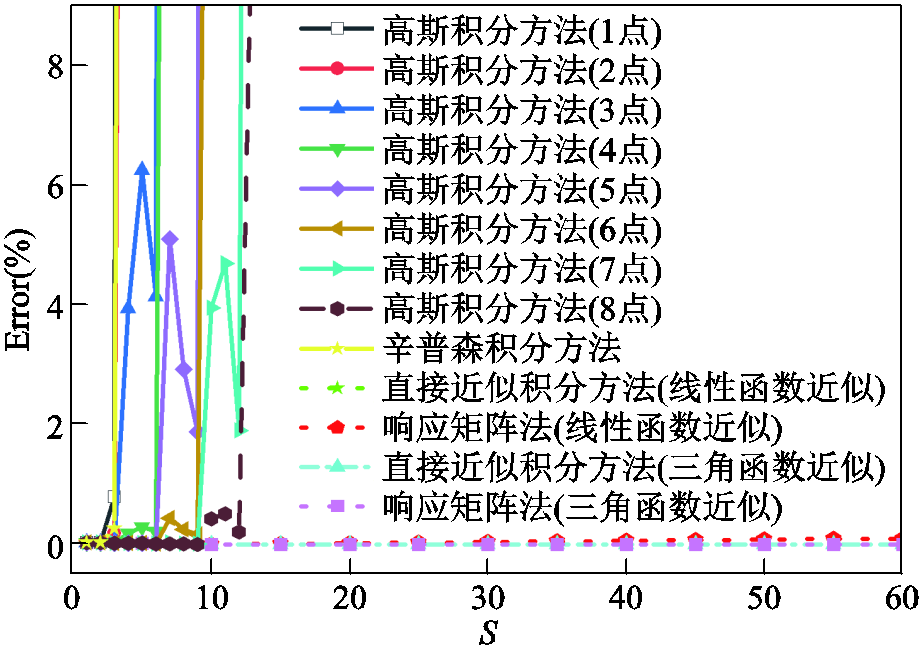
图2 不同矩阵积分计算方法在二维算例中的计算误差对比
Fig.2 Comparison of calculation errors between different matrix integral calculation methods in the two-dimensional example
从图2中可以看出,直接近似积分法在大时间步长下也可以保持较高的计算精度,但矩阵求逆运算过程极可能会产生数值不稳定现象,甚至出现逆矩阵不存在的情况。例如,当激励源为40 kHz的正弦波时,采用三角函数近似的直接近似积分方法需要求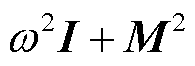 的逆矩阵,由于激励源频率较低,对奇异矩阵
的逆矩阵,由于激励源频率较低,对奇异矩阵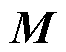 的影响增加,会导致矩阵
的影响增加,会导致矩阵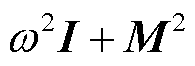 接近奇异,使得计算结果出现了如图3所示的非正常波动现象。虽然数值积分方法不涉及矩阵的逆运算,但在大时间步长下计算精度比较低,即使增加数值积分的点数,计算精度仍然不高。响应矩阵法的计算结果与直接近似积分方法几乎相同,即使在大时间步长下其计算误差也均小于0.5%。
接近奇异,使得计算结果出现了如图3所示的非正常波动现象。虽然数值积分方法不涉及矩阵的逆运算,但在大时间步长下计算精度比较低,即使增加数值积分的点数,计算精度仍然不高。响应矩阵法的计算结果与直接近似积分方法几乎相同,即使在大时间步长下其计算误差也均小于0.5%。
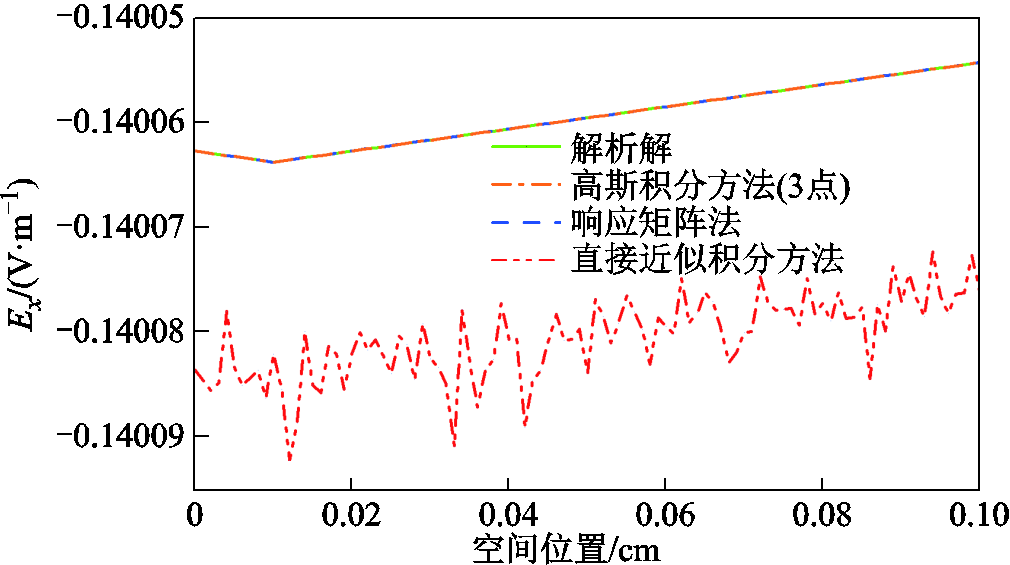
图3 40 kHz正弦波激励下电场的空间分布
Fig.3 Spatial distribution of electric field under 40 kHz sine wave excitation
以图4所示模型为例,对响应矩阵法在求解三维电磁波传播问题时的计算精度进行说明。如图4所示,在一个内阻为50 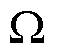 ,幅值为1 V,频率为500 MHz的电压源激励下,仿真模拟50
,幅值为1 V,频率为500 MHz的电压源激励下,仿真模拟50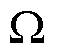 电阻两端的电压值。电压源和电阻之间通过两个电导率为2×104 S/m的平行导电薄层连接。采用空间步长为
电阻两端的电压值。电压源和电阻之间通过两个电导率为2×104 S/m的平行导电薄层连接。采用空间步长为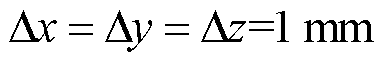 的网格对整个系统进行剖分,
的网格对整个系统进行剖分,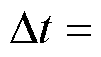 1.925 ps,在边界处设置Mur吸收边界条件进行截断。
1.925 ps,在边界处设置Mur吸收边界条件进行截断。
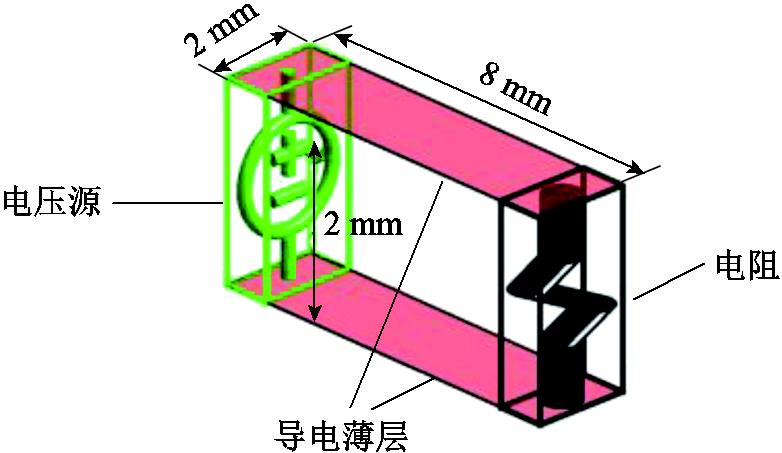
图4 电压源激励下的电阻
Fig.4 The resistance under a voltage source excitation
分别采用响应矩阵法、直接近似积分方法和数值积分方法来仿真获得电阻两端的电压值,并采用式(33)求解计算误差。计算误差的参考值由细网格剖分的FDTD法计算得到,细网格的空间步长为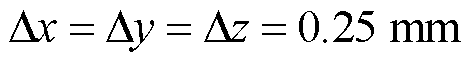 。得到的计算误差如图5所示。从图5中看出,在三维情况下,响应矩阵法的计算结果与直接近似积分方法基本保持一致,即使在大时间步长下其计算误差也均小于0.5%。数值积分方法在大时间步长下计算精度比较低,即使增加数值积分的点数,计算精度仍然不高。直接近似积分方法在大时间步长下可以保持较高的计算精度,但因包含矩阵求逆运算而易产生数值不稳定,甚至逆矩阵不存在的情况。在本仿真算例中,矩阵
。得到的计算误差如图5所示。从图5中看出,在三维情况下,响应矩阵法的计算结果与直接近似积分方法基本保持一致,即使在大时间步长下其计算误差也均小于0.5%。数值积分方法在大时间步长下计算精度比较低,即使增加数值积分的点数,计算精度仍然不高。直接近似积分方法在大时间步长下可以保持较高的计算精度,但因包含矩阵求逆运算而易产生数值不稳定,甚至逆矩阵不存在的情况。在本仿真算例中,矩阵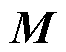 是不可逆的,因此无法采用线性函数近似的直接近似积分方法进行仿真。而采用三角函数近似的直接近似积分方法也会出现数值不稳定现象。例如,当激励源为1 MHz的正弦波时,计算结果出现了如图6所示的非正常波动现象,且电压幅值明显异常大于电压源幅值1 V。
是不可逆的,因此无法采用线性函数近似的直接近似积分方法进行仿真。而采用三角函数近似的直接近似积分方法也会出现数值不稳定现象。例如,当激励源为1 MHz的正弦波时,计算结果出现了如图6所示的非正常波动现象,且电压幅值明显异常大于电压源幅值1 V。
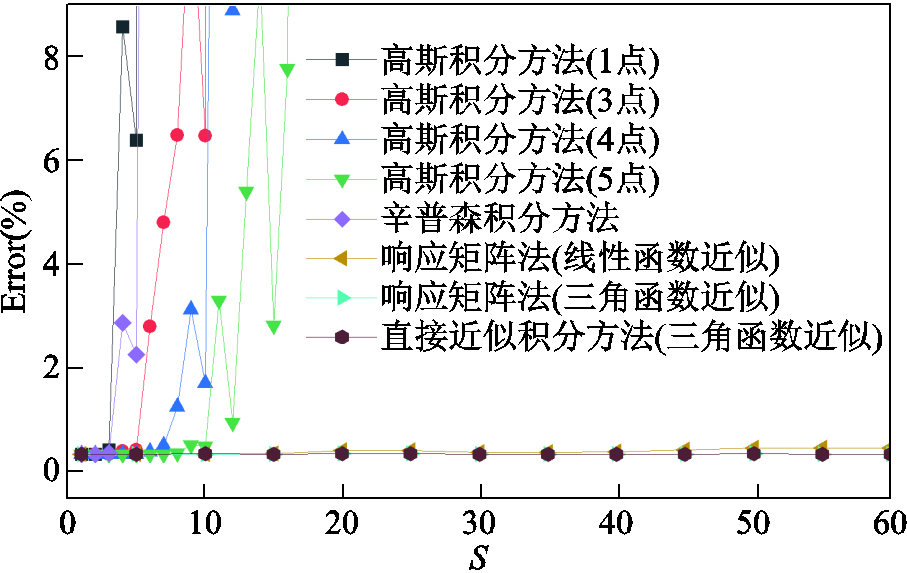
图5 不同矩阵积分计算方法在三维算例中的计算误差对比
Fig.5 Comparison of calculation errors between different matrix integral calculation methods in the three-dimensional example
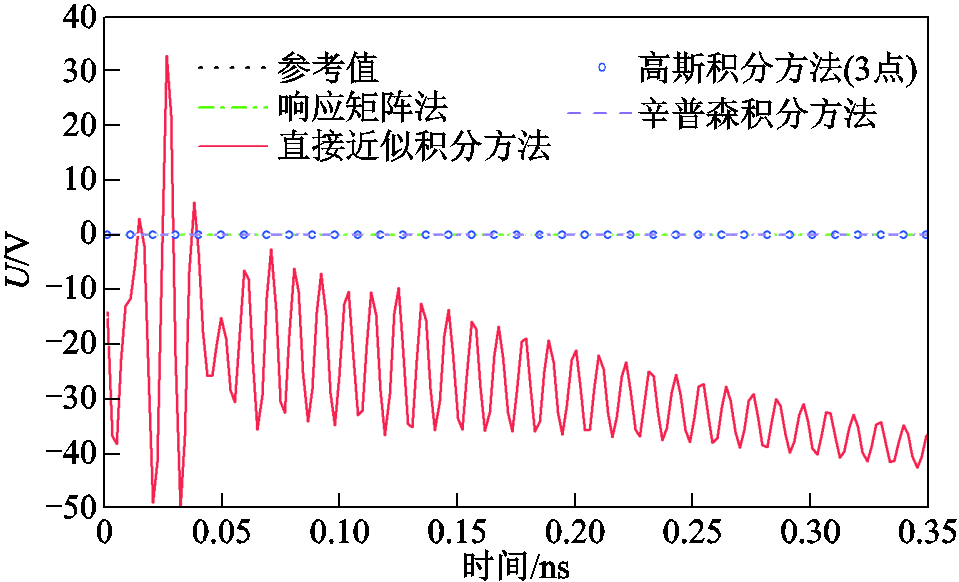
图6 1 MHz正弦波激励下电阻两端的电压值
Fig.6 The voltage of the resistor under 1 MHz sinusoidal excitation
根据以上分析,响应矩阵法在求解一维和三维电磁场传播问题时均具有良好的计算精度。事实上,无论是一维、二维还是三维电磁场传播问题,响应矩阵法始终只需以相同方式计算式(6)中形如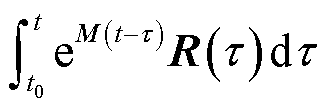 的矩阵积分项。也就是说,响应矩阵法在计算精度方面的表现,理论上不受电磁场传播问题维度的影响。同时,本文的算例结果说明,响应矩阵法能够在保证结果计算精度的前提下,增大时间步长的选择范围,为进一步提高算法的计算效率提供途径。
的矩阵积分项。也就是说,响应矩阵法在计算精度方面的表现,理论上不受电磁场传播问题维度的影响。同时,本文的算例结果说明,响应矩阵法能够在保证结果计算精度的前提下,增大时间步长的选择范围,为进一步提高算法的计算效率提供途径。
这里,以由皮肤-脂肪-肌肉组成的二维生物组织模型为例,比较响应矩阵法和数值积分方法的存储占用和计算效率。由皮肤-脂肪-肌肉组成的二维生物组织模型如图7所示,分析由源点发出的400 MHz正弦波对生物组织的影响。图中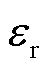 为相对介电常数,
为相对介电常数,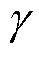 为电导率。采用空间步长
为电导率。采用空间步长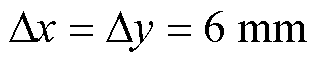 的正方形网格进行剖分,取时间步长
的正方形网格进行剖分,取时间步长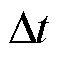 =12.73 ps,并在边界处设置吸收边界条件进行截断。以
=12.73 ps,并在边界处设置吸收边界条件进行截断。以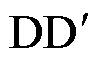 作为观测线,采集30.56 ns时刻观测线处的场值,然后采用式(33)计算结果误差。计算误差的参考值由细网格剖分的FDTD法计算得到,细网格的空间步长为
作为观测线,采集30.56 ns时刻观测线处的场值,然后采用式(33)计算结果误差。计算误差的参考值由细网格剖分的FDTD法计算得到,细网格的空间步长为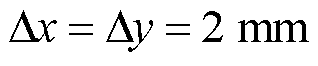 。
。
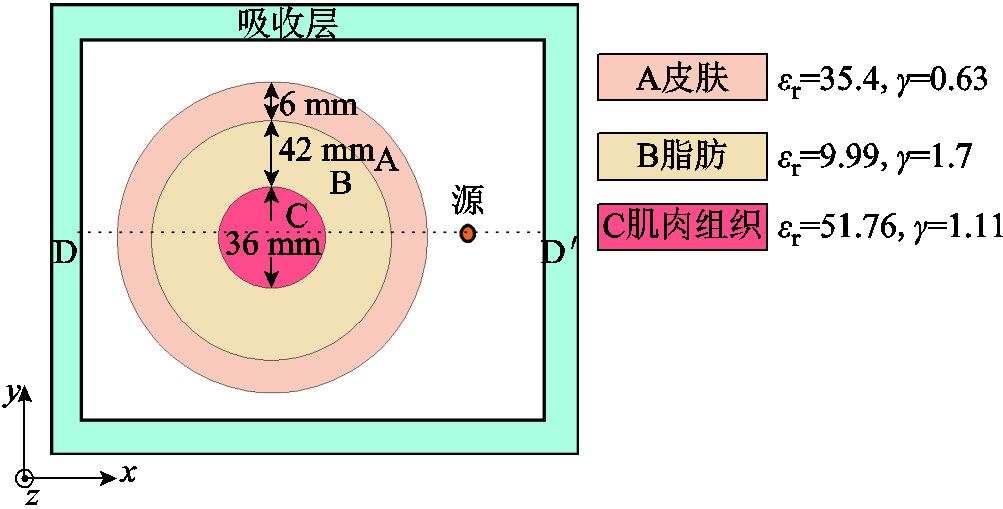
图7 由皮肤-脂肪-肌肉组成的二维生物组织模型
Fig.7 A two-dimensional biological tissue model composed of skin-fat-muscle
在保证计算误差控制在5%内的前提下,采用辛普森积分方法、三点高斯积分方法,S最大可取3;采用响应矩阵法,S最大可取到60。响应矩阵法与数值积分方法的存储占用及运行时间见表1,响应矩阵法的运行时间为57.28 s,分别为高斯积分方法的14.51%和辛普森积分方法的49.26%。响应矩阵法的存储占用为451.65 MB,为高斯积分方法的73.71%。显然,在保证计算精度的前提下,响应矩阵法的时间步长选取范围更加宽松、计算效率更高,存储占用也相对较低。
表1 响应矩阵法与数值积分方法的存储占用及运行时间
Tab.1 Memory occupation and running time of response matrix method and numerical integral methods

方法S时间步进次数运行时间/s存储占用/MB 辛普森积分法3800116.28306.62 高斯积分法3800394.68612.74 响应矩阵法604057.28451.65
为了说明在高斯脉冲源激励下,非齐次项采用升余弦函数近似的优点,以探地雷达为算例,分别采用升余弦函数、二次多项式函数以及三次多项式函数对非齐次项进行近似。探地雷达示意图如图8所示,电介质的参数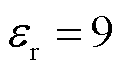 ,
,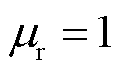 。电介质内设置了电导率为500 S/m的金属导电体。T点为探地雷达的发射天线,沿z方向发射高斯脉冲信号
。电介质内设置了电导率为500 S/m的金属导电体。T点为探地雷达的发射天线,沿z方向发射高斯脉冲信号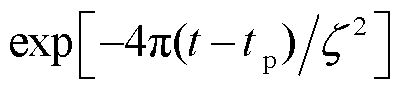 ,其中,
,其中,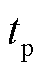 =
=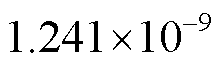 ,
,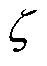 =
= 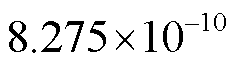 。信号经传播和反射后被R点处的接收天线捕捉到。采用空间步长
。信号经传播和反射后被R点处的接收天线捕捉到。采用空间步长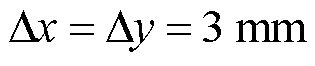 的正方形网格进行剖分,在边界处设置吸收边界条件进行截断,采用的时间步长
的正方形网格进行剖分,在边界处设置吸收边界条件进行截断,采用的时间步长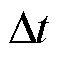 =6.37 ps。根据R点处采集到的磁场分量
=6.37 ps。根据R点处采集到的磁场分量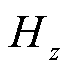 进行误差计算,升余弦函数与多项式函数的精度对比见表2。误差的参考值由细网格剖分的FDTD法计算得到,细网格的空间步长为
进行误差计算,升余弦函数与多项式函数的精度对比见表2。误差的参考值由细网格剖分的FDTD法计算得到,细网格的空间步长为 。
。
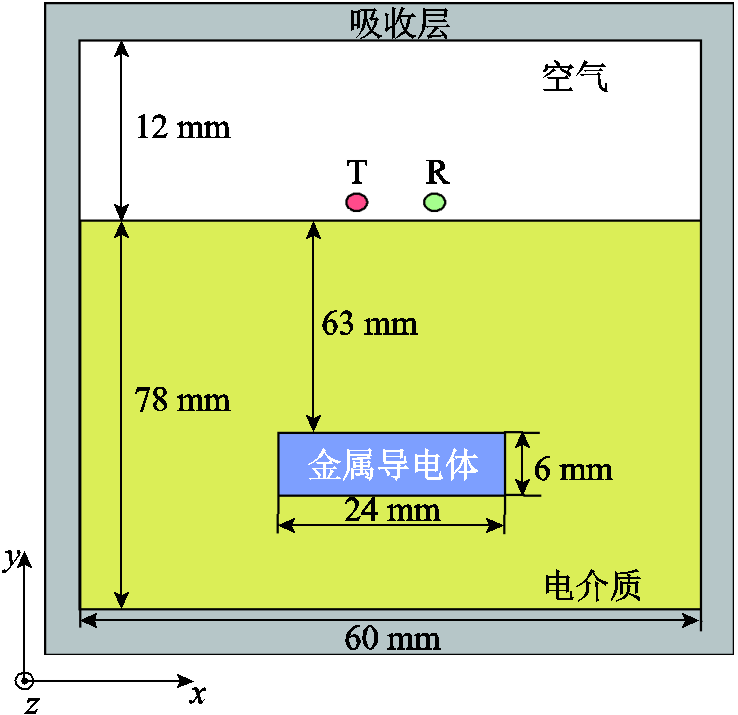
图8 探地雷达示意图
Fig.8 Schematic diagram of ground penetrating radar
表2 升余弦函数与多项式函数的精度对比
Tab.2 Comparison of accuracy between raised cosine function and polynomial function (%)
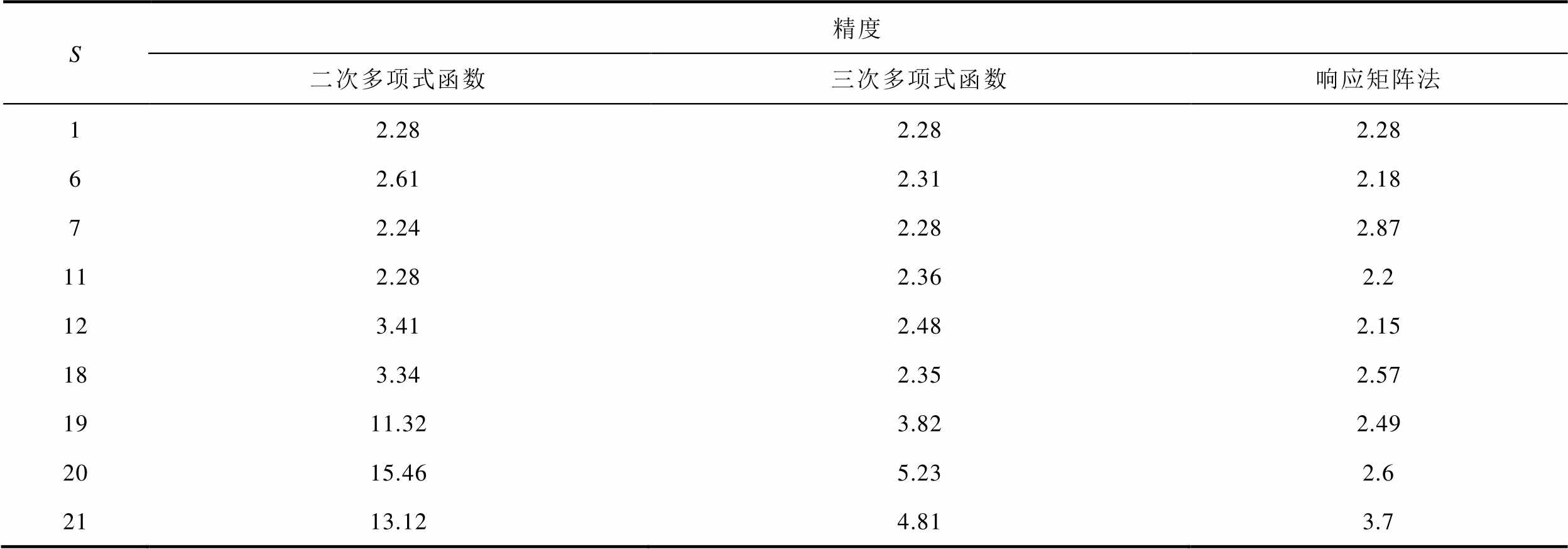
S精度 二次多项式函数三次多项式函数响应矩阵法 12.282.282.28 62.612.312.18 72.242.282.87 112.282.362.2 123.412.482.15 183.342.352.57 1911.323.822.49 2015.465.232.6 2113.124.813.7
从表2中看到,采用升余弦函数近似时,计算精度与采用三次多项式函数几乎一致,且基本不受时间步长的影响。若要保证计算误差在3%内,采用升余弦函数时,S最大可以取20,仿真消耗的时间为68.33 s,存储占用为397.72 MB;采用二次多项式函数和三次多项式函数时,S最大分别可以取11、18,仿真时间分别为82.71 s、86.86 s,存储占用分别为391.24 MB、492.93 MB。显然,采用升余弦函数,比采用多项式函数要节省约20%的仿真时间,且存储占用相对较低。
本文将响应矩阵法引入电磁波PITD仿真中,不仅避免了非齐次项矩阵积分的求逆运算,并且保证了在大时间步长下计算结果的高精度,进而提高了算法的计算效率。数值算例结果表明,在时间步长是CFL稳定性条件定义的时间步长的60倍时,响应矩阵法的结果仍然是准确的。与数值积分方法相比,响应矩阵法明显提高了PITD法的计算效率。此外,为了不失一般性,本文给出了多项式函数展开形式、e指数函数展开形式和升余弦函数展开形式的PITD法递推公式。根据递推公式可知,响应矩阵法避免了矩阵求逆运算,使得PITD法不再掣制于矩阵性态,不仅提高了算法的数值稳定性,更有利于扩展其应用范围。
随着材料技术和加工技术的发展,新型天线、微波器件等为了追求更高的性能,往往集成了非线性、色散的复杂先进材料,且器件的制备逐渐朝着亚毫米、纳米尺度发展,为了反映量子效应及原子细节,量子力学与电磁学的混合模拟趋势增强。本文方法可以处理各种性态的矩阵,更便于后续PITD法与具有色散、非线性性能的复杂材料的辅助方程等结合,以及与其他物理场混合模拟的实现,进而扩展其应用范围。
参考文献
[1] 胡亚楠, 包家立, 朱金俊, 等. 纳秒电脉冲对肝脏组织不可逆电穿孔消融区分布的时域有限差分法仿真[J]. 电工技术学报, 2021, 36(18): 3841-3850.
Hu Yanan, Bao Jiali, Zhu Jinjun, et al. The finite difference time domain simulation of the distribution of irreversible electroporation ablation area in liver tissue by nanosecond electrical pulse[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3841-3850.
[2] Masumnia-Bisheh K, Forooraghi K, Ghaffari-Miab M, et al. Geometrically stochastic FDTD method for uncertainty quantification of EM fields and SAR in biological tissues[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(12): 7466-7475.
[3] 叶志红, 张杰, 周健健, 等. 有耗介质层上多导体传输线的电磁耦合时域分析方法[J]. 物理学报, 2020, 69(6): 47-54.
Ye Zhihong, Zhang Jie, Zhou Jianjian, et al. Time domain hybrid method for coupling analysis of multi-conductor transmission lines on the lossy dielectric layer excited by ambient wave[J]. Acta Physica Sinica, 2020, 69(6): 47-54.
[4] Kogon A J, Sarris C D. An expedient approach to FDTD-based modeling of finite periodic structures[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(2): 1192-1204.
[5] Chen Juan. A review of hybrid implicit explicit finite difference time domain method[J]. Journal of Computational Physics, 2018, 363: 256-267.
[6] 周静, 康升扬, 李辉, 等. 内部压力不均对压接式IGBT器件电热特性的影响分析[J]. 电工技术学报, 2019, 34(16): 3408-3415.
Zhou Jing, Kang Shengyang, Li Hui, et al. Simulation of influence of unbalanced clamping force on electro-thermal characteristics of press-pack IGBT devices[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3408-3415.
[7] 丁雪妮, 陈民铀, 赖伟, 等. 多芯片并联IGBT模块老化特征参量甄选研究[J]. 电工技术学报, 2022, 37(13): 3304-3316, 3340.
Ding Xueni, Chen Minyou, Lai Wei, et al. Selection of aging characteristic parameter for multi-chips parallel IGBT module[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3304-3316, 3340.
[8] Elsherbeni A Z, Veysel D. The Finite-Difference Time-Domain Method for Electromagnetics with MATLAB Simulations[M]. Raleigh: SciTech Pub. Inc., 2009.
[9] 赵鑫泰, 马西奎. 一种求解Maxwell方程组的无条件稳定时域精细积分法[J]. 电子学报, 2006, 34(9): 1600-1604.
Zhao Xintai, Ma Xikui. An unconditionally stable precise integration time domain method for solving Maxwell’s equations[J]. Acta Electronica Sinica, 2006, 34(9): 1600-1604.
[10] Chen Zhizhang, Jiang Lele, Mao Junfa. Numerical dispersion characteristics of the three-dimensional precise integration time-domain method[C]//2007 IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 2007: 1971-1974.
[11] Jiang Lele, Chen Zhizhang, Mao Junfa. On the numerical stability of the precise integration time-domain (PITD) method[J]. IEEE Microwave and Wireless Components Letters, 2007, 17(7): 471-473.
[12] 白仲明, 赵彦珍, 马西奎. 子域精细积分方法在求解Maxwell方程组中的应用分析[J]. 电工技术学报, 2010, 25(4): 1-9.
Bai Zhongming, Zhao Yanzhen, Ma Xikui. Analysis and application of sub-domain precise integration method for solving Maxwell’s equations[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 1-9.
[13] Zhu Xiaojie, Ma Xikui, Shao Jinghui, et al. A memory-efficient formulation of precise-integration time-domain method with Riccati matrix differential equations[J]. IEEE Transactions on Magnetics, 2020, 56(2): 7507404.
[14] Zhu Xiaojie, Ma Xikui, Shao Jinghui. Low-memory implementation of PITD method using a thresholding scheme[J]. IEEE Microwave and Wireless Components Letters, 2021, 31(6): 537-540.
[15] Kang Zhen, Ma Xikui, Xu Zhuansun. An efficient 2-D compact precise-integration time-domain method for longitudinally invariant waveguiding structures[J]. IEEE Transactions on Microwave Theory and Techniques, 2013, 61(7): 2535-2544.
[16] Yang Hongwei, Wang Yuqi, Peng Shuo. Analysis of the propagation properties of photonic crystals with defect by the precise integration time domain method[J]. Journal of Electromagnetic Waves and Applications, 2019, 33(16): 2112-2125.
[17] Shao Jinghui, Ma Xikui, Kang Zhen, et al. Numerical treatment for electromagnetic wave in time-variant medium using generalized PITD method[J]. IEEE Microwave and Wireless Components Letters, 2020, 30(1): 4-7.
[18] Kang Zhen, Huang Ming, Li Weilin, et al. An efficient numerical formulation for wave propagation in magnetized plasma using PITD method[J]. Electronics, 2020, 9(10): 1575.
[19] Sirvent-Verdú J J, Francés J, Márquez A, et al. Precise-integration time-domain formulation for optical periodic media[J]. Materials, 2021, 14(24): 7896.
[20] Shao Jinghui, Mao Minyu, Wang Jiawei, et al. A numerical approach to modeling electromagnetic response of dynamic medium in arbitrary shape[J]. IEEE Microwave and Wireless Technology Letters, 2023, 33(7): 959-962.
[21] 谭述君, 钟万勰. 非齐次动力方程Duhamel项的精细积分[J]. 力学学报, 2007, 39(3): 374-381.
Tan Shujun, Zhong Wanxie. Precise integration method for Duhamel terms arising from non-homogenous dynamic systems[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(3): 374-381.
[22] 谭述君, 高强, 钟万勰. Duhamel项的精细积分方法在非线性微分方程数值求解中的应用[J]. 计算力学学报, 2010, 27(5): 752-758.
Tan Shujun, Gao Qiang, Zhong Wanxie. Applications of Duhamel term’s precise integration method in solving nonlinear differential equations[J]. Chinese Journal of Computational Mechanics, 2010, 27(5): 752-758.
Abstract With the improvement of processing technology, many devices are becoming more integrated and their sizes are developing towards sub-millimeter or nanometer scales, which makes electrically small systems, such as chips, an area of increasing interest. Therefore, it is significant to develop an efficient numerical method with a large time step size which is not strictly limited by the Courant Friedrichs Lewy (CFL) stability condition defined by the minimum spatial step size. The precise integration time domain (PITD) method is a full-wave electromagnetic numerical method with a relaxed numerical stability condition, especially its numerical dispersion error is almost independent of the time step size, which provides it with a natural advantage in enlarging the time step size and improving computational efficiency. As a consequence, it has attracted a lot of attention in the field of electromagnetism in recent years. However, the PITD method needs to calculate the matrix integral associated with the inhomogeneous term introduced by the excitation source when simulating in the active region. At present, the methods used to calculate the matrix integral are either easy to be unstable due to the existence of matrix inverse operation or difficult to maintain the accuracy of the calculation results at large time step sizes, which has become an urgent problem in the popularisation and application of the PITD method.
To address these issues, this paper introduces response matrix method into the PITD method. Firstly, the response matrix method transforms the computation of matrix integrals into the computation of a series of elementary form functions’ response matrices. Then, the values of these response matrices will be calculated based on the addition theorem and the incremental storage idea. Finally, the value of the matrix integral can be easily obtained. Considering the common types of excitation sources, the calculation formulas for the response matrix method are given in the form of exponential function, polynomial function and raised cosine function.
Based on these calculation formulas, it can be seen that the important advantage of the response matrix method is the avoidance of matrix inversion operation, which is computationally intensive, easily unstable and sometimes unsolvable. This makes it convenient to extend the PITD method's application and improve its numerical stability. Actually, the numerical integral methods commonly used at present, such as the Gaussian integral method and Simpson integral method, can also avoid the matrix inverse operation. However, these methods have a low computational accuracy of the results at large time step sizes.
On the contrary, the response matrix method has a good accuracy and can ensure the accuracy of the simulation results at large time step sizes. Simulations are carried out and the results show that the response matrix method is feasible and effective in ensuring the computational accuracy of the results under a large time step size which is 60 times as large as that limited by CFL stability condition. Compared with the commonly used numerical integral method, the response matrix method can obviously increase the time step size determined by the computational accuracy. This is beneficial to improve the computational efficiency of PITD simulation. The results of the two-dimensional biological tissue simulation model show that the simulation time of the response matrix method is only 14.51% of the Gaussian integral method and 49.26% of the Simpson integral method.
keywords:Numerical simulation of electromagnetic waves, matrix integral, matrix inverse problem, response matrix method
中图分类号:TM15
DOI: 10.19595/j.cnki.1000-6753.tces.231460
国家自然科学基金资助项目(52177008)。
收稿日期 2023-09-04
改稿日期 2023-11-21
迟明珺 女,1998年生,博士研究生,研究方向为电磁场数值计算。E-mail:3120104253@stu.xjtu.edu.cn(通信作者)
马西奎 男,1958年生,教授,博士生导师,研究方向为电气工程中的多种物理场的耦合理论及其数值分析和软件技术,通信与电子系统中的电磁场与电磁波,非线性电路与系统中的分歧与混沌,混沌的控制、同步及其应用等。E-mail:maxikui@xjtu.edu.cn
(编辑 赫 蕾)