Tab.1 The main parameters of the transformer after modification
参 数数 值 型号SFSZ7-31500/110 额定容量/(MVA)31.5 额定电压/kV(110±3×2.5%)/(38.5±2×2.5%)/10.5 额定电流/A165/472/1 732 接线方式Yyn0d11
摘要 为研究变压器短路冲击信号包含的物理特征与绕组形变之间的关系，提出一种基于绕组冲击响应时频特性的特征提取及形变判定方法。基于单自由度系统的相对位移模型构建绕组的短路冲击响应谱，得到其响应点频率偏移特征。对Hilbert能量谱进行非均匀频率带宽划分，修正累积效应的影响，提取不同频带范围内的能量带熵并计算加权能量带熵，表征特定频带内的能量混乱度；构建时频矩阵，量化能量密度分布、短时能量衰减变化等细节特征，对该矩阵进行奇异值分解，根据奇异值分布特性计算每个元素的权重值。据此提出基于加权能量带熵及基频奇异值畸变率的联合绕组状态判定方法，经三组共17次短路冲击试验数据验证，冲击信号的相对能量带熵增量变化与绕组产生的累积微应变呈高度正相关，基频奇异值畸变率与绕组发生形变的规律一致，发生形变时，该畸变率的值会大于2.0，证明了该判定方法的有效性。该方法可在变压器发生短路后对绕组的状态进行预判，进而考虑是否需要进一步处理，对变压器绕组状态的在线监测具有一定的指导意义。
关键词：短路试验 绕组形变 累积效应 冲击响应 时频矩阵
变压器作为电网输配电环节的关键设备，在长期运行过程中会遭受多次外部短路冲击作用，绕组受到多次累积的影响，会产生不可逆的变形，为电网的安全稳定运行带来巨大的隐患[1-3]。因此，对于遭受短路冲击后的绕组进行形变检测十分有必要。
变压器绕组所通过的最大短路电流可达正常运行时额定电流的数十倍，在一瞬间会产生巨大的电动力，可能导致绕组的失稳变形，从而造成变压器无法正常运行[4]。目前，绕组形变的检测方法主要包括低压脉冲法、短路电抗法及频率响应法[5-7]，但上述这些方法大都在离线状态下对变压器中的电气机械结构特性进行诊断，受现场电磁干扰的影响，难以满足带电或在线检测的要求[8]。通过对变压器油箱表面的振动信号进行收集和分析，无需电气连接就可以实现被测设备和在线监测系统之间的数据传输，进行实时在线监测，应用前景广阔[9-13]。
西安交通大学师愉航等对绕组的多倍频振动机理及特征进行了研究，提出当绕组固有频率满足电流激励的整数倍时，会出现参变共振多倍频振动[14]；张凡等对绕组振动特性及振动信号采集等方面的相关性进行了研究，为绕组机械状态监测提供了参考依据[15]；河海大学马宏忠等借助有限元仿真对绕组不同状态下的模态特性进行分析，并通过相关试验验证绕组松动会导致绕组的固有频率下降[16]。在绕组受到短路冲击时，从频谱的角度可对绕组的特征进行量化，然而受噪声的影响，实际的在运变压器振动信号较难收集到试验条件下的数据，且变压器运行过程中受到累积效应的影响，绕组不会一直维持在初始状态，因此仅单一特征下的绕组形变判断会存在较大的误差[8]。在频域上绘制绕组的冲击响应谱（Shock Response Spectrum, SRS）[17]，其响应加速度值仅和被测物体本身材料参数有关，可避免受其他信号干扰的问题，反映绕组的机械状态。
浙江大学熊卫华等对变压器振动信号进行了希尔伯特黄变换（Hilbert-Huang Transform, HHT），对变压器正常及故障状态振动时的能量分布进行了对比分析，实现了时频分析在变压器中的应用[18]；徐建源等通过联合短路电抗变化率以及经小波分解后得到的振动信号特征，对绕组变形进行了诊断，提高了绕组形变检测的灵敏度[19]；张坤等通过复小波变换法对变压器突发短路的振动信号进行时频分析，实现了绕组松动变形的高灵敏度检测[20]；杜厚贤等进行了多特征值的变压器故障研究，改进了振动基频占比、总谐波畸变率的计算，提高了故障检测的准确性[21]。结合前人的研究，针对绕组振动的倍频特征、能量分布特点，对短路冲击信号进行时频分析，可为辨别绕组的机械状态变化提供较好的依据。但目前的研究仍存在部分问题：①变压器运行受到累积效应的影响，以上研究均未对相关特征值进行去累积化的修正；②目前相关故障诊断分析主要针对变压器的振动基频信号，但正常运行时普遍存在500 Hz以内的倍频分量，暂态下包含更多的高次谐波，不充分考虑将影响诊断效果。
为解决以上问题，本文提出一种基于绕组冲击响应时频特性的特征提取及形变判定方法。基于某退役SFSZ7-31500/110型变压器，绘制绕组的冲击响应谱，对比冲击信号的频谱分析了不同冲击信号对绕组的影响程度，确定分析的频率范围。根据冲击响应谱的频率偏移情况对Hilbert能量谱进行多频带划分，提取其相对能量带熵。将能量谱转换为时频矩阵，计算其占比奇异值矩阵，根据奇异值的平面分布特性确定每个元素的权重参数。基于能量带熵及占比奇异值提出绕组状态的联合判定方法，每次短路冲击后的相对能量带熵增量变化作为表征绕组形变的特征参量；同时计算短路冲击信号的基频奇异值畸变率，作为辅助判定的手段弥补前者的不足。经试验数据验证了该方法的可靠性，可在变压器发生短路后对绕组的状态进行预判。
为了对变压器绕组遭受短路冲击时引起的形变问题进行研究，本文采用一台真型退役变压器作为试验模型，并对其进行改造，其参数见表1。
表1 改造变压器主要参数
Tab.1 The main parameters of the transformer after modification
参 数数 值 型号SFSZ7-31500/110 额定容量/(MVA)31.5 额定电压/kV(110±3×2.5%)/(38.5±2×2.5%)/10.5 额定电流/A165/472/1 732 接线方式Yyn0d11
为确定真型变压器冲击试验过程中传感器的布置位置，基于变压器绕组经典“质量-弹簧-阻尼”模型，计算得到短路工况下电动力达到幅值时绕组的振动规律，绕组1/4和3/4处产生的位移较大，如图1所示。
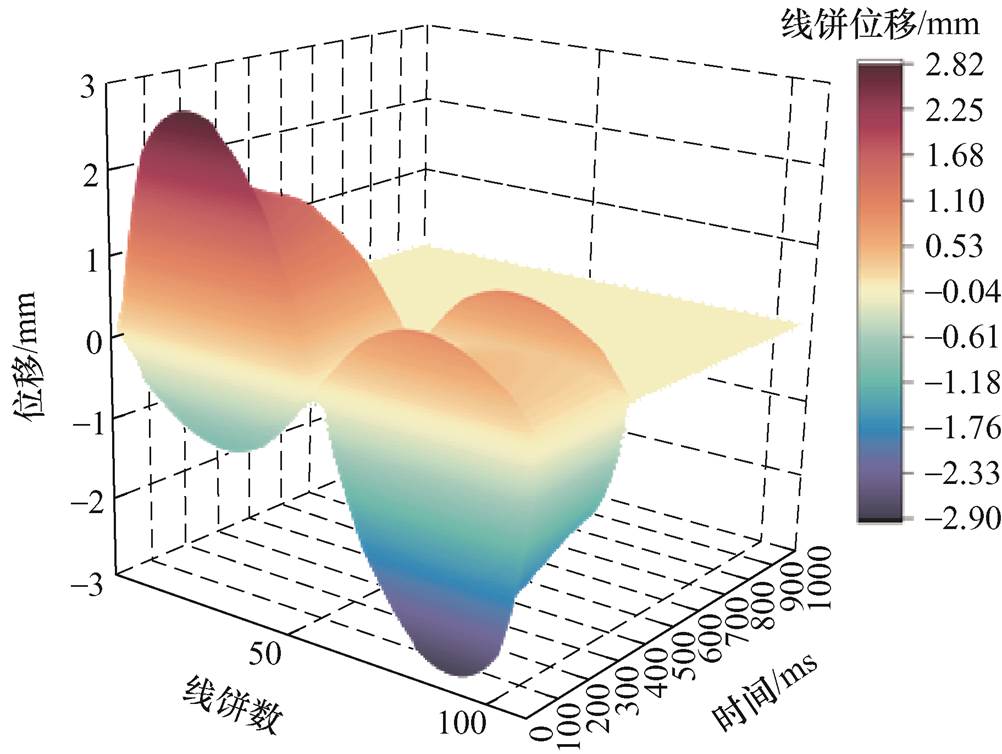
图1 绕组不同位置线饼振动位移分布
Fig.1 Vibration displacement distribution of winding cake at different positions
绕组振动强度大的线饼附近的油压以及质点振动速度高，可近似认为油箱壁上某测点的振动信号能够反映该测点附近绕组的振动情况[15]。因此，为同时监测到绕组振动幅值较大的位置，本试验选定变压器外壳靠近A、B、C三相绕组中心的位置安装冲击力传感器进行短路冲击信号的测量，如图2所示。经过改造的试验变压器已经通过全部出厂试验，传感器安装固定在变压器外壳，不会对变压器的正常运行造成任何影响。
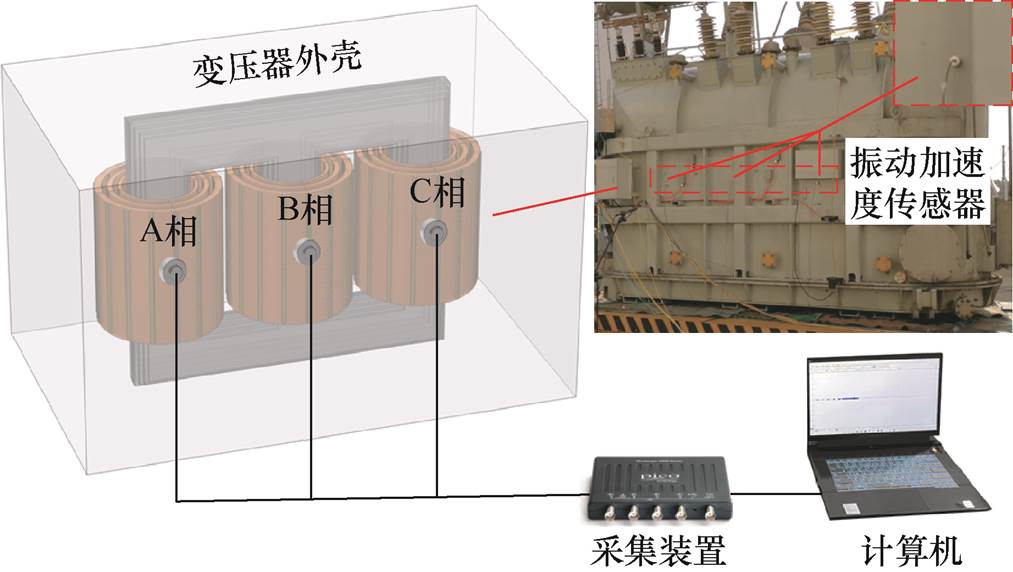
图2 试验平台搭建
Fig.2 Test platform construction
本次变压器短路承受能力试验依据GB 1094.5-2008中相关规定实施[22]，分别进行高-低、高-中、中-低等不同相的短路冲击试验。以高-中B相短路冲击试验（H-M B）为例，试验电路如图3所示。
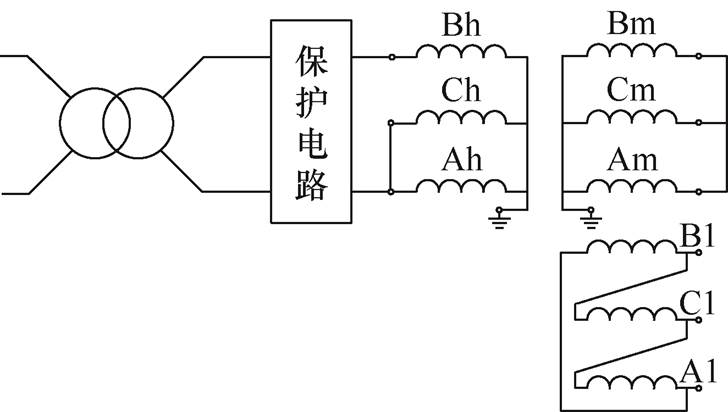
图3 试验电路
Fig.3 Test circuit diagram
变压器高压侧供电，对中压侧绕组进行三相短接，低压侧开路处理。通过调节高压侧电压，使B相高压侧电流依次达到表2中所示的值。
表2 短路电流设置
Tab.2 Short-circuit current setting
序号比例(%)-次数实际试验电流/A安全电流/A 160-19141 181 280-11 176 385-11 262 490-11 346 595-11 421 6100-11 483 7105-11 550 8105-21 551 9105-31 547 10105-41 552
每次短路冲击时间为(250±25) ms，两次试验间隔20 min。试验过程中采集短路冲击信号的实时波形，采样时间为0.1 ms，采样频率为10 kHz。由于短路试验属于破坏性试验，因此每次试验结束后均要测量绕组的电抗变化率，当电抗变化率超过2%时停止短路试验。
变压器绕组的振动因其辐向刚性较大，以轴向振动为主[23]。忽略垫块、撑条等因素的影响，绕组由多个线饼叠加而成，其每个线饼在振动时都可看作一个单自由度系统，故绕组整体可看作由一系列单自由度质量阻尼系统组成的系统[24]。每饼绕组的相对位移模型如图4所示。
图4 线饼相对位移模型
Fig.4 Coil cake relative displacement model
x(t)为线饼电磁力导致的位移，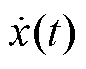
为激励的速度，
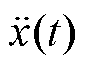为激励的加速度，y(t)为线饼实际振动产生的位移，
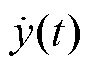为响应的速度，
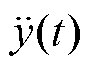为响应的加速度，z(t)为相对位移，k为弹性系数，c为阻尼系数，m为线饼质量。可知该系统的运动方程为
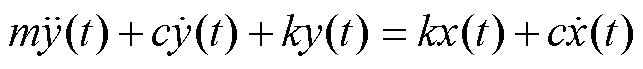（1）
设系统无阻尼固有频率为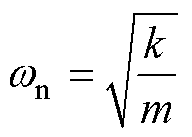
，阻尼比
，相对位移为z(t)=y(t)-x(t)，代入式（1）可得
（2）
绕组各层线饼的初始位移与初始加速度均为0，利用杜哈梅积分计算得到式（2）的位移响应解析式为
（3）
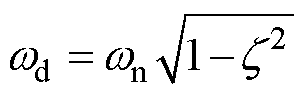（4）
式中，ωd为有阻尼固有频率；ωn为无阻尼固有频率；τ为时间积分变量。
对式（3）求二阶导，得初始位移和初始速度为0时的加速度响应为
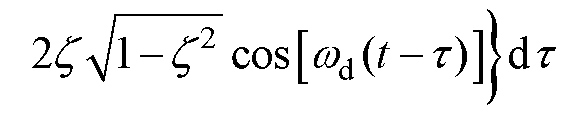（5）
在50 Hz的电网系统中，变压器绕组振动的基频为100 Hz[25]，并存在振动频率为电流各个倍频的短路冲击信号，导致时域振动冲击信号高频分量构成较为复杂，无法直接提取异常信号的特征。如图5所示，为H-M B试验中最后一次短路冲击下的信号时域波形，可以观察到B相波形区别于A、C两相，幅值降低约44.12%。
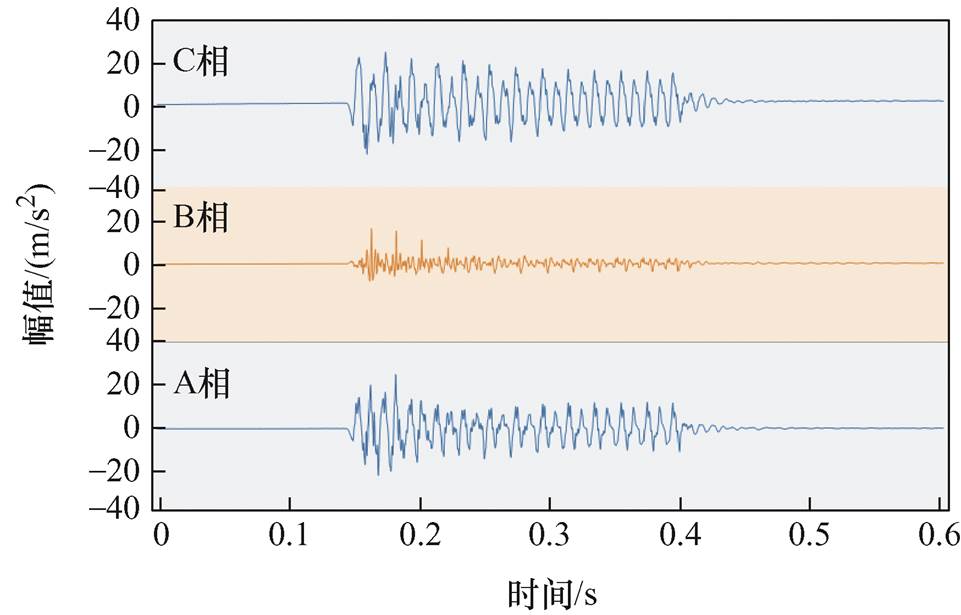
图5 绕组短路冲击信号波形
Fig.5 Winding short circuit impact signal waveforms
对17组试验后A、B、C三相绕组的电抗进行检测，并计算其电抗变化率，电抗变化及绕组变形情况如图6所示，参考GB 1094.5-2008的评价标准，在绕组发生形变的三组试验中，H-M B相试验B相绕组电抗变化率在第10次时超过2%，达到2.28%，为确定该绕组已经发生形变，加做一次试验，电抗变化率升高至2.32%，停止对B相的试验。然后，在M-L A相试验中，A相绕组电抗变化率在第5次冲击后达到1.49%，判断发生形变。M-L C相试验C相第二次冲击后产生7.81%的电抗变化率，自此，终止试验。
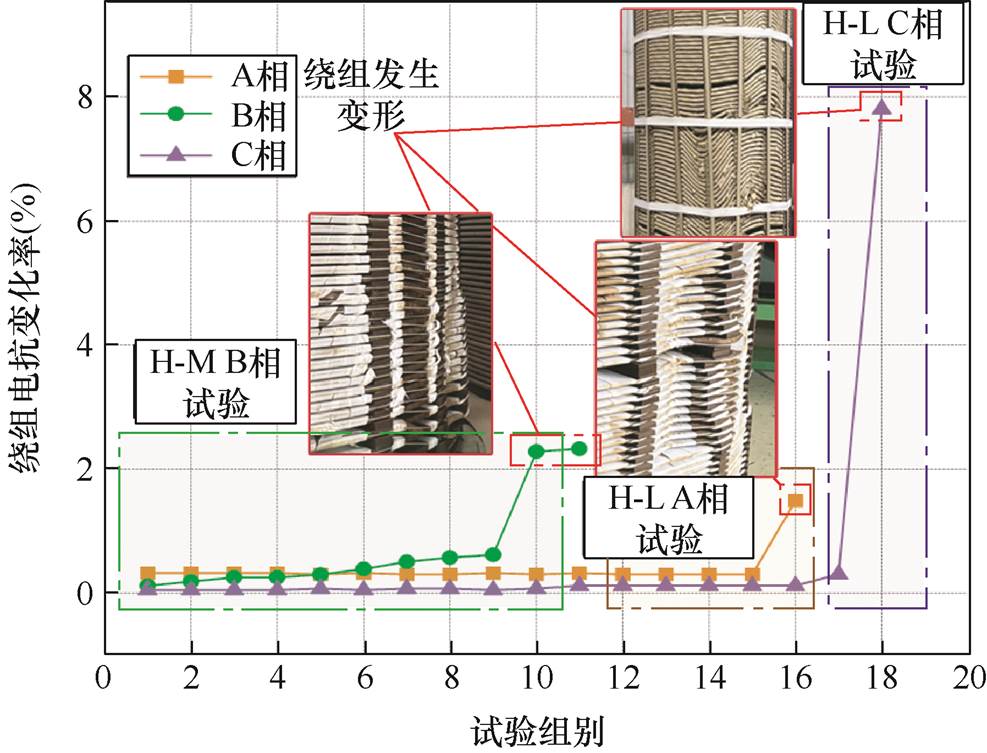
图6 三相绕组电抗变化率
Fig.6 Reactance change rate of three-phase winding
为了便于分析，以H-M B相试验为例，根据10次冲击结果，绘制短路冲击信号的冲击响应谱，如图7所示，同时绘制其10次响应的峰值包络线。可观察到，随着短路冲击电流的增加，绕组的冲击响应幅值逐渐增大，并且高频部分响应升高，最大值可达基频响应的4.78倍。在第10次即105%短路电流第4次冲击时，响应值骤减，因此判断产生此现象的原因与B相绕组发生形变相关。
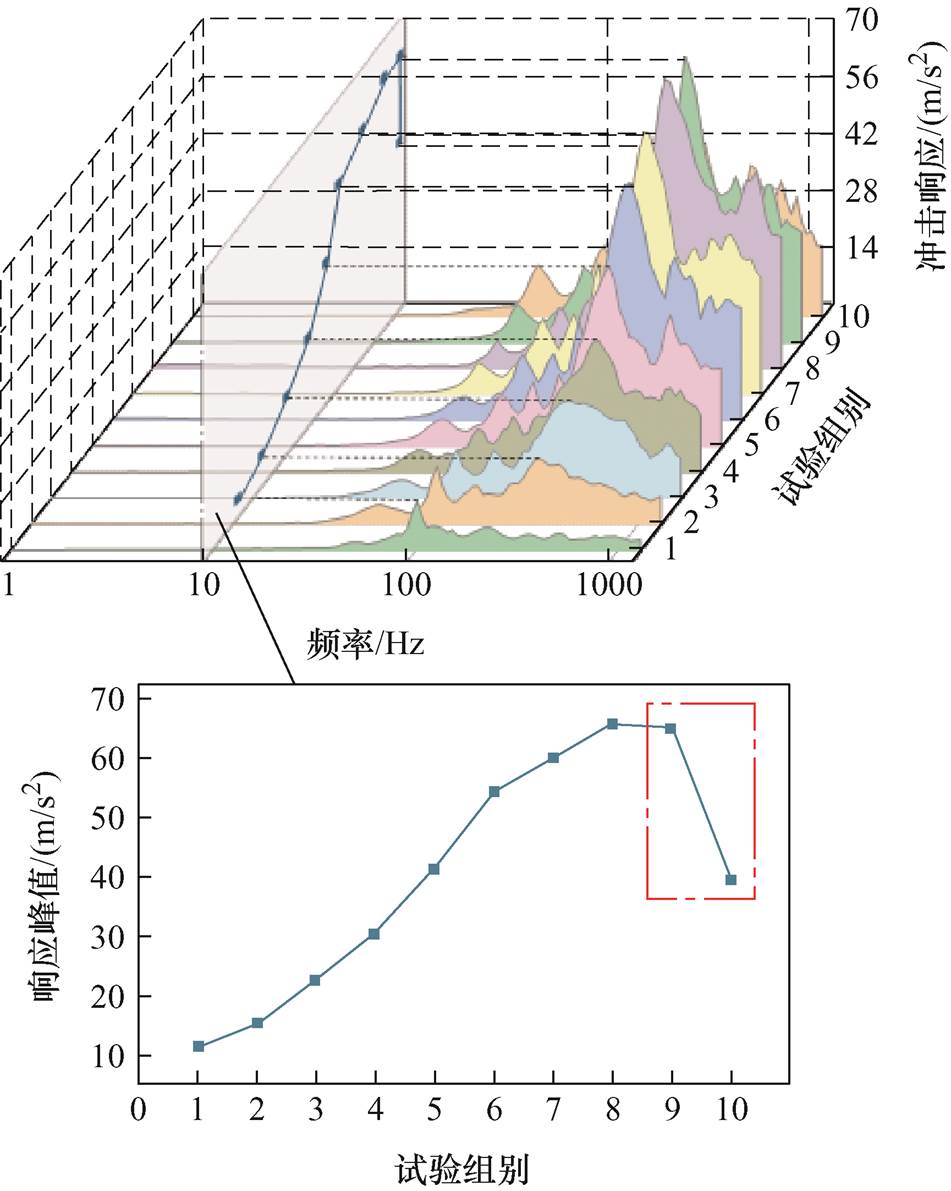
图7 B相绕组10次冲击响应谱及峰值包络线
Fig.7 10 shock response spectrum and peak envelope of B phase winding
对于短路冲击信号而言，仅从其响应峰值分析，发生形变时的信号仅表现为响应峰值的减小，并无明显区别于同响应水平的其他信号的特征，故还需对信号进行更加深入的剖析。
计算试验信号的频谱，与冲击响应谱一同进行归一化处理，方便二者进行对比分析，频谱与冲击响应谱分布变化情况如图8所示。通过短路冲击信号的频谱可以发现，信号能量集中在500 Hz以内，在此范围内低频信号的能量分布与产生的短路冲击响应分布规律一致，即能量-响应分布，随着短路冲击的进行，短路电流增加，绕组短路冲击信号在高频部分的能量分布依然维持在较低水平，但产生的短路响应峰值升高，且与频谱无明显的对应关系，高频部分响应值远超低频。
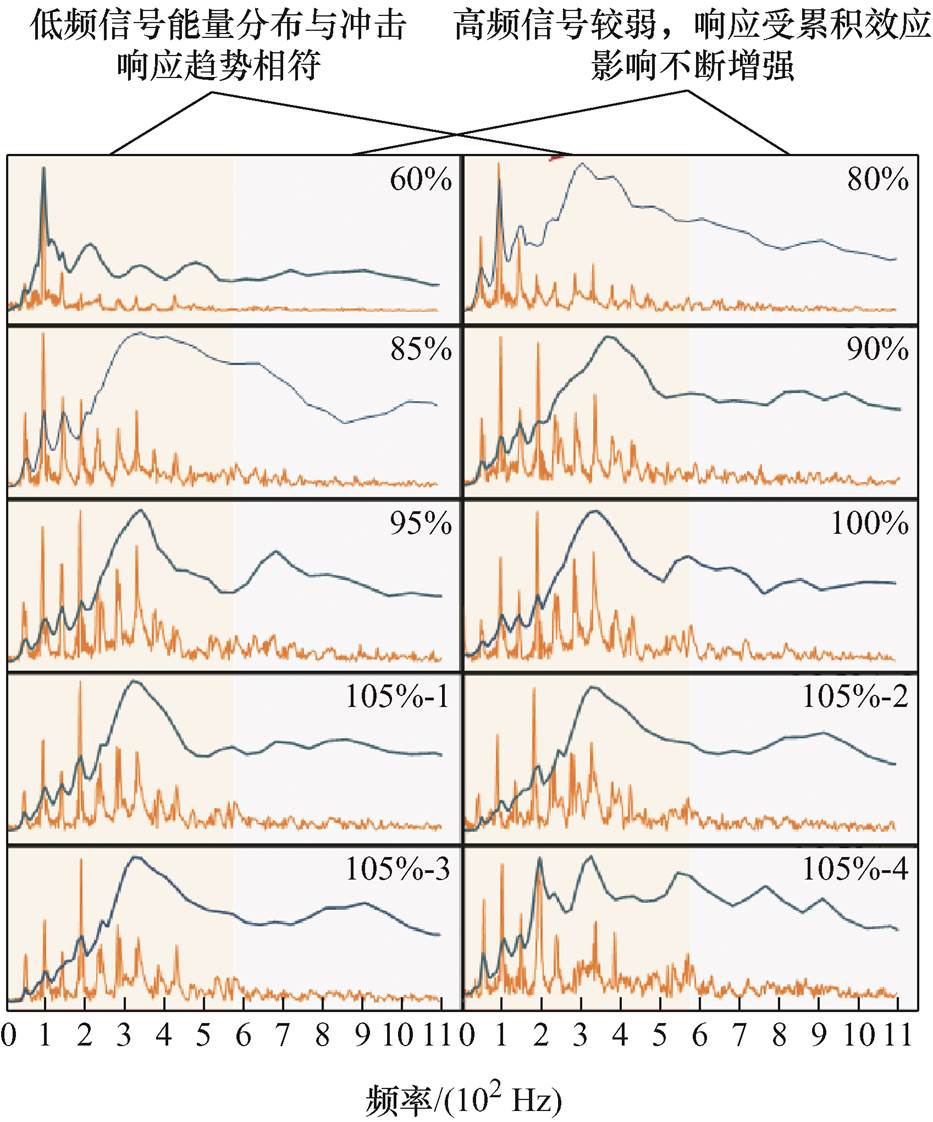
图8 频谱与冲击响应谱分布变化情况
Fig.8 Spectrum and shock response spectrum comparison
通过式（5）计算得到，信号高频分量产生相对较大的冲击响应。这是由于短路电流增加，引起初始的激励加速度增大，同时高频振动信号的能量占比在持续增加。随着固有频率ωn的升高，高频部分的响应持续增大。虽然冲击信号中高次谐波分量整体较少，但对于绕组稳定性造成的影响更加严重。因此，在进行信号分析时，本文选择对绕组产生主要冲击响应的0～1 000 Hz范围内的信号进行分析。
为量化分析共振点偏移的影响，借助总谐波畸变率的概念[26]，计算冲击响应谱的响应畸变率，来表征绕组形变引起的共振点偏移对绕组冲击响应的影响。
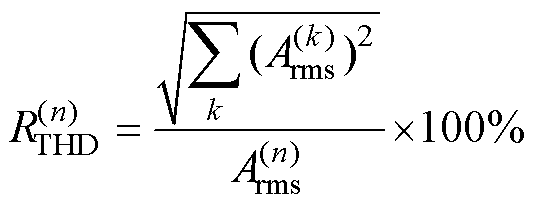（6）
式中，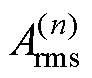
为n倍基频（2倍电流频率）冲击响应点幅值，本文取n=1, 3, 7进行相关分析；
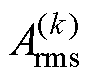为10倍基频以内除基频外各倍频点的冲击响应点分量，k=1, 2,
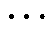, 10，且n≠k；
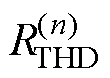为n倍基频的响应畸变率。B相试验10次冲击下RTHD值见表3。
表3 10次冲击下绕组响应的RTHD值
Tab.3 RTHD value of winding response under 10 shocks
试验组别比例(%)-次数 1600.846 51.678 35.314 2 2801.153 62.049 93.534 8 3851.474 72.232 83.417 5 4901.655 22.315 23.474 8 5951.924 22.415 22.513 2 61002.158 72.215 23.295 4 7105-12.288 62.215 23.144 7 8105-22.352 42.324 13.123 2 9105-32.423 22.212 12.925 4 10105-42.161 12.331 42.785 7
从冲击响应谱中选取100、300和700 Hz 3个响应幅值点，计算出绕组基频响应畸变率相关度较好，随着短路冲击次数及强度的增加，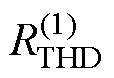
数值在形变组发生了突变，但没有非常明显的区别于其他数据的特征。高频响应畸变率
、
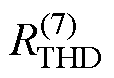的分布没有明显规律，无法为形变提供有效支撑。
仅通过频域信息得到的响应畸变率存在一定的局限性，寻找全面的状态分析方法更加重要。通过HHT建立短路冲击信号在时间、频率尺度下的能量分布，对信号进行降噪处理。通过集合经验模态分解（Ensemble Empirical Mode Decomposition, EEMD）分解，求得信号各阶具有物理意义的瞬时频率分量，保留高频分量，舍去残余分量，可实现高分辨率的时频分析[27]。经EEMD分解后的各阶内涵模态分量（Intrinsic Mode Functions, IMF）如图9所示。
忽略包含信息较少的低频分量，对前6阶IMF分量进行叠加，得到的信号记为S(t)，它的复信号为
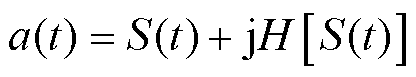（7）
也可表示为
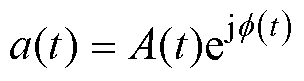（8）
式中，A(t)为复信号的幅值；
为瞬时相位表达式，
。
对时间求导得到瞬时频率
（9）
经Hilbert变换后的结果a(t)展开并对实部进行叠加，得到Hilbert符号谱为
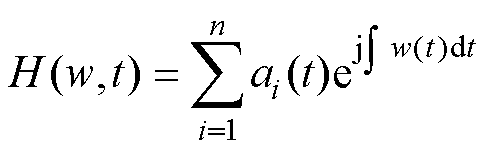（10）
式中，H2(w, t)为Hilbert能量谱，基于时频维度的能量分布可以反映信号的特征变化规律。如图10所示，该图谱绘制了短路电流为额定值60%、90%、105%的4次短路冲击能量的时频分布。
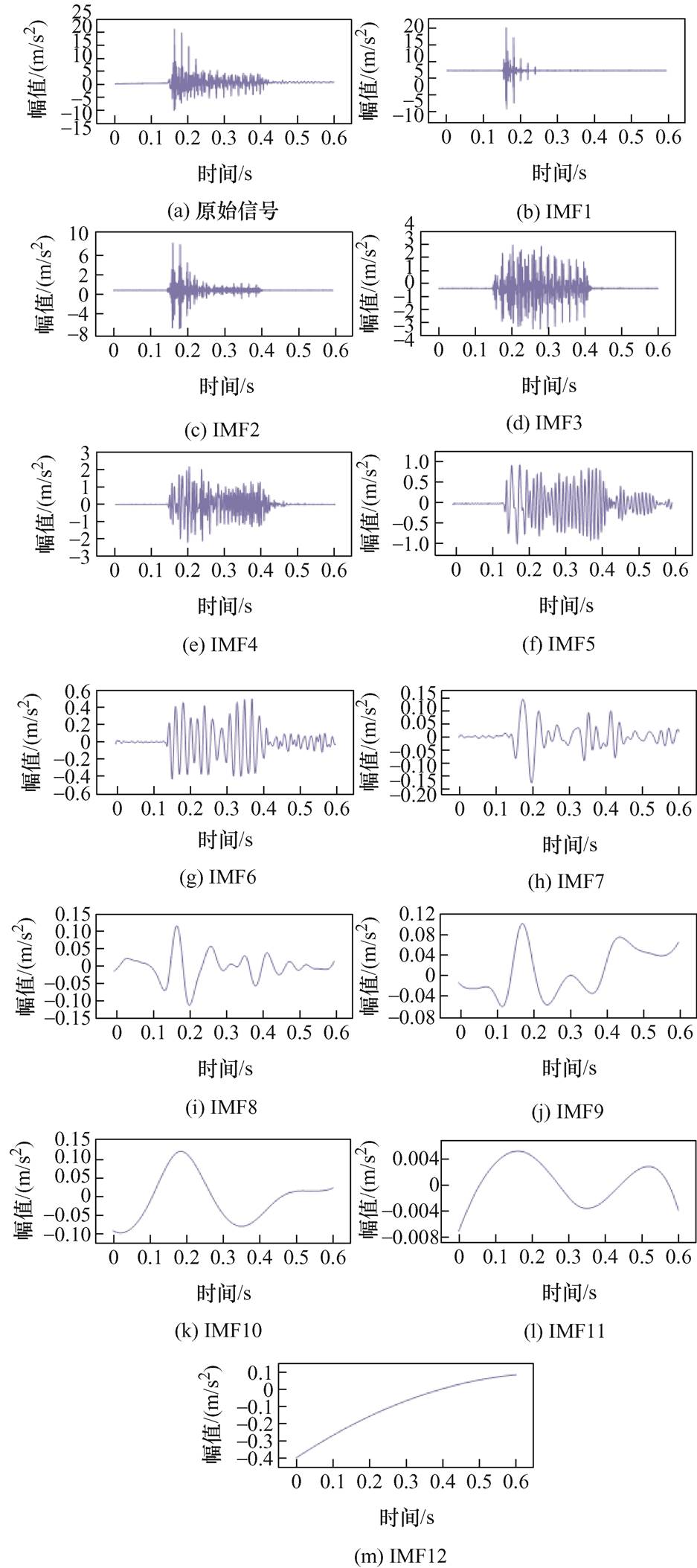
图9 原始信号的各阶IMF分量
Fig.9 IMF weight of each order of the original signal
观察图谱可以发现，经过HHT后，变压器的短路冲击信号能量分布在0～1 000 Hz范围内，并且其能量受累积效应影响，随着短路冲击次数的增加不断升高，在发生形变时，能量谱峰值出现了骤减的现象。
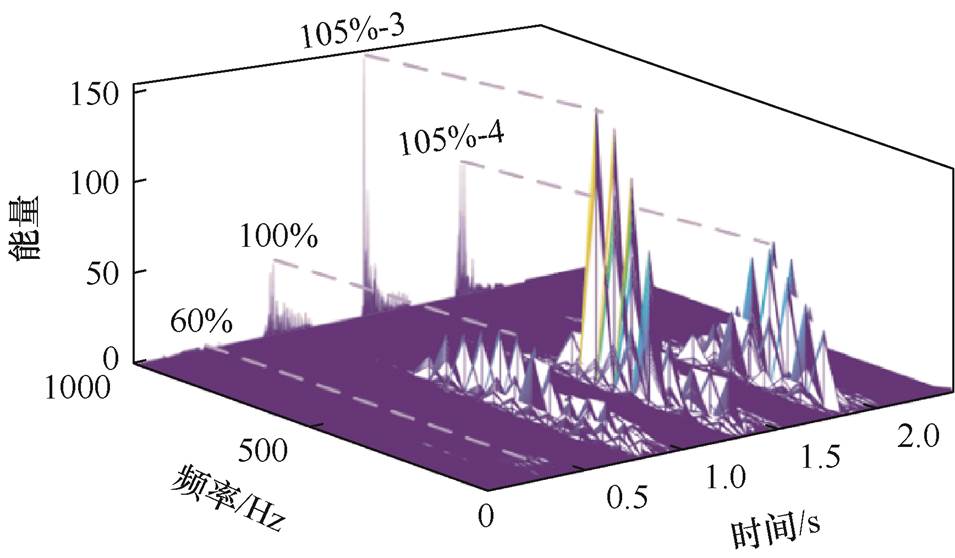
图10 三维Hilbert能量谱
Fig.10 Three dimensional Hilbert energy spectrum
4.1.1 能量带熵矩阵构建
由于变压器短路冲击信号的频率范围较大，构成复杂，无法直接提取有效特征值，通过提取其Hilbert谱熵来描述功率谱和熵率之间的关系，可表征每次短路冲击信号的能量分布混乱程度。
根据Shannon熵的定义，熵是复杂程度的统计度量，是对源信号在平均意义上的一种特征描述，表征了信号的随机性[28]。其公式为
（11）
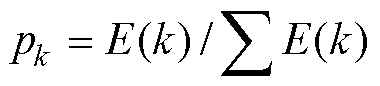（12）
式中，H为谱熵；pk为第k个取值出现的概率；E(k)为第k个取值的幅值。
整体的谱熵提取难以体现各组试验之间的差异，将短路冲击响应谱进行平面带状转化，三相绕组冲击响应点偏移情况如图11所示。试验初期短路电流相对较小，不产生累积效应，因此绕组的前四次冲击响应带并没有明显的变化。自第五次开始，受累积效应影响，A、C两相绕组基频短路冲击响应分别从约100 Hz升高至105.3 Hz和104.7 Hz，高频部分无明显变化特征。故障相B相基频短路冲击响应由101.5 Hz升高至107.6 Hz，主要响应峰值分布逐渐增加到200～550 Hz，在550～1 000 Hz内，绕组的冲击响应呈不均匀分布，同A、C两相产生明显的不同。
考虑到绕组机械状态的改变会引起共振点产生一定的偏移，响应峰值点也会随着累积效应的影响而变化，但并未引起绕组变形。因此，将B相绕组的Hilbert能量谱按照响应分布的规律进行细致划分，可避免累积效应的影响。以包含变压器基频振动响应偏移量的频率范围为第一块主子矩阵，即0～110 Hz，以110～550 Hz为第二块副子矩阵，550～1 000 Hz为第三块副子矩阵，通过公式分别计算其相对能量带熵，如图12所示。
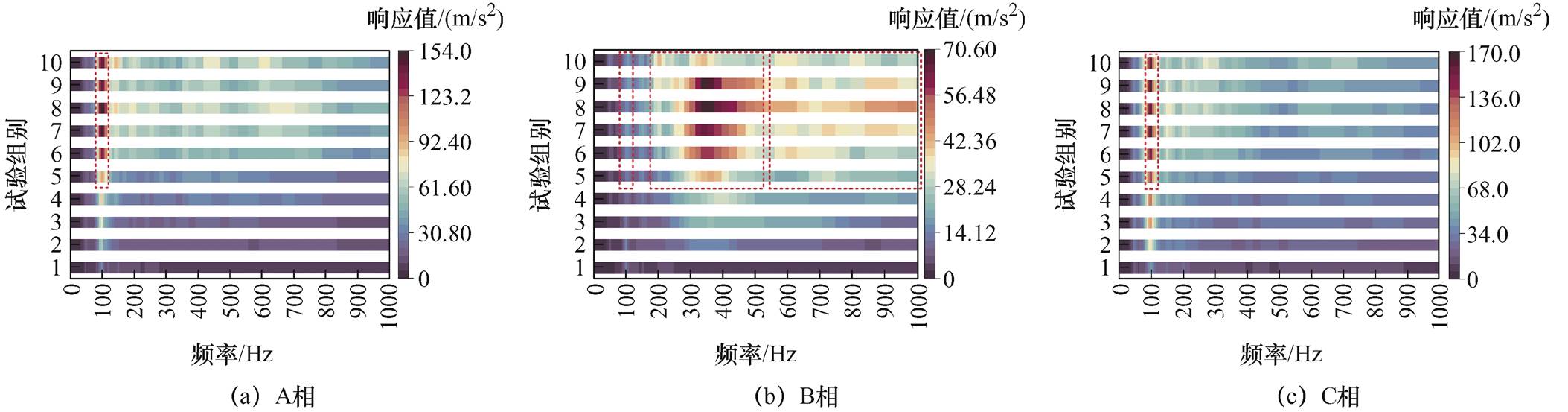
图11 三相绕组冲击响应点偏移情况
Fig.11 Offset of shock response point in three-phase winding
由图12中数据可以观察出，划分后的第10次短路冲击信号能量带熵与之前存在明显差异，主子矩阵的熵值相对占比下降，两块副子矩阵的熵值相对占比上升。同时，变压器解体吊罩后观察到B相中压绕组在第10次试验时发生了明显形变，证明绕组发生形变后信号不同频带的能量分布混乱程度与之前存在较大差异。
4.1.2 特征计算
对发生绕组变形的三组共17次试验的相对能量带熵的增量进行计算，其中H-M B短路冲击试验10组、M-L A短路冲击试验5组、M-L C短路冲击试验2组，共17组，结果如图13所示。可观察到，在发生形变的试验组，相对能量带熵的增量都发生了突变，说明绕组的突然形变会引起所有频段相对能量带熵熵值的突变。
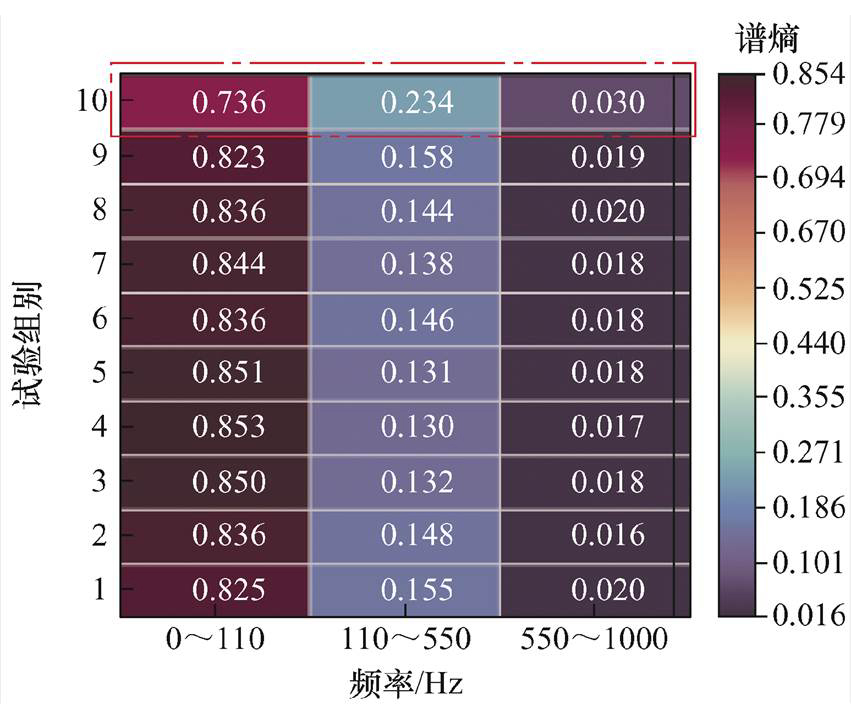
图12 Hilbert能量带熵及其相对占比情况
Fig.12 Hilbert spectrum entropy and its relative proportion
图13 各组试验不同频段的相对能量带熵增量变化
Fig.13 SVR model decision results of different optimization algorithms
三个频段内的相对能量带熵增量产生的突变证明其变化与绕组的形变具有相关性，对三个频段内的熵增量按各频段的占比进行加权求和得到一个加权熵增量，可作为绕组形变的评判标准。
加权熵增量目的在于记录绕组每次短路冲击后的变化，对绕组的基本状态随时进行记录，可实现提前预警，作为检修、维护的判定依据，避免发生事故后造成更大的损失。但是仅通过熵增量进行判断，有造成误判的可能，熵增量的阈值不易判断，同时对数据采集的要求较高，不能漏采误采，数据的缺失易造成无法判断。因此，通过其他方法进行辅助判断是非常有必要的。
4.2.1 时频矩阵构建
提取短路冲击信号的能量带熵，从频带分布角度，对绕组能量分布的混乱程度进行了整体上的区分，但未能表明绕组对短路冲击的响应变化情况，包括冲击信号的能量密度分布、短时内的能量衰减变化等特征。为了尽可能获得更多的包含其实际物理意义的信息，构建Hilbert能量谱的时频矩阵[29]，如图14所示。
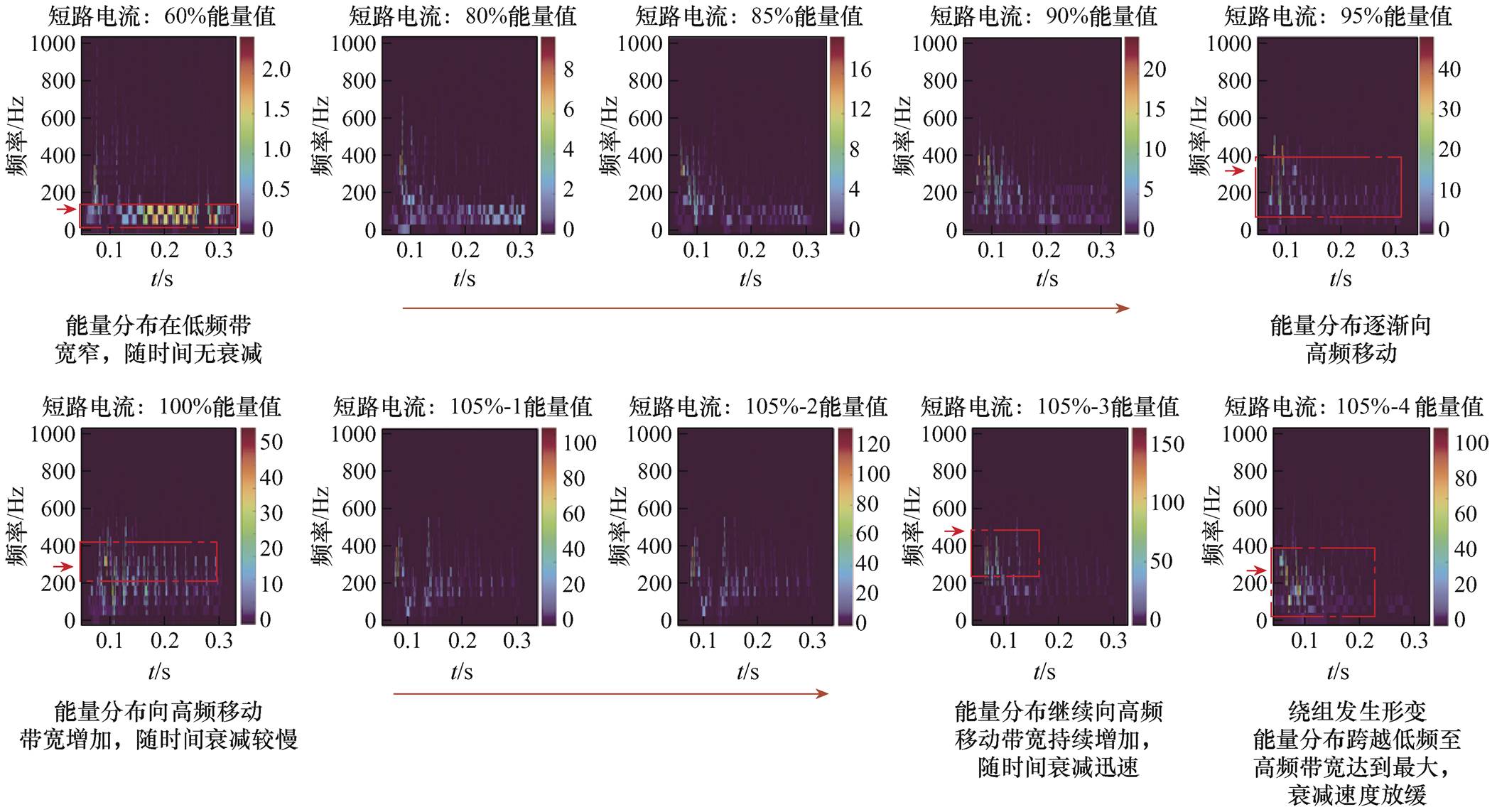
图14 Hilbert能量时频分布
Fig.14 Hilbert energy time-frequency distribution diagram
对比时频分布特征，可以观察到，前期受累积效应的影响较小，Hilbert能量峰值主要是简单地持续增大。随着短路冲击强度与次数的增加，能量主要集中的频带范围逐渐升高，冲击响应的衰减速度逐渐变快。但随着绕组突然变形，能量分布及衰减速度出现了与规律不符的情况，需对这种情况进行特征量化。
提取Hilbert时频谱图中每个时频窗格的能量值并构建相应的时频矩阵H，可表示为
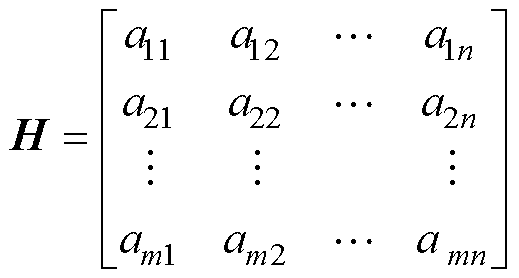（13）
每个时频窗格内的能量幅值记为ai,j，行表示信号的瞬时频率信息，列为时间信息。对矩阵进行细化，取频带宽度为100 Hz，划分为10×10的子矩阵块，形成新的时频矩阵Z，作为一次短路冲击信号的特征矩阵。
4.2.2 占比奇异值矩阵
对于得到的特征矩阵Z，可分解为Z=UΣVT的形式，U和V均为单位正交矩阵且分别为左、右奇异矩阵，Σ对角线上的值也就是奇异值。利用ZTZ= VΣTUTUΣVT=VΣTΣVT为对称矩阵，对其进行特征值分解，可得ΣTΣ为
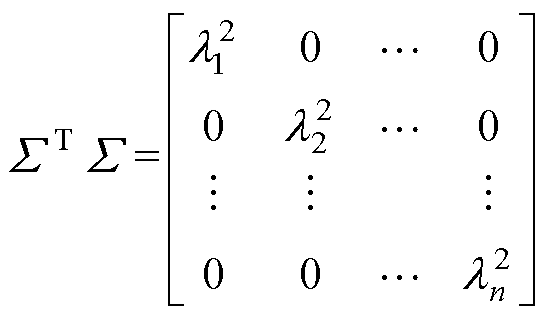（14）
得到λ1, λ2, …, λn为时频矩阵A的奇异值。同时，为弱化累积效应对能量幅值累积升高的影响，对奇异值矩阵进行占比奇异值矩阵的转化。转化后B相10次短路冲击试验的占比奇异值分布如图15所示。
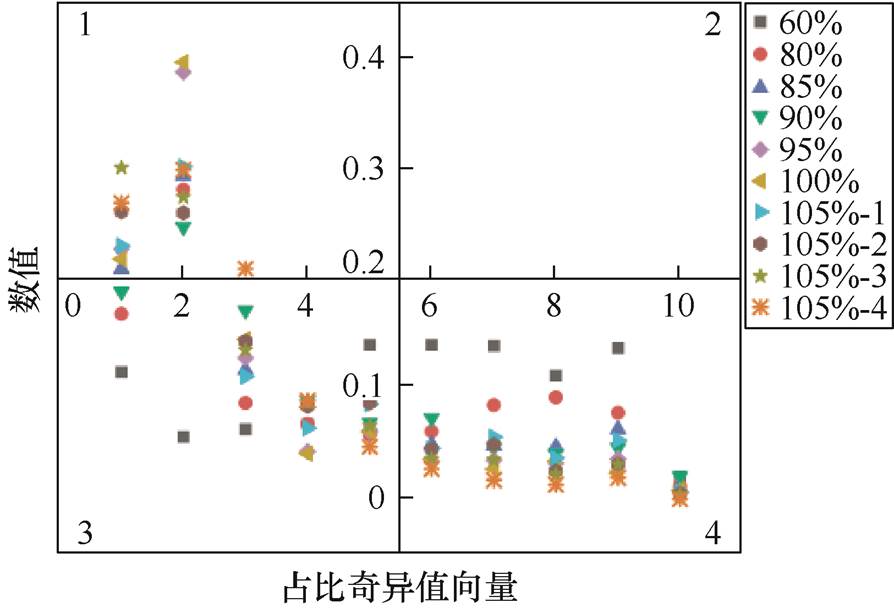
图15 占比奇异值分布
Fig.15 Proportion singular value distribution
将之均分为四部分，分别计算1～4号区域内占比奇异值的分布散乱度，以确定奇异值向量中各个元素的权重，其计算结果如图16所示。
图16 各区域分布散乱度
Fig.16 Degree of dispersion in each region
各区的域散乱度百分比记为Si，相应区域主要分布奇异值的位数及其个数记为Nj。以各区域内的散点分布为基准，按照式（15）确定奇异值各个元素的权重参数，计算得到短路冲击信号的加权占比奇异值。其中，区域4中奇异值差异较小，为优化判定流程，将此部分的奇异值舍去。
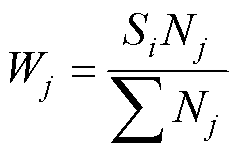（15）
4.2.3 占比奇异值分布及特征计算
绘制17次短路冲击剩余5个奇异值的比重分布变化，在绕组发生形变的试验组，1、2、5号值存在明显的不同，如图17所示。
前文分析到，对冲击响应谱的观察中，绕组基频响应畸变率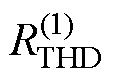
数值在形变组发生了突变。因此，为量化表示加权占比奇异值矩阵的特征，对此概念加以运用，将包含基频在内的子矩阵块的奇异值视作基频奇异值，计算短路冲击信号的基频奇异值畸变率。
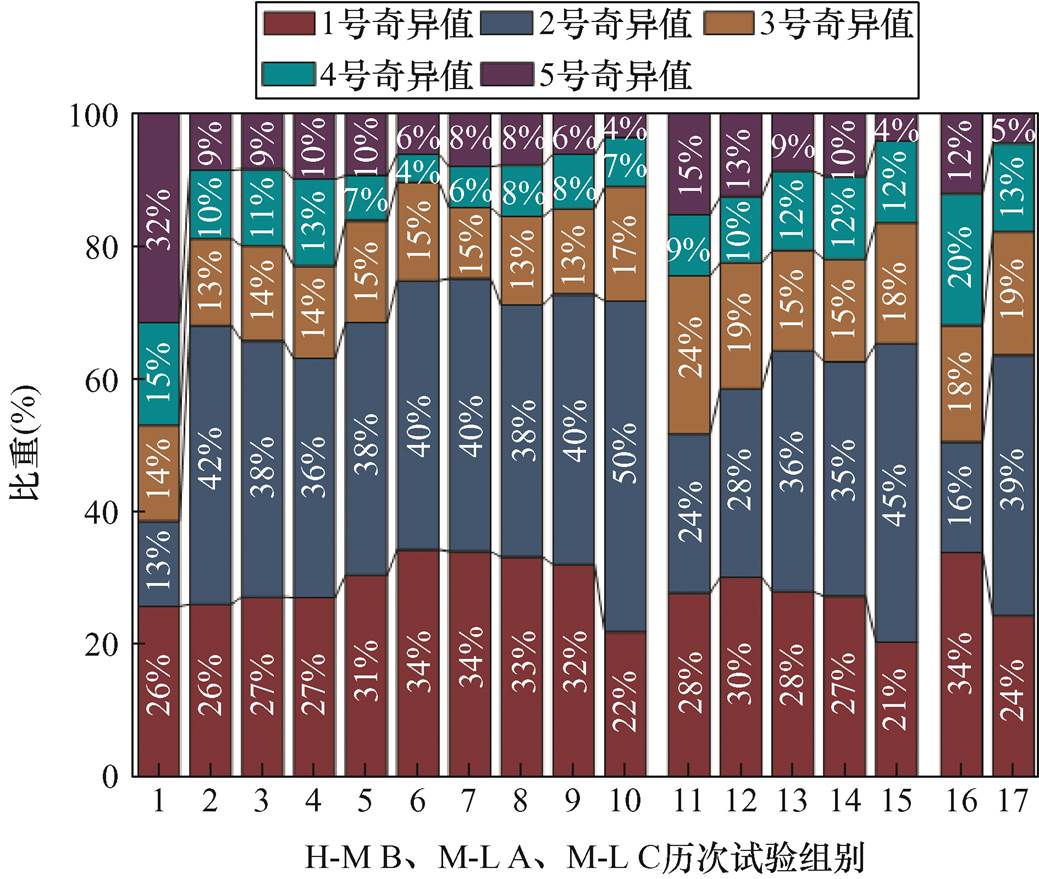
图17 17次短路冲击各加权占比奇异值的比重变化
Fig.17 The weight change of singular value of each weighted proportion of 17 short circuit impact
考虑累积效应的影响，提取短路冲击信号的相对能量带熵、加权占比奇异值，对绕组能量分布的混乱程度进行整体上的区分，避免累积效应影响的同时考虑绕组对短路冲击的响应变化，联合两种特征对绕组形变进行判定。短路冲击特征提取及绕组形变判定流程如图18所示。
对三组共17次短路试验获取的短路冲击信号依据本文所提方法进行处理，按照各频段占比对相对能量带熵增量进行累加得到加权熵增量，依据基频响应畸变率RTHD的计算公式计算基频奇异值畸变率，与提前布置好的光纤光栅应变传感器监测得到的绕组微应变进行对比。各组试验的加权熵增量以及基频奇异值畸变率这两种计算特征与试验测得的微应变累积量做对比，如图19所示。
除却因绕组倾塌导致的M-L A第5组应变数据缺失，其他试验组的加权熵增量在绕组发生变形阶段呈现出良好的正相关性，在绕组形变的同时发生突变，证明该特征可以表明绕组形变与否。同时，随着试验的进行，奇异值畸变率和绕组累积微应变的契合度非常高，在形变组呈现的规律保持较高的一致性，且未发生形变时，该畸变率的值不会超过2.0，作为辅助判断绕组形变与否的特征，可避免由于数据采集失误引起的漏判、错判。
图18 短路冲击特征提取及绕组形变判定流程
Fig.18 Short-circuit impact feature extraction and winding deformation determination process
图19 17次短路冲击熵增和微应变对比
Fig.19 Comparison of entropy increase and microstrain of 17 short circuit impact
本文提出的基于变压器绕组冲击响应时频特性的特征提取及形变判定方法，实现了对变压器突发短路冲击信号的特征提取，可准确判定绕组的形变。研究结果表明：
1）构造绕组的冲击响应谱，对比绕组的冲击响应谱和短路冲击信号的频谱特征，不论短路电流如何变化，频谱高频分量较少，但绕组对高频分量产生的响应水平较高，共振点振动加速度幅值较大。因此，对包含高频部分（1 000 Hz以内）的短路冲击信号进行全面分析是很有必要的。
2）根据冲击响应点频率偏移水平，将Hilbert能量谱划分为不均匀子矩阵并提取谱熵，计算不同频率范围内的相对能量带熵，其值在形变试验组发生了明显的不符规律的突变。其变化同冲击响应谱所体现出来的变化特征相符，表明短路冲击信号的相对能量带熵与绕组的形变具有一定的相关关系。
3）计算每次短路冲击后的相对能量带熵增量变化，加权叠加后同绕组累积微应变进行对比，二者呈高度正相关，证明加权熵增量的变化在工程中可作为绕组形变、失稳的判别方式；同时为提高判定准确度，计算短路冲击信号的基频奇异值畸变率与绕组发生形变的规律一致，发生形变时，该畸变率的值会大于2.0，联合二者共同判定，可在变压器发生短路后对绕组的状态进行预判。
本文研究的变压器绕组形变判定方法，去除累积效应带来的误差影响，可实现绕组形变的判定，具有重要的工程指导意义。但由于不同电压等级的变压器试验数据较少，是否能够对适用于本变压器的特征提取以及累积效应误差修正方法进行推广使用还有待研究。
参考文献
[1] 律方成, 汪鑫宇, 王平, 等. 基于振动偏离及加权熵的多次短路冲击下变压器绕组机械形变辨识[J]. 电工技术学报, 2023, 38(11): 3022-3032.
Lü Fangcheng, Wang Xinyu, Wang Ping, et al. Mechanical deformation identification of transformer winding under multiple short-circuit impacts based on vibration deviation and weighted entropy[J]. Transactions of China Electro- technical Society, 2023, 38(11): 3022-3032.
[2] 李典阳, 张育杰, 冯健, 等. 变压器故障样本多维诊断及结果可信度分析[J]. 电工技术学报, 2022, 37(3): 667-675.
Li Dianyang, Zhang Yujie, Feng Jian, et al. Multi- dimensional diagnosis of transformer fault sample and credibility analysis[J]. Transactions of China Electro- technical Society, 2022, 37(3): 667-675.
[3] 朱柯佳. 高噪声环境下变压器声纹特征提取方法研究[D]. 北京: 华北电力大学, 2021.
[4] 徐永明, 郭蓉, 张洪达. 电力变压器绕组短路电动力计算[J]. 电机与控制学报, 2014, 18(5): 36-42.
Xu Yongming, Guo Rong, Zhang Hongda. Calcu- lation of electrodynamic force with winding short- circuit in power transformers[J]. Electric Machines and Control, 2014, 18(5): 36-42.
[5] 李宏达, 黄鼎琨, 张彬, 等. 改进的低压脉冲法对变压器绕组变形的探测研究[J]. 南京理工大学学报, 2020, 44(1): 15-20.
Li Hongda, Huang Dingkun, Zhang Bin, et al. Research in detection of winding transformer variation based on improved LVI method[J]. Journal of Nanjing University of Science and Technology, 2020, 44(1): 15-20.
[6] 何为, 刘以刚, 胡国辉, 等. 基于短路电抗法的配电变压器绕组变形在线诊断[J]. 电测与仪表, 2014, 51(14): 47-51, 109.
He Wei, Liu Yigang, Hu Guohui, et al. On-line diagnosis of the distribution transformer winding deformation based on the short-circuit reactance method[J]. Electrical Measurement & Instrumentation, 2014, 51(14): 47-51, 109.
[7] Ludwikowski K, Siodla K, Ziomek W. Investigation of transformer model winding deformation using sweep frequency response analysis[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2012, 19(6): 1957-1961.
[8] 刘云鹏, 王博闻, 李欢, 等. 结合载纤绕组形变测量法的大型变压器绕组多次短路冲击暂态声纹特征[J]. 中国电机工程学报, 2022, 42(1): 434-447.
Liu Yunpeng, Wang Bowen, Li Huan, et al. Transient acoustics characteristics of large transformer windings under multiple short-circuit impulse combined with fiber-carrying winding deformation measurement[J]. Proceedings of the CSEE, 2022, 42(1): 434-447.
[9] 高树国, 汲胜昌, 孟令明, 等. 基于在线监测系统与声振特征预测模型的高压并联电抗器运行状态评估方法[J]. 电工技术学报, 2022, 37(9): 2179-2189.
Gao Shuguo, Ji Shengchang, Meng Lingming, et al. Operation state evaluation method of high-voltage shunt reactor based on on-line monitoring system and vibro-acoustic characteristic prediction model[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2179-2189.
[10] Komatowski E. Amplitude detection of power transformer tank vibrations signal[C]//2016 International Conferenceon Signalsand Electronic Systems (ICSES), Krakow, Poland, 2016: 41-46.
[11] 赵书涛, 许文杰, 刘会兰, 等. 基于振动信号谱形状熵特征的高压断路器操动状态辨识方法[J]. 电工技术学报, 2022, 37(9): 2170-2178.
Zhao Shutao, Xu Wenjie, Liu Huilan, et al. Identification method for operation state of high voltage circuit breakers based on spectral shape entropy characteristics of vibration signals[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(9): 2170-2178.
[12] 王丰华, 段若晨, 耿超, 等. 基于“磁–机械”耦合场理论的电力变压器绕组振动特性研究[J]. 中国电机工程学报, 2016, 36(9): 2555-2562.
Wang Fenghua, Duan Ruochen, Geng Chao, et al. Research of vibration characteristics of power transformer winding based on magnetic-mechanical coupling field theory[J]. Proceedings of the CSEE, 2016, 36(9): 2555-2562.
[13] 郭俊, 汲胜昌, 沈琪, 等. 盲源分离技术在振动法检测变压器故障中的应用[J]. 电工技术学报, 2012, 27(10): 68-78.
Guo Jun, Ji Shengchang, Shen Qi, et al. Blind source separation technology for the detection of transformer fault based on vibration method[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 68-78.
[14] 师愉航, 汲胜昌, 张凡, 等. 变压器绕组多倍频振动机理及特性[J]. 高电压技术, 2021, 47(7): 2536-2544.
Shi Yuhang, Ji Shengchang, Zhang Fan, et al. Multi- frequency vibration mechanism and characteristics of transformer windings[J]. High Voltage Engineering, 2021, 47(7): 2536-2544.
[15] 张凡, 汲胜昌, 师愉航, 等. 电力变压器绕组振动及传播特性研究[J]. 中国电机工程学报, 2018, 38(9): 2790-2798, 2849.
Zhang Fan, Ji Shengchang, Shi Yuhang, et al. Research on transformer winding vibration and propagation characteristics[J]. Proceedings of the CSEE, 2018, 38(9): 2790-2798, 2849.
[16] 马宏忠, 弓杰伟, 李凯, 等. 基于ANSYS Workbench的变压器绕组松动分析及判定方法[J]. 高电压技术, 2016, 42(1): 192-199.
Ma Hongzhong, Gong Jiewei, Li Kai, et al. Analysis and determination method for transformer winding looseness based on ANSYS Workbench[J]. High Voltage Engineering, 2016, 42(1): 192-199.
[17] 田聪. 中低频冲击谱测量装置研制及响应谱修正方法研究[D]. 沈阳: 沈阳工业大学, 2021.
[18] 熊卫华, 赵光宙. 基于希尔伯特-黄变换的变压器铁心振动特性分析[J]. 电工技术学报, 2006, 21(8): 9-13.
Xiong Weihua, Zhao Guangzhou. Analysis of transformer core vibration characteristics using Hilbert-Huang transformation[J]. Transactions of China Electrotechnical Society, 2006, 21(8): 9-13.
[19] 徐建源, 陈彦文, 李辉, 等. 基于短路电抗与振动信号联合分析的变压器绕组变形诊断[J]. 高电压技术, 2017, 43(6): 2001-2006.
Xu Jianyuan, Chen Yanwen, Li Hui, et al. Trans- former winding deformation analysis based on short-circuit reactance and vibration signal analysis[J]. High Voltage Engineering, 2017, 43(6): 2001-2006.
[20] 张坤, 王丰华, 廖天明, 等. 应用复小波变换检测突发短路时的电力变压器绕组状态[J]. 电工技术学报, 2014, 29(8): 327-332.
Zhang Kun, Wang Fenghua, Liao Tianming, et al. Detection of transformer winding deformation under sudden short-circuit impact based on complex wavelet algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 327-332.
[21] 杜厚贤, 刘昊, 雷龙武, 等. 基于振动信号多特征值的电力变压器故障检测研究[J]. 电工技术学报, 2023, 38(1): 83-94.
Du Houxian, Liu Hao, Lei Longwu, et al. Power transformer fault detection based on multi- eigenvalues of vibration signal[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 83-94.
[22] 中华人民共和国国家质量监督检验检疫总局. GB 1094.5-2008电力变压器第五部分:承受短路的能力[S]. 北京: 中国标准出版社, 2009.
[23] 张凡, 汲胜昌, 祝令瑜, 等. 短路冲击下变压器振动频响函数研究[J]. 西安交通大学学报, 2017, 51(2): 97-103, 154.
Zhang Fan, Ji Shengchang, Zhu Lingyu, et al. Frequency response function of short circuit vibration for power transformer[J]. Journal of Xi’an Jiaotong University, 2017, 51(2): 97-103, 154.
[24] 张凡, 吴书煜, 徐征宇, 等. 变压器绕组非线性动力学模型及多次短路冲击下的振动特征[J]. 高电压技术, 2022, 48(12): 4882-4892.
Zhang Fan, Wu Shuyu, Xu Zhengyu, et al. Nonlinear vibration model of transformer windings and their vibration characteristics during multiple short circuits[J]. High Voltage Engineering, 2022, 48(12): 4882-4892.
[25] 马宏忠, 耿志慧, 陈楷, 等. 基于振动的电力变压器绕组变形故障诊断新方法[J]. 电力系统自动化, 2013, 37(8): 89-95.
Ma Hongzhong, Geng Zhihui, Chen Kai, et al. A new fault diagnosis method for power transformer winding deformation based on vibration[J]. Automation of Electric Power Systems, 2013, 37(8): 89-95.
[26] 姜崇学, 马秀达, 邹强, 等. 柔性直流输电系统的高频谐波保护方法与工程实践[J]. 电力系统自动化, 2024, 48(3): 150-158.
Jiang Chongxue, Ma Xiuda, Zou Qiang, et al. High-frequency harmonic protection methods and engineering practice for flexible DC transmission systems[J]. Automation of Electric Power Systems, 2024, 48(3): 150-158.
[27] 张知先, 陈伟根, 汤思蕊, 等. 基于互补集总经验模态分解和局部异常因子的有载分接开关状态特征提取及异常状态诊断[J]. 电工技术学报, 2019, 34(21): 4508-4518.
Zhang Zhixian, Chen Weigen, Tang Sirui, et al. State feature extraction and anomaly diagnosis of on-load tap-changer based on complementary ensemble empirical mode decomposition and local outlier factor[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4508-4518.
[28] 杨挺, 张璐, 张亚健, 等. 基于信息熵计算模型的电力信息物理系统融合控制方法[J]. 电力系统自动化, 2021, 45(12): 65-74.
Yang Ting, Zhang Lu, Zhang Yajian, et al. Fusion control method for cyber-physical power system based on information entropy calculation model[J]. Automation of Electric Power Systems, 2021, 45(12): 65-74.
[29] 郭谋发, 徐丽兰, 缪希仁, 等. 采用时频矩阵奇异值分解的配电开关振动信号特征量提取方法[J]. 中国电机工程学报, 2014, 34(28): 4990-4997.
Guo Moufa, Xu Lilan, Miao Xiren, et al. A vibration signal feature extraction method for distribution switches based on singular value decomposition of time-frequency matrix[J]. Proceedings of the CSEE, 2014, 34(28): 4990-4997.
Abstract The transformer will suffer many external short-circuit impact during long-term operation, and the winding will be affected by many accumulations, which will produce irreversible deformation. However, there are still some problems in the study of on-line monitoring of winding mechanical status. The operation of transformer is affected by the accumulative effect, and the relevant studies have not modified the relevant eigenvalues by de-accumulation. The fault diagnosis is mainly aimed at the fundamental frequency vibration signal of the transformer, but the frequency doubling component within 500 Hz is generally present in normal operation, and the transient state contains more higher harmonics. To solve these problems, a feature extraction and deformation determination method based on time-frequency characteristics of shock response of winding is proposed in this paper, which can accurately judge the deformation of winding.
Firstly, based on the relative displacement model of the single degree-of-freedom system, the short-circuit shock response spectrum of the winding is constructed, and the distribution law of the vibration shock response of the winding considering the cumulative effect is obtained. The Fourier spectrum and shock response spectrum distribution of the measured signal are compared to determine the frequency analysis range. Secondly, the time-frequency energy distribution of the short-circuit impulse signal is calculated, and the frequency bands of the energy spectrum are divided according to the response distribution characteristics obtained by the impulse response spectrum to offset the influence of the cumulative effect, and the characteristic changes of the relative energy band entropy are obtained, and the weighted entropy increment is calculated. Thirdly, transform the energy spectrum into time-frequency matrix, decompose the signal by singular value decomposition (SVD), get the singular value vector, and calculate its weight according to the distribution characteristics of the singular value, can calculate the fundamental frequency singular value distortion rate of the signal. Finally, the calculated weighted entropy increment and the singular value distortion of fundamental frequency are compared with the measured cumulative microstrain.
After converting the shock response spectrum into a planar strip, it can be seen that there is basically no accumulative effect when the short-circuit current is relatively small, so the first four shock response bands do not change significantly. Since the fifth time, due to the accumulative effect, the base-frequency short-circuit impulse response of A and C two-phase winding increases from about 100 Hz to 105.3 Hz and 104.7 Hz respectively, but the high-frequency part does not change significantly. The shock response of the B-phase fundamental short-circuit increases from 101.5 Hz to 107.6 Hz, and the peak distribution of the main response gradually increases to 200～550 Hz. In the range of 550～1 000 Hz, the shock response of the winding is unevenly distributed. According to this, the frequency bands are divided, the accumulative effect is corrected, and the change of weighted entropy is calculated, which is highly correlated with the accumulative microstrain of the winding. However, because the threshold of entropy increment is not easy to judge, and the requirement of data acquisition is high, it can not be missed or miscollected, so the concept of fundamental frequency singular value distortion is proposed, and the distortion rate does not exceed 2.0 when there is no deformation, which can be used as an auxiliary judgment means.
Through the analysis of the feature extraction and deformation determination methods proposed in this paper, the following conclusions are drawn: (1) Less high-frequency components in the spectrum can cause a higher level of shock response in the winding, and it is necessary to conduct a comprehensive analysis of signals within 1 000 Hz. (2) Considering the offset degree of shock response points affected by cumulative effects, the relative energy band entropy in different frequency ranges is calculated, which is consistent with the law of winding burst deformation, indicating that it is correlated with winding deformation. (3) The weighted entropy increment of the short-circuit impact signal is calculated and compared with the cumulative microstrain of the winding. The two are linearly correlated. The calculated singular value distortion rate of the short-circuit impact signal does not exceed 2.0 when the winding is not deformed. The combination of the two can accurately predict whether the winding deformation occurs after short-circuit.
keywords：Short-circuit test, winding deformation, accumulative effect, impact response, time-frequency matrix
中图分类号：TM407
DOI: 10.19595/j.cnki.1000-6753.tces.231323
河北省自然科学基金资助项目（E2021521004）。
收稿日期 2023-08-16
改稿日期 2023-09-07
张子康 男，1997年生，硕士研究生，主要研究方向为电气设备在线监测与故障诊断。E-mail: 596450739@qq.com
耿江海 男，1980年生，博士，高级工程师，主要研究方向为高电压试验技术和外绝缘、电气设备在线监测与故障诊断等。E-mail: gengjianghai@163.com（通信作者）
（编辑 崔文静）