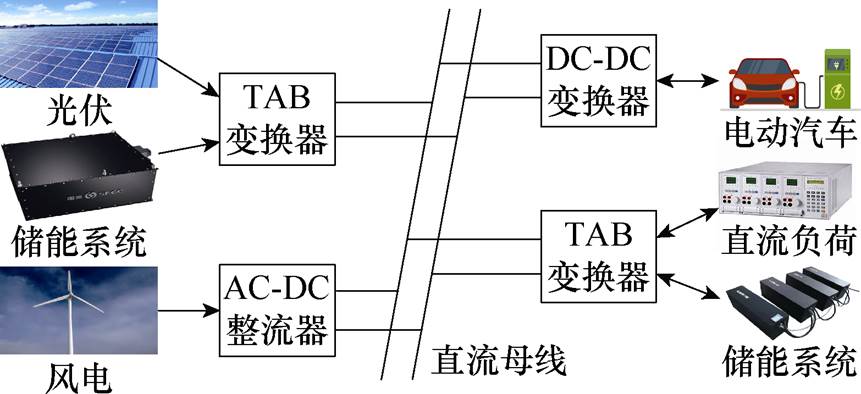
图1 含TAB变换器的直流电网
Fig.1 DC grid with triple active bridge converter
摘要 三有源桥DC-DC 变换器（TAB）作为可再生能源、电动汽车和储能等灵活接入直流电网的有效解决方案，在直流电网中应用前景十分广阔。该文针对TAB 在单移相控制（SPS）下电感电流有效值较大，而移相加脉宽控制（PS-PWM）下数学模型复杂难以求解的问题，提出一种基于电路分解模型的TAB 电感电流有效值优化控制策略。首先分析TAB 在PS-PWM 下的工作原理，建立PS-PWM 下的电路分解模型，得出不同工作模式下各端口功率和电感电流有效值的统一表达式，然后，构建TAB 各端口的电感电流有效值二次方和的优化数学模型，并采用遗传算法求解最优移相角。仿真和实验结果表明，所提分析方法和控制策略能够降低模型的复杂度及计算难度，有效减小各端口的电感电流有效值二次方和，并提高系统效率。
关键词：三有源桥 电流有效值 遗传算法 移相加脉宽调制 DC-DC 变换器
随着直流电网的快速发展，大量分布式可再生能源、电动汽车新型负荷以及储能接入直流电网，DC-DC变换器作为直流电网的重要组成部分，得到了广泛的关注并开展研究[1-4]。直流电网中的源荷储通过大量独立的DC-DC变换器连接，会导致系统结构复杂且效率较低，在源荷储可集中接入的应用场景中，采用三有源桥（Three Active Bridges, TAB）DC-DC变换器取代多个独立DC-DC变换器可以达到简化系统结构、减小装置体积、提高系统的效率和稳定性，以及降低建设成本的目的[5-7]，如图1所示。
目前，对TAB的研究工作主要集中在拓扑结构改进、解耦控制策略、建模方法、软开关特性等方面。文献[8]提出一种电压功率混合解耦控制策略，不仅能够实现电压功率混合控制，还能够实现零电压开关，提高系统效率。文献[9]针对混合储能系统中的TAB变换器，在蓄电池端口采用移相加脉宽控制策略，减小回流功率，提高系统的峰值效率。以上文献详细分析了TAB的软开关及解耦控制方法，但其并未对TAB的电流有效值及损耗进行分析。文献[10]提出基于三角波电流模式调制优化的控制策略，减小了TAB的导通损耗，提高了系统效率，实现了部分开关管的零电流软开关（Zero Current Switching, ZCS）。文献[11]提出一种移相加脉宽控制下TAB的简化傅里叶级数分析模型，简化了移相加脉宽控制下TAB的分析和计算难度，有效减小了无功功率及电感电流有效值，但其并未考虑时域角度下TAB电感电流有效值的分析。文献[12]基于移相加脉宽控制，采用相量法分析并构建最小无功优化问题，能够在宽电压范围内降低变换器的无功回流功率。文献[13]构建了TAB在双电源作用下等效电路的分解模型，进行了相应的开关管ZVS区域分析。文献[14]提出一种简易的TAB电感电流统一求解模型，推导得出电感电流的统一表达式，但其并未考虑TAB的电感电流有效值优化问题。根据以上文献分析可知，电感电流有效值与开关器件的导通损耗、变压器铜损等都有重要关系，因此电感电流有效值是影响TAB效率的重要指标，现有文献对于TAB电感电流有效值的优化研究相对较少。
图1 含TAB变换器的直流电网
Fig.1 DC grid with triple active bridge converter
单移相（Single Phase Shift, SPS）控制策略作为TAB最基本的控制策略，简便易行，但其控制自由度较少、灵活性低，并且由于回流功率的存在，使电感电流有效值增大，从而使TAB的损耗增加，降低系统运行效率。因此通常采用相移脉宽调制（Phase Shift Pulse Width Modulation, PS-PWM）控制策略对各个目标进行优化，但PS-PWM控制下数学模型更为复杂，采用传统的模态分析方法分析难度高、求解困难。为解决这一问题，智能优化算法提供了新的思路。目前粒子群算法、遗传算法（Genetic Algorithm, GA）等已被用于双有源桥（Dual Active Bridge, DAB）变换器的优化控制中[15-17]，文献[15, 17]利用粒子群算法计算DAB的移相角，对电感电流有效值和电流应力进行优化。文献[16]利用遗传算法分别对单模块DAB和多模块DAB的软开关和电流应力进行优化，提高了系统效率，相较于粒子群算法，遗传算法不容易掉入局部最优解中。可以看出，利用智能优化算法能够避免DC-DC变换器繁杂的分段化及非线性公式计算分析，一次运行即可得到全域最优解。基于智能优化算法计算得到DC-DC变换器所有运行工况下的最优移相角，嵌入程序代码供控制器查表使用，可有效减少实时运算量。相比于实时计算类的控制算法，可简化系统设计并提升其计算速度。
综上所述，本文首先提出一种基于电路分解模型的TAB电感电流有效值优化控制策略，构建了PS- PWM控制下TAB的电路分解模型，得出了不同工作模式下各端口功率及电感电流有效值的统一表达式，从而建立了电感电流有效值二次方和的优化数学模型，并采用遗传算法求解得出最优移相角。最后，通过实验验证了本文所提控制策略的可行性和有效性。
TAB拓扑如图2所示。图2中，各端口与高频变压器通过三个H桥模块连接在一起，端口1连接直流母线，端口2连接储能单元，端口3连接负载。本文定义由直流母线输出的功率流向为正方向，输入至储能单元和负载的功率流向为正方向。图2中，L1、L2、L3为各端口的功率传输电感，变压器绕组匝比为N1
N2N3，上标“′”表示折算到端口1的量。为便于分析，将端口2、3折算至端口1侧可得TAB的三角形和星形等效电路，如图3所示。图3中，L12、L13、L23分别为三角形等效电路中，端口1、端口2、端口3之间的等效电感。
图2 TAB拓扑结构
Fig.2 Topology of the TAB
图3 TAB等效电路
Fig.3 Equivalent circuit of TAB
TAB的SPS控制原理与传统DAB类似，通过控制各端口H桥的方波电压VHi（i=1, 2, 3）之间的移相角来调节各端口的输出功率。SPS控制下各端口H桥方波电压工作波形如图4所示。由图4可知，通过调节移相角的大小即可调整各端口间的传输功率。图4中，D12、D13分别为VH1和VH2、VH1和VH3之间的移相比。
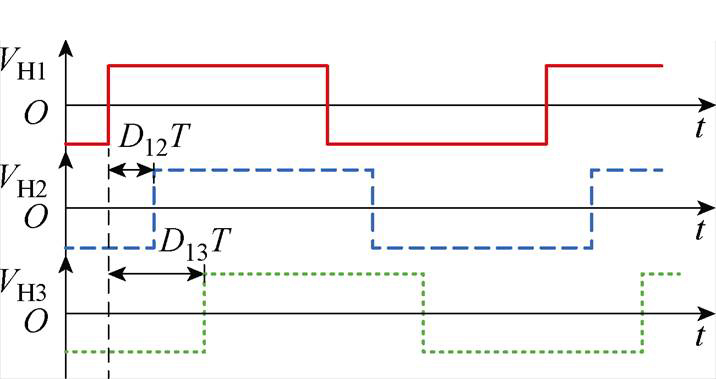
图4 TAB变换器的SPS控制策略
Fig.4 SPS control strategy for TAB converters
SPS控制下，当Dij=0.5时TAB各端口的传输功率达最大值Pmaxij，即
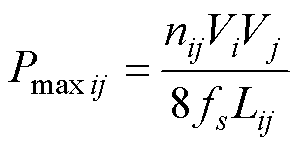（1）
式中，nij=Ni/Nj；fs为开关频率；Lij为三角形等效电路中电感。
与传统DAB类似，TAB的PS-PWM控制在SPS控制的基础上引入内移相比di（i=1, 2, 3）。TAB的PS-PWM控制策略如图5所示。PS-PWM实质是在SPS控制策略各端口方波电压VHi移相的基础上，增加了对VHi占空比的控制。在移相加脉宽控制策略下，TAB各端口的内移相比di存在多种取值和组合方式，增加了控制自由度，更为灵活。其中di的取值范围满足0≤di≤1。
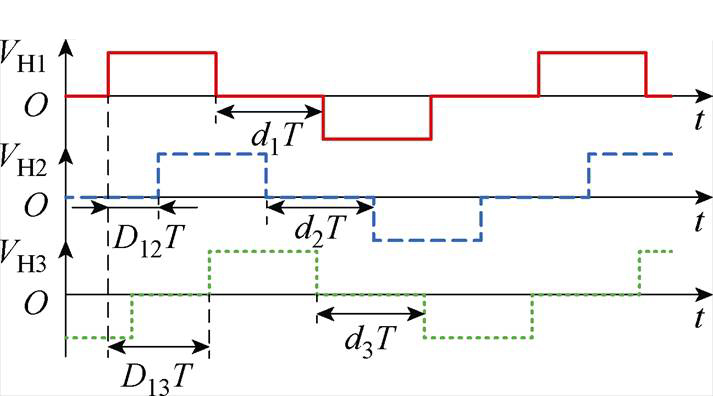
图5 TAB的PS-PWM控制策略
Fig.5 PS-PWM control strategy for TAB converters
TAB运行在稳态时，无论各开关器件都伴随着通态电流，都有通态压降的存在，从而产生通态损耗。通态损耗不仅与器件的特性相关，同时也受到电流波形的影响。对于TAB的通态损耗，由于高频变压器的磁化电感远大于漏感（Li
Lm），故漏感可忽略不计。此外，由于变压器及电感的铁心损耗远小于总损耗，为便于分析，变压器及电感的铁心损耗可忽略不计，因此本文主要考虑开关管的导通损耗和电流通过变压器绕线电阻产生的铜损。
一个周期内TAB中各开关管的导通损耗可表示为
（2）
式中，RDS(on)i为各个H桥中开关管的导通电阻；ILi为各端口磁化电感电流有效值。
变压器铜损可表示为
（3）
式中，RLi和Rtr,i分别为电感和高频变压器各个绕组的电阻。
由式（2）和式（3）可知，TAB的通态损耗与电感电流有效值的二次方和成正比。因此，可以通过减小各端口电感电流有效值降低开关管的导通损耗和变压器铜损。
基于电路分解模型的TAB电流有效值优化控制策略采用PS-PWM的控制方式，首先建立电路分解模型，得到各端口电感电流有效值表达式及不同工作模式下各端口功率表达式，然后构建TAB各端口的电感电流有效值二次方和的优化数学模型，最后采用遗传算法在给定端口功率及电压匹配比的情况下以电感电流有效值二次方和为优化目标求解最优移相角。
根据图5可知，PS-PWM控制下VHi均为三电平方波，其占空比为1-di。两电平方波合成三电平方波如图6所示。三电平方波可以分解为两个对称的两电平方波，S(t)是幅值为0.5、周期为2T的一个两电平方波函数，S(t-DT)是相位滞后S(t)的一个两电平方波函数，D为两个两电平方波的移相比。因此，占空比为1-di三电平方波可以表示为S(t)与S(t-DT)之和，其幅值为1，周期为2T。
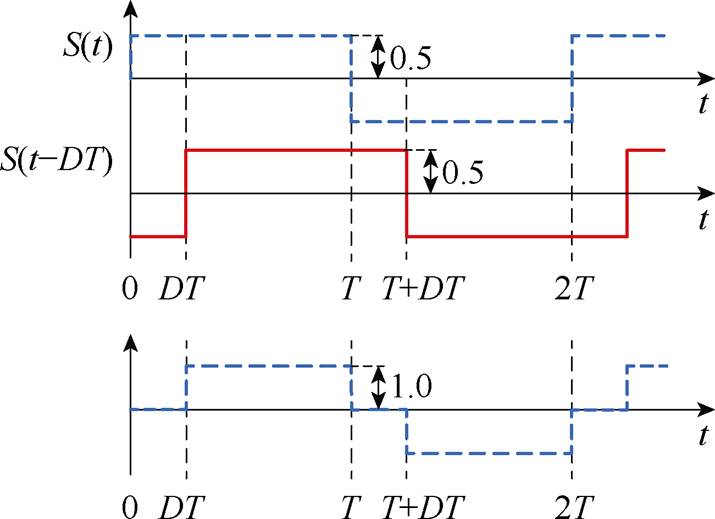
图6 两电平方波合成三电平方波
Fig.6 Synthesis of a two-electrode square wave into a three-electrode square wave
因此，VHi可表示为
（4）
式中，S(t)为标准的两电平方波函数；V1为输入直流电压，即VH1幅值；V2、V3分别为端口2、3直流电压，即VH2、VH3幅值。
因此，在PS-PWM控制下，TAB电路分解后的等效电路如图7所示。
图7 TAB电路分解后的等效模型
Fig.7 Equivalent model of the decomposed TAB circuit
为了简化分析，假设电路中的开关器件和磁性元件均是理想的[18]，则根据图7所示等效模型，可得电路分解后电感电流微分方程为
（5）
将式（4）代入式（5），并且根据电感伏秒平衡关系，并结合叠加定理，可解得基于电路分解模型的各端口电感电流表达式为
（6）
其中
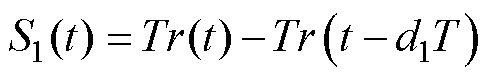
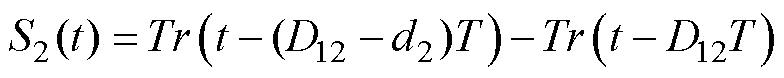
式中，Tr(t)为三角波。
由于电感电流波形半周期中心对称，因此Tr(t)是由S(t)积分得到的幅值为0.25T、周期为2T对称三角波，如图8所示。
图8 Tr(t)波形
Fig.8 The waveform of Tr(t)
从而可得基于电路分解模型的电感电流有效值表达式为
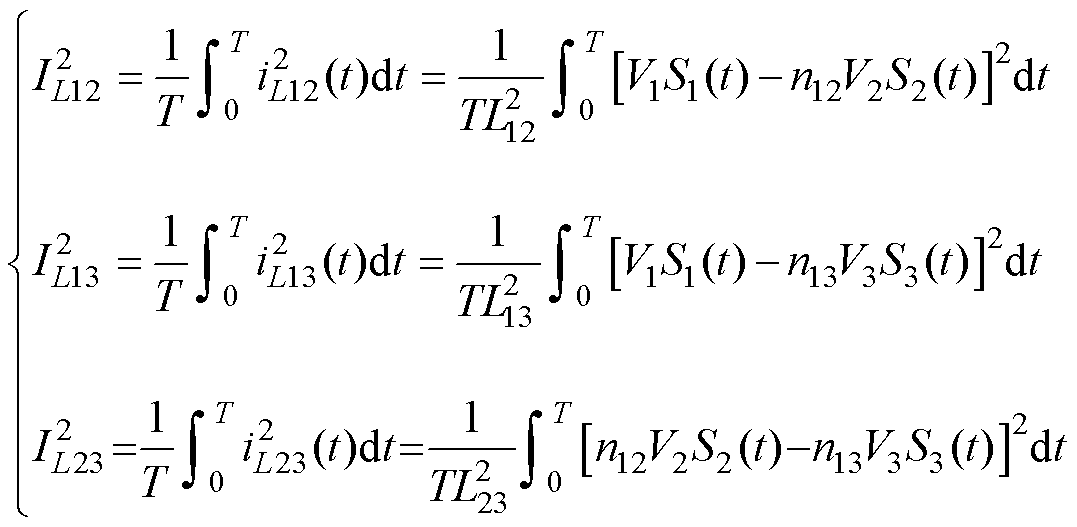（7）
对于式（7）的展开式中，每一项都具有相似的表达形式，满足
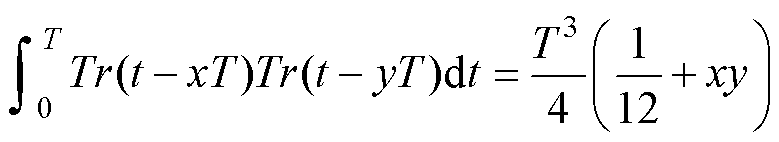（8）
因此，联立式（7）和式（8），即可解得基于电路分解模型的电感电流有效值表达式。三个内移相角的加入使得变量增多，分析更加复杂，为便于分析，本文仅讨论加入单个内移相比（即d2≠0）的情况。根据控制量D12、D13、d2之间的关系，PS-PWM控制方式可分为五种工作模式，如图9所示。各端口传输功率表达式可表示为
（9）
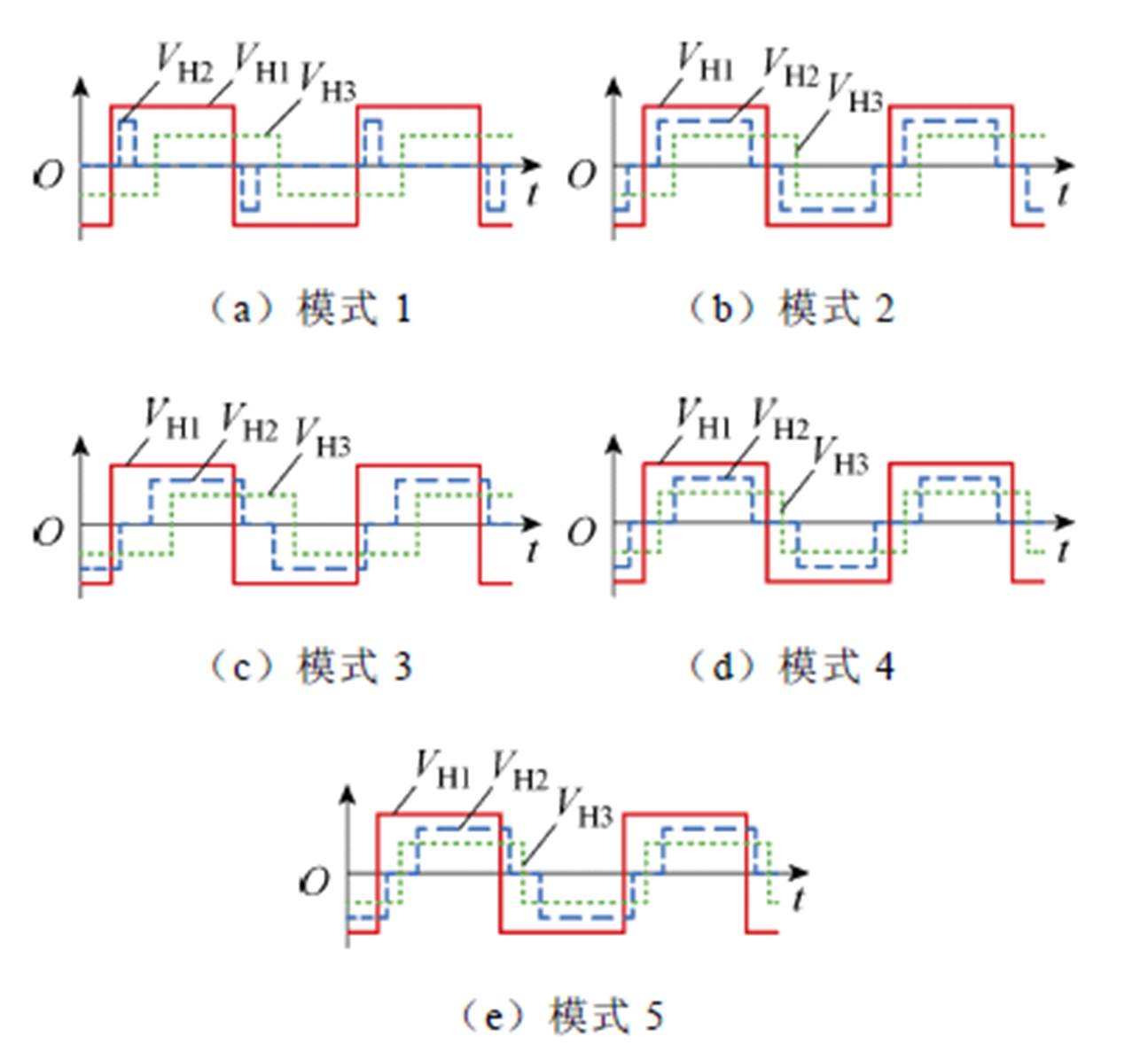
图9 PS-PWM控制下的五种工作模式
Fig.9 Five operating modes with PS-PWM control
根据各端口间功率传输关系可得五种工作模式下各端口功率表达式，见表1。基于电路分解模型的电感电流有效值表达式为
表1 PS-PWM控制下不同工作模式的功率表达式
Tab.1 Power expressions for different operating modes under PS-PWM control
工作模式移相比约束各端口功率表达式 模式1 模式2 模式3 模式4 模式5
（10）
式中，K=(TV1/
)2，L12=L13=L23=；g1=1/12+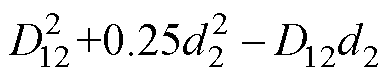 
；g2=1/6+
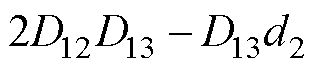；k21、k31分别为端口1、2和端口1、3的电压匹配比，取k21=n12V2/V1、k31=n13V3/V1。从而可得基于电路分解模型的电感电流有效值二次方和表达式为
（11）
因此，基于电路分解模型的电感电流有效值二次方和优化数学模型为
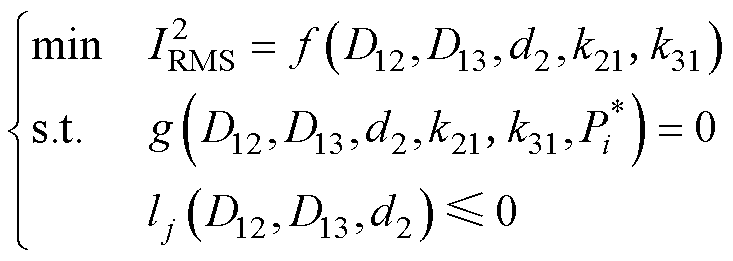（12）
式中，f(D12, D13, d2, k21, k31) 为电感电流有效值二次方和表达式；g(D12, D13, d2, k21, k31,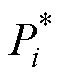 
)=0为功率约束；lj为工作模式j下的移相比约束。
为便于分析，本文取功率基准值和电感电流有效值二次方及基准值分别为
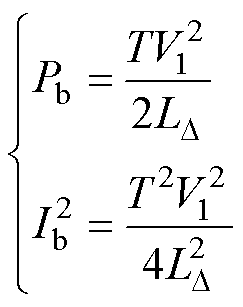（13）
由于在PS-PWM控制中，实现指定功率输出具有多个移相角组合，因此需要结合算法找到使电感电流有效值最小的最优组合。根据得到的电感电流有效值和功率模型，可以通过拉格朗日乘数法等数学方法求解最优移相角，但分析计算过程繁琐复杂，遇到多变量和非线性的约束时可能无法求出数值解。
利用智能算法，可以通过多次迭代计算、利用适应度函数评价来简化优化过程，通过加入罚函数对约束条件进行调制。遗传算法是一个将优化问题模拟成自然选择过程，根据适应度函数对优化结果进行搜索，相比于其他智能算法，通过调整遗传算法的初始参数，可以有效避开局部最优化结果。
遗传算法的具体流程如图10所示，包括编码、解码、遗传运算、适应度计算、评价等，初始化参数见表2。首先对遗传算法参数初始化，获取种群内各个个体的初始参数（D12, D13, d2），并计算适应度；其次对个体进行编码，根据设定的参数对种群进行选择、交叉、变异操作，操作过后进行解码，得到新种群的（D12, D13, d2），用本轮迭代的适应度与最优适应度比较，取较优结果更新最优适应度和最优解；最后当终止原则满足时结束运算。
图10 遗传算法流程
Fig.10 Genetic algorithm flow chart
表2 遗传算法初始参数
Tab.2 Initial parameters of the genetic algorithm
参 数数 值 种群规模100 进化代数50 交叉概率0.6 变异概率0.01
图11所示为基于电路分解模型采用遗传算法求解的电感电流有效值优化控制策略（Genetic Algorithm Optimal Strategy, GAOS）的实现框图。首先，在系统控制程序运行之前，通过遗传算法寻优得到 (P2, P3) 全功率范围内不同电压匹配比k21所对应的移相比d2，并将其形成表格存储到控制器中。然后通过检测端口2电感电流及端口3电压，分别与给定值作差，经过PI控制器后得出移相比（D12, D13），根据端口功率（P2, P3）、电压匹配比k21对d2进行在线查表，即得出优化后的移相比组合。
图11 电感电流有效值优化控制策略
Fig.11 Optimal control strategy for inductor current RMS
为验证本文所提GAOS控制策略的有效性，基于Matlab/Simulink平台搭建了TAB的仿真模型，主要仿真参数见表3。
由于端口2所接储能系统在接入用户配电系统时存在多个电压等级，因此本文考虑端口2在不同电压匹配比下系统运行状况。图12分别给出了k21=1、k21=1.2、k21=1.4时，TAB在SPS和GAOS控制策略下电感电流有效值二次方和
与端口2、3功率的三维关系对比图。由图12可知，电感电流有效值二次方和与端口功率成正比，且GAOS控制策略下明显小于SPS控制策略。
表3 主要仿真参数
Tab.3 Main simulation parameters
参 数数 值 端口1电压V1/V120 端口3电压V3/V240 开关频率fs/kHz20 变压器电压比N1N2N3112 功率传输电感L1, L2/mH21.33 功率传输电感L3/mH85.32
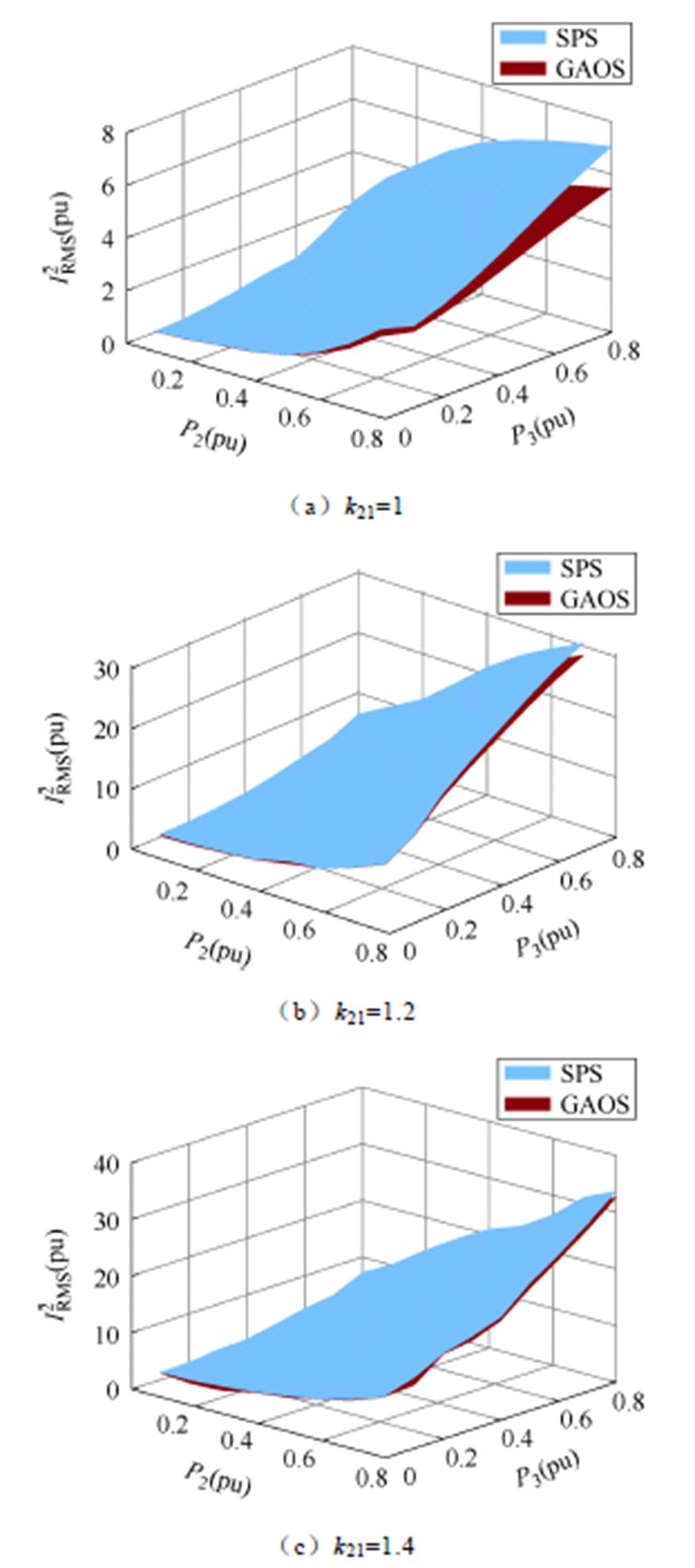
图12 两种控制策略下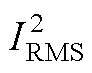
与各端口功率的三维对比图
Fig.12 3D plot of 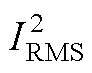vs. power at each port for the two control strategies
图13给出了k21=1, P2=0.6(pu), P3=0.1(pu)时，两种控制策略下各端口电压和电感电流波形。在此工况下，由GAOS控制策略计算得出的内移相比D22=0.007，GAOS控制策略下各端口电感电流有效值（标幺值）二次方和为1.452，SPS控制策略下各端口电感电流有效值（标幺值）二次方和为1.478。
图13 k21=1, P2=0.6(pu), P3=0.1(pu)时各端口工作波形
Fig.13 Waveforms at each port with k21=1, P2=0.6(pu), P3=0.1(pu)
图14给出了k21=1.2, P2=0.4(pu), P3=0.2(pu)时，两种控制策略下各端口电压和电感电流波形。在此工况下，由GAOS控制策略计算得出的内移相比dz=0.25，GAOS控制策略下各端口电感电流有效值（标幺值）二次方和为0.777，SPS控制策略下各端口电感电流有效值（标幺值）二次方和为0.803。
图14 k21=1.2, P2=0.4(pu), P3=0.2(pu)时各端口工作波形
Fig.14 Waveforms at each port with k21=1.2, P2=0.4(pu), P3=0.2(pu)
图15给出了k21=1.4, P2=0.2(pu), P3=0.4(pu)时，两种控制策略下各端口电压和电感电流波形。在此工况下，由GAOS控制策略计算得出的内移相比dz=0.275，GAOS控制策略下各端口电感电流有效值（标幺值）二次方和为0.782，SPS控制策略下各端口电感电流有效值（标幺值）二次方和为0.902。
图16a～图16c分别为端口3输入功率P3恒定时，不同电压匹配比下端口2输入功率P2与电流有效值二次方和的示意图。从图中可以看出，P3= 0.1(pu)时，电感电流有效值二次方和与P2成正比，并且在GAOS控制下电感电流有效值二次方和明显小于SPS控制。同理，P3=0.3(pu)和P3=0.5(pu)时电感电流有效值二次方和与P2也成正比例关系，在GAOS控制下电感电流有效值二次方和同样明显小于SPS控制，并且随着P3的增大电感电流有效值二次方和也随之增加。
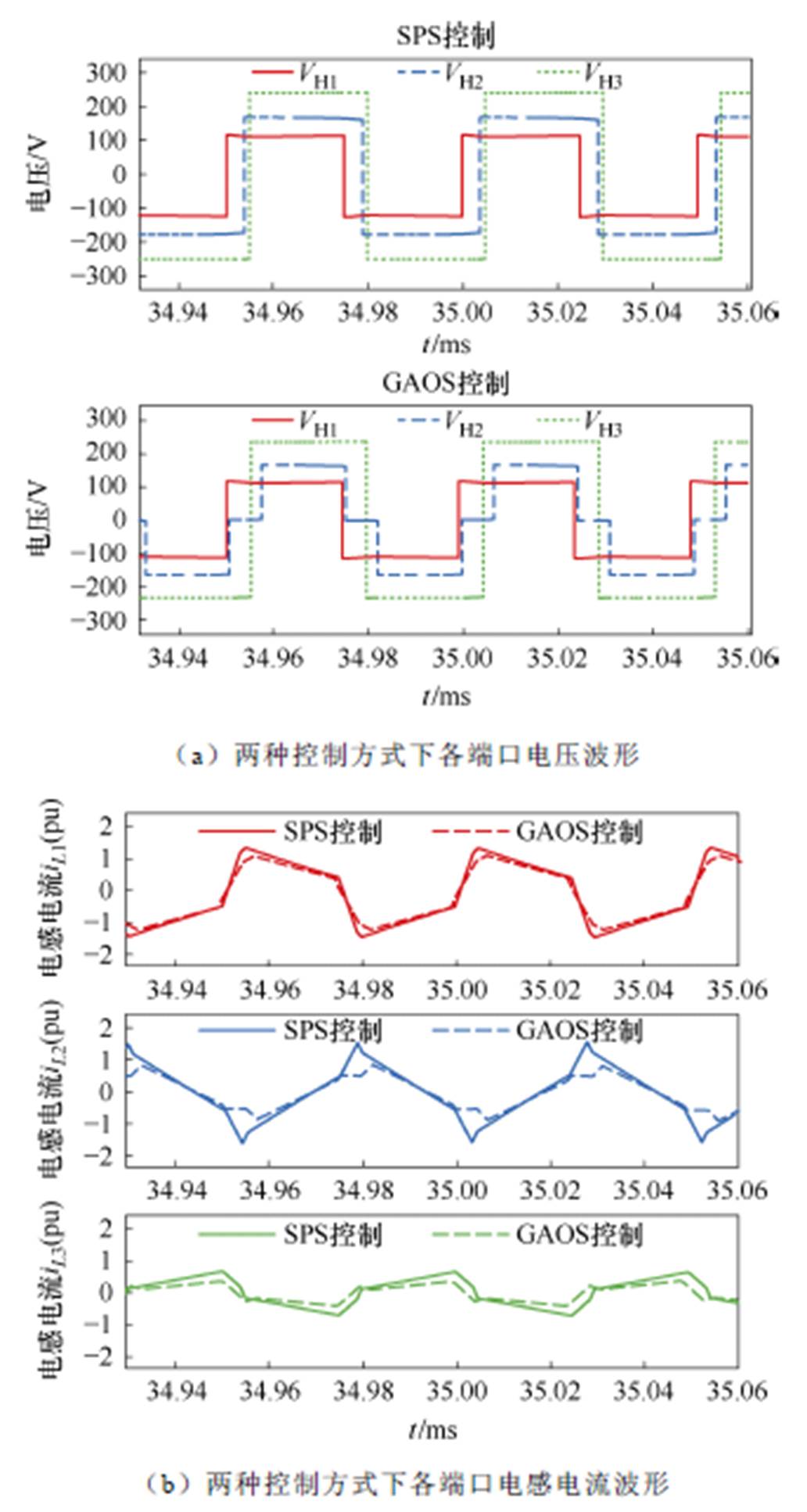
图15 k21=1.4, P2=0.2(pu), P3=0.4(pu)时各端口工作波形
Fig.15 Waveforms at each port with k21=1.4, P2=0.2(pu), P3=0.4(pu)
图16d～图16f分别为端口2输入功率P2恒定时，不同电压匹配比下端口3输入功率P3与电感电流有效值二次方和的示意图。从图中可以看出P2=0(pu)时，电感电流有效值二次方和与P3成正比，并且在GAOS控制下电感电流有效值二次方和明显小于SPS控制。同理，P2=0.2(pu)和P2=0.4(pu)时，电感电流有效值二次方和与P3也成正比例关系，在GAOS控制下电感电流有效值二次方和同样明显小于SPS控制，并且随着P2的增大电感电流有效值二次方和也随之增加。
由图16可知，电感电流有效值二次方和与端口2、3输入功率成正比，并且在不同电压匹配比k21下GAOS控制电感电流有效值二次方和均明显小于SPS控制。
图16 不同k21下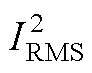与各端口功率的二维关系图
Fig.16 Two-dimensional plot of 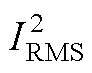versus power at each port for different k21
图17给出了两种控制方式下TAB的通态损耗对比曲线。从图17中可以看出，当P2、P3其中一个端口功率恒定时，TAB的通态损耗均随另一个端口功率的增大而增大，且GAOS控制下通态损耗明显小于SPS控制。结合图16分析可知，采用GAOS控制能够有效降低TAB的电感电流有效值的二次方和，进而降低TAB的通态损耗、提升变换器的效率，与前文理论分析一致。
为了验证本文提出的GAOS控制策略的有效性，本文基于RT-Lab实验平台进行了实验验证，如图18所示，实验主要参数见表4。
图17 两种控制下TAB的通态损耗对比曲线
Fig.17 Comparison curves of on-state loss of TAB under two controls modes
图18 RT-Lab半实物实验平台
Fig.18 RT-Lab semi-physical experimental platform
表4 实验主要参数
Tab.4 Main parameters of the experiment
参 数数 值 端口1电压V1/V120 端口3电压V3/V240 开关频率fs/kHz5 变压器电压比N1N2N3112 功率传输电感L1, L2/μH21.33 功率传输电感L3/μH85.32
图19给出了k21=1, P2=960 W, P3=480 W时，两种控制策略下各端口的实验波形。由实验图分析可知，SPS控制策略下各端口电感电流有效值（标幺值）二次方和为0.096，GAOS控制策略下各端口电感电流有效值（标幺值）二次方和为0.078。
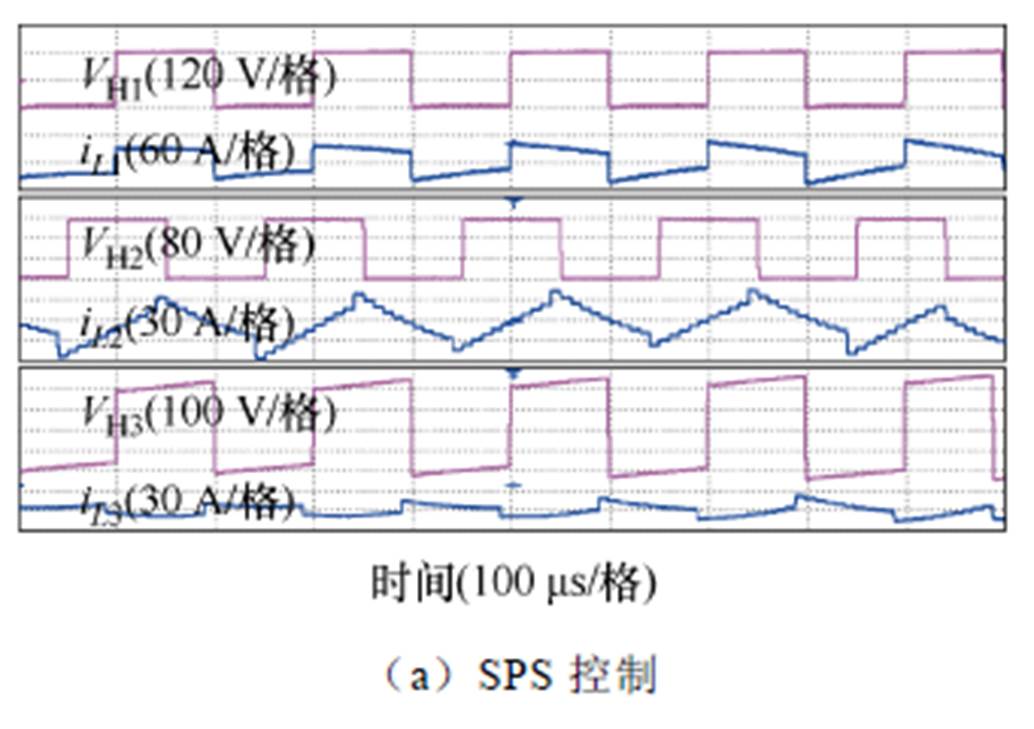
图19 k21=1, P2=960 W, P3=480 W时两种控制下的实验波形
Fig.19 Experimental waveforms under two control strategies when k21=1, P2=960 W, P3=480 W
图20给出了k21=1.2, P2=1 152 W, P3=230 W时，两种控制策略下各端口的实验波形。由实验图分析可知，SPS控制策略下各端口电感电流有效值（标幺值）二次方和为0.118，GAOS控制策略下各端口电感电流有效值（标幺值）二次方和为0.089。
图20 k21=1.2, P2=1 152 W, P3=230 W时两种控制下的实验波形
Fig.20 Experimental waveforms under two control strategies when k21=1.2, P2=1 152 W, P3=230 W
图21给出了k21=1.4, P2=840 W, P3=288 W时，两种控制策略下各端口的实验波形。由实验图分析可知，SPS控制策略下各端口电感电流有效值（标幺值）二次方和为0.6，GAOS控制策略下各端口电感电流有效值（标幺值）二次方和为0.428。
图21 k21=1.4, P2=840 W, P3=288 W时两种控制下的实验波形
Fig.21 Experimental waveforms under two control strategies when k21=1.4, P2=840 W, P3=288 W
由图19～图21可知，实验结果与仿真分析结果一致。因此，本文提出的优化控制策略能够有效降低电感电流有效值二次方和，从而降低通态损耗。
图22给出了TAB端口1输入电压为120 V、端口2负载突变时，端口2、3的输出电压及电流波形。从图22中可以看出，当端口2负载切换时，端口3输出电压仍然稳定在240 V，端口3输出电流仍然稳定在2.4 A，端口3功率保持恒定。因此，端口2负载突变时系统仍然能够保持稳定。
图22 端口2负载突变时端口2、3的输出波形
Fig.22 The output waveforms of ports 2 and 3 when the load of port 2 changes suddenly
图23给出了TAB端口1输入电压为120 V、端口3负载突变时，端口2、3的输出电压及电流波形。从图23中可以看出，当端口3负载切换时，端口2输出电压仍然稳定在144 V，端口2输出电流仍然稳定在5 A，端口2功率保持恒定。因此，端口3负载突变时系统仍然能够保持稳定。
图23 端口3负载突变时端口2、3的输出波形
Fig.23 The output waveforms of ports 2 and 3 when the load of port 3 changes suddenly
针对TAB在SPS控制下电感电流有效值较大且PS-PWM控制下数学模型复杂难以求解的问题，本文首先分析了TAB在PS-PWM控制下的工作原理，基于叠加定理将PS-PWM控制下TAB等效电路分解为两个方波电源共同作用的电路，构建了不同工作模式下各端口功率和电感电流有效值的统一表达式，从而建立了电感电流有效值二次方和的优化数学模型，并采用遗传算法进行模型求解。最后搭建了半实物实验平台，验证了本文所提控制策略的可行性与有效性，并得到以下结论：
1）TAB的通态损耗与电感电流有效值的二次方成正比，电感电流有效值二次方和仅与电压匹配比k21、k31以及各端口间移相角和开关管的占空比有关，为TAB电路分解模型的搭建提供了理论 基础。
2）基于PS-PWM控制的电路分解模型能够有效降低TAB的分析难度，遗传算法的引入使得电感电流有效值优化数学模型的复杂度及计算难度减小。
3）在电压匹配比k21＞1时，本文所提GAOS控制策略能够有效降低TAB电感电流有效值二次方和，减小变换器通态损耗，提高TAB功率传输效率。
参考文献
[1] 魏晓光, 王新颖, 高冲, 等. 用于直流电网的高压大容量DC/DC变换器拓扑研究[J]. 中国电机工程学报, 2014, 34(20): 218-224.
Wei Xiaoguang, Wang Xinying, Gao Chong, et al. Topology research of high voltage and high power DC/DC converters used in DC grids[J]. Proceedings of the CSEE, 2014, 34(20): 218-224.
[2] 孟祥齐, 贾燕冰, 任春光, 等. 直流微电网DAB变换器和直流固态变压器的非线性控制策略[J]. 电力系统自动化, 2023, 47(4): 180-189.
Meng Xiangqi, Jia Yanbing, Ren Chunguang, et al. Nonlinear control strategy of dual active bridge converter and DC solid state transformer in DC microgrid[J]. Automation of Electric Power Systems, 2023, 47(4): 180-189.
[3] 杨晓峰, 郑琼林, 林智钦, 等. 用于直流电网的大容量DC/DC变换器研究综述[J]. 电网技术, 2016, 40(3): 670-677.
Yang Xiaofeng, Zheng Trillon Q, Lin Zhiqin, et al. Survey of high-power DC/DC converter for HVDC grid application[J]. Power System Technology, 2016, 40(3): 670-677.
[4] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[5] Duarte J, Hendrix M, Simoes M. Three-port bidi- rectional converter for hybrid fuel cell systems[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 480-487.
[6] Krishnaswami H, Mohan N. Three-port series- resonant DC-DC converter to interface renewable energy sources with bidirectional load and energy storage ports[J]. IEEE Transactions on Power Elec- tronics, 2009, 24(10): 2289-2297.
[7] Bhattacharjee A K, Kutkut N, Batarseh I. Review of multi port converters for solar and energy storage integration[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(2): 1431-1445.
[8] 宋钊, 刘明. 模块化多端口无线电能DC-DC变换器建模及其多向功率流解耦控制策略[J]. 电工技术学报, 2022, 37(24): 6262-6271.
Song Zhao, Liu Ming. Modular multiport wireless DC-DC converter with multidirectional power flow and its decoupling control strategy[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6262- 6271
[9] Wang Chengshan, Li Wei, Wang Yifeng, et al. An isolated three-port bidirectional DC-DC converter with enlarged ZVS region for HESS applications in DC micro grids[J]. Energies, 2017, 10(4): 1-23.
[10] 涂春鸣, 栾思平, 肖凡, 等. 三端口直流能量路由器在TCM调制下的优化控制策略[J]. 电网技术, 2018, 42(8): 2503-2511.
Tu Chunming, Luan Siping, Xiao Fan, et al. Optimal control strategy of three-port DC energy router under TCM modulation[J]. Power System Technology, 2018, 42(8): 2503-2511.
[11] 刘贝, 帅智康, 肖凡, 等. 三有源桥变换器简化分析模型及优化控制策略[J]. 电工技术学报, 2021, 36(11): 2394-2407.
Liu Bei, Shuai Zhikang, Xiao Fan, et al. Simplified analysis model and optimal control strategy of triple active bridge converter[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2394-2407.
[12] 黄珺, 付亚楠, 吕晓飞, 等. 基于无功优化的三端口双向DC-DC变换器控制策略[J]. 电工技术学报, 2022, 37(8): 2086-2096.
Huang Jun, Fu Yanan, Lü Xiaofei, et al. Control strategy of three-port bidirectional DC-DC converter based on reactive power optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2086- 2096.
[13] Yu Xueping, Lan Zheng, Zeng Jinhui, et al. Time- domain based superposition analysis for triple active bridge and its application for ZVS and current stress optimization[J]. IEEE Transactions on Power Elec- tronics, 2023, 38(5): 5844-5857.
[14] 涂春鸣, 余雪萍, 肖凡, 等. TAB变换器高频链交流电流峰值与有效值统一求解模型[J]. 中国电机工程学报, 2021, 41(22): 7740-7751.
Tu Chunming, Yu Xueping, Xiao Fan, et al. A novel solution for high-frequency-link AC current of TAB converter[J]. Proceedings of the CSEE, 2021, 41(22): 7740-7751.
[15] Zhou Lu, Gao Yihan, Ma Hao, et al. Wide-load range multiobjective efficiency optimization produces closed-form control solutions for dual active bridge converter[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 8612-8616.
[16] Li Jia, Luo Quanming, Mou Di, et al. A hybrid five-variable modulation scheme for dual-active- bridge converter with minimal RMS current[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 336-346.
[17] Hebala O M, Aboushady A A, Ahmed K H, et al. Generic closed-loop controller for power regulation in dual active bridge DC-DC converter with current stress minimization[J]. IEEE Transactions on Indu- strial Electronics, 2019, 66(6): 4468-4478.
[18] 童安平, 杭丽君, 李国杰. 三重移相控制下DAB变换器全局优化控制策略及分析[J]. 中国电机工程学报, 2017, 37(20): 6037-6049.
Tong Anping, Hang Lijun, Li Guojie. Global optimized control strategy of dual active bridge converter controlled by triple-phase-shift modulation scheme and its analysis[J]. Proceedings of the CSEE, 2017, 37(20): 6037-6049.
Abstract As an effective solution for renewable energy, electric vehicles, and energy storage flexible access to the DC grid, the triple active bridge DC-DC converter (TAB) has widespread adoption in the DC grid. The main research of TAB involves topology improvement, decoupling control strategy, modeling methodology, and soft-switching characteristics. However, the rms value of the inductor current, as an important indicator affecting the efficiency of TAB, has few optimization studies. Therefore, this paper focuses on the rms value optimization for inductor current in TAB.
As the most basic control strategy of TAB, the SPS control strategy is simple and easy to implement. However, it has many shortcomings, such as few control degrees of freedom, low flexibility, increased loss, and reduced operating efficiency of the TAB. PS-PWM control strategy is usually used to optimize these objectives, but the mathematical model under PS-PWM control is complex. This paper proposes a TAB inductor current rms optimization control strategy based on the circuit decomposition model. Firstly, the operating principle of TAB under PS-PWM is analyzed, and the circuit decomposition model under PS-PWM is established. Then, the unified expressions for the power and the rms value of the inductor current at each port under different operating modes are derived. The optimized mathematical model for summing the rms value squares of the inductor current at each port of the TAB is constructed, and a genetic algorithm is applied to reduce the inductor current rms value by the optimal shift ratio. Simulation and experimental results show that the proposed analysis method and control strategy can reduce the complexity and computational difficulty of the model. The rms value of inductance current at each port is effectively reduced, and the system efficiency is improved.
The following conclusions can be drawn. (1) The on-state loss of the TAB is proportional to the square of the rms value of the inductor current. The sum of rms value squares of the inductor currents is primarily related to the voltage matching ratios k21 and k31, the phase shift angle between the ports, and the duty ratio of the switching tubes. These factors provide the theoretical basis for constructing the decomposition model of the TAB circuit. (2) The circuit decomposition model based on PS-PWM control can simplify the TAB circuit analysis. The complexity and computational difficulty of optimizing the mathematical model can be reduced by introducing a genetic algorithm. (3) When the voltage matching ratio k21＞1, the sum of rms value squares of the TAB inductor current can be effectively reduced, and the power transfer efficiency of the TAB can be improved by the proposed GAOS control strategy.
keywords：Three active bridges, current rms, genetic algorithm, phase shifting plus pulse width modulation, DC-DC converter
中图分类号：TM72
DOI: 10.19595/j.cnki.1000-6753.tces.231541
国家自然科学基金项目（51807058）、湖南省教育厅优秀青年项目（22B0603）和湖南省自然科学基金项目（2021JJ50059）资助。
收稿日期 2023-09-14
改稿日期 2023-09-25
兰 征 男，1985年生，副教授，硕士生导师，研究方向为多端口变换器、分布式电源并网技术、微电网控制等。E-mail: lanzheng20@foxmail.com
余雪萍 女，1990年生，博士，讲师，硕士生导师，研究方向为多端口变换器和电力电子技术在电力系统中的应用等。E-mail: Xuepingyu@163.com（通信作者）
（编辑 郭丽军）