图1 直流固态变压器的拓扑结构
Fig.1 Topology structure of the DC solid-state transformer
摘要 该文针对以输入串联-输出并联的双有源桥变换器为核心的直流固态变压器的控制策略展开研究。传统的由输出电压控制和输入均压控制构成的双环控制系统，各控制环的环路增益特性会随负载等工况发生显著变化，控制器参数的设计难以兼顾全工况下的动态性能。为此，该文利用双有源桥变换器的一阶模型特性，基于直流固态变压器的大信号模型，开发了一种新型的线性化控制策略，以实现输出电压控制和输入均压控制的环路模型的线性化，从而简化控制器参数的设计，并增强变换器对不同工况的适应能力。同时，该文所提出的控制策略保留了比例-积分控制的简洁性和鲁棒性，且实现了对负载的补偿作用。仿真和实验结果证实了所提的控制策略可以显著降低直流固态变压器的环路模型和动态特性对工况的敏感程度，有利于实现全工况范围内动态性能的综合优化。
关键词：直流固态变压器 双有源桥 线性化控制 输出电压控制 输入均压控制
随着光伏、风电等分布式电源、储能以及电动汽车等直流负荷在电网中的大规模集成，传统的交流配电网面临严峻的挑战。与交流配电网相比，直流配电网由于在接入可再生能源、减少电力转换阶段和传输损耗方面的优势成为当前的研究热点。其中，用于连接中低压直流母线的直流固态变压器（Solid-State Transformer, SST）是直流配网的核心设备。
受限于功率器件的耐压和耐流水平，直流固态变压器往往需要在输入侧串联以匹配较高的中压直流电压，在输出侧并联以实现足够大的传输功率。因而，基于输入串联-输出并联（Input-Series Output- Parallel, ISOP）的DC-DC结构成为直流固态变压器的典型拓扑结构。其中，双有源桥（Dual Active Bridge, DAB）变换器由于具有高功率密度、双向功率传输能力和动态性能优异等特点，成为直流固态变压器中应用最广泛的DC-DC单元。本文针对以ISOP-DAB为核心的直流固态变压器的控制策略展开研究。
直流固态变压器的正常运行首先要确保输出电压的稳定。对于直流固态变压器的输出电压控制，传统的纯反馈控制策略在负载等工况突变时难以保证足够快的响应速度[1]。为此，前馈控制[2]、直接功率控制[3-4]和虚拟直接功率控制[5]相继被提出，并被证明能够有效抑制负载和输入电压的扰动。同时，电流模式控制[6-7]也被引入直流固态变压器的输出电压控制中，即在输出电压外环的基础上，通过检测DAB变换器的变压器电流并让其参与控制，以进一步增强动态性能。为了减少传感器的数量，基于状态观测的输出电压控制策略被提出[8-9]。此外，一些文献还报道了滑模控制[10]、模型预测控制[11]等非线性控制策略在直流固态变压器输出电压控制中的应用。以上所述的输出电压控制策略在算法复杂度、动态响应速度、传感器数量以及鲁棒性等方面各有优劣[1,12]，可根据实际需求进行选择。
在直流固态变压器中，漏感、损耗等参数的不一致性会使单元间的电压和功率不均衡，这会增大DAB变换器输入输出电压的不匹配程度，导致损耗增加，甚至可能使单个单元的传输功率超出额定 值[13]。因而，除输出电压控制外，直流固态变压器还应控制所有子单元的均衡。文献[13]讨论了包含输出电压控制和输入均压控制的双环控制策略。每个DAB单元的移相比由输出电压环产生的公共移相比和输入均压环产生的移相比增量叠加得到。这种双环控制策略是ISOP系统最常用的均衡控制方案。文献[14]介绍了一些基于功率控制的均衡控制方法，如在线功率积分均衡控制[15]、直接功率均衡控制[16]和虚拟功率均衡控制[17]等。此外，模型预测控制[11]和状态观测[18]等方法也被引入直流固态变压器的均衡控制中。
然而，前面所述的输出电压控制和均衡控制策略存在的一个普遍问题是，其控制对象都是非线性的，因而环路增益会随负载等工况变化。为了保证直流固态变压器在全工况下的稳定性，控制器参数的设计需要满足最恶劣工况下的稳定性指标，从而牺牲了在其他工况下的动态性能。为了解决这一问题，文献[19]针对DAB变换器提出了一种线性化控制策略，通过将PI控制器的输出设置为移相比的非线性表达式，使得环路模型不随工况变化。然而，这种线性化方法只适用于输出侧接恒定阻性负载的情况。文献[20]采用自适应PI控制，通过检测控制对象的增益和极点位置，并令PI控制器的零点与控制对象的极点对消的同时，根据期望的开环截止频率实时计算PI控制器的参数。然而，这种方法一方面加重了实时运算的负担；另一方面没有改变控制对象的非线性特性，控制对象的传递函数依赖负载的类型和大小，限制了该方法的控制效果和适用范围。此外，目前鲜有文献讨论直流固态变压器均衡控制的工况适应性问题。
本文利用DAB变换器的一阶模型特性[1]，基于直流固态变压器的大信号模型，推导了输出电压控制和输入均压控制的线性化控制策略。所提出的控制策略可以消除原控制对象的非线性，从而简化控制器参数的设计，增强变换器对不同工况的适应能力，有利于实现全工况范围内动态性能的综合优化。同时，所提出的控制策略保留了比例-积分控制的简洁性和鲁棒性，且实现了对负载的补偿。仿真和实验结果验证了所提控制策略的有效性。
本文研究以ISOP-DAB为核心的直流固态变压器的拓扑结构如图1所示。图中，vin和iin分别为输入电压和输入电流，vout和iout分别为输出电压和输出电流，Cin和Cout分别为输入和输出侧的滤波电容，Lp和n分别为折算到变压器一次侧的功率电感和变压器电压比，N为子单元数量，vin,i为第i个DAB单元的输入电压，ip,i和is,i分别为第i个DAB单元的一次和二次电流。
图1 直流固态变压器的拓扑结构
Fig.1 Topology structure of the DC solid-state transformer
常用的DAB变换器建模方法主要包括降阶模型[21]、广义平均模型[22]和离散迭代模型[23]。文献[1]通过时域仿真得出，由于功率电感电流的低频分量为零，降阶模型可以准确地描述DAB变换器的动态响应。图2以单移相（Single Phase Shift, SPS）调制为例展示了基于DAB变换器降阶模型建立的直流固态变压器的大信号模型等效电路。gi可以表示为
图2 直流固态变压器的大信号模型等效电路
Fig.2 Equivalent circuit of the DC solid-state transformer based on the large-signal model
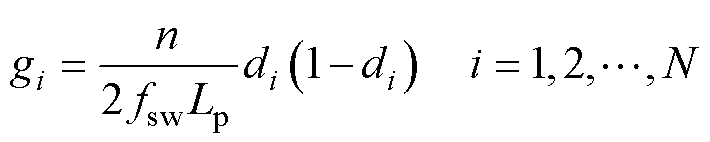（1）
式中，fsw为开关频率；di为第i个DAB单元的移相比。
图3展示了直流固态变压器最常用的双环控制方案[13]，图中，vin,avg为所有单元输入电压的平均值。输出电压环的PI控制器输出公共移相比指令
，每个DAB单元的输入均压环的PI控制器产生各自的移相比增量指令
，而各DAB单元的总移相比指令
由二者叠加得到。
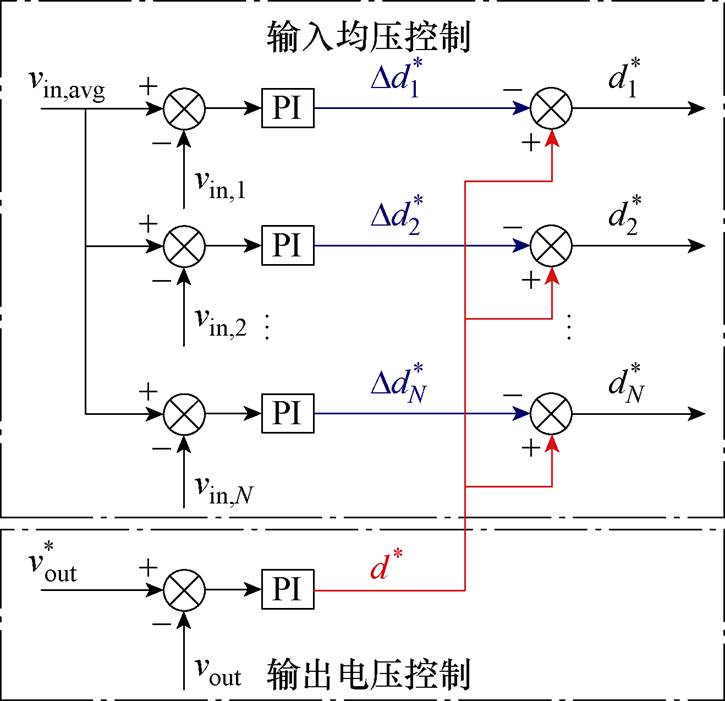
图3 直流固态变压器的传统双环控制策略
Fig.3 Traditional double closed-loop control strategy for the DC solid-state transformer
以输出侧接纯阻性负载为例，经推导可得输出电压环和输入均压环的控制对象的小信号模型分别为
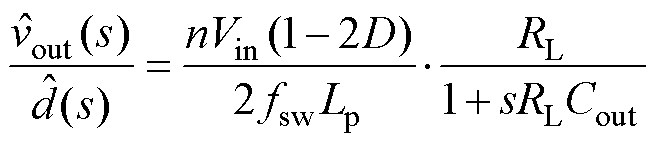（2）
（3）
式中，D为稳态移相比；RL为负载电阻；Vin和Vout分别为输入电压和输出电压的稳态值。详细推导过程见附录。
式（2）和式（3）中的RL随负载变化，而D不仅随负载变化，还随Vin变化。因此，不论是输出电压环还是输入均压环，其控制对象模型均与稳态工作点直接相关，表现出较强的非线性。为了保证所有工况下的稳定性，控制器参数的选取不得不十分保守，不利于动态性能的提高。这将在后续的仿真和实验中得到验证。
从式（2）和式（3）可以看出，在传统控制策略下，直流固态变压器的输出电压环和输入均压环控制对象的传递函数都依赖于稳态工作点，控制器参数的设计难以保证全工况范围内的动态性能。为了解决这一问题，本节将从图2所示的大信号模型出发，基于DAB变换器的一阶模型特性，推导直流固态变压器的线性化控制策略。
根据图2所示的大信号模型等效电路可得各子单元输入电压的状态方程为
（4）
将式（4）中的所有等式相加可得
（5）
进一步地，用式（5）减去式（4）可得
（6）
通过观察式（6）可以发现，等号左边为第i个单元的输入电压与平均电压的差，是均压环PI控制器的输入信号；等号右边是第i个单元的一次电流与所有单元一次电流的平均值，可以看做第i个单元的一次电流增量Dip,i。为了实现输入均压控制的线性化，将输入均压环PI控制器的输出信号设置为第i个单元的一次电流增量的指令值
，即令
（7）
式中，kp、ki分别为比例、积分常数。
另外，根据图2所示的大信号模型等效电路还可以得到输出电压的状态方程为
（8）
式中，is为所有DAB单元的二次电流之和。
与输入均压控制的线性化思路类似，可将输出电压环PI控制器的输出信号设置为
（9）
式中，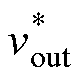
为输出电压指令值；
为二次电流指令值。
为了实现与输入均压环产生的一次电流增量指令叠加，式（9）得到的需要进一步转换为一次电流指令
。该转换过程可以根据输入输出的功率守恒得到，即
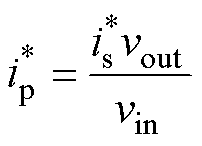（10）
根据式（7）、式（9）和式（10）可得本文所提出的新型线性化控制的完整控制框图，如图4所示。输出电压控制环PI控制器的输出叠加上输出电流iout，得到二次电流指令，并根据式（10）进一步得到公共一次电流指令。各子单元的均压环PI控制器输出一次电流增量的指令值，与输出电压控制环输出的公共指令叠加后得到各自的一次电流指令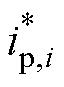
。进一步地，各子单元的移相比指令可根据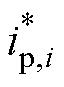和所采用的调制策略计算得到。式（11）以SPS调制为例展示了由一次电流指令计算移相比指令的公式。值得指出的是，图4所示控制框图也适用于其他的调制策略，如扩展移相调制[24]、双移相调制[25]、三移相调制[26]等，只需要更改式（11）所示的移相比计算式即可。
（11）
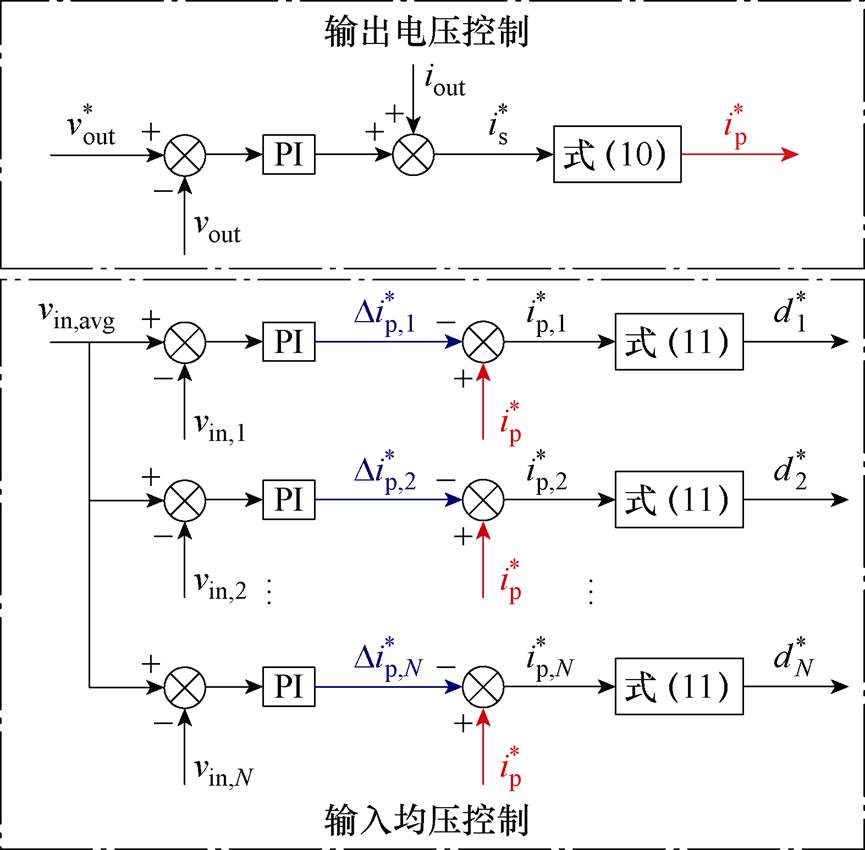
图4 直流固态变压器的新型线性化控制策略
Fig.4 The proposed novel linearization control strategy for the DC solid-state transformer
将图4与图3比较可得，为了实现输出电压环和输入电压环的线性化，本文对传统控制框图所做的改进包括：
（1）将输出电压环的PI控制器输出的控制指令由移相比改为电流指令，与输出电流iout叠加后生成二次电流指令。
（2）将输入均压环的PI控制器输出的控制指令由移相比增量改为一次电流增量。
（3）将两闭环的控制指令叠加方式由移相比叠加
，改为一次电流叠加
。
（4）各DAB的移相比不再由PI控制器直接输出，而是根据控制系统生成的输入电流指令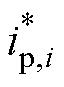和输入电压vin,i计算得到。
为了对图4所示的输出电压控制环和输入均压环的环路模型进行分析，首先推导由一次电流实际值与指令值之比定义的传递函数
。
由图2所示大信号模型等效电路和式（1）可得
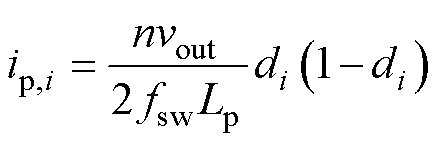（12）
图5展示了DAB变换器指令值与实际值之间的关系。图中，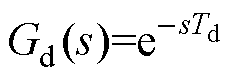
为由数字控制带来的延时，通常其对变换器低频段的频率特性的影响可以近似忽略，Td为控制延时。
图5 DAB变换器指令值与实际值之间的关系示意图
Fig.5 Illustration of the relationship between the command signals and the actual values of the DAB converter
文献[1]指出，稳态时DAB变换器的电感电流中不含低频成分，只含有开关频率整数倍的谐波分量，所以功率电感只影响高频段特性。由于决定电力电子变换器动态响应的是中低频段（这也是控制器设计所关心的频段），因而可以近似忽略功率电感的惯性对DAB变换器动态特性的影响。此时DAB变换器的动态响应只受输出滤波电容惯性的影响，可以用一阶模型来描述。本文称这一特性为DAB变换器的一阶模型特性。可以证明，一阶模型特性与所采用的调制策略无关，因此本文后续都以单移相为例进行讨论。
由于DAB变换器的一阶模型特性，图5中di到ip,i之间的惯性在低频段可以近似忽略。又因为式（11）是式（12）的反变换，所以当忽略数字控制延时的影响时，有
（13）
结合式（8）、式（9）和式（13），可以得到如图6所示的控制系统与原控制对象模型之间的关系示意图。显然，由于DAB变换器的一阶模型特性决定了
在中低频段内近似为1，原控制对象中的非线性可以被控制算法抵消。对PI控制器来讲，控制对象被简化为一个积分环节。
图6 控制系统与控制对象模型之间的关系示意图
Fig.6 Illustration of the relationship between the control system and the plant model
根据图6可得输出电压环的开环传递函数为
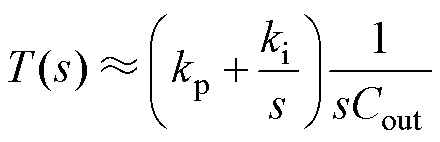（14）
可见，环路模型是线性的，与稳态工作点无关，从而简化了控制器参数的设计。
同理，结合式（6）、式（7）以及
=1可得输入均压环的开环传递函数如式（15）所示，同样实现了环路模型的线性化。
（15）
值得说明的是，严格来说，式（14）和式（15）所示结果只在控制延时为零时成立。当存在控制延时时，式（13）需要修改为
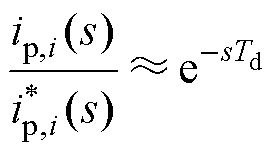（16）
结合图6可以看出，该控制延时会降低原控制对象中非线性的抵消效果，从而影响线性化控制的效果。所以，在实际系统中，控制延时的存在导致所提出的线性化控制策略无法完全消除原控制对象的非线性。也就是说，即使采用了所提出的线性化控制策略，控制系统的频率特性和动态性能也会因为负载、输入电压等工况的变化而有所变化。但是，与采用传统控制策略相比，这种变化已经大大减小了。后续将通过仿真和实验对这一点进行验证。
此外，从图4可以看出，线性化的过程利用了输出电流iout的信息。通过推导可得，输出电流扰动项iout(s)到vout(s)和vin,i(s)的传递函数理论上均等于零。可见，所提出的控制策略实现了对负载的补偿作用，这有利于增强直流固态变压器对负载扰动的抑制能力。
为了对本文提出的新型线性化控制策略的效果进行验证，在PLECS软件中进行了直流固态变压器的仿真，并搭建了一台由三个DAB单元构成的直流固态变压器实验样机。仿真和实验参数见表1。
表1 直流固态变压器的仿真和实验参数
Tab.1 Simulation and experimental parameters of the DC solid-state transformer
参 数数 值 额定功率PN/W250 输入电压Vin/V150 输出电压Vout/V50 子单元数N3 变压器电压比n1:1 功率电感Lp/mH260 开关频率fsw/kHz10 采样周期Tsam/ms100 输入滤波电容Cin/mF1 080 输出滤波电容Cout/mF60
图7展示了由主电路板和控制板组成的实验样机。其中主电路板由三块子模块板组成，上、下叠层放置，分别对应直流固态变压器的三个DAB单元。每个子模块板依次由DAB的输入滤波电容、MOSFET和驱动器组成的半桥模块、变压器和功率电感，以及输出滤波电容组成。同时，通过导线将不同DAB的输入侧串联、输出侧并联，以构建图1所示的直流固态变压器拓扑。
图7 直流固态变压器实验样机
Fig.7 Experimental prototype of the DC SST
控制板分为两块，一块为主板，型号为TMS320F28335的数字信号处理（Digital Signal Processing, DSP）和型号为EP4CE10E22的现场可编程门阵列（Field-Programmable Gate Array, FPGA）作为主控芯片，用于实现直流固态变压器的控制算法；另一块板上放置从机FPGA作为从机，用于收集每个DAB单元的电压和电流数据，并产生半桥模块的驱动信号。主控芯片与从机之间通过光纤进行通信。
下面对仿真和实验中所采用的各控制环的PI系数的选取进行简要说明。
开环频率特性可以直观地通过增益裕度和相位裕度反映稳定性，通过穿越频率反映快速性，在控制器参数的设计中取得了广泛应用。可通过绘制开环频率特性曲线（即伯德图）的方式来选取各控制环的PI系数。传统控制策略和新型控制策略下，输出电压环和输入均压环的开环传递函数分别如式（2）、式（3）、式（14）和式（15）所示。在设计各控制环的PI系数时，还需考虑数字控制延时，包括采样延时、计算延时、控制量更新延时和通信延时等。经估算和测量得到本实验中的总控制延时约为250 ms，即2.5个采样周期。因此，各控制环的开环传递函数需要在式（2）、式（3）、式（14）和式（15）基础上乘上
，其中Td=250 ms。
通过开环频率特性设计PI系数的原则是，在保证系统具有足够的相位裕度和增益裕度的前提下，尽可能提高穿越频率，从而实现在保证稳定性的前提下尽可能提高动态响应的快速性。为此，在伯德图上调整各控制环PI系数，在保证60°左右的相位裕度和10 dB左右的增益裕度的前提下，尽可能提高穿越频率。该过程可借助Matlab的sisotool工具箱完成。图8展示了新型控制策略下输出电压环校正后的开环频率特性曲线，可见通过调节PI系数为kp=0.12、ki=12，实现了58.5°的相位裕度和9.85 dB的增益裕度，以及319 Hz的穿越频率。
同理可得其他控制环的PI系数，见表2。值得说明的是，传统控制策略下开环传递函数和工况有关，本文按照半载工况进行PI设计，以便于验证频率特性和动态性能随负载的变化。
图8 校正后的输出电压控制环伯德图
Fig.8 Bode plot of the output voltage control loop after corrected
表2 仿真和实验中采用的PI系数
Tab.2 PI coefficients used in simulation and experiment
控制环比例系数积分系数穿越频率/Hz相位裕度/(°)增益裕度/dB 传统输出电压环0.005531657.610.1 输入均压环0.272730659.410.2 新型输出电压环0.121231958.59.85 输入均压环220029560.310.5
为了观察环路增益随工况的变化情况，在PLECS软件中进行了输出电压控制环和输入均压控制环的频率特性扫描。为了展示控制延时对所提出的控制策略的控制效果的影响，仿真中设置控制延时为250 ms，与实验中的控制延时的实测结果一致。图9展示了传统控制策略和新型控制策略下输出电压控制环的闭环增益的扫频结果。
从图9a可以看出，传统控制策略下，当负载较轻时，闭环增益的谐振峰较高，意味着此时稳定性较差，时域响应将表现出明显的振荡；而当负载较重时，谐振峰消失，意味着稳定性提高，但此时频带宽度较低，意味着快速性较低。因而，传统控制策略下的PI系数很难兼顾全工况的动态性能。
图9 输出电压环的闭环增益随负载的变化
Fig.9 Variation of the closed-loop gain of the output voltage loop with the load
相反地，当采用本文所提出的新型线性化控制策略时，如图9b所示，输出电压环的频率特性随负载变化不明显，从而有利于实现全工况范围内动态性能的综合优化。
图10展示了输入均压控制环的闭环增益的扫频结果。与输出电压控制环的扫频结果类似，输入均压环的闭环频率特性在传统控制策略下随负载显著变化，而当采用新型线性化控制策略时随负载变化不明显。
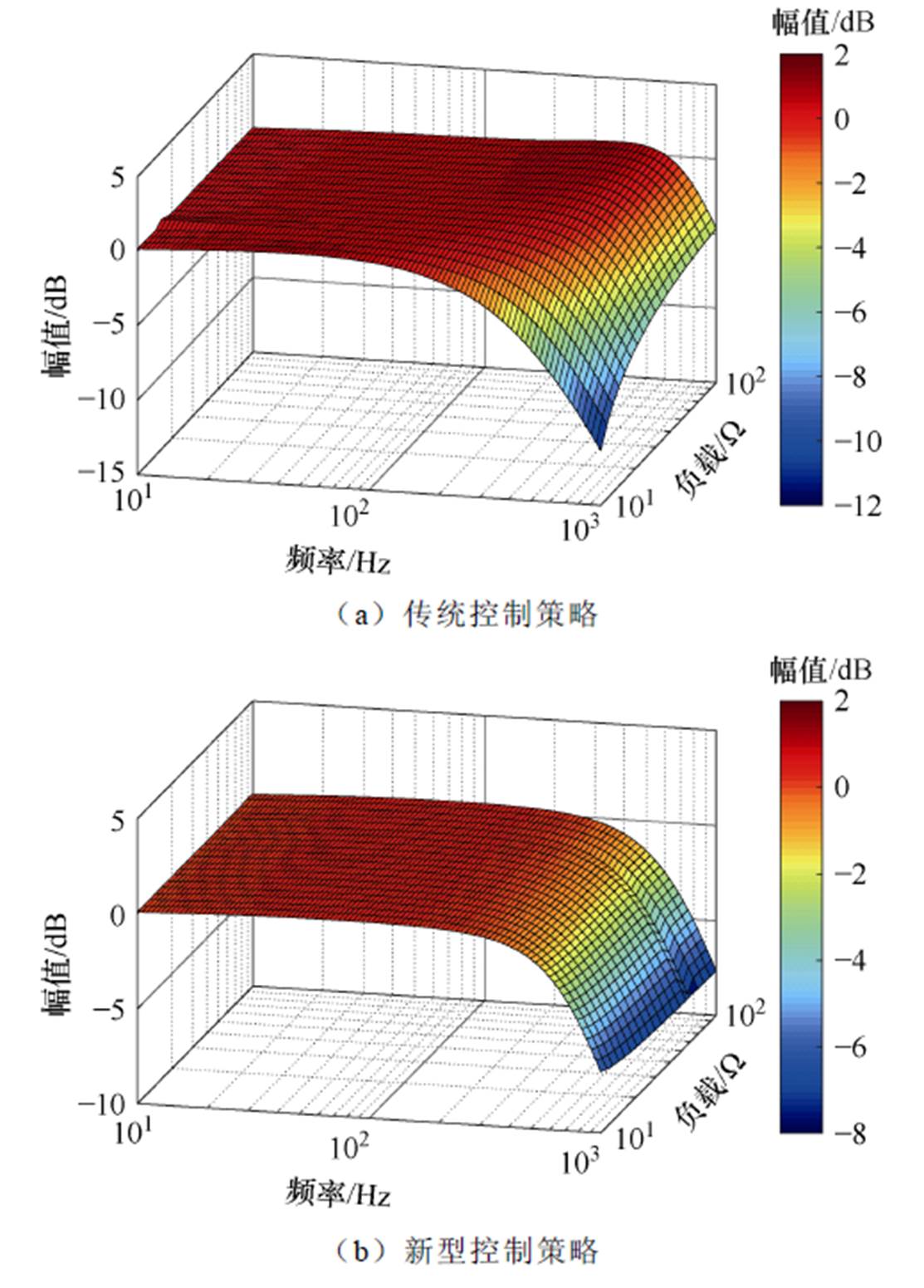
图10 输入均压环的闭环增益随负载的变化
Fig.10 Variation of the closed-loop gain of the input voltage sharing control loop with the load
理论上，根据式（14）和式（15），新型控制策略下输出电压环和输入均压环的闭环增益不随负载变化。但是由于控制延时的存在，它们随负载的改变仍呈现一定变化。但是，从图9和图10可以看出，与传统控制策略相比，这种变化已经大大降低了。可见，尽管有控制延时的存在，所提出的线性化控制策略仍然可以明显降低输出电压环和输入均压环的环路特性对工况的敏感程度，从而有利于简化控制器参数的设计和优化全工况下的动态性能。
此外，目前很多文献中提到了控制延时补偿策略[27]。这些补偿策略也可以引入到直流固态变压器的控制系统中，从而克服控制延时的影响，进一步提升所提出的线性化控制策略的效果。该内容不是本文的核心，不再展开。
图11为采用本文所提出的新型线性化控制策略时的满载输出电压和子单元1的电感电流波形。输出电压稳定在50 V，且每个DAB单元的输入输出电压匹配，电感电流接近方波，从而证明了所提出的输出电压控制算法的可行性。
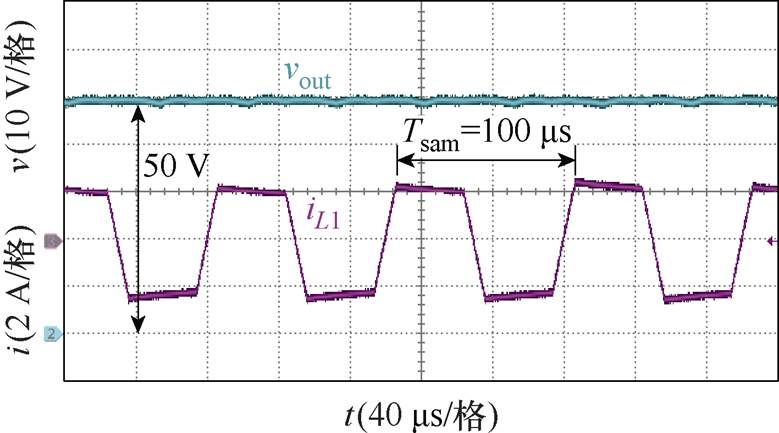
图11 输出电压与电感电流波形
Fig.11 Waveforms of the output voltage and the inductor current
图12为输入电压从135 V上升到150 V前后，各子单元的输入电压波形。可以看到，三个输入电压时刻保持均衡，证明了所提出的输入均压控制算法的可行性。
图12 不同子单元的输入电压波形
Fig.12 Input voltage waveforms of different subunits
图13为当采用传统控制策略时，不同负载条件下的输出电压阶跃响应波形，其中输出电压参考值由起始时刻的40 V突变至50 V。从图13可以看出，由于本实验中传统控制策略的PI系数是按照半载工况设计的，输出电压在此工况下跟随参考值的速度较快且超调较小；反之，满载工况下，输出电压的响应速度明显下降，而当负载降为10%时，超调量显著增加，意味着稳定性明显降低。
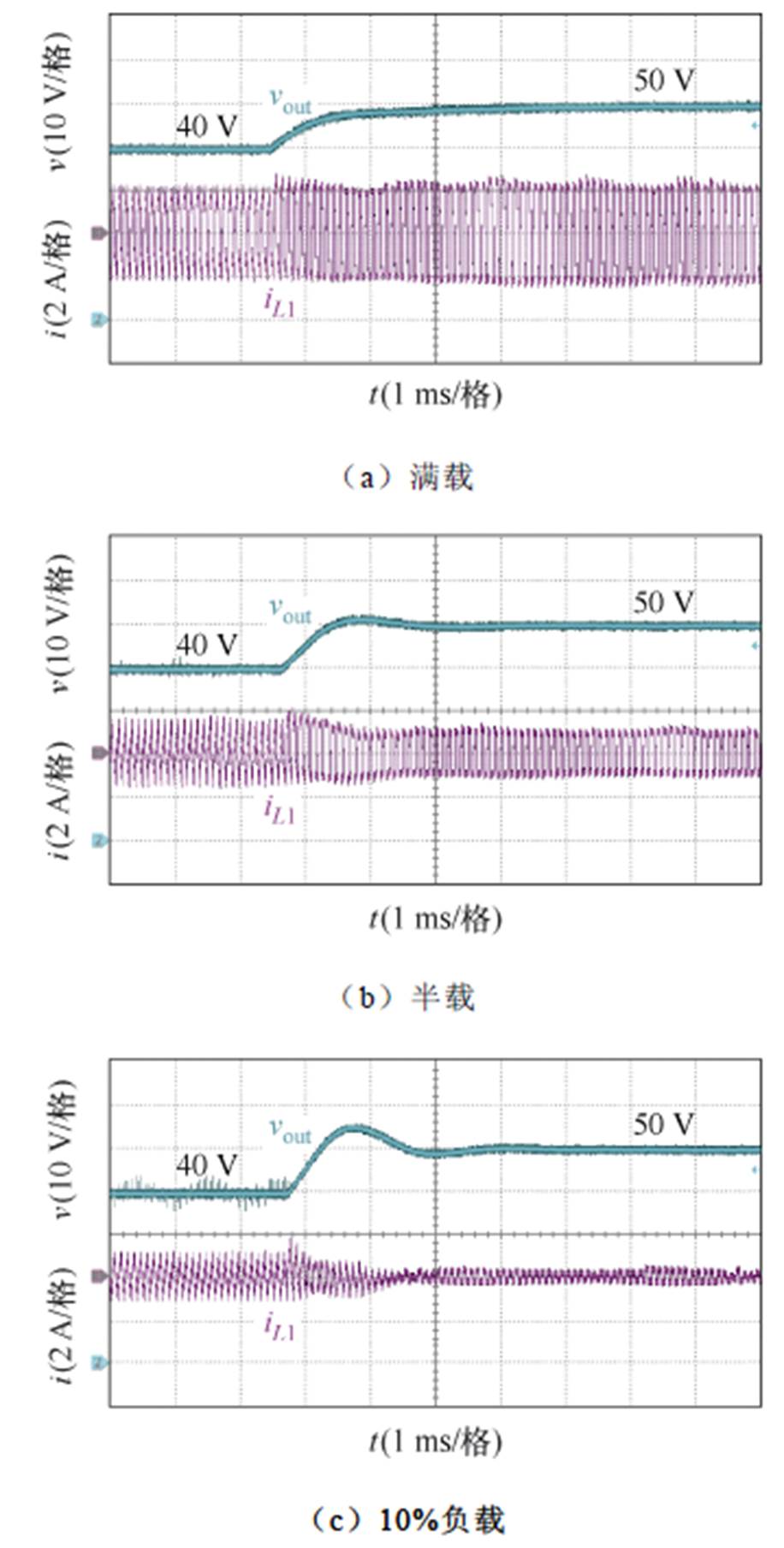
图13 传统控制策略下的输出电压阶跃波形
Fig.13 Step waveforms of the output voltage when the traditional control strategy is implemented
当改用本文所提出的新型线性化控制策略时，图14展示了各负载条件下的输出电压阶跃响应波形。可见各负载条件下的输出电压波形大致重合，稳定性和快速性均较高。
为了对两种控制策略下的动态性能进行定量比较，表3统计了不同负载条件下的输出电压阶跃响应指标。其中超调量定义为输出电压最大值与稳态值之差占阶跃值的百分比[28]，反映了系统的相对稳定性；上升时间定义为输出电压从阶跃值的10%上升到90%所需的时间，反映了系统的快速性；调节时间定义为输出电压与稳态值之间的误差保持在±2%以内所需的时间，同时反映了系统的快速性和相对稳定性。
图14 新型线性化控制策略下的输出电压阶跃波形
Fig.14 Step waveforms of the output voltage when the novel linearization control strategy is implemented
从表3可以看出，传统控制策略下，与半载工况相比，满载时的上升时间和调节时间均变长。而当负载降为10%时，尽管此时上升时间缩短，但超调过大，调节时间也明显上升。而当采用所提出的线性化控制策略时，不同负载条件的性能指标差距明显缩小，快速性和稳定性均较高。
表3 不同负载条件下的输出电压阶跃响应指标
Tab.3 Indexes of the output voltage step response under different load conditions
负载超调量(%)上升时间/ms调节时间/ms 传统满载2.12.506.15 半载14.80.603.24 10%负载50.60.395.61 新型满载10.40.794.18 半载10.50.674.30 10%负载11.00.514.10
图13、图14和表3所示的实验现象与3.2节中的频域仿真结果一致，也进一步说明了传统控制策略下的PI系数难以兼顾全工况下的稳定性和快速性，而所提出的线性化控制策略却明显地降低了系统动态性能对工况的敏感程度，从而有利于动态性能的综合优化。
为了验证所提出的控制策略在负载突变下的响应，通过空气开关投切负载电阻实现输出负载的切换。图15为负载由半载切换为满载时的输出电压瞬态波形。输出电压在负载突变后先下降，然后在控制系统的闭环调节下回升。值得说明的是，图15中的输出电压波形在下降过程中出现了短暂的回升，这是空气开关的抖动引起的。
图15 负载突变时的输出电压瞬态波形
Fig.15 Transient waveforms of the output voltage when the load changes suddenly
由图15可知，传统控制策略下的电压跌落约为13 V，恢复时间[29]约为5.4 ms。而当采用所提出的新型线性化控制策略时，电压跌落降为6 V，恢复时间缩短至2.1 ms。这说明所提出的线性化控制策略可以明显抑制负载的扰动。从第2.2节中的分析可以看出，这是因为所提出的控制策略在线性化的过程利用了输出电流iout的信息，如图4所示，因而能对负载电流的变化作出更及时的响应。这可以在一定程度上减少输出滤波电容的体积，有利于提升装置的功率密度。
本文针对以ISOP-DAB为核心的直流固态变压器的控制策略展开了研究。为了解决传统控制策略下各控制环的环路增益会随负载等条件变化，控制器参数设计难以兼顾全工况下的动态性能指标的问题，本文基于DAB变换器的一阶模型特性和直流固态变压器的大信号模型，提出了一种新型的线性化控制策略。
为了验证所提出的新型线性化控制策略的有效性，在PLECS软件中进行了直流固态变压器的仿真，并搭建了一台由3个DAB单元构成的直流固态变压器实验样机。频域仿真和实验波形表明，传统控制策略下直流固态变压器的闭环增益的谐振峰和频段宽度等频域指标，以及超调量、上升时间和调节时间等时域指标，均会随工况显著变化。而当采用本文所提出的线性化控制策略时，这些动态性能指标却随工况变化不明显，从而有利于实现全工况范围内动态性能的综合优化。
本文所提出的线性化控制策略仍然采用PI控制器实现，保留了比例-积分控制的简洁性和鲁棒性。同时，线性化的过程利用了输出电流的信息，实现了对负载的补偿。实验波形显示，所提出的控制策略可以显著降低负载突增时的输出电压跌落，并缩短恢复时间。这有利于增强直流固态变压器对负载扰动的抑制能力。
此外，本文所提出的线性化控制思路还可以拓展到其他包含DAB串并联结构的变换器中，如DAB的输入串联-输出串联和输入并联-输出并联结构，以及采用DAB变换器作为隔离级的CHB型和MMC型电力电子变压器。
附 录
推导传统控制策略下小信号模型。根据图2所示的大信号模型等效电路可得
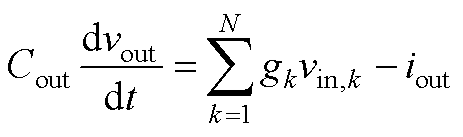（A1）
考虑输出侧接纯阻性负载的情况，将式（1）和di=d-Ddi代入式（A1）可得
（A2）
为求解输出电压环控制对象的传递函数，在稳态工作点附近对输出电压vout和公共移相比d做小信号扰动，并令其他变量的扰动为零，即
（A3）
将式（A3）代入式（A2），并忽略小信号的乘积项，即可得到输出电压环控制对象的传递函数，如式（2）所示。
根据图2还可以得到
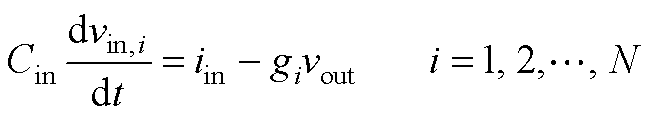（A4）
将式（A4）中的所有等式相加，并结合式（1）和di=d-Ddi可得
（A5）
根据图3所示控制框图，所有均压环的参考值之和与反馈值之和相等，且各均压环的PI系数一致，所以各均压环PI控制器输出的移相比增量之和为零，因而式（A5）可进一步化简为
（A6）
将式（A6）与式（A4）相减可得
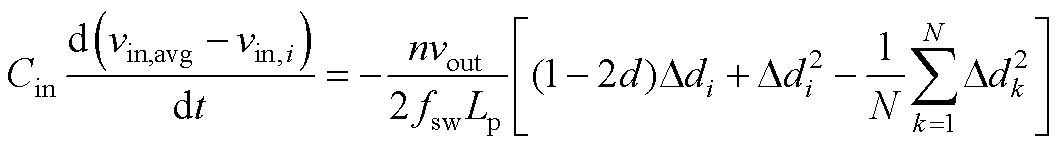（A7）
为了求解输入均压环的控制对象的传递函数，在稳态工作点附近对vin,i和
做小信号扰动，并令其他变量的扰动为零，即
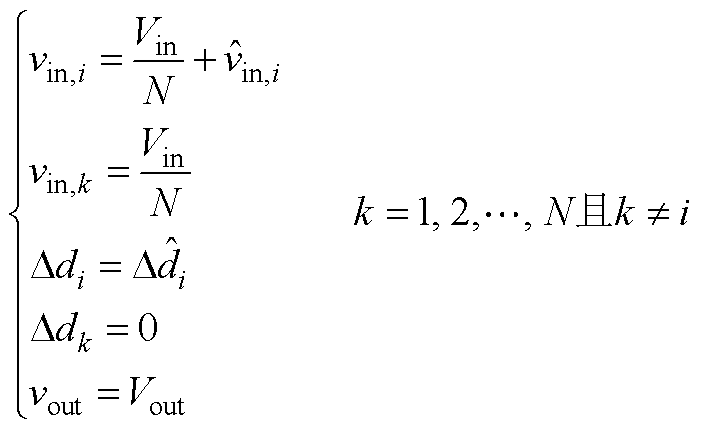（A8）
将式（A8）代入式（A7），并忽略小信号的乘积项，即可得到输入均压环控制对象的传递函数，如式（3）所示。
参考文献
[1] Shao Shuai, Chen Linglin, Shan Zhenyu, et al. Modeling and advanced control of dual-active-bridge DC-DC converters: a review[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1524-1547.
[2] Segaran D, Holmes D G, McGrath B P. Enhanced load step response for a bidirectional DC-DC con- verter[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 371-379.
[3] 侯聂, 宋文胜, 武明义. 全桥隔离DC/DC变换器的直接功率控制方法[J]. 电力系统自动化, 2016, 40(17): 204-209.
Hou Nie, Song Wensheng, Wu Mingyi. Direct power control scheme of full-bridge isolated DC/DC con- verters[J]. Automation of Electric Power Systems, 2016, 40(17): 204-209.
[4] 刘子薇, 孙兆龙, 刘宝龙, 等. 基于直接功率控制的双有源桥暂态直流偏置抑制策略[J]. 电工技术学报, 2023, 38(12): 3234-3247.
Liu Ziwei, Sun Zhaolong, Liu Baolong, et al. Transient DC bias suppression strategy of dual active bridge based on direct power control[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3234-3247.
[5] Song Wensheng, Hou Nie, Wu Mingyi. Virtual direct power control scheme of dual active bridge DC-DC converters for fast dynamic response[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(2): 1750-1759.
[6] Shan Zhenyu, Jatskevich J, Iu H H C, et al. Simplified load-feedforward control design for dual-active- bridge converters with current-mode modulation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 2073-2085.
[7] Dutta S, Hazra S, Bhattacharya S. A digital predictive current-mode controller for a single-phase high- frequency transformer-isolated dual-active bridge DC-to-DC converter[J]. IEEE Transactions on Indu- strial Electronics, 2016, 63(9): 5943-5952.
[8] Ali M, Yaqoob M, Cao Lingling, et al. Disturbance- observer-based DC-bus voltage control for ripple mitigation and improved dynamic response in two- stage single-phase inverter system[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(9): 6836- 6845.
[9] Wu Yuheng, Mahmud M H, Zhao Yue, et al. Uncertainty and disturbance estimator-based robust tracking control for dual-active- bridge converters[J]. IEEE Transactions on Transportation Electrification, 2020, 6(4): 1791-1800.
[10] Li Kerui, Yang Yun, Tan S C, et al. Sliding- mode-based direct power control of dual-active- bridge DC-DC converters[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 188-192.
[11] 安峰, 宋文胜, 杨柯欣. 电力电子变压器的双有源全桥DC-DC变换器模型预测控制及其功率均衡方法[J]. 中国电机工程学报, 2018, 38(13): 3921-3929, 4034.
An Feng, Song Wensheng, Yang Kexin. Model predictive control and power balance scheme of dual-active-bridge DC-DC converters in power electronic transformer[J]. Proceedings of the CSEE, 2018, 38(13): 3921-3929, 4034.
[12] 汤旭东, 王学梅. 双有源桥变换器动态响应影响因素及改善对策[J]. 电气自动化, 2021, 43(4): 1-6.
Tang Xudong, Wang Xuemei. Influencing factors and improving countermeasures of dynamic response of dual active bridge converter[J]. Electrical Automation, 2021, 43(4): 1-6.
[13] Zumel P, Ortega L, Lazaro A, et al. Control strategy for modular dual active bridge input series output parallel[C]//2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), Salt Lake City, UT, USA, 2013: 1-7.
[14] 孙志峰, 肖岚, 王勤. 输出并联型双有源全桥变换器控制技术研究综述[J]. 中国电机工程学报, 2021, 41(5): 1811-1831.
Sun Zhifeng, Xiao Lan, Wang Qin. Review research on control technology of output parallel dual-active- bridge-converters[J]. Proceedings of the CSEE, 2021, 41(5): 1811-1831.
[15] Zhao Tiefu, Wang Gangyao, Bhattacharya S, et al. Voltage and power balance control for a cascaded H-bridge converter-based solid-state transformer[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1523-1532.
[16] 武明义, 侯聂, 宋文胜, 等. 独立输入并联输出全桥隔离DC-DC变换器直接功率平衡控制[J]. 中国电机工程学报, 2018, 38(5): 1329-1337.
Wu Mingyi, Hou Nie, Song Wensheng, et al. Direct power balance control scheme of the Input- independent-output-parallel operated full-bridge isolated DC-DC converters[J]. Proceedings of the CSEE, 2018, 38(5): 1329-1337.
[17] 安峰, 宋文胜, 杨柯欣, 等. 输出并联双有源全桥DC-DC变换器虚拟功率均衡控制方法[J]. 电力系统自动化, 2018, 42(12): 106-112.
An Feng, Song Wensheng, Yang Kexin, et al. Virtual power balance control scheme of dual active bridge DC-DC converters with output-parallel structure[J]. Automation of Electric Power Systems, 2018, 42(12): 106-112.
[18] 曾进辉, 孙志峰, 雷敏, 等. 独立输入并联输出双有源全桥DC-DC变换器无电流传感器均流控制[J]. 中国电机工程学报, 2019, 39(7): 2144-2155.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Sensorless current sharing control strategy of independent-input- parallel-output dual-active-bridge converters[J]. Pro- ceedings of the CSEE, 2019, 39(7): 2144-2155.
[19] 李国文, 杭丽君, 钱语安, 等. 考虑损耗的DAB变换器简化模型及线性化控制方法[J]. 高电压技术, 2019, 45(7): 2074-2081.
Li Guowen, Hang Lijun, Qian Yu’an, et al. Simplified equivalent circuit model of DAB converter and the linearized control method with considering losses[J]. High Voltage Engineering, 2019, 45(7): 2074-2081.
[20] Segaran D, McGrath B P, Holmes D G. Adaptive dynamic control of a bi-directional DC-DC con- verter[C]//2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 2010: 1442- 1449.
[21] Rodríguez Alonso A R, Sebastian J, Lamar D G, et al. An overall study of a dual active bridge for bidirectional DC/DC conversion[C]//2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 2010: 1129-1135.
[22] Qin Hengsi, Kimball J W. Generalized average modeling of dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 2078-2084.
[23] Zhao Chuanhong, Round S D, Kolar J W. Full-order averaging modelling of zero-voltage-switching phase- shift bidirectional DC-DC converters[J]. IET Power Electronics, 2010, 3(3): 400-410.
[24] 涂春鸣, 管亮, 肖凡, 等. 基于扩展移相控制下双有源桥移相角优化选取与分析[J]. 电工技术学报, 2020, 35(4): 850-861.
Tu Chunming, Guan Liang, Xiao Fan, et al. Parameter optimization selection and analysis of dual active bridge based on extended phase shift control[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 850-861.
[25] 王仁龙, 杨庆新, 操孙鹏, 等. 一种优化电流应力的双有源桥式DC-DC变换器双重移相调制策略[J]. 电工技术学报, 2021, 36(增刊1): 274-282.
Wang Renlong, Yang Qingxin, Cao Sunpeng, et al. An optimized dual phase shift modulation strategy for dual active bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 274- 282.
[26] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[27] Lu Minghui, Wang Xiongfei, Loh P C, et al. Graphical evaluation of time-delay compensation techniques for digitally controlled converters[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2601-2614.
[28] 沈传文. 自动控制理论[M]. 西安: 西安交通大学出版社, 2007.
[29] 陈伯时. 电力拖动自动控制系统——运动控制系统[M]. 3版. 北京: 机械工业出版社, 2018.
Abstract The control system of the DC solid-state transformer with the input-series-output-parallel dual active bridge converters typically consists of output voltage control and input voltage sharing control. In the conventional control strategy, the loop gain characteristics of each control loop change considerably with the load and other working conditions, and the dynamic performance is ignored in the controller parameter design. This paper proposes a novel linearization control strategy to achieve the linearization of the loop models of both the output voltage control and input voltage sharing control, thereby simplifying the design of controller parameters and enhancing the adaptability of the converter.
Firstly, the control command output by the PI controller of the output voltage control loop is changed from the phase shift command to a current command. A secondary-side current command is generated after the control command is superimposed with the output current. Then, the control command output by the PI controller of the input voltage sharing control loop is changed from the phase shift increment to the primary-side current increment. The method for superimposing the control commands of the two loops is changed from the phase-shift superposition to the primary-side current superposition. Finally, the phase shift ratio of each DAB is calculated based on the input current command generated by the control system, which is no longer directly output by the PI controller.
In simulations, frequency sweep analyses are conducted on the output voltage control loop and input voltage sharing control loop. With the conventional control strategy, the closed-loop gain exhibits a high resonance peak with light loads. This peak disappears with heavier loads, but the bandwidth is low. In contrast, the frequency characteristics of the control loops change little with the load using the proposed linearization control strategy.
An experimental prototype of a DC solid-state transformer composed of three DAB units is built. Experimental results show that under full-load conditions, the output voltage’s response speed is slow using the conventional control strategy. When the load is reduced to 10%, the overshoot significantly increases, indicating a noticeable decrease in stability. In contrast, with the proposed linearization control strategy, the output voltage’s step response waveforms under various load conditions roughly overlap, demonstrating high stability and fast response. Moreover, when switching from half-load to full-load, the voltage drop and recovery time are significantly lower than those using the conventional control strategy.
The conclusions are as follows. (1) Using the conventional control strategy, the closed-loop gain's resonance frequency-domain indicators (peak, frequency bandwidth) and time-domain indicators (overshoot, rise time, and adjustment time) vary significantly with operating conditions. These dynamic performance indicators show slight variation using the proposed control strategy, facilitating the comprehensive optimization of dynamic performance. (2) The proposed control strategy enhances the suppression capability of the DC solid-state transformer against load disturbances using output current information for load compensation during the linearization process.
keywords：DC solid-state transformer, dual active bridge, linearization control, output voltage control, input voltage sharing control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231492
国家重点研发计划资助项目（2023YFB2407400）。
收稿日期 2023-09-09
改稿日期 2024-03-20
李志祥 男，1996年生，博士研究生，研究方向为电力电子变压器的拓扑、控制与设计技术。E-mail: lizhixiang951206@stu.xjtu.edu.cn
王来利 男，1982年生，教授，博士生导师，研究方向为宽禁带功率半导体器件封装集成及应用技术。E-mail: llwang@mail.xjtu.edu.cn（通信作者）
（编辑 崔文静）