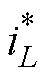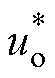、
，再经数字控制器计算产生离散调制波信号
，零阶保持器后的调制信号um经PWM生成开关器件驱动信号。Cdc为直流输入电容，ZL为负载。后续的分析基于如表1所示的逆变器设计参数展开。摘要 360～800 Hz宽变频交流电源系统是多电飞机电力系统的主要发展方向之一。为实现宽变频中频逆变电源在包括带整流型非线性负载等工况下的宽范围谐波抑制，保证其任意基准频率下的输出电压质量，提出一种基于频率基准自适应谐波准谐振控制器的控制策略。基于滤波电感电流反馈，设计了包含数字控制延迟补偿的有源阻尼方案，以抑制输出滤波器的谐振尖峰，对电压控制器的被控对象进行校正使系统得到简化；设计并采用积分与准比例谐振相结合的基波追踪控制器以消除基波频段的稳态误差；提出基准频率自适应的补偿角度设计方法以实现谐波准谐振控制在电压环控制带宽之外的谐波抑制。在理论分析的基础上，搭建了一台300～800 Hz/600 W单相逆变器样机并进行实验测试，结果表明，采用该控制策略的逆变器能够实现宽基波频段内任意基准频率下的宽范围谐波抑制，且具有良好的稳态和动态输出特性。
关键词：变频逆变电源 谐波抑制 准谐振控制 相位补偿 自适应控制
360～800 Hz宽变频航空交流电源系统具有结构简单、可靠性高、功率密度高、发电效率高等优点，是多电飞机电力系统的主要发展方向之一[1]。此外，在对多电飞机进行地面维护时，需要向机载设备提供类似飞机发电机输出的变频交流电，以满足设备的供电、测试和检修等保障需求。因此，研究高效率、高功率密度的高质量地面变频逆变电源具有重要的实际意义。
航空变频交流电源需要在宽的基波频率范围及复杂负载情况下输出满足规定要求的电压。随着多电飞机技术的发展，机载电力电子设备不断增多，出现了许多复杂的用电负载，包括整流型非线性负载，对逆变电源电压质量造成挑战[2-5]。据GJB 181B标准，变频交流供电系统的电压总谐波畸变率（Total Harmonic Distortion, THD）应小于5%，6 000 Hz及以下的各次谐波含量应不高于3.16 V[6]。
与工频逆变电源不同，中频电源的谐波频率较高，且往往位于控制带宽之外，甚至接近输出滤波器的谐振频率。由于被控对象在谐波频段的相位裕度小，电压控制器难以对谐波进行有效抑制[7-8]。因此，提升宽变频逆变电源电压质量的关键在于实现变基波频率基准条件下对电压控制器带宽之外的谐波抑制，即在保证稳定性的前提下提升系统在电压控制器带宽外的开环增益。
基于内模原理的重复控制器（Repetitive Con- troller, RC）能够实现基波及谐波处很高的系统开环增益，非常适合逆变器的输出电压谐波抑制，是应对周期性扰动的整流型非线性负载的有力工具[9-10]。RC的离散脉冲传递函数形式简洁，适合数字控制实现，但RC存在周期延迟环节，系统的动态特性较差，难以满足电源在变基准频率下的输出电压控制要求，尤其是频率突变工况下的动态特性要求。尽管已有众多文献研究了复合RC控制方案，以改善RC系统的动态特性[11-13]，但由于复合控制中快速响应环的控制带宽较为有限，难以在中频逆变场合获得满意的动态特性[14]。
基于单一频率交流信号内模的准比例谐振（Quasi Proportion Resonant, QPR）控制器能够实现基波频率处较高的系统开环增益，将多个准谐振环节并联形成谐波准谐振（Harmonics Quasi Resonant, HQR）控制器，能够实现多个谐波频率处的高增益，是另一种常用的谐波抑制手段[15-17]。但在中频逆变场合，由于基波频率较高，被控对象谐波频率处的相位裕度往往有限甚至为负，HQR控制器在其谐振频率处的相位跃变容易造成控制环路失稳。文献[18]提出采用带相位补偿（Phase Compensation, PC）的HQR控制器（Harmonics Quasi Resonant with Phase Compensation, HQR-PC）补偿被控对象的相位滞后。HQR-PC控制器有很高的自由度，可根据需要配置其在谐振频率处的系统开环增益和相位。但在变频场合，谐波频率随基准频率变化，实现任意基准频率下的宽范围谐波抑制HQR控制尚未见研究。
本文以实现高质量变频交流电压为逆变电源控制器的设计目标，提出结合数字控制延迟补偿的有源阻尼、被控对象校正和频率基准自适应的HQR- PC控制策略。主要贡献在于提出将被控对象相位补偿至特定角度的HQR-PC基准频率自适应律，以在宽变频基准下获得足够的稳定裕度，并通过系统开环频率响应分析和实验验证所提控制策略在宽变频逆变场合的宽范围谐波抑制能力。
逆变电源电路结构如图1所示，包括功率逆变单元、输出滤波器和数字控制系统。图1中，直流输入电压Udc经逆变桥电路变换为输出电压uinv；电感L和电容C构成二阶输出滤波器滤除uinv中的高次谐波；数字控制系统包括离散采样、数字控制器（Digital Controller, DC）和脉冲宽度调制（Pulse Width Modulation, PWM）与驱动生成。采样环节对电感电流iL和输出电压uo采样生成离散采样信号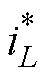、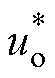，再经数字控制器计算产生离散调制波信号，零阶保持器后的调制信号um经PWM生成开关器件驱动信号。Cdc为直流输入电容，ZL为负载。后续的分析基于如表1所示的逆变器设计参数展开。
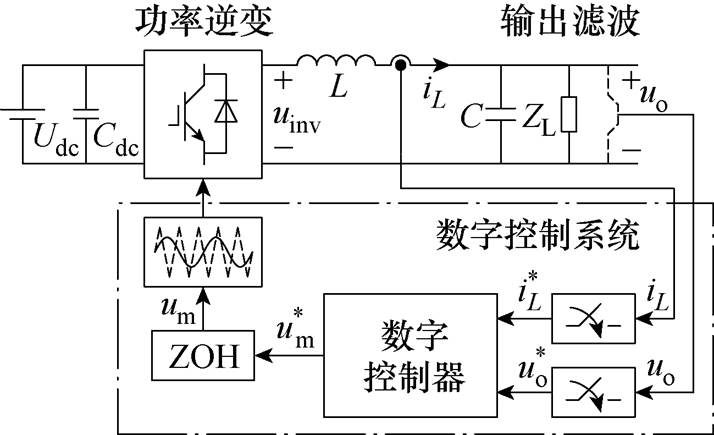
图1 逆变电源电路结构
Fig.1 Circuit configuration of inverter
表1 逆变器设计参数
Tab.1 Inverter hardware parameters
参 数数 值 输入电压Udc/V400 输出额定电压Uo/Vrms115 额定功率So/(V·A)600 输出频率fo/Hz300～800 滤波电感L/mH187 滤波电容C/mF27 谐振频率fr/kHz2.244 开关频率fsw/kHz19.2
LC输出滤波器会在其谐振频率fr处产生幅值较高的谐振尖峰和-180°相位跃变，极易造成系统失稳。通常需要采用有源阻尼（Active Damping, AD）校正被控对象，削弱LC谐振增益峰值，减缓相频变化，以克服LC谐振尖峰对系统稳定性的不利影响。采用滤波电感电流iL反馈可以构成AD，同时可兼顾逆变电源的过载和短路保护。
基于iL反馈AD的双闭环系统控制结构框图如图2所示。
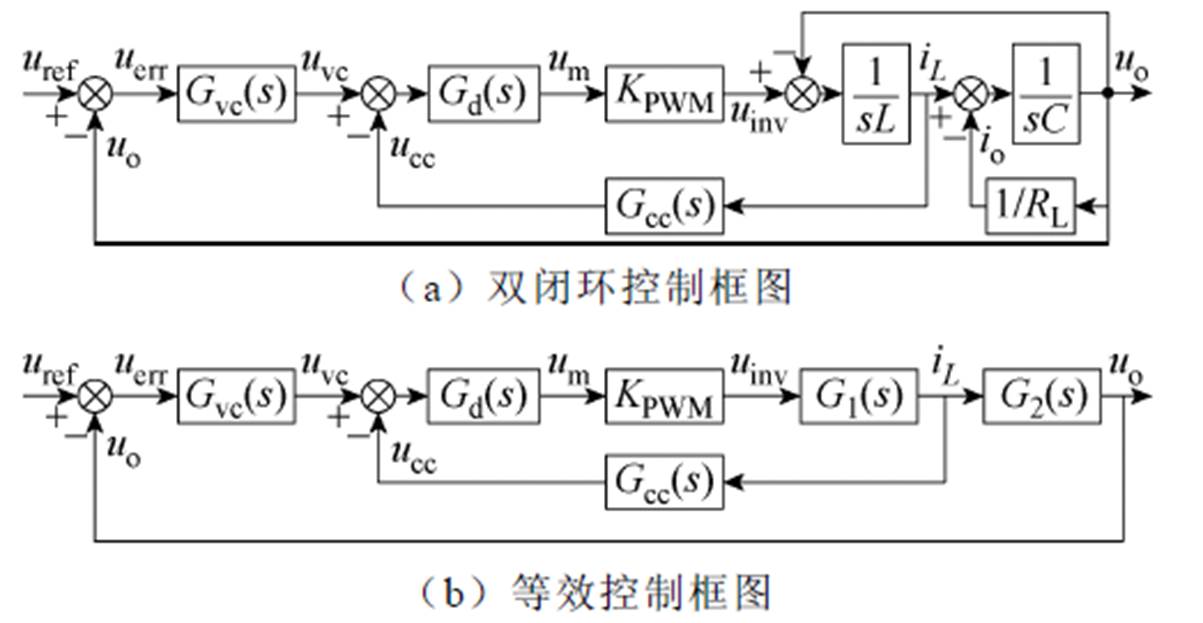
图2 逆变电源双闭环控制及其等效框图
Fig.2 Dual-loop control of inverter and its equivalent block diagram
在图2中，逆变桥输出uinv可视为对调制波um的比例放大KPWM；电压参考信号uref与反馈比较产生的电压误差信号uerr作为电压环控制器Gvc(s)的输入，电压环输出的控制量为uvc；Gcc(s)为有源阻尼环节，输出的控制量为ucc；控制信号经数字控制延迟Gd(s)后生成um。Gd(s)由离散采样环节ksam、数字控制器计算延迟Gcd(s)和PWM加载等效的零阶保持器GZOH(s)共同构成，即
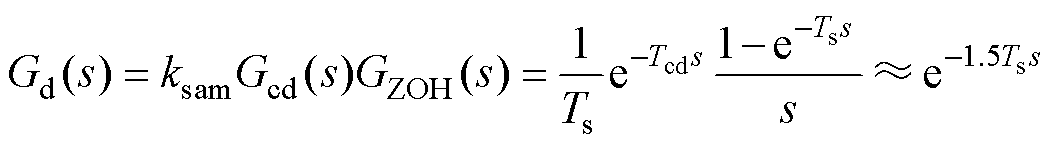（1）
式中，Ts为采样周期；Tcd为计算延迟。当采用不对称PWM装载规则时，采样时刻和调制波加载时刻位于三角载波的波峰和波谷处，Tcd即一个采样周期Ts。
观察图2a可以看出，若引出iL进行内环控制器设计，与uo反馈环路存在耦合。为简化分析，前向通道化简为uinv到iL和iL到uo两个环节的串联，分别记为传递函数G1(s)和G2(s)，即
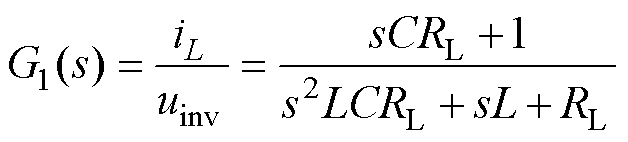（2）
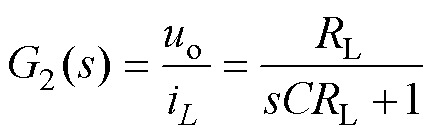（3）
式中，RL为负载电阻。
根据表1参数，输出滤波器谐振频率约为2 240 Hz，对于4 000 Hz以上的信号，滤波器有-20 dB以上的衰减能力，能够被很好地抑制。因此需要通过控制器设计抑制的谐波频率范围为900～4 000 Hz。
图3给出了系统应用AD后的开环频率响应曲线（蓝色实线），由图3可知，这一频率范围中大部分谐波频率位于电压环截止频率fvc以外，且相位变化宽（-124°～-272°）。因此，HQR控制器的被控对象谐波频率处增益小于零，且相位裕度较小，甚至为负裕度，控制器设计不当，极易造成开环频率响应在幅频曲线大于零时相频曲线穿越-(2k+1)× 180°，形成负穿越导致系统失稳。因此，为实现fvc以外的谐波抑制，采用如式（4）所示的HQR-PC控制器[19]。
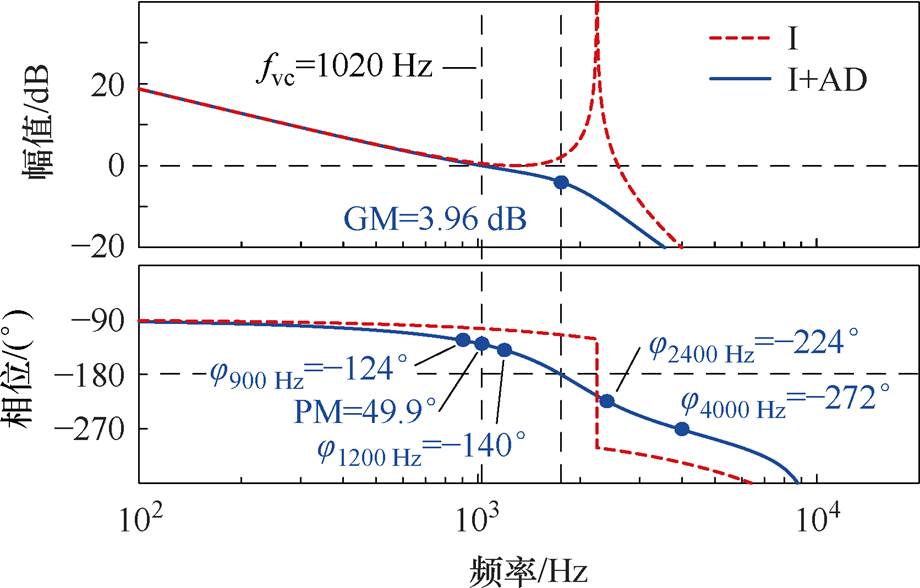
图3 有源阻尼实施前后Go(s)伯德图
Fig.3 Bode diagram of Go(s) before and after implementation of AD
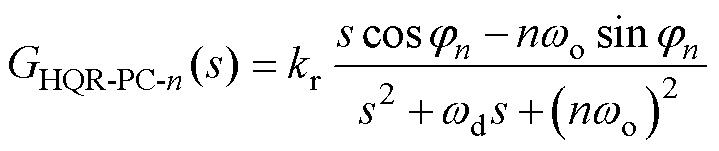（4）
式中，kr为谐振增益；wd为谐振截止角频率；n为谐波次数；jn为n次谐波频率谐振环节补偿角度。
图4以fo=400 Hz的3次谐波HQR设计为例，展示了不同jn对HQR环节频率响应的影响。为便于比较相位补偿的影响，图中控制器包含比例（Proportion, P）环节。由图4易知，当jn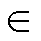
[0°, 90°]时，HQR-PC在n fo处具有相位超前补偿作用；当jn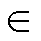
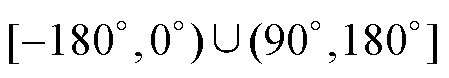时，在n fo处具有不同程度的相位滞后。当jn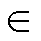
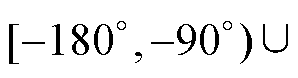
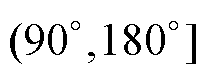时，在n fo处出现严重的相位滞后，相频曲线穿越-(2k+1)×180°而成为非最小相位环节。
图4 对应不同jn的GP-HQR-PC(s)伯德图
Fig.4 Bode diagram of GP-HQR-PC(s) with different jn
根据不同jn对HQR-PC控制器的补偿效果，对jn分类如下：①jn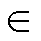[0°, 90°]时为HQR-PC具有最小相位特性的超前补偿区间；②jn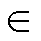[-90°, 0°
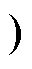时为HQR-PC具有最小相位特性的滞后区间；③jn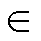
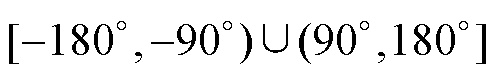时为HQR-PC具有非最小相位特性的滞后区间。
以400 Hz和800 Hz输出时的3次谐波抑制为例讨论宽变频基准下HQR控制的稳定性问题。
图5展示了基准频率400 Hz时Gvc(s)为带积分（Integration, I）的基波和3次谐波谐振控制器（I+ QPR+HQR-PC-3，HQR-PC-n代表n次谐波HQR-PC控制器）的系统开环Go(s)频率响应。
由图3的蓝色曲线可以看出，3次谐波频率1 200 Hz已超出fvc，应用HQR-PC-3后幅频曲线二次穿越0 dB，在幅频曲线大于0 dB时需避免相频曲线穿越-(2k+1)×180°以保证系统稳定，如图5a所示。若不对HQR进行相位补偿，相频曲线穿越-180°使得系统产生一次负穿越和一次正穿越，系统虽然稳定，但若在数字控制器实现过程中由于截断和舍入误差导致控制器增益降低，相频曲线正穿越可能消失，系统有失稳风险。图5b中采用j3=44°的相位补偿，使得相频曲线避免对-180°的穿越而增强稳定性。进一步地，若继续增加j3使得HQR控制器具有非最小相位特性，在足够的相位滞后下，幅频曲线小于0 dB时相频曲线越过-(2k+1)×180°而不造成负穿越，如图5c所示，此时j3=147°。若要避免负穿越，须保持图5c上的相位裕度PM＜0。若j3进一步增大，PM继续减小，有负穿越风险。可见，对于400 Hz的HQR-PC-3设计，示例中合适的j3取值范围为[44°, 147°]。
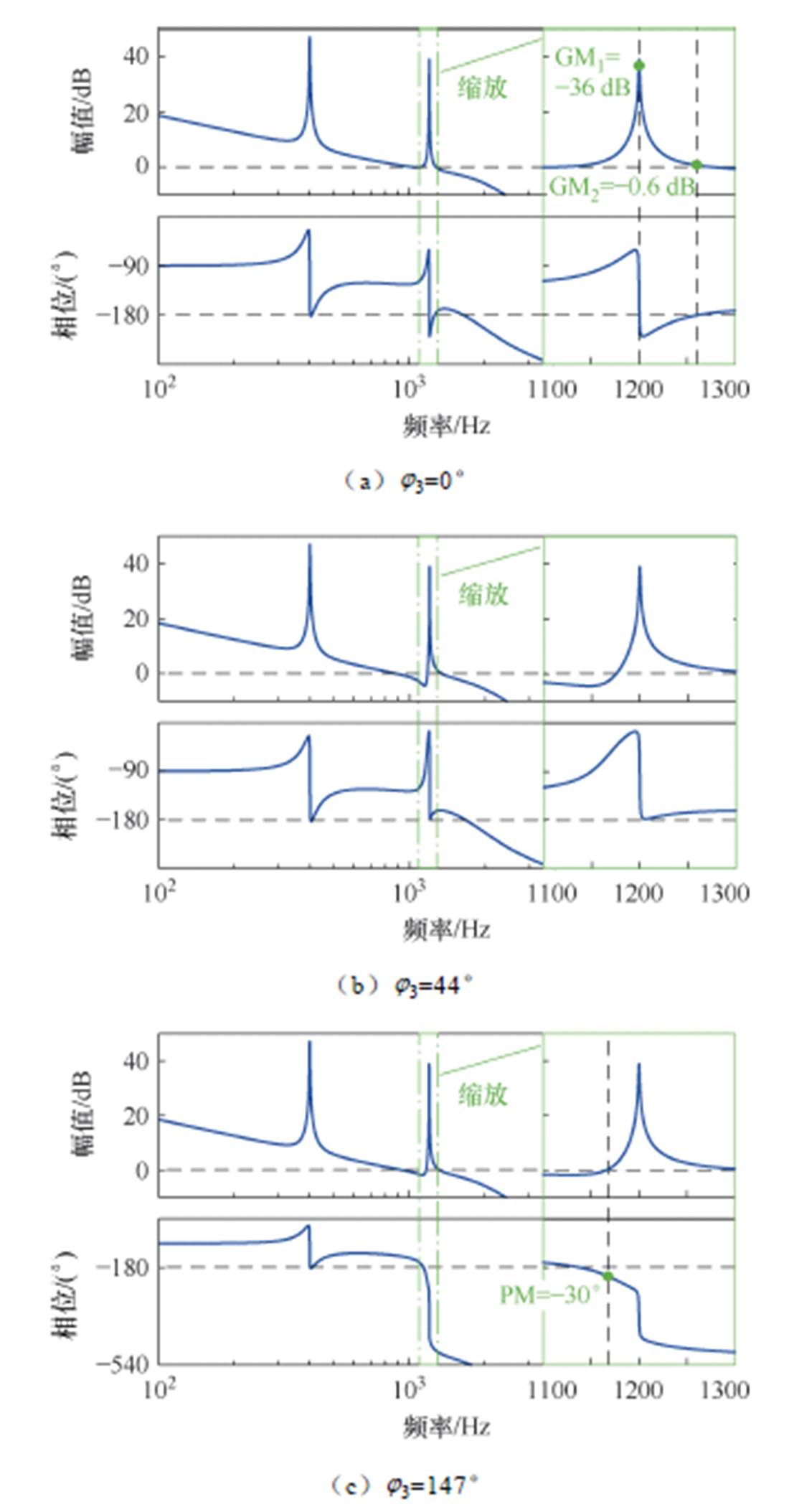
图5 不同j3下应用HQR-PC-3 Go(s)伯德图（fo=400 Hz）
Fig.5 Bodediagram of Go(s) after implementation of HQR-PC-3 with different j3 (fo=400 Hz)
图6为800 Hz基准时系统采用I+QPR+HQR- PC-3控制的开环频率响应曲线。
图6 不同j3下应用HQR-PC-3 Go(s)伯德图（fo=800 Hz）
Fig.6 Bode diagram of Go(s) after implementation of HQR-PC-3 with different j3 (fo=800 Hz)
在图6中，系统在3次谐波（2 400 Hz）处相位裕度为负（PM2400 Hz=j2400 Hz-(-180°)=-44°）。若不对HQR控制器附加相位补偿，如图6a所示，相频曲线在幅频曲线大于0 dB时单次越过-180°，系统失稳。若j3设计在常用的超前补偿区间[0°, 90°]，由于HQR控制器在谐振频率附近相位跃变超过90°，加之被控对象本身相位裕度为负，即使j3设计为90°，仍将出现负穿越。将j3设计在具有最小相位特性的滞后区间[-90°, 0°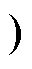，并施加足够相位滞后，可以避免负穿越。如图6b所示，j3设计为-40°时，相频特性在谐振频率附近完全低于-180°，系统稳定。进一步加大相位滞后，使得HQR-PC具有非最小相位特性，如图6c所示，j3设计在-178°，相频曲线的相位跃变而继续滞后越过-540°，此时须保持PM1＜0且PM2＞0才可以避免负穿越。若再加大相位滞后，则PM2裕度过小，系统可能失稳。因此，对于800 Hz的HQR-PC-3设计，示例中合适的j3取值范围是[-178°,-40°]。
将400 Hz和800 Hz的3次谐波HQR-PC的j3设计值进行对比，可发现两者取值范围交集为空。
上述分析表明，由于被控对象的谐波频率区间大部分位于开环截止频率之外，相位裕度较小或为负裕度，普通的相位超前补偿难以保证系统稳定；另一方面，被控对象在谐波频率区间相位特性变化较大，常用的恒定补偿角度jn整定方法在宽变频场合下不能满足HQR-PC控制器稳定应用的需求。因此，宽变频输出逆变器中采用HQR-PC控制器时，必须要进一步研究控制器的设计以保证系统稳定。
在采用基于iL反馈AD的双闭环控制结构基础上，针对HQR-PC的被控对象频率响应特性进行分析，进而提出基准频率自适应的HQR-PC策略，实现中频逆变电源在宽变频基准场合下电压环控制带宽外的低次谐波抑制。考虑到系统空载时稳定性最差，下述分析均围绕空载下系统特性展开。
数字控制延迟Gd(s)的存在会造成内环相位裕度下降，限制AD增益的取值范围，进而影响AD对LC谐振尖峰的抑制效果。通过设置数字控制延迟补偿环节Gad(s)可以补偿滞后相位[19]。因此，将AD控制器设计为Gcc(s)=Gad(s)kad，其中kad为AD的阻尼增益。采取如式（5）所示的二阶补偿器对Gd(s)在fr处产生的相位滞后实施补偿。
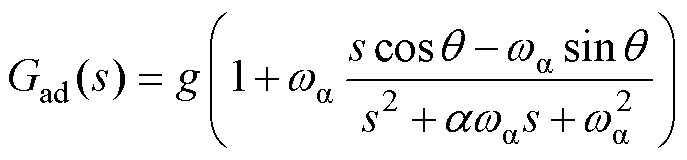（5）
式中，wa 为补偿环节谐振角频率；a 为补偿环节阻尼系数；q 为补偿角度；g为增益修正系数。
在wa之前的频段，Gad(s)能够对被控对象实施相位超前补偿。为避免补偿环节谐振幅值峰的影响，将wa 设计在系统的奈奎斯特（Nyquist）角频率处，即wa =2p fs/2。a 的合理设计能够平衡高频处Gad(s)的谐振峰值增益和补偿角度之间的关系，可折中选取a =1.414。进一步，以wr处Gd(s)产生的相位滞后尽可能地被补偿为目标，选取q，即ÐGad(jwr)=-ÐGd(jwr)，可由式（1）和式（5）联立，利用数值求解得到q = 45°。最后，令Gad(s)在wr处的幅值增益为1，且以高频段增益尽可能低为设计目标，选取g，在实现相位补偿的同时减少Gad(s)对内环增益的影响。令|Gad(jwr)|=1可以计算得到g=2.7，为削弱高频增益而折中选取g=1.8，Nyquist频率处Gad(s)增益在10 dB以下。
为比较延迟补偿效果，图7展示了Gd(s)、1/Gad(s)以及Gd(s)Gad(s)的频率响应曲线。1/Gad(s)呈现出Gad(s)的反相位特性，以便于与Gd(s)对比补偿偏差。可以看出，在中低频段Gad(s)较好地补偿Gd(s)产生的相位滞后，Gd(s)在fr处的相位滞后得到了较好的补偿，且Gd(s)Gad(s)在高频处的增益小于10 dB。
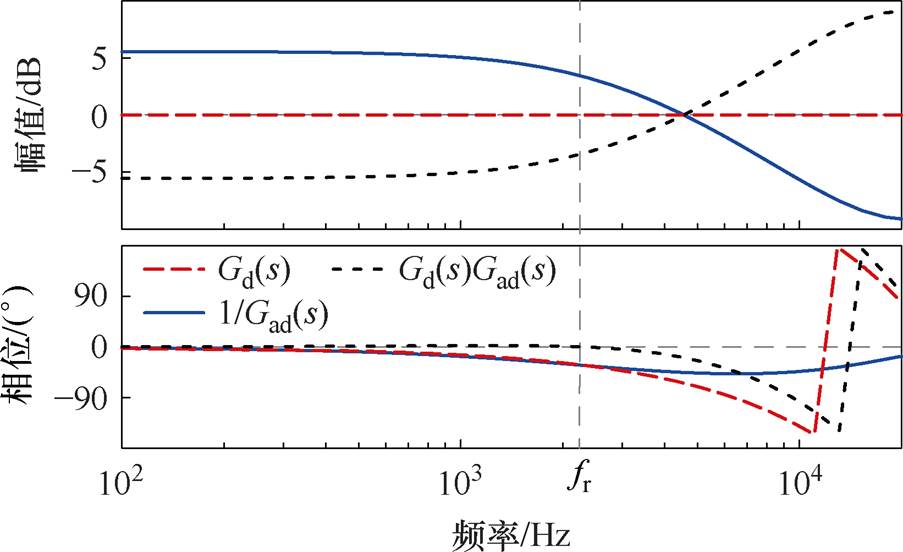
图7 Gd(s)、1/Gad(s)以及Gd(s)·Gad(s)的伯德图
Fig.7 Bodediagram of Gd(s), 1/Gad(s)and Gd(s)·Gad(s)
另一方面，AD中的阻尼增益kad若取值过小则不能起到有效的谐振阻尼作用，取值过大则可能在Gd(s)的影响下内环失稳成为非最小相位系统，这增加了Gvc(s)的设计难度。此外，过强的阻尼使得低频奇次谐波频段附近增益衰减严重，弱化了Gvc(s)的谐波抑制性能。
为简化Gvc(s)及HQR-PC的设计，以HQR-PC的被控对象具有合适的稳定裕度为目标选取kad，然后针对确定的Gvc(s)进行参数整定。
由图2b和式（2）、式（3）可得系统开环传递函数为
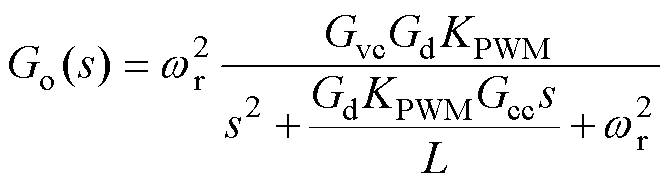（6）
其直流增益为一有限值，可以采用I与QPR控制器串联获得较高的低频增益，提升变频输出基波频段（300～800 Hz）的基准追踪能力。进一步地，将多个准谐振环节并联形成HQR控制。其中，由于基波频段位于电压环截止频率之内，一般具有充足的相位裕度而无需调整QPR的相位；谐波频段位于截止频率之外，需要采用HQR-PC控制器以调整系统开环相位从而维持系统稳定。
完整的电压控制器Gvc(s)表达式为
（7）
式中，ki为积分系数；kp为比例增益。
由系统开环截止频率fvc可确定ki。为保证基波频段在应用QPR控制器时具有一定的相位裕度，fvc需小于fr。I环节增益需要抵消被控对象在fvc处的增益，即|ki/(jwvc)||Go(jwvc)|=1。由于kad尚未整定，被控对象fvc处增益|Go(jwvc)|由尚未采用电流闭环的Go(s)近似计算，即令Gcc(s)=0；Go(s)中的KPWM可通过数字控制器中的载波幅值设计调整为1，可推得
（8）
fr=2.24 kHz，取fvc=1.3 kHz，计算可得ki=5 425。确定ki后可确定kad。为使QPR及HQR-PC控制器的被控对象具有合适的稳定裕度，取kad=4.26。
至此，系统的开环频率响应如图3所示，图中添加了未实施AD的控制方案（I方案，红色虚线）作为对比。可以看出，AD校正结果使得AD内环为最小相位系统，实施I+AD的控制方案系统截止频率（fvc=1.02 kHz）能够覆盖基波频段，且具有合适的稳定裕度（GM=3.96 dB，PM=49.9°），便于进一步设计QPR及HQR-PC控制器。
由图3可知，对于基波频段，QPR控制器的被控对象具有充足的相位裕度，因而无需增加相位补偿。kp会影响全频段增益进而影响截止频率，由于先前已由I环节确定fvc，因此kp取1即可。wd会影响QPR控制器的谐振通频带宽度，应在带宽能够包容数字控制器的截断误差和舍入误差的情况下尽可能地取小。参考一般的数字控制系统设计[20-21]，可折中选取wd=5 rad/s。本文以基波频率分量具有1%以内的稳态误差为QPR控制器的设计目标，即在wo处具有40 dB增益。当kp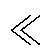
kr/wd时，QPR控制器在wo处增益可近似计算为20lg|GQPR(jwo)|≈20lg(kr/wd)，计算可得kr=500。
wo由图2a中参考信号uref中的频率基准给定。对于频率变化的uref，wo需要控制器实时根据基准信号计算。不同基准频率下应用QPR控制器的系统开环频率响应如图8所示。系统在大于400 Hz频段发生一次负穿越和一次正穿越；由于I环节作用，fvc=1 020 Hz，在小于fvc频段幅值增益大于0，根据对数频率稳定判据系统稳定。基波频段wo处最低增益为42 dB，因此设计的I+QPR控制器满足基波频段的增益需求。
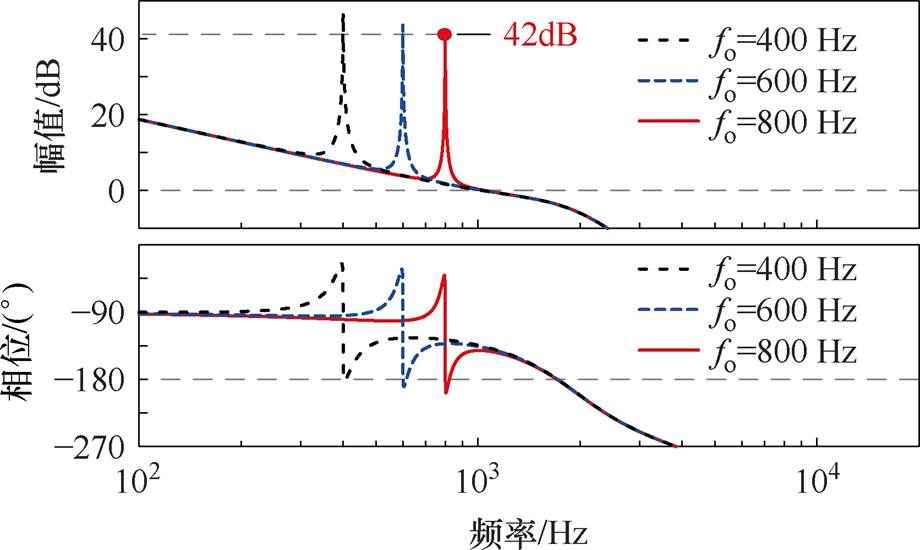
图8 应用QPR控制器的Go(s)伯德图
Fig.8 Bode diagram of Go(s) with controller QPR
为获得较高的谐波频率处增益，除jn外，HQR- PC与QPR控制器参数保持一致，即HQR-PC和QPR控制器具有相同的谐振增益。逆变电源在低次谐波频率处的增益与控制稳定性之间矛盾存在的原因，是电压控制器的被控对象谐波频率区间大部分位于开环截止频率之外，在低次谐波频率处的相位裕度不足甚至为负裕度。
以n fo处相位补偿至360°k（k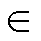Z）为目标，根据频率基准自适应选取jn，如式（9）所示。当n fo处相位为360°k时，控制器能够最大限度地获取相位裕度，避免相频曲线在n fo附近幅频曲线大于0 dB的区域穿越-(2k+1)×180°而使得控制环路失稳。
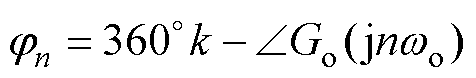（9）
以变频基准下HQR-PC-3控制器j3为例描述jn的自适应选取。将被控对象的相频特性以线性坐标轴重绘得到应用I+QPR控制器的Go(s)伯德图如图9所示。为便于在图9中展示，取k=-1，即j3= -360°-ÐGo(jnwo)。在线解析计算j3运算量过大，若以预置表形式又会占用较多存储空间。本文提出以形如P=an f n+an-1 f n-1+…+a1 f+a0的n次多项式P对ÐGo(jnwo)进行拟合以简化计算jn。例如，观察图9，3次谐波频段内可采用一次多项式拟合，结果为：P=-0.071°f-55.83°，j3-360°-P=0.071°f-304.17°。对于谐波频段较宽和相位变化不规则的情况，还可以用更高次数的多项式增强拟合精度。
图9 应用I+QPR控制器的Go(s)伯德图
Fig.9 Bode diagram of Go(s) with controller I+QPR
类似j3的整定过程，5次和7次谐波的HQR-PC参数设计结果见表2。
表2 HQR-PC控制器jn参数整定结果
Tab.2 Design results of parameter jn in HQR-PC
参数谐波频率范围/Hz拟合多项式P 整定结果 j3900～2 400-0.071°f-55.83° 0.071°f-304.17° j51 500～4 00010-5´1.6°f2-0.131°f -10-5´1.6°f2+0.131°f-360° j72 100～4 000-0.032 7°f-146.975° 0.032 7°f-213.025°
上述jn的整定方法可以归纳为：计算未计及QPR和HQR控制器被控对象谐波频率段开环相频特性ÐGo(jw)，可采用多项式P拟合近似，近似整定计算jn≈360°k-P。需要指出的是，这一方法不依赖特定的LC滤波器参数，可根据系统的开环相频ÐGo(jw)整定相应的补偿角度参数jn。
由前述jn设计过程可知，jn可视为fo的函数，控制器的其他参数不随fo变化。HQR-PC控制器在变频应用时可视为控制器中仅fo发生变化。
进一步研究fo变化下系统稳定性，以判断所设计的基准频率自适应HQR-PC控制策略的稳定性。根据式（6），可利用CAD软件直接绘制在频率基准范围内不同fo的系统闭环极点，获得关于参数fo的根轨迹以判断系统是否稳定。
不同fo下的闭环系统零极点如图10a所示。fo变化仅对原点附近的极点造成影响，远离原点的极点不受影响。放大图10a中原点附近红色方框标明的零极点，如图10b所示。图10b中不同根轨迹相互交叉而难以分辨，图10c～图10l将所有受fo变化影响的根轨迹放大展示并隐藏了与该条根轨迹无关的极点，标明了随fo增加闭环极点的变化方向，对于共轭极点只展示正虚部轨迹部分。图10i、图10j 的频率变化范围仅为300～560 Hz，是因为这两对极点与HQR-PC-7控制器有关：HQR-PC-7的谐波抑制频率范围在4 000 Hz以下，560～800 Hz频段的7次谐波已经超出该范围，此时HQR-PC-7输出为0，相应的闭环极点消失。对于图10l，该根轨迹随fo变化在实轴上折返。
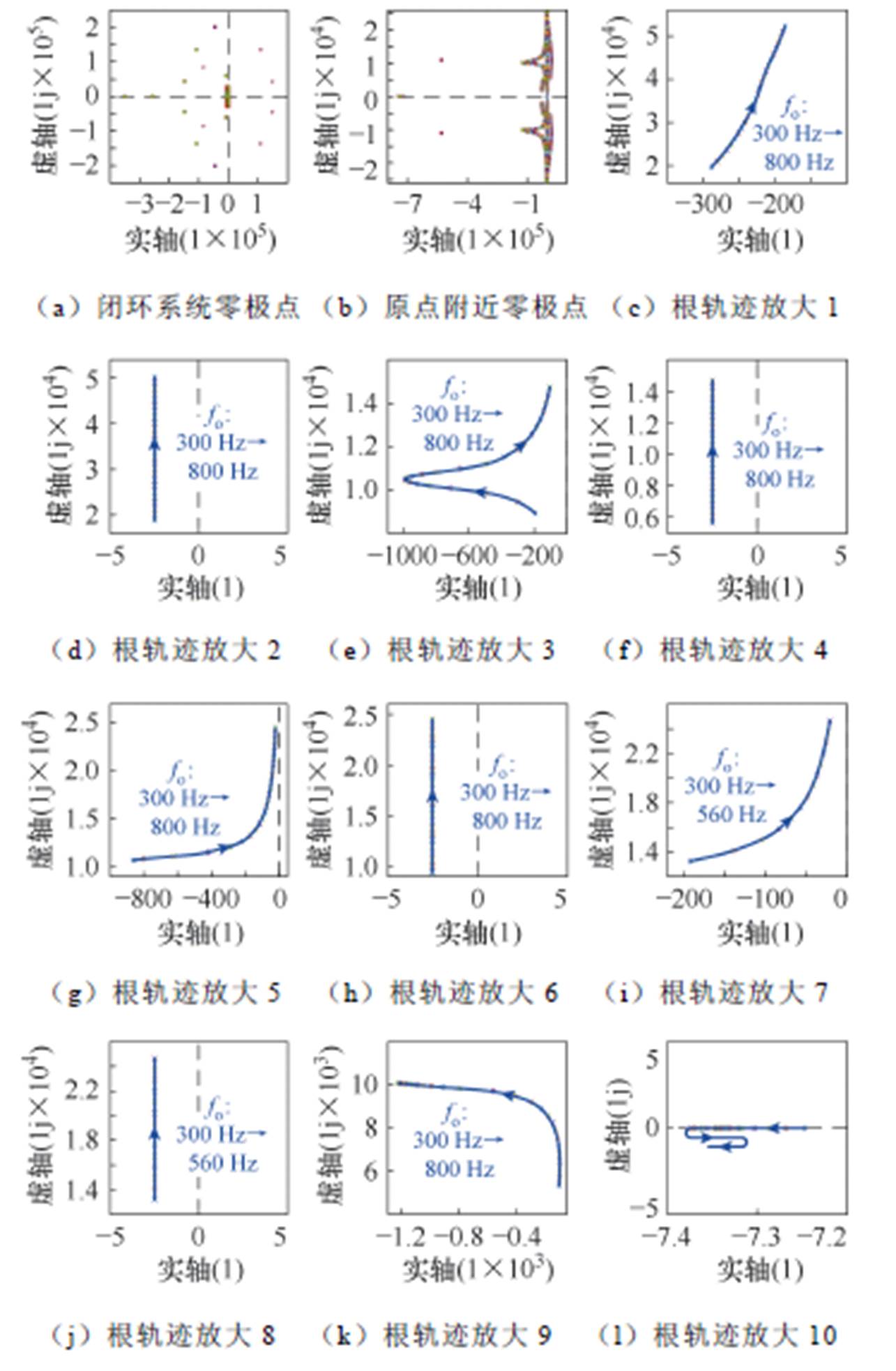
图10 fo变化时系统的闭环根轨迹图
Fig.10 Root locus of the system with different fo
总之，由图10可知，采用频率基准自适应的HQR-PC控制器，fo变化时系统根轨迹不会进入s平面右半部分，也就是说采用频率基准自适应的HQR-PC控制器能保证宽频率基准时的系统稳定。
图11为选取400、600、800 Hz基准下应用频率基准自适应的HQR-PC的系统开环频率响应曲线。图11中相频曲线表明系统具有一定的相位裕度（大于33.4°），无负穿越情况，系统稳定。对于3.0 kHz以下的谐波，系统开环增益接近25 dB，即稳态误差能够接近5%及以下，谐波抑制能力较好。对于3.0 kHz及以上频段，尽管增益相对较低，但已远离输出滤波器谐振频率，且高频谐波相对较小，滤波器本身的谐波衰减能力能够保证电压质量符合相关标准。
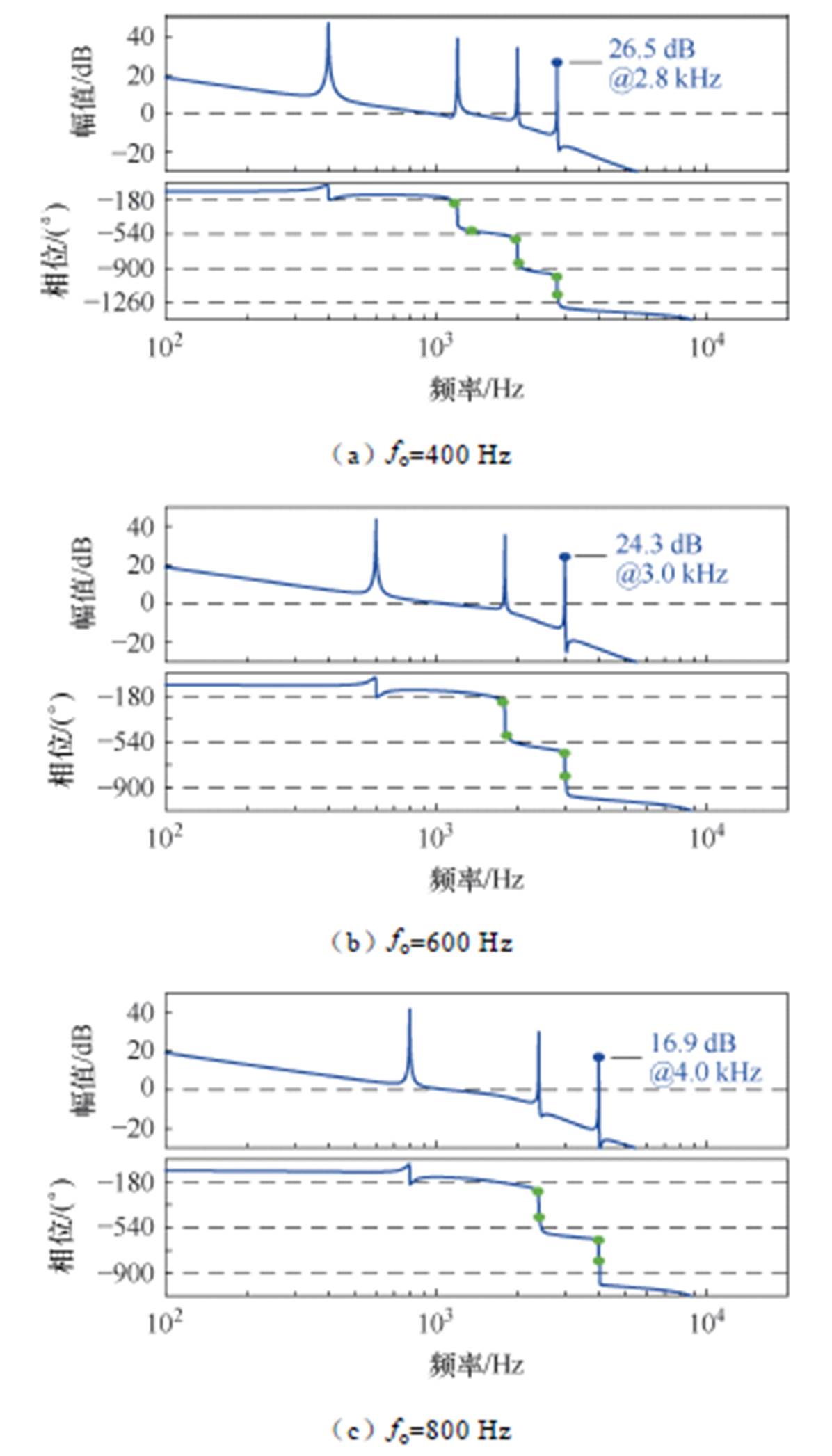
图11 应用频率基准自适应HQR-PC控制器Go(s)伯德图
Fig.11 Bode diagram of Go(s) with frequency reference adaptive HQR-PC
为验证频率基准自适应HQR-PC控制策略的有效性，搭建了600 W/300～800 Hz宽变频中频逆变电源样机进行实验验证，样机参数同表1，实验平台如图12所示。在图12的主控电路中，ARM芯片负责系统的总体控制，FPGA芯片用于产生功率电路的PWM控制信号。
分别采用频率基准自适应的HQR-PC控制和I控制，实验波形如图13和图14所示。
图12 实验平台
Fig.12 The experimental system
空载输出电压测试数据见表3。可以看出，较之于I控制，采用HQR-PC控制策略时，基准频率全频段内空载工况下输出电压THD明显降低，均小于2%，且低频奇次谐波电压有效值均小于1 V。
其次在阻性满载工况下进行实验测试，结果如图15所示。
图13 空载工况应用HQR-PC控制器的实验波形
Fig.13 Experimental waveforms with implementation of HQR-PC under no-load condition
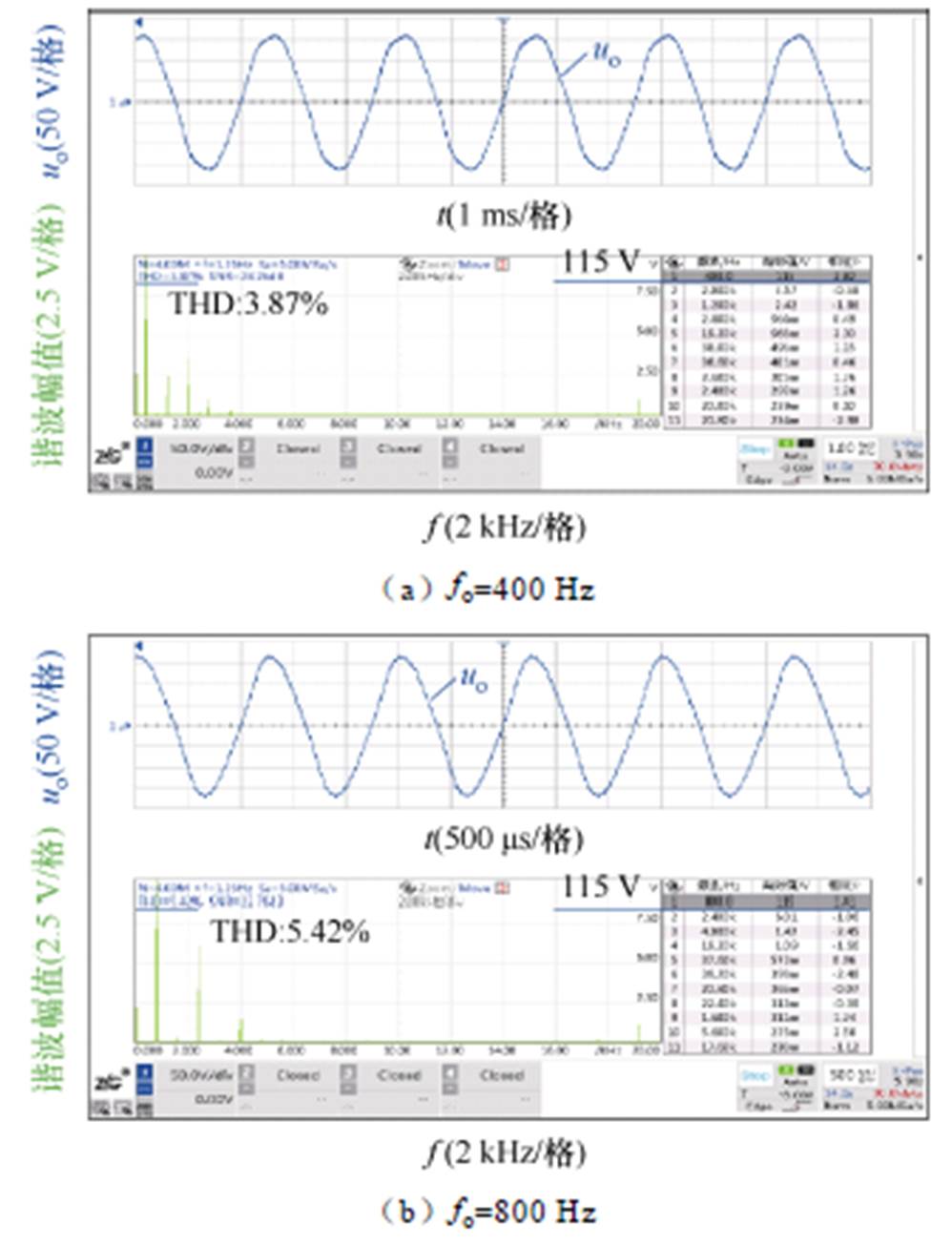
图14 空载工况应用I控制器的实验波形
Fig.14 Experimental waveforms with implementation of I under no-load condition
表3 空载工况应用HQR-PC控制器前后实验结果
Tab.3 Experiment results before and after implementation of HQR-PC under no-load condition
类别THD(%)谐波电压有效值/V 3次谐波5次谐波 400 Hz未应用3.872.423.57 应用0.47＜0.16＜0.16 600 Hz未应用4.985.361.84 应用0.82＜0.23＜0.23 800 Hz未应用5.426.011.42 应用1.63＜0.26＜0.26
图15 阻性满载工况应用HQR-PC控制器的实验波形
Fig.15 Experimental waveforms with implementation of HQR-PC under resistive full-load condition
根据实验测试，阻性满载工况下逆变器输出电压的THD均小于1%，低频奇次谐波电压有效值也均小于1 V。
根据HB 8432-2014行业标准[22]规定的非线性负载测试要求，以负载功率180 W、波峰系数为3的整流型负载作为测试条件。逆变器所连接的非线性负载电路如图16所示。非线性负载电路参数见表4。
图16 逆变器所连接的非线性负载电路
Fig.16 Nonlinear load circuit connected with the inverter
表4 非线性负载电路参数
Tab.4 Circuit parameters of the nonlinear load
参 数数 值 滤波电感L/mH100 滤波电容C/mF560 负载电阻RL/W140
非线性负载工况的实验波形如图17所示。
图17 非线性负载工况应用HQR-PC控制器的实验波形
Fig.17 Experimental waveforms with implementation of HQR-PC under non-linear load condition
由图17可知，该工况下输出电压的THD＜2.5%，低频奇次谐波电压有效值均小于1.5 V。
突加阻性满载的实验波形如图18所示。根据图18，输出电压跌落在10 V（6.15%）以内，调节时间均小于半个周期。
为验证系统对频率变化的适应性，设计了频率指令突变实验。HQR-PC控制策略频率指令突变实验波形如图19所示。在频率指令突增300 Hz的工况下，其调节时间约为一个周期。
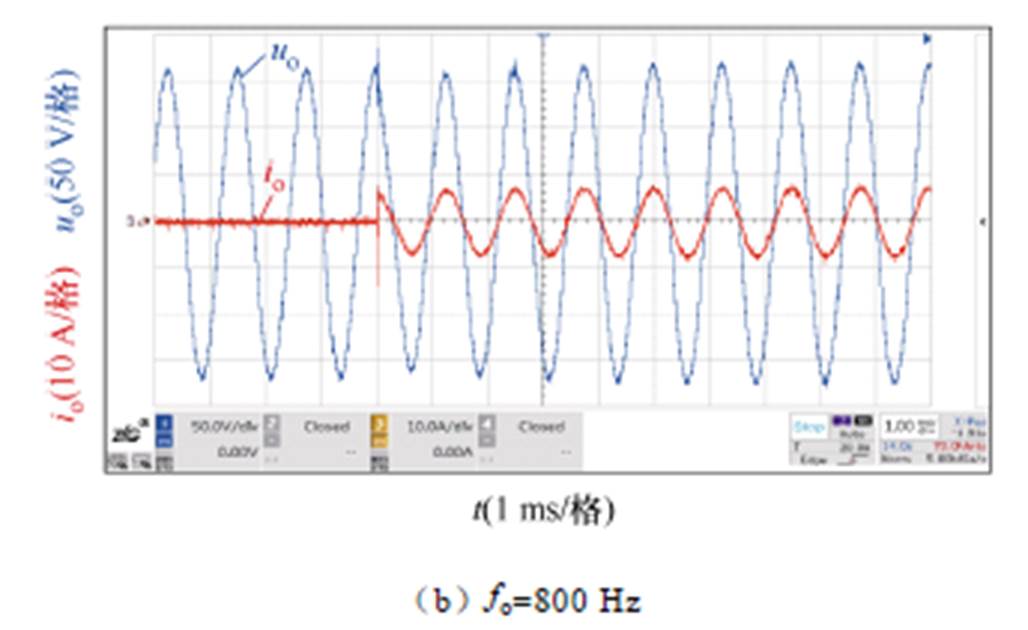
图18 应用HQR-PC控制器的动态实验波形
Fig.18 Experimental waveforms with implementation of HQR-PC under dynamic load condition
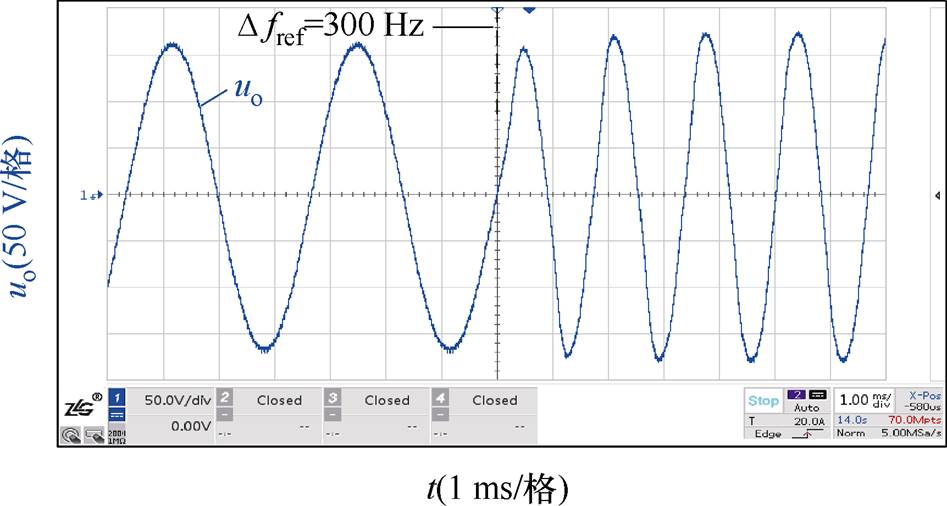
图19 HQR-PC控制策略频率指令突变实验波形
Fig.19 Experimental waveforms with implementation of HQR-PC under frequency variation dynamic condition
进一步验证频率基准全范围内的动态响应性能。图20展示了频率基准渐近递增变化下输出电压uo的波形，图20中，ufm为脉冲信号引导频率指令渐近变化。可以看出，uo的频率随指令ufm全频段变化过程中未产生明显的电压幅值变化，逆变器具有较好的动态性能和频率基准自适应能力。
综上所述，在空载、典型线性负载及典型非线性负载工况下，无论是稳态还是动态实验，应用HQR-PC控制的变频逆变器的输出均满足GJB 181B-2012标准。
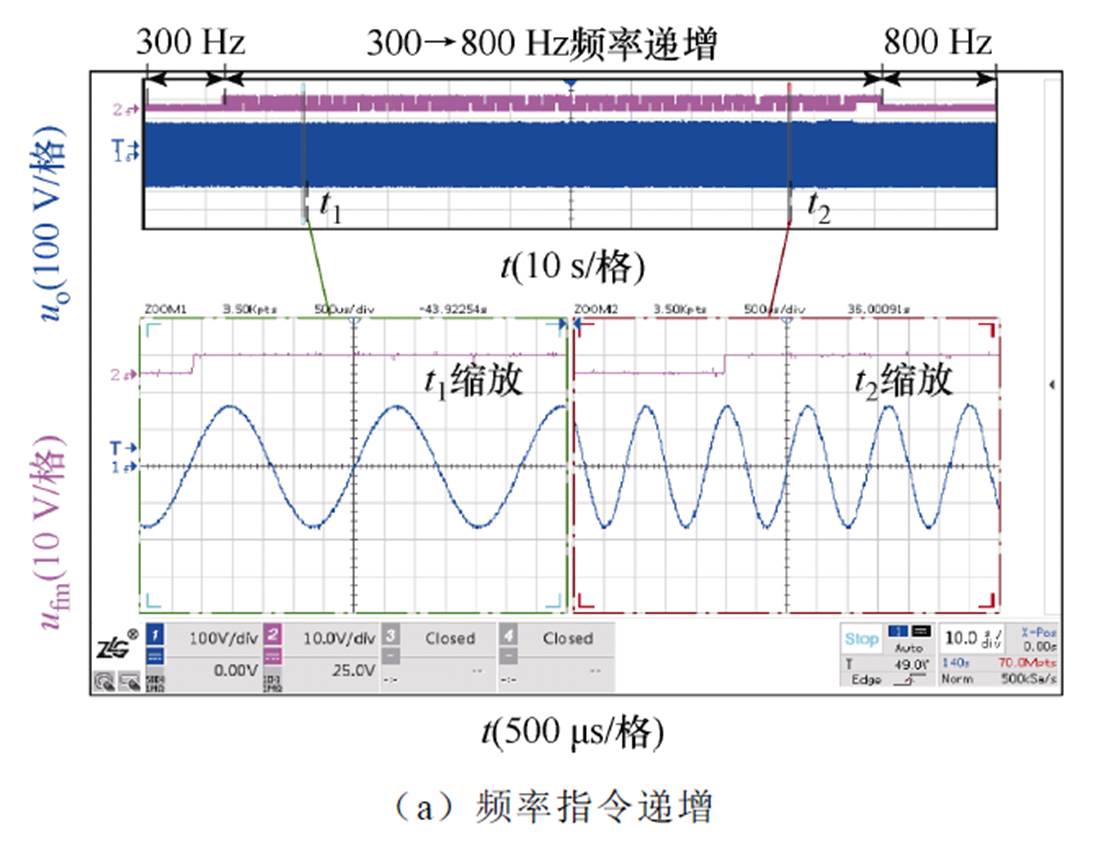
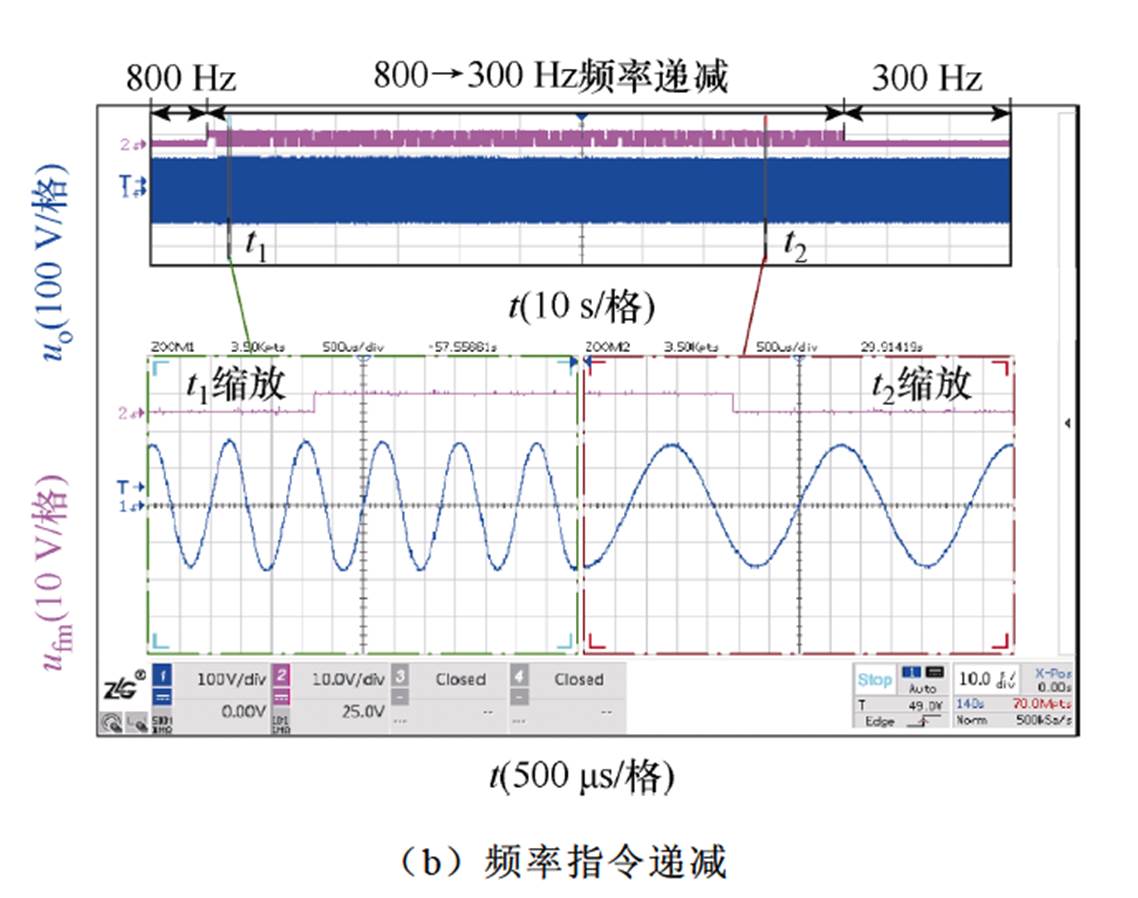
图20 HQR-PC控制策略频率指令渐近变化实验波形
Fig.20 Experimental waveforms with implementation of HQR-PC under frequency progressive variation
对于中频变频逆变电源，谐波频率区间大部分位于系统截止频率之外，相位裕度不足甚至为负，控制器增益设计难度高。此外，谐波频率处相位特性随基准频率宽范围变化，常规带相位补偿的谐波准谐振控制器难以兼顾谐波抑制与稳定性。
本文提出了一种结合数字控制延迟补偿的有源阻尼、基于积分（I）和准比例谐振（QPR）的基波追踪控制以及基准频率自适应的谐波准谐振控制策略，实现了任意频率基准下宽范围的谐波抑制；提出的相位补偿自适应律可兼顾控制带宽之外的谐波准谐振控制器增益和系统稳定性。
通过理论分析和实验验证，得出如下结论：
1）由于被控对象的谐波频率区间相位裕度较小或为负裕度，普通的相位超前补偿不能满足HQR-PC控制器的稳定应用要求；电压控制器被控对象在谐波频率区间相位特性变化较大，在宽变频场合下恒定的补偿角度不能满足HQR-PC控制器的稳定应用要求。
2）根轨迹分析表明所提出的控制方案在研究的频率基准范围内能够保持稳定，开环频率响应分析显示系统在基波频段具有40 dB增益，3 kHz以内频段具有约25 dB及以上增益的控制性能，本文设计的角度补偿自适应律实现了HQR控制器增益和稳定性的折中设计。
3）应用频率基准自适应HQR-PC控制器时，在相应的基准频率范围内，针对不同类型的负载，逆变器输出的稳态和动态性能符合相关标准要求。
参考文献
[1] 张卓然, 许彦武, 姚一鸣, 等. 多电飞机电力系统及其关键技术[J]. 南京航空航天大学学报, 2022, 54(5): 969-984.
Zhang Zhuoran, Xu Yanwu, Yao Yiming, et al. Electric power system and key technologies of more electric aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2022, 54(5): 969-984.
[2] Buticchi G, Bozhko S, Liserre M, et al. On-board microgrids for the more electric aircraft-technology review[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(7): 5588-5599.
[3] Arricibita D, Sanchis P, González R, et al. Impedance emulation for voltage harmonic compensation in PWM stand-alone inverters[J]. IEEE Transactions on Energy Conversion, 2017, 32(4): 1335-1344.
[4] Zhou Leming, Wu Wenhua, Chen Yandong, et al. Harmonic voltage distortion damping method for parallel-connected LCL-type inverters in islanded operation[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(11): 9032-9044.
[5] Chen Xinran, Ruan Xinbo, Yang Dongsheng, et al. Injected grid current quality improvement for a voltage-controlled grid-connected inverter[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1247-1258.
[6] 飞机供电特性: GJB 2573-1996[S].
[7] 钱强, 张犁, 过仕安, 等. 抗电感参数扰动的400Hz逆变器控制策略研究[J]. 中国电机工程学报, 2022, 42(增刊1): 256-268.
Qian Qiang, Zhang Li, Guo Shian, et al. Research on control strategy of 400Hz inverter against inductance parameter disturbance[J]. Proceedings of the CSEE, 2022, 42(S1): 256-268.
[8] 杨明, 杨倬, 李玉龙, 等. 弱电网下基于电网电压前馈的并网逆变器阻抗重塑控制策略[J]. 电工技术学报, 2024, 39(8): 2553-2566.
Yang Ming, Yang Zhuo, Li Yulong, et al. Impedance remodeling control strategy of grid-connected inverter based on feedforward voltage under weak grid[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2553-2566.
[9] Ramos G A, Ruget R I, Costa-Castelló R. Robust repetitive control of power inverters for standalone operation in DG systems[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 237-247.
[10] 朱元, 朱醴亭, 肖明康, 等. 基于几何约束优化的重复控制器及PMSM电流谐波抑制应用[J]. 电工技术学报, 2024, 39(4): 1059-1073.
Zhu Yuan, Zhu Liting, Xiao Mingkang, et al. Repetitive controller based on geometric constraint optimization and its application to current harmonic suppression of PMSM[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1059-1073.
[11] Zhao Qiangsong, Ye Yongqiang. A PIMR-type repetitive control for a grid-tied inverter: structure, analysis, and design[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2730-2739.
[12] 李金玉, 陈杰, 龚春英, 等. 一种提高级联H桥逆变器功率不平衡运行能力的控制策略[J]. 电工技术学报, 2023, 38(10): 2731-2743.
Li Jinyu, Chen Jie, Gong Chunying, et al. A control strategy to improve working ability of cascaded H-bridge inverter under power imbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(10): 2731-2743.
[13] Wang Yachao, Darwish A, Holliday D, et al. Plug-in repetitive control strategy for high-order wide-output range impedance-source converters[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(8): 6510-6522.
[14] Liu Zhichao, Zhou Keliang, Yang Yongheng, et al. Frequency-adaptive virtual variable sampling-based selective harmonic repetitive control of power inverters[J]. IEEE Transactions on Industrial Electronics, 2021, 68(11): 11339-11347.
[15] Alves A G P, Rolim L G B, da Silva Dias R F, et al. Analysis of grid-connected VSCs subject to voltage harmonic disturbances: prediction and design tool of resonant controllers[J]. IEEE Transactions on Energy Conversion, 2023, 38(1): 239-249.
[16] 黄仁志, 全相军, 吴在军, 等. 基于多重谐振控制器的参考值前馈自适应控制[J]. 电工技术学报, 2022, 37(16): 4212-4224.
Huang Renzhi, Quan Xiangjun, Wu Zaijun, et al. A multiple resonant based on reference feedforward adaptive voltage control of three-phase inverter[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4212-4224.
[17] Golestan S, Ebrahimzadeh E, Guerrero J M, et al. An adaptive resonant regulator for single-phase grid-tied VSCs[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 1867-1873.
[18] Peng Cong, Sun Jinji, Song Xinda, et al. Frequency- varying current harmonics for active magnetic bearing via multiple resonant controllers[J]. IEEE Transa- ctions on Industrial Electronics, 2017, 64(1): 517- 526.
[19] Qian Qiang, Xie Shaojun, Xu Jinming, et al. Passivity-based output admittance shaping of the converter-side current-controlled grid-tied inverter to improve the robustness to the grid impedance[J].IET Power Electronics, 2020, 13(10): 1956-1965.
[20] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[21] 施烨, 吴在军, 窦晓波, 等. 三相四线变换器相位补偿控制策略研究[J]. 中国电机工程学报, 2017, 37(10): 2971-2985.
Shi Ye, Wu Zaijun, Dou Xiaobo, et al. Research on phase compensation control schemes for three-phase four-wire converters[J]. Proceedings of the CSEE, 2017, 37(10): 2971-2985.
[22] 民用飞机地面电源供电特性要求: HB 93-2003[S].
Abstract With the development of more electric aircraft (MEA) and the increase of aircraft power system capability, AC power system of 360～800 Hz wide variable frequency has become one of the most important development trends due to its high reliability, high power density, and huge individual machine capability. However, since more and more electric and electronic equipment, especially nonlinear loads such as rectifiers, are applied in aircraft, the harmonics induced by those loads significantly impact the voltage quality of the aircraft grid. Unlike a 50 Hz inverter, the harmonic frequency of a medium-frequency inverter is very high, usually beyond the control band, which leads to a relatively small phase margin and great difficulty in control. Typical methods, such as repetitive control, do not satisfy the requirement when the power source frequency varies. QPR (quasi-proportional resonant) and HQR (harmonics quasi-resonant) control performs poor stability since its phase changes suddenly at the resonant frequency.
The paper focuses on harmonics suppression for 360～800 Hz wide variable frequency AC power inverter, as well as the stability of the voltage controller. First, the structure of a single-phase inverter with digital control is described, and then the delay of digital control, which greatly influences control stability, is derived. Next, the stability of the control system with the application of HQR is discussed. The system phase margin is very small, even negative. Due to large frequency variation, a constant angle compensation cannot ensure the control system’s stability. To simplify the design of the voltage controller, inductor current feedback active damping with digital control delay compensation is designed, which provides a suitable stability margin and minimum phase characteristic for the controlled object and suppresses the resonance peak. Furthermore, the I (integration)+QPR control scheme is proposed to improve the tracking ability of fundamental voltage.
As the frequency varies from 360 Hz to 800 Hz, for HQR, a constant angle compensation cannot guarantee the voltage controller’s stability. Accordingly, a frequency self-adapted HQR-PC (harmonics quasi-resonant with phase compensation) is proposed, compensating a specific angle for the control object to acquire a sufficient stability margin under a wide frequency reference range. After that, the stability of the control system is verified by root locus figures. The digital control implementation method of polynomial fitting of compensation angle is also given. It is indicated that the control scheme has high open-loop gain at fundamental and harmonics frequencies by open-loop frequency response, and harmonics can be suppressed with simulation verification.
Finally, an experimental platform of 600 W medium frequency inverter power supply with a wide output frequency range is built. The control performance of the proposed control methods is tested with resistive and nonlinear loads, respectively. The results show that the medium-frequency inverter can output voltage with small harmonics, and the total harmonics distortion of the output voltage conforms to the industrial power supply standard under the frequency reference range. Moreover, the inverter shows excellent static and dynamic performance.
keywords：Variable-frequency inverters, harmonics suppression, quasi resonant control, phase com- pensation, adaptive control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.231341
国家自然科学基金资助项目（52277183）。
收稿日期 2023-08-17
改稿日期 2023-09-20
刘海春 男，1977年生，博士，副教授，研究方向为功率电子变换技术和航空电源技术。E-mail: nualhc@163.com（通信作者）
过仕安 男，1998年生，硕士，研究方向为功率电子变换技术。E-mail: guoshian@nuaa.edu.cn
（编辑 郭丽军）