图1 典型DCTLI桥臂结构示意图
Fig.1 Schematic diagram of typical DCTLI bridge
摘要 针对二极管钳位型三电平逆变器存在的电容电压平衡问题和死区时间导致的输出波形失真问题，该文在分析死区时间对输出波形失真及电容电压平衡影响的基础上，提出一种可用于高频逆变器的数字调制方法及具体实现形式，分析量化与采样环节、数字隔离器件传输延时及采样时钟对所提方法的影响，并给出开关时钟分频倍数的设计准则。该方法独立于闭环控制系统其他环节，无需电流采样，实现容易且易于集成在数字控制器中；无需控制环路运算，可适用于更高开关频率和输出频率。仿真和实验表明，所提方法在不同开关频率、不同死区时间和不同负载类型下均能有效地降低死区时间导致的输出波形失真现象，且能够很好地解决电容电压平衡问题。此外，所提方法在开关频率高达400 kHz的情况下仍具有良好的效果。
关键词：三电平逆变器 电容电压平衡 死区时间补偿 数字调制 输出波形失真
二极管钳位型三电平逆变器（Diode-Clamped Three-Level Inverter, DCTLI）由于结构简单、控制容易被广泛应用于光/储并网变换器、高压直流输电、固态变压器及机车驱动器[1-4]等场合。随着宽禁带半导体的发展，DCTLI可以和SiC或GaN器件结合，通过实现高至200 kHz及以上的开关频率以提高系统的功率密度[5]。如航空逆变器可以通过GaN器件和DCTLI的结合实现更小的体积。但高开关频率意味着更小的开关和控制周期，一些应用于中低频场合的方法在高开关频率时难以获得良好的效果。
为了防止DCTLI桥臂上开关管的直通，需要在各开关管的驱动信号上增加死区时间，这会导致桥臂输出波形的平均值偏离控制信号，从而导致输出电压电流波形失真[6]。对死区时间影响的补偿，一般分为以下几种：
（1）基于电流极性的补偿方法[7-10]：文献[7]通过检测电流方向，然后利用逻辑电路在PWM信号上增加或减小相应的时间实现补偿；文献[8]综合死区时间、开关器件的开关延时、器件导通损耗等因素计算得到补偿脉冲，并根据电流极性对死区进行补偿；文献[9]通过预测电流消除了由通信延迟造成的电流过零点判断偏差；文献[10]提出一种应用于中点钳位（Neutral Point Clamped, NPC）变换器的多调制时间调制方法，根据电流极性选择不同的调制时间生成PWM信号，从而消除了死区时间的影响。还有很多基于电流极性的补偿方法[11-12]，受限于电流传感器的精度或算力的要求，这些方法在低开关频率和输出频率下具有良好的效果，但在更高频率的场合其补偿效果将受限。
（2）通过改进控制方法来消除死区时间的影响[13-15]：文献[13]利用免疫算法来补偿死区时间的影响；文献[14]则采用重复控制器来补偿死区时间；文献[15]将死区时间当作系统的非线性扰动，通过一种谐波分离方案直接提取出逆变器非线性因素并加以补偿消除了死区时间的影响。这些方法受限于额外的算力，在开关频率或输出频率较高时同样难以获得令人满意的效果。
（3）死区时间消除方法，通过修改电路或调制方式，等效地将桥臂构建成开关管串联二极管的形式[16-18]，因此也就不需要死区时间。但这些方法有些同样需要电流检测，有些则需要特殊的拓扑结构。此外，还有利用大量计算精确分析死区时间引起的谐波，然后生成补偿信号的方法[19]，也难以适应于高频的场合。
此外，DCTLI在运行过程中容易产生电容电压不平衡的问题，不仅会影响输出波形质量，严重时还会导致开关管过电压损坏[20]。虽然电容电压存在自然平衡特性[21]，但很多情况下仍然存在不平衡的问题。典型的电容电压平衡方法基本可以分为两类：
（1）通过修改调制策略来产生平衡电流，这一类方法又可以分为基于载波脉宽调制（Carrier- Based Pulse Width Modulation, CBPWM）[22-24]和基于空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）[25-26]两种。前者通常通过注入补偿电压来实现电压平衡，SVPWM一般通过调节冗余矢量来实现电压平衡，此外，还有通过在参考信号上增加偏置电压控制开关管在某些时刻不调制来实现电压平衡的非连续脉宽调制（Dis- continuous Pulse Width Modulation, DPWM）[27-28]。这些方法由于其调制的复杂性，也难以适合在高开关频率场合应用。
（2）通过增加额外电路强迫电容电压平衡[29-30]，这类方法至少需要一个开关管、一个二极管和一个电感，尽管具有良好的平衡效果，但增加的额外器件不利于更高功率密度的要求。此外，文献[31]提出了一种结合调制和额外电路的混合策略，但仍然面临上面提到的问题。
目前，针对死区时间补偿和电容电压平衡的解决方法一般是相互独立的，若要同时解决这两个问题就需要使用独立的两套解决方法，这会显著增加系统的复杂程度。尽管也有文献提出将两者结合的方法[32]，但过多运算难以应用于高开关频率的场合。
与中低频逆变器不同，开关频率高至200 kHz以上的逆变器，可用于执行控制算法的时间通常小于5 ms。若要通过额外控制环路或复杂的调制方式来解决上述问题，则必然会降低控制带宽。此外，受限于高频下传感器精度、带宽和体积，无传感器的方法有潜力提供更好的效果和功率密度。
为此，本文在死区时间对输出波形失真和电容电压平衡影响分析的基础上，提出一种无额外传感器的兼具电容电压平衡及死区时间补偿的数字调制方法，通过在调制环节引入桥臂输出波形和电容电压平衡状态，强迫桥臂输出波形的平均值跟踪控制器输出的控制信号，仅在调制环节即可消除死区时间的影响，同时调节控制信号使电容电压平衡。所提方法易于实现、便于集成，可应用于高输出频率和开关频率。本文详细分析了所提方法的原理及实现方法，并就量化与采样环节、数字隔离器件传输延时及采样时钟对所提方法产生的误差进行了详细分析，给出了开关时钟分频倍数的设计准则。最后，通过仿真与实验验证了所提方法的有效性。
典型的DCTLI桥臂的结构示意图如图1所示。图中，Udc为直流电源电压，us为桥臂实际的输出电压，i为桥臂的输出电流。当参考信号处于正半周时，根据桥臂输出电流的方向和桥臂输出电流的大小的不同，死区时间及由开关管结电容引起的开关暂态对桥臂输出波形的影响可以分为如图2所示的五种情况。参考信号处于负半周的情况类似，因此全文皆以正半周为例，参考信号为负半周的情况不再赘述。
图1 典型DCTLI桥臂结构示意图
Fig.1 Schematic diagram of typical DCTLI bridge
图2中，
为期望的桥臂输出波形，S1～S4为开关管S1～S4对应的驱动信号，uref为参考信号。以情况1和情况2为例详细分析死区时间td及结电容Cd引起的开关暂态对桥臂输出波形的影响。图3为情况1和情况2的放大图。
情况1和情况2的区别在于在死区时间内结电容能否完全充放电，而临界点就是死区时间恰好让电容电压完全充放电，此时桥臂输出电流满足
（1）
图2 不同输出电流情况下的桥臂输出波形
Fig.2 The output waveforms of the bridge under different output currents
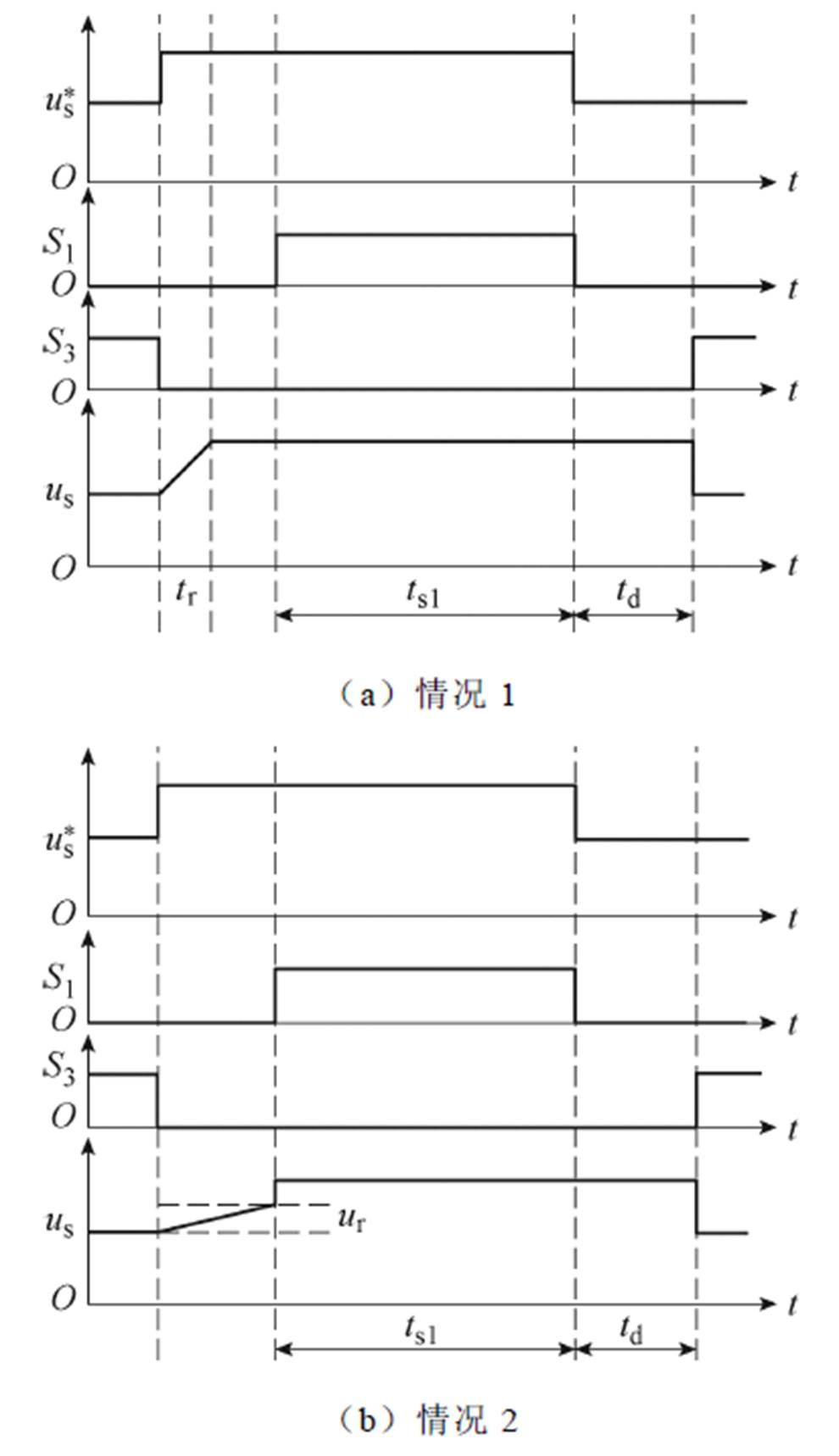
图3 情况1和情况2下各波形的放大图
Fig.3 Zoom-in graphs of waveforms in Case 1 and Case 2
情况1：当参考信号处于正半周，桥臂输出电流方向为负且幅值较大，即i≥UdcCd/td时，开关管的结电容Cd在死区时间内即可被完全充放电，可以得到充放电时间tr为
（2）
根据图3a可得，此时的面积为
（3）
式中，ts1为开关管S1导通的持续时间。
而实际输出us的面积为
（4）
因此，与实际输出us之间的误差uerr为
（5）
情况2：当参考信号处于正半周，桥臂输出电流方向为负但幅值较小，即i＜UdcCd/td时，结电容Cd在死区时间内无法被完全充放电，因此在死区时间结束时桥臂输出电压us会被强制从结电容电压切换至0.5Udc。在死区时间结束时结电容上的电压ur为
（6）
类似于之前的分析，此时的误差uerr为
（7）
通过类似的分析可以分别得出其余情况下的电压误差uerr。显然，当存在死区时间时，由于二极管的自然续流及结电容的充放电过程，桥臂实际的输出电压us会偏离，这会在桥臂的实际输出电压上引入额外的谐波，影响逆变器的输出波形质量。
尤其是考虑了由结电容引起的开关暂态过程后，与仅考虑死区时间不同，误差电压uerr变为与桥臂输出电流i和结电容Cd均相关的非线性关系，图4展示了在情况1和情况2时的这种非线性关系。其中，图4的纵坐标为电压误差与仅考虑死区时间时引入误差的比值，x轴为结电容与电流i的比值，用来同时描述二者的变化，y轴为死区时间。图4所示的这种非线性使得仅考虑死区时间影响的死区补偿方法并不能完全补偿死区时间的影响。
在不考虑开关管及二极管压降差异时，各开关管驱动回路之间的传输延时会使开关管之间的死区时间存在微弱的差异，这种差异使得直流侧电容的充放电时间也存在差异，从而导致电容电压不平衡。
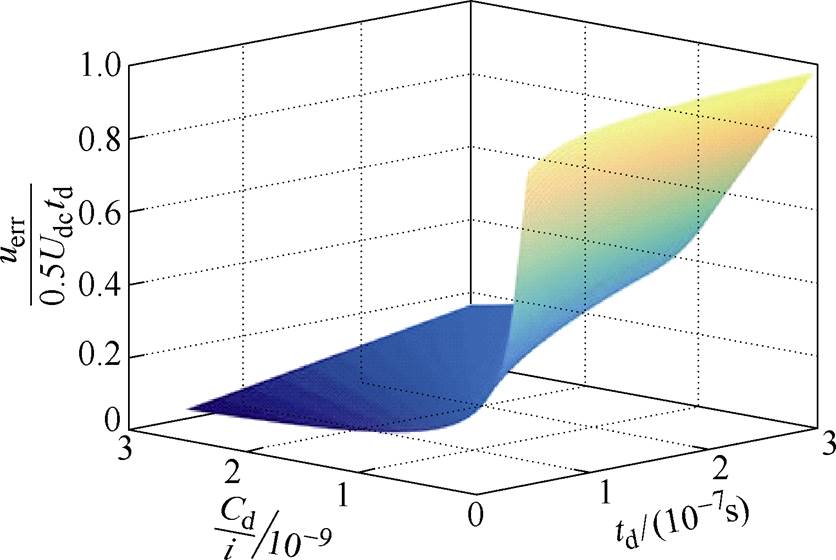
图4 开关暂态引起的电压误差非线性的示意图
Fig.4 Schematic illustration of voltage error nonlinearity due to switching transients
以全桥DCTLI为例，图5为存在死区延时时间不匹配时的桥臂输出波形、电感电流iL的波形和电容C1的电流iC1的波形。其中us1、us2分别为两个桥臂的输出波形，Dtd1、Dtd2分别为驱动的传输延时不匹配导致的us1、us2上升沿和下降沿之间的时间差。由电路可知，Dtd1、Dtd2内，流过电感的电流和电容的电流大小相同，方向不同，即可以表示为
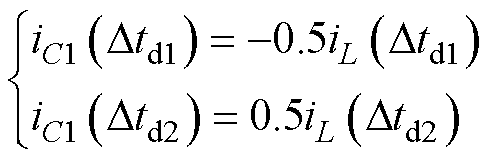（8）
图5 驱动存在传输延时不匹配时的各波形
Fig.5 The waveforms when the transmission delay mismatch exists in the driver circuit
在一个开关周期Ts内流过电容C1的总电流为
（9）
根据电感电流上升斜率的表达式，可得
（10）
（11）
式中，K为调制比；R为负载电阻；Lf为输出滤波电感；w 为输出波形的角频率。在一个开关周期内，流过电容C1的平均电流为
（12）
因此，在半个输出周期内电容电压的变化量为
（13）
由于全桥DCTLI共有8个开关管，任意两个开关管之间均可能存在延时不匹配，其他情况的分析可以依此类推。由式（9）～式（13）可见，当各开关管驱动回路存在延时不匹配时，每个输出波形周期内电容电压均会产生变化，且变化的方向是相同的，累积的电压变化最终会导致电容电压的不平衡。因此，需要采取额外的措施保证电容电压平衡。
以图1所示的单桥臂为例，逆变器的滤波截止频率通常远低于开关频率，因此输出波形在每个开关周期Ts内的值等价于桥臂实际的输出电压us在开关周期内的平均值，即
（14）
式中，uo为逆变器的输出电压。在无死区时，逆变器的输出电压uo为参考信号uref的等比例放大，由于DCTLI为三电平逆变器，比例放大倍数为0.5Udc，因此有如下关系
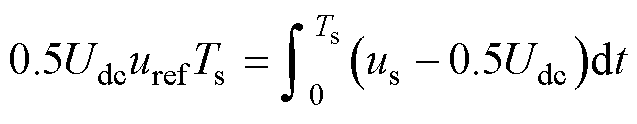（15）
式中，参考信号uref的取值范围为-1≤uref≤1。若定义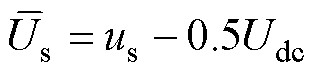
，则uref可以表示为
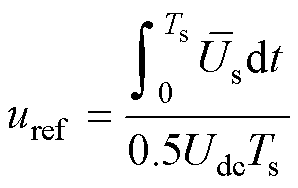（16）
若令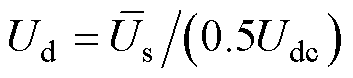
，则uref可以表示为
（17）
式中，Ud的取值范围为-1≤Ud≤1。根据定积分与黎曼和的关系，当分割的区间足够多时，定积分近似等于无数矩形的面积之和，因此，uref可以表示为
（18）
式中，N为每个开关周期Ts内分割的区间数量。由于在整个输出波形的周期内，绝大多数开关周期下桥臂的输出电流足以使开关管结电容完全充放电，因此绝大多数桥臂输出波形为图2中的情况1和情况5。在这两种情况下，桥臂输出波形均为矩形与三角形的组合，由于三角形面积等价于对应矩形面积的一半，因此若在每个区间定义数字信号为
（19）
用频率为N倍于开关频率的采样时钟对数字信号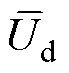
进行计数，则计数值
数值上等于
。根据式（18），若在每个开关周期内，当计数值等于Nuref时，生成驱动信号S1～S4，则可保证不论是否存在死区时间及开关暂态，均可使桥臂输出波形的平均值完全跟踪参考信号，这就消除了死区时间及开关暂态对输出波形的影响。
对于电容电压平衡来说，可以根据两电容电压的差值来修改参考信号的幅值，即修改驱动信号的占空比，当电容C1的电压高于电容C2的电压时，增大参考信号的幅值，使流过电容C1的电流增大，即可降低电容C1的电压；反之，亦然。周期性的这种操作即可使两个电容的电压趋于平衡。
根据上述分析，提出一种如图6a所示的用于DCTLI的数字调制器。数字调制器、桥臂波形采集模块、电容电压采集模块共同组成完整的数字调制方法。图6b给出了数字调制方法在实际逆变器系统中应用的连接关系。图6b中的数字隔离器是非必需的，若无隔离需求可舍去。数字调制器用来接收控制程序生成的控制指令并根据桥臂输出波形及电容电压平衡状态来生成PWM信号。电容电压采集模块用于采集不平衡状态电容电压，并将不平衡状态的电容电压转换为数字信号后送入计数器计数，计数结果与控制指令相结合生成修正后的控制指令。桥臂波形采集模块采集桥臂输出波形us并转换为数字信号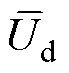，然后进行计数。当计数结果等于修正过的控制指令时，触发生成PWM信号驱动各个开关管。
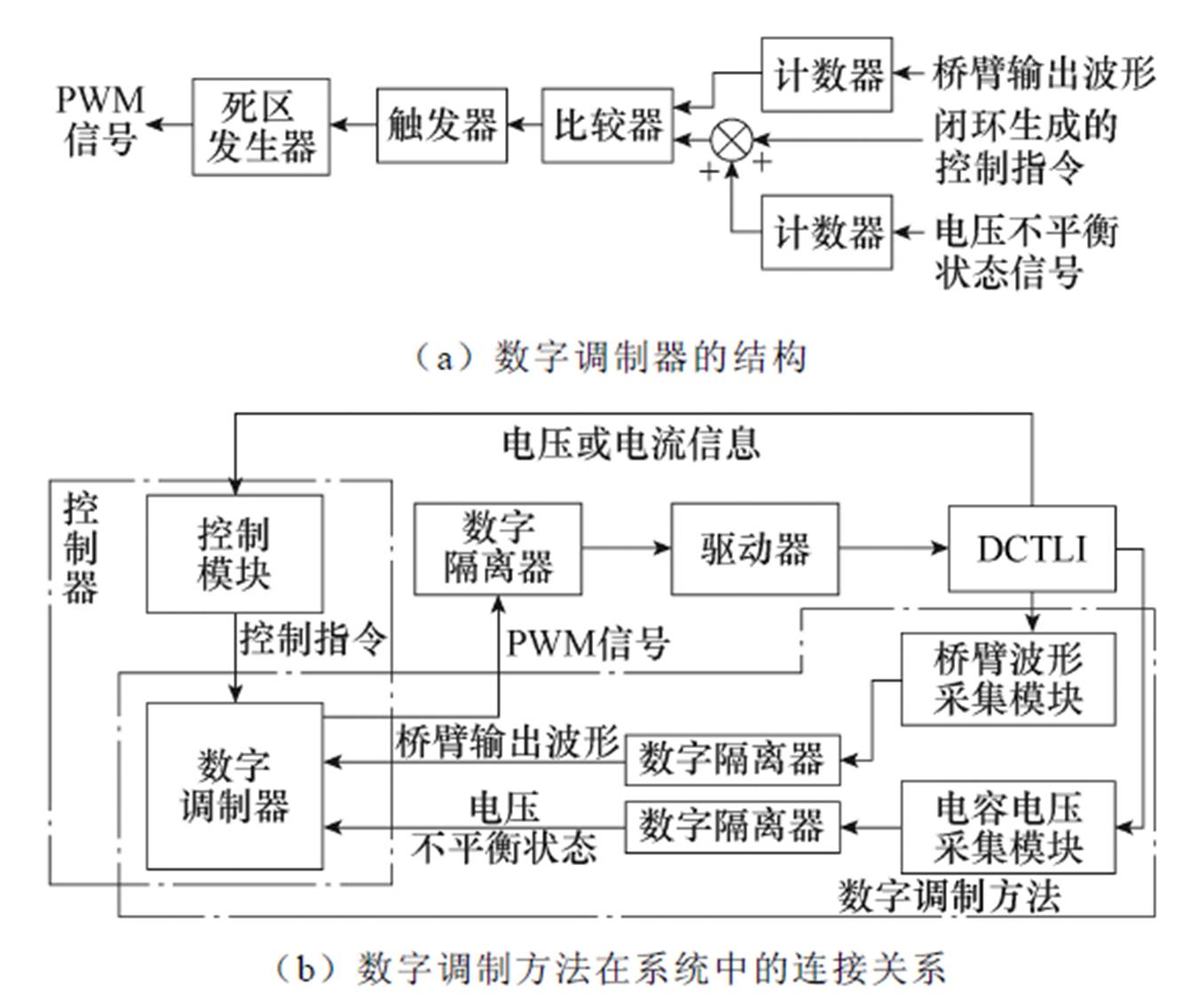
图6 数字调制方法示意图
Fig.6 Diagram of digital modulation method
这样，通过调制器本身即可同时补偿死区及开关暂态的影响并消除电容电压不平衡，无需控制环路的干预也无需额外的电流传感器。
根据2.1节提出的原理和如图6所示的数字调制方法结构，给出一种如图7所示的实现形式。其中计数器中的U代表增计数输入端，D代表减计数输入端，R代表复位端。逆变器桥臂波形采集模块和电容电压平衡状态检测模块分别由电阻采样网络和比较器组成。分别选取Rs1=-0.75R1+0.25R2，Rs2= -0.25R1+0.75R2，RC2=-0.5R1+0.5R2。Rs1所在的电阻网络目的是使比较器在us≥0.75Udc时输出高电平，Rs2所在的电阻网络目的是使比较器在us≤0.25Udc时输出高电平，这样，即使直流电压存在波动，所提方法也能够在满足式（19）的条件下正确生成数字信号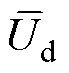。而RC2所在的电阻网络目的是使比较器在UC2≤0.5Udc时输出高电平，从而使得电容电压不平衡状态可以被正确转换为数字信号。
数字调制器中的电容电压平衡部分主要由逻辑门和增减计数器组成。采用开关时钟分频M倍作为计数时钟，M的选取方法可参照3.4节的分析。在每个计数时钟的上升沿，当电容电压平衡采集模块输出高电平时，增减计数器增计数；反之，则减计数，计数结果与控制量进行结合用来生成修正后的控制指令。同时，在每个参考信号从负到正过零时清零计数器的值，防止电容电压平衡过补偿。
调制器生成PWM信号的过程在参考信号的正负半周是类似的，死区补偿部分是对称的结构，因此后续仅分析控制量1所在的正半周的调制结构。以情况1为例，在一个开关周期内，调制器生成PWM信号的工作过程如图8所示。在开关时钟的上升沿即开关周期起始时，置位RS触发器输出高电平。在控制量1＞0即参考信号处于正半周时，RS触发器的输出经过数据选择器并增加死区时间后驱动S1和S3。当检测到桥臂输出波形为高，即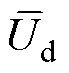为高电平时，计数器开始计数，当计数器的值等于修正后的控制指令时，复位RS触发器让其输出低电平，进而在增加死区时间后关断开关管S1，这样就可以强迫桥臂输出波形的平均值精确跟踪参考信号。由于此时参考信号处于正半周，控制量2为负，因此S4的驱动信号始终为低电平，用以满足调制时序。
图7 数字调制方法实现方式示意图
Fig.7 Schematic diagram of implementation of digital modulation method
图8 情况1下的数字调制器工作过程示意图
Fig.8 Schematic diagram of the working process of the digital modulator in Case 1
计数器由两个信号复位，其中一个当参考信号过零时复位计数器，防止计数器仍有计数值而无法关断S1。另一个复位信号来自RS触发器输出的反相，用于在RS触发器输出的下降沿即S1的驱动信号的下降沿复位计数器。以情况1为例，当开关管S1关断后，由于二极管的自然续流，桥臂仍然继续输出高电压，但这段时间无法被提前计数，因此将死区时间内的计数值作为下一个开关周期的计数初值。由于开关频率一般较高，相邻两个开关周期内桥臂输出波形基本具有相同的形式，因此这种生成计数初值的方法可以保证数字信号被提前完整地计数。
由于所提数字调制器仅由逻辑单元组成，因此可以利用控制器内部资源实现，无需额外分立器件，易于集成。
由于存在结电容引起的开关暂态过程，逆变器桥臂波形采集模块通过采样与量化生成的数字信号无法完全还原暂态过程，这必然引起误差。
以情况1和情况2为例，其桥臂输出波形和采样生成的数字信号对比如图9所示。
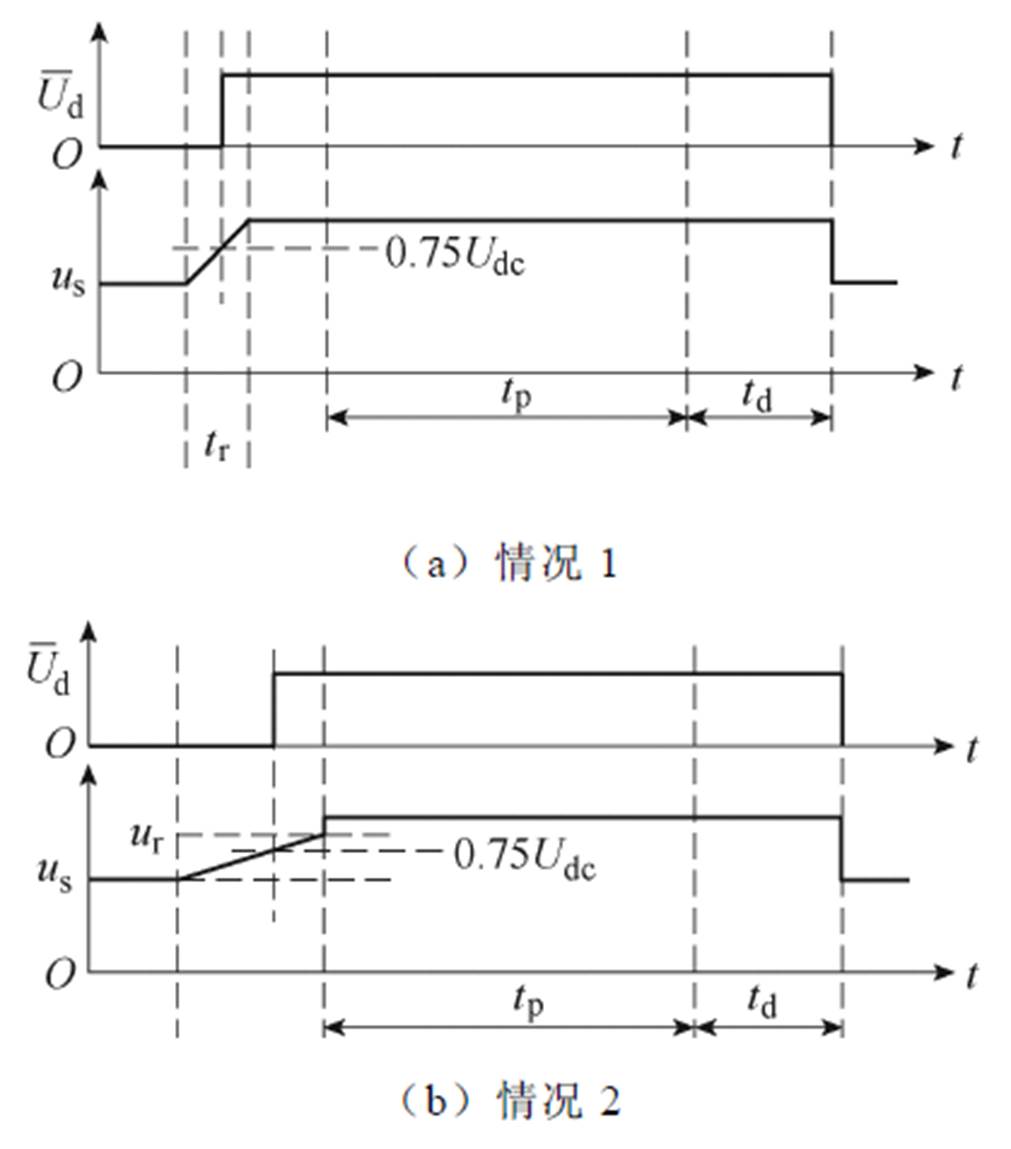
图9 桥臂输出波形及其采样生成的数字信号对比
Fig.9 A comparison of the output waveform of the bridge and the digital signal generated by sampling
由图9a可得，情况1下us的面积为
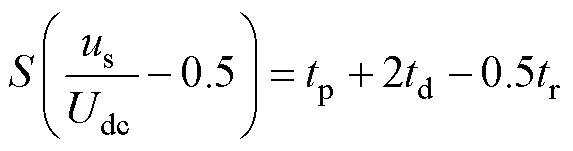（20）
采样生成的数字信号的面积为
（21）
可见，由于给出的逆变器桥臂波形采集模块的结构能够精确地在直流输入电压的3/4处生成数字信号，此时us与
的面积相同，没有误差。
由图9b可得，在情况2下桥臂输出波形和采样生成的数字信号的面积分别为
（22）
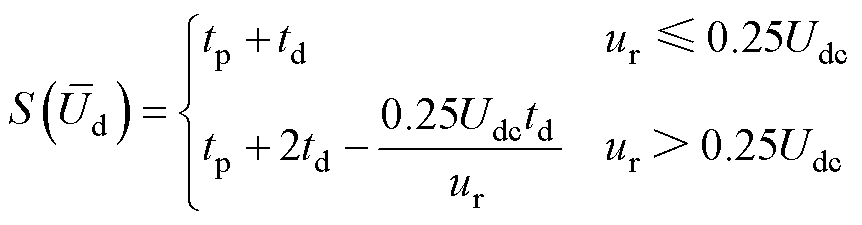（23）
将式（22）与式（23）作差并求极值后，可以得出在情况2时，us与的面积误差
最大为
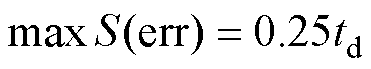（24）
但上述最大的误差仅出现在ur=0.25Udc时，其余情况下误差均小于该值。表1总结了其余情况下的最大误差。根据表1可知，仅在情况2、3和4这三种情况下量化与采样环节会引起误差，但这三种情况仅出现在输出电流穿越零点附近时，在整个输出波形周期内占比很小，且由于死区时间一般较短，因此量化与采样对所提方法造成的误差一般可忽略。
表1 不同情况下由量化采样和传输延时引起的误差
Tab.1 Errors caused by quantization sampling and transmission delay in different Cases
情况量化与采样引起的最大误差传输延时引起的误差 100 20.25td0 30.25td0 40.25td0 500
数字隔离器件通常存在不可避免的传输延时，随着开关频率的提高，传输延时相对于死区时间和开关周期的比例逐渐增大，可能会引起误差。但由于所提方法数字信号输入与PWM输出结构的对称性，消除了传输延时的影响。以情况1为例，图10展示了存在数字隔离器传输延时情况下的各波形。其中t1代表数字隔离器的传输延时时间。
图10 考虑传输延时时情况1的各波形
Fig.10 Waveforms in Case 1 when transmission delay is considered
当us=0.75Udc时，经过传输延时t1后，数字调制器接收到高电平开始计数。当计数结果等于参考量1时，RS触发器输出低电平；经过传输延时t1后开关管S1关断；经过死区时间td后，桥臂输出波形us变低；再经过传输延时t1后，数字调制器接收到低电平停止计数。因此，us的面积为
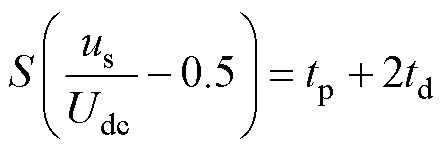（25）
采样生成的数字信号的面积为
（26）
二者面积相等，因此，传输延时不会产生误差。表1同样总结了其余情况下由传输延时引起的误差。
上述分析均认为采样间隔足够小，使得黎曼和能够完全代替积分。然而一般的数字控制器时钟频率仅在100～200 MHz之间，当开关频率较高时，比值N可能低于1 000，因此数字调制器接收到的数字信号无法完全复现桥臂输出波形，势必引起误差。
图11为考虑采样时钟频率有限时情况1的各波形，由图11可见，当采样时钟频率有限时，数字信号的面积与Ud的面积存在差异，二者面积分别为
（27）
（28）
式中，Dt为采样时钟的周期。数字信号与Ud的面积误差为
（29）
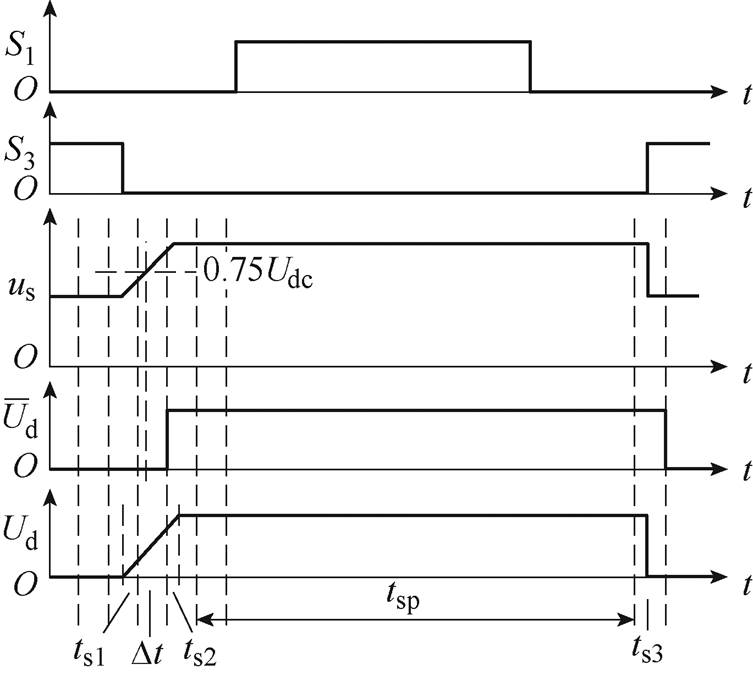
图11 采样时钟频率有限时情况1的各波形
Fig.11 The waveforms of Case 1 in the finite sampling clock
当且仅当ts2=Dt，ts1=0，ts3=-Dt时面积误差最大，最大误差为
（30）
其他情况下的分析与情况1类似，由于采样时钟的周期较小，因此由采样时钟引起的误差几乎可以忽略不计。由于所提的调制方法用于代替原有调制，因此所提方法的采样时钟可直接使用原有控制器的时钟，此时时钟频率对输出调节精度的影响与传统调制方法一致，不再分析。
本文所提方法仅有开关时钟分频倍数M需要设计：一方面M影响稳态时电容电压纹波；另一方面M影响电容电压平衡暂态的时间，需要折中考虑。
首先是基于电容电压平衡暂态时间的考虑。图12为电容电压平衡暂态过程中，一个开关周期内的关键波形。其中
为对电容电压平衡状态的计数值，MTs为当前开关周期内的值，DtC为所提方法在该开关周期内为保证电容电压平衡自动生成的桥臂波形偏移时间。由于处于电容电压暂态平衡，电容电压的偏差是单方向的，因此计数值单调上升。根据对图5的分析，该周期的值MTs会同时影响全桥DCTLI两个桥臂的占空比，因此两个桥臂输出波形的偏移时间总计为
（31）
由于此时单调上升，因此每个输出波形周期内每个开关周期DtC可表示为随时间变化的函数，即
（32）
图12 电容电压平衡暂态过程关键波形
Fig.12 Key waveforms of capacitor voltage balance transient
类似1.2节的分析，若忽略电感电流纹波，可得一个输出波形周期内电容电压的变化量DUC1m为
（33）
因此电容电压平衡暂态过程的时间tCb为
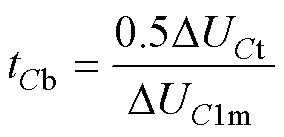（34）
式中，DUCt为电容电压不平衡的总差值。在这种情况下M的选取准则即为tCd≥tCb，tCd为期望的暂态时间。为简化计算，令正弦信号在半个周期内的平均值0.636代替式（33）中的正弦函数，因此DUC1m可近似为
（35）
设计M取值的另一个需要考虑的因素是稳态时的电容电压纹波。电容电压纹波最大的情况即为在一个输出波形周期内电容电压平衡状态计数器单调计数，在下一个周期向另一个方向单调计数。此时电容电压纹波DUCr最大为DUC1m，因此，M的选取要保证最大的DUC小于设计期望的电容电压纹波。
由于更快的电容电压平衡暂态意味着更大的稳态纹波，因此M的选取需折中考虑，一般取电容电压平衡状态计数器计数最大值小于5%KN即可。
以全桥结构DCTLI对图7所示的数字调制方法进行了仿真和实验验证，仿真与实验参数见表2。功率开关管采用GaN MOSFET，数字调制方法由Xilinx公司的spartan6型FPGA实现，同样可以由含可编程逻辑单元的DSP来实现。由于所提出的方法与控制系统其他部分无关，因此验证所提方法时系统采用开环控制，开环给定调制比为0.6。
表2 仿真与实验参数
Tab.2 Simulation and experimental parameters
参 数数 值(型号) 直流电源电压Udc/V270 电容C1, C2/mF1 000 开关频率fs/kHz200 采样频率fsamp/MHz200 输出滤波电容Cf/mF2.2 GaN开关管INN650DA140A 比较器LTC6752 死区时间td/ns200 开关时钟分频倍数M20 输出波形频率fo/Hz400 输出滤波电感Lf/mH450 输出负载R/W30 开关管结电容Cd/pF＜220 死区延时不匹配/ns100
由于逆变器的母线电容会存在二倍输出波形频率的纹波，纹波最大为
（36）
选取最大母线电容纹波为小于0.5%的电源电压，可得母线电容大于477 mF，因此C1、C2应大于954 mF，选取1 000 mF的常用型号。
图13给出了采用所提调制方法时参考信号与的累加值之间的差异。桥臂输出波形的平均值能够跟踪参考信号，消除了死区时间的影响。
图13 所提调制方法参考信号和数字信号累加值对比
Fig.13 Comparison of the cumulative value of the digital signal and the reference under proposed methods
图14对比了采用所提调制方法和典型的基于电流极性的死区时间补偿方法时的输出电压波形。图14a为基于电流极性判断的死区时间补偿方法，电流传感器设置带宽为50 kHz，符合常见参数。该方法受限于电流采样精度且无法补偿开关暂态，因此补偿效果不如图14b中的所提调制方法。
图15给出了电容电压平衡过程时的电容电压波形。图15a为采用所提方法，电容电压不平衡值为DUC=10 V，死区延时不匹配分别为100、200和400 ns的电容电压波形。所提方法在400 ns的不匹配时间下仍能保证电容电压平衡。采用额外电路的电容电压平衡方法[29]作为对比展示在图15b中，额外的储能电感为470 mH。尽管采用额外电路时电容电压的平衡过程速度快于所提方法，但本文所提方法具有无需额外电路、体积小、易于实现，且平衡过程比较平稳的优势。此外，图15c给出了DUC=70 V时的电容电压波形，表明在电容电压不平衡程度非常严重时，所提方法依然有效。
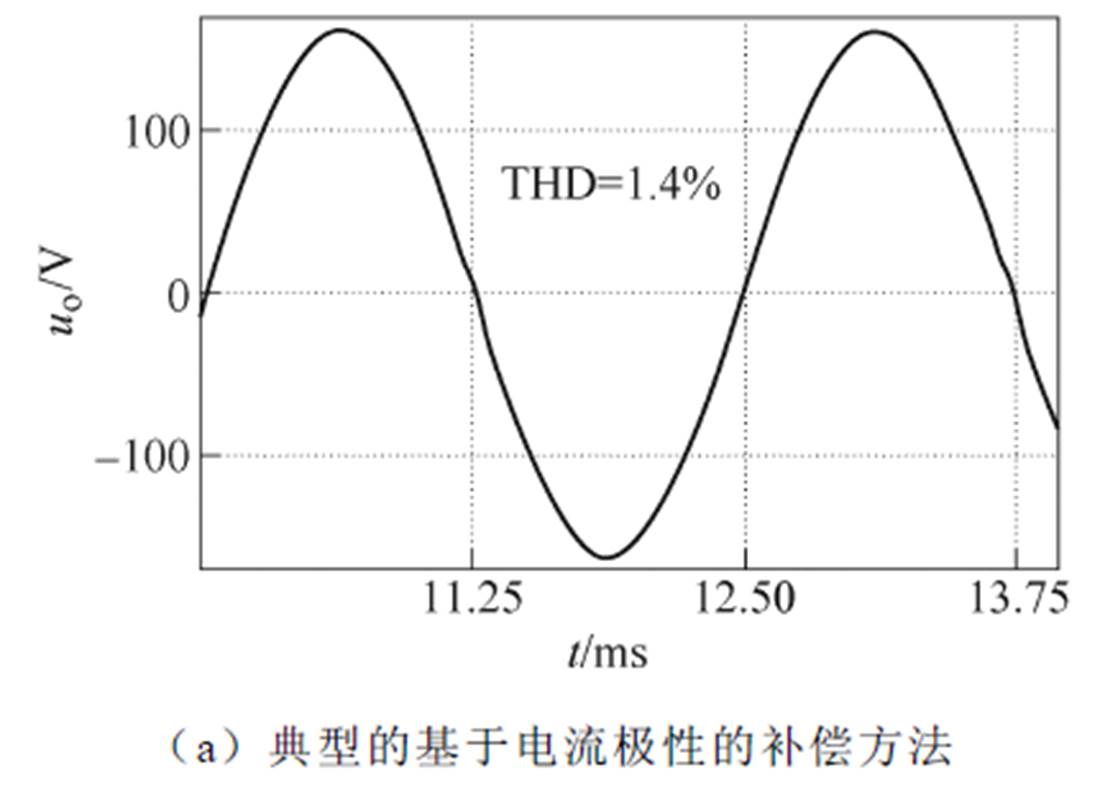
图14 不同补偿方法下输出电压波形对比
Fig.14 Comparison diagram of output voltage waveform under different compensation methods
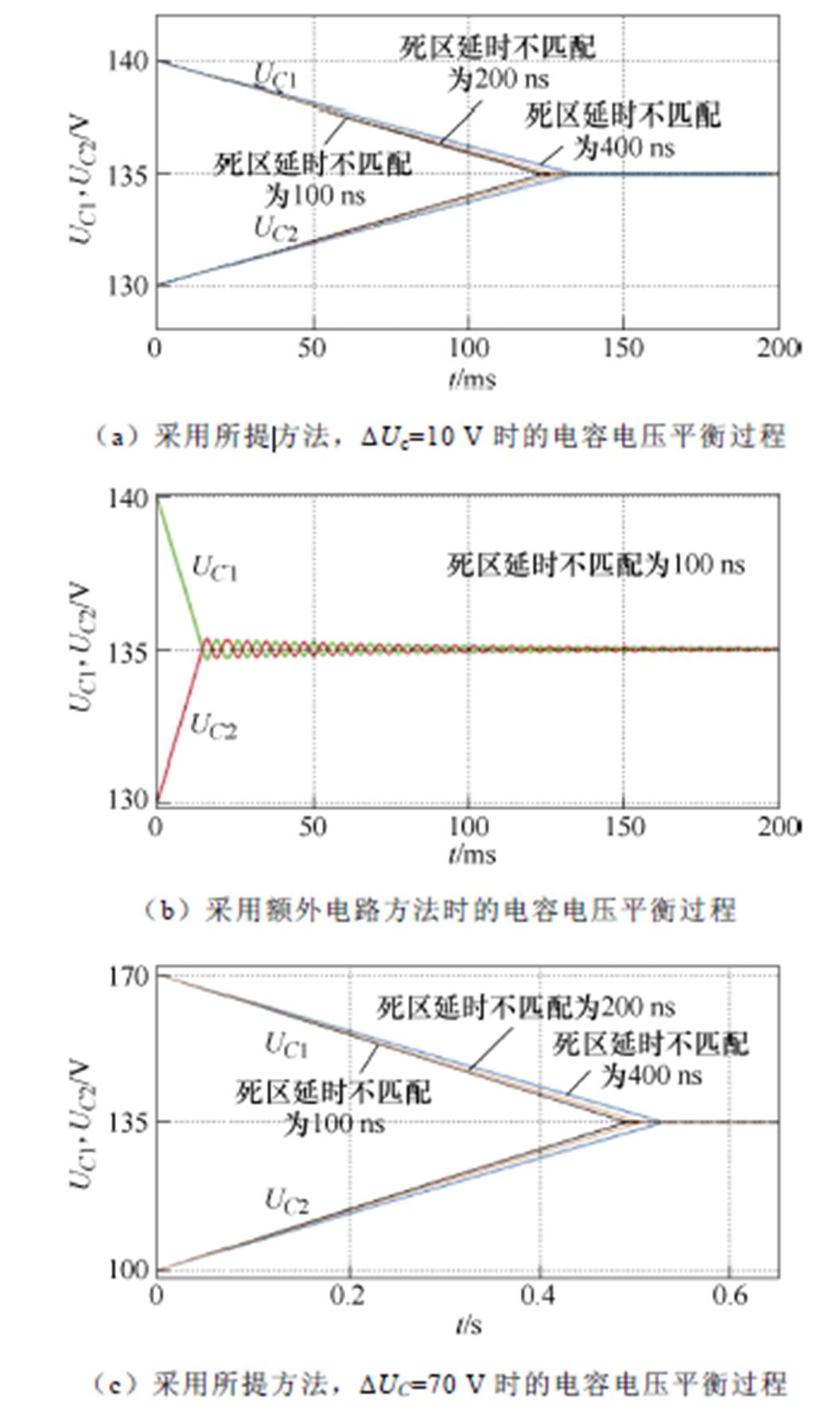
图15 电容电压平衡暂态过程波形
Fig.15 Waveforms of capacitor voltage balance process
根据2.2节的分析和图14、图15的结果，表3和表4分别总结了所提调制方法与其他典型的死区时间补偿方法和电容电压平衡方法的差异与优势。
表3 不同死区时间补偿方法对比
Tab.3 Comparison of dead-time compensation methods
指标所提方法基于电流极性的方法[7-12]基于额外控制的方法[13-15]死区时间消除方法[16-18] 传感器无需要需要 需要[17]，不需要[16, 18] THD较高中中高 灵活性高较高中低 算力需求无低[7]，较高[8-12]高较低 开关频率高中低较高 器件数量较高低低中 器件尺寸低中中高
表4 不同电压平衡方法对比
Tab.4 Comparison of various voltage balancing methods
指标所提方法基于CBPWM[22-24]基于SVPWM[25-26]额外电路[29-30] 灵活性高较高中高 算力需求无较高高中 开关频率高较低较低中 平衡速度低中中高 额外器件中低低高
相比之下，所提方法在灵活性、实现体积、算力需求及可实现的开关频率上均具有优势。
实验平台如图16所示，实现所提调制方法共用电阻20个，比较器5个，数字隔离器2个，总共占用面积为271 mm2，尺寸小，有利于提高功率密度。
图16 基于GaN的DCTLI实验平台
Fig.16 DCTLI experimental platform based on GaN
图17a给出了当采用传统调制方法时，负载从50 W 切换到19 W 的输出电压电流波形，输出波形始终存在失真，且失真程度随着负载电流的增大而加重。图17b为采用所提调制方法时的情况，不论负载电流如何变化，输出波形质量均较好，表明所提方法在负载范围内均能有效地补偿死区及开关暂态对输出波形的影响。此外，图17b表明在负载切变时，所提调制方法能够保持电容电压平衡。
图17 采用不同调制方法负载切变时的波形
Fig.17 Waveforms of step load with different modulations
图18为额定负载时直流电源电压Udc从270 V变化到240 V时的输出电压和电容电压波形，由于采用开环固定调制比，因此输出波形的幅值也发生了变化，但输出电压波形的总谐波畸变率（Total Harmonic Distortion, THD）几乎不变，表明无论直流电源电压如何变化，所提方法中的桥臂输出波形采样结构均能够正确地将桥臂输出波形信息转换为数字信号，进而能够有效补偿死区及开关暂态对输出波形的影响。电容电压波形也表明，输入电压变化时所提调制方法能够保持电容电压平衡。
图19为不同调制比时的输出电压、电流和电容电压波形。根据3.1节的分析，图2中情况2、情况3及情况4这三种情况下量化与采样环节会在所提方法中引入误差，当调制比较小时，这三种情况在整个输出波形周期内的占比较大，因此图19a的输出波形在过零点处存在失真，但THD也仅为2.48%，所提方法仍具有较好的补偿效果。由于实际PWM信号的占空比不能大于1，因此在所提方法中最大可实现的调制比为1-td/Ts，考虑到驱动等环节的影响，因此图19d给出了调制比为0.94的情况。图19表明，调制比不同时，所提方法均能够良好补偿死区时间和开关暂态的影响，并保证电容电压平衡。
图18 直流电源电压变化时的输出电压波形
Fig.18 The output voltage waveforms as the Udc changes
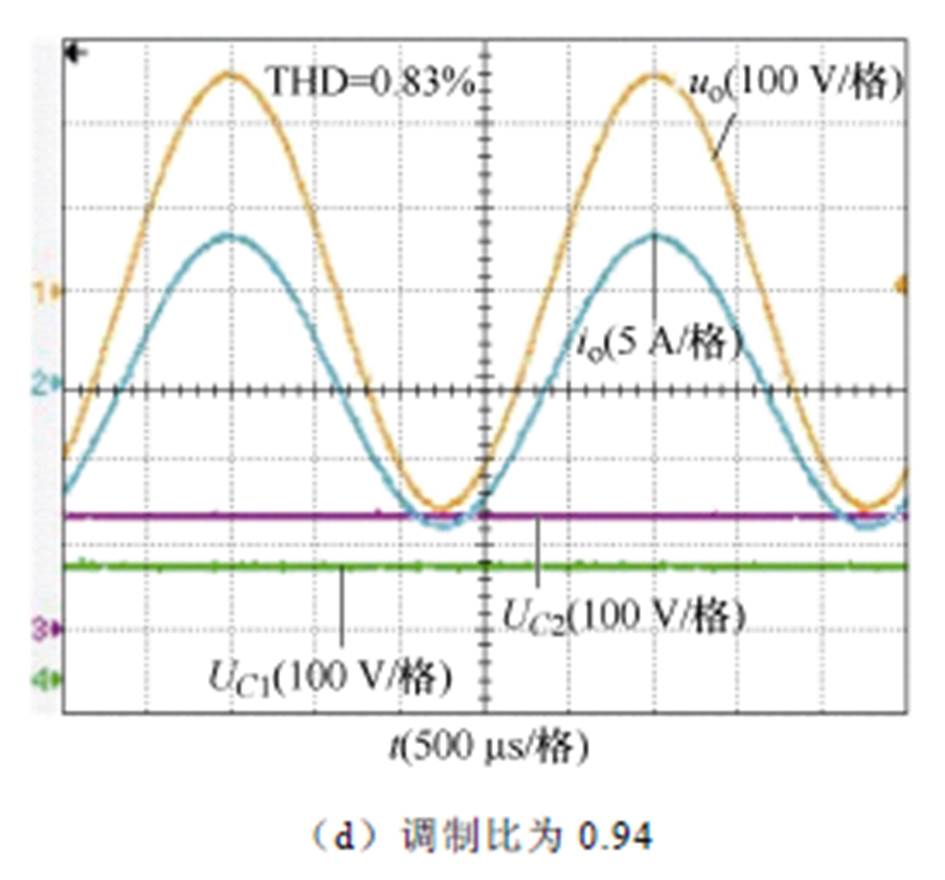
图19 不同调制比时的输出电压电流波形
Fig.19 Output voltage and current waveforms at different modulation ratios
图20分别给出了死区时间为200、300和400 ns时的输出电压波形和电容电压波形。死区时间不同时所提调制方法均能够保证电容电压平衡，且对死区时间和开关暂态均具有良好的补偿效果。
图21给出了不同开关频率下的输出电压和电容电压波形。不同开关频率下保持死区时间与开关周期的比值不变，并保持输出滤波器截止频率小于10%的开关频率。图21表明，不论开关频率较低还是较高，所提调制方法均能有效补偿死区时间和开关暂态的影响，并能保持电容电压平衡。由于低开关频率下，开关频率与输出波形频率的比值较低，开关谐波较难滤除，因此THD略有上升。
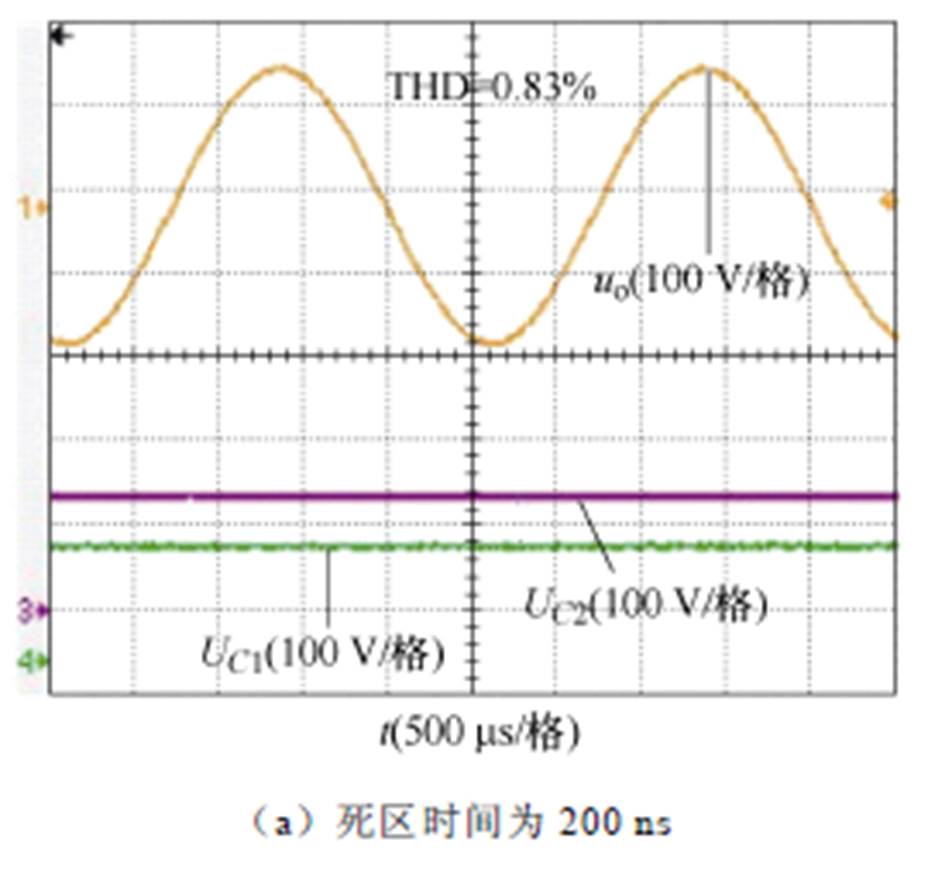
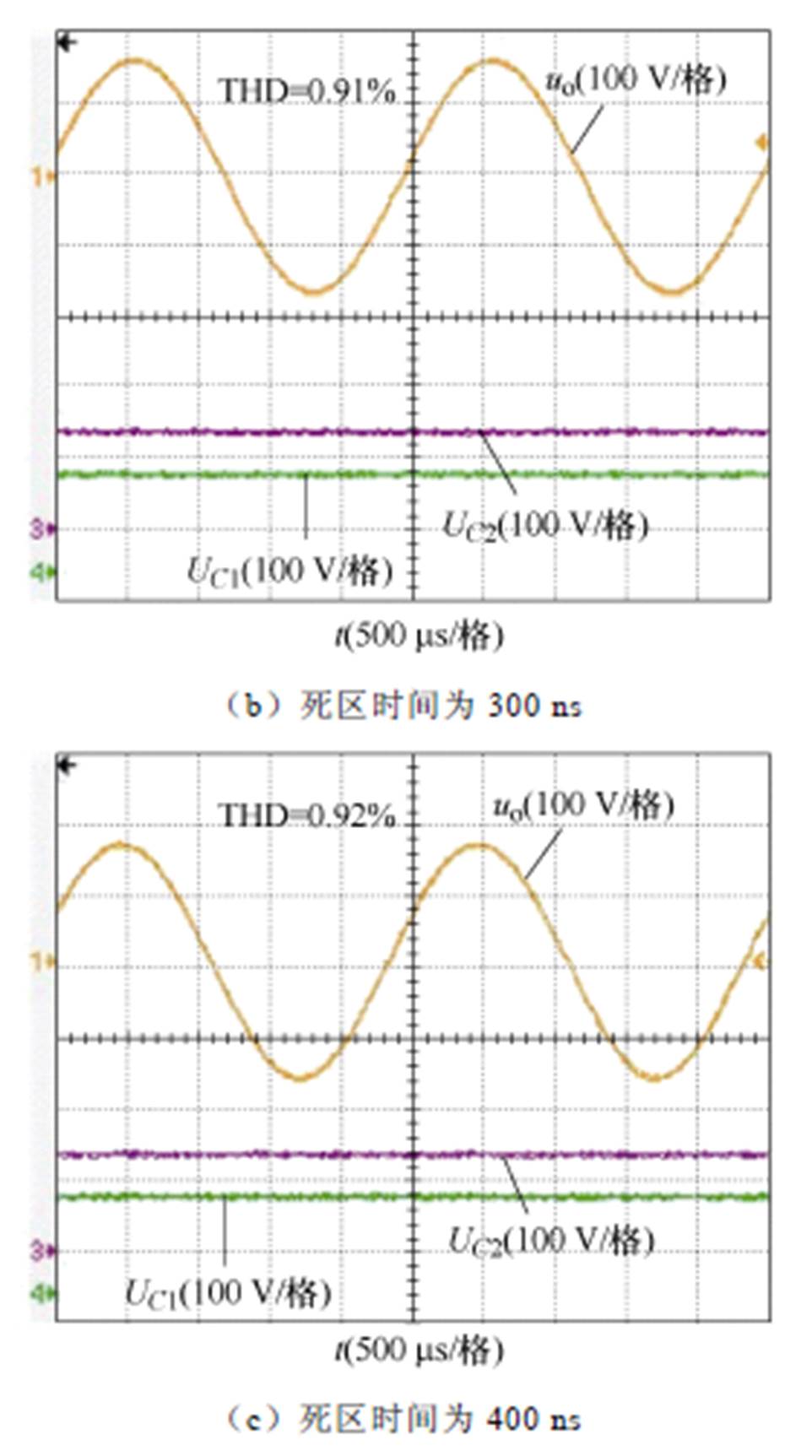
图20 不同死区时间下的输出电压和电容电压波形
Fig.20 Output voltage and capacitor voltage waveforms under different dead time
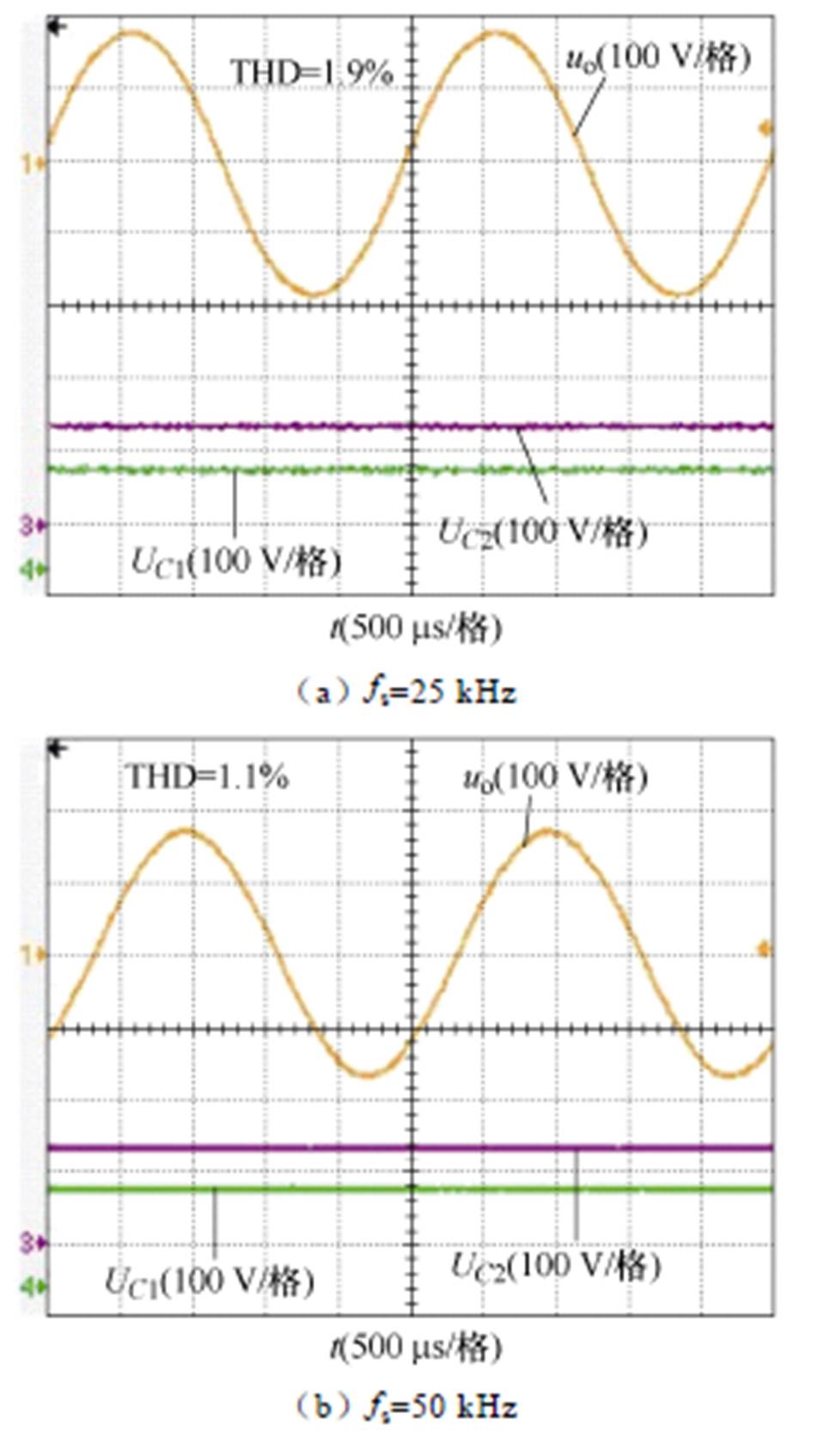
图21 不同开关频率下的输出电压和电容电压波形
Fig.21 Output voltage and capacitor voltage waveforms under different switching frequencies
为了验证所提方法在不同死区延时不匹配情况下的有效性，实验验证了死区延时不匹配分别为100、200和300 ns的输出电压波形和电容电压波形。300 ns的死区延时不匹配已经超出了实际中可能出现的情况。图22表明，即使死区延时不匹配达到300 ns，所提调制方法仍然能够有效保持电容电压平衡，同时保证输出波形质量。
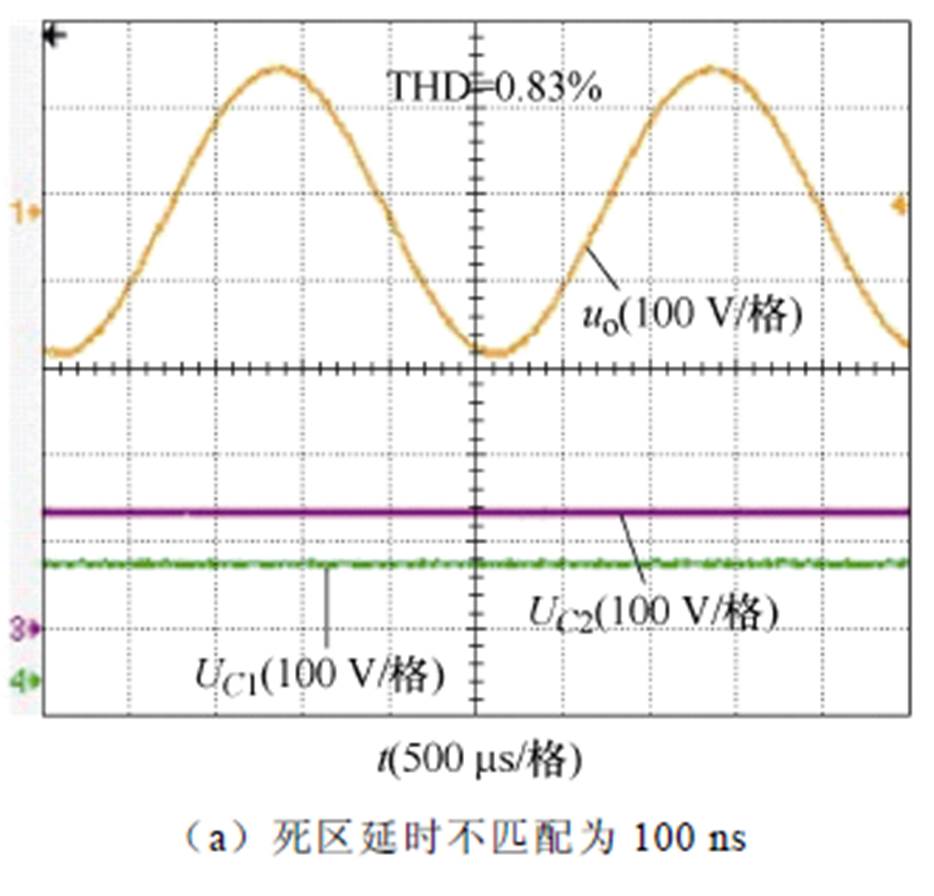
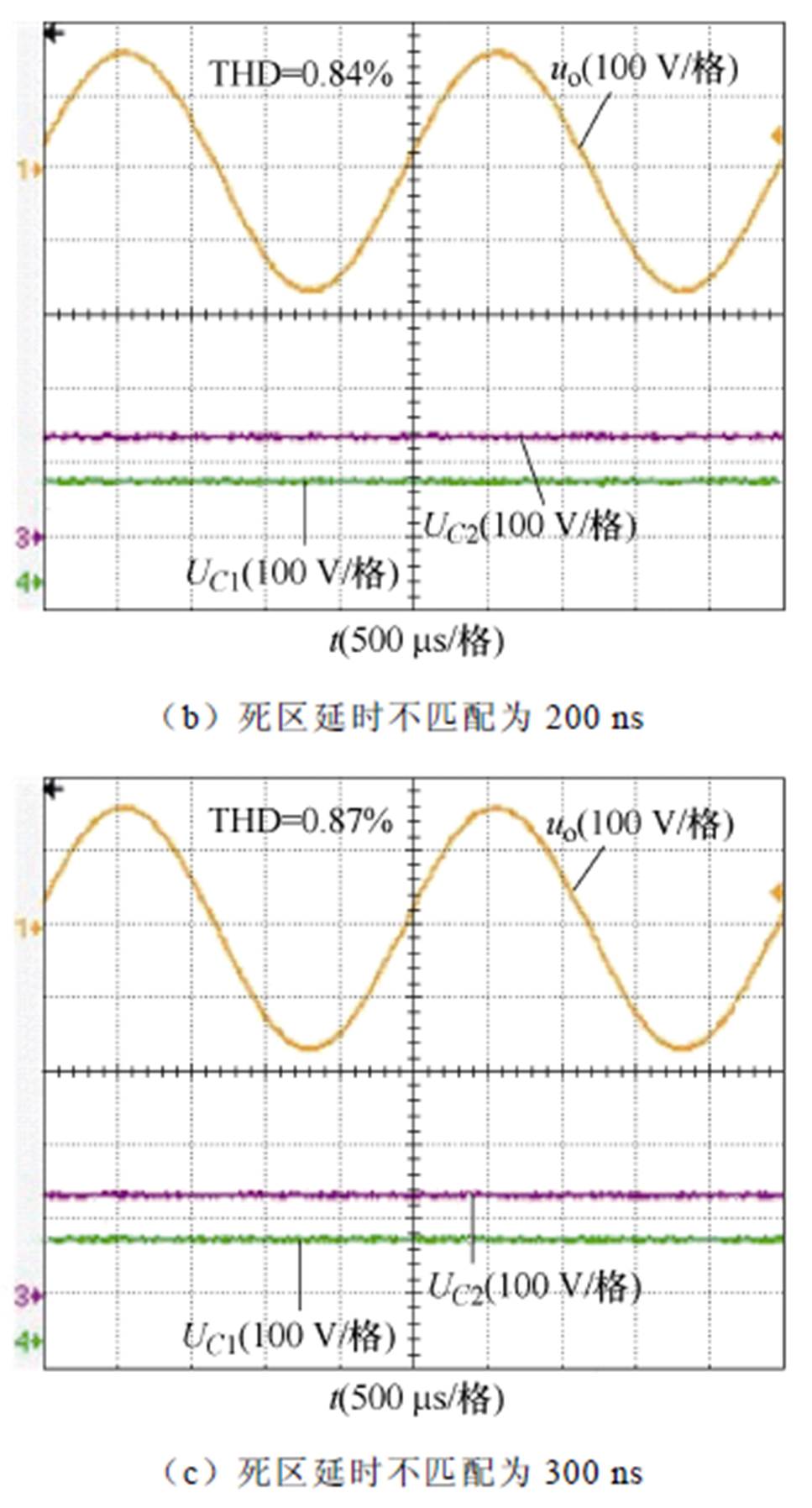
图22 不同死区延时不匹配下的输出电压和电容电压波形
Fig.22 Output voltage and capacitor voltage waveforms under different dead time delay mismatches
图23a给出了当负载为20 mH时的输出电压电流和电容电压波形。由于系统为开环固定调制比，在非阻性负载时输出电压波形受滤波参数、开关谐波及负载情况影响，无法完全说明所提调制方法对死区时间的补偿效果，因此图23b给出了桥臂输出波形的频谱。由于测试设备仅测到21次谐波，开关谐波成分被内部数字滤波器滤除，因此图23b仅包含基波及其谐波成分。图23b中的谐波成分占比很小，表明了所提调制方法在感性负载时仍具有良好的死区时间补偿效果。此外，在感性负载下所提方法能够有效平衡电容电压。
图23 感性负载下的输出电压电流及电容电压波形
Fig.23 Output voltage current and capacitance voltage waveforms under inductive load
图24给出了当负载为8 mF时的输出电压电流和电容电压波形及桥臂输出波形的频谱，表明容性负载下所提方法依然可以有效补偿死区时间及开关暂态的影响，并保持电容电压平衡。
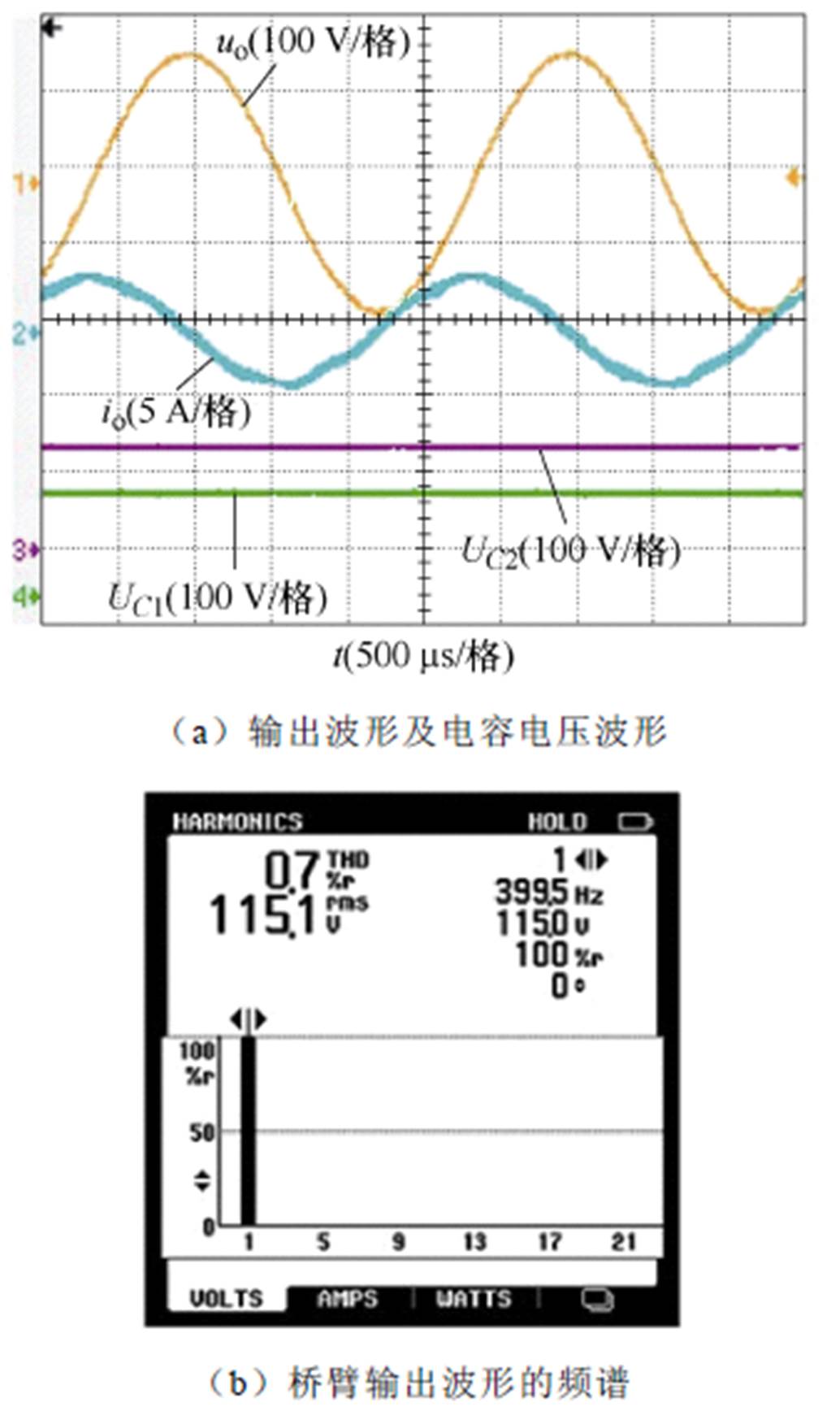
图24 容性负载下的输出电压电流及电容电压波形
Fig.24 Output voltage current and capacitance voltage waveforms under capacitive load
此外，图25a给出了输出带全桥整流并接4.7 mF电容并联30 W 电阻时的负载电压、逆变器输出电流及电容电压波形，图25b给出了桥臂输出波形的频谱。图25b表明，所提方法在整流性负载下仍能有效补偿死区时间及开关暂态的影响。同时，电容电压波形表明整流性负载下，所提调制方法能够保证电容电压平衡。
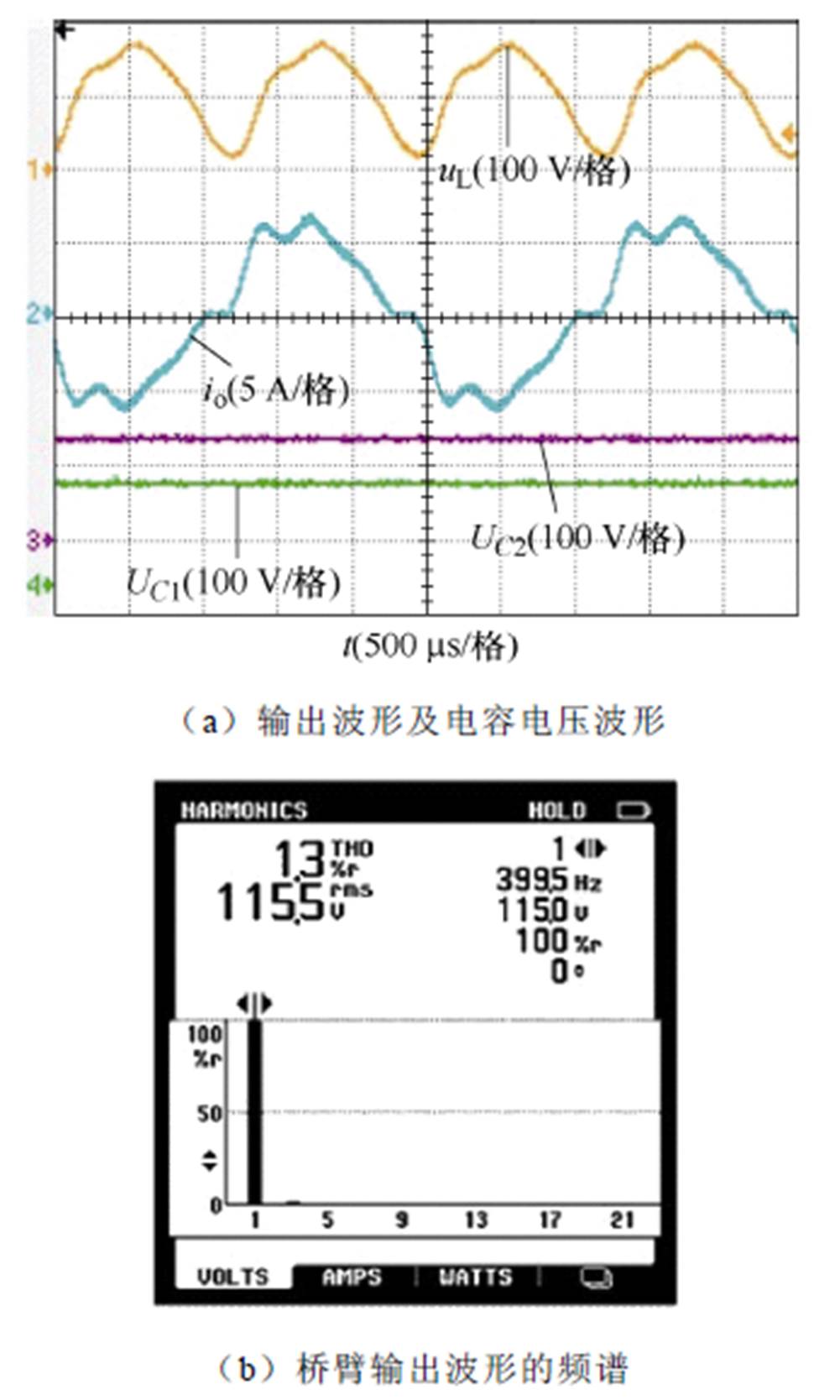
图25 整流性负载下的输出电压电流及电容电压波形
Fig.25 Output voltage current and capacitance voltage waveform under rectifier load
不同的电容电压平衡方法均能有效保持电容电压平衡，表5对比了不同方法实现所需的计算时间和实现尺寸。所提方法由数字电路实现，无需计算，因此可适用于更高开关频率，且具有较小的实现尺寸，因此可实现更高功率密度。
表5 不同电压平衡方法的指标对比
Tab.5 Comparison of various voltage balancing methods
指标所提方法CBPWMSVPWM额外电路 计算时间/ms0＞2[33]＞24[26]0.5 实现尺寸/mm2121137662453
图26总结并对比了不同工况下，无死区补偿、典型的基于电流极性的补偿方法和所提调制方法下的输出电压波形的THD。由于电流检测精度的原因，随着开关频率的升高，基于电流极性的死区时间补偿效果会降低。而所提方法无需电流检测，且能补偿开关暂态的影响，因此在高开关频率下仍具有良好效果。同样地，由于调制比较低时，电流极性的检测噪声增大，基于电流极性的死区补偿部分在低调制比下效果较差，而所提方法仍具有良好效果。由于基于电流极性的补偿方法需要知道死区时间的数值，而存在死区延时不匹配时，实际的死区时间与理论值不同，因此基于电流极性方法的效果也会随死区延时不匹配的上升而下降。但所提方法无需预先知道实际电路存在的死区时间，因此补偿效果几乎不变。图26的对比表明了在不同工况下，所提方法的效果均优于典型的死区时间补偿方法。
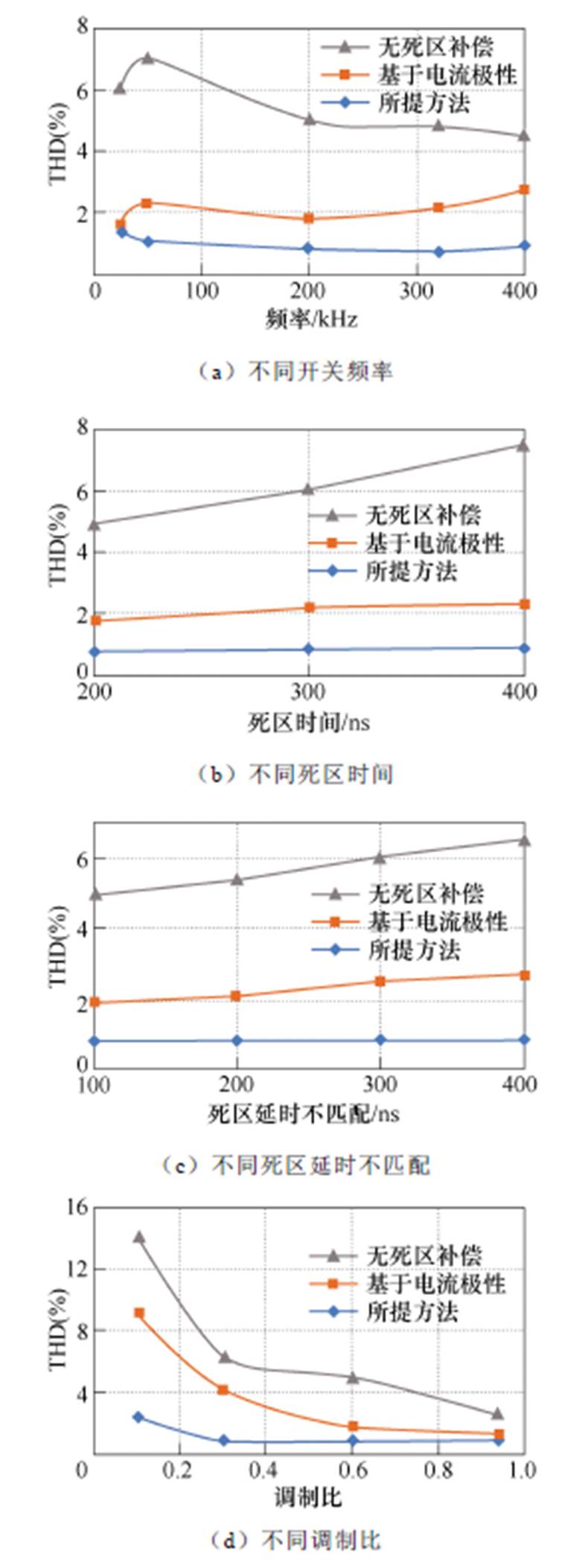
图26 不同工况下不同方法输出电压波形的THD的对比
Fig.26 Comparison of THD for output voltage waveforms of different methods under different operating conditions
本文提出了一种可以同时实现死区时间补偿和电容电压平衡的数字调制方法，该方法相比于传统方法，无需额外的电压电流传感器，无计算需求，可用于高开关频率，同时易于实现，具有明显的优势。同时，本文详细阐述了所提方法的原理与实现方法，并对引起误差的因素进行了分析。仿真与实验表明，所提调制方法在不同开关频率、死区时间及负载等情况下均能有效补偿死区时间及开关暂态的影响，改善输出电压波形质量，同时能够有效抑制电容电压的不平衡。本文的方法除采样环节外，均为全数字实现，易于实现和集成在现代微处理器中，且可拓展到其他多电平变换器中。
参考文献
[1] Khan M N H, Forouzesh M, Siwakoti Y P, et al. Transformerless inverter topologies for single-phase photovoltaic systems: a comparative review[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 805-835.
[2] 王金平, 刘斌, 董浩, 等. 中点钳位型三电平逆变器基于调制波分解的调制策略[J]. 电工技术学报, 2023, 38(12): 3221-3233.
Wang Jinping, Liu Bin, Dong Hao, et al. A modulation strategy based on modulation wave decomposition for neutral point clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3221-3233.
[3] 许水清, 黄文展, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开路故障诊断[J]. 电工技术学报, 2023, 38(4): 1010-1022.
Xu Shuiqing, Huang Wenzhan, He Yigang, et al. Open-circuit fault diagnosis method of neutral point clamped three-level grid-connected inverter based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1010- 1022.
[4] 卫炜, 高瞻, 赵牧天, 等. 基于切换调制波的三电平有源中点钳位逆变器优化容错技术研究[J]. 电工技术学报, 2022, 37(15): 3818-3833.
Wei Wei, Gao Zhan, Zhao Mutian, et al. Research on optimal fault-tolerant technique for three-level active- neutral-point-clamped inverter based on switching modulation wave[J]. Transactions of China Electro- technical Society, 2022, 37(15): 3818-3833.
[5] Zhang Li, Lou Xiutao, Li Chushan, et al. Evaluation of different Si/SiC hybrid three-level active NPC inverters for high power density[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(8): 8224-8236.
[6] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead- time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Elec- trotechnical Society, 2021, 36(8): 1671-1680.
[7] Jeong S G, Park M H. The analysis and compensation of dead-time effects in PWM inverters[J]. IEEE Transactions on Industrial Electronics, 1991, 38(2): 108-114.
[8] 倪瑞政, 李庭, 陈杰, 等. 一种脉冲式死区补偿方法的研究[J]. 电工技术学报, 2019, 34(增刊2): 553-559.
Ni Ruizheng, Li Ting, Chen Jie, et al. Research on a pulse dead zone compensation method[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(S2): 553-559.
[9] Li Baojin, Xu Jinbang, Ye Jie, et al. A new model- based dead-time compensation strategy for cascaded H-bridge converters[J]. IEEE Transactions on Indu- strial Electronics, 2023, 70(4): 3793-3802.
[10] Diao Naizhe, Sun Xianrui, Song Chonghui, et al. A multimodulation times SVPWM for dead-time effect elimination in three-level neutral point clamped converters[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(7): 5476-5485.
[11] 赵牧天, 葛琼璇, 张波, 等. 高速磁悬浮牵引系统大功率三电平整流器特定谐波消除脉宽调制策略[J]. 电工技术学报, 2022, 37(16): 4180-4192.
Zhao Mutian, Ge Qiongxuan, Zhang Bo, et al. Selective harmonic elimination pulse width modu- lation for high power three-level rectifier of high- speed maglev traction system[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4180- 4192.
[12] Yan Qingzeng, Yuan Xinbo. A double-modulation- wave PWM for dead-time-effect elimination and synchronous rectification in SiC-device-based high- switching-frequency converters[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13500-13513.
[13] Yuan Jiaxin, Zhao Zhen, Chen Baichao, et al. An immune-algorithm-based dead-time elimination PWM control strategy in a single-phase inverter[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3964-3975.
[14] Yang Yongheng, Zhou Keliang, Wang Huai, et al. Harmonics mitigation of dead time effects in PWM converters using a repetitive controller[C]//2015 IEEE Applied Power Electronics Conference and Expo- sition (APEC), Charlotte, NC, USA, 2015: 1479- 1486.
[15] 周世超, 刘侃, 丁荣军, 等. 基于谐波分离的逆变器非线性因素直接提取和补偿方法[J]. 中国电机工程学报, 2021, 41(22): 7763-7772.
Zhou Shichao, Liu Kan, Ding Rongjun, et al. Direct extraction and compensation of inverter nonlinearity based on harmonic separation[J]. Proceedings of the CSEE, 2021, 41(22): 7763-7772.
[16] Chen Lihua, Peng Fangzheng. Dead-time elimination for voltage source inverters[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 574-580.
[17] Yan Qingzeng, Xiao Langtao, Yuan Xinbo, et al. A double-modulation-wave PWM with reduced depen- dency on current polarities for dead-time-effect elimination in three-level T-type converters[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8413-8427.
[18] Ali Khan A, Ali Khan U, Ahmed H F, et al. Improved NPC inverters without short-circuit and dead-time issues[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2180-2190.
[19] Ye Jie, Huang Yukai, Huang Songtao, et al. An accurate dead time compensation method for SPWM voltage source inverters[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 4894-4908.
[20] 董志强, 王琛琛, 周明磊, 等. 基于SHEPWM的三电平三相逆变器中点电位主动平衡控制策略[J]. 电工技术学报, 2024, 39(4): 1147-1158.
Dong Zhiqiang, Wang Chenchen, Zhou Minglei, et al. Active NP voltage balance control strategy for three-level three phase inverter under SHEPWM[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1147-1158.
[21] du Toit Mouton H. Natural balancing of three-level neutral-point-clamped PWM inverters[J]. IEEE Transactions on Industrial Electronics, 2002, 49(5): 1017-1025.
[22] 陈仲, 许亚明, 那显龙. 基于中点电流的三电平NPC逆变器电容电压均衡控制分析[J]. 中国电机工程学报, 2016, 36(19): 5308-5317, 5413.
Chen Zhong, Xu Yaming, Na Xianlong. Analysis of a new voltage balance method for three-level NPC inverters based on neutral-point current[J]. Pro- ceedings of the CSEE, 2016, 36(19): 5308-5317, 5413.
[23] Wang Zhiqiang, Cui Fuyao, Zhang Guozheng, et al. Novel carrier-based PWM strategy with zero- sequence voltage injected for three-level NPC inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1442-1451.
[24] Zhu Jianxin, Wu Hongfei, Cao Li, et al. Modified CBPWM-controlled semi-two-stage AC-DC converter for low-frequency pulsed load[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 1470- 1482.
[25] 周冠卿, 张国荣, 解润生, 等. 改进的三电平逆变器变虚拟空间矢量调制策略[J]. 电力系统自动化, 2023, 47(1): 172-182.
Zhou Guanqing, Zhang Guorong, Xie Runsheng, et al. Improved variable virtual-space-vector modulation strategy for three-level inverter[J]. Automation of Electric Power Systems, 2023, 47(1): 172-182.
[26] Zorig A, Barkat S, Sangwongwanich A. Neutral point voltage balancing control based on adjusting application times of redundant vectors for three-level NPC inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(5): 5604-5613.
[27] Lee J S, Yoo S, Lee K B. Novel discontinuous PWM method of a three-level inverter for neutral-point voltage ripple reduction[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3344-3354.
[28] 孙青松, 吴学智, 唐芬. 考虑中点电位平衡的三电平逆变器断续脉宽调制策略研究[J]. 中国电机工程学报, 2017, 37(增刊1): 177-185.
Sun Qingsong, Wu Xuezhi, Tang Fen. Three-level inverter discontinuous pulse-width modulation strategy considering neutral point potential balance[J]. Proceedings of the CSEE, 2017, 37(S1): 177-185.
[29] Shukla A, Ghosh A, Joshi A. Flying-capacitor-based chopper circuit for DC capacitor voltage balancing in diode-clamped multilevel inverter[J]. IEEE Transa- ctions on Industrial Electronics, 2010, 57(7): 2249- 2261.
[30] Hasegawa K, Akagi H. A new DC-voltage-balancing circuit including a single coupled inductor for a five-level diode-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 2011, 47(2): 841-852.
[31] Wodajo E T, Elbuluk M E, Choi S, et al. Three parts modulation and hybrid DC capacitor voltage balancing for a single-phase two-leg five-level NPC inverter[J]. IEEE Transactions on Industrial Elec- tronics, 2023, 70(7): 6765-6775.
[32] Tan Guojun, Deng Qingwei, Liu Zhan. An optimized SVPWM strategy for five-level active NPC (5L- ANPC) converter[J]. IEEE Transactions on Power Electronics, 2013, 29(1): 386-395.
[33] Chen Fa, Qiao Wei, Wang Hongmei, et al. A simple zero-sequence voltage injection method for carrier- based pulsewidth modulation of the three-level NPC inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4687-4699.
Abstract With the development of wide bandgap semiconductor devices, high power density can be achieved by high switching frequencies combined with diode-clamped three-level inverters (DCTLI) and wide bandgap semiconductor devices like gallium nitride (GaN) and silicon carbide (SiC). However, problems that are well solved at low switching frequencies may be difficult to solve at high switching frequencies.
In DCTLI, there are two main problems: the influence of dead time and the capacitor voltage balance. Dead time introduces harmonics into the output waveform, degrading the output waveform quality. Unbalanced capacitor voltages reduce converter reliability and even damage transistors. In addition, delay mismatches associated with dead time affect capacitor voltage balance. However, limited by computing power requirements, existing methods are challenging to achieve good results at high switching frequencies, and the additional sensors required are not conducive to realizing high power density.
Therefore, the effects of dead time on the output waveform and capacitor voltage balance are analyzed. Then, a digital modulation method without additional sensors is proposed for high switching frequencies. The resistor divider network introduces the output voltage information of the bridge. The driving signal is generated by making the count value of the output voltage of the bridge equal to the reference signal. Accordingly, the average value of the inverter bridge output waveform is forced to track the reference signal, so dead time effects are compensated directly in the modulator section. The capacitor voltage balance state is collected through the resistor voltage dividing network, and the balance state is accumulated through the counter. As a result, the modulator obtains the degree of capacitor voltage imbalance and modifies the reference signal to balance the capacitor voltage.
In addition, the effects of the quantization and sampling, the propagation delay of the digital isolator, and the finite sampling clock on the proposed method are analyzed. It is shown that these factors have little impact on the proposed method. Design criteria for the capacitor voltage balancing frequency division coefficient M are given based on trade-off considerations for capacitor voltage balancing speed and steady-state ripple.
Finally, the proposed method is compared with traditional dead time compensation and capacitor voltage balancing methods through simulations. The advantages and disadvantages of the proposed methods are summarized. The effectiveness of the proposed method is verified under different loads (resistive load, resistive step load, capacitive load, inductive load, and rectifier load) and different conditions (switching frequency, modulation ratio, dead-time delay mismatch, and dead time). Simulation and experiments show that the proposed method can effectively suppress the impact of dead time and maintain capacitor voltage balance, which is effective at high switching frequencies.
keywords：Three-level inverter, capacitor voltage balance, dead time compensation, digital modulation, output waveform distortion
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.231325
收稿日期 2023-08-16
改稿日期 2023-10-11
宁继超 男，1995年生，博士研究生，研究方向为高频逆变器先进调制与控制。E-mail: 18B906005@stu.hit.edu.cn
贲洪奇 男，1965年生，教授，博士生导师，研究方向为高频开关电源及其控制。E-mail: benhq@hit.edu.cn（通信作者）
（编辑 陈 诚）