抽水蓄能电机转子匝间短路无传感器检测方法
齐 鹏 李永刚 马明晗
(华北电力大学电气与电子工程学院 保定 0710032)
摘要 定位筋作为抽水蓄能电机的固有部件,其感应电动势可有效反映转子绕组匝间绝缘健康水平。首先,通过引入衰减系数法推导了杂散磁通与气隙主磁通之间的关系,进而获取了定位筋感应电动势在匝间短路状态下的特征谐波,据此提出了谐波幅值比阈值检测法;其次,根据抽水蓄能电站服役机组运行参数搭建了二维电磁仿真模型,分析了匝间短路故障前后定位筋感应电动势时/频域特征的演变规律,并验证了谐波幅值比阈值检测法的有效性;最后,结合信号调理装置对动模实验机组不同匝间短路程度下的定位筋感应电动势信息进行采集。监测结果表明,故障磁极所对应的定位筋感应电动势时域特征幅值及基频幅值均呈衰减趋势,其频谱分数次谐波幅值呈递增趋势,进一步计算多个周期信号的谐波幅值比,据此构建统计箱线图并设定故障检测阈值,可有效为转子绕组匝间绝缘故障防御提供指导。
关键词:抽水蓄能电机 转子绕组 匝间短路 定位筋感应电动势 谐波幅值比阈值检测法
0 引言
抽水蓄能发电作为可再生清洁能源的重要组成部分,近年来一直呈高速发展趋势。由于抽水蓄能发电系统具有复杂性、非线性等特点,致使其运行过程中可能受到某些因素的影响而出现异常,导致供电质量不佳[1-4]。转子绕组匝间绝缘劣化过程缓慢,早期微弱故障不易及时发现,仍是困扰现场运检的难题[5-6]。为了避免匝间短路故障而导致严重的经济损失,需对转子绕组健康状态及剩余寿命进行准确评估[7-8]。传统的转子绕组匝间短路故障诊断方法主要采用交流阻抗法[9]和重复脉冲法[10]等离线方式,需在机组计划检修期间将转子抽出进行测试,操作步骤较为复杂。此外,由于实际运行中的动态匝间短路往往随着转子静止而减轻或消失,离线检测方式无法实现动态匝间短路的有效辨识与定位。
利用抽水蓄能电机运行中的电磁、机械及温度等参量实现对转子绕组匝间绝缘健康状态的实时跟踪,成为近年来的研究热点[11]。同时,根据监测参量的不同,在线检测方法又可细分为电流特征分析法、振动特征分析法、温度特征分析法以及磁通特征分析法[12]。电流特征分析法主要根据电机励磁电流、定子电流的变化规律实现对转子绕组匝间绝缘状态的预判。文献[13]通过分析发电机组正常状态与匝间短路状态下励磁电流的变化规律,并设置故障报警阈值,可及时排除匝间短路故障隐患。文献[14]在分析多回路理论的基础上,提取发电机定子支路不平衡电流分数次谐波有效值,实现励磁绕组匝间短路状态识别。文献[15]提出将光纤电流传感器安装于抽水蓄能电机定子绕组同相支路,用于监测同相支路的不平衡电流,以此实现转子绕组匝间短路的辨识与预警。振动特征分析法主要集中于对电机定子机壳、定子铁心及定子绕组振动信号的传感与分析。文献[16]通过分析水轮发电机组定子机壳振动频谱的故障特征谐波,实现转子绕组运行状态的在线监测。文献[17]提出采用光纤布拉格光栅传感器在线监测水轮发电机定子绕组振动特征量的变化,可为机组健康状态评估提供参考。文献[18]提出一种分布式光纤振动传感技术用于监测发电机定子铁心振动信号,并通过分析故障特征谐波幅值的变化判断转子绕组健康状态。温度特征分析法则主要针对电机转子铁心和定子铁心的运行温度进行监测与分析。文献[19]通过发电机三维有限元模型仿真以及模拟机组实验分析了不同匝间短路位置对转子表面温升的影响。文献[20]通过在发电机定子齿部布置基于拉曼散射的分布式光纤温度传感器,并以热成像的方式展示定子温度变化,可为匝间短路预测性维护提供指导。磁通特征分析法主要是对电机的气隙磁通和杂散磁通进行实时监测。文献[21]通过在电机不同区域的定子槽中安装磁场探测线圈,用以检测气隙磁场的变化规律,并根据故障特征谐波阈值实现匝间短路故障诊断。文献[22]提出将霍尔传感器安装于水轮发电机定子齿部用以监测气隙磁通的变化,可有效跟踪转子绕组匝间绝缘健康状态。文献[23]通过在水轮发电机组定子轭外部布置多匝感应线圈采集杂散磁通感应电压信号,并采用时频分析法完成对匝间短路故障特征的挖掘提取。
以上检测方法的提出丰富了匝间短路在线监测技术的多样性,为抽水蓄能电站安全运维提供了更多可行性选择。但电流特征分析法易受负载波动影响,振动特征分析法和温度特征分析法不能直接用于匝间短路判别,只能作为现场运检的一种辅助手段,因此磁通特征分析法无疑成为匝间短路状态监测最为直接有效的途径。出于抽水蓄能电站安全运行考虑,电站运检人员普遍难以接受后期在机组内部加装传感器,因此基于气隙磁通检测的侵入式方法难以大范围推广,而基于杂散磁通的非侵入式检测方法则在工程应用方面展现出巨大优势。目前,已有学者将多匝线圈布置于电机定子机壳或定子铁心外部,用于采集径向杂散磁通感应电压信号[24]。但感应电压信号易受现场高频电磁干扰影响,且现有研究多采用数字信号处理方法对采样信号进行降噪,未见在信号采集前端加设信号调理装置,导致信号分析效果并不理想。同时考虑到电机径向杂散磁通信号较为微弱,若要准确捕捉其感应电压信号需绕制几百匝甚至上千匝线圈,无疑会导致制作成本的增加。
鉴于现有杂散磁通检测方法的弊端,在综合考虑现场在线监测精度需求与工程应用经济性的基础上,本文首次利用机组固有部件定位筋作为传感器,并结合本团队设计的信号调理装置,搭建了基于定位筋感应电动势的匝间短路非侵入式检测系统,以期实现机组健康状态的高精度数据感知。首先,根据现场机组的运行特点,分析推理了杂散磁场的形成机制,建立了定位筋感应电动势与杂散磁通密度之间的数学关系,揭示了故障程度与感应电动势谐波演变规律的对应机制,并据此提出了谐波幅值比故障诊断判据,为现场制定故障防御策略提供了参考。其次,根据现场运行的抽水蓄能电机实际尺寸1 1搭建了二维有限元仿真模型,分析了不同故障程度下的径向杂散磁通密度特征,并据此计算了定位筋感应电动势的时/频域信息,重点研究了其随匝间短路程度变化的规律。最后,在动模实验机组定子铁心背部布置铜板用以模拟定位筋,同时在信号采集前端布置信号调理装置用于信号的滤波与放大,在此基础上分别采集空载/负载工况下不同状态的感应电动势信息用于时/频域分析,实验结果证明了该检测系统可有效屏蔽电磁干扰,凸显微弱的转子匝间短路故障特征。本文所提方法填补了大型水电机组非侵入式无传感器监测领域的空白,在保证故障辨识快速性与准确性的基础上,最大限度地提升状态监测与设备维护的经济性。
1搭建了二维有限元仿真模型,分析了不同故障程度下的径向杂散磁通密度特征,并据此计算了定位筋感应电动势的时/频域信息,重点研究了其随匝间短路程度变化的规律。最后,在动模实验机组定子铁心背部布置铜板用以模拟定位筋,同时在信号采集前端布置信号调理装置用于信号的滤波与放大,在此基础上分别采集空载/负载工况下不同状态的感应电动势信息用于时/频域分析,实验结果证明了该检测系统可有效屏蔽电磁干扰,凸显微弱的转子匝间短路故障特征。本文所提方法填补了大型水电机组非侵入式无传感器监测领域的空白,在保证故障辨识快速性与准确性的基础上,最大限度地提升状态监测与设备维护的经济性。
1 定位筋感应电动势检测理论研究
抽水蓄能电机定位筋切割定子铁心外部杂散磁力线而产生感应电动势,通过实时监测定位筋感应电动势的变化即可实现对转子绕组匝间绝缘健康状态的有效跟踪。
1.1 杂散磁通理论分析
由于定子铁心和空气均对径向气隙磁场的扩散产生衰减效应,因此本文引入衰减系数法[25]对径向杂散磁场进行解析计算,以期建立径向气隙磁场与径向杂散磁场之间的数学关系。
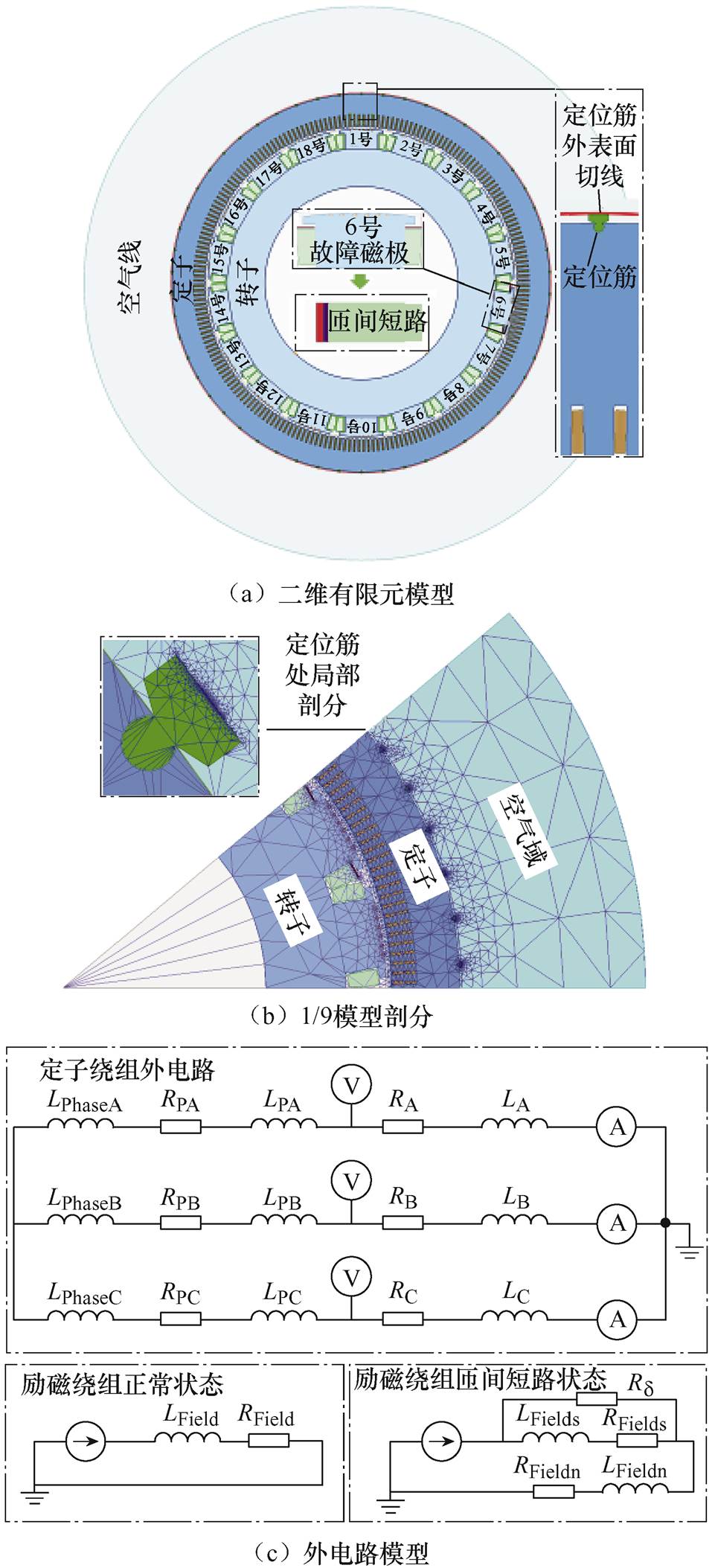
构建抽水蓄能电机的三维示意图如图1a所示,由于其定子机座为镂空设计,为了简化电磁计算过程,可将定位筋外部区域等效为空气域进行分析。同时为了便于对杂散磁通进行理论分析,构建二维平面图如图1b所示。
机组二维模型由内至外主要包括转轴、转子、定子、定位筋及定子机座五部分,图1中,Rsext为定子铁心外径,Rsint为定子铁心内径,r为定位筋外表面的某一点至机组转轴中心的距离,a 为定子圆周机械角。为了确定气隙磁通密度通过定子及空气的扩散,需利用麦克斯韦方程进行求解,其表达式[26]为
式中, 为磁矢量势;μ为介质磁导率;σ为介质电导率。由于在定子铁心及空气域中并不存在涡流效应,因此σ = 0,式(1)在极坐标系下的标量形式可表示为
为磁矢量势;μ为介质磁导率;σ为介质电导率。由于在定子铁心及空气域中并不存在涡流效应,因此σ = 0,式(1)在极坐标系下的标量形式可表示为
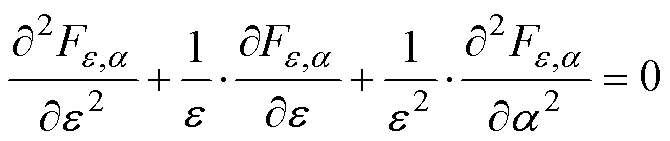 (2)
(2)
式中,ε为磁场求解点至转轴中心的距离。采用分离变量法进行求解,可得磁矢量势的标量表达式为
式中,p为极对数;k为奇数;ω为电角速度; 、
、 为系数。根据式(3)可求得气隙磁通密度的径向分量
为系数。根据式(3)可求得气隙磁通密度的径向分量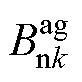 及切向分量
及切向分量 表达式分别为
表达式分别为
根据式(4),对不同区域的衰减系数进行分类计算如下:
(1)当磁场求解点处于定位筋外表面空气域,假设其至转轴中心的距离r趋于无穷大时,则有系数λ1=0,进而求解空气域中的径向磁通密度为
根据式(5)求解方法,进一步计算定子铁心外表面边界处(ε = Rsext)的径向磁通密度为
 (6)
(6)
综合式(5)和式(6),求解定位筋外表面空气域与定子铁心外表面边界处的径向磁通密度之间的关系为
由式(7)可知,定位筋外表面空气域衰减系数Ka表达式为
 (8)
(8)
(2)当磁场求解点处于定子铁心外表面时,其径向磁通密度幅值可表示为
其中
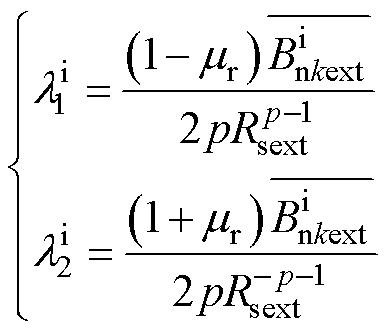 (10)
(10)
式中,μr为相对磁导率;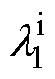 和
和 为系数。
为系数。
综合式(9)和式(10)进而求解定子铁心内表面和定子铁心外表面之间的径向磁通密度关系为
当磁场求解点位于定子铁心内表面与旋转气隙边界时,则有定子铁心内表面的径向磁通密度幅值与旋转气隙的径向磁通密度幅值相等,表示为
 (12)
(12)
综合式(11)和式(12)则可得定子铁心衰减系数Ks表达式为
式中,μr为常数,因此衰减系数Ka、Ks均为常数。
由式(8)和式(13)即可计算定位筋外表面处的径向杂散磁通密度 与径向气隙磁通密度
与径向气隙磁通密度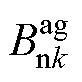 之间的关系为
之间的关系为
据式(14)可知,径向杂散磁通密度与径向气隙磁通密度呈线性关系。
1.2 定位筋感应电动势理论分析
抽水蓄能电机转子旋转过程中,定子铁心外部漏磁场的径向分量以同步速切割定位筋,并在定位筋上产生感应电动势,其表达式为
式中,L为定位筋的有效长度;R为定位筋外表面至转轴中心的距离;v为转子旋转速度;ωr为转子旋转的机械角速度。
在现场实际测量过程中,为了简化操作,可选取定位筋的某一段用于感应电动势的实时在线监测。同时为了有效滤除现场的高频电磁干扰,提升检测信号的信噪比,需在信号采集前端设置具有滤波放大功能的信号调理装置,定位筋感应电动势监测示意图如图2所示。
根据感应电动势式(15)可知,L、R、ωr均为常数,因此定位筋感应电动势E应与径向杂散磁通密度 呈线性关系。进一步以1.1节理论分析为基础,可知定位筋感应电动势亦与径向气隙磁通密度Bnk呈线性关系,由此可得出:
呈线性关系。进一步以1.1节理论分析为基础,可知定位筋感应电动势亦与径向气隙磁通密度Bnk呈线性关系,由此可得出:
(1)当抽水蓄能电机处于正常运行状态时,其径向气隙磁通频域信息仅包含基波及奇数次谐波,即k=1, 3, 5, , 2n-1,因此定位筋也将产生同频率感应电动势。
, 2n-1,因此定位筋也将产生同频率感应电动势。
(2)当抽水蓄能电机发生转子绕组匝间短路故障时,其径向气隙磁通频域信息不仅包含基波及奇数次谐波,而且包含分数次谐波,即v=1/p, 2/p, , n/p,此时定位筋感应电动势也将出现同频率故障特征谐波,且其幅值随匝间短路故障程度的增加呈递增趋势。
, n/p,此时定位筋感应电动势也将出现同频率故障特征谐波,且其幅值随匝间短路故障程度的增加呈递增趋势。
考虑到现场通过直观观察定位筋感应电动势的时/频域波形容易导致故障误判,本文提出谐波幅值比阈值检测法以期定量评估转子绕组匝间绝缘健康状况。首先,定义谐波幅值比为定位筋感应电动势频谱中各分数次谐波幅值之和与50 Hz基频幅值的比值,其表达式为
式中,f为频率。为了减小故障检测阈值预设的偏差,需要对转子绕组健康状态下的定位筋感应电动势信息进行多次采集与提取,据此构建谐波幅值比统计箱线图,并获取箱线图上边缘最大值。最后,为了避免发生误报警,留取边缘最大值的5%作为弹性裕度(即边缘最大值的1.05倍)[21],并将其设为临界阈值,从而及时有效地辨识微弱匝间绝缘缺陷。
综上所述,定位筋感应电动势特征信息可有效反映转子绕组的健康状态,因此定位筋可做为匝间短路故障检测的传感器进行使用,此技术方案的实施对提升现场状态监测的经济性与可靠性具有重大意义。
2 定位筋感应电动势检测仿真研究
本文根据抽水蓄能电站服役机组参数搭建了有功功率为250 MW、极对数为9的抽水蓄能发电机电磁仿真模型如图3所示。首先,由于定子机座镂空设计,可将定位筋外部设为空气域[23],并将Balloon设置为边界条件,便于计算定位筋外表面的杂散磁通密度。其次,进行转子绕组匝间短路故障设置,图3a中红色线匝代表短路2匝、紫色线匝代表短路4匝。然后,以1/9模型为例展示网格剖分设置,同时重点关注定位筋外表面处空气域的剖分细致程度,其剖分结果如图3b所示。最后,构建用于与Maxwell模型进行电磁耦合仿真的外电路模型,如图3c所示。
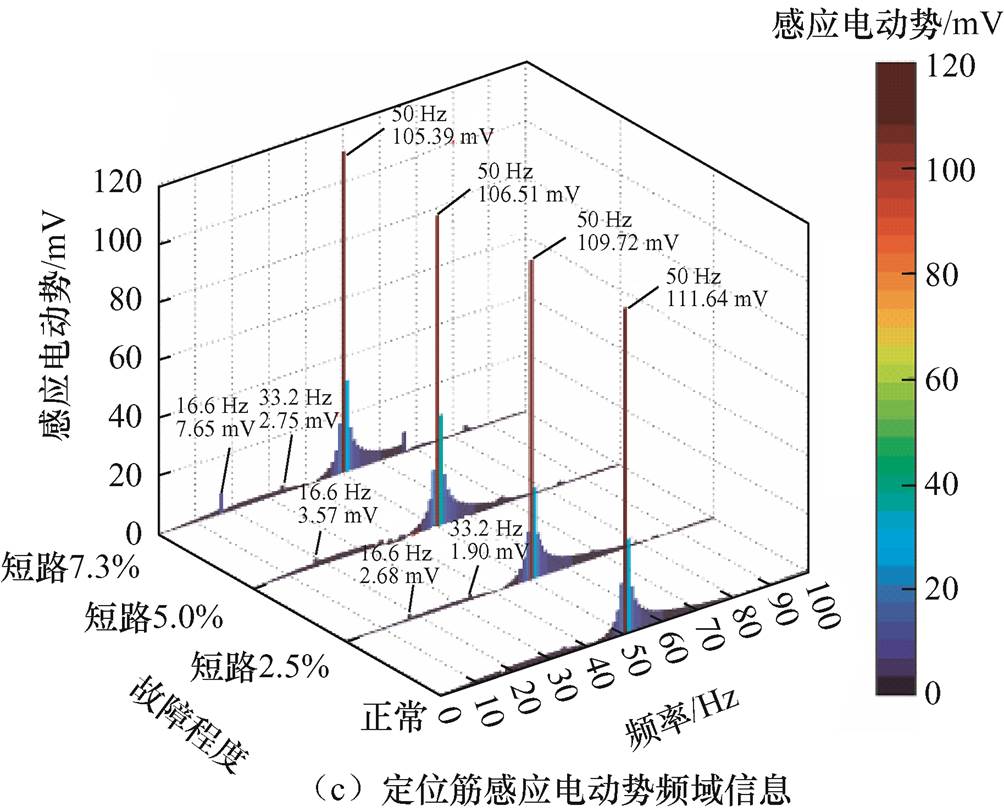
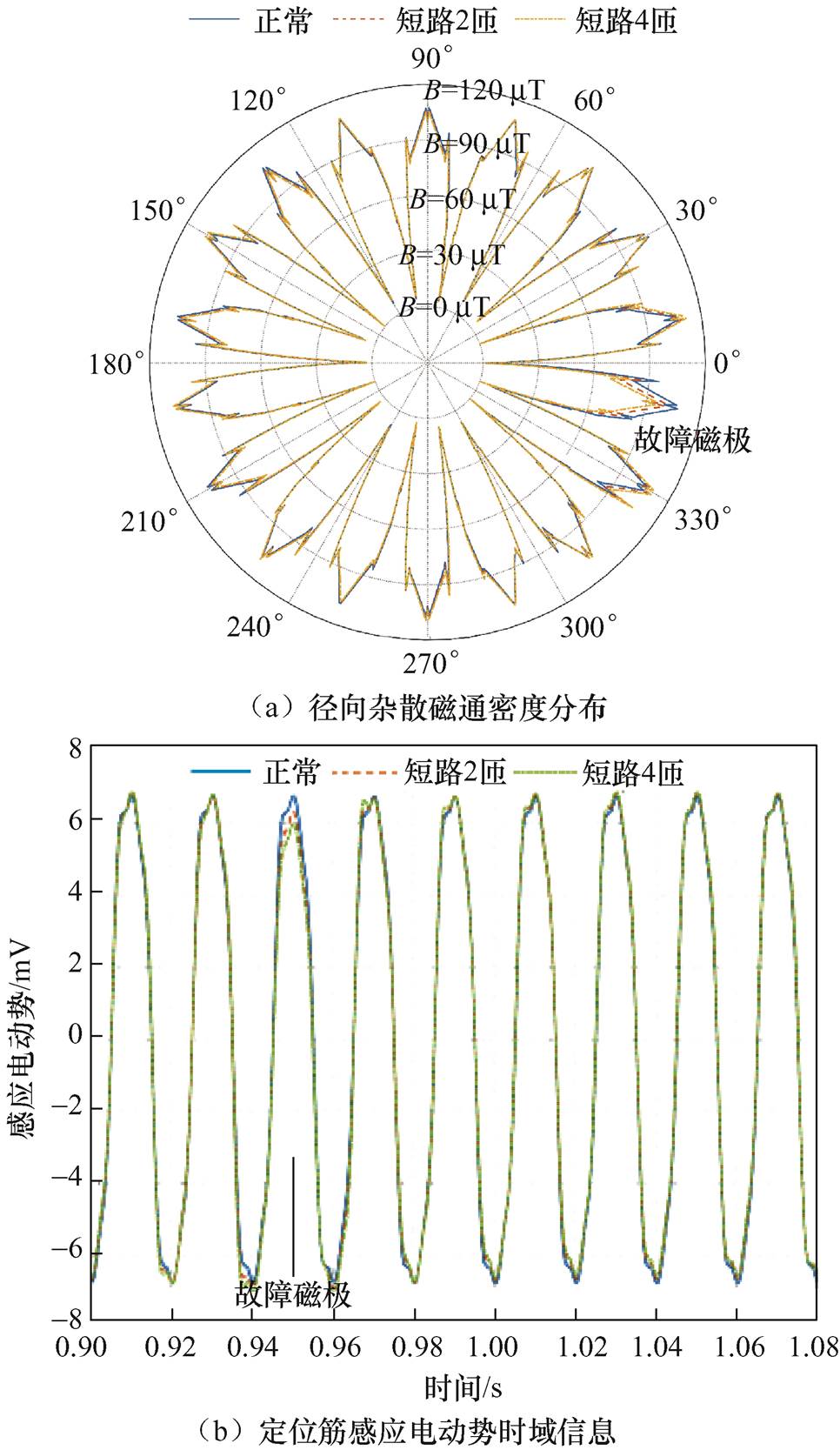
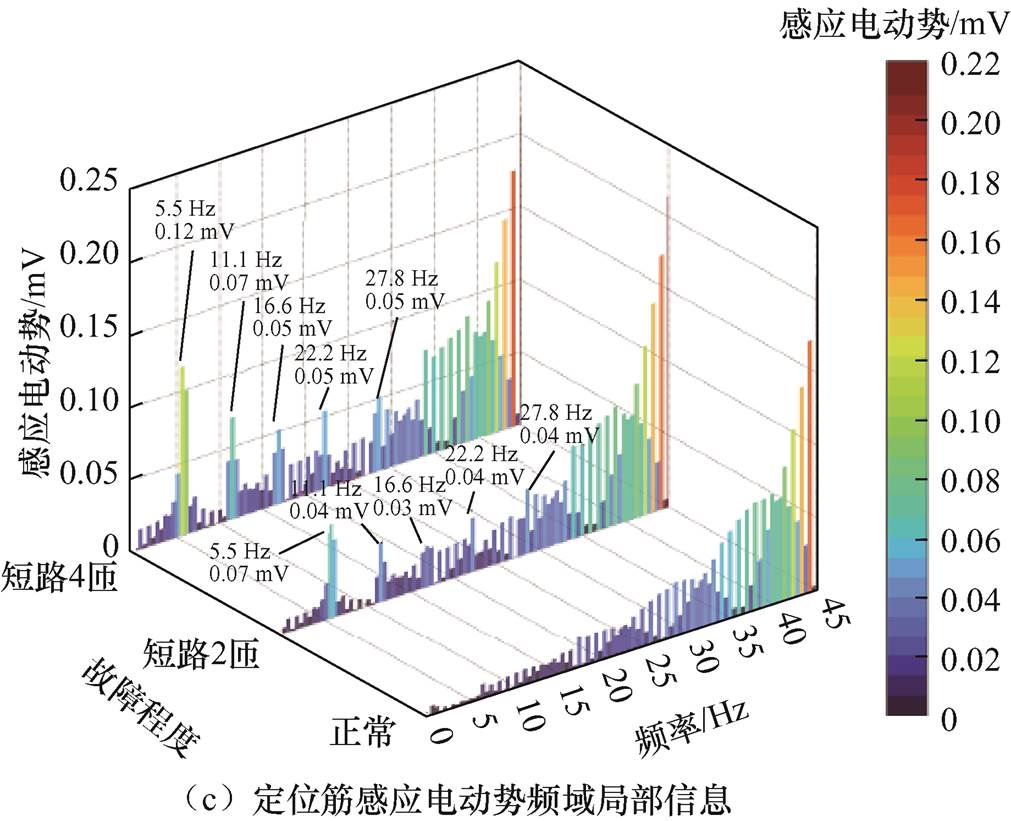
分别提取磁极绕组正常、短路2匝、短路4匝状态下所对应定位筋外表面切线处的径向杂散磁通密度分布信息进行分析,得到空载工况仿真结果如图4a所示,负载工况仿真结果如图5a所示。选取定位筋有效长度为0.5 m,并根据1.2节定位筋感应电动势式(15)进一步计算空载/负载工况下的杂散磁通感应电动势时域信息分别如图4b、图5b所示。对定位筋感应电动势信息进行频谱分析,得50 Hz频段以内的局部频谱分别如图4c、图5c所示。
为了减小故障检测的随机误差,分别截取发电机空载/负载工况正常、短路2匝、短路4匝状态下10个电周期的定位筋感应电动势进行频谱分析,提取各分数次谐波的峰值信息,并根据谐波幅值比计算式(16)得到各周期感应电动势的分数次谐波含量百分比,据此构建空载工况下的统计箱线图如图6a所示,负载工况下的统计箱线图如图6b所示。
由图4a、图5a可以得出,正常状态下径向杂散磁通密度的空载时域峰值约为106.5 μT,负载时域峰值约为110.5 μT。同时,负载工况由于存在电枢反应影响,使径向磁通密度波形不对称分布。此外,伴随匝间短路程度的增加,故障磁极的径向杂散磁通密度幅值均呈递减趋势。通过分析杂散磁通密度的演变规律,验证了二维有限元仿真建模的正确性。
由图4b、图5b可以得出,正常状态下定位筋感应电动势的空载时域峰值为6.74 mV,负载时域峰值为7.33 mV。当故障磁极发生匝间短路时,与之对应的空载时域峰值分别降为6.3 mV、5.96 mV,负载时域峰值分别降为6.72 mV、6.25 mV,均呈递减趋势。
由图4c、图5c可知,无论机组处于空载工况或是负载工况,匝间短路状态下,定位筋感应电动势频谱0~50 Hz频率段均出现了明显的v(v=1/9, 2/9, , n/9,且v≠np)次特征谐波,并于图中标记各谐波频率点所对应的幅值大小,发现其幅值随故障水平的增加而增大,由此验证了定位筋感应电动势检测理论的正确性。由于存在电枢反应干扰,负载正常状态亦出现了分数次故障特征谐波。
, n/9,且v≠np)次特征谐波,并于图中标记各谐波频率点所对应的幅值大小,发现其幅值随故障水平的增加而增大,由此验证了定位筋感应电动势检测理论的正确性。由于存在电枢反应干扰,负载正常状态亦出现了分数次故障特征谐波。
由图6a可以看出,空载工况正常状态下的分数次谐波幅值比最大值为9.37%,按照5%弹性裕度,可将Rnormal=9.83%设为故障检测阈值,与短路2匝状态下最小值14.39%存在4.56%差距,因此不会出现故障误判。由图6b可以看出,负载工况正常状态下的分数次谐波幅值比最大值为10.94%,考虑5%弹性裕度,可将Rnormal=11.49%设为检测阈值,与短路2匝状态下最小值12.31%相差0.82%,因此可有效区分不同运行状态。综上所述,通过将Rnormal设为故障检测阈值,即可精准识别匝间绝缘缺陷。
3 定位筋感应电动势检测实验研究
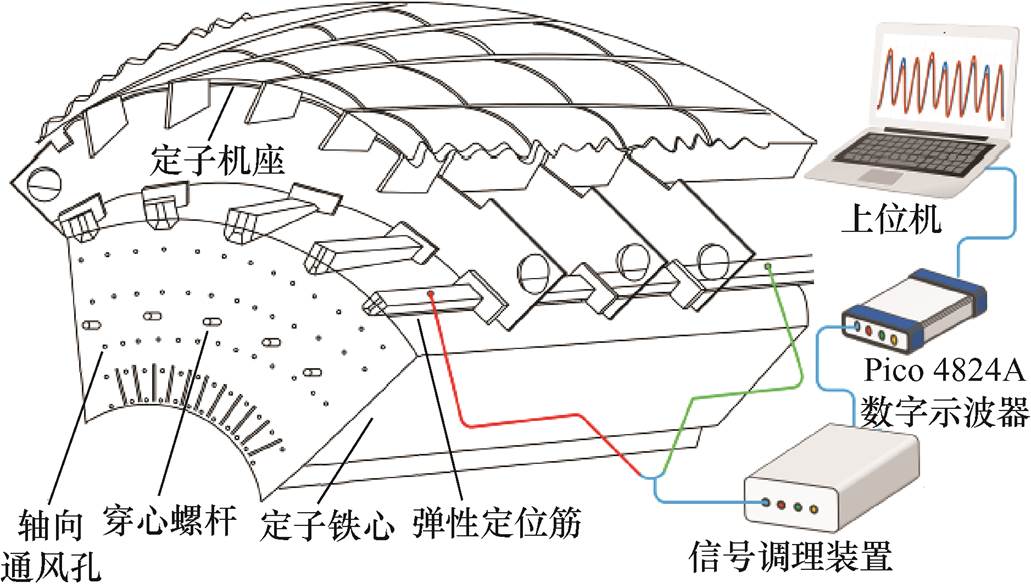
3.1 定位筋感应电动势检测实验平台
转子绕组匝间短路实验依托电力系统动态模拟实验室额定容量为30 kV A、极对数为3的同步发电机故障模拟平台,用于模拟抽水蓄能电机发电运行工况。首先,由于实验机组与抽水蓄能电机在结构上存在一定差别,实验机组定子铁心外部并无定位筋,因此本次实验将覆有绝缘漆的铜板粘固于定子铁心表面,用于模拟铁心外部定位筋。其次,在信号采集前端布置了本团队设计的滤波放大信号调理装置,并采用5 V开关电源进行供电,其工作电流为10 mA,低通截止频率最大可调至10 kHz,放大增益最大可调至100倍,可在0~75℃范围内稳定工作。本次实验将低通截止频率设为200 Hz,且将输出信号放大增益调至50倍。同时为了观察,与未滤波的原始定位筋感应电动势信号做对比,本次实验也对未滤波信号进行了采集。
A、极对数为3的同步发电机故障模拟平台,用于模拟抽水蓄能电机发电运行工况。首先,由于实验机组与抽水蓄能电机在结构上存在一定差别,实验机组定子铁心外部并无定位筋,因此本次实验将覆有绝缘漆的铜板粘固于定子铁心表面,用于模拟铁心外部定位筋。其次,在信号采集前端布置了本团队设计的滤波放大信号调理装置,并采用5 V开关电源进行供电,其工作电流为10 mA,低通截止频率最大可调至10 kHz,放大增益最大可调至100倍,可在0~75℃范围内稳定工作。本次实验将低通截止频率设为200 Hz,且将输出信号放大增益调至50倍。同时为了观察,与未滤波的原始定位筋感应电动势信号做对比,本次实验也对未滤波信号进行了采集。
同步发电机转子绕组匝间短路实验分为空载工况及负载工况(负载为4 kW),在匝间短路程度25%所对应的抽头之间串接滑动变阻器、电流表及断路器,其本质则是通过改变滑动变阻器分流 来减小流过故障模拟磁极的励磁电流If,从而有效模拟微弱匝间绝缘缺陷,并根据fault degree=
来减小流过故障模拟磁极的励磁电流If,从而有效模拟微弱匝间绝缘缺陷,并根据fault degree=  /
/ ×25%计算匝间短路故障程度。此外,机组线电压、相电流、励磁电流、定位筋感应电动势等电气特征参量信息均采用Pico 4824 A数字示波器进行同步采集,采样频率设为4 kHz,实验整体布置如图7所示。
×25%计算匝间短路故障程度。此外,机组线电压、相电流、励磁电流、定位筋感应电动势等电气特征参量信息均采用Pico 4824 A数字示波器进行同步采集,采样频率设为4 kHz,实验整体布置如图7所示。
3.2 定位筋感应电动势时/频域信息分析
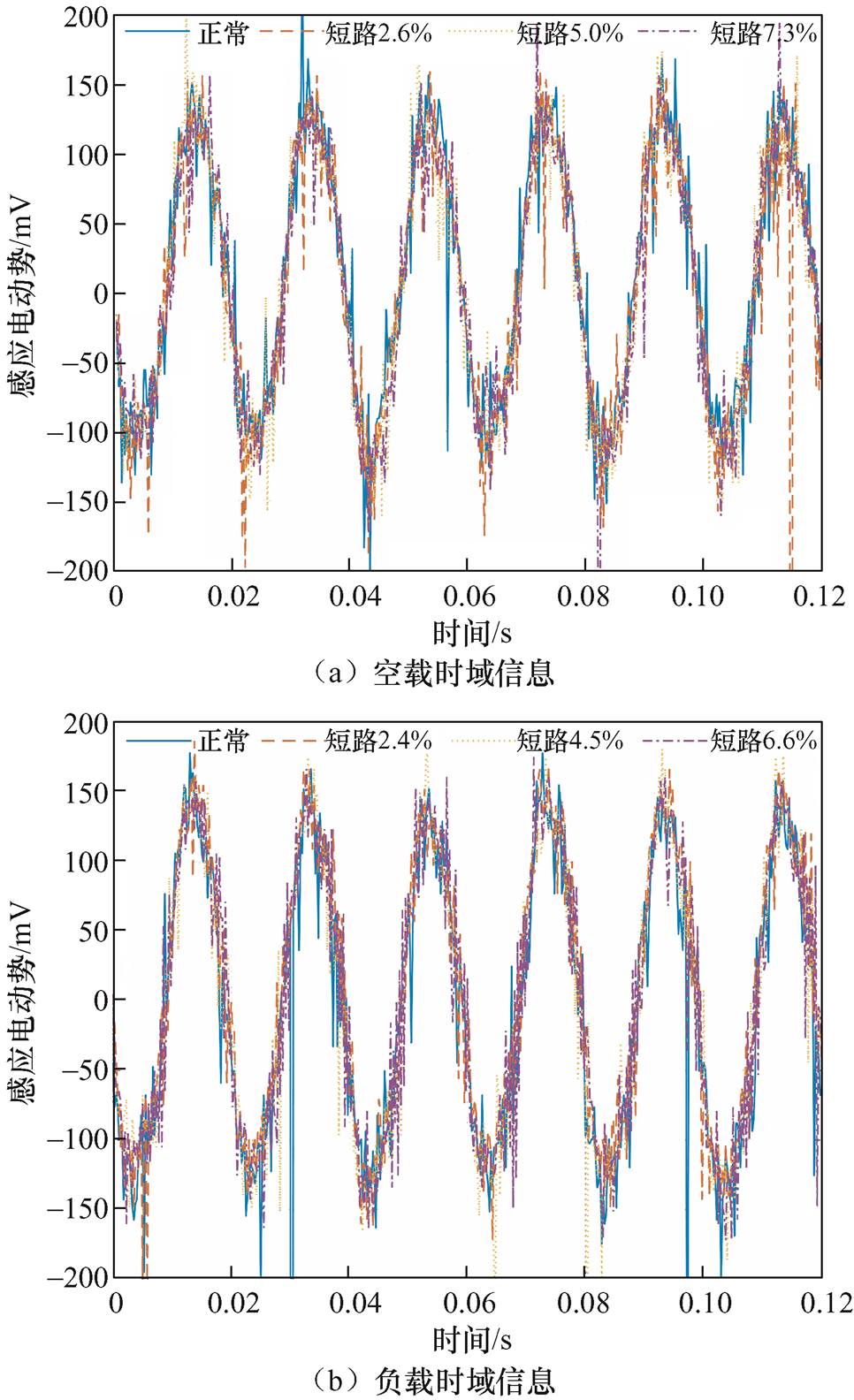
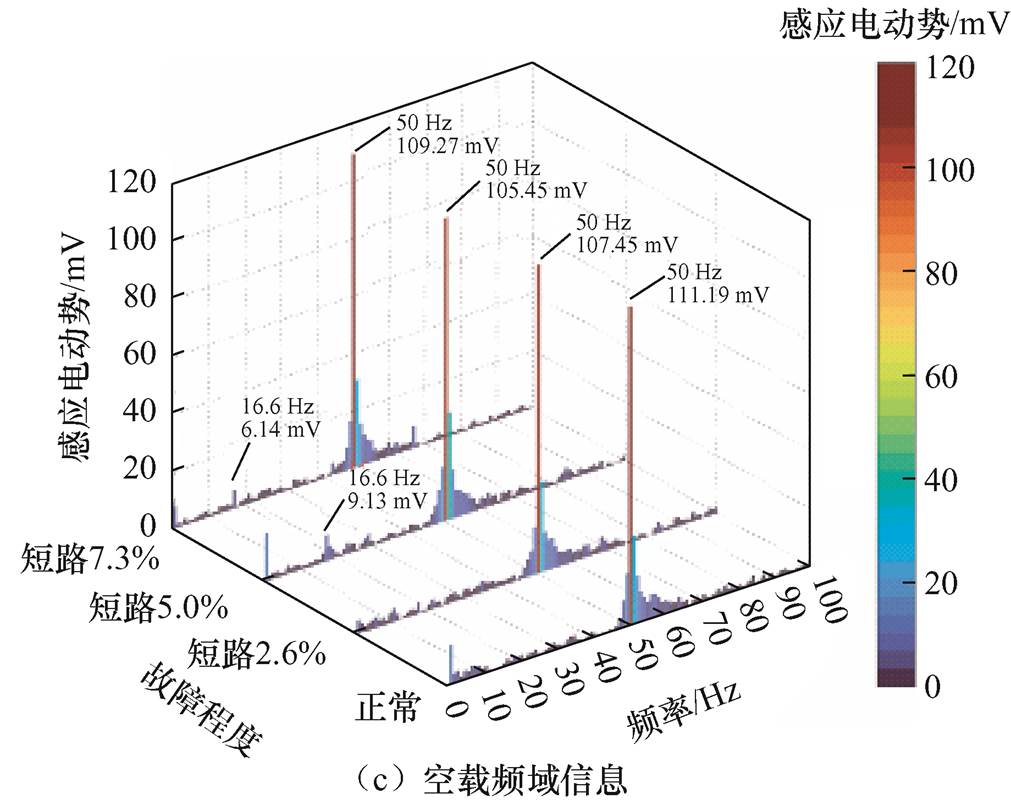
首先,对空载工况正常、匝间短路故障状态下的励磁电流数据及滑动变阻器分流数据进行分析,得到时域信息如图8a所示,据此计算励磁电流均值分别为0.96 A、0.98 A、1.01 A、1.03 A,滑动变阻器分流均值分别为0 A、0.1 A、0.2 A、0.3 A,从而得出匝间短路程度分别为2.6%、5.0%、7.3%。其次,提取负载工况正常、匝间短路故障状态下的励磁电流数据及滑动变阻器分流数据,绘制时域谱如图9a所示,据此计算励磁电流均值分别为1.04 A、1.06 A、1.11 A、1.14 A,滑动变阻器分流均值分别为0 A、0.1 A、0.2 A、0.3 A,进而得出匝间短路程度分别为2.4%、4.5%、6.6%。然后,随机提取同步发电机空载/负载工况下两个电周期的定位筋感应电动势信息(50倍增益输出数据)进行分析,得不同状态下的时域特征图谱分别如图8b、图9b所示。最后,对定位筋感应电动势信息进行傅里叶分析,得不同工况下的频谱特征谐波分别如图8c、图9c所示。
由图8b、图9b可以得到正常状态下定位筋感应电动势的空载时域峰值为120.07 mV,负载时域峰值为133.99 mV。故障磁极处的时域幅值伴随匝间短路故障程度的增加呈递减趋势,其中空载工况下故障磁极所对应的时域峰值分别为115.43 mV、112.24 mV、109.05 mV,负载工况下故障磁极所对应的时域峰值分别为130.22 mV、128.76 mV、125.58 mV。
由图8c、图9c可知,匝间短路状态下,定位筋感应电动势频谱在0~50 Hz频率段出现了明显的k/3(16.6 Hz、33.2 Hz)分数次特征谐波,且其幅值伴随匝间短路故障程度的增大而增加,而50 Hz基频幅值伴随匝间短路故障程度的增加出现了微小的衰减,对应幅值均已在频谱图中进行了标注。
同时,为了验证添加信号调理装置的合理性与有效性,随机提取空载/负载工况下未滤波的定位筋感应电动势信号进行对比实验分析,其中时域信息分别如图10a、图10b所示,频域信息分别如图10c、图10d所示。
图10a、图10b中的时域信息由于受高频电磁干扰,导致故障磁极处幅值衰减并不明显,从图中无法判断故障磁极。同时观查图10c中短路5.0%和短路7.3%所对应的频谱信息,发现其16.6 Hz处幅值随故障程度增加呈递减趋势(由9.13 mV衰减至6.14 mV),而50 Hz处幅值呈递增趋势(由105.45 mV增至109.27 mV),这与理论及仿真所得故障分数次特征谐波幅值随匝间短路程度增加呈递增趋势,50 Hz基波随匝间短路程度增加呈递减趋势相悖。图10d中短路4.5%和短路6.6%所对应的16.6 Hz处的幅值分别为5.23 mV、5.50 mV,而50 Hz处幅值分别为124.75 mV、124.22 mV,虽与理论及仿真所得结论相吻合,但不同故障程度的分数次谐波及基波幅值信息区分度较小,同时综合观察正常状态及短路2.4%所对应的频域信息,其50 Hz处幅值则呈无规律变化趋势,因此难以完成匝间绝缘健康与否的有效区分。
综上分析,通过对比实验结果发现,未经信号调理装置预处理的定位筋感应电动势易受电磁干扰影响,其时域检测信息中包含了大量高频噪声,且频谱特征谐波无规律变化,因此不利于匝间短路故障检测。而经过信号调理装置预处理的定位筋感应电动势信号,其时/频域信息则清晰地展现了匝间短路故障特征,可有效用于机组运行状态的在线监测。
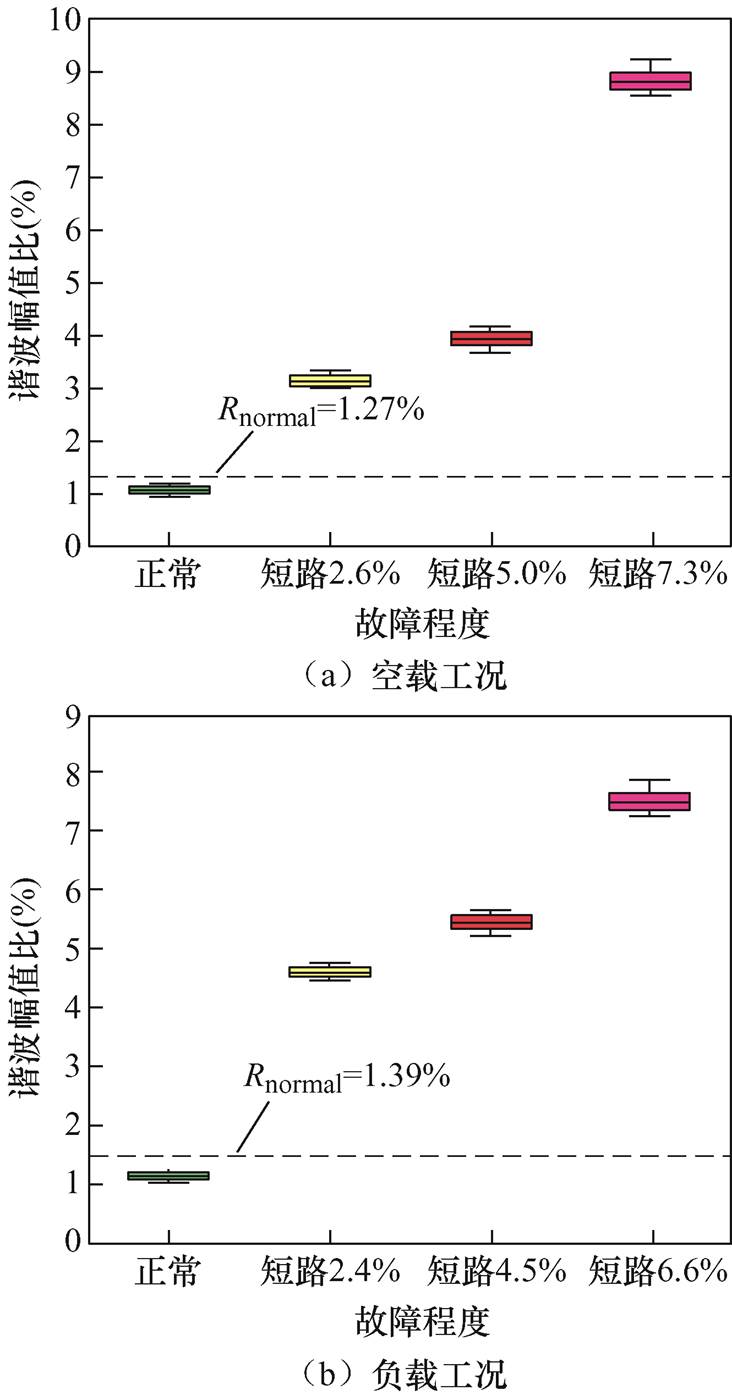
此外,为了有效通过量化数值辨识匝间绝缘缺陷,本文随机选取空载/负载工况下10个电周期的定位筋感应电动势信息(经信号调理装置预处理)进行频谱分析,并定位故障特征谐波幅值用于计算谐波幅值比,据此构建统计箱线图分别如图11a、图11b所示。
由图11a可以得出,空载工况正常状态下的分数次谐波幅值比最大值为1.21%,根据5%弹性裕度,可将Rnormal=1.27%设为故障检测阈值,与短路2.6%状态下最小值3.01%相差1.74%,因此可通过阈值法实现匝间短路的靶向防御。由图11b可以得出,负载工况正常状态下的分数次谐波幅值比最大值为1.32%,按照5%弹性裕度将Rnormal=1.39%设为检测阈值,与短路2.4%状态下最小值4.53%相差3.14%,因此利用阈值法可有效识别匝间绝缘缺陷。
4 结论
本文提出了抽水蓄能电机无传感器在线检测方法,并结合有限元仿真与机组实验对所提理论进行验证,总结如下:
1)采用抽水蓄能电机定子铁心外部定位筋作为转子绕组匝间短路的检测部件,其感应电动势信号可用于机组健康状态的在线监测。通过有限元仿真及同步发电机模拟实验,验证了该检测方法不受运行工况的限制,具有非侵入式、灵敏度高、成本低等优点。
2)通过对抽水蓄能电机有限元仿真及同步发电机组实验所得定位筋感应电动势信号进行数据分析,证明了转子绕组发生匝间短路故障后,定位筋感应电动势频谱会产生特有的分数次特征谐波,且其幅值随匝间短路程度的增加而增大,而50 Hz基波幅值则随匝间短路程度的增加而减小。
3)通过对定位筋感应电动势的时/频域特征信息进行深度分析与挖掘,提出了谐波幅值比阈值检测法,并通过服役抽蓄电机的有限元建模计算与动模机组实测进行有效性验证,填补了匝间短路状态感知在无传感器检测领域的研究空白,为现场运检提供了新的非侵入式在线监测方案。
综上所述,通过对机组不同状态下的定位筋感应电动势信息展开理论研究、电磁仿真分析及动模机组实测,有效论证了该非侵入式状态监测方法能够及时发现转子绕组微弱匝间短路故障,对提升设备状态感知能力和设备运维检修效率具有重要意义。
参考文献
[1] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[2] 谢小荣, 马宁嘉, 刘威, 等. 新型电力系统中储能应用功能的综述与展望[J]. 中国电机工程学报, 2023, 43(1): 158-169.
Xie Xiaorong, Ma Ningjia, Liu Wei, et al. Functions of energy storage in renewable energy dominated power systems: review and prospect[J]. Proceedings of the CSEE, 2023, 43(1): 158-169.
[3] Shaikh M F, Park J, Lee Sang bin. A non-intrusive leakage flux based method for detecting rotor faults in the starting transient of salient pole synchronous motors[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1262-1270.
[4] Ehya H, Nysveen A, Antonino-Daviu J A. Advanced fault detection of synchronous generators using stray magnetic field[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11675-11685.
[5] 赵方伟, 王秀和, 赵文良, 等. 内置式永磁同步电机动态偏心故障下的轴电压解析分析和削弱[J]. 电工技术学报, 2022, 37(4): 837-848.
Zhao Fangwei, Wang Xiuhe, Zhao Wenliang, et al. Analysis and reduction of shaft voltage in interior permanent magnet synchronous motors under dynamic eccentricity fault[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 837-848.
[6] Zamudio-Ramirez I, Osornio-Rios R A, Antonino- Daviu J A, et al. Magnetic flux analysis for the condition monitoring of electric machines: a review[J]. IEEE Transactions on Industrial Informatics, 2022, 18(5): 2895-2908.
[7] 孙宇光, 杜威, 桂林, 等. 用于多相无刷励磁机开路与短路故障检测的磁极探测线圈设计[J]. 电工技术学报, 2022, 37(14): 3542-3554.
Sun Yuguang, Du Wei, Gui Lin, et al. Design of pole detection coils for open-circuit and short-circuit faults in multiphase brushless exciter[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3542- 3554.
[8] 齐鹏, 李永刚, 马明晗, 等. 基于环流时频图谱的抽水蓄能机组励磁绕组匝间短路故障诊断[J]. 电工技术学报, 2023, 38(22): 6104-6120.
Qi Peng, Li Yonggang, Ma Minghan, et al. Diagnosis of inter-turn short circuit in excitation winding of pumped storage units based on time-frequency map of circulating current[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6104-6120.
[9] Kim H J, de la Morena J, Platero C A, et al. Influence of rotor eccentricity on the reliability of the pole drop test for salient pole synchronous machines[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2240-2243.
[10] 贾志东, 陈海, 张征平, 等. 采用重复脉冲法诊断发电机转子绕组匝间短路故障[J]. 高电压技术, 2012, 38(11): 2927-2933.
Jia Zhidong, Chen Hai, Zhang Zhengping, et al. Inter-turn short faults dignosis on rotor windings of generator using repetive surge oscilloscope[J]. High Voltage Engineering, 2012, 38(11): 2927-2933.
[11] 马明晗, 侯岳佳, 李永刚, 等. 基于MSK-CNN和多源机电信息融合的同步发电机故障诊断方法[J]. 电机与控制学报, 2023, 27(1): 1-11.
Ma Minghan, Hou Yuejia, Li Yonggang, et al. Synchronous generator fault diagnosis method based on MSK-CNN and multi-source electromechanical information fusion[J]. Electric Machines and Control, 2023, 27(1): 1-11.
[12] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Discrimination of interturn short-circuit and local demagnetization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[13] 李永刚, 李和明, 赵华. 汽轮发电机转子绕组匝间短路故障诊断新判据[J]. 中国电机工程学报, 2003, 23(6): 112-116, 169.
Li Yonggang, Li Heming, Zhao Hua. The new criterion on inter turn short-circuit fault diagnose of steam turbine generator rotor windings[J]. Proceedings of the CSEE, 2003, 23(6): 112-116, 169.
[14] 郝亮亮, 孙宇光, 邱阿瑞, 等. 同步发电机励磁绕组匝间短路故障稳态数学模型及仿真[J]. 电力系统自动化, 2010, 34(18): 51-56.
Hao Liangliang, Sun Yuguang, Qiu Arui, et al. Steady-state mathematical modeling and simulation of inter-turn short circuit of field windings in synchronous machines[J]. Automation of Electric Power Systems, 2010, 34(18): 51-56.
[15] 桂林, 陈俊, 王凯, 等. 基于柔性光学TA的发电电动机主保护优化设计[J]. 电力系统自动化, 2020, 44(18): 132-138.
Gui Lin, Chen Jun, Wang Kai, et al. Optimal design of main protection for generator-motor based on flexible optical current transformer[J]. Automation of Electric Power Systems, 2020, 44(18): 132-138.
[16] Cuevas M, Romary R, Lecointe J P, et al. Noninvasive detection of winding short-circuit faults in salient pole synchronous machine with squirrel-cage damper[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5988-5997.
[17] Dreyer U J, Mezzadri F, Dutra G, et al. Quasi- distributed optical fiber transducer for simultaneous temperature and vibration sensing in high-power generators[J]. IEEE Sensors Journal, 2018, 18(4): 1547-1554.
[18] Qi Peng, Li Yonggang, Ma Minghan, et al. Research on the vibration characteristics of pumped storage unit stator core based on fiber optic sensing[J]. IEEE Transactions on Energy Conversion, 2023, 38(3): 2179-2190.
[19] 何玉灵, 张文, 王烁, 等. 定子匝间短路位置对汽轮发电机转子铁心温升特性的影响[J]. 电机与控制学报, 2022, 26(10): 12-22.
He Yuling, Zhang Wen, Wang Shuo, et al. Impact of stator interturn short circuit position on rotor core temperature rising characteristics in turbo-generators[J]. Electric Machines and Control, 2022, 26(10): 12-22.
[20] Bazzo J P, Mezzadri F, da Silva E V, et al. Thermal imaging of hydroelectric generator stator using a DTS system[J]. IEEE Sensors Journal, 2015, 15(11): 6689- 6696.
[21] Afrandideh S, Milasi M E, Haghjoo F, et al. Turn to turn fault detection, discrimination, and faulty region identification in the stator and rotor windings of synchronous machines based on the rotational magnetic field distortion[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 292-301.
[22] Sasic M, Stone G C, Stein J, et al. Detecting turn shorts in rotor windings: a new test using magnetic flux monitoring[J]. IEEE Industry Applications Magazine, 2013, 19(2): 63-69.
[23] Ehya H, Nysveen A. Pattern recognition of interturn short circuit fault in a synchronous generator using magnetic flux[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3573-3581.
[24] Ehya H, Skreien T N, Nysveen A. Intelligent data- driven diagnosis of incipient interturn short circuit fault in field winding of salient pole synchronous generators[J]. IEEE Transactions on Industrial Informatics, 2022, 18(5): 3286-3294.
[25] Ramirez-Nunez J A, Antonino-Daviu J A, Climente- Alarcón V, et al. Evaluation of the detectability of electromechanical faults in induction motors via transient analysis of the stray flux[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4324-4332.
[26] Romary R, Roger D, Brudny J F. Analytical computation of an AC machine external magnetic field[J]. The European Physical Journal Applied Physics, 2009, 47(3): 31102.
Sensorless Detection Method of Rotor Inter-Turn Short Circuit in Pumped Storage Motors
Qi Peng Li Yonggang Ma Minghan
(School of Electrical and Electronic Engineering North China Electric Power University Baoding 0710032 China)
Abstract As an important part of renewable and clean energy, pumped storage power generation has been developing at a high rate in recent years. Due to the complexity and non-linearity of the pumped storage power generation system, its operation may be affected by certain factors and become abnormal, resulting in poor power supply quality. The rotor winding inter-turn insulation (ITI) deterioration process is slow, and the early weak faults are difficult to detect in time. This paper uses the positioning bar (PB) of pumped storage motors (PSMs) as a detection component to avoid inter-turn short circuit (ITSC) faults. Its induced electromotive force (IEMF) can effectively react to the health level of the rotor winding's ITI.
Firstly, the relationship between the stray and main flux is derived by introducing the attenuation coefficient method. The characteristic harmonics of the PB's IEMF in the ITSC state are obtained. Accordingly, the harmonic amplitude ratio (HAR) threshold detection method is proposed. Secondly, a two-dimensional electromagnetic simulation model is constructed according to the operating parameters of PSM, and the evolution law of the IEMF's time/frequency domain characteristics before and after the ITSC fault are analyzed. The HAR threshold detection method is verified. Finally, combined with the signal conditioning device, the PB's IEMF information under different ITSC degrees is collected. The HARs of multiple periodic signals are calculated, a statistical box plot is constructed, and the fault detection threshold is set.
The simulation results show that the IEMF's time-domain peak value of PB decreases under normal, 2 turns-ITSC, and 4 turns-ITSC states. The corresponding IEMF's time-domain peaks are 6.74 mV, 6.3 mV, and 5.96 mV under no-load conditions, while 7.33 mV, 6.72 mV, and 6.25 mV under load conditions. Meanwhile, the frequency band 0 to 50 Hz of the PB's IEMF spectrum shows obvious fractional characteristic harmonics, and their amplitudes increase with the fault level. According to the 5% elasticity margin, the fault detection thresholds under no-load/load conditions are set to 9.83% and 11.49%, respectively, which are 4.56% and 0.82% different from the minimum values of 14.39% and 12.31% in the 2 turns-ITSC states, so that the ITI defects can be identified accurately.
Experiments on the synchronous generator show that the peak time-domain values of the PB's IEMF corresponding to the faulty pole decrease with the increase of ITSC degree. The peak values of the time domain corresponding to normal, 2.6%-ITSC, 5%-ITSC, and 7.3%-ITSC under no-load conditions are 120.07 mV, 115.43 mV, 112.24 mV, and 109.05 mV, respectively. In contrast, 2.4%-ITSC, 4.5%-ITSC, and 6.6%-ITSC under load conditions are 133.99 mV, 130.22 mV, 128.76 mV, and 125.58 mV, respectively. According to the PB's IEMF spectrum, there are obvious fractional characteristic harmonics in the 0 – 50 Hz frequency band. Their amplitudes increase with the ITSC degree, and the amplitude of 50 Hz fundamental frequency decreases slightly. In addition, the PB's IEMF information for 10 electrical cycles under no-load/load conditions is randomly selected for calculating the HARs. Considering the 5% elasticity margin, the fault detection thresholds under no-load/load conditions are set to 1.27% and 1.39%, which are 1.74% and 3.14% different from the minimum values of 3.01% and 4.53% in the ITSC state. Therefore, the threshold method can be used to achieve the target defense of ITSC fault.
In conclusion, the HAR threshold detection method is proposed by analyzing and mining the IEMF's time/frequency domain characteristic information of PB. The proposed method verifies finite element modeling calculation of in-service PSM and the measurement of the synchronous generator, providing a non-intrusive on-line monitoring method for the on-site operation and maintenance.
keywords:Pumped storage motors, rotor winding, inter-turn short circuit, induced electromotive force of the positioning bar, harmonic amplitude ratio threshold detection method
中图分类号:TM311
DOI: 10.19595/j.cnki.1000-6753.tces.231455
国家自然科学基金(51777075)和国家自然科学基金青年科学基金(52307053)资助项目。
收稿日期 2023-09-04
改稿日期 2023-09-19
作者简介
齐 鹏 男,1991年生,博士研究生,研究方向为旋转电力设备运行特性分析及故障诊断。E-mail: qipeng91@foxmail.com
马明晗 男,1990年生,讲师,硕士生导师,研究方向为旋转电力设备运行特性分析及故障诊断。E-mail: NCEPU_MMH@outlook.com(通信作者)
(编辑 崔文静)
 1搭建了二维有限元仿真模型,分析了不同故障程度下的径向杂散磁通密度特征,并据此计算了定位筋感应电动势的时/频域信息,重点研究了其随匝间短路程度变化的规律。最后,在动模实验机组定子铁心背部布置铜板用以模拟定位筋,同时在信号采集前端布置信号调理装置用于信号的滤波与放大,在此基础上分别采集空载/负载工况下不同状态的感应电动势信息用于时/频域分析,实验结果证明了该检测系统可有效屏蔽电磁干扰,凸显微弱的转子匝间短路故障特征。本文所提方法填补了大型水电机组非侵入式无传感器监测领域的空白,在保证故障辨识快速性与准确性的基础上,最大限度地提升状态监测与设备维护的经济性。
1搭建了二维有限元仿真模型,分析了不同故障程度下的径向杂散磁通密度特征,并据此计算了定位筋感应电动势的时/频域信息,重点研究了其随匝间短路程度变化的规律。最后,在动模实验机组定子铁心背部布置铜板用以模拟定位筋,同时在信号采集前端布置信号调理装置用于信号的滤波与放大,在此基础上分别采集空载/负载工况下不同状态的感应电动势信息用于时/频域分析,实验结果证明了该检测系统可有效屏蔽电磁干扰,凸显微弱的转子匝间短路故障特征。本文所提方法填补了大型水电机组非侵入式无传感器监测领域的空白,在保证故障辨识快速性与准确性的基础上,最大限度地提升状态监测与设备维护的经济性。

 (1)
(1)
 为磁矢量势;μ为介质磁导率;σ为介质电导率。由于在定子铁心及空气域中并不存在涡流效应,因此σ = 0,式(1)在极坐标系下的标量形式可表示为
为磁矢量势;μ为介质磁导率;σ为介质电导率。由于在定子铁心及空气域中并不存在涡流效应,因此σ = 0,式(1)在极坐标系下的标量形式可表示为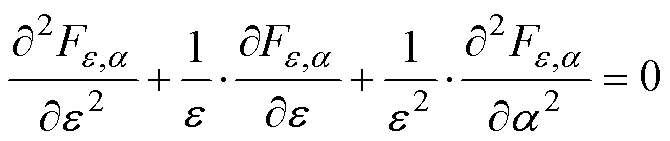 (2)
(2) (3)
(3)
 、
、 为系数。根据式(3)可求得气隙磁通密度的径向分量
为系数。根据式(3)可求得气隙磁通密度的径向分量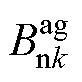 及切向分量
及切向分量 表达式分别为
表达式分别为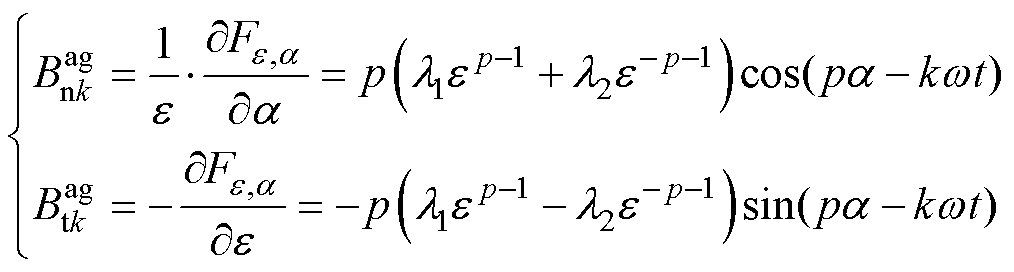 (4)
(4)
 (5)
(5)
 (6)
(6) (7)
(7)
 (8)
(8)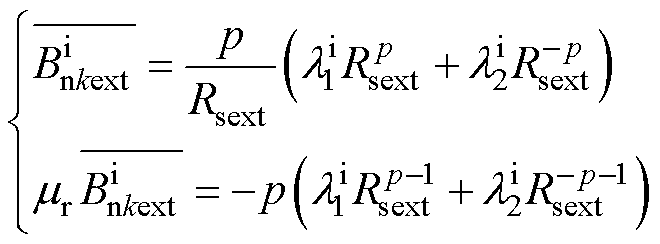 (9)
(9)
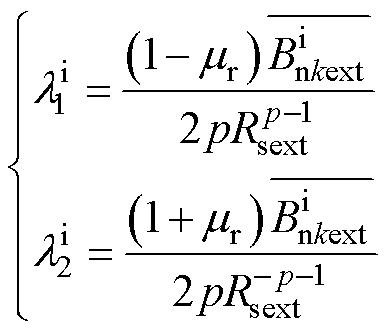 (10)
(10)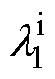 和
和 为系数。
为系数。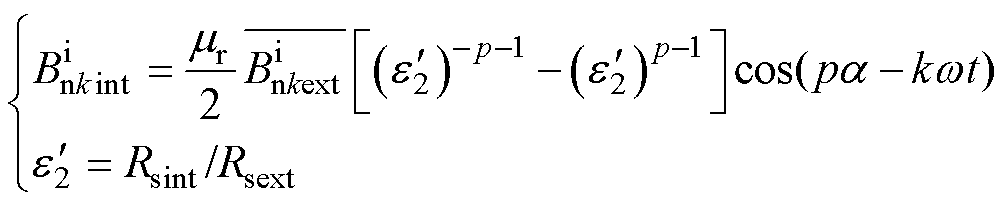 (11)
(11)
 (12)
(12) (13)
(13)
 与径向气隙磁通密度
与径向气隙磁通密度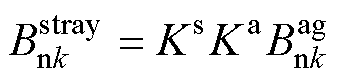 (14)
(14)
 (15)
(15)
 , 2n
, 2n (16)
(16)


 A、极对数为3的同步发电机故障模拟平台,用于模拟抽水蓄能电机发电运行工况。首先,由于实验机组与抽水蓄能电机在结构上存在一定差别,实验机组定子铁心外部并无定位筋,因此本次实验将覆有绝缘漆的铜板粘固于定子铁心表面,用于模拟铁心外部定位筋。其次,在信号采集前端布置了本团队设计的滤波放大信号调理装置,并采用5 V开关电源进行供电,其工作电流为10 mA,低通截止频率最大可调至10 kHz,放大增益最大可调至100倍,可在0~75℃范围内稳定工作。本次实验将低通截止频率设为200 Hz,且将输出信号放大增益调至50倍。同时为了观察,与未滤波的原始定位筋感应电动势信号做对比,本次实验也对未滤波信号进行了采集。
A、极对数为3的同步发电机故障模拟平台,用于模拟抽水蓄能电机发电运行工况。首先,由于实验机组与抽水蓄能电机在结构上存在一定差别,实验机组定子铁心外部并无定位筋,因此本次实验将覆有绝缘漆的铜板粘固于定子铁心表面,用于模拟铁心外部定位筋。其次,在信号采集前端布置了本团队设计的滤波放大信号调理装置,并采用5 V开关电源进行供电,其工作电流为10 mA,低通截止频率最大可调至10 kHz,放大增益最大可调至100倍,可在0~75℃范围内稳定工作。本次实验将低通截止频率设为200 Hz,且将输出信号放大增益调至50倍。同时为了观察,与未滤波的原始定位筋感应电动势信号做对比,本次实验也对未滤波信号进行了采集。 来减小流过故障模拟磁极的励磁电流I
来减小流过故障模拟磁极的励磁电流I ×25%计算匝间短路故障程度。此外,机组线电压、相电流、励磁电流、定位筋感应电动势等电气特征参量信息均采用Pico 4824 A数字示波器进行同步采集,采样频率设为4 kHz,实验整体布置如图7所示。
×25%计算匝间短路故障程度。此外,机组线电压、相电流、励磁电流、定位筋感应电动势等电气特征参量信息均采用Pico 4824 A数字示波器进行同步采集,采样频率设为4 kHz,实验整体布置如图7所示。