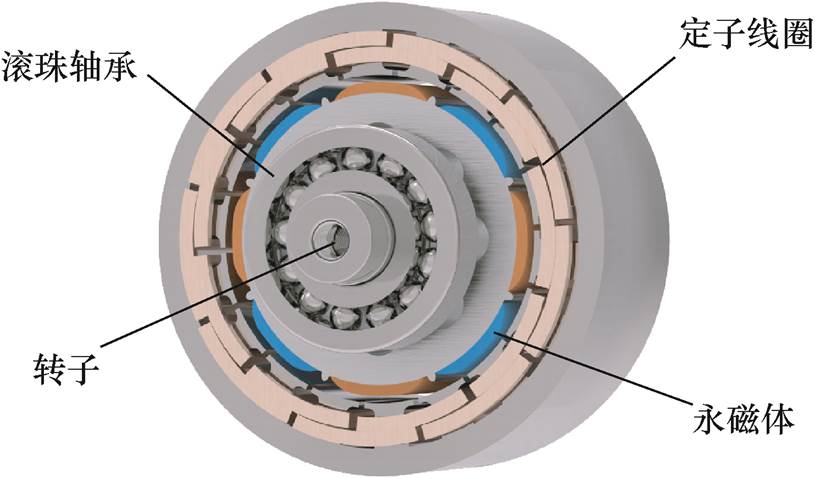
图1 PMSM三维拓扑结构
Fig.1 PMSM 3D topology
摘要 该文提出一种基于多通道信号二维递归融合和高效通道注意力机制新一代卷积神经网络(ECA-ConvNeXt)相结合的方法,以解决永磁同步电机高阻接触故障精细定量化诊断识别的问题。首先,建立永磁同步电机仿真模型获取三相电流信号作为有效故障信号;其次,引入递归图,将三相电流信号分别映射为二维图像并进行多通道融合,以提高故障特征信息的丰富性并消除人工特征提取的影响,实现故障特征的增强显示;然后,通过在ConvNeXt中引入高效通道注意力模块,提升了网络在通道维度上的适应性,得到ECA-ConvNeXt以实现永磁同步电机故障位置类型和严重程度的精确诊断分类,分类精度达到99.18%,并通过带噪声数据验证了该方法的鲁棒性;最后,搭建了样机实验平台,验证所提方法识别精度高达97.35%,能够准确识别永磁同步电机高阻接触故障位置和严重程度。
关键词:永磁同步电机 高阻接触故障 递归图 卷积神经网络 注意力机制
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)采用永磁体励磁,由于其高转矩、高效率、高功率因数等优点,已广泛应用于新能源汽车、工业自动化以及航空航天等领域[1-7]。
永磁同步电机常服役于复杂恶劣的工况环境中,容易产生多类型故障,甚至造成设备系统的损坏和报废,其中电气故障最为常见[8-10]。高阻接触(High-Resistance Connection, HRC)故障是一种常见的电气故障,尤其是在电机驱动系统中,其可能是由制造缺陷、热循环、腐蚀、点蚀或污染导致的接触表面损坏造成的[11-13]。HRC故障会引起连接处温度升高,加速接触面氧化,导致电阻进一步增大,进而可能演变为更严重的断路故障。因此,及时准确的诊断非常重要,可以防止发生严重损坏,并提高电机系统的可靠性。
传统的HRC故障诊断使用压降测量、红外热像仪等方法,测量误差较大,很难全面和定量地评估HRC故障。近年来,注入信号法[14-16]和零序分量检测法[17-18]在永磁同步电机HRC故障诊断中得到了应用。文献[14]提出了一种基于高频信号注入策略的三相感应电机HRC故障自动诊断方法;文献[16]中使用直流磁通注入法,在直接转矩控制系统的磁链控制回路中叠加磁链偏置,通过求解建立的电阻偏差二元线性方程组实现HRC故障的诊断。然而,这些基于信号注入策略方法属于侵入式诊断,可能对原有的驱动系统产生影响。为了避免信号注入的影响,文献[17-18]分别将零序电压分量(Zero- Sequence Voltage Component, ZSVC)的幅值和相位、基频和高频分量作为永磁同步电机的HRC故障指示器,用于故障诊断和定位。基于ZSVC的方法还被推广应用到直流无刷电机[19]和开关磁阻电机[20]的HRC故障诊断。然而,这类方法必须要中性点和额外的电阻网络,适用场景受到限制。
不同于上述方法,本文采用数据驱动的方法实现永磁同步电机HRC故障诊断,通过已有的大量的历史数据来建立系统的故障模式,不需要先验的已知模型或信号模式,可以很好地避免上述方法存在的问题。在数据驱动的电机故障诊断研究中,面临的挑战主要集中在故障信号处理和智能分类算法方面。
(1)故障信号处理方面。从故障信号中提取有用特征信息是故障诊断的基础。文献[21]中通过傅里叶变换,提取多通道振动和声音信号阶比分析处理后的频域特征,作为HRC故障检测和分类的指标;文献[22]基于双树复小波变换的方法检测电流信号振荡,从中提取电机故障特征信息。这些方法需要提取一维信号时域和频域细节特征,对信号处理相关专业能力依赖程度高,且易受噪声干扰。
(2)智能分类算法方面。用于电机故障诊断的智能分类模型主要有卷积神经网络、人工神经网络、支持向量机等。文献[21]利用双层双向长短期记忆网络从经过预处理的多传感器信号中提取和融合特征以识别电机HRC、霍尔断线等多种故障。文献[23]利用反向传播神经网络分析漏磁信号的时频特征实现电机HRC故障检测和定量分析。在这些分类方法中,随着网络层数的增加,会出现梯度弥散的现象,影响模型的分类精度和泛化能力。
针对以上方法中存在的问题,本文以三相永磁同步电机为研究对象,提出一种基于多通道信号二维递归融合和高效通道注意力机制新一代卷积神经网络(Effificient Channel Attention-Convolutional Neural Network Generation, ECA-ConvNeXt)的HRC故障诊断方法。首先,建立PMSM仿真模型获取三相电流信号作为有效故障信号。其次,创新性地引入递归图,将三相电流信号分别映射为二维递归图像并进行多通道融合,提升故障信息的丰富性,实现故障特征的互补增强显示。然后,引入ConvNeXt分类模型,利用卷积神经网络强大的特征提取能力实现数据分类识别,避免了故障信号处理时人工特征提取的影响。并通过融合注意力机制对传统ConvNeXt进行改进,得到新型ECA-ConvNeXt分类模型,提升了网络在通道维度上的适应性,增强了模型的泛化能力,有效解决了现有分类模型梯度弥散的问题。最后,搭建PMSM高阻接触故障诊断实验平台,验证了本文所提方法可实现PMSM高阻故障位置类型和严重程度的精确诊断分类,与其他方法的对比实验证明了所提方法具有较高的识别精度和鲁棒性。
永磁同步电机的三维拓扑结构如图1所示,该电机主要是由永磁体、定子线圈、转子铁心和轴承组成。本文的研究对象为一台4对极18槽表贴式的三相永磁同步电机,其主要的结构和部件参数见表1。

图1 PMSM三维拓扑结构
Fig.1 PMSM 3D topology
表1 永磁同步电机参数
Tab.1 PMSM motor parameters

参 数数 值参 数数 值 额定功率/W1 200额定转速/(r/min)2 000 额定电压/V 220额定电流/A4.5 额定转矩/(N·m)6转子惯量/(kg·cm2)7.6 定子电阻/Ω0.73电枢电感/mH2.35 极对数4永磁体磁链/Wb0.217
健康状态下,PMSM的三相电压方程为
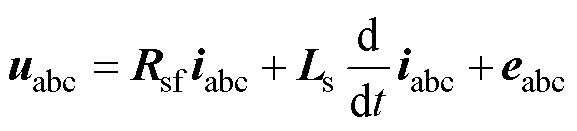 (1)
(1)
其中
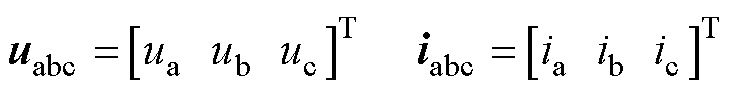
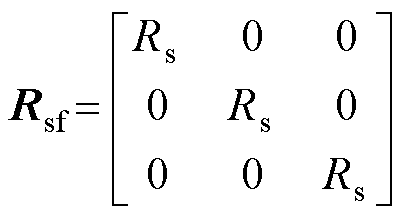 (2)
(2)
 (3)
(3)
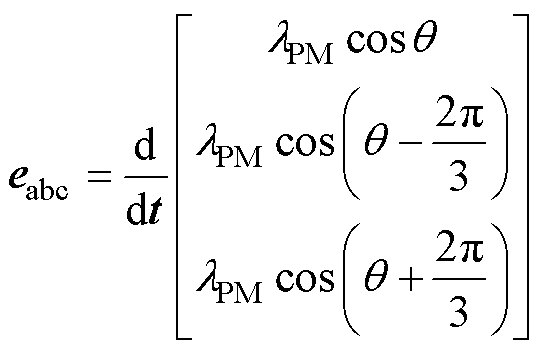 (4)
(4)
式中,uabc为定子电压矩阵;iabc为定子电流矩阵;Rsf为定子绕组电阻矩阵;Ls为定子绕组电感矩阵;eabc为空载电动势矩阵;L为定子相自感;M为定子相间互感;λPM为永磁体磁链;θ为转子的电角度。
当电机A相发生HRC故障时,定子绕组的电阻矩阵变为
 (5)
(5)
式中,Rs为定子电阻;Ra为A相定子绕组出现HRC故障时的附加电阻。
可以看出,HRC故障只影响到相电压方程中的电阻项。无论是否存在HRC故障,PMSM的机械运动方程都可表示为
 (6)
(6)
式中,ωm为电机的机械角速度;J为转动惯量;B为阻尼系数;TL为负载转矩;Te为电磁转矩。
根据式(6)中PMSM的电压方程和机械运动方程,本文采用id=0的矢量控制策略,基于Simulink平台建立PMSM控制仿真模型,如图2所示。HRC故障可能发生在PMSM中A、B、C三相中的任意相,如果假设HRC发生在A相,则可以通过将附加电阻Ra串联在A相的相线上来模拟HRC故障。
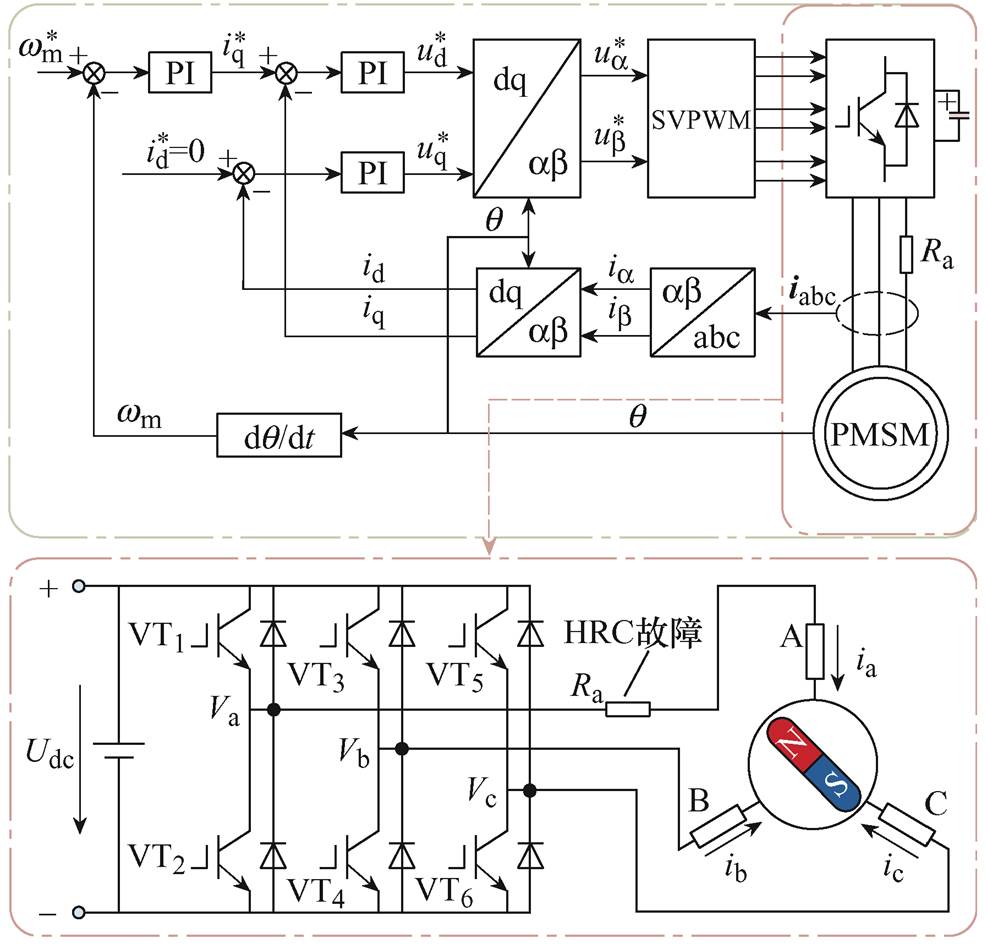
图2 永磁同步电机Simulink仿真模型
Fig.2 Simulink model of PMSM
本文将PMSM的HRC故障的严重程度按附加电阻Ra的阻值分为三类:轻微故障、中度故障和严重故障,对应附加电阻的阻值分别为0.1~0.3 Ω、0.4~1.0 Ω、1.1~2.0 Ω。针对HRC故障的不同位置和不同故障程度进行仿真生成原始电流信号。表2列出了预设的十种不同类型的永磁同步电机HRC故障及对应的标签,标签中的字母代表故障发生的位置,数字越大表示故障越严重。
表2 永磁同步电机高阻接触故障类型及标签
Tab.2 HRC fault types and labels of PMSM

Ra/Ω高阻接触故障程度故障位置标签 0无无Healthy 0.1~0.3轻微故障A相A1 B相B1 C相C1 0.4~1.0中度故障A相A2 B相B2 C相C2 1.1~2.0严重故障A相A3 B相B3 C相C3
通过仿真得到不同故障情况下的永磁同步电机三相电流信号如图3所示。其中,在0~0.1 s电机正常运行无故障,此时电机的三相电流处于平衡状态;0.1~0.2 s时电机A相出现中度HRC故障,A相电流幅值轻微减小,同时电机C相电流的幅值增加;0.2~0.3 s时电机A相故障演化为严重HRC故障,随着故障程度加深,电机的三相电流幅值变化更加显著。后续需要对电流信号进一步处理以增强故障特征。

图3 PMSM在Healthy、A2、A3情况下的仿真电流信号
Fig.3 PMSM simulation current signals of Healthy, A2, A3
递归图(Recurrence Plot, RP)是一种通过相空间可视化轨迹周期性的方法,已成功应用于电机轴承振动信号处理和故障诊断[24]、机械缺陷检测[25]等领域。RP能够保留原始一维信号中幅值与相位之间的相关信息,同时提高故障信息的丰富程度,实现故障特征的增强显示。基于二维递归图的输入已被证明可以有效提高模型的分类精度[26]。本研究创新性地将RP的方法引入永磁同步电机HRC故障诊断中,将一维电流数据编码为二维递归图像,为后续HRC故障分类和识别提供了基础。
基于二维递归融合的信号特征增强方法具体步骤如图4所示。首先利用RP的方法,将时域空间变换为相空间,计算状态之间的距离,从而得到相应的图像特征。对于给定的时间序列信号(I1, I2, , In),确定合适的嵌入维度m和延迟时间τ,进而对时间序列进行重构,重构后的轨迹为
, In),确定合适的嵌入维度m和延迟时间τ,进而对时间序列进行重构,重构后的轨迹为
 (7)
(7)
则递归图可以表示为
 (8)
(8)
式中, 为最小距离的阈值;
为最小距离的阈值; 为Heaviside函数。
为Heaviside函数。
 (9)
(9)

图4 原始三相电流信号到二维递归融合图的转换
Fig.4 Conversion of the original three-phase current signal to a 2D recursive fusion map
每600个点(采样率为10 kHz)转化为一张递归图,在得到A、B、C三相电流转化后的二维灰度递归图后,分别作为图像的R、G、B三个通道输入进行通道融合,得到最终的多通道递归融合图。不同类型的高阻故障转化后的递归融合图如图5所示。融合后的图像保留了每一相一维电流数据的细节和特征,为后续卷积神经网络提取故障特征奠定丰富的数据信息基础。

图5 不同类型高阻故障的递归融合图
Fig.5 Fusion recursive graph of different classes of HRC
卷积神经网络能有效地提取二维信号的特征信息,常用于解决数据的分类识别问题,已在电机轴承故障诊断[27]、目标检测[28]等领域得到广泛应用。
ConvNeXt[29]是在Swin Transformer的基础上改进的卷积神经网络,通过使用残差结构解决了随着网络深度增加带来的梯度弥散问题,进一步提高了分类的准确性。为了使网络能够自适应地锁定潜在的关键特征信息,本文在ConvNeXt的基础上,加入ECA[30]模块增强网络的性能,得到新的ECA-ConvNeXt分类模型用于永磁同步电机HRC故障的分类识别。
ECA-ConvNeXt分类模型的主要步骤如下:
(1)残差网络提取故障特征信息。残差模块是构成ECA-ConvNeXt的基本单元,其结构如图6所示,操作可表示为
 (10)
(10)
式中,X为输入矩阵;H(X)为模块输出;F(X)为残差,表示X和H(X)之间的误差。通过残差块中的恒等映射连接,输入的故障特征信息可以更快速地向前传播。
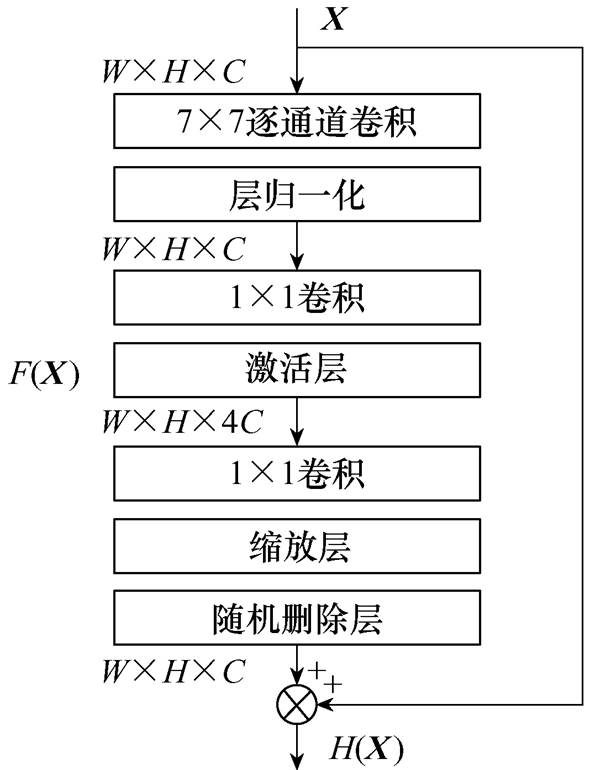
图6 残差模块结构
Fig.6 Structure of residual module
为了提高网络的非线性拟合能力,在残差模块中的卷积操作后跟随使用高斯误差线性单元(Gaussian Error Linear Unit, GELU)激活函数,有
 (11)
(11)
式中, 为x的高斯正态分布的累积分布,完整形式为
为x的高斯正态分布的累积分布,完整形式为
 (12)
(12)
最后,为防止过拟合并克服网络退化问题,通过Drop Path层将网络中的多分支结构的子路径随机删除。
(2)ECA实现局部跨通道交互,加强网络整体的通道特征。ECA结构如图7所示,对残差模块提取到的空间特征信息进行压缩,得到1×1×C的特征向量。为了对通道特征和通道之间的相关性进行学习,将得到的特征向量进行一维卷积操作,经过Sigmod激活函数后得到各个通道的权重p,该过程可表示为
 (13)
(13)
式中,k为一维卷积核的大小;y为全局平均池化后得到的1×1×C的输出。将权重p与原始输入中对应的通道相乘,得到最终融合了通道注意力机制的W×H×C的输出特征图。

图7 ECA结构
Fig.7 Structure of ECA
卷积核的大小k代表了局部跨信道交互的覆盖率,即该通道附近有多少相邻通道参与了这个信道的注意力预测。k的值与通道维数成正比,可以通过式(14)、式(15)自适应地确定。
 (14)
(14)
 (15)
(15)
式中,C为通道维数;符号“| |odd”表示k只能取奇数;γ和b用于改变通道数C和卷积核大小k之间的比例关系。
(3)全连接层整合特征信息,得到期望输出。将具有通道注意力的特征输出进行全局平均池化后,通过全连接层将分布式特征映射到样本标记空间,得到最后的分类识别结果。
基于上述分析,本文的故障诊断方法基本流程如图8所示。该方法主要分为三个部分:首先,从永磁同步电机中采集三相电流信号作为原始故障数据。然后,将电机每相的一维电流数据分别转化为二维递归图并进行通道融合处理。融合后的图像提供了在一维时间序列数据中无法观察到的额外特征,可以直观地识别和分类故障模式。最后,将融合了通道注意力机制的ECA-ConvNeXt作为一种高效的特征提取器用来从输入的图像中获得更多可区分故障模式和故障严重程度的特征,将提取的代表性特征向量用于分类,得到最终的永磁同步电机HRC故障分类识别结果。
本文提出的ECA-ConvNeXt,通过融合通道注意力机制,不仅构建了多尺度的可视化映射,还加强了特征通道的映射,细化了特征表示,能够抑制冗余特征,突出复杂工况下永磁同步电机的关键故障和通道位置。

图8 本文所提出方法的故障诊断流程
Fig.8 HRC fault diagnosis flow chart
使用PMSM转速为1 300 r/min,负载转矩为2 N·m时仿真得到的三相电流信号制作递归图像仿真数据集。采样率设为10 kHz,通过RP算法将三通道的电流信号转化为128×128×3的图像。训练集共4 000张图像,每一类故障中含有400张图,以A1类型故障为例,其中包含HRC故障发生在A相且Ra阻值分别为0.1、0.2、0.3 Ω时的递归图像各133、133、134张。测试集共4 000张图,与训练集不同的是,测试集的每一类故障中对应不同阻值Ra的递归图像数量是完全随机的。
ECA-ConvNeXt的训练过程如图9所示,精度随着迭代次数的增加而增加,最后收敛到99%。经过多次迭代训练,得到了一个训练良好的ECA- ConvNeXt模型。

图9 ECA-ConvNeXt训练精度和损失曲线
Fig.9 ECA-ConvNeXt training accuracy and loss curves
为了验证所提出方法的优越性,本文选取了相关研究中较为流行的GoogLeNet、ResNet和Swin Transformer模型作为对比。同时,将RP+ECA- ConvNeXt与未采用RP算法的1D+ECA-ConvNeXt进行对比以证明RP算法的有效性。为保证两者训练时模型的结构和输入数据相同,将三通道电流信号直接重构成32×32×3的矩阵,经过上采样后变成128×128×3的矩阵作为1D+ECA-ConvNeXt的输入。使用每类400个样本的测试数据集对训练过的模型进行测试,结果见表3。其中,分类精度是评估分类模型性能时最常用的指标,计算了分类正确的预测数与总预测数的比值。然而,在不均衡多分类问题中,仅凭分类精度评估模型是具有缺陷的,因此本文还引入了F1分数和感受性曲线下面积(Area Under Curve, AUC)作为模型的评价指标,这些指标越接近1,说明模型的性能越好。从表3中可以看出,1D+ECA- ConvNeXt的精度只有83.32%,各项性能指标都远低于其他采用了RP算法的模型,这证明了RP算法提升信号特征的有效性。都使用RP算法的情况下,ECA-ConvNeXt相较于基础的ConvNeXt在性能上有所提升,在测试集样本上的识别精度从98.05%提升到了99.18%。GoogLeNet、ResNet和Swin Transformer的精度分别为94.95%、94.43%、91.23%。对比这些模型,本文提出的ECA- ConvNeXt的各项性能指标都是最高,效果最好。
表3 测试结果对比(仿真)
Tab.3 Comparison of test results (simulation)

方 法精度(%)F1分数AUC RP+ECA-ConvNeXt99.180.991 70.995 9 1D+ECA-ConvNeXt83.320.838 80.916 6 RP+ConvNeXt98.050.980 50.990 2 RP+GoogLeNet94.950.948 80.974 7 RP+ResNet94.430.943 70.972 1 RP+Swin Transformer91.230.913 80.956 1
图10通过混淆矩阵可视化了不同模型经过训练后的最终分类结果,其中纵向和横向标签分别代表电机实际故障类型和预测故障类型,每种类型400个测试样本。当电机发生不同类型HRC故障时,电流信号相应发生变化,这进一步导致产生相互区分的递归融合图像。因此,通过ECA-ConvNeXt提取的特征图保证了来自不同电机故障的图像可以被分类到不同的组中。从图10中可以看出,本文提出的RP+ECA-ConvNeXt分类模型仅在A3、B3、C3这几类严重故障情况下存在少量标签预测错误,其他故障样本识别精度均为100%。这是由于在严重HRC故障时,附加电阻Ra的阻值范围更大,识别难度会更高。在识别A1类型故障时,ConvNeXt、GoogLeNet、ResNet、SwinTransformer均存在较多错误,400个样本中,分别有26、131、80、50个样本被错误地分类到了Healthy类型。未采用RP的1D+ECA-ConvNeXt预测错误的标签最多,有大量轻微和中等程度的故障样本被识别为Healthy。可以看出,RP算法丰富了故障特征信息,能大幅提高模型的训练精度,因此在后续的实验中,均采用RP算法处理数据。对比ConvNeXt、GoogLeNet、ResNet、Swin Transformer模型,本文提出的ECA- ConvNeXt性能更好,并且在识别早期HRC故障方面更具优势,可以帮助及时发现电机故障,防止进一步恶化。

图10 各方法测试结果的混淆矩阵
Fig.10 Confusion matrix of test results of each method
为了让数据更符合实际情况,分别在PMSM三相电流仿真数据中加入信噪比(Signal-to-Noise Ratio, SNR)为30、35、40 dB的高斯白噪声。使用带噪声的数据制作递归图像数据集对各个模型进行测试,测试结果如图11所示,各项指标对比见表4。
从测试结果可以看出,ECA-ConvNeXt在三种噪声情况下的测试精度、F1分数、AUC都是所有模型中最高的。当加入信噪比40 dB的噪声时,ECA- ConvNeXt模型精度为99.03%,几乎不受影响;加入信噪比为30 dB的噪声时,ECA-ConvNeXt仍有94.58%的精度,高于其他模型。结果表明,所提出的ECA-ConvNeXt分类模型具有较好的鲁棒性。

图11 加入噪声后模型的测试精度
Fig.11 Test accuracy of the model after adding noise
表4 加入噪声后各模型测试结果对比
Tab.4 Comparison of test results of each model after adding noise

模型SNR=40 dBSNR=35 dBSNR=30 dB 精度(%)F1分数AUC精度(%)F1分数AUC精度(%)F1分数AUC ECA-ConvNeXt99.030.990 20.995 197.930.979 30.989 694.580.945 80.972 9 ConvNeXt97.650.976 60.988 296.680.966 90.983 494.250.942 70.971 2 GoogLeNet94.920.948 60.974 694.580.945 30.972 994.000.939 80.969 9 ResNet93.430.934 50.967 193.580.935 80.967 992.400.924 30.962 0 Swin Transformer89.650.898 30.948 288.700.888 30.943 586.380.864 50.931 9
搭建了PMSM样机高阻故障诊断实验平台进一步验证本文所提方法的有效性,如图12所示。实验平台包括:测试PMSM(具体参数见表1)、负载PMSM、电机控制器、AC-DC整流器、电子负载、计算机、数据采集卡、电流探头。

图12 高阻接触故障诊断实验平台
Fig.12 Experimental platform of HRC fault diagnosis
实验流程如下:①测试电机通过联轴器连接到负载电机,负载电机产生的交流电经过AC-DC整流器接入一个电子负载,通过改变电子负载的阻值控制负载大小。实验过程中测试电机的转速为1 300 r/min,电子负载阻值设为10 Ω;②将电阻分别串联在A、B、C相的相线上模拟不同位置的HRC故障,电阻阻值为0.1~2.0 Ω,以0.1 Ω为间隔递增;③三个电流探头同时采集驱动电机A、B、C三相的电流信号,采集到的电流信号数据通过NI数据采集卡上传到计算机,采样频率为10 kHz。
实验测得永磁同步电机正常工作时和A相发生不同程度HRC故障时的三相电流波形。永磁同步电机HRC故障识别和分类过程如下:
(1)永磁同步电机HRC故障数据集制作。对实测电机三相电流信号进行多通道递归融合处理的步骤如图13所示。从采集到的原始三相电流信号中截取数据,每段包含600个数据点,采用递归算法将一维数据信号分别转化为二维灰度递归图,图片的大小为128×128×1。将A、B、C三相电流对应的灰度递归图分别作为RGB图像的R、G、B三个通道输入,得到最终的递归融合图,大小为128×128×3。按表2中的故障类型将生成的递归融合图划分为十类,使用与仿真数据集相同的方法制作高阻故障实验数据集用于后续验证。

图13 对实验数据进行多通道递归融合
Fig.13 Multi-channel RP fusion of experimental data
(2)永磁同步电机HRC故障诊断结果分析。使用训练集对ECA-ConvNeXt、ConvNeXt、GoogLeNet、ResNet和Swin Transformer等模型进行训练。训练后的各个模型对测试集的分类精度、F1分数、AUC和测试时间对比见表5。其中,测试时间是指从数据读入后,经过RP转化和模型分类识别所需的总时间,取十次测试时间的平均值作为最终结果。
表5 模型测试结果对比(实验)
Tab.5 Comparison of model test results (experiment)

模型精度(%)F1分数AUC测试时间/ms ECA-ConvNeXt97.350.973 40.986 7728 ConvNeXt96.530.965 00.982 6753 GoogLeNet94.250.941 00.971 2521 ResNet93.330.932 30.966 7717 Swin Transformer89.930.892 60.949 6823
从表5中可以看出,ECA-ConvNeXt的分类精度为97.35%,在所有模型中最高,F1分数和AUC都最接近1,说明模型的泛化能力强。ConvNeXt分类精度为96.53%,GoogLeNet、ResNet和Swin Transformer的分类精度分别为94.25%、93.33%、89.93%。ECA-ConvNeXt通过引入注意力机制,提升了模型在通道维度上的适应性,加强了特征通道的映射,细化了故障特征表示,相比基础的ConvNeXt精度提升了0.82%,同时测试时间也有所减少。ECA-ConvNeXt的测试时间为728 ms,相较于参数量较少的GoogLeNet,测试时间高出207 ms,但仍然能够在1 s完成故障的分类识别。综上所述,本文所提出的方法可以准确、有效地分类识别永磁同步电机HRC故障,同时具有良好的计算效率,未来可通过将该算法部署到边缘设备中,实现电机的实时故障诊断。
在实际的工程问题中,电机通常存在多种运行状况,因此模型在多工况下的故障分类识别能力同样重要。本文采集了电机在三种不同工况下的高阻故障数据,见表6。使用电机转速为1 300 r/min,电子负载为10 Ω的工况Ⅱ数据训练模型,用工况Ⅰ和Ⅲ的数据进行测试,得到的结果见表7。
表6 工况参数介绍
Tab.6 Working condition parameter introduction

工况ⅠⅡⅢ 转速/(r/min)1 2501 3001 300 电子负载阻值/Ω101011
表7 使用其他工况数据测试的结果
Tab.7 Test results using other operating data

模型精度(%) 工况Ⅰ工况Ⅲ ECA-ConvNeXt96.795.8 ConvNeXt93.591.3 GoogLeNet94.592.8 ResNet90.187.3 Swin Transformer87.285.9
由表7可知,本文提出的方法能准确识别其他转速转矩工况下的高阻故障,并且都取得了最高的故障识别精度。得益于ECA模块中的通道注意力机制,有效提高了ConvNeXt模型的全局特征提取能力,最终达到了提高模型泛化能力的效果。
本文针对永磁同步电机HRC故障,提出一种基于多通道信号递归融合和ECA-ConvNeXt分类模型相结合的HRC故障诊断方法,通过实验结果分析得到以下结论:
本文使用数据驱动诊断方法,创新性地引入二维递归图方法将PMSM三相电流信号进行融合转换,实现了电机高阻接触故障多通道特征的互补增强显示,为后续故障诊断提供了有效的特征数据基础。提出一种基于注意力机制的ECA-ConvNeXt永磁同步电机高阻故障诊断模型,增强了模型在通道维度上的适应性,对PMSM高阻故障的诊断精度达到了99.18%,通过和多种诊断识别分类框架的对比实验,验证了该方法的优越性。通过仿真和样机实验的验证,证明本文所提方法在不同工况下的诊断鲁棒性。
参考文献
[1] Chen Hao, He Jiangbiao, Guan Xing, et al. High- resistance connection diagnosis in five-phase PMSMs based on the method of magnetic field pendulous oscillation and symmetrical components[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 2288-2299.
[2] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Spatial distribution characteristics and influencing factors of demagnetization of permanent magnet motor for electric vehicle[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5959-5974.
[3] 沐俊文, 葛兴来, 朱丹. 地铁永磁牵引系统复矢量电流环稳定性研究[J]. 电气工程学报, 2022, 17(2): 92-100.
Mu Junwen, Ge Xinglai, Zhu Dan. Research on current loop stability of metro permanent magnet traction system[J]. Journal of Electrical Engineering, 2022, 17(2): 92-100.
[4] 陈少先, 丁树业, 申淑锋, 等. 船舶用表贴式永磁同步电机的电磁振动分析与抑制[J]. 电工技术学报, 2023, 38(5): 1275-1286, 1298.
Chen Shaoxian, Ding Shuye, Shen Shufeng, et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1275-1286, 1298.
[5] 周立, 苏美霞, 王杰. 永磁同步电机模糊多矢量模型预测控制[J]. 电气工程学报, 2022, 17(4): 181-192.
Zhou Li, Su Meixia, Wang Jie. Fuzzy multi-vector model predictive control of permanent magnet syn- chronous motor[J]. Journal of Electrical Engineering, 2022, 17(4): 181-192.
[6] 于艳君, 崔明恺, 柴凤. 双绕组永磁同步电机滑模变结构控制[J]. 电工技术学报, 2022, 37(22): 5799- 5807.
Yu Yanjun,Cui Mingkai, Chai Feng. Sliding mode variable structure control of a dual-winding per- manent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5799- 5807.
[7] 张伟伟, 肖飞, 刘计龙, 等. 轨道交通车辆永磁同步牵引系统断电区穿越控制策略[J]. 电工技术学报, 2021, 36(16): 3483-3492.
Zhang Weiwei, Xiao Fei, Liu Jilong, et al. Power-off area traversing control strategy of permanent magnet synchronous motor traction system in rail transit vehicle[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3483-3492.
[8] 杭俊, 孙无双, 赖江龙, 等. 基于跨极式探测线圈的双三相永磁同步电机故障诊断方法[J]. 电机与控制学报, 2023, 27(7): 163-173.
Hang Jun, Sun Wushuang, Lai Jianglong, et al. Fault diagnosis method of dual three phase permanent magnet synchronous motor based on transpolar search coil[J]. Electric Machines and Control, 2023, 27(7): 163-173.
[9] 陈昊, 张楠, 高彩霞, 等. 永磁同步电机匝间短路故障短路线圈定位方法[J]. 电机与控制学报, 2023, 27(3): 124-134.
Chen Hao, Zhang Nan, Gao Caixia, et al. Fault coil location approach of permanent magnet synchronous motor with interturn short circuit fault[J]. Electric Machines and Control, 2023, 27(3): 124-134.
[10] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Discrimination of interturn short-circuit and local demagnetization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[11] Hu Rongguang, Wang Jiabin, Mills A R, et al. High-frequency voltage injection based stator interturn fault detection in permanent magnet machines[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 785-794.
[12] 高彩霞, 苗壮, 陈昊, 等. 基于线圈子单元的永磁同步电机健康与定子绕组短路故障数学模型[J]. 电工技术学报, 2023, 38(4): 957-969.
Gao Caixia, Miao Zhuang, Chen Hao, et al. A mathematical model based on coil sub-element for permanent magnet synchronous motor with health and stator winding short-circuit fault[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 957-969.
[13] Kommuri S K, Park Y, Lee Sangbin. High-resistance fault control in permanent magnet synchronous motors[J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(1): 271-281.
[14] de la Barrera P M, Bossio G R, Solsona J A. High-resistance connection detection in induction motor drives using signal injection[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3563-3573.
[15] de la Barrera P M, Bossio G R, Leidhold R. Online voltage sensorles shigh-resistance connection diagnosis in induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4374-4384.
[16] Hang Jun, Wu Han, Ding Shichuan, et al. A DC-flux-injection method for fault diagnosis of high-resistance connection in direct-torque-controlled PMSM drive system[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 3029-3042.
[17] Hu Rongguang, Wang Jiabin, Mills A R, et al. Detection and classification of turn fault and high resistance connection fault in permanent magnet machines based on zero sequence voltage[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1922-1933.
[18] Zhang Jianzhong, Hang Jun, Ding Shichuan, et al. Online diagnosis and localization of high-resistance connection in PMSM with improved fault indicator[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3585-3594.
[19] Wang Hui, Lu Siliang, Qian Gang, et al. A two-step strategy for online fault detection of high-resistance connection in BLDC motor[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 3043-3053.
[20] Hang Jun, Zhang Jianzhong, Ding Shichuan, et al. Fault diagnosis of high-resistance connection in a nine-phase flux-switching permanent-magnet machine considering the neutral-point connection model[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6444-6454.
[21] 王骁贤, 陆思良, 何清波, 等. 变转速工况下基于多传感器信号深度特征融合的电机故障诊断研究[J]. 仪器仪表学报, 2022, 43(3): 59-67.
Wang Xiaoxian, Lu Siliang, He Qingbo, et al. Motor fault diagnosis based on deep feature fusion of multi-sensor data under variable speed condition[J]. Chinese Journal of Scientific Instrument, 2022, 43(3): 59-67.
[22] Seshadrinath J, Singh B, Panigrahi B K. Incipient turn fault detection and condition monitoring of induction machine using analytical wavelet transform[J]. IEEE Transactions on Industry Applications, 2014, 50(3): 2235-2242.
[23] 武智超, 王慧, 王吉亮, 等. 基于阵列漏磁信号分析的无刷直流电机高阻接触故障诊断研究[J]. 电子测量与仪器学报, 2021, 35(11): 108-114.
Wu Zhichao, Wang Hui, Wang Jiliang, et al. Fault diagnosis of high resistance connection in brushless DC motor based on analysis of array leakage flux signals[J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(11): 108-114.
[24] Liu Xiaoping, Xia Lijian, Shi Jian, et al. A fault diagnosis method of rolling bearing based on improved recurrence plot and convolutional neural network[J]. IEEE Sensors Journal, 2023, 23(10): 10767-10775.
[25] 杨秋玉, 阮江军, 张灿, 等. 基于定量递归分析的高压断路器机械缺陷辨识及应用[J]. 电工技术学报, 2020, 35(18): 3848-3859.
Yang Qiuyu, Ruan Jiangjun, Zhang Can, et al. Study and application of mechanical defect identification for high-voltage circuit breakers using recurrence quantification analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3848-3859.
[26] Wen Long, Li Xinyu, Gao Liang, et al. A new convolutional neural network-based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5990-5998.
[27] Lu Siliang, Qian Gang, He Qingbo, et al. In situ motor fault diagnosis using enhanced convolutional neural network in an embedded system[J]. IEEE Sensors Journal, 2020, 20(15): 8287-8296.
[28] Hu Yuan, Li Xiang, Zhou Nan, et al. A sample update-based convolutional neural network framework for object detection in large-area remote sensing images[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(6): 947-951.
[29] Liu Zhuang, Mao Hanzi, Wu Chaoyuan, et al. A ConvNet for the 2020s[C]//2022 IEEE/CVF Confer- ence on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 2022: 11966- 11976.
[30] Wang Qilong, Wu Banggu, Zhu Pengfei, et al. ECA-net: efficient channel attention for deep convolutional neural networks[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 2020: 11531-11539.
Abstract The measurement error of traditional high-resistance connection (HRC) fault diagnosis method for permanent magnet synchronous motor (PMSM) is typically high, and it is difficult to evaluate HRC fault comprehensively and quantitatively. Modern diagnosticmethods of HRC fault are realized by the symmetry monitoring system of injection signal method and zero-sequence component detection method. However, these methods based on signal injection strategy are invasive diagnostics, which may have an impact on the original drive system. The method based on zero sequence component must have neutral points and additional resistance network, and the application scenario is limited. To solve the above problems, this paper proposes a data-driven method to realize the HRC fault diagnosis of PMSM, and establishes the fault mode of the system through a large number of existing historical data, without the need for a prior known model or signal mode. Firstly, a simulated PMSM model is established to obtain the three-phase current signal as an effective fault signal. Secondly, the recursive graph method is innovatively introduced to map the three-phase current signals into two-dimensional recursive images and perform multi-channel fusion. The fused images contain more feature information and avoid the influence of artificial feature extraction during fault signal processing. Then, ConvNeXt is introduced to effectively solve the gradient dispersion problem of the existing classification model, and a new ECA-ConvNeXt classification model is obtained by integrating the attention mechanism, which improves the adaptability of the network in the channel dimension and enhances the generalization ability of the model. The simulation results show that compared with the basic ConvNeXt, the accuracy of ECA-ConvNeXt on the test set sample is improved from 98.05% to 99.18%. Compared with models such as GoogLeNet, ResNet and Swin Transformer, the ECA-ConvNeXt proposed in this paper also has higher performance indexes and more advantages in identifying early HRC faults. To verify the robustness of the model in the presence of input data noise, Gaussian noise is added to the original input data. The results show that the effect of these noises is not significant. Finally, through the establishment of prototype experimental platform verification, it is proved that the identification accuracy of the new method proposed in this paper is as high as 97.35%, and it can accurately identify the location and severity of high resistance contact faults of permanent magnet synchronous motors. Based on the analysis of simulation and test data, this paper draws the following conclusions: (1) This paper uses data-driven method to realize the non-invasive diagnosis of HRC fault of permanent magnet synchronous motor, avoiding the problem that the mathematical and electromagnetic relationship is too complicated in the model diagnosis method. (2) The two-dimensional recursive graph signal conversion method is innovatively introduced into the field of high resistance fault diagnosis of permanent magnet motors, and one-dimensional three-phase current signals are transformed into two-dimensional recursive images respectively and channel fusion is carried out to enhance fault characteristics, eliminate the influence of artificial feature extraction, and lay a rich fault information foundation for the classification and recognition of HRC faults of permanent magnet synchronous motors. (3) An ECA-ConvNeXt classification model with added attention mechanism was proposed to solve the gradient dispersion problem, improve the adaptability of the model in the channel dimension, and increase the classification accuracy of the model on the experimental data set from 96.53% to 97.35%. The comparison between the proposed method and other classification models proves the superiority of this classification model.
Keywords:Permanent magnet synchronous motor (PMSM), high-resistance connection (HRC) fault, recursive graph, convolutional neural network, attention mechanism
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.231091
国家自然科学基金项目(52207036, 62203010, 52075002)、安徽省自然科学基金项目(22080850E167)和安徽省教育厅自然科学重点项目(KJ2021A0018)资助。
收稿日期 2023-07-11
改稿日期 2023-10-07
丁 伟 男,2000年生,硕士研究生,研究方向为机电系统故障诊断。E-mail: Z21301120@stu.ahu.edu.cn
宋俊材 男,1992年生,博士,讲师,硕士生导师,研究方向为机电设备故障诊断与状态监测、电机优化设计与控制。E-mail: songjuncai@ahu.edu.cn(通信作者)
(编辑 崔文静)