, an。其中，n为磁钢层数，0＜an＜90°。摘要 针对内置式永磁同步电机转矩脉动大、转子结构复杂优化设计困难的问题，将转子上的隔磁桥抽象为转子虚槽，并研究转子虚槽位置对电机转矩性能的影响，在此基础上提出一种通用的优化转子结构降低转矩脉动的方法。首先，推导考虑转子虚槽影响的电机转矩的解析计算模型，并分析转子虚槽位置对电机转矩的影响规律，进而总结降低转矩脉动的电磁设计原则。对不同转子结构的内置式永磁同步电机进行有限元仿真计算，验证解析模型。然后，以一台8极48槽电动汽车用内置式永磁同步电机为例，根据降低转矩脉动的原则对转子结构进行优化。计算优化前后电机的电磁性能，结果表明该方法能够有效降低电机的转矩脉动。最后，通过样机试验验证了理论分析以及仿真的有效性，为解决电机转矩脉动大、转子结构优化困难提供了一种有效的方法。
关键词：内置式永磁电机 转矩脉动 转子虚槽 电动汽车
内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor, IPMSM）因具有高功率密度、高转矩密度、宽调速范围、弱磁能力强等优势，广泛地应用于电动汽车领域[1-2]。然而，内置式永磁电机也具有转矩脉动大、电磁振动及引发噪声等缺点，会对电动汽车的驾驶性能造成负面影响[3-4]。因此，电动汽车用内置式永磁同步电机的转矩脉动抑制问题成为近些年的研究热点[5-6]。
定子斜槽或转子错极能够有效地抑制电机的转矩脉动，但这些方法会增加电机的制造成本，并且降低电机的输出转矩[7-8]。优化内置式电机转子结构能有效地降低转矩脉动，同时不削弱电机的输出转矩，不明显提高电机的成本[9-10]。针对隔磁桥优化设计问题，国内外研究者进行了一系列研究。单层磁钢转子隔磁桥的设计参数较少，文献[11]采用穷举法来计算单层磁钢转子隔磁桥尺寸对电机转矩性能的影响，得到了转矩脉动最小的隔磁桥设计参数。文献[12]提出了几种单层磁钢转子的异形隔磁桥形式并给出了需要设计的参数，同样用穷举法探索这些设计参数对电机转矩脉动的影响。其研究的基本思路为通过优化设计隔磁桥来改变dq轴的磁阻，消除气隙磁通密度中的低次谐波，从而降低转矩脉动。然而研究以气隙总谐波畸变率为目标，缺乏针对性。
对于多层磁钢转子，文献[13-16]仍然使用穷举法获取隔磁桥的最优设计参数。但随着设计参数的增多，相关计算量呈指数级增长。为解决这一问题，文献[17-18]使用智能算法优化设计隔磁桥，以减小设计的计算量。尽管这种方法能够减小计算量，但对于电机的初期设计无法提供指导。文献[19-20]尝试对隔磁桥设计参数进行灵敏度分析，以获得设计参数的权重，为电机的电磁设计提供指导。
解析法在指导电机初期设计方面具有明显优势。通过解析方法，可以更精确地分析不同转子隔磁桥设计参数对转矩脉动的影响，并得出指导初期设计的设计原则。文献[21-22]通过解析法分别研究了双层和三层磁钢转子隔磁桥位置对转矩脉动的影响。其主要贡献是推导了隔磁桥位置对转子磁动势分布影响的解析公式，并确定了使转子磁动势谐波最小的隔磁桥位置，进而获得较低的转矩脉动。文献[23-24]推导出转矩脉动随转子磁动势谐波含量变化的解析公式，并指出与定子齿谐波次数相同的转子磁动势谐波对转矩脉动的贡献最大。基于这些解析公式，总结出了设计低转矩脉动转子隔磁桥的原则。
然而，以上基于解析计算的研究中，没有考虑隔磁桥对气隙比磁导率的影响。为此本文首先将不同内置式转子结构等效为转子虚槽位置。考虑转子虚槽位置对电机气隙比磁导率的影响，并推导电机转矩脉动的解析表达式。根据解析公式分析了单层磁钢及双层磁钢转子虚槽位置对转矩脉动的影响规律。在此基础上总结了一种任意层磁钢电机的低转矩脉动的电磁设计方法。使用有限元法计算一台实例电机的转矩性能，验证该方法的有效性。最后制作样机进行试验，试验结果验证了理论分析与仿真结果的合理性。
为了简化分析，做如下假设：①隔磁桥处的磁通密度深度饱和，其磁导率为真空磁导率；②所有隔磁桥对气隙比磁导率的影响相同，影响效果等效为一个槽深、槽宽已知的槽。
根据以上假设，可以用转子开槽等效转子隔磁桥对气隙比磁导率的影响，本文称为转子虚槽。转子虚槽位置的定义如图1所示，图1a和图1b的气隙比磁导率计算可以抽象表达为图1c的形式。图中，c为虚槽开口电角度。图1a和图1b两台永磁同步电机的转子结构虽然不同，但虚槽分布相同。虚槽分布相同的转子结构对气隙比磁导率的影响相同。定义转子虚槽位置为与q轴夹角的电角度，从靠近q轴到靠近d轴方向分别为a1, a2,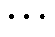, an。其中，n为磁钢层数，0＜an＜90°。
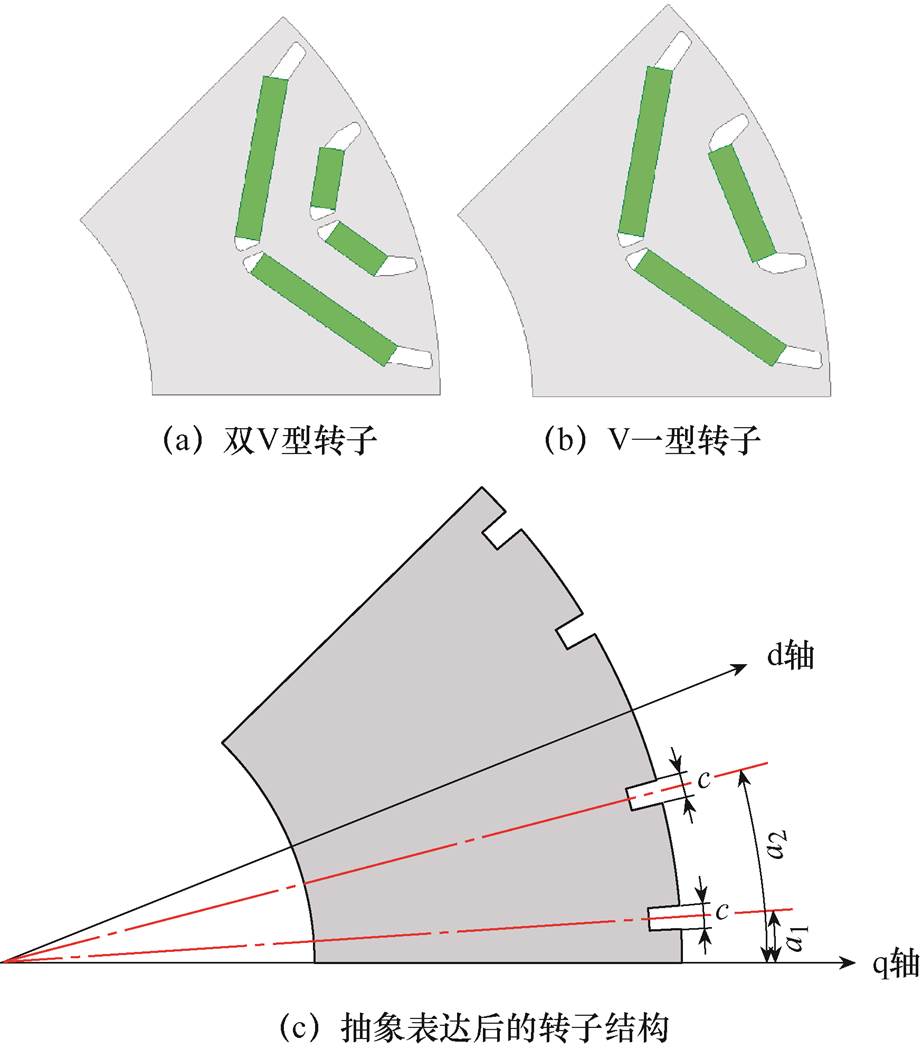
图1 转子虚槽位置的定义
Fig.1 Definition of the location of virtual slots
假设定子表面光滑，转子虚槽影响气隙比磁导率的等效深度为hR，气隙长度为hg，θ为极坐标下的空间角度，r为电机半径，转子开槽的气隙磁场计算模型如图2所示。
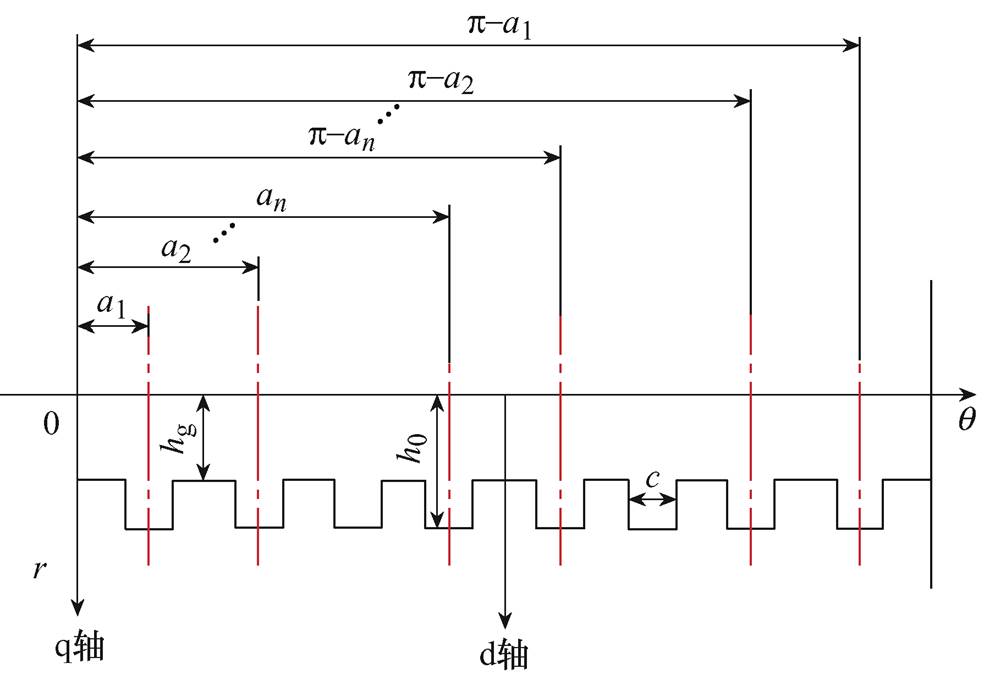
图2 转子开槽的气隙磁场计算模型
Fig.2 Air gap relative permeability calculation model considering virtual slot
一极下的气隙比磁导率可以表示[23]为
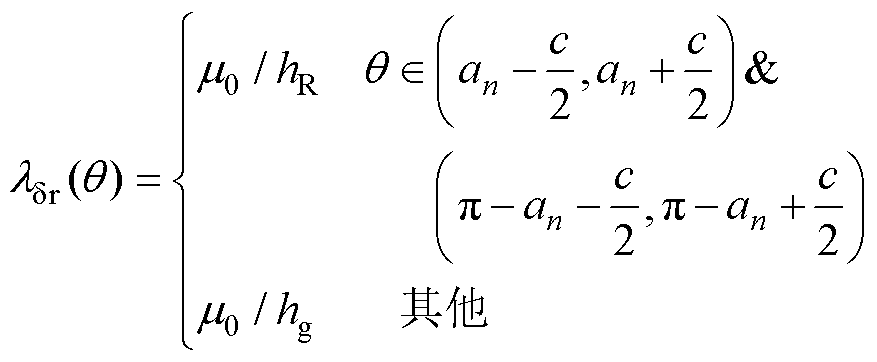
（1）
式中，μ0为真空磁导率；λδr为考虑转子开槽气隙比磁导率。
将一对极下的气隙比磁导率进行傅里叶分解可得
（2）
式中，λ0为气隙平均比磁导率；p为电机极对数；ω为电机角速度；t为时间；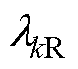
为转子开槽引起的谐波比磁导率各次幅值；kR为转子开槽引起谐波比磁导率的谐波次数，kR=2,4,6,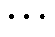且有
（3）
由转子虚槽引起的各次气隙谐波比磁导率幅值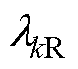受转子虚槽位置影响，整体呈现三角函数关系。因此，合理设计虚槽位置可以使得特定次数的转子虚槽引起的气隙比磁导率谐波的标幺值为0。
上述研究假设定子表面光滑，考虑定转子表面开槽后的气隙比磁导率可以表示[25]为
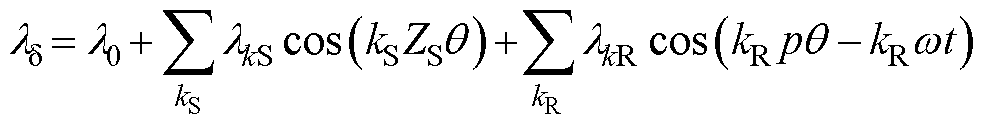（4）
式中，λδ为考虑定转子开槽的气隙比磁导率；ZS为定子槽数；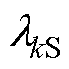
为定子开槽引起的谐波比磁导率各次幅值；kS为定子开槽引起谐波比磁导率的谐波次数，kS=1,3,5,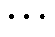且[25]有
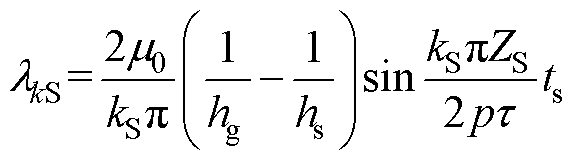（5）
式中，hs为定子开槽影响气隙比磁导率的等效深度；ts为定子齿宽；
为电机极距。
定转子开槽对气隙比磁导率的影响有两点不同：一是周期不同。由于定子槽沿着圆周均匀分布，受其影响引起的气隙谐波比磁导率在一个圆周内的周期数为ZS；而转子虚槽通常不会沿着转子圆周均匀分布，因此转子开虚槽引起的气隙谐波比磁导率在一个圆周的周期数为p。二是转速不同。坐标系设定在定子上时，定子开槽引起的气隙谐波比磁导率表达式为空间量，而转子开槽引起的气隙谐波比磁导率表达式为空间-时间量。
根据洛伦兹力法则，电机的转矩可以表示[6]为
（6）
式中，Te为电机转矩；Bg为气隙磁通密度；rg为气隙平均半径；lstk为电机的轴向长度；
为定子的磁动势。
定子的磁动势FS可以描述[6]为
（7）
转子的磁动势FR可以描述[6]为
（8）
式中，
为vR次永磁磁动势幅值；
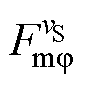为vS次电枢磁动势幅值；vR为转子磁动势的空间次数，vR=2k+1(k=0, 1, 2, 3,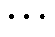)；vS为定子磁动势的空间次数，取负数时表示转向与基波磁动势相反，vS= ±(6k±1) (k=0,1,2,3,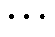)；φ为控制超前角。
将式（4）、式（7）、式（8）代入式（6），考虑定转子开槽的电机转矩可以表示为
（9）
式中，Te0为定转子磁动势与气隙平均比磁导率作用产生的转矩；TeS为定转子磁动势与定子开槽气隙谐波比磁导率作用产生的转矩；TeR为定转子磁动势与转子开虚槽气隙谐波比磁导率作用产生的转矩。
式（9）中，只有满足三角函数的空间阶数为0时，其积分结果不为0。Te0≠0需要满足vR±vS=0，因此，Te0是由谐波次数相同的定转子谐波磁动势与气隙平均比磁导率产生的转矩脉动。TeS与TeR不为0要分别满足(vR±vS)p±kSZS=0与(vR±vS)±kR=0，满足这两个等式的组合非常多。由于基波磁动势的幅值最大，对转矩脉动的影响也最大，因此只考虑TeS与TeR中有基波磁动势参与的磁动势组合。
以8极48槽，绕组短距电机为例，表1列出了式（9）中能形成转矩脉动的定转子磁动势组合形式。
表1 8极48槽电机转矩脉动来源
Tab.1 Source of torque ripple for 8-pole/48-slot PMSM
转矩脉动倍频数Te0TeSTeR vS, vRvS, vR, kSvS, vR, kR 6倍频-5, 57, 7—-5, 1, 67, 1, 6 12倍频-11, 1113, 131, 11, 11, 13, 1-11, 1, 1213, 1, 12 18倍频-17, 1719, 19—-17, 1, 1819, 1, 18 24倍频-23, 2325, 251, 23, 21, 25, 2-23, 1, 2425, 1, 24
由表1可知，Te0不包括基波磁动势的作用。TeS主要由定子基波磁动势、转子谐波磁动势与一阶二阶定子开槽气隙谐波比磁导率相互作用产生。TeR主要由转子基波磁动势、定子谐波磁动势与6k次转子开虚槽气隙谐波比磁导率相互作用产生。
8极48槽电机中，定子-11、13次谐波磁动势为定子齿谐波磁动势，幅值远大于其他次定子谐波磁动势。转矩脉动Te0和TeR的12倍频分量有-11、13定子次磁动势参与，因此Te0与TeR的12倍频分量要远大于Te0和TeR中其他频率的转矩脉动分量。根据式（5），一阶定子开槽气隙谐波比磁导率也远大于二阶，因此TeS中12倍频转矩脉动也要远大于24倍频转矩脉动。综上分析，对于8极48槽电机，12倍频转矩脉动的占比最大。
根据第1节分析，对于8极48槽电机，12倍频转矩脉动为转矩脉动的最主要分量，因此优化设计主要以减小12倍频转矩脉动为目标。暂不考虑定子侧的优化，减小12倍频转矩脉动需要减小12次转子开虚槽气隙谐波比磁导率标幺值与转子磁动势11、13次谐波，而它们都与转子虚槽位置有关。
从一层磁钢转子入手开始研究虚槽位置对转矩脉动的影响。式（3）中取n=1，12次转子开虚槽气隙谐波比磁导率的标幺值与虚槽位置的关系如图3所示。虚槽位于7.5°、22.5°、37.5°、52.5°、67.5°、82.5°电角度时，12次转子开虚槽气隙谐波比磁导率的标幺值为0。需要特别说明的是，12次谐波比磁导率标幺值为0的物理意义为气隙比磁导率函数傅里叶分解结果12次余弦级数的系数为0。虚槽位于15°、45°、75°电角度时，取得负最大值；虚槽位于30°、60°电角度时取得正最大值。
图3 12次谐波比磁导率与虚槽位置
Fig.3 12th airgap harmonic relative permeance vs virtual slot position
改变虚槽位置a1的值会导致转子磁动势分布以及磁动势谐波含量发生变化。图4为转子磁动势的空间分布以及11次和13次磁动势谐波的含量与虚槽位置的关系。随着a1变大，11、13次磁动势谐波振荡幅度变大；由于它们的振荡周期不同，二者同时接近0值的难度也增大。使11、13次磁动势谐波同时较小的a1值主要分布在5°～10°、20°～25°以及36°～40°电角度之间。
图4 转子磁动势与虚槽位置
Fig.4 Rotor magnetomotive force vs virtual slot position
由图3和图4可知，对于单层磁钢转子，使得转矩脉动较小的虚槽位置应该位于7.5°、22.5°和37.5°电角度附近。在这些位置上，12次转子开虚槽气隙谐波比磁导率标幺值以及11、13次转子磁动势谐波的幅值都相对较小。
利用有限元仿真建立8极48槽单层磁钢不同虚槽位置的仿真模型，探究其转矩特性，有限元仿真模型如图5所示，不同虚槽位置转矩脉动的结果如图6所示。由于虚槽位置小于10°或大于60°电角度在设计上十分不合理，这里不做讨论。
由图6可以得出，当转子虚槽位于15°、30°、45°和60°时，转矩脉动达到极大值；而当虚槽位于22.5°和37.5°时，转矩脉动取得极小值。最大转矩脉动出现在虚槽位置为45°处，转矩脉动达到48%；第二大和第三大的转矩脉动分别出现在电角度30°和15°处，转矩脉动分别为44%和40%；最小转矩脉动出现的虚槽位置为22.5°，转矩脉动仅为8%；第二小和第三小的转矩脉动出现在37.5°和57.5°处，转矩脉动分别为14%和15%。
图5 单层磁钢有限元仿真模型
Fig.5 Finite element model of single-layer permanent magnet rotor
图6 48槽8极的转矩脉动与虚槽位置
Fig.6 Torque ripple vs virtual position for 8-pole/48-slot
值得注意的是，转矩脉动随虚槽位置的变化规律与12次开虚槽气隙谐波比磁导率随虚槽变化的规律大致相同。在细节上，转矩脉动的变化趋势与转子磁动势的11次和13次谐波含量随虚槽位置的变化规律相似。这表明转子开虚槽对转矩脉动的影响远远大于定子开槽，即TeR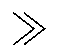
TeS。由此可见，虚槽位置主要通过影响气隙比磁导率来影响电机的转矩脉动，且对转矩脉动性能的影响很大。
以双层磁钢8极48槽电机为例，取式（3）中n=2，计算转子虚槽位置与12次转子开虚槽气隙谐波比磁导率标幺值的关系，结果如图7所示。12次转子开虚槽气隙谐波比磁导率标幺值绝对值较大的(a1，a2)组合主要有（15°，45°）、（15°，75°）、（30°，60°）、（45°，75°），使其值为0的（a1，a2）组合有（15°，30°）、（30°，45°）、（45°，60°）、（60°，75°），以及（15°，60°）、（45°，60°）、（60°，75°）。双层磁钢转子的磁动势谐波分布主要受最内层磁钢的分布影响[20]，因此其分布规律受虚槽位置的影响与图4b相似，这里不再赘述。利用有限元仿真计算8极48槽电机虚槽在不同位置时的转矩脉动，其有限元仿真模型如图8所示，结果如图9所示。
图7 12次转子开槽谐波比磁导率标幺值与虚槽位置
Fig.7 12 th airgap harmonic relative permeance vs virtual slot position for double-layer permanent magnet rotor
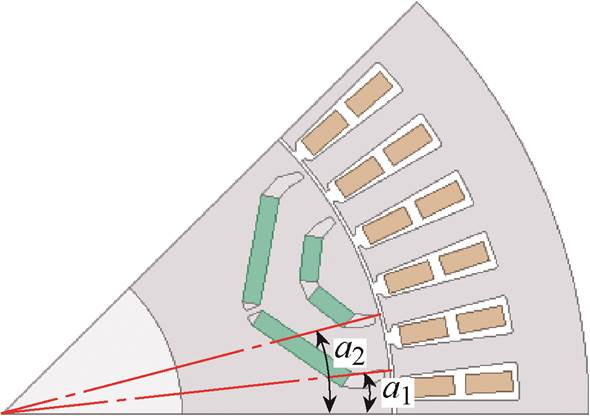
图8 双层磁钢有限元仿真模型
Fig.8 Finite element model of double-layer permanent magnet rotor
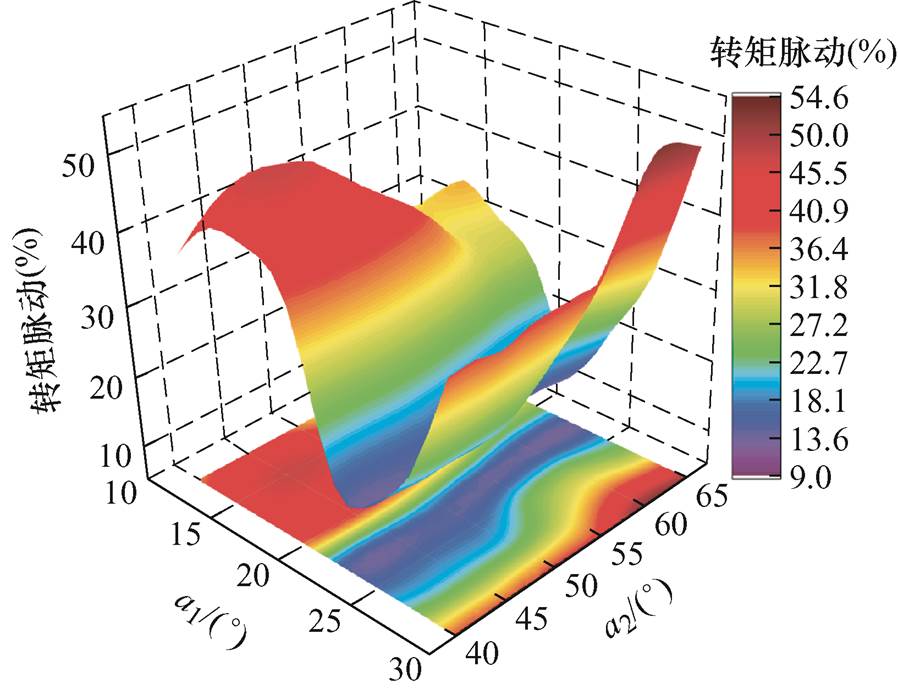
图9 双层磁钢转矩脉动与虚槽位置
Fig.9 Torque ripple vs virtual position for double layer permanent magnet rotor
根据图7，转子虚槽在（15°，45°）时，12次转子开虚槽气隙谐波比磁导率标幺值达到正最大值；而在（30°，60°）时，该谐波比磁导率达到负最大值。与之对应的是图9中转矩脉动的最大值在位置（30°，60°）处，达到了54.6%。第二大的转矩脉动值则出现在位置（15°，45°），达到了47.7%。这两个位置附近的区域也显示出相对较大的转矩脉动。而转矩脉动的最小值出现在位置（22.5°，65°），恰好与12次转子开虚槽气隙谐波比磁导率标幺值接近0的位置相符。在该位置，转矩脉动仅为9%。与图7中12次转子开虚槽气隙谐波比磁导率的变化趋势相比，图9中转矩脉动的变化规律基本相同，这些都与2.1节的分析相吻合。
针对极槽配合为ZS/p的整数槽永磁同步电机，获取转矩脉动最小的虚槽位置电磁设计流程如下：
（1）根据极槽配合，确定影响转矩脉动最大的转子开虚槽气隙谐波比磁导率的次数，应为ZS/p次。
（2）利用式（3）计算ZS/p次转子开虚槽气隙比磁导率谐波随虚槽位置的变化规律，找出使ZS/p次谐波接近0的虚槽位置组合。
（3）计算在ZS/p次谐波接近零的虚槽位置组合中，具有较小转子磁动势谐波的虚槽位置组合。
（4）考虑到转子设计还受其他参数影响，尽量选择接近步骤（3）中的虚槽位置组合，并进行其他电磁性能的验证计算。
利用2.3节提出的方法对一台8极48槽电动汽车永磁同步电机进行优化设计，减小其转矩脉动。电机的详细参数见表2。电机优化后的有限元仿真模型如图10所示。
表2 样机基本参数
Tab.2 Basic parameters of the prototype
参 数数 值 额定功率/kW30 额定转速/(r/min)3 000 额定转矩/(Nm)95.5 最大转速/(r/min)8 000 额定电流/A110 冷却方式强迫水冷 轴向长度/mm130 气隙长度/mm0.6 定子外径/mm225 永磁体厚度/mm3
原样机转子虚槽的位置为a1=14°，a2=42°。根据式（3）计算，12次转子开虚槽谐波相对比磁导率为0.74(pu)。基于2.3节总结的规律，对原样机进行优化。由于机械空间上不允许减小a1的值，选择增大a1值。为了保持磁钢用量不变，V型磁钢的夹角需要变小。同时，为了不影响电机的磁阻转矩利用以及弱磁性能，需要尽量保持电机的dq轴电感不发生变化，因此在增大a1的同时增大a2。优化后，a1=22°，a2=54°。12次转子开虚槽谐波相对比磁导率为0.1(pu)，比优化前大大降低。为了验证优化效果，同时对原样机做分段错极优化，转子分四段，错极角度为7.5°。
图10 优化前后的有限元仿真模型
Fig.10 Finite element analysis model before and after optimization
图11为基于有限元仿真计算的原样机、虚槽位置优化以及错极优化后的电机额定点转矩结果。显然，在虚槽位置优化前后，转矩的平均值基本保持不变，而转矩脉动分别为25.5%和6.8%。通过优化虚槽位置，转矩脉动下降了18.7%。错极优化方案中，转矩脉动下降至12.3%，平均转矩减小了约5%。
图11 不同方案转矩仿真结果
Fig.11 Torque results for different simulation models
电机额定点的其他主要电磁性能计算结果见表3。优化前后的dq轴电感变化很小，因此磁阻转矩、弱磁能力等性能变化也很小。优化前后主要电磁性能基本保持不变，但转矩脉动大幅下降。
表3 优化前后主要性能对比
Tab.3 Main performance comparison before and after optimization
参 数优化前优化后 千转反电动势/V41.543.3 额定电流/A113110 d轴电感/mH0.243 70.243 9 q轴电感/mH0.838 30.837 1 磁阻转矩占比(%)50.648.3 效率(%)96.5596.66 齿槽转矩/(Nm)3.870.98 转矩脉动(%)25.56.8
为探究电动汽车电机在典型工况下的转矩脉动优化情况，计算额定电流与最大电流全转速下的电机转矩脉动结果如图12所示。在恒转矩额定电流区，转矩脉动由25.5%下降至6.8%；恒转矩最大电流区，转矩脉动由32.2%下降至11.1%；额定电流弱磁区，转矩脉动由38.2%下降至10.8%；最大电流弱磁区，转矩脉动由71.2%下降至14.7%；优化转子虚槽位置对转矩脉动有很好的抑制效果，尤其在最大电流弱磁区域。
图12 优化前后最大/额定电流曲线转矩脉动结果
Fig.12 Torque ripple for maximum/rated current curves
为了验证仿真分析模型的正确性，制造样机并进行电机的空载与负载的电磁试验。其中，负载试验转速为3 000 r/min，试验功率为30 kW，控制器载波频率为10 kHz。图13为试验测试平台与优化前后转子冲片的示意图。试验中的两台样机转子均没有采用分段错极。
图14为优化前后的反电动势试验波形。其中，优化前的千转反电动势的有效值为40 V，优化后的千转反电动势有效值为42 V。
图13 样机转子冲片及试验平台
Fig.13 Rotor punching and experiment platformof the prototype
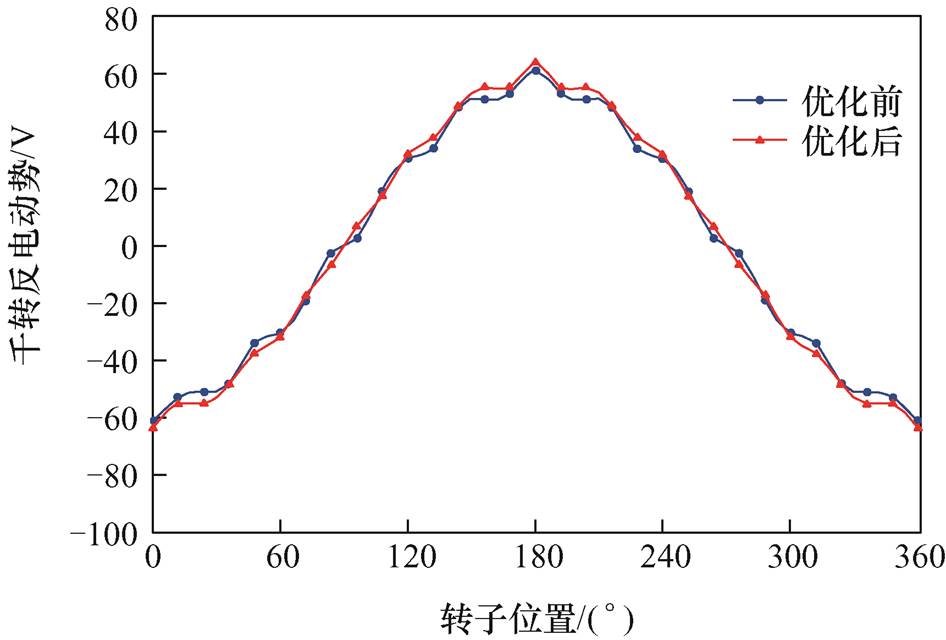
图14 优化前后的千转反电动势试验波形
Fig.14 Back-electromotive force per thousand turn test waveforms before and after optimization for the prototype
图15为优化后额定转矩试验与有限元仿真的对比结果。仿真与试验的具体数据对比结果见表4。其中，反电动势最大误差不超过3%，平均转矩误差不超过2%。误差原因是仿真中没有考虑装配过程造成的累积误差。而转矩脉动的误差较大，优化前的仿真与试验误差为10%。转矩试验结果比仿真结果多出一些高次谐波分量，这是由于仿真没有考虑由PWM载波引起的电枢电流谐波。电枢绕组中的高次电流谐波不能产生平均转矩，但能产生高频转矩脉动分量。因此，转矩平均值的仿真精度较高，而转矩脉动的精度稍低一些。经过傅里叶分解后发现，转矩脉动的低次谐波分量误差较小，仅在高频次处有误差。空载反电动势与负载转矩的仿真结果与试验结果基本一致，试验结果验证了有限元仿真的有效性。
图15 优化后转矩试验仿真值对比
Fig.15 Torque simulation and test result for the prototypes
表4 试验与仿真值对比
Tab.4 Comparison of simulation and test results
千转反电动势/V平均转矩/(Nm)转矩脉动(%) 仿真 试验仿真 试验仿真 试验 优化前41.5 40.295.7 96.425.5 35.1 优化后43.3 42.695.5 95.66.8 7.3
本文提出了一种用于分析转子虚槽位置对内置式永磁电机转矩脉动影响的解析模型，并得出如下结论：
1）转子虚槽通过影响气隙比磁导率来影响电机的转矩脉动。受转子虚槽影响的气隙谐波比磁导率会随转子虚槽位置的变化而变化，通过优化转子虚槽位置可以使得特定次转子开虚槽引起的气隙谐波比磁导率的标幺值为0。
2）对于极槽配合为ZS/p的整数槽永磁电机，ZS/p次转子开虚槽气隙谐波比磁导率与定子齿谐波磁动势、转子基波磁动势相互作用会产生转矩脉动，且该转矩脉动是电机转矩脉动中最大的分量。
3）通过优化转子虚槽位置可以有效地降低ZS/p次转子开虚槽气隙比磁导率谐波，从而减小转矩脉动的幅值，同时不明显改变电机的其他主要电磁性能。
参考文献
[1] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961-2970.
[2] Peng Chen, Wang Daohan, Feng Zhenkang, et al. A new segmented rotor to mitigate torque ripple and electromagnetic vibration of interior permanent magnet machine[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1367-1377.
[3] 王道涵, 彭晨, 王柄东, 等. 电动汽车新型转子内置式永磁同步电动机转矩脉动与电磁振动抑制研究[J]. 中国电机工程学报, 2022, 42(14): 5289-5300.
Wang Daohan, Peng Chen, Wang Bingdong, et al. Research on a novel interior permanent magnet machine with segmented rotor to mitigate torque ripple and electromagnetic vibration[J]. Proceedings of the CSEE, 2022, 42(14): 5289-5300.
[4] 王群京, 郑耀达, 刘先增. 基于结构参数优化的电机振动噪声的抑制研究[J]. 电气工程学报, 2023, 18(2): 16-25.
Wang Qunjing, Zheng Yaoda, Liu Xianzeng. Research on suppression of motor vibration and noise based on structural parameter optimization[J]. Journal of Electrical Engineering, 2023, 18(2): 16-25.
[5] 高锋阳, 齐晓东, 李晓峰, 等. 不等宽不等厚Halbach部分分段永磁同步电机电磁性能解析计算与优化分析[J]. 电工技术学报, 2022, 37(6): 1398- 1414.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Analytical calculation and optimization analysis of electromagnetic performance of Halbach partially- segmented permanent magnet synchronous motors with unequal width and thickness[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1398- 1414.
[6] 高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Optimization design of partially-segmented Halbach permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 787- 800.
[7] Zhao Wenliang, Lipo T A, Kwon B. Torque pulsation minimization in spoke-type interior permanent magnet motors with skewing and sinusoidal permanent magnet configurations[C]//2015 IEEE International Magnetics Conference (INTERMAG), Beijing, China, 2015, doi: 10. 1109/INTMAG. 2015. 7156886.
[8] Shi Zhou, Sun Xiaodong, Cai Yingfeng, et al. Torque analysis and dynamic performance improvement of a PMSM for EVs by skew angle optimization[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(2):0600305.
[9] Song C H, Kim D H, Kim K C. Design of a novel IPMSM bridge for torque ripple reduction[J]. IEEE Transactions on Magnetics, 2021, 57(2): 8201004.
[10] Liu Chengcheng, Huang Xiaorui, Zhang Wenfeng, et al. Shape optimization and demagnetization analysis of interior permanent magnet synchronous machine with hybrid cores[J]. AIP Advances, 2023, 13(3): 035215.
[11] Im Y H, Hwang S I, Jang S M, et al. Analysis of torque pulsation considering interior permanent magnet rotor rib shape using response surface methodology[J]. IEEE Transactions on Magnetics, 2012, 48(2): 979-982.
[12] Pan Zhicheng, Yang Kai, Wang Xiaojie. Optimal design of flux-barrier to improve torque performance of IPMSM for electric spindle[C]//2015 18 th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 2015: 773-778.
[13] Sarani E, Vaez-Zadeh S. Line start permanent magnet motors with double-barrier configuration for magnet conservation and performance improvement[J]. IET Electric Power Applications, 2017, 11(9): 1656-1663.
[14] Alotto P, Barcaro M, Bianchi N, et al. Optimization of interior PM motors with machaon rotor flux barriers[J]. IEEE Transactions on Magnetics, 2011, 47(5): 958-961.
[15] Fang Liang, Kim S I, Kwon S O, et al. Novel double-barrier rotor designs in interior-PM motor for reducing torque pulsation[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2183-2186.
[16] Zhu Shushu, Hu Yaohua, Liu Chuang, et al. Shaping of the air gap in a V-typed IPMSM for compressed-air system applications[J]. IEEE Transactions on Magnetics, 2021, 57(2): 8103705.
[17] 孙毅, 蔡顺, 林迎前, 等. 永磁辅助同步磁阻电机顶层优化设计[J]. 电工技术学报, 2022, 37(9): 2306-2318.
Sun Yi, Cai Shun, Lin Yingqian, et al. Top-level design pattern of PM-assisted synchronous reluctance machines[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2306-2318.
[18] 刘成成, 刘乾宇, 王韶鹏, 等. 低转矩脉动同步磁阻电机磁障形状分析与优化设计[J]. 电机与控制学报, 2022, 26(12): 38-47.
Liu Chengcheng, Liu Qianyu, Wang Shaopeng, et al. Flux barrier shape analysis and optimal design for low torque ripple synchronous reluctance machine[J]. Electric Machines and Control, 2022, 26(12): 38-47.
[19] Chen Yunyun, Cai Tongle, Zhu Xiaoyong, et al. Optimization of a new asymmetric-hybrid-PM machine with high torque density and low torque ripple considering the difference of magnetic materials[J]. IEEE Transactions on Magnetics, 2022, 58(2): 8103505.
[20] 张玉峰, 高文韬, 史乔宁, 等. 基于改进迭代田口法的双余度永磁同步电机优化设计[J]. 电工技术学报, 2023, 38(10): 2637-2647, 2685.
Zhang Yufeng, Gao Wentao, Shi Qiaoning, et al. Optimization design of dual-redundancy permanent magnet synchronous motor based on improved iterations taguchi method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2637-2647, 2685.
[21] Barcaro M, Bianchi N. Torque ripple reduction in fractional-slot interior PM machines optimizing the flux-barrier geometries[C]//International Conference on Electrical Machines, Marseille, France, 2012: 1496-1502.
[22] Hu Yaohua, Zhu Shushu, Liu Chuang, et al. Electromagnetic performance analysis of interior PM machines for electric vehicle applications[J]. IEEE Transactions on Energy Conversion, 2018, 33(1): 199-208.
[23] Han S H, Jahns T M, Zhu Z Q. Design tradeoffs between stator core loss and torque ripple in IPM machines[C]//2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 2008: 1-8.
[24] Han S H, Jahns T M, Soong W L. Torque ripple reduction in interior permanent magnet synchronous machines using the principle of mutual harmonics exclusion[C]//2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 2007: 558-565.
[25] 徐广人, 唐任远, 安忠良. 永磁同步电动机气隙磁场分析[J]. 沈阳电力高等专科学校学报, 2001(2): 1-4.
Xu Guangren, Tang Renyuan, An Zhongliang. The analysis of airgap magnetic field of permanent magnet synchronous motor[J]. Journal of Shenyang Electric Power Institute, 2001(2): 1-4.
Abstract The torque ripple of the interior permanent magnet synchronous motor (IPMSM) which affects the driving experience of electric vehicles (EVs), is the most important factor in assessing the quality of driving motors for EVs. Optimizing the rotor structure of the IPMSM is a solution to this drawback that does not significantly increase manufacturing costs. The traditional analytical methods for optimizing the rotor structure are mainly of two kinds: The first method is to make the rotor magnetomotive force (MMF) as close as possible to a sinusoidal waveform by optimizing the magnet distribution; The other method is to make the air gap flux density closer to a sinusoidal waveform by designing an uneven magnetic resistance. However, these methods did not consider the effect of the rotor structure on the air gap relative permeability. This paper proposes an analytical model for calculating the torque ripple of IPMSM, which takes into account the influence of rotor structure on the air gap relative permeability. The optimal design of the rotor structure can be quickly determined by analyzing the analytical model.
Firstly, based on the assumption of deep magnetic saturation of the ferromagnetic material at the flux barrier, the flux barrier is abstracted as a rotor virtual slot. Secondly, an air gap relative permeability equation is derived, which takes into account the effect of stator slotting and rotor virtual slotting on the air gap relative permeability. Thirdly, an analytical expression for the torque of IPMSM is obtained, by utilizing the stator MMF equation, rotor MMF equation and the air gap relative permeability equation. The relationship between the position of rotor virtual slot and torque ripple is derived by analyzing the analytical expression, based on which the design principle of IPMSM with low torque ripple is summarized. Finally, an IPMSM for EV with a rated power of 30 kW is optimally designed. The main electromagnetic properties of the original motorand the optimized motor are calculated. The torque ripple is significantly reduced after optimization, without affecting other electromagnetic performance.
For torque performance, compared to the original motor, the torque ripple of the optimized motor decreased from 25.5% to 6.8%, a decrease of 18.7%. For the cogging torque performance, compared to the original motor, the cogging torque of the optimized motor decreased from 3.87 Nm to 0.98 Nm. That is to say, optimizing design is beneficial for reducing cogging torque. For inductance performance, the d-axis inductance before and after optimization is 0.243 7 mH, 0.243 9 mH, and the q-axis inductance is 0.838 3 mH and 0.837 1 mH, respectively. The simulation results show that the inductance remains unchanged before and after optimization. Due to the influence of the inductance of IPMSM on its flux weaken ability and reluctance torque utilization, the unchanged inductance means that these properties remain unchanged. For voltage performance, compared to the original motor, the optimized back electromotive force increased from 41.5 V to 43.3 V. For efficiency performance, compared to the original motor, the optimized efficiency increased from 96.55% to 96.66%. The optimization design has little impact on voltage and efficiency performance. Meanwhile, the torque ripple under all operating conditions has been suppressed by optimized design, especially in the flux-weakened region of the maximum current.
The following conclusions can be drawn: The rotor virtual slot affects the torque ripple of IPMSM by affecting the air gap relative permeability. By optimizing the position of the rotor virtual slot, it is possible to make the value of the air gap relative permeability 0 for some specific order. For a ZS-slot p-pole IPMSM, the air gap relative permeability with ZS/p order can cause most of the torque ripple. By optimizing the position of the virtual slot, the torque ripple can be reduced without significantly altering the other main electromagnetic performance of the motor. This method is effective for all operating conditions of electric vehicles.
keywords：Interior permanent magnet synchronous motor (IPMSM), torque ripple, rotor virtual slot, electric vehicle
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.231345
收稿日期 2023-08-18
改稿日期 2023-11-10
王力新 男，1988年生，博士研究生，研究方向为电动汽车电机设计。E-mail: wanglixin_201031@tju.edu.cn（通信作者）
王晓远 男，1962年生，教授，博士生导师，研究方向为高速电机电磁设计、电动汽车永磁电机设计。E-mail: xywang62@tju.edu.cn
（编辑 崔文静）