图1 T型三电平逆变器供电的六相PMSM拓扑
Fig.1 The topology of six-phase PMSM powered by T-type three-level inverter
摘要 在三电平六相电机驱动系统中，存在中点电压不平衡及零序电流导致定子电流畸变等问题。为此，该文针对T型三电平逆变器供电的六相永磁同步电机，提出一种具有中点电压平衡与零序电流抑制功能的直接转矩控制（DTC）策略。为实现DTC的快速构建，该策略基于两电平三相电机DTC结构，利用精简后的开关状态，在六相绕组轴线上分别合成满足控制要求的4个电压矢量，然后通过两个滞环比较器结合简单的扇区划分，确定最优电压矢量所在轴线，同时构建中点电压与零序电流控制平面，并对系统在控制平面所处扇区进行判断。在此基础上，根据最优电压矢量所在绕组的相电流iy的极性，实现最优电压矢量的选择，并进一步构建DTC最优开关矢量表。最后，通过实验结果验证了所提控制策略的可行性和有效性。
关键词：T型三电平逆变器 六相永磁同步电机 直接转矩控制 中点电压平衡 零序电流抑制
随着一些工业与军事领域对于电机驱动系统的高可靠性和大功率要求的不断提高，传统三相电机驱动系统逐渐不能满足需求[1-3]。多相电机由于相数的增加，对逆变器开关管额定电流的要求降低，且电机在部分绕组开路情况下仍能容错运行。因此，多相电机驱动系统在这些领域的运用日益广泛[4-5]。
目前，多相电机驱动系统瞬时转矩控制策略主要有磁场定向的矢量控制和直接转矩控制（Direct Torque Control, DTC）[6-8]。DTC在各平面和轴系的控制均处于定子静止坐标系，对电机参数依赖性较低、算法简洁。此外，控制策略采用滞环比较器，对负载变化的适应能力较强。国内外学者对于多相电机直接转矩控制技术做了大量研究，从传统的滞环比较器结合开关表型DTC结构向现代控制理论构建的控制器结构演变。例如，文献[9]针对双三相永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）直接转矩控制系统提出一种基于12个新合成电压矢量的改进开关表，实现在一个开关周期内控制转矩的同时，能够消除电流谐波。文献[10]针对双三相PMSM提出一种基于虚拟电压矢量集的新型占空比调制直接转矩控制策略，分别定义动态工况和稳态工况的开关表及占空比的计算方法，实现对转矩脉动与谐波分量的抑制。文献[11]针对五相PMSM提出一种直接转矩模型预测控制方案，不仅减小了损耗，还降低了磁链和转矩脉动。
同时，随着电力电子技术的发展，多电平逆变器提高了输出电压的质量，减小了元件的电压应力，因此广泛应用于中、高压场合[12-14]。在多种多电平拓扑中，三电平逆变器由于结构简单且与两电平逆变器相比优势明显，已成为中压大功率领域最具吸引力的逆变器之一[15]。
近年来，将多相电机和三电平逆变器结合的三电平多相电机驱动系统受到了广泛的关注。三电平多相驱动系统实现了多相电机与三电平逆变器的优势互补，但存在中点电压不平衡与零序电流较大的问题。中点电压不平衡会导致输出电压畸变，零序电流较大会导致定子电流畸变、损耗增大等问题。文献[16-18]针对中点钳位（Neutral Point Clamped, NPC）型三电平五相、七相及六相逆变器提出一种基于空间矢量解耦的空间矢量调制方法，能够有效抑制谐波电流，但没有考虑对中点电压的平衡控制。文献[19]针对NPC型三电平六相逆变器提出一种基于空间矢量解耦的空间矢量调制策略，能够有效降低电流的谐波含量，同时具备中点电压平衡能力。文献[20]提出一种三电平多相逆变器的空间矢量调制策略，不仅能实现中点电压平衡与谐波电流抑制，还能降低开关频率。文献[21]针对T型三电平双三相PMSM驱动系统，提出一种基于双空间矢量调制的直接转矩控制，虽能有效抑制低次谐波电流，但没有实现系统的完全解耦。
目前，针对三电平多相驱动系统的研究主要集中在矢量控制，且多采用空间矢量调制，虽能有效抑制谐波，但扇区划分、开关序列选择、矢量合成等环节比较复杂，且需额外设计中点电压的平衡控制，实现过程复杂，以直接转矩控制为理论基础的研究却仍较少见。对称六相PMSM除了具有效率高、响应速率快等多相电机共有的优点外，相比其他多相电机，具有更强的容错能力，符合三电平多相驱动系统对高可靠性的要求。
为此，本文针对T型三电平逆变器供电的对称六相PMSM，提出了一种具有中点电压平衡与零序电流抑制的DTC策略。主要创新点为：①基于两电平三相电机DTC结构，利用精简后的开关状态合成六相绕组轴线电压矢量，并结合滞环比较器与简单的扇区划分，快速构建T型三电平逆变器供电的六相PMSM-DTC；②构建中点电压与零序电流控制平面，通过对系统在控制平面所处扇区判断，选择最优电压矢量，实现中点电压平衡与零序电流抑制。
图1为T型三电平逆变器供电的六相永磁同步电机拓扑。UDC为直流母线电压，通过两个相同的电容C1、C2串联分压。当电容C1、C2两端承受的电压相等时，中点电压经反串连开关管钳位为零电位，每相可以输出UDC/2、0和-UDC/2三种电压，用开关状态变量Sx（x=A～F）分别表示为2、1、0。以A相为例，当开关管Sa1与Sa2导通、Sa3与Sa4关断时，输出电压为UDC/2，SA=2；当开关管Sa2与Sa3导通、Sa1与Sa4关断时，输出电压为0，SA=1；当开关管Sa3与Sa4导通，Sa1与Sa2关断时，输出电压为-UDC/2，SA=0。T型三电平六相逆变器的开关状态变量组合SASBSCSDSESF=000000～222222，进一步用十进制值可表示为0～728，共计可产生36=729种开关状态。
图1 T型三电平逆变器供电的六相PMSM拓扑
Fig.1 The topology of six-phase PMSM powered by T-type three-level inverter
六相PMSM除了机电能量转换平面占用两个自由度外，还存在4个零序轴系z1～z4，由于电机采用星形联结，所以只有5个自由度可控，机电能量转换平面坐标系定义如图2所示。图中，yfs、ys分别为转子磁极磁链及定子磁链矢量；ab、dq分别为定子静止坐标系及转子磁场定向同步旋转坐标系；us、is分别为定子电压及电流矢量。矢量在各轴上投影的分量分别用对应的下标标识，d 为转矩角，qr为转子位置角。
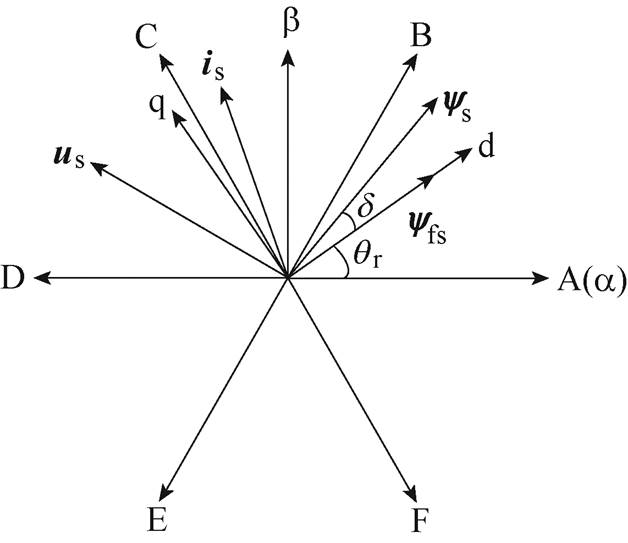
图2 机电能量转换平面坐标系定义
Fig.2 Definition of planar coordinate system for electromechanical energy conversion
根据文献[22]的理论给出六相PMSM关键数学模型结论如下。ab 坐标系及z1～z4零序轴系下的电压平衡方程式为
（1）
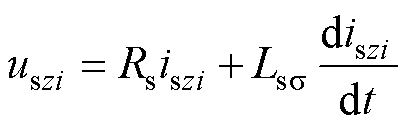（2）
式中，i=1, 2, 3, 4；Rs为定子电阻；Lss 为定子漏电感。从式（1）可知，利用ab 坐标系的空间电压矢量us可以瞬时控制定子磁链ys；z1～z4轴零序电压uszi与机电能量转换无关，却会产生零序电流iszi，引起定子电流畸变。
电磁转矩方程式为
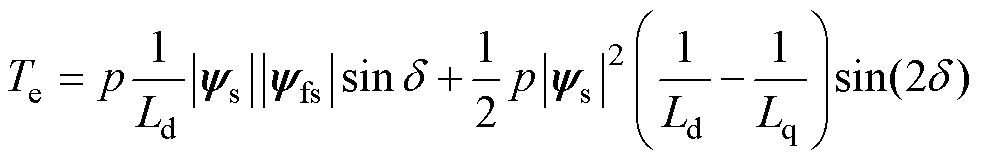（3）
其中
|yfs|=
yf
式中，yf、p、Ld、Lq分别为转子永磁体磁链矢量、极对数、电机直轴电感和交轴电感。
结合式（1）、式（3）可知，在定子磁链幅值|ys|恒定情况下，通过定子电压矢量us对定子磁链ys快速旋转控制，能够达到对转矩角d 的快速控制，最终实现对Te的直接控制。
根据图1中六相PMSM与逆变器之间的连接关系，六相PMSM各相绕组相电压usx（x=A～F）等于对应相绕组端点与直流母线电容中点N之间的电压uxN（x=A～F）和N与绕组中心点O之间的电压uNO之和，具体数学关系为
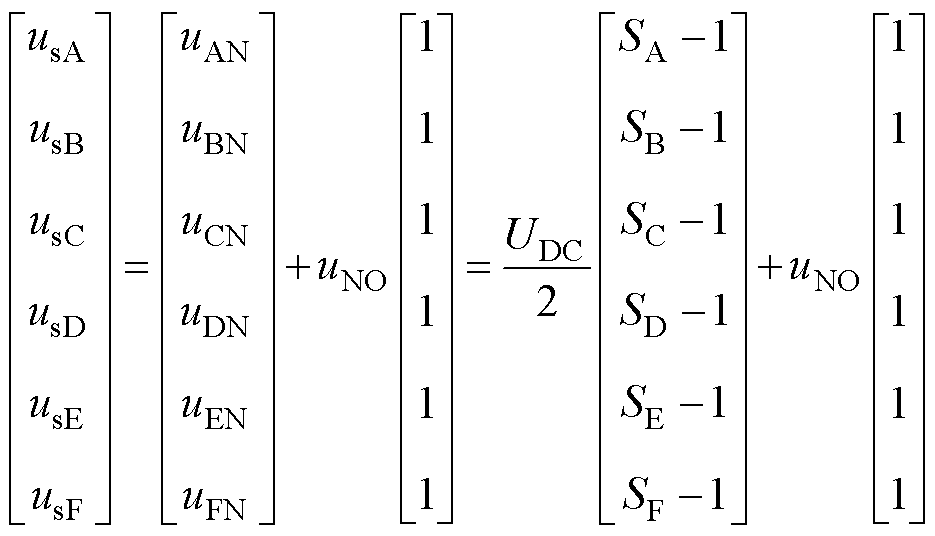（4）
六相绕组为对称星形结构，其六相电压之和为零，即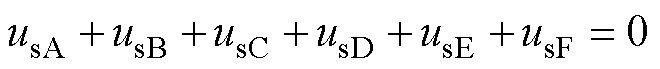
。则由式（4）可得uNO为
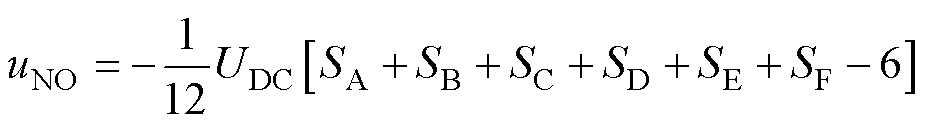（5）
采用恒功率正交变换矩阵T6，将式（4）中六相电压解耦变换到ab 轴系及z1～z4零序轴系上，再将式（5）代入，可得六相电压投影在各轴系上的电压分量为
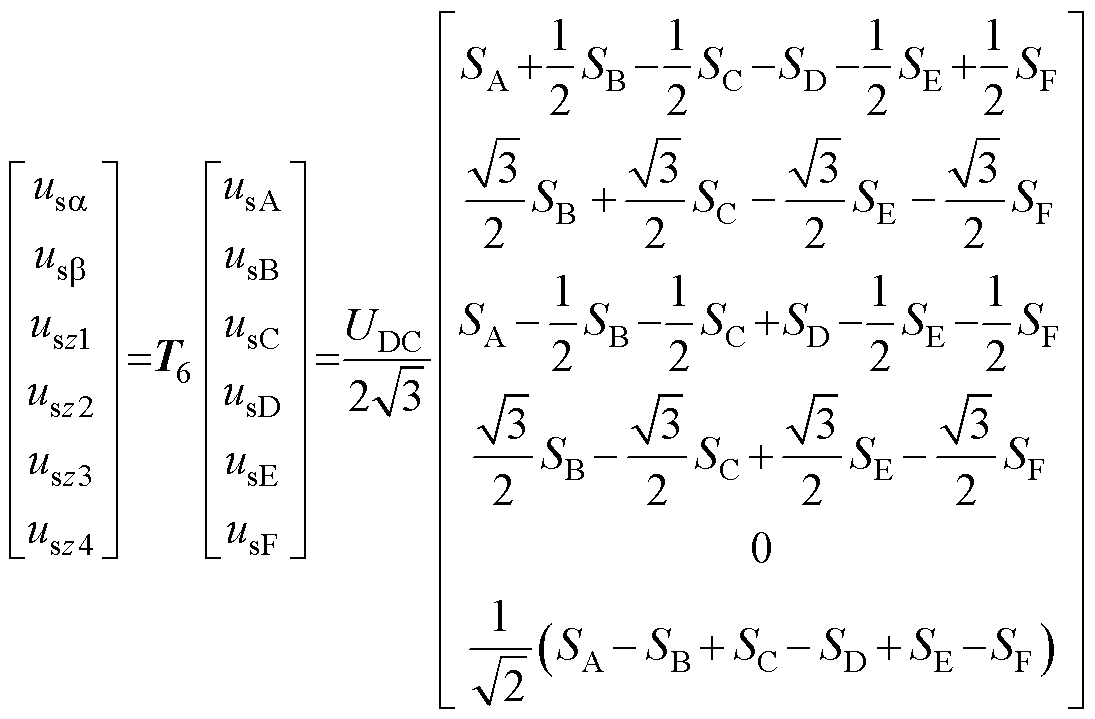（6）
其中
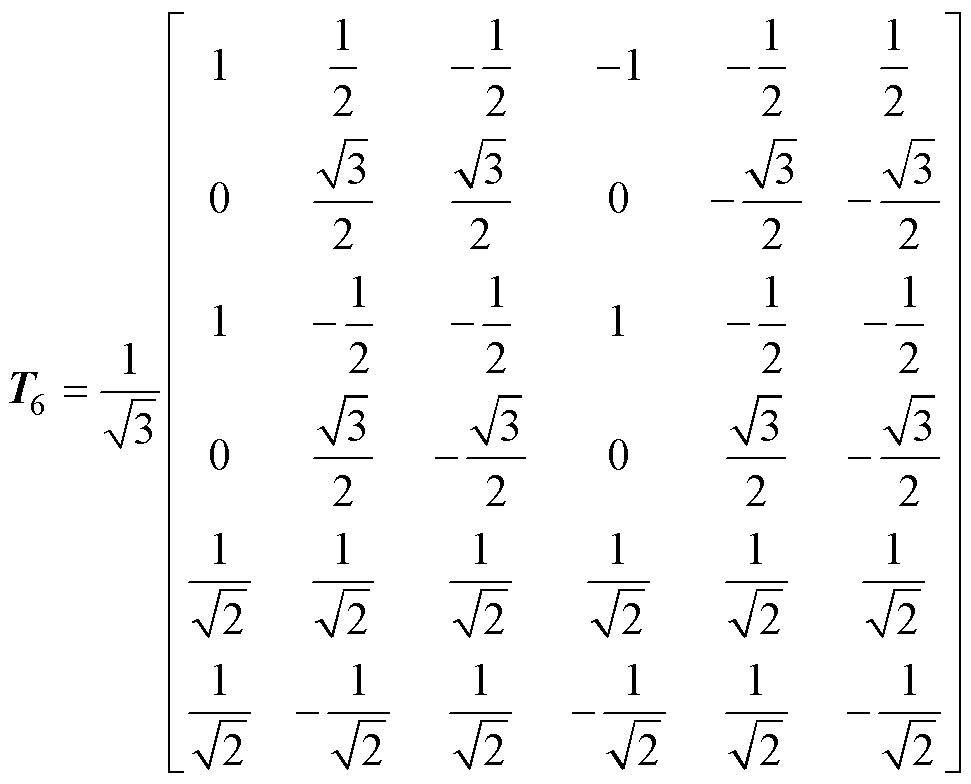（7）
由式（6）可知，a-b 平面电压矢量、z1-z2平面零序电压矢量、z3-z4轴系零序电压矢量分别为
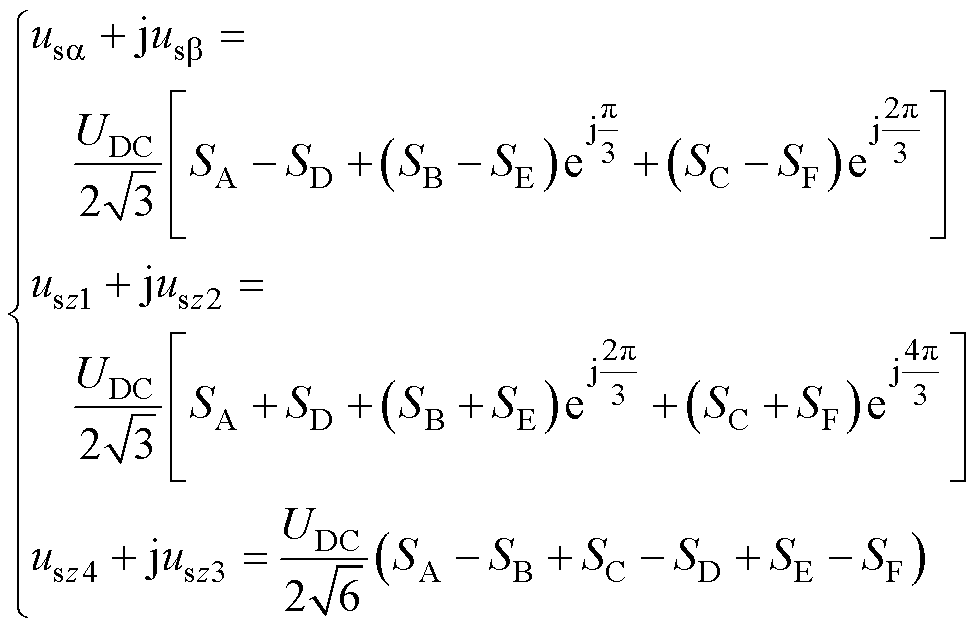（8）
由式（8）知，各平面及轴系电压矢量由开关状态决定。
根据图1中T型三电平逆变器的拓扑，推导中点电压的数学模型。当逆变器桥臂输出电压为0时，相电流经过两个反串连开关管流入中点N，分别对母线上下电容充放电，引起中点电压偏移。三电平逆变器流入中点电流io的瞬时值为
（9）
式中，Sx为状态变量；ix为相电流；x∈{A, B, C, D, E, F}。
中点电压偏移值uo定义为
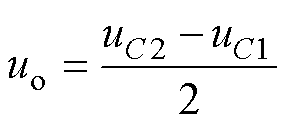（10）
式中，uC1、uC2分别为母线上下电容C1、C2电压。
由母线上下电容充放电特性可知
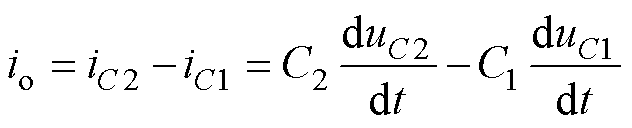（11）
式中，iC1、iC2分别为流入母线上、下电容的电流。将式（10）代入式（11）进一步得到中点电压变化率为
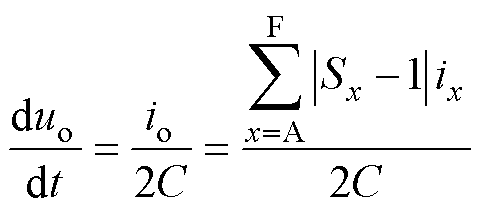（12）
式中，C为母线电容。由式（12）可知，中点电压的变化方向与开关状态相关。
两电平三相电机DTC结构提出最早，利用处于三相轴上的非零电压矢量结合简单的扇区划分，得到最优开关矢量表，实现对|ys|及Te的控制。两电平三相永磁同步电机DTC简介如图3所示，三相PMSM定子磁链ys位于q1时，非零电压矢量对三相PMSM的作用见表1。
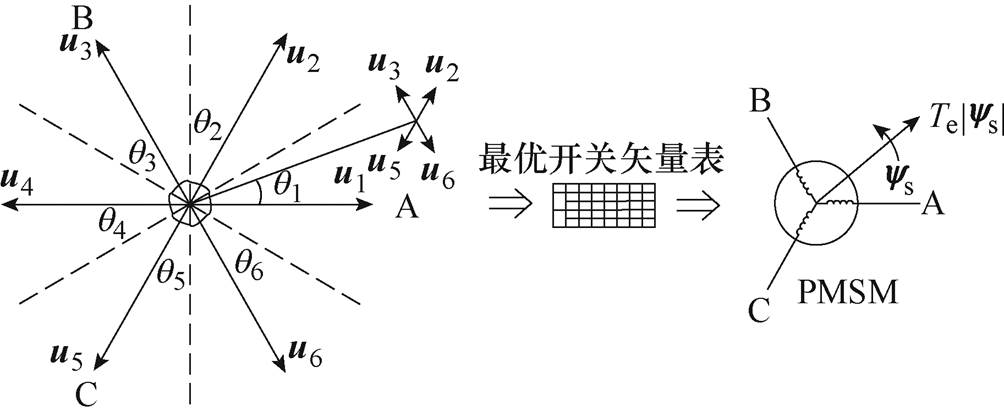
图3 两电平三相永磁同步电机DTC简介
Fig.3 Introduction to DTC for two-level three-PMSM
此外，两电平三相电机DTC研究最成熟，也是最基础的。若能借鉴上述两电平三相电机DTC通过相绕组轴线上电压矢量控制|ys|、Te的思路，可以实现本文T型三电平逆变器供电六相PMSM-DTC的快速构建。关键是如何获得具有中点电压平衡与零序电流抑制功能的六相绕组轴线电压矢量。根据1.3节分析，虽然存在六相绕组轴线电压矢量，但这些矢量不能同时满足中点电压平衡与零序电流抑制功能。例如，A相轴线电压矢量的开关状态355 (111011)能够使零序电流isz1减小、使零序电流isz4增大，却对零序电流isz2无影响，对中点电压的影响与流入中点的电流极性有关。因此，本文采用合成矢量的方法，得到满足控制条件的六相绕组轴线电压矢量。
表1 ys位于q1时，电压矢量选择
Tab.1 The choice of voltage vector for ys at q1
Te|ys|q1 增大增大u2 增大减小u3 减小增大u6 减小减小u5
2.2.1 开关状态精简
T型三电平六相逆变器有729种开关状态。按开关状态能否输出正弦的相电压，将其划分为有效开关状态和冗余开关状态。由于开关状态数量多、特性复杂、且存在冗余，直接选择开关状态合成电压矢量较为困难。
为此，本文采用了一种空间矢量投影的方法对开关状态进行精简。在a-b 平面每隔p/6弧度划分为一个扇区，将整个a-b 平面划分为12个扇区。位于各扇区的电压矢量与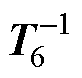
变换矩阵相乘得到六相电压分量。将六相电压分量按大小顺序排列，由式（4）可知，各相状态变量Sx与相电压usx呈线性正相关，大小顺序一致。将各扇区状态变量的大小顺序，作为该扇区的开关状态精简原则，剔除冗余开关状态。如冗余开关状态407 (120002)，位于S1扇区（0≤ q≤p/6），开关状态精简原则为SA≥SB≥SF≥SC≥ SE≥SD。407的状态变量SA＜SB，407被剔除。各扇区的开关状态精简原则见表2。
利用各扇区的精简原则，开关状态从729个精简为189个。精简后的开关状态在a-b 平面上的电压矢量分布，如图4所示。
精简后的189个开关状态在a-b 平面上产生61个电压矢量。除了零矢量，按电压矢量在a-b 平面所处的位置，将它们划分为顶点矢量、中点矢量和非交点矢量，共三类。
表2 各扇区开关状态精简原则
Tab.2 The principle of reduction of sector switch state
扇区各扇区开关精简原则 s1SA≥SB≥SF≥SC≥SE≥SD s2SB≥SA≥SC≥SF≥SD≥SE s3SB≥SC≥SA≥SD≥SF≥SE s4SC≥SB≥SD≥SA≥SE≥SF s5SC≥SD≥SB≥SE≥SA≥SF s6SD≥SC≥SE≥SB≥SF≥SA s7SD≥SE≥SC≥SF≥SB≥SA s8SE≥SD≥SF≥SC≥SA≥SB s9SE≥SF≥SD≥SA≥SC≥SB s10SF≥SE≥SA≥SD≥SB≥SC s11SF≥SA≥SE≥SB≥SD≥SC s12SA≥SF≥SB≥SE≥SC≥SD
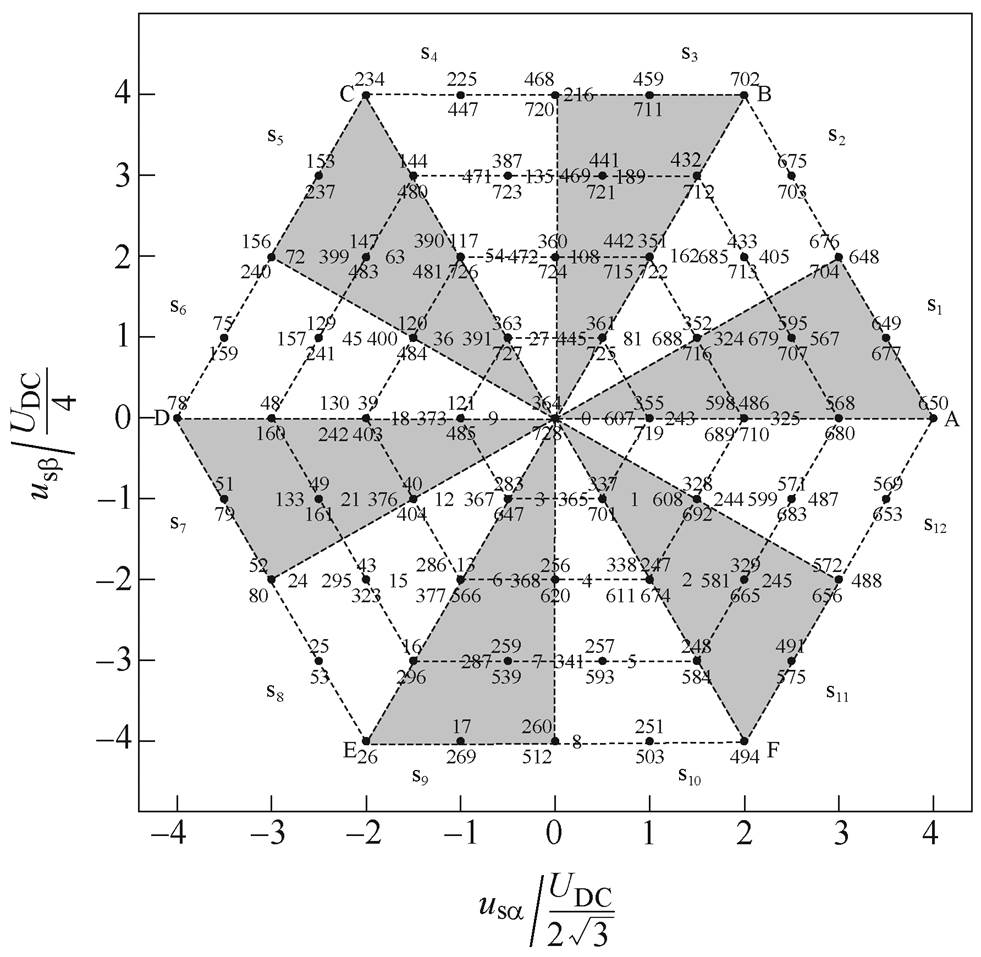
图4 精简后a-b 平面电压矢量分布
Fig.4 Distribution of the fined voltage vector in a-b plane
2.2.2 电压矢量合成
1）开关状态选择
由1.3节与1.4节可知，中点电压与零序电流均与开关状态有关，选择合适的开关状态，可以控制六相PMSM机电能量转换的同时，兼顾中点电压平衡与零序电流抑制。
以s1扇区为例，分析精简后的开关状态在a-b 平面、z1-z2平面、z3-z4轴的电压矢量分布及流入中点的电流，如图5所示。
在合成A相轴线电压矢量时，非交点矢量与中点矢量的开关状态参与矢量合成，会使流入中点的电流包含多相电流耦合。例如，s1扇区中点矢量352 (111001) 流入中点的电流为-(iA+iB)，非交点矢量679 (221011) 流入中点的电流为iB。这些开关状态参与矢量合成会导致对流入中点电流的分析变得复杂，因此，合成矢量时仅考虑顶点矢量的开关状态。
图5 s1扇区各平面及轴系电压矢量分布
Fig.5 Distribution of voltage vectors in planes and shafts of sector s1
A相轴线上顶点矢量的开关状态特性见表3。表中，us为a-b 平面的电压矢量幅值标幺值，单位长度为UDC/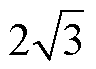
，io为流入中点的电流，uszz1-zz2为z1-z2平面的电压矢量幅值标幺值，单位长度为UDC/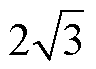，uszz4为z4轴上的电压分量标幺值，单位长度为UDC/
。
表3 A相顶点矢量的开关状态特性
Tab.3 The switching state characteristics of the vertex vector on the A-phase axis
us开关状态iouszz1-zz2uszz4 1355-iA11 1607iA11 1719iA11 1243-iA11 2598002 2486022 26892iA0-1 2710022 2325-2iA0-1 3568-iA10 3680iA10 465000-2
2）矢量合成顺序
电压矢量的合成分为两步：①利用轴线上的开关状态合成z1-z2平面电压矢量平均值为零的合成矢量；②利用合成的矢量，进一步合成z4轴电压分量标幺值分别为±|uszz4|的电压矢量。
3）占空比的最优确定
首先，选取表3中z1-z2平面电压矢量为反方向的两个开关状态，去合成z1-z2平面电压矢量平均值为零的合成矢量。两个开关状态的作用时间占比为
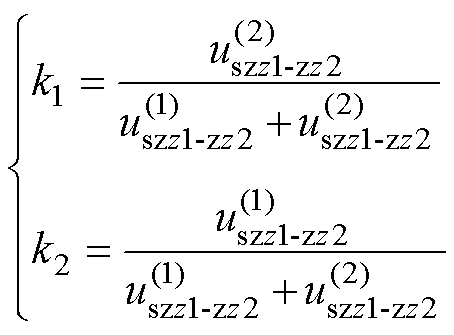（13）
式中，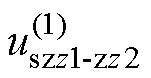
、
分别为两个开关状态在z1-z2平面的电压矢量幅值标幺值。例如，开关状态355与607，在z1-z2平面的电压矢量大小相等、方向相反，因此，两者作用时间各占0.5。
（14）
式中，uszz4为合成矢量在z4轴的电压分量标幺值。如开关状态355与607的合成矢量，us、io、uszz4分别为1、0、1。
利用A相轴线上开关状态合成无z1-z2平面分量合成的矢量，见表4。
表4 A相轴线上无z1-z2平面分量的合成矢量
Tab.4 Composite vectors without z1-z2plane components on the A-phase axis
us开关状态及占空比iouszz4 1355+607 (0.5+0.5)01 1355+243 (0.5+0.5)-iA1 4/3355+486 (2/3+1/3)-2/3iA1 2355+568 (0.5+0.5)-iA0.5 2607+719 (0.5+0.5)iA1 4/3607+710 (2/3+1/3)2/3iA1 2607+680 (0.5+0.5)iA0.5 1719+243 (0.5+0.5)01 4/3719+486 (2/3+1/3)2/3iA4/3 2719+568 (0.5+0.5)00.5 4/3243+710 (2/3+1/3)-2/3iA4/3 2243+680 (0.5+0.5)00.5 2598 (1)02 2486+710 (0.5+0.5)02 8/3486+680 (1/3+2/3)2/3iA2/3 2689 (1)2iA-1 8/3710+568 (1/3+2/3)-2/3iA2/3 2325 (1)-2iA-1 3568+680 (0.5+0.5)00 4650 (1)0-2
在此基础上，选取表4中z4轴电压分量极性相反的两个合成矢量，进一步合成能对零序电流isz4主动抑制的电压矢量。
此外，参与合成矢量的开关状态序列必须满足两个条件：①为了不引起各相输出电压跳变，开关状态序列的状态变量Sx（x=A～F）不能出现0-2及2-0的跳变；②为了保证输出的PWM波形对称，开关状态序列的状态变量Sx（x=A～F）不能出现0-1-0、1-0-1、1-2-1、2-1-2的变换。
综合以上条件，A相绕组轴线上可得到2个用于电压矢量合成的开关状态序列，见表5。
以开关状态序列1为例进行分析，两个矢量作用时间的占比与合成矢量的z4轴电压分量uszz4的关系为
表5 A相轴线开关状态序列
Tab.5 Sequences of switching states on the A-phase axis
序号矢量1矢量2 ①243+355 (100000+111011)689 (221112) ②325 (110001)607+719 (211111+222122)
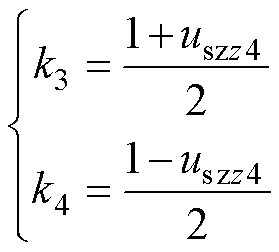（15）
开关状态序列1的合成矢量在a-b 平面的电压矢量幅值标幺值us1，流入中点的电流io1与z4轴电压分量标幺值uszz4的关系式为
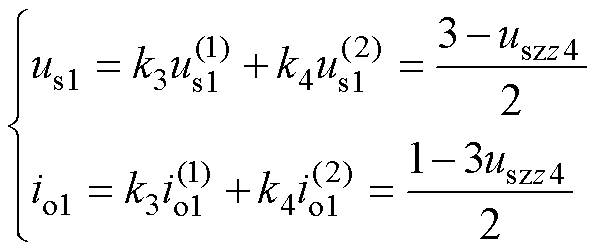（16）
同理可得，开关状态序列2的合成矢量状态us2、io2与uszz4的关系式为
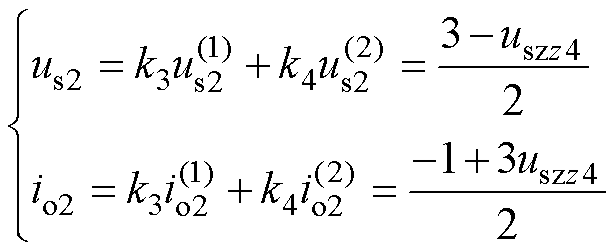（17）
为实现对零序电流iszz4的均衡抑制，控制同一开关状态序列分别合成z4轴零序电压标幺值uszz4为±|uszz4|的电压矢量。两个合成矢量分量在a-b 平面的电压矢量幅值标幺值之差Dus为
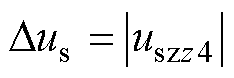（18）
将Dus、io1、io2与uszz4（-1＜uszz4＜1）的关系式在同一个坐标系中表示，如图6所示。
图6 uszz4最优取值的确定
Fig.6 Determination of the optimal value for uszz4
由图6可知，当uszz4=1/3时，流入中点的电流为0，uszz4越靠近1/3，对中点电压的平衡能力越弱，Dus随着|uszz4|的增大而增大，|uszz4|越小对零序电流isz4抑制能力越差。进一步分析可得，当0＜|uszz4|≤ 1/3时，|uszz4|取值靠近0，合成矢量对isz4的抑制能力较弱，|uszz4|取值靠近1/3，合成矢量的中点电压平衡能力不足；而当1/3≤|uszz4|＜1时，|uszz4|越大，合成矢量的中点电压平衡能力与对isz4的抑制能力越强，Dus越大。因此，在1/3≤|uszz4|＜1的范围内选取|uszz4|，在满足中点电压平衡的基础上，|uszz4|的取值应尽量靠近1/3，以使Dus维持在较小值，最终确定|uszz4|取值为0.5。
将|uszz4|的取值代入A相轴线上的两个开关状态序列中，得到4个合成矢量，见表6。
表6 A相轴线合成矢量分量
Tab.6 Composite vector components on the A-phase axis
us开关序列及占空比iouszz4 1.25325+607+719(0.25+0.375+0.375)0.25iA0.5 1.75243+355+689(0.125+0.125+0.75)1.25iA-0.5 1.25243+355+689(0.375+0.375+0.25)-0.25iA0.5 1.75325+607+719(0.75+0.125+0.125)-1.25iA-0.5
根据上述A相轴线上电压矢量合成阐述，进一步总结其合成步骤如图7所示。
图7 A相轴线电压矢量合成流程
Fig.7 Flowchart of A phase axis voltage vector synthesis
4）合成的六相轴线电压矢量
按照A相轴线电压矢量的合成方法，在六相轴线上分别合成4个电压矢量，见表7。其中，x为绕组相序，u为各轴线上合成矢量序号。
表7 六相轴线合成矢量分量
Tab.7 Composite vector components on the six-phase axis
xu开关序列及占空比iouszz4 Au11325+607+719(0.25+0.375+0.375)0.25iA0.5 u12243+355+689(0.125+0.125+0.75)1.25iA-0.5 u13243+355+689(0.375+0.375+0.25)-0.25iA0.5 u14325+607+719(0.75+0.125+0.125)-1.25iA-0.5
（续）
xu开关序列及占空比iouszz4 Bu2181+361+715(0.125+0.125+0.75)1.25iB0.5 u22351+445+725(0.25+0.375+0.375)0.25iB-0.5 u23351+445+725(0.75+0.125+0.125)-1.25iB0.5 u2481+361+715(0.375+0.375+0.25)-0.25iB-0.5 Cu31117+391+727(0.25+0.375+0.375)0.25iC0.5 u3227+363+481(0.125+0.125+0.75)1.25iC-0.5 u3327+363+481(0.375+0.375+0.25)-0.25iC0.5 u34117+391+727(0.75+0.125+0.125)-1.25iC-0.5 Du419+121+403(0.125+0.125+0.75)1.25iD0.5 u4239+373+727(0.25+0.375+0.375)0.25iD-0.5 u4339+373+727(0.75+0.125+0.125)-1.25iD0.5 u449+121+403(0.375+0.375+0.25)-0.25iD-0.5 Eu5113+367+647(0.25+0.375+0.375)0.25iE0.5 u523+283+377(0.125+0.125+0.75)1.25iE-0.5 u533+283+377(0.375+0.375+0.25)-0.25iE0.5 u5413+367+647(0.75+0.125+0.125)-1.25iE-0.5 Fu611+337+611(0.125+0.125+0.75)1.25iF0.5 u62247+365+701(0.25+0.375+0.375)0.25iF-0.5 u63247+365+701(0.75+0.125+0.125)-1.25iF0.5 u641+337+611(0.375+0.375+0.25)-0.25iF-0.5
2.3.1 最优电压矢量所在轴线判断
利用两个滞环比较器结合简单的扇区划分，确定最优电压矢量所在相绕组轴线y。最优电压矢量所在轴线判断见表8。
表8 最优电压矢量所在轴线判断
Tab.8 The axis where the optimal voltage vector lies
tq1q2q3q4q5q6 11BCDEFA 1-1FABCDE -11CDEFAB -1-1EFABCD
2.3.2 系统所处控制平面扇区判断
构建中点电压与零序电流的控制平面，控制平面被isz4轴与uo轴划分为4个扇区，利用变量isz4及uo的实时值，判断系统在控制平面所处的扇区m。判断条件见表9。
2.3.3 最优电压矢量选择
中点电压的变化方向由流入中点的电流极性决定，而六相轴线电压矢量流入中点的电流与其所在绕组的相电流有关。因此，在选择最优电压矢量时，还需要判断最优电压矢量所在绕组的相电流iy的极性。例如，定子磁链ys位于q1，且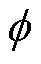
=1、t =1、m=1时，最优电压矢量选择，见表10。
表9 系统所处控制平面扇区判断
Tab.9 The control plane sector where the system lies
isz4uom ≤0≤01 ≤0＞02 ＞0≤03 ＞0＞04
表10 最优电压矢量选择
Tab.10 Selection of optimal voltage vector
tmiy (A～F)q1 111iB＞0u21 iB≤0u23
2.3.4 最优开关矢量
按照上述步骤，可快速构建最优开关矢量表。定子磁链ys位于q1的最优开关矢量见表11。其他扇区的最优开关矢量表构建方法与q1相同。
表11 ys位于q1时，最优开关矢量
Tab.11 The table of optimal switching vector for ys at q1
tmiy (A～F) iy＞0q1iy≤0q1 111iB＞0u21iB≤0u23 2u22u24 3u23u21 4u24u22 1-11iF＞0u61iF≤0u63 2u62u64 3u63u61 4u64u62 -111iC＞0u31iC≤0u33 2u32u34 3u33u31 4u34u32 -1-11iE＞0u51iE≤0u53 2u52u54 3u53u51 4u54u52
2.3.5 DTC的结构
本文所提出具有中点电压平衡与零序电流抑制的T型三电平逆变器供电六相PMSM-DTC与两电平三相电机DTC结构基本相同，首先通过两个滞环比较器结合简单的扇区划分，确定最优电压矢量所处轴线，然后利用isz4及uo的实时值，判断系统在控制平面所处扇区，最后根据最优电压矢量所在绕组的相电流iy的极性，实现电压矢量的最优选择。控制框图如图8所示。
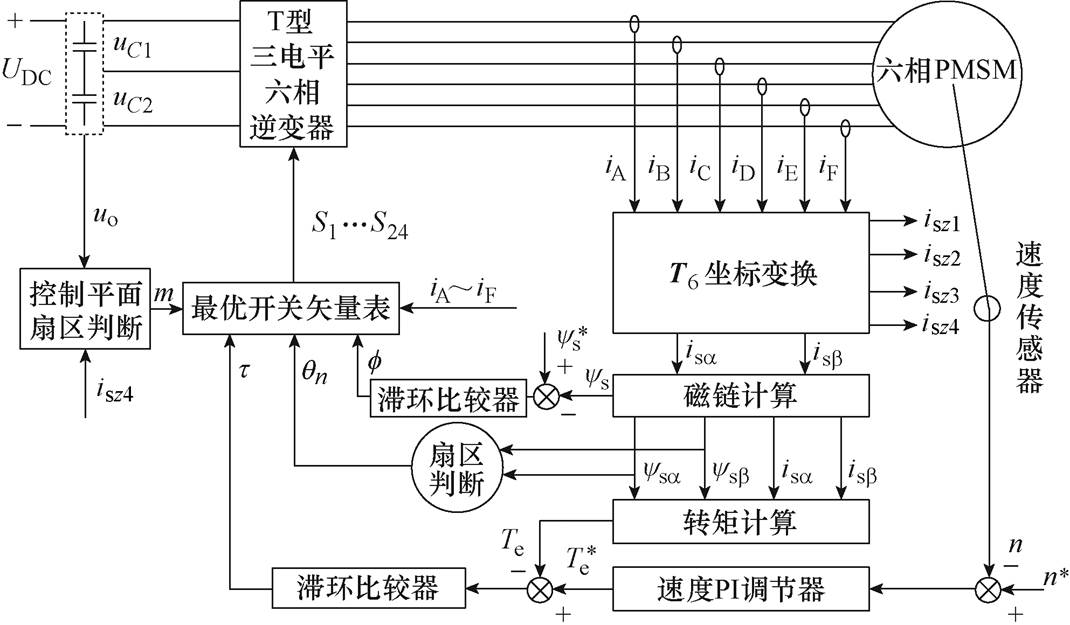
图8 控制策略框图
Fig.8 Block diagram of control strategy
为了验证所提DTC策略的有效性。本文搭建了以DSP（TMS320F28377D）为核心的T型三电平逆变器供电的六相PMSM实验平台。逆变器的母线电压由直流电源提供，IGBT的驱动信号由DSP产生。控制周期为100 ms，死区时间为3 ms。六相电流通过电流霍尔传感器采样得到，直流母线电压与半母线电压利用精密串联电阻分压接入运算放大器构成的电压跟随器采样得到。六相PMSM与装有增量式编码器的他励直流电机同轴相连，其中直流电机与滑动变阻器相连充当负载。六相PMSM参数见表12。实验平台如图9所示。
表12 六相PMSM参数
Tab.12 Data of six-phase PMSM
参 数数 值 额定功率/kW1.5 额定电流/A6.2 极对数2 定子电阻/W1.0 相绕组直轴电感/mH1.54 相绕组交轴电感/mH2.46 转子感应到相绕组磁链幅值/Wb0.198 5
传统的矢量合成方法，通过控制合成矢量的各零序电压分量平均值为0，以实现各零序电流的抑制。为了验证本文所提策略的有效性，利用传统的矢量合成方法，构建最优开关矢量表。在母线电压为100 V时，进行转速为200 r/min，负载为3 N∙m的稳态对比实验，实验结果如图10所示。由实验结果可知：传统方法下，零序电流isz1、isz2得到有效抑制，零序电流isz4出现3次谐波交流分量，相电流发生畸变，经快速傅里叶变换（Fast Fourier Transform, FFT）分析得A相电流中2、3次谐波含量分别为1.77%、30.37%。本文所提方法下，零序电流isz1、isz2及isz4均被有效抑制在0 A附近，相电流波形明显正弦化，经FFT分析得A相电流中2、3次谐波含量分别为5.02%、8.58%。
图9 实验平台
Fig.9 Experimental platform
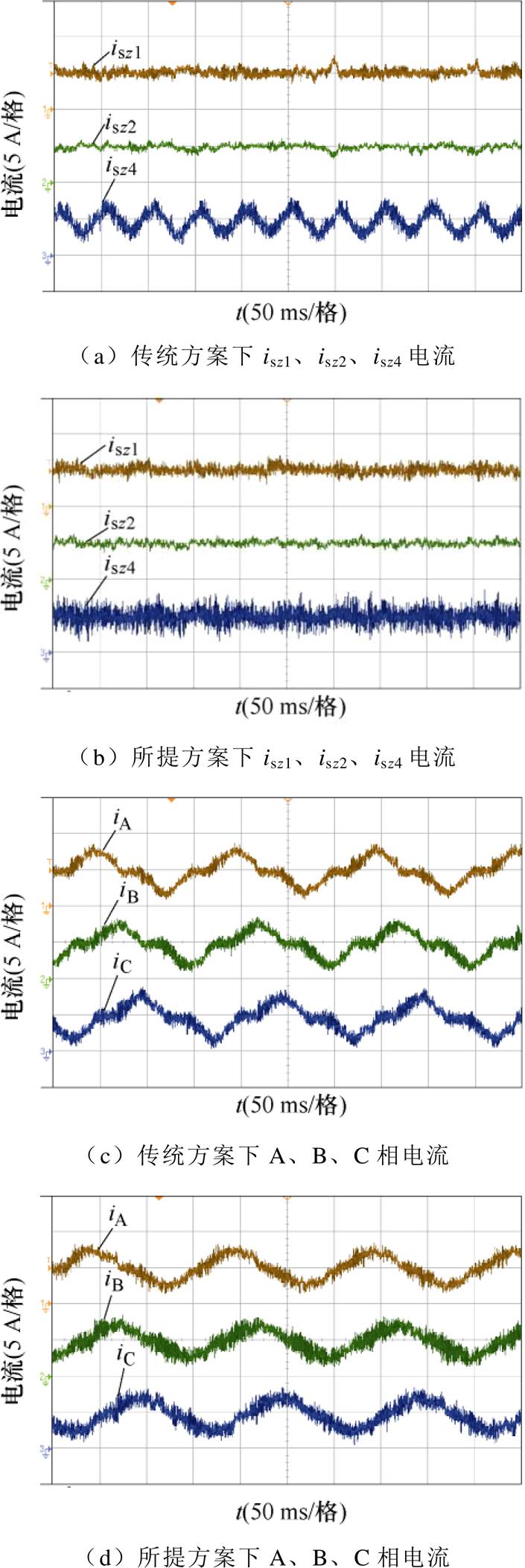
图10 200 r/min稳态带3 N∙m负载实验
Fig.10 Experiment with load 3 N∙m at 200 r/min speed
为了研究系统在所提方法下的稳态性能，在母线电压为150 V，电机带6 N∙m负载情况下，进行转速为500 r/min的稳态运行实验，实验结果如图11所示。由实验结果可知：零序电流isz1、isz2及isz4均被有效地抑制在0 A附近；母线上下电容均分母线电压，中点电压保持平衡，中点电压波动被控制在1 V以内；转速与电磁转矩均能较好地跟随给定值；定子a、b 磁链是一对相位相差90º的正弦波，幅值跟踪到给定值0.33 Wb；A相电压波形为三电平；相电流正弦度较高，FFT分析得A相电流中2、3次谐波含量为分别为3.27%、7.89%。
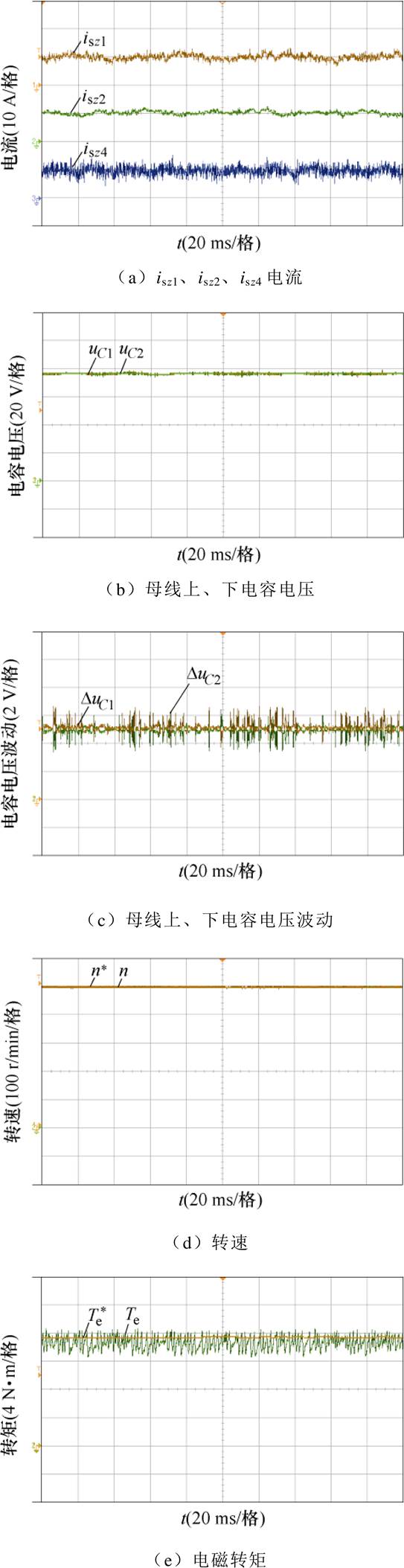
图11 500 r/min稳态带6 N∙m负载实验
Fig.11 Experiment with load 6 N∙m at 500 r/min speed
为了进一步分析系统在不同工况下的稳态性能差异，分别在200、300、400、500 r/min的转速下，进行带2、4、6 N∙m负载的稳态实验。不同工况下的A相电流2次及3次谐波含量、中点电压波动、转矩脉动及磁链脉动，见表13。由表13可知：A相电流2次谐波含量随负载增大而减小；3次谐波含量受转速和负载影响不大；转矩脉动随转速增大而减小，随负载增大而增大；中点电压波动及磁链脉动受转速和负载影响不大。
表13 不同工况下系统关键数据
Tab.13 Key data of different working conditions
n*/(r/min)/(N·m)THD (f2)(%)THD (f3)(%)DuC/VDTe/(N·m)|Dys|/Wb 20029.943.73±0.84±1.76±0.004 06 48.496.10±0.81±1.79±0.004 21 66.135.92±1.00±2.21±0.004 74 30028.607.18±0.96±1.66±0.004 09 46.468.13±0.96±1.92±0.004 41 62.437.76±0.88±2.18±0.004 61 400210.536.25±0.85±1.61±0.004 27 44.568.40±0.80±1.89±0.004 32 63.217.04±0.98±2.14±0.004 47 50027.827.67±1.06±1.40±0.004 26 44.195.20±0.97±1.64±0.004 28 63.277.89±0.99±2.06±0.004 26
为了验证所提控制策略运行下电机的动态性能，在电机给定转速为200 r/min空载运行时，进行给定转速为500 r/min的转速阶跃实验，实验结果如图12所示。在电机转速为500 r/min时，进行6 N∙m负载转矩的突加突卸负载实验，实验结果如图13所示。由实验结果可见，电机在转速阶跃与突加突卸负载时，零序电流isz1、isz2及isz4仍能较好地控制在0 A附近；中点电压虽有较小波动，但能快速调节至平衡状态；六相PMSM转速与电磁转矩均能快速地跟随跟定。
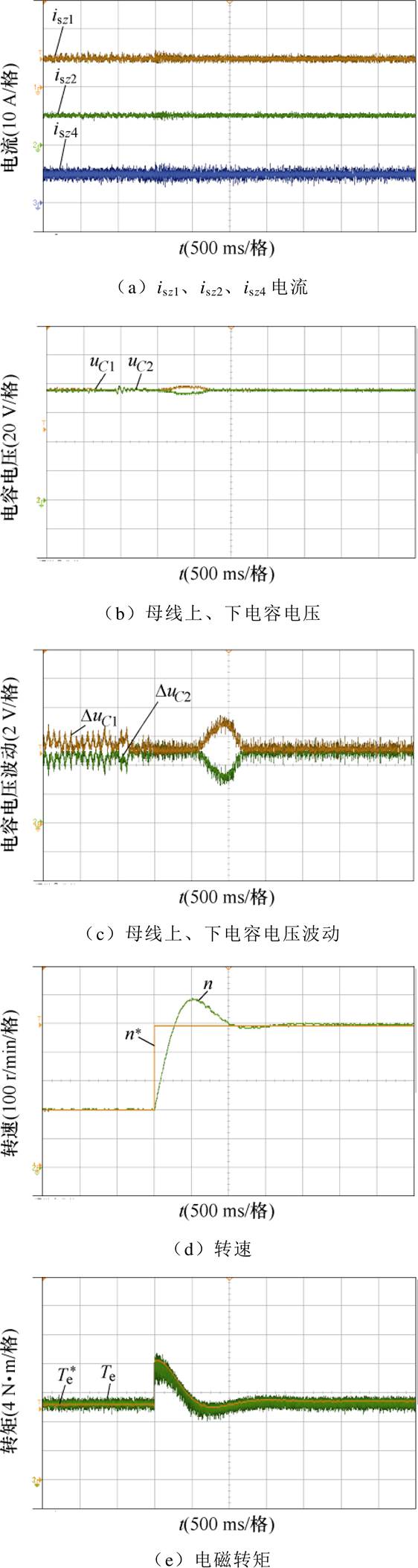
图12 空载时200 r/min至500 r/min转速阶跃实验
Fig.12 Experiments of speed step from 200 r/min to 500 r/min without load
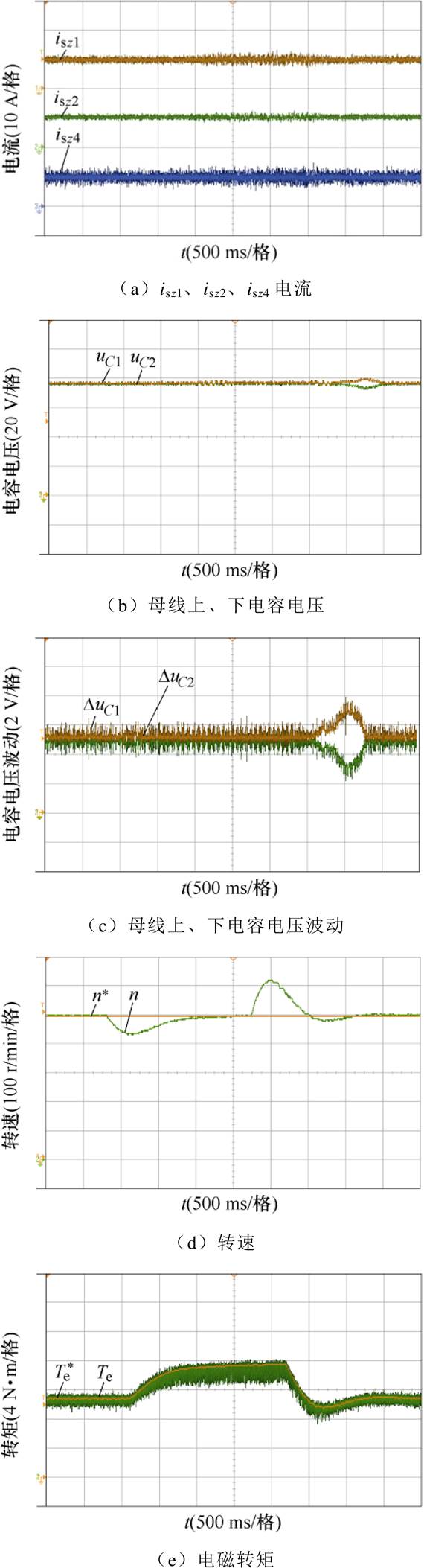
图13 500 r/min时突加突卸6 N∙m负载实验
Fig.13 Experiments involves two tests: the 6 N∙m sudden loading test and the sudden unloading test at 500 r/min
本文基于两电平三相PMSM的DTC方案通过相绕组轴线上电压矢量控制|ys|、Te的思路，快速构建了T型三电平逆变器供电对称六相PMSM-DTC策略。针对驱动系统中，存在中点电压不平衡与零序电流导致定子电流畸变等问题，首先采用合成矢量的方法，分别在六相绕组轴线上合成4个电压矢量；然后确定最优电压矢量所在相绕组轴线，并判断系统在控制平面所处扇区；最后根据最优电压矢量所在绕组的相电流iy的极性，实现电压矢量的最优选择。该策略可以在控制|ys|、Te的同时，兼顾中点电压平衡与零序电流抑制。通过实验验证了本文提出DTC策略的有效性。
参考文献
[1] Levi E. Multiphase electric machines for variable- speed applications[J]. IEEE Transactions on Indu- strial Electronics, 2008, 55(5): 1893-1909.
[2] Cao Wenping, Mecrow B C, Atkinson G J, et al. Overview of electric motor technologies used for more electric aircraft (MEA)[J]. IEEE Transactions on Industrial Electronics, 2012, 59(9): 3523-3531.
[3] 孙玉华, 赵文祥, 吉敬华, 等. 高转矩性能多相组永磁电机及其关键技术综述[J]. 电工技术学报, 2023, 38(6): 1403-1420.
Sun Yuhua, Zhao Wenxiang, Ji Jinghua, et al. Overview of multi-star multi-phase permanent magnet machines with high torque performance and its key technologies[J]. Transactions of China Electrotech- nical Society, 2023, 38(6): 1403-1420.
[4] 周长攀, 刘海峰, 景国秀, 等. 双三相永磁同步电机缺相容错运行虚拟矢量间接修正方法及其在直接转矩控制中应用[J]. 电工技术学报, 2023, 38(2): 451-464.
Zhou Changpan, Liu Haifeng, Jing Guoxiu, et al. The indirect correction method of virtual vectors for dual three-phase permanent magnet synchronous motors under the open-phase fault and its application in the direct torque control[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 451-464.
[5] 孙嘉伟, 郑泽东, 李驰, 等. 对称型多相电机断相容错运行下的电流谐波分析与补偿[J]. 电工技术学报, 2022, 37(21): 5424-5434.
Sun Jiawei, Zheng Zedong, Li Chi, et al. Analysis and compensation of current harmonics in symmetrical multiphase machines in fault-tolerant operation against open-phase faults[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5424-5434.
[6] Karttunen J, Kallio S, Peltoniemi P, et al. Decoupled vector control scheme for dual three-phase permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2185-2196.
[7] Yang Jiaqiang, Hu Haofeng, Huang Jin. Electronic pole changing technique of multiphase induction motor based on vector control[J]. International Transactions on Electrical Energy Systems, 2013, 23(7): 901-913.
[8] 陈涛, 周扬忠, 屈艾文, 等. 基于旋转高频电压注入的六相串联三相永磁同步电机系统转子初始位置解耦观测[J]. 电工技术学报, 2023, 38(8): 2073- 2085.
Chen Tao, Zhou Yangzhong, Qu Aiwen, et al. Decoupling observation of rotor initial position of six-phase and three-phase permanent magnet syn- chronous motors series-connected system based on rotating high-frequency voltage injection[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(8): 2073-2085.
[9] Ren Yuan, Zhu Z Q. Enhancement of steady-state performance in direct-torque-controlled dual three- phase permanent-magnet synchronous machine drives with modified switching table[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3338-3350.
[10] 黄林森, 赵文祥, 吉敬华, 等. 稳态性能改善的双三相永磁电机直接转矩控制[J]. 电工技术学报, 2022, 37(2): 355-367.
Huang Linsen, Zhao Wenxiang, Ji Jinghua, et al. Direct torque control for dual three-phase permanent- magnet machine with improved steady-state perfor- mance[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 355-367.
[11] Cao B, Grainger B M, Wang Xin, et al. Direct torque model predictive control of a five-phase permanent magnet synchronous motor[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2346-2360.
[12] 冯腾, 康龙云, 胡毕华, 等. 基于无差拍控制的T型三电平逆变器中点电位平衡策略[J]. 电工技术学报, 2018, 33(8): 1827-1834.
Feng Teng, Kang Longyun, Hu Bihua, et al. A neutral point potential balancing strategy for three-level T-type inverter based on deadbeat control[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1827-1834.
[13] 陈隆, 周扬忠. 一种基于虚拟矢量的T型三电平并网逆变器改进型模型预测控制策略[J]. 电气技术, 2022, 23(11): 37-43.
Chen Long, Zhou Yangzhong. An improved model predictive control based on virtual space vector for T-type three-level grid-connected inverters[J]. Elec- trical Engineering, 2022, 23(11): 37-43.
[14] 王金平, 刘斌, 董浩, 等. 中点钳位型三电平逆变器基于调制波分解的调制策略[J]. 电工技术学报, 2023, 38(12): 3221-3233.
Wang Jinping, Liu Bin, Dong Hao, et al. A modulation strategy based on modulation wave decomposition for neutral point clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3221-3233.
[15] Vancini L, Mengoni M, Rizzoli G, et al. Voltage balancing of the DC-link capacitors in three-level T-type multiphase inverters[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6450-6461.
[16] Gao Liliang, Fletcher J E. A space vector switching strategy for three-level five-phase inverter drives[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2332-2343.
[17] Dordevic O, Levi E, Jones M. A vector space decomposition based space vector PWM algorithm for a three-level seven-phase voltage source inverter[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 637-649.
[18] Engku Ariff E A R, Dordevic O, Jones M. A space vector PWM technique for a three-level symmetrical six-phase drive[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8396-8405.
[19] 陈健, 王政, 程明. 一种基于矢量空间解耦的三电平六相逆变器空间矢量调制策略[J]. 电工技术学报, 2016, 31(9): 101-111.
Chen Jian, Wang Zheng, Cheng Ming. Design of a space vector modulation strategy based on vector space decomposition for three-level six-phase inverters[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 101-111.
[20] 王一波, 王政. 一种新型基于矢量空间解耦的多相三电平逆变器空间矢量调制策略[J]. 中国电机工程学报, 2018, 38(11): 3316-3324.
Wang Yibo, Wang Zheng. A novel vector space decomposition based space vector modulation strategy for multiphase three-level inverter[J]. Proceedings of the CSEE, 2018, 38(11): 3316-3324.
[21] 王学庆, 王政, 程明. T型三电平逆变器馈电双三相PMSM直接转矩控制[J]. 电工技术学报, 2017, 32(增刊1): 116-123.
Wang Xueqing, Wang Zheng, Cheng Ming. Direct torque control of T-type three-level inverter fed dual three-phase PMSM drives[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 116-123.
[22] Hu Yashan, Zhu Ziqiang, Liu Kan. Current control for dual three-phase permanent magnet synchronous motors accounting for current unbalance and harmonics[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2): 272-284.
Abstract The three-level multi-phase drive system combines the advantages of multi-phase motors and three-level inverters. However, midpoint voltage imbalance and excessive zero-sequence current exist. Midpoint voltage imbalance can lead to output voltage distortion, while excessive zero-sequence current can cause distortion of the stator current and increased losses. Direct torque control (DTC) requires minimal dependence on motor parameters, with a simple algorithm and strong adaptability to load changes. However, research based on DTC theory is still relatively rare. The symmetrical six-phase permanent magnet synchronous motor (PMSM) has high efficiency, a fast response rate among multi-phase motors, and superior fault tolerance. Therefore, this paper proposes a DTC strategy for a symmetrical six-phase PMSM powered by a T-type three-level inverter to balance midpoint voltage and suppress zero-sequence current.
Firstly, by using a spatial vector projection method to remove the redundant switching states in the switching state, the switching states are reduced from 729 to 189. Secondly, based on the three-phase PMSM-DTC structure powered by the two-level inverter, the scheme synthesizes four voltage vectors to meet the control requirements on the six-phase axis using the simplified switching state. In addition, by combining flux linkage and torque hysteresis comparator with simple sector division, the axis of the optimal voltage vector is determined, and the midpoint voltage and zero-sequence current control plane are constructed. The sector where the system is located in the control plane is judged. According to the polarity of the winding phase current iy of the optimal voltage vector, the optimal voltage vector selection is realized, and the optimal switch vector table of DTC is further constructed.
Steady-state comparative experiments are conducted. Compared to the traditional approach, the proposed method maintains a balanced midpoint voltage, effectively suppresses zero-sequence current to approximately 0 A, and significantly sinusoidalize phase current. Steady-state running experiments are conducted at different speeds and loads to investigate the steady-state performance of the motor. The results show that zero-sequence current is effectively suppressed to approximately 0 A, and the midpoint voltage remains balanced. Speed step and sudden load change experiments are performed to validate the dynamic performance of the motor. The results demonstrate that the zero-sequence current can still be well controlled around 0 A, even during speed steps and sudden load changes. Although the midpoint voltage may fluctuate slightly, it can be quickly adjusted to a balanced state.
The following conclusions can be drawn. This paper proposes a DTC strategy for a symmetrical six-phase PMSM powered by a T-type three-level inverter, addressing the control of |ys| and Te, midpoint voltage balance, and zero-sequence current suppression.
keywords：T-type three-level inverter, six-phase permanent magnet synchronous motor, direct torque control, midpoint voltage balance, zero sequence current suppression
中图分类号：TM301.2
DOI: 10.19595/j.cnki.1000-6753.tces.231372
福建省自然科学基金重点资助项目-数控机床电主轴五自由度磁悬浮双定子无轴承磁通切换电机驱动控制关键技术研究（2021J02023）。
收稿日期 2023-08-22
改稿日期 2023-10-27
黄德猛 男，1999年生，硕士研究生，研究方向为现代调速系统。E-mail: 2833942966@qq.com
周扬忠 男，1971年生，博士，教授，博士生导师，研究方向为现代调速系统、新能源发电系统。E-mail: zhty_75313@sina.com（通信作者）
（编辑 陈 诚）