
图1 DR-PMSM的拓扑结构
Fig.1 Topological structure of DR-PMSM
摘要 双并列转子永磁同步电机由于部分定子铁心和绕组的缺失,存在较大的转矩脉动,限制了其在并行对驱类机械装备中的应用。该文对双并列转子永磁电机转矩脉动产生机理进行分析,并提出了相应的抑制方法。对比了N-N型、N-S型两种转子结构,阐明了N-S型转子结构的优越性。在此基础上,开展了转矩脉动产生机理研究,按照影响因素不同,逐次分析了齿槽效应、端部效应、永磁齿轮效应以及绕组参数不对称对电机转矩脉动的作用机理,构建了各个转矩分量的解析表达式。通过有限元模型,验证了理论分析的正确性。针对产生转矩脉动的不同分量,提出了相应的抑制方法,其中抑制空载转矩可以通过优化电机的结构参数来实现,抑制纹波转矩可以通过优化绕组位置分布来实现。搭建样机实验平台,验证了分析模型的准确性。
关键词:双并列转子 永磁同步电机 转矩脉动 空载转矩 结构优化
在挤压机、二辊轧机、双螺杆泵等并行对驱类机械装备中,目前的驱动方式为主从驱动,即由一台感应电机驱动主动轴,主动轴通过同步机械齿轮将转矩传递给从动轴,从而实现两轴的反向同步旋转。这种传递方式存在系统体积大、系统效率低、密封难度大、需要定期维护等问题。此外,由于两轴间距有着严格的尺寸限制,不能用两台独立电机分别直接驱动。因此,双并列转子永磁同步电机(Dual-parallel Rotor Permanent Magnet Synchronous Motor,DR-PMSM)逐渐进入人们的视野[1-4],由于其具有结构紧凑、系统效率高、少维护、主从动轴同步性严格等优点,可用于直接驱动负载。
DR-PMSM由于部分定子铁心和绕组的缺失,导致其存在较大的转矩脉动,影响电机运行时的稳定性和可靠性。从控制的角度看,转矩脉动不利于电机的精准控制[5];从机械的角度看,转矩脉动会带来电机的振动问题,导致轴承磨损,影响轴承寿命;从用户使用感受的角度看,转矩脉动会产生噪声污染,尤其是在低速直驱应用场合[6]。因此,研究DR-PMSM转矩脉动产生机理和抑制方法,对推进该类电机技术研究和工程应用具有实用价值。
DR-PMSM由于具有特殊的拓扑结构,使其既具有旋转电机的性质,又有直线电机的性质。目前,已有大量文献对旋转永磁电机的转矩脉动和直线永磁电机的推力波动进行研究。对于旋转永磁电机,文献[7]提出了一种抑制气隙磁场高频谐波分量的余弦削极转子结构,有效地降低了磁通切换永磁电机的齿槽转矩和转矩脉动。文献[8]基于极弧系数选择和分段倾斜磁极结构对表贴式永磁电机的齿槽转矩进行研究,提出了计算最佳极弧系数和分段斜极结构参数的解析模型。文献[9]提出一种采用不同极宽的分段转子来抑制永磁同步电机的转矩脉动。文献[10]基于相位分析研究了双定子低速大转矩永磁同步电机内外定子槽数配合及相对位置对转矩脉动的影响,采用叠加原理,分开研究了内外两个电机的转矩脉动。
对于直线永磁电机,其齿槽力与旋转永磁电机的齿槽转矩基本无异,因此,对其端部力和纹波推力的抑制是此类电机的研究热点[11]。文献[12]建立了无槽圆筒永磁直线同步电机的精确子域解析模型,提出了优化初级铁心长度、三相绕组位置及匝数分配的优化方法。文献[13-15]以精密运动领域永磁直线电机为对象,分析了齿槽效应、端部效应及绕组不对称对推力波动的作用机理,并提出了初级分段式结构以抑制推力波动。文献[16]提出了磁路互补型横向磁通切换直线电机,该种结构可以极大地削减定位力。文献[17]提出双向反向倾斜线圈的结构,实现了对永磁同步直线电机推力波动的抑制。以上是从电机本体角度出发,也有学者从控制的角度实现对永磁直线电机推力波动的抑制[18-19]。
以上研究成果能够为DR-PMSM转矩脉动产生机理和抑制方法提供有益参考和借鉴。从电机本体角度,DR-PMSM转矩脉动主要由齿槽转矩、端部效应力矩、永磁齿轮传递转矩和因绕组参数不对称而带来的纹波转矩所组成。由于电机结构的对称性,本文以左侧转子为对象,研究了这四部分转矩分量对转矩脉动的影响规律,从而揭示转矩脉动的产生机理,并针对不同的转矩分量,优化结构参数,实现对电机转矩脉动的抑制。
本文首先介绍DR-PMSM的拓扑结构,理论分析齿槽效应、端部效应、永磁齿轮效应和绕组参数不对称对电机转矩脉动的影响规律,建立电磁转矩谐波次数与各个转矩脉动来源之间的关系;然后,通过有限元法验证理论分析的正确性,针对不同的转矩分量,提出对应的抑制方法,实现对电机转矩脉动的优化;最后,通过实验验证模型的准确性并给结论。
本文所研究的DR-PMSM的拓扑结构如图1所示,图1a为整体结构,其由一个连体定子和左右侧两个转子共同组成。其中,连体定子包括连体定子铁心和左右两侧绕组;左右两侧转子由各自侧的转子铁心和永磁体组成。连体定子可以看成是由两个完全相同的传统结构电机定子各自切割掉部分单元电机后拼接而成,左右侧绕组沿非完整圆周分布,分别以逆时针和顺时针嵌放在定子槽内,沿中心线镜像对称位置的定子槽内绕组电流的流向完全相同。两个并列转子均为表贴式永磁转子结构,转子铁心上均匀分布永磁体。

图1 DR-PMSM的拓扑结构
Fig.1 Topological structure of DR-PMSM
按照永磁体极性排布位置的不同,DR-PMSM的转子结构有N-N型和N-S型两种,如图1b和图1c所示。在N-N型转子结构中,两侧转子永磁体沿中心线镜像对称位置的极性相同,即N极对N极、S极对S极;而在N-S型转子结构中,两侧转子永磁体沿中心线镜像对称位置的极性相反,即N极对S极、S极对N极。为了便于分析,把两个传统电机定子的拼接处,即转子之间沿单侧圆周无绕组分布的区域定义为耦合区,如图1a中虚线部分所示。当两套绕组通以三相对称电流时,左右两个电机分别形成两个反向旋转的磁场,与各自的转子相互作用,产生一对反向旋转的电磁转矩,实现两个转子反向同步旋转。
本文以某双螺杆泵驱动系统实际工程需求为背景,所研究的DR-PMSM的主要参数和尺寸见表1,尺寸参数为单侧电机尺寸参数。
表1 DR-PMSM的主要参数和尺寸
Tab.1 Main parameters and dimension of DR-PMSM

参 数数 值 额定功率/kW11 额定电压/V380 额定频率/Hz50 额定转速/(r/min)750 定子外径/mm260 定子内径/mm180 转子内径/mm110 叠片轴长/mm120
按照表1中的数据建立N-N型转子结构电机和N-S型转子结构电机的有限元模型,二者除永磁体排布不同外,其他结构尺寸完全相同,对两种结构的电机进行仿真和对比分析。模型中将定子铁心外径的边界设定为矢量磁位边界,并对整体进行精密的网格剖分,将左右侧两套绕组的电流激励均设置为0。两种结构的电机空载磁力线分布如图2所示。由图2a可知,在N-N型结构中,左侧电机的磁通与右侧电机的磁通无耦合,对称位置极性相同永磁体的安置起到了隔磁的作用,但此时需要注意定子铁心拼接处磁通密度的饱和情况,必要时需要增加两个永磁转子之间的距离,以防止定子铁心拼接处磁通密度过大问题;由图2b可知,在N-S型结构中,靠近耦合区处左侧电机的磁通与右侧电机的磁通存在耦合,左右两侧电机部分永磁体产生的磁通经连体定子铁心形成完整磁路,且磁力线分布较为均匀,不存在局部磁力线过于密集的情况。

图2 两种转子结构的空载磁力线分布
Fig.2 No-load flux distribution of two rotor structures
分别计算N-N型转子结构电机和N-S型转子结构单侧电机的空载反电动势E0、空载转矩T0、转子所受的不平衡电磁力F0和连体定子铁心的最大磁通密度Bsm,0,整理见表2。由表2可知,N-N型转子结构电机具有更高的反电动势,然而,其空载转矩与转子所受的不平衡电磁力比N-S型转子结构电机的空载转矩和转子所受的不平衡电磁力要大得多;N-N型转子结构电机定子铁心最大磁通密度高达2.20 T,出现在定子铁心拼接处,而N-S型转子结构电机定子铁心最大磁通密度仅为1.60 T,出现在定子齿部,定子铁心拼接处不存在过饱和的现象。
表2 两种转子结构的对比
Tab.2 Comparison of two rotor structures

转子结构E0/VT0/(Nm)F0/kNBsm,0/T N-N型215.7848.842.672.20 N-S型202.9427.420.651.60
究其原因,N-N型转子结构电机的左右两个转子永磁体之间为斥力,耦合区处永磁体产生的磁力线为完成闭合更倾向于向磁阻小的区域流通(即定子铁心端部),其产生端部力矩的切向分量助力了空载转矩,径向分量恶化了转子所受的不平衡电磁力,同时也造成了耦合区磁通密度的饱和,这使得N-N型的空载转矩、不平衡电磁力及耦合区域磁通密度都较大。而N-S型转子结构电机的左右两个转子永磁体之间为引力,耦合区处两侧永磁体产生的部分磁力线会直接交链另一侧转子,从而完成闭合,另一部分磁力线会流经铁心端部后再与另一侧转子交链,削弱了耦合区端部效应的影响,两个转子永磁体之间的吸引力缓解了转子所受的不平衡电磁力。
为了进一步说明转子所受的不平衡电磁力,以左侧转子为例进行分析,两种转子结构下转子所受的主要空载电磁力如图3所示。由图3可知,转子所受电磁力的主要分量包含三部分:耦合区外永磁体与定子齿之间的作用力F1,方向为径向,可知F1的合力方向水平向左;耦合区处永磁体与端部铁心之间的作用力Fend,方向为径向,可知Fend的合力方向水平向右;左右两侧转子永磁体之间的作用力Fmag,方向为水平。无论是N-N型转子结构还是N-S型转子结构的电机,F1+Fend的合力方向均为水平向左。在N-N型转子结构中,Fmag方向仍为向左,加剧了转子所受电磁力的不平衡,而N-N型转子结构的Fmag方向向右,缓解了转子所受电磁力的不平衡。因此,即使N-S型转子结构耦合区存在磁力线耦合,但其总不平衡电磁力反而更小。
此外,根据磁力齿轮原理,N-S型转子结构电机的左右两个转子能够更好地保持旋转的同步性。综合考虑,可认为N-S型转子结构电机优于N-N型转子结构电机,因此,后文以N-S型转子结构的DR-PMSM为对象,对其转矩脉动产生机理和抑制方法进行研究。

图3 两种转子结构的不平衡电磁力示意图
Fig.3 Unbalanced electromagnetic force diagram of two rotor structures
从电机本体角度出发,DR-PMSM的转矩脉动受齿槽效应、耦合区端部效应、永磁齿轮效应和绕组参数不对称的影响,分别对应齿槽转矩、端部效应力矩、永磁齿轮传递转矩和纹波转矩。其中,前三种转矩分量在电机空载时就存在,将其定义为DR-PMSM的空载转矩,其示意图如图4所示。换言之,DR-PMSM的转矩脉动由四个分量组成,即
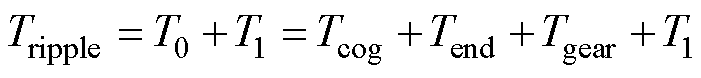 (1)
(1)
式中,Tripple为转矩脉动;T0为空载转矩;T1为纹波转矩;Tcog为齿槽转矩;Tend为端部效应力矩;Tgear为永磁齿轮传递转矩。

图4 DR-PMSM的空载转矩
Fig.4 No-load torque of DR-PMSM
齿槽转矩是永磁电机不通电时永磁磁极与电枢齿之间相互作用力的切向分量引起的,随转子位置变化的交变磁阻转矩[20]。在分析齿槽转矩时,可以从单个槽产生的齿槽转矩出发,利用叠加原理,进而分析所有槽产生的齿槽转矩。设电机的极距为τ(为便于分析,以转子极距所占的圆心角来定义),以2τ为基波周期时,单个槽产生的齿槽转矩Tst可以展开为傅里叶级数形式,表达式为
 (2)
(2)
式中,θ为转子位置角;Tnc为n阶谐波的幅值;θns为n阶谐波的初相位。第i个槽相对于第一个槽的角度位置相差
 (3)
(3)
式中,Ns为定子槽数;l为Ns与转子永磁体磁极对数p的最大公约数。电机总的齿槽转矩表达式为
 (4)
(4)
式中, 为Ns/l阶谐波的幅值;
为Ns/l阶谐波的幅值; 为Ns/l阶谐波的初相位。
为Ns/l阶谐波的初相位。
根据式(4)可知,齿槽转矩Tcog由Ns/l次谐波及其倍频组成,其他谐波成分均已抵消。经过分析和计算,对于本文所研究的DR-PMSM,齿槽转矩Tcog只包含12次及其倍数次谐波组成。
与常规永磁同步电机不同,DR-PMSM由于耦合区的存在,使得电机气隙磁通密度发生畸变,产生类似直线电机的端部效应,进而产生一个周期性的端部效应力矩。随着转子与定子位置的相对变化,端部气隙磁通密度也发生变化,上端部产生的力矩Tend1的波形和下端部产生的力矩Tend2的波形是完全一致的,仅仅是相位不同。由上端部产生的单端力矩用傅里叶级数表示为
 (5)
(5)
式中,T01为直流偏量;Tne为n阶谐波的幅值。由下端部产生的单端力矩用傅里叶级数表示为
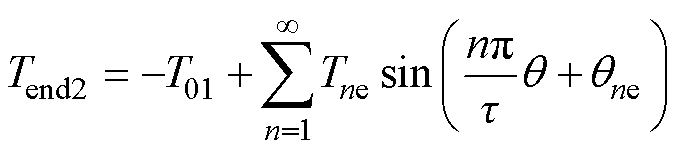 (6)
(6)
式中,θne为上、下两个端部的相位差。将式(5)与式(6)相加即可得到总端部效应力矩,表达式为
 (7)
(7)
根据式(7)可知,以2τ为基波周期时,端部效应力矩Tend只含有偶次谐波,即2次谐波及其倍数次谐波。同时可以看出,通过合理设计上、下两个端部的相位差θne使得cos(θne/2)=0,可以实现对某次谐波的消除,达到削弱端部效应力矩Tend的目的。
DR-PMSM的两个永磁转子并列放置,存在“磁齿轮效应”,当两个转子同步旋转时,左右两侧永磁体之间的磁耦合产生了传递转矩。由于左右两个永磁转子完全相同,且电机结构具有对称性,永磁齿轮传递转矩也可以展开为傅里叶级数的形式,有
 (8)
(8)
式中,Tng为n阶谐波的幅值;θng为n阶谐波的初相位。根据式(8)可知,以2τ为基波周期时,永磁齿轮传递转矩Tgear也只含有偶次谐波,即2次谐波及其倍数次谐波。
DR-PMSM耦合区的存在使得DR-PMSM绕组排布不连续,导致三相绕组参数不对称,进而产生一个周期性的转矩脉动。设左侧电机三相绕组分别为A相、B相、C相,右侧电机三相绕组分别为U相、V相、W相,以一个单元电机来说明三相绕组参数不对称的情况,如图5所示。

图5 单元电机
Fig.5 One unit motor
由图5可知,A相绕组和B相绕组位于一个单元电机的两端,它们之间的距离较远导致磁力线耦合程度较弱,使得A相绕组与B相绕组之间的互感值偏小。而C相绕组位于单元电机的中部,A相绕组与C相绕组之间的距离和B相绕组与C相绕组之间的距离较近且二者基本相等,使得A相绕组与C相绕组之间的互感值和B相绕组与C相绕组之间的互感值基本相等,且均大于A相绕组与B相绕组之间的互感值,三相互感存在不对称情况。当三个单元电机组成一个完整单侧电机时,互感不对称的情况与一个单元电机互感不对称的情况类似。三相自感主要是受每相磁阻不对称的影响,靠近耦合区定子铁心端部相磁路的磁阻与位于定子铁心中部相磁路的磁阻不同。此外,由于左右两侧定子铁心为连体结构,两侧绕组之间还存在互感。
DR-PMSM单侧电机的电压方程为
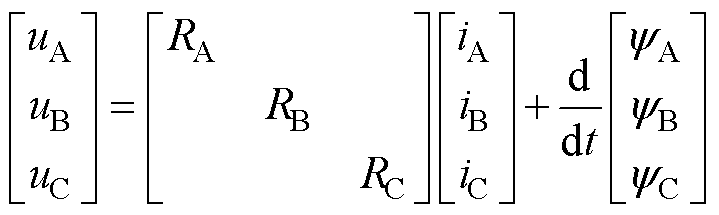 (9)
(9)
式中,u为绕组相电压;i为绕组相电流;R为绕组相电阻;ψ为一相绕组的全磁链,即
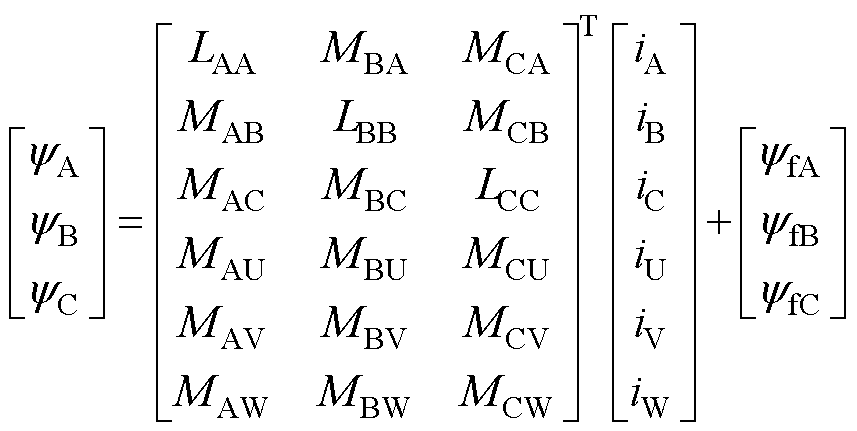 (10)
(10)
式中,L和M分别为绕组的自感和互感;ψf为永磁体磁链。
由式(9)和式(10)可知,当电机通以三相对称电流时,由于绕组之间电感参数不对称,导致三相磁链不对称。采用有限元法,计算各相绕组的电感参数,见表3。由表3可知,DR-PMSM的绕组自感不存在不对称的问题,而互感却存在不平衡问题,互感的不对称不仅体现在同侧电机的不同相之间,也体现在不同侧电机的不同相之间。单侧电机三相磁链波形如图6所示。由图6可知,A相磁链幅值和B相磁链幅值为0.948 Wb,C相磁链幅值为0.961 Wb,这是因为A相绕组和B相绕组包含端部线圈和非端部线圈,而C相绕组仅存在非端部线圈,因端部绕组匝链的磁通少于非端部绕组匝链的磁通所导致。通过以上分析可知,对于DR-PMSM而言,耦合区的存在产生两个端部,因而三相绕组在空间上分布不对称,具体表现为某两相绕组空间上对称,且不同于另一相绕组。这一现象导致电机电感、磁链等参数均存在三相不对称问题。
表3 DR-PMSM的电感参数
Tab.3 Inductance of DR-PMSM (单位: mH)

参 数数 值参 数数 值 LAA9.24MAW-0.215 LBB9.24MBU0.211 LCC9.24MBV0.218 MAB-0.804MBW-0.215 MBC-3.167MCU-0.215 MCA-3.167MCV-0.215 MAU0.218MCW0.214 MAV0.211

图6 单侧电机三相磁链
Fig.6 Flux linkage of three phase windings
建立考虑电机绕组参数不对称的DR-PMSM转矩模型。设三相绕组磁链分别为ψA0、ψB0、ψC0,将ψC0分为ψC01和ψC02两部分,MAB分为MAB1和MAB2两部分,MCU、MCV、MCW也做同样的分解,使得分解后的ψC01与ψA0、ψB0,MAB1与MBC、MCA,MCU1与MAU、MBU,MCV1与MAV、MBV, MCW1与MAW、MBW均实现三相对称,而ψC02、MAB2、MCU2、MCV2、MCW2作为额外的分量存在。因此,分析纹波转矩只需分析ψC02、MAB2、MCU2、MCV2、MCW2五个分量对电机纹波转矩的影响。设左右两侧电机的三相绕组电流iA、iB、iC和iU、iV、iW为
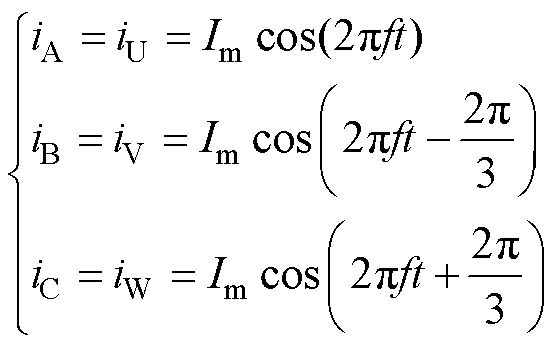 (11)
(11)
式中,Im为相电流幅值;f为相电流频率。ψC02可表示为
 (12)
(12)
式中,ψC02m为磁链的幅值。此时,受五个分量影响的额外三相端电压分量可以表示为
 (13)
(13)
进而产生的转矩脉动为
 (14)
(14)
 (15)
(15)
式中,Ω为角速度。
根据式(14)可知,绕组参数不对称产生的转矩可分为四部分:第一项为输出的恒定转矩,与电流幅值成正比;第二项是输出周期为τ的纹波转矩,与磁链的不对称分量ψC02有关,与电流幅值成正比;第三项受互感不对称分量MAB2的影响,与电流幅值的二次方成正比;第四项受MCU2、MCV2、MCW2的影响,与电流幅值的二次方成正比。同样取2τ为基波周期,纹波转矩T1只存在2次谐波及其倍数次谐波。
基于以上分析可知,齿槽转矩Tcog会给DR- PMSM输出的电磁转矩带来12次及其倍数次谐波,端部效应力矩Tend、永磁齿轮传递转矩Tgear、由绕组参数不对称引起的纹波转矩T1会给电磁转矩带来一系列偶次谐波。
采用有限元法对上述DR-PMSM转矩脉动理论分析的正确性进行验证。图7为DR-PMSM空载转矩波形,其峰峰值为27.42 Nm。以2τ为基波周期对其进行谐波分析,结果表明,空载转矩波形中以2次谐波、12次谐波和24次谐波为主,幅值分别为7.70、4.58和3.85 Nm,此外,还存在幅值很小的其他偶次谐波,这证明了2.1节对DR-PMSM空载转矩理论分析的正确性。

图7 空载转矩T0波形及谐波
Fig.7 Waveform and harmonic of no-load torque T0
进一步地,建立DR-PMSM的无槽有限元模型,如图8所示,该模型能够去除齿槽转矩的影响,计算出端部效应力矩与永磁齿轮传递转矩的和Tend+Tgear。图9为Tend+Tgear的波形,其峰峰值为16.38 Nm。以2τ为基波周期对其进行谐波分析,结果表明,Tend+Tgear中最主要的谐波次数为2次,幅值为7.92 Nm,除此之外还含有少量其他偶数次谐波。

图8 DR-PMSM的无槽有限元模型
Fig.8 Slot-less finite element model of DR-PMSM

图9 Tend+Tgear波形及谐波
Fig.9 Waveform and harmonic of Tend+Tgear
利用有槽模型计算出的空载转矩T0,与利用无槽模型计算出的Tend+Tgear,将二者做差即可得到齿槽转矩Tcog,波形如图10所示,其峰峰值为15.29 Nm。以2τ为基波周期对其进行谐波分析,结果表明,齿槽转矩Tcog中最主要的谐波次数为12次和24次,其幅值为4.58 Nm和3.58 Nm,此外还含有少量其他偶数次谐波。

图10 齿槽转矩Tcog波形及谐波
Fig.10 Waveform and harmonic of cogging torque Tcog
将DR-PMSM空载转矩T0中含量较大的谐波次数整理见表4。由表4可知,空载转矩的2次谐波、12次谐波、24次谐波是最主要的成分。其中,2次谐波主要是由端部效应力矩和永磁齿轮传递转矩Tend+Tgear产生的,12次谐波和24次谐波主要是由齿槽转矩Tcog产生的。
表4 DR-PMSM空载转矩中的谐波
Tab.4 No-load torque harmonic of DR-PMSM

谐波次数248121624 T0幅值/(Nm)7.700.270.404.580.343.85 Tend+Tgear幅值/(Nm)7.920.390.390.030.390.20 Tcog幅值/(Nm)0.290.340.034.580.183.58
当电机施加电流源激励时,能够得到电机负载时的电磁转矩T,当不考虑定子铁心的饱和效应时,其与空载转矩T0的差值即为电机的纹波转矩T1。图11给出了T0、T1、T的波形,并对T1、T进行了谐波分析。由图11可知,电机通电以后,转子产生70.44 Nm的恒定电磁转矩以及一系列偶次谐波,其中,2次、12次和24次谐波仍是最主要的成分;纹波转矩T1中最主要的谐波次数为12次,此外,2次、4次、6次、18次、24次谐波占有小部分的比例。
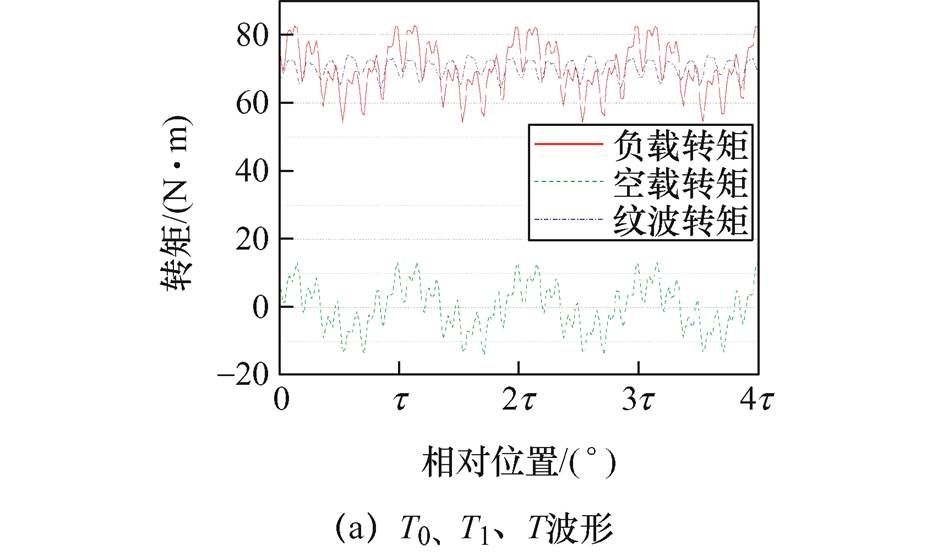

图11 T0、T1、T波形及T、T1的谐波
Fig.11 Waveforms of T0, T1, T and harmonic of T, T1
表5给出了DR-PMSM空载转矩谐波与负载转矩谐波的对比。由表5可知,负载情况下,可以认为输出转矩的2次、24次谐波来源于空载转矩,12次谐波由空载转矩和绕组参数不对称带来的纹波转矩共同产生。
表5 空载转矩谐波与负载转矩谐波的对比
Tab.5 Comparison of no-load torque harmonic and load torque harmonic

谐波次数0246121824 T0幅值/(Nm)07.700.270.124.580.113.85 T幅值/(Nm)70.447.710.800.605.520.603.91
以上负载分析是对电机施加额定电流,此时电流幅值Imax=13 A。工业用电机在设计时一般都会考虑其过载能力,对电机施加电流幅值分别为14、15、16 A的三相对称电流能够使电机短时运行。施加不同的电流以得到不同的负载转矩,并对其进行谐波分析,探讨对纹波转矩的影响,验证式(12)的正确性。图12为不同电流幅值下的负载转矩,表6为不同电流下负载转矩的谐波。由图12和表6可知,随着负载电流的增加,电机输出的负载转矩增大,各次谐波的幅值也都随之增加,其中,12次谐波受电流大小的影响最大,其增加的幅值最大;其他偶次谐波增加的幅值较小,基本可以忽略不计。

图12 不同电流下的负载转矩
Fig.12 Load torque at different current
表6 不同电流下的负载转矩谐波
Tab.6 Load torque harmonic at different current

Imax/A负载转矩谐波幅值/(Nm) 0次2次4次6次12次18次24次 1475.787.710.840.635.670.623.93 1581.167.720.890.675.830.653.95 1686.537.730.930.695.990.673.97
基于以上对空载转矩和负载转矩的有限元分析,验证了第2节理论分析的正确性。可以推断,对于本文所研究的DR-PMSM,转矩脉动最主要的来源为其空载转矩,因绕组不对称产生的纹波转矩是次要来源,这为对其转矩脉动的抑制提供了理论基础。
对于永磁同步电机而言,有大量文献表明,永磁体极弧系数和偏心距对齿槽转矩有显著影响[20],优先考虑优化这两个结构参数来抑制齿槽转矩。初始设计方案中,永磁体的极弧系数αp=0.80,偏心距h=22 mm,在有限元模型中对这两个参数进行参数化设置,其变化范围分别为[0.7,0.9]和[12 mm,32 mm],仿真步长分别为0.02和2 mm,每个参数在变化范围之内各有11个数据点。图13给出了永磁体极弧系数αp和偏心距h对空载转矩的影响。由图13可知,随着极弧系数的增加,空载转矩峰峰值先增大后减小再增大,当极弧系数为0.86时,空载转矩峰峰值有极小值;随着偏心距的增加,空载转矩峰峰值先减小后增大,当偏心距为26 mm时,空载转矩峰峰值有极小值。

图13 极弧系数和偏心距对空载转矩的影响
Fig.13 Influence of pole arc coefficient and eccentricity distance on no-load torque
采用有限元模型计算永磁体极弧系数为0.86、偏心距为26 mm下的空载转矩,并对其进行谐波分析,如图14所示。由图14可知,此时空载转矩峰峰值为18.52 Nm,空载转矩中的12次谐波幅值由4.58 Nm削弱到1.57 Nm,24次谐波幅值基本为0。由此可以推断,通过优化永磁体的极弧系数和偏心距,能够有效降低空载转矩中的齿槽转矩分量。同时,可以根据加工工艺水平,尽可能减小槽口宽度b0,以进一步削弱齿槽转矩。

图14 极弧系数为0.86、偏心距为26 mm下的空载转矩波形及谐波
Fig.14 Waveform and harmonic of no-load torque at αp is 0.86 and h is 26 mm
由于DR-PMSM中端部效应力矩和永磁齿轮传递转矩难以通过有限元模型进行分离,且二者都只产生偶次谐波,为方便分析,将二者同时进行考虑。DR-PMSM具有区别于传统电机的耦合区结构,增加了电机的结构参数。定义耦合区中沿单侧圆周被切掉的定子铁心区域为占空区,所对应的圆心角为占空角β;定义两个永磁转子之间的最小距离为耦合间距d,新增的两个结构参数的示意图如图15所示。由图15可知,占空角和耦合间距的大小对端部效应力矩和永磁齿轮传递转矩有重要影响,其中占空角的大小决定了上下端部的相位差,因此可以通过优化这两个结构参数实现对两种转矩的削弱。使用DR-PMSM的无槽有限元模型对其进行研究。图16给出了不同耦合间距d下,Tend+Tgear峰峰值随占空角β变化的情况。

图15 占空角β和耦合间距d
Fig.15 Duty angle β and coupling distance d
由图16可知,无论d的大小如何,β越小对Tend+Tgear的抑制作用越有效,因此,若不考虑加工工艺因素,占空角应该尽可能小;此外,当d=1.6 mm和d=2.4 mm时,Tend+Tgear峰峰值随β的增加而增加,但当d=3.2 mm、d=4.0 mm、d=4.8 mm和d= 5.6 mm时,Tend+Tgear随β的增加过程中会出现极小值,分别在β=42°、β=48°、β=48°、β=48°时取到。由此可以推断,当d不超过2.4 mm时,Tend+Tgear中的Tgear占主导作用,此时不能通过优化上下端部的相位差来对Tend进行抑制;当d超过2.4 mm时,Tend+Tgear中的Tend才开始出现作用,此时能通过优化上下端部的相位差来对Tend进行抑制。
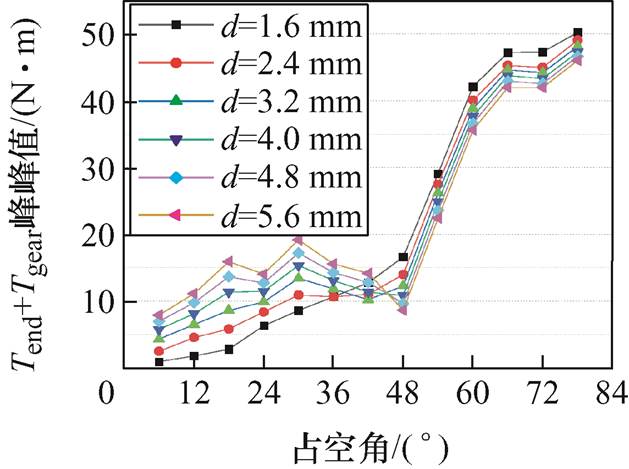
图16 不同耦合间距、不同占空角下的Tend+Tgear
Fig.16 Tend+Tgear at different d and different β
以d=3.2 mm、β=42°(此时Tend+Tgear取得极小值)的情况继续进行研究,对定子铁心拼接处端部采用圆弧形结构,圆弧角ang来定义端部圆弧的尺寸,如图17所示。图18给出了Tend+Tgear峰峰值随ang的变化情况,由图18可知,随着ang的增加,Tend+Tgear的峰峰值存在极小值的情况,在ang=2°的时候取得。因此,通过采用端部圆弧形结构,可以更进一步地实现对Tend+Tgear的抑制。

图17 具有圆弧形端部结构的无槽模型
Fig.17 Slotless model with circular end structure
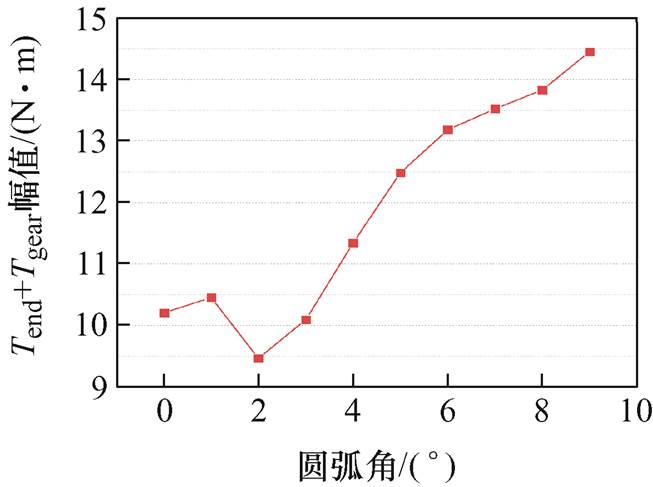
图18 不同圆弧角下的Tend+Tgear
Fig.18 Tend+Tgear at different ang
然而,耦合间距d受两个转子轴心距的限制,选择采用何种方法对Tend+Tgear进行抑制需要根据具体的工程应用需求及加工工艺水平来决定。图19给出了β=0°、d=1.6 mm时的Tend+Tgear波形及其谐波分析。由图19可知,此时Tend+Tgear峰峰值只有1.04 Nm,其谐波中2次、4次含量较大。图20给出了β=42°、d=3.2 mm、ang=2°时的Tend+Tgear波形及其谐波分析。由图20可知,此时Tend+Tgear峰峰值为9.46 Nm,其谐波中也是2次、4次含量较大。这两种情况下的Tend+Tgear相比于图9中的初始值而言,都得到了有效抑制。
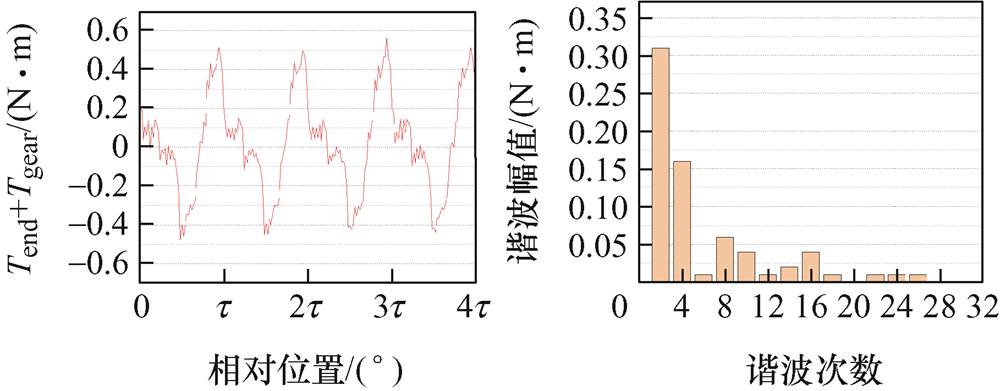
图19 占空角为0°、耦合间距为1.6 mm下的Tend+Tgear波形及谐波
Fig.19 Waveform and harmonic of Tend+Tgear at β is 0°and d is 1.6 mm

图20 占空角为42°、耦合间距为3.2 mm、圆弧角为2°下的Tend+Tgear波形及谐波
Fig.20 Waveform and harmonic of Tend+Tgear at β is 42°, d is 3.2 mm and ang is 2°
4.2节已对DR-PMSM的空载转矩进行了抑制,图21给出了空载转矩优化完成后(αp=0.86、h=26 mm、β=0°、d=1.6 mm)的负载转矩波形及谐波分析。由图21可知,电机的转矩脉动为4.91 Nm,占额定转矩的6.89%,与图11中优化前的负载转矩相比,占比较大的2次、24次谐波基本被完全消除,12次谐波被大大削弱,幅值为1.43 Nm。在此基础上,进一步对因绕组不对称所产生的纹波转矩进行抑制。
根据2.4节对纹波转矩的理论分析,电机绕组电感参数的不对称是产生纹波转矩的重要原因。采用有限元模型对电机的电感参数进行计算,由于结构参数发生了改变,经过有限元计算,此时左侧绕组和右侧绕组之间的互感几乎为0,同时各相自感仍然近似相等,可以推断,同侧电机绕组之间的互感产生了纹波转矩。因此,可以通过优化绕组位置排布来平衡各相之间的互感,如图22所示。令A相绕组对称分布在两端,B相绕组和C相绕组夹在中间,相比于图4中的常规绕组排布,能够增加各相之间的耦合程度,从而在一定程度上平衡各相之间的互感。图23给出了绕组位置优化后的负载转矩波形及谐波分析。由图23可知,此时转矩脉动为4.62 Nm,占额定转矩的6.49%,12次谐波的幅值被削弱到1.40 Nm。由于因绕组参数不对称产生的纹波转矩是转矩脉动的次要成分,因此对其进行优化对转矩脉动的抑制程度有限。

图21 优化后的负载转矩波形及谐波
Fig.21 Waveform and harmonic of load torque after optimization
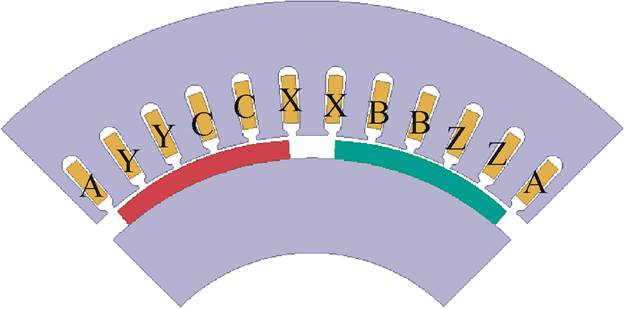
图22 优化后的绕组位置排布
Fig.22 Optimal windings position

图23 绕组位置优化后的负载转矩波形及谐波
Fig.23 Waveform and harmonic of load torque after windings position optimization
表7给出了绕组优化前后电机的三相互感,由表7可知,优化后的三相互感不对称程度得到了削弱,从而降低了纹波转矩。需要说明的是,绕组位置优化后,三相绕组的自感也发生了变化,即产生了自感不平衡的现象。因此,在对电机绕组位置进行优化时,应同时关注自感和互感的变化情况,必要时可采用不等匝数结构。
表7 绕组位置优化前后的三相互感
Tab.7 Three-phase mutual inductance before and after windings position optimization

MAB/mHMBC/mHMCA/mH不对称度 优化前-0.804-3.167-3.1670.64 优化后-2.002-3.492-2.0010.51
为了验证上述分析的可靠性,进行了相关的实验研究。实验基于一台优化前的DR-PMSM样机展开,实验平台如图24所示,DR-PMSM由一台变频器进行供电,为确保实验安全,在实验过程中使用温度巡检仪实时监测电机绕组温度。采用国家标准GB/T 22669空载实验方法中的最小电流法测量其空载反电动势。样机通过变频起动,在额定电压下空载运行到稳定。此时,通过变频器调节其外加电压,利用Mavowatt270-400型电能质量分析仪测量输入的电压和电流。当测得的空载电流达到最小时,记录此刻的电压,即为电机的空载反电动势。

图24 DR-PMSM实验平台
Fig.24 Test platform of DR-PMSM
图25给出了样机的实验值和仿真值,由图25可知,空载反电动势波形吻合度较好,A相空载反电动势的实验值幅值为273.48 V,仿真值幅值为282.28 V,误差仅为3.22%,证明了前述仿真模型和仿真结果的可靠性和准确性。由于样机仍在试制阶段,因此本文只对其进行了空载反电动势的实验研究。

图25 空载反电动势的实验结果和仿真结果
Fig.25 Experimental results and simulation results of no-load back EMF
本文提出一种双并列转子永磁同步电机,主要工作是针对N-S型转子结构电机的转矩脉动产生机理进行分析并提出了相应的抑制方法。得到的主要结论如下:
1)双并列转子永磁同步电机的转矩脉动来源于四个分量,分别为齿槽转矩、端部效应力矩、永磁齿轮传递转矩和因绕组参数不对称产生的纹波转矩,前三个分量统称为空载转矩。
2)空载转矩是转矩脉动的主要成分,纹波转矩是转矩脉动的次要成分。空载转矩中的2次、12次和24次谐波是最主要的成分。其中,2次谐波是由端部效应力矩和永磁齿轮传递转矩引起的,12次和24次谐波是由齿槽转矩引起的。纹波转矩中的12次谐波含量最大。
3)通过对电机结构参数的优化,如优化永磁体极弧系数、永磁体偏心距、占空角、耦合间距、拼接处铁心端部形状可以有效地抑制电机的空载转矩。通过优化绕组位置分布可以在一定程度上抑制纹波转矩。
本文所提双并列转子永磁同步电机为并行对驱类机械装备提供了一种全新的驱动思路,研究工作揭示了电机转矩脉动的产生机理,为研制低转矩脉动的此类电机提供了理论支撑,有助于此类电机的工业应用和推广。同时,本文对其他具有相似结构的双并列转子电机的研制也有一定的参考价值。
参考文献
[1] 戴思锐, 张炳义, 厉伟, 等. 一种定子连体双转子同步并行直驱永磁电机[J]. 电工技术学报, 2020, 35(10): 2107-2118.
Dai Sirui, Zhang Bingyi, Li Wei, et al. A parallel direct-driven permanent magnet synchronous motor with stator connected dual-rotors synchronous[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2107-2118.
[2] 陶大军, 陈阳, 李峥, 等. 双并列转子永磁直驱电机转子不平衡力分析与优化[J]. 电工技术学报, 2024, 39(10): 2961-2973.
Tao Dajun, Chen Yang, Li Zheng, et al. Analysis and optimization of unbalanced electromagnetic force on the rotor of dual-parallel rotor permanent magnet direct-driven motor[J]. Transactions of China Elec- trotechnical Society, 2024, 39(10): 2961-2973.
[3] 黄家楠, 章玮. 定子连体双轴永磁电机稳态特性分析[J]. 电机与控制学报, 2023, 27(6): 1-7.
Huang Jianan, Zhang Wei. Analysis of steady state characteristics of connected permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(6): 1-7.
[4] 陶大军, 陈阳, 李凌霄, 等. MW级双并列转子低速永磁直驱电机设计方法与性能分析[J]. 电机与控制学报, 2023, 27(9): 82-90.
Tao Dajun, Chen Yang, Li Lingxiao, et al. Design method and performance analysis of MW-level dual-parallel rotor low-speed permanent magnet direct-driven motor[J]. Electric Machines and Control, 2023, 27(9): 82-90.
[5] Zhang Chi, Chen Feixue, Qiu Shuheng, et al. A low detent force DS-PMSLM based on the modulation of cogging and end forces[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 721-730.
[6] Wang Tengguang, Zhu Xiaoyong, Xiang Zixuan, et al. Torque ripple suppression of a permanent magnet vernier motor from perspective of shifted air-gap permeance distribution[J]. IEEE Transactions on Magnetics, 2022, 58(8): 8203006.
[7] 王培欣, 花为, 胡铭觐, 等. 余弦削极转子磁通切换永磁电机设计与性能分析[J]. 中国电机工程学报, 2022, 42(22): 8372-8382.
Wang Peixin, Hua Wei, Hu Mingjin, et al. Design and performance analysis of flux-switching permanent magnet machine with cos-chamfering rotor[J]. Proceedings of the CSEE, 2022, 42(22): 8372-8382.
[8] 邢泽智, 王秀和, 赵文良. 基于不同极弧系数组合分段倾斜磁极的表贴式永磁同步电机齿槽转矩削弱措施研究[J]. 中国电机工程学报, 2021, 41(16): 5737-5748.
Xing Zezhi, Wang Xiuhe, Zhao Wenliang. Research on reduction methods of cogging torque based on segmented skewing magnetic poles with different combinations of pole-arc coefficients in surface- mounted permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2021, 41(16): 5737-5748.
[9] Peng Chen, Wang Daohan, Wang Bingdong, et al. Torque ripple and electromagnetic vibration suppression in permanent magnet synchronous motor using segmented rotor with different pole widths[J]. IEEE Transactions on Magnetics, 2022, 58(9): 8206505.
[10] 鲍晓华, 朱然, 刘佶炜, 等. 基于相位分析的双定子低速大转矩永磁同步电动机转矩脉动研究[J]. 电工技术学报, 2022, 37(22): 5660-5669.
Bao Xiaohua, Zhu Ran, Liu Jiwei, et al. Torque ripple analysis of dual-stator surface mounted low-speed high-torque permanent magnet synchronous motors based on phase analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5660-5669.
[11] 沈燚明, 卢琴芬. 初级励磁型永磁直线电机研究现状与展望[J]. 电工技术学报, 2021, 36(11): 2325- 2343.
Shen Yiming, Lu Qinfen. Overview of permanent magnet linear machines with primary excitation[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2325-2343.
[12] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883- 892.
[13] Tan Qiang, Wang Mingyi, Li Liyi, et al. Pulsating magnetic field of permanent magnet linear synchronous motor and its influence on detent force[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 703-712.
[14] Tan Qiang, Huang Xuzhen, Li Liyi, et al. Analysis of flux linkage and detent force for a modular tubular permanent magnet synchronous linear motor with large slots[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1532-1541.
[15] Tan Qiang, Huang Xuzhen, Li Liyi, et al. Research on inductance unbalance and thrust ripple suppression of slot-less tubular permanent magnet synchronous linear motor[J]. IEEE Access, 6: 51011-51020.
[16] 付东山, 吴康伊, 郑萍, 等. 磁路互补型横向磁通切换直线电机电磁推力计算与特性分析[J]. 电工技术学报, 2022, 37(22): 5717-5727.
Fu Dongshan, Wu Kangyi, Zheng Ping, et al. Analysis of electromagnetic thrust characteristics of magnetic circuit complementary transverse flux switching linear motor[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5717-5727.
[17] 汪伟涛, 赵吉文, 宋俊材, 等. 双层反向倾斜线圈永磁同步直线电机的设计与优化[J]. 中国电机工程学报, 2020, 40(3): 980-989.
Wang Weitao, Zhao Jiwen, Song Juncai, et al. Design and optimization of double layer reverse dip coil permanent magnet synchronous linear motors[J]. Proceedings of the CSEE, 2020, 40(3): 980-989.
[18] Chen Zhi, Kong Wubin, Zhang Xuhui, et al. Novel virtual winding current controller for suppression of linear permanent magnet machine electromagnetic thrust ripple[J]. IEEE Transactions on Industrial Electronics, 2023, 70(10): 9835-9846.
[19] Chen Zhi, Kong Wubin, Shi Chaojie, et al. A novel negative-sequence current injection method for reducing LVPMM electromagnetic thrust ripple considering static longitudinal end effect[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 1108-1117.
[20] 王秀和, 杨玉波, 朱常青, 等. 永磁同步电机: 基础理论、共性问题与电磁设计[M]. 北京: 机械工业出版社, 2022.
Abstract In extruder, two-roll mill, twin-screw pump and other parallel driving mechanical equipment, the current driving mode is an induction motor to drive the drive shaft, and the drive shaft transmits the torque to the driven shaft through the synchronous mechanical gear. This transmission mode has some problems, such as large system volume, low system efficiency, difficult sealing, and regular maintenance. Therefore, the dual-parallel rotor permanent magnet synchronous motor has gradually attracted attention.
Due to the absence of partial stator core and windings, the dual-parallel rotor permanent magnet synchronous motor has a large torque ripple, which limits its application in parallel drive machinery. In this paper, the mechanism of torque ripple in dual-parallel rotor permanent magnet motor is analyzed, and the corresponding suppression methods are proposed. Firstly, the advantage of N-S type rotor is illustrated by comparing the N-N type and N-S type two rotor structures. On this basis, the mechanism of torque ripple is studied. According to the different influencing factors, the mechanism of cogging effect, end effect, permanent magnet gear effect and winding parameter asymmetry on the motor torque ripple are analyzed step by step, and the analytical expression of each torque component is constructed. Secondly, the correctness of theoretical analysis is verified by finite element model. According to the different components of torque ripple, the corresponding suppression methods are proposed. The suppression of no-load torque can be realized by optimizing the structure parameters of the motor, and the suppression of ripple torque can further be realized by optimizing the windings position distribution. Finally, a prototype test platform is built to verify the accuracy of the analytical model.
The following conclusions can be drawn from the simulation analysis: (1) The torque ripple of dual-parallel rotor permanent magnet synchronous motor comes from four components, namely, cogging torque, end effect torque, permanent magnet gear transmission torque and ripple torque caused by asymmetry of winding parameters, and the first three components are collectively referred to as no-load torque. (2) No-load torque is the main component of torque ripple, ripple torque is a secondary component of torque ripple. The 2nd harmonics, 12th harmonics and 24th harmonics in no-load torque are the most important components. Among them, the 2nd harmonic is caused by the end effect torque and the permanent magnet gear transmission torque, the 12th harmonic and the 24th harmonic are caused by the cogging torque. The 12 harmonics content in ripple torque is the largest. (3) The no-load torque of the motor can be effectively suppressed by optimizing the structural parameters of the motor, such as the polar arc coefficient of the permanent magnet, the eccentricity of the permanent magnet, the duty angle, the coupling distance, and the shape of the core end at the splice. Ripple torque can be suppressed to some extent by optimizing the winding position distribution.
keywords:Dual-parallel rotor, permanent magnet synchronous motor, torque ripple, no-load torque, structure optimization
中图分类号:TM30
DOI: 10.19595/j.cnki.1000-6753.tces.231410
国家自然科学基金资助项目(51777048)。
收稿日期 2023-08-29
改稿日期 2023-09-25
陈 阳 男,1995年生,博士研究生,研究方向为永磁及特种电机的设计与分析。E-mail: chenyang2022@foxmail.com
陶大军 男,1982年生,教授,博士生导师,研究方向为大电机和特种电机的基础理论、设计与分析。E-mail: tao.dj@163.com(通信作者)
(编辑 崔文静)