 轴电感相等,参考系中第
轴电感相等,参考系中第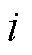 (
( )个永磁同步电机的数学模型描述为
)个永磁同步电机的数学模型描述为摘要 为了提高多电机转速协同控制精度,该文提出一种多智能体系统固定时间一致性的多永磁同步电机转速协同控制新思想。首先,将多永磁同步电机调速系统视为一个多智能体系统,设计了基于无向通信拓扑图的固定时间一致性协议;同时,设计了固定时间滑模观测器估计扰动并在一致性协议中引入前馈补偿,从而得到期望的q轴电流。然后,在矢量控制调速系统的框架下设计了固定时间互补滑模电流控制器,用于跟踪q轴参考电流。利用李雅普诺夫函数分别证明了控制器和观测器可以在与系统初始状态无关的情况下实现固定时间内收敛。最后,在三台永磁同步电机调速系统实验平台上与传统偏差耦合控制算法进行了对比实验验证,证明了所提控制算法的可行性和鲁棒性。
关键词:多永磁同步电机 多智能体系统 固定时间滑模观测器 固定时间互补滑模控制
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其具有高效率、高动态响应、高精度控制等优点,广泛应用于工业领域[1-3]。对于现代复杂的工业生产过程,如电动汽车[4]、航空航天等领域,速度同步控制的精度是多电机调速系统的一个重要性能指标。
目前,多电机调速系统常用的控制算法包括主从控制、交叉耦合控制、偏差耦合控制等[5]。主从控制策略是将一个电机设置为主电机,其他电机设置为从电机来跟踪主电机状态的变化,从而提高多电机协同控制系统的同步精度。然而,主电机上的干扰会传导到从电机,在起动和受到负载扰动时存在较大的同步误差,容易出现抖振现象[6]。因此,交叉耦合的概念被提出,利用两个电机之间速度的差异作为附加的反馈跟踪信号来实现多电机的协调控制。文献[7]将智能互补滑模控制技术结合到交叉耦合控制算法中,增强了双线性伺服电机系统的鲁棒性。但是交叉耦合的方法仅限于两个电机之间的协调控制,在存在多个电机时,会严重影响电机的同步性能。为了克服这一问题,提出了偏差耦合控制策略。文献[8]提出一种偏差耦合同步控制策略,这种控制策略在保证了系统同步性能的同时,也降低了多电机带来的控制结构的复杂性。
多智能体系统具有灵活性、可靠性以及强大的自组织能力等优点,因此多智能体系统一致性问题的研究成为当下的热点。由简单智能体组成网络系统的多智能体系统通常用于解决分布式控制问题,如多机器人协调[9]、无人机编队[10]、电池能量储存[11]等。考虑到多智能体系统一致性控制与多电机速度协同控制两者之间存在本质上的相似性,因此可以将每个电机系统视为一个多智能体,用图论来描述智能体之间的通信,将一致性概念引入到多电机速度协同控制中,为解决多电机之间的协同控制问题提供了新的思路和方法。
多智能体协同控制的一个重要性能指标是收敛速度。按照收敛时间可以分为渐近一致性稳定、有限时间一致性稳定、固定时间一致性稳定等。在文献[12]中提出了一种基于观测器变结构的一致性算法,有效地提高了系统的鲁棒性。然而,文中提出的协议只能实现渐近一致性稳定,这意味着在多永磁同步电机调速系统中,同步误差只能在时间趋近无穷时收敛为零。有限时间一致性可以更快地实现收敛,同时对外部不确定扰动有着更强的鲁棒性。有限时间收敛通常适用于要求系统在一定时间内快速收敛到一致性的情况。文献[13]分析了两种有限时间一致性协议,用于解决多智能体快速收敛一致性问题。然而,系统的初始状态会影响有限时间一致性的收敛时间,因此提出了固定时间一致性的理论。固定时间一致性无需考虑系统的初始状态,可以在一个预定的固定时间内到达一致性状态。通常适用于对多智能体系统性能和鲁棒性要求较为严格的应用,如飞行器的编队、卫星网络的同步[14]等。文献[15]所设计的一致性协议可以有效地抑制干扰信号,实现固定时间内收敛。文献[16]提出了一种非奇异终端滑模一致性协议,实现系统在固定时间内达到一致性收敛,系统性能明显优于有限时间一致性协议。
实现多电机协同控制系统的高品质转速同步控制不仅取决于多电机系统的结构和控制算法,也与单电机系统的电流环控制性能密切相关。目前,对电流环的研究包括自抗扰控制[17]、模型预测控 制[18]、滑模控制等方法。滑模控制具有高精度、强鲁棒性等优点被广泛应用于控制器设计中[19]。然而,单纯的滑模控制会导致系统抖振现象的发生。互补滑模控制不仅有效地减小了抖振,而且使系统的控制精度得到了提高[20]。与使用饱和函数的传统滑模控制相比,可以确保跟踪误差至少减少50%[21]。文献[22]提出一种动态边界层全局互补滑模控制,进一步提高了系统的鲁棒性,改善了系统的跟踪性能。
受上述研究发现的启发,本文提出了一种基于固定时间互补滑模电流控制器的固定时间多智能体系统一致性协议。创新点如下:
(1)创新性地将多电机调速系统视为多智能体系统,将多电机转速协同控制问题转换为多智能体系统一致性问题。
(2)设计了一种新颖的固定时间一致性协议,利用固定时间滑模观测器估计扰动并进行补偿,从而得到期望的q轴电流。
(3)在永磁同步电机矢量控制的框架下,设计了固定时间互补滑模电流控制器。同时,所设计的一致性协议、观测器、电流控制器都是在固定时间内收敛的,可以有效地缩短系统的响应时间。
本文研究的是表贴式永磁同步电机,其 轴电感相等,参考系中第
轴电感相等,参考系中第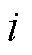 (
( )个永磁同步电机的数学模型描述为
)个永磁同步电机的数学模型描述为
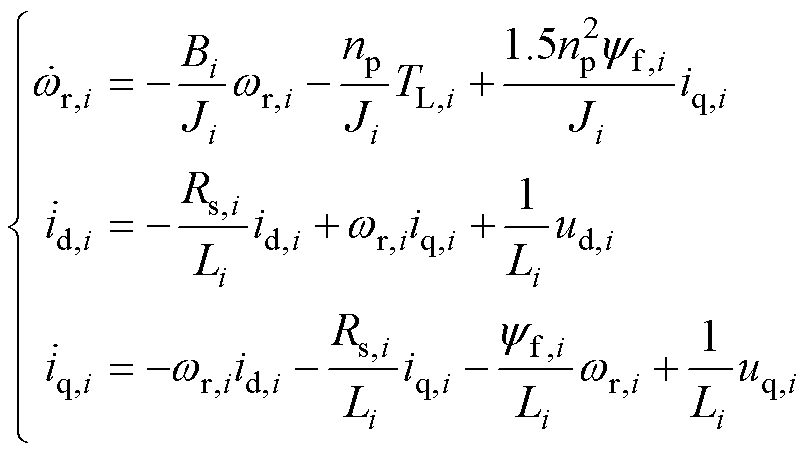 (1)
(1)
式中, 为电角速度;
为电角速度;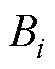 为摩擦系数;
为摩擦系数;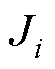 为转动惯量;np为极对数;
为转动惯量;np为极对数;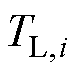 为负载转矩;
为负载转矩;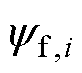 为永磁体磁链;
为永磁体磁链;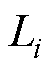 为定子绕组电感;
为定子绕组电感;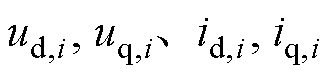 分别为d、q轴电压和电流;
分别为d、q轴电压和电流; 为定子电阻。
为定子电阻。
用一个图 来表示
来表示 个智能体所构成的网络。
个智能体所构成的网络。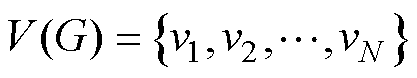 为
为 个智能体所构成的点集,
个智能体所构成的点集,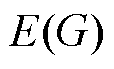

 为图
为图 的边集。图
的边集。图 中的无向边记为
中的无向边记为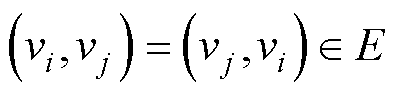 。若智能体
。若智能体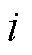 与智能体
与智能体 之间存在连接,则
之间存在连接,则 ;否则
;否则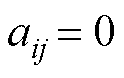 。矩阵
。矩阵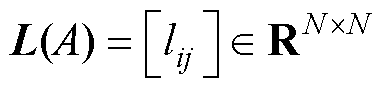 为图
为图 的拉普拉斯矩阵,其中
的拉普拉斯矩阵,其中 ,
, 。
。
本文将多永磁同步电机系统视为具有干扰的一阶多智能体系统。系统的动力学方程描述为
 (2)
(2)
其中


式中, 为控制系数;
为控制系数;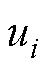 为控制输入,即为
为控制输入,即为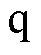 轴电流
轴电流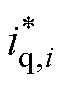 ;
;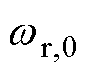 为领导者电角速度;
为领导者电角速度;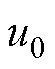 为领导者控制输入;本文采用静态领导者,因此
为领导者控制输入;本文采用静态领导者,因此 。
。
一致性误差定义为
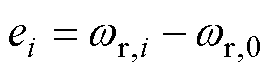 (3)
(3)
多永磁同步电机转速协同控制系统的主框图如图1所示。
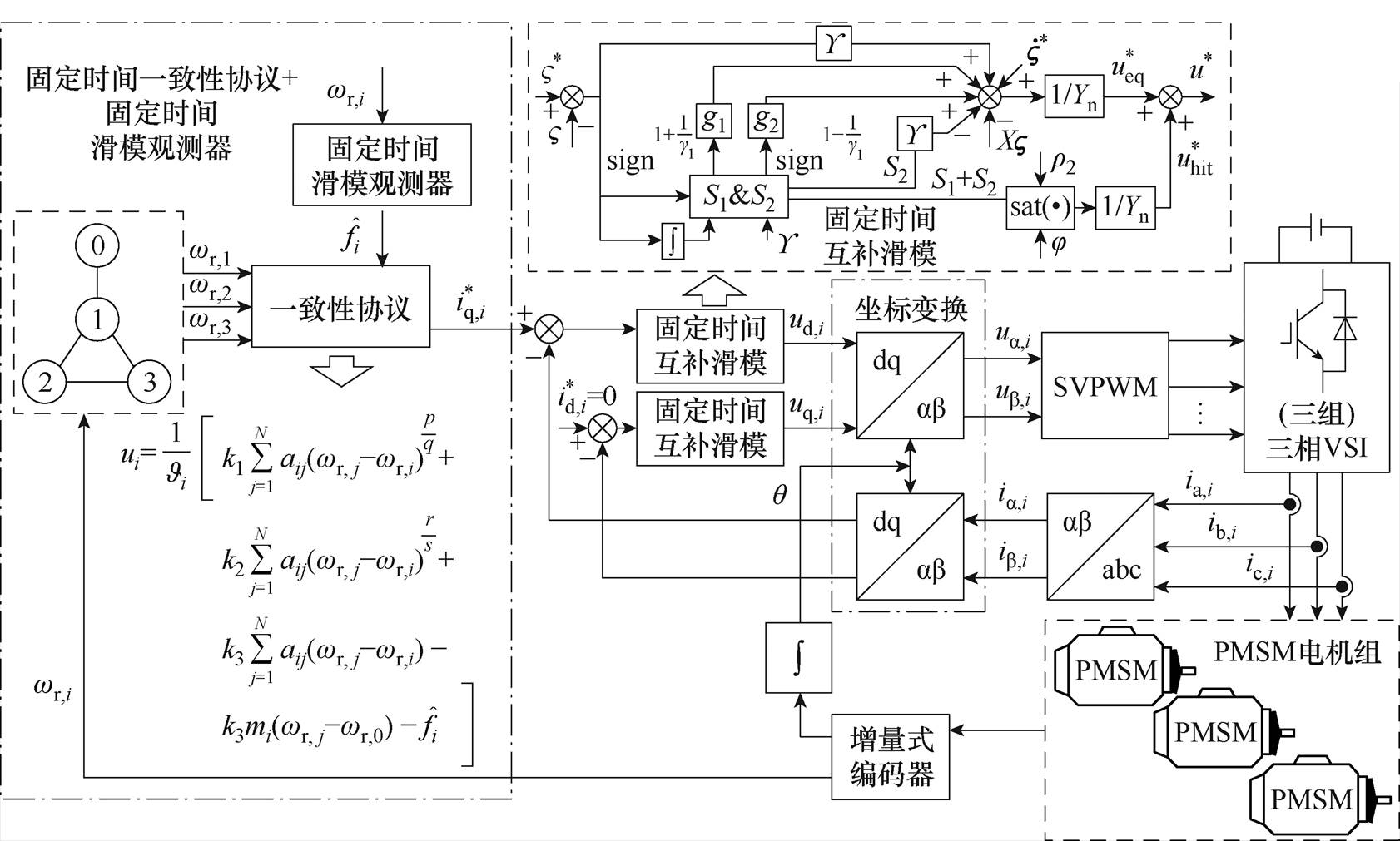
图1 多永磁同步电机转速协同控制系统的主框图
Fig.1 Schematic diagram of multi-PMSMs control method
引理1[23]:对于 ,
,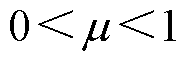 且
且 ,以下不等式成立。
,以下不等式成立。
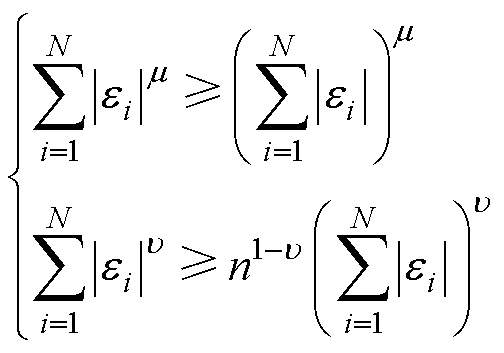 (4)
(4)
引理2[24]:对于一个无向拓扑图,关联的拉普拉斯矩阵为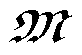 。对于任意向量
。对于任意向量 ,有
,有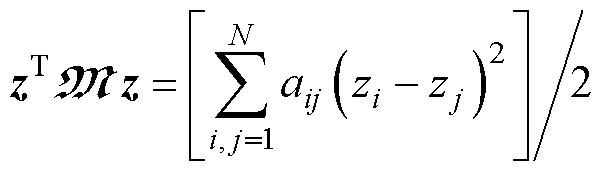 。其最小特征值为0,而所有其他特征值都是正实数,表示为
。其最小特征值为0,而所有其他特征值都是正实数,表示为
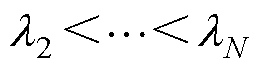 。
。
引理3[25]:假设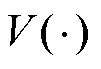 :
: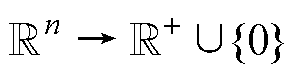 是一个连续的、在无穷远处趋于无穷的函数,并且满足
是一个连续的、在无穷远处趋于无穷的函数,并且满足
(1) 。
。
(2)系统的任何解满足
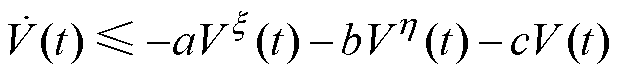
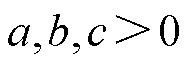 ,
,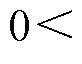
 ,
,
那么系统的原点可以实现固定时间稳定,并且
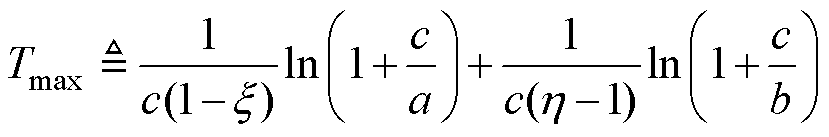 (5)
(5)
引理4[26]:考虑以下系统
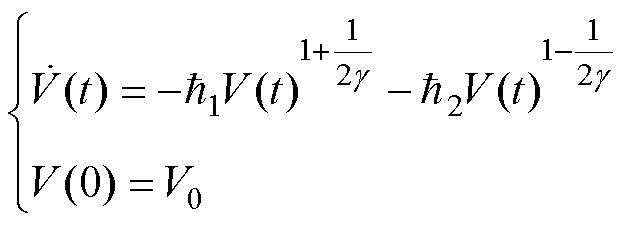 (6)
(6)
式中,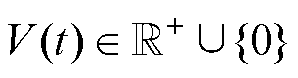 ;
;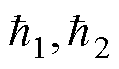 为正实数;
为正实数; 。系统式(6)的平衡点在全局范围内实现了固定时间稳定,其稳定时间上界为
。系统式(6)的平衡点在全局范围内实现了固定时间稳定,其稳定时间上界为
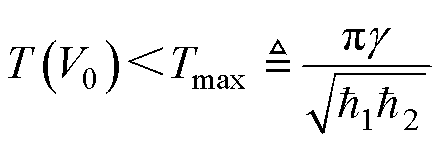 (7)
(7)
设计的固定时间一致性协议为

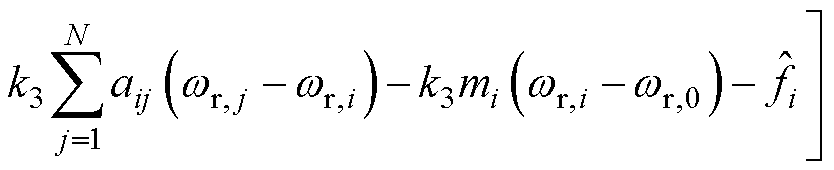 (8)
(8)
其中


式中,k1、k2、k3为控制增益,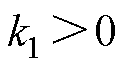 ,
, ,
, ;A为多智能体之间信息传输网络的邻接矩阵;p、q、r、s为正奇数,满足
;A为多智能体之间信息传输网络的邻接矩阵;p、q、r、s为正奇数,满足 ,
, 。
。
定理1:多永磁同步电机转速协同控制系统采用一致性协议式(8),在 的条件下,多电机转速在固定时间内达到一致性,且达到一致性的时间上界满足
的条件下,多电机转速在固定时间内达到一致性,且达到一致性的时间上界满足
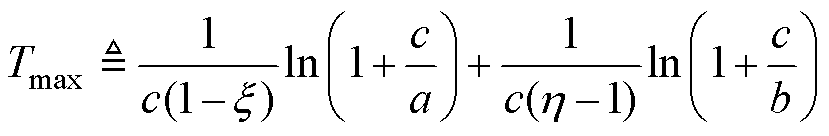
证明:由式(2)、式(3)可知,系统的误差方程为
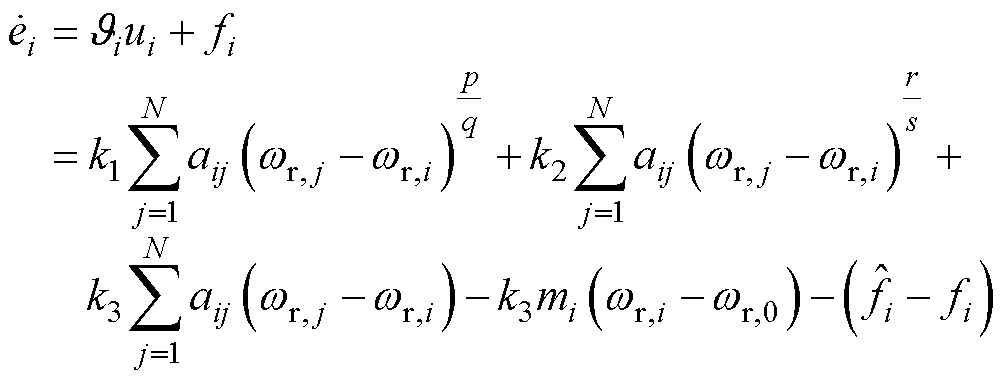 (9)
(9)
考虑以下李雅普诺夫函数
 (10)
(10)
求导可得
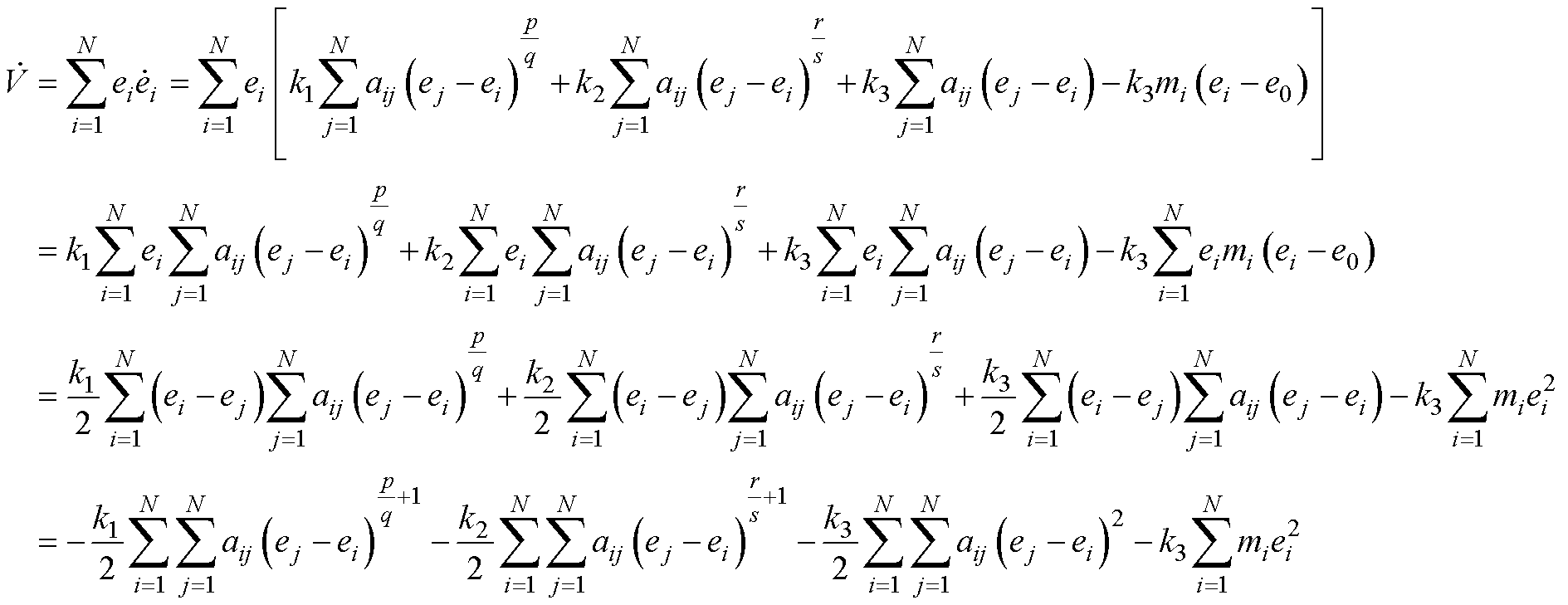 (11)
(11)
对式(11)的前两项进行变换,可得
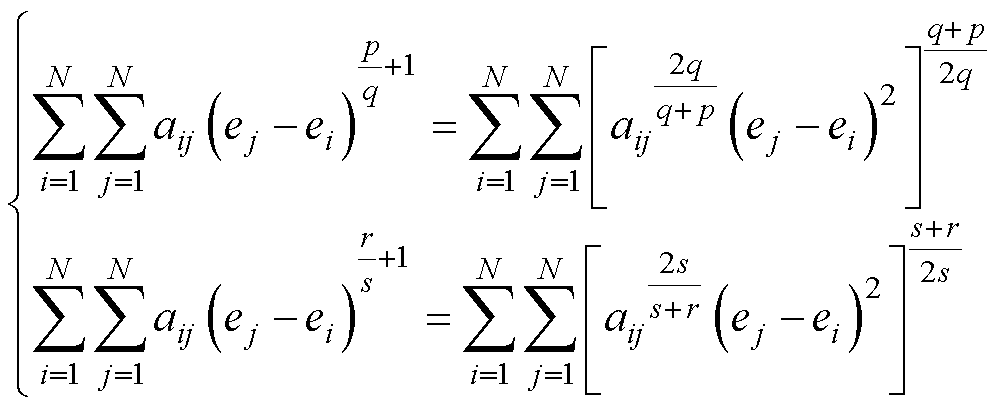 (12)
(12)
根据引理1,若 ,
, ;则
;则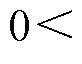

 ,
,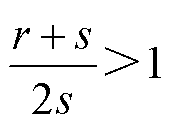 。可以得到不等式
。可以得到不等式
 (13)
(13)
根据引理2,定义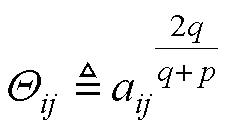 ;
;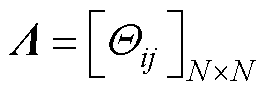 ;
;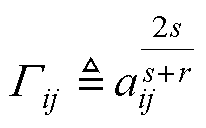 ;
;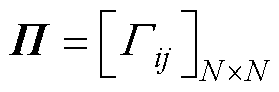 ,可得
,可得
 (14)
(14)
定义 ,
,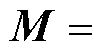
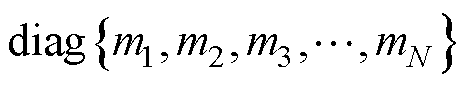 ,
,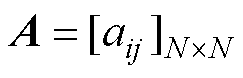 ,
,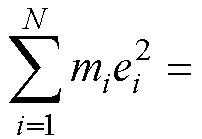
 ,
,
 ,可得
,可得
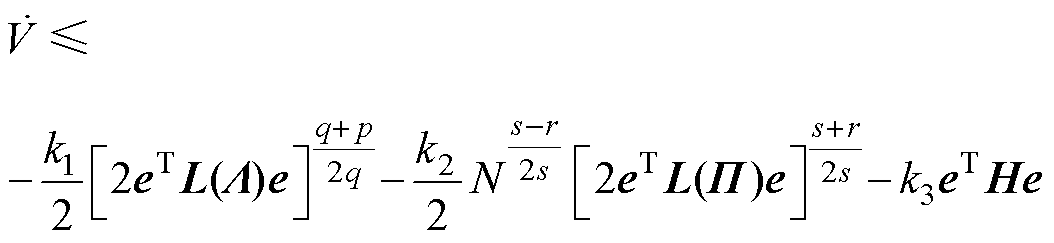 (15)
(15)
因为
 (16)
(16)
将式(12)~式(16)代入式(11)可得
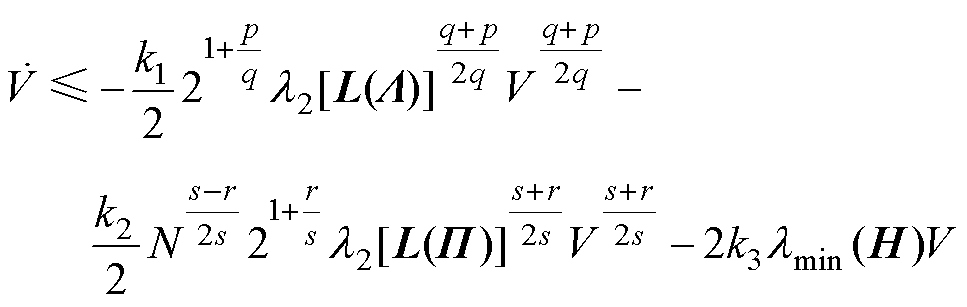 (17)
(17)
其中,定义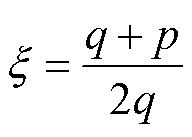 ,
,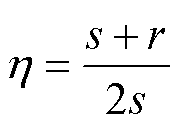 ,
,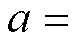
 ,
,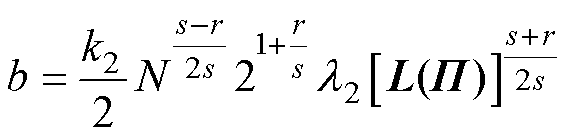 ,
,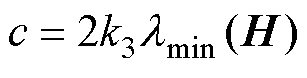 ,可得
,可得
 (18)
(18)
根据引理3,系统在固定时间内实现一致性。
定义变量 ,
,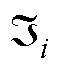 为辅助变量,定义
为辅助变量,定义
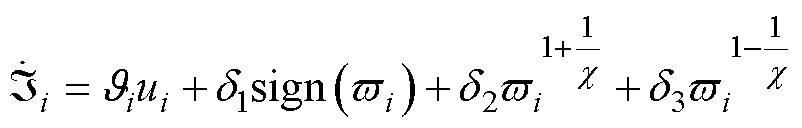 (19)
(19)
式中, ;
;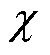 为待设计增益,
为待设计增益, 。
。
可得
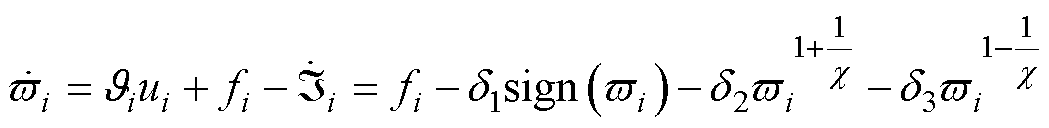 (20)
(20)
固定时间滑模观测器为
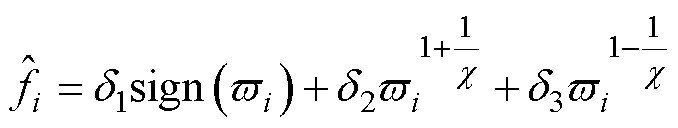 (21)
(21)
选取李雅普诺夫函数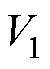 为
为
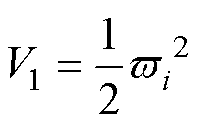 (22)
(22)
求导得
 (23)
(23)
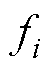 是有界的,
是有界的,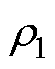 为给定正常数。则
为给定正常数。则
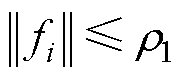 (24)
(24)
当 时有
时有
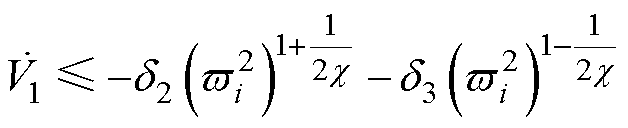 (25)
(25)
根据引理4可得,扰动观测器在固定时间内收敛,收敛时间为
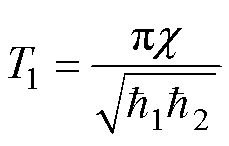 (26)
(26)
其中
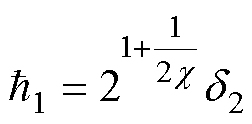
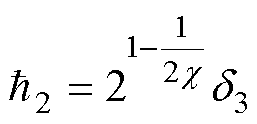
电流环采用一种基于 的控制策略,并设计了一个固定时间互补滑模控制律。固定时间互补滑模电流控制器的跟踪误差定义为
的控制策略,并设计了一个固定时间互补滑模控制律。固定时间互补滑模电流控制器的跟踪误差定义为
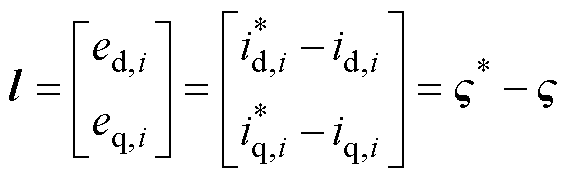 (27)
(27)
其中
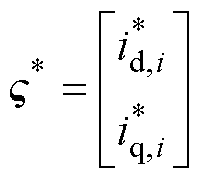

通过式(1)可得考虑扰动后的矩阵为
 (28)
(28)
其中
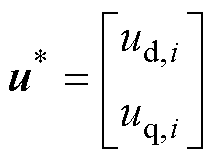

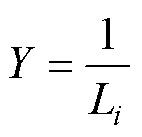

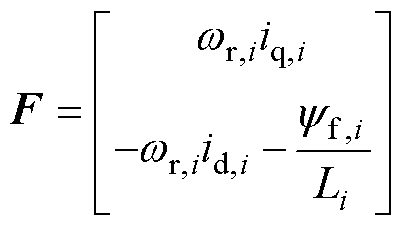
考虑到电机参数变化、摩擦力以及外部扰动,永磁同步电机调速系统可表述为
 (29)
(29)
式中,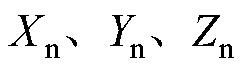 分别为
分别为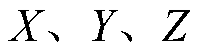 的标称值;
的标称值;

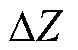 为参数变化量;
为参数变化量; 为集总不确定项,
为集总不确定项,
 ,且满足
,且满足
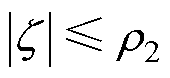 (30)
(30)
式中,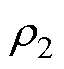 为给定正常数。
为给定正常数。
本文的滑模面以及定义的互补滑模面为
 (31)
(31)
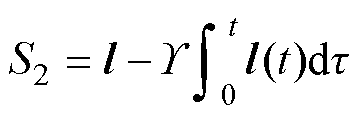 (32)
(32)
式中,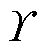 为给定正常数。对式(32)求导得
为给定正常数。对式(32)求导得
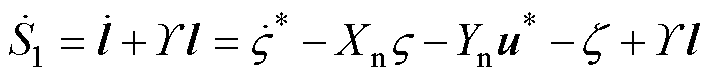 (33)
(33)
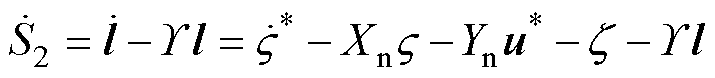 (34)
(34)
两个滑模面的和为
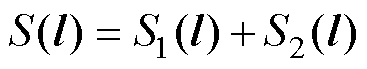 (35)
(35)
可得
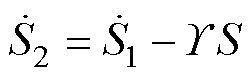 (36)
(36)
设计固定时间互补滑模控制律为
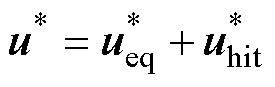 (37)
(37)
 (38)
(38)
 (39)
(39)
式中,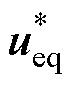 为等效控制律;
为等效控制律;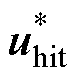 为切换控制律;
为切换控制律;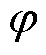 为饱和函数边界层厚度;g1、g2>0;
为饱和函数边界层厚度;g1、g2>0; 为饱和函数;
为饱和函数; 为待设计增益,
为待设计增益,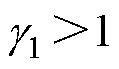 。
。
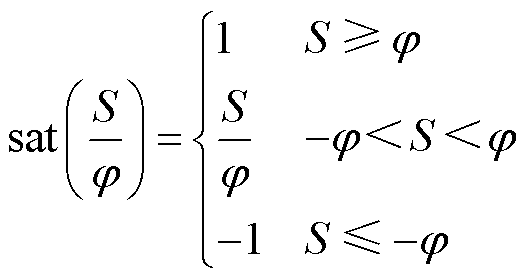 (40)
(40)
选择李雅普诺夫函数 ,求导得
,求导得
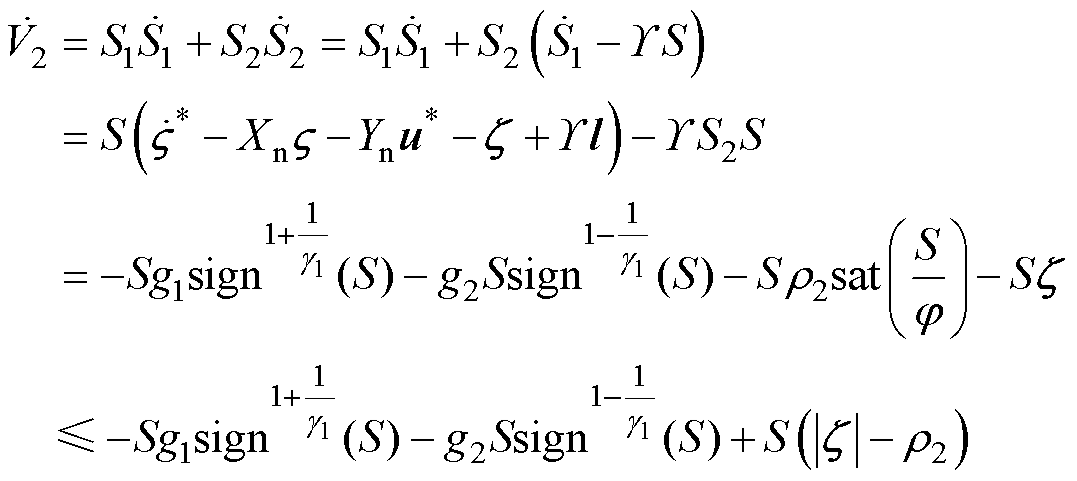
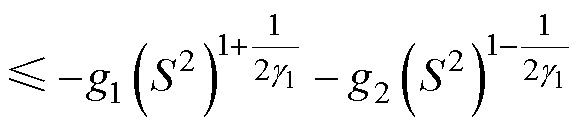 (41)
(41)
根据引理4得出系统固定时间稳定,收敛时间为
 (42)
(42)
其中
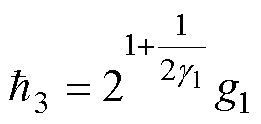
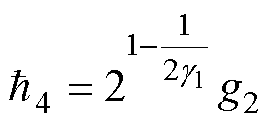
固定时间互补滑模结构示意图如图2所示。

图2 固定时间互补滑模控制器
Fig.2 Fixed-time complementary sliding mode control
为了验证本文提出的控制方法的可行性和鲁棒性,在图3中的半实物仿真实验平台上与传统多电机偏差耦合控制方法进行了对比实验验证。

图3 多电机调速与加载综合实验平台
Fig.3 Multi-motor speed control and load integration experimental platform
综合实验平台的永磁同步电机参数见表1,本文提出的控制方法的参数见表2,传统偏差耦合控制方法的参数见表3。考虑到在工程中的实际应用,本文对提出的控制方法进行了多永磁同步电机调速控制系统升降速、加减负载以及正反转等操作的对比实验验证。
表1 永磁同步电机参数
Tab.1 Parameters of PMSM

参 数数 值 定子电阻Rs/W0.5 绕线电感L/H0.01 摩擦系数B/(N·m·s)0.004 3 转动惯量J/(kg·m2)0.001 94 磁链yf/(V·s)0.1 极对数np2
表2 本文设计控制器参数
Tab.2 Design controller parameters

参 数数 值 k11 k2410 k3400 p3 q5 r7 s5 d10.5 d215 d335 c270 45 g10.1 g20.1 g160
表3 偏差耦合控制器参数
Tab.3 Bias-coupled controller parameters

参 数数 值 速度环Kp1.1 Ki3 电流环Kp4 Ki8
为了验证本文所提出控制方法的同步性能,进行了一个升降速对比实验,将多电机调速系统从初始速度0起动,升速到300 r/min,然后升速到600 r/min,最后降速到300 r/min。升降速对比实验的结果如图4所示。
从图4a中可以看出,在本文设计的控制方法下,每台电机都能准确跟踪上给定轨迹。与图4b对比可以看出,所设计的控制方法没有超调现象,过渡过程比较平滑,在稳态过程中,图4a的振幅在3 r/min左右,明显低于图4b 5 r/min左右的振幅。图4c相较图4d而言,抖振明显减小。从图4e与图4f可以看出,两种控制方法均有较好的同步性能,传统偏差耦合控制方法在起动过程中稍快一些。由此可知,本文所设计的控制方法能够有效减小系统的抖振现象,保证系统的跟踪性能。

图4 多电机调速系统升降速对比实验
Fig.4 Experimental comparison of speed increase and decrease in multi-motor speed control systems
为了验证本文所提出的控制方法的鲁棒性,进行了一个加减载实验,将多电机调速系统从初始速度0起动,升速到300 r/min,然后在不同时间向不同的电机施加或移除不同的负载。负载是由图3所示的负载电机组所完成的,加减载对比实验的结果如图5所示。
当出现负载扰动的情况下,两种方法下的响应时间相差不大,均能在短时间内将转速恢复到所设定的300 r/min,但图5a稳态时刻的3 r/min左右振幅明显优于图5b 5 r/min左右的振幅。由于本文设计了观测器估计并补偿扰动,因此负载扰动对多电机调速系统的影响被降低,当突加相同负载扰动时,图5c中电机3的转速波动为10 r/min,而图5d中电机3的转速波动为20 r/min。同时,由图5e可以看出,当一台电机的速度发生变化时,其他电机的速度也会相应进行调整,减小系统的同步误差。图5f在出现负载扰动的情况下同样有着很好的同步误差。由此可知,本文所设计的控制方法可以保证系统的鲁棒性能。

图5 多电机调速系统加减载对比实验
Fig.5 Experimental comparison of multi-motor speed control systems with load addition and reduction
图6为电机进行正反转时的对比实验,将多电机调速系统从初始速度0起动,升速到300 r/min,然后反转到-300 r/min。图6a相较图6b没有超调现象,进入反转的过程更加平稳。图6c的稳态误差优于图6d,但是在过渡时间上图6d相对较快。图6e的同步误差在3 r/min左右,优于图6f的6 r/min左右的同步误差。
综上所述,所进行的升降速实验、加减载实验、正反转实验能够很好地验证本文所提出的控制方法的可行性和鲁棒性,与传统偏差耦合控制方法相比具有较好的同步和跟随性能。
本文提出了一种多永磁同步电机转速协同控制方法,将多永磁同步电机的速度控制系统视为一个多智能体系统,在无向通信拓扑结构下设计了固定时间一致性协议。利用固定时间滑模观测器估计并补偿扰动,得到期望的q轴电流。在矢量控制系统的框架下,设计了固定时间互补滑模电流控制器,从而构成了多电机转速协同控制系统。通过与传统偏差耦合控制方法进行对比实验来验证系统具有良好的跟踪和同步性能,具有较快的收敛性和较强的鲁棒性。

图6 多电机调速系统正反转对比实验
Fig.6 Experimental comparison of forward and reverse rotation in multi-motor speed control systems
参考文献
[1] 赵凯辉, 刘文昌, 刘智诚, 等. 一种永磁同步电机无模型高阶滑模控制算法[J]. 电工技术学报, 2023, 38(6): 1472-1485.
Zhao Kaihui, Liu Wenchang, Liu Zhicheng, et al. Model-free high sliding mode control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1472-1485.
[2] 罗力岩, 樊启高. 一种改进型永磁同步电机无模型预测电流控制策略[J]. 电工技术学报, DOI: 10. 19595/j.cnki.1000-6753.tces.240101.
Luo Liyan, Fan Qigao. An improved model-free predictive current control strategy for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, DOI: 10.19595/j.cnki.1000- 6753.tces.240101.
[3] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Elec- trical Machines and Systems, 2020, 4(2): 151-160.
[4] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Spatial distribution characteristics and influencing factors of demagnetization of permanent magnet motor for electric vehicle[J]. Transactions of China Electro- technical Society, 2023, 38(22): 5959-5974.
[5] 叶宇豪, 彭飞, 黄允凯. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021, 36(14): 2922-2935.
Ye Yuhao, Peng Fei, Huang Yunkai. Overview of multi-motor synchronous motion control techno- logy[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2922-2935.
[6] Yeam T I, Lee D C. Design of sliding-mode speed controller with active damping control for single- inverter dual-PMSM drive systems[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(5): 5794- 5801.
[7] Lin F J, Chou Pohuan, Chen C S, et al. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control[J]. IEEE Transactions on Industrial Elec- tronics, 2012, 59(2): 1061-1073.
[8] Li Lebao, Sun Lingling, Zhang Shengzhou. Mean deviation coupling synchronous control for multiple motors via second-order adaptive sliding mode control[J]. ISA Transactions, 2016, 62: 222-235.
[9] He Guojun, Cui Shibo, Dai Yueyue, et al. Learning task-oriented channel allocation for multi-agent communication[J]. IEEE Transactions on Vehicular Technology, 2022, 71(11): 12016-12029.
[10] 郑长兵, 庞中华, 董燕飞, 等. 复杂通信约束下网络化多智能体系统的时变编队控制[J]. 控制与决策, 2024, 39(10): 3513-3520.
Zheng Changbing, Pang Zhonghua, Dong Yanfei, et al. Time-varying formation control of networked multi- agent systems with complex communication con- straints[J]. Control and Decision, 2024, 39(10): 3513-3520.
[11] 吕冬翔, 张志成, 朱立宏, 等. 基于多智能体的太阳能无人机能源控制[J]. 控制与决策, 2023, 38(2): 372-378.
Lü Dongxiang, Zhang Zhicheng, Zhu Lihong, et al. Multi-agent based energy control for solar unmanned aerial vehicles[J]. Control and Decision, 2023, 38(2): 372-378.
[12] Zhang Changfan, Wu Han, He Jing, et al. Consensus tracking for multi-motor system via observer based variable structure approach[J]. Journal of the Franklin Institute, 2015, 352(8): 3366-3377.
[13] He Sulan, Wang He, Yu Wenwu. Distributed fast finite-time tracking consensus of multi-agent systems with a dynamic leader[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(4): 2176-2180.
[14] Liu Jian, Wu Yongbao, Sun Mengwei, et al. Fixed- time cooperative tracking for delayed disturbed multi-agent systems under dynamic event-triggered control[J]. IEEE/CAA Journal of Automatica Sinica, 2022, 9(5): 930-933.
[15] 耿超, 武永宝, 孙佳, 等. 抗干扰的多智能体系统固定时间分布式优化算法[J]. 控制与决策, 2024, 39(2): 527-535.
Geng Chao, Wu Yongbao, Sun Jia, et al. Fixed-time distributed optimization algorithm for multi-agent systems with disturbance resistance[J]. Control and Decision, 2024, 39(2): 527-535.
[16] Ni Junkang, Tang Yang, Shi Peng. A new fixed-time consensus tracking approach for second-order multiagent systems under directed communication topology[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(4): 2488-2500.
[17] 王建渊, 王海啸, 尹忠刚, 等. 基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制研究[J]. 电工技术学报, 2024, 39(14): 4405-4421.
Wang Jianyuan, Wang Haixiao, Yin Zhonggang, et al. Research on sensorless control of synchronous reluctance motor based on first order linear active disturbance rejection controller[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4405-4421.
[18] 魏尧, 柯栋梁, 黄东晓, 等. 基于超局部化时间序列的永磁同步电机无模型预测电流滑模控制策略[J]. 电工技术学报, 2024, 39(4): 1022-1032.
Wei Yao, Ke Dongliang, Huang Dongxiao, et al. Model-free predictive sliding mode control using ultra-localized time-series for permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1022-1032.
[19] 赵鑫宇, 王丽梅. 永磁直线同步电机自适应分数阶终端滑模控制[J]. 电工技术学报, 2023, 38(20): 5434-5443.
Zhao Xinyu, Wang Limei. Adaptive fractional-order terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5434-5443.
[20] Hou Shixi, Chu Yundi, Fei Juntao. Intelligent global sliding mode control using recurrent feature selection neural network for active power filter[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 7320-7329.
[21] Lin F J, Hung Y C, Tsai M T. Fault-tolerant control for six-phase PMSM drive system via intelligent complementary sliding-mode control using TSKFNN- AMF[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5747-5762.
[22] 金鸿雁, 赵希梅, 原浩. 永磁直线同步电机动态边界层全局互补滑模控制[J]. 电工技术学报, 2020, 35(9): 1945-1951.
Jin Hongyan, Zhao Ximei, Yuan Hao. Dynamic boundary layer global complementary sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1945-1951.
[23] Zuo Zongyu, Tie Lin. A new class of finite-time nonlinear consensus protocols for multi-agent systems[J]. International Journal of Control, 2014, 87(2): 363-370.
[24] Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time- delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
[25] Chen Chuan, Li Lixiang, Peng Haipeng, et al. A new fixed-time stability theorem and its application to the fixed-time synchronization of neural networks[J]. Neural Networks, 2020, 123: 412-419.
[26] Parsegov S E, Polyakov A E, Shcherbakov P S. Nonlinear fixed-time control protocol for uniform allocation of agents on a segment[J]. Doklady Mathe- matics, 2013, 87(1): 133-136.
Abstract For modern complex industrial production processes, the speed synchronization control precision of multi-motor speed regulation systems is an extremely critical performance indicator. Therefore, this paper proposes a concept of fixed-time multi-agent consistency for the speed-coordinated control of multiple permanent magnet synchronous motors (multi-PMSMs).
Multi-agent systems (MASs) have advantages such as flexibility, reliability, and strong self-organizing capabilities. Considering the inherent similarity between consensus control of MASs and coordinated control of multi-motor speed, each motor system can be viewed as a MAS. Graph theory describes agent communication, and a fixed-time consensus protocol is designed. Meanwhile, a fixed-time sliding mode observer is utilized to estimate disturbances and introduced into the consensus protocol, thereby obtaining the desired q-axis current. Then, within the framework of the field-oriented control, a fixed-time complementary sliding mode current controller is designed to track the q-axis reference current. The fixed-time convergence of both the controller and observer is proven using Lyapunov functions regardless of the initial state of the system.
On the experimental platform with three PMSMs, the proposed control algorithm is validated and compared with the traditional deviation coupling control (DCC) algorithm through experiments involving speed-up and speed-down, load increase and decrease, and forward and reverse rotation. The speed-up and speed-down experiments indicate that the proposed control algorithm can accurately track the given speed. The transition process is relatively smooth without significant overshoot. During the steady-state process, the chattering amplitude of the proposed control algorithm is around 3 r/min, which is significantly lower than the approximately 5 r/min of the traditional DCC algorithm. The load increase and decrease experiments show that when load disturbances occur, the proposed control algorithm can restore the speed to the set value within a short time. Because an observer is designed to estimate and compensate for disturbances, the impact of load disturbances on the multi-motor speed regulation system is reduced. When the speed of one motor changes, the speeds of the other motors are correspondingly adjusted, reducing the system's synchronization error. When a sudden load disturbance of the same magnitude is applied, the proposed control algorithm results in a speed increase of 10 r/min, which is lower than the 20 r/min increase observed with the traditional DCC algorithm. The forward and reverse rotation experiments show that the proposed control algorithm does not exhibit significant overshoot. During the reverse rotation process, it transitions more smoothly than the traditional DCC algorithm.
The following conclusions can be drawn. (1) This paper treats the multi-motor speed regulation system as a MAS, transforming the problem of coordinated speed control of multiple motors into a consensus problem in MAS. (2) A fixed-time consensus protocol is designed. A fixed-time sliding mode observer estimates and compensates for disturbances, thereby obtaining the desired q-axis current. (3) Comparative experiments verify the feasibility and robustness of the proposed algorithm.
keywords:Multi permanent magnet synchronous motors, multi-agent system, fixed-time sliding mode disturbance observer, fixed-time complementary sliding mode control
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240119
国家自然科学基金资助项目(52177047)。
收稿日期 2024-01-18
改稿日期 2024-03-19
侯利民 男,1976年生,教授,博士生导师,研究方向为电力电子与电气传动、先进控制理论与控制工程。E-mail: hlm760410@163.com(通信作者)
兰骁儒 男,1998年生,硕士研究生,研究方向为永磁同步电机调速系统、多智能体系统一致性控制。E-mail: 472220400@stu.lntu.edu.cn
(编辑 崔文静)