图1 新型转子结构
Fig.1 New rotor structure
摘要 一种新型粉块层级转子结构可有效提高高速永磁电机转子强度。为了准确分析新型复合转子结构强度，需要准确预测转子复合磁性材料的力学性能。该文将新型磁粉胶膜复合材料看作由磁粉颗粒、界面和基体组成的三相复合材料，首先基于蒙特卡罗法构建了Abaqus-Python耦合的代表性体积单元参数化模型，然后依据细观力学等效三相球模型推导出界面层的弹性模量，最后基于虚功原理创建磁粉胶膜弹性模量有限元预测模型，并与拉伸试验结果进行比较分析，验证了模型的准确性。在此基础上，研究了细观结构和界面参数对磁粉胶膜弹性模量的影响规律，得到了磁性材料细观结构与力学性能的映射关系。
关键词：高速电机 复合转子 磁性复合材料 弹性模量 数值仿真
在飞轮储能系统、高速机床、压缩机、燃气轮机等领域[1-4]，高速永磁电机（High-Speed Permanent Magnet Motor, HSPMM）因其优越的效率、高功率密度和强大的动态响应能力而被广泛采用。为了提高转子强度、降低转子损耗[5-6]，项目组提出一种新型的复合转子结构如图1a所示。该新型复合转子包括转轴、烧结永磁体、磁粉胶膜/碳纤维（Magnetic Powder Film/ Carbon Fiber, MPF/CF）单元和碳纤维护套。MPF/CF单元是HSPMM转子的重要组成部分，由硬磁粉和环氧树脂复合成磁粉胶膜，再与碳纤维预侵布复合成MPF/CF复合材料，逐层均匀缠绕在永磁体外层，形成MPF/CF单元。MPF/CF复合材料完整结构示意图如图1b所示。这种磁性材料主要由碳纤维层承受载荷，使磁性材料的抗拉强度大大提高，可以大幅度提高转子线速度[7]；同时MPF/CF复合结构中硬磁材料呈离散粉末状态，无集中载荷，可有效降低转子损耗；复合磁性材料由于树脂黏合剂的加入可以切断黏合磁粉的涡流路径，降低电导率，从而有效地降低新型复合磁性材料的转子温升[8-9]，在电机领域得到了广泛的关注。
图1 新型转子结构
Fig.1 New rotor structure
MPF/CF复合材料的力学性能是保证转子强度及服役性能的关键。MPF是由磁粉与环氧树脂混合而成的高填充混胶体，具有多组分、非均质性的特点，材料组分的变化决定材料电磁及力学性能，对于MPF的力学性能而言，弹性模量是一项至关重要的参数，相对于宏观研究，细观尺度能考虑材料各组分的影响因素，因此备受关注。本文对MPF/CF材料中的MPF开展弹性模量预测，研究MPF材料细观结构与宏观性能的关系，为研究复合转子电磁及机械特性提供理论基础。
颗粒增强复合材料的细观模型可分为两大类：一类是单胞（Unit Cell, UC）模型，将整个复合材料简化为最小单元是单胞模型的特点，每个单元仅包含一个或多个颗粒，从而实现了材料的优化；另一类则是代表性的体积单元（Representative Volume Element, RVE）模型，该模型考虑了不同大小、形状及位置上颗粒对材料性能的影响，如宏观尺度下的等效刚度系数，且增强粒子的数量呈现出随机分布。RVE细观模型与复合材料的实际结构更为接近，因此被广泛采用。目前，一些国内外学者利用有限元的方法，预测了颗粒增强复合材料的有效弹性性能，并研究了其内部应力分布特征、强度和失效机理。田学亮等[10]建立了不包含界面的二维RVE有限元模型，研究了颗粒增强铝基复合材料中颗粒占比和颗粒形状对有效弹性模量的影响。李庆等[11]基于Abaqus有限元软件，建立了细观尺度的二维平面应变数值模型，分析填料粒子的粒径大小、刚度、体积分数以及随机分布形态等因素对复合材料宏观力学性能影响的变化规律。邵乐天等[12]构建了三维有限元模型，研究TiC颗粒尺寸在拉伸过程中对颗粒增强复合材料的力学性能所产生的影响。三维有限元模型相较于二维模型，在数值模拟、宏观和细观材料行为研究方面呈现出更为精准的表现。Meng Qinghua等[13]基于细观力学模型对颗粒增强金属基复合材料失效机理及界面强度进行预测，按体心立方结构对球形颗粒进行均匀排布，模型与实际细观结构有一定的差异。刘骏华等[14]建立了二维颗粒随机分布的细观模型，并将该模型与真实结构模型一同进行单轴拉伸试验，在此基础上进一步讨论了边界条件对两种模型仿真结果的影响。邱昆等[15]利用Abaqus软件，构建了一个具有代表性的体积单元模型，研究了颗粒间距、颗粒应变硬化指数以及颗粒体积分数对金属玻璃基复合材料强度和韧性的影响。综上所述，颗粒增强复合材料细观结构十分复杂，部分学者在分析中建立二维细观模型但很少考虑界面因素对力学性能的影响，且目前颗粒增强复合材料的研究大多是金属基材料，因此，对于环氧树脂基复合材料的细观力学数值模拟有待深入研究。
为了构建符合真实细观结构的MPF复合材料计算模型，实现三维MPF力学性能的准确仿真分析，本文从细观尺度将MPF看作由磁粉颗粒、界面层和树脂基体组成的三相复合材料，采用蒙特卡罗法，利用Python语言二次开发Abaqus软件内核[16]，实现了MPF细观结构三维球形随机颗粒模型的参数化建模，在考虑界面层影响的条件下计算不同磁粉含量的MPF弹性模量，并与拉伸试验结果进行比较分析，验证本文所建弹性模量数值预测模型的正确性；在此基础上进一步研究磁粉级配、界面弹性模量和界面厚度对MPF弹性模量的影响规律，建立MPF细观结构与力学性能的映射关系。
本文采用参数化建模方法，利用Python语言与Abaqus进行耦合，将随机颗粒生成、布尔切割合并以及网格划分进行自动操作，从而实现磁性胶膜细观结构的一体化设计。通过修改磁粉颗粒粒径、级配、组分配比及界面层厚度等参数生成不同磁粉组分的细观模型，同时对上述参数进行调控，建立材料细观结构与材料性能的映射关系。
在MPF复合材料中，将磁粉颗粒简化为球形，磁粉颗粒各种参数都是随机的，调用Python语言uniform函数，生成磁粉球形颗粒优化后的半径和球心坐标分别为
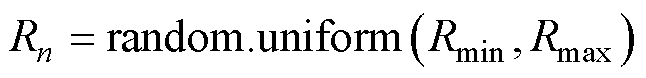（1）
（2）
式中，random.uniform(p, q)为生成一个p到q之间的随机浮点数；Rn为第n个磁粉颗粒的半径，为避免颗粒之间以及颗粒和容器内壁之间相接触，将半径Rn进行优化处理，即
；Rmin和Rmax分别为最小和最大磁粉颗粒粒径；xM、yM、zM分别为三个方向的投放边界上限；（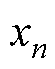
, 
, zn）为第n个磁粉颗粒的球心坐标。在Abaqus中使用脚本内置方法，得到已生成的磁粉颗粒的体积，并将其体积记录到对应的级配范围
（i=1～3）中，磁粉颗粒总体积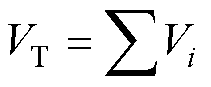
。按照级配顺序，每个级配中的磁粉粒按半径从大到小的顺序进行生成，颗粒生成流程如图2所示。
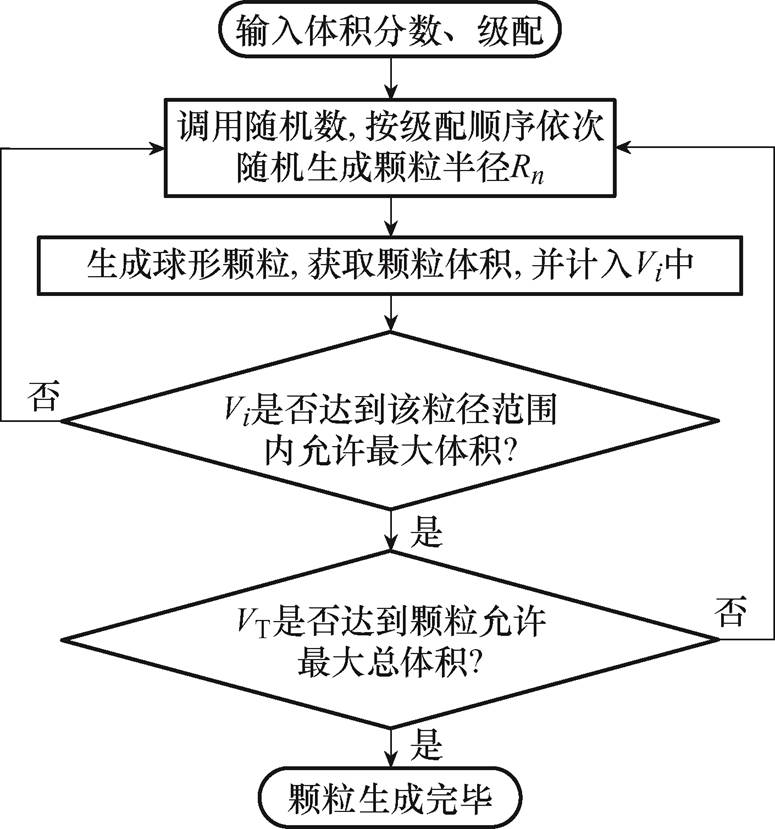
图2 颗粒生成流程
Fig.2 Particle generation process
按体分比及级配产生球形颗粒后，再做投放试验，其中入侵区分是投放颗粒的关键步骤，对球形颗粒进行判别，即
（3）
使用循环语句（for i in range (n)：）遍历前n-1个球形粒子，在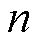
粒子和前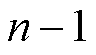
个粒子均未相交的情况下，粒子被成功地释放。具体设想如下：
（1）根据已生成的球形颗粒粒径尺寸，按从大到小顺序进行选取。
（2）调用随机数随机生成坐标，将选取的颗粒按照随机坐标投放到指定区域中。
（3）对第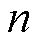个颗粒与前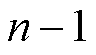个进行入侵判别操作，球心净距是否满足最小容差，若不满足最小容差，则投放失败；若满足最小容差，则投放成功。
（4）投放失败的颗粒回到第二部继续投放，投放成功的颗粒与前n-1个颗粒进行布尔合并。
（5）存储投放成功颗粒对应的坐标数据。
界面层（Interfacial Transition Zone, ITZ）是MPF复合材料中的重要相，由磁粉颗粒表面和树脂基体相互影响而产生，尽管界面层的区域很小，但它的性质在很大程度上决定和控制着复合材料的性质。
本文的界面层模型通过如下方法建立，首先生成实体球形颗粒，根据界面层厚度的参数设置，将球形颗粒表面向外平移对应距离生成新的颗粒，将新颗粒与平移前的颗粒进行布尔切割运算，将切割后的实体模型作为MPF界面层[17]。当球形颗粒被成功投放后，存储其位置坐标，同时颗粒界面层也将按照该坐标在指定区域内进行精准匹配。根据图3所示的颗粒投放流程，可以得到不同级配的颗粒和界面层。
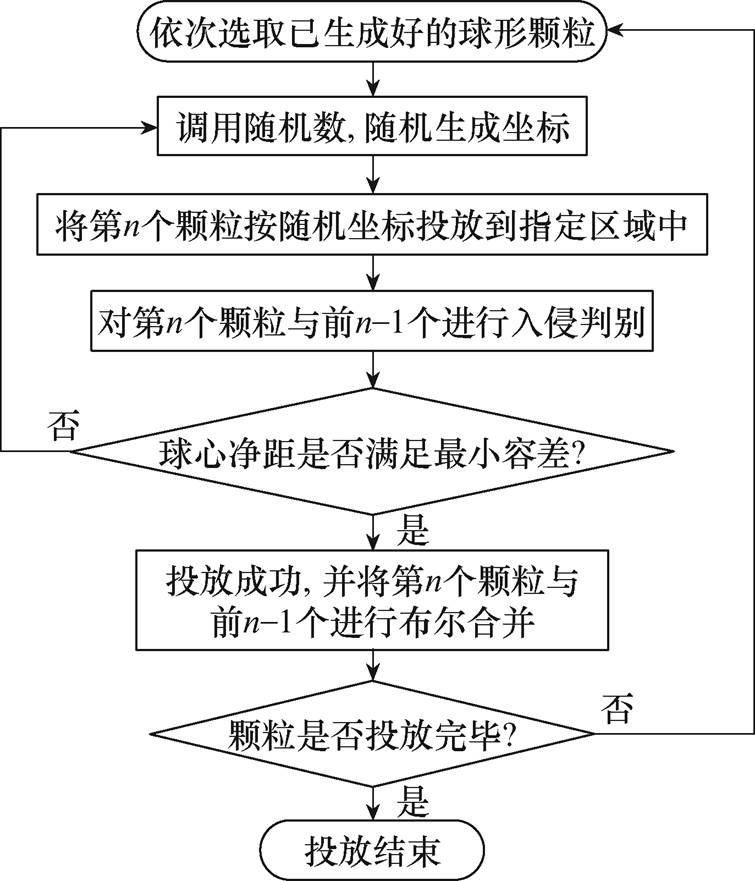
图3 颗粒投放流程
Fig.3 Particle dispensing process
图4给出了Ⅲ级级配的MPF细观随机模型，分别为球形颗粒、界面层和颗粒在基体中的分布，利用上述方法可有效生成各级配下整体分布均匀的球形颗粒，证明本文构建的Abaqus-Python耦合参数化RVE模型的正确性和适应性。
图4 MPFⅢ级级配RVE模型
Fig.4 Three graded RVE model for magnetic powder film
通过有限元方法计算RVE中的应力和应变分布。选择四面体单元的位移插值函数为
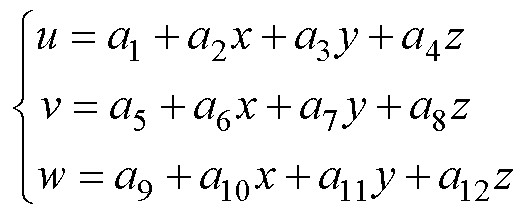（4）
式中，u、v、w为每个节点的三个位移分量；a1～a12为系数。得到单元位移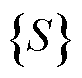
与节点位移
的关系为
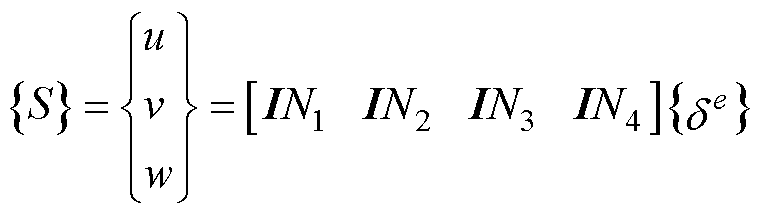（5）
式中，
（
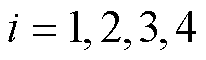）为三维四面体单元的形函数；I为三阶单位矩阵。
分析单元与节点的力学特性，单元应变
用几何方程可表示为
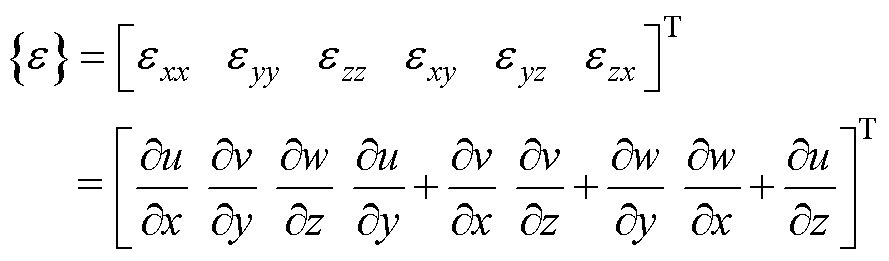（6）
将形函数代入式（6）可得单元应变与节点位移之间的关系为
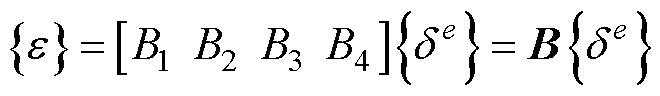（7）
式中，B为四面体单元的几何矩阵。
由本构关系（应力-应变关系）及单元应变与节点位移的关系得到单元应力
与节点位移的关系为
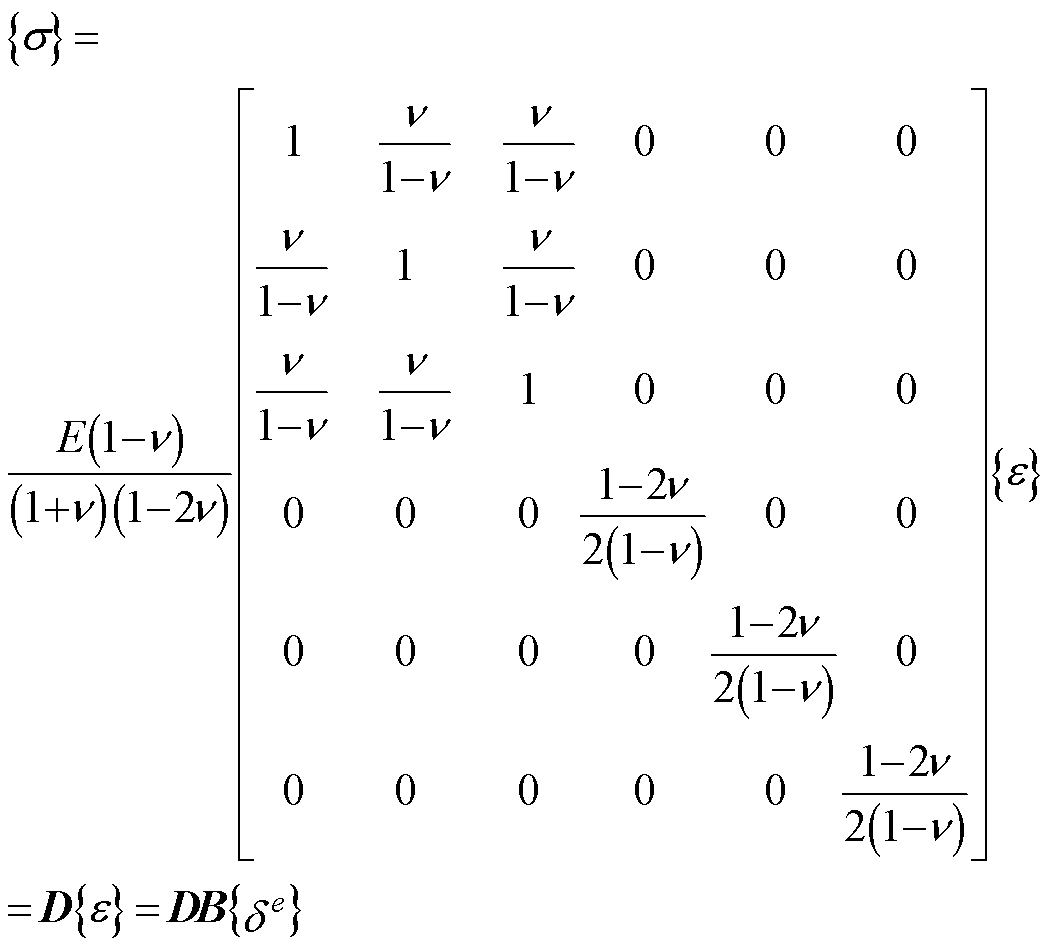（8）
式中，D为弹性矩阵；
为泊松比。
再由虚功原理得到单元刚度矩阵式（9），并用高斯积分进行求解，得到节点力与节点位移的关系，最后根据平衡条件和边界条件求出节点位移，从而得到各单元的应力和应变。
（9）
式中，K为单元刚度矩阵。
RVE的平均应力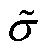
和平均应变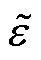
可以用体积分得到，有
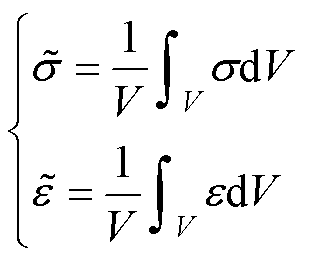（10）
将各单元的应力和应变与对应的体积相乘，再通过式（10）对整个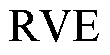
积分，从而求解中的平均应力和应变。最后得到模型弹性模量E为
（11）
2.2.1 界面层的厚度和体积分数
基于文献[18]的试验研究可知，颗粒填料填充E51环氧树脂复合材料中的颗粒体积分数、界面层厚度与复合材料性能的关系，即增加颗粒的体积分数，基体（树脂基体和界面层二部分之和）的密度随之增大；当颗粒体积分数达到一个临界值时，继续增加颗粒的体积分数，基体的密度不再改变，此时整个基体完全转变为界面层。该临界值处的颗粒体积分数为“临界颗粒体积分数”，记为fcr。在临界磁粉体积分数时，界面层的厚度为h，把磁粉颗粒近似看作理想球形粒子，其半径为r1，这时被界面层覆盖的磁粉颗粒的等效半径r2=r1+h，等效半径与临界磁粉体积分数关系[18]为
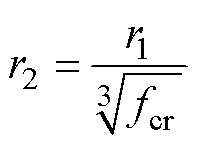（12）
又
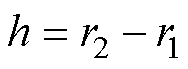（13）
则界面层厚度h为
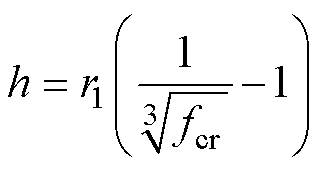（14）
在任意磁粉含量下，界面层的体积分数为
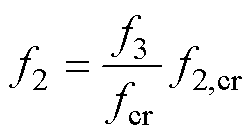（15）
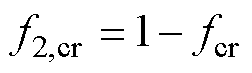（16）
式中，f3为磁粉体积分数；f2和f2,cr分别为界面层体积分数和在临界磁粉体积分数时界面层的体积分数。
2.2.2 界面层的弹性模量
将界面层和夹杂颗粒看作图5a所示的等效颗粒（即具有等效弹性，半径为b的均匀粒子），将等效粒子作为分离体，并利用等效颗粒将四相球模型简化为图5b所示的等效三相球模型[19]。
图5中，a、b、c分别为夹杂、界面和基体相的半径。阴影的无限区域是等效的复合材料介质。其他物理力学参数k0、m0、E0和
分别为等效复合材料介质的有效体积模量、剪切模量、弹性模量和泊松比。Ej、kj、mj和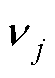
(j=1、2、3)分别为基体(j=1)、界面层(j=2)和夹杂颗粒(j=3)的弹性模量、体积模量、剪切模量和泊松比。
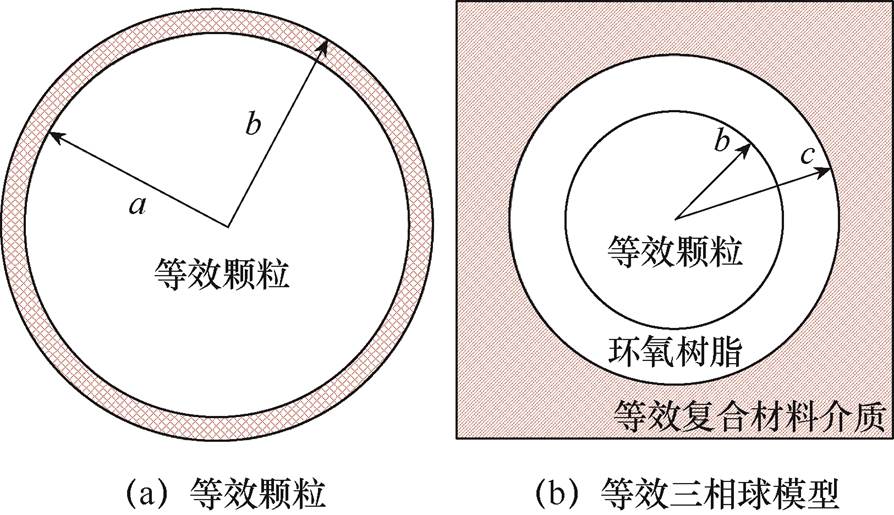
图5 等效模型
Fig.5 Equivalent model
利用弹性力学理论和Eshelby[19]等效理论证明了三相球体模型的有效体积模量计算公式为
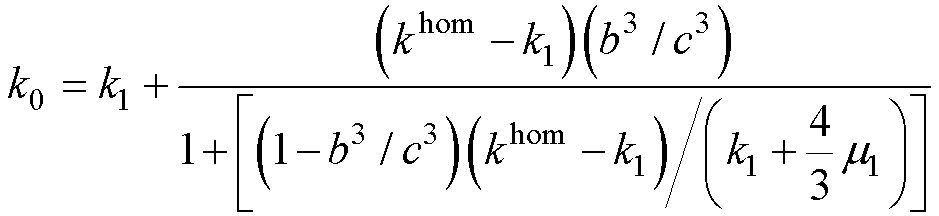（17）
式中，k0为图5b所示的三相球体模型的有效体积模量；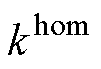
为等效颗粒的有效体积模量。对于图5a中的等效颗粒，可推导出有效体模量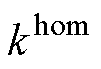的表达式为
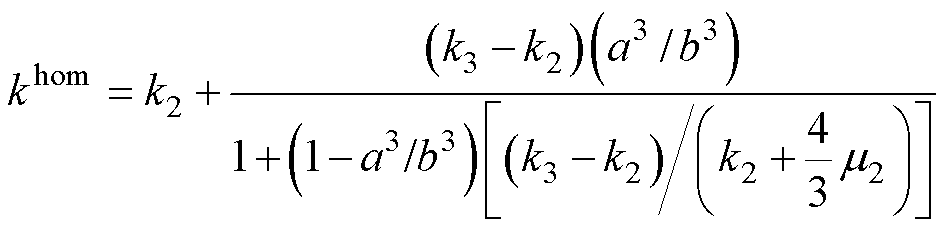（18）
b/c的值可通过界面和夹杂的体积分数计算，其关系式为
（19）
式中，f2、f3分别为界面层及夹杂颗粒的体积分数，本文的夹杂颗粒为磁粉颗粒。
假设夹杂相、界面相和基体相横向串联，则总横向应变e0为基体相横向应变e1、界面层横向应变e2和夹杂相横向应变e3之和。以各相的体积分数f1、f2、f3作为加权因子，得到
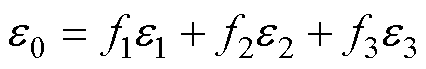（20）
式中，f1为基体的体积分数。
假设复合材料中的每个相均为轴向等应变（即每个相具有相同的轴向应变）。根据泊松比的定义（即横向应变与轴向应变比的负值），式（20）的两边分别除以e，从而得到估计复合材料有效泊松比为
（21）
弹性模量E、体积模量k、剪切模量m 和泊松比关系为
（22）
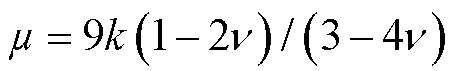（23）
已知磁粉颗粒和树脂基体的力学性能，MPF复合材料的体积模量k0、泊松比、临界磁粉含量和磁粉颗粒半径a，联立式（12）～式（23），则能计算界面层的弹性模量。
根据RVE模型需要满足的尺度关系（微元尺度对于结构尺度充分小，且对于夹杂尺度充分大），本文选取尺寸为400 µm×400 µm×400 µm的立方体模型。利用三明治填充模型建立了磁粉堆积模型[20]如图6所示，图中分别为Ⅱ级、Ⅲ级和Ⅳ级级配下的磁粉堆积模型，并研究了磁粉级配和配比对MPF孔隙率以及磁性性能的影响，综合考虑制备工艺及电磁性能要求，本文磁粉采用Ⅱ级级配，选取磁粉颗粒粒径分别为100 µm和50 µm，配比为1
1。磁粉颗粒弹性模量E3=137 GPa，n3=0.26，树脂基体弹性模量E1=1 GPa，n1=0.38。由于界面相的材料属性不能直接测得，利用界面层弹性模量计算公式，求得界面层弹性模量E2=83.7 MPa，泊松比n2=0.33。根据基体（界面层和树脂两部分之和）密度和磁粉体积分数的变化关系[18]，磁粉体积分数达到80%时，基体密度保持一个恒定值，故取临界磁粉体积分数fcr=0.8，由式（14）计算出大颗粒与小颗粒界面层厚度h分别为3.86 µm和1.93 µm。
图6 磁粉堆积模型
Fig.6 Magnetic particle stacking model
图7为本文细观模型网格划分结果，其中颗粒、基体和界面均用C3D10四面体单元。从局部网格截面图可以看出，网格划分质量较好，提高了后续有限元计算分析的效率。
图7 细观模型网格划分
Fig.7 Mesoscopic model mesh division
在相互作用模块中，对模型上方中心处设置基准点并作为参考点，将该点与模型上表面进行全耦合约束。根据ASTMD3039-2017试验标准对其顶部参考点加载位移荷载，然后在模型底部进行完全固定约束，完成边界条件创建。
经有限元计算分析，磁粉体积分数为30%的MPF应力云图如图8所示。图中直观形象地表现了MPF的应力分布规律，最大应力集中在球形颗粒区域，说明MPF复合磁性材料其力学性能主要由磁粉颗粒承担。颗粒顶部和底部的界面区域应力呈对称分布，而颗粒两侧处于受压状态，界面层中间部分的应力最小。计算随机生成的RVE模型，弹性模量数值计算结果为1.2 GPa。
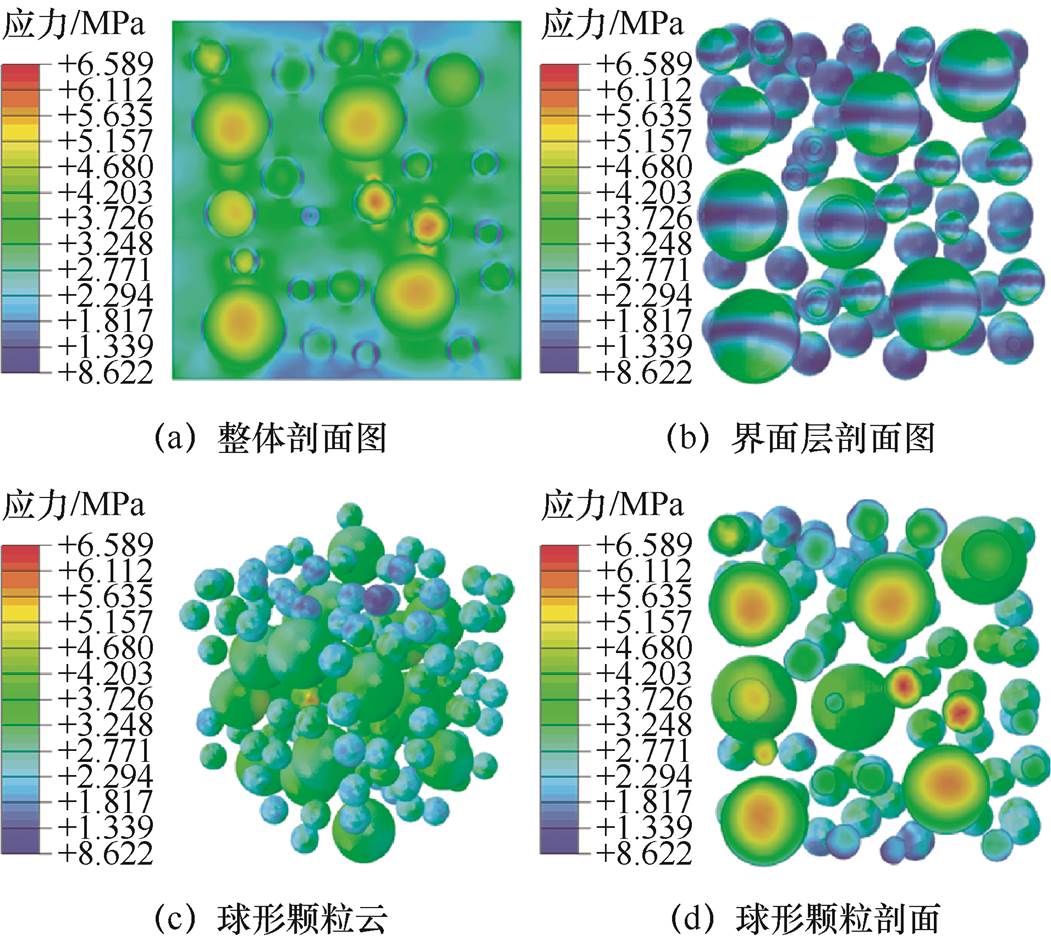
图8 单轴拉伸应力云图
Fig.8 Uniaxial tensile stress cloud map
根据ASTMD3039-2017的要求，对30%磁粉体积分数的五组样件做拉伸试验，测得其应力-应变曲线如图9所示，拉伸试验如图10所示，加载速率为2 mm/min。表1为测得的相关参数，样件测量的离散系数为4.84，因此，弹性模量取平均值为1.17 GPa，与仿真模型的误差较小，仅为2.6%，说明本文所建模型能较好地预测MPF弹性模量。
为研究不同磁粉配比对MPF弹性模量的影响，本文考虑工艺的难易程度[21]，采用了磁粉Ⅱ级级配模型。将大颗粒（d=100 µm）和小颗粒（d=50 µm）按11、21和31三种比例分别建立磁粉Ⅱ级级配模型，取界面厚度为2.5 μm，不同磁粉配比在不同磁粉体积分数下，MPF弹性模量变化趋势如图11所示。图12为30%磁粉体积分数下，三种磁粉配比的RVE轴向剖面应力云图。
图9 拉伸试验的应力-应变曲线
Fig.9 Stress-strain curves obtained from the longitudinal tensile experiment
图10 拉伸试验
Fig.10 Tensile test
表1 弹性模量数值计算与拉伸试验结果
Tab.1 The numerical results and experimental values of elastic modulus
试样编号拉伸强度/MPa弹性模量/GPa数值计算与试验结果比较误差值(%) 数值计算—1.2— 30%-119.61.24-3.2 30%-215.71.109.1 30%-318.21.163.4 30%-416.11.154.3 30%-518.81.21-0.8 平均值17.71.172.6
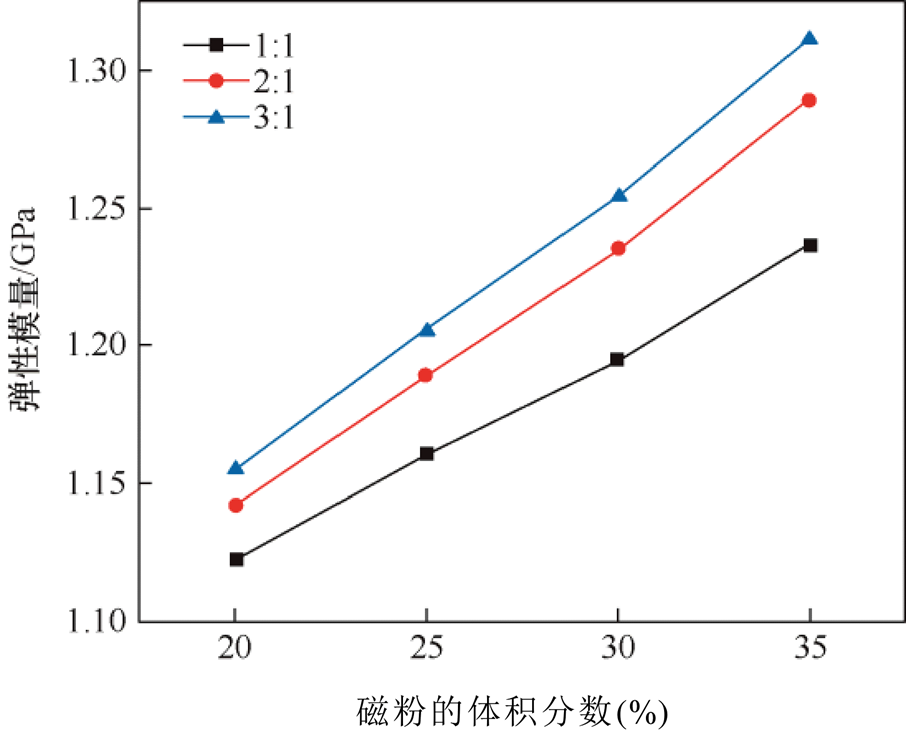
图11 磁粉配比对MPF弹性模量的影响
Fig.11 Effect of magnetic powder ratios on the elastic modulus of magnetic powder films
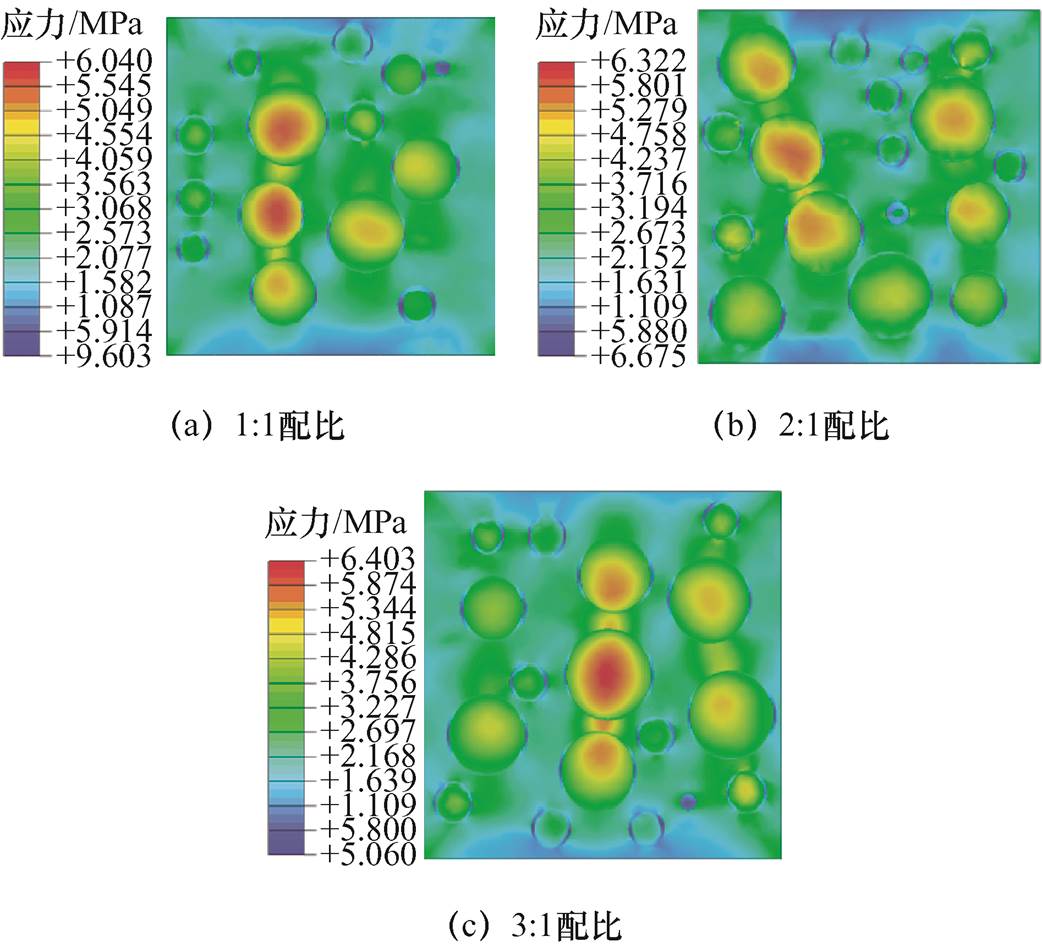
图12 三种磁粉配比RVE轴向剖面应力云图
Fig.12 Three types of magnetic powder ratios RVE axial profile stress cloud maps
从图11可以看出，随着磁粉体积分数的增大，三种不同配比的磁粉模型弹性模量均增大。当磁粉的体积分数相同时，磁粉级配模型中大颗粒磁粉的体积分数越多，小颗粒磁粉的体积分数就会相对减小。当界面厚度保持不变时，球形颗粒的总表面积会随之减小，进而导致模型界面层体积分数减小，MPF的弹性模量随之增加，且随着磁粉体积分数的增大，磁粉配比对MPF弹性模量影响越显著。图12表明，不同磁粉配比，球形颗粒中应力分布情况相同，模型最大应力值随着大颗粒体积分数的增加而增大。
为进一步探索MPF弹性模量受界面厚度的影响情况，利用文中建立的磁粉级配模型（设大、小磁粉颗粒体积分数分别为V1、V2），且V1
V2=11，在不同磁粉占比下，MPF弹性模量按照界面厚度分别为0、1、2、3 μm时的预测结果如图13所示。30%磁粉体积分数下，不同界面厚度的RVE轴向剖面应力云图如图14所示。
磁粉的体积分数(%)
图13 界面厚度对MPF弹性模量的影响
Fig.13 The effect of interface thickness on the elastic modulus of magnetic powder films
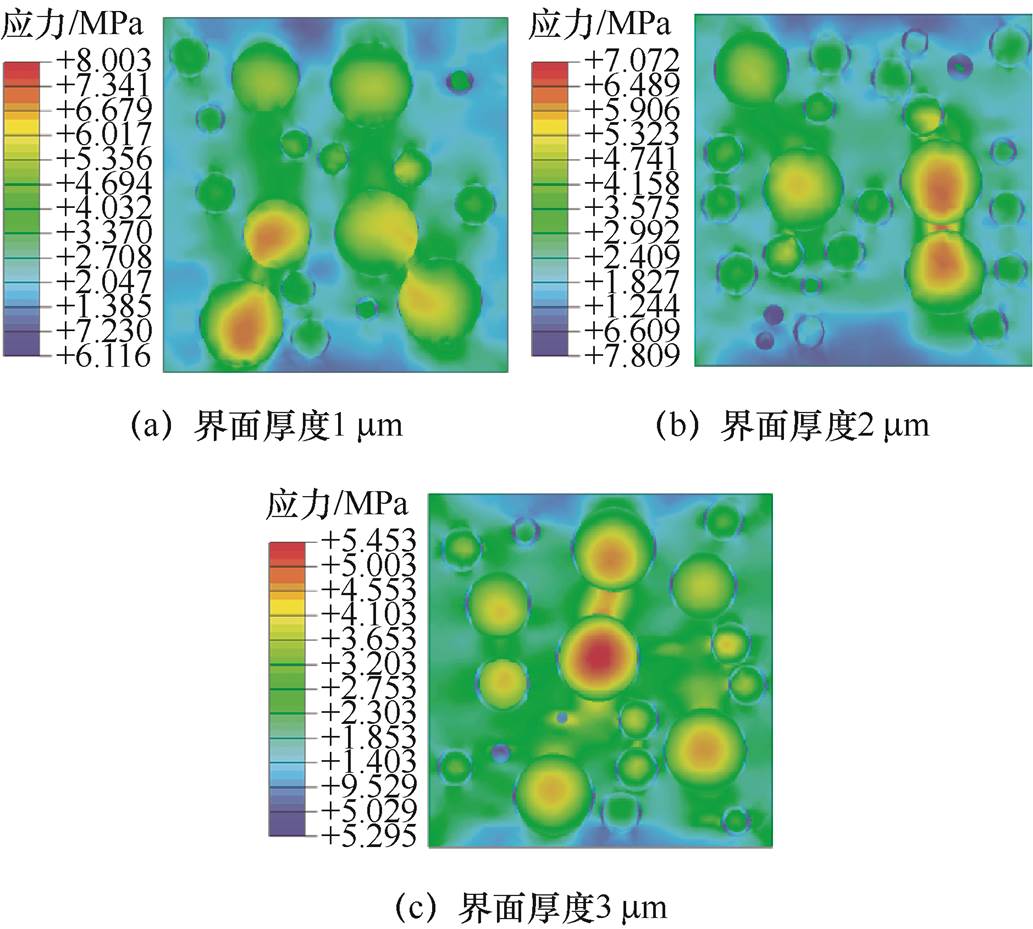
图14 不同界面厚度RVE轴向剖面应力云图
Fig.14 Stress nephogram of RVE axial profile with different interface thicknesses
从图13中可以看出，在不同磁粉的体积分数下，考虑界面层的MPF弹性模量预测值较小，且远小于界面层厚度为0时的MPF弹性模量模型预测值。由此可见，对于MPF的弹性模量，界面层的作用是不能忽略的。当界面厚度在1～3 μm时，在磁粉总表面积保持不变的条件下，增大界面层厚度，则界面层体积分数也会随之升高，此时MPF弹性模量逐渐减小，且随磁粉体积分数的增加，界面厚度对MPF弹性模量的影响程度越高。因此，控制界面层厚度可以调节MPF弹性模量。图14表明，不同界面厚度，界面层中应力分布情况相同，模型最大应力值随着界面层厚度的增加而减小。
为研究界面弹性模量对MPF弹性模量的影响，本文取界面弹性模量分别为40、80、120 MPa，磁粉Ⅱ级级配且V1V2=11，界面厚度为2.5 µm。不同界面弹性模量，在不同磁粉体积分数下，MPF弹性模量变化情况如图15所示。30%磁粉体积分数下，不同界面弹性模量RVE轴向剖面应力云图如图16所示。
图15 界面弹性模量对MPF弹性模量的影响
Fig.15 The impact of the interfacial modulus of elastic on magnetic powder film elastic modulus
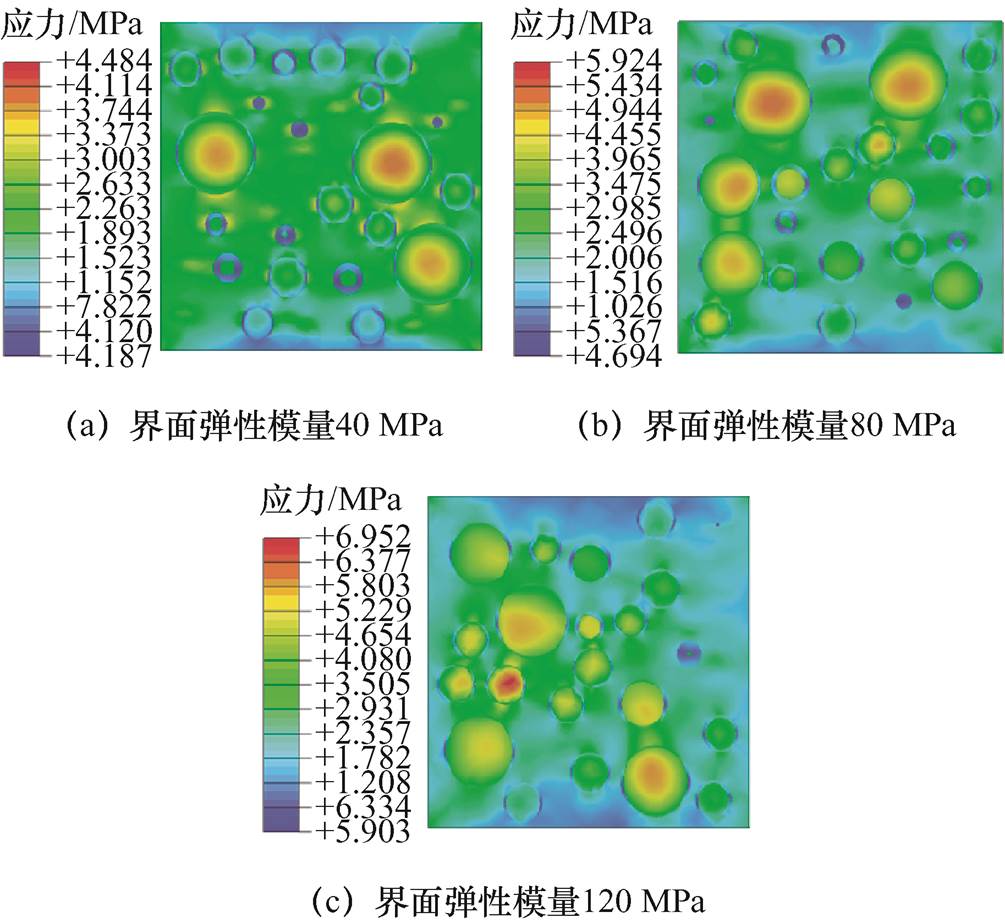
图16 不同界面弹性模量RVE轴向剖面应力云图
Fig.16 Stress nephogram of RVE axial profile with different interface elastic moduli
从图15中可以看出，不同磁粉体积分数下，当界面弹性模量为40 MPa时，MPF弹性模量基本保持不变；而当界面弹性模量取较大值时，增加磁粉体积分数，MPF弹性模量开始逐渐增大。当磁粉体积分数相同时，MPF弹性模量随着界面弹性模量的增加而增大，且随磁粉体积分数的增加，界面弹性模量对MPF弹性模量影响越加显著。图16表明，不同界面弹性模量，界面层中应力分布情况相同，模型最大应力值随着界面弹性模量的增加而增大。
为了建立新型磁性材料的力学性能与其细观结构之间的映射关系，本文基于细观力学建立了MPF弹性模量预测的数值模型，并通过拉伸试验结果验证了模型的正确性，为实现HSPMM复合转子的材料-结构一体化设计奠定了基础。所得到的主要结论如下：
1）MPF复合材料弹性模量与磁粉级配、界面层参数及界面弹性模量密切相关，可以通过调控材料细观结构参数改善材料力学性能。
2）当磁粉体积分数一定时，MPF的弹性模量随大颗粒含量的增多而增大，随着磁粉占比的增加，磁粉配比对MPF弹性模量的影响也会越来越显著。
3）界面层作为MPF弹性模量的影响因素不能被忽略。在磁粉总表面积保持不变的条件下，增大界面层厚度，界面层体积分数随之升高，MPF弹性模量逐渐减小。且随磁粉体积分数的增加，界面厚度对MPF弹性模量的影响程度越高。
4）当界面弹性模量值较小时，不同磁粉体积分数下，MPF弹性模量基本保持不变。当磁粉体积分数相同时，MPF弹性模量随着界面弹性模量的增加而增大，且随磁粉体积分数的增加，界面弹性模量对MPF弹性模量的影响越加显著。
参考文献
[1] 鲍旭聪, 王晓琳, 彭旭衡, 等. 高速电机驱动关键技术研究综述[J]. 中国电机工程学报, 2022, 42(18): 6856-6871.
Bao Xucong, Wang Xiaolin, Peng Xuheng, et al. Review of key technologies of high-speed motor drive[J]. Proceedings of the CSEE, 2022, 42(18): 6856-6871.
[2] 杨江涛, 王镇宇, 冯垚径, 等. 高速永磁电机转子过盈方式对转子应力的影响[J]. 电工技术学报, 2023, 38(16): 4263-4273.
Yang Jiangtao, Wang Zhenyu, Feng Yaojing, et al. Influence of shrink fitting modes on rotor stress of high speed permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4263-4273.
[3] 戴睿, 张岳, 王惠军, 等. 基于多物理场近似模型的高速永磁电机多目标优化设计[J]. 电工技术学报, 2022, 37(21): 5414-5423.
Dai Rui, Zhang Yue, Wang Huijun, et al. Multi-objective optimization design of high-speed permanent magnet machine based on multi-physics approximate model[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5414-5423.
[4] Qin Xuefei, Shen Jianxin, Nilssen R, et al. Design of high-speed PMSM considering multi-physics fields and power converter constraints[J]. Journal of Electrotechnical Society, 2022, 37(7): 1618-1633.
[5] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[6] 张文校, 胡岩, 曹力, 等. 高速永磁屏蔽电机摩擦损耗分析与计算[J]. 电工技术学报, 2023, 38(12): 3122-3129.
Zhang Wenxiao, Hu Yan, Cao Li, et al. Analysis and calculation of friction loss of high-speed permanent magnetic shielding motor[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3122-3129.
[7] Wang Zerun, Zhang Yue, Wang Tianyu, et al. Analytical model of mechanical properties of carbon fiber magnetic powder film-level magnetic materials for high-speed motors[J]. Energy Reports, 2022, 8: 374-383.
[8] Sato M, Takazawa K, Horiuchi M, et al. Reducing rotor temperature rise in concentrated winding motor by using magnetic powder mixed resin ring[J]. Energies, 2020, 13(24): 6721.
[9] Yao Jinyu, Wang Huijun, Zhang Yue, et al. Magnetic properties analysis of novel composite magnetic materials for HSPMSMs[J]. IEEE Transactions on Magnetics, 2022, 58(4): 8104310.
[10] 田学亮, 徐颖. 碳化硅颗粒增强铝基复合材料有效弹性模量预测[J]. 航空发动机, 2021, 47(5): 92-97.
Tian Xueliang, Xu Ying. Prediction of effective elastic modulus for SiC particle reinforced aluminium matrix composites[J]. Aeroengine, 2021, 47(5): 92-97.
[11] 李庆, 杨晓翔. 颗粒增强橡胶细观力学性能二维数值模拟[J]. 应用力学学报, 2012, 29(5): 607-612, 633.
Li Qing, Yang Xiaoxiang. Two-dimensional numerical simulation for mechanical behavior of particle reinforced rubber matrix composites[J]. Chinese Journal of Applied Mechanics, 2012, 29(5): 607-612, 633.
[12] 邵乐天, 尧军平, 胡启耀, 等. 颗粒尺寸对TiC/AZ91镁基复合材料力学性能的影响[J]. 材料热处理学报, 2019, 40(9): 1-7.
Shao Letian, Yao Junping, Hu Qiyao, et al. Effect of particle size on mechanical properties of TiC/AZ91 magnesium matrix composites[J]. Transactions of Materials and Heat Treatment, 2019, 40(9): 1-7.
[13] Meng Qinghua, Wang Zhenqing. Prediction of interfacial strength and failure mechanisms in particle-reinforced metal-matrix composites based on a micromechanical model[J]. Engineering Fracture Mechanics, 2015, 142: 170-183.
[14] 刘骏华, 张娟, 张晨, 等. 颗粒增强金属基复合材料细观有限元建模方法的对比[J]. 机械工程材料, 2022, 46(4): 82-88, 94.
Liu Junhua, Zhang Juan, Zhang Chen, et al. Comparison of meso finite element modeling methods for particle reinforced metal matrix composites[J]. Materials for Mechanical Engineering, 2022, 46(4): 82-88, 94.
[15] 邱昆, 姜云鹏, 史雪萍, 等. 新型颗粒增强金属玻璃复合材料的拉伸增韧机制[J]. 复合材料学报, 2018, 35(1): 124-131.
Qiu Kun, Jiang Yunpeng, Shi Xueping, et al. Tensile toughening mechanism of new particle reinforced metallic glass composites[J]. Acta Materiae Compositae Sinica, 2018, 35(1): 124-131.
[16] 田玉泰. 基于Python的Abaqus前、后处理GUI插件二次开发与应用[J]. 计算机辅助工程, 2022, 31(2): 63-68.
Tian Yutai. GUI plugin redevelopment and application of Abaqus pre-and post-processing based on Python[J]. Computer Aided Engineering, 2022, 31(2): 63-68.
[17] 吴宇航, 肖映雄, 徐亚飞. 基于Python-Abaqus的混凝土三维细观随机模型的建立[J]. 计算力学学报, 2022, 39(5): 566-573.
Wu Yuhang, Xiao Yingxiong, Xu Yafei. Establishment of mesoscopic stochastic models of concrete in three dimensions based on Python-Abaqus[J]. Chinese Journal of Computational Mechanics, 2022, 39(5): 566-573.
[18] 吴鑫森, 陈祥宝, 宋焕成. 颗粒增强复合材料中的界面层[J]. 复合材料学报, 1985, 2(3): 41-45, 118.
Wu Xinsen, Chen Xiangbao, Song Huancheng. Interface layer in particulate composites[J]. Acta Materiae Compositae Sinica, 1985, 2(3): 41-45, 118.
[19] Li Guoqiang, Zhao Yi, Pang Suseng. Four-phase sphere modeling of effective bulk modulus of concrete[J]. Cement and Concrete Research, 1999, 29(6): 839-845.
[20] Yao Jinyu, Zhang Yue, Wang Huijun, et al. Effect of multi-size magnetic powder gradation on magnetic properties of novel composite magnetic materials for HSPMSM[J]. IEEE Transactions on Transportation Electrification, 2022, 8(3): 3594-3605.
[21] 史平安, 万强, 张灿阳, 等. 铁凝胶的力磁耦合细观力学模型的建立[J]. 机械强度, 2017, 39(3): 564-571.
Shi Ping’an, Wan Qiang, Zhang Canyang, et al. Study on the micromechanical model of force-magnetic coupling for ferrogel materials[J]. Journal of Mechanical Strength, 2017, 39(3): 564-571.
Abstract The tensile strength of the conventional surface mount HSPMM (High-speed permanent magnet motor) rotor's permanent magnet is significantly low, posing a bottleneck for developing HSPMM. A novel composite rotor structure incorporating a powder block layer can effectively enhance the rotor strength of HSPMMs. The mechanical properties of these new composite magnetic materials play a crucial role in ensuring the structural strength and performance of magnetic components. Unlike traditional HSPMM rotors, the composite rotor structure consists of multiple layers of composite magnetic materials, necessitating a different approach to accurately analyze its mechanical strength. This paper employs micromechanics and finite element method techniques to predict the elastic modulus of magnetic composites based on an equivalent three-phase spherical model. Furthermore, the influence of microstructure, interface parameters, and magnetic powder grade on the elastic modulus of the magnetic powder film (MPF) is studied, and a mapping relationship between microstructure and mechanical properties is established.
Firstly, a representative volume element (RVE) calculation model is constructed for the MPF to capture its real microstructure. From a microscopic perspective, MPF is regarded as a three-phase composite material comprising magnetic particles, interface layers, and resin matrix. The Monte-Carlo method and Python language are utilized to develop the Abaqus software kernel for automating random particle generation, Boolean cutting and merging operations, and grid division. By adjusting parameters such as particle size, gradation, group distribution ratio, and interface layer thickness, mesoscale models representing different magnetic powder components are generated to establish the mapping relationship between mesoscopic structure and material properties. Secondly, the parameters of the interface in the RVE model are determined using elastic mechanics theory and Eshelby equivalent theory based on critical magnetic particle content. Crucial information, such as the interface layer's thickness, volume fraction, and elastic modulus, can be obtained. The proposed method ensures a uniform distribution of spherical particles at all levels. Finally, based on the virtual work principle, a finite element prediction model for the elastic modulus of the magnetic powder film is established. The predicted results can be effectively utilized in the structural design and analysis of magnetic composite materials, allowing rapid prediction of mechanical properties without complex, time-consuming testing procedures.
Based on the finite element model of micromechanics, the mechanical properties of magnetic materials are simulated and analyzed. The effects of magnetic particle gradation, interface layer parameters, and interface elastic modulus on the elastic modulus of magnetic materials are studied. The following conclusions can be drawn from the simulation analysis. (1) Magnetic particle gradation, interfacial layer parameters, and interfacial elastic modulus significantly influence the elastic modulus of MPF. Adjusting these microstructure parameters using a predictive model make it possible to enhance the material's mechanical properties. (2) Optimizing the gradation of magnetic powder using the proposed prediction model can improve the MPF elastic modulus when keeping the integral number of magnetic powder constant. (3) Accurate calculation of interface layer parameters can effectively enhance the accuracy of the prediction model.
keywords：High-speed motor, composite rotor, composite magnetic materials, elastic modulus, numerical simulation
中图分类号：TM355
DOI: 10.19595/j.cnki.1000-6753.tces.231481
国家自然科学基金项目（52077121）、辽宁省科技计划联合基金项目(2023-MSLH-215)和辽宁省教育厅基本科研项目（JYTMS20230297）资助。
收稿日期 2023-09-08
改稿日期 2023-11-20
王天煜 女，1968年生，教授，硕士生导师，研究方向为机械强度、转子动力学及多物理场耦合分析等。E-mail: 491129306@qq.com
白 斌 男，1979年生，副教授，硕士生导师，研究方向机械强度、多学科优化设计等。E-mail: kpbw@163.com（通信作者）
（编辑 崔文静）