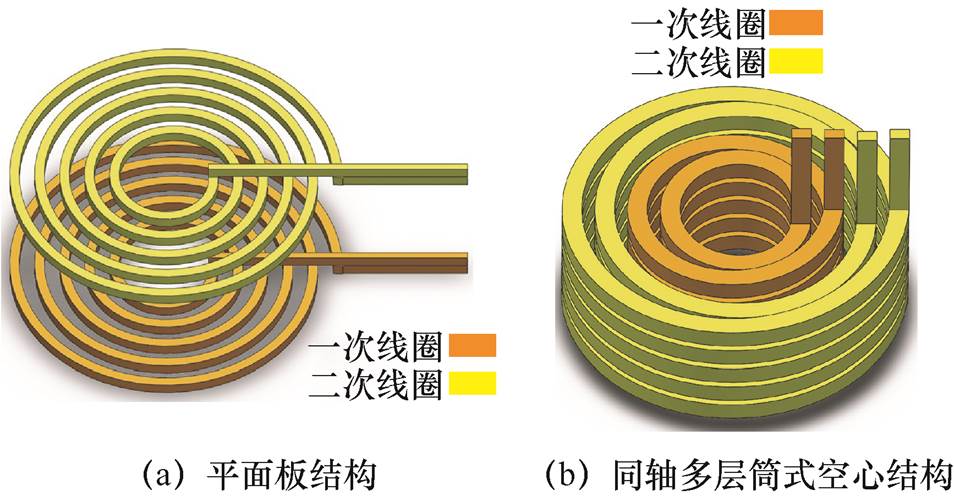
图1 线圈结构类型
Fig.1 Type of coil structure
摘要 在电磁耦合的无线电能传输系统中,准确获取线圈电感参数是设计和优化无线电能传输系统的重要理论依据。现有的无线电能传输系统研究大多针对平面板结构线圈,同轴多层筒式空心线圈相比于平面板线圈具有更高的传输功率和传输效率。因此,该文针对同轴多层筒式空心线圈,提出了一种考虑高频涡流效应的自感和互感解析计算方法。首先,将单匝线圈截面离散等效为数量众多、形状相同的网格带电圆环单元,采用离散等效求和法推导出单匝线圈的自感和线圈间互感的解析式;然后,基于筒式空心线圈的整体结构以及考虑高频涡流效应,推导出基于第一类、第二类完全椭圆积分和开尔文函数的一、二次线圈自感和总互感计算的理论解析式;最后,以两种不同排布方式的筒式空心线圈为例,对比解析计算、有限元计算和实验测量结果,验证了所提解析法的可行性,同时也为筒式空心线圈的设计提供参考依据。
关键词:无线电能传输 电感参数 筒式空心线圈 离散等效 涡流效应 解析计算
DC-DC变换器是现代大功率能量转换系统的重要组成部分,可应用于快速电动汽车充电器、数据中心电源、驱动系统和电动飞机等高功率领域[1-4]。LC串联谐振变换器(Series Resonant Converter, SRC)具有零电压开关特性,且可以有效减少开关管关断电流和中压隔离变压器电流中的高频谐波成分等优点[5],拓扑结构被广泛应用于DC-DC变换器。SRC中间的中压隔离变压器起到电压变换、功率传输和电气隔离的作用。按照中压隔离变压器是否含有磁心,可以分为有磁心式(Magnetic Core Transformer, MCT)和无磁心式(Air Core Transformer, ACT)两大类。其中,MCT具有工作磁通密度高和结构紧凑等优点,但是含磁心会造成质量大且存在散热效率低等缺点。ACT相比于MCT具有质量轻、功率密度高以及高于99.5%的效率等优势[6]。线圈结构类型如图1所示。如果ACT选择图1b所示的同轴多层筒式结构,在同等质量条件下,比图1a中传统的平面板结构线圈具有更高的耦合系数和传输效率[7]。类似于无线电能传输系统,如果将中压隔离变压器的自感和互感参数设计为合适大小,使电感与外电路串接电容发生谐振,可以提高变换器的传输效率和功率密度,降低整个变换器的质量和成本。然而,现有文献并未报道过同轴多层筒式线圈的自感和互感值解析计算方法,针对上述问题开展研究对大功率ACT的优化设计至关重要。

图1 线圈结构类型
Fig.1 Type of coil structure
在无线电能传输系统中采用圆形线圈相比于矩形和圆盘线圈在对称性上更具优势,稳定性更好,工作频率更高,因此无线电能传输系统大多采用圆形线圈传递功率。文献[8]基于电磁场理论推导出磁耦合线圈结构发生错位时的互感解析计算式,并以此优化了线圈结构。文献[9]基于磁路分析和磁阻建模法计算了磁心平面板耦合线圈的电感。文献[10]通过仿真和实验定量分析了平面板线圈间的角度对无线电能传输效率的影响。文献[11]通过矢量磁位和诺依曼公式推导出带双层有界磁屏蔽的盘式圆形线圈在不同相对位置下的自感和互感计算式。
上述文献都是针对无线电能传输系统的平面板线圈进行研究(见图1a),而计算类似ACT的同轴多层筒式结构线圈电感参数的研究大多仅针对单匝线圈。S. I. Babic[12]和W. G. Hurley[13]等分别推导了针对同轴具有矩形截面圆环线圈模型的自、互感通用解析式。J. T. Conway[14]则提出了一种与众不同的方法,采用贝塞尔函数计算具有矩形截面的平行轴空心线圈的自感和互感,该方法既适用于非同轴线圈,也适用于同轴线圈,但变量积分在一个高度振荡的被积函数的无限区间内进行。随后,罗垚等[15]采用五重积分的方法改进了其自感计算式,但编程较为复杂。Ren Yong等[16]采用二重积分的半解析法推导出空心矩形截面线圈的自感和互感表达式,然而推导过程复杂且不是完全的解析计算。Liang Sizhuang等[17]提出了一种利用反双曲函数计算同轴空心具有矩形截面线圈互感和自感的改进方法,但其适用范围较为单一。文献[18]和文献[19]分别采用等效圆环回路法和细分求和法对空心矩形截面线圈之间的互感进行计算,但都仅限于研究线圈之间相对位置距离与互感的关系。文献[20]结合上述研究内容与方法,推导出多层平面板结构的超导空心变压器的自、互感解析式,但没有考虑频率对电感的影响,只适用于低频情况。
在数值计算方面,空心线圈由于没有导磁材料,所以不具有特定的磁通路径,磁场不会被束缚于某一部分,而是分布于整个无限大空间,这意味着通常需要用有限元仿真去计算其自、互感值[21]。三维有限元虽然能够很好地计算出空间中的磁场分布,但构建模型较复杂、计算周期长,对计算机配置需求高,需要大量的存储空间和足够快的运算速度,且当线圈匝数较多时,通常将一层绕组等效为铜箔结构,计算精度有限,或者当线圈尺寸发生变化时,需要重新建模计算,使研究线圈参数间的相互关系变得较为困难,其使用受到一定的限制。
综上所述,一方面,有限元法具有一定的局限性,难以直接显示出线圈电感参数与线圈结构之间的关系,且当线圈结构发生改变时,需多次建模计算,计算成本较高;另一方面,目前大多文献都集中于研究平面板式线圈的电感参数解析计算或者只针对研究两匝空心导体线圈间互感参数的解析计算,并且都未考虑频率对线圈电感参数的影响。因此,本文以同轴多层筒式空心线圈作为研究对象,该研究模型不但具有多匝空心导体线圈,而且又不同于平面板式线圈,同时也考虑了频率因素。本文首先采用离散等效求和法推导出同轴多层筒式空心线圈在不同排布方式和任意频率下一、二次线圈自感和总互感解析计算式,然后利用有限元法和实验法,验证该解析公式的可行性,对筒式空心线圈参数化设计具有一定指导意义。
基于离散等效求和法的思想,建立求解筒式空心线圈在涡流效应条件下一、二次线圈自感和总互感的计算流程,如图2所示。

图2 筒式空心线圈电感参数计算流程
Fig.2 Flow chart for calculating inductance parameters of cylindrical hollow coil
图3为空间直角坐标系中的两个带电圆环,电流大小分别为I1、I2,半径分别为R1、R2。根据毕奥萨伐尔定律,通有电流I1的带电圆环1在带电圆环2上P点处产生的矢量磁位具有周向分量[22],表示为
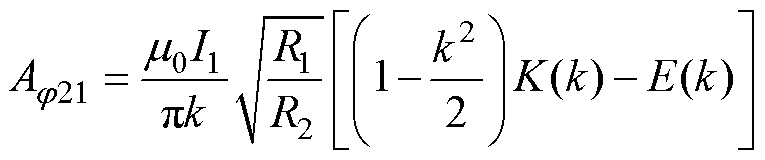 (1)
(1)
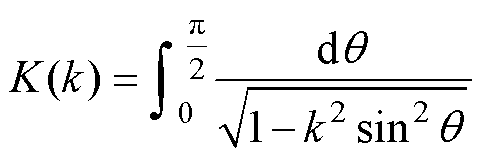 (2)
(2)
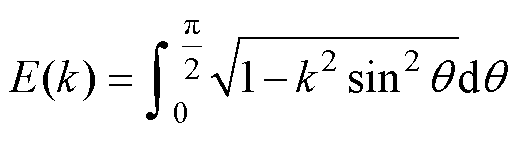 (3)
(3)
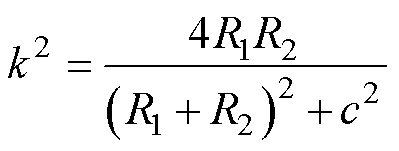 (4)
(4)
式中,c为两个带电圆环的垂直距离;K(k)和E(k)分别为第一类和第二类完全椭圆积分;k为完全椭圆积分中与带电圆环尺寸和圆环之间垂直距离相关的变量;q 为完全椭圆积分变量;m0为真空磁导率。
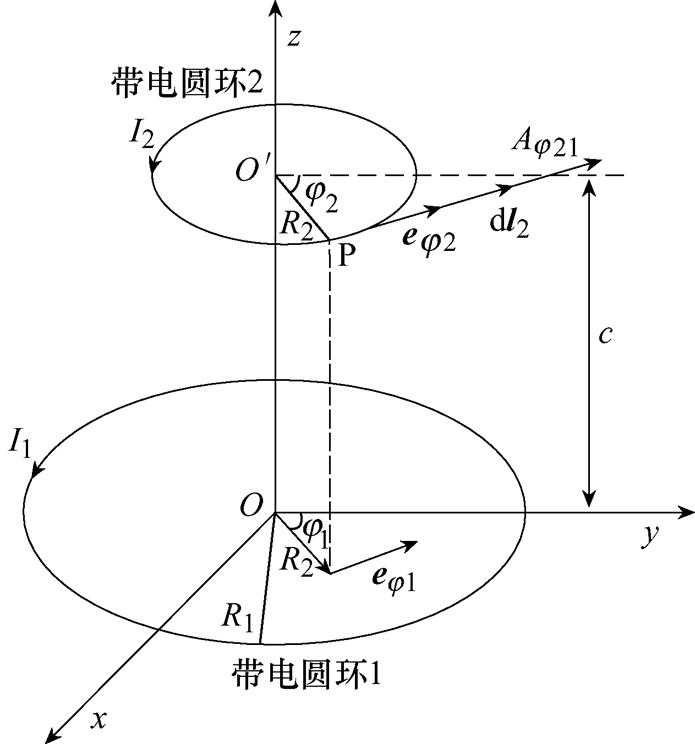
图3 带电圆环相对位置示意图
Fig.3 Schematic diagram of the relative positions of the charged circles
根据磁链法,可得带电圆环之间互感M的计算表达式为
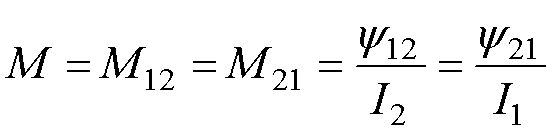 (5)
(5)
式中,M12与M21为带电圆环1与带电圆环2间互感;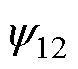 和
和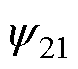 为带电圆环产生的磁链。
为带电圆环产生的磁链。
根据斯托克斯定理,带电圆环1产生的部分磁通交链带电圆环2时,产生的磁链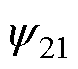 为
为
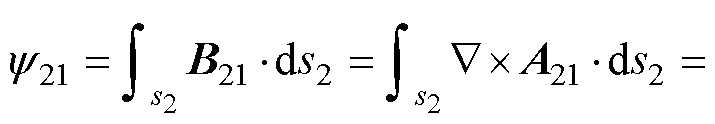
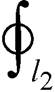
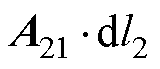 (6)
(6)
式中,B21为磁感应强度矢量;A21为矢量磁位;s2和l2分别为带电圆环2的截面和周长。
结合式(1)~式(6),单匝同轴平行带电圆环的互感M可表示为
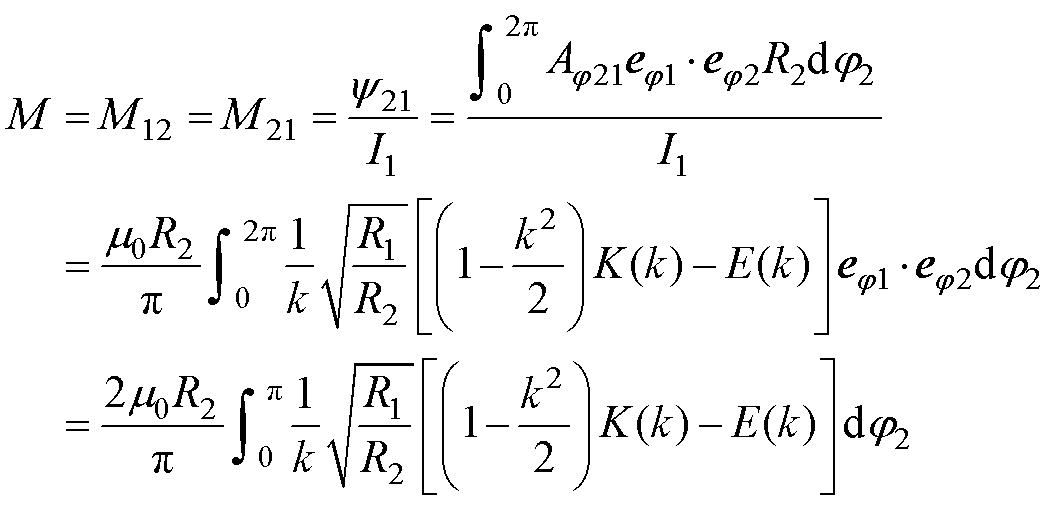
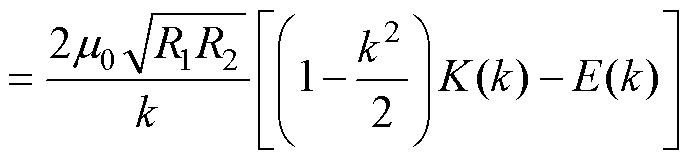 (7)
(7)
式中,eφ1和eφ2为单位长度的向量;φ2为积分变量。
式(7)表明,圆环之间的互感与电流大小无关,只与圆环尺寸和圆环之间的垂直距离有关。
单匝圆环的自感值Lself可采用文献[16]中的解析式计算,有
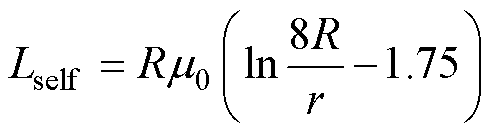 (8)
(8)
式中,R为圆环的内半径;r为圆导线的半径。
图4为两个空心矩形截面线圈相对位置示意图,由于单匝线圈的径向(横向)宽和轴向(竖直方向)高是有限的,因此可以将线圈截面在径向和轴向上离散等效为数量众多、形状相同的网格带电圆环单元。图中,R1为线圈1的内半径,R2为线圈2的内半径,Dw1和Dw2为不同线圈相邻网格单元之间的径向间距,Dh1和Dh2为不同线圈相邻网格单元之间的轴向间距,H0为线圈之间的轴向间距,m1和m2为不同线圈在径向上相邻网格单元的间距总数,n1和n2为不同线圈在轴向上相邻网格单元的间距总数,网格单元的编号原则如图中蓝色框所示,以左下角网格单元为起始点,编号为(1,1),线圈2的网格单元编号原则同理。
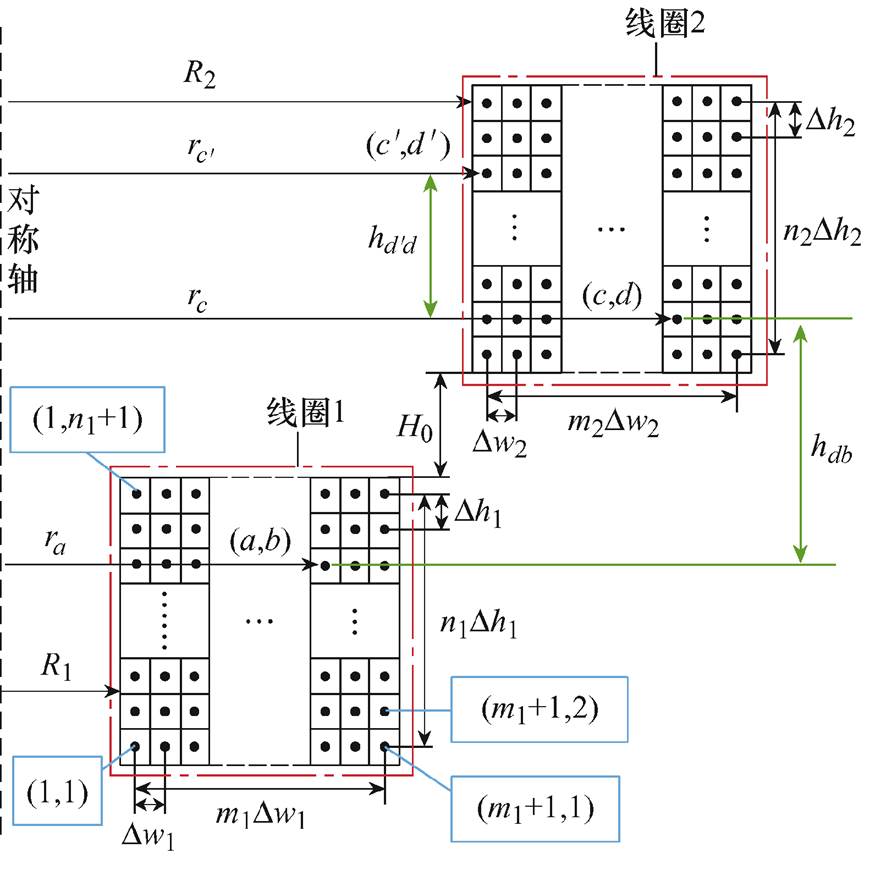
图4 同轴空心矩形截面线圈二维轴对称等效单元模型
Fig.4 2D axisymmetric equivalent element model of a coaxial hollow rectangular section coil
以线圈2为例,单匝线圈的自感可由总储存能量得到,总储存能量是由每个网格带电圆环单元的自感能量和网格带电圆环单元之间的互感能量组成,结合式(7)、式(8),可得总储存能量为
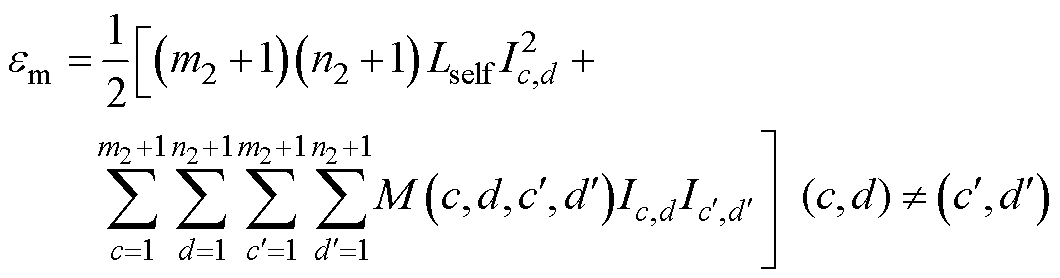 (9)
(9)
式中,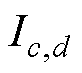 和
和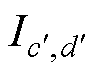 为通过网格带电圆环单元的电流值;M(c,d,c′,d′)为线圈2中编号为(c,d)与编号为(c′,d′)的网格带电圆环单元之间的互感。
为通过网格带电圆环单元的电流值;M(c,d,c′,d′)为线圈2中编号为(c,d)与编号为(c′,d′)的网格带电圆环单元之间的互感。
在低频条件下,由于电流的趋肤效应造成电流拥挤的现象可以忽略,所以可以认为线圈导体不受趋肤效应的影响,线圈截面电流均匀分布,所以离散等效后的每个网格带电圆环单元所通过的电流大小相等,即
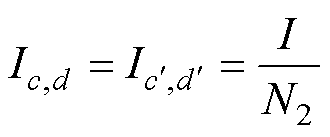 (10)
(10)
式中,N2为线圈2中离散等效的网格带电圆环单元总个数;I为通过单匝线圈的总电流。
结合式(7)~式(10)并代入总储能公式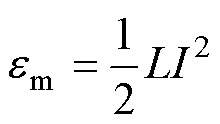 中,即可计算出单匝线圈的自感表达式为
中,即可计算出单匝线圈的自感表达式为
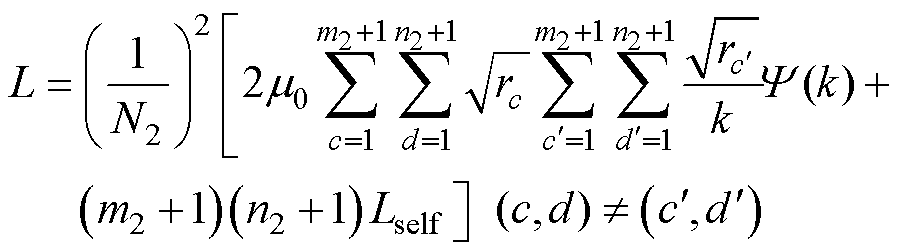 (11)
(11)
其中
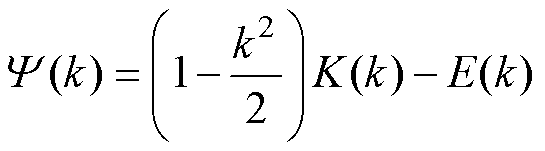
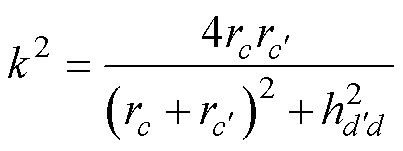
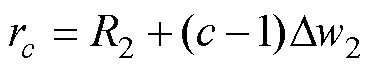
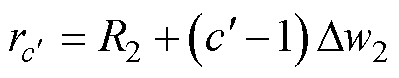
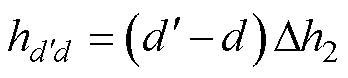
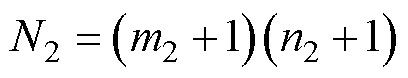
式中,m2+1为线圈2离散等效过程中的横向网格带电圆环单元的数量;n2+1为线圈2离散等效过程中的竖直方向网格带电圆环单元的数量;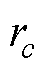 为编号(c,d)的网格带电圆环单元的半径;
为编号(c,d)的网格带电圆环单元的半径;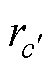 为编号(c′,d′)的网格带电圆环单元的半径;
为编号(c′,d′)的网格带电圆环单元的半径;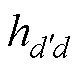 为编号(c′,d′)和编号(c,d)的两个网格带电圆环单元的轴向垂直距离;
为编号(c′,d′)和编号(c,d)的两个网格带电圆环单元的轴向垂直距离;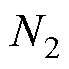 为线圈2中离散等效的网格带电圆环单元总个数。
为线圈2中离散等效的网格带电圆环单元总个数。
由于线圈1和线圈2之间存在互感,所以下面将对两个线圈之间的互感进行解析推导。同样在考虑低频条件以及两个线圈导体实际尺寸的情况下,将线圈截面离散为数量众多且大小相等的网格带电圆环单元,结合式(7),求解线圈1中网格带电圆环单元和线圈2中网格带电圆环单元之间的互感并叠加求和,即可得到线圈1和线圈2之间的互感M12为
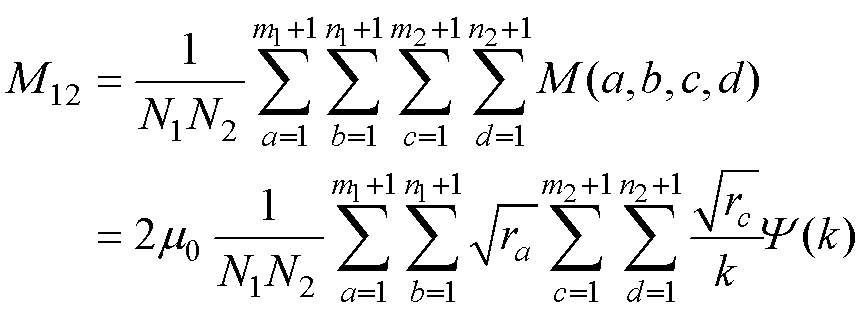 (12)
(12)
其中
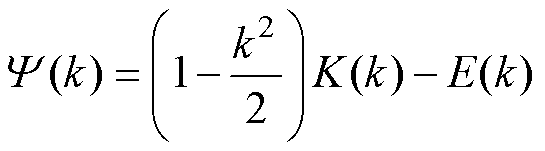
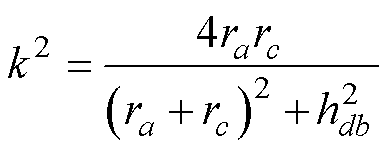
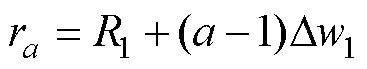
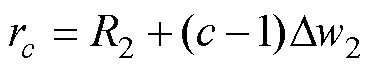
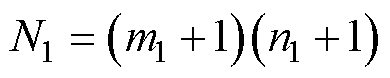
式中,M(a,b,c,d)为线圈1中编号为(a,b)与线圈2中编号为(c,d)的两个网格带电圆环单元之间的互感;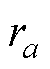 为编号(a,b)的网格带电圆环单元的半径;
为编号(a,b)的网格带电圆环单元的半径;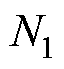 为线圈1中离散等效的网格带电圆环单元总个数;hdb为线圈1中编号为(a,b)与线圈2中编号为(c,d)的两个网格带电圆环单元之间的轴向垂直距离。当线圈1与线圈2呈同轴竖直排列(R1=R2)或如图4所示的位置关系时,hdb采用式(13)计算;当线圈1与线圈2呈同轴水平共面的位置关系时,hdb采用式(14)计算。
为线圈1中离散等效的网格带电圆环单元总个数;hdb为线圈1中编号为(a,b)与线圈2中编号为(c,d)的两个网格带电圆环单元之间的轴向垂直距离。当线圈1与线圈2呈同轴竖直排列(R1=R2)或如图4所示的位置关系时,hdb采用式(13)计算;当线圈1与线圈2呈同轴水平共面的位置关系时,hdb采用式(14)计算。
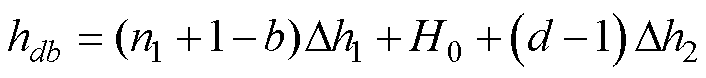 (13)
(13)
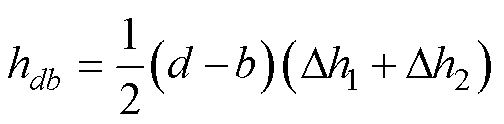 (14)
(14)
第1.2节所推导的解析式只针对低频条件下单匝空心矩形截面线圈而言,因此还需结合整个同轴多层筒式空心线圈的等效电路模型,计算出在低频条件下其一、二次线圈自感和总互感参数。
对于无线电能传输系统而言,一、二次线圈各自均采用串联的缠绕方式,所以本文研究的同轴多层筒式空心线圈也采用该缠绕方式。这里以一次线圈为例,分析其自感计算过程,等效电路如图5所示。
将筒式空心线圈中每匝一次线圈以单个电感表示,则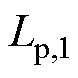 、
、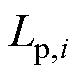 、
、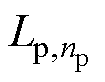 、
、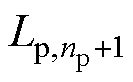 、
、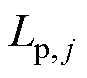 、
、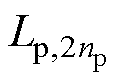 、
、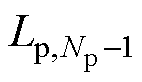 、
、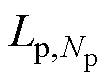 分别表示一次线圈中第1匝、第i匝、第np匝、第np+1匝、第j匝、第2np匝、第Np-1匝和第Np匝线圈的电感值,其中,np为一次线圈中一层的匝数,Np为一次线圈的总匝数。在一次线圈中,每匝线圈不仅存在自感,而且匝与匝间还存有互感,如图5中第i匝线圈不但存在自感值
分别表示一次线圈中第1匝、第i匝、第np匝、第np+1匝、第j匝、第2np匝、第Np-1匝和第Np匝线圈的电感值,其中,np为一次线圈中一层的匝数,Np为一次线圈的总匝数。在一次线圈中,每匝线圈不仅存在自感,而且匝与匝间还存有互感,如图5中第i匝线圈不但存在自感值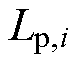 ,还与第1匝、第np匝、第np+1匝、第j匝、第2np匝、第Np-1匝和第Np匝等线圈之间存在互感。
,还与第1匝、第np匝、第np+1匝、第j匝、第2np匝、第Np-1匝和第Np匝等线圈之间存在互感。
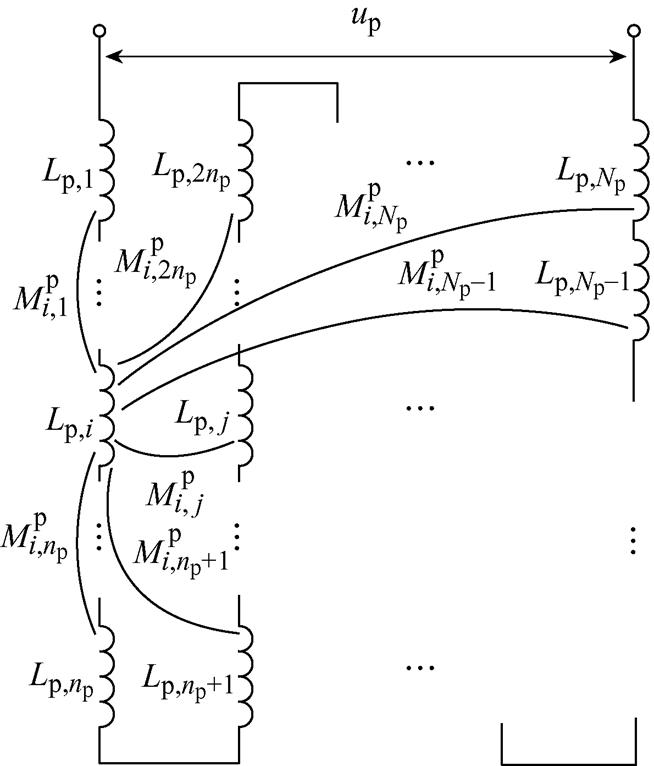
图5 一次线圈等效电路
Fig.5 Primary coil equivalent circuit
根据文献[23]的电路原理可知,对每匝线圈都做上述类似的分析,并将所有匝线圈的自感值和所有匝间互感值叠加求和,即可得到一次线圈的自感计算式为
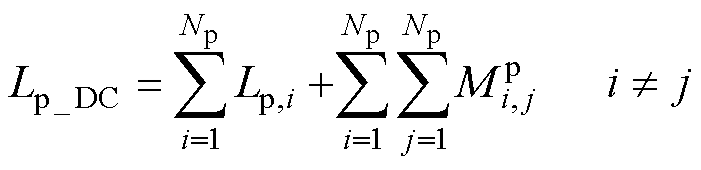 (15)
(15)
式中,Lp_DC为在低频条件下,同轴多层筒式空心线圈的一次线圈自感值;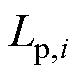 为第i匝线圈的自感值,根据式(11)计算;
为第i匝线圈的自感值,根据式(11)计算;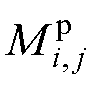 为在一次线圈中第i匝线圈与第j匝线圈间的互感,根据线圈间的相对位置关系,选用合适的hdb计算式,并结合式(12)计算第i匝线圈与第j匝线圈间的互感值。
为在一次线圈中第i匝线圈与第j匝线圈间的互感,根据线圈间的相对位置关系,选用合适的hdb计算式,并结合式(12)计算第i匝线圈与第j匝线圈间的互感值。
同理,同轴多层筒式空心线圈的二次线圈自感计算的分析过程与一次线圈一致,计算表达式为
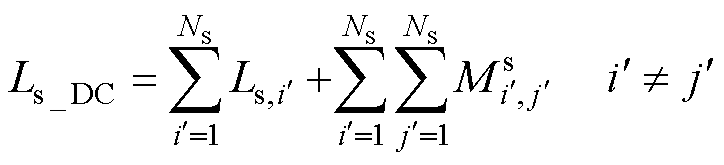 (16)
(16)
式中,Ls_DC为在低频条件下,同轴多层筒式空心线圈二次线圈自感值;Ns为二次线圈总匝数;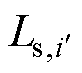 为第i′匝二次线圈的自感值,根据式(11)计算;
为第i′匝二次线圈的自感值,根据式(11)计算;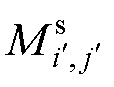 为在二次线圈中第i′匝线圈与第j′匝线圈间的互感,根据线圈间的相对位置关系,选用合适的hdb计算式,并结合式(12)从而计算第i′匝线圈与第j′匝线圈间的互感值。
为在二次线圈中第i′匝线圈与第j′匝线圈间的互感,根据线圈间的相对位置关系,选用合适的hdb计算式,并结合式(12)从而计算第i′匝线圈与第j′匝线圈间的互感值。
总互感计算等效电路如图6所示。图6中,ns为二次线圈中一层的匝数。
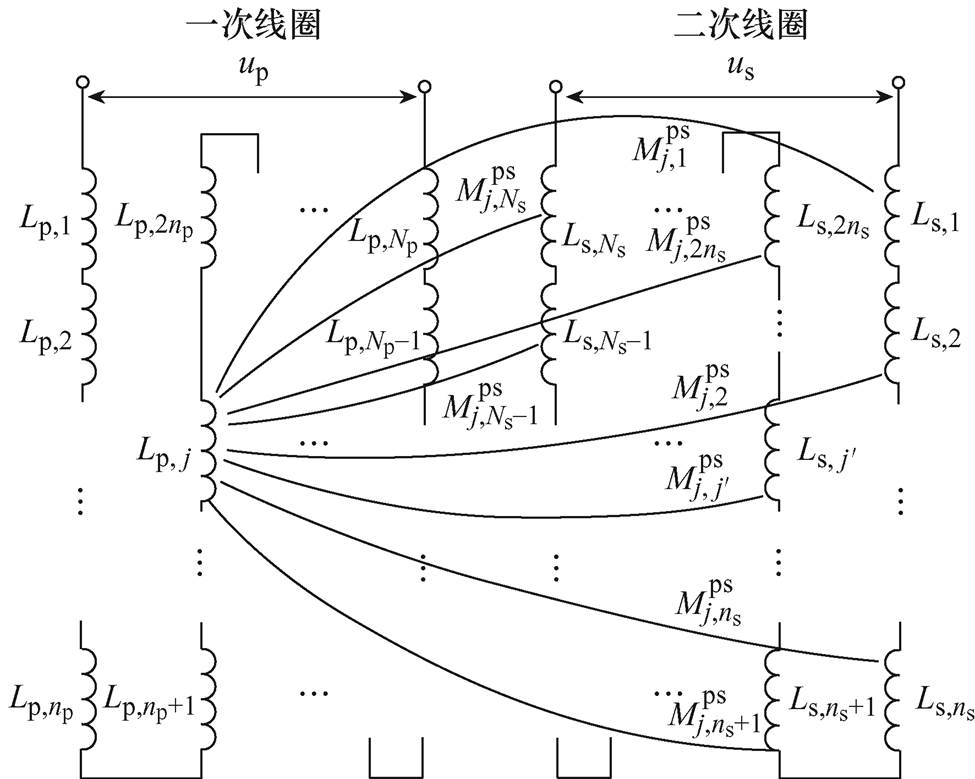
图6 总互感计算等效电路
Fig.6 Total mutual inductance calculation equivalent circuit
根据文献[23]的电路定理可知,每匝一次线圈和每匝二次线圈间的互感之和即为总互感,以一次线圈中第j匝线圈为例,如图6所示,其与每匝二次线圈间都存在互感,最终将每匝一次线圈与每匝二次线圈间的互感叠加求和,即可得到同轴多层筒式空心线圈的一、二次线圈间的总互感值,其计算表达式为
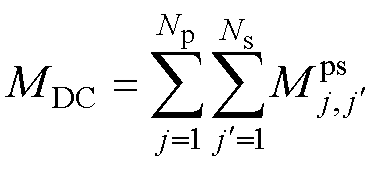 (17)
(17)
式中,MDC为在低频条件下,同轴多层筒式空心线圈一、二次线圈的总互感;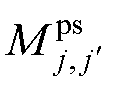 为第j匝一次线圈与第j′匝二次线圈之间的互感,根据线圈之间的相对位置关系选用合适的hdb计算式,并结合式(12)从而计算第j匝一次线圈与第j′匝二次线圈间的互感值。
为第j匝一次线圈与第j′匝二次线圈之间的互感,根据线圈之间的相对位置关系选用合适的hdb计算式,并结合式(12)从而计算第j匝一次线圈与第j′匝二次线圈间的互感值。
当圆形导线中通有高频交流电时会产生明显的趋肤效应,如图7所示,导线截面电流分布不均匀,电流集中分布于导线外侧,从而影响导线的电感值。
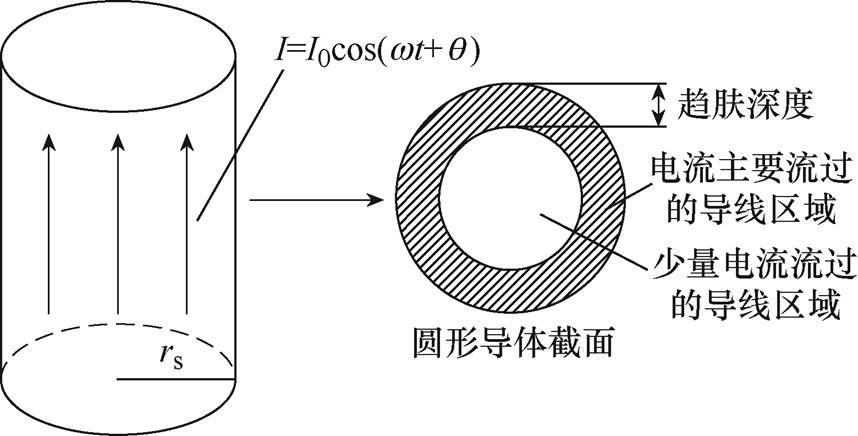
图7 导线的趋肤效应
Fig.7 Skin effect of the conductor
文献[24-25]对所有用于计算圆形导线交流阻抗的研究工作进行了比较,推导出了在考虑趋肤效应影响下,基于开尔文函数的单位长度圆形导线交流阻抗计算公式为
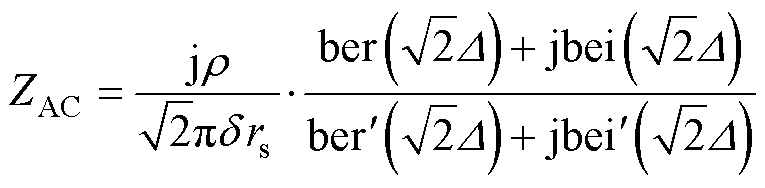 (18)
(18)
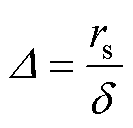 (19)
(19)
其中
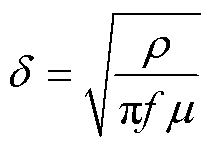 μ=μrμ0
μ=μrμ0
式中,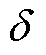 为趋肤深度;f为交流电的频率;m 为导体磁导率;mr为圆形导体的相对磁导率,当圆形导体为非磁性材料(如铜)时,mr=1;m0为真空磁导率;r 为导体的电阻率;rs为圆形导体半径。
为趋肤深度;f为交流电的频率;m 为导体磁导率;mr为圆形导体的相对磁导率,当圆形导体为非磁性材料(如铜)时,mr=1;m0为真空磁导率;r 为导体的电阻率;rs为圆形导体半径。
由式(18)可得单位长度圆形导体在趋肤效应的作用下,随频率变化的交流电感LAC与直流电感LDC的比值[24]为
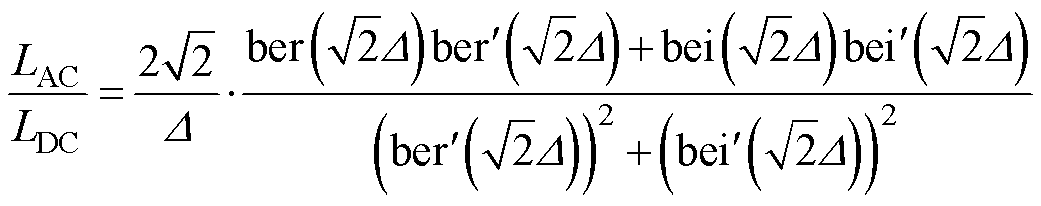 (20)
(20)
式中,ber和bei函数分别为第一类开尔文函数的实部和虚部,可以由以下无穷级数表示为
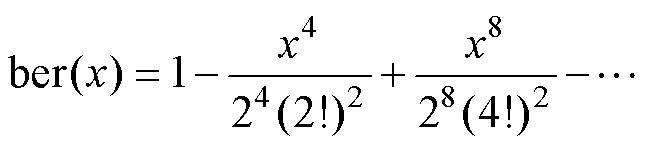 (21)
(21)
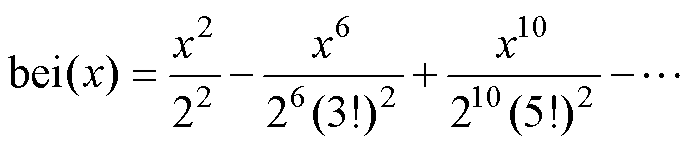 (22)
(22)
结合式(20)~式(22),可以得到式(20)的无穷级数表达式为
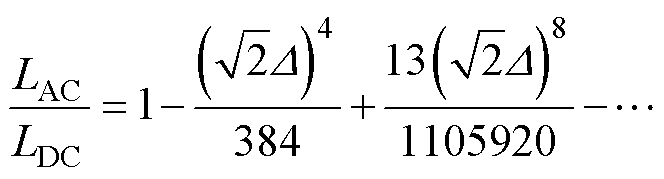 (23)
(23)
为方便运算,对式(23)保留3项多项式得到近似计算式(24),并对比精确计算式(20)和近似计算式(24)的计算精度,如图8所示。当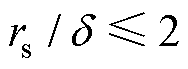 时,精确计算式(20)和近似计算式(24)的曲线分布趋势基本一致,具有相同的计算精度。
时,精确计算式(20)和近似计算式(24)的曲线分布趋势基本一致,具有相同的计算精度。
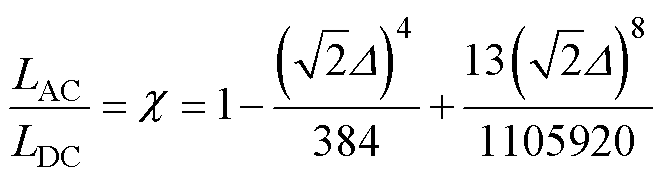 (24)
(24)
式中,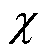 为电感修正系数。
为电感修正系数。
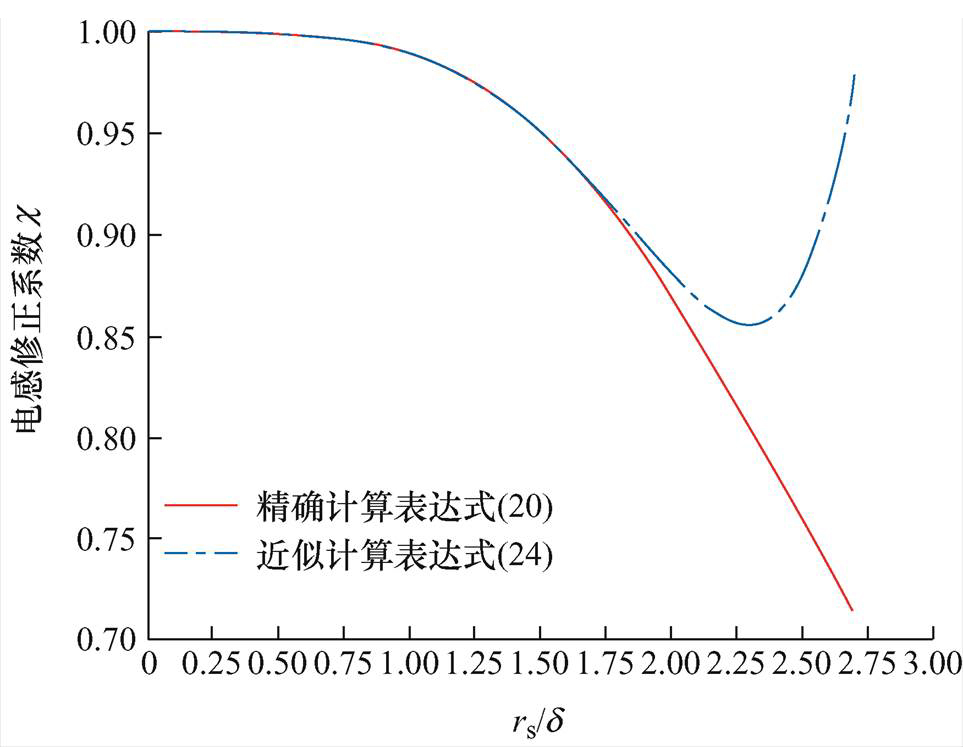
图8 计算精度对比
Fig.8 Comparison of calculation accuracy
由1.3节可知,同轴多层筒式空心线圈的一次线圈自感Lp_DC、二次线圈自感Ls_DC和总互感MDC的计算是基于导体截面电流均匀分布的条件下计算得到的,只适用于通有低频交流电的情况,忽略了通有高频交流电的影响。电感修正系数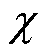 考虑了高频电流在导线截面上的分布,即可计算出在趋肤效应影响下圆导线的电感值。因此,基于对单根圆导线趋肤效应电感计算的研究,结合式(24),得到了同轴多层筒式空心线圈通有高频交流电时一、二次线圈自感Lp_AC、Ls_AC和总互感MAC的计算解析式,有
考虑了高频电流在导线截面上的分布,即可计算出在趋肤效应影响下圆导线的电感值。因此,基于对单根圆导线趋肤效应电感计算的研究,结合式(24),得到了同轴多层筒式空心线圈通有高频交流电时一、二次线圈自感Lp_AC、Ls_AC和总互感MAC的计算解析式,有
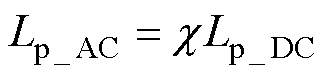 (25)
(25)
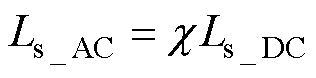 (26)
(26)
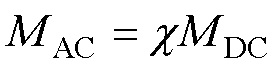 (27)
(27)
为了验证本文所提方法的计算可行性,分别采用解析法、仿真法和实验法对两种不同排布方式的同轴多层筒式空心变压器的一、二次线圈自感和互感参数进行分析计算。
图9给出了筒式空心线圈的两种不同排布方式。其中,图9a为无交叉换位式,即一次线圈的所有层连续排列构成一个区域,二次线圈的所有层连续排列构成另一区域;图9b为部分交叉换位式,即线圈分别等分成Q/2个区域(Q为一次线圈或二次线圈层数),每个线圈区域各包含两层一、二次线圈,不同线圈区域交替布置。根据图9所示的同轴多层筒式空心变压器线圈排布方式,设计制造了相应的实验模型,主要设计参数见表1。
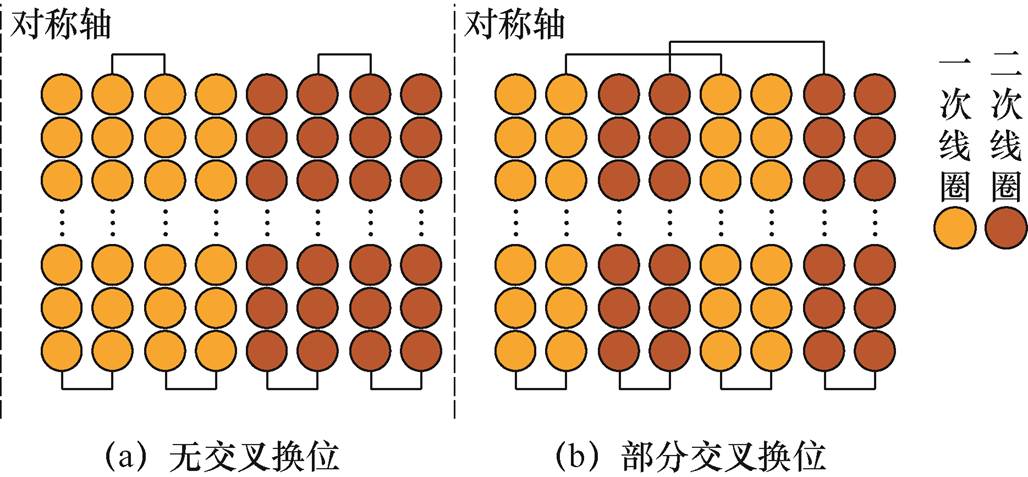
图9 同轴多层筒式空心线圈排布方式
Fig.9 Arrangement of coaxial multilayer cylindrical hollow coils
表1 线圈几何结构参数
Table 1 Parameters of coil geometry

参 数数 值 一、二次线圈匝数,形状80/80,圆导体 层间空气绝缘距离/mm0.15 线圈直径/mm0.8 匝间间距/mm0.03 线圈内半径/mm9.76
在实验验证方面,采用LCR-8205阻抗分析仪(阻抗量测精度±0.08%)对两种不同排布方式的同轴多层筒式空心变压器进行开路实验,得到一、二次线圈自感测量结果。由于电感参数的计算与电流大小无关,而只与交流电频率大小有关,如本文中式(25)~式(27)所示,所以通常采用阻抗分析仪(RCL表)的小信号测量线圈的自感和互感参数就已经可以满足测量精度。因此,在实际运行的大功率情况下,电流值的改变不会影响线圈自感值和线圈间的互感值。根据文献[11]的互感测量方法(见图10),首先将一次线圈与二次线圈同向连接,得到线圈两端的电感为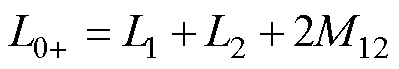 ,再将一次线圈与二次线圈反向连接,得到线圈两端的电感为
,再将一次线圈与二次线圈反向连接,得到线圈两端的电感为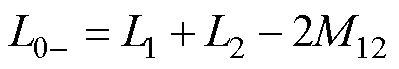 。其中,L1和L2分别为一次线圈和二次线圈的自感值,M12为当一次线圈与二次线圈同向连接或反向连接时的互感值。因此,一次线圈与二次线圈之间的互感
。其中,L1和L2分别为一次线圈和二次线圈的自感值,M12为当一次线圈与二次线圈同向连接或反向连接时的互感值。因此,一次线圈与二次线圈之间的互感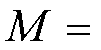
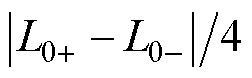 ,实验测量平台如图11所示。
,实验测量平台如图11所示。
本文所提出的解析法需要将导体截面离散等效为数量众多、形状大小相同的网格带电圆环单元,但由于圆形截面导体在离散等效过程中,不能确保各网格带电圆环单元形状相同,所以应当对该类型的导体线圈进行等效处理。考虑到线圈的层数和匝数较多,对圆形铜导体线圈进行有限元仿真建模时,其网格划分极其复杂且普通计算机难以承受如此巨大的计算压力,所以综合考虑线圈导体离散等效过程、计算运行成本和时间以及计算结果的可靠性,将具有圆形截面的线圈导体采用等面积法转换为方形导体进行解析和仿真建模计算。将每匝圆形铜导线等效后的方形导线离散为9个形状相同的网格带电圆环单元,每个网格带电圆环单元边长为0.236 mm,等效离散过程如图12所示。
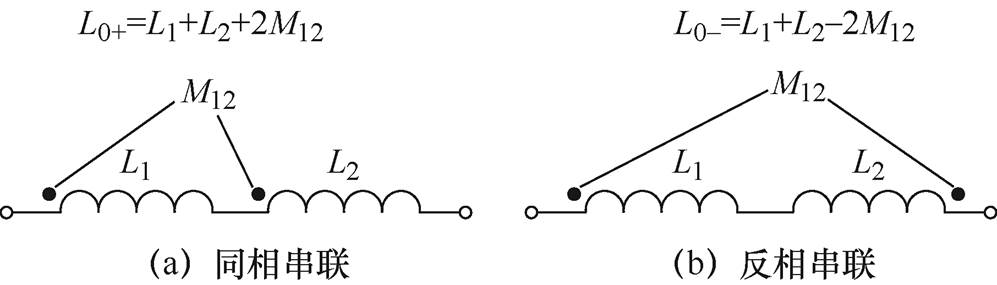
图10 互感测量实验原理
Fig.10 Schematic diagram of mutual inductance measurement experiment

图11 实验测量平台
Fig.11 Experimental measurement platform
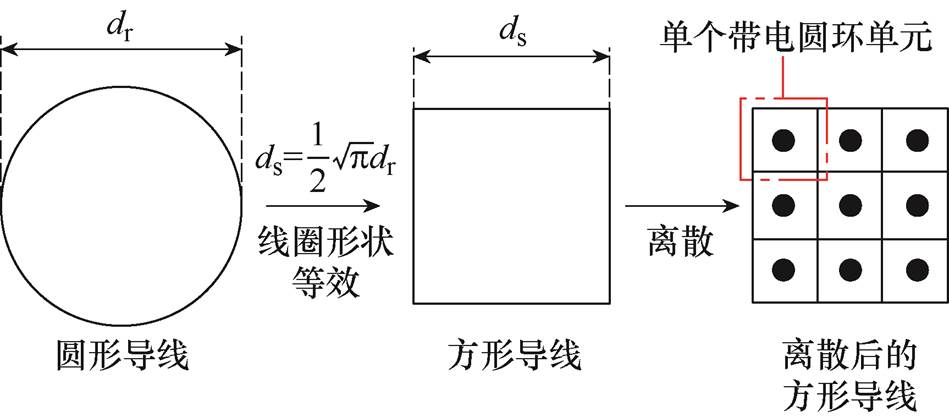
图12 圆导线等效离散过程
Fig.12 Equivalent discrete process of circular conductors
本文将借助于Ansys/Maxwell有限元仿真对两种不同排布方式的筒式空心线圈进行建模计算。由于空心线圈不包含磁心,磁场分布在空间中极不均匀,所以为接近其实际的磁场分布,求解域范围应尽可能扩大,但考虑到计算机的运行压力,这里设定求解域范围是仿真模型本身大小的5倍,选择涡流场求解模式,即考虑线圈导体的涡流效应,使仿真环境尽量接近实际,有限元仿真模型如图13所示。
上述所有的仿真计算和实验测试都是在1~100 kHz的频率下进行的,在该频率范围内,由于圆导线会受趋肤效应的影响,会对电感参数产生影响,所以应根据式(25)~式(27)对筒式空心线圈自感和互感进行计算。本文所提出的解析法的适用范围必须满足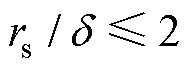 ,取决于导线半径与趋肤深度。实验空心线圈中圆导线半径为0.4 mm,当交流电频率f=100 kHz时,由于
,取决于导线半径与趋肤深度。实验空心线圈中圆导线半径为0.4 mm,当交流电频率f=100 kHz时,由于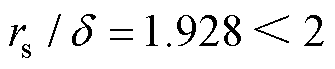 ,所以近似计算式(24)得到的计算结果与精确计算 式(20)的计算结果一致,因此为确保计算结果的准确性,结合上述分析,确定计算的频率范围为1~100 kHz。由近似计算式(24)得到的电感修正系数
,所以近似计算式(24)得到的计算结果与精确计算 式(20)的计算结果一致,因此为确保计算结果的准确性,结合上述分析,确定计算的频率范围为1~100 kHz。由近似计算式(24)得到的电感修正系数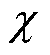 随频率变化的曲线如图14所示。
随频率变化的曲线如图14所示。
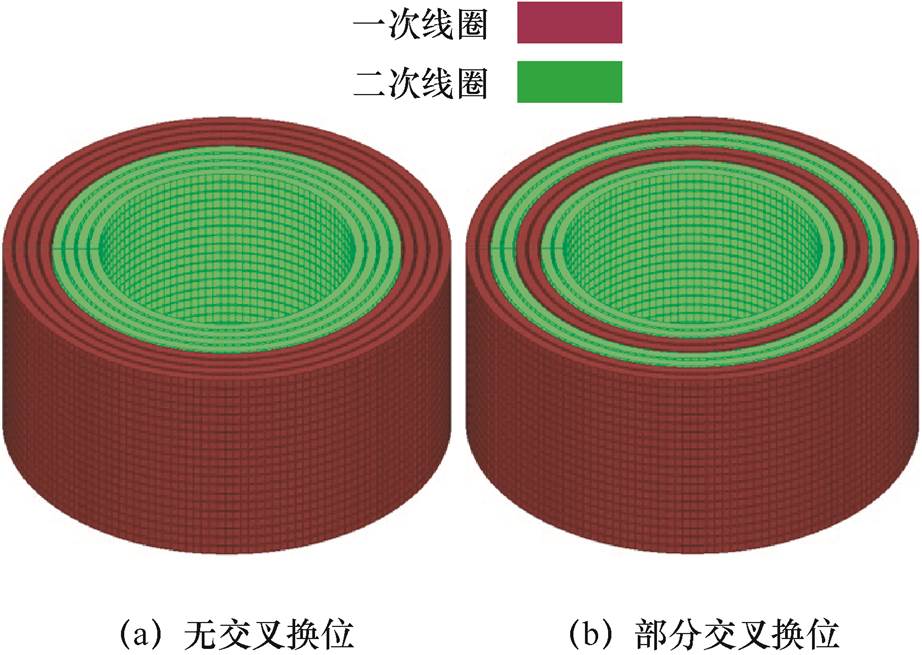
图13 有限元仿真模型
Fig.13 Finite element simulation model
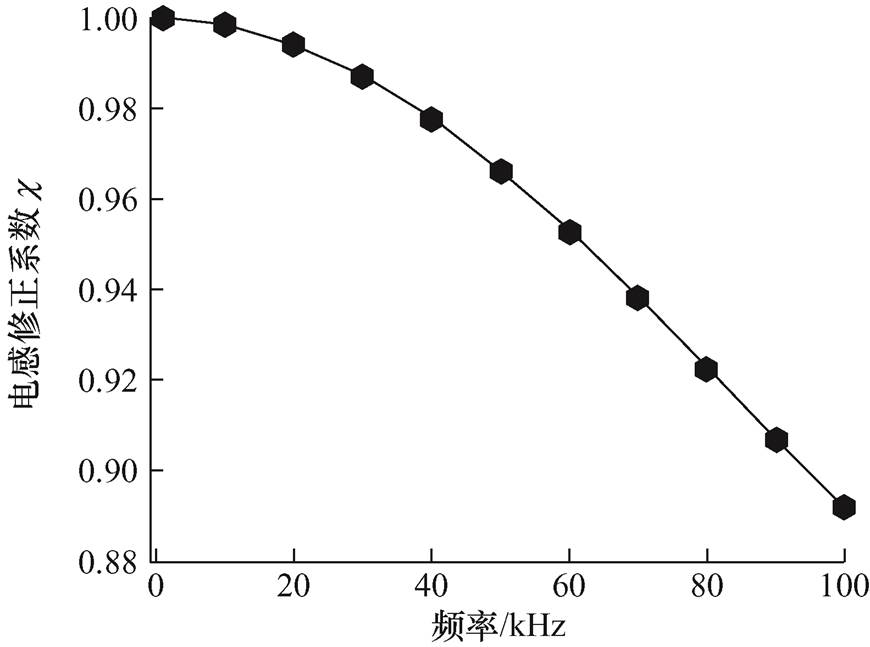
图14 电感修正系数χ曲线
Fig.14 Inductance correction factor χ curve
图15和图16展示了在不同频率下采用不同方法计算得到的筒式空心线圈自、互感值,其中解析法计算得到的一次线圈自感、二次线圈自感和总互感分别表示为LC1、LC2和MC;一次线圈自感、二次线圈自感和总互感的仿真值分别表示为LF1、LF2和MF;一次线圈自感、二次线圈自感和总互感的实验测量值分别表示为LE1、LE2和ME。
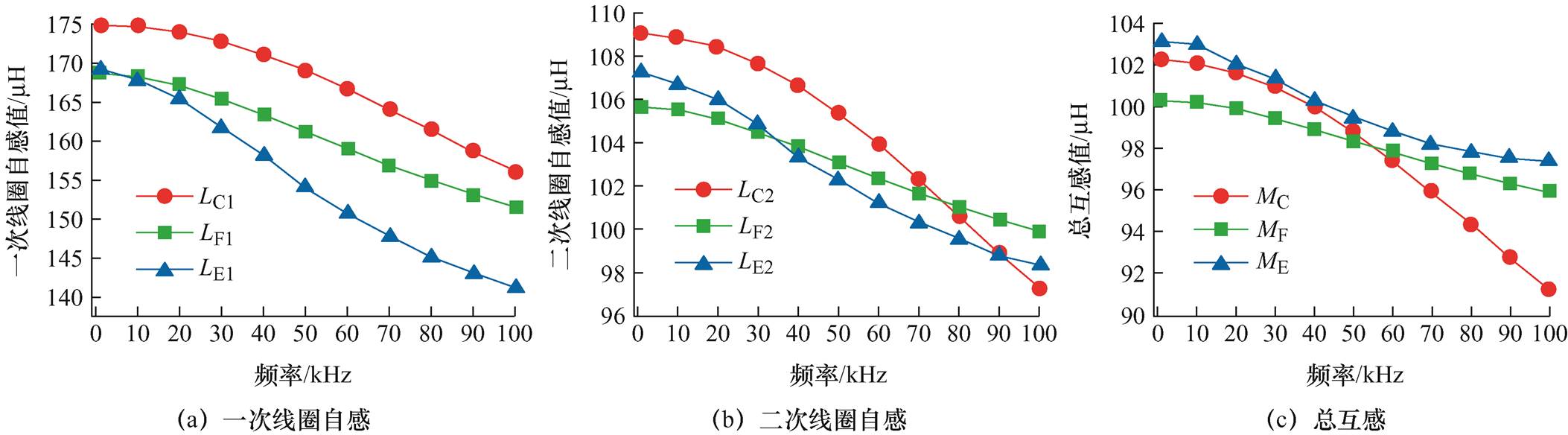
图15 不同频率下无交叉换位筒式空心线圈电感参数
Fig.15 Inductance parameters of the cartridge hollow coil without cross-transposition at different frequencies
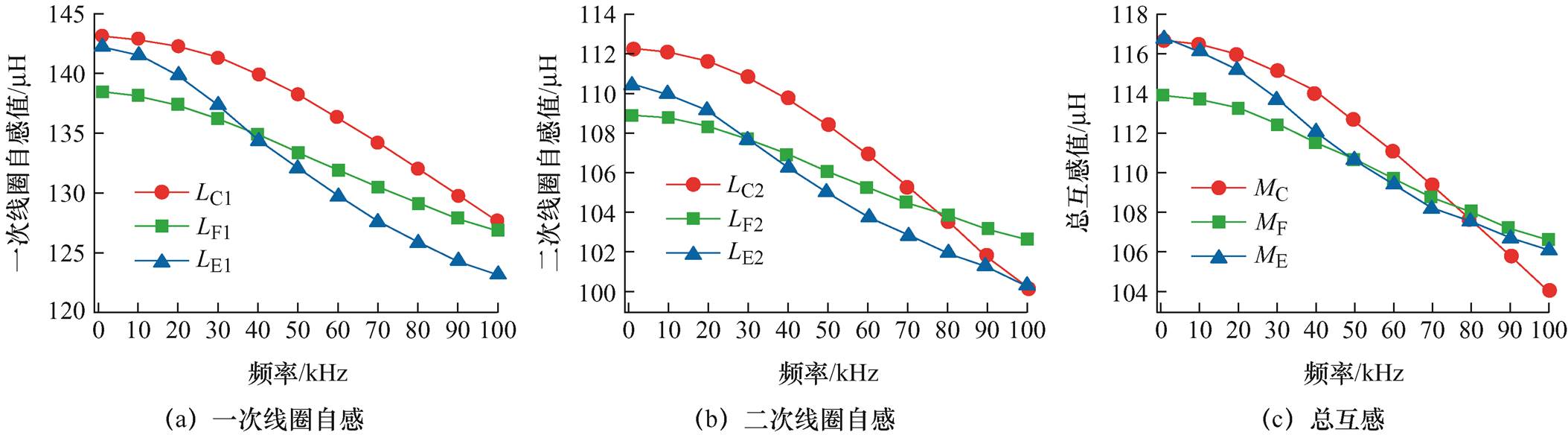
图16 不同频率下部分交叉换位筒式空心线圈电感参数
Fig.16 Inductance parameters of partially cross-transposition cartridge hollow coil at different frequencies
结合图15、图16可知,解析计算结果、仿真计算结果与实验测量数据之间的分布趋势与规律一致,即随着频率的升高,不同排布方式的同轴多层筒式空心线圈的一、二次自感和总互感逐渐减小,并且随着交叉换位程度的提高,互感增大。
为验证解析方法的计算结果的可行性,针对具有不同排布方式的筒式空心线圈模型,采用式(28)给出的相对偏差计算公式,对解析计算结果进行偏差分析,如图17所示。
 (28)
(28)
式中,LC1(i)、LC2(i)和MC(i)为第i个频率的解析计算值;LF1(i)、LF2(i)和MF(i)为第i个频率的仿真计算值;LE1(i)、LE2(i)和ME(i)为第i个频率的实验测量值;αC-F、αC-E分别为一次线圈自感解析计算值与仿真值、实验值的相对误差;bC-F、bC-E分别为二次线圈自感解析计算值与仿真值、实验值的相对误差;gC-F、gC-E分别为总互感解析计算值与仿真值、实验值的相对误差。
根据图17可知,对于无交叉换位的筒式空心线圈而言,以实验测量值为参照,计算值与实验测量值的平均相对误差为4.118%;以仿真值为参照,计算值与仿真值之间的平均相对误差为2.779%;对于部分交叉换位的筒式空心线圈而言,以实验测量值为参照,计算值与实验值之间的平均相对误差为2.200%;以仿真值为参照,计算值与仿真值之间的平均相对误差为2.278%。上述分析均体现出解析计算结果、仿真计算结果与实验测量结果具有较好的一致性,证明了本文所提解析方法的可行性。
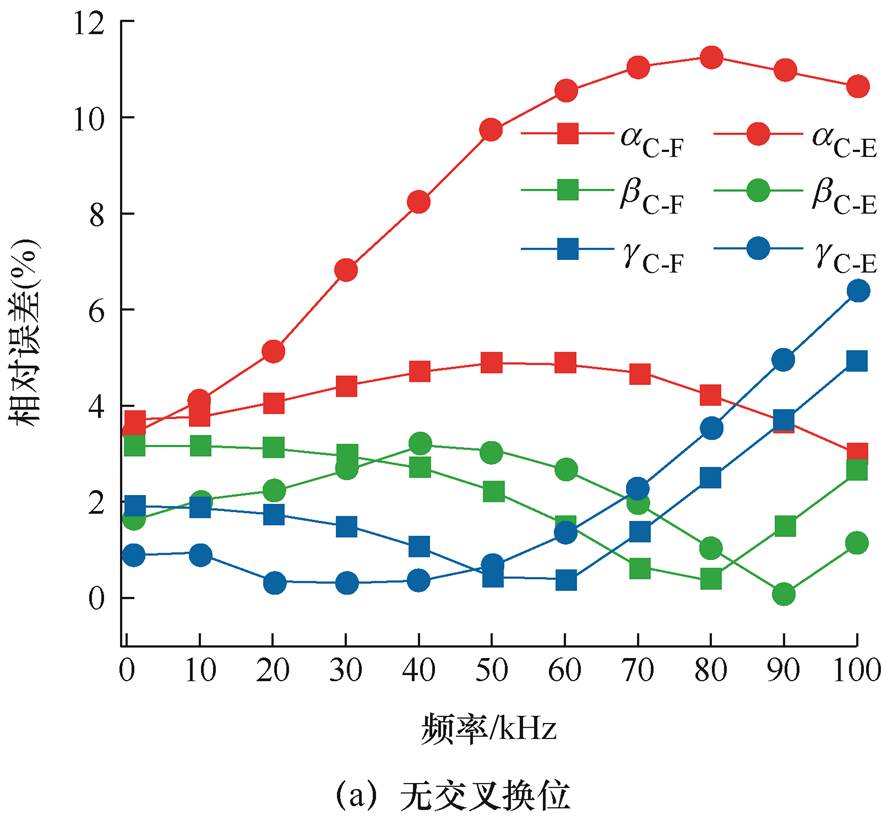
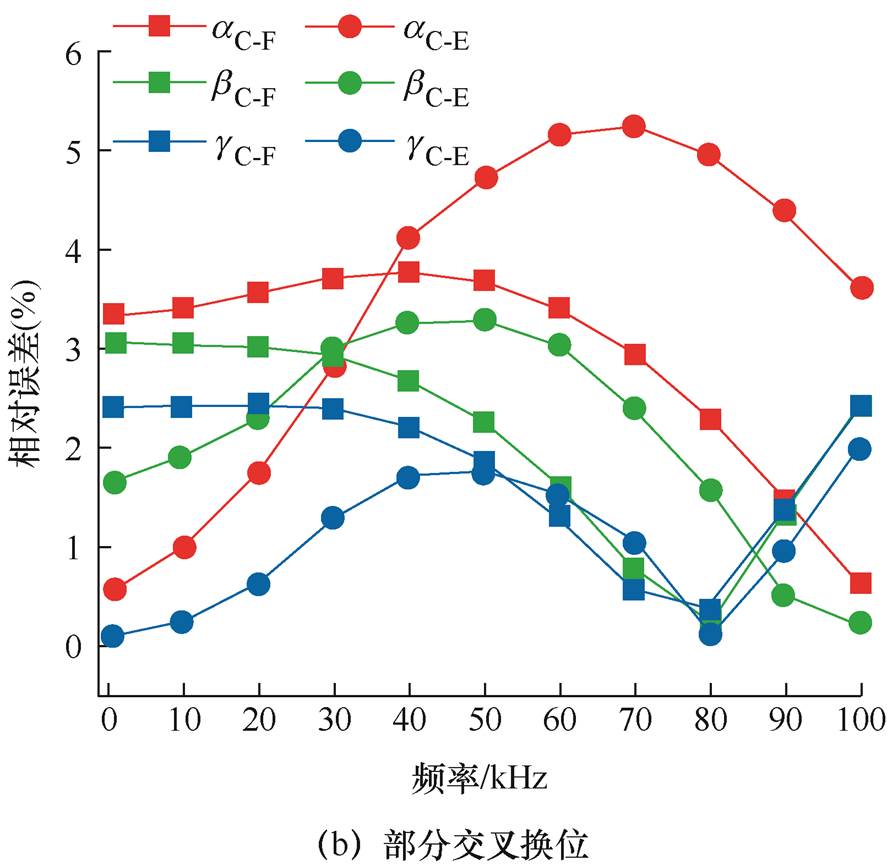
图17 不同频率下筒式空心线圈电感参数相对误差
Fig.17 Relative error of inductance parameters of a cartridge hollow coil at different frequencies
由于本文将实验测量的圆形导线采用面积等效法等效为方形导线,如图12所示,结合解析公式计算筒式空心线圈一、二次线圈自感和总互感值,导致电感计算的结果与实际测量的结果之间存在偏差。同时,由于多匝空心线圈的自感值不仅会受到趋肤效应的影响,而且也会受到邻近效应的影响,导致电感计算结果存在一定偏差,但两种效应对线圈自感值的影响程度不同。本文以具有无交叉换位方式的空心线圈模型为例(见图9a),以低频1 kHz二次线圈自感仿真计算值作为基准值,采用有限元仿真计算的方法研究在高频情况下,趋肤效应和邻近效应对二次线圈自感值的影响程度,并绘制了如图18所示的二次线圈的自感衰减率的变化规律。
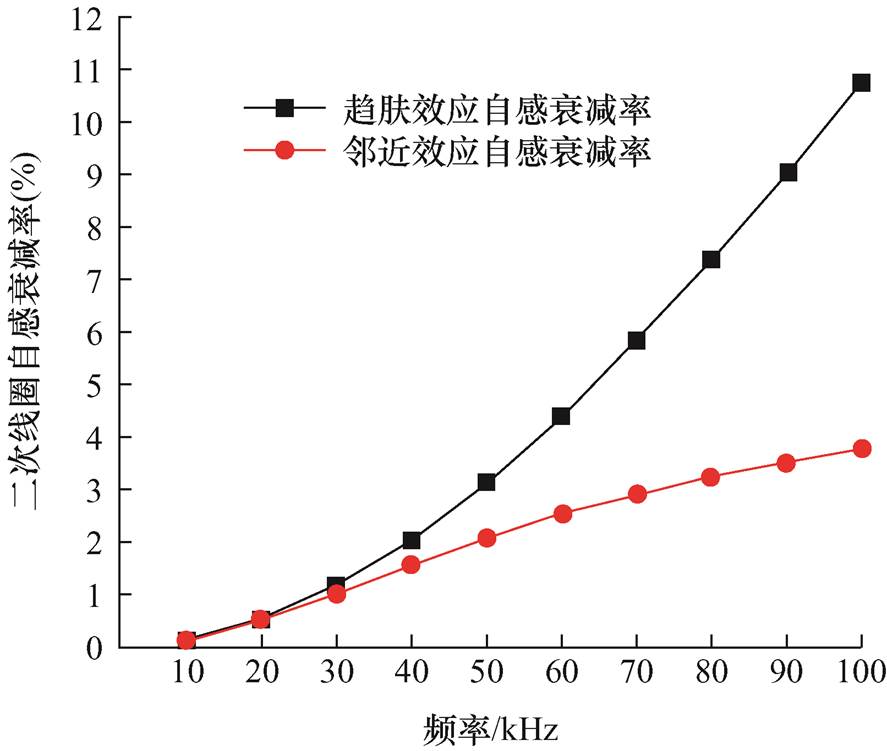
图18 二次线圈自感衰减率
Fig.18 Secondary coil self-inductance decay rate
从图18中可以得出,趋肤效应对二次线圈的自感影响程度较大,而邻近效应对二次线圈的自感也有影响,但影响程度较小。同理,一次线圈的自感衰减率也满足上述规律,并且对于具有无交叉换位的空心线圈而言,一次线圈位于该研究模型的外侧,其储存的自感能量相对较多,空间中的磁链分布也较为复杂,而邻近效应在相对较高的频率会对空间中的磁链分布产生一定的影响,但由于目前文献对于求解多匝导体线圈在邻近效应影响下的电流密度分布解析式较为困难,因此本文忽略了邻近效应对线圈自感的影响,在相对较高的频率下,aC-E的误差相对较大。
1)本文针对无线电能传输系统中的筒式空心线圈结构模型进行研究,考虑高频趋肤效应及筒式空心线圈的整体结构,采用离散等效求和法推导出包含第一类、第二类完全椭圆积分和开尔文函数的解析表达式用于计算不同排布方式的筒式空心线圈在不同频率下的一、二次线圈自感和总互感值。
2)通过实验测量和基于电磁场理论的有限元仿真计算可知,在1~100 kHz频率范围内,该解析法计算具有无交叉换位筒式空心线圈的电感值与仿真值、实验值的平均相对误差分别为2.779%和4.118%,计算具有部分交叉换位筒式空心线圈的电感值与仿真值、实验值的最大平均相对误差分别为2.278%和2.200%,验证了所提解析方法的可行性。
3)本文所提出的解析法可以根据筒式空心线圈结构参数和排布方式对一、二次线圈自感和总互感进行计算,因此可以利用该方法对筒式空心线圈进行电磁耦合分析,其计算结果可以为线圈参数化设计提供参考依据,具有重要的参考价值。
参考文献
[1] 刘乐, 毕恺韬, 朱一昕, 等. 适用于储能系统的准Z源模块化多电平双向DC-DC变换器的设计与控制[J]. 电工技术学报, 2022, 37(增刊1): 235-245.
Liu Yue, Bi Kaitao, Zhu Yixin, et al. Design and control of quasi-Z-source modular multilevel bidirectional DC-DC converter for energy storage system[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 235-245.
[2] 王武, 雷文浩, 蔡逢煌, 等. 结合电流应力优化的双有源全桥DC-DC变换器自抗扰控制[J]. 电工技术学报, 2022, 37(12): 3073-3086.
Wang Wu, Lei Wenhao, Cai Fenghuang, et al. Active disturbance rejection control of dual-active-bridge DC-DC converter with current stress optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3073-3086.
[3] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[4] Schröder D, Marquardt R. Solid-state transformers[M]. Berlin, Heidelberg: Springer, 2018.
[5] 范恩泽, 李耀华, 葛琼璇, 等. 基于优化移相的双有源串联谐振变换器前馈控制策略[J]. 电工技术学报, 2022, 37(20): 5324-5333.
Fan Enze, Li Yaohua, Ge Qiongxuan, et al. Feedforward control strategy of dual active bridge series resonant converter based on optimized phase shift[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5324-5333.
[6] Czyz P, Guillod T, Krismer F, et al. Design and experimental analysis of 166 kW medium-voltage medium-frequency air-core transformer for 1: 1-DCX applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(4): 3541-3560.
[7] Czyz P, Guillod T, Zhang Daifei, et al. Analysis of the performance limits of 166 kW/7 kV air-and magnetic-core medium-voltage medium-frequency transformers for 1: 1-DCX applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2989-3012.
[8] 张文杰, 毕鲁飞, 吝伶艳, 等. 磁耦合谐振式无线电能传输系统磁耦合结构错位性能的研究[J]. 高电压技术, 2020, 46(11): 4087-4095.
Zhang Wenjie, Bi Lufei, Lin Lingyan, et al. Research on misalignment performance of magnetic coupling structure in magnetically coupled resonant wireless power transfer system[J]. High Voltage Engineering, 2020, 46(11): 4087-4095.
[9] 陈雨晨, 陈凯楠, 郑树轩, 等. 无线电能传输平板型磁耦合机构电感解析建模方法[J]. 中国电机工程学报, 2023, 43(4): 1504-1517.
Chen Yuchen, Chen Kainan, Zheng Shuxuan, et al. Analytical modeling method for inductance of planar magnetic coupler in wireless power transfer[J]. Proceedings of the CSEE, 2023, 43(4): 1504-1517.
[10] Norodin N S A, Hotta M. Performance improvement of resonator-coupled wireless power transfer system using dual-spiral resonator with angular misalignments[J]. URSI Radio Science Bulletin, 2020, 372: 22-28.
[11] 李中启, 林志远, 杨鹏, 等. 无线电能传输系统带双层有界磁屏蔽任意位置圆形线圈的耦合系数计算[J]. 电工技术学报, 2022, 37(24): 6306-6318.
Li Zhongqi, Lin Zhiyuan, Yang Peng, et al. Calculation of the coupling coefficient of an arbitrarily positioned circular coil for wireless power transfer system with a double-layered finite magnetic shield[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6306-6318.
[12] Babic S I, Akyel C. New analytic-numerical solutions for the mutual inductance of two coaxial circular coils with rectangular cross section in air[J]. IEEE Transactions on Magnetics, 2006, 42(6): 1661-1669.
[13] Hurley W G, Duffy M C, Zhang Jun, et al. A unified approach to the calculation of self- and mutual- inductance for coaxial coils in air[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6155-6162.
[14] Conway J T. Inductance calculations for circular coils of rectangular cross section and parallel axes using Bessel and struve functions[J]. IEEE Transactions on Magnetics, 2010, 46(1): 75-81.
[15] 罗垚, 陈柏超. 空心矩形截面圆柱线圈自感计算的新方法[J]. 电工技术学报, 2012, 27(6): 1-5.
Luo Yao, Chen Baichao. New method for self- inductance calculations of air-core circular coils with rectangular cross-sections[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 1-5.
[16] Ren Yong, Kuang Guangli, Chen Wenge. Inductance of bitter coil with rectangular cross-section[J]. Journal of Superconductivity and Novel Magnetism, 2013, 26(6): 2159-2163.
[17] Liang Sizhuang, Fang Youtong. Analysis of inductance calculation of coaxial circular coils with rectangular cross section using inverse hyperbolic functions[J]. IEEE Transactions on Applied Super- conductivity, 2015, 25(4): 4901209.
[18] 罗垚, 陈柏超, 袁佳歆, 等. 倾斜轴空心矩形截面圆柱线圈互感计算[J]. 电工技术学报, 2012, 27(5): 132-136.
Luo Yao, Chen Baichao, Yuan Jiaxin, et al. Mutual inductance calculations of inclined axial air-core circular coils with rectangular cross-sections[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 132-136.
[19] 谢岳, 潘伟玲. 任意空间位置线圈的互感计算方法[J].电机与控制学报, 2016, 20(6): 63-67, 76.
Xie Yue, Pan Weiling. Mutual inductance calculation method of arbitrary space positioned coils[J]. Electric Machines and Control, 2016, 20(6): 63-67, 76.
[20] Hu Daoyu, Jie Sheng, Feng Wang, et al. A numerical method for calculating and optimizing the coupling factor of HTS air-core transformer[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(6): 5501106.
[21] Chen Bin, Tao Xin, Wan Nina, et al. Design method for high-power high-frequency magnetic-resonance air-core transformer[J]. COMPEL-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2023, 42(3): 740-756.
[22] Song K H, Feng J, Zhao R ,et al. A general mutual inductance formula for parallel non-coaxial circular coils[J]. Applied Computational Electromagnetics Society Journal, 2019, 34(9): 1385-1390.
[23] 邱关源原著,罗先觉修订. 电路[M]. 5版. 北京: 高等教育出版社, 2006.
[24] Morgan V T. The current distribution, resistance and internal inductance of linear power system conductors—a review of explicit equations[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1252-1262.
[25] Wu Mingli, Fan Yu. Numerical calculations of internal impedance of solid and tubular cylindrical conductors under large parameters[J]. IEE Proceedings-Generation, Transmission and Distribution, 2004, 151(1): 67.
Abstract In the electromagnetic coupling of wireless power transmission systems, accurate calculation of the coil inductance parameters is an important theoretical basis. The existing analytical calculations for coil inductance mostly focus on planar plate coils to study the relationship between coil inductance and coil structure, ignoring the influence of frequency. However, the coaxial multilayer cylindrical structure of the air-core transformer (ACT) has a higher coupling coefficient and transmission efficiency than the planar plate coil under the same quality conditions. However, since the ACT has no magnetic conductive material, it has no specific magnetic flux path, and the magnetic field cannot be bound to a certain part. Usually, it is calculated using the three-dimensional finite element method, which requires a high computer configuration, a large amount of storage space, and sufficiently fast computing speed, resulting in high computational costs. Therefore, this paper proposes an analytical calculation method for the self and mutual inductance of coaxial multilayer cylindrical hollow coils considering high-frequency eddy current effects.
Firstly, the magnetic chain method derives the analytical equations for the self and mutual inductance of a single-turn coaxial parallel charged circular ring. Secondly, the cross-section of the single-turn coil is discretized into grid-charged circular ring elements with the same shape. The analytical equations for the single-turn coil’s self-inductance and the coils' mutual inductance are derived using the discrete equivalent summation method. Based on the first and second types of complete elliptic integrals and Kelvin functions, analytical formulas are derived to calculate the self-inductance of the primary and secondary coils and the total mutual inductance. Finally, taking two different arrangements of cylindrical hollow coils as examples, the proposed analytical method is verified by comparing analytical calculations, finite element calculations, and experimental measurements. This method considers the effect of frequency on coil inductance parameters and significantly reduces the computational cost.
Within the frequency range of 1~100 kHz, the inductance's average relative errors of the proposed method and the simulated values are 2.779% and 4.118% for the cylindrical hollow coils without cross-transposition, and 2.278% and 2.200% for the partially cross-transposition cylindrical hollow coils. The proposed method can calculate the self-inductance and total mutual inductance of the primary and secondary coils of cylindrical hollow coils with different arrangements and frequencies. Therefore, the electromagnetic coupling of the cylindrical hollow coil can be analyzed, which provides a reference for the parametric design of the coil.
Keywords:Wireless power transmission, inductance parameter, cylindrical type hollow coil, discrete equivalence, eddy current effect, analytical calculation
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.231516
国家自然科学基金青年科学基金项目(52107006)和湖北省自然科学基金面上项目(2021CFB149)资助。
收稿日期 2023-09-13
改稿日期 2023-11-16
陈 彬 男,1989年生,博士,副教授,研究方向为电力装备电磁特性模拟与测量技术、电工新材料综合特性模拟与测量技术等。E-mail: chenbin@ctgu.edu.cn(通信作者)
姜鹏飞 男,1998年生,硕士研究生,研究方向为高频磁心损耗的模拟和空心变压器的优化设计等。E-mail: 2308679871@qq.com
(编辑 崔文静)