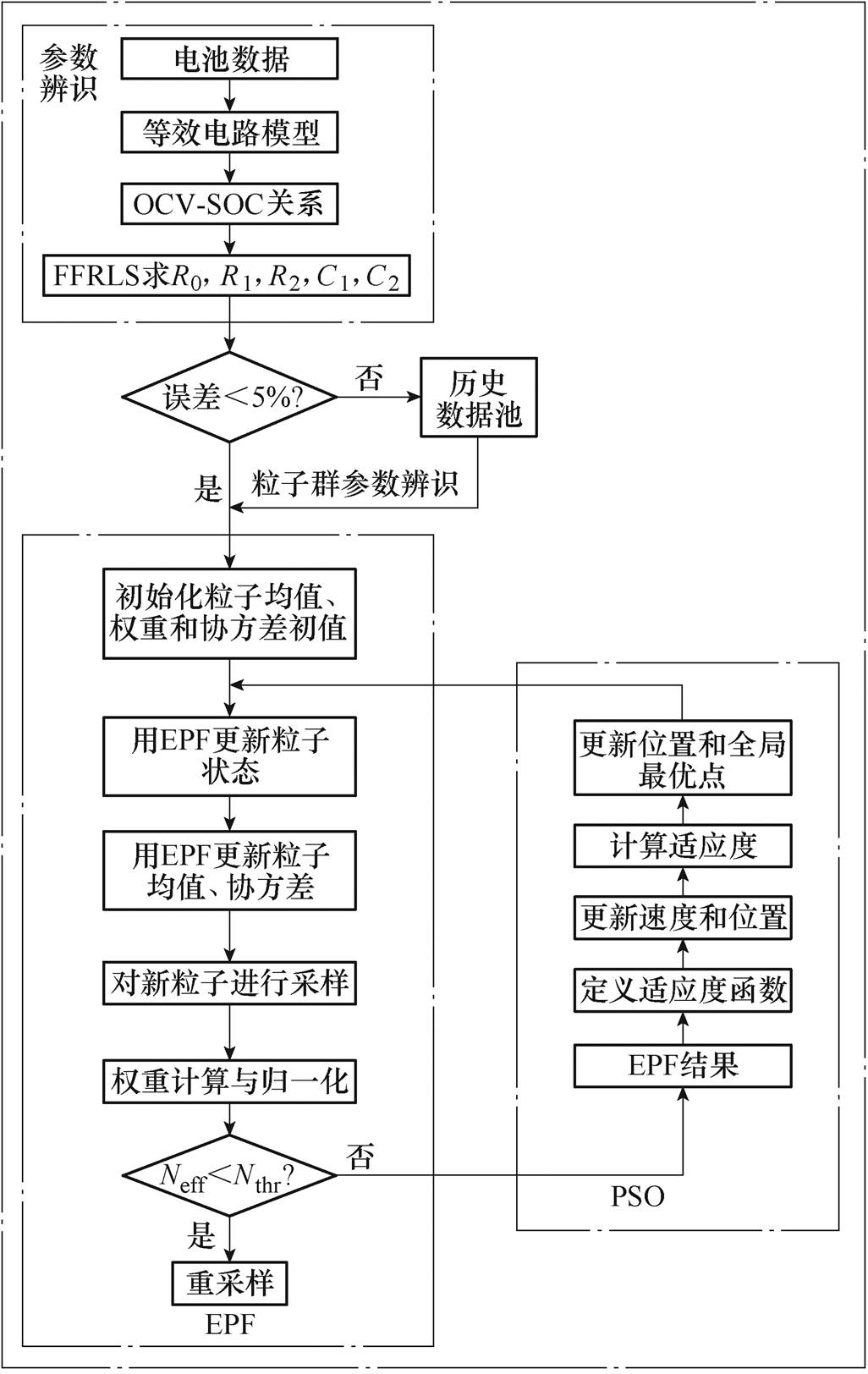
图1 PSO-EPF流程
Fig.1 PSO-EPF flow chart
摘要 提高参数辨识的精度和SOC算法的精度是提高SOC估计的关键，该文提出了基于联合参数辨识的粒子群优化扩展粒子滤波的荷电状态（SOC）估计方法。在参数辨识阶段，结合遗忘因子递推最小二乘法在线辨识的优势，弥补粒子群辨识精度高但前期缺乏数据无法实时辨识的劣势，联合进行参数辨识；在SOC估计阶段，利用扩展卡尔曼滤波生成重要性密度函数，去克服粒子退化，同时采用粒子群优化算法优化重采样策略改进采样过程缓解粒子贫化。最后在联邦城市运行（FUDS）和US06高速公路运行（US06）工况下将所提算法与F-PF、F-PSO-PF、FPSO-PSO-PF进行了对比，结果表明，在FUDS工况下，方均根误差分别提高了65.4%、56.3%和43.5%；在US06工况下，方均根误差分别提高了45.8%、35.9%和35.1%，验证了所提算法具有较好的适应性和鲁棒性。
关键词：锂电池 粒子群算法 扩展粒子滤波算法 荷电状态
随着燃油车对环境污染的加剧，电动汽车因其低噪声、低排放、能源效率高等特点越来越成为道路的主要交通工具之一[1]。目前，电动汽车的储能装置还是以锂离子电池为主，准确的荷电状态（State of Charge, SOC）对于电池管理系统实时监控电池的状态起到很重要的作用，研究锂电池的SOC对于电动汽车的安全行驶以及缓解续航焦虑有着非常重要的意义[2]。因此，对SOC的研究一直是学术界和汽车界研究的热点。
目前基于锂电池SOC的预测方法主要有安时积分法、基于数据驱动的方法和基于模型驱动的方法。安时积分法是应用广泛的一种方法[3]，在充放电阶段具有较高的精度，但是存在初值难以确定以及累计误差的问题。基于数据驱动的方法主要有神经网络方法[4]和随机森林方法[5]。数据驱动的方法通过样本数据的学习可以获得较高估计精度，但其对训练数据的数量和质量要求较高[5]。
与数据驱动方法不同的是，基于模型的方法不需要大量的数据训练，因而一直是众多研究人员研究的热点。基于模型的方法和所建模型以及辨识的参数精度有着直接的关系，目前基于模型的参数辨识方法有递推最小二乘法[6]、遗传算法[7]和粒子群算法[8]等。锂电池具有较强的非线性特性，模型参数会随着SOC的变化而变化，遗忘因子递推最小二乘法（Forgetting Factor Recursive Least Square, FFRLS）可以较好地进行参数的在线辨识，但是在低SOC区域参数会有较大波动，这也是SOC估计出现误差较大的区域[9]。群智能算法在参数辨识上取得了不错的效果，粒子群（Particle Swarm Optimi- zation, PSO）算法相较于遗传算法，参数更少、收敛更快、实现更容易，但由于前期缺少训练数据，更多适用于离线系统。所以在本文中，结合了FFRLS和PSO两者的优点，采用联合方法进行参数的辨识，在前期（误差小于5%）采用FFRLS进行在线辨识，在参数辨识的同时记录历史电压为粒子群；在后期（误差大于5%时）进行参数辨识积攒了训练所需的数据，PSO辨识的参数为固定参数，虽然得不到最优解，但是可以避免FFRLS在后期参数突变导致滤波产生更大的误差。
常见的基于模型的方法主要是基于卡尔曼滤波的方法[10-13]。扩展卡尔曼滤波（Extended Kalman Filter, EKF）[10]利用泰勒级数展开将非线性系统线性化，然后采用卡尔曼滤波对系统的状态进行估计，但是非线性系统在线性化过程中将引入线性化误差。无迹卡尔曼滤波（Unscented Kalman Filter, UKF）[11]通过无迹变换来取代EKF中的局部线性化，由于不需要计算Jacobian矩阵，会比EKF具有更小线性化误差，能够以至少二阶泰勒精度逼近非线性系统。UKF可以提高电池SOC的估计精度，但有可能因为误差协方差矩阵出现非正定矩阵而导致滤波发散[12]。EKF和UKF受高斯系统的限制，而粒子滤波（Particle Filter, PF）[13]可以用于非高斯系统中，其适应场合更广，但由于粒子退化以及重要密度函数等因素，粒子滤波在应用中估计效果并不理想。如何解决粒子退化和重要性密度函数已成为一个广泛关注的问题，文献[14]提出了采用遗传算法和粒子滤波结合的方法去改善粒子退化，增加粒子多样性，通过选择高质量的粒子去增加估计的精度，但试验工况较单一，没有显示不同温度时算法的性能[14]。文献[15]针对粒子退化问题，提出了改进重要性密度函数的辅助粒子滤波算法，主要适用于中、高SOC区域，在低SOC区域的精度有待进一步分析[15]。以上针对PF的研究取得了一些成果，但大都未考虑在低SOC区域参数辨识失准的情况以及不同温度工况下算法的适应性。
针对FFRLS在低SOC区域参数辨识准确度低以及粒子滤波存在的粒子退化和粒子短缺问题，本文提出了基于联合参数辨识的粒子群优化扩展粒子滤波的锂电池荷电状态估计方法，并对其在多工况、多温度条件下的适应性进行了研究。图1所示为粒子群优化-扩展粒子滤波（PSO-Extended Particle Filter, PSO-EPF）算法的流程示意图。首先建立了二阶等效电路模型，联合FFRLS和PSO进行模型参数的辨识，然后以辨识的参数为基础，通过EKF对粒子进行更新并将最后得到的近似后验概率作为PF的重要密度函数，去克服粒子退化，同时引入粒子群算法对粒子滤波重采样过程进行优化，增加粒子的多样性，解决粒子贫化问题。最后将本文提出的粒子群优化-扩展粒子滤波（PSO-EPF）算法和PF以及PSO-PF算法进行了比较，进而验证本文算法的鲁棒性和泛化能力。
图1 PSO-EPF流程
Fig.1 PSO-EPF flow chart
电池的等效电路模型能准确地表征锂电池的外部特征，同时计算量较小，锂电池的二阶RC等效电路模型如图2所示。
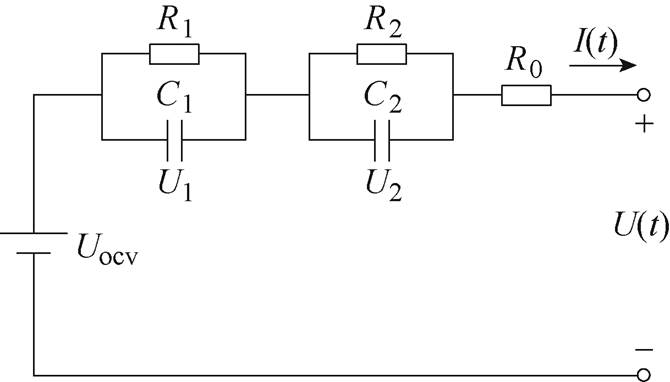
图2 二阶RC等效电路模型
Fig.2 Second order RC equivalent circuit model
图2中，Uocv为电池开路电压，U(t)为端电压，R0为电池欧姆内阻，I(t)为工作电流，R1、C1分别为电池极化电阻和极化电容，R2、C2分别为浓差极化电阻和浓差极化电容，U1、U2对应两个回路的电压，由电路模型可得
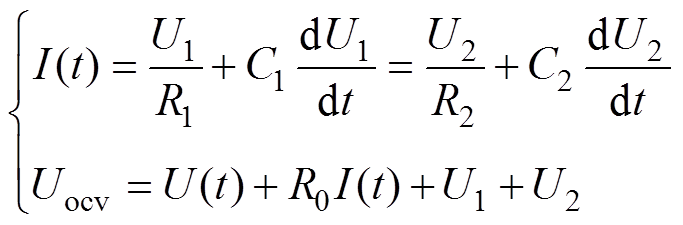（1）
选取SOC、U1、U2作为系统的状态变量，可得式（2）和式（3）电池的状态方程和观测方程。
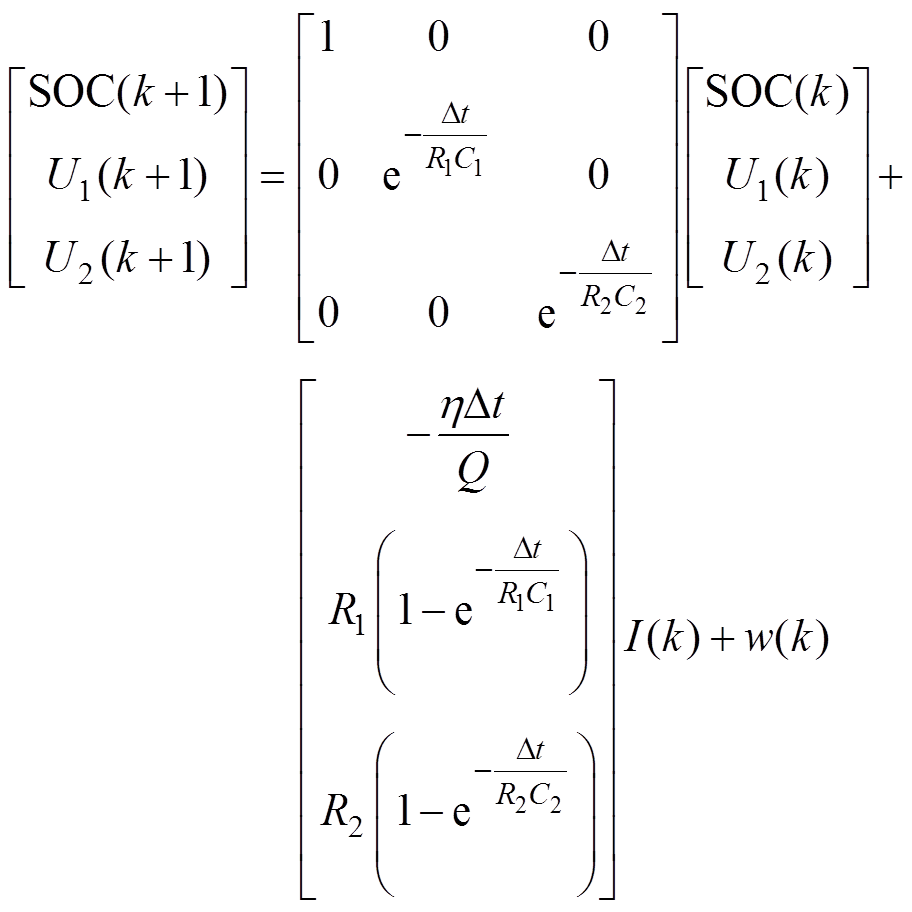（2）
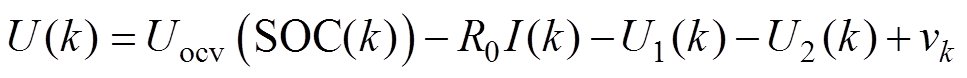（3）
式中，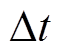
为采样周期；Q为电池容量；k为离散时间；
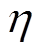为充放电效率；SOC(k)为k时刻的电池SOC；I(k)为k时刻的电流；
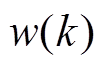为过程噪声；
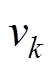为测量噪声。
马里兰大学18650电池在25℃时混合功率脉冲特性（Hybrid Pulse Power Characteristic, HPPC）实验的电压和电流如图3所示。利用Matlab中多项式拟合函数ployfit对OCV-SOC曲线进行六阶多项式拟合，拟合曲线如图4所示。
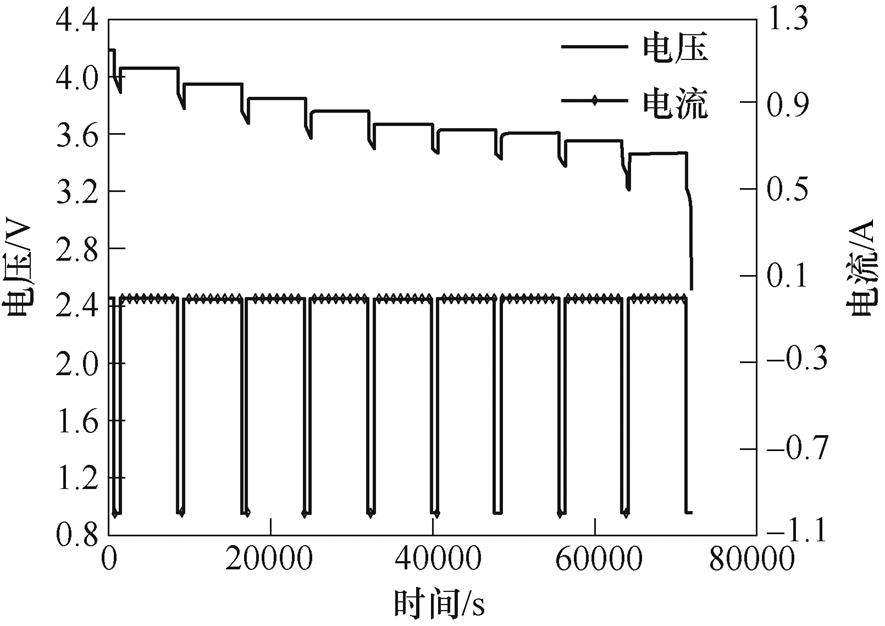
图3 HPPC实验的电流和电压
Fig.3 Current and voltage of HPPC test
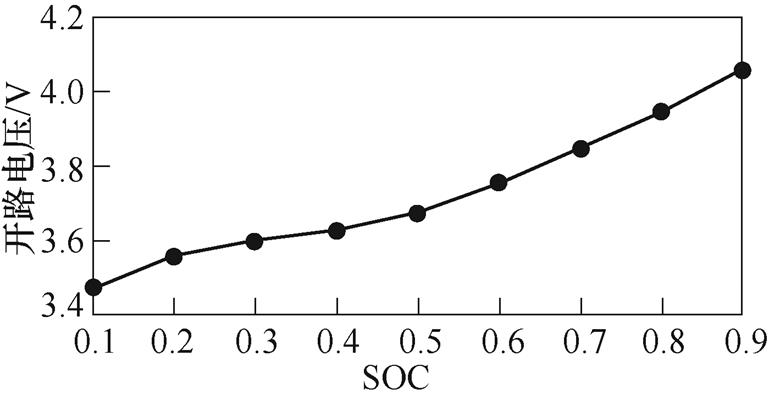
图4 OCV-SOC拟合曲线
Fig.4 OCV-SOC fitting curve
图4中六阶多项式拟合曲线的表达式为
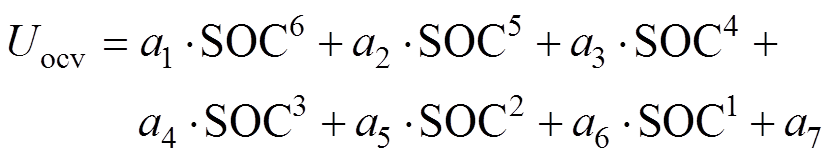（4）
式中，a1～a7为拟合参数。
为了对电路模型进行参数辨识，根据二阶RC等效电路模型，Uocv可以描述为
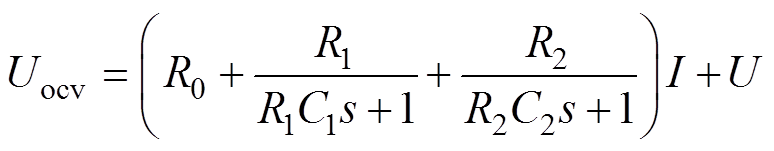（5）
令时间常数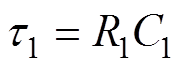
，
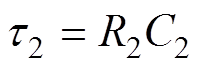，则式（5）为
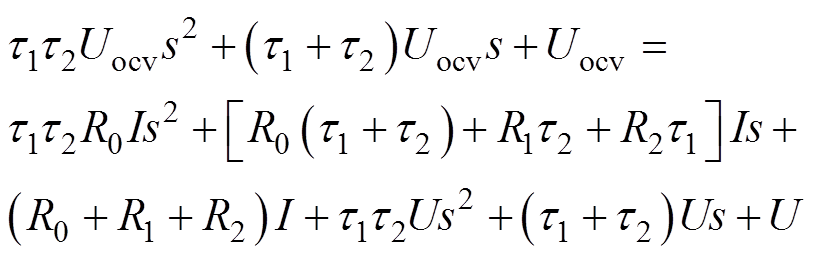（6）
设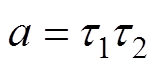
，
，
，
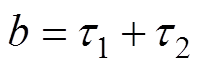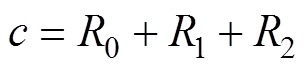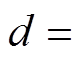
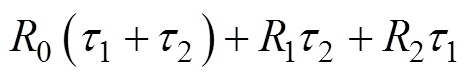，则式（6）可以简化为
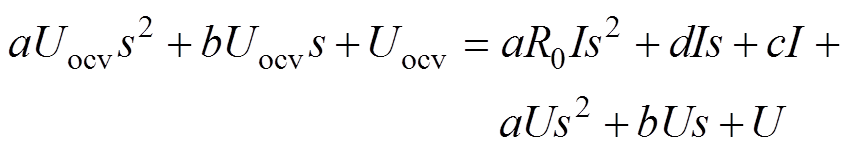（7）
将
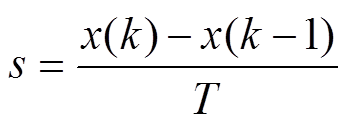
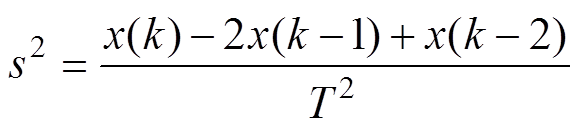
代入式（7）后进行离散化处理，整理后可得
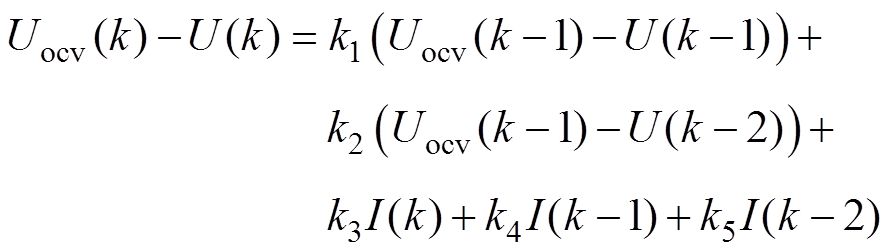（8）
遗忘因子递推最小二乘法是一种基于自适应滤波理论的模型参数辨识算法，通过对参数不断修正和更新，从而实现参数的实时估计。
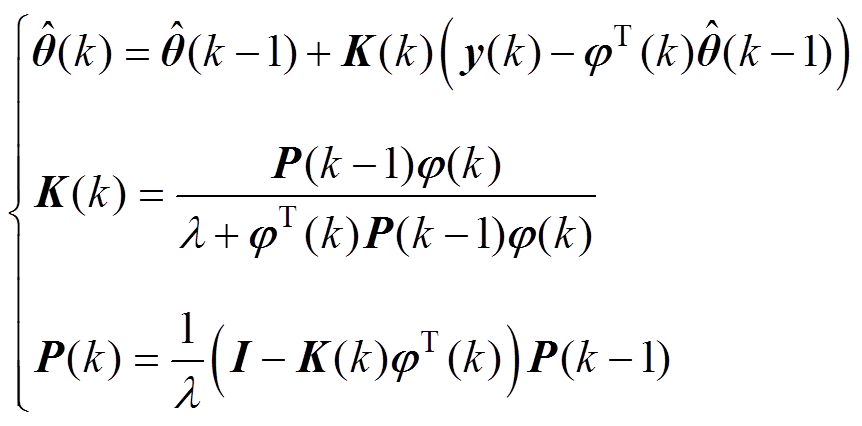（9）
式中，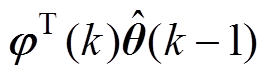
为观测值的预测结果，其中
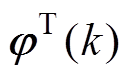为式（8）的转置向量，
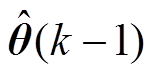为式（8）的系数向量；
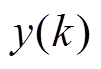为实际观测值；
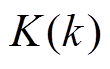为增益项；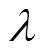
为遗忘因子，通常在0.95≤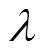≤1范围内；
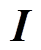为相应维数的单位矩阵；
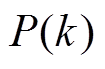为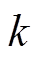
时刻的协方差。
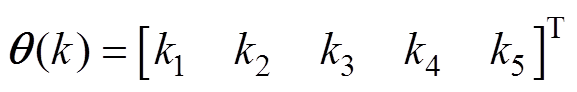（10）
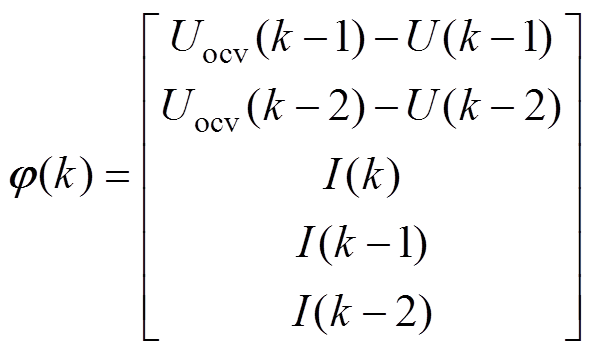（11）
将式（8）、式（10）、式（11）代入FFRLS方法中，进行参数辨识，辨识的参数包括电池欧姆内阻R0、极化电阻R1、极化电容C1、浓差极化电阻R2、浓差极化电容C2。
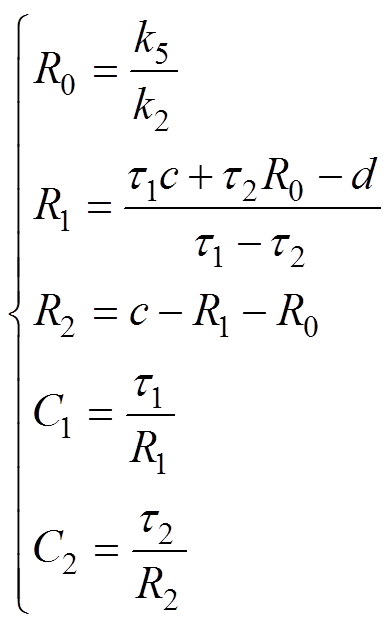（12）
在确定了电池的等效电路以后，需要对模型参数[R0 R1 C1 R2 C2]进行辨识，群智能算法[8]已经被用于参数辨识领域，在本研究中，在误差小于5%时采用FFRLS，在误差大于5%时，采用了PSO算法通过历史电压去获得模型参数。
考虑到电池模型是二阶等效电路模型，目标变量为[R0 R1 C1 R2 C2]，目标函数是真实电压和预测电压之间的误差值，目标函数表示为
（13）
式中，N为电压数据的样本量；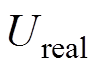
和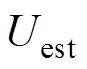
分别为真实电压值和预测电压值。
粒子滤波方法[16]是一种基于贝叶斯估计和蒙特卡罗方法的近似值求解方法，其基本思想是：首先依据系统状态向量的经验条件分布，在状态空间产生一组随机粒子，并以粒子代替积分运算，然后根据观测量，不断地调整粒子的权重和位置，通过调整后的粒子信息修正最初的条件分布。在锂电池SOC估计中，PF的状态方程和观测方程为
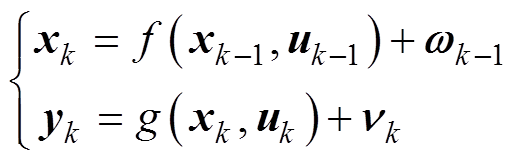（14）
式中，xk为系统的状态向量，在电池系统中表示SOC；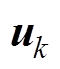
为电池电流；
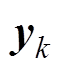为系统的测量向量，表示端电压；
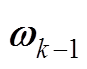和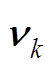
为过程噪声和测量噪声。
实施的主要步骤如下：
（1）初始化权值，SOC初始粒子是随机生成的。
（2）重要性抽样，从重要性密度函数中收集样本。
（3）权值归一化计算。
（4）重采样阶段，计算有效粒子。
（5）输出预测值。
为了解决PF算法中粒子退化的问题，将EKF算法作为一种重要性密度函数替代先验密度函数来实现粒子滤波算法，这种改进算法称为扩展粒子滤波（EPF）算法。EPF在状态预测阶段采用EKF来更新采样粒子，更新后的采样粒子包含了最新时刻的观测信息，使得这些采样粒子能更好地接近真实的分布，因而能够提高粒子滤波算法的精度。
为了克服在重采样过程中的粒子贫化问题，在EPF算法中引入了粒子群算法[17]，将EPF算法的输出作为PSO算法的输入，通过粒子的移动，搜索并更新粒子在重要性密度函数中的最优位置，驱动粒子移动到系统的最优位置，最终使粒子不断向真实值靠近。通过引入粒子群算法对重采样过程进行优化，增加粒子的多样性，从而解决粒子贫化问题。提出的组合算法（PSO-EPF）通过同时改进了粒子滤波的重要性密度函数和重采样过程，来改善粒子滤波算法的性能。
粒子群优化扩展粒子滤波算法的步骤如下。
1）初始化。
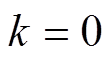时，构造采样点集
，
，
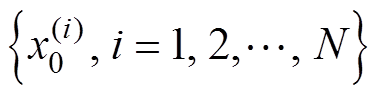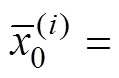
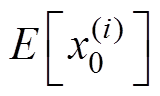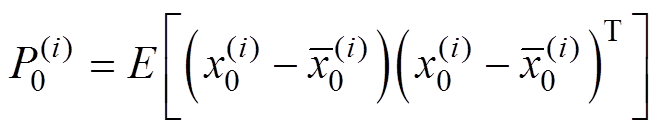，重要性权值
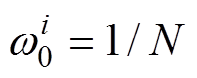。其中，E[×]表示数学期望。
2）重要性采样。
For k=1
T, For i=1N用EKF递推公式更新采样粒子
状态预测
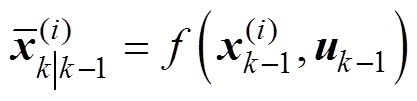（15）
式中，f(·) 为状态函数。
协方差预测
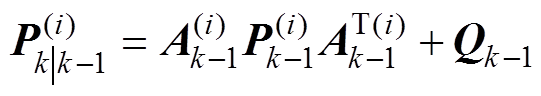（16）
式中，A为状态方程系数矩阵；P为误差协方差矩阵；Q为过程噪声的协方差矩阵；R为测量噪声的协方差矩阵。
卡尔曼增益
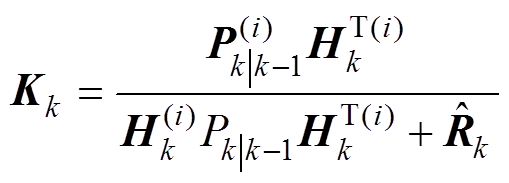（17）
式中，K为卡尔曼增益；H为观测方程的系数矩阵。
状态更新
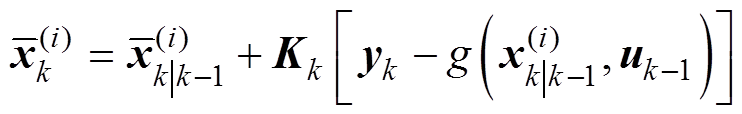（18）
式中，g(·)为观测函数。
协方差更新
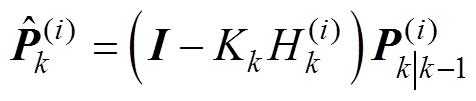（19）
采用粒子滤波算法计算权重并更新粒子
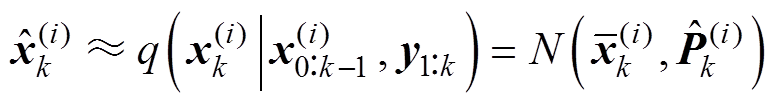（20）
3）计算权重和归一化。
For i=1N，计算粒子的权值
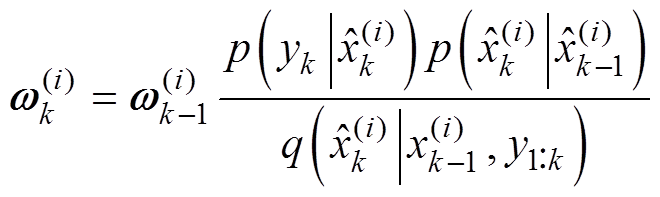（21）
式中，p(·)为后验概率分布；q(×)为先验概率分布。
For i=1N，归一化权值
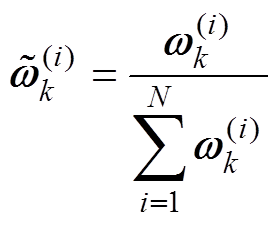（22）
4）计算有效粒子数。
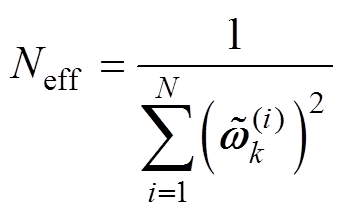（23）
如果Neff＜Nthr（Nthr为粒子数阈值），则进行重采样，否则转到步骤6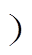
。
5）粒子群优化算法。
粒子群优化（PSO）算法不仅考虑了个体的位置信息，同时考虑速度信息，根据个体和群体的最优解更新位置和速度，粒子优化步骤如下：
（1）首先建立适应度函数。
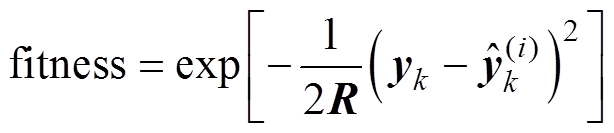（24）
式中，R为测量噪声方差；yk为k时刻测量值；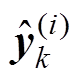
为第i个粒子预测测量值。粒子群优化算法通过计算适应度函数选择粒子的最优值来更新位置。
（2） 将EPF生成的样本集作为PSO的初始位置。
（3）根据式（25）更新每个粒子的速度和位置，并计算每个粒子的适应度值，根据适应度值，更新粒子个体和全局最优值，最终通过移动粒子向最优粒子靠近，获得最优估计值。
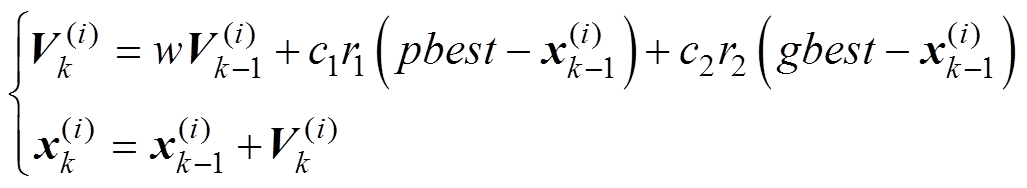（25）
式中，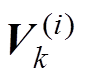
为第i个粒子k时刻的移动速度；
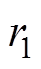和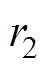
为0～1上的随机数；
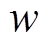为惯性权重；
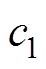和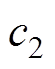
为学习因子；
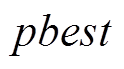为粒子个体最优解；
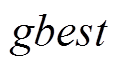为全局最优解。
（4）最大迭代次数达到时，停止搜索。
6）输出预测值。
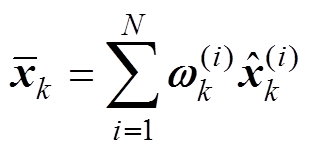（26）
式中，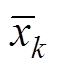
为k时刻SOC预测值。
本文中的锂离子电池数据来源于美国马里兰大学先进寿命周期工程中心（Center for Advanced Life Cycle Engineering, CALCE）电池组开源实验数据集（https://web.calce.umd.edu/batteries/data.htm），试验平台包括18650镍钴锰酸锂（LNMC）/石墨锂离子单体电池（2 A×h）、温度试验箱、Arbin BT2000电池测试系统和带有Arbin软件的计算机。本文选择联邦城市运行（FUDS）和US06高速公路运行（US06）工况在0℃、25℃、45℃的实验数据来验证本文SOC估计算法，电池初始SOC为0.8。
以FUDS 0℃为例采用基于联合参数辨识的PSO- EPF算法进行荷电状态估计，在前期采用FFRLS进行辨识参数，在误差大于5%时启动PSO进行参数辨识，如图5所示。
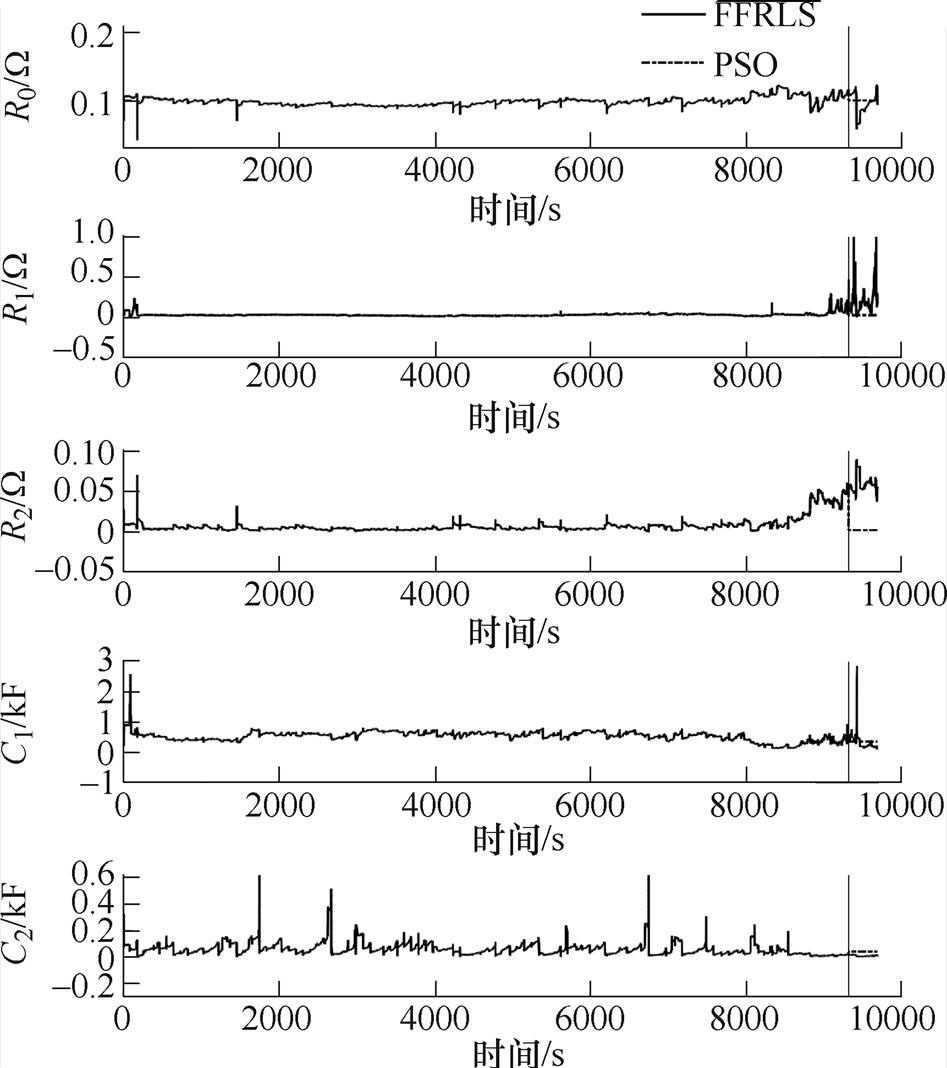
图5 FUDS 0℃工况下联合参数辨识
Fig.5 Joint parameter identification under FUDS at 0℃
图5中，PSO辨识的参数是固定值，即PSO-EPF在误差大于5%时，采用PSO辨识的固定参数进行荷电状态估计，PSO辨识的参数忽略了其时变特性。这样的好处是FFRLS在后期辨识的参数突变时，可以用粒子群辨识的固定参数继续进行计算，虽然达不到最优解，但是可以避免FFRLS在后期参数突变导致滤波产生更大的误差。
为了验证所提算法的可行性，在FUDS工况0℃、25℃、45℃三种温度下对PF、PSO-PF和PSO-EPF进行了对比，算法均是在二阶等效电路模型下进行的，图中算法1（F-PF）是基于FFRLS参数辨识的PF估计，算法2（F-PSO-PF）是基于FFRLS参数辨识的PSO-PF估计，算法3（FPSO-PSO-PF）是基于联合参数辨识的PSO-PF估计，算法4（FPSO- PSO-EPF）是基于联合参数辨识的PSO-EPF估计。图6～图11为算法在三种温度下SOC预测曲线和其对应的SOC预测误差曲线。
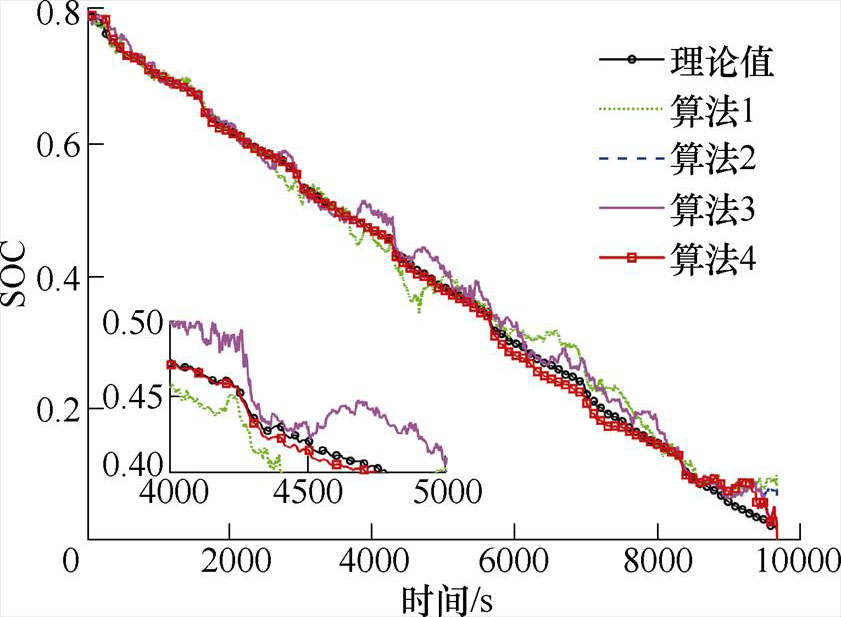
图6 FUDS 0℃工况下不同算法预测曲线
Fig.6 Different algorithms predict curves under FUDS at 0℃
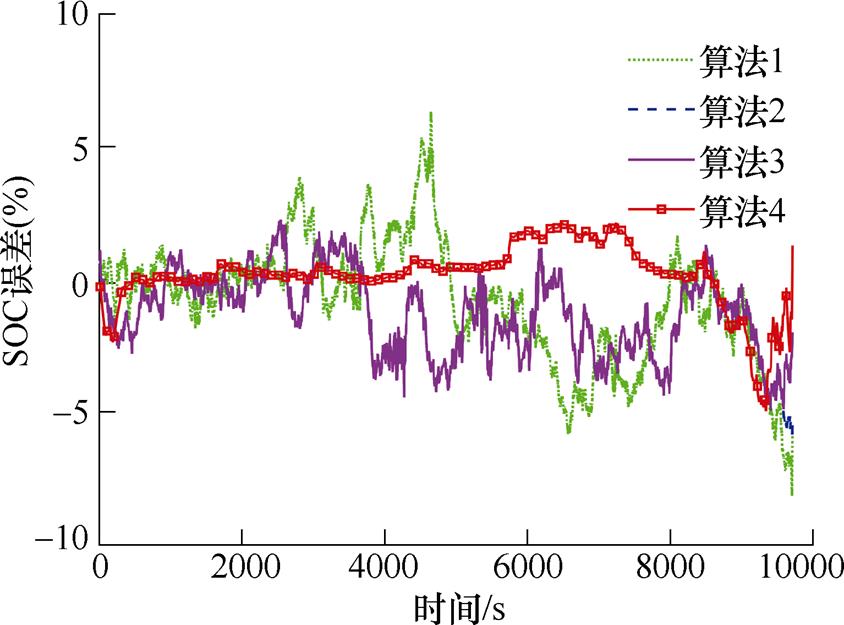
图7 FUDS 0℃工况下不同算法预测误差曲线
Fig.7 Different algorithms predict error curves under FUDS at 0℃
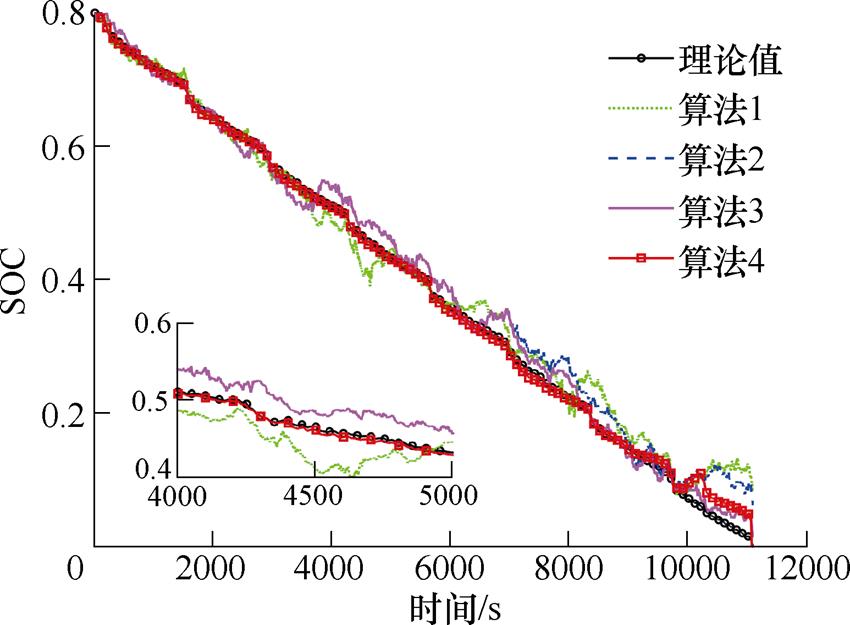
图8 FUDS 25℃工况下不同算法预测曲线
Fig.8 Different algorithms predict curves under FUDS at 25℃
从图6～图9可以看出，在FUDS 0℃和25℃工况下，基于FFRLS的PF和PSO-PF（算法1和算法2）在中期和后期波动都较大，基于联合参数辨识的PSO-PF（算法3）减弱了后期的波动幅度，而基于联合参数辨识的PSO-EPF（算法4）在前期波动较小，跟踪效果较好，在SOC处于0.05附近出现较大误差，经过粒子群重新辨识参数进行估计后，很快收敛。从图10和图11可以看出，在45℃时，PF和PSO-PF（算法1和算法2）在SOC估计中期出现较大误差，而PSO-EPF（算法4）总体较平稳，虽然在末期出现一点波动，但误差较小，且很快收敛。
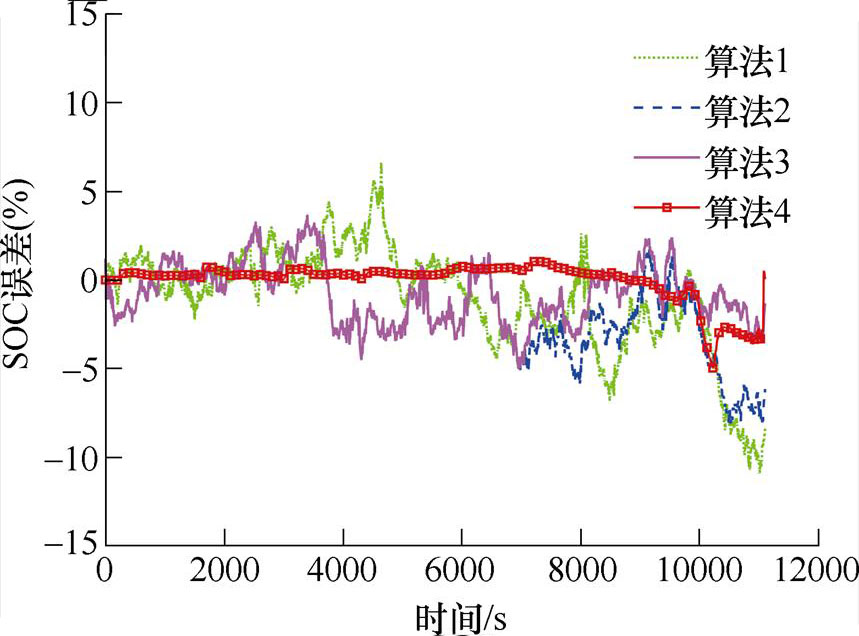
图9 FUDS 25℃工况下不同算法预测误差曲线
Fig.9 Different algorithms predict error curves under FUDS at 25℃
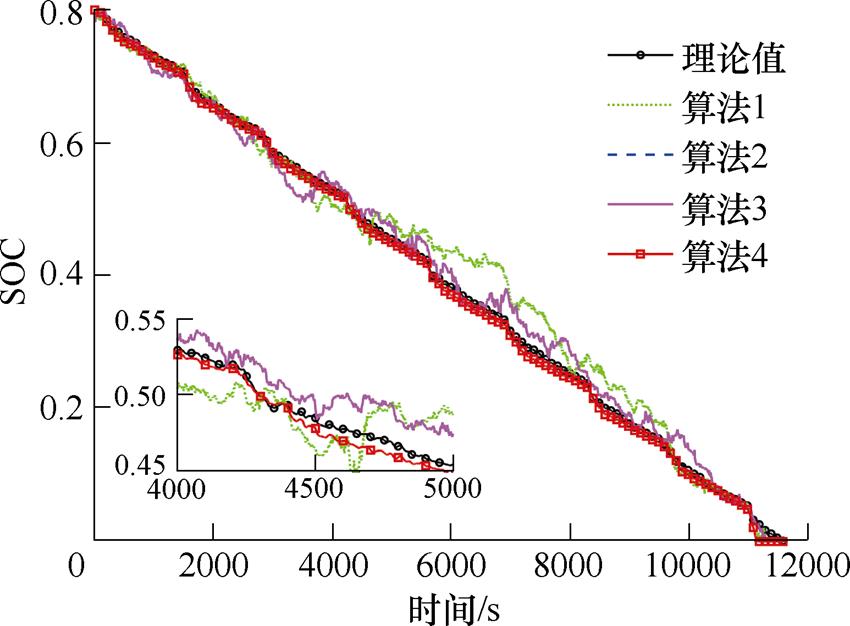
图10 FUDS 45℃工况下不同算法预测曲线
Fig.10 Different algorithms predict curves under FUDS at 45℃
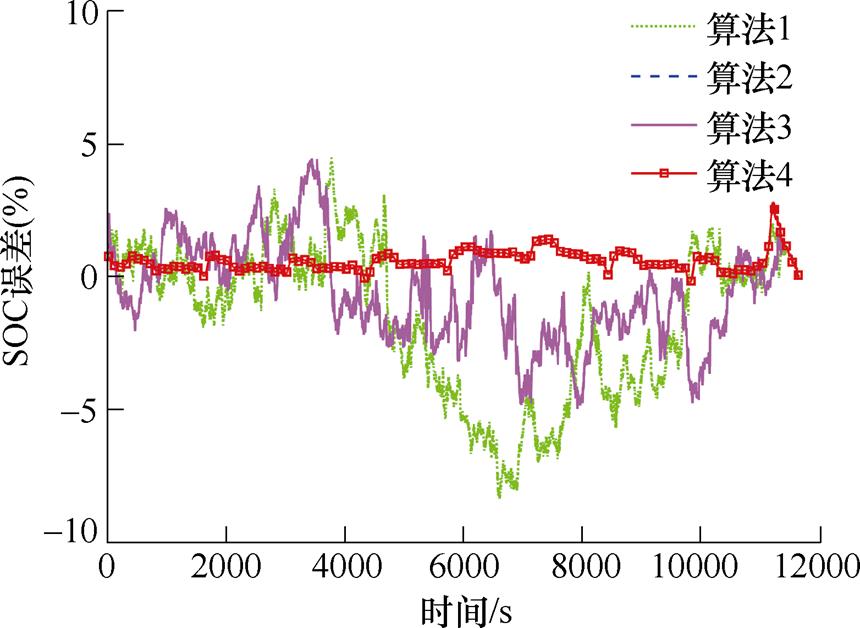
图11 FUDS 45℃工况下不同算法预测误差曲线
Fig.11 Different algorithms predict error curves under FUDS at 45℃
表1是算法在FUDS不同温度下的统计指标对比，粒子群算法对PF是起到了一定的效果，克服了部分粒子退化问题，但在0℃和25℃下还是存在误差过大的情况，经过联合参数辨识算法后，可以把误差控制在5%之内。在45℃工况下，基于FFRLS的PSO-PF（算法2）的准确度在5%之内，所以没有启动PSO进行参数辨识，算法2和算法3的数值是一样。经过联合参数辨识后PSO-PF（算法3）也可以提升准确度到5%之内，但经过EKF生成重要性密度函数后的PSO-EPF（算法4），相较于基于联合参数辨识的PSO-PF，三个指标有了进一步的提升。
表1 FUDS工况下统计指标对比
Tab.1 Comparison of statistical indicators under FUDS condition （%）
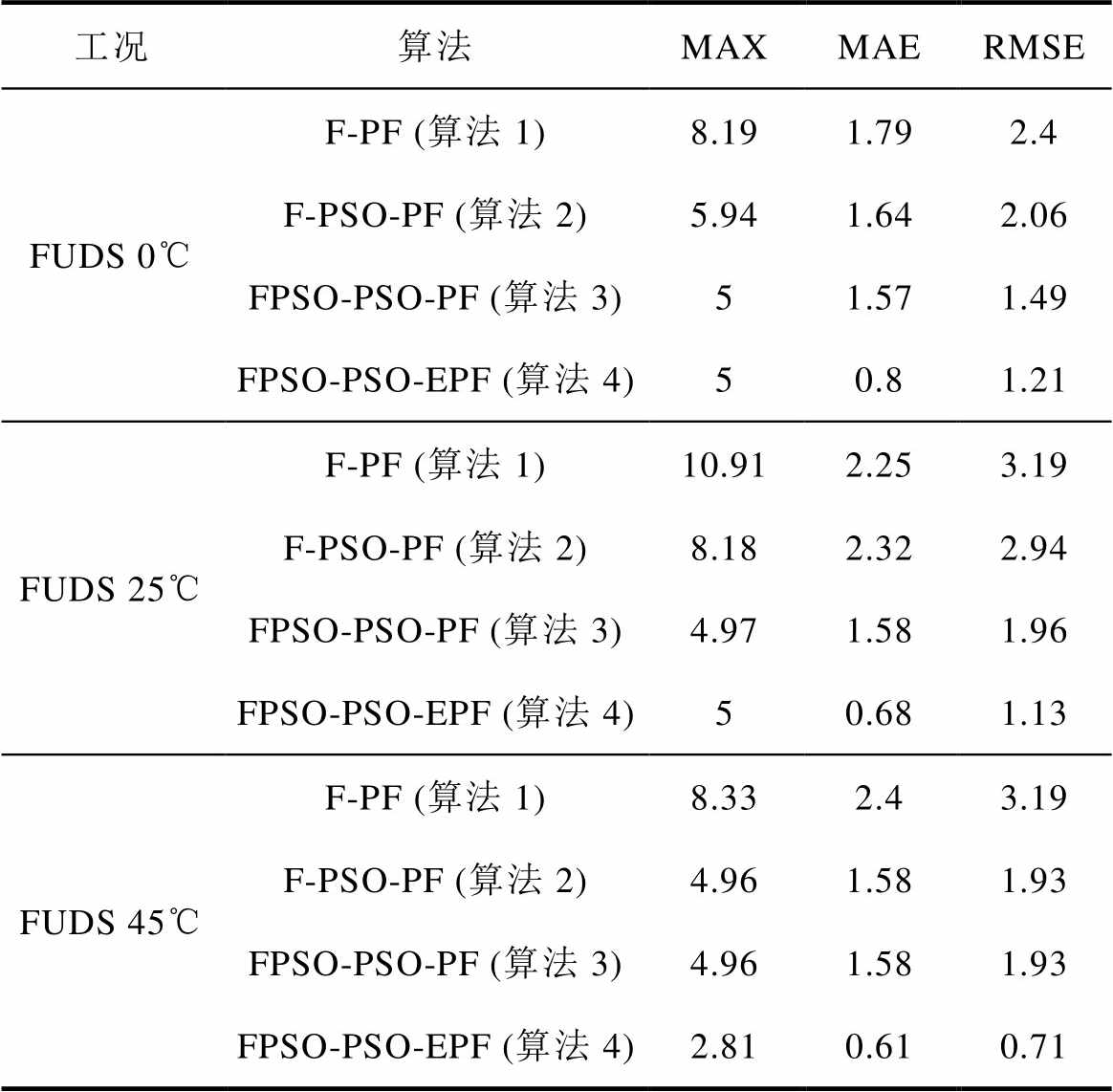
工况算法MAXMAERMSE FUDS 0℃F-PF (算法1)8.191.792.4 F-PSO-PF (算法2)5.941.642.06 FPSO-PSO-PF (算法3)51.571.49 FPSO-PSO-EPF (算法4)50.81.21 FUDS 25℃F-PF (算法1)10.912.253.19 F-PSO-PF (算法2)8.182.322.94 FPSO-PSO-PF (算法3)4.971.581.96 FPSO-PSO-EPF (算法4)50.681.13 FUDS 45℃F-PF (算法1)8.332.43.19 F-PSO-PF (算法2)4.961.581.93 FPSO-PSO-PF (算法3)4.961.581.93 FPSO-PSO-EPF (算法4)2.810.610.71
表2是三种温度平均指标对比结果，基于联合参数辨识的PSO-EPF（算法4）在三种统计指标上都获得了较好的提升，在最大误差上，基于联合参数辨识的PSO-EPF（算法4）比基于联合参数辨识的PSO-PF（算法3）平均提升了14.1%，比基于FFRLS的PSO-PF和PF（算法2和算法1）平均提升了32.9%和53.3%；在平均绝对误差（Mean Absolute Error, MAE）上，基于联合参数辨识的PSO-EPF（算法4）比基于联合参数辨识的PSO-PF（算法3）平均提升了56.05%，比基于FFRLS的PSO-PF和PF（算法2和算法1）平均提升了62.5%和67.8%；其方均根误差（Root Mean Square Error, RMSE），基于联合参数辨识的PSO-EPF（算法4）比基于联合参数辨识的PSO-PF（算法3）平均提升了43.6%，比基于FFRLS的PSO-PF和PF（算法2和算法1）平均提升了56.3%和65.4%。
表2 三种温度平均指标对比
Tab.2 Comparison of three temperature averageindicators （%）
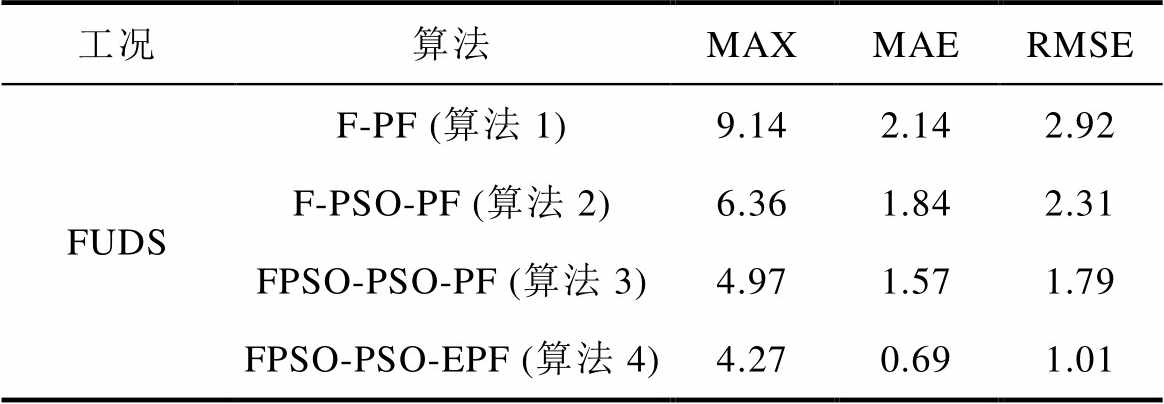
工况算法MAXMAERMSE FUDSF-PF (算法1)9.142.142.92 F-PSO-PF (算法2)6.361.842.31 FPSO-PSO-PF (算法3)4.971.571.79 FPSO-PSO-EPF (算法4)4.270.691.01
为了验证所提算法不同工况的适应性，在US06工况0℃、25℃、45℃三种温度下对PF、PSO-PF和PSO-EPF进行了对比。图12～图17为算法在三种温度下SOC预测曲线和其对应的SOC预测误差曲线。
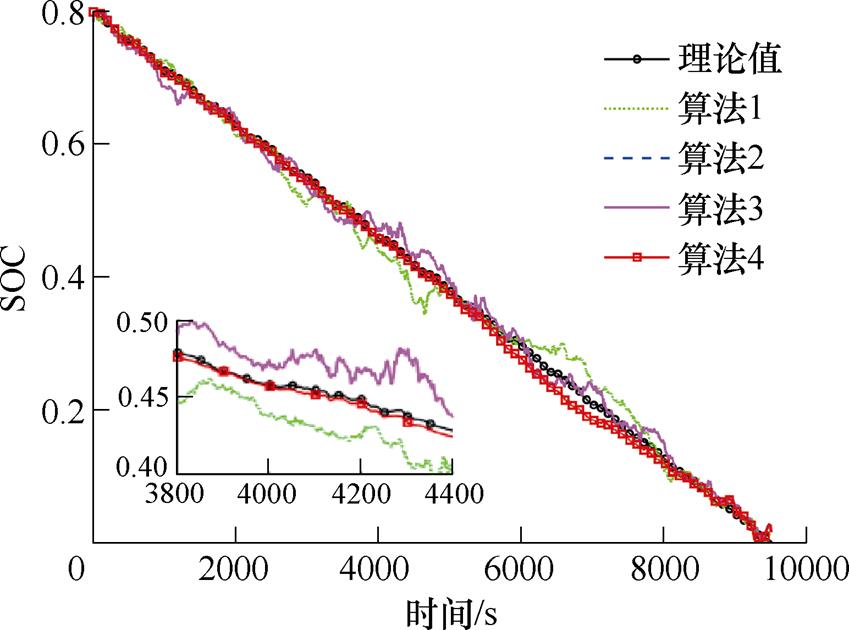
图12 US06 0℃工况下不同算法预测曲线
Fig.12 Different algorithms predict curves under US06 at 0℃
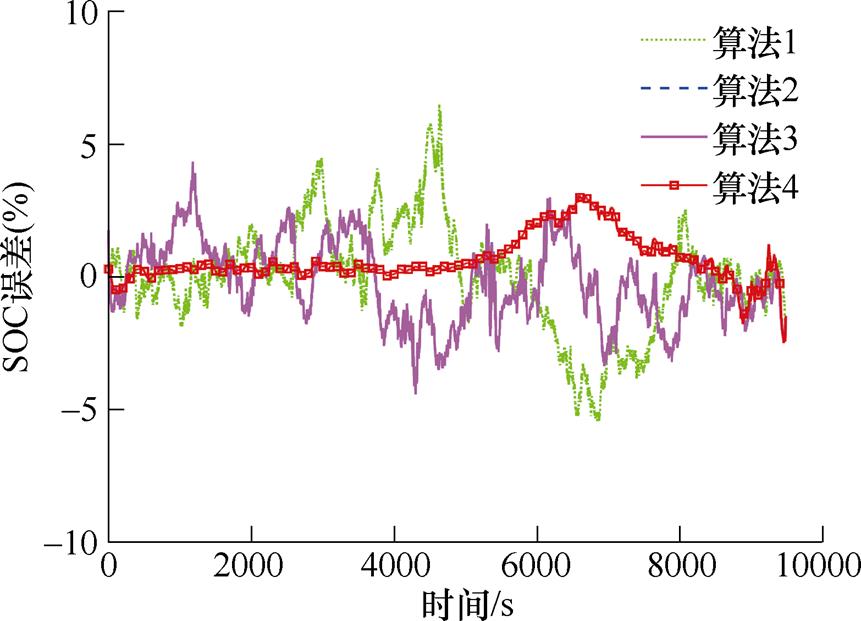
图13 US06 0℃工况下不同算法预测误差曲线
Fig.13 Different algorithms predict error curves under US06 at 0℃
从图12、图13以及图16和图17可以看出，在US06 0℃工况下，基于FFRLS的PF和PSO-PF（算法1和算法2）在中期波动都较大，基于联合参数辨识的PSO-EPF（算法4）总体波动较小，在US06 0℃工况中间阶段会有相对较大波动，在US06 45℃工况后期会有相对较大误差，但还在误差范围内。在US06 25℃工况下基于FFRLS的PF和PSO-PF（算法1和算法2）在中期和后期波动都较大，出现较大误差，基于联合参数辨识的PSO-PF（算法3）后期降低了波动，基于联合参数辨识的PSO-EPF（算法4）在前期较平稳，后期会有一个较大波动，但误差较小，且很快收敛。
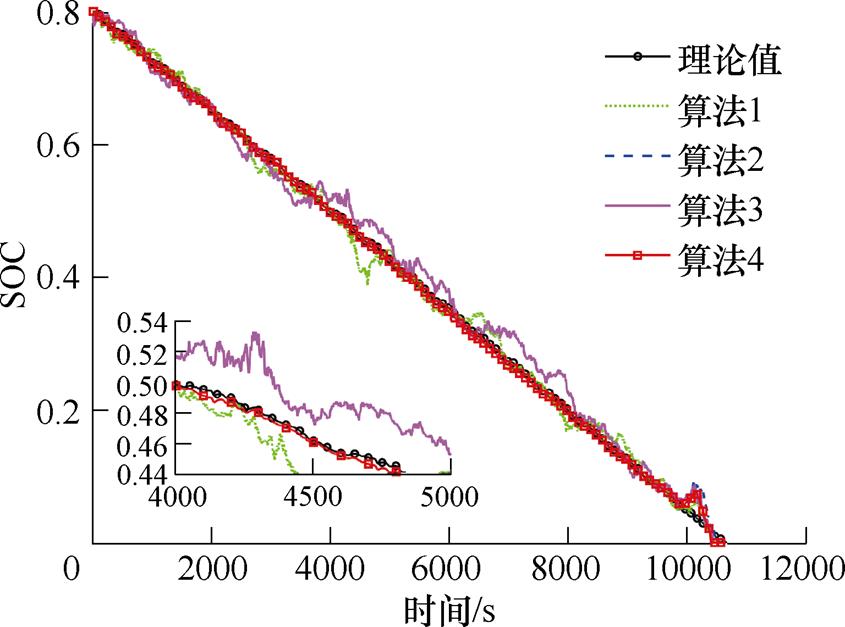
图14 US06 25℃工况下不同算法预测曲线
Fig.14 Different algorithms predict curves under US06 at 25℃
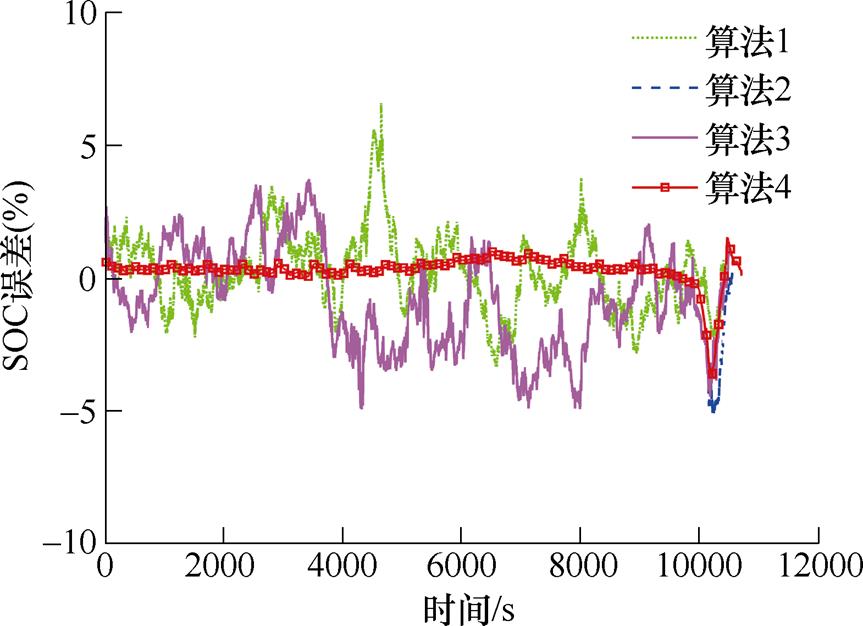
图15 US06 25℃工况下不同算法预测误差曲线
Fig.15 Different algorithms predict error curves under US06 at 25℃
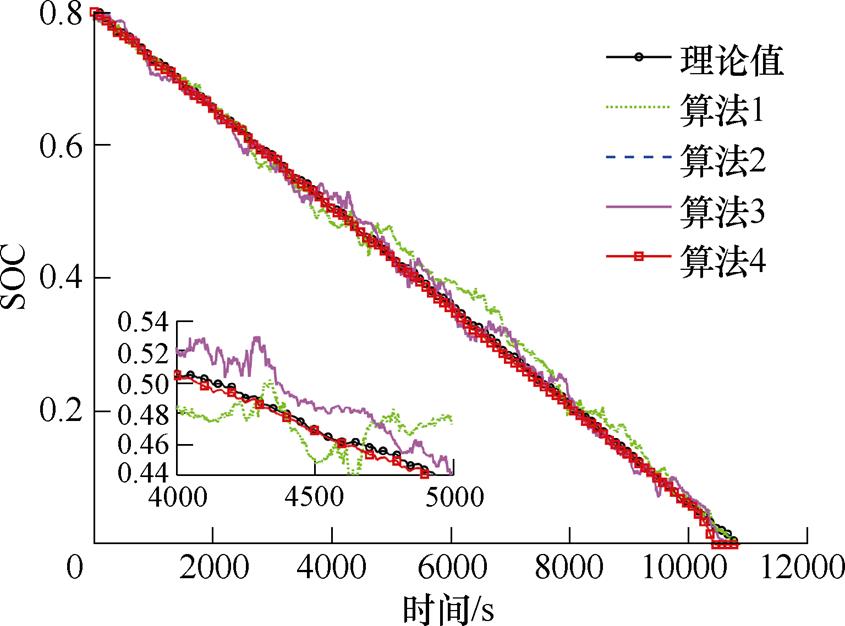
图16 US06 45℃工况下不同算法预测曲线
Fig.16 Different algorithms predict curves under US06 at 45℃
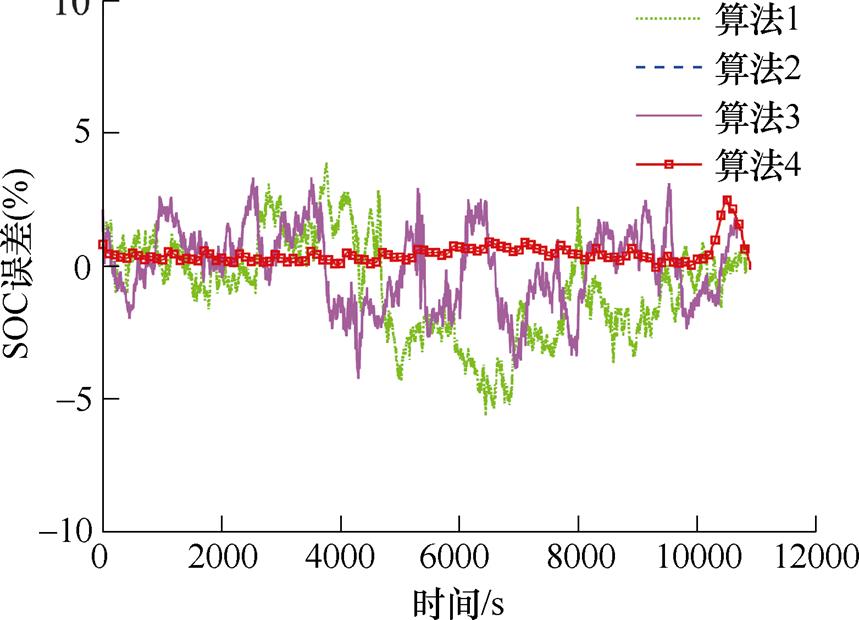
图17 US06 45℃工况下不同算法预测误差曲线
Fig.17 Different algorithms predict error curves under US06 at 45℃
表3是算法在US06工况下不同温度下的统计指标对比，同样可以看出粒子群算法对PF是起到了一定的效果，克服了部分粒子退化问题。在0℃和45℃，基于FFRLS的PSO-PF（算法2）误差较小，所以没有启动联合参数辨识。在25℃时，基于联合参数辨识的PSO-PF（算法3）虽然也可以把最大误差控制在5%附近，但经过EKF生成重要性密度函数后的PSO-EPF（算法4），MAE和RMSE的提升效果更加明显，MAE基本都在1%以内，RMSE除0℃外也在1%以内，相较于基于联合参数辨识的PSO-PF（算法3），基于联合参数辨识的PSO-EPF（算法4）的MAE和RMSE的提升效果更加明显。需要注意的是，基于FFRLS的PSO-PF（算法2）在25℃的MAE和RMSE分别为1.77%和2.13%，甚至比0℃时的估计结果差，这是因为用PF的时候，粒子是经过试参法得出的，可能是全局最优值，耗费了大量的时间，而PSO-PF（算法2）是使用粒子群优化（PSO）算法对粒子进行全局寻优，节省了大量的时间，但是PSO算法在其原理上存在陷入局部最优的可能性，导致选出的粒子并不是最优解，进而出现误差可能稍大一些的情况。
表3 US06工况下统计指标对比
Tab.3 Comparison of statistical indicators under US06 condition （%）
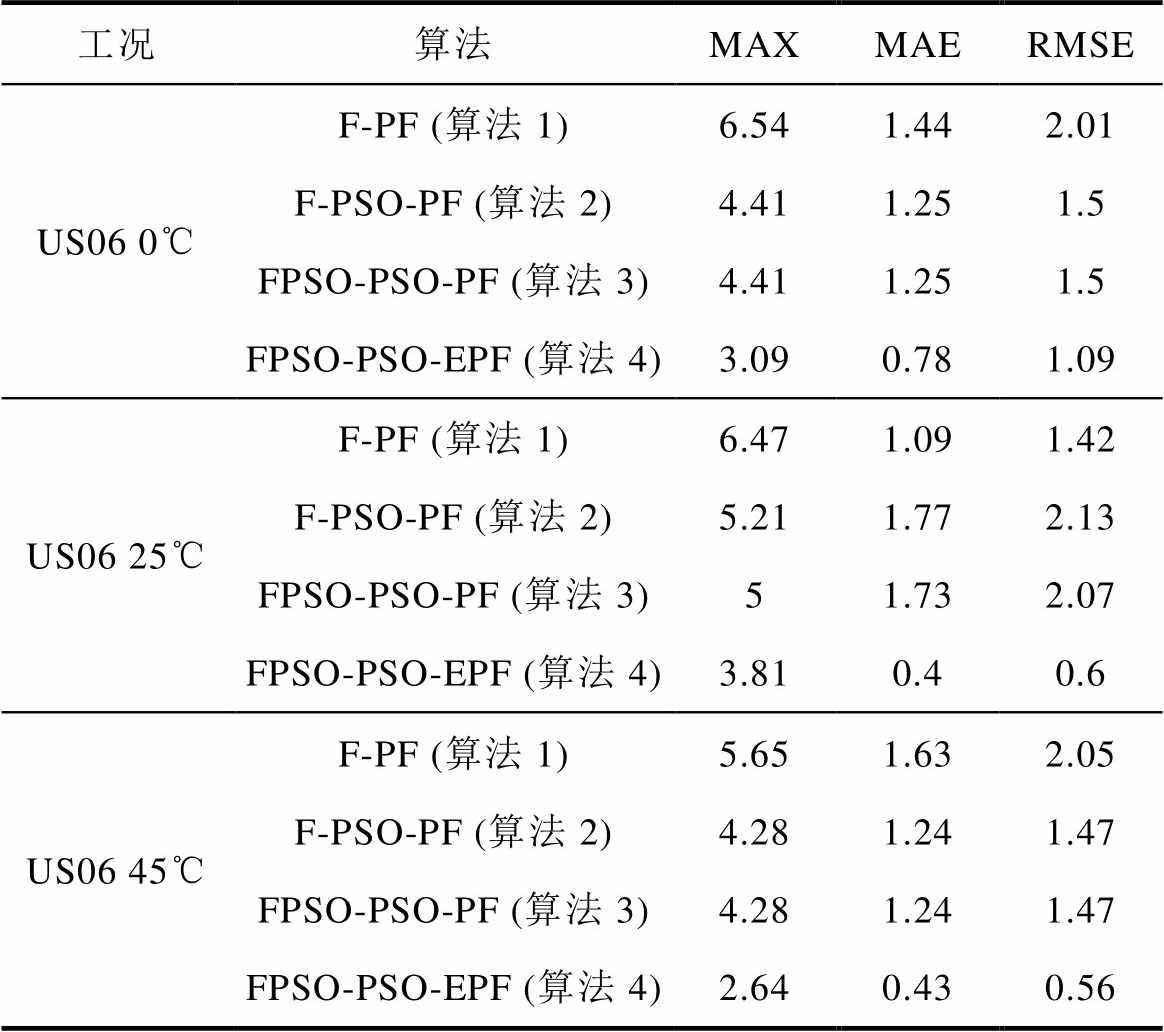
工况算法MAXMAERMSE US06 0℃F-PF (算法1)6.541.442.01 F-PSO-PF (算法2)4.411.251.5 FPSO-PSO-PF (算法3)4.411.251.5 FPSO-PSO-EPF (算法4)3.090.781.09 US06 25℃F-PF (算法1)6.471.091.42 F-PSO-PF (算法2)5.211.772.13 FPSO-PSO-PF (算法3)51.732.07 FPSO-PSO-EPF (算法4)3.810.40.6 US06 45℃F-PF (算法1)5.651.632.05 F-PSO-PF (算法2)4.281.241.47 FPSO-PSO-PF (算法3)4.281.241.47 FPSO-PSO-EPF (算法4)2.640.430.56
表4是算法三种温度平均指标对比结果，基于联合参数辨识的PSO-EPF（算法4）在三种统计指标上都获得了较好的提升，在最大误差上，基于联合参数辨识的PSO-EPF（算法4）比基于联合参数辨识的PSO-PF（算法3）平均提升了32.2%，比基于FFRLS的PSO-PF和PF（算法2和算法1）平均提升了33.3%和52.8%；在平均绝对误差上，基于联合参数辨识的PSO-EPF（算法4）比基于联合参数辨识的PSO-PF（算法3）平均提升了44.3%，比基于FFRLS的PSO-PF和PF（算法2和算法1）平均提升了45.1%和45.8%；在方均根误差方面，基于联合参数辨识的PSO-EPF（算法4）比基于联合参数辨识的PSO-PF（算法3）平均提升了35.1%，比基于FFRLS的PSO-PF和PF（算法2和算法1）平均提升了35.9%和45.8%。
表4 三种温度平均指标对比
Tab.4 Comparison of three temperature average indicators （%）
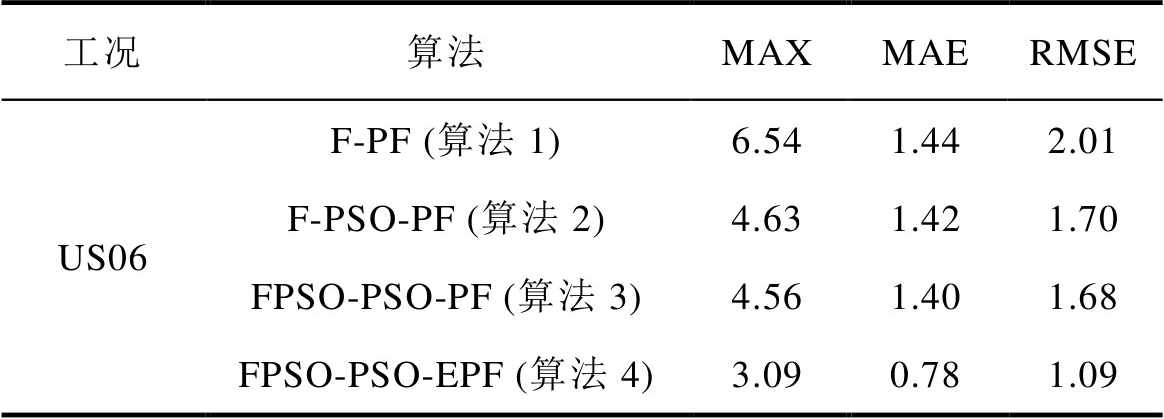
工况算法MAXMAERMSE US06F-PF (算法1)6.541.442.01 F-PSO-PF (算法2)4.631.421.70 FPSO-PSO-PF (算法3)4.561.401.68 FPSO-PSO-EPF (算法4)3.090.781.09
以上两种工况的结果显示，基于FFRLS参数辨的PSO-PF（算法2）比PF（算法1）准确度有所提升，证明了PSO可以增加粒子的多样性；而基于联合参数辨识的PSO-PF（算法3）比基于FFRLS的PSO-PF（算法2）准确度有提升，可见联合参数辨识方法是有效的；最后同样采用联合参数辨识方法的PSO-EPF（算法4）改进重要密度函数后比PSO-PF（算法3）三者指标均有所提升，验证了联合参数辨识方法以及粒子群优化扩展粒子滤波方法的有效性。
为了提高锂电池模型参数辨识的精度和SOC算法的估计精度，本文以电池二阶等效电路模型为基础，设计了以FFRLS和PSO联合参数辨识为基础的粒子群优化扩展粒子滤波的SOC评估算法。本文的主要结论如下：
1）针对FFRLS在低SOC区域的参数突变继而影响滤波效果的问题，在误差较大的低SOC区域，采用了PSO算法进行参数辨识，PSO以历史电压为输入，以最小压差为目标函数计算模型参数，相较于为了提高精度，把A工况的离线辨识的结果用到B工况进行在线估计的方法，联合参数辨识方法只需在一种工况即可进行。
2）针对PF在SOC估计中存在的粒子退化和粒子贫化问题，PSO-EPF利用EKF生成PF的重要性密度函数来克服粒子退化，同时在重采样过程中采用PSO算法缓解粒子贫化，仿真结果显示该方法具有较高的估计精度。
3）针对不同温度工况下的适应性问题，主要从优化算法本身以及在最容易产生累积误差的低SOC区域出发，在两种工况三种温度下的验证结果显示，提出的算法精度优于PF和PSO-PF，相较于很多关于SOC研究放电至20%的情况，该方法在低SOC区域显示了较好的效果，展现出了较强的鲁棒性和泛化能力。
本文在改进粒子滤波算法进行荷电状态估计上进行了一些研究，今后还需要从以下两个方面进行深入研究和探索：
1）研究基于容量和SOC关系的评估方案。随着电池的老化，电池容量必然也会发生改变，电池容量变化也会影响到荷电状态估计，考虑电池容量变化的SOC估计也是非常重要的。
2）研究基于电池组的SOC估计方法。单体电池的估计精度不能表征整个电池组的估计精度，从单体电池延伸到电池组，展开对电池组均衡管理技术的研究也是一个需要深入研究的方向。
参考文献
[1] 高德欣, 郑晓雨, 王义, 等. 电动汽车充电状态监测与多级安全预报警方法[J]. 电工技术学报, 2022, 37(9): 2252-2262.
Gao Dexin, Zheng Xiaoyu, Wang Yi, et al. A state monitoring and multi-level safety pre-warning method for electric vehicle charging process[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2252- 2262.
[2] 崔淑梅, 宋贝贝, 王志远. 电动汽车动态无线供电磁耦合机构研究综述[J]. 电工技术学报, 2022, 37(3): 537-554.
Cui Shumei, Song Beibei, Wang Zhiyuan. Overview of magnetic coupler for electric vehicles dynamic wireless charging[J]. Transactions of China Electro- technical Society, 2022, 37(3): 537-554.
[3] Xiong Xin, Wang Shunli, Fernandez C, et al. A novel practical state of charge estimation method: an adaptive improved ampere-hour method based on composite correction factor[J]. International Journal of Energy Research, 2020, 44(14): 11385-11404.
[4] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State-of- charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decompo- sition[J]. Automation of Electric Power Systems, 2022, 37(17): 4528-4536.
[5] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885.
Liu Suzhen, Yuan Luhang, Zhang Chuang, et al. State of charge estimation of LiFeO4 batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.
[6] 郭向伟, 邢程, 司阳, 等. RLS锂电池全工况自适应等效电路模型[J]. 电工技术学报, 2022, 37(16): 4029-4037.
Guo Xiangwei, Xing Cheng, Si Yang, et al. RLS adaptive equivalent circuit model of lithium battery under full working condition[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4029- 4037.
[7] He Lin, Wang Yangang, Wei Yujiang, et al. An adaptive central difference Kalman filter approach for state of charge estimation by fractional order model of lithium-ion battery[J]. Energy, 2022, 244: 122627.
[8] Wang Zuolu, Feng Guojin, Liu Xiongwei, et al. A novel method of parameter identification and state of charge estimation for lithium-ion battery energy storage system[J]. Journal of Energy Storage, 2022, 49: 104124.
[9] Shi Na, Chen Zewang, Niu Mu, et al. State-of-charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification[J]. Journal of Energy Storage, 2022, 45: 103518.
[10] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J].电工技术学报, 2021, 36(24): 5165-5175.
Wu Chunling, Hu Wenbo, Meng Jinhao, et al. state of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(24): 5165-5175.
[11] Li Guidan, Peng Kai, Li Bin, et al. A combined state-of-charge estimation method for lithium-ion battery using an improved BGRU network and UKF[J]. Energy, 2022, 259: 124933.
[12] Liu Fang, Shao Chen, Su Weixing, et al. Online joint estimator of key states for battery based on a new equivalent circuit model[J]. Journal of Energy Storage, 2022, 52: 104780.
[13] Li Bin, Peng Kai, Li Guidan. State-of-charge estimation for lithium-ion battery using the gauss- hermite particle filter technique[J]. Journal of Renewable and Sustainable Energy, 2018, 10(1): 014105.
[14] Li Guidan, Peng Kai, Li Bin, et al. An improved state of harge and state of power estimation method basedon genetic particle filter for lithium-ion batteries[J]. Energies, 2020, 13(2): 478.
[15] Liu Qinghe, Liu Shouzhi, Liu Haiwei, et al. Evaluation of LFP battery SOC estimation using auxiliary particle filter[J]. Energies, 2019, 12(11): 2041.
[16] Jouin M, Gouriveau R, Hissel D, et al. Particle filter-based prognostics: review, discussion and perspectives[J]. Mechanical Systems and Signal Pro- cessing, 2016, 72: 2-31.
[17] Chen Lei. Decreasing weight particle swarm opti- mization combined with unscented particle filter for the non-linear model for lithium battery state of charge estimation[J]. International Journal of Elec- trochemical Science, 2020, 15(10): 10104-10116.
State of Charge Estimation of Li-Ion Battery Using Particle Swarm Optimization Extended Kalman Particle Filter Based on Joint Parameter Identification
Abstract Improving the accuracy of parameter identification and SOC (state of charge) algorithm is the key to enhancing SOC estimation. Based on joint parameter identification, this paper proposed a SOC estimation method using particle swarm optimization extended Kalman particle filter (EPF). In the early stage of parameter identification, the forgetting factor recursive least squares (FFRLS) is used. However, when errors in the low SOC region become larger, the swarm optimization (PSO) algorithm is used for parameter identification. PSO uses the voltage data collected during the previous FFRLS parameter identification as input, employing the minimum voltage difference as the objective function to calculate the circuit model parameters. The joint parameter identification method can compensate for the accuracy issue of PSO identification but needs more data in the early stage. The SOC of the lithium battery is estimated based on parameter identification. Aimed at the problem of particle degradation and particle shortage in particle filter (PF), an extended Kalman filter algorithm is used to update each particle. The final approximate posterior probability density is used as the importance density function to overcome particle degradation. At the same time, the particle swarm optimization algorithm optimizes the resampling strategy to improve the sampling process and mitigate particle impoverishment. Finally, the proposed method is compared with PF and PSO-PF algorithms under federal urban driving schedule (FUDS) and US06 Highway Driving Schedule (US06) conditions.
Under the FUDS condition, regarding the maximum error, PSO-EPF based on joint identification is 14% higher than PSO-PF based on joint identification, 32.8% higher than PSO-PF based on FFRLS, and 53.2% higher than PF based on FFRLS. Regarding the mean absolute error, PSO-EPF is 56% higher than PSO-PF based on joint identification, 62.5% higher than PSO-PF based on FFRLS, and 67.7% higher than PF based on FFRLS. Regarding the root mean square error, PSO-EPF is 43.5% higher than PSO-PF based on joint identification, 56.2% higher than PSO-PF based on FFRLS, and 65.4% higher than PF based on FFRLS.
Under US06 condition, regarding the maximum error, PSO-EPF is 32.2% higher than PSO-PF based on joint identification, 33.2% higher than PSO-PF based on FFRLS, and 52.7% higher than PF based on FFRLS. Regarding the mean absolute error, PSO-EPF is 44.2% higher than PSO-PF based on joint identification, 45% higher than PSO-PF based on FFRLS, and 45.8% higher than PF based on FFRLS. Regarding the root mean square error, PSO-EPF is 35.1% higher than PSO-PF based on joint identification, 35.8% higher than PSO-PF based on FFRLS, and 45.7% higher than PF based on FFRLS.
The results show that the SOC estimation method of PSO-EPF for lithium batteries based on joint identification meets the accuracy requirements in the low SOC region. It has higher estimation accuracy than PF and PSO-PF, indicating the strong robustness and generalization ability of the proposed algorithm.
keywords：Li-ion battery, particle swarm optimization algorithm, extended Kalman particle filter, state of charge (SOC)
中图分类号：TM912
DOI: 10.19595/j.cnki.1000-6753.tces.222007
国家自然科学基金（61741126）和广西自然科学基金（2022GXNSFAA035533）资助项目。
收稿日期 2022-10-21
改稿日期 2023-03-30
贠 祥 男，1989年生，博士研究生，研究方向为智能化电器。E-mail: shengaowangluo@163.com
范兴明 男，1978年生，教授，博士生导师，研究方向为智能化电器和高电压新技术。E-mail: fanxm_627@163.com（通信作者）
（编辑 郭丽军）